About the Execution of LTSMin+red for BlocksWorld-PT-17
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 16197.688 | 513111.00 | 594582.00 | 1666.40 | 87 1 87 1 ? 1 ? ? 1 1 1 1 1 1 1 1 | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
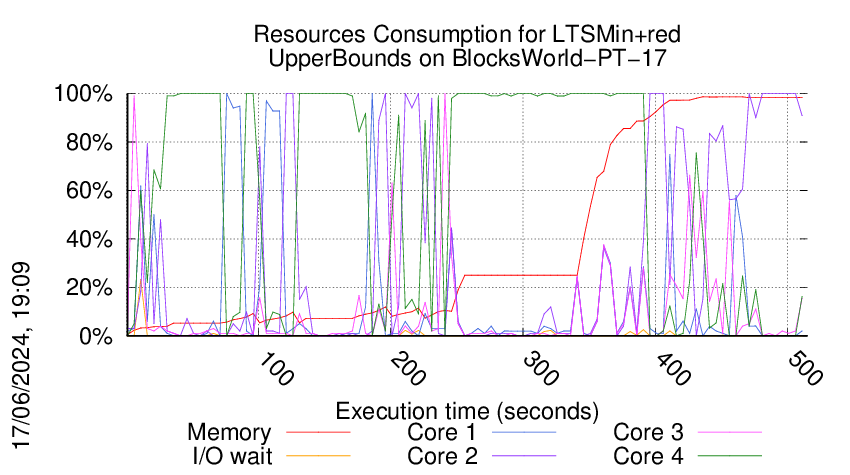
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r605-tall-171774427000293.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool ltsminxred
Input is BlocksWorld-PT-17, examination is UpperBounds
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r605-tall-171774427000293
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 127M
-rw-r--r-- 1 mcc users 2.3M Jun 7 06:38 CTLCardinality.txt
-rw-r--r-- 1 mcc users 11M Jun 7 06:38 CTLCardinality.xml
-rw-r--r-- 1 mcc users 4.0M Jun 7 06:38 CTLFireability.txt
-rw-r--r-- 1 mcc users 21M Jun 7 06:38 CTLFireability.xml
-rw-r--r-- 1 mcc users 49K Jun 7 06:44 LTLCardinality.txt
-rw-r--r-- 1 mcc users 152K Jun 7 06:44 LTLCardinality.xml
-rw-r--r-- 1 mcc users 1.7M Jun 7 06:44 LTLFireability.txt
-rw-r--r-- 1 mcc users 6.2M Jun 7 06:44 LTLFireability.xml
-rw-r--r-- 1 mcc users 1 Jun 7 06:26 NewModel
-rw-r--r-- 1 mcc users 4.2M Jun 7 06:39 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 19M Jun 7 06:39 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 8.2M Jun 7 06:39 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 43M Jun 7 06:39 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 338K Jun 7 06:43 UpperBounds.txt
-rw-r--r-- 1 mcc users 812K Jun 7 06:43 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Jun 7 06:26 equiv_col
-rw-r--r-- 1 mcc users 3 Jun 7 06:26 instance
-rw-r--r-- 1 mcc users 6 Jun 7 06:26 iscolored
-rw-r--r-- 1 mcc users 7.4M Jun 7 06:26 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of positive values
NUM_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-00
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-01
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-02
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-03
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-04
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-05
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-06
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-07
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-08
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-09
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-10
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-11
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-12
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-13
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-14
FORMULA_NAME BlocksWorld-PT-17-UpperBounds-15
=== Now, execution of the tool begins
BK_START 1717756943668
Invoking MCC driver with
BK_TOOL=ltsminxred
BK_EXAMINATION=UpperBounds
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=BlocksWorld-PT-17
BK_MEMORY_CONFINEMENT=16384
Applying reductions before tool ltsmin
Invoking reducer
Running Version 202405141337
[2024-06-07 10:42:24] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, UpperBounds, -timeout, 360, -rebuildPNML]
[2024-06-07 10:42:24] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-06-07 10:42:25] [INFO ] Load time of PNML (sax parser for PT used): 536 ms
[2024-06-07 10:42:25] [INFO ] Transformed 7831 places.
[2024-06-07 10:42:25] [INFO ] Transformed 15313 transitions.
[2024-06-07 10:42:25] [INFO ] Found NUPN structural information;
[2024-06-07 10:42:25] [INFO ] Completing missing partition info from NUPN : creating a component with [pred_on_table_0, pred_arm_empty_0, pred_on_table_1, pred_on_table_2, pred_on_table_3, pred_on_table_4, pred_on_table_5, pred_on_table_6, pred_on_table_7, pred_on_table_8, pred_on_table_9, pred_on_table_10, pred_on_table_11, pred_on_table_12, pred_on_table_13, pred_on_table_14, pred_on_table_15, pred_on_table_16, pred_on_table_17, pred_on_table_18, pred_on_table_19, pred_on_table_20, pred_on_table_21, pred_on_table_22, pred_on_table_23, pred_on_table_24, pred_on_table_25, pred_on_table_26, pred_on_table_27, pred_on_table_28, pred_on_table_29, pred_on_table_30, pred_on_table_31, pred_on_table_32, pred_on_table_33, pred_on_table_34, pred_on_table_35, pred_on_table_36, pred_on_table_37, pred_on_table_38, pred_on_table_39, pred_on_table_40, pred_on_table_41, pred_on_table_42, pred_on_table_43, pred_on_table_44, pred_on_table_45, pred_on_table_46, pred_on_table_47, pred_on_table_48, pred_on_table_49, pred_on_table_50, pred_on_table_51, pred_on_table_52, pred_on_table_53, pred_on_table_54, pred_on_table_55, pred_on_table_56, pred_on_table_57, pred_on_table_58, pred_on_table_59, pred_on_table_60, pred_on_table_61, pred_on_table_62, pred_on_table_63, pred_on_table_64, pred_on_table_65, pred_on_table_66, pred_on_table_67, pred_on_table_68, pred_on_table_69, pred_on_table_70, pred_on_table_71, pred_on_table_72, pred_on_table_73, pred_on_table_74, pred_on_table_75, pred_on_table_76, pred_on_table_77, pred_on_table_78, pred_on_table_79, pred_on_table_80, pred_on_table_81, pred_on_table_82, pred_on_table_83, pred_on_table_84, pred_on_table_85, pred_on_table_86]
[2024-06-07 10:42:25] [INFO ] Parsed PT model containing 7831 places and 15313 transitions and 76536 arcs in 730 ms.
Parsed 16 properties from file /home/mcc/execution/UpperBounds.xml in 59 ms.
Reduction of identical properties reduced properties to check from 16 to 9
Current structural bounds on expressions (Initially) : Max Seen:[7, 1, 0, 80, 0, 0, 0, 0, 0] Max Struct:[+inf, +inf, +inf, +inf, +inf, +inf, +inf, +inf, +inf]
Current structural bounds on expressions (Before main loop) : Max Seen:[7, 1, 0, 80, 0, 0, 0, 0, 0] Max Struct:[+inf, +inf, +inf, +inf, +inf, +inf, +inf, +inf, +inf]
// Phase 1: matrix 15313 rows 7831 cols
[2024-06-07 10:42:26] [INFO ] Computed 175 invariants in 244 ms
Current structural bounds on expressions (after invariants) : Max Seen:[7, 1, 0, 80, 0, 0, 0, 0, 0] Max Struct:[87, 1, 87, 7569, 1, 1, 1, 1, 1]
FORMULA BlocksWorld-PT-17-UpperBounds-10 1 TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BlocksWorld-PT-17-UpperBounds-13 1 TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BlocksWorld-PT-17-UpperBounds-14 1 TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BlocksWorld-PT-17-UpperBounds-01 1 TECHNIQUES TOPOLOGICAL INITIAL_STATE
RANDOM walk for 10000 steps (2 resets) in 3369 ms. (2 steps per ms)
FORMULA BlocksWorld-PT-17-UpperBounds-12 1 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-09 1 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-08 1 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
BEST_FIRST walk for 50005 steps (10 resets) in 2825 ms. (17 steps per ms)
Current structural bounds on expressions (after WALK) : Max Seen:[57, 1, 84, 0, 0] Max Struct:[87, 87, 7569, 1, 1]
[2024-06-07 10:42:32] [INFO ] Invariant cache hit.
[2024-06-07 10:42:34] [INFO ] [Real]Absence check using 175 positive place invariants in 371 ms returned sat
[2024-06-07 10:42:37] [INFO ] [Real]Absence check using state equation in 3468 ms returned unknown
[2024-06-07 10:42:38] [INFO ] [Real]Absence check using 175 positive place invariants in 171 ms returned unsat
[2024-06-07 10:42:40] [INFO ] [Real]Absence check using 175 positive place invariants in 938 ms returned unknown
[2024-06-07 10:42:41] [INFO ] [Real]Absence check using 175 positive place invariants in 294 ms returned sat
[2024-06-07 10:42:45] [INFO ] [Real]Absence check using state equation in 3936 ms returned unknown
[2024-06-07 10:42:46] [INFO ] [Real]Absence check using 175 positive place invariants in 278 ms returned sat
[2024-06-07 10:42:50] [INFO ] [Real]Absence check using state equation in 3934 ms returned unknown
Current structural bounds on expressions (after SMT) : Max Seen:[57, 1, 84, 0, 0] Max Struct:[87, 1, 7569, 1, 1]
FORMULA BlocksWorld-PT-17-UpperBounds-05 1 TECHNIQUES TOPOLOGICAL SAT_SMT RANDOM_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-03 1 TECHNIQUES TOPOLOGICAL SAT_SMT RANDOM_WALK
Current structural bounds on expressions (After Parikh guided walk) : Max Seen:[57, 84, 0, 0] Max Struct:[87, 7569, 1, 1]
Support contains 7656 out of 7831 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 7831/7831 places, 15313/15313 transitions.
Drop transitions (Empty/Sink Transition effects.) removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 0 with 1 rules applied. Total rules applied 1 place count 7831 transition count 15312
Applied a total of 1 rules in 4889 ms. Remains 7831 /7831 variables (removed 0) and now considering 15312/15313 (removed 1) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 4906 ms. Remains : 7831/7831 places, 15312/15313 transitions.
// Phase 1: matrix 15312 rows 7831 cols
[2024-06-07 10:42:55] [INFO ] Computed 175 invariants in 103 ms
Current structural bounds on expressions (after invariants) : Max Seen:[57, 84, 0, 0] Max Struct:[87, 7569, 1, 1]
RANDOM walk for 109756 steps (0 resets) in 30001 ms. (3 steps per ms)
FORMULA BlocksWorld-PT-17-UpperBounds-15 1 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-11 1 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-02 87 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA BlocksWorld-PT-17-UpperBounds-00 87 TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
BEST_FIRST walk for 538864 steps (1 resets) in 10002 ms. (53 steps per ms)
Current structural bounds on expressions (after WALK) : Max Seen:[86] Max Struct:[7569]
[2024-06-07 10:43:35] [INFO ] Invariant cache hit.
[2024-06-07 10:43:38] [INFO ] [Real]Absence check using 175 positive place invariants in 1997 ms returned sat
[2024-06-07 10:43:53] [INFO ] [Real]Absence check using state equation in 15200 ms returned sat
[2024-06-07 10:43:54] [INFO ] State equation strengthened by 160 read => feed constraints.
[2024-06-07 10:43:58] [INFO ] SMT solver returned unknown. Retrying;
[2024-06-07 10:44:02] [INFO ] [Real]Added 160 Read/Feed constraints in 7706 ms returned sat
[2024-06-07 10:44:02] [INFO ] Solution in real domain found non-integer solution.
[2024-06-07 10:44:05] [INFO ] [Nat]Absence check using 175 positive place invariants in 2095 ms returned sat
[2024-06-07 10:44:21] [INFO ] [Nat]Absence check using state equation in 16235 ms returned sat
[2024-06-07 10:44:26] [INFO ] SMT solver returned unknown. Retrying;
[2024-06-07 10:44:30] [INFO ] [Nat]Added 160 Read/Feed constraints in 9063 ms returned unknown
Current structural bounds on expressions (after SMT) : Max Seen:[86] Max Struct:[7569]
Current structural bounds on expressions (After Parikh guided walk) : Max Seen:[86] Max Struct:[7569]
Support contains 7569 out of 7831 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 7831/7831 places, 15312/15312 transitions.
Applied a total of 0 rules in 7236 ms. Remains 7831 /7831 variables (removed 0) and now considering 15312/15312 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 7237 ms. Remains : 7831/7831 places, 15312/15312 transitions.
[2024-06-07 10:44:38] [INFO ] Invariant cache hit.
Current structural bounds on expressions (after invariants) : Max Seen:[86] Max Struct:[7569]
RANDOM walk for 112646 steps (0 resets) in 30001 ms. (3 steps per ms)
BEST_FIRST walk for 31385 steps (0 resets) in 5001 ms. (6 steps per ms)
Current structural bounds on expressions (after WALK) : Max Seen:[86] Max Struct:[7569]
[2024-06-07 10:45:13] [INFO ] Invariant cache hit.
[2024-06-07 10:45:15] [INFO ] [Real]Absence check using 175 positive place invariants in 2060 ms returned sat
[2024-06-07 10:45:31] [INFO ] [Real]Absence check using state equation in 15675 ms returned sat
[2024-06-07 10:45:32] [INFO ] State equation strengthened by 160 read => feed constraints.
[2024-06-07 10:45:36] [INFO ] SMT solver returned unknown. Retrying;
[2024-06-07 10:45:39] [INFO ] [Real]Added 160 Read/Feed constraints in 6852 ms returned sat
[2024-06-07 10:45:39] [INFO ] Solution in real domain found non-integer solution.
[2024-06-07 10:45:42] [INFO ] [Nat]Absence check using 175 positive place invariants in 2017 ms returned sat
[2024-06-07 10:45:58] [INFO ] [Nat]Absence check using state equation in 15853 ms returned sat
[2024-06-07 10:46:02] [INFO ] SMT solver returned unknown. Retrying;
[2024-06-07 10:46:07] [INFO ] [Nat]Added 160 Read/Feed constraints in 9062 ms returned unknown
Current structural bounds on expressions (after SMT) : Max Seen:[86] Max Struct:[7569]
Current structural bounds on expressions (After Parikh guided walk) : Max Seen:[86] Max Struct:[7569]
Support contains 7569 out of 7831 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 7831/7831 places, 15312/15312 transitions.
Applied a total of 0 rules in 6798 ms. Remains 7831 /7831 variables (removed 0) and now considering 15312/15312 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 6798 ms. Remains : 7831/7831 places, 15312/15312 transitions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 7831/7831 places, 15312/15312 transitions.
Applied a total of 0 rules in 6563 ms. Remains 7831 /7831 variables (removed 0) and now considering 15312/15312 (removed 0) transitions.
[2024-06-07 10:46:20] [INFO ] Invariant cache hit.
[2024-06-07 10:46:25] [INFO ] Implicit Places using invariants in 5163 ms returned []
Implicit Place search using SMT only with invariants took 5198 ms to find 0 implicit places.
Running 15305 sub problems to find dead transitions.
[2024-06-07 10:46:26] [INFO ] Invariant cache hit.
[2024-06-07 10:46:26] [INFO ] State equation strengthened by 160 read => feed constraints.
Problem TDEAD1 is UNSAT
Problem TDEAD88 is UNSAT
Problem TDEAD262 is UNSAT
Problem TDEAD350 is UNSAT
Problem TDEAD438 is UNSAT
Problem TDEAD526 is UNSAT
Problem TDEAD614 is UNSAT
Problem TDEAD702 is UNSAT
Problem TDEAD790 is UNSAT
Problem TDEAD878 is UNSAT
Problem TDEAD966 is UNSAT
Problem TDEAD1054 is UNSAT
Problem TDEAD1142 is UNSAT
Problem TDEAD1230 is UNSAT
Problem TDEAD1406 is UNSAT
Problem TDEAD1494 is UNSAT
Problem TDEAD1582 is UNSAT
Problem TDEAD1670 is UNSAT
Problem TDEAD1758 is UNSAT
Problem TDEAD1846 is UNSAT
Problem TDEAD1934 is UNSAT
Problem TDEAD2110 is UNSAT
Problem TDEAD2198 is UNSAT
Problem TDEAD2286 is UNSAT
Problem TDEAD2374 is UNSAT
Problem TDEAD2462 is UNSAT
Problem TDEAD2550 is UNSAT
Problem TDEAD2638 is UNSAT
Problem TDEAD2726 is UNSAT
Problem TDEAD2814 is UNSAT
Problem TDEAD2902 is UNSAT
Problem TDEAD2990 is UNSAT
Problem TDEAD3078 is UNSAT
Problem TDEAD3166 is UNSAT
Problem TDEAD3254 is UNSAT
Problem TDEAD3342 is UNSAT
Problem TDEAD3430 is UNSAT
Problem TDEAD3606 is UNSAT
Problem TDEAD3694 is UNSAT
Problem TDEAD3782 is UNSAT
Problem TDEAD3870 is UNSAT
Problem TDEAD3958 is UNSAT
Problem TDEAD4046 is UNSAT
Problem TDEAD4134 is UNSAT
Problem TDEAD4222 is UNSAT
Problem TDEAD4310 is UNSAT
Problem TDEAD4398 is UNSAT
Problem TDEAD4486 is UNSAT
Problem TDEAD4662 is UNSAT
Problem TDEAD4750 is UNSAT
Problem TDEAD4838 is UNSAT
Problem TDEAD4926 is UNSAT
Problem TDEAD5014 is UNSAT
Problem TDEAD5102 is UNSAT
Problem TDEAD5190 is UNSAT
Problem TDEAD5278 is UNSAT
Problem TDEAD5366 is UNSAT
Problem TDEAD5454 is UNSAT
Problem TDEAD5542 is UNSAT
Problem TDEAD5630 is UNSAT
Problem TDEAD5718 is UNSAT
Problem TDEAD5806 is UNSAT
Problem TDEAD5894 is UNSAT
Problem TDEAD5982 is UNSAT
Problem TDEAD6070 is UNSAT
Problem TDEAD6158 is UNSAT
Problem TDEAD6246 is UNSAT
Problem TDEAD6334 is UNSAT
Problem TDEAD6422 is UNSAT
Problem TDEAD6510 is UNSAT
Problem TDEAD6598 is UNSAT
Problem TDEAD6686 is UNSAT
Problem TDEAD6774 is UNSAT
Problem TDEAD6862 is UNSAT
Problem TDEAD6950 is UNSAT
Problem TDEAD7038 is UNSAT
Problem TDEAD7126 is UNSAT
Problem TDEAD7302 is UNSAT
Problem TDEAD7390 is UNSAT
Problem TDEAD7478 is UNSAT
Problem TDEAD7566 is UNSAT
Problem TDEAD7654 is UNSAT
Problem TDEAD7742 is UNSAT
Problem TDEAD7830 is UNSAT
Problem TDEAD8002 is UNSAT
Problem TDEAD8172 is UNSAT
Problem TDEAD8340 is UNSAT
Problem TDEAD8506 is UNSAT
Problem TDEAD8670 is UNSAT
Problem TDEAD8832 is UNSAT
Problem TDEAD8992 is UNSAT
Problem TDEAD9150 is UNSAT
Problem TDEAD9306 is UNSAT
Problem TDEAD9460 is UNSAT
Problem TDEAD9612 is UNSAT
Problem TDEAD9910 is UNSAT
Problem TDEAD10056 is UNSAT
Problem TDEAD10200 is UNSAT
Problem TDEAD10342 is UNSAT
Problem TDEAD10482 is UNSAT
Problem TDEAD10620 is UNSAT
Problem TDEAD10756 is UNSAT
Problem TDEAD11022 is UNSAT
Problem TDEAD11152 is UNSAT
Problem TDEAD11280 is UNSAT
Problem TDEAD11406 is UNSAT
Problem TDEAD11530 is UNSAT
Problem TDEAD11652 is UNSAT
Problem TDEAD11772 is UNSAT
Problem TDEAD11890 is UNSAT
Problem TDEAD12006 is UNSAT
Problem TDEAD12120 is UNSAT
Problem TDEAD12232 is UNSAT
Problem TDEAD12342 is UNSAT
Problem TDEAD12450 is UNSAT
Problem TDEAD12556 is UNSAT
Problem TDEAD12660 is UNSAT
Problem TDEAD12762 is UNSAT
Problem TDEAD12960 is UNSAT
Problem TDEAD13056 is UNSAT
Problem TDEAD13150 is UNSAT
Problem TDEAD13242 is UNSAT
Problem TDEAD13332 is UNSAT
Problem TDEAD13420 is UNSAT
Problem TDEAD13506 is UNSAT
Problem TDEAD13590 is UNSAT
Problem TDEAD13672 is UNSAT
Problem TDEAD13752 is UNSAT
Problem TDEAD13830 is UNSAT
Problem TDEAD13980 is UNSAT
Problem TDEAD14052 is UNSAT
Problem TDEAD14122 is UNSAT
Problem TDEAD14190 is UNSAT
Problem TDEAD14256 is UNSAT
Problem TDEAD14320 is UNSAT
Problem TDEAD14382 is UNSAT
Problem TDEAD14442 is UNSAT
Problem TDEAD14500 is UNSAT
Problem TDEAD14556 is UNSAT
Problem TDEAD14610 is UNSAT
Problem TDEAD14662 is UNSAT
Problem TDEAD14712 is UNSAT
Problem TDEAD14760 is UNSAT
Problem TDEAD14806 is UNSAT
Problem TDEAD14850 is UNSAT
Problem TDEAD14892 is UNSAT
Problem TDEAD14932 is UNSAT
Problem TDEAD14970 is UNSAT
Problem TDEAD15006 is UNSAT
Problem TDEAD15040 is UNSAT
Problem TDEAD15072 is UNSAT
Problem TDEAD15102 is UNSAT
Problem TDEAD15130 is UNSAT
Problem TDEAD15156 is UNSAT
Problem TDEAD15180 is UNSAT
Problem TDEAD15202 is UNSAT
Problem TDEAD15222 is UNSAT
Problem TDEAD15240 is UNSAT
Problem TDEAD15270 is UNSAT
Problem TDEAD15282 is UNSAT
Problem TDEAD15292 is UNSAT
Problem TDEAD15300 is UNSAT
Problem TDEAD15306 is UNSAT
Problem TDEAD15310 is UNSAT
At refinement iteration 0 (INCLUDED_ONLY) 0/7824 variables, 163/163 constraints. Problems are: Problem set: 164 solved, 15141 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 7824/23143 variables, and 163 constraints, problems are : Problem set: 164 solved, 15141 unsolved in 30515 ms.
Refiners :[Positive P Invariants (semi-flows): 163/175 constraints, State Equation: 0/7831 constraints, ReadFeed: 0/160 constraints, PredecessorRefiner: 15223/7656 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 164 solved, 15141 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/7742 variables, 6/6 constraints. Problems are: Problem set: 164 solved, 15141 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 1)
(s1 1)
(s2 1)
(s3 0)
(s4 1)
(s5 1)
(s6 0)
(s7 1)
(s8 1)
(s9 0)
(s10 1)
(s11 1)
(s12 0)
(s13 1)
(s14 1)
(s15 0)
(s16 1)
(s17 1)
(s18 0)
(s19 1)
(s20 1)
(s21 0)
(s22 1)
(s23 1)
(s24 0)
(s25 1)
(s26 1)
(s27 0)
(s28 1)
(s29 1)
(s30 0)
(s31 1)
(s32 1)
(s33 0)
(s34 1)
(s35 1)
(s36 0)
(s37 1)
(s38 1)
(s39 0)
(s40 1)
(s41 0)
(s42 0)
(s43 1)
(s44 1)
(s45 0)
(s46 1)
(s47 1)
(s48 0)
(s49 1)
(s50 1)
(s51 0)
(s52 1)
(s53 1)
(s54 0)
(s55 1)
(s56 1)
(s57 0)
(s58 1)
(s59 1)
(s60 0)
(s61 1)
(s62 1)
(s63 0)
(s64 1)
(s65 0)
(s66 0)
(s67 1)
(s69 0)
(s70 1)
(s71 1)
(s72 0)
(s73 1)
(s74 1)
(s75 0)
(s76 1)
(s77 1)
(s78 0)
(s79 1)
(s80 1)
(s81 0)
(s82 1)
(s83 1)
(s84 0)
(s85 1)
(s86 1)
(s87 0)
(s88 1)
(s89 1)
(s90 0)
(s91 1)
(s92 1)
(s93 0)
(s94 1)
(s95 1)
(s96 0)
(s97 1)
(s98 1)
(s99 0)
(s100 1)
(s101 1)
(s102 0)
(s103 1)
(s104 1)
(s105 0)
(s106 1)
(s107 1)
(s108 0)
(s109 1)
(s110 1)
(s111 0)
(s112 1)
(s113 1)
(s114 0)
(s115 1)
(s116 0)
(s117 0)
(s118 1)
(s119 1)
(s120 0)
(s121 1)
(s122 1)
(s123 0)
(s124 1)
(s125 1)
(s126 0)
(s127 1)
(s128 1)
(s129 0)
(s130 1)
(s131 1)
(s132 0)
(s133 1)
(s134 1)
(s135 0)
(s136 1)
(s137 1)
(s138 0)
(s139 1)
(s140 1)
(s141 0)
(s142 1)
(s143 1)
(s144 0)
(s145 1)
(s146 1)
(s147 0)
(s148 1)
(s149 1)
(s150 0)
(s151 1)
(s152 0)
(s153 0)
(s154 1)
(s155 1)
(s156 0)
(s157 1)
(s158 1)
(s159 0)
(s160 1)
(s161 1)
(s162 0)
(s163 1)
(s164 1)
(s165 0)
(s166 1)
(s167 1)
(s168 0)
(s169 1)
(s170 1)
(s171 0)
(s172 1)
(s173 1)
(s174 0)
(s175 1)
(s176 1)
(s177 0)
(s178 1)
(s179 1)
(s180 0)
(s181 1)
(s182 1)
(s183 0)
(s184 1)
(s185 1)
(s186 0)
(s187 1)
(s188 1)
(s189 0)
(s190 1)
(s191 1)
(s192 0)
(s193 1)
(s194 1)
(s195 0)
(s196 1)
(s197 1)
(s198 0)
(s199 1)
(s200 1)
(s201 0)
(s202 1)
(s204 0)
(s205 1)
(s206 1)
(s207 0)
(s208 1)
(s209 1)
(s210 0)
(s211 1)
(s212 1)
(s213 0)
(s214 1)
(s215 1)
(s216 0)
(s217 1)
(s218 1)
(s219 0)
(s220 1)
(s221 1)
(s222 0)
(s223 1)
(s224 1)
(s225 0)
(s226 1)
(s227 1)
(s228 0)
(s229 1)
(s230 1)
(s231 0)
(s232 1)
(s233 1)
(s234 0)
(s235 1)
(s236 1)
(s237 0)
(s238 1)
(s239 1)
(s240 0)
(s241 1)
(s242 0)
(s243 0)
(s244 1)
(s245 1)
(s246 0)
(s247 1)
(s248 1)
(s249 0)
(s250 1)
(s251 1)
(s252 0)
(s253 1)
(s254 1)
(s255 0)
(s256 1)
(s257 1)
(s258 0)
(s259 1)
(s260 1)
(s261 0)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 0)
(s1394 0)
(s1395 0)
(s1396 0)
(s1397 0)
(s1398 0)
(s1399 0)
(s1400 0)
(s1401 0)
(s1402 0)
(s1403 0)
(s1404 0)
(s1405 0)
(s1406 0)
(s1407 0)
(s1408 0)
(s1409 0)
(s1410 0)
(s1411 0)
(s1412 0)
(s1413 0)
(s1414 0)
(s1415 0)
(s1416 0)
(s1417 0)
(s1418 0)
(s1419 0)
(s1420 0)
(s1421 0)
(s1422 0)
(s1423 0)
(s1424 0)
(s1425 0)
(s1426 0)
(s1427 0)
(s1428 0)
(s1429 0)
(s1430 0)
(s1431 0)
(s1432 0)
(s1433 0)
(s1434 0)
(s1435 0)
(s1436 0)
(s1437 0)
(s1438 0)
(s1439 0)
(s1440 0)
(s1441 0)
(s1442 0)
(s1443 0)
(s1444 0)
(s1445 0)
(s1446 0)
(s1447 0)
(s1448 0)
(s1449 0)
(s1450 0)
(s1451 0)
(s1452 0)
(s1453 0)
(s1454 0)
(s1455 0)
(s1456 0)
(s1457 0)
(s1458 0)
(s1459 0)
(s1460 0)
(s1461 0)
(s1462 0)
(s1463 0)
(s1464 0)
(s1465 0)
(s1466 0)
(s1467 0)
(s1468 0)
(s1469 0)
(s1470 0)
(s1471 0)
(s1472 0)
(s1473 0)
(s1474 0)
(s1475 0)
(s1476 0)
(s1477 0)
(s1478 0)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 0)
(s2090 0)
(s2091 0)
(s2092 0)
(s2093 0)
(s2094 0)
(s2095 0)
(s2096 0)
(s2097 0)
(s2098 0)
(s2099 0)
(s2100 0)
(s2101 0)
(s2102 0)
(s2103 0)
(s2104 0)
(s2105 0)
(s2106 0)
(s2107 0)
(s2108 0)
(s2109 0)
(s2110 0)
(s2111 0)
(s2112 0)
(s2113 0)
(s2114 0)
(s2115 0)
(s2116 0)
(s2117 0)
(s2118 0)
(s2119 0)
(s2120 0)
(s2121 0)
(s2122 0)
(s2123 0)
(s2124 0)
(s2125 0)
(s2126 0)
(s2127 0)
(s2128 0)
(s2129 0)
(s2130 0)
(s2131 0)
(s2132 0)
(s2133 0)
(s2134 0)
(s2135 0)
(s2136 0)
(s2137 0)
(s2138 0)
(s2139 0)
(s2140 0)
(s2141 0)
(s2142 0)
(s2143 0)
(s2144 0)
(s2145 0)
(s2146 0)
(s2147 0)
(s2148 0)
(s2149 0)
(s2150 0)
(s2151 0)
(s2152 0)
(s2153 0)
(s2154 0)
(s2155 0)
(s2156 0)
(s2157 0)
(s2158 0)
(s2159 0)
(s2160 0)
(s2161 0)
(s2162 0)
(s2163 0)
(s2164 0)
(s2165 0)
(s2166 0)
(s2167 0)
(s2168 0)
(s2169 0)
(s2170 0)
(s2171 0)
(s2172 0)
(s2173 0)
(s2174 0)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 1)
(s2577 1)
(s2578 1)
(s2579 1)
(s2580 1)
(s2581 1)
(s2582 1)
(s2583 1)
(s2584 1)
(s2585 1)
(s2586 1)
(s2587 1)
(s2588 1)
(s2589 1)
(s2590 1)
(s2591 1)
(s2592 1)
(s2593 1)
(s2594 1)
(s2595 1)
(s2596 1)
(s2597 1)
(s2598 1)
(s2599 1)
(s2600 1)
(s2601 1)
(s2602 1)
(s2603 1)
(s2604 1)
(s2605 1)
(s2606 1)
(s2607 1)
(s2608 1)
(s2609 1)
(s2610 1)
(s2611 1)
(s2612 1)
(s2613 1)
(s2614 1)
(s2615 1)
(s2616 1)
(s2617 1)
(s2618 1)
(s2619 1)
(s2620 1)
(s2621 1)
(s2622 1)
(s2623 1)
(s2624 1)
(s2625 1)
(s2626 1)
(s2627 1)
(s2628 1)
(s2629 1)
(s2630 1)
(s2631 1)
(s2632 1)
(s2633 1)
(s2634 1)
(s2635 1)
(s2636 1)
(s2637 1)
(s2639 1)
(s2640 1)
(s2641 1)
(s2642 1)
(s2643 1)
(s2644 1)
(s2645 1)
(s2646 1)
(s2647 1)
(s2648 1)
(s2649 1)
(s2650 1)
(s2651 1)
(s2652 1)
(s2653 1)
(s2654 1)
(s2655 1)
(s2656 1)
(s2657 1)
(s2658 1)
(s2659 1)
(s2660 1)
(s2661 1)
(s2662 1)
(s2663 1)
(s2664 1)
(s2665 1)
(s2666 1)
(s2667 1)
(s2668 1)
(s2669 1)
(s2670 1)
(s2671 1)
(s2672 1)
(s2673 1)
(s2674 1)
(s2675 1)
(s2676 1)
(s2677 1)
(s2678 1)
(s2679 1)
(s2680 1)
(s2681 1)
(s2682 1)
(s2683 1)
(s2684 1)
(s2685 1)
(s2686 1)
(s2687 1)
(s2688 1)
(s2689 1)
(s2690 1)
(s2691 1)
(s2692 1)
(s2693 1)
(s2694 1)
(s2695 1)
(s2696 1)
(s2697 1)
(s2698 1)
(s2699 1)
(s2700 1)
(s2701 1)
(s2702 1)
(s2703 1)
(s2704 1)
(s2705 1)
(s2706 1)
(s2707 1)
(s2708 1)
(s2709 1)
(s2710 1)
(s2711 1)
(s2712 1)
(s2713 1)
(s2714 1)
(s2715 1)
(s2716 1)
(s2717 1)
(s2718 1)
(s2720 1)
(s2721 1)
(s2722 1)
(s2723 1)
(s2724 1)
(s2725 1)
(s2727 1)
(s2728 1)
(s2729 1)
(s2730 1)
(s2731 1)
(s2732 1)
(s2733 1)
(s2734 1)
(s2735 1)
(s2736 1)
(s2737 1)
(s2738 1)
(s2739 1)
(s2740 1)
(s2741 1)
(s2742 1)
(s2743 1)
(s2744 1)
(s2745 1)
(s2746 1)
(s2747 1)
(s2748 1)
(s2749 1)
(s2750 1)
(s2751 1)
(s2752 1)
(s2753 1)
(s2754 1)
(s2755 1)
(s2756 1)
(s2757 1)
(s2758 1)
(s2759 1)
(s2760 1)
(s2761 1)
(s2762 1)
(s2763 1)
(s2764 1)
(s2765 1)
(s2766 1)
(s2767 1)
(s2768 1)
(s2769 1)
(s2770 1)
(s2771 1)
(s2772 1)
(s2773 1)
(s2774 1)
(s2775 1)
(s2776 1)
(s2777 1)
(s2778 1)
(s2779 1)
(s2780 1)
(s2781 1)
(s2782 1)
(s2783 1)
(s2784 1)
(s2785 1)
(s2786 1)
(s2787 1)
(s2788 1)
(s2789 1)
(s2790 1)
(s2791 1)
(s2792 1)
(s2793 1)
(s2794 1)
(s2795 1)
(s2796 1)
(s2797 1)
(s2798 1)
(s2799 1)
(s2800 1)
(s2801 1)
(s2802 1)
(s2803 1)
(s2804 1)
(s2805 1)
(s2806 1)
(s2807 1)
(s2808 1)
(s2809 1)
(s2810 1)
(s2811 1)
(s2812 1)
(s2813 1)
(s2815 1)
(s2816 1)
(s2817 1)
(s2818 1)
(s2819 1)
(s2820 1)
(s2821 1)
(s2822 1)
(s2823 1)
(s2824 1)
(s2825 1)
(s2826 1)
(s2827 1)
(s2828 1)
(s2829 1)
(s2830 1)
(s2831 1)
(s2832 1)
(s2833 1)
(s2834 1)
(s2835 1)
(s2836 1)
(s2837 1)
(s2838 1)
(s2839 1)
(s2840 1)
(s2841 1)
(s2842 1)
(s2843 1)
(s2844 1)
(s2845 1)
(s2846 1)
(s2847 1)
(s2848 1)
(s2849 1)
(s2850 1)
(s2851 1)
(s2852 1)
(s2853 1)
(s2854 1)
(s2855 1)
(s2856 1)
(s2857 1)
(s2858 1)
(s2859 1)
(s2860 1)
(s2861 1)
(s2862 1)
(s2863 1)
(s2864 1)
(s2865 1)
(s2866 1)
(s2867 1)
(s2868 1)
(s2869 1)
(s2870 1)
(s2871 1)
(s2872 1)
(s2873 1)
(s2874 1)
(s2875 1)
(s2876 1)
(s2877 1)
(s2878 1)
(s2879 1)
(s2880 1)
(s2881 1)
(s2882 1)
(s2883 1)
(s2884 1)
(s2885 1)
(s2886 1)
(s2887 1)
(s2888 1)
(s2889 1)
(s2890 1)
(s2891 1)
(s2892 1)
(s2893 1)
(s2894 1)
(s2895 1)
(s2896 1)
(s2897 1)
(s2898 1)
(s2899 1)
(s2900 1)
(s2901 1)
(s2903 1)
(s2904 1)
(s2905 1)
(s2906 1)
(s2907 1)
(s2908 1)
(s2909 1)
(s2910 1)
(s2911 1)
(s2912 1)
(s2913 1)
(s2914 1)
(s2915 1)
(s2916 1)
(s2917 1)
(s2918 1)
(s2919 1)
(s2920 1)
(s2921 1)
(s2922 1)
(s2923 1)
(s2924 1)
(s2925 1)
(s2926 1)
(s2927 1)
(s2928 1)
(s2929 1)
(s2930 1)
(s2931 1)
(s2932 1)
(s2933 1)
(s2934 1)
(s2935 1)
(s2936 1)
(s2937 1)
(s2938 1)
(s2939 1)
(s2940 1)
(s2941 1)
(s2942 1)
(s2943 1)
(s2944 1)
(s2945 1)
(s2946 1)
(s2947 1)
(s2948 1)
(s2949 1)
(s2950 1)
(s2951 1)
(s2952 1)
(s2953 1)
(s2954 1)
(s2955 1)
(s2956 1)
(s2957 1)
(s2958 1)
(s2959 1)
(s2960 1)
(s2961 1)
(s2962 1)
(s2963 1)
(s2964 1)
(s2965 1)
(s2966 1)
(s2967 1)
(s2968 1)
(s2969 1)
(s2970 1)
(s2971 1)
(s2972 1)
(s2973 1)
(s2974 1)
(s2975 1)
(s2976 1)
(s2977 1)
(s2978 1)
(s2979 1)
(s2980 1)
(s2981 1)
(s2982 1)
(s2983 1)
(s2984 1)
(s2985 1)
(s2986 1)
(s2987 1)
(s2988 1)
(s2989 1)
(s2991 1)
(s2992 1)
(s2993 1)
(s2994 1)
(s2995 1)
(s2996 1)
(s2997 1)
(s2998 1)
(s2999 1)
(s3000 1)
(s3001 1)
(s3002 1)
(s3003 1)
(s3004 1)
(s3005 1)
(s3006 1)
(s3007 1)
(s3008 1)
(s3009 1)
(s3010 1)
(s3011 1)
(s3012 1)
(s3013 1)
(s3014 1)
(s3015 1)
(s3016 1)
(s3017 1)
(s3018 1)
(s3019 1)
(s3020 1)
(s3021 1)
(s3022 1)
(s3023 1)
(s3024 1)
(s3025 1)
(s3026 1)
(s3027 1)
(s3028 1)
(s3029 1)
(s3030 1)
(s3031 1)
(s3032 1)
(s3033 1)
(s3034 1)
(s3035 1)
(s3036 1)
(s3037 1)
(s3038 1)
(s3039 1)
(s3040 1)
(s3041 1)
(s3042 1)
(s3043 1)
(s3044 1)
(s3045 1)
(s3046 1)
(s3047 1)
(s3048 1)
(s3049 1)
(s3050 1)
(s3051 1)
(s3052 1)
(s3053 1)
(s3054 1)
(s3055 1)
(s3056 1)
(s3057 1)
(s3058 1)
(s3059 1)
(s3060 1)
(s3061 1)
(s3062 1)
(s3063 1)
(s3064 1)
(s3065 1)
(s3066 1)
(s3067 1)
(s3068 1)
(s3069 1)
(s3070 1)
(s3071 1)
(s3072 1)
(s3073 1)
(s3074 1)
(s3075 1)
(s3076 1)
(s3077 1)
(s3079 1)
(s3080 1)
(s3081 1)
(s3082 1)
(s3083 1)
(s3084 1)
(s3085 1)
(s3086 1)
(s3087 1)
(s3088 1)
(s3089 1)
(s3090 1)
(s3091 1)
(s3092 1)
(s3093 1)
(s3094 1)
(s3095 1)
(s3096 1)
(s3097 1)
(s3098 1)
(s3099 1)
(s3100 1)
(s3101 1)
(s3102 1)
(s3103 1)
(s3104 1)
(s3105 1)
(s3106 1)
(s3107 1)
(s3108 1)
(s3109 1)
(s3110 1)
(s3111 1)
(s3112 1)
(s3113 1)
(s3114 1)
(s3115 1)
(s3116 1)
(s3117 1)
(s3118 1)
(s3119 1)
(s3120 1)
(s3121 1)
(s3122 1)
(s3123 1)
(s3124 1)
(s3125 1)
(s3126 1)
(s3127 1)
(s3128 1)
(s3129 1)
(s3130 1)
(s3131 1)
(s3132 1)
(s3133 1)
(s3134 1)
(s3135 1)
(s3136 1)
(s3137 1)
(s3138 1)
(s3139 1)
(s3140 1)
(s3141 1)
(s3142 1)
(s3143 1)
(s3144 1)
(s3145 1)
(s3146 1)
(s3147 1)
(s3148 1)
(s3149 1)
(s3150 1)
(s3151 1)
(s3152 1)
(s3153 1)
(s3154 1)
(s3155 1)
(s3156 1)
(s3157 1)
(s3158 1)
(s3159 1)
(s3160 1)
(s3161 1)
(s3162 1)
(s3163 1)
(s3164 1)
(s3165 1)
(s3167 1)
(s3168 1)
(s3169 1)
(s3170 1)
(s3171 1)
(s3172 1)
(s3173 1)
(s3174 1)
(s3175 1)
(s3176 1)
(s3177 1)
(s3178 1)
(s3179 1)
(s3180 1)
(s3181 1)
(s3182 1)
(s3183 1)
(s3184 1)
(s3185 1)
(s3186 1)
(s3187 1)
(s3188 1)
(s3189 1)
(s3190 1)
(s3191 1)
(s3192 1)
(s3193 1)
(s3194 1)
(s3195 1)
(s3196 1)
(s3197 1)
(s3198 1)
(s3199 1)
(s3200 1)
(s3201 1)
(s3202 1)
(s3203 1)
(s3204 1)
(s3205 1)
(s3206 1)
(s3207 1)
(s3208 1)
(s3209 1)
(s3210 1)
(s3211 1)
(s3212 1)
(s3213 1)
(s3214 1)
(s3215 1)
(s3216 1)
(s3217 1)
(s3218 1)
(s3219 1)
(s3220 1)
(s3221 1)
(s3222 1)
(s3223 1)
(s3224 1)
(s3225 1)
(s3226 1)
(s3227 1)
(s3228 1)
(s3229 1)
(s3230 1)
(s3231 1)
(s3232 1)
(s3233 1)
(s3234 1)
(s3235 1)
(s3236 1)
(s3237 1)
(s3238 1)
(s3239 1)
(s3240 1)
(s3241 1)
(s3242 1)
(s3243 1)
(s3244 1)
(s3245 1)
(s3246 1)
(s3247 1)
(s3248 1)
(s3249 1)
(s3250 1)
(s3251 1)
(s3252 1)
(s3253 1)
(s3255 1)
(s3256 1)
(s3257 1)
(s3258 1)
(s3259 1)
(s3260 1)
(s3261 1)
(s3262 1)
(s3263 1)
(s3264 1)
(s3265 1)
(s3266 1)
(s3267 1)
(s3268 1)
(s3269 1)
(s3270 1)
(s3271 1)
(s3272 1)
(s3273 1)
(s3274 1)
(s3275 1)
(s3276 1)
(s3277 1)
(s3278 1)
(s3279 1)
(s3280 1)
(s3281 1)
(s3282 1)
(s3283 1)
(s3284 1)
(s3285 1)
(s3286 1)
(s3287 1)
(s3288 1)
(s3289 1)
(s3290 1)
(s3291 1)
(s3292 1)
(s3293 1)
(s3294 1)
(s3295 1)
(s3296 1)
(s3297 1)
(s3298 1)
(s3299 1)
(s3300 1)
(s3301 1)
(s3302 1)
(s3303 1)
(s3304 1)
(s3305 1)
(s3306 1)
(s3307 1)
(s3308 1)
(s3309 1)
(s3310 1)
(s3311 1)
(s3312 1)
(s3313 1)
(s3314 1)
(s3315 1)
(s3316 1)
(s3317 1)
(s3318 1)
(s3319 1)
(s3320 1)
(s3321 1)
(s3322 1)
(s3323 1)
(s3324 1)
(s3325 1)
(s3326 1)
(s3327 1)
(s3328 1)
(s3329 1)
(s3330 1)
(s3331 1)
(s3332 1)
(s3333 1)
(s3334 1)
(s3335 1)
(s3336 1)
(s3337 1)
(s3338 1)
(s3339 1)
(s3340 1)
(s3341 1)
(s3343 1)
(s3344 1)
(s3345 1)
(s3346 1)
(s3347 1)
(s3348 1)
(s3349 1)
(s3350 1)
(s3351 1)
(s3352 1)
(s3353 1)
(s3354 1)
(s3355 1)
(s3356 1)
(s3357 1)
(s3358 1)
(s3359 1)
(s3360 1)
(s3361 1)
(s3362 1)
(s3363 1)
(s3364 1)
(s3365 1)
(s3366 1)
(s3367 1)
(s3368 1)
(s3369 1)
(s3370 1)
(s3371 1)
(s3372 1)
(s3373 1)
(s3374 1)
(s3375 1)
(s3376 1)
(s3377 1)
(s3378 1)
(s3379 1)
(s3380 1)
(s3381 1)
(s3382 1)
(s3383 1)
(s3384 1)
(s3385 1)
(s3386 1)
(s3387 1)
(s3388 1)
(s3389 1)
(s3390 1)
(s3391 1)
(s3392 1)
(s3393 1)
(s3394 1)
(s3395 1)
(s3396 1)
(s3397 1)
(s3398 1)
(s3399 1)
(s3400 1)
(s3401 1)
(s3402 1)
(s3403 1)
(s3404 1)
(s3405 1)
(s3406 1)
(s3407 1)
(s3408 1)
(s3409 1)
(s3410 1)
(s3411 1)
(s3412 1)
(s3413 1)
(s3414 1)
(s3415 1)
(s3416 1)
(s3417 1)
(s3418 1)
(s3419 1)
(s3420 1)
(s3421 1)
(s3422 1)
(s3423 1)
(s3424 1)
(s3425 1)
(s3426 1)
(s3427 1)
(s3428 1)
(s3429 1)
(s3431 1)
(s3432 1)
(s3433 1)
(s3434 1)
(s3435 1)
(s3436 1)
(s3437 1)
(s3438 1)
(s3439 1)
(s3440 1)
(s3441 1)
(s3442 1)
(s3443 1)
(s3444 1)
(s3445 1)
(s3446 1)
(s3447 1)
(s3448 1)
(s3449 1)
(s3450 1)
(s3451 1)
(s3452 1)
(s3453 1)
(s3454 1)
(s3455 1)
(s3456 1)
(s3457 1)
(s3458 1)
(s3459 1)
(s3460 1)
(s3461 1)
(s3462 1)
(s3463 1)
(s3464 1)
(s3465 1)
(s3466 1)
(s3467 1)
(s3468 1)
(s3469 1)
(s3470 1)
(s3471 1)
(s3472 1)
(s3473 1)
(s3474 1)
(s3475 1)
(s3476 1)
(s3477 1)
(s3478 1)
(s3479 1)
(s3480 1)
(s3481 1)
(s3482 1)
(s3483 1)
(s3484 1)
(s3485 1)
(s3486 1)
(s3487 1)
(s3488 1)
(s3489 1)
(s3490 1)
(s3491 1)
(s3492 1)
(s3493 1)
(s3494 1)
(s3495 1)
(s3496 1)
(s3497 1)
(s3498 1)
(s3499 1)
(s3500 1)
(s3501 1)
(s3502 1)
(s3503 1)
(s3504 1)
(s3505 1)
(s3506 1)
(s3507 1)
(s3508 1)
(s3509 1)
(s3510 1)
(s3511 1)
(s3512 1)
(s3513 1)
(s3514 1)
(s3515 1)
(s3516 1)
(s3517 1)
(s3519 1)
(s3520 1)
(s3521 1)
(s3522 1)
(s3523 1)
(s3524 1)
(s3525 1)
(s3526 1)
(s3527 1)
(s3528 1)
(s3529 1)
(s3530 1)
(s3531 1)
(s3532 1)
(s3533 1)
(s3534 1)
(s3535 1)
(s3536 1)
(s3537 1)
(s3538 1)
(s3539 1)
(s3540 1)
(s3541 1)
(s3542 1)
(s3543 1)
(s3544 1)
(s3545 1)
(s3546 1)
(s3547 1)
(s3548 1)
(s3549 1)
(s3550 1)
(s3551 1)
(s3552 1)
(s3553 1)
(s3554 1)
(s3555 1)
(s3556 1)
(s3557 1)
(s3558 1)
(s3559 1)
(s3560 1)
(s3561 1)
(s3562 1)
(s3563 1)
(s3564 1)
(s3565 1)
(s3566 1)
(s3567 1)
(s3568 0)
(s3569 0)
(s3570 0)
(s3571 0)
(s3572 0)
(s3573 0)
(s3574 0)
(s3575 0)
(s3576 0)
(s3577 0)
(s3578 0)
(s3579 0)
(s3580 0)
(s3581 0)
(s3582 0)
(s3583 0)
(s3584 0)
(s3585 0)
(s3586 0)
(s3587 0)
(s3588 0)
(s3589 0)
(s3590 0)
(s3591 0)
(s3592 0)
(s3593 0)
(s3594 0)
(s3595 0)
(s3596 0)
(s3597 0)
(s3598 0)
(s3599 0)
(s3600 0)
(s3601 0)
(s3602 0)
(s3603 0)
(s3604 0)
(s3605 0)
(s3606 0)
(s3607 0)
(s3608 0)
(s3609 0)
(s3610 0)
(s3611 0)
(s3612 0)
(s3613 0)
(s3614 0)
(s3615 0)
(s3616 0)
(s3617 0)
(s3618 0)
(s3619 0)
(s3620 0)
(s3621 0)
(s3622 0)
(s3623 0)
(s3624 0)
(s3625 0)
(s3626 0)
(s3627 0)
(s3628 0)
(s3629 0)
(s3630 0)
(s3631 0)
(s3632 0)
(s3633 0)
(s3634 0)
(s3635 0)
(s3636 0)
(s3637 0)
(s3638 0)
(s3639 0)
(s3640 0)
(s3641 0)
(s3642 0)
(s3643 0)
(s3644 0)
(s3645 0)
(s3646 0)
(s3647 0)
(s3648 0)
(s3649 0)
(s3650 0)
(s3651 0)
(s3652 0)
(s3653 0)
(s3654 1)
(s3655 1)
(s3656 1)
(s3657 1)
(s3658 1)
(s3659 1)
(s3660 1)
(s3661 1)
(s3662 1)
(s3663 1)
(s3664 1)
(s3665 1)
(s3666 1)
(s3667 1)
(s3668 1)
(s3669 1)
(s3670 1)
(s3671 1)
(s3672 1)
(s3673 1)
(s3674 1)
(s3675 1)
(s3676 1)
(s3677 1)
(s3678 1)
(s3679 1)
(s3680 1)
(s3681 1)
(s3682 1)
(s3683 1)
(s3684 1)
(s3685 1)
(s3686 1)
(s3687 1)
(s3688 1)
(s3689 1)
(s3690 1)
(s3691 1)
(s3692 1)
(s3693 1)
(s3695 1)
(s3696 1)
(s3697 1)
(s3698 1)
(s3699 1)
(s3700 1)
(s3701 1)
(s3702 1)
(s3703 1)
(s3704 1)
(s3705 1)
(s3706 1)
(s3707 1)
(s3708 1)
(s3709 1)
(s3710 1)
(s3711 1)
(s3712 1)
(s3713 1)
(s3714 1)
(s3715 1)
(s3716 1)
(s3717 1)
(s3718 1)
(s3719 1)
(s3720 1)
(s3721 1)
(s3722 1)
(s3723 1)
(s3724 1)
(s3725 1)
(s3726 1)
(s3727 1)
(s3728 1)
(s3729 1)
(s3730 1)
(s3731 1)
(s3732 1)
(s3733 1)
(s3734 1)
(s3735 1)
(s3736 1)
(s3737 1)
(s3738 1)
(s3739 1)
(s3740 1)
(s3741 1)
(s3742 1)
(s3743 1)
(s3744 1)
(s3745 1)
(s3746 1)
(s3747 1)
(s3748 1)
(s3749 1)
(s3750 1)
(s3751 1)
(s3752 1)
(s3753 1)
(s3754 1)
(s3755 1)
(s3756 1)
(s3757 1)
(s3758 1)
(s3759 1)
(s3760 1)
(s3761 1)
(s3762 1)
(s3763 1)
(s3764 1)
(s3765 1)
(s3766 1)
(s3767 1)
(s3768 1)
(s3769 1)
(s3770 1)
(s3771 1)
(s3772 1)
(s3773 1)
(s3774 1)
(s3775 1)
(s3776 1)
(s3777 1)
(s3778 1)
(s3779 1)
(s3780 1)
(s3781 1)
(s3783 1)
(s3784 1)
(s3785 1)
(s3786 1)
(s3787 1)
(s3788 1)
(s3789 1)
(s3790 1)
(s3791 1)
(s3792 1)
(s3793 1)
(s3794 1)
(s3795 1)
(s3796 1)
(s3797 1)
(s3798 1)
(s3799 1)
(s3800 1)
(s3801 1)
(s3802 1)
(s3803 1)
(s3804 1)
(s3805 1)
(s3806 1)
(s3807 1)
(s3808 1)
(s3809 1)
(s3810 1)
(s3811 1)
(s3812 1)
(s3813 1)
(s3814 1)
(s3815 1)
(s3816 1)
(s3817 1)
(s3818 1)
(s3819 1)
(s3820 1)
(s3821 1)
(s3822 1)
(s3823 1)
(s3824 1)
(s3825 1)
(s3826 1)
(s3827 1)
(s3828 1)
(s3829 1)
(s3830 1)
(s3831 1)
(s3832 1)
(s3833 1)
(s3834 1)
(s3835 1)
(s3836 1)
(s3837 1)
(s3838 1)
(s3839 1)
(s3840 1)
(s3841 1)
(s3842 1)
(s3843 1)
(s3844 1)
(s3845 1)
(s3846 1)
(s3847 1)
(s3848 1)
(s3849 1)
(s3850 1)
(s3851 1)
(s3852 1)
(s3853 1)
(s3854 1)
(s3855 1)
(s3856 1)
(s3857 1)
(s3858 1)
(s3859 1)
(s3860 1)
(s3861 1)
(s3862 1)
(s3863 1)
(s3864 1)
(s3865 1)
(s3866 1)
(s3867 1)
(s3868 1)
(s3869 1)
(s3871 1)
(s3872 1)
(s3873 1)
(s3874 1)
(s3875 1)
(s3876 1)
(s3877 1)
(s3878 1)
(s3879 1)
(s3880 1)
(s3881 1)
(s3882 1)
(s3883 1)
(s3884 1)
(s3885 1)
(s3886 1)
(s3887 1)
(s3888 1)
(s3889 1)
(s3890 1)
(s3891 1)
(s3892 1)
(s3893 1)
(s3894 1)
(s3895 1)
(s3896 1)
(s3897 1)
(s3898 1)
(s3899 1)
(s3900 1)
(s3901 1)
(s3902 1)
(s3903 1)
(s3904 1)
(s3905 1)
(s3906 1)
(s3907 1)
(s3908 1)
(s3909 1)
(s3910 1)
(s3911 1)
(s3912 1)
(s3913 1)
(s3914 1)
(s3915 1)
(s3916 1)
(s3917 1)
(s3918 1)
(s3919 1)
(s3920 1)
(s3921 1)
(s3922 1)
(s3923 1)
(s3924 1)
(s3925 1)
(s3926 1)
(s3927 1)
(s3928 1)
(s3929 1)
(s3930 1)
(s3931 1)
(s3932 1)
(s3933 1)
(s3934 1)
(s3935 1)
(s3936 1)
(s3937 1)
(s3938 1)
(s3939 1)
(s3940 1)
(s3941 1)
(s3942 1)
(s3943 1)
(s3944 1)
(s3945 1)
(s3946 1)
(s3947 1)
(s3948 1)
(s3949 1)
(s3950 1)
(s3951 1)
(s3952 1)
(s3953 1)
(s3954 1)
(s3955 1)
(s3956 1)
(s3957 1)
(s3959 1)
(s3960 1)
(s3961 1)
(s3962 1)
(s3963 1)
(s3964 1)
(s3965 1)
(s3966 1)
(s3967 1)
(s3968 1)
(s3969 1)
(s3970 1)
(s3971 1)
(s3972 1)
(s3973 1)
(s3974 1)
(s3975 1)
(s3976 1)
(s3977 1)
(s3978 1)
(s3979 1)
(s3980 1)
(s3981 1)
(s3982 1)
(s3983 1)
(s3984 1)
(s3985 1)
(s3986 1)
(s3987 1)
(s3988 1)
(s3989 1)
(s3990 1)
(s3991 1)
(s3992 1)
(s3993 1)
(s3994 1)
(s3995 1)
(s3996 1)
(s3997 1)
(s3998 1)
(s3999 1)
(s4000 1)
(s4001 1)
(s4002 1)
(s4003 1)
(s4004 1)
(s4005 1)
(s4006 1)
(s4007 1)
(s4008 1)
(s4009 1)
(s4010 1)
(s4011 1)
(s4012 1)
(s4013 1)
(s4014 1)
(s4015 1)
(s4016 1)
(s4017 1)
(s4018 1)
(s4019 1)
(s4020 1)
(s4021 1)
(s4022 1)
(s4023 1)
(s4024 1)
(s4025 1)
(s4026 1)
(s4027 1)
(s4028 1)
(s4029 1)
(s4030 1)
(s4031 1)
(s4032 1)
(s4033 1)
(s4034 1)
(s4035 1)
(s4036 1)
(s4037 1)
(s4038 1)
(s4039 1)
(s4040 1)
(s4041 1)
(s4042 1)
(s4043 1)
(s4044 1)
(s4045 1)
(s4047 1)
(s4048 1)
(s4049 1)
(s4050 1)
(s4051 1)
(s4052 1)
(s4053 1)
(s4054 1)
(s4055 1)
(s4056 1)
(s4057 1)
(s4058 1)
(s4059 1)
(s4060 1)
(s4061 1)
(s4062 1)
(s4063 1)
(s4064 1)
(s4065 1)
(s4066 1)
(s4067 1)
(s4068 1)
(s4069 1)
(s4070 1)
(s4071 1)
(s4072 1)
(s4073 1)
(s4074 1)
(s4075 1)
(s4076 1)
(s4077 1)
(s4078 1)
(s4079 1)
(s4080 1)
(s4081 1)
(s4082 1)
(s4083 1)
(s4084 1)
(s4085 1)
(s4086 1)
(s4087 1)
(s4088 1)
(s4089 1)
(s4090 1)
(s4091 1)
(s4092 1)
(s4093 1)
(s4094 1)
(s4095 1)
(s4096 1)
(s4097 1)
(s4098 1)
(s4099 1)
(s4100 1)
(s4101 1)
(s4102 1)
(s4103 1)
(s4104 1)
(s4105 1)
(s4106 1)
(s4107 1)
(s4108 1)
(s4109 1)
(s4110 1)
(s4111 1)
(s4112 1)
(s4113 1)
(s4114 1)
(s4115 1)
(s4116 1)
(s4117 1)
(s4118 1)
(s4119 1)
(s4120 1)
(s4121 1)
(s4122 1)
(s4123 1)
(s4124 1)
(s4125 1)
(s4126 1)
(s4127 1)
(s4128 1)
(s4129 1)
(s4130 1)
(s4131 1)
(s4132 1)
(s4133 1)
(s4135 1)
(s4136 1)
(s4137 1)
(s4138 1)
(s4139 1)
(s4140 1)
(s4141 1)
(s4142 1)
(s4143 1)
(s4144 1)
(s4145 1)
(s4146 1)
(s4147 1)
(s4148 1)
(s4149 1)
(s4150 1)
(s4151 1)
(s4152 1)
(s4153 1)
(s4154 1)
(s4155 1)
(s4156 1)
(s4157 1)
(s4158 1)
(s4159 1)
(s4160 1)
(s4161 1)
(s4162 1)
(s4163 1)
(s4164 1)
(s4165 1)
(s4166 1)
(s4167 1)
(s4168 1)
(s4169 1)
(s4170 1)
(s4171 1)
(s4172 1)
(s4173 1)
(s4174 1)
(s4175 1)
(s4176 1)
(s4177 1)
(s4178 1)
(s4179 1)
(s4180 1)
(s4181 1)
(s4182 1)
(s4183 1)
(s4184 1)
(s4185 1)
(s4186 1)
(s4187 1)
(s4188 1)
(s4189 1)
(s4190 1)
(s4191 1)
(s4192 1)
(s4193 1)
(s4194 1)
(s4195 1)
(s4196 1)
(s4197 1)
(s4198 1)
(s4199 1)
(s4200 1)
(s4201 1)
(s4202 1)
(s4203 1)
(s4204 1)
(s4205 1)
(s4206 1)
(s4207 1)
(s4208 1)
(s4209 1)
(s4210 1)
(s4211 1)
(s4212 1)
(s4213 1)
(s4214 1)
(s4215 1)
(s4216 1)
(s4217 1)
(s4218 1)
(s4219 1)
(s4220 1)
(s4221 1)
(s4223 1)
(s4224 1)
(s4225 1)
(s4226 1)
(s4227 1)
(s4228 1)
(s4229 1)
(s4230 1)
(s4231 1)
(s4232 1)
(s4233 1)
(s4234 1)
(s4235 1)
(s4236 1)
(s4237 1)
(s4238 1)
(s4239 1)
(s4240 1)
(s4241 1)
(s4242 1)
(s4243 1)
(s4244 1)
(s4245 1)
(s4246 1)
(s4247 1)
(s4248 1)
(s4249 1)
(s4250 1)
(s4251 1)
(s4252 1)
(s4253 1)
(s4254 1)
(s4255 1)
(s4256 1)
(s4257 1)
(s4258 1)
(s4259 1)
(s4260 1)
(s4261 1)
(s4262 1)
(s4263 1)
(s4264 1)
(s4265 1)
(s4266 1)
(s4267 1)
(s4268 1)
(s4269 1)
(s4270 1)
(s4271 1)
(s4272 1)
(s4273 1)
(s4274 1)
(s4275 1)
(s4276 1)
(s4277 1)
(s4278 1)
(s4279 1)
(s4280 1)
(s4281 1)
(s4282 1)
(s4283 1)
(s4284 1)
(s4285 1)
(s4286 1)
(s4287 1)
(s4288 1)
(s4289 1)
(s4290 1)
(s4291 1)
(s4292 1)
(s4293 1)
(s4294 1)
(s4295 1)
(s4296 1)
(s4297 1)
(s4298 1)
(s4299 1)
(s4300 1)
(s4301 1)
(s4302 1)
(s4303 1)
(s4304 1)
(s4305 1)
(s4306 1)
(s4307 1)
(s4308 1)
(s4309 1)
(s4311 1)
(s4312 1)
(s4313 1)
(s4314 1)
(s4315 1)
(s4316 1)
(s4317 1)
(s4318 1)
(s4319 1)
(s4320 1)
(s4321 1)
(s4322 1)
(s4323 1)
(s4324 1)
(s4325 1)
(s4326 1)
(s4327 1)
(s4328 1)
(s4329 1)
(s4330 1)
(s4331 1)
(s4332 1)
(s4333 1)
(s4334 1)
(s4335 1)
(s4336 1)
(s4337 1)
(s4338 1)
(s4339 1)
(s4340 1)
(s4341 1)
(s4342 1)
(s4343 1)
(s4344 1)
(s4345 1)
(s4346 1)
(s4347 1)
(s4348 1)
(s4349 1)
(s4350 1)
(s4351 1)
(s4352 1)
(s4353 1)
(s4354 1)
(s4355 1)
(s4356 1)
(s4357 1)
(s4358 1)
(s4359 1)
(s4360 1)
(s4361 1)
(s4362 1)
(s4363 1)
(s4364 1)
(s4365 1)
(s4366 1)
(s4367 1)
(s4368 1)
(s4369 1)
(s4370 1)
(s4371 1)
(s4372 1)
(s4373 1)
(s4374 1)
(s4375 1)
(s4376 1)
(s4377 1)
(s4378 1)
(s4379 1)
(s4380 1)
(s4381 1)
(s4382 1)
(s4383 1)
(s4384 1)
(s4385 1)
(s4386 1)
(s4387 1)
(s4388 1)
(s4389 1)
(s4390 1)
(s4391 1)
(s4392 1)
(s4393 1)
(s4394 1)
(s4395 1)
(s4396 1)
(s4397 1)
(s4399 1)
(s4400 1)
(s4401 1)
(s4402 1)
(s4403 1)
(s4404 1)
(s4405 1)
(s4406 1)
(s4407 1)
(s4408 1)
(s4409 1)
(s4410 1)
(s4411 1)
(s4412 1)
(s4413 1)
(s4414 1)
(s4415 1)
(s4416 1)
(s4417 1)
(s4418 1)
(s4419 1)
(s4420 1)
(s4421 1)
(s4422 1)
(s4423 1)
(s4424 1)
(s4425 1)
(s4426 1)
(s4427 1)
(s4428 1)
(s4429 1)
(s4430 1)
(s4431 1)
(s4432 1)
(s4433 1)
(s4434 1)
(s4435 1)
(s4436 1)
(s4437 1)
(s4438 1)
(s4439 1)
(s4440 1)
(s4441 1)
(s4442 1)
(s4443 1)
(s4444 1)
(s4445 1)timeout
(s4446 1)
(s4447 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 7742/23143 variables, and 6 constraints, problems are : Problem set: 164 solved, 15141 unsolved in 30218 ms.
Refiners :[Positive P Invariants (semi-flows): 6/175 constraints, State Equation: 0/7831 constraints, ReadFeed: 0/160 constraints, PredecessorRefiner: 7567/7656 constraints, Known Traps: 0/0 constraints]
After SMT, in 224695ms problems are : Problem set: 164 solved, 15141 unsolved
Search for dead transitions found 164 dead transitions in 224986ms
Found 164 dead transitions using SMT.
Drop transitions (Dead Transitions using SMT only with invariants) removed 164 transitions
Dead transitions reduction (with SMT) removed 164 transitions
Starting structural reductions in REACHABILITY mode, iteration 1 : 7831/7831 places, 15148/15312 transitions.
Deduced a syphon composed of 82 places in 10 ms
Applied a total of 0 rules in 6746 ms. Remains 7831 /7831 variables (removed 0) and now considering 15148/15148 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 2 iterations and 243631 ms. Remains : 7831/7831 places, 15148/15312 transitions.
Deduced a syphon composed of 82 places in 11 ms
Reduce places removed 82 places and 0 transitions.
// Phase 1: matrix 15148 rows 7749 cols
[2024-06-07 10:50:17] [INFO ] Computed 175 invariants in 99 ms
Current structural bounds on expressions (after invariants) : Max Seen:[86] Max Struct:[7487]
RANDOM walk for 119230 steps (0 resets) in 30001 ms. (3 steps per ms)
BEST_FIRST walk for 31523 steps (0 resets) in 5001 ms. (6 steps per ms)
Current structural bounds on expressions (after WALK) : Max Seen:[86] Max Struct:[7487]
[2024-06-07 10:50:52] [INFO ] Invariant cache hit.
[2024-06-07 10:50:55] [INFO ] [Real]Absence check using 175 positive place invariants in 1637 ms returned sat
Usage: pnml2lts-sym [-gvqh] [--order=
[--mu-opt] [--saturation=
[--sat-granularity=
[--guidance=
[--action=
[--trace=
[--mu=
[--ctl=
[--save-levels=STRING] [--pg-solve] [--attr=
[--saturating-attractor] [--write-strategy=
[--check-strategy] [--interactive-play] [--player]
[--pg-write=
[--edge-label=
[--mucalc=
[--allow-undefined-edges] [--allow-undefined-values]
[-p|--por=
[--weak=[valmari] (default: uses stronger left-commutativity)]
[--leap] [-r|--regroup=<(T,)+>] [--sloan-w1=
[--cw-max-cols=
[--mh-timeout=
[--graph-metrics] [--regroup-exit] [--regroup-time]
[-g|--pins-guards] [--vset=
[--ldd32-cache=
[--cache-ratio=
[--min-free-nodes=
[--fdd-reorder=
[--vset-cache-diff=
[--next-union] [--peak-nodes] [--maxsum=
[--block-size=
[--debug=
[--timeout=INT] [--version] [-h|--help] [--usage]
[OPTIONS]
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-00
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-01
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-02
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-03
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-04
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-05
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-06
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-07
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-08
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-09
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-10
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-11
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-12
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-13
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-14
Could not compute solution for formula : BlocksWorld-PT-17-UpperBounds-15
BK_STOP 1717757456779
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202405141337.jar
+ VERSION=202405141337
+ echo 'Running Version 202405141337'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination UpperBounds -timeout 360 -rebuildPNML
mcc2024
ub formula name BlocksWorld-PT-17-UpperBounds-00
ub formula formula --maxsum=/tmp/558/ub_0_
ub formula name BlocksWorld-PT-17-UpperBounds-01
ub formula formula --maxsum=/tmp/558/ub_1_
ub formula name BlocksWorld-PT-17-UpperBounds-02
ub formula formula --maxsum=/tmp/558/ub_2_
ub formula name BlocksWorld-PT-17-UpperBounds-03
ub formula formula --maxsum=/tmp/558/ub_3_
ub formula name BlocksWorld-PT-17-UpperBounds-04
ub formula formula --maxsum=/tmp/558/ub_4_
ub formula name BlocksWorld-PT-17-UpperBounds-05
ub formula formula --maxsum=/tmp/558/ub_5_
ub formula name BlocksWorld-PT-17-UpperBounds-06
ub formula formula --maxsum=/tmp/558/ub_6_
ub formula name BlocksWorld-PT-17-UpperBounds-07
ub formula formula --maxsum=/tmp/558/ub_7_
ub formula name BlocksWorld-PT-17-UpperBounds-08
ub formula formula --maxsum=/tmp/558/ub_8_
ub formula name BlocksWorld-PT-17-UpperBounds-09
ub formula formula --maxsum=/tmp/558/ub_9_
ub formula name BlocksWorld-PT-17-UpperBounds-10
ub formula formula --maxsum=/tmp/558/ub_10_
ub formula name BlocksWorld-PT-17-UpperBounds-11
ub formula formula --maxsum=/tmp/558/ub_11_
ub formula name BlocksWorld-PT-17-UpperBounds-12
ub formula formula --maxsum=/tmp/558/ub_12_
ub formula name BlocksWorld-PT-17-UpperBounds-13
ub formula formula --maxsum=/tmp/558/ub_13_
ub formula name BlocksWorld-PT-17-UpperBounds-14
ub formula formula --maxsum=/tmp/558/ub_14_
ub formula name BlocksWorld-PT-17-UpperBounds-15
ub formula formula --maxsum=/tmp/558/ub_15_
pnml2lts-sym, ** error **: unknown vector set implementation lddmc
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="BlocksWorld-PT-17"
export BK_EXAMINATION="UpperBounds"
export BK_TOOL="ltsminxred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool ltsminxred"
echo " Input is BlocksWorld-PT-17, examination is UpperBounds"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r605-tall-171774427000293"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/BlocksWorld-PT-17.tgz
mv BlocksWorld-PT-17 execution
cd execution
if [ "UpperBounds" = "ReachabilityDeadlock" ] || [ "UpperBounds" = "UpperBounds" ] || [ "UpperBounds" = "QuasiLiveness" ] || [ "UpperBounds" = "StableMarking" ] || [ "UpperBounds" = "Liveness" ] || [ "UpperBounds" = "OneSafe" ] || [ "UpperBounds" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "UpperBounds" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "UpperBounds" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "UpperBounds.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property UpperBounds.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "UpperBounds.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "UpperBounds" = "ReachabilityDeadlock" ] || [ "UpperBounds" = "QuasiLiveness" ] || [ "UpperBounds" = "StableMarking" ] || [ "UpperBounds" = "Liveness" ] || [ "UpperBounds" = "OneSafe" ] ; then
echo "FORMULA_NAME UpperBounds"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

