About the Execution of LTSMin+red for JoinFreeModules-PT-2000
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 11130.779 | 909336.00 | 1108633.00 | 1665.50 | T???T??F??TT??T? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
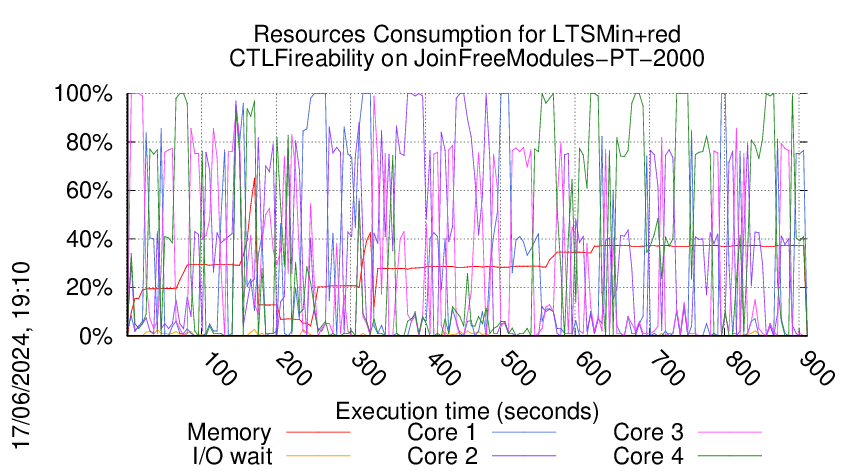
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r504-tall-171649612000082.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
..................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool ltsminxred
Input is JoinFreeModules-PT-2000, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r504-tall-171649612000082
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 6.6M
-rw-r--r-- 1 mcc users 9.1K May 14 13:22 CTLCardinality.txt
-rw-r--r-- 1 mcc users 102K May 14 13:22 CTLCardinality.xml
-rw-r--r-- 1 mcc users 6.9K May 14 13:22 CTLFireability.txt
-rw-r--r-- 1 mcc users 64K May 14 13:22 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 18 16:42 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K May 18 16:42 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 3.8K May 19 07:10 LTLCardinality.txt
-rw-r--r-- 1 mcc users 27K May 19 16:03 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.1K May 19 07:22 LTLFireability.txt
-rw-r--r-- 1 mcc users 16K May 19 18:34 LTLFireability.xml
-rw-r--r-- 1 mcc users 8.6K Apr 11 14:31 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 79K Apr 11 14:31 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 6.1K Apr 11 14:28 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 44K Apr 11 14:28 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.6K May 19 07:13 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K May 19 15:27 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 May 18 16:42 equiv_col
-rw-r--r-- 1 mcc users 5 May 18 16:42 instance
-rw-r--r-- 1 mcc users 6 May 18 16:42 iscolored
-rw-r--r-- 1 mcc users 6.2M May 18 16:42 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-00
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-01
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-02
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-03
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-04
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-05
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-06
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-07
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-08
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-09
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-10
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2024-11
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2023-12
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2023-13
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2023-14
FORMULA_NAME JoinFreeModules-PT-2000-CTLFireability-2023-15
=== Now, execution of the tool begins
BK_START 1717221282221
Invoking MCC driver with
BK_TOOL=ltsminxred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=JoinFreeModules-PT-2000
BK_MEMORY_CONFINEMENT=16384
Applying reductions before tool ltsmin
Invoking reducer
Running Version 202405141337
[2024-06-01 05:54:43] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2024-06-01 05:54:43] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-06-01 05:54:43] [INFO ] Load time of PNML (sax parser for PT used): 460 ms
[2024-06-01 05:54:43] [INFO ] Transformed 10001 places.
[2024-06-01 05:54:43] [INFO ] Transformed 16001 transitions.
[2024-06-01 05:54:43] [INFO ] Parsed PT model containing 10001 places and 16001 transitions and 46002 arcs in 622 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 18 ms.
Initial state reduction rules removed 5 formulas.
Reduce places removed 1 places and 0 transitions.
FORMULA JoinFreeModules-PT-2000-CTLFireability-2024-04 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA JoinFreeModules-PT-2000-CTLFireability-2024-07 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA JoinFreeModules-PT-2000-CTLFireability-2024-10 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA JoinFreeModules-PT-2000-CTLFireability-2024-11 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA JoinFreeModules-PT-2000-CTLFireability-2023-14 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 108 out of 10000 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 1403 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
// Phase 1: matrix 16001 rows 10000 cols
[2024-06-01 05:54:45] [INFO ] Computed 2000 invariants in 93 ms
[2024-06-01 05:54:45] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20260 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20134 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56864ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56991ms
[2024-06-01 05:55:42] [INFO ] Invariant cache hit.
[2024-06-01 05:55:44] [INFO ] Implicit Places using invariants in 2386 ms returned []
Implicit Place search using SMT only with invariants took 2390 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-06-01 05:55:45] [INFO ] Invariant cache hit.
[2024-06-01 05:55:45] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30126 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30120 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 77232ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 77322ms
Finished structural reductions in LTL mode , in 1 iterations and 138216 ms. Remains : 10000/10000 places, 16001/16001 transitions.
Support contains 108 out of 10000 places after structural reductions.
[2024-06-01 05:57:03] [INFO ] Flatten gal took : 619 ms
[2024-06-01 05:57:03] [INFO ] Flatten gal took : 432 ms
[2024-06-01 05:57:04] [INFO ] Input system was already deterministic with 16001 transitions.
Support contains 102 out of 10000 places (down from 108) after GAL structural reductions.
RANDOM walk for 41036 steps (8 resets) in 4191 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 430 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 422 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 403 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 384 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 403 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 391 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 395 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 503 ms. (7 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 390 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 378 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 389 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 366 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 380 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 366 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 380 ms. (10 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 547 ms. (7 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 489 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 501 ms. (7 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 447 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 429 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 430 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 432 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 465 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 616 ms. (6 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 478 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 437 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 443 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 438 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 435 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 485 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 475 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 629 ms. (6 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 514 ms. (7 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 443 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 450 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 436 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 429 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 440 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 452 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 605 ms. (6 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 474 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 439 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 439 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 432 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 434 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 437 ms. (9 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 444 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 587 ms. (6 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 482 ms. (8 steps per ms) remains 83/83 properties
BEST_FIRST walk for 4004 steps (0 resets) in 435 ms. (9 steps per ms) remains 83/83 properties
Probabilistic random walk after 129126 steps, saw 129068 distinct states, run finished after 21032 ms. (steps per millisecond=6 ) properties seen :11
[2024-06-01 05:57:33] [INFO ] Invariant cache hit.
[2024-06-01 05:57:33] [INFO ] State equation strengthened by 2000 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/89 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 72 unsolved
At refinement iteration 1 (OVERLAPS) 351/440 variables, 88/88 constraints. Problems are: Problem set: 0 solved, 72 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/440 variables, 0/88 constraints. Problems are: Problem set: 0 solved, 72 unsolved
All remaining problems are real, not stopping.
At refinement iteration 3 (OVERLAPS) 704/1144 variables, 440/528 constraints. Problems are: Problem set: 0 solved, 72 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/1144 variables, 88/616 constraints. Problems are: Problem set: 0 solved, 72 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/1144 variables, 0/616 constraints. Problems are: Problem set: 0 solved, 72 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 1144/26001 variables, and 616 constraints, problems are : Problem set: 0 solved, 72 unsolved in 5015 ms.
Refiners :[Positive P Invariants (semi-flows): 88/2000 constraints, State Equation: 440/10000 constraints, ReadFeed: 88/2000 constraints, PredecessorRefiner: 72/72 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 72 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/89 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 72 unsolved
At refinement iteration 1 (OVERLAPS) 351/440 variables, 88/88 constraints. Problems are: Problem set: 0 solved, 72 unsolved
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 90 ms of which 11 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 76 ms of which 2 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 62 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 75 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 64 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 60 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 58 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 56 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 56 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 53 ms of which 0 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 52 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 59 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 54 ms of which 1 ms to minimize.
[2024-06-01 05:57:40] [INFO ] Deduced a trap composed of 3 places in 48 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 50 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 50 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 49 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 48 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 45 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 47 ms of which 2 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/440 variables, 20/108 constraints. Problems are: Problem set: 0 solved, 72 unsolved
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 46 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 52 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 39 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 40 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 44 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 38 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 46 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 0 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 38 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 42 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 1 ms to minimize.
[2024-06-01 05:57:41] [INFO ] Deduced a trap composed of 3 places in 39 ms of which 1 ms to minimize.
[2024-06-01 05:57:42] [INFO ] Deduced a trap composed of 3 places in 35 ms of which 0 ms to minimize.
[2024-06-01 05:57:42] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 1 ms to minimize.
[2024-06-01 05:57:42] [INFO ] Deduced a trap composed of 3 places in 35 ms of which 1 ms to minimize.
[2024-06-01 05:57:42] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 0 ms to minimize.
At refinement iteration 3 (INCLUDED_ONLY) 0/440 variables, 17/125 constraints. Problems are: Problem set: 0 solved, 72 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 440/26001 variables, and 125 constraints, problems are : Problem set: 0 solved, 72 unsolved in 5008 ms.
Refiners :[Positive P Invariants (semi-flows): 88/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/72 constraints, Known Traps: 37/37 constraints]
After SMT, in 10312ms problems are : Problem set: 0 solved, 72 unsolved
Skipping Parikh replay, no witness traces provided.
Support contains 89 out of 10000 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Graph (complete) has 24000 edges and 10000 vertex of which 440 are kept as prefixes of interest. Removing 9560 places using SCC suffix rule.35 ms
Discarding 9560 places :
Also discarding 15296 output transitions
Drop transitions (Output transitions of discarded places.) removed 15296 transitions
Drop transitions (Empty/Sink Transition effects.) removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 0 with 1 rules applied. Total rules applied 2 place count 440 transition count 704
Applied a total of 2 rules in 105 ms. Remains 440 /10000 variables (removed 9560) and now considering 704/16001 (removed 15297) transitions.
Running 528 sub problems to find dead transitions.
// Phase 1: matrix 704 rows 440 cols
[2024-06-01 05:57:44] [INFO ] Computed 88 invariants in 4 ms
[2024-06-01 05:57:44] [INFO ] State equation strengthened by 88 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/352 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 1 (OVERLAPS) 88/440 variables, 88/88 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/440 variables, 0/88 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 3 (OVERLAPS) 704/1144 variables, 440/528 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/1144 variables, 88/616 constraints. Problems are: Problem set: 0 solved, 528 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 1144/1144 variables, and 616 constraints, problems are : Problem set: 0 solved, 528 unsolved in 20022 ms.
Refiners :[Positive P Invariants (semi-flows): 88/88 constraints, State Equation: 440/440 constraints, ReadFeed: 88/88 constraints, PredecessorRefiner: 528/528 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 528 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/352 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 1 (OVERLAPS) 88/440 variables, 88/88 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/440 variables, 0/88 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 3 (OVERLAPS) 704/1144 variables, 440/528 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/1144 variables, 88/616 constraints. Problems are: Problem set: 0 solved, 528 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/1144 variables, 528/1144 constraints. Problems are: Problem set: 0 solved, 528 unsolved
[2024-06-01 05:58:15] [INFO ] Deduced a trap composed of 3 places in 31 ms of which 1 ms to minimize.
[2024-06-01 05:58:15] [INFO ] Deduced a trap composed of 3 places in 19 ms of which 0 ms to minimize.
[2024-06-01 05:58:15] [INFO ] Deduced a trap composed of 3 places in 17 ms of which 1 ms to minimize.
[2024-06-01 05:58:15] [INFO ] Deduced a trap composed of 3 places in 17 ms of which 0 ms to minimize.
[2024-06-01 05:58:20] [INFO ] Deduced a trap composed of 3 places in 29 ms of which 0 ms to minimize.
[2024-06-01 05:58:20] [INFO ] Deduced a trap composed of 3 places in 18 ms of which 1 ms to minimize.
[2024-06-01 05:58:20] [INFO ] Deduced a trap composed of 3 places in 17 ms of which 1 ms to minimize.
[2024-06-01 05:58:20] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 1 ms to minimize.
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 1144/1144 variables, and 1152 constraints, problems are : Problem set: 0 solved, 528 unsolved in 20022 ms.
Refiners :[Positive P Invariants (semi-flows): 88/88 constraints, State Equation: 440/440 constraints, ReadFeed: 88/88 constraints, PredecessorRefiner: 528/528 constraints, Known Traps: 8/8 constraints]
After SMT, in 40116ms problems are : Problem set: 0 solved, 528 unsolved
Search for dead transitions found 0 dead transitions in 40121ms
Finished structural reductions in REACHABILITY mode , in 1 iterations and 40227 ms. Remains : 440/10000 places, 704/16001 transitions.
RANDOM walk for 40037 steps (8 resets) in 338 ms. (118 steps per ms) remains 68/72 properties
BEST_FIRST walk for 4004 steps (8 resets) in 32 ms. (121 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 26 ms. (148 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 29 ms. (133 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 27 ms. (143 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 31 ms. (125 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 27 ms. (143 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 29 ms. (133 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 32 ms. (121 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 24 ms. (160 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 24 ms. (160 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 38 ms. (102 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 24 ms. (160 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 27 ms. (143 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 21 ms. (182 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 33 ms. (117 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 26 ms. (148 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 30 ms. (129 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 30 ms. (129 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 27 ms. (143 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 38 ms. (102 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 28 ms. (138 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 21 ms. (182 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 33 ms. (117 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 27 ms. (143 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 23 ms. (166 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 51 ms. (77 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 38 ms. (102 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 31 ms. (125 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 31 ms. (125 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 33 ms. (117 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 25 ms. (154 steps per ms) remains 68/68 properties
BEST_FIRST walk for 4004 steps (8 resets) in 30 ms. (129 steps per ms) remains 68/68 properties
Interrupted probabilistic random walk after 92859 steps, run timeout after 3001 ms. (steps per millisecond=30 ) properties seen :0 out of 68
Probabilistic random walk after 92859 steps, saw 92086 distinct states, run finished after 3014 ms. (steps per millisecond=30 ) properties seen :0
[2024-06-01 05:58:27] [INFO ] Invariant cache hit.
[2024-06-01 05:58:27] [INFO ] State equation strengthened by 88 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/85 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 1 (OVERLAPS) 335/420 variables, 84/84 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/420 variables, 0/84 constraints. Problems are: Problem set: 0 solved, 68 unsolved
All remaining problems are real, not stopping.
At refinement iteration 3 (OVERLAPS) 672/1092 variables, 420/504 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/1092 variables, 84/588 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/1092 variables, 0/588 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 6 (OVERLAPS) 0/1092 variables, 0/588 constraints. Problems are: Problem set: 0 solved, 68 unsolved
No progress, stopping.
After SMT solving in domain Real declared 1092/1144 variables, and 588 constraints, problems are : Problem set: 0 solved, 68 unsolved in 4202 ms.
Refiners :[Positive P Invariants (semi-flows): 84/88 constraints, State Equation: 420/440 constraints, ReadFeed: 84/88 constraints, PredecessorRefiner: 68/68 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 68 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/85 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 1 (OVERLAPS) 335/420 variables, 84/84 constraints. Problems are: Problem set: 0 solved, 68 unsolved
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 38 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 85 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 54 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 44 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 33 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 2 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 62 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 57 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 52 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 75 ms of which 1 ms to minimize.
[2024-06-01 05:58:32] [INFO ] Deduced a trap composed of 3 places in 49 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 75 ms of which 4 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 38 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 32 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 32 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 29 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 28 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 28 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/420 variables, 20/104 constraints. Problems are: Problem set: 0 solved, 68 unsolved
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 28 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 24 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 22 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 20 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 19 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 17 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 20 ms of which 0 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 18 ms of which 1 ms to minimize.
[2024-06-01 05:58:33] [INFO ] Deduced a trap composed of 3 places in 19 ms of which 0 ms to minimize.
At refinement iteration 3 (INCLUDED_ONLY) 0/420 variables, 13/117 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/420 variables, 0/117 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 5 (OVERLAPS) 672/1092 variables, 420/537 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/1092 variables, 84/621 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/1092 variables, 68/689 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 8 (INCLUDED_ONLY) 0/1092 variables, 0/689 constraints. Problems are: Problem set: 0 solved, 68 unsolved
At refinement iteration 9 (OVERLAPS) 0/1092 variables, 0/689 constraints. Problems are: Problem set: 0 solved, 68 unsolved
No progress, stopping.
After SMT solving in domain Int declared 1092/1144 variables, and 689 constraints, problems are : Problem set: 0 solved, 68 unsolved in 10965 ms.
Refiners :[Positive P Invariants (semi-flows): 84/88 constraints, State Equation: 420/440 constraints, ReadFeed: 84/88 constraints, PredecessorRefiner: 68/68 constraints, Known Traps: 33/33 constraints]
After SMT, in 15183ms problems are : Problem set: 0 solved, 68 unsolved
Fused 68 Parikh solutions to 17 different solutions.
Finished Parikh walk after 109738 steps, including 0 resets, run visited all 68 properties in 3337 ms. (steps per millisecond=32 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 2 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Parikh walk visited 68 properties in 3355 ms.
[2024-06-01 05:58:46] [INFO ] Flatten gal took : 309 ms
[2024-06-01 05:58:46] [INFO ] Flatten gal took : 275 ms
[2024-06-01 05:58:47] [INFO ] Input system was already deterministic with 16001 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 3462 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
// Phase 1: matrix 16001 rows 10000 cols
[2024-06-01 05:58:52] [INFO ] Computed 2000 invariants in 51 ms
[2024-06-01 05:58:52] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20142 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20140 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56304ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56388ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 59872 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 05:59:48] [INFO ] Flatten gal took : 275 ms
[2024-06-01 05:59:49] [INFO ] Flatten gal took : 293 ms
[2024-06-01 05:59:49] [INFO ] Input system was already deterministic with 16001 transitions.
RANDOM walk for 40038 steps (8 resets) in 3176 ms. (12 steps per ms) remains 1/1 properties
BEST_FIRST walk for 40004 steps (8 resets) in 4314 ms. (9 steps per ms) remains 1/1 properties
Probabilistic random walk after 48034 steps, saw 48017 distinct states, run finished after 6025 ms. (steps per millisecond=7 ) properties seen :0
[2024-06-01 05:59:57] [INFO ] Invariant cache hit.
[2024-06-01 05:59:57] [INFO ] State equation strengthened by 2000 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/1 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 4/5 variables, 1/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/5 variables, 0/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 8/13 variables, 5/6 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/13 variables, 1/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/13 variables, 0/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (OVERLAPS) 0/13 variables, 0/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Real declared 13/26001 variables, and 7 constraints, problems are : Problem set: 0 solved, 1 unsolved in 97 ms.
Refiners :[Positive P Invariants (semi-flows): 1/2000 constraints, State Equation: 5/10000 constraints, ReadFeed: 1/2000 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 1 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/1 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 4/5 variables, 1/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
[2024-06-01 05:59:58] [INFO ] Deduced a trap composed of 3 places in 30 ms of which 1 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/5 variables, 1/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/5 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (OVERLAPS) 8/13 variables, 5/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/13 variables, 1/8 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/13 variables, 1/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/13 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 8 (OVERLAPS) 0/13 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Int declared 13/26001 variables, and 9 constraints, problems are : Problem set: 0 solved, 1 unsolved in 116 ms.
Refiners :[Positive P Invariants (semi-flows): 1/2000 constraints, State Equation: 5/10000 constraints, ReadFeed: 1/2000 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 1/1 constraints]
After SMT, in 276ms problems are : Problem set: 0 solved, 1 unsolved
Finished Parikh walk after 9 steps, including 0 resets, run visited all 1 properties in 3 ms. (steps per millisecond=3 )
FORMULA JoinFreeModules-PT-2000-CTLFireability-2024-00 TRUE TECHNIQUES PARIKH_WALK
Parikh walk visited 1 properties in 5 ms.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 1084 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 05:59:59] [INFO ] Invariant cache hit.
[2024-06-01 05:59:59] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: ((s0 5.0)
(s1 2.0)
(s3 4.0)
(s4 5.0)
(s5 5.0)
(s6 2.0)
(s8 4.0)
(s9 5.0)
(s10 5.0)
(s11 2.0)
(s13 4.0)
(s14 5.0)
(s15 5.0)
(s16 2.0)
(s18 4.0)
(s19 5.0)
(s20 5.0)
(s21 2.0)
(s23 4.0)
(s24 5.0)
(s25 5.0)
(s26 2.0)
(s28 4.0)
(s29 5.0)
(s30 5.0)
(s31 2.0)
(s33 4.0)
(s34 5.0)
(s35 5.0)
(s36 2.0)
(s38 4.0)
(s39 5.0)
(s40 5.0)
(s41 2.0)
(s43 4.0)
(s44 5.0)
(s45 5.0)
(s46 2.0)
(s48 4.0)
(s49 5.0)
(s50 5.0)
(s51 2.0)
(s53 4.0)
(s54 5.0)
(s55 5.0)
(s56 2.0)
(s58 4.0)
(s59 5.0)
(s60 5.0)
(s61 2.0)
(s63 4.0)
(s64 5.0)
(s65 5.0)
(s66 2.0)
(s68 4.0)
(s69 5.0)
(s70 5.0)
(s71 2.0)
(s73 4.0)
(s74 5.0)
(s75 5.0)
(s76 2.0)
(s78 4.0)
(s79 5.0)
(s80 5.0)
(s81 2.0)
(s83 4.0)
(s84 5.0)
(s85 5.0)
(s86 2.0)
(s88 4.0)
(s89 5.0)
(s90 5.0)
(s91 2.0)
(s93 4.0)
(s94 5.0)
(s95 5.0)
(s96 2.0)
(s98 4.0)
(s99 5.0)
(s100 5.0)
(s101 2.0)
(s103 4.0)
(s104 5.0)
(s105 5.0)
(s106 2.0)
(s108 4.0)
(s109 5.0)
(s110 5.0)
(s111 2.0)
(s113 4.0)
(s114 5.0)
(s115 5.0)
(s116 2.0)
(s118 4.0)
(s119 5.0)
(s120 5.0)
(s121 2.0)
(s123 4.0)
(s124 5.0)
(s125 5.0)
(s126 2.0)
(s128 4.0)
(s129 5.0)
(s130 5.0)
(s131 2.0)
(s133 4.0)
(s134 5.0)
(s135 5.0)
(s136 2.0)
(s138 4.0)
(s139 5.0)
(s140 5.0)
(s141 2.0)
(s143 4.0)
(s144 5.0)
(s145 5.0)
(s146 2.0)
(s148 4.0)
(s149 5.0)
(s150 5.0)
(s151 2.0)
(s153 4.0)
(s154 5.0)
(s155 5.0)
(s156 2.0)
(s158 4.0)
(s159 5.0)
(s160 5.0)
(s161 2.0)
(s163 4.0)
(s164 5.0)
(s165 5.0)
(s166 2.0)
(s168 4.0)
(s169 5.0)
(s170 5.0)
(s171 2.0)
(s173 4.0)
(s174 5.0)
(s175 5.0)
(s176 2.0)
(s178 4.0)
(s179 5.0)
(s180 5.0)
(s181 2.0)
(s183 4.0)
(s184 5.0)
(s185 5.0)
(s186 2.0)
(s188 4.0)
(s189 5.0)
(s190 5.0)
(s191 2.0)
(s193 4.0)
(s194 5.0)
(s195 5.0)
(s196 2.0)
(s198 4.0)
(s199 5.0)
(s200 5.0)
(s201 2.0)
(s203 4.0)
(s204 5.0)
(s205 5.0)
(s206 2.0)
(s208 4.0)
(s209 5.0)
(s210 5.0)
(s211 2.0)
(s213 4.0)
(s214 5.0)
(s215 5.0)
(s216 2.0)
(s218 4.0)
(s219 5.0)
(s220 5.0)
(s221 2.0)
(s223 4.0)
(s224 5.0)
(s225 5.0)
(s226 2.0)
(s228 4.0)
(s229 5.0)
(s230 5.0)
(s231 2.0)
(s233 4.0)
(s234 5.0)
(s235 5.0)
(s236 2.0)
(s238 4.0)
(s239 5.0)
(s240 5.0)
(s241 2.0)
(s243 4.0)
(s244 5.0)
(s245 5.0)
(s246 2.0)
(s248 4.0)
(s249 5.0)
(s250 5.0)
(s251 2.0)
(s253 4.0)
(s254 5.0)
(s255 5.0)
(s256 2.0)
(s258 4.0)
(s259 5.0)
(s260 5.0)
(s261 2.0)
(s263 4.0)
(s264 5.0)
(s265 5.0)
(s266 2.0)
(s268 4.0)
(s269 5.0)
(s270 5.0)
(s271 2.0)
(s273 4.0)
(s274 5.0)
(s275 5.0)
(s276 2.0)
(s278 4.0)
(s279 5.0)
(s280 5.0)
(s281 2.0)
(s283 4.0)
(s284 5.0)
(s285 5.0)
(s286 2.0)
(s288 4.0)
(s289 5.0)
(s290 5.0)
(s291 2.0)
(s293 4.0)
(s294 5.0)
(s295 5.0)
(s296 2.0)
(s298 4.0)
(s299 5.0)
(s300 5.0)
(s301 2.0)
(s303 4.0)
(s304 5.0)
(s305 5.0)
(s306 2.0)
(s308 4.0)
(s309 5.0)
(s310 5.0)
(s311 2.0)
(s313 4.0)
(s314 5.0)
(s315 5.0)
(s316 2.0)
(s318 4.0)
(s319 5.0)
(s320 5.0)
(s321 2.0)
(s323 4.0)
(s324 5.0)
(s325 5.0)
(s326 2.0)
(s328 4.0)
(s329 5.0)
(s330 5.0)
(s331 2.0)
(s333 4.0)
(s334 5.0)
(s335 5.0)
(s336 2.0)
(s338 4.0)
(s339 5.0)
(s340 5.0)
(s341 2.0)
(s343 4.0)
(s344 5.0)
(s345 5.0)
(s346 2.0)
(s348 4.0)
(s349 5.0)
(s350 5.0)
(s351 2.0)
(s353 4.0)
(s354 5.0)
(s355 5.0)
(s356 2.0)
(s358 4.0)
(s359 5.0)
(s360 5.0)
(s361 2.0)
(s363 4.0)
(s364 5.0)
(s365 5.0)
(s366 2.0)
(s368 4.0)
(s369 5.0)
(s370 5.0)
(s371 2.0)
(s373 4.0)
(s374 5.0)
(s375 5.0)
(s376 2.0)
(s378 4.0)
(s379 5.0)
(s380 5.0)
(s381 2.0)
(s383 4.0)
(s384 5.0)
(s385 5.0)
(s386 2.0)
(s388 4.0)
(s389 5.0)
(s390 5.0)
(s391 2.0)
(s393 4.0)
(s394 5.0)
(s395 5.0)
(s396 2.0)
(s398 4.0)
(s399 5.0)
(s400 5.0)
(s401 2.0)
(s403 4.0)
(s404 5.0)
(s405 5.0)
(s406 2.0)
(s408 4.0)
(s409 5.0)
(s410 5.0)
(s411 2.0)
(s413 4.0)
(s414 5.0)
(s415 5.0)
(s416 2.0)
(s418 4.0)
(s419 5.0)
(s420 5.0)
(s421 2.0)
(s423 4.0)
(s424 5.0)
(s425 5.0)
(s426 2.0)
(s428 4.0)
(s429 5.0)
(s430 5.0)
(s431 2.0)
(s433 4.0)
(s434 5.0)
(s435 5.0)
(s436 2.0)
(s438 4.0)
(s439 5.0)
(s440 5.0)
(s441 2.0)
(s443 4.0)
(s444 5.0)
(s445 5.0)
(s446 2.0)
(s448 4.0)
(s449 5.0)
(s450 5.0)
(s451 2.0)
(s453 4.0)
(s454 5.0)
(s455 5.0)
(s456 2.0)
(s458 4.0)
(s459 5.0)
(s460 5.0)
(s461 2.0)
(s463 4.0)
(s464 5.0)
(s465 5.0)
(s466 2.0)
(s468 4.0)
(s469 5.0)
(s470 5.0)
(s471 2.0)
(s473 4.0)
(s474 5.0)
(s475 5.0)
(s476 2.0)
(s478 4.0)
(s479 5.0)
(s480 5.0)
(s481 2.0)
(s483 4.0)
(s484 5.0)
(s485 5.0)
(s486 2.0)
(s488 4.0)
(s489 5.0)
(s490 5.0)
(s491 2.0)
(s493 4.0)
(s494 5.0)
(s495 5.0)
(s496 2.0)
(s498 4.0)
(s499 5.0)
(s500 5.0)
(s501 2.0)
(s503 4.0)
(s504 5.0)
(s505 5.0)
(s506 2.0)
(s508 4.0)
(s509 5.0)
(s510 5.0)
(s511 2.0)
(s513 4.0)
(s514 5.0)
(s515 5.0)
(s516 2.0)
(s518 4.0)
(s519 5.0)
(s520 5.0)
(s521 2.0)
(s523 4.0)
(s524 5.0)
(s525 5.0)
(s526 2.0)
(s528 4.0)
(s529 5.0)
(s530 5.0)
(s531 2.0)
(s533 4.0)
(s534 5.0)
(s535 5.0)
(s536 2.0)
(s538 4.0)
(s539 5.0)
(s540 5.0)
(s541 2.0)
(s543 4.0)
(s544 5.0)
(s545 5.0)
(s546 2.0)
(s548 4.0)
(s549 5.0)
(s550 5.0)
(s551 2.0)
(s553 4.0)
(s554 5.0)
(s555 5.0)
(s556 2.0)
(s558 4.0)
(s559 5.0)
(s560 5.0)
(s561 2.0)
(s563 4.0)
(s564 5.0)
(s565 5.0)
(s566 2.0)
(s568 4.0)
(s569 5.0)
(s570 5.0)
(s571 2.0)
(s573 4.0)
(s574 5.0)
(s575 5.0)
(s576 2.0)
(s578 4.0)
(s579 5.0)
(s580 5.0)
(s581 2.0)
(s583 4.0)
(s584 5.0)
(s585 5.0)
(s586 2.0)
(s588 4.0)
(s589 5.0)
(s590 5.0)
(s591 2.0)
(s593 4.0)
(s594 5.0)
(s595 5.0)
(s596 2.0)
(s598 4.0)
(s599 5.0)
(s600 5.0)
(s601 2.0)
(s603 4.0)
(s604 5.0)
(s605 5.0)
(s606 2.0)
(s608 4.0)
(s609 5.0)
(s610 5.0)
(s611 2.0)
(s613 4.0)
(s614 5.0)
(s615 5.0)
(s616 2.0)
(s618 4.0)
(s619 5.0)
(s620 5.0)
(s621 2.0)
(s623 4.0)
(s624 5.0)
(s625 5.0)
(s626 2.0)
(s628 4.0)
(s629 5.0)
(s630 5.0)
(s631 2.0)
(s633 4.0)
(s634 5.0)
(s635 5.0)
(s636 2.0)
(s638 4.0)
(s639 5.0)
(s640 5.0)
(s641 2.0)
(s643 4.0)
(s644 5.0)
(s645 5.0)
(s646 2.0)
(s648 4.0)
(s649 5.0)
(s650 5.0)
(s651 2.0)
(s653 4.0)
(s654 5.0)
(s655 5.0)
(s656 2.0)
(s658 4.0)
(s659 5.0)
(s660 5.0)
(s661 2.0)
(s663 4.0)
(s664 5.0)
(s665 5.0)
(s666 2.0)
(s668 4.0)
(s669 5.0)
(s670 5.0)
(s671 2.0)
(s673 4.0)
(s674 5.0)
(s675 5.0)
(s676 2.0)
(s678 4.0)
(s679 5.0)
(s680 5.0)
(s681 2.0)
(s683 4.0)
(s684 5.0)
(s685 5.0)
(s686 2.0)
(s688 4.0)
(s689 5.0)
(s690 5.0)
(s691 2.0)
(s693 4.0)
(s694 5.0)
(s695 5.0)
(s696 2.0)
(s698 4.0)
(s699 5.0)
(s700 5.0)
(s701 2.0)
(s703 4.0)
(s704 5.0)
(s705 5.0)
(s706 2.0)
(s708 4.0)
(s709 5.0)
(s710 5.0)
(s711 2.0)
(s713 4.0)
(s714 5.0)
(s715 5.0)
(s716 2.0)
(s718 4.0)
(s719 5.0)
(s720 5.0)
(s721 2.0)
(s723 4.0)
(s724 5.0)
(s725 5.0)
(s726 2.0)
(s728 4.0)
(s729 5.0)
(s730 5.0)
(s731 2.0)
(s733 4.0)
(s734 5.0)
(s735 5.0)
(s736 2.0)
(s738 4.0)
(s739 5.0)
(s740 5.0)
(s741 2.0)
(s743 4.0)
(s744 5.0)
(s745 5.0)
(s746 2.0)
(s748 4.0)
(s749 5.0)
(s750 5.0)
(s751 2.0)
(s753 4.0)
(s754 5.0)
(s755 5.0)
(s756 2.0)
(s758 4.0)
(s759 5.0)
(s760 5.0)
(s761 2.0)
(s763 4.0)
(s764 5.0)
(s765 5.0)
(s766 2.0)
(s768 4.0)
(s769 5.0)
(s770 5.0)
(s771 2.0)
(s773 4.0)
(s774 5.0)
(s775 5.0)
(s776 2.0)
(s778 4.0)
(s779 5.0)
(s780 5.0)
(s781 2.0)
(s783 4.0)
(s784 5.0)
(s785 5.0)
(s786 2.0)
(s788 4.0)
(s789 5.0)
(s790 5.0)
(s791 2.0)
(s793 4.0)
(s794 5.0)
(s795 5.0)
(s796 2.0)
(s798 4.0)
(s799 5.0)
(s800 5.0)
(s801 2.0)
(s803 4.0)
(s804 5.0)
(s805 5.0)
(s806 2.0)
(s808 4.0)
(s809 5.0)
(s810 5.0)
(s811 2.0)
(s813 4.0)
(s814 5.0)
(s815 5.0)
(s816 2.0)
(s818 4.0)
(s819 5.0)
(s820 5.0)
(s821 2.0)
(s823 4.0)
(s824 5.0)
(s825 5.0)
(s826 2.0)
(s828 4.0)
(s829 5.0)
(s830 5.0)
(s831 2.0)
(s833 4.0)
(s834 5.0)
(s835 5.0)
(s836 2.0)
(s838 4.0)
(s839 5.0)
(s840 5.0)
(s841 2.0)
(s843 4.0)
(s844 5.0)
(s845 5.0)
(s846 2.0)
(s848 4.0)
(s849 5.0)
(s850 5.0)
(s851 2.0)
(s853 4.0)
(s854 5.0)
(s855 5.0)
(s856 2.0)
(s858 4.0)
(s859 5.0)
(s860 5.0)
(s861 2.0)
(s863 4.0)
(s864 5.0)
(s865 5.0)
(s866 2.0)
(s868 4.0)
(s869 5.0)
(s870 5.0)
(s871 2.0)
(s873 4.0)
(s874 5.0)
(s875 5.0)
(s876 2.0)
(s878 4.0)
(s879 5.0)
(s880 5.0)
(s881 2.0)
(s883 4.0)
(s884 5.0)
(s885 5.0)
(s886 2.0)
(s888 4.0)
(s889 5.0)
(s890 5.0)
(s891 2.0)
(s893 4.0)
(s894 5.0)
(s895 5.0)
(s896 2.0)
(s898 4.0)
(s899 5.0)
(s900 5.0)
(s901 2.0)
(s903 4.0)
(s904 5.0)
(s905 5.0)
(s906 2.0)
(s908 4.0)
(s909 5.0)
(s910 5.0)
(s911 2.0)
(s913 4.0)
(s914 5.0)
(s915 5.0)
(s916 2.0)
(s918 4.0)
(s919 5.0)
(s920 5.0)
(s921 2.0)
(s923 4.0)
(s924 5.0)
(s925 5.0)
(s926 2.0)
(s928 4.0)
(s929 5.0)
(s930 5.0)
(s931 2.0)
(s933 4.0)
(s934 5.0)
(s935 5.0)
(s936 2.0)
(s938 4.0)
(s939 5.0)
(s940 5.0)
(s941 2.0)
(s943 4.0)
(s944 5.0)
(s945 5.0)
(s946 2.0)
(s948 4.0)
(s949 5.0)
(s950 5.0)
(s951 2.0)
(s953 4.0)
(s954 5.0)
(s955 5.0)
(s956 2.0)
(s958 4.0)
(s959 5.0)
(s960 5.0)
(s961 2.0)
(s963 4.0)
(s964 5.0)
(s965 5.0)
(s966 2.0)
(s968 4.0)
(s969 5.0)
(s970 5.0)
(s971 2.0)
(s973 4.0)
(s974 5.0)
(s975 5.0)
(s976 2.0)
(s978 4.0)
(s979 5.0)
(s980 5.0)
(s981 2.0)
(s983 4.0)
(s984 5.0)
(s985 5.0)
(s986 2.0)
(s988 4.0)
(s989 5.0)
(s990 5.0)
(s991 2.0)
(s993 4.0)
(s994 5.0)
(s995 5.0)
(s996 2.0)
(s998 4.0)
(s999 5.0)
(s1000 5.0)
(s1001 2.0)
(s1003 4.0)
(s1004 5.0)
(s1005 5.0)
(s1006 2.0)
(s1008 4.0)
(s1009 5.0)
(s1010 5.0)
(s1011 2.0)
(s1013 4.0)
(s1014 5.0)
(s1015 5.0)
(s1016 2.0)
(s1018 4.0)
(s1019 5.0)
(s1020 5.0)
(s1021 2.0)
(s1023 4.0)
(s1024 5.0)
(s1025 5.0)
(s1026 2.0)
(s1028 4.0)
(s1029 5.0)
(s1030 5.0)
(s1031 2.0)
(s1033 4.0)
(s1034 5.0)
(s1035 5.0)
(s1036 2.0)
(s1038 4.0)
(s1039 5.0)
(s1040 5.0)
(s1041 2.0)
(s1043 4.0)
(s1044 5.0)
(s1045 5.0)
(s1046 2.0)
(s1048 4.0)
(s1049 5.0)
(s1050 5.0)
(s1051 2.0)
(s1053 4.0)
(s1054 5.0)
(s1055 5.0)
(s1056 2.0)
(s1058 4.0)
(s1059 5.0)
(s1060 5.0)
(s1061 2.0)
(s1063 4.0)
(s1064 5.0)
(s1065 5.0)
(s1066 2.0)
(s1068 4.0)
(s1069 5.0)
(s1070 5.0)
(s1071 2.0)
(s1073 4.0)
(s1074 5.0)
(s1075 5.0)
(s1076 2.0)
(s1078 4.0)
(s1079 5.0)
(s1080 5.0)
(s1081 2.0)
(s1083 4.0)
(s1084 5.0)
(s1085 5.0)
(s1086 2.0)
(s1088 4.0)
(s1089 5.0)
(s1090 5.0)
(s1091 2.0)
(s1093 4.0)
(s1094 5.0)
(s1095 5.0)
(s1096 2.0)
(s1098 4.0)
(s1099 5.0)
(s1100 5.0)
(s1101 2.0)
(s1103 4.0)
(s1104 5.0)
(s1105 5.0)
(s1106 2.0)
(s1108 4.0)
(s1109 5.0)
(s1110 5.0)
(s1111 2.0)
(s1113 4.0)
(s1114 5.0)
(s1115 5.0)
(s1116 2.0)
(s1118 4.0)
(s1119 5.0)
(s1120 5.0)
(s1121 2.0)
(s1123 4.0)
(s1124 5.0)
(s1125 5.0)
(s1126 2.0)
(s1128 4.0)
(s1129 5.0)
(s1130 5.0)
(s1131 2.0)
(s1133 4.0)
(s1134 5.0)
(s1135 5.0)
(s1136 2.0)
(s1138 4.0)
(s1139 5.0)
(s1140 5.0)
(s1141 2.0)
(s1143 4.0)
(s1144 5.0)
(s1145 5.0)
(s1146 2.0)
(s1148 4.0)
(s1149 5.0)
(s1150 5.0)
(s1151 2.0)
(s1153 4.0)
(s1154 5.0)
(s1155 5.0)
(s1156 2.0)
(s1158 4.0)
(s1159 5.0)
(s1160 5.0)
(s1161 2.0)
(s1163 4.0)
(s1164 5.0)
(s1165 5.0)
(s1166 2.0)
(s1168 4.0)
(s1169 5.0)
(s1170 5.0)
(s1171 2.0)
(s1173 4.0)
(s1174 5.0)
(s1175 5.0)
(s1176 2.0)
(s1178 4.0)
(s1179 5.0)
(s1180 5.0)
(s1181 2.0)
(s1183 4.0)
(s1184 5.0)
(s1185 5.0)
(s1186 2.0)
(s1188 4.0)
(s1189 5.0)
(s1190 5.0)
(s1191 2.0)
(s1193 4.0)
(s1194 5.0)
(s1195 5.0)
(s1196 2.0)
(s1198 4.0)
(s1199 5.0)
(s1200 5.0)
(s1201 2.0)
(s1203 4.0)
(s1204 5.0)
(s1205 5.0)
(s1206 2.0)
(s1208 4.0)
(s1209 5.0)
(s1210 5.0)
(s1211 2.0)
(s1213 4.0)
(s1214 5.0)
(s1215 5.0)
(s1216 2.0)
(s1218 4.0)
(s1219 5.0)
(s1220 5.0)
(s1221 2.0)
(s1223 4.0)
(s1224 5.0)
(s1225 5.0)
(s1226 2.0)
(s1228 4.0)
(s1229 5.0)
(s1230 5.0)
(s1231 2.0)
(s1233 4.0)
(s1234 5.0)
(s1235 5.0)
(s1236 2.0)
(s1238 4.0)
(s1239 5.0)
(s1240 5.0)
(s1241 2.0)
(s1243 4.0)
(s1244 5.0)
(s1245 5.0)
(s1246 2.0)
(s1248 4.0)
(s1249 5.0)
(s1250 5.0)
(s1251 2.0)
(s1253 4.0)
(s1254 5.0)
(s1255 5.0)
(s1256 2.0)
(s1258 4.0)
(s1259 5.0)
(s1260 5.0)
(s1261 2.0)
(s1263 4.0)
(s1264 5.0)
(s1265 5.0)
(s1266 2.0)
(s1268 4.0)
(s1269 5.0)
(s1270 5.0)
(s1271 2.0)
(s1273 4.0)
(s1274 5.0)
(s1275 5.0)
(s1276 2.0)
(s1278 4.0)
(s1279 5.0)
(s1280 5.0)
(s1281 2.0)
(s1283 4.0)
(s1284 5.0)
(s1285 5.0)
(s1286 2.0)
(s1288 4.0)
(s1289 5.0)
(s1290 5.0)
(s1291 2.0)
(s1293 4.0)
(s1294 5.0)
(s1295 5.0)
(s1296 2.0)
(s1298 4.0)
(s1299 5.0)
(s1300 5.0)
(s1301 2.0)
(s1303 4.0)
(s1304 5.0)
(s1305 5.0)
(s1306 2.0)
(s1308 4.0)
(s1309 5.0)
(s1310 5.0)
(s1311 2.0)
(s1313 4.0)
(s1314 5.0)
(s1315 5.0)
(s1316 2.0)
(s1318 4.0)
(s1319 5.0)
(s1320 5.0)
(s1321 2.0)
(s1323 4.0)
(s1324 5.0)
(s1325 5.0)
(s1326 2.0)
(s1328 4.0)
(s1329 5.0)
(s1330 5.0)
(s1331 2.0)
(s1333 4.0)
(s1334 5.0)
(s1335 5.0)
(s1336 2.0)
(s1338 4.0)
(s1339 5.0)
(s1340 5.0)
(s1341 2.0)
(s1343 4.0)
(s1344 5.0)
(s1345 5.0)
(s1346 2.0)
(s1348 4.0)
(s1349 5.0)
(s1350 5.0)
(s1351 2.0)
(s1353 4.0)
(s1354 5.0)
(s1355 5.0)
(s1356 2.0)
(s1358 4.0)
(s1359 5.0)
(s1360 5.0)
(s1361 2.0)
(s1363 4.0)
(s1364 5.0)
(s1365 5.0)
(s1366 2.0)
(s1368 4.0)
(s1369 5.0)
(s1370 5.0)
(s1371 2.0)
(s1373 4.0)
(s1374 5.0)
(s1375 5.0)
(s1376 2.0)
(s1378 4.0)
(s1379 5.0)
(s1380 5.0)
(s1381 2.0)
(s1383 4.0)
(s1384 5.0)
(s1385 5.0)
(s1386 2.0)
(s1388 4.0)
(s1389 5.0)
(s1390 5.0)
(s1391 2.0)
(s1393 4.0)
(s1394 5.0)
(s1395 5.0)
(s1396 2.0)
(s1398 4.0)
(s1399 5.0)
(s1400 5.0)
(s1401 2.0)
(s1403 4.0)
(s1404 5.0)
(s1405 5.0)
(s1406 2.0)
(s1408 4.0)
(s1409 5.0)
(s1410 5.0)
(s1411 2.0)
(s1413 4.0)
(s1414 5.0)
(s1415 5.0)
(s1416 2.0)
(s1418 4.0)
(s1419 5.0)
(s1420 5.0)
(s1421 2.0)
(s1423 4.0)
(s1424 5.0)
(s1425 5.0)
(s1426 2.0)
(s1428 4.0)
(s1429 5.0)
(s1430 5.0)
(s1431 2.0)
(s1433 4.0)
(s1434 5.0)
(s1435 5.0)
(s1436 2.0)
(s1438 4.0)
(s1439 5.0)
(s1440 5.0)
(s1441 2.0)
(s1443 4.0)
(s1444 5.0)
(s1445 5.0)
(s1446 2.0)
(s1448 4.0)
(s1449 5.0)
(s1450 5.0)
(s1451 2.0)
(s1453 4.0)
(s1454 5.0)
(s1455 5.0)
(s1456 2.0)
(s1458 4.0)
(s1459 5.0)
(s1460 5.0)
(s1461 2.0)
(s1463 4.0)
(s1464 5.0)
(s1465 5.0)
(s1466 2.0)
(s1468 4.0)
(s1469 5.0)
(s1470 5.0)
(s1471 2.0)
(s1473 4.0)
(s1474 5.0)
(s1475 5.0)
(s1476 2.0)
(s1478 4.0)
(s1479 5.0)
(s1480 5.0)
(s1481 2.0)
(s1483 4.0)
(s1484 5.0)
(s1485 5.0)
(s1486 2.0)
(s1488 4.0)
(s1489 5.0)
(s1490 5.0)
(s1491 2.0)
(s1493 4.0)
(s1494 5.0)
(s1495 5.0)
(s1496 2.0)
(s1498 4.0)
(s1499 5.0)
(s1500 5.0)
(s1501 2.0)
(s1503 4.0)
(s1504 5.0)
(s1505 5.0)
(s1506 2.0)
(s1508 4.0)
(s1509 5.0)
(s1510 5.0)
(s1511 2.0)
(s1513 4.0)
(s1514 5.0)
(s1515 5.0)
(s1516 2.0)
(s1518 4.0)
(s1519 5.0)
(s1520 5.0)
(s1521 2.0)
(s1523 4.0)
(s1524 5.0)
(s1525 5.0)
(s1526 2.0)
(s1528 4.0)
(s1529 5.0)
(s1530 5.0)
(s1531 2.0)
(s1533 4.0)
(s1534 5.0)
(s1535 5.0)
(s1536 2.0)
(s1538 4.0)
(s1539 5.0)
(s1540 5.0)
(s1541 2.0)
(s1543 4.0)
(s1544 5.0)
(s1545 5.0)
(s1546 2.0)
(s1548 4.0)
(s1549 5.0)
(s1550 5.0)
(s1551 2.0)
(s1553 4.0)
(s1554 5.0)
(s1555 5.0)
(s1556 2.0)
(s1558 4.0)
(s1559 5.0)
(s1560 5.0)
(s1561 2.0)
(s1563 4.0)
(s1564 5.0)
(s1565 5.0)
(s1566 2.0)
(s1568 4.0)
(s1569 5.0)
(s1570 5.0)
(s1571 2.0)
(s1573 4.0)
(s1574 5.0)
(s1575 5.0)
(s1576 2.0)
(s1578 4.0)
(s1579 5.0)
(s1580 5.0)
(s1581 2.0)
(s1583 4.0)
(s1584 5.0)
(s1585 5.0)
(s1586 2.0)
(s1588 4.0)
(s1589 5.0)
(s1590 5.0)
(s1591 2.0)
(s1593 4.0)
(s1594 5.0)
(s1595 5.0)
(s1596 2.0)
(s1598 4.0)
(s1599 5.0)
(s1600 5.0)
(s1601 2.0)
(s1603 4.0)
(s1604 5.0)
(s1605 5.0)
(s1606 2.0)
(s1608 4.0)
(s1609 5.0)
(s1610 5.0)
(s1611 2.0)
(s1613 4.0)
(s1614 5.0)
(s1615 5.0)
(s1616 2.0)
(s1618 4.0)
(s1619 5.0)
(s1620 5.0)
(s1621 2.0)
(s1623 4.0)
(s1624 5.0)
(s1625 5.0)
(s1626 2.0)
(s1628 4.0)
(s1629 5.0)
(s1630 5.0)
(s1631 2.0)
(s1633 4.0)
(s1634 5.0)
(s1635 5.0)
(s1636 2.0)
(s1638 4.0)
(s1639 5.0)
(s1640 5.0)
(s1641 2.0)
(s1643 4.0)
(s1644 5.0)
(s1645 5.0)
(s1646 2.0)
(s1648 4.0)
(s1649 5.0)
(s1650 5.0)
(s1651 2.0)
(s1653 4.0)
(s1654 5.0)
(s1655 5.0)
(s1656 2.0)
(s1658 4.0)
(s1659 5.0)
(s1660 5.0)
(s1661 2.0)
(s1663 4.0)
(s1664 5.0)
(s1665 5.0)
(s1666 2.0)
(s1668 4.0)
(s1669 5.0)
(s1670 5.0)
(s1671 2.0)
(s1673 4.0)
(s1674 5.0)
(s1675 5.0)
(s1676 2.0)
(s1678 4.0)
(s1679 5.0)
(s1680 5.0)
(s1681 2.0)
(s1683 4.0)
(s1684 5.0)
(s1685 5.0)
(s1686 2.0)
(s1688 4.0)
(s1689 5.0)
(s1690 5.0)
(s1691 2.0)
(s1693 4.0)
(s1694 5.0)
(s1695 5.0)
(s1696 2.0)
(s1698 4.0)
(s1699 5.0)
(s1700 5.0)
(s1701 2.0)
(s1703 4.0)
(s1704 5.0)
(s1705 5.0)
(s1706 2.0)
(s1708 4.0)
(s1709 5.0)
(s1710 5.0)
(s1711 2.0)
(s1713 4.0)
(s1714 5.0)
(s1715 5.0)
(s1716 2.0)
(s1718 4.0)
(s1719 5.0)
(s1720 5.0)
(s1721 2.0)
(s1723 4.0)
(s1724 5.0)
(s1725 5.0)
(s1726 2.0)
(s1728 4.0)
(s1729 5.0)
(s1730 5.0)
(s1731 2.0)
(s1733 4.0)
(s1734 5.0)
(s1735 5.0)
(s1736 2.0)
(s1738 4.0)
(s1739 5.0)
(s1740 5.0)
(s1741 2.0)
(s1743 4.0)
(s1744 5.0)
(s1745 5.0)
(s1746 2.0)
(s1748 4.0)
(s1749 5.0)
(s1750 5.0)
(s1751 2.0)
(s1753 4.0)
(s1754 5.0)
(s1755 5.0)
(s1756 2.0)
(s1758 4.0)
(s1759 5.0)
(s1760 5.0)
(s1761 2.0)
(s1763 4.0)
(s1764 5.0)
(s1765 5.0)
(s1766 2.0)
(s1768 4.0)
(s1769 5.0)
(s1770 5.0)
(s1771 2.0)
(s1773 4.0)
(s1774 5.0)
(s1775 5.0)
(s1776 2.0)
(s1778 4.0)
(s1779 5.0)
(s1780 5.0)
(s1781 2.0)
(s1783 4.0)
(s1784 5.0)
(s1785 5.0)
(s1786 2.0)
(s1788 4.0)
(s1789 5.0)
(s1790 5.0)
(s1791 2.0)
(s1793 4.0)
(s1794 5.0)
(s1795 5.0)
(s1796 2.0)
(s1798 4.0)
(s1799 5.0)
(s1800 5.0)
(s1801 2.0)
(s1803 4.0)
(s1804 5.0)
(s1805 5.0)
(s1806 2.0)
(s1808 4.0)
(s1809 5.0)
(s1810 5.0)
(s1811 2.0)
(s1813 4.0)
(s1814 5.0)
(s1815 5.0)
(s1816 2.0)
(s1818 4.0)
(s1819 5.0)
(s1820 5.0)
(s1821 2.0)
(s1823 4.0)
(s1824 5.0)
(s1825 5.0)
(s1826 2.0)
(s1828 4.0)
(s1829 5.0)
(s1830 5.0)
(s1831 2.0)
(s1833 4.0)
(s1834 5.0)
(s1835 5.0)
(s1836 2.0)
(s1838 4.0)
(s1839 5.0)
(s1840 5.0)
(s1841 2.0)
(s1843 4.0)
(s1844 5.0)
(s1845 5.0)
(s1846 2.0)
(s1848 4.0)
(s1849 5.0)
(s1850 5.0)
(s1851 2.0)
(s1853 4.0)
(s1854 5.0)
(s1855 5.0)
(s1856 2.0)
(s1858 4.0)
(s1859 5.0)
(s1860 5.0)
(s1861 2.0)
(s1863 4.0)
(s1864 5.0)
(s1865 5.0)
(s1866 2.0)
(s1868 4.0)
(s1869 5.0)
(s1870 5.0)
(s1871 2.0)
(s1873 4.0)
(s1874 5.0)
(s1875 5.0)
(s1876 2.0)
(s1878 4.0)
(s1879 5.0)
(s1880 5.0)
(s1881 2.0)
(s1883 4.0)
(s1884 5.0)
(s1885 5.0)
(s1886 2.0)
(s1888 4.0)
(s1889 5.0)
(s1890 5.0)
(s1891 2.0)
(s1893 4.0)
(s1894 5.0)
(s1895 5.0)
(s1896 2.0)
(s1898 4.0)
(s1899 5.0)
(s1900 5.0)
(s1901 2.0)
(s1903 4.0)
(s1904 5.0)
(s1905 5.0)
(s1906 2.0)
(s1908 4.0)
(s1909 5.0)
(s1910 5.0)
(s1911 2.0)
(s1913 4.0)
(s1914 5.0)
(s1915 5.0)
(s1916 timeout
2.0) org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20134 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56597ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56682ms
Finished structural reductions in LTL mode , in 1 iterations and 57787 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:00:56] [INFO ] Flatten gal took : 317 ms
[2024-06-01 06:00:56] [INFO ] Flatten gal took : 336 ms
[2024-06-01 06:00:57] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 942 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:00:58] [INFO ] Invariant cache hit.
[2024-06-01 06:00:58] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20122 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20120 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 59163ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 59274ms
Finished structural reductions in LTL mode , in 1 iterations and 60237 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:01:58] [INFO ] Flatten gal took : 265 ms
[2024-06-01 06:01:58] [INFO ] Flatten gal took : 292 ms
[2024-06-01 06:01:58] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 861 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:01:59] [INFO ] Invariant cache hit.
[2024-06-01 06:01:59] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20135 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 timeout
5)
(s86 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20134 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 57231ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 57338ms
Finished structural reductions in LTL mode , in 1 iterations and 58214 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:02:57] [INFO ] Flatten gal took : 268 ms
[2024-06-01 06:02:57] [INFO ] Flatten gal took : 283 ms
[2024-06-01 06:02:58] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 898 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:02:59] [INFO ] Invariant cache hit.
[2024-06-01 06:02:59] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20125 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20126 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56054ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56133ms
Finished structural reductions in LTL mode , in 1 iterations and 57045 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:03:55] [INFO ] Flatten gal took : 269 ms
[2024-06-01 06:03:55] [INFO ] Flatten gal took : 292 ms
[2024-06-01 06:03:56] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 2532 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:03:59] [INFO ] Invariant cache hit.
[2024-06-01 06:03:59] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20123 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56665ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56742ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 59291 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:04:56] [INFO ] Flatten gal took : 264 ms
[2024-06-01 06:04:56] [INFO ] Flatten gal took : 282 ms
[2024-06-01 06:04:56] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 855 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:04:57] [INFO ] Invariant cache hit.
[2024-06-01 06:04:57] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20126 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20140 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56321ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56397ms
Finished structural reductions in LTL mode , in 1 iterations and 57266 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:05:54] [INFO ] Flatten gal took : 268 ms
[2024-06-01 06:05:54] [INFO ] Flatten gal took : 281 ms
[2024-06-01 06:05:55] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 907 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:05:56] [INFO ] Invariant cache hit.
[2024-06-01 06:05:56] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: ((s0 5.0)
(s1 2.0)
(s3 4.0)
(s4 5.0)
(s5 5.0)
(s6 2.0)
(s8 4.0)
(s9 5.0)
(s10 5.0)
(s11 2.0)
(s13 4.0)
(s14 5.0)
(s15 5.0)
(s16 2.0)
(s18 4.0)
(s19 5.0)
(s20 5.0)
(s21 2.0)
(s23 4.0)
(s24 5.0)
(s25 5.0)
(s26 2.0)
(s28 4.0)
(s29 5.0)
(s30 5.0)
(s31 2.0)
(s33 4.0)
(s34 5.0)
(s35 5.0)
(s36 2.0)
(s38 4.0)
(s39 5.0)
(s40 5.0)
(s41 2.0)
(s43 4.0)
(s44 5.0)
(s45 5.0)
(s46 2.0)
(s48 4.0)
(s49 5.0)
(s50 5.0)
(s51 2.0)
(s53 4.0)
(s54 5.0)
(s55 5.0)
(s56 2.0)
(s58 4.0)
(s59 5.0)
(s60 5.0)
(s61 2.0)
(s63 4.0)
(s64 5.0)
(s65 5.0)
(s66 2.0)
(s68 4.0)
(s69 5.0)
(s70 5.0)
(s71 2.0)
(s73 4.0)
(s74 5.0)
(s75 5.0)
(s76 2.0)
(s78 4.0)
(s79 5.0)
(s80 5.0)
(s81 2.0)
(s83 4.0)
(s84 5.0)
(s85 5.0)
(s86 2.0)
(s88 4.0)
(s89 5.0)
(s90 5.0)
(s91 2.0)
(s93 4.0)
(s94 5.0)
(s95 5.0)
(s96 2.0)
(s98 4.0)
(s99 5.0)
(s100 5.0)
(s101 2.0)
(s103 4.0)
(s104 5.0)
(s105 5.0)
(s106 2.0)
(s108 4.0)
(s109 5.0)
(s110 5.0)
(s111 2.0)
(s113 4.0)
(s114 5.0)
(s115 5.0)
(s116 2.0)
(s118 4.0)
(s119 5.0)
(s120 5.0)
(s121 2.0)
(s123 4.0)
(s124 5.0)
(s125 5.0)
(s126 2.0)
(s128 4.0)
(s129 5.0)
(s130 5.0)
(s131 2.0)
(s133 4.0)
(s134 5.0)
(s135 5.0)
(s136 2.0)
(s138 4.0)
(s139 5.0)
(s140 5.0)
(s141 2.0)
(s143 4.0)
(s144 5.0)
(s145 5.0)
(s146 2.0)
(s148 4.0)
(s149 5.0)
(s150 5.0)
(s151 2.0)
(s153 4.0)
(s154 5.0)
(s155 5.0)
(s156 2.0)
(s158 4.0)
(s159 5.0)
(s160 5.0)
(s161 2.0)
(s163 4.0)
(s164 5.0)
(s165 5.0)
(s166 2.0)
(s168 4.0)
(s169 5.0)
(s170 5.0)
(s171 2.0)
(s173 4.0)
(s174 5.0)
(s175 5.0)
(s176 2.0)
(s178 4.0)
(s179 5.0)
(s180 5.0)
(s181 2.0)
(s183 4.0)
(s184 5.0)
(s185 5.0)
(s186 2.0)
(s188 4.0)
(s189 5.0)
(s190 5.0)
(s191 2.0)
(s193 4.0)
(s194 5.0)
(s195 5.0)
(s196 2.0)
(s198 4.0)
(s199 5.0)
(s200 5.0)
(s201 2.0)
(s203 4.0)
(s204 5.0)
(s205 5.0)
(s206 2.0)
(s208 4.0)
(s209 5.0)
(s210 5.0)
(s211 2.0)
(s213 4.0)
(s214 5.0)
(s215 5.0)
(s216 2.0)
(s218 4.0)
(s219 5.0)
(s220 5.0)
(s221 2.0)
(s223 4.0)
(s224 5.0)
(s225 5.0)
(s226 2.0)
(s228 4.0)
(s229 5.0)
(s230 5.0)
(s231 2.0)
(s233 4.0)
(s234 5.0)
(s235 5.0)
(s236 2.0)
(s238 4.0)
(s239 5.0)
(s240 5.0)
(s241 2.0)
(s243 4.0)
(s244 5.0)
(s245 5.0)
(s246 2.0)
(s248 4.0)
(s249 5.0)
(s250 5.0)
(s251 2.0)
(s253 4.0)
(s254 5.0)
(s255 5.0)
(s256 2.0)
(s258 4.0)
(s259 5.0)
(s260 5.0)
(s261 2.0)
(s263 4.0)
(s264 5.0)
(s265 5.0)
(s266 2.0)
(s268 4.0)
(s269 5.0)
(s270 5.0)
(s271 2.0)
(s273 4.0)
(s274 5.0)
(s275 5.0)
(s276 2.0)
(s278 4.0)
(s279 5.0)
(s280 5.0)
(s281 2.0)
(s283 4.0)
(s284 5.0)
(s285 5.0)
(s286 2.0)
(s288 4.0)
(s289 5.0)
(s290 5.0)
(s291 2.0)
(s293 4.0)
(s294 5.0)
(s295 5.0)
(s296 2.0)
(s298 4.0)
(s299 5.0)
(s300 5.0)
(s301 2.0)
(s303 4.0)
(s304 5.0)
(s305 5.0)
(s306 2.0)
(s308 4.0)
(s309 5.0)
(s310 5.0)
(s311 2.0)
(s313 4.0)
(s314 5.0)
(s315 5.0)
(s316 2.0)
(s318 4.0)
(s319 5.0)
(s320 5.0)
(s321 2.0)
(s323 4.0)
(s324 5.0)
(s325 5.0)
(s326 2.0)
(s328 4.0)
(s329 5.0)
(s330 5.0)
(s331 2.0)
(s333 4.0)
(s334 5.0)
(s335 5.0)
(s336 2.0)
(s338 4.0)
(s339 5.0)
(s340 5.0)
(s341 2.0)
(s343 4.0)
(s344 5.0)
(s345 5.0)
(s346 2.0)
(s348 4.0)
(s349 5.0)
(s350 5.0)
(s351 2.0)
(s353 4.0)
(s354 5.0)
(s355 5.0)
(s356 2.0)
(s358 4.0)
(s359 5.0)
(s360 5.0)
(s361 2.0)
(s363 4.0)
(s364 5.0)
(s365 5.0)
(s366 2.0)
(s368 4.0)
(s369 5.0)
(s370 5.0)
(s371 2.0)
(s373 4.0)
(s374 5.0)
(s375 5.0)
(s376 2.0)
(s378 4.0)
(s379 5.0)
(s380 5.0)
(s381 2.0)
(s383 4.0)
(s384 5.0)
(s385 5.0)
(s386 2.0)
(s388 4.0)
(s389 5.0)
(s390 5.0)
(s391 2.0)
(s393 4.0)
(s394 5.0)
(s395 5.0)
(s396 2.0)
(s398 4.0)
(s399 5.0)
(s400 5.0)
(s401 2.0)
(s403 4.0)
(s404 5.0)
(s405 5.0)
(s406 2.0)
(s408 4.0)
(s409 5.0)
(s410 5.0)
(s411 2.0)
(s413 4.0)
(s414 5.0)
(s415 5.0)
(s416 2.0)
(s418 4.0)
(s419 5.0)
(s420 5.0)
(s421 2.0)
(s423 4.0)
(s424 5.0)
(s425 5.0)
(s426 2.0)
(s428 4.0)
(s429 5.0)
(s430 5.0)
(s431 2.0)
(s433 4.0)
(s434 5.0)
(s435 5.0)
(s436 2.0)
(s438 4.0)
(s439 5.0)
(s440 5.0)
(s441 2.0)
(s443 4.0)
(s444 5.0)
(s445 5.0)
(s446 2.0)
(s448 4.0)
(s449 5.0)
(s450 5.0)
(s451 2.0)
(s453 4.0)
(s454 5.0)
(s455 5.0)
(s456 2.0)
(s458 4.0)
(s459 5.0)
(s460 5.0)
(s461 2.0)
(s463 4.0)
(s464 5.0)
(s465 5.0)
(s466 2.0)
(s468 4.0)
(s469 5.0)
(s470 5.0)
(s471 2.0)
(s473 4.0)
(s474 5.0)
(s475 5.0)
(s476 2.0)
(s478 4.0)
(s479 5.0)
(s480 5.0)
(s481 2.0)
(s483 4.0)
(s484 5.0)
(s485 5.0)
(s486 2.0)
(s488 4.0)
(s489 5.0)
(s490 5.0)
(s491 2.0)
(s493 4.0)
(s494 5.0)
(s495 5.0)
(s496 2.0)
(s498 4.0)
(s499 5.0)
(s500 5.0)
(s501 2.0)
(s503 4.0)
(s504 5.0)
(s505 5.0)
(s506 2.0)
(s508 4.0)
(s509 5.0)
(s510 5.0)
(s511 2.0)
(s513 4.0)
(s514 5.0)
(s515 5.0)
(s516 2.0)
(s518 4.0)
(s519 5.0)
(s520 5.0)
(s521 2.0)
(s523 4.0)
(s524 5.0)
(s525 5.0)
(s526 2.0)
(s528 4.0)
(s529 5.0)
(s530 5.0)
(s531 2.0)
(s533 4.0)
(s534 5.0)
(s535 5.0)
(s536 2.0)
(s538 4.0)
(s539 5.0)
(s540 5.0)
(s541 2.0)
(s543 4.0)
(s544 5.0)
(s545 5.0)
(s546 2.0)
(s548 4.0)
(s549 5.0)
(s550 5.0)
(s551 2.0)
(s553 4.0)
(s554 5.0)
(s555 5.0)
(s556 2.0)
(s558 4.0)
(s559 5.0)
(s560 5.0)
(s561 2.0)
(s563 4.0)
(s564 5.0)
(s565 5.0)
(s566 2.0)
(s568 4.0)
(s569 5.0)
(s570 5.0)
(s571 2.0)
(s573 4.0)
(s574 5.0)
(s575 5.0)
(s576 2.0)
(s578 4.0)
(s579 5.0)
(s580 5.0)
(s581 2.0)
(s583 4.0)
(s584 5.0)
(s585 5.0)
(s586 2.0)
(s588 4.0)
(s589 5.0)
(s590 5.0)
(s591 2.0)
(s593 4.0)
(s594 5.0)
(s595 5.0)
(s596 2.0)
(s598 4.0)
(s599 5.0)
(s600 5.0)
(s601 2.0)
(s603 4.0)
(s604 5.0)
(s605 5.0)
(s606 2.0)
(s608 4.0)
(s609 5.0)
(s610 5.0)
(s611 2.0)
(s613 4.0)
(s614 5.0)
(s615 5.0)
(s616 2.0)
(s618 4.0)
(s619 5.0)
(s620 5.0)
(s621 2.0)
(s623 4.0)
(s624 5.0)
(s625 5.0)
(s626 2.0)
(s628 4.0)
(s629 5.0)
(s630 5.0)
(s631 2.0)
(s633 4.0)
(s634 5.0)
(s635 5.0)
(s636 2.0)
(s638 4.0)
(s639 5.0)
(s640 5.0)
(s641 2.0)
(s643 4.0)
(s644 5.0)
(s645 5.0)
(s646 2.0)
(s648 4.0)
(s649 5.0)
(s650 5.0)
(s651 2.0)
(s653 4.0)
(s654 5.0)
(s655 5.0)
(s656 2.0)
(s658 4.0)
(s659 5.0)
(s660 5.0)
(s661 2.0)
(s663 4.0)
(s664 5.0)
(s665 5.0)
(s666 2.0)
(s668 4.0)
(s669 5.0)
(s670 5.0)
(s671 2.0)
(s673 4.0)
(s674 5.0)
(s675 5.0)
(s676 2.0)
(s678 4.0)
(s679 5.0)
(s680 5.0)
(s681 2.0)
(s683 4.0)
(s684 5.0)
(s685 5.0)
(s686 2.0)
(s688 4.0)
(s689 5.0)
(s690 5.0)
(s691 2.0)
(s693 4.0)
(s694 5.0)
(s695 5.0)
(s696 2.0)
(s698 4.0)
(s699 5.0)
(s700 5.0)
(s701 2.0)
(s703 4.0)
(s704 5.0)
(s705 5.0)
(s706 2.0)
(s708 4.0)
(s709 5.0)
(s710 5.0)
(s711 2.0)
(s713 4.0)
(s714 5.0)
(s715 5.0)
(s716 2.0)
(s718 4.0)
(s719 5.0)
(s720 5.0)
(s721 2.0)
(s723 4.0)
(s724 5.0)
(s725 5.0)
(s726 2.0)
(s728 4.0)
(s729 5.0)
(s730 5.0)
(s731 2.0)
(s733 4.0)
(s734 5.0)
(s735 5.0)
(s736 2.0)
(s738 4.0)
(s739 5.0)
(s740 5.0)
(s741 2.0)
(s743 4.0)
(s744 5.0)
(s745 5.0)
(s746 2.0)
(s748 4.0)
(s749 5.0)
(s750 5.0)
(s751 2.0)
(s753 4.0)
(s754 5.0)
(s755 5.0)
(s756 2.0)
(s758 4.0)
(s759 5.0)
(s760 5.0)
(s761 2.0)
(s763 4.0)
(s764 5.0)
(s765 5.0)
(s766 2.0)
(s768 4.0)
(s769 5.0)
(s770 5.0)
(s771 2.0)
(s773 4.0)
(s774 5.0)
(s775 5.0)
(s776 2.0)
(s778 4.0)
(s779 5.0)
(s780 5.0)
(s781 2.0)
(s783 4.0)
(s784 5.0)
(s785 5.0)
(s786 2.0)
(s788 4.0)
(s789 5.0)
(s790 5.0)
(s791 2.0)
(s793 4.0)
(s794 5.0)
(s795 5.0)
(s796 2.0)
(s798 4.0)
(s799 5.0)
(s800 5.0)
(s801 2.0)
(s803 4.0)
(s804 5.0)
(s805 5.0)
(s806 2.0)
(s808 4.0)
(s809 5.0)
(s810 5.0)
(s811 2.0)
(s813 4.0)
(s814 5.0)
(s815 5.0)
(s816 2.0)
(s818 4.0)
(s819 5.0)
(s820 5.0)
(s821 2.0)
(s823 4.0)
(s824 5.0)
(s825 5.0)
(s826 2.0)
(s828 4.0)
(s829 5.0)
(s830 5.0)
(s831 2.0)
(s833 4.0)
(s834 5.0)
(s835 5.0)
(s836 2.0)
(s838 4.0)
(s839 5.0)
(s840 5.0)
(s841 2.0)
(s843 4.0)
(s844 5.0)
(s845 5.0)
(s846 2.0)
(s848 4.0)
(s849 5.0)
(s850 5.0)
(s851 2.0)
(s853 4.0)
(s854 5.0)
(s855 5.0)
(s856 2.0)
(s858 4.0)
(s859 5.0)
(s860 5.0)
(s861 2.0)
(s863 4.0)
(s864 5.0)
(s865 5.0)
(s866 2.0)
(s868 4.0)
(s869 5.0)
(s870 5.0)
(s871 2.0)
(s873 4.0)
(s874 5.0)
(s875 5.0)
(s876 2.0)
(s878 4.0)
(s879 5.0)
(s880 5.0)
(s881 2.0)
(s883 4.0)
(s884 5.0)
(s885 5.0)
(s886 2.0)
(s888 4.0)
(s889 5.0)
(s890 5.0)
(s891 2.0)
(s893 4.0)
(s894 5.0)
(s895 5.0)
(s896 2.0)
(s898 4.0)
(s899 5.0)
(s900 5.0)
(s901 2.0)
(s903 4.0)
(s904 5.0)
(s905 5.0)
(s906 2.0)
(s908 4.0)
(s909 5.0)
(s910 5.0)
(s911 2.0)
(s913 4.0)
(s914 5.0)
(s915 5.0)
(s916 2.0)
(s918 4.0)
(s919 5.0)
(s920 5.0)
(s921 2.0)
(s923 4.0)
(s924 5.0)
(s925 5.0)
(s926 2.0)
(s928 4.0)
(s929 5.0)
(s930 5.0)
(s931 2.0)
(s933 4.0)
(s934 5.0)
(s935 5.0)
(s936 2.0)
(s938 4.0)
(s939 5.0)
(s940 5.0)
(s941 2.0)
(s943 4.0)
(s944 5.0)
(s945 5.0)
(s946 2.0)
(s948 4.0)
(s949 5.0)
(s950 5.0)
(s951 2.0)
(s953 4.0)
(s954 5.0)
(s955 5.0)
(s956 2.0)
(s958 4.0)
(s959 5.0)
(s960 5.0)
(s961 2.0)
(s963 4.0)
(s964 5.0)
(s965 5.0)
(s966 2.0)
(s968 4.0)
(s969 5.0)
(s970 5.0)
(s971 2.0)
(s973 4.0)
(s974 5.0)
(s975 5.0)
(s976 2.0)
(s978 4.0)
(s979 5.0)
(s980 5.0)
(s981 2.0)
(s983 4.0)
(s984 5.0)
(s985 5.0)
(s986 2.0)
(s988 4.0)
(s989 5.0)
(s990 5.0)
(s991 2.0)
(s993 4.0)
(s994 5.0)
(s995 5.0)
(s996 2.0)
(s998 4.0)
(s999 5.0)
(s1000 5.0)
(s1001 2.0)
(s1003 4.0)
(s1004 5.0)
(s1005 5.0)
(s1006 2.0)
(s1008 4.0)
(s1009 5.0)
(s1010 5.0)
(s1011 2.0)
(s1013 4.0)
(s1014 5.0)
(s1015 5.0)
(s1016 2.0)
(s1018 4.0)
(s1019 5.0)
(s1020 5.0)
(s1021 2.0)
(s1023 4.0)
(s1024 5.0)
(s1025 5.0)
(s1026 2.0)
(s1028 4.0)
(s1029 5.0)
(s1030 5.0)
(s1031 2.0)
(s1033 4.0)
(s1034 5.0)
(s1035 5.0)
(s1036 2.0)
(s1038 4.0)
(s1039 5.0)
(s1040 5.0)
(s1041 2.0)
(s1043 4.0)
(s1044 5.0)
(s1045 5.0)
(s1046 2.0)
(s1048 4.0)
(s1049 5.0)
(s1050 5.0)
(s1051 2.0)
(s1053 4.0)
(s1054 5.0)
(s1055 5.0)
(s1056 2.0)
(s1058 4.0)
(s1059 5.0)
(s1060 5.0)
(s1061 2.0)
(s1063 4.0)
(s1064 5.0)
(s1065 5.0)
(s1066 2.0)
(s1068 4.0)
(s1069 5.0)
(s1070 5.0)
(s1071 2.0)
(s1073 4.0)
(s1074 5.0)
(s1075 5.0)
(s1076 2.0)
(s1078 4.0)
(s1079 5.0)
(s1080 5.0)
(s1081 2.0)
(s1083 4.0)
(s1084 5.0)
(s1085 5.0)
(s1086 2.0)
(s1088 4.0)
(s1089 5.0)
(s1090 5.0)
(s1091 2.0)
(s1093 4.0)
(s1094 5.0)
(s1095 5.0)
(s1096 2.0)
(s1098 4.0)
(s1099 5.0)
(s1100 5.0)
(s1101 2.0)
(s1103 4.0)
(s1104 5.0)
(s1105 5.0)
(s1106 2.0)
(s1108 4.0)
(s1109 5.0)
(s1110 5.0)
(s1111 2.0)
(s1113 4.0)
(s1114 5.0)
(s1115 5.0)
(s1116 2.0)
(s1118 4.0)
(s1119 5.0)
(s1120 5.0)
(s1121 2.0)
(s1123 4.0)
(s1124 5.0)
(s1125 5.0)
(s1126 2.0)
(s1128 4.0)
(s1129 5.0)
(s1130 5.0)
(s1131 2.0)
(s1133 4.0)
(s1134 5.0)
(s1135 5.0)
(s1136 2.0)
(s1138 4.0)
(s1139 5.0)
(s1140 5.0)
(s1141 2.0)
(s1143 4.0)
(s1144 5.0)
(s1145 5.0)
(s1146 2.0)
(s1148 4.0)
(s1149 5.0)
(s1150 5.0)
(s1151 2.0)
(s1153 4.0)
(s1154 5.0)
(s1155 5.0)
(s1156 2.0)
(s1158 4.0)
(s1159 5.0)
(s1160 5.0)
(s1161 2.0)
(s1163 4.0)
(s1164 5.0)
(s1165 5.0)
(s1166 2.0)
(s1168 4.0)
(s1169 5.0)
(s1170 5.0)
(s1171 2.0)
(s1173 4.0)
(s1174 5.0)
(s1175 5.0)
(s1176 2.0)
(s1178 4.0)
(s1179 5.0)
(s1180 5.0)
(s1181 2.0)
(s1183 4.0)
(s1184 5.0)
(s1185 5.0)
(s1186 2.0)
(s1188 4.0)
(s1189 5.0)
(s1190 5.0)
(s1191 2.0)
(s1193 4.0)
(s1194 5.0)
(s1195 5.0)
(s1196 2.0)
(s1198 4.0)
(s1199 5.0)
(s1200 5.0)
(s1201 2.0)
(s1203 4.0)
(s1204 5.0)
(s1205 5.0)
(s1206 2.0)
(s1208 4.0)
(s1209 5.0)
(s1210 5.0)
(s1211 2.0)
(s1213 4.0)
(s1214 5.0)
(s1215 5.0)
(s1216 2.0)
(s1218 4.0)
(s1219 5.0)
(s1220 5.0)
(s1221 2.0)
(s1223 4.0)
(s1224 5.0)
(s1225 5.0)
(s1226 2.0)
(s1228 4.0)
(s1229 5.0)
(s1230 5.0)
(s1231 2.0)
(s1233 4.0)
(s1234 5.0)
(s1235 5.0)
(s1236 2.0)
(s1238 4.0)
(s1239 5.0)
(s1240 5.0)
(s1241 2.0)
(s1243 4.0)
(s1244 5.0)
(s1245 5.0)
(s1246 2.0)
(s1248 4.0)
(s1249 5.0)
(s1250 5.0)
(s1251 2.0)
(s1253 4.0)
(s1254 5.0)
(s1255 5.0)
(s1256 2.0)
(s1258 4.0)
(s1259 5.0)
(s1260 5.0)
(s1261 2.0)
(s1263 4.0)
(s1264 5.0)
(s1265 5.0)
(s1266 2.0)
(s1268 4.0)
(s1269 5.0)
(s1270 5.0)
(s1271 2.0)
(s1273 4.0)
(s1274 5.0)
(s1275 5.0)
(s1276 2.0)
(s1278 4.0)
(s1279 5.0)
(s1280 5.0)
(s1281 2.0)
(s1283 4.0)
(s1284 5.0)
(s1285 5.0)
(s1286 2.0)
(s1288 4.0)
(s1289 5.0)
(s1290 5.0)
(s1291 2.0)
(s1293 4.0)
(s1294 5.0)
(s1295 5.0)
(s1296 2.0)
(s1298 4.0)
(s1299 5.0)
(s1300 5.0)
(s1301 2.0)
(s1303 4.0)
(s1304 5.0)
(s1305 5.0)
(s1306 2.0)
(s1308 4.0)
(s1309 5.0)
(s1310 5.0)
(s1311 2.0)
(s1313 4.0)
(s1314 5.0)
(s1315 5.0)
(s1316 2.0)
(s1318 4.0)
(s1319 5.0)
(s1320 5.0)
(s1321 2.0)
(s1323 4.0)
(s1324 5.0)
(s1325 5.0)
(s1326 2.0)
(s1328 4.0)
(s1329 5.0)
(s1330 5.0)
(s1331 2.0)
(s1333 4.0)
(s1334 5.0)
(s1335 5.0)
(s1336 2.0)
(s1338 4.0)
(s1339 5.0)
(s1340 5.0)
(s1341 2.0)
(s1343 4.0)
(s1344 5.0)
(s1345 5.0)
(s1346 2.0)
(s1348 4.0)
(s1349 5.0)
(s1350 5.0)
(s1351 2.0)
(s1353 4.0)
(s1354 5.0)
(s1355 5.0)
(s1356 2.0)
(s1358 4.0)
(s1359 5.0)
(s1360 5.0)
(s1361 2.0)
(s1363 4.0)
(s1364 5.0)
(s1365 5.0)
(s1366 2.0)
(s1368 4.0)
(s1369 5.0)
(s1370 5.0)
(s1371 2.0)
(s1373 4.0)
(s1374 5.0)
(s1375 5.0)
(s1376 2.0)
(s1378 4.0)
(s1379 5.0)
(s1380 5.0)
(s1381 2.0)
(s1383 4.0)
(s1384 5.0)
(s1385 5.0)
(s1386 2.0)
(s1388 4.0)
(s1389 5.0)
(s1390 5.0)
(s1391 2.0)
(s1393 4.0)
(s1394 5.0)
(s1395 5.0)
(s1396 2.0)
(s1398 4.0)
(s1399 5.0)
(s1400 5.0)
(s1401 2.0)
(s1403 4.0)
(s1404 5.0)
(s1405 5.0)
(s1406 2.0)
(s1408 4.0)
(s1409 5.0)
(s1410 5.0)
(s1411 2.0)
(s1413 4.0)
(s1414 5.0)
(s1415 5.0)
(s1416 2.0)
(s1418 4.0)
(s1419 5.0)
(s1420 5.0)
(s1421 2.0)
(s1423 4.0)
(s1424 5.0)
(s1425 5.0)
(s1426 2.0)
(s1428 4.0)
(s1429 5.0)
(s1430 5.0)
(s1431 2.0)
(s1433 4.0)
(s1434 5.0)
(s1435 5.0)
(s1436 2.0)
(s1438 4.0)
(s1439 5.0)
(s1440 5.0)
(s1441 2.0)
(s1443 4.0)
(s1444 5.0)
(s1445 5.0)
(s1446 2.0)
(s1448 4.0)
(s1449 5.0)
(s1450 5.0)
(s1451 2.0)
(s1453 4.0)
(s1454 5.0)
(s1455 5.0)
(s1456 2.0)
(s1458 4.0)
(s1459 5.0)
(s1460 5.0)
(s1461 2.0)
(s1463 4.0)
(s1464 5.0)
(s1465 5.0)
(s1466 2.0)
(s1468 4.0)
(s1469 5.0)
(s1470 5.0)
(s1471 2.0)
(s1473 4.0)
(s1474 5.0)
(s1475 5.0)
(s1476 2.0)
(s1478 4.0)
(s1479 5.0)
(s1480 5.0)
(s1481 2.0)
(s1483 4.0)
(s1484 5.0)
(s1485 5.0)
(s1486 2.0)
(s1488 4.0)
(s1489 5.0)
(s1490 5.0)
(s1491 2.0)
(s1493 4.0)
(s1494 5.0)
(s1495 5.0)
(s1496 2.0)
(s1498 4.0)
(s1499 5.0)
(s1500 5.0)
(s1501 2.0)
(s1503 4.0)
(s1504 5.0)
(s1505 5.0)
(s1506 2.0)
(s1508 4.0)
(s1509 5.0)
(s1510 5.0)
(s1511 2.0)
(s1513 4.0)
(s1514 5.0)
(s1515 5.0)
(s1516 2.0)
(s1518 4.0)
(s1519 5.0)
(s1520 5.0)
(s1521 2.0)
(s1523 4.0)
(s1524 5.0)
(s1525 5.0)
(s1526 2.0)
(s1528 4.0)
(s1529 5.0)
(s1530 5.0)
(s1531 2.0)
(s1533 4.0)
(s1534 5.0)
(s1535 5.0)
(s1536 2.0)
(s1538 4.0)
(s1539 5.0)
(s1540 5.0)
(s1541 2.0)
(s1543 4.0)
(s1544 5.0)
(s1545 5.0)
(s1546 2.0)
(s1548 4.0)
(s1549 5.0)
(s1550 5.0)
(s1551 2.0)
(s1553 4.0)
(s1554 5.0)
(s1555 5.0)
(s1556 2.0)
(s1558 4.0)
(s1559 5.0)
(s1560 5.0)
(s1561 2.0)
(s1563 4.0)
(s1564 5.0)
(s1565 5.0)
(s1566 2.0)
(s1568 4.0)
(s1569 5.0)
(s1570 5.0)
(s1571 2.0)
(s1573 4.0)
(s1574 5.0)
(s1575 5.0)
(s1576 2.0)
(s1578 4.0)
(s1579 5.0)
(s1580 5.0)
(s1581 2.0)
(s1583 4.0)
(s1584 5.0)
(s1585 5.0)
(s1586 2.0)
(s1588 4.0)
(s1589 5.0)
(s1590 5.0)
(s1591 2.0)
(s1593 4.0)
(s1594 5.0)
(s1595 5.0)
(s1596 2.0)
(s1598 4.0)
(s1599 5.0)
(s1600 5.0)
(s1601 2.0)
(s1603 4.0)
(s1604 5.0)
(s1605 5.0)
(s1606 2.0)
(s1608 4.0)
(s1609 5.0)
(s1610 5.0)
(s1611 2.0)
(s1613 4.0)
(s1614 5.0)
(s1615 5.0)
(s1616 2.0)
(s1618 4.0)
(s1619 5.0)
(s1620 5.0)
(s1621 2.0)
(s1623 4.0)
(s1624 5.0)
(s1625 5.0)
(s1626 2.0)
(s1628 4.0)
(s1629 5.0)
(s1630 5.0)
(s1631 2.0)
(s1633 4.0)
(s1634 5.0)
(s1635 5.0)
(s1636 2.0)
(s1638 4.0)
(s1639 5.0)
(s1640 5.0)
(s1641 2.0)
(s1643 4.0)
(s1644 5.0)
(s1645 5.0)
(s1646 2.0)
(s1648 4.0)
(s1649 5.0)
(s1650 5.0)
(s1651 2.0)
(s1653 4.0)
(s1654 5.0)
(s1655 5.0)
(s1656 2.0)
(s1658 4.0)
(s1659 5.0)
(s1660 5.0)
(s1661 2.0)
(s1663 4.0)
(s1664 5.0)
(s1665 5.0)
(s1666 2.0)
(s1668 4.0)
(s1669 5.0)
(s1670 5.0)
(s1671 2.0)
(s1673 4.0)
(s1674 5.0)
(s1675 5.0)
(s1676 2.0)
(s1678 4.0)
(s1679 5.0)
(s1680 5.0)
(s1681 2.0)
(s1683 4.0)
(s1684 5.0)
(s1685 5.0)
(s1686 2.0)
(s1688 4.0)
(s1689 5.0)
(s1690 5.0)
(s1691 2.0)
(s1693 4.0)
(s1694 5.0)
(s1695 5.0)
(s1696 2.0)
(s1698 4.0)
(s1699 5.0)
(s1700 5.0)
(s1701 2.0)
(s1703 4.0)
(s1704 5.0)
(s1705 5.0)
(s1706 2.0)
(s1708 4.0)
(s1709 5.0)
(s1710 5.0)
(s1711 2.0)
(s1713 4.0)
(s1714 5.0)
(s1715 5.0)
(s1716 2.0)
(s1718 4.0)
(s1719 5.0)
(s1720 5.0)
(s1721 2.0)
(s1723 4.0)
(s1724 5.0)
(s1725 5.0)
(s1726 2.0)
(s1728 4.0)
(s1729 5.0)
(s1730 5.0)
(s1731 2.0)
(s1733 4.0)
(s1734 5.0)
(s1735 5.0)
(s1736 2.0)
(s1738 4.0)
(s1739 5.0)
(s1740 5.0)
(s1741 2.0)
(s1743 4.0)
(s1744 5.0)
(s1745 5.0)
(s1746 2.0)
(s1748 4.0)
(s1749 5.0)
(s1750 5.0)
(s1751 2.0)
(s1753 4.0)
(s1754 5.0)
(s1755 5.0)
(s1756 2.0)
(s1758 4.0)
(s1759 5.0)
(s1760 5.0)
(s1761 2.0)
(s1763 4.0)
(s1764 5.0)
(s1765 5.0)
(s1766 2.0)
(s1768 4.0)
(s1769 5.0)
(s1770 5.0)
(s1771 2.0)
(s1773 4.0)
(s1774 5.0)
(s1775 5.0)
(s1776 2.0)
(s1778 4.0)
(s1779 5.0)
(s1780 5.0)
(s1781 2.0)
(s1783 4.0)
(s1784 5.0)
(s1785 5.0)
(s1786 2.0)
(s1788 4.0)
(s1789 5.0)
(s1790 5.0)
(s1791 2.0)
(s1793 4.0)
(s1794 5.0)
(s1795 5.0)
(s1796 2.0)
(s1798 4.0)
(s1799 5.0)
(s1800 5.0)
(s1801 2.0)
(s1803 4.0)
(s1804 5.0)
(s1805 5.0)
(s1806 2.0)
(s1808 4.0)
(s1809 5.0)
(s1810 5.0)
(s1811 2.0)
(s1813 4.0)
(s1814 5.0)
(s1815 5.0)
(s1816 2.0)
(s1818 4.0)
(s1819 5.0)
(s1820 5.0)
(s1821 2.0)
(s1823 4.0)
(s1824 5.0)
(s1825 5.0)
(s1826 2.0)
(s1828 4.0)
(s1829 5.0)
(s1830 5.0)
(s1831 2.0)
(s1833 4.0)
(s1834 5.0)
(s1835 5.0)
(s1836 2.0)
(s1838 4.0)
(s1839 5.0)
(s1840 5.0)
(s1841 2.0)
(s1843 4.0)
(s1844 5.0)
(s1845 5.0)
(s1846 2.0)
(s1848 4.0)
(s1849 5.0)
(s1850 5.0)
(s1851 2.0)
(s1853 4.0)
(s1854 5.0)
(s1855 5.0)
(s1856 2.0)
(s1858 4.0)
(s1859 5.0)
(s1860 5.0)
(s1861 2.0)
(s1863 4.0)
(s1864 5.0)
(s1865 5.0)
(s1866 2.0)
(s1868 4.0)
(s1869 5.0)
(s1870 5.0)
(s1871 2.0)
(s1873 4.0)
(s1874 5.0)
(s1875 5.0)
(s1876 2.0)
(s1878 4.0)
(s1879 5.0)
(s1880 5.0)
(s1881 2.0)
(s1883 4.0)
(s1884 5.0)
(s1885 5.0)
(s1886 2.0)
(s1888 4.0)
(s1889 5.0)
(s1890 5.0)
(s1891 2.0)
(s1893 4.0)
(s1894 5.0)
(s1895 5.0)
(s1896 2.0)
(s1898 4.0)
(s1899 5.0)
(s1900 5.0)
(s1901 2.0)
(s1903 4.0)
(s1904 5.0)
(s1905 5.0)
(s1906 2.0)
(s1908 4.0)
(s1909 5.0)
(s1910 5.0)
(s1911 2.0)
(s1913 4.0)
(s1914 5.0)
(s1915 5.0)
(s1916 2.0)
(s1918 4.0)
(s1919 5.0)
(s1920 5.0)
(s1921 2.0)
(s1923 4.0)
(s1924 5.0)
(s1925 5.0)
(s1926 2.0)
(s1928 4.0)
(s1929 5.0)
(s1930 5.0)
(s1931 2.0)
(s1933 4.0)
(s1934 5.0)
(s1935 5.0)
(s1936 2.0)
(s1938 4.0)
(s1939 5.0)
(s1940 5.0)
(s1941 2.0)
(s1943 4.0)
(s1944 5.0)
(s1945 5.0)
(s1946 2.0)
(s1948 4.0)
(s1949 5.0)
(s1950 5.0)
(s1951 2.0)
(s1953 4.0)
(s1954 5.0)
(s1955 5.0)
(s1956 2.0)
(s1958 4.0)
(s1959 5.0)
(s1960 5.0)
(s1961 2.0)
(s1963 4.0)
(s1964 5.0)
(s1965 5.0)
(s1966 2.0)
(s1968 4.0)
(s1969 5.0)
(s1970 5.0)
(s1971 2.0)
(s1973 4.0)
(s1974 5.0)
(s1975 5.0)
(s1976 2.0)
(s1978 4.0)
(s1979 5.0)
(s1980 5.0)
(s1981 2.0)
(s1983 4.0)
(s1984 5.0)
(s1985 5.0)
(s1986 2.0)
(s1988 4.0)
(s1989 5.0)
(s1990 5.0)
(s1991 2.0)
(s1993 4.0)
(s1994 5.0)
(s1995 5.0)
(s1996 2.0)
(s1998 4.0)
(s1999 5.0)
(s2000 5.0)
(s2001 2.0)
(s2003 4.0)
(s2004 5.0)
(s2005 5.0)
(s2006 2.0)
(s2008 4.0)
(s2009 5.0)
(s2010 5.0)
(s2011 2.0)
(s2013 4.0)
(s2014 5.0)
(s2015 5.0)
(s2016 2.0)
(s2018 4.0)
(s2019 5.0)
(s2020 5.0)
(s2021 2.0)
(s2023 4.0)
(s2024 5.0)
(s2025 5.0)
(s2026 2.0)
(s2028 4.0)
(s2029 5.0)
(s2030 5.0)
(s2031 2.0)
(s2033 4.0)
(s2034 5.0)
(s2035 5.0)
(s2036 2.0)
(s2038 4.0)
(s2039 5.0)
(s2040 5.0)
(s2041 2.0)
(s2043 4.0)
(s2044 5.0)
(s2045 5.0)
(s2046 2.0)
(s2048 4.0)
(s2049 5.0)
(s2050 5.0)
(s2051 2.0)
(s2053 4.0)
(s2054 5.0)
(s2055 5.0)
(s2056 2.0)
(s2058 4.0)
(s2059 5.0)
(s2060 5.0)
(s2061 2.0)
(s2063 4.0)
(s2064 5.0)
(s2065 5.0)
(s2066 2.0)
(s2068 4.0)
(s2069 5.0)
(s2070 5.0)
(s2071 2.0)
(s2073 4.0)
(s2074 5.0)
(s2075 5.0)
(s2076 2.0)
(s2078 4.0)
(s2079 5.0)
(s2080 5.0)
(s2081 2.0)
(s2083 4.0)
(s2084 5.0)
(s2085 5.0)
(s2086 2.0)
(s2088 4.0)
(s2089 5.0)
(s2090 5.0)
(s2091 2.0)
(s2093 4.0)
(s2094 5.0)
(s2095 5.0)
(s2096 2.0)
(s2098 4.0)
(s2099 5.0)
(s2100 5.0)
(s2101 2.0)
(s2103 4.0)
(s2104 5.0)
(s2105 5.0)
(s2106 2.0)
(s2108 4.0)
(s2109 5.0)
(s2110 5.0)
(s2111 2.0)
(s2113 4.0)
(s2114 5.0)
(s2115 5.0)
(s2116 2.0)
(s2118 4.0)
(s2119 5.0)
(s2120 5.0)
(s2121 2.0)
(s2123 4.0)
(s2124 5.0)
(s2125 5.0)
(s2126 2.0)
(s2128 4.0)
(s2129 5.0)
(s2130 5.0)
(s2131 2.0)
(s2133 4.0)
(s2134 5.0)
(s2135 5.0)
(s2136 2.0)
(s2138 4.0)
(s2139 5.0)
(s2140 5.0)
(s2141 2.0)
(s2143 4.0)
(s2144 5.0)
(s2145 5.0)
(s2146 2.0)
(s2148 4.0)
(s2149 5.0)
(s2150 5.0)
(s2151 2.0)
(s2153 4.0)
(s2154 5.0)
(s2155 5.0)
(s2156 2.0)
(s2158 4.0)
(s2159 5.0)
(s2160 5.0)
(s2161 2.0)
(s2163 4.0)
(s2164 5.0)
(s2165 5.0)
(s2166 2.0)
(s2168 4.0)
(s2169 5.0)
(s2170 5.0)
(s2171 2.0)
(s2173 4.0)
(s2174 5.0)
(s2175 5.0)
(s2176 2.0)
(s2178 4.0)
(s2179 5.0)
(s2180 5.0)
(s2181 2.0)
(s2183 4.0)
(s2184 5.0)
(s2185 5.0)
(s2186 2.0)
(s2188 4.0)
(s2189 5.0)
(s2190 5.0)
(s2191 2.0)
(s2193 4.0)
(s2194 5.0)
(s2195 5.0)
(s2196 2.0)
(s2198 4.0)
(s2199 5.0)
(s2200 5.0)
(s2201 2.0)
(s2203 4.0)
(s2204 5.0)
(s2205 5.0)
(s2206 2.0)
(s2208 4.0)
(s2209 5.0)
(s2210 5.0)
(s2211 2.0)
(s2213 4.0)
(s2214 5.0)
(s2215 5.0)
(s2216 2.0)
(s2218 4.0)
(s2219 5.0)
(s2220 5.0)
(s2221 2.0)
(s2223 4.0)
(s2224 5.0)
(s2225 5.0)
(s2226 2.0)
(s2228 4.0)
(s2229 5.0)
(s2230 5.0)
(s2231 2.0)
(s2233 4.0)
(s2234 5.0)
(s2235 5.0)
(s2236 2.0)
(s2238 4.0)
(s2239 5.0)
(s2240 5.0)
(s2241 2.0)
(s2243 4.0)
(s2244 5.0)
(s2245 5.0)
(s2246 2.0)
(s2248 4.0)
(s2249 5.0)
(s2250 5.0)
(s2251 2.0)
(s2253 4.0)
(s2254 5.0)
(s2255 5.0)
(s2256 2.0)
(s2258 4.0)
(s2259 5.0)
(s2260 5.0)
(s2261 2.0)
(s2263 4.0)
(s2264 5.0)
(s2265 5.0)
(s2266 2.0)
(s2268 4.0)
(s2269 5.0)
(s2270 5.0)
(s2271 2.0)
(s2273 4.0)
(s2274 5.0)
(s2275 5.0)
(s2276 2.0)
(s2278 4.0)
(s2279 5.0)
(s2280 5.0)
(s2281 2.0)
(s2283 4.0)
(s2284 5.0)
(s2285 5.0)
(s2286 2.0)
(s2288 4.0)
(s2289 5.0)
(s2290 5.0)
(s2291 2.0)
(s2293 4.0)
(s2294 5.0)
(s2295 5.0)
(s2296 2.0)
(s2298 4.0)
(s2299 5.0)
(s2300 5.0)
(s2301 2.0)
(s2303 4.0)
(s2304 5.0)
(s2305 5.0)
(s2306 2.0)
(s2308 4.0)
(s2309 5.0)
(s2310 5.0)
(s2311 2.0)
(s2313 4.0)
(s2314 5.0)
(s2315 5.0)
(s2316 2.0)
(s2318 4.0)
(s2319 5.0)
(s2320 5.0)
(s2321 2.0)
(s2323 4.0)
(s2324 5.0)
(s2325 5.0)
(s2326 2.0)
(s2328 4.0)
(s2329 5.0)
(s2330 5.0)
(s2331 2.0)
(s2333 4.0)
(s2334 5.0)
(s2335 5.0)
(s2336 2.0)
(s2338 4.0)
(s2339 5.0)
(s2340 5.0)
(s2341 2.0)
(s2343 4.0)
(s2344 5.0)
(s2345 5.0)
(s2346 2.0)
(s2348 4.0)
(s2349 5.0)
(s2350 5.0)
(s2351 2.0)
(s2353 4.0)
(s2354 5.0)
(s2355 5.0)
(s2356 2.0)
(s2358 4.0)
(s2359 5.0)
(s2360 5.0)
(s2361 2.0)
(s2363 4.0)
(s2364 5.0)
(s2365 5.0)
(s2366 2.0)
(s2368 4.0)
(s2369 5.0)
(s2370 5.0)
(s2371 2.0)
(s2373 4.0)
(s2374 5.0)
(s2375 5.0)
(s2376 2.0)
(s2378 4.0)
(s2379 5.0)
(s2380 5.0)
(s2381 2.0)
(s2383 4.0)
(s2384 5.0)
(s2385 5.0)
(s2386 2.0)
(s2388 4.0)
(s2389 5.0)
(s2390 5.0)
(s2391 2.0)
(s2393 4.0)
(s2394 5.0)
(s2395 5.0)
(s2396 2.0)
(s2398 4.0)
(s2399 5.0)
(s2400 5.0)
(s2401 2.0)
(s2403 4.0)
(s2404 5.0)
(s2405 5.0)
(s2406 2.0)
(s2408 4.0)
(s2409 5.0)
(s2410 5.0)
(s2411 2.0)
(s2413 4.0)
(s2414 5.0)
(s2415 5.0)
(s2416 2.0)
(s2418 4.0)
(s2419 5.0)
(s2420 5.0)
(s2421 2.0)
(s2423 4.0)
(s2424 5.0)
(s2425 5.0)
(s2426 2.0)
(s2428 4.0)
(s2429 5.0)
(s2430 5.0)
(s2431 2.0)
(s2433 4.0)
(s2434 5.0)
(s2435 5.0)
(s2436 2.0)
(s2438 4.0)
(s2439 5.0)
(s2440 5.0)
(s2441 2.0)
(s2443 4.0)
(s2444 5.0)
(s2445 5.0)
(s2446 2.0)
(s2448 4.0)
(s2449 5.0)
(s2450 5.0)
(s2451 2.0)
(s2453 4.0)
(s2454 5.0)
(s2455 5.0)
(s2456 2.0)
(s2458 4.0)
(s2459 5.0)
(s2460 5.0)
(s2461 2.0)
(s2463 4.0)
(s2464 5.0)
(s2465 5.0)
(s2466 2.0)
(s2468 4.0)
(s2469 5.0)
(s2470 5.0)
(s2471 2.0)
(s2473 4.0)
(s2474 5.0)
(s2475 5.0)
(s2476 2.0)
(s2478 4.0)
(s2479 5.0)
(s2480 5.0)
(s2481 2.0)
(s2483 4.0)
(s2484 5.0)
(s2485 5.0)
(s2486 2.0)
(s2488 4.0)
(s2489 5.0)
(s2490 5.0)
(s2491 2.0)
(s2493 4.0)
(s2494 5.0)
(s2495 5.0)
(s2496 2.0)
(s2498 4.0)
(s2499 5.0)
(s2500 5.0)
(s2501 2.0)
(s2503 4.0)
(s2504 5.0)
(s2505 5.0)
(s2506 2.0)
(s2508 4.0)
(s2509 5.0)
(s2510 5.0)
(s2511 2.0)
(s2513 4.0)
(s2514 5.0)
(s2515 5.0)
(s2516 2.0)
(s2518 4.0)
(s2519 5.0)
(s2520 5.0)
(s2521 2.0)
(s2523 4.0)
(s2524 5.0)
(s2525 5.0)
(s2526 2.0)
(s2528 4.0)
(s2529 5.0)
(s2530 5.0)
(s2531 2.0)
(s2533 4.0)
(s2534 5.0)
(s2535 5.0)
(s2536 2.0)
(s2538 4.0)
(s2539 5.0)
(s2540 5.0)
(s2541 2.0)
(s2543 4.0)
(s2544 5.0)
(s2545 5.0)
(s2546 2.0)
(s2548 4.0)
(s2549 5.0)
(s2550 5.0)
(s2551 2.0)
(s2553 4.0)
(s2554 5.0)
(s2555 5.0)
(s2556 2.0)
(s2558 4.0)
(s2559 5.0)
(s2560 5.0)
(s2561 2.0)
(s2563 4.0)
(s2564 5.0)
(s2565 5.0)
(s2566 2.0)
(s2568 4.0)
(s2569 5.0)
(s2570 5.0)
(s2571 2.0)
(s2573 4.0)
(s2574 5.0)
(s2575 5.0)
(s2576 2.0)
(s2578 4.0)
(s2579 5.0)
(s2580 5.0)
(s2581 2.0)
(s2583 4.0)
(s2584 5.0)
(s2585 5.0)
(s2586 2.0)
(s2588 4.0)
(s2589 5.0)
(s2590 5.0)
(s2591 2.0)
(s2593 4.0)
(s2594 5.0)
(s2595 5.0)
(s2596 2.0)
(s2598 4.0)
(s2599 5.0)
(s2600 5.0)
(s2601 2.0)
(s2603 4.0)
(s2604 5.0)
(s2605 5.0)
(s2606 2.0)
(s2608 4.0)
(s2609 5.0)
(s2610 5.0)
(s2611 2.0)
(s2613 4.0)
(s2614 5.0)
(s2615 5.0)
(s2616 2.0)
(s2618 4.0)
(s2619 5.0)
(s2620 5.0)
(s2621 2.0)
(s2623 4.0)
(s2624 5.0)
(s2625 5.0)
(s2626 2.0)
(s2628 4.0)
(s2629 5.0)
(s2630 5.0)
(s2631 2.0)
(s2633 4.0)
(s2634 5.0)
(s2635 5.0)
(s2636 2.0)
(s2638 4.0)
(s2639 5.0)
(s2640 5.0)
(s2641 2.0)
(s2643 4.0)
(s2644 5.0)
(s2645 5.0)
(s2646 2.0)
(s2648 4.0)
(s2649 5.0)
(s2650 5.0)
(s2651 2.0)
(s2653 4.0)
(s2654 5.0)
(s2655 5.0)
(s2656 2.0)
(s2658 4.0)
(s2659 5.0)
(s2660 5.0)
(s2661 2.0)
(s2663 4.0)
(s2664 5.0)
(s2665 5.0)
(s2666 2.0)
(s2668 4.0)
(s2669 5.0)
(s2670 5.0)
(s2671 2.0)
(s2673 4.0)
(s2674 5.0)
(s2675 5.0)
(s2676 2.0)
(s2678 4.0)
(s2679 5.0)
(s2680 5.0)
(s2681 2.0)
(s2683 4.0)
(s2684 5.0)
(s2685 5.0)
(s2686 2.0)
(s2688 4.0)
(s2689 5.0)
(s2690 5.0)
(s2691 2.0)
(s2693 4.0)
(s2694 5.0)
(s2695 5.0)
(s2696 2.0)
(s2698 4.0)
(s2699 5.0)
(s2700 5.0)
(s2701 2.0)
(s2703 4.0)
(s2704 5.0)
(s2705 5.0)
(s2706 2.0)
(s2708 4.0)
(s2709 5.0)
(s2710 5.0)
(s2711 2.0)
(s2713 4.0)
(s2714 5.0)
(s2715 5.0)
(s2716 2.0)
(s2718 4.0)
(s2719 5.0)
(s2720 5.0)
(s2721 2.0)
(s2723 4.0)
(s2724 5.0)
(s2725 5.0)
(s2726 2.0)
(s2728 4.0)
(s2729 5.0)
(s2730 5.0)
(s2731 2.0)
(s2733 4.0)
(s2734 5.0)
(s2735 5.0)
(s2736 2.0)
(s2738 4.0)
(s2739 5.0)
(s2740 5.0)
(s2741 2.0)
(s2743 4.0)
(s2744 5.0)
(s2745 5.0)
(s2746 2.0)
(s2748 4.0)
(s2749 5.0)
(s2750 5.0)
(s2751 2.0)
(s2753 4.0)
(s2754 5.0)
(s2755 5.0)
(s2756 2.0)
(s2758 4.0)
(s2759 5.0)
(s2760 5.0)
(s2761 2.0)
(s2763 4.0)
(s2764 5.0)
(s2765 5.0)
(s2766 2.0)
(s2768 4.0)
(s2769 5.0)
(s2770 5.0)
(s2771 2.0)
(s2773 4.0)
(s2774 5.0)
(s2775 5.0)
(s2776 2.0)
(s2778 4.0)
(s2779 5.0)
(s2780 5.0)
(s2781 2.0)
(s2783 4.0)
(s2784 5.0)
(s2785 5.0)
(s2786 2.0)
(s2788 4.0)
(s2789 5.0)
(s2790 5.0)
(s2791 2.0)
(s2793 4.0)
(s2794 5.0)
(s2795 5.0)
(s2796 2.0)
(s2798 4.0)
(s2799 5.0)
(s2800 5.0)
(s2801 2.0)
(s2803 4.0)
(s2804 5.0)
(s2805 5.0)
(s2806 2.0)
(s2808 4.0)
(s2809 5.0)
(s2810 5.0)
(s2811 2.0)
(s2813 4.0)
(s2814 5.0)
(s2815 5.0)
(s2816 2.0)
(s2818 4.0)
(s2819 5.0)
(s2820 5.0)
(s2821 2.0)
(s2823 4.0)
(s2824 5.0)
(s2825 5.0)
(s2826 2.0)
(s2828 4.0)
(s2829 5.0)
(s2830 5.0)
(s2831 2.0)
(s2833 4.0)
(s2834 5.0)
(s2835 5.0)
(s2836 2.0)
(s2838 4.0)
(s2839 5.0)
(s2840 5.0)
(s2841 2.0)
(s2843 4.0)
(s2844 5.0)
(s2845 5.0)
(s2846 2.0)
(s2848 4.0)
(s2849 5.0)
(s2850 5.0)
(s2851 2.0)
(s2853 4.0)
(s2854 5.0)
(s2855 5.0)
(s2856 2.0)
(s2858 4.0)
(s2859 5.0)
(s2860 5.0)
(s2861 2.0)
(s2863 4.0)
(s2864 5.0)
(s2865 5.0)
(s2866 2.0)
(s2868 4.0)
(s2869 5.0)
(s2870 5.0)
(s2871 2.0)
(s2873 4.0)
(s2874 5.0)
(s2875 5.0)
(s2876 2.0)
(s2878 4.0)
(s2879 5.0)
(s2880 5.0)
(s2881 2.0)
(s2883 4.0)
(s2884 5.0)
(s2885 5.0)
(s2886 2.0)
(s2888 4.0)
(s2889 5.0)
(s2890 5.0)
(s2891 2.0)
(s2893 4.0)
(s2894 5.0)
(s2895 5.0)
(s2896 2.0)
(s2898 4.0)
(s2899 5.0)
(s2900 5.0)
(s2901 2.0)
(s2903 4.0)
(s2904 5.0)
(s2905 5.0)
(s2906 2.0)
(s2908 4.0)
(s2909 5.0)
(s2910 5.0)
(s2911 2.0)
(s2913 4.0)
(s2914 5.0)
(s2915 5.0)
(s2916 2.0)
(s2918 4.0)
(s2919 5.0)
(s2920 5.0)
(s2921 2.0)
(s2923 4.0)
(s2924 5.0)
(s2925 5.0)
(s2926 2.0)
(s2928 4.0)
(s2929 5.0)
(s2930 5.0)
(s2931 2.0)
(s2933 4.0)
(s2934 5.0)
(s2935 5.0)
(s2936 2.0)
(s2938 4.0)
(s2939 5.0)
(s2940 5.0)
(s2941 2.0)
(s2943 4.0)
(s2944 5.0)
(s2945 5.0)
(s2946 2.0)
(s2948 4.0)
(s2949 5.0)
(s2950 5.0)
(s2951 2.0)
(s2953 4.0)
(s2954 5.0)
(s2955 5.0)
(s2956 2.0)
(s2958 4.0)
(s2959 5.0)
(s2960 5.0)
(s2961 2.0)
(s2963 4.0)
(s2964 5.0)
(s2965 5.0)
(s2966 2.0)
(s2968 4.0)
(s2969 5.0)
(s2970 5.0)
(s2971 2.0)
(s2973 4.0)
(s2974 5.0)
(s2975 5.0)
(s2976 2.0)
(s2978 4.0)
(s2979 5.0)
(s2980 5.0)
(s2981 2.0)
(s2983 4.0)
(s2984 5.0)
(s2985 5.0)
(s2986 2.0)
(s2988 4.0)
(s2989 5.0)
(s2990 5.0)
(s2991 2.0)
(s2993 4.0)
(s2994 5.0)
(s2995 5.0)
(s2996 2.0)
(s2998 4.0)
(s2999 5.0)
(s3000 5.0)
(s3001 2.0)
(s3003 4.0)
(s3004 5.0)
(s3005 5.0)
(s3006 2.0)
(s3008 4.0)
(s3009 5.0)
(s3010 5.0)
(s3011 2.0)
(s3013 4.0)
(s3014 5.0)
(s3015 5.0)
(s3016 2.0)
(s3018 4.0)
(s3019 5.0)
(s3020 5.0)
(s3021 2.0)
(s3023 4.0)
(s3024 5.0)
(s3025 5.0)
(s3026 2.0)
(s3028 4.0)
(s3029 5.0)
(s3030 5.0)
(s3031 2.0)
(s3033 4.0)
(s3034 5.0)
(s3035 5.0)
(s3036 2.0)
(s3038 4.0)
(s3039 5.0)
(s3040 5.0)
(s3041 2.0)
(s3043 4.0)
(s3044 5.0)
(s3045 5.0)
(s3046 2.0)
(s3048 4.0)
(s3049 5.0)
(s3050 5.0)
(s3051 2.0)
(s3053 4.0)
(s3054 5.0)
(s3055 5.0)
(s3056 2.0)
(s3058 4.0)
(s3059 5.0)
(s3060 5.0)
(s3061 2.0)
(s3063 4.0)
(s3064 5.0)
(s3065 5.0)
(s3066 2.0)
(s3068 4.0)
(s3069 5.0)
(s3070 5.0)
(s3071 2.0)
(s3073 4.0)
(s3074 5.0)
(s3075 5.0)
(s3076 2.0)
(s3078 4.0)
(s3079 5.0)
(s3080 5.0)
(s3081 2.0)
(s3083 4.0)
(s3084 5.0)
(s3085 5.0)
(s3086 2.0)
(s3088 4.0)
(s3089 5.0)
(s3090 5.0)
(s3091 2.0)
(s3093 4.0)
(s3094 5.0)
(s3095 5.0)
(s3096 2.0)
(s3098 4.0)
(s3099 5.0)
(s3100 5.0)
(s3101 2.0)
(s3103 4.0)
(s3104 5.0)
(s3105 5.0)
(s3106 2.0)
(s3108 4.0)
(s3109 5.0)
(s3110 5.0)
(s3111 2.0)
(s3113 4.0)
(s3114 5.0)
(s3115 5.0)
(s3116 2.0)
(s3118 4.0)
(s3119 5.0)
(s3120 5.0)
(s3121 2.0)
(s3123 4.0)
(s3124 5.0)
(s3125 5.0)
(s3126 2.0)
(s3128 4.0)
(s3129 5.0)
(s3130 5.0)
(s3131 2.0)
(s3133 4.0)
(s3134 5.0)
(s3135 5.0)
(s3136 2.0)
(s3138 4.0)
(s3139 5.0)
(s3140 5.0)
(s3141 2.0)
(s3143 4.0)
(s3144 5.0)
(s3145 5.0)
(s3146 2.0)
(s3148 4.0)
(s3149 5.0)
(s3150 5.0)
(s3151 2.0)
(s3153 4.0)
(s3154 5.0)
(s3155 5.0)
(s3156 2.0)
(s3158 4.0)
(s3159 5.0)
(s3160 5.0)
(s3161 2.0)
(s3163 4.0)
(s3164 5.0)
(s3165 5.0)
(s3166 2.0)
(s3168 4.0)
(s3169 5.0)
(s3170 5.0)
(s3171 2.0)
(s3173 4.0)
(s3174 5.0)
(s3175 5.0)
(s3176 2.0)
(s3178 4.0)
(s3179 5.0)
(s3180 5.0)
(s3181 2.0)
(s3183 4.0)
(s3184 5.0)
(s3185 5.0)
(s3186 2.0)
(s3188 4.0)
(s3189 5.0)
(s3190 5.0)
(s3191 2.0)
(s3193 4.0)
(s3194 5.0)
(s3195 5.0)
(s3196 2.0)
(s3198 4.0)
(s3199 5.0)
(s3200 5.0)
(s3201 2.0)
(s3203 4.0)
(s3204 5.0)
(s3205 5.0)
(s3206 2.0)
(s3208 4.0)
(s3209 5.0)
(s3210 5.0)
(s3211 2.0)
(s3213 4.0)
(s3214 5.0)
(s3215 5.0)
(s3216 2.0)
(s3218 4.0)
(s3219 5.0)
(s3220 5.0)
(s3221 2.0)
(s3223 4.0)
(s3224 5.0)
(s3225 5.0)
(s3226 2.0)
(s3228 4.0)
(s3229 5.0)
(s3230 5.0)
(s3231 2.0)
(s3233 4.0)
(s3234 5.0)
(s3235 5.0)
(s3236 2.0)
(s3238 4.0)
(s3239 5.0)
(s3240 5.0)
(s3241 2.0)
(s3243 4.0)
(s3244 5.0)
(s3245 5.0)
(s3246 2.0)
(s3248 4.0)
(s3249 5.0)
(s3250 5.0)
(s3251 2.0)
(s3253 4.0)
(s3254 5.0)
(s3255 5.0)
(s3256 2.0)
(s3258 4.0)
(s3259 5.0)
(s3260 5.0)
(s3261 2.0)
(s3263 4.0)
(s3264 5.0)
(s3265 5.0)
(s3266 2.0)
(s3268 4.0)
(s3269 5.0)
(s3270 5.0)
(s3271 2.0)
(s3273 4.0)
(s3274 5.0)
(s3275 5.0)
(s3276 2.0)
(s3278 4.0)
(s3279 5.0)
(s3280 5.0)
(s3281 2.0)
(s3283 4.0)
(s3284 5.0)
(s3285 5.0)
(s3286 2.0)
(s3288 4.0)
(s3289 5.0)
(s3290 5.0)
(s3291 2.0)
(s3293 4.0)
(s3294 5.0)
(s3295 5.0)
(s3296 2.0)
(s3298 4.0)
(s3299 5.0)
(s3300 5.0)
(s3301 2.0)
(s3303 4.0)
(s3304 5.0)
(s3305 5.0)
(s3306 2.0)
(s3308 4.0)
(s3309 5.0)
(s3310 5.0)
(s3311 2.0)
(s3313 4.0)
(s3314 5.0)
(s3315 5.0)
(s3316 2.0)
(s3318 4.0)
(s3319 5.0)
(s3320 5.0)
(s3321 2.0)
(s3323 4.0)
(s3324 5.0)
(s3325 5.0)
(s3326 2.0)
(s3328 4.0)
(s3329 5.0)
(s3330 5.0)
(s3331 2.0)
(s3333 4.0)
(s3334 5.0)
(s3335 5.0)
(s3336 2.0)
(s3338 4.0)
(s3339 5.0)
(s3340 5.0)
(s3341 2.0)
(s3343 4.0)
(s3344 5.0)
(s3345 5.0)
(s3346 2.0)
(s3348 4.0)
(s3349 5.0)
(s3350 5.0)
(s3351 2.0)
(s3353 4.0)
(s3354 5.0)
(s3355 5.0)
(s3356 2.0)
(s3358 4.0)
(s3359 5.0)
(s3360 5.0)
(s3361 2.0)
(s3363 4.0)
(s3364 5.0)
(s3365 5.0)
(s3366 2.0)
(s3368 4.0)
(s3369 5.0)
(s3370 5.0)
(s3371 2.0)
(s3373 4.0)
(s3374 5.0)
(s3375 5.0)
(s3376 2.0)
(s3378 4.0)
(s3379 5.0)
(s3380 5.0)
(s3381 2.0)
(s3383 4.0)
(s3384 5.0)
(s3385 5.0)
(s3386 2.0)
(s3388 4.0)
(s3389 5.0)
(s3390 5.0)
(s3391 2.0)
(s3393 4.0)
(s3394 5.0)
(s3395 5.0)
(s3396 2.0)
(s3398 4.0)
(s3399 5.0)
(s3400 5.0)
(s3401 2.0)
(s3403 4.0)
(s3404 5.0)
(s3405 5.0)
(s3406 2.0)
(s3408 4.0)
(s3409 5.0)
(s3410 5.0)
(s3411 2.0)
(s3413 4.0)
(s3414 5.0)
(s3415 5.0)
(s3416 2.0)
(s3418 4.0)
(s3419 5.0)
(s3420 5.0)
(s3421 2.0)
(s3423 4.0)
(s3424 5.0)
(s3425 5.0)
(s3426 2.0)
(s3428 4.0)
(s3429 5.0)
(s3430 5.0)
(s3431 2.0)
(s3433 4.0)
(s3434 5.0)
(s3435 5.0)
(s3436 2.0)
(s3438 4.0)
(s3439 5.0)
(s3440 5.0)
(s3441 2.0)
(s3443 4.0)
(s3444 5.0)
(s3445 5.0)
(s3446 2.0)
(s3448 4.0)
(s3449 5.0)
(s3450 5.0)
(s3451 2.0)
(s3453 4.0)
(s3454 5.0)
(s3455 5.0)
(s3456 2.0)
(s3458 4.0)
(s3459 5.0)
(s3460 5.0)
(s3461 2.0)
(s3463 4.0)
(s3464 5.0)
(s3465 5.0)
(s3466 2.0)
(s3468 4.0)
(s3469 5.0)
(s3470 5.0)
(s3471 2.0)
(s3473 4.0)
(s3474 5.0)
(s3475 5.0)
(s3476 2.0)
(s3478 4.0)
(s3479 5.0)
(s3480 5.0)
(s3481 2.0)
(s3483 4.0)
(s3484 5.0)
(s3485 5.0)
(s3486 2.0)
(s3488 4.0)
(s3489 5.0)
(s3490 5.0)
(s3491 2.0)
(s3493 4.0)
(s3494 5.0)
(s3495 5.0)
(s3496 2.0)
(s3498 4.0)
(s3499 5.0)
(s3500 5.0)
(s3501 2.0)
(s3503 4.0)
(s3504 5.0)
(s3505 5.0)
(s3506 2.0)
(s3508 4.0)
(s3509 5.0)
(s3510 5.0)
(s3511 2.0)
(s3513 4.0)
(s3514 5.0)
(s3515 5.0)
(s3516 2.0)
(s3518 4.0)
(s3519 5.0)
(s3520 5.0)
(s3521 2.0)
(s3523 4.0)
(s3524 5.0)
(s3525 5.0)
(s3526 2.0)
(s3528 4.0)
(s3529 5.0)
(s3530 5.0)
(s3531 2.0)
(s3533 4.0)
(s3534 5.0)
(s3535 5.0)
(s3536 2.0)
(s3538 4.0)
(s3539 5.0)
(s3540 5.0)
(s3541 2.0)
(s3543 4.0)
(s3544 5.0)
(s3545 5.0)
(s3546 2.0)
(s3548 4.0)
(s3549 5.0)
(s3550 5.0)
(s3551 2.0)
(s3553 4.0)
(s3554 5.0)
(s3555 5.0)
(s3556 2.0)
(s3558 4.0)
(s3559 5.0)
(s3560 5.0)
(s3561 2.0)
(s3563 4.0)
(s3564 5.0)
(s3565 5.0)
(s3566 2.0)
(s3568 4.0)
(s3569 5.0)
(s3570 5.0)
(s3571 2.0)
(s3573 4.0)
(s3574 5.0)
(s3575 5.0)
(s3576 2.0)
(s3578 4.0)
(s3579 5.0)
(s3580 5.0)
(s3581 2.0)
(s3583 4.0)
(s3584 5.0)
(s3585 5.0)
(s3586 2.0)
(s3588 4.0)
(s3589 5.0)
(s3590 5.0)
(s3591 2.0)
(s3593 4.0)
(s3594 5.0)
(s3595 5.0)
(s3596 2.0)
(s3598 4.0)
(s3599 5.0)
(s3600 5.0)
(s3601 2.0)
(s3603 4.0)
(s3604 5.0)
(s3605 5.0)
(s3606 2.0)
(s3608 4.0)
(s3609 5.0)
(s3610 5.0)
(s3611 2.0)
(s3613 4.0)
(s3614 5.0)
(s3615 5.0)
(s3616 2.0)
(s3618 4.0)
(s3619 5.0)
(s3620 5.0)
(s3621 2.0)
(s3623 4.0)
(s3624 5.0)
(s3625 5.0)
(s3626 2.0)
(s3628 4.0)
(s3629 5.0)
(s3630 5.0)
(s3631 2.0)
(s3633 4.0)
(s3634 5.0)
(s3635 5.0)
(s3636 2.0)
(s3638 4.0)
(s3639 5.0)
(s3640 5.0)
(s3641 2.0)
(s3643 4.0)
(s3644 5.0)
(s3645 5.0)
(s3646 2.0)
(s3648 4.0)
(s3649 5.0)
(s3650 5.0)
(s3651 2.0)
(s3653 4.0)
(s3654 5.0)
(s3655 5.0)
(s3656 2.0)
(s3658 4.0)
(s3659 5.0)
(s3660 5.0)
(s3661 2.0)
(s3663 4.0)
(s3664 5.0)
(s3665 5.0)
(s3666 2.0)
(s3668 4.0)
(s3669 5.0)
(s3670 5.0)
(s3671 2.0)
(s3673 4.0)
(s3674 5.0)
(s3675 5.0)
(s3676 2.0)
(s3678 4.0)
(s3679 5.0)
(s3680 5.0)
(s3681 2.0)
(s3683 4.0)
(s3684 5.0)
(s3685 5.0)
(s3686 2.0)
(s3688 4.0)
(s3689 5.0)
(s3690 5.0)
(s3691 2.0)
(s3693 4.0)
(s3694 5.0)
(s3695 5.0)
(s3696 2.0)
(s3698 4.0)
(s3699 5.0)
(s3700 5.0)
(s3701 2.0)
(s3703 4.0)
(s3704 5.0)
(s3705 5.0)
(s3706 2.0)
(s3708 4.0)
(s3709 5.0)
(s3710 5.0)
(s3711 2.0)
(s3713 4.0)
(s3714 5.0)
(s3715 5.0)
(s3716 2.0)
(s3718 4.0)
(s3719 5.0)
(s3720 5.0)
(s3721 2.0)
(s3723 4.0)
(s3724 5.0)
(s3725 5.0)
(s3726 2.0)
(s3728 4.0)
(s3729 5.0)
(s3730 5.0)
(s3731 2.0)
(s3733 4.0)
(s3734 5.0)
(s3735 5.0)
(s3736 2.0)
(s3738 4.0)
(s3739 5.0)
(s3740 5.0)
(s3741 2.0)
(s3743 4.0)
(s3744 5.0)
(s3745 5.0)
(s3746 2.0)
(s3748 4.0)
(s3749 5.0)
(s3750 5.0)
(s3751 2.0)
(s3753 4.0)
(s3754 5.0)
(s3755 5.0)
(s3756 2.0)
(s3758 4.0)
(s3759 5.0)
(s3760 5.0)
(s3761 2.0)
(s3763 4.0)
(s3764 5.0)
(s3765 5.0)
(s3766 2.0)
(s3768 4.0)
(s3769 5.0)
(s3770 5.0)
(s3771 2.0)
(s3773 4.0)
(s3774 5.0)
(s3775 5.0)
(s3776 2.0)
(s3778 4.0)
(s3779 5.0)
(s3780 5.0)
(s3781 2.0)
(s3783 4.0)
(s3784 5.0)
(s3785 5.0)
(s3786 2.0)
(s3788 4.0)
(s3789 5.0)
(s3790 5.0)
(s3791 2.0)
(s3793 4.0)
(s3794 5.0)
(s3795 5.0)
(s3796 2.0)
(s3798 4.0)
(s3799 5.0)
(s3800 5.0)
(s3801 2.0)
(s3803 4.0)
(s3804 5.0)
(s3805 5.0)
(s3806 2.0)
(s3808 4.0)
(s3809 5.0)
(s3810 5.0)
(s3811 2.0)
(s3813 4.0)
(s3814 5.0)
(s3815 5.0)
(s3816 2.0)
(s3818 4.0)
(s3819 5.0)
(s3820 5.0)
(s3821 2.0)
(s3823 4.0)
(s3824 5.0)
(s3825 5.0)
(s3826 2.0)
(s3828 4.0)
(s3829 5.0)
(s3830 5.0)
(s3831 2.0)
(s3833 4.0)
(s3834 5.0)
(s3835 5.0)
(s3836 2.0)
(s3838 4.0)
(s3839 5.0)
(s3840 5.0)
(s3841 2.0)
(s3843 4.0)
(s3844 5.0)
(s3845 5.0)
(s3846 2.0)
(s3848 4.0)
(s3849 5.0)
(s3850 5.0)
(s3851 2.0)
(s3853 4.0)
(s3854 5.0)
(s3855 5.0)
(s3856 2.0)
(s3858 4.0)
(s3859 5.0)
(s3860 5.0)
(s3861 2.0)
(s3863 4.0)
(s3864 5.0)
(s3865 5.0)
(s3866 2.0)
(s3868 4.0)
(s3869 5.0)
(s3870 5.0)
(s3871 2.0)
(s3873 4.0)
(s3874 5.0)
(s3875 5.0)
(s3876 2.0)
(s3878 4.0)
(s3879 5.0)
(s3880 5.0)
(s3881 2.0)
(s3883 4.0)
(s3884 5.0)
(s3885 5.0)
(s3886 2.0)
(s3888 4.0)
(s3889 5.0)
(s3890 5.0)
(s3891 2.0)
(s3893 4.0)
(s3894 5.0)
(s3895 5.0)
(s3896 2.0)
(s3898 4.0)
(s3899 5.0)
(s3900 5.0)
(s3901 2.0)
(s3903 4.0)
(s3904 5.0)
(s3905 5.0)
(s3906 2.0)
(s3908 4.0)
(s3909 5.0)
(s3910 5.0)
(s3911 2.0)
(s3913 4.0)
(s3914 5.0)
(s3915 5.0)
(s3916 2.0)
(s3918 4.0)
(s3919 5.0)
(s3920 5.0)
(s3921 2.0)
(s3923 4.0)
(s3924 5.0)
(s3925 5.0)
(s3926 2.0)
(s3928 4.0)
(s3929 5.0)
(s3930 5.0)
(s3931 2.0)
(s3933 4.0)
(s3934 5.0)
(s3935 5.0)
(s3936 2.0)
(s3938 4.0)
(s3939 5.0)
(s3940 5.0)
(s3941 2.0)
(s3943 4.0)
(s3944 5.0)
(s3945 5.0)
(s3946 2.0)
(s3948 4.0)
(s3949 5.0)
(s3950 5.0)
(s3951 2.0)
(s3953 4.0)
(s3954 5.0)
(s3955 5.0)
(s3956 2.0)
(s3958 4.0)
(s3959 5.0)
(s3960 5.0)
(s3961 2.0)
(s3963 4.0)
(s3964 5.0)
(s3965 5.0)
(s3966 2.0)
(s3968 4.0)
(s3969 5.0)
(s3970 5.0)
(s3971 2.0)
(s3973 4.0)
(s3974 5.0)
(s3975 5.0)
(s3976 2.0)
(s3978 4.0)
(s3979 5.0)
(s3980 5.0)
(s3981 2.0)
(s3983 4.0)
(s3984 5.0)
(s3985 5.0)
(s3986 2.0)
(s3988 4.0)
(s3989 5.0)
(s3990 5.0)
(s3991 2.0)
(s3993 4.0)
(s3994 5.0)
(s3995 5.0)
(s3996 2.0)
(s3998 4.0)
(s3999 5.0)
(s4000 5.0)
(s4001 2.0)
(s4003 4.0)
(s4004 5.0)
(s4005 5.0)
(s4006 2.0)
(s4008 4.0)
(s4009 5.0)
(s4010 5.0)
(s4011 2.0)
(s4013 4.0)
(s4014 5.0)
(s4015 5.0)
(s4016 2.0)
(s4018 4.0)
(s4019 5.0)
(s4020 5.0)
(s4021 2.0)
(s4023 4.0)
(s4024 5.0)
(s4025 5.0)
(s4026 2.0)
(s4028 4.0)
(s4029 5.0)
(s4030 5.0)
(s4031 2.0)
(s4033 4.0)
(s4034 5.0)
(s4035 5.0)
(s4036 2.0)
(s4038 4.0)
(s4039 5.0)
(s4040 5.0)
(s4041 2.0)
(s4043 4.0)
(s4044 5.0)
(s4045 5.0)
(s4046 2.0)
(s4048 4.0)
(s4049 5.0)
(s4050 5.0)
(s4051 2.0)
(s4053 4.0)
(s4054 5.0)
(s4055 5.0)
(s4056 2.0)
(s4058 4.0)
(s4059 5.0)
(s4060 5.0)
(s4061 2.0)
(s4063 4.0)
(s4064 5.0)
(s4065 5.0)
(s4066 2.0)
(s4068 4.0)
(s4069 5.0)
(s4070 5.0)
(s4071 2.0)
(s4073 4.0)
(s4074 5.0)
(s4075 5.0)
(s4076 2.0)
(s4078 4.0)
(s4079 5.0)
(s4080 5.0)
(s4081 2.0)
(s4083 4.0)
(s4084 5.0)
(s4085 5.0)
(s4086 2.0)
(s4088 4.0)
(s4089 5.0)
(s4090 5.0)
(s4091 2.0)
(s4093 4.0)
(s4094 5.0)
(s4095 5.0)
(s4096 2.0)
(s4098 4.0)
(s4099 5.0)
(s4100 5.0)
(s4101 2.0)
(s4103 4.0)
(s4104 5.0)
(s4105 5.0)
(s4106 2.0)
(s4108 4.0)
(s4109 5.0)
(s4110 5.0)
(s4111 2.0)
(s4113 4.0)
(s4114 5.0)
(s4115 5.0)
(s4116 2.0)
(s4118 4.0)
(s4119 5.0)
(s4120 5.0)
(s4121 2.0)
(s4123 4.0)
(s4124 5.0)
(s4125 5.0)
(s4126 2.0)
(s4128 4.0)
(s4129 5.0)
(s4130 5.0)
(s4131 2.0)
(s4133 4.0)
(s4134 5.0)
(s4135 5.0)
(s4136 2.0)
(s4138 4.0)
(s4139 5.0)
(s4140 5.0)
(s4141 2.0)
(s4143 4.0)
(s4144 5.0)
(s4145 5.0)
(s4146 2.0)
(s4148 4.0)
(s4149 5.0)
(s4150 5.0)
(s4151 2.0)
(s4153 4.0)
(s4154 5.0)
(s4155 5.0)
(s4156 2.0)
(s4158 4.0)
(s4159 5.0)
(s4160 5.0)
(s4161 2.0)
(s4163 4.0)
(s4164 5.0)
(s4165 5.0)
(s4166 2.0)
(s4168 4.0)
(s4169 5.0)
(s4170 5.0)
(s4171 2.0)
(s4173 4.0)
(s4174 5.0)
(s4175 5.0)
(s4176 2.0)
(s4178 4.0)
(s4179 5.0)
(s4180 5.0)
(s4181 2.0)
(s4183 4.0)
(s4184 5.0)
(s4185 5.0)
(s4186 2.0)
(s4188 4.0)
(s4189 5.0)
(s4190 5.0)
(s4191 2.0)
(s4193 4.0)
(s4194 5.0)
(s4195 5.0)
(s4196 2.0)
(s4198 4.0)
(s4199 5.0)
(s4200 5.0)
(s4201 2.0)
(s4203 4.0)
(s4204 5.0)
(s4205 5.0)
(s4206 2.0)
(s4208 4.0)
(s4209 5.0)
(s4210 5.0)
(s4211 2.0)
(s4213 4.0)
(s4214 5.0)
(s4215 5.0)
(s4216 2.0)
(s4218 4.0)
(s4219 5.0)
(s4220 5.0)
(s4221 2.0)
(s4223 4.0)
(s4224 5.0)
(s4225 5.0)
(s4226 2.0)
(s4228 4.0)
(s4229 5.0)
(s4230 5.0)
(s4231 2.0)
(s4233 4.0)
(s4234 5.0)
(s4235 5.0)
(s4236 2.0)
(s4238 4.0)
(s4239 5.0)
(s4240 5.0)
(s4241 2.0)
(s4243 4.0)
(s4244 5.0)
(s4245 5.0)
(s4246 2.0)
(s4248 4.0)
(s4249 5.0)
(s4250 5.0)
(s4251 2.0)
(s4253 4.0)
(s4254 5.0)
(s4255 5.0)
(s4256 2.0)
(s4258 4.0)
(s4259 5.0)
(s4260 5.0)
(s4261 2.0)
(s4263 4.0)
(s4264 5.0)
(s4265 5.0)
(s4266 2.0)
(s4268 4.0)
(s4269 5.0)
(s4270 5.0)
(s4271 2.0)
(s4273 4.0)
(s4274 5.0)
(s4275 5.0)
(s4276 2.0)
(s4278 4.0)
(s4279 5.0)
(s4280 5.0)
(s4281 2.0)
(s4283 4.0)
(s4284 5.0)
(s4285 5.0)
(s4286 2.0)
(s4288 4.0)
(s4289 5.0)
(s4290 5.0)
(s4291 2.0)
(s4293 4.0)
(s4294 5.0)
(s4295 5.0)
(s4296 2.0)
(s4298 4.0)
(s4299 5.0)
(s4300 5.0)
(s4301 2.0)
(s4303 4.0)
(s4304 5.0)
(s4305 5.0)
(s4306 2.0)
(s4308 4.0)
(s4309 5.0)
(s4310 5.0)
(s4311 2.0)
(s4313 4.0)
(s4314 5.0)
(s4315 5.0)
(s4316 2.0)
(s4318 4.0)
(s4319 5.0)
(s4320 5.0)
(s4321 2.0)
(s4323 4.0)
(s4324 5.0)
(s4325 5.0)
(s4326 2.0)
(s4328 4.0)
(s4329 5.0)
(s4330 5.0)
(s4331 2.0)
(s4333 4.0)
(s4334 5.0)
(s4335 5.0)
(s4336 2.0)
(s4338 4.0)
(s4339 5.0)
(s4340 5.0)
(s4341 2.0)
(s4343 4.0)
(s4344 5.0)
(s4345 5.0)
(s4346 2.0)
(s4348 4.0)
(s4349 5.0)
(s4350 5.0)
(s4351 2.0)
(s4353 4.0)
(s4354 5.0)
(s4355 5.0)
(s4356 2.0)
(s4358 4.0)
(s4359 5.0)
(s4360 5.0)
(s4361 2.0)
(s4363 4.0)
(s4364 5.0)
(s4365 5.0)
(s4366 2.0)
(s4368 4.0)
(s4369 5.0)
(s4370 5.0)
(s4371 2.0)
(s4373 4.0)
(s4374 5.0)
(s4375 5.0)
(s4376 2.0)
(s4378 4.0)
(s4379 5.0)
(s4380 5.0)
(s4381 2.0)
(s4383 4.0)
(s4384 5.0)
(s4385 5.0)
(s4386 2.0)
(s4388 4.0)
(s4389 5.0)
(s4390 5.0)
(s4391 2.0)
(s4393 4.0)
(s4394 timeout
5.0)
(s4395 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20131 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)
(s3653 4)
(s3654 5)
(s3655 5)
(s3656 2)
(s3658 4)
(s3659 5)
(s3660 5)
(s3661 2)
(s3663 4)
(s3664 5)
(s3665 5)
(s3666 2)
(s3668 4)
(s3669 5)
(s3670 5)
(s3671 2)
(s3673 4)
(s3674 5)
(s3675 5)
(s3676 2)
(s3678 4)
(s3679 5)
(s3680 5)
(s3681 2)
(s3683 4)
(s3684 5)
(s3685 5)
(s3686 2)
(s3688 4)
(s3689 5)
(s3690 5)
(s3691 2)
(s3693 4)
(s3694 5)
(s3695 5)
(s3696 2)
(s3698 4)
(s3699 5)
(s3700 5)
(s3701 2)
(s3703 4)
(s3704 5)
(s3705 5)
(s3706 2)
(s3708 4)
(s3709 5)
(s3710 5)
(s3711 2)
(s3713 4)
(s3714 5)
(s3715 5)
(s3716 2)
(s3718 4)
(s3719 5)
(s3720 5)
(s3721 2)
(s3723 4)
(s3724 5)
(s3725 5)
(s3726 2)
(s3728 4)
(s3729 5)
(s3730 5)
(s3731 2)
(s3733 4)
(s3734 5)
(s3735 5)
(s3736 2)
(s3738 4)
(s3739 5)
(s3740 5)
(s3741 2)
(s3743 4)
(s3744 5)
(s3745 5)
(s3746 2)
(s3748 4)
(s3749 5)
(s3750 5)
(s3751 2)
(s3753 4)
(s3754 5)
(s3755 5)
(s3756 2)
(s3758 4)
(s3759 5)
(s3760 5)
(s3761 2)
(s3763 4)
(s3764 5)
(s3765 5)
(s3766 2)
(s3768 4)
(s3769 5)
(s3770 5)
(s3771 2)
(s3773 4)
(s3774 5)
(s3775 5)
(s3776 2)
(s3778 4)
(s3779 5)
(s3780 5)
(s3781 2)
(s3783 4)
(s3784 5)
(s3785 5)
(s3786 2)
(s3788 4)
(s3789 5)
(s3790 5)
(s3791 2)
(s3793 4)
(s3794 5)
(s3795 5)
(s3796 2)
(s3798 4)
(s3799 5)
(s3800 5)
(s3801 2)
(s3803 4)
(s3804 5)
(s3805 5)
(s3806 2)
(s3808 4)
(s3809 5)
(s3810 5)
(s3811 2)
(s3813 4)
(s3814 5)
(s3815 5)
(s3816 2)
(s3818 4)
(s3819 5)
(s3820 5)
(s3821 2)
(s3823 4)
(s3824 5)
(s3825 5)
(s3826 2)
(s3828 4)
(s3829 5)
(s3830 5)
(s3831 2)
(s3833 4)
(s3834 5)
(s3835 5)
(s3836 2)
(s3838 4)
(s3839 5)
(s3840 5)
(s3841 2)
(s3843 4)
(s3844 5)
(s3845 5)
(s3846 2)
(s3848 4)
(s3849 5)
(s3850 5)
(s3851 2)
(s3853 4)
(s3854 5)
(s3855 5)
(s3856 2)
(s3858 4)
(s3859 5)
(s3860 5)
(s3861 2)
(s3863 4)
(s3864 5)
(s3865 5)
(s3866 2)
(s3868 4)
(s3869 5)
(s3870 5)
(s3871 2)
(s3873 4)
(s3874 5)
(s3875 5)
(s3876 2)
(s3878 4)
(s3879 5)
(s3880 5)
(s3881 2)
(s3883 4)
(s3884 5)
(s3885 5)
(s3886 2)
(s3888 4)
(s3889 5)
(s3890 5)
(s3891 2)
(s3893 4)
(s3894 5)
(s3895 5)
(s3896 2)
(s3898 4)
(s3899 5)
(s3900 5)
(s3901 2)
(s3903 4)
(s3904 5)
(s3905 5)
(s3906 2)
(s3908 4)
(s3909 5)
(s3910 5)
(s3911 2)
(s3913 4)
(s3914 5)
(s3915 5)
(s3916 2)
(s3918 4)
(s3919 5)
(s3920 5)
(s3921 2)
(s3923 4)
(s3924 5)
(s3925 5)
(s3926 2)
(s3928 4)
(s3929 5)
(s3930 5)
(s3931 2)
(s3933 4)
(s3934 5)
(s3935 5)
(s3936 2)
(s3938 4)
(s3939 5)
(s3940 5)
(s3941 2)
(s3943 4)
(s3944 5)
(s3945 5)
(s3946 2)
(s3948 4)
(s3949 5)
(s3950 5)
(s3951 2)
(s3953 4)
(s3954 5)
(s3955 5)
(s3956 2)
(s3958 4)
(s3959 5)
(s3960 5)
(s3961 2)
(s3963 4)
(s3964 5)
(s3965 5)
(s3966 2)
(s3968 4)
(s3969 5)
(s3970 5)
(s3971 2)
(s3973 4)
(s3974 5)
(s3975 5)
(s3976 2)
(s3978 4)
(s3979 5)
(s3980 5)
(s3981 2)
(s3983 4)
(s3984 5)
(s3985 5)
(s3986 2)
(s3988 4)
(s3989 5)
(s3990 5)
(s3991 2)
(s3993 4)
(s3994 5)
(s3995 5)
(s3996 2)
(s3998 4)
(s3999 5)
(s4000 5)
(s4001 2)
(s4003 4)
(s4004 5)
(s4005 5)
(s4006 2)
(s4008 4)
(s4009 5)
(s4010 5)
(s4011 2)
(s4013 4)
(s4014 5)
(s4015 5)
(s4016 2)
(s4018 4)
(s4019 5)
(s4020 5)
(s4021 2)
(s4023 4)
(s4024 5)
(s4025 5)
(s4026 2)
(s4028 4)
(s4029 5)
(s4030 5)
(s4031 2)
(s4033 4)
(s4034 5)
(s4035 5)
(s4036 2)
(s4038 4)
(s4039 5)
(s4040 5)
(s4041 2)
(s4043 4)
(s4044 5)
(s4045 5)
(s4046 2)
(s4048 4)
(s4049 5)
(s4050 5)
(s4051 2)
(s4053 4)
(s4054 5)
(s4055 5)
(s4056 2)
(s4058 4)
(s4059 5)
(s4060 5)
(s4061 2)
(s4063 4)
(s4064 5)
(s4065 5)
(s4066 2)
(s4068 4)
(s4069 5)
(s4070 5)
(s4071 2)
(s4073 4)
(s4074 5)
(s4075 5)
(s4076 2)
(s4078 4)
(s4079 5)
(s4080 5)
(s4081 2)
(s4083 4)
(s4084 5)
(s4085 5)
(s4086 2)
(s4088 4)
(s4089 5)
(s4090 5)
(s4091 2)
(s4093 4)
(s4094 5)
(s4095 5)
(s4096 2)
(s4098 4)
(s4099 5)
(s4100 5)
(s4101 2)
(s4103 4)
(s4104 5)
(s4105 5)
(s4106 2)
(s4108 4)
(s4109 5)
(s4110 5)
(s4111 2)
(s4113 4)
(s4114 5)
(s4115 5)
(s4116 2)
(s4118 4)
(s4119 5)
(s4120 5)
(s4121 2)
(s4123 4)
(s4124 5)
(s4125 5)
(s4126 2)
(s4128 4)
(s4129 5)
(s4130 5)
(s4131 2)
(s4133 4)
(s4134 5)
(s4135 5)
(s4136 2)
(s4138 4)
(s4139 5)
(s4140 5)
(s4141 2)
(s4143 4)
(s4144 5)
(s4145 5)
(s4146 2)
(s4148 4)
(s4149 5)
(s4150 5)
(s4151 2)
(s4153 4)
(s4154 5)
(s4155 5)
(s4156 2)
(s4158 4)
(s4159 5)
(s4160 5)
(s4161 2)
(s4163 4)
(s4164 5)
(s4165 5)
(s4166 2)
(s4168 4)
(s4169 5)
(s4170 5)
(s4171 2)
(s4173 4)
(s4174 5)
(s4175 5)
(s4176 2)
(s4178 4)
(s4179 5)
(s4180 5)
(s4181 2)
(s4183 4)
(s4184 5)
(s4185 5)
(s4186 2)
(s4188 4)
(s4189 5)
(s4190 5)
(s4191 2)
(s4193 4)
(s4194 5)
(s4195 5)
(s4196 2)
(s4198 4)
(s4199 5)
(s4200 5)
(s4201 2)
(s4203 4)
(s4204 5)
(s4205 5)
(s4206 2)
(s4208 4)
(s4209 5)
(s4210 5)
(s4211 2)
(s4213 4)
(s4214 5)
(s4215 5)
(s4216 2)
(s4218 4)
(s4219 5)
(s4220 5)
(s4221 2)
(s4223 4)
(s4224 5)
(s4225 5)
(s4226 2)
(s4228 4)
(s4229 5)
(s4230 5)
(s4231 2)
(s4233 4)
(s4234 5)
(s4235 5)
(s4236 2)
(s4238 4)
(s4239 5)
(s4240 5)
(s4241 2)
(s4243 4)
(s4244 5)
(s4245 5)
(s4246 2)
(s4248 4)
(s4249 5)
(s4250 5)
(s4251 2)
(s4253 4)
(s4254 5)
(s4255 5)
(s4256 2)
(s4258 4)
(s4259 5)
(s4260 5)
(s4261 2)
(s4263 4)
(s4264 5)
(s4265 5)
(s4266 2)
(s4268 4)
(s4269 5)
(s4270 5)
(s4271 2)
(s4273 4)
(s4274 5)
(s4275 5)
(s4276 2)
(s4278 4)
(s4279 5)
(s4280 5)
(s4281 2)
(s4283 4)
(s4284 5)
(s4285 5)
(s4286 2)
(s4288 4)
(s4289 5)
(s4290 5)
(s4291 2)
(s4293 4)
(s4294 5)
(s4295 5)
(s4296 2)
(s4298 4)
(s4299 5)
(s4300 5)
(s4301 2)
(s4303 4)
(s4304 5)
(s4305 5)
(s4306 2)
(s4308 4)
(s4309 5)
(s4310 5)
(s4311 2)
(s4313 4)
(s4314 5)
(s4315 5)
(s4316 2)
(s4318 4)
(s4319 5)
(s4320 5)
(s4321 2)
(s4323 4)
(s4324 5)
(s4325 5)
(s4326 2)
(s4328 4)
(s4329 5)
(s4330 5)
(s4331 2)
(s4333 4)
(s4334 5)
(s4335 5)
(s4336 2)
(s4338 4)
(s4339 5)
(s4340 5)
(s4341 2)
(s4343 4)
(s4344 5)
(s4345 5)
(s4346 2)
(s4348 4)
(s4349 5)
(s4350 5)
(s4351 2)
(s4353 4)
(s4354 5)
(s4355 5)
(s4356 2)
(s4358 4)
(s4359 5)
(s4360 5)
(s4361 2)
(s4363 4)
(s4364 5)
(s4365 5)
(s4366 2)
(s4368 4)
(s4369 5)
(s4370 5)
(s4371 2)
(s4373 4)
(s4374 5)
(s4375 5)
(s4376 2)
(s4378 4)
(s4379 5)
(s4380 5)
(s4381 2)
(s4383 4)
(s4384 5)
(s4385 5)
(s4386 2)
(s4388 4)
(s4389 5)
(s4390 5)
(s4391 2)
(s4393 4)
(s4394 5)
(s4395 5)
(s4396 2)
(s4398 4)
(s4399 5)
(s4400 5)
(s4401 2)
(s4403 4)
(s4404 5)
(s4405 5)
(s4406 2)
(s4408 4)
(s4409 5)
(s4410 5)
(s4411 2)
(s4413 4)
(s4414 5)
(s4415 5)
(s4416 2)
(s4418 4)
(s4419 5)
(s4420 5)
(s4421 2)
(s4423 4)
(s4424 5)
(s4425 5)
(s4426 2)
(s4428 4)
(s4429 5)
(s4430 5)
(s4431 2)
(s4433 4)
(s4434 5)
(s4435 5)
(s4436 2)
(s4438 4)
(s4439 5)
(s4440 5)
(s4441 2)
(s4443 4)
(s4444 5)
(s4445 5)
(s4446 2)
(s4448 4)
(s4449 5)
(s4450 5)
(s4451 2)
(s4453 4)
(s4454 5)
(s4455 5)
(s4456 2)
(s4458 4)
(s4459 5)
(s4460 5)
(s4461 2)
(s4463 4)
(s4464 5)
(s4465 5)
(s4466 2)
(s4468 4)
(s4469 5)
(s4470 5)
(s4471 2)
(s4473 4)
(s4474 5)
(s4475 5)
(s4476 2)
(s4478 4)
(s4479 5)
(s4480 5)
(s4481 2)
(s4483 4)
(s4484 5)
(s4485 5)
(s4486 2)
(s4488 4)
(s4489 5)
(s4490 5)
(s4491 2)
(s4493 4)
(s4494 5)
(s4495 5)
(s4496 2)
(s4498 4)
(s4499 5)
(s4500 5)
(s4501 2)
(s4503 4)
(s4504 5)
(s4505 5)
(s4506 2)
(s4508 4)
(s4509 5)
(s4510 5)
(s4511 2)
(s4513 4)
(s4514 5)
(s4515 5)
(s4516 2)
(s4518 4)
(s4519 5)
(s4520 5)
(s4521 2)
(s4523 4)
(s4524 5)
(s4525 5)
(s4526 2)
(s4528 4)
(s4529 5)
(s4530 5)
(s4531 2)
(s4533 4)
(s4534 5)
(s4535 5)
(s4536 2)
(s4538 4)
(s4539 5)
(s4540 5)
(s4541 2)
(s4543 4)
(s4544 5)
(s4545 5)
(s4546 2)
(s4548 4)
(s4549 5)
(s4550 5)
(s4551 2)
(s4553 4)
(s4554 5)
(s4555 5)
(s4556 2)
(s4558 4)
(s4559 5)
(s4560 5)
(s4561 2)
(s4563 4)
(s4564 5)
(s4565 5)
(s4566 2)
(s4568 4)
(s4569 5)
(s4570 5)
(s4571 2)
(s4573 4)
(s4574 5)
(s4575 5)
(s4576 2)
(s4578 4)
(s4579 5)
(s4580 5)
(s4581 2)
(s4583 4)
(s4584 5)
(s4585 5)
(s4586 2)
(s4588 4)
(s4589 5)
(s4590 5)
(s4591 2)
(s4593 4)
(s4594 5)
(s4595 5)
(s4596 2)
(s4598 4)
(s4599 5)
(s4600 5)
(s4601 2)
(s4603 4)
(s4604 5)
(s4605 5)
(s4606 2)
(s4608 4)
(s4609 5)
(s4610 5)
(s4611 2)
(s4613 4)
(s4614 5)
(s4615 5)
(s4616 2)
(s4618 4)
(s4619 5)
(s4620 5)
(s4621 2)
(s4623 4)
(s4624 5)
(s4625 5)
(s4626 2)
(s4628 4)
(s4629 5)
(s4630 5)
(s4631 2)
(s4633 4)
(s4634 5)
(s4635 5)
(s4636 2)
(s4638 4)
(s4639 5)
(s4640 5)
(s4641 2)
(s4643 4)
(s4644 5)
(s4645 5)
(s4646 2)
(s4648 4)
(s4649 5)
(s4650 5)
(s4651 2)
(s4653 4)
(s4654 5)
(s4655 5)
(s4656 2)
(s4658 4)
(s4659 5)
(s4660 5)
(s4661 2)
(s4663 4)
(s4664 5)
(s4665 5)
(s4666 2)
(s4668 4)
(s4669 5)
(s4670 5)
(s4671 2)
(s4673 4)
(s4674 5)
(s4675 5)
(s4676 2)
(s4678 4)
(s4679 5)
(s4680 5)
(s4681 2)
(s4683 4)
(s4684 5)
(s4685 5)
(s4686 2)
(s4688 4)
(s4689 5)
(s4690 5)
(s4691 2)
(s4693 4)
(s4694 5)
(s4695 5)
(s4696 2)
(s4698 4)
(s4699 5)
(s4700 5)
(s4701 2)
(s4703 4)
(s4704 5)
(s4705 5)
(s4706 2)
(s4708 4)
(s4709 5)
(s4710 5)
(s4711 2)
(s4713 4)
(s4714 5)
(s4715 5)
(s4716 2)
(s4718 4)
(s4719 5)
(s4720 5)
(s4721 2)
(s4723 4)
(s4724 5)
(s4725 5)
(s4726 2)
(s4728 4)
(s4729 5)
(s4730 5)
(s4731 2)
(s4733 4)
(s4734 5)
(s4735 5)
(s4736 2)
(s4738 4)
(s4739 5)
(s4740 5)
(s4741 2)
(s4743 4)
(s4744 5)
(s4745 5)
(s4746 2)
(s4748 4)
(s4749 5)
(s4750 5)
(s4751 2)
(s4753 4)
(s4754 5)
(s4755 5)
(s4756 2)
(s4758 4)
(s4759 5)
(s4760 5)
(s4761 2)
(s4763 4)
(s4764 5)
(s4765 5)
(s4766 2)
(s4768 4)
(s4769 5)
(s4770 5)
(s4771 2)
(s4773 4)
(s4774 5)
(s4775 5)
(s4776 2)
(s4778 4)
(s4779 5)
(s4780 5)
(s4781 2)
(s4783 4)
(s4784 5)
(s4785 5)
(s4786 2)
(s4788 4)
(s4789 5)
(s4790 5)
(s4791 2)
(s4793 4)
(s4794 5)
(s4795 5)
(s4796 2)
(s4798 4)
(s4799 5)
(s4800 5)
(s4801 2)
(s4803 4)
(s4804 5)
(s4805 5)
(s4806 2)
(s4808 4)
(s4809 5)
(s4810 5)
(s4811 2)
(s4813 4)
(s4814 5)
(s4815 5)
(s4816 2)
(s4818 4)
(s4819 5)
(s4820 5)
(s4821 2)
(s4823 4)
(s4824 5)
(s4825 5)
(s4826 2)
(s4828 4)
(s4829 5)
(s4830 5)
(s4831 2)
(s4833 4)
(s4834 5)
(s4835 5)
(s4836 2)
(s4838 4)
(s4839 5)
(s4840 5)
(s4841 2)
(s4843 4)
(s4844 5)
(s4845 5)
(s4846 2)
(s4848 4)
(s4849 5)
(s4850 5)
(s4851 2)
(s4853 4)
(s4854 5)
(s4855 5)
(s4856 2)
(s4858 4)
(s4859 5)
(s4860 5)
(s4861 2)
(s4863 4)
(s4864 5)
(s4865 5)
(s4866 2)
(s4868 4)
(s4869 5)
(s4870 5)
(s4871 2)
(s4873 4)
(s4874 5)
(s4875 5)
(s4876 2)
(s4878 4)
(s4879 5)
(s4880 5)
(s4881 2)
(s4883 4)
(s4884 5)
(s4885 5)
(s4886 2)
(s4888 4)
(s4889 5)
(s4890 5)
(s4891 2)
(s4893 4)
(s4894 5)
(s4895 5)
(s4896 2)
(s4898 4)
(s4899 5)
(s4900 5)
(s4901 2)
(s4903 4)
(s4904 5)
(s4905 5)
(s4906 2)
(s4908 4)
(s4909 5)
(s4910 5)
(s4911 2)
(s4913 4)
(s4914 5)
(s4915 5)
(s4916 2)
(s4918 4)
(s4919 5)
(s4920 5)
(s4921 2)
(s4923 4)
(s4924 5)
(s4925 5)
(s4926 2)
(s4928 4)
(s4929 5)
(s4930 5)
(s4931 2)
(s4933 4)
(s4934 5)
(s4935 5)
(s4936 2)
(s4938 4)
(s4939 5)
(s4940 5)
(s4941 2)
(s4943 4)
(s4944 5)
(s4945 5)
(s4946 2)
(s4948 4)
(s4949 5)
(s4950 5)
(s4951 2)
(s4953 4)
(s4954 5)
(s4955 5)
(s4956 2)
(s4958 4)
(s4959 5)
(s4960 5)
(s4961 2)
(s4963 4)
(s4964 5)
(s4965 5)
(s4966 2)
(s4968 4)
(s4969 5)
(s4970 5)
(s4971 2)
(s4973 4)
(s4974 5)
(s4975 5)
(s4976 2)
(s4978 4)
(s4979 5)
(s4980 5)
(s4981 2)
(s4983 4)
(s4984 5)
(s4985 5)
(s4986 2)
(s4988 4)
(s4989 5)
(s4990 5)
(s4991 2)
(s4993 4)
(s4994 5)
(s4995 5)
(s4996 2)
(s4998 4)
(s4999 5)
(s5000 5)
(s5001 2)
(s5003 4)
(s5004 5)
(s5005 5)
(s5006 2)
(s5008 4)
(s5009 5)
(s5010 5)
(s5011 2)
(s5013 4)
(s5014 5)
(s5015 5)
(s5016 2)
(s5018 4)
(s5019 5)
(s5020 5)
(s5021 2)
(s5023 4)
(s5024 5)
(s5025 5)
(s5026 2)
(s5028 4)
(s5029 5)
(s5030 5)
(s5031 2)
(s5033 4)
(s5034 5)
(s5035 5)
(s5036 2)
(s5038 4)
(s5039 5)
(s5040 5)
(s5041 2)
(s5043 4)
(s5044 5)
(s5045 5)
(s5046 2)
(s5048 4)
(s5049 5)
(s5050 5)
(s5051 2)
(s5053 4)
(s5054 5)
(s5055 5)
(s5056 2)
(s5058 4)
(s5059 5)
(s5060 5)
(s5061 2)
(s5063 4)
(s5064 5)
(s5065 5)
(s5066 2)
(s5068 4)
(s5069 5)
(s5070 5)
(s5071 2)
(s5073 4)
(s5074 5)
(s5075 5)
(s5076 2)
(s5078 4)
(s5079 5)
(s5080 5)
(s5081 2)
(s5083 4)
(s5084 5)
(s5085 5)
(s5086 2)
(s5088 4)
(s5089 5)
(s5090 5)
(s5091 2)
(s5093 4)
(s5094 5)
(s5095 5)
(s5096 2)
(s5098 4)
(s5099 5)
(s5100 5)
(s5101 2)
(s5103 4)
(s5104 5)
(s5105 5)
(s5106 2)
(s5108 4)
(s5109 5)
(s5110 5)
(s5111 2)
(s5113 4)
(s5114 5)
(s5115 5)
(s5116 2)
(s5118 4)
(s5119 5)
(s5120 5)
(s5121 2)
(s5123 4)
(s5124 5)
(s5125 5)
(s5126 2)
(s5128 4)
(s5129 5)
(s5130 5)
(s5131 2)
(s5133 4)
(s5134 5)
(s5135 5)
(s5136 2)
(s5138 4)
(s5139 5)
(s5140 5)
(s5141 2)
(s5143 4)
(s5144 5)
(s5145 5)
(s5146 2)
(s5148 4)
(s5149 5)
(s5150 5)
(s5151 2)
(s5153 4)
(s5154 5)
(s5155 5)
(s5156 2)
(s5158 4)
(s5159 5)
(s5160 5)
(s5161 2)
(s5163 4)
(s5164 5)
(s5165 5)
(s5166 2)
(s5168 4)
(s5169 5)
(s5170 5)
(s5171 2)
(s5173 4)
(s5174 5)
(s5175 5)
(s5176 2)
(s5178 4)
(s5179 5)
(s5180 5)
(s5181 2)
(s5183 4)
(s5184 5)
(s5185 5)
(s5186 2)
(s5188 4)
(s5189 5)
(s5190 5)
(s5191 2)
(s5193 4)
(s5194 5)
(s5195 5)
(s5196 2)
(s5198 4)
(s5199 5)
(s5200 5)
(s5201 2)
(s5203 4)
(s5204 5)
(s5205 5)
(s5206 2)
(s5208 4)
(s5209 5)
(s5210 5)
(s5211 2)
(s5213 4)
(s5214 5)
(s5215 5)
(s5216 2)
(s5218 4)
(s5219 5)
(s5220 5)
(s5221 2)
(s5223 4)
(s5224 5)
(s5225 5)
(s5226 2)
(s5228 4)
(s5229 5)
(s5230 5)
(s5231 2)
(s5233 4)
(s5234 5)
(s5235 5)
(s5236 2)
(s5238 4)
(s5239 5)
(s5240 5)
(s5241 2)
(s5243 4)
(s5244 5)
(s5245 5)
(s5246 2)
(s5248 4)
(s5249 5)
(s5250 5)
(s5251 2)
(s5253 4)
(s5254 5)
(s5255 5)
(s5256 2)
(s5258 4)
(s5259 5)
(s5260 5)
(s5261 2)
(s5263 4)
(s5264 5)
(s5265 5)
(s5266 2)
(s5268 4)
(s5269 5)
(s5270 5)
(s5271 2)
(s5273 4)
(s5274 5)
(s5275 5)
(s5276 2)
(s5278 4)
(s5279 5)
(s5280 5)
(s5281 2)
(s5283 4)
(s5284 5)
(s5285 5)
(s5286 2)
(s5288 4)
(s5289 5)
(s5290 5)
(s5291 2)
(s5293 4)
(s5294 5)
(s5295 5)
(s5296 2)
(s5298 4)
(s5299 5)
(s5300 5)
(s5301 2)
(s5303 4)
(s5304 5)
(s5305 5)
(s5306 2)
(s5308 4)
(s5309 5)
(s5310 5)
(s5311 2)
(s5313 4)
(s5314 5)
(s5315 5)
(s5316 2)
(s5318 4)
(s5319 5)
(s5320 5)
(s5321 2)
(s5323 4)
(s5324 5)
(s5325 5)
(s5326 2)
(s5328 4)
(s5329 5)
(s5330 5)
(s5331 2)
(s5333 4)
(s5334 5)
(s5335 5)
(s5336 2)
(s5338 4)
(s5339 5)
(s5340 5)
(s5341 2)
(s5343 4)
(s5344 5)
(s5345 5)
(s5346 2)
(s5348 4)
(s5349 5)
(s5350 5)
(s5351 2)
(s5353 4)
(s5354 5)
(s5355 5)
(s5356 2)
(s5358 4)
(s5359 5)
(s5360 5)
(s5361 2)
(s5363 4)
(s5364 5)
(s5365 5)
(s5366 2)
(s5368 4)
(s5369 5)
(s5370 5)
(s5371 2)
(s5373 4)
(s5374 5)
(s5375 5)
(s5376 2)
(s5378 4)
(s5379 5)
(s5380 5)
(s5381 2)
(s5383 4)
(s5384 5)
(s5385 5)
(s5386 2)
(s5388 4)
(s5389 5)
(s5390 5)
(s5391 2)
(s5393 4)
(s5394 5)
(s5395 5)
(s5396 2)
(s5398 4)
(s5399 5)
(s5400 5)
(s5401 2)
(s5403 4)
(s5404 5)
(s5405 5)
(s5406 2)
(s5408 4)
(s5409 5)
(s5410 5)
(s5411 2)
(s5413 4)
(s5414 5)
(s5415 5)
(s5416 2)
(s5418 4)
(s5419 5)
(s5420 5)
(s5421 2)
(s5423 4)
(s5424 5)
(s5425 5)
(s5426 2)
(s5428 4)
(s5429 5)
(s5430 5)
(s5431 2)
(s5433 4)
(s5434 5)
(s5435 5)
(s5436 2)
(s5438 4)
(s5439 5)
(s5440 5)
(s5441 2)
(s5443 4)
(s5444 5)
(s5445 5)
(s5446 2)
(s5448 4)
(s5449 5)
(s5450 5)
(s5451 2)
(s5453 4)
(s5454 5)
(s5455 5)
(s5456 2)
(s5458 4)
(s5459 5)
(s5460 5)
(s5461 2)
(s5463 4)
(s5464 5)
(s5465 5)
(s5466 2)
(s5468 4)
(s5469 5)
(s5470 5)
(s5471 2)
(s5473 4)
(s5474 5)
(s5475 5)
(s5476 2)
(s5478 4)
(s5479 5)
(s5480 5)
(s5481 2)
(s5483 4)
(s5484 5)
(s5485 5)
(s5486 2)
(s5488 4)
(s5489 5)
(s5490 5)
(s5491 2)
(s5493 4)
(s5494 5)
(s5495 5)
(s5496 2)
(s5498 4)
(s5499 5)
(s5500 5)
(s5501 2)
(s5503 4)
(s5504 5)
(s5505 5)
(s5506 2)
(s5508 4)
(s5509 5)
(s5510 5)
(s5511 2)
(s5513 4)
(s5514 5)
(s5515 5)
(s5516 2)
(s5518 4)
(s5519 5)
(s5520 5)
(s5521 2)
(s5523 4)
(s5524 5)
(s5525 5)
(s5526 2)
(s5528 4)
(s5529 5)
(s5530 5)
(s5531 2)
(s5533 4)
(s5534 5)
(s5535 5)
(s5536 2)
(s5538 4)
(s5539 5)
(s5540 5)
(s5541 2)
(s5543 4)
(s5544 5)
(s5545 5)
(s5546 2)
(s5548 4)
(s5549 5)
(s5550 5)
(s5551 2)
(s5553 4)
(s5554 5)
(s5555 5)
(s5556 2)
(s5558 4)
(s5559 5)
(s5560 5)
(s5561 2)
(s5563 4)
(s5564 5)
(s5565 5)
(s5566 2)
(s5568 4)
(s5569 5)
(s5570 5)
(s5571 2)
(s5573 4)
(s5574 5)
(s5575 5)
(s5576 2)
(s5578 4)
(s5579 5)
(s5580 5)
(s5581 2)
(s5583 4)
(s5584 5)
(s5585 5)
(s5586 2)
(s5588 4)
(s5589 5)
(s5590 5)
(s5591 2)
(s5593 4)
(s5594 5)
(s5595 5)
(s5596 2)
(s5598 4)
(s5599 5)
(s5600 5)
(s5601 2)
(s5603 4)
(s5604 5)
(s5605 5)
(s5606 2)
(s5608 4)
(s5609 5)
(s5610 5)
(s5611 2)
(s5613 4)
(s5614 5)
(s5615 5)
(s5616 2)
(s5618 4)
(s5619 5)
(s5620 5)
(s5621 2)
(s5623 4)
(s5624 5)
(s5625 5)
(s5626 2)
(s5628 4)
(s5629 5)
(s5630 5)
(s5631 2)
(s5633 4)
(s5634 5)
(s5635 5)
(s5636 2)
(s5638 4)
(s5639 5)
(s5640 5)
(s5641 2)
(s5643 4)
(s5644 5)
(s5645 5)
(s5646 2)
(s5648 4)
(s5649 5)
(s5650 5)
(s5651 2)
(s5653 4)
(s5654 5)
(s5655 5)
(s5656 2)
(s5658 4)
(s5659 5)
(s5660 5)
(s5661 2)
(s5663 4)
(s5664 5)
(s5665 5)
(s5666 2)
(s5668 4)
(s5669 5)
(s5670 5)
(s5671 2)
(s5673 4)
(s5674 5)
(s5675 5)
(s5676 2)
(s5678 4)
(s5679 5)
(s5680 5)
(s5681 2)
(s5683 4)
(s5684 5)
(s5685 5)
(s5686 2)
(s5688 4)
(s5689 5)
(s5690 5)
(s5691 2)
(s5693 4)
(s5694 5)
(s5695 5)
(s5696 2)
(s5698 4)
(s5699 5)
(s5700 5)
(s5701 2)
(s5703 4)
(s5704 5)
(s5705 5)
(s5706 2)
(s5708 4)
(s5709 5)
(s5710 5)
(s5711 2)
(s5713 4)
(s5714 5)
(s5715 5)
(s5716 2)
(s5718 4)
(s5719 5)
(s5720 5)
(s5721 2)
(s5723 4)
(s5724 5)
(s5725 5)
(s5726 2)
(s5728 4)
(s5729 5)
(s5730 5)
(s5731 2)
(s5733 4)
(s5734 5)
(s5735 5)
(s5736 2)
(s5738 4)
(s5739 5)
(s5740 5)
(s5741 2)
(s5743 4)
(s5744 5)
(s5745 5)
(s5746 2)
(s5748 4)
(s5749 5)
(s5750 5)
(s5751 2)
(s5753 4)
(s5754 5)
(s5755 5)
(s5756 2)
(s5758 4)
(s5759 5)
(s5760 5)
(s5761 2)
(s5763 4)
(s5764 5)
(s5765 5)
(s5766 2)
(s5768 4)
(s5769 5)
(s5770 5)
(s5771 2)
(s5773 4)
(s5774 5)
(s5775 5)
(s5776 2)
(s5778 4)
(s5779 5)
(s5780 5)
(s5781 2)
(s5783 4)
(s5784 5)
(s5785 5)
(s5786 2)
(s5788 4)
(s5789 5)
(s5790 5)
(s5791 2)
(s5793 4)
(s5794 5)
(s5795 5)
(s5796 2)
(s5798 4)
(s5799 5)
(s5800 5)
(s5801 2)
(s5803 4)
(s5804 5)
(s5805 5)
(s5806 2)
(s5808 4)
(s5809 5)
(s5810 5)
(s5811 2)
(s5813 4)
(s5814 5)
(s5815 5)
(s5816 2)
(s5818 4)
(s5819 5)
(s5820 5)
(s5821 2)
(s5823 4)
(s5824 5)
(s5825 5)
(s5826 2)
(s5828 4)
(s5829 5)
(s5830 5)
(s5831 2)
(s5833 4)
(s5834 5)
(s5835 5)
(s5836 2)
(s5838 4)
(s5839 5)
(s5840 5)
(s5841 2)
(s5843 4)
(s5844 5)
(s5845 5)
(s5846 2)
(s5848 4)
(s5849 5)
(s5850 5)
(s5851 2)
(s5853 4)
(s5854 5)
(s5855 5)
(s5856 2)
(s5858 4)
(s5859 5)
(s5860 5)
(s5861 2)
(s5863 4)
(s5864 5)
(s5865 5)
(s5866 2)
(s5868 4)
(s5869 5)
(s5870 5)
(s5871 2)
(s5873 4)
(s5874 5)
(s5875 5)
(s5876 2)
(s5878 4)
(s5879 5)
(s5880 5)
(s5881 2)
(s5883 4)
(s5884 5)
(s5885 5)
(s5886 2)
(s5888 4)
(s5889 5)
(s5890 5)
(s5891 2)
(s5893 4)
(s5894 5)
(s5895 5)
(s5896 2)
(s5898 4)
(s5899 5)
(s5900 5)
(s5901 2)
(s5903 4)
(s5904 5)
(s5905 5)
(s5906 2)
(s5908 4)
(s5909 5)
(s5910 5)
(s5911 2)
(s5913 4)
(s5914 5)
(s5915 5)
(s5916 2)
(s5918 4)
(s5919 5)
(s5920 5)
(s5921 2)
(s5923 4)
(s5924 5)
(s5925 5)
(s5926 2)
(s5928 4)
(s5929 5)
(s5930 5)
(s5931 2)
(s5933 4)
(s5934 5)
(s5935 5)
(s5936 2)
(s5938 4)
(s5939 5)
(s5940 5)
(s5941 2)
(s5943 4)
(s5944 5)
(s5945 5)
(s5946 2)
(s5948 4)
(s5949 5)
(s5950 5)
(s5951 2)
(s5953 4)
(s5954 5)
(s5955 5)
(s5956 2)
(s5958 4)
(s5959 5)
(s5960 5)
(s5961 2)
(s5963 4)
(s5964 5)
(s5965 5)
(s5966 2)
(s5968 4)
(s5969 5)
(s5970 5)
(s5971 2)
(s5973 4)
(s5974 5)
(s5975 5)
(s5976 2)
(s5978 4)
(s5979 5)
(s5980 5)
(s5981 2)
(s5983 4)
(s5984 5)
(s5985 5)
(s5986 2)
(s5988 4)
(s5989 5)
(s5990 5)
(s5991 2)
(s5993 4)
(s5994 5)
(s5995 5)
(s5996 2)
(s5998 4)
(s5999 5)
(s6000 5)
(s6001 2)
(s6003 4)
(s6004 5)
(s6005 5)
(s6006 2)
(s6008 4)
(s6009 5)
(s6010 5)
(s6011 2)
(s6013 4)
(s6014 5)
(s6015 5)
(s6016 2)
(s6018 4)
(s6019 5)
(s6020 5)
(s6021 2)
(s6023 4)
(s6024 5)
(s6025 5)
(s6026 2)
(s6028 4)
(s6029 5)
(s6030 5)
(s6031 2)
(s6033 4)
(s6034 5)
(s6035 5)
(s6036 2)
(s6038 4)
(s6039 5)
(s6040 5)
(s6041 2)
(s6043 4)
(s6044 5)
(s6045 5)
(s6046 2)
(s6048 4)
(s6049 5)
(s6050 5)
(s6051 2)
(s6053 4)
(s6054 5)
(s6055 5)
(s6056 2)
(s6058 4)
(s6059 5)
(s6060 5)
(s6061 2)
(s6063 4)
(s6064 5)
(s6065 5)
(s6066 2)
(s6068 4)
(s6069 5)
(s6070 5)
(s6071 2)
(s6073 4)
(s6074 5)
(s6075 5)
(s6076 2)
(s6078 4)
(s6079 5)
(s6080 5)
(s6081 2)
(s6083 4)
(s6084 5)
(s6085 5)
(s6086 2)
(s6088 4)
(s6089 5)
(s6090 5)
(s6091 2)
(s6093 4)
(s6094 5)
(s6095 5)
(s6096 2)
(s6098 4)
(s6099 5)
(s6100 5)
(s6101 2)
(s6103 4)
(s6104 5)
(s6105 5)
(s6106 2)
(s6108 4)
(s6109 5)
(s6110 5)
(s6111 2)
(s6113 4)
(s6114 5)
(s6115 5)
(s6116 2)
(s6118 4)
(s6119 5)
(s6120 5)
(s6121 2)
(s6123 4)
(s6124 5)
(s6125 5)
(s6126 2)
(s6128 4)
(s6129 5)
(s6130 5)
(s6131 2)
(s6133 4)
(s6134 5)
(s6135 5)
(s6136 2)
(s6138 4)
(s6139 5)
(s6140 5)
(s6141 2)
(s6143 4)
(s6144 5)
(s6145 5)
(s6146 2)
(s6148 4)
(s6149 5)
(s6150 5)
(s6151 2)
(s6153 4)
(s6154 5)
(s6155 5)
(s6156 2)
(s6158 4)
(s6159 5)
(s6160 5)
(s6161 2)
(s6163 4)
(s6164 5)
(s6165 5)
(s6166 2)
(s6168 4)
(s6169 5)
(s6170 5)
(s6171 2)
(s6173 4)
(s6174 5)
(s6175 5)
(s6176 2)
(s6178 4)
(s6179 5)
(s6180 5)
(s6181 2)
(s6183 4)
(s6184 5)
(s6185 5)
(s6186 2)
(s6188 4)
(s6189 5)
(s6190 5)
(s6191 2)
(s6193 4)
(s6194 5)
(s6195 5)
(s6196 2)
(s6198 4)
(s6199 5)
(s6200 5)
(s6201 2)
(s6203 4)
(s6204 5)
(s6205 5)
(s6206 2)
(s6208 4)
(s6209 5)
(s6210 5)
(s6211 2)
(s6213 4)
(s6214 5)
(s6215 5)
(s6216 2)
(s6218 4)
(s6219 5)
(s6220 5)
(s6221 2)
(s6223 4)
(s6224 5)
(s6225 5)
(s6226 2)
(s6228 4)
(s6229 5)
(s6230 5)
(s6231 2)
(s6233 4)
(s6234 5)
(s6235 5)
(s6236 2)
(s6238 4)
(s6239 5)
(s6240 5)
(s6241 2)
(s6243 4)
(s6244 5)
(s6245 5)
(s6246 2)
(s6248 4)
(s6249 5)
(s6250 5)
(s6251 2)
(s6253 4)
(s6254 5)
(s6255 5)
(s6256 2)
(s6258 4)
(s6259 5)
(s6260 5)
(s6261 2)
(s6263 4)
(s6264 5)
(s6265 5)
(s6266 2)
(s6268 4)
(s6269 5)
(s6270 5)
(s6271 2)
(s6273 4)
(s6274 5)
(s6275 5)
(s6276 2)
(s6278 4)
(s6279 5)
(s6280 5)
(s6281 2)
(s6283 4)
(s6284 5)
(s6285 5)
(s6286 2)
(s6288 4)
(s6289 5)
(s6290 5)
(s6291 2)
(s6293 4)
(s6294 5)
(s6295 5)
(s6296 2)
(s6298 4)
(s6299 5)
(s6300 5)
(s6301 2)
(s6303 4)
(s6304 5)
(s6305 5)
(s6306 2)
(s6308 4)
(s6309 5)
(s6310 5)
(s6311 2)
(s6313 4)
(s6314 5)
(s6315 5)
(s6316 2)
(s6318 4)
(s6319 5)
(s6320 5)
(s6321 2)
(s6323 4)
(s6324 5)
(s6325 5)
(s6326 2)
(s6328 4)
(s6329 5)
(s6330 5)
(s6331 2)
(s6333 4)
(s6334 5)
(s6335 5)
(s6336 2)
(s6338 4)
(s6339 5)
(s6340 5)
(s6341 2)
(s6343 4)
(s6344 5)
(s6345 5)
(s6346 2)
(s6348 4)
(s6349 5)
(s6350 5)
(s6351 2)
(s6353 4)
(s6354 5)
(s6355 5)
(s6356 2)
(s6358 4)
(s6359 5)
(s6360 5)
(s6361 2)
(s6363 4)
(s6364 5)
(s6365 5)
(s6366 2)
(s6368 4)
(s6369 5)
(s6370 5)
(s6371 2)
(s6373 4)
(s6374 5)
(s6375 5)
(s6376 2)
(s6378 4)
(s6379 5)
(s6380 5)
(s6381 2)
(s6383 4)
(s6384 5)
(s6385 5)
(s6386 2)
(s6388 4)
(s6389 5)
(s6390 5)
(s6391 2)
(s6393 4)
(s6394 5)
(s6395 5)
(s6396 2)
(s6398 4)
(s6399 5)
(s6400 5)
(s6401 2)
(s6403 4)
(s6404 5)
(s6405 5)
(s6406 2)
(s6408 4)
(s6409 5)
(s6410 5)
(s6411 2)
(s6413 4)
(s6414 5)
(s6415 5)
(s6416 2)
(s6418 4)
(s6419 5)
(s6420 5)
(s6421 2)
(s6423 4)
(s6424 5)
(s6425 5)
(s6426 2)
(s6428 4)
(s6429 5)
(s6430 5)
(s6431 2)
(s6433 4)
(s6434 5)
(s6435 5)
(s6436 2)
(s6438 4)
(s6439 5)
(s6440 5)
(s6441 2)
(s6443 4)
(s6444 5)
(s6445 5)
(s6446 2)
(s6448 4)
(s6449 5)
(s6450 5)
(s6451 2)
(s6453 4)
(s6454 5)
(s6455 5)
(s6456 2)
(s6458 4)
(s6459 5)
(s6460 5)
(s6461 2)
(s6463 4)
(s6464 5)
(s6465 5)
(s6466 2)
(s6468 4)
(s6469 5)
(s6470 5)
(s6471 2)
(s6473 4)
(s6474 5)
(s6475 5)
(s6476 2)
(s6478 4)
(s6479 5)
(s6480 5)
(s6481 2)
(s6483 4)
(s6484 5)
(s6485 5)
(s6486 2)
(s6488 4)
(s6489 5)
(s6490 5)
(s6491 2)
(s6493 4)
(s6494 5)
(s6495 5)
(s6496 2)
(s6498 4)
(s6499 5)
(s6500 5)
(s6501 2)
(s6503 4)
(s6504 5)
(s6505 5)
(s6506 2)
(s6508 4)
(s6509 5)
(s6510 5)
(s6511 2)
(s6513 4)
(s6514 5)
(s6515 5)
(s6516 2)
(s6518 4)
(s6519 5)
(s6520 5)
(s6521 2)
(s6523 4)
(s6524 5)
(s6525 5)
(s6526 2)
(s6528 4)
(s6529 5)
(s6530 5)
(s6531 2)
(s6533 4)
(s6534 5)
(s6535 5)
(s6536 2)
(s6538 4)
(s6539 5)
(s6540 5)
(s6541 2)
(s6543 4)
(s6544 5)
(s6545 5)
(s6546 2)
(s6548 4)
(s6549 5)
(s6550 5)
(s6551 2)
(s6553 4)
(s6554 5)
(s6555 5)
(s6556 2)
(s6558 4)
(s6559 5)
(s6560 5)
(s6561 2)
(s6563 4)
(s6564 5)
(s6565 5)
(s6566 2)
(s6568 4)
(s6569 5)
(s6570 5)
(s6571 2)
(s6573 4)
(s6574 5)
(s6575 5)
(s6576 2)
(s6578 4)
(s6579 5)
(s6580 5)
(s6581 2)
(s6583 4)
(s6584 5)
(s6585 5)
(s6586 2)
(s6588 4)
(s6589 5)
(s6590 5)
(s6591 2)
(s6593 4)
(s6594 5)
(s6595 5)
(s6596 2)
(s6598 4)
(s6599 5)
(s6600 5)
(s6601 2)
(s6603 4)
(s6604 5)
(s6605 5)
(s6606 2)
(s6608 4)
(s6609 5)
(s6610 5)
(s6611 2)
(s6613 4)
(s6614 5)
(s6615 5)
(s6616 2)
(s6618 4)
(s6619 5)
(s6620 5)
(s6621 2)
(s6623 4)
(s6624 5)
(s6625 5)
(s6626 2)
(s6628 4)
(s6629 5)
(s6630 5)
(s6631 2)
(s6633 4)
(s6634 5)
(s6635 5)
(s6636 2)
(s6638 4)
(s6639 5)
(s6640 5)
(s6641 2)
(s6643 4)
(s6644 5)
(s6645 5)
(s6646 2)
(s6648 4)
(s6649 5)
(s6650 5)
(s6651 2)
(s6653 4)
(s6654 5)
(s6655 5)
(s6656 2)
(s6658 4)
(s6659 5)
(s6660 5)
(s6661 2)
(s6663 4)
(s6664 5)
(s6665 5)
(s6666 2)
(s6668 4)
(s6669 5)
(s6670 5)
(s6671 2)
(s6673 4)
(s6674 5)
(s6675 5)
(s6676 2)
(s6678 4)
(s6679 5)
(s6680 5)
(s6681 2)
(s6683 4)
(s6684 5)
(s6685 5)
(s6686 2)
(s6688 4)
(s6689 5)
(s6690 5)
(s6691 2)
(s6693 4)
(s6694 5)
(s6695 5)
(s6696 2)
(s6698 4)
(s6699 5)
(s6700 5)
(s6701 2)
(s6703 4)
(s6704 5)
(s6705 5)
(s6706 2)
(s6708 4)
(s6709 5)
(s6710 5)
(s6711 2)
(s6713 4)
(s6714 5)
(s6715 5)
(s6716 2)
(s6718 4)
(s6719 5)
(s6720 5)
(s6721 2)
(s6723 4)
(s6724 5)
(s6725 5)
(s6726 2)
(s6728 4)
(s6729 5)
(s6730 5)
(s6731 2)
(s6733 4)
(s6734 5)
(s6735 5)
(s6736 2)
(s6738 4)
(s6739 5)
(s6740 5)
(s6741 2)
(s6743 4)
(s6744 5)
(s6745 5)
(s6746 2)
(s6748 4)
(s6749 5)
(s6750 5)
(s6751 2)
(s6753 4)
(s6754 5)
(s6755 5)
(s6756 2)
(s6758 4)
(s6759 5)
(s6760 5)
(s6761 2)
(s6763 4)
(s6764 5)
(s6765 5)
(s6766 2)
(s6768 4)
(s6769 5)
(s6770 5)
(s6771 2)
(s6773 4)
(s6774 5)
(s6775 5)
(s6776 2)
(s6778 4)
(s6779 5)
(s6780 5)
(s6781 2)
(s6783 4)
(s6784 5)
(s6785 5)
(s6786 2)
(s6788 4)
(s6789 5)
(s6790 5)
(s6791 2)
(s6793 4)
(s6794 5)
(s6795 5)
(s6796 2)
(s6798 4)
(s6799 5)
(s6800 5)
(s6801 2)
(s6803 4)
(s6804 5)
(s6805 5)
(s6806 2)
(s6808 4)
(s6809 5)
(s6810 5)
(s6811 2)
(s6813 4)
(s6814 5)
(s6815 5)
(s6816 2)
(s6818 4)
(s6819 5)
(s6820 5)
(s6821 2)
(s6823 4)
(s6824 5)
(s6825 5)
(s6826 2)
(s6828 4)
(s6829 5)
(s6830 5)
(s6831 2)
(s6833 4)
(s6834 5)
(s6835 5)
(s6836 2)
(s6838 4)
(s6839 5)
(s6840 5)
(s6841 2)
(s6843 4)
(s6844 5)
(s6845 5)
(s6846 2)
(s6848 4)
(s6849 5)
(s6850 5)
(s6851 2)
(s6853 4)
(s6854 5)
(s6855 5)
(s6856 2)
(s6858 4)
(s6859 5)
(s6860 5)
(s6861 2)
(s6863 4)
(s6864 5)
(s6865 5)
(s6866 2)
(s6868 4)
(s6869 5)
(s6870 5)
(s6871 2)
(s6873 4)
(s6874 5)
(s6875 5)
(s6876 2)
(s6878 4)
(s6879 5)
(s6880 5)
(s6881 2)
(s6883 4)
(s6884 5)
(s6885 5)
(s6886 2)
(s6888 4)
(s6889 5)
(s6890 5)
(s6891 2)
(s6893 4)
(s6894 5)
(s6895 5)
(s6896 2)
(s6898 4)
(s6899 5)
(s6900 5)
(s6901 2)
(s6903 4)
(s6904 5)
(s6905 5)
(s6906 2)
(s6908 4)
(s6909 5)
(s6910 5)
(s6911 2)
(s6913 4)
(s6914 5)
(s6915 5)
(s6916 2)
(s6918 4)
(s6919 5)
(s6920 5)
(s6921 2)
(s6923 4)
(s6924 5)
(s6925 5)
(s6926 2)
(s6928 4)
(s6929 5)
(s6930 5)
(s6931 2)
(s6933 4)
(s6934 5)
(s6935 5)
(s6936 2)
(s6938 4)
(s6939 5)
(s6940 5)
(s6941 2)
(s6943 4)
(s6944 5)
(s6945 5)
(s6946 2)
(s6948 4)
(s6949 5)
(s6950 5)
(s6951 2)
(s6953 4)
(s6954 5)
(s6955 5)
(s6956 2)
(s6958 4)
(s6959 5)
(s6960 5)
(s6961 2)
(s6963 4)
(s6964 5)
(s6965 5)
(s6966 2)
(s6968 4)
(s6969 5)
(s6970 5)
(s6971 2)
(s6973 4)
(s6974 5)
(s6975 5)
(s6976 2)
(s6978 4)
(s6979 5)
(s6980 5)
(s6981 2)
(s6983 4)
(s6984 5)
(s6985 5)
(s6986 2)
(s6988 4)
(s6989 5)
(s6990 5)
(s6991 2)
(s6993 4)
(s6994 5)
(s6995 5)
(s6996 2)
(s6998 4)
(s6999 5)
(s7000 5)
(s7001 2)
(s7003 4)
(s7004 5)
(s7005 5)
(s7006 2)
(s7008 4)
(s7009 5)
(s7010 5)
(s7011 2)
(s7013 4)
(s7014 5)
(s7015 5)
(s7016 2)
(s7018 4)
(s7019 5)
(s7020 5)
(s7021 2)
(s7023 4)
(s7024 5)
(s7025 5)
(s7026 2)
(s7028 4)
(s7029 5)
(s7030 5)
(s7031 2)
(s7033 4)
(s7034 5)
(s7035 5)
(s7036 2)
(s7038 4)
(s7039 5)
(s7040 5)
(s7041 2)
(s7043 4)
(s7044 5)
(s7045 5)
(s7046 2)
(s7048 4)
(s7049 5)
(s7050 5)
(s7051 2)
(s7053 4)
(s7054 5)
(s7055 5)
(s7056 2)
(s7058 4)
(s7059 5)
(s7060 5)
(s7061 2)
(s7063 4)
(s7064 5)
(s7065 5)
(s7066 2)
(s7068 4)
(s7069 5)
(s7070 5)
(s7071 2)
(s7073 4)
(s7074 5)
(s7075 5)
(s7076 2)
(s7078 4)
(s7079 5)
(s7080 5)
(s7081 2)
(s7083 4)
(s7084 5)
(s7085 5)
(s7086 2)
(s7088 4)
(s7089 5)
(s7090 5)
(s7091 2)
(s7093 4)
(s7094 5)
(s7095 5)
(s7096 2)
(s7098 4)
(s7099 5)
(s7100 5)
(s7101 2)
(s7103 4)
(s7104 5)
(s7105 5)
(s7106 2)
(s7108 4)
(s7109 5)
(s7110 5)
(s7111 2)
(s7113 4)
(s7114 5)
(s7115 5)
(s7116 2)
(s7118 4)
(s7119 5)
(s7120 5)
(s7121 2)
(s7123 4)
(s7124 5)
(s7125 5)
(s7126 2)
(s7128 4)
(s7129 5)
(s7130 5)
(s7131 2)
(s7133 4)
(s7134 5)
(s7135 5)
(s7136 2)
(s7138 4)
(s7139 5)
(s7140 5)
(s7141 2)
(s7143 4)
(s7144 5)
(s7145 5)
(s7146 2)
(s7148 4)
(s7149 5)
(s7150 5)
(s7151 2)
(s7153 4)
(s7154 5)
(s7155 5)
(s7156 2)
(s7158 4)
(s7159 5)
(s7160 5)
(s7161 2)
(s7163 4)
(s7164 5)
(s7165 5)
(s7166 2)
(s7168 4)
(s7169 5)
(s7170 5)
(s7171 2)
(s7173 4)
(s7174 5)
(s7175 5)
(s7176 2)
(s7178 4)
(s7179 5)
(s7180 5)
(s7181 2)
(s7183 4)
(s7184 5)
(s7185 5)
(s7186 2)
(s7188 4)
(s7189 5)
(s7190 5)
(s7191 2)
(s7193 4)
(s7194 5)
(s7195 5)
(s7196 2)
(s7198 4)
(s7199 5)
(s7200 5)
(s7201 2)
(s7203 4)
(s7204 5)
(s7205 5)
(s7206 2)
(s7208 4)
(s7209 5)
(s7210 5)
(s7211 2)
(s7213 4)
(s7214 5)
(s7215 5)
(s7216 2)
(s7218 4)
(s7219 5)
(s7220 5)
(s7221 2)
(s7223 4)
(s7224 5)
(s7225 5)
(s7226 2)
(s7228 4)
(s7229 5)
(s7230 5)
(s7231 2)
(s7233 4)
(s7234 5)
(s7235 5)
(s7236 2)
(s7238 4)
(s7239 5)
(s7240 5)
(s7241 2)
(s7243 4)
(s7244 5)
(s7245 5)
(s7246 2)
(s7248 4)
(s7249 5)
(s7250 5)
(s7251 2)
(s7253 4)
(s7254 5)
(s7255 5)
(s7256 2)
(s7258 4)
(s7259 5)
(s7260 5)
(s7261 2)
(s7263 4)
(s7264 5)
(s7265 5)
(s7266 2)
(s7268 4)
(s7269 5)
(s7270 5)
(s7271 2)
(s7273 4)
(s7274 5)
(s7275 5)
(s7276 2)
(s7278 4)
(s7279 5)
(s7280 5)
(s7281 2)
(s7283 4)
(s7284 5)
(s7285 5)
(s7286 2)
(s7288 4)
(s7289 5)
(s7290 5)
(s7291 2)
(s7293 4)
(s7294 5)
(s7295 5)
(s7296 2)
(s7298 4)
(s7299 5)
(s7300 5)
(s7301 2)
(s7303 4)
(s7304 5)
(s7305 5)
(s7306 2)
(s7308 4)
(s7309 5)
(s7310 5)
(s7311 2)
(s7313 4)
(s7314 5)
(s7315 5)
(s7316 2)
(s7318 4)
(s7319 5)
(s7320 5)
(s7321 2)
(s7323 4)
(s7324 5)
(s7325 5)
(s7326 2)
(s7328 4)
(s7329 5)
(s7330 5)
(s7331 2)
(s7333 4)
(s7334 5)
(s7335 5)
(s7336 2)
(s7338 4)
(s7339 5)
(s7340 5)
(s7341 2)
(s7343 4)
(s7344 5)
(s7345 5)
(s7346 2)
(s7348 4)
(s7349 5)
(s7350 5)
(s7351 2)
(s7353 4)
(s7354 5)
(s7355 5)
(s7356 2)
(s7358 4)
(s7359 5)
(s7360 5)
(s7361 2)
(s7363 4)
(s7364 5)
(s7365 5)
(s7366 2)
(s7368 4)
(s7369 5)
(s7370 5)
(s7371 2)
(s7373 4)
(s7374 5)
(s7375 5)
(s7376 2)
(s7378 4)
(s7379 5)
(s7380 5)
(s7381 2)
(s7383 4)
(s7384 5)
(s7385 5)
(s7386 2)
(s7388 4)
(s7389 5)
(s7390 5)
(s7391 2)
(s7393 4)
(s7394 5)
(s7395 5)
(s7396 2)
(s7398 4)
(s7399 5)
(s7400 5)
(s7401 2)
(s7403 4)
(s7404 5)
(s7405 5)
(s7406 2)
(s7408 4)
(s7409 5)
(s7410 5)
(s7411 2)
(s7413 4)
(s7414 5)
(s7415 5)
(s7416 2)
(s7418 4)
(s7419 5)
(s7420 5)
(s7421 2)
(s7423 4)
(s7424 5)
(s7425 5)
(s7426 2)
(s7428 4)
(s7429 5)
(s7430 5)
(s7431 2)
(s7433 4)
(s7434 5)
(s7435 5)
(s7436 2)
(s7438 4)
(s7439 5)
(s7440 5)
(s7441 2)
(s7443 4)
(s7444 5)
(s7445 5)
(s7446 2)
(s7448 4)
(s7449 5)
(s7450 5)
(s7451 2)
(s7453 4)
(s7454 5)
(s7455 5)
(s7456 2)
(s7458 4)
(s7459 5)
(s7460 5)
(s7461 2)
(s7463 4)
(s7464 5)
(s7465 5)
(s7466 2)
(s7468 4)
(s7469 5)
(s7470 5)
(s7471 2)
(s7473 4)
(s7474 5)
(s7475 5)
(s7476 2)
(s7478 4)
(s7479 5)
(s7480 5)
(s7481 2)
(s7483 4)
(s7484 5)
(s7485 5)
(s7486 2)
(s7488 4)
(s7489 5)
(s7490 5)
(s7491 2)
(s7493 4)
(s7494 5)
(s7495 5)
(s7496 2)
(s7498 4)
(s7499 5)
(s7500 5)
(s7501 2)
(s7503 4)
(s7504 5)
(s7505 5)
(s7506 2)
(s7508 4)
(s7509 5)
(s7510 5)
(s7511 2)
(s7513 4)
(s7514 5)
(s7515 5)
(s7516 2)
(s7518 4)
(s7519 5)
(s7520 5)
(s7521 2)
(s7523 4)
(s7524 5)
(s7525 5)
(s7526 2)
(s7528 4)
(s7529 5)
(s7530 5)
(s7531 2)
(s7533 4)
(s7534 5)
(s7535 5)
(s7536 2)
(s7538 4)
(s7539 5)
(s7540 5)
(s7541 2)
(s7543 4)
(s7544 5)
(s7545 5)
(s7546 2)
(s7548 4)
(s7549 5)
(s7550 5)
(s7551 2)
(s7553 4)
(s7554 5)
(s7555 5)
(s7556 2)
(s7558 4)
(s7559 5)
(s7560 5)
(s7561 2)
(s7563 4)
(s7564 5)
(s7565 5)
(s7566 2)
(s7568 4)
(s7569 5)
(s7570 5)
(s7571 2)
(s7573 4)
(s7574 5)
(s7575 5)
(s7576 2)
(s7578 4)
(s7579 5)
(s7580 5)
(s7581 2)
(s7583 4)
(s7584 5)
(s7585 5)
(s7586 2)
(s7588 4)
(s7589 5)
(s7590 5)
(s7591 2)
(s7593 4)
(s7594 5)
(s7595 5)
(s7596 2)
(s7598 4)
(s7599 5)
(s7600 5)
(s7601 2)
(s7603 4)
(s7604 5)
(s7605 5)
(s7606 2)
(s7608 4)
(s7609 5)
(s7610 5)
(s7611 2)
(s7613 4)
(s7614 5)
(s7615 5)
(s7616 2)
(s7618 4)
(s7619 5)
(s7620 5)
(s7621 2)
(s7623 4)
(s7624 5)
(s7625 5)
(s7626 2)
(s7628 4)
(s7629 5)
(s7630 5)
(s7631 2)
(s7633 4)
(s7634 5)
(s7635 5)
(s7636 2)
(s7638 4)
(s7639 5)
(s7640 5)
(s7641 2)
(s7643 4)
(s7644 5)
(s7645 5)
(s7646 2)
(s7648 4)
(s7649 5)
(s7650 5)
(s7651 2)
(s7653 4)
(s7654 5)
(s7655 5)
(s7656 2)
(s7658 4)
(s7659 5)
(s7660 5)
(s7661 2)
(s7663 4)
(s7664 5)
(s7665 5)
(s7666 2)
(s7668 4)
(s7669 5)
(s7670 5)
(s7671 2)
(s7673 4)
(s7674 5)
(s7675 5)
(s7676 2)
(s7678 4)
(s7679 5)
(s7680 5)
(s7681 2)
(s7683 4)
(s7684 5)
(s7685 5)
(s7686 2)
(s7688 4)
(s7689 5)
(s7690 5)
(s7691 2)
(s7693 4)
(s7694 5)
(s7695 5)
(s7696 2)
(s7698 4)
(s7699 5)
(s7700 5)
(s7701 2)
(s7703 4)
(s7704 5)
(s7705 5)
(s7706 2)
(s7708 4)
(s7709 5)
(s7710 5)
(s7711 2)
(s7713 4)
(s7714 5)
(s7715 5)
(s7716 2)
(s7718 4)
(s7719 5)
(s7720 5)
(s7721 2)
(s7723 4)
(s7724 5)
(s7725 5)
(s7726 2)
(s7728 4)
(s7729 5)
(s7730 5)
(s7731 2)
(s7733 4)
(s7734 5)
(s7735 5)
(s7736 2)
(s7738 4)
(s7739 5)
(s7740 5)
(s7741 2)
(s7743 4)
(s7744 5)
(s7745 5)
(s7746 2)
(s7748 4)
(s7749 5)
(s7750 5)
(s7751 2)
(s7753 4)
(s7754 5)
(s7755 5)
(s7756 2)
(s7758 4)
(s7759 5)
(s7760 5)
(s7761 2)
(s7763 4)
(s7764 5)
(s7765 5)
(s7766 2)
(s7768 4)
(s7769 5)
(s7770 5)
(s7771 2)
(s7773 4)
(s7774 5)
(s7775 5)
(s7776 2)
(s7778 4)
(s7779 5)
(s7780 5)
(s7781 2)
(s7783 4)
(s7784 5)
(s7785 5)
(s7786 2)
(s7788 4)
(s7789 5)
(s7790 5)
(s7791 2)
(s7793 4)
(s7794 5)
(s7795 5)
(s7796 2)
(s7798 4)
(s7799 5)
(s7800 5)
(s7801 2)
(s7803 4)
(s7804 5)
(s7805 5)
(s7806 2)
(s7808 4)
(s7809 5)
(s7810 5)
(s7811 2)
(s7813 4)
(s7814 5)
(s7815 5)
(s7816 2)
(s7818 4)
(s7819 5)
(s7820 5)
(s7821 2)
(s7823 4)
(s7824 5)
(s7825 5)
(s7826 2)
(s7828 4)
(s7829 5)
(s7830 5)
(s7831 2)
(s7833 4)
(s7834 5)
(s7835 5)
(s7836 2)
(s7838 4)
(s7839 5)
(s7840 5)
(s7841 2)
(s7843 4)
(s7844 5)
(s7845 5)
(s7846 2)
(s7848 4)
(s7849 5)
(s7850 5)
(s7851 2)
(s7853 4)
(s7854 5)
(s7855 5)
(s7856 2)
(s7858 4)
(s7859 5)
(s7860 5)
(s7861 2)
(s7863 4)
(s7864 5)
(s7865 5)
(s7866 2)
(s7868 4)
(s7869 5)
(s7870 5)
(s7871 2)
(s7873 4)
(s7874 5)
(s7875 5)
(s7876 2)
(s7878 4)
(s7879 5)
(s7880 5)
(s7881 2)
(s7883 4)
(s7884 5)
(s7885 5)
(s7886 2)
(s7888 4)
(s7889 5)
(s7890 5)
(s7891 2)
(s7893 4)
(s7894 5)
(s7895 5)
(s7896 2)
(s7898 4)
(s7899 5)
(s7900 5)
(s7901 2)
(s7903 4)
(s7904 5)
(s7905 5)
(s7906 2)
(s7908 4)
(s7909 5)
(s7910 5)
(s7911 2)
(s7913 4)
(s7914 5)
(s7915 5)
(s7916 2)
(s7918 4)
(s7919 5)
(s7920 5)
(s7921 2)
(s7923 4)
(s7924 5)
(s7925 5)
(s7926 2)
(s7928 4)
(s7929 5)
(s7930 5)
(s7931 2)
(s7933 4)
(s7934 5)
(s7935 5)
(s7936 2)
(s7938 4)
(s7939 5)
(s7940 5)
(s7941 2)
(s7943 4)
(s7944 5)
(s7945 5)
(s7946 2)
(s7948 4)
(s7949 5)
(s7950 5)
(s7951 2)
(s7953 4)
(s7954 5)
(s7955 5)
(s7956 2)
(s7958 4)
(s7959 5)
(s7960 5)
(s7961 2)
(s7963 4)
(s7964 5)
(s7965 5)
(s7966 2)
(s7968 4)
(s7969 5)
(s7970 5)
(s7971 2)
(s7973 4)
(s7974 5)
(s7975 5)
(s7976 2)
(s7978 4)
(s7979 5)
(s7980 5)
(s7981 2)
(s7983 4)
(s7984 5)
(s7985 5)
(s7986 2)
(s7988 4)
(s7989 5)
(s7990 5)
(s7991 2)
(s7993 4)
(s7994 5)
(s7995 5)
(s7996 2)
(s7998 4)
(s7999 5)
(s8000 5)
(s8001 2)
(s8003 4)
(s8004 5)
(s8005 5)
(s8006 2)
(s8008 4)
(s8009 5)
(s8010 5)
(s8011 2)
(s8013 4)
(s8014 5)
(s8015 5)
(s8016 2)
(s8018 4)
(s8019 5)
(s8020 5)
(s8021 2)
(s8023 4)
(s8024 5)
(s8025 5)
(s8026 2)
(s8028 4)
(s8029 5)
(s8030 5)
(s8031 2)
(s8033 4)
(s8034 5)
(s8035 5)
(s8036 2)
(s8038 4)
(s8039 5)
(s8040 5)
(s8041 2)
(s8043 4)
(s8044 5)
(s8045 5)
(s8046 2)
(s8048 4)
(s8049 5)
(s8050 5)
(s8051 2)
(s8053 4)
(s8054 5)
(s8055 5)
(s8056 2)
(s8058 4)
(s8059 5)
(s8060 5)
(s8061 2)
(s8063 4)
(s8064 5)
(s8065 5)
(s8066 2)
(s8068 4)
(s8069 5)
(s8070 5)
(s8071 2)
(s8073 4)
(s8074 5)
(s8075 5)
(s8076 2)
(s8078 4)
(s8079 5)
(s8080 5)
(s8081 2)
(s8083 4)
(s8084 5)
(s8085 5)
(s8086 2)
(s8088 4)
(s8089 5)
(s8090 5)
(s8091 2)
(s8093 4)
(s8094 5)
(s8095 5)
(s8096 2)
(s8098 4)
(s8099 5)
(s8100 5)
(s8101 2)
(s8103 4)
(s8104 5)
(s8105 5)
(s8106 2)
(s8108 4)
(s8109 5)
(s8110 5)
(s8111 2)
(s8113 4)
(s8114 5)
(s8115 5)
(s8116 2)
(s8118 4)
(s8119 5)
(s8120 5)
(s8121 2)
(s8123 4)
(s8124 5)
(s8125 5)
(s8126 2)
(s8128 4)
(s8129 5)
(s8130 5)
(s8131 2)
(s8133 4)
(s8134 5)
(s8135 5)
(s8136 2)
(s8138 4)
(s8139 5)
(s8140 5)
(s8141 2)
(s8143 4)
(s8144 5)
(s8145 5)
(s8146 2)
(s8148 4)
(s8149 5)
(s8150 5)
(s8151 2)
(s8153 4)
(s8154 5)
(s8155 5)
(s8156 2)
(s8158 4)
(s8159 5)
(s8160 5)
(s8161 2)
(s8163 4)
(s8164 5)
(s8165 5)
(s8166 2)
(s8168 4)
(s8169 5)
(s8170 5)
(s8171 2)
(s8173 4)
(s8174 5)
(s8175 5)
(s8176 2)
(s8178 4)
(s8179 5)
(s8180 5)
(s8181 2)
(s8183 4)
(s8184 5)
(s8185 5)
(s8186 2)
(s8188 4)
(s8189 5)
(s8190 5)
(s8191 2)
(s8193 4)
(s8194 5)
(s8195 5)
(s8196 2)
(s8198 4)
(s8199 5)
(s8200 5)
(s8201 2)
(s8203 4)
(s8204 5)
(s8205 5)
(s8206 2)
(s8208 4)
(s8209 5)
(s8210 5)
(s8211 2)
(s8213 4)
(s8214 5)
(s8215 5)
(s8216 2)
(s8218 4)
(s8219 5)
(s8220 5)
(s8221 2)
(s8223 4)
(s8224 5)
(s8225 5)
(s8226 2)
(s8228 4)
(s8229 5)
(s8230 5)
(s8231 2)
(s8233 4)
(s8234 5)
(s8235 5)
(s8236 2)
(s8238 4)
(s8239 5)
(s8240 5)
(s8241 2)
(s8243 4)
(s8244 5)
(s8245 5)
(s8246 2)
(s8248 4)
(s8249 5)
(s8250 5)
(s8251 2)
(s8253 4)
(s8254 5)
(s8255 5)
(s8256 2)
(s8258 4)
(s8259 5)
(s8260 5)
(s8261 2)
(s8263 4)
(s8264 5)
(s8265 5)
(s8266 2)
(s8268 4)
(s8269 5)
(s8270 5)
(s8271 2)
(s8273 4)
(s8274 5)
(s8275 5)
(s8276 2)
(s8278 4)
(s8279 5)
(s8280 5)
(s8281 2)
(s8283 4)
(s8284 5)
(s8285 5)
(s8286 2)
(s8288 4)
(s8289 5)
(s8290 5)
(s8291 2)
(s8293 4)
(s8294 5)
(s8295 5)
(s8296 2)
(s8298 4)
(s8299 5)
(s8300 5)
(s8301 2)
(s8303 4)
(s8304 5)
(s8305 5)
(s8306 2)
(s8308 4)
(s8309 5)
(s8310 5)
(s8311 2)
(s8313 4)
(s8314 5)
(s8315 5)
(s8316 2)
(s8318 4)
(s8319 5)
(s8320 5)
(s8321 2)
(s8323 4)
(s8324 5)
(s8325 5)
(s8326 2)
(s8328 4)
(s8329 5)
(s8330 5)
(s8331 2)
(s8333 4)
(s8334 5)
(s8335 5)
(s8336 2)
(s8338 4)
(s8339 5)
(s8340 5)
(s8341 2)
(s8343 4)
(s8344 5)
(s8345 5)
(s8346 2)
(s8348 4)
(s8349 5)
(s8350 5)
(s8351 2)
(s8353 4)
(s8354 5)
(s8355 5)
(s8356 2)
(s8358 4)
(s8359 5)
(s8360 5)
(s8361 2)
(s8363 4)
(s8364 5)
(s8365 5)
(s8366 2)
(s8368 4)
(s8369 5)
(s8370 5)
(s8371 2)
(s8373 4)
(s8374 5)
(s8375 5)
(s8376 2)
(s8378 4)
(s8379 5)
(s8380 5)
(s8381 2)
(s8383 4)
(s8384 5)
(s8385 5)
(s8386 2)
(s8388 4)
(s8389 5)
(s8390 5)
(s8391 2)
(s8393 4)
(s8394 5)
(s8395 5)
(s8396 2)
(s8398 4)
(s8399 5)
(s8400 5)
(s8401 2)
(s8403 4)
(s8404 5)
(s8405 5)
(s8406 2)
(s8408 4)
(s8409 5)
(s8410 5)
(s8411 2)
(s8413 4)
(s8414 5)
(s8415 5)
(s8416 2)
(s8418 4)
(s8419 5)
(s8420 5)
(s8421 2)
(s8423 4)
(s8424 5)
(s8425 5)
(s8426 2)
(s8428 4)
(s8429 5)
(s8430 5)
(s8431 2)
(s8433 4)
(s8434 5)
(s8435 5)
(s8436 2)
(s8438 4)
(s8439 5)
(s8440 5)
(s8441 2)
(s8443 4)
(s8444 5)
(s8445 5)
(s8446 2)
(s8448 4)
(s8449 5)
(s8450 5)
(s8451 2)
(s8453 4)
(s8454 5)
(s8455 5)
(s8456 2)
(s8458 4)
(s8459 5)
(s8460 5)
(s8461 2)
(s8463 4)
(s8464 5)
(s8465 5)
(s8466 2)
(s8468 4)
(s8469 5)
(s8470 5)
(s8471 2)
(s8473 4)
(s8474 5)
(s8475 5)
(s8476 2)
(s8478 4)
(s8479 5)
(s8480 5)
(s8481 2)
(s8483 4)
(s8484 5)
(s8485 5)
(s8486 2)
(s8488 4)
(s8489 5)
(s8490 5)
(s8491 2)
(s8493 4)
(s8494 5)
(s8495 5)
(s8496 2)
(s8498 4)
(s8499 5)
(s8500 5)
(s8501 2)
(s8503 4)
(s8504 5)
(s8505 5)
(s8506 2)
(s8508 4)
(s8509 5)
(s8510 5)
(s8511 2)
(s8513 4)
(s8514 5)
(s8515 5)
(s8516 2)
(s8518 4)
(s8519 5)
(s8520 5)
(s8521 2)
(s8523 4)
(s8524 5)
(s8525 5)
(s8526 2)
(s8528 4)
(s8529 5)
(s8530 5)
(s8531 2)
(s8533 4)
(s8534 5)
(s8535 5)
(s8536 2)
(s8538 4)
(s8539 5)
(s8540 5)
(s8541 2)
(s8543 4)
(s8544 5)
(s8545 5)
(s8546 2)
(s8548 4)
(s8549 5)
(s8550 5)
(s8551 2)
(s8553 4)
(s8554 5)
(s8555 5)
(s8556 2)
(s8558 4)
(s8559 5)
(s8560 5)
(s8561 2)
(s8563 4)
(s8564 5)
(s8565 5)
(s8566 2)
(s8568 4)
(s8569 5)
(s8570 5)
(s8571 2)
(s8573 4)
(s8574 5)
(s8575 5)
(s8576 2)
(s8578 4)
(s8579 5)
(s8580 5)
(s8581 2)
(s8583 4)
(s8584 5)
(s8585 5)
(s8586 2)
(s8588 4)
(s8589 5)
(s8590 5)
(s8591 2)
(s8593 4)
(s8594 5)
(s8595 5)
(s8596 2)
(s8598 4)
(s8599 5)
(s8600 5)
(s8601 2)
(s8603 4)
(s8604 5)
(s8605 5)
(s8606 2)
(s8608 4)
(s8609 5)
(s8610 5)
(s8611 2)
(s8613 4)
(s8614 5)
(s8615 5)
(s8616 2)
(s8618 4)
(s8619 5)
(s8620 5)
(s8621 2)
(s8623 4)
(s8624 5)
(s8625 5)
(s8626 2)
(s8628 4)
(s8629 5)
(s8630 5)
(s8631 2)
(s8633 4)
(s8634 5)
(s8635 5)
(s8636 2)
(s8638 4)
(s8639 5)
(s8640 5)
(s8641 2)
(s8643 4)
(s8644 5)
(s8645 5)
(s8646 2)
(s8648 4)
(s8649 5)
(s8650 5)
(s8651 2)
(s8653 4)
(s8654 5)
(s8655 5)
(s8656 2)
(s8658 4)
(s8659 5)
(s8660 5)
(s8661 2)
(s8663 4)
(s8664 5)
(s8665 5)
(s8666 2)
(s8668 4)
(s8669 5)
(s8670 5)
(s8671 2)
(s8673 4)
(s8674 5)
(s8675 5)
(s8676 2)
(s8678 4)
(s8679 5)
(s8680 5)
(s8681 2)
(s8683 4)
(s8684 5)
(s8685 5)
(s8686 2)
(s8688 4)
(s8689 5)
(s8690 5)
(s8691 2)
(s8693 4)
(s8694 5)
(s8695 5)
(s8696 2)
(s8698 4)
(s8699 5)
(s8700 5)
(s8701 2)
(s8703 4)
(s8704 5)
(s8705 5)
(s8706 2)
(s8708 4)
(s8709 5)
(s8710 5)
(s8711 2)
(s8713 4)
(s8714 5)
(s8715 5)
(s8716 2)
(s8718 4)
(s8719 5)
(s8720 5)
(s8721 2)
(s8723 4)
(s8724 5)
(s8725 5)
(s8726 2)
(s8728 4)
(s8729 5)
(s8730 5)
(s8731 2)
(s8733 4)
(s8734 5)
(s8735 5)
(s8736 2)
(s8738 4)
(s8739 5)
(s8740 5)
(s8741 2)
(s8743 4)
(s8744 5)
(s8745 5)
(s8746 2)
(s8748 4)
(s8749 5)
(s8750 5)
(s8751 2)
(s8753 4)
(s8754 5)
(s8755 5)
(s8756 2)
(s8758 4)
(s8759 5)
(s8760 5)
(s8761 2)
(s8763 4)
(s8764 5)
(s8765 5)
(s8766 2)
(s8768 4)
(s8769 5)
(s8770 5)
(s8771 2)
(s8773 4)
(s8774 5)
(s8775 5)
(s8776 2)
(s8778 4)
(s8779 5)
(s8780 5)
(s8781 2)
(s8783 4)
(s8784 5)
(s8785 5)
(s8786 2)
(s8788 4)
(s8789 5)
(s8790 5)
(s8791 2)
(s8793 4)
(s8794 5)
(s8795 5)
(s8796 2)
(s8798 4)
(s8799 5)
(s8800 5)
(s8801 2)
(s8803 4)
(s8804 5)
(s8805 5)
(s8806 2)
(s8808 4)
(s8809 5)
(s8810 5)
(s8811 2)
(s8813 4)
(s8814 5)
(s8815 5)
(s8816 2)
(s8818 4)
(s8819 5)
(s8820 5)
(s8821 2)
(s8823 4)
(s8824 5)
(s8825 5)
(s8826 2)
(s8828 4)
(s8829 5)
(s8830 5)
(s8831 2)
(s8833 4)
(s8834 5)
(s8835 5)
(s8836 2)
(s8838 4)
(s8839 5)
(s8840 5)
(s8841 2)
(s8843 4)
(s8844 5)
(s8845 5)
(s8846 2)
(s8848 4)
(s8849 5)
(s8850 5)
(s8851 2)
(s8853 4)
(s8854 5)
(s8855 5)
(s8856 2)
(s8858 4)
(s8859 5)
(s8860 5)
(s8861 2)
(s8863 4)
(s8864 5)
(s8865 5)
(s8866 2)
(s8868 4)
(s8869 5)
(s8870 5)
(s8871 2)
(s8873 4)
(s8874 5)
(s8875 5)
(s8876 2)
(s8878 4)
(s8879 5)
(s8880 5)
(s8881 2)
(s8883 4)
(s8884 5)
(s8885 5)
(s8886 2)
(s8888 4)
(s8889 5)
(s8890 5)
(s8891 2)
(s8893 4)
(s8894 5)
(s8895 5)
(s8896 2)
(s8898 4)
(s8899 5)
(s8900 5)
(s8901 2)
(s8903 4)
(s8904 5)
(s8905 5)
(s8906 2)
(s8908 4)
(s8909 5)
(s8910 5)
(s8911 2)
(s8913 4)
(s8914 5)
(s8915 5)
(s8916 2)
(s8918 4)
(s8919 5)
(s8920 5)
(s8921 2)
(s8923 4)
(s8924 5)
(s8925 5)
(s8926 2)
(s8928 4)
(s8929 5)
(s8930 5)
(s8931 2)
(s8933 4)
(s8934 5)
(s8935 5)
(s8936 2)
(s8938 4)
(s8939 5)
(s8940 5)
(s8941 2)
(s8943 4)
(s8944 5)
(s8945 5)
(s8946 2)
(s8948 4)
(s8949 5)
(s8950 5)
(s8951 2)
(s8953 4)
(s8954 5)
(s8955 5)
(s8956 2)
(s8958 4)
(s8959 5)
(s8960 5)
(s8961 2)
(s8963 4)
(s8964 5)
(s8965 5)
(s8966 2)
(s8968 4)
(s8969 5)
(s8970 5)
(s8971 2)
(s8973 4)
(s8974 5)
(s8975 5)
(s8976 2)
(s8978 4)
(s8979 5)
(s8980 5)
(s8981 2)
(s8983 4)
(s8984 5)
(s8985 5)
(s8986 2)
(s8988 4)
(s8989 5)
(s8990 5)
(s8991 2)
(s8993 4)
(s8994 5)
(s8995 5)
(s8996 2)
(s8998 4)
(s8999 5)
(s9000 5)
(s9001 2)
(s9003 4)
(s9004 5)
(s9005 5)
(s9006 2)
(s9008 4)
(s9009 5)
(s9010 5)
(s9011 2)
(s9013 4)
(s9014 5)
(s9015 5)
(s9016 2)
(s9018 4)
(s9019 5)
(s9020 5)
(s9021 2)
(s9023 4)
(s9024 5)
(s9025 5)
(s9026 2)
(s9028 4)
(s9029 5)
(s9030 5)
(s9031 2)
(s9033 4)
(s9034 5)
(s9035 5)
(s9036 2)
(s9038 4)
(s9039 5)
(s9040 5)
(s9041 2)
(s9043 4)
(s9044 5)
(s9045 5)
(s9046 2)
(s9048 4)
(s9049 5)
(s9050 5)
(s9051 2)
(s9053 4)
(s9054 5)
(s9055 5)
(s9056 2)
(s9058 4)
(s9059 5)
(s9060 5)
(s9061 2)
(s9063 4)
(s9064 5)
(s9065 5)
(s9066 2)
(s9068 4)
(s9069 5)
(s9070 5)
(s9071 2)
(s9073 4)
(s9074 5)
(s9075 5)
(s9076 2)
(s9078 4)
(s9079 5)
(s9080 5)
(s9081 2)
(s9083 4)
(s9084 5)
(s9085 5)
(s9086 2)
(s9088 4)
(s9089 5)
(s9090 5)
(s9091 2)
(s9093 4)
(s9094 5)
(s9095 5)
(s9096 2)
(s9098 4)
(s9099 5)
(s9100 5)
(s9101 2)
(s9103 4)
(s9104 5)
(s9105 5)
(s9106 2)
(s9108 4)
(s9109 5)
(s9110 5)
(s9111 2)
(s9113 4)
(s9114 5)
(s9115 5)
(s9116 2)
(s9118 4)
(s9119 5)
(s9120 5)
(s9121 2)
(s9123 4)
(s9124 5)
(s9125 5)
(s9126 2)
(s9128 4)
(s9129 5)
(s9130 5)
(s9131 2)
(s9133 4)
(s9134 5)
(s9135 5)
(s9136 2)
(s9138 4)
(s9139 5)
(s9140 5)
(s9141 2)
(s9143 4)
(s9144 5)
(s9145 5)
(s9146 2)
(s9148 4)
(s9149 5)
(s9150 5)
(s9151 2)
(s9153 4)
(s9154 5)
(s9155 5)
(s9156 2)
(s9158 4)
(s9159 5)
(s9160 5)
(s9161 2)
(s9163 4)
(s9164 5)
(s9165 5)
(s9166 2)
(s9168 4)
(s9169 5)
(s9170 5)
(s9171 2)
(s9173 4)
(s9174 5)
(s9175 5)
(s9176 2)
(s9178 4)
(s9179 5)
(s9180 5)
(s9181 2)
(s9183 4)
(s9184 5)
(s9185 5)
(s9186 2)
(s9188 4)
(s9189 5)
(s9190 5)
(s9191 2)
(s9193 4)
(s9194 5)
(s9195 5)
(s9196 2)
(s9198 4)
(s9199 5)
(s9200 5)
(s9201 2)
(s9203 4)
(s9204 5)
(s9205 5)
(s9206 2)
(s9208 4)
(s9209 5)
(s9210 5)
(s9211 2)
(s9213 4)
(s9214 5)
(s9215 5)
(s9216 2)
(s9218 4)
(s9219 5)
(s9220 5)
(s9221 2)
(s9223 4)
(s9224 5)
(s9225 5)
(s9226 2)
(s9228 4)
(s9229 5)
(s9230 5)
(s9231 2)
(s9233 4)
(s9234 5)
(s9235 5)
(s9236 2)
(s9238 4)
(s9239 5)
(s9240 5)
(s9241 2)
(s9243 4)
(s9244 5)
(s9245 5)
(s9246 2)
(s9248 4)
(s9249 5)
(s9250 5)
(s9251 2)
(s9253 4)
(s9254 5)
(s9255 5)
(s9256 2)
(s9258 4)
(s9259 5)
(s9260 5)
(s9261 2)
(s9263 4)
(s9264 5)
(s9265 5)
(s9266 2)
(s9268 4)
(s9269 5)
(s9270 5)
(s9271 2)
(s9273 4)
(s9274 5)
(s9275 5)
(s9276 2)
(s9278 4)
(s9279 5)
(s9280 5)
(s9281 2)
(s9283 4)
(s9284 5)
(s9285 5)
(s9286 2)
(s9288 4)
(s9289 5)
(s9290 5)
(s9291 2)
(s9293 4)
(s9294 5)
(s9295 5)
(s9296 2)
(s9298 4)
(s9299 5)
(s9300 5)
(s9301 2)
(s9303 4)
(s9304 5)
(s9305 5)
(s9306 2)
(s9308 4)
(s9309 5)
(s9310 5)
(s9311 2)
(s9313 4)
(s9314 5)
(s9315 5)
(s9316 2)
(s9318 4)
(s9319 5)
(s9320 5)
(s9321 2)
(s9323 4)
(s9324 5)
(s9325 5)
(s9326 2)
(s9328 4)
(s9329 5)
(s9330 5)
(s9331 2)
(s9333 4)
(s9334 5)
(s9335 5)
(s9336 2)
(s9338 4)
(s9339 5)
(s9340 5)
(s9341 2)
(s9343 4)
(s9344 5)
(s9345 5)
(s9346 2)
(s9348 4)
(s9349 5)
(s9350 5)
(s9351 2)
(s9353 4)
(s9354 5)
(s9355 5)
(s9356 2)
(s9358 4)
(s9359 5)
(s9360 5)
(s9361 2)
(s9363 4)
(s9364 5)
(s9365 5)
(s9366 2)
(s9368 4)
(s9369 5)
(s9370 5)
(s9371 2)
(s9373 4)
(s9374 5)
(s9375 5)
(s9376 2)
(s9378 4)
(s9379 5)
(s9380 5)
(s9381 2)
(s9383 4)
(s9384 5)
(s9385 5)
(s9386 2)
(s9388 4)
(s9389 5)
(s9390 5)
(s9391 2)
(s9393 4)
(s9394 5)
(s9395 5)
(s9396 2)
(s9398 4)
(s9399 5)
(s9400 5)
(s9401 2)
(s9403 4)
(s9404 5)
(s9405 5)
(s9406 2)
(s9408 4)
(s9409 5)
(s9410 5)
(s9411 2)
(s9413 4)
(s9414 5)
(s9415 5)
(s9416 2)
(s9418 4)
(s9419 5)
(s9420 5)
(s9421 2)
(s9423 4)
(s9424 5)
(s9425 5)
(s9426 2)
(s9428 4)
(s9429 5)
(s9430 5)
(s9431 2)
(s9433 4)
(s9434 5)
(s9435 5)
(s9436 2)
(s9438 4)
(s9439 5)
(s9440 5)
(s9441 2)
(s9443 4)
(s9444 5)
(s9445 5)
(s9446 2)
(s9448 4)
(s9449 5)
(s9450 5)
(s9451 2)
(s9453 4)
(s9454 5)
(s9455 5)
(s9456 2)
(s9458 4)
(s9459 5)
(s9460 5)
(s9461 2)
(s9463 4)
(s9464 5)
(s9465 5)
(s9466 2)
(s9468 4)
(s9469 5)
(s9470 5)
(s9471 2)
(s9473 4)
(s9474 5)
(s9475 5)
(s9476 2)
(s9478 4)
(s9479 5)
(s9480 5)
(s9481 2)
(s9483 4)
(s9484 5)
(s9485 5)
(s9486 2)
(s9488 4)
(s9489 5)
(s9490 5)
(s9491 2)
(s9493 4)
(s9494 5)
(s9495 5)
(s9496 2)
(s9498 4)
(s9499 5)
(s9500 5)
(s9501 2)
(s9503 4)
(s9504 5)
(s9505 5)
(s9506 2)
(s9508 4)
(s9509 5)
(s9510 5)
(s9511 2)
(s9513 4)
(s9514 5)
(s9515 5)
(s9516 2)
(s9518 4)
(s9519 5)
(s9520 5)
(s9521 2)
(s9523 4)
(s9524 5)
(s9525 5)
(s9526 2)
(s9528 4)
(s9529 5)
(s9530 5)
(s9531 2)
(s9533 4)
(s9534 5)
(s9535 5)
(s9536 2)
(s9538 4)
(s9539 5)
(s9540 5)
(s9541 2)
(s9543 4)
(s9544 5)
(s9545 5)
(s9546 2)
(s9548 4)
(s9549 5)
(s9550 5)
(s9551 2)
(s9553 4)
(s9554 5)
(s9555 5)
(s9556 2)
(s9558 4)
(s9559 5)
(s9560 5)
(s9561 2)
(s9563 4)
(s9564 5)
(s9565 5)
(s9566 2)
(s9568 4)
(s9569 5)
(s9570 5)
(s9571 2)
(s9573 4)
(s9574 5)
(s9575 5)
(s9576 2)
(s9578 4)
(s9579 5)
(s9580 5)
(s9581 2)
(s9583 4)
(s9584 5)
(s9585 5)
(s9586 2)
(s9588 4)
(s9589 5)
(s9590 5)
(s9591 2)
(s9593 4)
(s9594 5)
(s9595 5)
(s9596 2)
(s9598 4)
(s9599 5)
(s9600 5)
(s9601 2)
(s9603 4)
(s9604 5)
(s9605 5)
(s9606 2)
(s9608 4)
(s9609 5)
(s9610 5)
(s9611 2)
(s9613 4)
(s9614 5)
(s9615 5)
(s9616 2)
(s9618 4)
(s9619 5)
(s9620 5)
(s9621 2)
(s9623 4)
(s9624 5)
(s9625 5)
(s9626 2)
(s9628 4)
(s9629 5)
(s9630 5)
(s9631 2)
(s9633 4)
(s9634 5)
(s9635 5)
(s9636 2)
(s9638 4)
(s9639 5)
(s9640 5)
(s9641 2)
(s9643 4)
(s9644 5)
(s9645 5)
(s9646 2)
(s9648 4)
(s9649 5)
(s9650 5)
(s9651 2)
(s9653 4)
(s9654 5)
(s9655 5)
(s9656 2)
(s9658 4)
(s9659 5)
(s9660 5)
(s9661 2)
(s9663 4)
(s9664 5)
(s9665 5)
(s9666 2)
(s9668 4)
(s9669 5)
(s9670 5)
(s9671 2)
(s9673 4)
(s9674 5)
(s9675 5)
(s9676 2)
(s9678 4)
(s9679 5)
(s9680 5)
(s9681 2)
(s9683 4)
(s9684 5)
(s9685 5)
(s9686 2)
(s9688 4)
(s9689 5)
(s9690 5)
(s9691 2)
(s9693 4)
(s9694 5)
(s9695 5)
(s9696 2)
(s9698 4)
(s9699 5)
(s9700 5)
(s9701 2)
(s9703 4)
(s9704 5)
(s9705 5)
(s9706 2)
(s9708 4)
(s9709 5)
(s9710 5)
(s9711 2)
(s9713 4)
(s9714 5)
(s9715 5)
(s9716 2)
(s9718 4)
(s9719 5)
(s9720 5)
(s9721 2)
(s9723 4)
(s9724 5)
(s9725 5)
(s9726 2)
(s9728 4)
(s9729 5)
(s9730 5)
(s9731 2)
(s9733 4)
(s9734 5)
(s9735 5)
(s9736 2)
(s9738 4)
(s9739 5)
(s9740 5)
(s9741 timeout
2)
(s9743 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20142 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 55961ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56039ms
Finished structural reductions in LTL mode , in 1 iterations and 56968 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:06:52] [INFO ] Flatten gal took : 267 ms
[2024-06-01 06:06:52] [INFO ] Flatten gal took : 277 ms
[2024-06-01 06:06:53] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 2370 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:06:55] [INFO ] Invariant cache hit.
[2024-06-01 06:06:55] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20125 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20128 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56677ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56752ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 59135 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:07:52] [INFO ] Flatten gal took : 272 ms
[2024-06-01 06:07:53] [INFO ] Flatten gal took : 281 ms
[2024-06-01 06:07:53] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 857 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:07:54] [INFO ] Invariant cache hit.
[2024-06-01 06:07:54] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20137 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20151 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56762ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56840ms
Finished structural reductions in LTL mode , in 1 iterations and 57710 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:08:51] [INFO ] Flatten gal took : 277 ms
[2024-06-01 06:08:52] [INFO ] Flatten gal took : 281 ms
[2024-06-01 06:08:52] [INFO ] Input system was already deterministic with 16001 transitions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 886 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-06-01 06:08:53] [INFO ] Invariant cache hit.
[2024-06-01 06:08:53] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20128 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20122 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 55814ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 55897ms
Finished structural reductions in LTL mode , in 1 iterations and 56796 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-06-01 06:09:49] [INFO ] Flatten gal took : 280 ms
[2024-06-01 06:09:50] [INFO ] Flatten gal took : 285 ms
[2024-06-01 06:09:50] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-06-01 06:09:50] [INFO ] Flatten gal took : 273 ms
[2024-06-01 06:09:51] [INFO ] Flatten gal took : 286 ms
[2024-06-01 06:09:51] [INFO ] Export to MCC of 10 properties in file /home/mcc/execution/CTLFireability.sr.xml took 3 ms.
[2024-06-01 06:09:51] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 10000 places, 16001 transitions and 46000 arcs took 58 ms.
Total runtime 907964 ms.
There are residual formulas that ITS could not solve within timeout
Usage: pnml2lts-sym [-gvqh] [--order=
[--mu-opt] [--saturation=
[--sat-granularity=
[--guidance=
[--action=
[--trace=
[--mu=
[--ctl=
[--save-levels=STRING] [--pg-solve] [--attr=
[--saturating-attractor] [--write-strategy=
[--check-strategy] [--interactive-play] [--player]
[--pg-write=
[--edge-label=
[--mucalc=
[--allow-undefined-edges] [--allow-undefined-values]
[-p|--por=
[--weak=[valmari] (default: uses stronger left-commutativity)]
[--leap] [-r|--regroup=<(T,)+>] [--sloan-w1=
[--cw-max-cols=
[--mh-timeout=
[--graph-metrics] [--regroup-exit] [--regroup-time]
[-g|--pins-guards] [--vset=
[--ldd32-cache=
[--cache-ratio=
[--min-free-nodes=
[--fdd-reorder=
[--vset-cache-diff=
[--next-union] [--peak-nodes] [--maxsum=
[--block-size=
[--debug=
[--timeout=INT] [--version] [-h|--help] [--usage]
[OPTIONS]
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-01
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-02
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-03
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-05
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-06
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-08
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2024-09
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2023-12
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2023-13
Could not compute solution for formula : JoinFreeModules-PT-2000-CTLFireability-2023-15
BK_STOP 1717222191557
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202405141337.jar
+ VERSION=202405141337
+ echo 'Running Version 202405141337'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
mcc2024
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-01
ctl formula formula --ctl=/tmp/893/ctl_0_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-02
ctl formula formula --ctl=/tmp/893/ctl_1_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-03
ctl formula formula --ctl=/tmp/893/ctl_2_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-05
ctl formula formula --ctl=/tmp/893/ctl_3_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-06
ctl formula formula --ctl=/tmp/893/ctl_4_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-08
ctl formula formula --ctl=/tmp/893/ctl_5_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2024-09
ctl formula formula --ctl=/tmp/893/ctl_6_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2023-12
ctl formula formula --ctl=/tmp/893/ctl_7_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2023-13
ctl formula formula --ctl=/tmp/893/ctl_8_
ctl formula name JoinFreeModules-PT-2000-CTLFireability-2023-15
ctl formula formula --ctl=/tmp/893/ctl_9_
pnml2lts-sym, ** error **: unknown vector set implementation lddmc
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="JoinFreeModules-PT-2000"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="ltsminxred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool ltsminxred"
echo " Input is JoinFreeModules-PT-2000, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r504-tall-171649612000082"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/JoinFreeModules-PT-2000.tgz
mv JoinFreeModules-PT-2000 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

