About the Execution of LTSMin+red for BART-PT-050
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 16194.876 | 3600000.00 | 10973299.00 | 6769.70 | FF??FFTF?FFFFFFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
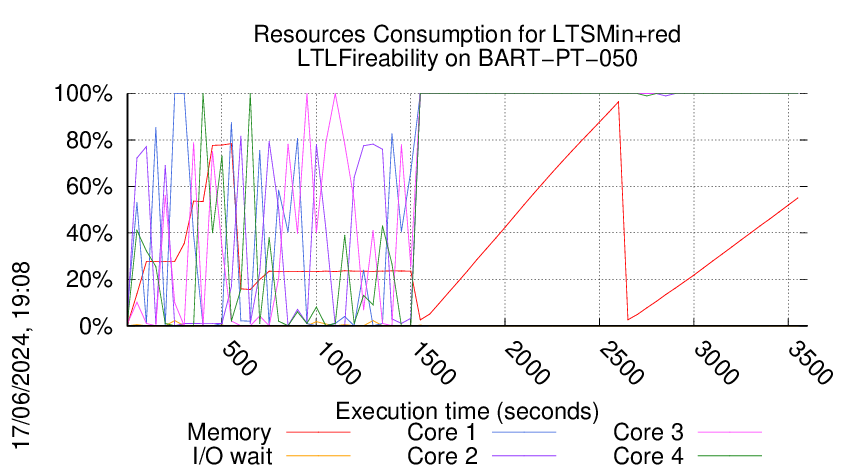
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r468-smll-171620167800492.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool ltsminxred
Input is BART-PT-050, examination is LTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r468-smll-171620167800492
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 97M
-rw-r--r-- 1 mcc users 2.6M Apr 13 01:31 CTLCardinality.txt
-rw-r--r-- 1 mcc users 9.1M Apr 13 01:31 CTLCardinality.xml
-rw-r--r-- 1 mcc users 3.5M Apr 12 22:08 CTLFireability.txt
-rw-r--r-- 1 mcc users 12M Apr 12 22:08 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 18 16:42 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.4K May 18 16:42 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 1.2M Apr 22 14:29 LTLCardinality.txt
-rw-r--r-- 1 mcc users 3.0M Apr 22 14:29 LTLCardinality.xml
-rw-r--r-- 1 mcc users 1.9M Apr 22 14:29 LTLFireability.txt
-rw-r--r-- 1 mcc users 4.7M Apr 22 14:29 LTLFireability.xml
-rw-r--r-- 1 mcc users 6.3M Apr 13 08:06 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 22M Apr 13 08:05 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 4.8M Apr 13 03:56 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 15M Apr 13 03:56 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 141K Apr 22 14:29 UpperBounds.txt
-rw-r--r-- 1 mcc users 283K Apr 22 14:29 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 May 18 16:42 equiv_col
-rw-r--r-- 1 mcc users 4 May 18 16:42 instance
-rw-r--r-- 1 mcc users 6 May 18 16:42 iscolored
-rw-r--r-- 1 mcc users 12M May 18 16:42 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME BART-PT-050-LTLFireability-00
FORMULA_NAME BART-PT-050-LTLFireability-01
FORMULA_NAME BART-PT-050-LTLFireability-02
FORMULA_NAME BART-PT-050-LTLFireability-03
FORMULA_NAME BART-PT-050-LTLFireability-04
FORMULA_NAME BART-PT-050-LTLFireability-05
FORMULA_NAME BART-PT-050-LTLFireability-06
FORMULA_NAME BART-PT-050-LTLFireability-07
FORMULA_NAME BART-PT-050-LTLFireability-08
FORMULA_NAME BART-PT-050-LTLFireability-09
FORMULA_NAME BART-PT-050-LTLFireability-10
FORMULA_NAME BART-PT-050-LTLFireability-11
FORMULA_NAME BART-PT-050-LTLFireability-12
FORMULA_NAME BART-PT-050-LTLFireability-13
FORMULA_NAME BART-PT-050-LTLFireability-14
FORMULA_NAME BART-PT-050-LTLFireability-15
=== Now, execution of the tool begins
BK_START 1717239847758
Invoking MCC driver with
BK_TOOL=ltsminxred
BK_EXAMINATION=LTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=BART-PT-050
BK_MEMORY_CONFINEMENT=16384
Applying reductions before tool ltsmin
Invoking reducer
Running Version 202405141337
[2024-06-01 11:04:10] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, LTLFireability, -timeout, 360, -rebuildPNML]
[2024-06-01 11:04:10] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-06-01 11:04:11] [INFO ] Load time of PNML (sax parser for PT used): 1124 ms
[2024-06-01 11:04:11] [INFO ] Transformed 6810 places.
[2024-06-01 11:04:11] [INFO ] Transformed 10100 transitions.
[2024-06-01 11:04:11] [INFO ] Found NUPN structural information;
[2024-06-01 11:04:11] [INFO ] Parsed PT model containing 6810 places and 10100 transitions and 81000 arcs in 1555 ms.
Parsed 16 properties from file /home/mcc/execution/LTLFireability.xml in 295 ms.
Working with output stream class java.io.PrintStream
Initial state reduction rules removed 4 formulas.
Reduce places removed 210 places and 0 transitions.
FORMULA BART-PT-050-LTLFireability-01 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BART-PT-050-LTLFireability-05 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BART-PT-050-LTLFireability-06 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA BART-PT-050-LTLFireability-13 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 6554 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Applied a total of 0 rules in 104 ms. Remains 6600 /6600 variables (removed 0) and now considering 10100/10100 (removed 0) transitions.
// Phase 1: matrix 10100 rows 6600 cols
[2024-06-01 11:04:13] [INFO ] Computed 50 invariants in 131 ms
[2024-06-01 11:04:16] [INFO ] Implicit Places using invariants in 3230 ms returned []
Implicit Place search using SMT only with invariants took 3277 ms to find 0 implicit places.
Running 8300 sub problems to find dead transitions.
[2024-06-01 11:04:16] [INFO ] Invariant cache hit.
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30476 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 8300/8300 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 8300 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30231 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 0/8300 constraints, Known Traps: 0/0 constraints]
After SMT, in 68978ms problems are : Problem set: 0 solved, 8300 unsolved
Search for dead transitions found 0 dead transitions in 69212ms
Finished structural reductions in LTL mode , in 1 iterations and 72702 ms. Remains : 6600/6600 places, 10100/10100 transitions.
Support contains 6554 out of 6600 places after structural reductions.
[2024-06-01 11:05:27] [INFO ] Flatten gal took : 617 ms
[2024-06-01 11:05:28] [INFO ] Flatten gal took : 385 ms
[2024-06-01 11:05:29] [INFO ] Input system was already deterministic with 10100 transitions.
Reduction of identical properties reduced properties to check from 22 to 18
RANDOM walk for 40000 steps (8 resets) in 3213 ms. (12 steps per ms) remains 2/18 properties
BEST_FIRST walk for 40004 steps (8 resets) in 194 ms. (205 steps per ms) remains 2/2 properties
BEST_FIRST walk for 40004 steps (8 resets) in 117 ms. (339 steps per ms) remains 2/2 properties
[2024-06-01 11:05:31] [INFO ] Invariant cache hit.
At refinement iteration 0 (INCLUDED_ONLY) 0/4 variables, 4/4 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (INCLUDED_ONLY) 0/4 variables, 0/4 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (OVERLAPS) 524/528 variables, 4/8 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/528 variables, 524/532 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/528 variables, 0/532 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (OVERLAPS) 808/1336 variables, 528/1060 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/1336 variables, 0/1060 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 7 (OVERLAPS) 0/1336 variables, 0/1060 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Real declared 1336/16700 variables, and 1060 constraints, problems are : Problem set: 0 solved, 2 unsolved in 1282 ms.
Refiners :[Domain max(s): 528/6600 constraints, Positive P Invariants (semi-flows): 4/50 constraints, State Equation: 528/6600 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/4 variables, 4/4 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (INCLUDED_ONLY) 0/4 variables, 0/4 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (OVERLAPS) 524/528 variables, 4/8 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/528 variables, 524/532 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/528 variables, 0/532 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (OVERLAPS) 808/1336 variables, 528/1060 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/1336 variables, 2/1062 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/1336 variables, 0/1062 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 8 (OVERLAPS) 0/1336 variables, 0/1062 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Int declared 1336/16700 variables, and 1062 constraints, problems are : Problem set: 0 solved, 2 unsolved in 1179 ms.
Refiners :[Domain max(s): 528/6600 constraints, Positive P Invariants (semi-flows): 4/50 constraints, State Equation: 528/6600 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
After SMT, in 2560ms problems are : Problem set: 0 solved, 2 unsolved
Finished Parikh walk after 26 steps, including 0 resets, run visited all 2 properties in 3 ms. (steps per millisecond=8 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Parikh walk visited 2 properties in 20 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!((G((X(p0)||(p0 U p1))) U (X(p0) U G(p0))))'
Support contains 6500 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Applied a total of 0 rules in 61 ms. Remains 6600 /6600 variables (removed 0) and now considering 10100/10100 (removed 0) transitions.
[2024-06-01 11:05:34] [INFO ] Invariant cache hit.
[2024-06-01 11:05:36] [INFO ] Implicit Places using invariants in 2120 ms returned []
Implicit Place search using SMT only with invariants took 2125 ms to find 0 implicit places.
Running 8300 sub problems to find dead transitions.
[2024-06-01 11:05:36] [INFO ] Invariant cache hit.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30228 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 8300/8300 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 8300 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30232 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 0/8300 constraints, Known Traps: 0/0 constraints]
After SMT, in 69010ms problems are : Problem set: 0 solved, 8300 unsolved
Search for dead transitions found 0 dead transitions in 69103ms
Finished structural reductions in LTL mode , in 1 iterations and 71316 ms. Remains : 6600/6600 places, 10100/10100 transitions.
Stuttering acceptance computed with spot in 442 ms :[(NOT p0), (NOT p0), (AND (NOT p0) (NOT p1)), true]
Running random walk in product with property : BART-PT-050-LTLFireability-00
Product exploration explored 100000 steps with 0 reset in 4830 ms.
Entered a terminal (fully accepting) state of product in 1 steps with 0 reset in 5 ms.
FORMULA BART-PT-050-LTLFireability-00 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-00 finished in 76795 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G((F(p0)||X(F((X(X(p1))&&F(p2)))))))'
Support contains 3450 out of 6600 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Drop transitions (Trivial Post-Agglo cleanup.) removed 150 transitions
Trivial Post-agglo rules discarded 150 transitions
Performed 150 trivial Post agglomeration. Transition count delta: 150
Iterating post reduction 0 with 150 rules applied. Total rules applied 150 place count 6600 transition count 9950
Reduce places removed 150 places and 0 transitions.
Performed 1300 Post agglomeration using F-continuation condition.Transition count delta: 1300
Iterating post reduction 1 with 1450 rules applied. Total rules applied 1600 place count 6450 transition count 8650
Reduce places removed 1300 places and 0 transitions.
Iterating post reduction 2 with 1300 rules applied. Total rules applied 2900 place count 5150 transition count 8650
Discarding 50 places :
Symmetric choice reduction at 3 with 50 rule applications. Total rules 2950 place count 5100 transition count 8600
Iterating global reduction 3 with 50 rules applied. Total rules applied 3000 place count 5100 transition count 8600
Performed 200 Post agglomeration using F-continuation condition.Transition count delta: 200
Deduced a syphon composed of 200 places in 3 ms
Reduce places removed 200 places and 0 transitions.
Iterating global reduction 3 with 400 rules applied. Total rules applied 3400 place count 4900 transition count 8400
Applied a total of 3400 rules in 1845 ms. Remains 4900 /6600 variables (removed 1700) and now considering 8400/10100 (removed 1700) transitions.
// Phase 1: matrix 8400 rows 4900 cols
[2024-06-01 11:06:53] [INFO ] Computed 50 invariants in 54 ms
[2024-06-01 11:06:54] [INFO ] Implicit Places using invariants in 1150 ms returned []
[2024-06-01 11:06:54] [INFO ] Invariant cache hit.
[2024-06-01 11:06:59] [INFO ] Implicit Places using invariants and state equation in 5331 ms returned []
Implicit Place search using SMT with State Equation took 6488 ms to find 0 implicit places.
[2024-06-01 11:07:00] [INFO ] Redundant transitions in 1364 ms returned []
Running 6600 sub problems to find dead transitions.
[2024-06-01 11:07:00] [INFO ] Invariant cache hit.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30177 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 6600/6600 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 6600 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30195 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 0/6600 constraints, Known Traps: 0/0 constraints]
After SMT, in 65854ms problems are : Problem set: 0 solved, 6600 unsolved
Search for dead transitions found 0 dead transitions in 65981ms
Starting structural reductions in SI_LTL mode, iteration 1 : 4900/6600 places, 8400/10100 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 75729 ms. Remains : 4900/6600 places, 8400/10100 transitions.
Stuttering acceptance computed with spot in 325 ms :[(OR (AND (NOT p0) (NOT p2)) (AND (NOT p0) (NOT p1))), (OR (AND (NOT p0) (NOT p1)) (AND (NOT p0) (NOT p2))), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p2) (NOT p1))]
Running random walk in product with property : BART-PT-050-LTLFireability-02
Product exploration explored 100000 steps with 1163 reset in 5199 ms.
Product exploration explored 100000 steps with 1211 reset in 4845 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND p0 (NOT p2) (NOT p1)), (X (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (X (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 5 factoid took 266 ms. Reduced automaton from 6 states, 10 edges and 3 AP (stutter insensitive) to 3 states, 6 edges and 3 AP (stutter insensitive).
Stuttering acceptance computed with spot in 166 ms :[(OR (AND (NOT p0) (NOT p2)) (AND (NOT p0) (NOT p1))), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p1))]
RANDOM walk for 40000 steps (8 resets) in 2183 ms. (18 steps per ms) remains 2/6 properties
BEST_FIRST walk for 40004 steps (8 resets) in 10466 ms. (3 steps per ms) remains 2/2 properties
BEST_FIRST walk for 40004 steps (8 resets) in 9188 ms. (4 steps per ms) remains 2/2 properties
[2024-06-01 11:08:41] [INFO ] Invariant cache hit.
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/3450 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (OVERLAPS) 1450/4900 variables, 50/50 constraints. Problems are: Problem set: 0 solved, 2 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 4900/13300 variables, and 50 constraints, problems are : Problem set: 0 solved, 2 unsolved in 5013 ms.
Refiners :[Positive P Invariants (semi-flows): 50/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 2/0 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/3450 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
Problem apf2 is UNSAT
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 4900/13300 variables, and 50 constraints, problems are : Problem set: 1 solved, 1 unsolved in 5012 ms.
Refiners :[Positive P Invariants (semi-flows): 50/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 2/0 constraints, Known Traps: 0/0 constraints]
After SMT, in 16230ms problems are : Problem set: 1 solved, 1 unsolved
Skipping Parikh replay, no witness traces provided.
Support contains 3450 out of 4900 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 4900/4900 places, 8400/8400 transitions.
Drop transitions (Redundant composition of simpler transitions.) removed 1750 transitions
Redundant transition composition rules discarded 1750 transitions
Iterating global reduction 0 with 1750 rules applied. Total rules applied 1750 place count 4900 transition count 6650
Applied a total of 1750 rules in 471 ms. Remains 4900 /4900 variables (removed 0) and now considering 6650/8400 (removed 1750) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 473 ms. Remains : 4900/4900 places, 6650/8400 transitions.
RANDOM walk for 40000 steps (8 resets) in 818 ms. (48 steps per ms) remains 1/1 properties
BEST_FIRST walk for 40004 steps (8 resets) in 9472 ms. (4 steps per ms) remains 1/1 properties
Interrupted probabilistic random walk after 967642 steps, run timeout after 6001 ms. (steps per millisecond=161 ) properties seen :0 out of 1
Probabilistic random walk after 967642 steps, saw 889864 distinct states, run finished after 6010 ms. (steps per millisecond=161 ) properties seen :0
// Phase 1: matrix 6650 rows 4900 cols
[2024-06-01 11:09:07] [INFO ] Computed 50 invariants in 22 ms
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/3450 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 1450/4900 variables, 50/50 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/4900 variables, 0/50 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 6650/11550 variables, 4900/4950 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/11550 variables, 0/4950 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (OVERLAPS) 0/11550 variables, 0/4950 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Real declared 11550/11550 variables, and 4950 constraints, problems are : Problem set: 0 solved, 1 unsolved in 13400 ms.
Refiners :[Positive P Invariants (semi-flows): 50/50 constraints, State Equation: 4900/4900 constraints, PredecessorRefiner: 1/0 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 1 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/3450 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
Problem apf3 is UNSAT
After SMT solving in domain Int declared 4900/11550 variables, and 50 constraints, problems are : Problem set: 1 solved, 0 unsolved in 2426 ms.
Refiners :[Positive P Invariants (semi-flows): 50/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 1/0 constraints, Known Traps: 0/0 constraints]
After SMT, in 19038ms problems are : Problem set: 1 solved, 0 unsolved
Skipping Parikh replay, no witness traces provided.
Found 2 invariant AP formulas.
Knowledge obtained : [(AND p0 (NOT p2) (NOT p1)), (X (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (X (NOT p2))), (G (OR p0 p2 p1)), (G (OR p0 p1))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0)), (F (NOT p0)), (F p1), (F p2), (F (NOT (OR p0 p2)))]
Knowledge based reduction with 7 factoid took 521 ms. Reduced automaton from 3 states, 6 edges and 3 AP (stutter insensitive) to 2 states, 3 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 103 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Stuttering acceptance computed with spot in 117 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Support contains 3450 out of 4900 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 4900/4900 places, 8400/8400 transitions.
Applied a total of 0 rules in 197 ms. Remains 4900 /4900 variables (removed 0) and now considering 8400/8400 (removed 0) transitions.
// Phase 1: matrix 8400 rows 4900 cols
[2024-06-01 11:09:27] [INFO ] Computed 50 invariants in 77 ms
[2024-06-01 11:09:28] [INFO ] Implicit Places using invariants in 1247 ms returned []
[2024-06-01 11:09:28] [INFO ] Invariant cache hit.
[2024-06-01 11:09:33] [INFO ] Implicit Places using invariants and state equation in 5182 ms returned []
Implicit Place search using SMT with State Equation took 6431 ms to find 0 implicit places.
[2024-06-01 11:09:34] [INFO ] Redundant transitions in 793 ms returned []
Running 6600 sub problems to find dead transitions.
[2024-06-01 11:09:34] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30184 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 6600/6600 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 6600 unsolved
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1582 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1670 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1758 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1846 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1934 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2022 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 1)
(s2090 1)
(s2091 1)
(s2092 1)
(s2093 1)
(s2094 1)
(s2095 1)
(s2096 1)
(s2097 1)
(s2098 1)
(s2099 1)
(s2100 1)
(s2101 1)
(s2102 1)
(s2103 1)
(s2104 1)
(s2105 1)
(s2106 1)
(s2107 1)
(s2108 1)
(s2109 1)
(s2110 1)
(s2111 1)
(s2112 1)
(s2113 1)
(s2114 1)
(s2115 1)
(s2116 1)
(s2117 1)
(s2118 1)
(s2119 1)
(s2120 1)
(s2121 1)
(s2122 1)
(s2123 1)
(s2124 1)
(s2125 1)
(s2126 1)
(s2127 1)
(s2128 1)
(s2129 1)
(s2130 1)
(s2131 1)
(s2132 1)
(s2133 1)
(s2134 1)
(s2135 1)
(s2136 1)
(s2137 1)
(s2138 1)
(s2139 1)
(s2140 1)
(s2141 1)
(s2142 1)
(s2143 1)
(s2144 1)
(s2145 1)
(s2146 1)
(s2147 1)
(s2148 1)
(s2149 1)
(s2150 1)
(s2151 1)
(s2152 1)
(s2153 1)
(s2154 1)
(s2155 1)
(s2156 1)
(s2157 1)
(s2158 1)
(s2159 1)
(s2160 1)
(s2161 1)
(s2162 1)
(s2163 1)
(s2164 1)
(s2165 1)
(s2166 1)
(s2167 1)
(s2168 1)
(s2169 1)
(s2170 1)
(s2171 1)
(s2172 1)
(s2173 1)
(s2174 1)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2198 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2286 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2374 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2462 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2550 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 1)
(s2577 1)
(s2578 1)
(s2579 1)
(s2580 1)
(s2581 1)
(s2582 1)
(s2583 1)
(s2584 1)
(s2585 1)
(s2586 1)
(s2587 1)
(s2588 1)
(s2589 1)
(s2590 1)
(s2591 1)
(s2592 1)
(s2593 1)
(s2594 1)
(s2595 1)
(s2596 1)
(s2597 1)
(s2598 1)
(s2599 1)
(s2600 1)
(s2601 1)
(s2602 1)
(s2603 1)
(s2604 1)
(s2605 1)
(s2606 1)
(s2607 1)
(s2608 1)
(s2609 1)
(s2610 1)
(s2611 1)
(s2612 1)
(s2613 1)
(s2614 1)
(s2615 1)
(s2616 1)
(s2617 1)
(s2618 1)
(s2619 1)
(s2620 1)
(s2621 1)
(s2622 1)
(s2623 1)
(s2624 1)
(s2625 1)
(s2626 1)
(s2627 1)
(s2628 1)
(s2629 1)
(s2630 1)
(s2631 1)
(s2632 1)
(s2633 1)
(s2634 1)
(s2635 1)
(s2636 1)
(s2637 1)
(s2638 1)
(s2639 1)
(s2640 1)
(s2641 1)
(s2642 1)
(s2643 1)
(s2644 1)
(s2645 1)
(s2646 1)
(s2647 1)
(s2648 1)
(s2649 1)
(s2650 1)
(s2651 1)
(s2652 1)
(s2653 1)
(s2654 1)
(s2655 1)
(s2656 1)
(s2657 1)
(s2658 1)
(s2659 1)
(s2660 1)
(s2661 1)
(s2662 1)
(s2663 1)
(s2664 1)
(s2665 1)
(s2666 1)
(s2667 1)
(s2668 1)
(s2669 1)
(s2670 1)
(s2671 1)
(s2672 1)
(s2673 1)
(s2674 1)
(s2675 1)
(s2676 1)
(s2677 1)
(s2678 1)
(s2679 1)
(s2680 1)
(s2681 1)
(s2682 1)
(s2683 1)
(s2684 1)
(s2685 1)
(s2686 1)
(s2687 1)
(s2688 1)
(s2689 1)
(s2690 1)
(s2691 1)
(s2692 1)
(s2693 1)
(s2694 1)
(s2695 1)
(s2696 1)
(s2697 1)
(s2698 1)
(s2699 1)
(s2700 1)
(s2701 1)
(s2702 1)
(s2703 1)
(s2704 1)
(s2705 1)
(s2706 1)
(s2707 1)
(s2708 1)
(s2709 1)
(s2710 1)
(s2711 1)
(s2712 1)
(s2713 1)
(s2714 1)
(s2715 1)
(s2716 1)
(s2717 1)
(s2718 1)
(s2719 1)
(s2720 1)
(s2721 1)
(s2722 1)
(s2723 1)
(s2724 1)
(s2725 1)
(s2726 1)
(s2727 1)
(s2728 1)
(s2729 1)
(s2730 1)
(s2731 1)
(s2732 1)
(s2733 1)
(s2734 1)
(s2735 1)
(s2736 1)
(s2737 1)
(s2738 1)
(s2739 1)
(s2740 1)
(s2741 1)
(s2742 1)
(s2743 1)
(s2744 1)
(s2745 1)
(s2746 1)
(s2747 1)
(s2748 1)
(s2749 1)
(s2750 1)
(s2751 1)
(s2752 1)
(s2753 1)
(s2754 1)
(s2755 1)
(s2756 1)
(s2757 1)
(s2758 1)
(s2759 1)
(s2760 1)
(s2761 1)
(s2762 1)
(s2763 1)
(s2764 1)
(s2765 1)
(s2766 1)
(s2767 1)
(s2768 1)
(s2769 1)
(s2770 1)
(s2771 1)
(s2772 1)
(s2773 1)
(s2774 1)
(s2775 1)
(s2776 1)
(s2777 1)
(s2778 1)
(s2779 1)
(s2780 1)
(s2781 1)
(s2782 1)
(s2783 1)
(s2784 1)
(s2785 1)
(s2786 1)
(s2787 1)
(s2788 1)
(s2789 1)
(s2790 1)
(s2791 1)
(s2792 1)
(s2793 1)
(s2794 1)
(s2795 1)
(s2796 1)
(s2797 1)
(s2798 1)
(s2799 1)
(s2800 1)
(s2801 1)
(s2802 1)
(s2803 1)
(s2804 1)
(s2805 1)
(s2806 1)
(s2807 1)
(s2808 1)
(s2809 1)
(s2810 1)
(s2811 1)
(s2812 1)
(s2813 1)
(s2814 1)
(s2815 1)
(s2816 1)
(s2817 1)
(s2818 1)
(s2819 1)
(s2820 1)
(s2821 1)
(s2822 1)
(s2823 1)
(s2824 1)
(s2825 1)
(s2826 1)
(s2827 1)
(s2828 1)
(s2829 1)
(s2830 1)
(s2831 1)
(s2832 1)
(s2833 1)
(s2834 1)
(s2835 1)
(s2836 1)
(s2837 1)
(s2838 1)
(s2839 1)
(s2840 1)
(s2841 1)
(s2842 1)
(s2843 1)
(s2844 1)
(s2845 1)
(s2846 1)
(s2847 1)
(s2848 1)
(s2849 1)
(s2850 1)
(s2851 1)
(s2852 1)
(s2853 1)
(s2854 1)
(s2855 1)
(s2856 1)
(s2857 1)
(s2858 1)
(s2859 1)
(s2860 1)
(s2861 1)
(s2862 1)
(s2863 1)
(s2864 1)
(s2865 1)
(s2866 1)
(s2867 1)
(s2868 1)
(s2869 1)
(s2870 1)
(s2871 1)
(s2872 1)
(s2873 1)
(s2874 1)
(s2875 1)
(s2876 1)
(s2877 1)
(s2878 1)
(s2879 1)
(s2880 1)
(s2881 1)
(s2882 1)
(s2883 1)
(s2884 1)
(s2885 1)
(s2886 1)
(s2887 1)
(s2888 1)
(s2889 1)
(s2890 1)
(s2891 1)
(s2892 1)
(s2893 1)
(s2894 1)
(s2895 1)
(s2896 1)
(s2897 1)
(s2898 1)
(s2899 1)
(s2900 1)
(s2901 1)
(s2902 1)
(s2903 1)
(s2904 1)
(s2905 1)
(s2906 1)
(s2907 1)
(s2908 1)
(s2909 1)
(s2910 1)
(s2911 1)
(s2912 1)
(s2913 1)
(s2914 1)
(s2915 1)
(s2916 1)
(s2917 1)
(s2918 1)
(s2919 1)
(s2920 1)
(s2921 1)
(s2922 1)
(s2923 1)
(s2924 1)
(s2925 1)
(s2926 1)
(s2927 1)
(s2928 1)
(s2929 1)
(s2930 1)
(s2931 1)
(s2932 1)
(s2933 1)
(s2934 1)
(s2935 1)
(s2936 1)
(s2937 1)
(s2938 1)
(s2939 1)
(s2940 1)
(s2941 1)
(s2942 1)
(s2943 1)
(s2944 1)
(s2945 1)
(s2946 1)
(s2947 1)
(s2948 1)
(s2949 1)
(s2950 1)
(s2951 1)
(s2952 1)
(s2953 1)
(s2954 1)
(s2955 1)
(s2956 1)
(s2957 1)
(s2958 1)
(s2959 1)
(s2960 1)
(s2961 1)
(s2962 1)
(s2963 1)
(s2964 1)
(s2965 1)
(s2966 1)
(s2967 1)
(s2968 1)
(s2969 1)
(s2970 1)
(s2971 1)
(s2972 1)
(s2973 1)
(s2974 1)
(s2975 1)
(s2976 1)
(s2977 1)
(s2978 1)
(s2979 1)
(s2980 1)
(s2981 1)
(s2982 1)
(s2983 1)
(s2984 1)
(s2985 1)
(s2986 1)
(s2987 1)
(s2988 1)
(s2989 1)
(s2990 1)
(s2991 1)
(s2992 1)
(s2993 1)
(s2994 1)
(s2995 1)
(s2996 1)
(s2997 1)
(s2998 1)
(s2999 1)
(s3000 1)
(s3001 1)
(s3002 1)
(s3003 1)
(s3004 1)
(s3005 1)
(s3006 1)
(s3007 1)
(s3008 1)
(s3009 1)
(s3010 1)
(s3011 1)
(s3012 1)
(s3013 1)
(s3014 1)
(s3015 1)
(s3016 1)
(s3017 1)
(s3018 1)
(s3019 1)
(s3020 1)
(s3021 1)
(s3022 1)
(s3023 1)
(s3024 1)
(s3025 1)
(s3026 1)
(s3027 1)
(s3028 1)
(s3029 1)
(s3030 1)
(s3031 1)
(s3032 1)
(s3033 1)
(s3034 1)
(s3035 1)
(s3036 1)
(s3037 1)
(s3038 1)
(s3039 1)
(s3040 1)
(s3041 1)
(s3042 1)
(s3043 1)
(s3044 1)
(s3045 1)
(s3046 1)
(s3047 1)
(s3048 1)
(s3049 1)
(s3050 1)
(s3051 1)
(s3052 1)
(s3053 1)
(s3054 1)
(s3055 1)
(s3056 1)
(s3057 1)
(s3058 1)
(s3059 1)
(s3060 1)
(s3061 1)
(s3062 1)
(s3063 1)
(s3064 1)
(s3065 1)
(s3066 1)
(s3067 1)
(s3068 1)
(s3069 1)
(s3070 1)
(s3071 1)
(s3072 1)
(s3073 1)
(s3074 1)
(s3075 1)
(s3076 1)
(s3077 1)
(s3078 1)
(s3079 1)
(s3080 1)
(s3081 1)
(s3082 1)
(s3083 1)
(s3084 1)
(s3085 1)
(s3086 1)
(s3087 1)
(s3088 1)
(s3089 1)
(s3090 1)
(s3091 1)
(s3092 1)
(s3093 1)
(s3094 1)
(s3095 1)
(s3096 1)
(s3097 1)
(s3098 1)
(s3099 1)
(s3100 1)
(s3101 1)
(s3102 1)
(s3103 1)
(s3104 1)
(s3105 1)
(s3106 1)
(s3107 1)
(s3108 1)
(s3109 1)
(s3110 1)
(s3111 1)
(s3112 1)
(s3113 1)
(s3114 1)
(s3115 1)
(s3116 1)
(s3117 1)
(s3118 1)
(s3119 1)
(s3120 1)
(s3121 1)
(s3122 1)
(s3123 1)
(s3124 1)
(s3125 1)
(s3126 1)
(s3127 1)
(s3128 1)
(s3129 1)
(s3130 1)
(s3131 1)
(s3132 1)
(s3133 1)
(s3134 1)
(s3135 1)
(s3136 1)
(s3137 1)
(s3138 1)
(s3139 1)
(s3140 1)
(s3141 1)
(s3142 1)
(s3143 1)
(s3144 1)
(s3145 1)
(s3146 1)
(s3147 1)
(s3148 1)
(s3149 1)
(s3150 1)
(s3151 1)
(s3152 1)
(s3153 1)
(s3154 1)
(s3155 1)
(s3156 1)
(s3157 1)
(s3158 1)
(s3159 1)
(s3160 1)
(s3161 1)
(s3162 1)
(s3163 1)
(s3164 1)
(s3165 1)
(s3166 1)
(s3167 1)
(s3168 1)
(s3169 1)
(s3170 1)
(s3171 1)
(s3172 1)
(s3173 1)
(s3174 1)
(s3175 1)
(s3176 1)
(s3177 1)
(s3178 1)
(s3179 1)
(s3180 1)
(s3181 1)
(s3182 1)
(s3183 1)
(s3184 1)
(s3185 1)
(s3186 1)
(s3187 1)
(s3188 1)
(s3189 1)
(s3190 1)
(s3191 1)
(s3192 1)
(s3193 1)
(s3194 1)
(s3195 1)
(s3196 1)
(s3197 1)
(s3198 1)
(s3199 1)
(s3200 1)
(s3201 1)
(s3202 1)
(s3203 1)
(s3204 1)
(s3205 1)
(s3206 1)
(s3207 1)
(s3208 1)
(s3209 1)
(s3210 1)
(s3211 1)
(s3212 1)
(s3213 1)
(s3214 1)
(s3215 1)
(s3216 1)
(s3217 1)
(s3218 1)
(s3219 1)
(s3220 1)
(s3221 1)
(s3222 1)
(s3223 1)
(s3224 1)
(s3225 1)
(s3226 1)
(s3227 1)
(s3228 1)
(s3229 1)
(s3230 1)
(s3231 1)
(s3232 1)
(s3233 1)
(s3234 1)
(s3235 1)
(s3236 1)
(s3237 1)
(s3238 1)
(s3239 1)
(s3240 1)
(s3241 1)
(s3242 1)
(s3243 1)
(s3244 1)
(s3245 1)
(s3246 1)
(s3247 1)
(s3248 1)
(s3249 1)
(s3250 1)
(s3251 1)
(s3252 1)
(s3253 1)
(s3254 1)
(s3255 1)
(s3256 1)
(s3257 1)
(s3258 1)
(s3259 1)
(s3260 1)
(s3261 1)
(s3262 1)
(s3263 1)
(s3264 1)
(s3265 1)
(s3266 1)
(s3267 1)
(s3268 1)
(s3269 1)
(s3270 1)
(s3271 1)
(s3272 1)
(s3273 1)
(s3274 1)
(s3275 1)
(s3276 1)
(s3277 1)
(s3278 1)
(s3279 1)
(s3280 1)
(s3281 1)
(s3282 1)
(s3283 1)
(s3284 1)
(s3285 1)
(s3286 1)
(s3287 1)
(s3288 1)
(s3289 1)
(s3290 1)
(s3291 1)
(s3292 1)
(s3293 1)
(s3294 1)
(s3295 1)
(s3296 1)
(s3297 1)
(s3298 1)
(s3299 1)
(s3300 1)
(s3301 1)
(s3302 1)
(s3303 1)
(s3304 1)
(s3305 1)
(s3306 1)
(s3307 1)
(s3308 1)
(s3309 1)
(s3310 1)
(s3311 1)
(s3312 1)
(s3313 1)
(s3314 1)
(s3315 1)
(s3316 1)
(s3317 1)
(s3318 1)
(s3319 1)
(s3320 1)
(s3321 1)
(s3322 1)
(s3323 1)
(s3324 1)
(s3325 1)
(s3326 1)
(s3327 1)
(s3328 1)
(s3329 1)
(s3330 1)
(s3331 1)
(s3332 1)
(s3333 1)
(s3334 1)
(s3335 1)
(s3336 1)
(s3337 1)
(s3338 1)
(s3339 1)
(s3340 1)
(s3341 1)
(s3342 1)
(s3343 1)
(s3344 1)
(s3345 1)
(s3346 1)
(s3347 1)
(s3348 1)
(s3349 1)
(s3350 1)
(s3351 1)
(s3352 1)
(s3353 1)
(s3354 1)
(s3355 1)
(s3356 1)
(s3357 1)
(s3358 1)
(s3359 1)
(s3360 1)
(s3361 1)
(s3362 1)
(s3363 1)
(s3364 1)
(s3365 1)
(s3366 1)
(s3367 1)
(s3368 1)
(s3369 1)
(s3370 1)
(s3371 1)
(s3372 1)
(s3373 1)
(s3374 1)
(s3375 1)
(s3376 1)
(s3377 1)
(s3378 1)
(s3379 1)
(s3380 1)
(s3381 1)
(s3382 1)
(s3383 1)
(s3384 1)
(s3385 1)
(s3386 1)
(s3387 1)
(s3388 1)
(s3389 1)
(s3390 1)
(s3391 1)
(s3392 1)
(s3393 1)
(s3394 1)
(s3395 1)
(s3396 1)
(s3397 1)
(s3398 1)
(s3399 1)
(s3400 1)
(s3401 1)
(s3402 1)
(s3403 1)
(s3404 1)
(s3405 1)
(s3406 1)
(s3407 1)
(s3408 1)
(s3409 1)
(s3410 1)
(s3411 1)
(s3412 1)
(s3413 1)
(s3414 1)
(s3415 1)
(s3416 1)
(s3417 1)
(s3418 1)
(s3419 1)
(s3420 1)
(s3421 1)
(s3422 1)
(s3423 1)
(s3424 1)
(s3425 1)
(s3426 1)
(s3427 1)
(s3428 1)
(s3429 1)
(s3430 1)
(s3431 1)
(s3432 1)
(s3433 1)
(s3434 1)
(s3435 1)
(s3436 1)
(s3437 1)
(s3438 1)
(s3439 1)
(s3440 1)
(s3441 1)
(s3442 1)
(s3443 1)
(s3444 1)
(s3445 1)
(s3446 1)
(s3447 1)
(s3448 1)
(s3449 1)
(s3450 1)
(s3451 1)
(s3452 1)
(s3453 1)
(s3454 1)
(s3455 1)
(s3456 1)
(s3457 1)
(s3458 1)
(s3459 1)
(s3460 1)
(s3461 1)
(s3462 1)
(s3463 1)
(s3464 1)
(s3465 1)
(s3466 1)
(s3467 1)
(s3468 1)
(s3469 1)
(s3470 1)
(s3471 1)
(s3472 1)
(s3473 1)
(s3474 1)
(s3475 1)
(s3476 1)
(s3477 1)
(s3478 1)
(s3479 1)
(s3480 1)
(s3481 1)
(s3482 1)
(s3483 1)
(s3484 1)
(s3485 1)
(s3486 1)
(s3487 1)
(s3488 1)
(s3489 1)
(s3490 1)
(s3491 1)
(s3492 1)
(s3493 1)
(s3494 1)
(s3495 1)
(s3496 1)
(s3497 1)
(s3498 1)
(s3499 1)
(s3500 1)
(s3501 1)
(s3502 1)
(s3503 1)
(s3504 1)
(s3505 1)
(s3506 1)
(s3507 1)
(s3508 1)
(s3509 1)
(s3510 1)
(s3511 1)
(s3512 1)
(s3513 1)
(s3514 1)
(s3515 1)
(s3516 1)
(s3517 1)
(s3518 1)
(s3519 1)
(s3520 1)
(s3521 1)
(s3522 1)
(s3523 1)
(s3524 1)
(s3525 1)
(s3526 1)
(s3527 1)
(s3528 1)
(s3529 1)
(s3530 1)
(s3531 1)
(s3532 1)
(s3533 1)
(s3534 1)
(s3535 1)
(s3536 1)
(s3537 1)
(s3538 1)
(s3539 1)
(s3540 1)
(s3541 1)
(s3542 1)
(s3543 1)
(s3544 1)
(s3545 1)
(s3546 1)
(s3547 1)
(s3548 1)
(s3549 1)
(s3550 1)
(s3551 1)
(s3552 1)
(s3553 1)
(s3554 1)
(s3555 1)
(s3556 1)
(s3557 1)
(s3558 1)
(s3559 1)
(s3560 1)
(s3561 1)
(s3562 1)
(s3563 1)
(s3564 1)
(s3565 1)
(s3566 1)
(s3567 1)
(s3568 1)
(s3569 1)
(s3570 1)
(s3571 1)
(s3572 1)
(s3573 1)
(s3574 1)
(s3575 1)
(s3576 1)
(s3577 1)
(s3578 1)
(s3579 1)
(s3580 1)
(s3581 1)
(s3582 1)
(s3583 1)
(s3584 1)
(s3585 1)
(s3586 1)
(s3587 1)
(s3588 1)
(s3589 1)
(s3590 1)
(s3591 1)
(s3592 1)
(s3593 1)
(s3594 1)
(s3595 1)
(s3596 1)
(s3597 1)
(s3598 1)
(s3599 1)
(s3600 1)
(s3601 1)
(s3602 1)
(s3603 1)
(s3604 1)
(s3605 1)
(s3606 1)
(s3607 1)
(s3608 1)
(s3609 1)
(s3610 1)
(s3611 1)
(s3612 1)
(s3613 1)
(s3614 1)
(s3615 1)
(s3616 1)
(s3617 1)
(s3618 1)
(s3619 1)
(s3620 1)
(s3621 1)
(s3622 1)
(s3623 1)
(s3624 1)
(s3625 1)
(s3626 1)
(s3627 1)
(s3628 1)
(s3629 1)
(s3630 1)
(s3631 1)
(s3632 1)
(s3633 1)
(s3634 1)
(s3635 1)
(s3636 1)
(s3637 1)
(s3638 1)
(s3639 1)
(s3640 1)
(s3641 1)
(s3642 1)
(s3643 1)
(s3644 1)
(s3645 1)
(s3646 1)
(s3647 1)
(s3648 1)
(s3649 1)
(s3650 1)
(s3651 1)
(s3652 1)
(s3653 1)
(s3654 1)
(s3655 1)
(s3656 1)
(s3657 1)
(s3658 1)
(s3659 1)
(s3660 1)
(s3661 1)
(s3662 1)
(s3663 1)
(s3664 1)
(s3665 1)
(s3666 1)
(s3667 1)
(s3668 1)
(s3669 1)
(s3670 1)
(s3671 1)
(s3672 1)
(s3673 1)
(s3674 1)
(s3675 1)
(s3676 1)
(s3677 1)
(s3678 1)
(s3679 1)
(s3680 1)
(s3681 1)
(s3682 1)
(s3683 1)
(s3684 1)
(s3685 1)
(s3686 1)
(s3687 1)
(s3688 1)
(s3689 1)
(s3690 1)
(s3691 1)
(s3692 1)
(s3693 1)
(s3694 1)
(s3695 1)
(s3696 1)
(s3697 1)
(s3698 1)
(s3699 1)
(s3700 1)
(s3701 1)
(s3702 1)
(s3703 1)
(s3704 1)
(s3705 1)
(s3706 1)
(s3707 1)
(s3708 1)
(s3709 1)
(s3710 1)
(s3711 1)
(s3712 1)
(s3713 1)
(s3714 1)
(s3715 1)
(s3716 1)
(s3717 1)
(s3718 1)
(s3719 1)
(s3720 1)
(s3721 1)
(s3722 1)
(s3723 1)
(s3724 1)
(s3725 1)
(s3726 1)
(s3727 1)
(s3728 1)
(s3729 1)
(s3730 1)
(s3731 1)
(s3732 1)
(s3733 1)
(s3734 1)
(s3735 1)
(s3736 1)
(s3737 1)
(s3738 1)
(s3739 1)
(s3740 1)
(s3741 1)
(s3742 1)
(s3743 1)
(s3744 1)
(s3745 1)
(s3746 1)
(s3747 1)
(s3748 1)
(s3749 1)
(s3750 1)
(s3751 1)
(s3752 1)
(s3753 1)
(s3754 1)
(s3755 1)
(s3756 1)
(s3757 1)
(s3758 1)
(s3759 1)
(s3760 1)
(s3761 1)
(s3762 1)
(s3763 1)
(s3764 1)
(s3765 1)
(s3766 1)
(s3767 1)
(s3768 1)
(s3769 1)
(s3770 1)
(s3771 1)
(s3772 1)
(s3773 1)
(s3774 1)
(s3775 1)
(s3776 1)
(s3777 1)
(s3778 1)
(s3779 1)
(s3780 1)
(s3781 1)
(s3782 1)
(s3783 1)
(s3784 1)
(s3785 1)
(s3786 1)
(s3787 1)
(s3788 1)
(s3789 1)
(s3790 1)
(s3791 1)
(s3792 1)
(s3793 1)
(s3794 1)
(s3795 1)
(s3796 1)
(s3797 1)
(s3798 1)
(s3799 1)
(s3800 1)
(s3801 1)
(s3802 1)
(s3803 1)
(s3804 1)
(s3805 1)
(s3806 1)
(s3807 1)
(s3808 1)
(s3809 1)
(s3810 1)
(s3811 1)
(s3812 1)
(s3813 1)
(s3814 1)
(s3815 1)
(s3816 1)
(s3817 1)
(s3818 1)
(s3819 1)
(s3820 1)
(s3821 1)
(s3822 1)
(s3823 1)
(s3824 1)
(s3825 1)
(s3826 1)
(s3827 1)
(s3828 1)
(s3829 1)
(s3830 1)
(s3831 1)
(s3832 1)
(s3833 1)
(s3834 1)
(s3835 1)
(s3836 1)
(s3837 1)
(s3838 1)
(s3839 1)
(s3840 1)
(s3841 1)
(s3842 1)
(s3843 1)
(s3844 1)
(s3845 1)
(s3846 1)
(s3847 1)
(s3848 1)
(s3849 1)
(s3850 1)
(s3851 1)
(s3852 1)
(s3853 1)
(s3854 1)
(s3855 1)
(s3856 1)
(s3857 1)
(s3858 1)
(s3859 1)
(s3860 1)
(s3861 1)
(s3862 1)
(s3863 1)
(s3864 1)
(s3865 1)
(s3866 1)
(s3867 1)
(s3868 1)
(s3869 1)
(s3870 1)
(s3871 1)
(s3872 1)
(s3873 1)
(s3874 1)
(s3875 1)
(s3876 1)
(s3877 1)
(s3878 1)
(s3879 1)
(s3880 1)
(s3881 1)
(s3882 1)
(s3883 1)
(s3884 1)
(s3885 1)
(s3886 1)
(s3887 1)
(s3888 1)
(s3889 1)
(s3890 1)
(s3891 1)
(s3892 1)
(s3893 1)
(s3894 1)
(s3895 1)
(s3896 1)
(s3897 1)
(s3898 1)
(s3899 1)
(s3900 1)
(s3901 1)
(s3902 1)
(s3903 1)
(s3904 1)
(s3905 1)
(s3906 1)
(s3907 1)
(s3908 1)
(s3909 1)
(s3910 1)
(s3911 1)
(s3912 1)
(s3913 1)
(s3914 1)
(s3915 1)
(s3916 1)
(s3917 1)
(s3918 1)
(s3919 1)
(s3920 1)
(s3921 1)
(s3922 1)
(s3923 1)
(s3924 1)
(s3925 1)
(s3926 1)
(s3927 1)
(s3928 1)
(s3929 1)
(s3930 1)
(s3931 1)
(s3932 1)
(s3933 1)
(s3934 1)
(s3935 1)
(s3936 1)
(s3937 1)
(s3938 1)
(s3939 1)
(s3940 1)
(s3941 1)
(s3942 1)
(s3943 1)
(s3944 1)
(s3945 1)
(s3946 1)
(s3947 1)
(s3948 1)
(s3949 1)
(s3950 1)
(s3951 1)
(s3952 1)
(s3953 1)
(s3954 1)
(s3955 1)
(s3956 1)
(s3957 1)
(s3958 1)
(s3959 1)
(s3960 1)
(s3961 1)
(s3962 1)
(s3963 1)
(s3964 1)
(s3965 1)
(s3966 1)
(s3967 1)
(s3968 1)
(s3969 1)
(s3970 1)
(s3971 1)
(s3972 1)
(s3973 1)
(s3974 1)
(s3975 1)
(s3976 1)
(s3977 1)
(s3978 1)
(s3979 1)
(s3980 1)
(s3981 1)
(s3982 1)
(s3983 1)
(s3984 1)
(s3985 1)
(s3986 1)
(s3987 1)
(s3988 1)
(s3989 1)
(s3990 1)
(s3991 1)
(s3992 1)
(s3993 1)
(s3994 1)
(s3995 1)
(s3996 1)
(s3997 1)
(s3998 1)
(s3999 1)
(s4000 1)
(s4001 1)
(s4002 1)
(s4003 1)
(s4004 1)
(s4005 1)
(s4006 1)
(s4007 1)
(s4008 1)
(s4009 1)
(s4010 1)
(s4011 1)
(s4012 1)
(s4013 1)
(s4014 1)
(s4015 1)
(s4016 1)
(s4017 1)
(s4018 1)
(s4019 1)
(s4020 1)
(s4021 1)
(s4022 1)
(s4023 1)
(s4024 1)
(s4025 1)
(s4026 1)
(s4027 1)
(s4028 1)
(s4029 1)
(s4030 1)
(s4031 1)
(s4032 1)
(s4033 1)
(s4034 1)
(s4035 1)
(s4036 1)
(s4037 1)
(s4038 1)
(s4039 1)
(s4040 1)
(s4041 1)
(s4042 1)
(s4043 1)
(s4044 1)
(s4045 1)
(s4046 1)
(s4047 1)
(s4048 1)
(s4049 1)
(s4050 1)
(s4051 1)
(s4052 1)
(s4053 1)
(s4054 1)
(s4055 1)
(s4056 1)
(s4057 1)
(s4058 1)
(s4059 1)
(s4060 1)
(s4061 1)
(s4062 1)
(s4063 1)
(s4064 1)
(s4065 1)
(s4066 1)
(s4067 1)
(s4068 1)
(s4069 1)
(s4070 1)
(s4071 1)
(s4072 1)
(s4073 1)
(s4074 1)
(s4075 1)
(s4076 1)
(s4077 1)
(s4078 1)
(s4079 1)
(s4080 1)
(s4081 1)
(s4082 1)
(s4083 1)
(s4084 1)
(s4085 1)
(s4086 1)
(s4087 1)
(s4088 1)
(s4089 1)
(s4090 1)
(s4091 1)
(s4092 1)
(s4093 1)
(s4094 1)
(s4095 1)
(s4096 1)
(s4097 1)
(s4098 1)
(s4099 1)
(s4100 1)
(s4101 1)
(s4102 1)
(s4103 1)
(s4104 1)
(s4105 1)
(s4106 1)
(s4107 1)
(s4108 1)
(s4109 1)
(s4110 1)
(s4111 1)
(s4112 1)
(s4113 1)
(s4114 1)
(s4115 1)
(s4116 1)
(s4117 1)
(s4118 1)
(s4119 1)
(s4120 1)
(s4121 1)
(s4122 1)
(s4123 1)
(s4124 1)
(s4125 1)
(s4126 1)
(s4127 1)
(s4128 1)
(s4129 1)
(s4130 1)
(s4131 1)
(s4132 1)
(s4133 1)
(s4134 1)
(s4135 1)
(s4136 1)
(s4137 1)
(s4138 1)
(s4139 1)
(s4140 1)
(s4141 1)
(s4142 1)
(s4143 1)
(s4144 1)
(s4145 1)
(s4146 1)
(s4147 1)
(s4148 1)
(s4149 1)
(s4150 1)
(s4151 1)
(s4152 1)
(s4153 1)
(s4154 1)
(s4155 1)
(s4156 1)
(s4157 1)
(s4158 1)
(s4159 1)
(s4160 1)
(s4161 1)
(s4162 1)
(s4163 1)
(s4164 1)
(s4165 1)
(s4166 1)
(s4167 1)
(s4168 1)
(s4169 1)
(s4170 1)
(s4171 1)
(s4172 1)
(s4173 1)
(s4174 1)
(s4175 1)
(s4176 1)
(s4177 1)
(s4178 1)
(s4179 1)
(s4180 1)
(s4181 1)
(s4182 1)
(s4183 1)
(s4184 1)
(s4185 1)
(s4186 1)
(s4187 1)
(s4188 1)
(s4189 1)
(s4190 1)
(s4191 1)
(s4192 1)
(s4193 1)
(s4194 1)
(s4195 1)
(s4196 1)
(s4197 1)
(s4198 1)
(s4199 1)
(s4200 1)
(s4201 1)
(s4202 1)
(s4203 1)
(s4204 1)
(s4205 1)
(s4206 1)
(s4207 1)
(s4208 1)
(s4209 1)
(s4210 1)
(s4211 1)
(s4212 1)
(s4213 1)
(s4214 1)
(s4215 1)
(s4216 1)
(s4217 1)
(s4218 1)
(s4219 1)
(s4220 1)
(s4221 1)
(s4222 1)
(s4223 1)
(s4224 1)
(s4225 1)
(s4226 1)
(s4227 1)
(s4228 1)
(s4229 1)
(s4230 1)
(s4231 1)
(s4232 1)
(s4233 1)
(s4234 1)
(s4235 1)
(s4236 1)
(s4237 1)
(s4238 1)
(s4239 1)
(s4240 1)
(s4241 1)
(s4242 1)
(s4243 1)
(s4244 1)
(s4245 1)
(s4246 1)
(s4247 1)
(s4248 1)
(s4249 1)
(s4250 1)
(s4251 1)
(s4252 1)
(s4253 1)
(s4254 1)
(s4255 1)
(s4256 1)
(s4257 1)
(s4258 1)
(s4259 1)
(s4260 1)
(s4261 1)
(s4262 1)
(s4263 1)
(s4264 1)
(s4265 1)
(s4266 1)
(s4267 1)
(s4268 1)
(s4269 1)
(s4270 1)
(s4271 1)
(s4272 1)
(s4273 1)
(s4274 1)
(s4275 1)
(s4276 1)timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30202 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 0/6600 constraints, Known Traps: 0/0 constraints]
After SMT, in 66095ms problems are : Problem set: 0 solved, 6600 unsolved
Search for dead transitions found 0 dead transitions in 66165ms
Finished structural reductions in SI_LTL mode , in 1 iterations and 73611 ms. Remains : 4900/4900 places, 8400/8400 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND p0 (NOT p2)), (X (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (X (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X p0)), (X (X (NOT p0)))]
Knowledge based reduction with 5 factoid took 189 ms. Reduced automaton from 2 states, 3 edges and 2 AP (stutter insensitive) to 2 states, 3 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 71 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
RANDOM walk for 660 steps (0 resets) in 30 ms. (21 steps per ms) remains 0/3 properties
Knowledge obtained : [(AND p0 (NOT p2)), (X (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (X (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X p0)), (X (X (NOT p0))), (F p2), (F (NOT p0)), (F (NOT (OR p0 p2)))]
Knowledge based reduction with 5 factoid took 265 ms. Reduced automaton from 2 states, 3 edges and 2 AP (stutter insensitive) to 2 states, 3 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 90 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Stuttering acceptance computed with spot in 91 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Stuttering acceptance computed with spot in 89 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Product exploration explored 100000 steps with 617 reset in 4208 ms.
Product exploration explored 100000 steps with 621 reset in 4318 ms.
Support contains 3450 out of 4900 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 4900/4900 places, 8400/8400 transitions.
Applied a total of 0 rules in 148 ms. Remains 4900 /4900 variables (removed 0) and now considering 8400/8400 (removed 0) transitions.
[2024-06-01 11:11:09] [INFO ] Invariant cache hit.
[2024-06-01 11:11:10] [INFO ] Implicit Places using invariants in 1146 ms returned []
[2024-06-01 11:11:10] [INFO ] Invariant cache hit.
[2024-06-01 11:11:16] [INFO ] Implicit Places using invariants and state equation in 5610 ms returned []
Implicit Place search using SMT with State Equation took 6763 ms to find 0 implicit places.
[2024-06-01 11:11:17] [INFO ] Redundant transitions in 1371 ms returned []
Running 6600 sub problems to find dead transitions.
[2024-06-01 11:11:17] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30180 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 6600/6600 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 6600 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 4850/13300 variables, and 0 constraints, problems are : Problem set: 0 solved, 6600 unsolved in 30170 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4900 constraints, PredecessorRefiner: 0/6600 constraints, Known Traps: 0/0 constraints]
After SMT, in 65989ms problems are : Problem set: 0 solved, 6600 unsolved
Search for dead transitions found 0 dead transitions in 66069ms
Finished structural reductions in SI_LTL mode , in 1 iterations and 74376 ms. Remains : 4900/4900 places, 8400/8400 transitions.
Treatment of property BART-PT-050-LTLFireability-02 finished in 333900 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X((p0||F(G(!p1))))))'
Support contains 4850 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Applied a total of 0 rules in 113 ms. Remains 6600 /6600 variables (removed 0) and now considering 10100/10100 (removed 0) transitions.
// Phase 1: matrix 10100 rows 6600 cols
[2024-06-01 11:12:25] [INFO ] Computed 50 invariants in 49 ms
[2024-06-01 11:12:27] [INFO ] Implicit Places using invariants in 2131 ms returned []
Implicit Place search using SMT only with invariants took 2132 ms to find 0 implicit places.
Running 8300 sub problems to find dead transitions.
[2024-06-01 11:12:27] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30206 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 8300/8300 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 8300 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30243 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 0/8300 constraints, Known Traps: 0/0 constraints]
After SMT, in 67751ms problems are : Problem set: 0 solved, 8300 unsolved
Search for dead transitions found 0 dead transitions in 67830ms
Finished structural reductions in LTL mode , in 1 iterations and 70093 ms. Remains : 6600/6600 places, 10100/10100 transitions.
Stuttering acceptance computed with spot in 204 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Running random walk in product with property : BART-PT-050-LTLFireability-03
Product exploration explored 100000 steps with 0 reset in 1643 ms.
Product exploration explored 100000 steps with 0 reset in 1511 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND p0 (NOT p1))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 1 factoid took 136 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 203 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
RANDOM walk for 390 steps (0 resets) in 37 ms. (10 steps per ms) remains 0/2 properties
Knowledge obtained : [(AND p0 (NOT p1))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0)), (F (NOT p0)), (F p1)]
Knowledge based reduction with 1 factoid took 164 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 220 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Stuttering acceptance computed with spot in 207 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Support contains 4850 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Applied a total of 0 rules in 190 ms. Remains 6600 /6600 variables (removed 0) and now considering 10100/10100 (removed 0) transitions.
[2024-06-01 11:13:42] [INFO ] Invariant cache hit.
[2024-06-01 11:13:45] [INFO ] Implicit Places using invariants in 2353 ms returned []
Implicit Place search using SMT only with invariants took 2360 ms to find 0 implicit places.
Running 8300 sub problems to find dead transitions.
[2024-06-01 11:13:45] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: ((s50 1.0)
(s51 1.0)
(s52 1.0)
(s53 1.0)
(s54 1.0)
(s55 1.0)
(s56 1.0)
(s57 1.0)
(s58 1.0)
(s59 1.0)
(s60 1.0)
(s61 1.0)
(s62 1.0)
(s63 1.0)
(s64 1.0)
(s65 1.0)
(s66 1.0)
(s67 1.0)
(s68 1.0)
(s69 1.0)
(s70 1.0)
(s71 1.0)
(s72 1.0)
(s73 1.0)
(s74 1.0)
(s75 1.0)
(s76 1.0)
(s77 1.0)
(s78 1.0)
(s79 1.0)
(s80 1.0)
(s81 1.0)
(s82 1.0)
(s83 1.0)
(s84 1.0)
(s85 1.0)
(s86 1.0)
(s87 1.0)
(s88 1.0)
(s89 1.0)
(s90 1.0)
(s91 1.0)
(s92 1.0)
(s93 1.0)
(s94 1.0)
(s95 1.0)
(s96 1.0)
(s97 1.0)
(s98 1.0)
(s99 1.0)
(s100 1.0)
(s101 1.0)
(s102 1.0)
(s103 1.0)
(s104 1.0)
(s105 1.0)
(s106 1.0)
(s107 1.0)
(s108 1.0)
(s109 1.0)
(s110 1.0)
(s111 1.0)
(s112 1.0)
(s113 1.0)
(s114 1.0)
(s115 1.0)
(s116 1.0)
(s117 1.0)
(s118 1.0)
(s119 1.0)
(s120 1.0)
(s121 1.0)
(s122 1.0)
(s123 1.0)
(s124 1.0)
(s125 1.0)
(s126 1.0)
(s127 1.0)
(s128 1.0)
(s129 1.0)
(s130 1.0)
(s131 1.0)
(s132 1.0)
(s133 1.0)
(s134 1.0)
(s135 1.0)
(s136 1.0)
(s137 1.0)
(s138 1.0)
(s139 1.0)
(s140 1.0)
(s141 1.0)
(s142 1.0)
(s143 1.0)
(s144 1.0)
(s145 1.0)
(s146 1.0)
(s147 1.0)
(s148 1.0)
(s149 1.0)
(s150 1.0)
(s151 1.0)
(s152 1.0)
(s153 1.0)
(s154 1.0)
(s155 1.0)
(s156 1.0)
(s157 1.0)
(s158 1.0)
(s159 1.0)
(s160 1.0)
(s161 1.0)
(s162 1.0)
(s163 1.0)
(s164 1.0)
(s165 1.0)
(s166 1.0)
(s167 1.0)
(s168 1.0)
(s169 1.0)
(s170 1.0)
(s171 1.0)
(s172 1.0)
(s173 1.0)
(s174 1.0)
(s175 1.0)
(s176 1.0)
(s177 1.0)
(s178 1.0)
(s179 1.0)
(s180 1.0)
(s181 1.0)
(s182 1.0)
(s183 1.0)
(s184 1.0)
(s185 1.0)
(s186 1.0)
(s187 1.0)
(s188 1.0)
(s189 1.0)
(s190 1.0)
(s191 1.0)
(s192 1.0)
(s193 1.0)
(s194 1.0)
(s195 1.0)
(s196 1.0)
(s197 1.0)
(s198 1.0)
(s199 1.0)
(s200 1.0)
(s201 1.0)
(s202 1.0)
(s203 1.0)
(s204 1.0)
(s205 1.0)
(s206 1.0)
(s207 1.0)
(s208 1.0)
(s209 1.0)
(s210 1.0)
(s211 1.0)
(s212 1.0)
(s213 1.0)
(s214 1.0)
(s215 1.0)
(s216 1.0)
(s217 1.0)
(s218 1.0)
(s219 1.0)
(s220 1.0)
(s221 1.0)
(s222 1.0)
(s223 1.0)
(s224 1.0)
(s225 1.0)
(s226 1.0)
(s227 1.0)
(s228 1.0)
(s229 1.0)
(s230 1.0)
(s231 1.0)
(s232 1.0)
(s233 1.0)
(s234 1.0)
(s235 1.0)
(s236 1.0)
(s237 1.0)
(s238 1.0)
(s239 1.0)
(s240 1.0)
(s241 1.0)
(s242 1.0)
(s243 1.0)
(s244 1.0)
(s245 1.0)
(s246 1.0)
(s247 1.0)
(s248 1.0)
(s249 1.0)
(s250 1.0)
(s251 1.0)
(s252 1.0)
(s253 1.0)
(s254 1.0)
(s255 1.0)
(s256 1.0)
(s257 1.0)
(s258 1.0)
(s259 1.0)
(s260 1.0)
(s261 1.0)
(s262 1.0)
(s263 1.0)
(s264 1.0)
(s265 1.0)
(s266 1.0)
(s267 1.0)
(s268 1.0)
(s269 1.0)
(s270 1.0)
(s271 1.0)
(s272 1.0)
(s273 1.0)
(s274 1.0)
(s275 1.0)
(s276 1.0)
(s277 1.0)
(s278 1.0)
(s279 1.0)
(s280 1.0)
(s281 1.0)
(s282 1.0)
(s283 1.0)
(s284 1.0)
(s285 1.0)
(s286 1.0)
(s287 1.0)
(s288 1.0)
(s289 1.0)
(s290 1.0)
(s291 1.0)
(s292 1.0)
(s293 1.0)
(s294 1.0)
(s295 1.0)
(s296 1.0)
(s297 1.0)
(s298 1.0)
(s299 1.0)
(s300 1.0)
(s301 1.0)
(s302 1.0)
(s303 1.0)
(s304 1.0)
(s305 1.0)
(s306 1.0)
(s307 1.0)
(s308 1.0)
(s309 1.0)
(s310 1.0)
(s311 1.0)
(s312 1.0)
(s313 1.0)
(s314 1.0)
(s315 1.0)
(s316 1.0)
(s317 1.0)
(s318 1.0)
(s319 1.0)
(s320 1.0)
(s321 1.0)
(s322 1.0)
(s323 1.0)
(s324 1.0)
(s325 1.0)
(s326 1.0)
(s327 1.0)
(s328 1.0)
(s329 1.0)
(s330 1.0)
(s331 1.0)
(s332 1.0)
(s333 1.0)
(s334 1.0)
(s335 1.0)
(s336 1.0)
(s337 1.0)
(s338 1.0)
(s339 1.0)
(s340 1.0)
(s341 1.0)
(s342 1.0)
(s343 1.0)
(s344 1.0)
(s345 1.0)
(s346 1.0)
(s347 1.0)
(s348 1.0)
(s349 1.0)
(s350 1.0)
(s351 1.0)
(s352 1.0)
(s353 1.0)
(s354 1.0)
(s355 1.0)
(s356 1.0)
(s357 1.0)
(s358 1.0)
(s359 1.0)
(s360 1.0)
(s361 1.0)
(s362 1.0)
(s363 1.0)
(s364 1.0)
(s365 1.0)
(s366 1.0)
(s367 1.0)
(s368 1.0)
(s369 1.0)
(s370 1.0)
(s371 1.0)
(s372 1.0)
(s373 1.0)
(s374 1.0)
(s375 1.0)
(s376 1.0)
(s377 1.0)
(s378 1.0)
(s379 1.0)
(s380 1.0)
(s381 1.0)
(s382 1.0)
(s383 1.0)
(s384 1.0)
(s385 1.0)
(s386 1.0)
(s387 1.0)
(s388 1.0)
(s389 1.0)
(s390 1.0)
(s391 1.0)
(s392 1.0)
(s393 1.0)
(s394 1.0)
(s395 1.0)
(s396 1.0)
(s397 1.0)
(s398 1.0)
(s399 1.0)
(s400 1.0)
(s401 1.0)
(s402 1.0)
(s403 1.0)
(s404 1.0)
(s405 1.0)
(s406 1.0)
(s407 1.0)
(s408 1.0)
(s409 1.0)
(s410 1.0)
(s411 1.0)
(s412 1.0)
(s413 1.0)
(s414 1.0)
(s415 1.0)
(s416 1.0)
(s417 1.0)
(s418 1.0)
(s419 1.0)
(s420 1.0)
(s421 1.0)
(s422 1.0)
(s423 1.0)
(s424 1.0)
(s425 1.0)
(s426 1.0)
(s427 1.0)
(s428 1.0)
(s429 1.0)
(s430 1.0)
(s431 1.0)
(s432 1.0)
(s433 1.0)
(s434 1.0)
(s435 1.0)
(s436 1.0)
(s437 1.0)
(s438 1.0)
(s439 1.0)
(s440 1.0)
(s441 1.0)
(s442 1.0)
(s443 1.0)
(s444 1.0)
(s445 1.0)
(s446 1.0)
(s447 1.0)
(s448 1.0)
(s449 1.0)
(s450 1.0)
(s451 1.0)
(s452 1.0)
(s453 1.0)
(s454 1.0)
(s455 1.0)
(s456 1.0)
(s457 1.0)
(s458 1.0)
(s459 1.0)
(s460 1.0)
(s461 1.0)
(s462 1.0)
(s463 1.0)
(s464 1.0)
(s465 1.0)
(s466 1.0)
(s467 1.0)
(s468 1.0)
(s469 1.0)
(s470 1.0)
(s471 1.0)
(s472 1.0)
(s473 1.0)
(s474 1.0)
(s475 1.0)
(s476 1.0)
(s477 1.0)
(s478 1.0)
(s479 1.0)
(s480 1.0)
(s481 1.0)
(s482 1.0)
(s483 1.0)
(s484 1.0)
(s485 1.0)
(s486 1.0)
(s487 1.0)
(s488 1.0)
(s489 1.0)
(s490 1.0)
(s491 1.0)
(s492 1.0)
(s493 1.0)
(s494 1.0)
(s495 1.0)
(s496 1.0)
(s497 1.0)
(s498 1.0)
(s499 1.0)
(s500 1.0)
(s501 1.0)
(s502 1.0)
(s503 1.0)
(s504 1.0)
(s505 1.0)
(s506 1.0)
(s507 1.0)
(s508 1.0)
(s509 1.0)
(s510 1.0)
(s511 1.0)
(s512 1.0)
(s513 1.0)
(s514 1.0)
(s515 1.0)
(s516 1.0)
(s517 1.0)
(s518 1.0)
(s519 1.0)
(s520 1.0)
(s521 1.0)
(s522 1.0)
(s523 1.0)
(s524 1.0)
(s525 1.0)
(s526 1.0)
(s527 1.0)
(s528 1.0)
(s529 1.0)
(s530 1.0)
(s531 1.0)
(s532 1.0)
(s533 1.0)
(s534 1.0)
(s535 1.0)
(s536 1.0)
(s537 1.0)
(s538 1.0)
(s539 1.0)
(s540 1.0)
(s541 1.0)
(s542 1.0)
(s543 1.0)
(s544 1.0)
(s545 1.0)
(s546 1.0)
(s547 1.0)
(s548 1.0)
(s549 1.0)
(s550 1.0)
(s551 1.0)
(s552 1.0)
(s553 1.0)
(s554 1.0)
(s555 1.0)
(s556 1.0)
(s557 1.0)
(s558 1.0)
(s559 1.0)
(s560 1.0)
(s561 1.0)
(s562 1.0)
(s563 1.0)
(s564 1.0)
(s565 1.0)
(s566 1.0)
(s567 1.0)
(s568 1.0)
(s569 1.0)
(s570 1.0)
(s571 1.0)
(s572 1.0)
(s573 1.0)
(s574 1.0)
(s575 1.0)
(s576 1.0)
(s577 1.0)
(s578 1.0)
(s579 1.0)
(s580 1.0)
(s581 1.0)
(s582 1.0)
(s583 1.0)
(s584 1.0)
(s585 1.0)
(s586 1.0)
(s587 1.0)
(s588 1.0)
(s589 1.0)
(s590 1.0)
(s591 1.0)
(s592 1.0)
(s593 1.0)
(s594 1.0)
(s595 1.0)
(s596 1.0)
(s597 1.0)
(s598 1.0)
(s599 1.0)
(s600 1.0)
(s601 1.0)
(s602 1.0)
(s603 1.0)
(s604 1.0)
(s605 1.0)
(s606 1.0)
(s607 1.0)
(s608 1.0)
(s609 1.0)
(s610 1.0)
(s611 1.0)
(s612 1.0)
(s613 1.0)
(s614 1.0)
(s615 1.0)
(s616 1.0)
(s617 1.0)
(s618 1.0)
(s619 1.0)
(s620 1.0)
(s621 1.0)
(s622 1.0)
(s623 1.0)
(s624 1.0)
(s625 1.0)
(s626 1.0)
(s627 1.0)
(s628 1.0)
(s629 1.0)
(s630 1.0)
(s631 1.0)
(s632 1.0)
(s633 1.0)
(s634 1.0)
(s635 1.0)
(s636 1.0)
(s637 1.0)
(s638 1.0)
(s639 1.0)
(s640 1.0)
(s641 1.0)
(s642 1.0)
(s643 1.0)
(s644 1.0)
(s645 1.0)
(s646 1.0)
(s647 1.0)
(s648 1.0)
(s649 1.0)
(s650 1.0)
(s651 1.0)
(s652 1.0)
(s653 1.0)
(s654 1.0)
(s655 1.0)
(s656 1.0)
(s657 1.0)
(s658 1.0)
(s659 1.0)
(s660 1.0)
(s661 1.0)
(s662 1.0)
(s663 1.0)
(s664 1.0)
(s665 1.0)
(s666 1.0)
(s667 1.0)
(s668 1.0)
(s669 1.0)
(s670 1.0)
(s671 1.0)
(s672 1.0)
(s673 1.0)
(s674 1.0)
(s675 1.0)
(s676 1.0)
(s677 1.0)
(s678 1.0)
(s679 1.0)
(s680 1.0)
(s681 1.0)
(s682 1.0)
(s683 1.0)
(s684 1.0)
(s685 1.0)
(s686 1.0)
(s687 1.0)
(s688 1.0)
(s689 1.0)
(s690 1.0)
(s691 1.0)
(s692 1.0)
(s693 1.0)
(s694 1.0)
(s695 1.0)
(s696 1.0)
(s697 1.0)
(s698 1.0)
(s699 1.0)
(s700 1.0)
(s701 1.0)
(s702 1.0)
(s703 1.0)
(s704 1.0)
(s705 1.0)
(s706 1.0)
(s707 1.0)
(s708 1.0)
(s709 1.0)
(s710 1.0)
(s711 1.0)
(s712 1.0)
(s713 1.0)
(s714 1.0)
(s715 1.0)
(s716 1.0)
(s717 1.0)
(s718 1.0)
(s719 1.0)
(s720 1.0)
(s721 1.0)
(s722 1.0)
(s723 1.0)
(s724 1.0)
(s725 1.0)
(s726 1.0)
(s727 1.0)
(s728 1.0)
(s729 1.0)
(s730 1.0)
(s731 1.0)
(s732 1.0)
(s733 1.0)
(s734 1.0)
(s735 1.0)
(s736 1.0)
(s737 1.0)
(s738 1.0)
(s739 1.0)
(s740 1.0)
(s741 1.0)
(s742 1.0)
(s743 1.0)
(s744 1.0)
(s745 1.0)
(s746 1.0)
(s747 1.0)
(s748 1.0)
(s749 1.0)
(s750 1.0)
(s751 1.0)
(s752 1.0)
(s753 1.0)
(s754 1.0)
(s755 1.0)
(s756 1.0)
(s757 1.0)
(s758 1.0)
(s759 1.0)
(s760 1.0)
(s761 1.0)
(s762 1.0)
(s763 1.0)
(s764 1.0)
(s765 1.0)
(s766 1.0)
(s767 1.0)
(s768 1.0)
(s769 1.0)
(s770 1.0)
(s771 1.0)
(s772 1.0)
(s773 1.0)
(s774 1.0)
(s775 1.0)
(s776 1.0)
(s777 1.0)
(s778 1.0)
(s779 1.0)
(s780 1.0)
(s781 1.0)
(s782 1.0)
(s783 1.0)
(s784 1.0)
(s785 1.0)
(s786 1.0)
(s787 1.0)
(s788 1.0)
(s789 1.0)
(s790 1.0)
(s791 1.0)
(s792 1.0)
(s793 1.0)
(s794 1.0)
(s795 1.0)
(s796 1.0)
(s797 1.0)
(s798 1.0)
(s799 1.0)
(s800 1.0)
(s801 1.0)
(s802 1.0)
(s803 1.0)
(s804 1.0)
(s805 1.0)
(s806 1.0)
(s807 1.0)
(s808 1.0)
(s809 1.0)
(s810 1.0)
(s811 1.0)
(s812 1.0)
(s813 1.0)
(s814 1.0)
(s815 1.0)
(s816 1.0)
(s817 1.0)
(s818 1.0)
(s819 1.0)
(s820 1.0)
(s821 1.0)
(s822 1.0)
(s823 1.0)
(s824 1.0)
(s825 1.0)
(s826 1.0)
(s827 1.0)
(s828 1.0)
(s829 1.0)
(s830 1.0)
(s831 1.0)
(s832 1.0)
(s833 1.0)
(s834 1.0)
(s835 1.0)
(s836 1.0)
(s837 1.0)
(s838 1.0)
(s839 1.0)
(s840 1.0)
(s841 1.0)
(s842 1.0)
(s843 1.0)
(s844 1.0)
(s845 1.0)
(s846 1.0)
(s847 1.0)
(s848 1.0)
(s849 1.0)
(s850 1.0)
(s851 1.0)
(s852 1.0)
(s853 1.0)
(s854 1.0)
(s855 1.0)
(s856 1.0)
(s857 1.0)
(s858 1.0)
(s859 1.0)
(s860 1.0)
(s861 1.0)
(s862 1.0)
(s863 1.0)
(s864 1.0)
(s865 1.0)
(s866 1.0)
(s867 1.0)
(s868 1.0)
(s869 1.0)
(s870 1.0)
(s871 1.0)
(s872 1.0)
(s873 1.0)
(s874 1.0)
(s875 1.0)
(s876 1.0)
(s877 1.0)
(s878 1.0)
(s879 1.0)
(s880 1.0)
(s881 1.0)
(s882 1.0)
(s883 1.0)
(s884 1.0)
(s885 1.0)
(s886 1.0)
(s887 1.0)
(s888 1.0)
(s889 1.0)
(s890 1.0)
(s891 1.0)
(s892 1.0)
(s893 1.0)
(s894 1.0)
(s895 1.0)
(s896 1.0)
(s897 1.0)
(s898 1.0)
(s899 1.0)
(s900 1.0)
(s901 1.0)
(s902 1.0)
(s903 1.0)
(s904 1.0)
(s905 1.0)
(s906 1.0)
(s907 1.0)
(s908 1.0)
(s909 1.0)
(s910 1.0)
(s911 1.0)
(s912 1.0)
(s913 1.0)
(s914 1.0)
(s915 1.0)
(s916 1.0)
(s917 1.0)
(s918 1.0)
(s919 1.0)
(s920 1.0)
(s921 1.0)
(s922 1.0)
(s923 1.0)
(s924 1.0)
(s925 1.0)
(s926 1.0)
(s927 1.0)
(s928 1.0)
(s929 1.0)
(s930 1.0)
(s931 1.0)
(s932 1.0)
(s933 1.0)
(s934 1.0)
(s935 1.0)
(s936 1.0)
(s937 1.0)
(s938 1.0)
(s939 1.0)
(s940 1.0)
(s941 1.0)
(s942 1.0)
(s943 1.0)
(s944 1.0)
(s945 1.0)
(s946 1.0)
(s947 1.0)
(s948 1.0)
(s949 1.0)
(s950 1.0)
(s951 1.0)
(s952 1.0)
(s953 1.0)
(s954 1.0)
(s955 1.0)
(s956 1.0)
(s957 1.0)
(s958 1.0)
(s959 1.0)
(s960 1.0)
(s961 1.0)
(s962 1.0)
(s963 1.0)
(s964 1.0)
(s965 1.0)
(s966 1.0)
(s967 1.0)
(s968 1.0)
(s969 1.0)
(s970 1.0)
(s971 1.0)
(s972 1.0)
(s973 1.0)
(s974 1.0)
(s975 1.0)
(s976 1.0)
(s977 1.0)
(s978 1.0)
(s979 1.0)
(s980 1.0)
(s981 1.0)
(s982 1.0)
(s983 1.0)
(s984 1.0)
(s985 1.0)
(s986 1.0)
(s987 1.0)
(s988 1.0)
(s989 1.0)
(s990 1.0)
(s991 1.0)
(s992 1.0)
(s993 1.0)
(s994 1.0)
(s995 1.0)
(s996 1.0)
(s997 1.0)
(s998 1.0)
(s999 1.0)
(s1000 1.0)
(s1001 1.0)
(s1002 1.0)
(s1003 1.0)
(s1004 1.0)
(s1005 1.0)
(s1006 1.0)
(s1007 1.0)
(s1008 1.0)
(s1009 1.0)
(s1010 1.0)
(s1011 1.0)
(s1012 1.0)
(s1013 1.0)
(s1014 1.0)
(s1015 1.0)
(s1016 1.0)
(s1017 1.0)
(s1018 1.0)
(s1019 1.0)
(s1020 1.0)
(s1021 1.0)
(s1022 1.0)
(s1023 1.0)
(s1024 1.0)
(s1025 1.0)
(s1026 1.0)
(s1027 1.0)
(s1028 1.0)
(s1029 1.0)
(s1030 1.0)
(s1031 1.0)
(s1032 1.0)
(s1033 1.0)
(s1034 1.0)
(s1035 1.0)
(s1036 1.0)
(s1037 1.0)
(s1038 1.0)
(s1039 1.0)
(s1040 1.0)
(s1041 1.0)
(s1042 1.0)
(s1043 1.0)
(s1044 1.0)
(s1045 1.0)
(s1046 1.0)
(s1047 1.0)
(s1048 1.0)
(s1049 1.0)
(s1050 1.0)
(s1051 1.0)
(s1052 1.0)
(s1053 1.0)
(s1054 1.0)
(s1055 1.0)
(s1056 1.0)
(s1057 1.0)
(s1058 1.0)
(s1059 1.0)
(s1060 1.0)
(s1061 1.0)
(s1062 1.0)
(s1063 1.0)
(s1064 1.0)
(s1065 1.0)
(s1066 1.0)
(s1067 1.0)
(s1068 1.0)
(s1069 1.0)
(s1070 1.0)
(s1071 1.0)
(s1072 1.0)
(s1073 1.0)
(s1074 1.0)
(s1075 1.0)
(s1076 1.0)
(s1077 1.0)
(s1078 1.0)
(s1079 1.0)
(s1080 1.0)
(s1081 1.0)
(s1082 1.0)
(s1083 1.0)
(s1084 1.0)
(s1085 1.0)
(s1086 1.0)
(s1087 1.0)
(s1088 1.0)
(s1089 1.0)
(s1090 1.0)
(s1091 1.0)
(s1092 1.0)
(s1093 1.0)
(s1094 1.0)
(s1095 1.0)
(s1096 1.0)
(s1097 1.0)
(s1098 1.0)
(s1099 1.0)
(s1100 1.0)
(s1101 1.0)
(s1102 1.0)
(s1103 1.0)
(s1104 1.0)
(s1105 1.0)
(s1106 1.0)
(s1107 1.0)
(s1108 1.0)
(s1109 1.0)
(s1110 1.0)
(s1111 1.0)
(s1112 1.0)
(s1113 1.0)
(s1114 1.0)
(s1115 1.0)
(s1116 1.0)
(s1117 1.0)
(s1118 1.0)
(s1119 1.0)
(s1120 1.0)
(s1121 1.0)
(s1122 1.0)
(s1123 1.0)
(s1124 1.0)
(s1125 1.0)
(s1126 1.0)
(s1127 1.0)
(s1128 1.0)
(s1129 1.0)
(s1130 1.0)
(s1131 1.0)
(s1132 1.0)
(s1133 1.0)
(s1134 1.0)
(s1135 1.0)
(s1136 1.0)
(s1137 1.0)
(s1138 1.0)
(s1139 1.0)
(s1140 1.0)
(s1141 1.0)
(s1142 1.0)
(s1143 1.0)
(s1144 1.0)
(s1145 1.0)
(s1146 1.0)
(s1147 1.0)
(s1148 1.0)
(s1149 1.0)
(s1150 1.0)
(s1151 1.0)
(s1152 1.0)
(s1153 1.0)
(s1154 1.0)
(s1155 1.0)
(s1156 1.0)
(s1157 1.0)
(s1158 1.0)
(s1159 1.0)
(s1160 1.0)
(s1161 1.0)
(s1162 1.0)
(s1163 1.0)
(s1164 1.0)
(s1165 1.0)
(s1166 1.0)
(s1167 1.0)
(s1168 1.0)
(s1169 1.0)
(s1170 1.0)
(s1171 1.0)
(s1172 1.0)
(s1173 1.0)
(s1174 1.0)
(s1175 1.0)
(s1176 1.0)
(s1177 1.0)
(s1178 1.0)
(s1179 1.0)
(s1180 1.0)
(s1181 1.0)
(s1182 1.0)
(s1183 1.0)
(s1184 1.0)
(s1185 1.0)
(s1186 1.0)
(s1187 1.0)
(s1188 1.0)
(s1189 1.0)
(s1190 1.0)
(s1191 1.0)
(s1192 1.0)
(s1193 1.0)
(s1194 1.0)
(s1195 1.0)
(s1196 1.0)
(s1197 1.0)
(s1198 1.0)
(s1199 1.0)
(s1200 1.0)
(s1201 1.0)
(s1202 1.0)
(s1203 1.0)
(s1204 1.0)
(s1205 1.0)
(s1206 1.0)
(s1207 1.0)
(s1208 1.0)
(s1209 1.0)
(s1210 1.0)
(s1211 1.0)
(s1212 1.0)
(s1213 1.0)
(s1214 1.0)
(s1215 1.0)
(s1216 1.0)
(s1217 1.0)
(s1218 1.0)
(s1219 1.0)
(s1220 1.0)
(s1221 1.0)
(s1222 1.0)
(s1223 1.0)
(s1224 1.0)
(s1225 1.0)
(s1226 1.0)
(s1227 1.0)
(s1228 1.0)
(s1229 1.0)
(s1230 1.0)
(s1231 1.0)
(s1232 1.0)
(s1233 1.0)
(s1234 timeout
1.0 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30218 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 8300/8300 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 8300 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1582 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1670 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1758 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1846 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1934 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2022 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 1)
(s2090 1)
(s2091 1)
(s2092 1)
(s2093 1)
(s2094 1)
(s2095 1)
(s2096 1)
(s2097 1)
(s2098 1)
(s2099 1)
(s2100 1)
(s2101 1)
(s2102 1)
(s2103 1)
(s2104 1)
(s2105 1)
(s2106 1)
(s2107 1)
(s2108 1)
(s2109 1)
(s2110 1)
(s2111 1)
(s2112 1)
(s2113 1)
(s2114 1)
(s2115 1)
(s2116 1)
(s2117 1)
(s2118 1)
(s2119 1)
(s2120 1)
(s2121 1)
(s2122 1)
(s2123 1)
(s2124 1)
(s2125 1)
(s2126 1)
(s2127 1)
(s2128 1)
(s2129 1)
(s2130 1)
(s2131 1)
(s2132 1)
(s2133 1)
(s2134 1)
(s2135 1)
(s2136 1)
(s2137 1)
(s2138 1)
(s2139 1)
(s2140 1)
(s2141 1)
(s2142 1)
(s2143 1)
(s2144 1)
(s2145 1)
(s2146 1)
(s2147 1)
(s2148 1)
(s2149 1)
(s2150 1)
(s2151 1)
(s2152 1)
(s2153 1)
(s2154 1)
(s2155 1)
(s2156 1)
(s2157 1)
(s2158 1)
(s2159 1)
(s2160 1)
(s2161 1)
(s2162 1)
(s2163 1)
(s2164 1)
(s2165 1)
(s2166 1)
(s2167 1)
(s2168 1)
(s2169 1)
(s2170 1)
(s2171 1)
(s2172 1)
(s2173 1)
(s2174 1)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2198 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2286 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2374 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2462 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2550 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 1)
(s2577 1)
(s2578 1)
(s2579 1)
(s2580 1)
(s2581 1)
(s2582 1)
(s2583 1)
(s2584 1)
(s2585 1)
(s2586 1)
(s2587 1)
(s2588 1)
(s2589 1)
(s2590 1)
(s2591 1)
(s2592 1)
(s2593 1)
(s2594 1)
(s2595 1)
(s2596 1)
(s2597 1)
(s2598 1)
(s2599 1)
(s2600 1)
(s2601 1)
(s2602 1)
(s2603 1)
(s2604 1)
(s2605 1)
(s2606 1)
(s2607 1)
(s2608 1)
(s2609 1)
(s2610 1)
(s2611 1)
(s2612 1)
(s2613 1)
(s2614 1)
(s2615 1)
(s2616 1)
(s2617 1)
(s2618 1)
(s2619 1)
(s2620 1)
(s2621 1)
(s2622 1)
(s2623 1)
(s2624 1)
(s2625 1)
(s2626 1)
(s2627 1)
(s2628 1)
(s2629 1)
(s2630 1)
(s2631 1)
(s2632 1)
(s2633 1)
(s2634 1)
(s2635 1)
(s2636 1)
(s2637 1)
(s2638 1)
(s2639 1)
(s2640 1)
(s2641 1)
(s2642 1)
(s2643 1)
(s2644 1)
(s2645 1)
(s2646 1)
(s2647 1)
(s2648 1)
(s2649 1)
(s2650 1)
(s2651 1)
(s2652 1)
(s2653 1)
(s2654 1)
(s2655 1)
(s2656 1)
(s2657 1)
(s2658 1)
(s2659 1)
(s2660 1)
(s2661 1)
(s2662 1)
(s2663 1)
(s2664 1)
(s2665 1)
(s2666 1)
(s2667 1)
(s2668 1)
(s2669 1)
(s2670 1)
(s2671 1)
(s2672 1)
(s2673 1)
(s2674 1)
(s2675 1)
(s2676 1)
(s2677 1)
(s2678 1)
(s2679 1)
(s2680 1)
(s2681 1)
(s2682 1)
(s2683 1)
(s2684 1)
(s2685 1)
(s2686 1)
(s2687 1)
(s2688 1)
(s2689 1)
(s2690 1)
(s2691 1)
(s2692 1)
(s2693 1)
(s2694 1)
(s2695 1)
(s2696 1)
(s2697 1)
(s2698 1)
(s2699 1)
(s2700 1)
(s2701 1)
(s2702 1)
(s2703 1)
(s2704 1)
(s2705 1)
(s2706 1)
(s2707 1)
(s2708 1)
(s2709 1)
(s2710 1)
(s2711 1)
(s2712 1)
(s2713 1)
(s2714 1)
(s2715 1)
(s2716 1)
(s2717 1)
(s2718 1)
(s2719 1)
(s2720 1)
(s2721 1)
(s2722 1)
(s2723 1)
(s2724 1)
(s2725 1)
(s2726 1)
(s2727 1)
(s2728 1)
(s2729 1)
(s2730 1)
(s2731 1)
(s2732 1)
(s2733 1)
(s2734 1)
(s2735 1)
(s2736 1)
(s2737 1)
(s2738 1)
(s2739 1)
(s2740 1)
(s2741 1)
(s2742 1)
(s2743 1)
(s2744 1)
(s2745 1)
(s2746 1)
(s2747 1)
(s2748 1)
(s2749 1)
(s2750 1)
(s2751 1)
(s2752 1)
(s2753 1)
(s2754 1)
(s2755 1)
(s2756 1)
(s2757 1)
(s2758 1)
(s2759 1)
(s2760 1)
(s2761 1)
(s2762 1)
(s2763 1)
(s2764 1)
(s2765 1)
(s2766 1)
(s2767 1)
(s2768 1)
(s2769 1)
(s2770 1)
(s2771 1)
(s2772 1)
(s2773 1)
(s2774 1)
(s2775 1)
(s2776 1)
(s2777 1)
(s2778 1)
(s2779 1)
(s2780 1)
(s2781 1)
(s2782 1)
(s2783 1)
(s2784 1)
(s2785 1)
(s2786 1)
(s2787 1)
(s2788 1)
(s2789 1)
(s2790 1)
(s2791 1)
(s2792 1)
(s2793 1)
(s2794 1)
(s2795 1)
(s2796 1)
(s2797 1)
(s2798 1)
(s2799 1)
(s2800 1)
(s2801 1)
(s2802 1)
(s2803 1)
(s2804 1)
(s2805 1)
(s2806 1)
(s2807 1)
(s2808 1)
(s2809 1)
(s2810 1)
(s2811 1)
(s2812 1)
(s2813 1)
(s2814 1)
(s2815 1)
(s2816 1)
(s2817 1)
(s2818 1)
(s2819 1)
(s2820 1)
(s2821 1)
(s2822 1)
(s2823 1)
(s2824 1)
(s2825 1)
(s2826 1)
(s2827 1)
(s2828 1)
(s2829 1)
(s2830 1)
(s2831 1)
(s2832 1)
(s2833 1)
(s2834 1)
(s2835 1)
(s2836 1)
(s2837 1)
(s2838 1)
(s2839 1)
(s2840 1)
(s2841 1)
(s2842 1)
(s2843 1)
(s2844 1)
(s2845 1)
(s2846 1)
(s2847 1)
(s2848 1)
(s2849 1)
(s2850 1)
(s2851 1)
(s2852 1)
(s2853 1)
(s2854 1)
(s2855 1)
(s2856 1)
(s2857 1)
(s2858 1)
(s2859 1)
(s2860 1)
(s2861 1)
(s2862 1)
(s2863 1)
(s2864 1)
(s2865 1)
(s2866 1)
(s2867 1)
(s2868 1)
(s2869 1)
(s2870 1)
(s2871 1)
(s2872 1)
(s2873 1)
(s2874 1)
(s2875 1)
(s2876 1)
(s2877 1)
(s2878 1)
(s2879 1)
(s2880 1)
(s2881 1)
(s2882 1)
(s2883 1)
(s2884 1)
(s2885 1)
(s2886 1)
(s2887 1)
(s2888 1)
(s2889 1)
(s2890 1)
(s2891 1)
(s2892 1)
(s2893 1)
(s2894 1)
(s2895 1)
(s2896 1)
(s2897 1)
(s2898 1)
(s2899 1)
(s2900 1)
(s2901 1)
(s2902 1)
(s2903 1)
(s2904 1)
(s2905 1)
(s2906 1)
(s2907 1)
(s2908 1)
(s2909 1)
(s2910 1)
(s2911 1)
(s2912 1)
(s2913 1)
(s2914 1)
(s2915 1)
(s2916 1)
(s2917 1)
(s2918 1)
(s2919 1)
(s2920 1)
(s2921 1)
(s2922 1)
(s2923 1)
(s2924 1)
(s2925 1)
(s2926 1)
(s2927 1)
(s2928 1)
(s2929 1)
(s2930 1)
(s2931 1)
(s2932 1)
(s2933 1)
(s2934 1)
(s2935 1)
(s2936 1)
(s2937 1)
(s2938 1)
(s2939 1)
(s2940 1)
(s2941 1)
(s2942 1)
(s2943 1)
(s2944 1)
(s2945 1)
(s2946 1)
(s2947 1)
(s2948 1)
(s2949 1)
(s2950 1)
(s2951 1)
(s2952 1)
(s2953 1)
(s2954 1)
(s2955 1)
(s2956 1)
(s2957 1)
(s2958 1)
(s2959 1)
(s2960 1)
(s2961 1)
(s2962 1)
(s2963 1)
(s2964 1)
(s2965 1)
(s2966 1)
(s2967 1)
(s2968 1)
(s2969 1)
(s2970 1)
(s2971 1)
(s2972 1)
(s2973 1)
(s2974 1)
(s2975 1)
(s2976 1)
(s2977 1)
(s2978 1)
(s2979 1)
(s2980 1)
(s2981 1)
(s2982 1)
(s2983 1)
(s2984 1)
(s2985 1)
(s2986 1)
(s2987 1)
(s2988 1)
(s2989 1)
(s2990 1)
(s2991 1)
(s2992 1)
(s2993 1)
(s2994 1)
(s2995 1)
(s2996 1)
(s2997 1)
(s2998 1)
(s2999 1)
(s3000 1)
(s3001 1)
(s3002 1)
(s3003 1)
(s3004 1)
(s3005 1)
(s3006 1)
(s3007 1)
(s3008 1)
(s3009 1)
(s3010 1)
(s3011 1)
(s3012 1)
(s3013 1)
(s3014 1)
(s3015 1)
(s3016 1)
(s3017 1)
(s3018 1)
(s3019 1)
(s3020 1)
(s3021 1)
(s3022 1)
(s3023 1)
(s3024 1)
(s3025 1)
(s3026 1)
(s3027 1)
(s3028 1)
(s3029 1)
(s3030 1)
(s3031 1)
(s3032 1)
(s3033 1)
(s3034 1)
(s3035 1)
(s3036 1)
(s3037 1)
(s3038 1)
(s3039 1)
(s3040 1)
(s3041 1)
(s3042 1)
(s3043 1)
(s3044 1)
(s3045 1)
(s3046 1)
(s3047 1)
(s3048 1)
(s3049 1)
(s3050 1)
(s3051 1)
(s3052 1)
(s3053 1)
(s3054 1)
(s3055 1)
(s3056 1)
(s3057 1)
(s3058 1)
(s3059 1)
(s3060 1)
(s3061 1)
(s3062 1)
(s3063 1)
(s3064 1)
(s3065 1)
(s3066 1)
(s3067 1)
(s3068 1)
(s3069 1)
(s3070 1)
(s3071 1)
(s3072 1)
(s3073 1)
(s3074 1)
(s3075 1)
(s3076 1)
(s3077 1)
(s3078 1)
(s3079 1)
(s3080 1)
(s3081 1)
(s3082 1)
(s3083 1)
(s3084 1)
(s3085 1)
(s3086 1)
(s3087 1)
(s3088 1)
(s3089 1)
(s3090 1)
(s3091 1)
(s3092 1)
(s3093 1)
(s3094 1)
(s3095 1)
(s3096 1)
(s3097 1)
(s3098 1)
(s3099 1)
(s3100 1)
(s3101 1)
(s3102 1)
(s3103 1)
(s3104 1)
(s3105 1)
(s3106 1)
(s3107 1)
(s3108 1)
(s3109 1)
(s3110 1)
(s3111 1)
(s3112 1)
(s3113 1)
(s3114 1)
(s3115 1)
(s3116 1)
(s3117 1)
(s3118 1)
(s3119 1)
(s3120 1)
(s3121 1)
(s3122 1)
(s3123 1)
(s3124 1)
(s3125 1)
(s3126 1)
(s3127 1)
(s3128 1)
(s3129 1)
(s3130 1)
(s3131 1)
(s3132 1)
(s3133 1)
(s3134 1)
(s3135 1)
(s3136 1)
(s3137 1)
(s3138 1)
(s3139 1)
(s3140 1)
(s3141 1)
(s3142 1)
(s3143 1)
(s3144 1)
(s3145 1)
(s3146 1)
(s3147 1)
(s3148 1)
(s3149 1)
(s3150 1)
(s3151 1)
(s3152 1)
(s3153 1)
(s3154 1)
(s3155 1)
(s3156 1)
(s3157 1)
(s3158 1)
(s3159 1)
(s3160 1)
(s3161 1)
(s3162 1)
(s3163 1)
(s3164 1)
(s3165 1)
(s3166 1)
(s3167 1)
(s3168 1)
(s3169 1)
(s3170 1)
(s3171 1)
(s3172 1)
(s3173 1)
(s3174 1)
(s3175 1)
(s3176 1)
(s3177 1)
(s3178 1)
(s3179 1)
(s3180 1)
(s3181 1)
(s3182 1)
(s3183 1)
(s3184 1)
(s3185 1)
(s3186 1)
(s3187 1)
(s3188 1)
(s3189 1)
(s3190 1)
(s3191 1)
(s3192 1)
(s3193 1)
(s3194 1)
(s3195 1)
(s3196 1)
(s3197 1)
(s3198 1)
(s3199 1)
(s3200 1)
(s3201 1)
(s3202 1)
(s3203 1)
(s3204 1)
(s3205 1)
(s3206 1)
(s3207 1)
(s3208 1)
(s3209 1)
(s3210 1)
(s3211 1)
(s3212 1)
(s3213 1)
(s3214 1)
(s3215 1)
(s3216 1)
(s3217 1)
(s3218 1)
(s3219 1)
(s3220 1)
(s3221 1)
(s3222 1)
(s3223 1)
(s3224 1)
(s3225 1)
(s3226 1)
(s3227 1)
(s3228 1)
(s3229 1)
(s3230 1)
(s3231 1)
(s3232 1)
(s3233 1)
(s3234 1)
(s3235 1)
(s3236 1)
(s3237 1)
(s3238 1)
(s3239 1)
(s3240 1)
(s3241 1)
(s3242 1)
(s3243 1)
(s3244 1)
(s3245 1)
(s3246 1)
(s3247 1)
(s3248 1)
(s3249 1)
(s3250 1)
(s3251 1)
(s3252 1)
(s3253 1)
(s3254 1)
(s3255 1)
(s3256 1)
(s3257 1)
(s3258 1)
(s3259 1)
(s3260 1)
(s3261 1)
(s3262 1)
(s3263 1)
(s3264 1)
(s3265 1)
(s3266 1)
(s3267 1)
(s3268 1)
(s3269 1)
(s3270 1)
(s3271 1)
(s3272 1)
(s3273 1)
(s3274 1)
(s3275 1)
(s3276 1)
(s3277 1)
(s3278 1)
(s3279 1)
(s3280 1)
(s3281 1)
(s3282 1)
(s3283 1)
(s3284 1)
(s3285 1)
(s3286 1)
(s3287 1)
(s3288 1)
(s3289 1)
(s3290 1)
(s3291 1)
(s3292 1)
(s3293 1)
(s3294 1)
(s3295 1)
(s3296 1)
(s3297 1)
(s3298 1)
(s3299 1)
(s3300 1)
(s3301 1)
(s3302 1)
(s3303 1)
(s3304 1)
(s3305 1)
(s3306 1)
(s3307 1)
(s3308 1)
(s3309 1)
(s3310 1)
(s3311 1)
(s3312 1)
(s3313 1)
(s3314 1)
(s3315 1)
(s3316 1)
(s3317 1)
(s3318 1)
(s3319 1)
(s3320 1)
(s3321 1)
(s3322 1)
(s3323 1)
(s3324 1)
(s3325 1)
(s3326 1)
(s3327 1)
(s3328 1)
(s3329 1)
(s3330 1)
(s3331 1)
(s3332 1)
(s3333 1)
(s3334 1)
(s3335 1)
(s3336 1)
(s3337 1)
(s3338 1)
(s3339 1)
(s3340 1)
(s3341 1)
(s3342 1)
(s3343 1)
(s3344 1)
(s3345 1)
(s3346 1)
(s3347 1)
(s3348 1)
(s3349 1)
(s3350 1)
(s3351 1)
(s3352 1)
(s3353 1)
(s3354 1)
(s3355 1)
(s3356 1)
(s3357 1)
(s3358 1)
(s3359 1)
(s3360 1)
(s3361 1)
(s3362 1)
(s3363 1)
(s3364 1)
(s3365 1)
(s3366 1)
(s3367 1)
(s3368 1)
(s3369 1)
(s3370 1)
(s3371 1)
(s3372 1)
(s3373 1)
(s3374 1)
(s3375 1)
(s3376 1)
(s3377 1)
(s3378 1)
(s3379 1)
(s3380 1)
(s3381 1)
(s3382 1)
(s3383 1)
(s3384 1)
(s3385 1)
(s3386 1)
(s3387 1)
(s3388 1)
(s3389 1)
(s3390 1)
(s3391 1)
(s3392 1)
(s3393 1)
(s3394 1)
(s3395 1)
(s3396 1)
(s3397 1)
(s3398 1)
(s3399 1)
(s3400 1)
(s3401 1)
(s3402 1)
(s3403 1)
(s3404 1)
(s3405 1)
(s3406 1)
(s3407 1)
(s3408 1)
(s3409 1)
(s3410 1)
(s3411 1)
(s3412 1)
(s3413 1)
(s3414 1)
(s3415 1)
(s3416 1)
(s3417 1)
(s3418 1)
(s3419 1)
(s3420 1)
(s3421 1)
(s3422 1)
(s3423 1)
(s3424 1)
(s3425 1)
(s3426 1)
(s3427 1)
(s3428 1)
(s3429 1)
(s3430 1)
(s3431 1)
(s3432 1)
(s3433 1)
(s3434 1)
(s3435 1)
(s3436 1)
(s3437 1)
(s3438 1)
(s3439 1)
(s3440 1)
(s3441 1)
(s3442 1)
(s3443 1)
(s3444 1)
(s3445 1)
(s3446 1)
(s3447 1)
(s3448 1)
(s3449 1)
(s3450 1)
(s3451 1)
(s3452 1)
(s3453 1)
(s3454 1)
(s3455 1)
(s3456 1)
(s3457 1)
(s3458 1)
(s3459 1)
(s3460 1)
(s3461 1)
(s3462 1)
(s3463 1)
(s3464 1)
(s3465 1)
(s3466 1)
(s3467 1)
(s3468 1)
(s3469 1)
(s3470 1)
(s3471 1)
(s3472 1)
(s3473 1)
(s3474 1)
(s3475 1)
(s3476 1)
(s3477 1)
(s3478 1)
(s3479 1)
(s3480 1)
(s3481 1)
(s3482 1)
(s3483 1)
(s3484 1)
(s3485 1)
(s3486 1)
(s3487 1)
(s3488 1)
(s3489 1)
(s3490 1)
(s3491 1)
(s3492 1)
(s3493 1)
(s3494 1)
(s3495 1)
(s3496 1)
(s3497 1)
(s3498 1)
(s3499 1)
(s3500 1)
(s3501 1)
(s3502 1)
(s3503 1)
(s3504 1)
(s3505 1)
(s3506 1)
(s3507 1)
(s3508 1)
(s3509 1)
(s3510 1)
(s3511 1)
(s3512 1)
(s3513 1)
(s3514 1)
(s3515 1)
(s3516 1)
(s3517 1)
(s3518 1)
(s3519 1)
(s3520 1)
(s3521 1)
(s3522 1)
(s3523 1)
(s3524 1)
(s3525 1)
(s3526 1)
(s3527 1)
(s3528 1)
(s3529 1)
(s3530 1)
(s3531 1)
(s3532 1)
(s3533 1)
(s3534 1)
(s3535 1)
(s3536 1)
(s3537 1)
(s3538 1)
(s3539 1)
(s3540 1)
(s3541 1)
(s3542 1)
(s3543 1)
(s3544 1)
(s3545 1)
(s3546 1)
(s3547 1)
(s3548 1)
(s3549 1)
(s3550 1)
(s3551 1)
(s3552 1)
(s3553 1)
(s3554 1)
(s3555 1)
(s3556 1)
(s3557 1)
(s3558 1)
(s3559 1)
(s3560 1)
(s3561 1)
(s3562 1)
(s3563 1)
(s3564 1)
(s3565 1)
(s3566 1)
(s3567 1)
(s3568 1)
(s3569 1)
(s3570 1)
(s3571 1)
(s3572 1)
(s3573 1)
(s3574 1)
(s3575 1)
(s3576 1)
(s3577 1)
(s3578 1)
(s3579 1)
(s3580 1)
(s3581 1)
(s3582 1)
(s3583 1)
(s3584 1)
(s3585 1)
(s3586 1)
(s3587 1)
(s3588 1)
(s3589 1)
(s3590 1)
(s3591 1)
(s3592 1)
(s3593 1)
(s3594 1)
(s3595 1)
(s3596 1)
(s3597 1)
(s3598 1)
(s3599 1)
(s3600 1)
(s3601 1)
(s3602 1)
(s3603 1)
(s3604 1)
(s3605 1)
(s3606 1)
(s3607 1)
(s3608 1)
(s3609 1)
(s3610 1)
(s3611 1)
(s3612 1)
(s3613 1)
(s3614 1)
(s3615 1)
(s3616 1)
(s3617 1)
(s3618 1)
(s3619 1)
(s3620 1)
(s3621 1)
(s3622 1)
(s3623 1)
(s3624 1)
(s3625 1)
(s3626 1)
(s3627 1)
(s3628 1)
(s3629 1)
(s3630 1)
(s3631 1)
(s3632 1)
(s3633 1)
(s3634 1)
(s3635 1)
(s3636 1)
(s3637 1)
(s3638 1)
(s3639 1)
(s3640 1)
(s3641 1)
(s3642 1)
(s3643 1)
(s3644 1)
(s3645 1)
(s3646 1)
(s3647 1)
(s3648 1)
(s3649 1)
(s3650 1)
(s3651 1)
(s3652 1)
(s3653 1)
(s3654 1)
(s3655 1)
(s3656 1)
(s3657 1)
(s3658 1)
(s3659 1)
(s3660 1)
(s3661 1)
(s3662 1)
(s3663 1)
(s3664 1)
(s3665 1)
(s3666 1)
(s3667 1)
(s3668 1)
(s3669 1)
(s3670 1)
(s3671 1)
(s3672 1)
(s3673 1)
(s3674 1)
(s3675 1)
(s3676 1)
(s3677 1)
(s3678 1)
(s3679 1)
(s3680 1)
(s3681 1)
(s3682 1)
(s3683 1)
(s3684 1)
(s3685 1)
(s3686 1)
(s3687 1)
(s3688 1)
(s3689 1)
(s3690 1)
(s3691 1)
(s3692 1)
(s3693 1)
(s3694 1)
(s3695 1)
(s3696 1)
(s3697 1)
(s3698 1)
(s3699 1)
(s3700 1)
(s3701 1)
(s3702 1)
(s3703 1)
(s3704 1)
(s3705 1)
(s3706 1)
(s3707 1)
(s3708 1)
(s3709 1)
(s3710 1)
(s3711 1)
(s3712 1)
(s3713 1)
(s3714 1)
(s3715 1)
(s3716 1)
(s3717 1)
(s3718 1)
(s3719 1)
(s3720 1)
(s3721 1)
(s3722 1)
(s3723 1)
(s3724 1)
(s3725 1)
(s3726 1)
(s3727 1)
(s3728 1)
(s3729 1)
(s3730 1)
(s3731 1)
(s3732 1)
(s3733 1)
(s3734 1)
(s3735 1)
(s3736 1)
(s3737 1)
(s3738 1)
(s3739 1)
(s3740 1)
(s3741 1)
(s3742 1)
(s3743 1)
(s3744 1)
(s3745 1)
(s3746 1)
(s3747 1)
(s3748 1)
(s3749 1)
(s3750 1)
(s3751 1)
(s3752 1)
(s3753 1)
(s3754 1)
(s3755 1)
(s3756 1)
(s3757 1)
(s3758 1)
(s3759 1)
(s3760 1)
(s3761 1)
(s3762 1)
(s3763 1)
(s3764 1)
(s3765 1)
(s3766 1)
(s3767 1)
(s3768 1)
(s3769 1)
(s3770 1)
(s3771 1)
(s3772 1)
(s3773 1)
(s3774 1)
(s3775 1)
(s3776 1)
(s3777 1)
(s3778 1)
(s3779 1)
(s3780 1)
(s3781 1)
(s3782 1)
(s3783 1)
(s3784 1)
(s3785 1)
(s3786 1)
(s3787 1)
(s3788 1)
(s3789 1)
(s3790 1)
(s3791 1)
(s3792 1)
(s3793 1)
(s3794 1)
(s3795 1)
(s3796 1)
(s3797 1)
(s3798 1)
(s3799 1)
(s3800 1)
(s3801 1)
(s3802 1)
(s3803 1)
(s3804 1)
(s3805 1)
(s3806 1)
(s3807 1)
(s3808 1)
(s3809 1)
(s3810 1)
(s3811 1)
(s3812 1)
(s3813 1)
(s3814 1)
(s3815 1)
(s3816 1)
(s3817 1)
(s3818 1)
(s3819 1)
(s3820 1)
(s3821 1)
(s3822 1)
(s3823 1)
(s3824 1)
(s3825 1)
(s3826 1)
(s3827 1)
(s3828 1)
(s3829 1)
(s3830 1)
(s3831 1)
(s3832 1)
(s3833 1)
(s3834 1)
(s3835 1)
(s3836 1)
(s3837 1)
(s3838 1)
(s3839 1)
(s3840 1)
(s3841 1)
(s3842 1)
(s3843 1)
(s3844 1)
(s3845 1)
(s3846 1)
(s3847 1)
(s3848 1)
(s3849 1)
(s3850 1)
(s3851 1)
(s3852 1)
(s3853 1)
(s3854 1)
(s3855 1)
(s3856 1)
(s3857 1)
(s3858 1)
(s3859 1)
(s3860 1)
(s3861 1)
(s3862 1)
(s3863 1)
(s3864 1)
(s3865 1)
(s3866 1)
(s3867 1)
(s3868 1)
(s3869 1)
(s3870 1)
(s3871 1)
(s3872 1)
(s3873 1)
(s3874 1)
(s3875 1)
(s3876 1)
(s3877 1)
(s3878 1)
(s3879 1)
(s3880 1)
(s3881 1)
(s3882 1)
(s3883 1)
(s3884 1)
(s3885 1)
(s3886 1)
(s3887 1)
(s3888 1)
(s3889 1)
(s3890 1)
(s3891 1)
(s3892 1)
(s3893 1)
(s3894 1)
(s3895 1)
(s3896 1)
(s3897 1)
(s3898 1)
(s3899 1)
(s3900 1)
(s3901 1)
(s3902 1)
(s3903 1)
(s3904 1)
(s3905 1)
(s3906 1)
(s3907 1)
(s3908 1)
(s3909 1)
(s3910 1)
(s3911 1)
(s3912 1)
(s3913 1)
(s3914 1)
(s3915 1)
(s3916 1)
(s3917 1)
(s3918 1)
(s3919 1)
(s3920 1)
(s3921 1)
(s3922 1)
(s3923 1)
(s3924 1)
(s3925 1)
(s3926 1)
(s3927 1)
(s3928 1)
(s3929 1)
(s3930 1)
(s3931 1)
(s3932 1)
(s3933 1)
(s3934 1)
(s3935 1)
(s3936 1)
(s3937 1)
(s3938 1)
(s3939 1)
(s3940 1)
(s3941 1)
(s3942 1)
(s3943 1)
(s3944 1)
(s3945 1)
(s3946 1)
(s3947 1)
(s3948 1)
(s3949 1)
(s3950 1)
(s3951 1)
(s3952 1)
(s3953 1)
(s3954 1)
(s3955 1)
(s3956 1)
(s3957 1)
(s3958 1)
(s3959 1)
(s3960 1)
(s3961 1)
(s3962 1)
(s3963 1)
(s3964 1)
(s3965 1)
(s3966 1)
(s3967 1)
(s3968 1)
(s3969 1)
(s3970 1)
(s3971 1)
(s3972 1)
(s3973 1)
(s3974 1)
(s3975 1)
(s3976 1)
(s3977 1)
(s3978 1)
(s3979 1)
(s3980 1)
(s3981 1)
(s3982 1)
(s3983 1)
(s3984 1)
(s3985 1)
(s3986 1)
(s3987 1)
(s3988 1)
(s3989 1)
(s3990 1)
(s3991 1)
(s3992 1)
(s3993 1)
(s3994 1)
(s3995 1)
(s3996 1)
(s3997 1)
(s3998 1)
(s3999 1)
(s4000 1)
(s4001 1)
(s4002 1)
(s4003 1)
(s4004 1)
(s4005 1)
(s4006 1)
(s4007 1)
(s4008 1)
(s4009 1)
(s4010 1)
(s4011 1)
(s4012 1)
(s4013 1)
(s4014 1)
(s4015 1)
(s4016 1)
(s4017 1)
(s4018 1)
(s4019 1)
(s4020 1)
(s4021 1)
(s4022 1)
(s4023 1)
(s4024 1)
(s4025 1)
(s4026 1)
(s4027 1)
(s4028 1)
(s4029 1)
(s4030 1)
(s4031 1)
(s4032 1)
(s4033 1)
(s4034 1)
(s4035 1)
(s4036 1)
(s4037 1)
(s4038 1)
(s4039 1)
(s4040 1)
(s4041 1)
(s4042 1)
(s4043 1)
(s4044 1)
(s4045 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30237 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 0/8300 constraints, Known Traps: 0/0 constraints]
After SMT, in 69361ms problems are : Problem set: 0 solved, 8300 unsolved
Search for dead transitions found 0 dead transitions in 69450ms
Finished structural reductions in LTL mode , in 1 iterations and 72025 ms. Remains : 6600/6600 places, 10100/10100 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND p0 (NOT p1))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 1 factoid took 116 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 140 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
RANDOM walk for 332 steps (0 resets) in 56 ms. (5 steps per ms) remains 0/2 properties
Knowledge obtained : [(AND p0 (NOT p1))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0)), (F (NOT p0)), (F p1)]
Knowledge based reduction with 1 factoid took 223 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 195 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Stuttering acceptance computed with spot in 202 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Stuttering acceptance computed with spot in 192 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Product exploration explored 100000 steps with 0 reset in 1582 ms.
Product exploration explored 100000 steps with 0 reset in 1781 ms.
Applying partial POR strategy [true, true, false, false]
Stuttering acceptance computed with spot in 200 ms :[(AND (NOT p0) p1), p1, (AND (NOT p0) p1), (AND (NOT p0) p1)]
Support contains 4850 out of 6600 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Graph (trivial) has 1300 edges and 6600 vertex of which 300 / 6600 are part of one of the 50 SCC in 8 ms
Free SCC test removed 250 places
Ensure Unique test removed 250 transitions
Reduce isomorphic transitions removed 250 transitions.
Performed 400 Post agglomeration using F-continuation condition.Transition count delta: 0
Iterating post reduction 0 with 400 rules applied. Total rules applied 401 place count 6350 transition count 9850
Performed 600 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 1000 places in 2 ms
Iterating global reduction 1 with 600 rules applied. Total rules applied 1001 place count 6350 transition count 9850
Discarding 600 places :
Symmetric choice reduction at 1 with 600 rule applications. Total rules 1601 place count 5750 transition count 9250
Deduced a syphon composed of 400 places in 2 ms
Iterating global reduction 1 with 600 rules applied. Total rules applied 2201 place count 5750 transition count 9250
Deduced a syphon composed of 400 places in 2 ms
Applied a total of 2201 rules in 1131 ms. Remains 5750 /6600 variables (removed 850) and now considering 9250/10100 (removed 850) transitions.
[2024-06-01 11:15:05] [INFO ] Redundant transitions in 991 ms returned []
Running 7450 sub problems to find dead transitions.
[2024-06-01 11:15:05] [INFO ] Flow matrix only has 9201 transitions (discarded 49 similar events)
// Phase 1: matrix 9201 rows 5750 cols
[2024-06-01 11:15:05] [INFO ] Computed 50 invariants in 64 ms
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 5700/14951 variables, and 0 constraints, problems are : Problem set: 0 solved, 7450 unsolved in 30176 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/5750 constraints, PredecessorRefiner: 7450/7450 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 7450 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 5700/14951 variables, and 0 constraints, problems are : Problem set: 0 solved, 7450 unsolved in 30185 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/5750 constraints, PredecessorRefiner: 0/7450 constraints, Known Traps: 0/0 constraints]
After SMT, in 67300ms problems are : Problem set: 0 solved, 7450 unsolved
Search for dead transitions found 0 dead transitions in 67379ms
Starting structural reductions in SI_LTL mode, iteration 1 : 5750/6600 places, 9250/10100 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 69529 ms. Remains : 5750/6600 places, 9250/10100 transitions.
Support contains 4850 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Applied a total of 0 rules in 517 ms. Remains 6600 /6600 variables (removed 0) and now considering 10100/10100 (removed 0) transitions.
// Phase 1: matrix 10100 rows 6600 cols
[2024-06-01 11:16:13] [INFO ] Computed 50 invariants in 46 ms
[2024-06-01 11:16:15] [INFO ] Implicit Places using invariants in 2006 ms returned []
Implicit Place search using SMT only with invariants took 2007 ms to find 0 implicit places.
Running 8300 sub problems to find dead transitions.
[2024-06-01 11:16:15] [INFO ] Invariant cache hit.
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30215 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 8300/8300 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 8300 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/6550 variables, 6550/6550 constraints. Problems are: Problem set: 0 solved, 8300 unsolved
(s5132 1timeout
^^^^^^^^
(error "Invalid token: 1timeout")
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1582 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1670 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1758 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1846 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1934 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2022 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 1)
(s2090 1)
(s2091 1)
(s2092 1)
(s2093 1)
(s2094 1)
(s2095 1)
(s2096 1)
(s2097 1)
(s2098 1)
(s2099 1)
(s2100 1)
(s2101 1)
(s2102 1)
(s2103 1)
(s2104 1)
(s2105 1)
(s2106 1)
(s2107 1)
(s2108 1)
(s2109 1)
(s2110 1)
(s2111 1)
(s2112 1)
(s2113 1)
(s2114 1)
(s2115 1)
(s2116 1)
(s2117 1)
(s2118 1)
(s2119 1)
(s2120 1)
(s2121 1)
(s2122 1)
(s2123 1)
(s2124 1)
(s2125 1)
(s2126 1)
(s2127 1)
(s2128 1)
(s2129 1)
(s2130 1)
(s2131 1)
(s2132 1)
(s2133 1)
(s2134 1)
(s2135 1)
(s2136 1)
(s2137 1)
(s2138 1)
(s2139 1)
(s2140 1)
(s2141 1)
(s2142 1)
(s2143 1)
(s2144 1)
(s2145 1)
(s2146 1)
(s2147 1)
(s2148 1)
(s2149 1)
(s2150 1)
(s2151 1)
(s2152 1)
(s2153 1)
(s2154 1)
(s2155 1)
(s2156 1)
(s2157 1)
(s2158 1)
(s2159 1)
(s2160 1)
(s2161 1)
(s2162 1)
(s2163 1)
(s2164 1)
(s2165 1)
(s2166 1)
(s2167 1)
(s2168 1)
(s2169 1)
(s2170 1)
(s2171 1)
(s2172 1)
(s2173 1)
(s2174 1)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2198 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2286 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2374 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2462 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2550 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 1)
(s2577 1)
(s2578 1)
(s2579 1)
(s2580 1)
(s2581 1)
(s2582 1)
(s2583 1)
(s2584 1)
(s2585 1)
(s2586 1)
(s2587 1)
(s2588 1)
(s2589 1)
(s2590 1)
(s2591 1)
(s2592 1)
(s2593 1)
(s2594 1)
(s2595 1)
(s2596 1)
(s2597 1)
(s2598 1)
(s2599 1)
(s2600 1)
(s2601 1)
(s2602 1)
(s2603 1)
(s2604 1)
(s2605 1)
(s2606 1)
(s2607 1)
(s2608 1)
(s2609 1)
(s2610 1)
(s2611 1)
(s2612 1)
(s2613 1)
(s2614 1)
(s2615 1)
(s2616 1)
(s2617 1)
(s2618 1)
(s2619 1)
(s2620 1)
(s2621 1)
(s2622 1)
(s2623 1)
(s2624 1)
(s2625 1)
(s2626 1)
(s2627 1)
(s2628 1)
(s2629 1)
(s2630 1)
(s2631 1)
(s2632 1)
(s2633 1)
(s2634 1)
(s2635 1)
(s2636 1)
(s2637 1)
(s2638 1)
(s2639 1)
(s2640 1)
(s2641 1)
(s2642 1)
(s2643 1)
(s2644 1)
(s2645 1)
(s2646 1)
(s2647 1)
(s2648 1)
(s2649 1)
(s2650 1)
(s2651 1)
(s2652 1)
(s2653 1)
(s2654 1)
(s2655 1)
(s2656 1)
(s2657 1)
(s2658 1)
(s2659 1)
(s2660 1)
(s2661 1)
(s2662 1)
(s2663 1)
(s2664 1)
(s2665 1)
(s2666 1)
(s2667 1)
(s2668 1)
(s2669 1)
(s2670 1)
(s2671 1)
(s2672 1)
(s2673 1)
(s2674 1)
(s2675 1)
(s2676 1)
(s2677 1)
(s2678 1)
(s2679 1)
(s2680 1)
(s2681 1)
(s2682 1)
(s2683 1)
(s2684 1)
(s2685 1)
(s2686 1)
(s2687 1)
(s2688 1)
(s2689 1)
(s2690 1)
(s2691 1)
(s2692 1)
(s2693 1)
(s2694 1)
(s2695 1)
(s2696 1)
(s2697 1)
(s2698 1)
(s2699 1)
(s2700 1)
(s2701 1)
(s2702 1)
(s2703 1)
(s2704 1)
(s2705 1)
(s2706 1)
(s2707 1)
(s2708 1)
(s2709 1)
(s2710 1)
(s2711 1)
(s2712 1)
(s2713 1)
(s2714 1)
(s2715 1)
(s2716 1)
(s2717 1)
(s2718 1)
(s2719 1)
(s2720 1)
(s2721 1)
(s2722 1)
(s2723 1)
(s2724 1)
(s2725 1)
(s2726 1)
(s2727 1)
(s2728 1)
(s2729 1)
(s2730 1)
(s2731 1)
(s2732 1)
(s2733 1)
(s2734 1)
(s2735 1)
(s2736 1)
(s2737 1)
(s2738 1)
(s2739 1)
(s2740 1)
(s2741 1)
(s2742 1)
(s2743 1)
(s2744 1)
(s2745 1)
(s2746 1)
(s2747 1)
(s2748 1)
(s2749 1)
(s2750 1)
(s2751 1)
(s2752 1)
(s2753 1)
(s2754 1)
(s2755 1)
(s2756 1)
(s2757 1)
(s2758 1)
(s2759 1)
(s2760 1)
(s2761 1)
(s2762 1)
(s2763 1)
(s2764 1)
(s2765 1)
(s2766 1)
(s2767 1)
(s2768 1)
(s2769 1)
(s2770 1)
(s2771 1)
(s2772 1)
(s2773 1)
(s2774 1)
(s2775 1)
(s2776 1)
(s2777 1)
(s2778 1)
(s2779 1)
(s2780 1)
(s2781 1)
(s2782 1)
(s2783 1)
(s2784 1)
(s2785 1)
(s2786 1)
(s2787 1)
(s2788 1)
(s2789 1)
(s2790 1)
(s2791 1)
(s2792 1)
(s2793 1)
(s2794 1)
(s2795 1)
(s2796 1)
(s2797 1)
(s2798 1)
(s2799 1)
(s2800 1)
(s2801 1)
(s2802 1)
(s2803 1)
(s2804 1)
(s2805 1)
(s2806 1)
(s2807 1)
(s2808 1)
(s2809 1)
(s2810 1)
(s2811 1)
(s2812 1)
(s2813 1)
(s2814 1)
(s2815 1)
(s2816 1)
(s2817 1)
(s2818 1)
(s2819 1)
(s2820 1)
(s2821 1)
(s2822 1)
(s2823 1)
(s2824 1)
(s2825 1)
(s2826 1)
(s2827 1)
(s2828 1)
(s2829 1)
(s2830 1)
(s2831 1)
(s2832 1)
(s2833 1)
(s2834 1)
(s2835 1)
(s2836 1)
(s2837 1)
(s2838 1)
(s2839 1)
(s2840 1)
(s2841 1)
(s2842 1)
(s2843 1)
(s2844 1)
(s2845 1)
(s2846 1)
(s2847 1)
(s2848 1)
(s2849 1)
(s2850 1)
(s2851 1)
(s2852 1)
(s2853 1)
(s2854 1)
(s2855 1)
(s2856 1)
(s2857 1)
(s2858 1)
(s2859 1)
(s2860 1)
(s2861 1)
(s2862 1)
(s2863 1)
(s2864 1)
(s2865 1)
(s2866 1)
(s2867 1)
(s2868 1)
(s2869 1)
(s2870 1)
(s2871 1)
(s2872 1)
(s2873 1)
(s2874 1)
(s2875 1)
(s2876 1)
(s2877 1)
(s2878 1)
(s2879 1)
(s2880 1)
(s2881 1)
(s2882 1)
(s2883 1)
(s2884 1)
(s2885 1)
(s2886 1)
(s2887 1)
(s2888 1)
(s2889 1)
(s2890 1)
(s2891 1)
(s2892 1)
(s2893 1)
(s2894 1)
(s2895 1)
(s2896 1)
(s2897 1)
(s2898 1)
(s2899 1)
(s2900 1)
(s2901 1)
(s2902 1)
(s2903 1)
(s2904 1)
(s2905 1)
(s2906 1)
(s2907 1)
(s2908 1)
(s2909 1)
(s2910 1)
(s2911 1)
(s2912 1)
(s2913 1)
(s2914 1)
(s2915 1)
(s2916 1)
(s2917 1)
(s2918 1)
(s2919 1)
(s2920 1)
(s2921 1)
(s2922 1)
(s2923 1)
(s2924 1)
(s2925 1)
(s2926 1)
(s2927 1)
(s2928 1)
(s2929 1)
(s2930 1)
(s2931 1)
(s2932 1)
(s2933 1)
(s2934 1)
(s2935 1)
(s2936 1)
(s2937 1)
(s2938 1)
(s2939 1)
(s2940 1)
(s2941 1)
(s2942 1)
(s2943 1)
(s2944 1)
(s2945 1)
(s2946 1)
(s2947 1)
(s2948 1)
(s2949 1)
(s2950 1)
(s2951 1)
(s2952 1)
(s2953 1)
(s2954 1)
(s2955 1)
(s2956 1)
(s2957 1)
(s2958 1)
(s2959 1)
(s2960 1)
(s2961 1)
(s2962 1)
(s2963 1)
(s2964 1)
(s2965 1)
(s2966 1)
(s2967 1)
(s2968 1)
(s2969 1)
(s2970 1)
(s2971 1)
(s2972 1)
(s2973 1)
(s2974 1)
(s2975 1)
(s2976 1)
(s2977 1)
(s2978 1)
(s2979 1)
(s2980 1)
(s2981 1)
(s2982 1)
(s2983 1)
(s2984 1)
(s2985 1)
(s2986 1)
(s2987 1)
(s2988 1)
(s2989 1)
(s2990 1)
(s2991 1)
(s2992 1)
(s2993 1)
(s2994 1)
(s2995 1)
(s2996 1)
(s2997 1)
(s2998 1)
(s2999 1)
(s3000 1)
(s3001 1)
(s3002 1)
(s3003 1)
(s3004 1)
(s3005 1)
(s3006 1)
(s3007 1)
(s3008 1)
(s3009 1)
(s3010 1)
(s3011 1)
(s3012 1)
(s3013 1)
(s3014 1)
(s3015 1)
(s3016 1)
(s3017 1)
(s3018 1)
(s3019 1)
(s3020 1)
(s3021 1)
(s3022 1)
(s3023 1)
(s3024 1)
(s3025 1)
(s3026 1)
(s3027 1)
(s3028 1)
(s3029 1)
(s3030 1)
(s3031 1)
(s3032 1)
(s3033 1)
(s3034 1)
(s3035 1)
(s3036 1)
(s3037 1)
(s3038 1)
(s3039 1)
(s3040 1)
(s3041 1)
(s3042 1)
(s3043 1)
(s3044 1)
(s3045 1)
(s3046 1)
(s3047 1)
(s3048 1)
(s3049 1)
(s3050 1)
(s3051 1)
(s3052 1)
(s3053 1)
(s3054 1)
(s3055 1)
(s3056 1)
(s3057 1)
(s3058 1)
(s3059 1)
(s3060 1)
(s3061 1)
(s3062 1)
(s3063 1)
(s3064 1)
(s3065 1)
(s3066 1)
(s3067 1)
(s3068 1)
(s3069 1)
(s3070 1)
(s3071 1)
(s3072 1)
(s3073 1)
(s3074 1)
(s3075 1)
(s3076 1)
(s3077 1)
(s3078 1)
(s3079 1)
(s3080 1)
(s3081 1)
(s3082 1)
(s3083 1)
(s3084 1)
(s3085 1)
(s3086 1)
(s3087 1)
(s3088 1)
(s3089 1)
(s3090 1)
(s3091 1)
(s3092 1)
(s3093 1)
(s3094 1)
(s3095 1)
(s3096 1)
(s3097 1)
(s3098 1)
(s3099 1)
(s3100 1)
(s3101 1)
(s3102 1)
(s3103 1)
(s3104 1)
(s3105 1)
(s3106 1)
(s3107 1)
(s3108 1)
(s3109 1)
(s3110 1)
(s3111 1)
(s3112 1)
(s3113 1)
(s3114 1)
(s3115 1)
(s3116 1)
(s3117 1)
(s3118 1)
(s3119 1)
(s3120 1)
(s3121 1)
(s3122 1)
(s3123 1)
(s3124 1)
(s3125 1)
(s3126 1)
(s3127 1)
(s3128 1)
(s3129 1)
(s3130 1)
(s3131 1)
(s3132 1)
(s3133 1)
(s3134 1)
(s3135 1)
(s3136 1)
(s3137 1)
(s3138 1)
(s3139 1)
(s3140 1)
(s3141 1)
(s3142 1)
(s3143 1)
(s3144 1)
(s3145 1)
(s3146 1)
(s3147 1)
(s3148 1)
(s3149 1)
(s3150 1)
(s3151 1)
(s3152 1)
(s3153 1)
(s3154 1)
(s3155 1)
(s3156 1)
(s3157 1)
(s3158 1)
(s3159 1)
(s3160 1)
(s3161 1)
(s3162 1)
(s3163 1)
(s3164 1)
(s3165 1)
(s3166 1)
(s3167 1)
(s3168 1)
(s3169 1)
(s3170 1)
(s3171 1)
(s3172 1)
(s3173 1)
(s3174 1)
(s3175 1)
(s3176 1)
(s3177 1)
(s3178 1)
(s3179 1)
(s3180 1)
(s3181 1)
(s3182 1)
(s3183 1)
(s3184 1)
(s3185 1)
(s3186 1)
(s3187 1)
(s3188 1)
(s3189 1)
(s3190 1)
(s3191 1)
(s3192 1)
(s3193 1)
(s3194 1)
(s3195 1)
(s3196 1)
(s3197 1)
(s3198 1)
(s3199 1)
(s3200 1)
(s3201 1)
(s3202 1)
(s3203 1)
(s3204 1)
(s3205 1)
(s3206 1)
(s3207 1)
(s3208 1)
(s3209 1)
(s3210 1)
(s3211 1)
(s3212 1)
(s3213 1)
(s3214 1)
(s3215 1)
(s3216 1)
(s3217 1)
(s3218 1)
(s3219 1)
(s3220 1)
(s3221 1)
(s3222 1)
(s3223 1)
(s3224 1)
(s3225 1)
(s3226 1)
(s3227 1)
(s3228 1)
(s3229 1)
(s3230 1)
(s3231 1)
(s3232 1)
(s3233 1)
(s3234 1)
(s3235 1)
(s3236 1)
(s3237 1)
(s3238 1)
(s3239 1)
(s3240 1)
(s3241 1)
(s3242 1)
(s3243 1)
(s3244 1)
(s3245 1)
(s3246 1)
(s3247 1)
(s3248 1)
(s3249 1)
(s3250 1)
(s3251 1)
(s3252 1)
(s3253 1)
(s3254 1)
(s3255 1)
(s3256 1)
(s3257 1)
(s3258 1)
(s3259 1)
(s3260 1)
(s3261 1)
(s3262 1)
(s3263 1)
(s3264 1)
(s3265 1)
(s3266 1)
(s3267 1)
(s3268 1)
(s3269 1)
(s3270 1)
(s3271 1)
(s3272 1)
(s3273 1)
(s3274 1)
(s3275 1)
(s3276 1)
(s3277 1)
(s3278 1)
(s3279 1)
(s3280 1)
(s3281 1)
(s3282 1)
(s3283 1)
(s3284 1)
(s3285 1)
(s3286 1)
(s3287 1)
(s3288 1)
(s3289 1)
(s3290 1)
(s3291 1)
(s3292 1)
(s3293 1)
(s3294 1)
(s3295 1)
(s3296 1)
(s3297 1)
(s3298 1)
(s3299 1)
(s3300 1)
(s3301 1)
(s3302 1)
(s3303 1)
(s3304 1)
(s3305 1)
(s3306 1)
(s3307 1)
(s3308 1)
(s3309 1)
(s3310 1)
(s3311 1)
(s3312 1)
(s3313 1)
(s3314 1)
(s3315 1)
(s3316 1)
(s3317 1)
(s3318 1)
(s3319 1)
(s3320 1)
(s3321 1)
(s3322 1)
(s3323 1)
(s3324 1)
(s3325 1)
(s3326 1)
(s3327 1)
(s3328 1)
(s3329 1)
(s3330 1)
(s3331 1)
(s3332 1)
(s3333 1)
(s3334 1)
(s3335 1)
(s3336 1)
(s3337 1)
(s3338 1)
(s3339 1)
(s3340 1)
(s3341 1)
(s3342 1)
(s3343 1)
(s3344 1)
(s3345 1)
(s3346 1)
(s3347 1)
(s3348 1)
(s3349 1)
(s3350 1)
(s3351 1)
(s3352 1)
(s3353 1)
(s3354 1)
(s3355 1)
(s3356 1)
(s3357 1)
(s3358 1)
(s3359 1)
(s3360 1)
(s3361 1)
(s3362 1)
(s3363 1)
(s3364 1)
(s3365 1)
(s3366 1)
(s3367 1)
(s3368 1)
(s3369 1)
(s3370 1)
(s3371 1)
(s3372 1)
(s3373 1)
(s3374 1)
(s3375 1)
(s3376 1)
(s3377 1)
(s3378 1)
(s3379 1)
(s3380 1)
(s3381 1)
(s3382 1)
(s3383 1)
(s3384 1)
(s3385 1)
(s3386 1)
(s3387 1)
(s3388 1)
(s3389 1)
(s3390 1)
(s3391 1)
(s3392 1)
(s3393 1)
(s3394 1)
(s3395 1)
(s3396 1)
(s3397 1)
(s3398 1)
(s3399 1)
(s3400 1)
(s3401 1)
(s3402 1)
(s3403 1)
(s3404 1)
(s3405 1)
(s3406 1)
(s3407 1)
(s3408 1)
(s3409 1)
(s3410 1)
(s3411 1)
(s3412 1)
(s3413 1)
(s3414 1)
(s3415 1)
(s3416 1)
(s3417 1)
(s3418 1)
(s3419 1)
(s3420 1)
(s3421 1)
(s3422 1)
(s3423 1)
(s3424 1)
(s3425 1)
(s3426 1)
(s3427 1)
(s3428 1)
(s3429 1)
(s3430 1)
(s3431 1)
(s3432 1)
(s3433 1)
(s3434 1)
(s3435 1)
(s3436 1)
(s3437 1)
(s3438 1)
(s3439 1)
(s3440 1)
(s3441 1)
(s3442 1)
(s3443 1)
(s3444 1)
(s3445 1)
(s3446 1)
(s3447 1)
(s3448 1)
(s3449 1)
(s3450 1)
(s3451 1)
(s3452 1)
(s3453 1)
(s3454 1)
(s3455 1)
(s3456 1)
(s3457 1)
(s3458 1)
(s3459 1)
(s3460 1)
(s3461 1)
(s3462 1)
(s3463 1)
(s3464 1)
(s3465 1)
(s3466 1)
(s3467 1)
(s3468 1)
(s3469 1)
(s3470 1)
(s3471 1)
(s3472 1)
(s3473 1)
(s3474 1)
(s3475 1)
(s3476 1)
(s3477 1)
(s3478 1)
(s3479 1)
(s3480 1)
(s3481 1)
(s3482 1)
(s3483 1)
(s3484 1)
(s3485 1)
(s3486 1)
(s3487 1)
(s3488 1)
(s3489 1)
(s3490 1)
(s3491 1)
(s3492 1)
(s3493 1)
(s3494 1)
(s3495 1)
(s3496 1)
(s3497 1)
(s3498 1)
(s3499 1)
(s3500 1)
(s3501 1)
(s3502 1)
(s3503 1)
(s3504 1)
(s3505 1)
(s3506 1)
(s3507 1)
(s3508 1)
(s3509 1)
(s3510 1)
(s3511 1)
(s3512 1)
(s3513 1)
(s3514 1)
(s3515 1)
(s3516 1)
(s3517 1)
(s3518 1)
(s3519 1)
(s3520 1)
(s3521 1)
(s3522 1)
(s3523 1)
(s3524 1)
(s3525 1)
(s3526 1)
(s3527 1)
(s3528 1)
(s3529 1)
(s3530 1)
(s3531 1)
(s3532 1)
(s3533 1)
(s3534 1)
(s3535 1)
(s3536 1)
(s3537 1)
(s3538 1)
(s3539 1)
(s3540 1)
(s3541 1)
(s3542 1)
(s3543 1)
(s3544 1)
(s3545 1)
(s3546 1)
(s3547 1)
(s3548 1)
(s3549 1)
(s3550 1)
(s3551 1)
(s3552 1)
(s3553 1)
(s3554 1)
(s3555 1)
(s3556 1)
(s3557 1)
(s3558 1)
(s3559 1)
(s3560 1)
(s3561 1)
(s3562 1)
(s3563 1)
(s3564 1)
(s3565 1)
(s3566 1)
(s3567 1)
(s3568 1)
(s3569 1)
(s3570 1)
(s3571 1)
(s3572 1)
(s3573 1)
(s3574 1)
(s3575 1)
(s3576 1)
(s3577 1)
(s3578 1)
(s3579 1)
(s3580 1)
(s3581 1)
(s3582 1)
(s3583 1)
(s3584 1)
(s3585 1)
(s3586 1)
(s3587 1)
(s3588 1)
(s3589 1)
(s3590 1)
(s3591 1)
(s3592 1)
(s3593 1)
(s3594 1)
(s3595 1)
(s3596 1)
(s3597 1)
(s3598 1)
(s3599 1)
(s3600 1)
(s3601 1)
(s3602 1)
(s3603 1)
(s3604 1)
(s3605 1)
(s3606 1)
(s3607 1)
(s3608 1)
(s3609 1)
(s3610 1)
(s3611 1)
(s3612 1)
(s3613 1)
(s3614 1)
(s3615 1)
(s3616 1)
(s3617 1)
(s3618 1)
(s3619 1)
(s3620 1)
(s3621 1)
(s3622 1)
(s3623 1)
(s3624 1)
(s3625 1)
(s3626 1)
(s3627 1)
(s3628 1)
(s3629 1)
(s3630 1)
(s3631 1)
(s3632 1)
(s3633 1)
(s3634 1)
(s3635 1)
(s3636 1)
(s3637 1)
(s3638 1)
(s3639 1)
(s3640 1)
(s3641 1)
(s3642 1)
(s3643 1)
(s3644 1)
(s3645 1)
(s3646 1)
(s3647 1)
(s3648 1)
(s3649 1)
(s3650 1)
(s3651 1)
(s3652 1)
(s3653 1)
(s3654 1)
(s3655 1)
(s3656 1)
(s3657 1)
(s3658 1)
(s3659 1)
(s3660 1)
(s3661 1)
(s3662 1)
(s3663 1)
(s3664 1)
(s3665 1)
(s3666 1)
(s3667 1)
(s3668 1)
(s3669 1)
(s3670 1)
(s3671 1)
(s3672 1)
(s3673 1)
(s3674 1)
(s3675 1)
(s3676 1)
(s3677 1)
(s3678 1)
(s3679 1)
(s3680 1)
(s3681 1)
(s3682 1)
(s3683 1)
(s3684 1)
(s3685 1)
(s3686 1)
(s3687 1)
(s3688 1)
(s3689 1)
(s3690 1)
(s3691 1)
(s3692 1)
(s3693 1)
(s3694 1)
(s3695 1)
(s3696 1)
(s3697 1)
(s3698 1)
(s3699 1)
(s3700 1)
(s3701 1)
(s3702 1)
(s3703 1)
(s3704 1)
(s3705 1)
(s3706 1)
(s3707 1)
(s3708 1)
(s3709 1)
(s3710 1)
(s3711 1)
(s3712 1)
(s3713 1)
(s3714 1)
(s3715 1)
(s3716 1)
(s3717 1)
(s3718 1)
(s3719 1)
(s3720 1)
(s3721 1)
(s3722 1)
(s3723 1)
(s3724 1)
(s3725 1)
(s3726 1)
(s3727 1)
(s3728 1)
(s3729 1)
(s3730 1)
(s3731 1)
(s3732 1)
(s3733 1)
(s3734 1)
(s3735 1)
(s3736 1)
(s3737 1)
(s3738 1)
(s3739 1)
(s3740 1)
(s3741 1)
(s3742 1)
(s3743 1)
(s3744 1)
(s3745 1)
(s3746 1)
(s3747 1)
(s3748 1)
(s3749 1)
(s3750 1)
(s3751 1)
(s3752 1)
(s3753 1)
(s3754 1)
(s3755 1)
(s3756 1)
(s3757 1)
(s3758 1)
(s3759 1)
(s3760 1)
(s3761 1)
(s3762 1)
(s3763 1)
(s3764 1)
(s3765 1)
(s3766 1)
(s3767 1)
(s3768 1)
(s3769 1)
(s3770 1)
(s3771 1)
(s3772 1)
(s3773 1)
(s3774 1)
(s3775 1)
(s3776 1)
(s3777 1)
(s3778 1)
(s3779 1)
(s3780 1)
(s3781 1)
(s3782 1)
(s3783 1)
(s3784 1)
(s3785 1)
(s3786 1)
(s3787 1)
(s3788 1)
(s3789 1)
(s3790 1)
(s3791 1)
(s3792 1)
(s3793 1)
(s3794 1)
(s3795 1)
(s3796 1)
(s3797 1)
(s3798 1)
(s3799 1)
(s3800 1)
(s3801 1)
(s3802 1)
(s3803 1)
(s3804 1)
(s3805 1)
(s3806 1)
(s3807 1)
(s3808 1)
(s3809 1)
(s3810 1)
(s3811 1)
(s3812 1)
(s3813 1)
(s3814 1)
(s3815 1)
(s3816 1)
(s3817 1)
(s3818 1)
(s3819 1)
(s3820 1)
(s3821 1)
(s3822 1)
(s3823 1)
(s3824 1)
(s3825 1)
(s3826 1)
(s3827 1)
(s3828 1)
(s3829 1)
(s3830 1)
(s3831 1)
(s3832 1)
(s3833 1)
(s3834 1)
(s3835 1)
(s3836 1)
(s3837 1)
(s3838 1)
(s3839 1)
(s3840 1)
(s3841 1)
(s3842 1)
(s3843 1)
(s3844 1)
(s3845 1)
(s3846 1)
(s3847 1)
(s3848 1)
(s3849 1)
(s3850 1)
(s3851 1)
(s3852 1)
(s3853 1)
(s3854 1)
(s3855 1)
(s3856 1)
(s3857 1)
(s3858 1)
(s3859 1)
(s3860 1)
(s3861 1)
(s3862 1)
(s3863 1)
(s3864 1)
(s3865 1)
(s3866 1)
(s3867 1)
(s3868 1)
(s3869 1)
(s3870 1)
(s3871 1)
(s3872 1)
(s3873 1)
(s3874 1)
(s3875 1)
(s3876 1)
(s3877 1)
(s3878 1)
(s3879 1)
(s3880 1)
(s3881 1)
(s3882 1)
(s3883 1)
(s3884 1)
(s3885 1)
(s3886 1)
(s3887 1)
(s3888 1)
(s3889 1)
(s3890 1)
(s3891 1)
(s3892 1)
(s3893 1)
(s3894 1)
(s3895 1)
(s3896 1)
(s3897 1)
(s3898 1)
(s3899 1)
(s3900 1)
(s3901 1)
(s3902 1)
(s3903 1)
(s3904 1)
(s3905 1)
(s3906 1)
(s3907 1)
(s3908 1)
(s3909 1)
(s3910 1)
(s3911 1)
(s3912 1)
(s3913 1)
(s3914 1)
(s3915 1)
(s3916 1)
(s3917 1)
(s3918 1)
(s3919 1)
(s3920 1)
(s3921 1)
(s3922 1)
(s3923 1)
(s3924 1)
(s3925 1)
(s3926 1)
(s3927 1)
(s3928 1)
(s3929 1)
(s3930 1)
(s3931 1)
(s3932 1)
(s3933 1)
(s3934 1)
(s3935 1)
(s3936 1)
(s3937 1)
(s3938 1)
(s3939 1)
(s3940 1)
(s3941 1)
(s3942 1)
(s3943 1)
(s3944 1)
(s3945 1)
(s3946 1)
(s3947 1)
(s3948 1)
(s3949 1)
(s3950 1)
(s3951 1)
(s3952 1)
(s3953 1)
(s3954 1)
(s3955 1)
(s3956 1)
(s3957 1)
(s3958 1)
(s3959 1)
(s3960 1)
(s3961 1)
(s3962 1)
(s3963 1)
(s3964 1)
(s3965 1)
(s3966 1)
(s3967 1)
(s3968 1)
(s3969 1)
(s3970 1)
(s3971 1)
(s3972 1)
(s3973 1)
(s3974 1)
(s3975 1)
(s3976 1)
(s3977 1)
(s3978 1)
(s3979 1)
(s3980 1)
(s3981 1)
(s3982 1)
(s3983 1)
(s3984 1)
(s3985 1)
(s3986 1)
(s3987 1)
(s3988 1)
(s3989 1)
(s3990 1)
(s3991 1)
(s3992 1)
(s3993 1)
(s3994 1)
(s3995 1)
(s3996 1)
(s3997 1)
(s3998 1)
(s3999 1)
(s4000 1)
(s4001 1)
(s4002 1)
(s4003 1)
(s4004 1)
(s4005 1)
(s4006 1)
(s4007 1)
(s4008 1)
(s4009 1)
(s4010 1)
(s4011 1)
(s4012 1)
(s4013 1)
(s4014 1)
(s4015 1)
(s4016 1)
(s4017 1)
(s4018 1)
(s4019 1)
(s4020 1)
(s4021 1)
(s4022 1)
(s4023 1)
(s4024 1)
(s4025 1)
(s4026 1)
(s4027 1)
(s4028 1)
(s4029 1)
(s4030 1)
(s4031 1)
(s4032 1)
(s4033 1)
(s4034 1)
(s4035 1)
(s4036 1)
(s4037 1)
(s4038 1)
(s4039 1)
(s4040 1)
(s4041 1)
(s4042 1)
(s4043 1)
(s4044 1)
(s4045 1)
(s4046 1)
(s4047 1)
(s4048 1)
(s4049 1)
(s4050 1)
(s4051 1)
(s4052 1)
(s4053 1)
(s4054 1)
(s4055 1)
(s4056 1)
(s4057 1)
(s4058 1)
(s4059 1)
(s4060 1)
(s4061 1)
(s4062 1)
(s4063 1)
(s4064 1)
(s4065 1)
(s4066 1)
(s4067 1)
(s4068 1)
(s4069 1)
(s4070 1)
(s4071 1)
(s4072 1)
(s4073 1)
(s4074 1)
(s4075 1)
(s4076 1)
(s4077 1)
(s4078 1)
(s4079 1)
(s4080 1)
(s4081 1)
(s4082 1)
(s4083 1)
(s4084 1)
(s4085 1)
(s4086 1)
(s4087 1)
(s4088 1)
(s4089 1)
(s4090 1)
(s4091 1)
(s4092 1)
(s4093 1)
(s4094 1)
(s4095 1)
(s4096 1)
(s4097 1)
(s4098 1)
(s4099 1)
(s4100 1)
(s4101 1)
(s4102 1)
(s4103 1)
(s4104 1)
(s4105 1)
(s4106 1)
(s4107 1)
(s4108 1)
(s4109 1)
(s4110 1)
(s4111 1)
(s4112 1)
(s4113 1)
(s4114 1)
(s4115 1)
(s4116 1)
(s4117 1)
(s4118 1)
(s4119 1)
(s4120 1)
(s4121 1)
(s4122 1)
(s4123 1)
(s4124 1)
(s4125 1)
(s4126 1)
(s4127 1)
(s4128 1)
(s4129 1)
(s4130 1)
(s4131 1)
(s4132 1)
(s4133 1)
(s4134 1)
(s4135 1)
(s4136 1)
(s4137 1)
(s4138 1)
(s4139 1)
(s4140 1)
(s4141 1)
(s4142 1)
(s4143 1)
(s4144 1)
(s4145 1)
(s4146 1)
(s4147 1)
(s4148 1)
(s4149 1)
(s4150 1)
(s4151 1)
(s4152 1)
(s4153 1)
(s4154 1)
(s4155 1)
(s4156 1)
(s4157 1)
(s4158 1)
(s4159 1)
(s4160 1)
(s4161 1)
(s4162 1)
(s4163 1)
(s4164 1)
(s4165 1)
(s4166 1)
(s4167 1)
(s4168 1)
(s4169 1)
(s4170 1)
(s4171 1)
(s4172 1)
(s4173 1)
(s4174 1)
(s4175 1)
(s4176 1)
(s4177 1)
(s4178 1)
(s4179 1)
(s4180 1)
(s4181 1)
(s4182 1)
(s4183 1)
(s4184 1)
(s4185 1)
(s4186 1)
(s4187 1)
(s4188 1)
(s4189 1)
(s4190 1)
(s4191 1)
(s4192 1)
(s4193 1)
(s4194 1)
(s4195 1)
(s4196 1)
(s4197 1)
(s4198 1)
(s4199 1)
(s4200 1)
(s4201 1)
(s4202 1)
(s4203 1)
(s4204 1)
(s4205 1)
(s4206 1)
(s4207 1)
(s4208 1)
(s4209 1)
(s4210 1)
(s4211 1)
(s4212 1)
(s4213 1)
(s4214 1)
(s4215 1)
(s4216 1)
(s4217 1)
(s4218 1)
(s4219 1)
(s4220 1)
(s4221 1)
(s4222 1)
(s4223 1)
(s4224 1)
(s4225 1)
(s4226 1)
(s4227 1)
(s4228 1)
(s4229 1)
(s4230 1)
(s4231 1)
(s4232 1)
(s4233 1)
(s4234 1)
(s4235 1)
(s4236 1)
(s4237 1)
(s4238 1)
(s4239 1)
(s4240 1)
(s4241 1)
(s4242 1)
(s4243 1)
(s4244 1)
(s4245 1)
(s4246 1)
(s4247 1)
(s4248 1)
(s4249 1)
(s4250 1)
(s4251 1)
(s4252 1)
(s4253 1)
(s4254 1)
(s4255 1)
(s4256 1)
(s4257 1)
(s4258 1)
(s4259 1)
(s4260 1)
(s4261 1)
(s4262 1)
(s4263 1)
(s4264 1)
(s4265 1)
(s4266 1)
(s4267 1)
(s4268 1)
(s4269 1)
(s4270 1)
(s4271 1)
(s4272 1)
(s4273 1)
(s4274 1)
(s4275 1)
(s4276 1)
(s4277 1)
(s4278 1)
(s4279 1)
(s4280 1)
(s4281 1)
(s4282 1)
(s4283 1)
(s4284 1)
(s4285 1)
(s4286 1)
(s4287 1)
(s4288 1)
(s4289 1)
(s4290 1)
(s4291 1)
(s4292 1)
(s4293 1)
(s4294 1)
(s4295 1)
(s4296 1)
(s4297 1)
(s4298 1)
(s4299 1)
(s4300 1)
(s4301 1)
(s4302 1)
(s4303 1)
(s4304 1)
(s4305 1)
(s4306 1)
(s4307 1)
(s4308 1)
(s4309 1)
(s4310 1)
(s4311 1)
(s4312 1)
(s4313 1)
(s4314 1)
(s4315 1)
(s4316 1)
(s4317 1)
(s4318 1)
(s4319 1)
(s4320 1)
(s4321 1)
(s4322 1)
(s4323 1)
(s4324 1)
(s4325 1)
(s4326 1)
(s4327 1)
(s4328 1)
(s4329 1)
(s4330 1)
(s4331 1)
(s4332 1)
(s4333 1)
(s4334 1)
(s4335 1)
(s4336 1)
(s4337 1)
(s4338 1)
(s4339 1)
(s4340 1)
(s4341 1)
(s4342 1)
(s4343 1)
(s4344 1)
(s4345 1)
(s4346 1)
(s4347 1)
(s4348 1)
(s4349 1)
(s4350 1)
(s4351 1)
(s4352 1)
(s4353 1)
(s4354 1)
(s4355 1)
(s4356 1)
(s4357 1)
(s4358 1)
(s4359 1)
(s4360 1)
(s4361 1)
(s4362 1)
(s4363 1)
(s4364 1)
(s4365 1)
(s4366 1)
(s4367 1)
(s4368 1)
(s4369 1)
(s4370 1)
(s4371 1)
(s4372 1)
(s4373 1)
(s4374 1)
(s4375 1)
(s4376 1)
(s4377 1)
(s4378 1)
(s4379 1)
(s4380 1)
(s4381 1)
(s4382 1)
(s4383 1)
(s4384 1)
(s4385 1)
(s4386 1)
(s4387 1)
(s4388 1)
(s4389 1)
(s4390 1)
(s4391 1)
(s4392 1)
(s4393 1)
(s4394 1)
(s4395 1)
(s4396 1)
(s4397 1)
(s4398 1)
(s4399 1)
(s4400 1)
(s4401 1)
(s4402 1)
(s4403 1)
(s4404 1)
(s4405 1)
(s4406 1)
(s4407 1)
(s4408 1)
(s4409 1)
(s4410 1)
(s4411 1)
(s4412 1)
(s4413 1)
(s4414 1)
(s4415 1)
(s4416 1)
(s4417 1)
(s4418 1)
(s4419 1)
(s4420 1)
(s4421 1)
(s4422 1)
(s4423 1)
(s4424 1)
(s4425 1)
(s4426 1)
(s4427 1)
(s4428 1)
(s4429 1)
(s4430 1)
(s4431 1)
(s4432 1)
(s4433 1)
(s4434 1)
(s4435 1)
(s4436 1)
(s4437 1)
(s4438 1)
(s4439 1)
(s4440 1)
(s4441 1)
(s4442 1)
(s4443 1)
(s4444 1)
(s4445 1)
(s4446 1)
(s4447 1)
(s4448 1)
(s4449 1)
(s4450 1)
(s4451 1)
(s4452 1)
(s4453 1)
(s4454 1)
(s4455 1)
(s4456 1)
(s4457 1)
(s4458 1)
(s4459 1)
(s4460 1)
(s4461 1)
(s4462 1)
(s4463 1)
(s4464 1)
(s4465 1)
(s4466 1)
(s4467 1)
(s4468 1)
(s4469 1)
(s4470 1)
(s4471 1)
(s4472 1)
(s4473 1)
(s4474 1)
(s4475 1)
(s4476 1)
(s4477 1)
(s4478 1)
(s4479 1)
(s4480 1)
(s4481 1)
(s4482 1)
(s4483 1)
(s4484 1)
(s4485 1)
(s4486 1)
(s4487 1)
(s4488 1)
(s4489 1)
(s4490 1)
(s4491 1)
(s4492 1)
(s4493 1)
(s4494 1)
(s4495 1)
(s4496 1)
(s4497 1)
(s4498 1)
(s4499 1)
(s4500 1)
(s4501 1)
(s4502 1)
(s4503 1)
(s4504 1)
(s4505 1)
(s4506 1)
(s4507 1)
(s4508 1)
(s4509 1)
(s4510 1)
(s4511 1)
(s4512 1)
(s4513 1)
(s4514 1)
(s4515 1)
(s4516 1)
(s4517 1)
(s4518 1)
(s4519 1)
(s4520 1)
(s4521 1)
(s4522 1)
(s4523 1)
(s4524 1)
(s4525 1)
(s4526 1)
(s4527 1)
(s4528 1)
(s4529 1)
(s4530 1)
(s4531 1)
(s4532 1)
(s4533 1)
(s4534 1)
(s4535 1)
(s4536 1)
(s4537 1)
(s4538 1)
(s4539 1)
(s4540 1)
(s4541 1)
(s4542 1)
(s4543 1)
(s4544 1)
(s4545 1)
(s4546 1)
(s4547 1)
(s4548 1)
(s4549 1)
(s4550 1)
(s4551 1)
(s4552 1)
(s4553 1)
(s4554 1)
(s4555 1)
(s4556 1)
(s4557 1)
(s4558 1)
(s4559 1)
(s4560 1)
(s4561 1)
(s4562 1)
(s4563 1)
(s4564 1)
(s4565 1)
(s4566 1)
(s4567 1)
(s4568 1)
(s4569 1)
(s4570 1)
(s4571 1)
(s4572 1)
(s4573 1)
(s4574 1)
(s4575 1)
(s4576 1)
(s4577 1)
(s4578 1)
(s4579 1)
(s4580 1)
(s4581 1)
(s4582 1)
(s4583 1)
(s4584 1)
(s4585 1)
(s4586 1)
(s4587 1)
(s4588 1)
(s4589 1)
(s4590 1)
(s4591 1)
(s4592 1)
(s4593 1)
(s4594 1)
(s4595 1)
(s4596 1)
(s4597 1)
(s4598 1)
(s4599 1)
(s4600 1)
(s4601 1)
(s4602 1)
(s4603 1)
(s4604 1)
(s4605 1)
(s4606 1)
(s4607 1)
(s4608 1)
(s4609 1)
(s4610 1)
(s4611 1)
(s4612 1)
(s4613 1)
(s4614 1)
(s4615 1)
(s4616 1)
(s4617 1)
(s4618 1)
(s4619 1)
(s4620 1)
(s4621 1)
(s4622 1)
(s4623 1)
(s4624 1)
(s4625 1)
(s4626 1)
(s4627 1)
(s4628 1)
(s4629 1)
(s4630 1)
(s4631 1)
(s4632 1)
(s4633 1)
(s4634 1)
(s4635 1)
(s4636 1)
(s4637 1)
(s4638 1)
(s4639 1)
(s4640 1)
(s4641 1)
(s4642 1)
(s4643 1)
(s4644 1)
(s4645 1)
(s4646 1)
(s4647 1)
(s4648 1)
(s4649 1)
(s4650 1)
(s4651 1)
(s4652 1)
(s4653 1)
(s4654 1)
(s4655 1)
(s4656 1)
(s4657 1)
(s4658 1)
(s4659 1)
(s4660 1)
(s4661 1)
(s4662 1)
(s4663 1)
(s4664 1)
(s4665 1)
(s4666 1)
(s4667 1)
(s4668 1)
(s4669 1)
(s4670 1)
(s4671 1)
(s4672 1)
(s4673 1)
(s4674 1)
(s4675 1)
(s4676 1)
(s4677 1)
(s4678 1)
(s4679 1)
(s4680 1)
(s4681 1)
(s4682 1)
(s4683 1)
(s4684 1)
(s4685 1)
(s4686 1)
(s4687 1)
(s4688 1)
(s4689 1)
(s4690 1)
(s4691 1)
(s4692 1)
(s4693 1)
(s4694 1)
(s4695 1)
(s4696 1)
(s4697 1)
(s4698 1)
(s4699 1)
(s4700 1)
(s4701 1)
(s4702 1)
(s4703 1)
(s4704 1)
(s4705 1)
(s4706 1)
(s4707 1)
(s4708 1)
(s4709 1)
(s4710 1)
(s4711 1)
(s4712 1)
(s4713 1)
(s4714 1)
(s4715 1)
(s4716 1)
(s4717 1)
(s4718 1)
(s4719 1)
(s4720 1)
(s4721 1)
(s4722 1)
(s4723 1)
(s4724 1)
(s4725 1)
(s4726 1)
(s4727 1)
(s4728 1)
(s4729 1)
(s4730 1)
(s4731 1)
(s4732 1)
(s4733 1)
(s4734 1)
(s4735 1)
(s4736 1)
(s4737 1)
(s4738 1)
(s4739 1)
(s4740 1)
(s4741 1)
(s4742 1)
(s4743 1)
(s4744 1)
(s4745 1)
(s4746 1)
(s4747 1)
(s4748 1)
(s4749 1)
(s4750 1)
(s4751 1)
(s4752 1)
(s4753 1)
(s4754 1)
(s4755 1)
(s4756 1)
(s4757 1)
(s4758 1)
(s4759 1)
(s4760 1)
(s4761 1)
(s4762 1)
(s4763 1)
(s4764 1)
(s4765 1)
(s4766 1)
(s4767 1)
(s4768 1)
(s4769 1)
(s4770 1)
(s4771 1)
(s4772 1)
(s4773 1)
(s4774 1)
(s4775 1)
(s4776 1)
(s4777 1)
(s4778 1)
(s4779 1)
(s4780 1)
(s4781 1)
(s4782 1)
(s4783 1)
(s4784 1)
(s4785 1)
(s4786 1)
(s4787 1)
(s4788 1)
(s4789 1)
(s4790 1)
(s4791 1)
(s4792 1)
(s4793 1)
(s4794 1)
(s4795 1)
(s4796 1)
(s4797 1)
(s4798 1)
(s4799 1)
(s4800 1)
(s4801 1)
(s4802 1)
(s4803 1)
(s4804 1)
(s4805 1)
(s4806 1)
(s4807 1)
(s4808 1)
(s4809 1)
(s4810 1)
(s4811 1)
(s4812 1)
(s4813 1)
(s4814 1)
(s4815 1)
(s4816 1)
(s4817 1)
(s4818 1)
(s4819 1)
(s4820 1)
(s4821 1)
(s4822 1)
(s4823 1)
(s4824 1)
(s4825 1)
(s4826 1)
(s4827 1)
(s4828 1)
(s4829 1)
(s4830 1)
(s4831 1)
(s4832 1)
(s4833 1)
(s4834 1)
(s4835 1)
(s4836 1)
(s4837 1)
(s4838 1)
(s4839 1)
(s4840 1)
(s4841 1)
(s4842 1)
(s4843 1)
(s4844 1)
(s4845 1)
(s4846 1)
(s4847 1)
(s4848 1)
(s4849 1)
(s4850 1)
(s4851 1)
(s4852 1)
(s4853 1)
(s4854 1)
(s4855 1)
(s4856 1)
(s4857 1)
(s4858 1)
(s4859 1)
(s4860 1)
(s4861 1)
(s4862 1)
(s4863 1)
(s4864 1)
(s4865 1)
(s4866 1)
(s4867 1)
(s4868 1)
(s4869 1)
(s4870 1)
(s4871 1)
(s4872 1)
(s4873 1)
(s4874 1)
(s4875 1)
(s4876 1)
(s4877 1)
(s4878 1)
(s4879 1)
(s4880 1)
(s4881 1)
(s4882 1)
(s4883 1)
(s4884 1)
(s4885 1)
(s4886 1)
(s4887 1)
(s4888 1)
(s4889 1)
(s4890 1)
(s4891 1)
(s4892 1)
(s4893 1)
(s4894 1)
(s4895 1)
(s4896 1)
(s4897 1)
(s4898 1)
(s4899 1)
(s4900 1)
(s4901 1)
(s4902 1)
(s4903 1)
(s4904 1)
(s4905 1)
(s4906 1)
(s4907 1)
(s4908 1)
(s4909 1)
(s4910 1)
(s4911 1)
(s4912 1)
(s4913 1)
(s4914 1)
(s4915 1)
(s4916 1)
(s4917 1)
(s4918 1)
(s4919 1)
(s4920 1)
(s4921 1)
(s4922 1)
(s4923 1)
(s4924 1)
(s4925 1)
(s4926 1)
(s4927 1)
(s4928 1)
(s4929 1)
(s4930 1)
(s4931 1)
(s4932 1)
(s4933 1)
(s4934 1)
(s4935 1)
(s4936 1)
(s4937 1)
(s4938 1)
(s4939 1)
(s4940 1)
(s4941 1)
(s4942 1)
(s4943 1)
(s4944 1)
(s4945 1)
(s4946 1)
(s4947 1)
(s4948 1)
(s4949 1)
(s4950 1)
(s4951 1)
(s4952 1)
(s4953 1)
(s4954 1)
(s4955 1)
(s4956 1)
(s4957 1)
(s4958 1)
(s4959 1)
(s4960 1)
(s4961 1)
(s4962 1)
(s4963 1)
(s4964 1)
(s4965 1)
(s4966 1)
(s4967 1)
(s4968 1)
(s4969 1)
(s4970 1)
(s4971 1)
(s4972 1)
(s4973 1)
(s4974 1)
(s4975 1)
(s4976 1)
(s4977 1)
(s4978 1)
(s4979 1)
(s4980 1)
(s4981 1)
(s4982 1)
(s4983 1)
(s4984 1)
(s4985 1)
(s4986 1)
(s4987 1)
(s4988 1)
(s4989 1)
(s4990 1)
(s4991 1)
(s4992 1)
(s4993 1)
(s4994 1)
(s4995 1)
(s4996 1)
(s4997 1)
(s4998 1)
(s4999 1)
(s5000 1)
(s5001 1)
(s5002 1)
(s5003 1)
(s5004 1)
(s5005 1)
(s5006 1)
(s5007 1)
(s5008 1)
(s5009 1)
(s5010 1)
(s5011 1)
(s5012 1)
(s5013 1)
(s5014 1)
(s5015 1)
(s5016 1)
(s5017 1)
(s5018 1)
(s5019 1)
(s5020 1)
(s5021 1)
(s5022 1)
(s5023 1)
(s5024 1)
(s5025 1)
(s5026 1)
(s5027 1)
(s5028 1)
(s5029 1)
(s5030 1)
(s5031 1)
(s5032 1)
(s5033 1)
(s5034 1)
(s5035 1)
(s5036 1)
(s5037 1)
(s5038 1)
(s5039 1)
(s5040 1)
(s5041 1)
(s5042 1)
(s5043 1)
(s5044 1)
(s5045 1)
(s5046 1)
(s5047 1)
(s5048 1)
(s5049 1)
(s5050 1)
(s5051 1)
(s5052 1)
(s5053 1)
(s5054 1)
(s5055 1)
(s5056 1)
(s5057 1)
(s5058 1)
(s5059 1)
(s5060 1)
(s5061 1)
(s5062 1)
(s5063 1)
(s5064 1)
(s5065 1)
(s5066 1)
(s5067 1)
(s5068 1)
(s5069 1)
(s5070 1)
(s5071 1)
(s5072 1)
(s5073 1)
(s5074 1)
(s5075 1)
(s5076 1)
(s5077 1)
(s5078 1)
(s5079 1)
(s5080 1)
(s5081 1)
(s5082 1)
(s5083 1)
(s5084 1)
(s5085 1)
(s5086 1)
(s5087 1)
(s5088 1)
(s5089 1)
(s5090 1)
(s5091 1)
(s5092 1)
(s5093 1)
(s5094 1)
(s5095 1)
(s5096 1)
(s5097 1)
(s5098 1)
(s5099 1)
(s5100 1)
(s5101 1)
(s5102 1)
(s5103 1)
(s5104 1)
(s5105 1)
(s5106 1)
(s5107 1)
(s5108 1)
(s5109 1)
(s5110 1)
(s5111 1)
(s5112 1)
(s5113 1)
(s5114 1)
(s5115 1)
(s5116 1)
(s5117 1)
(s5118 1)
(s5119 1)
(s5120 1)
(s5121 1)
(s5122 1)
(s5123 1)
(s5124 1)
(s5125 1)
(s5126 1)
(s5127 1)
(s5128 1)
(s5129 1)
(s5130 1)
(s5131 1)
(s5132 1timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 6550/16700 variables, and 6550 constraints, problems are : Problem set: 0 solved, 8300 unsolved in 30262 ms.
Refiners :[Domain max(s): 6550/6600 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/6600 constraints, PredecessorRefiner: 0/8300 constraints, Known Traps: 0/0 constraints]
After SMT, in 68167ms problems are : Problem set: 0 solved, 8300 unsolved
Search for dead transitions found 0 dead transitions in 68283ms
Finished structural reductions in LTL mode , in 1 iterations and 70818 ms. Remains : 6600/6600 places, 10100/10100 transitions.
Treatment of property BART-PT-050-LTLFireability-03 finished in 298903 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G(F((p0||G(p1)))))'
Support contains 4450 out of 6600 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Drop transitions (Trivial Post-Agglo cleanup.) removed 100 transitions
Trivial Post-agglo rules discarded 100 transitions
Performed 100 trivial Post agglomeration. Transition count delta: 100
Iterating post reduction 0 with 100 rules applied. Total rules applied 100 place count 6600 transition count 10000
Reduce places removed 100 places and 0 transitions.
Performed 450 Post agglomeration using F-continuation condition.Transition count delta: 450
Iterating post reduction 1 with 550 rules applied. Total rules applied 650 place count 6500 transition count 9550
Reduce places removed 450 places and 0 transitions.
Iterating post reduction 2 with 450 rules applied. Total rules applied 1100 place count 6050 transition count 9550
Performed 200 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 200 Pre rules applied. Total rules applied 1100 place count 6050 transition count 9350
Deduced a syphon composed of 200 places in 3 ms
Reduce places removed 200 places and 0 transitions.
Iterating global reduction 3 with 400 rules applied. Total rules applied 1500 place count 5850 transition count 9350
Discarding 300 places :
Symmetric choice reduction at 3 with 300 rule applications. Total rules 1800 place count 5550 transition count 9050
Iterating global reduction 3 with 300 rules applied. Total rules applied 2100 place count 5550 transition count 9050
Ensure Unique test removed 50 transitions
Reduce isomorphic transitions removed 50 transitions.
Iterating post reduction 3 with 50 rules applied. Total rules applied 2150 place count 5550 transition count 9000
Discarding 150 places :
Symmetric choice reduction at 4 with 150 rule applications. Total rules 2300 place count 5400 transition count 8850
Iterating global reduction 4 with 150 rules applied. Total rules applied 2450 place count 5400 transition count 8850
Discarding 150 places :
Symmetric choice reduction at 4 with 150 rule applications. Total rules 2600 place count 5250 transition count 8700
Iterating global reduction 4 with 150 rules applied. Total rules applied 2750 place count 5250 transition count 8700
Discarding 150 places :
Symmetric choice reduction at 4 with 150 rule applications. Total rules 2900 place count 5100 transition count 8550
Iterating global reduction 4 with 150 rules applied. Total rules applied 3050 place count 5100 transition count 8550
Discarding 100 places :
Symmetric choice reduction at 4 with 100 rule applications. Total rules 3150 place count 5000 transition count 8450
Iterating global reduction 4 with 100 rules applied. Total rules applied 3250 place count 5000 transition count 8450
Discarding 100 places :
Symmetric choice reduction at 4 with 100 rule applications. Total rules 3350 place count 4900 transition count 8350
Iterating global reduction 4 with 100 rules applied. Total rules applied 3450 place count 4900 transition count 8350
Discarding 50 places :
Symmetric choice reduction at 4 with 50 rule applications. Total rules 3500 place count 4850 transition count 8300
Iterating global reduction 4 with 50 rules applied. Total rules applied 3550 place count 4850 transition count 8300
Performed 300 Post agglomeration using F-continuation condition.Transition count delta: 300
Deduced a syphon composed of 300 places in 1 ms
Reduce places removed 300 places and 0 transitions.
Iterating global reduction 4 with 600 rules applied. Total rules applied 4150 place count 4550 transition count 8000
Applied a total of 4150 rules in 1005 ms. Remains 4550 /6600 variables (removed 2050) and now considering 8000/10100 (removed 2100) transitions.
// Phase 1: matrix 8000 rows 4550 cols
[2024-06-01 11:17:24] [INFO ] Computed 50 invariants in 39 ms
[2024-06-01 11:17:25] [INFO ] Implicit Places using invariants in 899 ms returned []
[2024-06-01 11:17:25] [INFO ] Invariant cache hit.
[2024-06-01 11:17:30] [INFO ] Implicit Places using invariants and state equation in 4436 ms returned []
Implicit Place search using SMT with State Equation took 5337 ms to find 0 implicit places.
[2024-06-01 11:17:31] [INFO ] Redundant transitions in 908 ms returned []
Running 6200 sub problems to find dead transitions.
[2024-06-01 11:17:31] [INFO ] Invariant cache hit.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 4500/12550 variables, and 0 constraints, problems are : Problem set: 0 solved, 6200 unsolved in 30159 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4550 constraints, PredecessorRefiner: 6200/6200 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 6200 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 4500/12550 variables, and 0 constraints, problems are : Problem set: 0 solved, 6200 unsolved in 30162 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/4550 constraints, PredecessorRefiner: 0/6200 constraints, Known Traps: 0/0 constraints]
After SMT, in 65025ms problems are : Problem set: 0 solved, 6200 unsolved
Search for dead transitions found 0 dead transitions in 65081ms
Starting structural reductions in SI_LTL mode, iteration 1 : 4550/6600 places, 8000/10100 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 72344 ms. Remains : 4550/6600 places, 8000/10100 transitions.
Stuttering acceptance computed with spot in 113 ms :[(AND (NOT p1) (NOT p0)), (AND (NOT p1) (NOT p0))]
Running random walk in product with property : BART-PT-050-LTLFireability-04
Product exploration explored 100000 steps with 1 reset in 3246 ms.
Stack based approach found an accepted trace after 15603 steps with 0 reset with depth 15604 and stack size 15604 in 469 ms.
FORMULA BART-PT-050-LTLFireability-04 FALSE TECHNIQUES STACK_TEST
Treatment of property BART-PT-050-LTLFireability-04 finished in 76226 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((G(p0)&&X(G(p1)))))'
Support contains 4850 out of 6600 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Graph (trivial) has 1300 edges and 6600 vertex of which 300 / 6600 are part of one of the 50 SCC in 2 ms
Free SCC test removed 250 places
Ensure Unique test removed 250 transitions
Reduce isomorphic transitions removed 250 transitions.
Performed 400 Post agglomeration using F-continuation condition.Transition count delta: 400
Iterating post reduction 0 with 400 rules applied. Total rules applied 401 place count 6350 transition count 9450
Reduce places removed 400 places and 0 transitions.
Iterating post reduction 1 with 400 rules applied. Total rules applied 801 place count 5950 transition count 9450
Performed 600 Post agglomeration using F-continuation condition.Transition count delta: 600
Deduced a syphon composed of 600 places in 2 ms
Reduce places removed 600 places and 0 transitions.
Iterating global reduction 2 with 1200 rules applied. Total rules applied 2001 place count 5350 transition count 8850
Applied a total of 2001 rules in 480 ms. Remains 5350 /6600 variables (removed 1250) and now considering 8850/10100 (removed 1250) transitions.
[2024-06-01 11:18:40] [INFO ] Flow matrix only has 8801 transitions (discarded 49 similar events)
// Phase 1: matrix 8801 rows 5350 cols
[2024-06-01 11:18:40] [INFO ] Computed 50 invariants in 34 ms
[2024-06-01 11:18:42] [INFO ] Implicit Places using invariants in 1820 ms returned []
[2024-06-01 11:18:42] [INFO ] Flow matrix only has 8801 transitions (discarded 49 similar events)
[2024-06-01 11:18:42] [INFO ] Invariant cache hit.
[2024-06-01 11:18:48] [INFO ] Implicit Places using invariants and state equation in 6283 ms returned []
Implicit Place search using SMT with State Equation took 8110 ms to find 0 implicit places.
[2024-06-01 11:18:49] [INFO ] Redundant transitions in 1052 ms returned []
Running 7050 sub problems to find dead transitions.
[2024-06-01 11:18:49] [INFO ] Flow matrix only has 8801 transitions (discarded 49 similar events)
[2024-06-01 11:18:49] [INFO ] Invariant cache hit.
At refinement iteration 0 (INCLUDED_ONLY) 0/5300 variables, 5300/5300 constraints. Problems are: Problem set: 0 solved, 7050 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 5300/14151 variables, and 5300 constraints, problems are : Problem set: 0 solved, 7050 unsolved in 30183 ms.
Refiners :[Domain max(s): 5300/5350 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/5350 constraints, PredecessorRefiner: 7050/7050 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 7050 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/5300 variables, 5300/5300 constraints. Problems are: Problem set: 0 solved, 7050 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 5300/14151 variables, and 5300 constraints, problems are : Problem set: 0 solved, 7050 unsolved in 30180 ms.
Refiners :[Domain max(s): 5300/5350 constraints, Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/5350 constraints, PredecessorRefiner: 0/7050 constraints, Known Traps: 0/0 constraints]
After SMT, in 66050ms problems are : Problem set: 0 solved, 7050 unsolved
Search for dead transitions found 0 dead transitions in 66112ms
Starting structural reductions in SI_LTL mode, iteration 1 : 5350/6600 places, 8850/10100 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 75766 ms. Remains : 5350/6600 places, 8850/10100 transitions.
Stuttering acceptance computed with spot in 151 ms :[(OR (NOT p0) (NOT p1)), (NOT p0), (NOT p1)]
Running random walk in product with property : BART-PT-050-LTLFireability-07
Stuttering criterion allowed to conclude after 0 steps with 0 reset in 2 ms.
FORMULA BART-PT-050-LTLFireability-07 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-07 finished in 75964 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(((p0 U X(p1))||X(X(G(p2)))))'
Support contains 4 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1598 places :
Symmetric choice reduction at 0 with 1598 rule applications. Total rules 1598 place count 5002 transition count 8502
Iterating global reduction 0 with 1598 rules applied. Total rules applied 3196 place count 5002 transition count 8502
Discarding 1348 places :
Symmetric choice reduction at 0 with 1348 rule applications. Total rules 4544 place count 3654 transition count 7154
Iterating global reduction 0 with 1348 rules applied. Total rules applied 5892 place count 3654 transition count 7154
Discarding 199 places :
Symmetric choice reduction at 0 with 199 rule applications. Total rules 6091 place count 3455 transition count 6955
Iterating global reduction 0 with 199 rules applied. Total rules applied 6290 place count 3455 transition count 6955
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 6439 place count 3306 transition count 6806
Iterating global reduction 0 with 149 rules applied. Total rules applied 6588 place count 3306 transition count 6806
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 6737 place count 3157 transition count 6657
Iterating global reduction 0 with 149 rules applied. Total rules applied 6886 place count 3157 transition count 6657
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7035 place count 3008 transition count 6508
Iterating global reduction 0 with 149 rules applied. Total rules applied 7184 place count 3008 transition count 6508
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7333 place count 2859 transition count 6359
Iterating global reduction 0 with 149 rules applied. Total rules applied 7482 place count 2859 transition count 6359
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7631 place count 2710 transition count 6210
Iterating global reduction 0 with 149 rules applied. Total rules applied 7780 place count 2710 transition count 6210
Discarding 99 places :
Symmetric choice reduction at 0 with 99 rule applications. Total rules 7879 place count 2611 transition count 6111
Iterating global reduction 0 with 99 rules applied. Total rules applied 7978 place count 2611 transition count 6111
Discarding 99 places :
Symmetric choice reduction at 0 with 99 rule applications. Total rules 8077 place count 2512 transition count 6012
Iterating global reduction 0 with 99 rules applied. Total rules applied 8176 place count 2512 transition count 6012
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 8226 place count 2462 transition count 5962
Iterating global reduction 0 with 50 rules applied. Total rules applied 8276 place count 2462 transition count 5962
Applied a total of 8276 rules in 4632 ms. Remains 2462 /6600 variables (removed 4138) and now considering 5962/10100 (removed 4138) transitions.
// Phase 1: matrix 5962 rows 2462 cols
[2024-06-01 11:20:00] [INFO ] Computed 50 invariants in 18 ms
[2024-06-01 11:20:01] [INFO ] Implicit Places using invariants in 599 ms returned []
[2024-06-01 11:20:01] [INFO ] Invariant cache hit.
[2024-06-01 11:20:04] [INFO ] Implicit Places using invariants and state equation in 2882 ms returned []
Implicit Place search using SMT with State Equation took 3483 ms to find 0 implicit places.
Running 4162 sub problems to find dead transitions.
[2024-06-01 11:20:04] [INFO ] Invariant cache hit.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2412/8424 variables, and 0 constraints, problems are : Problem set: 0 solved, 4162 unsolved in 30108 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2462 constraints, PredecessorRefiner: 4162/4162 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4162 unsolved
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2412/8424 variables, and 0 constraints, problems are : Problem set: 0 solved, 4162 unsolved in 30113 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2462 constraints, PredecessorRefiner: 0/4162 constraints, Known Traps: 0/0 constraints]
After SMT, in 62448ms problems are : Problem set: 0 solved, 4162 unsolved
Search for dead transitions found 0 dead transitions in 62486ms
Starting structural reductions in LTL mode, iteration 1 : 2462/6600 places, 5962/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70606 ms. Remains : 2462/6600 places, 5962/10100 transitions.
Stuttering acceptance computed with spot in 442 ms :[true, (AND (NOT p1) (NOT p2)), (NOT p2), (AND (NOT p2) (NOT p1)), (AND (NOT p1) (NOT p2)), (NOT p1), (NOT p1), (AND (NOT p2) (NOT p1)), (AND (NOT p1) (NOT p2))]
Running random walk in product with property : BART-PT-050-LTLFireability-08
Product exploration explored 100000 steps with 7 reset in 1195 ms.
Product exploration explored 100000 steps with 14 reset in 1007 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND (NOT p0) p2 p1), (X (NOT (AND p0 (NOT p1)))), (X (NOT p0)), (X (X (NOT (AND (NOT p0) (NOT p1) (NOT p2))))), (X (X p2)), (X (X (NOT (AND (NOT p1) (NOT p2))))), (X (X (NOT (AND p0 (NOT p1) p2)))), (X (X (NOT p0))), (X (X (NOT (AND p0 (NOT p1) (NOT p2)))))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X (NOT p1)), (X p1), (X (X (AND (NOT p0) (NOT p1) p2))), (X (X (NOT (AND (NOT p0) (NOT p1) p2)))), (X (X (AND (NOT p1) p2))), (X (X (NOT (AND (NOT p1) p2)))), (X (X p1)), (X (X (NOT p1)))]
Knowledge based reduction with 9 factoid took 440 ms. Reduced automaton from 9 states, 17 edges and 3 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 159 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
RANDOM walk for 40000 steps (8 resets) in 621 ms. (64 steps per ms) remains 1/2 properties
BEST_FIRST walk for 40004 steps (8 resets) in 115 ms. (344 steps per ms) remains 1/1 properties
[2024-06-01 11:21:15] [INFO ] Invariant cache hit.
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 98/100 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/100 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 240/340 variables, 100/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/340 variables, 0/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (OVERLAPS) 0/340 variables, 0/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Real declared 340/8424 variables, and 102 constraints, problems are : Problem set: 0 solved, 1 unsolved in 158 ms.
Refiners :[Positive P Invariants (semi-flows): 2/50 constraints, State Equation: 100/2462 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 1 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 98/100 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/100 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 240/340 variables, 100/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/340 variables, 1/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/340 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (OVERLAPS) 0/340 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Int declared 340/8424 variables, and 103 constraints, problems are : Problem set: 0 solved, 1 unsolved in 205 ms.
Refiners :[Positive P Invariants (semi-flows): 2/50 constraints, State Equation: 100/2462 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
After SMT, in 387ms problems are : Problem set: 0 solved, 1 unsolved
Finished Parikh walk after 24 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=24 )
Parikh walk visited 1 properties in 2 ms.
Knowledge obtained : [(AND (NOT p0) p2 p1), (X (NOT (AND p0 (NOT p1)))), (X (NOT p0)), (X (X (NOT (AND (NOT p0) (NOT p1) (NOT p2))))), (X (X p2)), (X (X (NOT (AND (NOT p1) (NOT p2))))), (X (X (NOT (AND p0 (NOT p1) p2)))), (X (X (NOT p0))), (X (X (NOT (AND p0 (NOT p1) (NOT p2)))))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X (NOT p1)), (X p1), (X (X (AND (NOT p0) (NOT p1) p2))), (X (X (NOT (AND (NOT p0) (NOT p1) p2)))), (X (X (AND (NOT p1) p2))), (X (X (NOT (AND (NOT p1) p2)))), (X (X p1)), (X (X (NOT p1))), (F (NOT p2)), (F (NOT p1))]
Knowledge based reduction with 9 factoid took 763 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 162 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Stuttering acceptance computed with spot in 161 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Support contains 3 out of 2462 places. Attempting structural reductions.
Property had overlarge support with respect to TGBA, discarding it for now.
Starting structural reductions in LTL mode, iteration 0 : 2462/2462 places, 5962/5962 transitions.
Applied a total of 0 rules in 349 ms. Remains 2462 /2462 variables (removed 0) and now considering 5962/5962 (removed 0) transitions.
[2024-06-01 11:21:17] [INFO ] Invariant cache hit.
[2024-06-01 11:21:18] [INFO ] Implicit Places using invariants in 641 ms returned []
[2024-06-01 11:21:18] [INFO ] Invariant cache hit.
[2024-06-01 11:21:20] [INFO ] Implicit Places using invariants and state equation in 2770 ms returned []
Implicit Place search using SMT with State Equation took 3425 ms to find 0 implicit places.
Running 4162 sub problems to find dead transitions.
[2024-06-01 11:21:20] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2412/8424 variables, and 0 constraints, problems are : Problem set: 0 solved, 4162 unsolved in 30114 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2462 constraints, PredecessorRefiner: 4162/4162 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4162 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2412/8424 variables, and 0 constraints, problems are : Problem set: 0 solved, 4162 unsolved in 30114 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2462 constraints, PredecessorRefiner: 0/4162 constraints, Known Traps: 0/0 constraints]
After SMT, in 62564ms problems are : Problem set: 0 solved, 4162 unsolved
Search for dead transitions found 0 dead transitions in 62601ms
Finished structural reductions in LTL mode , in 1 iterations and 66382 ms. Remains : 2462/2462 places, 5962/5962 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND p2 p1), (X (X p2))]
False Knowledge obtained : [(X (NOT p1)), (X p1)]
Knowledge based reduction with 2 factoid took 114 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 148 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
RANDOM walk for 40000 steps (8 resets) in 755 ms. (52 steps per ms) remains 1/2 properties
BEST_FIRST walk for 40004 steps (8 resets) in 110 ms. (360 steps per ms) remains 1/1 properties
[2024-06-01 11:22:28] [INFO ] Invariant cache hit.
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 98/100 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/100 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 240/340 variables, 100/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/340 variables, 0/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (OVERLAPS) 0/340 variables, 0/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Real declared 340/8424 variables, and 102 constraints, problems are : Problem set: 0 solved, 1 unsolved in 154 ms.
Refiners :[Positive P Invariants (semi-flows): 2/50 constraints, State Equation: 100/2462 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 1 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 98/100 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/100 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 240/340 variables, 100/102 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/340 variables, 1/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/340 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (OVERLAPS) 0/340 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Int declared 340/8424 variables, and 103 constraints, problems are : Problem set: 0 solved, 1 unsolved in 213 ms.
Refiners :[Positive P Invariants (semi-flows): 2/50 constraints, State Equation: 100/2462 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
After SMT, in 381ms problems are : Problem set: 0 solved, 1 unsolved
Finished Parikh walk after 24 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=24 )
Parikh walk visited 1 properties in 2 ms.
Knowledge obtained : [(AND p2 p1), (X (X p2))]
False Knowledge obtained : [(X (NOT p1)), (X p1), (F (NOT p2)), (F (NOT p1))]
Knowledge based reduction with 2 factoid took 231 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 4 states, 5 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 166 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Stuttering acceptance computed with spot in 158 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Stuttering acceptance computed with spot in 158 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Product exploration explored 100000 steps with 47 reset in 1163 ms.
Product exploration explored 100000 steps with 13 reset in 882 ms.
Applying partial POR strategy [true, false, true, false]
Stuttering acceptance computed with spot in 107 ms :[true, (AND (NOT p2) (NOT p1)), (NOT p2), (AND (NOT p2) (NOT p1))]
Support contains 3 out of 2462 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 2462/2462 places, 5962/5962 transitions.
Graph (trivial) has 5886 edges and 2462 vertex of which 2362 / 2462 are part of one of the 48 SCC in 2 ms
Free SCC test removed 2314 places
Ensure Unique test removed 5673 transitions
Reduce isomorphic transitions removed 5673 transitions.
Reduce places removed 47 places and 0 transitions.
Ensure Unique test removed 46 transitions
Reduce isomorphic transitions removed 46 transitions.
Performed 4 Post agglomeration using F-continuation condition.Transition count delta: 0
Iterating post reduction 0 with 50 rules applied. Total rules applied 51 place count 101 transition count 243
Performed 2 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 1 with 2 Pre rules applied. Total rules applied 51 place count 101 transition count 243
Deduced a syphon composed of 6 places in 1 ms
Iterating global reduction 1 with 2 rules applied. Total rules applied 53 place count 101 transition count 243
Discarding 4 places :
Symmetric choice reduction at 1 with 4 rule applications. Total rules 57 place count 97 transition count 239
Deduced a syphon composed of 2 places in 0 ms
Iterating global reduction 1 with 4 rules applied. Total rules applied 61 place count 97 transition count 239
Performed 20 Post agglomeration using F-continuation condition.Transition count delta: -2
Deduced a syphon composed of 22 places in 0 ms
Iterating global reduction 1 with 20 rules applied. Total rules applied 81 place count 97 transition count 241
Ensure Unique test removed 6 transitions
Reduce isomorphic transitions removed 6 transitions.
Iterating post reduction 1 with 6 rules applied. Total rules applied 87 place count 97 transition count 235
Discarding 16 places :
Symmetric choice reduction at 2 with 16 rule applications. Total rules 103 place count 81 transition count 219
Deduced a syphon composed of 6 places in 1 ms
Iterating global reduction 2 with 16 rules applied. Total rules applied 119 place count 81 transition count 219
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 2 with 2 rules applied. Total rules applied 121 place count 81 transition count 219
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 2 with 4 rules applied. Total rules applied 125 place count 81 transition count 215
Discarding 2 places :
Symmetric choice reduction at 3 with 2 rule applications. Total rules 127 place count 79 transition count 213
Deduced a syphon composed of 6 places in 1 ms
Iterating global reduction 3 with 2 rules applied. Total rules applied 129 place count 79 transition count 213
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 3 with 2 rules applied. Total rules applied 131 place count 79 transition count 213
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 3 with 4 rules applied. Total rules applied 135 place count 79 transition count 209
Discarding 2 places :
Symmetric choice reduction at 4 with 2 rule applications. Total rules 137 place count 77 transition count 207
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 4 with 2 rules applied. Total rules applied 139 place count 77 transition count 207
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 4 with 2 rules applied. Total rules applied 141 place count 77 transition count 207
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 4 with 4 rules applied. Total rules applied 145 place count 77 transition count 203
Discarding 2 places :
Symmetric choice reduction at 5 with 2 rule applications. Total rules 147 place count 75 transition count 201
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 5 with 2 rules applied. Total rules applied 149 place count 75 transition count 201
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 5 with 2 rules applied. Total rules applied 151 place count 75 transition count 201
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 5 with 4 rules applied. Total rules applied 155 place count 75 transition count 197
Discarding 2 places :
Symmetric choice reduction at 6 with 2 rule applications. Total rules 157 place count 73 transition count 195
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 6 with 2 rules applied. Total rules applied 159 place count 73 transition count 195
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 6 with 2 rules applied. Total rules applied 161 place count 73 transition count 195
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 6 with 4 rules applied. Total rules applied 165 place count 73 transition count 191
Discarding 2 places :
Symmetric choice reduction at 7 with 2 rule applications. Total rules 167 place count 71 transition count 189
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 7 with 2 rules applied. Total rules applied 169 place count 71 transition count 189
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 7 with 2 rules applied. Total rules applied 171 place count 71 transition count 189
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 7 with 4 rules applied. Total rules applied 175 place count 71 transition count 185
Discarding 2 places :
Symmetric choice reduction at 8 with 2 rule applications. Total rules 177 place count 69 transition count 183
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 8 with 2 rules applied. Total rules applied 179 place count 69 transition count 183
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 8 with 2 rules applied. Total rules applied 181 place count 69 transition count 183
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 8 with 4 rules applied. Total rules applied 185 place count 69 transition count 179
Discarding 2 places :
Symmetric choice reduction at 9 with 2 rule applications. Total rules 187 place count 67 transition count 177
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 9 with 2 rules applied. Total rules applied 189 place count 67 transition count 177
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 9 with 2 rules applied. Total rules applied 191 place count 67 transition count 177
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 9 with 4 rules applied. Total rules applied 195 place count 67 transition count 173
Discarding 2 places :
Symmetric choice reduction at 10 with 2 rule applications. Total rules 197 place count 65 transition count 171
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 10 with 2 rules applied. Total rules applied 199 place count 65 transition count 171
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 10 with 2 rules applied. Total rules applied 201 place count 65 transition count 171
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 10 with 4 rules applied. Total rules applied 205 place count 65 transition count 167
Discarding 2 places :
Symmetric choice reduction at 11 with 2 rule applications. Total rules 207 place count 63 transition count 165
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 11 with 2 rules applied. Total rules applied 209 place count 63 transition count 165
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 11 with 2 rules applied. Total rules applied 211 place count 63 transition count 165
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 11 with 4 rules applied. Total rules applied 215 place count 63 transition count 161
Discarding 2 places :
Symmetric choice reduction at 12 with 2 rule applications. Total rules 217 place count 61 transition count 159
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 12 with 2 rules applied. Total rules applied 219 place count 61 transition count 159
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 12 with 2 rules applied. Total rules applied 221 place count 61 transition count 159
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 12 with 4 rules applied. Total rules applied 225 place count 61 transition count 155
Discarding 2 places :
Symmetric choice reduction at 13 with 2 rule applications. Total rules 227 place count 59 transition count 153
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 13 with 2 rules applied. Total rules applied 229 place count 59 transition count 153
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 13 with 2 rules applied. Total rules applied 231 place count 59 transition count 153
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 13 with 4 rules applied. Total rules applied 235 place count 59 transition count 149
Discarding 2 places :
Symmetric choice reduction at 14 with 2 rule applications. Total rules 237 place count 57 transition count 147
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 14 with 2 rules applied. Total rules applied 239 place count 57 transition count 147
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 1 ms
Iterating global reduction 14 with 2 rules applied. Total rules applied 241 place count 57 transition count 147
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 14 with 4 rules applied. Total rules applied 245 place count 57 transition count 143
Discarding 2 places :
Symmetric choice reduction at 15 with 2 rule applications. Total rules 247 place count 55 transition count 141
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 15 with 2 rules applied. Total rules applied 249 place count 55 transition count 141
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 15 with 2 rules applied. Total rules applied 251 place count 55 transition count 141
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 15 with 4 rules applied. Total rules applied 255 place count 55 transition count 137
Discarding 2 places :
Symmetric choice reduction at 16 with 2 rule applications. Total rules 257 place count 53 transition count 135
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 16 with 2 rules applied. Total rules applied 259 place count 53 transition count 135
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 16 with 2 rules applied. Total rules applied 261 place count 53 transition count 135
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 16 with 4 rules applied. Total rules applied 265 place count 53 transition count 131
Discarding 2 places :
Symmetric choice reduction at 17 with 2 rule applications. Total rules 267 place count 51 transition count 129
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 17 with 2 rules applied. Total rules applied 269 place count 51 transition count 129
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 17 with 2 rules applied. Total rules applied 271 place count 51 transition count 129
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 17 with 4 rules applied. Total rules applied 275 place count 51 transition count 125
Discarding 2 places :
Symmetric choice reduction at 18 with 2 rule applications. Total rules 277 place count 49 transition count 123
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 18 with 2 rules applied. Total rules applied 279 place count 49 transition count 123
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 18 with 2 rules applied. Total rules applied 281 place count 49 transition count 123
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 18 with 4 rules applied. Total rules applied 285 place count 49 transition count 119
Discarding 2 places :
Symmetric choice reduction at 19 with 2 rule applications. Total rules 287 place count 47 transition count 117
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 19 with 2 rules applied. Total rules applied 289 place count 47 transition count 117
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 19 with 2 rules applied. Total rules applied 291 place count 47 transition count 117
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 19 with 4 rules applied. Total rules applied 295 place count 47 transition count 113
Discarding 2 places :
Symmetric choice reduction at 20 with 2 rule applications. Total rules 297 place count 45 transition count 111
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 20 with 2 rules applied. Total rules applied 299 place count 45 transition count 111
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 20 with 2 rules applied. Total rules applied 301 place count 45 transition count 111
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 20 with 4 rules applied. Total rules applied 305 place count 45 transition count 107
Discarding 2 places :
Symmetric choice reduction at 21 with 2 rule applications. Total rules 307 place count 43 transition count 105
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 21 with 2 rules applied. Total rules applied 309 place count 43 transition count 105
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 21 with 2 rules applied. Total rules applied 311 place count 43 transition count 105
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 21 with 4 rules applied. Total rules applied 315 place count 43 transition count 101
Discarding 2 places :
Symmetric choice reduction at 22 with 2 rule applications. Total rules 317 place count 41 transition count 99
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 22 with 2 rules applied. Total rules applied 319 place count 41 transition count 99
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 22 with 2 rules applied. Total rules applied 321 place count 41 transition count 99
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 22 with 4 rules applied. Total rules applied 325 place count 41 transition count 95
Discarding 2 places :
Symmetric choice reduction at 23 with 2 rule applications. Total rules 327 place count 39 transition count 93
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 23 with 2 rules applied. Total rules applied 329 place count 39 transition count 93
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 23 with 2 rules applied. Total rules applied 331 place count 39 transition count 93
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 23 with 4 rules applied. Total rules applied 335 place count 39 transition count 89
Discarding 2 places :
Symmetric choice reduction at 24 with 2 rule applications. Total rules 337 place count 37 transition count 87
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 24 with 2 rules applied. Total rules applied 339 place count 37 transition count 87
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 24 with 2 rules applied. Total rules applied 341 place count 37 transition count 87
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 24 with 4 rules applied. Total rules applied 345 place count 37 transition count 83
Discarding 2 places :
Symmetric choice reduction at 25 with 2 rule applications. Total rules 347 place count 35 transition count 81
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 25 with 2 rules applied. Total rules applied 349 place count 35 transition count 81
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 25 with 2 rules applied. Total rules applied 351 place count 35 transition count 81
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 25 with 4 rules applied. Total rules applied 355 place count 35 transition count 77
Discarding 2 places :
Symmetric choice reduction at 26 with 2 rule applications. Total rules 357 place count 33 transition count 75
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 26 with 2 rules applied. Total rules applied 359 place count 33 transition count 75
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 26 with 2 rules applied. Total rules applied 361 place count 33 transition count 75
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 26 with 4 rules applied. Total rules applied 365 place count 33 transition count 71
Discarding 2 places :
Symmetric choice reduction at 27 with 2 rule applications. Total rules 367 place count 31 transition count 69
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 27 with 2 rules applied. Total rules applied 369 place count 31 transition count 69
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 27 with 2 rules applied. Total rules applied 371 place count 31 transition count 69
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 27 with 4 rules applied. Total rules applied 375 place count 31 transition count 65
Discarding 2 places :
Symmetric choice reduction at 28 with 2 rule applications. Total rules 377 place count 29 transition count 63
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 28 with 2 rules applied. Total rules applied 379 place count 29 transition count 63
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 28 with 2 rules applied. Total rules applied 381 place count 29 transition count 63
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 28 with 4 rules applied. Total rules applied 385 place count 29 transition count 59
Discarding 2 places :
Symmetric choice reduction at 29 with 2 rule applications. Total rules 387 place count 27 transition count 57
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 29 with 2 rules applied. Total rules applied 389 place count 27 transition count 57
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 29 with 2 rules applied. Total rules applied 391 place count 27 transition count 57
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 29 with 4 rules applied. Total rules applied 395 place count 27 transition count 53
Discarding 2 places :
Symmetric choice reduction at 30 with 2 rule applications. Total rules 397 place count 25 transition count 51
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 30 with 2 rules applied. Total rules applied 399 place count 25 transition count 51
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 30 with 2 rules applied. Total rules applied 401 place count 25 transition count 51
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 30 with 4 rules applied. Total rules applied 405 place count 25 transition count 47
Discarding 2 places :
Symmetric choice reduction at 31 with 2 rule applications. Total rules 407 place count 23 transition count 45
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 31 with 2 rules applied. Total rules applied 409 place count 23 transition count 45
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 31 with 2 rules applied. Total rules applied 411 place count 23 transition count 45
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 31 with 4 rules applied. Total rules applied 415 place count 23 transition count 41
Discarding 2 places :
Symmetric choice reduction at 32 with 2 rule applications. Total rules 417 place count 21 transition count 39
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 32 with 2 rules applied. Total rules applied 419 place count 21 transition count 39
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 32 with 2 rules applied. Total rules applied 421 place count 21 transition count 39
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 32 with 4 rules applied. Total rules applied 425 place count 21 transition count 35
Discarding 2 places :
Symmetric choice reduction at 33 with 2 rule applications. Total rules 427 place count 19 transition count 33
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 33 with 2 rules applied. Total rules applied 429 place count 19 transition count 33
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 33 with 2 rules applied. Total rules applied 431 place count 19 transition count 33
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 33 with 4 rules applied. Total rules applied 435 place count 19 transition count 29
Discarding 2 places :
Symmetric choice reduction at 34 with 2 rule applications. Total rules 437 place count 17 transition count 27
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 34 with 2 rules applied. Total rules applied 439 place count 17 transition count 27
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 34 with 2 rules applied. Total rules applied 441 place count 17 transition count 27
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 34 with 4 rules applied. Total rules applied 445 place count 17 transition count 23
Discarding 2 places :
Symmetric choice reduction at 35 with 2 rule applications. Total rules 447 place count 15 transition count 21
Deduced a syphon composed of 6 places in 0 ms
Iterating global reduction 35 with 2 rules applied. Total rules applied 449 place count 15 transition count 21
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 8 places in 0 ms
Iterating global reduction 35 with 2 rules applied. Total rules applied 451 place count 15 transition count 21
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 35 with 4 rules applied. Total rules applied 455 place count 15 transition count 17
Discarding 4 places :
Symmetric choice reduction at 36 with 4 rule applications. Total rules 459 place count 11 transition count 13
Deduced a syphon composed of 4 places in 0 ms
Iterating global reduction 36 with 4 rules applied. Total rules applied 463 place count 11 transition count 13
Deduced a syphon composed of 4 places in 0 ms
Drop transitions (Redundant composition of simpler transitions.) removed 1 transitions
Redundant transition composition rules discarded 1 transitions
Iterating global reduction 36 with 1 rules applied. Total rules applied 464 place count 11 transition count 12
Performed 1 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 36 with 1 Pre rules applied. Total rules applied 464 place count 11 transition count 12
Deduced a syphon composed of 5 places in 0 ms
Iterating global reduction 36 with 1 rules applied. Total rules applied 465 place count 11 transition count 12
Deduced a syphon composed of 5 places in 0 ms
Applied a total of 465 rules in 76 ms. Remains 11 /2462 variables (removed 2451) and now considering 12/5962 (removed 5950) transitions.
[2024-06-01 11:22:31] [INFO ] Redundant transitions in 0 ms returned []
Running 8 sub problems to find dead transitions.
// Phase 1: matrix 12 rows 11 cols
[2024-06-01 11:22:31] [INFO ] Computed 3 invariants in 1 ms
At refinement iteration 0 (INCLUDED_ONLY) 0/8 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 8 unsolved
At refinement iteration 1 (OVERLAPS) 3/11 variables, 3/3 constraints. Problems are: Problem set: 0 solved, 8 unsolved
[2024-06-01 11:22:31] [INFO ] Deduced a trap composed of 2 places in 29 ms of which 7 ms to minimize.
Problem TDEAD0 is UNSAT
[2024-06-01 11:22:31] [INFO ] Deduced a trap composed of 2 places in 24 ms of which 2 ms to minimize.
Problem TDEAD1 is UNSAT
[2024-06-01 11:22:31] [INFO ] Deduced a trap composed of 2 places in 22 ms of which 1 ms to minimize.
Problem TDEAD2 is UNSAT
Problem TDEAD4 is UNSAT
Problem TDEAD5 is UNSAT
At refinement iteration 2 (INCLUDED_ONLY) 0/11 variables, 3/6 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/11 variables, 0/6 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 4 (OVERLAPS) 11/22 variables, 11/17 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/22 variables, 0/17 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 6 (OVERLAPS) 0/22 variables, 0/17 constraints. Problems are: Problem set: 5 solved, 3 unsolved
No progress, stopping.
After SMT solving in domain Real declared 22/23 variables, and 17 constraints, problems are : Problem set: 5 solved, 3 unsolved in 435 ms.
Refiners :[Positive P Invariants (semi-flows): 3/3 constraints, State Equation: 11/11 constraints, PredecessorRefiner: 8/8 constraints, Known Traps: 3/3 constraints]
Escalating to Integer solving :Problem set: 5 solved, 3 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/3 variables, 0/0 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 1 (OVERLAPS) 8/11 variables, 3/3 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/11 variables, 3/6 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/11 variables, 0/6 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 4 (OVERLAPS) 11/22 variables, 11/17 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/22 variables, 3/20 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/22 variables, 0/20 constraints. Problems are: Problem set: 5 solved, 3 unsolved
At refinement iteration 7 (OVERLAPS) 0/22 variables, 0/20 constraints. Problems are: Problem set: 5 solved, 3 unsolved
No progress, stopping.
After SMT solving in domain Int declared 22/23 variables, and 20 constraints, problems are : Problem set: 5 solved, 3 unsolved in 70 ms.
Refiners :[Positive P Invariants (semi-flows): 3/3 constraints, State Equation: 11/11 constraints, PredecessorRefiner: 3/8 constraints, Known Traps: 3/3 constraints]
After SMT, in 510ms problems are : Problem set: 5 solved, 3 unsolved
Search for dead transitions found 5 dead transitions in 510ms
Found 5 dead transitions using SMT.
Drop transitions (Dead Transitions using SMT only with invariants) removed 5 transitions
Dead transitions reduction (with SMT) removed 5 transitions
Starting structural reductions in SI_LTL mode, iteration 1 : 11/2462 places, 7/5962 transitions.
Graph (complete) has 6 edges and 11 vertex of which 6 are kept as prefixes of interest. Removing 5 places using SCC suffix rule.1 ms
Discarding 5 places :
Also discarding 0 output transitions
Applied a total of 1 rules in 3 ms. Remains 6 /11 variables (removed 5) and now considering 7/7 (removed 0) transitions.
Starting structural reductions in SI_LTL mode, iteration 2 : 6/2462 places, 7/5962 transitions.
Finished structural reductions in SI_LTL mode , in 2 iterations and 615 ms. Remains : 6/2462 places, 7/5962 transitions.
Support contains 3 out of 2462 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2462/2462 places, 5962/5962 transitions.
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 1 place count 2461 transition count 5961
Iterating global reduction 0 with 1 rules applied. Total rules applied 2 place count 2461 transition count 5961
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 3 place count 2460 transition count 5960
Iterating global reduction 0 with 1 rules applied. Total rules applied 4 place count 2460 transition count 5960
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 5 place count 2459 transition count 5959
Iterating global reduction 0 with 1 rules applied. Total rules applied 6 place count 2459 transition count 5959
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 7 place count 2458 transition count 5958
Iterating global reduction 0 with 1 rules applied. Total rules applied 8 place count 2458 transition count 5958
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 9 place count 2457 transition count 5957
Iterating global reduction 0 with 1 rules applied. Total rules applied 10 place count 2457 transition count 5957
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 11 place count 2456 transition count 5956
Iterating global reduction 0 with 1 rules applied. Total rules applied 12 place count 2456 transition count 5956
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 13 place count 2455 transition count 5955
Iterating global reduction 0 with 1 rules applied. Total rules applied 14 place count 2455 transition count 5955
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 15 place count 2454 transition count 5954
Iterating global reduction 0 with 1 rules applied. Total rules applied 16 place count 2454 transition count 5954
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 17 place count 2453 transition count 5953
Iterating global reduction 0 with 1 rules applied. Total rules applied 18 place count 2453 transition count 5953
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 19 place count 2452 transition count 5952
Iterating global reduction 0 with 1 rules applied. Total rules applied 20 place count 2452 transition count 5952
Applied a total of 20 rules in 2716 ms. Remains 2452 /2462 variables (removed 10) and now considering 5952/5962 (removed 10) transitions.
// Phase 1: matrix 5952 rows 2452 cols
[2024-06-01 11:22:34] [INFO ] Computed 50 invariants in 16 ms
[2024-06-01 11:22:35] [INFO ] Implicit Places using invariants in 611 ms returned []
[2024-06-01 11:22:35] [INFO ] Invariant cache hit.
[2024-06-01 11:22:38] [INFO ] Implicit Places using invariants and state equation in 2977 ms returned []
Implicit Place search using SMT with State Equation took 3599 ms to find 0 implicit places.
Running 4152 sub problems to find dead transitions.
[2024-06-01 11:22:38] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: ((s50 1.0)
(s51 1.0)
(s52 1.0)
(s53 1.0)
(s54 1.0)
(s55 1.0)
(s56 1.0)
(s57 1.0)
(s58 1.0)
(s59 1.0)
(s60 1.0)
(s61 1.0)
(s62 1.0)
(s63 1.0)
(s64 1.0)
(s65 1.0)
(s66 1.0)
(s67 1.0)
(s68 1.0)
(s69 1.0)
(s70 1.0)
(s71 1.0)
(s72 1.0)
(s73 1.0)
(s74 1.0)
(s75 1.0)
(s76 1.0)
(s77 1.0)
(s78 1.0)
(s79 1.0)
(s80 1.0)
(s81 1.0)
(s82 1.0)
(s83 1.0)
(s84 1.0)
(s85 1.0)
(s86 1.0)
(s87 1.0)
(s88 1.0)
(s89 1.0)
(s90 1.0)
(s91 1.0)
(s92 1.0)
(s93 1.0)
(s94 1.0)
(s95 1.0)
(s96 1.0)
(s97 1.0)
(s98 1.0)
(s99 1.0)
(s100 1.0)
(s101 1.0)
(s102 1.0)
(s103 1.0)
(s104 1.0)
(s105 1.0)
(s106 1.0)
(s107 1.0)
(s108 1.0)
(s109 1.0)
(s110 1.0)
(s111 1.0)
(s112 1.0)
(s113 1.0)
(s114 1.0)
(s115 1.0)
(s116 1.0)
(s117 1.0)
(s118 1.0)
(s119 1.0)
(s120 1.0)
(s121 1.0)
(s122 1.0)
(s123 1.0)
(s124 1.0)
(s125 1.0)
(s126 1.0)
(s127 1.0)
(s128 1.0)
(s129 1.0)
(s130 1.0)
(s131 1.0)
(s132 1.0)
(s133 1.0)
(s134 1.0)
(s135 1.0)
(s136 1.0)
(s137 1.0)
(s138 1.0)
(s139 1.0)
(s140 1.0)
(s141 1.0)
(s142 1.0)
(s143 1.0)
(s144 1.0)
(s145 1.0)
(s146 1.0)
(s147 1.0)
(s148 1.0)
(s149 1.0)
(s150 1.0)
(s151 1.0)
(s152 1.0)
(s153 1.0)
(s154 1.0)
(s155 1.0)
(s156 1.0)
(s157 1.0)
(s158 1.0)
(s159 1.0)
(s160 1.0)
(s161 1.0)
(s162 1.0)
(s163 1.0)
(s164 1.0)
(s165 1.0)
(s166 1.0)
(s167 1.0)
(s168 1.0)
(s169 1.0)
(s170 1.0)
(s171 1.0)
(s172 1.0)
(s173 1.0)
(s174 1.0)
(s175 1.0)
(s176 1.0)
(s177 1.0)
(s178 1.0)
(s179 1.0)
(s180 1.0)
(s181 1.0)
(s182 1.0)
(s183 1.0)
(s184 1.0)
(s185 1.0)
(s186 1.0)
(s187 1.0)
(s188 1.0)
(s189 1.0)
(s190 1.0)
(s191 1.0)
(s192 1.0)
(s193 1.0)
(s194 1.0)
(s195 1.0)
(s196 1.0)
(s197 1.0)
(s198 1.0)
(s199 1.0)
(s200 1.0)
(s201 1.0)
(s202 1.0)
(s203 1.0)
(s204 1.0)
(s205 1.0)
(s206 1.0)
(s207 1.0)
(s208 1.0)
(s209 1.0)
(s210 1.0)
(s211 1.0)
(s212 1.0)
(s213 1.0)
(s214 1.0)
(s215 1.0)
(s216 1.0)
(s217 1.0)
(s218 1.0)
(s219 1.0)
(s220 1.0)
(s221 1.0)
(s222 1.0)
(s223 1.0)
(s224 1.0)
(s225 1.0)
(s226 1.0)
(s227 1.0)
(s228 1.0)
(s229 1.0)
(s230 1.0)
(s231 1.0)
(s232 1.0)
(s233 1.0)
(s234 1.0)
(s235 1.0)
(s236 1.0)
(s237 1.0)
(s238 1.0)
(s239 1.0)
(s240 1.0)
(s241 1.0)
(s242 1.0)
(s243 1.0)
(s244 1.0)
(s245 1.0)
(s246 1.0)
(s247 1.0)
(s248 1.0)
(s249 1.0)
(s250 1.0)
(s251 1.0)
(s252 1.0)
(s253 1.0)
(s254 1.0)
(s255 1.0)
(s256 1.0)
(s257 1.0)
(s258 1.0)
(s259 1.0)
(s260 1.0)
(s261 1.0)
(s262 1.0)
(s263 1.0)
(s264 1.0)
(s265 1.0)
(s266 1.0)
(s267 1.0)
(s268 1.0)
(s269 1.0)
(s270 1.0)
(s271 1.0)
(s272 1.0)
(s273 1.0)
(s274 1.0)
(s275 1.0)
(s276 1.0)
(s277 1.0)
(s278 1.0)
(s279 1.0)
(s280 1.0)
(s281 1.0)
(s282 1.0)
(s283 1.0)
(s284 1.0)
(s285 1.0)
(s286 1.0)
(s287 1.0)
(s288 1.0)
(s289 1.0)
(s290 1.0)
(s291 1.0)
(s292 1.0)
(s293 1.0)
(s294 1.0)
(s295 1.0)
(s296 1.0)
(s297 1.0)
(s298 1.0)
(s299 1.0)
(s300 1.0)
(s301 1.0)
(s302 1.0)
(s303 1.0)
(s304 1.0)
(s305 1.0)
(s306 1.0)
(s307 1.0)
(s308 1.0)
(s309 1.0)
(s310 1.0)
(s311 1.0)
(s312 1.0)
(s313 1.0)
(s314 1.0)
(s315 1.0)
(s316 1.0)
(s317 1.0)
(s318 1.0)
(s319 1.0)
(s320 1.0)
(s321 1.0)
(s322 1.0)
(s323 1.0)
(s324 1.0)
(s325 1.0)
(s326 1.0)
(s327 1.0)
(s328 1.0)
(s329 1.0)
(s330 1.0)
(s331 1.0)
(s332 1.0)
(s333 1.0)
(s334 1.0)
(s335 1.0)
(s336 1.0)
(s337 1.0)
(s338 1.0)
(s339 1.0)
(s340 1.0)
(s341 1.0)
(s342 1.0)
(s343 1.0)
(s344 1.0)
(s345 1.0)
(s346 1.0)
(s347 1.0)
(s348 1.0)
(s349 1.0)
(s350 1.0)
(s351 1.0)
(s352 1.0)
(s353 1.0)
(s354 1.0)
(s355 1.0)
(s356 1.0)
(s357 1.0)
(s358 1.0)
(s359 1.0)
(s360 1.0)
(s361 1.0)
(s362 1.0)
(s363 1.0)
(s364 1.0)
(s365 1.0)
(s366 1.0)
(s367 1.0)
(s368 1.0)
(s369 1.0)
(s370 1.0)
(s371 1.0)
(s372 1.0)
(s373 1.0)
(s374 1.0)
(s375 1.0)
(s376 1.0)
(s377 1.0)
(s378 1.0)
(s379 1.0)
(s380 1.0)
(s381 1.0)
(s382 1.0)
(s383 1.0)
(s384 1.0)
(s385 1.0)
(s386 1.0)
(s387 1.0)
(s388 1.0)
(s389 1.0)
(s390 1.0)
(s391 1.0)
(s392 1.0)
(s393 1.0)
(s394 1.0)
(s395 1.0)
(s396 1.0)
(s397 1.0)
(s398 1.0)
(s399 1.0)
(s400 1.0)
(s401 1.0)
(s402 1.0)
(s403 1.0)
(s404 1.0)
(s405 1.0)
(s406 1.0)
(s407 1.0)
(s408 1.0)
(s409 1.0)
(s410 1.0)
(s411 1.0)
(s412 1.0)
(s413 1.0)
(s414 1.0)
(s415 1.0)
(s416 1.0)
(s417 1.0)
(s418 1.0)
(s419 1.0)
(s420 1.0)
(s421 1.0)
(s422 1.0)
(s423 1.0)
(s424 1.0)
(s425 1.0)
(s426 1.0)
(s427 1.0)
(s428 1.0)
(s429 1.0)
(s430 1.0)
(s431 1.0)
(s432 1.0)
(s433 1.0)
(s434 1.0)
(s435 1.0)
(s436 1.0)
(s437 1.0)
(s438 1.0)
(s439 1.0)
(s440 1.0)
(s441 1.0)
(s442 1.0)
(s443 1.0)
(s444 1.0)
(s445 1.0)
(s446 1.0)
(s447 1.0)
(s448 1.0)
(s449 1.0)
(s450 1.0)
(s451 1.0)
(s452 1.0)
(s453 1.0)
(s454 1.0)
(s455 1.0)
(s456 1.0)
(s457 1.0)
(s458 1.0)
(s459 1.0)
(s460 1.0)
(s461 1.0)
(s462 1.0)
(s463 1.0)
(s464 1.0)
(s465 1.0)
(s466 1.0)
(s467 1.0)
(s468 1.0)
(s469 1.0)
(s470 1.0)
(s471 1.0)
(s472 1.0)
(s473 1.0)
(s474 1.0)
(s475 1.0)
(s476 1.0)
(s477 1.0)
(s478 1.0)
(s479 1.0)
(s480 1.0)
(s481 1.0)
(s482 1.0)
(s483 1.0)
(s484 1.0)
(s485 1.0)
(s486 1.0)
(s487 1.0)
(s488 1.0)
(s489 1.0)
(s490 1.0)
(s491 1.0)
(s492 1.0)
(s493 1.0)
(s494 1.0)
(s495 1.0)
(s496 1.0)
(s497 1.0)
(s498 1.0)
(s499 1.0)
(s500 1.0)
(s501 1.0)
(s502 1.0)
(s503 1.0)
(s504 1.0)
(s505 1.0)
(s506 1.0)
(s507 1.0)
(s508 1.0)
(s509 1.0)
(s510 1.0)
(s511 1.0)
(s512 1.0)
(s513 1.0)
(s514 1.0)
(s515 1.0)
(s516 1.0)
(s517 1.0)
(s518 1.0)
(s519 1.0)
(s520 1.0)
(s521 1.0)
(s522 1.0)
(s523 1.0)
(s524 1.0)
(s525 1.0)
(s526 1.0)
(s527 1.0)
(s528 1.0)
(s529 1.0)
(s530 1.0)
(s531 1.0)
(s532 1.0)
(s533 1.0)
(s534 1.0)
(s535 1.0)
(s536 1.0)
(s537 1.0)
(s538 1.0)
(s539 1.0)
(s540 1.0)
(s541 1.0)
(s542 1.0)
(s543 1.0)
(s544 1.0)
(s545 1.0)
(s546 1.0)
(s547 1.0)
(s548 1.0)
(s549 1.0)
(s550 1.0)
(s551 1.0)
(s552 1.0)
(s553 1.0)
(s554 1.0)
(s555 1.0)
(s556 1.0)
(s557 1.0)
(s558 1.0)
(s559 1.0)
(s560 1.0)
(s561 1.0)
(s562 1.0)
(s563 1.0)
(s564 1.0)
(s565 1.0)
(s566 1.0)
(s567 1.0)
(s568 1.0)
(s569 1.0)
(s570 1.0)
(s571 1.0)
(s572 1.0)
(s573 1.0)
(s574 1.0)
(s575 1.0)
(s576 1.0)
(s577 1.0)
(s578 1.0)
(s579 1.0)
(s580 1.0)
(s581 1.0)
(s582 1.0)
(s583 1.0)
(s584 1.0)
(s585 1.0)
(s586 1.0)
(s587 1.0)
(s588 1.0)
(s589 1.0)
(s590 1.0)
(s591 1.0)
(s592 1.0)
(s593 1.0)
(s594 1.0)
(s595 1.0)
(s596 1.0)
(s597 1.0)
(s598 1.0)
(s599 1.0)
(s600 1.0)
(s601 1.0)
(s602 1.0)
(s603 1.0)
(s604 1.0)
(s605 1.0)
(s606 1.0)
(s607 1.0)
(s608 1.0)
(s609 1.0)
(s610 1.0)
(s611 1.0)
(s612 1.0)
(s613 1.0)
(s614 1.0)
(s615 1.0)
(s616 1.0)
(s617 1.0)
(s618 1.0)
(s619 1.0)
(s620 1.0)
(s621 1.0)
(s622 1.0)
(s623 1.0)
(s624 1.0)
(s625 1.0)
(s626 1.0)
(s627 1.0)
(s628 1.0)
(s629 1.0)
(s630 1.0)
(s631 1.0)
(s632 1.0)
(s633 1.0)
(s634 1.0)
(s635 1.0)
(s636 1.0)
(s637 1.0)
(s638 1.0)
(s639 1.0)
(s640 1.0)
(s641 1.0)
(s642 1.0)
(s643 1.0)
(s644 1.0)
(s645 1.0)
(s646 1.0)
(s647 1.0)
(s648 1.0)
(s649 1.0)
(s650 1.0)
(s651 1.0)
(s652 1.0)
(s653 1.0)
(s654 1.0)
(s655 1.0)
(s656 1.0)
(s657 1.0)
(s658 1.0)
(s659 1.0)
(s660 1.0)
(s661 1.0)
(s662 1.0)
(s663 1.0)
(s664 1.0)
(s665 1.0)
(s666 1.0)
(s667 1.0)
(s668 1.0)
(s669 1.0)
(s670 1.0)
(s671 1.0)
(s672 1.0)
(s673 1.0)
(s674 1.0)
(s675 1.0)
(s676 1.0)
(s677 1.0)
(s678 1.0)
(s679 1.0)
(s680 1.0)
(s681 1.0)
(s682 1.0)
(s683 1.0)
(s684 1.0)
(s685 1.0)
(s686 1.0)
(s687 1.0)
(s688 1.0)
(s689 1.0)
(s690 1.0)
(s691 1.0)
(s692 1.0)
(s693 1.0)
(s694 1.0)
(s695 1.0)
(s696 1.0)
(s697 1.0)
(s698 1.0)
(s699 1.0)
(s700 1.0)
(s701 1.0)
(s702 1.0)
(s703 1.0)
(s704 1.0)
(s705 1.0)
(s706 1.0)
(s707 1.0)
(s708 1.0)
(s709 1.0)
(s710 1.0)
(s711 1.0)
(s712 1.0)
(s713 1.0)
(s714 1.0)
(s715 1.0)
(s716 1.0)
(s717 1.0)
(s718 1.0)
(s719 1.0)
(s720 1.0)
(s721 1.0)
(s722 1.0)
(s723 1.0)
(s724 1.0)
(s725 1.0)
(s726 1.0)
(s727 1.0)
(s728 1.0)
(s729 1.0)
(s730 1.0)
(s731 1.0)
(s732 1.0)
(s733 1.0)
(s734 1.0)
(s735 1.0)
(s736 1.0)
(s737 1.0)
(s738 1.0)
(s739 1.0)
(s740 1.0)
(s741 1.0)
(s742 1.0)
(s743 1.0)
(s744 1.0)
(s745 1.0)
(s746 1.0)
(s747 1.0)
(s748 1.0)
(s749 1.0)
(s750 1.0)
(s751 1.0)
(s752 1.0)
(s753 1.0)
(s754 1.0)
(s755 1.0)
(s756 1.0)
(s757 1.0)
(s758 1.0)
(s759 1.0)
(s760 1.0)
(s761 1.0)
(s762 1.0)
(s763 1.0)
(s764 1.0)
(s765 1.0)
(s766 1.0)
(s767 1.0)
(s768 1.0)
(s769 1.0)
(s770 1.0)
(s771 1.0)
(s772 1.0)
(s773 1.0)
(s774 1.0)
(s775 1.0)
(s776 1.0)
(s777 1.0)
(s778 1.0)
(s779 1.0)
(s780 1.0)
(s781 1.0)
(s782 1.0)
(s783 1.0)
(s784 1.0)
(s785 1.0)
(s786 1.0)
(s787 1.0)
(s788 1.0)
(s789 1.0)
(s790 1.0)
(s791 1.0)
(s792 1.0)
(s793 1.0)
(s794 1.0)
(s795 1.0)
(s796 1.0)
(s797 1.0)
(s798 1.0)
(s799 1.0)
(s800 1.0)
(s801 1.0)
(s802 1.0)
(s803 1.0)
(s804 1.0)
(s805 1.0)
(s806 1.0)
(s807 1.0)
(s808 1.0)
(s809 1.0)
(s810 1.0)
(s811 1.0)
(s812 1.0)
(s813 1.0)
(s814 1.0)
(s815 1.0)
(s816 1.0)
(s817 1.0)
(s818 1.0)
(s819 1.0)
(s820 1.0)
(s821 1.0)
(s822 1.0)
(s823 1.0)
(s824 1.0)
(s825 1.0)
(s826 1.0)
(s827 1.0)
(s828 1.0)
(s829 1.0)
(s830 1.0)
(s831 1.0)
(s832 1.0)
(s833 1.0)
(s834 1.0)
(s835 1.0)
(s836 1.0)
(s837 1.0)
(s838 1.0)
(s839 1.0)
(s840 1.0)
(s841 1.0)
(s842 1.0)
(s843 1.0)
(s844 1.0)
(s845 1.0)
(s846 1.0)
(s847 1.0)
(s848 1.0)
(s849 1.0)
(s850 1.0)
(s851 1.0)
(s852 1.0)
(s853 1.0)
(s854 1.0)
(s855 1.0)
(s856 1.0)
(s857 1.0)
(s858 1.0)
(s859 1.0)
(s860 1.0)
(s861 1.0)
(s862 1.0)
(s863 1.0)
(s864 1.0)
(s865 1.0)
(s866 1.0)
(s867 1.0)
(s868 1.0)
(s869 1.0)
(s870 1.0)
(s871 1.0)
(s872 1.0)
(s873 1.0)
(s874 1.0)
(s875 1.0)
(s876 1.0)
(s877 1.0)
(s878 1.0)
(s879 1.0)
(s880 1.0)
(s881 1.0)
(s882 1.0)
(s883 1.0)
(s884 1.0)
(s885 1.0)
(s886 1.0)
(s887 1.0)
(s888 1.0)
(s889 1.0)
(s890 1.0)
(s891 1.0)
(s892 1.0)
(s893 1.0)
(s894 1.0)
(s895 1.0)
(s896 1.0)
(s897 1.0)
(s898 1.0)
(s899 1.0)
(s900 1.0)
(s901 1.0)
(s902 1.0)
(s903 1.0)
(s904 1.0)
(s905 1.0)
(s906 1.0)
(s907 1.0)
(s908 1.0)
(s909 1.0)
(s910 1.0)
(s911 1.0)
(s912 1.0)
(s913 1.0)
(s914 1.0)
(s915 1.0)
(s916 1.0)
(s917 1.0)
(s918 1.0)
(s919 1.0)
(s920 1.0)
(s921 1.0)
(s922 1.0)
(s923 1.0)
(s924 1.0)
(s925 1.0)
(s926 1.0)
(s927 1.0)
(s928 1.0)
(s929 1.0)
(s930 1.0)
(s931 1.0)
(s932 1.0)
(s933 1.0)
(s934 1.0)
(s935 1.0)
(s936 1.0)
(s937 1.0)
(s938 1.0)
(s939 1.0)
(s940 1.0)
(s941 1.0)
(s942 1.0)
(s943 1.0)
(s944 1.0)
(s945 1.0)
(s946 1.0)
(s947 1.0)
(s948 1.0)
(s949 1.0)
(s950 1.0)
(s951 1.0)
(s952 1.0)
(s953 1.0)
(s954 1.0)
(s955 1.0)
(s956 1.0)
(s957 1.0)
(s958 1.0)
(s959 1.0)
(s960 1.0)
(s961 1.0)
(s962 1.0)
(s963 1.0)
(s964 1.0)
(s965 1.0)
(s966 1.0)
(s967 1.0)
(s968 1.0)
(s969 1.0)
(s970 1.0)
(s971 1.0)
(s972 1.0)
(s973 1.0)
(s974 1.0)
(s975 1.0)
(s976 1.0)
(s977 1.0)
(s978 1.0)
(s979 1.0)
(s980 1.0)
(s981 1.0)
(s982 1.0)
(s983 1.0)
(s984 1.0)
(s985 1.0)
(s986 1.0)
(s987 1.0)
(s988 1.0)
(s989 1.0)
(s990 1.0)
(s991 1.0)
(s992 1.0)
(s993 1.0)
(s994 1.0)
(s995 1.0)
(s996 1.0)
(s997 1.0)
(s998 1.0)
(s999 1.0)
(s1000 1.0)
(s1001 1.0)
(s1002 1.0)
(s1003 1.0)
(s1004 1.0)
(s1005 1.0)
(s1006 1.0)
(s1007 1.0)
(s1008 1.0)
(s1009 1.0)
(s1010 1.0)
(s1011 1.0)
(s1012 1.0)
(s1013 1.0)
(s1014 1.0)
(s1015 1.0)
(s1016 1.0)
(s1017 1.0)
(s1018 1.0)
(s1019 1.0)
(s1020 1.0)
(s1021 1.0)
(s1022 1.0)
(s1023 1.0)
(s1024 1.0)
(s1025 1.0)
(s1026 1.0)
(s1027 1.0)
(s1028 1.0)
(s1029 1.0)
(s1030 1.0)
(s1031 1.0)
(s1032 1.0)
(s1033 1.0)
(s1034 1.0)
(s1035 1.0)
(s1036 1.0)
(s1037 1.0)
(s1038 1.0)
(s1039 1.0)
(s1040 1.0)
(s1041 1.0)
(s1042 1.0)
(s1043 1.0)
(s1044 1.0)
(s1045 1.0)
(s1046 1.0)
(s1047 1.0)
(s1048 1.0)
(s1049 1.0)
(s1050 1.0)
(s1051 1.0)
(s1052 1.0)
(s1053 1.0)
(s1054 1.0)
(s1055 1.0)
(s1056 1.0)
(s1057 1.0)
(s1058 1.0)
(s1059 1.0)
(s1060 1.0)
(s1061 1.0)
(s1062 1.0)
(s1063 1.0)
(s1064 1.0)
(s1065 1.0)
(s1066 1.0)
(s1067 1.0)
(s1068 1.0)
(s1069 1.0)
(s1070 1.0)
(s1071 1.0)
(s1072 1.0)
(s1073 1.0)
(s1074 1.0)
(s1075 1.0)
(s1076 1.0)
(s1077 1.0)
(s1078 1.0)
(s1079 1.0)
(s1080 1.0)
(s1081 1.0)
(s1082 1.0)
(s1083 1.0)
(s1084 1.0)
(s1085 1.0)
(s1086 1.0)
(s1087 1.0)
(s1088 1.0)
(s1089 1.0)
(s1090 1.0)
(s1091 1.0)
(s1092 1.0)
(s1093 1.0)
(s1094 1.0)
(s1095 1.0)
(s1096 1.0)
(s1097 1.0)
(s1098 1.0)
(s1099 1.0)
(s1100 1.0)
(s1101 1.0)
(s1102 1.0)
(s1103 1.0)
(s1104 1.0)
(s1105 1.0)
(s1106 1.0)
(s1107 1.0)
(s1108 1.0)
(s1109 1.0)
(s1110 1.0)
(s1111 1.0)
(s1112 1.0)
(s1113 1.0)
(s1114 1.0)
(s1115 1.0)
(s1116 1.0)
(s1117 1.0)
(s1118 1.0)
(s1119 1.0)
(s1120 1.0)
(s1121 1.0)
(s1122 1.0)
(s1123 1.0)
(s1124 1.0)
(s1125 1.0)
(s1126 1.0)
(s1127 1.0)
(s1128 1.0)
(s1129 1.0)
(s1130 1.0)
(s1131 1.0)
(s1132 1.0)
(s1133 1.0)
(s1134 1.0)
(s1135 1.0)
(s1136 1.0)
(s1137 1.0)
(s1138 1.0)
(s1139 1.0)
(s1140 1.0)
(s1141 1.0)
(s1142 1.0)
(s1143 1.0)
(s1144 1.0)
(s1145 1.0)
(s1146 1.0)
(s1147 1.0)
(s1148 1.0)
(s1149 1.0)
(s1150 1.0)
(s1151 1.0)
(s1152 1.0)
(s1153 1.0)
(s1154 1.0)
(s1155 1.0)
(s1156 1.0)
(s1157 1.0)
(s1158 1.0)
(s1159 1.0)
(s1160 1.0)
(s1161 1.0)
(s1162 1.0)
(s1163 1.0)
(s1164 1.0)
(s1165 1.0)
(s1166 1.0)
(s1167 1.0)
(s1168 1.0)
(s1169 1.0)
(s1170 1.0)
(s1171 1.0)
(s1172 1.0)
(s1173 1.0)
(s1174 1.0)
(s1175 1.0)
(s1176 1.0)
(s1177 1.0)
(s1178 1.0)
(s1179 1.0)
(s1180 1.0)
(s1181 1.0)
(s1182 1.0)
(s1183 1.0)
(s1184 1.0)
(s1185 1.0)
(s1186 1.0)
(s1187 1.0)
(s1188 1.0)
(s1189 1.0)
(s1190 1.0)
(s1191 1.0)
(s1192 1.0)
(s1193 1.0)
(s1194 1.0)
(s1195 1.0)
(s1196 1.0)
(s1197 1.0)
(s1198 1.0)
(s1199 1.0)
(s1200 1.0)
(s1201 1.0)
(s1202 1.0)
(s1203 1.0)
(s1204 1.0)
(s1205 1.0)
(s1206 1.0)
(s1207 1.0)
(s1208 1.0)
(s1209 1.0)
(s1210 1.0)
(s1211 1.0)
(s1212 1.0)
(s1213 1.0)
(s1214 1.0)
(s1215 1.0)
(s1216 1.0)
(s1217 1.0)
(s1218 1.0)
(s1219 1.0)
(s1220 1.0)
(s1221 1.0)
(s1222 1.0)
(s1223 1.0)
(s1224 1.0)
(s1225 1.0)
(s1226 1.0)
(s1227 1.0)
(s1228 1.0)
(s1229 1.0)
(s1230 1.0)
(s1231 1.0)
(s1232 1.0)
(s1233 1.0)
(s1234 1.0)
(s1235 1.0)
(s1236 1.0)
(s1237 1.0)
(s1238 1.0)
(s1239 1.0)
(s1240 1.0)
(s1241 1.0)
(s1242 1.0)
(s1243 1.0)
(s1244 1.0)
(s1245 1.0)
(s1246 1.0)
(s1247 1.0)
(s1248 1.0)
(s1249 1.0)
(s1250 1.0)
(s1251 1.0)
(s1252 1.0)
(s1253 1.0)
(s1254 1.0)
(s1255 1.0)
(s1256 1.0)
(s1257 1.0)
(s1258 1.0)
(s1259 1.0)
(s1260 1.0)
(s1261 1.0)
(s1262 1.0)
(s1263 1.0)
(s1264 1.0)
(s1265 1.0)
(s1266 1.0)
(s1267 1.0)
(s1268 1.0)
(s1269 1.0)
(s1270 1.0)
(s1271 1.0)
(s1272 1.0)
(s1273 1.0)
(s1274 1.0)
(s1275 1.0)
(s1276 1.0)
(s1277 1.0)
(s1278 1.0)
(s1279 1.0)
(s1280 1.0)
(s1281 1.0)
(s1282 1.0)
(s1283 1.0)
(s1284 1.0)
(s1285 1.0)
(s1286 1.0)
(s1287 1.0)
(s1288 1.0)
(s1289 1.0)
(s1290 1.0)
(s1291 1.0)
(s1292 1.0)
(s1293 1.0)
(s1294 1.0)
(s1295 1.0)
(s1296 1.0)
(s1297 1.0)
(s1298 1.0)
(s1299 1.0)
(s1300 1.0)
(s1301 1.0)
(s1302 1.0)
(s1303 1.0)
(s1304 1.0)
(s1305 1.0)
(s1306 1.0)
(s1307 1.0)
(s1308 1.0)
(s1309 1.0)
(s1310 1.0)
(s1311 1.0)
(s1312 1.0)
(s1313 1.0)
(s1314 1.0)
(s1315 1.0)
(s1316 1.0)
(s1317 1.0)
(s1318 1.0)
(s1319 1.0)
(s1320 1.0)
(s1321 1.0)
(s1322 1.0)
(s1323 1.0)
(s1324 1.0)
(s1325 1.0)
(s1326 1.0)
(s1327 1.0)
(s1328 1.0)
(s1329 1.0)
(s1330 1.0)
(s1331 1.0)
(s1332 1.0)
(s1333 1.0)
(s1334 1.0)
(s1335 1.0)
(s1336 1.0)
(s1337 1.0)
(s1338 1.0)
(s1339 1.0)
(s1340 1.0)
(s1341 1.0)
(s1342 1.0)
(s1343 1.0)
(s1344 1.0)
(s1345 1.0)
(s1346 1.0)
(s1347 1.0)
(s1348 1.0)
(s1349 1.0)
(s1350 1.0)
(s1351 1.0)
(s1352 1.0)
(s1353 1.0)
(s1354 1.0)
(s1355 1.0)
(s1356 1.0)
(s1357 1.0)
(s1358 1.0)
(s1359 1.0)
(s1360 1.0)
(s1361 1.0)
(s1362 1.0)
(s1363 1.0)
(s1364 1.0)
(s1365 1.0)
(s1366 1.0)
(s1367 1.0)
(s1368 1.0)
(s1369 1.0)
(s1370 1.0)
(s1371 1.0)
(s1372 1.0)
(s1373 1.0)
(s1374 1.0)
(s1375 1.0)
(s1376 1.0)
(s1377 1.0)
(s1378 1.0)
(s1379 1.0)
(s1380 1.0)
(s1381 1.0)
(s1382 1.0)
(s1383 1.0)
(s1384 1.0)
(s1385 1.0)
(s1386 1.0)
(s1387 1.0)
(s1388 1.0)
(s1389 1.0)
(s1390 1.0)
(s1391 1.0)
(s1392 1.0)
(s1393 1.0)
(s1394 1.0)
(s1395 1.0)
(s1396 1.0)
(s1397 1.0)
(s1398 1.0)
(s1399 1.0)
(s1400 1.0)
(s1401 1.0)
(s1402 1.0)
(s1403 1.0)
(s1404 1.0)
(s1405 1.0)
(s1406 1.0)
(s1407 1.0)
(s1408 1.0)
(s1409 1.0)
(s1410 1.0)
(s1411 1.0)
(s1412 1.0)
(s1413 1.0)
(s1414 1.0)
(s1415 1.0)
(s1416 1.0)
(s1417 1.0)
(s1418 1.0)
(s1419 1.0)
(s1420 1.0)
(s1421 1.0)
(s1422 1.0)
(s1423 1.0)
(s1424 1.0)
(s1425 1.0)
(s1426 1.0)
(s1427 1.0)
(s1428 1.0)
(s1429 1.0)
(s1430 1.0)
(s1431 1.0)
(s1432 1.0)
(s1433 1.0)
(s1434 1.0)
(s1435 1.0)
(s1436 1.0)
(s1437 1.0)
(s1438 1.0)
(s1439 1.0)
(s1440 1.0)
(s1441 1.0)
(s1442 1.0)
(s1443 1.0)
(s1444 1.0)
(s1445 1.0)
(s1446 1.0)
(s1447 1.0)
(s1448 1.0)
(s1449 1.0)
(s1450 1.0)
(s1451 1.0)
(s1452 1.0)
(s1453 1.0)
(s1454 1.0)
(s1455 1.0)
(s1456 1.0)
(s1457 1.0)
(s1458 1.0)
(s1459 1.0)
(s1460 1.0)
(s1461 1.0)
(s1462 1.0)
(s1463 1.0)
(s1464 1.0)
(s1465 1.0)
(s1466 1.0)
(s1467 1.0)
(s1468 1.0)
(s1469 1.0)
(s1470 1.0)
(s1471 1.0)
(s1472 1.0)
(s1473 1.0)
(s1474 1.0)
(s1475 1.0)
(s1476 1.0)
(s1477 1.0)
(s1478 1.0)
(s1479 1.0)
(s1480 1.0)
(s1481 1.0)
(s1482 1.0)
(s1483 1.0)
(s1484 1.0)
(s1485 1.0)
(s1486 1.0)
(s1487 1.0)
(s1488 1.0)
(s1489 1.0)
(s1490 1.0)
(s1491 1.0)
(s1492 1.0)
(s1493 1.0)
(s1494 1.0)
(s1495 1.0)
(s1496 1.0)
(s1497 1.0)
(s1498 1.0)
(s1499 1.0)
(s1500 1.0)
(s1501 1.0)
(s1502 1.0)
(s1503 1.0)
(s1504 1.0)
(s1505 1.0)
(s1506 1.0)
(s1507 1.0)
(s1508 1.0)
(s1509 1.0)
(s1510 1.0)
(s1511 1.0)
(s1512 1.0)
(s1513 1.0)
(s1514 1.0)
(s1515 1.0)
(s1516 1.0)
(s1517 1.0)
(s1518 1.0)
(s1519 1.0)
(s1520 1.0)
(s1521 1.0)
(s1522 1.0)
(s1523 1.0)
(s1524 1.0)
(s1525 1.0)
(s1526 1.0)
(s1527 1.0)
(s1528 1.0)
(s1529 1.0)
(s1530 1.0)
(s1531 1.0)
(s1532 1.0)
(s1533 1.0)
(s1534 1.0)
(s1535 1.0)
(s1536 1.0)
(s1537 1.0)
(s1538 1.0)
(s1539 1.0)
(s1540 1.0)
(s1541 1.0)
(s1542 1.0)
(s1543 1.0)
(s1544 1.0)
(s1545 1.0)
(s1546 1.0)
(s1547 1.0)
(s1548 1.0)
(s1549 1.0)
(s1550 1.0)
(s1551 1.0)
(s1552 1.0)
(s1553 1.0)
(s1554 1.0)
(s1555 1.0)
(s1556 1.0)
(s1557 1.0)
(s1558 1.0)
(s1559 1.0)
(s1560 1.0)
(s1561 1.0)
(s1562 1.0)
(s1563 1.0)
(s1564 1.0)
(s1565 1.0)
(s1566 1.0)
(s1567 1.0)
(s1568 1.0)
(s1569 1.0)
(s1570 1.0)
(s1571 1.0)
(s1572 1.0)
(s1573 1.0)
(s1574 1.0)
(s1575 1.0)
(s1576 1.0)
(s1577 1.0)
(s1578 1.0)
(s1579 1.0)
(s1580 1.0)
(s1581 1.0)
(s1582 1.0)
(s1583 1.0)
(s1584 1.0)
(s1585 1.0)
(s1586 1.0)
(s1587 1.0)
(s1588 1.0)
(s1589 1.0)
(s1590 1.0)
(s1591 1.0)
(s1592 1.0)
(s1593 1.0)
(s1594 1.0)
(s1595 1.0)
(s1596 1.0)
(s1597 1.0)
(s1598 1.0)
(s1599 1.0)
(s1600 1.0)
(s1601 1.0)
(s1602 1.0)
(s1603 1.0)
(s1604 1.0)
(s1605 1.0)
(s1606 1.0)
(s1607 1.0)
(s1608 1.0)
(s1609 1.0)
(s1610 1.0)
(s1611 1.0)
(s1612 1.0)
(s1613 1.0)
(s1614 1.0)
(s1615 1.0)
(s1616 1.0)
(s1617 1.0)
(s1618 1.0)
(s1619 1.0)
(s1620 1.0)
(s1621 1.0)
(s1622 1.0)
(s1623 1.0)
(s1624 1.0)
(s1625 1.0)
(s1626 1.0)
(s1627 1.0)
(s1628 1.0)
(s1629 1.0)
(s1630 1.0)
(s1631 1.0)
(s1632 1.0)
(s1633 1.0)
(s1634 1.0)
(s1635 1.0)
(s1636 1.0)
(s1637 1.0)
(s1638 1.0)
(s1639 1.0)
(s1640 1.0)
(s1641 1.0)
(s1642 1.0)
(s1643 1.0)
(s1644 1.0)
(s1645 1.0)
(s1646 1.0)
(s1647 1.0)
(s1648 1.0)
(s1649 1.0)
(s1650 1.0)
(s1651 1.0)
(s1652 1.0)
(s1653 1.0)
(s1654 1.0)
(s1655 1.0)
(s1656 1.0)
(s1657 1.0)
(s1658 1.0)
(s1659 1.0)
(s1660 1.0)
(s1661 1.0)
(s1662 1.0)
(s1663 1.0)
(s1664 1.0)
(s1665 1.0)
(s1666 1.0)
(s1667 1.0)
(s1668 1.0)
(s1669 1.0)
(s1670 1.0)
(s1671 1.0)
(s1672 1.0)
(s1673 1.0)
(s1674 1.0)
(s1675 1.0)
(s1676 1.0)
(s1677 1.0)
(s1678 1.0)
(s1679 1.0)
(s1680 1.0)
(s1681 1.0)
(s1682 1.0)
(s1683 1.0)
(s1684 1.0)
(s1685 1.0)
(s1686 1.0)
(s1687 1.0)
(s1688 1.0)
(s1689 1.0)
(s1690 1.0)
(s1691 1.0)
(s1692 1.0)
(s1693 1.0)
(s1694 1.0)
(s1695 1.0)
(s1696 1.0)
(s1697 1.0)
(s1698 1.0)
(s1699 1.0)
(s1700 1.0)
(s1701 1.0)
(s1702 1.0)
(s1703 1.0)
(s1704 1.0)
(s1705 1.0)
(s1706 1.0)
(s1707 1.0)
(s1708 1.0)
(s1709 1.0)
(s1710 1.0)
(s1711 1.0)
(s1712 1.0)
(s1713 1.0)
(s1714 1.0)
(s1715 1.0)
(s1716 1.0)
(s1717 1.0)
(s1718 1.0)
(s1719 1.0)
(s1720 1.0)
(s1721 1.0)
(s1722 1.0)
(s1723 1.0)
(s1724 1.0)
(s1725 1.0)
(s1726 1.0)
(s1727 1.0)
(s1728 1.0)
(s1729 1.0)
(s1730 1.0)
(s1731 1.0)
(s1732 1.0)
(s1733 1.0)
(s1734 1.0)
(s1735 1.0)
(s1736 1.0)
(s1737 1.0)
(s1738 1.0)
(s1739 1.0)
(s1740 1.0)
(s1741 1.0)
(s1742 1.0)
(s1743 1.0)
(s1744 1.0)
(s1745 1.0)
(s1746 1.0)
(s1747 1.0)
(s1748 1.0)
(s1749 1.0)
(s1750 1.0)
(s1751 1.0)
(s1752 1.0)
(s1753 1.0)
(s1754 1.0)
(s1755 1.0)
(s1756 1.0)
(s1757 1.0)
(s1758 1.0)
(s1759 1.0)
(s1760 1.0)
(s1761 1.0)
(s1762 1.0)
(s1763 1.0)
(s1764 1.0)
(s1765 1.0)
(s1766 1.0)
(s1767 1.0)
(s1768 1.0)
(s1769 1.0)
(s1770 1.0)
(s1771 1.0)
(s1772 1.0)
(s1773 1.0)
(s1774 1.0)
(s1775 1.0)
(s1776 1.0)
(s1777 1.0)
(s1778 1.0)
(s1779 1.0)
(s1780 1.0)
(s1781 1.0)
(s1782 1.0)
(s1783 1.0)
(s1784 1.0)
(s1785 1.0)
(s1786 1.0)
(s1787 1.0)
(s1788 1.0)
(s1789 1.0)
(s1790 1.0)
(s1791 1.0)
(s1792 1.0)
(s1793 1.0)
(s1794 1.0)
(s1795 1.0)
(s1796 1.0)
(s1797 1.0)
(s1798 1.0)
(s1799 1.0)
(s1800 1.0)
(s1801 1.0)
(s1802 1.0)
(s1803 1.0)
(s1804 1.0)
(s1805 1.0)
(s1806 1.0)
(s1807 1.0)
(s1808 1.0)
(s1809 1.0)
(s1810 1.0)
(s1811 1.0)
(s1812 1.0)
(s1813 1.0)
(s1814 1.0)
(s1815 1.0)
(s1816 1.0)
(s1817 1.0)
(s1818 1.0)
(s1819 1.0)
(s1820 1.0)
(s1821 1.0)
(s1822 1.0)
(s1823 1.0)
(s1824 1.0)
(s1825 1.0)
(s1826 1.0)
(s1827 1.0)
(s1828 1.0)
(s1829 1.0)
(s1830 1.0)
(s1831 1.0)
(s1832 1.0)
(s1833 1.0)
(s1834 1.0)
(s1835 1.0)
(s1836 1.0)
(s1837 1.0)
(s1838 1.0)
(s1839 1.0)
(s1840 1.0)
(s1841 1.0)
(s1842 1.0)
(s1843 1.0)
(s1844 1.0)
(s1845 1.0)
(s1846 1.0)
(s1847 1.0)
(s1848 1.0)
(s1849 1.0)
(s1850 1.0)
(s1851 1.0)
(s1852 1.0)
(s1853 1.0)
(s1854 1.0)
(s1855 1.0)
(s1856 1.0)
(s1857 1.0)
(s1858 1.0)
(s1859 1.0)
(s1860 1.0)
(s1861 1.0)
(s1862 1.0)
(s1863 1.0)
(s1864 1.0)
(s1865 1.0)
(s1866 1.0)
(s1867 1.0)
(s1868 1.0)
(s1869 1.0)
(s1870 1.0)
(s1871 1.0)
(s1872 1.0)
(s1873 1.0)
(s1874 1.0)
(s1875 1.0)
(s1876 1.0)
(s1877 1.0)
(s1878 1.0)
(s1879 1.0)
(s1880 1.0)
(s1881 1.0)
(s1882 1.0)
(s1883 1.0)
(s1884 1.0)
(s1885 1.0)
(s1886 1.0)
(s1887 1.0)
(s1888 1.0)
(s1889 1.0)
(s1890 1.0)
(s1891 1.0)
(s1892 1.0)
(s1893 1.0)
(s1894 1.0)
(s1895 1.0)
(s1896 1.0)
(s1897 1.0)
(s1898 1.0)
(s1899 1.0)
(s1900 1.0)
(s1901 1.0)
(s1902 1.0)
(s1903 1.0)
(s1904 1.0)
(s1905 1.0)
(s1906 1.0)
(s1907 1.0)
(s1908 1.0)
(s1909 1.0)
(s1910 1.0)
(s1911 1.0)
(s1912 1.0)
(s1913 1.0)
(s1914 1.0)
(s1915 1.0)
(s1916 1.0)
(s1917 1.0)
(s1918 1.0)
(s1919 1.0)
(s1920 1.0)
(s1921 1.0)
(s1922 1.0)
(s1923 1.0)
(s1924 1.0)
(s1925 1.0)timeout
(s1926 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2402/8404 variables, and 0 constraints, problems are : Problem set: 0 solved, 4152 unsolved in 30134 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2452 constraints, PredecessorRefiner: 4152/4152 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4152 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2402/8404 variables, and 0 constraints, problems are : Problem set: 0 solved, 4152 unsolved in 30117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2452 constraints, PredecessorRefiner: 0/4152 constraints, Known Traps: 0/0 constraints]
After SMT, in 62621ms problems are : Problem set: 0 solved, 4152 unsolved
Search for dead transitions found 0 dead transitions in 62659ms
Starting structural reductions in LTL mode, iteration 1 : 2452/2462 places, 5952/5962 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68980 ms. Remains : 2452/2462 places, 5952/5962 transitions.
Treatment of property BART-PT-050-LTLFireability-08 finished in 225542 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X((F(p0)&&G(p1))))'
Support contains 2 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1599 places :
Symmetric choice reduction at 0 with 1599 rule applications. Total rules 1599 place count 5001 transition count 8501
Iterating global reduction 0 with 1599 rules applied. Total rules applied 3198 place count 5001 transition count 8501
Discarding 1349 places :
Symmetric choice reduction at 0 with 1349 rule applications. Total rules 4547 place count 3652 transition count 7152
Iterating global reduction 0 with 1349 rules applied. Total rules applied 5896 place count 3652 transition count 7152
Discarding 200 places :
Symmetric choice reduction at 0 with 200 rule applications. Total rules 6096 place count 3452 transition count 6952
Iterating global reduction 0 with 200 rules applied. Total rules applied 6296 place count 3452 transition count 6952
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6446 place count 3302 transition count 6802
Iterating global reduction 0 with 150 rules applied. Total rules applied 6596 place count 3302 transition count 6802
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6746 place count 3152 transition count 6652
Iterating global reduction 0 with 150 rules applied. Total rules applied 6896 place count 3152 transition count 6652
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7045 place count 3003 transition count 6503
Iterating global reduction 0 with 149 rules applied. Total rules applied 7194 place count 3003 transition count 6503
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7343 place count 2854 transition count 6354
Iterating global reduction 0 with 149 rules applied. Total rules applied 7492 place count 2854 transition count 6354
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7641 place count 2705 transition count 6205
Iterating global reduction 0 with 149 rules applied. Total rules applied 7790 place count 2705 transition count 6205
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 7890 place count 2605 transition count 6105
Iterating global reduction 0 with 100 rules applied. Total rules applied 7990 place count 2605 transition count 6105
Discarding 99 places :
Symmetric choice reduction at 0 with 99 rule applications. Total rules 8089 place count 2506 transition count 6006
Iterating global reduction 0 with 99 rules applied. Total rules applied 8188 place count 2506 transition count 6006
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 8238 place count 2456 transition count 5956
Iterating global reduction 0 with 50 rules applied. Total rules applied 8288 place count 2456 transition count 5956
Applied a total of 8288 rules in 4365 ms. Remains 2456 /6600 variables (removed 4144) and now considering 5956/10100 (removed 4144) transitions.
// Phase 1: matrix 5956 rows 2456 cols
[2024-06-01 11:23:46] [INFO ] Computed 50 invariants in 19 ms
[2024-06-01 11:23:46] [INFO ] Implicit Places using invariants in 604 ms returned []
[2024-06-01 11:23:46] [INFO ] Invariant cache hit.
[2024-06-01 11:23:49] [INFO ] Implicit Places using invariants and state equation in 2640 ms returned []
Implicit Place search using SMT with State Equation took 3247 ms to find 0 implicit places.
Running 4156 sub problems to find dead transitions.
[2024-06-01 11:23:49] [INFO ] Invariant cache hit.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2406/8412 variables, and 0 constraints, problems are : Problem set: 0 solved, 4156 unsolved in 30116 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2456 constraints, PredecessorRefiner: 4156/4156 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4156 unsolved
(s1534 1timeout
^^^^^^^^
(error "Invalid token: 1timeout")
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2406/8412 variables, and 0 constraints, problems are : Problem set: 0 solved, 4156 unsolved in 30120 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2456 constraints, PredecessorRefiner: 0/4156 constraints, Known Traps: 0/0 constraints]
After SMT, in 62595ms problems are : Problem set: 0 solved, 4156 unsolved
Search for dead transitions found 0 dead transitions in 62633ms
Starting structural reductions in LTL mode, iteration 1 : 2456/6600 places, 5956/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70250 ms. Remains : 2456/6600 places, 5956/10100 transitions.
Stuttering acceptance computed with spot in 176 ms :[(NOT p1), (OR (NOT p0) (NOT p1)), true, (OR (NOT p1) (NOT p0))]
Running random walk in product with property : BART-PT-050-LTLFireability-09
Entered a terminal (fully accepting) state of product in 1 steps with 0 reset in 1 ms.
FORMULA BART-PT-050-LTLFireability-09 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-09 finished in 70464 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X((G(p0)||(p1&&X(p2)))))'
Support contains 3 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1599 places :
Symmetric choice reduction at 0 with 1599 rule applications. Total rules 1599 place count 5001 transition count 8501
Iterating global reduction 0 with 1599 rules applied. Total rules applied 3198 place count 5001 transition count 8501
Discarding 1349 places :
Symmetric choice reduction at 0 with 1349 rule applications. Total rules 4547 place count 3652 transition count 7152
Iterating global reduction 0 with 1349 rules applied. Total rules applied 5896 place count 3652 transition count 7152
Discarding 200 places :
Symmetric choice reduction at 0 with 200 rule applications. Total rules 6096 place count 3452 transition count 6952
Iterating global reduction 0 with 200 rules applied. Total rules applied 6296 place count 3452 transition count 6952
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6446 place count 3302 transition count 6802
Iterating global reduction 0 with 150 rules applied. Total rules applied 6596 place count 3302 transition count 6802
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6746 place count 3152 transition count 6652
Iterating global reduction 0 with 150 rules applied. Total rules applied 6896 place count 3152 transition count 6652
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7046 place count 3002 transition count 6502
Iterating global reduction 0 with 150 rules applied. Total rules applied 7196 place count 3002 transition count 6502
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7346 place count 2852 transition count 6352
Iterating global reduction 0 with 150 rules applied. Total rules applied 7496 place count 2852 transition count 6352
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7646 place count 2702 transition count 6202
Iterating global reduction 0 with 150 rules applied. Total rules applied 7796 place count 2702 transition count 6202
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 7896 place count 2602 transition count 6102
Iterating global reduction 0 with 100 rules applied. Total rules applied 7996 place count 2602 transition count 6102
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 8096 place count 2502 transition count 6002
Iterating global reduction 0 with 100 rules applied. Total rules applied 8196 place count 2502 transition count 6002
Discarding 49 places :
Symmetric choice reduction at 0 with 49 rule applications. Total rules 8245 place count 2453 transition count 5953
Iterating global reduction 0 with 49 rules applied. Total rules applied 8294 place count 2453 transition count 5953
Applied a total of 8294 rules in 4657 ms. Remains 2453 /6600 variables (removed 4147) and now considering 5953/10100 (removed 4147) transitions.
// Phase 1: matrix 5953 rows 2453 cols
[2024-06-01 11:24:56] [INFO ] Computed 50 invariants in 16 ms
[2024-06-01 11:24:57] [INFO ] Implicit Places using invariants in 459 ms returned []
[2024-06-01 11:24:57] [INFO ] Invariant cache hit.
[2024-06-01 11:24:59] [INFO ] Implicit Places using invariants and state equation in 2560 ms returned []
Implicit Place search using SMT with State Equation took 3028 ms to find 0 implicit places.
Running 4153 sub problems to find dead transitions.
[2024-06-01 11:24:59] [INFO ] Invariant cache hit.
(s1097 1.0timeout
^^^^^^^^^^
(error "Invalid token: 1.0timeout")
Error getting values : (error "ParserException while parsing response: ((s50 1.0)
(s51 1.0)
(s52 1.0)
(s53 1.0)
(s54 1.0)
(s55 1.0)
(s56 1.0)
(s57 1.0)
(s58 1.0)
(s59 1.0)
(s60 1.0)
(s61 1.0)
(s62 1.0)
(s63 1.0)
(s64 1.0)
(s65 1.0)
(s66 1.0)
(s67 1.0)
(s68 1.0)
(s69 1.0)
(s70 1.0)
(s71 1.0)
(s72 1.0)
(s73 1.0)
(s74 1.0)
(s75 1.0)
(s76 1.0)
(s77 1.0)
(s78 1.0)
(s79 1.0)
(s80 1.0)
(s81 1.0)
(s82 1.0)
(s83 1.0)
(s84 1.0)
(s85 1.0)
(s86 1.0)
(s87 1.0)
(s88 1.0)
(s89 1.0)
(s90 1.0)
(s91 1.0)
(s92 1.0)
(s93 1.0)
(s94 1.0)
(s95 1.0)
(s96 1.0)
(s97 1.0)
(s98 1.0)
(s99 1.0)
(s100 1.0)
(s101 1.0)
(s102 1.0)
(s103 1.0)
(s104 1.0)
(s105 1.0)
(s106 1.0)
(s107 1.0)
(s108 1.0)
(s109 1.0)
(s110 1.0)
(s111 1.0)
(s112 1.0)
(s113 1.0)
(s114 1.0)
(s115 1.0)
(s116 1.0)
(s117 1.0)
(s118 1.0)
(s119 1.0)
(s120 1.0)
(s121 1.0)
(s122 1.0)
(s123 1.0)
(s124 1.0)
(s125 1.0)
(s126 1.0)
(s127 1.0)
(s128 1.0)
(s129 1.0)
(s130 1.0)
(s131 1.0)
(s132 1.0)
(s133 1.0)
(s134 1.0)
(s135 1.0)
(s136 1.0)
(s137 1.0)
(s138 1.0)
(s139 1.0)
(s140 1.0)
(s141 1.0)
(s142 1.0)
(s143 1.0)
(s144 1.0)
(s145 1.0)
(s146 1.0)
(s147 1.0)
(s148 1.0)
(s149 1.0)
(s150 1.0)
(s151 1.0)
(s152 1.0)
(s153 1.0)
(s154 1.0)
(s155 1.0)
(s156 1.0)
(s157 1.0)
(s158 1.0)
(s159 1.0)
(s160 1.0)
(s161 1.0)
(s162 1.0)
(s163 1.0)
(s164 1.0)
(s165 1.0)
(s166 1.0)
(s167 1.0)
(s168 1.0)
(s169 1.0)
(s170 1.0)
(s171 1.0)
(s172 1.0)
(s173 1.0)
(s174 1.0)
(s175 1.0)
(s176 1.0)
(s177 1.0)
(s178 1.0)
(s179 1.0)
(s180 1.0)
(s181 1.0)
(s182 1.0)
(s183 1.0)
(s184 1.0)
(s185 1.0)
(s186 1.0)
(s187 1.0)
(s188 1.0)
(s189 1.0)
(s190 1.0)
(s191 1.0)
(s192 1.0)
(s193 1.0)
(s194 1.0)
(s195 1.0)
(s196 1.0)
(s197 1.0)
(s198 1.0)
(s199 1.0)
(s200 1.0)
(s201 1.0)
(s202 1.0)
(s203 1.0)
(s204 1.0)
(s205 1.0)
(s206 1.0)
(s207 1.0)
(s208 1.0)
(s209 1.0)
(s210 1.0)
(s211 1.0)
(s212 1.0)
(s213 1.0)
(s214 1.0)
(s215 1.0)
(s216 1.0)
(s217 1.0)
(s218 1.0)
(s219 1.0)
(s220 1.0)
(s221 1.0)
(s222 1.0)
(s223 1.0)
(s224 1.0)
(s225 1.0)
(s226 1.0)
(s227 1.0)
(s228 1.0)
(s229 1.0)
(s230 1.0)
(s231 1.0)
(s232 1.0)
(s233 1.0)
(s234 1.0)
(s235 1.0)
(s236 1.0)
(s237 1.0)
(s238 1.0)
(s239 1.0)
(s240 1.0)
(s241 1.0)
(s242 1.0)
(s243 1.0)
(s244 1.0)
(s245 1.0)
(s246 1.0)
(s247 1.0)
(s248 1.0)
(s249 1.0)
(s250 1.0)
(s251 1.0)
(s252 1.0)
(s253 1.0)
(s254 1.0)
(s255 1.0)
(s256 1.0)
(s257 1.0)
(s258 1.0)
(s259 1.0)
(s260 1.0)
(s261 1.0)
(s262 1.0)
(s263 1.0)
(s264 1.0)
(s265 1.0)
(s266 1.0)
(s267 1.0)
(s268 1.0)
(s269 1.0)
(s270 1.0)
(s271 1.0)
(s272 1.0)
(s273 1.0)
(s274 1.0)
(s275 1.0)
(s276 1.0)
(s277 1.0)
(s278 1.0)
(s279 1.0)
(s280 1.0)
(s281 1.0)
(s282 1.0)
(s283 1.0)
(s284 1.0)
(s285 1.0)
(s286 1.0)
(s287 1.0)
(s288 1.0)
(s289 1.0)
(s290 1.0)
(s291 1.0)
(s292 1.0)
(s293 1.0)
(s294 1.0)
(s295 1.0)
(s296 1.0)
(s297 1.0)
(s298 1.0)
(s299 1.0)
(s300 1.0)
(s301 1.0)
(s302 1.0)
(s303 1.0)
(s304 1.0)
(s305 1.0)
(s306 1.0)
(s307 1.0)
(s308 1.0)
(s309 1.0)
(s310 1.0)
(s311 1.0)
(s312 1.0)
(s313 1.0)
(s314 1.0)
(s315 1.0)
(s316 1.0)
(s317 1.0)
(s318 1.0)
(s319 1.0)
(s320 1.0)
(s321 1.0)
(s322 1.0)
(s323 1.0)
(s324 1.0)
(s325 1.0)
(s326 1.0)
(s327 1.0)
(s328 1.0)
(s329 1.0)
(s330 1.0)
(s331 1.0)
(s332 1.0)
(s333 1.0)
(s334 1.0)
(s335 1.0)
(s336 1.0)
(s337 1.0)
(s338 1.0)
(s339 1.0)
(s340 1.0)
(s341 1.0)
(s342 1.0)
(s343 1.0)
(s344 1.0)
(s345 1.0)
(s346 1.0)
(s347 1.0)
(s348 1.0)
(s349 1.0)
(s350 1.0)
(s351 1.0)
(s352 1.0)
(s353 1.0)
(s354 1.0)
(s355 1.0)
(s356 1.0)
(s357 1.0)
(s358 1.0)
(s359 1.0)
(s360 1.0)
(s361 1.0)
(s362 1.0)
(s363 1.0)
(s364 1.0)
(s365 1.0)
(s366 1.0)
(s367 1.0)
(s368 1.0)
(s369 1.0)
(s370 1.0)
(s371 1.0)
(s372 1.0)
(s373 1.0)
(s374 1.0)
(s375 1.0)
(s376 1.0)
(s377 1.0)
(s378 1.0)
(s379 1.0)
(s380 1.0)
(s381 1.0)
(s382 1.0)
(s383 1.0)
(s384 1.0)
(s385 1.0)
(s386 1.0)
(s387 1.0)
(s388 1.0)
(s389 1.0)
(s390 1.0)
(s391 1.0)
(s392 1.0)
(s393 1.0)
(s394 1.0)
(s395 1.0)
(s396 1.0)
(s397 1.0)
(s398 1.0)
(s399 1.0)
(s400 1.0)
(s401 1.0)
(s402 1.0)
(s403 1.0)
(s404 1.0)
(s405 1.0)
(s406 1.0)
(s407 1.0)
(s408 1.0)
(s409 1.0)
(s410 1.0)
(s411 1.0)
(s412 1.0)
(s413 1.0)
(s414 1.0)
(s415 1.0)
(s416 1.0)
(s417 1.0)
(s418 1.0)
(s419 1.0)
(s420 1.0)
(s421 1.0)
(s422 1.0)
(s423 1.0)
(s424 1.0)
(s425 1.0)
(s426 1.0)
(s427 1.0)
(s428 1.0)
(s429 1.0)
(s430 1.0)
(s431 1.0)
(s432 1.0)
(s433 1.0)
(s434 1.0)
(s435 1.0)
(s436 1.0)
(s437 1.0)
(s438 1.0)
(s439 1.0)
(s440 1.0)
(s441 1.0)
(s442 1.0)
(s443 1.0)
(s444 1.0)
(s445 1.0)
(s446 1.0)
(s447 1.0)
(s448 1.0)
(s449 1.0)
(s450 1.0)
(s451 1.0)
(s452 1.0)
(s453 1.0)
(s454 1.0)
(s455 1.0)
(s456 1.0)
(s457 1.0)
(s458 1.0)
(s459 1.0)
(s460 1.0)
(s461 1.0)
(s462 1.0)
(s463 1.0)
(s464 1.0)
(s465 1.0)
(s466 1.0)
(s467 1.0)
(s468 1.0)
(s469 1.0)
(s470 1.0)
(s471 1.0)
(s472 1.0)
(s473 1.0)
(s474 1.0)
(s475 1.0)
(s476 1.0)
(s477 1.0)
(s478 1.0)
(s479 1.0)
(s480 1.0)
(s481 1.0)
(s482 1.0)
(s483 1.0)
(s484 1.0)
(s485 1.0)
(s486 1.0)
(s487 1.0)
(s488 1.0)
(s489 1.0)
(s490 1.0)
(s491 1.0)
(s492 1.0)
(s493 1.0)
(s494 1.0)
(s495 1.0)
(s496 1.0)
(s497 1.0)
(s498 1.0)
(s499 1.0)
(s500 1.0)
(s501 1.0)
(s502 1.0)
(s503 1.0)
(s504 1.0)
(s505 1.0)
(s506 1.0)
(s507 1.0)
(s508 1.0)
(s509 1.0)
(s510 1.0)
(s511 1.0)
(s512 1.0)
(s513 1.0)
(s514 1.0)
(s515 1.0)
(s516 1.0)
(s517 1.0)
(s518 1.0)
(s519 1.0)
(s520 1.0)
(s521 1.0)
(s522 1.0)
(s523 1.0)
(s524 1.0)
(s525 1.0)
(s526 1.0)
(s527 1.0)
(s528 1.0)
(s529 1.0)
(s530 1.0)
(s531 1.0)
(s532 1.0)
(s533 1.0)
(s534 1.0)
(s535 1.0)
(s536 1.0)
(s537 1.0)
(s538 1.0)
(s539 1.0)
(s540 1.0)
(s541 1.0)
(s542 1.0)
(s543 1.0)
(s544 1.0)
(s545 1.0)
(s546 1.0)
(s547 1.0)
(s548 1.0)
(s549 1.0)
(s550 1.0)
(s551 1.0)
(s552 1.0)
(s553 1.0)
(s554 1.0)
(s555 1.0)
(s556 1.0)
(s557 1.0)
(s558 1.0)
(s559 1.0)
(s560 1.0)
(s561 1.0)
(s562 1.0)
(s563 1.0)
(s564 1.0)
(s565 1.0)
(s566 1.0)
(s567 1.0)
(s568 1.0)
(s569 1.0)
(s570 1.0)
(s571 1.0)
(s572 1.0)
(s573 1.0)
(s574 1.0)
(s575 1.0)
(s576 1.0)
(s577 1.0)
(s578 1.0)
(s579 1.0)
(s580 1.0)
(s581 1.0)
(s582 1.0)
(s583 1.0)
(s584 1.0)
(s585 1.0)
(s586 1.0)
(s587 1.0)
(s588 1.0)
(s589 1.0)
(s590 1.0)
(s591 1.0)
(s592 1.0)
(s593 1.0)
(s594 1.0)
(s595 1.0)
(s596 1.0)
(s597 1.0)
(s598 1.0)
(s599 1.0)
(s600 1.0)
(s601 1.0)
(s602 1.0)
(s603 1.0)
(s604 1.0)
(s605 1.0)
(s606 1.0)
(s607 1.0)
(s608 1.0)
(s609 1.0)
(s610 1.0)
(s611 1.0)
(s612 1.0)
(s613 1.0)
(s614 1.0)
(s615 1.0)
(s616 1.0)
(s617 1.0)
(s618 1.0)
(s619 1.0)
(s620 1.0)
(s621 1.0)
(s622 1.0)
(s623 1.0)
(s624 1.0)
(s625 1.0)
(s626 1.0)
(s627 1.0)
(s628 1.0)
(s629 1.0)
(s630 1.0)
(s631 1.0)
(s632 1.0)
(s633 1.0)
(s634 1.0)
(s635 1.0)
(s636 1.0)
(s637 1.0)
(s638 1.0)
(s639 1.0)
(s640 1.0)
(s641 1.0)
(s642 1.0)
(s643 1.0)
(s644 1.0)
(s645 1.0)
(s646 1.0)
(s647 1.0)
(s648 1.0)
(s649 1.0)
(s650 1.0)
(s651 1.0)
(s652 1.0)
(s653 1.0)
(s654 1.0)
(s655 1.0)
(s656 1.0)
(s657 1.0)
(s658 1.0)
(s659 1.0)
(s660 1.0)
(s661 1.0)
(s662 1.0)
(s663 1.0)
(s664 1.0)
(s665 1.0)
(s666 1.0)
(s667 1.0)
(s668 1.0)
(s669 1.0)
(s670 1.0)
(s671 1.0)
(s672 1.0)
(s673 1.0)
(s674 1.0)
(s675 1.0)
(s676 1.0)
(s677 1.0)
(s678 1.0)
(s679 1.0)
(s680 1.0)
(s681 1.0)
(s682 1.0)
(s683 1.0)
(s684 1.0)
(s685 1.0)
(s686 1.0)
(s687 1.0)
(s688 1.0)
(s689 1.0)
(s690 1.0)
(s691 1.0)
(s692 1.0)
(s693 1.0)
(s694 1.0)
(s695 1.0)
(s696 1.0)
(s697 1.0)
(s698 1.0)
(s699 1.0)
(s700 1.0)
(s701 1.0)
(s702 1.0)
(s703 1.0)
(s704 1.0)
(s705 1.0)
(s706 1.0)
(s707 1.0)
(s708 1.0)
(s709 1.0)
(s710 1.0)
(s711 1.0)
(s712 1.0)
(s713 1.0)
(s714 1.0)
(s715 1.0)
(s716 1.0)
(s717 1.0)
(s718 1.0)
(s719 1.0)
(s720 1.0)
(s721 1.0)
(s722 1.0)
(s723 1.0)
(s724 1.0)
(s725 1.0)
(s726 1.0)
(s727 1.0)
(s728 1.0)
(s729 1.0)
(s730 1.0)
(s731 1.0)
(s732 1.0)
(s733 1.0)
(s734 1.0)
(s735 1.0)
(s736 1.0)
(s737 1.0)
(s738 1.0)
(s739 1.0)
(s740 1.0)
(s741 1.0)
(s742 1.0)
(s743 1.0)
(s744 1.0)
(s745 1.0)
(s746 1.0)
(s747 1.0)
(s748 1.0)
(s749 1.0)
(s750 1.0)
(s751 1.0)
(s752 1.0)
(s753 1.0)
(s754 1.0)
(s755 1.0)
(s756 1.0)
(s757 1.0)
(s758 1.0)
(s759 1.0)
(s760 1.0)
(s761 1.0)
(s762 1.0)
(s763 1.0)
(s764 1.0)
(s765 1.0)
(s766 1.0)
(s767 1.0)
(s768 1.0)
(s769 1.0)
(s770 1.0)
(s771 1.0)
(s772 1.0)
(s773 1.0)
(s774 1.0)
(s775 1.0)
(s776 1.0)
(s777 1.0)
(s778 1.0)
(s779 1.0)
(s780 1.0)
(s781 1.0)
(s782 1.0)
(s783 1.0)
(s784 1.0)
(s785 1.0)
(s786 1.0)
(s787 1.0)
(s788 1.0)
(s789 1.0)
(s790 1.0)
(s791 1.0)
(s792 1.0)
(s793 1.0)
(s794 1.0)
(s795 1.0)
(s796 1.0)
(s797 1.0)
(s798 1.0)
(s799 1.0)
(s800 1.0)
(s801 1.0)
(s802 1.0)
(s803 1.0)
(s804 1.0)
(s805 1.0)
(s806 1.0)
(s807 1.0)
(s808 1.0)
(s809 1.0)
(s810 1.0)
(s811 1.0)
(s812 1.0)
(s813 1.0)
(s814 1.0)
(s815 1.0)
(s816 1.0)
(s817 1.0)
(s818 1.0)
(s819 1.0)
(s820 1.0)
(s821 1.0)
(s822 1.0)
(s823 1.0)
(s824 1.0)
(s825 1.0)
(s826 1.0)
(s827 1.0)
(s828 1.0)
(s829 1.0)
(s830 1.0)
(s831 1.0)
(s832 1.0)
(s833 1.0)
(s834 1.0)
(s835 1.0)
(s836 1.0)
(s837 1.0)
(s838 1.0)
(s839 1.0)
(s840 1.0)
(s841 1.0)
(s842 1.0)
(s843 1.0)
(s844 1.0)
(s845 1.0)
(s846 1.0)
(s847 1.0)
(s848 1.0)
(s849 1.0)
(s850 1.0)
(s851 1.0)
(s852 1.0)
(s853 1.0)
(s854 1.0)
(s855 1.0)
(s856 1.0)
(s857 1.0)
(s858 1.0)
(s859 1.0)
(s860 1.0)
(s861 1.0)
(s862 1.0)
(s863 1.0)
(s864 1.0)
(s865 1.0)
(s866 1.0)
(s867 1.0)
(s868 1.0)
(s869 1.0)
(s870 1.0)
(s871 1.0)
(s872 1.0)
(s873 1.0)
(s874 1.0)
(s875 1.0)
(s876 1.0)
(s877 1.0)
(s878 1.0)
(s879 1.0)
(s880 1.0)
(s881 1.0)
(s882 1.0)
(s883 1.0)
(s884 1.0)
(s885 1.0)
(s886 1.0)
(s887 1.0)
(s888 1.0)
(s889 1.0)
(s890 1.0)
(s891 1.0)
(s892 1.0)
(s893 1.0)
(s894 1.0)
(s895 1.0)
(s896 1.0)
(s897 1.0)
(s898 1.0)
(s899 1.0)
(s900 1.0)
(s901 1.0)
(s902 1.0)
(s903 1.0)
(s904 1.0)
(s905 1.0)
(s906 1.0)
(s907 1.0)
(s908 1.0)
(s909 1.0)
(s910 1.0)
(s911 1.0)
(s912 1.0)
(s913 1.0)
(s914 1.0)
(s915 1.0)
(s916 1.0)
(s917 1.0)
(s918 1.0)
(s919 1.0)
(s920 1.0)
(s921 1.0)
(s922 1.0)
(s923 1.0)
(s924 1.0)
(s925 1.0)
(s926 1.0)
(s927 1.0)
(s928 1.0)
(s929 1.0)
(s930 1.0)
(s931 1.0)
(s932 1.0)
(s933 1.0)
(s934 1.0)
(s935 1.0)
(s936 1.0)
(s937 1.0)
(s938 1.0)
(s939 1.0)
(s940 1.0)
(s941 1.0)
(s942 1.0)
(s943 1.0)
(s944 1.0)
(s945 1.0)
(s946 1.0)
(s947 1.0)
(s948 1.0)
(s949 1.0)
(s950 1.0)
(s951 1.0)
(s952 1.0)
(s953 1.0)
(s954 1.0)
(s955 1.0)
(s956 1.0)
(s957 1.0)
(s958 1.0)
(s959 1.0)
(s960 1.0)
(s961 1.0)
(s962 1.0)
(s963 1.0)
(s964 1.0)
(s965 1.0)
(s966 1.0)
(s967 1.0)
(s968 1.0)
(s969 1.0)
(s970 1.0)
(s971 1.0)
(s972 1.0)
(s973 1.0)
(s974 1.0)
(s975 1.0)
(s976 1.0)
(s977 1.0)
(s978 1.0)
(s979 1.0)
(s980 1.0)
(s981 1.0)
(s982 1.0)
(s983 1.0)
(s984 1.0)
(s985 1.0)
(s986 1.0)
(s987 1.0)
(s988 1.0)
(s989 1.0)
(s990 1.0)
(s991 1.0)
(s992 1.0)
(s993 1.0)
(s994 1.0)
(s995 1.0)
(s996 1.0)
(s997 1.0)
(s998 1.0)
(s999 1.0)
(s1000 1.0)
(s1001 1.0)
(s1002 1.0)
(s1003 1.0)
(s1004 1.0)
(s1005 1.0)
(s1006 1.0)
(s1007 1.0)
(s1008 1.0)
(s1009 1.0)
(s1010 1.0)
(s1011 1.0)
(s1012 1.0)
(s1013 1.0)
(s1014 1.0)
(s1015 1.0)
(s1016 1.0)
(s1017 1.0)
(s1018 1.0)
(s1019 1.0)
(s1020 1.0)
(s1021 1.0)
(s1022 1.0)
(s1023 1.0)
(s1024 1.0)
(s1025 1.0)
(s1026 1.0)
(s1027 1.0)
(s1028 1.0)
(s1029 1.0)
(s1030 1.0)
(s1031 1.0)
(s1032 1.0)
(s1033 1.0)
(s1034 1.0)
(s1035 1.0)
(s1036 1.0)
(s1037 1.0)
(s1038 1.0)
(s1039 1.0)
(s1040 1.0)
(s1041 1.0)
(s1042 1.0)
(s1043 1.0)
(s1044 1.0)
(s1045 1.0)
(s1046 1.0)
(s1047 1.0)
(s1048 1.0)
(s1049 1.0)
(s1050 1.0)
(s1051 1.0)
(s1052 1.0)
(s1053 1.0)
(s1054 1.0)
(s1055 1.0)
(s1056 1.0)
(s1057 1.0)
(s1058 1.0)
(s1059 1.0)
(s1060 1.0)
(s1061 1.0)
(s1062 1.0)
(s1063 1.0)
(s1064 1.0)
(s1065 1.0)
(s1066 1.0)
(s1067 1.0)
(s1068 1.0)
(s1069 1.0)
(s1070 1.0)
(s1071 1.0)
(s1072 1.0)
(s1073 1.0)
(s1074 1.0)
(s1075 1.0)
(s1076 1.0)
(s1077 1.0)
(s1078 1.0)
(s1079 1.0)
(s1080 1.0)
(s1081 1.0)
(s1082 1.0)
(s1083 1.0)
(s1084 1.0)
(s1085 1.0)
(s1086 1.0)
(s1087 1.0)
(s1088 1.0)
(s1089 1.0)
(s1090 1.0)
(s1091 1.0)
(s1092 1.0)
(s1093 1.0)
(s1094 1.0)
(s1095 1.0)
(s1096 1.0)
(s1097 1.0timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2403/8406 variables, and 0 constraints, problems are : Problem set: 0 solved, 4153 unsolved in 30118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2453 constraints, PredecessorRefiner: 4153/4153 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4153 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2403/8406 variables, and 0 constraints, problems are : Problem set: 0 solved, 4153 unsolved in 30118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2453 constraints, PredecessorRefiner: 0/4153 constraints, Known Traps: 0/0 constraints]
After SMT, in 62516ms problems are : Problem set: 0 solved, 4153 unsolved
Search for dead transitions found 0 dead transitions in 62553ms
Starting structural reductions in LTL mode, iteration 1 : 2453/6600 places, 5953/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70243 ms. Remains : 2453/6600 places, 5953/10100 transitions.
Stuttering acceptance computed with spot in 284 ms :[true, (NOT p2), (OR (AND (NOT p0) (NOT p2)) (AND (NOT p0) (NOT p1))), (OR (AND (NOT p0) (NOT p1)) (AND (NOT p0) (NOT p2))), (NOT p0), (AND (NOT p0) (NOT p2))]
Running random walk in product with property : BART-PT-050-LTLFireability-10
Entered a terminal (fully accepting) state of product in 36425 steps with 0 reset in 475 ms.
FORMULA BART-PT-050-LTLFireability-10 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-10 finished in 71038 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X(G(p0))))'
Support contains 2 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1600 places :
Symmetric choice reduction at 0 with 1600 rule applications. Total rules 1600 place count 5000 transition count 8500
Iterating global reduction 0 with 1600 rules applied. Total rules applied 3200 place count 5000 transition count 8500
Discarding 1349 places :
Symmetric choice reduction at 0 with 1349 rule applications. Total rules 4549 place count 3651 transition count 7151
Iterating global reduction 0 with 1349 rules applied. Total rules applied 5898 place count 3651 transition count 7151
Discarding 200 places :
Symmetric choice reduction at 0 with 200 rule applications. Total rules 6098 place count 3451 transition count 6951
Iterating global reduction 0 with 200 rules applied. Total rules applied 6298 place count 3451 transition count 6951
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6448 place count 3301 transition count 6801
Iterating global reduction 0 with 150 rules applied. Total rules applied 6598 place count 3301 transition count 6801
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6748 place count 3151 transition count 6651
Iterating global reduction 0 with 150 rules applied. Total rules applied 6898 place count 3151 transition count 6651
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7048 place count 3001 transition count 6501
Iterating global reduction 0 with 150 rules applied. Total rules applied 7198 place count 3001 transition count 6501
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7348 place count 2851 transition count 6351
Iterating global reduction 0 with 150 rules applied. Total rules applied 7498 place count 2851 transition count 6351
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7648 place count 2701 transition count 6201
Iterating global reduction 0 with 150 rules applied. Total rules applied 7798 place count 2701 transition count 6201
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 7898 place count 2601 transition count 6101
Iterating global reduction 0 with 100 rules applied. Total rules applied 7998 place count 2601 transition count 6101
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 8098 place count 2501 transition count 6001
Iterating global reduction 0 with 100 rules applied. Total rules applied 8198 place count 2501 transition count 6001
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 8248 place count 2451 transition count 5951
Iterating global reduction 0 with 50 rules applied. Total rules applied 8298 place count 2451 transition count 5951
Applied a total of 8298 rules in 4566 ms. Remains 2451 /6600 variables (removed 4149) and now considering 5951/10100 (removed 4149) transitions.
// Phase 1: matrix 5951 rows 2451 cols
[2024-06-01 11:26:07] [INFO ] Computed 50 invariants in 18 ms
[2024-06-01 11:26:08] [INFO ] Implicit Places using invariants in 591 ms returned []
[2024-06-01 11:26:08] [INFO ] Invariant cache hit.
[2024-06-01 11:26:11] [INFO ] Implicit Places using invariants and state equation in 2931 ms returned []
Implicit Place search using SMT with State Equation took 3525 ms to find 0 implicit places.
Running 4151 sub problems to find dead transitions.
[2024-06-01 11:26:11] [INFO ] Invariant cache hit.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2401/8402 variables, and 0 constraints, problems are : Problem set: 0 solved, 4151 unsolved in 30108 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2451 constraints, PredecessorRefiner: 4151/4151 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4151 unsolved
Error getting values : (error "ParserException while parsing response: ((s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2401/8402 variables, and 0 constraints, problems are : Problem set: 0 solved, 4151 unsolved in 30109 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2451 constraints, PredecessorRefiner: 0/4151 constraints, Known Traps: 0/0 constraints]
After SMT, in 62775ms problems are : Problem set: 0 solved, 4151 unsolved
Search for dead transitions found 0 dead transitions in 62836ms
Starting structural reductions in LTL mode, iteration 1 : 2451/6600 places, 5951/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70933 ms. Remains : 2451/6600 places, 5951/10100 transitions.
Stuttering acceptance computed with spot in 165 ms :[true, (NOT p0), (NOT p0), (NOT p0)]
Running random walk in product with property : BART-PT-050-LTLFireability-11
Entered a terminal (fully accepting) state of product in 2 steps with 0 reset in 0 ms.
FORMULA BART-PT-050-LTLFireability-11 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-11 finished in 71130 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G(((F(G((G(p0) U p1))) U p1)&&F(p0))))'
Support contains 2 out of 6600 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Graph (trivial) has 10059 edges and 6600 vertex of which 6465 / 6600 are part of one of the 49 SCC in 7 ms
Free SCC test removed 6416 places
Ensure Unique test removed 9844 transitions
Reduce isomorphic transitions removed 9844 transitions.
Reduce places removed 48 places and 0 transitions.
Ensure Unique test removed 47 transitions
Reduce isomorphic transitions removed 47 transitions.
Drop transitions (Trivial Post-Agglo cleanup.) removed 65 transitions
Trivial Post-agglo rules discarded 65 transitions
Performed 65 trivial Post agglomeration. Transition count delta: 65
Iterating post reduction 0 with 112 rules applied. Total rules applied 113 place count 136 transition count 144
Reduce places removed 65 places and 0 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 1 with 66 rules applied. Total rules applied 179 place count 71 transition count 143
Reduce places removed 1 places and 0 transitions.
Ensure Unique test removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 2 with 2 rules applied. Total rules applied 181 place count 70 transition count 142
Performed 5 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 5 Pre rules applied. Total rules applied 181 place count 70 transition count 137
Deduced a syphon composed of 5 places in 0 ms
Reduce places removed 5 places and 0 transitions.
Iterating global reduction 3 with 10 rules applied. Total rules applied 191 place count 65 transition count 137
Discarding 6 places :
Symmetric choice reduction at 3 with 6 rule applications. Total rules 197 place count 59 transition count 131
Iterating global reduction 3 with 6 rules applied. Total rules applied 203 place count 59 transition count 131
Ensure Unique test removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 3 with 1 rules applied. Total rules applied 204 place count 59 transition count 130
Discarding 4 places :
Symmetric choice reduction at 4 with 4 rule applications. Total rules 208 place count 55 transition count 126
Iterating global reduction 4 with 4 rules applied. Total rules applied 212 place count 55 transition count 126
Discarding 3 places :
Symmetric choice reduction at 4 with 3 rule applications. Total rules 215 place count 52 transition count 123
Iterating global reduction 4 with 3 rules applied. Total rules applied 218 place count 52 transition count 123
Discarding 3 places :
Symmetric choice reduction at 4 with 3 rule applications. Total rules 221 place count 49 transition count 120
Iterating global reduction 4 with 3 rules applied. Total rules applied 224 place count 49 transition count 120
Discarding 2 places :
Symmetric choice reduction at 4 with 2 rule applications. Total rules 226 place count 47 transition count 118
Iterating global reduction 4 with 2 rules applied. Total rules applied 228 place count 47 transition count 118
Discarding 2 places :
Symmetric choice reduction at 4 with 2 rule applications. Total rules 230 place count 45 transition count 116
Iterating global reduction 4 with 2 rules applied. Total rules applied 232 place count 45 transition count 116
Discarding 1 places :
Symmetric choice reduction at 4 with 1 rule applications. Total rules 233 place count 44 transition count 115
Iterating global reduction 4 with 1 rules applied. Total rules applied 234 place count 44 transition count 115
Performed 7 Post agglomeration using F-continuation condition.Transition count delta: 7
Deduced a syphon composed of 7 places in 0 ms
Reduce places removed 7 places and 0 transitions.
Iterating global reduction 4 with 14 rules applied. Total rules applied 248 place count 37 transition count 108
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 4 with 4 rules applied. Total rules applied 252 place count 37 transition count 104
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 5 with 4 rules applied. Total rules applied 256 place count 35 transition count 102
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 5 with 4 rules applied. Total rules applied 260 place count 35 transition count 98
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 6 with 4 rules applied. Total rules applied 264 place count 33 transition count 96
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 6 with 4 rules applied. Total rules applied 268 place count 33 transition count 92
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 7 with 4 rules applied. Total rules applied 272 place count 31 transition count 90
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 7 with 4 rules applied. Total rules applied 276 place count 31 transition count 86
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 8 with 4 rules applied. Total rules applied 280 place count 29 transition count 84
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 8 with 4 rules applied. Total rules applied 284 place count 29 transition count 80
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 9 with 4 rules applied. Total rules applied 288 place count 27 transition count 78
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 9 with 4 rules applied. Total rules applied 292 place count 27 transition count 74
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 10 with 4 rules applied. Total rules applied 296 place count 25 transition count 72
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 10 with 4 rules applied. Total rules applied 300 place count 25 transition count 68
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 11 with 4 rules applied. Total rules applied 304 place count 23 transition count 66
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 11 with 4 rules applied. Total rules applied 308 place count 23 transition count 62
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 12 with 4 rules applied. Total rules applied 312 place count 21 transition count 60
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 12 with 4 rules applied. Total rules applied 316 place count 21 transition count 56
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 13 with 4 rules applied. Total rules applied 320 place count 19 transition count 54
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 13 with 4 rules applied. Total rules applied 324 place count 19 transition count 50
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 14 with 4 rules applied. Total rules applied 328 place count 17 transition count 48
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 14 with 4 rules applied. Total rules applied 332 place count 17 transition count 44
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 15 with 4 rules applied. Total rules applied 336 place count 15 transition count 42
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 15 with 4 rules applied. Total rules applied 340 place count 15 transition count 38
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 16 with 4 rules applied. Total rules applied 344 place count 13 transition count 36
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 16 with 4 rules applied. Total rules applied 348 place count 13 transition count 32
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 17 with 4 rules applied. Total rules applied 352 place count 11 transition count 30
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 17 with 4 rules applied. Total rules applied 356 place count 11 transition count 26
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 18 with 4 rules applied. Total rules applied 360 place count 9 transition count 24
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 18 with 4 rules applied. Total rules applied 364 place count 9 transition count 20
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 19 with 4 rules applied. Total rules applied 368 place count 7 transition count 18
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Iterating post reduction 19 with 4 rules applied. Total rules applied 372 place count 7 transition count 14
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 20 with 4 rules applied. Total rules applied 376 place count 5 transition count 12
Ensure Unique test removed 4 transitions
Reduce isomorphic transitions removed 4 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 20 with 5 rules applied. Total rules applied 381 place count 5 transition count 7
Reduce places removed 1 places and 0 transitions.
Ensure Unique test removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 21 with 2 rules applied. Total rules applied 383 place count 4 transition count 6
Drop transitions (Redundant composition of simpler transitions.) removed 1 transitions
Redundant transition composition rules discarded 1 transitions
Iterating global reduction 22 with 1 rules applied. Total rules applied 384 place count 4 transition count 5
Applied a total of 384 rules in 92 ms. Remains 4 /6600 variables (removed 6596) and now considering 5/10100 (removed 10095) transitions.
// Phase 1: matrix 5 rows 4 cols
[2024-06-01 11:27:14] [INFO ] Computed 2 invariants in 0 ms
[2024-06-01 11:27:14] [INFO ] Implicit Places using invariants in 24 ms returned []
[2024-06-01 11:27:14] [INFO ] Invariant cache hit.
[2024-06-01 11:27:14] [INFO ] Implicit Places using invariants and state equation in 27 ms returned []
Implicit Place search using SMT with State Equation took 53 ms to find 0 implicit places.
[2024-06-01 11:27:14] [INFO ] Redundant transitions in 0 ms returned []
Running 2 sub problems to find dead transitions.
[2024-06-01 11:27:14] [INFO ] Invariant cache hit.
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (OVERLAPS) 2/4 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/4 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (OVERLAPS) 4/8 variables, 4/6 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/8 variables, 0/6 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (OVERLAPS) 0/8 variables, 0/6 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Real declared 8/9 variables, and 6 constraints, problems are : Problem set: 0 solved, 2 unsolved in 43 ms.
Refiners :[Positive P Invariants (semi-flows): 2/2 constraints, State Equation: 4/4 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/2 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (OVERLAPS) 2/4 variables, 2/2 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/4 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (OVERLAPS) 4/8 variables, 4/6 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/8 variables, 2/8 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/8 variables, 0/8 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 6 (OVERLAPS) 0/8 variables, 0/8 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Int declared 8/9 variables, and 8 constraints, problems are : Problem set: 0 solved, 2 unsolved in 47 ms.
Refiners :[Positive P Invariants (semi-flows): 2/2 constraints, State Equation: 4/4 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
After SMT, in 97ms problems are : Problem set: 0 solved, 2 unsolved
Search for dead transitions found 0 dead transitions in 97ms
Starting structural reductions in SI_LTL mode, iteration 1 : 4/6600 places, 5/10100 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 250 ms. Remains : 4/6600 places, 5/10100 transitions.
Stuttering acceptance computed with spot in 368 ms :[(OR (NOT p0) (NOT p1)), (NOT p1), (NOT p1), (NOT p0), (AND (NOT p1) (NOT p0)), (NOT p1)]
Running random walk in product with property : BART-PT-050-LTLFireability-12
Stuttering criterion allowed to conclude after 0 steps with 0 reset in 1 ms.
FORMULA BART-PT-050-LTLFireability-12 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-12 finished in 651 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X((p0 U p1))))'
Support contains 2 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1599 places :
Symmetric choice reduction at 0 with 1599 rule applications. Total rules 1599 place count 5001 transition count 8501
Iterating global reduction 0 with 1599 rules applied. Total rules applied 3198 place count 5001 transition count 8501
Discarding 1349 places :
Symmetric choice reduction at 0 with 1349 rule applications. Total rules 4547 place count 3652 transition count 7152
Iterating global reduction 0 with 1349 rules applied. Total rules applied 5896 place count 3652 transition count 7152
Discarding 200 places :
Symmetric choice reduction at 0 with 200 rule applications. Total rules 6096 place count 3452 transition count 6952
Iterating global reduction 0 with 200 rules applied. Total rules applied 6296 place count 3452 transition count 6952
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6446 place count 3302 transition count 6802
Iterating global reduction 0 with 150 rules applied. Total rules applied 6596 place count 3302 transition count 6802
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 6745 place count 3153 transition count 6653
Iterating global reduction 0 with 149 rules applied. Total rules applied 6894 place count 3153 transition count 6653
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7043 place count 3004 transition count 6504
Iterating global reduction 0 with 149 rules applied. Total rules applied 7192 place count 3004 transition count 6504
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7341 place count 2855 transition count 6355
Iterating global reduction 0 with 149 rules applied. Total rules applied 7490 place count 2855 transition count 6355
Discarding 149 places :
Symmetric choice reduction at 0 with 149 rule applications. Total rules 7639 place count 2706 transition count 6206
Iterating global reduction 0 with 149 rules applied. Total rules applied 7788 place count 2706 transition count 6206
Discarding 99 places :
Symmetric choice reduction at 0 with 99 rule applications. Total rules 7887 place count 2607 transition count 6107
Iterating global reduction 0 with 99 rules applied. Total rules applied 7986 place count 2607 transition count 6107
Discarding 99 places :
Symmetric choice reduction at 0 with 99 rule applications. Total rules 8085 place count 2508 transition count 6008
Iterating global reduction 0 with 99 rules applied. Total rules applied 8184 place count 2508 transition count 6008
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 8234 place count 2458 transition count 5958
Iterating global reduction 0 with 50 rules applied. Total rules applied 8284 place count 2458 transition count 5958
Applied a total of 8284 rules in 4688 ms. Remains 2458 /6600 variables (removed 4142) and now considering 5958/10100 (removed 4142) transitions.
// Phase 1: matrix 5958 rows 2458 cols
[2024-06-01 11:27:19] [INFO ] Computed 50 invariants in 30 ms
[2024-06-01 11:27:20] [INFO ] Implicit Places using invariants in 594 ms returned []
[2024-06-01 11:27:20] [INFO ] Invariant cache hit.
[2024-06-01 11:27:22] [INFO ] Implicit Places using invariants and state equation in 2569 ms returned []
Implicit Place search using SMT with State Equation took 3169 ms to find 0 implicit places.
Running 4158 sub problems to find dead transitions.
[2024-06-01 11:27:22] [INFO ] Invariant cache hit.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2408/8416 variables, and 0 constraints, problems are : Problem set: 0 solved, 4158 unsolved in 30117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2458 constraints, PredecessorRefiner: 4158/4158 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4158 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2408/8416 variables, and 0 constraints, problems are : Problem set: 0 solved, 4158 unsolved in 30109 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2458 constraints, PredecessorRefiner: 0/4158 constraints, Known Traps: 0/0 constraints]
After SMT, in 62500ms problems are : Problem set: 0 solved, 4158 unsolved
Search for dead transitions found 0 dead transitions in 62539ms
Starting structural reductions in LTL mode, iteration 1 : 2458/6600 places, 5958/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70402 ms. Remains : 2458/6600 places, 5958/10100 transitions.
Stuttering acceptance computed with spot in 186 ms :[(NOT p1), (NOT p1), true, (NOT p1)]
Running random walk in product with property : BART-PT-050-LTLFireability-14
Entered a terminal (fully accepting) state of product in 2 steps with 0 reset in 1 ms.
FORMULA BART-PT-050-LTLFireability-14 FALSE TECHNIQUES STUTTER_TEST
Treatment of property BART-PT-050-LTLFireability-14 finished in 70620 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(G((G(p0)||F(p1)))))'
Support contains 2 out of 6600 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 6600/6600 places, 10100/10100 transitions.
Discarding 1599 places :
Symmetric choice reduction at 0 with 1599 rule applications. Total rules 1599 place count 5001 transition count 8501
Iterating global reduction 0 with 1599 rules applied. Total rules applied 3198 place count 5001 transition count 8501
Discarding 1349 places :
Symmetric choice reduction at 0 with 1349 rule applications. Total rules 4547 place count 3652 transition count 7152
Iterating global reduction 0 with 1349 rules applied. Total rules applied 5896 place count 3652 transition count 7152
Discarding 200 places :
Symmetric choice reduction at 0 with 200 rule applications. Total rules 6096 place count 3452 transition count 6952
Iterating global reduction 0 with 200 rules applied. Total rules applied 6296 place count 3452 transition count 6952
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6446 place count 3302 transition count 6802
Iterating global reduction 0 with 150 rules applied. Total rules applied 6596 place count 3302 transition count 6802
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 6746 place count 3152 transition count 6652
Iterating global reduction 0 with 150 rules applied. Total rules applied 6896 place count 3152 transition count 6652
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7046 place count 3002 transition count 6502
Iterating global reduction 0 with 150 rules applied. Total rules applied 7196 place count 3002 transition count 6502
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7346 place count 2852 transition count 6352
Iterating global reduction 0 with 150 rules applied. Total rules applied 7496 place count 2852 transition count 6352
Discarding 150 places :
Symmetric choice reduction at 0 with 150 rule applications. Total rules 7646 place count 2702 transition count 6202
Iterating global reduction 0 with 150 rules applied. Total rules applied 7796 place count 2702 transition count 6202
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 7896 place count 2602 transition count 6102
Iterating global reduction 0 with 100 rules applied. Total rules applied 7996 place count 2602 transition count 6102
Discarding 100 places :
Symmetric choice reduction at 0 with 100 rule applications. Total rules 8096 place count 2502 transition count 6002
Iterating global reduction 0 with 100 rules applied. Total rules applied 8196 place count 2502 transition count 6002
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 8246 place count 2452 transition count 5952
Iterating global reduction 0 with 50 rules applied. Total rules applied 8296 place count 2452 transition count 5952
Applied a total of 8296 rules in 4393 ms. Remains 2452 /6600 variables (removed 4148) and now considering 5952/10100 (removed 4148) transitions.
// Phase 1: matrix 5952 rows 2452 cols
[2024-06-01 11:28:29] [INFO ] Computed 50 invariants in 16 ms
[2024-06-01 11:28:30] [INFO ] Implicit Places using invariants in 448 ms returned []
[2024-06-01 11:28:30] [INFO ] Invariant cache hit.
[2024-06-01 11:28:32] [INFO ] Implicit Places using invariants and state equation in 2596 ms returned []
Implicit Place search using SMT with State Equation took 3046 ms to find 0 implicit places.
Running 4152 sub problems to find dead transitions.
[2024-06-01 11:28:32] [INFO ] Invariant cache hit.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2402/8404 variables, and 0 constraints, problems are : Problem set: 0 solved, 4152 unsolved in 30111 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2452 constraints, PredecessorRefiner: 4152/4152 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 4152 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2402/8404 variables, and 0 constraints, problems are : Problem set: 0 solved, 4152 unsolved in 30110 ms.
Refiners :[Positive P Invariants (semi-flows): 0/50 constraints, State Equation: 0/2452 constraints, PredecessorRefiner: 0/4152 constraints, Known Traps: 0/0 constraints]
After SMT, in 62571ms problems are : Problem set: 0 solved, 4152 unsolved
Search for dead transitions found 0 dead transitions in 62607ms
Starting structural reductions in LTL mode, iteration 1 : 2452/6600 places, 5952/10100 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 70049 ms. Remains : 2452/6600 places, 5952/10100 transitions.
Stuttering acceptance computed with spot in 158 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p1)]
Running random walk in product with property : BART-PT-050-LTLFireability-15
Product exploration explored 100000 steps with 5 reset in 1164 ms.
Product exploration explored 100000 steps with 11 reset in 937 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Computed a total of 0 stabilizing places and 0 stable transitions
Knowledge obtained : [(AND (NOT p0) (NOT p1)), (X (NOT p1)), (X (X (NOT p1)))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X p0), (X (NOT p0)), (X (X (AND (NOT p0) (NOT p1)))), (X (X (NOT (AND (NOT p0) (NOT p1))))), (X (X p0)), (X (X (NOT p0)))]
Knowledge based reduction with 3 factoid took 262 ms. Reduced automaton from 3 states, 4 edges and 2 AP (stutter sensitive) to 3 states, 4 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 103 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p1)]
RANDOM walk for 32404 steps (6 resets) in 563 ms. (57 steps per ms) remains 0/3 properties
Knowledge obtained : [(AND (NOT p0) (NOT p1)), (X (NOT p1)), (X (X (NOT p1)))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X p0), (X (NOT p0)), (X (X (AND (NOT p0) (NOT p1)))), (X (X (NOT (AND (NOT p0) (NOT p1))))), (X (X p0)), (X (X (NOT p0))), (F (NOT (AND (NOT p0) (NOT p1)))), (F p1), (F p0)]
Knowledge based reduction with 3 factoid took 484 ms. Reduced automaton from 3 states, 4 edges and 2 AP (stutter sensitive) to 3 states, 4 edges and 2 AP (stutter sensitive).
Stuttering acceptance computed with spot in 146 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p1)]
Stuttering acceptance computed with spot in 152 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p1)]
[2024-06-01 11:29:42] [INFO ] Invariant cache hit.
[2024-06-01 11:29:47] [INFO ] [Real]Absence check using 50 positive place invariants in 4 ms returned unsat
Proved EG (AND (NOT p0) (NOT p1))
Knowledge obtained : [(AND (NOT p0) (NOT p1)), (X (NOT p1)), (X (X (NOT p1)))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X p0), (X (NOT p0)), (X (X (AND (NOT p0) (NOT p1)))), (X (X (NOT (AND (NOT p0) (NOT p1))))), (X (X p0)), (X (X (NOT p0))), (F (NOT (AND (NOT p0) (NOT p1)))), (F p1), (F p0), (G (AND (NOT p0) (NOT p1)))]
Property proved to be false thanks to negative knowledge :(G (AND (NOT p0) (NOT p1)))
Knowledge based reduction with 3 factoid took 344 ms. Reduced automaton from 3 states, 4 edges and 2 AP (stutter sensitive) to 1 states, 1 edges and 0 AP (stutter insensitive).
FORMULA BART-PT-050-LTLFireability-15 FALSE TECHNIQUES KNOWLEDGE
Treatment of property BART-PT-050-LTLFireability-15 finished in 82002 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G((F(p0)||X(F((X(X(p1))&&F(p2)))))))'
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X((p0||F(G(!p1))))))'
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(((p0 U X(p1))||X(X(G(p2)))))'
[2024-06-01 11:29:48] [INFO ] Flatten gal took : 392 ms
[2024-06-01 11:29:48] [INFO ] Export to MCC of 3 properties in file /home/mcc/execution/LTLFireability.sr.xml took 68 ms.
[2024-06-01 11:29:48] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 6600 places, 10100 transitions and 20200 arcs took 45 ms.
Total runtime 1538522 ms.
There are residual formulas that ITS could not solve within timeout
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202405141337.jar
+ VERSION=202405141337
+ echo 'Running Version 202405141337'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination LTLFireability -timeout 360 -rebuildPNML
mcc2024
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="BART-PT-050"
export BK_EXAMINATION="LTLFireability"
export BK_TOOL="ltsminxred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool ltsminxred"
echo " Input is BART-PT-050, examination is LTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r468-smll-171620167800492"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/BART-PT-050.tgz
mv BART-PT-050 execution
cd execution
if [ "LTLFireability" = "ReachabilityDeadlock" ] || [ "LTLFireability" = "UpperBounds" ] || [ "LTLFireability" = "QuasiLiveness" ] || [ "LTLFireability" = "StableMarking" ] || [ "LTLFireability" = "Liveness" ] || [ "LTLFireability" = "OneSafe" ] || [ "LTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "LTLFireability" = "ReachabilityDeadlock" ] || [ "LTLFireability" = "QuasiLiveness" ] || [ "LTLFireability" = "StableMarking" ] || [ "LTLFireability" = "Liveness" ] || [ "LTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME LTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

