About the Execution of ITS-Tools for ViralEpidemic-PT-S03D1C1A06
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 1664.768 | 912481.00 | 1102974.00 | 3119.10 | TFTTTTFFFFTFTFFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
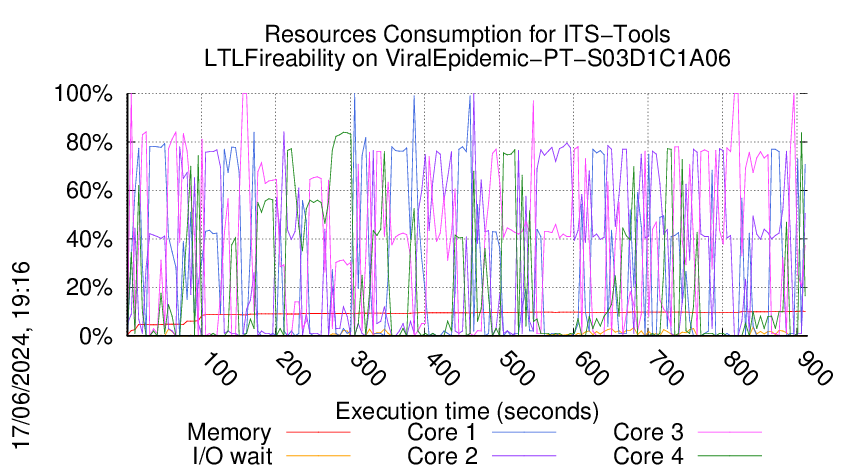
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r444-smll-171701111300332.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool itstools
Input is ViralEpidemic-PT-S03D1C1A06, examination is LTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r444-smll-171701111300332
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 3.5M
-rw-r--r-- 1 mcc users 9.0K May 14 13:22 CTLCardinality.txt
-rw-r--r-- 1 mcc users 82K May 14 13:22 CTLCardinality.xml
-rw-r--r-- 1 mcc users 6.6K May 14 13:22 CTLFireability.txt
-rw-r--r-- 1 mcc users 53K May 14 13:22 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 18 16:43 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.8K May 18 16:43 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 4.6K May 19 07:18 LTLCardinality.txt
-rw-r--r-- 1 mcc users 28K May 19 16:47 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.8K May 19 07:39 LTLFireability.txt
-rw-r--r-- 1 mcc users 19K May 19 19:30 LTLFireability.xml
-rw-r--r-- 1 mcc users 13K Apr 12 04:33 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 105K Apr 12 04:33 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 9.4K Apr 12 04:24 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 66K Apr 12 04:24 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.9K Apr 23 08:04 UpperBounds.txt
-rw-r--r-- 1 mcc users 4.0K Apr 23 08:04 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 May 18 16:43 equiv_col
-rw-r--r-- 1 mcc users 11 May 18 16:43 instance
-rw-r--r-- 1 mcc users 6 May 18 16:43 iscolored
-rw-r--r-- 1 mcc users 3.1M May 18 16:43 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-00
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-01
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-02
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-03
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-04
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-05
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-06
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-07
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-08
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-09
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-10
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-11
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-12
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-13
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-14
FORMULA_NAME ViralEpidemic-PT-S03D1C1A06-LTLFireability-15
=== Now, execution of the tool begins
BK_START 1717170586054
Invoking MCC driver with
BK_TOOL=itstools
BK_EXAMINATION=LTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=ViralEpidemic-PT-S03D1C1A06
BK_MEMORY_CONFINEMENT=16384
Not applying reductions.
Model is PT
LTLFireability PT
Running Version 202405141337
[2024-05-31 15:49:47] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, LTLFireability, -its, -ltsmin, -greatspnpath, /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/, -order, META, -manyOrder, -smt, -timeout, 3600]
[2024-05-31 15:49:47] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-05-31 15:49:48] [INFO ] Load time of PNML (sax parser for PT used): 730 ms
[2024-05-31 15:49:48] [INFO ] Transformed 5466 places.
[2024-05-31 15:49:48] [INFO ] Transformed 7651 transitions.
[2024-05-31 15:49:48] [INFO ] Found NUPN structural information;
[2024-05-31 15:49:48] [INFO ] Parsed PT model containing 5466 places and 7651 transitions and 17488 arcs in 1164 ms.
Parsed 16 properties from file /home/mcc/execution/LTLFireability.xml in 27 ms.
Working with output stream class java.io.PrintStream
Initial state reduction rules removed 1 formulas.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-11 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 71 out of 5466 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 5466/5466 places, 7651/7651 transitions.
Discarding 2497 places :
Symmetric choice reduction at 0 with 2497 rule applications. Total rules 2497 place count 2969 transition count 3013
Iterating global reduction 0 with 2497 rules applied. Total rules applied 4994 place count 2969 transition count 3013
Applied a total of 4994 rules in 1665 ms. Remains 2969 /5466 variables (removed 2497) and now considering 3013/7651 (removed 4638) transitions.
// Phase 1: matrix 3013 rows 2969 cols
[2024-05-31 15:49:51] [INFO ] Invariants computation overflowed in 322 ms
[2024-05-31 15:49:53] [INFO ] Implicit Places using invariants in 2609 ms returned []
// Phase 1: matrix 3013 rows 2969 cols
[2024-05-31 15:49:54] [INFO ] Invariants computation overflowed in 340 ms
[2024-05-31 15:49:58] [INFO ] Implicit Places using invariants and state equation in 4934 ms returned []
Implicit Place search using SMT with State Equation took 7592 ms to find 0 implicit places.
Running 3012 sub problems to find dead transitions.
// Phase 1: matrix 3013 rows 2969 cols
[2024-05-31 15:49:58] [INFO ] Invariants computation overflowed in 74 ms
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2968/5982 variables, and 0 constraints, problems are : Problem set: 0 solved, 3012 unsolved in 30149 ms.
Refiners :[State Equation: 0/2969 constraints, PredecessorRefiner: 3012/3012 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 3012 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2968/5982 variables, and 0 constraints, problems are : Problem set: 0 solved, 3012 unsolved in 30058 ms.
Refiners :[State Equation: 0/2969 constraints, PredecessorRefiner: 0/3012 constraints, Known Traps: 0/0 constraints]
After SMT, in 61835ms problems are : Problem set: 0 solved, 3012 unsolved
Search for dead transitions found 0 dead transitions in 61915ms
Starting structural reductions in LTL mode, iteration 1 : 2969/5466 places, 3013/7651 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 71230 ms. Remains : 2969/5466 places, 3013/7651 transitions.
Support contains 71 out of 2969 places after structural reductions.
[2024-05-31 15:51:01] [INFO ] Flatten gal took : 294 ms
[2024-05-31 15:51:01] [INFO ] Flatten gal took : 180 ms
[2024-05-31 15:51:01] [INFO ] Input system was already deterministic with 3013 transitions.
Support contains 69 out of 2969 places (down from 71) after GAL structural reductions.
Reduction of identical properties reduced properties to check from 40 to 39
RANDOM walk for 40000 steps (294 resets) in 4048 ms. (9 steps per ms) remains 2/39 properties
BEST_FIRST walk for 40004 steps (16 resets) in 1656 ms. (24 steps per ms) remains 2/2 properties
BEST_FIRST walk for 40004 steps (11 resets) in 1354 ms. (29 steps per ms) remains 2/2 properties
// Phase 1: matrix 3013 rows 2969 cols
[2024-05-31 15:51:03] [INFO ] Invariants computation overflowed in 62 ms
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/9 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (OVERLAPS) 21/30 variables, 9/9 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/30 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (OVERLAPS) 49/79 variables, 21/30 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/79 variables, 0/30 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (OVERLAPS) 99/178 variables, 39/69 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/178 variables, 0/69 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 7 (OVERLAPS) 229/407 variables, 86/155 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 8 (INCLUDED_ONLY) 0/407 variables, 0/155 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 9 (OVERLAPS) 587/994 variables, 217/372 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 10 (INCLUDED_ONLY) 0/994 variables, 0/372 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 11 (OVERLAPS) 999/1993 variables, 405/777 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 12 (INCLUDED_ONLY) 0/1993 variables, 0/777 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 13 (OVERLAPS) 1112/3105 variables, 551/1328 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 14 (INCLUDED_ONLY) 0/3105 variables, 0/1328 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 15 (OVERLAPS) 1519/4624 variables, 682/2010 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 16 (INCLUDED_ONLY) 0/4624 variables, 0/2010 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 17 (OVERLAPS) 973/5597 variables, 574/2584 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 18 (INCLUDED_ONLY) 0/5597 variables, 0/2584 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 19 (OVERLAPS) 385/5982 variables, 385/2969 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 20 (INCLUDED_ONLY) 0/5982 variables, 0/2969 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 21 (OVERLAPS) 0/5982 variables, 0/2969 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Real declared 5982/5982 variables, and 2969 constraints, problems are : Problem set: 0 solved, 2 unsolved in 2543 ms.
Refiners :[State Equation: 2969/2969 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/9 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 1 (OVERLAPS) 21/30 variables, 9/9 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/30 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 3 (OVERLAPS) 49/79 variables, 21/30 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/79 variables, 2/32 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/79 variables, 0/32 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 6 (OVERLAPS) 99/178 variables, 39/71 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/178 variables, 0/71 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 8 (OVERLAPS) 229/407 variables, 86/157 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 9 (INCLUDED_ONLY) 0/407 variables, 0/157 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 10 (OVERLAPS) 587/994 variables, 217/374 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 11 (INCLUDED_ONLY) 0/994 variables, 0/374 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 12 (OVERLAPS) 999/1993 variables, 405/779 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 13 (INCLUDED_ONLY) 0/1993 variables, 0/779 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 14 (OVERLAPS) 1112/3105 variables, 551/1330 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 15 (INCLUDED_ONLY) 0/3105 variables, 0/1330 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 16 (OVERLAPS) 1519/4624 variables, 682/2012 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 17 (INCLUDED_ONLY) 0/4624 variables, 0/2012 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 18 (OVERLAPS) 973/5597 variables, 574/2586 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 19 (INCLUDED_ONLY) 0/5597 variables, 0/2586 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 20 (OVERLAPS) 385/5982 variables, 385/2971 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 21 (INCLUDED_ONLY) 0/5982 variables, 0/2971 constraints. Problems are: Problem set: 0 solved, 2 unsolved
At refinement iteration 22 (OVERLAPS) 0/5982 variables, 0/2971 constraints. Problems are: Problem set: 0 solved, 2 unsolved
No progress, stopping.
After SMT solving in domain Int declared 5982/5982 variables, and 2971 constraints, problems are : Problem set: 0 solved, 2 unsolved in 3409 ms.
Refiners :[State Equation: 2969/2969 constraints, PredecessorRefiner: 2/2 constraints, Known Traps: 0/0 constraints]
After SMT, in 6043ms problems are : Problem set: 0 solved, 2 unsolved
Finished Parikh walk after 111 steps, including 0 resets, run visited all 2 properties in 6 ms. (steps per millisecond=18 )
Finished Parikh walk after 0 steps, including 0 resets, run visited all 0 properties in 1 ms. (steps per millisecond=0 )
Parikh walk visited 2 properties in 16 ms.
Computed a total of 2969 stabilizing places and 3013 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2969 transition count 3013
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X((p0||G(F(p1)))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 50 place count 2919 transition count 2920
Iterating global reduction 0 with 50 rules applied. Total rules applied 100 place count 2919 transition count 2920
Applied a total of 100 rules in 395 ms. Remains 2919 /2969 variables (removed 50) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:51:11] [INFO ] Invariants computation overflowed in 80 ms
[2024-05-31 15:51:12] [INFO ] Implicit Places using invariants in 1787 ms returned []
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:51:12] [INFO ] Invariants computation overflowed in 94 ms
[2024-05-31 15:51:17] [INFO ] Implicit Places using invariants and state equation in 4648 ms returned []
Implicit Place search using SMT with State Equation took 6443 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:51:17] [INFO ] Invariants computation overflowed in 59 ms
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30074 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 1)
(s2 1)
(s3 1)
(s4 1)
(s5 1)
(s6 1)
(s7 1)
(s8 1)
(s9 1)
(s10 1)
(s11 1)
(s12 1)
(s13 1)
(s14 1)
(s15 1)
(s16 1)
(s17 1)
(s18 1)
(s19 1)
(s20 1)
(s21 1)
(s22 1)
(s23 1)
(s24 1)
(s25 1)
(s26 1)
(s27 1)
(s28 1)
(s29 1)
(s30 1)
(s31 1)
(s32 1)
(s33 1)
(s34 1)
(s35 1)
(s36 1)
(s37 1)
(s38 1)
(s39 1)
(s40 1)
(s41 1)
(s42 1)
(s43 1)
(s44 1)
(s45 1)
(s46 1)
(s47 1)
(s48 1)
(s49 1)
(s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1582 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1670 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1758 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1846 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1934 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2022 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 1)
(s2090 1)
(s2091 1)
(s2092 1)
(s2093 1)
(s2094 1)
(s2095 1)
(s2096 1)
(s2097 1)
(s2098 1)
(s2099 1)
(s2100 1)
(s2101 1)
(s2102 1)
(s2103 1)
(s2104 1)
(s2105 1)
(s2106 1)
(s2107 1)
(s2108 1)
(s2109 1)
(s2110 1)
(s2111 1)
(s2112 1)
(s2113 1)
(s2114 1)
(s2115 1)
(s2116 1)
(s2117 1)
(s2118 1)
(s2119 1)
(s2120 1)
(s2121 1)
(s2122 1)
(s2123 1)
(s2124 1)
(s2125 1)
(s2126 1)
(s2127 1)
(s2128 1)
(s2129 1)
(s2130 1)
(s2131 1)
(s2132 1)
(s2133 1)
(s2134 1)
(s2135 1)
(s2136 1)
(s2137 1)
(s2138 1)
(s2139 1)
(s2140 1)
(s2141 1)
(s2142 1)
(s2143 1)
(s2144 1)
(s2145 1)
(s2146 1)
(s2147 1)
(s2148 1)
(s2149 1)
(s2150 1)
(s2151 1)
(s2152 1)
(s2153 1)
(s2154 1)
(s2155 1)
(s2156 1)
(s2157 1)
(s2158 1)
(s2159 1)
(s2160 1)
(s2161 1)
(s2162 1)
(s2163 1)
(s2164 1)
(s2165 1)
(s2166 1)
(s2167 1)
(s2168 1)
(s2169 1)
(s2170 1)
(s2171 1)
(s2172 1)
(s2173 1)
(s2174 1)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2198 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2286 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2374 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2462 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2550 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30068 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61312ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61355ms
Starting structural reductions in LTL mode, iteration 1 : 2919/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68205 ms. Remains : 2919/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 449 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p1), (NOT p1)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-00
Product exploration explored 100000 steps with 822 reset in 3227 ms.
Product exploration explored 100000 steps with 840 reset in 3710 ms.
Computed a total of 2919 stabilizing places and 2920 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2919 transition count 2920
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) p1), (X (NOT (AND (NOT p0) (NOT p1)))), (X (NOT p0)), (X p1), (X (X p1)), (F (G (NOT p0))), (F (G p1))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 7 factoid took 22 ms. Reduced automaton from 4 states, 6 edges and 2 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-00 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-00 finished in 77229 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(G((F(p0) U (p0||G(p1))))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 50 place count 2919 transition count 2920
Iterating global reduction 0 with 50 rules applied. Total rules applied 100 place count 2919 transition count 2920
Applied a total of 100 rules in 570 ms. Remains 2919 /2969 variables (removed 50) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:52:28] [INFO ] Invariants computation overflowed in 59 ms
[2024-05-31 15:52:30] [INFO ] Implicit Places using invariants in 2444 ms returned []
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:52:30] [INFO ] Invariants computation overflowed in 60 ms
[2024-05-31 15:52:35] [INFO ] Implicit Places using invariants and state equation in 4374 ms returned []
Implicit Place search using SMT with State Equation took 6825 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:52:35] [INFO ] Invariants computation overflowed in 58 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30095 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 1)
(s2 1)
(s3 1)
(s4 1)
(s5 1)
(s6 1)
(s7 1)
(s8 1)
(s9 1)
(s10 1)
(s11 1)
(s12 1)
(s13 1)
(s14 1)
(s15 1)
(s16 1)
(s17 1)
(s18 1)
(s19 1)
(s20 1)
(s21 1)
(s22 1)
(s23 1)
(s24 1)
(s25 1)
(s26 1)
(s27 1)
(s28 1)
(s29 1)
(s30 1)
(s31 1)
(s32 1)
(s33 1)
(s34 1)
(s35 1)
(s36 1)
(s37 1)
(s38 1)
(s39 1)
(s40 1)
(s41 1)
(s42 1)
(s43 1)
(s44 1)
(s45 1)
(s46 1)
(s47 1)
(s48 1)
(s49 1)
(s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30090 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61308ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61342ms
Starting structural reductions in LTL mode, iteration 1 : 2919/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68745 ms. Remains : 2919/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 157 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (NOT p0)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-01
Stuttering criterion allowed to conclude after 202 steps with 0 reset in 6 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-01 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-01 finished in 68941 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!((G(p0)||F(G(p1))))'
Support contains 2 out of 2969 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Graph (complete) has 1842 edges and 2969 vertex of which 23 are kept as prefixes of interest. Removing 2946 places using SCC suffix rule.12 ms
Discarding 2946 places :
Also discarding 2978 output transitions
Drop transitions (Output transitions of discarded places.) removed 2978 transitions
Reduce places removed 1 places and 1 transitions.
Ensure Unique test removed 2 transitions
Reduce isomorphic transitions removed 2 transitions.
Iterating post reduction 0 with 2 rules applied. Total rules applied 3 place count 22 transition count 32
Discarding 2 places :
Symmetric choice reduction at 1 with 2 rule applications. Total rules 5 place count 20 transition count 28
Iterating global reduction 1 with 2 rules applied. Total rules applied 7 place count 20 transition count 28
Applied a total of 7 rules in 64 ms. Remains 20 /2969 variables (removed 2949) and now considering 28/3013 (removed 2985) transitions.
// Phase 1: matrix 28 rows 20 cols
[2024-05-31 15:53:36] [INFO ] Computed 0 invariants in 1 ms
[2024-05-31 15:53:36] [INFO ] Implicit Places using invariants in 40 ms returned []
[2024-05-31 15:53:36] [INFO ] Invariant cache hit.
[2024-05-31 15:53:36] [INFO ] Implicit Places using invariants and state equation in 49 ms returned []
Implicit Place search using SMT with State Equation took 92 ms to find 0 implicit places.
[2024-05-31 15:53:36] [INFO ] Redundant transitions in 28 ms returned [5, 15]
Found 2 redundant transitions using SMT.
Drop transitions (Redundant Transitions using SMT with State Equation) removed 2 transitions
Redundant transitions reduction (with SMT) removed 2 transitions.
Running 18 sub problems to find dead transitions.
// Phase 1: matrix 26 rows 20 cols
[2024-05-31 15:53:36] [INFO ] Computed 0 invariants in 0 ms
At refinement iteration 0 (INCLUDED_ONLY) 0/17 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 1 (OVERLAPS) 23/40 variables, 17/17 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/40 variables, 0/17 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 3 (OVERLAPS) 2/42 variables, 1/18 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/42 variables, 0/18 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 5 (OVERLAPS) 2/44 variables, 1/19 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/44 variables, 0/19 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 7 (OVERLAPS) 2/46 variables, 1/20 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 8 (INCLUDED_ONLY) 0/46 variables, 0/20 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 9 (OVERLAPS) 0/46 variables, 0/20 constraints. Problems are: Problem set: 0 solved, 18 unsolved
No progress, stopping.
After SMT solving in domain Real declared 46/46 variables, and 20 constraints, problems are : Problem set: 0 solved, 18 unsolved in 430 ms.
Refiners :[State Equation: 20/20 constraints, PredecessorRefiner: 18/18 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 18 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/17 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 1 (OVERLAPS) 23/40 variables, 17/17 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/40 variables, 18/35 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/40 variables, 0/35 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 4 (OVERLAPS) 2/42 variables, 1/36 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/42 variables, 0/36 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 6 (OVERLAPS) 2/44 variables, 1/37 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/44 variables, 0/37 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 8 (OVERLAPS) 2/46 variables, 1/38 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 9 (INCLUDED_ONLY) 0/46 variables, 0/38 constraints. Problems are: Problem set: 0 solved, 18 unsolved
At refinement iteration 10 (OVERLAPS) 0/46 variables, 0/38 constraints. Problems are: Problem set: 0 solved, 18 unsolved
No progress, stopping.
After SMT solving in domain Int declared 46/46 variables, and 38 constraints, problems are : Problem set: 0 solved, 18 unsolved in 393 ms.
Refiners :[State Equation: 20/20 constraints, PredecessorRefiner: 18/18 constraints, Known Traps: 0/0 constraints]
After SMT, in 831ms problems are : Problem set: 0 solved, 18 unsolved
Search for dead transitions found 0 dead transitions in 832ms
Starting structural reductions in SI_LTL mode, iteration 1 : 20/2969 places, 26/3013 transitions.
Graph (complete) has 10 edges and 20 vertex of which 18 are kept as prefixes of interest. Removing 2 places using SCC suffix rule.1 ms
Discarding 2 places :
Also discarding 2 output transitions
Drop transitions (Output transitions of discarded places.) removed 2 transitions
Applied a total of 1 rules in 2 ms. Remains 18 /20 variables (removed 2) and now considering 24/26 (removed 2) transitions.
// Phase 1: matrix 24 rows 18 cols
[2024-05-31 15:53:37] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 15:53:37] [INFO ] Implicit Places using invariants in 25 ms returned []
[2024-05-31 15:53:37] [INFO ] Invariant cache hit.
[2024-05-31 15:53:37] [INFO ] Implicit Places using invariants and state equation in 33 ms returned []
Implicit Place search using SMT with State Equation took 67 ms to find 0 implicit places.
Starting structural reductions in SI_LTL mode, iteration 2 : 18/2969 places, 24/3013 transitions.
Finished structural reductions in SI_LTL mode , in 2 iterations and 1095 ms. Remains : 18/2969 places, 24/3013 transitions.
Stuttering acceptance computed with spot in 77 ms :[(AND (NOT p0) (NOT p1)), (NOT p1)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-02
Product exploration explored 100000 steps with 7117 reset in 150 ms.
Product exploration explored 100000 steps with 7137 reset in 129 ms.
Computed a total of 18 stabilizing places and 24 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 18 transition count 24
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) p1), (X (NOT p0)), (X p1), (X (X (NOT p0))), (X (X p1)), (F (G (NOT p0))), (F (G p1))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 7 factoid took 15 ms. Reduced automaton from 2 states, 4 edges and 2 AP (stutter insensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-02 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-02 finished in 1515 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G((p0||F((G(p1)&&X(X(p2)))))))'
Support contains 6 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 49 places :
Symmetric choice reduction at 0 with 49 rule applications. Total rules 49 place count 2920 transition count 2923
Iterating global reduction 0 with 49 rules applied. Total rules applied 98 place count 2920 transition count 2923
Applied a total of 98 rules in 410 ms. Remains 2920 /2969 variables (removed 49) and now considering 2923/3013 (removed 90) transitions.
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:53:38] [INFO ] Invariants computation overflowed in 92 ms
[2024-05-31 15:53:41] [INFO ] Implicit Places using invariants in 2722 ms returned []
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:53:41] [INFO ] Invariants computation overflowed in 59 ms
[2024-05-31 15:53:45] [INFO ] Implicit Places using invariants and state equation in 4362 ms returned []
Implicit Place search using SMT with State Equation took 7087 ms to find 0 implicit places.
Running 2922 sub problems to find dead transitions.
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:53:45] [INFO ] Invariants computation overflowed in 86 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2919/5843 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30101 ms.
Refiners :[State Equation: 0/2920 constraints, PredecessorRefiner: 2922/2922 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2922 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2919/5843 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30084 ms.
Refiners :[State Equation: 0/2920 constraints, PredecessorRefiner: 0/2922 constraints, Known Traps: 0/0 constraints]
After SMT, in 61516ms problems are : Problem set: 0 solved, 2922 unsolved
Search for dead transitions found 0 dead transitions in 61549ms
Starting structural reductions in LTL mode, iteration 1 : 2920/2969 places, 2923/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 69060 ms. Remains : 2920/2969 places, 2923/3013 transitions.
Stuttering acceptance computed with spot in 402 ms :[(OR (AND (NOT p0) (NOT p1)) (AND (NOT p0) (NOT p2))), (OR (NOT p1) (NOT p2)), (NOT p1), (NOT p2), (NOT p2), (AND (NOT p1) (NOT p2)), (NOT p2)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-03
Product exploration explored 100000 steps with 1605 reset in 3066 ms.
Product exploration explored 100000 steps with 1531 reset in 3588 ms.
Computed a total of 2920 stabilizing places and 2923 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2920 transition count 2923
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) p1 p2), (X p1), (X (X p2)), (X (X (NOT (AND p1 (NOT p2))))), (X (X (NOT (AND (NOT p1) (NOT p2))))), (X (X p1)), (F (G (NOT p0))), (F (G p1)), (F (G p2))]
False Knowledge obtained : []
Property proved to be true thanks to conjunction of knowledge (Minato strategy)
Knowledge based reduction with 9 factoid took 247 ms. Reduced automaton from 7 states, 20 edges and 3 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-03 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-03 finished in 78041 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(G((p0||X(X(X(p1)))))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 51 places :
Symmetric choice reduction at 0 with 51 rule applications. Total rules 51 place count 2918 transition count 2920
Iterating global reduction 0 with 51 rules applied. Total rules applied 102 place count 2918 transition count 2920
Applied a total of 102 rules in 674 ms. Remains 2918 /2969 variables (removed 51) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:54:57] [INFO ] Invariants computation overflowed in 92 ms
[2024-05-31 15:54:59] [INFO ] Implicit Places using invariants in 2206 ms returned []
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:54:59] [INFO ] Invariants computation overflowed in 57 ms
[2024-05-31 15:55:04] [INFO ] Implicit Places using invariants and state equation in 5207 ms returned []
Implicit Place search using SMT with State Equation took 7417 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:55:04] [INFO ] Invariants computation overflowed in 59 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30081 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 1)
(s2 1)
(s3 1)
(s4 1)
(s5 1)
(s6 1)
(s7 1)
(s8 1)
(s9 1)
(s10 1)
(s11 1)
(s12 1)
(s13 1)
(s14 1)
(s15 1)
(s16 1)
(s17 1)
(s18 1)
(s19 1)
(s20 1)
(s21 1)
(s22 1)
(s23 1)
(s24 1)
(s25 1)
(s26 1)
(s27 1)
(s28 1)
(s29 1)
(s30 1)
(s31 1)
(s32 1)
(s33 1)
(s34 1)
(s35 1)
(s36 1)
(s37 1)
(s38 1)
(s39 1)
(s40 1)
(s41 1)
(s42 1)
(s43 1)
(s44 1)
(s45 1)
(s46 1)
(s47 1)
(s48 1)
(s49 1)
(s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 1)
(s441 1)
(s442 1)
(s443 1)
(s444 1)
(s445 1)
(s446 1)
(s447 1)
(s448 1)
(s449 1)
(s450 1)
(s451 1)
(s452 1)
(s453 1)
(s454 1)
(s455 1)
(s456 1)
(s457 1)
(s458 1)
(s459 1)
(s460 1)
(s461 1)
(s462 1)
(s463 1)
(s464 1)
(s465 1)
(s466 1)
(s467 1)
(s468 1)
(s469 1)
(s470 1)
(s471 1)
(s472 1)
(s473 1)
(s474 1)
(s475 1)
(s476 1)
(s477 1)
(s478 1)
(s479 1)
(s480 1)
(s481 1)
(s482 1)
(s483 1)
(s484 1)
(s485 1)
(s486 1)
(s487 1)
(s488 1)
(s489 1)
(s490 1)
(s491 1)
(s492 1)
(s493 1)
(s494 1)
(s495 1)
(s496 1)
(s497 1)
(s498 1)
(s499 1)
(s500 1)
(s501 1)
(s502 1)
(s503 1)
(s504 1)
(s505 1)
(s506 1)
(s507 1)
(s508 1)
(s509 1)
(s510 1)
(s511 1)
(s512 1)
(s513 1)
(s514 1)
(s515 1)
(s516 1)
(s517 1)
(s518 1)
(s519 1)
(s520 1)
(s521 1)
(s522 1)
(s523 1)
(s524 1)
(s525 1)
(s526 1)
(s527 1)
(s528 1)
(s529 1)
(s530 1)
(s531 1)
(s532 1)
(s533 1)
(s534 1)
(s535 1)
(s536 1)
(s537 1)
(s538 1)
(s539 1)
(s540 1)
(s541 1)
(s542 1)
(s543 1)
(s544 1)
(s545 1)
(s546 1)
(s547 1)
(s548 1)
(s549 1)
(s550 1)
(s551 1)
(s552 1)
(s553 1)
(s554 1)
(s555 1)
(s556 1)
(s557 1)
(s558 1)
(s559 1)
(s560 1)
(s561 1)
(s562 1)
(s563 1)
(s564 1)
(s565 1)
(s566 1)
(s567 1)
(s568 1)
(s569 1)
(s570 1)
(s571 1)
(s572 1)
(s573 1)
(s574 1)
(s575 1)
(s576 1)
(s577 1)
(s578 1)
(s579 1)
(s580 1)
(s581 1)
(s582 1)
(s583 1)
(s584 1)
(s585 1)
(s586 1)
(s587 1)
(s588 1)
(s589 1)
(s590 1)
(s591 1)
(s592 1)
(s593 1)
(s594 1)
(s595 1)
(s596 1)
(s597 1)
(s598 1)
(s599 1)
(s600 1)
(s601 1)
(s602 1)
(s603 1)
(s604 1)
(s605 1)
(s606 1)
(s607 1)
(s608 1)
(s609 1)
(s610 1)
(s611 1)
(s612 1)
(s613 1)
(s614 1)
(s615 1)
(s616 1)
(s617 1)
(s618 1)
(s619 1)
(s620 1)
(s621 1)
(s622 1)
(s623 1)
(s624 1)
(s625 1)
(s626 1)
(s627 1)
(s628 1)
(s629 1)
(s630 1)
(s631 1)
(s632 1)
(s633 1)
(s634 1)
(s635 1)
(s636 1)
(s637 1)
(s638 1)
(s639 1)
(s640 1)
(s641 1)
(s642 1)
(s643 1)
(s644 1)
(s645 1)
(s646 1)
(s647 1)
(s648 1)
(s649 1)
(s650 1)
(s651 1)
(s652 1)
(s653 1)
(s654 1)
(s655 1)
(s656 1)
(s657 1)
(s658 1)
(s659 1)
(s660 1)
(s661 1)
(s662 1)
(s663 1)
(s664 1)
(s665 1)
(s666 1)
(s667 1)
(s668 1)
(s669 1)
(s670 1)
(s671 1)
(s672 1)
(s673 1)
(s674 1)
(s675 1)
(s676 1)
(s677 1)
(s678 1)
(s679 1)
(s680 1)
(s681 1)
(s682 1)
(s683 1)
(s684 1)
(s685 1)
(s686 1)
(s687 1)
(s688 1)
(s689 1)
(s690 1)
(s691 1)
(s692 1)
(s693 1)
(s694 1)
(s695 1)
(s696 1)
(s697 1)
(s698 1)
(s699 1)
(s700 1)
(s701 1)
(s702 1)
(s703 1)
(s704 1)
(s705 1)
(s706 1)
(s707 1)
(s708 1)
(s709 1)
(s710 1)
(s711 1)
(s712 1)
(s713 1)
(s714 1)
(s715 1)
(s716 1)
(s717 1)
(s718 1)
(s719 1)
(s720 1)
(s721 1)
(s722 1)
(s723 1)
(s724 1)
(s725 1)
(s726 1)
(s727 1)
(s728 1)
(s729 1)
(s730 1)
(s731 1)
(s732 1)
(s733 1)
(s734 1)
(s735 1)
(s736 1)
(s737 1)
(s738 1)
(s739 1)
(s740 1)
(s741 1)
(s742 1)
(s743 1)
(s744 1)
(s745 1)
(s746 1)
(s747 1)
(s748 1)
(s749 1)
(s750 1)
(s751 1)
(s752 1)
(s753 1)
(s754 1)
(s755 1)
(s756 1)
(s757 1)
(s758 1)
(s759 1)
(s760 1)
(s761 1)
(s762 1)
(s763 1)
(s764 1)
(s765 1)
(s766 1)
(s767 1)
(s768 1)
(s769 1)
(s770 1)
(s771 1)
(s772 1)
(s773 1)
(s774 1)
(s775 1)
(s776 1)
(s777 1)
(s778 1)
(s779 1)
(s780 1)
(s781 1)
(s782 1)
(s783 1)
(s784 1)
(s785 1)
(s786 1)
(s787 1)
(s788 1)
(s789 1)
(s790 1)
(s791 1)
(s792 1)
(s793 1)
(s794 1)
(s795 1)
(s796 1)
(s797 1)
(s798 1)
(s799 1)
(s800 1)
(s801 1)
(s802 1)
(s803 1)
(s804 1)
(s805 1)
(s806 1)
(s807 1)
(s808 1)
(s809 1)
(s810 1)
(s811 1)
(s812 1)
(s813 1)
(s814 1)
(s815 1)
(s816 1)
(s817 1)
(s818 1)
(s819 1)
(s820 1)
(s821 1)
(s822 1)
(s823 1)
(s824 1)
(s825 1)
(s826 1)
(s827 1)
(s828 1)
(s829 1)
(s830 1)
(s831 1)
(s832 1)
(s833 1)
(s834 1)
(s835 1)
(s836 1)
(s837 1)
(s838 1)
(s839 1)
(s840 1)
(s841 1)
(s842 1)
(s843 1)
(s844 1)
(s845 1)
(s846 1)
(s847 1)
(s848 1)
(s849 1)
(s850 1)
(s851 1)
(s852 1)
(s853 1)
(s854 1)
(s855 1)
(s856 1)
(s857 1)
(s858 1)
(s859 1)
(s860 1)
(s861 1)
(s862 1)
(s863 1)
(s864 1)
(s865 1)
(s866 1)
(s867 1)
(s868 1)
(s869 1)
(s870 1)
(s871 1)
(s872 1)
(s873 1)
(s874 1)
(s875 1)
(s876 1)
(s877 1)
(s878 1)
(s879 1)
(s880 1)
(s881 1)
(s882 1)
(s883 1)
(s884 1)
(s885 1)
(s886 1)
(s887 1)
(s888 1)
(s889 1)
(s890 1)
(s891 1)
(s892 1)
(s893 1)
(s894 1)
(s895 1)
(s896 1)
(s897 1)
(s898 1)
(s899 1)
(s900 1)
(s901 1)
(s902 1)
(s903 1)
(s904 1)
(s905 1)
(s906 1)
(s907 1)
(s908 1)
(s909 1)
(s910 1)
(s911 1)
(s912 1)
(s913 1)
(s914 1)
(s915 1)
(s916 1)
(s917 1)
(s918 1)
(s919 1)
(s920 1)
(s921 1)
(s922 1)
(s923 1)
(s924 1)
(s925 1)
(s926 1)
(s927 1)
(s928 1)
(s929 1)
(s930 1)
(s931 1)
(s932 1)
(s933 1)
(s934 1)
(s935 1)
(s936 1)
(s937 1)
(s938 1)
(s939 1)
(s940 1)
(s941 1)
(s942 1)
(s943 1)
(s944 1)
(s945 1)
(s946 1)
(s947 1)
(s948 1)
(s949 1)
(s950 1)
(s951 1)
(s952 1)
(s953 1)
(s954 1)
(s955 1)
(s956 1)
(s957 1)
(s958 1)
(s959 1)
(s960 1)
(s961 1)
(s962 1)
(s963 1)
(s964 1)
(s965 1)
(s966 1)
(s967 1)
(s968 1)
(s969 1)
(s970 1)
(s971 1)
(s972 1)
(s973 1)
(s974 1)
(s975 1)
(s976 1)
(s977 1)
(s978 1)
(s979 1)
(s980 1)
(s981 1)
(s982 1)
(s983 1)
(s984 1)
(s985 1)
(s986 1)
(s987 1)
(s988 1)
(s989 1)
(s990 1)
(s991 1)
(s992 1)
(s993 1)
(s994 1)
(s995 1)
(s996 1)
(s997 1)
(s998 1)
(s999 1)
(s1000 1)
(s1001 1)
(s1002 1)
(s1003 1)
(s1004 1)
(s1005 1)
(s1006 1)
(s1007 1)
(s1008 1)
(s1009 1)
(s1010 1)
(s1011 1)
(s1012 1)
(s1013 1)
(s1014 1)
(s1015 1)
(s1016 1)
(s1017 1)
(s1018 1)
(s1019 1)
(s1020 1)
(s1021 1)
(s1022 1)
(s1023 1)
(s1024 1)
(s1025 1)
(s1026 1)
(s1027 1)
(s1028 1)
(s1029 1)
(s1030 1)
(s1031 1)
(s1032 1)
(s1033 1)
(s1034 1)
(s1035 1)
(s1036 1)
(s1037 1)
(s1038 1)
(s1039 1)
(s1040 1)
(s1041 1)
(s1042 1)
(s1043 1)
(s1044 1)
(s1045 1)
(s1046 1)
(s1047 1)
(s1048 1)
(s1049 1)
(s1050 1)
(s1051 1)
(s1052 1)
(s1053 1)
(s1054 1)
(s1055 1)
(s1056 1)
(s1057 1)
(s1058 1)
(s1059 1)
(s1060 1)
(s1061 1)
(s1062 1)
(s1063 1)
(s1064 1)
(s1065 1)
(s1066 1)
(s1067 1)
(s1068 1)
(s1069 1)
(s1070 1)
(s1071 1)
(s1072 1)
(s1073 1)
(s1074 1)
(s1075 1)
(s1076 1)
(s1077 1)
(s1078 1)
(s1079 1)
(s1080 1)
(s1081 1)
(s1082 1)
(s1083 1)
(s1084 1)
(s1085 1)
(s1086 1)
(s1087 1)
(s1088 1)
(s1089 1)
(s1090 1)
(s1091 1)
(s1092 1)
(s1093 1)
(s1094 1)
(s1095 1)
(s1096 1)
(s1097 1)
(s1098 1)
(s1099 1)
(s1100 1)
(s1101 1)
(s1102 1)
(s1103 1)
(s1104 1)
(s1105 1)
(s1106 1)
(s1107 1)
(s1108 1)
(s1109 1)
(s1110 1)
(s1111 1)
(s1112 1)
(s1113 1)
(s1114 1)
(s1115 1)
(s1116 1)
(s1117 1)
(s1118 1)
(s1119 1)
(s1120 1)
(s1121 1)
(s1122 1)
(s1123 1)
(s1124 1)
(s1125 1)
(s1126 1)
(s1127 1)
(s1128 1)
(s1129 1)
(s1130 1)
(s1131 1)
(s1132 1)
(s1133 1)
(s1134 1)
(s1135 1)
(s1136 1)
(s1137 1)
(s1138 1)
(s1139 1)
(s1140 1)
(s1141 1)
(s1142 1)
(s1143 1)
(s1144 1)
(s1145 1)
(s1146 1)
(s1147 1)
(s1148 1)
(s1149 1)
(s1150 1)
(s1151 1)
(s1152 1)
(s1153 1)
(s1154 1)
(s1155 1)
(s1156 1)
(s1157 1)
(s1158 1)
(s1159 1)
(s1160 1)
(s1161 1)
(s1162 1)
(s1163 1)
(s1164 1)
(s1165 1)
(s1166 1)
(s1167 1)
(s1168 1)
(s1169 1)
(s1170 1)
(s1171 1)
(s1172 1)
(s1173 1)
(s1174 1)
(s1175 1)
(s1176 1)
(s1177 1)
(s1178 1)
(s1179 1)
(s1180 1)
(s1181 1)
(s1182 1)
(s1183 1)
(s1184 1)
(s1185 1)
(s1186 1)
(s1187 1)
(s1188 1)
(s1189 1)
(s1190 1)
(s1191 1)
(s1192 1)
(s1193 1)
(s1194 1)
(s1195 1)
(s1196 1)
(s1197 1)
(s1198 1)
(s1199 1)
(s1200 1)
(s1201 1)
(s1202 1)
(s1203 1)
(s1204 1)
(s1205 1)
(s1206 1)
(s1207 1)
(s1208 1)
(s1209 1)
(s1210 1)
(s1211 1)
(s1212 1)
(s1213 1)
(s1214 1)
(s1215 1)
(s1216 1)
(s1217 1)
(s1218 1)
(s1219 1)
(s1220 1)
(s1221 1)
(s1222 1)
(s1223 1)
(s1224 1)
(s1225 1)
(s1226 1)
(s1227 1)
(s1228 1)
(s1229 1)
(s1230 1)
(s1231 1)
(s1232 1)
(s1233 1)
(s1234 1)
(s1235 1)
(s1236 1)
(s1237 1)
(s1238 1)
(s1239 1)
(s1240 1)
(s1241 1)
(s1242 1)
(s1243 1)
(s1244 1)
(s1245 1)
(s1246 1)
(s1247 1)
(s1248 1)
(s1249 1)
(s1250 1)
(s1251 1)
(s1252 1)
(s1253 1)
(s1254 1)
(s1255 1)
(s1256 1)
(s1257 1)
(s1258 1)
(s1259 1)
(s1260 1)
(s1261 1)
(s1262 1)
(s1263 1)
(s1264 1)
(s1265 1)
(s1266 1)
(s1267 1)
(s1268 1)
(s1269 1)
(s1270 1)
(s1271 1)
(s1272 1)
(s1273 1)
(s1274 1)
(s1275 1)
(s1276 1)
(s1277 1)
(s1278 1)
(s1279 1)
(s1280 1)
(s1281 1)
(s1282 1)
(s1283 1)
(s1284 1)
(s1285 1)
(s1286 1)
(s1287 1)
(s1288 1)
(s1289 1)
(s1290 1)
(s1291 1)
(s1292 1)
(s1293 1)
(s1294 1)
(s1295 1)
(s1296 1)
(s1297 1)
(s1298 1)
(s1299 1)
(s1300 1)
(s1301 1)
(s1302 1)
(s1303 1)
(s1304 1)
(s1305 1)
(s1306 1)
(s1307 1)
(s1308 1)
(s1309 1)
(s1310 1)
(s1311 1)
(s1312 1)
(s1313 1)
(s1314 1)
(s1315 1)
(s1316 1)
(s1317 1)
(s1318 1)
(s1319 1)
(s1320 1)
(s1321 1)
(s1322 1)
(s1323 1)
(s1324 1)
(s1325 1)
(s1326 1)
(s1327 1)
(s1328 1)
(s1329 1)
(s1330 1)
(s1331 1)
(s1332 1)
(s1333 1)
(s1334 1)
(s1335 1)
(s1336 1)
(s1337 1)
(s1338 1)
(s1339 1)
(s1340 1)
(s1341 1)
(s1342 1)
(s1343 1)
(s1344 1)
(s1345 1)
(s1346 1)
(s1347 1)
(s1348 1)
(s1349 1)
(s1350 1)
(s1351 1)
(s1352 1)
(s1353 1)
(s1354 1)
(s1355 1)
(s1356 1)
(s1357 1)
(s1358 1)
(s1359 1)
(s1360 1)
(s1361 1)
(s1362 1)
(s1363 1)
(s1364 1)
(s1365 1)
(s1366 1)
(s1367 1)
(s1368 1)
(s1369 1)
(s1370 1)
(s1371 1)
(s1372 1)
(s1373 1)
(s1374 1)
(s1375 1)
(s1376 1)
(s1377 1)
(s1378 1)
(s1379 1)
(s1380 1)
(s1381 1)
(s1382 1)
(s1383 1)
(s1384 1)
(s1385 1)
(s1386 1)
(s1387 1)
(s1388 1)
(s1389 1)
(s1390 1)
(s1391 1)
(s1392 1)
(s1393 1)
(s1394 1)
(s1395 1)
(s1396 1)
(s1397 1)
(s1398 1)
(s1399 1)
(s1400 1)
(s1401 1)
(s1402 1)
(s1403 1)
(s1404 1)
(s1405 1)
(s1406 1)
(s1407 1)
(s1408 1)
(s1409 1)
(s1410 1)
(s1411 1)
(s1412 1)
(s1413 1)
(s1414 1)
(s1415 1)
(s1416 1)
(s1417 1)
(s1418 1)
(s1419 1)
(s1420 1)
(s1421 1)
(s1422 1)
(s1423 1)
(s1424 1)
(s1425 1)
(s1426 1)
(s1427 1)
(s1428 1)
(s1429 1)
(s1430 1)
(s1431 1)
(s1432 1)
(s1433 1)
(s1434 1)
(s1435 1)
(s1436 1)
(s1437 1)
(s1438 1)
(s1439 1)
(s1440 1)
(s1441 1)
(s1442 1)
(s1443 1)
(s1444 1)
(s1445 1)
(s1446 1)
(s1447 1)
(s1448 1)
(s1449 1)
(s1450 1)
(s1451 1)
(s1452 1)
(s1453 1)
(s1454 1)
(s1455 1)
(s1456 1)
(s1457 1)
(s1458 1)
(s1459 1)
(s1460 1)
(s1461 1)
(s1462 1)
(s1463 1)
(s1464 1)
(s1465 1)
(s1466 1)
(s1467 1)
(s1468 1)
(s1469 1)
(s1470 1)
(s1471 1)
(s1472 1)
(s1473 1)
(s1474 1)
(s1475 1)
(s1476 1)
(s1477 1)
(s1478 1)
(s1479 1)
(s1480 1)
(s1481 1)
(s1482 1)
(s1483 1)
(s1484 1)
(s1485 1)
(s1486 1)
(s1487 1)
(s1488 1)
(s1489 1)
(s1490 1)
(s1491 1)
(s1492 1)
(s1493 1)
(s1494 1)
(s1495 1)
(s1496 1)
(s1497 1)
(s1498 1)
(s1499 1)
(s1500 1)
(s1501 1)
(s1502 1)
(s1503 1)
(s1504 1)
(s1505 1)
(s1506 1)
(s1507 1)
(s1508 1)
(s1509 1)
(s1510 1)
(s1511 1)
(s1512 1)
(s1513 1)
(s1514 1)
(s1515 1)
(s1516 1)
(s1517 1)
(s1518 1)
(s1519 1)
(s1520 1)
(s1521 1)
(s1522 1)
(s1523 1)
(s1524 1)
(s1525 1)
(s1526 1)
(s1527 1)
(s1528 1)
(s1529 1)
(s1530 1)
(s1531 1)
(s1532 1)
(s1533 1)
(s1534 1)
(s1535 1)
(s1536 1)
(s1537 1)
(s1538 1)
(s1539 1)
(s1540 1)
(s1541 1)
(s1542 1)
(s1543 1)
(s1544 1)
(s1545 1)
(s1546 1)
(s1547 1)
(s1548 1)
(s1549 1)
(s1550 1)
(s1551 1)
(s1552 1)
(s1553 1)
(s1554 1)
(s1555 1)
(s1556 1)
(s1557 1)
(s1558 1)
(s1559 1)
(s1560 1)
(s1561 1)
(s1562 1)
(s1563 1)
(s1564 1)
(s1565 1)
(s1566 1)
(s1567 1)
(s1568 1)
(s1569 1)
(s1570 1)
(s1571 1)
(s1572 1)
(s1573 1)
(s1574 1)
(s1575 1)
(s1576 1)
(s1577 1)
(s1578 1)
(s1579 1)
(s1580 1)
(s1581 1)
(s1582 1)
(s1583 1)
(s1584 1)
(s1585 1)
(s1586 1)
(s1587 1)
(s1588 1)
(s1589 1)
(s1590 1)
(s1591 1)
(s1592 1)
(s1593 1)
(s1594 1)
(s1595 1)
(s1596 1)
(s1597 1)
(s1598 1)
(s1599 1)
(s1600 1)
(s1601 1)
(s1602 1)
(s1603 1)
(s1604 1)
(s1605 1)
(s1606 1)
(s1607 1)
(s1608 1)
(s1609 1)
(s1610 1)
(s1611 1)
(s1612 1)
(s1613 1)
(s1614 1)
(s1615 1)
(s1616 1)
(s1617 1)
(s1618 1)
(s1619 1)
(s1620 1)
(s1621 1)
(s1622 1)
(s1623 1)
(s1624 1)
(s1625 1)
(s1626 1)
(s1627 1)
(s1628 1)
(s1629 1)
(s1630 1)
(s1631 1)
(s1632 1)
(s1633 1)
(s1634 1)
(s1635 1)
(s1636 1)
(s1637 1)
(s1638 1)
(s1639 1)
(s1640 1)
(s1641 1)
(s1642 1)
(s1643 1)
(s1644 1)
(s1645 1)
(s1646 1)
(s1647 1)
(s1648 1)
(s1649 1)
(s1650 1)
(s1651 1)
(s1652 1)
(s1653 1)
(s1654 1)
(s1655 1)
(s1656 1)
(s1657 1)
(s1658 1)
(s1659 1)
(s1660 1)
(s1661 1)
(s1662 1)
(s1663 1)
(s1664 1)
(s1665 1)
(s1666 1)
(s1667 1)
(s1668 1)
(s1669 1)
(s1670 1)
(s1671 1)
(s1672 1)
(s1673 1)
(s1674 1)
(s1675 1)
(s1676 1)
(s1677 1)
(s1678 1)
(s1679 1)
(s1680 1)
(s1681 1)
(s1682 1)
(s1683 1)
(s1684 1)
(s1685 1)
(s1686 1)
(s1687 1)
(s1688 1)
(s1689 1)
(s1690 1)
(s1691 1)
(s1692 1)
(s1693 1)
(s1694 1)
(s1695 1)
(s1696 1)
(s1697 1)
(s1698 1)
(s1699 1)
(s1700 1)
(s1701 1)
(s1702 1)
(s1703 1)
(s1704 1)
(s1705 1)
(s1706 1)
(s1707 1)
(s1708 1)
(s1709 1)
(s1710 1)
(s1711 1)
(s1712 1)
(s1713 1)
(s1714 1)
(s1715 1)
(s1716 1)
(s1717 1)
(s1718 1)
(s1719 1)
(s1720 1)
(s1721 1)
(s1722 1)
(s1723 1)
(s1724 1)
(s1725 1)
(s1726 1)
(s1727 1)
(s1728 1)
(s1729 1)
(s1730 1)
(s1731 1)
(s1732 1)
(s1733 1)
(s1734 1)
(s1735 1)
(s1736 1)
(s1737 1)
(s1738 1)
(s1739 1)
(s1740 1)
(s1741 1)
(s1742 1)
(s1743 1)
(s1744 1)
(s1745 1)
(s1746 1)
(s1747 1)
(s1748 1)
(s1749 1)
(s1750 1)
(s1751 1)
(s1752 1)
(s1753 1)
(s1754 1)
(s1755 1)
(s1756 1)
(s1757 1)
(s1758 1)
(s1759 1)
(s1760 1)
(s1761 1)
(s1762 1)
(s1763 1)
(s1764 1)
(s1765 1)
(s1766 1)
(s1767 1)
(s1768 1)
(s1769 1)
(s1770 1)
(s1771 1)
(s1772 1)
(s1773 1)
(s1774 1)
(s1775 1)
(s1776 1)
(s1777 1)
(s1778 1)
(s1779 1)
(s1780 1)
(s1781 1)
(s1782 1)
(s1783 1)
(s1784 1)
(s1785 1)
(s1786 1)
(s1787 1)
(s1788 1)
(s1789 1)
(s1790 1)
(s1791 1)
(s1792 1)
(s1793 1)
(s1794 1)
(s1795 1)
(s1796 1)
(s1797 1)
(s1798 1)
(s1799 1)
(s1800 1)
(s1801 1)
(s1802 1)
(s1803 1)
(s1804 1)
(s1805 1)
(s1806 1)
(s1807 1)
(s1808 1)
(s1809 1)
(s1810 1)
(s1811 1)
(s1812 1)
(s1813 1)
(s1814 1)
(s1815 1)
(s1816 1)
(s1817 1)
(s1818 1)
(s1819 1)
(s1820 1)
(s1821 1)
(s1822 1)
(s1823 1)
(s1824 1)
(s1825 1)
(s1826 1)
(s1827 1)
(s1828 1)
(s1829 1)
(s1830 1)
(s1831 1)
(s1832 1)
(s1833 1)
(s1834 1)
(s1835 1)
(s1836 1)
(s1837 1)
(s1838 1)
(s1839 1)
(s1840 1)
(s1841 1)
(s1842 1)
(s1843 1)
(s1844 1)
(s1845 1)
(s1846 1)
(s1847 1)
(s1848 1)
(s1849 1)
(s1850 1)
(s1851 1)
(s1852 1)
(s1853 1)
(s1854 1)
(s1855 1)
(s1856 1)
(s1857 1)
(s1858 1)
(s1859 1)
(s1860 1)
(s1861 1)
(s1862 1)
(s1863 1)
(s1864 1)
(s1865 1)
(s1866 1)
(s1867 1)
(s1868 1)
(s1869 1)
(s1870 1)
(s1871 1)
(s1872 1)
(s1873 1)
(s1874 1)
(s1875 1)
(s1876 1)
(s1877 1)
(s1878 1)
(s1879 1)
(s1880 1)
(s1881 1)
(s1882 1)
(s1883 1)
(s1884 1)
(s1885 1)
(s1886 1)
(s1887 1)
(s1888 1)
(s1889 1)
(s1890 1)
(s1891 1)
(s1892 1)
(s1893 1)
(s1894 1)
(s1895 1)
(s1896 1)
(s1897 1)
(s1898 1)
(s1899 1)
(s1900 1)
(s1901 1)
(s1902 1)
(s1903 1)
(s1904 1)
(s1905 1)
(s1906 1)
(s1907 1)
(s1908 1)
(s1909 1)
(s1910 1)
(s1911 1)
(s1912 1)
(s1913 1)
(s1914 1)
(s1915 1)
(s1916 1)
(s1917 1)
(s1918 1)
(s1919 1)
(s1920 1)
(s1921 1)
(s1922 1)
(s1923 1)
(s1924 1)
(s1925 1)
(s1926 1)
(s1927 1)
(s1928 1)
(s1929 1)
(s1930 1)
(s1931 1)
(s1932 1)
(s1933 1)
(s1934 1)
(s1935 1)
(s1936 1)
(s1937 1)
(s1938 1)
(s1939 1)
(s1940 1)
(s1941 1)
(s1942 1)
(s1943 1)
(s1944 1)
(s1945 1)
(s1946 1)
(s1947 1)
(s1948 1)
(s1949 1)
(s1950 1)
(s1951 1)
(s1952 1)
(s1953 1)
(s1954 1)
(s1955 1)
(s1956 1)
(s1957 1)
(s1958 1)
(s1959 1)
(s1960 1)
(s1961 1)
(s1962 1)
(s1963 1)
(s1964 1)
(s1965 1)
(s1966 1)
(s1967 1)
(s1968 1)
(s1969 1)
(s1970 1)
(s1971 1)
(s1972 1)
(s1973 1)
(s1974 1)
(s1975 1)
(s1976 1)
(s1977 1)
(s1978 1)
(s1979 1)
(s1980 1)
(s1981 1)
(s1982 1)
(s1983 1)
(s1984 1)
(s1985 1)
(s1986 1)
(s1987 1)
(s1988 1)
(s1989 1)
(s1990 1)
(s1991 1)
(s1992 1)
(s1993 1)
(s1994 1)
(s1995 1)
(s1996 1)
(s1997 1)
(s1998 1)
(s1999 1)
(s2000 1)
(s2001 1)
(s2002 1)
(s2003 1)
(s2004 1)
(s2005 1)
(s2006 1)
(s2007 1)
(s2008 1)
(s2009 1)
(s2010 1)
(s2011 1)
(s2012 1)
(s2013 1)
(s2014 1)
(s2015 1)
(s2016 1)
(s2017 1)
(s2018 1)
(s2019 1)
(s2020 1)
(s2021 1)
(s2022 1)
(s2023 1)
(s2024 1)
(s2025 1)
(s2026 1)
(s2027 1)
(s2028 1)
(s2029 1)
(s2030 1)
(s2031 1)
(s2032 1)
(s2033 1)
(s2034 1)
(s2035 1)
(s2036 1)
(s2037 1)
(s2038 1)
(s2039 1)
(s2040 1)
(s2041 1)
(s2042 1)
(s2043 1)
(s2044 1)
(s2045 1)
(s2046 1)
(s2047 1)
(s2048 1)
(s2049 1)
(s2050 1)
(s2051 1)
(s2052 1)
(s2053 1)
(s2054 1)
(s2055 1)
(s2056 1)
(s2057 1)
(s2058 1)
(s2059 1)
(s2060 1)
(s2061 1)
(s2062 1)
(s2063 1)
(s2064 1)
(s2065 1)
(s2066 1)
(s2067 1)
(s2068 1)
(s2069 1)
(s2070 1)
(s2071 1)
(s2072 1)
(s2073 1)
(s2074 1)
(s2075 1)
(s2076 1)
(s2077 1)
(s2078 1)
(s2079 1)
(s2080 1)
(s2081 1)
(s2082 1)
(s2083 1)
(s2084 1)
(s2085 1)
(s2086 1)
(s2087 1)
(s2088 1)
(s2089 1)
(s2090 1)
(s2091 1)
(s2092 1)
(s2093 1)
(s2094 1)
(s2095 1)
(s2096 1)
(s2097 1)
(s2098 1)
(s2099 1)
(s2100 1)
(s2101 1)
(s2102 1)
(s2103 1)
(s2104 1)
(s2105 1)
(s2106 1)
(s2107 1)
(s2108 1)
(s2109 1)
(s2110 1)
(s2111 1)
(s2112 1)
(s2113 1)
(s2114 1)
(s2115 1)
(s2116 1)
(s2117 1)
(s2118 1)
(s2119 1)
(s2120 1)
(s2121 1)
(s2122 1)
(s2123 1)
(s2124 1)
(s2125 1)
(s2126 1)
(s2127 1)
(s2128 1)
(s2129 1)
(s2130 1)
(s2131 1)
(s2132 1)
(s2133 1)
(s2134 1)
(s2135 1)
(s2136 1)
(s2137 1)
(s2138 1)
(s2139 1)
(s2140 1)
(s2141 1)
(s2142 1)
(s2143 1)
(s2144 1)
(s2145 1)
(s2146 1)
(s2147 1)
(s2148 1)
(s2149 1)
(s2150 1)
(s2151 1)
(s2152 1)
(s2153 1)
(s2154 1)
(s2155 1)
(s2156 1)
(s2157 1)
(s2158 1)
(s2159 1)
(s2160 1)
(s2161 1)
(s2162 1)
(s2163 1)
(s2164 1)
(s2165 1)
(s2166 1)
(s2167 1)
(s2168 1)
(s2169 1)
(s2170 1)
(s2171 1)
(s2172 1)
(s2173 1)
(s2174 1)
(s2175 1)
(s2176 1)
(s2177 1)
(s2178 1)
(s2179 1)
(s2180 1)
(s2181 1)
(s2182 1)
(s2183 1)
(s2184 1)
(s2185 1)
(s2186 1)
(s2187 1)
(s2188 1)
(s2189 1)
(s2190 1)
(s2191 1)
(s2192 1)
(s2193 1)
(s2194 1)
(s2195 1)
(s2196 1)
(s2197 1)
(s2198 1)
(s2199 1)
(s2200 1)
(s2201 1)
(s2202 1)
(s2203 1)
(s2204 1)
(s2205 1)
(s2206 1)
(s2207 1)
(s2208 1)
(s2209 1)
(s2210 1)
(s2211 1)
(s2212 1)
(s2213 1)
(s2214 1)
(s2215 1)
(s2216 1)
(s2217 1)
(s2218 1)
(s2219 1)
(s2220 1)
(s2221 1)
(s2222 1)
(s2223 1)
(s2224 1)
(s2225 1)
(s2226 1)
(s2227 1)
(s2228 1)
(s2229 1)
(s2230 1)
(s2231 1)
(s2232 1)
(s2233 1)
(s2234 1)
(s2235 1)
(s2236 1)
(s2237 1)
(s2238 1)
(s2239 1)
(s2240 1)
(s2241 1)
(s2242 1)
(s2243 1)
(s2244 1)
(s2245 1)
(s2246 1)
(s2247 1)
(s2248 1)
(s2249 1)
(s2250 1)
(s2251 1)
(s2252 1)
(s2253 1)
(s2254 1)
(s2255 1)
(s2256 1)
(s2257 1)
(s2258 1)
(s2259 1)
(s2260 1)
(s2261 1)
(s2262 1)
(s2263 1)
(s2264 1)
(s2265 1)
(s2266 1)
(s2267 1)
(s2268 1)
(s2269 1)
(s2270 1)
(s2271 1)
(s2272 1)
(s2273 1)
(s2274 1)
(s2275 1)
(s2276 1)
(s2277 1)
(s2278 1)
(s2279 1)
(s2280 1)
(s2281 1)
(s2282 1)
(s2283 1)
(s2284 1)
(s2285 1)
(s2286 1)
(s2287 1)
(s2288 1)
(s2289 1)
(s2290 1)
(s2291 1)
(s2292 1)
(s2293 1)
(s2294 1)
(s2295 1)
(s2296 1)
(s2297 1)
(s2298 1)
(s2299 1)
(s2300 1)
(s2301 1)
(s2302 1)
(s2303 1)
(s2304 1)
(s2305 1)
(s2306 1)
(s2307 1)
(s2308 1)
(s2309 1)
(s2310 1)
(s2311 1)
(s2312 1)
(s2313 1)
(s2314 1)
(s2315 1)
(s2316 1)
(s2317 1)
(s2318 1)
(s2319 1)
(s2320 1)
(s2321 1)
(s2322 1)
(s2323 1)
(s2324 1)
(s2325 1)
(s2326 1)
(s2327 1)
(s2328 1)
(s2329 1)
(s2330 1)
(s2331 1)
(s2332 1)
(s2333 1)
(s2334 1)
(s2335 1)
(s2336 1)
(s2337 1)
(s2338 1)
(s2339 1)
(s2340 1)
(s2341 1)
(s2342 1)
(s2343 1)
(s2344 1)
(s2345 1)
(s2346 1)
(s2347 1)
(s2348 1)
(s2349 1)
(s2350 1)
(s2351 1)
(s2352 1)
(s2353 1)
(s2354 1)
(s2355 1)
(s2356 1)
(s2357 1)
(s2358 1)
(s2359 1)
(s2360 1)
(s2361 1)
(s2362 1)
(s2363 1)
(s2364 1)
(s2365 1)
(s2366 1)
(s2367 1)
(s2368 1)
(s2369 1)
(s2370 1)
(s2371 1)
(s2372 1)
(s2373 1)
(s2374 1)
(s2375 1)
(s2376 1)
(s2377 1)
(s2378 1)
(s2379 1)
(s2380 1)
(s2381 1)
(s2382 1)
(s2383 1)
(s2384 1)
(s2385 1)
(s2386 1)
(s2387 1)
(s2388 1)
(s2389 1)
(s2390 1)
(s2391 1)
(s2392 1)
(s2393 1)
(s2394 1)
(s2395 1)
(s2396 1)
(s2397 1)
(s2398 1)
(s2399 1)
(s2400 1)
(s2401 1)
(s2402 1)
(s2403 1)
(s2404 1)
(s2405 1)
(s2406 1)
(s2407 1)
(s2408 1)
(s2409 1)
(s2410 1)
(s2411 1)
(s2412 1)
(s2413 1)
(s2414 1)
(s2415 1)
(s2416 1)
(s2417 1)
(s2418 1)
(s2419 1)
(s2420 1)
(s2421 1)
(s2422 1)
(s2423 1)
(s2424 1)
(s2425 1)
(s2426 1)
(s2427 1)
(s2428 1)
(s2429 1)
(s2430 1)
(s2431 1)
(s2432 1)
(s2433 1)
(s2434 1)
(s2435 1)
(s2436 1)
(s2437 1)
(s2438 1)
(s2439 1)
(s2440 1)
(s2441 1)
(s2442 1)
(s2443 1)
(s2444 1)
(s2445 1)
(s2446 1)
(s2447 1)
(s2448 1)
(s2449 1)
(s2450 1)
(s2451 1)
(s2452 1)
(s2453 1)
(s2454 1)
(s2455 1)
(s2456 1)
(s2457 1)
(s2458 1)
(s2459 1)
(s2460 1)
(s2461 1)
(s2462 1)
(s2463 1)
(s2464 1)
(s2465 1)
(s2466 1)
(s2467 1)
(s2468 1)
(s2469 1)
(s2470 1)
(s2471 1)
(s2472 1)
(s2473 1)
(s2474 1)
(s2475 1)
(s2476 1)
(s2477 1)
(s2478 1)
(s2479 1)
(s2480 1)
(s2481 1)
(s2482 1)
(s2483 1)
(s2484 1)
(s2485 1)
(s2486 1)
(s2487 1)
(s2488 1)
(s2489 1)
(s2490 1)
(s2491 1)
(s2492 1)
(s2493 1)
(s2494 1)
(s2495 1)
(s2496 1)
(s2497 1)
(s2498 1)
(s2499 1)
(s2500 1)
(s2501 1)
(s2502 1)
(s2503 1)
(s2504 1)
(s2505 1)
(s2506 1)
(s2507 1)
(s2508 1)
(s2509 1)
(s2510 1)
(s2511 1)
(s2512 1)
(s2513 1)
(s2514 1)
(s2515 1)
(s2516 1)
(s2517 1)
(s2518 1)
(s2519 1)
(s2520 1)
(s2521 1)
(s2522 1)
(s2523 1)
(s2524 1)
(s2525 1)
(s2526 1)
(s2527 1)
(s2528 1)
(s2529 1)
(s2530 1)
(s2531 1)
(s2532 1)
(s2533 1)
(s2534 1)
(s2535 1)
(s2536 1)
(s2537 1)
(s2538 1)
(s2539 1)
(s2540 1)
(s2541 1)
(s2542 1)
(s2543 1)
(s2544 1)
(s2545 1)
(s2546 1)
(s2547 1)
(s2548 1)
(s2549 1)
(s2550 1)
(s2551 1)
(s2552 1)
(s2553 1)
(s2554 1)
(s2555 1)
(s2556 1)
(s2557 1)
(s2558 1)
(s2559 1)
(s2560 1)
(s2561 1)
(s2562 1)
(s2563 1)
(s2564 1)
(s2565 1)
(s2566 1)
(s2567 1)
(s2568 1)
(s2569 1)
(s2570 1)
(s2571 1)
(s2572 1)
(s2573 1)
(s2574 1)
(s2575 1)
(s2576 1)
(s2577 1)
(s2578 1)
(s2579 1)
(s2580 1)
(s2581 1)
(s2582 1)
(s2583 1)
(s2584 1)
(s2585 1)
(s2586 1)
(s2587 1)
(s2588 1)
(s2589 1)
(s2590 1)
(s2591 1)
(s2592 1)
(s2593 1)
(s2594 1)
(s2595 1)
(s2596 1)
(s2597 1)
(s2598 1)
(s2599 1)
(s2600 1)
(s2601 1)
(s2602 1)
(s2603 1)
(s2604 1)
(s2605 1)
(s2606 1)
(s2607 1)
(s2608 1)
(s2609 1)
(s2610 1)
(s2611 1)
(s2612 1)
(s2613 1)
(s2614 1)
(s2615 1)
(s2616 1)
(s2617 1)
(s2618 1)
(s2619 1)
(s2620 1)
(s2621 1)
(s2622 1)
(s2623 1)
(s2624 1)
(s2625 1)
(s2626 1)
(s2627 1)
(s2628 1)
(s2629 1)
(s2630 1)
(s2631 1)
(s2632 1)
(s2633 1)
(s2634 1)
(s2635 1)
(s2636 1)
(s2637 1)
(s2638 1)
(s2639 1)
(s2640 1)
(s2641 1)
(s2642 1)
(s2643 1)
(s2644 1)
(s2645 1)
(s2646 1)
(s2647 1)
(s2648 1)
(s2649 1)
(s2650 1)
(s2651 1)
(s2652 1)
(s2653 1)
(s2654 1)
(s2655 1)
(s2656 1)
(s2657 1)
(s2658 1)
(s2659 1)
(s2660 1)
(s2661 1)
(s2662 1)
(s2663 1)
(s2664 1)
(s2665 1)
(s2666 1)
(s2667 1)
(s2668 1)
(s2669 1)
(s2670 1)
(s2671 1)
(s2672 1)
(s2673 1)
(s2674 1)
(s2675 1)
(s2676 1)
(s2677 1)
(s2678 1)
(s2679 1)
(s2680 1)
(s2681 1)
(s2682 1)
(s2683 1)
(s2684 1)
(s2685 1)
(s2686 1)
(s2687 1)
(s2688 1)
(s2689 1)
(s2690 1)
(s2691 1)
(s2692 1)
(s2693 1)
(s2694 1)
(s2695 1)
(s2696 1)
(s2697 1)
(s2698 1)
(s2699 1)
(s2700 1)
(s2701 1)
(s2702 1)
(s2703 1)
(s2704 1)
(s2705 1)
(s2706 1)
(s2707 1)
(s2708 1)
(s2709 1)
(s2710 1)
(s2711 1)
(s2712 1)
(s2713 1)
(s2714 1)
(s2715 1)
(s2716 1)
(s2717 1)
(s2718 1)
(s2719 1)
(s2720 1)
(s2721 1)
(s2722 1)
(s2723 1)
(s2724 1)
(s2725 1)
(s2726 1)
(s2727 1)
(s2728 1)
(s2729 1)
(s2730 1)
(s2731 1)
(s2732 1)
(s2733 1)
(s2734 1)
(s2735 1)
(s2736 1)
(s2737 1)
(s2738 1)
(s2739 1)
(s2740 1)
(s2741 1)
(s2742 1)
(s2743 1)
(s2744 1)
(s2745 1)
(s2746 1)
(s2747 1)
(s2748 1)
(s2749 1)
(s2750 1)
(s2751 1)
(s2752 1)
(s2753 1)
(s2754 1)
(s2755 1)
(s2756 1)
(s2757 1)
(s2758 1)
(s2759 1)
(s2760 1)
(s2761 1)
(s2762 1)
(s2763 1)
(s2764 1)
(s2765 1)
(s2766 1)
(s2767 1)
(s2768 1)
(s2769 1)
(s2770 1)
(s2771 1)
(s2772 1)
(s2773 1)
(s2774 1)
(s2775 1)
(s2776 1)
(s2777 1)
(s2778 1)
(s2779 1)
(s2780 1)
(s2781 1)
(s2782 1)
(s2783 1)
(s2784 1)
(s2785 1)
(s2786 1)
(s2787 1)
(s2788 1)
(s2789 1)
(s2790 1)
(s2791 1)
(s2792 1)
(s2793 1)
(s2794 1)
(s2795 1)
(s2796 1)
(s2797 1)
(s2798 1)
(s2799 1)
(s2800 1)
(s2801 1)
(s2802 1)
(s2803 timeout
1 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30097 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61216ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61248ms
Starting structural reductions in LTL mode, iteration 1 : 2918/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 69350 ms. Remains : 2918/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 225 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-04
Product exploration explored 100000 steps with 20001 reset in 3289 ms.
Product exploration explored 100000 steps with 19953 reset in 4081 ms.
Computed a total of 2918 stabilizing places and 2920 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2918 transition count 2920
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) p1), (F (G (NOT p0))), (F (G p1))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 3 factoid took 16 ms. Reduced automaton from 4 states, 5 edges and 2 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-04 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-04 finished in 78278 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((p0||X((p1||F((G(F(!p2))||(F(!p2)&&X(!p1)))))))))'
Support contains 6 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 49 places :
Symmetric choice reduction at 0 with 49 rule applications. Total rules 49 place count 2920 transition count 2923
Iterating global reduction 0 with 49 rules applied. Total rules applied 98 place count 2920 transition count 2923
Applied a total of 98 rules in 525 ms. Remains 2920 /2969 variables (removed 49) and now considering 2923/3013 (removed 90) transitions.
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:56:15] [INFO ] Invariants computation overflowed in 93 ms
[2024-05-31 15:56:17] [INFO ] Implicit Places using invariants in 2496 ms returned []
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:56:17] [INFO ] Invariants computation overflowed in 89 ms
[2024-05-31 15:56:22] [INFO ] Implicit Places using invariants and state equation in 5138 ms returned []
Implicit Place search using SMT with State Equation took 7645 ms to find 0 implicit places.
Running 2922 sub problems to find dead transitions.
// Phase 1: matrix 2923 rows 2920 cols
[2024-05-31 15:56:22] [INFO ] Invariants computation overflowed in 80 ms
Error getting values : (error "ParserException while parsing response: ((s0 1.0)
(s2 1.0)
(s3 1.0)
(s4 1.0)
(s5 1.0)
(s6 1.0)
(s7 1.0)
(s8 1.0)
(s9 1.0)
(s10 1.0)
(s11 1.0)
(s12 1.0)
(s13 1.0)
(s14 1.0)
(s15 1.0)
(s16 1.0)
(s17 1.0)
(s18 1.0)
(s19 1.0)
(s20 1.0)
(s21 1.0)
(s22 1.0)
(s23 1.0)
(s24 1.0)
(s25 1.0)
(s26 1.0)
(s27 1.0)
(s28 1.0)
(s29 1.0)
(s30 1.0)
(s31 1.0)
(s32 1.0)
(s33 1.0)
(s34 1.0)
(s35 1.0)
(s36 1.0)
(s37 1.0)
(s38 1.0)
(s39 1.0)
(s40 1.0)
(s41 1.0)
(s42 1.0)
(s43 1.0)
(s44 1.0)
(s45 1.0)
(s46 1.0)
(s47 1.0)
(s48 1.0)
(s49 1.0)
(s50 1.0)
(s51 1.0)
(s52 1.0)
(s53 1.0)
(s54 1.0)
(s55 1.0)
(s56 1.0)
(s57 1.0)
(s58 1.0)
(s59 1.0)
(s60 1.0)
(s61 1.0)
(s62 1.0)
(s63 1.0)
(s64 1.0)
(s65 1.0)
(s66 1.0)
(s67 1.0)
(s68 1.0)
(s69 1.0)
(s70 1.0)
(s71 1.0)
(s72 1.0)
(s73 1.0)
(s74 1.0)
(s75 1.0)
(s76 1.0)
(s77 1.0)
(s78 1.0)
(s79 1.0)
(s80 1.0)
(s81 1.0)
(s82 1.0)
(s83 1.0)
(s84 1.0)
(s85 1.0)
(s86 1.0)
(s87 1.0)
(s88 1.0)
(s89 1.0)
(s90 1.0)
(s91 1.0)
(s92 1.0)
(s93 1.0)
(s94 1.0)
(s95 1.0)
(s96 1.0)
(s97 1.0)
(s98 1.0)
(s99 1.0)
(s100 1.0)
(s101 1.0)
(s102 1.0)
(s103 1.0)
(s104 1.0)
(s105 1.0)
(s106 1.0)
(s107 1.0)
(s108 1.0)
(s109 1.0)
(s110 1.0)
(s111 1.0)
(s112 1.0)
(s113 1.0)
(s114 1.0)
(s115 1.0)
(s116 1.0)
(s117 1.0)
(s118 1.0)
(s119 1.0)
(s120 1.0)
(s121 1.0)
(s122 1.0)
(s123 1.0)
(s124 1.0)
(s125 1.0)
(s126 1.0)
(s127 1.0)
(s128 1.0)
(s129 1.0)
(s130 1.0)
(s131 1.0)
(s132 1.0)
(s133 1.0)
(s134 1.0)
(s135 1.0)
(s136 1.0)
(s137 1.0)
(s138 1.0)
(s139 1.0)
(s140 1.0)
(s141 1.0)
(s142 1.0)
(s143 1.0)
(s144 1.0)
(s145 1.0)
(s146 1.0)
(s147 1.0)
(s148 1.0)
(s149 1.0)
(s150 1.0)
(s151 1.0)
(s152 1.0)
(s153 1.0)
(s154 1.0)
(s155 1.0)
(s156 1.0)
(s157 1.0)
(s158 1.0)
(s159 1.0)
(s160 1.0)
(s161 1.0)
(s162 1.0)
(s163 1.0)
(s164 1.0)
(s165 1.0)
(s166 1.0)
(s167 1.0)
(s168 1.0)
(s169 1.0)
(s170 1.0)
(s171 1.0)
(s172 1.0)
(s173 1.0)
(s174 1.0)
(s175 1.0)
(s176 1.0)
(s177 1.0)
(s178 1.0)
(s179 1.0)
(s180 1.0)
(s181 1.0)
(s182 1.0)
(s183 1.0)
(s184 1.0)
(s185 1.0)
(s186 1.0)
(s187 1.0)
(s188 1.0)
(s189 1.0)
(s190 1.0)
(s191 1.0)
(s192 1.0)
(s193 1.0)
(s194 1.0)
(s195 1.0)
(s196 1.0)
(s197 1.0)
(s198 1.0)
(s199 1.0)
(s200 1.0)
(s201 1.0)
(s202 1.0)
(s203 1.0)
(s204 1.0)
(s205 1.0)
(s206 1.0)
(s207 1.0)
(s208 1.0)
(s209 1.0)
(s210 1.0)
(s211 1.0)
(s212 1.0)
(s213 1.0)
(s214 1.0)
(s215 1.0)
(s216 1.0)
(s217 1.0)
(s218 1.0)
(s219 1.0)
(s220 1.0)
(s221 1.0)
(s222 1.0)
(s223 1.0)
(s224 1.0)
(s225 1.0)
(s226 1.0)
(s227 1.0)
(s228 1.0)
(s229 1.0)
(s230 1.0)
(s231 1.0)
(s232 1.0)
(s233 1.0)
(s234 1.0)
(s235 1.0)
(s236 1.0)
(s237 1.0)
(s238 1.0)
(s239 1.0)
(s240 1.0)
(s241 1.0)
(s242 1.0)
(s243 1.0)
(s244 1.0)
(s245 1.0)
(s246 1.0)
(s247 1.0)
(s248 1.0)
(s249 1.0)
(s250 1.0)
(s251 1.0)
(s252 1.0)
(s253 1.0)
(s254 1.0)
(s255 1.0)
(s256 1.0)
(s257 1.0)
(s258 1.0)
(s259 1.0)
(s260 1.0)
(s261 1.0)
(s262 1.0)
(s263 1.0)
(s264 1.0)
(s265 1.0)
(s266 1.0)
(s267 1.0)
(s268 1.0)
(s269 1.0)
(s270 1.0)
(s271 1.0)
(s272 1.0)
(s273 1.0)
(s274 1.0)
(s275 1.0)
(s276 1.0)
(s277 1.0)
(s278 1.0)
(s279 1.0)
(s280 1.0)
(s281 1.0)
(s282 1.0)
(s283 1.0)
(s284 1.0)
(s285 1.0)
(s286 1.0)
(s287 1.0)
(s288 1.0)
(s289 1.0)
(s290 1.0)
(s291 1.0)
(s292 1.0)
(s293 1.0)
(s294 1.0)
(s295 1.0)
(s296 1.0)
(s297 1.0)
(s298 1.0)
(s299 1.0)
(s300 1.0)
(s301 1.0)
(s302 1.0)
(s303 1.0)
(s304 1.0)
(s305 1.0)
(s306 1.0)
(s307 1.0)
(s308 1.0)
(s309 1.0)
(s310 1.0)
(s311 1.0)
(s312 1.0)
(s313 1.0)
(s314 1.0)
(s315 1.0)
(s316 1.0)
(s317 1.0)
(s318 1.0)
(s319 1.0)
(s320 1.0)
(s321 1.0)
(s322 1.0)
(s323 1.0)
(s324 1.0)
(s325 1.0)
(s326 1.0)
(s327 1.0)
(s328 1.0)
(s329 1.0)
(s330 1.0)
(s331 1.0)
(s332 1.0)
(s333 1.0)
(s334 1.0)
(s335 1.0)
(s336 1.0)
(s337 1.0)
(s338 1.0)
(s339 1.0)
(s340 1.0)
(s341 1.0)
(s342 1.0)
(s343 1.0)
(s344 1.0)
(s345 1.0)
(s346 1.0)
(s347 1.0)
(s348 1.0)
(s349 1.0)
(s350 1.0)
(s351 1.0)
(s352 1.0)
(s353 1.0)
(s354 1.0)
(s355 1.0)
(s356 1.0)
(s357 1.0)
(s358 1.0)
(s359 1.0)
(s360 1.0)
(s361 1.0)
(s362 1.0)
(s363 1.0)
(s364 1.0)
(s365 1.0)
(s366 1.0)
(s367 1.0)
(s368 1.0)
(s369 1.0)
(s370 1.0)
(s371 1.0)
(s372 1.0)
(s373 1.0)
(s374 1.0)
(s375 1.0)
(s376 1.0)
(s377 1.0)
(s378 1.0)
(s379 1.0)
(s380 1.0)
(s381 1.0)
(s382 1.0)
(s383 1.0)
(s384 1.0)
(s385 1.0)
(s386 1.0)
(s387 1.0)
(s388 1.0)
(s389 1.0)
(s390 1.0)
(s391 1.0)
(s392 1.0)
(s393 1.0)
(s394 1.0)
(s395 1.0)
(s396 1.0)
(s397 1.0)
(s398 1.0)
(s399 1.0)
(s400 1.0)
(s401 1.0)
(s402 1.0)
(s403 1.0)
(s404 1.0)
(s405 1.0)
(s406 1.0)
(s407 1.0)
(s408 1.0)
(s409 1.0)
(s410 1.0)
(s411 1.0)
(s412 1.0)
(s413 1.0)
(s414 1.0)
(s415 1.0)
(s416 1.0)
(s417 1.0)
(s418 1.0)
(s419 1.0)
(s420 1.0)
(s421 1.0)
(s422 1.0)
(s423 1.0)
(s424 1.0)
(s425 1.0)
(s426 1.0)
(s427 1.0)
(s428 1.0)
(s429 1.0)
(s430 1.0)
(s431 1.0)
(s432 1.0)
(s433 1.0)
(s434 1.0)
(s435 1.0)
(s436 1.0)
(s437 1.0)
(s438 1.0)
(s439 1.0)
(s440 1.0)
(s441 1.0)
(s442 1.0)
(s443 1.0)
(s444 1.0)
(s445 1.0)
(s446 1.0)
(s447 1.0)
(s448 1.0)
(s449 1.0)
(s450 1.0)
(s451 1.0)
(s452 1.0)
(s453 1.0)
(s454 1.0)
(s455 1.0)
(s456 1.0)
(s457 1.0)
(s458 1.0)
(s459 1.0)
(s460 1.0)
(s461 1.0)
(s462 1.0)
(s463 1.0)
(s464 1.0)
(s465 1.0)
(s466 1.0)
(s467 1.0)
(s468 1.0)
(s469 1.0)
(s470 1.0)
(s471 1.0)
(s472 1.0)
(s473 1.0)
(s474 1.0)
(s475 1.0)
(s476 1.0)
(s477 1.0)
(s478 1.0)
(s479 1.0)
(s480 1.0)
(s481 1.0)
(s482 1.0)
(s483 1.0)
(s484 1.0)
(s485 1.0)
(s486 1.0)
(s487 1.0)
(s488 1.0)
(s489 1.0)
(s490 1.0)
(s491 1.0)
(s492 1.0)
(s493 1.0)
(s494 1.0)
(s495 1.0)
(s496 1.0)
(s497 1.0)
(s498 1.0)
(s499 1.0)
(s500 1.0)
(s501 1.0)
(s502 1.0)
(s503 1.0)
(s504 1.0)
(s505 1.0)
(s506 1.0)
(s507 1.0)
(s508 1.0)
(s509 1.0)
(s510 1.0)
(s511 1.0)
(s512 1.0)
(s513 1.0)
(s514 1.0)
(s515 1.0)
(s516 1.0)
(s517 1.0)
(s518 1.0)
(s519 1.0)
(s520 1.0)
(s521 1.0)
(s522 1.0)
(s523 1.0)
(s524 1.0)
(s525 1.0)
(s526 1.0)
(s527 1.0)
(s528 1.0)
(s529 1.0)
(s530 1.0)
(s531 1.0)
(s532 1.0)
(s533 1.0)
(s534 1.0)
(s535 1.0)
(s536 1.0)
(s537 1.0)
(s538 1.0)
(s539 1.0)
(s540 1.0)
(s541 1.0)
(s542 1.0)
(s543 1.0)
(s544 1.0)
(s545 1.0)
(s546 1.0)
(s547 1.0)
(s548 1.0)
(s549 1.0)
(s550 1.0)
(s551 1.0)
(s552 1.0)
(s553 1.0)
(s554 1.0)
(s555 1.0)
(s556 1.0)
(s557 1.0)
(s558 1.0)
(s559 1.0)
(s560 1.0)
(s561 1.0)
(s562 1.0)
(s563 1.0)
(s564 1.0)
(s565 1.0)
(s566 1.0)
(s567 1.0)
(s568 1.0)
(s569 1.0)
(s570 1.0)
(s571 1.0)
(s572 1.0)
(s573 1.0)
(s574 1.0)
(s575 1.0)
(s576 1.0)
(s577 1.0)
(s578 1.0)
(s579 1.0)
(s580 1.0)
(s581 1.0)
(s582 1.0)
(s583 1.0)
(s584 1.0)
(s585 1.0)
(s586 1.0)
(s587 1.0)
(s588 1.0)
(s589 1.0)
(s590 1.0)
(s591 1.0)
(s592 1.0)
(s593 1.0)
(s594 1.0)
(s595 1.0)
(s596 1.0)
(s597 1.0)
(s598 1.0)
(s599 1.0)
(s600 1.0)
(s601 1.0)
(s602 1.0)
(s603 1.0)
(s604 1.0)
(s605 1.0)
(s606 1.0)
(s607 1.0)
(s608 1.0)
(s609 1.0)
(s610 1.0)
(s611 1.0)
(s612 1.0)
(s613 1.0)
(s614 1.0)
(s615 1.0)
(s616 1.0)
(s617 1.0)
(s618 1.0)
(s619 1.0)
(s620 1.0)
(s621 1.0)
(s622 1.0)
(s623 1.0)
(s624 1.0)
(s625 1.0)
(s626 1.0)
(s627 1.0)
(s628 1.0)
(s629 1.0)
(s630 1.0)
(s631 1.0)
(s632 1.0)
(s633 1.0)
(s634 1.0)
(s635 1.0)
(s636 1.0)
(s637 1.0)
(s638 1.0)
(s639 1.0)
(s640 1.0)
(s641 1.0)
(s642 1.0)
(s643 1.0)
(s644 1.0)
(s645 1.0)
(s646 1.0)
(s647 1.0)
(s648 1.0)
(s649 1.0)
(s650 1.0)
(s651 1.0)
(s652 1.0)
(s653 1.0)
(s654 1.0)
(s655 1.0)
(s656 1.0)
(s657 1.0)
(s658 1.0)
(s659 1.0)
(s660 1.0)
(s661 1.0)
(s662 1.0)
(s663 1.0)
(s664 1.0)
(s665 1.0)
(s666 1.0)
(s667 1.0)
(s668 1.0)
(s669 1.0)
(s670 1.0)
(s671 1.0)
(s672 1.0)
(s673 1.0)
(s674 1.0)
(s675 1.0)
(s676 1.0)
(s677 1.0)
(s678 1.0)
(s679 1.0)
(s680 1.0)
(s681 1.0)
(s682 1.0)
(s683 1.0)
(s684 1.0)
(s685 1.0)
(s686 1.0)
(s687 1.0)
(s688 1.0)
(s689 1.0)
(s690 1.0)
(s691 1.0)
(s692 1.0)
(s693 1.0)
(s694 1.0)
(s695 1.0)
(s696 1.0)
(s697 1.0)
(s698 1.0)
(s699 1.0)
(s700 1.0)
(s701 1.0)
(s702 1.0)
(s703 1.0)
(s704 1.0)
(s705 1.0)
(s706 1.0)
(s707 1.0)
(s708 1.0)
(s709 1.0)
(s710 1.0)
(s711 1.0)
(s712 1.0)
(s713 1.0)
(s714 1.0)
(s715 1.0)
(s716 1.0)
(s717 1.0)
(s718 1.0)
(s719 1.0)
(s720 1.0)
(s721 1.0)
(s722 1.0)
(s723 1.0)
(s724 1.0)
(s725 1.0)
(s726 1.0)
(s727 1.0)
(s728 1.0)
(s729 1.0)
(s730 1.0)
(s731 1.0)
(s732 1.0)
(s733 1.0)
(s734 1.0)
(s735 1.0)
(s736 1.0)
(s737 1.0)
(s738 1.0)
(s739 1.0)
(s740 1.0)
(s741 1.0)
(s742 1.0)
(s743 1.0)
(s744 1.0)
(s745 1.0)
(s746 1.0)
(s747 1.0)
(s748 1.0)
(s749 1.0)
(s750 1.0)
(s751 1.0)
(s752 1.0)
(s753 1.0)
(s754 1.0)
(s755 1.0)
(s756 1.0)
(s757 1.0)
(s758 1.0)
(s759 1.0)
(s760 1.0)
(s761 1.0)
(s762 1.0)
(s763 1.0)
(s764 1.0)
(s765 1.0)
(s766 1.0)
(s767 1.0)
(s768 1.0)
(s769 1.0)
(s770 1.0)
(s771 1.0)
(s772 1.0)
(s773 1.0)
(s774 1.0)
(s775 1.0)
(s776 1.0)
(s777 1.0)
(s778 1.0)
(s779 1.0)
(s780 1.0)
(s781 1.0)
(s782 1.0)
(s783 1.0)
(s784 1.0)
(s785 1.0)
(s786 1.0)
(s787 1.0)
(s788 1.0)
(s789 1.0)
(s790 1.0)
(s791 1.0)
(s792 1.0)
(s793 1.0)
(s794 1.0)
(s795 1.0)
(s796 1.0)
(s797 1.0)
(s798 1.0)
(s799 1.0)
(s800 1.0)
(s801 1.0)
(s802 1.0)
(s803 1.0)
(s804 1.0)
(s805 1.0)
(s806 1.0)
(s807 1.0)
(s808 1.0)
(s809 1.0)
(s810 1.0)
(s811 1.0)
(s812 1.0)
(s813 1.0)
(s814 1.0)
(s815 1.0)
(s816 1.0)
(s817 1.0)
(s818 1.0)
(s819 1.0)
(s820 1.0)
(s821 1.0)
(s822 1.0)
(s823 1.0)
(s824 1.0)
(s825 1.0)
(s826 1.0)
(s827 1.0)
(s828 1.0)
(s829 1.0)
(s830 1.0)
(s831 1.0)
(s832 1.0)
(s833 1.0)
(s834 1.0)
(s835 1.0)
(s836 1.0)
(s837 1.0)
(s838 1.0)
(s839 1.0)
(s840 1.0)
(s841 1.0)
(s842 1.0)
(s843 1.0)
(s844 1.0)
(s845 1.0)
(s846 1.0)
(s847 1.0)
(s848 1.0)
(s849 1.0)
(s850 1.0)
(s851 1.0)
(s852 1.0)
(s853 1.0)
(s854 1.0)
(s855 1.0)
(s856 1.0)
(s857 1.0)
(s858 1.0)
(s859 1.0)
(s860 1.0)
(s861 1.0)
(s862 1.0)
(s863 1.0)
(s864 1.0)
(s865 1.0)
(s866 1.0)
(s867 1.0)
(s868 1.0)
(s869 1.0)
(s870 1.0)
(s871 1.0)
(s872 1.0)
(s873 1.0)
(s874 1.0)
(s875 1.0)
(s876 1.0)
(s877 1.0)
(s878 1.0)
(s879 1.0)
(s880 1.0)
(s881 1.0)
(s882 1.0)
(s883 1.0)
(s884 1.0)
(s885 1.0)
(s886 1.0)
(s887 1.0)
(s888 1.0)
(s889 1.0)
(s890 1.0)
(s891 1.0)
(s892 1.0)
(s893 1.0)
(s894 1.0)
(s895 1.0)
(s896 1.0)
(s897 1.0)
(s898 1.0)
(s899 1.0)
(s900 1.0)
(s901 1.0)
(s902 1.0)
(s903 1.0)
(s904 1.0)
(s905 1.0)
(s906 1.0)
(s907 1.0)
(s908 1.0)
(s909 1.0)
(s910 1.0)
(s911 1.0)
(s912 1.0)
(s913 1.0)
(s914 1.0)
(s915 1.0)
(s916 1.0)
(s917 1.0)
(s918 1.0)
(s919 1.0)
(s920 1.0)
(s921 1.0)
(s922 1.0)
(s923 1.0)
(s924 1.0)
(s925 1.0)
(s926 1.0)
(s927 1.0)
(s928 1.0)
(s929 1.0)
(s930 1.0)
(s931 1.0)
(s932 1.0)
(s933 1.0)
(s934 1.0)
(s935 1.0)
(s936 1.0)
(s937 1.0)
(s938 1.0)
(s939 1.0)
(s940 1.0)
(s941 1.0)
(s942 1.0)
(s943 1.0)
(s944 1.0)
(s945 1.0)
(s946 1.0)
(s947 1.0)
(s948 1.0)
(s949 1.0)
(s950 1.0)
(s951 1.0)
(s952 1.0)
(s953 1.0)
(s954 1.0)
(s955 1.0)
(s956 1.0)
(s957 1.0)
(s958 1.0)
(s959 1.0)
(s960 1.0)
(s961 1.0)
(s962 1.0)
(s963 1.0)
(s964 1.0)
(s965 1.0)
(s966 1.0)
(s967 1.0)
(s968 1.0)
(s969 1.0)
(s970 1.0)
(s971 1.0)
(s972 1.0)
(s973 1.0)
(s974 1.0)
(s975 1.0)
(s976 1.0)
(s977 1.0)
(s978 1.0)
(s979 1.0)
(s980 1.0)
(s981 1.0)
(s982 1.0)
(s983 1.0)
(s984 1.0)
(s985 1.0)
(s986 1.0)
(s987 1.0)
(s988 1.0)
(s989 1.0)
(s990 1.0)
(s991 1.0)
(s992 1.0)
(s993 1.0)
(s994 1.0)
(s995 1.0)
(s996 1.0)
(s997 1.0)
(s998 1.0)
(s999 1.0)
(s1000 1.0)
(s1001 1.0)
(s1002 1.0)
(s1003 1.0)
(s1004 1.0)
(s1005 1.0)
(s1006 1.0)
(s1007 1.0)
(s1008 1.0)
(s1009 1.0)
(s1010 1.0)
(s1011 1.0)
(s1012 1.0)
(s1013 1.0)
(s1014 1.0)
(s1015 1.0)
(s1016 1.0)
(s1017 1.0)
(s1018 1.0)
(s1019 1.0)
(s1020 1.0)
(s1021 1.0)
(s1022 1.0)
(s1023 1.0)
(s1024 1.0)
(s1025 1.0)
(s1026 1.0)
(s1027 1.0)
(s1028 1.0)
(s1029 1.0)
(s1030 1.0)
(s1031 1.0)
(s1032 1.0)
(s1033 1.0)
(s1034 1.0)
(s1035 1.0)
(s1036 1.0)
(s1037 1.0)
(s1038 1.0)
(s1039 1.0)
(s1040 1.0)
(s1041 1.0)
(s1042 1.0)
(s1043 1.0)
(s1044 1.0)
(s1045 1.0)
(s1046 1.0)
(s1047 1.0)
(s1048 1.0)
(s1049 1.0)
(s1050 1.0)
(s1051 1.0)
(s1052 1.0)
(s1053 1.0)
(s1054 1.0)
(s1055 1.0)
(s1056 1.0)
(s1057 1.0)
(s1058 1.0)
(s1059 1.0)
(s1060 1.0)
(s1061 1.0)
(s1062 1.0)
(s1063 1.0)
(s1064 1.0)
(s1065 1.0)
(s1066 1.0)
(s1067 1.0)
(s1068 1.0)
(s1069 1.0)
(s1070 1.0)
(s1071 1.0)
(s1072 1.0)
(s1073 1.0)
(s1074 1.0)
(s1075 1.0)
(s1076 1.0)
(s1077 1.0)
(s1078 1.0)
(s1079 1.0)
(s1080 1.0)
(s1081 1.0)
(s1082 1.0)
(s1083 1.0)
(s1084 1.0)
(s1085 1.0)
(s1086 1.0)
(s1087 1.0)
(s1088 1.0)
(s1089 1.0)
(s1090 1.0)
(s1091 1.0)
(s1092 1.0)
(s1093 1.0)
(s1094 1.0)
(s1095 1.0)
(s1096 1.0)
(s1097 1.0)
(s1098 1.0)
(s1099 1.0)
(s1100 1.0)
(s1101 1.0)
(s1102 1.0)
(s1103 1.0)
(s1104 1.0)
(s1105 1.0)
(s1106 1.0)
(s1107 1.0)
(s1108 1.0)
(s1109 1.0)
(s1110 1.0)
(s1111 1.0)
(s1112 1.0)
(s1113 1.0)
(s1114 1.0)
(s1115 1.0)
(s1116 1.0)
(s1117 1.0)
(s1118 1.0)
(s1119 1.0)
(s1120 1.0)
(s1121 1.0)
(s1122 1.0)
(s1123 1.0)
(s1124 1.0)
(s1125 1.0)
(s1126 1.0)
(s1127 1.0)
(s1128 1.0)
(s1129 1.0)
(s1130 1.0)
(s1131 1.0)
(s1132 1.0)
(s1133 1.0)
(s1134 1.0)
(s1135 1.0)
(s1136 1.0)
(s1137 1.0)
(s1138 1.0)
(s1139 1.0)
(s1140 1.0)
(s1141 1.0)
(s1142 1.0)
(s1143 1.0)
(s1144 1.0)
(s1145 1.0)
(s1146 1.0)
(s1147 1.0)
(s1148 1.0)
(s1149 1.0)
(s1150 1.0)
(s1151 1.0)
(s1152 1.0)
(s1153 1.0)
(s1154 1.0)
(s1155 1.0)
(s1156 1.0)
(s1157 1.0)
(s1158 1.0)
(s1159 1.0)
(s1160 1.0)
(s1161 1.0)
(s1162 1.0)
(s1163 1.0)
(s1164 1.0)
(s1165 1.0)
(s1166 1.0)
(s1167 1.0)
(s1168 1.0)
(s1169 1.0)
(s1170 1.0)
(s1171 1.0)
(s1172 1.0)
(s1173 1.0)
(s1174 1.0)
(s1175 1.0)
(s1176 1.0)
(s1177 1.0)
(s1178 1.0)
(s1179 1.0)
(s1180 1.0)
(s1181 1.0)
(s1182 1.0)
(s1183 1.0)
(s1184 1.0)
(s1185 1.0)
(s1186 1.0)
(s1187 1.0)
(s1188 1.0)
(s1189 1.0)
(s1190 1.0)
(s1191 1.0)
(s1192 1.0)
(s1193 1.0)
(s1194 1.0)
(s1195 1.0)
(s1196 1.0)
(s1197 1.0)
(s1198 1.0)
(s1199 1.0)
(s1200 1.0)
(s1201 1.0)
(s1202 1.0)
(s1203 1.0)
(s1204 1.0)
(s1205 1.0)
(s1206 1.0)
(s1207 1.0)
(s1208 1.0)
(s1209 1.0)
(s1210 1.0)
(s1211 1.0)
(s1212 1.0)
(s1213 1.0)
(s1214 1.0)
(s1215 1.0)
(s1216 1.0)
(s1217 1.0)
(s1218 1.0)
(s1219 1.0)
(s1220 1.0)
(s1221 1.0)
(s1222 1.0)
(s1223 1.0)
(s1224 1.0)
(s1225 1.0)
(s1226 1.0)
(s1227 1.0)
(s1228 1.0)
(s1229 1.0)
(s1230 1.0)
(s1231 1.0)
(s1232 1.0)
(s1233 1.0)
(s1234 1.0)
(s1235 1.0)
(s1236 1.0)
(s1237 1.0)
(s1238 1.0)
(s1239 1.0)
(s1240 1.0)
(s1241 1.0)
(s1242 1.0)
(s1243 1.0)
(s1244 1.0)
(s1245 1.0)
(s1246 1.0)
(s1247 1.0)
(s1248 1.0)
(s1249 1.0)
(s1250 1.0)
(s1251 1.0)
(s1252 1.0)
(s1253 1.0)
(s1254 1.0)
(s1255 1.0)
(s1256 1.0)
(s1257 1.0)
(s1258 1.0)
(s1259 1.0)
(s1260 1.0)
(s1261 1.0)
(s1262 1.0)
(s1263 1.0)
(s1264 1.0)
(s1265 1.0)
(s1266 1.0)
(s1267 1.0)
(s1268 1.0)
(s1269 1.0)
(s1270 1.0)
(s1271 1.0)
(s1272 1.0)
(s1273 1.0)
(s1274 1.0)
(s1275 1.0)
(s1276 1.0)
(s1277 1.0)
(s1278 1.0)
(s1279 1.0)
(s1280 1.0)
(s1281 1.0)
(s1282 1.0)
(s1283 1.0)
(s1284 1.0)
(s1285 1.0)
(s1286 1.0)
(s1287 1.0)
(s1288 1.0)
(s1289 1.0)
(s1290 1.0)
(s1291 1.0)
(s1292 1.0)
(s1293 1.0)
(s1294 1.0)
(s1295 1.0)
(s1296 1.0)
(s1297 1.0)
(s1298 1.0)
(s1299 1.0)
(s1300 1.0)
(s1301 1.0)
(s1302 1.0)
(s1303 1.0)
(s1304 1.0)
(s1305 1.0)
(s1306 1.0)
(s1307 1.0)
(s1308 1.0)
(s1309 1.0)
(s1310 1.0)
(s1311 1.0)
(s1312 1.0)
(s1313 1.0)
(s1314 1.0)
(s1315 1.0)
(s1316 1.0)
(s1317 1.0)
(s1318 1.0)
(s1319 1.0)
(s1320 1.0)
(s1321 1.0)
(s1322 1.0)
(s1323 1.0)
(s1324 1.0)
(s1325 1.0)
(s1326 1.0)
(s1327 1.0)
(s1328 1.0)
(s1329 1.0)
(s1330 1.0)
(s1331 1.0)
(s1332 1.0)
(s1333 1.0)
(s1334 1.0)
(s1335 1.0)
(s1336 1.0)
(s1337 1.0)
(s1338 1.0)
(s1339 1.0)
(s1340 1.0)
(s1341 1.0)
(s1342 1.0)
(s1343 1.0)
(s1344 1.0)
(s1345 1.0)
(s1346 1.0)
(s1347 1.0)
(s1348 1.0)
(s1349 1.0)
(s1350 1.0)
(s1351 1.0)
(s1352 1.0)
(s1353 1.0)
(s1354 1.0)
(s1355 1.0)
(s1356 1.0)
(s1357 1.0)
(s1358 1.0)
(s1359 1.0)
(s1360 1.0)
(s1361 1.0)
(s1362 1.0)
(s1363 1.0)
(s1364 1.0)
(s1365 1.0)
(s1366 1.0)
(s1367 1.0)
(s1368 1.0)
(s1369 1.0)
(s1370 1.0)
(s1371 1.0)
(s1372 1.0)
(s1373 1.0)
(s1374 1.0)
(s1375 1.0)
(s1376 1.0)
(s1377 1.0)
(s1378 1.0)
(s1379 1.0)
(s1380 1.0)
(s1381 1.0)
(s1382 1.0)
(s1383 1.0)
(s1384 1.0)
(s1385 1.0)
(s1386 1.0)
(s1387 1.0)
(s1388 1.0)
(s1389 1.0)
(s1390 1.0)
(s1391 1.0)
(s1392 1.0)
(s1393 1.0)
(s1394 1.0)
(s1395 1.0)
(s1396 1.0)
(s1397 1.0)
(s1398 1.0)
(s1399 1.0)
(s1400 1.0)
(s1401 1.0)
(s1402 1.0)
(s1403 1.0)
(s1404 1.0)
(s1405 1.0)
(s1406 1.0)
(s1407 1.0)
(s1408 1.0)
(s1409 1.0)
(s1410 1.0)
(s1411 1.0)
(s1412 1.0)
(s1413 1.0)
(s1414 1.0)
(s1415 1.0)
(s1416 1.0)
(s1417 1.0)
(s1418 1.0)
(s1419 1.0)
(s1420 1.0)
(s1421 1.0)
(s1422 1.0)
(s1423 1.0)
(s1424 1.0)
(s1425 1.0)
(s1426 1.0)
(s1427 1.0)
(s1428 1.0)
(s1429 1.0)
(s1430 1.0)
(s1431 1.0)
(s1432 1.0)
(s1433 1.0)
(s1434 1.0)
(s1435 1.0)
(s1436 1.0)
(s1437 1.0)
(s1438 1.0)
(s1439 1.0)
(s1440 1.0)
(s1441 1.0)
(s1442 1.0)
(s1443 1.0)
(s1444 1.0)
(s1445 1.0)
(s1446 1.0)
(s1447 1.0)
(s1448 1.0)
(s1449 1.0)
(s1450 1.0)
(s1451 1.0)
(s1452 1.0)
(s1453 1.0)
(s1454 1.0)
(s1455 1.0)
(s1456 1.0)
(s1457 1.0)
(s1458 1.0)
(s1459 1.0)
(s1460 1.0)
(s1461 1.0)
(s1462 1.0)
(s1463 1.0)
(s1464 1.0)
(s1465 1.0)
(s1466 1.0)
(s1467 1.0)
(s1468 1.0)
(s1469 1.0)
(s1470 1.0)
(s1471 1.0)
(s1472 1.0)
(s1473 1.0)
(s1474 1.0)
(s1475 1.0)
(s1476 1.0)
(s1477 1.0)
(s1478 1.0)
(s1479 1.0)
(s1480 1.0)
(s1481 1.0)
(s1482 1.0)
(s1483 1.0)
(s1484 1.0)
(s1485 1.0)
(s1486 1.0)
(s1487 1.0)
(s1488 1.0)
(s1489 1.0)
(s1490 1.0)
(s1491 1.0)
(s1492 1.0)
(s1493 1.0)
(s1494 1.0)
(s1495 1.0)
(s1496 1.0)
(s1497 1.0)
(s1498 1.0)
(s1499 1.0)
(s1500 1.0)
(s1501 1.0)
(s1502 1.0)
(s1503 1.0)
(s1504 1.0)
(s1505 1.0)
(s1506 1.0)
(s1507 1.0)
(s1508 1.0)
(s1509 1.0)
(s1510 1.0)
(s1511 1.0)
(s1512 1.0)
(s1513 1.0)
(s1514 1.0)
(s1515 1.0)
(s1516 1.0)
(s1517 1.0)
(s1518 1.0)
(s1519 1.0)
(s1520 1.0)
(s1521 1.0)
(s1522 1.0)
(s1523 1.0)
(s1524 1.0)
(s1525 1.0)
(s1526 1.0)
(s1527 1.0)
(s1528 1.0)
(s1529 1.0)
(s1530 1.0)
(s1531 1.0)
(s1532 1.0)
(s1533 1.0)
(s1534 1.0)
(s1535 1.0)
(s1536 1.0)
(s1537 1.0)
(s1538 1.0)
(s1539 1.0)
(s1540 1.0)
(s1541 1.0)
(s1542 1.0)
(s1543 1.0)
(s1544 1.0)
(s1545 1.0)
(s1546 1.0)
(s1547 1.0)
(s1548 1.0)
(s1549 1.0)
(s1550 1.0)
(s1551 1.0)
(s1552 1.0)
(s1553 1.0)
(s1554 1.0)
(s1555 1.0)
(s1556 1.0)
(s1557 1.0)
(s1558 1.0)
(s1559 1.0)
(s1560 1.0)
(s1561 1.0)
(s1562 1.0)
(s1563 1.0)
(s1564 1.0)
(s1565 1.0)
(s1566 1.0)
(s1567 1.0)
(s1568 1.0)
(s1569 1.0)
(s1570 1.0)
(s1571 1.0)
(s1572 1.0)
(s1573 1.0)
(s1574 1.0)
(s1575 1.0)
(s1576 1.0)
(s1577 1.0)
(s1578 1.0)
(s1579 1.0)
(s1580 1.0)
(s1581 1.0)
(s1582 1.0)
(s1583 1.0)
(s1584 1.0)
(s1585 1.0)
(s1586 1.0)
(s1587 1.0)
(s1588 1.0)
(s1589 1.0)
(s1590 1.0)
(s1591 1.0)
(s1592 1.0)
(s1593 1.0)
(s1594 1.0)
(s1595 1.0)
(s1596 1.0)
(s1597 1.0)
(s1598 1.0)
(s1599 1.0)
(s1600 1.0)
(s1601 1.0)
(s1602 1.0)
(s1603 1.0)
(s1604 1.0)
(s1605 1.0)
(s1606 1.0)
(s1607 1.0)
(s1608 1.0)
(s1609 1.0)
(s1610 1.0)
(s1611 1.0)
(s1612 1.0)
(s1613 1.0)
(s1614 1.0)
(s1615 1.0)
(s1616 1.0)
(s1617 1.0)
(s1618 1.0)
(s1619 1.0)
(s1620 1.0)
(s1621 1.0)
(s1622 1.0)
(s1623 1.0)
(s1624 1.0)
(s1625 1.0)
(s1626 1.0)
(s1627 1.0)
(s1628 1.0)
(s1629 1.0)
(s1630 1.0)
(s1631 1.0)
(s1632 1.0)
(s1633 1.0)
(s1634 1.0)
(s1635 1.0)
(s1636 1.0)
(s1637 1.0)
(s1638 1.0)
(s1639 1.0)
(s1640 1.0)
(s1641 1.0)
(s1642 1.0)
(s1643 1.0)
(s1644 1.0)
(s1645 1.0)
(s1646 1.0)
(s1647 1.0)
(s1648 1.0)
(s1649 1.0)
(s1650 1.0)
(s1651 1.0)
(s1652 1.0)
(s1653 1.0)
(s1654 1.0)
(s1655 1.0)
(s1656 1.0)
(s1657 1.0)
(s1658 1.0)
(s1659 1.0)
(s1660 1.0)
(s1661 1.0)
(s1662 1.0)
(s1663 1.0)
(s1664 1.0)
(s1665 1.0)
(s1666 1.0)
(s1667 1.0)
(s1668 1.0)
(s1669 1.0)
(s1670 1.0)
(s1671 1.0)
(s1672 1.0)
(s1673 1.0)
(s1674 1.0)
(s1675 1.0)
(s1676 1.0)
(s1677 1.0)
(s1678 1.0)
(s1679 1.0)
(s1680 1.0)
(s1681 1.0)
(s1682 1.0)
(s1683 1.0)
(s1684 1.0)
(s1685 1.0)
(s1686 1.0)
(s1687 1.0)
(s1688 1.0)
(s1689 1.0)
(s1690 1.0)
(s1691 1.0)
(s1692 1.0)
(s1693 1.0)
(s1694 1.0)
(s1695 1.0)
(s1696 1.0)
(s1697 1.0)
(s1698 1.0)
(s1699 1.0)
(s1700 1.0)
(s1701 1.0)
(s1702 1.0)
(s1703 1.0)
(s1704 1.0)
(s1705 1.0)
(s1706 1.0)
(s1707 1.0)
(s1708 1.0)
(s1709 1.0)
(s1710 1.0)
(s1711 1.0)
(s1712 1.0)
(s1713 1.0)
(s1714 1.0)
(s1715 1.0)
(s1716 1.0)
(s1717 1.0)
(s1718 1.0)
(s1719 1.0)
(s1720 1.0)
(s1721 1.0)
(s1722 1.0)
(s1723 1.0)
(s1724 1.0)
(s1725 1.0)
(s1726 1.0)
(s1727 1.0)
(s1728 1.0)
(s1729 1.0)
(s1730 1.0)
(s1731 1.0)
(s1732 1.0)
(s1733 1.0)
(s1734 1.0)
(s1735 1.0)
(s1736 1.0)
(s1737 1.0)
(s1738 1.0)
(s1739 1.0)
(s1740 1.0)
(s1741 1.0)
(s1742 1.0)
(s1743 1.0)
(s1744 1.0)
(s1745 1.0)
(s1746 1.0)
(s1747 1.0)timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2919/5843 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30089 ms.
Refiners :[State Equation: 0/2920 constraints, PredecessorRefiner: 2922/2922 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2922 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2919/5843 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30083 ms.
Refiners :[State Equation: 0/2920 constraints, PredecessorRefiner: 0/2922 constraints, Known Traps: 0/0 constraints]
After SMT, in 61741ms problems are : Problem set: 0 solved, 2922 unsolved
Search for dead transitions found 0 dead transitions in 61773ms
Starting structural reductions in LTL mode, iteration 1 : 2920/2969 places, 2923/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 69951 ms. Remains : 2920/2969 places, 2923/3013 transitions.
Stuttering acceptance computed with spot in 116 ms :[(AND (NOT p0) (NOT p1) p2), (AND (NOT p0) (NOT p1) p2)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-05
Product exploration explored 100000 steps with 50000 reset in 3277 ms.
Product exploration explored 100000 steps with 50000 reset in 3596 ms.
Computed a total of 2920 stabilizing places and 2923 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2920 transition count 2923
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) (NOT p1) (NOT p2)), (X (NOT p2)), (X (NOT (AND (NOT p0) (NOT p1) p2))), (X (NOT p0)), (X (NOT p1)), (X (X (NOT p2))), (X (X (NOT (AND (NOT p0) (NOT p1) p2)))), (X (X (NOT p0))), (X (X (NOT p1))), (F (G (NOT p0))), (F (G (NOT p1))), (F (G (NOT p2)))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 12 factoid took 16 ms. Reduced automaton from 2 states, 2 edges and 3 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-05 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-05 finished in 78596 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((X(X((X(X(F(p2)))&&p1)))&&p0)))'
Support contains 6 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 51 places :
Symmetric choice reduction at 0 with 51 rule applications. Total rules 51 place count 2918 transition count 2923
Iterating global reduction 0 with 51 rules applied. Total rules applied 102 place count 2918 transition count 2923
Applied a total of 102 rules in 538 ms. Remains 2918 /2969 variables (removed 51) and now considering 2923/3013 (removed 90) transitions.
// Phase 1: matrix 2923 rows 2918 cols
[2024-05-31 15:57:33] [INFO ] Invariants computation overflowed in 85 ms
[2024-05-31 15:57:35] [INFO ] Implicit Places using invariants in 2234 ms returned []
// Phase 1: matrix 2923 rows 2918 cols
[2024-05-31 15:57:35] [INFO ] Invariants computation overflowed in 55 ms
[2024-05-31 15:57:40] [INFO ] Implicit Places using invariants and state equation in 4491 ms returned []
Implicit Place search using SMT with State Equation took 6731 ms to find 0 implicit places.
Running 2922 sub problems to find dead transitions.
// Phase 1: matrix 2923 rows 2918 cols
[2024-05-31 15:57:40] [INFO ] Invariants computation overflowed in 55 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2917/5841 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30080 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 2922/2922 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2922 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2917/5841 variables, and 0 constraints, problems are : Problem set: 0 solved, 2922 unsolved in 30077 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 0/2922 constraints, Known Traps: 0/0 constraints]
After SMT, in 61469ms problems are : Problem set: 0 solved, 2922 unsolved
Search for dead transitions found 0 dead transitions in 61499ms
Starting structural reductions in LTL mode, iteration 1 : 2918/2969 places, 2923/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68775 ms. Remains : 2918/2969 places, 2923/3013 transitions.
Stuttering acceptance computed with spot in 367 ms :[(OR (NOT p2) (NOT p1)), (OR (NOT p2) (NOT p0) (NOT p1)), (OR (NOT p2) (NOT p1)), (OR (NOT p1) (NOT p2)), (NOT p2), (NOT p2)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-06
Stuttering criterion allowed to conclude after 23 steps with 0 reset in 2 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-06 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-06 finished in 69169 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!((F(X(p0))&&(!X(p1) U p0)))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 50 place count 2919 transition count 2920
Iterating global reduction 0 with 50 rules applied. Total rules applied 100 place count 2919 transition count 2920
Applied a total of 100 rules in 655 ms. Remains 2919 /2969 variables (removed 50) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:58:43] [INFO ] Invariants computation overflowed in 61 ms
[2024-05-31 15:58:45] [INFO ] Implicit Places using invariants in 2762 ms returned []
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:58:45] [INFO ] Invariants computation overflowed in 62 ms
[2024-05-31 15:58:49] [INFO ] Implicit Places using invariants and state equation in 4157 ms returned []
Implicit Place search using SMT with State Equation took 6921 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 15:58:49] [INFO ] Invariants computation overflowed in 54 ms
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30079 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30087 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61301ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61331ms
Starting structural reductions in LTL mode, iteration 1 : 2919/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68913 ms. Remains : 2919/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 183 ms :[(NOT p0), (OR (NOT p0) p1), true, (NOT p0)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-07
Stuttering criterion allowed to conclude after 132 steps with 0 reset in 8 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-07 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-07 finished in 69133 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!((p0 U X((p1||F(G(p1))))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 51 places :
Symmetric choice reduction at 0 with 51 rule applications. Total rules 51 place count 2918 transition count 2920
Iterating global reduction 0 with 51 rules applied. Total rules applied 102 place count 2918 transition count 2920
Applied a total of 102 rules in 670 ms. Remains 2918 /2969 variables (removed 51) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:59:52] [INFO ] Invariants computation overflowed in 89 ms
[2024-05-31 15:59:54] [INFO ] Implicit Places using invariants in 2665 ms returned []
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:59:54] [INFO ] Invariants computation overflowed in 57 ms
[2024-05-31 15:59:59] [INFO ] Implicit Places using invariants and state equation in 4273 ms returned []
Implicit Place search using SMT with State Equation took 6944 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 15:59:59] [INFO ] Invariants computation overflowed in 57 ms
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30079 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 1)
(s2 1)
(s3 1)
(s4 1)
(s5 1)
(s6 1)
(s7 1)
(s8 1)
(s9 1)
(s10 1)
(s11 1)
(s12 1)
(s13 1)
(s14 1)
(s15 1)
(s16 1)
(s17 1)
(s18 1)
(s19 1)
(s20 1)
(s21 1)
(s22 1)
(s23 1)
(s24 1)
(s25 1)
(s26 1)
(s27 1)
(s28 1)
(s29 1)
(s30 1)
(s31 1)
(s32 1)
(s33 1)
(s34 1)
(s35 1)
(s36 1)
(s37 1)
(s38 1)
(s39 1)
(s40 1)
(s41 1)
(s42 1)
(s43 1)
(s44 1)
(s45 1)
(s46 1)
(s47 1)
(s48 1)
(s49 1)
(s50 1)
(s51 1)
(s52 1)
(s53 1)
(s54 1)
(s55 1)
(s56 1)
(s57 1)
(s58 1)
(s59 1)
(s60 1)
(s61 1)
(s62 1)
(s63 1)
(s64 1)
(s65 1)
(s66 1)
(s67 1)
(s68 1)
(s69 1)
(s70 1)
(s71 1)
(s72 1)
(s73 1)
(s74 1)
(s75 1)
(s76 1)
(s77 1)
(s78 1)
(s79 1)
(s80 1)
(s81 1)
(s82 1)
(s83 1)
(s84 1)
(s85 1)
(s86 1)
(s87 1)
(s88 1)
(s89 1)
(s90 1)
(s91 1)
(s92 1)
(s93 1)
(s94 1)
(s95 1)
(s96 1)
(s97 1)
(s98 1)
(s99 1)
(s100 1)
(s101 1)
(s102 1)
(s103 1)
(s104 1)
(s105 1)
(s106 1)
(s107 1)
(s108 1)
(s109 1)
(s110 1)
(s111 1)
(s112 1)
(s113 1)
(s114 1)
(s115 1)
(s116 1)
(s117 1)
(s118 1)
(s119 1)
(s120 1)
(s121 1)
(s122 1)
(s123 1)
(s124 1)
(s125 1)
(s126 1)
(s127 1)
(s128 1)
(s129 1)
(s130 1)
(s131 1)
(s132 1)
(s133 1)
(s134 1)
(s135 1)
(s136 1)
(s137 1)
(s138 1)
(s139 1)
(s140 1)
(s141 1)
(s142 1)
(s143 1)
(s144 1)
(s145 1)
(s146 1)
(s147 1)
(s148 1)
(s149 1)
(s150 1)
(s151 1)
(s152 1)
(s153 1)
(s154 1)
(s155 1)
(s156 1)
(s157 1)
(s158 1)
(s159 1)
(s160 1)
(s161 1)
(s162 1)
(s163 1)
(s164 1)
(s165 1)
(s166 1)
(s167 1)
(s168 1)
(s169 1)
(s170 1)
(s171 1)
(s172 1)
(s173 1)
(s174 1)
(s175 1)
(s176 1)
(s177 1)
(s178 1)
(s179 1)
(s180 1)
(s181 1)
(s182 1)
(s183 1)
(s184 1)
(s185 1)
(s186 1)
(s187 1)
(s188 1)
(s189 1)
(s190 1)
(s191 1)
(s192 1)
(s193 1)
(s194 1)
(s195 1)
(s196 1)
(s197 1)
(s198 1)
(s199 1)
(s200 1)
(s201 1)
(s202 1)
(s203 1)
(s204 1)
(s205 1)
(s206 1)
(s207 1)
(s208 1)
(s209 1)
(s210 1)
(s211 1)
(s212 1)
(s213 1)
(s214 1)
(s215 1)
(s216 1)
(s217 1)
(s218 1)
(s219 1)
(s220 1)
(s221 1)
(s222 1)
(s223 1)
(s224 1)
(s225 1)
(s226 1)
(s227 1)
(s228 1)
(s229 1)
(s230 1)
(s231 1)
(s232 1)
(s233 1)
(s234 1)
(s235 1)
(s236 1)
(s237 1)
(s238 1)
(s239 1)
(s240 1)
(s241 1)
(s242 1)
(s243 1)
(s244 1)
(s245 1)
(s246 1)
(s247 1)
(s248 1)
(s249 1)
(s250 1)
(s251 1)
(s252 1)
(s253 1)
(s254 1)
(s255 1)
(s256 1)
(s257 1)
(s258 1)
(s259 1)
(s260 1)
(s261 1)
(s262 1)
(s263 1)
(s264 1)
(s265 1)
(s266 1)
(s267 1)
(s268 1)
(s269 1)
(s270 1)
(s271 1)
(s272 1)
(s273 1)
(s274 1)
(s275 1)
(s276 1)
(s277 1)
(s278 1)
(s279 1)
(s280 1)
(s281 1)
(s282 1)
(s283 1)
(s284 1)
(s285 1)
(s286 1)
(s287 1)
(s288 1)
(s289 1)
(s290 1)
(s291 1)
(s292 1)
(s293 1)
(s294 1)
(s295 1)
(s296 1)
(s297 1)
(s298 1)
(s299 1)
(s300 1)
(s301 1)
(s302 1)
(s303 1)
(s304 1)
(s305 1)
(s306 1)
(s307 1)
(s308 1)
(s309 1)
(s310 1)
(s311 1)
(s312 1)
(s313 1)
(s314 1)
(s315 1)
(s316 1)
(s317 1)
(s318 1)
(s319 1)
(s320 1)
(s321 1)
(s322 1)
(s323 1)
(s324 1)
(s325 1)
(s326 1)
(s327 1)
(s328 1)
(s329 1)
(s330 1)
(s331 1)
(s332 1)
(s333 1)
(s334 1)
(s335 1)
(s336 1)
(s337 1)
(s338 1)
(s339 1)
(s340 1)
(s341 1)
(s342 1)
(s343 1)
(s344 1)
(s345 1)
(s346 1)
(s347 1)
(s348 1)
(s349 1)
(s350 1)
(s351 1)
(s352 1)
(s353 1)
(s354 1)
(s355 1)
(s356 1)
(s357 1)
(s358 1)
(s359 1)
(s360 1)
(s361 1)
(s362 1)
(s363 1)
(s364 1)
(s365 1)
(s366 1)
(s367 1)
(s368 1)
(s369 1)
(s370 1)
(s371 1)
(s372 1)
(s373 1)
(s374 1)
(s375 1)
(s376 1)
(s377 1)
(s378 1)
(s379 1)
(s380 1)
(s381 1)
(s382 1)
(s383 1)
(s384 1)
(s385 1)
(s386 1)
(s387 1)
(s388 1)
(s389 1)
(s390 1)
(s391 1)
(s392 1)
(s393 1)
(s394 1)
(s395 1)
(s396 1)
(s397 1)
(s398 1)
(s399 1)
(s400 1)
(s401 1)
(s402 1)
(s403 1)
(s404 1)
(s405 1)
(s406 1)
(s407 1)
(s408 1)
(s409 1)
(s410 1)
(s411 1)
(s412 1)
(s413 1)
(s414 1)
(s415 1)
(s416 1)
(s417 1)
(s418 1)
(s419 1)
(s420 1)
(s421 1)
(s422 1)
(s423 1)
(s424 1)
(s425 1)
(s426 1)
(s427 1)
(s428 1)
(s429 1)
(s430 1)
(s431 1)
(s432 1)
(s433 1)
(s434 1)
(s435 1)
(s436 1)
(s437 1)
(s438 1)
(s439 1)
(s440 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30081 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61321ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61351ms
Starting structural reductions in LTL mode, iteration 1 : 2918/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68972 ms. Remains : 2918/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 217 ms :[(NOT p1), (NOT p1), (NOT p1), (NOT p1)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-08
Stuttering criterion allowed to conclude after 273 steps with 0 reset in 15 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-08 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-08 finished in 69235 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(F((F(G(p0))&&((!p0||X(p1)) U (G((!p0||X(p1)))||(!p2&&(!p0||X(p1)))))))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 53 places :
Symmetric choice reduction at 0 with 53 rule applications. Total rules 53 place count 2916 transition count 2917
Iterating global reduction 0 with 53 rules applied. Total rules applied 106 place count 2916 transition count 2917
Applied a total of 106 rules in 637 ms. Remains 2916 /2969 variables (removed 53) and now considering 2917/3013 (removed 96) transitions.
// Phase 1: matrix 2917 rows 2916 cols
[2024-05-31 16:01:01] [INFO ] Invariants computation overflowed in 55 ms
[2024-05-31 16:01:03] [INFO ] Implicit Places using invariants in 2547 ms returned []
// Phase 1: matrix 2917 rows 2916 cols
[2024-05-31 16:01:03] [INFO ] Invariants computation overflowed in 54 ms
[2024-05-31 16:01:08] [INFO ] Implicit Places using invariants and state equation in 5139 ms returned []
Implicit Place search using SMT with State Equation took 7688 ms to find 0 implicit places.
Running 2916 sub problems to find dead transitions.
// Phase 1: matrix 2917 rows 2916 cols
[2024-05-31 16:01:09] [INFO ] Invariants computation overflowed in 54 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2915/5833 variables, and 0 constraints, problems are : Problem set: 0 solved, 2916 unsolved in 30100 ms.
Refiners :[State Equation: 0/2916 constraints, PredecessorRefiner: 2916/2916 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2916 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2915/5833 variables, and 0 constraints, problems are : Problem set: 0 solved, 2916 unsolved in 30089 ms.
Refiners :[State Equation: 0/2916 constraints, PredecessorRefiner: 0/2916 constraints, Known Traps: 0/0 constraints]
After SMT, in 61140ms problems are : Problem set: 0 solved, 2916 unsolved
Search for dead transitions found 0 dead transitions in 61170ms
Starting structural reductions in LTL mode, iteration 1 : 2916/2969 places, 2917/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 69501 ms. Remains : 2916/2969 places, 2917/3013 transitions.
Stuttering acceptance computed with spot in 317 ms :[(OR (NOT p0) (NOT p1)), (OR (NOT p0) (NOT p1)), (NOT p0), (AND p0 (NOT p1)), (AND p0 (NOT p1))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-09
Stuttering criterion allowed to conclude after 58 steps with 0 reset in 4 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-09 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-09 finished in 69864 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X((F(p0)||X(X(G(p1))))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 51 places :
Symmetric choice reduction at 0 with 51 rule applications. Total rules 51 place count 2918 transition count 2920
Iterating global reduction 0 with 51 rules applied. Total rules applied 102 place count 2918 transition count 2920
Applied a total of 102 rules in 668 ms. Remains 2918 /2969 variables (removed 51) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 16:02:11] [INFO ] Invariants computation overflowed in 88 ms
[2024-05-31 16:02:13] [INFO ] Implicit Places using invariants in 2001 ms returned []
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 16:02:13] [INFO ] Invariants computation overflowed in 59 ms
[2024-05-31 16:02:17] [INFO ] Implicit Places using invariants and state equation in 4647 ms returned []
Implicit Place search using SMT with State Equation took 6654 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2918 cols
[2024-05-31 16:02:18] [INFO ] Invariants computation overflowed in 91 ms
Error getting values : (error "ParserException while parsing response: ((s0 1.0)
(s2 1.0)
(s3 1.0)
(s4 1.0)
(s5 1.0)
(s6 1.0)
(s7 1.0)
(s8 1.0)
(s9 1.0)
(s10 1.0)
(s11 1.0)
(s12 1.0)
(s13 1.0)
(s14 1.0)
(s15 1.0)
(s16 1.0)
(s17 1.0)
(s18 1.0)
(s19 1.0)
(s20 1.0)
(s21 1.0)
(s22 1.0)
(s23 1.0)
(s24 1.0)
(s25 1.0)
(s26 1.0)
(s27 1.0)
(s28 1.0)
(s29 1.0)
(s30 1.0)
(s31 1.0)
(s32 1.0)
(s33 1.0)
(s34 1.0)
(s35 1.0)
(s36 1.0)
(s37 1.0)
(s38 1.0)
(s39 1.0)
(s40 1.0)
(s41 1.0)
(s42 1.0)
(s43 1.0)
(s44 1.0)
(s45 1.0)
(s46 1.0)
(s47 1.0)
(s48 1.0)
(s49 1.0)
(s50 1.0)
(s51 1.0)
(s52 1.0)
(s53 1.0)
(s54 1.0)
(s55 1.0)
(s56 1.0)
(s57 1.0)
(s58 1.0)
(s59 1.0)
(s60 1.0)
(s61 1.0)
(s62 1.0)
(s63 1.0)
(s64 1.0)
(s65 1.0)
(s66 1.0)
(s67 1.0)
(s68 1.0)
(s69 1.0)
(s70 1.0)
(s71 1.0)
(s72 1.0)
(s73 1.0)
(s74 1.0)
(s75 1.0)
(s76 1.0)
(s77 1.0)
(s78 1.0)
(s79 1.0)
(s80 1.0)
(s81 1.0)
(s82 1.0)
(s83 1.0)
(s84 1.0)
(s85 1.0)
(s86 1.0)
(s87 1.0)
(s88 1.0)
(s89 1.0)
(s90 1.0)
(s91 1.0)
(s92 1.0)
(s93 1.0)
(s94 1.0)
(s95 1.0)
(s96 1.0)
(s97 1.0)
(s98 1.0)
(s99 1.0)
(s100 1.0)
(s101 1.0)
(s102 1.0)
(s103 1.0)
(s104 1.0)
(s105 1.0)
(s106 1.0)
(s107 1.0)
(s108 1.0)
(s109 1.0)
(s110 1.0)
(s111 1.0)
(s112 1.0)
(s113 1.0)
(s114 1.0)
(s115 1.0)
(s116 1.0)
(s117 1.0)
(s118 1.0)
(s119 1.0)
(s120 1.0)
(s121 1.0)
(s122 1.0)
(s123 1.0)
(s124 1.0)
(s125 1.0)
(s126 1.0)
(s127 1.0)
(s128 1.0)
(s129 1.0)
(s130 1.0)
(s131 1.0)
(s132 1.0)
(s133 1.0)
(s134 1.0)
(s135 1.0)
(s136 1.0)
(s137 1.0)
(s138 1.0)
(s139 1.0)
(s140 1.0)
(s141 1.0)
(s142 1.0)
(s143 1.0)
(s144 1.0)
(s145 1.0)
(s146 1.0)
(s147 1.0)
(s148 1.0)
(s149 1.0)
(s150 1.0)
(s151 1.0)
(s152 1.0)
(s153 1.0)
(s154 1.0)
(s155 1.0)
(s156 1.0)
(s157 1.0)
(s158 1.0)
(s159 1.0)
(s160 1.0)
(s161 1.0)
(s162 1.0)
(s163 1.0)
(s164 1.0)
(s165 1.0)
(s166 1.0)
(s167 1.0)
(s168 1.0)
(s169 1.0)
(s170 1.0)
(s171 1.0)
(s172 1.0)
(s173 1.0)
(s174 1.0)
(s175 1.0)
(s176 1.0)
(s177 1.0)
(s178 1.0)
(s179 1.0)
(s180 1.0)
(s181 1.0)
(s182 1.0)
(s183 1.0)
(s184 1.0)
(s185 1.0)
(s186 1.0)
(s187 1.0)
(s188 1.0)
(s189 1.0)
(s190 1.0)
(s191 1.0)
(s192 1.0)
(s193 1.0)
(s194 1.0)
(s195 1.0)
(s196 1.0)
(s197 1.0)
(s198 1.0)
(s199 1.0)
(s200 1.0)
(s201 1.0)
(s202 1.0)
(s203 1.0)
(s204 1.0)
(s205 1.0)
(s206 1.0)
(s207 1.0)
(s208 1.0)
(s209 1.0)
(s210 1.0)
(s211 1.0)
(s212 1.0)
(s213 1.0)
(s214 1.0)
(s215 1.0)
(s216 1.0)
(s217 1.0)
(s218 1.0)
(s219 1.0)
(s220 1.0)
(s221 1.0)
(s222 1.0)
(s223 1.0)
(s224 1.0)
(s225 1.0)
(s226 1.0)
(s227 1.0)
(s228 1.0)
(s229 1.0)
(s230 1.0)
(s231 1.0)
(s232 1.0)
(s233 1.0)
(s234 1.0)
(s235 1.0)
(s236 1.0)
(s237 1.0)
(s238 1.0)
(s239 1.0)
(s240 1.0)
(s241 1.0)
(s242 1.0)
(s243 1.0)
(s244 1.0)
(s245 1.0)
(s246 1.0)
(s247 1.0)
(s248 1.0)
(s249 1.0)
(s250 1.0)
(s251 1.0)
(s252 1.0)
(s253 1.0)
(s254 1.0)
(s255 1.0)
(s256 1.0)
(s257 1.0)
(s258 1.0)
(s259 1.0)
(s260 1.0)
(s261 1.0)
(s262 1.0)
(s263 1.0)
(s264 1.0)
(s265 1.0)
(s266 1.0)
(s267 1.0)
(s268 1.0)
(s269 1.0)
(s270 1.0)
(s271 1.0)
(s272 1.0)
(s273 1.0)
(s274 1.0)
(s275 1.0)
(s276 1.0)
(s277 1.0)
(s278 1.0)
(s279 1.0)
(s280 1.0)
(s281 1.0)
(s282 1.0)
(s283 1.0)
(s284 1.0)
(s285 1.0)
(s286 1.0)
(s287 1.0)
(s288 1.0)
(s289 1.0)
(s290 1.0)
(s291 1.0)
(s292 1.0)
(s293 1.0)
(s294 1.0)
(s295 1.0)
(s296 1.0)
(s297 1.0)
(s298 1.0)
(s299 1.0)
(s300 1.0)
(s301 1.0)
(s302 1.0)
(s303 1.0)
(s304 1.0)
(s305 1.0)
(s306 1.0)
(s307 1.0)
(s308 1.0)
(s309 1.0)
(s310 1.0)
(s311 1.0)
(s312 1.0)
(s313 1.0)
(s314 1.0)
(s315 1.0)
(s316 1.0)
(s317 1.0)
(s318 1.0)
(s319 1.0)
(s320 1.0)
(s321 1.0)
(s322 1.0)
(s323 1.0)
(s324 1.0)
(s325 1.0)
(s326 1.0)
(s327 1.0)
(s328 1.0)
(s329 1.0)
(s330 1.0)
(s331 1.0)
(s332 1.0)
(s333 1.0)
(s334 1.0)
(s335 1.0)
(s336 1.0)
(s337 1.0)
(s338 1.0)
(s339 1.0)
(s340 1.0)
(s341 1.0)
(s342 1.0)
(s343 1.0)
(s344 1.0)
(s345 1.0)
(s346 1.0)
(s347 1.0)
(s348 1.0)
(s349 1.0)
(s350 1.0)
(s351 1.0)
(s352 1.0)
(s353 1.0)
(s354 1.0)
(s355 1.0)
(s356 1.0)
(s357 1.0)
(s358 1.0)
(s359 1.0)
(s360 1.0)
(s361 1.0)
(s362 1.0)
(s363 1.0)
(s364 1.0)
(s365 1.0)
(s366 1.0)
(s367 1.0)
(s368 1.0)
(s369 1.0)
(s370 1.0)
(s371 1.0)
(s372 1.0)
(s373 1.0)
(s374 1.0)
(s375 1.0)
(s376 1.0)
(s377 1.0)
(s378 1.0)
(s379 1.0)
(s380 1.0)
(s381 1.0)
(s382 1.0)
(s383 1.0)
(s384 1.0)
(s385 1.0)
(s386 1.0)
(s387 1.0)
(s388 1.0)
(s389 1.0)
(s390 1.0)
(s391 1.0)
(s392 1.0)
(s393 1.0)
(s394 1.0)
(s395 1.0)
(s396 1.0)
(s397 1.0)
(s398 1.0)
(s399 1.0)
(s400 1.0)
(s401 1.0)
(s402 1.0)
(s403 1.0)
(s404 1.0)
(s405 1.0)
(s406 1.0)
(s407 1.0)
(s408 1.0)
(s409 1.0)
(s410 1.0)
(s411 1.0)
(s412 1.0)
(s413 1.0)
(s414 1.0)
(s415 1.0)
(s416 1.0)
(s417 1.0)
(s418 1.0)
(s419 1.0)
(s420 1.0)
(s421 1.0)
(s422 1.0)
(s423 1.0)
(s424 1.0)
(s425 1.0)
(s426 1.0)
(s427 1.0)
(s428 1.0)
(s429 1.0)
(s430 1.0)
(s431 1.0)
(s432 1.0)
(s433 1.0)
(s434 1.0)
(s435 1.0)
(s436 1.0)
(s437 1.0)
(s438 1.0)
(s439 1.0)
(s440 1.0)
(s441 1.0)
(s442 1.0)
(s443 1.0)
(s444 1.0)
(s445 1.0)
(s446 1.0)
(s447 1.0)
(s448 1.0)
(s449 1.0)
(s450 1.0)
(s451 1.0)
(s452 1.0)
(s453 1.0)
(s454 1.0)
(s455 1.0)
(s456 1.0)
(s457 1.0)
(s458 1.0)
(s459 1.0)
(s460 1.0)
(s461 1.0)
(s462 1.0)
(s463 1.0)
(s464 1.0)
(s465 1.0)
(s466 1.0)
(s467 1.0)
(s468 1.0)
(s469 1.0)
(s470 1.0)
(s471 1.0)
(s472 1.0)
(s473 1.0)
(s474 1.0)
(s475 1.0)
(s476 1.0)
(s477 1.0)
(s478 1.0)
(s479 1.0)
(s480 1.0)
(s481 1.0)
(s482 1.0)
(s483 1.0)
(s484 1.0)
(s485 1.0)
(s486 1.0)
(s487 1.0)
(s488 1.0)
(s489 1.0)
(s490 1.0)
(s491 1.0)
(s492 1.0)
(s493 1.0)
(s494 1.0)
(s495 1.0)
(s496 1.0)
(s497 1.0)
(s498 1.0)
(s499 1.0)
(s500 1.0)
(s501 1.0)
(s502 1.0)
(s503 1.0)
(s504 1.0)
(s505 1.0)
(s506 1.0)
(s507 1.0)
(s508 1.0)
(s509 1.0)
(s510 1.0)
(s511 1.0)
(s512 1.0)
(s513 1.0)
(s514 1.0)
(s515 1.0)
(s516 1.0)
(s517 1.0)
(s518 1.0)
(s519 1.0)
(s520 1.0)
(s521 1.0)
(s522 1.0)
(s523 1.0)
(s524 1.0)
(s525 1.0)
(s526 1.0)
(s527 1.0)
(s528 1.0)
(s529 1.0)
(s530 1.0)
(s531 1.0)
(s532 1.0)
(s533 1.0)
(s534 1.0)
(s535 1.0)
(s536 1.0)
(s537 1.0)
(s538 1.0)
(s539 1.0)
(s540 1.0)
(s541 1.0)
(s542 1.0)
(s543 1.0)
(s544 1.0)
(s545 1.0)
(s546 1.0)
(s547 1.0)
(s548 1.0)
(s549 1.0)
(s550 1.0)
(s551 1.0)
(s552 1.0)
(s553 1.0)
(s554 1.0)
(s555 1.0)
(s556 1.0)
(s557 1.0)
(s558 1.0)
(s559 1.0)
(s560 1.0)
(s561 1.0)
(s562 1.0)
(s563 1.0)
(s564 1.0)
(s565 1.0)
(s566 1.0)
(s567 1.0)
(s568 1.0)
(s569 1.0)
(s570 1.0)
(s571 1.0)
(s572 1.0)
(s573 1.0)
(s574 1.0)
(s575 1.0)
(s576 1.0)
(s577 1.0)
(s578 1.0)
(s579 1.0)
(s580 1.0)
(s581 1.0)
(s582 1.0)
(s583 1.0)
(s584 1.0)
(s585 1.0)
(s586 1.0)
(s587 1.0)
(s588 1.0)
(s589 1.0)
(s590 1.0)
(s591 1.0)
(s592 1.0)
(s593 1.0)
(s594 1.0)
(s595 1.0)
(s596 1.0)
(s597 1.0)
(s598 1.0)
(s599 1.0)
(s600 1.0)
(s601 1.0)
(s602 1.0)
(s603 1.0)
(s604 1.0)
(s605 1.0)
(s606 1.0)
(s607 1.0)
(s608 1.0)
(s609 1.0)
(s610 1.0)
(s611 1.0)
(s612 1.0)
(s613 1.0)
(s614 1.0)
(s615 1.0)
(s616 1.0)
(s617 1.0)
(s618 1.0)
(s619 1.0)
(s620 1.0)
(s621 1.0)
(s622 1.0)
(s623 1.0)
(s624 1.0)
(s625 1.0)
(s626 1.0)
(s627 1.0)
(s628 1.0)
(s629 1.0)
(s630 1.0)
(s631 1.0)
(s632 1.0)
(s633 1.0)
(s634 1.0)
(s635 1.0)
(s636 1.0)
(s637 1.0)
(s638 1.0)
(s639 1.0)
(s640 1.0)
(s641 1.0)
(s642 1.0)
(s643 1.0)
(s644 1.0)
(s645 1.0)
(s646 1.0)
(s647 1.0)
(s648 1.0)
(s649 1.0)
(s650 1.0)
(s651 1.0)
(s652 1.0)
(s653 1.0)
(s654 1.0)
(s655 1.0)
(s656 1.0)
(s657 1.0)
(s658 1.0)
(s659 1.0)
(s660 1.0)
(s661 1.0)
(s662 1.0)
(s663 1.0)
(s664 1.0)
(s665 1.0)
(s666 1.0)
(s667 1.0)
(s668 1.0)
(s669 1.0)
(s670 1.0)
(s671 1.0)
(s672 1.0)
(s673 1.0)
(s674 1.0)
(s675 1.0)
(s676 1.0)
(s677 1.0)
(s678 1.0)
(s679 1.0)
(s680 1.0)
(s681 1.0)
(s682 1.0)
(s683 1.0)
(s684 1.0)
(s685 1.0)
(s686 1.0)
(s687 1.0)
(s688 1.0)
(s689 1.0)
(s690 1.0)
(s691 1.0)
(s692 1.0)
(s693 1.0)
(s694 1.0)
(s695 1.0)
(s696 1.0)
(s697 1.0)
(s698 1.0)
(s699 1.0)
(s700 1.0)
(s701 1.0)
(s702 1.0)
(s703 1.0)
(s704 1.0)
(s705 1.0)
(s706 1.0)
(s707 1.0)
(s708 1.0)
(s709 1.0)
(s710 1.0)
(s711 1.0)
(s712 1.0)
(s713 1.0)
(s714 1.0)
(s715 1.0)
(s716 1.0)
(s717 1.0)
(s718 1.0)
(s719 1.0)
(s720 1.0)
(s721 1.0)
(s722 1.0)
(s723 1.0)
(s724 1.0)
(s725 1.0)
(s726 1.0)
(s727 1.0)
(s728 1.0)
(s729 1.0)
(s730 1.0)
(s731 1.0)
(s732 1.0)
(s733 1.0)
(s734 1.0)
(s735 1.0)
(s736 1.0)
(s737 1.0)
(s738 1.0)
(s739 1.0)
(s740 1.0)
(s741 1.0)
(s742 1.0)
(s743 1.0)
(s744 1.0)
(s745 1.0)
(s746 1.0)
(s747 1.0)
(s748 1.0)
(s749 1.0)
(s750 1.0)
(s751 1.0)
(s752 1.0)
(s753 1.0)
(s754 1.0)
(s755 1.0)
(s756 1.0)
(s757 1.0)
(s758 1.0)
(s759 1.0)
(s760 1.0)
(s761 1.0)
(s762 1.0)
(s763 1.0)
(s764 1.0)
(s765 1.0)
(s766 1.0)
(s767 1.0)
(s768 1.0)
(s769 1.0)
(s770 1.0)
(s771 1.0)
(s772 1.0)
(s773 1.0)
(s774 1.0)
(s775 1.0)
(s776 1.0)
(s777 1.0)
(s778 1.0)
(s779 1.0)
(s780 1.0)
(s781 1.0)
(s782 1.0)
(s783 1.0)
(s784 1.0)
(s785 1.0)
(s786 1.0)
(s787 1.0)
(s788 1.0)
(s789 1.0)
(s790 1.0)
(s791 1.0)
(s792 1.0)
(s793 1.0)
(s794 1.0)
(s795 1.0)
(s796 1.0)
(s797 1.0)
(s798 1.0)
(s799 1.0)
(s800 1.0)
(s801 1.0)
(s802 1.0)
(s803 1.0)
(s804 1.0)
(s805 1.0)
(s806 1.0)
(s807 1.0)
(s808 1.0)
(s809 1.0)
(s810 1.0)
(s811 1.0)
(s812 1.0)
(s813 1.0)
(s814 1.0)
(s815 1.0)
(s816 1.0)
(s817 1.0)
(s818 1.0)
(s819 1.0)
(s820 1.0)
(s821 1.0)
(s822 1.0)
(s823 1.0)
(s824 1.0)
(s825 1.0)
(s826 1.0)
(s827 1.0)
(s828 1.0)
(s829 1.0)
(s830 1.0)
(s831 1.0)
(s832 1.0)
(s833 1.0)
(s834 1.0)
(s835 1.0)
(s836 1.0)
(s837 1.0)
(s838 1.0)
(s839 1.0)
(s840 1.0)
(s841 1.0)
(s842 1.0)
(s843 1.0)
(s844 1.0)
(s845 1.0)
(s846 1.0)
(s847 1.0)
(s848 1.0)
(s849 1.0)
(s850 1.0)
(s851 1.0)
(s852 1.0)
(s853 1.0)
(s854 1.0)
(s855 1.0)
(s856 1.0)
(s857 1.0)
(s858 1.0)
(s859 1.0)
(s860 1.0)
(s861 1.0)
(s862 1.0)
(s863 1.0)
(s864 1.0)
(s865 1.0)
(s866 1.0)
(s867 1.0)
(s868 1.0)
(s869 1.0)
(s870 1.0)
(s871 1.0)
(s872 1.0)
(s873 1.0)
(s874 1.0)
(s875 1.0)
(s876 1.0)
(s877 1.0)
(s878 1.0)
(s879 1.0)
(s880 1.0)
(s881 1.0)
(s882 1.0)
(s883 1.0)
(s884 1.0)
(s885 1.0)
(s886 1.0)
(s887 1.0)
(s888 1.0)
(s889 1.0)
(s890 1.0)
(s891 1.0)
(s892 1.0)
(s893 1.0)
(s894 1.0)
(s895 1.0)
(s896 1.0)
(s897 1.0)
(s898 1.0)
(s899 1.0)
(s900 1.0)
(s901 1.0)
(s902 1.0)
(s903 1.0)
(s904 1.0)
(s905 1.0)
(s906 1.0)
(s907 1.0)
(s908 1.0)
(s909 1.0)
(s910 1.0)
(s911 1.0)
(s912 1.0)
(s913 1.0)
(s914 1.0)
(s915 1.0)
(s916 1.0)
(s917 1.0)
(s918 1.0)
(s919 1.0)
(s920 1.0)
(s921 1.0)
(s922 1.0)
(s923 1.0)
(s924 1.0)
(s925 1.0)
(s926 1.0)
(s927 1.0)
(s928 1.0)
(s929 1.0)
(s930 1.0)
(s931 1.0)
(s932 1.0)
(s933 1.0)
(s934 1.0)
(s935 1.0)
(s936 1.0)
(s937 1.0)
(s938 1.0)
(s939 1.0)
(s940 1.0)
(s941 1.0)
(s942 1.0)
(s943 1.0)
(s944 1.0)
(s945 1.0)
(s946 1.0)
(s947 1.0)
(s948 1.0)
(s949 1.0)
(s950 1.0)
(s951 1.0)
(s952 1.0)
(s953 1.0)
(s954 1.0)
(s955 1.0)
(s956 1.0)
(s957 1.0)
(s958 1.0)
(s959 1.0)
(s960 1.0)
(s961 1.0)
(s962 1.0)
(s963 1.0)
(s964 1.0)
(s965 1.0)
(s966 1.0)
(s967 1.0)
(s968 1.0)
(s969 1.0)
(s970 1.0)
(s971 1.0)
(s972 1.0)
(s973 1.0)
(s974 1.0)
(s975 1.0)
(s976 1.0)
(s977 1.0)
(s978 1.0)
(s979 1.0)
(s980 1.0)
(s981 1.0)
(s982 1.0)
(s983 1.0)
(s984 1.0)
(s985 1.0)
(s986 1.0)
(s987 1.0)
(s988 1.0)
(s989 1.0)
(s990 1.0)
(s991 1.0)
(s992 1.0)
(s993 1.0)
(s994 1.0)
(s995 1.0)
(s996 1.0)
(s997 1.0)
(s998 1.0)
(s999 1.0)
(s1000 1.0)
(s1001 1.0)
(s1002 1.0)
(s1003 1.0)
(s1004 1.0)
(s1005 1.0)
(s1006 1.0)
(s1007 1.0)
(s1008 1.0)
(s1009 1.0)
(s1010 1.0)
(s1011 1.0)
(s1012 1.0)
(s1013 1.0)
(s1014 1.0)
(s1015 1.0)
(s1016 1.0)
(s1017 1.0)
(s1018 1.0)
(s1019 1.0)
(s1020 1.0)
(s1021 1.0)
(s1022 1.0)
(s1023 1.0)
(s1024 1.0)
(s1025 1.0)
(s1026 1.0)
(s1027 1.0)
(s1028 1.0)
(s1029 1.0)
(s1030 1.0)
(s1031 1.0)
(s1032 1.0)
(s1033 1.0)
(s1034 1.0)
(s1035 1.0)
(s1036 1.0)
(s1037 1.0)
(s1038 1.0)
(s1039 1.0)
(s1040 1.0)
(s1041 1.0)
(s1042 1.0)
(s1043 1.0)
(s1044 1.0)
(s1045 1.0)
(s1046 1.0)
(s1047 1.0)
(s1048 1.0)
(s1049 1.0)
(s1050 1.0)
(s1051 1.0)
(s1052 1.0)
(s1053 1.0)
(s1054 1.0)
(s1055 1.0)
(s1056 1.0)
(s1057 1.0)
(s1058 1.0)
(s1059 1.0)
(s1060 1.0)
(s1061 1.0)
(s1062 1.0)
(s1063 1.0)
(s1064 1.0)
(s1065 1.0)
(s1066 1.0)
(s1067 1.0)
(s1068 1.0)
(s1069 1.0)
(s1070 1.0)
(s1071 1.0)
(s1072 1.0)
(s1073 1.0)
(s1074 1.0)
(s1075 1.0)
(s1076 1.0)
(s1077 1.0)
(s1078 1.0)
(s1079 1.0)
(s1080 1.0)
(s1081 1.0)
(s1082 1.0)
(s1083 1.0)
(s1084 1.0)
(s1085 1.0)
(s1086 1.0)
(s1087 1.0)
(s1088 1.0)
(s1089 1.0)
(s1090 1.0)
(s1091 1.0)
(s1092 1.0)
(s1093 1.0)
(s1094 1.0)
(s1095 1.0)
(s1096 1.0)
(s1097 1.0)
(s1098 1.0)
(s1099 1.0)
(s1100 1.0)
(s1101 1.0)
(s1102 1.0)
(s1103 1.0)
(s1104 1.0)
(s1105 1.0)
(s1106 1.0)
(s1107 1.0)
(s1108 1.0)
(s1109 1.0)
(s1110 1.0)
(s1111 1.0)
(s1112 1.0)
(s1113 1.0)
(s1114 1.0)
(s1115 1.0)
(s1116 1.0)
(s1117 1.0)
(s1118 1.0)
(s1119 1.0)
(s1120 1.0)
(s1121 1.0)
(s1122 1.0)
(s1123 1.0)
(s1124 1.0)
(s1125 1.0)
(s1126 1.0)
(s1127 1.0)
(s1128 1.0)
(s1129 1.0)
(s1130 1.0)
(s1131 1.0)
(s1132 1.0)
(s1133 1.0)
(s1134 1.0)
(s1135 1.0)
(s1136 1.0)
(s1137 1.0)
(s1138 1.0)
(s1139 1.0)
(s1140 1.0)
(s1141 1.0)
(s1142 1.0)
(s1143 1.0)
(s1144 1.0)
(s1145 1.0)
(s1146 1.0)
(s1147 1.0)
(s1148 1.0)
(s1149 1.0)
(s1150 1.0)
(s1151 1.0)
(s1152 1.0)
(s1153 1.0)
(s1154 1.0)
(s1155 1.0)
(s1156 1.0)
(s1157 1.0)
(s1158 1.0)
(s1159 1.0)
(s1160 1.0)
(s1161 1.0)
(s1162 1.0)
(s1163 1.0)
(s1164 1.0)
(s1165 1.0)
(s1166 1.0)
(s1167 1.0)
(s1168 1.0)
(s1169 1.0)
(s1170 1.0)
(s1171 1.0)
(s1172 1.0)
(s1173 1.0)
(s1174 1.0)
(s1175 1.0)
(s1176 1.0)
(s1177 1.0)
(s1178 1.0)
(s1179 1.0)
(s1180 1.0)
(s1181 1.0)
(s1182 1.0)
(s1183 1.0)
(s1184 1.0)
(s1185 1.0)
(s1186 1.0)
(s1187 1.0)
(s1188 1.0)
(s1189 1.0)
(s1190 1.0)
(s1191 1.0)
(s1192 1.0)
(s1193 1.0)
(s1194 1.0)
(s1195 1.0)
(s1196 1.0)
(s1197 1.0)
(s1198 1.0)
(s1199 1.0)
(s1200 1.0)
(s1201 1.0)
(s1202 1.0)
(s1203 1.0)
(s1204 1.0)
(s1205 1.0)
(s1206 1.0)
(s1207 1.0)
(s1208 1.0)
(s1209 1.0)
(s1210 1.0)
(s1211 1.0)
(s1212 1.0)
(s1213 1.0)
(s1214 1.0)
(s1215 1.0)
(s1216 1.0)
(s1217 1.0)
(s1218 1.0)
(s1219 1.0)
(s1220 1.0)
(s1221 1.0)
(s1222 1.0)
(s1223 1.0)
(s1224 1.0)
(s1225 1.0)
(s1226 1.0)
(s1227 1.0)
(s1228 1.0)
(s1229 1.0)
(s1230 1.0)
(s1231 1.0)
(s1232 1.0)
(s1233 1.0)
(s1234 1.0)
(s1235 1.0)
(s1236 1.0)
(s1237 1.0)
(s1238 1.0)
(s1239 1.0)
(s1240 1.0)
(s1241 1.0)
(s1242 1.0)
(s1243 1.0)
(s1244 1.0)
(s1245 1.0)
(s1246 1.0)
(s1247 1.0)
(s1248 1.0)
(s1249 1.0)
(s1250 1.0)
(s1251 1.0)
(s1252 1.0)
(s1253 1.0)
(s1254 1.0)
(s1255 1.0)
(s1256 1.0)
(s1257 1.0)
(s1258 1.0)
(s1259 1.0)
(s1260 1.0)
(s1261 1.0)
(s1262 1.0)
(s1263 1.0)
(s1264 1.0)
(s1265 1.0)
(s1266 1.0)
(s1267 1.0)
(s1268 1.0)
(s1269 1.0)
(s1270 1.0)
(s1271 1.0)
(s1272 1.0)
(s1273 1.0)
(s1274 1.0)
(s1275 1.0)
(s1276 1.0)
(s1277 1.0)
(s1278 1.0)
(s1279 1.0)
(s1280 1.0)
(s1281 1.0)
(s1282 1.0)
(s1283 1.0)
(s1284 1.0)
(s1285 1.0)
(s1286 1.0)
(s1287 1.0)
(s1288 1.0)
(s1289 1.0)
(s1290 1.0)
(s1291 1.0)
(s1292 1.0)
(s1293 1.0)
(s1294 1.0)
(s1295 1.0)
(s1296 1.0)
(s1297 1.0)
(s1298 1.0)
(s1299 1.0)
(s1300 1.0)
(s1301 1.0)
(s1302 1.0)
(s1303 1.0)
(s1304 1.0)
(s1305 1.0)
(s1306 1.0)
(s1307 1.0)
(s1308 1.0)
(s1309 1.0)
(s1310 1.0)
(s1311 1.0)
(s1312 1.0)
(s1313 1.0)
(s1314 1.0)
(s1315 1.0)
(s1316 1.0)
(s1317 1.0)
(s1318 1.0)
(s1319 1.0)
(s1320 1.0)
(s1321 1.0)
(s1322 1.0)
(s1323 1.0)
(s1324 1.0)
(s1325 1.0)
(s1326 1.0)
(s1327 1.0)
(s1328 1.0)
(s1329 1.0)
(s1330 1.0)
(s1331 1.0)
(s1332 1.0)
(s1333 1.0)
(s1334 1.0)
(s1335 1.0)
(s1336 1.0)
(s1337 1.0)
(s1338 1.0)
(s1339 1.0)
(s1340 1.0)
(s1341 1.0)
(s1342 1.0)
(s1343 1.0)
(s1344 1.0)
(s1345 1.0)
(s1346 1.0)
(s1347 1.0)
(s1348 1.0)
(s1349 1.0)
(s1350 1.0)
(s1351 1.0)
(s1352 1.0)
(s1353 1.0)
(s1354 1.0)
(s1355 1.0)
(s1356 1.0)
(s1357 1.0)
(s1358 1.0)
(s1359 1.0)
(s1360 1.0)
(s1361 1.0)
(s1362 1.0)
(s1363 1.0)
(s1364 1.0)
(s1365 1.0)
(s1366 1.0)
(s1367 1.0)
(s1368 1.0)
(s1369 1.0)
(s1370 1.0)
(s1371 1.0)
(s1372 1.0)
(s1373 1.0)
(s1374 1.0)
(s1375 1.0)
(s1376 1.0)
(s1377 1.0)
(s1378 1.0)
(s1379 1.0)
(s1380 1.0)
(s1381 1.0)
(s1382 1.0)
(s1383 1.0)
(s1384 1.0)
(s1385 1.0)
(s1386 1.0)
(s1387 1.0)
(s1388 1.0)
(s1389 1.0)
(s1390 1.0)
(s1391 1.0)
(s1392 1.0)
(s1393 1.0)
(s1394 1.0)
(s1395 1.0)
(s1396 1.0)
(s1397 1.0)
(s1398 1.0)
(s1399 1.0)
(s1400 1.0)
(s1401 1.0)
(s1402 1.0)
(s1403 1.0)
(s1404 1.0)
(s1405 1.0)
(s1406 1.0)
(s1407 1.0)
(s1408 1.0)
(s1409 1.0)
(s1410 1.0)
(s1411 1.0)
(s1412 1.0)
(s1413 1.0)
(s1414 1.0)
(s1415 1.0)
(s1416 1.0)
(s1417 1.0)
(s1418 1.0)
(s1419 1.0)
(s1420 1.0)
(s1421 1.0)
(s1422 1.0)
(s1423 1.0)
(s1424 1.0)
(s1425 1.0)
(s1426 1.0)
(s1427 1.0)
(s1428 1.0)
(s1429 1.0)
(s1430 1.0)
(s1431 1.0)
(s1432 1.0)
(s1433 1.0)
(s1434 1.0)
(s1435 1.0)
(s1436 1.0)
(s1437 1.0)
(s1438 1.0)
(s1439 1.0)
(s1440 1.0)
(s1441 1.0)
(s1442 1.0)
(s1443 1.0)
(s1444 1.0)
(s1445 1.0)
(s1446 1.0)
(s1447 1.0)
(s1448 1.0)
(s1449 1.0)
(s1450 1.0)
(s1451 1.0)
(s1452 1.0)
(s1453 1.0)
(s1454 1.0)
(s1455 1.0)
(s1456 1.0)
(s1457 1.0)
(s1458 1.0)
(s1459 1.0)
(s1460 1.0)
(s1461 1.0)
(s1462 1.0)
(s1463 1.0)
(s1464 1.0)
(s1465 1.0)
(s1466 1.0)
(s1467 1.0)
(s1468 1.0)
(s1469 1.0)
(s1470 1.0)
(s1471 1.0)
(s1472 1.0)
(s1473 1.0)
(s1474 1.0)
(s1475 1.0)
(s1476 1.0)
(s1477 1.0)
(s1478 1.0)
(s1479 1.0)
(s1480 1.0)
(s1481 1.0)
(s1482 1.0)
(s1483 1.0)
(s1484 1.0)
(s1485 1.0)
(s1486 1.0)
(s1487 1.0)
(s1488 1.0)
(s1489 1.0)
(s1490 1.0)
(s1491 1.0)
(s1492 1.0)
(s1493 1.0)
(s1494 1.0)
(s1495 1.0)
(s1496 1.0)
(s1497 1.0)
(s1498 1.0)
(s1499 1.0)
(s1500 1.0)
(s1501 1.0)
(s1502 1.0)
(s1503 1.0)
(s1504 1.0)
(s1505 1.0)
(s1506 1.0)
(s1507 1.0)
(s1508 1.0)
(s1509 1.0)
(s1510 1.0)
(s1511 1.0)
(s1512 1.0)
(s1513 1.0)
(s1514 1.0)
(s1515 1.0)
(s1516 1.0)
(s1517 1.0)
(s1518 1.0)
(s1519 1.0)
(s1520 1.0)
(s1521 1.0)
(s1522 1.0)
(s1523 1.0)
(s1524 1.0)
(s1525 1.0)
(s1526 1.0)
(s1527 1.0)
(s1528 1.0)
(s1529 1.0)
(s1530 1.0)
(s1531 1.0)
(s1532 1.0)
(s1533 1.0)
(s1534 1.0)
(s1535 1.0)
(s1536 1.0)
(s1537 1.0)
(s1538 1.0)
(s1539 1.0)
(s1540 1.0)
(s1541 1.0)
(s1542 1.0)
(s1543 1.0)
(s1544 1.0)
(s1545 1.0)
(s1546 1.0)
(s1547 1.0)
(s1548 1.0)
(s1549 1.0)
(s1550 1.0)
(s1551 1.0)
(s1552 1.0)
(s1553 1.0)
(s1554 1.0)
(s1555 1.0)
(s1556 1.0)
(s1557 1.0)
(s1558 1.0)
(s1559 1.0)
(s1560 1.0)
(s1561 1.0)
(s1562 1.0)
(s1563 1.0)
(s1564 1.0)
(s1565 1.0)
(s1566 1.0)
(s1567 1.0)
(s1568 1.0)
(s1569 1.0)
(s1570 1.0)
(s1571 1.0)
(s1572 1.0)
(s1573 1.0)
(s1574 1.0)
(s1575 1.0)
(s1576 1.0)
(s1577 1.0)
(s1578 1.0)
(s1579 1.0)
(s1580 1.0)
(s1581 1.0)
(s1582 1.0)
(s1583 1.0)
(s1584 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30087 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2917/5838 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30087 ms.
Refiners :[State Equation: 0/2918 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61446ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61498ms
Starting structural reductions in LTL mode, iteration 1 : 2918/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 68840 ms. Remains : 2918/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 273 ms :[(NOT p0), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-10
Product exploration explored 100000 steps with 50000 reset in 3109 ms.
Product exploration explored 100000 steps with 50000 reset in 3632 ms.
Computed a total of 2918 stabilizing places and 2920 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2918 transition count 2920
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND p0 p1), (X p0), (X (X p0)), (F (G p0)), (F (G p1))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 5 factoid took 38 ms. Reduced automaton from 5 states, 6 edges and 2 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-10 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-10 finished in 77586 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X((p0&&(G(F(p1))||F(G(p0))||G(p2)))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Discarding 50 places :
Symmetric choice reduction at 0 with 50 rule applications. Total rules 50 place count 2919 transition count 2920
Iterating global reduction 0 with 50 rules applied. Total rules applied 100 place count 2919 transition count 2920
Applied a total of 100 rules in 578 ms. Remains 2919 /2969 variables (removed 50) and now considering 2920/3013 (removed 93) transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 16:03:28] [INFO ] Invariants computation overflowed in 89 ms
[2024-05-31 16:03:31] [INFO ] Implicit Places using invariants in 2523 ms returned []
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 16:03:31] [INFO ] Invariants computation overflowed in 75 ms
[2024-05-31 16:03:36] [INFO ] Implicit Places using invariants and state equation in 5093 ms returned []
Implicit Place search using SMT with State Equation took 7619 ms to find 0 implicit places.
Running 2919 sub problems to find dead transitions.
// Phase 1: matrix 2920 rows 2919 cols
[2024-05-31 16:03:36] [INFO ] Invariants computation overflowed in 54 ms
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30081 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 2919/2919 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 2919 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 2918/5839 variables, and 0 constraints, problems are : Problem set: 0 solved, 2919 unsolved in 30082 ms.
Refiners :[State Equation: 0/2919 constraints, PredecessorRefiner: 0/2919 constraints, Known Traps: 0/0 constraints]
After SMT, in 61459ms problems are : Problem set: 0 solved, 2919 unsolved
Search for dead transitions found 0 dead transitions in 61491ms
Starting structural reductions in LTL mode, iteration 1 : 2919/2969 places, 2920/3013 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 69698 ms. Remains : 2919/2969 places, 2920/3013 transitions.
Stuttering acceptance computed with spot in 305 ms :[(NOT p0), (NOT p0), true, (AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1) (NOT p2)), (AND (NOT p0) (NOT p1))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-12
Product exploration explored 100000 steps with 827 reset in 3020 ms.
Product exploration explored 100000 steps with 826 reset in 3725 ms.
Computed a total of 2919 stabilizing places and 2920 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 2919 transition count 2920
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND p0 p2 (NOT p1)), (X p2), (X p0), (X (NOT (AND p0 (NOT p2)))), (X (AND p0 p2)), (X (X (NOT (AND (NOT p0) (NOT p1))))), (X (X (NOT (AND (NOT p0) (NOT p2) (NOT p1))))), (X (X p2)), (X (X p0)), (X (X (NOT p1))), (F (G p0)), (F (G p2)), (F (G (NOT p1)))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 13 factoid took 16 ms. Reduced automaton from 6 states, 12 edges and 3 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-12 TRUE TECHNIQUES KNOWLEDGE
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-12 finished in 78365 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(G(((p1||(p2 U p3))&&p0))))'
Support contains 8 out of 2969 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Graph (complete) has 1842 edges and 2969 vertex of which 71 are kept as prefixes of interest. Removing 2898 places using SCC suffix rule.7 ms
Discarding 2898 places :
Also discarding 2900 output transitions
Drop transitions (Output transitions of discarded places.) removed 2900 transitions
Reduce places removed 1 places and 1 transitions.
Ensure Unique test removed 6 transitions
Reduce isomorphic transitions removed 6 transitions.
Iterating post reduction 0 with 6 rules applied. Total rules applied 7 place count 70 transition count 106
Discarding 7 places :
Symmetric choice reduction at 1 with 7 rule applications. Total rules 14 place count 63 transition count 90
Iterating global reduction 1 with 7 rules applied. Total rules applied 21 place count 63 transition count 90
Applied a total of 21 rules in 17 ms. Remains 63 /2969 variables (removed 2906) and now considering 90/3013 (removed 2923) transitions.
// Phase 1: matrix 90 rows 63 cols
[2024-05-31 16:04:46] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 16:04:46] [INFO ] Implicit Places using invariants in 45 ms returned []
[2024-05-31 16:04:46] [INFO ] Invariant cache hit.
[2024-05-31 16:04:46] [INFO ] Implicit Places using invariants and state equation in 67 ms returned []
Implicit Place search using SMT with State Equation took 114 ms to find 0 implicit places.
[2024-05-31 16:04:46] [INFO ] Redundant transitions in 18 ms returned [5, 38, 42, 59]
Found 4 redundant transitions using SMT.
Drop transitions (Redundant Transitions using SMT with State Equation) removed 4 transitions
Redundant transitions reduction (with SMT) removed 4 transitions.
Running 70 sub problems to find dead transitions.
// Phase 1: matrix 86 rows 63 cols
[2024-05-31 16:04:46] [INFO ] Computed 0 invariants in 1 ms
At refinement iteration 0 (INCLUDED_ONLY) 0/59 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 1 (OVERLAPS) 83/142 variables, 59/59 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/142 variables, 0/59 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 3 (OVERLAPS) 6/148 variables, 3/62 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/148 variables, 0/62 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 5 (OVERLAPS) 1/149 variables, 1/63 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/149 variables, 0/63 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 7 (OVERLAPS) 0/149 variables, 0/63 constraints. Problems are: Problem set: 0 solved, 70 unsolved
No progress, stopping.
After SMT solving in domain Real declared 149/149 variables, and 63 constraints, problems are : Problem set: 0 solved, 70 unsolved in 2287 ms.
Refiners :[State Equation: 63/63 constraints, PredecessorRefiner: 70/70 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 70 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/59 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 1 (OVERLAPS) 83/142 variables, 59/59 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/142 variables, 70/129 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/142 variables, 0/129 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 4 (OVERLAPS) 6/148 variables, 3/132 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/148 variables, 0/132 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 6 (OVERLAPS) 1/149 variables, 1/133 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/149 variables, 0/133 constraints. Problems are: Problem set: 0 solved, 70 unsolved
At refinement iteration 8 (OVERLAPS) 0/149 variables, 0/133 constraints. Problems are: Problem set: 0 solved, 70 unsolved
No progress, stopping.
After SMT solving in domain Int declared 149/149 variables, and 133 constraints, problems are : Problem set: 0 solved, 70 unsolved in 2327 ms.
Refiners :[State Equation: 63/63 constraints, PredecessorRefiner: 70/70 constraints, Known Traps: 0/0 constraints]
After SMT, in 4622ms problems are : Problem set: 0 solved, 70 unsolved
Search for dead transitions found 0 dead transitions in 4622ms
Starting structural reductions in SI_LTL mode, iteration 1 : 63/2969 places, 86/3013 transitions.
Graph (complete) has 35 edges and 63 vertex of which 59 are kept as prefixes of interest. Removing 4 places using SCC suffix rule.0 ms
Discarding 4 places :
Also discarding 4 output transitions
Drop transitions (Output transitions of discarded places.) removed 4 transitions
Applied a total of 1 rules in 5 ms. Remains 59 /63 variables (removed 4) and now considering 82/86 (removed 4) transitions.
// Phase 1: matrix 82 rows 59 cols
[2024-05-31 16:04:51] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 16:04:51] [INFO ] Implicit Places using invariants in 48 ms returned []
[2024-05-31 16:04:51] [INFO ] Invariant cache hit.
[2024-05-31 16:04:51] [INFO ] Implicit Places using invariants and state equation in 105 ms returned []
Implicit Place search using SMT with State Equation took 154 ms to find 0 implicit places.
Starting structural reductions in SI_LTL mode, iteration 2 : 59/2969 places, 82/3013 transitions.
Finished structural reductions in SI_LTL mode , in 2 iterations and 4936 ms. Remains : 59/2969 places, 82/3013 transitions.
Stuttering acceptance computed with spot in 143 ms :[(OR (NOT p0) (AND (NOT p1) (NOT p3))), (OR (AND (NOT p0) (NOT p3)) (AND (NOT p1) (NOT p3)))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-13
Stuttering criterion allowed to conclude after 34 steps with 0 reset in 0 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-13 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-13 finished in 5100 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((p0||G((F(p2)&&F(p3)&&p1)))))'
Support contains 6 out of 2969 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Graph (complete) has 1842 edges and 2969 vertex of which 56 are kept as prefixes of interest. Removing 2913 places using SCC suffix rule.8 ms
Discarding 2913 places :
Also discarding 2929 output transitions
Drop transitions (Output transitions of discarded places.) removed 2929 transitions
Reduce places removed 1 places and 1 transitions.
Ensure Unique test removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 0 with 1 rules applied. Total rules applied 2 place count 55 transition count 82
Discarding 7 places :
Symmetric choice reduction at 1 with 7 rule applications. Total rules 9 place count 48 transition count 67
Iterating global reduction 1 with 7 rules applied. Total rules applied 16 place count 48 transition count 67
Applied a total of 16 rules in 20 ms. Remains 48 /2969 variables (removed 2921) and now considering 67/3013 (removed 2946) transitions.
// Phase 1: matrix 67 rows 48 cols
[2024-05-31 16:04:51] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 16:04:51] [INFO ] Implicit Places using invariants in 40 ms returned []
[2024-05-31 16:04:51] [INFO ] Invariant cache hit.
[2024-05-31 16:04:51] [INFO ] Implicit Places using invariants and state equation in 84 ms returned []
Implicit Place search using SMT with State Equation took 127 ms to find 0 implicit places.
[2024-05-31 16:04:51] [INFO ] Redundant transitions in 20 ms returned [2, 18, 58]
Found 3 redundant transitions using SMT.
Drop transitions (Redundant Transitions using SMT with State Equation) removed 3 transitions
Redundant transitions reduction (with SMT) removed 3 transitions.
Running 56 sub problems to find dead transitions.
// Phase 1: matrix 64 rows 48 cols
[2024-05-31 16:04:51] [INFO ] Computed 0 invariants in 1 ms
At refinement iteration 0 (INCLUDED_ONLY) 0/45 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 1 (OVERLAPS) 61/106 variables, 45/45 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/106 variables, 0/45 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 3 (OVERLAPS) 2/108 variables, 1/46 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/108 variables, 0/46 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 5 (OVERLAPS) 2/110 variables, 1/47 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/110 variables, 0/47 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 7 (OVERLAPS) 0/110 variables, 0/47 constraints. Problems are: Problem set: 0 solved, 56 unsolved
No progress, stopping.
After SMT solving in domain Real declared 110/112 variables, and 47 constraints, problems are : Problem set: 0 solved, 56 unsolved in 1609 ms.
Refiners :[State Equation: 47/48 constraints, PredecessorRefiner: 56/56 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 56 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/45 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 1 (OVERLAPS) 61/106 variables, 45/45 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/106 variables, 56/101 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/106 variables, 0/101 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 4 (OVERLAPS) 2/108 variables, 1/102 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/108 variables, 0/102 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 6 (OVERLAPS) 2/110 variables, 1/103 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/110 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 56 unsolved
At refinement iteration 8 (OVERLAPS) 0/110 variables, 0/103 constraints. Problems are: Problem set: 0 solved, 56 unsolved
No progress, stopping.
After SMT solving in domain Int declared 110/112 variables, and 103 constraints, problems are : Problem set: 0 solved, 56 unsolved in 1710 ms.
Refiners :[State Equation: 47/48 constraints, PredecessorRefiner: 56/56 constraints, Known Traps: 0/0 constraints]
After SMT, in 3334ms problems are : Problem set: 0 solved, 56 unsolved
Search for dead transitions found 0 dead transitions in 3335ms
Starting structural reductions in SI_LTL mode, iteration 1 : 48/2969 places, 64/3013 transitions.
Graph (complete) has 28 edges and 48 vertex of which 45 are kept as prefixes of interest. Removing 3 places using SCC suffix rule.0 ms
Discarding 3 places :
Also discarding 3 output transitions
Drop transitions (Output transitions of discarded places.) removed 3 transitions
Applied a total of 1 rules in 2 ms. Remains 45 /48 variables (removed 3) and now considering 61/64 (removed 3) transitions.
// Phase 1: matrix 61 rows 45 cols
[2024-05-31 16:04:55] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 16:04:55] [INFO ] Implicit Places using invariants in 42 ms returned []
[2024-05-31 16:04:55] [INFO ] Invariant cache hit.
[2024-05-31 16:04:55] [INFO ] Implicit Places using invariants and state equation in 83 ms returned []
Implicit Place search using SMT with State Equation took 127 ms to find 0 implicit places.
Starting structural reductions in SI_LTL mode, iteration 2 : 45/2969 places, 61/3013 transitions.
Finished structural reductions in SI_LTL mode , in 2 iterations and 3639 ms. Remains : 45/2969 places, 61/3013 transitions.
Stuttering acceptance computed with spot in 176 ms :[(OR (AND (NOT p0) (NOT p1)) (AND (NOT p0) (NOT p2)) (AND (NOT p0) (NOT p3))), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p3))]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-14
Stuttering criterion allowed to conclude after 28 steps with 0 reset in 0 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-14 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-14 finished in 3841 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202405141337/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!((F(p0)||G((p1||G(p2)))))'
Support contains 4 out of 2969 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 2969/2969 places, 3013/3013 transitions.
Graph (complete) has 1842 edges and 2969 vertex of which 41 are kept as prefixes of interest. Removing 2928 places using SCC suffix rule.8 ms
Discarding 2928 places :
Also discarding 2950 output transitions
Drop transitions (Output transitions of discarded places.) removed 2950 transitions
Reduce places removed 1 places and 1 transitions.
Ensure Unique test removed 3 transitions
Reduce isomorphic transitions removed 3 transitions.
Iterating post reduction 0 with 3 rules applied. Total rules applied 4 place count 40 transition count 59
Discarding 4 places :
Symmetric choice reduction at 1 with 4 rule applications. Total rules 8 place count 36 transition count 51
Iterating global reduction 1 with 4 rules applied. Total rules applied 12 place count 36 transition count 51
Applied a total of 12 rules in 17 ms. Remains 36 /2969 variables (removed 2933) and now considering 51/3013 (removed 2962) transitions.
// Phase 1: matrix 51 rows 36 cols
[2024-05-31 16:04:55] [INFO ] Computed 0 invariants in 1 ms
[2024-05-31 16:04:55] [INFO ] Implicit Places using invariants in 33 ms returned []
[2024-05-31 16:04:55] [INFO ] Invariant cache hit.
[2024-05-31 16:04:55] [INFO ] Implicit Places using invariants and state equation in 64 ms returned []
Implicit Place search using SMT with State Equation took 109 ms to find 0 implicit places.
[2024-05-31 16:04:55] [INFO ] Redundant transitions in 18 ms returned [8, 18]
Found 2 redundant transitions using SMT.
Drop transitions (Redundant Transitions using SMT with State Equation) removed 2 transitions
Redundant transitions reduction (with SMT) removed 2 transitions.
Running 38 sub problems to find dead transitions.
// Phase 1: matrix 49 rows 36 cols
[2024-05-31 16:04:55] [INFO ] Computed 0 invariants in 0 ms
At refinement iteration 0 (INCLUDED_ONLY) 0/32 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 1 (OVERLAPS) 45/77 variables, 32/32 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/77 variables, 0/32 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 3 (OVERLAPS) 4/81 variables, 2/34 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/81 variables, 0/34 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 5 (OVERLAPS) 2/83 variables, 1/35 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/83 variables, 0/35 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 7 (OVERLAPS) 2/85 variables, 1/36 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 8 (INCLUDED_ONLY) 0/85 variables, 0/36 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 9 (OVERLAPS) 0/85 variables, 0/36 constraints. Problems are: Problem set: 0 solved, 38 unsolved
No progress, stopping.
After SMT solving in domain Real declared 85/85 variables, and 36 constraints, problems are : Problem set: 0 solved, 38 unsolved in 1168 ms.
Refiners :[State Equation: 36/36 constraints, PredecessorRefiner: 38/38 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 38 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/32 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 1 (OVERLAPS) 45/77 variables, 32/32 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/77 variables, 38/70 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/77 variables, 0/70 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 4 (OVERLAPS) 4/81 variables, 2/72 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/81 variables, 0/72 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 6 (OVERLAPS) 2/83 variables, 1/73 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/83 variables, 0/73 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 8 (OVERLAPS) 2/85 variables, 1/74 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 9 (INCLUDED_ONLY) 0/85 variables, 0/74 constraints. Problems are: Problem set: 0 solved, 38 unsolved
At refinement iteration 10 (OVERLAPS) 0/85 variables, 0/74 constraints. Problems are: Problem set: 0 solved, 38 unsolved
No progress, stopping.
After SMT solving in domain Int declared 85/85 variables, and 74 constraints, problems are : Problem set: 0 solved, 38 unsolved in 1099 ms.
Refiners :[State Equation: 36/36 constraints, PredecessorRefiner: 38/38 constraints, Known Traps: 0/0 constraints]
After SMT, in 2276ms problems are : Problem set: 0 solved, 38 unsolved
Search for dead transitions found 0 dead transitions in 2277ms
Starting structural reductions in SI_LTL mode, iteration 1 : 36/2969 places, 49/3013 transitions.
Graph (complete) has 20 edges and 36 vertex of which 34 are kept as prefixes of interest. Removing 2 places using SCC suffix rule.1 ms
Discarding 2 places :
Also discarding 2 output transitions
Drop transitions (Output transitions of discarded places.) removed 2 transitions
Applied a total of 1 rules in 2 ms. Remains 34 /36 variables (removed 2) and now considering 47/49 (removed 2) transitions.
// Phase 1: matrix 47 rows 34 cols
[2024-05-31 16:04:57] [INFO ] Computed 0 invariants in 0 ms
[2024-05-31 16:04:57] [INFO ] Implicit Places using invariants in 36 ms returned []
[2024-05-31 16:04:57] [INFO ] Invariant cache hit.
[2024-05-31 16:04:57] [INFO ] Implicit Places using invariants and state equation in 68 ms returned []
Implicit Place search using SMT with State Equation took 106 ms to find 0 implicit places.
Starting structural reductions in SI_LTL mode, iteration 2 : 34/2969 places, 47/3013 transitions.
Finished structural reductions in SI_LTL mode , in 2 iterations and 2535 ms. Remains : 34/2969 places, 47/3013 transitions.
Stuttering acceptance computed with spot in 162 ms :[(AND (NOT p0) (NOT p1) (NOT p2)), (AND (NOT p0) (NOT p2)), (NOT p0)]
Running random walk in product with property : ViralEpidemic-PT-S03D1C1A06-LTLFireability-15
Stuttering criterion allowed to conclude after 13 steps with 0 reset in 0 ms.
FORMULA ViralEpidemic-PT-S03D1C1A06-LTLFireability-15 FALSE TECHNIQUES STUTTER_TEST
Treatment of property ViralEpidemic-PT-S03D1C1A06-LTLFireability-15 finished in 2718 ms.
All properties solved by simple procedures.
Total runtime 910335 ms.
BK_STOP 1717171498535
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
+ BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ LTLFireability = StateSpace ]]
+ /home/mcc/BenchKit/bin//../itstools/bin//..//runeclipse.sh /home/mcc/execution LTLFireability -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202405141337.jar
+ VERSION=202405141337
+ echo 'Running Version 202405141337'
+ /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/its-tools -pnfolder /home/mcc/execution -examination LTLFireability -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="ViralEpidemic-PT-S03D1C1A06"
export BK_EXAMINATION="LTLFireability"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool itstools"
echo " Input is ViralEpidemic-PT-S03D1C1A06, examination is LTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r444-smll-171701111300332"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/ViralEpidemic-PT-S03D1C1A06.tgz
mv ViralEpidemic-PT-S03D1C1A06 execution
cd execution
if [ "LTLFireability" = "ReachabilityDeadlock" ] || [ "LTLFireability" = "UpperBounds" ] || [ "LTLFireability" = "QuasiLiveness" ] || [ "LTLFireability" = "StableMarking" ] || [ "LTLFireability" = "Liveness" ] || [ "LTLFireability" = "OneSafe" ] || [ "LTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "LTLFireability" = "ReachabilityDeadlock" ] || [ "LTLFireability" = "QuasiLiveness" ] || [ "LTLFireability" = "StableMarking" ] || [ "LTLFireability" = "Liveness" ] || [ "LTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME LTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

