About the Execution of 2023-gold for NeoElection-PT-6
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 502.703 | 20829.00 | 33429.00 | 957.30 | FTFFTFFFFFFTTTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
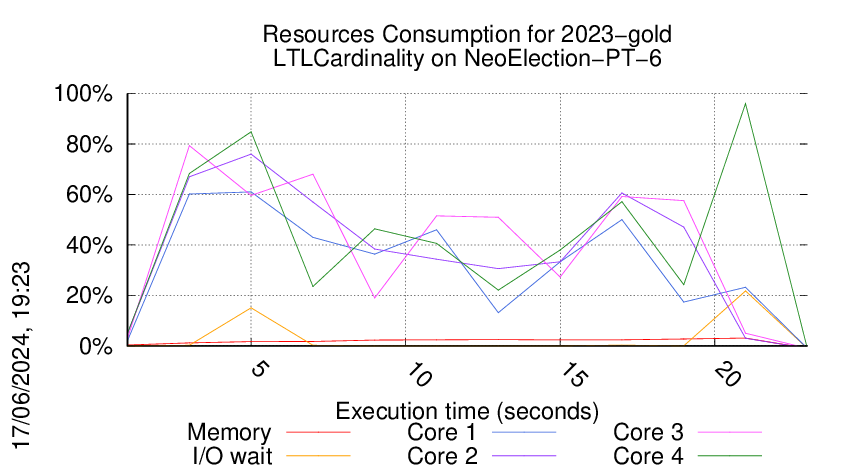
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r263-tall-171654372600332.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.............................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool gold2023
Input is NeoElection-PT-6, examination is LTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r263-tall-171654372600332
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 23M
-rw-r--r-- 1 mcc users 420K Apr 11 19:45 CTLCardinality.txt
-rw-r--r-- 1 mcc users 1.4M Apr 11 19:45 CTLCardinality.xml
-rw-r--r-- 1 mcc users 812K Apr 11 19:27 CTLFireability.txt
-rw-r--r-- 1 mcc users 2.7M Apr 11 19:27 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 18 16:43 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.6K May 18 16:43 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 236K Apr 23 07:40 LTLCardinality.txt
-rw-r--r-- 1 mcc users 585K Apr 23 07:40 LTLCardinality.xml
-rw-r--r-- 1 mcc users 164K Apr 23 07:41 LTLFireability.txt
-rw-r--r-- 1 mcc users 447K Apr 23 07:41 LTLFireability.xml
-rw-r--r-- 1 mcc users 1.6M Apr 11 21:10 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 5.1M Apr 11 21:10 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 514K Apr 11 20:29 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 1.5M Apr 11 20:29 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 62K Apr 23 07:41 UpperBounds.txt
-rw-r--r-- 1 mcc users 109K Apr 23 07:41 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 May 18 16:43 equiv_col
-rw-r--r-- 1 mcc users 2 May 18 16:43 instance
-rw-r--r-- 1 mcc users 6 May 18 16:43 iscolored
-rw-r--r-- 1 mcc users 7.5M May 18 16:43 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-6-LTLCardinality-00
FORMULA_NAME NeoElection-PT-6-LTLCardinality-01
FORMULA_NAME NeoElection-PT-6-LTLCardinality-02
FORMULA_NAME NeoElection-PT-6-LTLCardinality-03
FORMULA_NAME NeoElection-PT-6-LTLCardinality-04
FORMULA_NAME NeoElection-PT-6-LTLCardinality-05
FORMULA_NAME NeoElection-PT-6-LTLCardinality-06
FORMULA_NAME NeoElection-PT-6-LTLCardinality-07
FORMULA_NAME NeoElection-PT-6-LTLCardinality-08
FORMULA_NAME NeoElection-PT-6-LTLCardinality-09
FORMULA_NAME NeoElection-PT-6-LTLCardinality-10
FORMULA_NAME NeoElection-PT-6-LTLCardinality-11
FORMULA_NAME NeoElection-PT-6-LTLCardinality-12
FORMULA_NAME NeoElection-PT-6-LTLCardinality-13
FORMULA_NAME NeoElection-PT-6-LTLCardinality-14
FORMULA_NAME NeoElection-PT-6-LTLCardinality-15
=== Now, execution of the tool begins
BK_START 1716688357958
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=gold2023
BK_EXAMINATION=LTLCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=NeoElection-PT-6
Not applying reductions.
Model is PT
LTLCardinality PT
Running Version 202304061127
[2024-05-26 01:52:39] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, LTLCardinality, -its, -ltsmin, -greatspnpath, /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/, -order, META, -manyOrder, -smt, -timeout, 3600]
[2024-05-26 01:52:39] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-05-26 01:52:39] [INFO ] Load time of PNML (sax parser for PT used): 343 ms
[2024-05-26 01:52:39] [INFO ] Transformed 4830 places.
[2024-05-26 01:52:39] [INFO ] Transformed 8435 transitions.
[2024-05-26 01:52:39] [INFO ] Found NUPN structural information;
[2024-05-26 01:52:40] [INFO ] Completing missing partition info from NUPN : creating a component with [P_crashed_0, P_crashed_1, P_crashed_2, P_crashed_3, P_crashed_4, P_crashed_5, P_crashed_6, P_dead_0, P_dead_1, P_dead_2, P_dead_3, P_dead_4, P_dead_5, P_dead_6, P_electedPrimary_0, P_electedPrimary_1, P_electedPrimary_2, P_electedPrimary_3, P_electedPrimary_4, P_electedPrimary_5, P_electedPrimary_6, P_electedSecondary_0, P_electedSecondary_1, P_electedSecondary_2, P_electedSecondary_3, P_electedSecondary_4, P_electedSecondary_5, P_electedSecondary_6, P_electionFailed_0, P_electionFailed_1, P_electionFailed_2, P_electionFailed_3, P_electionFailed_4, P_electionFailed_5, P_electionFailed_6, P_electionInit_0, P_electionInit_1, P_electionInit_2, P_electionInit_3, P_electionInit_4, P_electionInit_5, P_electionInit_6, P_masterList_0_1_0, P_masterList_0_1_1, P_masterList_0_1_2, P_masterList_0_1_3, P_masterList_0_1_4, P_masterList_0_1_5, P_masterList_0_1_6, P_masterList_0_2_0, P_masterList_0_2_1, P_masterList_0_2_2, P_masterList_0_2_3, P_masterList_0_2_4, P_masterList_0_2_5, P_masterList_0_2_6, P_masterList_0_3_0, P_masterList_0_3_1, P_masterList_0_3_2, P_masterList_0_3_3, P_masterList_0_3_4, P_masterList_0_3_5, P_masterList_0_3_6, P_masterList_0_4_0, P_masterList_0_4_1, P_masterList_0_4_2, P_masterList_0_4_3, P_masterList_0_4_4, P_masterList_0_4_5, P_masterList_0_4_6, P_masterList_0_5_0, P_masterList_0_5_1, P_masterList_0_5_2, P_masterList_0_5_3, P_masterList_0_5_4, P_masterList_0_5_5, P_masterList_0_5_6, P_masterList_0_6_0, P_masterList_0_6_1, P_masterList_0_6_2, P_masterList_0_6_3, P_masterList_0_6_4, P_masterList_0_6_5, P_masterList_0_6_6, P_masterList_1_1_0, P_masterList_1_1_1, P_masterList_1_1_2, P_masterList_1_1_3, P_masterList_1_1_4, P_masterList_1_1_5, P_masterList_1_1_6, P_masterList_1_2_0, P_masterList_1_2_1, P_masterList_1_2_2, P_masterList_1_2_3, P_masterList_1_2_4, P_masterList_1_2_5, P_masterList_1_2_6, P_masterList_1_3_0, P_masterList_1_3_1, P_masterList_1_3_2, P_masterList_1_3_3, P_masterList_1_3_4, P_masterList_1_3_5, P_masterList_1_3_6, P_masterList_1_4_0, P_masterList_1_4_1, P_masterList_1_4_2, P_masterList_1_4_3, P_masterList_1_4_4, P_masterList_1_4_5, P_masterList_1_4_6, P_masterList_1_5_0, P_masterList_1_5_1, P_masterList_1_5_2, P_masterList_1_5_3, P_masterList_1_5_4, P_masterList_1_5_5, P_masterList_1_5_6, P_masterList_1_6_0, P_masterList_1_6_1, P_masterList_1_6_2, P_masterList_1_6_3, P_masterList_1_6_4, P_masterList_1_6_5, P_masterList_1_6_6, P_masterList_2_1_0, P_masterList_2_1_1, P_masterList_2_1_2, P_masterList_2_1_3, P_masterList_2_1_4, P_masterList_2_1_5, P_masterList_2_1_6, P_masterList_2_2_0, P_masterList_2_2_1, P_masterList_2_2_2, P_masterList_2_2_3, P_masterList_2_2_4, P_masterList_2_2_5, P_masterList_2_2_6, P_masterList_2_3_0, P_masterList_2_3_1, P_masterList_2_3_2, P_masterList_2_3_3, P_masterList_2_3_4, P_masterList_2_3_5, P_masterList_2_3_6, P_masterList_2_4_0, P_masterList_2_4_1, P_masterList_2_4_2, P_masterList_2_4_3, P_masterList_2_4_4, P_masterList_2_4_5, P_masterList_2_4_6, P_masterList_2_5_0, P_masterList_2_5_1, P_masterList_2_5_2, P_masterList_2_5_3, P_masterList_2_5_4, P_masterList_2_5_5, P_masterList_2_5_6, P_masterList_2_6_0, P_masterList_2_6_1, P_masterList_2_6_2, P_masterList_2_6_3, P_masterList_2_6_4, P_masterList_2_6_5, P_masterList_2_6_6, P_masterList_3_1_0, P_masterList_3_1_1, P_masterList_3_1_2, P_masterList_3_1_3, P_masterList_3_1_4, P_masterList_3_1_5, P_masterList_3_1_6, P_masterList_3_2_0, P_masterList_3_2_1, P_masterList_3_2_2, P_masterList_3_2_3, P_masterList_3_2_4, P_masterList_3_2_5, P_masterList_3_2_6, P_masterList_3_3_0, P_masterList_3_3_1, P_masterList_3_3_2, P_masterList_3_3_3, P_masterList_3_3_4, P_masterList_3_3_5, P_masterList_3_3_6, P_masterList_3_4_0, P_masterList_3_4_1, P_masterList_3_4_2, P_masterList_3_4_3, P_masterList_3_4_4, P_masterList_3_4_5, P_masterList_3_4_6, P_masterList_3_5_0, P_masterList_3_5_1, P_masterList_3_5_2, P_masterList_3_5_3, P_masterList_3_5_4, P_masterList_3_5_5, P_masterList_3_5_6, P_masterList_3_6_0, P_masterList_3_6_1, P_masterList_3_6_2, P_masterList_3_6_3, P_masterList_3_6_4, P_masterList_3_6_5, P_masterList_3_6_6, P_masterList_4_1_0, P_masterList_4_1_1, P_masterList_4_1_2, P_masterList_4_1_3, P_masterList_4_1_4, P_masterList_4_1_5, P_masterList_4_1_6, P_masterList_4_2_0, P_masterList_4_2_1, P_masterList_4_2_2, P_masterList_4_2_3, P_masterList_4_2_4, P_masterList_4_2_5, P_masterList_4_2_6, P_masterList_4_3_0, P_masterList_4_3_1, P_masterList_4_3_2, P_masterList_4_3_3, P_masterList_4_3_4, P_masterList_4_3_5, P_masterList_4_3_6, P_masterList_4_4_0, P_masterList_4_4_1, P_masterList_4_4_2, P_masterList_4_4_3, P_masterList_4_4_4, P_masterList_4_4_5, P_masterList_4_4_6, P_masterList_4_5_0, P_masterList_4_5_1, P_masterList_4_5_2, P_masterList_4_5_3, P_masterList_4_5_4, P_masterList_4_5_5, P_masterList_4_5_6, P_masterList_4_6_0, P_masterList_4_6_1, P_masterList_4_6_2, P_masterList_4_6_3, P_masterList_4_6_4, P_masterList_4_6_5, P_masterList_4_6_6, P_masterList_5_1_0, P_masterList_5_1_1, P_masterList_5_1_2, P_masterList_5_1_3, P_masterList_5_1_4, P_masterList_5_1_5, P_masterList_5_1_6, P_masterList_5_2_0, P_masterList_5_2_1, P_masterList_5_2_2, P_masterList_5_2_3, P_masterList_5_2_4, P_masterList_5_2_5, P_masterList_5_2_6, P_masterList_5_3_0, P_masterList_5_3_1, P_masterList_5_3_2, P_masterList_5_3_3, P_masterList_5_3_4, P_masterList_5_3_5, P_masterList_5_3_6, P_masterList_5_4_0, P_masterList_5_4_1, P_masterList_5_4_2, P_masterList_5_4_3, P_masterList_5_4_4, P_masterList_5_4_5, P_masterList_5_4_6, P_masterList_5_5_0, P_masterList_5_5_1, P_masterList_5_5_2, P_masterList_5_5_3, P_masterList_5_5_4, P_masterList_5_5_5, P_masterList_5_5_6, P_masterList_5_6_0, P_masterList_5_6_1, P_masterList_5_6_2, P_masterList_5_6_3, P_masterList_5_6_4, P_masterList_5_6_5, P_masterList_5_6_6, P_masterList_6_1_0, P_masterList_6_1_1, P_masterList_6_1_2, P_masterList_6_1_3, P_masterList_6_1_4, P_masterList_6_1_5, P_masterList_6_1_6, P_masterList_6_2_0, P_masterList_6_2_1, P_masterList_6_2_2, P_masterList_6_2_3, P_masterList_6_2_4, P_masterList_6_2_5, P_masterList_6_2_6, P_masterList_6_3_0, P_masterList_6_3_1, P_masterList_6_3_2, P_masterList_6_3_3, P_masterList_6_3_4, P_masterList_6_3_5, P_masterList_6_3_6, P_masterList_6_4_0, P_masterList_6_4_1, P_masterList_6_4_2, P_masterList_6_4_3, P_masterList_6_4_4, P_masterList_6_4_5, P_masterList_6_4_6, P_masterList_6_5_0, P_masterList_6_5_1, P_masterList_6_5_2, P_masterList_6_5_3, P_masterList_6_5_4, P_masterList_6_5_5, P_masterList_6_5_6, P_masterList_6_6_0, P_masterList_6_6_1, P_masterList_6_6_2, P_masterList_6_6_3, P_masterList_6_6_4, P_masterList_6_6_5, P_masterList_6_6_6, P_masterState_0_F_0, P_masterState_0_F_1, P_masterState_0_F_2, P_masterState_0_F_3, P_masterState_0_F_4, P_masterState_0_F_5, P_masterState_0_F_6, P_masterState_0_T_0, P_masterState_0_T_1, P_masterState_0_T_2, P_masterState_0_T_3, P_masterState_0_T_4, P_masterState_0_T_5, P_masterState_0_T_6, P_masterState_1_F_0, P_masterState_1_F_1, P_masterState_1_F_2, P_masterState_1_F_3, P_masterState_1_F_4, P_masterState_1_F_5, P_masterState_1_F_6, P_masterState_1_T_0, P_masterState_1_T_1, P_masterState_1_T_2, P_masterState_1_T_3, P_masterState_1_T_4, P_masterState_1_T_5, P_masterState_1_T_6, P_masterState_2_F_0, P_masterState_2_F_1, P_masterState_2_F_2, P_masterState_2_F_3, P_masterState_2_F_4, P_masterState_2_F_5, P_masterState_2_F_6, P_masterState_2_T_0, P_masterState_2_T_1, P_masterState_2_T_2, P_masterState_2_T_3, P_masterState_2_T_4, P_masterState_2_T_5, P_masterState_2_T_6, P_masterState_3_F_0, P_masterState_3_F_1, P_masterState_3_F_2, P_masterState_3_F_3, P_masterState_3_F_4, P_masterState_3_F_5, P_masterState_3_F_6, P_masterState_3_T_0, P_masterState_3_T_1, P_masterState_3_T_2, P_masterState_3_T_3, P_masterState_3_T_4, P_masterState_3_T_5, P_masterState_3_T_6, P_masterState_4_F_0, P_masterState_4_F_1, P_masterState_4_F_2, P_masterState_4_F_3, P_masterState_4_F_4, P_masterState_4_F_5, P_masterState_4_F_6, P_masterState_4_T_0, P_masterState_4_T_1, P_masterState_4_T_2, P_masterState_4_T_3, P_masterState_4_T_4, P_masterState_4_T_5, P_masterState_4_T_6, P_masterState_5_F_0, P_masterState_5_F_1, P_masterState_5_F_2, P_masterState_5_F_3, P_masterState_5_F_4, P_masterState_5_F_5, P_masterState_5_F_6, P_masterState_5_T_0, P_masterState_5_T_1, P_masterState_5_T_2, P_masterState_5_T_3, P_masterState_5_T_4, P_masterState_5_T_5, P_masterState_5_T_6, P_masterState_6_F_0, P_masterState_6_F_1, P_masterState_6_F_2, P_masterState_6_F_3, P_masterState_6_F_4, P_masterState_6_F_5, P_masterState_6_F_6, P_masterState_6_T_0, P_masterState_6_T_1, P_masterState_6_T_2, P_masterState_6_T_3, P_masterState_6_T_4, P_masterState_6_T_5, P_masterState_6_T_6, P_negotiation_0_0_NONE, P_negotiation_0_0_CO, P_negotiation_0_0_DONE, P_negotiation_0_1_NONE, P_negotiation_0_1_CO, P_negotiation_0_1_DONE, P_negotiation_0_2_NONE, P_negotiation_0_2_CO, P_negotiation_0_2_DONE, P_negotiation_0_3_NONE, P_negotiation_0_3_CO, P_negotiation_0_3_DONE, P_negotiation_0_4_NONE, P_negotiation_0_4_CO, P_negotiation_0_4_DONE, P_negotiation_0_5_NONE, P_negotiation_0_5_CO, P_negotiation_0_5_DONE, P_negotiation_0_6_NONE, P_negotiation_0_6_CO, P_negotiation_0_6_DONE, P_negotiation_1_0_NONE, P_negotiation_1_0_CO, P_negotiation_1_0_DONE, P_negotiation_1_1_NONE, P_negotiation_1_1_CO, P_negotiation_1_1_DONE, P_negotiation_1_2_NONE, P_negotiation_1_2_CO, P_negotiation_1_2_DONE, P_negotiation_1_3_NONE, P_negotiation_1_3_CO, P_negotiation_1_3_DONE, P_negotiation_1_4_NONE, P_negotiation_1_4_CO, P_negotiation_1_4_DONE, P_negotiation_1_5_NONE, P_negotiation_1_5_CO, P_negotiation_1_5_DONE, P_negotiation_1_6_NONE, P_negotiation_1_6_CO, P_negotiation_1_6_DONE, P_negotiation_2_0_NONE, P_negotiation_2_0_CO, P_negotiation_2_0_DONE, P_negotiation_2_1_NONE, P_negotiation_2_1_CO, P_negotiation_2_1_DONE, P_negotiation_2_2_NONE, P_negotiation_2_2_CO, P_negotiation_2_2_DONE, P_negotiation_2_3_NONE, P_negotiation_2_3_CO, P_negotiation_2_3_DONE, P_negotiation_2_4_NONE, P_negotiation_2_4_CO, P_negotiation_2_4_DONE, P_negotiation_2_5_NONE, P_negotiation_2_5_CO, P_negotiation_2_5_DONE, P_negotiation_2_6_NONE, P_negotiation_2_6_CO, P_negotiation_2_6_DONE, P_negotiation_3_0_NONE, P_negotiation_3_0_CO, P_negotiation_3_0_DONE, P_negotiation_3_1_NONE, P_negotiation_3_1_CO, P_negotiation_3_1_DONE, P_negotiation_3_2_NONE, P_negotiation_3_2_CO, P_negotiation_3_2_DONE, P_negotiation_3_3_NONE, P_negotiation_3_3_CO, P_negotiation_3_3_DONE, P_negotiation_3_4_NONE, P_negotiation_3_4_CO, P_negotiation_3_4_DONE, P_negotiation_3_5_NONE, P_negotiation_3_5_CO, P_negotiation_3_5_DONE, P_negotiation_3_6_NONE, P_negotiation_3_6_CO, P_negotiation_3_6_DONE, P_negotiation_4_0_NONE, P_negotiation_4_0_CO, P_negotiation_4_0_DONE, P_negotiation_4_1_NONE, P_negotiation_4_1_CO, P_negotiation_4_1_DONE, P_negotiation_4_2_NONE, P_negotiation_4_2_CO, P_negotiation_4_2_DONE, P_negotiation_4_3_NONE, P_negotiation_4_3_CO, P_negotiation_4_3_DONE, P_negotiation_4_4_NONE, P_negotiation_4_4_CO, P_negotiation_4_4_DONE, P_negotiation_4_5_NONE, P_negotiation_4_5_CO, P_negotiation_4_5_DONE, P_negotiation_4_6_NONE, P_negotiation_4_6_CO, P_negotiation_4_6_DONE, P_negotiation_5_0_NONE, P_negotiation_5_0_CO, P_negotiation_5_0_DONE, P_negotiation_5_1_NONE, P_negotiation_5_1_CO, P_negotiation_5_1_DONE, P_negotiation_5_2_NONE, P_negotiation_5_2_CO, P_negotiation_5_2_DONE, P_negotiation_5_3_NONE, P_negotiation_5_3_CO, P_negotiation_5_3_DONE, P_negotiation_5_4_NONE, P_negotiation_5_4_CO, P_negotiation_5_4_DONE, P_negotiation_5_5_NONE, P_negotiation_5_5_CO, P_negotiation_5_5_DONE, P_negotiation_5_6_NONE, P_negotiation_5_6_CO, P_negotiation_5_6_DONE, P_negotiation_6_0_NONE, P_negotiation_6_0_CO, P_negotiation_6_0_DONE, P_negotiation_6_1_NONE, P_negotiation_6_1_CO, P_negotiation_6_1_DONE, P_negotiation_6_2_NONE, P_negotiation_6_2_CO, P_negotiation_6_2_DONE, P_negotiation_6_3_NONE, P_negotiation_6_3_CO, P_negotiation_6_3_DONE, P_negotiation_6_4_NONE, P_negotiation_6_4_CO, P_negotiation_6_4_DONE, P_negotiation_6_5_NONE, P_negotiation_6_5_CO, P_negotiation_6_5_DONE, P_negotiation_6_6_NONE, P_negotiation_6_6_CO, P_negotiation_6_6_DONE, P_network_0_0_AskP_0, P_network_0_0_AskP_1, P_network_0_0_AskP_2, P_network_0_0_AskP_3, P_network_0_0_AskP_4, P_network_0_0_AskP_5, P_network_0_0_AskP_6, P_network_0_0_AnsP_0, P_network_0_0_AnsP_1, P_network_0_0_AnsP_2, P_network_0_0_AnsP_3, P_network_0_0_AnsP_4, P_network_0_0_AnsP_5, P_network_0_0_AnsP_6, P_network_0_0_RI_0, P_network_0_0_RI_1, P_network_0_0_RI_2, P_network_0_0_RI_3, P_network_0_0_RI_4, P_network_0_0_RI_5, P_network_0_0_RI_6, P_network_0_0_AI_0, P_network_0_0_AI_1, P_network_0_0_AI_2, P_network_0_0_AI_3, P_network_0_0_AI_4, P_network_0_0_AI_5, P_network_0_0_AI_6, P_network_0_0_AnnP_0, P_network_0_0_AnnP_1, P_network_0_0_AnnP_2, P_network_0_0_AnnP_3, P_network_0_0_AnnP_4, P_network_0_0_AnnP_5, P_network_0_0_AnnP_6, P_network_0_0_RP_0, P_network_0_0_RP_1, P_network_0_0_RP_2, P_network_0_0_RP_3, P_network_0_0_RP_4, P_network_0_0_RP_5, P_network_0_0_RP_6, P_network_0_1_AskP_0, P_network_0_1_AskP_1, P_network_0_1_AskP_2, P_network_0_1_AskP_3, P_network_0_1_AskP_4, P_network_0_1_AskP_5, P_network_0_1_AskP_6, P_network_0_1_AnsP_0, P_network_0_1_AnsP_1, P_network_0_1_AnsP_2, P_network_0_1_AnsP_3, P_network_0_1_AnsP_4, P_network_0_1_AnsP_5, P_network_0_1_AnsP_6, P_network_0_1_RI_0, P_network_0_1_RI_1, P_network_0_1_RI_2, P_network_0_1_RI_3, P_network_0_1_RI_4, P_network_0_1_RI_5, P_network_0_1_RI_6, P_network_0_1_AI_0, P_network_0_1_AI_1, P_network_0_1_AI_2, P_network_0_1_AI_3, P_network_0_1_AI_4, P_network_0_1_AI_5, P_network_0_1_AI_6, P_network_0_1_AnnP_0, P_network_0_1_AnnP_1, P_network_0_1_AnnP_2, P_network_0_1_AnnP_3, P_network_0_1_AnnP_4, P_network_0_1_AnnP_5, P_network_0_1_AnnP_6, P_network_0_1_RP_0, P_network_0_1_RP_1, P_network_0_1_RP_2, P_network_0_1_RP_3, P_network_0_1_RP_4, P_network_0_1_RP_5, P_network_0_1_RP_6, P_network_0_2_AskP_0, P_network_0_2_AskP_1, P_network_0_2_AskP_2, P_network_0_2_AskP_3, P_network_0_2_AskP_4, P_network_0_2_AskP_5, P_network_0_2_AskP_6, P_network_0_2_AnsP_0, P_network_0_2_AnsP_1, P_network_0_2_AnsP_2, P_network_0_2_AnsP_3, P_network_0_2_AnsP_4, P_network_0_2_AnsP_5, P_network_0_2_AnsP_6, P_network_0_2_RI_0, P_network_0_2_RI_1, P_network_0_2_RI_2, P_network_0_2_RI_3, P_network_0_2_RI_4, P_network_0_2_RI_5, P_network_0_2_RI_6, P_network_0_2_AI_0, P_network_0_2_AI_1, P_network_0_2_AI_2, P_network_0_2_AI_3, P_network_0_2_AI_4, P_network_0_2_AI_5, P_network_0_2_AI_6, P_network_0_2_AnnP_0, P_network_0_2_AnnP_1, P_network_0_2_AnnP_2, P_network_0_2_AnnP_3, P_network_0_2_AnnP_4, P_network_0_2_AnnP_5, P_network_0_2_AnnP_6, P_network_0_2_RP_0, P_network_0_2_RP_1, P_network_0_2_RP_2, P_network_0_2_RP_3, P_network_0_2_RP_4, P_network_0_2_RP_5, P_network_0_2_RP_6, P_network_0_3_AskP_0, P_network_0_3_AskP_1, P_network_0_3_AskP_2, P_network_0_3_AskP_3, P_network_0_3_AskP_4, P_network_0_3_AskP_5, P_network_0_3_AskP_6, P_network_0_3_AnsP_0, P_network_0_3_AnsP_1, P_network_0_3_AnsP_2, P_network_0_3_AnsP_3, P_network_0_3_AnsP_4, P_network_0_3_AnsP_5, P_network_0_3_AnsP_6, P_network_0_3_RI_0, P_network_0_3_RI_1, P_network_0_3_RI_2, P_network_0_3_RI_3, P_network_0_3_RI_4, P_network_0_3_RI_5, P_network_0_3_RI_6, P_network_0_3_AI_0, P_network_0_3_AI_1, P_network_0_3_AI_2, P_network_0_3_AI_3, P_network_0_3_AI_4, P_network_0_3_AI_5, P_network_0_3_AI_6, P_network_0_3_AnnP_0, P_network_0_3_AnnP_1, P_network_0_3_AnnP_2, P_network_0_3_AnnP_3, P_network_0_3_AnnP_4, P_network_0_3_AnnP_5, P_network_0_3_AnnP_6, P_network_0_3_RP_0, P_network_0_3_RP_1, P_network_0_3_RP_2, P_network_0_3_RP_3, P_network_0_3_RP_4, P_network_0_3_RP_5, P_network_0_3_RP_6, P_network_0_4_AskP_0, P_network_0_4_AskP_1, P_network_0_4_AskP_2, P_network_0_4_AskP_3, P_network_0_4_AskP_4, P_network_0_4_AskP_5, P_network_0_4_AskP_6, P_network_0_4_AnsP_0, P_network_0_4_AnsP_1, P_network_0_4_AnsP_2, P_network_0_4_AnsP_3, P_network_0_4_AnsP_4, P_network_0_4_AnsP_5, P_network_0_4_AnsP_6, P_network_0_4_RI_0, P_network_0_4_RI_1, P_network_0_4_RI_2, P_network_0_4_RI_3, P_network_0_4_RI_4, P_network_0_4_RI_5, P_network_0_4_RI_6, P_network_0_4_AI_0, P_network_0_4_AI_1, P_network_0_4_AI_2, P_network_0_4_AI_3, P_network_0_4_AI_4, P_network_0_4_AI_5, P_network_0_4_AI_6, P_network_0_4_AnnP_0, P_network_0_4_AnnP_1, P_network_0_4_AnnP_2, P_network_0_4_AnnP_3, P_network_0_4_AnnP_4, P_network_0_4_AnnP_5, P_network_0_4_AnnP_6, P_network_0_4_RP_0, P_network_0_4_RP_1, P_network_0_4_RP_2, P_network_0_4_RP_3, P_network_0_4_RP_4, P_network_0_4_RP_5, P_network_0_4_RP_6, P_network_0_5_AskP_0, P_network_0_5_AskP_1, P_network_0_5_AskP_2, P_network_0_5_AskP_3, P_network_0_5_AskP_4, P_network_0_5_AskP_5, P_network_0_5_AskP_6, P_network_0_5_AnsP_0, P_network_0_5_AnsP_1, P_network_0_5_AnsP_2, P_network_0_5_AnsP_3, P_network_0_5_AnsP_4, P_network_0_5_AnsP_5, P_network_0_5_AnsP_6, P_network_0_5_RI_0, P_network_0_5_RI_1, P_network_0_5_RI_2, P_network_0_5_RI_3, P_network_0_5_RI_4, P_network_0_5_RI_5, P_network_0_5_RI_6, P_network_0_5_AI_0, P_network_0_5_AI_1, P_network_0_5_AI_2, P_network_0_5_AI_3, P_network_0_5_AI_4, P_network_0_5_AI_5, P_network_0_5_AI_6, P_network_0_5_AnnP_0, P_network_0_5_AnnP_1, P_network_0_5_AnnP_2, P_network_0_5_AnnP_3, P_network_0_5_AnnP_4, P_network_0_5_AnnP_5, P_network_0_5_AnnP_6, P_network_0_5_RP_0, P_network_0_5_RP_1, P_network_0_5_RP_2, P_network_0_5_RP_3, P_network_0_5_RP_4, P_network_0_5_RP_5, P_network_0_5_RP_6, P_network_0_6_AskP_0, P_network_0_6_AskP_1, P_network_0_6_AskP_2, P_network_0_6_AskP_3, P_network_0_6_AskP_4, P_network_0_6_AskP_5, P_network_0_6_AskP_6, P_network_0_6_AnsP_0, P_network_0_6_AnsP_1, P_network_0_6_AnsP_2, P_network_0_6_AnsP_3, P_network_0_6_AnsP_4, P_network_0_6_AnsP_5, P_network_0_6_AnsP_6, P_network_0_6_RI_0, P_network_0_6_RI_1, P_network_0_6_RI_2, P_network_0_6_RI_3, P_network_0_6_RI_4, P_network_0_6_RI_5, P_network_0_6_RI_6, P_network_0_6_AI_0, P_network_0_6_AI_1, P_network_0_6_AI_2, P_network_0_6_AI_3, P_network_0_6_AI_4, P_network_0_6_AI_5, P_network_0_6_AI_6, P_network_0_6_AnnP_0, P_network_0_6_AnnP_1, P_network_0_6_AnnP_2, P_network_0_6_AnnP_3, P_network_0_6_AnnP_4, P_network_0_6_AnnP_5, P_network_0_6_AnnP_6, P_network_0_6_RP_0, P_network_0_6_RP_1, P_network_0_6_RP_2, P_network_0_6_RP_3, P_network_0_6_RP_4, P_network_0_6_RP_5, P_network_0_6_RP_6, P_network_1_0_AskP_0, P_network_1_0_AskP_1, P_network_1_0_AskP_2, P_network_1_0_AskP_3, P_network_1_0_AskP_4, P_network_1_0_AskP_5, P_network_1_0_AskP_6, P_network_1_0_AnsP_0, P_network_1_0_AnsP_1, P_network_1_0_AnsP_2, P_network_1_0_AnsP_3, P_network_1_0_AnsP_4, P_network_1_0_AnsP_5, P_network_1_0_AnsP_6, P_network_1_0_RI_0, P_network_1_0_RI_1, P_network_1_0_RI_2, P_network_1_0_RI_3, P_network_1_0_RI_4, P_network_1_0_RI_5, P_network_1_0_RI_6, P_network_1_0_AI_0, P_network_1_0_AI_1, P_network_1_0_AI_2, P_network_1_0_AI_3, P_network_1_0_AI_4, P_network_1_0_AI_5, P_network_1_0_AI_6, P_network_1_0_AnnP_0, P_network_1_0_AnnP_1, P_network_1_0_AnnP_2, P_network_1_0_AnnP_3, P_network_1_0_AnnP_4, P_network_1_0_AnnP_5, P_network_1_0_AnnP_6, P_network_1_0_RP_0, P_network_1_0_RP_1, P_network_1_0_RP_2, P_network_1_0_RP_3, P_network_1_0_RP_4, P_network_1_0_RP_5, P_network_1_0_RP_6, P_network_1_1_AskP_0, P_network_1_1_AskP_1, P_network_1_1_AskP_2, P_network_1_1_AskP_3, P_network_1_1_AskP_4, P_network_1_1_AskP_5, P_network_1_1_AskP_6, P_network_1_1_AnsP_0, P_network_1_1_AnsP_1, P_network_1_1_AnsP_2, P_network_1_1_AnsP_3, P_network_1_1_AnsP_4, P_network_1_1_AnsP_5, P_network_1_1_AnsP_6, P_network_1_1_RI_0, P_network_1_1_RI_1, P_network_1_1_RI_2, P_network_1_1_RI_3, P_network_1_1_RI_4, P_network_1_1_RI_5, P_network_1_1_RI_6, P_network_1_1_AI_0, P_network_1_1_AI_1, P_network_1_1_AI_2, P_network_1_1_AI_3, P_network_1_1_AI_4, P_network_1_1_AI_5, P_network_1_1_AI_6, P_network_1_1_AnnP_0, P_network_1_1_AnnP_1, P_network_1_1_AnnP_2, P_network_1_1_AnnP_3, P_network_1_1_AnnP_4, P_network_1_1_AnnP_5, P_network_1_1_AnnP_6, P_network_1_1_RP_0, P_network_1_1_RP_1, P_network_1_1_RP_2, P_network_1_1_RP_3, P_network_1_1_RP_4, P_network_1_1_RP_5, P_network_1_1_RP_6, P_network_1_2_AskP_0, P_network_1_2_AskP_1, P_network_1_2_AskP_2, P_network_1_2_AskP_3, P_network_1_2_AskP_4, P_network_1_2_AskP_5, P_network_1_2_AskP_6, P_network_1_2_AnsP_0, P_network_1_2_AnsP_1, P_network_1_2_AnsP_2, P_network_1_2_AnsP_3, P_network_1_2_AnsP_4, P_network_1_2_AnsP_5, P_network_1_2_AnsP_6, P_network_1_2_RI_0, P_network_1_2_RI_1, P_network_1_2_RI_2, P_network_1_2_RI_3, P_network_1_2_RI_4, P_network_1_2_RI_5, P_network_1_2_RI_6, P_network_1_2_AI_0, P_network_1_2_AI_1, P_network_1_2_AI_2, P_network_1_2_AI_3, P_network_1_2_AI_4, P_network_1_2_AI_5, P_network_1_2_AI_6, P_network_1_2_AnnP_0, P_network_1_2_AnnP_1, P_network_1_2_AnnP_2, P_network_1_2_AnnP_3, P_network_1_2_AnnP_4, P_network_1_2_AnnP_5, P_network_1_2_AnnP_6, P_network_1_2_RP_0, P_network_1_2_RP_1, P_network_1_2_RP_2, P_network_1_2_RP_3, P_network_1_2_RP_4, P_network_1_2_RP_5, P_network_1_2_RP_6, P_network_1_3_AskP_0, P_network_1_3_AskP_1, P_network_1_3_AskP_2, P_network_1_3_AskP_3, P_network_1_3_AskP_4, P_network_1_3_AskP_5, P_network_1_3_AskP_6, P_network_1_3_AnsP_0, P_network_1_3_AnsP_1, P_network_1_3_AnsP_2, P_network_1_3_AnsP_3, P_network_1_3_AnsP_4, P_network_1_3_AnsP_5, P_network_1_3_AnsP_6, P_network_1_3_RI_0, P_network_1_3_RI_1, P_network_1_3_RI_2, P_network_1_3_RI_3, P_network_1_3_RI_4, P_network_1_3_RI_5, P_network_1_3_RI_6, P_network_1_3_AI_0, P_network_1_3_AI_1, P_network_1_3_AI_2, P_network_1_3_AI_3, P_network_1_3_AI_4, P_network_1_3_AI_5, P_network_1_3_AI_6, P_network_1_3_AnnP_0, P_network_1_3_AnnP_1, P_network_1_3_AnnP_2, P_network_1_3_AnnP_3, P_network_1_3_AnnP_4, P_network_1_3_AnnP_5, P_network_1_3_AnnP_6, P_network_1_3_RP_0, P_network_1_3_RP_1, P_network_1_3_RP_2, P_network_1_3_RP_3, P_network_1_3_RP_4, P_network_1_3_RP_5, P_network_1_3_RP_6, P_network_1_4_AskP_0, P_network_1_4_AskP_1, P_network_1_4_AskP_2, P_network_1_4_AskP_3, P_network_1_4_AskP_4, P_network_1_4_AskP_5, P_network_1_4_AskP_6, P_network_1_4_AnsP_0, P_network_1_4_AnsP_1, P_network_1_4_AnsP_2, P_network_1_4_AnsP_3, P_network_1_4_AnsP_4, P_network_1_4_AnsP_5, P_network_1_4_AnsP_6, P_network_1_4_RI_0, P_network_1_4_RI_1, P_network_1_4_RI_2, P_network_1_4_RI_3, P_network_1_4_RI_4, P_network_1_4_RI_5, P_network_1_4_RI_6, P_network_1_4_AI_0, P_network_1_4_AI_1, P_network_1_4_AI_2, P_network_1_4_AI_3, P_network_1_4_AI_4, P_network_1_4_AI_5, P_network_1_4_AI_6, P_network_1_4_AnnP_0, P_network_1_4_AnnP_1, P_network_1_4_AnnP_2, P_network_1_4_AnnP_3, P_network_1_4_AnnP_4, P_network_1_4_AnnP_5, P_network_1_4_AnnP_6, P_network_1_4_RP_0, P_network_1_4_RP_1, P_network_1_4_RP_2, P_network_1_4_RP_3, P_network_1_4_RP_4, P_network_1_4_RP_5, P_network_1_4_RP_6, P_network_1_5_AskP_0, P_network_1_5_AskP_1, P_network_1_5_AskP_2, P_network_1_5_AskP_3, P_network_1_5_AskP_4, P_network_1_5_AskP_5, P_network_1_5_AskP_6, P_network_1_5_AnsP_0, P_network_1_5_AnsP_1, P_network_1_5_AnsP_2, P_network_1_5_AnsP_3, P_network_1_5_AnsP_4, P_network_1_5_AnsP_5, P_network_1_5_AnsP_6, P_network_1_5_RI_0, P_network_1_5_RI_1, P_network_1_5_RI_2, P_network_1_5_RI_3, P_network_1_5_RI_4, P_network_1_5_RI_5, P_network_1_5_RI_6, P_network_1_5_AI_0, P_network_1_5_AI_1, P_network_1_5_AI_2, P_network_1_5_AI_3, P_network_1_5_AI_4, P_network_1_5_AI_5, P_network_1_5_AI_6, P_network_1_5_AnnP_0, P_network_1_5_AnnP_1, P_network_1_5_AnnP_2, P_network_1_5_AnnP_3, P_network_1_5_AnnP_4, P_network_1_5_AnnP_5, P_network_1_5_AnnP_6, P_network_1_5_RP_0, P_network_1_5_RP_1, P_network_1_5_RP_2, P_network_1_5_RP_3, P_network_1_5_RP_4, P_network_1_5_RP_5, P_network_1_5_RP_6, P_network_1_6_AskP_0, P_network_1_6_AskP_1, P_network_1_6_AskP_2, P_network_1_6_AskP_3, P_network_1_6_AskP_4, P_network_1_6_AskP_5, P_network_1_6_AskP_6, P_network_1_6_AnsP_0, P_network_1_6_AnsP_1, P_network_1_6_AnsP_2, P_network_1_6_AnsP_3, P_network_1_6_AnsP_4, P_network_1_6_AnsP_5, P_network_1_6_AnsP_6, P_network_1_6_RI_0, P_network_1_6_RI_1, P_network_1_6_RI_2, P_network_1_6_RI_3, P_network_1_6_RI_4, P_network_1_6_RI_5, P_network_1_6_RI_6, P_network_1_6_AI_0, P_network_1_6_AI_1, P_network_1_6_AI_2, P_network_1_6_AI_3, P_network_1_6_AI_4, P_network_1_6_AI_5, P_network_1_6_AI_6, P_network_1_6_AnnP_0, P_network_1_6_AnnP_1, P_network_1_6_AnnP_2, P_network_1_6_AnnP_3, P_network_1_6_AnnP_4, P_network_1_6_AnnP_5, P_network_1_6_AnnP_6, P_network_1_6_RP_0, P_network_1_6_RP_1, P_network_1_6_RP_2, P_network_1_6_RP_3, P_network_1_6_RP_4, P_network_1_6_RP_5, P_network_1_6_RP_6, P_network_2_0_AskP_0, P_network_2_0_AskP_1, P_network_2_0_AskP_2, P_network_2_0_AskP_3, P_network_2_0_AskP_4, P_network_2_0_AskP_5, P_network_2_0_AskP_6, P_network_2_0_AnsP_0, P_network_2_0_AnsP_1, P_network_2_0_AnsP_2, P_network_2_0_AnsP_3, P_network_2_0_AnsP_4, P_network_2_0_AnsP_5, P_network_2_0_AnsP_6, P_network_2_0_RI_0, P_network_2_0_RI_1, P_network_2_0_RI_2, P_network_2_0_RI_3, P_network_2_0_RI_4, P_network_2_0_RI_5, P_network_2_0_RI_6, P_network_2_0_AI_0, P_network_2_0_AI_1, P_network_2_0_AI_2, P_network_2_0_AI_3, P_network_2_0_AI_4, P_network_2_0_AI_5, P_network_2_0_AI_6, P_network_2_0_AnnP_0, P_network_2_0_AnnP_1, P_network_2_0_AnnP_2, P_network_2_0_AnnP_3, P_network_2_0_AnnP_4, P_network_2_0_AnnP_5, P_network_2_0_AnnP_6, P_network_2_0_RP_0, P_network_2_0_RP_1, P_network_2_0_RP_2, P_network_2_0_RP_3, P_network_2_0_RP_4, P_network_2_0_RP_5, P_network_2_0_RP_6, P_network_2_1_AskP_0, P_network_2_1_AskP_1, P_network_2_1_AskP_2, P_network_2_1_AskP_3, P_network_2_1_AskP_4, P_network_2_1_AskP_5, P_network_2_1_AskP_6, P_network_2_1_AnsP_0, P_network_2_1_AnsP_1, P_network_2_1_AnsP_2, P_network_2_1_AnsP_3, P_network_2_1_AnsP_4, P_network_2_1_AnsP_5, P_network_2_1_AnsP_6, P_network_2_1_RI_0, P_network_2_1_RI_1, P_network_2_1_RI_2, P_network_2_1_RI_3, P_network_2_1_RI_4, P_network_2_1_RI_5, P_network_2_1_RI_6, P_network_2_1_AI_0, P_network_2_1_AI_1, P_network_2_1_AI_2, P_network_2_1_AI_3, P_network_2_1_AI_4, P_network_2_1_AI_5, P_network_2_1_AI_6, P_network_2_1_AnnP_0, P_network_2_1_AnnP_1, P_network_2_1_AnnP_2, P_network_2_1_AnnP_3, P_network_2_1_AnnP_4, P_network_2_1_AnnP_5, P_network_2_1_AnnP_6, P_network_2_1_RP_0, P_network_2_1_RP_1, P_network_2_1_RP_2, P_network_2_1_RP_3, P_network_2_1_RP_4, P_network_2_1_RP_5, P_network_2_1_RP_6, P_network_2_2_AskP_0, P_network_2_2_AskP_1, P_network_2_2_AskP_2, P_network_2_2_AskP_3, P_network_2_2_AskP_4, P_network_2_2_AskP_5, P_network_2_2_AskP_6, P_network_2_2_AnsP_0, P_network_2_2_AnsP_1, P_network_2_2_AnsP_2, P_network_2_2_AnsP_3, P_network_2_2_AnsP_4, P_network_2_2_AnsP_5, P_network_2_2_AnsP_6, P_network_2_2_RI_0, P_network_2_2_RI_1, P_network_2_2_RI_2, P_network_2_2_RI_3, P_network_2_2_RI_4, P_network_2_2_RI_5, P_network_2_2_RI_6, P_network_2_2_AI_0, P_network_2_2_AI_1, P_network_2_2_AI_2, P_network_2_2_AI_3, P_network_2_2_AI_4, P_network_2_2_AI_5, P_network_2_2_AI_6, P_network_2_2_AnnP_0, P_network_2_2_AnnP_1, P_network_2_2_AnnP_2, P_network_2_2_AnnP_3, P_network_2_2_AnnP_4, P_network_2_2_AnnP_5, P_network_2_2_AnnP_6, P_network_2_2_RP_0, P_network_2_2_RP_1, P_network_2_2_RP_2, P_network_2_2_RP_3, P_network_2_2_RP_4, P_network_2_2_RP_5, P_network_2_2_RP_6, P_network_2_3_AskP_0, P_network_2_3_AskP_1, P_network_2_3_AskP_2, P_network_2_3_AskP_3, P_network_2_3_AskP_4, P_network_2_3_AskP_5, P_network_2_3_AskP_6, P_network_2_3_AnsP_0, P_network_2_3_AnsP_1, P_network_2_3_AnsP_2, P_network_2_3_AnsP_3, P_network_2_3_AnsP_4, P_network_2_3_AnsP_5, P_network_2_3_AnsP_6, P_network_2_3_RI_0, P_network_2_3_RI_1, P_network_2_3_RI_2, P_network_2_3_RI_3, P_network_2_3_RI_4, P_network_2_3_RI_5, P_network_2_3_RI_6, P_network_2_3_AI_0, P_network_2_3_AI_1, P_network_2_3_AI_2, P_network_2_3_AI_3, P_network_2_3_AI_4, P_network_2_3_AI_5, P_network_2_3_AI_6, P_network_2_3_AnnP_0, P_network_2_3_AnnP_1, P_network_2_3_AnnP_2, P_network_2_3_AnnP_3, P_network_2_3_AnnP_4, P_network_2_3_AnnP_5, P_network_2_3_AnnP_6, P_network_2_3_RP_0, P_network_2_3_RP_1, P_network_2_3_RP_2, P_network_2_3_RP_3, P_network_2_3_RP_4, P_network_2_3_RP_5, P_network_2_3_RP_6, P_network_2_4_AskP_0, P_network_2_4_AskP_1, P_network_2_4_AskP_2, P_network_2_4_AskP_3, P_network_2_4_AskP_4, P_network_2_4_AskP_5, P_network_2_4_AskP_6, P_network_2_4_AnsP_0, P_network_2_4_AnsP_1, P_network_2_4_AnsP_2, P_network_2_4_AnsP_3, P_network_2_4_AnsP_4, P_network_2_4_AnsP_5, P_network_2_4_AnsP_6, P_network_2_4_RI_0, P_network_2_4_RI_1, P_network_2_4_RI_2, P_network_2_4_RI_3, P_network_2_4_RI_4, P_network_2_4_RI_5, P_network_2_4_RI_6, P_network_2_4_AI_0, P_network_2_4_AI_1, P_network_2_4_AI_2, P_network_2_4_AI_3, P_network_2_4_AI_4, P_network_2_4_AI_5, P_network_2_4_AI_6, P_network_2_4_AnnP_0, P_network_2_4_AnnP_1, P_network_2_4_AnnP_2, P_network_2_4_AnnP_3, P_network_2_4_AnnP_4, P_network_2_4_AnnP_5, P_network_2_4_AnnP_6, P_network_2_4_RP_0, P_network_2_4_RP_1, P_network_2_4_RP_2, P_network_2_4_RP_3, P_network_2_4_RP_4, P_network_2_4_RP_5, P_network_2_4_RP_6, P_network_2_5_AskP_0, P_network_2_5_AskP_1, P_network_2_5_AskP_2, P_network_2_5_AskP_3, P_network_2_5_AskP_4, P_network_2_5_AskP_5, P_network_2_5_AskP_6, P_network_2_5_AnsP_0, P_network_2_5_AnsP_1, P_network_2_5_AnsP_2, P_network_2_5_AnsP_3, P_network_2_5_AnsP_4, P_network_2_5_AnsP_5, P_network_2_5_AnsP_6, P_network_2_5_RI_0, P_network_2_5_RI_1, P_network_2_5_RI_2, P_network_2_5_RI_3, P_network_2_5_RI_4, P_network_2_5_RI_5, P_network_2_5_RI_6, P_network_2_5_AI_0, P_network_2_5_AI_1, P_network_2_5_AI_2, P_network_2_5_AI_3, P_network_2_5_AI_4, P_network_2_5_AI_5, P_network_2_5_AI_6, P_network_2_5_AnnP_0, P_network_2_5_AnnP_1, P_network_2_5_AnnP_2, P_network_2_5_AnnP_3, P_network_2_5_AnnP_4, P_network_2_5_AnnP_5, P_network_2_5_AnnP_6, P_network_2_5_RP_0, P_network_2_5_RP_1, P_network_2_5_RP_2, P_network_2_5_RP_3, P_network_2_5_RP_4, P_network_2_5_RP_5, P_network_2_5_RP_6, P_network_2_6_AskP_0, P_network_2_6_AskP_1, P_network_2_6_AskP_2, P_network_2_6_AskP_3, P_network_2_6_AskP_4, P_network_2_6_AskP_5, P_network_2_6_AskP_6, P_network_2_6_AnsP_0, P_network_2_6_AnsP_1, P_network_2_6_AnsP_2, P_network_2_6_AnsP_3, P_network_2_6_AnsP_4, P_network_2_6_AnsP_5, P_network_2_6_AnsP_6, P_network_2_6_RI_0, P_network_2_6_RI_1, P_network_2_6_RI_2, P_network_2_6_RI_3, P_network_2_6_RI_4, P_network_2_6_RI_5, P_network_2_6_RI_6, P_network_2_6_AI_0, P_network_2_6_AI_1, P_network_2_6_AI_2, P_network_2_6_AI_3, P_network_2_6_AI_4, P_network_2_6_AI_5, P_network_2_6_AI_6, P_network_2_6_AnnP_0, P_network_2_6_AnnP_1, P_network_2_6_AnnP_2, P_network_2_6_AnnP_3, P_network_2_6_AnnP_4, P_network_2_6_AnnP_5, P_network_2_6_AnnP_6, P_network_2_6_RP_0, P_network_2_6_RP_1, P_network_2_6_RP_2, P_network_2_6_RP_3, P_network_2_6_RP_4, P_network_2_6_RP_5, P_network_2_6_RP_6, P_network_3_0_AskP_0, P_network_3_0_AskP_1, P_network_3_0_AskP_2, P_network_3_0_AskP_3, P_network_3_0_AskP_4, P_network_3_0_AskP_5, P_network_3_0_AskP_6, P_network_3_0_AnsP_0, P_network_3_0_AnsP_1, P_network_3_0_AnsP_2, P_network_3_0_AnsP_3, P_network_3_0_AnsP_4, P_network_3_0_AnsP_5, P_network_3_0_AnsP_6, P_network_3_0_RI_0, P_network_3_0_RI_1, P_network_3_0_RI_2, P_network_3_0_RI_3, P_network_3_0_RI_4, P_network_3_0_RI_5, P_network_3_0_RI_6, P_network_3_0_AI_0, P_network_3_0_AI_1, P_network_3_0_AI_2, P_network_3_0_AI_3, P_network_3_0_AI_4, P_network_3_0_AI_5, P_network_3_0_AI_6, P_network_3_0_AnnP_0, P_network_3_0_AnnP_1, P_network_3_0_AnnP_2, P_network_3_0_AnnP_3, P_network_3_0_AnnP_4, P_network_3_0_AnnP_5, P_network_3_0_AnnP_6, P_network_3_0_RP_0, P_network_3_0_RP_1, P_network_3_0_RP_2, P_network_3_0_RP_3, P_network_3_0_RP_4, P_network_3_0_RP_5, P_network_3_0_RP_6, P_network_3_1_AskP_0, P_network_3_1_AskP_1, P_network_3_1_AskP_2, P_network_3_1_AskP_3, P_network_3_1_AskP_4, P_network_3_1_AskP_5, P_network_3_1_AskP_6, P_network_3_1_AnsP_0, P_network_3_1_AnsP_1, P_network_3_1_AnsP_2, P_network_3_1_AnsP_3, P_network_3_1_AnsP_4, P_network_3_1_AnsP_5, P_network_3_1_AnsP_6, P_network_3_1_RI_0, P_network_3_1_RI_1, P_network_3_1_RI_2, P_network_3_1_RI_3, P_network_3_1_RI_4, P_network_3_1_RI_5, P_network_3_1_RI_6, P_network_3_1_AI_0, P_network_3_1_AI_1, P_network_3_1_AI_2, P_network_3_1_AI_3, P_network_3_1_AI_4, P_network_3_1_AI_5, P_network_3_1_AI_6, P_network_3_1_AnnP_0, P_network_3_1_AnnP_1, P_network_3_1_AnnP_2, P_network_3_1_AnnP_3, P_network_3_1_AnnP_4, P_network_3_1_AnnP_5, P_network_3_1_AnnP_6, P_network_3_1_RP_0, P_network_3_1_RP_1, P_network_3_1_RP_2, P_network_3_1_RP_3, P_network_3_1_RP_4, P_network_3_1_RP_5, P_network_3_1_RP_6, P_network_3_2_AskP_0, P_network_3_2_AskP_1, P_network_3_2_AskP_2, P_network_3_2_AskP_3, P_network_3_2_AskP_4, P_network_3_2_AskP_5, P_network_3_2_AskP_6, P_network_3_2_AnsP_0, P_network_3_2_AnsP_1, P_network_3_2_AnsP_2, P_network_3_2_AnsP_3, P_network_3_2_AnsP_4, P_network_3_2_AnsP_5, P_network_3_2_AnsP_6, P_network_3_2_RI_0, P_network_3_2_RI_1, P_network_3_2_RI_2, P_network_3_2_RI_3, P_network_3_2_RI_4, P_network_3_2_RI_5, P_network_3_2_RI_6, P_network_3_2_AI_0, P_network_3_2_AI_1, P_network_3_2_AI_2, P_network_3_2_AI_3, P_network_3_2_AI_4, P_network_3_2_AI_5, P_network_3_2_AI_6, P_network_3_2_AnnP_0, P_network_3_2_AnnP_1, P_network_3_2_AnnP_2, P_network_3_2_AnnP_3, P_network_3_2_AnnP_4, P_network_3_2_AnnP_5, P_network_3_2_AnnP_6, P_network_3_2_RP_0, P_network_3_2_RP_1, P_network_3_2_RP_2, P_network_3_2_RP_3, P_network_3_2_RP_4, P_network_3_2_RP_5, P_network_3_2_RP_6, P_network_3_3_AskP_0, P_network_3_3_AskP_1, P_network_3_3_AskP_2, P_network_3_3_AskP_3, P_network_3_3_AskP_4, P_network_3_3_AskP_5, P_network_3_3_AskP_6, P_network_3_3_AnsP_0, P_network_3_3_AnsP_1, P_network_3_3_AnsP_2, P_network_3_3_AnsP_3, P_network_3_3_AnsP_4, P_network_3_3_AnsP_5, P_network_3_3_AnsP_6, P_network_3_3_RI_0, P_network_3_3_RI_1, P_network_3_3_RI_2, P_network_3_3_RI_3, P_network_3_3_RI_4, P_network_3_3_RI_5, P_network_3_3_RI_6, P_network_3_3_AI_0, P_network_3_3_AI_1, P_network_3_3_AI_2, P_network_3_3_AI_3, P_network_3_3_AI_4, P_network_3_3_AI_5, P_network_3_3_AI_6, P_network_3_3_AnnP_0, P_network_3_3_AnnP_1, P_network_3_3_AnnP_2, P_network_3_3_AnnP_3, P_network_3_3_AnnP_4, P_network_3_3_AnnP_5, P_network_3_3_AnnP_6, P_network_3_3_RP_0, P_network_3_3_RP_1, P_network_3_3_RP_2, P_network_3_3_RP_3, P_network_3_3_RP_4, P_network_3_3_RP_5, P_network_3_3_RP_6, P_network_3_4_AskP_0, P_network_3_4_AskP_1, P_network_3_4_AskP_2, P_network_3_4_AskP_3, P_network_3_4_AskP_4, P_network_3_4_AskP_5, P_network_3_4_AskP_6, P_network_3_4_AnsP_0, P_network_3_4_AnsP_1, P_network_3_4_AnsP_2, P_network_3_4_AnsP_3, P_network_3_4_AnsP_4, P_network_3_4_AnsP_5, P_network_3_4_AnsP_6, P_network_3_4_RI_0, P_network_3_4_RI_1, P_network_3_4_RI_2, P_network_3_4_RI_3, P_network_3_4_RI_4, P_network_3_4_RI_5, P_network_3_4_RI_6, P_network_3_4_AI_0, P_network_3_4_AI_1, P_network_3_4_AI_2, P_network_3_4_AI_3, P_network_3_4_AI_4, P_network_3_4_AI_5, P_network_3_4_AI_6, P_network_3_4_AnnP_0, P_network_3_4_AnnP_1, P_network_3_4_AnnP_2, P_network_3_4_AnnP_3, P_network_3_4_AnnP_4, P_network_3_4_AnnP_5, P_network_3_4_AnnP_6, P_network_3_4_RP_0, P_network_3_4_RP_1, P_network_3_4_RP_2, P_network_3_4_RP_3, P_network_3_4_RP_4, P_network_3_4_RP_5, P_network_3_4_RP_6, P_network_3_5_AskP_0, P_network_3_5_AskP_1, P_network_3_5_AskP_2, P_network_3_5_AskP_3, P_network_3_5_AskP_4, P_network_3_5_AskP_5, P_network_3_5_AskP_6, P_network_3_5_AnsP_0, P_network_3_5_AnsP_1, P_network_3_5_AnsP_2, P_network_3_5_AnsP_3, P_network_3_5_AnsP_4, P_network_3_5_AnsP_5, P_network_3_5_AnsP_6, P_network_3_5_RI_0, P_network_3_5_RI_1, P_network_3_5_RI_2, P_network_3_5_RI_3, P_network_3_5_RI_4, P_network_3_5_RI_5, P_network_3_5_RI_6, P_network_3_5_AI_0, P_network_3_5_AI_1, P_network_3_5_AI_2, P_network_3_5_AI_3, P_network_3_5_AI_4, P_network_3_5_AI_5, P_network_3_5_AI_6, P_network_3_5_AnnP_0, P_network_3_5_AnnP_1, P_network_3_5_AnnP_2, P_network_3_5_AnnP_3, P_network_3_5_AnnP_4, P_network_3_5_AnnP_5, P_network_3_5_AnnP_6, P_network_3_5_RP_0, P_network_3_5_RP_1, P_network_3_5_RP_2, P_network_3_5_RP_3, P_network_3_5_RP_4, P_network_3_5_RP_5, P_network_3_5_RP_6, P_network_3_6_AskP_0, P_network_3_6_AskP_1, P_network_3_6_AskP_2, P_network_3_6_AskP_3, P_network_3_6_AskP_4, P_network_3_6_AskP_5, P_network_3_6_AskP_6, P_network_3_6_AnsP_0, P_network_3_6_AnsP_1, P_network_3_6_AnsP_2, P_network_3_6_AnsP_3, P_network_3_6_AnsP_4, P_network_3_6_AnsP_5, P_network_3_6_AnsP_6, P_network_3_6_RI_0, P_network_3_6_RI_1, P_network_3_6_RI_2, P_network_3_6_RI_3, P_network_3_6_RI_4, P_network_3_6_RI_5, P_network_3_6_RI_6, P_network_3_6_AI_0, P_network_3_6_AI_1, P_network_3_6_AI_2, P_network_3_6_AI_3, P_network_3_6_AI_4, P_network_3_6_AI_5, P_network_3_6_AI_6, P_network_3_6_AnnP_0, P_network_3_6_AnnP_1, P_network_3_6_AnnP_2, P_network_3_6_AnnP_3, P_network_3_6_AnnP_4, P_network_3_6_AnnP_5, P_network_3_6_AnnP_6, P_network_3_6_RP_0, P_network_3_6_RP_1, P_network_3_6_RP_2, P_network_3_6_RP_3, P_network_3_6_RP_4, P_network_3_6_RP_5, P_network_3_6_RP_6, P_network_4_0_AskP_0, P_network_4_0_AskP_1, P_network_4_0_AskP_2, P_network_4_0_AskP_3, P_network_4_0_AskP_4, P_network_4_0_AskP_5, P_network_4_0_AskP_6, P_network_4_0_AnsP_0, P_network_4_0_AnsP_1, P_network_4_0_AnsP_2, P_network_4_0_AnsP_3, P_network_4_0_AnsP_4, P_network_4_0_AnsP_5, P_network_4_0_AnsP_6, P_network_4_0_RI_0, P_network_4_0_RI_1, P_network_4_0_RI_2, P_network_4_0_RI_3, P_network_4_0_RI_4, P_network_4_0_RI_5, P_network_4_0_RI_6, P_network_4_0_AI_0, P_network_4_0_AI_1, P_network_4_0_AI_2, P_network_4_0_AI_3, P_network_4_0_AI_4, P_network_4_0_AI_5, P_network_4_0_AI_6, P_network_4_0_AnnP_0, P_network_4_0_AnnP_1, P_network_4_0_AnnP_2, P_network_4_0_AnnP_3, P_network_4_0_AnnP_4, P_network_4_0_AnnP_5, P_network_4_0_AnnP_6, P_network_4_0_RP_0, P_network_4_0_RP_1, P_network_4_0_RP_2, P_network_4_0_RP_3, P_network_4_0_RP_4, P_network_4_0_RP_5, P_network_4_0_RP_6, P_network_4_1_AskP_0, P_network_4_1_AskP_1, P_network_4_1_AskP_2, P_network_4_1_AskP_3, P_network_4_1_AskP_4, P_network_4_1_AskP_5, P_network_4_1_AskP_6, P_network_4_1_AnsP_0, P_network_4_1_AnsP_1, P_network_4_1_AnsP_2, P_network_4_1_AnsP_3, P_network_4_1_AnsP_4, P_network_4_1_AnsP_5, P_network_4_1_AnsP_6, P_network_4_1_RI_0, P_network_4_1_RI_1, P_network_4_1_RI_2, P_network_4_1_RI_3, P_network_4_1_RI_4, P_network_4_1_RI_5, P_network_4_1_RI_6, P_network_4_1_AI_0, P_network_4_1_AI_1, P_network_4_1_AI_2, P_network_4_1_AI_3, P_network_4_1_AI_4, P_network_4_1_AI_5, P_network_4_1_AI_6, P_network_4_1_AnnP_0, P_network_4_1_AnnP_1, P_network_4_1_AnnP_2, P_network_4_1_AnnP_3, P_network_4_1_AnnP_4, P_network_4_1_AnnP_5, P_network_4_1_AnnP_6, P_network_4_1_RP_0, P_network_4_1_RP_1, P_network_4_1_RP_2, P_network_4_1_RP_3, P_network_4_1_RP_4, P_network_4_1_RP_5, P_network_4_1_RP_6, P_network_4_2_AskP_0, P_network_4_2_AskP_1, P_network_4_2_AskP_2, P_network_4_2_AskP_3, P_network_4_2_AskP_4, P_network_4_2_AskP_5, P_network_4_2_AskP_6, P_network_4_2_AnsP_0, P_network_4_2_AnsP_1, P_network_4_2_AnsP_2, P_network_4_2_AnsP_3, P_network_4_2_AnsP_4, P_network_4_2_AnsP_5, P_network_4_2_AnsP_6, P_network_4_2_RI_0, P_network_4_2_RI_1, P_network_4_2_RI_2, P_network_4_2_RI_3, P_network_4_2_RI_4, P_network_4_2_RI_5, P_network_4_2_RI_6, P_network_4_2_AI_0, P_network_4_2_AI_1, P_network_4_2_AI_2, P_network_4_2_AI_3, P_network_4_2_AI_4, P_network_4_2_AI_5, P_network_4_2_AI_6, P_network_4_2_AnnP_0, P_network_4_2_AnnP_1, P_network_4_2_AnnP_2, P_network_4_2_AnnP_3, P_network_4_2_AnnP_4, P_network_4_2_AnnP_5, P_network_4_2_AnnP_6, P_network_4_2_RP_0, P_network_4_2_RP_1, P_network_4_2_RP_2, P_network_4_2_RP_3, P_network_4_2_RP_4, P_network_4_2_RP_5, P_network_4_2_RP_6, P_network_4_3_AskP_0, P_network_4_3_AskP_1, P_network_4_3_AskP_2, P_network_4_3_AskP_3, P_network_4_3_AskP_4, P_network_4_3_AskP_5, P_network_4_3_AskP_6, P_network_4_3_AnsP_0, P_network_4_3_AnsP_1, P_network_4_3_AnsP_2, P_network_4_3_AnsP_3, P_network_4_3_AnsP_4, P_network_4_3_AnsP_5, P_network_4_3_AnsP_6, P_network_4_3_RI_0, P_network_4_3_RI_1, P_network_4_3_RI_2, P_network_4_3_RI_3, P_network_4_3_RI_4, P_network_4_3_RI_5, P_network_4_3_RI_6, P_network_4_3_AI_0, P_network_4_3_AI_1, P_network_4_3_AI_2, P_network_4_3_AI_3, P_network_4_3_AI_4, P_network_4_3_AI_5, P_network_4_3_AI_6, P_network_4_3_AnnP_0, P_network_4_3_AnnP_1, P_network_4_3_AnnP_2, P_network_4_3_AnnP_3, P_network_4_3_AnnP_4, P_network_4_3_AnnP_5, P_network_4_3_AnnP_6, P_network_4_3_RP_0, P_network_4_3_RP_1, P_network_4_3_RP_2, P_network_4_3_RP_3, P_network_4_3_RP_4, P_network_4_3_RP_5, P_network_4_3_RP_6, P_network_4_4_AskP_0, P_network_4_4_AskP_1, P_network_4_4_AskP_2, P_network_4_4_AskP_3, P_network_4_4_AskP_4, P_network_4_4_AskP_5, P_network_4_4_AskP_6, P_network_4_4_AnsP_0, P_network_4_4_AnsP_1, P_network_4_4_AnsP_2, P_network_4_4_AnsP_3, P_network_4_4_AnsP_4, P_network_4_4_AnsP_5, P_network_4_4_AnsP_6, P_network_4_4_RI_0, P_network_4_4_RI_1, P_network_4_4_RI_2, P_network_4_4_RI_3, P_network_4_4_RI_4, P_network_4_4_RI_5, P_network_4_4_RI_6, P_network_4_4_AI_0, P_network_4_4_AI_1, P_network_4_4_AI_2, P_network_4_4_AI_3, P_network_4_4_AI_4, P_network_4_4_AI_5, P_network_4_4_AI_6, P_network_4_4_AnnP_0, P_network_4_4_AnnP_1, P_network_4_4_AnnP_2, P_network_4_4_AnnP_3, P_network_4_4_AnnP_4, P_network_4_4_AnnP_5, P_network_4_4_AnnP_6, P_network_4_4_RP_0, P_network_4_4_RP_1, P_network_4_4_RP_2, P_network_4_4_RP_3, P_network_4_4_RP_4, P_network_4_4_RP_5, P_network_4_4_RP_6, P_network_4_5_AskP_0, P_network_4_5_AskP_1, P_network_4_5_AskP_2, P_network_4_5_AskP_3, P_network_4_5_AskP_4, P_network_4_5_AskP_5, P_network_4_5_AskP_6, P_network_4_5_AnsP_0, P_network_4_5_AnsP_1, P_network_4_5_AnsP_2, P_network_4_5_AnsP_3, P_network_4_5_AnsP_4, P_network_4_5_AnsP_5, P_network_4_5_AnsP_6, P_network_4_5_RI_0, P_network_4_5_RI_1, P_network_4_5_RI_2, P_network_4_5_RI_3, P_network_4_5_RI_4, P_network_4_5_RI_5, P_network_4_5_RI_6, P_network_4_5_AI_0, P_network_4_5_AI_1, P_network_4_5_AI_2, P_network_4_5_AI_3, P_network_4_5_AI_4, P_network_4_5_AI_5, P_network_4_5_AI_6, P_network_4_5_AnnP_0, P_network_4_5_AnnP_1, P_network_4_5_AnnP_2, P_network_4_5_AnnP_3, P_network_4_5_AnnP_4, P_network_4_5_AnnP_5, P_network_4_5_AnnP_6, P_network_4_5_RP_0, P_network_4_5_RP_1, P_network_4_5_RP_2, P_network_4_5_RP_3, P_network_4_5_RP_4, P_network_4_5_RP_5, P_network_4_5_RP_6, P_network_4_6_AskP_0, P_network_4_6_AskP_1, P_network_4_6_AskP_2, P_network_4_6_AskP_3, P_network_4_6_AskP_4, P_network_4_6_AskP_5, P_network_4_6_AskP_6, P_network_4_6_AnsP_0, P_network_4_6_AnsP_1, P_network_4_6_AnsP_2, P_network_4_6_AnsP_3, P_network_4_6_AnsP_4, P_network_4_6_AnsP_5, P_network_4_6_AnsP_6, P_network_4_6_RI_0, P_network_4_6_RI_1, P_network_4_6_RI_2, P_network_4_6_RI_3, P_network_4_6_RI_4, P_network_4_6_RI_5, P_network_4_6_RI_6, P_network_4_6_AI_0, P_network_4_6_AI_1, P_network_4_6_AI_2, P_network_4_6_AI_3, P_network_4_6_AI_4, P_network_4_6_AI_5, P_network_4_6_AI_6, P_network_4_6_AnnP_0, P_network_4_6_AnnP_1, P_network_4_6_AnnP_2, P_network_4_6_AnnP_3, P_network_4_6_AnnP_4, P_network_4_6_AnnP_5, P_network_4_6_AnnP_6, P_network_4_6_RP_0, P_network_4_6_RP_1, P_network_4_6_RP_2, P_network_4_6_RP_3, P_network_4_6_RP_4, P_network_4_6_RP_5, P_network_4_6_RP_6, P_network_5_0_AskP_0, P_network_5_0_AskP_1, P_network_5_0_AskP_2, P_network_5_0_AskP_3, P_network_5_0_AskP_4, P_network_5_0_AskP_5, P_network_5_0_AskP_6, P_network_5_0_AnsP_0, P_network_5_0_AnsP_1, P_network_5_0_AnsP_2, P_network_5_0_AnsP_3, P_network_5_0_AnsP_4, P_network_5_0_AnsP_5, P_network_5_0_AnsP_6, P_network_5_0_RI_0, P_network_5_0_RI_1, P_network_5_0_RI_2, P_network_5_0_RI_3, P_network_5_0_RI_4, P_network_5_0_RI_5, P_network_5_0_RI_6, P_network_5_0_AI_0, P_network_5_0_AI_1, P_network_5_0_AI_2, P_network_5_0_AI_3, P_network_5_0_AI_4, P_network_5_0_AI_5, P_network_5_0_AI_6, P_network_5_0_AnnP_0, P_network_5_0_AnnP_1, P_network_5_0_AnnP_2, P_network_5_0_AnnP_3, P_network_5_0_AnnP_4, P_network_5_0_AnnP_5, P_network_5_0_AnnP_6, P_network_5_0_RP_0, P_network_5_0_RP_1, P_network_5_0_RP_2, P_network_5_0_RP_3, P_network_5_0_RP_4, P_network_5_0_RP_5, P_network_5_0_RP_6, P_network_5_1_AskP_0, P_network_5_1_AskP_1, P_network_5_1_AskP_2, P_network_5_1_AskP_3, P_network_5_1_AskP_4, P_network_5_1_AskP_5, P_network_5_1_AskP_6, P_network_5_1_AnsP_0, P_network_5_1_AnsP_1, P_network_5_1_AnsP_2, P_network_5_1_AnsP_3, P_network_5_1_AnsP_4, P_network_5_1_AnsP_5, P_network_5_1_AnsP_6, P_network_5_1_RI_0, P_network_5_1_RI_1, P_network_5_1_RI_2, P_network_5_1_RI_3, P_network_5_1_RI_4, P_network_5_1_RI_5, P_network_5_1_RI_6, P_network_5_1_AI_0, P_network_5_1_AI_1, P_network_5_1_AI_2, P_network_5_1_AI_3, P_network_5_1_AI_4, P_network_5_1_AI_5, P_network_5_1_AI_6, P_network_5_1_AnnP_0, P_network_5_1_AnnP_1, P_network_5_1_AnnP_2, P_network_5_1_AnnP_3, P_network_5_1_AnnP_4, P_network_5_1_AnnP_5, P_network_5_1_AnnP_6, P_network_5_1_RP_0, P_network_5_1_RP_1, P_network_5_1_RP_2, P_network_5_1_RP_3, P_network_5_1_RP_4, P_network_5_1_RP_5, P_network_5_1_RP_6, P_network_5_2_AskP_0, P_network_5_2_AskP_1, P_network_5_2_AskP_2, P_network_5_2_AskP_3, P_network_5_2_AskP_4, P_network_5_2_AskP_5, P_network_5_2_AskP_6, P_network_5_2_AnsP_0, P_network_5_2_AnsP_1, P_network_5_2_AnsP_2, P_network_5_2_AnsP_3, P_network_5_2_AnsP_4, P_network_5_2_AnsP_5, P_network_5_2_AnsP_6, P_network_5_2_RI_0, P_network_5_2_RI_1, P_network_5_2_RI_2, P_network_5_2_RI_3, P_network_5_2_RI_4, P_network_5_2_RI_5, P_network_5_2_RI_6, P_network_5_2_AI_0, P_network_5_2_AI_1, P_network_5_2_AI_2, P_network_5_2_AI_3, P_network_5_2_AI_4, P_network_5_2_AI_5, P_network_5_2_AI_6, P_network_5_2_AnnP_0, P_network_5_2_AnnP_1, P_network_5_2_AnnP_2, P_network_5_2_AnnP_3, P_network_5_2_AnnP_4, P_network_5_2_AnnP_5, P_network_5_2_AnnP_6, P_network_5_2_RP_0, P_network_5_2_RP_1, P_network_5_2_RP_2, P_network_5_2_RP_3, P_network_5_2_RP_4, P_network_5_2_RP_5, P_network_5_2_RP_6, P_network_5_3_AskP_0, P_network_5_3_AskP_1, P_network_5_3_AskP_2, P_network_5_3_AskP_3, P_network_5_3_AskP_4, P_network_5_3_AskP_5, P_network_5_3_AskP_6, P_network_5_3_AnsP_0, P_network_5_3_AnsP_1, P_network_5_3_AnsP_2, P_network_5_3_AnsP_3, P_network_5_3_AnsP_4, P_network_5_3_AnsP_5, P_network_5_3_AnsP_6, P_network_5_3_RI_0, P_network_5_3_RI_1, P_network_5_3_RI_2, P_network_5_3_RI_3, P_network_5_3_RI_4, P_network_5_3_RI_5, P_network_5_3_RI_6, P_network_5_3_AI_0, P_network_5_3_AI_1, P_network_5_3_AI_2, P_network_5_3_AI_3, P_network_5_3_AI_4, P_network_5_3_AI_5, P_network_5_3_AI_6, P_network_5_3_AnnP_0, P_network_5_3_AnnP_1, P_network_5_3_AnnP_2, P_network_5_3_AnnP_3, P_network_5_3_AnnP_4, P_network_5_3_AnnP_5, P_network_5_3_AnnP_6, P_network_5_3_RP_0, P_network_5_3_RP_1, P_network_5_3_RP_2, P_network_5_3_RP_3, P_network_5_3_RP_4, P_network_5_3_RP_5, P_network_5_3_RP_6, P_network_5_4_AskP_0, P_network_5_4_AskP_1, P_network_5_4_AskP_2, P_network_5_4_AskP_3, P_network_5_4_AskP_4, P_network_5_4_AskP_5, P_network_5_4_AskP_6, P_network_5_4_AnsP_0, P_network_5_4_AnsP_1, P_network_5_4_AnsP_2, P_network_5_4_AnsP_3, P_network_5_4_AnsP_4, P_network_5_4_AnsP_5, P_network_5_4_AnsP_6, P_network_5_4_RI_0, P_network_5_4_RI_1, P_network_5_4_RI_2, P_network_5_4_RI_3, P_network_5_4_RI_4, P_network_5_4_RI_5, P_network_5_4_RI_6, P_network_5_4_AI_0, P_network_5_4_AI_1, P_network_5_4_AI_2, P_network_5_4_AI_3, P_network_5_4_AI_4, P_network_5_4_AI_5, P_network_5_4_AI_6, P_network_5_4_AnnP_0, P_network_5_4_AnnP_1, P_network_5_4_AnnP_2, P_network_5_4_AnnP_3, P_network_5_4_AnnP_4, P_network_5_4_AnnP_5, P_network_5_4_AnnP_6, P_network_5_4_RP_0, P_network_5_4_RP_1, P_network_5_4_RP_2, P_network_5_4_RP_3, P_network_5_4_RP_4, P_network_5_4_RP_5, P_network_5_4_RP_6, P_network_5_5_AskP_0, P_network_5_5_AskP_1, P_network_5_5_AskP_2, P_network_5_5_AskP_3, P_network_5_5_AskP_4, P_network_5_5_AskP_5, P_network_5_5_AskP_6, P_network_5_5_AnsP_0, P_network_5_5_AnsP_1, P_network_5_5_AnsP_2, P_network_5_5_AnsP_3, P_network_5_5_AnsP_4, P_network_5_5_AnsP_5, P_network_5_5_AnsP_6, P_network_5_5_RI_0, P_network_5_5_RI_1, P_network_5_5_RI_2, P_network_5_5_RI_3, P_network_5_5_RI_4, P_network_5_5_RI_5, P_network_5_5_RI_6, P_network_5_5_AI_0, P_network_5_5_AI_1, P_network_5_5_AI_2, P_network_5_5_AI_3, P_network_5_5_AI_4, P_network_5_5_AI_5, P_network_5_5_AI_6, P_network_5_5_AnnP_0, P_network_5_5_AnnP_1, P_network_5_5_AnnP_2, P_network_5_5_AnnP_3, P_network_5_5_AnnP_4, P_network_5_5_AnnP_5, P_network_5_5_AnnP_6, P_network_5_5_RP_0, P_network_5_5_RP_1, P_network_5_5_RP_2, P_network_5_5_RP_3, P_network_5_5_RP_4, P_network_5_5_RP_5, P_network_5_5_RP_6, P_network_5_6_AskP_0, P_network_5_6_AskP_1, P_network_5_6_AskP_2, P_network_5_6_AskP_3, P_network_5_6_AskP_4, P_network_5_6_AskP_5, P_network_5_6_AskP_6, P_network_5_6_AnsP_0, P_network_5_6_AnsP_1, P_network_5_6_AnsP_2, P_network_5_6_AnsP_3, P_network_5_6_AnsP_4, P_network_5_6_AnsP_5, P_network_5_6_AnsP_6, P_network_5_6_RI_0, P_network_5_6_RI_1, P_network_5_6_RI_2, P_network_5_6_RI_3, P_network_5_6_RI_4, P_network_5_6_RI_5, P_network_5_6_RI_6, P_network_5_6_AI_0, P_network_5_6_AI_1, P_network_5_6_AI_2, P_network_5_6_AI_3, P_network_5_6_AI_4, P_network_5_6_AI_5, P_network_5_6_AI_6, P_network_5_6_AnnP_0, P_network_5_6_AnnP_1, P_network_5_6_AnnP_2, P_network_5_6_AnnP_3, P_network_5_6_AnnP_4, P_network_5_6_AnnP_5, P_network_5_6_AnnP_6, P_network_5_6_RP_0, P_network_5_6_RP_1, P_network_5_6_RP_2, P_network_5_6_RP_3, P_network_5_6_RP_4, P_network_5_6_RP_5, P_network_5_6_RP_6, P_network_6_0_AskP_0, P_network_6_0_AskP_1, P_network_6_0_AskP_2, P_network_6_0_AskP_3, P_network_6_0_AskP_4, P_network_6_0_AskP_5, P_network_6_0_AskP_6, P_network_6_0_AnsP_0, P_network_6_0_AnsP_1, P_network_6_0_AnsP_2, P_network_6_0_AnsP_3, P_network_6_0_AnsP_4, P_network_6_0_AnsP_5, P_network_6_0_AnsP_6, P_network_6_0_RI_0, P_network_6_0_RI_1, P_network_6_0_RI_2, P_network_6_0_RI_3, P_network_6_0_RI_4, P_network_6_0_RI_5, P_network_6_0_RI_6, P_network_6_0_AI_0, P_network_6_0_AI_1, P_network_6_0_AI_2, P_network_6_0_AI_3, P_network_6_0_AI_4, P_network_6_0_AI_5, P_network_6_0_AI_6, P_network_6_0_AnnP_0, P_network_6_0_AnnP_1, P_network_6_0_AnnP_2, P_network_6_0_AnnP_3, P_network_6_0_AnnP_4, P_network_6_0_AnnP_5, P_network_6_0_AnnP_6, P_network_6_0_RP_0, P_network_6_0_RP_1, P_network_6_0_RP_2, P_network_6_0_RP_3, P_network_6_0_RP_4, P_network_6_0_RP_5, P_network_6_0_RP_6, P_network_6_1_AskP_0, P_network_6_1_AskP_1, P_network_6_1_AskP_2, P_network_6_1_AskP_3, P_network_6_1_AskP_4, P_network_6_1_AskP_5, P_network_6_1_AskP_6, P_network_6_1_AnsP_0, P_network_6_1_AnsP_1, P_network_6_1_AnsP_2, P_network_6_1_AnsP_3, P_network_6_1_AnsP_4, P_network_6_1_AnsP_5, P_network_6_1_AnsP_6, P_network_6_1_RI_0, P_network_6_1_RI_1, P_network_6_1_RI_2, P_network_6_1_RI_3, P_network_6_1_RI_4, P_network_6_1_RI_5, P_network_6_1_RI_6, P_network_6_1_AI_0, P_network_6_1_AI_1, P_network_6_1_AI_2, P_network_6_1_AI_3, P_network_6_1_AI_4, P_network_6_1_AI_5, P_network_6_1_AI_6, P_network_6_1_AnnP_0, P_network_6_1_AnnP_1, P_network_6_1_AnnP_2, P_network_6_1_AnnP_3, P_network_6_1_AnnP_4, P_network_6_1_AnnP_5, P_network_6_1_AnnP_6, P_network_6_1_RP_0, P_network_6_1_RP_1, P_network_6_1_RP_2, P_network_6_1_RP_3, P_network_6_1_RP_4, P_network_6_1_RP_5, P_network_6_1_RP_6, P_network_6_2_AskP_0, P_network_6_2_AskP_1, P_network_6_2_AskP_2, P_network_6_2_AskP_3, P_network_6_2_AskP_4, P_network_6_2_AskP_5, P_network_6_2_AskP_6, P_network_6_2_AnsP_0, P_network_6_2_AnsP_1, P_network_6_2_AnsP_2, P_network_6_2_AnsP_3, P_network_6_2_AnsP_4, P_network_6_2_AnsP_5, P_network_6_2_AnsP_6, P_network_6_2_RI_0, P_network_6_2_RI_1, P_network_6_2_RI_2, P_network_6_2_RI_3, P_network_6_2_RI_4, P_network_6_2_RI_5, P_network_6_2_RI_6, P_network_6_2_AI_0, P_network_6_2_AI_1, P_network_6_2_AI_2, P_network_6_2_AI_3, P_network_6_2_AI_4, P_network_6_2_AI_5, P_network_6_2_AI_6, P_network_6_2_AnnP_0, P_network_6_2_AnnP_1, P_network_6_2_AnnP_2, P_network_6_2_AnnP_3, P_network_6_2_AnnP_4, P_network_6_2_AnnP_5, P_network_6_2_AnnP_6, P_network_6_2_RP_0, P_network_6_2_RP_1, P_network_6_2_RP_2, P_network_6_2_RP_3, P_network_6_2_RP_4, P_network_6_2_RP_5, P_network_6_2_RP_6, P_network_6_3_AskP_0, P_network_6_3_AskP_1, P_network_6_3_AskP_2, P_network_6_3_AskP_3, P_network_6_3_AskP_4, P_network_6_3_AskP_5, P_network_6_3_AskP_6, P_network_6_3_AnsP_0, P_network_6_3_AnsP_1, P_network_6_3_AnsP_2, P_network_6_3_AnsP_3, P_network_6_3_AnsP_4, P_network_6_3_AnsP_5, P_network_6_3_AnsP_6, P_network_6_3_RI_0, P_network_6_3_RI_1, P_network_6_3_RI_2, P_network_6_3_RI_3, P_network_6_3_RI_4, P_network_6_3_RI_5, P_network_6_3_RI_6, P_network_6_3_AI_0, P_network_6_3_AI_1, P_network_6_3_AI_2, P_network_6_3_AI_3, P_network_6_3_AI_4, P_network_6_3_AI_5, P_network_6_3_AI_6, P_network_6_3_AnnP_0, P_network_6_3_AnnP_1, P_network_6_3_AnnP_2, P_network_6_3_AnnP_3, P_network_6_3_AnnP_4, P_network_6_3_AnnP_5, P_network_6_3_AnnP_6, P_network_6_3_RP_0, P_network_6_3_RP_1, P_network_6_3_RP_2, P_network_6_3_RP_3, P_network_6_3_RP_4, P_network_6_3_RP_5, P_network_6_3_RP_6, P_network_6_4_AskP_0, P_network_6_4_AskP_1, P_network_6_4_AskP_2, P_network_6_4_AskP_3, P_network_6_4_AskP_4, P_network_6_4_AskP_5, P_network_6_4_AskP_6, P_network_6_4_AnsP_0, P_network_6_4_AnsP_1, P_network_6_4_AnsP_2, P_network_6_4_AnsP_3, P_network_6_4_AnsP_4, P_network_6_4_AnsP_5, P_network_6_4_AnsP_6, P_network_6_4_RI_0, P_network_6_4_RI_1, P_network_6_4_RI_2, P_network_6_4_RI_3, P_network_6_4_RI_4, P_network_6_4_RI_5, P_network_6_4_RI_6, P_network_6_4_AI_0, P_network_6_4_AI_1, P_network_6_4_AI_2, P_network_6_4_AI_3, P_network_6_4_AI_4, P_network_6_4_AI_5, P_network_6_4_AI_6, P_network_6_4_AnnP_0, P_network_6_4_AnnP_1, P_network_6_4_AnnP_2, P_network_6_4_AnnP_3, P_network_6_4_AnnP_4, P_network_6_4_AnnP_5, P_network_6_4_AnnP_6, P_network_6_4_RP_0, P_network_6_4_RP_1, P_network_6_4_RP_2, P_network_6_4_RP_3, P_network_6_4_RP_4, P_network_6_4_RP_5, P_network_6_4_RP_6, P_network_6_5_AskP_0, P_network_6_5_AskP_1, P_network_6_5_AskP_2, P_network_6_5_AskP_3, P_network_6_5_AskP_4, P_network_6_5_AskP_5, P_network_6_5_AskP_6, P_network_6_5_AnsP_0, P_network_6_5_AnsP_1, P_network_6_5_AnsP_2, P_network_6_5_AnsP_3, P_network_6_5_AnsP_4, P_network_6_5_AnsP_5, P_network_6_5_AnsP_6, P_network_6_5_RI_0, P_network_6_5_RI_1, P_network_6_5_RI_2, P_network_6_5_RI_3, P_network_6_5_RI_4, P_network_6_5_RI_5, P_network_6_5_RI_6, P_network_6_5_AI_0, P_network_6_5_AI_1, P_network_6_5_AI_2, P_network_6_5_AI_3, P_network_6_5_AI_4, P_network_6_5_AI_5, P_network_6_5_AI_6, P_network_6_5_AnnP_0, P_network_6_5_AnnP_1, P_network_6_5_AnnP_2, P_network_6_5_AnnP_3, P_network_6_5_AnnP_4, P_network_6_5_AnnP_5, P_network_6_5_AnnP_6, P_network_6_5_RP_0, P_network_6_5_RP_1, P_network_6_5_RP_2, P_network_6_5_RP_3, P_network_6_5_RP_4, P_network_6_5_RP_5, P_network_6_5_RP_6, P_network_6_6_AskP_0, P_network_6_6_AskP_1, P_network_6_6_AskP_2, P_network_6_6_AskP_3, P_network_6_6_AskP_4, P_network_6_6_AskP_5, P_network_6_6_AskP_6, P_network_6_6_AnsP_0, P_network_6_6_AnsP_1, P_network_6_6_AnsP_2, P_network_6_6_AnsP_3, P_network_6_6_AnsP_4, P_network_6_6_AnsP_5, P_network_6_6_AnsP_6, P_network_6_6_RI_0, P_network_6_6_RI_1, P_network_6_6_RI_2, P_network_6_6_RI_3, P_network_6_6_RI_4, P_network_6_6_RI_5, P_network_6_6_RI_6, P_network_6_6_AI_0, P_network_6_6_AI_1, P_network_6_6_AI_2, P_network_6_6_AI_3, P_network_6_6_AI_4, P_network_6_6_AI_5, P_network_6_6_AI_6, P_network_6_6_AnnP_0, P_network_6_6_AnnP_1, P_network_6_6_AnnP_2, P_network_6_6_AnnP_3, P_network_6_6_AnnP_4, P_network_6_6_AnnP_5, P_network_6_6_AnnP_6, P_network_6_6_RP_0, P_network_6_6_RP_1, P_network_6_6_RP_2, P_network_6_6_RP_3, P_network_6_6_RP_4, P_network_6_6_RP_5, P_network_6_6_RP_6, P_poll__handlingMessage_0, P_poll__handlingMessage_1, P_poll__handlingMessage_2, P_poll__handlingMessage_3, P_poll__handlingMessage_4, P_poll__handlingMessage_5, P_poll__handlingMessage_6, P_poll__networl_0_0_AskP_0, P_poll__networl_0_0_AskP_1, P_poll__networl_0_0_AskP_2, P_poll__networl_0_0_AskP_3, P_poll__networl_0_0_AskP_4, P_poll__networl_0_0_AskP_5, P_poll__networl_0_0_AskP_6, P_poll__networl_0_0_AnsP_0, P_poll__networl_0_0_AnsP_1, P_poll__networl_0_0_AnsP_2, P_poll__networl_0_0_AnsP_3, P_poll__networl_0_0_AnsP_4, P_poll__networl_0_0_AnsP_5, P_poll__networl_0_0_AnsP_6, P_poll__networl_0_0_RI_0, P_poll__networl_0_0_RI_1, P_poll__networl_0_0_RI_2, P_poll__networl_0_0_RI_3, P_poll__networl_0_0_RI_4, P_poll__networl_0_0_RI_5, P_poll__networl_0_0_RI_6, P_poll__networl_0_0_AI_0, P_poll__networl_0_0_AI_1, P_poll__networl_0_0_AI_2, P_poll__networl_0_0_AI_3, P_poll__networl_0_0_AI_4, P_poll__networl_0_0_AI_5, P_poll__networl_0_0_AI_6, P_poll__networl_0_0_AnnP_0, P_poll__networl_0_0_AnnP_1, P_poll__networl_0_0_AnnP_2, P_poll__networl_0_0_AnnP_3, P_poll__networl_0_0_AnnP_4, P_poll__networl_0_0_AnnP_5, P_poll__networl_0_0_AnnP_6, P_poll__networl_0_0_RP_0, P_poll__networl_0_0_RP_1, P_poll__networl_0_0_RP_2, P_poll__networl_0_0_RP_3, P_poll__networl_0_0_RP_4, P_poll__networl_0_0_RP_5, P_poll__networl_0_0_RP_6, P_poll__networl_0_1_AskP_0, P_poll__networl_0_1_AskP_1, P_poll__networl_0_1_AskP_2, P_poll__networl_0_1_AskP_3, P_poll__networl_0_1_AskP_4, P_poll__networl_0_1_AskP_5, P_poll__networl_0_1_AskP_6, P_poll__networl_0_1_AnsP_0, P_poll__networl_0_1_AnsP_1, P_poll__networl_0_1_AnsP_2, P_poll__networl_0_1_AnsP_3, P_poll__networl_0_1_AnsP_4, P_poll__networl_0_1_AnsP_5, P_poll__networl_0_1_AnsP_6, P_poll__networl_0_1_RI_0, P_poll__networl_0_1_RI_1, P_poll__networl_0_1_RI_2, P_poll__networl_0_1_RI_3, P_poll__networl_0_1_RI_4, P_poll__networl_0_1_RI_5, P_poll__networl_0_1_RI_6, P_poll__networl_0_1_AI_0, P_poll__networl_0_1_AI_1, P_poll__networl_0_1_AI_2, P_poll__networl_0_1_AI_3, P_poll__networl_0_1_AI_4, P_poll__networl_0_1_AI_5, P_poll__networl_0_1_AI_6, P_poll__networl_0_1_AnnP_0, P_poll__networl_0_1_AnnP_1, P_poll__networl_0_1_AnnP_2, P_poll__networl_0_1_AnnP_3, P_poll__networl_0_1_AnnP_4, P_poll__networl_0_1_AnnP_5, P_poll__networl_0_1_AnnP_6, P_poll__networl_0_1_RP_0, P_poll__networl_0_1_RP_1, P_poll__networl_0_1_RP_2, P_poll__networl_0_1_RP_3, P_poll__networl_0_1_RP_4, P_poll__networl_0_1_RP_5, P_poll__networl_0_1_RP_6, P_poll__networl_0_2_AskP_0, P_poll__networl_0_2_AskP_1, P_poll__networl_0_2_AskP_2, P_poll__networl_0_2_AskP_3, P_poll__networl_0_2_AskP_4, P_poll__networl_0_2_AskP_5, P_poll__networl_0_2_AskP_6, P_poll__networl_0_2_AnsP_0, P_poll__networl_0_2_AnsP_1, P_poll__networl_0_2_AnsP_2, P_poll__networl_0_2_AnsP_3, P_poll__networl_0_2_AnsP_4, P_poll__networl_0_2_AnsP_5, P_poll__networl_0_2_AnsP_6, P_poll__networl_0_2_RI_0, P_poll__networl_0_2_RI_1, P_poll__networl_0_2_RI_2, P_poll__networl_0_2_RI_3, P_poll__networl_0_2_RI_4, P_poll__networl_0_2_RI_5, P_poll__networl_0_2_RI_6, P_poll__networl_0_2_AI_0, P_poll__networl_0_2_AI_1, P_poll__networl_0_2_AI_2, P_poll__networl_0_2_AI_3, P_poll__networl_0_2_AI_4, P_poll__networl_0_2_AI_5, P_poll__networl_0_2_AI_6, P_poll__networl_0_2_AnnP_0, P_poll__networl_0_2_AnnP_1, P_poll__networl_0_2_AnnP_2, P_poll__networl_0_2_AnnP_3, P_poll__networl_0_2_AnnP_4, P_poll__networl_0_2_AnnP_5, P_poll__networl_0_2_AnnP_6, P_poll__networl_0_2_RP_0, P_poll__networl_0_2_RP_1, P_poll__networl_0_2_RP_2, P_poll__networl_0_2_RP_3, P_poll__networl_0_2_RP_4, P_poll__networl_0_2_RP_5, P_poll__networl_0_2_RP_6, P_poll__networl_0_3_AskP_0, P_poll__networl_0_3_AskP_1, P_poll__networl_0_3_AskP_2, P_poll__networl_0_3_AskP_3, P_poll__networl_0_3_AskP_4, P_poll__networl_0_3_AskP_5, P_poll__networl_0_3_AskP_6, P_poll__networl_0_3_AnsP_0, P_poll__networl_0_3_AnsP_1, P_poll__networl_0_3_AnsP_2, P_poll__networl_0_3_AnsP_3, P_poll__networl_0_3_AnsP_4, P_poll__networl_0_3_AnsP_5, P_poll__networl_0_3_AnsP_6, P_poll__networl_0_3_RI_0, P_poll__networl_0_3_RI_1, P_poll__networl_0_3_RI_2, P_poll__networl_0_3_RI_3, P_poll__networl_0_3_RI_4, P_poll__networl_0_3_RI_5, P_poll__networl_0_3_RI_6, P_poll__networl_0_3_AI_0, P_poll__networl_0_3_AI_1, P_poll__networl_0_3_AI_2, P_poll__networl_0_3_AI_3, P_poll__networl_0_3_AI_4, P_poll__networl_0_3_AI_5, P_poll__networl_0_3_AI_6, P_poll__networl_0_3_AnnP_0, P_poll__networl_0_3_AnnP_1, P_poll__networl_0_3_AnnP_2, P_poll__networl_0_3_AnnP_3, P_poll__networl_0_3_AnnP_4, P_poll__networl_0_3_AnnP_5, P_poll__networl_0_3_AnnP_6, P_poll__networl_0_3_RP_0, P_poll__networl_0_3_RP_1, P_poll__networl_0_3_RP_2, P_poll__networl_0_3_RP_3, P_poll__networl_0_3_RP_4, P_poll__networl_0_3_RP_5, P_poll__networl_0_3_RP_6, P_poll__networl_0_4_AskP_0, P_poll__networl_0_4_AskP_1, P_poll__networl_0_4_AskP_2, P_poll__networl_0_4_AskP_3, P_poll__networl_0_4_AskP_4, P_poll__networl_0_4_AskP_5, P_poll__networl_0_4_AskP_6, P_poll__networl_0_4_AnsP_0, P_poll__networl_0_4_AnsP_1, P_poll__networl_0_4_AnsP_2, P_poll__networl_0_4_AnsP_3, P_poll__networl_0_4_AnsP_4, P_poll__networl_0_4_AnsP_5, P_poll__networl_0_4_AnsP_6, P_poll__networl_0_4_RI_0, P_poll__networl_0_4_RI_1, P_poll__networl_0_4_RI_2, P_poll__networl_0_4_RI_3, P_poll__networl_0_4_RI_4, P_poll__networl_0_4_RI_5, P_poll__networl_0_4_RI_6, P_poll__networl_0_4_AI_0, P_poll__networl_0_4_AI_1, P_poll__networl_0_4_AI_2, P_poll__networl_0_4_AI_3, P_poll__networl_0_4_AI_4, P_poll__networl_0_4_AI_5, P_poll__networl_0_4_AI_6, P_poll__networl_0_4_AnnP_0, P_poll__networl_0_4_AnnP_1, P_poll__networl_0_4_AnnP_2, P_poll__networl_0_4_AnnP_3, P_poll__networl_0_4_AnnP_4, P_poll__networl_0_4_AnnP_5, P_poll__networl_0_4_AnnP_6, P_poll__networl_0_4_RP_0, P_poll__networl_0_4_RP_1, P_poll__networl_0_4_RP_2, P_poll__networl_0_4_RP_3, P_poll__networl_0_4_RP_4, P_poll__networl_0_4_RP_5, P_poll__networl_0_4_RP_6, P_poll__networl_0_5_AskP_0, P_poll__networl_0_5_AskP_1, P_poll__networl_0_5_AskP_2, P_poll__networl_0_5_AskP_3, P_poll__networl_0_5_AskP_4, P_poll__networl_0_5_AskP_5, P_poll__networl_0_5_AskP_6, P_poll__networl_0_5_AnsP_0, P_poll__networl_0_5_AnsP_1, P_poll__networl_0_5_AnsP_2, P_poll__networl_0_5_AnsP_3, P_poll__networl_0_5_AnsP_4, P_poll__networl_0_5_AnsP_5, P_poll__networl_0_5_AnsP_6, P_poll__networl_0_5_RI_0, P_poll__networl_0_5_RI_1, P_poll__networl_0_5_RI_2, P_poll__networl_0_5_RI_3, P_poll__networl_0_5_RI_4, P_poll__networl_0_5_RI_5, P_poll__networl_0_5_RI_6, P_poll__networl_0_5_AI_0, P_poll__networl_0_5_AI_1, P_poll__networl_0_5_AI_2, P_poll__networl_0_5_AI_3, P_poll__networl_0_5_AI_4, P_poll__networl_0_5_AI_5, P_poll__networl_0_5_AI_6, P_poll__networl_0_5_AnnP_0, P_poll__networl_0_5_AnnP_1, P_poll__networl_0_5_AnnP_2, P_poll__networl_0_5_AnnP_3, P_poll__networl_0_5_AnnP_4, P_poll__networl_0_5_AnnP_5, P_poll__networl_0_5_AnnP_6, P_poll__networl_0_5_RP_0, P_poll__networl_0_5_RP_1, P_poll__networl_0_5_RP_2, P_poll__networl_0_5_RP_3, P_poll__networl_0_5_RP_4, P_poll__networl_0_5_RP_5, P_poll__networl_0_5_RP_6, P_poll__networl_0_6_AskP_0, P_poll__networl_0_6_AskP_1, P_poll__networl_0_6_AskP_2, P_poll__networl_0_6_AskP_3, P_poll__networl_0_6_AskP_4, P_poll__networl_0_6_AskP_5, P_poll__networl_0_6_AskP_6, P_poll__networl_0_6_AnsP_0, P_poll__networl_0_6_AnsP_1, P_poll__networl_0_6_AnsP_2, P_poll__networl_0_6_AnsP_3, P_poll__networl_0_6_AnsP_4, P_poll__networl_0_6_AnsP_5, P_poll__networl_0_6_AnsP_6, P_poll__networl_0_6_RI_0, P_poll__networl_0_6_RI_1, P_poll__networl_0_6_RI_2, P_poll__networl_0_6_RI_3, P_poll__networl_0_6_RI_4, P_poll__networl_0_6_RI_5, P_poll__networl_0_6_RI_6, P_poll__networl_0_6_AI_0, P_poll__networl_0_6_AI_1, P_poll__networl_0_6_AI_2, P_poll__networl_0_6_AI_3, P_poll__networl_0_6_AI_4, P_poll__networl_0_6_AI_5, P_poll__networl_0_6_AI_6, P_poll__networl_0_6_AnnP_0, P_poll__networl_0_6_AnnP_1, P_poll__networl_0_6_AnnP_2, P_poll__networl_0_6_AnnP_3, P_poll__networl_0_6_AnnP_4, P_poll__networl_0_6_AnnP_5, P_poll__networl_0_6_AnnP_6, P_poll__networl_0_6_RP_0, P_poll__networl_0_6_RP_1, P_poll__networl_0_6_RP_2, P_poll__networl_0_6_RP_3, P_poll__networl_0_6_RP_4, P_poll__networl_0_6_RP_5, P_poll__networl_0_6_RP_6, P_poll__networl_1_0_AskP_0, P_poll__networl_1_0_AskP_1, P_poll__networl_1_0_AskP_2, P_poll__networl_1_0_AskP_3, P_poll__networl_1_0_AskP_4, P_poll__networl_1_0_AskP_5, P_poll__networl_1_0_AskP_6, P_poll__networl_1_0_AnsP_0, P_poll__networl_1_0_AnsP_1, P_poll__networl_1_0_AnsP_2, P_poll__networl_1_0_AnsP_3, P_poll__networl_1_0_AnsP_4, P_poll__networl_1_0_AnsP_5, P_poll__networl_1_0_AnsP_6, P_poll__networl_1_0_RI_0, P_poll__networl_1_0_RI_1, P_poll__networl_1_0_RI_2, P_poll__networl_1_0_RI_3, P_poll__networl_1_0_RI_4, P_poll__networl_1_0_RI_5, P_poll__networl_1_0_RI_6, P_poll__networl_1_0_AI_0, P_poll__networl_1_0_AI_1, P_poll__networl_1_0_AI_2, P_poll__networl_1_0_AI_3, P_poll__networl_1_0_AI_4, P_poll__networl_1_0_AI_5, P_poll__networl_1_0_AI_6, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_0_AnnP_2, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_AnnP_4, P_poll__networl_1_0_AnnP_5, P_poll__networl_1_0_AnnP_6, P_poll__networl_1_0_RP_0, P_poll__networl_1_0_RP_1, P_poll__networl_1_0_RP_2, P_poll__networl_1_0_RP_3, P_poll__networl_1_0_RP_4, P_poll__networl_1_0_RP_5, P_poll__networl_1_0_RP_6, P_poll__networl_1_1_AskP_0, P_poll__networl_1_1_AskP_1, P_poll__networl_1_1_AskP_2, P_poll__networl_1_1_AskP_3, P_poll__networl_1_1_AskP_4, P_poll__networl_1_1_AskP_5, P_poll__networl_1_1_AskP_6, P_poll__networl_1_1_AnsP_0, P_poll__networl_1_1_AnsP_1, P_poll__networl_1_1_AnsP_2, P_poll__networl_1_1_AnsP_3, P_poll__networl_1_1_AnsP_4, P_poll__networl_1_1_AnsP_5, P_poll__networl_1_1_AnsP_6, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_RI_1, P_poll__networl_1_1_RI_2, P_poll__networl_1_1_RI_3, P_poll__networl_1_1_RI_4, P_poll__networl_1_1_RI_5, P_poll__networl_1_1_RI_6, P_poll__networl_1_1_AI_0, P_poll__networl_1_1_AI_1, P_poll__networl_1_1_AI_2, P_poll__networl_1_1_AI_3, P_poll__networl_1_1_AI_4, P_poll__networl_1_1_AI_5, P_poll__networl_1_1_AI_6, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_1_AnnP_1, P_poll__networl_1_1_AnnP_2, P_poll__networl_1_1_AnnP_3, P_poll__networl_1_1_AnnP_4, P_poll__networl_1_1_AnnP_5, P_poll__networl_1_1_AnnP_6, P_poll__networl_1_1_RP_0, P_poll__networl_1_1_RP_1, P_poll__networl_1_1_RP_2, P_poll__networl_1_1_RP_3, P_poll__networl_1_1_RP_4, P_poll__networl_1_1_RP_5, P_poll__networl_1_1_RP_6, P_poll__networl_1_2_AskP_0, P_poll__networl_1_2_AskP_1, P_poll__networl_1_2_AskP_2, P_poll__networl_1_2_AskP_3, P_poll__networl_1_2_AskP_4, P_poll__networl_1_2_AskP_5, P_poll__networl_1_2_AskP_6, P_poll__networl_1_2_AnsP_0, P_poll__networl_1_2_AnsP_1, P_poll__networl_1_2_AnsP_2, P_poll__networl_1_2_AnsP_3, P_poll__networl_1_2_AnsP_4, P_poll__networl_1_2_AnsP_5, P_poll__networl_1_2_AnsP_6, P_poll__networl_1_2_RI_0, P_poll__networl_1_2_RI_1, P_poll__networl_1_2_RI_2, P_poll__networl_1_2_RI_3, P_poll__networl_1_2_RI_4, P_poll__networl_1_2_RI_5, P_poll__networl_1_2_RI_6, P_poll__networl_1_2_AI_0, P_poll__networl_1_2_AI_1, P_poll__networl_1_2_AI_2, P_poll__networl_1_2_AI_3, P_poll__networl_1_2_AI_4, P_poll__networl_1_2_AI_5, P_poll__networl_1_2_AI_6, P_poll__networl_1_2_AnnP_0, P_poll__networl_1_2_AnnP_1, P_poll__networl_1_2_AnnP_2, P_poll__networl_1_2_AnnP_3, P_poll__networl_1_2_AnnP_4, P_poll__networl_1_2_AnnP_5, P_poll__networl_1_2_AnnP_6, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_RP_1, P_poll__networl_1_2_RP_2, P_poll__networl_1_2_RP_3, P_poll__networl_1_2_RP_4, P_poll__networl_1_2_RP_5, P_poll__networl_1_2_RP_6, P_poll__networl_1_3_AskP_0, P_poll__networl_1_3_AskP_1, P_poll__networl_1_3_AskP_2, P_poll__networl_1_3_AskP_3, P_poll__networl_1_3_AskP_4, P_poll__networl_1_3_AskP_5, P_poll__networl_1_3_AskP_6, P_poll__networl_1_3_AnsP_0, P_poll__networl_1_3_AnsP_1, P_poll__networl_1_3_AnsP_2, P_poll__networl_1_3_AnsP_3, P_poll__networl_1_3_AnsP_4, P_poll__networl_1_3_AnsP_5, P_poll__networl_1_3_AnsP_6, P_poll__networl_1_3_RI_0, P_poll__networl_1_3_RI_1, P_poll__networl_1_3_RI_2, P_poll__networl_1_3_RI_3, P_poll__networl_1_3_RI_4, P_poll__networl_1_3_RI_5, P_poll__networl_1_3_RI_6, P_poll__networl_1_3_AI_0, P_poll__networl_1_3_AI_1, P_poll__networl_1_3_AI_2, P_poll__networl_1_3_AI_3, P_poll__networl_1_3_AI_4, P_poll__networl_1_3_AI_5, P_poll__networl_1_3_AI_6, P_poll__networl_1_3_AnnP_0, P_poll__networl_1_3_AnnP_1, P_poll__networl_1_3_AnnP_2, P_poll__networl_1_3_AnnP_3, P_poll__networl_1_3_AnnP_4, P_poll__networl_1_3_AnnP_5, P_poll__networl_1_3_AnnP_6, P_poll__networl_1_3_RP_0, P_poll__networl_1_3_RP_1, P_poll__networl_1_3_RP_2, P_poll__networl_1_3_RP_3, P_poll__networl_1_3_RP_4, P_poll__networl_1_3_RP_5, P_poll__networl_1_3_RP_6, P_poll__networl_1_4_AskP_0, P_poll__networl_1_4_AskP_1, P_poll__networl_1_4_AskP_2, P_poll__networl_1_4_AskP_3, P_poll__networl_1_4_AskP_4, P_poll__networl_1_4_AskP_5, P_poll__networl_1_4_AskP_6, P_poll__networl_1_4_AnsP_0, P_poll__networl_1_4_AnsP_1, P_poll__networl_1_4_AnsP_2, P_poll__networl_1_4_AnsP_3, P_poll__networl_1_4_AnsP_4, P_poll__networl_1_4_AnsP_5, P_poll__networl_1_4_AnsP_6, P_poll__networl_1_4_RI_0, P_poll__networl_1_4_RI_1, P_poll__networl_1_4_RI_2, P_poll__networl_1_4_RI_3, P_poll__networl_1_4_RI_4, P_poll__networl_1_4_RI_5, P_poll__networl_1_4_RI_6, P_poll__networl_1_4_AI_0, P_poll__networl_1_4_AI_1, P_poll__networl_1_4_AI_2, P_poll__networl_1_4_AI_3, P_poll__networl_1_4_AI_4, P_poll__networl_1_4_AI_5, P_poll__networl_1_4_AI_6, P_poll__networl_1_4_AnnP_0, P_poll__networl_1_4_AnnP_1, P_poll__networl_1_4_AnnP_2, P_poll__networl_1_4_AnnP_3, P_poll__networl_1_4_AnnP_4, P_poll__networl_1_4_AnnP_5, P_poll__networl_1_4_AnnP_6, P_poll__networl_1_4_RP_0, P_poll__networl_1_4_RP_1, P_poll__networl_1_4_RP_2, P_poll__networl_1_4_RP_3, P_poll__networl_1_4_RP_4, P_poll__networl_1_4_RP_5, P_poll__networl_1_4_RP_6, P_poll__networl_1_5_AskP_0, P_poll__networl_1_5_AskP_1, P_poll__networl_1_5_AskP_2, P_poll__networl_1_5_AskP_3, P_poll__networl_1_5_AskP_4, P_poll__networl_1_5_AskP_5, P_poll__networl_1_5_AskP_6, P_poll__networl_1_5_AnsP_0, P_poll__networl_1_5_AnsP_1, P_poll__networl_1_5_AnsP_2, P_poll__networl_1_5_AnsP_3, P_poll__networl_1_5_AnsP_4, P_poll__networl_1_5_AnsP_5, P_poll__networl_1_5_AnsP_6, P_poll__networl_1_5_RI_0, P_poll__networl_1_5_RI_1, P_poll__networl_1_5_RI_2, P_poll__networl_1_5_RI_3, P_poll__networl_1_5_RI_4, P_poll__networl_1_5_RI_5, P_poll__networl_1_5_RI_6, P_poll__networl_1_5_AI_0, P_poll__networl_1_5_AI_1, P_poll__networl_1_5_AI_2, P_poll__networl_1_5_AI_3, P_poll__networl_1_5_AI_4, P_poll__networl_1_5_AI_5, P_poll__networl_1_5_AI_6, P_poll__networl_1_5_AnnP_0, P_poll__networl_1_5_AnnP_1, P_poll__networl_1_5_AnnP_2, P_poll__networl_1_5_AnnP_3, P_poll__networl_1_5_AnnP_4, P_poll__networl_1_5_AnnP_5, P_poll__networl_1_5_AnnP_6, P_poll__networl_1_5_RP_0, P_poll__networl_1_5_RP_1, P_poll__networl_1_5_RP_2, P_poll__networl_1_5_RP_3, P_poll__networl_1_5_RP_4, P_poll__networl_1_5_RP_5, P_poll__networl_1_5_RP_6, P_poll__networl_1_6_AskP_0, P_poll__networl_1_6_AskP_1, P_poll__networl_1_6_AskP_2, P_poll__networl_1_6_AskP_3, P_poll__networl_1_6_AskP_4, P_poll__networl_1_6_AskP_5, P_poll__networl_1_6_AskP_6, P_poll__networl_1_6_AnsP_0, P_poll__networl_1_6_AnsP_1, P_poll__networl_1_6_AnsP_2, P_poll__networl_1_6_AnsP_3, P_poll__networl_1_6_AnsP_4, P_poll__networl_1_6_AnsP_5, P_poll__networl_1_6_AnsP_6, P_poll__networl_1_6_RI_0, P_poll__networl_1_6_RI_1, P_poll__networl_1_6_RI_2, P_poll__networl_1_6_RI_3, P_poll__networl_1_6_RI_4, P_poll__networl_1_6_RI_5, P_poll__networl_1_6_RI_6, P_poll__networl_1_6_AI_0, P_poll__networl_1_6_AI_1, P_poll__networl_1_6_AI_2, P_poll__networl_1_6_AI_3, P_poll__networl_1_6_AI_4, P_poll__networl_1_6_AI_5, P_poll__networl_1_6_AI_6, P_poll__networl_1_6_AnnP_0, P_poll__networl_1_6_AnnP_1, P_poll__networl_1_6_AnnP_2, P_poll__networl_1_6_AnnP_3, P_poll__networl_1_6_AnnP_4, P_poll__networl_1_6_AnnP_5, P_poll__networl_1_6_AnnP_6, P_poll__networl_1_6_RP_0, P_poll__networl_1_6_RP_1, P_poll__networl_1_6_RP_2, P_poll__networl_1_6_RP_3, P_poll__networl_1_6_RP_4, P_poll__networl_1_6_RP_5, P_poll__networl_1_6_RP_6, P_poll__networl_2_0_AskP_0, P_poll__networl_2_0_AskP_1, P_poll__networl_2_0_AskP_2, P_poll__networl_2_0_AskP_3, P_poll__networl_2_0_AskP_4, P_poll__networl_2_0_AskP_5, P_poll__networl_2_0_AskP_6, P_poll__networl_2_0_AnsP_0, P_poll__networl_2_0_AnsP_1, P_poll__networl_2_0_AnsP_2, P_poll__networl_2_0_AnsP_3, P_poll__networl_2_0_AnsP_4, P_poll__networl_2_0_AnsP_5, P_poll__networl_2_0_AnsP_6, P_poll__networl_2_0_RI_0, P_poll__networl_2_0_RI_1, P_poll__networl_2_0_RI_2, P_poll__networl_2_0_RI_3, P_poll__networl_2_0_RI_4, P_poll__networl_2_0_RI_5, P_poll__networl_2_0_RI_6, P_poll__networl_2_0_AI_0, P_poll__networl_2_0_AI_1, P_poll__networl_2_0_AI_2, P_poll__networl_2_0_AI_3, P_poll__networl_2_0_AI_4, P_poll__networl_2_0_AI_5, P_poll__networl_2_0_AI_6, P_poll__networl_2_0_AnnP_0, P_poll__networl_2_0_AnnP_1, P_poll__networl_2_0_AnnP_2, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_0_AnnP_4, P_poll__networl_2_0_AnnP_5, P_poll__networl_2_0_AnnP_6, P_poll__networl_2_0_RP_0, P_poll__networl_2_0_RP_1, P_poll__networl_2_0_RP_2, P_poll__networl_2_0_RP_3, P_poll__networl_2_0_RP_4, P_poll__networl_2_0_RP_5, P_poll__networl_2_0_RP_6, P_poll__networl_2_1_AskP_0, P_poll__networl_2_1_AskP_1, P_poll__networl_2_1_AskP_2, P_poll__networl_2_1_AskP_3, P_poll__networl_2_1_AskP_4, P_poll__networl_2_1_AskP_5, P_poll__networl_2_1_AskP_6, P_poll__networl_2_1_AnsP_0, P_poll__networl_2_1_AnsP_1, P_poll__networl_2_1_AnsP_2, P_poll__networl_2_1_AnsP_3, P_poll__networl_2_1_AnsP_4, P_poll__networl_2_1_AnsP_5, P_poll__networl_2_1_AnsP_6, P_poll__networl_2_1_RI_0, P_poll__networl_2_1_RI_1, P_poll__networl_2_1_RI_2, P_poll__networl_2_1_RI_3, P_poll__networl_2_1_RI_4, P_poll__networl_2_1_RI_5, P_poll__networl_2_1_RI_6, P_poll__networl_2_1_AI_0, P_poll__networl_2_1_AI_1, P_poll__networl_2_1_AI_2, P_poll__networl_2_1_AI_3, P_poll__networl_2_1_AI_4, P_poll__networl_2_1_AI_5, P_poll__networl_2_1_AI_6, P_poll__networl_2_1_AnnP_0, P_poll__networl_2_1_AnnP_1, P_poll__networl_2_1_AnnP_2, P_poll__networl_2_1_AnnP_3, P_poll__networl_2_1_AnnP_4, P_poll__networl_2_1_AnnP_5, P_poll__networl_2_1_AnnP_6, P_poll__networl_2_1_RP_0, P_poll__networl_2_1_RP_1, P_poll__networl_2_1_RP_2, P_poll__networl_2_1_RP_3, P_poll__networl_2_1_RP_4, P_poll__networl_2_1_RP_5, P_poll__networl_2_1_RP_6, P_poll__networl_2_2_AskP_0, P_poll__networl_2_2_AskP_1, P_poll__networl_2_2_AskP_2, P_poll__networl_2_2_AskP_3, P_poll__networl_2_2_AskP_4, P_poll__networl_2_2_AskP_5, P_poll__networl_2_2_AskP_6, P_poll__networl_2_2_AnsP_0, P_poll__networl_2_2_AnsP_1, P_poll__networl_2_2_AnsP_2, P_poll__networl_2_2_AnsP_3, P_poll__networl_2_2_AnsP_4, P_poll__networl_2_2_AnsP_5, P_poll__networl_2_2_AnsP_6, P_poll__networl_2_2_RI_0, P_poll__networl_2_2_RI_1, P_poll__networl_2_2_RI_2, P_poll__networl_2_2_RI_3, P_poll__networl_2_2_RI_4, P_poll__networl_2_2_RI_5, P_poll__networl_2_2_RI_6, P_poll__networl_2_2_AI_0, P_poll__networl_2_2_AI_1, P_poll__networl_2_2_AI_2, P_poll__networl_2_2_AI_3, P_poll__networl_2_2_AI_4, P_poll__networl_2_2_AI_5, P_poll__networl_2_2_AI_6, P_poll__networl_2_2_AnnP_0, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_2_AnnP_2, P_poll__networl_2_2_AnnP_3, P_poll__networl_2_2_AnnP_4, P_poll__networl_2_2_AnnP_5, P_poll__networl_2_2_AnnP_6, P_poll__networl_2_2_RP_0, P_poll__networl_2_2_RP_1, P_poll__networl_2_2_RP_2, P_poll__networl_2_2_RP_3, P_poll__networl_2_2_RP_4, P_poll__networl_2_2_RP_5, P_poll__networl_2_2_RP_6, P_poll__networl_2_3_AskP_0, P_poll__networl_2_3_AskP_1, P_poll__networl_2_3_AskP_2, P_poll__networl_2_3_AskP_3, P_poll__networl_2_3_AskP_4, P_poll__networl_2_3_AskP_5, P_poll__networl_2_3_AskP_6, P_poll__networl_2_3_AnsP_0, P_poll__networl_2_3_AnsP_1, P_poll__networl_2_3_AnsP_2, P_poll__networl_2_3_AnsP_3, P_poll__networl_2_3_AnsP_4, P_poll__networl_2_3_AnsP_5, P_poll__networl_2_3_AnsP_6, P_poll__networl_2_3_RI_0, P_poll__networl_2_3_RI_1, P_poll__networl_2_3_RI_2, P_poll__networl_2_3_RI_3, P_poll__networl_2_3_RI_4, P_poll__networl_2_3_RI_5, P_poll__networl_2_3_RI_6, P_poll__networl_2_3_AI_0, P_poll__networl_2_3_AI_1, P_poll__networl_2_3_AI_2, P_poll__networl_2_3_AI_3, P_poll__networl_2_3_AI_4, P_poll__networl_2_3_AI_5, P_poll__networl_2_3_AI_6, P_poll__networl_2_3_AnnP_0, P_poll__networl_2_3_AnnP_1, P_poll__networl_2_3_AnnP_2, P_poll__networl_2_3_AnnP_3, P_poll__networl_2_3_AnnP_4, P_poll__networl_2_3_AnnP_5, P_poll__networl_2_3_AnnP_6, P_poll__networl_2_3_RP_0, P_poll__networl_2_3_RP_1, P_poll__networl_2_3_RP_2, P_poll__networl_2_3_RP_3, P_poll__networl_2_3_RP_4, P_poll__networl_2_3_RP_5, P_poll__networl_2_3_RP_6, P_poll__networl_2_4_AskP_0, P_poll__networl_2_4_AskP_1, P_poll__networl_2_4_AskP_2, P_poll__networl_2_4_AskP_3, P_poll__networl_2_4_AskP_4, P_poll__networl_2_4_AskP_5, P_poll__networl_2_4_AskP_6, P_poll__networl_2_4_AnsP_0, P_poll__networl_2_4_AnsP_1, P_poll__networl_2_4_AnsP_2, P_poll__networl_2_4_AnsP_3, P_poll__networl_2_4_AnsP_4, P_poll__networl_2_4_AnsP_5, P_poll__networl_2_4_AnsP_6, P_poll__networl_2_4_RI_0, P_poll__networl_2_4_RI_1, P_poll__networl_2_4_RI_2, P_poll__networl_2_4_RI_3, P_poll__networl_2_4_RI_4, P_poll__networl_2_4_RI_5, P_poll__networl_2_4_RI_6, P_poll__networl_2_4_AI_0, P_poll__networl_2_4_AI_1, P_poll__networl_2_4_AI_2, P_poll__networl_2_4_AI_3, P_poll__networl_2_4_AI_4, P_poll__networl_2_4_AI_5, P_poll__networl_2_4_AI_6, P_poll__networl_2_4_AnnP_0, P_poll__networl_2_4_AnnP_1, P_poll__networl_2_4_AnnP_2, P_poll__networl_2_4_AnnP_3, P_poll__networl_2_4_AnnP_4, P_poll__networl_2_4_AnnP_5, P_poll__networl_2_4_AnnP_6, P_poll__networl_2_4_RP_0, P_poll__networl_2_4_RP_1, P_poll__networl_2_4_RP_2, P_poll__networl_2_4_RP_3, P_poll__networl_2_4_RP_4, P_poll__networl_2_4_RP_5, P_poll__networl_2_4_RP_6, P_poll__networl_2_5_AskP_0, P_poll__networl_2_5_AskP_1, P_poll__networl_2_5_AskP_2, P_poll__networl_2_5_AskP_3, P_poll__networl_2_5_AskP_4, P_poll__networl_2_5_AskP_5, P_poll__networl_2_5_AskP_6, P_poll__networl_2_5_AnsP_0, P_poll__networl_2_5_AnsP_1, P_poll__networl_2_5_AnsP_2, P_poll__networl_2_5_AnsP_3, P_poll__networl_2_5_AnsP_4, P_poll__networl_2_5_AnsP_5, P_poll__networl_2_5_AnsP_6, P_poll__networl_2_5_RI_0, P_poll__networl_2_5_RI_1, P_poll__networl_2_5_RI_2, P_poll__networl_2_5_RI_3, P_poll__networl_2_5_RI_4, P_poll__networl_2_5_RI_5, P_poll__networl_2_5_RI_6, P_poll__networl_2_5_AI_0, P_poll__networl_2_5_AI_1, P_poll__networl_2_5_AI_2, P_poll__networl_2_5_AI_3, P_poll__networl_2_5_AI_4, P_poll__networl_2_5_AI_5, P_poll__networl_2_5_AI_6, P_poll__networl_2_5_AnnP_0, P_poll__networl_2_5_AnnP_1, P_poll__networl_2_5_AnnP_2, P_poll__networl_2_5_AnnP_3, P_poll__networl_2_5_AnnP_4, P_poll__networl_2_5_AnnP_5, P_poll__networl_2_5_AnnP_6, P_poll__networl_2_5_RP_0, P_poll__networl_2_5_RP_1, P_poll__networl_2_5_RP_2, P_poll__networl_2_5_RP_3, P_poll__networl_2_5_RP_4, P_poll__networl_2_5_RP_5, P_poll__networl_2_5_RP_6, P_poll__networl_2_6_AskP_0, P_poll__networl_2_6_AskP_1, P_poll__networl_2_6_AskP_2, P_poll__networl_2_6_AskP_3, P_poll__networl_2_6_AskP_4, P_poll__networl_2_6_AskP_5, P_poll__networl_2_6_AskP_6, P_poll__networl_2_6_AnsP_0, P_poll__networl_2_6_AnsP_1, P_poll__networl_2_6_AnsP_2, P_poll__networl_2_6_AnsP_3, P_poll__networl_2_6_AnsP_4, P_poll__networl_2_6_AnsP_5, P_poll__networl_2_6_AnsP_6, P_poll__networl_2_6_RI_0, P_poll__networl_2_6_RI_1, P_poll__networl_2_6_RI_2, P_poll__networl_2_6_RI_3, P_poll__networl_2_6_RI_4, P_poll__networl_2_6_RI_5, P_poll__networl_2_6_RI_6, P_poll__networl_2_6_AI_0, P_poll__networl_2_6_AI_1, P_poll__networl_2_6_AI_2, P_poll__networl_2_6_AI_3, P_poll__networl_2_6_AI_4, P_poll__networl_2_6_AI_5, P_poll__networl_2_6_AI_6, P_poll__networl_2_6_AnnP_0, P_poll__networl_2_6_AnnP_1, P_poll__networl_2_6_AnnP_2, P_poll__networl_2_6_AnnP_3, P_poll__networl_2_6_AnnP_4, P_poll__networl_2_6_AnnP_5, P_poll__networl_2_6_AnnP_6, P_poll__networl_2_6_RP_0, P_poll__networl_2_6_RP_1, P_poll__networl_2_6_RP_2, P_poll__networl_2_6_RP_3, P_poll__networl_2_6_RP_4, P_poll__networl_2_6_RP_5, P_poll__networl_2_6_RP_6, P_poll__networl_3_0_AskP_0, P_poll__networl_3_0_AskP_1, P_poll__networl_3_0_AskP_2, P_poll__networl_3_0_AskP_3, P_poll__networl_3_0_AskP_4, P_poll__networl_3_0_AskP_5, P_poll__networl_3_0_AskP_6, P_poll__networl_3_0_AnsP_0, P_poll__networl_3_0_AnsP_1, P_poll__networl_3_0_AnsP_2, P_poll__networl_3_0_AnsP_3, P_poll__networl_3_0_AnsP_4, P_poll__networl_3_0_AnsP_5, P_poll__networl_3_0_AnsP_6, P_poll__networl_3_0_RI_0, P_poll__networl_3_0_RI_1, P_poll__networl_3_0_RI_2, P_poll__networl_3_0_RI_3, P_poll__networl_3_0_RI_4, P_poll__networl_3_0_RI_5, P_poll__networl_3_0_RI_6, P_poll__networl_3_0_AI_0, P_poll__networl_3_0_AI_1, P_poll__networl_3_0_AI_2, P_poll__networl_3_0_AI_3, P_poll__networl_3_0_AI_4, P_poll__networl_3_0_AI_5, P_poll__networl_3_0_AI_6, P_poll__networl_3_0_AnnP_0, P_poll__networl_3_0_AnnP_1, P_poll__networl_3_0_AnnP_2, P_poll__networl_3_0_AnnP_3, P_poll__networl_3_0_AnnP_4, P_poll__networl_3_0_AnnP_5, P_poll__networl_3_0_AnnP_6, P_poll__networl_3_0_RP_0, P_poll__networl_3_0_RP_1, P_poll__networl_3_0_RP_2, P_poll__networl_3_0_RP_3, P_poll__networl_3_0_RP_4, P_poll__networl_3_0_RP_5, P_poll__networl_3_0_RP_6, P_poll__networl_3_1_AskP_0, P_poll__networl_3_1_AskP_1, P_poll__networl_3_1_AskP_2, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AskP_4, P_poll__networl_3_1_AskP_5, P_poll__networl_3_1_AskP_6, P_poll__networl_3_1_AnsP_0, P_poll__networl_3_1_AnsP_1, P_poll__networl_3_1_AnsP_2, P_poll__networl_3_1_AnsP_3, P_poll__networl_3_1_AnsP_4, P_poll__networl_3_1_AnsP_5, P_poll__networl_3_1_AnsP_6, P_poll__networl_3_1_RI_0, P_poll__networl_3_1_RI_1, P_poll__networl_3_1_RI_2, P_poll__networl_3_1_RI_3, P_poll__networl_3_1_RI_4, P_poll__networl_3_1_RI_5, P_poll__networl_3_1_RI_6, P_poll__networl_3_1_AI_0, P_poll__networl_3_1_AI_1, P_poll__networl_3_1_AI_2, P_poll__networl_3_1_AI_3, P_poll__networl_3_1_AI_4, P_poll__networl_3_1_AI_5, P_poll__networl_3_1_AI_6, P_poll__networl_3_1_AnnP_0, P_poll__networl_3_1_AnnP_1, P_poll__networl_3_1_AnnP_2, P_poll__networl_3_1_AnnP_3, P_poll__networl_3_1_AnnP_4, P_poll__networl_3_1_AnnP_5, P_poll__networl_3_1_AnnP_6, P_poll__networl_3_1_RP_0, P_poll__networl_3_1_RP_1, P_poll__networl_3_1_RP_2, P_poll__networl_3_1_RP_3, P_poll__networl_3_1_RP_4, P_poll__networl_3_1_RP_5, P_poll__networl_3_1_RP_6, P_poll__networl_3_2_AskP_0, P_poll__networl_3_2_AskP_1, P_poll__networl_3_2_AskP_2, P_poll__networl_3_2_AskP_3, P_poll__networl_3_2_AskP_4, P_poll__networl_3_2_AskP_5, P_poll__networl_3_2_AskP_6, P_poll__networl_3_2_AnsP_0, P_poll__networl_3_2_AnsP_1, P_poll__networl_3_2_AnsP_2, P_poll__networl_3_2_AnsP_3, P_poll__networl_3_2_AnsP_4, P_poll__networl_3_2_AnsP_5, P_poll__networl_3_2_AnsP_6, P_poll__networl_3_2_RI_0, P_poll__networl_3_2_RI_1, P_poll__networl_3_2_RI_2, P_poll__networl_3_2_RI_3, P_poll__networl_3_2_RI_4, P_poll__networl_3_2_RI_5, P_poll__networl_3_2_RI_6, P_poll__networl_3_2_AI_0, P_poll__networl_3_2_AI_1, P_poll__networl_3_2_AI_2, P_poll__networl_3_2_AI_3, P_poll__networl_3_2_AI_4, P_poll__networl_3_2_AI_5, P_poll__networl_3_2_AI_6, P_poll__networl_3_2_AnnP_0, P_poll__networl_3_2_AnnP_1, P_poll__networl_3_2_AnnP_2, P_poll__networl_3_2_AnnP_3, P_poll__networl_3_2_AnnP_4, P_poll__networl_3_2_AnnP_5, P_poll__networl_3_2_AnnP_6, P_poll__networl_3_2_RP_0, P_poll__networl_3_2_RP_1, P_poll__networl_3_2_RP_2, P_poll__networl_3_2_RP_3, P_poll__networl_3_2_RP_4, P_poll__networl_3_2_RP_5, P_poll__networl_3_2_RP_6, P_poll__networl_3_3_AskP_0, P_poll__networl_3_3_AskP_1, P_poll__networl_3_3_AskP_2, P_poll__networl_3_3_AskP_3, P_poll__networl_3_3_AskP_4, P_poll__networl_3_3_AskP_5, P_poll__networl_3_3_AskP_6, P_poll__networl_3_3_AnsP_0, P_poll__networl_3_3_AnsP_1, P_poll__networl_3_3_AnsP_2, P_poll__networl_3_3_AnsP_3, P_poll__networl_3_3_AnsP_4, P_poll__networl_3_3_AnsP_5, P_poll__networl_3_3_AnsP_6, P_poll__networl_3_3_RI_0, P_poll__networl_3_3_RI_1, P_poll__networl_3_3_RI_2, P_poll__networl_3_3_RI_3, P_poll__networl_3_3_RI_4, P_poll__networl_3_3_RI_5, P_poll__networl_3_3_RI_6, P_poll__networl_3_3_AI_0, P_poll__networl_3_3_AI_1, P_poll__networl_3_3_AI_2, P_poll__networl_3_3_AI_3, P_poll__networl_3_3_AI_4, P_poll__networl_3_3_AI_5, P_poll__networl_3_3_AI_6, P_poll__networl_3_3_AnnP_0, P_poll__networl_3_3_AnnP_1, P_poll__networl_3_3_AnnP_2, P_poll__networl_3_3_AnnP_3, P_poll__networl_3_3_AnnP_4, P_poll__networl_3_3_AnnP_5, P_poll__networl_3_3_AnnP_6, P_poll__networl_3_3_RP_0, P_poll__networl_3_3_RP_1, P_poll__networl_3_3_RP_2, P_poll__networl_3_3_RP_3, P_poll__networl_3_3_RP_4, P_poll__networl_3_3_RP_5, P_poll__networl_3_3_RP_6, P_poll__networl_3_4_AskP_0, P_poll__networl_3_4_AskP_1, P_poll__networl_3_4_AskP_2, P_poll__networl_3_4_AskP_3, P_poll__networl_3_4_AskP_4, P_poll__networl_3_4_AskP_5, P_poll__networl_3_4_AskP_6, P_poll__networl_3_4_AnsP_0, P_poll__networl_3_4_AnsP_1, P_poll__networl_3_4_AnsP_2, P_poll__networl_3_4_AnsP_3, P_poll__networl_3_4_AnsP_4, P_poll__networl_3_4_AnsP_5, P_poll__networl_3_4_AnsP_6, P_poll__networl_3_4_RI_0, P_poll__networl_3_4_RI_1, P_poll__networl_3_4_RI_2, P_poll__networl_3_4_RI_3, P_poll__networl_3_4_RI_4, P_poll__networl_3_4_RI_5, P_poll__networl_3_4_RI_6, P_poll__networl_3_4_AI_0, P_poll__networl_3_4_AI_1, P_poll__networl_3_4_AI_2, P_poll__networl_3_4_AI_3, P_poll__networl_3_4_AI_4, P_poll__networl_3_4_AI_5, P_poll__networl_3_4_AI_6, P_poll__networl_3_4_AnnP_0, P_poll__networl_3_4_AnnP_1, P_poll__networl_3_4_AnnP_2, P_poll__networl_3_4_AnnP_3, P_poll__networl_3_4_AnnP_4, P_poll__networl_3_4_AnnP_5, P_poll__networl_3_4_AnnP_6, P_poll__networl_3_4_RP_0, P_poll__networl_3_4_RP_1, P_poll__networl_3_4_RP_2, P_poll__networl_3_4_RP_3, P_poll__networl_3_4_RP_4, P_poll__networl_3_4_RP_5, P_poll__networl_3_4_RP_6, P_poll__networl_3_5_AskP_0, P_poll__networl_3_5_AskP_1, P_poll__networl_3_5_AskP_2, P_poll__networl_3_5_AskP_3, P_poll__networl_3_5_AskP_4, P_poll__networl_3_5_AskP_5, P_poll__networl_3_5_AskP_6, P_poll__networl_3_5_AnsP_0, P_poll__networl_3_5_AnsP_1, P_poll__networl_3_5_AnsP_2, P_poll__networl_3_5_AnsP_3, P_poll__networl_3_5_AnsP_4, P_poll__networl_3_5_AnsP_5, P_poll__networl_3_5_AnsP_6, P_poll__networl_3_5_RI_0, P_poll__networl_3_5_RI_1, P_poll__networl_3_5_RI_2, P_poll__networl_3_5_RI_3, P_poll__networl_3_5_RI_4, P_poll__networl_3_5_RI_5, P_poll__networl_3_5_RI_6, P_poll__networl_3_5_AI_0, P_poll__networl_3_5_AI_1, P_poll__networl_3_5_AI_2, P_poll__networl_3_5_AI_3, P_poll__networl_3_5_AI_4, P_poll__networl_3_5_AI_5, P_poll__networl_3_5_AI_6, P_poll__networl_3_5_AnnP_0, P_poll__networl_3_5_AnnP_1, P_poll__networl_3_5_AnnP_2, P_poll__networl_3_5_AnnP_3, P_poll__networl_3_5_AnnP_4, P_poll__networl_3_5_AnnP_5, P_poll__networl_3_5_AnnP_6, P_poll__networl_3_5_RP_0, P_poll__networl_3_5_RP_1, P_poll__networl_3_5_RP_2, P_poll__networl_3_5_RP_3, P_poll__networl_3_5_RP_4, P_poll__networl_3_5_RP_5, P_poll__networl_3_5_RP_6, P_poll__networl_3_6_AskP_0, P_poll__networl_3_6_AskP_1, P_poll__networl_3_6_AskP_2, P_poll__networl_3_6_AskP_3, P_poll__networl_3_6_AskP_4, P_poll__networl_3_6_AskP_5, P_poll__networl_3_6_AskP_6, P_poll__networl_3_6_AnsP_0, P_poll__networl_3_6_AnsP_1, P_poll__networl_3_6_AnsP_2, P_poll__networl_3_6_AnsP_3, P_poll__networl_3_6_AnsP_4, P_poll__networl_3_6_AnsP_5, P_poll__networl_3_6_AnsP_6, P_poll__networl_3_6_RI_0, P_poll__networl_3_6_RI_1, P_poll__networl_3_6_RI_2, P_poll__networl_3_6_RI_3, P_poll__networl_3_6_RI_4, P_poll__networl_3_6_RI_5, P_poll__networl_3_6_RI_6, P_poll__networl_3_6_AI_0, P_poll__networl_3_6_AI_1, P_poll__networl_3_6_AI_2, P_poll__networl_3_6_AI_3, P_poll__networl_3_6_AI_4, P_poll__networl_3_6_AI_5, P_poll__networl_3_6_AI_6, P_poll__networl_3_6_AnnP_0, P_poll__networl_3_6_AnnP_1, P_poll__networl_3_6_AnnP_2, P_poll__networl_3_6_AnnP_3, P_poll__networl_3_6_AnnP_4, P_poll__networl_3_6_AnnP_5, P_poll__networl_3_6_AnnP_6, P_poll__networl_3_6_RP_0, P_poll__networl_3_6_RP_1, P_poll__networl_3_6_RP_2, P_poll__networl_3_6_RP_3, P_poll__networl_3_6_RP_4, P_poll__networl_3_6_RP_5, P_poll__networl_3_6_RP_6, P_poll__networl_4_0_AskP_0, P_poll__networl_4_0_AskP_1, P_poll__networl_4_0_AskP_2, P_poll__networl_4_0_AskP_3, P_poll__networl_4_0_AskP_4, P_poll__networl_4_0_AskP_5, P_poll__networl_4_0_AskP_6, P_poll__networl_4_0_AnsP_0, P_poll__networl_4_0_AnsP_1, P_poll__networl_4_0_AnsP_2, P_poll__networl_4_0_AnsP_3, P_poll__networl_4_0_AnsP_4, P_poll__networl_4_0_AnsP_5, P_poll__networl_4_0_AnsP_6, P_poll__networl_4_0_RI_0, P_poll__networl_4_0_RI_1, P_poll__networl_4_0_RI_2, P_poll__networl_4_0_RI_3, P_poll__networl_4_0_RI_4, P_poll__networl_4_0_RI_5, P_poll__networl_4_0_RI_6, P_poll__networl_4_0_AI_0, P_poll__networl_4_0_AI_1, P_poll__networl_4_0_AI_2, P_poll__networl_4_0_AI_3, P_poll__networl_4_0_AI_4, P_poll__networl_4_0_AI_5, P_poll__networl_4_0_AI_6, P_poll__networl_4_0_AnnP_0, P_poll__networl_4_0_AnnP_1, P_poll__networl_4_0_AnnP_2, P_poll__networl_4_0_AnnP_3, P_poll__networl_4_0_AnnP_4, P_poll__networl_4_0_AnnP_5, P_poll__networl_4_0_AnnP_6, P_poll__networl_4_0_RP_0, P_poll__networl_4_0_RP_1, P_poll__networl_4_0_RP_2, P_poll__networl_4_0_RP_3, P_poll__networl_4_0_RP_4, P_poll__networl_4_0_RP_5, P_poll__networl_4_0_RP_6, P_poll__networl_4_1_AskP_0, P_poll__networl_4_1_AskP_1, P_poll__networl_4_1_AskP_2, P_poll__networl_4_1_AskP_3, P_poll__networl_4_1_AskP_4, P_poll__networl_4_1_AskP_5, P_poll__networl_4_1_AskP_6, P_poll__networl_4_1_AnsP_0, P_poll__networl_4_1_AnsP_1, P_poll__networl_4_1_AnsP_2, P_poll__networl_4_1_AnsP_3, P_poll__networl_4_1_AnsP_4, P_poll__networl_4_1_AnsP_5, P_poll__networl_4_1_AnsP_6, P_poll__networl_4_1_RI_0, P_poll__networl_4_1_RI_1, P_poll__networl_4_1_RI_2, P_poll__networl_4_1_RI_3, P_poll__networl_4_1_RI_4, P_poll__networl_4_1_RI_5, P_poll__networl_4_1_RI_6, P_poll__networl_4_1_AI_0, P_poll__networl_4_1_AI_1, P_poll__networl_4_1_AI_2, P_poll__networl_4_1_AI_3, P_poll__networl_4_1_AI_4, P_poll__networl_4_1_AI_5, P_poll__networl_4_1_AI_6, P_poll__networl_4_1_AnnP_0, P_poll__networl_4_1_AnnP_1, P_poll__networl_4_1_AnnP_2, P_poll__networl_4_1_AnnP_3, P_poll__networl_4_1_AnnP_4, P_poll__networl_4_1_AnnP_5, P_poll__networl_4_1_AnnP_6, P_poll__networl_4_1_RP_0, P_poll__networl_4_1_RP_1, P_poll__networl_4_1_RP_2, P_poll__networl_4_1_RP_3, P_poll__networl_4_1_RP_4, P_poll__networl_4_1_RP_5, P_poll__networl_4_1_RP_6, P_poll__networl_4_2_AskP_0, P_poll__networl_4_2_AskP_1, P_poll__networl_4_2_AskP_2, P_poll__networl_4_2_AskP_3, P_poll__networl_4_2_AskP_4, P_poll__networl_4_2_AskP_5, P_poll__networl_4_2_AskP_6, P_poll__networl_4_2_AnsP_0, P_poll__networl_4_2_AnsP_1, P_poll__networl_4_2_AnsP_2, P_poll__networl_4_2_AnsP_3, P_poll__networl_4_2_AnsP_4, P_poll__networl_4_2_AnsP_5, P_poll__networl_4_2_AnsP_6, P_poll__networl_4_2_RI_0, P_poll__networl_4_2_RI_1, P_poll__networl_4_2_RI_2, P_poll__networl_4_2_RI_3, P_poll__networl_4_2_RI_4, P_poll__networl_4_2_RI_5, P_poll__networl_4_2_RI_6, P_poll__networl_4_2_AI_0, P_poll__networl_4_2_AI_1, P_poll__networl_4_2_AI_2, P_poll__networl_4_2_AI_3, P_poll__networl_4_2_AI_4, P_poll__networl_4_2_AI_5, P_poll__networl_4_2_AI_6, P_poll__networl_4_2_AnnP_0, P_poll__networl_4_2_AnnP_1, P_poll__networl_4_2_AnnP_2, P_poll__networl_4_2_AnnP_3, P_poll__networl_4_2_AnnP_4, P_poll__networl_4_2_AnnP_5, P_poll__networl_4_2_AnnP_6, P_poll__networl_4_2_RP_0, P_poll__networl_4_2_RP_1, P_poll__networl_4_2_RP_2, P_poll__networl_4_2_RP_3, P_poll__networl_4_2_RP_4, P_poll__networl_4_2_RP_5, P_poll__networl_4_2_RP_6, P_poll__networl_4_3_AskP_0, P_poll__networl_4_3_AskP_1, P_poll__networl_4_3_AskP_2, P_poll__networl_4_3_AskP_3, P_poll__networl_4_3_AskP_4, P_poll__networl_4_3_AskP_5, P_poll__networl_4_3_AskP_6, P_poll__networl_4_3_AnsP_0, P_poll__networl_4_3_AnsP_1, P_poll__networl_4_3_AnsP_2, P_poll__networl_4_3_AnsP_3, P_poll__networl_4_3_AnsP_4, P_poll__networl_4_3_AnsP_5, P_poll__networl_4_3_AnsP_6, P_poll__networl_4_3_RI_0, P_poll__networl_4_3_RI_1, P_poll__networl_4_3_RI_2, P_poll__networl_4_3_RI_3, P_poll__networl_4_3_RI_4, P_poll__networl_4_3_RI_5, P_poll__networl_4_3_RI_6, P_poll__networl_4_3_AI_0, P_poll__networl_4_3_AI_1, P_poll__networl_4_3_AI_2, P_poll__networl_4_3_AI_3, P_poll__networl_4_3_AI_4, P_poll__networl_4_3_AI_5, P_poll__networl_4_3_AI_6, P_poll__networl_4_3_AnnP_0, P_poll__networl_4_3_AnnP_1, P_poll__networl_4_3_AnnP_2, P_poll__networl_4_3_AnnP_3, P_poll__networl_4_3_AnnP_4, P_poll__networl_4_3_AnnP_5, P_poll__networl_4_3_AnnP_6, P_poll__networl_4_3_RP_0, P_poll__networl_4_3_RP_1, P_poll__networl_4_3_RP_2, P_poll__networl_4_3_RP_3, P_poll__networl_4_3_RP_4, P_poll__networl_4_3_RP_5, P_poll__networl_4_3_RP_6, P_poll__networl_4_4_AskP_0, P_poll__networl_4_4_AskP_1, P_poll__networl_4_4_AskP_2, P_poll__networl_4_4_AskP_3, P_poll__networl_4_4_AskP_4, P_poll__networl_4_4_AskP_5, P_poll__networl_4_4_AskP_6, P_poll__networl_4_4_AnsP_0, P_poll__networl_4_4_AnsP_1, P_poll__networl_4_4_AnsP_2, P_poll__networl_4_4_AnsP_3, P_poll__networl_4_4_AnsP_4, P_poll__networl_4_4_AnsP_5, P_poll__networl_4_4_AnsP_6, P_poll__networl_4_4_RI_0, P_poll__networl_4_4_RI_1, P_poll__networl_4_4_RI_2, P_poll__networl_4_4_RI_3, P_poll__networl_4_4_RI_4, P_poll__networl_4_4_RI_5, P_poll__networl_4_4_RI_6, P_poll__networl_4_4_AI_0, P_poll__networl_4_4_AI_1, P_poll__networl_4_4_AI_2, P_poll__networl_4_4_AI_3, P_poll__networl_4_4_AI_4, P_poll__networl_4_4_AI_5, P_poll__networl_4_4_AI_6, P_poll__networl_4_4_AnnP_0, P_poll__networl_4_4_AnnP_1, P_poll__networl_4_4_AnnP_2, P_poll__networl_4_4_AnnP_3, P_poll__networl_4_4_AnnP_4, P_poll__networl_4_4_AnnP_5, P_poll__networl_4_4_AnnP_6, P_poll__networl_4_4_RP_0, P_poll__networl_4_4_RP_1, P_poll__networl_4_4_RP_2, P_poll__networl_4_4_RP_3, P_poll__networl_4_4_RP_4, P_poll__networl_4_4_RP_5, P_poll__networl_4_4_RP_6, P_poll__networl_4_5_AskP_0, P_poll__networl_4_5_AskP_1, P_poll__networl_4_5_AskP_2, P_poll__networl_4_5_AskP_3, P_poll__networl_4_5_AskP_4, P_poll__networl_4_5_AskP_5, P_poll__networl_4_5_AskP_6, P_poll__networl_4_5_AnsP_0, P_poll__networl_4_5_AnsP_1, P_poll__networl_4_5_AnsP_2, P_poll__networl_4_5_AnsP_3, P_poll__networl_4_5_AnsP_4, P_poll__networl_4_5_AnsP_5, P_poll__networl_4_5_AnsP_6, P_poll__networl_4_5_RI_0, P_poll__networl_4_5_RI_1, P_poll__networl_4_5_RI_2, P_poll__networl_4_5_RI_3, P_poll__networl_4_5_RI_4, P_poll__networl_4_5_RI_5, P_poll__networl_4_5_RI_6, P_poll__networl_4_5_AI_0, P_poll__networl_4_5_AI_1, P_poll__networl_4_5_AI_2, P_poll__networl_4_5_AI_3, P_poll__networl_4_5_AI_4, P_poll__networl_4_5_AI_5, P_poll__networl_4_5_AI_6, P_poll__networl_4_5_AnnP_0, P_poll__networl_4_5_AnnP_1, P_poll__networl_4_5_AnnP_2, P_poll__networl_4_5_AnnP_3, P_poll__networl_4_5_AnnP_4, P_poll__networl_4_5_AnnP_5, P_poll__networl_4_5_AnnP_6, P_poll__networl_4_5_RP_0, P_poll__networl_4_5_RP_1, P_poll__networl_4_5_RP_2, P_poll__networl_4_5_RP_3, P_poll__networl_4_5_RP_4, P_poll__networl_4_5_RP_5, P_poll__networl_4_5_RP_6, P_poll__networl_4_6_AskP_0, P_poll__networl_4_6_AskP_1, P_poll__networl_4_6_AskP_2, P_poll__networl_4_6_AskP_3, P_poll__networl_4_6_AskP_4, P_poll__networl_4_6_AskP_5, P_poll__networl_4_6_AskP_6, P_poll__networl_4_6_AnsP_0, P_poll__networl_4_6_AnsP_1, P_poll__networl_4_6_AnsP_2, P_poll__networl_4_6_AnsP_3, P_poll__networl_4_6_AnsP_4, P_poll__networl_4_6_AnsP_5, P_poll__networl_4_6_AnsP_6, P_poll__networl_4_6_RI_0, P_poll__networl_4_6_RI_1, P_poll__networl_4_6_RI_2, P_poll__networl_4_6_RI_3, P_poll__networl_4_6_RI_4, P_poll__networl_4_6_RI_5, P_poll__networl_4_6_RI_6, P_poll__networl_4_6_AI_0, P_poll__networl_4_6_AI_1, P_poll__networl_4_6_AI_2, P_poll__networl_4_6_AI_3, P_poll__networl_4_6_AI_4, P_poll__networl_4_6_AI_5, P_poll__networl_4_6_AI_6, P_poll__networl_4_6_AnnP_0, P_poll__networl_4_6_AnnP_1, P_poll__networl_4_6_AnnP_2, P_poll__networl_4_6_AnnP_3, P_poll__networl_4_6_AnnP_4, P_poll__networl_4_6_AnnP_5, P_poll__networl_4_6_AnnP_6, P_poll__networl_4_6_RP_0, P_poll__networl_4_6_RP_1, P_poll__networl_4_6_RP_2, P_poll__networl_4_6_RP_3, P_poll__networl_4_6_RP_4, P_poll__networl_4_6_RP_5, P_poll__networl_4_6_RP_6, P_poll__networl_5_0_AskP_0, P_poll__networl_5_0_AskP_1, P_poll__networl_5_0_AskP_2, P_poll__networl_5_0_AskP_3, P_poll__networl_5_0_AskP_4, P_poll__networl_5_0_AskP_5, P_poll__networl_5_0_AskP_6, P_poll__networl_5_0_AnsP_0, P_poll__networl_5_0_AnsP_1, P_poll__networl_5_0_AnsP_2, P_poll__networl_5_0_AnsP_3, P_poll__networl_5_0_AnsP_4, P_poll__networl_5_0_AnsP_5, P_poll__networl_5_0_AnsP_6, P_poll__networl_5_0_RI_0, P_poll__networl_5_0_RI_1, P_poll__networl_5_0_RI_2, P_poll__networl_5_0_RI_3, P_poll__networl_5_0_RI_4, P_poll__networl_5_0_RI_5, P_poll__networl_5_0_RI_6, P_poll__networl_5_0_AI_0, P_poll__networl_5_0_AI_1, P_poll__networl_5_0_AI_2, P_poll__networl_5_0_AI_3, P_poll__networl_5_0_AI_4, P_poll__networl_5_0_AI_5, P_poll__networl_5_0_AI_6, P_poll__networl_5_0_AnnP_0, P_poll__networl_5_0_AnnP_1, P_poll__networl_5_0_AnnP_2, P_poll__networl_5_0_AnnP_3, P_poll__networl_5_0_AnnP_4, P_poll__networl_5_0_AnnP_5, P_poll__networl_5_0_AnnP_6, P_poll__networl_5_0_RP_0, P_poll__networl_5_0_RP_1, P_poll__networl_5_0_RP_2, P_poll__networl_5_0_RP_3, P_poll__networl_5_0_RP_4, P_poll__networl_5_0_RP_5, P_poll__networl_5_0_RP_6, P_poll__networl_5_1_AskP_0, P_poll__networl_5_1_AskP_1, P_poll__networl_5_1_AskP_2, P_poll__networl_5_1_AskP_3, P_poll__networl_5_1_AskP_4, P_poll__networl_5_1_AskP_5, P_poll__networl_5_1_AskP_6, P_poll__networl_5_1_AnsP_0, P_poll__networl_5_1_AnsP_1, P_poll__networl_5_1_AnsP_2, P_poll__networl_5_1_AnsP_3, P_poll__networl_5_1_AnsP_4, P_poll__networl_5_1_AnsP_5, P_poll__networl_5_1_AnsP_6, P_poll__networl_5_1_RI_0, P_poll__networl_5_1_RI_1, P_poll__networl_5_1_RI_2, P_poll__networl_5_1_RI_3, P_poll__networl_5_1_RI_4, P_poll__networl_5_1_RI_5, P_poll__networl_5_1_RI_6, P_poll__networl_5_1_AI_0, P_poll__networl_5_1_AI_1, P_poll__networl_5_1_AI_2, P_poll__networl_5_1_AI_3, P_poll__networl_5_1_AI_4, P_poll__networl_5_1_AI_5, P_poll__networl_5_1_AI_6, P_poll__networl_5_1_AnnP_0, P_poll__networl_5_1_AnnP_1, P_poll__networl_5_1_AnnP_2, P_poll__networl_5_1_AnnP_3, P_poll__networl_5_1_AnnP_4, P_poll__networl_5_1_AnnP_5, P_poll__networl_5_1_AnnP_6, P_poll__networl_5_1_RP_0, P_poll__networl_5_1_RP_1, P_poll__networl_5_1_RP_2, P_poll__networl_5_1_RP_3, P_poll__networl_5_1_RP_4, P_poll__networl_5_1_RP_5, P_poll__networl_5_1_RP_6, P_poll__networl_5_2_AskP_0, P_poll__networl_5_2_AskP_1, P_poll__networl_5_2_AskP_2, P_poll__networl_5_2_AskP_3, P_poll__networl_5_2_AskP_4, P_poll__networl_5_2_AskP_5, P_poll__networl_5_2_AskP_6, P_poll__networl_5_2_AnsP_0, P_poll__networl_5_2_AnsP_1, P_poll__networl_5_2_AnsP_2, P_poll__networl_5_2_AnsP_3, P_poll__networl_5_2_AnsP_4, P_poll__networl_5_2_AnsP_5, P_poll__networl_5_2_AnsP_6, P_poll__networl_5_2_RI_0, P_poll__networl_5_2_RI_1, P_poll__networl_5_2_RI_2, P_poll__networl_5_2_RI_3, P_poll__networl_5_2_RI_4, P_poll__networl_5_2_RI_5, P_poll__networl_5_2_RI_6, P_poll__networl_5_2_AI_0, P_poll__networl_5_2_AI_1, P_poll__networl_5_2_AI_2, P_poll__networl_5_2_AI_3, P_poll__networl_5_2_AI_4, P_poll__networl_5_2_AI_5, P_poll__networl_5_2_AI_6, P_poll__networl_5_2_AnnP_0, P_poll__networl_5_2_AnnP_1, P_poll__networl_5_2_AnnP_2, P_poll__networl_5_2_AnnP_3, P_poll__networl_5_2_AnnP_4, P_poll__networl_5_2_AnnP_5, P_poll__networl_5_2_AnnP_6, P_poll__networl_5_2_RP_0, P_poll__networl_5_2_RP_1, P_poll__networl_5_2_RP_2, P_poll__networl_5_2_RP_3, P_poll__networl_5_2_RP_4, P_poll__networl_5_2_RP_5, P_poll__networl_5_2_RP_6, P_poll__networl_5_3_AskP_0, P_poll__networl_5_3_AskP_1, P_poll__networl_5_3_AskP_2, P_poll__networl_5_3_AskP_3, P_poll__networl_5_3_AskP_4, P_poll__networl_5_3_AskP_5, P_poll__networl_5_3_AskP_6, P_poll__networl_5_3_AnsP_0, P_poll__networl_5_3_AnsP_1, P_poll__networl_5_3_AnsP_2, P_poll__networl_5_3_AnsP_3, P_poll__networl_5_3_AnsP_4, P_poll__networl_5_3_AnsP_5, P_poll__networl_5_3_AnsP_6, P_poll__networl_5_3_RI_0, P_poll__networl_5_3_RI_1, P_poll__networl_5_3_RI_2, P_poll__networl_5_3_RI_3, P_poll__networl_5_3_RI_4, P_poll__networl_5_3_RI_5, P_poll__networl_5_3_RI_6, P_poll__networl_5_3_AI_0, P_poll__networl_5_3_AI_1, P_poll__networl_5_3_AI_2, P_poll__networl_5_3_AI_3, P_poll__networl_5_3_AI_4, P_poll__networl_5_3_AI_5, P_poll__networl_5_3_AI_6, P_poll__networl_5_3_AnnP_0, P_poll__networl_5_3_AnnP_1, P_poll__networl_5_3_AnnP_2, P_poll__networl_5_3_AnnP_3, P_poll__networl_5_3_AnnP_4, P_poll__networl_5_3_AnnP_5, P_poll__networl_5_3_AnnP_6, P_poll__networl_5_3_RP_0, P_poll__networl_5_3_RP_1, P_poll__networl_5_3_RP_2, P_poll__networl_5_3_RP_3, P_poll__networl_5_3_RP_4, P_poll__networl_5_3_RP_5, P_poll__networl_5_3_RP_6, P_poll__networl_5_4_AskP_0, P_poll__networl_5_4_AskP_1, P_poll__networl_5_4_AskP_2, P_poll__networl_5_4_AskP_3, P_poll__networl_5_4_AskP_4, P_poll__networl_5_4_AskP_5, P_poll__networl_5_4_AskP_6, P_poll__networl_5_4_AnsP_0, P_poll__networl_5_4_AnsP_1, P_poll__networl_5_4_AnsP_2, P_poll__networl_5_4_AnsP_3, P_poll__networl_5_4_AnsP_4, P_poll__networl_5_4_AnsP_5, P_poll__networl_5_4_AnsP_6, P_poll__networl_5_4_RI_0, P_poll__networl_5_4_RI_1, P_poll__networl_5_4_RI_2, P_poll__networl_5_4_RI_3, P_poll__networl_5_4_RI_4, P_poll__networl_5_4_RI_5, P_poll__networl_5_4_RI_6, P_poll__networl_5_4_AI_0, P_poll__networl_5_4_AI_1, P_poll__networl_5_4_AI_2, P_poll__networl_5_4_AI_3, P_poll__networl_5_4_AI_4, P_poll__networl_5_4_AI_5, P_poll__networl_5_4_AI_6, P_poll__networl_5_4_AnnP_0, P_poll__networl_5_4_AnnP_1, P_poll__networl_5_4_AnnP_2, P_poll__networl_5_4_AnnP_3, P_poll__networl_5_4_AnnP_4, P_poll__networl_5_4_AnnP_5, P_poll__networl_5_4_AnnP_6, P_poll__networl_5_4_RP_0, P_poll__networl_5_4_RP_1, P_poll__networl_5_4_RP_2, P_poll__networl_5_4_RP_3, P_poll__networl_5_4_RP_4, P_poll__networl_5_4_RP_5, P_poll__networl_5_4_RP_6, P_poll__networl_5_5_AskP_0, P_poll__networl_5_5_AskP_1, P_poll__networl_5_5_AskP_2, P_poll__networl_5_5_AskP_3, P_poll__networl_5_5_AskP_4, P_poll__networl_5_5_AskP_5, P_poll__networl_5_5_AskP_6, P_poll__networl_5_5_AnsP_0, P_poll__networl_5_5_AnsP_1, P_poll__networl_5_5_AnsP_2, P_poll__networl_5_5_AnsP_3, P_poll__networl_5_5_AnsP_4, P_poll__networl_5_5_AnsP_5, P_poll__networl_5_5_AnsP_6, P_poll__networl_5_5_RI_0, P_poll__networl_5_5_RI_1, P_poll__networl_5_5_RI_2, P_poll__networl_5_5_RI_3, P_poll__networl_5_5_RI_4, P_poll__networl_5_5_RI_5, P_poll__networl_5_5_RI_6, P_poll__networl_5_5_AI_0, P_poll__networl_5_5_AI_1, P_poll__networl_5_5_AI_2, P_poll__networl_5_5_AI_3, P_poll__networl_5_5_AI_4, P_poll__networl_5_5_AI_5, P_poll__networl_5_5_AI_6, P_poll__networl_5_5_AnnP_0, P_poll__networl_5_5_AnnP_1, P_poll__networl_5_5_AnnP_2, P_poll__networl_5_5_AnnP_3, P_poll__networl_5_5_AnnP_4, P_poll__networl_5_5_AnnP_5, P_poll__networl_5_5_AnnP_6, P_poll__networl_5_5_RP_0, P_poll__networl_5_5_RP_1, P_poll__networl_5_5_RP_2, P_poll__networl_5_5_RP_3, P_poll__networl_5_5_RP_4, P_poll__networl_5_5_RP_5, P_poll__networl_5_5_RP_6, P_poll__networl_5_6_AskP_0, P_poll__networl_5_6_AskP_1, P_poll__networl_5_6_AskP_2, P_poll__networl_5_6_AskP_3, P_poll__networl_5_6_AskP_4, P_poll__networl_5_6_AskP_5, P_poll__networl_5_6_AskP_6, P_poll__networl_5_6_AnsP_0, P_poll__networl_5_6_AnsP_1, P_poll__networl_5_6_AnsP_2, P_poll__networl_5_6_AnsP_3, P_poll__networl_5_6_AnsP_4, P_poll__networl_5_6_AnsP_5, P_poll__networl_5_6_AnsP_6, P_poll__networl_5_6_RI_0, P_poll__networl_5_6_RI_1, P_poll__networl_5_6_RI_2, P_poll__networl_5_6_RI_3, P_poll__networl_5_6_RI_4, P_poll__networl_5_6_RI_5, P_poll__networl_5_6_RI_6, P_poll__networl_5_6_AI_0, P_poll__networl_5_6_AI_1, P_poll__networl_5_6_AI_2, P_poll__networl_5_6_AI_3, P_poll__networl_5_6_AI_4, P_poll__networl_5_6_AI_5, P_poll__networl_5_6_AI_6, P_poll__networl_5_6_AnnP_0, P_poll__networl_5_6_AnnP_1, P_poll__networl_5_6_AnnP_2, P_poll__networl_5_6_AnnP_3, P_poll__networl_5_6_AnnP_4, P_poll__networl_5_6_AnnP_5, P_poll__networl_5_6_AnnP_6, P_poll__networl_5_6_RP_0, P_poll__networl_5_6_RP_1, P_poll__networl_5_6_RP_2, P_poll__networl_5_6_RP_3, P_poll__networl_5_6_RP_4, P_poll__networl_5_6_RP_5, P_poll__networl_5_6_RP_6, P_poll__networl_6_0_AskP_0, P_poll__networl_6_0_AskP_1, P_poll__networl_6_0_AskP_2, P_poll__networl_6_0_AskP_3, P_poll__networl_6_0_AskP_4, P_poll__networl_6_0_AskP_5, P_poll__networl_6_0_AskP_6, P_poll__networl_6_0_AnsP_0, P_poll__networl_6_0_AnsP_1, P_poll__networl_6_0_AnsP_2, P_poll__networl_6_0_AnsP_3, P_poll__networl_6_0_AnsP_4, P_poll__networl_6_0_AnsP_5, P_poll__networl_6_0_AnsP_6, P_poll__networl_6_0_RI_0, P_poll__networl_6_0_RI_1, P_poll__networl_6_0_RI_2, P_poll__networl_6_0_RI_3, P_poll__networl_6_0_RI_4, P_poll__networl_6_0_RI_5, P_poll__networl_6_0_RI_6, P_poll__networl_6_0_AI_0, P_poll__networl_6_0_AI_1, P_poll__networl_6_0_AI_2, P_poll__networl_6_0_AI_3, P_poll__networl_6_0_AI_4, P_poll__networl_6_0_AI_5, P_poll__networl_6_0_AI_6, P_poll__networl_6_0_AnnP_0, P_poll__networl_6_0_AnnP_1, P_poll__networl_6_0_AnnP_2, P_poll__networl_6_0_AnnP_3, P_poll__networl_6_0_AnnP_4, P_poll__networl_6_0_AnnP_5, P_poll__networl_6_0_AnnP_6, P_poll__networl_6_0_RP_0, P_poll__networl_6_0_RP_1, P_poll__networl_6_0_RP_2, P_poll__networl_6_0_RP_3, P_poll__networl_6_0_RP_4, P_poll__networl_6_0_RP_5, P_poll__networl_6_0_RP_6, P_poll__networl_6_1_AskP_0, P_poll__networl_6_1_AskP_1, P_poll__networl_6_1_AskP_2, P_poll__networl_6_1_AskP_3, P_poll__networl_6_1_AskP_4, P_poll__networl_6_1_AskP_5, P_poll__networl_6_1_AskP_6, P_poll__networl_6_1_AnsP_0, P_poll__networl_6_1_AnsP_1, P_poll__networl_6_1_AnsP_2, P_poll__networl_6_1_AnsP_3, P_poll__networl_6_1_AnsP_4, P_poll__networl_6_1_AnsP_5, P_poll__networl_6_1_AnsP_6, P_poll__networl_6_1_RI_0, P_poll__networl_6_1_RI_1, P_poll__networl_6_1_RI_2, P_poll__networl_6_1_RI_3, P_poll__networl_6_1_RI_4, P_poll__networl_6_1_RI_5, P_poll__networl_6_1_RI_6, P_poll__networl_6_1_AI_0, P_poll__networl_6_1_AI_1, P_poll__networl_6_1_AI_2, P_poll__networl_6_1_AI_3, P_poll__networl_6_1_AI_4, P_poll__networl_6_1_AI_5, P_poll__networl_6_1_AI_6, P_poll__networl_6_1_AnnP_0, P_poll__networl_6_1_AnnP_1, P_poll__networl_6_1_AnnP_2, P_poll__networl_6_1_AnnP_3, P_poll__networl_6_1_AnnP_4, P_poll__networl_6_1_AnnP_5, P_poll__networl_6_1_AnnP_6, P_poll__networl_6_1_RP_0, P_poll__networl_6_1_RP_1, P_poll__networl_6_1_RP_2, P_poll__networl_6_1_RP_3, P_poll__networl_6_1_RP_4, P_poll__networl_6_1_RP_5, P_poll__networl_6_1_RP_6, P_poll__networl_6_2_AskP_0, P_poll__networl_6_2_AskP_1, P_poll__networl_6_2_AskP_2, P_poll__networl_6_2_AskP_3, P_poll__networl_6_2_AskP_4, P_poll__networl_6_2_AskP_5, P_poll__networl_6_2_AskP_6, P_poll__networl_6_2_AnsP_0, P_poll__networl_6_2_AnsP_1, P_poll__networl_6_2_AnsP_2, P_poll__networl_6_2_AnsP_3, P_poll__networl_6_2_AnsP_4, P_poll__networl_6_2_AnsP_5, P_poll__networl_6_2_AnsP_6, P_poll__networl_6_2_RI_0, P_poll__networl_6_2_RI_1, P_poll__networl_6_2_RI_2, P_poll__networl_6_2_RI_3, P_poll__networl_6_2_RI_4, P_poll__networl_6_2_RI_5, P_poll__networl_6_2_RI_6, P_poll__networl_6_2_AI_0, P_poll__networl_6_2_AI_1, P_poll__networl_6_2_AI_2, P_poll__networl_6_2_AI_3, P_poll__networl_6_2_AI_4, P_poll__networl_6_2_AI_5, P_poll__networl_6_2_AI_6, P_poll__networl_6_2_AnnP_0, P_poll__networl_6_2_AnnP_1, P_poll__networl_6_2_AnnP_2, P_poll__networl_6_2_AnnP_3, P_poll__networl_6_2_AnnP_4, P_poll__networl_6_2_AnnP_5, P_poll__networl_6_2_AnnP_6, P_poll__networl_6_2_RP_0, P_poll__networl_6_2_RP_1, P_poll__networl_6_2_RP_2, P_poll__networl_6_2_RP_3, P_poll__networl_6_2_RP_4, P_poll__networl_6_2_RP_5, P_poll__networl_6_2_RP_6, P_poll__networl_6_3_AskP_0, P_poll__networl_6_3_AskP_1, P_poll__networl_6_3_AskP_2, P_poll__networl_6_3_AskP_3, P_poll__networl_6_3_AskP_4, P_poll__networl_6_3_AskP_5, P_poll__networl_6_3_AskP_6, P_poll__networl_6_3_AnsP_0, P_poll__networl_6_3_AnsP_1, P_poll__networl_6_3_AnsP_2, P_poll__networl_6_3_AnsP_3, P_poll__networl_6_3_AnsP_4, P_poll__networl_6_3_AnsP_5, P_poll__networl_6_3_AnsP_6, P_poll__networl_6_3_RI_0, P_poll__networl_6_3_RI_1, P_poll__networl_6_3_RI_2, P_poll__networl_6_3_RI_3, P_poll__networl_6_3_RI_4, P_poll__networl_6_3_RI_5, P_poll__networl_6_3_RI_6, P_poll__networl_6_3_AI_0, P_poll__networl_6_3_AI_1, P_poll__networl_6_3_AI_2, P_poll__networl_6_3_AI_3, P_poll__networl_6_3_AI_4, P_poll__networl_6_3_AI_5, P_poll__networl_6_3_AI_6, P_poll__networl_6_3_AnnP_0, P_poll__networl_6_3_AnnP_1, P_poll__networl_6_3_AnnP_2, P_poll__networl_6_3_AnnP_3, P_poll__networl_6_3_AnnP_4, P_poll__networl_6_3_AnnP_5, P_poll__networl_6_3_AnnP_6, P_poll__networl_6_3_RP_0, P_poll__networl_6_3_RP_1, P_poll__networl_6_3_RP_2, P_poll__networl_6_3_RP_3, P_poll__networl_6_3_RP_4, P_poll__networl_6_3_RP_5, P_poll__networl_6_3_RP_6, P_poll__networl_6_4_AskP_0, P_poll__networl_6_4_AskP_1, P_poll__networl_6_4_AskP_2, P_poll__networl_6_4_AskP_3, P_poll__networl_6_4_AskP_4, P_poll__networl_6_4_AskP_5, P_poll__networl_6_4_AskP_6, P_poll__networl_6_4_AnsP_0, P_poll__networl_6_4_AnsP_1, P_poll__networl_6_4_AnsP_2, P_poll__networl_6_4_AnsP_3, P_poll__networl_6_4_AnsP_4, P_poll__networl_6_4_AnsP_5, P_poll__networl_6_4_AnsP_6, P_poll__networl_6_4_RI_0, P_poll__networl_6_4_RI_1, P_poll__networl_6_4_RI_2, P_poll__networl_6_4_RI_3, P_poll__networl_6_4_RI_4, P_poll__networl_6_4_RI_5, P_poll__networl_6_4_RI_6, P_poll__networl_6_4_AI_0, P_poll__networl_6_4_AI_1, P_poll__networl_6_4_AI_2, P_poll__networl_6_4_AI_3, P_poll__networl_6_4_AI_4, P_poll__networl_6_4_AI_5, P_poll__networl_6_4_AI_6, P_poll__networl_6_4_AnnP_0, P_poll__networl_6_4_AnnP_1, P_poll__networl_6_4_AnnP_2, P_poll__networl_6_4_AnnP_3, P_poll__networl_6_4_AnnP_4, P_poll__networl_6_4_AnnP_5, P_poll__networl_6_4_AnnP_6, P_poll__networl_6_4_RP_0, P_poll__networl_6_4_RP_1, P_poll__networl_6_4_RP_2, P_poll__networl_6_4_RP_3, P_poll__networl_6_4_RP_4, P_poll__networl_6_4_RP_5, P_poll__networl_6_4_RP_6, P_poll__networl_6_5_AskP_0, P_poll__networl_6_5_AskP_1, P_poll__networl_6_5_AskP_2, P_poll__networl_6_5_AskP_3, P_poll__networl_6_5_AskP_4, P_poll__networl_6_5_AskP_5, P_poll__networl_6_5_AskP_6, P_poll__networl_6_5_AnsP_0, P_poll__networl_6_5_AnsP_1, P_poll__networl_6_5_AnsP_2, P_poll__networl_6_5_AnsP_3, P_poll__networl_6_5_AnsP_4, P_poll__networl_6_5_AnsP_5, P_poll__networl_6_5_AnsP_6, P_poll__networl_6_5_RI_0, P_poll__networl_6_5_RI_1, P_poll__networl_6_5_RI_2, P_poll__networl_6_5_RI_3, P_poll__networl_6_5_RI_4, P_poll__networl_6_5_RI_5, P_poll__networl_6_5_RI_6, P_poll__networl_6_5_AI_0, P_poll__networl_6_5_AI_1, P_poll__networl_6_5_AI_2, P_poll__networl_6_5_AI_3, P_poll__networl_6_5_AI_4, P_poll__networl_6_5_AI_5, P_poll__networl_6_5_AI_6, P_poll__networl_6_5_AnnP_0, P_poll__networl_6_5_AnnP_1, P_poll__networl_6_5_AnnP_2, P_poll__networl_6_5_AnnP_3, P_poll__networl_6_5_AnnP_4, P_poll__networl_6_5_AnnP_5, P_poll__networl_6_5_AnnP_6, P_poll__networl_6_5_RP_0, P_poll__networl_6_5_RP_1, P_poll__networl_6_5_RP_2, P_poll__networl_6_5_RP_3, P_poll__networl_6_5_RP_4, P_poll__networl_6_5_RP_5, P_poll__networl_6_5_RP_6, P_poll__networl_6_6_AskP_0, P_poll__networl_6_6_AskP_1, P_poll__networl_6_6_AskP_2, P_poll__networl_6_6_AskP_3, P_poll__networl_6_6_AskP_4, P_poll__networl_6_6_AskP_5, P_poll__networl_6_6_AskP_6, P_poll__networl_6_6_AnsP_0, P_poll__networl_6_6_AnsP_1, P_poll__networl_6_6_AnsP_2, P_poll__networl_6_6_AnsP_3, P_poll__networl_6_6_AnsP_4, P_poll__networl_6_6_AnsP_5, P_poll__networl_6_6_AnsP_6, P_poll__networl_6_6_RI_0, P_poll__networl_6_6_RI_1, P_poll__networl_6_6_RI_2, P_poll__networl_6_6_RI_3, P_poll__networl_6_6_RI_4, P_poll__networl_6_6_RI_5, P_poll__networl_6_6_RI_6, P_poll__networl_6_6_AI_0, P_poll__networl_6_6_AI_1, P_poll__networl_6_6_AI_2, P_poll__networl_6_6_AI_3, P_poll__networl_6_6_AI_4, P_poll__networl_6_6_AI_5, P_poll__networl_6_6_AI_6, P_poll__networl_6_6_AnnP_0, P_poll__networl_6_6_AnnP_1, P_poll__networl_6_6_AnnP_2, P_poll__networl_6_6_AnnP_3, P_poll__networl_6_6_AnnP_4, P_poll__networl_6_6_AnnP_5, P_poll__networl_6_6_AnnP_6, P_poll__networl_6_6_RP_0, P_poll__networl_6_6_RP_1, P_poll__networl_6_6_RP_2, P_poll__networl_6_6_RP_3, P_poll__networl_6_6_RP_4, P_poll__networl_6_6_RP_5, P_poll__networl_6_6_RP_6, P_poll__pollEnd_0, P_poll__pollEnd_1, P_poll__pollEnd_2, P_poll__pollEnd_3, P_poll__pollEnd_4, P_poll__pollEnd_5, P_poll__pollEnd_6, P_poll__waitingMessage_0, P_poll__waitingMessage_1, P_poll__waitingMessage_2, P_poll__waitingMessage_3, P_poll__waitingMessage_4, P_poll__waitingMessage_5, P_poll__waitingMessage_6, P_polling_0, P_polling_1, P_polling_2, P_polling_3, P_polling_4, P_polling_5, P_polling_6, P_sendAnnPs__broadcasting_0_1, P_sendAnnPs__broadcasting_0_2, P_sendAnnPs__broadcasting_0_3, P_sendAnnPs__broadcasting_0_4, P_sendAnnPs__broadcasting_0_5, P_sendAnnPs__broadcasting_0_6, P_sendAnnPs__broadcasting_1_1, P_sendAnnPs__broadcasting_1_2, P_sendAnnPs__broadcasting_1_3, P_sendAnnPs__broadcasting_1_4, P_sendAnnPs__broadcasting_1_5, P_sendAnnPs__broadcasting_1_6, P_sendAnnPs__broadcasting_2_1, P_sendAnnPs__broadcasting_2_2, P_sendAnnPs__broadcasting_2_3, P_sendAnnPs__broadcasting_2_4, P_sendAnnPs__broadcasting_2_5, P_sendAnnPs__broadcasting_2_6, P_sendAnnPs__broadcasting_3_1, P_sendAnnPs__broadcasting_3_2, P_sendAnnPs__broadcasting_3_3, P_sendAnnPs__broadcasting_3_4, P_sendAnnPs__broadcasting_3_5, P_sendAnnPs__broadcasting_3_6, P_sendAnnPs__broadcasting_4_1, P_sendAnnPs__broadcasting_4_2, P_sendAnnPs__broadcasting_4_3, P_sendAnnPs__broadcasting_4_4, P_sendAnnPs__broadcasting_4_5, P_sendAnnPs__broadcasting_4_6, P_sendAnnPs__broadcasting_5_1, P_sendAnnPs__broadcasting_5_2, P_sendAnnPs__broadcasting_5_3, P_sendAnnPs__broadcasting_5_4, P_sendAnnPs__broadcasting_5_5, P_sendAnnPs__broadcasting_5_6, P_sendAnnPs__broadcasting_6_1, P_sendAnnPs__broadcasting_6_2, P_sendAnnPs__broadcasting_6_3, P_sendAnnPs__broadcasting_6_4, P_sendAnnPs__broadcasting_6_5, P_sendAnnPs__broadcasting_6_6, P_stage_0_NEG, P_stage_0_PRIM, P_stage_0_SEC, P_stage_1_NEG, P_stage_1_PRIM, P_stage_1_SEC, P_stage_2_NEG, P_stage_2_PRIM, P_stage_2_SEC, P_stage_3_NEG, P_stage_3_PRIM, P_stage_3_SEC, P_stage_4_NEG, P_stage_4_PRIM, P_stage_4_SEC, P_stage_5_NEG, P_stage_5_PRIM, P_stage_5_SEC, P_stage_6_NEG, P_stage_6_PRIM, P_stage_6_SEC, P_startNeg__broadcasting_0_1, P_startNeg__broadcasting_0_2, P_startNeg__broadcasting_0_3, P_startNeg__broadcasting_0_4, P_startNeg__broadcasting_0_5, P_startNeg__broadcasting_0_6, P_startNeg__broadcasting_1_1, P_startNeg__broadcasting_1_2, P_startNeg__broadcasting_1_3, P_startNeg__broadcasting_1_4, P_startNeg__broadcasting_1_5, P_startNeg__broadcasting_1_6, P_startNeg__broadcasting_2_1, P_startNeg__broadcasting_2_2, P_startNeg__broadcasting_2_3, P_startNeg__broadcasting_2_4, P_startNeg__broadcasting_2_5, P_startNeg__broadcasting_2_6, P_startNeg__broadcasting_3_1, P_startNeg__broadcasting_3_2, P_startNeg__broadcasting_3_3, P_startNeg__broadcasting_3_4, P_startNeg__broadcasting_3_5, P_startNeg__broadcasting_3_6, P_startNeg__broadcasting_4_1, P_startNeg__broadcasting_4_2, P_startNeg__broadcasting_4_3, P_startNeg__broadcasting_4_4, P_startNeg__broadcasting_4_5, P_startNeg__broadcasting_4_6, P_startNeg__broadcasting_5_1, P_startNeg__broadcasting_5_2, P_startNeg__broadcasting_5_3, P_startNeg__broadcasting_5_4, P_startNeg__broadcasting_5_5, P_startNeg__broadcasting_5_6, P_startNeg__broadcasting_6_1, P_startNeg__broadcasting_6_2, P_startNeg__broadcasting_6_3, P_startNeg__broadcasting_6_4, P_startNeg__broadcasting_6_5, P_startNeg__broadcasting_6_6]
[2024-05-26 01:52:40] [INFO ] Parsed PT model containing 4830 places and 8435 transitions and 49028 arcs in 672 ms.
Parsed 16 properties from file /home/mcc/execution/LTLCardinality.xml in 121 ms.
Working with output stream class java.io.PrintStream
Initial state reduction rules removed 1 formulas.
Deduced a syphon composed of 4507 places in 21 ms
Reduce places removed 4537 places and 8041 transitions.
Reduce places removed 13 places and 0 transitions.
Initial state reduction rules removed 2 formulas.
FORMULA NeoElection-PT-6-LTLCardinality-02 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-04 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-07 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-09 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-10 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-11 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-12 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-15 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-LTLCardinality-08 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 181 out of 280 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 280/280 places, 394/394 transitions.
Reduce places removed 30 places and 0 transitions.
Iterating post reduction 0 with 30 rules applied. Total rules applied 30 place count 250 transition count 394
Discarding 24 places :
Symmetric choice reduction at 1 with 24 rule applications. Total rules 54 place count 226 transition count 214
Iterating global reduction 1 with 24 rules applied. Total rules applied 78 place count 226 transition count 214
Applied a total of 78 rules in 18 ms. Remains 226 /280 variables (removed 54) and now considering 214/394 (removed 180) transitions.
[2024-05-26 01:52:40] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
// Phase 1: matrix 189 rows 226 cols
[2024-05-26 01:52:40] [INFO ] Computed 47 invariants in 23 ms
[2024-05-26 01:52:40] [INFO ] Implicit Places using invariants in 255 ms returned [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51]
Discarding 36 places :
Implicit Place search using SMT only with invariants took 279 ms to find 36 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 190/280 places, 214/394 transitions.
Applied a total of 0 rules in 1 ms. Remains 190 /190 variables (removed 0) and now considering 214/214 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 300 ms. Remains : 190/280 places, 214/394 transitions.
Support contains 181 out of 190 places after structural reductions.
[2024-05-26 01:52:40] [INFO ] Flatten gal took : 44 ms
[2024-05-26 01:52:40] [INFO ] Flatten gal took : 24 ms
[2024-05-26 01:52:40] [INFO ] Input system was already deterministic with 214 transitions.
Incomplete random walk after 10000 steps, including 24 resets, run finished after 240 ms. (steps per millisecond=41 ) properties (out of 13) seen :11
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 31 ms. (steps per millisecond=322 ) properties (out of 2) seen :0
Incomplete Best-First random walk after 10001 steps, including 4 resets, run finished after 34 ms. (steps per millisecond=294 ) properties (out of 2) seen :0
Running SMT prover for 2 properties.
[2024-05-26 01:52:41] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
// Phase 1: matrix 189 rows 190 cols
[2024-05-26 01:52:41] [INFO ] Computed 11 invariants in 10 ms
[2024-05-26 01:52:41] [INFO ] [Real]Absence check using 11 positive place invariants in 8 ms returned sat
[2024-05-26 01:52:41] [INFO ] After 62ms SMT Verify possible using all constraints in real domain returned unsat :2 sat :0
Fused 2 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 0 ms.
Successfully simplified 2 atomic propositions for a total of 7 simplifications.
FORMULA NeoElection-PT-6-LTLCardinality-03 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Computed a total of 190 stabilizing places and 214 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 190 transition count 214
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(G(p0)))'
Support contains 6 out of 190 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Discarding 26 places :
Symmetric choice reduction at 0 with 26 rule applications. Total rules 26 place count 164 transition count 178
Iterating global reduction 0 with 26 rules applied. Total rules applied 52 place count 164 transition count 178
Applied a total of 52 rules in 14 ms. Remains 164 /190 variables (removed 26) and now considering 178/214 (removed 36) transitions.
[2024-05-26 01:52:42] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
// Phase 1: matrix 153 rows 164 cols
[2024-05-26 01:52:42] [INFO ] Computed 11 invariants in 1 ms
[2024-05-26 01:52:42] [INFO ] Implicit Places using invariants in 92 ms returned []
[2024-05-26 01:52:42] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
[2024-05-26 01:52:42] [INFO ] Invariant cache hit.
[2024-05-26 01:52:42] [INFO ] State equation strengthened by 5 read => feed constraints.
[2024-05-26 01:52:42] [INFO ] Implicit Places using invariants and state equation in 143 ms returned []
Implicit Place search using SMT with State Equation took 236 ms to find 0 implicit places.
[2024-05-26 01:52:42] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
[2024-05-26 01:52:42] [INFO ] Invariant cache hit.
[2024-05-26 01:52:42] [INFO ] Dead Transitions using invariants and state equation in 81 ms found 0 transitions.
Starting structural reductions in LTL mode, iteration 1 : 164/190 places, 178/214 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 332 ms. Remains : 164/190 places, 178/214 transitions.
ANTLR Tool version 4.9.3 used for code generation does not match the current runtime version 4.7.2ANTLR Runtime version 4.9.3 used for parser compilation does not match the current runtime version 4.7.2ANTLR Tool version 4.9.3 used for code generation does not match the current runtime version 4.7.2ANTLR Runtime version 4.9.3 used for parser compilation does not match the current runtime version 4.7.2Stuttering acceptance computed with spot in 181 ms :[true, (NOT p0), (NOT p0)]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-00 automaton TGBA Formula[mat=[[{ cond=true, acceptance={0} source=0 dest: 0}], [{ cond=true, acceptance={} source=1 dest: 2}], [{ cond=(NOT p0), acceptance={} source=2 dest: 0}, { cond=p0, acceptance={} source=2 dest: 2}]], initial=1, aps=[p0:(GT (ADD s116 s117 s118 s119 s120 s121) 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, complete, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-sensitive, terminal, very-weak, weak, inherently-weak], stateDesc=[null, null, null][false, false, false]]
Entered a terminal (fully accepting) state of product in 1 steps with 0 reset in 3 ms.
FORMULA NeoElection-PT-6-LTLCardinality-00 FALSE TECHNIQUES STUTTER_TEST
Treatment of property NeoElection-PT-6-LTLCardinality-00 finished in 1388 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(F((p0||X(((p1 U p0)||G(F(p2))))))))'
Support contains 126 out of 190 places. Attempting structural reductions.
Property had overlarge support with respect to TGBA, discarding it for now.
Starting structural reductions in LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Applied a total of 0 rules in 4 ms. Remains 190 /190 variables (removed 0) and now considering 214/214 (removed 0) transitions.
[2024-05-26 01:52:42] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
// Phase 1: matrix 189 rows 190 cols
[2024-05-26 01:52:42] [INFO ] Computed 11 invariants in 1 ms
[2024-05-26 01:52:43] [INFO ] Implicit Places using invariants in 57 ms returned []
[2024-05-26 01:52:43] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:43] [INFO ] Invariant cache hit.
[2024-05-26 01:52:43] [INFO ] State equation strengthened by 15 read => feed constraints.
[2024-05-26 01:52:43] [INFO ] Implicit Places using invariants and state equation in 108 ms returned []
Implicit Place search using SMT with State Equation took 168 ms to find 0 implicit places.
[2024-05-26 01:52:43] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:43] [INFO ] Invariant cache hit.
[2024-05-26 01:52:43] [INFO ] Dead Transitions using invariants and state equation in 96 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 273 ms. Remains : 190/190 places, 214/214 transitions.
Stuttering acceptance computed with spot in 109 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2))]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-01 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 1}], [{ cond=(NOT p0), acceptance={} source=1 dest: 1}, { cond=(AND (NOT p0) (NOT p2)), acceptance={} source=1 dest: 2}], [{ cond=(AND (NOT p0) (NOT p2)), acceptance={0} source=2 dest: 2}]], initial=0, aps=[p0:(LEQ 1 (ADD s16 s17 s18 s19 s20 s21 s22 s23 s24 s25 s26 s27 s28 s29 s30 s31 s32 s33 s34 s35 s36 s37 s38 s39 s40 s41 s42 s43 s44 s45 s46 s47 s48 s49 s50...], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-sensitive], stateDesc=[null, null, null][false, false, false]]
Product exploration explored 100000 steps with 20879 reset in 453 ms.
Product exploration explored 100000 steps with 20889 reset in 352 ms.
Computed a total of 190 stabilizing places and 214 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 190 transition count 214
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (F (OR (G p0) (G (NOT p0)))), (F (G (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0))]
Knowledge sufficient to adopt a stutter insensitive property.
Knowledge based reduction with 5 factoid took 248 ms. Reduced automaton from 3 states, 4 edges and 2 AP (stutter sensitive) to 5 states, 11 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 217 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
Finished random walk after 46 steps, including 0 resets, run visited all 4 properties in 4 ms. (steps per millisecond=11 )
Parikh walk visited 0 properties in 0 ms.
Knowledge obtained : [(AND (NOT p0) (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (F (OR (G p0) (G (NOT p0)))), (F (G (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0)), (F p0), (F (NOT (AND (NOT p0) (NOT p2)))), (F (AND p0 p2)), (F (AND p0 (NOT p2)))]
Knowledge based reduction with 5 factoid took 360 ms. Reduced automaton from 5 states, 11 edges and 2 AP (stutter insensitive) to 5 states, 11 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 190 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
Stuttering acceptance computed with spot in 178 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
[2024-05-26 01:52:45] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:45] [INFO ] Invariant cache hit.
[2024-05-26 01:52:45] [INFO ] [Real]Absence check using 11 positive place invariants in 13 ms returned sat
[2024-05-26 01:52:45] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2024-05-26 01:52:45] [INFO ] [Real]Absence check using state equation in 155 ms returned sat
[2024-05-26 01:52:45] [INFO ] Solution in real domain found non-integer solution.
[2024-05-26 01:52:46] [INFO ] [Nat]Absence check using 11 positive place invariants in 4 ms returned sat
[2024-05-26 01:52:46] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2024-05-26 01:52:46] [INFO ] [Nat]Absence check using state equation in 63 ms returned sat
[2024-05-26 01:52:46] [INFO ] State equation strengthened by 15 read => feed constraints.
[2024-05-26 01:52:46] [INFO ] [Nat]Added 15 Read/Feed constraints in 4 ms returned sat
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 7 places in 79 ms of which 2 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 8 places in 80 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 6 places in 64 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 7 places in 62 ms of which 2 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 6 places in 55 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 7 places in 57 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 9 places in 54 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 7 places in 37 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 8 places in 28 ms of which 0 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 6 places in 53 ms of which 1 ms to minimize.
[2024-05-26 01:52:46] [INFO ] Deduced a trap composed of 7 places in 58 ms of which 0 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 10 places in 31 ms of which 1 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 7 places in 54 ms of which 0 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 8 places in 51 ms of which 1 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 7 places in 54 ms of which 0 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 7 places in 53 ms of which 0 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 7 places in 53 ms of which 0 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Deduced a trap composed of 4 places in 62 ms of which 1 ms to minimize.
[2024-05-26 01:52:47] [INFO ] Trap strengthening (SAT) tested/added 19/18 trap constraints in 1179 ms
[2024-05-26 01:52:47] [INFO ] Computed and/alt/rep : 202/498/177 causal constraints (skipped 6 transitions) in 11 ms.
[2024-05-26 01:52:47] [INFO ] Added : 0 causal constraints over 0 iterations in 27 ms. Result :sat
Could not prove EG (AND (NOT p0) (NOT p2))
Support contains 126 out of 190 places. Attempting structural reductions.
Property had overlarge support with respect to TGBA, discarding it for now.
Starting structural reductions in SI_LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Applied a total of 0 rules in 16 ms. Remains 190 /190 variables (removed 0) and now considering 214/214 (removed 0) transitions.
[2024-05-26 01:52:47] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:47] [INFO ] Invariant cache hit.
[2024-05-26 01:52:47] [INFO ] Implicit Places using invariants in 47 ms returned []
[2024-05-26 01:52:47] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:47] [INFO ] Invariant cache hit.
[2024-05-26 01:52:47] [INFO ] State equation strengthened by 15 read => feed constraints.
[2024-05-26 01:52:47] [INFO ] Implicit Places using invariants and state equation in 98 ms returned []
Implicit Place search using SMT with State Equation took 148 ms to find 0 implicit places.
[2024-05-26 01:52:47] [INFO ] Redundant transitions in 7 ms returned []
[2024-05-26 01:52:47] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:47] [INFO ] Invariant cache hit.
[2024-05-26 01:52:47] [INFO ] Dead Transitions using invariants and state equation in 102 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 280 ms. Remains : 190/190 places, 214/214 transitions.
Computed a total of 190 stabilizing places and 214 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 190 transition count 214
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (NOT (AND p0 (NOT p2)))), (X (NOT (AND p0 p2))), (X (X (NOT (AND p0 p2)))), (F (OR (G p0) (G (NOT p0)))), (F (G (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0)), (X (X (AND p0 (NOT p2)))), (X (X (NOT (AND p0 (NOT p2)))))]
Knowledge based reduction with 8 factoid took 401 ms. Reduced automaton from 5 states, 11 edges and 2 AP (stutter insensitive) to 5 states, 11 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 185 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
Finished random walk after 40 steps, including 0 resets, run visited all 4 properties in 3 ms. (steps per millisecond=13 )
Parikh walk visited 0 properties in 0 ms.
Knowledge obtained : [(AND (NOT p0) (NOT p2)), (X (AND (NOT p0) (NOT p2))), (X (NOT p0)), (X (NOT (AND p0 (NOT p2)))), (X (NOT (AND p0 p2))), (X (X (NOT (AND p0 p2)))), (F (OR (G p0) (G (NOT p0)))), (F (G (NOT p2)))]
False Knowledge obtained : [(X (X (AND (NOT p0) (NOT p2)))), (X (X (NOT (AND (NOT p0) (NOT p2))))), (X (X (NOT p0))), (X (X p0)), (X (X (AND p0 (NOT p2)))), (X (X (NOT (AND p0 (NOT p2))))), (F p0), (F (NOT (AND (NOT p0) (NOT p2)))), (F (AND p0 p2)), (F (AND p0 (NOT p2)))]
Knowledge based reduction with 8 factoid took 536 ms. Reduced automaton from 5 states, 11 edges and 2 AP (stutter insensitive) to 5 states, 11 edges and 2 AP (stutter insensitive).
Stuttering acceptance computed with spot in 206 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
Stuttering acceptance computed with spot in 202 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
[2024-05-26 01:52:49] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:49] [INFO ] Invariant cache hit.
[2024-05-26 01:52:49] [INFO ] [Real]Absence check using 11 positive place invariants in 7 ms returned sat
[2024-05-26 01:52:49] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2024-05-26 01:52:49] [INFO ] [Real]Absence check using state equation in 164 ms returned sat
[2024-05-26 01:52:49] [INFO ] Solution in real domain found non-integer solution.
[2024-05-26 01:52:50] [INFO ] [Nat]Absence check using 11 positive place invariants in 2 ms returned sat
[2024-05-26 01:52:50] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2024-05-26 01:52:50] [INFO ] [Nat]Absence check using state equation in 62 ms returned sat
[2024-05-26 01:52:50] [INFO ] State equation strengthened by 15 read => feed constraints.
[2024-05-26 01:52:50] [INFO ] [Nat]Added 15 Read/Feed constraints in 4 ms returned sat
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 7 places in 68 ms of which 0 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 8 places in 76 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 6 places in 70 ms of which 0 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 7 places in 64 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 6 places in 60 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 7 places in 57 ms of which 0 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 9 places in 48 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 7 places in 45 ms of which 0 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 8 places in 35 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 6 places in 69 ms of which 0 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 7 places in 61 ms of which 1 ms to minimize.
[2024-05-26 01:52:50] [INFO ] Deduced a trap composed of 10 places in 32 ms of which 0 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 7 places in 55 ms of which 1 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 8 places in 57 ms of which 0 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 7 places in 64 ms of which 0 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 7 places in 61 ms of which 1 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 7 places in 60 ms of which 3 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Deduced a trap composed of 4 places in 59 ms of which 0 ms to minimize.
[2024-05-26 01:52:51] [INFO ] Trap strengthening (SAT) tested/added 19/18 trap constraints in 1247 ms
[2024-05-26 01:52:51] [INFO ] Computed and/alt/rep : 202/498/177 causal constraints (skipped 6 transitions) in 12 ms.
[2024-05-26 01:52:51] [INFO ] Added : 0 causal constraints over 0 iterations in 26 ms. Result :sat
Could not prove EG (AND (NOT p0) (NOT p2))
Stuttering acceptance computed with spot in 199 ms :[(AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), (AND (NOT p0) (NOT p2)), false, false]
Product exploration explored 100000 steps with 20974 reset in 368 ms.
Product exploration explored 100000 steps with 20888 reset in 354 ms.
Built C files in :
/tmp/ltsmin4839198759640039751
[2024-05-26 01:52:52] [INFO ] Computing symmetric may disable matrix : 214 transitions.
[2024-05-26 01:52:52] [INFO ] Computation of Complete disable matrix. took 1 ms. Total solver calls (SAT/UNSAT): 0(0/0)
[2024-05-26 01:52:52] [INFO ] Computing symmetric may enable matrix : 214 transitions.
[2024-05-26 01:52:52] [INFO ] Computation of Complete enable matrix. took 1 ms. Total solver calls (SAT/UNSAT): 0(0/0)
[2024-05-26 01:52:52] [INFO ] Computing Do-Not-Accords matrix : 214 transitions.
[2024-05-26 01:52:52] [INFO ] Computation of Completed DNA matrix. took 3 ms. Total solver calls (SAT/UNSAT): 0(0/0)
[2024-05-26 01:52:52] [INFO ] Built C files in 35ms conformant to PINS (ltsmin variant)in folder :/tmp/ltsmin4839198759640039751
Running compilation step : cd /tmp/ltsmin4839198759640039751;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.ltsmin.binaries_1.0.0.202304061127/bin/limit_time.pl' '3' 'gcc' '-c' '-I/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.ltsmin.binaries_1.0.0.202304061127/bin/include/' '-I.' '-std=c99' '-fPIC' '-O0' 'model.c'
Compilation finished in 508 ms.
Running link step : cd /tmp/ltsmin4839198759640039751;'gcc' '-shared' '-o' 'gal.so' 'model.o'
Link finished in 47 ms.
Running LTSmin : cd /tmp/ltsmin4839198759640039751;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.ltsmin.binaries_1.0.0.202304061127/bin/pins2lts-mc-linux64' './gal.so' '--threads=8' '-p' '--pins-guards' '--when' '--hoa' '/tmp/stateBased1403422167848548084.hoa' '--buchi-type=spotba'
LTSmin run took 425 ms.
FORMULA NeoElection-PT-6-LTLCardinality-01 TRUE TECHNIQUES PARTIAL_ORDER EXPLICIT LTSMIN SAT_SMT
Treatment of property NeoElection-PT-6-LTLCardinality-01 finished in 10459 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(G((X(p0)&&(G(p0)||F(p1))))))'
Support contains 162 out of 190 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Applied a total of 0 rules in 2 ms. Remains 190 /190 variables (removed 0) and now considering 214/214 (removed 0) transitions.
[2024-05-26 01:52:53] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:53] [INFO ] Invariant cache hit.
[2024-05-26 01:52:53] [INFO ] Implicit Places using invariants in 61 ms returned []
[2024-05-26 01:52:53] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:53] [INFO ] Invariant cache hit.
[2024-05-26 01:52:53] [INFO ] State equation strengthened by 15 read => feed constraints.
[2024-05-26 01:52:53] [INFO ] Implicit Places using invariants and state equation in 106 ms returned []
Implicit Place search using SMT with State Equation took 169 ms to find 0 implicit places.
[2024-05-26 01:52:53] [INFO ] Flow matrix only has 189 transitions (discarded 25 similar events)
[2024-05-26 01:52:53] [INFO ] Invariant cache hit.
[2024-05-26 01:52:53] [INFO ] Dead Transitions using invariants and state equation in 87 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 258 ms. Remains : 190/190 places, 214/214 transitions.
Stuttering acceptance computed with spot in 170 ms :[(NOT p0), true, (NOT p0), (OR (NOT p0) (NOT p1)), (NOT p0)]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-05 automaton TGBA Formula[mat=[[{ cond=(AND (NOT p0) (NOT p1)), acceptance={} source=0 dest: 3}, { cond=(OR p0 p1), acceptance={} source=0 dest: 4}], [{ cond=true, acceptance={0} source=1 dest: 1}], [{ cond=true, acceptance={} source=2 dest: 0}], [{ cond=(NOT p0), acceptance={0} source=3 dest: 1}, { cond=(AND p0 (NOT p1)), acceptance={0} source=3 dest: 3}, { cond=(AND p0 p1), acceptance={0} source=3 dest: 4}], [{ cond=(NOT p0), acceptance={} source=4 dest: 1}, { cond=p0, acceptance={} source=4 dest: 4}]], initial=2, aps=[p0:(LEQ 2 (ADD s154 s155 s156 s157 s158 s159 s160 s161 s162 s163 s164 s165 s166 s167 s168 s169 s170 s171 s172 s173 s174 s175 s176 s177 s178 s179 s180 s181...], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, complete, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-sensitive, very-weak, weak, inherently-weak], stateDesc=[null, null, null, null, null][false, false, false, false, false]]
Entered a terminal (fully accepting) state of product in 2 steps with 0 reset in 1 ms.
FORMULA NeoElection-PT-6-LTLCardinality-05 FALSE TECHNIQUES STUTTER_TEST
Treatment of property NeoElection-PT-6-LTLCardinality-05 finished in 451 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(G(F(p0)))'
Support contains 6 out of 190 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Reduce places removed 6 places and 6 transitions.
Performed 6 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 6 Pre rules applied. Total rules applied 0 place count 184 transition count 202
Deduced a syphon composed of 6 places in 0 ms
Reduce places removed 6 places and 0 transitions.
Iterating global reduction 0 with 12 rules applied. Total rules applied 12 place count 178 transition count 202
Discarding 20 places :
Symmetric choice reduction at 0 with 20 rule applications. Total rules 32 place count 158 transition count 172
Iterating global reduction 0 with 20 rules applied. Total rules applied 52 place count 158 transition count 172
Performed 30 Post agglomeration using F-continuation condition.Transition count delta: 30
Deduced a syphon composed of 30 places in 0 ms
Reduce places removed 30 places and 0 transitions.
Iterating global reduction 0 with 60 rules applied. Total rules applied 112 place count 128 transition count 142
Reduce places removed 6 places and 6 transitions.
Iterating global reduction 0 with 6 rules applied. Total rules applied 118 place count 122 transition count 136
Applied a total of 118 rules in 34 ms. Remains 122 /190 variables (removed 68) and now considering 136/214 (removed 78) transitions.
[2024-05-26 01:52:53] [INFO ] Flow matrix only has 111 transitions (discarded 25 similar events)
// Phase 1: matrix 111 rows 122 cols
[2024-05-26 01:52:53] [INFO ] Computed 11 invariants in 1 ms
[2024-05-26 01:52:53] [INFO ] Implicit Places using invariants in 64 ms returned []
[2024-05-26 01:52:53] [INFO ] Flow matrix only has 111 transitions (discarded 25 similar events)
[2024-05-26 01:52:53] [INFO ] Invariant cache hit.
[2024-05-26 01:52:53] [INFO ] State equation strengthened by 5 read => feed constraints.
[2024-05-26 01:52:54] [INFO ] Implicit Places using invariants and state equation in 97 ms returned []
Implicit Place search using SMT with State Equation took 162 ms to find 0 implicit places.
[2024-05-26 01:52:54] [INFO ] Redundant transitions in 3 ms returned []
[2024-05-26 01:52:54] [INFO ] Flow matrix only has 111 transitions (discarded 25 similar events)
[2024-05-26 01:52:54] [INFO ] Invariant cache hit.
[2024-05-26 01:52:54] [INFO ] Dead Transitions using invariants and state equation in 67 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 122/190 places, 136/214 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 272 ms. Remains : 122/190 places, 136/214 transitions.
Stuttering acceptance computed with spot in 67 ms :[(NOT p0), (NOT p0)]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-06 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 0}, { cond=(NOT p0), acceptance={} source=0 dest: 1}], [{ cond=(NOT p0), acceptance={0} source=1 dest: 1}]], initial=0, aps=[p0:(LEQ 6 (ADD s110 s111 s112 s113 s114 s115))], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-invariant, very-weak, weak, inherently-weak], stateDesc=[null, null][true, true]]
Product exploration explored 100000 steps with 8792 reset in 367 ms.
Product exploration explored 100000 steps with 8844 reset in 391 ms.
Computed a total of 122 stabilizing places and 136 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 122 transition count 136
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X (NOT p0)), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 4 factoid took 84 ms. Reduced automaton from 2 states, 3 edges and 1 AP (stutter insensitive) to 2 states, 3 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 66 ms :[(NOT p0), (NOT p0)]
Finished random walk after 10 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=10 )
Parikh walk visited 0 properties in 0 ms.
Knowledge obtained : [(NOT p0), (X (NOT p0)), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Property proved to be false thanks to negative knowledge :(F p0)
Knowledge based reduction with 4 factoid took 95 ms. Reduced automaton from 2 states, 3 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 0 AP (stutter insensitive).
FORMULA NeoElection-PT-6-LTLCardinality-06 FALSE TECHNIQUES KNOWLEDGE
Treatment of property NeoElection-PT-6-LTLCardinality-06 finished in 1432 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((p0||X(p1))))'
Support contains 2 out of 190 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Discarding 26 places :
Symmetric choice reduction at 0 with 26 rule applications. Total rules 26 place count 164 transition count 178
Iterating global reduction 0 with 26 rules applied. Total rules applied 52 place count 164 transition count 178
Applied a total of 52 rules in 7 ms. Remains 164 /190 variables (removed 26) and now considering 178/214 (removed 36) transitions.
[2024-05-26 01:52:55] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
// Phase 1: matrix 153 rows 164 cols
[2024-05-26 01:52:55] [INFO ] Computed 11 invariants in 2 ms
[2024-05-26 01:52:55] [INFO ] Implicit Places using invariants in 78 ms returned []
[2024-05-26 01:52:55] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
[2024-05-26 01:52:55] [INFO ] Invariant cache hit.
[2024-05-26 01:52:55] [INFO ] State equation strengthened by 5 read => feed constraints.
[2024-05-26 01:52:55] [INFO ] Implicit Places using invariants and state equation in 117 ms returned []
Implicit Place search using SMT with State Equation took 197 ms to find 0 implicit places.
[2024-05-26 01:52:55] [INFO ] Flow matrix only has 153 transitions (discarded 25 similar events)
[2024-05-26 01:52:55] [INFO ] Invariant cache hit.
[2024-05-26 01:52:55] [INFO ] Dead Transitions using invariants and state equation in 78 ms found 0 transitions.
Starting structural reductions in LTL mode, iteration 1 : 164/190 places, 178/214 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 283 ms. Remains : 164/190 places, 178/214 transitions.
Stuttering acceptance computed with spot in 73 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1))]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-13 automaton TGBA Formula[mat=[[{ cond=(NOT p0), acceptance={} source=0 dest: 1}], [{ cond=(AND (NOT p0) (NOT p1)), acceptance={0} source=1 dest: 1}]], initial=0, aps=[p0:(EQ s4 0), p1:(EQ s11 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-sensitive, very-weak, weak, inherently-weak], stateDesc=[null, null][false, false]]
Product exploration explored 100000 steps with 14306 reset in 150 ms.
Product exploration explored 100000 steps with 14396 reset in 173 ms.
Computed a total of 164 stabilizing places and 178 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 164 transition count 178
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND (NOT p0) (NOT p1)), (F (G p0)), (F (OR (G p1) (G (NOT p1))))]
False Knowledge obtained : [(X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X (X (AND (NOT p0) (NOT p1)))), (X (X (NOT (AND (NOT p0) (NOT p1)))))]
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 3 factoid took 16 ms. Reduced automaton from 2 states, 2 edges and 2 AP (stutter sensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA NeoElection-PT-6-LTLCardinality-13 TRUE TECHNIQUES KNOWLEDGE
Treatment of property NeoElection-PT-6-LTLCardinality-13 finished in 764 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202304061127/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F((G(p0)||G(F(p1)))))'
Support contains 2 out of 190 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 190/190 places, 214/214 transitions.
Reduce places removed 4 places and 4 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 0 with 1 rules applied. Total rules applied 1 place count 186 transition count 209
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 1 with 1 rules applied. Total rules applied 2 place count 185 transition count 209
Performed 6 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 6 Pre rules applied. Total rules applied 2 place count 185 transition count 203
Deduced a syphon composed of 6 places in 0 ms
Reduce places removed 6 places and 0 transitions.
Iterating global reduction 2 with 12 rules applied. Total rules applied 14 place count 179 transition count 203
Discarding 26 places :
Symmetric choice reduction at 2 with 26 rule applications. Total rules 40 place count 153 transition count 167
Iterating global reduction 2 with 26 rules applied. Total rules applied 66 place count 153 transition count 167
Performed 6 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 6 Pre rules applied. Total rules applied 66 place count 153 transition count 161
Deduced a syphon composed of 6 places in 0 ms
Reduce places removed 6 places and 0 transitions.
Iterating global reduction 2 with 12 rules applied. Total rules applied 78 place count 147 transition count 161
Performed 24 Post agglomeration using F-continuation condition.Transition count delta: 24
Deduced a syphon composed of 24 places in 0 ms
Reduce places removed 24 places and 0 transitions.
Iterating global reduction 2 with 48 rules applied. Total rules applied 126 place count 123 transition count 137
Reduce places removed 4 places and 4 transitions.
Iterating global reduction 2 with 4 rules applied. Total rules applied 130 place count 119 transition count 133
Reduce places removed 4 places and 0 transitions.
Graph (complete) has 296 edges and 115 vertex of which 99 are kept as prefixes of interest. Removing 16 places using SCC suffix rule.1 ms
Discarding 16 places :
Also discarding 16 output transitions
Drop transitions removed 16 transitions
Drop transitions removed 9 transitions
Trivial Post-agglo rules discarded 9 transitions
Performed 9 trivial Post agglomeration. Transition count delta: 9
Iterating post reduction 2 with 14 rules applied. Total rules applied 144 place count 99 transition count 108
Reduce places removed 9 places and 0 transitions.
Iterating post reduction 3 with 9 rules applied. Total rules applied 153 place count 90 transition count 108
Performed 11 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 4 with 11 Pre rules applied. Total rules applied 153 place count 90 transition count 97
Deduced a syphon composed of 11 places in 0 ms
Reduce places removed 11 places and 0 transitions.
Iterating global reduction 4 with 22 rules applied. Total rules applied 175 place count 79 transition count 97
Discarding 16 places :
Symmetric choice reduction at 4 with 16 rule applications. Total rules 191 place count 63 transition count 78
Iterating global reduction 4 with 16 rules applied. Total rules applied 207 place count 63 transition count 78
Performed 1 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 4 with 1 Pre rules applied. Total rules applied 207 place count 63 transition count 77
Deduced a syphon composed of 1 places in 0 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 4 with 2 rules applied. Total rules applied 209 place count 62 transition count 77
Discarding 9 places :
Symmetric choice reduction at 4 with 9 rule applications. Total rules 218 place count 53 transition count 64
Iterating global reduction 4 with 9 rules applied. Total rules applied 227 place count 53 transition count 64
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 4 with 4 rules applied. Total rules applied 231 place count 51 transition count 62
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 4 with 4 rules applied. Total rules applied 235 place count 49 transition count 60
Applied a total of 235 rules in 45 ms. Remains 49 /190 variables (removed 141) and now considering 60/214 (removed 154) transitions.
[2024-05-26 01:52:56] [INFO ] Flow matrix only has 42 transitions (discarded 18 similar events)
// Phase 1: matrix 42 rows 49 cols
[2024-05-26 01:52:56] [INFO ] Computed 7 invariants in 0 ms
[2024-05-26 01:52:56] [INFO ] Implicit Places using invariants in 37 ms returned []
[2024-05-26 01:52:56] [INFO ] Flow matrix only has 42 transitions (discarded 18 similar events)
[2024-05-26 01:52:56] [INFO ] Invariant cache hit.
[2024-05-26 01:52:56] [INFO ] State equation strengthened by 24 read => feed constraints.
[2024-05-26 01:52:56] [INFO ] Implicit Places using invariants and state equation in 50 ms returned []
Implicit Place search using SMT with State Equation took 89 ms to find 0 implicit places.
[2024-05-26 01:52:56] [INFO ] Redundant transitions in 0 ms returned []
[2024-05-26 01:52:56] [INFO ] Flow matrix only has 42 transitions (discarded 18 similar events)
[2024-05-26 01:52:56] [INFO ] Invariant cache hit.
[2024-05-26 01:52:56] [INFO ] Dead Transitions using invariants and state equation in 34 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 49/190 places, 60/214 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 174 ms. Remains : 49/190 places, 60/214 transitions.
Stuttering acceptance computed with spot in 71 ms :[(AND (NOT p0) (NOT p1)), (AND (NOT p0) (NOT p1))]
Running random walk in product with property : NeoElection-PT-6-LTLCardinality-14 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 0}, { cond=(AND (NOT p0) (NOT p1)), acceptance={} source=0 dest: 1}], [{ cond=(AND p0 (NOT p1)), acceptance={} source=1 dest: 1}, { cond=(AND (NOT p0) (NOT p1)), acceptance={0} source=1 dest: 1}]], initial=0, aps=[p0:(EQ s48 0), p1:(EQ s1 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-invariant], stateDesc=[null, null][true, true]]
Product exploration explored 100000 steps with 2180 reset in 258 ms.
Product exploration explored 100000 steps with 2179 reset in 268 ms.
Computed a total of 49 stabilizing places and 60 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 49 transition count 60
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(AND p0 (NOT p1)), (F (G p0)), (F (G p1))]
False Knowledge obtained : [(X (AND p0 (NOT p1))), (X (NOT (AND p0 (NOT p1)))), (X (AND (NOT p0) (NOT p1))), (X (NOT (AND (NOT p0) (NOT p1)))), (X (X (AND p0 (NOT p1)))), (X (X (NOT (AND p0 (NOT p1))))), (X (X (AND (NOT p0) (NOT p1)))), (X (X (NOT (AND (NOT p0) (NOT p1)))))]
Property proved to be true thanks to knowledge (Minato strategy)
Knowledge based reduction with 3 factoid took 19 ms. Reduced automaton from 2 states, 4 edges and 2 AP (stutter insensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA NeoElection-PT-6-LTLCardinality-14 TRUE TECHNIQUES KNOWLEDGE
Treatment of property NeoElection-PT-6-LTLCardinality-14 finished in 838 ms.
All properties solved by simple procedures.
Total runtime 17461 ms.
BK_STOP 1716688378787
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
+ BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ LTLCardinality = StateSpace ]]
+ /home/mcc/BenchKit/bin//../itstools/bin//..//runeclipse.sh /home/mcc/execution LTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202304061127.jar
+ VERSION=202304061127
+ echo 'Running Version 202304061127'
+ /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/its-tools -pnfolder /home/mcc/execution -examination LTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-6"
export BK_EXAMINATION="LTLCardinality"
export BK_TOOL="gold2023"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool gold2023"
echo " Input is NeoElection-PT-6, examination is LTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r263-tall-171654372600332"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-6.tgz
mv NeoElection-PT-6 execution
cd execution
if [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "UpperBounds" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] || [ "LTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME LTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

