About the Execution of ITS-Tools for JoinFreeModules-PT-2000
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 9242.604 | 3600000.00 | 4014270.00 | 9556.40 | ??????????????F? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
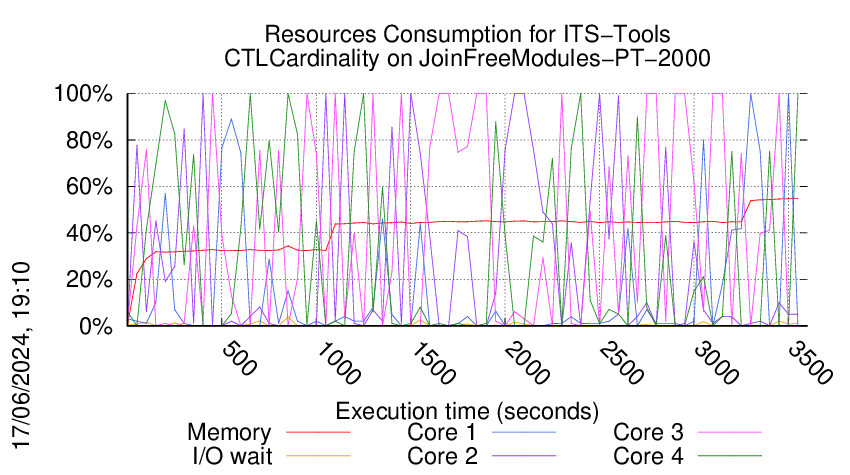
Trace from the execution
Formatting '/data/fkordon/mcc2024-input.r224-tall-171649612000081.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2024-input.qcow2 backing_fmt=qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
...................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5568
Executing tool itstools
Input is JoinFreeModules-PT-2000, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r224-tall-171649612000081
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 6.6M
-rw-r--r-- 1 mcc users 9.1K May 14 13:22 CTLCardinality.txt
-rw-r--r-- 1 mcc users 102K May 14 13:22 CTLCardinality.xml
-rw-r--r-- 1 mcc users 6.9K May 14 13:22 CTLFireability.txt
-rw-r--r-- 1 mcc users 64K May 14 13:22 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 18 16:42 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K May 18 16:42 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 3.8K May 19 07:10 LTLCardinality.txt
-rw-r--r-- 1 mcc users 27K May 19 16:03 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.1K May 19 07:22 LTLFireability.txt
-rw-r--r-- 1 mcc users 16K May 19 18:34 LTLFireability.xml
-rw-r--r-- 1 mcc users 8.6K Apr 11 14:31 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 79K Apr 11 14:31 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 6.1K Apr 11 14:28 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 44K Apr 11 14:28 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.6K May 19 07:13 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K May 19 15:27 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 May 18 16:42 equiv_col
-rw-r--r-- 1 mcc users 5 May 18 16:42 instance
-rw-r--r-- 1 mcc users 6 May 18 16:42 iscolored
-rw-r--r-- 1 mcc users 6.2M May 18 16:42 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-00
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-01
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-02
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-03
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-04
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-05
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-06
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-07
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-08
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-09
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-10
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2024-11
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2023-12
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2023-13
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2023-14
FORMULA_NAME JoinFreeModules-PT-2000-CTLCardinality-2023-15
=== Now, execution of the tool begins
BK_START 1716544245233
Invoking MCC driver with
BK_TOOL=itstools
BK_EXAMINATION=CTLCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=JoinFreeModules-PT-2000
BK_MEMORY_CONFINEMENT=16384
Not applying reductions.
Model is PT
CTLCardinality PT
Running Version 202405141337
[2024-05-24 09:50:46] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLCardinality, -its, -ltsmin, -greatspnpath, /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/, -order, META, -manyOrder, -smt, -timeout, 3600]
[2024-05-24 09:50:46] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2024-05-24 09:50:46] [INFO ] Load time of PNML (sax parser for PT used): 466 ms
[2024-05-24 09:50:47] [INFO ] Transformed 10001 places.
[2024-05-24 09:50:47] [INFO ] Transformed 16001 transitions.
[2024-05-24 09:50:47] [INFO ] Parsed PT model containing 10001 places and 16001 transitions and 46002 arcs in 685 ms.
Parsed 16 properties from file /home/mcc/execution/CTLCardinality.xml in 44 ms.
Reduce places removed 1 places and 0 transitions.
Support contains 211 out of 10000 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 1333 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
// Phase 1: matrix 16001 rows 10000 cols
[2024-05-24 09:50:49] [INFO ] Computed 2000 invariants in 113 ms
[2024-05-24 09:50:49] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20245 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20151 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56664ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56825ms
[2024-05-24 09:51:45] [INFO ] Invariant cache hit.
[2024-05-24 09:51:48] [INFO ] Implicit Places using invariants in 2542 ms returned []
Implicit Place search using SMT only with invariants took 2552 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 09:51:48] [INFO ] Invariant cache hit.
[2024-05-24 09:51:48] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30156 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30131 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76800ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76927ms
Finished structural reductions in LTL mode , in 1 iterations and 137758 ms. Remains : 10000/10000 places, 16001/16001 transitions.
Support contains 211 out of 10000 places after structural reductions.
[2024-05-24 09:53:05] [INFO ] Flatten gal took : 552 ms
[2024-05-24 09:53:06] [INFO ] Flatten gal took : 375 ms
[2024-05-24 09:53:07] [INFO ] Input system was already deterministic with 16001 transitions.
Support contains 210 out of 10000 places (down from 211) after GAL structural reductions.
RANDOM walk for 40033 steps (8 resets) in 4123 ms. (9 steps per ms) remains 128/129 properties
BEST_FIRST walk for 404 steps (0 resets) in 71 ms. (5 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 49 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 48 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 48 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 53 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 54 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 54 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 55 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 61 ms. (6 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 60 ms. (6 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 66 ms. (6 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 60 ms. (6 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 47 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 48 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 44 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 52 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 51 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 48 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 44 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 54 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 53 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 44 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 158 ms. (2 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 52 ms. (7 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 46 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 44 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 43 ms. (9 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 45 ms. (8 steps per ms) remains 128/128 properties
BEST_FIRST walk for 404 steps (0 resets) in 44 ms. (8 steps per ms) remains 128/128 properties
Probabilistic random walk after 17005 steps, saw 17001 distinct states, run finished after 3096 ms. (steps per millisecond=5 ) properties seen :17
[2024-05-24 09:53:12] [INFO ] Invariant cache hit.
[2024-05-24 09:53:12] [INFO ] State equation strengthened by 2000 read => feed constraints.
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/170 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 111 unsolved
At refinement iteration 1 (OVERLAPS) 640/810 variables, 162/162 constraints. Problems are: Problem set: 0 solved, 111 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/810 variables, 0/162 constraints. Problems are: Problem set: 0 solved, 111 unsolved
At refinement iteration 3 (OVERLAPS) 1296/2106 variables, 810/972 constraints. Problems are: Problem set: 0 solved, 111 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/2106 variables, 162/1134 constraints. Problems are: Problem set: 0 solved, 111 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 2106/26001 variables, and 1134 constraints, problems are : Problem set: 0 solved, 111 unsolved in 5022 ms.
Refiners :[Positive P Invariants (semi-flows): 162/2000 constraints, State Equation: 810/10000 constraints, ReadFeed: 162/2000 constraints, PredecessorRefiner: 111/111 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 111 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/170 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 111 unsolved
At refinement iteration 1 (OVERLAPS) 640/810 variables, 162/162 constraints. Problems are: Problem set: 0 solved, 111 unsolved
[2024-05-24 09:53:19] [INFO ] Deduced a trap composed of 3 places in 155 ms of which 19 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 154 ms of which 2 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 125 ms of which 2 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 119 ms of which 2 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 106 ms of which 2 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 104 ms of which 2 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 98 ms of which 1 ms to minimize.
[2024-05-24 09:53:20] [INFO ] Deduced a trap composed of 3 places in 110 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 102 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 96 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 96 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 93 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 96 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 93 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 93 ms of which 1 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 96 ms of which 2 ms to minimize.
[2024-05-24 09:53:21] [INFO ] Deduced a trap composed of 3 places in 89 ms of which 2 ms to minimize.
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 91 ms of which 2 ms to minimize.
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 85 ms of which 3 ms to minimize.
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 99 ms of which 1 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/810 variables, 20/182 constraints. Problems are: Problem set: 0 solved, 111 unsolved
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 79 ms of which 1 ms to minimize.
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 79 ms of which 2 ms to minimize.
[2024-05-24 09:53:22] [INFO ] Deduced a trap composed of 3 places in 79 ms of which 1 ms to minimize.
SMT process timed out in 10378ms, After SMT, problems are : Problem set: 0 solved, 111 unsolved
Fused 111 Parikh solutions to 1 different solutions.
Parikh walk visited 0 properties in 0 ms.
Support contains 170 out of 10000 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Graph (complete) has 24000 edges and 10000 vertex of which 810 are kept as prefixes of interest. Removing 9190 places using SCC suffix rule.21 ms
Discarding 9190 places :
Also discarding 14704 output transitions
Drop transitions (Output transitions of discarded places.) removed 14704 transitions
Drop transitions (Empty/Sink Transition effects.) removed 1 transitions
Reduce isomorphic transitions removed 1 transitions.
Iterating post reduction 0 with 1 rules applied. Total rules applied 2 place count 810 transition count 1296
Applied a total of 2 rules in 116 ms. Remains 810 /10000 variables (removed 9190) and now considering 1296/16001 (removed 14705) transitions.
Running 972 sub problems to find dead transitions.
// Phase 1: matrix 1296 rows 810 cols
[2024-05-24 09:53:22] [INFO ] Computed 162 invariants in 3 ms
[2024-05-24 09:53:22] [INFO ] State equation strengthened by 162 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/648 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 972 unsolved
At refinement iteration 1 (OVERLAPS) 162/810 variables, 162/162 constraints. Problems are: Problem set: 0 solved, 972 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 810/2106 variables, and 162 constraints, problems are : Problem set: 0 solved, 972 unsolved in 20021 ms.
Refiners :[Positive P Invariants (semi-flows): 162/162 constraints, State Equation: 0/810 constraints, ReadFeed: 0/162 constraints, PredecessorRefiner: 972/972 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 972 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/648 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 972 unsolved
At refinement iteration 1 (OVERLAPS) 162/810 variables, 162/162 constraints. Problems are: Problem set: 0 solved, 972 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s2 0)
(s3 1991)
(s4 5)
(s5 5)
(s6 2)
(s7 0)
(s8 1991)
(s9 5)
(s10 5)
(s11 2)
(s12 1987)
(s13 4)
(s14 5)
(s15 1992)
(s16 2)
(s17 0)
(s18 4)
(s19 5)
(s20 5)
(s21 1989)
(s22 0)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s27 0)
(s28 4)
(s29 1992)
(s30 5)
(s31 2)
(s32 1987)
(s33 4)
(s34 5)
(s35 5)
(s36 1989)
(s37 0)
(s38 4)
(s39 5)
(s40 5)
(s41 1989)
(s42 0)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s47 1987)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s52 0)
(s53 1991)
(s54 5)
(s55 5)
(s56 2)
(s57 0)
(s58 4)
(s59 1992)
(s60 5)
(s61 2)
(s62 1987)
(s63 4)
(s64 5)
(s65 1992)
(s66 2)
(s67 0)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s72 0)
(s73 1991)
(s74 5)
(s75 1992)
(s76 2)
(s77 0)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s82 0)
(s83 1991)
(s84 5)
(s85 5)
(s86 2)
(s87 0)
(s88 4)
(s89 1992)
(s90 5)
(s91 1989)
(s92 0)
(s93 4)
(s94 5)
(s95 1992)
(s96 2)
(s97 0)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s102 1987)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s107 1987)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s112 0)
(s113 4)
(s114 1992)
(s115 5)
(s116 2)
(s117 1987)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s122 0)
(s123 1991)
(s124 5)
(s125 5)
(s126 2)
(s127 0)
(s128 1991)
(s129 5)
(s130 5)
(s131 1989)
(s132 0)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s137 1987)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s142 0)
(s143 1991)
(s144 5)
(s145 5)
(s146 2)
(s147 0)
(s148 1991)
(s149 5)
(s150 5)
(s151 2)
(s152 0)
(s153 4)
(s154 1992)
(s155 5)
(s156 2)
(s157 0)
(s158 4)
(s159 1992)
(s160 5)
(s161 2)
(s162 0)
(s163 1991)
(s164 5)
(s165 5)
(s166 2)
(s167 1987)
(s168 4)
(s169 5)
(s170 5)
(s171 1989)
(s172 0)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s177 0)
(s178 4)
(s179 1992)
(s180 5)
(s181 2)
(s182 0)
(s183 1991)
(s184 5)
(s185 1992)
(s186 2)
(s187 0)
(s188 4)
(s189 5)
(s190 5)
(s191 1989)
(s192 0)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s197 0)
(s198 1991)
(s199 5)
(s200 1992)
(s201 2)
(s202 0)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s207 0)
(s208 4)
(s209 1992)
(s210 1992)
(s211 2)
(s212 0)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s217 1987)
(s218 4)
(s219 5)
(s220 5)
(s221 timeout
1989 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 810/2106 variables, and 162 constraints, problems are : Problem set: 0 solved, 972 unsolved in 20021 ms.
Refiners :[Positive P Invariants (semi-flows): 162/162 constraints, State Equation: 0/810 constraints, ReadFeed: 0/162 constraints, PredecessorRefiner: 0/972 constraints, Known Traps: 0/0 constraints]
After SMT, in 40195ms problems are : Problem set: 0 solved, 972 unsolved
Search for dead transitions found 0 dead transitions in 40203ms
Finished structural reductions in REACHABILITY mode , in 1 iterations and 40321 ms. Remains : 810/10000 places, 1296/16001 transitions.
RANDOM walk for 41036 steps (8 resets) in 423 ms. (96 steps per ms) remains 103/111 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 10 ms. (36 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 9 ms. (40 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 9 ms. (40 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 10 ms. (36 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 12 ms. (31 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 10 ms. (36 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 9 ms. (40 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 8 ms. (44 steps per ms) remains 103/103 properties
BEST_FIRST walk for 404 steps (0 resets) in 7 ms. (50 steps per ms) remains 103/103 properties
Interrupted probabilistic random walk after 82062 steps, run timeout after 3001 ms. (steps per millisecond=27 ) properties seen :0 out of 103
Probabilistic random walk after 82062 steps, saw 81691 distinct states, run finished after 3005 ms. (steps per millisecond=27 ) properties seen :0
[2024-05-24 09:54:06] [INFO ] Invariant cache hit.
[2024-05-24 09:54:06] [INFO ] State equation strengthened by 162 read => feed constraints.
All remaining problems are real, not stopping.
At refinement iteration 0 (INCLUDED_ONLY) 0/159 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 1 (OVERLAPS) 596/755 variables, 151/151 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/755 variables, 0/151 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 3 (OVERLAPS) 1208/1963 variables, 755/906 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/1963 variables, 151/1057 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/1963 variables, 0/1057 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 6 (OVERLAPS) 0/1963 variables, 0/1057 constraints. Problems are: Problem set: 0 solved, 103 unsolved
No progress, stopping.
After SMT solving in domain Real declared 1963/2106 variables, and 1057 constraints, problems are : Problem set: 0 solved, 103 unsolved in 9596 ms.
Refiners :[Positive P Invariants (semi-flows): 151/162 constraints, State Equation: 755/810 constraints, ReadFeed: 151/162 constraints, PredecessorRefiner: 103/103 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 103 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/159 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 1 (OVERLAPS) 596/755 variables, 151/151 constraints. Problems are: Problem set: 0 solved, 103 unsolved
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 66 ms of which 1 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 69 ms of which 2 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 64 ms of which 1 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 75 ms of which 1 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 70 ms of which 2 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 65 ms of which 2 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 64 ms of which 2 ms to minimize.
[2024-05-24 09:54:16] [INFO ] Deduced a trap composed of 3 places in 66 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 61 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 61 ms of which 2 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 59 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 66 ms of which 3 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 65 ms of which 2 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 56 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 55 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 4 places in 54 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 4 places in 54 ms of which 2 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 55 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 54 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 4 places in 52 ms of which 2 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/755 variables, 20/171 constraints. Problems are: Problem set: 0 solved, 103 unsolved
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 53 ms of which 1 ms to minimize.
[2024-05-24 09:54:17] [INFO ] Deduced a trap composed of 3 places in 56 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 57 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 49 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 48 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 50 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 49 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 53 ms of which 2 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 56 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 46 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 64 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 58 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 46 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 44 ms of which 2 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 53 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 40 ms of which 1 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 0 ms to minimize.
[2024-05-24 09:54:18] [INFO ] Deduced a trap composed of 3 places in 44 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 45 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 44 ms of which 1 ms to minimize.
At refinement iteration 3 (INCLUDED_ONLY) 0/755 variables, 20/191 constraints. Problems are: Problem set: 0 solved, 103 unsolved
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 40 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 38 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 40 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 37 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 41 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 32 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 31 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 32 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 32 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 36 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 30 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 30 ms of which 1 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 28 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
[2024-05-24 09:54:19] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 1 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
At refinement iteration 4 (INCLUDED_ONLY) 0/755 variables, 20/211 constraints. Problems are: Problem set: 0 solved, 103 unsolved
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 27 ms of which 1 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 0 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 27 ms of which 0 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 22 ms of which 1 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 21 ms of which 0 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 21 ms of which 1 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 20 ms of which 1 ms to minimize.
[2024-05-24 09:54:20] [INFO ] Deduced a trap composed of 3 places in 21 ms of which 1 ms to minimize.
At refinement iteration 5 (INCLUDED_ONLY) 0/755 variables, 8/219 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/755 variables, 0/219 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 7 (OVERLAPS) 1208/1963 variables, 755/974 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 8 (INCLUDED_ONLY) 0/1963 variables, 151/1125 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 9 (INCLUDED_ONLY) 0/1963 variables, 103/1228 constraints. Problems are: Problem set: 0 solved, 103 unsolved
[2024-05-24 09:54:25] [INFO ] Deduced a trap composed of 3 places in 35 ms of which 0 ms to minimize.
[2024-05-24 09:54:25] [INFO ] Deduced a trap composed of 3 places in 31 ms of which 0 ms to minimize.
[2024-05-24 09:54:25] [INFO ] Deduced a trap composed of 3 places in 31 ms of which 0 ms to minimize.
[2024-05-24 09:54:25] [INFO ] Deduced a trap composed of 3 places in 27 ms of which 0 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 29 ms of which 1 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 27 ms of which 1 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 21 ms of which 0 ms to minimize.
[2024-05-24 09:54:26] [INFO ] Deduced a trap composed of 3 places in 22 ms of which 0 ms to minimize.
[2024-05-24 09:54:30] [INFO ] Deduced a trap composed of 3 places in 25 ms of which 1 ms to minimize.
[2024-05-24 09:54:30] [INFO ] Deduced a trap composed of 3 places in 24 ms of which 1 ms to minimize.
[2024-05-24 09:54:30] [INFO ] Deduced a trap composed of 3 places in 26 ms of which 0 ms to minimize.
[2024-05-24 09:54:30] [INFO ] Deduced a trap composed of 3 places in 21 ms of which 1 ms to minimize.
[2024-05-24 09:54:30] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
[2024-05-24 09:54:31] [INFO ] Deduced a trap composed of 3 places in 19 ms of which 0 ms to minimize.
[2024-05-24 09:54:33] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
[2024-05-24 09:54:34] [INFO ] Deduced a trap composed of 3 places in 15 ms of which 1 ms to minimize.
[2024-05-24 09:54:34] [INFO ] Deduced a trap composed of 3 places in 23 ms of which 0 ms to minimize.
At refinement iteration 10 (INCLUDED_ONLY) 0/1963 variables, 20/1248 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 11 (INCLUDED_ONLY) 0/1963 variables, 0/1248 constraints. Problems are: Problem set: 0 solved, 103 unsolved
At refinement iteration 12 (OVERLAPS) 0/1963 variables, 0/1248 constraints. Problems are: Problem set: 0 solved, 103 unsolved
No progress, stopping.
After SMT solving in domain Int declared 1963/2106 variables, and 1248 constraints, problems are : Problem set: 0 solved, 103 unsolved in 45015 ms.
Refiners :[Positive P Invariants (semi-flows): 151/162 constraints, State Equation: 755/810 constraints, ReadFeed: 151/162 constraints, PredecessorRefiner: 103/103 constraints, Known Traps: 88/88 constraints]
After SMT, in 54640ms problems are : Problem set: 0 solved, 103 unsolved
Skipping Parikh replay, no witness traces provided.
Support contains 159 out of 810 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 810/810 places, 1296/1296 transitions.
Graph (complete) has 1944 edges and 810 vertex of which 755 are kept as prefixes of interest. Removing 55 places using SCC suffix rule.1 ms
Discarding 55 places :
Also discarding 88 output transitions
Drop transitions (Output transitions of discarded places.) removed 88 transitions
Applied a total of 1 rules in 73 ms. Remains 755 /810 variables (removed 55) and now considering 1208/1296 (removed 88) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 73 ms. Remains : 755/810 places, 1208/1296 transitions.
[2024-05-24 09:55:01] [INFO ] Flatten gal took : 313 ms
[2024-05-24 09:55:01] [INFO ] Flatten gal took : 301 ms
[2024-05-24 09:55:02] [INFO ] Input system was already deterministic with 16001 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 952 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
// Phase 1: matrix 16001 rows 10000 cols
[2024-05-24 09:55:04] [INFO ] Computed 2000 invariants in 40 ms
[2024-05-24 09:55:04] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20163 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56596ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56692ms
[2024-05-24 09:56:00] [INFO ] Invariant cache hit.
[2024-05-24 09:56:03] [INFO ] Implicit Places using invariants in 2454 ms returned []
Implicit Place search using SMT only with invariants took 2455 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 09:56:03] [INFO ] Invariant cache hit.
[2024-05-24 09:56:03] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30140 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)
(s3653 4)
(s3654 5)
(s3655 5)
(s3656 2)
(s3658 4)
(s3659 5)
(s3660 5)
(s3661 2)
(s3663 4)
(s3664 5)
(s3665 5)
(s3666 2)
(s3668 4)
(s3669 5)
(s3670 5)
(s3671 2)
(s3673 4)
(s3674 5)
(s3675 5)
(s3676 2)
(s3678 4)
(s3679 5)
(s3680 5)
(s3681 2)
(s3683 4)
(s3684 5)
(s3685 5)
(s3686 2)
(s3688 4)
(s3689 5)
(s3690 5)
(s3691 2)
(s3693 4)
(s3694 5)
(s3695 5)
(s3696 2)
(s3698 4)
(s3699 5)
(s3700 5)
(s3701 2)
(s3703 4)
(s3704 5)
(s3705 5)
(s3706 2)
(s3708 4)
(s3709 5)
(s3710 5)
(s3711 2)
(s3713 4)
(s3714 5)
(s3715 5)
(s3716 2)
(s3718 4)
(s3719 5)
(s3720 5)
(s3721 2)
(s3723 4)
(s3724 5)
(s3725 5)
(s3726 2)
(s3728 4)
(s3729 5)
(s3730 5)
(s3731 2)
(s3733 4)
(s3734 5)
(s3735 5)
(s3736 2)
(s3738 4)
(s3739 5)
(s3740 5)
(s3741 2)
(s3743 4)
(s3744 5)
(s3745 5)
(s3746 2)
(s3748 4)
(s3749 5)
(s3750 5)
(s3751 2)
(s3753 4)
(s3754 5)
(s3755 5)
(s3756 2)
(s3758 4)
(s3759 5)
(s3760 5)
(s3761 2)
(s3763 4)
(s3764 5)
(s3765 5)
(s3766 2)
(s3768 4)
(s3769 5)
(s3770 5)
(s3771 2)
(s3773 4)
(s3774 5)
(s3775 5)
(s3776 2)
(s3778 4)
(s3779 5)
(s3780 5)
(s3781 2)
(s3783 4)
(s3784 5)
(s3785 5)
(s3786 2)
(s3788 4)
(s3789 5)
(s3790 5)
(s3791 2)
(s3793 4)
(s3794 5)
(s3795 5)
(s3796 2)
(s3798 4)
(s3799 5)
(s3800 5)
(s3801 2)
(s3803 4)
(s3804 5)
(s3805 5)
(s3806 2)
(s3808 4)
(s3809 5)
(s3810 5)
(s3811 2)
(s3813 4)
(s3814 5)
(s3815 5)
(s3816 2)
(s3818 4)
(s3819 5)
(s3820 5)
(s3821 2)
(s3823 4)
(s3824 5)
(s3825 5)
(s3826 2)
(s3828 4)
(s3829 5)
(s3830 5)
(s3831 2)
(s3833 4)
(s3834 5)
(s3835 5)
(s3836 2)
(s3838 4)
(s3839 5)
(s3840 5)
(s3841 2)
(s3843 4)
(s3844 5)
(s3845 5)
(s3846 2)
(s3848 4)
(s3849 5)
(s3850 5)
(s3851 2)
(s3853 4)
(s3854 5)
(s3855 5)
(s3856 2)
(s3858 4)
(s3859 5)
(s3860 5)
(s3861 2)
(s3863 4)
(s3864 5)
(s3865 5)
(s3866 2)
(s3868 4)
(s3869 5)
(s3870 5)
(s3871 2)
(s3873 4)
(s3874 5)
(s3875 5)
(s3876 2)
(s3878 4)
(s3879 5)
(s3880 5)
(s3881 2)
(s3883 4)
(s3884 5)
(s3885 5)
(s3886 2)
(s3888 4)
(s3889 5)
(s3890 5)
(s3891 2)
(s3893 4)
(s3894 5)
(s3895 5)
(s3896 2)
(s3898 4)
(s3899 5)
(s3900 5)
(s3901 2)
(s3903 4)
(s3904 5)
(s3905 5)
(s3906 2)
(s3908 4)
(s3909 5)
(s3910 5)
(s3911 2)
(s3913 4)
(s3914 5)
(s3915 5)
(s3916 2)
(s3918 4)
(s3919 5)
(s3920 5)
(s3921 2)
(s3923 4)
(s3924 5)
(s3925 5)
(s3926 2)
(s3928 4)
(s3929 5)
(s3930 5)
(s3931 2)
(s3933 4)
(s3934 5)
(s3935 5)
(s3936 2)
(s3938 4)
(s3939 5)
(s3940 5)
(s3941 2)
(s3943 4)
(s3944 5)
(s3945 5)
(s3946 2)
(s3948 4)
(s3949 5)
(s3950 5)
(s3951 2)
(s3953 4)
(s3954 5)
(s3955 5)
(s3956 2)
(s3958 4)
(s3959 5)
(s3960 5)
(s3961 2)
(s3963 4)
(s3964 5)
(s3965 5)
(s3966 2)
(s3968 4)
(s3969 5)
(s3970 5)
(s3971 2)
(s3973 4)
(s3974 5)
(s3975 5)
(s3976 2)
(s3978 4)
(s3979 5)
(s3980 5)
(s3981 2)
(s3983 4)
(s3984 5)
(s3985 5)
(s3986 2)
(s3988 4)
(s3989 5)
(s3990 5)
(s3991 2)
(s3993 4)
(s3994 5)
(s3995 5)
(s3996 2)
(s3998 4)
(s3999 5)
(s4000 5)
(s4001 2)
(s4003 4)
(s4004 5)
(s4005 5)
(s4006 2)
(s4008 4)
(s4009 5)
(s4010 5)
(s4011 2)
(s4013 4)
(s4014 5)
(s4015 5)
(s4016 2)
(s4018 4)
(s4019 5)
(s4020 5)
(s4021 2)
(s4023 4)
(s4024 5)
(s4025 5)
(s4026 2)
(s4028 4)
(s4029 5)
(s4030 5)
(s4031 2)
(s4033 4)
(s4034 5)
(s4035 5)
(s4036 2)
(s4038 4)
(s4039 5)
(s4040 5)
(s4041 2)
(s4043 4)
(s4044 5)
(s4045 5)
(s4046 2)
(s4048 4)
(s4049 5)
(s4050 5)
(s4051 2)
(s4053 4)
(s4054 5)
(s4055 5)
(s4056 2)
(s4058 4)
(s4059 5)
(s4060 5)
(s4061 2)
(s4063 4)
(s4064 5)
(s4065 5)
(s4066 2)
(s4068 4)
(s4069 5)
(s4070 5)
(s4071 2)
(s4073 4)
(s4074 5)
(s4075 5)
(s4076 2)
(s4078 4)
(s4079 5)
(s4080 5)
(s4081 2)
(s4083 4)
(s4084 5)
(s4085 5)
(s4086 2)
(s4088 4)
(s4089 5)
(s4090 5)
(s4091 2)
(s4093 4)
(s4094 5)
(s4095 5)
(s4096 2)
(s4098 4)
(s4099 5)
(s4100 5)
(s4101 2)
(s4103 4)
(s4104 5)
(s4105 5)
(s4106 2)
(s4108 4)
(s4109 5)
(s4110 5)
(s4111 2)
(s4113 4)
(s4114 5)
(s4115 5)
(s4116 2)
(s4118 4)
(s4119 5)
(s4120 5)
(s4121 2)
(s4123 4)
(s4124 5)
(s4125 5)
(s4126 2)
(s4128 4)
(s4129 5)
(s4130 5)
(s4131 2)
(s4133 4)
(s4134 5)
(s4135 5)
(s4136 2)
(s4138 4)
(s4139 5)
(s4140 5)
(s4141 2)
(s4143 4)
(s4144 5)
(s4145 5)
(s4146 2)
(s4148 4)
(s4149 5)
(s4150 5)
(s4151 2)
(s4153 4)
(s4154 5)
(s4155 5)
(s4156 2)
(s4158 4)
(s4159 5)
(s4160 5)
(s4161 2)
(s4163 4)
(s4164 5)
(s4165 5)
(s4166 2)
(s4168 4)
(s4169 5)
(s4170 5)
(s4171 2)
(s4173 4)
(s4174 5)
(s4175 5)
(s4176 2)
(s4178 4)
(s4179 5)
(s4180 5)
(s4181 2)
(s4183 4)
(s4184 5)
(s4185 5)
(s4186 2)
(s4188 4)
(s4189 5)
(s4190 5)
(s4191 2)
(s4193 4)
(s4194 5)
(s4195 5)
(s4196 2)
(s4198 4)
(s4199 5)
(s4200 5)
(s4201 2)
(s4203 4)
(s4204 5)
(s4205 5)
(s4206 2)
(s4208 4)
(s4209 5)
(s4210 5)
(s4211 2)
(s4213 4)
(s4214 5)
(s4215 5)
(s4216 2)
(s4218 4)
(s4219 5)
(s4220 5)
(s4221 2)
(s4223 4)
(s4224 5)
(s4225 5)
(s4226 2)
(s4228 4)
(s4229 5)
(s4230 5)
(s4231 2)
(s4233 4)
(s4234 5)
(s4235 5)
(s4236 2)
(s4238 4)
(s4239 5)
(s4240 5)
(s4241 2)
(s4243 4)
(s4244 5)
(s4245 5)
(s4246 2)
(s4248 4)
(s4249 5)
(s4250 5)
(s4251 2)
(s4253 4)
(s4254 5)
(s4255 5)
(s4256 2)
(s4258 4)
(s4259 5)
(s4260 5)
(s4261 2)
(s4263 4)
(s4264 5)
(s4265 5)
(s4266 2)
(s4268 4)
(s4269 5)
(s4270 5)
(s4271 2)
(s4273 4)
(s4274 5)
(s4275 5)
(s4276 2)
(s4278 4)
(s4279 5)
(s4280 5)
(s4281 2)
(s4283 4)
(s4284 5)
(s4285 5)
(s4286 2)
(s4288 4)
(s4289 5)
(s4290 5)
(s4291 2)
(s4293 4)
(s4294 5)
(s4295 5)
(s4296 2)
(s4298 4)
(s4299 5)
(s4300 5)
(s4301 2)
(s4303 4)
(s4304 5)
(s4305 5)
(s4306 2)
(s4308 4)
(s4309 5)
(s4310 5)
(s4311 2)
(s4313 4)
(s4314 5)
(s4315 5)
(s4316 2)
(s4318 4)
(s4319 5)
(s4320 5)
(s4321 2)
(s4323 4)
(s4324 5)
(s4325 5)
(s4326 2)
(s4328 4)
(s4329 5)
(s4330 5)
(s4331 2)
(s4333 4)
(s4334 5)
(s4335 5)
(s4336 2)
(s4338 4)
(s4339 5)
(s4340 5)
(s4341 2)
(s4343 4)
(s4344 5)
(s4345 5)
(s4346 2)
(s4348 4)
(s4349 5)
(s4350 5)
(s4351 2)
(s4353 4)
(s4354 5)
(s4355 5)
(s4356 2)
(s4358 4)
(s4359 5)
(s4360 5)
(s4361 2)
(s4363 4)
(s4364 5)
(s4365 5)
(s4366 2)
(s4368 4)
(s4369 5)
(s4370 5)
(s4371 2)
(s4373 4)
(s4374 5)
(s4375 5)
(s4376 2)
(s4378 4)
(s4379 5)
(s4380 5)
(s4381 2)
(s4383 4)
(s4384 5)
(s4385 5)
(s4386 2)
(s4388 4)
(s4389 5)
(s4390 5)
(s4391 2)
(s4393 4)
(s4394 5)
(s4395 5)
(s4396 2)
(s4398 4)
(s4399 5)
(s4400 5)
(s4401 2)
(s4403 4)
(s4404 5)
(s4405 5)
(s4406 2)
(s4408 4)
(s4409 5)
(s4410 5)
(s4411 2)
(s4413 4)
(s4414 5)
(s4415 5)
(s4416 2)
(s4418 4)
(s4419 5)
(s4420 5)
(s4421 2)
(s4423 4)
(s4424 5)
(s4425 5)
(s4426 2)
(s4428 4)
(s4429 5)
(s4430 5)
(s4431 2)
(s4433 4)
(s4434 5)
(s4435 5)
(s4436 2)
(s4438 4)
(s4439 5)
(s4440 5)
(s4441 2)
(s4443 4)
(s4444 5)
(s4445 5)
(s4446 2)
(s4448 4)
(s4449 5)
(s4450 5)
(s4451 2)
(s4453 4)
(s4454 5)
(s4455 5)
(s4456 2)
(s4458 4)
(s4459 5)
(s4460 5)
(s4461 2)
(s4463 4)
(s4464 5)
(s4465 5)
(s4466 2)
(s4468 4)
(s4469 5)
(s4470 5)
(s4471 2)
(s4473 4)
(s4474 5)
(s4475 5)
(s4476 2)
(s4478 4)
(s4479 5)
(s4480 5)
(s4481 2)
(s4483 4)
(s4484 5)
(s4485 5)
(s4486 2)
(s4488 4)
(s4489 5)
(s4490 5)
(s4491 2)
(s4493 4)
(s4494 5)
(s4495 5)
(s4496 2)
(s4498 4)
(s4499 5)
(s4500 5)
(s4501 2)
(s4503 4)
(s4504 5)
(s4505 5)
(s4506 2)
(s4508 4)
(s4509 5)
(s4510 5)
(s4511 2)
(s4513 4)
(s4514 5)
(s4515 5)
(s4516 2)
(s4518 4)
(s4519 5)
(s4520 5)
(s4521 2)
(s4523 4)
(s4524 5)
(s4525 5)
(s4526 2)
(s4528 4)
(s4529 5)
(s4530 5)
(s4531 2)
(s4533 4)
(s4534 5)
(s4535 5)
(s4536 2)
(s4538 4)
(s4539 5)
(s4540 5)
(s4541 2)
(s4543 4)
(s4544 5)
(s4545 5)
(s4546 2)
(s4548 4)
(s4549 5)
(s4550 5)
(s4551 2)
(s4553 4)
(s4554 5)
(s4555 5)
(s4556 2)
(s4558 4)
(s4559 5)
(s4560 5)
(s4561 2)
(s4563 4)
(s4564 5)
(s4565 5)
(s4566 2)
(s4568 4)
(s4569 5)
(s4570 5)
(s4571 2)
(s4573 4)
(s4574 5)
(s4575 5)
(s4576 2)
(s4578 4)
(s4579 5)
(s4580 5)
(s4581 2)
(s4583 4)
(s4584 5)
(s4585 5)
(s4586 2)
(s4588 4)
(s4589 5)
(s4590 5)
(s4591 2)
(s4593 4)
(s4594 5)
(s4595 5)
(s4596 2)
(s4598 4)
(s4599 5)
(s4600 5)
(s4601 2)
(s4603 4)
(s4604 5)
(s4605 5)
(s4606 2)
(s4608 4)
(s4609 5)
(s4610 5)
(s4611 2)
(s4613 4)
(s4614 5)
(s4615 5)
(s4616 2)
(s4618 4)
(s4619 5)
(s4620 5)
(s4621 2)
(s4623 4)
(s4624 5)
(s4625 5)
(s4626 2)
(s4628 4)
(s4629 5)
(s4630 5)
(s4631 2)
(s4633 4)
(s4634 5)
(s4635 5)
(s4636 2)
(s4638 4)
(s4639 5)
(s4640 5)
(s4641 2)
(s4643 4)
(s4644 5)
(s4645 5)
(s4646 2)
(s4648 4)
(s4649 5)
(s4650 5)
(s4651 2)
(s4653 4)
(s4654 5)
(s4655 5)
(s4656 2)
(s4658 4)
(s4659 5)
(s4660 5)
(s4661 2)
(s4663 4)
(s4664 5)
(s4665 5)
(s4666 2)
(s4668 4)
(s4669 5)
(s4670 5)
(s4671 2)
(s4673 4)
(s4674 5)
(s4675 5)
(s4676 2)
(s4678 4)
(s4679 5)
(s4680 5)
(s4681 2)
(s4683 4)
(s4684 5)
(s4685 5)
(s4686 2)
(s4688 4)
(s4689 5)
(s4690 5)
(s4691 2)
(s4693 4)
(s4694 5)
(s4695 5)
(s4696 2)
(s4698 4)
(s4699 5)
(s4700 5)
(s4701 2)
(s4703 4)
(s4704 5)
(s4705 5)
(s4706 2)
(s4708 4)
(s4709 5)
(s4710 5)
(s4711 2)
(s4713 4)
(s4714 5)
(s4715 5)
(s4716 2)
(s4718 4)
(s4719 5)
(s4720 5)
(s4721 2)
(s4723 4)
(s4724 5)
(s4725 5)
(s4726 2)
(s4728 4)
(s4729 5)
(s4730 5)
(s4731 2)
(s4733 4)
(s4734 5)
(s4735 5)
(s4736 2)
(s4738 4)
(s4739 5)
(s4740 5)
(s4741 2)
(s4743 4)
(s4744 5)
(s4745 5)
(s4746 2)
(s4748 4)
(s4749 5)
(s4750 5)
(s4751 2)
(s4753 4)
(s4754 5)
(s4755 5)
(s4756 2)
(s4758 4)
(s4759 5)
(s4760 5)
(s4761 2)
(s4763 4)
(s4764 5)
(s4765 5)
(s4766 2)
(s4768 4)
(s4769 5)
(s4770 5)
(s4771 2)
(s4773 4)
(s4774 5)
(s4775 5)
(s4776 2)
(s4778 4)
(s4779 5)
(s4780 5)
(s4781 2)
(s4783 4)
(s4784 5)
(s4785 5)
(s4786 2)
(s4788 4)
(s4789 5)
(s4790 5)
(s4791 2)
(s4793 4)
(s4794 5)
(s4795 5)
(s4796 2)
(s4798 4)
(s4799 5)
(s4800 5)
(s4801 2)
(s4803 4)
(s4804 5)
(s4805 5)
(s4806 2)
(s4808 4)
(s4809 5)
(s4810 5)
(s4811 2)
(s4813 4)
(s4814 5)
(s4815 5)
(s4816 2)
(s4818 4)
(s4819 5)
(s4820 5)
(s4821 2)
(s4823 4)
(s4824 5)
(s4825 5)
(s4826 2)
(s4828 4)
(s4829 5)
(s4830 5)
(s4831 2)
(s4833 4)
(s4834 5)
(s4835 5)
(s4836 2)
(s4838 4)
(s4839 5)
(s4840 5)
(s4841 2)
(s4843 4)
(s4844 5)
(s4845 5)
(s4846 2)
(s4848 4)
(s4849 5)
(s4850 5)
(s4851 2)
(s4853 4)
(s4854 5)
(s4855 5)
(s4856 2)
(s4858 4)
(s4859 5)
(s4860 5)
(s4861 2)
(s4863 4)
(s4864 5)
(s4865 5)
(s4866 2)
(s4868 4)
(s4869 5)
(s4870 5)
(s4871 2)
(s4873 4)
(s4874 5)
(s4875 5)
(s4876 2)
(s4878 4)
(s4879 5)
(s4880 5)
(s4881 2)
(s4883 4)
(s4884 5)
(s4885 5)
(s4886 2)
(s4888 4)
(s4889 5)
(s4890 5)
(s4891 2)
(s4893 4)
(s4894 5)
(s4895 5)
(s4896 2)
(s4898 4)
(s4899 5)
(s4900 5)
(s4901 2)
(s4903 4)
(s4904 5)
(s4905 5)
(s4906 2)
(s4908 4)
(s4909 5)
(s4910 5)
(s4911 2)
(s4913 4)
(s4914 5)
(s4915 5)
(s4916 2)
(s4918 4)
(s4919 5)
(s4920 5)
(s4921 2)
(s4923 4)
(s4924 5)
(s4925 5)
(s4926 2)
(s4928 4)
(s4929 5)
(s4930 5)
(s4931 2)
(s4933 4)
(s4934 5)
(s4935 5)
(s4936 2)
(s4938 4)
(s4939 5)
(s4940 5)
(s4941 2)
(s4943 4)
(s4944 5)
(s4945 5)
(s4946 2)
(s4948 4)
(s4949 5)
(s4950 5)
(s4951 2)
(s4953 4)
(s4954 5)
(s4955 5)
(s4956 2)
(s4958 4)
(s4959 5)
(s4960 5)
(s4961 2)
(s4963 4)
(s4964 5)
(s4965 5)
(s4966 2)
(s4968 4)
(s4969 5)
(s4970 5)
(s4971 2)
(s4973 4)
(s4974 5)
(s4975 5)
(s4976 2)
(s4978 4)
(s4979 5)
(s4980 5)
(s4981 2)
(s4983 4)
(s4984 5)
(s4985 5)
(s4986 2)
(s4988 4)
(s4989 5)
(s4990 5)
(s4991 2)
(s4993 4)
(s4994 5)
(s4995 5)
(s4996 2)
(s4998 4)
(s4999 5)
(s5000 5)
(s5001 2)
(s5003 4)
(s5004 5)
(s5005 5)
(s5006 2)
(s5008 4)
(s5009 5)
(s5010 5)
(s5011 2)
(s5013 4)
(s5014 5)
(s5015 5)
(s5016 2)
(s5018 4)
(s5019 5)
(s5020 5)
(s5021 2)
(s5023 4)
(s5024 5)
(s5025 5)
(s5026 2)
(s5028 4)
(s5029 5)
(s5030 5)
(s5031 2)
(s5033 4)
(s5034 5)
(s5035 5)
(s5036 2)
(s5038 4)
(s5039 5)
(s5040 5)
(s5041 2)
(s5043 4)
(s5044 5)
(s5045 5)
(s5046 2)
(s5048 4)
(s5049 5)
(s5050 5)
(s5051 2)
(s5053 4)
(s5054 5)
(s5055 5)
(s5056 2)
(s5058 4)
(s5059 5)
(s5060 5)
(s5061 2)
(s5063 4)
(s5064 5)
(s5065 5)
(s5066 2)
(s5068 4)
(s5069 5)
(s5070 5)
(s5071 2)
(s5073 4)
(s5074 5)
(s5075 5)
(s5076 2)
(s5078 4)
(s5079 5)
(s5080 5)
(s5081 2)
(s5083 4)
(s5084 5)
(s5085 5)
(s5086 2)
(s5088 4)
(s5089 5)
(s5090 5)
(s5091 2)
(s5093 4)
(s5094 5)
(s5095 5)
(s5096 2)
(s5098 4)
(s5099 5)
(s5100 5)
(s5101 2)
(s5103 4)
(s5104 5)
(s5105 5)
(s5106 2)
(s5108 4)
(s5109 5)
(s5110 5)
(s5111 2)
(s5113 4)
(s5114 5)
(s5115 5)
(s5116 2)
(s5118 4)
(s5119 5)
(s5120 5)
(s5121 2)
(s5123 4)
(s5124 5)
(s5125 5)
(s5126 2)
(s5128 4)
(s5129 5)
(s5130 5)
(s5131 2)
(s5133 4)
(s5134 5)
(s5135 5)
(s5136 2)
(s5138 4)
(s5139 5)
(s5140 5)
(s5141 2)
(s5143 4)
(s5144 5)
(s5145 5)
(s5146 2)
(s5148 4)
(s5149 5)
(s5150 5)
(s5151 2)
(s5153 4)
(s5154 5)
(s5155 5)
(s5156 2)
(s5158 4)
(s5159 5)
(s5160 5)
(s5161 2)
(s5163 4)
(s5164 5)
(s5165 5)
(s5166 2)
(s5168 4)
(s5169 5)
(s5170 5)
(s5171 2)
(s5173 4)
(s5174 5)
(s5175 5)
(s5176 2)
(s5178 4)
(s5179 5)
(s5180 5)
(s5181 2)
(s5183 4)
(s5184 5)
(s5185 5)
(s5186 2)
(s5188 4)
(s5189 5)
(s5190 5)
(s5191 2)
(s5193 4)
(s5194 5)
(s5195 5)
(s5196 2)
(s5198 4)
(s5199 5)
(s5200 5)
(s5201 2)
(s5203 4)
(s5204 5)
(s5205 5)
(s5206 2)
(s5208 4)
(s5209 5)
(s5210 5)
(s5211 2)
(s5213 4)
(s5214 5)
(s5215 5)
(s5216 2)
(s5218 4)
(s5219 5)
(s5220 5)
(s5221 2)
(s5223 4)
(s5224 5)
(s5225 5)
(s5226 2)
(s5228 4)
(s5229 5)
(s5230 5)
(s5231 2)
(s5233 4)
(s5234 5)
(s5235 5)
(s5236 2)
(s5238 4)
(s5239 5)
(s5240 5)
(s5241 2)
(s5243 4)
(s5244 5)
(s5245 5)
(s5246 2)
(s5248 4)
(s5249 5)
(s5250 5)
(s5251 2)
(s5253 4)
(s5254 5)
(s5255 5)
(s5256 2)
(s5258 4)
(s5259 5)
(s5260 5)
(s5261 2)
(s5263 4)
(s5264 5)
(s5265 5)
(s5266 2)
(s5268 4)
(s5269 5)
(s5270 5)
(s5271 2)
(s5273 4)
(s5274 5)
(s5275 5)
(s5276 2)
(s5278 4)
(s5279 5)
(s5280 5)
(s5281 2)
(s5283 4)
(s5284 5)
(s5285 5)
(s5286 2)
(s5288 4)
(s5289 5)
(s5290 5)
(s5291 2)
(s5293 4)
(s5294 5)
(s5295 5)
(s5296 2)
(s5298 4)
(s5299 5)
(s5300 5)
(s5301 2)
(s5303 4)
(s5304 5)
(s5305 5)
(s5306 2)
(s5308 4)
(s5309 5)
(s5310 5)
(s5311 2)
(s5313 4)
(s5314 5)
(s5315 5)
(s5316 2)
(s5318 4)
(s5319 5)
(s5320 5)
(s5321 2)
(s5323 4)
(s5324 5)
(s5325 5)
(s5326 2)
(s5328 4)
(s5329 5)
(s5330 5)
(s5331 2)
(s5333 4)
(s5334 5)
(s5335 5)
(s5336 2)
(s5338 4)
(s5339 5)
(s5340 5)
(s5341 2)
(s5343 4)
(s5344 5)
(s5345 5)
(s5346 2)
(s5348 4)
(s5349 5)
(s5350 5)
(s5351 2)
(s5353 4)
(s5354 5)
(s5355 5)
(s5356 2)
(s5358 4)
(s5359 5)
(s5360 5)
(s5361 2)
(s5363 4)
(s5364 5)
(s5365 5)
(s5366 2)
(s5368 4)
(s5369 5)
(s5370 5)
(s5371 2)
(s5373 4)
(s5374 5)
(s5375 5)
(s5376 2)
(s5378 4)
(s5379 5)
(s5380 5)
(s5381 2)
(s5383 4)
(s5384 5)
(s5385 5)
(s5386 2)
(s5388 4)
(s5389 5)
(s5390 5)
(s5391 2)
(s5393 4)
(s5394 5)
(s5395 5)
(s5396 2)
(s5398 4)
(s5399 5)
(s5400 5)
(s5401 2)
(s5403 4)
(s5404 5)
(s5405 5)
(s5406 2)
(s5408 4)
(s5409 5)
(s5410 5)
(s5411 2)
(s5413 4)
(s5414 5)
(s5415 5)
(s5416 2)
(s5418 4)
(s5419 5)
(s5420 5)
(s5421 2)
(s5423 4)
(s5424 5)
(s5425 5)
(s5426 2)
(s5428 4)
(s5429 5)
(s5430 5)
(s5431 2)
(s5433 4)
(s5434 5)
(s5435 5)
(s5436 2)
(s5438 4)
(s5439 5)
(s5440 5)
(s5441 2)
(s5443 4)
(s5444 5)
(s5445 5)
(s5446 2)
(s5448 4)
(s5449 5)
(s5450 5)
(s5451 2)
(s5453 4)
(s5454 5)
(s5455 5)
(s5456 2)
(s5458 4)
(s5459 5)
(s5460 5)
(s5461 2)
(s5463 4)
(s5464 5)
(s5465 5)
(s5466 2)
(s5468 4)
(s5469 5)
(s5470 5)
(s5471 2)
(s5473 4)
(s5474 5)
(s5475 5)
(s5476 2)
(s5478 4)
(s5479 5)
(s5480 5)
(s5481 2)
(s5483 4)
(s5484 5)
(s5485 5)
(s5486 2)
(s5488 4)
(s5489 5)
(s5490 5)
(s5491 2)
(s5493 4)
(s5494 5)
(s5495 5)
(s5496 2)
(s5498 4)
(s5499 5)
(s5500 5)
(s5501 2)
(s5503 4)
(s5504 5)
(s5505 5)
(s5506 2)
(s5508 4)
(s5509 5)
(s5510 5)
(s5511 2)
(s5513 4)
(s5514 5)
(s5515 5)
(s5516 2)
(s5518 4)
(s5519 5)
(s5520 5)
(s5521 2)
(s5523 4)
(s5524 5)
(s5525 5)
(s5526 2)
(s5528 4)
(s5529 5)
(s5530 5)
(s5531 2)
(s5533 4)
(s5534 5)
(s5535 5)
(s5536 2)
(s5538 4)
(s5539 5)
(s5540 5)
(s5541 2)
(s5543 4)
(s5544 5)
(s5545 5)
(s5546 2)
(s5548 4)
(s5549 5)
(s5550 5)
(s5551 2)
(s5553 4)
(s5554 5)
(s5555 5)
(s5556 2)
(s5558 4)
(s5559 5)
(s5560 5)
(s5561 2)
(s5563 4)
(s5564 5)
(s5565 5)
(s5566 2)
(s5568 4)
(s5569 5)
(s5570 5)
(s5571 2)
(s5573 4)
(s5574 5)
(s5575 5)
(s5576 2)
(s5578 4)
(s5579 5)
(s5580 5)
(s5581 2)
(s5583 4)
(s5584 5)
(s5585 5)
(s5586 2)
(s5588 4)
(s5589 5)
(s5590 5)
(s5591 2)
(s5593 4)
(s5594 5)
(s5595 5)
(s5596 2)
(s5598 4)
(s5599 5)
(s5600 5)
(s5601 2)
(s5603 4)
(s5604 5)
(s5605 5)
(s5606 2)
(s5608 4)
(s5609 5)
(s5610 5)
(s5611 2)
(s5613 4)
(s5614 5)
(s5615 5)
(s5616 2)
(s5618 4)
(s5619 5)
(s5620 5)
(s5621 2)
(s5623 4)
(s5624 5)
(s5625 5)
(s5626 2)
(s5628 4)
(s5629 5)
(s5630 5)
(s5631 2)
(s5633 4)
(s5634 5)
(s5635 5)
(s5636 2)
(s5638 4)
(s5639 5)
(s5640 5)
(s5641 2)
(s5643 4)
(s5644 5)
(s5645 5)
(s5646 2)
(s5648 4)
(s5649 5)
(s5650 5)
(s5651 2)
(s5653 4)
(s5654 5)
(s5655 5)
(s5656 2)
(s5658 4)
(s5659 5)
(s5660 5)
(s5661 2)
(s5663 4)
(s5664 5)
(s5665 5)
(s5666 2)
(s5668 4)
(s5669 5)
(s5670 5)
(s5671 2)
(s5673 4)
(s5674 5)
(s5675 5)
(s5676 2)
(s5678 4)
(s5679 5)
(s5680 5)
(s5681 2)
(s5683 4)
(s5684 5)
(s5685 5)
(s5686 2)
(s5688 4)
(s5689 5)
(s5690 5)
(s5691 2)
(s5693 4)
(s5694 5)
(s5695 5)
(s5696 2)
(s5698 4)
(s5699 5)
(s5700 5)
(s5701 2)
(s5703 4)
(s5704 5)
(s5705 5)
(s5706 2)
(s5708 4)
(s5709 5)
(s5710 5)
(s5711 2)
(s5713 4)
(s5714 5)
(s5715 5)
(s5716 2)
(s5718 4)
(s5719 5)
(s5720 5)
(s5721 2)
(s5723 4)
(s5724 5)
(s5725 5)
(s5726 2)
(s5728 4)
(s5729 5)
(s5730 5)
(s5731 2)
(s5733 4)
(s5734 5)
(s5735 5)
(s5736 2)
(s5738 4)
(s5739 5)
(s5740 5)
(s5741 2)
(s5743 4)
(s5744 5)
(s5745 5)
(s5746 2)
(s5748 4)
(s5749 5)
(s5750 5)
(s5751 2)
(s5753 4)
(s5754 5)
(s5755 5)
(s5756 2)
(s5758 4)
(s5759 5)
(s5760 5)
(s5761 2)
(s5763 4)
(s5764 5)
(s5765 5)
(s5766 2)
(s5768 4)
(s5769 5)
(s5770 5)
(s5771 2)
(s5773 4)
(s5774 5)
(s5775 5)
(s5776 2)
(s5778 4)
(s5779 5)
(s5780 5)
(s5781 2)
(s5783 4)
(s5784 5)
(s5785 5)
(s5786 2)
(s5788 4)
(s5789 5)
(s5790 5)
(s5791 2)
(s5793 4)
(s5794 5)
(s5795 5)
(s5796 2)
(s5798 4)
(s5799 5)
(s5800 5)
(s5801 2)
(s5803 4)
(s5804 5)
(s5805 5)
(s5806 2)
(s5808 4)
(s5809 5)
(s5810 5)
(s5811 2)
(s5813 4)
(s5814 5)
(s5815 5)
(s5816 2)
(s5818 4)
(s5819 5)
(s5820 5)
(s5821 2)
(s5823 4)
(s5824 5)
(s5825 5)
(s5826 2)
(s5828 4)
(s5829 5)
(s5830 5)
(s5831 2)
(s5833 4)
(s5834 5)
(s5835 5)
(s5836 2)
(s5838 4)
(s5839 5)
(s5840 5)
(s5841 2)
(s5843 4)
(s5844 5)
(s5845 5)
(s5846 2)
(s5848 4)
(s5849 5)
(s5850 5)
(s5851 2)
(s5853 4)
(s5854 5)
(s5855 5)
(s5856 2)
(s5858 4)
(s5859 5)
(s5860 5)
(s5861 2)
(s5863 4)
(s5864 5)
(s5865 5)
(s5866 2)
(s5868 4)
(s5869 5)
(s5870 5)
(s5871 2)
(s5873 4)
(s5874 5)
(s5875 5)
(s5876 2)
(s5878 4)
(s5879 5)
(s5880 5)
(s5881 2)
(s5883 4)
(s5884 5)
(s5885 5)
(s5886 2)
(s5888 4)
(s5889 5)
(s5890 5)
(s5891 2)
(s5893 4)
(s5894 5)
(s5895 5)
(s5896 2)
(s5898 4)
(s5899 5)
(s5900 5)
(s5901 2)
(s5903 4)
(s5904 5)
(s5905 5)
(s5906 2)
(s5908 4)
(s5909 5)
(s5910 5)
(s5911 2)
(s5913 4)
(s5914 5)
(s5915 5)
(s5916 2)
(s5918 4)
(s5919 5)
(s5920 5)
(s5921 2)
(s5923 4)
(s5924 5)
(s5925 5)
(s5926 2)
(s5928 4)
(s5929 5)
(s5930 5)
(s5931 2)
(s5933 4)
(s5934 5)
(s5935 5)
(s5936 2)
(s5938 4)
(s5939 5)
(s5940 5)
(s5941 2)
(s5943 4)
(s5944 5)
(s5945 5)
(s5946 2)
(s5948 4)
(s5949 5)
(s5950 5)
(s5951 2)
(s5953 4)
(s5954 5)
(s5955 5)
(s5956 2)
(s5958 4)
(s5959 5)
(s5960 5)
(s5961 2)
(s5963 4)
(s5964 5)
(s5965 5)
(s5966 2)
(s5968 4)
(s5969 5)
(s5970 5)
(s5971 2)
(s5973 4)
(s5974 5)
(s5975 5)
(s5976 2)
(s5978 4)
(s5979 5)
(s5980 5)
(s5981 2)
(s5983 4)
(s5984 5)
(s5985 5)
(s5986 2)
(s5988 4)
(s5989 5)
(s5990 5)
(s5991 2)
(s5993 4)
(s5994 5)
(s5995 5)
(s5996 2)
(s5998 4)
(s5999 5)
(s6000 5)
(s6001 2)
(s6003 4)
(s6004 5)
(s6005 5)
(s6006 2)
(s6008 4)
(s6009 5)
(s6010 5)
(s6011 2)
(s6013 4)
(s6014 5)
(s6015 5)
(s6016 2)
(s6018 4)
(s6019 5)
(s6020 5)
(s6021 2)
(s6023 4)
(s6024 5)
(s6025 5)
(s6026 2)
(s6028 4)
(s6029 5)
(s6030 5)
(s6031 2)
(s6033 4)
(s6034 5)
(s6035 5)
(s6036 2)
(s6038 4)
(s6039 5)
(s6040 5)
(s6041 2)
(s6043 4)
(s6044 5)
(s6045 5)
(s6046 2)
(s6048 4)
(s6049 5)
(s6050 5)
(s6051 2)
(s6053 4)
(s6054 5)
(s6055 5)
(s6056 2)
(s6058 4)
(s6059 5)
(s6060 5)
(s6061 2)
(s6063 4)
(s6064 5)
(s6065 5)
(s6066 2)
(s6068 4)
(s6069 5)
(s6070 5)
(s6071 2)
(s6073 4)
(s6074 5)
(s6075 5)
(s6076 2)
(s6078 4)
(s6079 5)
(s6080 5)
(s6081 2)
(s6083 4)
(s6084 5)
(s6085 5)
(s6086 2)
(s6088 4)
(s6089 5)
(s6090 5)
(s6091 2)
(s6093 4)
(s6094 5)
(s6095 5)
(s6096 2)
(s6098 4)
(s6099 5)
(s6100 5)
(s6101 2)
(s6103 4)
(s6104 5)
(s6105 5)
(s6106 2)
(s6108 4)
(s6109 5)
(s6110 5)
(s6111 2)
(s6113 4)
(s6114 5)
(s6115 5)
(s6116 2)
(s6118 4)
(s6119 5)
(s6120 5)
(s6121 2)
(s6123 4)
(s6124 5)
(s6125 5)
(s6126 2)
(s6128 4)
(s6129 5)
(s6130 5)
(s6131 2)
(s6133 4)
(s6134 5)
(s6135 5)
(s6136 2)
(s6138 4)
(s6139 5)
(s6140 5)
(s6141 2)
(s6143 4)
(s6144 5)
(s6145 5)
(s6146 2)
(s6148 4)
(s6149 5)
(s6150 5)
(s6151 2)
(s6153 4)
(s6154 5)
(s6155 5)
(s6156 2)
(s6158 4)
(s6159 5)
(s6160 5)
(s6161 2)
(s6163 4)
(s6164 5)
(s6165 5)
(s6166 2)
(s6168 4)
(s6169 5)
(s6170 5)
(s6171 2)
(s6173 4)
(s6174 5)
(s6175 5)
(s6176 2)
(s6178 4)
(s6179 5)
(s6180 5)
(s6181 2)
(s6183 4)
(s6184 5)
(s6185 5)
(s6186 2)
(s6188 4)
(s6189 5)
(s6190 5)
(s6191 2)
(s6193 4)
(s6194 5)
(s6195 5)
(s6196 2)
(s6198 4)
(s6199 5)
(s6200 5)
(s6201 2)
(s6203 4)
(s6204 5)
(s6205 5)
(s6206 2)
(s6208 4)
(s6209 5)
(s6210 5)
(s6211 2)
(s6213 4)
(s6214 5)
(s6215 5)
(s6216 2)
(s6218 4)
(s6219 5)
(s6220 5)
(s6221 2)
(s6223 4)
(s6224 5)
(s6225 5)
(s6226 2)
(s6228 4)
(s6229 5)
(s6230 5)
(s6231 2)
(s6233 4)
(s6234 5)
(s6235 5)
(s6236 2)
(s6238 4)
(s6239 5)
(s6240 5)
(s6241 2)
(s6243 4)
(s6244 5)
(s6245 5)
(s6246 2)
(s6248 4)
(s6249 5)
(s6250 5)
(s6251 2)
(s6253 4)
(s6254 5)
(s6255 5)
(s6256 2)
(s6258 4)
(s6259 5)
(s6260 5)
(s6261 2)
(s6263 4)
(s6264 5)
(s6265 5)
(s6266 2)
(s6268 4)
(s6269 5)
(s6270 5)
(s6271 2)
(s6273 4)
(s6274 5)
(s6275 5)
(s6276 2)
(s6278 4)
(s6279 5)
(s6280 5)
(s6281 2)
(s6283 4)
(s6284 5)
(s6285 5)
(s6286 2)
(s6288 4)
(s6289 5)
(s6290 5)
(s6291 2)
(s6293 4)
(s6294 5)
(s6295 5)
(s6296 2)
(s6298 4)
(s6299 5)
(s6300 5)
(s6301 2)
(s6303 4)
(s6304 5)
(s6305 5)
(s6306 2)
(s6308 4)
(s6309 5)
(s6310 5)
(s6311 2)
(s6313 4)
(s6314 5)
(s6315 5)
(s6316 2)
(s6318 4)
(s6319 5)
(s6320 5)
(s6321 2)
(s6323 4)
(s6324 5)
(s6325 5)
(s6326 2)
(s6328 4)
(s6329 5)
(s6330 5)
(s6331 2)
(s6333 4)
(s6334 5)
(s6335 5)
(s6336 2)
(s6338 4)
(s6339 5)
(s6340 5)
(s6341 2)
(s6343 4)
(s6344 5)
(s6345 5)
(s6346 2)
(s6348 4)
(s6349 5)
(s6350 5)
(s6351 2)
(s6353 4)
(s6354 5)
(s6355 5)
(s6356 2)
(s6358 4)
(s6359 5)
(s6360 5)
(s6361 2)
(s6363 4)
(s6364 5)
(s6365 5)
(s6366 2)
(s6368 4)
(s6369 5)
(s6370 5)
(s6371 2)
(s6373 4)
(s6374 5)
(s6375 5)
(s6376 2)
(s6378 4)
(s6379 5)
(s6380 5)
(s6381 2)
(s6383 4)
(s6384 5)
(s6385 5)
(s6386 2)
(s6388 4)
(s6389 5)
(s6390 5)
(s6391 2)
(s6393 4)
(s6394 5)
(s6395 5)
(s6396 2)
(s6398 4)
(s6399 5)
(s6400 5)
(s6401 2)
(s6403 4)
(s6404 5)
(s6405 5)
(s6406 2)
(s6408 4)
(s6409 5)
(s6410 5)
(s6411 2)
(s6413 4)
(s6414 5)
(s6415 5)
(s6416 2)
(s6418 4)
(s6419 5)
(s6420 5)
(s6421 2)
(s6423 4)
(s6424 5)
(s6425 5)
(s6426 2)
(s6428 4)
(s6429 5)
(s6430 5)
(s6431 2)
(s6433 4)
(s6434 5)
(s6435 5)
(s6436 2)
(s6438 4)
(s6439 5)
(s6440 5)
(s6441 2)
(s6443 4)
(s6444 5)
(s6445 5)
(s6446 2)
(s6448 4)
(s6449 5)
(s6450 5)
(s6451 2)
(s6453 4)
(s6454 5)
(s6455 5)
(s6456 2)
(s6458 4)
(s6459 5)
(s6460 5)
(s6461 2)
(s6463 4)
(s6464 5)
(s6465 5)
(s6466 2)
(s6468 4)
(s6469 5)
(s6470 5)
(s6471 2)
(s6473 4)
(s6474 5)
(s6475 5)
(s6476 2)
(s6478 4)
(s6479 5)
(s6480 5)
(s6481 2)
(s6483 4)
(s6484 5)
(s6485 5)
(s6486 2)
(s6488 4)
(s6489 5)
(s6490 5)
(s6491 2)
(s6493 4)
(s6494 5)
(s6495 5)
(s6496 2)
(s6498 4)
(s6499 5)
(s6500 5)
(s6501 2)
(s6503 4)
(s6504 5)
(s6505 5)
(s6506 2)
(s6508 4)
(s6509 5)
(s6510 5)
(s6511 2)
(s6513 4)
(s6514 5)
(s6515 5)
(s6516 2)
(s6518 4)
(s6519 5)
(s6520 5)
(s6521 2)
(s6523 4)
(s6524 5)
(s6525 5)
(s6526 2)
(s6528 4)
(s6529 5)
(s6530 5)
(s6531 2)
(s6533 4)
(s6534 5)
(s6535 5)
(s6536 2)
(s6538 4)
(s6539 5)
(s6540 5)
(s6541 2)
(s6543 4)
(s6544 5)
(s6545 5)
(s6546 2)
(s6548 4)
(s6549 5)
(s6550 5)
(s6551 2)
(s6553 4)
(s6554 5)
(s6555 5)
(s6556 2)
(s6558 4)
(s6559 5)
(s6560 5)
(s6561 2)
(s6563 4)
(s6564 5)
(s6565 5)
(s6566 2)
(s6568 4)
(s6569 5)
(s6570 5)
(s6571 2)
(s6573 4)
(s6574 5)
(s6575 5)
(s6576 2)
(s6578 4)
(s6579 5)
(s6580 5)
(s6581 2)
(s6583 4)
(s6584 5)
(s6585 5)
(s6586 2)
(s6588 4)
(s6589 5)
(s6590 5)
(s6591 2)
(s6593 4)
(s6594 5)
(s6595 5)
(s6596 2)
(s6598 4)
(s6599 5)
(s6600 5)
(s6601 2)
(s6603 4)
(s6604 5)
(s6605 5)
(s6606 2)
(s6608 4)
(s6609 5)
(s6610 5)
(s6611 2)
(s6613 4)
(s6614 5)
(s6615 5)
(s6616 2)
(s6618 4)
(s6619 5)
(s6620 5)
(s6621 2)
(s6623 4)
(s6624 5)
(s6625 5)
(s6626 2)
(s6628 4)
(s6629 5)
(s6630 5)
(s6631 2)
(s6633 4)
(s6634 5)
(s6635 5)
(s6636 2)
(s6638 4)
(s6639 5)
(s6640 5)
(s6641 2)
(s6643 4)
(s6644 5)
(s6645 5)
(s6646 2)
(s6648 4)
(s6649 5)
(s6650 5)
(s6651 2)
(s6653 4)
(s6654 5)
(s6655 5)
(s6656 2)
(s6658 4)
(s6659 5)
(s6660 5)
(s6661 2)
(s6663 4)
(s6664 5)
(s6665 5)
(s6666 2)
(s6668 4)
(s6669 5)
(s6670 5)
(s6671 2)
(s6673 4)
(s6674 5)
(s6675 5)
(s6676 2)
(s6678 4)
(s6679 5)
(s6680 5)
(s6681 2)
(s6683 4)
(s6684 5)
(s6685 5)
(s6686 2)
(s6688 4)
(s6689 5)
(s6690 timeout
5)
(s6691 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30142 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76109ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76200ms
Finished structural reductions in LTL mode , in 1 iterations and 136348 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 09:57:19] [INFO ] Flatten gal took : 276 ms
[2024-05-24 09:57:20] [INFO ] Flatten gal took : 288 ms
[2024-05-24 09:57:20] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 09:57:20] [INFO ] Flatten gal took : 277 ms
[2024-05-24 09:57:21] [INFO ] Flatten gal took : 270 ms
[2024-05-24 09:57:21] [INFO ] Time to serialize gal into /tmp/CTLCardinality8333151120784525821.gal : 99 ms
[2024-05-24 09:57:21] [INFO ] Time to serialize properties into /tmp/CTLCardinality8797201743729827756.ctl : 2 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality8333151120784525821.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality8797201743729827756.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 09:57:51] [INFO ] Flatten gal took : 266 ms
[2024-05-24 09:57:51] [INFO ] Applying decomposition
[2024-05-24 09:57:51] [INFO ] Flatten gal took : 279 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph10372094188598353730.txt' '-o' '/tmp/graph10372094188598353730.bin' '-w' '/tmp/graph10372094188598353730.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph10372094188598353730.bin' '-l' '-1' '-v' '-w' '/tmp/graph10372094188598353730.weights' '-q' '0' '-e' '0.001'
[2024-05-24 09:57:53] [INFO ] Decomposing Gal with order
[2024-05-24 09:57:53] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 09:57:59] [INFO ] Removed a total of 1 redundant transitions.
[2024-05-24 09:57:59] [INFO ] Flatten gal took : 462 ms
[2024-05-24 09:58:00] [INFO ] Fuse similar labels procedure discarded/fused a total of 2 labels/synchronizations in 785 ms.
[2024-05-24 09:58:00] [INFO ] Time to serialize gal into /tmp/CTLCardinality8181372474054814448.gal : 151 ms
[2024-05-24 09:58:00] [INFO ] Time to serialize properties into /tmp/CTLCardinality9328252608198002873.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality8181372474054814448.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality9328252608198002873.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 969 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 09:58:31] [INFO ] Invariant cache hit.
[2024-05-24 09:58:31] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20131 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20110 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56245ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56336ms
[2024-05-24 09:59:27] [INFO ] Invariant cache hit.
[2024-05-24 09:59:30] [INFO ] Implicit Places using invariants in 2166 ms returned []
Implicit Place search using SMT only with invariants took 2169 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 09:59:30] [INFO ] Invariant cache hit.
[2024-05-24 09:59:30] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30129 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30169 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 78658ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 78746ms
Finished structural reductions in LTL mode , in 1 iterations and 138250 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:00:49] [INFO ] Flatten gal took : 360 ms
[2024-05-24 10:00:49] [INFO ] Flatten gal took : 306 ms
[2024-05-24 10:00:50] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:00:50] [INFO ] Flatten gal took : 279 ms
[2024-05-24 10:00:50] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:00:50] [INFO ] Time to serialize gal into /tmp/CTLCardinality18415418879228047027.gal : 52 ms
[2024-05-24 10:00:50] [INFO ] Time to serialize properties into /tmp/CTLCardinality1299132412212167167.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality18415418879228047027.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality1299132412212167167.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:01:21] [INFO ] Flatten gal took : 281 ms
[2024-05-24 10:01:21] [INFO ] Applying decomposition
[2024-05-24 10:01:21] [INFO ] Flatten gal took : 288 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph14409071601732778484.txt' '-o' '/tmp/graph14409071601732778484.bin' '-w' '/tmp/graph14409071601732778484.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph14409071601732778484.bin' '-l' '-1' '-v' '-w' '/tmp/graph14409071601732778484.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:01:22] [INFO ] Decomposing Gal with order
[2024-05-24 10:01:22] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:01:27] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:01:27] [INFO ] Flatten gal took : 339 ms
[2024-05-24 10:01:28] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 490 ms.
[2024-05-24 10:01:28] [INFO ] Time to serialize gal into /tmp/CTLCardinality15366557384735779977.gal : 54 ms
[2024-05-24 10:01:28] [INFO ] Time to serialize properties into /tmp/CTLCardinality7876961978939687526.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality15366557384735779977.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality7876961978939687526.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 906 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:01:59] [INFO ] Invariant cache hit.
[2024-05-24 10:01:59] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20123 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20115 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56746ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56833ms
[2024-05-24 10:02:56] [INFO ] Invariant cache hit.
[2024-05-24 10:02:58] [INFO ] Implicit Places using invariants in 2114 ms returned []
Implicit Place search using SMT only with invariants took 2114 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:02:58] [INFO ] Invariant cache hit.
[2024-05-24 10:02:58] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30137 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30116 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76110ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76199ms
Finished structural reductions in LTL mode , in 1 iterations and 136087 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:04:14] [INFO ] Flatten gal took : 276 ms
[2024-05-24 10:04:15] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:04:15] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:04:16] [INFO ] Flatten gal took : 279 ms
[2024-05-24 10:04:16] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:04:16] [INFO ] Time to serialize gal into /tmp/CTLCardinality7663464731492213575.gal : 50 ms
[2024-05-24 10:04:16] [INFO ] Time to serialize properties into /tmp/CTLCardinality340011321238887971.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality7663464731492213575.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality340011321238887971.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...282
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:04:46] [INFO ] Flatten gal took : 275 ms
[2024-05-24 10:04:46] [INFO ] Applying decomposition
[2024-05-24 10:04:47] [INFO ] Flatten gal took : 287 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph1925264532693215819.txt' '-o' '/tmp/graph1925264532693215819.bin' '-w' '/tmp/graph1925264532693215819.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph1925264532693215819.bin' '-l' '-1' '-v' '-w' '/tmp/graph1925264532693215819.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:04:47] [INFO ] Decomposing Gal with order
[2024-05-24 10:04:48] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:04:53] [INFO ] Removed a total of 6 redundant transitions.
[2024-05-24 10:04:53] [INFO ] Flatten gal took : 348 ms
[2024-05-24 10:04:53] [INFO ] Fuse similar labels procedure discarded/fused a total of 12 labels/synchronizations in 502 ms.
[2024-05-24 10:04:54] [INFO ] Time to serialize gal into /tmp/CTLCardinality16365052664061257871.gal : 55 ms
[2024-05-24 10:04:54] [INFO ] Time to serialize properties into /tmp/CTLCardinality3652251702768622187.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality16365052664061257871.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality3652251702768622187.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 899 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:05:25] [INFO ] Invariant cache hit.
[2024-05-24 10:05:25] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: ((s0 5.0)
(s1 2.0)
(s3 4.0)
(s4 5.0)
(s5 5.0)
(s6 2.0)
(s8 4.0)
(s9 5.0)
(s10 5.0)
(s11 2.0)
(s13 4.0)
(s14 5.0)
(s15 5.0)
(s16 2.0)
(s18 4.0)
(s19 5.0)
(s20 5.0)
(s21 2.0)
(s23 4.0)
(s24 5.0)
(s25 5.0)
(s26 2.0)
(s28 4.0)
(s29 5.0)
(s30 5.0)
(s31 2.0)
(s33 4.0)
(s34 5.0)
(s35 5.0)
(s36 2.0)
(s38 4.0)
(s39 5.0)
(s40 5.0)
(s41 2.0)
(s43 4.0)
(s44 5.0)
(s45 5.0)
(s46 2.0)
(s48 4.0)
(s49 5.0)
(s50 5.0)
(s51 2.0)
(s53 4.0)
(s54 5.0)
(s55 5.0)
(s56 2.0)
(s58 4.0)
(s59 5.0)
(s60 5.0)
(s61 2.0)
(s63 4.0)
(s64 5.0)
(s65 5.0)
(s66 2.0)
(s68 4.0)
(s69 5.0)
(s70 5.0)
(s71 2.0)
(s73 4.0)
(s74 5.0)
(s75 5.0)
(s76 2.0)
(s78 4.0)
(s79 5.0)
(s80 5.0)
(s81 2.0)
(s83 4.0)
(s84 5.0)
(s85 5.0)
(s86 2.0)
(s88 4.0)
(s89 5.0)
(s90 5.0)
(s91 2.0)
(s93 4.0)
(s94 5.0)
(s95 5.0)
(s96 2.0)
(s98 4.0)
(s99 5.0)
(s100 5.0)
(s101 2.0)
(s103 4.0)
(s104 5.0)
(s105 5.0)
(s106 2.0)
(s108 4.0)
(s109 5.0)
(s110 5.0)
(s111 2.0)
(s113 4.0)
(s114 5.0)
(s115 5.0)
(s116 2.0)
(s118 4.0)
(s119 5.0)
(s120 5.0)
(s121 2.0)
(s123 4.0)
(s124 5.0)
(s125 5.0)
(s126 2.0)
(s128 4.0)
(s129 5.0)
(s130 5.0)
(s131 2.0)
(s133 4.0)
(s134 5.0)
(s135 5.0)
(s136 2.0)
(s138 4.0)
(s139 5.0)
(s140 5.0)
(s141 2.0)
(s143 4.0)
(s144 5.0)
(s145 5.0)
(s146 2.0)
(s148 4.0)
(s149 5.0)
(s150 5.0)
(s151 2.0)
(s153 4.0)
(s154 5.0)
(s155 5.0)
(s156 2.0)
(s158 4.0)
(s159 5.0)
(s160 5.0)
(s161 2.0)
(s163 4.0)
(s164 5.0)
(s165 5.0)
(s166 2.0)
(s168 4.0)
(s169 5.0)
(s170 5.0)
(s171 2.0)
(s173 4.0)
(s174 5.0)
(s175 5.0)
(s176 2.0)
(s178 4.0)
(s179 5.0)
(s180 5.0)
(s181 2.0)
(s183 4.0)
(s184 5.0)
(s185 5.0)
(s186 2.0)
(s188 4.0)
(s189 5.0)
(s190 5.0)
(s191 2.0)
(s193 4.0)
(s194 5.0)
(s195 5.0)
(s196 2.0)
(s198 4.0)
(s199 5.0)
(s200 5.0)
(s201 2.0)
(s203 4.0)
(s204 5.0)
(s205 5.0)
(s206 2.0)
(s208 4.0)
(s209 5.0)
(s210 5.0)
(s211 2.0)
(s213 4.0)
(s214 5.0)
(s215 5.0)
(s216 2.0)
(s218 4.0)
(s219 5.0)
(s220 5.0)
(s221 2.0)
(s223 4.0)
(s224 5.0)
(s225 5.0)
(s226 2.0)
(s228 4.0)
(s229 5.0)
(s230 5.0)
(s231 2.0)
(s233 4.0)
(s234 5.0)
(s235 5.0)
(s236 2.0)
(s238 4.0)
(s239 5.0)
(s240 5.0)
(s241 2.0)
(s243 4.0)
(s244 5.0)
(s245 5.0)
(s246 2.0)
(s248 4.0)
(s249 5.0)
(s250 5.0)
(s251 2.0)
(s253 4.0)
(s254 5.0)
(s255 5.0)
(s256 2.0)
(s258 4.0)
(s259 5.0)
(s260 5.0)
(s261 2.0)
(s263 4.0)
(s264 5.0)
(s265 5.0)
(s266 2.0)
(s268 4.0)
(s269 5.0)
(s270 5.0)
(s271 2.0)
(s273 4.0)
(s274 5.0)
(s275 5.0)
(s276 2.0)
(s278 4.0)
(s279 5.0)
(s280 5.0)
(s281 2.0)
(s283 4.0)
(s284 5.0)
(s285 5.0)
(s286 2.0)
(s288 4.0)
(s289 5.0)
(s290 5.0)
(s291 2.0)
(s293 4.0)
(s294 5.0)
(s295 5.0)
(s296 2.0)
(s298 4.0)
(s299 5.0)
(s300 5.0)
(s301 2.0)
(s303 4.0)
(s304 5.0)
(s305 5.0)
(s306 2.0)
(s308 4.0)
(s309 5.0)
(s310 5.0)
(s311 2.0)
(s313 4.0)
(s314 5.0)
(s315 5.0)
(s316 2.0)
(s318 4.0)
(s319 5.0)
(s320 5.0)
(s321 2.0)
(s323 4.0)
(s324 5.0)
(s325 5.0)
(s326 2.0)
(s328 4.0)
(s329 5.0)
(s330 5.0)
(s331 2.0)
(s333 4.0)
(s334 5.0)
(s335 5.0)
(s336 2.0)
(s338 4.0)
(s339 5.0)
(s340 5.0)
(s341 2.0)
(s343 4.0)
(s344 5.0)
(s345 5.0)
(s346 2.0)
(s348 4.0)
(s349 5.0)
(s350 5.0)
(s351 2.0)
(s353 4.0)
(s354 5.0)
(s355 5.0)
(s356 2.0)
(s358 4.0)
(s359 5.0)
(s360 5.0)
(s361 2.0)
(s363 4.0)
(s364 5.0)
(s365 5.0)
(s366 2.0)
(s368 4.0)
(s369 5.0)
(s370 5.0)
(s371 2.0)
(s373 4.0)
(s374 5.0)
(s375 5.0)
(s376 2.0)
(s378 4.0)
(s379 5.0)
(s380 5.0)
(s381 2.0)
(s383 4.0)
(s384 5.0)
(s385 5.0)
(s386 2.0)
(s388 4.0)
(s389 5.0)
(s390 5.0)
(s391 2.0)
(s393 4.0)
(s394 5.0)
(s395 5.0)
(s396 2.0)
(s398 4.0)
(s399 5.0)
(s400 5.0)
(s401 2.0)
(s403 4.0)
(s404 5.0)
(s405 5.0)
(s406 2.0)
(s408 4.0)
(s409 5.0)
(s410 5.0)
(s411 2.0)
(s413 4.0)
(s414 5.0)
(s415 5.0)
(s416 2.0)
(s418 4.0)
(s419 5.0)
(s420 5.0)
(s421 2.0)
(s423 4.0)
(s424 5.0)
(s425 5.0)
(s426 2.0)
(s428 4.0)
(s429 5.0)
(s430 5.0)
(s431 2.0)
(s433 4.0)
(s434 5.0)
(s435 5.0)
(s436 2.0)
(s438 4.0)
(s439 5.0)
(s440 5.0)
(s441 2.0)
(s443 4.0)
(s444 5.0)
(s445 5.0)
(s446 2.0)
(s448 4.0)
(s449 5.0)
(s450 5.0)
(s451 2.0)
(s453 4.0)
(s454 5.0)
(s455 5.0)
(s456 2.0)
(s458 4.0)
(s459 5.0)
(s460 5.0)
(s461 2.0)
(s463 4.0)
(s464 5.0)
(s465 5.0)
(s466 2.0)
(s468 4.0)
(s469 5.0)
(s470 5.0)
(s471 2.0)
(s473 4.0)
(s474 5.0)
(s475 5.0)
(s476 2.0)
(s478 4.0)
(s479 5.0)
(s480 5.0)
(s481 2.0)
(s483 4.0)
(s484 5.0)
(s485 5.0)
(s486 2.0)
(s488 4.0)
(s489 5.0)
(s490 5.0)
(s491 2.0)
(s493 4.0)
(s494 5.0)
(s495 5.0)
(s496 2.0)
(s498 4.0)
(s499 5.0)
(s500 5.0)
(s501 2.0)
(s503 4.0)
(s504 5.0)
(s505 5.0)
(s506 2.0)
(s508 4.0)
(s509 5.0)
(s510 5.0)
(s511 2.0)
(s513 4.0)
(s514 5.0)
(s515 5.0)
(s516 2.0)
(s518 4.0)
(s519 5.0)
(s520 5.0)
(s521 2.0)
(s523 4.0)
(s524 5.0)
(s525 5.0)
(s526 2.0)
(s528 4.0)
(s529 5.0)
(s530 5.0)
(s531 2.0)
(s533 4.0)
(s534 5.0)
(s535 5.0)
(s536 2.0)
(s538 4.0)
(s539 5.0)
(s540 5.0)
(s541 2.0)
(s543 4.0)
(s544 5.0)
(s545 5.0)
(s546 2.0)
(s548 4.0)
(s549 5.0)
(s550 5.0)
(s551 2.0)
(s553 4.0)
(s554 5.0)
(s555 5.0)
(s556 2.0)
(s558 4.0)
(s559 5.0)
(s560 5.0)
(s561 2.0)
(s563 4.0)
(s564 5.0)
(s565 5.0)
(s566 2.0)
(s568 4.0)
(s569 5.0)
(s570 5.0)
(s571 2.0)
(s573 4.0)
(s574 5.0)
(s575 5.0)
(s576 2.0)
(s578 4.0)
(s579 5.0)
(s580 5.0)
(s581 2.0)
(s583 4.0)
(s584 5.0)
(s585 5.0)
(s586 2.0)
(s588 4.0)
(s589 5.0)
(s590 5.0)
(s591 2.0)
(s593 4.0)
(s594 5.0)
(s595 5.0)
(s596 2.0)
(s598 4.0)
(s599 5.0)
(s600 5.0)
(s601 2.0)
(s603 4.0)
(s604 5.0)
(s605 5.0)
(s606 2.0)
(s608 4.0)
(s609 5.0)
(s610 5.0)
(s611 2.0)
(s613 4.0)
(s614 5.0)
(s615 5.0)
(s616 2.0)
(s618 4.0)
(s619 5.0)
(s620 5.0)
(s621 2.0)
(s623 4.0)
(s624 5.0)
(s625 5.0)
(s626 2.0)
(s628 4.0)
(s629 5.0)
(s630 5.0)
(s631 2.0)
(s633 4.0)
(s634 5.0)
(s635 5.0)
(s636 2.0)
(s638 4.0)
(s639 5.0)
(s640 5.0)
(s641 2.0)
(s643 4.0)
(s644 5.0)
(s645 5.0)
(s646 2.0)
(s648 4.0)
(s649 5.0)
(s650 5.0)
(s651 2.0)
(s653 4.0)
(s654 5.0)
(s655 5.0)
(s656 2.0)
(s658 4.0)
(s659 5.0)
(s660 5.0)
(s661 2.0)
(s663 4.0)
(s664 5.0)
(s665 5.0)
(s666 2.0)
(s668 4.0)
(s669 5.0)
(s670 5.0)
(s671 2.0)
(s673 4.0)
(s674 5.0)
(s675 5.0)
(s676 2.0)
(s678 4.0)
(s679 5.0)
(s680 5.0)
(s681 2.0)
(s683 4.0)
(s684 5.0)
(s685 5.0)
(s686 2.0)
(s688 4.0)
(s689 5.0)
(s690 5.0)
(s691 2.0)
(s693 4.0)
(s694 5.0)
(s695 5.0)
(s696 2.0)
(s698 4.0)
(s699 5.0)
(s700 5.0)
(s701 2.0)
(s703 4.0)
(s704 5.0)
(s705 5.0)
(s706 2.0)
(s708 4.0)
(s709 5.0)
(s710 5.0)
(s711 2.0)
(s713 4.0)
(s714 5.0)
(s715 5.0)
(s716 2.0)
(s718 4.0)
(s719 5.0)
(s720 5.0)
(s721 2.0)
(s723 4.0)
(s724 5.0)
(s725 5.0)
(s726 2.0)
(s728 4.0)
(s729 5.0)
(s730 5.0)
(s731 2.0)
(s733 4.0)
(s734 5.0)
(s735 5.0)
(s736 2.0)
(s738 4.0)
(s739 5.0)
(s740 5.0)
(s741 2.0)
(s743 4.0)
(s744 5.0)
(s745 5.0)
(s746 2.0)
(s748 4.0)
(s749 5.0)
(s750 5.0)
(s751 2.0)
(s753 4.0)
(s754 5.0)
(s755 5.0)
(s756 2.0)
(s758 4.0)
(s759 5.0)
(s760 5.0)
(s761 2.0)
(s763 4.0)
(s764 5.0)
(s765 5.0)
(s766 2.0)
(s768 4.0)
(s769 5.0)
(s770 5.0)
(s771 2.0)
(s773 4.0)
(s774 5.0)
(s775 5.0)
(s776 2.0)
(s778 4.0)
(s779 5.0)
(s780 5.0)
(s781 2.0)
(s783 4.0)
(s784 5.0)
(s785 5.0)
(s786 2.0)
(s788 4.0)
(s789 5.0)
(s790 5.0)
(s791 2.0)
(s793 4.0)
(s794 5.0)
(s795 5.0)
(s796 2.0)
(s798 4.0)
(s799 5.0)
(s800 5.0)
(s801 2.0)
(s803 4.0)
(s804 5.0)
(s805 5.0)
(s806 2.0)
(s808 4.0)
(s809 5.0)
(s810 5.0)
(s811 2.0)
(s813 4.0)
(s814 5.0)
(s815 5.0)
(s816 2.0)
(s818 4.0)
(s819 5.0)
(s820 5.0)
(s821 2.0)
(s823 4.0)
(s824 5.0)
(s825 5.0)
(s826 2.0)
(s828 4.0)
(s829 5.0)
(s830 5.0)
(s831 2.0)
(s833 4.0)
(s834 5.0)
(s835 5.0)
(s836 2.0)
(s838 4.0)
(s839 5.0)
(s840 5.0)
(s841 2.0)
(s843 4.0)
(s844 5.0)
(s845 5.0)
(s846 2.0)
(s848 4.0)
(s849 5.0)
(s850 5.0)
(s851 2.0)
(s853 4.0)
(s854 5.0)
(s855 5.0)
(s856 2.0)
(s858 4.0)
(s859 5.0)
(s860 5.0)
(s861 2.0)
(s863 4.0)
(s864 5.0)
(s865 5.0)
(s866 2.0)
(s868 4.0)
(s869 5.0)
(s870 5.0)
(s871 2.0)
(s873 4.0)
(s874 5.0)
(s875 5.0)
(s876 2.0)
(s878 4.0)
(s879 5.0)
(s880 5.0)
(s881 2.0)
(s883 4.0)
(s884 5.0)
(s885 5.0)
(s886 2.0)
(s888 4.0)
(s889 5.0)
(s890 5.0)
(s891 2.0)
(s893 4.0)
(s894 5.0)
(s895 5.0)
(s896 2.0)
(s898 4.0)
(s899 5.0)
(s900 5.0)
(s901 2.0)
(s903 4.0)
(s904 5.0)
(s905 5.0)
(s906 2.0)
(s908 4.0)
(s909 5.0)
(s910 5.0)
(s911 2.0)
(s913 4.0)
(s914 5.0)
(s915 5.0)
(s916 2.0)
(s918 4.0)
(s919 5.0)
(s920 5.0)
(s921 2.0)
(s923 4.0)
(s924 5.0)
(s925 5.0)
(s926 2.0)
(s928 4.0)
(s929 5.0)
(s930 5.0)
(s931 2.0)
(s933 4.0)
(s934 5.0)
(s935 5.0)
(s936 2.0)
(s938 4.0)
(s939 5.0)
(s940 5.0)
(s941 2.0)
(s943 4.0)
(s944 5.0)
(s945 5.0)
(s946 2.0)
(s948 4.0)
(s949 5.0)
(s950 5.0)
(s951 2.0)
(s953 4.0)
(s954 5.0)
(s955 5.0)
(s956 2.0)
(s958 4.0)
(s959 5.0)
(s960 5.0)
(s961 2.0)
(s963 4.0)
(s964 5.0)
(s965 5.0)
(s966 2.0)
(s968 4.0)
(s969 5.0)
(s970 5.0)
(s971 2.0)
(s973 4.0)
(s974 5.0)
(s975 5.0)
(s976 2.0)
(s978 4.0)
(s979 5.0)
(s980 5.0)
(s981 2.0)
(s983 4.0)
(s984 5.0)
(s985 5.0)
(s986 2.0)
(s988 4.0)
(s989 5.0)
(s990 5.0)
(s991 2.0)
(s993 4.0)
(s994 5.0)
(s995 5.0)
(s996 2.0)
(s998 4.0)
(s999 5.0)
(s1000 5.0)
(s1001 2.0)
(s1003 4.0)
(s1004 5.0)
(s1005 5.0)
(s1006 2.0)
(s1008 4.0)
(s1009 5.0)
(s1010 5.0)
(s1011 2.0)
(s1013 4.0)
(s1014 5.0)
(s1015 5.0)
(s1016 2.0)
(s1018 4.0)
(s1019 5.0)
(s1020 5.0)
(s1021 2.0)
(s1023 4.0)
(s1024 5.0)
(s1025 5.0)
(s1026 2.0)
(s1028 4.0)
(s1029 5.0)
(s1030 5.0)
(s1031 2.0)
(s1033 4.0)
(s1034 5.0)
(s1035 5.0)
(s1036 2.0)
(s1038 4.0)
(s1039 5.0)
(s1040 5.0)
(s1041 2.0)
(s1043 4.0)
(s1044 5.0)
(s1045 5.0)
(s1046 2.0)
(s1048 4.0)
(s1049 5.0)
(s1050 5.0)
(s1051 2.0)
(s1053 4.0)
(s1054 5.0)
(s1055 5.0)
(s1056 2.0)
(s1058 4.0)
(s1059 5.0)
(s1060 5.0)
(s1061 2.0)
(s1063 4.0)
(s1064 5.0)
(s1065 5.0)
(s1066 2.0)
(s1068 4.0)
(s1069 5.0)
(s1070 5.0)
(s1071 2.0)
(s1073 4.0)
(s1074 5.0)
(s1075 5.0)
(s1076 2.0)
(s1078 4.0)
(s1079 5.0)
(s1080 5.0)
(s1081 2.0)
(s1083 4.0)
(s1084 5.0)
(s1085 5.0)
(s1086 2.0)
(s1088 4.0)
(s1089 5.0)
(s1090 5.0)
(s1091 2.0)
(s1093 4.0)
(s1094 5.0)
(s1095 5.0)
(s1096 2.0)
(s1098 4.0)
(s1099 5.0)
(s1100 5.0)
(s1101 2.0)
(s1103 4.0)
(s1104 5.0)
(s1105 5.0)
(s1106 2.0)
(s1108 4.0)
(s1109 5.0)
(s1110 5.0)
(s1111 2.0)
(s1113 4.0)
(s1114 5.0)
(s1115 5.0)
(s1116 2.0)
(s1118 4.0)
(s1119 5.0)
(s1120 5.0)
(s1121 2.0)
(s1123 4.0)
(s1124 5.0)
(s1125 5.0)
(s1126 2.0)
(s1128 4.0)
(s1129 5.0)
(s1130 5.0)
(s1131 2.0)
(s1133 4.0)
(s1134 5.0)
(s1135 5.0)
(s1136 2.0)
(s1138 4.0)
(s1139 5.0)
(s1140 5.0)
(s1141 2.0)
(s1143 4.0)
(s1144 5.0)
(s1145 5.0)
(s1146 2.0)
(s1148 4.0)
(s1149 5.0)
(s1150 5.0)
(s1151 2.0)
(s1153 4.0)
(s1154 5.0)
(s1155 5.0)
(s1156 2.0)
(s1158 4.0)
(s1159 5.0)
(s1160 5.0)
(s1161 2.0)
(s1163 4.0)
(s1164 5.0)
(s1165 5.0)
(s1166 2.0)
(s1168 4.0)
(s1169 5.0)
(s1170 5.0)
(s1171 2.0)
(s1173 4.0)
(s1174 5.0)
(s1175 5.0)
(s1176 2.0)
(s1178 4.0)
(s1179 5.0)
(s1180 5.0)
(s1181 2.0)
(s1183 4.0)
(s1184 5.0)
(s1185 5.0)
(s1186 2.0)
(s1188 4.0)
(s1189 5.0)
(s1190 5.0)
(s1191 2.0)
(s1193 4.0)
(s1194 5.0)
(s1195 5.0)
(s1196 2.0)
(s1198 4.0)
(s1199 5.0)
(s1200 5.0)
(s1201 2.0)
(s1203 4.0)
(s1204 5.0)
(s1205 5.0)
(s1206 2.0)
(s1208 4.0)
(s1209 5.0)
(s1210 5.0)
(s1211 2.0)
(s1213 4.0)
(s1214 5.0)
(s1215 5.0)
(s1216 2.0)
(s1218 4.0)
(s1219 5.0)
(s1220 5.0)
(s1221 2.0)
(s1223 4.0)
(s1224 5.0)
(s1225 5.0)
(s1226 2.0)
(s1228 4.0)
(s1229 5.0)
(s1230 5.0)
(s1231 2.0)
(s1233 4.0)
(s1234 5.0)
(s1235 5.0)
(s1236 2.0)
(s1238 4.0)
(s1239 5.0)
(s1240 5.0)
(s1241 2.0)
(s1243 4.0)
(s1244 5.0)
(s1245 5.0)
(s1246 2.0)
(s1248 4.0)
(s1249 5.0)
(s1250 5.0)
(s1251 2.0)
(s1253 4.0)
(s1254 5.0)
(s1255 5.0)
(s1256 2.0)
(s1258 4.0)
(s1259 5.0)
(s1260 5.0)
(s1261 2.0)
(s1263 4.0)
(s1264 5.0)
(s1265 5.0)
(s1266 2.0)
(s1268 4.0)
(s1269 5.0)
(s1270 5.0)
(s1271 2.0)
(s1273 4.0)
(s1274 5.0)
(s1275 5.0)
(s1276 2.0)
(s1278 4.0)
(s1279 5.0)
(s1280 5.0)
(s1281 2.0)
(s1283 4.0)
(s1284 5.0)
(s1285 5.0)
(s1286 2.0)
(s1288 4.0)
(s1289 5.0)
(s1290 5.0)
(s1291 2.0)
(s1293 4.0)
(s1294 5.0)
(s1295 5.0)
(s1296 2.0)
(s1298 4.0)
(s1299 5.0)
(s1300 5.0)
(s1301 2.0)
(s1303 4.0)
(s1304 5.0)
(s1305 5.0)
(s1306 2.0)
(s1308 4.0)
(s1309 5.0)
(s1310 5.0)
(s1311 2.0)
(s1313 4.0)
(s1314 5.0)
(s1315 5.0)
(s1316 2.0)
(s1318 4.0)
(s1319 5.0)
(s1320 5.0)
(s1321 2.0)
(s1323 4.0)
(s1324 5.0)
(s1325 5.0)
(s1326 2.0)
(s1328 4.0)
(s1329 5.0)
(s1330 5.0)
(s1331 2.0)
(s1333 4.0)
(s1334 5.0)
(s1335 5.0)
(s1336 2.0)
(s1338 4.0)
(s1339 5.0)
(s1340 5.0)
(s1341 2.0)
(s1343 4.0)
(s1344 5.0)
(s1345 5.0)
(s1346 2.0)
(s1348 4.0)
(s1349 5.0)
(s1350 5.0)
(s1351 2.0)
(s1353 4.0)
(s1354 5.0)
(s1355 5.0)
(s1356 2.0)
(s1358 4.0)
(s1359 5.0)
(s1360 5.0)
(s1361 2.0)
(s1363 4.0)
(s1364 5.0)
(s1365 5.0)
(s1366 2.0)
(s1368 4.0)
(s1369 5.0)
(s1370 5.0)
(s1371 2.0)
(s1373 4.0)
(s1374 5.0)
(s1375 5.0)
(s1376 2.0)
(s1378 4.0)
(s1379 5.0)
(s1380 5.0)
(s1381 2.0)
(s1383 4.0)
(s1384 5.0)
(s1385 5.0)
(s1386 2.0)
(s1388 4.0)
(s1389 5.0)
(s1390 5.0)
(s1391 2.0)
(s1393 4.0)
(s1394 5.0)
(s1395 5.0)
(s1396 2.0)
(s1398 4.0)
(s1399 5.0)
(s1400 5.0)
(s1401 2.0)
(s1403 4.0)
(s1404 5.0)
(s1405 5.0)
(s1406 2.0)
(s1408 4.0)
(s1409 5.0)
(s1410 5.0)
(s1411 2.0)
(s1413 4.0)
(s1414 5.0)
(s1415 5.0)
(s1416 2.0)
(s1418 4.0)
(s1419 5.0)
(s1420 5.0)
(s1421 2.0)
(s1423 4.0)
(s1424 5.0)
(s1425 5.0)
(s1426 2.0)
(s1428 4.0)
(s1429 5.0)
(s1430 5.0)
(s1431 2.0)
(s1433 4.0)
(s1434 5.0)
(s1435 5.0)
(s1436 2.0)
(s1438 4.0)
(s1439 5.0)
(s1440 5.0)
(s1441 2.0)
(s1443 4.0)
(s1444 5.0)
(s1445 5.0)
(s1446 2.0)
(s1448 4.0)
(s1449 5.0)
(s1450 5.0)
(s1451 2.0)
(s1453 4.0)
(s1454 5.0)
(s1455 5.0)
(s1456 2.0)
(s1458 4.0)
(s1459 5.0)
(s1460 5.0)
(s1461 2.0)
(s1463 4.0)
(s1464 5.0)
(s1465 5.0)
(s1466 2.0)
(s1468 4.0)
(s1469 5.0)
(s1470 5.0)
(s1471 2.0)
(s1473 4.0)
(s1474 5.0)
(s1475 5.0)
(s1476 2.0)
(s1478 4.0)
(s1479 5.0)
(s1480 5.0)
(s1481 2.0)
(s1483 4.0)
(s1484 5.0)
(s1485 5.0)
(s1486 2.0)
(s1488 4.0)
(s1489 5.0)
(s1490 5.0)
(s1491 2.0)
(s1493 4.0)
(s1494 5.0)
(s1495 5.0)
(s1496 2.0)
(s1498 4.0)
(s1499 5.0)
(s1500 5.0)
(s1501 2.0)
(s1503 4.0)
(s1504 5.0)
(s1505 5.0)
(s1506 2.0)
(s1508 4.0)
(s1509 5.0)
(s1510 5.0)
(s1511 2.0)
(s1513 4.0)
(s1514 5.0)
(s1515 5.0)
(s1516 2.0)
(s1518 4.0)
(s1519 5.0)
(s1520 5.0)
(s1521 2.0)
(s1523 4.0)
(s1524 5.0)
(s1525 5.0)
(s1526 2.0)
(s1528 4.0)
(s1529 5.0)
(s1530 5.0)
(s1531 2.0)
(s1533 4.0)
(s1534 5.0)
(s1535 5.0)
(s1536 2.0)
(s1538 4.0)
(s1539 5.0)
(s1540 5.0)
(s1541 2.0)
(s1543 4.0)
(s1544 5.0)
(s1545 5.0)
(s1546 2.0)
(s1548 4.0)
(s1549 5.0)
(s1550 5.0)
(s1551 2.0)
(s1553 4.0)
(s1554 5.0)
(s1555 5.0)
(s1556 2.0)
(s1558 4.0)
(s1559 5.0)
(s1560 5.0)
(s1561 2.0)
(s1563 4.0)
(s1564 5.0)
(s1565 5.0)
(s1566 2.0)
(s1568 4.0)
(s1569 5.0)
(s1570 5.0)
(s1571 2.0)
(s1573 4.0)
(s1574 5.0)
(s1575 5.0)
(s1576 2.0)
(s1578 4.0)
(s1579 5.0)
(s1580 5.0)
(s1581 2.0)
(s1583 4.0)
(s1584 5.0)
(s1585 5.0)
(s1586 2.0)
(s1588 4.0)
(s1589 5.0)
(s1590 5.0)
(s1591 2.0)
(s1593 4.0)
(s1594 5.0)
(s1595 5.0)
(s1596 2.0)
(s1598 4.0)
(s1599 5.0)
(s1600 5.0)
(s1601 2.0)
(s1603 4.0)
(s1604 5.0)
(s1605 5.0)
(s1606 2.0)
(s1608 4.0)
(s1609 5.0)
(s1610 5.0)
(s1611 2.0)
(s1613 4.0)
(s1614 5.0)
(s1615 5.0)
(s1616 2.0)
(s1618 4.0)
(s1619 5.0)
(s1620 5.0)
(s1621 2.0)
(s1623 4.0)
(s1624 5.0)
(s1625 5.0)
(s1626 2.0)
(s1628 4.0)
(s1629 5.0)
(s1630 5.0)
(s1631 2.0)
(s1633 4.0)
(s1634 5.0)
(s1635 5.0)
(s1636 2.0)
(s1638 4.0)
(s1639 5.0)
(s1640 5.0)
(s1641 2.0)
(s1643 4.0)
(s1644 5.0)
(s1645 5.0)
(s1646 2.0)
(s1648 4.0)
(s1649 5.0)
(s1650 5.0)
(s1651 2.0)
(s1653 4.0)
(s1654 5.0)
(s1655 5.0)
(s1656 2.0)
(s1658 4.0)
(s1659 5.0)
(s1660 5.0)
(s1661 2.0)
(s1663 4.0)
(s1664 5.0)
(s1665 5.0)
(s1666 2.0)
(s1668 4.0)
(s1669 5.0)
(s1670 5.0)
(s1671 2.0)
(s1673 4.0)
(s1674 5.0)
(s1675 5.0)
(s1676 2.0)
(s1678 4.0)
(s1679 5.0)
(s1680 5.0)
(s1681 2.0)
(s1683 4.0)
(s1684 5.0)
(s1685 5.0)
(s1686 2.0)
(s1688 4.0)
(s1689 5.0)
(s1690 5.0)
(s1691 2.0)
(s1693 4.0)
(s1694 5.0)
(s1695 5.0)
(s1696 2.0)
(s1698 4.0)
(s1699 5.0)
(s1700 5.0)
(s1701 2.0)
(s1703 4.0)
(s1704 5.0)
(s1705 5.0)
(s1706 2.0)
(s1708 4.0)
(s1709 5.0)
(s1710 5.0)
(s1711 2.0)
(s1713 4.0)
(s1714 5.0)
(s1715 5.0)
(s1716 2.0)
(s1718 4.0)
(s1719 5.0)
(s1720 5.0)
(s1721 2.0)
(s1723 4.0)
(s1724 5.0)
(s1725 5.0)
(s1726 2.0)
(s1728 4.0)
(s1729 5.0)
(s1730 5.0)
(s1731 2.0)
(s1733 4.0)
(s1734 5.0)
(s1735 5.0)
(s1736 2.0)
(s1738 4.0)
(s1739 5.0)
(s1740 5.0)
(s1741 2.0)
(s1743 4.0)
(s1744 5.0)
(s1745 5.0)
(s1746 2.0)
(s1748 4.0)
(s1749 5.0)
(s1750 5.0)
(s1751 2.0)
(s1753 4.0)
(s1754 5.0)
(s1755 5.0)
(s1756 2.0)
(s1758 4.0)
(s1759 5.0)
(s1760 5.0)
(s1761 2.0)
(s1763 4.0)
(s1764 5.0)
(s1765 5.0)
(s1766 2.0)
(s1768 4.0)
(s1769 5.0)
(s1770 5.0)
(s1771 2.0)
(s1773 4.0)
(s1774 5.0)
(s1775 5.0)
(s1776 2.0)
(s1778 4.0)
(s1779 5.0)
(s1780 5.0)
(s1781 2.0)
(s1783 4.0)
(s1784 5.0)
(s1785 5.0)
(s1786 2.0)
(s1788 4.0)
(s1789 5.0)
(s1790 5.0)
(s1791 2.0)
(s1793 4.0)
(s1794 5.0)
(s1795 5.0)
(s1796 2.0)
(s1798 4.0)
(s1799 5.0)
(s1800 5.0)
(s1801 2.0)
(s1803 4.0)
(s1804 5.0)
(s1805 5.0)
(s1806 2.0)
(s1808 4.0)
(s1809 5.0)
(s1810 5.0)
(s1811 2.0)
(s1813 4.0)
(s1814 5.0)
(s1815 5.0)
(s1816 2.0)
(s1818 4.0)
(s1819 5.0)
(s1820 5.0)
(s1821 2.0)
(s1823 4.0)
(s1824 5.0)
(s1825 5.0)
(s1826 2.0)
(s1828 4.0)
(s1829 5.0)
(s1830 5.0)
(s1831 2.0)
(s1833 4.0)
(s1834 5.0)
(s1835 5.0)
(s1836 2.0)
(s1838 4.0)
(s1839 5.0)
(s1840 5.0)
(s1841 2.0)
(s1843 4.0)
(s1844 5.0)
(s1845 5.0)
(s1846 2.0)
(s1848 4.0)
(s1849 5.0)
(s1850 5.0)
(s1851 2.0)
(s1853 4.0)
(s1854 5.0)
(s1855 5.0)
(s1856 2.0)
(s1858 4.0)
(s1859 5.0)
(s1860 5.0)
(s1861 2.0)
(s1863 4.0)
(s1864 5.0)
(s1865 5.0)
(s1866 2.0)
(s1868 4.0)
(s1869 5.0)
(s1870 5.0)
(s1871 2.0)
(s1873 4.0)
(s1874 5.0)
(s1875 5.0)
(s1876 2.0)
(s1878 4.0)
(s1879 5.0)
(s1880 5.0)
(s1881 2.0)
(s1883 4.0)
(s1884 5.0)
(s1885 5.0)
(s1886 2.0)
(s1888 4.0)
(s1889 5.0)
(s1890 5.0)
(s1891 2.0)
(s1893 4.0)
(s1894 5.0)
(s1895 5.0)
(s1896 2.0)
(s1898 4.0)
(s1899 5.0)
(s1900 5.0)
(s1901 2.0)
(s1903 4.0)
(s1904 5.0)
(s1905 5.0)
(s1906 2.0)
(s1908 4.0)
(s1909 5.0)
(s1910 5.0)
(s1911 2.0)
(s1913 4.0)
(s1914 5.0)
(s1915 5.0)
(s1916 2.0)
(s1918 4.0)
(s1919 5.0)
(s1920 5.0)
(s1921 2.0)
(s1923 4.0)
(s1924 5.0)
(s1925 5.0)
(s1926 2.0)
(s1928 4.0)
(s1929 5.0)
(s1930 5.0)
(s1931 2.0)
(s1933 4.0)
(s1934 5.0)
(s1935 5.0)
(s1936 2.0)
(s1938 4.0)
(s1939 5.0)
(s1940 5.0)
(s1941 2.0)
(s1943 4.0)
(s1944 5.0)
(s1945 5.0)
(s1946 2.0)
(s1948 4.0)
(s1949 5.0)
(s1950 5.0)
(s1951 2.0)
(s1953 4.0)
(s1954 5.0)
(s1955 5.0)
(s1956 2.0)
(s1958 4.0)
(s1959 5.0)
(s1960 5.0)
(s1961 2.0)
(s1963 4.0)
(s1964 5.0)
(s1965 5.0)
(s1966 2.0)
(s1968 4.0)
(s1969 5.0)
(s1970 5.0)
(s1971 2.0)
(s1973 4.0)
(s1974 5.0)
(s1975 5.0)
(s1976 2.0)
(s1978 4.0)
(s1979 5.0)
(s1980 5.0)
(s1981 2.0)
(s1983 4.0)
(s1984 5.0)
(s1985 5.0)
(s1986 2.0)
(s1988 4.0)
(s1989 5.0)
(s1990 5.0)
(s1991 2.0)
(s1993 4.0)
(s1994 5.0)
(s1995 5.0)
(s1996 2.0)
(s1998 4.0)
(s1999 5.0)
(s2000 5.0)
(s2001 2.0)
(s2003 4.0)
(s2004 5.0)
(s2005 5.0)
(s2006 2.0)
(s2008 4.0)
(s2009 5.0)
(s2010 5.0)
(s2011 2.0)
(s2013 4.0)
(s2014 5.0)
(s2015 5.0)
(s2016 2.0)
(s2018 4.0)
(s2019 5.0)
(s2020 5.0)
(s2021 2.0)
(s2023 4.0)
(s2024 5.0)
(s2025 5.0)
(s2026 2.0)
(s2028 4.0)
(s2029 5.0)
(s2030 5.0)
(s2031 2.0)
(s2033 4.0)
(s2034 5.0)
(s2035 5.0)
(s2036 2.0)
(s2038 4.0)
(s2039 5.0)
(s2040 5.0)
(s2041 2.0)
(s2043 4.0)
(s2044 5.0)
(s2045 5.0)
(s2046 2.0)
(s2048 4.0)
(s2049 5.0)
(s2050 5.0)
(s2051 2.0)
(s2053 4.0)
(s2054 5.0)
(s2055 5.0)
(s2056 2.0)
(s2058 4.0)
(s2059 5.0)
(s2060 5.0)
(s2061 2.0)
(s2063 4.0)
(s2064 5.0)
(s2065 5.0)
(s2066 2.0)
(s2068 4.0)
(s2069 5.0)
(s2070 5.0)
(s2071 2.0)
(s2073 4.0)
(s2074 5.0)
(s2075 5.0)
(s2076 2.0)
(s2078 4.0)
(s2079 5.0)
(s2080 5.0)
(s2081 2.0)
(s2083 4.0)
(s2084 5.0)
(s2085 5.0)
(s2086 2.0)
(s2088 4.0)
(s2089 5.0)
(s2090 5.0)
(s2091 2.0)
(s2093 4.0)
(s2094 5.0)
(s2095 5.0)
(s2096 2.0)
(s2098 4.0)
(s2099 5.0)
(s2100 5.0)
(s2101 2.0)
(s2103 4.0)
(s2104 5.0)
(s2105 5.0)
(s2106 2.0)
(s2108 4.0)
(s2109 5.0)
(s2110 5.0)
(s2111 2.0)
(s2113 4.0)
(s2114 5.0)
(s2115 5.0)
(s2116 2.0)
(s2118 4.0)
(s2119 5.0)
(s2120 5.0)
(s2121 2.0)
(s2123 4.0)
(s2124 5.0)
(s2125 5.0)
(s2126 2.0)
(s2128 4.0)
(s2129 5.0)
(s2130 5.0)
(s2131 2.0)
(s2133 4.0)
(s2134 5.0)
(s2135 5.0)
(s2136 2.0)
(s2138 4.0)
(s2139 5.0)
(s2140 5.0)
(s2141 2.0)
(s2143 4.0)
(s2144 5.0)
(s2145 5.0)
(s2146 2.0)
(s2148 4.0)
(s2149 5.0)
(s2150 5.0)
(s2151 2.0)
(s2153 4.0)
(s2154 5.0)
(s2155 5.0)
(s2156 2.0)
(s2158 4.0)
(s2159 5.0)
(s2160 5.0)
(s2161 2.0)
(s2163 4.0)
(s2164 5.0)
(s2165 5.0)
(s2166 2.0)
(s2168 4.0)
(s2169 5.0)
(s2170 5.0)
(s2171 2.0)
(s2173 4.0)
(s2174 5.0)
(s2175 5.0)
(s2176 2.0)
(s2178 4.0)
(s2179 5.0)
(s2180 5.0)
(s2181 2.0)
(s2183 4.0)
(s2184 5.0)
(s2185 5.0)
(s2186 2.0)
(s2188 4.0)
(s2189 5.0)
(s2190 5.0)
(s2191 2.0)
(s2193 4.0)
(s2194 5.0)
(s2195 5.0)
(s2196 2.0)
(s2198 4.0)
(s2199 5.0)
(s2200 5.0)
(s2201 2.0)
(s2203 4.0)
(s2204 5.0)
(s2205 5.0)
(s2206 2.0)
(s2208 4.0)
(s2209 5.0)
(s2210 5.0)
(s2211 2.0)
(s2213 4.0)
(s2214 5.0)
(s2215 5.0)
(s2216 2.0)
(s2218 4.0)
(s2219 5.0)
(s2220 5.0)
(s2221 2.0)
(s2223 4.0)
(s2224 5.0)
(s2225 5.0)
(s2226 2.0)
(s2228 4.0)
(s2229 5.0)
(s2230 5.0)
(s2231 2.0)
(s2233 4.0)
(s2234 5.0)
(s2235 5.0)
(s2236 2.0)
(s2238 4.0)
(s2239 5.0)
(s2240 5.0)
(s2241 2.0)
(s2243 4.0)
(s2244 5.0)
(s2245 5.0)
(s2246 2.0)
(s2248 4.0)
(s2249 5.0)
(s2250 5.0)
(s2251 2.0)
(s2253 4.0)
(s2254 5.0)
(s2255 5.0)
(s2256 2.0)
(s2258 4.0)
(s2259 5.0)
(s2260 5.0)
(s2261 2.0)
(s2263 4.0)
(s2264 5.0)
(s2265 5.0)
(s2266 2.0)
(s2268 4.0)
(s2269 5.0)
(s2270 5.0)
(s2271 2.0)
(s2273 4.0)
(s2274 5.0)
(s2275 5.0)
(s2276 2.0)
(s2278 4.0)
(s2279 5.0)
(s2280 5.0)
(s2281 2.0)
(s2283 4.0)
(s2284 5.0)
(s2285 5.0)
(s2286 2.0)
(s2288 4.0)
(s2289 5.0)
(s2290 5.0)
(s2291 2.0)
(s2293 4.0)
(s2294 5.0)
(s2295 5.0)
(s2296 2.0)
(s2298 4.0)
(s2299 5.0)
(s2300 5.0)
(s2301 2.0)
(s2303 4.0)
(s2304 5.0)
(s2305 5.0)
(s2306 2.0)
(s2308 4.0)
(s2309 5.0)
(s2310 5.0)
(s2311 2.0)
(s2313 4.0)
(s2314 5.0)
(s2315 5.0)
(s2316 2.0)
(s2318 4.0)
(s2319 5.0)
(s2320 5.0)
(s2321 2.0)
(s2323 4.0)
(s2324 5.0)
(s2325 5.0)
(s2326 2.0)
(s2328 4.0)
(s2329 5.0)
(s2330 5.0)
(s2331 2.0)
(s2333 4.0)
(s2334 5.0)
(s2335 5.0)
(s2336 2.0)
(s2338 4.0)
(s2339 5.0)
(s2340 5.0)
(s2341 2.0)
(s2343 4.0)
(s2344 5.0)
(s2345 5.0)
(s2346 2.0)
(s2348 4.0)
(s2349 5.0)
(s2350 5.0)
(s2351 2.0)
(s2353 4.0)
(s2354 5.0)
(s2355 5.0)
(s2356 2.0)
(s2358 4.0)
(s2359 5.0)
(s2360 5.0)
(s2361 2.0)
(s2363 4.0)
(s2364 5.0)
(s2365 5.0)
(s2366 2.0)
(s2368 4.0)
(s2369 5.0)
(s2370 5.0)
(s2371 2.0)
(s2373 4.0)
(s2374 5.0)
(s2375 5.0)
(s2376 2.0)
(s2378 4.0)
(s2379 5.0)
(s2380 5.0)
(s2381 2.0)
(s2383 4.0)
(s2384 5.0)
(s2385 5.0)
(s2386 2.0)
(s2388 4.0)
(s2389 5.0)
(s2390 5.0)
(s2391 2.0)
(s2393 4.0)
(s2394 5.0)
(s2395 5.0)
(s2396 2.0)
(s2398 4.0)
(s2399 5.0)
(s2400 5.0)
(s2401 2.0)
(s2403 4.0)
(s2404 5.0)
(s2405 5.0)
(s2406 2.0)
(s2408 4.0)
(s2409 5.0)
(s2410 5.0)
(s2411 2.0)
(s2413 4.0)
(s2414 5.0)
(s2415 5.0)
(s2416 2.0)
(s2418 4.0)
(s2419 5.0)
(s2420 5.0)
(s2421 2.0)
(s2423 4.0)
(s2424 5.0)
(s2425 5.0)
(s2426 2.0)
(s2428 4.0)
(s2429 5.0)
(s2430 5.0)
(s2431 2.0)
(s2433 4.0)
(s2434 5.0)
(s2435 5.0)
(s2436 2.0)
(s2438 4.0)
(s2439 5.0)
(s2440 5.0)
(s2441 2.0)
(s2443 4.0)
(s2444 5.0)
(s2445 5.0)
(s2446 2.0)
(s2448 4.0)
(s2449 5.0)
(s2450 5.0)
(s2451 2.0)
(s2453 4.0)
(s2454 5.0)
(s2455 5.0)
(s2456 2.0)
(s2458 4.0)
(s2459 5.0)
(s2460 5.0)
(s2461 2.0)
(s2463 4.0)
(s2464 5.0)
(s2465 5.0)
(s2466 2.0)
(s2468 4.0)
(s2469 5.0)
(s2470 5.0)
(s2471 2.0)
(s2473 4.0)
(s2474 5.0)
(s2475 5.0)
(s2476 2.0)
(s2478 4.0)
(s2479 5.0)
(s2480 5.0)
(s2481 2.0)
(s2483 4.0)
(s2484 5.0)
(s2485 5.0)
(s2486 2.0)
(s2488 4.0)
(s2489 5.0)
(s2490 5.0)
(s2491 2.0)
(s2493 4.0)
(s2494 5.0)
(s2495 5.0)
(s2496 2.0)
(s2498 4.0)
(s2499 5.0)
(s2500 5.0)
(s2501 2.0)
(s2503 4.0)
(s2504 5.0)
(s2505 5.0)
(s2506 2.0)
(s2508 4.0)
(s2509 5.0)
(s2510 5.0)
(s2511 2.0)
(s2513 4.0)
(s2514 5.0)
(s2515 5.0)
(s2516 2.0)
(s2518 4.0)
(s2519 5.0)
(s2520 5.0)
(s2521 2.0)
(s2523 4.0)
(s2524 5.0)
(s2525 5.0)
(s2526 2.0)
(s2528 4.0)
(s2529 5.0)
(s2530 5.0)
(s2531 2.0)
(s2533 4.0)
(s2534 5.0)
(s2535 5.0)
(s2536 2.0)
(s2538 4.0)
(s2539 5.0)
(s2540 5.0)
(s2541 2.0)
(s2543 4.0)
(s2544 5.0)
(s2545 5.0)
(s2546 2.0)
(s2548 4.0)
(s2549 5.0)
(s2550 5.0)
(s2551 2.0)
(s2553 4.0)
(s2554 5.0)
(s2555 5.0)
(s2556 2.0)
(s2558 4.0)
(s2559 5.0)
(s2560 5.0)
(s2561 2.0)
(s2563 4.0)
(s2564 5.0)
(s2565 5.0)
(s2566 2.0)
(s2568 4.0)
(s2569 5.0)
(s2570 5.0)
(s2571 2.0)
(s2573 4.0)
(s2574 5.0)
(s2575 5.0)
(s2576 2.0)
(s2578 4.0)
(s2579 5.0)
(s2580 5.0)
(s2581 2.0)
(s2583 4.0)
(s2584 5.0)
(s2585 5.0)
(s2586 2.0)
(s2588 4.0)
(s2589 5.0)
(s2590 5.0)
(s2591 2.0)
(s2593 4.0)
(s2594 5.0)
(s2595 5.0)
(s2596 2.0)
(s2598 4.0)
(s2599 5.0)
(s2600 5.0)
(s2601 2.0)
(s2603 4.0)
(s2604 5.0)
(s2605 5.0)
(s2606 2.0)
(s2608 4.0)
(s2609 5.0)
(s2610 5.0)
(s2611 2.0)
(s2613 4.0)
(s2614 5.0)
(s2615 5.0)
(s2616 timeout
2.0)
(s2618 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20129 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56367ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56453ms
[2024-05-24 10:06:21] [INFO ] Invariant cache hit.
[2024-05-24 10:06:23] [INFO ] Implicit Places using invariants in 2128 ms returned []
Implicit Place search using SMT only with invariants took 2130 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:06:23] [INFO ] Invariant cache hit.
[2024-05-24 10:06:23] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30115 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30114 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76255ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76340ms
Finished structural reductions in LTL mode , in 1 iterations and 135848 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:07:40] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:07:40] [INFO ] Flatten gal took : 294 ms
[2024-05-24 10:07:41] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:07:41] [INFO ] Flatten gal took : 285 ms
[2024-05-24 10:07:41] [INFO ] Flatten gal took : 275 ms
[2024-05-24 10:07:41] [INFO ] Time to serialize gal into /tmp/CTLCardinality1671580840470899857.gal : 49 ms
[2024-05-24 10:07:41] [INFO ] Time to serialize properties into /tmp/CTLCardinality3377885450830750035.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality1671580840470899857.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality3377885450830750035.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:08:11] [INFO ] Flatten gal took : 278 ms
[2024-05-24 10:08:11] [INFO ] Applying decomposition
[2024-05-24 10:08:12] [INFO ] Flatten gal took : 289 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph15425861607266490378.txt' '-o' '/tmp/graph15425861607266490378.bin' '-w' '/tmp/graph15425861607266490378.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph15425861607266490378.bin' '-l' '-1' '-v' '-w' '/tmp/graph15425861607266490378.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:08:12] [INFO ] Decomposing Gal with order
[2024-05-24 10:08:13] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:08:18] [INFO ] Flatten gal took : 294 ms
[2024-05-24 10:08:18] [INFO ] Fuse similar labels procedure discarded/fused a total of 0 labels/synchronizations in 244 ms.
[2024-05-24 10:08:18] [INFO ] Time to serialize gal into /tmp/CTLCardinality4380875798956327247.gal : 63 ms
[2024-05-24 10:08:18] [INFO ] Time to serialize properties into /tmp/CTLCardinality14883792903303136742.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality4380875798956327247.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality14883792903303136742.ctl'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...263
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 3334 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:08:51] [INFO ] Invariant cache hit.
[2024-05-24 10:08:52] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20176 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20123 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56492ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56579ms
[2024-05-24 10:09:48] [INFO ] Invariant cache hit.
[2024-05-24 10:09:50] [INFO ] Implicit Places using invariants in 2157 ms returned []
Implicit Place search using SMT only with invariants took 2158 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:09:50] [INFO ] Invariant cache hit.
[2024-05-24 10:09:50] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30126 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76116ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76202ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 138299 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:11:07] [INFO ] Flatten gal took : 279 ms
[2024-05-24 10:11:07] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:11:07] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:11:08] [INFO ] Flatten gal took : 275 ms
[2024-05-24 10:11:08] [INFO ] Flatten gal took : 287 ms
[2024-05-24 10:11:08] [INFO ] Time to serialize gal into /tmp/CTLCardinality6270676994182841267.gal : 48 ms
[2024-05-24 10:11:08] [INFO ] Time to serialize properties into /tmp/CTLCardinality17987076225467927158.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality6270676994182841267.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality17987076225467927158.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:11:38] [INFO ] Flatten gal took : 280 ms
[2024-05-24 10:11:38] [INFO ] Applying decomposition
[2024-05-24 10:11:39] [INFO ] Flatten gal took : 293 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph5598413453139110976.txt' '-o' '/tmp/graph5598413453139110976.bin' '-w' '/tmp/graph5598413453139110976.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph5598413453139110976.bin' '-l' '-1' '-v' '-w' '/tmp/graph5598413453139110976.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:11:39] [INFO ] Decomposing Gal with order
[2024-05-24 10:11:40] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:11:45] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:11:45] [INFO ] Flatten gal took : 335 ms
[2024-05-24 10:11:45] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 489 ms.
[2024-05-24 10:11:45] [INFO ] Time to serialize gal into /tmp/CTLCardinality3887840364384493195.gal : 56 ms
[2024-05-24 10:11:45] [INFO ] Time to serialize properties into /tmp/CTLCardinality4084833052448419953.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality3887840364384493195.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality4084833052448419953.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 895 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:12:17] [INFO ] Invariant cache hit.
[2024-05-24 10:12:17] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20134 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56330ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56417ms
[2024-05-24 10:13:13] [INFO ] Invariant cache hit.
[2024-05-24 10:13:15] [INFO ] Implicit Places using invariants in 2182 ms returned []
Implicit Place search using SMT only with invariants took 2183 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:13:15] [INFO ] Invariant cache hit.
[2024-05-24 10:13:15] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76542ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76631ms
Finished structural reductions in LTL mode , in 1 iterations and 136151 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:14:32] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:14:32] [INFO ] Flatten gal took : 287 ms
[2024-05-24 10:14:33] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:14:33] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:14:33] [INFO ] Flatten gal took : 294 ms
[2024-05-24 10:14:33] [INFO ] Time to serialize gal into /tmp/CTLCardinality13691056878797328482.gal : 46 ms
[2024-05-24 10:14:33] [INFO ] Time to serialize properties into /tmp/CTLCardinality6374644674384473255.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality13691056878797328482.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality6374644674384473255.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:15:04] [INFO ] Flatten gal took : 288 ms
[2024-05-24 10:15:04] [INFO ] Applying decomposition
[2024-05-24 10:15:04] [INFO ] Flatten gal took : 297 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph7441330354605667740.txt' '-o' '/tmp/graph7441330354605667740.bin' '-w' '/tmp/graph7441330354605667740.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph7441330354605667740.bin' '-l' '-1' '-v' '-w' '/tmp/graph7441330354605667740.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:15:05] [INFO ] Decomposing Gal with order
[2024-05-24 10:15:06] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:15:10] [INFO ] Removed a total of 1 redundant transitions.
[2024-05-24 10:15:10] [INFO ] Flatten gal took : 336 ms
[2024-05-24 10:15:11] [INFO ] Fuse similar labels procedure discarded/fused a total of 2 labels/synchronizations in 489 ms.
[2024-05-24 10:15:11] [INFO ] Time to serialize gal into /tmp/CTLCardinality2527020805033442987.gal : 54 ms
[2024-05-24 10:15:11] [INFO ] Time to serialize properties into /tmp/CTLCardinality2319811143114758474.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality2527020805033442987.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality2319811143114758474.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 932 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:15:42] [INFO ] Invariant cache hit.
[2024-05-24 10:15:42] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20122 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)
(s3653 4)
(s3654 5)
(s3655 5)
(s3656 2)
(s3658 4)
(s3659 5)
(s3660 5)
(s3661 2)
(s3663 4)
(s3664 5)
(s3665 5)
(s3666 2)
(s3668 4)
(s3669 5)
(s3670 5)
(s3671 2)
(s3673 4)
(s3674 5)
(s3675 5)
(s3676 2)
(s3678 4)
(s3679 5)
(s3680 5)
(s3681 2)
(s3683 4)
(s3684 5)
(s3685 5)
(s3686 2)
(s3688 4)
(s3689 5)
(s3690 5)
(s3691 2)
(s3693 4)
(s3694 5)
(s3695 5)
(s3696 2)
(s3698 4)
(s3699 5)
(s3700 5)
(s3701 2)
(s3703 4)
(s3704 5)
(s3705 5)
(s3706 2)
(s3708 4)
(s3709 5)
(s3710 5)
(s3711 2)
(s3713 4)
(s3714 5)
(s3715 5)
(s3716 2)
(s3718 4)
(s3719 5)
(s3720 5)
(s3721 2)
(s3723 4)
(s3724 5)
(s3725 5)
(s3726 2)
(s3728 4)
(s3729 5)
(s3730 5)
(s3731 2)
(s3733 4)
(s3734 5)
(s3735 5)
(s3736 2)
(s3738 4)
(s3739 5)
(s3740 5)
(s3741 2)
(s3743 4)
(s3744 5)
(s3745 5)
(s3746 2)
(s3748 4)
(s3749 5)
(s3750 5)
(s3751 2)
(s3753 4)
(s3754 5)
(s3755 5)
(s3756 2)
(s3758 4)
(s3759 5)
(s3760 5)
(s3761 2)
(s3763 4)
(s3764 5)
(s3765 5)
(s3766 2)
(s3768 4)
(s3769 5)
(s3770 5)
(s3771 2)
(s3773 4)
(s3774 5)
(s3775 5)
(s3776 2)
(s3778 4)
(s3779 5)
(s3780 5)
(s3781 2)
(s3783 4)
(s3784 5)
(s3785 5)
(s3786 2)
(s3788 4)
(s3789 5)
(s3790 5)
(s3791 2)
(s3793 4)
(s3794 5)
(s3795 5)
(s3796 2)
(s3798 4)
(s3799 5)
(s3800 5)
(s3801 2)
(s3803 4)
(s3804 5)
(s3805 5)
(s3806 2)
(s3808 4)
(s3809 5)
(s3810 5)
(s3811 2)
(s3813 4)
(s3814 5)
(s3815 5)
(s3816 2)
(s3818 4)
(s3819 5)
(s3820 5)
(s3821 2)
(s3823 4)
(s3824 5)
(s3825 5)
(s3826 2)
(s3828 4)
(s3829 5)
(s3830 5)
(s3831 2)
(s3833 4)
(s3834 5)
(s3835 5)
(s3836 2)
(s3838 4)
(s3839 5)
(s3840 5)
(s3841 2)
(s3843 4)
(s3844 5)
(s3845 5)
(s3846 2)
(s3848 4)
(s3849 5)
(s3850 5)
(s3851 2)
(s3853 4)
(s3854 5)
(s3855 5)
(s3856 2)
(s3858 4)
(s3859 5)
(s3860 5)
(s3861 2)
(s3863 4)
(s3864 5)
(s3865 5)
(s3866 2)
(s3868 4)
(s3869 5)
(s3870 5)
(s3871 2)
(s3873 4)
(s3874 5)
(s3875 5)
(s3876 2)
(s3878 4)
(s3879 5)
(s3880 5)
(s3881 2)
(s3883 4)
(s3884 5)
(s3885 5)
(s3886 2)
(s3888 4)
(s3889 5)
(s3890 5)
(s3891 2)
(s3893 4)
(s3894 5)
(s3895 5)
(s3896 2)
(s3898 4)
(s3899 5)
(s3900 5)
(s3901 2)
(s3903 4)
(s3904 5)
(s3905 5)
(s3906 2)
(s3908 4)
(s3909 5)
(s3910 5)
(s3911 2)
(s3913 4)
(s3914 5)
(s3915 5)
(s3916 2)
(s3918 4)
(s3919 5)
(s3920 5)
(s3921 2)
(s3923 4)
(s3924 5)
(s3925 5)
(s3926 2)
(s3928 4)
(s3929 5)
(s3930 5)
(s3931 2)
(s3933 4)
(s3934 5)
(s3935 5)
(s3936 2)
(s3938 4)
(s3939 5)
(s3940 5)
(s3941 2)
(s3943 4)
(s3944 5)
(s3945 5)
(s3946 2)
(s3948 4)
(s3949 5)
(s3950 5)
(s3951 2)
(s3953 4)
(s3954 5)
(s3955 5)
(s3956 2)
(s3958 4)
(s3959 5)
(s3960 5)
(s3961 2)
(s3963 4)
(s3964 5)
(s3965 5)
(s3966 2)
(s3968 4)
(s3969 5)
(s3970 5)
(s3971 2)
(s3973 4)
(s3974 5)
(s3975 5)
(s3976 2)
(s3978 4)
(s3979 5)
(s3980 5)
(s3981 2)
(s3983 4)
(s3984 5)
(s3985 5)
(s3986 2)
(s3988 4)
(s3989 5)
(s3990 5)
(s3991 2)
(s3993 4)
(s3994 5)
(s3995 5)
(s3996 2)
(s3998 4)
(s3999 5)
(s4000 5)
(s4001 2)
(s4003 4)
(s4004 5)
(s4005 5)
(s4006 2)
(s4008 4)
(s4009 5)
(s4010 5)
(s4011 2)
(s4013 4)
(s4014 5)
(s4015 5)
(s4016 2)
(s4018 4)
(s4019 5)
(s4020 5)
(s4021 2)
(s4023 4)
(s4024 5)
(s4025 5)
(s4026 2)
(s4028 4)
(s4029 5)
(s4030 5)
(s4031 2)
(s4033 4)
(s4034 5)
(s4035 5)
(s4036 2)
(s4038 4)
(s4039 5)
(s4040 5)
(s4041 2)
(s4043 4)
(s4044 5)
(s4045 5)
(s4046 2)
(s4048 4)
(s4049 5)
(s4050 5)
(s4051 2)
(s4053 4)
(s4054 5)
(s4055 5)
(s4056 2)
(s4058 4)
(s4059 5)
(s4060 5)
(s4061 2)
(s4063 4)
(s4064 5)
(s4065 5)
(s4066 2)
(s4068 4)
(s4069 5)
(s4070 5)
(s4071 2)
(s4073 4)
(s4074 5)
(s4075 5)
(s4076 2)
(s4078 4)
(s4079 5)
(s4080 5)
(s4081 2)
(s4083 4)
(s4084 5)
(s4085 5)
(s4086 2)
(s4088 4)
(s4089 5)
(s4090 5)
(s4091 2)
(s4093 4)
(s4094 5)
(s4095 5)
(s4096 2)
(s4098 4)
(s4099 5)
(s4100 5)
(s4101 2)
(s4103 4)
(s4104 5)
(s4105 5)
(s4106 2)
(s4108 4)
(s4109 5)
(s4110 5)
(s4111 2)
(s4113 4)
(s4114 5)
(s4115 5)
(s4116 2)
(s4118 4)
(s4119 5)
(s4120 5)
(s4121 2)
(s4123 4)
(s4124 5)
(s4125 5)
(s4126 2)
(s4128 4)
(s4129 5)
(s4130 5)
(s4131 2)
(s4133 4)
(s4134 5)
(s4135 5)
(s4136 2)
(s4138 4)
(s4139 5)
(s4140 5)
(s4141 2)
(s4143 4)
(s4144 5)
(s4145 5)
(s4146 2)
(s4148 4)
(s4149 5)
(s4150 5)
(s4151 2)
(s4153 4)
(s4154 5)
(s4155 5)
(s4156 2)
(s4158 4)
(s4159 5)
(s4160 5)
(s4161 2)
(s4163 4)
(s4164 5)
(s4165 5)
(s4166 2)
(s4168 4)
(s4169 5)
(s4170 5)
(s4171 2)
(s4173 4)
(s4174 5)
(s4175 5)
(s4176 2)
(s4178 4)
(s4179 5)
(s4180 5)
(s4181 2)
(s4183 4)
(s4184 5)
(s4185 5)
(s4186 2)
(s4188 4)
(s4189 5)
(s4190 5)
(s4191 2)
(s4193 4)
(s4194 5)
(s4195 5)
(s4196 2)
(s4198 4)
(s4199 5)
(s4200 5)
(s4201 2)
(s4203 4)
(s4204 5)
(s4205 5)
(s4206 2)
(s4208 4)
(s4209 5)
(s4210 5)
(s4211 2)
(s4213 4)
(s4214 5)
(s4215 5)
(s4216 2)
(s4218 4)
(s4219 5)
(s4220 5)
(s4221 2)
(s4223 4)
(s4224 5)
(s4225 5)
(s4226 2)
(s4228 4)
(s4229 5)
(s4230 5)
(s4231 2)
(s4233 4)
(s4234 5)
(s4235 5)
(s4236 2)
(s4238 4)
(s4239 5)
(s4240 5)
(s4241 2)
(s4243 4)
(s4244 5)
(s4245 5)
(s4246 2)
(s4248 4)
(s4249 5)
(s4250 5)
(s4251 2)
(s4253 4)
(s4254 5)
(s4255 5)
(s4256 2)
(s4258 4)
(s4259 5)
(s4260 5)
(s4261 2)
(s4263 4)
(s4264 5)
(s4265 5)
(s4266 2)
(s4268 4)
(s4269 5)
(s4270 5)
(s4271 2)
(s4273 4)
(s4274 5)
(s4275 5)
(s4276 2)
(s4278 4)
(s4279 5)
(s4280 5)
(s4281 2)
(s4283 4)
(s4284 5)
(s4285 5)
(s4286 2)
(s4288 4)
(s4289 5)
(s4290 5)
(s4291 2)
(s4293 4)
(s4294 5)
(s4295 5)
(s4296 2)
(s4298 4)
(s4299 5)
(s4300 5)
(s4301 2)
(s4303 4)
(s4304 5)
(s4305 5)
(s4306 2)
(s4308 4)
(s4309 5)
(s4310 5)
(s4311 2)
(s4313 4)
(s4314 5)
(s4315 5)
(s4316 2)
(s4318 4)
(s4319 5)
(s4320 5)
(s4321 2)
(s4323 4)
(s4324 5)
(s4325 5)
(s4326 2)
(s4328 4)
(s4329 5)
(s4330 5)
(s4331 2)
(s4333 4)
(s4334 5)
(s4335 5)
(s4336 2)
(s4338 4)
(s4339 5)
(s4340 5)
(s4341 2)
(s4343 4)
(s4344 5)
(s4345 5)
(s4346 2)
(s4348 4)
(s4349 5)
(s4350 5)
(s4351 2)
(s4353 4)
(s4354 5)
(s4355 5)
(s4356 2)
(s4358 4)
(s4359 5)
(s4360 5)
(s4361 2)
(s4363 4)
(s4364 5)
(s4365 5)
(s4366 2)
(s4368 4)
(s4369 5)
(s4370 5)
(s4371 2)
(s4373 4)
(s4374 5)
(s4375 5)
(s4376 2)
(s4378 4)
(s4379 5)
(s4380 5)
(s4381 2)
(s4383 4)
(s4384 5)
(s4385 5)
(s4386 2)
(s4388 4)
(s4389 5)
(s4390 5)
(s4391 2)
(s4393 4)
(s4394 5)
(s4395 5)
(s4396 2)
(s4398 4)
(s4399 5)
(s4400 5)
(s4401 2)
(s4403 4)
(s4404 5)
(s4405 5)
(s4406 2)
(s4408 4)
(s4409 5)
(s4410 5)
(s4411 2)
(s4413 4)
(s4414 5)
(s4415 5)
(s4416 2)
(s4418 4)
(s4419 5)
(s4420 5)
(s4421 2)
(s4423 4)
(s4424 5)
(s4425 5)
(s4426 2)
(s4428 4)
(s4429 5)
(s4430 5)
(s4431 2)
(s4433 4)
(s4434 5)
(s4435 5)
(s4436 2)
(s4438 4)
(s4439 5)
(s4440 5)
(s4441 2)
(s4443 4)
(s4444 5)
(s4445 5)
(s4446 2)
(s4448 4)
(s4449 5)
(s4450 5)
(s4451 2)
(s4453 4)
(s4454 5)
(s4455 5)
(s4456 2)
(s4458 4)
(s4459 5)
(s4460 5)
(s4461 2)
(s4463 4)
(s4464 5)
(s4465 5)
(s4466 2)
(s4468 4)
(s4469 5)
(s4470 5)
(s4471 2)
(s4473 4)
(s4474 5)
(s4475 5)
(s4476 2)
(s4478 4)
(s4479 5)
(s4480 5)
(s4481 2)
(s4483 4)
(s4484 5)
(s4485 5)
(s4486 2)
(s4488 4)
(s4489 5)
(s4490 5)
(s4491 2)
(s4493 4)
(s4494 5)
(s4495 5)
(s4496 2)
(s4498 4)
(s4499 5)
(s4500 5)
(s4501 2)
(s4503 4)
(s4504 5)
(s4505 5)
(s4506 2)
(s4508 4)
(s4509 5)
(s4510 5)
(s4511 2)
(s4513 4)
(s4514 5)
(s4515 5)
(s4516 2)
(s4518 4)
(s4519 5)
(s4520 5)
(s4521 2)
(s4523 4)
(s4524 5)
(s4525 5)
(s4526 2)
(s4528 4)
(s4529 5)
(s4530 5)
(s4531 2)
(s4533 4)
(s4534 5)
(s4535 5)
(s4536 2)
(s4538 4)
(s4539 5)
(s4540 5)
(s4541 2)
(s4543 4)
(s4544 5)
(s4545 5)
(s4546 2)
(s4548 4)
(s4549 5)
(s4550 5)
(s4551 2)
(s4553 4)
(s4554 5)
(s4555 5)
(s4556 2)
(s4558 4)
(s4559 5)
(s4560 5)
(s4561 2)
(s4563 4)
(s4564 5)
(s4565 5)
(s4566 2)
(s4568 4)
(s4569 5)
(s4570 5)
(s4571 2)
(s4573 4)
(s4574 5)
(s4575 5)
(s4576 2)
(s4578 4)
(s4579 5)
(s4580 5)
(s4581 2)
(s4583 4)
(s4584 5)
(s4585 5)
(s4586 2)
(s4588 4)
(s4589 5)
(s4590 5)
(s4591 2)
(s4593 4)
(s4594 5)
(s4595 5)
(s4596 2)
(s4598 4)
(s4599 5)
(s4600 5)
(s4601 2)
(s4603 4)
(s4604 5)
(s4605 5)
(s4606 2)
(s4608 4)
(s4609 5)
(s4610 5)
(s4611 2)
(s4613 4)
(s4614 5)
(s4615 5)
(s4616 2)
(s4618 4)
(s4619 5)
(s4620 5)
(s4621 2)
(s4623 4)
(s4624 5)
(s4625 5)
(s4626 2)
(s4628 4)
(s4629 5)
(s4630 5)
(s4631 2)
(s4633 4)
(s4634 5)
(s4635 5)
(s4636 2)
(s4638 4)
(s4639 5)
(s4640 5)
(s4641 2)
(s4643 4)
(s4644 5)
(s4645 5)
(s4646 2)
(s4648 4)
(s4649 5)
(s4650 5)
(s4651 2)
(s4653 4)
(s4654 5)
(s4655 5)
(s4656 2)
(s4658 4)
(s4659 5)
(s4660 5)
(s4661 2)
(s4663 4)
(s4664 5)
(s4665 5)
(s4666 2)
(s4668 4)
(s4669 5)
(s4670 5)
(s4671 2)
(s4673 4)
(s4674 5)
(s4675 5)
(s4676 2)
(s4678 4)
(s4679 5)
(s4680 5)
(s4681 2)
(s4683 4)
(s4684 5)
(s4685 5)
(s4686 2)
(s4688 4)
(s4689 5)
(s4690 5)
(s4691 2)
(s4693 4)
(s4694 5)
(s4695 5)
(s4696 2)
(s4698 4)
(s4699 5)
(s4700 5)
(s4701 2)
(s4703 4)
(s4704 5)
(s4705 5)
(s4706 2)
(s4708 4)
(s4709 5)
(s4710 5)
(s4711 2)
(s4713 4)
(s4714 5)
(s4715 5)
(s4716 2)
(s4718 4)
(s4719 5)
(s4720 5)
(s4721 2)
(s4723 4)
(s4724 5)
(s4725 5)
(s4726 2)
(s4728 4)
(s4729 5)
(s4730 5)
(s4731 2)
(s4733 4)
(s4734 5)
(s4735 5)
(s4736 2)
(s4738 4)
(s4739 5)
(s4740 5)
(s4741 2)
(s4743 4)
(s4744 5)
(s4745 5)
(s4746 2)
(s4748 4)
(s4749 5)
(s4750 5)
(s4751 2)
(s4753 4)
(s4754 5)
(s4755 5)
(s4756 2)
(s4758 4)
(s4759 5)
(s4760 5)
(s4761 2)
(s4763 4)
(s4764 5)
(s4765 5)
(s4766 2)
(s4768 4)
(s4769 5)
(s4770 5)
(s4771 2)
(s4773 4)
(s4774 5)
(s4775 5)
(s4776 2)
(s4778 4)
(s4779 5)
(s4780 5)
(s4781 2)
(s4783 4)
(s4784 5)
(s4785 5)
(s4786 2)
(s4788 4)
(s4789 5)
(s4790 5)
(s4791 2)
(s4793 4)
(s4794 5)
(s4795 5)
(s4796 2)
(s4798 4)
(s4799 5)
(s4800 5)
(s4801 2)
(s4803 4)
(s4804 5)
(s4805 5)
(s4806 2)
(s4808 4)
(s4809 5)
(s4810 5)
(s4811 2)
(s4813 4)
(s4814 5)
(s4815 5)
(s4816 2)
(s4818 4)
(s4819 5)
(s4820 5)
(s4821 2)
(s4823 4)
(s4824 5)
(s4825 5)
(s4826 2)
(s4828 4)
(s4829 5)
(s4830 5)
(s4831 2)
(s4833 4)
(s4834 5)
(s4835 5)
(s4836 2)
(s4838 4)
(s4839 5)
(s4840 5)
(s4841 2)
(s4843 4)
(s4844 5)
(s4845 5)
(s4846 2)
(s4848 4)
(s4849 5)
(s4850 5)
(s4851 2)
(s4853 4)
(s4854 5)
(s4855 5)
(s4856 2)
(s4858 4)
(s4859 5)
(s4860 5)
(s4861 2)
(s4863 4)
(s4864 5)
(s4865 5)
(s4866 2)
(s4868 4)
(s4869 5)
(s4870 5)
(s4871 2)
(s4873 4)
(s4874 5)
(s4875 5)
(s4876 2)
(s4878 4)
(s4879 5)
(s4880 5)
(s4881 2)
(s4883 4)
(s4884 5)
(s4885 5)
(s4886 2)
(s4888 4)
(s4889 5)
(s4890 5)
(s4891 2)
(s4893 4)
(s4894 5)
(s4895 5)
(s4896 2)
(s4898 4)
(s4899 5)
(s4900 5)
(s4901 2)
(s4903 4)
(s4904 5)
(s4905 5)
(s4906 2)
(s4908 4)
(s4909 5)
(s4910 5)
(s4911 2)
(s4913 4)
(s4914 5)
(s4915 5)
(s4916 2)
(s4918 4)
(s4919 5)
(s4920 5)
(s4921 2)
(s4923 4)
(s4924 5)
(s4925 5)
(s4926 2)
(s4928 4)
(s4929 5)
(s4930 5)
(s4931 2)
(s4933 4)
(s4934 5)
(s4935 5)
(s4936 2)
(s4938 4)
(s4939 5)
(s4940 5)
(s4941 2)
(s4943 4)
(s4944 5)
(s4945 5)
(s4946 2)
(s4948 4)
(s4949 5)
(s4950 5)
(s4951 2)
(s4953 4)
(s4954 5)
(s4955 5)
(s4956 2)
(s4958 4)
(s4959 5)
(s4960 5)
(s4961 2)
(s4963 4)
(s4964 5)
(s4965 5)
(s4966 2)
(s4968 4)
(s4969 5)
(s4970 5)
(s4971 2)
(s4973 4)
(s4974 5)
(s4975 5)
(s4976 2)
(s4978 4)
(s4979 5)
(s4980 5)
(s4981 2)
(s4983 4)
(s4984 5)
(s4985 5)
(s4986 2)
(s4988 4)
(s4989 5)
(s4990 5)
(s4991 2)
(s4993 4)
(s4994 5)
(s4995 5)
(s4996 2)
(s4998 4)
(s4999 5)
(s5000 5)
(s5001 2)
(s5003 4)
(s5004 5)
(s5005 5)
(s5006 2)
(s5008 4)
(s5009 5)
(s5010 5)
(s5011 2)
(s5013 4)
(s5014 5)
(s5015 5)
(s5016 2)
(s5018 4)
(s5019 5)
(s5020 5)
(s5021 2)
(s5023 4)
(s5024 5)
(s5025 5)
(s5026 2)
(s5028 4)
(s5029 5)
(s5030 5)
(s5031 2)
(s5033 4)
(s5034 5)
(s5035 5)
(s5036 2)
(s5038 4)
(s5039 5)
(s5040 5)
(s5041 2)
(s5043 4)
(s5044 5)
(s5045 5)
(s5046 2)
(s5048 4)
(s5049 5)
(s5050 5)
(s5051 2)
(s5053 4)
(s5054 5)
(s5055 5)
(s5056 2)
(s5058 4)
(s5059 5)
(s5060 5)
(s5061 2)
(s5063 4)
(s5064 5)
(s5065 5)
(s5066 2)
(s5068 4)
(s5069 5)
(s5070 5)
(s5071 2)
(s5073 4)
(s5074 5)
(s5075 5)
(s5076 2)
(s5078 4)
(s5079 5)
(s5080 5)
(s5081 2)
(s5083 4)
(s5084 5)
(s5085 5)
(s5086 2)
(s5088 4)
(s5089 5)
(s5090 5)
(s5091 2)
(s5093 4)
(s5094 5)
(s5095 5)
(s5096 2)
(s5098 4)
(s5099 5)
(s5100 5)
(s5101 2)
(s5103 4)
(s5104 5)
(s5105 5)
(s5106 2)
(s5108 4)
(s5109 5)
(s5110 5)
(s5111 2)
(s5113 4)
(s5114 5)
(s5115 5)
(s5116 2)
(s5118 4)
(s5119 5)
(s5120 5)
(s5121 2)
(s5123 4)
(s5124 5)
(s5125 5)
(s5126 2)
(s5128 4)
(s5129 5)
(s5130 5)
(s5131 2)
(s5133 4)
(s5134 5)
(s5135 5)
(s5136 2)
(s5138 4)
(s5139 5)
(s5140 5)
(s5141 2)
(s5143 4)
(s5144 5)
(s5145 5)
(s5146 2)
(s5148 4)
(s5149 5)
(s5150 5)
(s5151 2)
(s5153 4)
(s5154 5)
(s5155 5)
(s5156 2)
(s5158 4)
(s5159 5)
(s5160 5)
(s5161 2)
(s5163 4)
(s5164 5)
(s5165 5)
(s5166 2)
(s5168 4)
(s5169 5)
(s5170 5)
(s5171 2)
(s5173 4)
(s5174 5)
(s5175 5)
(s5176 2)
(s5178 4)
(s5179 5)
(s5180 5)
(s5181 2)
(s5183 4)
(s5184 5)
(s5185 5)
(s5186 2)
(s5188 4)
(s5189 5)
(s5190 5)
(s5191 2)
(s5193 4)
(s5194 5)
(s5195 5)
(s5196 2)
(s5198 4)
(s5199 5)
(s5200 5)
(s5201 2)
(s5203 4)
(s5204 5)
(s5205 5)
(s5206 2)
(s5208 4)
(s5209 5)
(s5210 5)
(s5211 2)
(s5213 4)
(s5214 5)
(s5215 5)
(s5216 2)
(s5218 4)
(s5219 5)
(s5220 5)
(s5221 2)
(s5223 4)
(s5224 5)
(s5225 5)
(s5226 2)
(s5228 4)
(s5229 5)
(s5230 5)
(s5231 2)
(s5233 4)
(s5234 5)
(s5235 5)
(s5236 2)
(s5238 4)
(s5239 5)
(s5240 5)
(s5241 2)
(s5243 4)
(s5244 5)
(s5245 5)
(s5246 2)
(s5248 4)
(s5249 5)
(s5250 5)
(s5251 2)
(s5253 4)
(s5254 5)
(s5255 5)
(s5256 2)
(s5258 4)
(s5259 5)
(s5260 5)
(s5261 2)
(s5263 4)
(s5264 5)
(s5265 5)
(s5266 2)
(s5268 4)
(s5269 5)
(s5270 5)
(s5271 2)
(s5273 4)
(s5274 5)
(s5275 5)
(s5276 2)
(s5278 4)
(s5279 5)
(s5280 5)
(s5281 2)
(s5283 4)
(s5284 5)
(s5285 5)
(s5286 2)
(s5288 4)
(s5289 5)
(s5290 5)
(s5291 2)
(s5293 4)
(s5294 5)
(s5295 5)
(s5296 2)
(s5298 4)
(s5299 5)
(s5300 5)
(s5301 2)
(s5303 4)
(s5304 5)
(s5305 5)
(s5306 2)
(s5308 4)
(s5309 5)
(s5310 5)
(s5311 2)
(s5313 4)
(s5314 5)
(s5315 5)
(s5316 2)
(s5318 4)
(s5319 5)
(s5320 5)
(s5321 2)
(s5323 4)
(s5324 5)
(s5325 5)
(s5326 2)
(s5328 4)
(s5329 5)
(s5330 5)
(s5331 2)
(s5333 4)
(s5334 5)
(s5335 5)
(s5336 2)
(s5338 4)
(s5339 5)
(s5340 5)
(s5341 2)
(s5343 4)
(s5344 5)
(s5345 5)
(s5346 2)
(s5348 4)
(s5349 5)
(s5350 5)
(s5351 2)
(s5353 4)
(s5354 5)
(s5355 5)
(s5356 2)
(s5358 4)
(s5359 5)
(s5360 5)
(s5361 2)
(s5363 4)
(s5364 5)
(s5365 5)
(s5366 2)
(s5368 4)
(s5369 5)
(s5370 5)
(s5371 2)
(s5373 4)
(s5374 5)
(s5375 5)
(s5376 2)
(s5378 4)
(s5379 5)
(s5380 5)
(s5381 2)
(s5383 4)
(s5384 5)
(s5385 5)
(s5386 2)
(s5388 4)
(s5389 5)
(s5390 5)
(s5391 2)
(s5393 4)
(s5394 5)
(s5395 5)
(s5396 2)
(s5398 4)
(s5399 5)
(s5400 5)
(s5401 2)
(s5403 4)
(s5404 5)
(s5405 5)
(s5406 2)
(s5408 4)
(s5409 5)
(s5410 5)
(s5411 2)
(s5413 4)
(s5414 5)
(s5415 5)
(s5416 2)
(s5418 4)
(s5419 5)
(s5420 5)
(s5421 2)
(s5423 4)
(s5424 5)
(s5425 5)
(s5426 2)
(s5428 4)
(s5429 5)
(s5430 5)
(s5431 2)
(s5433 4)
(s5434 5)
(s5435 5)
(s5436 2)
(s5438 4)
(s5439 5)
(s5440 5)
(s5441 2)
(s5443 4)
(s5444 5)
(s5445 5)
(s5446 2)
(s5448 4)
(s5449 5)
(s5450 5)
(s5451 2)
(s5453 4)
(s5454 5)
(s5455 5)
(s5456 2)
(s5458 4)
(s5459 5)
(s5460 5)
(s5461 2)
(s5463 4)
(s5464 5)
(s5465 5)
(s5466 2)
(s5468 4)
(s5469 5)
(s5470 5)
(s5471 2)
(s5473 4)
(s5474 5)
(s5475 5)
(s5476 2)
(s5478 4)
(s5479 5)
(s5480 5)
(s5481 2)
(s5483 4)
(s5484 5)
(s5485 5)
(s5486 2)
(s5488 4)
(s5489 5)
(s5490 5)
(s5491 2)
(s5493 4)
(s5494 5)
(s5495 5)
(s5496 2)
(s5498 4)
(s5499 5)
(s5500 5)
(s5501 2)
(s5503 4)
(s5504 5)
(s5505 5)
(s5506 2)
(s5508 4)
(s5509 5)
(s5510 5)
(s5511 2)
(s5513 4)
(s5514 5)
(s5515 5)
(s5516 2)
(s5518 4)
(s5519 5)
(s5520 5)
(s5521 2)
(s5523 4)
(s5524 5)
(s5525 5)
(s5526 2)
(s5528 4)
(s5529 5)
(s5530 5)
(s5531 2)
(s5533 4)
(s5534 5)
(s5535 5)
(s5536 2)
(s5538 4)
(s5539 5)
(s5540 5)
(s5541 2)
(s5543 4)
(s5544 5)
(s5545 5)
(s5546timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20125 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56598ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56683ms
[2024-05-24 10:16:39] [INFO ] Invariant cache hit.
[2024-05-24 10:16:41] [INFO ] Implicit Places using invariants in 2105 ms returned []
Implicit Place search using SMT only with invariants took 2110 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:16:41] [INFO ] Invariant cache hit.
[2024-05-24 10:16:41] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76212ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76299ms
Finished structural reductions in LTL mode , in 1 iterations and 136049 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:17:57] [INFO ] Flatten gal took : 285 ms
[2024-05-24 10:17:58] [INFO ] Flatten gal took : 288 ms
[2024-05-24 10:17:58] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:17:59] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:17:59] [INFO ] Flatten gal took : 289 ms
[2024-05-24 10:17:59] [INFO ] Time to serialize gal into /tmp/CTLCardinality3084957354603099764.gal : 49 ms
[2024-05-24 10:17:59] [INFO ] Time to serialize properties into /tmp/CTLCardinality10551901786317495538.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality3084957354603099764.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality10551901786317495538.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:18:29] [INFO ] Flatten gal took : 285 ms
[2024-05-24 10:18:29] [INFO ] Applying decomposition
[2024-05-24 10:18:30] [INFO ] Flatten gal took : 299 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph4338502712141166071.txt' '-o' '/tmp/graph4338502712141166071.bin' '-w' '/tmp/graph4338502712141166071.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph4338502712141166071.bin' '-l' '-1' '-v' '-w' '/tmp/graph4338502712141166071.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:18:30] [INFO ] Decomposing Gal with order
[2024-05-24 10:18:31] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:18:36] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:18:36] [INFO ] Flatten gal took : 339 ms
[2024-05-24 10:18:36] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 491 ms.
[2024-05-24 10:18:36] [INFO ] Time to serialize gal into /tmp/CTLCardinality8189902441375222409.gal : 55 ms
[2024-05-24 10:18:36] [INFO ] Time to serialize properties into /tmp/CTLCardinality384416504559826317.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality8189902441375222409.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality384416504559826317.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...282
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 2570 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:19:09] [INFO ] Invariant cache hit.
[2024-05-24 10:19:09] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20123 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56266ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56353ms
[2024-05-24 10:20:05] [INFO ] Invariant cache hit.
[2024-05-24 10:20:08] [INFO ] Implicit Places using invariants in 2087 ms returned []
Implicit Place search using SMT only with invariants took 2088 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:20:08] [INFO ] Invariant cache hit.
[2024-05-24 10:20:08] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30113 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)
(s3653 4)
(s3654 5)
(s3655 5)
(s3656 2)
(s3658 4)
(s3659 5)
(s3660 5)
(s3661 2)
(s3663 4)
(s3664 5)
(s3665 5)
(s3666 2)
(s3668 4)
(s3669 5)
(s3670 5)
(s3671 2)
(s3673 4)
(s3674 5)
(s3675 5)
(s3676 2)
(s3678 4)
(s3679 5)
(s3680 5)
(s3681 2)
(s3683 4)
(s3684 5)
(s3685 5)
(s3686 2)
(s3688 4)
(s3689 5)
(s3690 5)
(s3691 2)
(s3693 4)
(s3694 5)
(s3695 5)
(s3696 2)
(s3698 4)
(s3699 5)
(s3700 5)
(s3701 2)
(s3703 4)
(s3704 5)
(s3705 5)
(s3706 2)
(s3708 4)
(s3709 5)
(s3710 5)
(s3711 2)
(s3713 4)
(s3714 5)
(s3715 5)
(s3716 2)
(s3718 4)
(s3719 5)
(s3720 5)
(s3721 2)
(s3723 4)
(s3724 5)
(s3725 5)
(s3726 2)
(s3728 4)
(s3729 5)
(s3730 5)
(s3731 2)
(s3733 4)
(s3734 5)
(s3735 5)
(s3736 2)
(s3738 4)
(s3739 5)
(s3740 5)
(s3741 2)
(s3743 4)
(s3744 5)
(s3745 5)
(s3746 2)
(s3748 4)
(s3749 5)
(s3750 5)
(s3751 2)
(s3753 4)
(s3754 5)
(s3755 5)
(s3756 2)
(s3758 4)
(s3759 5)
(s3760 5)
(s3761 2)
(s3763 4)
(s3764 5)
(s3765 5)
(s3766 2)
(s3768 4)
(s3769 5)
(s3770 5)
(s3771 2)
(s3773 4)
(s3774 5)
(s3775 5)
(s3776 2)
(s3778 4)
(s3779 5)
(s3780 5)
(s3781 2)
(s3783 4)
(s3784 5)
(s3785 5)
(s3786 2)
(s3788 4)
(s3789 5)
(s3790 5)
(s3791 2)
(s3793 4)
(s3794 5)
(s3795 5)
(s3796 2)
(s3798 4)
(s3799 5)
(s3800 5)
(s3801 2)
(s3803 4)
(s3804 5)
(s3805 5)
(s3806 2)
(s3808 4)
(s3809 5)
(s3810 5)
(s3811 2)
(s3813 4)
(s3814 5)
(s3815 5)
(s3816 2)
(s3818 4)
(s3819 5)
(s3820 5)
(s3821 2)
(s3823 4)
(s3824 5)
(s3825 5)
(s3826 2)
(s3828 4)
(s3829 5)
(s3830 5)
(s3831 2)
(s3833 4)
(s3834 5)
(s3835 5)
(s3836 2)
(s3838 4)
(s3839 5)
(s3840 5)
(s3841 2)
(s3843 4)
(s3844 5)
(s3845 5)
(s3846 2)
(s3848 4)
(s3849 5)
(s3850 5)
(s3851 2)
(s3853 4)
(s3854 5)
(s3855 5)
(s3856 2)
(s3858 4)
(s3859 5)
(s3860 5)
(s3861 2)
(s3863 4)
(s3864 5)
(s3865 5)
(s3866 2)
(s3868 4)
(s3869 5)
(s3870 5)
(s3871 2)
(s3873 4)
(s3874 5)
(s3875 5)
(s3876 2)
(s3878 4)
(s3879 5)
(s3880 5)
(s3881 2)
(s3883 4)
(s3884 5)
(s3885 5)
(s3886 2)
(s3888 4)
(s3889 5)
(s3890 5)
(s3891 2)
(s3893 4)
(s3894 5)
(s3895 5)
(s3896 2)
(s3898 4)
(s3899 5)
(s3900 5)
(s3901 2)
(s3903 4)
(s3904 5)
(s3905 5)
(s3906 2)
(s3908 4)
(s3909 5)
(s3910 5)
(s3911 2)
(s3913 4)
(s3914 5)
(s3915 5)
(s3916 2)
(s3918 4)
(s3919 5)
(s3920 5)
(s3921 2)
(s3923 4)
(s3924 5)
(s3925 5)
(s3926 2)
(s3928 4)
(s3929 5)
(s3930 5)
(s3931 2)
(s3933 4)
(s3934 5)
(s3935 5)
(s3936 2)
(s3938 4)
(s3939 5)
(s3940 5)
(s3941 2)
(s3943 4)
(s3944 5)
(s3945 5)
(s3946 2)
(s3948 4)
(s3949 5)
(s3950 5)
(s3951 2)
(s3953 4)
(s3954 5)
(s3955 5)
(s3956 2)
(s3958 4)
(s3959 5)
(s3960 5)
(s3961 2)
(s3963 4)
(s3964 5)
(s3965 5)
(s3966 2)
(s3968 4)
(s3969 5)
(s3970 5)
(s3971 2)
(s3973 4)
(s3974 5)
(s3975 5)
(s3976 2)
(s3978 4)
(s3979 5)
(s3980 5)
(s3981 2)
(s3983 4)
(s3984 5)
(s3985 5)
(s3986 2)
(s3988 4)
(s3989 5)
(s3990 5)
(s3991 2)
(s3993 4)
(s3994 5)
(s3995 5)
(s3996 2)
(s3998 4)
(s3999 5)
(s4000 5)
(s4001 2)
(s4003 4)
(s4004 5)
(s4005 5)
(s4006 2)
(s4008 4)
(s4009 5)
(s4010 5)
(s4011 2)
(s4013 4)
(s4014 5)
(s4015 5)
(s4016 2)
(s4018 4)
(s4019 5)
(s4020 5)
(s4021 2)
(s4023 4)
(s4024 5)
(s4025 5)
(s4026 2)
(s4028 4)
(s4029 5)
(s4030 5)
(s4031 2)
(s4033 4)
(s4034 5)
(s4035 5)
(s4036 2)
(s4038 4)
(s4039 5)
(s4040 5)
(s4041 2)
(s4043 4)
(s4044 5)
(s4045 5)
(s4046 2)
(s4048 4)
(s4049 5)
(s4050 5)
(s4051 2)
(s4053 4)
(s4054 5)
(s4055 5)
(s4056 2)
(s4058 4)
(s4059 5)
(s4060 5)
(s4061 2)
(s4063 4)
(s4064 5)
(s4065 5)
(s4066 2)
(s4068 4)
(s4069 5)
(s4070 5)
(s4071 2)
(s4073 4)
(s4074 5)
(s4075 5)
(s4076 2)
(s4078 4)
(s4079 5)
(s4080 5)
(s4081 2)
(s4083 4)
(s4084 5)
(s4085 5)
(s4086 2)
(s4088 4)
(s4089 5)
(s4090 5)
(s4091 2)
(s4093 4)
(s4094 5)
(s4095 5)
(s4096 2)
(s4098 4)
(s4099 5)
(s4100 5)
(s4101 2)
(s4103 4)
(s4104 5)
(s4105 5)
(s4106 2)
(s4108 4)
(s4109 5)
(s4110 5)
(s4111 2)
(s4113 4)
(s4114 5)
(s4115 5)
(s4116 2)
(s4118 4)
(s4119 5)
(s4120 5)
(s4121 2)
(s4123 4)
(s4124 5)
(s4125 5)
(s4126 2)
(s4128 4)
(s4129 5)
(s4130 5)
(s4131 2)
(s4133 4)
(s4134 5)
(s4135 5)
(s4136 2)
(s4138 4)
(s4139 5)
(s4140 5)
(s4141 2)
(s4143 4)
(s4144 5)
(s4145 5)
(s4146 2)
(s4148 4)
(s4149 5)
(s4150 5)
(s4151 2)
(s4153 4)
(s4154 5)
(s4155 5)
(s4156 2)
(s4158 4)
(s4159 5)
(s4160 5)
(s4161 2)
(s4163 4)
(s4164 5)
(s4165 5)
(s4166 2)
(s4168 4)
(s4169 5)
(s4170 5)
(s4171 2)
(s4173 4)
(s4174 5)
(s4175 5)
(s4176 2)
(s4178 4)
(s4179 5)
(s4180 5)
(s4181 2)
(s4183 4)
(s4184 5)
(s4185 5)
(s4186 2)
(s4188 4)
(s4189 5)
(s4190 5)
(s4191 2)
(s4193 4)
(s4194 5)
(s4195 5)
(s4196 2)
(s4198 4)
(s4199 5)
(s4200 5)
(s4201 2)
(s4203 4)
(s4204 5)
(s4205 5)
(s4206 2)
(s4208 4)
(s4209 5)
(s4210 5)
(s4211 2)
(s4213 4)
(s4214 5)
(s4215 5)
(s4216 2)
(s4218 4)
(s4219 5)
(s4220 5)
(s4221 2)
(s4223 4)
(s4224 5)
(s4225 5)
(s4226 2)
(s4228 4)
(s4229 5)
(s4230 5)
(s4231 2)
(s4233 4)
(s4234 5)
(s4235 5)
(s4236 2)
(s4238 4)
(s4239 5)
(s4240 5)
(s4241 2)
(s4243 4)
(s4244 5)
(s4245 5)
(s4246 2)
(s4248 4)
(s4249 5)
(s4250 5)
(s4251 2)
(s4253 4)
(s4254 5)
(s4255 5)
(s4256 2)
(s4258 4)
(s4259 5)
(s4260 5)
(s4261 2)
(s4263 4)
(s4264 5)
(s4265 5)
(s4266 2)
(s4268 4)
(s4269 5)
(s4270 5)
(s4271 2)
(s4273 4)
(s4274 5)
(s4275 5)
(s4276 2)
(s4278 4)
(s4279 5)
(s4280 5)
(s4281 2)
(s4283 4)
(s4284 5)
(s4285 5)
(s4286 2)
(s4288 4)
(s4289 5)
(s4290 5)
(s4291 2)
(s4293 4)
(s4294 5)
(s4295 5)
(s4296 2)
(s4298 4)
(s4299 5)
(s4300 5)
(s4301 2)
(s4303 4)
(s4304 5)
(s4305 5)
(s4306 2)
(s4308 4)
(s4309 5)
(s4310 5)
(s4311 2)
(s4313 4)
(s4314 5)
(s4315 5)
(s4316 2)
(s4318 4)
(s4319 5)
(s4320 5)
(s4321 2)
(s4323 4)
(s4324 5)
(s4325 5)
(s4326 2)
(s4328 4)
(s4329 5)
(s4330 5)
(s4331 2)
(s4333 4)
(s4334 5)
(s4335 5)
(s4336 2)
(s4338 4)
(s4339 5)
(s4340 5)
(s4341 2)
(s4343 4)
(s4344 5)
(s4345 5)
(s4346 2)
(s4348 4)
(s4349 5)
(s4350 5)
(s4351 2)
(s4353 4)
(s4354 5)
(s4355 5)
(s4356 2)
(s4358 4)
(s4359 5)
(s4360 5)
(s4361 2)
(s4363 4)
(s4364 5)
(s4365 5)
(s4366 2)
(s4368 4)
(s4369 5)
(s4370 5)
(s4371 2)
(s4373 4)
(s4374 5)
(s4375 5)
(s4376 2)
(s4378 4)
(s4379 5)
(s4380 5)
(s4381 2)
(s4383 4)
(s4384 5)
(s4385 5)
(s4386 2)
(s4388 4)
(s4389 5)
(s4390 5)
(s4391 2)
(s4393 4)
(s4394 5)
(s4395 5)
(s4396 2)
(s4398 4)
(s4399 5)
(s4400 5)
(s4401 2)
(s4403 4)
(s4404 5)
(s4405 5)
(s4406 2)
(s4408 4)
(s4409 5)
(s4410 5)
(s4411 2)
(s4413 4)
(s4414 5)
(s4415 5)
(s4416 2)
(s4418 4)
(s4419 5)
(s4420 5)
(s4421 2)
(s4423 4)
(s4424 5)
(s4425 5)
(s4426 2)
(s4428 4)
(s4429 5)
(s4430 5)
(s4431 2)
(s4433 4)
(s4434 5)
(s4435 5)
(s4436 2)
(s4438 4)
(s4439 5)
(s4440 5)
(s4441 2)
(s4443 4)
(s4444 5)
(s4445 5)
(s4446 2)
(s4448 4)
(s4449 5)
(s4450 5)
(s4451 2)
(s4453 4)
(s4454 5)
(s4455 5)
(s4456 2)
(s4458 4)
(s4459 5)
(s4460 5)
(s4461 2)
(s4463 4)
(s4464 5)
(s4465 5)
(s4466 2)
(s4468 4)
(s4469 5)
(s4470 5)
(s4471 2)
(s4473 4)
(s4474 5)
(s4475 5)
(s4476 2)
(s4478 4)
(s4479 5)
(s4480 5)
(s4481 2)
(s4483 4)
(s4484 5)
(s4485 5)
(s4486 2)
(s4488 4)
(s4489 5)
(s4490 5)
(s4491 2)
(s4493 4)
(s4494 5)
(s4495 5)
(s4496 2)
(s4498 4)
(s4499 5)
(s4500 5)
(s4501 2)
(s4503 4)
(s4504 5)
(s4505 5)
(s4506 2)
(s4508 4)
(s4509 5)
(s4510 5)
(s4511 2)
(s4513 4)
(s4514 5)
(s4515 5)
(s4516 2)
(s4518 4)
(s4519 5)
(s4520 5)
(s4521 2)
(s4523 4)
(s4524 5)
(s4525 5)
(s4526 2)
(s4528 4)
(s4529 5)
(s4530 5)
(s4531 2)
(s4533 4)
(s4534 5)
(s4535 5)
(s4536 2)
(s4538 4)
(s4539 5)
(s4540 5)
(s4541 2)
(s4543 4)
(s4544 5)
(s4545 5)
(s4546 2)
(s4548 4)
(s4549 5)
(s4550 5)
(s4551 2)
(s4553 4)
(s4554 5)
(s4555 5)
(s4556 2)
(s4558 4)
(s4559 5)
(s4560 5)
(s4561 2)
(s4563 4)
(s4564 5)
(s4565 5)
(s4566 2)
(s4568 4)
(s4569 5)
(s4570 5)
(s4571 2)
(s4573 4)
(s4574 5)
(s4575 5)
(s4576 2)
(s4578 4)
(s4579 5)
(s4580 5)
(s4581 2)
(s4583 4)
(s4584 5)
(s4585 5)
(s4586 2)
(s4588 4)
(s4589 5)
(s4590 5)
(s4591 2)
(s4593 4)
(s4594 5)
(s4595 5)
(s4596 2)
(s4598 4)
(s4599 5)
(s4600 5)
(s4601 2)
(s4603 4)
(s4604 5)
(s4605 5)
(s4606 2)
(s4608 4)
(s4609 5)
(s4610 5)
(s4611 2)
(s4613 4)
(s4614 5)
(s4615 5)
(s4616 2)
(s4618 4)
(s4619 5)
(s4620 5)
(s4621 2)
(s4623 4)
(s4624 5)
(s4625 5)
(s4626 2)
(s4628 4)
(s4629 5)
(s4630 5)
(s4631 2)
(s4633 4)
(s4634 5)
(s4635 5)
(s4636 2)
(s4638 4)
(s4639 5)
(s4640 5)
(s4641 2)
(s4643 4)
(s4644 5)
(s4645 5)
(s4646 2)
(s4648 4)
(s4649 5)
(s4650 5)
(s4651 2)
(s4653 4)
(s4654 5)
(s4655 5)
(s4656 2)
(s4658 4)
(s4659 5)
(s4660 5)
(s4661 2)
(s4663 4)
(s4664 5)
(s4665 5)
(s4666 2)
(s4668 4)
(s4669 5)
(s4670 5)
(s4671 2)
(s4673 4)
(s4674 5)
(s4675 5)
(s4676 2)
(s4678 4)
(s4679 5)
(s4680 5)
(s4681 2)
(s4683 4)
(s4684 5)
(s4685 5)
(s4686 2)
(s4688 4)
(s4689 5)
(s4690 5)
(s4691 2)
(s4693 4)
(s4694 5)
(s4695 5)
(s4696 2)
(s4698 4)
(s4699 5)
(s4700 5)
(s4701 2)
(s4703 4)
(s4704 5)
(s4705 5)
(s4706 2)
(s4708 4)
(s4709 5)
(s4710 5)
(s4711 2)
(s4713 4)
(s4714 5)
(s4715 5)
(s4716 2)
(s4718 4)
(s4719 5)
(s4720 5)
(s4721 2)
(s4723 4)
(s4724 5)
(s4725 5)
(s4726 2)
(s4728 4)
(s4729 5)
(s4730 5)
(s4731 2)
(s4733 4)
(s4734 5)
(s4735 5)
(s4736 2)
(s4738 4)
(s4739 5)
(s4740 5)
(s4741 2)
(s4743 4)
(s4744 5)
(s4745 5)
(s4746 2)
(s4748 4)
(s4749 5)
(s4750 5)
(s4751 2)
(s4753 4)
(s4754 5)
(s4755 5)
(s4756 2)
(s4758 4)
(s4759 5)
(s4760 5)
(s4761 2)
(s4763 4)
(s4764 5)
(s4765 5)
(s4766 2)
(s4768 4)
(s4769 5)
(s4770 5)
(s4771 2)
(s4773 4)
(s4774 5)
(s4775 5)
(s4776 2)
(s4778 4)
(s4779 5)
(s4780 5)
(s4781 2)
(s4783 4)
(s4784 5)
(s4785 5)
(s4786 2)
(s4788 4)
(s4789 5)
(s4790 5)
(s4791 2)
(s4793 4)
(s4794 5)
(s4795 5)
(s4796 2)
(s4798 4)
(s4799 5)
(s4800 5)
(s4801 2)
(s4803 4)
(s4804 5)
(s4805 5)
(s4806 2)
(s4808 4)
(s4809 5)
(s4810 5)
(s4811 2)
(s4813 4)
(s4814 5)
(s4815 5)
(s4816 2)
(s4818 4)
(s4819 5)
(s4820 5)
(s4821 2)
(s4823 4)
(s4824 5)
(s4825 5)
(s4826 2)
(s4828 4)
(s4829 5)
(s4830 5)
(s4831 2)
(s4833 4)
(s4834 5)
(s4835 5)
(s4836 2)
(s4838 4)
(s4839 5)
(s4840 5)
(s4841 2)
(s4843 4)
(s4844 5)
(s4845 5)
(s4846 2)
(s4848 4)
(s4849 5)
(s4850 5)
(s4851 2)
(s4853 4)
(s4854 5)
(s4855 5)
(s4856 2)
(s4858 4)
(s4859 5)
(s4860 5)
(s4861 2)
(s4863 4)
(s4864 5)
(s4865 5)
(s4866 2)
(s4868 4)
(s4869 5)
(s4870 5)
(s4871 2)
(s4873 4)
(s4874 5)
(s4875 5)
(s4876 2)
(s4878 4)
(s4879 5)
(s4880 5)
(s4881 2)
(s4883 4)
(s4884 5)
(s4885 5)
(s4886 2)
(s4888 4)
(s4889 5)
(s4890 5)
(s4891 2)
(s4893 4)
(s4894 5)
(s4895 5)
(s4896 2)
(s4898 4)
(s4899 5)
(s4900 5)
(s4901 2)
(s4903 4)
(s4904 5)
(s4905 5)
(s4906 2)
(s4908 4)
(s4909 5)
(s4910 5)
(s4911 2)
(s4913 4)
(s4914 5)
(s4915 5)
(s4916 2)
(s4918 4)
(s4919 5)
(s4920 5)
(s4921 2)
(s4923 4)
(s4924 5)
(s4925 5)
(s4926 2)
(s4928 4)
(s4929 5)
(s4930 5)
(s4931 2)
(s4933 4)
(s4934 5)
(s4935 5)
(s4936 2)
(s4938 4)
(s4939 5)
(s4940 5)
(s4941 2)
(s4943 4)
(s4944 5)
(s4945 5)
(s4946 2)
(s4948 4)
(s4949 5)
(s4950 5)
(s4951 2)
(s4953 4)
(s4954 5)
(s4955 5)
(s4956 2)
(s4958 4)
(s4959 5)
(s4960 5)
(s4961 2)
(s4963 4)
(s4964 5)
(s4965 5)
(s4966 2)
(s4968 4)
(s4969 5)
(s4970 5)
(s4971 2)
(s4973 4)
(s4974 5)
(s4975 5)
(s4976 2)
(s4978 4)
(s4979 5)
(s4980 5)
(s4981 2)
(s4983 4)
(s4984 5)
(s4985 5)
(s4986 2)
(s4988 4)
(s4989 5)
(s4990 5)
(s4991 2)
(s4993 4)
(s4994 5)
(s4995 5)
(s4996 2)
(s4998 4)
(s4999 5)
(s5000 5)
(s5001 2)
(s5003 4)
(s5004 5)
(s5005 5)
(s5006 2)
(s5008 4)
(s5009 5)
(s5010 5)
(s5011 2)
(s5013 4)
(s5014 5)
(s5015 5)
(s5016 2)
(s5018 4)
(s5019 5)
(s5020 5)
(s5021 2)
(s5023 4)
(s5024 5)
(s5025 5)
(s5026 2)
(s5028 4)
(s5029 5)
(s5030 5)
(s5031 2)
(s5033 4)
(s5034 5)
(s5035 5)
(s5036 2)
(s5038 4)
(s5039 5)
(s5040 5)
(s5041 2)
(s5043 4)
(s5044 5)
(s5045 5)
(s5046 2)
(s5048 4)
(s5049 5)
(s5050 5)
(s5051 2)
(s5053 4)
(s5054 5)
(s5055 5)
(s5056 2)
(s5058 4)
(s5059 5)
(s5060 5)
(s5061 2)
(s5063 4)
(s5064 5)
(s5065 5)
(s5066 2)
(s5068 4)
(s5069 5)
(s5070 5)
(s5071 2)
(s5073 4)
(s5074 5)
(s5075 5)
(s5076 2)
(s5078 4)
(s5079 5)
(s5080 5)
(s5081 2)
(s5083 4)
(s5084 5)
(s5085 5)
(s5086 2)
(s5088 4)
(s5089 5)
(s5090 5)
(s5091 2)
(s5093 4)
(s5094 5)
(s5095 5)
(s5096 2)
(s5098 4)
(s5099 5)
(s5100 5)
(s5101 2)
(s5103 4)
(s5104 5)
(s5105 5)
(s5106 2)
(s5108 4)
(s5109 5)
(s5110 5)
(s5111 2)
(s5113 4)
(s5114 5)
(s5115 5)
(s5116 2)
(s5118 4)
(s5119 5)
(s5120 5)
(s5121 2)
(s5123 4)
(s5124 5)
(s5125 5)
(s5126 2)
(s5128 4)
(s5129 5)
(s5130 5)
(s5131 2)
(s5133 4)
(s5134 5)
(s5135 5)
(s5136 2)
(s5138 4)
(s5139 5)
(s5140 5)
(s5141 2)
(s5143 4)
(s5144 5)
(s5145 5)
(s5146 2)
(s5148 4)
(s5149 5)
(s5150 5)
(s5151 2)
(s5153 4)
(s5154 5)
(s5155 5)
(s5156 2)
(s5158 4)
(s5159 5)
(s5160 5)
(s5161 2)
(s5163 4)
(s5164 5)
(s5165 5)
(s5166 2)
(s5168 4)
(s5169 5)
(s5170 5)
(s5171 2)
(s5173 4)
(s5174 5)
(s5175 5)
(s5176 2)
(s5178 4)
(s5179 5)
(s5180 5)
(s5181 2)
(s5183 4)
(s5184 5)
(s5185 5)
(s5186 2)
(s5188 4)
(s5189 5)
(s5190 5)
(s5191 2)
(s5193 4)
(s5194 5)
(s5195 5)
(s5196 2)
(s5198 4)
(s5199 5)
(s5200 5)
(s5201 2)
(s5203 4)
(s5204 5)
(s5205 5)
(s5206 2)
(s5208 4)
(s5209 5)
(s5210 5)
(s5211 2)
(s5213 4)
(s5214 5)
(s5215 5)
(s5216 2)
(s5218 4)
(s5219 5)
(s5220 5)
(s5221 2)
(s5223 4)
(s5224 5)
(s5225 5)
(s5226 2)
(s5228 4)
(s5229 5)
(s5230 5)
(s5231 2)
(s5233 4)
(s5234 5)
(s5235 5)
(s5236 2)
(s5238 4)
(s5239 5)
(s5240 5)
(s5241 2)
(s5243 4)
(s5244 5)
(s5245 5)
(s5246 2)
(s5248 4)
(s5249 5)
(s5250 5)
(s5251 2)
(s5253 4)
(s5254 5)
(s5255 5)
(s5256 2)
(s5258 4)
(s5259 5)
(s5260 5)
(s5261 2)
(s5263 4)
(s5264 5)
(s5265 5)
(s5266 2)
(s5268 4)
(s5269 5)
(s5270 5)
(s5271 2)
(s5273 4)
(s5274 5)
(s5275 5)
(s5276 2)
(s5278 4)
(s5279 5)
(s5280 5)
(s5281 2)
(s5283 4)
(s5284 5)
(s5285 5)
(s5286 2)
(s5288 4)
(s5289 5)
(s5290 5)
(s5291 2)
(s5293 4)
(s5294 5)
(s5295 5)
(s5296 2)
(s5298 4)
(s5299 5)
(s5300 5)
(s5301 2)
(s5303 4)
(s5304 5)
(s5305 5)
(s5306 2)
(s5308 4)
(s5309 5)
(s5310 5)
(s5311 2)
(s5313 4)
(s5314 5)
(s5315 5)
(s5316 2)
(s5318 4)
(s5319 5)
(s5320 5)
(s5321 2)
(s5323 4)
(s5324 5)
(s5325 5)
(s5326 2)
(s5328 4)
(s5329 5)
(s5330 5)
(s5331 2)
(s5333 4)
(s5334 5)
(s5335 5)
(s5336 2)
(s5338 4)
(s5339 5)
(s5340 5)
(s5341 2)
(s5343 4)
(s5344 5)
(s5345 5)
(s5346 2)
(s5348 4)
(s5349 5)
(s5350 5)
(s5351 2)
(s5353 4)
(s5354 5)
(s5355 5)
(s5356 2)
(s5358 4)
(s5359 5)
(s5360 5)
(s5361 2)
(s5363 4)
(s5364 5)
(s5365 5)
(s5366 2)
(s5368 4)
(s5369 5)
(s5370 5)
(s5371 2)
(s5373 4)
(s5374 5)
(s5375 5)
(s5376 2)
(s5378 4)
(s5379 5)
(s5380 5)
(s5381 2)
(s5383 4)
(s5384 5)
(s5385 5)
(s5386 2)
(s5388 4)
(s5389 5)
(s5390 5)
(s5391 2)
(s5393 4)
(s5394 5)
(s5395 5)
(s5396 2)
(s5398 4)
(s5399 5)
(s5400 5)
(s5401 2)
(s5403 4)
(s5404 5)
(s5405 5)
(s5406 2)
(s5408 4)
(s5409 5)
(s5410 5)
(s5411 2)
(s5413 4)
(s5414 5)
(s5415 5)
(s5416 2)
(s5418 4)
(s5419 5)
(s5420 5)
(s5421 2)
(s5423 4)
(s5424 5)
(s5425 5)
(s5426 2)
(s5428 4)
(s5429 5)
(s5430 5)
(s5431 2)
(s5433 4)
(s5434 5)
(s5435 5)
(s5436 2)
(s5438 4)
(s5439 5)
(s5440 5)
(s5441 2)
(s5443 4)
(s5444 5)
(s5445 5)
(s5446 2)
(s5448 4)
(s5449 5)
(s5450 5)
(s5451 2)
(s5453 4)
(s5454 5)
(s5455 5)
(s5456 2)
(s5458 4)
(s5459 5)
(s5460 5)
(s5461 2)
(s5463 4)
(s5464 5)
(s5465 5)
(s5466 2)
(s5468 4)
(s5469 5)
(s5470 5)
(s5471 2)
(s5473 4)
(s5474 5)
(s5475 5)
(s5476 2)
(s5478 4)
(s5479 5)
(s5480 5)
(s5481 2)
(s5483 4)
(s5484 5)
(s5485 5)
(s5486 2)
(s5488 4)
(s5489 5)
(s5490 5)
(s5491 2)
(s5493 4)
(s5494 5)
(s5495 5)
(s5496 2)
(s5498 4)
(s5499 5)
(s5500 5)
(s5501 2)
(s5503 4)
(s5504 5)
(s5505 5)
(s5506 2)
(s5508 4)
(s5509 5)
(s5510 5)
(s5511 2)
(s5513 4)
(s5514 5)
(s5515 5)
(s5516 2)
(s5518 4)
(s5519 5)
(s5520 5)
(s5521 2)
(s5523 4)
(s5524 5)
(s5525 5)
(s5526 2)
(s5528 4)
(s5529 5)
(s5530 5)
(s5531 2)
(s5533 4)
(s5534 5)
(s5535 5)
(s5536 2)
(s5538 4)
(s5539 5)
(s5540 5)
(s5541 2)
(s5543 4)
(s5544 5)
(s5545 5)
(s5546 2)
(s5548 4)
(s5549 5)
(s5550 5)
(s5551 2)
(s5553 4)
(s5554 5)
(s5555 5)
(s5556 2)
(s5558 4)
(s5559 5)
(s5560 5)
(s5561 2)
(s5563 4)
(s5564 5)
(s5565 5)
(s5566 2)
(s5568 4)
(s5569 5)
(s5570 5)
(s5571 2)
(s5573 4)
(s5574 5)
(s5575 5)
(s5576 2)
(s5578 4)
(s5579 5)
(s5580 5)
(s5581 2)
(s5583 4)
(s5584 5)
(s5585 5)
(s5586 2)
(s5588 4)
(s5589 5)
(s5590 5)
(s5591 2)
(s5593 4)
(s5594 5)
(s5595 5)
(s5596 2)
(s5598 4)
(s5599 5)
(s5600 5)
(s5601 2)
(s5603 4)
(s5604 5)
(s5605 5)
(s5606 2)
(s5608 4)
(s5609 5)
(s5610 5)
(s5611 2)
(s5613 4)
(s5614 5)
(s5615 5)
(s5616 2)
(s5618 4)
(s5619 5)
(s5620 5)
(s5621 2)
(s5623 4)
(s5624 5)
(s5625 5)
(s5626 2)
(s5628 4)
(s5629 5)
(s5630 5)
(s5631 2)
(s5633 4)
(s5634 5)
(s5635 5)
(s5636 2)
(s5638 4)
(s5639 5)
(s5640 5)
(s5641 2)
(s5643 4)
(s5644 5)
(s5645 5)
(s5646 2)
(s5648 4)
(s5649 5)
(s5650 5)
(s5651 2)
(s5653 4)
(s5654 5)
(s5655 5)
(s5656 2)
(s5658 4)
(s5659 5)
(s5660 5)
(s5661 2)
(s5663 4)
(s5664 5)
(s5665 5)
(s5666 2)
(s5668 4)
(s5669 5)
(s5670 5)
(s5671 2)
(s5673 4)
(s5674 5)
(s5675 5)
(s5676 2)
(s5678 4)
(s5679 5)
(s5680 5)
(s5681 2)
(s5683 4)
(s5684 5)
(s5685 5)
(s5686 2)
(s5688 4)
(s5689 5)
(s5690 5)
(s5691 2)
(s5693 4)
(s5694 5)
(s5695 5)
(s5696 2)
(s5698 4)
(s5699 5)
(s5700 5)
(s5701 2)
(s5703 4)
(s5704 5)
(s5705 5)
(s5706 2)
(s5708 4)
(s5709 5)
(s5710 5)
(s5711 2)
(s5713 4)
(s5714 5)
(s5715 5)
(s5716 2)
(s5718 4)
(s5719 5)
(s5720 5)
(s5721 2)
(s5723 4)
(s5724 5)
(s5725 5)
(s5726 2)
(s5728 4)
(s5729 5)
(s5730 5)
(s5731 2)
(s5733 4)
(s5734 5)
(s5735 5)
(s5736 2)
(s5738 4)
(s5739 5)
(s5740 5)
(s5741 2)
(s5743 4)
(s5744 5)
(s5745 5)
(s5746 2)
(s5748 4)
(s5749 5)
(s5750 5)
(s5751 2)
(s5753 4)
(s5754 5)
(s5755 5)
(s5756 2)
(s5758 4)
(s5759 5)
(s5760 5)
(s5761 2)
(s5763 4)
(s5764 5)
(s5765 5)
(s5766 2)
(s5768 4)
(s5769 5)
(s5770 5)
(s5771 2)
(s5773 4)
(s5774 5)
(s5775 5)
(s5776 2)
(s5778 4)
(s5779 5)
(s5780 5)
(s5781 2)
(s5783 4)
(s5784 5)
(s5785 5)
(s5786 2)
(s5788 4)
(s5789 5)
(s5790 5)
(s5791 2)
(s5793 4)
(s5794 5)
(s5795 5)
(s5796 2)
(s5798 4)
(s5799 5)
(s5800 5)
(s5801 2)
(s5803 4)
(s5804 5)
(s5805 5)
(s5806 2)
(s5808 4)
(s5809 5)
(s5810 5)
(s5811 2)
(s5813 4)
(s5814 5)
(s5815 5)
(s5816 2)
(s5818 4)
(s5819 5)
(s5820 5)
(s5821 2)
(s5823 4)
(s5824 5)
(s5825 5)
(s5826 2)
(s5828 4)
(s5829 5)
(s5830 5)
(s5831 2)
(s5833 4)
(s5834 5)
(s5835 5)
(s5836 2)
(s5838 4)
(s5839 5)
(s5840 5)
(s5841 2)
(s5843 4)
(s5844 5)
(s5845 5)
(s5846 2)
(s5848 4)
(s5849 5)
(s5850 5)
(s5851 2)
(s5853 4)
(s5854 5)
(s5855 5)
(s5856 2)
(s5858 4)
(s5859 5)
(s5860 5)
(s5861 2)
(s5863 4)
(s5864 5)
(s5865 5)
(s5866 2)
(s5868 4)
(s5869 5)
(s5870 5)
(s5871 2)
(s5873 4)
(s5874 5)
(s5875 5)
(s5876 2)
(s5878 4)
(s5879 5)
(s5880 5)
(s5881 2)
(s5883 4)
(s5884 5)
(s5885 5)
(s5886 2)
(s5888 4)
(s5889 5)
(s5890 5)
(s5891 2)
(s5893 4)
(s5894 5)
(s5895 5)
(s5896 2)
(s5898 4)
(s5899 5)
(s5900 5)
(s5901 2)
(s5903 4)
(s5904 5)
(s5905 5)
(s5906 2)
(s5908 4)
(s5909 5)
(s5910 5)
(s5911 2)
(s5913 4)
(s5914 5)
(s5915 5)
(s5916 2)
(s5918 4)
(s5919 5)
(s5920 5)
(s5921 2)
(s5923 4)
(s5924 5)
(s5925 5)
(s5926 2)
(s5928 4)
(s5929 5)
(s5930 5)
(s5931 2)
(s5933 4)
(s5934 5)
(s5935 5)
(s5936 2)
(s5938 4)
(s5939 5)
(s5940 5)
(s5941 2)
(s5943 4)
(s5944 5)
(s5945 5)
(s5946 2)
(s5948 4)
(s5949 5)
(s5950 5)
(s5951 2)
(s5953 4)
(s5954 5)
(s5955 5)
(s5956 2)
(s5958 4)
(s5959 5)
(s5960 5)
(s5961 2)
(s5963 4)
(s5964 5)
(s5965 5)
(s5966 2)
(s5968 4)
(s5969 5)
(s5970 5)
(s5971 2)
(s5973 4)
(s5974 5)
(s5975 5)
(s5976 2)
(s5978 4)
(s5979 5)
(s5980 5)
(s5981 2)
(s5983 4)
(s5984 5)
(s5985 5)
(s5986 2)
(s5988 4)
(s5989 5)
(s5990 5)
(s5991 2)
(s5993 4)
(s5994 5)
(s5995 5)
(s5996 2)
(s5998 4)
(s5999 5)
(s6000 5)
(s6001 2)
(s6003 4)
(s6004 5)
(s6005 5)
(s6006 2)
(s6008 4)
(s6009 5)
(s6010 5)
(s6011 2)
(s6013 4)
(s6014 5)
(s6015 5)
(s6016 2)
(s6018 4)
(s6019 5)
(s6020 5)
(s6021 2)
(s6023 4)
(s6024 5)
(s6025 5)
(s6026 2)
(s6028 4)
(s6029 5)
(s6030 5)
(s6031 2)
(s6033 4)
(s6034 5)
(s6035 5)
(s6036 2)
(s6038 4)
(s6039 5)
(s6040 5)
(s6041 2)
(s6043 4)
(s6044 5)
(s6045 5)
(s6046 2)
(s6048 4)
(s6049 5)
(s6050 5)
(s6051 2)
(s6053 4)
(s6054 5)
(s6055 5)
(s6056 2)
(s6058 4)
(s6059 5)
(s6060 5)
(s6061 2)
(s6063 4)
(s6064 5)
(s6065 5)
(s6066 2)
(s6068 4)
(s6069 5)
(s6070 5)
(s6071 2)
(s6073 4)
(s6074 5)
(s6075 5)
(s6076 2)
(s6078 4)
(s6079 5)
(s6080 5)
(s6081 2)
(s6083 4)
(s6084 5)
(s6085 5)
(s6086 2)
(s6088 4)
(s6089 5)
(s6090 5)
(s6091 2)
(s6093 4)
(s6094 5)
(s6095 5)
(s6096 2)
(s6098 4)
(s6099 5)
(s6100 5)
(s6101 2)
(s6103 4)
(s6104 5)
(s6105 5)
(s6106 2)
(s6108 4)
(s6109 5)
(s6110 5)
(s6111 2)
(s6113 4)
(s6114 5)
(s6115 5)
(s6116 2)
(s6118 4)
(s6119 5)
(s6120 5)
(s6121 2)
(s6123 4)
(s6124 5)
(s6125 5)
(s6126 2)
(s6128 4)
(s6129 5)
(s6130 5)
(s6131 2)
(s6133 4)
(s6134 5)
(s6135 5)
(s6136 2)
(s6138 4)
(s6139 5)
(s6140 5)
(s6141 2)
(s6143 4)
(s6144 5)
(s6145 5)
(s6146 2)
(s6148 4)
(s6149 5)
(s6150 5)
(s6151 2)
(s6153 4)
(s6154 5)
(s6155 5)
(s6156 2)
(s6158 4)
(s6159 5)
(s6160 5)
(s6161 2)
(s6163 4)
(s6164 5)
(s6165 5)
(s6166 2)
(s6168 4)
(s6169 5)
(s6170 5)
(s6171 2)
(s6173 4)
(s6174 5)
(s6175 5)
(s6176 2)
(s6178 4)
(s6179 5)
(s6180 5)
(s6181 2)
(s6183 4)
(s6184 5)
(s6185 5)
(s6186 2)
(s6188 4)
(s6189 5)
(s6190 5)
(s6191 2)
(s6193 4)
(s6194 timeout
5)
(s6195 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30132 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76595ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76680ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 137718 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:21:25] [INFO ] Flatten gal took : 276 ms
[2024-05-24 10:21:25] [INFO ] Flatten gal took : 292 ms
[2024-05-24 10:21:25] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:21:26] [INFO ] Flatten gal took : 280 ms
[2024-05-24 10:21:26] [INFO ] Flatten gal took : 291 ms
[2024-05-24 10:21:26] [INFO ] Time to serialize gal into /tmp/CTLCardinality9582150062344072030.gal : 47 ms
[2024-05-24 10:21:26] [INFO ] Time to serialize properties into /tmp/CTLCardinality15054803111894720624.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality9582150062344072030.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality15054803111894720624.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:21:56] [INFO ] Flatten gal took : 284 ms
[2024-05-24 10:21:56] [INFO ] Applying decomposition
[2024-05-24 10:21:57] [INFO ] Flatten gal took : 294 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph1706206544119402129.txt' '-o' '/tmp/graph1706206544119402129.bin' '-w' '/tmp/graph1706206544119402129.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph1706206544119402129.bin' '-l' '-1' '-v' '-w' '/tmp/graph1706206544119402129.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:21:57] [INFO ] Decomposing Gal with order
[2024-05-24 10:21:58] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:22:03] [INFO ] Flatten gal took : 300 ms
[2024-05-24 10:22:03] [INFO ] Fuse similar labels procedure discarded/fused a total of 0 labels/synchronizations in 245 ms.
[2024-05-24 10:22:03] [INFO ] Time to serialize gal into /tmp/CTLCardinality1959877196954019379.gal : 52 ms
[2024-05-24 10:22:03] [INFO ] Time to serialize properties into /tmp/CTLCardinality12343328021025576360.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality1959877196954019379.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality12343328021025576360.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 928 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:22:34] [INFO ] Invariant cache hit.
[2024-05-24 10:22:34] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 timeout
4) org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20125 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56363ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56446ms
[2024-05-24 10:23:31] [INFO ] Invariant cache hit.
[2024-05-24 10:23:33] [INFO ] Implicit Places using invariants in 2130 ms returned []
Implicit Place search using SMT only with invariants took 2130 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:23:33] [INFO ] Invariant cache hit.
[2024-05-24 10:23:33] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76169ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76256ms
Finished structural reductions in LTL mode , in 1 iterations and 135786 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:24:49] [INFO ] Flatten gal took : 279 ms
[2024-05-24 10:24:50] [INFO ] Flatten gal took : 291 ms
[2024-05-24 10:24:50] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:24:50] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:24:51] [INFO ] Flatten gal took : 293 ms
[2024-05-24 10:24:51] [INFO ] Time to serialize gal into /tmp/CTLCardinality16046004170865767282.gal : 147 ms
[2024-05-24 10:24:51] [INFO ] Time to serialize properties into /tmp/CTLCardinality4718595875017490671.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality16046004170865767282.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality4718595875017490671.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:25:21] [INFO ] Flatten gal took : 287 ms
[2024-05-24 10:25:21] [INFO ] Applying decomposition
[2024-05-24 10:25:22] [INFO ] Flatten gal took : 296 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph17487573674883616384.txt' '-o' '/tmp/graph17487573674883616384.bin' '-w' '/tmp/graph17487573674883616384.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph17487573674883616384.bin' '-l' '-1' '-v' '-w' '/tmp/graph17487573674883616384.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:25:22] [INFO ] Decomposing Gal with order
[2024-05-24 10:25:23] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:25:28] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:25:28] [INFO ] Flatten gal took : 347 ms
[2024-05-24 10:25:28] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 502 ms.
[2024-05-24 10:25:29] [INFO ] Time to serialize gal into /tmp/CTLCardinality12968922052001993062.gal : 75 ms
[2024-05-24 10:25:29] [INFO ] Time to serialize properties into /tmp/CTLCardinality8187385152423432185.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality12968922052001993062.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality8187385152423432185.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 950 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:26:00] [INFO ] Invariant cache hit.
[2024-05-24 10:26:00] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20127 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56389ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56476ms
[2024-05-24 10:26:56] [INFO ] Invariant cache hit.
[2024-05-24 10:26:58] [INFO ] Implicit Places using invariants in 2098 ms returned []
Implicit Place search using SMT only with invariants took 2099 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:26:58] [INFO ] Invariant cache hit.
[2024-05-24 10:26:58] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: ((s0 5.0)
(s1 2.0)
(s3 4.0)
(s4 5.0)
(s5 5.0)
(s6 2.0)
(s8 4.0)
(s9 5.0)
(s10 5.0)
(s11 2.0)
(s13 4.0)
(s14 5.0)
(s15 5.0)
(s16 2.0)
(s18 4.0)
(s19 5.0)
(s20 5.0)
(s21 2.0)
(s23 4.0)
(s24 5.0)
(s25 5.0)
(s26 2.0)
(s28 4.0)
(s29 5.0)
(s30 5.0)
(s31 2.0)
(s33 4.0)
(s34 5.0)
(s35 5.0)
(s36 2.0)
(s38 4.0)
(s39 5.0)
(s40 5.0)
(s41 2.0)
(s43 4.0)
(s44 5.0)
(s45 5.0)
(s46 2.0)
(s48 4.0)
(s49 5.0)
(s50 5.0)
(s51 2.0)
(s53 4.0)
(s54 5.0)
(s55 5.0)
(s56 2.0)
(s58 4.0)
(s59 5.0)
(s60 5.0)
(s61 2.0)
(s63 4.0)
(s64 5.0)
(s65 5.0)
(s66 2.0)
(s68 4.0)
(s69 5.0)
(s70 5.0)
(s71 2.0)
(s73 4.0)
(s74 5.0)
(s75 5.0)
(s76 2.0)
(s78 4.0)
(s79 5.0)
(s80 5.0)
(s81 2.0)
(s83 4.0)
(s84 5.0)
(s85 5.0)
(s86 2.0)
(s88 4.0)
(s89 5.0)
(s90 5.0)
(s91 2.0)
(s93 4.0)
(s94 5.0)
(s95 5.0)
(s96 2.0)
(s98 4.0)
(s99 5.0)
(s100 5.0)
(s101 2.0)
(s103 4.0)
(s104 5.0)
(s105 5.0)
(s106 2.0)
(s108 4.0)
(s109 5.0)
(s110 5.0)
(s111 2.0)
(s113 4.0)
(s114 5.0)
(s115 5.0)
(s116 2.0)
(s118 4.0)
(s119 5.0)
(s120 5.0)
(s121 2.0)
(s123 4.0)
(s124 5.0)
(s125 5.0)
(s126 2.0)
(s128 4.0)
(s129 5.0)
(s130 5.0)
(s131 2.0)
(s133 4.0)
(s134 5.0)
(s135 5.0)
(s136 2.0)
(s138 4.0)
(s139 5.0)
(s140 5.0)
(s141 2.0)
(s143 4.0)
(s144 5.0)
(s145 5.0)
(s146 2.0)
(s148 4.0)
(s149 5.0)
(s150 5.0)
(s151 2.0)
(s153 4.0)
(s154 5.0)
(s155 5.0)
(s156 2.0)
(s158 4.0)
(s159 5.0)
(s160 5.0)
(s161 2.0)
(s163 4.0)
(s164 5.0)
(s165 5.0)
(s166 2.0)
(s168 4.0)
(s169 5.0)
(s170 5.0)
(s171 2.0)
(s173 4.0)
(s174 5.0)
(s175 5.0)
(s176 2.0)
(s178 4.0)
(s179 5.0)
(s180 5.0)
(s181 2.0)
(s183 4.0)
(s184 5.0)
(s185 5.0)
(s186 2.0)
(s188 4.0)
(s189 5.0)
(s190 5.0)
(s191 2.0)
(s193 4.0)
(s194 5.0)
(s195 5.0)
(s196 2.0)
(s198 4.0)
(s199 5.0)
(s200 5.0)
(s201 2.0)
(s203 4.0)
(s204 5.0)
(s205 5.0)
(s206 2.0)
(s208 4.0)
(s209 5.0)
(s210 5.0)
(s211 2.0)
(s213 4.0)
(s214 5.0)
(s215 5.0)
(s216 2.0)
(s218 4.0)
(s219 5.0)
(s220 5.0)
(s221 2.0)
(s223 4.0)
(s224 5.0)
(s225 5.0)
(s226 2.0)
(s228 4.0)
(s229 5.0)
(s230 5.0)
(s231 2.0)
(s233 4.0)
(s234 5.0)
(s235 5.0)
(s236 2.0)
(s238 4.0)
(s239 5.0)
(s240 5.0)
(s241 2.0)
(s243 4.0)
(s244 5.0)
(s245 5.0)
(s246 2.0)
(s248 4.0)
(s249 5.0)
(s250 5.0)
(s251 2.0)
(s253 4.0)
(s254 5.0)
(s255 5.0)
(s256 2.0)
(s258 4.0)
(s259 5.0)
(s260 5.0)
(s261 2.0)
(s263 4.0)
(s264 5.0)
(s265 5.0)
(s266 2.0)
(s268 4.0)
(s269 5.0)
(s270 5.0)
(s271 2.0)
(s273 4.0)
(s274 5.0)
(s275 5.0)
(s276 2.0)
(s278 4.0)
(s279 5.0)
(s280 5.0)
(s281 2.0)
(s283 4.0)
(s284 5.0)
(s285 5.0)
(s286 2.0)
(s288 4.0)
(s289 5.0)
(s290 5.0)
(s291 2.0)
(s293 4.0)
(s294 5.0)
(s295 5.0)
(s296 2.0)
(s298 4.0)
(s299 5.0)
(s300 5.0)
(s301 2.0)
(s303 4.0)
(s304 5.0)
(s305 5.0)
(s306 2.0)
(s308 4.0)
(s309 5.0)
(s310 5.0)
(s311 2.0)
(s313 4.0)
(s314 5.0)
(s315 5.0)
(s316 2.0)
(s318 4.0)
(s319 5.0)
(s320 5.0)
(s321 2.0)
(s323 4.0)
(s324 5.0)
(s325 5.0)
(s326 2.0)
(s328 4.0)
(s329 5.0)
(s330 5.0)
(s331 2.0)
(s333 4.0)
(s334 5.0)
(s335 5.0)
(s336 2.0)
(s338 4.0)
(s339 5.0)
(s340 5.0)
(s341 2.0)
(s343 4.0)
(s344 5.0)
(s345 5.0)
(s346 2.0)
(s348 4.0)
(s349 5.0)
(s350 5.0)
(s351 2.0)
(s353 4.0)
(s354 5.0)
(s355 5.0)
(s356 2.0)
(s358 4.0)
(s359 5.0)
(s360 5.0)
(s361 2.0)
(s363 4.0)
(s364 5.0)
(s365 5.0)
(s366 2.0)
(s368 4.0)
(s369 5.0)
(s370 5.0)
(s371 2.0)
(s373 4.0)
(s374 5.0)
(s375 5.0)
(s376 2.0)
(s378 4.0)
(s379 5.0)
(s380 5.0)
(s381 2.0)
(s383 4.0)
(s384 5.0)
(s385 5.0)
(s386 2.0)
(s388 4.0)
(s389 5.0)
(s390 5.0)
(s391 2.0)
(s393 4.0)
(s394 5.0)
(s395 5.0)
(s396 2.0)
(s398 4.0)
(s399 5.0)
(s400 5.0)
(s401 2.0)
(s403 4.0)
(s404 5.0)
(s405 5.0)
(s406 2.0)
(s408 4.0)
(s409 5.0)
(s410 5.0)
(s411 2.0)
(s413 4.0)
(s414 5.0)
(s415 5.0)
(s416 2.0)
(s418 4.0)
(s419 5.0)
(s420 5.0)
(s421 2.0)
(s423 4.0)
(s424 5.0)
(s425 5.0)
(s426 2.0)
(s428 4.0)
(s429 5.0)
(s430 5.0)
(s431 2.0)
(s433 4.0)
(s434 5.0)
(s435 5.0)
(s436 2.0)
(s438 4.0)
(s439 5.0)
(s440 5.0)
(s441 2.0)
(s443 4.0)
(s444 5.0)
(s445 5.0)
(s446 2.0)
(s448 4.0)
(s449 5.0)
(s450 5.0)
(s451 2.0)
(s453 4.0)
(s454 5.0)
(s455 5.0)
(s456 2.0)
(s458 4.0)
(s459 5.0)
(s460 5.0)
(s461 2.0)
(s463 4.0)
(s464 5.0)
(s465 5.0)
(s466 2.0)
(s468 4.0)
(s469 5.0)
(s470 5.0)
(s471 2.0)
(s473 4.0)
(s474 5.0)
(s475 5.0)
(s476 2.0)
(s478 4.0)
(s479 5.0)
(s480 5.0)
(s481 2.0)
(s483 4.0)
(s484 5.0)
(s485 5.0)
(s486 2.0)
(s488 4.0)
(s489 5.0)
(s490 5.0)
(s491 2.0)
(s493 4.0)
(s494 5.0)
(s495 5.0)
(s496 2.0)
(s498 4.0)
(s499 5.0)
(s500 5.0)
(s501 2.0)
(s503 4.0)
(s504 5.0)
(s505 5.0)
(s506 2.0)
(s508 4.0)
(s509 5.0)
(s510 5.0)
(s511 2.0)
(s513 4.0)
(s514 5.0)
(s515 5.0)
(s516 2.0)
(s518 4.0)
(s519 5.0)
(s520 5.0)
(s521 2.0)
(s523 4.0)
(s524 5.0)
(s525 5.0)
(s526 2.0)
(s528 4.0)
(s529 5.0)
(s530 5.0)
(s531 2.0)
(s533 4.0)
(s534 5.0)
(s535 5.0)
(s536 2.0)
(s538 4.0)
(s539 5.0)
(s540 5.0)
(s541 2.0)
(s543 4.0)
(s544 5.0)
(s545 5.0)
(s546 2.0)
(s548 4.0)
(s549 5.0)
(s550 5.0)
(s551 2.0)
(s553 4.0)
(s554 5.0)
(s555 5.0)
(s556 2.0)
(s558 4.0)
(s559 5.0)
(s560 5.0)
(s561 2.0)
(s563 4.0)
(s564 5.0)
(s565 5.0)
(s566 2.0)
(s568 4.0)
(s569 5.0)
(s570 5.0)
(s571 2.0)
(s573 4.0)
(s574 5.0)
(s575 5.0)
(s576 2.0)
(s578 4.0)
(s579 5.0)
(s580 5.0)
(s581 2.0)
(s583 4.0)
(s584 5.0)
(s585 5.0)
(s586 2.0)
(s588 4.0)
(s589 5.0)
(s590 5.0)
(s591 2.0)
(s593 4.0)
(s594 5.0)
(s595 5.0)
(s596 2.0)
(s598 4.0)
(s599 5.0)
(s600 5.0)
(s601 2.0)
(s603 4.0)
(s604 5.0)
(s605 5.0)
(s606 2.0)
(s608 4.0)
(s609 5.0)
(s610 5.0)
(s611 2.0)
(s613 4.0)
(s614 5.0)
(s615 5.0)
(s616 2.0)
(s618 4.0)
(s619 5.0)
(s620 5.0)
(s621 2.0)
(s623 4.0)
(s624 5.0)
(s625 5.0)
(s626 2.0)
(s628 4.0)
(s629 5.0)
(s630 5.0)
(s631 2.0)
(s633 4.0)
(s634 5.0)
(s635 5.0)
(s636 2.0)
(s638 4.0)
(s639 5.0)
(s640 5.0)
(s641 2.0)
(s643 4.0)
(s644 5.0)
(s645 5.0)
(s646 2.0)
(s648 4.0)
(s649 5.0)
(s650 5.0)
(s651 2.0)
(s653 4.0)
(s654 5.0)
(s655 5.0)
(s656 2.0)
(s658 4.0)
(s659 5.0)
(s660 5.0)
(s661 2.0)
(s663 4.0)
(s664 5.0)
(s665 5.0)
(s666 2.0)
(s668 4.0)
(s669 5.0)
(s670 5.0)
(s671 2.0)
(s673 4.0)
(s674 5.0)
(s675 5.0)
(s676 2.0)
(s678 4.0)
(s679 5.0)
(s680 5.0)
(s681 2.0)
(s683 4.0)
(s684 5.0)
(s685 5.0)
(s686 2.0)
(s688 4.0)
(s689 5.0)
(s690 5.0)
(s691 2.0)
(s693 4.0)
(s694 5.0)
(s695 5.0)
(s696 2.0)
(s698 4.0)
(s699 5.0)
(s700 5.0)
(s701 2.0)
(s703 4.0)
(s704 5.0)
(s705 5.0)
(s706 2.0)
(s708 4.0)
(s709 5.0)
(s710 5.0)
(s711 2.0)
(s713 4.0)
(s714 5.0)
(s715 5.0)
(s716 2.0)
(s718 4.0)
(s719 5.0)
(s720 5.0)
(s721 2.0)
(s723 4.0)
(s724 5.0)
(s725 5.0)
(s726 2.0)
(s728 4.0)
(s729 5.0)
(s730 5.0)
(s731 2.0)
(s733 4.0)
(s734 5.0)
(s735 5.0)
(s736 2.0)
(s738 4.0)
(s739 5.0)
(s740 5.0)
(s741 2.0)
(s743 4.0)
(s744 5.0)
(s745 5.0)
(s746 2.0)
(s748 4.0)
(s749 5.0)
(s750 5.0)
(s751 2.0)
(s753 4.0)
(s754 5.0)
(s755 5.0)
(s756 2.0)
(s758 4.0)
(s759 5.0)
(s760 5.0)
(s761 2.0)
(s763 4.0)
(s764 5.0)
(s765 5.0)
(s766 2.0)
(s768 4.0)
(s769 5.0)
(s770 5.0)
(s771 2.0)
(s773 4.0)
(s774 5.0)
(s775 5.0)
(s776 2.0)
(s778 4.0)
(s779 5.0)
(s780 5.0)
(s781 2.0)
(s783 4.0)
(s784 5.0)
(s785 5.0)
(s786 2.0)
(s788 4.0)
(s789 5.0)
(s790 5.0)
(s791 2.0)
(s793 4.0)
(s794 5.0)
(s795 5.0)
(s796 2.0)
(s798 4.0)
(s799 5.0)
(s800 5.0)
(s801 2.0)
(s803 4.0)
(s804 5.0)
(s805 5.0)
(s806 2.0)
(s808 4.0)
(s809 5.0)
(s810 5.0)
(s811 2.0)
(s813 4.0)
(s814 5.0)
(s815 5.0)
(s816 2.0)
(s818 4.0)
(s819 5.0)
(s820 5.0)
(s821 2.0)
(s823 4.0)
(s824 5.0)
(s825 5.0)
(s826 2.0)
(s828 4.0)
(s829 5.0)
(s830 5.0)
(s831 2.0)
(s833 4.0)
(s834 5.0)
(s835 5.0)
(s836 2.0)
(s838 4.0)
(s839 5.0)
(s840 5.0)
(s841 2.0)
(s843 4.0)
(s844 5.0)
(s845 5.0)
(s846 2.0)
(s848 4.0)
(s849 5.0)
(s850 5.0)
(s851 2.0)
(s853 4.0)
(s854 5.0)
(s855 5.0)
(s856 2.0)
(s858 4.0)
(s859 5.0)
(s860 5.0)
(s861 2.0)
(s863 4.0)
(s864 5.0)
(s865 5.0)
(s866 2.0)
(s868 4.0)
(s869 5.0)
(s870 5.0)
(s871 2.0)
(s873 4.0)
(s874 5.0)
(s875 5.0)
(s876 2.0)
(s878 4.0)
(s879 5.0)
(s880 5.0)
(s881 2.0)
(s883 4.0)
(s884 5.0)
(s885 5.0)
(s886 2.0)
(s888 4.0)
(s889 5.0)
(s890 5.0)
(s891 2.0)
(s893 4.0)
(s894 5.0)
(s895 5.0)
(s896 2.0)
(s898 4.0)
(s899 5.0)
(s900 5.0)
(s901 2.0)
(s903 4.0)
(s904 5.0)
(s905 5.0)
(s906 2.0)
(s908 4.0)
(s909 5.0)
(s910 5.0)
(s911 2.0)
(s913 4.0)
(s914 5.0)
(s915 5.0)
(s916 2.0)
(s918 4.0)
(s919 5.0)
(s920 5.0)
(s921 2.0)
(s923 4.0)
(s924 5.0)
(s925 5.0)
(s926 2.0)
(s928 4.0)
(s929 5.0)
(s930 5.0)
(s931 2.0)
(s933 4.0)
(s934 5.0)
(s935 5.0)
(s936 2.0)
(s938 4.0)
(s939 5.0)
(s940 5.0)
(s941 2.0)
(s943 4.0)
(s944 5.0)
(s945 5.0)
(s946 2.0)
(s948 4.0)
(s949 5.0)
(s950 5.0)
(s951 2.0)
(s953 4.0)
(s954 5.0)
(s955 5.0)
(s956 2.0)
(s958 4.0)
(s959 5.0)
(s960 5.0)
(s961 2.0)
(s963 4.0)
(s964 5.0)
(s965 5.0)
(s966 2.0)
(s968 4.0)
(s969 5.0)
(s970 5.0)
(s971 2.0)
(s973 4.0)
(s974 5.0)
(s975 5.0)
(s976 2.0)
(s978 4.0)
(s979 5.0)
(s980 5.0)
(s981 2.0)
(s983 4.0)
(s984 5.0)
(s985 5.0)
(s986 2.0)
(s988 4.0)
(s989 5.0)
(s990 5.0)
(s991 2.0)
(s993 4.0)
(s994 5.0)
(s995 5.0)
(s996 2.0)
(s998 4.0)
(s999 5.0)
(s1000 5.0)
(s1001 2.0)
(s1003 4.0)
(s1004 5.0)
(s1005 5.0)
(s1006 2.0)
(s1008 4.0)
(s1009 5.0)
(s1010 5.0)
(s1011 2.0)
(s1013 4.0)
(s1014 5.0)
(s1015 5.0)
(s1016 2.0)
(s1018 4.0)
(s1019 5.0)
(s1020 5.0)
(s1021 2.0)
(s1023 4.0)
(s1024 5.0)
(s1025 5.0)
(s1026 2.0)
(s1028 4.0)
(s1029 5.0)
(s1030 5.0)
(s1031 2.0)
(s1033 4.0)
(s1034 5.0)
(s1035 5.0)
(s1036 2.0)
(s1038 4.0)
(s1039 5.0)
(s1040 5.0)
(s1041 2.0)
(s1043 4.0)
(s1044 5.0)
(s1045 5.0)
(s1046 2.0)
(s1048 4.0)
(s1049 5.0)
(s1050 5.0)
(s1051 2.0)
(s1053 4.0)
(s1054 5.0)
(s1055 5.0)
(s1056 2.0)
(s1058 4.0)
(s1059 5.0)
(s1060 5.0)
(s1061 2.0)
(s1063 4.0)
(s1064 5.0)
(s1065 5.0)
(s1066 2.0)
(s1068 4.0)
(s1069 5.0)
(s1070 5.0)
(s1071 2.0)
(s1073 4.0)
(s1074 5.0)
(s1075 5.0)
(s1076 2.0)
(s1078 4.0)
(s1079 5.0)
(s1080 5.0)
(s1081 2.0)
(s1083 4.0)
(s1084 5.0)
(s1085 5.0)
(s1086 2.0)
(s1088 4.0)
(s1089 5.0)
(s1090 5.0)
(s1091 2.0)
(s1093 4.0)
(s1094 5.0)
(s1095 5.0)
(s1096 2.0)
(s1098 4.0)
(s1099 5.0)
(s1100 5.0)
(s1101 2.0)
(s1103 4.0)
(s1104 5.0)
(s1105 5.0)
(s1106 2.0)
(s1108 4.0)
(s1109 5.0)
(s1110 5.0)
(s1111 2.0)
(s1113 4.0)
(s1114 5.0)
(s1115 5.0)
(s1116 2.0)
(s1118 4.0)
(s1119 5.0)
(s1120 5.0)
(s1121 2.0)
(s1123 4.0)
(s1124 5.0)
(s1125 5.0)
(s1126 2.0)
(s1128 4.0)
(s1129 5.0)
(s1130 5.0)
(s1131 2.0)
(s1133 4.0)
(s1134 5.0)
(s1135 5.0)
(s1136 2.0)
(s1138 4.0)
(s1139 5.0)
(s1140 5.0)
(s1141 2.0)
(s1143 4.0)
(s1144 5.0)
(s1145 5.0)
(s1146 2.0)
(s1148 4.0)
(s1149 5.0)
(s1150 5.0)
(s1151 2.0)
(s1153 4.0)
(s1154 5.0)
(s1155 5.0)
(s1156 2.0)
(s1158 4.0)
(s1159 5.0)
(s1160 5.0)
(s1161 2.0)
(s1163 4.0)
(s1164 5.0)
(s1165 5.0)
(s1166 2.0)
(s1168 4.0)
(s1169 5.0)
(s1170 5.0)
(s1171 2.0)
(s1173 4.0)
(s1174 5.0)
(s1175 5.0)
(s1176 2.0)
(s1178 4.0)
(s1179 5.0)
(s1180 5.0)
(s1181 2.0)
(s1183 4.0)
(s1184 5.0)
(s1185 5.0)
(s1186 2.0)
(s1188 4.0)
(s1189 5.0)
(s1190 5.0)
(s1191 2.0)
(s1193 4.0)
(s1194 5.0)
(s1195 5.0)
(s1196 2.0)
(s1198 4.0)
(s1199 5.0)
(s1200 5.0)
(s1201 2.0)
(s1203 4.0)
(s1204 5.0)
(s1205 5.0)
(s1206 2.0)
(s1208 4.0)
(s1209 5.0)
(s1210 5.0)
(s1211 2.0)
(s1213 4.0)
(s1214 5.0)
(s1215 5.0)
(s1216 2.0)
(s1218 4.0)
(s1219 5.0)
(s1220 5.0)
(s1221 2.0)
(s1223 4.0)
(s1224 5.0)
(s1225 5.0)
(s1226 2.0)
(s1228 4.0)
(s1229 5.0)
(s1230 5.0)
(s1231 2.0)
(s1233 4.0)
(s1234 5.0)
(s1235 5.0)
(s1236 2.0)
(s1238 4.0)
(s1239 5.0)
(s1240 5.0)
(s1241 2.0)
(s1243 4.0)
(s1244 5.0)
(s1245 5.0)
(s1246 2.0)
(s1248 4.0)
(s1249 5.0)
(s1250 5.0)
(s1251 2.0)
(s1253 4.0)
(s1254 5.0)
(s1255 5.0)
(s1256 2.0)
(s1258 4.0)
(s1259 5.0)
(s1260 5.0)
(s1261 2.0)
(s1263 4.0)
(s1264 5.0)
(s1265 5.0)
(s1266 2.0)
(s1268 4.0)
(s1269 5.0)
(s1270 5.0)
(s1271 2.0)
(s1273 4.0)
(s1274 5.0)
(s1275 5.0)
(s1276 2.0)
(s1278 4.0)
(s1279 5.0)
(s1280 5.0)
(s1281 2.0)
(s1283 4.0)
(s1284 5.0)
(s1285 5.0)
(s1286 2.0)
(s1288 4.0)
(s1289 5.0)
(s1290 5.0)
(s1291 2.0)
(s1293 4.0)
(s1294 5.0)
(s1295 5.0)
(s1296 2.0)
(s1298 4.0)
(s1299 5.0)
(s1300 5.0)
(s1301 2.0)
(s1303 4.0)
(s1304 5.0)
(s1305 5.0)
(s1306 2.0)
(s1308 4.0)
(s1309 5.0)
(s1310 5.0)
(s1311 2.0)
(s1313 4.0)
(s1314 5.0)
(s1315 5.0)
(s1316 2.0)
(s1318 4.0)
(s1319 5.0)
(s1320 5.0)
(s1321 2.0)
(s1323 4.0)
(s1324 5.0)
(s1325 5.0)
(s1326 2.0)
(s1328 4.0)
(s1329 5.0)
(s1330 5.0)
(s1331 2.0)
(s1333 4.0)
(s1334 5.0)
(s1335 5.0)
(s1336 2.0)
(s1338 4.0)
(s1339 5.0)
(s1340 5.0)
(s1341 2.0)
(s1343 4.0)
(s1344 5.0)
(s1345 5.0)
(s1346 2.0)
(s1348 4.0)
(s1349 5.0)
(s1350 5.0)
(s1351 2.0)
(s1353 4.0)
(s1354 5.0)
(s1355 5.0)
(s1356 2.0)
(s1358 4.0)
(s1359 5.0)
(s1360 5.0)
(s1361 2.0)
(s1363 4.0)
(s1364 5.0)
(s1365 5.0)
(s1366 2.0)
(s1368 4.0)
(s1369 5.0)
(s1370 5.0)
(s1371 2.0)
(s1373 4.0)
(s1374 5.0)
(s1375 5.0)
(s1376 2.0)
(s1378 4.0)
(s1379 5.0)
(s1380 5.0)
(s1381 2.0)
(s1383 4.0)
(s1384 5.0)
(s1385 5.0)
(s1386 2.0)
(s1388 4.0)
(s1389 5.0)
(s1390 5.0)
(s1391 2.0)
(s1393 4.0)
(s1394 5.0)
(s1395 5.0)
(s1396 2.0)
(s1398 4.0)
(s1399 5.0)
(s1400 5.0)
(s1401 2.0)
(s1403 4.0)
(s1404 5.0)
(s1405 5.0)
(s1406 2.0)
(s1408 4.0)
(s1409 5.0)
(s1410 5.0)
(s1411 2.0)
(s1413 4.0)
(s1414 5.0)
(s1415 5.0)
(s1416 2.0)
(s1418 4.0)
(s1419 5.0)
(s1420 5.0)
(s1421 2.0)
(s1423 4.0)
(s1424 5.0)
(s1425 5.0)
(s1426 2.0)
(s1428 4.0)
(s1429 5.0)
(s1430 5.0)
(s1431 2.0)
(s1433 4.0)
(s1434 5.0)
(s1435 5.0)
(s1436 2.0)
(s1438 4.0)
(s1439 5.0)
(s1440 5.0)
(s1441 2.0)
(s1443 4.0)
(s1444 5.0)
(s1445 5.0)
(s1446 2.0)
(s1448 4.0)
(s1449 5.0)
(s1450 5.0)
(s1451 2.0)
(s1453 4.0)
(s1454 5.0)
(s1455 5.0)
(s1456 2.0)
(s1458 4.0)
(s1459 5.0)
(s1460 5.0)
(s1461 2.0)
(s1463 4.0)
(s1464 5.0)
(s1465 5.0)
(s1466 2.0)
(s1468 4.0)
(s1469 5.0)
(s1470 5.0)
(s1471 2.0)
(s1473 4.0)
(s1474 5.0)
(s1475 5.0)
(s1476 2.0)
(s1478 4.0)
(s1479 5.0)
(s1480 5.0)
(s1481 2.0)
(s1483 4.0)
(s1484 5.0)
(s1485 5.0)
(s1486 2.0)
(s1488 4.0)
(s1489 5.0)
(s1490 5.0)
(s1491 2.0)
(s1493 4.0)
(s1494 5.0)
(s1495 5.0)
(s1496 2.0)
(s1498 4.0)
(s1499 5.0)
(s1500 5.0)
(s1501 2.0)
(s1503 4.0)
(s1504 5.0)
(s1505 5.0)
(s1506 2.0)
(s1508 4.0)
(s1509 5.0)
(s1510 5.0)
(s1511 2.0)
(s1513 4.0)
(s1514 5.0)
(s1515 5.0)
(s1516 2.0)
(s1518 4.0)
(s1519 5.0)
(s1520 5.0)
(s1521 2.0)
(s1523 4.0)
(s1524 5.0)
(s1525 5.0)
(s1526 2.0)
(s1528 4.0)
(s1529 5.0)
(s1530 5.0)
(s1531 2.0)
(s1533 4.0)
(s1534 5.0)
(s1535 5.0)
(s1536 2.0)
(s1538 4.0)
(s1539 5.0)
(s1540 5.0)
(s1541 2.0)
(s1543 4.0)
(s1544 5.0)
(s1545 5.0)
(s1546 2.0)
(s1548 4.0)
(s1549 5.0)
(s1550 5.0)
(s1551 2.0)
(s1553 4.0)
(s1554 5.0)
(s1555 5.0)
(s1556 2.0)
(s1558 4.0)
(s1559 5.0)
(s1560 5.0)
(s1561 2.0)
(s1563 4.0)
(s1564 5.0)
(s1565 5.0)
(s1566 2.0)
(s1568 4.0)
(s1569 5.0)
(s1570 5.0)
(s1571 2.0)
(s1573 4.0)
(s1574 5.0)
(s1575 5.0)
(s1576 2.0)
(s1578 4.0)
(s1579 5.0)
(s1580 5.0)
(s1581 2.0)
(s1583 4.0)
(s1584 5.0)
(s1585 5.0)
(s1586 2.0)
(s1588 4.0)
(s1589 5.0)
(s1590 5.0)
(s1591 2.0)
(s1593 4.0)
(s1594 5.0)
(s1595 5.0)
(s1596 2.0)
(s1598 4.0)
(s1599 5.0)
(s1600 5.0)
(s1601 2.0)
(s1603 4.0)
(s1604 5.0)
(s1605 5.0)
(s1606 2.0)
(s1608 4.0)
(s1609 5.0)
(s1610 5.0)
(s1611 2.0)
(s1613 4.0)
(s1614 5.0)
(s1615 5.0)
(s1616 2.0)
(s1618 4.0)
(s1619 5.0)
(s1620 5.0)
(s1621 2.0)
(s1623 4.0)
(s1624 5.0)
(s1625 5.0)
(s1626 2.0)
(s1628 4.0)
(s1629 5.0)
(s1630 5.0)
(s1631 2.0)
(s1633 4.0)
(s1634 5.0)
(s1635 5.0)
(s1636 2.0)
(s1638 4.0)
(s1639 5.0)
(s1640 5.0)
(s1641 2.0)
(s1643 4.0)
(s1644 5.0)
(s1645 5.0)
(s1646 2.0)
(s1648 4.0)
(s1649 5.0)
(s1650 5.0)
(s1651 2.0)
(s1653 4.0)
(s1654 5.0)
(s1655 5.0)
(s1656 2.0)
(s1658 4.0)
(s1659 5.0)
(s1660 5.0)
(s1661 2.0)
(s1663 4.0)
(s1664 5.0)
(s1665 5.0)
(s1666 2.0)
(s1668 4.0)
(s1669 5.0)
(s1670 5.0)
(s1671 2.0)
(s1673 4.0)
(s1674 5.0)
(s1675 5.0)
(s1676 2.0)
(s1678 4.0)
(s1679 5.0)
(s1680 5.0)
(s1681 2.0)
(s1683 4.0)
(s1684 5.0)
(s1685 5.0)
(s1686 2.0)
(s1688 4.0)
(s1689 5.0)
(s1690 5.0)
(s1691 2.0)
(s1693 4.0)
(s1694 5.0)
(s1695 5.0)
(s1696 2.0)
(s1698 4.0)
(s1699 5.0)
(s1700 5.0)
(s1701 2.0)
(s1703 4.0)
(s1704 5.0)
(s1705 5.0)
(s1706 2.0)
(s1708 4.0)
(s1709 5.0)
(s1710 5.0)
(s1711 2.0)
(s1713 4.0)
(s1714 5.0)
(s1715 5.0)
(s1716 2.0)
(s1718 4.0)
(s1719 5.0)
(s1720 5.0)
(s1721 2.0)
(s1723 4.0)
(s1724 5.0)
(s1725 5.0)
(s1726 2.0)
(s1728 4.0)
(s1729 5.0)
(s1730 5.0)
(s1731 2.0)
(s1733 4.0)
(s1734 5.0)
(s1735 5.0)
(s1736 2.0)
(s1738 4.0)
(s1739 5.0)
(s1740 5.0)
(s1741 2.0)
(s1743 4.0)
(s1744 5.0)
(s1745 5.0)
(s1746 2.0)
(s1748 4.0)
(s1749 5.0)
(s1750 5.0)
(s1751 2.0)
(s1753 4.0)
(s1754 5.0)
(s1755 5.0)
(s1756 2.0)
(s1758 4.0)
(s1759 5.0)
(s1760 5.0)
(s1761 2.0)
(s1763 4.0)
(s1764 5.0)
(s1765 5.0)
(s1766 2.0)
(s1768 4.0)
(s1769 5.0)
(s1770 5.0)
(s1771 2.0)
(s1773 4.0)
(s1774 5.0)
(s1775 5.0)
(s1776 2.0)
(s1778 4.0)
(s1779 5.0)
(s1780 5.0)
(s1781 2.0)
(s1783 4.0)
(s1784 5.0)
(s1785 5.0)
(s1786 2.0)
(s1788 4.0)
(s1789 5.0)
(s1790 5.0)
(s1791 2.0)
(s1793 4.0)
(s1794 5.0)
(s1795 5.0)
(s1796 2.0)
(s1798 4.0)
(s1799 5.0)
(s1800 5.0)
(s1801 2.0)
(s1803 4.0)
(s1804 5.0)
(s1805 5.0)
(s1806 2.0)
(s1808 4.0)
(s1809 5.0)
(s1810 5.0)
(s1811 2.0)
(s1813 4.0)
(s1814 5.0)
(s1815 5.0)
(s1816 2.0)
(s1818 4.0)
(s1819 5.0)
(s1820 5.0)
(s1821 2.0)
(s1823 4.0)
(s1824 5.0)
(s1825 5.0)
(s1826 2.0)
(s1828 4.0)
(s1829 5.0)
(s1830 5.0)
(s1831 2.0)
(s1833 4.0)
(s1834 5.0)
(s1835 5.0)
(s1836 2.0)
(s1838 4.0)
(s1839 5.0)
(s1840 5.0)
(s1841 2.0)
(s1843 4.0)
(s1844 5.0)
(s1845 5.0)
(s1846 2.0)
(s1848 4.0)
(s1849 5.0)
(s1850 5.0)
(s1851 2.0)
(s1853 4.0)
(s1854 5.0)
(s1855 5.0)
(s1856 2.0)
(s1858 4.0)
(s1859 5.0)
(s1860 5.0)
(s1861 2.0)
(s1863 4.0)
(s1864 5.0)
(s1865 5.0)
(s1866 2.0)
(s1868 4.0)
(s1869 5.0)
(s1870 5.0)
(s1871 2.0)
(s1873 4.0)
(s1874 5.0)
(s1875 5.0)
(s1876 2.0)
(s1878 4.0)
(s1879 5.0)
(s1880 5.0)
(s1881 2.0)
(s1883 4.0)
(s1884 5.0)
(s1885 5.0)
(s1886 2.0)
(s1888 4.0)
(s1889 5.0)
(s1890 5.0)
(s1891 2.0)
(s1893 4.0)
(s1894 5.0)
(s1895 5.0)
(s1896 2.0)
(s1898 4.0)
(s1899 5.0)
(s1900 5.0)
(s1901 2.0)
(s1903 4.0)
(s1904 5.0)
(s1905 5.0)
(s1906 2.0)
(s1908 4.0)
(s1909 5.0)
(s1910 5.0)
(s1911 2.0)
(s1913 4.0)
(s1914 5.0)
(s1915 5.0)
(s1916 2.0)
(s1918 4.0)
(s1919 5.0)
(s1920 5.0)
(s1921 2.0)
(s1923 4.0)
(s1924 5.0)
(s1925 5.0)
(s1926 2.0)
(s1928 4.0)
(s1929 5.0)
(s1930 5.0)
(s1931 2.0)
(s1933 4.0)
(s1934 5.0)
(s1935 5.0)
(s1936 2.0)
(s1938 4.0)
(s1939 5.0)
(s1940 5.0)
(s1941 2.0)
(s1943 4.0)
(s1944 5.0)
(s1945 5.0)
(s1946 2.0)
(s1948 4.0)
(s1949 5.0)
(s1950 5.0)
(s1951 2.0)
(s1953 4.0)
(s1954 5.0)
(s1955 5.0)
(s1956 2.0)
(s1958 4.0)
(s1959 5.0)
(s1960 5.0)
(s1961 2.0)
(s1963 4.0)
(s1964 5.0)
(s1965 5.0)
(s1966 2.0)
(s1968 4.0)
(s1969 5.0)
(s1970 5.0)
(s1971 2.0)
(s1973 4.0)
(s1974 5.0)
(s1975 5.0)
(s1976 2.0)
(s1978 4.0)
(s1979 5.0)
(s1980 5.0)
(s1981 2.0)
(s1983 4.0)
(s1984 5.0)
(s1985 5.0)
(s1986 2.0)
(s1988 4.0)
(s1989 5.0)
(s1990 5.0)
(s1991 2.0)
(s1993 4.0)
(s1994 5.0)
(s1995 5.0)
(s1996 2.0)
(s1998 4.0)
(s1999 5.0)
(s2000 5.0)
(s2001 2.0)
(s2003 4.0)
(s2004 5.0)
(s2005 5.0)
(s2006 2.0)
(s2008 4.0)
(s2009 5.0)
(s2010 5.0)
(s2011 2.0)
(s2013 4.0)
(s2014 5.0)
(s2015 5.0)
(s2016 2.0)
(s2018 4.0)
(s2019 5.0)
(s2020 5.0)
(s2021 2.0)
(s2023 4.0)
(s2024 5.0)
(s2025 5.0)
(s2026 2.0)
(s2028 4.0)
(s2029 5.0)
(s2030 5.0)
(s2031 2.0)
(s2033 4.0)
(s2034 5.0)
(s2035 5.0)
(s2036 2.0)
(s2038 4.0)
(s2039 5.0)
(s2040 5.0)
(s2041 2.0)
(s2043 4.0)
(s2044 5.0)
(s2045 5.0)
(s2046 2.0)
(s2048 4.0)
(s2049 5.0)
(s2050 5.0)
(s2051 2.0)
(s2053 4.0)
(s2054 5.0)
(s2055 5.0)
(s2056 2.0)
(s2058 4.0)
(s2059 5.0)
(s2060 5.0)
(s2061 2.0)
(s2063 4.0)
(s2064 5.0)
(s2065 5.0)
(s2066 2.0)
(s2068 4.0)
(s2069 5.0)
(s2070 5.0)
(s2071 2.0)
(s2073 4.0)
(s2074 5.0)
(s2075 5.0)
(s2076 2.0)
(s2078 4.0)
(s2079 5.0)
(s2080 5.0)
(s2081 2.0)
(s2083 4.0)
(s2084 5.0)
(s2085 5.0)
(s2086 2.0)
(s2088 4.0)
(s2089 5.0)
(s2090 5.0)
(s2091 2.0)
(s2093 4.0)
(s2094 5.0)
(s2095 5.0)
(s2096 2.0)
(s2098 4.0)
(s2099 5.0)
(s2100 5.0)
(s2101 2.0)
(s2103 4.0)
(s2104 5.0)
(s2105 5.0)
(s2106 2.0)
(s2108 4.0)
(s2109 5.0)
(s2110 5.0)
(s2111 2.0)
(s2113 4.0)
(s2114 5.0)
(s2115 5.0)
(s2116 2.0)
(s2118 4.0)
(s2119 5.0)
(s2120 5.0)
(s2121 2.0)
(s2123 4.0)
(s2124 5.0)
(s2125 5.0)
(s2126 2.0)
(s2128 4.0)
(s2129 5.0)
(s2130 5.0)
(s2131 2.0)
(s2133 4.0)
(s2134 5.0)
(s2135 5.0)
(s2136 2.0)
(s2138 4.0)
(s2139 5.0)
(s2140 5.0)
(s2141 2.0)
(s2143 4.0)
(s2144 5.0)
(s2145 5.0)
(s2146 2.0)
(s2148 4.0)
(s2149 5.0)
(s2150 5.0)
(s2151 2.0)
(s2153 4.0)
(s2154 5.0)
(s2155 5.0)
(s2156 2.0)
(s2158 4.0)
(s2159 5.0)
(s2160 5.0)
(s2161 2.0)
(s2163 4.0)
(s2164 5.0)
(s2165 5.0)
(s2166 2.0)
(s2168 4.0)
(s2169 5.0)
(s2170 5.0)
(s2171 2.0)
(s2173 4.0)
(s2174 5.0)
(s2175 5.0)
(s2176 2.0)
(s2178 4.0)
(s2179 5.0)
(s2180 5.0)
(s2181 2.0)
(s2183 4.0)
(s2184 5.0)
(s2185 5.0)
(s2186 2.0)
(s2188 4.0)
(s2189 5.0)
(s2190 5.0)
(s2191 2.0)
(s2193 4.0)
(s2194 5.0)
(s2195 5.0)
(s2196 2.0)
(s2198 4.0)
(s2199 5.0)
(s2200 5.0)
(s2201 2.0)
(s2203 4.0)
(s2204 5.0)
(s2205 5.0)
(s2206 2.0)
(s2208 4.0)
(s2209 5.0)
(s2210 5.0)
(s2211 2.0)
(s2213 4.0)
(s2214 5.0)
(s2215 5.0)
(s2216 2.0)
(s2218 4.0)
(s2219 5.0)
(s2220 5.0)
(s2221 2.0)
(s2223 4.0)
(s2224 5.0)
(s2225 5.0)
(s2226 2.0)
(s2228 4.0)
(s2229 5.0)
(s2230 5.0)
(s2231 2.0)
(s2233 4.0)
(s2234 5.0)
(s2235 5.0)
(s2236 2.0)
(s2238 4.0)
(s2239 5.0)
(s2240 5.0)
(s2241 2.0)
(s2243 4.0)
(s2244 5.0)
(s2245 5.0)
(s2246 2.0)
(s2248 4.0)
(s2249 5.0)
(s2250 5.0)
(s2251 2.0)
(s2253 4.0)
(s2254 5.0)
(s2255 5.0)
(s2256 2.0)
(s2258 4.0)
(s2259 5.0)
(s2260 5.0)
(s2261 2.0)
(s2263 4.0)
(s2264 5.0)
(s2265 5.0)
(s2266 2.0)
(s2268 4.0)
(s2269 5.0)
(s2270 5.0)
(s2271 2.0)
(s2273 4.0)
(s2274 5.0)
(s2275 5.0)
(s2276 2.0)
(s2278 4.0)
(s2279 5.0)
(s2280 5.0)
(s2281 2.0)
(s2283 4.0)
(s2284 5.0)
(s2285 5.0)
(s2286 2.0)
(s2288 4.0)
(s2289 5.0)
(s2290 5.0)
(s2291 2.0)
(s2293 4.0)
(s2294 5.0)
(s2295 5.0)
(s2296 2.0)
(s2298 4.0)
(s2299 5.0)
(s2300 5.0)
(s2301 2.0)
(s2303 4.0)
(s2304 5.0)
(s2305 5.0)
(s2306 2.0)
(s2308 4.0)
(s2309 5.0)
(s2310 5.0)
(s2311 2.0)
(s2313 4.0)
(s2314 5.0)
(s2315 5.0)
(s2316 2.0)
(s2318 4.0)
(s2319 5.0)
(s2320 5.0)
(s2321 2.0)
(s2323 4.0)
(s2324 5.0)
(s2325 5.0)
(s2326 2.0)
(s2328 4.0)
(s2329 5.0)
(s2330 5.0)
(s2331 2.0)
(s2333 4.0)
(s2334 5.0)
(s2335 5.0)
(s2336 2.0)
(s2338 4.0)
(s2339 5.0)
(s2340 5.0)
(s2341 2.0)
(s2343 4.0)
(s2344 5.0)
(s2345 5.0)
(s2346 2.0)
(s2348 4.0)
(s2349 5.0)
(s2350 5.0)
(s2351 2.0)
(s2353 4.0)
(s2354 5.0)
(s2355 5.0)
(s2356 2.0)
(s2358 4.0)
(s2359 5.0)
(s2360 5.0)
(s2361 2.0)
(s2363 4.0)
(s2364 5.0)
(s2365 5.0)
(s2366 2.0)
(s2368 4.0)
(s2369 5.0)
(s2370 5.0)
(s2371 2.0)
(s2373 4.0)
(s2374 5.0)
(s2375 5.0)
(s2376 2.0)
(s2378 4.0)
(s2379 5.0)
(s2380 5.0)
(s2381 2.0)
(s2383 4.0)
(s2384 5.0)
(s2385 5.0)
(s2386 2.0)
(s2388 4.0)
(s2389 5.0)
(s2390 5.0)
(s2391 2.0)
(s2393 4.0)
(s2394 5.0)
(s2395 5.0)
(s2396 2.0)
(s2398 4.0)
(s2399 5.0)
(s2400 5.0)
(s2401 2.0)
(s2403 4.0)
(s2404 5.0)
(s2405 5.0)
(s2406 2.0)
(s2408 4.0)
(s2409 5.0)
(s2410 5.0)
(s2411 2.0)
(s2413 4.0)
(s2414 5.0)
(s2415 5.0)
(s2416 2.0)
(s2418 4.0)
(s2419 5.0)
(s2420 5.0)
(s2421 2.0)
(s2423 4.0)
(s2424 5.0)
(s2425 5.0)
(s2426 2.0)
(s2428 4.0)
(s2429 5.0)
(s2430 5.0)
(s2431 2.0)
(s2433 4.0)
(s2434 5.0)
(s2435 5.0)
(s2436 2.0)
(s2438 4.0)
(s2439 5.0)
(s2440 5.0)
(s2441 2.0)
(s2443 4.0)
(s2444 5.0)
(s2445 5.0)
(s2446 2.0)
(s2448 4.0)
(s2449 5.0)
(s2450 5.0)
(s2451 2.0)
(s2453 4.0)
(s2454 5.0)
(s2455 5.0)
(s2456 2.0)
(s2458 4.0)
(s2459 5.0)
(s2460 5.0)
(s2461 2.0)
(s2463 4.0)
(s2464 5.0)
(s2465 5.0)
(s2466 2.0)
(s2468 4.0)
(s2469 5.0)
(s2470 5.0)
(s2471 2.0)
(s2473 4.0)
(s2474 5.0)
(s2475 5.0)
(s2476 2.0)
(s2478 4.0)
(s2479 5.0)
(s2480 5.0)
(s2481 2.0)
(s2483 4.0)
(s2484 5.0)
(s2485 5.0)
(s2486 2.0)
(s2488 4.0)
(s2489 5.0)
(s2490 5.0)
(s2491 2.0)
(s2493 4.0)
(s2494 5.0)
(s2495 5.0)
(s2496 2.0)
(s2498 4.0)
(s2499 5.0)
(s2500 5.0)
(s2501 2.0)
(s2503 4.0)
(s2504 5.0)
(s2505 5.0)
(s2506 2.0)
(s2508 4.0)
(s2509 5.0)
(s2510 5.0)
(s2511 2.0)
(s2513 4.0)
(s2514 5.0)
(s2515 5.0)
(s2516 2.0)
(s2518 4.0)
(s2519 5.0)
(s2520 5.0)
(s2521 2.0)
(s2523 4.0)
(s2524 5.0)
(s2525 5.0)
(s2526 2.0)
(s2528 4.0)
(s2529 5.0)
(s2530 5.0)
(s2531 2.0)
(s2533 4.0)
(s2534 5.0)
(s2535 5.0)
(s2536 2.0)
(s2538 4.0)
(s2539 5.0)
(s2540 5.0)
(s2541 2.0)
(s2543 4.0)
(s2544 5.0)
(s2545 5.0)
(s2546 2.0)
(s2548 4.0)
(s2549 5.0)
(s2550 5.0)
(s2551 2.0)
(s2553 4.0)
(s2554 5.0)
(s2555 5.0)
(s2556 2.0)
(s2558 4.0)
(s2559 5.0)
(s2560 5.0)
(s2561 2.0)
(s2563 4.0)
(s2564 5.0)
(s2565 5.0)
(s2566 2.0)
(s2568 4.0)
(s2569 5.0)
(s2570 5.0)
(s2571 2.0)
(s2573 4.0)
(s2574 5.0)
(s2575 5.0)
(s2576 2.0)
(s2578 4.0)
(s2579 5.0)
(s2580 5.0)
(s2581 2.0)
(s2583 4.0)
(s2584 5.0)
(s2585 5.0)
(s2586 2.0)
(s2588 4.0)
(s2589 5.0)
(s2590 5.0)
(s2591 2.0)
(s2593 4.0)
(s2594 5.0)
(s2595 5.0)
(s2596 2.0)
(s2598 4.0)
(s2599 5.0)
(s2600 5.0)
(s2601 2.0)
(s2603 4.0)
(s2604 5.0)
(s2605 5.0)
(s2606 2.0)
(s2608 4.0)
(s2609 5.0)
(s2610 5.0)
(s2611 2.0)
(s2613 4.0)
(s2614 5.0)
(s2615 5.0)
(s2616 2.0)
(s2618 4.0)
(s2619 5.0)
(s2620 5.0)
(s2621 2.0)
(s2623 4.0)
(s2624 5.0)
(s2625 5.0)
(s2626 2.0)
(s2628 4.0)
(s2629 5.0)
(s2630 5.0)
(s2631 2.0)
(s2633 4.0)
(s2634 5.0)
(s2635 5.0)
(s2636 2.0)
(s2638 4.0)
(s2639 5.0)
(s2640 5.0)
(s2641 2.0)
(s2643 4.0)
(s2644 5.0)
(s2645 5.0)
(s2646 2.0)
(s2648 4.0)
(s2649 5.0)
(s2650 5.0)
(s2651 2.0)
(s2653 4.0)
(s2654 5.0)
(s2655 5.0)
(s2656 2.0)
(s2658 4.0)
(s2659 5.0)
(s2660 5.0)
(s2661 2.0)
(s2663 4.0)
(s2664 5.0)
(s2665 5.0)
(s2666 2.0)
(s2668 4.0)
(s2669 5.0)
(s2670 5.0)
(s2671 2.0)
(s2673 4.0)
(s2674 5.0)
(s2675 5.0)
(s2676 2.0)
(s2678 4.0)
(s2679 5.0)
(s2680 5.0)
(s2681 2.0)
(s2683 4.0)
(s2684 5.0)
(s2685 5.0)
(s2686 2.0)
(s2688 4.0)
(s2689 5.0)
(s2690 5.0)
(s2691 2.0)
(s2693 4.0)
(s2694 5.0)
(s2695 5.0)
(s2696 2.0)
(s2698 4.0)
(s2699 5.0)
(s2700 5.0)
(s2701 2.0)
(s2703 4.0)
(s2704 5.0)
(s2705 5.0)
(s2706 2.0)
(s2708 4.0)
(s2709 5.0)
(s2710 5.0)
(s2711 2.0)
(s2713 4.0)
(s2714 5.0)
(s2715 5.0)
(s2716 2.0)
(s2718 4.0)
(s2719 5.0)
(s2720 5.0)
(s2721 2.0)
(s2723 4.0)
(s2724 5.0)
(s2725 5.0)
(s2726 2.0)
(s2728 4.0)
(s2729 5.0)
(s2730 5.0)
(s2731 2.0)
(s2733 4.0)
(s2734 5.0)
(s2735 5.0)
(s2736 2.0)
(s2738 4.0)
(s2739 5.0)
(s2740 5.0)
(s2741 2.0)
(s2743 4.0)
(s2744 5.0)
(s2745 5.0)
(s2746 2.0)
(s2748 4.0)
(s2749 5.0)
(s2750 5.0)
(s2751 2.0)
(s2753 4.0)
(s2754 5.0)
(s2755 5.0)
(s2756 2.0)
(s2758 4.0)
(s2759 5.0)
(s2760 5.0)
(s2761 2.0)
(s2763 4.0)
(s2764 5.0)
(s2765 5.0)
(s2766 2.0)
(s2768 4.0)
(s2769 5.0)
(s2770 5.0)
(s2771 2.0)
(s2773 4.0)
(s2774 5.0)
(s2775 5.0)
(s2776 2.0)
(s2778 4.0)
(s2779 5.0)
(s2780 5.0)
(s2781 2.0)
(s2783 4.0)
(s2784 5.0)
(s2785 5.0)
(s2786 2.0)
(s2788 4.0)
(s2789 5.0)
(s2790 5.0)
(s2791 2.0)
(s2793 4.0)
(s2794 5.0)
(s2795 5.0)
(s2796 2.0)
(s2798 4.0)
(s2799 5.0)
(s2800 5.0)
(s2801 2.0)
(s2803 4.0)
(s2804 5.0)
(s2805 5.0)
(s2806 2.0)
(s2808 4.0)
(s2809 5.0)
(s2810 5.0)
(s2811 2.0)
(s2813 4.0)
(s2814 5.0)
(s2815 5.0)
(s2816 2.0)
(s2818 4.0)
(s2819 5.0)
(s2820 5.0)
(s2821 2.0)
(s2823 4.0)
(s2824 5.0)
(s2825 5.0)
(s2826 2.0)
(s2828 4.0)
(s2829 5.0)
(s2830 5.0)
(s2831 2.0)
(s2833 4.0)
(s2834 5.0)
(s2835 5.0)
(s2836 2.0)
(s2838 4.0)
(s2839 5.0)
(s2840 5.0)
(s2841 2.0)
(s2843 4.0)
(s2844 5.0)
(s2845 5.0)
(s2846 2.0)
(s2848 4.0)
(s2849 5.0)
(s2850 5.0)
(s2851 2.0)
(s2853 4.0)
(s2854 5.0)
(s2855 5.0)
(s2856 2.0)
(s2858 4.0)
(s2859 5.0)
(s2860 5.0)
(s2861 2.0)
(s2863 4.0)
(s2864 5.0)
(s2865 5.0)
(s2866 2.0)
(s2868 4.0)
(s2869 5.0)
(s2870 5.0)
(s2871 2.0)
(s2873 4.0)
(s2874 5.0)
(s2875 5.0)
(s2876 2.0)
(s2878 4.0)
(s2879 5.0)
(s2880 5.0)
(s2881 2.0)
(s2883 4.0)
(s2884 5.0)
(s2885 5.0)
(s2886 2.0)
(s2888 4.0)
(s2889 5.0)
(s2890 5.0)
(s2891 2.0)
(s2893 4.0)
(s2894 5.0)
(s2895 5.0)
(s2896 2.0)
(s2898 4.0)
(s2899 5.0)
(s2900 5.0)
(s2901 2.0)
(s2903 4.0)
(s2904 5.0)
(s2905 5.0)
(s2906 2.0)
(s2908 4.0)
(s2909 5.0)
(s2910 5.0)
(s2911 2.0)
(s2913 4.0)
(s2914 5.0)
(s2915 5.0)
(s2916 2.0)
(s2918 4.0)
(s2919 5.0)
(s2920 5.0)
(s2921 2.0)
(s2923 4.0)
(s2924 5.0)
(s2925 5.0)
(s2926 2.0)
(s2928 4.0)
(s2929 5.0)
(s2930 5.0)
(s2931 2.0)
(s2933 4.0)
(s2934 5.0)
(s2935 5.0)
(s2936 2.0)
(s2938 4.0)
(s2939 5.0)
(s2940 5.0)
(s2941 2.0)
(s2943 4.0)
(s2944 5.0)
(s2945 5.0)
(s2946 2.0)
(s2948 4.0)
(s2949 5.0)
(s2950 5.0)
(s2951 2.0)
(s2953 4.0)
(s2954 5.0)
(s2955 5.0)
(s2956 2.0)
(s2958 4.0)
(s2959 5.0)
(s2960 5.0)
(s2961 2.0)
(s2963 4.0)
(s2964 5.0)
(s2965 5.0)
(s2966 2.0)
(s2968 4.0)
(s2969 5.0)
(s2970 5.0)
(s2971 2.0)
(s2973 4.0)
(s2974 5.0)
(s2975 5.0)
(s2976 2.0)
(s2978 4.0)
(s2979 5.0)
(s2980 5.0)
(s2981 2.0)
(s2983 4.0)
(s2984 5.0)
(s2985 5.0)
(s2986 2.0)
(s2988 4.0)
(s2989 5.0)
(s2990 5.0)
(s2991 2.0)
(s2993 4.0)
(s2994 5.0)
(s2995 5.0)
(s2996 2.0)
(s2998 4.0)
(s2999 5.0)
(s3000 5.0)
(s3001 2.0)
(s3003 4.0)
(s3004 5.0)
(s3005 5.0)
(s3006 2.0)
(s3008 4.0)
(s3009 5.0)
(s3010 5.0)
(s3011 2.0)
(s3013 4.0)
(s3014 5.0)
(s3015 5.0)
(s3016 2.0)
(s3018 4.0)
(s3019 5.0)
(s3020 5.0)
(s3021 2.0)
(s3023 4.0)
(s3024 5.0)
(s3025 5.0)
(s3026 2.0)
(s3028 4.0)
(s3029 5.0)
(s3030 5.0)
(s3031 2.0)
(s3033 4.0)
(s3034 5.0)
(s3035 5.0)
(s3036 2.0)
(s3038 4.0)
(s3039 5.0)
(s3040 5.0)
(s3041 2.0)
(s3043 4.0)
(s3044 5.0)
(s3045 5.0)
(s3046 2.0)
(s3048 4.0)
(s3049 5.0)
(s3050 5.0)
(s3051 2.0)
(s3053 4.0)
(s3054 5.0)
(s3055 5.0)
(s3056 2.0)
(s3058 4.0)
(s3059 5.0)
(s3060 5.0)
(s3061 2.0)
(s3063 4.0)
(s3064 5.0)
(s3065 5.0)
(s3066 2.0)
(s3068 4.0)
(s3069 5.0)
(s3070 5.0)
(s3071 2.0)
(s3073 4.0)
(s3074 5.0)
(s3075 5.0)
(s3076 2.0)
(s3078 4.0)
(s3079 5.0)
(s3080 5.0)
(s3081 2.0)
(s3083 4.0)
(s3084 5.0)
(s3085 5.0)
(s3086 2.0)
(s3088 4.0)
(s3089 5.0)
(s3090 5.0)
(s3091 2.0)
(s3093 4.0)
(s3094 5.0)
(s3095 5.0)
(s3096 2.0)
(s3098 4.0)
(s3099 5.0)
(s3100 5.0)
(s3101 2.0)
(s3103 4.0)
(s3104 5.0)
(s3105 5.0)
(s3106 2.0)
(s3108 4.0)
(s3109 5.0)
(s3110 5.0)
(s3111 2.0)
(s3113 4.0)
(s3114 5.0)
(s3115 5.0)
(s3116 2.0)
(s3118 4.0)
(s3119 5.0)
(s3120 5.0)
(s3121 2.0)
(s3123 4.0)
(s3124 5.0)
(s3125 5.0)
(s3126 2.0)
(s3128 4.0)
(s3129 5.0)
(s3130 5.0)
(s3131 2.0)
(s3133 4.0)
(s3134 5.0)
(s3135 5.0)
(s3136 2.0)
(s3138 4.0)
(s3139 5.0)
(s3140 5.0)
(s3141 2.0)
(s3143 4.0)
(s3144 5.0)
(s3145 5.0)
(s3146 2.0)
(s3148 4.0)
(s3149 5.0)
(s3150 5.0)
(s3151 2.0)
(s3153 4.0)
(s3154 5.0)
(s3155 5.0)
(s3156 2.0)
(s3158 4.0)
(s3159 5.0)
(s3160 5.0)
(s3161 2.0)
(s3163 4.0)
(s3164 5.0)
(s3165 5.0)
(s3166 2.0)
(s3168 4.0)
(s3169 5.0)
(s3170 5.0)
(s3171 2.0)
(s3173 4.0)
(s3174 5.0)
(s3175 5.0)
(s3176 2.0)
(s3178 4.0)
(s3179 5.0)
(s3180 5.0)
(s3181 2.0)
(s3183 4.0)
(s3184 5.0)
(s3185 5.0)
(s3186 2.0)
(s3188 4.0)
(s3189 5.0)
(s3190 5.0)
(s3191 2.0)
(s3193 4.0)
(s3194 5.0)
(s3195 5.0)
(s3196 2.0)
(s3198 4.0)
(s3199 5.0)
(s3200 5.0)
(s3201 2.0)
(s3203 4.0)
(s3204 5.0)
(s3205 5.0)
(s3206 2.0)
(s3208 4.0)
(s3209 5.0)
(s3210 5.0)
(s3211 2.0)
(s3213 4.0)
(s3214 5.0)
(s3215 5.0)
(s3216 2.0)
(s3218 4.0)
(s3219 5.0)
(s3220 5.0)
(s3221 2.0)
(s3223 4.0)
(s3224 5.0)
(s3225 5.0)
(s3226 2.0)
(s3228 4.0)
(s3229 5.0)
(s3230 5.0)
(s3231 2.0)
(s3233 4.0)
(s3234 5.0)
(s3235 5.0)
(s3236 2.0)
(s3238 4.0)
(s3239 5.0)
(s3240 5.0)
(s3241 2.0)
(s3243 4.0)
(s3244 5.0)
(s3245 5.0)
(s3246 2.0)
(s3248 4.0)
(s3249 5.0)
(s3250 5.0)
(s3251 2.0)
(s3253 4.0)
(s3254 5.0)
(s3255 5.0)
(s3256 2.0)
(s3258 4.0)
(s3259 5.0)
(s3260 5.0)
(s3261 2.0)
(s3263 4.0)
(s3264 5.0)
(s3265 5.0)
(s3266 2.0)
(s3268 4.0)
(s3269 5.0)
(s3270 5.0)
(s3271 2.0)
(s3273 4.0)
(s3274 5.0)
(s3275 5.0)
(s3276 2.0)
(s3278 4.0)
(s3279 5.0)
(s3280 5.0)
(s3281 2.0)
(s3283 4.0)
(s3284 5.0)
(s3285 5.0)
(s3286 2.0)
(s3288 4.0)
(s3289 5.0)
(s3290 5.0)
(s3291 2.0)
(s3293 4.0)
(s3294 5.0)
(s3295 5.0)
(s3296 2.0)
(s3298 4.0)
(s3299 5.0)
(s3300 5.0)
(s3301 2.0)
(s3303 4.0)
(s3304 5.0)
(s3305 5.0)
(s3306 2.0)
(s3308 4.0)
(s3309 5.0)
(s3310 5.0)
(s3311 2.0)
(s3313 4.0)
(s3314 5.0)
(s3315 5.0)
(s3316 2.0)
(s3318 4.0)
(s3319 5.0)
(s3320 5.0)
(s3321 2.0)
(s3323 4.0)
(s3324 5.0)
(s3325 5.0)
(s3326 2.0)
(s3328 4.0)
(s3329 5.0)
(s3330 5.0)
(s3331 2.0)
(s3333 4.0)
(s3334 5.0)
(s3335 5.0)
(s3336 2.0)
(s3338 4.0)
(s3339 5.0)
(s3340 5.0)timeout
(s3341 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30128 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 79266ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 79352ms
Finished structural reductions in LTL mode , in 1 iterations and 138902 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:28:18] [INFO ] Flatten gal took : 334 ms
[2024-05-24 10:28:18] [INFO ] Flatten gal took : 343 ms
[2024-05-24 10:28:19] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:28:19] [INFO ] Flatten gal took : 320 ms
[2024-05-24 10:28:20] [INFO ] Flatten gal took : 341 ms
[2024-05-24 10:28:20] [INFO ] Time to serialize gal into /tmp/CTLCardinality18288498252532602354.gal : 54 ms
[2024-05-24 10:28:20] [INFO ] Time to serialize properties into /tmp/CTLCardinality11897436483759795029.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality18288498252532602354.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality11897436483759795029.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...285
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:28:50] [INFO ] Flatten gal took : 327 ms
[2024-05-24 10:28:50] [INFO ] Applying decomposition
[2024-05-24 10:28:50] [INFO ] Flatten gal took : 348 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph11568109420363935381.txt' '-o' '/tmp/graph11568109420363935381.bin' '-w' '/tmp/graph11568109420363935381.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph11568109420363935381.bin' '-l' '-1' '-v' '-w' '/tmp/graph11568109420363935381.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:28:51] [INFO ] Decomposing Gal with order
[2024-05-24 10:28:52] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:28:57] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:28:57] [INFO ] Flatten gal took : 388 ms
[2024-05-24 10:28:57] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 506 ms.
[2024-05-24 10:28:58] [INFO ] Time to serialize gal into /tmp/CTLCardinality3457768756664394356.gal : 64 ms
[2024-05-24 10:28:58] [INFO ] Time to serialize properties into /tmp/CTLCardinality15132565072422225582.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality3457768756664394356.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality15132565072422225582.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 949 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:29:29] [INFO ] Invariant cache hit.
[2024-05-24 10:29:29] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20121 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 59479ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 59587ms
[2024-05-24 10:30:28] [INFO ] Invariant cache hit.
[2024-05-24 10:30:30] [INFO ] Implicit Places using invariants in 2168 ms returned []
Implicit Place search using SMT only with invariants took 2170 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:30:30] [INFO ] Invariant cache hit.
[2024-05-24 10:30:30] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30127 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76227ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76317ms
Finished structural reductions in LTL mode , in 1 iterations and 139053 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:31:47] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:31:47] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:31:48] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:31:48] [INFO ] Flatten gal took : 276 ms
[2024-05-24 10:31:48] [INFO ] Flatten gal took : 293 ms
[2024-05-24 10:31:48] [INFO ] Time to serialize gal into /tmp/CTLCardinality14130182711768605083.gal : 48 ms
[2024-05-24 10:31:48] [INFO ] Time to serialize properties into /tmp/CTLCardinality1383020182612595093.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality14130182711768605083.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality1383020182612595093.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:32:19] [INFO ] Flatten gal took : 283 ms
[2024-05-24 10:32:19] [INFO ] Applying decomposition
[2024-05-24 10:32:19] [INFO ] Flatten gal took : 302 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph17735212008716421591.txt' '-o' '/tmp/graph17735212008716421591.bin' '-w' '/tmp/graph17735212008716421591.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph17735212008716421591.bin' '-l' '-1' '-v' '-w' '/tmp/graph17735212008716421591.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:32:20] [INFO ] Decomposing Gal with order
[2024-05-24 10:32:20] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:32:25] [INFO ] Removed a total of 4 redundant transitions.
[2024-05-24 10:32:25] [INFO ] Flatten gal took : 330 ms
[2024-05-24 10:32:26] [INFO ] Fuse similar labels procedure discarded/fused a total of 8 labels/synchronizations in 488 ms.
[2024-05-24 10:32:26] [INFO ] Time to serialize gal into /tmp/CTLCardinality17283932231346759399.gal : 53 ms
[2024-05-24 10:32:26] [INFO ] Time to serialize properties into /tmp/CTLCardinality3742462106181350350.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality17283932231346759399.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality3742462106181350350.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 928 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:32:57] [INFO ] Invariant cache hit.
[2024-05-24 10:32:57] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20120 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20119 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56325ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56408ms
[2024-05-24 10:33:53] [INFO ] Invariant cache hit.
[2024-05-24 10:33:55] [INFO ] Implicit Places using invariants in 2134 ms returned []
Implicit Place search using SMT only with invariants took 2135 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:33:56] [INFO ] Invariant cache hit.
[2024-05-24 10:33:56] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30115 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 77576ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 77663ms
Finished structural reductions in LTL mode , in 1 iterations and 137161 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:35:13] [INFO ] Flatten gal took : 278 ms
[2024-05-24 10:35:14] [INFO ] Flatten gal took : 290 ms
[2024-05-24 10:35:14] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:35:15] [INFO ] Flatten gal took : 278 ms
[2024-05-24 10:35:15] [INFO ] Flatten gal took : 291 ms
[2024-05-24 10:35:15] [INFO ] Time to serialize gal into /tmp/CTLCardinality2566604300028848129.gal : 47 ms
[2024-05-24 10:35:15] [INFO ] Time to serialize properties into /tmp/CTLCardinality14759783681447024874.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality2566604300028848129.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality14759783681447024874.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:35:45] [INFO ] Flatten gal took : 281 ms
[2024-05-24 10:35:45] [INFO ] Applying decomposition
[2024-05-24 10:35:46] [INFO ] Flatten gal took : 291 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph12723989346099308756.txt' '-o' '/tmp/graph12723989346099308756.bin' '-w' '/tmp/graph12723989346099308756.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph12723989346099308756.bin' '-l' '-1' '-v' '-w' '/tmp/graph12723989346099308756.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:35:46] [INFO ] Decomposing Gal with order
[2024-05-24 10:35:47] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:35:52] [INFO ] Removed a total of 3 redundant transitions.
[2024-05-24 10:35:52] [INFO ] Flatten gal took : 329 ms
[2024-05-24 10:35:52] [INFO ] Fuse similar labels procedure discarded/fused a total of 6 labels/synchronizations in 486 ms.
[2024-05-24 10:35:52] [INFO ] Time to serialize gal into /tmp/CTLCardinality8129778142800895859.gal : 53 ms
[2024-05-24 10:35:52] [INFO ] Time to serialize properties into /tmp/CTLCardinality17602480421420343443.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality8129778142800895859.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality17602480421420343443.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 924 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:36:24] [INFO ] Invariant cache hit.
[2024-05-24 10:36:24] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20125 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56257ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56343ms
[2024-05-24 10:37:20] [INFO ] Invariant cache hit.
[2024-05-24 10:37:22] [INFO ] Implicit Places using invariants in 2132 ms returned []
Implicit Place search using SMT only with invariants took 2135 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:37:22] [INFO ] Invariant cache hit.
[2024-05-24 10:37:22] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30124 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76240ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76325ms
Finished structural reductions in LTL mode , in 1 iterations and 135753 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:38:39] [INFO ] Flatten gal took : 270 ms
[2024-05-24 10:38:39] [INFO ] Flatten gal took : 285 ms
[2024-05-24 10:38:39] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:38:40] [INFO ] Flatten gal took : 274 ms
[2024-05-24 10:38:40] [INFO ] Flatten gal took : 283 ms
[2024-05-24 10:38:40] [INFO ] Time to serialize gal into /tmp/CTLCardinality10607085761546804561.gal : 48 ms
[2024-05-24 10:38:40] [INFO ] Time to serialize properties into /tmp/CTLCardinality9180108984929717154.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality10607085761546804561.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality9180108984929717154.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:39:10] [INFO ] Flatten gal took : 277 ms
[2024-05-24 10:39:10] [INFO ] Applying decomposition
[2024-05-24 10:39:11] [INFO ] Flatten gal took : 288 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph8582611491711328985.txt' '-o' '/tmp/graph8582611491711328985.bin' '-w' '/tmp/graph8582611491711328985.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph8582611491711328985.bin' '-l' '-1' '-v' '-w' '/tmp/graph8582611491711328985.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:39:11] [INFO ] Decomposing Gal with order
[2024-05-24 10:39:12] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:39:16] [INFO ] Removed a total of 1 redundant transitions.
[2024-05-24 10:39:17] [INFO ] Flatten gal took : 332 ms
[2024-05-24 10:39:17] [INFO ] Fuse similar labels procedure discarded/fused a total of 2 labels/synchronizations in 485 ms.
[2024-05-24 10:39:17] [INFO ] Time to serialize gal into /tmp/CTLCardinality8878866661105714967.gal : 54 ms
[2024-05-24 10:39:17] [INFO ] Time to serialize properties into /tmp/CTLCardinality72133014244488035.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality8878866661105714967.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality72133014244488035.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...281
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 954 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:39:48] [INFO ] Invariant cache hit.
[2024-05-24 10:39:48] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20115 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 4)
(s1874 5)
(s1875 5)
(s1876 2)
(s1878 4)
(s1879 5)
(s1880 5)
(s1881 2)
(s1883 4)
(s1884 5)
(s1885 5)
(s1886 2)
(s1888 4)
(s1889 5)
(s1890 5)
(s1891 2)
(s1893 4)
(s1894 5)
(s1895 5)
(s1896 2)
(s1898 4)
(s1899 5)
(s1900 5)
(s1901 2)
(s1903 4)
(s1904 5)
(s1905 5)
(s1906 2)
(s1908 4)
(s1909 5)
(s1910 5)
(s1911 2)
(s1913 4)
(s1914 5)
(s1915 5)
(s1916 2)
(s1918 4)
(s1919 5)
(s1920 5)
(s1921 2)
(s1923 4)
(s1924 5)
(s1925 5)
(s1926 2)
(s1928 4)
(s1929 5)
(s1930 5)
(s1931 2)
(s1933 4)
(s1934 5)
(s1935 5)
(s1936 2)
(s1938 4)
(s1939 5)
(s1940 5)
(s1941 2)
(s1943 4)
(s1944 5)
(s1945 5)
(s1946 2)
(s1948 4)
(s1949 5)
(s1950 5)
(s1951 2)
(s1953 4)
(s1954 5)
(s1955 5)
(s1956 2)
(s1958 4)
(s1959 5)
(s1960 5)
(s1961 2)
(s1963 4)
(s1964 5)
(s1965 5)
(s1966 2)
(s1968 4)
(s1969 5)
(s1970 5)
(s1971 2)
(s1973 4)
(s1974 5)
(s1975 5)
(s1976 2)
(s1978 4)
(s1979 5)
(s1980 5)
(s1981 2)
(s1983 4)
(s1984 5)
(s1985 5)
(s1986 2)
(s1988 4)
(s1989 5)
(s1990 5)
(s1991 2)
(s1993 4)
(s1994 5)
(s1995 5)
(s1996 2)
(s1998 4)
(s1999 5)
(s2000 5)
(s2001 2)
(s2003 4)
(s2004 5)
(s2005 5)
(s2006 2)
(s2008 4)
(s2009 5)
(s2010 5)
(s2011 2)
(s2013 4)
(s2014 5)
(s2015 5)
(s2016 2)
(s2018 4)
(s2019 5)
(s2020 5)
(s2021 2)
(s2023 4)
(s2024 5)
(s2025 5)
(s2026 2)
(s2028 4)
(s2029 5)
(s2030 5)
(s2031 2)
(s2033 4)
(s2034 5)
(s2035 5)
(s2036 2)
(s2038 4)
(s2039 5)
(s2040 5)
(s2041 2)
(s2043 4)
(s2044 5)
(s2045 5)
(s2046 2)
(s2048 4)
(s2049 5)
(s2050 5)
(s2051 2)
(s2053 4)
(s2054 5)
(s2055 5)
(s2056 2)
(s2058 4)
(s2059 5)
(s2060 5)
(s2061 2)
(s2063 4)
(s2064 5)
(s2065 5)
(s2066 2)
(s2068 4)
(s2069 5)
(s2070 5)
(s2071 2)
(s2073 4)
(s2074 5)
(s2075 5)
(s2076 2)
(s2078 4)
(s2079 5)
(s2080 5)
(s2081 2)
(s2083 4)
(s2084 5)
(s2085 5)
(s2086 2)
(s2088 4)
(s2089 5)
(s2090 5)
(s2091 2)
(s2093 4)
(s2094 5)
(s2095 5)
(s2096 2)
(s2098 4)
(s2099 5)
(s2100 5)
(s2101 2)
(s2103 4)
(s2104 5)
(s2105 5)
(s2106 2)
(s2108 4)
(s2109 5)
(s2110 5)
(s2111 2)
(s2113 4)
(s2114 5)
(s2115 5)
(s2116 2)
(s2118 4)
(s2119 5)
(s2120 5)
(s2121 2)
(s2123 4)
(s2124 5)
(s2125 5)
(s2126 2)
(s2128 4)
(s2129 5)
(s2130 5)
(s2131 2)
(s2133 4)
(s2134 5)
(s2135 5)
(s2136 2)
(s2138 4)
(s2139 5)
(s2140 5)
(s2141 2)
(s2143 4)
(s2144 5)
(s2145 5)
(s2146 2)
(s2148 4)
(s2149 5)
(s2150 5)
(s2151 2)
(s2153 4)
(s2154 5)
(s2155 5)
(s2156 2)
(s2158 4)
(s2159 5)
(s2160 5)
(s2161 2)
(s2163 4)
(s2164 5)
(s2165 5)
(s2166 2)
(s2168 4)
(s2169 5)
(s2170 5)
(s2171 2)
(s2173 4)
(s2174 5)
(s2175 5)
(s2176 2)
(s2178 4)
(s2179 5)
(s2180 5)
(s2181 2)
(s2183 4)
(s2184 5)
(s2185 5)
(s2186 2)
(s2188 4)
(s2189 5)
(s2190 5)
(s2191 2)
(s2193 4)
(s2194 5)
(s2195 5)
(s2196 2)
(s2198 4)
(s2199 5)
(s2200 5)
(s2201 2)
(s2203 4)
(s2204 5)
(s2205 5)
(s2206 2)
(s2208 4)
(s2209 5)
(s2210 5)
(s2211 2)
(s2213 4)
(s2214 5)
(s2215 5)
(s2216 2)
(s2218 4)
(s2219 5)
(s2220 5)
(s2221 2)
(s2223 4)
(s2224 5)
(s2225 5)
(s2226 2)
(s2228 4)
(s2229 5)
(s2230 5)
(s2231 2)
(s2233 4)
(s2234 5)
(s2235 5)
(s2236 2)
(s2238 4)
(s2239 5)
(s2240 5)
(s2241 2)
(s2243 4)
(s2244 5)
(s2245 5)
(s2246 2)
(s2248 4)
(s2249 5)
(s2250 5)
(s2251 2)
(s2253 4)
(s2254 5)
(s2255 5)
(s2256 2)
(s2258 4)
(s2259 5)
(s2260 5)
(s2261 2)
(s2263 4)
(s2264 5)
(s2265 5)
(s2266 2)
(s2268 4)
(s2269 5)
(s2270 5)
(s2271 2)
(s2273 4)
(s2274 5)
(s2275 5)
(s2276 2)
(s2278 4)
(s2279 5)
(s2280 5)
(s2281 2)
(s2283 4)
(s2284 5)
(s2285 5)
(s2286 2)
(s2288 4)
(s2289 5)
(s2290 5)
(s2291 2)
(s2293 4)
(s2294 5)
(s2295 5)
(s2296 2)
(s2298 4)
(s2299 5)
(s2300 5)
(s2301 2)
(s2303 4)
(s2304 5)
(s2305 5)
(s2306 2)
(s2308 4)
(s2309 5)
(s2310 5)
(s2311 2)
(s2313 4)
(s2314 5)
(s2315 5)
(s2316 2)
(s2318 4)
(s2319 5)
(s2320 5)
(s2321 2)
(s2323 4)
(s2324 5)
(s2325 5)
(s2326 2)
(s2328 4)
(s2329 5)
(s2330 5)
(s2331 2)
(s2333 4)
(s2334 5)
(s2335 5)
(s2336 2)
(s2338 4)
(s2339 5)
(s2340 5)
(s2341 2)
(s2343 4)
(s2344 5)
(s2345 5)
(s2346 2)
(s2348 4)
(s2349 5)
(s2350 5)
(s2351 2)
(s2353 4)
(s2354 5)
(s2355 5)
(s2356 2)
(s2358 4)
(s2359 5)
(s2360 5)
(s2361 2)
(s2363 4)
(s2364 5)
(s2365 5)
(s2366 2)
(s2368 4)
(s2369 5)
(s2370 5)
(s2371 2)
(s2373 4)
(s2374 5)
(s2375 5)
(s2376 2)
(s2378 4)
(s2379 5)
(s2380 5)
(s2381 2)
(s2383 4)
(s2384 5)
(s2385 5)
(s2386 2)
(s2388 4)
(s2389 5)
(s2390 5)
(s2391 2)
(s2393 4)
(s2394 5)
(s2395 5)
(s2396 2)
(s2398 4)
(s2399 5)
(s2400 5)
(s2401 2)
(s2403 4)
(s2404 5)
(s2405 5)
(s2406 2)
(s2408 4)
(s2409 5)
(s2410 5)
(s2411 2)
(s2413 4)
(s2414 5)
(s2415 5)
(s2416 2)
(s2418 4)
(s2419 5)
(s2420 5)
(s2421 2)
(s2423 4)
(s2424 5)
(s2425 5)
(s2426 2)
(s2428 4)
(s2429 5)
(s2430 5)
(s2431 2)
(s2433 4)
(s2434 5)
(s2435 5)
(s2436 2)
(s2438 4)
(s2439 5)
(s2440 5)
(s2441 2)
(s2443 4)
(s2444 5)
(s2445 5)
(s2446 2)
(s2448 4)
(s2449 5)
(s2450 5)
(s2451 2)
(s2453 4)
(s2454 5)
(s2455 5)
(s2456 2)
(s2458 4)
(s2459 5)
(s2460 5)
(s2461 2)
(s2463 4)
(s2464 5)
(s2465 5)
(s2466 2)
(s2468 4)
(s2469 5)
(s2470 5)
(s2471 2)
(s2473 4)
(s2474 5)
(s2475 5)
(s2476 2)
(s2478 4)
(s2479 5)
(s2480 5)
(s2481 2)
(s2483 4)
(s2484 5)
(s2485 5)
(s2486 2)
(s2488 4)
(s2489 5)
(s2490 5)
(s2491 2)
(s2493 4)
(s2494 5)
(s2495 5)
(s2496 2)
(s2498 4)
(s2499 5)
(s2500 5)
(s2501 2)
(s2503 4)
(s2504 5)
(s2505 5)
(s2506 2)
(s2508 4)
(s2509 5)
(s2510 5)
(s2511 2)
(s2513 4)
(s2514 5)
(s2515 5)
(s2516 2)
(s2518 4)
(s2519 5)
(s2520 5)
(s2521 2)
(s2523 4)
(s2524 5)
(s2525 5)
(s2526 2)
(s2528 4)
(s2529 5)
(s2530 5)
(s2531 2)
(s2533 4)
(s2534 5)
(s2535 5)
(s2536 2)
(s2538 4)
(s2539 5)
(s2540 5)
(s2541 2)
(s2543 4)
(s2544 5)
(s2545 5)
(s2546 2)
(s2548 4)
(s2549 5)
(s2550 5)
(s2551 2)
(s2553 4)
(s2554 5)
(s2555 5)
(s2556 2)
(s2558 4)
(s2559 5)
(s2560 5)
(s2561 2)
(s2563 4)
(s2564 5)
(s2565 5)
(s2566 2)
(s2568 4)
(s2569 5)
(s2570 5)
(s2571 2)
(s2573 4)
(s2574 5)
(s2575 5)
(s2576 2)
(s2578 4)
(s2579 5)
(s2580 5)
(s2581 2)
(s2583 4)
(s2584 5)
(s2585 5)
(s2586 2)
(s2588 4)
(s2589 5)
(s2590 5)
(s2591 2)
(s2593 4)
(s2594 5)
(s2595 5)
(s2596 2)
(s2598 4)
(s2599 5)
(s2600 5)
(s2601 2)
(s2603 4)
(s2604 5)
(s2605 5)
(s2606 2)
(s2608 4)
(s2609 5)
(s2610 5)
(s2611 2)
(s2613 4)
(s2614 5)
(s2615 5)
(s2616 2)
(s2618 4)
(s2619 5)
(s2620 5)
(s2621 2)
(s2623 4)
(s2624 5)
(s2625 5)
(s2626 2)
(s2628 4)
(s2629 5)
(s2630 5)
(s2631 2)
(s2633 4)
(s2634 5)
(s2635 5)
(s2636 2)
(s2638 4)
(s2639 5)
(s2640 5)
(s2641 2)
(s2643 4)
(s2644 5)
(s2645 5)
(s2646 2)
(s2648 4)
(s2649 5)
(s2650 5)
(s2651 2)
(s2653 4)
(s2654 5)
(s2655 5)
(s2656 2)
(s2658 4)
(s2659 5)
(s2660 5)
(s2661 2)
(s2663 4)
(s2664 5)
(s2665 5)
(s2666 2)
(s2668 4)
(s2669 5)
(s2670 5)
(s2671 2)
(s2673 4)
(s2674 5)
(s2675 5)
(s2676 2)
(s2678 4)
(s2679 5)
(s2680 5)
(s2681 2)
(s2683 4)
(s2684 5)
(s2685 5)
(s2686 2)
(s2688 4)
(s2689 5)
(s2690 5)
(s2691 2)
(s2693 4)
(s2694 5)
(s2695 5)
(s2696 2)
(s2698 4)
(s2699 5)
(s2700 5)
(s2701 2)
(s2703 4)
(s2704 5)
(s2705 5)
(s2706 2)
(s2708 4)
(s2709 5)
(s2710 5)
(s2711 2)
(s2713 4)
(s2714 5)
(s2715 5)
(s2716 2)
(s2718 4)
(s2719 5)
(s2720 5)
(s2721 2)
(s2723 4)
(s2724 5)
(s2725 5)
(s2726 2)
(s2728 4)
(s2729 5)
(s2730 5)
(s2731 2)
(s2733 4)
(s2734 5)
(s2735 5)
(s2736 2)
(s2738 4)
(s2739 5)
(s2740 5)
(s2741 2)
(s2743 4)
(s2744 5)
(s2745 5)
(s2746 2)
(s2748 4)
(s2749 5)
(s2750 5)
(s2751 2)
(s2753 4)
(s2754 5)
(s2755 5)
(s2756 2)
(s2758 4)
(s2759 5)
(s2760 5)
(s2761 2)
(s2763 4)
(s2764 5)
(s2765 5)
(s2766 2)
(s2768 4)
(s2769 5)
(s2770 5)
(s2771 2)
(s2773 4)
(s2774 5)
(s2775 5)
(s2776 2)
(s2778 4)
(s2779 5)
(s2780 5)
(s2781 2)
(s2783 4)
(s2784 5)
(s2785 5)
(s2786 2)
(s2788 4)
(s2789 5)
(s2790 5)
(s2791 2)
(s2793 4)
(s2794 5)
(s2795 5)
(s2796 2)
(s2798 4)
(s2799 5)
(s2800 5)
(s2801 2)
(s2803 4)
(s2804 5)
(s2805 5)
(s2806 2)
(s2808 4)
(s2809 5)
(s2810 5)
(s2811 2)
(s2813 4)
(s2814 5)
(s2815 5)
(s2816 2)
(s2818 4)
(s2819 5)
(s2820 5)
(s2821 2)
(s2823 4)
(s2824 5)
(s2825 5)
(s2826 2)
(s2828 4)
(s2829 5)
(s2830 5)
(s2831 2)
(s2833 4)
(s2834 5)
(s2835 5)
(s2836 2)
(s2838 4)
(s2839 5)
(s2840 5)
(s2841 2)
(s2843 4)
(s2844 5)
(s2845 5)
(s2846 2)
(s2848 4)
(s2849 5)
(s2850 5)
(s2851 2)
(s2853 4)
(s2854 5)
(s2855 5)
(s2856 2)
(s2858 4)
(s2859 5)
(s2860 5)
(s2861 2)
(s2863 4)
(s2864 5)
(s2865 5)
(s2866 2)
(s2868 4)
(s2869 5)
(s2870 5)
(s2871 2)
(s2873 4)
(s2874 5)
(s2875 5)
(s2876 2)
(s2878 4)
(s2879 5)
(s2880 5)
(s2881 2)
(s2883 4)
(s2884 5)
(s2885 5)
(s2886 2)
(s2888 4)
(s2889 5)
(s2890 5)
(s2891 2)
(s2893 4)
(s2894 5)
(s2895 5)
(s2896 2)
(s2898 4)
(s2899 5)
(s2900 5)
(s2901 2)
(s2903 4)
(s2904 5)
(s2905 5)
(s2906 2)
(s2908 4)
(s2909 5)
(s2910 5)
(s2911 2)
(s2913 4)
(s2914 5)
(s2915 5)
(s2916 2)
(s2918 4)
(s2919 5)
(s2920 5)
(s2921 2)
(s2923 4)
(s2924 5)
(s2925 5)
(s2926 2)
(s2928 4)
(s2929 5)
(s2930 5)
(s2931 2)
(s2933 4)
(s2934 5)
(s2935 5)
(s2936 2)
(s2938 4)
(s2939 5)
(s2940 5)
(s2941 2)
(s2943 4)
(s2944 5)
(s2945 5)
(s2946 2)
(s2948 4)
(s2949 5)
(s2950 5)
(s2951 2)
(s2953 4)
(s2954 5)
(s2955 5)
(s2956 2)
(s2958 4)
(s2959 5)
(s2960 5)
(s2961 2)
(s2963 4)
(s2964 5)
(s2965 5)
(s2966 2)
(s2968 4)
(s2969 5)
(s2970 5)
(s2971 2)
(s2973 4)
(s2974 5)
(s2975 5)
(s2976 2)
(s2978 4)
(s2979 5)
(s2980 5)
(s2981 2)
(s2983 4)
(s2984 5)
(s2985 5)
(s2986 2)
(s2988 4)
(s2989 5)
(s2990 5)
(s2991 2)
(s2993 4)
(s2994 5)
(s2995 5)
(s2996 2)
(s2998 4)
(s2999 5)
(s3000 5)
(s3001 2)
(s3003 4)
(s3004 5)
(s3005 5)
(s3006 2)
(s3008 4)
(s3009 5)
(s3010 5)
(s3011 2)
(s3013 4)
(s3014 5)
(s3015 5)
(s3016 2)
(s3018 4)
(s3019 5)
(s3020 5)
(s3021 2)
(s3023 4)
(s3024 5)
(s3025 5)
(s3026 2)
(s3028 4)
(s3029 5)
(s3030 5)
(s3031 2)
(s3033 4)
(s3034 5)
(s3035 5)
(s3036 2)
(s3038 4)
(s3039 5)
(s3040 5)
(s3041 2)
(s3043 4)
(s3044 5)
(s3045 5)
(s3046 2)
(s3048 4)
(s3049 5)
(s3050 5)
(s3051 2)
(s3053 4)
(s3054 5)
(s3055 5)
(s3056 2)
(s3058 4)
(s3059 5)
(s3060 5)
(s3061 2)
(s3063 4)
(s3064 5)
(s3065 5)
(s3066 2)
(s3068 4)
(s3069 5)
(s3070 5)
(s3071 2)
(s3073 4)
(s3074 5)
(s3075 5)
(s3076 2)
(s3078 4)
(s3079 5)
(s3080 5)
(s3081 2)
(s3083 4)
(s3084 5)
(s3085 5)
(s3086 2)
(s3088 4)
(s3089 5)
(s3090 5)
(s3091 2)
(s3093 4)
(s3094 5)
(s3095 5)
(s3096 2)
(s3098 4)
(s3099 5)
(s3100 5)
(s3101 2)
(s3103 4)
(s3104 5)
(s3105 5)
(s3106 2)
(s3108 4)
(s3109 5)
(s3110 5)
(s3111 2)
(s3113 4)
(s3114 5)
(s3115 5)
(s3116 2)
(s3118 4)
(s3119 5)
(s3120 5)
(s3121 2)
(s3123 4)
(s3124 5)
(s3125 5)
(s3126 2)
(s3128 4)
(s3129 5)
(s3130 5)
(s3131 2)
(s3133 4)
(s3134 5)
(s3135 5)
(s3136 2)
(s3138 4)
(s3139 5)
(s3140 5)
(s3141 2)
(s3143 4)
(s3144 5)
(s3145 5)
(s3146 2)
(s3148 4)
(s3149 5)
(s3150 5)
(s3151 2)
(s3153 4)
(s3154 5)
(s3155 5)
(s3156 2)
(s3158 4)
(s3159 5)
(s3160 5)
(s3161 2)
(s3163 4)
(s3164 5)
(s3165 5)
(s3166 2)
(s3168 4)
(s3169 5)
(s3170 5)
(s3171 2)
(s3173 4)
(s3174 5)
(s3175 5)
(s3176 2)
(s3178 4)
(s3179 5)
(s3180 5)
(s3181 2)
(s3183 4)
(s3184 5)
(s3185 5)
(s3186 2)
(s3188 4)
(s3189 5)
(s3190 5)
(s3191 2)
(s3193 4)
(s3194 5)
(s3195 5)
(s3196 2)
(s3198 4)
(s3199 5)
(s3200 5)
(s3201 2)
(s3203 4)
(s3204 5)
(s3205 5)
(s3206 2)
(s3208 4)
(s3209 5)
(s3210 5)
(s3211 2)
(s3213 4)
(s3214 5)
(s3215 5)
(s3216 2)
(s3218 4)
(s3219 5)
(s3220 5)
(s3221 2)
(s3223 4)
(s3224 5)
(s3225 5)
(s3226 2)
(s3228 4)
(s3229 5)
(s3230 5)
(s3231 2)
(s3233 4)
(s3234 5)
(s3235 5)
(s3236 2)
(s3238 4)
(s3239 5)
(s3240 5)
(s3241 2)
(s3243 4)
(s3244 5)
(s3245 5)
(s3246 2)
(s3248 4)
(s3249 5)
(s3250 5)
(s3251 2)
(s3253 4)
(s3254 5)
(s3255 5)
(s3256 2)
(s3258 4)
(s3259 5)
(s3260 5)
(s3261 2)
(s3263 4)
(s3264 5)
(s3265 5)
(s3266 2)
(s3268 4)
(s3269 5)
(s3270 5)
(s3271 2)
(s3273 4)
(s3274 5)
(s3275 5)
(s3276 2)
(s3278 4)
(s3279 5)
(s3280 5)
(s3281 2)
(s3283 4)
(s3284 5)
(s3285 5)
(s3286 2)
(s3288 4)
(s3289 5)
(s3290 5)
(s3291 2)
(s3293 4)
(s3294 5)
(s3295 5)
(s3296 2)
(s3298 4)
(s3299 5)
(s3300 5)
(s3301 2)
(s3303 4)
(s3304 5)
(s3305 5)
(s3306 2)
(s3308 4)
(s3309 5)
(s3310 5)
(s3311 2)
(s3313 4)
(s3314 5)
(s3315 5)
(s3316 2)
(s3318 4)
(s3319 5)
(s3320 5)
(s3321 2)
(s3323 4)
(s3324 5)
(s3325 5)
(s3326 2)
(s3328 4)
(s3329 5)
(s3330 5)
(s3331 2)
(s3333 4)
(s3334 5)
(s3335 5)
(s3336 2)
(s3338 4)
(s3339 5)
(s3340 5)
(s3341 2)
(s3343 4)
(s3344 5)
(s3345 5)
(s3346 2)
(s3348 4)
(s3349 5)
(s3350 5)
(s3351 2)
(s3353 4)
(s3354 5)
(s3355 5)
(s3356 2)
(s3358 4)
(s3359 5)
(s3360 5)
(s3361 2)
(s3363 4)
(s3364 5)
(s3365 5)
(s3366 2)
(s3368 4)
(s3369 5)
(s3370 5)
(s3371 2)
(s3373 4)
(s3374 5)
(s3375 5)
(s3376 2)
(s3378 4)
(s3379 5)
(s3380 5)
(s3381 2)
(s3383 4)
(s3384 5)
(s3385 5)
(s3386 2)
(s3388 4)
(s3389 5)
(s3390 5)
(s3391 2)
(s3393 4)
(s3394 5)
(s3395 5)
(s3396 2)
(s3398 4)
(s3399 5)
(s3400 5)
(s3401 2)
(s3403 4)
(s3404 5)
(s3405 5)
(s3406 2)
(s3408 4)
(s3409 5)
(s3410 5)
(s3411 2)
(s3413 4)
(s3414 5)
(s3415 5)
(s3416 2)
(s3418 4)
(s3419 5)
(s3420 5)
(s3421 2)
(s3423 4)
(s3424 5)
(s3425 5)
(s3426 2)
(s3428 4)
(s3429 5)
(s3430 5)
(s3431 2)
(s3433 4)
(s3434 5)
(s3435 5)
(s3436 2)
(s3438 4)
(s3439 5)
(s3440 5)
(s3441 2)
(s3443 4)
(s3444 5)
(s3445 5)
(s3446 2)
(s3448 4)
(s3449 5)
(s3450 5)
(s3451 2)
(s3453 4)
(s3454 5)
(s3455 5)
(s3456 2)
(s3458 4)
(s3459 5)
(s3460 5)
(s3461 2)
(s3463 4)
(s3464 5)
(s3465 5)
(s3466 2)
(s3468 4)
(s3469 5)
(s3470 5)
(s3471 2)
(s3473 4)
(s3474 5)
(s3475 5)
(s3476 2)
(s3478 4)
(s3479 5)
(s3480 5)
(s3481 2)
(s3483 4)
(s3484 5)
(s3485 5)
(s3486 2)
(s3488 4)
(s3489 5)
(s3490 5)
(s3491 2)
(s3493 4)
(s3494 5)
(s3495 5)
(s3496 2)
(s3498 4)
(s3499 5)
(s3500 5)
(s3501 2)
(s3503 4)
(s3504 5)
(s3505 5)
(s3506 2)
(s3508 4)
(s3509 5)
(s3510 5)
(s3511 2)
(s3513 4)
(s3514 5)
(s3515 5)
(s3516 2)
(s3518 4)
(s3519 5)
(s3520 5)
(s3521 2)
(s3523 4)
(s3524 5)
(s3525 5)
(s3526 2)
(s3528 4)
(s3529 5)
(s3530 5)
(s3531 2)
(s3533 4)
(s3534 5)
(s3535 5)
(s3536 2)
(s3538 4)
(s3539 5)
(s3540 5)
(s3541 2)
(s3543 4)
(s3544 5)
(s3545 5)
(s3546 2)
(s3548 4)
(s3549 5)
(s3550 5)
(s3551 2)
(s3553 4)
(s3554 5)
(s3555 5)
(s3556 2)
(s3558 4)
(s3559 5)
(s3560 5)
(s3561 2)
(s3563 4)
(s3564 5)
(s3565 5)
(s3566 2)
(s3568 4)
(s3569 5)
(s3570 5)
(s3571 2)
(s3573 4)
(s3574 5)
(s3575 5)
(s3576 2)
(s3578 4)
(s3579 5)
(s3580 5)
(s3581 2)
(s3583 4)
(s3584 5)
(s3585 5)
(s3586 2)
(s3588 4)
(s3589 5)
(s3590 5)
(s3591 2)
(s3593 4)
(s3594 5)
(s3595 5)
(s3596 2)
(s3598 4)
(s3599 5)
(s3600 5)
(s3601 2)
(s3603 4)
(s3604 5)
(s3605 5)
(s3606 2)
(s3608 4)
(s3609 5)
(s3610 5)
(s3611 2)
(s3613 4)
(s3614 5)
(s3615 5)
(s3616 2)
(s3618 4)
(s3619 5)
(s3620 5)
(s3621 2)
(s3623 4)
(s3624 5)
(s3625 5)
(s3626 2)
(s3628 4)
(s3629 5)
(s3630 5)
(s3631 2)
(s3633 4)
(s3634 5)
(s3635 5)
(s3636 2)
(s3638 4)
(s3639 5)
(s3640 5)
(s3641 2)
(s3643 4)
(s3644 5)
(s3645 5)
(s3646 2)
(s3648 4)
(s3649 5)
(s3650 5)
(s3651 2)
(s3653 4)
(s3654 5)
(s3655 5)
(s3656 2)
(s3658 4)
(s3659 5)
(s3660 5)
(s3661 2)
(s3663 4)
(s3664 5)
(s3665 5)
(s3666 2)
(s3668 4)
(s3669 5)
(s3670 5)
(s3671 2)
(s3673 4)
(s3674 5)
(s3675 5)
(s3676 2)
(s3678 4)
(s3679 5)
(s3680 5)
(s3681 2)
(s3683 4)
(s3684 5)
(s3685 5)
(s3686 2)
(s3688 4)
(s3689 5)
(s3690 5)
(s3691 2)
(s3693 4)
(s3694 5)
(s3695 5)
(s3696 2)
(s3698 4)
(s3699 5)
(s3700 5)
(s3701 2)
(s3703 4)
(s3704 5)
(s3705 5)
(s3706 2)
(s3708 4)
(s3709 5)
(s3710 5)
(s3711 2)
(s3713 4)
(s3714 5)
(s3715 5)
(s3716 2)
(s3718 4)
(s3719 5)
(s3720 5)
(s3721 2)
(s3723 4)
(s3724 5)
(s3725 5)
(s3726 2)
(s3728 4)
(s3729 5)
(s3730 5)
(s3731 2)
(s3733 4)
(s3734 5)
(s3735 5)
(s3736 2)
(s3738 4)
(s3739 5)
(s3740 5)
(s3741 2)
(s3743 4)
(s3744 5)
(s3745 5)
(s3746 2)
(s3748 4)
(s3749 5)
(s3750 5)
(s3751 2)
(s3753 4)
(s3754 5)
(s3755 5)
(s3756 2)
(s3758 4)
(s3759 5)
(s3760 5)
(s3761 2)
(s3763 4)
(s3764 5)
(s3765 5)
(s3766 2)
(s3768 4)
(s3769 5)
(s3770 5)
(s3771 2)
(s3773 4)
(s3774 5)
(s3775 5)
(s3776 2)
(s3778 4)
(s3779 5)
(s3780 5)
(s3781 2)
(s3783 4)
(s3784 5)
(s3785 5)
(s3786 2)
(s3788 4)
(s3789 5)
(s3790 5)
(s3791 2)
(s3793 4)
(s3794 5)
(s3795 5)
(s3796 2)
(s3798 4)
(s3799 5)
(s3800 5)
(s3801 2)
(s3803 4)
(s3804 5)
(s3805 5)
(s3806 2)
(s3808 4)
(s3809 5)
(s3810 5)
(s3811 2)
(s3813 4)
(s3814 5)
(s3815 5)
(s3816 2)
(s3818 4)
(s3819 5)
(s3820 5)
(s3821 2)
(s3823 4)
(s3824 5)
(s3825 5)
(s3826 2)
(s3828 4)
(s3829 5)
(s3830 5)
(s3831 2)
(s3833 4)
(s3834 5)
(s3835 5)
(s3836 2)
(s3838 4)
(s3839 5)
(s3840 5)
(s3841 2)
(s3843 4)
(s3844 5)
(s3845 5)
(s3846 2)
(s3848 4)
(s3849 5)
(s3850 5)
(s3851 2)
(s3853 4)
(s3854 5)
(s3855 5)
(s3856 2)
(s3858 4)
(s3859 5)
(s3860 5)
(s3861 2)
(s3863 4)
(s3864 5)
(s3865 5)
(s3866 2)
(s3868 4)
(s3869 5)
(s3870 5)
(s3871 2)
(s3873 4)
(s3874 5)
(s3875 5)
(s3876 2)
(s3878 4)
(s3879 5)
(s3880 5)
(s3881 2)
(s3883 4)
(s3884 5)
(s3885 5)
(s3886 2)
(s3888 4)
(s3889 5)
(s3890 5)
(s3891 2)
(s3893 4)
(s3894 5)
(s3895 5)
(s3896 2)
(s3898 4)
(s3899 5)
(s3900 5)
(s3901 2)
(s3903 4)
(s3904 5)
(s3905 5)
(s3906 2)
(s3908 4)
(s3909 5)
(s3910 5)
(s3911 2)
(s3913 4)
(s3914 5)
(s3915 5)
(s3916 2)
(s3918 4)
(s3919 5)
(s3920 5)
(s3921 2)
(s3923 4)
(s3924 5)
(s3925 5)
(s3926 2)
(s3928 4)
(s3929 5)
(s3930 5)
(s3931 2)
(s3933 4)
(s3934 5)
(s3935 5)
(s3936 2)
(s3938 4)
(s3939 5)
(s3940 5)
(s3941 2)
(s3943 4)
(s3944 5)
(s3945 5)
(s3946 2)
(s3948 4)
(s3949 5)
(s3950 5)
(s3951 2)
(s3953 4)
(s3954 5)
(s3955 5)
(s3956 2)
(s3958 4)
(s3959 5)
(s3960 5)
(s3961 2)
(s3963 4)
(s3964 5)
(s3965 5)
(s3966 2)
(s3968 4)
(s3969 5)
(s3970 5)
(s3971 2)
(s3973 4)
(s3974 5)
(s3975 5)
(s3976 2)
(s3978 4)
(s3979 5)
(s3980 5)
(s3981 2)
(s3983 4)
(s3984 5)
(s3985 5)
(s3986 2)
(s3988 4)
(s3989 5)
(s3990 5)
(s3991 2)
(s3993 4)
(s3994 5)
(s3995 5)
(s3996 2)
(s3998 4)
(s3999 5)
(s4000 5)
(s4001 2)
(s4003 4)
(s4004 5)
(s4005 5)
(s4006 2)
(s4008 4)
(s4009 5)
(s4010 5)
(s4011 2)
(s4013 4)
(s4014 5)
(s4015 5)
(s4016 2)
(s4018 4)
(s4019 5)
(s4020 5)
(s4021 2)
(s4023 4)
(s4024 5)
(s4025 5)
(s4026 2)
(s4028 4)
(s4029 5)
(s4030 5)
(s4031 2)
(s4033 4)
(s4034 5)
(s4035 5)
(s4036 2)
(s4038 4)
(s4039 5)
(s4040 5)
(s4041 2)
(s4043 4)
(s4044 5)
(s4045 5)
(s4046 2)
(s4048 4)
(s4049 5)
(s4050 5)
(s4051 2)
(s4053 4)
(s4054 5)
(s4055 5)
(s4056 2)
(s4058 4)
(s4059 5)
(s4060 5)
(s4061 2)
(s4063 4)
(s4064 5)
(s4065 5)
(s4066 2)
(s4068 4)
(s4069 5)
(s4070 5)
(s4071 2)
(s4073 4)
(s4074 5)
(s4075 5)
(s4076 2)
(s4078 4)
(s4079 5)
(s4080 5)
(s4081 2)
(s4083 4)
(s4084 5)
(s4085 5)
(s4086 2)
(s4088 4)
(s4089 5)
(s4090 5)
(s4091 2)
(s4093 4)
(s4094 5)
(s4095 5)
(s4096 2)
(s4098 4)
(s4099 5)
(s4100 5)
(s4101 2)
(s4103 4)
(s4104 5)
(s4105 5)
(s4106 2)
(s4108 4)
(s4109 5)
(s4110 5)
(s4111 2)
(s4113 4)
(s4114 5)
(s4115 5)
(s4116 2)
(s4118 4)
(s4119 5)
(s4120 5)
(s4121 2)
(s4123 4)
(s4124 5)
(s4125 5)
(s4126 2)
(s4128 4)
(s4129 5)
(s4130 5)
(s4131 2)
(s4133 4)
(s4134 5)
(s4135 5)
(s4136 2)
(s4138 4)
(s4139 5)
(s4140 5)
(s4141 2)
(s4143 4)
(s4144 5)
(s4145 5)
(s4146 2)
(s4148 4)
(s4149 5)
(s4150 5)
(s4151 2)
(s4153 4)
(s4154 5)
(s4155 5)
(s4156 2)
(s4158 4)
(s4159 5)
(s4160 5)
(s4161 2)
(s4163 4)
(s4164 5)
(s4165 5)
(s4166 2)
(s4168 4)
(s4169 5)
(s4170 5)
(s4171 2)
(s4173 4)
(s4174 5)
(s4175 5)
(s4176 2)
(s4178 4)
(s4179 5)
(s4180 5)
(s4181 2)
(s4183 4)
(s4184 5)
(s4185 5)
(s4186 2)
(s4188 4)
(s4189 5)
(s4190 5)
(s4191 2)
(s4193 4)
(s4194 5)
(s4195 5)
(s4196 2)
(s4198 4)
(s4199 5)
(s4200 5)
(s4201 2)
(s4203 4)
(s4204 5)
(s4205 5)
(s4206 2)
(s4208 4)
(s4209 5)
(s4210 5)
(s4211 2)
(s4213 4)
(s4214 5)
(s4215 5)
(s4216 2)
(s4218 4)
(s4219 5)
(s4220 5)
(s4221 2)
(s4223 4)
(s4224 5)
(s4225 5)
(s4226 2)
(s4228 4)
(s4229 5)
(s4230 5)
(s4231 2)
(s4233 4)
(s4234 5)
(s4235 5)
(s4236 2)
(s4238 4)
(s4239 5)
(s4240 5)
(s4241 2)
(s4243 4)
(s4244 5)
(s4245 5)
(s4246 2)
(s4248 4)
(s4249 5)
(s4250 5)
(s4251 2)
(s4253 4)
(s4254 5)
(s4255 5)
(s4256 2)
(s4258 4)
(s4259 5)
(s4260 5)
(s4261 2)
(s4263 4)
(s4264 5)
(s4265 5)
(s4266 2)
(s4268 4)
(s4269 5)
(s4270 5)
(s4271 2)
(s4273 4)
(s4274 5)
(s4275 5)
(s4276 2)
(s4278 4)
(s4279 5)
(s4280 5)
(s4281 2)
(s4283 4)
(s4284 5)
(s4285 5)
(s4286 2)
(s4288 4)
(s4289 5)
(s4290 5)
(s4291 2)
(s4293 4)
(s4294 5)
(s4295 5)
(s4296 2)
(s4298 4)
(s4299 5)
(s4300 5)
(s4301 2)
(s4303 4)
(s4304 5)
(s4305 5)
(s4306 2)
(s4308 4)
(s4309 5)
(s4310 5)
(s4311 2)
(s4313 4)
(s4314 5)
(s4315 5)
(s4316 2)
(s4318 4)
(s4319 5)
(s4320 5)
(s4321 2)
(s4323 4)
(s4324 5)
(s4325 5)
(s4326 2)
(s4328 4)
(s4329 5)
(s4330 5)
(s4331 2)
(s4333 4)
(s4334 5)
(s4335 5)
(s4336 2)
(s4338 4)
(s4339 5)
(s4340 5)
(s4341 2)
(s4343 4)
(s4344 5)
(s4345 5)
(s4346 2)
(s4348 4)
(s4349 5)
(s4350 5)
(s4351 2)
(s4353 4)
(s4354 5)
(s4355 5)
(s4356 2)
(s4358 4)
(s4359 5)
(s4360 5)
(s4361 2)
(s4363 4)
(s4364 5)
(s4365 5)
(s4366 2)
(s4368 4)
(s4369 5)
(s4370 5)
(s4371 2)
(s4373 4)
(s4374 5)
(s4375 5)
(s4376 2)
(s4378 4)
(s4379 5)
(s4380 5)
(s4381 2)
(s4383 4)
(s4384 5)
(s4385 5)
(s4386 2)
(s4388 4)
(s4389 5)
(s4390 5)
(s4391 2)
(s4393 4)
(s4394 5)
(s4395 5)
(s4396 2)
(s4398 4)
(s4399 5)
(s4400 5)
(s4401 2)
(s4403 4)
(s4404 5)
(s4405 5)
(s4406 2)
(s4408 4)
(s4409 5)
(s4410 5)
(s4411 2)
(s4413 4)
(s4414 5)
(s4415 5)
(s4416 2)
(s4418 4)
(s4419 5)
(s4420 5)
(s4421 2)
(s4423 4)
(s4424 5)
(s4425 5)
(s4426 2)
(s4428 4)
(s4429 5)
(s4430 5)
(s4431 2)
(s4433 4)
(s4434 5)
(s4435 5)
(s4436 2)
(s4438 4)
(s4439 5)
(s4440 5)
(s4441 2)
(s4443 4)
(s4444 5)
(s4445 5)
(s4446 2)
(s4448 4)
(s4449 5)
(s4450 5)
(s4451 2)
(s4453 4)
(s4454 5)
(s4455 5)
(s4456 2)
(s4458 4)
(s4459 5)
(s4460 5)
(s4461 2)
(s4463 4)
(s4464 5)
(s4465 5)
(s4466 2)
(s4468 4)
(s4469 5)
(s4470 5)
(s4471 2)
(s4473 4)
(s4474 5)
(s4475 5)
(s4476 2)
(s4478 4)
(s4479 5)
(s4480 5)
(s4481 2)
(s4483 4)
(s4484 5)
(s4485 5)
(s4486 2)
(s4488 4)
(s4489 5)
(s4490 5)
(s4491 2)
(s4493 4)
(s4494 5)
(s4495 5)
(s4496 2)
(s4498 4)
(s4499 5)
(s4500 5)
(s4501 2)
(s4503 4)
(s4504 5)
(s4505 5)
(s4506 2)
(s4508 4)
(s4509 5)
(s4510 5)
(s4511 2)
(s4513 4)
(s4514 5)
(s4515 5)
(s4516 2)
(s4518 4)
(s4519 5)
(s4520 5)
(s4521 2)
(s4523 4)
(s4524 5)
(s4525 5)
(s4526 2)
(s4528 4)
(s4529 5)
(s4530 5)
(s4531 2)
(s4533 4)
(s4534 5)
(s4535 5)
(s4536 2)
(s4538 4)
(s4539 5)
(s4540 5)
(s4541 2)
(s4543 4)
(s4544 5)
(s4545 5)
(s4546 2)
(s4548 4)
(s4549 5)
(s4550 5)
(s4551 2)
(s4553 4)
(s4554 5)
(s4555 5)
(s4556 2)
(s4558 4)
(s4559 5)
(s4560 5)
(s4561 2)
(s4563 4)
(s4564 5)
(s4565 5)
(s4566 2)
(s4568 4)
(s4569 5)
(s4570 5)
(s4571 2)
(s4573 4)
(s4574 5)
(s4575 5)
(s4576 2)
(s4578 4)
(s4579 5)
(s4580 5)
(s4581 2)
(s4583 4)
(s4584 5)
(s4585 5)
(s4586 2)
(s4588 4)
(s4589 5)
(s4590 5)
(s4591 2)
(s4593 4)
(s4594 5)
(s4595 5)
(s4596 2)
(s4598 4)
(s4599 5)
(s4600 5)
(s4601 2)
(s4603 4)
(s4604 5)
(s4605 5)
(s4606 2)
(s4608 4)
(s4609 5)
(s4610 5)
(s4611 2)
(s4613 4)
(s4614 5)
(s4615 5)
(s4616 2)
(s4618 4)
(s4619 5)
(s4620 5)
(s4621 2)
(s4623 4)
(s4624 5)
(s4625 5)
(s4626 2)
(s4628 4)
(s4629 5)
(s4630 5)
(s4631 2)
(s4633 4)
(s4634 5)
(s4635 5)
(s4636 2)
(s4638 4)
(s4639 5)
(s4640 5)
(s4641 2)
(s4643 4)
(s4644 5)
(s4645 5)
(s4646 2)
(s4648 4)
(s4649 5)
(s4650 5)
(s4651 2)
(s4653 4)
(s4654 5)
(s4655 5)
(s4656 2)
(s4658 4)
(s4659 5)
(s4660 5)
(s4661 2)
(s4663 4)
(s4664 5)
(s4665 5)
(s4666 2)
(s4668 4)
(s4669 5)
(s4670 5)
(s4671 2)
(s4673 4)
(s4674 5)
(s4675 5)
(s4676 2)
(s4678 4)
(s4679 5)
(s4680 5)
(s4681 2)
(s4683 4)
(s4684 5)
(s4685 5)
(s4686 2)
(s4688 4)
(s4689 5)
(s4690 5)
(s4691 2)
(s4693 4)
(s4694 5)
(s4695 5)
(s4696 2)
(s4698 4)
(s4699 5)
(s4700 5)
(s4701 2)
(s4703 4)
(s4704 5)
(s4705 5)
(s4706 2)
(s4708 4)
(s4709 5)
(s4710 5)
(s4711 2)
(s4713 4)
(s4714 5)
(s4715 5)
(s4716 2)
(s4718 4)
(s4719 5)
(s4720 5)
(s4721 2)
(s4723 4)
(s4724 5)
(s4725 5)
(s4726 2)
(s4728 4)
(s4729 5)
(s4730 5)
(s4731 2)
(s4733 4)
(s4734 5)
(s4735 5)
(s4736 2)
(s4738 4)
(s4739 5)
(s4740 5)
(s4741 2)
(s4743 4)
(s4744 5)
(s4745 5)
(s4746 2)
(s4748 4)
(s4749 5)
(s4750 5)
(s4751 2)
(s4753 4)
(s4754 5)
(s4755 5)
(s4756 2)
(s4758 4)
(s4759 5)
(s4760 5)
(s4761 2)
(s4763 4)
(s4764 5)
(s4765 5)
(s4766 2)
(s4768 4)
(s4769 5)
(s4770 5)
(s4771 2)
(s4773 4)
(s4774 5)
(s4775 5)
(s4776 2)
(s4778 4)
(s4779 5)
(s4780 5)
(s4781 2)
(s4783 4)
(s4784 5)
(s4785 5)
(s4786 2)
(s4788 4)
(s4789 5)
(s4790 5)
(s4791 2)
(s4793 4)
(s4794 5)
(s4795 5)
(s4796 2)
(s4798 4)
(s4799 5)
(s4800 5)
(s4801 2)
(s4803 4)
(s4804 5)
(s4805 5)
(s4806 2)
(s4808 4)
(s4809 5)
(s4810 5)
(s4811 2)
(s4813 4)
(s4814 5)
(s4815 5)
(s4816 2)
(s4818 4)
(s4819 5)
(s4820 5)
(s4821 2)
(s4823 4)
(s4824 5)
(s4825 5)
(s4826 2)
(s4828 4)
(s4829 5)
(s4830 5)
(s4831 2)
(s4833 4)
(s4834 5)
(s4835 5)
(s4836 2)
(s4838 4)
(s4839 5)
(s4840 5)
(s4841 2)
(s4843 4)
(s4844 5)
(s4845 5)
(s4846 2)
(s4848 4)
(s4849 5)
(s4850 5)
(s4851 2)
(s4853 4)
(s4854 5)
(s4855 5)
(s4856 2)
(s4858 4)
(s4859 5)
(s4860 5)
(s4861 2)
(s4863 4)
(s4864 5)
(s4865 5)
(s4866 2)
(s4868 4)
(s4869 5)
(s4870 5)
(s4871 2)
(s4873 4)
(s4874 5)
(s4875 5)
(s4876 2)
(s4878 4)
(s4879 5)
(s4880 5)
(s4881 2)
(s4883 4)
(s4884 5)
(s4885 5)
(s4886 2)
(s4888 4)
(s4889 5)
(s4890 5)
(s4891 2)
(s4893 4)
(s4894 5)
(s4895 5)
(s4896 2)
(s4898 4)
(s4899 5)
(s4900 5)
(s4901 2)
(s4903 4)
(s4904 5)
(s4905 5)
(s4906 2)
(s4908 4)
(s4909 5)
(s4910 5)
(s4911 2)
(s4913 4)
(s4914 5)
(s4915 5)
(s4916 2)
(s4918 4)
(s4919 5)
(s4920 5)
(s4921 2)
(s4923 4)
(s4924 5)
(s4925 5)
(s4926 2)
(s4928 4)
(s4929 5)
(s4930 5)
(s4931 2)
(s4933 4)
(s4934 5)
(s4935 5)
(s4936 2)
(s4938 4)
(s4939 5)
(s4940 5)
(s4941 2)
(s4943 4)
(s4944 5)
(s4945 5)
(s4946 2)
(s4948 4)
(s4949 5)
(s4950 5)
(s4951 2)
(s4953 4)
(s4954 5)
(s4955 5)
(s4956 2)
(s4958 4)
(s4959 5)
(s4960 5)
(s4961 2)
(s4963 4)
(s4964 5)
(s4965 5)
(s4966 2)
(s4968 4)
(s4969 5)
(s4970 5)
(s4971 2)
(s4973 4)
(s4974 5)
(s4975 5)
(s4976 2)
(s4978 4)
(s4979 5)
(s4980 5)
(s4981 2)
(s4983 4)
(s4984 5)
(s4985 5)
(s4986 2)
(s4988 4)
(s4989 5)
(s4990 5)
(s4991 2)
(s4993 4)
(s4994 5)
(s4995 5)
(s4996 2)
(s4998 4)
(s4999 5)
(s5000 5)
(s5001 2)
(s5003 4)
(s5004 5)
(s5005 5)
(s5006 2)
(s5008 4)
(s5009 5)
(s5010 5)
(s5011 2)
(s5013 4)
(s5014 5)
(s5015 5)
(s5016 2)
(s5018 4)
(s5019 5)
(s5020 5)
(s5021 2)
(s5023 4)
(s5024 5)
(s5025 5)
(s5026 2)
(s5028 4)
(s5029 5)
(s5030 5)
(s5031 2)
(s5033 4)
(s5034 5)
(s5035 5)
(s5036 2)
(s5038 4)
(s5039 5)
(s5040 5)
(s5041 2)
(s5043 4)
(s5044 5)
(s5045 5)
(s5046 2)
(s5048 4)
(s5049 5)
(s5050 5)
(s5051 2)
(s5053 4)
(s5054 5)
(s5055 5)
(s5056 2)
(s5058 4)
(s5059 5)
(s5060 5)
(s5061 2)
(s5063 4)
(s5064 5)
(s5065 5)
(s5066 2)
(s5068 4)
(s5069 5)
(s5070 5)
(s5071 2)
(s5073 4)
(s5074 5)
(s5075 5)
(s5076 2)
(s5078 4)
(s5079 5)
(s5080 5)
(s5081 2)
(s5083 4)
(s5084 5)
(s5085 5)
(s5086 2)
(s5088 4)
(s5089 5)
(s5090 5)
(s5091 2)
(s5093 4)
(s5094 5)
(s5095 5)
(s5096 2)
(s5098 4)
(s5099 5)
(s5100 5)
(s5101 2)
(s5103 4)
(s5104 5)
(s5105 5)
(s5106 2)
(s5108 4)
(s5109 5)
(s5110 5)
(s5111 2)
(s5113 4)
(s5114 5)
(s5115 5)
(s5116 2)
(s5118 4)
(s5119 5)
(s5120 5)
(s5121 2)
(s5123 4)
(s5124 5)
(s5125 5)
(s5126 2)
(s5128 4)
(s5129 5)
(s5130 5)
(s5131 2)
(s5133 4)
(s5134 5)
(s5135 5)
(s5136 2)
(s5138 4)
(s5139 5)
(s5140 5)
(s5141 2)
(s5143 4)
(s5144 5)
(s5145 5)
(s5146 2)
(s5148 4)
(s5149 5)
(s5150 5)
(s5151 2)
(s5153 4)
(s5154 5)
(s5155 5)
(s5156 2)
(s5158 4)
(s5159 5)
(s5160 5)
(s5161 2)
(s5163 4)
(s5164 5)
(s5165 5)
(s5166 2)
(s5168 4)
(s5169 5)
(s5170 5)
(s5171 2)
(s5173 4)
(s5174 5)
(s5175 5)
(s5176 2)
(s5178 4)
(s5179 5)
(s5180 5)
(s5181 2)
(s5183 4)
(s5184 5)
(s5185 5)
(s5186 2)
(s5188 4)
(s5189 5)
(s5190 5)
(s5191 2)
(s5193 4)
(s5194 5)
(s5195 5)
(s5196 2)
(s5198 4)
(s5199 5)
(s5200 5)
(s5201 2)
(s5203 4)
(s5204 5)
(s5205 5)
(s5206 2)
(s5208 4)
(s5209 5)
(s5210 5)
(s5211 2)
(s5213 4)
(s5214 5)
(s5215 5)
(s5216 2)
(s5218 4)
(s5219 5)
(s5220 5)
(s5221 2)
(s5223 4)
(s5224 5)
(s5225 5)
(s5226 2)
(s5228 4)
(s5229 5)
(s5230 5)
(s5231 2)
(s5233 4)
(s5234 5)
(s5235 5)
(s5236 2)
(s5238 4)
(s5239 5)
(s5240 5)
(s5241 2)
(s5243 4)
(s5244 5)
(s5245 5)
(s5246 2)
(s5248 4)
(s5249 5)
(s5250 5)
(s5251 2)
(s5253 4)
(s5254 5)
(s5255 5)
(s5256 2)
(s5258 4)
(s5259 5)
(s5260 5)
(s5261 2)
(s5263 4)
(s5264 5)
(s5265 5)
(s5266 2)
(s5268 4)
(s5269 5)
(s5270 5)
(s5271 2)
(s5273 4)
(s5274 5)
(s5275 5)
(s5276 2)
(s5278 4)
(s5279 5)
(s5280 5)
(s5281 2)
(s5283 4)
(s5284 5)
(s5285 5)
(s5286 2)
(s5288 4)
(s5289 5)
(s5290 5)
(s5291 2)
(s5293 4)
(s5294 5)
(s5295 5)
(s5296 2)
(s5298 4)
(s5299 5)
(s5300 5)
(s5301 2)
(s5303 4)
(s5304 5)
(s5305 5)
(s5306 2)
(s5308 4)
(s5309 5)
(s5310 5)
(s5311 2)
(s5313 4)
(s5314 5)
(s5315 5)
(s5316 2)
(s5318 4)
(s5319 5)
(s5320 5)
(s5321 2)
(s5323 4)
(s5324 5)
(s5325 5)
(s5326 2)
(s5328 4)
(s5329 5)
(s5330 5)
(s5331 2)
(s5333 4)
(s5334 5)
(s5335 5)
(s5336 2)
(s5338 4)
(s5339 5)
(s5340 5)
(s5341 2)
(s5343 4)
(s5344 5)
(s5345 5)
(s5346 2)
(s5348 4)
(s5349 5)
(s5350 5)
(s5351 2)
(s5353 4)
(s5354 5)
(s5355 5)
(s5356 2)
(s5358 4)
(s5359 5)
(s5360 5)
(s5361 2)
(s5363 4)
(s5364 5)
(s5365 5)
(s5366 2)
(s5368 4)
(s5369 5)
(s5370 5)
(s5371 2)
(s5373 4)
(s5374 5)
(s5375 5)
(s5376 2)
(s5378 4)
(s5379 5)
(s5380 5)
(s5381 2)
(s5383 4)
(s5384 5)
(s5385 5)
(s5386 2)
(s5388 4)
(s5389 5)
(s5390 5)
(s5391 2)
(s5393 4)
(s5394 5)
(s5395 5)
(s5396 2)
(s5398 4)
(s5399 5)
(s5400 5)
(s5401 2)
(s5403 4)
(s5404 5)
(s5405 5)
(s5406 2)
(s5408 4)
(s5409 5)
(s5410 5)
(s5411 2)
(s5413 4)
(s5414 5)
(s5415 5)
(s5416 2)
(s5418 4)
(s5419 5)
(s5420 5)
(s5421 2)
(s5423 4)
(s5424 5)
(s5425 5)
(s5426 2)
(s5428 4)
(s5429 5)
(s5430 5)
(s5431 2)
(s5433 4)
(s5434 5)
(s5435 5)
(s5436 2)
(s5438 4)
(s5439 5)
(s5440 5)
(s5441 2)
(s5443 4)
(s5444 5)
(s5445 5)
(s5446 2)
(s5448 4)
(s5449 5)
(s5450 5)
(s5451 2)
(s5453 4)
(s5454 5)
(s5455 5)
(s5456 2)
(s5458 4)
(s5459 5)
(s5460 5)
(s5461 2)
(s5463 4)
(s5464 5)
(s5465 5)
(s5466 2)
(s5468 4)
(s5469 5)
(s5470 5)
(s5471 2)
(s5473 4)
(s5474 5)
(s5475 5)
(s5476 2)
(s5478 4)
(s5479 5)
(s5480 5)
(s5481 2)
(s5483 4)
(s5484 5)
(s5485 5)
(s5486 2)
(s5488 4)
(s5489 5)
(s5490 5)
(s5491 2)
(s5493 4)
(s5494 5)
(s5495 5)
(s5496 2)
(s5498 4)
(s5499 5)
(s5500 5)
(s5501 2)
(s5503 4)
(s5504 5)
(s5505 5)
(s5506 2)
(s5508 4)
(s5509 5)
(s5510 5)
(s5511 2)
(s5513 4)
(s5514 5)
(s5515 5)
(s5516 2)
(s5518 4)
(s5519 5)
(s5520 5)
(s5521 2)
(s5523 4)
(s5524 5)
(s5525 5)
(s5526 2)
(s5528 4)
(s5529 5)
(s5530 5)
(s5531 2)
(s5533 4)
(s5534 5)
(s5535 5)
(s5536 2)
(s5538 4)
(s5539 5)
(s5540 5)
(s5541 2)
(s5543 4)
(s5544 5)
(s5545 5)
(s5546 2)
(s5548 4)
(s5549 5)
(s5550 5)
(s5551 2)
(s5553 4)
(s5554 5)
(s5555 5)
(s5556 2)
(s5558 4)
(s5559 5)
(s5560 5)
(s5561 2)
(s5563 4)
(s5564 5)
(s5565 5)
(s5566 2)
(s5568 4)
(s5569 5)
(s5570 5)
(s5571 2)
(s5573 4)
(s5574 5)
(s5575 5)
(s5576 2)
(s5578 4)
(s5579 5)
(s5580 5)
(s5581 2)
(s5583 4)
(s5584 5)
(s5585 5)
(s5586 2)
(s5588 4)
(s5589 5)
(s5590 5)
(s5591 2)
(s5593 4)
(s5594 5)
(s5595 5)
(s5596 2)
(s5598 4)
(s5599 5)
(s5600 5)
(s5601 2)
(s5603 4)
(s5604 5)
(s5605 5)
(s5606 2)
(s5608 4)
(s5609 5)
(s5610 5)
(s5611 2)
(s5613 4)
(s5614 5)
(s5615 5)
(s5616 2)
(s5618 4)
(s5619 5)
(s5620 5)
(s5621 2)
(s5623 4)
(s5624 5)
(s5625 5)
(s5626 2)
(s5628 4)
(s5629 5)
(s5630 5)
(s5631 2)
(s5633 4)
(s5634 5)
(s5635 5)
(s5636 2)
(s5638 4)
(s5639 5)
(s5640 5)
(s5641 2)
(s5643 4)
(s5644 5)
(s5645 5)
(s5646 2)
(s5648 4)
(s5649 5)
(s5650 5)
(s5651 2)
(s5653 4)
(s5654 5)
(s5655 5)
(s5656 2)
(s5658 4)
(s5659 5)
(s5660 5)
(s5661 2)
(s5663 4)
(s5664 5)
(s5665 5)
(s5666 2)
(s5668 4)
(s5669 5)
(s5670 5)
(s5671 2)
(s5673 4)
(s5674 5)
(s5675 5)
(s5676 2)
(s5678 4)
(s5679 5)
(s5680 5)
(s5681 2)
(s5683 4)
(s5684 5)
(s5685 5)
(s5686 2)
(s5688 4)
(s5689 5)
(s5690 5)
(s5691 2)
(s5693 4)
(s5694 5)
(s5695 5)
(s5696 2)
(s5698 4)
(s5699 5)
(s5700 5)
(s5701 2)
(s5703 4)
(s5704 5)
(s5705 5)
(s5706 2)
(s5708 4)
(s5709 5)
(s5710 5)
(s5711 2)
(s5713 4)
(s5714 5)
(s5715 5)
(s5716 2)
(s5718 4)
(s5719 5)
(s5720 5)
(s5721 2)
(s5723 4)
(s5724 5)
(s5725 5)
(s5726 2)
(s5728 4)
(s5729 5)
(s5730 5)
(s5731 2)
(s5733 4)
(s5734 5)
(s5735 5)
(s5736 2)
(s5738 4)
(s5739 5)
(s5740 5)
(s5741 2)
(s5743 4)
(s5744 5)
(s5745 5)
(s5746 2)
(s5748 4)
(s5749 5)
(s5750 5)
(s5751 2)
(s5753 4)
(s5754 5)
(s5755 5)
(s5756 2)
(s5758 4)
(s5759 5)
(s5760 5)
(s5761 2)
(s5763 4)
(s5764 5)
(s5765 5)
(s5766 2)
(s5768 4)
(s5769 5)
(s5770 5)
(s5771 2)
(s5773 4)
(s5774 5)
(s5775 5)
(s5776 2)
(s5778 4)
(s5779 5)
(s5780 5)
(s5781 2)
(s5783 4)
(s5784 5)
(s5785 5)
(s5786 2)
(s5788 4)
(s5789 5)
(s5790 5)
(s5791 2)
(s5793 4)
(s5794 5)
(s5795 5)
(s5796 2)
(s5798 4)
(s5799 5)
(s5800 5)
(s5801 2)
(s5803 4)
(s5804 5)
(s5805 5)
(s5806 2)
(s5808 4)
(s5809 5)
(s5810 5)
(s5811 2)
(s5813 4)
(s5814 5)
(s5815 5)
(s5816 2)
(s5818 4)
(s5819 5)
(s5820 5)
(s5821 2)
(s5823 4)
(s5824 5)
(s5825 5)
(s5826 2)
(s5828 4)
(s5829 5)
(s5830 5)
(s5831 2)
(s5833 4)
(s5834 5)
(s5835 5)
(s5836 2)
(s5838 4)
(s5839 5)
(s5840 5)
(s5841 2)
(s5843 4)
(s5844 5)
(s5845 5)
(s5846 2)
(s5848 4)
(s5849 5)
(s5850 5)
(s5851 2)
(s5853 4)
(s5854 5)
(s5855 5)
(s5856 2)
(s5858 4)
(s5859 5)
(s5860 5)
(s5861 2)
(s5863 4)
(s5864 5)
(s5865 5)
(s5866 2)
(s5868 4)
(s5869 5)
(s5870 5)
(s5871 2)
(s5873 4)
(s5874 5)
(s5875 5)
(s5876 2)
(s5878 4)
(s5879 5)
(s5880 5)
(s5881 2)
(s5883 4)
(s5884 5)
(s5885 5)
(s5886 2)
(s5888 4)
(s5889 5)
(s5890 5)
(s5891 2)
(s5893 4)
(s5894 5)
(s5895 5)
(s5896 2)
(s5898 4)
(s5899 5)
(s5900 5)
(s5901 2)
(s5903 4)
(s5904 5)
(s5905 5)
(s5906 2)
(s5908 4)
(s5909 5)
(s5910 5)
(s5911 2)
(s5913 4)
(s5914 5)
(s5915 5)
(s5916 2)
(s5918 4)
(s5919 5)
(s5920 5)
(s5921 2)
(s5923 4)
(s5924 5)
(s5925 5)
(s5926 2)
(s5928 4)
(s5929 5)
(s5930 5)
(s5931 2)
(s5933 4)
(s5934 5)
(s5935 5)
(s5936 2)
(s5938 4)
(s5939 5)
(s5940 5)
(s5941 2)
(s5943 4)
(s5944 5)
(s5945 5)
(s5946 2)
(s5948 4)
(s5949 5)
(s5950 5)
(s5951 2)
(s5953 4)
(s5954 5)
(s5955 5)
(s5956 2)
(s5958 4)
(s5959 5)
(s5960 5)
(s5961 2)
(s5963 4)
(s5964 5)
(s5965 5)
(s5966 2)
(s5968 4)
(s5969 5)
(s5970 5)
(s5971 2)
(s5973 4)
(s5974 5)
(s5975 5)
(s5976 2)
(s5978 4)
(s5979 5)
(s5980 5)
(s5981 2)
(s5983 4)
(s5984 5)
(s5985 5)
(s5986 2)
(s5988 4)
(s5989 5)
(s5990 5)
(s5991 2)
(s5993 4)
(s5994 5)
(s5995 5)
(s5996 2)
(s5998 4)
(s5999 5)
(s6000 5)
(s6001 2)
(s6003 4)
(s6004 5)
(s6005 5)
(s6006 2)
(s6008 4)
(s6009 5)
(s6010 5)
(s6011 2)
(s6013 4)
(s6014 5)
(s6015 5)
(s6016 2)
(s6018 4)
(s6019 5)
(s6020 5)
(s6021 2)
(s6023 4)
(s6024 5)
(s6025 5)
(s6026 2)
(s6028 4)
(s6029 5)
(s6030 5)
(s6031 2)
(s6033 4)
(s6034 5)
(s6035 5)
(s6036 2)
(s6038 4)
(s6039 5)
(s6040 5)
(s6041 2)
(s6043 4)
(s6044 5)
(s6045 5)
(s6046 2)
(s6048 4)
(s6049 5)
(s6050 5)
(s6051 2)
(s6053 4)
(s6054 5)
(s6055 5)
(s6056 2)
(s6058 4)
(s6059 5)
(s6060 5)
(s6061 2)
(s6063 4)
(s6064 5)
(s6065 5)
(s6066 2)
(s6068 4)
(s6069 5)
(s6070 5)
(s6071 2)
(s6073 4)
(s6074 5)
(s6075 5)
(s6076 2)
(s6078 4)
(s6079 5)
(s6080 5)
(s6081 2)
(s6083 4)
(s6084 5)
(s6085 5)
(s6086 2)
(s6088 4)
(s6089 5)
(s6090 5)
(s6091 2)
(s6093 4)
(s6094 5)
(s6095 5)
(s6096 2)
(s6098 4)
(s6099 5)
(s6100 5)
(s6101 2)
(s6103 4)
(s6104 5)
(s6105 5)
(s6106 2)
(s6108 4)
(s6109 5)
(s6110 5)
(s6111 2)
(s6113 4)
(s6114 5)
(s6115 5)
(s6116 2)
(s6118 4)
(s6119 5)
(s6120 5)
(s6121 2)
(s6123 4)
(s6124 5)
(s6125 5)
(s6126 2)
(s6128 4)
(s6129 5)
(s6130 5)
(s6131 2)
(s6133 4)
(s6134 5)
(s6135 5)
(s6136 2)
(s6138 4)
(s6139 5)
(s6140 5)
(s6141 2)
(s6143 4)
(s6144 5)
(s6145 5)
(s6146 2)
(s6148 4)
(s6149 5)
(s6150 5)
(s6151 2)
(s6153 4)
(s6154 5)
(s6155 5)
(s6156 2)
(s6158 4)
(s6159 5)
(s6160 5)
(s6161 2)
(s6163 4)
(s6164 5)
(s6165 5)
(s6166 2)
(s6168 4)
(s6169 5)
(s6170 5)
(s6171 2)
(s6173 4)
(s6174 5)
(s6175 5)
(s6176 2)
(s6178 4)
(s6179 5)
(s6180 5)
(s6181 2)
(s6183 4)
(s6184 5)
(s6185 5)
(s6186 2)
(s6188 4)
(s6189 5)
(s6190 5)
(s6191 2)
(s6193 4)
(s6194 5)
(s6195 5)
(s6196 2)
(s6198 4)
(s6199 5)
(s6200 5)
(s6201 2)
(s6203 4)
(s6204 5)
(s6205 5)
(s6206 2)
(s6208 4)
(s6209 5)
(s6210 5)
(s6211 2)
(s6213 4)
(s6214 5)
(s6215 5)
(s6216 2)
(s6218 4)
(s6219 5)
(s6220 5)
(s6221 2)
(s6223 4)
(s6224 5)
(s6225 5)
(s6226 2)
(s6228 4)
(s6229 5)
(s6230 5)
(s6231 2)
(s6233 4)
(s6234 5)
(s6235 5)
(s6236 2)
(s6238 4)
(s6239 5)
(s6240 5)
(s6241 2)
(s6243 4)
(s6244 5)
(s6245 5)
(s6246 2)
(s6248 4)
(s6249 5)
(s6250 5)
(s6251 2)
(s6253 4)
(s6254 5)
(s6255 5)
(s6256 2)
(s6258 4)
(s6259 5)
(s6260 5)
(s6261 2)
(s6263 4)
(s6264 5)
(s6265 5)
(s6266 2)
(s6268 4)
(s6269 5)
(s6270 5)
(s6271 2)
(s6273 4)
(s6274 5)
(s6275 5)
(s6276 2)
(s6278 4)
(s6279 5)
(s6280 5)
(s6281 2)
(s6283 4)
(s6284 5)
(s6285 5)
(s6286 2)
(s6288 4)
(s6289 5)
(s6290 5)
(s6291 2)
(s6293 4)
(s6294 5)
(s6295 5)
(s6296 2)
(s6298 4)
(s6299 5)
(s6300 5)
(s6301 2)
(s6303 4)
(s6304 5)
(s6305 5)
(s6306 2)
(s6308 4)
(s6309 5)
(s6310 5)
(s6311 2)
(s6313 4)
(s6314 5)
(s6315 5)
(s6316 2)
(s6318 4)
(s6319 5)
(s6320 5)
(s6321 2)
(s6323 4)
(s6324 5)
(s6325 5)
(s6326 2)
(s6328 4)
(s6329 5)
(s6330 5)
(s6331 2)
(s6333 4)
(s6334 5)
(s6335 5)
(s6336 2)
(s6338 4)
(s6339 5)
(s6340 5)
(s6341 2)
(s6343 4)
(s6344 5)
(s6345 5)
(s6346 2)
(s6348 4)
(s6349 5)
(s6350 5)
(s6351 2)
(s6353 4)
(s6354 5)
(s6355 5)
(s6356 2)
(s6358 4)
(s6359 5)
(s6360 5)
(s6361 2)
(s6363 4)
(s6364 5)
(s6365 5)
(s6366 2)
(s6368 4)
(s6369 5)
(s6370 5)
(s6371 2)
(s6373 4)
(s6374 5)
(s6375 5)
(s6376 2)
(s6378 4)
(s6379 5)
(s6380 5)
(s6381 2)
(s6383 4)
(s6384 5)
(s6385 5)
(s6386 2)
(s6388 4)
(s6389 5)
(s6390 5)
(s6391 2)
(s6393 4)
(s6394 5)
(s6395 5)
(s6396 2)
(s6398 4)
(s6399 5)
(s6400 5)
(s6401 2)
(s6403 4)
(s6404 5)
(s6405 5)
(s6406 2)
(s6408 4)
(s6409 5)
(s6410 5)
(s6411 2)
(s6413 4)
(s6414 5)
(s6415 5)
(s6416 2)
(s6418 4)
(s6419 5)
(s6420 5)
(s6421 2)
(s6423 4)
(s6424 5)
(s6425 5)
(s6426 2)
(s6428 4)
(s6429 5)
(s6430 5)
(s6431 2)
(s6433 4)
(s6434 5)
(s6435 5)
(s6436 2)
(s6438 4)
(s6439 5)
(s6440 5)
(s6441 2)
(s6443 4)
(s6444 5)
(s6445 5)
(s6446 2)
(s6448 4)
(s6449 5)
(s6450 5)
(s6451 2)
(s6453 4)
(s6454 5)
(s6455 5)
(s6456 2)
(s6458 4)
(s6459 5)
(s6460 5)
(s6461 2)
(s6463 4)
(s6464 5)
(s6465 5)
(s6466 2)
(s6468 4)
(s6469 5)
(s6470 5)
(s6471 2)
(s6473 4)
(s6474 5)
(s6475 5)
(s6476 2)
(s6478 4)
(s6479 5)
(s6480 5)
(s6481 2)
(s6483 4)
(s6484 5)
(s6485 5)
(s6486 2)
(s6488 4)
(s6489 5)
(s6490 5)
(s6491 2)
(s6493 4)
(s6494 5)
(s6495 5)
(s6496 2)
(s6498 4)
(s6499 5)
(s6500 5)
(s6501 2)
(s6503 4)
(s6504 5)
(s6505 5)
(s6506 2)
(s6508 4)
(s6509 5)
(s6510 5)
(s6511 2)
(s6513 4)
(s6514 5)
(s6515 5)
(s6516 2)
(s6518 4)
(s6519 5)
(s6520 5)
(s6521 2)
(s6523 4)
(s6524 5)
(s6525 5)
(s6526 2)
(s6528 4)
(s6529 5)
(s6530 5)
(s6531 2)
(s6533 4)
(s6534 5)
(s6535 5)
(s6536 2)
(s6538 4)
(s6539 5)
(s6540 5)
(s6541 2)
(s6543 4)
(s6544 5)
(s6545 5)
(s6546 2)
(s6548 4)
(s6549 5)
(s6550 5)
(s6551 2)
(s6553 4)
(s6554 5)
(s6555 5)
(s6556 2)
(s6558 4)
(s6559 5)
(s6560 5)
(s6561 2)
(s6563 4)
(s6564 5)
(s6565 5)
(s6566 2)
(s6568 4)
(s6569 5)
(s6570 5)
(s6571 2)
(s6573 4)
(s6574 5)
(s6575 5)
(s6576 2)
(s6578 4)
(s6579 5)
(s6580 5)
(s6581 2)
(s6583 4)
(s6584 5)
(s6585 5)
(s6586 2)
(s6588 4)
(s6589 5)
(s6590 5)
(s6591 2)
(s6593 4)
(s6594 5)
(s6595 5)
(s6596 2)
(s6598 4)
(s6599 5)
(s6600 5)
(s6601 2)
(s6603 4)
(s6604 5)
(s6605 5)
(s6606 2)
(s6608 4)
(s6609 5)
(s6610 5)
(s6611 2)
(s6613 4)
(s6614 5)
(s6615 5)
(s6616 2)
(s6618 4)
(s6619 5)
(s6620 5)
(s6621 2)
(s6623 4)
(s6624 5)
(s6625 5)
(s6626 2)
(s6628 4)
(s6629 5)
(s6630 5)
(s6631 2)
(s6633 4)
(s6634 5)
(s6635 5)
(s6636 2)
(s6638 4)
(s6639 5)
(s6640 5)
(s6641 2)
(s6643 4)
(s6644 5)
(s6645 5)
(s6646 2)
(s6648 4)
(s6649 5)
(s6650 5)
(s6651 2)
(s6653 4)
(s6654 5)
(s6655 5)
(s6656 2)
(s6658 4)
(s6659 5)
(s6660 5)
(s6661 2)
(s6663 4)
(s6664 5)
(s6665 5)
(s6666 2)
(s6668 4)
(s6669 5)
(s6670 5)
(s6671 2)
(s6673 4)
(s6674 5)
(s6675 5)
(s6676 2)
(s6678 4)
(s6679 5)
(s6680 5)
(s6681 2)
(s6683 4)
(s6684 5)
(s6685 5)
(s6686 2)
(s6688 4)
(s6689 5)
(s6690 5)
(s6691 2)
(s6693 4)
(s6694 5)
(s6695 5)
(s6696 2)
(s6698 4)
(s6699 5)
(s6700 5)
(s6701 2)
(s6703 4)
(s6704 5)
(s6705 5)
(s6706 2)
(s6708 4)
(s6709 5)
(s6710 5)
(s6711 2)
(s6713 4)
(s6714 5)
(s6715 5)
(s6716 2)
(s6718 4)
(s6719 5)
(s6720 5)
(s6721 2)
(s6723 4)
(s6724 5)
(s6725 5)
(s6726 2)
(s6728 4)
(s6729 5)
(s6730 5)
(s6731 2)
(s6733 4)
(s6734 5)
(s6735 5)
(s6736 2)
(s6738 4)
(s6739 5)
(s6740 5)
(s6741 2)
(s6743 4)
(s6744 5)
(s6745 5)
(s6746 2)
(s6748 4)
(s6749 5)
(s6750 5)
(s6751 2)
(s6753 4)
(s6754 5)
(s6755 5)
(s6756 2)
(s6758 4)
(s6759 5)
(s6760 5)
(s6761 2)
(s6763 4)
(s6764 5)
(s6765 5)
(s6766 2)
(s6768 4)
(s6769 5)
(s6770 5)
(s6771 2)
(s6773 4)
(s6774 5)
(s6775 5)
(s6776 2)
(s6778 4)
(s6779 5)
(s6780 5)
(s6781 2)
(s6783 4)
(s6784 5)
(s6785 5)
(s6786 2)
(s6788 4)
(s6789 5)
(s6790 5)
(s6791 2)
(s6793 4)
(s6794 5)
(s6795 5)
(s6796 2)
(s6798 4)
(s6799 5)
(s6800 5)
(s6801 2)
(s6803 4)
(s6804 5)
(s6805 5)
(s6806 2)
(s6808 4)
(s6809 5)
(s6810 5)
(s6811 2)
(s6813 4)
(s6814 5)
(s6815 5)
(s6816 2)
(s6818 4)
(s6819 5)
(s6820 5)
(s6821 2)
(s6823 4)
(s6824 5)
(s6825 5)
(s6826 2)
(s6828 4)
(s6829 5)
(s6830 5)
(s6831 2)
(s6833 4)
(s6834 5)
(s6835 5)
(s6836 2)
(s6838 4)
(s6839 5)
(s6840 5)
(s6841 2)
(s6843 4)
(s6844 5)
(s6845 5)
(s6846 2)
(s6848 4)
(s6849 5)
(s6850 5)
(s6851 2)
(s6853 4)
(s6854 5)
(s6855 5)
(s6856 2)
(s6858 4)
(s6859 5)
(s6860 5)
(s6861 2)
(s6863 4)
(s6864 5)
(s6865 5)
(s6866 2)
(s6868 4)
(s6869 5)
(s6870 5)
(s6871 2)
(s6873 4)
(s6874 5)
(s6875 5)
(s6876 2)
(s6878 4)
(s6879 5)
(s6880 5)
(s6881 2)
(s6883 4)
(s6884 5)
(s6885 5)
(s6886 2)
(s6888 4)
(s6889 5)
(s6890 5)
(s6891 2)
(s6893 4)
(s6894 5)
(s6895 5)
(s6896 2)
(s6898 4)
(s6899 5)
(s6900 5)
(s6901 2)
(s6903 4)
(s6904 5)
(s6905 5)
(s6906 2)
(s6908 4)
(s6909 5)
(s6910 5)
(s6911 2)
(s6913 4)
(s6914 5)
(s6915 5)
(s6916 2)
(s6918 4)
(s6919 5)
(s6920 5)
(s6921 2)
(s6923 4)
(s6924 5)
(s6925 5)
(s6926 2)
(s6928 4)
(s6929 5)
(s6930 5)
(s6931 2)
(s6933 4)
(s6934 5)
(s6935 5)
(s6936 2)
(s6938 4)
(s6939 5)
(s6940 5)
(s6941 2)
(s6943 4)
(s6944 5)
(s6945 5)
(s6946 2)
(s6948 4)
(s6949 5)
(s6950 5)
(s6951 2)
(s6953 4)
(s6954 5)
(s6955 5)
(s6956 2)
(s6958 4)
(s6959 5)
(s6960 5)
(s6961 2)
(s6963 4)
(s6964 5)
(s6965 5)
(s6966 2)
(s6968 4)
(s6969 5)
(s6970 5)
(s6971 2)
(s6973 4)
(s6974 5)
(s6975 5)
(s6976 2)
(s6978 4)
(s6979 5)
(s6980 5)
(s6981 2)
(s6983 4)
(s6984 5)
(s6985 5)
(s6986 2)
(s6988 4)
(s6989 5)
(s6990 5)
(s6991 2)
(s6993 4)
(s6994 5)
(s6995 5)
(s6996 2)
(s6998 4)
(s6999 5)
(s7000 5)
(s7001 2)
(s7003 4)
(s7004 5)
(s7005 5)
(s7006 2)
(s7008 4)
(s7009 5)
(s7010 5)
(s7011 2)
(s7013 4)
(s7014 5)
(s7015 5)
(s7016 2)
(s7018 4)
(s7019 5)
(s7020 5)
(s7021 2)
(s7023 4)
(s7024 5)
(s7025 5)
(s7026 2)
(s7028 4)
(s7029 5)
(s7030 5)
(s7031 2)
(s7033 4)
(s7034 5)
(s7035 5)
(s7036 2)
(s7038 4)
(s7039 5)
(s7040 5)
(s7041 2)
(s7043 4)
(s7044 5)
(s7045 5)
(s7046 2)
(s7048 4)
(s7049 5)
(s7050 5)
(s7051 2)
(s7053 4)
(s7054 5)
(s7055 5)
(s7056 2)
(s7058 4)
(s7059 5)
(s7060 5)
(s7061 2)
(s7063 4)
(s7064 5)
(s7065 5)
(s7066 2)
(s7068 4)
(s7069 5)
(s7070 5)
(s7071 2)
(s7073 4)
(s7074 5)
(s7075 5)
(s7076 2)
(s7078 4)
(s7079 5)
(s7080 5)
(s7081 2)
(s7083 4)
(s7084 5)
(s7085 5)
(s7086 2)
(s7088 4)
(s7089 5)
(s7090 5)
(s7091 2)
(s7093 4)
(s7094 5)
(s7095 5)
(s7096 2)
(s7098 4)
(s7099 5)
(s7100 5)
(s7101 2)
(s7103 4)
(s7104 5)
(s7105 5)
(s7106 2)
(s7108 4)
(s7109 5)
(s7110 5)
(s7111 2)
(s7113 4)
(s7114 5)
(s7115 5)
(s7116 2)
(s7118 4)
(s7119 5)
(s7120 5)
(s7121 2)
(s7123 4)
(s7124 5)
(s7125 5)
(s7126 2)
(s7128 4)
(s7129 5)
(s7130 5)
(s7131 2)
(s7133 4)
(s7134 5)
(s7135 5)
(s7136 2)
(s7138 4)
(s7139 5)
(s7140 5)
(s7141 2)
(s7143 4)
(s7144 5)
(s7145 5)
(s7146 2)
(s7148 4)
(s7149 5)
(s7150 5)
(s7151 2)
(s7153 4)
(s7154 5)
(s7155 5)
(s7156 2)
(s7158 4)
(s7159 5)
(s7160 5)
(s7161 2)
(s7163 4)
(s7164 5)
(s7165 5)
(s7166 2)
(s7168 4)
(s7169 5)
(s7170 5)
(s7171 2)
(s7173 4)
(s7174 5)
(s7175 5)
(s7176 2)
(s7178 4)
(s7179 5)
(s7180 5)
(s7181 2)
(s7183 4)
(s7184 5)
(s7185 5)
(s7186 2)
(s7188 4)
(s7189 5)
(s7190 5)
(s7191 2)
(s7193 4)
(s7194 5)
(s7195 5)
(s7196 2)
(s7198 4)
(s7199 5)
(s7200 5)
(s7201 2)
(s7203 4)
(s7204 5)
(s7205 5)
(s7206 2)
(s7208 4)
(s7209 5)
(s7210 5)
(s7211 2)
(s7213 4)
(s7214 5)
(s7215 5)
(s7216 2)
(s7218 4)
(s7219 5)
(s7220 5)
(s7221 2)
(s7223 4)
(s7224 5)
(s7225 5)
(s7226 2)
(s7228 4)
(s7229 5)
(s7230 5)
(s7231 2)
(s7233 4)
(s7234 5)
(s7235 5)
(s7236 2)
(s7238 4)
(s7239 5)
(s7240 5)
(s7241 2)
(s7243 4)
(s7244 5)
(s7245 5)
(s7246 2)
(s7248 4)
(s7249 5)
(s7250 5)
(s7251 2)
(s7253 4)
(s7254 5)
(s7255 5)
(s7256 2)
(s7258 4)
(s7259 5)
(s7260 5)
(s7261 2)
(s7263 4)
(s7264 5)
(s7265 5)
(s7266 2)
(s7268 4)
(s7269 5)
(s7270 5)
(s7271 2)
(s7273 4)
(s7274 5)
(s7275 5)
(s7276 2)
(s7278 4)
(s7279 5)
(s7280 5)
(s7281 2)
(s7283 4)
(s7284 5)
(s7285 5)
(s7286 2)
(s7288 4)
(s7289 5)
(s7290 5)
(s7291 2)
(s7293 4)
(s7294 5)
(s7295 5)
(s7296 2)
(s7298 4)
(s7299 5)
(s7300 5)
(s7301 2)
(s7303 4)
(s7304 5)
(s7305 5)
(s7306 2)
(s7308 4)
(s7309 5)
(s7310 5)
(s7311 2)
(s7313 4)
(s7314 5)
(s7315 5)
(s7316 2)
(s7318 4)
(s7319 5)
(s7320 5)
(s7321 2)
(s7323 4)
(s7324 5)
(s7325 5)
(s7326 2)
(s7328 4)
(s7329 5)
(s7330 5)
(s7331 2)
(s7333 4)
(s7334 5)
(s7335 5)
(s7336 2)
(s7338 4)
(s7339 5)
(s7340 5)
(s7341 2)
(s7343 4)
(s7344 5)
(s7345 5)
(s7346 2)
(s7348 4)
(s7349 5)
(s7350 5)
(s7351 2)
(s7353 4)
(s7354 5)
(s7355 5)
(s7356 2)
(s7358 4)
(s7359 5)
(s7360 5)
(s7361 2)
(s7363 4)
(s7364 5)
(s7365 5)
(s7366 2)
(s7368 4)
(s7369 5)
(s7370 5)
(s7371 2)
(s7373 4)
(s7374 5)
(s7375 5)
(s7376 2)
(s7378 4)
(s7379 5)
(s7380 5)
(s7381 2)
(s7383 4)
(s7384 5)
(s7385 5)
(s7386 2)
(s7388 4)
(s7389 5)
(s7390 5)
(s7391 2)
(s7393 4)
(s7394 5)
(s7395 5)
(s7396 2)
(s7398 4)
(s7399 5)
(s7400 5)
(s7401 2)
(s7403 4)
(s7404 5)
(s7405 5)
(s7406 2)
(s7408 4)
(s7409 5)
(s7410 5)
(s7411 2)
(s7413 4)
(s7414 5)
(s7415 5)
(s7416 2)
(s7418 4)
(s7419 5)
(s7420 5)
(s7421 2)
(s7423 4)
(s7424 5)
(s7425 5)
(s7426 2)
(s7428 4)
(s7429 5)
(s7430 5)
(s7431 2)
(s7433 4)
(s7434 5)
(s7435 5)
(s7436 2)
(s7438 4)
(s7439 5)
(s7440 5)
(s7441 2)
(s7443 4)
(s7444 5)
(s7445 5)
(s7446 2)
(s7448 4)
(s7449 5)
(s7450 5)
(s7451 2)
(s7453 4)
(s7454 5)
(s7455 5)
(s7456 2)
(s7458 4)
(s7459 5)
(s7460 5)
(s7461 2)
(s7463 4)
(s7464 5)
(s7465 5)
(s7466 2)
(s7468 4)
(s7469 5)
(s7470 5)
(s7471 2)
(s7473 4)
(s7474 5)
(s7475 5)
(s7476 2)
(s7478 4)
(s7479 5)
(s7480 5)
(s7481 2)
(s7483 4)
(s7484 5)
(s7485 5)
(s7486 2)
(s7488 4)
(s7489 5)
(s7490 5)
(s7491 2)
(s7493 4)
(s7494 5)
(s7495 5)
(s7496 2)
(s7498 4)
(s7499 5)
(s7500 5)
(s7501 2)
(s7503 4)
(s7504 5)
(s7505 5)
(s7506 2)
(s7508 4)
(s7509 5)
(s7510 5)
(s7511 2)
(s7513 4)
(s7514 5)
(s7515 5)
(s7516 2)
(s7518 4)
(s7519 5)
(s7520 5)
(s7521 2)
(s7523 4)
(s7524 5)
(s7525 5)
(s7526 2)
(s7528 4)
(s7529 5)
(s7530 5)
(s7531 2)
(s7533 4)
(s7534 5)
(s7535 5)
(s7536 2)
(s7538 4)
(s7539 5)
(s7540 5)
(s7541 2)
(s7543 4)
(s7544 5)
(s7545 5)
(s7546 2)
(s7548 4)
(s7549 5)
(s7550 5)
(s7551 2)
(s7553 4)
(s7554 5)
(s7555 5)
(s7556 2)
(s7558 4)
(s7559 5)
(s7560 5)
(s7561 2)
(s7563 4)
(s7564 5)
(s7565 5)
(s7566 2)
(s7568 4)
(s7569 5)
(s7570 5)
(s7571 2)
(s7573 4)
(s7574 5)
(s7575 5)
(s7576 2)
(s7578 4)
(s7579 5)
(s7580 5)
(s7581 2)
(s7583 4)
(s7584 5)
(s7585 5)
(s7586 2)
(s7588 4)
(s7589 5)
(s7590 5)
(s7591 2)
(s7593 4)
(s7594 5)
(s7595 5)
(s7596 2)
(s7598 4)
(s7599 5)
(s7600 5)
(s7601 2)
(s7603 4)
(s7604 5)
(s7605 5)
(s7606 2)
(s7608 4)
(s7609 5)
(s7610 5)
(s7611 2)
(s7613 4)
(s7614 5)
(s7615 5)
(s7616 2)
(s7618 4)
(s7619 5)
(s7620 5)
(s7621 2)
(s7623 4)
(s7624 5)
(s7625 5)
(s7626 2)
(s7628 4)
(s7629 5)
(s7630 5)
(s7631 2)
(s7633 4)
(s7634 5)
(s7635 5)
(s7636 2)
(s7638 4)
(s7639 5)
(s7640 5)
(s7641 2)
(s7643 4)
(s7644 5)
(s7645 5)
(s7646 2)
(s7648 4)
(s7649 5)
(s7650 5)
(s7651 2)
(s7653 4)
(s7654 5)
(s7655 5)
(s7656 2)
(s7658 4)
(s7659 5)
(s7660 5)
(s7661 2)
(s7663 4)
(s7664 5)
(s7665 5)
(s7666 2)
(s7668 4)
(s7669 5)
(s7670 5)
(s7671 2)
(s7673 4)
(s7674 5)
(s7675 5)
(s7676 2)
(s7678 4)
(s7679 5)
(s7680 5)
(s7681 2)
(s7683 4)
(s7684 5)
(s7685 5)
(s7686 2)
(s7688 4)
(s7689 5)
(s7690 5)
(s7691 2)
(s7693 4)
(s7694 5)
(s7695 5)
(s7696 2)
(s7698 4)
(s7699 5)
(s7700 5)
(s7701 2)
(s7703 4)
(s7704 5)
(s7705 5)
(s7706 2)
(s7708 4)
(s7709 5)
(s7710 5)
(s7711 2)
(s7713 4)
(s7714 5)
(s7715 5)
(s7716 2)
(s7718 4)
(s7719 5)
(s7720 5)
(s7721 2)
(s7723 4)
(s7724 5)
(s7725 5)
(s7726 2)
(s7728 4)
(s7729 5)
(s7730 5)
(s7731 2)
(s7733 4)
(s7734 5)
(s7735 5)
(s7736 2)
(s7738 4)
(s7739 5)
(s7740 5)
(s7741 2)
(s7743 4)
(s7744 5)
(s7745 5)
(s7746 2)
(s7748 4)
(s7749 5)
(s7750 5)
(s7751 2)
(s7753 4)
(s7754 5)
(s7755 5)
(s7756 2)
(s7758 4)
(s7759 5)
(s7760 5)
(s7761 2)
(s7763 4)
(s7764 5)
(s7765 5)
(s7766 2)
(s7768 4)
(s7769 5)
(s7770 5)
(s7771 2)
(s7773 4)
(s7774 5)
(s7775 5)
(s7776 2)
(s7778 4)
(s7779 5)
(s7780 5)
(s7781 2)
(s7783 4)
(s7784 5)
(s7785 5)
(s7786 2)
(s7788 4)
(s7789 5)
(s7790 5)
(s7791 2)
(s7793 4)
(s7794 5)
(s7795 5)
(s7796 2)
(s7798 4)
(s7799 5)
(s7800 5)
(s7801 2)
(s7803 4)
(s7804 5)
(s7805 5)
(s7806 2)
(s7808 4)
(s7809 5)
(s7810 5)
(s7811 2)
(s7813 4)
(s7814 5)
(s7815 5)
(s7816 2)
(s7818 4)
(s7819 5)
(s7820 5)
(s7821 2)
(s7823 4)
(s7824 5)
(s7825 5)
(s7826 2)
(s7828 4)
(s7829 5)
(s7830 5)
(s7831 2)
(s7833 4)
(s7834 5)
(s7835 5)
(s7836 2)
(s7838 4)
(s7839 5)
(s7840 5)
(s7841 2)
(s7843 4)
(s7844 5)
(s7845 5)
(s7846 2)
(s7848 4)
(s7849 5)
(s7850 5)
(s7851 2)
(s7853 4)
(s7854 5)
(s7855 5)
(s7856 2)
(s7858 4)
(s7859 5)
(s7860 5)
(s7861 2)
(s7863 4)
(s7864 5)
(s7865 5)
(s7866 2)
(s7868 4)
(s7869 5)
(s7870 5)
(s7871 2)
(s7873 4)
(s7874 5)
(s7875 5)
(s7876 2)
(s7878 4)
(s7879 5)
(s7880 5)
(s7881 2)
(s7883 4)
(s7884 5)
(s7885 5)
(s7886 2)
(s7888 4)
(s7889 5)
(s7890 5)
(s7891 2)
(s7893 4)
(s7894 5)
(s7895 5)
(s7896 2)
(s7898 4)
(s7899 5)
(s7900 5)
(s7901 2)
(s7903 4)
(s7904 5)
(s7905 5)
(s7906 2)
(s7908 4)
(s7909 5)
(s7910 5)
(s7911 2)
(s7913 4)
(s7914 5)
(s7915 5)
(s7916 2)
(s7918 4)
(s7919 5)
(s7920 5)
(s7921 2)
(s7923 4)
(s7924 5)
(s7925 5)
(s7926 2)
(s7928 4)
(s7929 5)
(s7930 5)
(s7931 2)
(s7933 4)
(s7934 5)
(s7935 5)
(s7936 2)
(s7938 4)
(s7939 5)
(s7940 5)
(s7941 2)
(s7943 4)
(s7944 5)
(s7945 5)
(s7946 2)
(s7948 4)
(s7949 5)
(s7950 5)
(s7951 2)
(s7953 4)
(s7954 5)
(s7955 5)
(s7956 2)
(s7958 4)
(s7959 5)
(s7960 5)
(s7961 2)
(s7963 4)
(s7964 5)
(s7965 5)
(s7966 2)
(s7968 4)
(s7969 5)
(s7970 5)
(s7971 2)
(s7973 4)
(s7974 5)
(s7975 5)
(s7976 2)
(s7978 4)
(s7979 5)
(s7980 5)
(s7981 2)
(s7983 4)
(s7984 5)
(s7985 5)
(s7986 2)
(s7988 4)
(s7989 5)
(s7990 5)
(s7991 2)
(s7993 4)
(s7994 5)
(s7995 5)
(s7996 2)
(s7998 4)
(s7999 5)
(s8000 5)
(s8001 2)
(s8003 4)
(s8004 5)
(s8005 5)
(s8006 2)
(s8008 4)
(s8009 5)
(s8010 5)
(s8011 2)
(s8013 4)
(s8014 5)
(s8015 5)
(s8016 2)
(s8018 4)
(s8019 5)
(s8020 5)
(s8021 2)
(s8023 4)
(s8024 5)
(s8025 5)
(s8026 2)
(s8028 4)
(s8029 5)
(s8030 5)
(s8031 2)
(s8033 4)
(s8034 5)
(s8035 5)
(s8036 2)
(s8038 4)
(s8039 5)
(s8040 5)
(s8041 2)
(s8043 4)
(s8044 5)
(s8045 5)
(s8046 2)
(s8048 4)
(s8049 5)
(s8050 5)
(s8051 2)
(s8053 4)
(s8054 5)
(s8055 5)
(s8056 2)
(s8058 4)
(s8059 5)
(s8060 5)
(s8061 2)
(s8063 4)
(s8064 5)
(s8065 5)
(s8066 2)
(s8068 4)
(s8069 5)
(s8070 5)
(s8071 2)
(s8073 4)
(s8074 5)
(s8075 5)
(s8076 2)
(s8078 4)
(s8079 5)
(s8080 5)
(s8081 2)
(s8083 4)
(s8084 5)
(s8085 5)
(s8086 2)
(s8088 4)
(s8089 5)
(s8090 5)
(s8091 2)
(s8093 4)
(s8094 5)
(s8095 5)
(s8096 2)
(s8098 4)
(s8099 5)
(s8100 5)
(s8101 2)
(s8103 4)
(s8104 5)
(s8105 5)
(s8106 2)
(s8108 4)
(s8109 5)
(s8110 5)
(s8111 2)
(s8113 4)
(s8114 5)
(s8115 5)
(s8116 2)
(s8118 4)
(s8119 5)
(s8120 5)
(s8121 2)
(s8123 4)
(s8124 5)
(s8125 5)
(s8126 2)
(s8128 4)
(s8129 5)
(s8130 5)
(s8131 2)
(s8133 4)
(s8134 5)
(s8135 5)
(s8136 2)
(s8138 4)
(s8139 5)
(s8140 5)
(s8141 2)
(s8143 4)
(s8144 5)
(s8145 5)
(s8146 2)
(s8148 4)
(s8149 5)
(s8150 5)
(s8151 2)
(s8153 4)
(s8154 5)
(s8155 5)
(s8156 2)
(s8158 4)
(s8159 5)
(s8160 5)
(s8161 2)
(s8163 4)
(s8164 5)
(s8165 5)
(s8166 2)
(s8168 4)
(s8169 5)
(s8170 5)
(s8171 2)
(s8173 4)
(s8174 5)
(s8175 5)
(s8176 2)
(s8178 4)
(s8179 5)
(s8180 5)
(s8181 2)
(s8183 4)
(s8184 5)
(s8185 5)
(s8186 2)
(s8188 4)
(s8189 5)
(s8190 5)
(s8191 2)
(s8193 4)
(s8194 5)
(s8195 5)
(s8196 2)
(s8198 4)
(s8199 5)
(s8200 5)
(s8201 2)
(s8203 4)
(s8204 5)
(s8205 5)
(s8206 2)
(s8208 4)
(s8209 5)
(s8210 5)
(s8211 2)
(s8213 4)
(s8214 5)
(s8215 5)
(s8216 2)
(s8218 4)
(s8219 5)
(s8220 5)
(s8221 2)
(s8223 4)
(s8224 5)
(s8225 5)
(s8226 2)
(s8228 4)
(s8229 5)
(s8230 5)
(s8231 2)
(s8233 4)
(s8234 5)
(s8235 5)
(s8236 2)
(s8238 4)
(s8239 5)
(s8240 5)
(s8241 2)
(s8243 4)
(s8244 5)
(s8245 5)
(s8246 2)
(s8248 4)
(s8249 5)
(s8250 5)
(s8251 2)
(s8253 4)
(s8254 5)
(s8255 5)
(s8256 2)
(s8258 4)
(s8259 5)
(s8260 5)
(s8261 timeout
2) org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20133 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56219ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56305ms
[2024-05-24 10:40:45] [INFO ] Invariant cache hit.
[2024-05-24 10:40:47] [INFO ] Implicit Places using invariants in 2109 ms returned []
Implicit Place search using SMT only with invariants took 2109 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:40:47] [INFO ] Invariant cache hit.
[2024-05-24 10:40:47] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30122 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30116 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76219ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76305ms
Finished structural reductions in LTL mode , in 1 iterations and 135699 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:42:03] [INFO ] Flatten gal took : 273 ms
[2024-05-24 10:42:04] [INFO ] Flatten gal took : 287 ms
[2024-05-24 10:42:04] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:42:04] [INFO ] Flatten gal took : 274 ms
[2024-05-24 10:42:05] [INFO ] Flatten gal took : 286 ms
[2024-05-24 10:42:05] [INFO ] Time to serialize gal into /tmp/CTLCardinality9884850643376914902.gal : 47 ms
[2024-05-24 10:42:05] [INFO ] Time to serialize properties into /tmp/CTLCardinality16581151801726130921.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality9884850643376914902.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality16581151801726130921.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:42:35] [INFO ] Flatten gal took : 271 ms
[2024-05-24 10:42:35] [INFO ] Applying decomposition
[2024-05-24 10:42:35] [INFO ] Flatten gal took : 283 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph5588162976992932983.txt' '-o' '/tmp/graph5588162976992932983.bin' '-w' '/tmp/graph5588162976992932983.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph5588162976992932983.bin' '-l' '-1' '-v' '-w' '/tmp/graph5588162976992932983.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:42:36] [INFO ] Decomposing Gal with order
[2024-05-24 10:42:37] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:42:41] [INFO ] Removed a total of 1 redundant transitions.
[2024-05-24 10:42:41] [INFO ] Flatten gal took : 325 ms
[2024-05-24 10:42:42] [INFO ] Fuse similar labels procedure discarded/fused a total of 2 labels/synchronizations in 483 ms.
[2024-05-24 10:42:42] [INFO ] Time to serialize gal into /tmp/CTLCardinality11984243173026280691.gal : 52 ms
[2024-05-24 10:42:42] [INFO ] Time to serialize properties into /tmp/CTLCardinality14420224904742412988.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality11984243173026280691.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality14420224904742412988.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...285
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
Starting structural reductions in SI_CTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 2624 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:43:15] [INFO ] Invariant cache hit.
[2024-05-24 10:43:15] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20117 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20118 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 56120ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 56206ms
[2024-05-24 10:44:11] [INFO ] Invariant cache hit.
[2024-05-24 10:44:13] [INFO ] Implicit Places using invariants in 2098 ms returned []
Implicit Place search using SMT only with invariants took 2098 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:44:13] [INFO ] Invariant cache hit.
[2024-05-24 10:44:13] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30115 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: ((s0 5)
(s1 2)
(s3 4)
(s4 5)
(s5 5)
(s6 2)
(s8 4)
(s9 5)
(s10 5)
(s11 2)
(s13 4)
(s14 5)
(s15 5)
(s16 2)
(s18 4)
(s19 5)
(s20 5)
(s21 2)
(s23 4)
(s24 5)
(s25 5)
(s26 2)
(s28 4)
(s29 5)
(s30 5)
(s31 2)
(s33 4)
(s34 5)
(s35 5)
(s36 2)
(s38 4)
(s39 5)
(s40 5)
(s41 2)
(s43 4)
(s44 5)
(s45 5)
(s46 2)
(s48 4)
(s49 5)
(s50 5)
(s51 2)
(s53 4)
(s54 5)
(s55 5)
(s56 2)
(s58 4)
(s59 5)
(s60 5)
(s61 2)
(s63 4)
(s64 5)
(s65 5)
(s66 2)
(s68 4)
(s69 5)
(s70 5)
(s71 2)
(s73 4)
(s74 5)
(s75 5)
(s76 2)
(s78 4)
(s79 5)
(s80 5)
(s81 2)
(s83 4)
(s84 5)
(s85 5)
(s86 2)
(s88 4)
(s89 5)
(s90 5)
(s91 2)
(s93 4)
(s94 5)
(s95 5)
(s96 2)
(s98 4)
(s99 5)
(s100 5)
(s101 2)
(s103 4)
(s104 5)
(s105 5)
(s106 2)
(s108 4)
(s109 5)
(s110 5)
(s111 2)
(s113 4)
(s114 5)
(s115 5)
(s116 2)
(s118 4)
(s119 5)
(s120 5)
(s121 2)
(s123 4)
(s124 5)
(s125 5)
(s126 2)
(s128 4)
(s129 5)
(s130 5)
(s131 2)
(s133 4)
(s134 5)
(s135 5)
(s136 2)
(s138 4)
(s139 5)
(s140 5)
(s141 2)
(s143 4)
(s144 5)
(s145 5)
(s146 2)
(s148 4)
(s149 5)
(s150 5)
(s151 2)
(s153 4)
(s154 5)
(s155 5)
(s156 2)
(s158 4)
(s159 5)
(s160 5)
(s161 2)
(s163 4)
(s164 5)
(s165 5)
(s166 2)
(s168 4)
(s169 5)
(s170 5)
(s171 2)
(s173 4)
(s174 5)
(s175 5)
(s176 2)
(s178 4)
(s179 5)
(s180 5)
(s181 2)
(s183 4)
(s184 5)
(s185 5)
(s186 2)
(s188 4)
(s189 5)
(s190 5)
(s191 2)
(s193 4)
(s194 5)
(s195 5)
(s196 2)
(s198 4)
(s199 5)
(s200 5)
(s201 2)
(s203 4)
(s204 5)
(s205 5)
(s206 2)
(s208 4)
(s209 5)
(s210 5)
(s211 2)
(s213 4)
(s214 5)
(s215 5)
(s216 2)
(s218 4)
(s219 5)
(s220 5)
(s221 2)
(s223 4)
(s224 5)
(s225 5)
(s226 2)
(s228 4)
(s229 5)
(s230 5)
(s231 2)
(s233 4)
(s234 5)
(s235 5)
(s236 2)
(s238 4)
(s239 5)
(s240 5)
(s241 2)
(s243 4)
(s244 5)
(s245 5)
(s246 2)
(s248 4)
(s249 5)
(s250 5)
(s251 2)
(s253 4)
(s254 5)
(s255 5)
(s256 2)
(s258 4)
(s259 5)
(s260 5)
(s261 2)
(s263 4)
(s264 5)
(s265 5)
(s266 2)
(s268 4)
(s269 5)
(s270 5)
(s271 2)
(s273 4)
(s274 5)
(s275 5)
(s276 2)
(s278 4)
(s279 5)
(s280 5)
(s281 2)
(s283 4)
(s284 5)
(s285 5)
(s286 2)
(s288 4)
(s289 5)
(s290 5)
(s291 2)
(s293 4)
(s294 5)
(s295 5)
(s296 2)
(s298 4)
(s299 5)
(s300 5)
(s301 2)
(s303 4)
(s304 5)
(s305 5)
(s306 2)
(s308 4)
(s309 5)
(s310 5)
(s311 2)
(s313 4)
(s314 5)
(s315 5)
(s316 2)
(s318 4)
(s319 5)
(s320 5)
(s321 2)
(s323 4)
(s324 5)
(s325 5)
(s326 2)
(s328 4)
(s329 5)
(s330 5)
(s331 2)
(s333 4)
(s334 5)
(s335 5)
(s336 2)
(s338 4)
(s339 5)
(s340 5)
(s341 2)
(s343 4)
(s344 5)
(s345 5)
(s346 2)
(s348 4)
(s349 5)
(s350 5)
(s351 2)
(s353 4)
(s354 5)
(s355 5)
(s356 2)
(s358 4)
(s359 5)
(s360 5)
(s361 2)
(s363 4)
(s364 5)
(s365 5)
(s366 2)
(s368 4)
(s369 5)
(s370 5)
(s371 2)
(s373 4)
(s374 5)
(s375 5)
(s376 2)
(s378 4)
(s379 5)
(s380 5)
(s381 2)
(s383 4)
(s384 5)
(s385 5)
(s386 2)
(s388 4)
(s389 5)
(s390 5)
(s391 2)
(s393 4)
(s394 5)
(s395 5)
(s396 2)
(s398 4)
(s399 5)
(s400 5)
(s401 2)
(s403 4)
(s404 5)
(s405 5)
(s406 2)
(s408 4)
(s409 5)
(s410 5)
(s411 2)
(s413 4)
(s414 5)
(s415 5)
(s416 2)
(s418 4)
(s419 5)
(s420 5)
(s421 2)
(s423 4)
(s424 5)
(s425 5)
(s426 2)
(s428 4)
(s429 5)
(s430 5)
(s431 2)
(s433 4)
(s434 5)
(s435 5)
(s436 2)
(s438 4)
(s439 5)
(s440 5)
(s441 2)
(s443 4)
(s444 5)
(s445 5)
(s446 2)
(s448 4)
(s449 5)
(s450 5)
(s451 2)
(s453 4)
(s454 5)
(s455 5)
(s456 2)
(s458 4)
(s459 5)
(s460 5)
(s461 2)
(s463 4)
(s464 5)
(s465 5)
(s466 2)
(s468 4)
(s469 5)
(s470 5)
(s471 2)
(s473 4)
(s474 5)
(s475 5)
(s476 2)
(s478 4)
(s479 5)
(s480 5)
(s481 2)
(s483 4)
(s484 5)
(s485 5)
(s486 2)
(s488 4)
(s489 5)
(s490 5)
(s491 2)
(s493 4)
(s494 5)
(s495 5)
(s496 2)
(s498 4)
(s499 5)
(s500 5)
(s501 2)
(s503 4)
(s504 5)
(s505 5)
(s506 2)
(s508 4)
(s509 5)
(s510 5)
(s511 2)
(s513 4)
(s514 5)
(s515 5)
(s516 2)
(s518 4)
(s519 5)
(s520 5)
(s521 2)
(s523 4)
(s524 5)
(s525 5)
(s526 2)
(s528 4)
(s529 5)
(s530 5)
(s531 2)
(s533 4)
(s534 5)
(s535 5)
(s536 2)
(s538 4)
(s539 5)
(s540 5)
(s541 2)
(s543 4)
(s544 5)
(s545 5)
(s546 2)
(s548 4)
(s549 5)
(s550 5)
(s551 2)
(s553 4)
(s554 5)
(s555 5)
(s556 2)
(s558 4)
(s559 5)
(s560 5)
(s561 2)
(s563 4)
(s564 5)
(s565 5)
(s566 2)
(s568 4)
(s569 5)
(s570 5)
(s571 2)
(s573 4)
(s574 5)
(s575 5)
(s576 2)
(s578 4)
(s579 5)
(s580 5)
(s581 2)
(s583 4)
(s584 5)
(s585 5)
(s586 2)
(s588 4)
(s589 5)
(s590 5)
(s591 2)
(s593 4)
(s594 5)
(s595 5)
(s596 2)
(s598 4)
(s599 5)
(s600 5)
(s601 2)
(s603 4)
(s604 5)
(s605 5)
(s606 2)
(s608 4)
(s609 5)
(s610 5)
(s611 2)
(s613 4)
(s614 5)
(s615 5)
(s616 2)
(s618 4)
(s619 5)
(s620 5)
(s621 2)
(s623 4)
(s624 5)
(s625 5)
(s626 2)
(s628 4)
(s629 5)
(s630 5)
(s631 2)
(s633 4)
(s634 5)
(s635 5)
(s636 2)
(s638 4)
(s639 5)
(s640 5)
(s641 2)
(s643 4)
(s644 5)
(s645 5)
(s646 2)
(s648 4)
(s649 5)
(s650 5)
(s651 2)
(s653 4)
(s654 5)
(s655 5)
(s656 2)
(s658 4)
(s659 5)
(s660 5)
(s661 2)
(s663 4)
(s664 5)
(s665 5)
(s666 2)
(s668 4)
(s669 5)
(s670 5)
(s671 2)
(s673 4)
(s674 5)
(s675 5)
(s676 2)
(s678 4)
(s679 5)
(s680 5)
(s681 2)
(s683 4)
(s684 5)
(s685 5)
(s686 2)
(s688 4)
(s689 5)
(s690 5)
(s691 2)
(s693 4)
(s694 5)
(s695 5)
(s696 2)
(s698 4)
(s699 5)
(s700 5)
(s701 2)
(s703 4)
(s704 5)
(s705 5)
(s706 2)
(s708 4)
(s709 5)
(s710 5)
(s711 2)
(s713 4)
(s714 5)
(s715 5)
(s716 2)
(s718 4)
(s719 5)
(s720 5)
(s721 2)
(s723 4)
(s724 5)
(s725 5)
(s726 2)
(s728 4)
(s729 5)
(s730 5)
(s731 2)
(s733 4)
(s734 5)
(s735 5)
(s736 2)
(s738 4)
(s739 5)
(s740 5)
(s741 2)
(s743 4)
(s744 5)
(s745 5)
(s746 2)
(s748 4)
(s749 5)
(s750 5)
(s751 2)
(s753 4)
(s754 5)
(s755 5)
(s756 2)
(s758 4)
(s759 5)
(s760 5)
(s761 2)
(s763 4)
(s764 5)
(s765 5)
(s766 2)
(s768 4)
(s769 5)
(s770 5)
(s771 2)
(s773 4)
(s774 5)
(s775 5)
(s776 2)
(s778 4)
(s779 5)
(s780 5)
(s781 2)
(s783 4)
(s784 5)
(s785 5)
(s786 2)
(s788 4)
(s789 5)
(s790 5)
(s791 2)
(s793 4)
(s794 5)
(s795 5)
(s796 2)
(s798 4)
(s799 5)
(s800 5)
(s801 2)
(s803 4)
(s804 5)
(s805 5)
(s806 2)
(s808 4)
(s809 5)
(s810 5)
(s811 2)
(s813 4)
(s814 5)
(s815 5)
(s816 2)
(s818 4)
(s819 5)
(s820 5)
(s821 2)
(s823 4)
(s824 5)
(s825 5)
(s826 2)
(s828 4)
(s829 5)
(s830 5)
(s831 2)
(s833 4)
(s834 5)
(s835 5)
(s836 2)
(s838 4)
(s839 5)
(s840 5)
(s841 2)
(s843 4)
(s844 5)
(s845 5)
(s846 2)
(s848 4)
(s849 5)
(s850 5)
(s851 2)
(s853 4)
(s854 5)
(s855 5)
(s856 2)
(s858 4)
(s859 5)
(s860 5)
(s861 2)
(s863 4)
(s864 5)
(s865 5)
(s866 2)
(s868 4)
(s869 5)
(s870 5)
(s871 2)
(s873 4)
(s874 5)
(s875 5)
(s876 2)
(s878 4)
(s879 5)
(s880 5)
(s881 2)
(s883 4)
(s884 5)
(s885 5)
(s886 2)
(s888 4)
(s889 5)
(s890 5)
(s891 2)
(s893 4)
(s894 5)
(s895 5)
(s896 2)
(s898 4)
(s899 5)
(s900 5)
(s901 2)
(s903 4)
(s904 5)
(s905 5)
(s906 2)
(s908 4)
(s909 5)
(s910 5)
(s911 2)
(s913 4)
(s914 5)
(s915 5)
(s916 2)
(s918 4)
(s919 5)
(s920 5)
(s921 2)
(s923 4)
(s924 5)
(s925 5)
(s926 2)
(s928 4)
(s929 5)
(s930 5)
(s931 2)
(s933 4)
(s934 5)
(s935 5)
(s936 2)
(s938 4)
(s939 5)
(s940 5)
(s941 2)
(s943 4)
(s944 5)
(s945 5)
(s946 2)
(s948 4)
(s949 5)
(s950 5)
(s951 2)
(s953 4)
(s954 5)
(s955 5)
(s956 2)
(s958 4)
(s959 5)
(s960 5)
(s961 2)
(s963 4)
(s964 5)
(s965 5)
(s966 2)
(s968 4)
(s969 5)
(s970 5)
(s971 2)
(s973 4)
(s974 5)
(s975 5)
(s976 2)
(s978 4)
(s979 5)
(s980 5)
(s981 2)
(s983 4)
(s984 5)
(s985 5)
(s986 2)
(s988 4)
(s989 5)
(s990 5)
(s991 2)
(s993 4)
(s994 5)
(s995 5)
(s996 2)
(s998 4)
(s999 5)
(s1000 5)
(s1001 2)
(s1003 4)
(s1004 5)
(s1005 5)
(s1006 2)
(s1008 4)
(s1009 5)
(s1010 5)
(s1011 2)
(s1013 4)
(s1014 5)
(s1015 5)
(s1016 2)
(s1018 4)
(s1019 5)
(s1020 5)
(s1021 2)
(s1023 4)
(s1024 5)
(s1025 5)
(s1026 2)
(s1028 4)
(s1029 5)
(s1030 5)
(s1031 2)
(s1033 4)
(s1034 5)
(s1035 5)
(s1036 2)
(s1038 4)
(s1039 5)
(s1040 5)
(s1041 2)
(s1043 4)
(s1044 5)
(s1045 5)
(s1046 2)
(s1048 4)
(s1049 5)
(s1050 5)
(s1051 2)
(s1053 4)
(s1054 5)
(s1055 5)
(s1056 2)
(s1058 4)
(s1059 5)
(s1060 5)
(s1061 2)
(s1063 4)
(s1064 5)
(s1065 5)
(s1066 2)
(s1068 4)
(s1069 5)
(s1070 5)
(s1071 2)
(s1073 4)
(s1074 5)
(s1075 5)
(s1076 2)
(s1078 4)
(s1079 5)
(s1080 5)
(s1081 2)
(s1083 4)
(s1084 5)
(s1085 5)
(s1086 2)
(s1088 4)
(s1089 5)
(s1090 5)
(s1091 2)
(s1093 4)
(s1094 5)
(s1095 5)
(s1096 2)
(s1098 4)
(s1099 5)
(s1100 5)
(s1101 2)
(s1103 4)
(s1104 5)
(s1105 5)
(s1106 2)
(s1108 4)
(s1109 5)
(s1110 5)
(s1111 2)
(s1113 4)
(s1114 5)
(s1115 5)
(s1116 2)
(s1118 4)
(s1119 5)
(s1120 5)
(s1121 2)
(s1123 4)
(s1124 5)
(s1125 5)
(s1126 2)
(s1128 4)
(s1129 5)
(s1130 5)
(s1131 2)
(s1133 4)
(s1134 5)
(s1135 5)
(s1136 2)
(s1138 4)
(s1139 5)
(s1140 5)
(s1141 2)
(s1143 4)
(s1144 5)
(s1145 5)
(s1146 2)
(s1148 4)
(s1149 5)
(s1150 5)
(s1151 2)
(s1153 4)
(s1154 5)
(s1155 5)
(s1156 2)
(s1158 4)
(s1159 5)
(s1160 5)
(s1161 2)
(s1163 4)
(s1164 5)
(s1165 5)
(s1166 2)
(s1168 4)
(s1169 5)
(s1170 5)
(s1171 2)
(s1173 4)
(s1174 5)
(s1175 5)
(s1176 2)
(s1178 4)
(s1179 5)
(s1180 5)
(s1181 2)
(s1183 4)
(s1184 5)
(s1185 5)
(s1186 2)
(s1188 4)
(s1189 5)
(s1190 5)
(s1191 2)
(s1193 4)
(s1194 5)
(s1195 5)
(s1196 2)
(s1198 4)
(s1199 5)
(s1200 5)
(s1201 2)
(s1203 4)
(s1204 5)
(s1205 5)
(s1206 2)
(s1208 4)
(s1209 5)
(s1210 5)
(s1211 2)
(s1213 4)
(s1214 5)
(s1215 5)
(s1216 2)
(s1218 4)
(s1219 5)
(s1220 5)
(s1221 2)
(s1223 4)
(s1224 5)
(s1225 5)
(s1226 2)
(s1228 4)
(s1229 5)
(s1230 5)
(s1231 2)
(s1233 4)
(s1234 5)
(s1235 5)
(s1236 2)
(s1238 4)
(s1239 5)
(s1240 5)
(s1241 2)
(s1243 4)
(s1244 5)
(s1245 5)
(s1246 2)
(s1248 4)
(s1249 5)
(s1250 5)
(s1251 2)
(s1253 4)
(s1254 5)
(s1255 5)
(s1256 2)
(s1258 4)
(s1259 5)
(s1260 5)
(s1261 2)
(s1263 4)
(s1264 5)
(s1265 5)
(s1266 2)
(s1268 4)
(s1269 5)
(s1270 5)
(s1271 2)
(s1273 4)
(s1274 5)
(s1275 5)
(s1276 2)
(s1278 4)
(s1279 5)
(s1280 5)
(s1281 2)
(s1283 4)
(s1284 5)
(s1285 5)
(s1286 2)
(s1288 4)
(s1289 5)
(s1290 5)
(s1291 2)
(s1293 4)
(s1294 5)
(s1295 5)
(s1296 2)
(s1298 4)
(s1299 5)
(s1300 5)
(s1301 2)
(s1303 4)
(s1304 5)
(s1305 5)
(s1306 2)
(s1308 4)
(s1309 5)
(s1310 5)
(s1311 2)
(s1313 4)
(s1314 5)
(s1315 5)
(s1316 2)
(s1318 4)
(s1319 5)
(s1320 5)
(s1321 2)
(s1323 4)
(s1324 5)
(s1325 5)
(s1326 2)
(s1328 4)
(s1329 5)
(s1330 5)
(s1331 2)
(s1333 4)
(s1334 5)
(s1335 5)
(s1336 2)
(s1338 4)
(s1339 5)
(s1340 5)
(s1341 2)
(s1343 4)
(s1344 5)
(s1345 5)
(s1346 2)
(s1348 4)
(s1349 5)
(s1350 5)
(s1351 2)
(s1353 4)
(s1354 5)
(s1355 5)
(s1356 2)
(s1358 4)
(s1359 5)
(s1360 5)
(s1361 2)
(s1363 4)
(s1364 5)
(s1365 5)
(s1366 2)
(s1368 4)
(s1369 5)
(s1370 5)
(s1371 2)
(s1373 4)
(s1374 5)
(s1375 5)
(s1376 2)
(s1378 4)
(s1379 5)
(s1380 5)
(s1381 2)
(s1383 4)
(s1384 5)
(s1385 5)
(s1386 2)
(s1388 4)
(s1389 5)
(s1390 5)
(s1391 2)
(s1393 4)
(s1394 5)
(s1395 5)
(s1396 2)
(s1398 4)
(s1399 5)
(s1400 5)
(s1401 2)
(s1403 4)
(s1404 5)
(s1405 5)
(s1406 2)
(s1408 4)
(s1409 5)
(s1410 5)
(s1411 2)
(s1413 4)
(s1414 5)
(s1415 5)
(s1416 2)
(s1418 4)
(s1419 5)
(s1420 5)
(s1421 2)
(s1423 4)
(s1424 5)
(s1425 5)
(s1426 2)
(s1428 4)
(s1429 5)
(s1430 5)
(s1431 2)
(s1433 4)
(s1434 5)
(s1435 5)
(s1436 2)
(s1438 4)
(s1439 5)
(s1440 5)
(s1441 2)
(s1443 4)
(s1444 5)
(s1445 5)
(s1446 2)
(s1448 4)
(s1449 5)
(s1450 5)
(s1451 2)
(s1453 4)
(s1454 5)
(s1455 5)
(s1456 2)
(s1458 4)
(s1459 5)
(s1460 5)
(s1461 2)
(s1463 4)
(s1464 5)
(s1465 5)
(s1466 2)
(s1468 4)
(s1469 5)
(s1470 5)
(s1471 2)
(s1473 4)
(s1474 5)
(s1475 5)
(s1476 2)
(s1478 4)
(s1479 5)
(s1480 5)
(s1481 2)
(s1483 4)
(s1484 5)
(s1485 5)
(s1486 2)
(s1488 4)
(s1489 5)
(s1490 5)
(s1491 2)
(s1493 4)
(s1494 5)
(s1495 5)
(s1496 2)
(s1498 4)
(s1499 5)
(s1500 5)
(s1501 2)
(s1503 4)
(s1504 5)
(s1505 5)
(s1506 2)
(s1508 4)
(s1509 5)
(s1510 5)
(s1511 2)
(s1513 4)
(s1514 5)
(s1515 5)
(s1516 2)
(s1518 4)
(s1519 5)
(s1520 5)
(s1521 2)
(s1523 4)
(s1524 5)
(s1525 5)
(s1526 2)
(s1528 4)
(s1529 5)
(s1530 5)
(s1531 2)
(s1533 4)
(s1534 5)
(s1535 5)
(s1536 2)
(s1538 4)
(s1539 5)
(s1540 5)
(s1541 2)
(s1543 4)
(s1544 5)
(s1545 5)
(s1546 2)
(s1548 4)
(s1549 5)
(s1550 5)
(s1551 2)
(s1553 4)
(s1554 5)
(s1555 5)
(s1556 2)
(s1558 4)
(s1559 5)
(s1560 5)
(s1561 2)
(s1563 4)
(s1564 5)
(s1565 5)
(s1566 2)
(s1568 4)
(s1569 5)
(s1570 5)
(s1571 2)
(s1573 4)
(s1574 5)
(s1575 5)
(s1576 2)
(s1578 4)
(s1579 5)
(s1580 5)
(s1581 2)
(s1583 4)
(s1584 5)
(s1585 5)
(s1586 2)
(s1588 4)
(s1589 5)
(s1590 5)
(s1591 2)
(s1593 4)
(s1594 5)
(s1595 5)
(s1596 2)
(s1598 4)
(s1599 5)
(s1600 5)
(s1601 2)
(s1603 4)
(s1604 5)
(s1605 5)
(s1606 2)
(s1608 4)
(s1609 5)
(s1610 5)
(s1611 2)
(s1613 4)
(s1614 5)
(s1615 5)
(s1616 2)
(s1618 4)
(s1619 5)
(s1620 5)
(s1621 2)
(s1623 4)
(s1624 5)
(s1625 5)
(s1626 2)
(s1628 4)
(s1629 5)
(s1630 5)
(s1631 2)
(s1633 4)
(s1634 5)
(s1635 5)
(s1636 2)
(s1638 4)
(s1639 5)
(s1640 5)
(s1641 2)
(s1643 4)
(s1644 5)
(s1645 5)
(s1646 2)
(s1648 4)
(s1649 5)
(s1650 5)
(s1651 2)
(s1653 4)
(s1654 5)
(s1655 5)
(s1656 2)
(s1658 4)
(s1659 5)
(s1660 5)
(s1661 2)
(s1663 4)
(s1664 5)
(s1665 5)
(s1666 2)
(s1668 4)
(s1669 5)
(s1670 5)
(s1671 2)
(s1673 4)
(s1674 5)
(s1675 5)
(s1676 2)
(s1678 4)
(s1679 5)
(s1680 5)
(s1681 2)
(s1683 4)
(s1684 5)
(s1685 5)
(s1686 2)
(s1688 4)
(s1689 5)
(s1690 5)
(s1691 2)
(s1693 4)
(s1694 5)
(s1695 5)
(s1696 2)
(s1698 4)
(s1699 5)
(s1700 5)
(s1701 2)
(s1703 4)
(s1704 5)
(s1705 5)
(s1706 2)
(s1708 4)
(s1709 5)
(s1710 5)
(s1711 2)
(s1713 4)
(s1714 5)
(s1715 5)
(s1716 2)
(s1718 4)
(s1719 5)
(s1720 5)
(s1721 2)
(s1723 4)
(s1724 5)
(s1725 5)
(s1726 2)
(s1728 4)
(s1729 5)
(s1730 5)
(s1731 2)
(s1733 4)
(s1734 5)
(s1735 5)
(s1736 2)
(s1738 4)
(s1739 5)
(s1740 5)
(s1741 2)
(s1743 4)
(s1744 5)
(s1745 5)
(s1746 2)
(s1748 4)
(s1749 5)
(s1750 5)
(s1751 2)
(s1753 4)
(s1754 5)
(s1755 5)
(s1756 2)
(s1758 4)
(s1759 5)
(s1760 5)
(s1761 2)
(s1763 4)
(s1764 5)
(s1765 5)
(s1766 2)
(s1768 4)
(s1769 5)
(s1770 5)
(s1771 2)
(s1773 4)
(s1774 5)
(s1775 5)
(s1776 2)
(s1778 4)
(s1779 5)
(s1780 5)
(s1781 2)
(s1783 4)
(s1784 5)
(s1785 5)
(s1786 2)
(s1788 4)
(s1789 5)
(s1790 5)
(s1791 2)
(s1793 4)
(s1794 5)
(s1795 5)
(s1796 2)
(s1798 4)
(s1799 5)
(s1800 5)
(s1801 2)
(s1803 4)
(s1804 5)
(s1805 5)
(s1806 2)
(s1808 4)
(s1809 5)
(s1810 5)
(s1811 2)
(s1813 4)
(s1814 5)
(s1815 5)
(s1816 2)
(s1818 4)
(s1819 5)
(s1820 5)
(s1821 2)
(s1823 4)
(s1824 5)
(s1825 5)
(s1826 2)
(s1828 4)
(s1829 5)
(s1830 5)
(s1831 2)
(s1833 4)
(s1834 5)
(s1835 5)
(s1836 2)
(s1838 4)
(s1839 5)
(s1840 5)
(s1841 2)
(s1843 4)
(s1844 5)
(s1845 5)
(s1846 2)
(s1848 4)
(s1849 5)
(s1850 5)
(s1851 2)
(s1853 4)
(s1854 5)
(s1855 5)
(s1856 2)
(s1858 4)
(s1859 5)
(s1860 5)
(s1861 2)
(s1863 4)
(s1864 5)
(s1865 5)
(s1866 2)
(s1868 4)
(s1869 5)
(s1870 5)
(s1871 2)
(s1873 timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30120 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76623ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76706ms
Finished structural reductions in SI_CTL mode , in 1 iterations and 137660 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:45:30] [INFO ] Flatten gal took : 304 ms
[2024-05-24 10:45:30] [INFO ] Flatten gal took : 288 ms
[2024-05-24 10:45:31] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:45:32] [INFO ] Flatten gal took : 473 ms
[2024-05-24 10:45:32] [INFO ] Flatten gal took : 345 ms
[2024-05-24 10:45:32] [INFO ] Time to serialize gal into /tmp/ReachabilityCardinality5859859771576101495.gal : 85 ms
[2024-05-24 10:45:32] [INFO ] Time to serialize properties into /tmp/ReachabilityCardinality14604854786605410767.prop : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-reach-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/ReachabilityCardinality5859859771576101495.gal' '-t' 'CGAL' '-reachable-file' '/tmp/ReachabilityCardinality14604854786605410767.prop' '--nowitness' '--gen-order' 'FOLLOW'
its-reach command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-reach-linux64 --gc-threshold 2000000 --quiet ...329
RANDOM walk for 43035 steps (8 resets) in 4365 ms. (9 steps per ms) remains 1/1 properties
BEST_FIRST walk for 40004 steps (8 resets) in 4422 ms. (9 steps per ms) remains 1/1 properties
Loading property file /tmp/ReachabilityCardinality14604854786605410767.prop.
Probabilistic random walk after 44028 steps, saw 44012 distinct states, run finished after 6173 ms. (steps per millisecond=7 ) properties seen :0
[2024-05-24 10:45:40] [INFO ] Invariant cache hit.
[2024-05-24 10:45:40] [INFO ] State equation strengthened by 2000 read => feed constraints.
At refinement iteration 0 (INCLUDED_ONLY) 0/1 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 4/5 variables, 1/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 2 (INCLUDED_ONLY) 0/5 variables, 0/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (OVERLAPS) 8/13 variables, 5/6 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (INCLUDED_ONLY) 0/13 variables, 1/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/13 variables, 0/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (OVERLAPS) 0/13 variables, 0/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Real declared 13/26001 variables, and 7 constraints, problems are : Problem set: 0 solved, 1 unsolved in 120 ms.
Refiners :[Positive P Invariants (semi-flows): 1/2000 constraints, State Equation: 5/10000 constraints, ReadFeed: 1/2000 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 1 unsolved
At refinement iteration 0 (INCLUDED_ONLY) 0/1 variables, 0/0 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 1 (OVERLAPS) 4/5 variables, 1/1 constraints. Problems are: Problem set: 0 solved, 1 unsolved
[2024-05-24 10:45:40] [INFO ] Deduced a trap composed of 3 places in 30 ms of which 1 ms to minimize.
At refinement iteration 2 (INCLUDED_ONLY) 0/5 variables, 1/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 3 (INCLUDED_ONLY) 0/5 variables, 0/2 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 4 (OVERLAPS) 8/13 variables, 5/7 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 5 (INCLUDED_ONLY) 0/13 variables, 1/8 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 6 (INCLUDED_ONLY) 0/13 variables, 1/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 7 (INCLUDED_ONLY) 0/13 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
At refinement iteration 8 (OVERLAPS) 0/13 variables, 0/9 constraints. Problems are: Problem set: 0 solved, 1 unsolved
No progress, stopping.
After SMT solving in domain Int declared 13/26001 variables, and 9 constraints, problems are : Problem set: 0 solved, 1 unsolved in 147 ms.
Refiners :[Positive P Invariants (semi-flows): 1/2000 constraints, State Equation: 5/10000 constraints, ReadFeed: 1/2000 constraints, PredecessorRefiner: 1/1 constraints, Known Traps: 1/1 constraints]
After SMT, in 317ms problems are : Problem set: 0 solved, 1 unsolved
Finished Parikh walk after 179 steps, including 0 resets, run visited all 1 properties in 19 ms. (steps per millisecond=9 )
FORMULA JoinFreeModules-PT-2000-CTLCardinality-2023-14 FALSE TECHNIQUES PARIKH_WALK
Parikh walk visited 1 properties in 31 ms.
ITS runner timed out or was interrupted.
ITS tools runner thread asked to quit. Dying gracefully.
Starting structural reductions in LTL mode, iteration 0 : 10000/10000 places, 16001/16001 transitions.
Applied a total of 0 rules in 940 ms. Remains 10000 /10000 variables (removed 0) and now considering 16001/16001 (removed 0) transitions.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:45:41] [INFO ] Invariant cache hit.
[2024-05-24 10:45:41] [INFO ] State equation strengthened by 2000 read => feed constraints.
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20130 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "ParserException while parsing response: (timeout
org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 20123 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 59206ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 59317ms
[2024-05-24 10:46:40] [INFO ] Invariant cache hit.
[2024-05-24 10:46:42] [INFO ] Implicit Places using invariants in 2167 ms returned []
Implicit Place search using SMT only with invariants took 2168 ms to find 0 implicit places.
Running 12000 sub problems to find dead transitions.
[2024-05-24 10:46:43] [INFO ] Invariant cache hit.
[2024-05-24 10:46:43] [INFO ] State equation strengthened by 2000 read => feed constraints.
Error getting values : (error "ParserException while parsing response: ((s0 5.0)
(s1 2.0)
(s3 4.0)
(s4 5.0)
(s5 5.0)
(s6 2.0)
(s8 4.0)
(s9 5.0)
(s10 5.0)
(s11 2.0)
(s13 4.0)
(s14 5.0)
(s15 5.0)
(s16 2.0)
(s18 4.0)
(s19 5.0)
(s20 5.0)
(s21 2.0)
(s23 4.0)
(s24 5.0)
(s25 5.0)
(s26 2.0)
(s28 4.0)
(s29 5.0)
(s30 5.0)
(s31 2.0)
(s33 4.0)
(s34 5.0)
(s35 5.0)
(s36 2.0)
(s38 4.0)
(s39 5.0)
(s40 5.0)
(s41 2.0)
(s43 4.0)
(s44 5.0)
(s45 5.0)
(s46 2.0)
(s48 4.0)
(s49 5.0)
(s50 5.0)
(s51 2.0)
(s53 4.0)
(s54 5.0)
(s55 5.0)
(s56 2.0)
(s58 4.0)
(s59 5.0)
(s60 5.0)
(s61 2.0)
(s63 4.0)
(s64 5.0)
(s65 5.0)
(s66 2.0)
(s68 4.0)
(s69 5.0)
(s70 5.0)
(s71 2.0)
(s73 4.0)
(s74 5.0)
(s75 5.0)
(s76 2.0)
(s78 4.0)
(s79 5.0)
(s80 5.0)
(s81 2.0)
(s83 4.0)
(s84 5.0)
(s85 5.0)
(s86 2.0)
(s88 4.0)
(s89 5.0)
(s90 5.0)
(s91 2.0)
(s93 4.0)
(s94 5.0)
(s95 5.0)
(s96 2.0)
(s98 4.0)
(s99 5.0)
(s100 5.0)
(s101 2.0)
(s103 4.0)
(s104 5.0)
(s105 5.0)
(s106 2.0)
(s108 4.0)
(s109 5.0)
(s110 5.0)
(s111 2.0)
(s113 4.0)
(s114 5.0)
(s115 5.0)
(s116 2.0)
(s118 4.0)
(s119 5.0)
(s120 5.0)
(s121 2.0)
(s123 4.0)
(s124 5.0)
(s125 5.0)
(s126 2.0)
(s128 4.0)
(s129 5.0)
(s130 5.0)
(s131 2.0)
(s133 4.0)
(s134 5.0)
(s135 5.0)
(s136 2.0)
(s138 4.0)
(s139 5.0)
(s140 5.0)
(s141 2.0)
(s143 4.0)
(s144 5.0)
(s145 5.0)
(s146 2.0)
(s148 4.0)
(s149 5.0)
(s150 5.0)
(s151 2.0)
(s153 4.0)
(s154 5.0)
(s155 5.0)
(s156 2.0)
(s158 4.0)
(s159 5.0)
(s160 5.0)
(s161 2.0)
(s163 4.0)
(s164 5.0)
(s165 5.0)
(s166 2.0)
(s168 4.0)
(s169 5.0)
(s170 5.0)
(s171 2.0)
(s173 4.0)
(s174 5.0)
(s175 5.0)
(s176 2.0)
(s178 4.0)
(s179 5.0)
(s180 5.0)
(s181 2.0)
(s183 4.0)
(s184 5.0)
(s185 5.0)
(s186 2.0)
(s188 4.0)
(s189 5.0)
(s190 5.0)
(s191 2.0)
(s193 4.0)
(s194 5.0)
(s195 5.0)
(s196 2.0)
(s198 4.0)
(s199 5.0)
(s200 5.0)
(s201 2.0)
(s203 4.0)
(s204 5.0)
(s205 5.0)
(s206 2.0)
(s208 4.0)
(s209 5.0)
(s210 5.0)
(s211 2.0)
(s213 4.0)
(s214 5.0)
(s215 5.0)
(s216 2.0)
(s218 4.0)
(s219 5.0)
(s220 5.0)
(s221 2.0)
(s223 4.0)
(s224 5.0)
(s225 5.0)
(s226 2.0)
(s228 4.0)
(s229 5.0)
(s230 5.0)
(s231 2.0)
(s233 4.0)
(s234 5.0)
(s235 5.0)
(s236 2.0)
(s238 4.0)
(s239 5.0)
(s240 5.0)
(s241 2.0)
(s243 4.0)
(s244 5.0)
(s245 5.0)
(s246 2.0)
(s248 4.0)
(s249 5.0)
(s250 5.0)
(s251 2.0)
(s253 4.0)
(s254 5.0)
(s255 5.0)
(s256 2.0)
(s258 4.0)
(s259 5.0)
(s260 5.0)
(s261 2.0)
(s263 4.0)
(s264 5.0)
(s265 5.0)
(s266 2.0)
(s268 4.0)
(s269 5.0)
(s270 5.0)
(s271 2.0)
(s273 4.0)
(s274 5.0)
(s275 5.0)
(s276 2.0)
(s278 4.0)
(s279 5.0)
(s280 5.0)
(s281 2.0)
(s283 4.0)
(s284 5.0)
(s285 5.0)
(s286 2.0)
(s288 4.0)
(s289 5.0)
(s290 5.0)
(s291 2.0)
(s293 4.0)
(s294 5.0)
(s295 5.0)
(s296 2.0)
(s298 4.0)
(s299 5.0)
(s300 5.0)
(s301 2.0)
(s303 4.0)
(s304 5.0)
(s305 5.0)
(s306 2.0)
(s308 4.0)
(s309 5.0)
(s310 5.0)
(s311 2.0)
(s313 4.0)
(s314 5.0)
(s315 5.0)
(s316 2.0)
(s318 4.0)
(s319 5.0)
(s320 5.0)
(s321 2.0)
(s323 4.0)
(s324 5.0)
(s325 5.0)
(s326 2.0)
(s328 4.0)
(s329 5.0)
(s330 5.0)
(s331 2.0)
(s333 4.0)
(s334 5.0)
(s335 5.0)
(s336 2.0)
(s338 4.0)
(s339 5.0)
(s340 5.0)
(s341 2.0)
(s343 4.0)
(s344 5.0)
(s345 5.0)
(s346 2.0)
(s348 4.0)
(s349 5.0)
(s350 5.0)
(s351 2.0)
(s353 4.0)
(s354 5.0)
(s355 5.0)
(s356 2.0)
(s358 4.0)
(s359 5.0)
(s360 5.0)
(s361 2.0)
(s363 4.0)
(s364 5.0)
(s365 5.0)
(s366 2.0)
(s368 4.0)
(s369 5.0)
(s370 5.0)
(s371 2.0)
(s373 4.0)
(s374 5.0)
(s375 5.0)
(s376 2.0)
(s378 4.0)
(s379 5.0)
(s380 5.0)
(s381 2.0)
(s383 4.0)
(s384 5.0)
(s385 5.0)
(s386 2.0)
(s388 4.0)
(s389 5.0)
(s390 5.0)
(s391 2.0)
(s393 4.0)
(s394 5.0)
(s395 5.0)
(s396 2.0)
(s398 4.0)
(s399 5.0)
(s400 5.0)
(s401 2.0)
(s403 4.0)
(s404 5.0)
(s405 5.0)
(s406 2.0)
(s408 4.0)
(s409 5.0)
(s410 5.0)
(s411 2.0)
(s413 4.0)
(s414 5.0)
(s415 5.0)
(s416 2.0)
(s418 4.0)
(s419 5.0)
(s420 5.0)
(s421 2.0)
(s423 4.0)
(s424 5.0)
(s425 5.0)
(s426 2.0)
(s428 4.0)
(s429 5.0)
(s430 5.0)
(s431 2.0)
(s433 4.0)
(s434 5.0)
(s435 5.0)
(s436 2.0)
(s438 4.0)
(s439 5.0)
(s440 5.0)
(s441 2.0)
(s443 4.0)
(s444 5.0)
(s445 5.0)
(s446 2.0)
(s448 4.0)
(s449 5.0)
(s450 5.0)
(s451 2.0)
(s453 4.0)
(s454 5.0)
(s455 5.0)
(s456 2.0)
(s458 4.0)
(s459 5.0)
(s460 5.0)
(s461 2.0)
(s463 4.0)
(s464 5.0)
(s465 5.0)
(s466 2.0)
(s468 4.0)
(s469 5.0)
(s470 5.0)
(s471 2.0)
(s473 4.0)
(s474 5.0)
(s475 5.0)
(s476 2.0)
(s478 4.0)
(s479 5.0)
(s480 5.0)
(s481 2.0)
(s483 4.0)
(s484 5.0)
(s485 5.0)
(s486 2.0)
(s488 4.0)
(s489 5.0)
(s490 5.0)
(s491 2.0)
(s493 4.0)
(s494 5.0)
(s495 5.0)
(s496 2.0)
(s498 4.0)
(s499 5.0)
(s500 5.0)
(s501 2.0)
(s503 4.0)
(s504 5.0)
(s505 5.0)
(s506 2.0)
(s508 4.0)
(s509 5.0)
(s510 5.0)
(s511 2.0)
(s513 4.0)
(s514 5.0)
(s515 5.0)
(s516 2.0)
(s518 4.0)
(s519 5.0)
(s520 5.0)
(s521 2.0)
(s523 4.0)
(s524 5.0)
(s525 5.0)
(s526 2.0)
(s528 4.0)
(s529 5.0)
(s530 5.0)
(s531 2.0)
(s533 4.0)
(s534 5.0)
(s535 5.0)
(s536 2.0)
(s538 4.0)
(s539 5.0)
(s540 5.0)
(s541 2.0)
(s543 4.0)
(s544 5.0)
(s545 5.0)
(s546 2.0)
(s548 4.0)
(s549 5.0)
(s550 5.0)
(s551 2.0)
(s553 4.0)
(s554 5.0)
(s555 5.0)
(s556 2.0)
(s558 4.0)
(s559 5.0)
(s560 5.0)
(s561 2.0)
(s563 4.0)
(s564 5.0)
(s565 5.0)
(s566 2.0)
(s568 4.0)
(s569 5.0)
(s570 5.0)
(s571 2.0)
(s573 4.0)
(s574 5.0)
(s575 5.0)
(s576 2.0)
(s578 4.0)
(s579 5.0)
(s580 5.0)
(s581 2.0)
(s583 4.0)
(s584 5.0)
(s585 5.0)
(s586 2.0)
(s588 4.0)
(s589 5.0)
(s590 5.0)
(s591 2.0)
(s593 4.0)
(s594 5.0)
(s595 5.0)
(s596 2.0)
(s598 4.0)
(s599 5.0)
(s600 5.0)
(s601 2.0)
(s603 4.0)
(s604 5.0)
(s605 5.0)
(s606 2.0)
(s608 4.0)
(s609 5.0)
(s610 5.0)
(s611 2.0)
(s613 4.0)
(s614 5.0)
(s615 5.0)
(s616 2.0)
(s618 4.0)
(s619 5.0)
(s620 5.0)
(s621 2.0)
(s623 4.0)
(s624 5.0)
(s625 5.0)
(s626 2.0)
(s628 4.0)
(s629 5.0)
(s630 5.0)
(s631 2.0)
(s633 4.0)
(s634 5.0)
(s635 5.0)
(s636 2.0)
(s638 4.0)
(s639 5.0)
(s640 5.0)
(s641 2.0)
(s643 4.0)
(s644 5.0)
(s645 5.0)
(s646 2.0)
(s648 4.0)
(s649 5.0)
(s650 5.0)
(s651 2.0)
(s653 4.0)
(s654 5.0)
(s655 5.0)
(s656 2.0)
(s658 4.0)
(s659 5.0)
(s660 5.0)
(s661 2.0)
(s663 4.0)
(s664 5.0)
(s665 5.0)
(s666 2.0)
(s668 4.0)
(s669 5.0)
(s670 5.0)
(s671 2.0)
(s673 4.0)
(s674 5.0)
(s675 5.0)
(s676 2.0)
(s678 4.0)
(s679 5.0)
(s680 5.0)
(s681 2.0)
(s683 4.0)
(s684 5.0)
(s685 5.0)
(s686 2.0)
(s688 4.0)
(s689 5.0)
(s690 5.0)
(s691 2.0)
(s693 4.0)
(s694 5.0)
(s695 5.0)
(s696 2.0)
(s698 4.0)
(s699 5.0)
(s700 5.0)
(s701 2.0)
(s703 4.0)
(s704 5.0)
(s705 5.0)
(s706 2.0)
(s708 4.0)
(s709 5.0)
(s710 5.0)
(s711 2.0)
(s713 4.0)
(s714 5.0)
(s715 5.0)
(s716 2.0)
(s718 4.0)
(s719 5.0)
(s720 5.0)
(s721 2.0)
(s723 4.0)
(s724 5.0)
(s725 5.0)
(s726 2.0)
(s728 4.0)
(s729 5.0)
(s730 5.0)
(s731 2.0)
(s733 4.0)
(s734 5.0)
(s735 5.0)
(s736 2.0)
(s738 4.0)
(s739 5.0)
(s740 5.0)
(s741 2.0)
(s743 4.0)
(s744 5.0)
(s745 5.0)
(s746 2.0)
(s748 4.0)
(s749 5.0)
(s750 5.0)
(s751 2.0)
(s753 4.0)
(s754 5.0)
(s755 5.0)
(s756 2.0)
(s758 4.0)
(s759 5.0)
(s760 5.0)
(s761 2.0)
(s763 4.0)
(s764 5.0)
(s765 5.0)
(s766 2.0)
(s768 4.0)
(s769 5.0)
(s770 5.0)
(s771 2.0)
(s773 4.0)
(s774 5.0)
(s775 5.0)
(s776 2.0)
(s778 4.0)
(s779 5.0)
(s780 5.0)
(s781 2.0)
(s783 4.0)
(s784 5.0)
(s785 5.0)
(s786 2.0)
(s788 4.0)
(s789 5.0)
(s790 5.0)
(s791 2.0)
(s793 4.0)
(s794 5.0)
(s795 5.0)
(s796 2.0)
(s798 4.0)
(s799 5.0)
(s800 5.0)
(s801 2.0)
(s803 4.0)
(s804 5.0)
(s805 5.0)
(s806 2.0)
(s808 4.0)
(s809 5.0)
(s810 5.0)
(s811 2.0)
(s813 4.0)
(s814 5.0)
(s815 5.0)
(s816 2.0)
(s818 4.0)
(s819 5.0)
(s820 5.0)
(s821 2.0)
(s823 4.0)
(s824 5.0)
(s825 5.0)
(s826 2.0)
(s828 4.0)
(s829 5.0)
(s830 5.0)
(s831 2.0)
(s833 4.0)
(s834 5.0)
(s835 5.0)
(s836 2.0)
(s838 4.0)
(s839 5.0)
(s840 5.0)
(s841 2.0)
(s843 4.0)
(s844 5.0)
(s845 5.0)
(s846 2.0)
(s848 4.0)
(s849 5.0)
(s850 5.0)
(s851 2.0)
(s853 4.0)
(s854 5.0)
(s855 5.0)
(s856 2.0)
(s858 4.0)
(s859 5.0)
(s860 5.0)
(s861 2.0)
(s863 4.0)
(s864 5.0)
(s865 5.0)
(s866 2.0)
(s868 4.0)
(s869 5.0)
(s870 5.0)
(s871 2.0)
(s873 4.0)
(s874 5.0)
(s875 5.0)
(s876 2.0)
(s878 4.0)
(s879 5.0)
(s880 5.0)
(s881 2.0)
(s883 4.0)
(s884 5.0)
(s885 5.0)
(s886 2.0)
(s888 4.0)
(s889 5.0)
(s890 5.0)
(s891 2.0)
(s893 4.0)
(s894 5.0)
(s895 5.0)
(s896 2.0)
(s898 4.0)
(s899 5.0)
(s900 5.0)
(s901 2.0)
(s903 4.0)
(s904 5.0)
(s905 5.0)
(s906 2.0)
(s908 4.0)
(s909 5.0)
(s910 5.0)
(s911 2.0)
(s913 4.0)
(s914 5.0)
(s915 5.0)
(s916 2.0)
(s918 4.0)
(s919 5.0)
(s920 5.0)
(s921 2.0)
(s923 4.0)
(s924 5.0)
(s925 5.0)
(s926 2.0)
(s928 4.0)
(s929 5.0)
(s930 5.0)
(s931 2.0)
(s933 4.0)
(s934 5.0)
(s935 5.0)
(s936 2.0)
(s938 4.0)
(s939 5.0)
(s940 5.0)
(s941 2.0)
(s943 4.0)
(s944 5.0)
(s945 5.0)
(s946 2.0)
(s948 4.0)
(s949 5.0)
(s950 5.0)
(s951 2.0)
(s953 4.0)
(s954 5.0)
(s955 5.0)
(s956 2.0)
(s958 4.0)
(s959 5.0)
(s960 5.0)
(s961 2.0)
(s963 4.0)
(s964 5.0)
(s965 5.0)
(s966 2.0)
(s968 4.0)
(s969 5.0)
(s970 5.0)
(s971 2.0)
(s973 4.0)
(s974 5.0)
(s975 5.0)
(s976 2.0)
(s978 4.0)
(s979 5.0)
(s980 5.0)
(s981 2.0)
(s983 4.0)
(s984 5.0)
(s985 5.0)
(s986 2.0)
(s988 4.0)
(s989 5.0)
(s990 5.0)
(s991 2.0)
(s993 4.0)
(s994 5.0)
(s995 5.0)
(s996 2.0)
(s998 4.0)
(s999 5.0)
(s1000 5.0)
(s1001 2.0)
(s1003 4.0)
(s1004 5.0)
(s1005 5.0)
(s1006 2.0)
(s1008 4.0)
(s1009 5.0)
(s1010 5.0)
(s1011 2.0)
(s1013 4.0)
(s1014 5.0)
(s1015 5.0)
(s1016 2.0)
(s1018 4.0)
(s1019 5.0)
(s1020 5.0)
(s1021 2.0)
(s1023 4.0)
(s1024 5.0)
(s1025 5.0)
(s1026 2.0)
(s1028 4.0)
(s1029 5.0)
(s1030 5.0)
(s1031 2.0)
(s1033 4.0)
(s1034 5.0)
(s1035 5.0)
(s1036 2.0)
(s1038 4.0)
(s1039 5.0)
(s1040 5.0)
(s1041 2.0)
(s1043 4.0)
(s1044 5.0)
(s1045 5.0)
(s1046 2.0)
(s1048 4.0)
(s1049 5.0)
(s1050 5.0)
(s1051 2.0)
(s1053 4.0)
(s1054 5.0)
(s1055 5.0)
(s1056 2.0)
(s1058 4.0)
(s1059 5.0)
(s1060 5.0)
(s1061 2.0)
(s1063 4.0)
(s1064 5.0)
(s1065 5.0)
(s1066 2.0)
(s1068 4.0)
(s1069 5.0)
(s1070 5.0)
(s1071 2.0)
(s1073 4.0)
(s1074 5.0)
(s1075 5.0)
(s1076 2.0)
(s1078 4.0)
(s1079 5.0)
(s1080 5.0)
(s1081 2.0)
(s1083 4.0)
(s1084 5.0)
(s1085 5.0)
(s1086 2.0)
(s1088 4.0)
(s1089 5.0)
(s1090 5.0)
(s1091 2.0)
(s1093 4.0)
(s1094 5.0)
(s1095 5.0)
(s1096 2.0)
(s1098 4.0)
(s1099 5.0)
(s1100 5.0)
(s1101 2.0)
(s1103 4.0)
(s1104 5.0)
(s1105 5.0)
(s1106 2.0)
(s1108 4.0)
(s1109 5.0)
(s1110 5.0)
(s1111 2.0)
(s1113 4.0)
(s1114 5.0)
(s1115 5.0)
(s1116 2.0)
(s1118 4.0)
(s1119 5.0)
(s1120 5.0)
(s1121 2.0)
(s1123 4.0)
(s1124 5.0)
(s1125 5.0)
(s1126 2.0)
(s1128 4.0)
(s1129 5.0)
(s1130 5.0)
(s1131 2.0)
(s1133 4.0)
(s1134 5.0)
(s1135 5.0)
(s1136 2.0)
(s1138 4.0)
(s1139 5.0)
(s1140 5.0)
(s1141 2.0)
(s1143 4.0)
(s1144 5.0)
(s1145 5.0)
(s1146 2.0)
(s1148 4.0)
(s1149 5.0)
(s1150 5.0)
(s1151 2.0)
(s1153 4.0)
(s1154 5.0)
(s1155 5.0)
(s1156 2.0)
(s1158 4.0)
(s1159 5.0)
(s1160 5.0)
(s1161 2.0)
(s1163 4.0)
(s1164 5.0)
(s1165 5.0)
(s1166 2.0)
(s1168 4.0)
(s1169 5.0)
(s1170 5.0)
(s1171 2.0)
(s1173 4.0)
(s1174 5.0)
(s1175 5.0)
(s1176 2.0)
(s1178 4.0)
(s1179 5.0)
(s1180 5.0)
(s1181 2.0)
(s1183 4.0)
(s1184 5.0)
(s1185 5.0)
(s1186 2.0)
(s1188 4.0)
(s1189 5.0)
(s1190 5.0)
(s1191 2.0)
(s1193 4.0)
(s1194 5.0)
(s1195 5.0)
(s1196 2.0)
(s1198 4.0)
(s1199 5.0)
(s1200 5.0)
(s1201 2.0)
(s1203 4.0)
(s1204 5.0)
(s1205 5.0)
(s1206 2.0)
(s1208 4.0)
(s1209 5.0)
(s1210 5.0)
(s1211 2.0)
(s1213 4.0)
(s1214 5.0)
(s1215 5.0)
(s1216 2.0)
(s1218 4.0)
(s1219 5.0)
(s1220 5.0)
(s1221 2.0)
(s1223 4.0)
(s1224 5.0)
(s1225 5.0)
(s1226 2.0)
(s1228 4.0)
(s1229 5.0)
(s1230 5.0)
(s1231 2.0)
(s1233 4.0)
(s1234 5.0)
(s1235 5.0)
(s1236 2.0)
(s1238 4.0)
(s1239 5.0)
(s1240 5.0)
(s1241 2.0)
(s1243 4.0)
(s1244 5.0)
(s1245 5.0)
(s1246 2.0)
(s1248 4.0)
(s1249 5.0)
(s1250 5.0)
(s1251 2.0)
(s1253 4.0)
(s1254 5.0)
(s1255 5.0)
(s1256 2.0)
(s1258 4.0)
(s1259 5.0)
(s1260 5.0)
(s1261 2.0)
(s1263 4.0)
(s1264 5.0)
(s1265 5.0)
(s1266 2.0)
(s1268 4.0)
(s1269 5.0)
(s1270 5.0)
(s1271 2.0)
(s1273 4.0)
(s1274 5.0)
(s1275 5.0)
(s1276 2.0)
(s1278 4.0)
(s1279 5.0)
(s1280 5.0)
(s1281 2.0)
(s1283 4.0)
(s1284 5.0)
(s1285 5.0)
(s1286 2.0)
(s1288 4.0)
(s1289 5.0)
(s1290 5.0)
(s1291 2.0)
(s1293 4.0)
(s1294 5.0)
(s1295 5.0)
(s1296 2.0)
(s1298 4.0)
(s1299 5.0)
(s1300 5.0)
(s1301 2.0)
(s1303 4.0)
(s1304 5.0)
(s1305 5.0)
(s1306 2.0)
(s1308 4.0)
(s1309 5.0)
(s1310 5.0)
(s1311 2.0)
(s1313 4.0)
(s1314 5.0)
(s1315 5.0)
(s1316 2.0)
(s1318 4.0)
(s1319 5.0)
(s1320 5.0)
(s1321 2.0)
(s1323 4.0)
(s1324 5.0)
(s1325 5.0)
(s1326 2.0)
(s1328 4.0)
(s1329 5.0)
(s1330 5.0)
(s1331 2.0)
(s1333 4.0)
(s1334 5.0)
(s1335 5.0)
(s1336 2.0)
(s1338 4.0)
(s1339 5.0)
(s1340 5.0)
(s1341 2.0)
(s1343 4.0)
(s1344 5.0)
(s1345 5.0)
(s1346 2.0)
(s1348 4.0)
(s1349 5.0)
(s1350 5.0)
(s1351 2.0)
(s1353 4.0)
(s1354 5.0)
(s1355 5.0)
(s1356 2.0)
(s1358 4.0)
(s1359 5.0)
(s1360 5.0)
(s1361 2.0)
(s1363 4.0)
(s1364 5.0)
(s1365 5.0)
(s1366 2.0)
(s1368 4.0)
(s1369 5.0)
(s1370 5.0)
(s1371 2.0)
(s1373 4.0)
(s1374 5.0)
(s1375 5.0)
(s1376 2.0)
(s1378 4.0)
(s1379 5.0)
(s1380 5.0)
(s1381 2.0)
(s1383 4.0)
(s1384 5.0)
(s1385 5.0)
(s1386 2.0)
(s1388 4.0)
(s1389 5.0)
(s1390 5.0)
(s1391 2.0)
(s1393 4.0)
(s1394 5.0)
(s1395 5.0)
(s1396 2.0)
(s1398 4.0)
(s1399 5.0)
(s1400 5.0)
(s1401 2.0)
(s1403 4.0)
(s1404 5.0)
(s1405 5.0)
(s1406 2.0)
(s1408 4.0)
(s1409 5.0)
(s1410 5.0)
(s1411 2.0)
(s1413 4.0)
(s1414 5.0)
(s1415 5.0)
(s1416 2.0)
(s1418 4.0)
(s1419 5.0)
(s1420 5.0)
(s1421 2.0)
(s1423 4.0)
(s1424 5.0)
(s1425 5.0)
(s1426 2.0)
(s1428 4.0)
(s1429 5.0)
(s1430 5.0)
(s1431 2.0)
(s1433 4.0)
(s1434 5.0)
(s1435 5.0)
(s1436 2.0)
(s1438 4.0)
(s1439 5.0)
(s1440 5.0)
(s1441 2.0)
(s1443 4.0)
(s1444 5.0)
(s1445 5.0)
(s1446 2.0)
(s1448 4.0)
(s1449 5.0)
(s1450 5.0)
(s1451 2.0)
(s1453 4.0)
(s1454 5.0)
(s1455 5.0)
(s1456 2.0)
(s1458 4.0)
(s1459 5.0)
(s1460 5.0)
(s1461 2.0)
(s1463 4.0)
(s1464 5.0)
(s1465 5.0)
(s1466 2.0)
(s1468 4.0)
(s1469 5.0)
(s1470 5.0)
(s1471 2.0)
(s1473 4.0)
(s1474 5.0)
(s1475 5.0)
(s1476 2.0)
(s1478 4.0)
(s1479 5.0)
(s1480 5.0)
(s1481 2.0)
(s1483 4.0)
(s1484 5.0)
(s1485 5.0)
(s1486 2.0)
(s1488 4.0)
(s1489 5.0)
(s1490 5.0)
(s1491 2.0)
(s1493 4.0)
(s1494 5.0)
(s1495 5.0)
(s1496 2.0)
(s1498 4.0)
(s1499 5.0)
(s1500 5.0)
(s1501 2.0)
(s1503 4.0)
(s1504 5.0)
(s1505 5.0)
(s1506 2.0)
(s1508 4.0)
(s1509 5.0)
(s1510 5.0)
(s1511 2.0)
(s1513 4.0)
(s1514 5.0)
(s1515 5.0)
(s1516 2.0)
(s1518 4.0)
(s1519 5.0)
(s1520 5.0)
(s1521 2.0)
(s1523 4.0)
(s1524 5.0)
(s1525 5.0)
(s1526 2.0)
(s1528 4.0)
(s1529 5.0)
(s1530 5.0)
(s1531 2.0)
(s1533 4.0)
(s1534 5.0)
(s1535 5.0)
(s1536 2.0)
(s1538 4.0)
(s1539 5.0)
(s1540 5.0)
(s1541 2.0)
(s1543 4.0)
(s1544 5.0)
(s1545 5.0)
(s1546 2.0)
(s1548 4.0)
(s1549 5.0)
(s1550 5.0)
(s1551 2.0)
(s1553 4.0)
(s1554 5.0)
(s1555 5.0)
(s1556 2.0)
(s1558 4.0)
(s1559 5.0)
(s1560 5.0)
(s1561 2.0)
(s1563 4.0)
(s1564 5.0)
(s1565 5.0)
(s1566 2.0)
(s1568 4.0)
(s1569 5.0)
(s1570 5.0)
(s1571 2.0)
(s1573 4.0)
(s1574 5.0)
(s1575 5.0)
(s1576 2.0)
(s1578 4.0)
(s1579 5.0)
(s1580 5.0)
(s1581 2.0)
(s1583 4.0)
(s1584 5.0)
(s1585 5.0)
(s1586 2.0)
(s1588 4.0)
(s1589 5.0)
(s1590 5.0)
(s1591 2.0)
(s1593 4.0)
(s1594 5.0)
(s1595 5.0)
(s1596 2.0)
(s1598 4.0)
(s1599 5.0)
(s1600 5.0)
(s1601 2.0)
(s1603 4.0)
(s1604 5.0)
(s1605 5.0)
(s1606 2.0)
(s1608 4.0)
(s1609 5.0)
(s1610 5.0)
(s1611 2.0)
(s1613 4.0)
(s1614 5.0)
(s1615 5.0)
(s1616 2.0)
(s1618 4.0)
(s1619 5.0)
(s1620 5.0)
(s1621 2.0)
(s1623 4.0)
(s1624 5.0)
(s1625 5.0)
(s1626 2.0)
(s1628 4.0)
(s1629 5.0)
(s1630 5.0)
(s1631 2.0)
(s1633 4.0)
(s1634 5.0)
(s1635 5.0)
(s1636 2.0)
(s1638 4.0)
(s1639 5.0)
(s1640 5.0)
(s1641 2.0)
(s1643 4.0)
(s1644 5.0)
(s1645 5.0)
(s1646 2.0)
(s1648 4.0)
(s1649 5.0)
(s1650 5.0)
(s1651 2.0)
(s1653 4.0)
(s1654 5.0)
(s1655 5.0)
(s1656 2.0)
(s1658 4.0)
(s1659 5.0)
(s1660 5.0)
(s1661 2.0)
(s1663 4.0)
(s1664 5.0)
(s1665 5.0)
(s1666 2.0)
(s1668 4.0)
(s1669 5.0)
(s1670 5.0)
(s1671 2.0)
(s1673 4.0)
(s1674 5.0)
(s1675 5.0)
(s1676 2.0)
(s1678 4.0)
(s1679 5.0)
(s1680 5.0)
(s1681 2.0)
(s1683 4.0)
(s1684 5.0)
(s1685 5.0)
(s1686 2.0)
(s1688 4.0)
(s1689 5.0)
(s1690 5.0)
(s1691 2.0)
(s1693 4.0)
(s1694 5.0)
(s1695 5.0)
(s1696 2.0)
(s1698 4.0)
(s1699 5.0)
(s1700 5.0)
(s1701 2.0)
(s1703 4.0)
(s1704 5.0)
(s1705 5.0)
(s1706 2.0)
(s1708 4.0)
(s1709 5.0)
(s1710 5.0)
(s1711 2.0)
(s1713 4.0)
(s1714 5.0)
(s1715 5.0)
(s1716 2.0)
(s1718 4.0)
(s1719 5.0)
(s1720 5.0)
(s1721 2.0)
(s1723 4.0)
(s1724 5.0)
(s1725 5.0)
(s1726 2.0)
(s1728 4.0)
(s1729 5.0)
(s1730 5.0)
(s1731 2.0)
(s1733 4.0)
(s1734 5.0)
(s1735 5.0)
(s1736 2.0)
(s1738 4.0)
(s1739 5.0)
(s1740 5.0)
(s1741 2.0)
(s1743 4.0)
(s1744 5.0)
(s1745 5.0)
(s1746 2.0)
(s1748 4.0)
(s1749 5.0)
(s1750 5.0)
(s1751 2.0)
(s1753 4.0)
(s1754 5.0)
(s1755 5.0)
(s1756 2.0)
(s1758 4.0)
(s1759 5.0)
(s1760 5.0)
(s1761 2.0)
(s1763 4.0)
(s1764 5.0)
(s1765 5.0)
(s1766 2.0)
(s1768 4.0)
(s1769 5.0)
(s1770 5.0)
(s1771 2.0)
(s1773 4.0)
(s1774 5.0)
(s1775 5.0)
(s1776 2.0)
(s1778 4.0)
(s1779 5.0)
(s1780 5.0)
(s1781 2.0)
(s1783 4.0)
(s1784 5.0)
(s1785 5.0)
(s1786 2.0)
(s1788 4.0)
(s1789 5.0)
(s1790 5.0)
(s1791 2.0)
(s1793 4.0)
(s1794 5.0)
(s1795 5.0)
(s1796 2.0)
(s1798 4.0)
(s1799 5.0)
(s1800 5.0)
(s1801 2.0)
(s1803 4.0)
(s1804 5.0)
(s1805 5.0)
(s1806 2.0)
(s1808 4.0)
(s1809 5.0)
(s1810 5.0)
(s1811 2.0)
(s1813 4.0)
(s1814 5.0)
(s1815 5.0)
(s1816 2.0)
(s1818 4.0)
(s1819 5.0)
(s1820 5.0)
(s1821 2.0)
(s1823 4.0)
(s1824 5.0)
(s1825 5.0)
(s1826 2.0)
(s1828 4.0)
(s1829 5.0)
(s1830 5.0)
(s1831 2.0)
(s1833 4.0)
(s1834 5.0)
(s1835 5.0)
(s1836 2.0)
(s1838 4.0)
(s1839 5.0)
(s1840 5.0)
(s1841 2.0)
(s1843 4.0)
(s1844 5.0)
(s1845 5.0)
(s1846 2.0)
(s1848 4.0)
(s1849 5.0)
(s1850 5.0)
(s1851 2.0)
(s1853 4.0)
(s1854 5.0)
(s1855 5.0)
(s1856 2.0)
(s1858 4.0)
(s1859 5.0)
(s1860 5.0)
(s1861 2.0)
(s1863 4.0)
(s1864 5.0)
(s1865 5.0)
(s1866 2.0)
(s1868 4.0)
(s1869 5.0)
(s1870 5.0)
(s1871 2.0)
(s1873 4.0)
(s1874 5.0)
(s1875 5.0)
(s1876 2.0)
(s1878 4.0)
(s1879 5.0)
(s1880 5.0)
(s1881 2.0)
(s1883 4.0)
(s1884 5.0)
(s1885 5.0)
(s1886 2.0)
(s1888 4.0)
(s1889 5.0)
(s1890 5.0)
(s1891 2.0)
(s1893 4.0)
(s1894 5.0)
(s1895 5.0)
(s1896 2.0)
(s1898 4.0)
(s1899 5.0)
(s1900 5.0)
(s1901 2.0)
(s1903 4.0)
(s1904 5.0)
(s1905 5.0)
(s1906 2.0)
(s1908 4.0)
(s1909 5.0)
(s1910 5.0)
(s1911 2.0)
(s1913 4.0)
(s1914 5.0)
(s1915 5.0)
(s1916 2.0)
(s1918 4.0)
(s1919 5.0)
(s1920 5.0)
(s1921 2.0)
(s1923 4.0)
(s1924 5.0)
(s1925 5.0)
(s1926 2.0)
(s1928 4.0)
(s1929 5.0)
(s1930 5.0)
(s1931 2.0)
(s1933 4.0)
(s1934 5.0)
(s1935 5.0)
(s1936 2.0)
(s1938 4.0)
(s1939 5.0)
(s1940 5.0)
(s1941 2.0)
(s1943 4.0)
(s1944 5.0)
(s1945 5.0)
(s1946 2.0)
(s1948 4.0)
(s1949 5.0)
(s1950 5.0)
(s1951 2.0)
(s1953 4.0)
(s1954 5.0)
(s1955 5.0)
(s1956 2.0)
(s1958 4.0)
(s1959 5.0)
(s1960 5.0)
(s1961 2.0)
(s1963 4.0)
(s1964 5.0)
(s1965 5.0)
(s1966 2.0)
(s1968 4.0)
(s1969 5.0)
(s1970 5.0)
(s1971 2.0)
(s1973 4.0)
(s1974 5.0)
(s1975 5.0)
(s1976 2.0)
(s1978 4.0)
(s1979 5.0)
(s1980 5.0)
(s1981 2.0)
(s1983 4.0)
(s1984 5.0)
(s1985 5.0)
(s1986 2.0)
(s1988 4.0)
(s1989 5.0)
(s1990 5.0)
(s1991 2.0)
(s1993 4.0)
(s1994 5.0)
(s1995 5.0)
(s1996 2.0)
(s1998 4.0)
(s1999 5.0)
(s2000 5.0)
(s2001 2.0)
(s2003 4.0)
(s2004 5.0)
(s2005 5.0)
(s2006 2.0)
(s2008 4.0)
(s2009 5.0)
(s2010 5.0)
(s2011 2.0)
(s2013 4.0)
(s2014 5.0)
(s2015 5.0)
(s2016 2.0)
(s2018 4.0)
(s2019 5.0)
(s2020 5.0)
(s2021 2.0)
(s2023 4.0)
(s2024 5.0)
(s2025 5.0)
(s2026 2.0)
(s2028 4.0)
(s2029 5.0)
(s2030 5.0)
(s2031 2.0)
(s2033 4.0)
(s2034 5.0)
(s2035 5.0)
(s2036 2.0)
(s2038 4.0)
(s2039 5.0)
(s2040 5.0)
(s2041 2.0)
(s2043 4.0)
(s2044 5.0)
(s2045 5.0)
(s2046 2.0)
(s2048 4.0)
(s2049 5.0)
(s2050 5.0)
(s2051 2.0)
(s2053 4.0)
(s2054 5.0)
(s2055 5.0)
(s2056 2.0)
(s2058 4.0)
(s2059 5.0)
(s2060 5.0)
(s2061 2.0)
(s2063 4.0)
(s2064 5.0)
(s2065 5.0)
(s2066 2.0)
(s2068 4.0)
(s2069 5.0)
(s2070 5.0)
(s2071 2.0)
(s2073 4.0)
(s2074 5.0)
(s2075 5.0)
(s2076 2.0)
(s2078 4.0)
(s2079 5.0)
(s2080 5.0)
(s2081 2.0)
(s2083 4.0)
(s2084 5.0)
(s2085 5.0)
(s2086 2.0)
(s2088 4.0)
(s2089 5.0)
(s2090 5.0)
(s2091 2.0)
(s2093 4.0)
(s2094 5.0)
(s2095 5.0)
(s2096 2.0)
(s2098 4.0)
(s2099 5.0)
(s2100 5.0)
(s2101 2.0)
(s2103 4.0)
(s2104 5.0)
(s2105 5.0)
(s2106 2.0)
(s2108 4.0)
(s2109 5.0)
(s2110 5.0)
(s2111 2.0)
(s2113 4.0)
(s2114 5.0)
(s2115 5.0)
(s2116 2.0)
(s2118 4.0)
(s2119 5.0)
(s2120 5.0)
(s2121 2.0)
(s2123 4.0)
(s2124 5.0)
(s2125 5.0)
(s2126 2.0)
(s2128 4.0)
(s2129 5.0)
(s2130 5.0)
(s2131 2.0)
(s2133 4.0)
(s2134 5.0)
(s2135 5.0)
(s2136 2.0)
(s2138 4.0)
(s2139 5.0)
(s2140 5.0)
(s2141 2.0)
(s2143 4.0)
(s2144 5.0)
(s2145 5.0)
(s2146 2.0)
(s2148 4.0)
(s2149 5.0)
(s2150 5.0)
(s2151 2.0)
(s2153 4.0)
(s2154 5.0)
(s2155 5.0)
(s2156 2.0)
(s2158 4.0)
(s2159 5.0)
(s2160 5.0)
(s2161 2.0)
(s2163 4.0)
(s2164 5.0)
(s2165 5.0)
(s2166 2.0)
(s2168 4.0)
(s2169 5.0)
(s2170 5.0)
(s2171 2.0)
(s2173 4.0)
(s2174 5.0)
(s2175 5.0)
(s2176 2.0)
(s2178 4.0)
(s2179 5.0)
(s2180 5.0)
(s2181 2.0)
(s2183 4.0)
(s2184 5.0)
(s2185 5.0)
(s2186 2.0)
(s2188 4.0)
(s2189 5.0)
(s2190 5.0)
(s2191 2.0)
(s2193 4.0)
(s2194 5.0)
(s2195 5.0)
(s2196 2.0)
(s2198 4.0)
(s2199 5.0)
(s2200 5.0)
(s2201 2.0)
(s2203 4.0)
(s2204 5.0)
(s2205 5.0)
(s2206 2.0)
(s2208 4.0)
(s2209 5.0)
(s2210 5.0)
(s2211 2.0)
(s2213 4.0)
(s2214 5.0)
(s2215 5.0)
(s2216 2.0)
(s2218 4.0)
(s2219 5.0)
(s2220 5.0)
(s2221 2.0)
(s2223 4.0)
(s2224 5.0)
(s2225 5.0)
(s2226 2.0)
(s2228 4.0)
(s2229 5.0)
(s2230 5.0)
(s2231 2.0)
(s2233 4.0)
(s2234 5.0)
(s2235 5.0)
(s2236 2.0)
(s2238 4.0)
(s2239 5.0)
(s2240 5.0)
(s2241 2.0)
(s2243 4.0)
(s2244 5.0)
(s2245 5.0)
(s2246 2.0)
(s2248 4.0)
(s2249 5.0)
(s2250 5.0)
(s2251 2.0)
(s2253 4.0)
(s2254 5.0)
(s2255 5.0)
(s2256 2.0)
(s2258 4.0)
(s2259 5.0)
(s2260 5.0)
(s2261 2.0)
(s2263 4.0)
(s2264 5.0)
(s2265 5.0)
(s2266 2.0)
(s2268 4.0)
(s2269 5.0)
(s2270 5.0)
(s2271 2.0)
(s2273 4.0)
(s2274 5.0)
(s2275 5.0)
(s2276 2.0)
(s2278 4.0)
(s2279 5.0)
(s2280 5.0)
(s2281 2.0)
(s2283 4.0)
(s2284 5.0)
(s2285 5.0)
(s2286 2.0)
(s2288 4.0)
(s2289 5.0)
(s2290 5.0)
(s2291 2.0)
(s2293 4.0)
(s2294 5.0)
(s2295 5.0)
(s2296 2.0)
(s2298 4.0)
(s2299 5.0)
(s2300 5.0)
(s2301 2.0)
(s2303 4.0)
(s2304 5.0)
(s2305 5.0)
(s2306 2.0)
(s2308 4.0)
(s2309 5.0)
(s2310 5.0)
(s2311 2.0)
(s2313 4.0)
(s2314 5.0)
(s2315 5.0)
(s2316 2.0)
(s2318 4.0)
(s2319 5.0)
(s2320 5.0)
(s2321 2.0)
(s2323 4.0)
(s2324 5.0)
(s2325 5.0)
(s2326 2.0)
(s2328 4.0)
(s2329 5.0)
(s2330 5.0)
(s2331 2.0)
(s2333 4.0)
(s2334 5.0)
(s2335 5.0)
(s2336 2.0)
(s2338 4.0)
(s2339 5.0)
(s2340 5.0)
(s2341 2.0)
(s2343 4.0)
(s2344 5.0)
(s2345 5.0)
(s2346 2.0)
(s2348 4.0)
(s2349 5.0)
(s2350 5.0)
(s2351 2.0)
(s2353 4.0)
(s2354 5.0)
(s2355 5.0)
(s2356 2.0)
(s2358 4.0)
(s2359 5.0)
(s2360 5.0)
(s2361 2.0)
(s2363 4.0)
(s2364 5.0)
(s2365 5.0)
(s2366 2.0)
(s2368 4.0)
(s2369 5.0)
(s2370 5.0)
(s2371 2.0)
(s2373 4.0)
(s2374 5.0)
(s2375 5.0)
(s2376 2.0)
(s2378 4.0)
(s2379 5.0)
(s2380 5.0)
(s2381 2.0)
(s2383 4.0)
(s2384 5.0)
(s2385 5.0)
(s2386 2.0)
(s2388 4.0)
(s2389 5.0)
(s2390 5.0)
(s2391 2.0)
(s2393 4.0)
(s2394 5.0)
(s2395 5.0)
(s2396 2.0)
(s2398 4.0)
(s2399 5.0)
(s2400 5.0)
(s2401 2.0)
(s2403 4.0)
(s2404 5.0)
(s2405 5.0)
(s2406 2.0)
(s2408 4.0)
(s2409 5.0)
(s2410 5.0)
(s2411 2.0)
(s2413 4.0)
(s2414 5.0)
(s2415 5.0)
(s2416 2.0)
(s2418 4.0)
(s2419 5.0)
(s2420 5.0)
(s2421 2.0)
(s2423 4.0)
(s2424 5.0)
(s2425 5.0)
(s2426 2.0)
(s2428 4.0)
(s2429 5.0)
(s2430 5.0)
(s2431 2.0)
(s2433 4.0)
(s2434 5.0)
(s2435 5.0)
(s2436 2.0)
(s2438 4.0)
(s2439 5.0)
(s2440 5.0)
(s2441 2.0)
(s2443 4.0)
(s2444 5.0)
(s2445 5.0)
(s2446 2.0)
(s2448 4.0)
(s2449 5.0)
(s2450 5.0)
(s2451 2.0)
(s2453 4.0)
(s2454 5.0)
(s2455 5.0)
(s2456 2.0)
(s2458 4.0)
(s2459 5.0)
(s2460 5.0)
(s2461 2.0)
(s2463 4.0)
(s2464 5.0)
(s2465 5.0)
(s2466 2.0)
(s2468 4.0)
(s2469 5.0)
(s2470 5.0)
(s2471 2.0)
(s2473 4.0)
(s2474 5.0)
(s2475 5.0)
(s2476 2.0)
(s2478 4.0)
(s2479 5.0)
(s2480 5.0)
(s2481 2.0)
(s2483 4.0)
(s2484 5.0)
(s2485 5.0)
(s2486 2.0)
(s2488 4.0)
(s2489 5.0)
(s2490 5.0)
(s2491 2.0)
(s2493 4.0)
(s2494 5.0)
(s2495 5.0)
(s2496 2.0)
(s2498 4.0)
(s2499 5.0)
(s2500 5.0)
(s2501 2.0)
(s2503 4.0)
(s2504 5.0)
(s2505 5.0)
(s2506 2.0)
(s2508 4.0)
(s2509 5.0)
(s2510 5.0)
(s2511 2.0)
(s2513 4.0)
(s2514 5.0)
(s2515 5.0)
(s2516 2.0)
(s2518 4.0)
(s2519 5.0)
(s2520 5.0)
(s2521 2.0)
(s2523 4.0)
(s2524 5.0)
(s2525 5.0)
(s2526 2.0)
(s2528 4.0)
(s2529 5.0)
(s2530 5.0)
(s2531 2.0)
(s2533 4.0)
(s2534 5.0)
(s2535 5.0)
(s2536 2.0)
(s2538 4.0)
(s2539 5.0)
(s2540 5.0)
(s2541 2.0)
(s2543 4.0)
(s2544 5.0)
(s2545 5.0)
(s2546 2.0)
(s2548 4.0)
(s2549 5.0)
(s2550 5.0)
(s2551 2.0)
(s2553 4.0)
(s2554 5.0)
(s2555 5.0)
(s2556 2.0)
(s2558 4.0)
(s2559 5.0)
(s2560 5.0)
(s2561 2.0)
(s2563 4.0)
(s2564 5.0)
(s2565 5.0)
(s2566 2.0)
(s2568 4.0)
(s2569 5.0)
(s2570 5.0)
(s2571 2.0)
(s2573 4.0)
(s2574 5.0)
(s2575 5.0)
(s2576 2.0)
(s2578 4.0)
(s2579 5.0)
(s2580 5.0)
(s2581 2.0)
(s2583 4.0)
(s2584 5.0)
(s2585 5.0)
(s2586 2.0)
(s2588 4.0)
(s2589 5.0)
(s2590 5.0)
(s2591 2.0)
(s2593 4.0)
(s2594 5.0)
(s2595 5.0)
(s2596 2.0)
(s2598 4.0)
(s2599 5.0)
(s2600 5.0)
(s2601 2.0)
(s2603 4.0)
(s2604 5.0)
(s2605 5.0)
(s2606 2.0)
(s2608 4.0)
(s2609 5.0)
(s2610 5.0)
(s2611 2.0)
(s2613 4.0)
(s2614 5.0)
(s2615 5.0)
(s2616 2.0)
(s2618 4.0)
(s2619 5.0)
(s2620 5.0)
(s2621 2.0)
(s2623 4.0)
(s2624 5.0)
(s2625 5.0)
(s2626 2.0)
(s2628 4.0)
(s2629 5.0)
(s2630 5.0)
(s2631 2.0)
(s2633 4.0)
(s2634 5.0)
(s2635 5.0)
(s2636 2.0)
(s2638 4.0)
(s2639 5.0)
(s2640 5.0)
(s2641 2.0)
(s2643 4.0)
(s2644 5.0)
(s2645 5.0)
(s2646 2.0)
(s2648 4.0)
(s2649 5.0)
(s2650 5.0)
(s2651 2.0)
(s2653 4.0)
(s2654 5.0)
(s2655 5.0)
(s2656 2.0)
(s2658 4.0)
(s2659 5.0)
(s2660 5.0)
(s2661 2.0)
(s2663 4.0)
(s2664 5.0)
(s2665 5.0)
(s2666 2.0)
(s2668 4.0)
(s2669 5.0)
(s2670 5.0)
(s2671 2.0)
(s2673 4.0)
(s2674 5.0)
(s2675 5.0)
(s2676 2.0)
(s2678 4.0)
(s2679 5.0)
(s2680 5.0)
(s2681 2.0)
(s2683 4.0)
(s2684 5.0)
(s2685 5.0)
(s2686 2.0)
(s2688 4.0)
(s2689 5.0)
(s2690 5.0)
(s2691 2.0)
(s2693 4.0)
(s2694 5.0)
(s2695 5.0)
(s2696 2.0)
(s2698 4.0)
(s2699 5.0)
(s2700 5.0)
(s2701 2.0)
(s2703 4.0)
(s2704 5.0)
(s2705 5.0)
(s2706 2.0)
(s2708 4.0)
(s2709 5.0)
(s2710 5.0)
(s2711 2.0)
(s2713 4.0)
(s2714 5.0)
(s2715 5.0)
(s2716 2.0)
(s2718 4.0)
(s2719 5.0)
(s2720 5.0)
(s2721 2.0)
(s2723 4.0)
(s2724 5.0)
(s2725 5.0)
(s2726 2.0)
(s2728 4.0)
(s2729 5.0)
(s2730 5.0)
(s2731 2.0)
(s2733 4.0)
(s2734 5.0)
(s2735 5.0)
(s2736 2.0)
(s2738 4.0)
(s2739 5.0)
(s2740 5.0)
(s2741 2.0)
(s2743 4.0)
(s2744 5.0)
(s2745 5.0)
(s2746 2.0)
(s2748 4.0)
(s2749 5.0)
(s2750 5.0)
(s2751 2.0)
(s2753 4.0)
(s2754 5.0)
(s2755 5.0)
(s2756 2.0)
(s2758 4.0)
(s2759 5.0)
(s2760 5.0)
(s2761 2.0)
(s2763 4.0)
(s2764 5.0)
(s2765 5.0)
(s2766 2.0)
(s2768 4.0)
(s2769 5.0)
(s2770 5.0)
(s2771 2.0)
(s2773 4.0)
(s2774 5.0)
(s2775 5.0)
(s2776 2.0)
(s2778 4.0)
(s2779 5.0)
(s2780 5.0)
(s2781 2.0)
(s2783 4.0)
(s2784 5.0)
(s2785 5.0)
(s2786 2.0)
(s2788 4.0)
(s2789 5.0)
(s2790 5.0)
(s2791 2.0)
(s2793 4.0)
(s2794 5.0)
(s2795 5.0)
(s2796 2.0)
(s2798 4.0)
(s2799 5.0)
(s2800 5.0)
(s2801 2.0)
(s2803 4.0)
(s2804 5.0)
(s2805 5.0)
(s2806 2.0)
(s2808 4.0)
(s2809 5.0)
(s2810 5.0)
(s2811 2.0)
(s2813 4.0)
(s2814 5.0)
(s2815 5.0)
(s2816 2.0)
(s2818 4.0)
(s2819 5.0)
(s2820 5.0)
(s2821 2.0)
(s2823 4.0)
(s2824 5.0)
(s2825 5.0)
(s2826 2.0)
(s2828 4.0)
(s2829 5.0)
(s2830 5.0)
(s2831 2.0)
(s2833 4.0)
(s2834 5.0)
(s2835 5.0)
(s2836 2.0)
(s2838 4.0)
(s2839 5.0)
(s2840 5.0)
(s2841 2.0)
(s2843 4.0)
(s2844 5.0)
(s2845 5.0)
(s2846 2.0)
(s2848 4.0)
(s2849 5.0)
(s2850 5.0)
(s2851 2.0)
(s2853 4.0)
(s2854 5.0)
(s2855 5.0)
(s2856 2.0)
(s2858 4.0)
(s2859 5.0)
(s2860 5.0)
(s2861 2.0)
(s2863 4.0)
(s2864 5.0)
(s2865 5.0)
(s2866 2.0)
(s2868 4.0)
(s2869 5.0)
(s2870 5.0)
(s2871 2.0)
(s2873 4.0)
(s2874 5.0)
(s2875 5.0)
(s2876 2.0)
(s2878 4.0)
(s2879 5.0)
(s2880 5.0)
(s2881 2.0)
(s2883 4.0)
(s2884 5.0)
(s2885 5.0)
(s2886 2.0)
(s2888 4.0)
(s2889 5.0)
(s2890 5.0)
(s2891 2.0)
(s2893 4.0)
(s2894 5.0)
(s2895 5.0)
(s2896 2.0)
(s2898 4.0)
(s2899 5.0)
(s2900 5.0)
(s2901 2.0)
(s2903 4.0)
(s2904 5.0)
(s2905 5.0)
(s2906 2.0)
(s2908 4.0)
(s2909 5.0)
(s2910 5.0)
(s2911 2.0)
(s2913 4.0)
(s2914 5.0)
(s2915 5.0)
(s2916 2.0)
(s2918 4.0)
(s2919 5.0)
(s2920 5.0)
(s2921 2.0)
(s2923 4.0)
(s2924 5.0)
(s2925 5.0)
(s2926 2.0)
(s2928 4.0)
(s2929 5.0)
(s2930 5.0)
(s2931 2.0)
(s2933 4.0)
(s2934 5.0)
(s2935 5.0)
(s2936 2.0)
(s2938 4.0)
(s2939 5.0)
(s2940 5.0)
(s2941 2.0)
(s2943 4.0)
(s2944 5.0)
(s2945 5.0)
(s2946 2.0)
(s2948 4.0)
(s2949 5.0)
(s2950 5.0)
(s2951 2.0)
(s2953 4.0)
(s2954 5.0)
(s2955 5.0)
(s2956 2.0)
(s2958 4.0)
(s2959 5.0)
(s2960 5.0)
(s2961 2.0)
(s2963 4.0)
(s2964 5.0)
(s2965 5.0)
(s2966 2.0)
(s2968 4.0)
(s2969 5.0)
(s2970 5.0)
(s2971 2.0)
(s2973 4.0)
(s2974 5.0)
(s2975 5.0)
(s2976 2.0)
(s2978 4.0)
(s2979 5.0)
(s2980 5.0)
(s2981 2.0)
(s2983 4.0)
(s2984 5.0)
(s2985 5.0)
(s2986 2.0)
(s2988 4.0)
(s2989 5.0)
(s2990 5.0)
(s2991 2.0)
(s2993 4.0)
(s2994 5.0)
(s2995 5.0)
(s2996 2.0)
(s2998 4.0)
(s2999 5.0)
(s3000 5.0)
(s3001 2.0)
(s3003 4.0)
(s3004 5.0)
(s3005 5.0)
(s3006 2.0)
(s3008 4.0)
(s3009 5.0)
(s3010 5.0)
(s3011 2.0)
(s3013 4.0)
(s3014 5.0)
(s3015 5.0)
(s3016 2.0)
(s3018 4.0)
(s3019 5.0)
(s3020 5.0)
(s3021 2.0)
(s3023 4.0)
(s3024 5.0)
(s3025 5.0)
(s3026 2.0)
(s3028 4.0)
(s3029 5.0)
(s3030 5.0)
(s3031 2.0)
(s3033 4.0)
(s3034 5.0)
(s3035 5.0)
(s3036 2.0)
(s3038 4.0)
(s3039 5.0)
(s3040 5.0)
(s3041 2.0)
(s3043 4.0)
(s3044 5.0)
(s3045 5.0)
(s3046 2.0)
(s3048 4.0)
(s3049 5.0)
(s3050 5.0)
(s3051 2.0)
(s3053 4.0)
(s3054 5.0)
(s3055 5.0)
(s3056 2.0)
(s3058 4.0)
(s3059 5.0)
(s3060 5.0)
(s3061 2.0)
(s3063 4.0)
(s3064 5.0)
(s3065 5.0)
(s3066 2.0)
(s3068 4.0)
(s3069 5.0)
(s3070 5.0)
(s3071 2.0)
(s3073 4.0)
(s3074 5.0)
(s3075 5.0)
(s3076 2.0)
(s3078 4.0)
(s3079 5.0)
(s3080 5.0)
(s3081 2.0)
(s3083 4.0)
(s3084 5.0)
(s3085 5.0)
(s3086 2.0)
(s3088 4.0)
(s3089 5.0)
(s3090 5.0)
(s3091 2.0)
(s3093 4.0)
(s3094 5.0)
(s3095 5.0)
(s3096 2.0)
(s3098 4.0)
(s3099 5.0)
(s3100 5.0)
(s3101 2.0)
(s3103 4.0)
(s3104 5.0)
(s3105 5.0)
(s3106 2.0)
(s3108 4.0)
(s3109 5.0)
(s3110 5.0)
(s3111 2.0)
(s3113 4.0)
(s3114 5.0)
(s3115 5.0)
(s3116 2.0)
(s3118 4.0)
(s3119 5.0)
(s3120 5.0)
(s3121 2.0)
(s3123 4.0)
(s3124 5.0)
(s3125 5.0)
(s3126 2.0)
(s3128 4.0)
(s3129 5.0)
(s3130 5.0)
(s3131 2.0)
(s3133 4.0)
(s3134 5.0)
(s3135 5.0)
(s3136 2.0)
(s3138 4.0)
(s3139 5.0)
(s3140 5.0)
(s3141 2.0)
(s3143 4.0)
(s3144 5.0)
(s3145 5.0)
(s3146 2.0)
(s3148 4.0)
(s3149 5.0)
(s3150 5.0)
(s3151 2.0)
(s3153 4.0)
(s3154 5.0)
(s3155 5.0)
(s3156 2.0)
(s3158 4.0)
(s3159 5.0)
(s3160 5.0)
(s3161 2.0)
(s3163 4.0)
(s3164 5.0)
(s3165 5.0)
(s3166 2.0)
(s3168 4.0)
(s3169 5.0)
(s3170 5.0)
(s3171 2.0)
(s3173 4.0)
(s3174 5.0)
(s3175 5.0)
(s3176 2.0)
(s3178 4.0)
(s3179 5.0)
(s3180 5.0)
(s3181 2.0)
(s3183 4.0)
(s3184 5.0)
(s3185 5.0)
(s3186 2.0)
(s3188 4.0)
(s3189 5.0)
(s3190 5.0)
(s3191 2.0)
(s3193 4.0)
(s3194 5.0)
(s3195 5.0)
(s3196 2.0)
(s3198 4.0)
(s3199 5.0)
(s3200 5.0)
(s3201 2.0)
(s3203 4.0)
(s3204 5.0)
(s3205 5.0)
(s3206 2.0)
(s3208 4.0)
(s3209 5.0)
(s3210 5.0)
(s3211 2.0)
(s3213 4.0)
(s3214 5.0)
(s3215 5.0)
(s3216 2.0)
(s3218 4.0)
(s3219 5.0)
(s3220 5.0)
(s3221 2.0)
(s3223 4.0)
(s3224 5.0)
(s3225 5.0)
(s3226 2.0)
(s3228 4.0)
(s3229 5.0)
(s3230 5.0)
(s3231 2.0)
(s3233 4.0)
(s3234 5.0)
(s3235 5.0)
(s3236 2.0)
(s3238 4.0)
(s3239 5.0)
(s3240 5.0)
(s3241 2.0)
(s3243 4.0)
(s3244 5.0)
(s3245 5.0)
(s3246 2.0)
(s3248 4.0)
(s3249 5.0)
(s3250 5.0)
(s3251 2.0)
(s3253 4.0)
(s3254 5.0)
(s3255 5.0)
(s3256 2.0)
(s3258 4.0)
(s3259 5.0)
(s3260 5.0)
(s3261 2.0)
(s3263 4.0)
(s3264 5.0)
(s3265 5.0)
(s3266 2.0)
(s3268 4.0)
(s3269 5.0)
(s3270 5.0)
(s3271 2.0)
(s3273 4.0)
(s3274 5.0)
(s3275 5.0)
(s3276 2.0)
(s3278 4.0)
(s3279 5.0)
(s3280 5.0)
(s3281 2.0)
(s3283 4.0)
(s3284 5.0)
(s3285 5.0)
(s3286 2.0)
(s3288 4.0)
(s3289 5.0)
(s3290 5.0)
(s3291 2.0)
(s3293 4.0)
(s3294 5.0)
(s3295 5.0)
(s3296 2.0)
(s3298 4.0)
(s3299 5.0)
(s3300 5.0)
(s3301 2.0)
(s3303 4.0)
(s3304 5.0)
(s3305 5.0)
(s3306 2.0)
(s3308 4.0)
(s3309 5.0)
(s3310 5.0)
(s3311 2.0)
(s3313 4.0)
(s3314 5.0)
(s3315 5.0)
(s3316 2.0)
(s3318 4.0)
(s3319 5.0)
(s3320 5.0)
(s3321 2.0)
(s3323 4.0)
(s3324 5.0)
(s3325 5.0)
(s3326 2.0)
(s3328 4.0)
(s3329 5.0)
(s3330 5.0)
(s3331 2.0)
(s3333 4.0)
(s3334 5.0)
(s3335 5.0)
(s3336 2.0)
(s3338 4.0)
(s3339 5.0)
(s3340 5.0)
(s3341 2.0)
(s3343 4.0)
(s3344 5.0)
(s3345 5.0)
(s3346 2.0)
(s3348 4.0)
(s3349 5.0)
(s3350 5.0)
(s3351 2.0)
(s3353 4.0)
(s3354 5.0)
(s3355 5.0)
(s3356 2.0)
(s3358 4.0)
(s3359 5.0)
(s3360 5.0)
(s3361 2.0)
(s3363 4.0)
(s3364 5.0)
(s3365 5.0)
(s3366 2.0)
(s3368 4.0)
(s3369 5.0)
(s3370 5.0)
(s3371 2.0)
(s3373 4.0)
(s3374 5.0)
(s3375 5.0)
(s3376 2.0)
(s3378 4.0)
(s3379 5.0)
(s3380 5.0)
(s3381 2.0)
(s3383 4.0)
(s3384 5.0)
(s3385 5.0)
(s3386 2.0)
(s3388 4.0)
(s3389 5.0)
(s3390 5.0)
(s3391 2.0)
(s3393 4.0)
(s3394 5.0)
(s3395 5.0)
(s3396 2.0)
(s3398 4.0)
(s3399 5.0)
(s3400 5.0)
(s3401 2.0)
(s3403 4.0)
(s3404 5.0)
(s3405 5.0)
(s3406 2.0)
(s3408 4.0)
(s3409 5.0)
(s3410 5.0)
(s3411 2.0)
(s3413 4.0)
(s3414 5.0)
(s3415 5.0)
(s3416 2.0)
(s3418 4.0)
(s3419 5.0)
(s3420 5.0)
(s3421 2.0)
(s3423 4.0)
(s3424 5.0)
(s3425 5.0)
(s3426 2.0)
(s3428 4.0)
(s3429 5.0)
(s3430 5.0)
(s3431 2.0)
(s3433 4.0)
(s3434 5.0)
(s3435 5.0)
(s3436 2.0)
(s3438 4.0)
(s3439 5.0)
(s3440 5.0)
(s3441 2.0)
(s3443 4.0)
(s3444 5.0)
(s3445 5.0)
(s3446 2.0)
(s3448 4.0)
(s3449 5.0)
(s3450 5.0)
(s3451 2.0)
(s3453 4.0)
(s3454 5.0)
(s3455 5.0)
(s3456 2.0)
(s3458 4.0)
(s3459 5.0)
(s3460 5.0)
(s3461 2.0)
(s3463 4.0)
(s3464 5.0)
(s3465 5.0)
(s3466 2.0)
(s3468 4.0)
(s3469 5.0)
(s3470 5.0)
(s3471 2.0)
(s3473 4.0)
(s3474 5.0)
(s3475 5.0)
(s3476 2.0)
(s3478 4.0)
(s3479 5.0)
(s3480 5.0)
(s3481 2.0)
(s3483 4.0)
(s3484 5.0)
(s3485 5.0)
(s3486 2.0)
(s3488 4.0)
(s3489 5.0)
(s3490 5.0)
(s3491 2.0)
(s3493 4.0)
(s3494 5.0)
(s3495 5.0)
(s3496 2.0)
(s3498 4.0)
(s3499 5.0)
(s3500 5.0)
(s3501 2.0)
(s3503 4.0)
(s3504 5.0)
(s3505 5.0)
(s3506 2.0)
(s3508 4.0)
(s3509 5.0)
(s3510 5.0)
(s3511 2.0)
(s3513 4.0)
(s3514 5.0)
(s3515 5.0)
(s3516 2.0)
(s3518 4.0)
(s3519 5.0)
(s3520 5.0)
(s3521 2.0)
(s3523 4.0)
(s3524 5.0)
(s3525 5.0)
(s3526 2.0)
(s3528 4.0)
(s3529 5.0)
(s3530 5.0)
(s3531 2.0)
(s3533 4.0)
(s3534 5.0)
(s3535 5.0)
(s3536 2.0)
(s3538 4.0)
(s3539 5.0)
(s3540 5.0)
(s3541 2.0)
(s3543 4.0)
(s3544 5.0)
(s3545 5.0)
(s3546 2.0)
(s3548 4.0)
(s3549 5.0)
(s3550 5.0)
(s3551 2.0)
(s3553 4.0)
(s3554 5.0)
(s3555 5.0)
(s3556 2.0)
(s3558 4.0)
(s3559 5.0)
(s3560 5.0)
(s3561 2.0)
(s3563 4.0)
(s3564 5.0)
(s3565 5.0)
(s3566 2.0)
(s3568 4.0)
(s3569 5.0)
(s3570 5.0)
(s3571 2.0)
(s3573 4.0)
(s3574 5.0)
(s3575 5.0)
(s3576 2.0)
(s3578 4.0)
(s3579 5.0)
(s3580 5.0)
(s3581 2.0)
(s3583 4.0)
(s3584 5.0)
(s3585 5.0)
(s3586 2.0)
(s3588 4.0)
(s3589 5.0)
(s3590 5.0)
(s3591 2.0)
(s3593 4.0)
(s3594 5.0)
(s3595 5.0)
(s3596 2.0)
(s3598 4.0)
(s3599 5.0)
(s3600 5.0)
(s3601 2.0)
(s3603 4.0)
(s3604 5.0)
(s3605 5.0)
(s3606 2.0)
(s3608 4.0)
(s3609 5.0)
(s3610 5.0)
(s3611 2.0)
(s3613 4.0)
(s3614 5.0)
(s3615 5.0)
(s3616 2.0)
(s3618 4.0)
(s3619 5.0)
(s3620 5.0)
(s3621 2.0)
(s3623 4.0)
(s3624 5.0)
(s3625 5.0)
(s3626 2.0)
(s3628 4.0)
(s3629 5.0)
(s3630 5.0)
(s3631 2.0)
(s3633 4.0)
(s3634 5.0)
(s3635 5.0)
(s3636 2.0)
(s3638 4.0)
(s3639 5.0)
(s3640 5.0)
(s3641 2.0)
(s3643 4.0)
(s3644 5.0)
(s3645 5.0)
(s3646 2.0)
(s3648 4.0)
(s3649 5.0)
(s3650 5.0)
(s3651 2.0)
(s3653 4.0)
(s3654 5.0)
(s3655 5.0)
(s3656 2.0)
(s3658 4.0)
(s3659 5.0)
(s3660 5.0)
(s3661 2.0)
(s3663 4.0)
(s3664 5.0)
(s3665 5.0)
(s3666 2.0)
(s3668 4.0)
(s3669 5.0)
(s3670 5.0)
(s3671 2.0)
(s3673 4.0)
(s3674 5.0)
(s3675 5.0)
(s3676 2.0)
(s3678 4.0)
(s3679 5.0)
(s3680 5.0)
(s3681 2.0)
(s3683 4.0)
(s3684 5.0)
(s3685 5.0)
(s3686 2.0)
(s3688 4.0)
(s3689 5.0)
(s3690 5.0)
(s3691 2.0)
(s3693 4.0)
(s3694 5.0)
(s3695 5.0)
(s3696 2.0)
(s3698 4.0)
(s3699 5.0)
(s3700 5.0)
(s3701 2.0)
(s3703 4.0)
(s3704 5.0)
(s3705 5.0)
(s3706 2.0)
(s3708 4.0)
(s3709 5.0)
(s3710 5.0)
(s3711 2.0)
(s3713 4.0)
(s3714 5.0)
(s3715 5.0)
(s3716 2.0)
(s3718 4.0)
(s3719 5.0)
(s3720 5.0)
(s3721 2.0)
(s3723 4.0)
(s3724 5.0)
(s3725 5.0)
(s3726 2.0)
(s3728 4.0)
(s3729 5.0)
(s3730 5.0)
(s3731 2.0)
(s3733 4.0)
(s3734 5.0)
(s3735 5.0)
(s3736 2.0)
(s3738 4.0)
(s3739 5.0)
(s3740 5.0)
(s3741 2.0)
(s3743 4.0)
(s3744 5.0)
(s3745 5.0)
(s3746 2.0)
(s3748 4.0)
(s3749 5.0)
(s3750 5.0)
(s3751 2.0)
(s3753 4.0)
(s3754 5.0)
(s3755 5.0)
(s3756 2.0)
(s3758 4.0)
(s3759 5.0)
(s3760 5.0)
(s3761 2.0)
(s3763 4.0)
(s3764 5.0)
(s3765 5.0)
(s3766 2.0)
(s3768 4.0)
(s3769 5.0)
(s3770 5.0)
(s3771 2.0)
(s3773 4.0)
(s3774 5.0)
(s3775 5.0)
(s3776 2.0)
(s3778 4.0)
(s3779 5.0)
(s3780 5.0)
(s3781 2.0)
(s3783 4.0)
(s3784 5.0)
(s3785 5.0)
(s3786 2.0)
(s3788 4.0)
(s3789 5.0)
(s3790 5.0)
(s3791 2.0)
(s3793 4.0)
(s3794 5.0)
(s3795 5.0)
(s3796 2.0)
(s3798 4.0)
(s3799 5.0)
(s3800 5.0)
(s3801 2.0)
(s3803 4.0)
(s3804 5.0)
(s3805 5.0)
(s3806 2.0)
(s3808 4.0)
(s3809 5.0)
(s3810 5.0)
(s3811 2.0)
(s3813 4.0)
(s3814 5.0)
(s3815 5.0)
(s3816 2.0)
(s3818 4.0)
(s3819 5.0)
(s3820 5.0)
(s3821 2.0)
(s3823 4.0)
(s3824 5.0)
(s3825 5.0)
(s3826 2.0)
(s3828 4.0)
(s3829 5.0)
(s3830 5.0)
(s3831 2.0)
(s3833 4.0)
(s3834 5.0)
(s3835 5.0)
(s3836 2.0)
(s3838 4.0)
(s3839 5.0)
(s3840 5.0)
(s3841 2.0)
(s3843 4.0)
(s3844 5.0)
(s3845 5.0)
(s3846 2.0)
(s3848 4.0)
(s3849 5.0)
(s3850 5.0)
(s3851 2.0)
(s3853 4.0)
(s3854 5.0)
(s3855 5.0)
(s3856 2.0)
(s3858 4.0)
(s3859 5.0)
(s3860 5.0)
(s3861 2.0)
(s3863 4.0)
(s3864 5.0)
(s3865 5.0)
(s3866 2.0)
(s3868 4.0)
(s3869 5.0)
(s3870 5.0)
(s3871 2.0)
(s3873 4.0)
(s3874 5.0)
(s3875 5.0)
(s3876 2.0)
(s3878 4.0)
(s3879 5.0)
(s3880 5.0)
(s3881 2.0)
(s3883 4.0)
(s3884 5.0)
(s3885 5.0)
(s3886 2.0)
(s3888 4.0)
(s3889 5.0)
(s3890 5.0)
(s3891 2.0)
(s3893 4.0)
(s3894 5.0)
(s3895 5.0)
(s3896 2.0)
(s3898 4.0)
(s3899 5.0)
(s3900 5.0)
(s3901 2.0)
(s3903 4.0)
(s3904 5.0)
(s3905 5.0)
(s3906 2.0)
(s3908 4.0)
(s3909 5.0)
(s3910 5.0)
(s3911 2.0)
(s3913 4.0)
(s3914 5.0)
(s3915 5.0)
(s3916 2.0)
(s3918 4.0)
(s3919 5.0)
(s3920 5.0)
(s3921 2.0)
(s3923 4.0)
(s3924 5.0)
(s3925 5.0)
(s3926 2.0)
(s3928 4.0)
(s3929 5.0)
(s3930 5.0)
(s3931 2.0)
(s3933 4.0)
(s3934 5.0)
(s3935 5.0)
(s3936 2.0)
(s3938 4.0)
(s3939 5.0)
(s3940 5.0)
(s3941 2.0)
(s3943 4.0)
(s3944 5.0)
(s3945 5.0)
(s3946 2.0)
(s3948 4.0)
(s3949 5.0)
(s3950 5.0)
(s3951 2.0)
(s3953 4.0)
(s3954 5.0)
(s3955 5.0)
(s3956 2.0)
(s3958 4.0)
(s3959 5.0)
(s3960 5.0)
(s3961 2.0)
(s3963 4.0)
(s3964 5.0)
(s3965 5.0)
(s3966 2.0)
(s3968 4.0)
(s3969 5.0)
(s3970 5.0)
(s3971 2.0)
(s3973 4.0)
(s3974 5.0)
(s3975 5.0)
(s3976 2.0)
(s3978 4.0)
(s3979 5.0)
(s3980 5.0)
(s3981 2.0)
(s3983 4.0)
(s3984 5.0)
(s3985 5.0)
(s3986 2.0)
(s3988 4.0)
(s3989 5.0)
(s3990 5.0)
(s3991 2.0)
(s3993 4.0)
(s3994 5.0)
(s3995 5.0)
(s3996 2.0)
(s3998 4.0)
(s3999 5.0)
(s4000 5.0)
(s4001 2.0)
(s4003 4.0)
(s4004 5.0)
(s4005 5.0)
(s4006 2.0)
(s4008 4.0)
(s4009 5.0)
(s4010 5.0)
(s4011 2.0)
(s4013 4.0)
(s4014 5.0)
(s4015 5.0)
(s4016 2.0)
(s4018 4.0)
(s4019 5.0)
(s4020 5.0)
(s4021 2.0)
(s4023 4.0)
(s4024 5.0)
(s4025 5.0)
(s4026 2.0)
(s4028 4.0)
(s4029 5.0)
(s4030 5.0)
(s4031 2.0)
(s4033 4.0)
(s4034 5.0)
(s4035 5.0)
(s4036 2.0)
(s4038 4.0)
(s4039 5.0)
(s4040 5.0)
(s4041 2.0)
(s4043 4.0)
(s4044 5.0)
(s4045 5.0)
(s4046 2.0)
(s4048 4.0)
(s4049 5.0)
(s4050 5.0)
(s4051 2.0)
(s4053 4.0)
(s4054 5.0)
(s4055 5.0)
(s4056 2.0)
(s4058 4.0)
(s4059 5.0)
(s4060 5.0)
(s4061 2.0)
(s4063 4.0)
(s4064 5.0)
(s4065 5.0)
(s4066 2.0)
(s4068 4.0)
(s4069 5.0)
(s4070 5.0)
(s4071 2.0)
(s4073 4.0)
(s4074 5.0)
(s4075 5.0)
(s4076 2.0)
(s4078 4.0)
(s4079 5.0)
(s4080 5.0)
(s4081 2.0)
(s4083 4.0)
(s4084 5.0)
(s4085 5.0)
(s4086 2.0)
(s4088 4.0)
(s4089 5.0)
(s4090 5.0)
(s4091 2.0)
(s4093 4.0)
(s4094 5.0)
(s4095 5.0)
(s4096 2.0)
(s4098 4.0)
(s4099 5.0)
(s4100 5.0)
(s4101 2.0)
(s4103 4.0)
(s4104 5.0)
(s4105 5.0)
(s4106 2.0)
(s4108 4.0)
(s4109 5.0)
(s4110 5.0)
(s4111 2.0)
(s4113 4.0)
(s4114 5.0)
(s4115 5.0)
(s4116 2.0)
(s4118 4.0)
(s4119 5.0)
(s4120 5.0)
(s4121 2.0)
(s4123 4.0)
(s4124 5.0)
(s4125 5.0)
(s4126 2.0)
(s4128 4.0)
(s4129 5.0)
(s4130 5.0)
(s4131 2.0)
(s4133 4.0)
(s4134 5.0)
(s4135 5.0)
(s4136 2.0)
(s4138 4.0)
(s4139 5.0)
(s4140 5.0)
(s4141 2.0)
(s4143 4.0)
(s4144 5.0)
(s4145 5.0)
(s4146 2.0)
(s4148 4.0)
(s4149 5.0)
(s4150 5.0)
(s4151 2.0)
(s4153 4.0)
(s4154 5.0)
(s4155 5.0)
(s4156 2.0)
(s4158 4.0)
(s4159 5.0)
(s4160 5.0)
(s4161 2.0)
(s4163 4.0)
(s4164 5.0)
(s4165 5.0)
(s4166 2.0)
(s4168 4.0)
(s4169 5.0)
(s4170 5.0)
(s4171 2.0)
(s4173 4.0)
(s4174 5.0)
(s4175 5.0)
(s4176 2.0)
(s4178 4.0)
(s4179 5.0)
(s4180 5.0)
(s4181 2.0)
(s4183 4.0)
(s4184 5.0)
(s4185 5.0)
(s4186 2.0)
(s4188 4.0)
(s4189 5.0)
(s4190 5.0)
(s4191 2.0)
(s4193 4.0)
(s4194 5.0)
(s4195 5.0)
(s4196 2.0)
(s4198 4.0)
(s4199 5.0)
(s4200 5.0)
(s4201 2.0)
(s4203 4.0)
(s4204 5.0)
(s4205 5.0)
(s4206 2.0)
(s4208 4.0)
(s4209 5.0)
(s4210 5.0)
(s4211 2.0)
(s4213 4.0)
(s4214 5.0)
(s4215 5.0)
(s4216 2.0)
(s4218 4.0)
(s4219 5.0)
(s4220 5.0)
(s4221 2.0)
(s4223 4.0)
(s4224 5.0)
(s4225 5.0)
(s4226 2.0)
(s4228 4.0)
(s4229 5.0)
(s4230 5.0)
(s4231 2.0)
(s4233 4.0)
(s4234 5.0)
(s4235 5.0)
(s4236 2.0)
(s4238 4.0)
(s4239 5.0)
(s4240 5.0)
(s4241 2.0)
(s4243 4.0)
(s4244 5.0)
(s4245 5.0)
(s4246 2.0)
(s4248 4.0)
(s4249 5.0)
(s4250 5.0)
(s4251 2.0)
(s4253 4.0)
(s4254 5.0)
(s4255 5.0)
(s4256 2.0)
(s4258 4.0)
(s4259 5.0)
(s4260 5.0)
(s4261 2.0)
(s4263 4.0)
(s4264 5.0)
(s4265 5.0)
(s4266 2.0)
(s4268 4.0)
(s4269 5.0)
(s4270 5.0)
(s4271 2.0)
(s4273 4.0)
(s4274 5.0)
(s4275 5.0)
(s4276 2.0)
(s4278 4.0)
(s4279 5.0)
(s4280 5.0)
(s4281 2.0)
(s4283 4.0)
(s4284 5.0)
(s4285 5.0)
(s4286 2.0)
(s4288 4.0)
(s4289 5.0)
(s4290 5.0)
(s4291 2.0)
(s4293 4.0)
(s4294 5.0)
(s4295 5.0)
(s4296 2.0)
(s4298 4.0)
(s4299 5.0)
(s4300 5.0)
(s4301 2.0)
(s4303 4.0)
(s4304 5.0)
(s4305 5.0)
(s4306 2.0)
(s4308 4.0)
(s4309 5.0)
(s4310 5.0)
(s4311 2.0)
(s4313 4.0)
(s4314 5.0)
(s4315 5.0)
(s4316 2.0)
(s4318 4.0)
(s4319 5.0)
(s4320 5.0)
(s4321 2.0)
(s4323 4.0)
(s4324 5.0)
(s4325 5.0)
(s4326 2.0)
(s4328 4.0)
(s4329 5.0)
(s4330 5.0)
(s4331 2.0)
(s4333 4.0)
(s4334 5.0)
(s4335 5.0)
(s4336 2.0)
(s4338 4.0)
(s4339 5.0)
(s4340 5.0)
(s4341 2.0)
(s4343 4.0)
(s4344 5.0)
(s4345 5.0)
(s4346 2.0)
(s4348 4.0)
(s4349 5.0)
(s4350 5.0)
(s4351 2.0)
(s4353 4.0)
(s4354 5.0)
(s4355 5.0)
(s4356 2.0)
(s4358 4.0)
(s4359 5.0)
(s4360 5.0)
(s4361 2.0)
(s4363 4.0)
(s4364 5.0)
(s4365 5.0)
(s4366 2.0)
(s4368 4.0)
(s4369 5.0)
(s4370 5.0)
(s4371 2.0)
(s4373 4.0)
(s4374 5.0)
(s4375 5.0)
(s4376 2.0)
(s4378 4.0)
(s4379 5.0)
(s4380 5.0)
(s4381 2.0)
(s4383 4.0)
(s4384 5.0)
(s4385 5.0)
(s4386 2.0)
(s4388 4.0)
(s4389 5.0)
(s4390 5.0)
(s4391 2.0)
(s4393 4.0)
(s4394 5.0)
(s4395 5.0)
(s4396 2.0)
(s4398 4.0)
(s4399 5.0)
(s4400 5.0)
(s4401 2.0)
(s4403 4.0)
(s4404 5.0)
(s4405 5.0)
(s4406 2.0)
(s4408 4.0)
(s4409 5.0)
(s4410 5.0)
(s4411 2.0)
(s4413 4.0)
(s4414 5.0)
(s4415 5.0)
(s4416 2.0)
(s4418 4.0)
(s4419 5.0)
(s4420 5.0)
(s4421 2.0)
(s4423 4.0)
(s4424 5.0)
(s4425 5.0)
(s4426 2.0)
(s4428 4.0)
(s4429 5.0)
(s4430 5.0)
(s4431 2.0)
(s4433 4.0)
(s4434 5.0)
(s4435 5.0)
(s4436 2.0)
(s4438 4.0)
(s4439 5.0)
(s4440 5.0)
(s4441 2.0)
(s4443 4.0)
(s4444 5.0)
(s4445 5.0)
(s4446 2.0)
(s4448 4.0)
(s4449 5.0)
(s4450 5.0)
(s4451 2.0)
(s4453 4.0)
(s4454 5.0)
(s4455 5.0)
(s4456 2.0)
(s4458 4.0)
(s4459 5.0)
(s4460 5.0)
(s4461 2.0)
(s4463 4.0)
(s4464 5.0)
(s4465 5.0)
(s4466 2.0)
(s4468 4.0)
(s4469 5.0)
(s4470 5.0)
(s4471 2.0)
(s4473 4.0)
(s4474 5.0)
(s4475 5.0)
(s4476 2.0)
(s4478 4.0)
(s4479 5.0)
(s4480 5.0)
(s4481 2.0)
(s4483 4.0)
(s4484 5.0)
(s4485 5.0)
(s4486 2.0)
(s4488 4.0)
(s4489 5.0)
(s4490 5.0)
(s4491 2.0)
(s4493 4.0)
(s4494 5.0)
(s4495 5.0)
(s4496 2.0)
(s4498 4.0)
(s4499 5.0)
(s4500 5.0)
(s4501 2.0)
(s4503 4.0)
(s4504 5.0)
(s4505 5.0)
(s4506 2.0)
(s4508 4.0)
(s4509 5.0)
(s4510 5.0)
(s4511 2.0)
(s4513 4.0)
(s4514 5.0)
(s4515 5.0)
(s4516 2.0)
(s4518 4.0)
(s4519 5.0)
(s4520 5.0)
(s4521 2.0)
(s4523 4.0)
(s4524 5.0)
(s4525 5.0)
(s4526 2.0)
(s4528 4.0)
(s4529 5.0)
(s4530 5.0)
(s4531 2.0)
(s4533 4.0)
(s4534 5.0)
(s4535 5.0)
(s4536 2.0)
(s4538 4.0)
(s4539 5.0)
(s4540 5.0)
(s4541 2.0)
(s4543 4.0)
(s4544 5.0)
(s4545 5.0)
(s4546 2.0)
(s4548 4.0)
(s4549 5.0)
(s4550 5.0)
(s4551 2.0)
(s4553 4.0)
(s4554 5.0)
(s4555 5.0)
(s4556 2.0)
(s4558 4.0)
(s4559 5.0)
(s4560 5.0)
(s4561 2.0)
(s4563 4.0)
(s4564 5.0)
(s4565 5.0)
(s4566 2.0)
(s4568 4.0)
(s4569 5.0)
(s4570 5.0)
(s4571 2.0)
(s4573 4.0)
(s4574 5.0)
(s4575 5.0)
(s4576 2.0)
(s4578 4.0)
(s4579 5.0)
(s4580 5.0)
(s4581 2.0)
(s4583 4.0)
(s4584 5.0)
(s4585 5.0)
(s4586 2.0)
(s4588 4.0)
(s4589 5.0)
(s4590 5.0)
(s4591 2.0)
(s4593 4.0)
(s4594 5.0)
(s4595 5.0)
(s4596 2.0)
(s4598 4.0)
(s4599 5.0)
(s4600 5.0)
(s4601 2.0)
(s4603 4.0)
(s4604 5.0)
(s4605 5.0)
(s4606 2.0)
(s4608 4.0)
(s4609 5.0)
(s4610 5.0)
(s4611 2.0)
(s4613 4.0)
(s4614 5.0)
(s4615 5.0)
(s4616 2.0)
(s4618 4.0)
(s4619 5.0)
(s4620 5.0)
(s4621 2.0)
(s4623 4.0)
(s4624 5.0)
(s4625 5.0)
(s4626 2.0)
(s4628 4.0)
(s4629 5.0)
(s4630 5.0)
(s4631 2.0)
(s4633 4.0)
(s4634 5.0)
(s4635 5.0)
(s4636 2.0)
(s4638 4.0)
(s4639 5.0)
(s4640 5.0)
(s4641 2.0)
(s4643 4.0)
(s4644 5.0)
(s4645 5.0)
(s4646 2.0)
(s4648 4.0)
(s4649 5.0)
(s4650 5.0)
(s4651 2.0)
(s4653 4.0)
(s4654 5.0)
(s4655 5.0)
(s4656 2.0)
(s4658 4.0)
(s4659 5.0)
(s4660 5.0)
(s4661 2.0)
(s4663 4.0)
(s4664 5.0)
(s4665 5.0)
(s4666 2.0)
(s4668 4.0)
(s4669 5.0)
(s4670 5.0)
(s4671 2.0)
(s4673 4.0)
(s4674 5.0)
(s4675 5.0)
(s4676 2.0)
(s4678 4.0)
(s4679 5.0)
(s4680 5.0)
(s4681 2.0)
(s4683 4.0)
(s4684 5.0)
(s4685 5.0)
(s4686 2.0)
(s4688 4.0)
(s4689 5.0)
(s4690 5.0)
(s4691 2.0)
(s4693 4.0)
(s4694 5.0)
(s4695 5.0)
(s4696 2.0)
(s4698 4.0)
(s4699 5.0)
(s4700 5.0)
(s4701 2.0)
(s4703 4.0)
(s4704 5.0)
(s4705 5.0)
(s4706 2.0)
(s4708 4.0)
(s4709 5.0)
(s4710 5.0)
(s4711 2.0)
(s4713 4.0)
(s4714 5.0)
(s4715 5.0)
(s4716 2.0)
(s4718 4.0)
(s4719 5.0)
(s4720 5.0)
(s4721 2.0)
(s4723 4.0)
(s4724 5.0)
(s4725 5.0)
(s4726 2.0)
(s4728 4.0)
(s4729 5.0)
(s4730 5.0)
(s4731 2.0)
(s4733 4.0)
(s4734 5.0)
(s4735 5.0)
(s4736 2.0)
(s4738 4.0)
(s4739 5.0)
(s4740 5.0)
(s4741 2.0)
(s4743 4.0)
(s4744 5.0)
(s4745 5.0)
(s4746 2.0)
(s4748 4.0)
(s4749 5.0)
(s4750 5.0)
(s4751 2.0)
(s4753 4.0)
(s4754 5.0)
(s4755 5.0)
(s4756 2.0)
(s4758 4.0)
(s4759 5.0)
(s4760 5.0)
(s4761 2.0)
(s4763 4.0)
(s4764 5.0)
(s4765 5.0)
(s4766 2.0)
(s4768 4.0)
(s4769 5.0)
(s4770 5.0)
(s4771 2.0)
(s4773 4.0)
(s4774 5.0)
(s4775 5.0)
(s4776 2.0)
(s4778 4.0)
(s4779 5.0)
(s4780 5.0)
(s4781 2.0)
(s4783 4.0)
(s4784 5.0)
(s4785 5.0)
(s4786 2.0)
(s4788 4.0)
(s4789 5.0)
(s4790 5.0)
(s4791 2.0)
(s4793 4.0)
(s4794 5.0)
(s4795 5.0)
(s4796 2.0)
(s4798 4.0)
(s4799 5.0)
(s4800 5.0)
(s4801 2.0)
(s4803 4.0)
(s4804 5.0)
(s4805 5.0)
(s4806 2.0)
(s4808 4.0)
(s4809 5.0)
(s4810 5.0)
(s4811 2.0)
(s4813 4.0)
(s4814 5.0)
(s4815 5.0)
(s4816 2.0)
(s4818 4.0)
(s4819 5.0)
(s4820 5.0)
(s4821 2.0)
(s4823 4.0)
(s4824 5.0)
(s4825 5.0)
(s4826 2.0)
(s4828 4.0)
(s4829 5.0)
(s4830 5.0)
(s4831 2.0)
(s4833 4.0)
(s4834 5.0)
(s4835 5.0)
(s4836 2.0)
(s4838 4.0)
(s4839 5.0)
(s4840 5.0)
(s4841 2.0)
(s4843 4.0)
(s4844 5.0)
(s4845 5.0)
(s4846 2.0)
(s4848 4.0)
(s4849 5.0)
(s4850 5.0)
(s4851 2.0)
(s4853 4.0)
(s4854 5.0)
(s4855 5.0)
(s4856 2.0)
(s4858 4.0)
(s4859 5.0)
(s4860 5.0)
(s4861 2.0)
(s4863 4.0)
(s4864 5.0)
(s4865 5.0)
(s4866 2.0)
(s4868 4.0)
(s4869 5.0)
(s4870 5.0)
(s4871 2.0)
(s4873 4.0)
(s4874 5.0)
(s4875 5.0)
(s4876 2.0)
(s4878 4.0)
(s4879 5.0)
(s4880 5.0)
(s4881 2.0)
(s4883 4.0)
(s4884 5.0)
(s4885 5.0)
(s4886 2.0)
(s4888 4.0)
(s4889 5.0)
(s4890 5.0)
(s4891 2.0)
(s4893 4.0)
(s4894 5.0)
(s4895 5.0)
(s4896 2.0)
(s4898 4.0)
(s4899 5.0)
(s4900 5.0)
(s4901 2.0)
(s4903 4.0)
(s4904 5.0)
(s4905 5.0)
(s4906 2.0)
(s4908 4.0)
(s4909 5.0)
(s4910 5.0)
(s4911 2.0)
(s4913 4.0)
(s4914 5.0)
(s4915 5.0)
(s4916 2.0)
(s4918 4.0)
(s4919 5.0)
(s4920 5.0)
(s4921 2.0)
(s4923 4.0)
(s4924 5.0)
(s4925 5.0)
(s4926 2.0)
(s4928 4.0)
(s4929 5.0)
(s4930 5.0)
(s4931 2.0)
(s4933 4.0)
(s4934 5.0)
(s4935 5.0)
(s4936 2.0)
(s4938 4.0)
(s4939 5.0)
(s4940 5.0)
(s4941 2.0)
(s4943 4.0)
(s4944 5.0)
(s4945 5.0)
(s4946 2.0)
(s4948 4.0)
(s4949 5.0)
(s4950 5.0)
(s4951 2.0)
(s4953 4.0)
(s4954 5.0)
(s4955 5.0)
(s4956 2.0)
(s4958 4.0)
(s4959 5.0)
(s4960 5.0)
(s4961 2.0)
(s4963 4.0)
(s4964 5.0)
(s4965 5.0)
(s4966 2.0)
(s4968 4.0)
(s4969 5.0)
(s4970 5.0)
(s4971 2.0)
(s4973 4.0)
(s4974 5.0)
(s4975 5.0)
(s4976 2.0)
(s4978 4.0)
(s4979 5.0)
(s4980 5.0)
(s4981 2.0)
(s4983 4.0)
(s4984 5.0)
(s4985 5.0)
(s4986 2.0)
(s4988 4.0)
(s4989 5.0)
(s4990 5.0)
(s4991 2.0)
(s4993 4.0)
(s4994 5.0)
(s4995 5.0)
(s4996 2.0)
(s4998 4.0)
(s4999 5.0)
(s5000 5.0)
(s5001 2.0)
(s5003 4.0)
(s5004 5.0)
(s5005 5.0)
(s5006 2.0)
(s5008 4.0)
(s5009 5.0)
(s5010 5.0)
(s5011 2.0)
(s5013 4.0)
(s5014 5.0)
(s5015 5.0)
(s5016 2.0)
(s5018 4.0)
(s5019 5.0)
(s5020 5.0)
(s5021 2.0)
(s5023 4.0)
(s5024 5.0)
(s5025 5.0)
(s5026 2.0)
(s5028 4.0)
(s5029 5.0)
(s5030 5.0)
(s5031 2.0)
(s5033 4.0)
(s5034 5.0)
(s5035 5.0)
(s5036 2.0)
(s5038 4.0)
(s5039 5.0)
(s5040 5.0)
(s5041 2.0)
(s5043 4.0)
(s5044 5.0)
(s5045 5.0)
(s5046 2.0)
(s5048 4.0)
(s5049 5.0)
(s5050 5.0)
(s5051 2.0)
(s5053 4.0)
(s5054 5.0)
(s5055 5.0)
(s5056 2.0)
(s5058 4.0)
(s5059 5.0)
(s5060 5.0)
(s5061 2.0)
(s5063 4.0)
(s5064 5.0)
(s5065 5.0)
(s5066 2.0)
(s5068 4.0)
(s5069 5.0)
(s5070 5.0)
(s5071 2.0)
(s5073 4.0)
(s5074 5.0)
(s5075 5.0)
(s5076 2.0)
(s5078 4.0)
(s5079 5.0)
(s5080 5.0)
(s5081 2.0)
(s5083 4.0)
(s5084 5.0)
(s5085 5.0)
(s5086 2.0)
(s5088 4.0)
(s5089 5.0)
(s5090 5.0)
(s5091 2.0)
(s5093 4.0)
(s5094 5.0)
(s5095 5.0)
(s5096 2.0)
(s5098 4.0)
(s5099 5.0)
(s5100 5.0)
(s5101 2.0)
(s5103 4.0)
(s5104 5.0)
(s5105 5.0)
(s5106 2.0)
(s5108 4.0)
(s5109 5.0)
(s5110 5.0)
(s5111 2.0)
(s5113 4.0)
(s5114 5.0)
(s5115 5.0)
(s5116 2.0)
(s5118 4.0)
(s5119 5.0)
(s5120 5.0)
(s5121 2.0)
(s5123 4.0)
(s5124 5.0)
(s5125 5.0)
(s5126 2.0)
(s5128 4.0)
(s5129 5.0)
(s5130 timeout
5.0)
(s5131 org.smtlib.IParser$ParserException: Unbalanced parentheses at end of input")
Solver is answering 'unknown', stopping.
After SMT solving in domain Real declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30122 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 12000/12000 constraints, Known Traps: 0/0 constraints]
Escalating to Integer solving :Problem set: 0 solved, 12000 unsolved
Error getting values : (error "Error writing to Z3 solver: java.io.IOException: Broken pipe")
Solver is answering 'unknown', stopping.
After SMT solving in domain Int declared 8000/26001 variables, and 0 constraints, problems are : Problem set: 0 solved, 12000 unsolved in 30135 ms.
Refiners :[Positive P Invariants (semi-flows): 0/2000 constraints, State Equation: 0/10000 constraints, ReadFeed: 0/2000 constraints, PredecessorRefiner: 0/12000 constraints, Known Traps: 0/0 constraints]
After SMT, in 76093ms problems are : Problem set: 0 solved, 12000 unsolved
Search for dead transitions found 0 dead transitions in 76180ms
Finished structural reductions in LTL mode , in 1 iterations and 138634 ms. Remains : 10000/10000 places, 16001/16001 transitions.
[2024-05-24 10:47:59] [INFO ] Flatten gal took : 309 ms
[2024-05-24 10:47:59] [INFO ] Flatten gal took : 330 ms
[2024-05-24 10:48:00] [INFO ] Input system was already deterministic with 16001 transitions.
[2024-05-24 10:48:00] [INFO ] Flatten gal took : 317 ms
[2024-05-24 10:48:01] [INFO ] Flatten gal took : 341 ms
[2024-05-24 10:48:01] [INFO ] Time to serialize gal into /tmp/CTLCardinality3268658016599411554.gal : 59 ms
[2024-05-24 10:48:01] [INFO ] Time to serialize properties into /tmp/CTLCardinality8639011588248500051.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality3268658016599411554.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality8639011588248500051.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:48:31] [INFO ] Flatten gal took : 273 ms
[2024-05-24 10:48:31] [INFO ] Applying decomposition
[2024-05-24 10:48:31] [INFO ] Flatten gal took : 289 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph7624564934989927443.txt' '-o' '/tmp/graph7624564934989927443.bin' '-w' '/tmp/graph7624564934989927443.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph7624564934989927443.bin' '-l' '-1' '-v' '-w' '/tmp/graph7624564934989927443.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:48:32] [INFO ] Decomposing Gal with order
[2024-05-24 10:48:33] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:48:37] [INFO ] Removed a total of 2 redundant transitions.
[2024-05-24 10:48:37] [INFO ] Flatten gal took : 341 ms
[2024-05-24 10:48:38] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 490 ms.
[2024-05-24 10:48:38] [INFO ] Time to serialize gal into /tmp/CTLCardinality3813637513974845860.gal : 56 ms
[2024-05-24 10:48:38] [INFO ] Time to serialize properties into /tmp/CTLCardinality13266593810993907222.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality3813637513974845860.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality13266593810993907222.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Detected timeout of ITS tools.
[2024-05-24 10:49:09] [INFO ] Flatten gal took : 294 ms
[2024-05-24 10:49:09] [INFO ] Flatten gal took : 320 ms
[2024-05-24 10:49:09] [INFO ] Applying decomposition
[2024-05-24 10:49:09] [INFO ] Flatten gal took : 328 ms
Converted graph to binary with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/convert-linux64' '-i' '/tmp/graph10720829560791595092.txt' '-o' '/tmp/graph10720829560791595092.bin' '-w' '/tmp/graph10720829560791595092.weights'
Built communities with : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202405141337/bin/louvain-linux64' '/tmp/graph10720829560791595092.bin' '-l' '-1' '-v' '-w' '/tmp/graph10720829560791595092.weights' '-q' '0' '-e' '0.001'
[2024-05-24 10:49:10] [INFO ] Decomposing Gal with order
[2024-05-24 10:49:11] [INFO ] Rewriting arrays to variables to allow decomposition.
[2024-05-24 10:49:17] [INFO ] Removed a total of 1 redundant transitions.
[2024-05-24 10:49:17] [INFO ] Flatten gal took : 368 ms
[2024-05-24 10:49:18] [INFO ] Fuse similar labels procedure discarded/fused a total of 0 labels/synchronizations in 331 ms.
[2024-05-24 10:49:18] [INFO ] Time to serialize gal into /tmp/CTLCardinality6032156590359452274.gal : 66 ms
[2024-05-24 10:49:18] [INFO ] Time to serialize properties into /tmp/CTLCardinality10989426790476134846.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality6032156590359452274.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality10989426790476134846.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202405141337/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 15 CTL formulae.
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
+ BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ CTLCardinality = StateSpace ]]
+ /home/mcc/BenchKit/bin//../itstools/bin//..//runeclipse.sh /home/mcc/execution CTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202405141337.jar
+ VERSION=202405141337
+ echo 'Running Version 202405141337'
+ /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="JoinFreeModules-PT-2000"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5568"
echo " Executing tool itstools"
echo " Input is JoinFreeModules-PT-2000, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r224-tall-171649612000081"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/JoinFreeModules-PT-2000.tgz
mv JoinFreeModules-PT-2000 execution
cd execution
if [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "UpperBounds" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] || [ "CTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

