About the Execution of Marcie+red for PGCD-COL-D03N050
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 16216.180 | 3321434.00 | 2987906.00 | 205834.90 | FFTFTTFFFFTFTFTT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
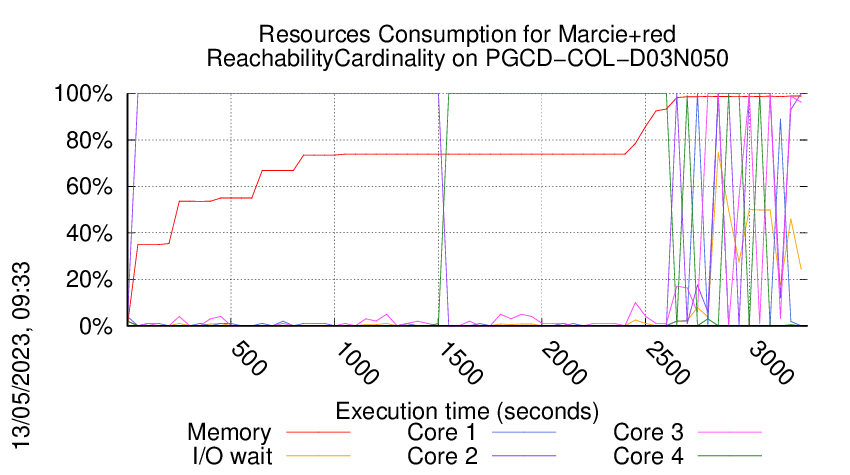
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r522-tall-167987247300406.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is PGCD-COL-D03N050, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r522-tall-167987247300406
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 420K
-rw-r--r-- 1 mcc users 7.2K Mar 23 15:25 CTLCardinality.txt
-rw-r--r-- 1 mcc users 83K Mar 23 15:25 CTLCardinality.xml
-rw-r--r-- 1 mcc users 5.4K Mar 23 15:22 CTLFireability.txt
-rw-r--r-- 1 mcc users 54K Mar 23 15:22 CTLFireability.xml
-rw-r--r-- 1 mcc users 3.3K Mar 23 07:07 LTLCardinality.txt
-rw-r--r-- 1 mcc users 25K Mar 23 07:07 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.0K Mar 23 07:07 LTLFireability.txt
-rw-r--r-- 1 mcc users 16K Mar 23 07:07 LTLFireability.xml
-rw-r--r-- 1 mcc users 1 Mar 26 22:42 NewModel
-rw-r--r-- 1 mcc users 9.3K Mar 23 15:28 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 100K Mar 23 15:28 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 6.2K Mar 23 15:27 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 55K Mar 23 15:27 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.6K Mar 23 07:07 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.6K Mar 23 07:07 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 equiv_pt
-rw-r--r-- 1 mcc users 8 Mar 26 22:42 instance
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 iscolored
-rw-r--r-- 1 mcc users 11K Mar 31 16:48 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-00
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-01
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-02
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-03
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-04
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-05
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-06
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-07
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-08
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-09
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-10
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-11
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-12
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-13
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-14
FORMULA_NAME PGCD-COL-D03N050-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1680811072794
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=ReachabilityCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=PGCD-COL-D03N050
Applying reductions before tool marcie
Invoking reducer
Running Version 202304061127
[2023-04-06 19:57:54] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, ReachabilityCardinality, -timeout, 360, -rebuildPNML]
[2023-04-06 19:57:54] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-04-06 19:57:54] [INFO ] Detected file is not PT type :http://www.pnml.org/version-2009/grammar/symmetricnet
log4j:WARN No appenders could be found for logger (org.apache.axiom.locator.DefaultOMMetaFactoryLocator).
log4j:WARN Please initialize the log4j system properly.
log4j:WARN See http://logging.apache.org/log4j/1.2/faq.html#noconfig for more info.
[2023-04-06 19:57:54] [WARNING] Using fallBack plugin, rng conformance not checked
[2023-04-06 19:57:54] [INFO ] Load time of PNML (colored model parsed with PNMLFW) : 408 ms
[2023-04-06 19:57:54] [INFO ] Imported 3 HL places and 3 HL transitions for a total of 12 PT places and 12.0 transition bindings in 19 ms.
Parsed 16 properties from file /home/mcc/execution/ReachabilityCardinality.xml in 22 ms.
Working with output stream class java.io.PrintStream
[2023-04-06 19:57:54] [INFO ] Built PT skeleton of HLPN with 3 places and 3 transitions 14 arcs in 4 ms.
[2023-04-06 19:57:54] [INFO ] Skeletonized 16 HLPN properties in 1 ms.
Remains 16 properties that can be checked using skeleton over-approximation.
Initial state reduction rules removed 7 formulas.
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-00 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-02 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-05 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-06 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-07 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-11 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-15 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Computed a total of 0 stabilizing places and 0 stable transitions
[2023-04-06 19:57:54] [INFO ] Flatten gal took : 13 ms
[2023-04-06 19:57:54] [INFO ] Flatten gal took : 1 ms
Arc [2:1*[(MOD (ADD $x 1) 4)]] contains successor/predecessor on variables of sort CD
[2023-04-06 19:57:54] [INFO ] Unfolded HLPN to a Petri net with 12 places and 12 transitions 56 arcs in 5 ms.
[2023-04-06 19:57:54] [INFO ] Unfolded 9 HLPN properties in 0 ms.
Incomplete random walk after 10050 steps, including 2 resets, run finished after 88 ms. (steps per millisecond=114 ) properties (out of 9) seen :3
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-12 TRUE TECHNIQUES TOPOLOGICAL RANDOM_WALK
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-04 TRUE TECHNIQUES TOPOLOGICAL RANDOM_WALK
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-01 FALSE TECHNIQUES TOPOLOGICAL RANDOM_WALK
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 95 ms. (steps per millisecond=105 ) properties (out of 6) seen :1
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-09 FALSE TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 52 ms. (steps per millisecond=192 ) properties (out of 5) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 18 ms. (steps per millisecond=555 ) properties (out of 5) seen :2
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-14 TRUE TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-10 TRUE TECHNIQUES TOPOLOGICAL BESTFIRST_WALK
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 20 ms. (steps per millisecond=500 ) properties (out of 3) seen :0
Running SMT prover for 3 properties.
// Phase 1: matrix 12 rows 12 cols
[2023-04-06 19:57:55] [INFO ] Computed 5 invariants in 5 ms
[2023-04-06 19:57:55] [INFO ] [Real]Absence check using 2 positive place invariants in 2 ms returned sat
[2023-04-06 19:57:55] [INFO ] [Real]Absence check using 2 positive and 3 generalized place invariants in 2 ms returned sat
[2023-04-06 19:57:55] [INFO ] After 136ms SMT Verify possible using all constraints in real domain returned unsat :3 sat :0
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-13 FALSE TECHNIQUES STRUCTURAL_REDUCTION TOPOLOGICAL SAT_SMT
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-08 FALSE TECHNIQUES STRUCTURAL_REDUCTION TOPOLOGICAL SAT_SMT
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-03 FALSE TECHNIQUES STRUCTURAL_REDUCTION TOPOLOGICAL SAT_SMT
Fused 3 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 0 ms.
All properties solved without resorting to model-checking.
Total runtime 1179 ms.
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Unfolding complete |P|=12|T|=12|A|=56
Time for unfolding: 0m 0.200sec
Net: PGCD_COL_D03N050
(NrP: 12 NrTr: 12 NrArc: 56)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 2.704sec
RS generation: 0m10.063sec
-> reachability set: #nodes 34961 (3.5e+04) #states 417,214,571,243 (11)
starting MCC model checker
--------------------------
checking: AG [~ [69<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]
normalized: ~ [E [true U 69<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]
abstracting: (69<=sum(p2_c3, p2_c2, p2_c1, p2_c0))
states: 341,306,278,844 (11)
MC time: 3m45.111sec
checking: EF [25<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]
normalized: E [true U 25<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]
abstracting: (25<=sum(p2_c3, p2_c2, p2_c1, p2_c0))
states: 414,437,574,213 (11)
-> the formula is TRUE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-04 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m15.948sec
checking: AG [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82]]
normalized: ~ [E [true U sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82]]
abstracting: (sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82)
states: 125,966,690,196 (11)
MC time: 3m32.198sec
checking: EF [~ [17<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]
normalized: E [true U ~ [17<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]
abstracting: (17<=sum(p1_c3, p1_c2, p1_c1, p1_c0))
states: 416,488,631,936 (11)
MC time: 3m17.112sec
checking: EF [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=53]
normalized: E [true U sum(p0_c3, p0_c2, p0_c1, p0_c0)<=53]
abstracting: (sum(p0_c3, p0_c2, p0_c1, p0_c0)<=53)
states: 36,320,070,927 (10)
MC time: 3m 4.051sec
checking: EF [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]
normalized: E [true U sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]
abstracting: (sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0))
MC time: 2m52.000sec
checking: EF [[~ [29<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & 71<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]
normalized: E [true U [71<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & ~ [29<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]
abstracting: (29<=sum(p1_c3, p1_c2, p1_c1, p1_c0))
MC time: 2m41.000sec
checking: AG [[51<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=95 & 46<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]
normalized: ~ [E [true U ~ [[51<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=95 & 46<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]
abstracting: (46<=sum(p2_c3, p2_c2, p2_c1, p2_c0))
MC time: 2m30.002sec
checking: EF [~ [[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 52<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=9]]]
normalized: E [true U ~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=9 & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 52<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]]
abstracting: (52<=sum(p0_c3, p0_c2, p0_c1, p0_c0))
MC time: 2m20.001sec
checking: EF [~ [[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=56] | [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=50 | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=51]] | ~ [[[44<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=25] & ~ [[~ [62<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | 38<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]]]]]]]
normalized: E [true U ~ [[[[~ [[~ [[38<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | ~ [62<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]] & [44<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=25]]] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=50 | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=51 & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]] & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=56]]]]
abstracting: (sum(p0_c3, p0_c2, p0_c1, p0_c0)<=56)
MC time: 2m11.000sec
checking: EF [[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=34] | [[[~ [[~ [[[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & [88<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 37<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]] | [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=38 | 71<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=4 & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]] | ~ [[[[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & ~ [37<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] & [54<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | [29<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=100]]]]] & [1<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=56 | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=38]]]
normalized: E [true U [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=38 | [[1<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=56 | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] & [~ [[[54<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | [29<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=100]] & [~ [37<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] | ~ [[[[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=4 & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=38 | 71<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | ~ [[[88<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 37<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]]]]]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=34]]]
abstracting: (sum(p0_c3, p0_c2, p0_c1, p0_c0)<=34)
MC time: 2m 2.000sec
checking: AG [[[[[~ [[19<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [~ [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=83 & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & [[20<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=67] & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=25]]]]] & ~ [[17<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=78] & [~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=62] | [~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=20]]] | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & ~ [[[[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=89 | 78<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] & ~ [[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=49] | [66<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 88<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] | [~ [[~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=25] & [96<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] & 72<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]]
normalized: ~ [E [true U ~ [[[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & ~ [[[72<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & ~ [[~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=25] & [96<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] | [~ [[[66<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 88<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=49]]] & [~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=89 | 78<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]] | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=20 | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=62]] & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=78 & [~ [[17<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] & ~ [[19<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [[~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=25] & [20<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=67]] & ~ [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=83 & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]]]]]]]]
abstracting: (sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0))
MC time: 1m54.000sec
checking: EF [[[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=98] | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=21 | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=59 & 36<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | [~ [56<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=95 | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] & [94<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=7]]] & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] & [[~ [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 89<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [[~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 40<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=42 & ~ [53<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]] & 70<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & [~ [12<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | ~ [[[~ [54<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=53]]]]]]
normalized: E [true U [[[~ [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=53 | [~ [54<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] | ~ [12<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] & [70<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & ~ [[~ [[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=42 & ~ [53<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] & ~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 40<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 89<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]] & [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & [[94<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=7] & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=21 | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=95 | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | ~ [56<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] | [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=59 & 36<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=98]]]]
abstracting: (sum(p0_c3, p0_c2, p0_c1, p0_c0)<=98)
MC time: 1m46.001sec
checking: AG [[[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & ~ [[18<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=16]]] & [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [[[94<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=62] & ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=54]]]] | [31<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 18<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] & [[[~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | 4<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & ~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 40<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]] | [[~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | 73<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] | [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 33<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=0 & 96<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] | ~ [[[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | [49<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=81]]]]]]]] | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 96<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]
normalized: ~ [E [true U ~ [[[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 96<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | [[[[[~ [[[49<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=81] | [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=0 & 96<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 33<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | ~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | 73<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]] | [[~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | 40<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] & [4<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] & [[31<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 18<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] | [94<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [[~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=54] & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=62]] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]]] & ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & ~ [[18<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=16]]]]]]]]
abstracting: (sum(p0_c3, p0_c2, p0_c1, p0_c0)<=16)
MC time: 1m39.000sec
checking: EF [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=12 & [[[28<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & 14<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [[~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=57 & 36<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=19] & [~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & 68<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] | [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=60] & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=49]] | [[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & ~ [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=32 | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]]]] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] & ~ [[[~ [[61<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=0 | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=44]] | [[[[33<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=98] & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=62]] & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=68 & [54<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & 9<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=35 | ~ [[66<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]]]]]]
normalized: E [true U [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=12 & [[~ [[[[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=35 | ~ [[66<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] | [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=68 & [54<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & 9<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] & [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=62] & [33<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=98]]]] | [~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=44] | ~ [[61<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=0 | sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]] & [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & ~ [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=32 | [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]]] | [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=49 & [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=60]] | ~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & 68<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]] & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=19 & ~ [[sum(p2_c3, p2_c2, p2_c1, p2_c0)<=57 & 36<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]] & [28<=sum(p2_c3, p2_c2, p2_c1, p2_c0) & 14<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]
abstracting: (14<=sum(p1_c3, p1_c2, p1_c1, p1_c0))
MC time: 1m32.001sec
checking: AG [[[[~ [[[[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=1 & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=100] | 47<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] | [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | 68<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]]] | 69<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=75] & [~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=5] | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=19 & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=52]] | ~ [[~ [[~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=81] | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=18]] | 33<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]] & [[[[[[[[67<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | 3<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & [61<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=32]] & [62<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | ~ [[95<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & 19<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | 82<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & ~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | [[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=59] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=5]]]]] & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0)]] & ~ [[[[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & ~ [40<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=62] | [[56<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 38<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] & sum(p0_c3, p0_c2, p0_c1, p0_c0)<=51] | ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=21]]]]]]
normalized: ~ [E [true U ~ [[[~ [[~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=21] | [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=51 & [[[~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [56<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & 38<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=62]] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & ~ [40<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]]]] & [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & ~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=5] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=59]]]]]] | [82<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | [~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)] & [[~ [[95<=sum(p0_c3, p0_c2, p0_c1, p0_c0) & 19<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]] & [[62<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | sum(p0_c3, p0_c2, p0_c1, p0_c0)<=sum(p2_c3, p2_c2, p2_c1, p2_c0)] & [[61<=sum(p1_c3, p1_c2, p1_c1, p1_c0) & sum(p2_c3, p2_c2, p2_c1, p2_c0)<=32] & [67<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | 3<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]]]]]]] & [[[~ [[33<=sum(p2_c3, p2_c2, p2_c1, p2_c0) | ~ [[sum(p0_c3, p0_c2, p0_c1, p0_c0)<=18 | ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=81]]]]] | [~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=52] | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=19 & ~ [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]]] | ~ [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=5]] & [sum(p0_c3, p0_c2, p0_c1, p0_c0)<=75 & ~ [[69<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [[[sum(p1_c3, p1_c2, p1_c1, p1_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0) | 68<=sum(p0_c3, p0_c2, p0_c1, p0_c0)] & ~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]] | [47<=sum(p0_c3, p0_c2, p0_c1, p0_c0) | [sum(p1_c3, p1_c2, p1_c1, p1_c0)<=1 & sum(p1_c3, p1_c2, p1_c1, p1_c0)<=100]]]]]]]]]]]
abstracting: (sum(p1_c3, p1_c2, p1_c1, p1_c0)<=100)
MC time: 1m26.000sec
checking: AG [~ [69<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]
normalized: ~ [E [true U 69<=sum(p2_c3, p2_c2, p2_c1, p2_c0)]]
abstracting: (69<=sum(p2_c3, p2_c2, p2_c1, p2_c0))
states: 341,306,278,844 (11)
-> the formula is FALSE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-01 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m28.644sec
checking: AG [~ [sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82]]
normalized: ~ [E [true U sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82]]
abstracting: (sum(p2_c3, p2_c2, p2_c1, p2_c0)<=82)
states: 125,966,690,196 (11)
-> the formula is FALSE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-06 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m 6.045sec
checking: EF [~ [17<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]
normalized: E [true U ~ [17<=sum(p1_c3, p1_c2, p1_c1, p1_c0)]]
abstracting: (17<=sum(p1_c3, p1_c2, p1_c1, p1_c0))
states: 416,488,631,936 (11)
-> the formula is TRUE
FORMULA PGCD-COL-D03N050-ReachabilityCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
BK_STOP 1680814394228
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202304061127.jar
+ VERSION=202304061127
+ echo 'Running Version 202304061127'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination ReachabilityCardinality -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:11549 (962), effective:3858 (321)
initing FirstDep: 0m 0.000sec
sat_reach.icc:155: Timeout: after 224 sec
iterations count:482 (40), effective:148 (12)
sat_reach.icc:155: Timeout: after 211 sec
sat_reach.icc:155: Timeout: after 196 sec
sat_reach.icc:155: Timeout: after 183 sec
idd.h:1025: Timeout: after 171 sec
idd.h:1025: Timeout: after 160 sec
idd.h:1025: Timeout: after 149 sec
idd.h:1025: Timeout: after 139 sec
idd.h:1025: Timeout: after 130 sec
idd.h:1025: Timeout: after 121 sec
idd.h:1025: Timeout: after 113 sec
idd.h:1025: Timeout: after 105 sec
idd.h:1025: Timeout: after 98 sec
idd.h:1025: Timeout: after 91 sec
idd.h:1025: Timeout: after 85 sec
iterations count:1472 (122), effective:456 (38)
iterations count:1620 (135), effective:493 (41)
iterations count:4161 (346), effective:1292 (107)
/home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin//../BenchKit_head.sh: line 16: 450 Killed ${MARCIE} --net-file=model.pnml --mcc-file=${BK_EXAMINATION}.xml ${MARCIE_CONFIG}
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="PGCD-COL-D03N050"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is PGCD-COL-D03N050, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r522-tall-167987247300406"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/PGCD-COL-D03N050.tgz
mv PGCD-COL-D03N050 execution
cd execution
if [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "UpperBounds" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] || [ "ReachabilityCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME ReachabilityCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

