About the Execution of Marcie+red for Murphy-COL-D2N050
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 8145.308 | 49502.00 | 62311.00 | 604.40 | TTFFFFFTFTFTTFFT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
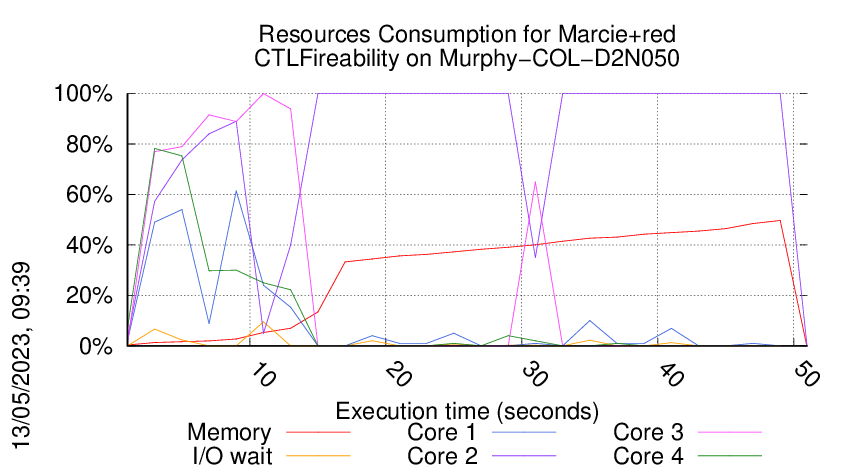
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r522-tall-167987247200290.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is Murphy-COL-D2N050, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r522-tall-167987247200290
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 476K
-rw-r--r-- 1 mcc users 6.4K Mar 23 15:21 CTLCardinality.txt
-rw-r--r-- 1 mcc users 70K Mar 23 15:21 CTLCardinality.xml
-rw-r--r-- 1 mcc users 5.1K Mar 23 15:20 CTLFireability.txt
-rw-r--r-- 1 mcc users 49K Mar 23 15:20 CTLFireability.xml
-rw-r--r-- 1 mcc users 3.5K Mar 23 07:07 LTLCardinality.txt
-rw-r--r-- 1 mcc users 25K Mar 23 07:07 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.1K Mar 23 07:07 LTLFireability.txt
-rw-r--r-- 1 mcc users 17K Mar 23 07:07 LTLFireability.xml
-rw-r--r-- 1 mcc users 1 Mar 26 22:42 NewModel
-rw-r--r-- 1 mcc users 12K Mar 23 15:23 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 128K Mar 23 15:23 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 8.7K Mar 23 15:22 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 84K Mar 23 15:22 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.6K Mar 23 07:07 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.6K Mar 23 07:07 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 equiv_pt
-rw-r--r-- 1 mcc users 7 Mar 26 22:42 instance
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 iscolored
-rw-r--r-- 1 mcc users 20K Mar 31 16:48 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-00
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-01
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-02
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-03
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-04
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-05
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-06
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-07
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-08
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-09
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-10
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-11
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-12
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-13
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-14
FORMULA_NAME Murphy-COL-D2N050-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1680887861064
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=Murphy-COL-D2N050
Applying reductions before tool marcie
Invoking reducer
Running Version 202304061127
[2023-04-07 17:17:42] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2023-04-07 17:17:42] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-04-07 17:17:42] [INFO ] Detected file is not PT type :http://www.pnml.org/version-2009/grammar/symmetricnet
log4j:WARN No appenders could be found for logger (org.apache.axiom.locator.DefaultOMMetaFactoryLocator).
log4j:WARN Please initialize the log4j system properly.
log4j:WARN See http://logging.apache.org/log4j/1.2/faq.html#noconfig for more info.
[2023-04-07 17:17:42] [WARNING] Using fallBack plugin, rng conformance not checked
[2023-04-07 17:17:43] [INFO ] Load time of PNML (colored model parsed with PNMLFW) : 546 ms
[2023-04-07 17:17:43] [INFO ] Imported 6 HL places and 7 HL transitions for a total of 18 PT places and 21.0 transition bindings in 16 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 13 ms.
[2023-04-07 17:17:43] [INFO ] Built PT skeleton of HLPN with 6 places and 7 transitions 27 arcs in 3 ms.
[2023-04-07 17:17:43] [INFO ] Skeletonized 16 HLPN properties in 2 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Remains 4 properties that can be checked using skeleton over-approximation.
Computed a total of 0 stabilizing places and 0 stable transitions
Finished random walk after 4 steps, including 0 resets, run visited all 3 properties in 6 ms. (steps per millisecond=0 )
Parikh walk visited 0 properties in 0 ms.
[2023-04-07 17:17:43] [INFO ] Flatten gal took : 13 ms
[2023-04-07 17:17:43] [INFO ] Flatten gal took : 1 ms
Arc [2:1*[(MOD (ADD $x 1) 3)]] contains successor/predecessor on variables of sort CD
[2023-04-07 17:17:43] [INFO ] Unfolded HLPN to a Petri net with 18 places and 21 transitions 81 arcs in 7 ms.
[2023-04-07 17:17:43] [INFO ] Unfolded 16 HLPN properties in 1 ms.
Initial state reduction rules removed 1 formulas.
FORMULA Murphy-COL-D2N050-CTLFireability-14 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 18 out of 18 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 5 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
// Phase 1: matrix 21 rows 18 cols
[2023-04-07 17:17:43] [INFO ] Computed 4 invariants in 3 ms
[2023-04-07 17:17:43] [INFO ] Dead Transitions using invariants and state equation in 155 ms found 0 transitions.
[2023-04-07 17:17:43] [INFO ] Invariant cache hit.
[2023-04-07 17:17:43] [INFO ] Implicit Places using invariants in 23 ms returned []
[2023-04-07 17:17:43] [INFO ] Invariant cache hit.
[2023-04-07 17:17:43] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:43] [INFO ] Implicit Places using invariants and state equation in 51 ms returned []
Implicit Place search using SMT with State Equation took 78 ms to find 0 implicit places.
[2023-04-07 17:17:43] [INFO ] Invariant cache hit.
[2023-04-07 17:17:43] [INFO ] Dead Transitions using invariants and state equation in 38 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 278 ms. Remains : 18/18 places, 21/21 transitions.
Support contains 18 out of 18 places after structural reductions.
[2023-04-07 17:17:43] [INFO ] Flatten gal took : 7 ms
[2023-04-07 17:17:43] [INFO ] Flatten gal took : 7 ms
[2023-04-07 17:17:43] [INFO ] Input system was already deterministic with 21 transitions.
Incomplete random walk after 10038 steps, including 2 resets, run finished after 147 ms. (steps per millisecond=68 ) properties (out of 35) seen :28
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 72 ms. (steps per millisecond=138 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 41 ms. (steps per millisecond=243 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 37 ms. (steps per millisecond=270 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 36 ms. (steps per millisecond=277 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 29 ms. (steps per millisecond=344 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 23 ms. (steps per millisecond=434 ) properties (out of 7) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 23 ms. (steps per millisecond=434 ) properties (out of 7) seen :0
Running SMT prover for 7 properties.
[2023-04-07 17:17:44] [INFO ] Invariant cache hit.
[2023-04-07 17:17:44] [INFO ] [Real]Absence check using 2 positive place invariants in 1 ms returned sat
[2023-04-07 17:17:44] [INFO ] [Real]Absence check using 2 positive and 2 generalized place invariants in 1 ms returned sat
[2023-04-07 17:17:44] [INFO ] After 54ms SMT Verify possible using all constraints in real domain returned unsat :1 sat :0 real:6
[2023-04-07 17:17:44] [INFO ] [Nat]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:44] [INFO ] [Nat]Absence check using 2 positive and 2 generalized place invariants in 1 ms returned sat
[2023-04-07 17:17:44] [INFO ] After 26ms SMT Verify possible using state equation in natural domain returned unsat :1 sat :6
[2023-04-07 17:17:44] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:44] [INFO ] After 30ms SMT Verify possible using 6 Read/Feed constraints in natural domain returned unsat :1 sat :6
[2023-04-07 17:17:44] [INFO ] After 55ms SMT Verify possible using trap constraints in natural domain returned unsat :1 sat :6
Attempting to minimize the solution found.
Minimization took 28 ms.
[2023-04-07 17:17:44] [INFO ] After 162ms SMT Verify possible using all constraints in natural domain returned unsat :1 sat :6
Fused 7 Parikh solutions to 6 different solutions.
Parikh walk visited 0 properties in 70 ms.
Support contains 18 out of 18 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 4 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:44] [INFO ] Invariant cache hit.
[2023-04-07 17:17:44] [INFO ] Dead Transitions using invariants and state equation in 36 ms found 0 transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 41 ms. Remains : 18/18 places, 21/21 transitions.
Incomplete random walk after 10000 steps, including 2 resets, run finished after 38 ms. (steps per millisecond=263 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 27 ms. (steps per millisecond=370 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 17 ms. (steps per millisecond=588 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 21 ms. (steps per millisecond=476 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 19 ms. (steps per millisecond=526 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 20 ms. (steps per millisecond=500 ) properties (out of 6) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 19 ms. (steps per millisecond=526 ) properties (out of 6) seen :0
Interrupted probabilistic random walk after 334809 steps, run timeout after 3001 ms. (steps per millisecond=111 ) properties seen :{}
Probabilistic random walk after 334809 steps, saw 215918 distinct states, run finished after 3002 ms. (steps per millisecond=111 ) properties seen :0
Running SMT prover for 6 properties.
[2023-04-07 17:17:47] [INFO ] Invariant cache hit.
[2023-04-07 17:17:47] [INFO ] [Real]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:47] [INFO ] [Real]Absence check using 2 positive and 2 generalized place invariants in 0 ms returned sat
[2023-04-07 17:17:47] [INFO ] After 27ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:6
[2023-04-07 17:17:47] [INFO ] [Nat]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:47] [INFO ] [Nat]Absence check using 2 positive and 2 generalized place invariants in 1 ms returned sat
[2023-04-07 17:17:47] [INFO ] After 22ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :6
[2023-04-07 17:17:47] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:47] [INFO ] After 31ms SMT Verify possible using 6 Read/Feed constraints in natural domain returned unsat :0 sat :6
[2023-04-07 17:17:47] [INFO ] After 52ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :6
Attempting to minimize the solution found.
Minimization took 21 ms.
[2023-04-07 17:17:47] [INFO ] After 123ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :6
Parikh walk visited 0 properties in 53 ms.
Support contains 18 out of 18 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 1 ms. Remains : 18/18 places, 21/21 transitions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:47] [INFO ] Invariant cache hit.
[2023-04-07 17:17:47] [INFO ] Implicit Places using invariants in 16 ms returned []
[2023-04-07 17:17:47] [INFO ] Invariant cache hit.
[2023-04-07 17:17:47] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:47] [INFO ] Implicit Places using invariants and state equation in 33 ms returned []
Implicit Place search using SMT with State Equation took 51 ms to find 0 implicit places.
[2023-04-07 17:17:47] [INFO ] Redundant transitions in 0 ms returned []
[2023-04-07 17:17:47] [INFO ] Invariant cache hit.
[2023-04-07 17:17:47] [INFO ] Dead Transitions using invariants and state equation in 23 ms found 0 transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 78 ms. Remains : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
Running SMT prover for 6 properties.
[2023-04-07 17:17:47] [INFO ] Invariant cache hit.
[2023-04-07 17:17:47] [INFO ] [Real]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:47] [INFO ] [Real]Absence check using 2 positive and 2 generalized place invariants in 1 ms returned sat
[2023-04-07 17:17:47] [INFO ] After 30ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:6
[2023-04-07 17:17:47] [INFO ] [Nat]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:47] [INFO ] [Nat]Absence check using 2 positive and 2 generalized place invariants in 3 ms returned sat
[2023-04-07 17:17:47] [INFO ] After 23ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :6
[2023-04-07 17:17:47] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:47] [INFO ] After 19ms SMT Verify possible using 6 Read/Feed constraints in natural domain returned unsat :0 sat :6
[2023-04-07 17:17:47] [INFO ] Deduced a trap composed of 2 places in 17 ms of which 1 ms to minimize.
[2023-04-07 17:17:47] [INFO ] Trap strengthening (SAT) tested/added 2/1 trap constraints in 21 ms
[2023-04-07 17:17:48] [INFO ] After 71ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :6
Attempting to minimize the solution found.
Minimization took 22 ms.
[2023-04-07 17:17:48] [INFO ] After 146ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :6
Successfully simplified 1 atomic propositions for a total of 15 simplifications.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 4 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 4 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 27 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 29 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 28 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 30 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 3 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 23 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 23 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 22 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 23 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 30 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 31 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 2 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:48] [INFO ] Invariant cache hit.
[2023-04-07 17:17:48] [INFO ] Dead Transitions using invariants and state equation in 23 ms found 0 transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 25 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:48] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:48] [INFO ] Input system was already deterministic with 21 transitions.
Incomplete random walk after 10003 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=2000 ) properties (out of 1) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 6 ms. (steps per millisecond=1666 ) properties (out of 1) seen :0
Interrupted probabilistic random walk after 2457024 steps, run timeout after 3001 ms. (steps per millisecond=818 ) properties seen :{}
Probabilistic random walk after 2457024 steps, saw 1545713 distinct states, run finished after 3001 ms. (steps per millisecond=818 ) properties seen :0
Running SMT prover for 1 properties.
[2023-04-07 17:17:51] [INFO ] Invariant cache hit.
[2023-04-07 17:17:51] [INFO ] [Real]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:51] [INFO ] [Real]Absence check using 2 positive and 2 generalized place invariants in 0 ms returned sat
[2023-04-07 17:17:51] [INFO ] After 29ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:1
[2023-04-07 17:17:51] [INFO ] [Nat]Absence check using 2 positive place invariants in 0 ms returned sat
[2023-04-07 17:17:51] [INFO ] [Nat]Absence check using 2 positive and 2 generalized place invariants in 0 ms returned sat
[2023-04-07 17:17:51] [INFO ] After 11ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :1
[2023-04-07 17:17:51] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-04-07 17:17:51] [INFO ] After 3ms SMT Verify possible using 6 Read/Feed constraints in natural domain returned unsat :0 sat :1
[2023-04-07 17:17:51] [INFO ] After 6ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :1
Attempting to minimize the solution found.
Minimization took 3 ms.
[2023-04-07 17:17:51] [INFO ] After 50ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :1
Parikh walk visited 0 properties in 4 ms.
Support contains 6 out of 18 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 18/18 places, 21/21 transitions.
Graph (complete) has 69 edges and 18 vertex of which 9 are kept as prefixes of interest. Removing 9 places using SCC suffix rule.1 ms
Discarding 9 places :
Also discarding 6 output transitions
Drop transitions removed 6 transitions
Drop transitions removed 3 transitions
Reduce isomorphic transitions removed 3 transitions.
Iterating post reduction 0 with 3 rules applied. Total rules applied 4 place count 9 transition count 12
Applied a total of 4 rules in 3 ms. Remains 9 /18 variables (removed 9) and now considering 12/21 (removed 9) transitions.
// Phase 1: matrix 12 rows 9 cols
[2023-04-07 17:17:51] [INFO ] Computed 0 invariants in 2 ms
[2023-04-07 17:17:51] [INFO ] Dead Transitions using invariants and state equation in 24 ms found 0 transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 27 ms. Remains : 9/18 places, 12/21 transitions.
Incomplete random walk after 1000000 steps, including 2 resets, run finished after 798 ms. (steps per millisecond=1253 ) properties (out of 1) seen :0
Incomplete Best-First random walk after 1000001 steps, including 2 resets, run finished after 422 ms. (steps per millisecond=2369 ) properties (out of 1) seen :0
Probably explored full state space saw : 216 states, properties seen :0
Probabilistic random walk after 1080 steps, saw 216 distinct states, run finished after 5 ms. (steps per millisecond=216 ) properties seen :0
Explored full state space saw : 216 states, properties seen :0
Exhaustive walk after 1080 steps, saw 216 distinct states, run finished after 2 ms. (steps per millisecond=540 ) properties seen :0
FORMULA Murphy-COL-D2N050-CTLFireability-05 FALSE TECHNIQUES TOPOLOGICAL EXHAUSTIVE_WALK
Parikh walk visited 0 properties in 0 ms.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
// Phase 1: matrix 21 rows 18 cols
[2023-04-07 17:17:52] [INFO ] Computed 4 invariants in 2 ms
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 48 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 50 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 23 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 24 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 22 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 23 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 24 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 24 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 28 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 29 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 29 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 31 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 21 ms found 0 transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 22 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Finished random walk after 5 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=5 )
FORMULA Murphy-COL-D2N050-CTLFireability-12 TRUE TECHNIQUES TOPOLOGICAL RANDOM_WALK
Parikh walk visited 0 properties in 0 ms.
Starting structural reductions in LTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 0 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 24 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 24 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 18/18 places, 21/21 transitions.
Applied a total of 0 rules in 1 ms. Remains 18 /18 variables (removed 0) and now considering 21/21 (removed 0) transitions.
[2023-04-07 17:17:52] [INFO ] Invariant cache hit.
[2023-04-07 17:17:52] [INFO ] Dead Transitions using invariants and state equation in 20 ms found 0 transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 22 ms. Remains : 18/18 places, 21/21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 1 ms
[2023-04-07 17:17:52] [INFO ] Input system was already deterministic with 21 transitions.
[2023-04-07 17:17:52] [INFO ] Flatten gal took : 2 ms
[2023-04-07 17:17:53] [INFO ] Flatten gal took : 3 ms
[2023-04-07 17:17:53] [INFO ] Export to MCC of 13 properties in file /home/mcc/execution/CTLFireability.sr.xml took 4 ms.
[2023-04-07 17:17:53] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 18 places, 21 transitions and 81 arcs took 1 ms.
Total runtime 10586 ms.
There are residual formulas that ITS could not solve within timeout
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLFireability.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Petri
(NrP: 18 NrTr: 21 NrArc: 81)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 2.683sec
RS generation: 0m 2.329sec
-> reachability set: #nodes 15348 (1.5e+04) #states 41,538,421,296 (10)
starting MCC model checker
--------------------------
checking: AX [1<=0]
normalized: ~ [EX [~ [1<=0]]]
abstracting: (1<=0)
states: 0
.-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-03 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.158sec
checking: AX [AF [[1<=p9 | [1<=p10 | 1<=p11]]]]
normalized: ~ [EX [EG [~ [[[1<=p10 | 1<=p11] | 1<=p9]]]]]
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
......
EG iterations: 6
.-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-08 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.432sec
checking: EX [[[p0<=2 | [p6<=0 | p12<=0]] & [[p1<=2 | [p7<=0 | p13<=0]] & [p2<=2 | [p8<=0 | p14<=0]]]]]
normalized: EX [[[[p2<=2 | [p8<=0 | p14<=0]] & [p1<=2 | [p7<=0 | p13<=0]]] & [p0<=2 | [p6<=0 | p12<=0]]]]
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p0<=2)
states: 3,826,043,208 (9)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p1<=2)
states: 3,826,043,208 (9)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p2<=2)
states: 3,826,043,208 (9)
.-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-09 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.235sec
checking: EG [A [~ [EX [~ [EF [~ [[[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]]]]]] U ~ [AX [[[[p0<=0 | p3<=0] & [p1<=0 | p4<=0]] & [[p2<=0 | p5<=0] & AF [~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]]]]]]]
normalized: EG [[~ [EG [~ [EX [~ [[[~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] & [p2<=0 | p5<=0]] & [[p1<=0 | p4<=0] & [p0<=0 | p3<=0]]]]]]]] & ~ [E [~ [EX [~ [[[~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] & [p2<=0 | p5<=0]] & [[p1<=0 | p4<=0] & [p0<=0 | p3<=0]]]]]] U [EX [~ [E [true U ~ [[[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]]]]]] & ~ [EX [~ [[[~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] & [p2<=0 | p5<=0]] & [[p1<=0 | p4<=0] & [p0<=0 | p3<=0]]]]]]]]]]]
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
.abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
.abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
.abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
..
EG iterations: 1
EG iterations: 0
-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.132sec
checking: EG [E [AG [~ [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]]] U [[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]] | [[1<=p2 & [1<=p5 & 1<=p8]] | [[1<=p0 & [1<=p3 & 1<=p6]] | [1<=p1 & [1<=p4 & 1<=p7]]]]]]]
normalized: EG [E [~ [E [true U [[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]]] U [[[[1<=p1 & [1<=p4 & 1<=p7]] | [1<=p0 & [1<=p3 & 1<=p6]]] | [1<=p2 & [1<=p5 & 1<=p8]]] | [[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]]]]]
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.173sec
checking: AX [[[AF [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]] & [~ [E [[[[1<=p2 & [1<=p5 & 1<=p8]] | [[1<=p0 & [1<=p3 & 1<=p6]] | [1<=p1 & [1<=p4 & 1<=p7]]]] | [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]] U [[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]] & [[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]]]]] & p15<=2]] & [p16<=2 & [p17<=2 & [[1<=p13 | 1<=p14] | 1<=p12]]]]]
normalized: ~ [EX [~ [[[p16<=2 & [p17<=2 & [1<=p12 | [1<=p13 | 1<=p14]]]] & [[p15<=2 & ~ [E [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] | [[[1<=p1 & [1<=p4 & 1<=p7]] | [1<=p0 & [1<=p3 & 1<=p6]]] | [1<=p2 & [1<=p5 & 1<=p8]]]] U [[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[2<=p9 & 1<=p12] | [[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]]]]]]] & ~ [EG [~ [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]]]]]]]]]
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (p15<=2)
states: 34,615,351,080 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (p17<=2)
states: 34,615,351,080 (10)
abstracting: (p16<=2)
states: 34,615,351,080 (10)
.-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-02 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.225sec
checking: [E [EG [E [[AX [[1<=p12 | [1<=p13 | 1<=p14]]] | EF [~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]] U ~ [[[1<=p12 | [1<=p13 | 1<=p14]] & [1<=p9 | [1<=p10 | 1<=p11]]]]]] U [EG [~ [AF [~ [[p9<=0 & [p10<=0 & p11<=0]]]]]] & [[EF [~ [[[[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]] & [1<=p9 | [1<=p10 | 1<=p11]]]]] | 1<=p12] | [1<=p13 | 1<=p14]]]] & AG [E [AF [[3<=p15 | [3<=p16 | 3<=p17]]] U ~ [[[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]]]]]
normalized: [~ [E [true U ~ [E [~ [EG [~ [[3<=p15 | [3<=p16 | 3<=p17]]]]] U ~ [[[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]]]]]]] & E [EG [E [[E [true U ~ [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] | ~ [EX [~ [[1<=p12 | [1<=p13 | 1<=p14]]]]]] U ~ [[[1<=p9 | [1<=p10 | 1<=p11]] & [1<=p12 | [1<=p13 | 1<=p14]]]]]] U [[[1<=p13 | 1<=p14] | [1<=p12 | E [true U ~ [[[1<=p9 | [1<=p10 | 1<=p11]] & [[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]]]]]] & EG [EG [[p9<=0 & [p10<=0 & p11<=0]]]]]]]
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
......
EG iterations: 6
.
EG iterations: 1
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
.abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
EG iterations: 0
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
......
EG iterations: 6
-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-04 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.907sec
checking: EF [AX [[EF [[[[1<=p14 | 1<=p13] | 1<=p12] | [[[1<=p0 & 1<=p3] | [1<=p1 & 1<=p4]] | [[1<=p2 & 1<=p5] | [[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]] & [3<=p15 | [3<=p16 | 3<=p17]]]]]]] | [EF [[p9<=0 & [p10<=0 & p11<=0]]] & [[[p15<=2 & [p16<=2 & p17<=2]] | [[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]] & [AG [[[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]] | EX [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]]]]]]
normalized: E [true U ~ [EX [~ [[[[[EX [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]] | ~ [E [true U ~ [[[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]]]]]] & [[[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]] | [p15<=2 & [p16<=2 & p17<=2]]]] & E [true U [p9<=0 & [p10<=0 & p11<=0]]]] | E [true U [[[[[3<=p15 | [3<=p16 | 3<=p17]] & [[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]]] | [1<=p2 & 1<=p5]] | [[1<=p1 & 1<=p4] | [1<=p0 & 1<=p3]]] | [1<=p12 | [1<=p14 | 1<=p13]]]]]]]]]
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p17<=2)
states: 34,615,351,080 (10)
abstracting: (p16<=2)
states: 34,615,351,080 (10)
abstracting: (p15<=2)
states: 34,615,351,080 (10)
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
..-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-00 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.097sec
checking: [E [[~ [AG [A [~ [[p9<=0 & [p10<=0 & p11<=0]]] U ~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]]] & EX [~ [[[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]]]] U [~ [EF [AG [~ [[[p9<=1 | p12<=0] & [[p10<=1 | p13<=0] & [p11<=1 | p14<=0]]]]]]] & E [[A [~ [[p9<=0 & [p10<=0 & p11<=0]]] U [3<=p15 | [3<=p16 | 3<=p17]]] | AF [[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]]] U AF [[[3<=p15 | [3<=p16 | 3<=p17]] | [1<=p12 | [1<=p13 | 1<=p14]]]]]]] | EF [[p15<=2 & [p16<=2 & p17<=2]]]]
normalized: [E [true U [p15<=2 & [p16<=2 & p17<=2]]] | E [[EX [~ [[[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]]]] & E [true U ~ [[~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] & ~ [E [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]] U [[p9<=0 & [p10<=0 & p11<=0]] & [[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]]]]]]] U [E [[~ [EG [~ [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]] | [~ [EG [~ [[3<=p15 | [3<=p16 | 3<=p17]]]]] & ~ [E [~ [[3<=p15 | [3<=p16 | 3<=p17]]] U [[p9<=0 & [p10<=0 & p11<=0]] & ~ [[3<=p15 | [3<=p16 | 3<=p17]]]]]]]] U ~ [EG [~ [[[1<=p12 | [1<=p13 | 1<=p14]] | [3<=p15 | [3<=p16 | 3<=p17]]]]]]] & ~ [E [true U ~ [E [true U [[[p11<=1 | p14<=0] & [p10<=1 | p13<=0]] & [p9<=1 | p12<=0]]]]]]]]]
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
..
EG iterations: 2
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
......
EG iterations: 6
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.....
EG iterations: 5
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p9<=1)
states: 41,538,421,296 (10)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p10<=1)
states: 41,538,421,296 (10)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p11<=1)
states: 41,538,421,296 (10)
.abstracting: (p17<=2)
states: 34,615,351,080 (10)
abstracting: (p16<=2)
states: 34,615,351,080 (10)
abstracting: (p15<=2)
states: 34,615,351,080 (10)
-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-01 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.791sec
checking: [EF [[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]] & [EX [AF [E [[[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]] & [3<=p15 | [3<=p16 | 3<=p17]]] U AF [~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]]]] | E [~ [EG [E [[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]] U ~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]]] U AX [AF [[[1<=p9 | [1<=p10 | 1<=p11]] | [1<=p12 | [1<=p13 | 1<=p14]]]]]]]]
normalized: [[E [~ [EG [E [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]] U ~ [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]]]] U ~ [EX [EG [~ [[[1<=p12 | [1<=p13 | 1<=p14]] | [1<=p9 | [1<=p10 | 1<=p11]]]]]]]] | EX [~ [EG [~ [E [[[3<=p15 | [3<=p16 | 3<=p17]] & [[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]]] U ~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]]]]]]]] & E [true U [[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]]]]
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
.
EG iterations: 1
.abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
..
EG iterations: 2
.abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.
EG iterations: 1
-> the formula is TRUE
FORMULA Murphy-COL-D2N050-CTLFireability-07 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.737sec
checking: AG [[AX [AF [[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]]] & [[A [[[[[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]] | [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]] & [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]] U ~ [EG [~ [[p9<=0 & [p10<=0 & p11<=0]]]]]] | A [EF [[3<=p15 | [3<=p16 | 3<=p17]]] U EF [[1<=p12 | [1<=p13 | 1<=p14]]]]] & [[A [AX [~ [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]]] U [~ [[p9<=0 & [p10<=0 & p11<=0]]] & EX [~ [[p9<=0 & [p10<=0 & p11<=0]]]]]] | [3<=p0 & [1<=p6 & 1<=p12]]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]]]]
normalized: ~ [E [true U ~ [[[[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [[3<=p0 & [1<=p6 & 1<=p12]] | [~ [EG [~ [[EX [~ [[p9<=0 & [p10<=0 & p11<=0]]]] & ~ [[p9<=0 & [p10<=0 & p11<=0]]]]]]] & ~ [E [~ [[EX [~ [[p9<=0 & [p10<=0 & p11<=0]]]] & ~ [[p9<=0 & [p10<=0 & p11<=0]]]]] U [EX [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]] & ~ [[EX [~ [[p9<=0 & [p10<=0 & p11<=0]]]] & ~ [[p9<=0 & [p10<=0 & p11<=0]]]]]]]]]]] & [[~ [EG [~ [E [true U [1<=p12 | [1<=p13 | 1<=p14]]]]]] & ~ [E [~ [E [true U [1<=p12 | [1<=p13 | 1<=p14]]]] U [~ [E [true U [3<=p15 | [3<=p16 | 3<=p17]]]] & ~ [E [true U [1<=p12 | [1<=p13 | 1<=p14]]]]]]]] | [~ [EG [EG [~ [[p9<=0 & [p10<=0 & p11<=0]]]]]] & ~ [E [EG [~ [[p9<=0 & [p10<=0 & p11<=0]]]] U [~ [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] | [[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]]]]] & EG [~ [[p9<=0 & [p10<=0 & p11<=0]]]]]]]]]] & ~ [EX [EG [~ [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]]]]]]]
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.....
EG iterations: 5
.abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.
EG iterations: 1
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.
EG iterations: 1
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.
EG iterations: 1
.
EG iterations: 1
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
.
EG iterations: 1
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
.abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
.......
EG iterations: 6
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m11.472sec
checking: EF [[AF [[[[EX [[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]] & AX [[[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]]]] | EF [[[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]]]] | [1<=p9 | [1<=p10 | 1<=p11]]]] & [EF [[E [[1<=p12 | [1<=p13 | 1<=p14]] U ~ [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]]] & [[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]] & [[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]]]]] & [EF [[[[1<=p9 | 1<=p10] | [1<=p11 | [2<=p9 & 1<=p12]]] | [[[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]] | [3<=p15 | [3<=p16 | 3<=p17]]]]] | [EX [A [[1<=p12 | [1<=p13 | 1<=p14]] U ~ [[[p2<=0 | [p5<=0 | p8<=0]] & [[p0<=0 | [p3<=0 | p6<=0]] & [p1<=0 | [p4<=0 | p7<=0]]]]]]] | [AG [[p9<=0 & [p10<=0 & p11<=0]]] & [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]] | [[p0<=2 | [p6<=0 | p12<=0]] & [[p1<=2 | [p7<=0 | p13<=0]] & [p2<=2 | [p8<=0 | p14<=0]]]]]]]]]]]
normalized: E [true U [[[[[[[[[p2<=2 | [p8<=0 | p14<=0]] & [p1<=2 | [p7<=0 | p13<=0]]] & [p0<=2 | [p6<=0 | p12<=0]]] | [[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]] & ~ [E [true U ~ [[p9<=0 & [p10<=0 & p11<=0]]]]]] | EX [[~ [EG [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]] & ~ [E [[[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]] U [~ [[1<=p12 | [1<=p13 | 1<=p14]]] & [[[p1<=0 | [p4<=0 | p7<=0]] & [p0<=0 | [p3<=0 | p6<=0]]] & [p2<=0 | [p5<=0 | p8<=0]]]]]]]]] | E [true U [[[3<=p15 | [3<=p16 | 3<=p17]] | [[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]]] | [[1<=p11 | [2<=p9 & 1<=p12]] | [1<=p9 | 1<=p10]]]]] & E [true U [[[[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]] & [[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]] & E [[1<=p12 | [1<=p13 | 1<=p14]] U ~ [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]]]]]] & ~ [EG [~ [[[1<=p9 | [1<=p10 | 1<=p11]] | [E [true U [[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]] | [~ [EX [~ [[[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]]]] & EX [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]]]]]]]]
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
.abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
......
EG iterations: 6
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
.abstracting: (p11<=0)
states: 20,769,210,648 (10)
abstracting: (p10<=0)
states: 20,769,210,648 (10)
abstracting: (p9<=0)
states: 20,769,210,648 (10)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p0<=2)
states: 3,826,043,208 (9)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p1<=2)
states: 3,826,043,208 (9)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p2<=2)
states: 3,826,043,208 (9)
-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-06 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.435sec
checking: [EF [[[EX [EG [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]]] & [AG [[[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]] | [[p0<=2 | [p6<=0 | p12<=0]] & [[p1<=2 | [p7<=0 | p13<=0]] & [p2<=2 | [p8<=0 | p14<=0]]]]]] & ~ [A [[[1<=p12 | [1<=p13 | 1<=p14]] | [3<=p15 | [3<=p16 | 3<=p17]]] U [[[2<=p9 & 1<=p12] | [[2<=p10 & 1<=p13] | [2<=p11 & 1<=p14]]] & [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]]]]]] & [[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]]] | [AF [[[[[[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]] & [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]] | [[[1<=p2 & [1<=p5 & 1<=p8]] | [[1<=p0 & [1<=p3 & 1<=p6]] | [1<=p1 & [1<=p4 & 1<=p7]]]] & [[1<=p0 & 1<=p3] | [[1<=p1 & 1<=p4] | [1<=p2 & 1<=p5]]]]] & [A [~ [[[p0<=0 | p3<=0] & [[p1<=0 | p4<=0] & [p2<=0 | p5<=0]]]] U [[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]] | [[1<=p9 | [1<=p10 | 1<=p11]] & [[3<=p0 & [1<=p6 & 1<=p12]] | [[3<=p1 & [1<=p7 & 1<=p13]] | [3<=p2 & [1<=p8 & 1<=p14]]]]]]]] & E [AX [EF [[1<=p12 | [1<=p13 | 1<=p14]]]] U E [AF [[1<=p12 | [1<=p13 | 1<=p14]]] U [[1<=p9 | [1<=p10 | 1<=p11]] & [3<=p15 | [3<=p16 | 3<=p17]]]]]]]
normalized: [[E [~ [EX [~ [E [true U [1<=p12 | [1<=p13 | 1<=p14]]]]]] U E [~ [EG [~ [[1<=p12 | [1<=p13 | 1<=p14]]]]] U [[3<=p15 | [3<=p16 | 3<=p17]] & [1<=p9 | [1<=p10 | 1<=p11]]]]] & ~ [EG [~ [[[[[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]] & [1<=p9 | [1<=p10 | 1<=p11]]] | [~ [EG [~ [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]] & ~ [E [~ [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]] U [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]] & ~ [[[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]]]]] & [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[1<=p1 & [1<=p4 & 1<=p7]] | [1<=p0 & [1<=p3 & 1<=p6]]] | [1<=p2 & [1<=p5 & 1<=p8]]]] | [[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[3<=p2 & [1<=p8 & 1<=p14]] | [3<=p1 & [1<=p7 & 1<=p13]]] | [3<=p0 & [1<=p6 & 1<=p12]]]]]]]]]] | E [true U [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]] & [[~ [[~ [EG [~ [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]]]]] & ~ [E [~ [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]]] U [~ [[[3<=p15 | [3<=p16 | 3<=p17]] | [1<=p12 | [1<=p13 | 1<=p14]]]] & ~ [[[[[1<=p2 & 1<=p5] | [1<=p1 & 1<=p4]] | [1<=p0 & 1<=p3]] & [[[2<=p11 & 1<=p14] | [2<=p10 & 1<=p13]] | [2<=p9 & 1<=p12]]]]]]]]] & ~ [E [true U ~ [[[[[p2<=2 | [p8<=0 | p14<=0]] & [p1<=2 | [p7<=0 | p13<=0]]] & [p0<=2 | [p6<=0 | p12<=0]]] | [[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]]]]]] & EX [EG [[[[p2<=0 | p5<=0] & [p1<=0 | p4<=0]] & [p0<=0 | p3<=0]]]]]]]]
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
.
EG iterations: 1
.abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (p12<=0)
states: 13,846,140,432 (10)
abstracting: (p6<=0)
states: 1,296,166,536 (9)
abstracting: (p0<=2)
states: 3,826,043,208 (9)
abstracting: (p13<=0)
states: 13,846,140,432 (10)
abstracting: (p7<=0)
states: 1,296,166,536 (9)
abstracting: (p1<=2)
states: 3,826,043,208 (9)
abstracting: (p14<=0)
states: 13,846,140,432 (10)
abstracting: (p8<=0)
states: 1,296,166,536 (9)
abstracting: (p2<=2)
states: 3,826,043,208 (9)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (2<=p9)
states: 0
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (2<=p10)
states: 0
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (2<=p11)
states: 0
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
EG iterations: 0
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p3)
states: 40,240,327,608 (10)
abstracting: (1<=p0)
states: 40,242,254,760 (10)
abstracting: (1<=p4)
states: 40,240,327,608 (10)
abstracting: (1<=p1)
states: 40,242,254,760 (10)
abstracting: (1<=p5)
states: 40,240,327,608 (10)
abstracting: (1<=p2)
states: 40,242,254,760 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
abstracting: (p3<=0)
states: 1,298,093,688 (9)
abstracting: (p0<=0)
states: 1,296,166,536 (9)
abstracting: (p4<=0)
states: 1,298,093,688 (9)
abstracting: (p1<=0)
states: 1,296,166,536 (9)
abstracting: (p5<=0)
states: 1,298,093,688 (9)
abstracting: (p2<=0)
states: 1,296,166,536 (9)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.....
EG iterations: 5
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
abstracting: (1<=p6)
states: 40,242,254,760 (10)
abstracting: (3<=p0)
states: 37,712,378,088 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p7)
states: 40,242,254,760 (10)
abstracting: (3<=p1)
states: 37,712,378,088 (10)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p8)
states: 40,242,254,760 (10)
abstracting: (3<=p2)
states: 37,712,378,088 (10)
.
EG iterations: 1
abstracting: (1<=p11)
states: 20,769,210,648 (10)
abstracting: (1<=p10)
states: 20,769,210,648 (10)
abstracting: (1<=p9)
states: 20,769,210,648 (10)
abstracting: (3<=p17)
states: 6,923,070,216 (9)
abstracting: (3<=p16)
states: 6,923,070,216 (9)
abstracting: (3<=p15)
states: 6,923,070,216 (9)
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
.....
EG iterations: 5
abstracting: (1<=p14)
states: 27,692,280,864 (10)
abstracting: (1<=p13)
states: 27,692,280,864 (10)
abstracting: (1<=p12)
states: 27,692,280,864 (10)
.-> the formula is FALSE
FORMULA Murphy-COL-D2N050-CTLFireability-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m11.304sec
totally nodes used: 8596595 (8.6e+06)
number of garbage collections: 0
fire ops cache: hits/miss/sum: 137998127 15868058 153866185
used/not used/entry size/cache size: 19728466 47380398 16 1024MB
basic ops cache: hits/miss/sum: 55606113 8974660 64580773
used/not used/entry size/cache size: 9434354 7342862 12 192MB
unary ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 8 128MB
abstract ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 12 192MB
state nr cache: hits/miss/sum: 642581 118923 761504
used/not used/entry size/cache size: 118016 8270592 32 256MB
max state cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 8388608 32 256MB
uniqueHash elements/entry size/size: 67108864 4 256MB
0 59689748
1 6601726
2 708171
3 80399
4 15390
5 7614
6 1495
7 389
8 218
9 81
>= 10 3633
Total processing time: 0m36.596sec
BK_STOP 1680887910566
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202304061127.jar
++ perl -pe 's/.*\.//g'
+ VERSION=202304061127
+ echo 'Running Version 202304061127'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:7459 (355), effective:1786 (85)
initing FirstDep: 0m 0.000sec
iterations count:995 (47), effective:299 (14)
iterations count:21 (1), effective:0 (0)
iterations count:21 (1), effective:0 (0)
iterations count:59 (2), effective:9 (0)
iterations count:53 (2), effective:8 (0)
iterations count:54 (2), effective:9 (0)
iterations count:21 (1), effective:0 (0)
iterations count:28 (1), effective:2 (0)
iterations count:33 (1), effective:3 (0)
iterations count:21 (1), effective:0 (0)
iterations count:21 (1), effective:0 (0)
iterations count:33 (1), effective:3 (0)
iterations count:21 (1), effective:0 (0)
iterations count:33 (1), effective:3 (0)
iterations count:995 (47), effective:299 (14)
iterations count:21 (1), effective:0 (0)
iterations count:30 (1), effective:3 (0)
iterations count:59 (2), effective:9 (0)
iterations count:21 (1), effective:0 (0)
iterations count:52 (2), effective:7 (0)
iterations count:21 (1), effective:0 (0)
iterations count:995 (47), effective:299 (14)
iterations count:28 (1), effective:2 (0)
iterations count:33 (1), effective:3 (0)
iterations count:28 (1), effective:2 (0)
iterations count:28 (1), effective:2 (0)
iterations count:994 (47), effective:298 (14)
iterations count:2248 (107), effective:446 (21)
iterations count:59 (2), effective:9 (0)
iterations count:29 (1), effective:2 (0)
iterations count:45 (2), effective:6 (0)
iterations count:32 (1), effective:3 (0)
iterations count:120 (5), effective:24 (1)
iterations count:78 (3), effective:15 (0)
iterations count:2697 (128), effective:669 (31)
iterations count:799 (38), effective:379 (18)
iterations count:28 (1), effective:2 (0)
iterations count:177 (8), effective:151 (7)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="Murphy-COL-D2N050"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is Murphy-COL-D2N050, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r522-tall-167987247200290"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/Murphy-COL-D2N050.tgz
mv Murphy-COL-D2N050 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

