About the Execution of Marcie for Murphy-PT-D2N050
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 10730.396 | 94185.00 | 94040.00 | 0.00 | FFTFTFTFTTFTTTTT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
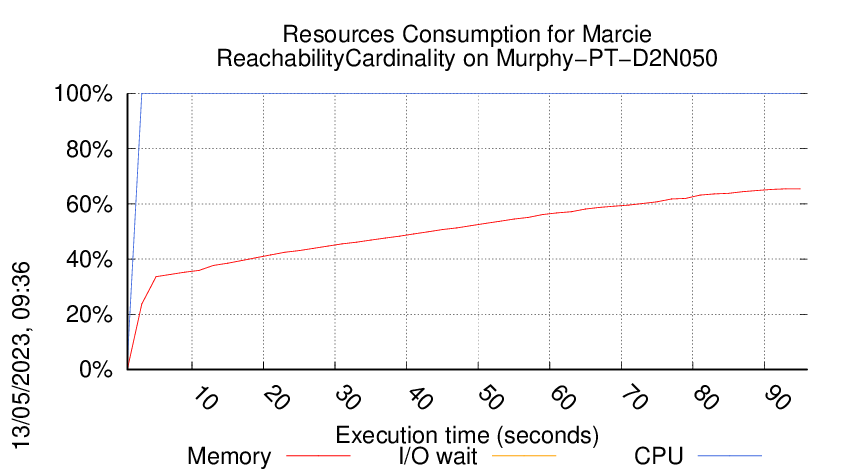
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r513-tall-167987240900342.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.........................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marcie
Input is Murphy-PT-D2N050, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r513-tall-167987240900342
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 464K
-rw-r--r-- 1 mcc users 7.2K Mar 23 15:22 CTLCardinality.txt
-rw-r--r-- 1 mcc users 76K Mar 23 15:22 CTLCardinality.xml
-rw-r--r-- 1 mcc users 4.5K Mar 23 15:21 CTLFireability.txt
-rw-r--r-- 1 mcc users 38K Mar 23 15:21 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.1K Mar 23 07:07 LTLCardinality.txt
-rw-r--r-- 1 mcc users 26K Mar 23 07:07 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.1K Mar 23 07:07 LTLFireability.txt
-rw-r--r-- 1 mcc users 17K Mar 23 07:07 LTLFireability.xml
-rw-r--r-- 1 mcc users 1 Mar 26 22:42 NewModel
-rw-r--r-- 1 mcc users 12K Mar 23 15:23 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 118K Mar 23 15:23 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 9.1K Mar 23 15:23 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 83K Mar 23 15:23 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.8K Mar 23 07:07 UpperBounds.txt
-rw-r--r-- 1 mcc users 4.3K Mar 23 07:07 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 equiv_col
-rw-r--r-- 1 mcc users 7 Mar 26 22:42 instance
-rw-r--r-- 1 mcc users 6 Mar 26 22:42 iscolored
-rw-r--r-- 1 mcc users 14K Mar 26 22:42 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-00
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-01
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-02
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-03
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-04
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-05
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-06
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-07
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-08
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-09
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-10
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-11
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-12
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-13
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-14
FORMULA_NAME Murphy-PT-D2N050-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1679894137787
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marcie
BK_EXAMINATION=ReachabilityCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=Murphy-PT-D2N050
Not applying reductions.
Model is PT
ReachabilityCardinality PT
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../marcie/bin/marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Murphy_COL_D2_N50
(NrP: 18 NrTr: 21 NrArc: 81)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 2.816sec
RS generation: 0m 2.658sec
-> reachability set: #nodes 15348 (1.5e+04) #states 41,538,421,296 (10)
starting MCC model checker
--------------------------
checking: EF [17<=p4_3]
normalized: E [true U 17<=p4_3]
abstracting: (17<=p4_3)
states: 0
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-05 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: AG [p3_1<=34]
normalized: ~ [E [true U ~ [p3_1<=34]]]
abstracting: (p3_1<=34)
states: 41,538,421,296 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-06 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.007sec
checking: EF [23<=p3_2]
normalized: E [true U 23<=p3_2]
abstracting: (23<=p3_2)
states: 0
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [17<=p0_2]
normalized: E [true U 17<=p0_2]
abstracting: (17<=p0_2)
states: 23,337,895,392 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.626sec
checking: AG [p4_1<=46]
normalized: ~ [E [true U ~ [p4_1<=46]]]
abstracting: (p4_1<=46)
states: 41,538,421,296 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.009sec
checking: AG [p5_2<=p5_2]
normalized: ~ [E [true U ~ [p5_2<=p5_2]]]
abstracting: (p5_2<=p5_2)
states: 41,538,421,296 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [[[~ [p1_3<=7] & 29<=p4_2] & [16<=p5_2 & p0_3<=p4_2]]]
normalized: E [true U [[16<=p5_2 & p0_3<=p4_2] & [29<=p4_2 & ~ [p1_3<=7]]]]
abstracting: (p1_3<=7)
states: 9,616,292,784 (9)
abstracting: (29<=p4_2)
states: 0
abstracting: (p0_3<=p4_2)
states: 2,571,946,128 (9)
abstracting: (16<=p5_2)
states: 0
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-07 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.033sec
checking: EF [~ [[[20<=p1_3 | p4_3<=p2_2] | ~ [[p5_3<=p4_1 | p2_1<=p2_1]]]]]
normalized: E [true U ~ [[~ [[p5_3<=p4_1 | p2_1<=p2_1]] | [20<=p1_3 | p4_3<=p2_2]]]]
abstracting: (p4_3<=p2_2)
states: 40,241,822,904 (10)
abstracting: (20<=p1_3)
states: 20,911,983,840 (10)
abstracting: (p2_1<=p2_1)
states: 41,538,421,296 (10)
abstracting: (p5_3<=p4_1)
states: 20,769,210,648 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.143sec
checking: AG [[~ [[[[~ [[p0_1<=p2_1 & p1_2<=23]] | p4_3<=p3_2] & ~ [[p2_2<=p0_1 & ~ [23<=p3_3]]]] & ~ [[[20<=p0_2 | p0_2<=p1_3] & ~ [p1_1<=p5_2]]]]] | p2_1<=24]]
normalized: ~ [E [true U ~ [[p2_1<=24 | ~ [[~ [[[20<=p0_2 | p0_2<=p1_3] & ~ [p1_1<=p5_2]]] & [~ [[p2_2<=p0_1 & ~ [23<=p3_3]]] & [p4_3<=p3_2 | ~ [[p0_1<=p2_1 & p1_2<=23]]]]]]]]]]
abstracting: (p1_2<=23)
states: 23,527,435,824 (10)
abstracting: (p0_1<=p2_1)
states: 41,538,421,296 (10)
abstracting: (p4_3<=p3_2)
states: 20,769,210,648 (10)
abstracting: (23<=p3_3)
states: 0
abstracting: (p2_2<=p0_1)
states: 21,101,462,280 (10)
abstracting: (p1_1<=p5_2)
states: 3,201,442,596 (9)
abstracting: (p0_2<=p1_3)
states: 21,100,781,880 (10)
abstracting: (20<=p0_2)
states: 20,914,008,192 (10)
abstracting: (p2_1<=24)
states: 24,187,766,832 (10)
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-00 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m46.122sec
checking: EF [~ [[[~ [[[[[~ [31<=p4_2] | p3_2<=4] | ~ [[32<=p5_2 | p3_2<=p0_1]]] | 26<=p3_1] | p1_2<=43]] | [p1_2<=p0_2 | [[~ [[~ [50<=p3_3] & p1_2<=p3_2]] & ~ [[33<=p2_3 & [39<=p5_1 | p4_3<=p0_1]]]] & [[[[27<=p3_2 | p5_2<=p0_3] | 31<=p1_2] | p1_2<=p5_3] | 5<=p2_2]]]] | p0_1<=41]]]
normalized: E [true U ~ [[p0_1<=41 | [[p1_2<=p0_2 | [[5<=p2_2 | [p1_2<=p5_3 | [31<=p1_2 | [27<=p3_2 | p5_2<=p0_3]]]] & [~ [[33<=p2_3 & [39<=p5_1 | p4_3<=p0_1]]] & ~ [[p1_2<=p3_2 & ~ [50<=p3_3]]]]]] | ~ [[p1_2<=43 | [26<=p3_1 | [~ [[32<=p5_2 | p3_2<=p0_1]] | [p3_2<=4 | ~ [31<=p4_2]]]]]]]]]]
abstracting: (31<=p4_2)
states: 0
abstracting: (p3_2<=4)
states: 41,538,421,296 (10)
abstracting: (p3_2<=p0_1)
states: 40,890,338,028 (10)
abstracting: (32<=p5_2)
states: 0
abstracting: (26<=p3_1)
states: 0
abstracting: (p1_2<=43)
states: 33,621,901,200 (10)
abstracting: (50<=p3_3)
states: 0
abstracting: (p1_2<=p3_2)
states: 1,947,140,532 (9)
abstracting: (p4_3<=p0_1)
states: 40,241,822,904 (10)
abstracting: (39<=p5_1)
states: 0
abstracting: (33<=p2_3)
states: 12,660,502,176 (10)
abstracting: (p5_2<=p0_3)
states: 39,604,149,036 (10)
abstracting: (27<=p3_2)
states: 0
abstracting: (31<=p1_2)
states: 13,722,395,976 (10)
abstracting: (p1_2<=p5_3)
states: 3,201,442,596 (9)
abstracting: (5<=p2_2)
states: 35,310,733,920 (10)
abstracting: (p1_2<=p0_2)
states: 20,770,490,016 (10)
abstracting: (p0_1<=41)
states: 32,887,386,288 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-04 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 4.963sec
checking: AG [[p4_3<=p1_1 | [~ [[~ [[[[[p0_2<=11 & p3_1<=42] | ~ [p4_3<=50]] & p1_1<=p1_3] | ~ [[p4_2<=p5_1 | p5_1<=p2_2]]]] | [[~ [p2_3<=28] & [35<=p5_1 | [[21<=p0_2 | 35<=p1_1] & [p5_1<=p1_1 & 40<=p1_2]]]] & [p1_1<=42 | [~ [p1_3<=p5_1] & [~ [p4_2<=p5_2] | [p1_3<=29 | p3_2<=p3_2]]]]]]] & p0_2<=5]]]
normalized: ~ [E [true U ~ [[p4_3<=p1_1 | [p0_2<=5 & ~ [[[[p1_1<=42 | [[[p1_3<=29 | p3_2<=p3_2] | ~ [p4_2<=p5_2]] & ~ [p1_3<=p5_1]]] & [[35<=p5_1 | [[p5_1<=p1_1 & 40<=p1_2] & [21<=p0_2 | 35<=p1_1]]] & ~ [p2_3<=28]]] | ~ [[~ [[p4_2<=p5_1 | p5_1<=p2_2]] | [p1_1<=p1_3 & [~ [p4_3<=50] | [p0_2<=11 & p3_1<=42]]]]]]]]]]]]
abstracting: (p3_1<=42)
states: 41,538,421,296 (10)
abstracting: (p0_2<=11)
states: 13,702,477,104 (10)
abstracting: (p4_3<=50)
states: 41,538,421,296 (10)
abstracting: (p1_1<=p1_3)
states: 21,102,118,056 (10)
abstracting: (p5_1<=p2_2)
states: 39,604,149,036 (10)
abstracting: (p4_2<=p5_1)
states: 32,307,661,008 (10)
abstracting: (p2_3<=28)
states: 26,680,372,272 (10)
abstracting: (35<=p1_1)
states: 11,662,251,480 (10)
abstracting: (21<=p0_2)
states: 20,167,079,328 (10)
abstracting: (40<=p1_2)
states: 9,436,017,024 (9)
abstracting: (p5_1<=p1_1)
states: 39,602,227,284 (10)
abstracting: (35<=p5_1)
states: 0
abstracting: (p1_3<=p5_1)
states: 3,201,442,596 (9)
abstracting: (p4_2<=p5_2)
states: 27,692,280,864 (10)
abstracting: (p3_2<=p3_2)
states: 41,538,421,296 (10)
abstracting: (p1_3<=29)
states: 27,267,074,064 (10)
abstracting: (p1_1<=42)
states: 33,255,368,856 (10)
abstracting: (p0_2<=5)
states: 7,396,916,976 (9)
abstracting: (p4_3<=p1_1)
states: 40,240,327,608 (10)
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-03 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 5.966sec
checking: AG [[[~ [8<=p3_3] | [[[37<=p3_2 | ~ [[[[p3_1<=17 | p1_1<=15] | 13<=p5_2] & ~ [[p1_1<=p4_1 & 12<=p0_3]]]]] & ~ [28<=p2_2]] | [~ [[[~ [[p5_3<=p1_3 | p5_1<=p3_3]] | [[p5_2<=24 | p3_2<=20] & [p0_3<=7 | 30<=p1_2]]] & ~ [[[p3_3<=p4_2 | p1_3<=0] & [17<=p4_3 & p1_3<=p3_1]]]]] | [~ [32<=p4_2] & p3_3<=35]]]] & [p3_2<=p3_2 | [p1_2<=p3_1 & 28<=p1_2]]]]
normalized: ~ [E [true U ~ [[[p3_2<=p3_2 | [p1_2<=p3_1 & 28<=p1_2]] & [[[[p3_3<=35 & ~ [32<=p4_2]] | ~ [[~ [[[17<=p4_3 & p1_3<=p3_1] & [p3_3<=p4_2 | p1_3<=0]]] & [[[p0_3<=7 | 30<=p1_2] & [p5_2<=24 | p3_2<=20]] | ~ [[p5_3<=p1_3 | p5_1<=p3_3]]]]]] | [~ [28<=p2_2] & [37<=p3_2 | ~ [[~ [[p1_1<=p4_1 & 12<=p0_3]] & [13<=p5_2 | [p3_1<=17 | p1_1<=15]]]]]]] | ~ [8<=p3_3]]]]]]
abstracting: (8<=p3_3)
states: 0
abstracting: (p1_1<=15)
states: 17,363,177,712 (10)
abstracting: (p3_1<=17)
states: 41,538,421,296 (10)
abstracting: (13<=p5_2)
states: 0
abstracting: (12<=p0_3)
states: 27,835,944,192 (10)
abstracting: (p1_1<=p4_1)
states: 2,574,294,336 (9)
abstracting: (37<=p3_2)
states: 0
abstracting: (28<=p2_2)
states: 15,443,011,584 (10)
abstracting: (p5_1<=p3_3)
states: 13,846,140,432 (10)
abstracting: (p5_3<=p1_3)
states: 39,602,227,284 (10)
abstracting: (p3_2<=20)
states: 41,538,421,296 (10)
abstracting: (p5_2<=24)
states: 41,538,421,296 (10)
abstracting: (30<=p1_2)
states: 14,271,347,232 (10)
abstracting: (p0_3<=7)
states: 9,613,897,776 (9)
abstracting: (p1_3<=0)
states: 1,298,093,688 (9)
abstracting: (p3_3<=p4_2)
states: 34,615,351,080 (10)
abstracting: (p1_3<=p3_1)
states: 1,947,140,532 (9)
abstracting: (17<=p4_3)
states: 0
abstracting: (32<=p4_2)
states: 0
abstracting: (p3_3<=35)
states: 41,538,421,296 (10)
abstracting: (28<=p1_2)
states: 15,441,217,056 (10)
abstracting: (p1_2<=p3_1)
states: 1,947,140,532 (9)
abstracting: (p3_2<=p3_2)
states: 41,538,421,296 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.692sec
checking: AG [[~ [[[~ [[~ [p4_1<=p1_1] | p0_3<=14]] & [[[[p2_2<=p2_1 | p4_2<=p0_1] & [p5_3<=p0_2 & p3_1<=p2_3]] & [[26<=p1_1 & p3_1<=44] & [p3_3<=27 & 46<=p3_1]]] | [[[p4_1<=38 & p4_2<=2] & ~ [p1_3<=p5_2]] & [31<=p4_3 | [42<=p2_1 | p5_2<=p0_2]]]]] | 43<=p4_2]] & [[[[p4_2<=4 | ~ [[~ [[p3_1<=8 & 13<=p3_2]] & ~ [[p3_3<=26 & p1_1<=p5_2]]]]] | p2_3<=35] & ~ [48<=p4_1]] & p2_2<=p2_2]]]
normalized: ~ [E [true U ~ [[[p2_2<=p2_2 & [~ [48<=p4_1] & [p2_3<=35 | [p4_2<=4 | ~ [[~ [[p3_3<=26 & p1_1<=p5_2]] & ~ [[p3_1<=8 & 13<=p3_2]]]]]]]] & ~ [[43<=p4_2 | [[[[31<=p4_3 | [42<=p2_1 | p5_2<=p0_2]] & [~ [p1_3<=p5_2] & [p4_1<=38 & p4_2<=2]]] | [[[p3_3<=27 & 46<=p3_1] & [26<=p1_1 & p3_1<=44]] & [[p5_3<=p0_2 & p3_1<=p2_3] & [p2_2<=p2_1 | p4_2<=p0_1]]]] & ~ [[p0_3<=14 | ~ [p4_1<=p1_1]]]]]]]]]]
abstracting: (p4_1<=p1_1)
states: 40,240,327,608 (10)
abstracting: (p0_3<=14)
states: 16,472,158,704 (10)
abstracting: (p4_2<=p0_1)
states: 40,241,822,904 (10)
abstracting: (p2_2<=p2_1)
states: 21,101,462,280 (10)
abstracting: (p3_1<=p2_3)
states: 40,890,338,028 (10)
abstracting: (p5_3<=p0_2)
states: 39,604,149,036 (10)
abstracting: (p3_1<=44)
states: 41,538,421,296 (10)
abstracting: (26<=p1_1)
states: 16,686,565,056 (10)
abstracting: (46<=p3_1)
states: 0
abstracting: (p3_3<=27)
states: 41,538,421,296 (10)
abstracting: (p4_2<=2)
states: 41,538,421,296 (10)
abstracting: (p4_1<=38)
states: 41,538,421,296 (10)
abstracting: (p1_3<=p5_2)
states: 3,201,442,596 (9)
abstracting: (p5_2<=p0_2)
states: 39,604,149,036 (10)
abstracting: (42<=p2_1)
states: 8,651,035,008 (9)
abstracting: (31<=p4_3)
states: 0
abstracting: (43<=p4_2)
states: 0
abstracting: (13<=p3_2)
states: 0
abstracting: (p3_1<=8)
states: 41,538,421,296 (10)
abstracting: (p1_1<=p5_2)
states: 3,201,442,596 (9)
abstracting: (p3_3<=26)
states: 41,538,421,296 (10)
abstracting: (p4_2<=4)
states: 41,538,421,296 (10)
abstracting: (p2_3<=35)
states: 30,356,529,840 (10)
abstracting: (48<=p4_1)
states: 0
abstracting: (p2_2<=p2_2)
states: 41,538,421,296 (10)
-> the formula is FALSE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-01 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 8.340sec
checking: AG [~ [[[[p0_2<=23 | ~ [[[[19<=p1_1 | p2_3<=p1_3] | ~ [28<=p3_1]] | ~ [[p5_3<=45 & 22<=p0_1]]]]] | [[[[[p1_1<=p0_2 & 24<=p4_1] & [p0_3<=p5_2 & 32<=p5_1]] | [~ [p4_3<=p1_1] & p2_3<=27]] & [p2_2<=p3_3 & p3_1<=28]] | [p2_3<=p1_1 | p2_3<=33]]] & [~ [[[~ [50<=p1_3] | [[p0_1<=p2_1 & p4_3<=32] | [p1_1<=p4_3 & p0_3<=p1_1]]] | p1_2<=p0_2]] & p2_3<=p3_3]]]]
normalized: ~ [E [true U [[p2_3<=p3_3 & ~ [[p1_2<=p0_2 | [[[p0_1<=p2_1 & p4_3<=32] | [p1_1<=p4_3 & p0_3<=p1_1]] | ~ [50<=p1_3]]]]] & [[[p2_3<=p1_1 | p2_3<=33] | [[p2_2<=p3_3 & p3_1<=28] & [[p2_3<=27 & ~ [p4_3<=p1_1]] | [[p0_3<=p5_2 & 32<=p5_1] & [p1_1<=p0_2 & 24<=p4_1]]]]] | [p0_2<=23 | ~ [[~ [[p5_3<=45 & 22<=p0_1]] | [~ [28<=p3_1] | [19<=p1_1 | p2_3<=p1_3]]]]]]]]]
abstracting: (p2_3<=p1_3)
states: 20,767,931,280 (10)
abstracting: (19<=p1_1)
states: 21,704,136,408 (10)
abstracting: (28<=p3_1)
states: 0
abstracting: (22<=p0_1)
states: 19,420,150,464 (10)
abstracting: (p5_3<=45)
states: 41,538,421,296 (10)
abstracting: (p0_2<=23)
states: 23,525,528,112 (10)
abstracting: (24<=p4_1)
states: 0
abstracting: (p1_1<=p0_2)
states: 21,103,405,416 (10)
abstracting: (32<=p5_1)
states: 0
abstracting: (p0_3<=p5_2)
states: 3,198,994,668 (9)
abstracting: (p4_3<=p1_1)
states: 40,240,327,608 (10)
abstracting: (p2_3<=27)
states: 26,095,409,712 (10)
abstracting: (p3_1<=28)
states: 41,538,421,296 (10)
abstracting: (p2_2<=p3_3)
states: 1,944,897,588 (9)
abstracting: (p2_3<=33)
states: 29,392,573,680 (10)
abstracting: (p2_3<=p1_1)
states: 21,100,781,880 (10)
abstracting: (50<=p1_3)
states: 6,010,065,216 (9)
abstracting: (p0_3<=p1_1)
states: 21,100,781,880 (10)
abstracting: (p1_1<=p4_3)
states: 2,574,294,336 (9)
abstracting: (p4_3<=32)
states: 41,538,421,296 (10)
abstracting: (p0_1<=p2_1)
states: 41,538,421,296 (10)
abstracting: (p1_2<=p0_2)
states: 20,770,490,016 (10)
abstracting: (p2_3<=p3_3)
states: 1,944,897,588 (9)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-09 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.494sec
checking: AG [[[~ [[[[p3_3<=31 | p2_2<=p4_2] & [[31<=p2_2 | p3_2<=14] & [~ [[p0_2<=p4_2 & p1_2<=p2_2]] & p5_2<=p3_2]]] | [[[p4_2<=p2_1 & p1_2<=p3_1] | p2_1<=p2_3] & ~ [[p5_3<=p5_1 & [p1_3<=p5_2 & [p3_1<=50 | 19<=p5_1]]]]]]] & [[~ [[29<=p3_3 | 41<=p5_2]] & [p1_2<=p0_1 & [[[[p2_2<=8 | p4_1<=26] | [p4_2<=10 | p0_1<=p2_1]] | p1_3<=p0_1] & [p4_3<=p4_3 & p3_3<=p1_3]]]] & [~ [p1_1<=0] & ~ [[p4_3<=p1_1 | p0_1<=p3_2]]]]] | ~ [[[50<=p5_1 & ~ [[[p4_3<=p3_2 & [[27<=p5_1 & p2_2<=20] | [p0_2<=p2_2 | p4_2<=19]]] | [~ [p0_3<=12] | ~ [[p4_3<=2 | p5_2<=29]]]]]] & ~ [[~ [[p1_2<=p3_3 & [1<=p1_3 & p0_3<=p5_1]]] | [p2_1<=p0_2 | [[p4_3<=19 & p4_1<=8] & [17<=p5_3 | p5_3<=p3_2]]]]]]]]]
normalized: ~ [E [true U ~ [[~ [[~ [[[p2_1<=p0_2 | [[17<=p5_3 | p5_3<=p3_2] & [p4_3<=19 & p4_1<=8]]] | ~ [[p1_2<=p3_3 & [1<=p1_3 & p0_3<=p5_1]]]]] & [50<=p5_1 & ~ [[[~ [[p4_3<=2 | p5_2<=29]] | ~ [p0_3<=12]] | [p4_3<=p3_2 & [[p0_2<=p2_2 | p4_2<=19] | [27<=p5_1 & p2_2<=20]]]]]]]] | [[[~ [[p4_3<=p1_1 | p0_1<=p3_2]] & ~ [p1_1<=0]] & [[p1_2<=p0_1 & [[p4_3<=p4_3 & p3_3<=p1_3] & [p1_3<=p0_1 | [[p4_2<=10 | p0_1<=p2_1] | [p2_2<=8 | p4_1<=26]]]]] & ~ [[29<=p3_3 | 41<=p5_2]]]] & ~ [[[~ [[p5_3<=p5_1 & [p1_3<=p5_2 & [p3_1<=50 | 19<=p5_1]]]] & [p2_1<=p2_3 | [p4_2<=p2_1 & p1_2<=p3_1]]] | [[[p5_2<=p3_2 & ~ [[p0_2<=p4_2 & p1_2<=p2_2]]] & [31<=p2_2 | p3_2<=14]] & [p3_3<=31 | p2_2<=p4_2]]]]]]]]]
abstracting: (p2_2<=p4_2)
states: 2,571,946,128 (9)
abstracting: (p3_3<=31)
states: 41,538,421,296 (10)
abstracting: (p3_2<=14)
states: 41,538,421,296 (10)
abstracting: (31<=p2_2)
states: 13,724,121,600 (10)
abstracting: (p1_2<=p2_2)
states: 20,770,490,016 (10)
abstracting: (p0_2<=p4_2)
states: 2,571,946,128 (9)
abstracting: (p5_2<=p3_2)
states: 13,846,140,432 (10)
abstracting: (p1_2<=p3_1)
states: 1,947,140,532 (9)
abstracting: (p4_2<=p2_1)
states: 40,241,822,904 (10)
abstracting: (p2_1<=p2_3)
states: 21,101,462,280 (10)
abstracting: (19<=p5_1)
states: 0
abstracting: (p3_1<=50)
states: 41,538,421,296 (10)
abstracting: (p1_3<=p5_2)
states: 3,201,442,596 (9)
abstracting: (p5_3<=p5_1)
states: 26,538,435,828 (10)
abstracting: (41<=p5_2)
states: 0
abstracting: (29<=p3_3)
states: 0
abstracting: (p4_1<=26)
states: 41,538,421,296 (10)
abstracting: (p2_2<=8)
states: 10,664,046,576 (10)
abstracting: (p0_1<=p2_1)
states: 41,538,421,296 (10)
abstracting: (p4_2<=10)
states: 41,538,421,296 (10)
abstracting: (p1_3<=p0_1)
states: 21,103,405,416 (10)
abstracting: (p3_3<=p1_3)
states: 40,889,374,452 (10)
abstracting: (p4_3<=p4_3)
states: 41,538,421,296 (10)
abstracting: (p1_2<=p0_1)
states: 21,103,405,416 (10)
abstracting: (p1_1<=0)
states: 1,298,093,688 (9)
abstracting: (p0_1<=p3_2)
states: 1,944,897,588 (9)
abstracting: (p4_3<=p1_1)
states: 40,240,327,608 (10)
abstracting: (p2_2<=20)
states: 21,371,341,968 (10)
abstracting: (27<=p5_1)
states: 0
abstracting: (p4_2<=19)
states: 41,538,421,296 (10)
abstracting: (p0_2<=p2_2)
states: 41,538,421,296 (10)
abstracting: (p4_3<=p3_2)
states: 20,769,210,648 (10)
abstracting: (p0_3<=12)
states: 14,642,880,624 (10)
abstracting: (p5_2<=29)
states: 41,538,421,296 (10)
abstracting: (p4_3<=2)
states: 41,538,421,296 (10)
abstracting: (50<=p5_1)
states: 0
abstracting: (p0_3<=p5_1)
states: 3,198,994,668 (9)
abstracting: (1<=p1_3)
states: 40,240,327,608 (10)
abstracting: (p1_2<=p3_3)
states: 1,947,140,532 (9)
abstracting: (p4_1<=8)
states: 41,538,421,296 (10)
abstracting: (p4_3<=19)
states: 41,538,421,296 (10)
abstracting: (p5_3<=p3_2)
states: 13,846,140,432 (10)
abstracting: (17<=p5_3)
states: 0
abstracting: (p2_1<=p0_2)
states: 21,101,462,280 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-02 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 6.301sec
checking: EF [[[~ [[[[p0_1<=42 | p0_1<=26] | [[[[p3_2<=p3_3 | 29<=p2_2] | ~ [p0_2<=10]] & ~ [[p0_3<=p0_3 | p2_2<=11]]] & p3_3<=p0_2]] & [16<=p0_1 | [p1_2<=2 | [p2_3<=43 | [~ [35<=p0_2] | ~ [p5_2<=20]]]]]]] & [[[p0_3<=p4_3 | [[[23<=p3_1 | ~ [p0_1<=10]] | [[9<=p0_2 & p0_1<=p0_3] | ~ [p3_1<=p3_1]]] | [50<=p2_1 | ~ [36<=p0_2]]]] | ~ [p2_1<=p2_3]] | ~ [[p2_3<=p4_1 & [[p3_3<=23 & p4_1<=49] | ~ [p5_1<=p2_2]]]]]] & [[[[p0_2<=33 & p2_3<=p4_2] & [p4_3<=p0_2 & p0_2<=26]] & [[~ [2<=p2_1] | [[11<=p4_2 & ~ [[38<=p4_1 & 25<=p0_3]]] | [p5_1<=p2_2 | ~ [[p2_2<=p1_2 & p5_3<=49]]]]] | ~ [[[~ [p1_1<=33] | [17<=p5_2 | p2_3<=19]] | [~ [p3_2<=p4_2] | ~ [p3_2<=12]]]]]] | [[[~ [p5_2<=p1_3] | p4_1<=7] & [p2_3<=p0_1 | [[~ [p5_3<=36] & [[p1_1<=p0_2 & p1_3<=32] & [42<=p4_2 & p2_2<=p5_3]]] & [p2_1<=p4_3 | 44<=p5_3]]]] & [[~ [[[p3_3<=p2_2 & 31<=p2_1] | [p4_1<=16 | p5_1<=p2_2]]] | p1_2<=13] & p0_2<=26]]]]]
normalized: E [true U [[[[p0_2<=26 & [p1_2<=13 | ~ [[[p4_1<=16 | p5_1<=p2_2] | [p3_3<=p2_2 & 31<=p2_1]]]]] & [[p2_3<=p0_1 | [[p2_1<=p4_3 | 44<=p5_3] & [[[42<=p4_2 & p2_2<=p5_3] & [p1_1<=p0_2 & p1_3<=32]] & ~ [p5_3<=36]]]] & [p4_1<=7 | ~ [p5_2<=p1_3]]]] | [[~ [[[~ [p3_2<=12] | ~ [p3_2<=p4_2]] | [[17<=p5_2 | p2_3<=19] | ~ [p1_1<=33]]]] | [[[p5_1<=p2_2 | ~ [[p2_2<=p1_2 & p5_3<=49]]] | [11<=p4_2 & ~ [[38<=p4_1 & 25<=p0_3]]]] | ~ [2<=p2_1]]] & [[p4_3<=p0_2 & p0_2<=26] & [p0_2<=33 & p2_3<=p4_2]]]] & [[~ [[p2_3<=p4_1 & [~ [p5_1<=p2_2] | [p3_3<=23 & p4_1<=49]]]] | [~ [p2_1<=p2_3] | [p0_3<=p4_3 | [[50<=p2_1 | ~ [36<=p0_2]] | [[~ [p3_1<=p3_1] | [9<=p0_2 & p0_1<=p0_3]] | [23<=p3_1 | ~ [p0_1<=10]]]]]]] & ~ [[[16<=p0_1 | [p1_2<=2 | [p2_3<=43 | [~ [p5_2<=20] | ~ [35<=p0_2]]]]] & [[p3_3<=p0_2 & [~ [[p0_3<=p0_3 | p2_2<=11]] & [~ [p0_2<=10] | [p3_2<=p3_3 | 29<=p2_2]]]] | [p0_1<=42 | p0_1<=26]]]]]]]
abstracting: (p0_1<=26)
states: 25,472,707,632 (10)
abstracting: (p0_1<=42)
states: 33,253,955,568 (10)
abstracting: (29<=p2_2)
states: 14,858,049,024 (10)
abstracting: (p3_2<=p3_3)
states: 31,153,815,972 (10)
abstracting: (p0_2<=10)
states: 12,708,336,240 (10)
abstracting: (p2_2<=11)
states: 13,702,477,104 (10)
abstracting: (p0_3<=p0_3)
states: 41,538,421,296 (10)
abstracting: (p3_3<=p0_2)
states: 40,890,338,028 (10)
abstracting: (35<=p0_2)
states: 11,663,869,536 (10)
abstracting: (p5_2<=20)
states: 41,538,421,296 (10)
abstracting: (p2_3<=43)
states: 33,620,524,848 (10)
abstracting: (p1_2<=2)
states: 3,828,601,944 (9)
abstracting: (16<=p0_1)
states: 24,177,388,032 (10)
abstracting: (p0_1<=10)
states: 12,708,336,240 (10)
abstracting: (23<=p3_1)
states: 0
abstracting: (p0_1<=p0_3)
states: 21,101,462,280 (10)
abstracting: (9<=p0_2)
states: 30,874,374,720 (10)
abstracting: (p3_1<=p3_1)
states: 41,538,421,296 (10)
abstracting: (36<=p0_2)
states: 11,181,891,456 (10)
abstracting: (50<=p2_1)
states: 6,011,299,008 (9)
abstracting: (p0_3<=p4_3)
states: 2,571,946,128 (9)
abstracting: (p2_1<=p2_3)
states: 21,101,462,280 (10)
abstracting: (p4_1<=49)
states: 41,538,421,296 (10)
abstracting: (p3_3<=23)
states: 41,538,421,296 (10)
abstracting: (p5_1<=p2_2)
states: 39,604,149,036 (10)
abstracting: (p2_3<=p4_1)
states: 2,571,946,128 (9)
abstracting: (p2_3<=p4_2)
states: 2,571,946,128 (9)
abstracting: (p0_2<=33)
states: 29,392,573,680 (10)
abstracting: (p0_2<=26)
states: 25,472,707,632 (10)
abstracting: (p4_3<=p0_2)
states: 40,241,822,904 (10)
abstracting: (2<=p2_1)
states: 38,944,792,656 (10)
abstracting: (25<=p0_3)
states: 17,350,654,464 (10)
abstracting: (38<=p4_1)
states: 0
abstracting: (11<=p4_2)
states: 0
abstracting: (p5_3<=49)
states: 41,538,421,296 (10)
abstracting: (p2_2<=p1_2)
states: 20,767,931,280 (10)
abstracting: (p5_1<=p2_2)
states: 39,604,149,036 (10)
abstracting: (p1_1<=33)
states: 29,394,204,912 (10)
abstracting: (p2_3<=19)
states: 20,624,413,104 (10)
abstracting: (17<=p5_2)
states: 0
abstracting: (p3_2<=p4_2)
states: 34,615,351,080 (10)
abstracting: (p3_2<=12)
states: 41,538,421,296 (10)
abstracting: (p5_2<=p1_3)
states: 39,602,227,284 (10)
abstracting: (p4_1<=7)
states: 41,538,421,296 (10)
abstracting: (p5_3<=36)
states: 41,538,421,296 (10)
abstracting: (p1_3<=32)
states: 28,879,590,528 (10)
abstracting: (p1_1<=p0_2)
states: 21,103,405,416 (10)
abstracting: (p2_2<=p5_3)
states: 3,198,994,668 (9)
abstracting: (42<=p4_2)
states: 0
abstracting: (44<=p5_3)
states: 0
abstracting: (p2_1<=p4_3)
states: 2,571,946,128 (9)
abstracting: (p2_3<=p0_1)
states: 21,101,462,280 (10)
abstracting: (31<=p2_1)
states: 13,724,121,600 (10)
abstracting: (p3_3<=p2_2)
states: 40,890,338,028 (10)
abstracting: (p5_1<=p2_2)
states: 39,604,149,036 (10)
abstracting: (p4_1<=16)
states: 41,538,421,296 (10)
abstracting: (p1_2<=13)
states: 15,585,489,936 (10)
abstracting: (p0_2<=26)
states: 25,472,707,632 (10)
-> the formula is TRUE
FORMULA Murphy-PT-D2N050-ReachabilityCardinality-08 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 7.713sec
totally nodes used: 18677968 (1.9e+07)
number of garbage collections: 0
fire ops cache: hits/miss/sum: 288610133 27607082 316217215
used/not used/entry size/cache size: 31033643 36075221 16 1024MB
basic ops cache: hits/miss/sum: 154557972 28903461 183461433
used/not used/entry size/cache size: 15134575 1642641 12 192MB
unary ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 8 128MB
abstract ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 12 192MB
state nr cache: hits/miss/sum: 3804399 908323 4712722
used/not used/entry size/cache size: 860277 7528331 32 256MB
max state cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 8388608 32 256MB
uniqueHash elements/entry size/size: 67108864 4 256MB
0 52406788
1 11960802
2 2263540
3 340526
4 61436
5 17370
6 12574
7 8291
8 6934
9 5375
>= 10 25228
Total processing time: 1m34.112sec
BK_STOP 1679894231972
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:7459 (355), effective:1786 (85)
initing FirstDep: 0m 0.000sec
iterations count:1108 (52), effective:246 (11)
iterations count:1324 (63), effective:303 (14)
iterations count:3317 (157), effective:772 (36)
iterations count:2756 (131), effective:618 (29)
iterations count:1244 (59), effective:389 (18)
iterations count:1000 (47), effective:262 (12)
iterations count:3533 (168), effective:758 (36)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="Murphy-PT-D2N050"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marcie"
echo " Input is Murphy-PT-D2N050, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r513-tall-167987240900342"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/Murphy-PT-D2N050.tgz
mv Murphy-PT-D2N050 execution
cd execution
if [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "UpperBounds" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] || [ "ReachabilityCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME ReachabilityCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

