About the Execution of Marcie for CryptoMiner-COL-D03N010
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5472.279 | 14892.00 | 15000.00 | 39.60 | FTFTTTTFFTTFFFFT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
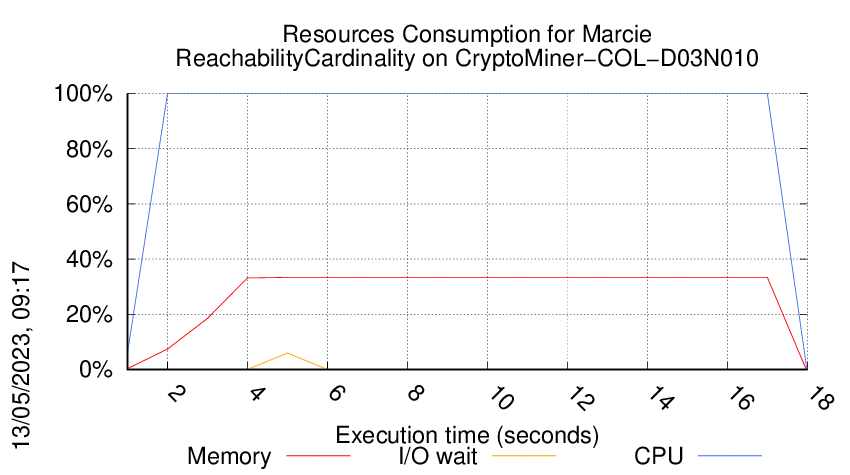
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r513-tall-167987240600086.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marcie
Input is CryptoMiner-COL-D03N010, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r513-tall-167987240600086
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 440K
-rw-r--r-- 1 mcc users 6.9K Mar 23 15:22 CTLCardinality.txt
-rw-r--r-- 1 mcc users 67K Mar 23 15:22 CTLCardinality.xml
-rw-r--r-- 1 mcc users 6.7K Mar 23 15:19 CTLFireability.txt
-rw-r--r-- 1 mcc users 59K Mar 23 15:19 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K Mar 23 07:06 LTLCardinality.txt
-rw-r--r-- 1 mcc users 26K Mar 23 07:06 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.4K Mar 23 07:06 LTLFireability.txt
-rw-r--r-- 1 mcc users 16K Mar 23 07:06 LTLFireability.xml
-rw-r--r-- 1 mcc users 1 Mar 26 22:42 NewModel
-rw-r--r-- 1 mcc users 8.9K Mar 23 15:24 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 82K Mar 23 15:24 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 11K Mar 23 15:24 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 90K Mar 23 15:24 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.8K Mar 23 07:06 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Mar 23 07:06 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 equiv_pt
-rw-r--r-- 1 mcc users 8 Mar 26 22:42 instance
-rw-r--r-- 1 mcc users 5 Mar 26 22:42 iscolored
-rw-r--r-- 1 mcc users 18K Mar 26 22:42 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-00
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-01
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-02
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-03
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-04
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-05
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-06
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-07
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-08
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-09
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-10
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-11
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-12
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-13
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-14
FORMULA_NAME CryptoMiner-COL-D03N010-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1679880800860
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marcie
BK_EXAMINATION=ReachabilityCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=CryptoMiner-COL-D03N010
Not applying reductions.
Model is COL
ReachabilityCardinality COL
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../marcie/bin/marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Unfolding complete |P|=12|T|=12|A|=34
Time for unfolding: 0m 0.250sec
Net: CryptoMinerB_COL_D3_N10
(NrP: 12 NrTr: 12 NrArc: 34)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 2.902sec
RS generation: 0m 0.013sec
-> reachability set: #nodes 121 (1.2e+02) #states 10,636 (4)
starting MCC model checker
--------------------------
checking: AG [sum(state_c3, state_c2, state_c1, state_c0)<=45]
normalized: ~ [E [true U ~ [sum(state_c3, state_c2, state_c1, state_c0)<=45]]]
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=45)
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-03 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.089sec
checking: AG [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=37]
normalized: ~ [E [true U ~ [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=37]]]
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=37)
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-05 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.021sec
checking: EF [~ [sum(state_c3, state_c2, state_c1, state_c0)<=68]]
normalized: E [true U ~ [sum(state_c3, state_c2, state_c1, state_c0)<=68]]
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=68)
states: 10,636 (4)
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-07 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.021sec
checking: EF [99<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]
normalized: E [true U 99<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]
abstracting: (99<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-08 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.021sec
checking: EF [27<=sum(state_c3, state_c2, state_c1, state_c0)]
normalized: E [true U 27<=sum(state_c3, state_c2, state_c1, state_c0)]
abstracting: (27<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.021sec
checking: AG [~ [86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]
normalized: ~ [E [true U 86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]
abstracting: (86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.026sec
checking: AG [[sum(state_c3, state_c2, state_c1, state_c0)<=46 | sum(state_c3, state_c2, state_c1, state_c0)<=91]]
normalized: ~ [E [true U ~ [[sum(state_c3, state_c2, state_c1, state_c0)<=46 | sum(state_c3, state_c2, state_c1, state_c0)<=91]]]]
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=91)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=46)
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-01 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.042sec
checking: EF [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7 & ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=87]]]
normalized: E [true U [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=87] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7]]
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7)
states: 6,621 (3)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=87)
states: 10,636 (4)
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-02 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.052sec
checking: AG [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]
normalized: ~ [E [true U ~ [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]]]
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-04 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [[97<=sum(state_c3, state_c2, state_c1, state_c0) & ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=56]]]
normalized: E [true U [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=56] & 97<=sum(state_c3, state_c2, state_c1, state_c0)]]
abstracting: (97<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=56)
states: 10,636 (4)
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.047sec
checking: AG [[[sum(state_c3, state_c2, state_c1, state_c0)<=37 & sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | ~ [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]]
normalized: ~ [E [true U ~ [[[~ [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] | [sum(state_c3, state_c2, state_c1, state_c0)<=37 & sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]]]
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=37)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 9,098 (3)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-09 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 4.651sec
checking: AG [~ [[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=21] | [~ [[[~ [[[80<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 80<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] & [35<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=13]] & [[[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & ~ [70<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | 4<=sum(state_c3, state_c2, state_c1, state_c0)] & [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=88 | [81<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 24<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]] & 61<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]]
normalized: ~ [E [true U [[~ [[[~ [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 80<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & [80<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] & [35<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=13]] & [[[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | 4<=sum(state_c3, state_c2, state_c1, state_c0)] & [[81<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 24<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=88]] | [[~ [70<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]] & 61<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=21]]]]
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=21)
states: 10,636 (4)
abstracting: (61<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (70<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=88)
states: 10,636 (4)
abstracting: (24<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (81<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (4<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 211
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=13)
states: 10,636 (4)
abstracting: (35<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (80<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (80<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.392sec
checking: EF [[~ [[[82<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=44 | 37<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [68<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12]] | 50<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0) | [55<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 28<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]] & [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=3 | [83<=sum(state_c3, state_c2, state_c1, state_c0) & [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=50 | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12] & 73<=sum(state_c3, state_c2, state_c1, state_c0)]] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=71 & ~ [6<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]
normalized: E [true U [[[[[[~ [6<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=71] | [[[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=50 | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12] & 73<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] & 83<=sum(state_c3, state_c2, state_c1, state_c0)] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=3] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & ~ [[[[55<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 28<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] & [[[[68<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=44 | 37<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] | 50<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | 82<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]
abstracting: (82<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (50<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (37<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=44)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12)
states: 10,636 (4)
abstracting: (68<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
abstracting: (28<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (55<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 9,098 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=3)
states: 8,031 (3)
abstracting: (83<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 10,636 (4)
abstracting: (73<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=12)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=50)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=71)
states: 10,636 (4)
abstracting: (6<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 652
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.319sec
checking: EF [~ [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | [[[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=42 | ~ [[[[sum(state_c3, state_c2, state_c1, state_c0)<=89 & 21<=sum(state_c3, state_c2, state_c1, state_c0)] & 6<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [~ [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]] & ~ [[[[sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & [18<=sum(state_c3, state_c2, state_c1, state_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=64]] | [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41 | 92<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=25]] | [[30<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & ~ [[1<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]] & [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & ~ [[[39<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=64]] | [~ [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] & [5<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=10]]]]]]]]]
normalized: E [true U ~ [[[[~ [[[[5<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=10] & ~ [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]] | [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=64] | 39<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] & ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [~ [[[~ [[1<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] & [30<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] | [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41 | 92<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=25] | [[18<=sum(state_c3, state_c2, state_c1, state_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=64] & sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]] & [~ [[[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | ~ [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]] | [[sum(state_c3, state_c2, state_c1, state_c0)<=89 & 21<=sum(state_c3, state_c2, state_c1, state_c0)] & 6<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=42]]] | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=42)
states: 10,636 (4)
abstracting: (6<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 652
abstracting: (21<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=89)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=64)
states: 10,636 (4)
abstracting: (18<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=25)
states: 10,636 (4)
abstracting: (92<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 2,243 (3)
abstracting: (30<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (1<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,569 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (39<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=64)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 3,129 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 3,129 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=10)
states: 10,636 (4)
abstracting: (5<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 1,364 (3)
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 4.773sec
checking: AG [[~ [[[[[[sum(state_c3, state_c2, state_c1, state_c0)<=18 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=33] & [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=82 | sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=76] & [[[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=46] | [2<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & 38<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & 21<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] | ~ [[sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & [[[[[[sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & 30<=sum(state_c3, state_c2, state_c1, state_c0)] | [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=13] & [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & [5<=sum(state_c3, state_c2, state_c1, state_c0) | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=94]] & [[20<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=48]]]] | [~ [[84<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & ~ [16<=sum(state_c3, state_c2, state_c1, state_c0)]]] | [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=32 & ~ [sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [~ [54<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [35<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=18]]]]] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=83 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]]
normalized: ~ [E [true U ~ [[~ [[[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=83 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [[[[[35<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=18] | ~ [54<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] & [~ [sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=32]] | ~ [[~ [16<=sum(state_c3, state_c2, state_c1, state_c0)] & 84<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]] | [[[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=48] | [20<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] & [[5<=sum(state_c3, state_c2, state_c1, state_c0) | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=94] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [[[sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0) & sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | [sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & 30<=sum(state_c3, state_c2, state_c1, state_c0)]] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=13]]]] & sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] | ~ [[[[[[2<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=46]] & 38<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & [[[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=82 | sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & [sum(state_c3, state_c2, state_c1, state_c0)<=18 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=33]] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=76]] & 21<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]]
abstracting: (21<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=76)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=33)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=18)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=82)
states: 10,636 (4)
abstracting: (38<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=46)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (86<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (2<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,353 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=13)
states: 10,636 (4)
abstracting: (30<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=94)
states: 10,636 (4)
abstracting: (5<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (20<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=48)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 9,098 (3)
abstracting: (84<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (16<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=32)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (54<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=18)
states: 10,636 (4)
abstracting: (35<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=83)
states: 10,636 (4)
-> the formula is TRUE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-06 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.452sec
checking: EF [[[[[~ [[~ [[[5<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 96<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87 | 98<=sum(state_c3, state_c2, state_c1, state_c0)]]] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8]] & ~ [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7 & [sum(state_c3, state_c2, state_c1, state_c0)<=42 & sum(state_c3, state_c2, state_c1, state_c0)<=2]] & [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0) | 72<=sum(state_c3, state_c2, state_c1, state_c0)]]]]]] & ~ [[[~ [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]] | [~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | 77<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=32]]]] | [[[53<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & [[[[sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0) & 81<=sum(state_c3, state_c2, state_c1, state_c0)] & ~ [69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7] | [sum(state_c3, state_c2, state_c1, state_c0)<=27 & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]] & 91<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & [sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) | [~ [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=18 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87] | ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=11]]] & 86<=sum(state_c3, state_c2, state_c1, state_c0)]]] | [~ [[69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | [[[45<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=88] | ~ [sum(state_c3, state_c2, state_c1, state_c0)<=58]] | sum(state_c3, state_c2, state_c1, state_c0)<=100]]] & ~ [[sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & [[[sum(state_c3, state_c2, state_c1, state_c0)<=88 & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(state_c3, state_c2, state_c1, state_c0)<=23] | ~ [[93<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=71]]]]]]]] & ~ [[~ [[[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=49 | [[sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 6<=sum(state_c3, state_c2, state_c1, state_c0)] & [24<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 71<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] | 13<=sum(state_c3, state_c2, state_c1, state_c0)] & [sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0) & [[70<=sum(state_c3, state_c2, state_c1, state_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=24] | [51<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & 39<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]]]]] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41]]]]
normalized: E [true U [~ [[~ [[[[[[51<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & 39<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] | [70<=sum(state_c3, state_c2, state_c1, state_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=24]] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & [[[[24<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 71<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0) & 6<=sum(state_c3, state_c2, state_c1, state_c0)]] | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=49] | 13<=sum(state_c3, state_c2, state_c1, state_c0)]]] & sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41]] & [[[~ [[[~ [[93<=sum(state_c3, state_c2, state_c1, state_c0) | sum(state_c3, state_c2, state_c1, state_c0)<=71]] | [[sum(state_c3, state_c2, state_c1, state_c0)<=88 & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] & sum(state_c3, state_c2, state_c1, state_c0)<=23]] & sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]] & ~ [[[[~ [sum(state_c3, state_c2, state_c1, state_c0)<=58] | [45<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=88]] | sum(state_c3, state_c2, state_c1, state_c0)<=100] | 69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]] | [[[~ [[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=11] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=18 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87]]] & 86<=sum(state_c3, state_c2, state_c1, state_c0)] | sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)] & [[[[[sum(state_c3, state_c2, state_c1, state_c0)<=27 & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | [sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7]] & [~ [69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & [sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0) & 81<=sum(state_c3, state_c2, state_c1, state_c0)]]] & 91<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] & 53<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]]] | [~ [[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=32] & [[~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0)] | 77<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)] | ~ [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8 | sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0)]]]]] & [~ [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) & [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0) | 72<=sum(state_c3, state_c2, state_c1, state_c0)] | ~ [sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0)]] & [[sum(state_c3, state_c2, state_c1, state_c0)<=42 & sum(state_c3, state_c2, state_c1, state_c0)<=2] & sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7]]]] & ~ [[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8 & ~ [[[sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87 | 98<=sum(state_c3, state_c2, state_c1, state_c0)] | [5<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0) | 96<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)]]]]]]]]]]
abstracting: (96<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (5<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 8,143 (3)
abstracting: (98<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8)
states: 10,607 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7)
states: 6,621 (3)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=2)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=42)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 2,243 (3)
abstracting: (72<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 3,129 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 9,098 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 3,129 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=8)
states: 10,607 (4)
abstracting: (77<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 211
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=32)
states: 10,636 (4)
abstracting: (53<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (91<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (81<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 10,636 (4)
abstracting: (69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=7)
states: 6,621 (3)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 9,098 (3)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=27)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 9,492 (3)
abstracting: (86<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=87)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=18)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=11)
states: 10,636 (4)
abstracting: (69<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=100)
states: 10,636 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=88)
states: 10,636 (4)
abstracting: (45<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=58)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=23)
states: 10,636 (4)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 211
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=88)
states: 10,636 (4)
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=71)
states: 10,636 (4)
abstracting: (93<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=41)
states: 10,636 (4)
abstracting: (13<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=49)
states: 10,636 (4)
abstracting: (6<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 2,243 (3)
abstracting: (71<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (24<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
abstracting: (sum(state_c3, state_c2, state_c1, state_c0)<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 10,592 (4)
abstracting: (sum(resource_c3, resource_c2, resource_c1, resource_c0)<=sum(state_c3, state_c2, state_c1, state_c0))
states: 3,129 (3)
abstracting: (sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0)<=24)
states: 10,636 (4)
abstracting: (70<=sum(state_c3, state_c2, state_c1, state_c0))
states: 0
abstracting: (39<=sum(resource_c3, resource_c2, resource_c1, resource_c0))
states: 0
abstracting: (51<=sum(capacity_c3, capacity_c2, capacity_c1, capacity_c0))
states: 0
-> the formula is FALSE
FORMULA CryptoMiner-COL-D03N010-ReachabilityCardinality-00 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.726sec
totally nodes used: 1917 (1.9e+03)
number of garbage collections: 0
fire ops cache: hits/miss/sum: 2819 2819 5638
used/not used/entry size/cache size: 3140 67105724 16 1024MB
basic ops cache: hits/miss/sum: 6618 5001 11619
used/not used/entry size/cache size: 6926 16770290 12 192MB
unary ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 8 128MB
abstract ops cache: hits/miss/sum: 0 2433827 2433827
used/not used/entry size/cache size: 1 16777215 12 192MB
state nr cache: hits/miss/sum: 929 563 1492
used/not used/entry size/cache size: 563 8388045 32 256MB
max state cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 8388608 32 256MB
uniqueHash elements/entry size/size: 67108864 4 256MB
0 67107095
1 1668
2 95
3 2
4 0
5 0
6 0
7 1
8 0
9 0
>= 10 3
Total processing time: 0m16.447sec
BK_STOP 1679880817356
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:223 (18), effective:54 (4)
initing FirstDep: 0m 0.000sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="CryptoMiner-COL-D03N010"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marcie"
echo " Input is CryptoMiner-COL-D03N010, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r513-tall-167987240600086"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/CryptoMiner-COL-D03N010.tgz
mv CryptoMiner-COL-D03N010 execution
cd execution
if [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "UpperBounds" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] || [ "ReachabilityCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME ReachabilityCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

