About the Execution of Marcie for TriangularGrid-PT-3026
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 13783.420 | 3600000.00 | 3600090.00 | 30.30 | T???FTFT?TTFT?FT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
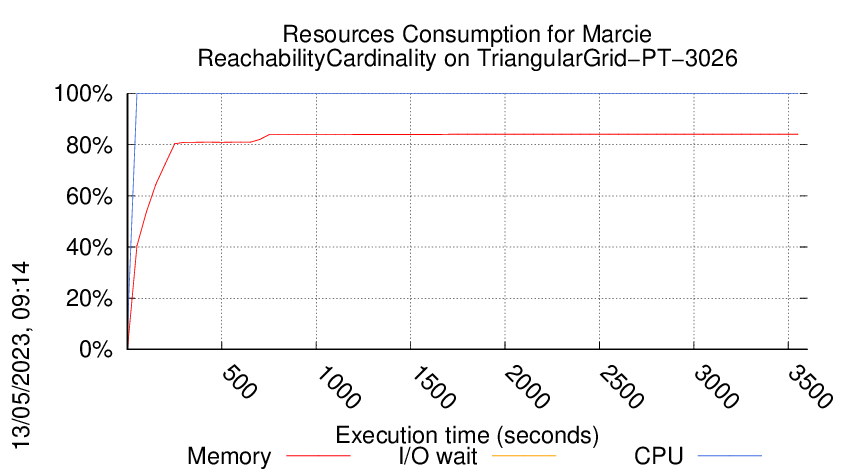
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r481-tall-167912692400742.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.......................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marcie
Input is TriangularGrid-PT-3026, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r481-tall-167912692400742
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 580K
-rw-r--r-- 1 mcc users 7.7K Feb 26 01:36 CTLCardinality.txt
-rw-r--r-- 1 mcc users 82K Feb 26 01:36 CTLCardinality.xml
-rw-r--r-- 1 mcc users 5.4K Feb 26 01:32 CTLFireability.txt
-rw-r--r-- 1 mcc users 43K Feb 26 01:32 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:41 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.4K Jan 29 11:41 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 3.9K Feb 25 17:22 LTLCardinality.txt
-rw-r--r-- 1 mcc users 25K Feb 25 17:22 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.6K Feb 25 17:22 LTLFireability.txt
-rw-r--r-- 1 mcc users 18K Feb 25 17:22 LTLFireability.xml
-rw-r--r-- 1 mcc users 15K Feb 26 01:39 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 151K Feb 26 01:39 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 11K Feb 26 01:38 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 89K Feb 26 01:38 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.8K Feb 25 17:22 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Feb 25 17:22 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 Mar 5 18:23 equiv_col
-rw-r--r-- 1 mcc users 5 Mar 5 18:23 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:23 iscolored
-rwxr-xr-x 1 mcc users 70K Mar 5 18:23 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-00
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-01
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-02
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-03
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-04
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-05
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-06
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-07
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-08
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-09
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-10
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-11
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-12
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-13
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-14
FORMULA_NAME TriangularGrid-PT-3026-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1679865106485
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marcie
BK_EXAMINATION=ReachabilityCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=TriangularGrid-PT-3026
Not applying reductions.
Model is PT
ReachabilityCardinality PT
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../marcie/bin/marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: TriangularGrid_PT_3026
(NrP: 108 NrTr: 90 NrArc: 360)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.001sec
net check time: 0m 0.000sec
init dd package: 0m 2.827sec
RS generation: 0m12.378sec
-> reachability set: #nodes 18981 (1.9e+04) #states 37,521,523,305,029,950,498,059,512,971 (28)
starting MCC model checker
--------------------------
checking: AG [pil2_3_3<=5]
normalized: ~ [E [true U ~ [pil2_3_3<=5]]]
abstracting: (pil2_3_3<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-09 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.006sec
checking: AG [[2<=pb1_1_1 | 1<=pb3_3_3]]
normalized: ~ [E [true U ~ [[2<=pb1_1_1 | 1<=pb3_3_3]]]]
abstracting: (1<=pb3_3_3)
states: 23,030,706,901,103,003,554,928,168,344 (28)
abstracting: (2<=pb1_1_1)
states: 13,926,906,088,048,385,023,070,108,577 (28)
-> the formula is FALSE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 5.544sec
checking: AG [~ [[po1_3_1<=4 & [4<=pil2_1_1 & 3<=po2_3_3]]]]
normalized: ~ [E [true U [po1_3_1<=4 & [4<=pil2_1_1 & 3<=po2_3_3]]]]
abstracting: (3<=po2_3_3)
states: 0
abstracting: (4<=pil2_1_1)
states: 0
abstracting: (po1_3_1<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-07 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.025sec
checking: EF [[~ [pil2_2_1<=pol2_2_1] & ~ [pi2_1_1<=po1_3_3]]]
normalized: E [true U [~ [pi2_1_1<=po1_3_3] & ~ [pil2_2_1<=pol2_2_1]]]
abstracting: (pil2_2_1<=pol2_2_1)
states: 28,621,414,119,829,765,828,867,656,493 (28)
abstracting: (pi2_1_1<=po1_3_3)
states: 28,621,450,933,514,325,343,354,951,981 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m33.493sec
checking: AG [[~ [2<=po2_2_1] & [1<=pb1_1_1 | [[2<=pbl_3_1 | 6<=pil2_1_1] & [pol1_3_1<=pol1_3_1 & pb1_2_2<=pbl_3_4]]]]]
normalized: ~ [E [true U ~ [[[1<=pb1_1_1 | [[pol1_3_1<=pol1_3_1 & pb1_2_2<=pbl_3_4] & [2<=pbl_3_1 | 6<=pil2_1_1]]] & ~ [2<=po2_2_1]]]]]
abstracting: (2<=po2_2_1)
states: 0
abstracting: (6<=pil2_1_1)
states: 0
abstracting: (2<=pbl_3_1)
states: 36,296,747,650,057,826,381,913,333,323 (28)
abstracting: (pb1_2_2<=pbl_3_4)
states: 36,287,651,688,888,520,492,624,355,297 (28)
abstracting: (pol1_3_1<=pol1_3_1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=pb1_1_1)
states: 23,030,754,140,338,062,066,726,775,282 (28)
before gc: list nodes free: 1060682
after gc: idd nodes used:600878, unused:63399122; list nodes free:496639053
MC time: 4m56.243sec
checking: AG [[[~ [[~ [pb3_3_5<=pol2_3_5] & [~ [[[pil1_3_1<=0 | 2<=pi1_2_3] & ~ [pol1_3_3<=4]]] & ~ [1<=pil2_1_1]]]] | 6<=pol1_2_3] | ~ [[po2_2_3<=4 & 6<=po2_3_1]]]]
normalized: ~ [E [true U ~ [[~ [[po2_2_3<=4 & 6<=po2_3_1]] | [6<=pol1_2_3 | ~ [[[~ [1<=pil2_1_1] & ~ [[~ [pol1_3_3<=4] & [pil1_3_1<=0 | 2<=pi1_2_3]]]] & ~ [pb3_3_5<=pol2_3_5]]]]]]]]
abstracting: (pb3_3_5<=pol2_3_5)
states: 20,086,276,489,886,602,670,273,248,183 (28)
abstracting: (2<=pi1_2_3)
states: 0
abstracting: (pil1_3_1<=0)
states: 14,413,891,169,425,439,652,546,685,691 (28)
abstracting: (pol1_3_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=pil2_1_1)
states: 23,107,632,135,604,510,845,512,827,280 (28)
abstracting: (6<=pol1_2_3)
states: 0
abstracting: (6<=po2_3_1)
states: 0
abstracting: (po2_2_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-05 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.188sec
checking: EF [[~ [2<=pbl_3_1] & [[1<=pil2_3_3 | ~ [[[~ [[5<=pi1_3_1 & pi3_3_5<=pbl_3_2]] & ~ [pi3_3_5<=po1_3_5]] | ~ [[~ [pi3_2_1<=6] | [pil3_3_1<=5 | pb1_3_5<=pb2_2_3]]]]]] | ~ [[~ [5<=po1_3_3] | [pil2_1_1<=0 | [pol1_2_3<=6 & pol1_2_3<=po3_3_3]]]]]]]
normalized: E [true U [[~ [[[pil2_1_1<=0 | [pol1_2_3<=6 & pol1_2_3<=po3_3_3]] | ~ [5<=po1_3_3]]] | [1<=pil2_3_3 | ~ [[~ [[[pil3_3_1<=5 | pb1_3_5<=pb2_2_3] | ~ [pi3_2_1<=6]]] | [~ [pi3_3_5<=po1_3_5] & ~ [[5<=pi1_3_1 & pi3_3_5<=pbl_3_2]]]]]]] & ~ [2<=pbl_3_1]]]
abstracting: (2<=pbl_3_1)
states: 36,296,747,650,057,826,381,913,333,323 (28)
abstracting: (pi3_3_5<=pbl_3_2)
states: 37,345,039,183,080,796,205,314,757,519 (28)
abstracting: (5<=pi1_3_1)
states: 0
abstracting: (pi3_3_5<=po1_3_5)
states: 28,621,450,933,514,325,282,844,282,157 (28)
abstracting: (pi3_2_1<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb1_3_5<=pb2_2_3)
states: 23,256,715,533,632,277,575,190,292,105 (28)
abstracting: (pil3_3_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=pil2_3_3)
states: 23,107,575,231,653,133,629,205,217,232 (28)
abstracting: (5<=po1_3_3)
states: 0
abstracting: (pol1_2_3<=po3_3_3)
states: 23,314,057,258,577,001,454,877,822,489 (28)
abstracting: (pol1_2_3<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil2_1_1<=0)
states: 14,413,891,169,425,439,652,546,685,691 (28)
MC time: 4m56.028sec
checking: AG [[[[[~ [1<=pil3_3_1] & [pb2_1_1<=pi1_3_5 & ~ [pol3_3_3<=po3_1_1]]] | [[[po3_3_5<=6 & ~ [[~ [2<=pbl_2_2] & [3<=pol3_2_3 & 1<=pol1_2_3]]]] | ~ [6<=po1_3_1]] & [pil1_2_3<=1 & ~ [[pi2_3_1<=1 & 3<=pol3_2_1]]]]] & pb1_2_1<=4] | [pil3_3_1<=pol3_3_3 | ~ [4<=pol2_2_3]]]]
normalized: ~ [E [true U ~ [[[pil3_3_1<=pol3_3_3 | ~ [4<=pol2_2_3]] | [pb1_2_1<=4 & [[[pil1_2_3<=1 & ~ [[pi2_3_1<=1 & 3<=pol3_2_1]]] & [~ [6<=po1_3_1] | [po3_3_5<=6 & ~ [[[3<=pol3_2_3 & 1<=pol1_2_3] & ~ [2<=pbl_2_2]]]]]] | [[pb2_1_1<=pi1_3_5 & ~ [pol3_3_3<=po3_1_1]] & ~ [1<=pil3_3_1]]]]]]]]
abstracting: (1<=pil3_3_1)
states: 23,107,632,135,604,510,845,512,827,280 (28)
abstracting: (pol3_3_3<=po3_1_1)
states: 23,314,057,258,577,001,427,371,630,105 (28)
abstracting: (pb2_1_1<=pi1_3_5)
states: 17,999,109,891,786,851,228,926,066,012 (28)
abstracting: (2<=pbl_2_2)
states: 36,296,660,608,530,049,507,674,160,419 (28)
abstracting: (1<=pol1_2_3)
states: 23,107,575,231,653,133,629,205,217,232 (28)
abstracting: (3<=pol3_2_3)
states: 0
abstracting: (po3_3_5<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (6<=po1_3_1)
states: 0
abstracting: (3<=pol3_2_1)
states: 0
abstracting: (pi2_3_1<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil1_2_3<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb1_2_1<=4)
states: 34,776,379,038,957,839,595,102,357,243 (28)
abstracting: (4<=pol2_2_3)
states: 0
abstracting: (pil3_3_1<=pol3_3_3)
states: 28,621,394,029,562,948,141,125,314,413 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.499sec
checking: AG [~ [[~ [pi3_3_5<=pb2_2_3] & [[~ [[~ [pil1_3_3<=po1_3_5] & [[5<=pb3_3_5 | 3<=pil3_1_1] & 3<=pil1_3_5]]] & [[[[6<=pi2_3_1 | 3<=pb3_2_2] | [pi3_3_5<=pil3_1_1 & pil1_2_3<=pi2_3_3]] | pb1_2_2<=pb3_2_2] | 2<=pi3_3_5]] | ~ [[[pb1_2_2<=pil2_3_5 | ~ [[pol2_2_1<=0 | 3<=pb1_2_3]]] & ~ [[~ [pbl_1_1<=3] | ~ [pi2_3_1<=pbl_2_1]]]]]]]]]
normalized: ~ [E [true U [[~ [[~ [[~ [pi2_3_1<=pbl_2_1] | ~ [pbl_1_1<=3]]] & [pb1_2_2<=pil2_3_5 | ~ [[pol2_2_1<=0 | 3<=pb1_2_3]]]]] | [[2<=pi3_3_5 | [pb1_2_2<=pb3_2_2 | [[pi3_3_5<=pil3_1_1 & pil1_2_3<=pi2_3_3] | [6<=pi2_3_1 | 3<=pb3_2_2]]]] & ~ [[[3<=pil1_3_5 & [5<=pb3_3_5 | 3<=pil3_1_1]] & ~ [pil1_3_3<=po1_3_5]]]]] & ~ [pi3_3_5<=pb2_2_3]]]]
abstracting: (pi3_3_5<=pb2_2_3)
states: 31,900,844,466,060,408,069,930,669,228 (28)
abstracting: (pil1_3_3<=po1_3_5)
states: 23,314,057,258,577,001,468,955,794,969 (28)
abstracting: (3<=pil3_1_1)
states: 0
abstracting: (5<=pb3_3_5)
states: 2,745,147,524,639,531,155,350,814,158 (27)
abstracting: (3<=pil1_3_5)
states: 0
abstracting: (3<=pb3_2_2)
states: 8,279,888,162,938,987,157,905,096,879 (27)
abstracting: (6<=pi2_3_1)
states: 0
abstracting: (pil1_2_3<=pi2_3_3)
states: 23,314,057,258,577,001,496,461,987,353 (28)
abstracting: (pi3_3_5<=pil3_1_1)
states: 32,007,704,507,120,136,005,715,673,326 (28)
abstracting: (pb1_2_2<=pb3_2_2)
states: 23,202,605,238,810,575,536,869,293,373 (28)
abstracting: (2<=pi3_3_5)
states: 0
abstracting: (3<=pb1_2_3)
states: 8,279,888,162,938,987,107,935,485,661 (27)
abstracting: (pol2_2_1<=0)
states: 14,413,948,073,376,816,868,854,295,739 (28)
abstracting: (pb1_2_2<=pil2_3_5)
states: 20,086,323,729,121,661,246,667,891,509 (28)
abstracting: (pbl_1_1<=3)
states: 3,833,820,178,000,510,225,676,992,861 (27)
abstracting: (pi2_3_1<=pbl_2_1)
states: 37,345,039,006,023,272,696,616,856,489 (28)
-> the formula is FALSE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-06 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m50.447sec
checking: AG [[[[~ [[[pol3_3_1<=2 & po2_3_1<=5] | [pbl_2_1<=po2_2_3 | pil3_2_1<=pil2_3_5]]] & ~ [[pol1_3_3<=1 | [pi3_3_3<=1 & [[[pb1_3_4<=4 | pi2_3_5<=4] & [3<=pol1_3_5 | pil2_2_3<=0]] & ~ [[pil1_3_1<=1 & pb2_3_4<=5]]]]]]] & 1<=po1_1_1] | [5<=pol2_3_3 | [[~ [[[~ [pil2_2_1<=2] | 2<=po3_2_1] & po3_3_5<=po3_3_3]] | [[[pb1_2_1<=5 & [[pol1_3_1<=pil3_1_1 | 2<=pb3_3_1] | pol2_3_5<=3]] | [pb3_3_1<=6 | ~ [pol2_2_1<=2]]] & ~ [pol3_3_5<=po3_3_5]]] | pb3_3_4<=4]]]]
normalized: ~ [E [true U ~ [[[5<=pol2_3_3 | [pb3_3_4<=4 | [[~ [pol3_3_5<=po3_3_5] & [[pb3_3_1<=6 | ~ [pol2_2_1<=2]] | [pb1_2_1<=5 & [pol2_3_5<=3 | [pol1_3_1<=pil3_1_1 | 2<=pb3_3_1]]]]] | ~ [[po3_3_5<=po3_3_3 & [2<=po3_2_1 | ~ [pil2_2_1<=2]]]]]]] | [1<=po1_1_1 & [~ [[pol1_3_3<=1 | [pi3_3_3<=1 & [~ [[pil1_3_1<=1 & pb2_3_4<=5]] & [[3<=pol1_3_5 | pil2_2_3<=0] & [pb1_3_4<=4 | pi2_3_5<=4]]]]]] & ~ [[[pbl_2_1<=po2_2_3 | pil3_2_1<=pil2_3_5] | [pol3_3_1<=2 & po2_3_1<=5]]]]]]]]]
abstracting: (po2_3_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pol3_3_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil3_2_1<=pil2_3_5)
states: 28,621,450,933,514,325,343,354,951,981 (28)
abstracting: (pbl_2_1<=po2_2_3)
states: 757,059,766,904,645,110,401,938,339 (26)
abstracting: (pi2_3_5<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb1_3_4<=4)
states: 34,776,379,038,957,839,605,671,127,952 (28)
abstracting: (pil2_2_3<=0)
states: 14,413,948,073,376,816,818,572,306,619 (28)
abstracting: (3<=pol1_3_5)
states: 0
abstracting: (pb2_3_4<=5)
states: 36,006,661,863,332,322,967,860,326,010 (28)
abstracting: (pil1_3_1<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pi3_3_3<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pol1_3_3<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=po1_1_1)
states: 14,413,891,169,425,439,652,546,685,691 (28)
abstracting: (pil2_2_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (2<=po3_2_1)
states: 0
abstracting: (po3_3_5<=po3_3_3)
states: 28,621,450,933,514,325,307,150,935,341 (28)
abstracting: (2<=pb3_3_1)
states: 13,926,906,088,048,385,023,070,108,577 (28)
abstracting: (pol1_3_1<=pil3_1_1)
states: 28,621,394,029,562,948,154,553,534,317 (28)
abstracting: (pol2_3_5<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb1_2_1<=5)
states: 36,006,661,863,332,322,917,809,686,334 (28)
abstracting: (pol2_2_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb3_3_1<=6)
states: 36,718,240,116,213,218,745,761,244,164 (28)
abstracting: (pol3_3_5<=po3_3_5)
states: 14,413,891,169,425,439,652,546,685,691 (28)
abstracting: (pb3_3_4<=4)
states: 34,776,379,038,957,839,645,154,466,793 (28)
abstracting: (5<=pol2_3_3)
states: 0
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-00 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.506sec
checking: AG [[pil2_2_3<=4 | ~ [[[~ [[~ [[[pi3_2_3<=pil2_3_1 | 3<=pi1_3_1] | [3<=pbl_2_3 & pi3_2_3<=5]]] | [[[pb3_2_3<=pbl_1_1 & pbl_2_3<=po1_2_1] & [6<=pb2_3_4 | po1_1_1<=pil2_3_3]] & ~ [[1<=pb1_2_1 | pbl_3_3<=po2_2_1]]]]] | [pbl_3_1<=pb1_2_3 | [~ [[[pol3_3_5<=pi2_1_1 & pol2_1_1<=pil2_1_1] & [pil1_3_3<=po3_2_1 | pb1_3_1<=pil2_1_1]]] & 1<=po1_1_1]]] & [[pi1_3_1<=pol2_3_1 | pil3_3_3<=pb1_3_4] | pb3_3_5<=po1_1_1]]]]]
normalized: ~ [E [true U ~ [[pil2_2_3<=4 | ~ [[[pb3_3_5<=po1_1_1 | [pi1_3_1<=pol2_3_1 | pil3_3_3<=pb1_3_4]] & [[pbl_3_1<=pb1_2_3 | [1<=po1_1_1 & ~ [[[pil1_3_3<=po3_2_1 | pb1_3_1<=pil2_1_1] & [pol3_3_5<=pi2_1_1 & pol2_1_1<=pil2_1_1]]]]] | ~ [[[~ [[1<=pb1_2_1 | pbl_3_3<=po2_2_1]] & [[6<=pb2_3_4 | po1_1_1<=pil2_3_3] & [pb3_2_3<=pbl_1_1 & pbl_2_3<=po1_2_1]]] | ~ [[[3<=pbl_2_3 & pi3_2_3<=5] | [pi3_2_3<=pil2_3_1 | 3<=pi1_3_1]]]]]]]]]]]]
abstracting: (3<=pi1_3_1)
states: 0
abstracting: (pi3_2_3<=pil2_3_1)
states: 32,007,684,416,853,318,262,311,193,902 (28)
abstracting: (pi3_2_3<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (3<=pbl_2_3)
states: 35,219,465,405,716,284,978,548,371,526 (28)
abstracting: (pbl_2_3<=po1_2_1)
states: 757,059,766,904,645,110,401,938,339 (26)
abstracting: (pb3_2_3<=pbl_1_1)
states: 36,287,698,383,391,423,493,952,150,314 (28)
abstracting: (po1_1_1<=pil2_3_3)
states: 32,007,704,507,120,136,000,217,388,270 (28)
abstracting: (6<=pb2_3_4)
states: 1,514,861,441,697,627,530,199,186,961 (27)
abstracting: (pbl_3_3<=po2_2_1)
states: 757,059,766,904,645,110,401,938,339 (26)
abstracting: (1<=pb1_2_1)
states: 23,030,706,901,103,003,554,928,168,344 (28)
abstracting: (pol2_1_1<=pil2_1_1)
states: 28,621,394,029,562,948,085,463,177,069 (28)
abstracting: (pol3_3_5<=pi2_1_1)
states: 23,313,983,631,196,033,633,268,695,065 (28)
abstracting: (pb1_3_1<=pil2_1_1)
states: 20,086,290,911,156,761,225,477,775,159 (28)
abstracting: (pil1_3_3<=po3_2_1)
states: 23,314,057,258,577,001,503,500,973,593 (28)
abstracting: (1<=po1_1_1)
states: 14,413,891,169,425,439,652,546,685,691 (28)
abstracting: (pbl_3_1<=pb1_2_3)
states: 2,269,924,224,676,008,764,086,496,807 (27)
abstracting: (pil3_3_3<=pb1_3_4)
states: 28,651,411,847,746,955,903,029,926,126 (28)
abstracting: (pi1_3_1<=pol2_3_1)
states: 32,007,704,507,120,136,060,728,058,094 (28)
abstracting: (pb3_3_5<=po1_1_1)
states: 17,999,095,470,516,692,680,844,366,924 (28)
before gc: list nodes free: 931493
after gc: idd nodes used:2416008, unused:61583992; list nodes free:512331141
abstracting: (pil2_2_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
-> the formula is TRUE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m12.892sec
checking: EF [[5<=pol3_2_1 & ~ [[[[6<=pi1_3_5 | [[[[5<=po3_3_3 | pi1_3_5<=1] | [po1_2_3<=4 | pol2_1_1<=6]] | [[pi1_2_3<=pi3_3_5 & 1<=pi1_3_1] & po1_3_5<=4]] | ~ [[3<=pol1_1_1 & 1<=pb3_1_1]]]] & [3<=pol2_2_1 & 6<=po2_2_3]] & ~ [[[[[pol1_2_1<=pb2_3_5 & [pi1_2_1<=2 & pbl_3_5<=pil3_3_3]] & [[po1_1_1<=pi3_1_1 & pb1_2_3<=pb3_2_1] | [pbl_2_2<=po3_3_1 & 3<=pb2_2_2]]] & [~ [3<=pol1_2_3] & [[4<=pil1_1_1 & 3<=pb3_3_5] | pil2_3_1<=6]]] & [~ [5<=pb3_3_2] & ~ [[~ [pi3_2_3<=pil1_2_1] & [2<=pil2_3_5 & pb3_3_2<=po1_2_1]]]]]]]]]]
normalized: E [true U [5<=pol3_2_1 & ~ [[~ [[[~ [[[2<=pil2_3_5 & pb3_3_2<=po1_2_1] & ~ [pi3_2_3<=pil1_2_1]]] & ~ [5<=pb3_3_2]] & [[[pil2_3_1<=6 | [4<=pil1_1_1 & 3<=pb3_3_5]] & ~ [3<=pol1_2_3]] & [[[pbl_2_2<=po3_3_1 & 3<=pb2_2_2] | [po1_1_1<=pi3_1_1 & pb1_2_3<=pb3_2_1]] & [pol1_2_1<=pb2_3_5 & [pi1_2_1<=2 & pbl_3_5<=pil3_3_3]]]]]] & [[3<=pol2_2_1 & 6<=po2_2_3] & [6<=pi1_3_5 | [~ [[3<=pol1_1_1 & 1<=pb3_1_1]] | [[po1_3_5<=4 & [pi1_2_3<=pi3_3_5 & 1<=pi1_3_1]] | [[po1_2_3<=4 | pol2_1_1<=6] | [5<=po3_3_3 | pi1_3_5<=1]]]]]]]]]]
abstracting: (pi1_3_5<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (5<=po3_3_3)
states: 0
abstracting: (pol2_1_1<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (po1_2_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=pi1_3_1)
states: 14,413,891,169,425,439,652,546,685,691 (28)
abstracting: (pi1_2_3<=pi3_3_5)
states: 28,621,394,029,562,948,127,047,341,933 (28)
abstracting: (po1_3_5<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (1<=pb3_1_1)
states: 23,030,666,360,838,071,143,158,361,137 (28)
abstracting: (3<=pol1_1_1)
states: 0
abstracting: (6<=pi1_3_5)
states: 0
abstracting: (6<=po2_2_3)
states: 0
abstracting: (3<=pol2_2_1)
states: 0
abstracting: (pbl_3_5<=pil3_3_3)
states: 956,817,594,947,932,176,278,246,492 (26)
abstracting: (pi1_2_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pol1_2_1<=pb2_3_5)
states: 28,651,442,644,023,923,099,500,695,954 (28)
abstracting: (pb1_2_3<=pb3_2_1)
states: 23,256,658,561,172,037,587,028,056,814 (28)
abstracting: (po1_1_1<=pi3_1_1)
states: 28,621,450,933,514,325,282,844,282,157 (28)
abstracting: (3<=pb2_2_2)
states: 8,279,888,162,938,987,118,421,758,038 (27)
abstracting: (pbl_2_2<=po3_3_1)
states: 757,059,437,025,192,725,714,129,776 (26)
abstracting: (3<=pol1_2_3)
states: 0
abstracting: (3<=pb3_3_5)
states: 8,279,901,115,204,979,072,751,695,217 (27)
abstracting: (4<=pil1_1_1)
states: 0
abstracting: (pil2_3_1<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (5<=pb3_3_2)
states: 2,745,144,266,072,110,852,905,046,178 (27)
abstracting: (pi3_2_3<=pil1_2_1)
states: 32,007,684,416,853,318,265,510,733,102 (28)
abstracting: (pb3_3_2<=po1_2_1)
states: 17,999,149,287,518,676,811,083,112,353 (28)
abstracting: (2<=pil2_3_5)
states: 0
abstracting: (5<=pol3_2_1)
states: 0
-> the formula is FALSE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-04 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.930sec
checking: EF [[~ [[~ [[[pi2_3_3<=6 & [~ [pi2_2_1<=1] | pb2_1_1<=4]] | ~ [[pb2_3_5<=pb2_1_1 & 2<=pbl_3_3]]]] & [6<=pi1_2_1 & ~ [pb1_3_1<=1]]]] & [[pb1_3_5<=0 & [5<=pb2_3_3 & ~ [[[[[pol2_3_1<=2 | po2_2_1<=5] & 2<=po3_3_1] | [~ [5<=pb2_1_1] | 3<=pi1_2_1]] | [[[5<=pb2_3_3 | po1_3_5<=pi3_3_1] | [5<=pol3_2_3 | pil2_2_3<=po1_3_5]] & ~ [[pol3_3_3<=po1_2_1 | 1<=pb3_3_2]]]]]]] | ~ [[[[~ [4<=pbl_2_3] | [po3_2_3<=pbl_3_5 | ~ [[po2_1_1<=3 & pb1_3_2<=5]]]] & [[~ [[pol3_3_1<=po2_2_1 | pi2_2_1<=pol2_2_3]] | [[5<=pi2_1_1 | pil2_3_5<=pil3_3_5] | [pb2_2_3<=4 & pb2_2_1<=pb2_2_1]]] & 3<=pol3_3_5]] | ~ [[4<=pi3_3_1 | ~ [[2<=pbl_2_1 | [pol1_3_5<=0 | 3<=pb1_2_1]]]]]]]]]]
normalized: E [true U [[~ [[~ [[4<=pi3_3_1 | ~ [[2<=pbl_2_1 | [pol1_3_5<=0 | 3<=pb1_2_1]]]]] | [[3<=pol3_3_5 & [[[pb2_2_3<=4 & pb2_2_1<=pb2_2_1] | [5<=pi2_1_1 | pil2_3_5<=pil3_3_5]] | ~ [[pol3_3_1<=po2_2_1 | pi2_2_1<=pol2_2_3]]]] & [[po3_2_3<=pbl_3_5 | ~ [[po2_1_1<=3 & pb1_3_2<=5]]] | ~ [4<=pbl_2_3]]]]] | [pb1_3_5<=0 & [5<=pb2_3_3 & ~ [[[~ [[pol3_3_3<=po1_2_1 | 1<=pb3_3_2]] & [[5<=pol3_2_3 | pil2_2_3<=po1_3_5] | [5<=pb2_3_3 | po1_3_5<=pi3_3_1]]] | [[3<=pi1_2_1 | ~ [5<=pb2_1_1]] | [2<=po3_3_1 & [pol2_3_1<=2 | po2_2_1<=5]]]]]]]] & ~ [[[6<=pi1_2_1 & ~ [pb1_3_1<=1]] & ~ [[~ [[pb2_3_5<=pb2_1_1 & 2<=pbl_3_3]] | [pi2_3_3<=6 & [pb2_1_1<=4 | ~ [pi2_2_1<=1]]]]]]]]]
abstracting: (pi2_2_1<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb2_1_1<=4)
states: 34,776,375,780,390,419,342,708,698,813 (28)
abstracting: (pi2_3_3<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (2<=pbl_3_3)
states: 36,296,660,608,530,049,518,241,279,268 (28)
abstracting: (pb2_3_5<=pb2_1_1)
states: 23,256,644,191,963,933,795,949,811,595 (28)
abstracting: (pb1_3_1<=1)
states: 23,594,617,216,981,565,474,989,404,394 (28)
abstracting: (6<=pi1_2_1)
states: 0
abstracting: (po2_2_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pol2_3_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (2<=po3_3_1)
states: 0
abstracting: (5<=pb2_1_1)
states: 2,745,147,524,639,531,155,350,814,158 (27)
abstracting: (3<=pi1_2_1)
states: 0
abstracting: (po1_3_5<=pi3_3_1)
states: 28,621,394,029,562,948,154,553,534,317 (28)
abstracting: (5<=pb2_3_3)
states: 2,745,144,266,072,110,842,339,579,189 (27)
abstracting: (pil2_2_3<=po1_3_5)
states: 23,314,057,258,577,001,461,916,808,729 (28)
abstracting: (5<=pol3_2_3)
states: 0
abstracting: (1<=pb3_3_2)
states: 23,030,706,901,103,003,502,560,570,640 (28)
abstracting: (pol3_3_3<=po1_2_1)
states: 23,314,057,258,577,001,420,332,643,865 (28)
abstracting: (5<=pb2_3_3)
states: 2,745,144,266,072,110,842,339,579,189 (27)
abstracting: (pb1_3_5<=0)
states: 14,490,856,944,191,879,354,901,151,834 (28)
abstracting: (4<=pbl_2_3)
states: 33,687,618,467,687,012,325,018,844,971 (28)
abstracting: (pb1_3_2<=5)
states: 36,006,661,863,332,322,967,860,326,010 (28)
abstracting: (po2_1_1<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (po3_2_3<=pbl_3_5)
states: 37,345,069,802,300,239,940,741,200,369 (28)
abstracting: (pi2_2_1<=pol2_2_3)
states: 32,007,684,416,853,318,272,549,719,342 (28)
abstracting: (pol3_3_1<=po2_2_1)
states: 23,314,020,444,892,442,023,558,856,729 (28)
abstracting: (pil2_3_5<=pil3_3_5)
states: 28,621,394,029,562,948,099,541,149,549 (28)
abstracting: (5<=pi2_1_1)
states: 0
abstracting: (pb2_2_1<=pb2_2_1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb2_2_3<=4)
states: 34,776,379,038,957,839,595,102,357,243 (28)
abstracting: (3<=pol3_3_5)
states: 0
abstracting: (3<=pb1_2_1)
states: 8,279,888,162,938,987,168,553,062,200 (27)
abstracting: (pol1_3_5<=0)
states: 14,413,948,073,376,816,835,849,818,299 (28)
abstracting: (2<=pbl_2_1)
states: 36,296,660,608,530,049,518,241,279,268 (28)
abstracting: (4<=pi3_3_1)
states: 0
MC time: 8m 2.430sec
checking: EF [[[[[[2<=pi2_3_1 & [[pi1_3_3<=0 | po1_3_5<=1] & [pb1_3_3<=1 | [~ [6<=pi1_2_1] & [2<=pbl_3_2 | po3_2_1<=pbl_2_1]]]]] | [pi1_3_3<=5 & [[pb1_3_3<=pi2_3_3 | [[pi1_3_5<=pb1_3_4 & po2_3_1<=pi1_2_1] & [3<=pb2_2_2 | 6<=pil2_2_1]]] | pb3_3_2<=po2_3_1]]] | [~ [[~ [pi2_3_1<=2] & [[pbl_1_1<=pb1_3_1 & [pb1_2_1<=pi2_2_3 & 5<=po2_3_3]] & ~ [[po3_1_1<=pi3_3_3 & 4<=pb1_2_1]]]]] & [[[[[pol2_1_1<=pb2_3_4 | 4<=pbl_3_2] | ~ [6<=pol3_1_1]] | [[pbl_3_3<=0 & po3_1_1<=pol2_3_5] & [3<=po2_2_1 & pi2_2_3<=4]]] | [3<=pi1_3_3 & po2_3_1<=5]] | pb2_3_3<=1]]] & [3<=pb3_1_1 | [1<=pil3_3_5 & 4<=pb2_3_1]]] & [~ [1<=po3_2_1] & [6<=pi3_2_3 & 4<=pil3_3_5]]]]
normalized: E [true U [[[6<=pi3_2_3 & 4<=pil3_3_5] & ~ [1<=po3_2_1]] & [[3<=pb3_1_1 | [1<=pil3_3_5 & 4<=pb2_3_1]] & [[[pb2_3_3<=1 | [[3<=pi1_3_3 & po2_3_1<=5] | [[[3<=po2_2_1 & pi2_2_3<=4] & [pbl_3_3<=0 & po3_1_1<=pol2_3_5]] | [~ [6<=pol3_1_1] | [pol2_1_1<=pb2_3_4 | 4<=pbl_3_2]]]]] & ~ [[[~ [[po3_1_1<=pi3_3_3 & 4<=pb1_2_1]] & [pbl_1_1<=pb1_3_1 & [pb1_2_1<=pi2_2_3 & 5<=po2_3_3]]] & ~ [pi2_3_1<=2]]]] | [[pi1_3_3<=5 & [pb3_3_2<=po2_3_1 | [pb1_3_3<=pi2_3_3 | [[3<=pb2_2_2 | 6<=pil2_2_1] & [pi1_3_5<=pb1_3_4 & po2_3_1<=pi1_2_1]]]]] | [2<=pi2_3_1 & [[pb1_3_3<=1 | [[2<=pbl_3_2 | po3_2_1<=pbl_2_1] & ~ [6<=pi1_2_1]]] & [pi1_3_3<=0 | po1_3_5<=1]]]]]]]]
abstracting: (po1_3_5<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pi1_3_3<=0)
states: 23,107,575,231,653,133,629,205,217,232 (28)
abstracting: (6<=pi1_2_1)
states: 0
abstracting: (po3_2_1<=pbl_2_1)
states: 37,345,039,006,023,272,705,255,612,329 (28)
abstracting: (2<=pbl_3_2)
states: 36,296,660,608,530,049,507,674,160,419 (28)
abstracting: (pb1_3_3<=1)
states: 23,594,642,191,447,389,594,182,866,119 (28)
abstracting: (2<=pi2_3_1)
states: 0
abstracting: (po2_3_1<=pi1_2_1)
states: 28,621,414,119,829,765,854,715,010,861 (28)
abstracting: (pi1_3_5<=pb1_3_4)
states: 31,900,818,358,385,998,138,770,327,905 (28)
abstracting: (6<=pil2_2_1)
states: 0
abstracting: (3<=pb2_2_2)
states: 8,279,888,162,938,987,118,421,758,038 (27)
abstracting: (pb1_3_3<=pi2_3_3)
states: 17,999,149,287,518,676,828,075,617,469 (28)
abstracting: (pb3_3_2<=po2_3_1)
states: 17,999,149,287,518,676,819,506,710,701 (28)
abstracting: (pi1_3_3<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pi2_3_1<=2)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (5<=po2_3_3)
states: 0
abstracting: (pb1_2_1<=pi2_2_3)
states: 17,999,149,287,518,676,752,150,430,238 (28)
abstracting: (pbl_1_1<=pb1_3_1)
states: 2,269,925,215,643,992,516,548,703,711 (27)
abstracting: (4<=pb1_2_1)
states: 4,825,510,724,751,101,142,808,532,312 (27)
abstracting: (po3_1_1<=pi3_3_3)
states: 28,621,414,119,829,765,889,260,189,485 (28)
abstracting: (4<=pbl_3_2)
states: 33,687,618,467,687,012,314,451,728,553 (28)
abstracting: (pol2_1_1<=pb2_3_4)
states: 28,651,385,740,072,545,945,964,277,199 (28)
abstracting: (6<=pol3_1_1)
states: 0
abstracting: (po3_1_1<=pol2_3_5)
states: 32,007,704,507,120,136,005,715,673,326 (28)
abstracting: (pbl_3_3<=0)
states: 489,101,858,644,044,786,765,002,885 (26)
abstracting: (pi2_2_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (3<=po2_2_1)
states: 0
abstracting: (po2_3_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (3<=pi1_3_3)
states: 0
abstracting: (pb2_3_3<=1)
states: 23,594,642,191,447,389,594,182,866,119 (28)
abstracting: (4<=pb2_3_1)
states: 4,825,429,521,265,642,670,941,692,634 (27)
abstracting: (1<=pil3_3_5)
states: 23,107,632,135,604,510,845,512,827,280 (28)
abstracting: (3<=pb3_1_1)
states: 8,279,813,335,704,988,149,183,281,072 (27)
abstracting: (1<=po3_2_1)
states: 14,413,948,073,376,816,868,854,295,739 (28)
abstracting: (4<=pil3_3_5)
states: 0
abstracting: (6<=pi3_2_3)
states: 0
-> the formula is FALSE
FORMULA TriangularGrid-PT-3026-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.475sec
checking: EF [~ [[[[~ [[[[pil1_3_3<=1 | ~ [6<=pol2_3_5]] & [[pil3_3_3<=pbl_3_5 & pil3_3_5<=5] & [3<=pb2_1_1 | 3<=po2_2_3]]] | [[pbl_2_2<=pil3_3_1 & [pbl_2_3<=pil2_3_1 | pi1_2_3<=po2_1_1]] | [[po3_3_5<=pi3_2_1 | pil2_2_3<=3] | pbl_2_1<=3]]]] | ~ [[[~ [pb1_3_3<=po3_3_3] & ~ [pb1_3_3<=pi3_3_1]] & [[pb2_3_5<=po2_3_5 & pil2_2_1<=0] & ~ [pb2_3_5<=pol1_3_3]]]]] & [[po1_2_1<=pil1_3_5 | [[pol3_3_5<=pil1_3_3 & [[po1_2_3<=po2_1_1 & pol2_1_1<=pil3_3_1] | 2<=pi1_2_3]] | [[[pi1_3_3<=pb3_2_1 | pb2_2_1<=3] | [pb3_2_3<=pil3_3_1 & 4<=pb3_3_4]] | pil3_1_1<=pb1_3_3]]] | [pol2_1_1<=5 | 3<=pb1_3_2]]] | [[[5<=pil3_1_1 & [~ [[pb3_3_4<=pil3_2_3 & po3_1_1<=pb2_1_1]] | 6<=pbl_3_2]] & [pol2_3_5<=6 & ~ [[3<=pbl_3_5 | [[pol3_3_3<=6 | 4<=pil1_1_1] | [pb2_2_3<=pil2_2_1 | 2<=pb2_3_2]]]]]] & ~ [[~ [[~ [pil3_1_1<=pb3_3_1] | pol3_3_3<=4]] | [pi1_1_1<=6 & 5<=pol2_3_5]]]]]]]
normalized: E [true U ~ [[[~ [[[pi1_1_1<=6 & 5<=pol2_3_5] | ~ [[pol3_3_3<=4 | ~ [pil3_1_1<=pb3_3_1]]]]] & [[pol2_3_5<=6 & ~ [[3<=pbl_3_5 | [[pb2_2_3<=pil2_2_1 | 2<=pb2_3_2] | [pol3_3_3<=6 | 4<=pil1_1_1]]]]] & [5<=pil3_1_1 & [6<=pbl_3_2 | ~ [[pb3_3_4<=pil3_2_3 & po3_1_1<=pb2_1_1]]]]]] | [[[pol2_1_1<=5 | 3<=pb1_3_2] | [po1_2_1<=pil1_3_5 | [[pil3_1_1<=pb1_3_3 | [[pb3_2_3<=pil3_3_1 & 4<=pb3_3_4] | [pi1_3_3<=pb3_2_1 | pb2_2_1<=3]]] | [pol3_3_5<=pil1_3_3 & [2<=pi1_2_3 | [po1_2_3<=po2_1_1 & pol2_1_1<=pil3_3_1]]]]]] & [~ [[[~ [pb2_3_5<=pol1_3_3] & [pb2_3_5<=po2_3_5 & pil2_2_1<=0]] & [~ [pb1_3_3<=pi3_3_1] & ~ [pb1_3_3<=po3_3_3]]]] | ~ [[[[pbl_2_1<=3 | [po3_3_5<=pi3_2_1 | pil2_2_3<=3]] | [pbl_2_2<=pil3_3_1 & [pbl_2_3<=pil2_3_1 | pi1_2_3<=po2_1_1]]] | [[[3<=pb2_1_1 | 3<=po2_2_3] & [pil3_3_3<=pbl_3_5 & pil3_3_5<=5]] & [pil1_3_3<=1 | ~ [6<=pol2_3_5]]]]]]]]]]
abstracting: (6<=pol2_3_5)
states: 0
abstracting: (pil1_3_3<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil3_3_5<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil3_3_3<=pbl_3_5)
states: 37,208,962,472,286,437,143,770,801,857 (28)
abstracting: (3<=po2_2_3)
states: 0
abstracting: (3<=pb2_1_1)
states: 8,279,901,115,204,979,072,751,695,217 (27)
abstracting: (pi1_2_3<=po2_1_1)
states: 28,621,394,029,562,948,099,541,149,549 (28)
abstracting: (pbl_2_3<=pil2_3_1)
states: 956,904,788,239,300,656,181,298,249 (26)
abstracting: (pbl_2_2<=pil3_3_1)
states: 956,905,118,118,753,062,003,344,510 (26)
abstracting: (pil2_2_3<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (po3_3_5<=pi3_2_1)
states: 28,621,450,933,514,325,343,354,951,981 (28)
abstracting: (pbl_2_1<=3)
states: 3,833,904,837,342,938,173,040,668,000 (27)
abstracting: (pb1_3_3<=po3_3_3)
states: 17,999,149,287,518,676,828,075,617,469 (28)
abstracting: (pb1_3_3<=pi3_3_1)
states: 17,999,134,866,252,675,346,818,757,277 (28)
abstracting: (pil2_2_1<=0)
states: 14,413,948,073,376,816,868,854,295,739 (28)
abstracting: (pb2_3_5<=po2_3_5)
states: 17,999,109,891,786,851,236,048,893,900 (28)
abstracting: (pb2_3_5<=pol1_3_3)
states: 20,086,276,489,886,602,672,051,649,731 (28)
abstracting: (pol2_1_1<=pil3_3_1)
states: 28,621,430,843,259,356,517,337,503,597 (28)
abstracting: (po1_2_3<=po2_1_1)
states: 28,621,394,029,562,948,099,541,149,549 (28)
abstracting: (2<=pi1_2_3)
states: 0
abstracting: (pol3_3_5<=pil1_3_3)
states: 28,621,394,029,562,948,127,047,341,933 (28)
abstracting: (pb2_2_1<=3)
states: 32,696,012,580,278,849,415,868,557,198 (28)
abstracting: (pi1_3_3<=pb3_2_1)
states: 31,900,818,358,385,998,089,340,178,650 (28)
abstracting: (4<=pb3_3_4)
states: 4,825,510,724,751,101,092,745,592,348 (27)
abstracting: (pb3_2_3<=pil3_3_1)
states: 20,086,323,729,121,661,256,457,456,348 (28)
abstracting: (pil3_1_1<=pb1_3_3)
states: 28,651,411,847,746,955,878,432,673,096 (28)
abstracting: (po1_2_1<=pil1_3_5)
states: 32,007,684,416,853,318,271,009,018,158 (28)
abstracting: (3<=pb1_3_2)
states: 8,279,888,162,938,987,118,421,758,038 (27)
abstracting: (pol2_1_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (po3_1_1<=pb2_1_1)
states: 31,900,834,801,344,089,408,761,730,977 (28)
abstracting: (pb3_3_4<=pil3_2_3)
states: 20,086,309,307,855,659,760,066,604,977 (28)
abstracting: (6<=pbl_3_2)
states: 28,772,315,181,658,757,456,293,247,843 (28)
abstracting: (5<=pil3_1_1)
states: 0
abstracting: (4<=pil1_1_1)
states: 0
abstracting: (pol3_3_3<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (2<=pb2_3_2)
states: 13,926,881,113,582,560,953,468,478,465 (28)
abstracting: (pb2_2_3<=pil2_2_1)
states: 20,086,309,307,855,659,716,122,605,621 (28)
abstracting: (3<=pbl_3_5)
states: 35,219,551,576,770,621,065,800,899,425 (28)
abstracting: (pol2_3_5<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil3_1_1<=pb3_3_1)
states: 28,651,442,644,023,923,112,921,481,616 (28)
abstracting: (pol3_3_3<=4)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (5<=pol2_3_5)
states: 0
abstracting: (pi1_1_1<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
before gc: list nodes free: 20024185
after gc: idd nodes used:1946961, unused:62053039; list nodes free:515300724
MC time: 8m 1.099sec
checking: AG [[[[[[[[[[pil1_3_5<=pb3_3_5 & pol3_2_3<=pil3_2_1] | [3<=po1_1_1 | 5<=pb2_3_3]] & [[pil1_3_5<=pil2_3_5 | pil3_3_1<=3] | ~ [5<=pil2_3_1]]] & pi3_2_1<=0] | pbl_3_3<=pil1_3_3] | [~ [[pb2_1_1<=pbl_3_3 | pi2_3_1<=pi2_2_1]] & [~ [pol2_2_1<=po2_3_5] | [[[3<=pb3_3_2 & po1_1_1<=3] & pi2_3_5<=6] | ~ [[pil1_3_3<=1 & pol2_3_3<=pol2_1_1]]]]]] | [pol3_3_1<=pb1_3_4 | [~ [[[1<=pb1_2_2 & 1<=pol3_3_1] | [~ [po2_2_1<=pol3_3_5] & 5<=pbl_2_1]]] | pb2_3_3<=pil1_3_3]]] | [~ [[[[pi1_1_1<=pb2_3_5 | [3<=pi1_1_1 & ~ [pil1_2_1<=5]]] & po2_2_3<=pi3_3_3] & ~ [[~ [[pb2_2_2<=0 & 4<=pb2_3_1]] | ~ [[pb2_2_1<=pol1_2_3 | 5<=pb3_3_5]]]]]] & [[pol2_3_3<=po1_2_3 & pb3_3_2<=1] | [[pil3_2_3<=3 | ~ [1<=po3_1_1]] | ~ [[~ [2<=pb3_2_2] & pi2_3_1<=pi2_2_1]]]]]] | [[pb2_1_1<=pol2_3_5 & [~ [[[~ [pb2_3_4<=0] & [[pb2_2_2<=4 & po2_3_1<=3] & [2<=pol3_3_1 & pol3_3_5<=pil3_2_3]]] & [~ [[5<=pil2_3_1 & pol3_1_1<=pil2_1_1]] | pb2_2_2<=2]]] & pol3_1_1<=pol2_1_1]] & pbl_2_2<=5]]]
normalized: ~ [E [true U ~ [[[[[[[[~ [[pil1_3_3<=1 & pol2_3_3<=pol2_1_1]] | [pi2_3_5<=6 & [3<=pb3_3_2 & po1_1_1<=3]]] | ~ [pol2_2_1<=po2_3_5]] & ~ [[pb2_1_1<=pbl_3_3 | pi2_3_1<=pi2_2_1]]] | [pbl_3_3<=pil1_3_3 | [pi3_2_1<=0 & [[~ [5<=pil2_3_1] | [pil1_3_5<=pil2_3_5 | pil3_3_1<=3]] & [[3<=po1_1_1 | 5<=pb2_3_3] | [pil1_3_5<=pb3_3_5 & pol3_2_3<=pil3_2_1]]]]]] | [pol3_3_1<=pb1_3_4 | [pb2_3_3<=pil1_3_3 | ~ [[[5<=pbl_2_1 & ~ [po2_2_1<=pol3_3_5]] | [1<=pb1_2_2 & 1<=pol3_3_1]]]]]] | [[[~ [[pi2_3_1<=pi2_2_1 & ~ [2<=pb3_2_2]]] | [pil3_2_3<=3 | ~ [1<=po3_1_1]]] | [pol2_3_3<=po1_2_3 & pb3_3_2<=1]] & ~ [[~ [[~ [[pb2_2_1<=pol1_2_3 | 5<=pb3_3_5]] | ~ [[pb2_2_2<=0 & 4<=pb2_3_1]]]] & [po2_2_3<=pi3_3_3 & [pi1_1_1<=pb2_3_5 | [3<=pi1_1_1 & ~ [pil1_2_1<=5]]]]]]]] | [pbl_2_2<=5 & [pb2_1_1<=pol2_3_5 & [pol3_1_1<=pol2_1_1 & ~ [[[pb2_2_2<=2 | ~ [[5<=pil2_3_1 & pol3_1_1<=pil2_1_1]]] & [[[2<=pol3_3_1 & pol3_3_5<=pil3_2_3] & [pb2_2_2<=4 & po2_3_1<=3]] & ~ [pb2_3_4<=0]]]]]]]]]]]
abstracting: (pb2_3_4<=0)
states: 14,490,816,403,926,946,995,498,942,331 (28)
abstracting: (po2_3_1<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pb2_2_2<=4)
states: 34,776,379,038,957,839,645,154,466,793 (28)
abstracting: (pol3_3_5<=pil3_2_3)
states: 28,621,394,029,562,948,099,541,149,549 (28)
abstracting: (2<=pol3_3_1)
states: 0
abstracting: (pol3_1_1<=pil2_1_1)
states: 28,621,450,933,514,325,282,844,282,157 (28)
abstracting: (5<=pil2_3_1)
states: 0
abstracting: (pb2_2_2<=2)
states: 29,241,635,142,090,963,379,637,754,933 (28)
abstracting: (pol3_1_1<=pol2_1_1)
states: 28,621,450,933,514,325,282,844,282,157 (28)
abstracting: (pb2_1_1<=pol2_3_5)
states: 20,086,290,911,156,761,225,477,775,159 (28)
abstracting: (pbl_2_2<=5)
states: 8,749,208,123,371,193,041,766,265,128 (27)
abstracting: (pil1_2_1<=5)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (3<=pi1_1_1)
states: 0
abstracting: (pi1_1_1<=pb2_3_5)
states: 31,900,860,909,011,611,064,881,159,300 (28)
abstracting: (po2_2_3<=pi3_3_3)
states: 28,621,414,119,829,765,896,299,175,725 (28)
abstracting: (4<=pb2_3_1)
states: 4,825,429,521,265,642,670,941,692,634 (27)
abstracting: (pb2_2_2<=0)
states: 14,490,816,403,926,946,995,498,942,331 (28)
abstracting: (5<=pb3_3_5)
states: 2,745,147,524,639,531,155,350,814,158 (27)
abstracting: (pb2_2_1<=pol1_2_3)
states: 20,086,309,307,855,659,776,740,182,160 (28)
abstracting: (pb3_3_2<=1)
states: 23,594,642,191,447,389,584,074,373,347 (28)
abstracting: (pol2_3_3<=po1_2_3)
states: 23,314,057,258,577,001,496,461,987,353 (28)
abstracting: (1<=po3_1_1)
states: 14,413,948,073,376,816,835,849,818,299 (28)
abstracting: (pil3_2_3<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (2<=pb3_2_2)
states: 13,926,881,113,582,560,953,468,478,465 (28)
abstracting: (pi2_3_1<=pi2_2_1)
states: 28,621,414,119,829,765,897,958,013,741 (28)
abstracting: (1<=pol3_3_1)
states: 23,107,632,135,604,510,845,512,827,280 (28)
abstracting: (1<=pb1_2_2)
states: 23,030,706,901,103,003,502,560,570,640 (28)
abstracting: (po2_2_1<=pol3_3_5)
states: 32,007,704,507,120,136,000,217,388,270 (28)
abstracting: (5<=pbl_2_1)
states: 31,577,448,623,370,092,618,196,778,191 (28)
abstracting: (pb2_3_3<=pil1_3_3)
states: 20,086,309,307,855,659,769,856,169,816 (28)
abstracting: (pol3_3_1<=pb1_3_4)
states: 28,651,385,740,072,545,978,968,754,639 (28)
abstracting: (pol3_2_3<=pil3_2_1)
states: 28,621,414,119,829,765,870,451,821,357 (28)
abstracting: (pil1_3_5<=pb3_3_5)
states: 28,651,442,644,023,923,156,024,557,276 (28)
abstracting: (5<=pb2_3_3)
states: 2,745,144,266,072,110,842,339,579,189 (27)
abstracting: (3<=po1_1_1)
states: 0
abstracting: (pil3_3_1<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pil1_3_5<=pil2_3_5)
states: 28,621,450,933,514,325,282,844,282,157 (28)
abstracting: (5<=pil2_3_1)
states: 0
abstracting: (pi3_2_1<=0)
states: 23,107,575,231,653,133,629,205,217,232 (28)
abstracting: (pbl_3_3<=pil1_3_3)
states: 956,904,788,239,300,656,181,298,249 (26)
abstracting: (pi2_3_1<=pi2_2_1)
states: 28,621,414,119,829,765,897,958,013,741 (28)
abstracting: (pb2_1_1<=pbl_3_3)
states: 36,287,651,144,156,364,876,228,802,047 (28)
abstracting: (pol2_2_1<=po2_3_5)
states: 23,314,020,444,892,442,023,558,856,729 (28)
abstracting: (po1_1_1<=3)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (3<=pb3_3_2)
states: 8,279,888,162,938,987,118,421,758,038 (27)
abstracting: (pi2_3_5<=6)
states: 37,521,523,305,029,950,498,059,512,971 (28)
abstracting: (pol2_3_3<=pol2_1_1)
states: 28,621,450,933,514,325,343,354,951,981 (28)
abstracting: (pil1_3_3<=1)
states: 37,521,523,305,029,950,498,059,512,971 (28)
before gc: list nodes free: 29723396
after gc: idd nodes used:7517012, unused:56482988; list nodes free:474068397
before gc: list nodes free: 77833704
after gc: idd nodes used:12139726, unused:51860274; list nodes free:441935367
TIME LIMIT: Killed by timeout after 3600 seconds
MemTotal: 16393932 kB
MemFree: 2440280 kB
After kill :
MemTotal: 16393932 kB
MemFree: 16179124 kB
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:96798 (1075), effective:13697 (152)
initing FirstDep: 0m 0.000sec
iterations count:2756 (30), effective:358 (3)
iterations count:5121 (56), effective:559 (6)
sat_reach.icc:155: Timeout: after 295 sec
sat_reach.icc:155: Timeout: after 295 sec
iterations count:6444 (71), effective:838 (9)
sat_reach.icc:155: Timeout: after 481 sec
sat_reach.icc:155: Timeout: after 480 sec
sat_reach.icc:155: Timeout: after 384 sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="TriangularGrid-PT-3026"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marcie"
echo " Input is TriangularGrid-PT-3026, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r481-tall-167912692400742"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/TriangularGrid-PT-3026.tgz
mv TriangularGrid-PT-3026 execution
cd execution
if [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "UpperBounds" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] || [ "ReachabilityCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "ReachabilityCardinality" = "ReachabilityDeadlock" ] || [ "ReachabilityCardinality" = "QuasiLiveness" ] || [ "ReachabilityCardinality" = "StableMarking" ] || [ "ReachabilityCardinality" = "Liveness" ] || [ "ReachabilityCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME ReachabilityCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

