MCC'2023- Execution of r265-smll-167863539700211

About the Execution of LTSMin+red for NeoElection-PT-7

Execution Summary
Max Memory Used (MB)	Time wait (ms)	CPU Usage (ms)	I/O Wait (ms)	Computed Result	Execution Status
726.836	947101.00	3650524.00	894.20	?T?TFFT?FFFTF?FF	normal

Execution Chart

We display below the execution chart for this examination (boot time has been removed).

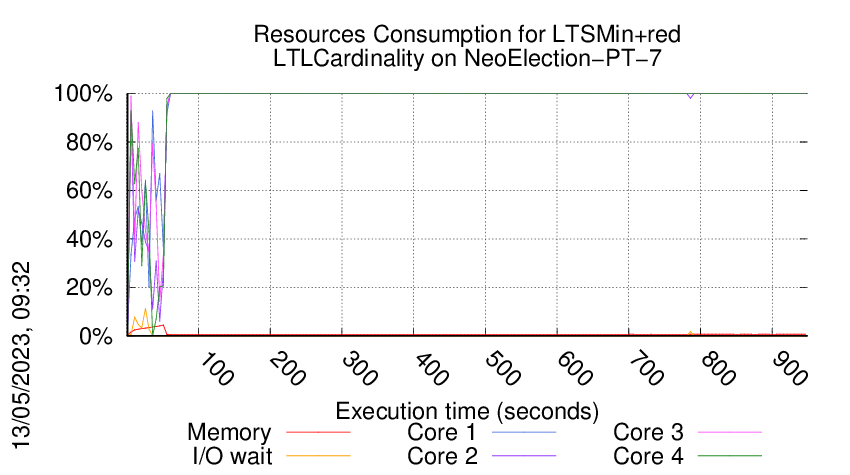
Trace from the execution

Formatting '/data/fkordon/mcc2023-input.r265-smll-167863539700211.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool ltsminxred
Input is NeoElection-PT-7, examination is LTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r265-smll-167863539700211
=====================================================================

--------------------
preparation of the directory to be used:
/home/mcc/execution
total 41M
-rw-r--r-- 1 mcc users 979K Feb 26 17:35 CTLCardinality.txt
-rw-r--r-- 1 mcc users 3.0M Feb 26 17:35 CTLCardinality.xml
-rw-r--r-- 1 mcc users 947K Feb 26 16:53 CTLFireability.txt
-rw-r--r-- 1 mcc users 3.2M Feb 26 16:53 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.6K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 507K Feb 25 16:28 LTLCardinality.txt
-rw-r--r-- 1 mcc users 1.3M Feb 25 16:28 LTLCardinality.xml
-rw-r--r-- 1 mcc users 176K Feb 25 16:28 LTLFireability.txt
-rw-r--r-- 1 mcc users 447K Feb 25 16:28 LTLFireability.xml
-rw-r--r-- 1 mcc users 2.1M Feb 26 19:11 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 6.6M Feb 26 19:11 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 2.1M Feb 26 18:43 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 6.8M Feb 26 18:43 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 75K Feb 25 16:28 UpperBounds.txt
-rw-r--r-- 1 mcc users 147K Feb 25 16:28 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 5 18:23 equiv_col
-rw-r--r-- 1 mcc users 2 Mar 5 18:23 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:23 iscolored
-rw-r--r-- 1 mcc users 13M Mar 5 18:23 model.pnml

--------------------
content from stdout:

=== Data for post analysis generated by BenchKit (invocation template)

The expected result is a vector of booleans
BOOL_VECTOR

here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-7-LTLCardinality-00
FORMULA_NAME NeoElection-PT-7-LTLCardinality-01
FORMULA_NAME NeoElection-PT-7-LTLCardinality-02
FORMULA_NAME NeoElection-PT-7-LTLCardinality-03
FORMULA_NAME NeoElection-PT-7-LTLCardinality-04
FORMULA_NAME NeoElection-PT-7-LTLCardinality-05
FORMULA_NAME NeoElection-PT-7-LTLCardinality-06
FORMULA_NAME NeoElection-PT-7-LTLCardinality-07
FORMULA_NAME NeoElection-PT-7-LTLCardinality-08
FORMULA_NAME NeoElection-PT-7-LTLCardinality-09
FORMULA_NAME NeoElection-PT-7-LTLCardinality-10
FORMULA_NAME NeoElection-PT-7-LTLCardinality-11
FORMULA_NAME NeoElection-PT-7-LTLCardinality-12
FORMULA_NAME NeoElection-PT-7-LTLCardinality-13
FORMULA_NAME NeoElection-PT-7-LTLCardinality-14
FORMULA_NAME NeoElection-PT-7-LTLCardinality-15

=== Now, execution of the tool begins

BK_START 1678831118872

bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=ltsminxred
BK_EXAMINATION=LTLCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=NeoElection-PT-7
Applying reductions before tool ltsmin
Invoking reducer
Running Version 202303021504
[2023-03-14 21:58:41] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, LTLCardinality, -timeout, 360, -rebuildPNML]
[2023-03-14 21:58:41] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-14 21:58:42] [INFO ] Load time of PNML (sax parser for PT used): 864 ms
[2023-03-14 21:58:42] [INFO ] Transformed 7128 places.
[2023-03-14 21:58:42] [INFO ] Transformed 14112 transitions.
[2023-03-14 21:58:42] [INFO ] Found NUPN structural information;
[2023-03-14 21:58:42] [INFO ] Completing missing partition info from NUPN : creating a component with [P_crashed_0, P_crashed_1, P_crashed_2, P_crashed_3, P_crashed_4, P_crashed_5, P_crashed_6, P_crashed_7, P_dead_0, P_dead_1, P_dead_2, P_dead_3, P_dead_4, P_dead_5, P_dead_6, P_dead_7, P_electedPrimary_0, P_electedPrimary_1, P_electedPrimary_2, P_electedPrimary_3, P_electedPrimary_4, P_electedPrimary_5, P_electedPrimary_6, P_electedPrimary_7, P_electedSecondary_0, P_electedSecondary_1, P_electedSecondary_2, P_electedSecondary_3, P_electedSecondary_4, P_electedSecondary_5, P_electedSecondary_6, P_electedSecondary_7, P_electionFailed_0, P_electionFailed_1, P_electionFailed_2, P_electionFailed_3, P_electionFailed_4, P_electionFailed_5, P_electionFailed_6, P_electionFailed_7, P_electionInit_0, P_electionInit_1, P_electionInit_2, P_electionInit_3, P_electionInit_4, P_electionInit_5, P_electionInit_6, P_electionInit_7, P_masterList_0_1_0, P_masterList_0_1_1, P_masterList_0_1_2, P_masterList_0_1_3, P_masterList_0_1_4, P_masterList_0_1_5, P_masterList_0_1_6, P_masterList_0_1_7, P_masterList_0_2_0, P_masterList_0_2_1, P_masterList_0_2_2, P_masterList_0_2_3, P_masterList_0_2_4, P_masterList_0_2_5, P_masterList_0_2_6, P_masterList_0_2_7, P_masterList_0_3_0, P_masterList_0_3_1, P_masterList_0_3_2, P_masterList_0_3_3, P_masterList_0_3_4, P_masterList_0_3_5, P_masterList_0_3_6, P_masterList_0_3_7, P_masterList_0_4_0, P_masterList_0_4_1, P_masterList_0_4_2, P_masterList_0_4_3, P_masterList_0_4_4, P_masterList_0_4_5, P_masterList_0_4_6, P_masterList_0_4_7, P_masterList_0_5_0, P_masterList_0_5_1, P_masterList_0_5_2, P_masterList_0_5_3, P_masterList_0_5_4, P_masterList_0_5_5, P_masterList_0_5_6, P_masterList_0_5_7, P_masterList_0_6_0, P_masterList_0_6_1, P_masterList_0_6_2, P_masterList_0_6_3, P_masterList_0_6_4, P_masterList_0_6_5, P_masterList_0_6_6, P_masterList_0_6_7, P_masterList_0_7_0, P_masterList_0_7_1, P_masterList_0_7_2, P_masterList_0_7_3, P_masterList_0_7_4, P_masterList_0_7_5, P_masterList_0_7_6, P_masterList_0_7_7, P_masterList_1_1_0, P_masterList_1_1_1, P_masterList_1_1_2, P_masterList_1_1_3, P_masterList_1_1_4, P_masterList_1_1_5, P_masterList_1_1_6, P_masterList_1_1_7, P_masterList_1_2_0, P_masterList_1_2_1, P_masterList_1_2_2, P_masterList_1_2_3, P_masterList_1_2_4, P_masterList_1_2_5, P_masterList_1_2_6, P_masterList_1_2_7, P_masterList_1_3_0, P_masterList_1_3_1, P_masterList_1_3_2, P_masterList_1_3_3, P_masterList_1_3_4, P_masterList_1_3_5, P_masterList_1_3_6, P_masterList_1_3_7, P_masterList_1_4_0, P_masterList_1_4_1, P_masterList_1_4_2, P_masterList_1_4_3, P_masterList_1_4_4, P_masterList_1_4_5, P_masterList_1_4_6, P_masterList_1_4_7, P_masterList_1_5_0, P_masterList_1_5_1, P_masterList_1_5_2, P_masterList_1_5_3, P_masterList_1_5_4, P_masterList_1_5_5, P_masterList_1_5_6, P_masterList_1_5_7, P_masterList_1_6_0, P_masterList_1_6_1, P_masterList_1_6_2, P_masterList_1_6_3, P_masterList_1_6_4, P_masterList_1_6_5, P_masterList_1_6_6, P_masterList_1_6_7, P_masterList_1_7_0, P_masterList_1_7_1, P_masterList_1_7_2, P_masterList_1_7_3, P_masterList_1_7_4, P_masterList_1_7_5, P_masterList_1_7_6, P_masterList_1_7_7, P_masterList_2_1_0, P_masterList_2_1_1, P_masterList_2_1_2, P_masterList_2_1_3, P_masterList_2_1_4, P_masterList_2_1_5, P_masterList_2_1_6, P_masterList_2_1_7, P_masterList_2_2_0, P_masterList_2_2_1, P_masterList_2_2_2, P_masterList_2_2_3, P_masterList_2_2_4, P_masterList_2_2_5, P_masterList_2_2_6, P_masterList_2_2_7, P_masterList_2_3_0, P_masterList_2_3_1, P_masterList_2_3_2, P_masterList_2_3_3, P_masterList_2_3_4, P_masterList_2_3_5, P_masterList_2_3_6, P_masterList_2_3_7, P_masterList_2_4_0, P_masterList_2_4_1, P_masterList_2_4_2, P_masterList_2_4_3, P_masterList_2_4_4, P_masterList_2_4_5, P_masterList_2_4_6, P_masterList_2_4_7, P_masterList_2_5_0, P_masterList_2_5_1, P_masterList_2_5_2, P_masterList_2_5_3, P_masterList_2_5_4, P_masterList_2_5_5, P_masterList_2_5_6, P_masterList_2_5_7, P_masterList_2_6_0, P_masterList_2_6_1, P_masterList_2_6_2, P_masterList_2_6_3, P_masterList_2_6_4, P_masterList_2_6_5, P_masterList_2_6_6, P_masterList_2_6_7, P_masterList_2_7_0, P_masterList_2_7_1, P_masterList_2_7_2, P_masterList_2_7_3, P_masterList_2_7_4, P_masterList_2_7_5, P_masterList_2_7_6, P_masterList_2_7_7, P_masterList_3_1_0, P_masterList_3_1_1, P_masterList_3_1_2, P_masterList_3_1_3, P_masterList_3_1_4, P_masterList_3_1_5, P_masterList_3_1_6, P_masterList_3_1_7, P_masterList_3_2_0, P_masterList_3_2_1, P_masterList_3_2_2, P_masterList_3_2_3, P_masterList_3_2_4, P_masterList_3_2_5, P_masterList_3_2_6, P_masterList_3_2_7, P_masterList_3_3_0, P_masterList_3_3_1, P_masterList_3_3_2, P_masterList_3_3_3, P_masterList_3_3_4, P_masterList_3_3_5, P_masterList_3_3_6, P_masterList_3_3_7, P_masterList_3_4_0, P_masterList_3_4_1, P_masterList_3_4_2, P_masterList_3_4_3, P_masterList_3_4_4, P_masterList_3_4_5, P_masterList_3_4_6, P_masterList_3_4_7, P_masterList_3_5_0, P_masterList_3_5_1, P_masterList_3_5_2, P_masterList_3_5_3, P_masterList_3_5_4, P_masterList_3_5_5, P_masterList_3_5_6, P_masterList_3_5_7, P_masterList_3_6_0, P_masterList_3_6_1, P_masterList_3_6_2, P_masterList_3_6_3, P_masterList_3_6_4, P_masterList_3_6_5, P_masterList_3_6_6, P_masterList_3_6_7, P_masterList_3_7_0, P_masterList_3_7_1, P_masterList_3_7_2, P_masterList_3_7_3, P_masterList_3_7_4, P_masterList_3_7_5, P_masterList_3_7_6, P_masterList_3_7_7, P_masterList_4_1_0, P_masterList_4_1_1, P_masterList_4_1_2, P_masterList_4_1_3, P_masterList_4_1_4, P_masterList_4_1_5, P_masterList_4_1_6, P_masterList_4_1_7, P_masterList_4_2_0, P_masterList_4_2_1, P_masterList_4_2_2, P_masterList_4_2_3, P_masterList_4_2_4, P_masterList_4_2_5, P_masterList_4_2_6, P_masterList_4_2_7, P_masterList_4_3_0, P_masterList_4_3_1, P_masterList_4_3_2, P_masterList_4_3_3, P_masterList_4_3_4, P_masterList_4_3_5, P_masterList_4_3_6, P_masterList_4_3_7, P_masterList_4_4_0, P_masterList_4_4_1, P_masterList_4_4_2, P_masterList_4_4_3, P_masterList_4_4_4, P_masterList_4_4_5, P_masterList_4_4_6, P_masterList_4_4_7, P_masterList_4_5_0, P_masterList_4_5_1, P_masterList_4_5_2, P_masterList_4_5_3, P_masterList_4_5_4, P_masterList_4_5_5, P_masterList_4_5_6, P_masterList_4_5_7, P_masterList_4_6_0, P_masterList_4_6_1, P_masterList_4_6_2, P_masterList_4_6_3, P_masterList_4_6_4, P_masterList_4_6_5, P_masterList_4_6_6, P_masterList_4_6_7, P_masterList_4_7_0, P_masterList_4_7_1, P_masterList_4_7_2, P_masterList_4_7_3, P_masterList_4_7_4, P_masterList_4_7_5, P_masterList_4_7_6, P_masterList_4_7_7, P_masterList_5_1_0, P_masterList_5_1_1, P_masterList_5_1_2, P_masterList_5_1_3, P_masterList_5_1_4, P_masterList_5_1_5, P_masterList_5_1_6, P_masterList_5_1_7, P_masterList_5_2_0, P_masterList_5_2_1, P_masterList_5_2_2, P_masterList_5_2_3, P_masterList_5_2_4, P_masterList_5_2_5, P_masterList_5_2_6, P_masterList_5_2_7, P_masterList_5_3_0, P_masterList_5_3_1, P_masterList_5_3_2, P_masterList_5_3_3, P_masterList_5_3_4, P_masterList_5_3_5, P_masterList_5_3_6, P_masterList_5_3_7, P_masterList_5_4_0, P_masterList_5_4_1, P_masterList_5_4_2, P_masterList_5_4_3, P_masterList_5_4_4, P_masterList_5_4_5, P_masterList_5_4_6, P_masterList_5_4_7, P_masterList_5_5_0, P_masterList_5_5_1, P_masterList_5_5_2, P_masterList_5_5_3, P_masterList_5_5_4, P_masterList_5_5_5, P_masterList_5_5_6, P_masterList_5_5_7, P_masterList_5_6_0, P_masterList_5_6_1, P_masterList_5_6_2, P_masterList_5_6_3, P_masterList_5_6_4, P_masterList_5_6_5, P_masterList_5_6_6, P_masterList_5_6_7, P_masterList_5_7_0, P_masterList_5_7_1, P_masterList_5_7_2, P_masterList_5_7_3, P_masterList_5_7_4, P_masterList_5_7_5, P_masterList_5_7_6, P_masterList_5_7_7, P_masterList_6_1_0, P_masterList_6_1_1, P_masterList_6_1_2, P_masterList_6_1_3, P_masterList_6_1_4, P_masterList_6_1_5, P_masterList_6_1_6, P_masterList_6_1_7, P_masterList_6_2_0, P_masterList_6_2_1, P_masterList_6_2_2, P_masterList_6_2_3, P_masterList_6_2_4, P_masterList_6_2_5, P_masterList_6_2_6, P_masterList_6_2_7, P_masterList_6_3_0, P_masterList_6_3_1, P_masterList_6_3_2, P_masterList_6_3_3, P_masterList_6_3_4, P_masterList_6_3_5, P_masterList_6_3_6, P_masterList_6_3_7, P_masterList_6_4_0, P_masterList_6_4_1, P_masterList_6_4_2, P_masterList_6_4_3, P_masterList_6_4_4, P_masterList_6_4_5, P_masterList_6_4_6, P_masterList_6_4_7, P_masterList_6_5_0, P_masterList_6_5_1, P_masterList_6_5_2, P_masterList_6_5_3, P_masterList_6_5_4, P_masterList_6_5_5, P_masterList_6_5_6, P_masterList_6_5_7, P_masterList_6_6_0, P_masterList_6_6_1, P_masterList_6_6_2, P_masterList_6_6_3, P_masterList_6_6_4, P_masterList_6_6_5, P_masterList_6_6_6, P_masterList_6_6_7, P_masterList_6_7_0, P_masterList_6_7_1, P_masterList_6_7_2, P_masterList_6_7_3, P_masterList_6_7_4, P_masterList_6_7_5, P_masterList_6_7_6, P_masterList_6_7_7, P_masterList_7_1_0, P_masterList_7_1_1, P_masterList_7_1_2, P_masterList_7_1_3, P_masterList_7_1_4, P_masterList_7_1_5, P_masterList_7_1_6, P_masterList_7_1_7, P_masterList_7_2_0, P_masterList_7_2_1, P_masterList_7_2_2, P_masterList_7_2_3, P_masterList_7_2_4, P_masterList_7_2_5, P_masterList_7_2_6, P_masterList_7_2_7, P_masterList_7_3_0, P_masterList_7_3_1, P_masterList_7_3_2, P_masterList_7_3_3, P_masterList_7_3_4, P_masterList_7_3_5, P_masterList_7_3_6, P_masterList_7_3_7, P_masterList_7_4_0, P_masterList_7_4_1, P_masterList_7_4_2, P_masterList_7_4_3, P_masterList_7_4_4, P_masterList_7_4_5, P_masterList_7_4_6, P_masterList_7_4_7, P_masterList_7_5_0, P_masterList_7_5_1, P_masterList_7_5_2, P_masterList_7_5_3, P_masterList_7_5_4, P_masterList_7_5_5, P_masterList_7_5_6, P_masterList_7_5_7, P_masterList_7_6_0, P_masterList_7_6_1, P_masterList_7_6_2, P_masterList_7_6_3, P_masterList_7_6_4, P_masterList_7_6_5, P_masterList_7_6_6, P_masterList_7_6_7, P_masterList_7_7_0, P_masterList_7_7_1, P_masterList_7_7_2, P_masterList_7_7_3, P_masterList_7_7_4, P_masterList_7_7_5, P_masterList_7_7_6, P_masterList_7_7_7, P_masterState_0_F_0, P_masterState_0_F_1, P_masterState_0_F_2, P_masterState_0_F_3, P_masterState_0_F_4, P_masterState_0_F_5, P_masterState_0_F_6, P_masterState_0_F_7, P_masterState_0_T_0, P_masterState_0_T_1, P_masterState_0_T_2, P_masterState_0_T_3, P_masterState_0_T_4, P_masterState_0_T_5, P_masterState_0_T_6, P_masterState_0_T_7, P_masterState_1_F_0, P_masterState_1_F_1, P_masterState_1_F_2, P_masterState_1_F_3, P_masterState_1_F_4, P_masterState_1_F_5, P_masterState_1_F_6, P_masterState_1_F_7, P_masterState_1_T_0, P_masterState_1_T_1, P_masterState_1_T_2, P_masterState_1_T_3, P_masterState_1_T_4, P_masterState_1_T_5, P_masterState_1_T_6, P_masterState_1_T_7, P_masterState_2_F_0, P_masterState_2_F_1, P_masterState_2_F_2, P_masterState_2_F_3, P_masterState_2_F_4, P_masterState_2_F_5, P_masterState_2_F_6, P_masterState_2_F_7, P_masterState_2_T_0, P_masterState_2_T_1, P_masterState_2_T_2, P_masterState_2_T_3, P_masterState_2_T_4, P_masterState_2_T_5, P_masterState_2_T_6, P_masterState_2_T_7, P_masterState_3_F_0, P_masterState_3_F_1, P_masterState_3_F_2, P_masterState_3_F_3, P_masterState_3_F_4, P_masterState_3_F_5, P_masterState_3_F_6, P_masterState_3_F_7, P_masterState_3_T_0, P_masterState_3_T_1, P_masterState_3_T_2, P_masterState_3_T_3, P_masterState_3_T_4, P_masterState_3_T_5, P_masterState_3_T_6, P_masterState_3_T_7, P_masterState_4_F_0, P_masterState_4_F_1, P_masterState_4_F_2, P_masterState_4_F_3, P_masterState_4_F_4, P_masterState_4_F_5, P_masterState_4_F_6, P_masterState_4_F_7, P_masterState_4_T_0, P_masterState_4_T_1, P_masterState_4_T_2, P_masterState_4_T_3, P_masterState_4_T_4, P_masterState_4_T_5, P_masterState_4_T_6, P_masterState_4_T_7, P_masterState_5_F_0, P_masterState_5_F_1, P_masterState_5_F_2, P_masterState_5_F_3, P_masterState_5_F_4, P_masterState_5_F_5, P_masterState_5_F_6, P_masterState_5_F_7, P_masterState_5_T_0, P_masterState_5_T_1, P_masterState_5_T_2, P_masterState_5_T_3, P_masterState_5_T_4, P_masterState_5_T_5, P_masterState_5_T_6, P_masterState_5_T_7, P_masterState_6_F_0, P_masterState_6_F_1, P_masterState_6_F_2, P_masterState_6_F_3, P_masterState_6_F_4, P_masterState_6_F_5, P_masterState_6_F_6, P_masterState_6_F_7, P_masterState_6_T_0, P_masterState_6_T_1, P_masterState_6_T_2, P_masterState_6_T_3, P_masterState_6_T_4, P_masterState_6_T_5, P_masterState_6_T_6, P_masterState_6_T_7, P_masterState_7_F_0, P_masterState_7_F_1, P_masterState_7_F_2, P_masterState_7_F_3, P_masterState_7_F_4, P_masterState_7_F_5, P_masterState_7_F_6, P_masterState_7_F_7, P_masterState_7_T_0, P_masterState_7_T_1, P_masterState_7_T_2, P_masterState_7_T_3, P_masterState_7_T_4, P_masterState_7_T_5, P_masterState_7_T_6, P_masterState_7_T_7, P_negotiation_0_0_NONE, P_negotiation_0_0_CO, P_negotiation_0_0_DONE, P_negotiation_0_1_NONE, P_negotiation_0_1_CO, P_negotiation_0_1_DONE, P_negotiation_0_2_NONE, P_negotiation_0_2_CO, P_negotiation_0_2_DONE, P_negotiation_0_3_NONE, P_negotiation_0_3_CO, P_negotiation_0_3_DONE, P_negotiation_0_4_NONE, P_negotiation_0_4_CO, P_negotiation_0_4_DONE, P_negotiation_0_5_NONE, P_negotiation_0_5_CO, P_negotiation_0_5_DONE, P_negotiation_0_6_NONE, P_negotiation_0_6_CO, P_negotiation_0_6_DONE, P_negotiation_0_7_NONE, P_negotiation_0_7_CO, P_negotiation_0_7_DONE, P_negotiation_1_0_NONE, P_negotiation_1_0_CO, P_negotiation_1_0_DONE, P_negotiation_1_1_NONE, P_negotiation_1_1_CO, P_negotiation_1_1_DONE, P_negotiation_1_2_NONE, P_negotiation_1_2_CO, P_negotiation_1_2_DONE, P_negotiation_1_3_NONE, P_negotiation_1_3_CO, P_negotiation_1_3_DONE, P_negotiation_1_4_NONE, P_negotiation_1_4_CO, P_negotiation_1_4_DONE, P_negotiation_1_5_NONE, P_negotiation_1_5_CO, P_negotiation_1_5_DONE, P_negotiation_1_6_NONE, P_negotiation_1_6_CO, P_negotiation_1_6_DONE, P_negotiation_1_7_NONE, P_negotiation_1_7_CO, P_negotiation_1_7_DONE, P_negotiation_2_0_NONE, P_negotiation_2_0_CO, P_negotiation_2_0_DONE, P_negotiation_2_1_NONE, P_negotiation_2_1_CO, P_negotiation_2_1_DONE, P_negotiation_2_2_NONE, P_negotiation_2_2_CO, P_negotiation_2_2_DONE, P_negotiation_2_3_NONE, P_negotiation_2_3_CO, P_negotiation_2_3_DONE, P_negotiation_2_4_NONE, P_negotiation_2_4_CO, P_negotiation_2_4_DONE, P_negotiation_2_5_NONE, P_negotiation_2_5_CO, P_negotiation_2_5_DONE, P_negotiation_2_6_NONE, P_negotiation_2_6_CO, P_negotiation_2_6_DONE, P_negotiation_2_7_NONE, P_negotiation_2_7_CO, P_negotiation_2_7_DONE, P_negotiation_3_0_NONE, P_negotiation_3_0_CO, P_negotiation_3_0_DONE, P_negotiation_3_1_NONE, P_negotiation_3_1_CO, P_negotiation_3_1_DONE, P_negotiation_3_2_NONE, P_negotiation_3_2_CO, P_negotiation_3_2_DONE, P_negotiation_3_3_NONE, P_negotiation_3_3_CO, P_negotiation_3_3_DONE, P_negotiation_3_4_NONE, P_negotiation_3_4_CO, P_negotiation_3_4_DONE, P_negotiation_3_5_NONE, P_negotiation_3_5_CO, P_negotiation_3_5_DONE, P_negotiation_3_6_NONE, P_negotiation_3_6_CO, P_negotiation_3_6_DONE, P_negotiation_3_7_NONE, P_negotiation_3_7_CO, P_negotiation_3_7_DONE, P_negotiation_4_0_NONE, P_negotiation_4_0_CO, P_negotiation_4_0_DONE, P_negotiation_4_1_NONE, P_negotiation_4_1_CO, P_negotiation_4_1_DONE, P_negotiation_4_2_NONE, P_negotiation_4_2_CO, P_negotiation_4_2_DONE, P_negotiation_4_3_NONE, P_negotiation_4_3_CO, P_negotiation_4_3_DONE, P_negotiation_4_4_NONE, P_negotiation_4_4_CO, P_negotiation_4_4_DONE, P_negotiation_4_5_NONE, P_negotiation_4_5_CO, P_negotiation_4_5_DONE, P_negotiation_4_6_NONE, P_negotiation_4_6_CO, P_negotiation_4_6_DONE, P_negotiation_4_7_NONE, P_negotiation_4_7_CO, P_negotiation_4_7_DONE, P_negotiation_5_0_NONE, P_negotiation_5_0_CO, P_negotiation_5_0_DONE, P_negotiation_5_1_NONE, P_negotiation_5_1_CO, P_negotiation_5_1_DONE, P_negotiation_5_2_NONE, P_negotiation_5_2_CO, P_negotiation_5_2_DONE, P_negotiation_5_3_NONE, P_negotiation_5_3_CO, P_negotiation_5_3_DONE, P_negotiation_5_4_NONE, P_negotiation_5_4_CO, P_negotiation_5_4_DONE, P_negotiation_5_5_NONE, P_negotiation_5_5_CO, P_negotiation_5_5_DONE, P_negotiation_5_6_NONE, P_negotiation_5_6_CO, P_negotiation_5_6_DONE, P_negotiation_5_7_NONE, P_negotiation_5_7_CO, P_negotiation_5_7_DONE, P_negotiation_6_0_NONE, P_negotiation_6_0_CO, P_negotiation_6_0_DONE, P_negotiation_6_1_NONE, P_negotiation_6_1_CO, P_negotiation_6_1_DONE, P_negotiation_6_2_NONE, P_negotiation_6_2_CO, P_negotiation_6_2_DONE, P_negotiation_6_3_NONE, P_negotiation_6_3_CO, P_negotiation_6_3_DONE, P_negotiation_6_4_NONE, P_negotiation_6_4_CO, P_negotiation_6_4_DONE, P_negotiation_6_5_NONE, P_negotiation_6_5_CO, P_negotiation_6_5_DONE, P_negotiation_6_6_NONE, P_negotiation_6_6_CO, P_negotiation_6_6_DONE, P_negotiation_6_7_NONE, P_negotiation_6_7_CO, P_negotiation_6_7_DONE, P_negotiation_7_0_NONE, P_negotiation_7_0_CO, P_negotiation_7_0_DONE, P_negotiation_7_1_NONE, P_negotiation_7_1_CO, P_negotiation_7_1_DONE, P_negotiation_7_2_NONE, P_negotiation_7_2_CO, P_negotiation_7_2_DONE, P_negotiation_7_3_NONE, P_negotiation_7_3_CO, P_negotiation_7_3_DONE, P_negotiation_7_4_NONE, P_negotiation_7_4_CO, P_negotiation_7_4_DONE, P_negotiation_7_5_NONE, P_negotiation_7_5_CO, P_negotiation_7_5_DONE, P_negotiation_7_6_NONE, P_negotiation_7_6_CO, P_negotiation_7_6_DONE, P_negotiation_7_7_NONE, P_negotiation_7_7_CO, P_negotiation_7_7_DONE, P_network_0_0_AskP_0, P_network_0_0_AskP_1, P_network_0_0_AskP_2, P_network_0_0_AskP_3, P_network_0_0_AskP_4, P_network_0_0_AskP_5, P_network_0_0_AskP_6, P_network_0_0_AskP_7, P_network_0_0_AnsP_0, P_network_0_0_AnsP_1, P_network_0_0_AnsP_2, P_network_0_0_AnsP_3, P_network_0_0_AnsP_4, P_network_0_0_AnsP_5, P_network_0_0_AnsP_6, P_network_0_0_AnsP_7, P_network_0_0_RI_0, P_network_0_0_RI_1, P_network_0_0_RI_2, P_network_0_0_RI_3, P_network_0_0_RI_4, P_network_0_0_RI_5, P_network_0_0_RI_6, P_network_0_0_RI_7, P_network_0_0_AI_0, P_network_0_0_AI_1, P_network_0_0_AI_2, P_network_0_0_AI_3, P_network_0_0_AI_4, P_network_0_0_AI_5, P_network_0_0_AI_6, P_network_0_0_AI_7, P_network_0_0_AnnP_0, P_network_0_0_AnnP_1, P_network_0_0_AnnP_2, P_network_0_0_AnnP_3, P_network_0_0_AnnP_4, P_network_0_0_AnnP_5, P_network_0_0_AnnP_6, P_network_0_0_AnnP_7, P_network_0_0_RP_0, P_network_0_0_RP_1, P_network_0_0_RP_2, P_network_0_0_RP_3, P_network_0_0_RP_4, P_network_0_0_RP_5, P_network_0_0_RP_6, P_network_0_0_RP_7, P_network_0_1_AskP_0, P_network_0_1_AskP_1, P_network_0_1_AskP_2, P_network_0_1_AskP_3, P_network_0_1_AskP_4, P_network_0_1_AskP_5, P_network_0_1_AskP_6, P_network_0_1_AskP_7, P_network_0_1_AnsP_0, P_network_0_1_AnsP_1, P_network_0_1_AnsP_2, P_network_0_1_AnsP_3, P_network_0_1_AnsP_4, P_network_0_1_AnsP_5, P_network_0_1_AnsP_6, P_network_0_1_AnsP_7, P_network_0_1_RI_0, P_network_0_1_RI_1, P_network_0_1_RI_2, P_network_0_1_RI_3, P_network_0_1_RI_4, P_network_0_1_RI_5, P_network_0_1_RI_6, P_network_0_1_RI_7, P_network_0_1_AI_0, P_network_0_1_AI_1, P_network_0_1_AI_2, P_network_0_1_AI_3, P_network_0_1_AI_4, P_network_0_1_AI_5, P_network_0_1_AI_6, P_network_0_1_AI_7, P_network_0_1_AnnP_0, P_network_0_1_AnnP_1, P_network_0_1_AnnP_2, P_network_0_1_AnnP_3, P_network_0_1_AnnP_4, P_network_0_1_AnnP_5, P_network_0_1_AnnP_6, P_network_0_1_AnnP_7, P_network_0_1_RP_0, P_network_0_1_RP_1, P_network_0_1_RP_2, P_network_0_1_RP_3, P_network_0_1_RP_4, P_network_0_1_RP_5, P_network_0_1_RP_6, P_network_0_1_RP_7, P_network_0_2_AskP_0, P_network_0_2_AskP_1, P_network_0_2_AskP_2, P_network_0_2_AskP_3, P_network_0_2_AskP_4, P_network_0_2_AskP_5, P_network_0_2_AskP_6, P_network_0_2_AskP_7, P_network_0_2_AnsP_0, P_network_0_2_AnsP_1, P_network_0_2_AnsP_2, P_network_0_2_AnsP_3, P_network_0_2_AnsP_4, P_network_0_2_AnsP_5, P_network_0_2_AnsP_6, P_network_0_2_AnsP_7, P_network_0_2_RI_0, P_network_0_2_RI_1, P_network_0_2_RI_2, P_network_0_2_RI_3, P_network_0_2_RI_4, P_network_0_2_RI_5, P_network_0_2_RI_6, P_network_0_2_RI_7, P_network_0_2_AI_0, P_network_0_2_AI_1, P_network_0_2_AI_2, P_network_0_2_AI_3, P_network_0_2_AI_4, P_network_0_2_AI_5, P_network_0_2_AI_6, P_network_0_2_AI_7, P_network_0_2_AnnP_0, P_network_0_2_AnnP_1, P_network_0_2_AnnP_2, P_network_0_2_AnnP_3, P_network_0_2_AnnP_4, P_network_0_2_AnnP_5, P_network_0_2_AnnP_6, P_network_0_2_AnnP_7, P_network_0_2_RP_0, P_network_0_2_RP_1, P_network_0_2_RP_2, P_network_0_2_RP_3, P_network_0_2_RP_4, P_network_0_2_RP_5, P_network_0_2_RP_6, P_network_0_2_RP_7, P_network_0_3_AskP_0, P_network_0_3_AskP_1, P_network_0_3_AskP_2, P_network_0_3_AskP_3, P_network_0_3_AskP_4, P_network_0_3_AskP_5, P_network_0_3_AskP_6, P_network_0_3_AskP_7, P_network_0_3_AnsP_0, P_network_0_3_AnsP_1, P_network_0_3_AnsP_2, P_network_0_3_AnsP_3, P_network_0_3_AnsP_4, P_network_0_3_AnsP_5, P_network_0_3_AnsP_6, P_network_0_3_AnsP_7, P_network_0_3_RI_0, P_network_0_3_RI_1, P_network_0_3_RI_2, P_network_0_3_RI_3, P_network_0_3_RI_4, P_network_0_3_RI_5, P_network_0_3_RI_6, P_network_0_3_RI_7, P_network_0_3_AI_0, P_network_0_3_AI_1, P_network_0_3_AI_2, P_network_0_3_AI_3, P_network_0_3_AI_4, P_network_0_3_AI_5, P_network_0_3_AI_6, P_network_0_3_AI_7, P_network_0_3_AnnP_0, P_network_0_3_AnnP_1, P_network_0_3_AnnP_2, P_network_0_3_AnnP_3, P_network_0_3_AnnP_4, P_network_0_3_AnnP_5, P_network_0_3_AnnP_6, P_network_0_3_AnnP_7, P_network_0_3_RP_0, P_network_0_3_RP_1, P_network_0_3_RP_2, P_network_0_3_RP_3, P_network_0_3_RP_4, P_network_0_3_RP_5, P_network_0_3_RP_6, P_network_0_3_RP_7, P_network_0_4_AskP_0, P_network_0_4_AskP_1, P_network_0_4_AskP_2, P_network_0_4_AskP_3, P_network_0_4_AskP_4, P_network_0_4_AskP_5, P_network_0_4_AskP_6, P_network_0_4_AskP_7, P_network_0_4_AnsP_0, P_network_0_4_AnsP_1, P_network_0_4_AnsP_2, P_network_0_4_AnsP_3, P_network_0_4_AnsP_4, P_network_0_4_AnsP_5, P_network_0_4_AnsP_6, P_network_0_4_AnsP_7, P_network_0_4_RI_0, P_network_0_4_RI_1, P_network_0_4_RI_2, P_network_0_4_RI_3, P_network_0_4_RI_4, P_network_0_4_RI_5, P_network_0_4_RI_6, P_network_0_4_RI_7, P_network_0_4_AI_0, P_network_0_4_AI_1, P_network_0_4_AI_2, P_network_0_4_AI_3, P_network_0_4_AI_4, P_network_0_4_AI_5, P_network_0_4_AI_6, P_network_0_4_AI_7, P_network_0_4_AnnP_0, P_network_0_4_AnnP_1, P_network_0_4_AnnP_2, P_network_0_4_AnnP_3, P_network_0_4_AnnP_4, P_network_0_4_AnnP_5, P_network_0_4_AnnP_6, P_network_0_4_AnnP_7, P_network_0_4_RP_0, P_network_0_4_RP_1, P_network_0_4_RP_2, P_network_0_4_RP_3, P_network_0_4_RP_4, P_network_0_4_RP_5, P_network_0_4_RP_6, P_network_0_4_RP_7, P_network_0_5_AskP_0, P_network_0_5_AskP_1, P_network_0_5_AskP_2, P_network_0_5_AskP_3, P_network_0_5_AskP_4, P_network_0_5_AskP_5, P_network_0_5_AskP_6, P_network_0_5_AskP_7, P_network_0_5_AnsP_0, P_network_0_5_AnsP_1, P_network_0_5_AnsP_2, P_network_0_5_AnsP_3, P_network_0_5_AnsP_4, P_network_0_5_AnsP_5, P_network_0_5_AnsP_6, P_network_0_5_AnsP_7, P_network_0_5_RI_0, P_network_0_5_RI_1, P_network_0_5_RI_2, P_network_0_5_RI_3, P_network_0_5_RI_4, P_network_0_5_RI_5, P_network_0_5_RI_6, P_network_0_5_RI_7, P_network_0_5_AI_0, P_network_0_5_AI_1, P_network_0_5_AI_2, P_network_0_5_AI_3, P_network_0_5_AI_4, P_network_0_5_AI_5, P_network_0_5_AI_6, P_network_0_5_AI_7, P_network_0_5_AnnP_0, P_network_0_5_AnnP_1, P_network_0_5_AnnP_2, P_network_0_5_AnnP_3, P_network_0_5_AnnP_4, P_network_0_5_AnnP_5, P_network_0_5_AnnP_6, P_network_0_5_AnnP_7, P_network_0_5_RP_0, P_network_0_5_RP_1, P_network_0_5_RP_2, P_network_0_5_RP_3, P_network_0_5_RP_4, P_network_0_5_RP_5, P_network_0_5_RP_6, P_network_0_5_RP_7, P_network_0_6_AskP_0, P_network_0_6_AskP_1, P_network_0_6_AskP_2, P_network_0_6_AskP_3, P_network_0_6_AskP_4, P_network_0_6_AskP_5, P_network_0_6_AskP_6, P_network_0_6_AskP_7, P_network_0_6_AnsP_0, P_network_0_6_AnsP_1, P_network_0_6_AnsP_2, P_network_0_6_AnsP_3, P_network_0_6_AnsP_4, P_network_0_6_AnsP_5, P_network_0_6_AnsP_6, P_network_0_6_AnsP_7, P_network_0_6_RI_0, P_network_0_6_RI_1, P_network_0_6_RI_2, P_network_0_6_RI_3, P_network_0_6_RI_4, P_network_0_6_RI_5, P_network_0_6_RI_6, P_network_0_6_RI_7, P_network_0_6_AI_0, P_network_0_6_AI_1, P_network_0_6_AI_2, P_network_0_6_AI_3, P_network_0_6_AI_4, P_network_0_6_AI_5, P_network_0_6_AI_6, P_network_0_6_AI_7, P_network_0_6_AnnP_0, P_network_0_6_AnnP_1, P_network_0_6_AnnP_2, P_network_0_6_AnnP_3, P_network_0_6_AnnP_4, P_network_0_6_AnnP_5, P_network_0_6_AnnP_6, P_network_0_6_AnnP_7, P_network_0_6_RP_0, P_network_0_6_RP_1, P_network_0_6_RP_2, P_network_0_6_RP_3, P_network_0_6_RP_4, P_network_0_6_RP_5, P_network_0_6_RP_6, P_network_0_6_RP_7, P_network_0_7_AskP_0, P_network_0_7_AskP_1, P_network_0_7_AskP_2, P_network_0_7_AskP_3, P_network_0_7_AskP_4, P_network_0_7_AskP_5, P_network_0_7_AskP_6, P_network_0_7_AskP_7, P_network_0_7_AnsP_0, P_network_0_7_AnsP_1, P_network_0_7_AnsP_2, P_network_0_7_AnsP_3, P_network_0_7_AnsP_4, P_network_0_7_AnsP_5, P_network_0_7_AnsP_6, P_network_0_7_AnsP_7, P_network_0_7_RI_0, P_network_0_7_RI_1, P_network_0_7_RI_2, P_network_0_7_RI_3, P_network_0_7_RI_4, P_network_0_7_RI_5, P_network_0_7_RI_6, P_network_0_7_RI_7, P_network_0_7_AI_0, P_network_0_7_AI_1, P_network_0_7_AI_2, P_network_0_7_AI_3, P_network_0_7_AI_4, P_network_0_7_AI_5, P_network_0_7_AI_6, P_network_0_7_AI_7, P_network_0_7_AnnP_0, P_network_0_7_AnnP_1, P_network_0_7_AnnP_2, P_network_0_7_AnnP_3, P_network_0_7_AnnP_4, P_network_0_7_AnnP_5, P_network_0_7_AnnP_6, P_network_0_7_AnnP_7, P_network_0_7_RP_0, P_network_0_7_RP_1, P_network_0_7_RP_2, P_network_0_7_RP_3, P_network_0_7_RP_4, P_network_0_7_RP_5, P_network_0_7_RP_6, P_network_0_7_RP_7, P_network_1_0_AskP_0, P_network_1_0_AskP_1, P_network_1_0_AskP_2, P_network_1_0_AskP_3, P_network_1_0_AskP_4, P_network_1_0_AskP_5, P_network_1_0_AskP_6, P_network_1_0_AskP_7, P_network_1_0_AnsP_0, P_network_1_0_AnsP_1, P_network_1_0_AnsP_2, P_network_1_0_AnsP_3, P_network_1_0_AnsP_4, P_network_1_0_AnsP_5, P_network_1_0_AnsP_6, P_network_1_0_AnsP_7, P_network_1_0_RI_0, P_network_1_0_RI_1, P_network_1_0_RI_2, P_network_1_0_RI_3, P_network_1_0_RI_4, P_network_1_0_RI_5, P_network_1_0_RI_6, P_network_1_0_RI_7, P_network_1_0_AI_0, P_network_1_0_AI_1, P_network_1_0_AI_2, P_network_1_0_AI_3, P_network_1_0_AI_4, P_network_1_0_AI_5, P_network_1_0_AI_6, P_network_1_0_AI_7, P_network_1_0_AnnP_0, P_network_1_0_AnnP_1, P_network_1_0_AnnP_2, P_network_1_0_AnnP_3, P_network_1_0_AnnP_4, P_network_1_0_AnnP_5, P_network_1_0_AnnP_6, P_network_1_0_AnnP_7, P_network_1_0_RP_0, P_network_1_0_RP_1, P_network_1_0_RP_2, P_network_1_0_RP_3, P_network_1_0_RP_4, P_network_1_0_RP_5, P_network_1_0_RP_6, P_network_1_0_RP_7, P_network_1_1_AskP_0, P_network_1_1_AskP_1, P_network_1_1_AskP_2, P_network_1_1_AskP_3, P_network_1_1_AskP_4, P_network_1_1_AskP_5, P_network_1_1_AskP_6, P_network_1_1_AskP_7, P_network_1_1_AnsP_0, P_network_1_1_AnsP_1, P_network_1_1_AnsP_2, P_network_1_1_AnsP_3, P_network_1_1_AnsP_4, P_network_1_1_AnsP_5, P_network_1_1_AnsP_6, P_network_1_1_AnsP_7, P_network_1_1_RI_0, P_network_1_1_RI_1, P_network_1_1_RI_2, P_network_1_1_RI_3, P_network_1_1_RI_4, P_network_1_1_RI_5, P_network_1_1_RI_6, P_network_1_1_RI_7, P_network_1_1_AI_0, P_network_1_1_AI_1, P_network_1_1_AI_2, P_network_1_1_AI_3, P_network_1_1_AI_4, P_network_1_1_AI_5, P_network_1_1_AI_6, P_network_1_1_AI_7, P_network_1_1_AnnP_0, P_network_1_1_AnnP_1, P_network_1_1_AnnP_2, P_network_1_1_AnnP_3, P_network_1_1_AnnP_4, P_network_1_1_AnnP_5, P_network_1_1_AnnP_6, P_network_1_1_AnnP_7, P_network_1_1_RP_0, P_network_1_1_RP_1, P_network_1_1_RP_2, P_network_1_1_RP_3, P_network_1_1_RP_4, P_network_1_1_RP_5, P_network_1_1_RP_6, P_network_1_1_RP_7, P_network_1_2_AskP_0, P_network_1_2_AskP_1, P_network_1_2_AskP_2, P_network_1_2_AskP_3, P_network_1_2_AskP_4, P_network_1_2_AskP_5, P_network_1_2_AskP_6, P_network_1_2_AskP_7, P_network_1_2_AnsP_0, P_network_1_2_AnsP_1, P_network_1_2_AnsP_2, P_network_1_2_AnsP_3, P_network_1_2_AnsP_4, P_network_1_2_AnsP_5, P_network_1_2_AnsP_6, P_network_1_2_AnsP_7, P_network_1_2_RI_0, P_network_1_2_RI_1, P_network_1_2_RI_2, P_network_1_2_RI_3, P_network_1_2_RI_4, P_network_1_2_RI_5, P_network_1_2_RI_6, P_network_1_2_RI_7, P_network_1_2_AI_0, P_network_1_2_AI_1, P_network_1_2_AI_2, P_network_1_2_AI_3, P_network_1_2_AI_4, P_network_1_2_AI_5, P_network_1_2_AI_6, P_network_1_2_AI_7, P_network_1_2_AnnP_0, P_network_1_2_AnnP_1, P_network_1_2_AnnP_2, P_network_1_2_AnnP_3, P_network_1_2_AnnP_4, P_network_1_2_AnnP_5, P_network_1_2_AnnP_6, P_network_1_2_AnnP_7, P_network_1_2_RP_0, P_network_1_2_RP_1, P_network_1_2_RP_2, P_network_1_2_RP_3, P_network_1_2_RP_4, P_network_1_2_RP_5, P_network_1_2_RP_6, P_network_1_2_RP_7, P_network_1_3_AskP_0, P_network_1_3_AskP_1, P_network_1_3_AskP_2, P_network_1_3_AskP_3, P_network_1_3_AskP_4, P_network_1_3_AskP_5, P_network_1_3_AskP_6, P_network_1_3_AskP_7, P_network_1_3_AnsP_0, P_network_1_3_AnsP_1, P_network_1_3_AnsP_2, P_network_1_3_AnsP_3, P_network_1_3_AnsP_4, P_network_1_3_AnsP_5, P_network_1_3_AnsP_6, P_network_1_3_AnsP_7, P_network_1_3_RI_0, P_network_1_3_RI_1, P_network_1_3_RI_2, P_network_1_3_RI_3, P_network_1_3_RI_4, P_network_1_3_RI_5, P_network_1_3_RI_6, P_network_1_3_RI_7, P_network_1_3_AI_0, P_network_1_3_AI_1, P_network_1_3_AI_2, P_network_1_3_AI_3, P_network_1_3_AI_4, P_network_1_3_AI_5, P_network_1_3_AI_6, P_network_1_3_AI_7, P_network_1_3_AnnP_0, P_network_1_3_AnnP_1, P_network_1_3_AnnP_2, P_network_1_3_AnnP_3, P_network_1_3_AnnP_4, P_network_1_3_AnnP_5, P_network_1_3_AnnP_6, P_network_1_3_AnnP_7, P_network_1_3_RP_0, P_network_1_3_RP_1, P_network_1_3_RP_2, P_network_1_3_RP_3, P_network_1_3_RP_4, P_network_1_3_RP_5, P_network_1_3_RP_6, P_network_1_3_RP_7, P_network_1_4_AskP_0, P_network_1_4_AskP_1, P_network_1_4_AskP_2, P_network_1_4_AskP_3, P_network_1_4_AskP_4, P_network_1_4_AskP_5, P_network_1_4_AskP_6, P_network_1_4_AskP_7, P_network_1_4_AnsP_0, P_network_1_4_AnsP_1, P_network_1_4_AnsP_2, P_network_1_4_AnsP_3, P_network_1_4_AnsP_4, P_network_1_4_AnsP_5, P_network_1_4_AnsP_6, P_network_1_4_AnsP_7, P_network_1_4_RI_0, P_network_1_4_RI_1, P_network_1_4_RI_2, P_network_1_4_RI_3, P_network_1_4_RI_4, P_network_1_4_RI_5, P_network_1_4_RI_6, P_network_1_4_RI_7, P_network_1_4_AI_0, P_network_1_4_AI_1, P_network_1_4_AI_2, P_network_1_4_AI_3, P_network_1_4_AI_4, P_network_1_4_AI_5, P_network_1_4_AI_6, P_network_1_4_AI_7, P_network_1_4_AnnP_0, P_network_1_4_AnnP_1, P_network_1_4_AnnP_2, P_network_1_4_AnnP_3, P_network_1_4_AnnP_4, P_network_1_4_AnnP_5, P_network_1_4_AnnP_6, P_network_1_4_AnnP_7, P_network_1_4_RP_0, P_network_1_4_RP_1, P_network_1_4_RP_2, P_network_1_4_RP_3, P_network_1_4_RP_4, P_network_1_4_RP_5, P_network_1_4_RP_6, P_network_1_4_RP_7, P_network_1_5_AskP_0, P_network_1_5_AskP_1, P_network_1_5_AskP_2, P_network_1_5_AskP_3, P_network_1_5_AskP_4, P_network_1_5_AskP_5, P_network_1_5_AskP_6, P_network_1_5_AskP_7, P_network_1_5_AnsP_0, P_network_1_5_AnsP_1, P_network_1_5_AnsP_2, P_network_1_5_AnsP_3, P_network_1_5_AnsP_4, P_network_1_5_AnsP_5, P_network_1_5_AnsP_6, P_network_1_5_AnsP_7, P_network_1_5_RI_0, P_network_1_5_RI_1, P_network_1_5_RI_2, P_network_1_5_RI_3, P_network_1_5_RI_4, P_network_1_5_RI_5, P_network_1_5_RI_6, P_network_1_5_RI_7, P_network_1_5_AI_0, P_network_1_5_AI_1, P_network_1_5_AI_2, P_network_1_5_AI_3, P_network_1_5_AI_4, P_network_1_5_AI_5, P_network_1_5_AI_6, P_network_1_5_AI_7, P_network_1_5_AnnP_0, P_network_1_5_AnnP_1, P_network_1_5_AnnP_2, P_network_1_5_AnnP_3, P_network_1_5_AnnP_4, P_network_1_5_AnnP_5, P_network_1_5_AnnP_6, P_network_1_5_AnnP_7, P_network_1_5_RP_0, P_network_1_5_RP_1, P_network_1_5_RP_2, P_network_1_5_RP_3, P_network_1_5_RP_4, P_network_1_5_RP_5, P_network_1_5_RP_6, P_network_1_5_RP_7, P_network_1_6_AskP_0, P_network_1_6_AskP_1, P_network_1_6_AskP_2, P_network_1_6_AskP_3, P_network_1_6_AskP_4, P_network_1_6_AskP_5, P_network_1_6_AskP_6, P_network_1_6_AskP_7, P_network_1_6_AnsP_0, P_network_1_6_AnsP_1, P_network_1_6_AnsP_2, P_network_1_6_AnsP_3, P_network_1_6_AnsP_4, P_network_1_6_AnsP_5, P_network_1_6_AnsP_6, P_network_1_6_AnsP_7, P_network_1_6_RI_0, P_network_1_6_RI_1, P_network_1_6_RI_2, P_network_1_6_RI_3, P_network_1_6_RI_4, P_network_1_6_RI_5, P_network_1_6_RI_6, P_network_1_6_RI_7, P_network_1_6_AI_0, P_network_1_6_AI_1, P_network_1_6_AI_2, P_network_1_6_AI_3, P_network_1_6_AI_4, P_network_1_6_AI_5, P_network_1_6_AI_6, P_network_1_6_AI_7, P_network_1_6_AnnP_0, P_network_1_6_AnnP_1, P_network_1_6_AnnP_2, P_network_1_6_AnnP_3, P_network_1_6_AnnP_4, P_network_1_6_AnnP_5, P_network_1_6_AnnP_6, P_network_1_6_AnnP_7, P_network_1_6_RP_0, P_network_1_6_RP_1, P_network_1_6_RP_2, P_network_1_6_RP_3, P_network_1_6_RP_4, P_network_1_6_RP_5, P_network_1_6_RP_6, P_network_1_6_RP_7, P_network_1_7_AskP_0, P_network_1_7_AskP_1, P_network_1_7_AskP_2, P_network_1_7_AskP_3, P_network_1_7_AskP_4, P_network_1_7_AskP_5, P_network_1_7_AskP_6, P_network_1_7_AskP_7, P_network_1_7_AnsP_0, P_network_1_7_AnsP_1, P_network_1_7_AnsP_2, P_network_1_7_AnsP_3, P_network_1_7_AnsP_4, P_network_1_7_AnsP_5, P_network_1_7_AnsP_6, P_network_1_7_AnsP_7, P_network_1_7_RI_0, P_network_1_7_RI_1, P_network_1_7_RI_2, P_network_1_7_RI_3, P_network_1_7_RI_4, P_network_1_7_RI_5, P_network_1_7_RI_6, P_network_1_7_RI_7, P_network_1_7_AI_0, P_network_1_7_AI_1, P_network_1_7_AI_2, P_network_1_7_AI_3, P_network_1_7_AI_4, P_network_1_7_AI_5, P_network_1_7_AI_6, P_network_1_7_AI_7, P_network_1_7_AnnP_0, P_network_1_7_AnnP_1, P_network_1_7_AnnP_2, P_network_1_7_AnnP_3, P_network_1_7_AnnP_4, P_network_1_7_AnnP_5, P_network_1_7_AnnP_6, P_network_1_7_AnnP_7, P_network_1_7_RP_0, P_network_1_7_RP_1, P_network_1_7_RP_2, P_network_1_7_RP_3, P_network_1_7_RP_4, P_network_1_7_RP_5, P_network_1_7_RP_6, P_network_1_7_RP_7, P_network_2_0_AskP_0, P_network_2_0_AskP_1, P_network_2_0_AskP_2, P_network_2_0_AskP_3, P_network_2_0_AskP_4, P_network_2_0_AskP_5, P_network_2_0_AskP_6, P_network_2_0_AskP_7, P_network_2_0_AnsP_0, P_network_2_0_AnsP_1, P_network_2_0_AnsP_2, P_network_2_0_AnsP_3, P_network_2_0_AnsP_4, P_network_2_0_AnsP_5, P_network_2_0_AnsP_6, P_network_2_0_AnsP_7, P_network_2_0_RI_0, P_network_2_0_RI_1, P_network_2_0_RI_2, P_network_2_0_RI_3, P_network_2_0_RI_4, P_network_2_0_RI_5, P_network_2_0_RI_6, P_network_2_0_RI_7, P_network_2_0_AI_0, P_network_2_0_AI_1, P_network_2_0_AI_2, P_network_2_0_AI_3, P_network_2_0_AI_4, P_network_2_0_AI_5, P_network_2_0_AI_6, P_network_2_0_AI_7, P_network_2_0_AnnP_0, P_network_2_0_AnnP_1, P_network_2_0_AnnP_2, P_network_2_0_AnnP_3, P_network_2_0_AnnP_4, P_network_2_0_AnnP_5, P_network_2_0_AnnP_6, P_network_2_0_AnnP_7, P_network_2_0_RP_0, P_network_2_0_RP_1, P_network_2_0_RP_2, P_network_2_0_RP_3, P_network_2_0_RP_4, P_network_2_0_RP_5, P_network_2_0_RP_6, P_network_2_0_RP_7, P_network_2_1_AskP_0, P_network_2_1_AskP_1, P_network_2_1_AskP_2, P_network_2_1_AskP_3, P_network_2_1_AskP_4, P_network_2_1_AskP_5, P_network_2_1_AskP_6, P_network_2_1_AskP_7, P_network_2_1_AnsP_0, P_network_2_1_AnsP_1, P_network_2_1_AnsP_2, P_network_2_1_AnsP_3, P_network_2_1_AnsP_4, P_network_2_1_AnsP_5, P_network_2_1_AnsP_6, P_network_2_1_AnsP_7, P_network_2_1_RI_0, P_network_2_1_RI_1, P_network_2_1_RI_2, P_network_2_1_RI_3, P_network_2_1_RI_4, P_network_2_1_RI_5, P_network_2_1_RI_6, P_network_2_1_RI_7, P_network_2_1_AI_0, P_network_2_1_AI_1, P_network_2_1_AI_2, P_network_2_1_AI_3, P_network_2_1_AI_4, P_network_2_1_AI_5, P_network_2_1_AI_6, P_network_2_1_AI_7, P_network_2_1_AnnP_0, P_network_2_1_AnnP_1, P_network_2_1_AnnP_2, P_network_2_1_AnnP_3, P_network_2_1_AnnP_4, P_network_2_1_AnnP_5, P_network_2_1_AnnP_6, P_network_2_1_AnnP_7, P_network_2_1_RP_0, P_network_2_1_RP_1, P_network_2_1_RP_2, P_network_2_1_RP_3, P_network_2_1_RP_4, P_network_2_1_RP_5, P_network_2_1_RP_6, P_network_2_1_RP_7, P_network_2_2_AskP_0, P_network_2_2_AskP_1, P_network_2_2_AskP_2, P_network_2_2_AskP_3, P_network_2_2_AskP_4, P_network_2_2_AskP_5, P_network_2_2_AskP_6, P_network_2_2_AskP_7, P_network_2_2_AnsP_0, P_network_2_2_AnsP_1, P_network_2_2_AnsP_2, P_network_2_2_AnsP_3, P_network_2_2_AnsP_4, P_network_2_2_AnsP_5, P_network_2_2_AnsP_6, P_network_2_2_AnsP_7, P_network_2_2_RI_0, P_network_2_2_RI_1, P_network_2_2_RI_2, P_network_2_2_RI_3, P_network_2_2_RI_4, P_network_2_2_RI_5, P_network_2_2_RI_6, P_network_2_2_RI_7, P_network_2_2_AI_0, P_network_2_2_AI_1, P_network_2_2_AI_2, P_network_2_2_AI_3, P_network_2_2_AI_4, P_network_2_2_AI_5, P_network_2_2_AI_6, P_network_2_2_AI_7, P_network_2_2_AnnP_0, P_network_2_2_AnnP_1, P_network_2_2_AnnP_2, P_network_2_2_AnnP_3, P_network_2_2_AnnP_4, P_network_2_2_AnnP_5, P_network_2_2_AnnP_6, P_network_2_2_AnnP_7, P_network_2_2_RP_0, P_network_2_2_RP_1, P_network_2_2_RP_2, P_network_2_2_RP_3, P_network_2_2_RP_4, P_network_2_2_RP_5, P_network_2_2_RP_6, P_network_2_2_RP_7, P_network_2_3_AskP_0, P_network_2_3_AskP_1, P_network_2_3_AskP_2, P_network_2_3_AskP_3, P_network_2_3_AskP_4, P_network_2_3_AskP_5, P_network_2_3_AskP_6, P_network_2_3_AskP_7, P_network_2_3_AnsP_0, P_network_2_3_AnsP_1, P_network_2_3_AnsP_2, P_network_2_3_AnsP_3, P_network_2_3_AnsP_4, P_network_2_3_AnsP_5, P_network_2_3_AnsP_6, P_network_2_3_AnsP_7, P_network_2_3_RI_0, P_network_2_3_RI_1, P_network_2_3_RI_2, P_network_2_3_RI_3, P_network_2_3_RI_4, P_network_2_3_RI_5, P_network_2_3_RI_6, P_network_2_3_RI_7, P_network_2_3_AI_0, P_network_2_3_AI_1, P_network_2_3_AI_2, P_network_2_3_AI_3, P_network_2_3_AI_4, P_network_2_3_AI_5, P_network_2_3_AI_6, P_network_2_3_AI_7, P_network_2_3_AnnP_0, P_network_2_3_AnnP_1, P_network_2_3_AnnP_2, P_network_2_3_AnnP_3, P_network_2_3_AnnP_4, P_network_2_3_AnnP_5, P_network_2_3_AnnP_6, P_network_2_3_AnnP_7, P_network_2_3_RP_0, P_network_2_3_RP_1, P_network_2_3_RP_2, P_network_2_3_RP_3, P_network_2_3_RP_4, P_network_2_3_RP_5, P_network_2_3_RP_6, P_network_2_3_RP_7, P_network_2_4_AskP_0, P_network_2_4_AskP_1, P_network_2_4_AskP_2, P_network_2_4_AskP_3, P_network_2_4_AskP_4, P_network_2_4_AskP_5, P_network_2_4_AskP_6, P_network_2_4_AskP_7, P_network_2_4_AnsP_0, P_network_2_4_AnsP_1, P_network_2_4_AnsP_2, P_network_2_4_AnsP_3, P_network_2_4_AnsP_4, P_network_2_4_AnsP_5, P_network_2_4_AnsP_6, P_network_2_4_AnsP_7, P_network_2_4_RI_0, P_network_2_4_RI_1, P_network_2_4_RI_2, P_network_2_4_RI_3, P_network_2_4_RI_4, P_network_2_4_RI_5, P_network_2_4_RI_6, P_network_2_4_RI_7, P_network_2_4_AI_0, P_network_2_4_AI_1, P_network_2_4_AI_2, P_network_2_4_AI_3, P_network_2_4_AI_4, P_network_2_4_AI_5, P_network_2_4_AI_6, P_network_2_4_AI_7, P_network_2_4_AnnP_0, P_network_2_4_AnnP_1, P_network_2_4_AnnP_2, P_network_2_4_AnnP_3, P_network_2_4_AnnP_4, P_network_2_4_AnnP_5, P_network_2_4_AnnP_6, P_network_2_4_AnnP_7, P_network_2_4_RP_0, P_network_2_4_RP_1, P_network_2_4_RP_2, P_network_2_4_RP_3, P_network_2_4_RP_4, P_network_2_4_RP_5, P_network_2_4_RP_6, P_network_2_4_RP_7, P_network_2_5_AskP_0, P_network_2_5_AskP_1, P_network_2_5_AskP_2, P_network_2_5_AskP_3, P_network_2_5_AskP_4, P_network_2_5_AskP_5, P_network_2_5_AskP_6, P_network_2_5_AskP_7, P_network_2_5_AnsP_0, P_network_2_5_AnsP_1, P_network_2_5_AnsP_2, P_network_2_5_AnsP_3, P_network_2_5_AnsP_4, P_network_2_5_AnsP_5, P_network_2_5_AnsP_6, P_network_2_5_AnsP_7, P_network_2_5_RI_0, P_network_2_5_RI_1, P_network_2_5_RI_2, P_network_2_5_RI_3, P_network_2_5_RI_4, P_network_2_5_RI_5, P_network_2_5_RI_6, P_network_2_5_RI_7, P_network_2_5_AI_0, P_network_2_5_AI_1, P_network_2_5_AI_2, P_network_2_5_AI_3, P_network_2_5_AI_4, P_network_2_5_AI_5, P_network_2_5_AI_6, P_network_2_5_AI_7, P_network_2_5_AnnP_0, P_network_2_5_AnnP_1, P_network_2_5_AnnP_2, P_network_2_5_AnnP_3, P_network_2_5_AnnP_4, P_network_2_5_AnnP_5, P_network_2_5_AnnP_6, P_network_2_5_AnnP_7, P_network_2_5_RP_0, P_network_2_5_RP_1, P_network_2_5_RP_2, P_network_2_5_RP_3, P_network_2_5_RP_4, P_network_2_5_RP_5, P_network_2_5_RP_6, P_network_2_5_RP_7, P_network_2_6_AskP_0, P_network_2_6_AskP_1, P_network_2_6_AskP_2, P_network_2_6_AskP_3, P_network_2_6_AskP_4, P_network_2_6_AskP_5, P_network_2_6_AskP_6, P_network_2_6_AskP_7, P_network_2_6_AnsP_0, P_network_2_6_AnsP_1, P_network_2_6_AnsP_2, P_network_2_6_AnsP_3, P_network_2_6_AnsP_4, P_network_2_6_AnsP_5, P_network_2_6_AnsP_6, P_network_2_6_AnsP_7, P_network_2_6_RI_0, P_network_2_6_RI_1, P_network_2_6_RI_2, P_network_2_6_RI_3, P_network_2_6_RI_4, P_network_2_6_RI_5, P_network_2_6_RI_6, P_network_2_6_RI_7, P_network_2_6_AI_0, P_network_2_6_AI_1, P_network_2_6_AI_2, P_network_2_6_AI_3, P_network_2_6_AI_4, P_network_2_6_AI_5, P_network_2_6_AI_6, P_network_2_6_AI_7, P_network_2_6_AnnP_0, P_network_2_6_AnnP_1, P_network_2_6_AnnP_2, P_network_2_6_AnnP_3, P_network_2_6_AnnP_4, P_network_2_6_AnnP_5, P_network_2_6_AnnP_6, P_network_2_6_AnnP_7, P_network_2_6_RP_0, P_network_2_6_RP_1, P_network_2_6_RP_2, P_network_2_6_RP_3, P_network_2_6_RP_4, P_network_2_6_RP_5, P_network_2_6_RP_6, P_network_2_6_RP_7, P_network_2_7_AskP_0, P_network_2_7_AskP_1, P_network_2_7_AskP_2, P_network_2_7_AskP_3, P_network_2_7_AskP_4, P_network_2_7_AskP_5, P_network_2_7_AskP_6, P_network_2_7_AskP_7, P_network_2_7_AnsP_0, P_network_2_7_AnsP_1, P_network_2_7_AnsP_2, P_network_2_7_AnsP_3, P_network_2_7_AnsP_4, P_network_2_7_AnsP_5, P_network_2_7_AnsP_6, P_network_2_7_AnsP_7, P_network_2_7_RI_0, P_network_2_7_RI_1, P_network_2_7_RI_2, P_network_2_7_RI_3, P_network_2_7_RI_4, P_network_2_7_RI_5, P_network_2_7_RI_6, P_network_2_7_RI_7, P_network_2_7_AI_0, P_network_2_7_AI_1, P_network_2_7_AI_2, P_network_2_7_AI_3, P_network_2_7_AI_4, P_network_2_7_AI_5, P_network_2_7_AI_6, P_network_2_7_AI_7, P_network_2_7_AnnP_0, P_network_2_7_AnnP_1, P_network_2_7_AnnP_2, P_network_2_7_AnnP_3, P_network_2_7_AnnP_4, P_network_2_7_AnnP_5, P_network_2_7_AnnP_6, P_network_2_7_AnnP_7, P_network_2_7_RP_0, P_network_2_7_RP_1, P_network_2_7_RP_2, P_network_2_7_RP_3, P_network_2_7_RP_4, P_network_2_7_RP_5, P_network_2_7_RP_6, P_network_2_7_RP_7, P_network_3_0_AskP_0, P_network_3_0_AskP_1, P_network_3_0_AskP_2, P_network_3_0_AskP_3, P_network_3_0_AskP_4, P_network_3_0_AskP_5, P_network_3_0_AskP_6, P_network_3_0_AskP_7, P_network_3_0_AnsP_0, P_network_3_0_AnsP_1, P_network_3_0_AnsP_2, P_network_3_0_AnsP_3, P_network_3_0_AnsP_4, P_network_3_0_AnsP_5, P_network_3_0_AnsP_6, P_network_3_0_AnsP_7, P_network_3_0_RI_0, P_network_3_0_RI_1, P_network_3_0_RI_2, P_network_3_0_RI_3, P_network_3_0_RI_4, P_network_3_0_RI_5, P_network_3_0_RI_6, P_network_3_0_RI_7, P_network_3_0_AI_0, P_network_3_0_AI_1, P_network_3_0_AI_2, P_network_3_0_AI_3, P_network_3_0_AI_4, P_network_3_0_AI_5, P_network_3_0_AI_6, P_network_3_0_AI_7, P_network_3_0_AnnP_0, P_network_3_0_AnnP_1, P_network_3_0_AnnP_2, P_network_3_0_AnnP_3, P_network_3_0_AnnP_4, P_network_3_0_AnnP_5, P_network_3_0_AnnP_6, P_network_3_0_AnnP_7, P_network_3_0_RP_0, P_network_3_0_RP_1, P_network_3_0_RP_2, P_network_3_0_RP_3, P_network_3_0_RP_4, P_network_3_0_RP_5, P_network_3_0_RP_6, P_network_3_0_RP_7, P_network_3_1_AskP_0, P_network_3_1_AskP_1, P_network_3_1_AskP_2, P_network_3_1_AskP_3, P_network_3_1_AskP_4, P_network_3_1_AskP_5, P_network_3_1_AskP_6, P_network_3_1_AskP_7, P_network_3_1_AnsP_0, P_network_3_1_AnsP_1, P_network_3_1_AnsP_2, P_network_3_1_AnsP_3, P_network_3_1_AnsP_4, P_network_3_1_AnsP_5, P_network_3_1_AnsP_6, P_network_3_1_AnsP_7, P_network_3_1_RI_0, P_network_3_1_RI_1, P_network_3_1_RI_2, P_network_3_1_RI_3, P_network_3_1_RI_4, P_network_3_1_RI_5, P_network_3_1_RI_6, P_network_3_1_RI_7, P_network_3_1_AI_0, P_network_3_1_AI_1, P_network_3_1_AI_2, P_network_3_1_AI_3, P_network_3_1_AI_4, P_network_3_1_AI_5, P_network_3_1_AI_6, P_network_3_1_AI_7, P_network_3_1_AnnP_0, P_network_3_1_AnnP_1, P_network_3_1_AnnP_2, P_network_3_1_AnnP_3, P_network_3_1_AnnP_4, P_network_3_1_AnnP_5, P_network_3_1_AnnP_6, P_network_3_1_AnnP_7, P_network_3_1_RP_0, P_network_3_1_RP_1, P_network_3_1_RP_2, P_network_3_1_RP_3, P_network_3_1_RP_4, P_network_3_1_RP_5, P_network_3_1_RP_6, P_network_3_1_RP_7, P_network_3_2_AskP_0, P_network_3_2_AskP_1, P_network_3_2_AskP_2, P_network_3_2_AskP_3, P_network_3_2_AskP_4, P_network_3_2_AskP_5, P_network_3_2_AskP_6, P_network_3_2_AskP_7, P_network_3_2_AnsP_0, P_network_3_2_AnsP_1, P_network_3_2_AnsP_2, P_network_3_2_AnsP_3, P_network_3_2_AnsP_4, P_network_3_2_AnsP_5, P_network_3_2_AnsP_6, P_network_3_2_AnsP_7, P_network_3_2_RI_0, P_network_3_2_RI_1, P_network_3_2_RI_2, P_network_3_2_RI_3, P_network_3_2_RI_4, P_network_3_2_RI_5, P_network_3_2_RI_6, P_network_3_2_RI_7, P_network_3_2_AI_0, P_network_3_2_AI_1, P_network_3_2_AI_2, P_network_3_2_AI_3, P_network_3_2_AI_4, P_network_3_2_AI_5, P_network_3_2_AI_6, P_network_3_2_AI_7, P_network_3_2_AnnP_0, P_network_3_2_AnnP_1, P_network_3_2_AnnP_2, P_network_3_2_AnnP_3, P_network_3_2_AnnP_4, P_network_3_2_AnnP_5, P_network_3_2_AnnP_6, P_network_3_2_AnnP_7, P_network_3_2_RP_0, P_network_3_2_RP_1, P_network_3_2_RP_2, P_network_3_2_RP_3, P_network_3_2_RP_4, P_network_3_2_RP_5, P_network_3_2_RP_6, P_network_3_2_RP_7, P_network_3_3_AskP_0, P_network_3_3_AskP_1, P_network_3_3_AskP_2, P_network_3_3_AskP_3, P_network_3_3_AskP_4, P_network_3_3_AskP_5, P_network_3_3_AskP_6, P_network_3_3_AskP_7, P_network_3_3_AnsP_0, P_network_3_3_AnsP_1, P_network_3_3_AnsP_2, P_network_3_3_AnsP_3, P_network_3_3_AnsP_4, P_network_3_3_AnsP_5, P_network_3_3_AnsP_6, P_network_3_3_AnsP_7, P_network_3_3_RI_0, P_network_3_3_RI_1, P_network_3_3_RI_2, P_network_3_3_RI_3, P_network_3_3_RI_4, P_network_3_3_RI_5, P_network_3_3_RI_6, P_network_3_3_RI_7, P_network_3_3_AI_0, P_network_3_3_AI_1, P_network_3_3_AI_2, P_network_3_3_AI_3, P_network_3_3_AI_4, P_network_3_3_AI_5, P_network_3_3_AI_6, P_network_3_3_AI_7, P_network_3_3_AnnP_0, P_network_3_3_AnnP_1, P_network_3_3_AnnP_2, P_network_3_3_AnnP_3, P_network_3_3_AnnP_4, P_network_3_3_AnnP_5, P_network_3_3_AnnP_6, P_network_3_3_AnnP_7, P_network_3_3_RP_0, P_network_3_3_RP_1, P_network_3_3_RP_2, P_network_3_3_RP_3, P_network_3_3_RP_4, P_network_3_3_RP_5, P_network_3_3_RP_6, P_network_3_3_RP_7, P_network_3_4_AskP_0, P_network_3_4_AskP_1, P_network_3_4_AskP_2, P_network_3_4_AskP_3, P_network_3_4_AskP_4, P_network_3_4_AskP_5, P_network_3_4_AskP_6, P_network_3_4_AskP_7, P_network_3_4_AnsP_0, P_network_3_4_AnsP_1, P_network_3_4_AnsP_2, P_network_3_4_AnsP_3, P_network_3_4_AnsP_4, P_network_3_4_AnsP_5, P_network_3_4_AnsP_6, P_network_3_4_AnsP_7, P_network_3_4_RI_0, P_network_3_4_RI_1, P_network_3_4_RI_2, P_network_3_4_RI_3, P_network_3_4_RI_4, P_network_3_4_RI_5, P_network_3_4_RI_6, P_network_3_4_RI_7, P_network_3_4_AI_0, P_network_3_4_AI_1, P_network_3_4_AI_2, P_network_3_4_AI_3, P_network_3_4_AI_4, P_network_3_4_AI_5, P_network_3_4_AI_6, P_network_3_4_AI_7, P_network_3_4_AnnP_0, P_network_3_4_AnnP_1, P_network_3_4_AnnP_2, P_network_3_4_AnnP_3, P_network_3_4_AnnP_4, P_network_3_4_AnnP_5, P_network_3_4_AnnP_6, P_network_3_4_AnnP_7, P_network_3_4_RP_0, P_network_3_4_RP_1, P_network_3_4_RP_2, P_network_3_4_RP_3, P_network_3_4_RP_4, P_network_3_4_RP_5, P_network_3_4_RP_6, P_network_3_4_RP_7, P_network_3_5_AskP_0, P_network_3_5_AskP_1, P_network_3_5_AskP_2, P_network_3_5_AskP_3, P_network_3_5_AskP_4, P_network_3_5_AskP_5, P_network_3_5_AskP_6, P_network_3_5_AskP_7, P_network_3_5_AnsP_0, P_network_3_5_AnsP_1, P_network_3_5_AnsP_2, P_network_3_5_AnsP_3, P_network_3_5_AnsP_4, P_network_3_5_AnsP_5, P_network_3_5_AnsP_6, P_network_3_5_AnsP_7, P_network_3_5_RI_0, P_network_3_5_RI_1, P_network_3_5_RI_2, P_network_3_5_RI_3, P_network_3_5_RI_4, P_network_3_5_RI_5, P_network_3_5_RI_6, P_network_3_5_RI_7, P_network_3_5_AI_0, P_network_3_5_AI_1, P_network_3_5_AI_2, P_network_3_5_AI_3, P_network_3_5_AI_4, P_network_3_5_AI_5, P_network_3_5_AI_6, P_network_3_5_AI_7, P_network_3_5_AnnP_0, P_network_3_5_AnnP_1, P_network_3_5_AnnP_2, P_network_3_5_AnnP_3, P_network_3_5_AnnP_4, P_network_3_5_AnnP_5, P_network_3_5_AnnP_6, P_network_3_5_AnnP_7, P_network_3_5_RP_0, P_network_3_5_RP_1, P_network_3_5_RP_2, P_network_3_5_RP_3, P_network_3_5_RP_4, P_network_3_5_RP_5, P_network_3_5_RP_6, P_network_3_5_RP_7, P_network_3_6_AskP_0, P_network_3_6_AskP_1, P_network_3_6_AskP_2, P_network_3_6_AskP_3, P_network_3_6_AskP_4, P_network_3_6_AskP_5, P_network_3_6_AskP_6, P_network_3_6_AskP_7, P_network_3_6_AnsP_0, P_network_3_6_AnsP_1, P_network_3_6_AnsP_2, P_network_3_6_AnsP_3, P_network_3_6_AnsP_4, P_network_3_6_AnsP_5, P_network_3_6_AnsP_6, P_network_3_6_AnsP_7, P_network_3_6_RI_0, P_network_3_6_RI_1, P_network_3_6_RI_2, P_network_3_6_RI_3, P_network_3_6_RI_4, P_network_3_6_RI_5, P_network_3_6_RI_6, P_network_3_6_RI_7, P_network_3_6_AI_0, P_network_3_6_AI_1, P_network_3_6_AI_2, P_network_3_6_AI_3, P_network_3_6_AI_4, P_network_3_6_AI_5, P_network_3_6_AI_6, P_network_3_6_AI_7, P_network_3_6_AnnP_0, P_network_3_6_AnnP_1, P_network_3_6_AnnP_2, P_network_3_6_AnnP_3, P_network_3_6_AnnP_4, P_network_3_6_AnnP_5, P_network_3_6_AnnP_6, P_network_3_6_AnnP_7, P_network_3_6_RP_0, P_network_3_6_RP_1, P_network_3_6_RP_2, P_network_3_6_RP_3, P_network_3_6_RP_4, P_network_3_6_RP_5, P_network_3_6_RP_6, P_network_3_6_RP_7, P_network_3_7_AskP_0, P_network_3_7_AskP_1, P_network_3_7_AskP_2, P_network_3_7_AskP_3, P_network_3_7_AskP_4, P_network_3_7_AskP_5, P_network_3_7_AskP_6, P_network_3_7_AskP_7, P_network_3_7_AnsP_0, P_network_3_7_AnsP_1, P_network_3_7_AnsP_2, P_network_3_7_AnsP_3, P_network_3_7_AnsP_4, P_network_3_7_AnsP_5, P_network_3_7_AnsP_6, P_network_3_7_AnsP_7, P_network_3_7_RI_0, P_network_3_7_RI_1, P_network_3_7_RI_2, P_network_3_7_RI_3, P_network_3_7_RI_4, P_network_3_7_RI_5, P_network_3_7_RI_6, P_network_3_7_RI_7, P_network_3_7_AI_0, P_network_3_7_AI_1, P_network_3_7_AI_2, P_network_3_7_AI_3, P_network_3_7_AI_4, P_network_3_7_AI_5, P_network_3_7_AI_6, P_network_3_7_AI_7, P_network_3_7_AnnP_0, P_network_3_7_AnnP_1, P_network_3_7_AnnP_2, P_network_3_7_AnnP_3, P_network_3_7_AnnP_4, P_network_3_7_AnnP_5, P_network_3_7_AnnP_6, P_network_3_7_AnnP_7, P_network_3_7_RP_0, P_network_3_7_RP_1, P_network_3_7_RP_2, P_network_3_7_RP_3, P_network_3_7_RP_4, P_network_3_7_RP_5, P_network_3_7_RP_6, P_network_3_7_RP_7, P_network_4_0_AskP_0, P_network_4_0_AskP_1, P_network_4_0_AskP_2, P_network_4_0_AskP_3, P_network_4_0_AskP_4, P_network_4_0_AskP_5, P_network_4_0_AskP_6, P_network_4_0_AskP_7, P_network_4_0_AnsP_0, P_network_4_0_AnsP_1, P_network_4_0_AnsP_2, P_network_4_0_AnsP_3, P_network_4_0_AnsP_4, P_network_4_0_AnsP_5, P_network_4_0_AnsP_6, P_network_4_0_AnsP_7, P_network_4_0_RI_0, P_network_4_0_RI_1, P_network_4_0_RI_2, P_network_4_0_RI_3, P_network_4_0_RI_4, P_network_4_0_RI_5, P_network_4_0_RI_6, P_network_4_0_RI_7, P_network_4_0_AI_0, P_network_4_0_AI_1, P_network_4_0_AI_2, P_network_4_0_AI_3, P_network_4_0_AI_4, P_network_4_0_AI_5, P_network_4_0_AI_6, P_network_4_0_AI_7, P_network_4_0_AnnP_0, P_network_4_0_AnnP_1, P_network_4_0_AnnP_2, P_network_4_0_AnnP_3, P_network_4_0_AnnP_4, P_network_4_0_AnnP_5, P_network_4_0_AnnP_6, P_network_4_0_AnnP_7, P_network_4_0_RP_0, P_network_4_0_RP_1, P_network_4_0_RP_2, P_network_4_0_RP_3, P_network_4_0_RP_4, P_network_4_0_RP_5, P_network_4_0_RP_6, P_network_4_0_RP_7, P_network_4_1_AskP_0, P_network_4_1_AskP_1, P_network_4_1_AskP_2, P_network_4_1_AskP_3, P_network_4_1_AskP_4, P_network_4_1_AskP_5, P_network_4_1_AskP_6, P_network_4_1_AskP_7, P_network_4_1_AnsP_0, P_network_4_1_AnsP_1, P_network_4_1_AnsP_2, P_network_4_1_AnsP_3, P_network_4_1_AnsP_4, P_network_4_1_AnsP_5, P_network_4_1_AnsP_6, P_network_4_1_AnsP_7, P_network_4_1_RI_0, P_network_4_1_RI_1, P_network_4_1_RI_2, P_network_4_1_RI_3, P_network_4_1_RI_4, P_network_4_1_RI_5, P_network_4_1_RI_6, P_network_4_1_RI_7, P_network_4_1_AI_0, P_network_4_1_AI_1, P_network_4_1_AI_2, P_network_4_1_AI_3, P_network_4_1_AI_4, P_network_4_1_AI_5, P_network_4_1_AI_6, P_network_4_1_AI_7, P_network_4_1_AnnP_0, P_network_4_1_AnnP_1, P_network_4_1_AnnP_2, P_network_4_1_AnnP_3, P_network_4_1_AnnP_4, P_network_4_1_AnnP_5, P_network_4_1_AnnP_6, P_network_4_1_AnnP_7, P_network_4_1_RP_0, P_network_4_1_RP_1, P_network_4_1_RP_2, P_network_4_1_RP_3, P_network_4_1_RP_4, P_network_4_1_RP_5, P_network_4_1_RP_6, P_network_4_1_RP_7, P_network_4_2_AskP_0, P_network_4_2_AskP_1, P_network_4_2_AskP_2, P_network_4_2_AskP_3, P_network_4_2_AskP_4, P_network_4_2_AskP_5, P_network_4_2_AskP_6, P_network_4_2_AskP_7, P_network_4_2_AnsP_0, P_network_4_2_AnsP_1, P_network_4_2_AnsP_2, P_network_4_2_AnsP_3, P_network_4_2_AnsP_4, P_network_4_2_AnsP_5, P_network_4_2_AnsP_6, P_network_4_2_AnsP_7, P_network_4_2_RI_0, P_network_4_2_RI_1, P_network_4_2_RI_2, P_network_4_2_RI_3, P_network_4_2_RI_4, P_network_4_2_RI_5, P_network_4_2_RI_6, P_network_4_2_RI_7, P_network_4_2_AI_0, P_network_4_2_AI_1, P_network_4_2_AI_2, P_network_4_2_AI_3, P_network_4_2_AI_4, P_network_4_2_AI_5, P_network_4_2_AI_6, P_network_4_2_AI_7, P_network_4_2_AnnP_0, P_network_4_2_AnnP_1, P_network_4_2_AnnP_2, P_network_4_2_AnnP_3, P_network_4_2_AnnP_4, P_network_4_2_AnnP_5, P_network_4_2_AnnP_6, P_network_4_2_AnnP_7, P_network_4_2_RP_0, P_network_4_2_RP_1, P_network_4_2_RP_2, P_network_4_2_RP_3, P_network_4_2_RP_4, P_network_4_2_RP_5, P_network_4_2_RP_6, P_network_4_2_RP_7, P_network_4_3_AskP_0, P_network_4_3_AskP_1, P_network_4_3_AskP_2, P_network_4_3_AskP_3, P_network_4_3_AskP_4, P_network_4_3_AskP_5, P_network_4_3_AskP_6, P_network_4_3_AskP_7, P_network_4_3_AnsP_0, P_network_4_3_AnsP_1, P_network_4_3_AnsP_2, P_network_4_3_AnsP_3, P_network_4_3_AnsP_4, P_network_4_3_AnsP_5, P_network_4_3_AnsP_6, P_network_4_3_AnsP_7, P_network_4_3_RI_0, P_network_4_3_RI_1, P_network_4_3_RI_2, P_network_4_3_RI_3, P_network_4_3_RI_4, P_network_4_3_RI_5, P_network_4_3_RI_6, P_network_4_3_RI_7, P_network_4_3_AI_0, P_network_4_3_AI_1, P_network_4_3_AI_2, P_network_4_3_AI_3, P_network_4_3_AI_4, P_network_4_3_AI_5, P_network_4_3_AI_6, P_network_4_3_AI_7, P_network_4_3_AnnP_0, P_network_4_3_AnnP_1, P_network_4_3_AnnP_2, P_network_4_3_AnnP_3, P_network_4_3_AnnP_4, P_network_4_3_AnnP_5, P_network_4_3_AnnP_6, P_network_4_3_AnnP_7, P_network_4_3_RP_0, P_network_4_3_RP_1, P_network_4_3_RP_2, P_network_4_3_RP_3, P_network_4_3_RP_4, P_network_4_3_RP_5, P_network_4_3_RP_6, P_network_4_3_RP_7, P_network_4_4_AskP_0, P_network_4_4_AskP_1, P_network_4_4_AskP_2, P_network_4_4_AskP_3, P_network_4_4_AskP_4, P_network_4_4_AskP_5, P_network_4_4_AskP_6, P_network_4_4_AskP_7, P_network_4_4_AnsP_0, P_network_4_4_AnsP_1, P_network_4_4_AnsP_2, P_network_4_4_AnsP_3, P_network_4_4_AnsP_4, P_network_4_4_AnsP_5, P_network_4_4_AnsP_6, P_network_4_4_AnsP_7, P_network_4_4_RI_0, P_network_4_4_RI_1, P_network_4_4_RI_2, P_network_4_4_RI_3, P_network_4_4_RI_4, P_network_4_4_RI_5, P_network_4_4_RI_6, P_network_4_4_RI_7, P_network_4_4_AI_0, P_network_4_4_AI_1, P_network_4_4_AI_2, P_network_4_4_AI_3, P_network_4_4_AI_4, P_network_4_4_AI_5, P_network_4_4_AI_6, P_network_4_4_AI_7, P_network_4_4_AnnP_0, P_network_4_4_AnnP_1, P_network_4_4_AnnP_2, P_network_4_4_AnnP_3, P_network_4_4_AnnP_4, P_network_4_4_AnnP_5, P_network_4_4_AnnP_6, P_network_4_4_AnnP_7, P_network_4_4_RP_0, P_network_4_4_RP_1, P_network_4_4_RP_2, P_network_4_4_RP_3, P_network_4_4_RP_4, P_network_4_4_RP_5, P_network_4_4_RP_6, P_network_4_4_RP_7, P_network_4_5_AskP_0, P_network_4_5_AskP_1, P_network_4_5_AskP_2, P_network_4_5_AskP_3, P_network_4_5_AskP_4, P_network_4_5_AskP_5, P_network_4_5_AskP_6, P_network_4_5_AskP_7, P_network_4_5_AnsP_0, P_network_4_5_AnsP_1, P_network_4_5_AnsP_2, P_network_4_5_AnsP_3, P_network_4_5_AnsP_4, P_network_4_5_AnsP_5, P_network_4_5_AnsP_6, P_network_4_5_AnsP_7, P_network_4_5_RI_0, P_network_4_5_RI_1, P_network_4_5_RI_2, P_network_4_5_RI_3, P_network_4_5_RI_4, P_network_4_5_RI_5, P_network_4_5_RI_6, P_network_4_5_RI_7, P_network_4_5_AI_0, P_network_4_5_AI_1, P_network_4_5_AI_2, P_network_4_5_AI_3, P_network_4_5_AI_4, P_network_4_5_AI_5, P_network_4_5_AI_6, P_network_4_5_AI_7, P_network_4_5_AnnP_0, P_network_4_5_AnnP_1, P_network_4_5_AnnP_2, P_network_4_5_AnnP_3, P_network_4_5_AnnP_4, P_network_4_5_AnnP_5, P_network_4_5_AnnP_6, P_network_4_5_AnnP_7, P_network_4_5_RP_0, P_network_4_5_RP_1, P_network_4_5_RP_2, P_network_4_5_RP_3, P_network_4_5_RP_4, P_network_4_5_RP_5, P_network_4_5_RP_6, P_network_4_5_RP_7, P_network_4_6_AskP_0, P_network_4_6_AskP_1, P_network_4_6_AskP_2, P_network_4_6_AskP_3, P_network_4_6_AskP_4, P_network_4_6_AskP_5, P_network_4_6_AskP_6, P_network_4_6_AskP_7, P_network_4_6_AnsP_0, P_network_4_6_AnsP_1, P_network_4_6_AnsP_2, P_network_4_6_AnsP_3, P_network_4_6_AnsP_4, P_network_4_6_AnsP_5, P_network_4_6_AnsP_6, P_network_4_6_AnsP_7, P_network_4_6_RI_0, P_network_4_6_RI_1, P_network_4_6_RI_2, P_network_4_6_RI_3, P_network_4_6_RI_4, P_network_4_6_RI_5, P_network_4_6_RI_6, P_network_4_6_RI_7, P_network_4_6_AI_0, P_network_4_6_AI_1, P_network_4_6_AI_2, P_network_4_6_AI_3, P_network_4_6_AI_4, P_network_4_6_AI_5, P_network_4_6_AI_6, P_network_4_6_AI_7, P_network_4_6_AnnP_0, P_network_4_6_AnnP_1, P_network_4_6_AnnP_2, P_network_4_6_AnnP_3, P_network_4_6_AnnP_4, P_network_4_6_AnnP_5, P_network_4_6_AnnP_6, P_network_4_6_AnnP_7, P_network_4_6_RP_0, P_network_4_6_RP_1, P_network_4_6_RP_2, P_network_4_6_RP_3, P_network_4_6_RP_4, P_network_4_6_RP_5, P_network_4_6_RP_6, P_network_4_6_RP_7, P_network_4_7_AskP_0, P_network_4_7_AskP_1, P_network_4_7_AskP_2, P_network_4_7_AskP_3, P_network_4_7_AskP_4, P_network_4_7_AskP_5, P_network_4_7_AskP_6, P_network_4_7_AskP_7, P_network_4_7_AnsP_0, P_network_4_7_AnsP_1, P_network_4_7_AnsP_2, P_network_4_7_AnsP_3, P_network_4_7_AnsP_4, P_network_4_7_AnsP_5, P_network_4_7_AnsP_6, P_network_4_7_AnsP_7, P_network_4_7_RI_0, P_network_4_7_RI_1, P_network_4_7_RI_2, P_network_4_7_RI_3, P_network_4_7_RI_4, P_network_4_7_RI_5, P_network_4_7_RI_6, P_network_4_7_RI_7, P_network_4_7_AI_0, P_network_4_7_AI_1, P_network_4_7_AI_2, P_network_4_7_AI_3, P_network_4_7_AI_4, P_network_4_7_AI_5, P_network_4_7_AI_6, P_network_4_7_AI_7, P_network_4_7_AnnP_0, P_network_4_7_AnnP_1, P_network_4_7_AnnP_2, P_network_4_7_AnnP_3, P_network_4_7_AnnP_4, P_network_4_7_AnnP_5, P_network_4_7_AnnP_6, P_network_4_7_AnnP_7, P_network_4_7_RP_0, P_network_4_7_RP_1, P_network_4_7_RP_2, P_network_4_7_RP_3, P_network_4_7_RP_4, P_network_4_7_RP_5, P_network_4_7_RP_6, P_network_4_7_RP_7, P_network_5_0_AskP_0, P_network_5_0_AskP_1, P_network_5_0_AskP_2, P_network_5_0_AskP_3, P_network_5_0_AskP_4, P_network_5_0_AskP_5, P_network_5_0_AskP_6, P_network_5_0_AskP_7, P_network_5_0_AnsP_0, P_network_5_0_AnsP_1, P_network_5_0_AnsP_2, P_network_5_0_AnsP_3, P_network_5_0_AnsP_4, P_network_5_0_AnsP_5, P_network_5_0_AnsP_6, P_network_5_0_AnsP_7, P_network_5_0_RI_0, P_network_5_0_RI_1, P_network_5_0_RI_2, P_network_5_0_RI_3, P_network_5_0_RI_4, P_network_5_0_RI_5, P_network_5_0_RI_6, P_network_5_0_RI_7, P_network_5_0_AI_0, P_network_5_0_AI_1, P_network_5_0_AI_2, P_network_5_0_AI_3, P_network_5_0_AI_4, P_network_5_0_AI_5, P_network_5_0_AI_6, P_network_5_0_AI_7, P_network_5_0_AnnP_0, P_network_5_0_AnnP_1, P_network_5_0_AnnP_2, P_network_5_0_AnnP_3, P_network_5_0_AnnP_4, P_network_5_0_AnnP_5, P_network_5_0_AnnP_6, P_network_5_0_AnnP_7, P_network_5_0_RP_0, P_network_5_0_RP_1, P_network_5_0_RP_2, P_network_5_0_RP_3, P_network_5_0_RP_4, P_network_5_0_RP_5, P_network_5_0_RP_6, P_network_5_0_RP_7, P_network_5_1_AskP_0, P_network_5_1_AskP_1, P_network_5_1_AskP_2, P_network_5_1_AskP_3, P_network_5_1_AskP_4, P_network_5_1_AskP_5, P_network_5_1_AskP_6, P_network_5_1_AskP_7, P_network_5_1_AnsP_0, P_network_5_1_AnsP_1, P_network_5_1_AnsP_2, P_network_5_1_AnsP_3, P_network_5_1_AnsP_4, P_network_5_1_AnsP_5, P_network_5_1_AnsP_6, P_network_5_1_AnsP_7, P_network_5_1_RI_0, P_network_5_1_RI_1, P_network_5_1_RI_2, P_network_5_1_RI_3, P_network_5_1_RI_4, P_network_5_1_RI_5, P_network_5_1_RI_6, P_network_5_1_RI_7, P_network_5_1_AI_0, P_network_5_1_AI_1, P_network_5_1_AI_2, P_network_5_1_AI_3, P_network_5_1_AI_4, P_network_5_1_AI_5, P_network_5_1_AI_6, P_network_5_1_AI_7, P_network_5_1_AnnP_0, P_network_5_1_AnnP_1, P_network_5_1_AnnP_2, P_network_5_1_AnnP_3, P_network_5_1_AnnP_4, P_network_5_1_AnnP_5, P_network_5_1_AnnP_6, P_network_5_1_AnnP_7, P_network_5_1_RP_0, P_network_5_1_RP_1, P_network_5_1_RP_2, P_network_5_1_RP_3, P_network_5_1_RP_4, P_network_5_1_RP_5, P_network_5_1_RP_6, P_network_5_1_RP_7, P_network_5_2_AskP_0, P_network_5_2_AskP_1, P_network_5_2_AskP_2, P_network_5_2_AskP_3, P_network_5_2_AskP_4, P_network_5_2_AskP_5, P_network_5_2_AskP_6, P_network_5_2_AskP_7, P_network_5_2_AnsP_0, P_network_5_2_AnsP_1, P_network_5_2_AnsP_2, P_network_5_2_AnsP_3, P_network_5_2_AnsP_4, P_network_5_2_AnsP_5, P_network_5_2_AnsP_6, P_network_5_2_AnsP_7, P_network_5_2_RI_0, P_network_5_2_RI_1, P_network_5_2_RI_2, P_network_5_2_RI_3, P_network_5_2_RI_4, P_network_5_2_RI_5, P_network_5_2_RI_6, P_network_5_2_RI_7, P_network_5_2_AI_0, P_network_5_2_AI_1, P_network_5_2_AI_2, P_network_5_2_AI_3, P_network_5_2_AI_4, P_network_5_2_AI_5, P_network_5_2_AI_6, P_network_5_2_AI_7, P_network_5_2_AnnP_0, P_network_5_2_AnnP_1, P_network_5_2_AnnP_2, P_network_5_2_AnnP_3, P_network_5_2_AnnP_4, P_network_5_2_AnnP_5, P_network_5_2_AnnP_6, P_network_5_2_AnnP_7, P_network_5_2_RP_0, P_network_5_2_RP_1, P_network_5_2_RP_2, P_network_5_2_RP_3, P_network_5_2_RP_4, P_network_5_2_RP_5, P_network_5_2_RP_6, P_network_5_2_RP_7, P_network_5_3_AskP_0, P_network_5_3_AskP_1, P_network_5_3_AskP_2, P_network_5_3_AskP_3, P_network_5_3_AskP_4, P_network_5_3_AskP_5, P_network_5_3_AskP_6, P_network_5_3_AskP_7, P_network_5_3_AnsP_0, P_network_5_3_AnsP_1, P_network_5_3_AnsP_2, P_network_5_3_AnsP_3, P_network_5_3_AnsP_4, P_network_5_3_AnsP_5, P_network_5_3_AnsP_6, P_network_5_3_AnsP_7, P_network_5_3_RI_0, P_network_5_3_RI_1, P_network_5_3_RI_2, P_network_5_3_RI_3, P_network_5_3_RI_4, P_network_5_3_RI_5, P_network_5_3_RI_6, P_network_5_3_RI_7, P_network_5_3_AI_0, P_network_5_3_AI_1, P_network_5_3_AI_2, P_network_5_3_AI_3, P_network_5_3_AI_4, P_network_5_3_AI_5, P_network_5_3_AI_6, P_network_5_3_AI_7, P_network_5_3_AnnP_0, P_network_5_3_AnnP_1, P_network_5_3_AnnP_2, P_network_5_3_AnnP_3, P_network_5_3_AnnP_4, P_network_5_3_AnnP_5, P_network_5_3_AnnP_6, P_network_5_3_AnnP_7, P_network_5_3_RP_0, P_network_5_3_RP_1, P_network_5_3_RP_2, P_network_5_3_RP_3, P_network_5_3_RP_4, P_network_5_3_RP_5, P_network_5_3_RP_6, P_network_5_3_RP_7, P_network_5_4_AskP_0, P_network_5_4_AskP_1, P_network_5_4_AskP_2, P_network_5_4_AskP_3, P_network_5_4_AskP_4, P_network_5_4_AskP_5, P_network_5_4_AskP_6, P_network_5_4_AskP_7, P_network_5_4_AnsP_0, P_network_5_4_AnsP_1, P_network_5_4_AnsP_2, P_network_5_4_AnsP_3, P_network_5_4_AnsP_4, P_network_5_4_AnsP_5, P_network_5_4_AnsP_6, P_network_5_4_AnsP_7, P_network_5_4_RI_0, P_network_5_4_RI_1, P_network_5_4_RI_2, P_network_5_4_RI_3, P_network_5_4_RI_4, P_network_5_4_RI_5, P_network_5_4_RI_6, P_network_5_4_RI_7, P_network_5_4_AI_0, P_network_5_4_AI_1, P_network_5_4_AI_2, P_network_5_4_AI_3, P_network_5_4_AI_4, P_network_5_4_AI_5, P_network_5_4_AI_6, P_network_5_4_AI_7, P_network_5_4_AnnP_0, P_network_5_4_AnnP_1, P_network_5_4_AnnP_2, P_network_5_4_AnnP_3, P_network_5_4_AnnP_4, P_network_5_4_AnnP_5, P_network_5_4_AnnP_6, P_network_5_4_AnnP_7, P_network_5_4_RP_0, P_network_5_4_RP_1, P_network_5_4_RP_2, P_network_5_4_RP_3, P_network_5_4_RP_4, P_network_5_4_RP_5, P_network_5_4_RP_6, P_network_5_4_RP_7, P_network_5_5_AskP_0, P_network_5_5_AskP_1, P_network_5_5_AskP_2, P_network_5_5_AskP_3, P_network_5_5_AskP_4, P_network_5_5_AskP_5, P_network_5_5_AskP_6, P_network_5_5_AskP_7, P_network_5_5_AnsP_0, P_network_5_5_AnsP_1, P_network_5_5_AnsP_2, P_network_5_5_AnsP_3, P_network_5_5_AnsP_4, P_network_5_5_AnsP_5, P_network_5_5_AnsP_6, P_network_5_5_AnsP_7, P_network_5_5_RI_0, P_network_5_5_RI_1, P_network_5_5_RI_2, P_network_5_5_RI_3, P_network_5_5_RI_4, P_network_5_5_RI_5, P_network_5_5_RI_6, P_network_5_5_RI_7, P_network_5_5_AI_0, P_network_5_5_AI_1, P_network_5_5_AI_2, P_network_5_5_AI_3, P_network_5_5_AI_4, P_network_5_5_AI_5, P_network_5_5_AI_6, P_network_5_5_AI_7, P_network_5_5_AnnP_0, P_network_5_5_AnnP_1, P_network_5_5_AnnP_2, P_network_5_5_AnnP_3, P_network_5_5_AnnP_4, P_network_5_5_AnnP_5, P_network_5_5_AnnP_6, P_network_5_5_AnnP_7, P_network_5_5_RP_0, P_network_5_5_RP_1, P_network_5_5_RP_2, P_network_5_5_RP_3, P_network_5_5_RP_4, P_network_5_5_RP_5, P_network_5_5_RP_6, P_network_5_5_RP_7, P_network_5_6_AskP_0, P_network_5_6_AskP_1, P_network_5_6_AskP_2, P_network_5_6_AskP_3, P_network_5_6_AskP_4, P_network_5_6_AskP_5, P_network_5_6_AskP_6, P_network_5_6_AskP_7, P_network_5_6_AnsP_0, P_network_5_6_AnsP_1, P_network_5_6_AnsP_2, P_network_5_6_AnsP_3, P_network_5_6_AnsP_4, P_network_5_6_AnsP_5, P_network_5_6_AnsP_6, P_network_5_6_AnsP_7, P_network_5_6_RI_0, P_network_5_6_RI_1, P_network_5_6_RI_2, P_network_5_6_RI_3, P_network_5_6_RI_4, P_network_5_6_RI_5, P_network_5_6_RI_6, P_network_5_6_RI_7, P_network_5_6_AI_0, P_network_5_6_AI_1, P_network_5_6_AI_2, P_network_5_6_AI_3, P_network_5_6_AI_4, P_network_5_6_AI_5, P_network_5_6_AI_6, P_network_5_6_AI_7, P_network_5_6_AnnP_0, P_network_5_6_AnnP_1, P_network_5_6_AnnP_2, P_network_5_6_AnnP_3, P_network_5_6_AnnP_4, P_network_5_6_AnnP_5, P_network_5_6_AnnP_6, P_network_5_6_AnnP_7, P_network_5_6_RP_0, P_network_5_6_RP_1, P_network_5_6_RP_2, P_network_5_6_RP_3, P_network_5_6_RP_4, P_network_5_6_RP_5, P_network_5_6_RP_6, P_network_5_6_RP_7, P_network_5_7_AskP_0, P_network_5_7_AskP_1, P_network_5_7_AskP_2, P_network_5_7_AskP_3, P_network_5_7_AskP_4, P_network_5_7_AskP_5, P_network_5_7_AskP_6, P_network_5_7_AskP_7, P_network_5_7_AnsP_0, P_network_5_7_AnsP_1, P_network_5_7_AnsP_2, P_network_5_7_AnsP_3, P_network_5_7_AnsP_4, P_network_5_7_AnsP_5, P_network_5_7_AnsP_6, P_network_5_7_AnsP_7, P_network_5_7_RI_0, P_network_5_7_RI_1, P_network_5_7_RI_2, P_network_5_7_RI_3, P_network_5_7_RI_4, P_network_5_7_RI_5, P_network_5_7_RI_6, P_network_5_7_RI_7, P_network_5_7_AI_0, P_network_5_7_AI_1, P_network_5_7_AI_2, P_network_5_7_AI_3, P_network_5_7_AI_4, P_network_5_7_AI_5, P_network_5_7_AI_6, P_network_5_7_AI_7, P_network_5_7_AnnP_0, P_network_5_7_AnnP_1, P_network_5_7_AnnP_2, P_network_5_7_AnnP_3, P_network_5_7_AnnP_4, P_network_5_7_AnnP_5, P_network_5_7_AnnP_6, P_network_5_7_AnnP_7, P_network_5_7_RP_0, P_network_5_7_RP_1, P_network_5_7_RP_2, P_network_5_7_RP_3, P_network_5_7_RP_4, P_network_5_7_RP_5, P_network_5_7_RP_6, P_network_5_7_RP_7, P_network_6_0_AskP_0, P_network_6_0_AskP_1, P_network_6_0_AskP_2, P_network_6_0_AskP_3, P_network_6_0_AskP_4, P_network_6_0_AskP_5, P_network_6_0_AskP_6, P_network_6_0_AskP_7, P_network_6_0_AnsP_0, P_network_6_0_AnsP_1, P_network_6_0_AnsP_2, P_network_6_0_AnsP_3, P_network_6_0_AnsP_4, P_network_6_0_AnsP_5, P_network_6_0_AnsP_6, P_network_6_0_AnsP_7, P_network_6_0_RI_0, P_network_6_0_RI_1, P_network_6_0_RI_2, P_network_6_0_RI_3, P_network_6_0_RI_4, P_network_6_0_RI_5, P_network_6_0_RI_6, P_network_6_0_RI_7, P_network_6_0_AI_0, P_network_6_0_AI_1, P_network_6_0_AI_2, P_network_6_0_AI_3, P_network_6_0_AI_4, P_network_6_0_AI_5, P_network_6_0_AI_6, P_network_6_0_AI_7, P_network_6_0_AnnP_0, P_network_6_0_AnnP_1, P_network_6_0_AnnP_2, P_network_6_0_AnnP_3, P_network_6_0_AnnP_4, P_network_6_0_AnnP_5, P_network_6_0_AnnP_6, P_network_6_0_AnnP_7, P_network_6_0_RP_0, P_network_6_0_RP_1, P_network_6_0_RP_2, P_network_6_0_RP_3, P_network_6_0_RP_4, P_network_6_0_RP_5, P_network_6_0_RP_6, P_network_6_0_RP_7, P_network_6_1_AskP_0, P_network_6_1_AskP_1, P_network_6_1_AskP_2, P_network_6_1_AskP_3, P_network_6_1_AskP_4, P_network_6_1_AskP_5, P_network_6_1_AskP_6, P_network_6_1_AskP_7, P_network_6_1_AnsP_0, P_network_6_1_AnsP_1, P_network_6_1_AnsP_2, P_network_6_1_AnsP_3, P_network_6_1_AnsP_4, P_network_6_1_AnsP_5, P_network_6_1_AnsP_6, P_network_6_1_AnsP_7, P_network_6_1_RI_0, P_network_6_1_RI_1, P_network_6_1_RI_2, P_network_6_1_RI_3, P_network_6_1_RI_4, P_network_6_1_RI_5, P_network_6_1_RI_6, P_network_6_1_RI_7, P_network_6_1_AI_0, P_network_6_1_AI_1, P_network_6_1_AI_2, P_network_6_1_AI_3, P_network_6_1_AI_4, P_network_6_1_AI_5, P_network_6_1_AI_6, P_network_6_1_AI_7, P_network_6_1_AnnP_0, P_network_6_1_AnnP_1, P_network_6_1_AnnP_2, P_network_6_1_AnnP_3, P_network_6_1_AnnP_4, P_network_6_1_AnnP_5, P_network_6_1_AnnP_6, P_network_6_1_AnnP_7, P_network_6_1_RP_0, P_network_6_1_RP_1, P_network_6_1_RP_2, P_network_6_1_RP_3, P_network_6_1_RP_4, P_network_6_1_RP_5, P_network_6_1_RP_6, P_network_6_1_RP_7, P_network_6_2_AskP_0, P_network_6_2_AskP_1, P_network_6_2_AskP_2, P_network_6_2_AskP_3, P_network_6_2_AskP_4, P_network_6_2_AskP_5, P_network_6_2_AskP_6, P_network_6_2_AskP_7, P_network_6_2_AnsP_0, P_network_6_2_AnsP_1, P_network_6_2_AnsP_2, P_network_6_2_AnsP_3, P_network_6_2_AnsP_4, P_network_6_2_AnsP_5, P_network_6_2_AnsP_6, P_network_6_2_AnsP_7, P_network_6_2_RI_0, P_network_6_2_RI_1, P_network_6_2_RI_2, P_network_6_2_RI_3, P_network_6_2_RI_4, P_network_6_2_RI_5, P_network_6_2_RI_6, P_network_6_2_RI_7, P_network_6_2_AI_0, P_network_6_2_AI_1, P_network_6_2_AI_2, P_network_6_2_AI_3, P_network_6_2_AI_4, P_network_6_2_AI_5, P_network_6_2_AI_6, P_network_6_2_AI_7, P_network_6_2_AnnP_0, P_network_6_2_AnnP_1, P_network_6_2_AnnP_2, P_network_6_2_AnnP_3, P_network_6_2_AnnP_4, P_network_6_2_AnnP_5, P_network_6_2_AnnP_6, P_network_6_2_AnnP_7, P_network_6_2_RP_0, P_network_6_2_RP_1, P_network_6_2_RP_2, P_network_6_2_RP_3, P_network_6_2_RP_4, P_network_6_2_RP_5, P_network_6_2_RP_6, P_network_6_2_RP_7, P_network_6_3_AskP_0, P_network_6_3_AskP_1, P_network_6_3_AskP_2, P_network_6_3_AskP_3, P_network_6_3_AskP_4, P_network_6_3_AskP_5, P_network_6_3_AskP_6, P_network_6_3_AskP_7, P_network_6_3_AnsP_0, P_network_6_3_AnsP_1, P_network_6_3_AnsP_2, P_network_6_3_AnsP_3, P_network_6_3_AnsP_4, P_network_6_3_AnsP_5, P_network_6_3_AnsP_6, P_network_6_3_AnsP_7, P_network_6_3_RI_0, P_network_6_3_RI_1, P_network_6_3_RI_2, P_network_6_3_RI_3, P_network_6_3_RI_4, P_network_6_3_RI_5, P_network_6_3_RI_6, P_network_6_3_RI_7, P_network_6_3_AI_0, P_network_6_3_AI_1, P_network_6_3_AI_2, P_network_6_3_AI_3, P_network_6_3_AI_4, P_network_6_3_AI_5, P_network_6_3_AI_6, P_network_6_3_AI_7, P_network_6_3_AnnP_0, P_network_6_3_AnnP_1, P_network_6_3_AnnP_2, P_network_6_3_AnnP_3, P_network_6_3_AnnP_4, P_network_6_3_AnnP_5, P_network_6_3_AnnP_6, P_network_6_3_AnnP_7, P_network_6_3_RP_0, P_network_6_3_RP_1, P_network_6_3_RP_2, P_network_6_3_RP_3, P_network_6_3_RP_4, P_network_6_3_RP_5, P_network_6_3_RP_6, P_network_6_3_RP_7, P_network_6_4_AskP_0, P_network_6_4_AskP_1, P_network_6_4_AskP_2, P_network_6_4_AskP_3, P_network_6_4_AskP_4, P_network_6_4_AskP_5, P_network_6_4_AskP_6, P_network_6_4_AskP_7, P_network_6_4_AnsP_0, P_network_6_4_AnsP_1, P_network_6_4_AnsP_2, P_network_6_4_AnsP_3, P_network_6_4_AnsP_4, P_network_6_4_AnsP_5, P_network_6_4_AnsP_6, P_network_6_4_AnsP_7, P_network_6_4_RI_0, P_network_6_4_RI_1, P_network_6_4_RI_2, P_network_6_4_RI_3, P_network_6_4_RI_4, P_network_6_4_RI_5, P_network_6_4_RI_6, P_network_6_4_RI_7, P_network_6_4_AI_0, P_network_6_4_AI_1, P_network_6_4_AI_2, P_network_6_4_AI_3, P_network_6_4_AI_4, P_network_6_4_AI_5, P_network_6_4_AI_6, P_network_6_4_AI_7, P_network_6_4_AnnP_0, P_network_6_4_AnnP_1, P_network_6_4_AnnP_2, P_network_6_4_AnnP_3, P_network_6_4_AnnP_4, P_network_6_4_AnnP_5, P_network_6_4_AnnP_6, P_network_6_4_AnnP_7, P_network_6_4_RP_0, P_network_6_4_RP_1, P_network_6_4_RP_2, P_network_6_4_RP_3, P_network_6_4_RP_4, P_network_6_4_RP_5, P_network_6_4_RP_6, P_network_6_4_RP_7, P_network_6_5_AskP_0, P_network_6_5_AskP_1, P_network_6_5_AskP_2, P_network_6_5_AskP_3, P_network_6_5_AskP_4, P_network_6_5_AskP_5, P_network_6_5_AskP_6, P_network_6_5_AskP_7, P_network_6_5_AnsP_0, P_network_6_5_AnsP_1, P_network_6_5_AnsP_2, P_network_6_5_AnsP_3, P_network_6_5_AnsP_4, P_network_6_5_AnsP_5, P_network_6_5_AnsP_6, P_network_6_5_AnsP_7, P_network_6_5_RI_0, P_network_6_5_RI_1, P_network_6_5_RI_2, P_network_6_5_RI_3, P_network_6_5_RI_4, P_network_6_5_RI_5, P_network_6_5_RI_6, P_network_6_5_RI_7, P_network_6_5_AI_0, P_network_6_5_AI_1, P_network_6_5_AI_2, P_network_6_5_AI_3, P_network_6_5_AI_4, P_network_6_5_AI_5, P_network_6_5_AI_6, P_network_6_5_AI_7, P_network_6_5_AnnP_0, P_network_6_5_AnnP_1, P_network_6_5_AnnP_2, P_network_6_5_AnnP_3, P_network_6_5_AnnP_4, P_network_6_5_AnnP_5, P_network_6_5_AnnP_6, P_network_6_5_AnnP_7, P_network_6_5_RP_0, P_network_6_5_RP_1, P_network_6_5_RP_2, P_network_6_5_RP_3, P_network_6_5_RP_4, P_network_6_5_RP_5, P_network_6_5_RP_6, P_network_6_5_RP_7, P_network_6_6_AskP_0, P_network_6_6_AskP_1, P_network_6_6_AskP_2, P_network_6_6_AskP_3, P_network_6_6_AskP_4, P_network_6_6_AskP_5, P_network_6_6_AskP_6, P_network_6_6_AskP_7, P_network_6_6_AnsP_0, P_network_6_6_AnsP_1, P_network_6_6_AnsP_2, P_network_6_6_AnsP_3, P_network_6_6_AnsP_4, P_network_6_6_AnsP_5, P_network_6_6_AnsP_6, P_network_6_6_AnsP_7, P_network_6_6_RI_0, P_network_6_6_RI_1, P_network_6_6_RI_2, P_network_6_6_RI_3, P_network_6_6_RI_4, P_network_6_6_RI_5, P_network_6_6_RI_6, P_network_6_6_RI_7, P_network_6_6_AI_0, P_network_6_6_AI_1, P_network_6_6_AI_2, P_network_6_6_AI_3, P_network_6_6_AI_4, P_network_6_6_AI_5, P_network_6_6_AI_6, P_network_6_6_AI_7, P_network_6_6_AnnP_0, P_network_6_6_AnnP_1, P_network_6_6_AnnP_2, P_network_6_6_AnnP_3, P_network_6_6_AnnP_4, P_network_6_6_AnnP_5, P_network_6_6_AnnP_6, P_network_6_6_AnnP_7, P_network_6_6_RP_0, P_network_6_6_RP_1, P_network_6_6_RP_2, P_network_6_6_RP_3, P_network_6_6_RP_4, P_network_6_6_RP_5, P_network_6_6_RP_6, P_network_6_6_RP_7, P_network_6_7_AskP_0, P_network_6_7_AskP_1, P_network_6_7_AskP_2, P_network_6_7_AskP_3, P_network_6_7_AskP_4, P_network_6_7_AskP_5, P_network_6_7_AskP_6, P_network_6_7_AskP_7, P_network_6_7_AnsP_0, P_network_6_7_AnsP_1, P_network_6_7_AnsP_2, P_network_6_7_AnsP_3, P_network_6_7_AnsP_4, P_network_6_7_AnsP_5, P_network_6_7_AnsP_6, P_network_6_7_AnsP_7, P_network_6_7_RI_0, P_network_6_7_RI_1, P_network_6_7_RI_2, P_network_6_7_RI_3, P_network_6_7_RI_4, P_network_6_7_RI_5, P_network_6_7_RI_6, P_network_6_7_RI_7, P_network_6_7_AI_0, P_network_6_7_AI_1, P_network_6_7_AI_2, P_network_6_7_AI_3, P_network_6_7_AI_4, P_network_6_7_AI_5, P_network_6_7_AI_6, P_network_6_7_AI_7, P_network_6_7_AnnP_0, P_network_6_7_AnnP_1, P_network_6_7_AnnP_2, P_network_6_7_AnnP_3, P_network_6_7_AnnP_4, P_network_6_7_AnnP_5, P_network_6_7_AnnP_6, P_network_6_7_AnnP_7, P_network_6_7_RP_0, P_network_6_7_RP_1, P_network_6_7_RP_2, P_network_6_7_RP_3, P_network_6_7_RP_4, P_network_6_7_RP_5, P_network_6_7_RP_6, P_network_6_7_RP_7, P_network_7_0_AskP_0, P_network_7_0_AskP_1, P_network_7_0_AskP_2, P_network_7_0_AskP_3, P_network_7_0_AskP_4, P_network_7_0_AskP_5, P_network_7_0_AskP_6, P_network_7_0_AskP_7, P_network_7_0_AnsP_0, P_network_7_0_AnsP_1, P_network_7_0_AnsP_2, P_network_7_0_AnsP_3, P_network_7_0_AnsP_4, P_network_7_0_AnsP_5, P_network_7_0_AnsP_6, P_network_7_0_AnsP_7, P_network_7_0_RI_0, P_network_7_0_RI_1, P_network_7_0_RI_2, P_network_7_0_RI_3, P_network_7_0_RI_4, P_network_7_0_RI_5, P_network_7_0_RI_6, P_network_7_0_RI_7, P_network_7_0_AI_0, P_network_7_0_AI_1, P_network_7_0_AI_2, P_network_7_0_AI_3, P_network_7_0_AI_4, P_network_7_0_AI_5, P_network_7_0_AI_6, P_network_7_0_AI_7, P_network_7_0_AnnP_0, P_network_7_0_AnnP_1, P_network_7_0_AnnP_2, P_network_7_0_AnnP_3, P_network_7_0_AnnP_4, P_network_7_0_AnnP_5, P_network_7_0_AnnP_6, P_network_7_0_AnnP_7, P_network_7_0_RP_0, P_network_7_0_RP_1, P_network_7_0_RP_2, P_network_7_0_RP_3, P_network_7_0_RP_4, P_network_7_0_RP_5, P_network_7_0_RP_6, P_network_7_0_RP_7, P_network_7_1_AskP_0, P_network_7_1_AskP_1, P_network_7_1_AskP_2, P_network_7_1_AskP_3, P_network_7_1_AskP_4, P_network_7_1_AskP_5, P_network_7_1_AskP_6, P_network_7_1_AskP_7, P_network_7_1_AnsP_0, P_network_7_1_AnsP_1, P_network_7_1_AnsP_2, P_network_7_1_AnsP_3, P_network_7_1_AnsP_4, P_network_7_1_AnsP_5, P_network_7_1_AnsP_6, P_network_7_1_AnsP_7, P_network_7_1_RI_0, P_network_7_1_RI_1, P_network_7_1_RI_2, P_network_7_1_RI_3, P_network_7_1_RI_4, P_network_7_1_RI_5, P_network_7_1_RI_6, P_network_7_1_RI_7, P_network_7_1_AI_0, P_network_7_1_AI_1, P_network_7_1_AI_2, P_network_7_1_AI_3, P_network_7_1_AI_4, P_network_7_1_AI_5, P_network_7_1_AI_6, P_network_7_1_AI_7, P_network_7_1_AnnP_0, P_network_7_1_AnnP_1, P_network_7_1_AnnP_2, P_network_7_1_AnnP_3, P_network_7_1_AnnP_4, P_network_7_1_AnnP_5, P_network_7_1_AnnP_6, P_network_7_1_AnnP_7, P_network_7_1_RP_0, P_network_7_1_RP_1, P_network_7_1_RP_2, P_network_7_1_RP_3, P_network_7_1_RP_4, P_network_7_1_RP_5, P_network_7_1_RP_6, P_network_7_1_RP_7, P_network_7_2_AskP_0, P_network_7_2_AskP_1, P_network_7_2_AskP_2, P_network_7_2_AskP_3, P_network_7_2_AskP_4, P_network_7_2_AskP_5, P_network_7_2_AskP_6, P_network_7_2_AskP_7, P_network_7_2_AnsP_0, P_network_7_2_AnsP_1, P_network_7_2_AnsP_2, P_network_7_2_AnsP_3, P_network_7_2_AnsP_4, P_network_7_2_AnsP_5, P_network_7_2_AnsP_6, P_network_7_2_AnsP_7, P_network_7_2_RI_0, P_network_7_2_RI_1, P_network_7_2_RI_2, P_network_7_2_RI_3, P_network_7_2_RI_4, P_network_7_2_RI_5, P_network_7_2_RI_6, P_network_7_2_RI_7, P_network_7_2_AI_0, P_network_7_2_AI_1, P_network_7_2_AI_2, P_network_7_2_AI_3, P_network_7_2_AI_4, P_network_7_2_AI_5, P_network_7_2_AI_6, P_network_7_2_AI_7, P_network_7_2_AnnP_0, P_network_7_2_AnnP_1, P_network_7_2_AnnP_2, P_network_7_2_AnnP_3, P_network_7_2_AnnP_4, P_network_7_2_AnnP_5, P_network_7_2_AnnP_6, P_network_7_2_AnnP_7, P_network_7_2_RP_0, P_network_7_2_RP_1, P_network_7_2_RP_2, P_network_7_2_RP_3, P_network_7_2_RP_4, P_network_7_2_RP_5, P_network_7_2_RP_6, P_network_7_2_RP_7, P_network_7_3_AskP_0, P_network_7_3_AskP_1, P_network_7_3_AskP_2, P_network_7_3_AskP_3, P_network_7_3_AskP_4, P_network_7_3_AskP_5, P_network_7_3_AskP_6, P_network_7_3_AskP_7, P_network_7_3_AnsP_0, P_network_7_3_AnsP_1, P_network_7_3_AnsP_2, P_network_7_3_AnsP_3, P_network_7_3_AnsP_4, P_network_7_3_AnsP_5, P_network_7_3_AnsP_6, P_network_7_3_AnsP_7, P_network_7_3_RI_0, P_network_7_3_RI_1, P_network_7_3_RI_2, P_network_7_3_RI_3, P_network_7_3_RI_4, P_network_7_3_RI_5, P_network_7_3_RI_6, P_network_7_3_RI_7, P_network_7_3_AI_0, P_network_7_3_AI_1, P_network_7_3_AI_2, P_network_7_3_AI_3, P_network_7_3_AI_4, P_network_7_3_AI_5, P_network_7_3_AI_6, P_network_7_3_AI_7, P_network_7_3_AnnP_0, P_network_7_3_AnnP_1, P_network_7_3_AnnP_2, P_network_7_3_AnnP_3, P_network_7_3_AnnP_4, P_network_7_3_AnnP_5, P_network_7_3_AnnP_6, P_network_7_3_AnnP_7, P_network_7_3_RP_0, P_network_7_3_RP_1, P_network_7_3_RP_2, P_network_7_3_RP_3, P_network_7_3_RP_4, P_network_7_3_RP_5, P_network_7_3_RP_6, P_network_7_3_RP_7, P_network_7_4_AskP_0, P_network_7_4_AskP_1, P_network_7_4_AskP_2, P_network_7_4_AskP_3, P_network_7_4_AskP_4, P_network_7_4_AskP_5, P_network_7_4_AskP_6, P_network_7_4_AskP_7, P_network_7_4_AnsP_0, P_network_7_4_AnsP_1, P_network_7_4_AnsP_2, P_network_7_4_AnsP_3, P_network_7_4_AnsP_4, P_network_7_4_AnsP_5, P_network_7_4_AnsP_6, P_network_7_4_AnsP_7, P_network_7_4_RI_0, P_network_7_4_RI_1, P_network_7_4_RI_2, P_network_7_4_RI_3, P_network_7_4_RI_4, P_network_7_4_RI_5, P_network_7_4_RI_6, P_network_7_4_RI_7, P_network_7_4_AI_0, P_network_7_4_AI_1, P_network_7_4_AI_2, P_network_7_4_AI_3, P_network_7_4_AI_4, P_network_7_4_AI_5, P_network_7_4_AI_6, P_network_7_4_AI_7, P_network_7_4_AnnP_0, P_network_7_4_AnnP_1, P_network_7_4_AnnP_2, P_network_7_4_AnnP_3, P_network_7_4_AnnP_4, P_network_7_4_AnnP_5, P_network_7_4_AnnP_6, P_network_7_4_AnnP_7, P_network_7_4_RP_0, P_network_7_4_RP_1, P_network_7_4_RP_2, P_network_7_4_RP_3, P_network_7_4_RP_4, P_network_7_4_RP_5, P_network_7_4_RP_6, P_network_7_4_RP_7, P_network_7_5_AskP_0, P_network_7_5_AskP_1, P_network_7_5_AskP_2, P_network_7_5_AskP_3, P_network_7_5_AskP_4, P_network_7_5_AskP_5, P_network_7_5_AskP_6, P_network_7_5_AskP_7, P_network_7_5_AnsP_0, P_network_7_5_AnsP_1, P_network_7_5_AnsP_2, P_network_7_5_AnsP_3, P_network_7_5_AnsP_4, P_network_7_5_AnsP_5, P_network_7_5_AnsP_6, P_network_7_5_AnsP_7, P_network_7_5_RI_0, P_network_7_5_RI_1, P_network_7_5_RI_2, P_network_7_5_RI_3, P_network_7_5_RI_4, P_network_7_5_RI_5, P_network_7_5_RI_6, P_network_7_5_RI_7, P_network_7_5_AI_0, P_network_7_5_AI_1, P_network_7_5_AI_2, P_network_7_5_AI_3, P_network_7_5_AI_4, P_network_7_5_AI_5, P_network_7_5_AI_6, P_network_7_5_AI_7, P_network_7_5_AnnP_0, P_network_7_5_AnnP_1, P_network_7_5_AnnP_2, P_network_7_5_AnnP_3, P_network_7_5_AnnP_4, P_network_7_5_AnnP_5, P_network_7_5_AnnP_6, P_network_7_5_AnnP_7, P_network_7_5_RP_0, P_network_7_5_RP_1, P_network_7_5_RP_2, P_network_7_5_RP_3, P_network_7_5_RP_4, P_network_7_5_RP_5, P_network_7_5_RP_6, P_network_7_5_RP_7, P_network_7_6_AskP_0, P_network_7_6_AskP_1, P_network_7_6_AskP_2, P_network_7_6_AskP_3, P_network_7_6_AskP_4, P_network_7_6_AskP_5, P_network_7_6_AskP_6, P_network_7_6_AskP_7, P_network_7_6_AnsP_0, P_network_7_6_AnsP_1, P_network_7_6_AnsP_2, P_network_7_6_AnsP_3, P_network_7_6_AnsP_4, P_network_7_6_AnsP_5, P_network_7_6_AnsP_6, P_network_7_6_AnsP_7, P_network_7_6_RI_0, P_network_7_6_RI_1, P_network_7_6_RI_2, P_network_7_6_RI_3, P_network_7_6_RI_4, P_network_7_6_RI_5, P_network_7_6_RI_6, P_network_7_6_RI_7, P_network_7_6_AI_0, P_network_7_6_AI_1, P_network_7_6_AI_2, P_network_7_6_AI_3, P_network_7_6_AI_4, P_network_7_6_AI_5, P_network_7_6_AI_6, P_network_7_6_AI_7, P_network_7_6_AnnP_0, P_network_7_6_AnnP_1, P_network_7_6_AnnP_2, P_network_7_6_AnnP_3, P_network_7_6_AnnP_4, P_network_7_6_AnnP_5, P_network_7_6_AnnP_6, P_network_7_6_AnnP_7, P_network_7_6_RP_0, P_network_7_6_RP_1, P_network_7_6_RP_2, P_network_7_6_RP_3, P_network_7_6_RP_4, P_network_7_6_RP_5, P_network_7_6_RP_6, P_network_7_6_RP_7, P_network_7_7_AskP_0, P_network_7_7_AskP_1, P_network_7_7_AskP_2, P_network_7_7_AskP_3, P_network_7_7_AskP_4, P_network_7_7_AskP_5, P_network_7_7_AskP_6, P_network_7_7_AskP_7, P_network_7_7_AnsP_0, P_network_7_7_AnsP_1, P_network_7_7_AnsP_2, P_network_7_7_AnsP_3, P_network_7_7_AnsP_4, P_network_7_7_AnsP_5, P_network_7_7_AnsP_6, P_network_7_7_AnsP_7, P_network_7_7_RI_0, P_network_7_7_RI_1, P_network_7_7_RI_2, P_network_7_7_RI_3, P_network_7_7_RI_4, P_network_7_7_RI_5, P_network_7_7_RI_6, P_network_7_7_RI_7, P_network_7_7_AI_0, P_network_7_7_AI_1, P_network_7_7_AI_2, P_network_7_7_AI_3, P_network_7_7_AI_4, P_network_7_7_AI_5, P_network_7_7_AI_6, P_network_7_7_AI_7, P_network_7_7_AnnP_0, P_network_7_7_AnnP_1, P_network_7_7_AnnP_2, P_network_7_7_AnnP_3, P_network_7_7_AnnP_4, P_network_7_7_AnnP_5, P_network_7_7_AnnP_6, P_network_7_7_AnnP_7, P_network_7_7_RP_0, P_network_7_7_RP_1, P_network_7_7_RP_2, P_network_7_7_RP_3, P_network_7_7_RP_4, P_network_7_7_RP_5, P_network_7_7_RP_6, P_network_7_7_RP_7, P_poll__handlingMessage_0, P_poll__handlingMessage_1, P_poll__handlingMessage_2, P_poll__handlingMessage_3, P_poll__handlingMessage_4, P_poll__handlingMessage_5, P_poll__handlingMessage_6, P_poll__handlingMessage_7, P_poll__networl_0_0_AskP_0, P_poll__networl_0_0_AskP_1, P_poll__networl_0_0_AskP_2, P_poll__networl_0_0_AskP_3, P_poll__networl_0_0_AskP_4, P_poll__networl_0_0_AskP_5, P_poll__networl_0_0_AskP_6, P_poll__networl_0_0_AskP_7, P_poll__networl_0_0_AnsP_0, P_poll__networl_0_0_AnsP_1, P_poll__networl_0_0_AnsP_2, P_poll__networl_0_0_AnsP_3, P_poll__networl_0_0_AnsP_4, P_poll__networl_0_0_AnsP_5, P_poll__networl_0_0_AnsP_6, P_poll__networl_0_0_AnsP_7, P_poll__networl_0_0_RI_0, P_poll__networl_0_0_RI_1, P_poll__networl_0_0_RI_2, P_poll__networl_0_0_RI_3, P_poll__networl_0_0_RI_4, P_poll__networl_0_0_RI_5, P_poll__networl_0_0_RI_6, P_poll__networl_0_0_RI_7, P_poll__networl_0_0_AI_0, P_poll__networl_0_0_AI_1, P_poll__networl_0_0_AI_2, P_poll__networl_0_0_AI_3, P_poll__networl_0_0_AI_4, P_poll__networl_0_0_AI_5, P_poll__networl_0_0_AI_6, P_poll__networl_0_0_AI_7, P_poll__networl_0_0_AnnP_0, P_poll__networl_0_0_AnnP_1, P_poll__networl_0_0_AnnP_2, P_poll__networl_0_0_AnnP_3, P_poll__networl_0_0_AnnP_4, P_poll__networl_0_0_AnnP_5, P_poll__networl_0_0_AnnP_6, P_poll__networl_0_0_AnnP_7, P_poll__networl_0_0_RP_0, P_poll__networl_0_0_RP_1, P_poll__networl_0_0_RP_2, P_poll__networl_0_0_RP_3, P_poll__networl_0_0_RP_4, P_poll__networl_0_0_RP_5, P_poll__networl_0_0_RP_6, P_poll__networl_0_0_RP_7, P_poll__networl_0_1_AskP_0, P_poll__networl_0_1_AskP_1, P_poll__networl_0_1_AskP_2, P_poll__networl_0_1_AskP_3, P_poll__networl_0_1_AskP_4, P_poll__networl_0_1_AskP_5, P_poll__networl_0_1_AskP_6, P_poll__networl_0_1_AskP_7, P_poll__networl_0_1_AnsP_0, P_poll__networl_0_1_AnsP_1, P_poll__networl_0_1_AnsP_2, P_poll__networl_0_1_AnsP_3, P_poll__networl_0_1_AnsP_4, P_poll__networl_0_1_AnsP_5, P_poll__networl_0_1_AnsP_6, P_poll__networl_0_1_AnsP_7, P_poll__networl_0_1_RI_0, P_poll__networl_0_1_RI_1, P_poll__networl_0_1_RI_2, P_poll__networl_0_1_RI_3, P_poll__networl_0_1_RI_4, P_poll__networl_0_1_RI_5, P_poll__networl_0_1_RI_6, P_poll__networl_0_1_RI_7, P_poll__networl_0_1_AI_0, P_poll__networl_0_1_AI_1, P_poll__networl_0_1_AI_2, P_poll__networl_0_1_AI_3, P_poll__networl_0_1_AI_4, P_poll__networl_0_1_AI_5, P_poll__networl_0_1_AI_6, P_poll__networl_0_1_AI_7, P_poll__networl_0_1_AnnP_0, P_poll__networl_0_1_AnnP_1, P_poll__networl_0_1_AnnP_2, P_poll__networl_0_1_AnnP_3, P_poll__networl_0_1_AnnP_4, P_poll__networl_0_1_AnnP_5, P_poll__networl_0_1_AnnP_6, P_poll__networl_0_1_AnnP_7, P_poll__networl_0_1_RP_0, P_poll__networl_0_1_RP_1, P_poll__networl_0_1_RP_2, P_poll__networl_0_1_RP_3, P_poll__networl_0_1_RP_4, P_poll__networl_0_1_RP_5, P_poll__networl_0_1_RP_6, P_poll__networl_0_1_RP_7, P_poll__networl_0_2_AskP_0, P_poll__networl_0_2_AskP_1, P_poll__networl_0_2_AskP_2, P_poll__networl_0_2_AskP_3, P_poll__networl_0_2_AskP_4, P_poll__networl_0_2_AskP_5, P_poll__networl_0_2_AskP_6, P_poll__networl_0_2_AskP_7, P_poll__networl_0_2_AnsP_0, P_poll__networl_0_2_AnsP_1, P_poll__networl_0_2_AnsP_2, P_poll__networl_0_2_AnsP_3, P_poll__networl_0_2_AnsP_4, P_poll__networl_0_2_AnsP_5, P_poll__networl_0_2_AnsP_6, P_poll__networl_0_2_AnsP_7, P_poll__networl_0_2_RI_0, P_poll__networl_0_2_RI_1, P_poll__networl_0_2_RI_2, P_poll__networl_0_2_RI_3, P_poll__networl_0_2_RI_4, P_poll__networl_0_2_RI_5, P_poll__networl_0_2_RI_6, P_poll__networl_0_2_RI_7, P_poll__networl_0_2_AI_0, P_poll__networl_0_2_AI_1, P_poll__networl_0_2_AI_2, P_poll__networl_0_2_AI_3, P_poll__networl_0_2_AI_4, P_poll__networl_0_2_AI_5, P_poll__networl_0_2_AI_6, P_poll__networl_0_2_AI_7, P_poll__networl_0_2_AnnP_0, P_poll__networl_0_2_AnnP_1, P_poll__networl_0_2_AnnP_2, P_poll__networl_0_2_AnnP_3, P_poll__networl_0_2_AnnP_4, P_poll__networl_0_2_AnnP_5, P_poll__networl_0_2_AnnP_6, P_poll__networl_0_2_AnnP_7, P_poll__networl_0_2_RP_0, P_poll__networl_0_2_RP_1, P_poll__networl_0_2_RP_2, P_poll__networl_0_2_RP_3, P_poll__networl_0_2_RP_4, P_poll__networl_0_2_RP_5, P_poll__networl_0_2_RP_6, P_poll__networl_0_2_RP_7, P_poll__networl_0_3_AskP_0, P_poll__networl_0_3_AskP_1, P_poll__networl_0_3_AskP_2, P_poll__networl_0_3_AskP_3, P_poll__networl_0_3_AskP_4, P_poll__networl_0_3_AskP_5, P_poll__networl_0_3_AskP_6, P_poll__networl_0_3_AskP_7, P_poll__networl_0_3_AnsP_0, P_poll__networl_0_3_AnsP_1, P_poll__networl_0_3_AnsP_2, P_poll__networl_0_3_AnsP_3, P_poll__networl_0_3_AnsP_4, P_poll__networl_0_3_AnsP_5, P_poll__networl_0_3_AnsP_6, P_poll__networl_0_3_AnsP_7, P_poll__networl_0_3_RI_0, P_poll__networl_0_3_RI_1, P_poll__networl_0_3_RI_2, P_poll__networl_0_3_RI_3, P_poll__networl_0_3_RI_4, P_poll__networl_0_3_RI_5, P_poll__networl_0_3_RI_6, P_poll__networl_0_3_RI_7, P_poll__networl_0_3_AI_0, P_poll__networl_0_3_AI_1, P_poll__networl_0_3_AI_2, P_poll__networl_0_3_AI_3, P_poll__networl_0_3_AI_4, P_poll__networl_0_3_AI_5, P_poll__networl_0_3_AI_6, P_poll__networl_0_3_AI_7, P_poll__networl_0_3_AnnP_0, P_poll__networl_0_3_AnnP_1, P_poll__networl_0_3_AnnP_2, P_poll__networl_0_3_AnnP_3, P_poll__networl_0_3_AnnP_4, P_poll__networl_0_3_AnnP_5, P_poll__networl_0_3_AnnP_6, P_poll__networl_0_3_AnnP_7, P_poll__networl_0_3_RP_0, P_poll__networl_0_3_RP_1, P_poll__networl_0_3_RP_2, P_poll__networl_0_3_RP_3, P_poll__networl_0_3_RP_4, P_poll__networl_0_3_RP_5, P_poll__networl_0_3_RP_6, P_poll__networl_0_3_RP_7, P_poll__networl_0_4_AskP_0, P_poll__networl_0_4_AskP_1, P_poll__networl_0_4_AskP_2, P_poll__networl_0_4_AskP_3, P_poll__networl_0_4_AskP_4, P_poll__networl_0_4_AskP_5, P_poll__networl_0_4_AskP_6, P_poll__networl_0_4_AskP_7, P_poll__networl_0_4_AnsP_0, P_poll__networl_0_4_AnsP_1, P_poll__networl_0_4_AnsP_2, P_poll__networl_0_4_AnsP_3, P_poll__networl_0_4_AnsP_4, P_poll__networl_0_4_AnsP_5, P_poll__networl_0_4_AnsP_6, P_poll__networl_0_4_AnsP_7, P_poll__networl_0_4_RI_0, P_poll__networl_0_4_RI_1, P_poll__networl_0_4_RI_2, P_poll__networl_0_4_RI_3, P_poll__networl_0_4_RI_4, P_poll__networl_0_4_RI_5, P_poll__networl_0_4_RI_6, P_poll__networl_0_4_RI_7, P_poll__networl_0_4_AI_0, P_poll__networl_0_4_AI_1, P_poll__networl_0_4_AI_2, P_poll__networl_0_4_AI_3, P_poll__networl_0_4_AI_4, P_poll__networl_0_4_AI_5, P_poll__networl_0_4_AI_6, P_poll__networl_0_4_AI_7, P_poll__networl_0_4_AnnP_0, P_poll__networl_0_4_AnnP_1, P_poll__networl_0_4_AnnP_2, P_poll__networl_0_4_AnnP_3, P_poll__networl_0_4_AnnP_4, P_poll__networl_0_4_AnnP_5, P_poll__networl_0_4_AnnP_6, P_poll__networl_0_4_AnnP_7, P_poll__networl_0_4_RP_0, P_poll__networl_0_4_RP_1, P_poll__networl_0_4_RP_2, P_poll__networl_0_4_RP_3, P_poll__networl_0_4_RP_4, P_poll__networl_0_4_RP_5, P_poll__networl_0_4_RP_6, P_poll__networl_0_4_RP_7, P_poll__networl_0_5_AskP_0, P_poll__networl_0_5_AskP_1, P_poll__networl_0_5_AskP_2, P_poll__networl_0_5_AskP_3, P_poll__networl_0_5_AskP_4, P_poll__networl_0_5_AskP_5, P_poll__networl_0_5_AskP_6, P_poll__networl_0_5_AskP_7, P_poll__networl_0_5_AnsP_0, P_poll__networl_0_5_AnsP_1, P_poll__networl_0_5_AnsP_2, P_poll__networl_0_5_AnsP_3, P_poll__networl_0_5_AnsP_4, P_poll__networl_0_5_AnsP_5, P_poll__networl_0_5_AnsP_6, P_poll__networl_0_5_AnsP_7, P_poll__networl_0_5_RI_0, P_poll__networl_0_5_RI_1, P_poll__networl_0_5_RI_2, P_poll__networl_0_5_RI_3, P_poll__networl_0_5_RI_4, P_poll__networl_0_5_RI_5, P_poll__networl_0_5_RI_6, P_poll__networl_0_5_RI_7, P_poll__networl_0_5_AI_0, P_poll__networl_0_5_AI_1, P_poll__networl_0_5_AI_2, P_poll__networl_0_5_AI_3, P_poll__networl_0_5_AI_4, P_poll__networl_0_5_AI_5, P_poll__networl_0_5_AI_6, P_poll__networl_0_5_AI_7, P_poll__networl_0_5_AnnP_0, P_poll__networl_0_5_AnnP_1, P_poll__networl_0_5_AnnP_2, P_poll__networl_0_5_AnnP_3, P_poll__networl_0_5_AnnP_4, P_poll__networl_0_5_AnnP_5, P_poll__networl_0_5_AnnP_6, P_poll__networl_0_5_AnnP_7, P_poll__networl_0_5_RP_0, P_poll__networl_0_5_RP_1, P_poll__networl_0_5_RP_2, P_poll__networl_0_5_RP_3, P_poll__networl_0_5_RP_4, P_poll__networl_0_5_RP_5, P_poll__networl_0_5_RP_6, P_poll__networl_0_5_RP_7, P_poll__networl_0_6_AskP_0, P_poll__networl_0_6_AskP_1, P_poll__networl_0_6_AskP_2, P_poll__networl_0_6_AskP_3, P_poll__networl_0_6_AskP_4, P_poll__networl_0_6_AskP_5, P_poll__networl_0_6_AskP_6, P_poll__networl_0_6_AskP_7, P_poll__networl_0_6_AnsP_0, P_poll__networl_0_6_AnsP_1, P_poll__networl_0_6_AnsP_2, P_poll__networl_0_6_AnsP_3, P_poll__networl_0_6_AnsP_4, P_poll__networl_0_6_AnsP_5, P_poll__networl_0_6_AnsP_6, P_poll__networl_0_6_AnsP_7, P_poll__networl_0_6_RI_0, P_poll__networl_0_6_RI_1, P_poll__networl_0_6_RI_2, P_poll__networl_0_6_RI_3, P_poll__networl_0_6_RI_4, P_poll__networl_0_6_RI_5, P_poll__networl_0_6_RI_6, P_poll__networl_0_6_RI_7, P_poll__networl_0_6_AI_0, P_poll__networl_0_6_AI_1, P_poll__networl_0_6_AI_2, P_poll__networl_0_6_AI_3, P_poll__networl_0_6_AI_4, P_poll__networl_0_6_AI_5, P_poll__networl_0_6_AI_6, P_poll__networl_0_6_AI_7, P_poll__networl_0_6_AnnP_0, P_poll__networl_0_6_AnnP_1, P_poll__networl_0_6_AnnP_2, P_poll__networl_0_6_AnnP_3, P_poll__networl_0_6_AnnP_4, P_poll__networl_0_6_AnnP_5, P_poll__networl_0_6_AnnP_6, P_poll__networl_0_6_AnnP_7, P_poll__networl_0_6_RP_0, P_poll__networl_0_6_RP_1, P_poll__networl_0_6_RP_2, P_poll__networl_0_6_RP_3, P_poll__networl_0_6_RP_4, P_poll__networl_0_6_RP_5, P_poll__networl_0_6_RP_6, P_poll__networl_0_6_RP_7, P_poll__networl_0_7_AskP_0, P_poll__networl_0_7_AskP_1, P_poll__networl_0_7_AskP_2, P_poll__networl_0_7_AskP_3, P_poll__networl_0_7_AskP_4, P_poll__networl_0_7_AskP_5, P_poll__networl_0_7_AskP_6, P_poll__networl_0_7_AskP_7, P_poll__networl_0_7_AnsP_0, P_poll__networl_0_7_AnsP_1, P_poll__networl_0_7_AnsP_2, P_poll__networl_0_7_AnsP_3, P_poll__networl_0_7_AnsP_4, P_poll__networl_0_7_AnsP_5, P_poll__networl_0_7_AnsP_6, P_poll__networl_0_7_AnsP_7, P_poll__networl_0_7_RI_0, P_poll__networl_0_7_RI_1, P_poll__networl_0_7_RI_2, P_poll__networl_0_7_RI_3, P_poll__networl_0_7_RI_4, P_poll__networl_0_7_RI_5, P_poll__networl_0_7_RI_6, P_poll__networl_0_7_RI_7, P_poll__networl_0_7_AI_0, P_poll__networl_0_7_AI_1, P_poll__networl_0_7_AI_2, P_poll__networl_0_7_AI_3, P_poll__networl_0_7_AI_4, P_poll__networl_0_7_AI_5, P_poll__networl_0_7_AI_6, P_poll__networl_0_7_AI_7, P_poll__networl_0_7_AnnP_0, P_poll__networl_0_7_AnnP_1, P_poll__networl_0_7_AnnP_2, P_poll__networl_0_7_AnnP_3, P_poll__networl_0_7_AnnP_4, P_poll__networl_0_7_AnnP_5, P_poll__networl_0_7_AnnP_6, P_poll__networl_0_7_AnnP_7, P_poll__networl_0_7_RP_0, P_poll__networl_0_7_RP_1, P_poll__networl_0_7_RP_2, P_poll__networl_0_7_RP_3, P_poll__networl_0_7_RP_4, P_poll__networl_0_7_RP_5, P_poll__networl_0_7_RP_6, P_poll__networl_0_7_RP_7, P_poll__networl_1_0_AskP_0, P_poll__networl_1_0_AskP_1, P_poll__networl_1_0_AskP_2, P_poll__networl_1_0_AskP_3, P_poll__networl_1_0_AskP_4, P_poll__networl_1_0_AskP_5, P_poll__networl_1_0_AskP_6, P_poll__networl_1_0_AskP_7, P_poll__networl_1_0_AnsP_0, P_poll__networl_1_0_AnsP_1, P_poll__networl_1_0_AnsP_2, P_poll__networl_1_0_AnsP_3, P_poll__networl_1_0_AnsP_4, P_poll__networl_1_0_AnsP_5, P_poll__networl_1_0_AnsP_6, P_poll__networl_1_0_AnsP_7, P_poll__networl_1_0_RI_0, P_poll__networl_1_0_RI_1, P_poll__networl_1_0_RI_2, P_poll__networl_1_0_RI_3, P_poll__networl_1_0_RI_4, P_poll__networl_1_0_RI_5, P_poll__networl_1_0_RI_6, P_poll__networl_1_0_RI_7, P_poll__networl_1_0_AI_0, P_poll__networl_1_0_AI_1, P_poll__networl_1_0_AI_2, P_poll__networl_1_0_AI_3, P_poll__networl_1_0_AI_4, P_poll__networl_1_0_AI_5, P_poll__networl_1_0_AI_6, P_poll__networl_1_0_AI_7, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_0_AnnP_2, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_AnnP_4, P_poll__networl_1_0_AnnP_5, P_poll__networl_1_0_AnnP_6, P_poll__networl_1_0_AnnP_7, P_poll__networl_1_0_RP_0, P_poll__networl_1_0_RP_1, P_poll__networl_1_0_RP_2, P_poll__networl_1_0_RP_3, P_poll__networl_1_0_RP_4, P_poll__networl_1_0_RP_5, P_poll__networl_1_0_RP_6, P_poll__networl_1_0_RP_7, P_poll__networl_1_1_AskP_0, P_poll__networl_1_1_AskP_1, P_poll__networl_1_1_AskP_2, P_poll__networl_1_1_AskP_3, P_poll__networl_1_1_AskP_4, P_poll__networl_1_1_AskP_5, P_poll__networl_1_1_AskP_6, P_poll__networl_1_1_AskP_7, P_poll__networl_1_1_AnsP_0, P_poll__networl_1_1_AnsP_1, P_poll__networl_1_1_AnsP_2, P_poll__networl_1_1_AnsP_3, P_poll__networl_1_1_AnsP_4, P_poll__networl_1_1_AnsP_5, P_poll__networl_1_1_AnsP_6, P_poll__networl_1_1_AnsP_7, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_RI_1, P_poll__networl_1_1_RI_2, P_poll__networl_1_1_RI_3, P_poll__networl_1_1_RI_4, P_poll__networl_1_1_RI_5, P_poll__networl_1_1_RI_6, P_poll__networl_1_1_RI_7, P_poll__networl_1_1_AI_0, P_poll__networl_1_1_AI_1, P_poll__networl_1_1_AI_2, P_poll__networl_1_1_AI_3, P_poll__networl_1_1_AI_4, P_poll__networl_1_1_AI_5, P_poll__networl_1_1_AI_6, P_poll__networl_1_1_AI_7, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_1_AnnP_1, P_poll__networl_1_1_AnnP_2, P_poll__networl_1_1_AnnP_3, P_poll__networl_1_1_AnnP_4, P_poll__networl_1_1_AnnP_5, P_poll__networl_1_1_AnnP_6, P_poll__networl_1_1_AnnP_7, P_poll__networl_1_1_RP_0, P_poll__networl_1_1_RP_1, P_poll__networl_1_1_RP_2, P_poll__networl_1_1_RP_3, P_poll__networl_1_1_RP_4, P_poll__networl_1_1_RP_5, P_poll__networl_1_1_RP_6, P_poll__networl_1_1_RP_7, P_poll__networl_1_2_AskP_0, P_poll__networl_1_2_AskP_1, P_poll__networl_1_2_AskP_2, P_poll__networl_1_2_AskP_3, P_poll__networl_1_2_AskP_4, P_poll__networl_1_2_AskP_5, P_poll__networl_1_2_AskP_6, P_poll__networl_1_2_AskP_7, P_poll__networl_1_2_AnsP_0, P_poll__networl_1_2_AnsP_1, P_poll__networl_1_2_AnsP_2, P_poll__networl_1_2_AnsP_3, P_poll__networl_1_2_AnsP_4, P_poll__networl_1_2_AnsP_5, P_poll__networl_1_2_AnsP_6, P_poll__networl_1_2_AnsP_7, P_poll__networl_1_2_RI_0, P_poll__networl_1_2_RI_1, P_poll__networl_1_2_RI_2, P_poll__networl_1_2_RI_3, P_poll__networl_1_2_RI_4, P_poll__networl_1_2_RI_5, P_poll__networl_1_2_RI_6, P_poll__networl_1_2_RI_7, P_poll__networl_1_2_AI_0, P_poll__networl_1_2_AI_1, P_poll__networl_1_2_AI_2, P_poll__networl_1_2_AI_3, P_poll__networl_1_2_AI_4, P_poll__networl_1_2_AI_5, P_poll__networl_1_2_AI_6, P_poll__networl_1_2_AI_7, P_poll__networl_1_2_AnnP_0, P_poll__networl_1_2_AnnP_1, P_poll__networl_1_2_AnnP_2, P_poll__networl_1_2_AnnP_3, P_poll__networl_1_2_AnnP_4, P_poll__networl_1_2_AnnP_5, P_poll__networl_1_2_AnnP_6, P_poll__networl_1_2_AnnP_7, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_RP_1, P_poll__networl_1_2_RP_2, P_poll__networl_1_2_RP_3, P_poll__networl_1_2_RP_4, P_poll__networl_1_2_RP_5, P_poll__networl_1_2_RP_6, P_poll__networl_1_2_RP_7, P_poll__networl_1_3_AskP_0, P_poll__networl_1_3_AskP_1, P_poll__networl_1_3_AskP_2, P_poll__networl_1_3_AskP_3, P_poll__networl_1_3_AskP_4, P_poll__networl_1_3_AskP_5, P_poll__networl_1_3_AskP_6, P_poll__networl_1_3_AskP_7, P_poll__networl_1_3_AnsP_0, P_poll__networl_1_3_AnsP_1, P_poll__networl_1_3_AnsP_2, P_poll__networl_1_3_AnsP_3, P_poll__networl_1_3_AnsP_4, P_poll__networl_1_3_AnsP_5, P_poll__networl_1_3_AnsP_6, P_poll__networl_1_3_AnsP_7, P_poll__networl_1_3_RI_0, P_poll__networl_1_3_RI_1, P_poll__networl_1_3_RI_2, P_poll__networl_1_3_RI_3, P_poll__networl_1_3_RI_4, P_poll__networl_1_3_RI_5, P_poll__networl_1_3_RI_6, P_poll__networl_1_3_RI_7, P_poll__networl_1_3_AI_0, P_poll__networl_1_3_AI_1, P_poll__networl_1_3_AI_2, P_poll__networl_1_3_AI_3, P_poll__networl_1_3_AI_4, P_poll__networl_1_3_AI_5, P_poll__networl_1_3_AI_6, P_poll__networl_1_3_AI_7, P_poll__networl_1_3_AnnP_0, P_poll__networl_1_3_AnnP_1, P_poll__networl_1_3_AnnP_2, P_poll__networl_1_3_AnnP_3, P_poll__networl_1_3_AnnP_4, P_poll__networl_1_3_AnnP_5, P_poll__networl_1_3_AnnP_6, P_poll__networl_1_3_AnnP_7, P_poll__networl_1_3_RP_0, P_poll__networl_1_3_RP_1, P_poll__networl_1_3_RP_2, P_poll__networl_1_3_RP_3, P_poll__networl_1_3_RP_4, P_poll__networl_1_3_RP_5, P_poll__networl_1_3_RP_6, P_poll__networl_1_3_RP_7, P_poll__networl_1_4_AskP_0, P_poll__networl_1_4_AskP_1, P_poll__networl_1_4_AskP_2, P_poll__networl_1_4_AskP_3, P_poll__networl_1_4_AskP_4, P_poll__networl_1_4_AskP_5, P_poll__networl_1_4_AskP_6, P_poll__networl_1_4_AskP_7, P_poll__networl_1_4_AnsP_0, P_poll__networl_1_4_AnsP_1, P_poll__networl_1_4_AnsP_2, P_poll__networl_1_4_AnsP_3, P_poll__networl_1_4_AnsP_4, P_poll__networl_1_4_AnsP_5, P_poll__networl_1_4_AnsP_6, P_poll__networl_1_4_AnsP_7, P_poll__networl_1_4_RI_0, P_poll__networl_1_4_RI_1, P_poll__networl_1_4_RI_2, P_poll__networl_1_4_RI_3, P_poll__networl_1_4_RI_4, P_poll__networl_1_4_RI_5, P_poll__networl_1_4_RI_6, P_poll__networl_1_4_RI_7, P_poll__networl_1_4_AI_0, P_poll__networl_1_4_AI_1, P_poll__networl_1_4_AI_2, P_poll__networl_1_4_AI_3, P_poll__networl_1_4_AI_4, P_poll__networl_1_4_AI_5, P_poll__networl_1_4_AI_6, P_poll__networl_1_4_AI_7, P_poll__networl_1_4_AnnP_0, P_poll__networl_1_4_AnnP_1, P_poll__networl_1_4_AnnP_2, P_poll__networl_1_4_AnnP_3, P_poll__networl_1_4_AnnP_4, P_poll__networl_1_4_AnnP_5, P_poll__networl_1_4_AnnP_6, P_poll__networl_1_4_AnnP_7, P_poll__networl_1_4_RP_0, P_poll__networl_1_4_RP_1, P_poll__networl_1_4_RP_2, P_poll__networl_1_4_RP_3, P_poll__networl_1_4_RP_4, P_poll__networl_1_4_RP_5, P_poll__networl_1_4_RP_6, P_poll__networl_1_4_RP_7, P_poll__networl_1_5_AskP_0, P_poll__networl_1_5_AskP_1, P_poll__networl_1_5_AskP_2, P_poll__networl_1_5_AskP_3, P_poll__networl_1_5_AskP_4, P_poll__networl_1_5_AskP_5, P_poll__networl_1_5_AskP_6, P_poll__networl_1_5_AskP_7, P_poll__networl_1_5_AnsP_0, P_poll__networl_1_5_AnsP_1, P_poll__networl_1_5_AnsP_2, P_poll__networl_1_5_AnsP_3, P_poll__networl_1_5_AnsP_4, P_poll__networl_1_5_AnsP_5, P_poll__networl_1_5_AnsP_6, P_poll__networl_1_5_AnsP_7, P_poll__networl_1_5_RI_0, P_poll__networl_1_5_RI_1, P_poll__networl_1_5_RI_2, P_poll__networl_1_5_RI_3, P_poll__networl_1_5_RI_4, P_poll__networl_1_5_RI_5, P_poll__networl_1_5_RI_6, P_poll__networl_1_5_RI_7, P_poll__networl_1_5_AI_0, P_poll__networl_1_5_AI_1, P_poll__networl_1_5_AI_2, P_poll__networl_1_5_AI_3, P_poll__networl_1_5_AI_4, P_poll__networl_1_5_AI_5, P_poll__networl_1_5_AI_6, P_poll__networl_1_5_AI_7, P_poll__networl_1_5_AnnP_0, P_poll__networl_1_5_AnnP_1, P_poll__networl_1_5_AnnP_2, P_poll__networl_1_5_AnnP_3, P_poll__networl_1_5_AnnP_4, P_poll__networl_1_5_AnnP_5, P_poll__networl_1_5_AnnP_6, P_poll__networl_1_5_AnnP_7, P_poll__networl_1_5_RP_0, P_poll__networl_1_5_RP_1, P_poll__networl_1_5_RP_2, P_poll__networl_1_5_RP_3, P_poll__networl_1_5_RP_4, P_poll__networl_1_5_RP_5, P_poll__networl_1_5_RP_6, P_poll__networl_1_5_RP_7, P_poll__networl_1_6_AskP_0, P_poll__networl_1_6_AskP_1, P_poll__networl_1_6_AskP_2, P_poll__networl_1_6_AskP_3, P_poll__networl_1_6_AskP_4, P_poll__networl_1_6_AskP_5, P_poll__networl_1_6_AskP_6, P_poll__networl_1_6_AskP_7, P_poll__networl_1_6_AnsP_0, P_poll__networl_1_6_AnsP_1, P_poll__networl_1_6_AnsP_2, P_poll__networl_1_6_AnsP_3, P_poll__networl_1_6_AnsP_4, P_poll__networl_1_6_AnsP_5, P_poll__networl_1_6_AnsP_6, P_poll__networl_1_6_AnsP_7, P_poll__networl_1_6_RI_0, P_poll__networl_1_6_RI_1, P_poll__networl_1_6_RI_2, P_poll__networl_1_6_RI_3, P_poll__networl_1_6_RI_4, P_poll__networl_1_6_RI_5, P_poll__networl_1_6_RI_6, P_poll__networl_1_6_RI_7, P_poll__networl_1_6_AI_0, P_poll__networl_1_6_AI_1, P_poll__networl_1_6_AI_2, P_poll__networl_1_6_AI_3, P_poll__networl_1_6_AI_4, P_poll__networl_1_6_AI_5, P_poll__networl_1_6_AI_6, P_poll__networl_1_6_AI_7, P_poll__networl_1_6_AnnP_0, P_poll__networl_1_6_AnnP_1, P_poll__networl_1_6_AnnP_2, P_poll__networl_1_6_AnnP_3, P_poll__networl_1_6_AnnP_4, P_poll__networl_1_6_AnnP_5, P_poll__networl_1_6_AnnP_6, P_poll__networl_1_6_AnnP_7, P_poll__networl_1_6_RP_0, P_poll__networl_1_6_RP_1, P_poll__networl_1_6_RP_2, P_poll__networl_1_6_RP_3, P_poll__networl_1_6_RP_4, P_poll__networl_1_6_RP_5, P_poll__networl_1_6_RP_6, P_poll__networl_1_6_RP_7, P_poll__networl_1_7_AskP_0, P_poll__networl_1_7_AskP_1, P_poll__networl_1_7_AskP_2, P_poll__networl_1_7_AskP_3, P_poll__networl_1_7_AskP_4, P_poll__networl_1_7_AskP_5, P_poll__networl_1_7_AskP_6, P_poll__networl_1_7_AskP_7, P_poll__networl_1_7_AnsP_0, P_poll__networl_1_7_AnsP_1, P_poll__networl_1_7_AnsP_2, P_poll__networl_1_7_AnsP_3, P_poll__networl_1_7_AnsP_4, P_poll__networl_1_7_AnsP_5, P_poll__networl_1_7_AnsP_6, P_poll__networl_1_7_AnsP_7, P_poll__networl_1_7_RI_0, P_poll__networl_1_7_RI_1, P_poll__networl_1_7_RI_2, P_poll__networl_1_7_RI_3, P_poll__networl_1_7_RI_4, P_poll__networl_1_7_RI_5, P_poll__networl_1_7_RI_6, P_poll__networl_1_7_RI_7, P_poll__networl_1_7_AI_0, P_poll__networl_1_7_AI_1, P_poll__networl_1_7_AI_2, P_poll__networl_1_7_AI_3, P_poll__networl_1_7_AI_4, P_poll__networl_1_7_AI_5, P_poll__networl_1_7_AI_6, P_poll__networl_1_7_AI_7, P_poll__networl_1_7_AnnP_0, P_poll__networl_1_7_AnnP_1, P_poll__networl_1_7_AnnP_2, P_poll__networl_1_7_AnnP_3, P_poll__networl_1_7_AnnP_4, P_poll__networl_1_7_AnnP_5, P_poll__networl_1_7_AnnP_6, P_poll__networl_1_7_AnnP_7, P_poll__networl_1_7_RP_0, P_poll__networl_1_7_RP_1, P_poll__networl_1_7_RP_2, P_poll__networl_1_7_RP_3, P_poll__networl_1_7_RP_4, P_poll__networl_1_7_RP_5, P_poll__networl_1_7_RP_6, P_poll__networl_1_7_RP_7, P_poll__networl_2_0_AskP_0, P_poll__networl_2_0_AskP_1, P_poll__networl_2_0_AskP_2, P_poll__networl_2_0_AskP_3, P_poll__networl_2_0_AskP_4, P_poll__networl_2_0_AskP_5, P_poll__networl_2_0_AskP_6, P_poll__networl_2_0_AskP_7, P_poll__networl_2_0_AnsP_0, P_poll__networl_2_0_AnsP_1, P_poll__networl_2_0_AnsP_2, P_poll__networl_2_0_AnsP_3, P_poll__networl_2_0_AnsP_4, P_poll__networl_2_0_AnsP_5, P_poll__networl_2_0_AnsP_6, P_poll__networl_2_0_AnsP_7, P_poll__networl_2_0_RI_0, P_poll__networl_2_0_RI_1, P_poll__networl_2_0_RI_2, P_poll__networl_2_0_RI_3, P_poll__networl_2_0_RI_4, P_poll__networl_2_0_RI_5, P_poll__networl_2_0_RI_6, P_poll__networl_2_0_RI_7, P_poll__networl_2_0_AI_0, P_poll__networl_2_0_AI_1, P_poll__networl_2_0_AI_2, P_poll__networl_2_0_AI_3, P_poll__networl_2_0_AI_4, P_poll__networl_2_0_AI_5, P_poll__networl_2_0_AI_6, P_poll__networl_2_0_AI_7, P_poll__networl_2_0_AnnP_0, P_poll__networl_2_0_AnnP_1, P_poll__networl_2_0_AnnP_2, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_0_AnnP_4, P_poll__networl_2_0_AnnP_5, P_poll__networl_2_0_AnnP_6, P_poll__networl_2_0_AnnP_7, P_poll__networl_2_0_RP_0, P_poll__networl_2_0_RP_1, P_poll__networl_2_0_RP_2, P_poll__networl_2_0_RP_3, P_poll__networl_2_0_RP_4, P_poll__networl_2_0_RP_5, P_poll__networl_2_0_RP_6, P_poll__networl_2_0_RP_7, P_poll__networl_2_1_AskP_0, P_poll__networl_2_1_AskP_1, P_poll__networl_2_1_AskP_2, P_poll__networl_2_1_AskP_3, P_poll__networl_2_1_AskP_4, P_poll__networl_2_1_AskP_5, P_poll__networl_2_1_AskP_6, P_poll__networl_2_1_AskP_7, P_poll__networl_2_1_AnsP_0, P_poll__networl_2_1_AnsP_1, P_poll__networl_2_1_AnsP_2, P_poll__networl_2_1_AnsP_3, P_poll__networl_2_1_AnsP_4, P_poll__networl_2_1_AnsP_5, P_poll__networl_2_1_AnsP_6, P_poll__networl_2_1_AnsP_7, P_poll__networl_2_1_RI_0, P_poll__networl_2_1_RI_1, P_poll__networl_2_1_RI_2, P_poll__networl_2_1_RI_3, P_poll__networl_2_1_RI_4, P_poll__networl_2_1_RI_5, P_poll__networl_2_1_RI_6, P_poll__networl_2_1_RI_7, P_poll__networl_2_1_AI_0, P_poll__networl_2_1_AI_1, P_poll__networl_2_1_AI_2, P_poll__networl_2_1_AI_3, P_poll__networl_2_1_AI_4, P_poll__networl_2_1_AI_5, P_poll__networl_2_1_AI_6, P_poll__networl_2_1_AI_7, P_poll__networl_2_1_AnnP_0, P_poll__networl_2_1_AnnP_1, P_poll__networl_2_1_AnnP_2, P_poll__networl_2_1_AnnP_3, P_poll__networl_2_1_AnnP_4, P_poll__networl_2_1_AnnP_5, P_poll__networl_2_1_AnnP_6, P_poll__networl_2_1_AnnP_7, P_poll__networl_2_1_RP_0, P_poll__networl_2_1_RP_1, P_poll__networl_2_1_RP_2, P_poll__networl_2_1_RP_3, P_poll__networl_2_1_RP_4, P_poll__networl_2_1_RP_5, P_poll__networl_2_1_RP_6, P_poll__networl_2_1_RP_7, P_poll__networl_2_2_AskP_0, P_poll__networl_2_2_AskP_1, P_poll__networl_2_2_AskP_2, P_poll__networl_2_2_AskP_3, P_poll__networl_2_2_AskP_4, P_poll__networl_2_2_AskP_5, P_poll__networl_2_2_AskP_6, P_poll__networl_2_2_AskP_7, P_poll__networl_2_2_AnsP_0, P_poll__networl_2_2_AnsP_1, P_poll__networl_2_2_AnsP_2, P_poll__networl_2_2_AnsP_3, P_poll__networl_2_2_AnsP_4, P_poll__networl_2_2_AnsP_5, P_poll__networl_2_2_AnsP_6, P_poll__networl_2_2_AnsP_7, P_poll__networl_2_2_RI_0, P_poll__networl_2_2_RI_1, P_poll__networl_2_2_RI_2, P_poll__networl_2_2_RI_3, P_poll__networl_2_2_RI_4, P_poll__networl_2_2_RI_5, P_poll__networl_2_2_RI_6, P_poll__networl_2_2_RI_7, P_poll__networl_2_2_AI_0, P_poll__networl_2_2_AI_1, P_poll__networl_2_2_AI_2, P_poll__networl_2_2_AI_3, P_poll__networl_2_2_AI_4, P_poll__networl_2_2_AI_5, P_poll__networl_2_2_AI_6, P_poll__networl_2_2_AI_7, P_poll__networl_2_2_AnnP_0, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_2_AnnP_2, P_poll__networl_2_2_AnnP_3, P_poll__networl_2_2_AnnP_4, P_poll__networl_2_2_AnnP_5, P_poll__networl_2_2_AnnP_6, P_poll__networl_2_2_AnnP_7, P_poll__networl_2_2_RP_0, P_poll__networl_2_2_RP_1, P_poll__networl_2_2_RP_2, P_poll__networl_2_2_RP_3, P_poll__networl_2_2_RP_4, P_poll__networl_2_2_RP_5, P_poll__networl_2_2_RP_6, P_poll__networl_2_2_RP_7, P_poll__networl_2_3_AskP_0, P_poll__networl_2_3_AskP_1, P_poll__networl_2_3_AskP_2, P_poll__networl_2_3_AskP_3, P_poll__networl_2_3_AskP_4, P_poll__networl_2_3_AskP_5, P_poll__networl_2_3_AskP_6, P_poll__networl_2_3_AskP_7, P_poll__networl_2_3_AnsP_0, P_poll__networl_2_3_AnsP_1, P_poll__networl_2_3_AnsP_2, P_poll__networl_2_3_AnsP_3, P_poll__networl_2_3_AnsP_4, P_poll__networl_2_3_AnsP_5, P_poll__networl_2_3_AnsP_6, P_poll__networl_2_3_AnsP_7, P_poll__networl_2_3_RI_0, P_poll__networl_2_3_RI_1, P_poll__networl_2_3_RI_2, P_poll__networl_2_3_RI_3, P_poll__networl_2_3_RI_4, P_poll__networl_2_3_RI_5, P_poll__networl_2_3_RI_6, P_poll__networl_2_3_RI_7, P_poll__networl_2_3_AI_0, P_poll__networl_2_3_AI_1, P_poll__networl_2_3_AI_2, P_poll__networl_2_3_AI_3, P_poll__networl_2_3_AI_4, P_poll__networl_2_3_AI_5, P_poll__networl_2_3_AI_6, P_poll__networl_2_3_AI_7, P_poll__networl_2_3_AnnP_0, P_poll__networl_2_3_AnnP_1, P_poll__networl_2_3_AnnP_2, P_poll__networl_2_3_AnnP_3, P_poll__networl_2_3_AnnP_4, P_poll__networl_2_3_AnnP_5, P_poll__networl_2_3_AnnP_6, P_poll__networl_2_3_AnnP_7, P_poll__networl_2_3_RP_0, P_poll__networl_2_3_RP_1, P_poll__networl_2_3_RP_2, P_poll__networl_2_3_RP_3, P_poll__networl_2_3_RP_4, P_poll__networl_2_3_RP_5, P_poll__networl_2_3_RP_6, P_poll__networl_2_3_RP_7, P_poll__networl_2_4_AskP_0, P_poll__networl_2_4_AskP_1, P_poll__networl_2_4_AskP_2, P_poll__networl_2_4_AskP_3, P_poll__networl_2_4_AskP_4, P_poll__networl_2_4_AskP_5, P_poll__networl_2_4_AskP_6, P_poll__networl_2_4_AskP_7, P_poll__networl_2_4_AnsP_0, P_poll__networl_2_4_AnsP_1, P_poll__networl_2_4_AnsP_2, P_poll__networl_2_4_AnsP_3, P_poll__networl_2_4_AnsP_4, P_poll__networl_2_4_AnsP_5, P_poll__networl_2_4_AnsP_6, P_poll__networl_2_4_AnsP_7, P_poll__networl_2_4_RI_0, P_poll__networl_2_4_RI_1, P_poll__networl_2_4_RI_2, P_poll__networl_2_4_RI_3, P_poll__networl_2_4_RI_4, P_poll__networl_2_4_RI_5, P_poll__networl_2_4_RI_6, P_poll__networl_2_4_RI_7, P_poll__networl_2_4_AI_0, P_poll__networl_2_4_AI_1, P_poll__networl_2_4_AI_2, P_poll__networl_2_4_AI_3, P_poll__networl_2_4_AI_4, P_poll__networl_2_4_AI_5, P_poll__networl_2_4_AI_6, P_poll__networl_2_4_AI_7, P_poll__networl_2_4_AnnP_0, P_poll__networl_2_4_AnnP_1, P_poll__networl_2_4_AnnP_2, P_poll__networl_2_4_AnnP_3, P_poll__networl_2_4_AnnP_4, P_poll__networl_2_4_AnnP_5, P_poll__networl_2_4_AnnP_6, P_poll__networl_2_4_AnnP_7, P_poll__networl_2_4_RP_0, P_poll__networl_2_4_RP_1, P_poll__networl_2_4_RP_2, P_poll__networl_2_4_RP_3, P_poll__networl_2_4_RP_4, P_poll__networl_2_4_RP_5, P_poll__networl_2_4_RP_6, P_poll__networl_2_4_RP_7, P_poll__networl_2_5_AskP_0, P_poll__networl_2_5_AskP_1, P_poll__networl_2_5_AskP_2, P_poll__networl_2_5_AskP_3, P_poll__networl_2_5_AskP_4, P_poll__networl_2_5_AskP_5, P_poll__networl_2_5_AskP_6, P_poll__networl_2_5_AskP_7, P_poll__networl_2_5_AnsP_0, P_poll__networl_2_5_AnsP_1, P_poll__networl_2_5_AnsP_2, P_poll__networl_2_5_AnsP_3, P_poll__networl_2_5_AnsP_4, P_poll__networl_2_5_AnsP_5, P_poll__networl_2_5_AnsP_6, P_poll__networl_2_5_AnsP_7, P_poll__networl_2_5_RI_0, P_poll__networl_2_5_RI_1, P_poll__networl_2_5_RI_2, P_poll__networl_2_5_RI_3, P_poll__networl_2_5_RI_4, P_poll__networl_2_5_RI_5, P_poll__networl_2_5_RI_6, P_poll__networl_2_5_RI_7, P_poll__networl_2_5_AI_0, P_poll__networl_2_5_AI_1, P_poll__networl_2_5_AI_2, P_poll__networl_2_5_AI_3, P_poll__networl_2_5_AI_4, P_poll__networl_2_5_AI_5, P_poll__networl_2_5_AI_6, P_poll__networl_2_5_AI_7, P_poll__networl_2_5_AnnP_0, P_poll__networl_2_5_AnnP_1, P_poll__networl_2_5_AnnP_2, P_poll__networl_2_5_AnnP_3, P_poll__networl_2_5_AnnP_4, P_poll__networl_2_5_AnnP_5, P_poll__networl_2_5_AnnP_6, P_poll__networl_2_5_AnnP_7, P_poll__networl_2_5_RP_0, P_poll__networl_2_5_RP_1, P_poll__networl_2_5_RP_2, P_poll__networl_2_5_RP_3, P_poll__networl_2_5_RP_4, P_poll__networl_2_5_RP_5, P_poll__networl_2_5_RP_6, P_poll__networl_2_5_RP_7, P_poll__networl_2_6_AskP_0, P_poll__networl_2_6_AskP_1, P_poll__networl_2_6_AskP_2, P_poll__networl_2_6_AskP_3, P_poll__networl_2_6_AskP_4, P_poll__networl_2_6_AskP_5, P_poll__networl_2_6_AskP_6, P_poll__networl_2_6_AskP_7, P_poll__networl_2_6_AnsP_0, P_poll__networl_2_6_AnsP_1, P_poll__networl_2_6_AnsP_2, P_poll__networl_2_6_AnsP_3, P_poll__networl_2_6_AnsP_4, P_poll__networl_2_6_AnsP_5, P_poll__networl_2_6_AnsP_6, P_poll__networl_2_6_AnsP_7, P_poll__networl_2_6_RI_0, P_poll__networl_2_6_RI_1, P_poll__networl_2_6_RI_2, P_poll__networl_2_6_RI_3, P_poll__networl_2_6_RI_4, P_poll__networl_2_6_RI_5, P_poll__networl_2_6_RI_6, P_poll__networl_2_6_RI_7, P_poll__networl_2_6_AI_0, P_poll__networl_2_6_AI_1, P_poll__networl_2_6_AI_2, P_poll__networl_2_6_AI_3, P_poll__networl_2_6_AI_4, P_poll__networl_2_6_AI_5, P_poll__networl_2_6_AI_6, P_poll__networl_2_6_AI_7, P_poll__networl_2_6_AnnP_0, P_poll__networl_2_6_AnnP_1, P_poll__networl_2_6_AnnP_2, P_poll__networl_2_6_AnnP_3, P_poll__networl_2_6_AnnP_4, P_poll__networl_2_6_AnnP_5, P_poll__networl_2_6_AnnP_6, P_poll__networl_2_6_AnnP_7, P_poll__networl_2_6_RP_0, P_poll__networl_2_6_RP_1, P_poll__networl_2_6_RP_2, P_poll__networl_2_6_RP_3, P_poll__networl_2_6_RP_4, P_poll__networl_2_6_RP_5, P_poll__networl_2_6_RP_6, P_poll__networl_2_6_RP_7, P_poll__networl_2_7_AskP_0, P_poll__networl_2_7_AskP_1, P_poll__networl_2_7_AskP_2, P_poll__networl_2_7_AskP_3, P_poll__networl_2_7_AskP_4, P_poll__networl_2_7_AskP_5, P_poll__networl_2_7_AskP_6, P_poll__networl_2_7_AskP_7, P_poll__networl_2_7_AnsP_0, P_poll__networl_2_7_AnsP_1, P_poll__networl_2_7_AnsP_2, P_poll__networl_2_7_AnsP_3, P_poll__networl_2_7_AnsP_4, P_poll__networl_2_7_AnsP_5, P_poll__networl_2_7_AnsP_6, P_poll__networl_2_7_AnsP_7, P_poll__networl_2_7_RI_0, P_poll__networl_2_7_RI_1, P_poll__networl_2_7_RI_2, P_poll__networl_2_7_RI_3, P_poll__networl_2_7_RI_4, P_poll__networl_2_7_RI_5, P_poll__networl_2_7_RI_6, P_poll__networl_2_7_RI_7, P_poll__networl_2_7_AI_0, P_poll__networl_2_7_AI_1, P_poll__networl_2_7_AI_2, P_poll__networl_2_7_AI_3, P_poll__networl_2_7_AI_4, P_poll__networl_2_7_AI_5, P_poll__networl_2_7_AI_6, P_poll__networl_2_7_AI_7, P_poll__networl_2_7_AnnP_0, P_poll__networl_2_7_AnnP_1, P_poll__networl_2_7_AnnP_2, P_poll__networl_2_7_AnnP_3, P_poll__networl_2_7_AnnP_4, P_poll__networl_2_7_AnnP_5, P_poll__networl_2_7_AnnP_6, P_poll__networl_2_7_AnnP_7, P_poll__networl_2_7_RP_0, P_poll__networl_2_7_RP_1, P_poll__networl_2_7_RP_2, P_poll__networl_2_7_RP_3, P_poll__networl_2_7_RP_4, P_poll__networl_2_7_RP_5, P_poll__networl_2_7_RP_6, P_poll__networl_2_7_RP_7, P_poll__networl_3_0_AskP_0, P_poll__networl_3_0_AskP_1, P_poll__networl_3_0_AskP_2, P_poll__networl_3_0_AskP_3, P_poll__networl_3_0_AskP_4, P_poll__networl_3_0_AskP_5, P_poll__networl_3_0_AskP_6, P_poll__networl_3_0_AskP_7, P_poll__networl_3_0_AnsP_0, P_poll__networl_3_0_AnsP_1, P_poll__networl_3_0_AnsP_2, P_poll__networl_3_0_AnsP_3, P_poll__networl_3_0_AnsP_4, P_poll__networl_3_0_AnsP_5, P_poll__networl_3_0_AnsP_6, P_poll__networl_3_0_AnsP_7, P_poll__networl_3_0_RI_0, P_poll__networl_3_0_RI_1, P_poll__networl_3_0_RI_2, P_poll__networl_3_0_RI_3, P_poll__networl_3_0_RI_4, P_poll__networl_3_0_RI_5, P_poll__networl_3_0_RI_6, P_poll__networl_3_0_RI_7, P_poll__networl_3_0_AI_0, P_poll__networl_3_0_AI_1, P_poll__networl_3_0_AI_2, P_poll__networl_3_0_AI_3, P_poll__networl_3_0_AI_4, P_poll__networl_3_0_AI_5, P_poll__networl_3_0_AI_6, P_poll__networl_3_0_AI_7, P_poll__networl_3_0_AnnP_0, P_poll__networl_3_0_AnnP_1, P_poll__networl_3_0_AnnP_2, P_poll__networl_3_0_AnnP_3, P_poll__networl_3_0_AnnP_4, P_poll__networl_3_0_AnnP_5, P_poll__networl_3_0_AnnP_6, P_poll__networl_3_0_AnnP_7, P_poll__networl_3_0_RP_0, P_poll__networl_3_0_RP_1, P_poll__networl_3_0_RP_2, P_poll__networl_3_0_RP_3, P_poll__networl_3_0_RP_4, P_poll__networl_3_0_RP_5, P_poll__networl_3_0_RP_6, P_poll__networl_3_0_RP_7, P_poll__networl_3_1_AskP_0, P_poll__networl_3_1_AskP_1, P_poll__networl_3_1_AskP_2, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AskP_4, P_poll__networl_3_1_AskP_5, P_poll__networl_3_1_AskP_6, P_poll__networl_3_1_AskP_7, P_poll__networl_3_1_AnsP_0, P_poll__networl_3_1_AnsP_1, P_poll__networl_3_1_AnsP_2, P_poll__networl_3_1_AnsP_3, P_poll__networl_3_1_AnsP_4, P_poll__networl_3_1_AnsP_5, P_poll__networl_3_1_AnsP_6, P_poll__networl_3_1_AnsP_7, P_poll__networl_3_1_RI_0, P_poll__networl_3_1_RI_1, P_poll__networl_3_1_RI_2, P_poll__networl_3_1_RI_3, P_poll__networl_3_1_RI_4, P_poll__networl_3_1_RI_5, P_poll__networl_3_1_RI_6, P_poll__networl_3_1_RI_7, P_poll__networl_3_1_AI_0, P_poll__networl_3_1_AI_1, P_poll__networl_3_1_AI_2, P_poll__networl_3_1_AI_3, P_poll__networl_3_1_AI_4, P_poll__networl_3_1_AI_5, P_poll__networl_3_1_AI_6, P_poll__networl_3_1_AI_7, P_poll__networl_3_1_AnnP_0, P_poll__networl_3_1_AnnP_1, P_poll__networl_3_1_AnnP_2, P_poll__networl_3_1_AnnP_3, P_poll__networl_3_1_AnnP_4, P_poll__networl_3_1_AnnP_5, P_poll__networl_3_1_AnnP_6, P_poll__networl_3_1_AnnP_7, P_poll__networl_3_1_RP_0, P_poll__networl_3_1_RP_1, P_poll__networl_3_1_RP_2, P_poll__networl_3_1_RP_3, P_poll__networl_3_1_RP_4, P_poll__networl_3_1_RP_5, P_poll__networl_3_1_RP_6, P_poll__networl_3_1_RP_7, P_poll__networl_3_2_AskP_0, P_poll__networl_3_2_AskP_1, P_poll__networl_3_2_AskP_2, P_poll__networl_3_2_AskP_3, P_poll__networl_3_2_AskP_4, P_poll__networl_3_2_AskP_5, P_poll__networl_3_2_AskP_6, P_poll__networl_3_2_AskP_7, P_poll__networl_3_2_AnsP_0, P_poll__networl_3_2_AnsP_1, P_poll__networl_3_2_AnsP_2, P_poll__networl_3_2_AnsP_3, P_poll__networl_3_2_AnsP_4, P_poll__networl_3_2_AnsP_5, P_poll__networl_3_2_AnsP_6, P_poll__networl_3_2_AnsP_7, P_poll__networl_3_2_RI_0, P_poll__networl_3_2_RI_1, P_poll__networl_3_2_RI_2, P_poll__networl_3_2_RI_3, P_poll__networl_3_2_RI_4, P_poll__networl_3_2_RI_5, P_poll__networl_3_2_RI_6, P_poll__networl_3_2_RI_7, P_poll__networl_3_2_AI_0, P_poll__networl_3_2_AI_1, P_poll__networl_3_2_AI_2, P_poll__networl_3_2_AI_3, P_poll__networl_3_2_AI_4, P_poll__networl_3_2_AI_5, P_poll__networl_3_2_AI_6, P_poll__networl_3_2_AI_7, P_poll__networl_3_2_AnnP_0, P_poll__networl_3_2_AnnP_1, P_poll__networl_3_2_AnnP_2, P_poll__networl_3_2_AnnP_3, P_poll__networl_3_2_AnnP_4, P_poll__networl_3_2_AnnP_5, P_poll__networl_3_2_AnnP_6, P_poll__networl_3_2_AnnP_7, P_poll__networl_3_2_RP_0, P_poll__networl_3_2_RP_1, P_poll__networl_3_2_RP_2, P_poll__networl_3_2_RP_3, P_poll__networl_3_2_RP_4, P_poll__networl_3_2_RP_5, P_poll__networl_3_2_RP_6, P_poll__networl_3_2_RP_7, P_poll__networl_3_3_AskP_0, P_poll__networl_3_3_AskP_1, P_poll__networl_3_3_AskP_2, P_poll__networl_3_3_AskP_3, P_poll__networl_3_3_AskP_4, P_poll__networl_3_3_AskP_5, P_poll__networl_3_3_AskP_6, P_poll__networl_3_3_AskP_7, P_poll__networl_3_3_AnsP_0, P_poll__networl_3_3_AnsP_1, P_poll__networl_3_3_AnsP_2, P_poll__networl_3_3_AnsP_3, P_poll__networl_3_3_AnsP_4, P_poll__networl_3_3_AnsP_5, P_poll__networl_3_3_AnsP_6, P_poll__networl_3_3_AnsP_7, P_poll__networl_3_3_RI_0, P_poll__networl_3_3_RI_1, P_poll__networl_3_3_RI_2, P_poll__networl_3_3_RI_3, P_poll__networl_3_3_RI_4, P_poll__networl_3_3_RI_5, P_poll__networl_3_3_RI_6, P_poll__networl_3_3_RI_7, P_poll__networl_3_3_AI_0, P_poll__networl_3_3_AI_1, P_poll__networl_3_3_AI_2, P_poll__networl_3_3_AI_3, P_poll__networl_3_3_AI_4, P_poll__networl_3_3_AI_5, P_poll__networl_3_3_AI_6, P_poll__networl_3_3_AI_7, P_poll__networl_3_3_AnnP_0, P_poll__networl_3_3_AnnP_1, P_poll__networl_3_3_AnnP_2, P_poll__networl_3_3_AnnP_3, P_poll__networl_3_3_AnnP_4, P_poll__networl_3_3_AnnP_5, P_poll__networl_3_3_AnnP_6, P_poll__networl_3_3_AnnP_7, P_poll__networl_3_3_RP_0, P_poll__networl_3_3_RP_1, P_poll__networl_3_3_RP_2, P_poll__networl_3_3_RP_3, P_poll__networl_3_3_RP_4, P_poll__networl_3_3_RP_5, P_poll__networl_3_3_RP_6, P_poll__networl_3_3_RP_7, P_poll__networl_3_4_AskP_0, P_poll__networl_3_4_AskP_1, P_poll__networl_3_4_AskP_2, P_poll__networl_3_4_AskP_3, P_poll__networl_3_4_AskP_4, P_poll__networl_3_4_AskP_5, P_poll__networl_3_4_AskP_6, P_poll__networl_3_4_AskP_7, P_poll__networl_3_4_AnsP_0, P_poll__networl_3_4_AnsP_1, P_poll__networl_3_4_AnsP_2, P_poll__networl_3_4_AnsP_3, P_poll__networl_3_4_AnsP_4, P_poll__networl_3_4_AnsP_5, P_poll__networl_3_4_AnsP_6, P_poll__networl_3_4_AnsP_7, P_poll__networl_3_4_RI_0, P_poll__networl_3_4_RI_1, P_poll__networl_3_4_RI_2, P_poll__networl_3_4_RI_3, P_poll__networl_3_4_RI_4, P_poll__networl_3_4_RI_5, P_poll__networl_3_4_RI_6, P_poll__networl_3_4_RI_7, P_poll__networl_3_4_AI_0, P_poll__networl_3_4_AI_1, P_poll__networl_3_4_AI_2, P_poll__networl_3_4_AI_3, P_poll__networl_3_4_AI_4, P_poll__networl_3_4_AI_5, P_poll__networl_3_4_AI_6, P_poll__networl_3_4_AI_7, P_poll__networl_3_4_AnnP_0, P_poll__networl_3_4_AnnP_1, P_poll__networl_3_4_AnnP_2, P_poll__networl_3_4_AnnP_3, P_poll__networl_3_4_AnnP_4, P_poll__networl_3_4_AnnP_5, P_poll__networl_3_4_AnnP_6, P_poll__networl_3_4_AnnP_7, P_poll__networl_3_4_RP_0, P_poll__networl_3_4_RP_1, P_poll__networl_3_4_RP_2, P_poll__networl_3_4_RP_3, P_poll__networl_3_4_RP_4, P_poll__networl_3_4_RP_5, P_poll__networl_3_4_RP_6, P_poll__networl_3_4_RP_7, P_poll__networl_3_5_AskP_0, P_poll__networl_3_5_AskP_1, P_poll__networl_3_5_AskP_2, P_poll__networl_3_5_AskP_3, P_poll__networl_3_5_AskP_4, P_poll__networl_3_5_AskP_5, P_poll__networl_3_5_AskP_6, P_poll__networl_3_5_AskP_7, P_poll__networl_3_5_AnsP_0, P_poll__networl_3_5_AnsP_1, P_poll__networl_3_5_AnsP_2, P_poll__networl_3_5_AnsP_3, P_poll__networl_3_5_AnsP_4, P_poll__networl_3_5_AnsP_5, P_poll__networl_3_5_AnsP_6, P_poll__networl_3_5_AnsP_7, P_poll__networl_3_5_RI_0, P_poll__networl_3_5_RI_1, P_poll__networl_3_5_RI_2, P_poll__networl_3_5_RI_3, P_poll__networl_3_5_RI_4, P_poll__networl_3_5_RI_5, P_poll__networl_3_5_RI_6, P_poll__networl_3_5_RI_7, P_poll__networl_3_5_AI_0, P_poll__networl_3_5_AI_1, P_poll__networl_3_5_AI_2, P_poll__networl_3_5_AI_3, P_poll__networl_3_5_AI_4, P_poll__networl_3_5_AI_5, P_poll__networl_3_5_AI_6, P_poll__networl_3_5_AI_7, P_poll__networl_3_5_AnnP_0, P_poll__networl_3_5_AnnP_1, P_poll__networl_3_5_AnnP_2, P_poll__networl_3_5_AnnP_3, P_poll__networl_3_5_AnnP_4, P_poll__networl_3_5_AnnP_5, P_poll__networl_3_5_AnnP_6, P_poll__networl_3_5_AnnP_7, P_poll__networl_3_5_RP_0, P_poll__networl_3_5_RP_1, P_poll__networl_3_5_RP_2, P_poll__networl_3_5_RP_3, P_poll__networl_3_5_RP_4, P_poll__networl_3_5_RP_5, P_poll__networl_3_5_RP_6, P_poll__networl_3_5_RP_7, P_poll__networl_3_6_AskP_0, P_poll__networl_3_6_AskP_1, P_poll__networl_3_6_AskP_2, P_poll__networl_3_6_AskP_3, P_poll__networl_3_6_AskP_4, P_poll__networl_3_6_AskP_5, P_poll__networl_3_6_AskP_6, P_poll__networl_3_6_AskP_7, P_poll__networl_3_6_AnsP_0, P_poll__networl_3_6_AnsP_1, P_poll__networl_3_6_AnsP_2, P_poll__networl_3_6_AnsP_3, P_poll__networl_3_6_AnsP_4, P_poll__networl_3_6_AnsP_5, P_poll__networl_3_6_AnsP_6, P_poll__networl_3_6_AnsP_7, P_poll__networl_3_6_RI_0, P_poll__networl_3_6_RI_1, P_poll__networl_3_6_RI_2, P_poll__networl_3_6_RI_3, P_poll__networl_3_6_RI_4, P_poll__networl_3_6_RI_5, P_poll__networl_3_6_RI_6, P_poll__networl_3_6_RI_7, P_poll__networl_3_6_AI_0, P_poll__networl_3_6_AI_1, P_poll__networl_3_6_AI_2, P_poll__networl_3_6_AI_3, P_poll__networl_3_6_AI_4, P_poll__networl_3_6_AI_5, P_poll__networl_3_6_AI_6, P_poll__networl_3_6_AI_7, P_poll__networl_3_6_AnnP_0, P_poll__networl_3_6_AnnP_1, P_poll__networl_3_6_AnnP_2, P_poll__networl_3_6_AnnP_3, P_poll__networl_3_6_AnnP_4, P_poll__networl_3_6_AnnP_5, P_poll__networl_3_6_AnnP_6, P_poll__networl_3_6_AnnP_7, P_poll__networl_3_6_RP_0, P_poll__networl_3_6_RP_1, P_poll__networl_3_6_RP_2, P_poll__networl_3_6_RP_3, P_poll__networl_3_6_RP_4, P_poll__networl_3_6_RP_5, P_poll__networl_3_6_RP_6, P_poll__networl_3_6_RP_7, P_poll__networl_3_7_AskP_0, P_poll__networl_3_7_AskP_1, P_poll__networl_3_7_AskP_2, P_poll__networl_3_7_AskP_3, P_poll__networl_3_7_AskP_4, P_poll__networl_3_7_AskP_5, P_poll__networl_3_7_AskP_6, P_poll__networl_3_7_AskP_7, P_poll__networl_3_7_AnsP_0, P_poll__networl_3_7_AnsP_1, P_poll__networl_3_7_AnsP_2, P_poll__networl_3_7_AnsP_3, P_poll__networl_3_7_AnsP_4, P_poll__networl_3_7_AnsP_5, P_poll__networl_3_7_AnsP_6, P_poll__networl_3_7_AnsP_7, P_poll__networl_3_7_RI_0, P_poll__networl_3_7_RI_1, P_poll__networl_3_7_RI_2, P_poll__networl_3_7_RI_3, P_poll__networl_3_7_RI_4, P_poll__networl_3_7_RI_5, P_poll__networl_3_7_RI_6, P_poll__networl_3_7_RI_7, P_poll__networl_3_7_AI_0, P_poll__networl_3_7_AI_1, P_poll__networl_3_7_AI_2, P_poll__networl_3_7_AI_3, P_poll__networl_3_7_AI_4, P_poll__networl_3_7_AI_5, P_poll__networl_3_7_AI_6, P_poll__networl_3_7_AI_7, P_poll__networl_3_7_AnnP_0, P_poll__networl_3_7_AnnP_1, P_poll__networl_3_7_AnnP_2, P_poll__networl_3_7_AnnP_3, P_poll__networl_3_7_AnnP_4, P_poll__networl_3_7_AnnP_5, P_poll__networl_3_7_AnnP_6, P_poll__networl_3_7_AnnP_7, P_poll__networl_3_7_RP_0, P_poll__networl_3_7_RP_1, P_poll__networl_3_7_RP_2, P_poll__networl_3_7_RP_3, P_poll__networl_3_7_RP_4, P_poll__networl_3_7_RP_5, P_poll__networl_3_7_RP_6, P_poll__networl_3_7_RP_7, P_poll__networl_4_0_AskP_0, P_poll__networl_4_0_AskP_1, P_poll__networl_4_0_AskP_2, P_poll__networl_4_0_AskP_3, P_poll__networl_4_0_AskP_4, P_poll__networl_4_0_AskP_5, P_poll__networl_4_0_AskP_6, P_poll__networl_4_0_AskP_7, P_poll__networl_4_0_AnsP_0, P_poll__networl_4_0_AnsP_1, P_poll__networl_4_0_AnsP_2, P_poll__networl_4_0_AnsP_3, P_poll__networl_4_0_AnsP_4, P_poll__networl_4_0_AnsP_5, P_poll__networl_4_0_AnsP_6, P_poll__networl_4_0_AnsP_7, P_poll__networl_4_0_RI_0, P_poll__networl_4_0_RI_1, P_poll__networl_4_0_RI_2, P_poll__networl_4_0_RI_3, P_poll__networl_4_0_RI_4, P_poll__networl_4_0_RI_5, P_poll__networl_4_0_RI_6, P_poll__networl_4_0_RI_7, P_poll__networl_4_0_AI_0, P_poll__networl_4_0_AI_1, P_poll__networl_4_0_AI_2, P_poll__networl_4_0_AI_3, P_poll__networl_4_0_AI_4, P_poll__networl_4_0_AI_5, P_poll__networl_4_0_AI_6, P_poll__networl_4_0_AI_7, P_poll__networl_4_0_AnnP_0, P_poll__networl_4_0_AnnP_1, P_poll__networl_4_0_AnnP_2, P_poll__networl_4_0_AnnP_3, P_poll__networl_4_0_AnnP_4, P_poll__networl_4_0_AnnP_5, P_poll__networl_4_0_AnnP_6, P_poll__networl_4_0_AnnP_7, P_poll__networl_4_0_RP_0, P_poll__networl_4_0_RP_1, P_poll__networl_4_0_RP_2, P_poll__networl_4_0_RP_3, P_poll__networl_4_0_RP_4, P_poll__networl_4_0_RP_5, P_poll__networl_4_0_RP_6, P_poll__networl_4_0_RP_7, P_poll__networl_4_1_AskP_0, P_poll__networl_4_1_AskP_1, P_poll__networl_4_1_AskP_2, P_poll__networl_4_1_AskP_3, P_poll__networl_4_1_AskP_4, P_poll__networl_4_1_AskP_5, P_poll__networl_4_1_AskP_6, P_poll__networl_4_1_AskP_7, P_poll__networl_4_1_AnsP_0, P_poll__networl_4_1_AnsP_1, P_poll__networl_4_1_AnsP_2, P_poll__networl_4_1_AnsP_3, P_poll__networl_4_1_AnsP_4, P_poll__networl_4_1_AnsP_5, P_poll__networl_4_1_AnsP_6, P_poll__networl_4_1_AnsP_7, P_poll__networl_4_1_RI_0, P_poll__networl_4_1_RI_1, P_poll__networl_4_1_RI_2, P_poll__networl_4_1_RI_3, P_poll__networl_4_1_RI_4, P_poll__networl_4_1_RI_5, P_poll__networl_4_1_RI_6, P_poll__networl_4_1_RI_7, P_poll__networl_4_1_AI_0, P_poll__networl_4_1_AI_1, P_poll__networl_4_1_AI_2, P_poll__networl_4_1_AI_3, P_poll__networl_4_1_AI_4, P_poll__networl_4_1_AI_5, P_poll__networl_4_1_AI_6, P_poll__networl_4_1_AI_7, P_poll__networl_4_1_AnnP_0, P_poll__networl_4_1_AnnP_1, P_poll__networl_4_1_AnnP_2, P_poll__networl_4_1_AnnP_3, P_poll__networl_4_1_AnnP_4, P_poll__networl_4_1_AnnP_5, P_poll__networl_4_1_AnnP_6, P_poll__networl_4_1_AnnP_7, P_poll__networl_4_1_RP_0, P_poll__networl_4_1_RP_1, P_poll__networl_4_1_RP_2, P_poll__networl_4_1_RP_3, P_poll__networl_4_1_RP_4, P_poll__networl_4_1_RP_5, P_poll__networl_4_1_RP_6, P_poll__networl_4_1_RP_7, P_poll__networl_4_2_AskP_0, P_poll__networl_4_2_AskP_1, P_poll__networl_4_2_AskP_2, P_poll__networl_4_2_AskP_3, P_poll__networl_4_2_AskP_4, P_poll__networl_4_2_AskP_5, P_poll__networl_4_2_AskP_6, P_poll__networl_4_2_AskP_7, P_poll__networl_4_2_AnsP_0, P_poll__networl_4_2_AnsP_1, P_poll__networl_4_2_AnsP_2, P_poll__networl_4_2_AnsP_3, P_poll__networl_4_2_AnsP_4, P_poll__networl_4_2_AnsP_5, P_poll__networl_4_2_AnsP_6, P_poll__networl_4_2_AnsP_7, P_poll__networl_4_2_RI_0, P_poll__networl_4_2_RI_1, P_poll__networl_4_2_RI_2, P_poll__networl_4_2_RI_3, P_poll__networl_4_2_RI_4, P_poll__networl_4_2_RI_5, P_poll__networl_4_2_RI_6, P_poll__networl_4_2_RI_7, P_poll__networl_4_2_AI_0, P_poll__networl_4_2_AI_1, P_poll__networl_4_2_AI_2, P_poll__networl_4_2_AI_3, P_poll__networl_4_2_AI_4, P_poll__networl_4_2_AI_5, P_poll__networl_4_2_AI_6, P_poll__networl_4_2_AI_7, P_poll__networl_4_2_AnnP_0, P_poll__networl_4_2_AnnP_1, P_poll__networl_4_2_AnnP_2, P_poll__networl_4_2_AnnP_3, P_poll__networl_4_2_AnnP_4, P_poll__networl_4_2_AnnP_5, P_poll__networl_4_2_AnnP_6, P_poll__networl_4_2_AnnP_7, P_poll__networl_4_2_RP_0, P_poll__networl_4_2_RP_1, P_poll__networl_4_2_RP_2, P_poll__networl_4_2_RP_3, P_poll__networl_4_2_RP_4, P_poll__networl_4_2_RP_5, P_poll__networl_4_2_RP_6, P_poll__networl_4_2_RP_7, P_poll__networl_4_3_AskP_0, P_poll__networl_4_3_AskP_1, P_poll__networl_4_3_AskP_2, P_poll__networl_4_3_AskP_3, P_poll__networl_4_3_AskP_4, P_poll__networl_4_3_AskP_5, P_poll__networl_4_3_AskP_6, P_poll__networl_4_3_AskP_7, P_poll__networl_4_3_AnsP_0, P_poll__networl_4_3_AnsP_1, P_poll__networl_4_3_AnsP_2, P_poll__networl_4_3_AnsP_3, P_poll__networl_4_3_AnsP_4, P_poll__networl_4_3_AnsP_5, P_poll__networl_4_3_AnsP_6, P_poll__networl_4_3_AnsP_7, P_poll__networl_4_3_RI_0, P_poll__networl_4_3_RI_1, P_poll__networl_4_3_RI_2, P_poll__networl_4_3_RI_3, P_poll__networl_4_3_RI_4, P_poll__networl_4_3_RI_5, P_poll__networl_4_3_RI_6, P_poll__networl_4_3_RI_7, P_poll__networl_4_3_AI_0, P_poll__networl_4_3_AI_1, P_poll__networl_4_3_AI_2, P_poll__networl_4_3_AI_3, P_poll__networl_4_3_AI_4, P_poll__networl_4_3_AI_5, P_poll__networl_4_3_AI_6, P_poll__networl_4_3_AI_7, P_poll__networl_4_3_AnnP_0, P_poll__networl_4_3_AnnP_1, P_poll__networl_4_3_AnnP_2, P_poll__networl_4_3_AnnP_3, P_poll__networl_4_3_AnnP_4, P_poll__networl_4_3_AnnP_5, P_poll__networl_4_3_AnnP_6, P_poll__networl_4_3_AnnP_7, P_poll__networl_4_3_RP_0, P_poll__networl_4_3_RP_1, P_poll__networl_4_3_RP_2, P_poll__networl_4_3_RP_3, P_poll__networl_4_3_RP_4, P_poll__networl_4_3_RP_5, P_poll__networl_4_3_RP_6, P_poll__networl_4_3_RP_7, P_poll__networl_4_4_AskP_0, P_poll__networl_4_4_AskP_1, P_poll__networl_4_4_AskP_2, P_poll__networl_4_4_AskP_3, P_poll__networl_4_4_AskP_4, P_poll__networl_4_4_AskP_5, P_poll__networl_4_4_AskP_6, P_poll__networl_4_4_AskP_7, P_poll__networl_4_4_AnsP_0, P_poll__networl_4_4_AnsP_1, P_poll__networl_4_4_AnsP_2, P_poll__networl_4_4_AnsP_3, P_poll__networl_4_4_AnsP_4, P_poll__networl_4_4_AnsP_5, P_poll__networl_4_4_AnsP_6, P_poll__networl_4_4_AnsP_7, P_poll__networl_4_4_RI_0, P_poll__networl_4_4_RI_1, P_poll__networl_4_4_RI_2, P_poll__networl_4_4_RI_3, P_poll__networl_4_4_RI_4, P_poll__networl_4_4_RI_5, P_poll__networl_4_4_RI_6, P_poll__networl_4_4_RI_7, P_poll__networl_4_4_AI_0, P_poll__networl_4_4_AI_1, P_poll__networl_4_4_AI_2, P_poll__networl_4_4_AI_3, P_poll__networl_4_4_AI_4, P_poll__networl_4_4_AI_5, P_poll__networl_4_4_AI_6, P_poll__networl_4_4_AI_7, P_poll__networl_4_4_AnnP_0, P_poll__networl_4_4_AnnP_1, P_poll__networl_4_4_AnnP_2, P_poll__networl_4_4_AnnP_3, P_poll__networl_4_4_AnnP_4, P_poll__networl_4_4_AnnP_5, P_poll__networl_4_4_AnnP_6, P_poll__networl_4_4_AnnP_7, P_poll__networl_4_4_RP_0, P_poll__networl_4_4_RP_1, P_poll__networl_4_4_RP_2, P_poll__networl_4_4_RP_3, P_poll__networl_4_4_RP_4, P_poll__networl_4_4_RP_5, P_poll__networl_4_4_RP_6, P_poll__networl_4_4_RP_7, P_poll__networl_4_5_AskP_0, P_poll__networl_4_5_AskP_1, P_poll__networl_4_5_AskP_2, P_poll__networl_4_5_AskP_3, P_poll__networl_4_5_AskP_4, P_poll__networl_4_5_AskP_5, P_poll__networl_4_5_AskP_6, P_poll__networl_4_5_AskP_7, P_poll__networl_4_5_AnsP_0, P_poll__networl_4_5_AnsP_1, P_poll__networl_4_5_AnsP_2, P_poll__networl_4_5_AnsP_3, P_poll__networl_4_5_AnsP_4, P_poll__networl_4_5_AnsP_5, P_poll__networl_4_5_AnsP_6, P_poll__networl_4_5_AnsP_7, P_poll__networl_4_5_RI_0, P_poll__networl_4_5_RI_1, P_poll__networl_4_5_RI_2, P_poll__networl_4_5_RI_3, P_poll__networl_4_5_RI_4, P_poll__networl_4_5_RI_5, P_poll__networl_4_5_RI_6, P_poll__networl_4_5_RI_7, P_poll__networl_4_5_AI_0, P_poll__networl_4_5_AI_1, P_poll__networl_4_5_AI_2, P_poll__networl_4_5_AI_3, P_poll__networl_4_5_AI_4, P_poll__networl_4_5_AI_5, P_poll__networl_4_5_AI_6, P_poll__networl_4_5_AI_7, P_poll__networl_4_5_AnnP_0, P_poll__networl_4_5_AnnP_1, P_poll__networl_4_5_AnnP_2, P_poll__networl_4_5_AnnP_3, P_poll__networl_4_5_AnnP_4, P_poll__networl_4_5_AnnP_5, P_poll__networl_4_5_AnnP_6, P_poll__networl_4_5_AnnP_7, P_poll__networl_4_5_RP_0, P_poll__networl_4_5_RP_1, P_poll__networl_4_5_RP_2, P_poll__networl_4_5_RP_3, P_poll__networl_4_5_RP_4, P_poll__networl_4_5_RP_5, P_poll__networl_4_5_RP_6, P_poll__networl_4_5_RP_7, P_poll__networl_4_6_AskP_0, P_poll__networl_4_6_AskP_1, P_poll__networl_4_6_AskP_2, P_poll__networl_4_6_AskP_3, P_poll__networl_4_6_AskP_4, P_poll__networl_4_6_AskP_5, P_poll__networl_4_6_AskP_6, P_poll__networl_4_6_AskP_7, P_poll__networl_4_6_AnsP_0, P_poll__networl_4_6_AnsP_1, P_poll__networl_4_6_AnsP_2, P_poll__networl_4_6_AnsP_3, P_poll__networl_4_6_AnsP_4, P_poll__networl_4_6_AnsP_5, P_poll__networl_4_6_AnsP_6, P_poll__networl_4_6_AnsP_7, P_poll__networl_4_6_RI_0, P_poll__networl_4_6_RI_1, P_poll__networl_4_6_RI_2, P_poll__networl_4_6_RI_3, P_poll__networl_4_6_RI_4, P_poll__networl_4_6_RI_5, P_poll__networl_4_6_RI_6, P_poll__networl_4_6_RI_7, P_poll__networl_4_6_AI_0, P_poll__networl_4_6_AI_1, P_poll__networl_4_6_AI_2, P_poll__networl_4_6_AI_3, P_poll__networl_4_6_AI_4, P_poll__networl_4_6_AI_5, P_poll__networl_4_6_AI_6, P_poll__networl_4_6_AI_7, P_poll__networl_4_6_AnnP_0, P_poll__networl_4_6_AnnP_1, P_poll__networl_4_6_AnnP_2, P_poll__networl_4_6_AnnP_3, P_poll__networl_4_6_AnnP_4, P_poll__networl_4_6_AnnP_5, P_poll__networl_4_6_AnnP_6, P_poll__networl_4_6_AnnP_7, P_poll__networl_4_6_RP_0, P_poll__networl_4_6_RP_1, P_poll__networl_4_6_RP_2, P_poll__networl_4_6_RP_3, P_poll__networl_4_6_RP_4, P_poll__networl_4_6_RP_5, P_poll__networl_4_6_RP_6, P_poll__networl_4_6_RP_7, P_poll__networl_4_7_AskP_0, P_poll__networl_4_7_AskP_1, P_poll__networl_4_7_AskP_2, P_poll__networl_4_7_AskP_3, P_poll__networl_4_7_AskP_4, P_poll__networl_4_7_AskP_5, P_poll__networl_4_7_AskP_6, P_poll__networl_4_7_AskP_7, P_poll__networl_4_7_AnsP_0, P_poll__networl_4_7_AnsP_1, P_poll__networl_4_7_AnsP_2, P_poll__networl_4_7_AnsP_3, P_poll__networl_4_7_AnsP_4, P_poll__networl_4_7_AnsP_5, P_poll__networl_4_7_AnsP_6, P_poll__networl_4_7_AnsP_7, P_poll__networl_4_7_RI_0, P_poll__networl_4_7_RI_1, P_poll__networl_4_7_RI_2, P_poll__networl_4_7_RI_3, P_poll__networl_4_7_RI_4, P_poll__networl_4_7_RI_5, P_poll__networl_4_7_RI_6, P_poll__networl_4_7_RI_7, P_poll__networl_4_7_AI_0, P_poll__networl_4_7_AI_1, P_poll__networl_4_7_AI_2, P_poll__networl_4_7_AI_3, P_poll__networl_4_7_AI_4, P_poll__networl_4_7_AI_5, P_poll__networl_4_7_AI_6, P_poll__networl_4_7_AI_7, P_poll__networl_4_7_AnnP_0, P_poll__networl_4_7_AnnP_1, P_poll__networl_4_7_AnnP_2, P_poll__networl_4_7_AnnP_3, P_poll__networl_4_7_AnnP_4, P_poll__networl_4_7_AnnP_5, P_poll__networl_4_7_AnnP_6, P_poll__networl_4_7_AnnP_7, P_poll__networl_4_7_RP_0, P_poll__networl_4_7_RP_1, P_poll__networl_4_7_RP_2, P_poll__networl_4_7_RP_3, P_poll__networl_4_7_RP_4, P_poll__networl_4_7_RP_5, P_poll__networl_4_7_RP_6, P_poll__networl_4_7_RP_7, P_poll__networl_5_0_AskP_0, P_poll__networl_5_0_AskP_1, P_poll__networl_5_0_AskP_2, P_poll__networl_5_0_AskP_3, P_poll__networl_5_0_AskP_4, P_poll__networl_5_0_AskP_5, P_poll__networl_5_0_AskP_6, P_poll__networl_5_0_AskP_7, P_poll__networl_5_0_AnsP_0, P_poll__networl_5_0_AnsP_1, P_poll__networl_5_0_AnsP_2, P_poll__networl_5_0_AnsP_3, P_poll__networl_5_0_AnsP_4, P_poll__networl_5_0_AnsP_5, P_poll__networl_5_0_AnsP_6, P_poll__networl_5_0_AnsP_7, P_poll__networl_5_0_RI_0, P_poll__networl_5_0_RI_1, P_poll__networl_5_0_RI_2, P_poll__networl_5_0_RI_3, P_poll__networl_5_0_RI_4, P_poll__networl_5_0_RI_5, P_poll__networl_5_0_RI_6, P_poll__networl_5_0_RI_7, P_poll__networl_5_0_AI_0, P_poll__networl_5_0_AI_1, P_poll__networl_5_0_AI_2, P_poll__networl_5_0_AI_3, P_poll__networl_5_0_AI_4, P_poll__networl_5_0_AI_5, P_poll__networl_5_0_AI_6, P_poll__networl_5_0_AI_7, P_poll__networl_5_0_AnnP_0, P_poll__networl_5_0_AnnP_1, P_poll__networl_5_0_AnnP_2, P_poll__networl_5_0_AnnP_3, P_poll__networl_5_0_AnnP_4, P_poll__networl_5_0_AnnP_5, P_poll__networl_5_0_AnnP_6, P_poll__networl_5_0_AnnP_7, P_poll__networl_5_0_RP_0, P_poll__networl_5_0_RP_1, P_poll__networl_5_0_RP_2, P_poll__networl_5_0_RP_3, P_poll__networl_5_0_RP_4, P_poll__networl_5_0_RP_5, P_poll__networl_5_0_RP_6, P_poll__networl_5_0_RP_7, P_poll__networl_5_1_AskP_0, P_poll__networl_5_1_AskP_1, P_poll__networl_5_1_AskP_2, P_poll__networl_5_1_AskP_3, P_poll__networl_5_1_AskP_4, P_poll__networl_5_1_AskP_5, P_poll__networl_5_1_AskP_6, P_poll__networl_5_1_AskP_7, P_poll__networl_5_1_AnsP_0, P_poll__networl_5_1_AnsP_1, P_poll__networl_5_1_AnsP_2, P_poll__networl_5_1_AnsP_3, P_poll__networl_5_1_AnsP_4, P_poll__networl_5_1_AnsP_5, P_poll__networl_5_1_AnsP_6, P_poll__networl_5_1_AnsP_7, P_poll__networl_5_1_RI_0, P_poll__networl_5_1_RI_1, P_poll__networl_5_1_RI_2, P_poll__networl_5_1_RI_3, P_poll__networl_5_1_RI_4, P_poll__networl_5_1_RI_5, P_poll__networl_5_1_RI_6, P_poll__networl_5_1_RI_7, P_poll__networl_5_1_AI_0, P_poll__networl_5_1_AI_1, P_poll__networl_5_1_AI_2, P_poll__networl_5_1_AI_3, P_poll__networl_5_1_AI_4, P_poll__networl_5_1_AI_5, P_poll__networl_5_1_AI_6, P_poll__networl_5_1_AI_7, P_poll__networl_5_1_AnnP_0, P_poll__networl_5_1_AnnP_1, P_poll__networl_5_1_AnnP_2, P_poll__networl_5_1_AnnP_3, P_poll__networl_5_1_AnnP_4, P_poll__networl_5_1_AnnP_5, P_poll__networl_5_1_AnnP_6, P_poll__networl_5_1_AnnP_7, P_poll__networl_5_1_RP_0, P_poll__networl_5_1_RP_1, P_poll__networl_5_1_RP_2, P_poll__networl_5_1_RP_3, P_poll__networl_5_1_RP_4, P_poll__networl_5_1_RP_5, P_poll__networl_5_1_RP_6, P_poll__networl_5_1_RP_7, P_poll__networl_5_2_AskP_0, P_poll__networl_5_2_AskP_1, P_poll__networl_5_2_AskP_2, P_poll__networl_5_2_AskP_3, P_poll__networl_5_2_AskP_4, P_poll__networl_5_2_AskP_5, P_poll__networl_5_2_AskP_6, P_poll__networl_5_2_AskP_7, P_poll__networl_5_2_AnsP_0, P_poll__networl_5_2_AnsP_1, P_poll__networl_5_2_AnsP_2, P_poll__networl_5_2_AnsP_3, P_poll__networl_5_2_AnsP_4, P_poll__networl_5_2_AnsP_5, P_poll__networl_5_2_AnsP_6, P_poll__networl_5_2_AnsP_7, P_poll__networl_5_2_RI_0, P_poll__networl_5_2_RI_1, P_poll__networl_5_2_RI_2, P_poll__networl_5_2_RI_3, P_poll__networl_5_2_RI_4, P_poll__networl_5_2_RI_5, P_poll__networl_5_2_RI_6, P_poll__networl_5_2_RI_7, P_poll__networl_5_2_AI_0, P_poll__networl_5_2_AI_1, P_poll__networl_5_2_AI_2, P_poll__networl_5_2_AI_3, P_poll__networl_5_2_AI_4, P_poll__networl_5_2_AI_5, P_poll__networl_5_2_AI_6, P_poll__networl_5_2_AI_7, P_poll__networl_5_2_AnnP_0, P_poll__networl_5_2_AnnP_1, P_poll__networl_5_2_AnnP_2, P_poll__networl_5_2_AnnP_3, P_poll__networl_5_2_AnnP_4, P_poll__networl_5_2_AnnP_5, P_poll__networl_5_2_AnnP_6, P_poll__networl_5_2_AnnP_7, P_poll__networl_5_2_RP_0, P_poll__networl_5_2_RP_1, P_poll__networl_5_2_RP_2, P_poll__networl_5_2_RP_3, P_poll__networl_5_2_RP_4, P_poll__networl_5_2_RP_5, P_poll__networl_5_2_RP_6, P_poll__networl_5_2_RP_7, P_poll__networl_5_3_AskP_0, P_poll__networl_5_3_AskP_1, P_poll__networl_5_3_AskP_2, P_poll__networl_5_3_AskP_3, P_poll__networl_5_3_AskP_4, P_poll__networl_5_3_AskP_5, P_poll__networl_5_3_AskP_6, P_poll__networl_5_3_AskP_7, P_poll__networl_5_3_AnsP_0, P_poll__networl_5_3_AnsP_1, P_poll__networl_5_3_AnsP_2, P_poll__networl_5_3_AnsP_3, P_poll__networl_5_3_AnsP_4, P_poll__networl_5_3_AnsP_5, P_poll__networl_5_3_AnsP_6, P_poll__networl_5_3_AnsP_7, P_poll__networl_5_3_RI_0, P_poll__networl_5_3_RI_1, P_poll__networl_5_3_RI_2, P_poll__networl_5_3_RI_3, P_poll__networl_5_3_RI_4, P_poll__networl_5_3_RI_5, P_poll__networl_5_3_RI_6, P_poll__networl_5_3_RI_7, P_poll__networl_5_3_AI_0, P_poll__networl_5_3_AI_1, P_poll__networl_5_3_AI_2, P_poll__networl_5_3_AI_3, P_poll__networl_5_3_AI_4, P_poll__networl_5_3_AI_5, P_poll__networl_5_3_AI_6, P_poll__networl_5_3_AI_7, P_poll__networl_5_3_AnnP_0, P_poll__networl_5_3_AnnP_1, P_poll__networl_5_3_AnnP_2, P_poll__networl_5_3_AnnP_3, P_poll__networl_5_3_AnnP_4, P_poll__networl_5_3_AnnP_5, P_poll__networl_5_3_AnnP_6, P_poll__networl_5_3_AnnP_7, P_poll__networl_5_3_RP_0, P_poll__networl_5_3_RP_1, P_poll__networl_5_3_RP_2, P_poll__networl_5_3_RP_3, P_poll__networl_5_3_RP_4, P_poll__networl_5_3_RP_5, P_poll__networl_5_3_RP_6, P_poll__networl_5_3_RP_7, P_poll__networl_5_4_AskP_0, P_poll__networl_5_4_AskP_1, P_poll__networl_5_4_AskP_2, P_poll__networl_5_4_AskP_3, P_poll__networl_5_4_AskP_4, P_poll__networl_5_4_AskP_5, P_poll__networl_5_4_AskP_6, P_poll__networl_5_4_AskP_7, P_poll__networl_5_4_AnsP_0, P_poll__networl_5_4_AnsP_1, P_poll__networl_5_4_AnsP_2, P_poll__networl_5_4_AnsP_3, P_poll__networl_5_4_AnsP_4, P_poll__networl_5_4_AnsP_5, P_poll__networl_5_4_AnsP_6, P_poll__networl_5_4_AnsP_7, P_poll__networl_5_4_RI_0, P_poll__networl_5_4_RI_1, P_poll__networl_5_4_RI_2, P_poll__networl_5_4_RI_3, P_poll__networl_5_4_RI_4, P_poll__networl_5_4_RI_5, P_poll__networl_5_4_RI_6, P_poll__networl_5_4_RI_7, P_poll__networl_5_4_AI_0, P_poll__networl_5_4_AI_1, P_poll__networl_5_4_AI_2, P_poll__networl_5_4_AI_3, P_poll__networl_5_4_AI_4, P_poll__networl_5_4_AI_5, P_poll__networl_5_4_AI_6, P_poll__networl_5_4_AI_7, P_poll__networl_5_4_AnnP_0, P_poll__networl_5_4_AnnP_1, P_poll__networl_5_4_AnnP_2, P_poll__networl_5_4_AnnP_3, P_poll__networl_5_4_AnnP_4, P_poll__networl_5_4_AnnP_5, P_poll__networl_5_4_AnnP_6, P_poll__networl_5_4_AnnP_7, P_poll__networl_5_4_RP_0, P_poll__networl_5_4_RP_1, P_poll__networl_5_4_RP_2, P_poll__networl_5_4_RP_3, P_poll__networl_5_4_RP_4, P_poll__networl_5_4_RP_5, P_poll__networl_5_4_RP_6, P_poll__networl_5_4_RP_7, P_poll__networl_5_5_AskP_0, P_poll__networl_5_5_AskP_1, P_poll__networl_5_5_AskP_2, P_poll__networl_5_5_AskP_3, P_poll__networl_5_5_AskP_4, P_poll__networl_5_5_AskP_5, P_poll__networl_5_5_AskP_6, P_poll__networl_5_5_AskP_7, P_poll__networl_5_5_AnsP_0, P_poll__networl_5_5_AnsP_1, P_poll__networl_5_5_AnsP_2, P_poll__networl_5_5_AnsP_3, P_poll__networl_5_5_AnsP_4, P_poll__networl_5_5_AnsP_5, P_poll__networl_5_5_AnsP_6, P_poll__networl_5_5_AnsP_7, P_poll__networl_5_5_RI_0, P_poll__networl_5_5_RI_1, P_poll__networl_5_5_RI_2, P_poll__networl_5_5_RI_3, P_poll__networl_5_5_RI_4, P_poll__networl_5_5_RI_5, P_poll__networl_5_5_RI_6, P_poll__networl_5_5_RI_7, P_poll__networl_5_5_AI_0, P_poll__networl_5_5_AI_1, P_poll__networl_5_5_AI_2, P_poll__networl_5_5_AI_3, P_poll__networl_5_5_AI_4, P_poll__networl_5_5_AI_5, P_poll__networl_5_5_AI_6, P_poll__networl_5_5_AI_7, P_poll__networl_5_5_AnnP_0, P_poll__networl_5_5_AnnP_1, P_poll__networl_5_5_AnnP_2, P_poll__networl_5_5_AnnP_3, P_poll__networl_5_5_AnnP_4, P_poll__networl_5_5_AnnP_5, P_poll__networl_5_5_AnnP_6, P_poll__networl_5_5_AnnP_7, P_poll__networl_5_5_RP_0, P_poll__networl_5_5_RP_1, P_poll__networl_5_5_RP_2, P_poll__networl_5_5_RP_3, P_poll__networl_5_5_RP_4, P_poll__networl_5_5_RP_5, P_poll__networl_5_5_RP_6, P_poll__networl_5_5_RP_7, P_poll__networl_5_6_AskP_0, P_poll__networl_5_6_AskP_1, P_poll__networl_5_6_AskP_2, P_poll__networl_5_6_AskP_3, P_poll__networl_5_6_AskP_4, P_poll__networl_5_6_AskP_5, P_poll__networl_5_6_AskP_6, P_poll__networl_5_6_AskP_7, P_poll__networl_5_6_AnsP_0, P_poll__networl_5_6_AnsP_1, P_poll__networl_5_6_AnsP_2, P_poll__networl_5_6_AnsP_3, P_poll__networl_5_6_AnsP_4, P_poll__networl_5_6_AnsP_5, P_poll__networl_5_6_AnsP_6, P_poll__networl_5_6_AnsP_7, P_poll__networl_5_6_RI_0, P_poll__networl_5_6_RI_1, P_poll__networl_5_6_RI_2, P_poll__networl_5_6_RI_3, P_poll__networl_5_6_RI_4, P_poll__networl_5_6_RI_5, P_poll__networl_5_6_RI_6, P_poll__networl_5_6_RI_7, P_poll__networl_5_6_AI_0, P_poll__networl_5_6_AI_1, P_poll__networl_5_6_AI_2, P_poll__networl_5_6_AI_3, P_poll__networl_5_6_AI_4, P_poll__networl_5_6_AI_5, P_poll__networl_5_6_AI_6, P_poll__networl_5_6_AI_7, P_poll__networl_5_6_AnnP_0, P_poll__networl_5_6_AnnP_1, P_poll__networl_5_6_AnnP_2, P_poll__networl_5_6_AnnP_3, P_poll__networl_5_6_AnnP_4, P_poll__networl_5_6_AnnP_5, P_poll__networl_5_6_AnnP_6, P_poll__networl_5_6_AnnP_7, P_poll__networl_5_6_RP_0, P_poll__networl_5_6_RP_1, P_poll__networl_5_6_RP_2, P_poll__networl_5_6_RP_3, P_poll__networl_5_6_RP_4, P_poll__networl_5_6_RP_5, P_poll__networl_5_6_RP_6, P_poll__networl_5_6_RP_7, P_poll__networl_5_7_AskP_0, P_poll__networl_5_7_AskP_1, P_poll__networl_5_7_AskP_2, P_poll__networl_5_7_AskP_3, P_poll__networl_5_7_AskP_4, P_poll__networl_5_7_AskP_5, P_poll__networl_5_7_AskP_6, P_poll__networl_5_7_AskP_7, P_poll__networl_5_7_AnsP_0, P_poll__networl_5_7_AnsP_1, P_poll__networl_5_7_AnsP_2, P_poll__networl_5_7_AnsP_3, P_poll__networl_5_7_AnsP_4, P_poll__networl_5_7_AnsP_5, P_poll__networl_5_7_AnsP_6, P_poll__networl_5_7_AnsP_7, P_poll__networl_5_7_RI_0, P_poll__networl_5_7_RI_1, P_poll__networl_5_7_RI_2, P_poll__networl_5_7_RI_3, P_poll__networl_5_7_RI_4, P_poll__networl_5_7_RI_5, P_poll__networl_5_7_RI_6, P_poll__networl_5_7_RI_7, P_poll__networl_5_7_AI_0, P_poll__networl_5_7_AI_1, P_poll__networl_5_7_AI_2, P_poll__networl_5_7_AI_3, P_poll__networl_5_7_AI_4, P_poll__networl_5_7_AI_5, P_poll__networl_5_7_AI_6, P_poll__networl_5_7_AI_7, P_poll__networl_5_7_AnnP_0, P_poll__networl_5_7_AnnP_1, P_poll__networl_5_7_AnnP_2, P_poll__networl_5_7_AnnP_3, P_poll__networl_5_7_AnnP_4, P_poll__networl_5_7_AnnP_5, P_poll__networl_5_7_AnnP_6, P_poll__networl_5_7_AnnP_7, P_poll__networl_5_7_RP_0, P_poll__networl_5_7_RP_1, P_poll__networl_5_7_RP_2, P_poll__networl_5_7_RP_3, P_poll__networl_5_7_RP_4, P_poll__networl_5_7_RP_5, P_poll__networl_5_7_RP_6, P_poll__networl_5_7_RP_7, P_poll__networl_6_0_AskP_0, P_poll__networl_6_0_AskP_1, P_poll__networl_6_0_AskP_2, P_poll__networl_6_0_AskP_3, P_poll__networl_6_0_AskP_4, P_poll__networl_6_0_AskP_5, P_poll__networl_6_0_AskP_6, P_poll__networl_6_0_AskP_7, P_poll__networl_6_0_AnsP_0, P_poll__networl_6_0_AnsP_1, P_poll__networl_6_0_AnsP_2, P_poll__networl_6_0_AnsP_3, P_poll__networl_6_0_AnsP_4, P_poll__networl_6_0_AnsP_5, P_poll__networl_6_0_AnsP_6, P_poll__networl_6_0_AnsP_7, P_poll__networl_6_0_RI_0, P_poll__networl_6_0_RI_1, P_poll__networl_6_0_RI_2, P_poll__networl_6_0_RI_3, P_poll__networl_6_0_RI_4, P_poll__networl_6_0_RI_5, P_poll__networl_6_0_RI_6, P_poll__networl_6_0_RI_7, P_poll__networl_6_0_AI_0, P_poll__networl_6_0_AI_1, P_poll__networl_6_0_AI_2, P_poll__networl_6_0_AI_3, P_poll__networl_6_0_AI_4, P_poll__networl_6_0_AI_5, P_poll__networl_6_0_AI_6, P_poll__networl_6_0_AI_7, P_poll__networl_6_0_AnnP_0, P_poll__networl_6_0_AnnP_1, P_poll__networl_6_0_AnnP_2, P_poll__networl_6_0_AnnP_3, P_poll__networl_6_0_AnnP_4, P_poll__networl_6_0_AnnP_5, P_poll__networl_6_0_AnnP_6, P_poll__networl_6_0_AnnP_7, P_poll__networl_6_0_RP_0, P_poll__networl_6_0_RP_1, P_poll__networl_6_0_RP_2, P_poll__networl_6_0_RP_3, P_poll__networl_6_0_RP_4, P_poll__networl_6_0_RP_5, P_poll__networl_6_0_RP_6, P_poll__networl_6_0_RP_7, P_poll__networl_6_1_AskP_0, P_poll__networl_6_1_AskP_1, P_poll__networl_6_1_AskP_2, P_poll__networl_6_1_AskP_3, P_poll__networl_6_1_AskP_4, P_poll__networl_6_1_AskP_5, P_poll__networl_6_1_AskP_6, P_poll__networl_6_1_AskP_7, P_poll__networl_6_1_AnsP_0, P_poll__networl_6_1_AnsP_1, P_poll__networl_6_1_AnsP_2, P_poll__networl_6_1_AnsP_3, P_poll__networl_6_1_AnsP_4, P_poll__networl_6_1_AnsP_5, P_poll__networl_6_1_AnsP_6, P_poll__networl_6_1_AnsP_7, P_poll__networl_6_1_RI_0, P_poll__networl_6_1_RI_1, P_poll__networl_6_1_RI_2, P_poll__networl_6_1_RI_3, P_poll__networl_6_1_RI_4, P_poll__networl_6_1_RI_5, P_poll__networl_6_1_RI_6, P_poll__networl_6_1_RI_7, P_poll__networl_6_1_AI_0, P_poll__networl_6_1_AI_1, P_poll__networl_6_1_AI_2, P_poll__networl_6_1_AI_3, P_poll__networl_6_1_AI_4, P_poll__networl_6_1_AI_5, P_poll__networl_6_1_AI_6, P_poll__networl_6_1_AI_7, P_poll__networl_6_1_AnnP_0, P_poll__networl_6_1_AnnP_1, P_poll__networl_6_1_AnnP_2, P_poll__networl_6_1_AnnP_3, P_poll__networl_6_1_AnnP_4, P_poll__networl_6_1_AnnP_5, P_poll__networl_6_1_AnnP_6, P_poll__networl_6_1_AnnP_7, P_poll__networl_6_1_RP_0, P_poll__networl_6_1_RP_1, P_poll__networl_6_1_RP_2, P_poll__networl_6_1_RP_3, P_poll__networl_6_1_RP_4, P_poll__networl_6_1_RP_5, P_poll__networl_6_1_RP_6, P_poll__networl_6_1_RP_7, P_poll__networl_6_2_AskP_0, P_poll__networl_6_2_AskP_1, P_poll__networl_6_2_AskP_2, P_poll__networl_6_2_AskP_3, P_poll__networl_6_2_AskP_4, P_poll__networl_6_2_AskP_5, P_poll__networl_6_2_AskP_6, P_poll__networl_6_2_AskP_7, P_poll__networl_6_2_AnsP_0, P_poll__networl_6_2_AnsP_1, P_poll__networl_6_2_AnsP_2, P_poll__networl_6_2_AnsP_3, P_poll__networl_6_2_AnsP_4, P_poll__networl_6_2_AnsP_5, P_poll__networl_6_2_AnsP_6, P_poll__networl_6_2_AnsP_7, P_poll__networl_6_2_RI_0, P_poll__networl_6_2_RI_1, P_poll__networl_6_2_RI_2, P_poll__networl_6_2_RI_3, P_poll__networl_6_2_RI_4, P_poll__networl_6_2_RI_5, P_poll__networl_6_2_RI_6, P_poll__networl_6_2_RI_7, P_poll__networl_6_2_AI_0, P_poll__networl_6_2_AI_1, P_poll__networl_6_2_AI_2, P_poll__networl_6_2_AI_3, P_poll__networl_6_2_AI_4, P_poll__networl_6_2_AI_5, P_poll__networl_6_2_AI_6, P_poll__networl_6_2_AI_7, P_poll__networl_6_2_AnnP_0, P_poll__networl_6_2_AnnP_1, P_poll__networl_6_2_AnnP_2, P_poll__networl_6_2_AnnP_3, P_poll__networl_6_2_AnnP_4, P_poll__networl_6_2_AnnP_5, P_poll__networl_6_2_AnnP_6, P_poll__networl_6_2_AnnP_7, P_poll__networl_6_2_RP_0, P_poll__networl_6_2_RP_1, P_poll__networl_6_2_RP_2, P_poll__networl_6_2_RP_3, P_poll__networl_6_2_RP_4, P_poll__networl_6_2_RP_5, P_poll__networl_6_2_RP_6, P_poll__networl_6_2_RP_7, P_poll__networl_6_3_AskP_0, P_poll__networl_6_3_AskP_1, P_poll__networl_6_3_AskP_2, P_poll__networl_6_3_AskP_3, P_poll__networl_6_3_AskP_4, P_poll__networl_6_3_AskP_5, P_poll__networl_6_3_AskP_6, P_poll__networl_6_3_AskP_7, P_poll__networl_6_3_AnsP_0, P_poll__networl_6_3_AnsP_1, P_poll__networl_6_3_AnsP_2, P_poll__networl_6_3_AnsP_3, P_poll__networl_6_3_AnsP_4, P_poll__networl_6_3_AnsP_5, P_poll__networl_6_3_AnsP_6, P_poll__networl_6_3_AnsP_7, P_poll__networl_6_3_RI_0, P_poll__networl_6_3_RI_1, P_poll__networl_6_3_RI_2, P_poll__networl_6_3_RI_3, P_poll__networl_6_3_RI_4, P_poll__networl_6_3_RI_5, P_poll__networl_6_3_RI_6, P_poll__networl_6_3_RI_7, P_poll__networl_6_3_AI_0, P_poll__networl_6_3_AI_1, P_poll__networl_6_3_AI_2, P_poll__networl_6_3_AI_3, P_poll__networl_6_3_AI_4, P_poll__networl_6_3_AI_5, P_poll__networl_6_3_AI_6, P_poll__networl_6_3_AI_7, P_poll__networl_6_3_AnnP_0, P_poll__networl_6_3_AnnP_1, P_poll__networl_6_3_AnnP_2, P_poll__networl_6_3_AnnP_3, P_poll__networl_6_3_AnnP_4, P_poll__networl_6_3_AnnP_5, P_poll__networl_6_3_AnnP_6, P_poll__networl_6_3_AnnP_7, P_poll__networl_6_3_RP_0, P_poll__networl_6_3_RP_1, P_poll__networl_6_3_RP_2, P_poll__networl_6_3_RP_3, P_poll__networl_6_3_RP_4, P_poll__networl_6_3_RP_5, P_poll__networl_6_3_RP_6, P_poll__networl_6_3_RP_7, P_poll__networl_6_4_AskP_0, P_poll__networl_6_4_AskP_1, P_poll__networl_6_4_AskP_2, P_poll__networl_6_4_AskP_3, P_poll__networl_6_4_AskP_4, P_poll__networl_6_4_AskP_5, P_poll__networl_6_4_AskP_6, P_poll__networl_6_4_AskP_7, P_poll__networl_6_4_AnsP_0, P_poll__networl_6_4_AnsP_1, P_poll__networl_6_4_AnsP_2, P_poll__networl_6_4_AnsP_3, P_poll__networl_6_4_AnsP_4, P_poll__networl_6_4_AnsP_5, P_poll__networl_6_4_AnsP_6, P_poll__networl_6_4_AnsP_7, P_poll__networl_6_4_RI_0, P_poll__networl_6_4_RI_1, P_poll__networl_6_4_RI_2, P_poll__networl_6_4_RI_3, P_poll__networl_6_4_RI_4, P_poll__networl_6_4_RI_5, P_poll__networl_6_4_RI_6, P_poll__networl_6_4_RI_7, P_poll__networl_6_4_AI_0, P_poll__networl_6_4_AI_1, P_poll__networl_6_4_AI_2, P_poll__networl_6_4_AI_3, P_poll__networl_6_4_AI_4, P_poll__networl_6_4_AI_5, P_poll__networl_6_4_AI_6, P_poll__networl_6_4_AI_7, P_poll__networl_6_4_AnnP_0, P_poll__networl_6_4_AnnP_1, P_poll__networl_6_4_AnnP_2, P_poll__networl_6_4_AnnP_3, P_poll__networl_6_4_AnnP_4, P_poll__networl_6_4_AnnP_5, P_poll__networl_6_4_AnnP_6, P_poll__networl_6_4_AnnP_7, P_poll__networl_6_4_RP_0, P_poll__networl_6_4_RP_1, P_poll__networl_6_4_RP_2, P_poll__networl_6_4_RP_3, P_poll__networl_6_4_RP_4, P_poll__networl_6_4_RP_5, P_poll__networl_6_4_RP_6, P_poll__networl_6_4_RP_7, P_poll__networl_6_5_AskP_0, P_poll__networl_6_5_AskP_1, P_poll__networl_6_5_AskP_2, P_poll__networl_6_5_AskP_3, P_poll__networl_6_5_AskP_4, P_poll__networl_6_5_AskP_5, P_poll__networl_6_5_AskP_6, P_poll__networl_6_5_AskP_7, P_poll__networl_6_5_AnsP_0, P_poll__networl_6_5_AnsP_1, P_poll__networl_6_5_AnsP_2, P_poll__networl_6_5_AnsP_3, P_poll__networl_6_5_AnsP_4, P_poll__networl_6_5_AnsP_5, P_poll__networl_6_5_AnsP_6, P_poll__networl_6_5_AnsP_7, P_poll__networl_6_5_RI_0, P_poll__networl_6_5_RI_1, P_poll__networl_6_5_RI_2, P_poll__networl_6_5_RI_3, P_poll__networl_6_5_RI_4, P_poll__networl_6_5_RI_5, P_poll__networl_6_5_RI_6, P_poll__networl_6_5_RI_7, P_poll__networl_6_5_AI_0, P_poll__networl_6_5_AI_1, P_poll__networl_6_5_AI_2, P_poll__networl_6_5_AI_3, P_poll__networl_6_5_AI_4, P_poll__networl_6_5_AI_5, P_poll__networl_6_5_AI_6, P_poll__networl_6_5_AI_7, P_poll__networl_6_5_AnnP_0, P_poll__networl_6_5_AnnP_1, P_poll__networl_6_5_AnnP_2, P_poll__networl_6_5_AnnP_3, P_poll__networl_6_5_AnnP_4, P_poll__networl_6_5_AnnP_5, P_poll__networl_6_5_AnnP_6, P_poll__networl_6_5_AnnP_7, P_poll__networl_6_5_RP_0, P_poll__networl_6_5_RP_1, P_poll__networl_6_5_RP_2, P_poll__networl_6_5_RP_3, P_poll__networl_6_5_RP_4, P_poll__networl_6_5_RP_5, P_poll__networl_6_5_RP_6, P_poll__networl_6_5_RP_7, P_poll__networl_6_6_AskP_0, P_poll__networl_6_6_AskP_1, P_poll__networl_6_6_AskP_2, P_poll__networl_6_6_AskP_3, P_poll__networl_6_6_AskP_4, P_poll__networl_6_6_AskP_5, P_poll__networl_6_6_AskP_6, P_poll__networl_6_6_AskP_7, P_poll__networl_6_6_AnsP_0, P_poll__networl_6_6_AnsP_1, P_poll__networl_6_6_AnsP_2, P_poll__networl_6_6_AnsP_3, P_poll__networl_6_6_AnsP_4, P_poll__networl_6_6_AnsP_5, P_poll__networl_6_6_AnsP_6, P_poll__networl_6_6_AnsP_7, P_poll__networl_6_6_RI_0, P_poll__networl_6_6_RI_1, P_poll__networl_6_6_RI_2, P_poll__networl_6_6_RI_3, P_poll__networl_6_6_RI_4, P_poll__networl_6_6_RI_5, P_poll__networl_6_6_RI_6, P_poll__networl_6_6_RI_7, P_poll__networl_6_6_AI_0, P_poll__networl_6_6_AI_1, P_poll__networl_6_6_AI_2, P_poll__networl_6_6_AI_3, P_poll__networl_6_6_AI_4, P_poll__networl_6_6_AI_5, P_poll__networl_6_6_AI_6, P_poll__networl_6_6_AI_7, P_poll__networl_6_6_AnnP_0, P_poll__networl_6_6_AnnP_1, P_poll__networl_6_6_AnnP_2, P_poll__networl_6_6_AnnP_3, P_poll__networl_6_6_AnnP_4, P_poll__networl_6_6_AnnP_5, P_poll__networl_6_6_AnnP_6, P_poll__networl_6_6_AnnP_7, P_poll__networl_6_6_RP_0, P_poll__networl_6_6_RP_1, P_poll__networl_6_6_RP_2, P_poll__networl_6_6_RP_3, P_poll__networl_6_6_RP_4, P_poll__networl_6_6_RP_5, P_poll__networl_6_6_RP_6, P_poll__networl_6_6_RP_7, P_poll__networl_6_7_AskP_0, P_poll__networl_6_7_AskP_1, P_poll__networl_6_7_AskP_2, P_poll__networl_6_7_AskP_3, P_poll__networl_6_7_AskP_4, P_poll__networl_6_7_AskP_5, P_poll__networl_6_7_AskP_6, P_poll__networl_6_7_AskP_7, P_poll__networl_6_7_AnsP_0, P_poll__networl_6_7_AnsP_1, P_poll__networl_6_7_AnsP_2, P_poll__networl_6_7_AnsP_3, P_poll__networl_6_7_AnsP_4, P_poll__networl_6_7_AnsP_5, P_poll__networl_6_7_AnsP_6, P_poll__networl_6_7_AnsP_7, P_poll__networl_6_7_RI_0, P_poll__networl_6_7_RI_1, P_poll__networl_6_7_RI_2, P_poll__networl_6_7_RI_3, P_poll__networl_6_7_RI_4, P_poll__networl_6_7_RI_5, P_poll__networl_6_7_RI_6, P_poll__networl_6_7_RI_7, P_poll__networl_6_7_AI_0, P_poll__networl_6_7_AI_1, P_poll__networl_6_7_AI_2, P_poll__networl_6_7_AI_3, P_poll__networl_6_7_AI_4, P_poll__networl_6_7_AI_5, P_poll__networl_6_7_AI_6, P_poll__networl_6_7_AI_7, P_poll__networl_6_7_AnnP_0, P_poll__networl_6_7_AnnP_1, P_poll__networl_6_7_AnnP_2, P_poll__networl_6_7_AnnP_3, P_poll__networl_6_7_AnnP_4, P_poll__networl_6_7_AnnP_5, P_poll__networl_6_7_AnnP_6, P_poll__networl_6_7_AnnP_7, P_poll__networl_6_7_RP_0, P_poll__networl_6_7_RP_1, P_poll__networl_6_7_RP_2, P_poll__networl_6_7_RP_3, P_poll__networl_6_7_RP_4, P_poll__networl_6_7_RP_5, P_poll__networl_6_7_RP_6, P_poll__networl_6_7_RP_7, P_poll__networl_7_0_AskP_0, P_poll__networl_7_0_AskP_1, P_poll__networl_7_0_AskP_2, P_poll__networl_7_0_AskP_3, P_poll__networl_7_0_AskP_4, P_poll__networl_7_0_AskP_5, P_poll__networl_7_0_AskP_6, P_poll__networl_7_0_AskP_7, P_poll__networl_7_0_AnsP_0, P_poll__networl_7_0_AnsP_1, P_poll__networl_7_0_AnsP_2, P_poll__networl_7_0_AnsP_3, P_poll__networl_7_0_AnsP_4, P_poll__networl_7_0_AnsP_5, P_poll__networl_7_0_AnsP_6, P_poll__networl_7_0_AnsP_7, P_poll__networl_7_0_RI_0, P_poll__networl_7_0_RI_1, P_poll__networl_7_0_RI_2, P_poll__networl_7_0_RI_3, P_poll__networl_7_0_RI_4, P_poll__networl_7_0_RI_5, P_poll__networl_7_0_RI_6, P_poll__networl_7_0_RI_7, P_poll__networl_7_0_AI_0, P_poll__networl_7_0_AI_1, P_poll__networl_7_0_AI_2, P_poll__networl_7_0_AI_3, P_poll__networl_7_0_AI_4, P_poll__networl_7_0_AI_5, P_poll__networl_7_0_AI_6, P_poll__networl_7_0_AI_7, P_poll__networl_7_0_AnnP_0, P_poll__networl_7_0_AnnP_1, P_poll__networl_7_0_AnnP_2, P_poll__networl_7_0_AnnP_3, P_poll__networl_7_0_AnnP_4, P_poll__networl_7_0_AnnP_5, P_poll__networl_7_0_AnnP_6, P_poll__networl_7_0_AnnP_7, P_poll__networl_7_0_RP_0, P_poll__networl_7_0_RP_1, P_poll__networl_7_0_RP_2, P_poll__networl_7_0_RP_3, P_poll__networl_7_0_RP_4, P_poll__networl_7_0_RP_5, P_poll__networl_7_0_RP_6, P_poll__networl_7_0_RP_7, P_poll__networl_7_1_AskP_0, P_poll__networl_7_1_AskP_1, P_poll__networl_7_1_AskP_2, P_poll__networl_7_1_AskP_3, P_poll__networl_7_1_AskP_4, P_poll__networl_7_1_AskP_5, P_poll__networl_7_1_AskP_6, P_poll__networl_7_1_AskP_7, P_poll__networl_7_1_AnsP_0, P_poll__networl_7_1_AnsP_1, P_poll__networl_7_1_AnsP_2, P_poll__networl_7_1_AnsP_3, P_poll__networl_7_1_AnsP_4, P_poll__networl_7_1_AnsP_5, P_poll__networl_7_1_AnsP_6, P_poll__networl_7_1_AnsP_7, P_poll__networl_7_1_RI_0, P_poll__networl_7_1_RI_1, P_poll__networl_7_1_RI_2, P_poll__networl_7_1_RI_3, P_poll__networl_7_1_RI_4, P_poll__networl_7_1_RI_5, P_poll__networl_7_1_RI_6, P_poll__networl_7_1_RI_7, P_poll__networl_7_1_AI_0, P_poll__networl_7_1_AI_1, P_poll__networl_7_1_AI_2, P_poll__networl_7_1_AI_3, P_poll__networl_7_1_AI_4, P_poll__networl_7_1_AI_5, P_poll__networl_7_1_AI_6, P_poll__networl_7_1_AI_7, P_poll__networl_7_1_AnnP_0, P_poll__networl_7_1_AnnP_1, P_poll__networl_7_1_AnnP_2, P_poll__networl_7_1_AnnP_3, P_poll__networl_7_1_AnnP_4, P_poll__networl_7_1_AnnP_5, P_poll__networl_7_1_AnnP_6, P_poll__networl_7_1_AnnP_7, P_poll__networl_7_1_RP_0, P_poll__networl_7_1_RP_1, P_poll__networl_7_1_RP_2, P_poll__networl_7_1_RP_3, P_poll__networl_7_1_RP_4, P_poll__networl_7_1_RP_5, P_poll__networl_7_1_RP_6, P_poll__networl_7_1_RP_7, P_poll__networl_7_2_AskP_0, P_poll__networl_7_2_AskP_1, P_poll__networl_7_2_AskP_2, P_poll__networl_7_2_AskP_3, P_poll__networl_7_2_AskP_4, P_poll__networl_7_2_AskP_5, P_poll__networl_7_2_AskP_6, P_poll__networl_7_2_AskP_7, P_poll__networl_7_2_AnsP_0, P_poll__networl_7_2_AnsP_1, P_poll__networl_7_2_AnsP_2, P_poll__networl_7_2_AnsP_3, P_poll__networl_7_2_AnsP_4, P_poll__networl_7_2_AnsP_5, P_poll__networl_7_2_AnsP_6, P_poll__networl_7_2_AnsP_7, P_poll__networl_7_2_RI_0, P_poll__networl_7_2_RI_1, P_poll__networl_7_2_RI_2, P_poll__networl_7_2_RI_3, P_poll__networl_7_2_RI_4, P_poll__networl_7_2_RI_5, P_poll__networl_7_2_RI_6, P_poll__networl_7_2_RI_7, P_poll__networl_7_2_AI_0, P_poll__networl_7_2_AI_1, P_poll__networl_7_2_AI_2, P_poll__networl_7_2_AI_3, P_poll__networl_7_2_AI_4, P_poll__networl_7_2_AI_5, P_poll__networl_7_2_AI_6, P_poll__networl_7_2_AI_7, P_poll__networl_7_2_AnnP_0, P_poll__networl_7_2_AnnP_1, P_poll__networl_7_2_AnnP_2, P_poll__networl_7_2_AnnP_3, P_poll__networl_7_2_AnnP_4, P_poll__networl_7_2_AnnP_5, P_poll__networl_7_2_AnnP_6, P_poll__networl_7_2_AnnP_7, P_poll__networl_7_2_RP_0, P_poll__networl_7_2_RP_1, P_poll__networl_7_2_RP_2, P_poll__networl_7_2_RP_3, P_poll__networl_7_2_RP_4, P_poll__networl_7_2_RP_5, P_poll__networl_7_2_RP_6, P_poll__networl_7_2_RP_7, P_poll__networl_7_3_AskP_0, P_poll__networl_7_3_AskP_1, P_poll__networl_7_3_AskP_2, P_poll__networl_7_3_AskP_3, P_poll__networl_7_3_AskP_4, P_poll__networl_7_3_AskP_5, P_poll__networl_7_3_AskP_6, P_poll__networl_7_3_AskP_7, P_poll__networl_7_3_AnsP_0, P_poll__networl_7_3_AnsP_1, P_poll__networl_7_3_AnsP_2, P_poll__networl_7_3_AnsP_3, P_poll__networl_7_3_AnsP_4, P_poll__networl_7_3_AnsP_5, P_poll__networl_7_3_AnsP_6, P_poll__networl_7_3_AnsP_7, P_poll__networl_7_3_RI_0, P_poll__networl_7_3_RI_1, P_poll__networl_7_3_RI_2, P_poll__networl_7_3_RI_3, P_poll__networl_7_3_RI_4, P_poll__networl_7_3_RI_5, P_poll__networl_7_3_RI_6, P_poll__networl_7_3_RI_7, P_poll__networl_7_3_AI_0, P_poll__networl_7_3_AI_1, P_poll__networl_7_3_AI_2, P_poll__networl_7_3_AI_3, P_poll__networl_7_3_AI_4, P_poll__networl_7_3_AI_5, P_poll__networl_7_3_AI_6, P_poll__networl_7_3_AI_7, P_poll__networl_7_3_AnnP_0, P_poll__networl_7_3_AnnP_1, P_poll__networl_7_3_AnnP_2, P_poll__networl_7_3_AnnP_3, P_poll__networl_7_3_AnnP_4, P_poll__networl_7_3_AnnP_5, P_poll__networl_7_3_AnnP_6, P_poll__networl_7_3_AnnP_7, P_poll__networl_7_3_RP_0, P_poll__networl_7_3_RP_1, P_poll__networl_7_3_RP_2, P_poll__networl_7_3_RP_3, P_poll__networl_7_3_RP_4, P_poll__networl_7_3_RP_5, P_poll__networl_7_3_RP_6, P_poll__networl_7_3_RP_7, P_poll__networl_7_4_AskP_0, P_poll__networl_7_4_AskP_1, P_poll__networl_7_4_AskP_2, P_poll__networl_7_4_AskP_3, P_poll__networl_7_4_AskP_4, P_poll__networl_7_4_AskP_5, P_poll__networl_7_4_AskP_6, P_poll__networl_7_4_AskP_7, P_poll__networl_7_4_AnsP_0, P_poll__networl_7_4_AnsP_1, P_poll__networl_7_4_AnsP_2, P_poll__networl_7_4_AnsP_3, P_poll__networl_7_4_AnsP_4, P_poll__networl_7_4_AnsP_5, P_poll__networl_7_4_AnsP_6, P_poll__networl_7_4_AnsP_7, P_poll__networl_7_4_RI_0, P_poll__networl_7_4_RI_1, P_poll__networl_7_4_RI_2, P_poll__networl_7_4_RI_3, P_poll__networl_7_4_RI_4, P_poll__networl_7_4_RI_5, P_poll__networl_7_4_RI_6, P_poll__networl_7_4_RI_7, P_poll__networl_7_4_AI_0, P_poll__networl_7_4_AI_1, P_poll__networl_7_4_AI_2, P_poll__networl_7_4_AI_3, P_poll__networl_7_4_AI_4, P_poll__networl_7_4_AI_5, P_poll__networl_7_4_AI_6, P_poll__networl_7_4_AI_7, P_poll__networl_7_4_AnnP_0, P_poll__networl_7_4_AnnP_1, P_poll__networl_7_4_AnnP_2, P_poll__networl_7_4_AnnP_3, P_poll__networl_7_4_AnnP_4, P_poll__networl_7_4_AnnP_5, P_poll__networl_7_4_AnnP_6, P_poll__networl_7_4_AnnP_7, P_poll__networl_7_4_RP_0, P_poll__networl_7_4_RP_1, P_poll__networl_7_4_RP_2, P_poll__networl_7_4_RP_3, P_poll__networl_7_4_RP_4, P_poll__networl_7_4_RP_5, P_poll__networl_7_4_RP_6, P_poll__networl_7_4_RP_7, P_poll__networl_7_5_AskP_0, P_poll__networl_7_5_AskP_1, P_poll__networl_7_5_AskP_2, P_poll__networl_7_5_AskP_3, P_poll__networl_7_5_AskP_4, P_poll__networl_7_5_AskP_5, P_poll__networl_7_5_AskP_6, P_poll__networl_7_5_AskP_7, P_poll__networl_7_5_AnsP_0, P_poll__networl_7_5_AnsP_1, P_poll__networl_7_5_AnsP_2, P_poll__networl_7_5_AnsP_3, P_poll__networl_7_5_AnsP_4, P_poll__networl_7_5_AnsP_5, P_poll__networl_7_5_AnsP_6, P_poll__networl_7_5_AnsP_7, P_poll__networl_7_5_RI_0, P_poll__networl_7_5_RI_1, P_poll__networl_7_5_RI_2, P_poll__networl_7_5_RI_3, P_poll__networl_7_5_RI_4, P_poll__networl_7_5_RI_5, P_poll__networl_7_5_RI_6, P_poll__networl_7_5_RI_7, P_poll__networl_7_5_AI_0, P_poll__networl_7_5_AI_1, P_poll__networl_7_5_AI_2, P_poll__networl_7_5_AI_3, P_poll__networl_7_5_AI_4, P_poll__networl_7_5_AI_5, P_poll__networl_7_5_AI_6, P_poll__networl_7_5_AI_7, P_poll__networl_7_5_AnnP_0, P_poll__networl_7_5_AnnP_1, P_poll__networl_7_5_AnnP_2, P_poll__networl_7_5_AnnP_3, P_poll__networl_7_5_AnnP_4, P_poll__networl_7_5_AnnP_5, P_poll__networl_7_5_AnnP_6, P_poll__networl_7_5_AnnP_7, P_poll__networl_7_5_RP_0, P_poll__networl_7_5_RP_1, P_poll__networl_7_5_RP_2, P_poll__networl_7_5_RP_3, P_poll__networl_7_5_RP_4, P_poll__networl_7_5_RP_5, P_poll__networl_7_5_RP_6, P_poll__networl_7_5_RP_7, P_poll__networl_7_6_AskP_0, P_poll__networl_7_6_AskP_1, P_poll__networl_7_6_AskP_2, P_poll__networl_7_6_AskP_3, P_poll__networl_7_6_AskP_4, P_poll__networl_7_6_AskP_5, P_poll__networl_7_6_AskP_6, P_poll__networl_7_6_AskP_7, P_poll__networl_7_6_AnsP_0, P_poll__networl_7_6_AnsP_1, P_poll__networl_7_6_AnsP_2, P_poll__networl_7_6_AnsP_3, P_poll__networl_7_6_AnsP_4, P_poll__networl_7_6_AnsP_5, P_poll__networl_7_6_AnsP_6, P_poll__networl_7_6_AnsP_7, P_poll__networl_7_6_RI_0, P_poll__networl_7_6_RI_1, P_poll__networl_7_6_RI_2, P_poll__networl_7_6_RI_3, P_poll__networl_7_6_RI_4, P_poll__networl_7_6_RI_5, P_poll__networl_7_6_RI_6, P_poll__networl_7_6_RI_7, P_poll__networl_7_6_AI_0, P_poll__networl_7_6_AI_1, P_poll__networl_7_6_AI_2, P_poll__networl_7_6_AI_3, P_poll__networl_7_6_AI_4, P_poll__networl_7_6_AI_5, P_poll__networl_7_6_AI_6, P_poll__networl_7_6_AI_7, P_poll__networl_7_6_AnnP_0, P_poll__networl_7_6_AnnP_1, P_poll__networl_7_6_AnnP_2, P_poll__networl_7_6_AnnP_3, P_poll__networl_7_6_AnnP_4, P_poll__networl_7_6_AnnP_5, P_poll__networl_7_6_AnnP_6, P_poll__networl_7_6_AnnP_7, P_poll__networl_7_6_RP_0, P_poll__networl_7_6_RP_1, P_poll__networl_7_6_RP_2, P_poll__networl_7_6_RP_3, P_poll__networl_7_6_RP_4, P_poll__networl_7_6_RP_5, P_poll__networl_7_6_RP_6, P_poll__networl_7_6_RP_7, P_poll__networl_7_7_AskP_0, P_poll__networl_7_7_AskP_1, P_poll__networl_7_7_AskP_2, P_poll__networl_7_7_AskP_3, P_poll__networl_7_7_AskP_4, P_poll__networl_7_7_AskP_5, P_poll__networl_7_7_AskP_6, P_poll__networl_7_7_AskP_7, P_poll__networl_7_7_AnsP_0, P_poll__networl_7_7_AnsP_1, P_poll__networl_7_7_AnsP_2, P_poll__networl_7_7_AnsP_3, P_poll__networl_7_7_AnsP_4, P_poll__networl_7_7_AnsP_5, P_poll__networl_7_7_AnsP_6, P_poll__networl_7_7_AnsP_7, P_poll__networl_7_7_RI_0, P_poll__networl_7_7_RI_1, P_poll__networl_7_7_RI_2, P_poll__networl_7_7_RI_3, P_poll__networl_7_7_RI_4, P_poll__networl_7_7_RI_5, P_poll__networl_7_7_RI_6, P_poll__networl_7_7_RI_7, P_poll__networl_7_7_AI_0, P_poll__networl_7_7_AI_1, P_poll__networl_7_7_AI_2, P_poll__networl_7_7_AI_3, P_poll__networl_7_7_AI_4, P_poll__networl_7_7_AI_5, P_poll__networl_7_7_AI_6, P_poll__networl_7_7_AI_7, P_poll__networl_7_7_AnnP_0, P_poll__networl_7_7_AnnP_1, P_poll__networl_7_7_AnnP_2, P_poll__networl_7_7_AnnP_3, P_poll__networl_7_7_AnnP_4, P_poll__networl_7_7_AnnP_5, P_poll__networl_7_7_AnnP_6, P_poll__networl_7_7_AnnP_7, P_poll__networl_7_7_RP_0, P_poll__networl_7_7_RP_1, P_poll__networl_7_7_RP_2, P_poll__networl_7_7_RP_3, P_poll__networl_7_7_RP_4, P_poll__networl_7_7_RP_5, P_poll__networl_7_7_RP_6, P_poll__networl_7_7_RP_7, P_poll__pollEnd_0, P_poll__pollEnd_1, P_poll__pollEnd_2, P_poll__pollEnd_3, P_poll__pollEnd_4, P_poll__pollEnd_5, P_poll__pollEnd_6, P_poll__pollEnd_7, P_poll__waitingMessage_0, P_poll__waitingMessage_1, P_poll__waitingMessage_2, P_poll__waitingMessage_3, P_poll__waitingMessage_4, P_poll__waitingMessage_5, P_poll__waitingMessage_6, P_poll__waitingMessage_7, P_polling_0, P_polling_1, P_polling_2, P_polling_3, P_polling_4, P_polling_5, P_polling_6, P_polling_7, P_sendAnnPs__broadcasting_0_1, P_sendAnnPs__broadcasting_0_2, P_sendAnnPs__broadcasting_0_3, P_sendAnnPs__broadcasting_0_4, P_sendAnnPs__broadcasting_0_5, P_sendAnnPs__broadcasting_0_6, P_sendAnnPs__broadcasting_0_7, P_sendAnnPs__broadcasting_1_1, P_sendAnnPs__broadcasting_1_2, P_sendAnnPs__broadcasting_1_3, P_sendAnnPs__broadcasting_1_4, P_sendAnnPs__broadcasting_1_5, P_sendAnnPs__broadcasting_1_6, P_sendAnnPs__broadcasting_1_7, P_sendAnnPs__broadcasting_2_1, P_sendAnnPs__broadcasting_2_2, P_sendAnnPs__broadcasting_2_3, P_sendAnnPs__broadcasting_2_4, P_sendAnnPs__broadcasting_2_5, P_sendAnnPs__broadcasting_2_6, P_sendAnnPs__broadcasting_2_7, P_sendAnnPs__broadcasting_3_1, P_sendAnnPs__broadcasting_3_2, P_sendAnnPs__broadcasting_3_3, P_sendAnnPs__broadcasting_3_4, P_sendAnnPs__broadcasting_3_5, P_sendAnnPs__broadcasting_3_6, P_sendAnnPs__broadcasting_3_7, P_sendAnnPs__broadcasting_4_1, P_sendAnnPs__broadcasting_4_2, P_sendAnnPs__broadcasting_4_3, P_sendAnnPs__broadcasting_4_4, P_sendAnnPs__broadcasting_4_5, P_sendAnnPs__broadcasting_4_6, P_sendAnnPs__broadcasting_4_7, P_sendAnnPs__broadcasting_5_1, P_sendAnnPs__broadcasting_5_2, P_sendAnnPs__broadcasting_5_3, P_sendAnnPs__broadcasting_5_4, P_sendAnnPs__broadcasting_5_5, P_sendAnnPs__broadcasting_5_6, P_sendAnnPs__broadcasting_5_7, P_sendAnnPs__broadcasting_6_1, P_sendAnnPs__broadcasting_6_2, P_sendAnnPs__broadcasting_6_3, P_sendAnnPs__broadcasting_6_4, P_sendAnnPs__broadcasting_6_5, P_sendAnnPs__broadcasting_6_6, P_sendAnnPs__broadcasting_6_7, P_sendAnnPs__broadcasting_7_1, P_sendAnnPs__broadcasting_7_2, P_sendAnnPs__broadcasting_7_3, P_sendAnnPs__broadcasting_7_4, P_sendAnnPs__broadcasting_7_5, P_sendAnnPs__broadcasting_7_6, P_sendAnnPs__broadcasting_7_7, P_stage_0_NEG, P_stage_0_PRIM, P_stage_0_SEC, P_stage_1_NEG, P_stage_1_PRIM, P_stage_1_SEC, P_stage_2_NEG, P_stage_2_PRIM, P_stage_2_SEC, P_stage_3_NEG, P_stage_3_PRIM, P_stage_3_SEC, P_stage_4_NEG, P_stage_4_PRIM, P_stage_4_SEC, P_stage_5_NEG, P_stage_5_PRIM, P_stage_5_SEC, P_stage_6_NEG, P_stage_6_PRIM, P_stage_6_SEC, P_stage_7_NEG, P_stage_7_PRIM, P_stage_7_SEC, P_startNeg__broadcasting_0_1, P_startNeg__broadcasting_0_2, P_startNeg__broadcasting_0_3, P_startNeg__broadcasting_0_4, P_startNeg__broadcasting_0_5, P_startNeg__broadcasting_0_6, P_startNeg__broadcasting_0_7, P_startNeg__broadcasting_1_1, P_startNeg__broadcasting_1_2, P_startNeg__broadcasting_1_3, P_startNeg__broadcasting_1_4, P_startNeg__broadcasting_1_5, P_startNeg__broadcasting_1_6, P_startNeg__broadcasting_1_7, P_startNeg__broadcasting_2_1, P_startNeg__broadcasting_2_2, P_startNeg__broadcasting_2_3, P_startNeg__broadcasting_2_4, P_startNeg__broadcasting_2_5, P_startNeg__broadcasting_2_6, P_startNeg__broadcasting_2_7, P_startNeg__broadcasting_3_1, P_startNeg__broadcasting_3_2, P_startNeg__broadcasting_3_3, P_startNeg__broadcasting_3_4, P_startNeg__broadcasting_3_5, P_startNeg__broadcasting_3_6, P_startNeg__broadcasting_3_7, P_startNeg__broadcasting_4_1, P_startNeg__broadcasting_4_2, P_startNeg__broadcasting_4_3, P_startNeg__broadcasting_4_4, P_startNeg__broadcasting_4_5, P_startNeg__broadcasting_4_6, P_startNeg__broadcasting_4_7, P_startNeg__broadcasting_5_1, P_startNeg__broadcasting_5_2, P_startNeg__broadcasting_5_3, P_startNeg__broadcasting_5_4, P_startNeg__broadcasting_5_5, P_startNeg__broadcasting_5_6, P_startNeg__broadcasting_5_7, P_startNeg__broadcasting_6_1, P_startNeg__broadcasting_6_2, P_startNeg__broadcasting_6_3, P_startNeg__broadcasting_6_4, P_startNeg__broadcasting_6_5, P_startNeg__broadcasting_6_6, P_startNeg__broadcasting_6_7, P_startNeg__broadcasting_7_1, P_startNeg__broadcasting_7_2, P_startNeg__broadcasting_7_3, P_startNeg__broadcasting_7_4, P_startNeg__broadcasting_7_5, P_startNeg__broadcasting_7_6, P_startNeg__broadcasting_7_7]
[2023-03-14 21:58:42] [INFO ] Parsed PT model containing 7128 places and 14112 transitions and 81968 arcs in 1143 ms.
Parsed 16 properties from file /home/mcc/execution/LTLCardinality.xml in 499 ms.
Working with output stream class java.io.PrintStream
Initial state reduction rules removed 3 formulas.
Deduced a syphon composed of 6688 places in 47 ms
Reduce places removed 6730 places and 13502 transitions.
Reduce places removed 15 places and 0 transitions.
FORMULA NeoElection-PT-7-LTLCardinality-04 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-06 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-08 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-12 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-14 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-15 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-01 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-09 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-10 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-7-LTLCardinality-11 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 238 out of 383 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 383/383 places, 610/610 transitions.
Reduce places removed 42 places and 0 transitions.
Iterating post reduction 0 with 42 rules applied. Total rules applied 42 place count 341 transition count 610
Discarding 35 places :
Symmetric choice reduction at 1 with 35 rule applications. Total rules 77 place count 306 transition count 295
Iterating global reduction 1 with 35 rules applied. Total rules applied 112 place count 306 transition count 295
Applied a total of 112 rules in 41 ms. Remains 306 /383 variables (removed 77) and now considering 295/610 (removed 315) transitions.
[2023-03-14 21:58:43] [INFO ] Flow matrix only has 259 transitions (discarded 36 similar events)
// Phase 1: matrix 259 rows 306 cols
[2023-03-14 21:58:43] [INFO ] Computed 62 place invariants in 38 ms
[2023-03-14 21:58:44] [INFO ] Implicit Places using invariants in 469 ms returned [19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67]
Discarding 49 places :
Implicit Place search using SMT only with invariants took 522 ms to find 49 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 257/383 places, 295/610 transitions.
Applied a total of 0 rules in 4 ms. Remains 257 /257 variables (removed 0) and now considering 295/295 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 567 ms. Remains : 257/383 places, 295/610 transitions.
Support contains 238 out of 257 places after structural reductions.
[2023-03-14 21:58:44] [INFO ] Flatten gal took : 81 ms
[2023-03-14 21:58:44] [INFO ] Flatten gal took : 40 ms
[2023-03-14 21:58:44] [INFO ] Input system was already deterministic with 295 transitions.
Incomplete random walk after 10000 steps, including 17 resets, run finished after 367 ms. (steps per millisecond=27 ) properties (out of 8) seen :6
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 69 ms. (steps per millisecond=144 ) properties (out of 2) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 41 ms. (steps per millisecond=243 ) properties (out of 2) seen :0
Running SMT prover for 2 properties.
[2023-03-14 21:58:45] [INFO ] Flow matrix only has 259 transitions (discarded 36 similar events)
// Phase 1: matrix 259 rows 257 cols
[2023-03-14 21:58:45] [INFO ] Computed 13 place invariants in 3 ms
[2023-03-14 21:58:45] [INFO ] [Real]Absence check using 13 positive place invariants in 5 ms returned sat
[2023-03-14 21:58:45] [INFO ] After 143ms SMT Verify possible using all constraints in real domain returned unsat :2 sat :0
Fused 2 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 0 ms.
Successfully simplified 2 atomic propositions for a total of 6 simplifications.
Computed a total of 257 stabilizing places and 295 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 257 transition count 295
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(G(p0)))'
Support contains 7 out of 257 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Reduce places removed 7 places and 7 transitions.
Performed 7 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 7 Pre rules applied. Total rules applied 0 place count 250 transition count 281
Deduced a syphon composed of 7 places in 1 ms
Reduce places removed 7 places and 0 transitions.
Iterating global reduction 0 with 14 rules applied. Total rules applied 14 place count 243 transition count 281
Discarding 37 places :
Symmetric choice reduction at 0 with 37 rule applications. Total rules 51 place count 206 transition count 229
Iterating global reduction 0 with 37 rules applied. Total rules applied 88 place count 206 transition count 229
Performed 35 Post agglomeration using F-continuation condition.Transition count delta: 35
Deduced a syphon composed of 35 places in 0 ms
Reduce places removed 35 places and 0 transitions.
Iterating global reduction 0 with 70 rules applied. Total rules applied 158 place count 171 transition count 194
Reduce places removed 7 places and 7 transitions.
Iterating global reduction 0 with 7 rules applied. Total rules applied 165 place count 164 transition count 187
Applied a total of 165 rules in 89 ms. Remains 164 /257 variables (removed 93) and now considering 187/295 (removed 108) transitions.
[2023-03-14 21:58:45] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
// Phase 1: matrix 151 rows 164 cols
[2023-03-14 21:58:45] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:58:45] [INFO ] Implicit Places using invariants in 201 ms returned []
[2023-03-14 21:58:45] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:45] [INFO ] Invariant cache hit.
[2023-03-14 21:58:45] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:46] [INFO ] Implicit Places using invariants and state equation in 259 ms returned []
Implicit Place search using SMT with State Equation took 463 ms to find 0 implicit places.
[2023-03-14 21:58:46] [INFO ] Redundant transitions in 8 ms returned []
[2023-03-14 21:58:46] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:46] [INFO ] Invariant cache hit.
[2023-03-14 21:58:46] [INFO ] Dead Transitions using invariants and state equation in 161 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 164/257 places, 187/295 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 729 ms. Remains : 164/257 places, 187/295 transitions.
Stuttering acceptance computed with spot in 197 ms :[(NOT p0)]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-00 automaton TGBA Formula[mat=[[{ cond=p0, acceptance={} source=0 dest: 0}, { cond=(NOT p0), acceptance={0} source=0 dest: 0}]], initial=0, aps=[p0:(GT (ADD s150 s151 s152 s153 s154 s155 s156) 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, complete, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-invariant], stateDesc=[null][true]]
Product exploration explored 100000 steps with 290 reset in 616 ms.
Product exploration explored 100000 steps with 290 reset in 501 ms.
Computed a total of 164 stabilizing places and 187 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 164 transition count 187
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X p0)), (X (X (NOT p0)))]
Knowledge based reduction with 3 factoid took 180 ms. Reduced automaton from 1 states, 2 edges and 1 AP (stutter insensitive) to 1 states, 2 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 38 ms :[(NOT p0)]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), (X p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X p0)), (X (X (NOT p0))), (F p0)]
Knowledge based reduction with 3 factoid took 193 ms. Reduced automaton from 1 states, 2 edges and 1 AP (stutter insensitive) to 1 states, 2 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 38 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 38 ms :[(NOT p0)]
[2023-03-14 21:58:48] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:48] [INFO ] Invariant cache hit.
[2023-03-14 21:58:48] [INFO ] [Real]Absence check using 13 positive place invariants in 5 ms returned sat
[2023-03-14 21:58:48] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:48] [INFO ] [Real]Absence check using state equation in 99 ms returned sat
[2023-03-14 21:58:48] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:58:48] [INFO ] [Nat]Absence check using 13 positive place invariants in 9 ms returned sat
[2023-03-14 21:58:48] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:49] [INFO ] [Nat]Absence check using state equation in 183 ms returned sat
[2023-03-14 21:58:49] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:49] [INFO ] [Nat]Added 6 Read/Feed constraints in 4 ms returned sat
[2023-03-14 21:58:49] [INFO ] Computed and/alt/rep : 180/369/144 causal constraints (skipped 0 transitions) in 49 ms.
[2023-03-14 21:58:49] [INFO ] Added : 54 causal constraints over 11 iterations in 308 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 7 out of 164 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 164/164 places, 187/187 transitions.
Applied a total of 0 rules in 10 ms. Remains 164 /164 variables (removed 0) and now considering 187/187 (removed 0) transitions.
[2023-03-14 21:58:49] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:49] [INFO ] Invariant cache hit.
[2023-03-14 21:58:49] [INFO ] Implicit Places using invariants in 175 ms returned []
[2023-03-14 21:58:49] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:49] [INFO ] Invariant cache hit.
[2023-03-14 21:58:49] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:49] [INFO ] Implicit Places using invariants and state equation in 266 ms returned []
Implicit Place search using SMT with State Equation took 450 ms to find 0 implicit places.
[2023-03-14 21:58:49] [INFO ] Redundant transitions in 8 ms returned []
[2023-03-14 21:58:49] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:49] [INFO ] Invariant cache hit.
[2023-03-14 21:58:50] [INFO ] Dead Transitions using invariants and state equation in 150 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 626 ms. Remains : 164/164 places, 187/187 transitions.
Computed a total of 164 stabilizing places and 187 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 164 transition count 187
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X p0)), (X (X (NOT p0)))]
Knowledge based reduction with 3 factoid took 169 ms. Reduced automaton from 1 states, 2 edges and 1 AP (stutter insensitive) to 1 states, 2 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 39 ms :[(NOT p0)]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), (X p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X p0)), (X (X (NOT p0))), (F p0)]
Knowledge based reduction with 3 factoid took 200 ms. Reduced automaton from 1 states, 2 edges and 1 AP (stutter insensitive) to 1 states, 2 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 37 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 45 ms :[(NOT p0)]
[2023-03-14 21:58:50] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:50] [INFO ] Invariant cache hit.
[2023-03-14 21:58:50] [INFO ] [Real]Absence check using 13 positive place invariants in 5 ms returned sat
[2023-03-14 21:58:50] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:50] [INFO ] [Real]Absence check using state equation in 93 ms returned sat
[2023-03-14 21:58:50] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:58:51] [INFO ] [Nat]Absence check using 13 positive place invariants in 5 ms returned sat
[2023-03-14 21:58:51] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:51] [INFO ] [Nat]Absence check using state equation in 116 ms returned sat
[2023-03-14 21:58:51] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:51] [INFO ] [Nat]Added 6 Read/Feed constraints in 4 ms returned sat
[2023-03-14 21:58:51] [INFO ] Computed and/alt/rep : 180/369/144 causal constraints (skipped 0 transitions) in 14 ms.
[2023-03-14 21:58:51] [INFO ] Added : 54 causal constraints over 11 iterations in 177 ms. Result :sat
Could not prove EG (NOT p0)
Stuttering acceptance computed with spot in 55 ms :[(NOT p0)]
Product exploration explored 100000 steps with 290 reset in 403 ms.
Product exploration explored 100000 steps with 290 reset in 440 ms.
Support contains 7 out of 164 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 164/164 places, 187/187 transitions.
Applied a total of 0 rules in 10 ms. Remains 164 /164 variables (removed 0) and now considering 187/187 (removed 0) transitions.
[2023-03-14 21:58:52] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:52] [INFO ] Invariant cache hit.
[2023-03-14 21:58:52] [INFO ] Implicit Places using invariants in 178 ms returned []
[2023-03-14 21:58:52] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:52] [INFO ] Invariant cache hit.
[2023-03-14 21:58:52] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:52] [INFO ] Implicit Places using invariants and state equation in 250 ms returned []
Implicit Place search using SMT with State Equation took 443 ms to find 0 implicit places.
[2023-03-14 21:58:52] [INFO ] Redundant transitions in 2 ms returned []
[2023-03-14 21:58:52] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:58:52] [INFO ] Invariant cache hit.
[2023-03-14 21:58:52] [INFO ] Dead Transitions using invariants and state equation in 148 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 614 ms. Remains : 164/164 places, 187/187 transitions.
Treatment of property NeoElection-PT-7-LTLCardinality-00 finished in 7556 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(((p0 U X(p0))&&X(X(p0)))))'
Support contains 49 out of 257 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Discarding 30 places :
Symmetric choice reduction at 0 with 30 rule applications. Total rules 30 place count 227 transition count 250
Iterating global reduction 0 with 30 rules applied. Total rules applied 60 place count 227 transition count 250
Applied a total of 60 rules in 8 ms. Remains 227 /257 variables (removed 30) and now considering 250/295 (removed 45) transitions.
[2023-03-14 21:58:53] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
// Phase 1: matrix 214 rows 227 cols
[2023-03-14 21:58:53] [INFO ] Computed 13 place invariants in 2 ms
[2023-03-14 21:58:53] [INFO ] Implicit Places using invariants in 381 ms returned []
[2023-03-14 21:58:53] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:53] [INFO ] Invariant cache hit.
[2023-03-14 21:58:53] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:53] [INFO ] Implicit Places using invariants and state equation in 294 ms returned []
Implicit Place search using SMT with State Equation took 679 ms to find 0 implicit places.
[2023-03-14 21:58:53] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:53] [INFO ] Invariant cache hit.
[2023-03-14 21:58:53] [INFO ] Dead Transitions using invariants and state equation in 217 ms found 0 transitions.
Starting structural reductions in LTL mode, iteration 1 : 227/257 places, 250/295 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 907 ms. Remains : 227/257 places, 250/295 transitions.
Stuttering acceptance computed with spot in 166 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-02 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 1}], [{ cond=(NOT p0), acceptance={} source=1 dest: 2}, { cond=true, acceptance={} source=1 dest: 3}], [{ cond=(NOT p0), acceptance={} source=2 dest: 4}], [{ cond=true, acceptance={} source=3 dest: 2}], [{ cond=true, acceptance={} source=4 dest: 4}]], initial=0, aps=[p0:(LEQ 1 (ADD s178 s179 s180 s181 s182 s183 s184 s185 s186 s187 s188 s189 s190 s191 s192 s193 s194 s195 s196 s197 s198 s199 s200 s201 s202 s203 s204 s205...], nbAcceptance=0, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-sensitive, very-weak, weak, inherently-weak], stateDesc=[null, null, null, null, null][false, false, false, false, false]]
Product exploration explored 100000 steps with 25000 reset in 304 ms.
Product exploration explored 100000 steps with 25000 reset in 265 ms.
Computed a total of 227 stabilizing places and 250 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 227 transition count 250
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X p0), true, (X (X p0)), (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 5 factoid took 224 ms. Reduced automaton from 5 states, 6 edges and 1 AP (stutter sensitive) to 5 states, 5 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 169 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), (X p0), true, (X (X p0)), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Knowledge based reduction with 5 factoid took 235 ms. Reduced automaton from 5 states, 5 edges and 1 AP (stutter sensitive) to 5 states, 5 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 164 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Stuttering acceptance computed with spot in 166 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
[2023-03-14 21:58:55] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:55] [INFO ] Invariant cache hit.
[2023-03-14 21:58:55] [INFO ] [Real]Absence check using 13 positive place invariants in 7 ms returned sat
[2023-03-14 21:58:55] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:56] [INFO ] [Real]Absence check using state equation in 188 ms returned sat
[2023-03-14 21:58:56] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:58:56] [INFO ] [Nat]Absence check using 13 positive place invariants in 4 ms returned sat
[2023-03-14 21:58:56] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:56] [INFO ] [Nat]Absence check using state equation in 187 ms returned sat
[2023-03-14 21:58:56] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:56] [INFO ] [Nat]Added 6 Read/Feed constraints in 6 ms returned sat
[2023-03-14 21:58:56] [INFO ] Deduced a trap composed of 6 places in 131 ms of which 5 ms to minimize.
[2023-03-14 21:58:56] [INFO ] Deduced a trap composed of 7 places in 138 ms of which 1 ms to minimize.
[2023-03-14 21:58:57] [INFO ] Deduced a trap composed of 9 places in 101 ms of which 1 ms to minimize.
[2023-03-14 21:58:57] [INFO ] Deduced a trap composed of 8 places in 113 ms of which 2 ms to minimize.
[2023-03-14 21:58:57] [INFO ] Trap strengthening (SAT) tested/added 5/4 trap constraints in 560 ms
[2023-03-14 21:58:57] [INFO ] Computed and/alt/rep : 236/510/200 causal constraints (skipped 7 transitions) in 23 ms.
[2023-03-14 21:58:57] [INFO ] Added : 26 causal constraints over 6 iterations in 168 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 49 out of 227 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 227/227 places, 250/250 transitions.
Applied a total of 0 rules in 4 ms. Remains 227 /227 variables (removed 0) and now considering 250/250 (removed 0) transitions.
[2023-03-14 21:58:57] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:57] [INFO ] Invariant cache hit.
[2023-03-14 21:58:57] [INFO ] Implicit Places using invariants in 163 ms returned []
[2023-03-14 21:58:57] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:57] [INFO ] Invariant cache hit.
[2023-03-14 21:58:57] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:57] [INFO ] Implicit Places using invariants and state equation in 294 ms returned []
Implicit Place search using SMT with State Equation took 462 ms to find 0 implicit places.
[2023-03-14 21:58:57] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:57] [INFO ] Invariant cache hit.
[2023-03-14 21:58:58] [INFO ] Dead Transitions using invariants and state equation in 206 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 673 ms. Remains : 227/227 places, 250/250 transitions.
Computed a total of 227 stabilizing places and 250 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 227 transition count 250
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), true, (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 3 factoid took 210 ms. Reduced automaton from 5 states, 5 edges and 1 AP (stutter sensitive) to 5 states, 5 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 168 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), true, (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Knowledge based reduction with 3 factoid took 157 ms. Reduced automaton from 5 states, 5 edges and 1 AP (stutter sensitive) to 5 states, 5 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 160 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Stuttering acceptance computed with spot in 180 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
[2023-03-14 21:58:59] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:58:59] [INFO ] Invariant cache hit.
[2023-03-14 21:58:59] [INFO ] [Real]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:58:59] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:59] [INFO ] [Real]Absence check using state equation in 193 ms returned sat
[2023-03-14 21:58:59] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:58:59] [INFO ] [Nat]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:58:59] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:58:59] [INFO ] [Nat]Absence check using state equation in 183 ms returned sat
[2023-03-14 21:58:59] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:58:59] [INFO ] [Nat]Added 6 Read/Feed constraints in 5 ms returned sat
[2023-03-14 21:59:00] [INFO ] Deduced a trap composed of 6 places in 112 ms of which 2 ms to minimize.
[2023-03-14 21:59:00] [INFO ] Deduced a trap composed of 7 places in 117 ms of which 0 ms to minimize.
[2023-03-14 21:59:00] [INFO ] Deduced a trap composed of 9 places in 112 ms of which 0 ms to minimize.
[2023-03-14 21:59:00] [INFO ] Deduced a trap composed of 8 places in 126 ms of which 1 ms to minimize.
[2023-03-14 21:59:00] [INFO ] Trap strengthening (SAT) tested/added 5/4 trap constraints in 555 ms
[2023-03-14 21:59:00] [INFO ] Computed and/alt/rep : 236/510/200 causal constraints (skipped 7 transitions) in 20 ms.
[2023-03-14 21:59:00] [INFO ] Added : 26 causal constraints over 6 iterations in 177 ms. Result :sat
Could not prove EG (NOT p0)
Stuttering acceptance computed with spot in 167 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Product exploration explored 100000 steps with 25000 reset in 169 ms.
Product exploration explored 100000 steps with 25000 reset in 176 ms.
Applying partial POR strategy [true, false, false, false, true]
Stuttering acceptance computed with spot in 160 ms :[(NOT p0), (NOT p0), (NOT p0), (NOT p0), true]
Support contains 49 out of 227 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 227/227 places, 250/250 transitions.
Performed 14 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 14 places in 0 ms
Iterating global reduction 0 with 14 rules applied. Total rules applied 14 place count 227 transition count 250
Discarding 7 places :
Symmetric choice reduction at 0 with 7 rule applications. Total rules 21 place count 220 transition count 243
Deduced a syphon composed of 7 places in 1 ms
Iterating global reduction 0 with 7 rules applied. Total rules applied 28 place count 220 transition count 243
Deduced a syphon composed of 7 places in 0 ms
Applied a total of 28 rules in 41 ms. Remains 220 /227 variables (removed 7) and now considering 243/250 (removed 7) transitions.
[2023-03-14 21:59:01] [INFO ] Redundant transitions in 3 ms returned []
[2023-03-14 21:59:01] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
// Phase 1: matrix 207 rows 220 cols
[2023-03-14 21:59:01] [INFO ] Computed 13 place invariants in 2 ms
[2023-03-14 21:59:01] [INFO ] Dead Transitions using invariants and state equation in 285 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 220/227 places, 243/250 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 337 ms. Remains : 220/227 places, 243/250 transitions.
Support contains 49 out of 227 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 227/227 places, 250/250 transitions.
Applied a total of 0 rules in 3 ms. Remains 227 /227 variables (removed 0) and now considering 250/250 (removed 0) transitions.
[2023-03-14 21:59:01] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
// Phase 1: matrix 214 rows 227 cols
[2023-03-14 21:59:01] [INFO ] Computed 13 place invariants in 2 ms
[2023-03-14 21:59:02] [INFO ] Implicit Places using invariants in 169 ms returned []
[2023-03-14 21:59:02] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:59:02] [INFO ] Invariant cache hit.
[2023-03-14 21:59:02] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:02] [INFO ] Implicit Places using invariants and state equation in 347 ms returned []
Implicit Place search using SMT with State Equation took 519 ms to find 0 implicit places.
[2023-03-14 21:59:02] [INFO ] Flow matrix only has 214 transitions (discarded 36 similar events)
[2023-03-14 21:59:02] [INFO ] Invariant cache hit.
[2023-03-14 21:59:02] [INFO ] Dead Transitions using invariants and state equation in 175 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 698 ms. Remains : 227/227 places, 250/250 transitions.
Treatment of property NeoElection-PT-7-LTLCardinality-02 finished in 9608 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(F(p0)))'
Support contains 168 out of 257 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Discarding 7 places :
Symmetric choice reduction at 0 with 7 rule applications. Total rules 7 place count 250 transition count 288
Iterating global reduction 0 with 7 rules applied. Total rules applied 14 place count 250 transition count 288
Applied a total of 14 rules in 4 ms. Remains 250 /257 variables (removed 7) and now considering 288/295 (removed 7) transitions.
[2023-03-14 21:59:02] [INFO ] Flow matrix only has 252 transitions (discarded 36 similar events)
// Phase 1: matrix 252 rows 250 cols
[2023-03-14 21:59:02] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:02] [INFO ] Implicit Places using invariants in 153 ms returned []
[2023-03-14 21:59:02] [INFO ] Flow matrix only has 252 transitions (discarded 36 similar events)
[2023-03-14 21:59:02] [INFO ] Invariant cache hit.
[2023-03-14 21:59:02] [INFO ] State equation strengthened by 21 read => feed constraints.
[2023-03-14 21:59:03] [INFO ] Implicit Places using invariants and state equation in 260 ms returned []
Implicit Place search using SMT with State Equation took 415 ms to find 0 implicit places.
[2023-03-14 21:59:03] [INFO ] Flow matrix only has 252 transitions (discarded 36 similar events)
[2023-03-14 21:59:03] [INFO ] Invariant cache hit.
[2023-03-14 21:59:03] [INFO ] Dead Transitions using invariants and state equation in 202 ms found 0 transitions.
Starting structural reductions in LTL mode, iteration 1 : 250/257 places, 288/295 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 637 ms. Remains : 250/257 places, 288/295 transitions.
Stuttering acceptance computed with spot in 297 ms :[(NOT p0), (NOT p0)]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-03 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 1}], [{ cond=(NOT p0), acceptance={0} source=1 dest: 1}]], initial=0, aps=[p0:(GT (ADD s19 s20 s21 s22 s23 s24 s25 s26 s27 s28 s29 s30 s31 s32 s33 s34 s35 s36 s37 s38 s39 s40 s41 s42 s43 s44 s45 s46 s47 s48 s49 s50 s51 s52 s53 s5...], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-sensitive, very-weak, weak, inherently-weak], stateDesc=[null, null][false, false]]
Product exploration explored 100000 steps with 19859 reset in 367 ms.
Product exploration explored 100000 steps with 19982 reset in 363 ms.
Computed a total of 250 stabilizing places and 288 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 250 transition count 288
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X (NOT p0)), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 3 factoid took 151 ms. Reduced automaton from 2 states, 2 edges and 1 AP (stutter sensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 33 ms :[(NOT p0)]
Finished random walk after 7 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=7 )
Knowledge obtained : [(NOT p0), (X (NOT p0)), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0)), (F p0)]
Knowledge based reduction with 3 factoid took 167 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 34 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 34 ms :[(NOT p0)]
[2023-03-14 21:59:04] [INFO ] Flow matrix only has 252 transitions (discarded 36 similar events)
[2023-03-14 21:59:04] [INFO ] Invariant cache hit.
[2023-03-14 21:59:05] [INFO ] [Real]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:05] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:05] [INFO ] [Real]Absence check using state equation in 154 ms returned sat
[2023-03-14 21:59:05] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:05] [INFO ] [Nat]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:05] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:05] [INFO ] [Nat]Absence check using state equation in 151 ms returned sat
[2023-03-14 21:59:05] [INFO ] State equation strengthened by 21 read => feed constraints.
[2023-03-14 21:59:05] [INFO ] [Nat]Added 21 Read/Feed constraints in 10 ms returned sat
[2023-03-14 21:59:05] [INFO ] Deduced a trap composed of 6 places in 130 ms of which 1 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 9 places in 134 ms of which 1 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 7 places in 125 ms of which 0 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 9 places in 144 ms of which 1 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 7 places in 151 ms of which 1 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 7 places in 144 ms of which 1 ms to minimize.
[2023-03-14 21:59:06] [INFO ] Deduced a trap composed of 7 places in 153 ms of which 0 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 6 places in 135 ms of which 1 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 7 places in 113 ms of which 1 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 9 places in 100 ms of which 0 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 9 places in 85 ms of which 0 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 10 places in 69 ms of which 0 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 11 places in 51 ms of which 1 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 4 places in 113 ms of which 1 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 7 places in 130 ms of which 0 ms to minimize.
[2023-03-14 21:59:07] [INFO ] Deduced a trap composed of 11 places in 123 ms of which 1 ms to minimize.
[2023-03-14 21:59:08] [INFO ] Deduced a trap composed of 7 places in 136 ms of which 1 ms to minimize.
[2023-03-14 21:59:08] [INFO ] Trap strengthening (SAT) tested/added 18/17 trap constraints in 2379 ms
[2023-03-14 21:59:08] [INFO ] Computed and/alt/rep : 262/656/232 causal constraints (skipped 13 transitions) in 26 ms.
[2023-03-14 21:59:08] [INFO ] Added : 0 causal constraints over 0 iterations in 60 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 168 out of 250 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 250/250 places, 288/288 transitions.
Reduce places removed 7 places and 7 transitions.
Drop transitions removed 7 transitions
Trivial Post-agglo rules discarded 7 transitions
Performed 7 trivial Post agglomeration. Transition count delta: 7
Iterating post reduction 0 with 7 rules applied. Total rules applied 7 place count 243 transition count 274
Reduce places removed 7 places and 0 transitions.
Iterating post reduction 1 with 7 rules applied. Total rules applied 14 place count 236 transition count 274
Performed 7 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 7 Pre rules applied. Total rules applied 14 place count 236 transition count 267
Deduced a syphon composed of 7 places in 0 ms
Reduce places removed 7 places and 0 transitions.
Iterating global reduction 2 with 14 rules applied. Total rules applied 28 place count 229 transition count 267
Applied a total of 28 rules in 29 ms. Remains 229 /250 variables (removed 21) and now considering 267/288 (removed 21) transitions.
[2023-03-14 21:59:08] [INFO ] Flow matrix only has 231 transitions (discarded 36 similar events)
// Phase 1: matrix 231 rows 229 cols
[2023-03-14 21:59:08] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:08] [INFO ] Implicit Places using invariants in 91 ms returned []
[2023-03-14 21:59:08] [INFO ] Flow matrix only has 231 transitions (discarded 36 similar events)
[2023-03-14 21:59:08] [INFO ] Invariant cache hit.
[2023-03-14 21:59:08] [INFO ] State equation strengthened by 189 read => feed constraints.
[2023-03-14 21:59:08] [INFO ] Implicit Places using invariants and state equation in 247 ms returned []
Implicit Place search using SMT with State Equation took 340 ms to find 0 implicit places.
[2023-03-14 21:59:08] [INFO ] Redundant transitions in 2 ms returned []
[2023-03-14 21:59:08] [INFO ] Flow matrix only has 231 transitions (discarded 36 similar events)
[2023-03-14 21:59:08] [INFO ] Invariant cache hit.
[2023-03-14 21:59:08] [INFO ] Dead Transitions using invariants and state equation in 199 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 229/250 places, 267/288 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 576 ms. Remains : 229/250 places, 267/288 transitions.
Computed a total of 229 stabilizing places and 267 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 229 transition count 267
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X p0), (X (X p0)), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : []
Property proved to be true thanks to knowledge :(X p0)
Knowledge based reduction with 4 factoid took 76 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 0 edges and 0 AP (stutter insensitive).
FORMULA NeoElection-PT-7-LTLCardinality-03 TRUE TECHNIQUES KNOWLEDGE
Treatment of property NeoElection-PT-7-LTLCardinality-03 finished in 6396 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(p0))'
Support contains 7 out of 257 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Reduce places removed 7 places and 7 transitions.
Performed 7 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 7 Pre rules applied. Total rules applied 0 place count 250 transition count 281
Deduced a syphon composed of 7 places in 1 ms
Reduce places removed 7 places and 0 transitions.
Iterating global reduction 0 with 14 rules applied. Total rules applied 14 place count 243 transition count 281
Discarding 30 places :
Symmetric choice reduction at 0 with 30 rule applications. Total rules 44 place count 213 transition count 236
Iterating global reduction 0 with 30 rules applied. Total rules applied 74 place count 213 transition count 236
Performed 42 Post agglomeration using F-continuation condition.Transition count delta: 42
Deduced a syphon composed of 42 places in 0 ms
Reduce places removed 42 places and 0 transitions.
Iterating global reduction 0 with 84 rules applied. Total rules applied 158 place count 171 transition count 194
Reduce places removed 7 places and 7 transitions.
Iterating global reduction 0 with 7 rules applied. Total rules applied 165 place count 164 transition count 187
Applied a total of 165 rules in 35 ms. Remains 164 /257 variables (removed 93) and now considering 187/295 (removed 108) transitions.
[2023-03-14 21:59:09] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
// Phase 1: matrix 151 rows 164 cols
[2023-03-14 21:59:09] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:09] [INFO ] Implicit Places using invariants in 180 ms returned []
[2023-03-14 21:59:09] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:59:09] [INFO ] Invariant cache hit.
[2023-03-14 21:59:09] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:09] [INFO ] Implicit Places using invariants and state equation in 298 ms returned []
Implicit Place search using SMT with State Equation took 480 ms to find 0 implicit places.
[2023-03-14 21:59:09] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:09] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:59:09] [INFO ] Invariant cache hit.
[2023-03-14 21:59:09] [INFO ] Dead Transitions using invariants and state equation in 164 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 164/257 places, 187/295 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 686 ms. Remains : 164/257 places, 187/295 transitions.
Stuttering acceptance computed with spot in 36 ms :[(NOT p0)]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-05 automaton TGBA Formula[mat=[[{ cond=(NOT p0), acceptance={0} source=0 dest: 0}]], initial=0, aps=[p0:(LEQ 3 (ADD s150 s151 s152 s153 s154 s155 s156))], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, colored, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-invariant, very-weak, weak, inherently-weak], stateDesc=[null][true]]
Product exploration explored 100000 steps with 23919 reset in 614 ms.
Product exploration explored 100000 steps with 23908 reset in 657 ms.
Computed a total of 164 stabilizing places and 187 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 164 transition count 187
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X (NOT p0)), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 4 factoid took 149 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 35 ms :[(NOT p0)]
Finished random walk after 3 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=3 )
Knowledge obtained : [(NOT p0), (X (NOT p0)), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Knowledge based reduction with 4 factoid took 167 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 36 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 36 ms :[(NOT p0)]
[2023-03-14 21:59:11] [INFO ] Flow matrix only has 151 transitions (discarded 36 similar events)
[2023-03-14 21:59:11] [INFO ] Invariant cache hit.
Proved EG (NOT p0)
Knowledge obtained : [(NOT p0), (X (NOT p0)), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0), (G (NOT p0))]
Property proved to be false thanks to negative knowledge :(G (NOT p0))
Knowledge based reduction with 4 factoid took 93 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 0 AP (stutter insensitive).
FORMULA NeoElection-PT-7-LTLCardinality-05 FALSE TECHNIQUES KNOWLEDGE
Treatment of property NeoElection-PT-7-LTLCardinality-05 finished in 2786 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X((F(p0)&&F(G(!p0))))))'
Support contains 7 out of 257 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Discarding 37 places :
Symmetric choice reduction at 0 with 37 rule applications. Total rules 37 place count 220 transition count 243
Iterating global reduction 0 with 37 rules applied. Total rules applied 74 place count 220 transition count 243
Applied a total of 74 rules in 5 ms. Remains 220 /257 variables (removed 37) and now considering 243/295 (removed 52) transitions.
[2023-03-14 21:59:11] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
// Phase 1: matrix 207 rows 220 cols
[2023-03-14 21:59:11] [INFO ] Computed 13 place invariants in 2 ms
[2023-03-14 21:59:11] [INFO ] Implicit Places using invariants in 189 ms returned []
[2023-03-14 21:59:11] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:11] [INFO ] Invariant cache hit.
[2023-03-14 21:59:12] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:12] [INFO ] Implicit Places using invariants and state equation in 331 ms returned []
Implicit Place search using SMT with State Equation took 522 ms to find 0 implicit places.
[2023-03-14 21:59:12] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:12] [INFO ] Invariant cache hit.
[2023-03-14 21:59:12] [INFO ] Dead Transitions using invariants and state equation in 193 ms found 0 transitions.
Starting structural reductions in LTL mode, iteration 1 : 220/257 places, 243/295 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 721 ms. Remains : 220/257 places, 243/295 transitions.
Stuttering acceptance computed with spot in 190 ms :[true, true, true, (NOT p0), p0]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-07 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 1}], [{ cond=true, acceptance={} source=1 dest: 2}], [{ cond=(NOT p0), acceptance={} source=2 dest: 3}, { cond=true, acceptance={} source=2 dest: 4}], [{ cond=(NOT p0), acceptance={0} source=3 dest: 3}], [{ cond=(NOT p0), acceptance={} source=4 dest: 4}, { cond=p0, acceptance={0} source=4 dest: 4}]], initial=0, aps=[p0:(GT (ADD s171 s172 s173 s174 s175 s176 s177) 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-sensitive], stateDesc=[null, null, null, null, null][false, false, false, false, false]]
Product exploration explored 100000 steps with 365 reset in 455 ms.
Product exploration explored 100000 steps with 330 reset in 431 ms.
Computed a total of 220 stabilizing places and 243 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 220 transition count 243
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), true, (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 4 factoid took 237 ms. Reduced automaton from 5 states, 7 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 107 ms :[(NOT p0), (NOT p0), (NOT p0)]
Finished random walk after 26 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=26 )
Knowledge obtained : [(NOT p0), true, (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Knowledge based reduction with 4 factoid took 183 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 114 ms :[(NOT p0), (NOT p0), (NOT p0)]
Stuttering acceptance computed with spot in 107 ms :[(NOT p0), (NOT p0), (NOT p0)]
[2023-03-14 21:59:14] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:14] [INFO ] Invariant cache hit.
[2023-03-14 21:59:14] [INFO ] [Real]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:14] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:14] [INFO ] [Real]Absence check using state equation in 162 ms returned sat
[2023-03-14 21:59:14] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:15] [INFO ] [Nat]Absence check using 13 positive place invariants in 7 ms returned sat
[2023-03-14 21:59:15] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:15] [INFO ] [Nat]Absence check using state equation in 161 ms returned sat
[2023-03-14 21:59:15] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:15] [INFO ] [Nat]Added 6 Read/Feed constraints in 4 ms returned sat
[2023-03-14 21:59:15] [INFO ] Computed and/alt/rep : 229/496/193 causal constraints (skipped 7 transitions) in 18 ms.
[2023-03-14 21:59:15] [INFO ] Added : 111 causal constraints over 23 iterations in 526 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 7 out of 220 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 220/220 places, 243/243 transitions.
Applied a total of 0 rules in 2 ms. Remains 220 /220 variables (removed 0) and now considering 243/243 (removed 0) transitions.
[2023-03-14 21:59:15] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:15] [INFO ] Invariant cache hit.
[2023-03-14 21:59:15] [INFO ] Implicit Places using invariants in 177 ms returned []
[2023-03-14 21:59:15] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:15] [INFO ] Invariant cache hit.
[2023-03-14 21:59:16] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:16] [INFO ] Implicit Places using invariants and state equation in 333 ms returned []
Implicit Place search using SMT with State Equation took 515 ms to find 0 implicit places.
[2023-03-14 21:59:16] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:16] [INFO ] Invariant cache hit.
[2023-03-14 21:59:16] [INFO ] Dead Transitions using invariants and state equation in 190 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 709 ms. Remains : 220/220 places, 243/243 transitions.
Computed a total of 220 stabilizing places and 243 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 220 transition count 243
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : []
Knowledge based reduction with 3 factoid took 127 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 109 ms :[(NOT p0), (NOT p0), (NOT p0)]
Finished random walk after 30 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=30 )
Knowledge obtained : [(NOT p0), (X (X (NOT p0))), (F (G (NOT p0)))]
False Knowledge obtained : [(F p0)]
Knowledge based reduction with 3 factoid took 154 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 105 ms :[(NOT p0), (NOT p0), (NOT p0)]
Stuttering acceptance computed with spot in 105 ms :[(NOT p0), (NOT p0), (NOT p0)]
[2023-03-14 21:59:17] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:17] [INFO ] Invariant cache hit.
[2023-03-14 21:59:17] [INFO ] [Real]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:17] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:17] [INFO ] [Real]Absence check using state equation in 158 ms returned sat
[2023-03-14 21:59:17] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:17] [INFO ] [Nat]Absence check using 13 positive place invariants in 5 ms returned sat
[2023-03-14 21:59:17] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:17] [INFO ] [Nat]Absence check using state equation in 159 ms returned sat
[2023-03-14 21:59:17] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:17] [INFO ] [Nat]Added 6 Read/Feed constraints in 4 ms returned sat
[2023-03-14 21:59:18] [INFO ] Computed and/alt/rep : 229/496/193 causal constraints (skipped 7 transitions) in 18 ms.
[2023-03-14 21:59:18] [INFO ] Added : 111 causal constraints over 23 iterations in 494 ms. Result :sat
Could not prove EG (NOT p0)
Stuttering acceptance computed with spot in 108 ms :[(NOT p0), (NOT p0), (NOT p0)]
Product exploration explored 100000 steps with 2987 reset in 186 ms.
Product exploration explored 100000 steps with 2985 reset in 220 ms.
Applying partial POR strategy [true, false, false]
Stuttering acceptance computed with spot in 106 ms :[(NOT p0), (NOT p0), (NOT p0)]
Support contains 7 out of 220 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 220/220 places, 243/243 transitions.
Performed 7 Post agglomeration using F-continuation condition.Transition count delta: 0
Iterating post reduction 0 with 7 rules applied. Total rules applied 7 place count 220 transition count 243
Performed 35 Post agglomeration using F-continuation condition.Transition count delta: 0
Deduced a syphon composed of 42 places in 0 ms
Iterating global reduction 1 with 35 rules applied. Total rules applied 42 place count 220 transition count 243
Deduced a syphon composed of 42 places in 0 ms
Applied a total of 42 rules in 18 ms. Remains 220 /220 variables (removed 0) and now considering 243/243 (removed 0) transitions.
[2023-03-14 21:59:19] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:19] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
// Phase 1: matrix 207 rows 220 cols
[2023-03-14 21:59:19] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:19] [INFO ] Dead Transitions using invariants and state equation in 200 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 220/220 places, 243/243 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 227 ms. Remains : 220/220 places, 243/243 transitions.
Support contains 7 out of 220 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 220/220 places, 243/243 transitions.
Applied a total of 0 rules in 2 ms. Remains 220 /220 variables (removed 0) and now considering 243/243 (removed 0) transitions.
[2023-03-14 21:59:19] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
// Phase 1: matrix 207 rows 220 cols
[2023-03-14 21:59:19] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:19] [INFO ] Implicit Places using invariants in 199 ms returned []
[2023-03-14 21:59:19] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:19] [INFO ] Invariant cache hit.
[2023-03-14 21:59:19] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:20] [INFO ] Implicit Places using invariants and state equation in 336 ms returned []
Implicit Place search using SMT with State Equation took 537 ms to find 0 implicit places.
[2023-03-14 21:59:20] [INFO ] Flow matrix only has 207 transitions (discarded 36 similar events)
[2023-03-14 21:59:20] [INFO ] Invariant cache hit.
[2023-03-14 21:59:20] [INFO ] Dead Transitions using invariants and state equation in 190 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 731 ms. Remains : 220/220 places, 243/243 transitions.
Treatment of property NeoElection-PT-7-LTLCardinality-07 finished in 8487 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(p0))'
Support contains 1 out of 257 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Reduce places removed 7 places and 7 transitions.
Performed 7 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 7 Pre rules applied. Total rules applied 0 place count 250 transition count 281
Deduced a syphon composed of 7 places in 0 ms
Reduce places removed 7 places and 0 transitions.
Iterating global reduction 0 with 14 rules applied. Total rules applied 14 place count 243 transition count 281
Discarding 37 places :
Symmetric choice reduction at 0 with 37 rule applications. Total rules 51 place count 206 transition count 229
Iterating global reduction 0 with 37 rules applied. Total rules applied 88 place count 206 transition count 229
Performed 6 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 6 Pre rules applied. Total rules applied 88 place count 206 transition count 223
Deduced a syphon composed of 6 places in 0 ms
Reduce places removed 6 places and 0 transitions.
Iterating global reduction 0 with 12 rules applied. Total rules applied 100 place count 200 transition count 223
Performed 35 Post agglomeration using F-continuation condition.Transition count delta: 35
Deduced a syphon composed of 35 places in 0 ms
Reduce places removed 35 places and 0 transitions.
Iterating global reduction 0 with 70 rules applied. Total rules applied 170 place count 165 transition count 188
Reduce places removed 7 places and 7 transitions.
Iterating global reduction 0 with 7 rules applied. Total rules applied 177 place count 158 transition count 181
Reduce places removed 6 places and 0 transitions.
Graph (complete) has 338 edges and 152 vertex of which 117 are kept as prefixes of interest. Removing 35 places using SCC suffix rule.3 ms
Discarding 35 places :
Also discarding 35 output transitions
Drop transitions removed 35 transitions
Drop transitions removed 20 transitions
Trivial Post-agglo rules discarded 20 transitions
Performed 20 trivial Post agglomeration. Transition count delta: 20
Iterating post reduction 0 with 27 rules applied. Total rules applied 204 place count 117 transition count 126
Reduce places removed 20 places and 0 transitions.
Iterating post reduction 1 with 20 rules applied. Total rules applied 224 place count 97 transition count 126
Performed 9 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 9 Pre rules applied. Total rules applied 224 place count 97 transition count 117
Deduced a syphon composed of 9 places in 0 ms
Reduce places removed 9 places and 0 transitions.
Iterating global reduction 2 with 18 rules applied. Total rules applied 242 place count 88 transition count 117
Discarding 28 places :
Symmetric choice reduction at 2 with 28 rule applications. Total rules 270 place count 60 transition count 79
Iterating global reduction 2 with 28 rules applied. Total rules applied 298 place count 60 transition count 79
Performed 3 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 3 Pre rules applied. Total rules applied 298 place count 60 transition count 76
Deduced a syphon composed of 3 places in 0 ms
Reduce places removed 3 places and 0 transitions.
Iterating global reduction 2 with 6 rules applied. Total rules applied 304 place count 57 transition count 76
Discarding 7 places :
Symmetric choice reduction at 2 with 7 rule applications. Total rules 311 place count 50 transition count 66
Iterating global reduction 2 with 7 rules applied. Total rules applied 318 place count 50 transition count 66
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 2 with 4 rules applied. Total rules applied 322 place count 48 transition count 64
Applied a total of 322 rules in 43 ms. Remains 48 /257 variables (removed 209) and now considering 64/295 (removed 231) transitions.
[2023-03-14 21:59:20] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
// Phase 1: matrix 41 rows 48 cols
[2023-03-14 21:59:20] [INFO ] Computed 7 place invariants in 1 ms
[2023-03-14 21:59:20] [INFO ] Implicit Places using invariants in 60 ms returned []
[2023-03-14 21:59:20] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:20] [INFO ] Invariant cache hit.
[2023-03-14 21:59:20] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:20] [INFO ] Implicit Places using invariants and state equation in 99 ms returned []
Implicit Place search using SMT with State Equation took 170 ms to find 0 implicit places.
[2023-03-14 21:59:20] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:20] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:20] [INFO ] Invariant cache hit.
[2023-03-14 21:59:20] [INFO ] Dead Transitions using invariants and state equation in 50 ms found 0 transitions.
Starting structural reductions in SI_LTL mode, iteration 1 : 48/257 places, 64/295 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 270 ms. Remains : 48/257 places, 64/295 transitions.
Stuttering acceptance computed with spot in 35 ms :[(NOT p0)]
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-13 automaton TGBA Formula[mat=[[{ cond=(NOT p0), acceptance={0} source=0 dest: 0}]], initial=0, aps=[p0:(NEQ s46 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, colored, deterministic, no-univ-branch, unambiguous, semi-deterministic, stutter-invariant, very-weak, weak, inherently-weak], stateDesc=[null][true]]
Product exploration explored 100000 steps with 5791 reset in 287 ms.
Product exploration explored 100000 steps with 5760 reset in 281 ms.
Computed a total of 48 stabilizing places and 64 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 48 transition count 64
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (NOT p0)), (X p0), (X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 2 factoid took 163 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 35 ms :[(NOT p0)]
Finished random walk after 7 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=7 )
Knowledge obtained : [(NOT p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (NOT p0)), (X p0), (X (X (NOT p0))), (X (X p0)), (F p0)]
Knowledge based reduction with 2 factoid took 184 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 36 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 37 ms :[(NOT p0)]
[2023-03-14 21:59:21] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:21] [INFO ] Invariant cache hit.
[2023-03-14 21:59:21] [INFO ] [Real]Absence check using 7 positive place invariants in 2 ms returned sat
[2023-03-14 21:59:21] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:21] [INFO ] [Real]Absence check using state equation in 27 ms returned sat
[2023-03-14 21:59:21] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:21] [INFO ] [Nat]Absence check using 7 positive place invariants in 2 ms returned sat
[2023-03-14 21:59:21] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:21] [INFO ] [Nat]Absence check using state equation in 24 ms returned sat
[2023-03-14 21:59:21] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:21] [INFO ] [Nat]Added 6 Read/Feed constraints in 2 ms returned sat
[2023-03-14 21:59:21] [INFO ] Computed and/alt/rep : 18/30/15 causal constraints (skipped 0 transitions) in 4 ms.
[2023-03-14 21:59:21] [INFO ] Added : 5 causal constraints over 1 iterations in 19 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 1 out of 48 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 48/48 places, 64/64 transitions.
Applied a total of 0 rules in 3 ms. Remains 48 /48 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2023-03-14 21:59:21] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:21] [INFO ] Invariant cache hit.
[2023-03-14 21:59:21] [INFO ] Implicit Places using invariants in 56 ms returned []
[2023-03-14 21:59:21] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:21] [INFO ] Invariant cache hit.
[2023-03-14 21:59:21] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:21] [INFO ] Implicit Places using invariants and state equation in 71 ms returned []
Implicit Place search using SMT with State Equation took 127 ms to find 0 implicit places.
[2023-03-14 21:59:21] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:21] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:21] [INFO ] Invariant cache hit.
[2023-03-14 21:59:22] [INFO ] Dead Transitions using invariants and state equation in 51 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 190 ms. Remains : 48/48 places, 64/64 transitions.
Computed a total of 48 stabilizing places and 64 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 48 transition count 64
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (NOT p0)), (X p0), (X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 2 factoid took 166 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 36 ms :[(NOT p0)]
Finished random walk after 42 steps, including 0 resets, run visited all 1 properties in 2 ms. (steps per millisecond=21 )
Knowledge obtained : [(NOT p0), (F (OR (G p0) (G (NOT p0))))]
False Knowledge obtained : [(X (NOT p0)), (X p0), (X (X (NOT p0))), (X (X p0)), (F p0)]
Knowledge based reduction with 2 factoid took 185 ms. Reduced automaton from 1 states, 1 edges and 1 AP (stutter insensitive) to 1 states, 1 edges and 1 AP (stutter insensitive).
Stuttering acceptance computed with spot in 39 ms :[(NOT p0)]
Stuttering acceptance computed with spot in 35 ms :[(NOT p0)]
[2023-03-14 21:59:22] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:22] [INFO ] Invariant cache hit.
[2023-03-14 21:59:22] [INFO ] [Real]Absence check using 7 positive place invariants in 2 ms returned sat
[2023-03-14 21:59:22] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:22] [INFO ] [Real]Absence check using state equation in 22 ms returned sat
[2023-03-14 21:59:22] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:22] [INFO ] [Nat]Absence check using 7 positive place invariants in 3 ms returned sat
[2023-03-14 21:59:22] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:22] [INFO ] [Nat]Absence check using state equation in 24 ms returned sat
[2023-03-14 21:59:22] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:22] [INFO ] [Nat]Added 6 Read/Feed constraints in 2 ms returned sat
[2023-03-14 21:59:22] [INFO ] Computed and/alt/rep : 18/30/15 causal constraints (skipped 0 transitions) in 3 ms.
[2023-03-14 21:59:22] [INFO ] Added : 5 causal constraints over 1 iterations in 16 ms. Result :sat
Could not prove EG (NOT p0)
Stuttering acceptance computed with spot in 35 ms :[(NOT p0)]
Product exploration explored 100000 steps with 5755 reset in 254 ms.
Product exploration explored 100000 steps with 5693 reset in 285 ms.
Support contains 1 out of 48 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 48/48 places, 64/64 transitions.
Applied a total of 0 rules in 2 ms. Remains 48 /48 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2023-03-14 21:59:23] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:23] [INFO ] Invariant cache hit.
[2023-03-14 21:59:23] [INFO ] Implicit Places using invariants in 61 ms returned []
[2023-03-14 21:59:23] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:23] [INFO ] Invariant cache hit.
[2023-03-14 21:59:23] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:23] [INFO ] Implicit Places using invariants and state equation in 68 ms returned []
Implicit Place search using SMT with State Equation took 131 ms to find 0 implicit places.
[2023-03-14 21:59:23] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:23] [INFO ] Flow matrix only has 41 transitions (discarded 23 similar events)
[2023-03-14 21:59:23] [INFO ] Invariant cache hit.
[2023-03-14 21:59:23] [INFO ] Dead Transitions using invariants and state equation in 50 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 191 ms. Remains : 48/48 places, 64/64 transitions.
Treatment of property NeoElection-PT-7-LTLCardinality-13 finished in 3259 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(G(p0)))'
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(((p0 U X(p0))&&X(X(p0)))))'
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(X(X((F(p0)&&F(G(!p0))))))'
Found a Shortening insensitive property : NeoElection-PT-7-LTLCardinality-07
Stuttering acceptance computed with spot in 181 ms :[true, true, true, (NOT p0), p0]
Support contains 7 out of 257 places. Attempting structural reductions.
Starting structural reductions in LI_LTL mode, iteration 0 : 257/257 places, 295/295 transitions.
Reduce places removed 7 places and 7 transitions.
Discarding 37 places :
Symmetric choice reduction at 0 with 37 rule applications. Total rules 37 place count 213 transition count 236
Iterating global reduction 0 with 37 rules applied. Total rules applied 74 place count 213 transition count 236
Performed 35 Post agglomeration using F-continuation condition.Transition count delta: 35
Deduced a syphon composed of 35 places in 0 ms
Reduce places removed 35 places and 0 transitions.
Iterating global reduction 0 with 70 rules applied. Total rules applied 144 place count 178 transition count 201
Reduce places removed 7 places and 7 transitions.
Iterating global reduction 0 with 7 rules applied. Total rules applied 151 place count 171 transition count 194
Applied a total of 151 rules in 37 ms. Remains 171 /257 variables (removed 86) and now considering 194/295 (removed 101) transitions.
[2023-03-14 21:59:24] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
// Phase 1: matrix 158 rows 171 cols
[2023-03-14 21:59:24] [INFO ] Computed 13 place invariants in 1 ms
[2023-03-14 21:59:24] [INFO ] Implicit Places using invariants in 141 ms returned []
[2023-03-14 21:59:24] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:24] [INFO ] Invariant cache hit.
[2023-03-14 21:59:24] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:24] [INFO ] Implicit Places using invariants and state equation in 265 ms returned []
Implicit Place search using SMT with State Equation took 421 ms to find 0 implicit places.
[2023-03-14 21:59:24] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:24] [INFO ] Invariant cache hit.
[2023-03-14 21:59:24] [INFO ] Dead Transitions using invariants and state equation in 145 ms found 0 transitions.
Starting structural reductions in LI_LTL mode, iteration 1 : 171/257 places, 194/295 transitions.
Finished structural reductions in LI_LTL mode , in 1 iterations and 604 ms. Remains : 171/257 places, 194/295 transitions.
Running random walk in product with property : NeoElection-PT-7-LTLCardinality-07 automaton TGBA Formula[mat=[[{ cond=true, acceptance={} source=0 dest: 1}], [{ cond=true, acceptance={} source=1 dest: 2}], [{ cond=(NOT p0), acceptance={} source=2 dest: 3}, { cond=true, acceptance={} source=2 dest: 4}], [{ cond=(NOT p0), acceptance={0} source=3 dest: 3}], [{ cond=(NOT p0), acceptance={} source=4 dest: 4}, { cond=p0, acceptance={0} source=4 dest: 4}]], initial=0, aps=[p0:(GT (ADD s164 s165 s166 s167 s168 s169 s170) 0)], nbAcceptance=1, properties=[trans-labels, explicit-labels, trans-acc, no-univ-branch, stutter-sensitive, cl-invariant], stateDesc=[null, null, null, null, null][false, false, false, false, false]]
Product exploration explored 100000 steps with 210 reset in 331 ms.
Product exploration explored 100000 steps with 203 reset in 367 ms.
Computed a total of 171 stabilizing places and 194 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 171 transition count 194
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), true, (F (G (NOT p0)))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 3 factoid took 177 ms. Reduced automaton from 5 states, 7 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 107 ms :[(NOT p0), (NOT p0), (NOT p0)]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), true, (F (G (NOT p0)))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0)), (F p0)]
Knowledge based reduction with 3 factoid took 188 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 105 ms :[(NOT p0), (NOT p0), (NOT p0)]
Stuttering acceptance computed with spot in 106 ms :[(NOT p0), (NOT p0), (NOT p0)]
[2023-03-14 21:59:26] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:26] [INFO ] Invariant cache hit.
[2023-03-14 21:59:26] [INFO ] [Real]Absence check using 13 positive place invariants in 7 ms returned sat
[2023-03-14 21:59:26] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:26] [INFO ] [Real]Absence check using state equation in 108 ms returned sat
[2023-03-14 21:59:26] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:26] [INFO ] [Nat]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:26] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:26] [INFO ] [Nat]Absence check using state equation in 118 ms returned sat
[2023-03-14 21:59:26] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:26] [INFO ] [Nat]Added 6 Read/Feed constraints in 3 ms returned sat
[2023-03-14 21:59:26] [INFO ] Computed and/alt/rep : 187/376/151 causal constraints (skipped 0 transitions) in 14 ms.
[2023-03-14 21:59:26] [INFO ] Added : 46 causal constraints over 10 iterations in 163 ms. Result :sat
Could not prove EG (NOT p0)
Support contains 7 out of 171 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 171/171 places, 194/194 transitions.
Applied a total of 0 rules in 2 ms. Remains 171 /171 variables (removed 0) and now considering 194/194 (removed 0) transitions.
[2023-03-14 21:59:26] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:26] [INFO ] Invariant cache hit.
[2023-03-14 21:59:27] [INFO ] Implicit Places using invariants in 163 ms returned []
[2023-03-14 21:59:27] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:27] [INFO ] Invariant cache hit.
[2023-03-14 21:59:27] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:27] [INFO ] Implicit Places using invariants and state equation in 304 ms returned []
Implicit Place search using SMT with State Equation took 469 ms to find 0 implicit places.
[2023-03-14 21:59:27] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:27] [INFO ] Invariant cache hit.
[2023-03-14 21:59:27] [INFO ] Dead Transitions using invariants and state equation in 151 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 622 ms. Remains : 171/171 places, 194/194 transitions.
Computed a total of 171 stabilizing places and 194 stable transitions
Complete graph has no SCC; deadlocks are unavoidable. place count 171 transition count 194
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge (and all enablings converge to false).
Detected that all paths lead to deadlock. Applying this knowledge to assert that all AP eventually converge : F ( (Ga|G!a) & (Gb|G!b)...)
Knowledge obtained : [(NOT p0), (F (G (NOT p0)))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0))]
Knowledge based reduction with 2 factoid took 135 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 106 ms :[(NOT p0), (NOT p0), (NOT p0)]
Finished random walk after 1 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=1 )
Knowledge obtained : [(NOT p0), (F (G (NOT p0)))]
False Knowledge obtained : [(X (X (NOT p0))), (X (X p0)), (F p0)]
Knowledge based reduction with 2 factoid took 153 ms. Reduced automaton from 3 states, 3 edges and 1 AP (stutter sensitive) to 3 states, 3 edges and 1 AP (stutter sensitive).
Stuttering acceptance computed with spot in 109 ms :[(NOT p0), (NOT p0), (NOT p0)]
Stuttering acceptance computed with spot in 106 ms :[(NOT p0), (NOT p0), (NOT p0)]
[2023-03-14 21:59:28] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:28] [INFO ] Invariant cache hit.
[2023-03-14 21:59:28] [INFO ] [Real]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:28] [INFO ] [Real]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:28] [INFO ] [Real]Absence check using state equation in 109 ms returned sat
[2023-03-14 21:59:28] [INFO ] Solution in real domain found non-integer solution.
[2023-03-14 21:59:28] [INFO ] [Nat]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-14 21:59:28] [INFO ] [Nat]Adding state equation constraints to refine reachable states.
[2023-03-14 21:59:28] [INFO ] [Nat]Absence check using state equation in 119 ms returned sat
[2023-03-14 21:59:28] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:28] [INFO ] [Nat]Added 6 Read/Feed constraints in 3 ms returned sat
[2023-03-14 21:59:28] [INFO ] Computed and/alt/rep : 187/376/151 causal constraints (skipped 0 transitions) in 16 ms.
[2023-03-14 21:59:28] [INFO ] Added : 46 causal constraints over 10 iterations in 166 ms. Result :sat
Could not prove EG (NOT p0)
Stuttering acceptance computed with spot in 108 ms :[(NOT p0), (NOT p0), (NOT p0)]
Product exploration explored 100000 steps with 31136 reset in 220 ms.
Product exploration explored 100000 steps with 31112 reset in 261 ms.
Applying partial POR strategy [true, false, false]
Stuttering acceptance computed with spot in 210 ms :[(NOT p0), (NOT p0), (NOT p0)]
Support contains 7 out of 171 places. Attempting structural reductions.
Starting structural reductions in SI_LTL mode, iteration 0 : 171/171 places, 194/194 transitions.
Applied a total of 0 rules in 6 ms. Remains 171 /171 variables (removed 0) and now considering 194/194 (removed 0) transitions.
[2023-03-14 21:59:29] [INFO ] Redundant transitions in 0 ms returned []
[2023-03-14 21:59:29] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:29] [INFO ] Invariant cache hit.
[2023-03-14 21:59:29] [INFO ] Dead Transitions using invariants and state equation in 142 ms found 0 transitions.
Finished structural reductions in SI_LTL mode , in 1 iterations and 156 ms. Remains : 171/171 places, 194/194 transitions.
Support contains 7 out of 171 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 171/171 places, 194/194 transitions.
Applied a total of 0 rules in 2 ms. Remains 171 /171 variables (removed 0) and now considering 194/194 (removed 0) transitions.
[2023-03-14 21:59:29] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:29] [INFO ] Invariant cache hit.
[2023-03-14 21:59:30] [INFO ] Implicit Places using invariants in 162 ms returned []
[2023-03-14 21:59:30] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:30] [INFO ] Invariant cache hit.
[2023-03-14 21:59:30] [INFO ] State equation strengthened by 6 read => feed constraints.
[2023-03-14 21:59:30] [INFO ] Implicit Places using invariants and state equation in 301 ms returned []
Implicit Place search using SMT with State Equation took 467 ms to find 0 implicit places.
[2023-03-14 21:59:30] [INFO ] Flow matrix only has 158 transitions (discarded 36 similar events)
[2023-03-14 21:59:30] [INFO ] Invariant cache hit.
[2023-03-14 21:59:30] [INFO ] Dead Transitions using invariants and state equation in 152 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 622 ms. Remains : 171/171 places, 194/194 transitions.
Treatment of property NeoElection-PT-7-LTLCardinality-07 finished in 6910 ms.
Running Spot : '/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.ltl.spot.binaries_1.0.0.202303021504/bin/ltl2tgba-linux64' '--check=stutter' '--hoaf=tv' '-f' '!(F(p0))'
[2023-03-14 21:59:30] [INFO ] Flatten gal took : 42 ms
[2023-03-14 21:59:30] [INFO ] Export to MCC of 4 properties in file /home/mcc/execution/LTLCardinality.sr.xml took 3 ms.
[2023-03-14 21:59:30] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 257 places, 295 transitions and 1247 arcs took 7 ms.
Total runtime 49345 ms.
There are residual formulas that ITS could not solve within timeout
pnml2lts-mc model.pnml -s80% --procs=4 --ltl=/tmp/1807/ltl_0_ --buchi-type=spotba --strategy=ufscc --ltl-semantics=spin --state=tree
pnml2lts-mc model.pnml -s80% --procs=4 --ltl=/tmp/1807/ltl_1_ --buchi-type=spotba --strategy=ufscc --ltl-semantics=spin --state=tree
TIME LIMIT: Killed by timeout after 892 seconds
MemTotal: 16393232 kB
MemFree: 16031684 kB
After kill :
MemTotal: 16393232 kB
MemFree: 16079900 kB
pnml2lts-mc model.pnml -s80% --procs=4 --ltl=/tmp/1807/ltl_2_ --buchi-type=spotba --strategy=ufscc --ltl-semantics=spin --state=tree
pnml2lts-mc model.pnml -s80% --procs=4 --ltl=/tmp/1807/ltl_3_ --buchi-type=spotba --strategy=ufscc --ltl-semantics=spin --state=tree
Could not compute solution for formula : NeoElection-PT-7-LTLCardinality-00
Could not compute solution for formula : NeoElection-PT-7-LTLCardinality-02
Could not compute solution for formula : NeoElection-PT-7-LTLCardinality-07
Could not compute solution for formula : NeoElection-PT-7-LTLCardinality-13

BK_STOP 1678832065973

--------------------
content from stderr:

+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination LTLCardinality -timeout 360 -rebuildPNML
mcc2023
ltl formula name NeoElection-PT-7-LTLCardinality-00
ltl formula formula --ltl=/tmp/1807/ltl_0_
pnml2lts-mc: =============================================================================
pnml2lts-mc: Runtime environment could only preallocate 15 GB while requesting 240 GB.
pnml2lts-mc: Configure your system limits to exploit all memory.
pnml2lts-mc: =============================================================================
pnml2lts-mc( 0/ 4): Loading model from model.pnml
pnml2lts-mc( 0/ 4): Edge label is id
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): Petri net has 257 places, 295 transitions and 1247 arcs
pnml2lts-mc( 0/ 4): Petri net Petri analyzed
pnml2lts-mc( 0/ 4): There are no safe places
pnml2lts-mc( 0/ 4): Loading Petri net took 0.080 real 0.010 user 0.010 sys
pnml2lts-mc( 0/ 4): LTL layer: formula: /tmp/1807/ltl_0_
pnml2lts-mc( 3/ 4): LTL layer: formula: /tmp/1807/ltl_0_
pnml2lts-mc( 2/ 4): LTL layer: formula: /tmp/1807/ltl_0_
pnml2lts-mc( 1/ 4): LTL layer: formula: /tmp/1807/ltl_0_
pnml2lts-mc( 0/ 4): buchi has 2 states
pnml2lts-mc( 0/ 4), ** error **: area memory exhausted
ltl formula name NeoElection-PT-7-LTLCardinality-02
ltl formula formula --ltl=/tmp/1807/ltl_1_
pnml2lts-mc: =============================================================================
pnml2lts-mc: Runtime environment could only preallocate 15 GB while requesting 240 GB.
pnml2lts-mc: Configure your system limits to exploit all memory.
pnml2lts-mc: =============================================================================
pnml2lts-mc( 0/ 4): Loading model from model.pnml
pnml2lts-mc( 0/ 4): Edge label is id
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): Petri net has 257 places, 295 transitions and 1247 arcs
pnml2lts-mc( 0/ 4): Petri net Petri analyzed
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): There are no safe places
pnml2lts-mc( 0/ 4): Loading Petri net took 0.060 real 0.000 user 0.020 sys
pnml2lts-mc( 1/ 4): LTL layer: formula: /tmp/1807/ltl_1_
pnml2lts-mc( 0/ 4): LTL layer: formula: /tmp/1807/ltl_1_
pnml2lts-mc( 2/ 4): LTL layer: formula: /tmp/1807/ltl_1_
pnml2lts-mc( 3/ 4): LTL layer: formula: /tmp/1807/ltl_1_
Killing (15) : 1819 1820 1821 1822 1823
Killing (9) : 1819 1820 1821 1822 1823
ltl formula name NeoElection-PT-7-LTLCardinality-07
ltl formula formula --ltl=/tmp/1807/ltl_2_
pnml2lts-mc: =============================================================================
pnml2lts-mc: Runtime environment could only preallocate 15 GB while requesting 240 GB.
pnml2lts-mc: Configure your system limits to exploit all memory.
pnml2lts-mc: =============================================================================
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): Loading model from model.pnml
pnml2lts-mc( 0/ 4): Edge label is id
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): Petri net has 257 places, 295 transitions and 1247 arcs
pnml2lts-mc( 0/ 4): Petri net Petri analyzed
pnml2lts-mc( 0/ 4): There are no safe places
pnml2lts-mc( 0/ 4): Loading Petri net took 0.050 real 0.000 user 0.020 sys
pnml2lts-mc( 2/ 4): LTL layer: formula: /tmp/1807/ltl_2_
pnml2lts-mc( 1/ 4): LTL layer: formula: /tmp/1807/ltl_2_
pnml2lts-mc( 0/ 4): LTL layer: formula: /tmp/1807/ltl_2_
pnml2lts-mc( 3/ 4): LTL layer: formula: /tmp/1807/ltl_2_
pnml2lts-mc( 0/ 4): buchi has 6 states
pnml2lts-mc( 0/ 4), ** error **: area memory exhausted
ltl formula name NeoElection-PT-7-LTLCardinality-13
ltl formula formula --ltl=/tmp/1807/ltl_3_
pnml2lts-mc: =============================================================================
pnml2lts-mc: Runtime environment could only preallocate 15 GB while requesting 240 GB.
pnml2lts-mc: Configure your system limits to exploit all memory.
pnml2lts-mc: =============================================================================
pnml2lts-mc( 0/ 4): Loading model from model.pnml
pnml2lts-mc( 0/ 4): Edge label is id
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
Warning: program compiled against libxml 210 using older 209
pnml2lts-mc( 0/ 4): Petri net has 257 places, 295 transitions and 1247 arcs
pnml2lts-mc( 0/ 4): Petri net Petri analyzed
pnml2lts-mc( 0/ 4): There are no safe places
pnml2lts-mc( 0/ 4): Loading Petri net took 0.040 real 0.010 user 0.010 sys
pnml2lts-mc( 2/ 4): LTL layer: formula: /tmp/1807/ltl_3_
pnml2lts-mc( 3/ 4): LTL layer: formula: /tmp/1807/ltl_3_
pnml2lts-mc( 0/ 4): LTL layer: formula: /tmp/1807/ltl_3_
pnml2lts-mc( 1/ 4): LTL layer: formula: /tmp/1807/ltl_3_
pnml2lts-mc( 0/ 4): buchi has 1 states
pnml2lts-mc( 0/ 4): Weak Buchi automaton detected, adding non-accepting as progress label.
pnml2lts-mc( 0/ 4), ** error **: area memory exhausted
*** segmentation fault ***

Please send information on how to reproduce this problem to:
ltsmin-support@lists.utwente.nl
along with all output preceding this message.
In addition, include the following information:
Package: ltsmin 3.1.0
Stack trace:
0: pnml2lts-mc(+0xa23f4) [0x5644cc02d3f4]
1: pnml2lts-mc(+0xa2496) [0x5644cc02d496]
2: /lib/x86_64-linux-gnu/libpthread.so.0(+0x13140) [0x7fd0a10e4140]
3: pnml2lts-mc(+0x405be5) [0x5644cc390be5]
4: pnml2lts-mc(+0x16b3f9) [0x5644cc0f63f9]
5: pnml2lts-mc(+0x164ac4) [0x5644cc0efac4]
6: pnml2lts-mc(+0x272e0a) [0x5644cc1fde0a]
7: pnml2lts-mc(+0xb61f0) [0x5644cc0411f0]
8: /lib/x86_64-linux-gnu/libc.so.6(+0x3b4d7) [0x7fd0a0f374d7]
9: /lib/x86_64-linux-gnu/libc.so.6(+0x3b67a) [0x7fd0a0f3767a]
10: pnml2lts-mc(+0xa1581) [0x5644cc02c581]
11: pnml2lts-mc(+0xa1910) [0x5644cc02c910]
12: pnml2lts-mc(+0xa32a2) [0x5644cc02e2a2]
13: pnml2lts-mc(+0xa50f4) [0x5644cc0300f4]
14: pnml2lts-mc(+0xa516b) [0x5644cc03016b]
15: pnml2lts-mc(+0x3f34b3) [0x5644cc37e4b3]
16: pnml2lts-mc(+0x7c63d) [0x5644cc00763d]
17: pnml2lts-mc(+0x67d86) [0x5644cbff2d86]
18: pnml2lts-mc(+0x60a8a) [0x5644cbfeba8a]
19: pnml2lts-mc(+0x5eb15) [0x5644cbfe9b15]
20: /lib/x86_64-linux-gnu/libc.so.6(__libc_start_main+0xea) [0x7fd0a0f1fd0a]
21: pnml2lts-mc(+0x6075e) [0x5644cbfeb75e]

Sequence of Actions to be Executed by the VM

This is useful if one wants to reexecute the tool in the VM from the submitted image disk.

set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-7"
export BK_EXAMINATION="LTLCardinality"
export BK_TOOL="ltsminxred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"

# this is specific to your benchmark or test

export BIN_DIR="$HOME/BenchKit/bin"

# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi

# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool ltsminxred"
echo " Input is NeoElection-PT-7, examination is LTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r265-smll-167863539700211"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"

tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-7.tgz
mv NeoElection-PT-7 execution
cd execution
if [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "UpperBounds" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] || [ "LTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh

echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '' LTLCardinality.xml | cut -d '>' -f 2 | cut -d '<' -f 1 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME LTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;