About the Execution of Marcie+red for LamportFastMutEx-PT-6
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 10184.775 | 3600000.00 | 3639099.00 | 7325.50 | ???????????FT?T? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
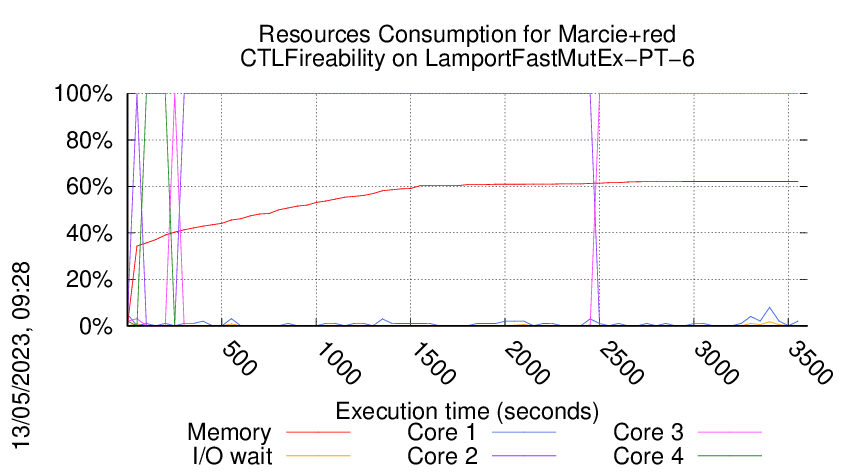
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r234-tall-167856420300426.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is LamportFastMutEx-PT-6, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r234-tall-167856420300426
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 1.4M
-rw-r--r-- 1 mcc users 16K Feb 25 13:41 CTLCardinality.txt
-rw-r--r-- 1 mcc users 97K Feb 25 13:41 CTLCardinality.xml
-rw-r--r-- 1 mcc users 31K Feb 25 13:40 CTLFireability.txt
-rw-r--r-- 1 mcc users 175K Feb 25 13:40 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.6K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 12K Feb 25 16:20 LTLCardinality.txt
-rw-r--r-- 1 mcc users 51K Feb 25 16:20 LTLCardinality.xml
-rw-r--r-- 1 mcc users 13K Feb 25 16:20 LTLFireability.txt
-rw-r--r-- 1 mcc users 56K Feb 25 16:20 LTLFireability.xml
-rw-r--r-- 1 mcc users 30K Feb 25 13:45 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 200K Feb 25 13:45 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 68K Feb 25 13:44 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 349K Feb 25 13:44 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 3.0K Feb 25 16:20 UpperBounds.txt
-rw-r--r-- 1 mcc users 7.0K Feb 25 16:20 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 equiv_col
-rw-r--r-- 1 mcc users 2 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 iscolored
-rw-r--r-- 1 mcc users 208K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-00
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-01
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-02
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-03
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-04
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-05
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-06
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-07
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-08
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-09
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-10
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-11
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-12
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-13
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-14
FORMULA_NAME LamportFastMutEx-PT-6-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1679495712982
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=LamportFastMutEx-PT-6
Applying reductions before tool marcie
Invoking reducer
Running Version 202303021504
[2023-03-22 14:35:14] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2023-03-22 14:35:14] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-22 14:35:14] [INFO ] Load time of PNML (sax parser for PT used): 62 ms
[2023-03-22 14:35:14] [INFO ] Transformed 217 places.
[2023-03-22 14:35:14] [INFO ] Transformed 420 transitions.
[2023-03-22 14:35:14] [INFO ] Found NUPN structural information;
[2023-03-22 14:35:14] [INFO ] Completing missing partition info from NUPN : creating a component with [P_start_1_0, P_start_1_1, P_start_1_2, P_start_1_3, P_start_1_4, P_start_1_5, P_start_1_6, P_b_0_false, P_b_0_true, P_b_1_false, P_b_1_true, P_b_2_false, P_b_2_true, P_b_3_false, P_b_3_true, P_b_4_false, P_b_4_true, P_b_5_false, P_b_5_true, P_b_6_false, P_b_6_true, P_setx_3_0, P_setx_3_1, P_setx_3_2, P_setx_3_3, P_setx_3_4, P_setx_3_5, P_setx_3_6, P_setbi_5_0, P_setbi_5_1, P_setbi_5_2, P_setbi_5_3, P_setbi_5_4, P_setbi_5_5, P_setbi_5_6, P_ify0_4_0, P_ify0_4_1, P_ify0_4_2, P_ify0_4_3, P_ify0_4_4, P_ify0_4_5, P_ify0_4_6, P_sety_9_0, P_sety_9_1, P_sety_9_2, P_sety_9_3, P_sety_9_4, P_sety_9_5, P_sety_9_6, P_ifxi_10_0, P_ifxi_10_1, P_ifxi_10_2, P_ifxi_10_3, P_ifxi_10_4, P_ifxi_10_5, P_ifxi_10_6, P_setbi_11_0, P_setbi_11_1, P_setbi_11_2, P_setbi_11_3, P_setbi_11_4, P_setbi_11_5, P_setbi_11_6, P_fordo_12_0, P_fordo_12_1, P_fordo_12_2, P_fordo_12_3, P_fordo_12_4, P_fordo_12_5, P_fordo_12_6, P_wait_0_0, P_wait_0_1, P_wait_0_2, P_wait_0_3, P_wait_0_4, P_wait_0_5, P_wait_0_6, P_wait_1_0, P_wait_1_1, P_wait_1_2, P_wait_1_3, P_wait_1_4, P_wait_1_5, P_wait_1_6, P_wait_2_0, P_wait_2_1, P_wait_2_2, P_wait_2_3, P_wait_2_4, P_wait_2_5, P_wait_2_6, P_wait_3_0, P_wait_3_1, P_wait_3_2, P_wait_3_3, P_wait_3_4, P_wait_3_5, P_wait_3_6, P_wait_4_0, P_wait_4_1, P_wait_4_2, P_wait_4_3, P_wait_4_4, P_wait_4_5, P_wait_4_6, P_wait_5_0, P_wait_5_1, P_wait_5_2, P_wait_5_3, P_wait_5_4, P_wait_5_5, P_wait_5_6, P_wait_6_0, P_wait_6_1, P_wait_6_2, P_wait_6_3, P_wait_6_4, P_wait_6_5, P_wait_6_6, P_await_13_0, P_await_13_1, P_await_13_2, P_await_13_3, P_await_13_4, P_await_13_5, P_await_13_6, P_done_0_0, P_done_0_1, P_done_0_2, P_done_0_3, P_done_0_4, P_done_0_5, P_done_0_6, P_done_1_0, P_done_1_1, P_done_1_2, P_done_1_3, P_done_1_4, P_done_1_5, P_done_1_6, P_done_2_0, P_done_2_1, P_done_2_2, P_done_2_3, P_done_2_4, P_done_2_5, P_done_2_6, P_done_3_0, P_done_3_1, P_done_3_2, P_done_3_3, P_done_3_4, P_done_3_5, P_done_3_6, P_done_4_0, P_done_4_1, P_done_4_2, P_done_4_3, P_done_4_4, P_done_4_5, P_done_4_6, P_done_5_0, P_done_5_1, P_done_5_2, P_done_5_3, P_done_5_4, P_done_5_5, P_done_5_6, P_done_6_0, P_done_6_1, P_done_6_2, P_done_6_3, P_done_6_4, P_done_6_5, P_done_6_6, P_ifyi_15_0, P_ifyi_15_1, P_ifyi_15_2, P_ifyi_15_3, P_ifyi_15_4, P_ifyi_15_5, P_ifyi_15_6, P_awaity_0, P_awaity_1, P_awaity_2, P_awaity_3, P_awaity_4, P_awaity_5, P_awaity_6, P_CS_21_0, P_CS_21_1, P_CS_21_2, P_CS_21_3, P_CS_21_4, P_CS_21_5, P_CS_21_6, P_setbi_24_0, P_setbi_24_1, P_setbi_24_2, P_setbi_24_3, P_setbi_24_4, P_setbi_24_5, P_setbi_24_6]
[2023-03-22 14:35:14] [INFO ] Parsed PT model containing 217 places and 420 transitions and 1834 arcs in 124 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 15 ms.
Deduced a syphon composed of 41 places in 3 ms
Reduce places removed 41 places and 66 transitions.
Support contains 176 out of 176 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 12 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
[2023-03-22 14:35:14] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
// Phase 1: matrix 264 rows 176 cols
[2023-03-22 14:35:14] [INFO ] Computed 50 place invariants in 19 ms
[2023-03-22 14:35:14] [INFO ] Implicit Places using invariants in 390 ms returned []
[2023-03-22 14:35:14] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 14:35:14] [INFO ] Invariant cache hit.
[2023-03-22 14:35:15] [INFO ] State equation strengthened by 72 read => feed constraints.
[2023-03-22 14:35:15] [INFO ] Implicit Places using invariants and state equation in 157 ms returned []
Implicit Place search using SMT with State Equation took 576 ms to find 0 implicit places.
[2023-03-22 14:35:15] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 14:35:15] [INFO ] Invariant cache hit.
[2023-03-22 14:35:15] [INFO ] Dead Transitions using invariants and state equation in 177 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 767 ms. Remains : 176/176 places, 354/354 transitions.
Support contains 176 out of 176 places after structural reductions.
[2023-03-22 14:35:15] [INFO ] Flatten gal took : 63 ms
[2023-03-22 14:35:15] [INFO ] Flatten gal took : 50 ms
[2023-03-22 14:35:15] [INFO ] Input system was already deterministic with 354 transitions.
Incomplete random walk after 10000 steps, including 2 resets, run finished after 527 ms. (steps per millisecond=18 ) properties (out of 75) seen :62
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 85 ms. (steps per millisecond=117 ) properties (out of 13) seen :1
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 35 ms. (steps per millisecond=285 ) properties (out of 12) seen :1
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 46 ms. (steps per millisecond=217 ) properties (out of 11) seen :0
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 46 ms. (steps per millisecond=217 ) properties (out of 11) seen :1
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 46 ms. (steps per millisecond=217 ) properties (out of 10) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 40 ms. (steps per millisecond=250 ) properties (out of 10) seen :0
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 42 ms. (steps per millisecond=238 ) properties (out of 10) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 34 ms. (steps per millisecond=294 ) properties (out of 10) seen :0
Incomplete Best-First random walk after 10000 steps, including 2 resets, run finished after 43 ms. (steps per millisecond=232 ) properties (out of 10) seen :1
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 35 ms. (steps per millisecond=285 ) properties (out of 9) seen :2
Running SMT prover for 7 properties.
[2023-03-22 14:35:17] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 14:35:17] [INFO ] Invariant cache hit.
[2023-03-22 14:35:17] [INFO ] [Real]Absence check using 50 positive place invariants in 8 ms returned sat
[2023-03-22 14:35:17] [INFO ] After 191ms SMT Verify possible using all constraints in real domain returned unsat :4 sat :0 real:3
[2023-03-22 14:35:17] [INFO ] [Nat]Absence check using 50 positive place invariants in 8 ms returned sat
[2023-03-22 14:35:17] [INFO ] After 131ms SMT Verify possible using state equation in natural domain returned unsat :4 sat :3
[2023-03-22 14:35:17] [INFO ] State equation strengthened by 72 read => feed constraints.
[2023-03-22 14:35:17] [INFO ] After 123ms SMT Verify possible using 72 Read/Feed constraints in natural domain returned unsat :4 sat :3
[2023-03-22 14:35:17] [INFO ] Deduced a trap composed of 9 places in 81 ms of which 4 ms to minimize.
[2023-03-22 14:35:17] [INFO ] Deduced a trap composed of 13 places in 76 ms of which 0 ms to minimize.
[2023-03-22 14:35:17] [INFO ] Deduced a trap composed of 9 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:17] [INFO ] Deduced a trap composed of 15 places in 64 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 16 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 16 places in 57 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 15 places in 56 ms of which 0 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 31 places in 52 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 27 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 17 places in 66 ms of which 0 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 21 places in 59 ms of which 0 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 46 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 15 places in 67 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 29 places in 59 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 9 places in 58 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 22 places in 55 ms of which 1 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 8 places in 57 ms of which 0 ms to minimize.
[2023-03-22 14:35:18] [INFO ] Deduced a trap composed of 9 places in 57 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 17 places in 52 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 16 places in 61 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 9 places in 59 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 20 places in 54 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 19 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 47 places in 51 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 17 places in 52 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 25 places in 52 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 18 places in 67 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 9 places in 51 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 17 places in 58 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 26 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 38 places in 50 ms of which 1 ms to minimize.
[2023-03-22 14:35:19] [INFO ] Deduced a trap composed of 22 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 18 places in 46 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 21 places in 67 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 15 places in 44 ms of which 4 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 9 places in 19 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 15 places in 63 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 31 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 19 places in 44 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 9 places in 26 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 17 places in 46 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 19 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 15 places in 64 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 25 places in 59 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 10 places in 58 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 16 places in 45 ms of which 1 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 17 places in 57 ms of which 0 ms to minimize.
[2023-03-22 14:35:20] [INFO ] Deduced a trap composed of 15 places in 58 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 34 places in 56 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 15 places in 52 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 9 places in 40 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 17 places in 44 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 22 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 18 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 15 places in 42 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 8 places in 56 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 15 places in 55 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 8 places in 55 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 16 places in 55 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 8 places in 54 ms of which 1 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 26 places in 64 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 15 places in 57 ms of which 0 ms to minimize.
[2023-03-22 14:35:21] [INFO ] Deduced a trap composed of 17 places in 63 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 42 places in 61 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 16 places in 63 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 26 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 26 places in 62 ms of which 1 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 21 places in 61 ms of which 2 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 25 places in 63 ms of which 1 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 21 places in 60 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 27 places in 60 ms of which 1 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 22 places in 59 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 14 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 17 places in 56 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 16 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:22] [INFO ] Deduced a trap composed of 17 places in 68 ms of which 1 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 16 places in 47 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 18 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 19 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 16 places in 47 ms of which 1 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 26 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 22 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 21 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 15 places in 55 ms of which 1 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 23 places in 57 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 28 places in 52 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 26 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 19 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 30 places in 58 ms of which 0 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 29 places in 53 ms of which 1 ms to minimize.
[2023-03-22 14:35:23] [INFO ] Deduced a trap composed of 26 places in 57 ms of which 1 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 17 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 25 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 25 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 16 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 17 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 32 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 27 places in 48 ms of which 1 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 16 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 28 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 16 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 21 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 30 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 27 places in 43 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 31 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 19 places in 54 ms of which 1 ms to minimize.
[2023-03-22 14:35:24] [INFO ] Deduced a trap composed of 15 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 21 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 27 places in 55 ms of which 1 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 17 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 25 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 25 places in 59 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 27 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 9 places in 55 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 16 places in 56 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 23 places in 57 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 32 places in 55 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 29 places in 52 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 28 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 24 places in 55 ms of which 0 ms to minimize.
[2023-03-22 14:35:25] [INFO ] Deduced a trap composed of 25 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 18 places in 47 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 23 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 20 places in 42 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 28 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 16 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 26 places in 58 ms of which 1 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 24 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 26 places in 56 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 25 places in 51 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 16 places in 54 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 24 places in 52 ms of which 4 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 23 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 17 places in 47 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 24 places in 58 ms of which 0 ms to minimize.
[2023-03-22 14:35:26] [INFO ] Deduced a trap composed of 24 places in 54 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 18 places in 44 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 18 places in 48 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 20 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 16 places in 45 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 16 places in 49 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 19 places in 43 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 23 places in 50 ms of which 2 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 54 places in 53 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 18 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 15 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 19 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 22 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 16 places in 50 ms of which 0 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 16 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 19 places in 49 ms of which 1 ms to minimize.
[2023-03-22 14:35:27] [INFO ] Deduced a trap composed of 22 places in 44 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 19 places in 41 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 15 places in 42 ms of which 1 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 23 places in 53 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 27 places in 50 ms of which 1 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 17 places in 46 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Trap strengthening procedure managed to obtain unsat after adding 157 trap constraints in 10655 ms
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 8 places in 47 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Deduced a trap composed of 8 places in 40 ms of which 0 ms to minimize.
[2023-03-22 14:35:28] [INFO ] Trap strengthening procedure managed to obtain unsat after adding 2 trap constraints in 105 ms
[2023-03-22 14:35:28] [INFO ] After 10977ms SMT Verify possible using trap constraints in natural domain returned unsat :7 sat :0
[2023-03-22 14:35:28] [INFO ] After 11193ms SMT Verify possible using all constraints in natural domain returned unsat :7 sat :0
Fused 7 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 0 ms.
Successfully simplified 7 atomic propositions for a total of 16 simplifications.
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 25 ms
[2023-03-22 14:35:28] [INFO ] Initial state reduction rules for CTL removed 1 formulas.
FORMULA LamportFastMutEx-PT-6-CTLFireability-12 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 43 ms
[2023-03-22 14:35:28] [INFO ] Input system was already deterministic with 354 transitions.
Computed a total of 1 stabilizing places and 6 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 7 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 8 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 16 ms
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 16 ms
[2023-03-22 14:35:28] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 4 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 14 ms
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 15 ms
[2023-03-22 14:35:28] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 17 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 17 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 14 ms
[2023-03-22 14:35:28] [INFO ] Flatten gal took : 14 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 6 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 6 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 15 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 14 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 4 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 12 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 14 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 18 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 18 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 29 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 15 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 5 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 5 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 4 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 11 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Performed 5 Post agglomeration using F-continuation condition.Transition count delta: 5
Deduced a syphon composed of 5 places in 0 ms
Reduce places removed 5 places and 0 transitions.
Iterating global reduction 0 with 10 rules applied. Total rules applied 10 place count 171 transition count 349
Applied a total of 10 rules in 19 ms. Remains 171 /176 variables (removed 5) and now considering 349/354 (removed 5) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 19 ms. Remains : 171/176 places, 349/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 349 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 9 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 9 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 9 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 25 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 3 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 9 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 24 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 3 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 10 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Performed 5 Post agglomeration using F-continuation condition.Transition count delta: 5
Deduced a syphon composed of 5 places in 1 ms
Reduce places removed 5 places and 0 transitions.
Iterating global reduction 0 with 10 rules applied. Total rules applied 10 place count 171 transition count 349
Applied a total of 10 rules in 14 ms. Remains 171 /176 variables (removed 5) and now considering 349/354 (removed 5) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 14 ms. Remains : 171/176 places, 349/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 9 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 16 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 349 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 9 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 9 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 24 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 11 ms
[2023-03-22 14:35:29] [INFO ] Input system was already deterministic with 354 transitions.
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 18 ms
[2023-03-22 14:35:29] [INFO ] Flatten gal took : 19 ms
[2023-03-22 14:35:30] [INFO ] Export to MCC of 15 properties in file /home/mcc/execution/CTLFireability.sr.xml took 18 ms.
[2023-03-22 14:35:30] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 176 places, 354 transitions and 1536 arcs took 1 ms.
Total runtime 15699 ms.
There are residual formulas that ITS could not solve within timeout
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLFireability.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Petri
(NrP: 176 NrTr: 354 NrArc: 1536)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.007sec
net check time: 0m 0.000sec
init dd package: 0m 2.691sec
RS generation: 24m48.182sec
-> reachability set: #nodes 706675 (7.1e+05) #states 547,231,759,144 (11)
starting MCC model checker
--------------------------
checking: AG [[EF [EX [0<=0]] | [[p11<=1 & 1<=p11] & [p56<=1 & 1<=p56]]]]
normalized: ~ [E [true U ~ [[E [true U EX [0<=0]] | [[p56<=1 & 1<=p56] & [p11<=1 & 1<=p11]]]]]]
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (0<=0)
states: 547,231,759,144 (11)
before gc: list nodes free: 1578418
after gc: idd nodes used:1817129, unused:62182871; list nodes free:275164461
.
before gc: list nodes free: 1104819
after gc: idd nodes used:1256064, unused:62743936; list nodes free:277606683
MC time: 2m21.141sec
checking: AG [EF [[[p24<=1 & 1<=p24] & [[p94<=1 & 1<=p94] & [p113<=1 & 1<=p113]]]]]
normalized: ~ [E [true U ~ [E [true U [[[p113<=1 & 1<=p113] & [p94<=1 & 1<=p94]] & [p24<=1 & 1<=p24]]]]]]
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p94)
states: 200,549,728,448 (11)
abstracting: (p94<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 1936393
after gc: idd nodes used:1331977, unused:62668023; list nodes free:281468001
MC time: 2m12.134sec
checking: EF [[EX [EX [[[p15<=1 & 1<=p15] & [p47<=1 & 1<=p47]]]] & AX [[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]]]]]
normalized: E [true U [~ [EX [~ [[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]]]]] & EX [EX [[[p47<=1 & 1<=p47] & [p15<=1 & 1<=p15]]]]]]
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (p47<=1)
states: 547,231,759,144 (11)
..abstracting: (1<=p169)
states: 9,580,362,816 (9)
abstracting: (p169<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 5965940
after gc: idd nodes used:3674874, unused:60325126; list nodes free:270741074
.-> the formula is FALSE
FORMULA LamportFastMutEx-PT-6-CTLFireability-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m58.568sec
checking: AF [[AG [[[~ [[p71<=1 & 1<=p71]] & [~ [[p70<=1 & 1<=p70]] & ~ [[p73<=1 & 1<=p73]]]] & [~ [[p72<=1 & 1<=p72]] & [~ [[p69<=1 & 1<=p69]] & ~ [[p68<=1 & 1<=p68]]]]]] & EX [0<=0]]]
normalized: ~ [EG [~ [[EX [0<=0] & ~ [E [true U ~ [[[[~ [[p68<=1 & 1<=p68]] & ~ [[p69<=1 & 1<=p69]]] & ~ [[p72<=1 & 1<=p72]]] & [[~ [[p73<=1 & 1<=p73]] & ~ [[p70<=1 & 1<=p70]]] & ~ [[p71<=1 & 1<=p71]]]]]]]]]]]
abstracting: (1<=p71)
states: 6,677,072,160 (9)
abstracting: (p71<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p70)
states: 6,677,072,160 (9)
abstracting: (p70<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p73)
states: 6,677,072,160 (9)
abstracting: (p73<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p72)
states: 6,677,072,160 (9)
abstracting: (p72<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p69)
states: 6,677,072,160 (9)
abstracting: (p69<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p68)
states: 6,677,072,160 (9)
abstracting: (p68<=1)
states: 547,231,759,144 (11)
MC time: 2m 3.256sec
checking: [EG [[EF [EX [0<=0]] & [AX [[[p17<=1 & 1<=p17] & [p48<=1 & 1<=p48]]] | [[p19<=0 & 0<=p19] | [p52<=0 & 0<=p52]]]]] & A [EG [EF [[[p18<=1 & 1<=p18] & [p169<=1 & 1<=p169]]]] U [EG [AF [[[p30<=1 & 1<=p30] & [[p79<=1 & 1<=p79] & [p110<=1 & 1<=p110]]]]] | EF [AX [[[p12<=1 & 1<=p12] & [p35<=1 & 1<=p35]]]]]]]
normalized: [[~ [EG [~ [[EG [~ [EG [~ [[[[p110<=1 & 1<=p110] & [p79<=1 & 1<=p79]] & [p30<=1 & 1<=p30]]]]]] | E [true U ~ [EX [~ [[[p35<=1 & 1<=p35] & [p12<=1 & 1<=p12]]]]]]]]]] & ~ [E [~ [[EG [~ [EG [~ [[[[p110<=1 & 1<=p110] & [p79<=1 & 1<=p79]] & [p30<=1 & 1<=p30]]]]]] | E [true U ~ [EX [~ [[[p35<=1 & 1<=p35] & [p12<=1 & 1<=p12]]]]]]]] U [~ [[EG [~ [EG [~ [[[[p110<=1 & 1<=p110] & [p79<=1 & 1<=p79]] & [p30<=1 & 1<=p30]]]]]] | E [true U ~ [EX [~ [[[p35<=1 & 1<=p35] & [p12<=1 & 1<=p12]]]]]]]] & ~ [EG [E [true U [[p169<=1 & 1<=p169] & [p18<=1 & 1<=p18]]]]]]]]] & EG [[[[[p52<=0 & 0<=p52] | [p19<=0 & 0<=p19]] | ~ [EX [~ [[[p48<=1 & 1<=p48] & [p17<=1 & 1<=p17]]]]]] & E [true U EX [0<=0]]]]]
abstracting: (0<=0)
states: 547,231,759,144 (11)
before gc: list nodes free: 4911853
after gc: idd nodes used:3209374, unused:60790626; list nodes free:273226217
.MC time: 1m54.297sec
checking: ~ [A [[A [[[p10<=1 & 1<=p10] & [p37<=1 & 1<=p37]] U [[p19<=1 & 1<=p19] & [p155<=1 & 1<=p155]]] | ~ [[[p22<=1 & 1<=p22] & [[p99<=1 & 1<=p99] & [p114<=1 & 1<=p114]]]]] U AG [[AF [[[p18<=1 & 1<=p18] & [p164<=1 & 1<=p164]]] | AF [[[p17<=1 & 1<=p17] & [p153<=1 & 1<=p153]]]]]]]
normalized: ~ [[~ [EG [E [true U ~ [[~ [EG [~ [[[p153<=1 & 1<=p153] & [p17<=1 & 1<=p17]]]]] | ~ [EG [~ [[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]]]]]]]]]] & ~ [E [E [true U ~ [[~ [EG [~ [[[p153<=1 & 1<=p153] & [p17<=1 & 1<=p17]]]]] | ~ [EG [~ [[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]]]]]]]] U [~ [[~ [[[[p114<=1 & 1<=p114] & [p99<=1 & 1<=p99]] & [p22<=1 & 1<=p22]]] | [~ [EG [~ [[[p155<=1 & 1<=p155] & [p19<=1 & 1<=p19]]]]] & ~ [E [~ [[[p155<=1 & 1<=p155] & [p19<=1 & 1<=p19]]] U [~ [[[p37<=1 & 1<=p37] & [p10<=1 & 1<=p10]]] & ~ [[[p155<=1 & 1<=p155] & [p19<=1 & 1<=p19]]]]]]]]] & E [true U ~ [[~ [EG [~ [[[p153<=1 & 1<=p153] & [p17<=1 & 1<=p17]]]]] | ~ [EG [~ [[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]]]]]]]]]]]]]
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p164)
states: 9,580,362,816 (9)
abstracting: (p164<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 5309343
after gc: idd nodes used:3853058, unused:60146942; list nodes free:270349824
.MC time: 1m46.162sec
checking: A [~ [E [[EF [[[p19<=1 & 1<=p19] & [p44<=1 & 1<=p44]]] | AX [[[p14<=1 & 1<=p14] & [p54<=1 & 1<=p54]]]] U EX [EX [[[p8<=1 & 1<=p8] & [p35<=1 & 1<=p35]]]]]] U [EF [[[p19<=1 & 1<=p19] & [p153<=1 & 1<=p153]]] | [AX [EG [[[p19<=1 & 1<=p19] & [p51<=1 & 1<=p51]]]] | [EF [[AF [[[p15<=1 & 1<=p15] & [p48<=1 & 1<=p48]]] & EF [[[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]]]]] & [[p15<=1 & 1<=p15] & [p155<=1 & 1<=p155]]]]]]
normalized: [~ [EG [~ [[[[E [true U [E [true U [[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]]] & ~ [EG [~ [[[p48<=1 & 1<=p48] & [p15<=1 & 1<=p15]]]]]]] & [[p155<=1 & 1<=p155] & [p15<=1 & 1<=p15]]] | ~ [EX [~ [EG [[[p51<=1 & 1<=p51] & [p19<=1 & 1<=p19]]]]]]] | E [true U [[p153<=1 & 1<=p153] & [p19<=1 & 1<=p19]]]]]]] & ~ [E [~ [[[[E [true U [E [true U [[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]]] & ~ [EG [~ [[[p48<=1 & 1<=p48] & [p15<=1 & 1<=p15]]]]]]] & [[p155<=1 & 1<=p155] & [p15<=1 & 1<=p15]]] | ~ [EX [~ [EG [[[p51<=1 & 1<=p51] & [p19<=1 & 1<=p19]]]]]]] | E [true U [[p153<=1 & 1<=p153] & [p19<=1 & 1<=p19]]]]] U [~ [[[[E [true U [E [true U [[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]]] & ~ [EG [~ [[[p48<=1 & 1<=p48] & [p15<=1 & 1<=p15]]]]]]] & [[p155<=1 & 1<=p155] & [p15<=1 & 1<=p15]]] | ~ [EX [~ [EG [[[p51<=1 & 1<=p51] & [p19<=1 & 1<=p19]]]]]]] | E [true U [[p153<=1 & 1<=p153] & [p19<=1 & 1<=p19]]]]] & E [[~ [EX [~ [[[p54<=1 & 1<=p54] & [p14<=1 & 1<=p14]]]]] | E [true U [[p44<=1 & 1<=p44] & [p19<=1 & 1<=p19]]]] U EX [EX [[[p35<=1 & 1<=p35] & [p8<=1 & 1<=p8]]]]]]]]]
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
..abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (p44<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 4492355
after gc: idd nodes used:4175921, unused:59824079; list nodes free:268931811
MC time: 1m39.032sec
checking: AG [[[EX [0<=0] | EX [[AF [[[p13<=1 & 1<=p13] & [p152<=1 & 1<=p152]]] | [[p12<=1 & 1<=p12] & [p36<=1 & 1<=p36]]]]] | [[[p18<=1 & 1<=p18] & [p167<=1 & 1<=p167]] | [[[[p8<=1 & 1<=p8] & [[p33<=1 & 1<=p33] & [p26<=1 & 1<=p26]]] & [[p95<=1 & 1<=p95] & [[p113<=1 & 1<=p113] & [AX [1<=0] | AX [[[p15<=1 & 1<=p15] & [p50<=1 & 1<=p50]]]]]]] | [~ [A [AX [[[p14<=1 & 1<=p14] & [p54<=1 & 1<=p54]]] U [[p0<=1 & 1<=p0] & [p20<=1 & 1<=p20]]]] & [[p27<=0 & 0<=p27] | [p173<=0 & 0<=p173]]]]]]]
normalized: ~ [E [true U ~ [[[[[[[[~ [EX [~ [[[p50<=1 & 1<=p50] & [p15<=1 & 1<=p15]]]]] | ~ [EX [~ [1<=0]]]] & [p113<=1 & 1<=p113]] & [p95<=1 & 1<=p95]] & [[[p26<=1 & 1<=p26] & [p33<=1 & 1<=p33]] & [p8<=1 & 1<=p8]]] | [[[p173<=0 & 0<=p173] | [p27<=0 & 0<=p27]] & ~ [[~ [EG [~ [[[p20<=1 & 1<=p20] & [p0<=1 & 1<=p0]]]]] & ~ [E [~ [[[p20<=1 & 1<=p20] & [p0<=1 & 1<=p0]]] U [EX [~ [[[p54<=1 & 1<=p54] & [p14<=1 & 1<=p14]]]] & ~ [[[p20<=1 & 1<=p20] & [p0<=1 & 1<=p0]]]]]]]]]] | [[p167<=1 & 1<=p167] & [p18<=1 & 1<=p18]]] | [EX [[[[p36<=1 & 1<=p36] & [p12<=1 & 1<=p12]] | ~ [EG [~ [[[p152<=1 & 1<=p152] & [p13<=1 & 1<=p13]]]]]]] | EX [0<=0]]]]]]
abstracting: (0<=0)
states: 547,231,759,144 (11)
MC time: 1m32.214sec
checking: EG [[[AX [[[[[p13<=0 & 0<=p13] | [p163<=0 & 0<=p163]] & [[[p13<=0 & 0<=p13] | [p160<=0 & 0<=p160]] & [[p13<=0 & 0<=p13] | [p159<=0 & 0<=p159]]]] & [[[p13<=0 & 0<=p13] | [p162<=0 & 0<=p162]] & [[[p13<=0 & 0<=p13] | [p161<=0 & 0<=p161]] & [[p13<=0 & 0<=p13] | [p158<=0 & 0<=p158]]]]]] | AX [AX [[[[[p13<=0 & 0<=p13] | [p47<=0 & 0<=p47]] & [[[p13<=0 & 0<=p13] | [p46<=0 & 0<=p46]] & [[p13<=0 & 0<=p13] | [p45<=0 & 0<=p45]]]] & [[[p13<=0 & 0<=p13] | [p44<=0 & 0<=p44]] & [[[p13<=0 & 0<=p13] | [p49<=0 & 0<=p49]] & [[p13<=0 & 0<=p13] | [p48<=0 & 0<=p48]]]]]]]] | [EG [[[[[[p110<=0 & 0<=p110] | [[p116<=0 & 0<=p116] | [p117<=0 & 0<=p117]]] | [[[p118<=0 & 0<=p118] | [p119<=0 & 0<=p119]] | [[p120<=0 & 0<=p120] | [p121<=0 & 0<=p121]]]] & [[[[p114<=0 & 0<=p114] | [[p140<=0 & 0<=p140] | [p141<=0 & 0<=p141]]] | [[[p142<=0 & 0<=p142] | [p143<=0 & 0<=p143]] | [[p144<=0 & 0<=p144] | [p145<=0 & 0<=p145]]]] & [[[p111<=0 & 0<=p111] | [[p122<=0 & 0<=p122] | [p123<=0 & 0<=p123]]] | [[[p124<=0 & 0<=p124] | [p125<=0 & 0<=p125]] | [[p126<=0 & 0<=p126] | [p127<=0 & 0<=p127]]]]]] & [[[[p115<=0 & 0<=p115] | [[p146<=0 & 0<=p146] | [p147<=0 & 0<=p147]]] | [[[p148<=0 & 0<=p148] | [p149<=0 & 0<=p149]] | [[p150<=0 & 0<=p150] | [p151<=0 & 0<=p151]]]] & [[[[p113<=0 & 0<=p113] | [[p134<=0 & 0<=p134] | [p135<=0 & 0<=p135]]] | [[[p136<=0 & 0<=p136] | [p137<=0 & 0<=p137]] | [[p138<=0 & 0<=p138] | [p139<=0 & 0<=p139]]]] & [[[p112<=0 & 0<=p112] | [[p128<=0 & 0<=p128] | [p129<=0 & 0<=p129]]] | [[[p130<=0 & 0<=p130] | [p131<=0 & 0<=p131]] | [[p132<=0 & 0<=p132] | [p133<=0 & 0<=p133]]]]]]]] | [[[[[[[p13<=0 & 0<=p13] | [p167<=0 & 0<=p167]] & [[p13<=0 & 0<=p13] | [p169<=0 & 0<=p169]]] & [[[p18<=0 & 0<=p18] | [p166<=0 & 0<=p166]] & [[[p13<=0 & 0<=p13] | [p165<=0 & 0<=p165]] & [[p18<=0 & 0<=p18] | [p168<=0 & 0<=p168]]]]] & [[[[p17<=0 & 0<=p17] | [p164<=0 & 0<=p164]] & [[p14<=0 & 0<=p14] | [p169<=0 & 0<=p169]]] & [[[p19<=0 & 0<=p19] | [p166<=0 & 0<=p166]] & [[[p19<=0 & 0<=p19] | [p164<=0 & 0<=p164]] & [[p19<=0 & 0<=p19] | [p168<=0 & 0<=p168]]]]]] & [[[[[p16<=0 & 0<=p16] | [p166<=0 & 0<=p166]] & [[p15<=0 & 0<=p15] | [p169<=0 & 0<=p169]]] & [[[p16<=0 & 0<=p16] | [p164<=0 & 0<=p164]] & [[[p15<=0 & 0<=p15] | [p164<=0 & 0<=p164]] & [[p16<=0 & 0<=p16] | [p169<=0 & 0<=p169]]]]] & [[[[p15<=0 & 0<=p15] | [p166<=0 & 0<=p166]] & [[[p16<=0 & 0<=p16] | [p167<=0 & 0<=p167]] & [[p14<=0 & 0<=p14] | [p164<=0 & 0<=p164]]]] & [[[p14<=0 & 0<=p14] | [p168<=0 & 0<=p168]] & [[[p17<=0 & 0<=p17] | [p169<=0 & 0<=p169]] & [[p14<=0 & 0<=p14] | [p166<=0 & 0<=p166]]]]]]] & [[[[[[p17<=0 & 0<=p17] | [p167<=0 & 0<=p167]] & [[p18<=0 & 0<=p18] | [p169<=0 & 0<=p169]]] & [[[p13<=0 & 0<=p13] | [p166<=0 & 0<=p166]] & [[[p13<=0 & 0<=p13] | [p168<=0 & 0<=p168]] & [[p18<=0 & 0<=p18] | [p165<=0 & 0<=p165]]]]] & [[[[p18<=0 & 0<=p18] | [p167<=0 & 0<=p167]] & [[p13<=0 & 0<=p13] | [p164<=0 & 0<=p164]]] & [[[p17<=0 & 0<=p17] | [p165<=0 & 0<=p165]] & [[[p19<=0 & 0<=p19] | [p167<=0 & 0<=p167]] & [[p19<=0 & 0<=p19] | [p165<=0 & 0<=p165]]]]]] & [[[[[p19<=0 & 0<=p19] | [p169<=0 & 0<=p169]] & [[p16<=0 & 0<=p16] | [p165<=0 & 0<=p165]]] & [[[p15<=0 & 0<=p15] | [p168<=0 & 0<=p168]] & [[[p15<=0 & 0<=p15] | [p165<=0 & 0<=p165]] & [[p15<=0 & 0<=p15] | [p167<=0 & 0<=p167]]]]] & [[[[p16<=0 & 0<=p16] | [p168<=0 & 0<=p168]] & [[[p17<=0 & 0<=p17] | [p168<=0 & 0<=p168]] & [[p17<=0 & 0<=p17] | [p166<=0 & 0<=p166]]]] & [[[p14<=0 & 0<=p14] | [p167<=0 & 0<=p167]] & [[[p14<=0 & 0<=p14] | [p165<=0 & 0<=p165]] & [[p18<=0 & 0<=p18] | [p164<=0 & 0<=p164]]]]]]]]]]]
normalized: EG [[[[[[[[[[[p164<=0 & 0<=p164] | [p18<=0 & 0<=p18]] & [[p165<=0 & 0<=p165] | [p14<=0 & 0<=p14]]] & [[p167<=0 & 0<=p167] | [p14<=0 & 0<=p14]]] & [[[[p166<=0 & 0<=p166] | [p17<=0 & 0<=p17]] & [[p168<=0 & 0<=p168] | [p17<=0 & 0<=p17]]] & [[p168<=0 & 0<=p168] | [p16<=0 & 0<=p16]]]] & [[[[[p167<=0 & 0<=p167] | [p15<=0 & 0<=p15]] & [[p165<=0 & 0<=p165] | [p15<=0 & 0<=p15]]] & [[p168<=0 & 0<=p168] | [p15<=0 & 0<=p15]]] & [[[p165<=0 & 0<=p165] | [p16<=0 & 0<=p16]] & [[p169<=0 & 0<=p169] | [p19<=0 & 0<=p19]]]]] & [[[[[[p165<=0 & 0<=p165] | [p19<=0 & 0<=p19]] & [[p167<=0 & 0<=p167] | [p19<=0 & 0<=p19]]] & [[p165<=0 & 0<=p165] | [p17<=0 & 0<=p17]]] & [[[p164<=0 & 0<=p164] | [p13<=0 & 0<=p13]] & [[p167<=0 & 0<=p167] | [p18<=0 & 0<=p18]]]] & [[[[[p165<=0 & 0<=p165] | [p18<=0 & 0<=p18]] & [[p168<=0 & 0<=p168] | [p13<=0 & 0<=p13]]] & [[p166<=0 & 0<=p166] | [p13<=0 & 0<=p13]]] & [[[p169<=0 & 0<=p169] | [p18<=0 & 0<=p18]] & [[p167<=0 & 0<=p167] | [p17<=0 & 0<=p17]]]]]] & [[[[[[[p166<=0 & 0<=p166] | [p14<=0 & 0<=p14]] & [[p169<=0 & 0<=p169] | [p17<=0 & 0<=p17]]] & [[p168<=0 & 0<=p168] | [p14<=0 & 0<=p14]]] & [[[[p164<=0 & 0<=p164] | [p14<=0 & 0<=p14]] & [[p167<=0 & 0<=p167] | [p16<=0 & 0<=p16]]] & [[p166<=0 & 0<=p166] | [p15<=0 & 0<=p15]]]] & [[[[[p169<=0 & 0<=p169] | [p16<=0 & 0<=p16]] & [[p164<=0 & 0<=p164] | [p15<=0 & 0<=p15]]] & [[p164<=0 & 0<=p164] | [p16<=0 & 0<=p16]]] & [[[p169<=0 & 0<=p169] | [p15<=0 & 0<=p15]] & [[p166<=0 & 0<=p166] | [p16<=0 & 0<=p16]]]]] & [[[[[[p168<=0 & 0<=p168] | [p19<=0 & 0<=p19]] & [[p164<=0 & 0<=p164] | [p19<=0 & 0<=p19]]] & [[p166<=0 & 0<=p166] | [p19<=0 & 0<=p19]]] & [[[p169<=0 & 0<=p169] | [p14<=0 & 0<=p14]] & [[p164<=0 & 0<=p164] | [p17<=0 & 0<=p17]]]] & [[[[[p168<=0 & 0<=p168] | [p18<=0 & 0<=p18]] & [[p165<=0 & 0<=p165] | [p13<=0 & 0<=p13]]] & [[p166<=0 & 0<=p166] | [p18<=0 & 0<=p18]]] & [[[p169<=0 & 0<=p169] | [p13<=0 & 0<=p13]] & [[p167<=0 & 0<=p167] | [p13<=0 & 0<=p13]]]]]]] | EG [[[[[[[[p133<=0 & 0<=p133] | [p132<=0 & 0<=p132]] | [[p131<=0 & 0<=p131] | [p130<=0 & 0<=p130]]] | [[[p129<=0 & 0<=p129] | [p128<=0 & 0<=p128]] | [p112<=0 & 0<=p112]]] & [[[[p139<=0 & 0<=p139] | [p138<=0 & 0<=p138]] | [[p137<=0 & 0<=p137] | [p136<=0 & 0<=p136]]] | [[[p135<=0 & 0<=p135] | [p134<=0 & 0<=p134]] | [p113<=0 & 0<=p113]]]] & [[[[p151<=0 & 0<=p151] | [p150<=0 & 0<=p150]] | [[p149<=0 & 0<=p149] | [p148<=0 & 0<=p148]]] | [[[p147<=0 & 0<=p147] | [p146<=0 & 0<=p146]] | [p115<=0 & 0<=p115]]]] & [[[[[[p127<=0 & 0<=p127] | [p126<=0 & 0<=p126]] | [[p125<=0 & 0<=p125] | [p124<=0 & 0<=p124]]] | [[[p123<=0 & 0<=p123] | [p122<=0 & 0<=p122]] | [p111<=0 & 0<=p111]]] & [[[[p145<=0 & 0<=p145] | [p144<=0 & 0<=p144]] | [[p143<=0 & 0<=p143] | [p142<=0 & 0<=p142]]] | [[[p141<=0 & 0<=p141] | [p140<=0 & 0<=p140]] | [p114<=0 & 0<=p114]]]] & [[[[p121<=0 & 0<=p121] | [p120<=0 & 0<=p120]] | [[p119<=0 & 0<=p119] | [p118<=0 & 0<=p118]]] | [[[p117<=0 & 0<=p117] | [p116<=0 & 0<=p116]] | [p110<=0 & 0<=p110]]]]]]] | [~ [EX [EX [~ [[[[[[p48<=0 & 0<=p48] | [p13<=0 & 0<=p13]] & [[p49<=0 & 0<=p49] | [p13<=0 & 0<=p13]]] & [[p44<=0 & 0<=p44] | [p13<=0 & 0<=p13]]] & [[[[p45<=0 & 0<=p45] | [p13<=0 & 0<=p13]] & [[p46<=0 & 0<=p46] | [p13<=0 & 0<=p13]]] & [[p47<=0 & 0<=p47] | [p13<=0 & 0<=p13]]]]]]]] | ~ [EX [~ [[[[[[p158<=0 & 0<=p158] | [p13<=0 & 0<=p13]] & [[p161<=0 & 0<=p161] | [p13<=0 & 0<=p13]]] & [[p162<=0 & 0<=p162] | [p13<=0 & 0<=p13]]] & [[[[p159<=0 & 0<=p159] | [p13<=0 & 0<=p13]] & [[p160<=0 & 0<=p160] | [p13<=0 & 0<=p13]]] & [[p163<=0 & 0<=p163] | [p13<=0 & 0<=p13]]]]]]]]]]
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p163)
states: 547,231,759,144 (11)
abstracting: (p163<=0)
states: 530,678,972,010 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p160)
states: 547,231,759,144 (11)
abstracting: (p160<=0)
states: 530,678,972,010 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p159)
states: 547,231,759,144 (11)
abstracting: (p159<=0)
states: 530,678,972,010 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p162)
states: 547,231,759,144 (11)
abstracting: (p162<=0)
states: 530,678,972,010 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p161)
states: 547,231,759,144 (11)
abstracting: (p161<=0)
states: 530,678,972,010 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p158)
states: 547,231,759,144 (11)
abstracting: (p158<=0)
before gc: list nodes free: 5360824
after gc: idd nodes used:5313229, unused:58686771; list nodes free:264037340
states: 530,678,972,010 (11)
.abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p47)
states: 547,231,759,144 (11)
abstracting: (p47<=0)
states: 529,752,753,288 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p46)
states: 547,231,759,144 (11)
abstracting: (p46<=0)
states: 529,752,753,288 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p45)
states: 547,231,759,144 (11)
abstracting: (p45<=0)
states: 529,752,753,288 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p44)
states: 547,231,759,144 (11)
abstracting: (p44<=0)
states: 529,752,753,288 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p49)
states: 547,231,759,144 (11)
abstracting: (p49<=0)
states: 529,752,753,288 (11)
abstracting: (0<=p13)
states: 547,231,759,144 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (0<=p48)
states: 547,231,759,144 (11)
abstracting: (p48<=0)
states: 529,752,753,288 (11)
.MC time: 1m25.265sec
checking: [E [~ [EF [[[[[[p70<=1 & 1<=p70] | [p73<=1 & 1<=p73]] | [p71<=1 & 1<=p71]] | [[p72<=1 & 1<=p72] | [[p69<=1 & 1<=p69] | [p68<=1 & 1<=p68]]]] | [[[[p13<=1 & 1<=p13] & [p163<=1 & 1<=p163]] | [[[p13<=1 & 1<=p13] & [p160<=1 & 1<=p160]] | [[p13<=1 & 1<=p13] & [p159<=1 & 1<=p159]]]] | [[[p13<=1 & 1<=p13] & [p162<=1 & 1<=p162]] | [[[p13<=1 & 1<=p13] & [p161<=1 & 1<=p161]] | [[p13<=1 & 1<=p13] & [p158<=1 & 1<=p158]]]]]]]] U [[[[[[[p17<=1 & 1<=p17] & [p55<=1 & 1<=p55]] | [[p16<=1 & 1<=p16] & [p53<=1 & 1<=p53]]] | [[[p16<=1 & 1<=p16] & [p55<=1 & 1<=p55]] | [[[p16<=1 & 1<=p16] & [p51<=1 & 1<=p51]] | [[p13<=1 & 1<=p13] & [p54<=1 & 1<=p54]]]]] | [[[[p13<=1 & 1<=p13] & [p52<=1 & 1<=p52]] | [[p13<=1 & 1<=p13] & [p50<=1 & 1<=p50]]] | [[[p17<=1 & 1<=p17] & [p53<=1 & 1<=p53]] | [[[p17<=1 & 1<=p17] & [p51<=1 & 1<=p51]] | [[p14<=1 & 1<=p14] & [p51<=1 & 1<=p51]]]]]] | [[[[[p19<=1 & 1<=p19] & [p54<=1 & 1<=p54]] | [[p19<=1 & 1<=p19] & [p50<=1 & 1<=p50]]] | [[[p14<=1 & 1<=p14] & [p53<=1 & 1<=p53]] | [[[p14<=1 & 1<=p14] & [p55<=1 & 1<=p55]] | [[p18<=1 & 1<=p18] & [p50<=1 & 1<=p50]]]]] | [[[[p18<=1 & 1<=p18] & [p52<=1 & 1<=p52]] | [[[p18<=1 & 1<=p18] & [p54<=1 & 1<=p54]] | [[p15<=1 & 1<=p15] & [p55<=1 & 1<=p55]]]] | [[[p15<=1 & 1<=p15] & [p53<=1 & 1<=p53]] | [[[p15<=1 & 1<=p15] & [p51<=1 & 1<=p51]] | [[p19<=1 & 1<=p19] & [p52<=1 & 1<=p52]]]]]]] | [[[[[[p16<=1 & 1<=p16] & [p52<=1 & 1<=p52]] | [[p16<=1 & 1<=p16] & [p54<=1 & 1<=p54]]] | [[[p16<=1 & 1<=p16] & [p50<=1 & 1<=p50]] | [[[p13<=1 & 1<=p13] & [p53<=1 & 1<=p53]] | [[p13<=1 & 1<=p13] & [p51<=1 & 1<=p51]]]]] | [[[[p13<=1 & 1<=p13] & [p55<=1 & 1<=p55]] | [[p17<=1 & 1<=p17] & [p50<=1 & 1<=p50]]] | [[[p17<=1 & 1<=p17] & [p54<=1 & 1<=p54]] | [[[p17<=1 & 1<=p17] & [p52<=1 & 1<=p52]] | [[p19<=1 & 1<=p19] & [p53<=1 & 1<=p53]]]]]] | [[[[[p14<=1 & 1<=p14] & [p50<=1 & 1<=p50]] | [[p19<=1 & 1<=p19] & [p55<=1 & 1<=p55]]] | [[[p14<=1 & 1<=p14] & [p52<=1 & 1<=p52]] | [[[p14<=1 & 1<=p14] & [p54<=1 & 1<=p54]] | [[p18<=1 & 1<=p18] & [p51<=1 & 1<=p51]]]]] | [[[[p18<=1 & 1<=p18] & [p53<=1 & 1<=p53]] | [[[p18<=1 & 1<=p18] & [p55<=1 & 1<=p55]] | [[p15<=1 & 1<=p15] & [p54<=1 & 1<=p54]]]] | [[[p15<=1 & 1<=p15] & [p52<=1 & 1<=p52]] | [[[p15<=1 & 1<=p15] & [p50<=1 & 1<=p50]] | [[p19<=1 & 1<=p19] & [p51<=1 & 1<=p51]]]]]]]]] | [AF [AX [EG [[[[[p13<=0 & 0<=p13] | [p163<=0 & 0<=p163]] & [[[p13<=0 & 0<=p13] | [p160<=0 & 0<=p160]] & [[p13<=0 & 0<=p13] | [p159<=0 & 0<=p159]]]] & [[[p13<=0 & 0<=p13] | [p162<=0 & 0<=p162]] & [[[p13<=0 & 0<=p13] | [p161<=0 & 0<=p161]] & [[p13<=0 & 0<=p13] | [p158<=0 & 0<=p158]]]]]]]] | AG [AX [[EG [[[[[[p21<=0 & 0<=p21] | [p170<=0 & 0<=p170]] & [[[p26<=0 & 0<=p26] | [p173<=0 & 0<=p173]] & [[p24<=0 & 0<=p24] | [p172<=0 & 0<=p172]]]] & [[[p23<=0 & 0<=p23] | [p171<=0 & 0<=p171]] & [[[p27<=0 & 0<=p27] | [p173<=0 & 0<=p173]] & [[p29<=0 & 0<=p29] | [p174<=0 & 0<=p174]]]]] & [[[[p31<=0 & 0<=p31] | [p175<=0 & 0<=p175]] & [[[p30<=0 & 0<=p30] | [p175<=0 & 0<=p175]] & [[p25<=0 & 0<=p25] | [p172<=0 & 0<=p172]]]] & [[[p22<=0 & 0<=p22] | [p171<=0 & 0<=p171]] & [[[p20<=0 & 0<=p20] | [p170<=0 & 0<=p170]] & [[p28<=0 & 0<=p28] | [p174<=0 & 0<=p174]]]]]]] & [[AX [[[[[[p23<=1 & 1<=p23] & [p39<=1 & 1<=p39]] | [[[p28<=1 & 1<=p28] & [p42<=1 & 1<=p42]] | [[p26<=1 & 1<=p26] & [p41<=1 & 1<=p41]]]] | [[[p31<=1 & 1<=p31] & [p43<=1 & 1<=p43]] | [[[p25<=1 & 1<=p25] & [p40<=1 & 1<=p40]] | [[p21<=1 & 1<=p21] & [p38<=1 & 1<=p38]]]]] | [[[[p27<=1 & 1<=p27] & [p41<=1 & 1<=p41]] | [[[p22<=1 & 1<=p22] & [p39<=1 & 1<=p39]] | [[p30<=1 & 1<=p30] & [p43<=1 & 1<=p43]]]] | [[[p29<=1 & 1<=p29] & [p42<=1 & 1<=p42]] | [[[p20<=1 & 1<=p20] & [p38<=1 & 1<=p38]] | [[p24<=1 & 1<=p24] & [p40<=1 & 1<=p40]]]]]]] | [[p71<=1 & 1<=p71] | [p70<=1 & 1<=p70]]] | [[[p73<=1 & 1<=p73] | [p72<=1 & 1<=p72]] | [[p69<=1 & 1<=p69] | [p68<=1 & 1<=p68]]]]]]]]]
normalized: [[~ [E [true U EX [~ [[[[[[p68<=1 & 1<=p68] | [p69<=1 & 1<=p69]] | [[p72<=1 & 1<=p72] | [p73<=1 & 1<=p73]]] | [[[p70<=1 & 1<=p70] | [p71<=1 & 1<=p71]] | ~ [EX [~ [[[[[[[p40<=1 & 1<=p40] & [p24<=1 & 1<=p24]] | [[p38<=1 & 1<=p38] & [p20<=1 & 1<=p20]]] | [[p42<=1 & 1<=p42] & [p29<=1 & 1<=p29]]] | [[[[p43<=1 & 1<=p43] & [p30<=1 & 1<=p30]] | [[p39<=1 & 1<=p39] & [p22<=1 & 1<=p22]]] | [[p41<=1 & 1<=p41] & [p27<=1 & 1<=p27]]]] | [[[[[p38<=1 & 1<=p38] & [p21<=1 & 1<=p21]] | [[p40<=1 & 1<=p40] & [p25<=1 & 1<=p25]]] | [[p43<=1 & 1<=p43] & [p31<=1 & 1<=p31]]] | [[[[p41<=1 & 1<=p41] & [p26<=1 & 1<=p26]] | [[p42<=1 & 1<=p42] & [p28<=1 & 1<=p28]]] | [[p39<=1 & 1<=p39] & [p23<=1 & 1<=p23]]]]]]]]]] & EG [[[[[[[p174<=0 & 0<=p174] | [p28<=0 & 0<=p28]] & [[p170<=0 & 0<=p170] | [p20<=0 & 0<=p20]]] & [[p171<=0 & 0<=p171] | [p22<=0 & 0<=p22]]] & [[[[p172<=0 & 0<=p172] | [p25<=0 & 0<=p25]] & [[p175<=0 & 0<=p175] | [p30<=0 & 0<=p30]]] & [[p175<=0 & 0<=p175] | [p31<=0 & 0<=p31]]]] & [[[[[p174<=0 & 0<=p174] | [p29<=0 & 0<=p29]] & [[p173<=0 & 0<=p173] | [p27<=0 & 0<=p27]]] & [[p171<=0 & 0<=p171] | [p23<=0 & 0<=p23]]] & [[[[p172<=0 & 0<=p172] | [p24<=0 & 0<=p24]] & [[p173<=0 & 0<=p173] | [p26<=0 & 0<=p26]]] & [[p170<=0 & 0<=p170] | [p21<=0 & 0<=p21]]]]]]]]]]] | ~ [EG [EX [~ [EG [[[[[[p158<=0 & 0<=p158] | [p13<=0 & 0<=p13]] & [[p161<=0 & 0<=p161] | [p13<=0 & 0<=p13]]] & [[p162<=0 & 0<=p162] | [p13<=0 & 0<=p13]]] & [[[[p159<=0 & 0<=p159] | [p13<=0 & 0<=p13]] & [[p160<=0 & 0<=p160] | [p13<=0 & 0<=p13]]] & [[p163<=0 & 0<=p163] | [p13<=0 & 0<=p13]]]]]]]]]] | E [~ [E [true U [[[[[[p158<=1 & 1<=p158] & [p13<=1 & 1<=p13]] | [[p161<=1 & 1<=p161] & [p13<=1 & 1<=p13]]] | [[p162<=1 & 1<=p162] & [p13<=1 & 1<=p13]]] | [[[[p159<=1 & 1<=p159] & [p13<=1 & 1<=p13]] | [[p160<=1 & 1<=p160] & [p13<=1 & 1<=p13]]] | [[p163<=1 & 1<=p163] & [p13<=1 & 1<=p13]]]] | [[[[p68<=1 & 1<=p68] | [p69<=1 & 1<=p69]] | [p72<=1 & 1<=p72]] | [[p71<=1 & 1<=p71] | [[p73<=1 & 1<=p73] | [p70<=1 & 1<=p70]]]]]]] U [[[[[[[[p51<=1 & 1<=p51] & [p19<=1 & 1<=p19]] | [[p50<=1 & 1<=p50] & [p15<=1 & 1<=p15]]] | [[p52<=1 & 1<=p52] & [p15<=1 & 1<=p15]]] | [[[[p54<=1 & 1<=p54] & [p15<=1 & 1<=p15]] | [[p55<=1 & 1<=p55] & [p18<=1 & 1<=p18]]] | [[p53<=1 & 1<=p53] & [p18<=1 & 1<=p18]]]] | [[[[[p51<=1 & 1<=p51] & [p18<=1 & 1<=p18]] | [[p54<=1 & 1<=p54] & [p14<=1 & 1<=p14]]] | [[p52<=1 & 1<=p52] & [p14<=1 & 1<=p14]]] | [[[p55<=1 & 1<=p55] & [p19<=1 & 1<=p19]] | [[p50<=1 & 1<=p50] & [p14<=1 & 1<=p14]]]]] | [[[[[[p53<=1 & 1<=p53] & [p19<=1 & 1<=p19]] | [[p52<=1 & 1<=p52] & [p17<=1 & 1<=p17]]] | [[p54<=1 & 1<=p54] & [p17<=1 & 1<=p17]]] | [[[p50<=1 & 1<=p50] & [p17<=1 & 1<=p17]] | [[p55<=1 & 1<=p55] & [p13<=1 & 1<=p13]]]] | [[[[[p51<=1 & 1<=p51] & [p13<=1 & 1<=p13]] | [[p53<=1 & 1<=p53] & [p13<=1 & 1<=p13]]] | [[p50<=1 & 1<=p50] & [p16<=1 & 1<=p16]]] | [[[p54<=1 & 1<=p54] & [p16<=1 & 1<=p16]] | [[p52<=1 & 1<=p52] & [p16<=1 & 1<=p16]]]]]] | [[[[[[[p52<=1 & 1<=p52] & [p19<=1 & 1<=p19]] | [[p51<=1 & 1<=p51] & [p15<=1 & 1<=p15]]] | [[p53<=1 & 1<=p53] & [p15<=1 & 1<=p15]]] | [[[[p55<=1 & 1<=p55] & [p15<=1 & 1<=p15]] | [[p54<=1 & 1<=p54] & [p18<=1 & 1<=p18]]] | [[p52<=1 & 1<=p52] & [p18<=1 & 1<=p18]]]] | [[[[[p50<=1 & 1<=p50] & [p18<=1 & 1<=p18]] | [[p55<=1 & 1<=p55] & [p14<=1 & 1<=p14]]] | [[p53<=1 & 1<=p53] & [p14<=1 & 1<=p14]]] | [[[p50<=1 & 1<=p50] & [p19<=1 & 1<=p19]] | [[p54<=1 & 1<=p54] & [p19<=1 & 1<=p19]]]]] | [[[[[[p51<=1 & 1<=p51] & [p14<=1 & 1<=p14]] | [[p51<=1 & 1<=p51] & [p17<=1 & 1<=p17]]] | [[p53<=1 & 1<=p53] & [p17<=1 & 1<=p17]]] | [[[p50<=1 & 1<=p50] & [p13<=1 & 1<=p13]] | [[p52<=1 & 1<=p52] & [p13<=1 & 1<=p13]]]] | [[[[[p54<=1 & 1<=p54] & [p13<=1 & 1<=p13]] | [[p51<=1 & 1<=p51] & [p16<=1 & 1<=p16]]] | [[p55<=1 & 1<=p55] & [p16<=1 & 1<=p16]]] | [[[p53<=1 & 1<=p53] & [p16<=1 & 1<=p16]] | [[p55<=1 & 1<=p55] & [p17<=1 & 1<=p17]]]]]]]]]
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p70)
states: 6,677,072,160 (9)
abstracting: (p70<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p73)
states: 6,677,072,160 (9)
abstracting: (p73<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p71)
states: 6,677,072,160 (9)
abstracting: (p71<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p72)
states: 6,677,072,160 (9)
abstracting: (p72<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p69)
states: 6,677,072,160 (9)
abstracting: (p69<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p68)
states: 6,677,072,160 (9)
abstracting: (p68<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p163)
states: 16,552,787,134 (10)
abstracting: (p163<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p160)
states: 16,552,787,134 (10)
abstracting: (p160<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p159)
states: 16,552,787,134 (10)
abstracting: (p159<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p162)
states: 16,552,787,134 (10)
abstracting: (p162<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p161)
states: 16,552,787,134 (10)
abstracting: (p161<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p158)
states: 16,552,787,134 (10)
abstracting: (p158<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 6171506
after gc: idd nodes used:11024825, unused:52975175; list nodes free:239008883
MC time: 1m20.209sec
checking: EG [AF [[AF [AG [[[[[[p110<=1 & 1<=p110] & [[p116<=1 & 1<=p116] & [p117<=1 & 1<=p117]]] & [[[p118<=1 & 1<=p118] & [p119<=1 & 1<=p119]] & [[p120<=1 & 1<=p120] & [p121<=1 & 1<=p121]]]] | [[[[p114<=1 & 1<=p114] & [[p140<=1 & 1<=p140] & [p141<=1 & 1<=p141]]] & [[[p142<=1 & 1<=p142] & [p143<=1 & 1<=p143]] & [[p144<=1 & 1<=p144] & [p145<=1 & 1<=p145]]]] | [[[p111<=1 & 1<=p111] & [[p122<=1 & 1<=p122] & [p123<=1 & 1<=p123]]] & [[[p124<=1 & 1<=p124] & [p125<=1 & 1<=p125]] & [[p126<=1 & 1<=p126] & [p127<=1 & 1<=p127]]]]]] | [[[[p115<=1 & 1<=p115] & [[p146<=1 & 1<=p146] & [p147<=1 & 1<=p147]]] & [[[p148<=1 & 1<=p148] & [p149<=1 & 1<=p149]] & [[p150<=1 & 1<=p150] & [p151<=1 & 1<=p151]]]] | [[[[p113<=1 & 1<=p113] & [[p134<=1 & 1<=p134] & [p135<=1 & 1<=p135]]] & [[[p136<=1 & 1<=p136] & [p137<=1 & 1<=p137]] & [[p138<=1 & 1<=p138] & [p139<=1 & 1<=p139]]]] | [[[p112<=1 & 1<=p112] & [[p128<=1 & 1<=p128] & [p129<=1 & 1<=p129]]] & [[[p130<=1 & 1<=p130] & [p131<=1 & 1<=p131]] & [[p132<=1 & 1<=p132] & [p133<=1 & 1<=p133]]]]]]]]] | [AG [[[[[[[[p26<=1 & 1<=p26] & [[p83<=1 & 1<=p83] & [p111<=1 & 1<=p111]]] | [[p24<=1 & 1<=p24] & [[p100<=1 & 1<=p100] & [p114<=1 & 1<=p114]]]] | [[[p22<=1 & 1<=p22] & [[p93<=1 & 1<=p93] & [p113<=1 & 1<=p113]]] | [[p30<=1 & 1<=p30] & [[p103<=1 & 1<=p103] & [p114<=1 & 1<=p114]]]]] | [[[[p28<=1 & 1<=p28] & [[p90<=1 & 1<=p90] & [p112<=1 & 1<=p112]]] | [[p20<=1 & 1<=p20] & [[p86<=1 & 1<=p86] & [p112<=1 & 1<=p112]]]] | [[[p30<=1 & 1<=p30] & [[p79<=1 & 1<=p79] & [p110<=1 & 1<=p110]]] | [[[p24<=1 & 1<=p24] & [[p106<=1 & 1<=p106] & [p115<=1 & 1<=p115]]] | [[p20<=1 & 1<=p20] & [[p74<=1 & 1<=p74] & [p110<=1 & 1<=p110]]]]]]] | [[[[[p22<=1 & 1<=p22] & [[p99<=1 & 1<=p99] & [p114<=1 & 1<=p114]]] | [[p30<=1 & 1<=p30] & [[p97<=1 & 1<=p97] & [p113<=1 & 1<=p113]]]] | [[[p20<=1 & 1<=p20] & [[p104<=1 & 1<=p104] & [p115<=1 & 1<=p115]]] | [[p24<=1 & 1<=p24] & [[p82<=1 & 1<=p82] & [p111<=1 & 1<=p111]]]]] | [[[[p30<=1 & 1<=p30] & [[p85<=1 & 1<=p85] & [p111<=1 & 1<=p111]]] | [[p28<=1 & 1<=p28] & [[p96<=1 & 1<=p96] & [p113<=1 & 1<=p113]]]] | [[[p26<=1 & 1<=p26] & [[p89<=1 & 1<=p89] & [p112<=1 & 1<=p112]]] | [[[p26<=1 & 1<=p26] & [[p107<=1 & 1<=p107] & [p115<=1 & 1<=p115]]] | [[p28<=1 & 1<=p28] & [[p108<=1 & 1<=p108] & [p115<=1 & 1<=p115]]]]]]]] | [[[[[[p22<=1 & 1<=p22] & [[p105<=1 & 1<=p105] & [p115<=1 & 1<=p115]]] | [[p28<=1 & 1<=p28] & [[p78<=1 & 1<=p78] & [p110<=1 & 1<=p110]]]] | [[[p22<=1 & 1<=p22] & [[p75<=1 & 1<=p75] & [p110<=1 & 1<=p110]]] | [[p26<=1 & 1<=p26] & [[p101<=1 & 1<=p101] & [p114<=1 & 1<=p114]]]]] | [[[[p22<=1 & 1<=p22] & [[p81<=1 & 1<=p81] & [p111<=1 & 1<=p111]]] | [[p20<=1 & 1<=p20] & [[p92<=1 & 1<=p92] & [p113<=1 & 1<=p113]]]] | [[[p26<=1 & 1<=p26] & [[p95<=1 & 1<=p95] & [p113<=1 & 1<=p113]]] | [[[p24<=1 & 1<=p24] & [[p88<=1 & 1<=p88] & [p112<=1 & 1<=p112]]] | [[p24<=1 & 1<=p24] & [[p94<=1 & 1<=p94] & [p113<=1 & 1<=p113]]]]]]] | [[[[[p26<=1 & 1<=p26] & [[p77<=1 & 1<=p77] & [p110<=1 & 1<=p110]]] | [[p28<=1 & 1<=p28] & [[p84<=1 & 1<=p84] & [p111<=1 & 1<=p111]]]] | [[[p28<=1 & 1<=p28] & [[p102<=1 & 1<=p102] & [p114<=1 & 1<=p114]]] | [[p24<=1 & 1<=p24] & [[p76<=1 & 1<=p76] & [p110<=1 & 1<=p110]]]]] | [[[[p22<=1 & 1<=p22] & [[p87<=1 & 1<=p87] & [p112<=1 & 1<=p112]]] | [[p30<=1 & 1<=p30] & [[p91<=1 & 1<=p91] & [p112<=1 & 1<=p112]]]] | [[[p30<=1 & 1<=p30] & [[p109<=1 & 1<=p109] & [p115<=1 & 1<=p115]]] | [[[p20<=1 & 1<=p20] & [[p80<=1 & 1<=p80] & [p111<=1 & 1<=p111]]] | [[p20<=1 & 1<=p20] & [[p98<=1 & 1<=p98] & [p114<=1 & 1<=p114]]]]]]]]]] & [[[[[[EF [[[[[[[[p13<=1 & 1<=p13] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p169<=1 & 1<=p169]]] | [[[p18<=1 & 1<=p18] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p168<=1 & 1<=p168]]]]] | [[[[p17<=1 & 1<=p17] & [p164<=1 & 1<=p164]] | [[p14<=1 & 1<=p14] & [p169<=1 & 1<=p169]]] | [[[p19<=1 & 1<=p19] & [p166<=1 & 1<=p166]] | [[[p19<=1 & 1<=p19] & [p164<=1 & 1<=p164]] | [[p19<=1 & 1<=p19] & [p168<=1 & 1<=p168]]]]]] | [[[[[p16<=1 & 1<=p16] & [p166<=1 & 1<=p166]] | [[p15<=1 & 1<=p15] & [p169<=1 & 1<=p169]]] | [[[p16<=1 & 1<=p16] & [p164<=1 & 1<=p164]] | [[[p15<=1 & 1<=p15] & [p164<=1 & 1<=p164]] | [[p16<=1 & 1<=p16] & [p169<=1 & 1<=p169]]]]] | [[[[p15<=1 & 1<=p15] & [p166<=1 & 1<=p166]] | [[[p16<=1 & 1<=p16] & [p167<=1 & 1<=p167]] | [[p14<=1 & 1<=p14] & [p164<=1 & 1<=p164]]]] | [[[p14<=1 & 1<=p14] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]] | [[p14<=1 & 1<=p14] & [p166<=1 & 1<=p166]]]]]]] | [[[[[[p17<=1 & 1<=p17] & [p167<=1 & 1<=p167]] | [[p18<=1 & 1<=p18] & [p169<=1 & 1<=p169]]] | [[[p13<=1 & 1<=p13] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p168<=1 & 1<=p168]] | [[p18<=1 & 1<=p18] & [p165<=1 & 1<=p165]]]]] | [[[[p18<=1 & 1<=p18] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p164<=1 & 1<=p164]]] | [[[p17<=1 & 1<=p17] & [p165<=1 & 1<=p165]] | [[[p19<=1 & 1<=p19] & [p167<=1 & 1<=p167]] | [[p19<=1 & 1<=p19] & [p165<=1 & 1<=p165]]]]]] | [[[[[p19<=1 & 1<=p19] & [p169<=1 & 1<=p169]] | [[p16<=1 & 1<=p16] & [p165<=1 & 1<=p165]]] | [[[p15<=1 & 1<=p15] & [p168<=1 & 1<=p168]] | [[[p15<=1 & 1<=p15] & [p165<=1 & 1<=p165]] | [[p15<=1 & 1<=p15] & [p167<=1 & 1<=p167]]]]] | [[[[p16<=1 & 1<=p16] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p168<=1 & 1<=p168]] | [[p17<=1 & 1<=p17] & [p166<=1 & 1<=p166]]]] | [[[p14<=1 & 1<=p14] & [p167<=1 & 1<=p167]] | [[[p14<=1 & 1<=p14] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p164<=1 & 1<=p164]]]]]]]]] & [[[p71<=1 & 1<=p71] | [[p70<=1 & 1<=p70] | [p73<=1 & 1<=p73]]] | [[p72<=1 & 1<=p72] | [[p69<=1 & 1<=p69] | [p68<=1 & 1<=p68]]]]] | [[p16<=1 & 1<=p16] & [p46<=1 & 1<=p46]]] | [[[p16<=1 & 1<=p16] & [p45<=1 & 1<=p45]] | [[p16<=1 & 1<=p16] & [p48<=1 & 1<=p48]]]] | [[[[p16<=1 & 1<=p16] & [p47<=1 & 1<=p47]] | [[p16<=1 & 1<=p16] & [p44<=1 & 1<=p44]]] | [[[p16<=1 & 1<=p16] & [p49<=1 & 1<=p49]] | [[[p17<=1 & 1<=p17] & [p47<=1 & 1<=p47]] | [[p17<=1 & 1<=p17] & [p46<=1 & 1<=p46]]]]]] | [[[[[p17<=1 & 1<=p17] & [p45<=1 & 1<=p45]] | [[p17<=1 & 1<=p17] & [p44<=1 & 1<=p44]]] | [[[p17<=1 & 1<=p17] & [p49<=1 & 1<=p49]] | [[p17<=1 & 1<=p17] & [p48<=1 & 1<=p48]]]] | [[[[p18<=1 & 1<=p18] & [p44<=1 & 1<=p44]] | [[p19<=1 & 1<=p19] & [p49<=1 & 1<=p49]]] | [[[p19<=1 & 1<=p19] & [p48<=1 & 1<=p48]] | [[[p18<=1 & 1<=p18] & [p46<=1 & 1<=p46]] | [[p19<=1 & 1<=p19] & [p47<=1 & 1<=p47]]]]]]] | [[[[[[p18<=1 & 1<=p18] & [p45<=1 & 1<=p45]] | [[p19<=1 & 1<=p19] & [p46<=1 & 1<=p46]]] | [[[p14<=1 & 1<=p14] & [p44<=1 & 1<=p44]] | [[p19<=1 & 1<=p19] & [p45<=1 & 1<=p45]]]] | [[[[p18<=1 & 1<=p18] & [p48<=1 & 1<=p48]] | [[p19<=1 & 1<=p19] & [p44<=1 & 1<=p44]]] | [[[p18<=1 & 1<=p18] & [p47<=1 & 1<=p47]] | [[[p14<=1 & 1<=p14] & [p46<=1 & 1<=p46]] | [[p14<=1 & 1<=p14] & [p45<=1 & 1<=p45]]]]]] | [[[[[p18<=1 & 1<=p18] & [p49<=1 & 1<=p49]] | [[p14<=1 & 1<=p14] & [p48<=1 & 1<=p48]]] | [[[p14<=1 & 1<=p14] & [p47<=1 & 1<=p47]] | [[[p14<=1 & 1<=p14] & [p49<=1 & 1<=p49]] | [[p15<=1 & 1<=p15] & [p49<=1 & 1<=p49]]]]] | [[[[p15<=1 & 1<=p15] & [p48<=1 & 1<=p48]] | [[p15<=1 & 1<=p15] & [p47<=1 & 1<=p47]]] | [[[p15<=1 & 1<=p15] & [1<=p46 & p46<=1]] | [[[p15<=1 & 1<=p15] & [p45<=1 & 1<=p45]] | [[p15<=1 & 1<=p15] & [p44<=1 & 1<=p44]]]]]]]]]]]]
normalized: EG [~ [EG [~ [[[[[[[[[[p44<=1 & 1<=p44] & [p19<=1 & 1<=p19]] | [[p48<=1 & 1<=p48] & [p18<=1 & 1<=p18]]] | [[[[p45<=1 & 1<=p45] & [p14<=1 & 1<=p14]] | [[p46<=1 & 1<=p46] & [p14<=1 & 1<=p14]]] | [[p47<=1 & 1<=p47] & [p18<=1 & 1<=p18]]]] | [[[[p45<=1 & 1<=p45] & [p19<=1 & 1<=p19]] | [[p44<=1 & 1<=p44] & [p14<=1 & 1<=p14]]] | [[[p46<=1 & 1<=p46] & [p19<=1 & 1<=p19]] | [[p45<=1 & 1<=p45] & [p18<=1 & 1<=p18]]]]] | [[[[[[p44<=1 & 1<=p44] & [p15<=1 & 1<=p15]] | [[p45<=1 & 1<=p45] & [p15<=1 & 1<=p15]]] | [[1<=p46 & p46<=1] & [p15<=1 & 1<=p15]]] | [[[p47<=1 & 1<=p47] & [p15<=1 & 1<=p15]] | [[p48<=1 & 1<=p48] & [p15<=1 & 1<=p15]]]] | [[[[[p49<=1 & 1<=p49] & [p15<=1 & 1<=p15]] | [[p49<=1 & 1<=p49] & [p14<=1 & 1<=p14]]] | [[p47<=1 & 1<=p47] & [p14<=1 & 1<=p14]]] | [[[p48<=1 & 1<=p48] & [p14<=1 & 1<=p14]] | [[p49<=1 & 1<=p49] & [p18<=1 & 1<=p18]]]]]] | [[[[[[p49<=1 & 1<=p49] & [p19<=1 & 1<=p19]] | [[p44<=1 & 1<=p44] & [p18<=1 & 1<=p18]]] | [[[[p47<=1 & 1<=p47] & [p19<=1 & 1<=p19]] | [[p46<=1 & 1<=p46] & [p18<=1 & 1<=p18]]] | [[p48<=1 & 1<=p48] & [p19<=1 & 1<=p19]]]] | [[[[p48<=1 & 1<=p48] & [p17<=1 & 1<=p17]] | [[p49<=1 & 1<=p49] & [p17<=1 & 1<=p17]]] | [[[p44<=1 & 1<=p44] & [p17<=1 & 1<=p17]] | [[p45<=1 & 1<=p45] & [p17<=1 & 1<=p17]]]]] | [[[[[[p46<=1 & 1<=p46] & [p17<=1 & 1<=p17]] | [[p47<=1 & 1<=p47] & [p17<=1 & 1<=p17]]] | [[p49<=1 & 1<=p49] & [p16<=1 & 1<=p16]]] | [[[p44<=1 & 1<=p44] & [p16<=1 & 1<=p16]] | [[p47<=1 & 1<=p47] & [p16<=1 & 1<=p16]]]] | [[[[p48<=1 & 1<=p48] & [p16<=1 & 1<=p16]] | [[p45<=1 & 1<=p45] & [p16<=1 & 1<=p16]]] | [[[p46<=1 & 1<=p46] & [p16<=1 & 1<=p16]] | [[[[[p68<=1 & 1<=p68] | [p69<=1 & 1<=p69]] | [p72<=1 & 1<=p72]] | [[[p73<=1 & 1<=p73] | [p70<=1 & 1<=p70]] | [p71<=1 & 1<=p71]]] & E [true U [[[[[[[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p14<=1 & 1<=p14]]] | [[p167<=1 & 1<=p167] & [p14<=1 & 1<=p14]]] | [[[[p166<=1 & 1<=p166] & [p17<=1 & 1<=p17]] | [[p168<=1 & 1<=p168] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p16<=1 & 1<=p16]]]] | [[[[[p167<=1 & 1<=p167] & [p15<=1 & 1<=p15]] | [[p165<=1 & 1<=p165] & [p15<=1 & 1<=p15]]] | [[p168<=1 & 1<=p168] & [p15<=1 & 1<=p15]]] | [[[p165<=1 & 1<=p165] & [p16<=1 & 1<=p16]] | [[p169<=1 & 1<=p169] & [p19<=1 & 1<=p19]]]]] | [[[[[[p165<=1 & 1<=p165] & [p19<=1 & 1<=p19]] | [[p167<=1 & 1<=p167] & [p19<=1 & 1<=p19]]] | [[p165<=1 & 1<=p165] & [p17<=1 & 1<=p17]]] | [[[p164<=1 & 1<=p164] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p18<=1 & 1<=p18]]]] | [[[[[p165<=1 & 1<=p165] & [p18<=1 & 1<=p18]] | [[p168<=1 & 1<=p168] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p13<=1 & 1<=p13]]] | [[[p169<=1 & 1<=p169] & [p18<=1 & 1<=p18]] | [[p167<=1 & 1<=p167] & [p17<=1 & 1<=p17]]]]]] | [[[[[[[p166<=1 & 1<=p166] & [p14<=1 & 1<=p14]] | [[p169<=1 & 1<=p169] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p14<=1 & 1<=p14]]] | [[[[p164<=1 & 1<=p164] & [p14<=1 & 1<=p14]] | [[p167<=1 & 1<=p167] & [p16<=1 & 1<=p16]]] | [[p166<=1 & 1<=p166] & [p15<=1 & 1<=p15]]]] | [[[[[p169<=1 & 1<=p169] & [p16<=1 & 1<=p16]] | [[p164<=1 & 1<=p164] & [p15<=1 & 1<=p15]]] | [[p164<=1 & 1<=p164] & [p16<=1 & 1<=p16]]] | [[[p169<=1 & 1<=p169] & [p15<=1 & 1<=p15]] | [[p166<=1 & 1<=p166] & [p16<=1 & 1<=p16]]]]] | [[[[[[p168<=1 & 1<=p168] & [p19<=1 & 1<=p19]] | [[p164<=1 & 1<=p164] & [p19<=1 & 1<=p19]]] | [[p166<=1 & 1<=p166] & [p19<=1 & 1<=p19]]] | [[[p169<=1 & 1<=p169] & [p14<=1 & 1<=p14]] | [[p164<=1 & 1<=p164] & [p17<=1 & 1<=p17]]]] | [[[[[p168<=1 & 1<=p168] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p18<=1 & 1<=p18]]] | [[[p169<=1 & 1<=p169] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p13<=1 & 1<=p13]]]]]]]]]]]]]] & ~ [E [true U ~ [[[[[[[[[[p114<=1 & 1<=p114] & [p98<=1 & 1<=p98]] & [p20<=1 & 1<=p20]] | [[[p111<=1 & 1<=p111] & [p80<=1 & 1<=p80]] & [p20<=1 & 1<=p20]]] | [[[p115<=1 & 1<=p115] & [p109<=1 & 1<=p109]] & [p30<=1 & 1<=p30]]] | [[[[p112<=1 & 1<=p112] & [p91<=1 & 1<=p91]] & [p30<=1 & 1<=p30]] | [[[p112<=1 & 1<=p112] & [p87<=1 & 1<=p87]] & [p22<=1 & 1<=p22]]]] | [[[[[p110<=1 & 1<=p110] & [p76<=1 & 1<=p76]] & [p24<=1 & 1<=p24]] | [[[p114<=1 & 1<=p114] & [p102<=1 & 1<=p102]] & [p28<=1 & 1<=p28]]] | [[[[p111<=1 & 1<=p111] & [p84<=1 & 1<=p84]] & [p28<=1 & 1<=p28]] | [[[p110<=1 & 1<=p110] & [p77<=1 & 1<=p77]] & [p26<=1 & 1<=p26]]]]] | [[[[[[[p113<=1 & 1<=p113] & [p94<=1 & 1<=p94]] & [p24<=1 & 1<=p24]] | [[[p112<=1 & 1<=p112] & [p88<=1 & 1<=p88]] & [p24<=1 & 1<=p24]]] | [[[p113<=1 & 1<=p113] & [p95<=1 & 1<=p95]] & [p26<=1 & 1<=p26]]] | [[[[p113<=1 & 1<=p113] & [p92<=1 & 1<=p92]] & [p20<=1 & 1<=p20]] | [[[p111<=1 & 1<=p111] & [p81<=1 & 1<=p81]] & [p22<=1 & 1<=p22]]]] | [[[[[p114<=1 & 1<=p114] & [p101<=1 & 1<=p101]] & [p26<=1 & 1<=p26]] | [[[p110<=1 & 1<=p110] & [p75<=1 & 1<=p75]] & [p22<=1 & 1<=p22]]] | [[[[p110<=1 & 1<=p110] & [p78<=1 & 1<=p78]] & [p28<=1 & 1<=p28]] | [[[p115<=1 & 1<=p115] & [p105<=1 & 1<=p105]] & [p22<=1 & 1<=p22]]]]]] | [[[[[[[[p115<=1 & 1<=p115] & [p108<=1 & 1<=p108]] & [p28<=1 & 1<=p28]] | [[[p115<=1 & 1<=p115] & [p107<=1 & 1<=p107]] & [p26<=1 & 1<=p26]]] | [[[p112<=1 & 1<=p112] & [p89<=1 & 1<=p89]] & [p26<=1 & 1<=p26]]] | [[[[p113<=1 & 1<=p113] & [p96<=1 & 1<=p96]] & [p28<=1 & 1<=p28]] | [[[p111<=1 & 1<=p111] & [p85<=1 & 1<=p85]] & [p30<=1 & 1<=p30]]]] | [[[[[p111<=1 & 1<=p111] & [p82<=1 & 1<=p82]] & [p24<=1 & 1<=p24]] | [[[p115<=1 & 1<=p115] & [p104<=1 & 1<=p104]] & [p20<=1 & 1<=p20]]] | [[[[p113<=1 & 1<=p113] & [p97<=1 & 1<=p97]] & [p30<=1 & 1<=p30]] | [[[p114<=1 & 1<=p114] & [p99<=1 & 1<=p99]] & [p22<=1 & 1<=p22]]]]] | [[[[[[[p110<=1 & 1<=p110] & [p74<=1 & 1<=p74]] & [p20<=1 & 1<=p20]] | [[[p115<=1 & 1<=p115] & [p106<=1 & 1<=p106]] & [p24<=1 & 1<=p24]]] | [[[p110<=1 & 1<=p110] & [p79<=1 & 1<=p79]] & [p30<=1 & 1<=p30]]] | [[[[p112<=1 & 1<=p112] & [p86<=1 & 1<=p86]] & [p20<=1 & 1<=p20]] | [[[p112<=1 & 1<=p112] & [p90<=1 & 1<=p90]] & [p28<=1 & 1<=p28]]]] | [[[[[p114<=1 & 1<=p114] & [p103<=1 & 1<=p103]] & [p30<=1 & 1<=p30]] | [[[p113<=1 & 1<=p113] & [p93<=1 & 1<=p93]] & [p22<=1 & 1<=p22]]] | [[[[p114<=1 & 1<=p114] & [p100<=1 & 1<=p100]] & [p24<=1 & 1<=p24]] | [[[p111<=1 & 1<=p111] & [p83<=1 & 1<=p83]] & [p26<=1 & 1<=p26]]]]]]]]]]] | ~ [EG [E [true U ~ [[[[[[[[p133<=1 & 1<=p133] & [p132<=1 & 1<=p132]] & [[p131<=1 & 1<=p131] & [p130<=1 & 1<=p130]]] & [[[p129<=1 & 1<=p129] & [p128<=1 & 1<=p128]] & [p112<=1 & 1<=p112]]] | [[[[p139<=1 & 1<=p139] & [p138<=1 & 1<=p138]] & [[p137<=1 & 1<=p137] & [p136<=1 & 1<=p136]]] & [[[p135<=1 & 1<=p135] & [p134<=1 & 1<=p134]] & [p113<=1 & 1<=p113]]]] | [[[[p151<=1 & 1<=p151] & [p150<=1 & 1<=p150]] & [[p149<=1 & 1<=p149] & [p148<=1 & 1<=p148]]] & [[[p147<=1 & 1<=p147] & [p146<=1 & 1<=p146]] & [p115<=1 & 1<=p115]]]] | [[[[[[p127<=1 & 1<=p127] & [p126<=1 & 1<=p126]] & [[p125<=1 & 1<=p125] & [p124<=1 & 1<=p124]]] & [[[p123<=1 & 1<=p123] & [p122<=1 & 1<=p122]] & [p111<=1 & 1<=p111]]] | [[[[p145<=1 & 1<=p145] & [p144<=1 & 1<=p144]] & [[p143<=1 & 1<=p143] & [p142<=1 & 1<=p142]]] & [[[p141<=1 & 1<=p141] & [p140<=1 & 1<=p140]] & [p114<=1 & 1<=p114]]]] | [[[[p121<=1 & 1<=p121] & [p120<=1 & 1<=p120]] & [[p119<=1 & 1<=p119] & [p118<=1 & 1<=p118]]] & [[[p117<=1 & 1<=p117] & [p116<=1 & 1<=p116]] & [p110<=1 & 1<=p110]]]]]]]]]]]]]]
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p116)
states: 197,739,387,520 (11)
abstracting: (p116<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p117)
states: 194,929,046,592 (11)
abstracting: (p117<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p118)
states: 194,929,046,592 (11)
abstracting: (p118<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p119)
states: 194,929,046,592 (11)
abstracting: (p119<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p120)
states: 194,929,046,592 (11)
abstracting: (p120<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p121)
states: 194,929,046,592 (11)
abstracting: (p121<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p140)
states: 194,929,046,592 (11)
abstracting: (p140<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p141)
states: 194,929,046,592 (11)
abstracting: (p141<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p142)
states: 194,929,046,592 (11)
abstracting: (p142<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p143)
states: 194,929,046,592 (11)
abstracting: (p143<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p144)
states: 197,739,387,520 (11)
abstracting: (p144<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p145)
states: 194,929,046,592 (11)
abstracting: (p145<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p122)
states: 194,929,046,592 (11)
abstracting: (p122<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p123)
states: 197,739,387,520 (11)
abstracting: (p123<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p124)
states: 194,929,046,592 (11)
abstracting: (p124<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p125)
states: 194,929,046,592 (11)
abstracting: (p125<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p126)
states: 194,929,046,592 (11)
abstracting: (p126<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p127)
states: 194,929,046,592 (11)
abstracting: (p127<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p146)
states: 194,929,046,592 (11)
abstracting: (p146<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p147)
states: 194,929,046,592 (11)
abstracting: (p147<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p148)
states: 194,929,046,592 (11)
abstracting: (p148<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p149)
states: 194,929,046,592 (11)
abstracting: (p149<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p150)
states: 194,929,046,592 (11)
abstracting: (p150<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p151)
states: 197,739,387,520 (11)
abstracting: (p151<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p134)
states: 194,929,046,592 (11)
abstracting: (p134<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p135)
states: 194,929,046,592 (11)
abstracting: (p135<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p136)
states: 194,929,046,592 (11)
abstracting: (p136<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p137)
states: 197,739,387,520 (11)
abstracting: (p137<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p138)
states: 194,929,046,592 (11)
abstracting: (p138<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p139)
states: 194,929,046,592 (11)
abstracting: (p139<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p128)
states: 194,929,046,592 (11)
abstracting: (p128<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p129)
states: 194,929,046,592 (11)
abstracting: (p129<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p130)
states: 197,739,387,520 (11)
abstracting: (p130<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p131)
states: 194,929,046,592 (11)
abstracting: (p131<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p132)
states: 194,929,046,592 (11)
abstracting: (p132<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p133)
states: 194,929,046,592 (11)
abstracting: (p133<=1)
states: 547,231,759,144 (11)
MC time: 1m13.344sec
checking: [EF [[[[[[[[[p10<=1 & 1<=p10] & [p33<=1 & 1<=p33]] | [[p10<=1 & 1<=p10] & [p35<=1 & 1<=p35]]] | [[[p10<=1 & 1<=p10] & [p37<=1 & 1<=p37]] | [[[p11<=1 & 1<=p11] & [p37<=1 & 1<=p37]] | [[p9<=1 & 1<=p9] & [p33<=1 & 1<=p33]]]]] | [[[[p11<=1 & 1<=p11] & [p35<=1 & 1<=p35]] | [[p11<=1 & 1<=p11] & [p33<=1 & 1<=p33]]] | [[[p9<=1 & 1<=p9] & [p37<=1 & 1<=p37]] | [[[p6<=1 & 1<=p6] & [p32<=1 & 1<=p32]] | [[p9<=1 & 1<=p9] & [p35<=1 & 1<=p35]]]]]] | [[[[[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]] | [[p6<=1 & 1<=p6] & [p36<=1 & 1<=p36]]] | [[[p8<=1 & 1<=p8] & [p36<=1 & 1<=p36]] | [[[p7<=1 & 1<=p7] & [p34<=1 & 1<=p34]] | [[p7<=1 & 1<=p7] & [p32<=1 & 1<=p32]]]]] | [[[[p7<=1 & 1<=p7] & [p36<=1 & 1<=p36]] | [[[p8<=1 & 1<=p8] & [p32<=1 & 1<=p32]] | [[p12<=1 & 1<=p12] & [p35<=1 & 1<=p35]]]] | [[[p8<=1 & 1<=p8] & [p34<=1 & 1<=p34]] | [[[p12<=1 & 1<=p12] & [p37<=1 & 1<=p37]] | [[p12<=1 & 1<=p12] & [p33<=1 & 1<=p33]]]]]]] | [[[[[[p10<=1 & 1<=p10] & [p34<=1 & 1<=p34]] | [[p10<=1 & 1<=p10] & [p36<=1 & 1<=p36]]] | [[[p6<=1 & 1<=p6] & [p37<=1 & 1<=p37]] | [[[p11<=1 & 1<=p11] & [p36<=1 & 1<=p36]] | [[p9<=1 & 1<=p9] & [p32<=1 & 1<=p32]]]]] | [[[[p11<=1 & 1<=p11] & [p34<=1 & 1<=p34]] | [[p11<=1 & 1<=p11] & [p32<=1 & 1<=p32]]] | [[[p9<=1 & 1<=p9] & [p36<=1 & 1<=p36]] | [[[p9<=1 & 1<=p9] & [p34<=1 & 1<=p34]] | [[p6<=1 & 1<=p6] & [p33<=1 & 1<=p33]]]]]] | [[[[[p6<=1 & 1<=p6] & [p35<=1 & 1<=p35]] | [[p10<=1 & 1<=p10] & [p32<=1 & 1<=p32]]] | [[[p8<=1 & 1<=p8] & [p35<=1 & 1<=p35]] | [[[p8<=1 & 1<=p8] & [p37<=1 & 1<=p37]] | [[p7<=1 & 1<=p7] & [p35<=1 & 1<=p35]]]]] | [[[[p7<=1 & 1<=p7] & [p33<=1 & 1<=p33]] | [[[p7<=1 & 1<=p7] & [p37<=1 & 1<=p37]] | [[p12<=1 & 1<=p12] & [p36<=1 & 1<=p36]]]] | [[[p8<=1 & 1<=p8] & [p33<=1 & 1<=p33]] | [[[p12<=1 & 1<=p12] & [p32<=1 & 1<=p32]] | [[p12<=1 & 1<=p12] & [p34<=1 & 1<=p34]]]]]]]] & [AG [[[[[[p19<=0 & 0<=p19] | [p157<=0 & 0<=p157]] & [[[p14<=0 & 0<=p14] | [p152<=0 & 0<=p152]] & [[p15<=0 & 0<=p15] | [p153<=0 & 0<=p153]]]] & [[[p16<=0 & 0<=p16] | [p154<=0 & 0<=p154]] & [[[p17<=0 & 0<=p17] | [p155<=0 & 0<=p155]] & [[p18<=0 & 0<=p18] | [p156<=0 & 0<=p156]]]]] | [[[[[p21<=0 & 0<=p21] | [p170<=0 & 0<=p170]] & [[[p26<=0 & 0<=p26] | [p173<=0 & 0<=p173]] & [[p24<=0 & 0<=p24] | [p172<=0 & 0<=p172]]]] & [[[p23<=0 & 0<=p23] | [p171<=0 & 0<=p171]] & [[[p27<=0 & 0<=p27] | [p173<=0 & 0<=p173]] & [[p29<=0 & 0<=p29] | [p174<=0 & 0<=p174]]]]] & [[[[p31<=0 & 0<=p31] | [p175<=0 & 0<=p175]] & [[[p30<=0 & 0<=p30] | [p175<=0 & 0<=p175]] & [[p25<=0 & 0<=p25] | [p172<=0 & 0<=p172]]]] & [[[p22<=0 & 0<=p22] | [p171<=0 & 0<=p171]] & [[[p20<=0 & 0<=p20] | [p170<=0 & 0<=p170]] & [[p28<=0 & 0<=p28] | [p174<=0 & 0<=p174]]]]]]]] | [[[[[p7<=0 & 0<=p7] | [p56<=0 & 0<=p56]] & [[[p8<=0 & 0<=p8] | [p57<=0 & 0<=p57]] & [[p9<=0 & 0<=p9] | [p58<=0 & 0<=p58]]]] & [[[p10<=0 & 0<=p10] | [p59<=0 & 0<=p59]] & [[[p11<=0 & 0<=p11] | [p60<=0 & 0<=p60]] & [[p12<=0 & 0<=p12] | [p61<=0 & 0<=p61]]]]] | [[[[[[[p16<=0 & 0<=p16] | [p46<=0 & 0<=p46]] & [[p16<=0 & 0<=p16] | [p45<=0 & 0<=p45]]] & [[[p16<=0 & 0<=p16] | [p48<=0 & 0<=p48]] & [[p16<=0 & 0<=p16] | [p47<=0 & 0<=p47]]]] & [[[[p16<=0 & 0<=p16] | [p44<=0 & 0<=p44]] & [[p16<=0 & 0<=p16] | [p49<=0 & 0<=p49]]] & [[[p17<=0 & 0<=p17] | [p47<=0 & 0<=p47]] & [[[p17<=0 & 0<=p17] | [p46<=0 & 0<=p46]] & [[p17<=0 & 0<=p17] | [p45<=0 & 0<=p45]]]]]] & [[[[[p17<=0 & 0<=p17] | [p44<=0 & 0<=p44]] & [[p17<=0 & 0<=p17] | [p49<=0 & 0<=p49]]] & [[[p17<=0 & 0<=p17] | [p48<=0 & 0<=p48]] & [[p18<=0 & 0<=p18] | [p44<=0 & 0<=p44]]]] & [[[[p19<=0 & 0<=p19] | [p49<=0 & 0<=p49]] & [[p19<=0 & 0<=p19] | [p48<=0 & 0<=p48]]] & [[[p18<=0 & 0<=p18] | [p46<=0 & 0<=p46]] & [[[p19<=0 & 0<=p19] | [p47<=0 & 0<=p47]] & [[p18<=0 & 0<=p18] | [p45<=0 & 0<=p45]]]]]]] & [[[[[[p19<=0 & 0<=p19] | [p46<=0 & 0<=p46]] & [[p14<=0 & 0<=p14] | [p44<=0 & 0<=p44]]] & [[[p19<=0 & 0<=p19] | [p45<=0 & 0<=p45]] & [[p18<=0 & 0<=p18] | [p48<=0 & 0<=p48]]]] & [[[[p19<=0 & 0<=p19] | [p44<=0 & 0<=p44]] & [[p18<=0 & 0<=p18] | [p47<=0 & 0<=p47]]] & [[[p14<=0 & 0<=p14] | [p46<=0 & 0<=p46]] & [[[p14<=0 & 0<=p14] | [p45<=0 & 0<=p45]] & [[p18<=0 & 0<=p18] | [p49<=0 & 0<=p49]]]]]] & [[[[[p14<=0 & 0<=p14] | [p48<=0 & 0<=p48]] & [[p14<=0 & 0<=p14] | [p47<=0 & 0<=p47]]] & [[[p14<=0 & 0<=p14] | [p49<=0 & 0<=p49]] & [[p15<=0 & 0<=p15] | [p49<=0 & 0<=p49]]]] & [[[[p15<=0 & 0<=p15] | [p48<=0 & 0<=p48]] & [[p15<=0 & 0<=p15] | [p47<=0 & 0<=p47]]] & [[[p15<=0 & 0<=p15] | [p46<=0 & 0<=p46]] & [[[p15<=0 & 0<=p15] | [p45<=0 & 0<=p45]] & [[p15<=0 & 0<=p15] | [p44<=0 & 0<=p44]]]]]]]]]]]] & EX [EX [[[[[[EG [[[[[p19<=1 & 1<=p19] & [p157<=1 & 1<=p157]] | [[[p14<=1 & 1<=p14] & [p152<=1 & 1<=p152]] | [[p15<=1 & 1<=p15] & [p153<=1 & 1<=p153]]]] | [[[p16<=1 & 1<=p16] & [p154<=1 & 1<=p154]] | [[[p17<=1 & 1<=p17] & [p155<=1 & 1<=p155]] | [[p18<=1 & 1<=p18] & [p156<=1 & 1<=p156]]]]]] | AX [[[[[[p28<=1 & 1<=p28] & [p66<=1 & 1<=p66]] | [[[p20<=1 & 1<=p20] & [p62<=1 & 1<=p62]] | [[p25<=1 & 1<=p25] & [p64<=1 & 1<=p64]]]] | [[[p23<=1 & 1<=p23] & [p63<=1 & 1<=p63]] | [[[p26<=1 & 1<=p26] & [p65<=1 & 1<=p65]] | [[p30<=1 & 1<=p30] & [p67<=1 & 1<=p67]]]]] | [[[[p29<=1 & 1<=p29] & [p66<=1 & 1<=p66]] | [[[p27<=1 & 1<=p27] & [p65<=1 & 1<=p65]] | [[p24<=1 & 1<=p24] & [p64<=1 & 1<=p64]]]] | [[[p21<=1 & 1<=p21] & [p62<=1 & 1<=p62]] | [[[p22<=1 & 1<=p22] & [p63<=1 & 1<=p63]] | [[p31<=1 & 1<=p31] & [p67<=1 & 1<=p67]]]]]]]] | [EG [EF [[[[[p13<=1 & 1<=p13] & [p47<=1 & 1<=p47]] | [[[p13<=1 & 1<=p13] & [p46<=1 & 1<=p46]] | [[p13<=1 & 1<=p13] & [p45<=1 & 1<=p45]]]] | [[[p13<=1 & 1<=p13] & [p44<=1 & 1<=p44]] | [[[p13<=1 & 1<=p13] & [p49<=1 & 1<=p49]] | [[p13<=1 & 1<=p13] & [p48<=1 & 1<=p48]]]]]]] | [[[p13<=1 & 1<=p13] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p169<=1 & 1<=p169]]]]] | [[[[p18<=1 & 1<=p18] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p168<=1 & 1<=p168]]]] | [[[p17<=1 & 1<=p17] & [p164<=1 & 1<=p164]] | [[[p14<=1 & 1<=p14] & [p169<=1 & 1<=p169]] | [[p19<=1 & 1<=p19] & [p166<=1 & 1<=p166]]]]]] | [[[[[p19<=1 & 1<=p19] & [p164<=1 & 1<=p164]] | [[p19<=1 & 1<=p19] & [p168<=1 & 1<=p168]]] | [[[p16<=1 & 1<=p16] & [p166<=1 & 1<=p166]] | [[[p15<=1 & 1<=p15] & [p169<=1 & 1<=p169]] | [[p16<=1 & 1<=p16] & [p164<=1 & 1<=p164]]]]] | [[[[p15<=1 & 1<=p15] & [p164<=1 & 1<=p164]] | [[[p16<=1 & 1<=p16] & [p169<=1 & 1<=p169]] | [[p15<=1 & 1<=p15] & [p166<=1 & 1<=p166]]]] | [[[p16<=1 & 1<=p16] & [p167<=1 & 1<=p167]] | [[[p14<=1 & 1<=p14] & [p164<=1 & 1<=p164]] | [[p14<=1 & 1<=p14] & [p168<=1 & 1<=p168]]]]]]] | [[[[[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]] | [[p14<=1 & 1<=p14] & [p166<=1 & 1<=p166]]] | [[[p17<=1 & 1<=p17] & [p167<=1 & 1<=p167]] | [[[p18<=1 & 1<=p18] & [p169<=1 & 1<=p169]] | [[p13<=1 & 1<=p13] & [p166<=1 & 1<=p166]]]]] | [[[[p13<=1 & 1<=p13] & [p168<=1 & 1<=p168]] | [[[p18<=1 & 1<=p18] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p167<=1 & 1<=p167]]]] | [[[p13<=1 & 1<=p13] & [p164<=1 & 1<=p164]] | [[[p17<=1 & 1<=p17] & [p165<=1 & 1<=p165]] | [[p19<=1 & 1<=p19] & [p167<=1 & 1<=p167]]]]]] | [[[[[p19<=1 & 1<=p19] & [p165<=1 & 1<=p165]] | [[[p19<=1 & 1<=p19] & [p169<=1 & 1<=p169]] | [[p16<=1 & 1<=p16] & [p165<=1 & 1<=p165]]]] | [[[p15<=1 & 1<=p15] & [p168<=1 & 1<=p168]] | [[[p15<=1 & 1<=p15] & [p165<=1 & 1<=p165]] | [[p15<=1 & 1<=p15] & [p167<=1 & 1<=p167]]]]] | [[[[p16<=1 & 1<=p16] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p168<=1 & 1<=p168]] | [[p17<=1 & 1<=p17] & [p166<=1 & 1<=p166]]]] | [[[p14<=1 & 1<=p14] & [p167<=1 & 1<=p167]] | [[[p14<=1 & 1<=p14] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p164<=1 & 1<=p164]]]]]]]]]]]
normalized: [EX [EX [[[[[[[[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p14<=1 & 1<=p14]]] | [[p167<=1 & 1<=p167] & [p14<=1 & 1<=p14]]] | [[[[p166<=1 & 1<=p166] & [p17<=1 & 1<=p17]] | [[p168<=1 & 1<=p168] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p16<=1 & 1<=p16]]]] | [[[[[p167<=1 & 1<=p167] & [p15<=1 & 1<=p15]] | [[p165<=1 & 1<=p165] & [p15<=1 & 1<=p15]]] | [[p168<=1 & 1<=p168] & [p15<=1 & 1<=p15]]] | [[[[p165<=1 & 1<=p165] & [p16<=1 & 1<=p16]] | [[p169<=1 & 1<=p169] & [p19<=1 & 1<=p19]]] | [[p165<=1 & 1<=p165] & [p19<=1 & 1<=p19]]]]] | [[[[[[p167<=1 & 1<=p167] & [p19<=1 & 1<=p19]] | [[p165<=1 & 1<=p165] & [p17<=1 & 1<=p17]]] | [[p164<=1 & 1<=p164] & [p13<=1 & 1<=p13]]] | [[[[p167<=1 & 1<=p167] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p18<=1 & 1<=p18]]] | [[p168<=1 & 1<=p168] & [p13<=1 & 1<=p13]]]] | [[[[[p166<=1 & 1<=p166] & [p13<=1 & 1<=p13]] | [[p169<=1 & 1<=p169] & [p18<=1 & 1<=p18]]] | [[p167<=1 & 1<=p167] & [p17<=1 & 1<=p17]]] | [[[p166<=1 & 1<=p166] & [p14<=1 & 1<=p14]] | [[p169<=1 & 1<=p169] & [p17<=1 & 1<=p17]]]]]] | [[[[[[[p168<=1 & 1<=p168] & [p14<=1 & 1<=p14]] | [[p164<=1 & 1<=p164] & [p14<=1 & 1<=p14]]] | [[p167<=1 & 1<=p167] & [p16<=1 & 1<=p16]]] | [[[[p166<=1 & 1<=p166] & [p15<=1 & 1<=p15]] | [[p169<=1 & 1<=p169] & [p16<=1 & 1<=p16]]] | [[p164<=1 & 1<=p164] & [p15<=1 & 1<=p15]]]] | [[[[[p164<=1 & 1<=p164] & [p16<=1 & 1<=p16]] | [[p169<=1 & 1<=p169] & [p15<=1 & 1<=p15]]] | [[p166<=1 & 1<=p166] & [p16<=1 & 1<=p16]]] | [[[p168<=1 & 1<=p168] & [p19<=1 & 1<=p19]] | [[p164<=1 & 1<=p164] & [p19<=1 & 1<=p19]]]]] | [[[[[[p166<=1 & 1<=p166] & [p19<=1 & 1<=p19]] | [[p169<=1 & 1<=p169] & [p14<=1 & 1<=p14]]] | [[p164<=1 & 1<=p164] & [p17<=1 & 1<=p17]]] | [[[[p168<=1 & 1<=p168] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p18<=1 & 1<=p18]]]] | [[[[[p169<=1 & 1<=p169] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p13<=1 & 1<=p13]]] | EG [E [true U [[[[[p48<=1 & 1<=p48] & [p13<=1 & 1<=p13]] | [[p49<=1 & 1<=p49] & [p13<=1 & 1<=p13]]] | [[p44<=1 & 1<=p44] & [p13<=1 & 1<=p13]]] | [[[[p45<=1 & 1<=p45] & [p13<=1 & 1<=p13]] | [[p46<=1 & 1<=p46] & [p13<=1 & 1<=p13]]] | [[p47<=1 & 1<=p47] & [p13<=1 & 1<=p13]]]]]]] | [~ [EX [~ [[[[[[[p67<=1 & 1<=p67] & [p31<=1 & 1<=p31]] | [[p63<=1 & 1<=p63] & [p22<=1 & 1<=p22]]] | [[p62<=1 & 1<=p62] & [p21<=1 & 1<=p21]]] | [[[[p64<=1 & 1<=p64] & [p24<=1 & 1<=p24]] | [[p65<=1 & 1<=p65] & [p27<=1 & 1<=p27]]] | [[p66<=1 & 1<=p66] & [p29<=1 & 1<=p29]]]] | [[[[[p67<=1 & 1<=p67] & [p30<=1 & 1<=p30]] | [[p65<=1 & 1<=p65] & [p26<=1 & 1<=p26]]] | [[p63<=1 & 1<=p63] & [p23<=1 & 1<=p23]]] | [[[[p64<=1 & 1<=p64] & [p25<=1 & 1<=p25]] | [[p62<=1 & 1<=p62] & [p20<=1 & 1<=p20]]] | [[p66<=1 & 1<=p66] & [p28<=1 & 1<=p28]]]]]]]] | EG [[[[[[p156<=1 & 1<=p156] & [p18<=1 & 1<=p18]] | [[p155<=1 & 1<=p155] & [p17<=1 & 1<=p17]]] | [[p154<=1 & 1<=p154] & [p16<=1 & 1<=p16]]] | [[[[p153<=1 & 1<=p153] & [p15<=1 & 1<=p15]] | [[p152<=1 & 1<=p152] & [p14<=1 & 1<=p14]]] | [[p157<=1 & 1<=p157] & [p19<=1 & 1<=p19]]]]]]]]]]]] & E [true U [[[[[[[[[[[p45<=0 & 0<=p45] | [p18<=0 & 0<=p18]] & [[p47<=0 & 0<=p47] | [p19<=0 & 0<=p19]]] & [[p46<=0 & 0<=p46] | [p18<=0 & 0<=p18]]] & [[[p48<=0 & 0<=p48] | [p19<=0 & 0<=p19]] & [[p49<=0 & 0<=p49] | [p19<=0 & 0<=p19]]]] & [[[[p44<=0 & 0<=p44] | [p18<=0 & 0<=p18]] & [[p48<=0 & 0<=p48] | [p17<=0 & 0<=p17]]] & [[[p49<=0 & 0<=p49] | [p17<=0 & 0<=p17]] & [[p44<=0 & 0<=p44] | [p17<=0 & 0<=p17]]]]] & [[[[[[p45<=0 & 0<=p45] | [p17<=0 & 0<=p17]] & [[p46<=0 & 0<=p46] | [p17<=0 & 0<=p17]]] & [[p47<=0 & 0<=p47] | [p17<=0 & 0<=p17]]] & [[[p49<=0 & 0<=p49] | [p16<=0 & 0<=p16]] & [[p44<=0 & 0<=p44] | [p16<=0 & 0<=p16]]]] & [[[[p47<=0 & 0<=p47] | [p16<=0 & 0<=p16]] & [[p48<=0 & 0<=p48] | [p16<=0 & 0<=p16]]] & [[[p45<=0 & 0<=p45] | [p16<=0 & 0<=p16]] & [[p46<=0 & 0<=p46] | [p16<=0 & 0<=p16]]]]]] & [[[[[[[p44<=0 & 0<=p44] | [p15<=0 & 0<=p15]] & [[p45<=0 & 0<=p45] | [p15<=0 & 0<=p15]]] & [[p46<=0 & 0<=p46] | [p15<=0 & 0<=p15]]] & [[[p47<=0 & 0<=p47] | [p15<=0 & 0<=p15]] & [[p48<=0 & 0<=p48] | [p15<=0 & 0<=p15]]]] & [[[[p49<=0 & 0<=p49] | [p15<=0 & 0<=p15]] & [[p49<=0 & 0<=p49] | [p14<=0 & 0<=p14]]] & [[[p47<=0 & 0<=p47] | [p14<=0 & 0<=p14]] & [[p48<=0 & 0<=p48] | [p14<=0 & 0<=p14]]]]] & [[[[[[p49<=0 & 0<=p49] | [p18<=0 & 0<=p18]] & [[p45<=0 & 0<=p45] | [p14<=0 & 0<=p14]]] & [[p46<=0 & 0<=p46] | [p14<=0 & 0<=p14]]] & [[[p47<=0 & 0<=p47] | [p18<=0 & 0<=p18]] & [[p44<=0 & 0<=p44] | [p19<=0 & 0<=p19]]]] & [[[[p48<=0 & 0<=p48] | [p18<=0 & 0<=p18]] & [[p45<=0 & 0<=p45] | [p19<=0 & 0<=p19]]] & [[[p44<=0 & 0<=p44] | [p14<=0 & 0<=p14]] & [[p46<=0 & 0<=p46] | [p19<=0 & 0<=p19]]]]]]] | [[[[[p61<=0 & 0<=p61] | [p12<=0 & 0<=p12]] & [[p60<=0 & 0<=p60] | [p11<=0 & 0<=p11]]] & [[p59<=0 & 0<=p59] | [p10<=0 & 0<=p10]]] & [[[[p58<=0 & 0<=p58] | [p9<=0 & 0<=p9]] & [[p57<=0 & 0<=p57] | [p8<=0 & 0<=p8]]] & [[p56<=0 & 0<=p56] | [p7<=0 & 0<=p7]]]]] | ~ [E [true U ~ [[[[[[[[p174<=0 & 0<=p174] | [p28<=0 & 0<=p28]] & [[p170<=0 & 0<=p170] | [p20<=0 & 0<=p20]]] & [[p171<=0 & 0<=p171] | [p22<=0 & 0<=p22]]] & [[[[p172<=0 & 0<=p172] | [p25<=0 & 0<=p25]] & [[p175<=0 & 0<=p175] | [p30<=0 & 0<=p30]]] & [[p175<=0 & 0<=p175] | [p31<=0 & 0<=p31]]]] & [[[[[p174<=0 & 0<=p174] | [p29<=0 & 0<=p29]] & [[p173<=0 & 0<=p173] | [p27<=0 & 0<=p27]]] & [[p171<=0 & 0<=p171] | [p23<=0 & 0<=p23]]] & [[[[p172<=0 & 0<=p172] | [p24<=0 & 0<=p24]] & [[p173<=0 & 0<=p173] | [p26<=0 & 0<=p26]]] & [[p170<=0 & 0<=p170] | [p21<=0 & 0<=p21]]]]] | [[[[[p156<=0 & 0<=p156] | [p18<=0 & 0<=p18]] & [[p155<=0 & 0<=p155] | [p17<=0 & 0<=p17]]] & [[p154<=0 & 0<=p154] | [p16<=0 & 0<=p16]]] & [[[[p153<=0 & 0<=p153] | [p15<=0 & 0<=p15]] & [[p152<=0 & 0<=p152] | [p14<=0 & 0<=p14]]] & [[p157<=0 & 0<=p157] | [p19<=0 & 0<=p19]]]]]]]]] & [[[[[[[[p34<=1 & 1<=p34] & [p12<=1 & 1<=p12]] | [[p32<=1 & 1<=p32] & [p12<=1 & 1<=p12]]] | [[p33<=1 & 1<=p33] & [p8<=1 & 1<=p8]]] | [[[[p36<=1 & 1<=p36] & [p12<=1 & 1<=p12]] | [[p37<=1 & 1<=p37] & [p7<=1 & 1<=p7]]] | [[p33<=1 & 1<=p33] & [p7<=1 & 1<=p7]]]] | [[[[[p35<=1 & 1<=p35] & [p7<=1 & 1<=p7]] | [[p37<=1 & 1<=p37] & [p8<=1 & 1<=p8]]] | [[p35<=1 & 1<=p35] & [p8<=1 & 1<=p8]]] | [[[p32<=1 & 1<=p32] & [p10<=1 & 1<=p10]] | [[p35<=1 & 1<=p35] & [p6<=1 & 1<=p6]]]]] | [[[[[[p33<=1 & 1<=p33] & [p6<=1 & 1<=p6]] | [[p34<=1 & 1<=p34] & [p9<=1 & 1<=p9]]] | [[p36<=1 & 1<=p36] & [p9<=1 & 1<=p9]]] | [[[p32<=1 & 1<=p32] & [p11<=1 & 1<=p11]] | [[p34<=1 & 1<=p34] & [p11<=1 & 1<=p11]]]] | [[[[[p32<=1 & 1<=p32] & [p9<=1 & 1<=p9]] | [[p36<=1 & 1<=p36] & [p11<=1 & 1<=p11]]] | [[p37<=1 & 1<=p37] & [p6<=1 & 1<=p6]]] | [[[p36<=1 & 1<=p36] & [p10<=1 & 1<=p10]] | [[p34<=1 & 1<=p34] & [p10<=1 & 1<=p10]]]]]] | [[[[[[[p33<=1 & 1<=p33] & [p12<=1 & 1<=p12]] | [[p37<=1 & 1<=p37] & [p12<=1 & 1<=p12]]] | [[p34<=1 & 1<=p34] & [p8<=1 & 1<=p8]]] | [[[[p35<=1 & 1<=p35] & [p12<=1 & 1<=p12]] | [[p32<=1 & 1<=p32] & [p8<=1 & 1<=p8]]] | [[p36<=1 & 1<=p36] & [p7<=1 & 1<=p7]]]] | [[[[[p32<=1 & 1<=p32] & [p7<=1 & 1<=p7]] | [[p34<=1 & 1<=p34] & [p7<=1 & 1<=p7]]] | [[p36<=1 & 1<=p36] & [p8<=1 & 1<=p8]]] | [[[p36<=1 & 1<=p36] & [p6<=1 & 1<=p6]] | [[p34<=1 & 1<=p34] & [p6<=1 & 1<=p6]]]]] | [[[[[[p35<=1 & 1<=p35] & [p9<=1 & 1<=p9]] | [[p32<=1 & 1<=p32] & [p6<=1 & 1<=p6]]] | [[p37<=1 & 1<=p37] & [p9<=1 & 1<=p9]]] | [[[p33<=1 & 1<=p33] & [p11<=1 & 1<=p11]] | [[p35<=1 & 1<=p35] & [p11<=1 & 1<=p11]]]] | [[[[[p33<=1 & 1<=p33] & [p9<=1 & 1<=p9]] | [[p37<=1 & 1<=p37] & [p11<=1 & 1<=p11]]] | [[p37<=1 & 1<=p37] & [p10<=1 & 1<=p10]]] | [[[p35<=1 & 1<=p35] & [p10<=1 & 1<=p10]] | [[p33<=1 & 1<=p33] & [p10<=1 & 1<=p10]]]]]]]]]]
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (p35<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (p37<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (p36<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (p33<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (p32<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (p34<=1)
states: 547,231,759,144 (11)
abstracting: (0<=p19)
states: 547,231,759,144 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p157)
states: 547,231,759,144 (11)
abstracting: (p157<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p14)
states: 547,231,759,144 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p152)
states: 547,231,759,144 (11)
abstracting: (p152<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p15)
states: 547,231,759,144 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p153)
states: 547,231,759,144 (11)
abstracting: (p153<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p16)
states: 547,231,759,144 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p154)
states: 547,231,759,144 (11)
abstracting: (p154<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p17)
states: 547,231,759,144 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p155)
states: 547,231,759,144 (11)
abstracting: (p155<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p18)
states: 547,231,759,144 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (0<=p156)
states: 547,231,759,144 (11)
abstracting: (p156<=0)
states: 541,439,115,624 (11)
abstracting: (0<=p21)
states: 547,231,759,144 (11)
abstracting: (p21<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p170)
states: 547,231,759,144 (11)
abstracting: (p170<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p26)
states: 547,231,759,144 (11)
abstracting: (p26<=0)
states: 98,914,841,322 (10)
abstracting: (0<=p173)
states: 547,231,759,144 (11)
abstracting: (p173<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p24)
states: 547,231,759,144 (11)
abstracting: (p24<=0)
states: 98,914,841,322 (10)
abstracting: (0<=p172)
states: 547,231,759,144 (11)
abstracting: (p172<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p23)
states: 547,231,759,144 (11)
abstracting: (p23<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p171)
states: 547,231,759,144 (11)
abstracting: (p171<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p27)
states: 547,231,759,144 (11)
abstracting: (p27<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p173)
states: 547,231,759,144 (11)
abstracting: (p173<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p29)
states: 547,231,759,144 (11)
abstracting: (p29<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p174)
states: 547,231,759,144 (11)
abstracting: (p174<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p31)
states: 547,231,759,144 (11)
abstracting: (p31<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p175)
states: 547,231,759,144 (11)
abstracting: (p175<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p30)
states: 547,231,759,144 (11)
abstracting: (p30<=0)
states: 98,914,841,322 (10)
abstracting: (0<=p175)
states: 547,231,759,144 (11)
abstracting: (p175<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p25)
states: 547,231,759,144 (11)
abstracting: (p25<=0)
states: 448,316,917,822 (11)
abstracting: (0<=p172)
states: 547,231,759,144 (11)
abstracting: (p172<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p22)
states: 547,231,759,144 (11)
abstracting: (p22<=0)
before gc: list nodes free: 7038474
after gc: idd nodes used:26552087, unused:37447913; list nodes free:171132034
states: 98,914,841,322 (10)
abstracting: (0<=p171)
states: 547,231,759,144 (11)
abstracting: (p171<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p20)
states: 547,231,759,144 (11)
abstracting: (p20<=0)
states: 98,914,841,322 (10)
abstracting: (0<=p170)
states: 547,231,759,144 (11)
abstracting: (p170<=0)
states: 530,705,059,848 (11)
abstracting: (0<=p28)
states: 547,231,759,144 (11)
abstracting: (p28<=0)
states: 98,914,841,322 (10)
abstracting: (0<=p174)
states: 547,231,759,144 (11)
abstracting: (p174<=0)
states: 530,705,059,848 (11)
MC time: 1m 8.023sec
checking: [AG [AF [E [[[[[[[[p17<=1 & 1<=p17] & [p157<=1 & 1<=p157]] | [[p17<=1 & 1<=p17] & [p156<=1 & 1<=p156]]] | [[[p17<=1 & 1<=p17] & [p153<=1 & 1<=p153]] | [[p17<=1 & 1<=p17] & [p152<=1 & 1<=p152]]]] | [[[[p17<=1 & 1<=p17] & [p154<=1 & 1<=p154]] | [[p16<=1 & 1<=p16] & [p152<=1 & 1<=p152]]] | [[[p13<=1 & 1<=p13] & [p157<=1 & 1<=p157]] | [[[p13<=1 & 1<=p13] & [p156<=1 & 1<=p156]] | [[p13<=1 & 1<=p13] & [p153<=1 & 1<=p153]]]]]] | [[[[[p13<=1 & 1<=p13] & [p152<=1 & 1<=p152]] | [[p13<=1 & 1<=p13] & [p155<=1 & 1<=p155]]] | [[[p13<=1 & 1<=p13] & [p154<=1 & 1<=p154]] | [[p16<=1 & 1<=p16] & [p157<=1 & 1<=p157]]]] | [[[[p16<=1 & 1<=p16] & [p156<=1 & 1<=p156]] | [[p16<=1 & 1<=p16] & [p155<=1 & 1<=p155]]] | [[[p16<=1 & 1<=p16] & [p153<=1 & 1<=p153]] | [[[p19<=1 & 1<=p19] & [p153<=1 & 1<=p153]] | [[p19<=1 & 1<=p19] & [p152<=1 & 1<=p152]]]]]]] | [[[[[[p14<=1 & 1<=p14] & [p154<=1 & 1<=p154]] | [[p19<=1 & 1<=p19] & [p155<=1 & 1<=p155]]] | [[[p14<=1 & 1<=p14] & [p153<=1 & 1<=p153]] | [[p19<=1 & 1<=p19] & [p154<=1 & 1<=p154]]]] | [[[[p19<=1 & 1<=p19] & [p156<=1 & 1<=p156]] | [[p15<=1 & 1<=p15] & [p155<=1 & 1<=p155]]] | [[[p15<=1 & 1<=p15] & [p154<=1 & 1<=p154]] | [[[p15<=1 & 1<=p15] & [p157<=1 & 1<=p157]] | [[p15<=1 & 1<=p15] & [p156<=1 & 1<=p156]]]]]] | [[[[[p18<=1 & 1<=p18] & [p154<=1 & 1<=p154]] | [[p18<=1 & 1<=p18] & [p153<=1 & 1<=p153]]] | [[[p18<=1 & 1<=p18] & [p152<=1 & 1<=p152]] | [[p18<=1 & 1<=p18] & [p157<=1 & 1<=p157]]]] | [[[[p15<=1 & 1<=p15] & [p152<=1 & 1<=p152]] | [[p18<=1 & 1<=p18] & [p155<=1 & 1<=p155]]] | [[[p14<=1 & 1<=p14] & [p157<=1 & 1<=p157]] | [[[p14<=1 & 1<=p14] & [p156<=1 & 1<=p156]] | [[p14<=1 & 1<=p14] & [p155<=1 & 1<=p155]]]]]]]] U [[[[[[[p17<=1 & 1<=p17] & [p55<=1 & 1<=p55]] | [[p16<=1 & 1<=p16] & [p53<=1 & 1<=p53]]] | [[[p16<=1 & 1<=p16] & [p55<=1 & 1<=p55]] | [[[p16<=1 & 1<=p16] & [p51<=1 & 1<=p51]] | [[p13<=1 & 1<=p13] & [p54<=1 & 1<=p54]]]]] | [[[[p13<=1 & 1<=p13] & [p52<=1 & 1<=p52]] | [[p13<=1 & 1<=p13] & [p50<=1 & 1<=p50]]] | [[[p17<=1 & 1<=p17] & [p53<=1 & 1<=p53]] | [[[p17<=1 & 1<=p17] & [p51<=1 & 1<=p51]] | [[p14<=1 & 1<=p14] & [p51<=1 & 1<=p51]]]]]] | [[[[[p19<=1 & 1<=p19] & [p54<=1 & 1<=p54]] | [[p19<=1 & 1<=p19] & [p50<=1 & 1<=p50]]] | [[[p14<=1 & 1<=p14] & [p53<=1 & 1<=p53]] | [[[p14<=1 & 1<=p14] & [p55<=1 & 1<=p55]] | [[p18<=1 & 1<=p18] & [p50<=1 & 1<=p50]]]]] | [[[[p18<=1 & 1<=p18] & [p52<=1 & 1<=p52]] | [[[p18<=1 & 1<=p18] & [p54<=1 & 1<=p54]] | [[p15<=1 & 1<=p15] & [p55<=1 & 1<=p55]]]] | [[[p15<=1 & 1<=p15] & [p53<=1 & 1<=p53]] | [[[p15<=1 & 1<=p15] & [p51<=1 & 1<=p51]] | [[p19<=1 & 1<=p19] & [p52<=1 & 1<=p52]]]]]]] | [[[[[[p16<=1 & 1<=p16] & [p52<=1 & 1<=p52]] | [[p16<=1 & 1<=p16] & [p54<=1 & 1<=p54]]] | [[[p16<=1 & 1<=p16] & [p50<=1 & 1<=p50]] | [[[p13<=1 & 1<=p13] & [p53<=1 & 1<=p53]] | [[p13<=1 & 1<=p13] & [p51<=1 & 1<=p51]]]]] | [[[[p13<=1 & 1<=p13] & [p55<=1 & 1<=p55]] | [[p17<=1 & 1<=p17] & [p50<=1 & 1<=p50]]] | [[[p17<=1 & 1<=p17] & [p54<=1 & 1<=p54]] | [[[p17<=1 & 1<=p17] & [p52<=1 & 1<=p52]] | [[p19<=1 & 1<=p19] & [p53<=1 & 1<=p53]]]]]] | [[[[[p14<=1 & 1<=p14] & [p50<=1 & 1<=p50]] | [[p19<=1 & 1<=p19] & [p55<=1 & 1<=p55]]] | [[[p14<=1 & 1<=p14] & [p52<=1 & 1<=p52]] | [[[p14<=1 & 1<=p14] & [p54<=1 & 1<=p54]] | [[p18<=1 & 1<=p18] & [p51<=1 & 1<=p51]]]]] | [[[[p18<=1 & 1<=p18] & [p53<=1 & 1<=p53]] | [[[p18<=1 & 1<=p18] & [p55<=1 & 1<=p55]] | [[p15<=1 & 1<=p15] & [p54<=1 & 1<=p54]]]] | [[[p15<=1 & 1<=p15] & [p52<=1 & 1<=p52]] | [[[p15<=1 & 1<=p15] & [p50<=1 & 1<=p50]] | [[p19<=1 & 1<=p19] & [p51<=1 & 1<=p51]]]]]]]]]]] | EG [AX [[[[[[[[[[p13<=0 & 0<=p13] | [p167<=0 & 0<=p167]] & [[[p13<=0 & 0<=p13] | [p169<=0 & 0<=p169]] & [[p18<=0 & 0<=p18] | [p166<=0 & 0<=p166]]]] & [[[p13<=0 & 0<=p13] | [p165<=0 & 0<=p165]] & [[[p18<=0 & 0<=p18] | [p168<=0 & 0<=p168]] & [[p17<=0 & 0<=p17] | [p164<=0 & 0<=p164]]]]] & [[[[p14<=0 & 0<=p14] | [p169<=0 & 0<=p169]] & [[[p19<=0 & 0<=p19] | [p166<=0 & 0<=p166]] & [[p19<=0 & 0<=p19] | [p164<=0 & 0<=p164]]]] & [[[p19<=0 & 0<=p19] | [p168<=0 & 0<=p168]] & [[[p16<=0 & 0<=p16] | [p166<=0 & 0<=p166]] & [[p15<=0 & 0<=p15] | [p169<=0 & 0<=p169]]]]]] & [[[[[p16<=0 & 0<=p16] | [p164<=0 & 0<=p164]] & [[[p15<=0 & 0<=p15] | [p164<=0 & 0<=p164]] & [[p16<=0 & 0<=p16] | [p169<=0 & 0<=p169]]]] & [[[p15<=0 & 0<=p15] | [p166<=0 & 0<=p166]] & [[[p16<=0 & 0<=p16] | [p167<=0 & 0<=p167]] & [[p14<=0 & 0<=p14] | [p164<=0 & 0<=p164]]]]] & [[[[p14<=0 & 0<=p14] | [p168<=0 & 0<=p168]] & [[[p17<=0 & 0<=p17] | [p169<=0 & 0<=p169]] & [[p14<=0 & 0<=p14] | [p166<=0 & 0<=p166]]]] & [[[p17<=0 & 0<=p17] | [p167<=0 & 0<=p167]] & [[[p18<=0 & 0<=p18] | [p169<=0 & 0<=p169]] & [[p13<=0 & 0<=p13] | [p166<=0 & 0<=p166]]]]]]] & [[[[[[p13<=0 & 0<=p13] | [p168<=0 & 0<=p168]] & [[[p18<=0 & 0<=p18] | [p165<=0 & 0<=p165]] & [[p18<=0 & 0<=p18] | [p167<=0 & 0<=p167]]]] & [[[p13<=0 & 0<=p13] | [p164<=0 & 0<=p164]] & [[[p17<=0 & 0<=p17] | [p165<=0 & 0<=p165]] & [[p19<=0 & 0<=p19] | [p167<=0 & 0<=p167]]]]] & [[[[p19<=0 & 0<=p19] | [p165<=0 & 0<=p165]] & [[[p19<=0 & 0<=p19] | [p169<=0 & 0<=p169]] & [[p16<=0 & 0<=p16] | [p165<=0 & 0<=p165]]]] & [[[p15<=0 & 0<=p15] | [p168<=0 & 0<=p168]] & [[[p15<=0 & 0<=p15] | [p165<=0 & 0<=p165]] & [[p15<=0 & 0<=p15] | [p167<=0 & 0<=p167]]]]]] & [[[[[p16<=0 & 0<=p16] | [p168<=0 & 0<=p168]] & [[[p17<=0 & 0<=p17] | [p168<=0 & 0<=p168]] & [[p17<=0 & 0<=p17] | [p166<=0 & 0<=p166]]]] & [[[p14<=0 & 0<=p14] | [p167<=0 & 0<=p167]] & [[[p14<=0 & 0<=p14] | [p165<=0 & 0<=p165]] & [[p18<=0 & 0<=p18] | [p164<=0 & 0<=p164]]]]] & [[[p71<=0 & 0<=p71] & [[p70<=0 & 0<=p70] & [p73<=0 & 0<=p73]]] & [[p72<=0 & 0<=p72] & [[p69<=0 & 0<=p69] & [p68<=0 & 0<=p68]]]]]]] | EX [[[[[[[[p10<=0 & 0<=p10] | [p33<=0 & 0<=p33]] & [[p10<=0 & 0<=p10] | [p35<=0 & 0<=p35]]] & [[[p10<=0 & 0<=p10] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p37<=0 & 0<=p37]] & [[p9<=0 & 0<=p9] | [p33<=0 & 0<=p33]]]]] & [[[[p11<=0 & 0<=p11] | [p35<=0 & 0<=p35]] & [[p11<=0 & 0<=p11] | [p33<=0 & 0<=p33]]] & [[[p9<=0 & 0<=p9] | [p37<=0 & 0<=p37]] & [[[p6<=0 & 0<=p6] | [p32<=0 & 0<=p32]] & [[p9<=0 & 0<=p9] | [p35<=0 & 0<=p35]]]]]] & [[[[[p6<=0 & 0<=p6] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p36<=0 & 0<=p36]]] & [[[p8<=0 & 0<=p8] | [p36<=0 & 0<=p36]] & [[[p7<=0 & 0<=p7] | [p34<=0 & 0<=p34]] & [[p7<=0 & 0<=p7] | [p32<=0 & 0<=p32]]]]] & [[[[p7<=0 & 0<=p7] | [p36<=0 & 0<=p36]] & [[[p8<=0 & 0<=p8] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p35<=0 & 0<=p35]]]] & [[[p8<=0 & 0<=p8] | [p34<=0 & 0<=p34]] & [[[p12<=0 & 0<=p12] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p33<=0 & 0<=p33]]]]]]] & [[[[[[p10<=0 & 0<=p10] | [p34<=0 & 0<=p34]] & [[p10<=0 & 0<=p10] | [p36<=0 & 0<=p36]]] & [[[p6<=0 & 0<=p6] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p36<=0 & 0<=p36]] & [[p9<=0 & 0<=p9] | [p32<=0 & 0<=p32]]]]] & [[[[p11<=0 & 0<=p11] | [p34<=0 & 0<=p34]] & [[p11<=0 & 0<=p11] | [p32<=0 & 0<=p32]]] & [[[p9<=0 & 0<=p9] | [p36<=0 & 0<=p36]] & [[[p9<=0 & 0<=p9] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p33<=0 & 0<=p33]]]]]] & [[[[[p6<=0 & 0<=p6] | [p35<=0 & 0<=p35]] & [[p10<=0 & 0<=p10] | [p32<=0 & 0<=p32]]] & [[[p8<=0 & 0<=p8] | [p35<=0 & 0<=p35]] & [[[p8<=0 & 0<=p8] | [p37<=0 & 0<=p37]] & [[p7<=0 & 0<=p7] | [p35<=0 & 0<=p35]]]]] & [[[[p7<=0 & 0<=p7] | [p33<=0 & 0<=p33]] & [[[p7<=0 & 0<=p7] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p36<=0 & 0<=p36]]]] & [[[p8<=0 & 0<=p8] | [p33<=0 & 0<=p33]] & [[[p12<=0 & 0<=p12] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p34<=0 & 0<=p34]]]]]]]]]] & [[[[[[p23<=1 & 1<=p23] & [p39<=1 & 1<=p39]] | [[[p28<=1 & 1<=p28] & [p42<=1 & 1<=p42]] | [[p26<=1 & 1<=p26] & [p41<=1 & 1<=p41]]]] | [[[p31<=1 & 1<=p31] & [p43<=1 & 1<=p43]] | [[[p25<=1 & 1<=p25] & [p40<=1 & 1<=p40]] | [[p21<=1 & 1<=p21] & [p38<=1 & 1<=p38]]]]] | [[[[p27<=1 & 1<=p27] & [p41<=1 & 1<=p41]] | [[[p22<=1 & 1<=p22] & [p39<=1 & 1<=p39]] | [[p30<=1 & 1<=p30] & [p43<=1 & 1<=p43]]]] | [[[p29<=1 & 1<=p29] & [p42<=1 & 1<=p42]] | [[[p20<=1 & 1<=p20] & [p38<=1 & 1<=p38]] | [[p24<=1 & 1<=p24] & [p40<=1 & 1<=p40]]]]]] & [[[[[[[p13<=1 & 1<=p13] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p169<=1 & 1<=p169]]] | [[[p18<=1 & 1<=p18] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p168<=1 & 1<=p168]]]]] | [[[[p17<=1 & 1<=p17] & [p164<=1 & 1<=p164]] | [[p14<=1 & 1<=p14] & [p169<=1 & 1<=p169]]] | [[[p19<=1 & 1<=p19] & [p166<=1 & 1<=p166]] | [[[p19<=1 & 1<=p19] & [p164<=1 & 1<=p164]] | [[p19<=1 & 1<=p19] & [p168<=1 & 1<=p168]]]]]] | [[[[[p16<=1 & 1<=p16] & [p166<=1 & 1<=p166]] | [[p15<=1 & 1<=p15] & [p169<=1 & 1<=p169]]] | [[[p16<=1 & 1<=p16] & [p164<=1 & 1<=p164]] | [[[p15<=1 & 1<=p15] & [p164<=1 & 1<=p164]] | [[p16<=1 & 1<=p16] & [p169<=1 & 1<=p169]]]]] | [[[[p15<=1 & 1<=p15] & [p166<=1 & 1<=p166]] | [[[p16<=1 & 1<=p16] & [p167<=1 & 1<=p167]] | [[p14<=1 & 1<=p14] & [p164<=1 & 1<=p164]]]] | [[[p14<=1 & 1<=p14] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]] | [[p14<=1 & 1<=p14] & [p166<=1 & 1<=p166]]]]]]] | [[[[[[p17<=1 & 1<=p17] & [p167<=1 & 1<=p167]] | [[p18<=1 & 1<=p18] & [p169<=1 & 1<=p169]]] | [[[p13<=1 & 1<=p13] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p168<=1 & 1<=p168]] | [[p18<=1 & 1<=p18] & [p165<=1 & 1<=p165]]]]] | [[[[p18<=1 & 1<=p18] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p164<=1 & 1<=p164]]] | [[[p17<=1 & 1<=p17] & [p165<=1 & 1<=p165]] | [[[p19<=1 & 1<=p19] & [p167<=1 & 1<=p167]] | [[p19<=1 & 1<=p19] & [p165<=1 & 1<=p165]]]]]] | [[[[[p19<=1 & 1<=p19] & [p169<=1 & 1<=p169]] | [[p16<=1 & 1<=p16] & [p165<=1 & 1<=p165]]] | [[[p15<=1 & 1<=p15] & [p168<=1 & 1<=p168]] | [[[p15<=1 & 1<=p15] & [p165<=1 & 1<=p165]] | [[p15<=1 & 1<=p15] & [p167<=1 & 1<=p167]]]]] | [[[[p16<=1 & 1<=p16] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p168<=1 & 1<=p168]] | [[p17<=1 & 1<=p17] & [p166<=1 & 1<=p166]]]] | [[[p14<=1 & 1<=p14] & [p167<=1 & 1<=p167]] | [[[p14<=1 & 1<=p14] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p164<=1 & 1<=p164]]]]]]]]]]]]]
normalized: [EG [~ [EX [~ [[[[[[[[[[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p14<=1 & 1<=p14]]] | [[p167<=1 & 1<=p167] & [p14<=1 & 1<=p14]]] | [[[[p166<=1 & 1<=p166] & [p17<=1 & 1<=p17]] | [[p168<=1 & 1<=p168] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p16<=1 & 1<=p16]]]] | [[[[[p167<=1 & 1<=p167] & [p15<=1 & 1<=p15]] | [[p165<=1 & 1<=p165] & [p15<=1 & 1<=p15]]] | [[p168<=1 & 1<=p168] & [p15<=1 & 1<=p15]]] | [[[p165<=1 & 1<=p165] & [p16<=1 & 1<=p16]] | [[p169<=1 & 1<=p169] & [p19<=1 & 1<=p19]]]]] | [[[[[[p165<=1 & 1<=p165] & [p19<=1 & 1<=p19]] | [[p167<=1 & 1<=p167] & [p19<=1 & 1<=p19]]] | [[p165<=1 & 1<=p165] & [p17<=1 & 1<=p17]]] | [[[p164<=1 & 1<=p164] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p18<=1 & 1<=p18]]]] | [[[[[p165<=1 & 1<=p165] & [p18<=1 & 1<=p18]] | [[p168<=1 & 1<=p168] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p13<=1 & 1<=p13]]] | [[[p169<=1 & 1<=p169] & [p18<=1 & 1<=p18]] | [[p167<=1 & 1<=p167] & [p17<=1 & 1<=p17]]]]]] | [[[[[[[p166<=1 & 1<=p166] & [p14<=1 & 1<=p14]] | [[p169<=1 & 1<=p169] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p14<=1 & 1<=p14]]] | [[[[p164<=1 & 1<=p164] & [p14<=1 & 1<=p14]] | [[p167<=1 & 1<=p167] & [p16<=1 & 1<=p16]]] | [[p166<=1 & 1<=p166] & [p15<=1 & 1<=p15]]]] | [[[[[p169<=1 & 1<=p169] & [p16<=1 & 1<=p16]] | [[p164<=1 & 1<=p164] & [p15<=1 & 1<=p15]]] | [[p164<=1 & 1<=p164] & [p16<=1 & 1<=p16]]] | [[[p169<=1 & 1<=p169] & [p15<=1 & 1<=p15]] | [[p166<=1 & 1<=p166] & [p16<=1 & 1<=p16]]]]] | [[[[[[p168<=1 & 1<=p168] & [p19<=1 & 1<=p19]] | [[p164<=1 & 1<=p164] & [p19<=1 & 1<=p19]]] | [[p166<=1 & 1<=p166] & [p19<=1 & 1<=p19]]] | [[[p169<=1 & 1<=p169] & [p14<=1 & 1<=p14]] | [[p164<=1 & 1<=p164] & [p17<=1 & 1<=p17]]]] | [[[[[p168<=1 & 1<=p168] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p18<=1 & 1<=p18]]] | [[[p169<=1 & 1<=p169] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p13<=1 & 1<=p13]]]]]]] & [[[[[[p40<=1 & 1<=p40] & [p24<=1 & 1<=p24]] | [[p38<=1 & 1<=p38] & [p20<=1 & 1<=p20]]] | [[p42<=1 & 1<=p42] & [p29<=1 & 1<=p29]]] | [[[[p43<=1 & 1<=p43] & [p30<=1 & 1<=p30]] | [[p39<=1 & 1<=p39] & [p22<=1 & 1<=p22]]] | [[p41<=1 & 1<=p41] & [p27<=1 & 1<=p27]]]] | [[[[[p38<=1 & 1<=p38] & [p21<=1 & 1<=p21]] | [[p40<=1 & 1<=p40] & [p25<=1 & 1<=p25]]] | [[p43<=1 & 1<=p43] & [p31<=1 & 1<=p31]]] | [[[[p41<=1 & 1<=p41] & [p26<=1 & 1<=p26]] | [[p42<=1 & 1<=p42] & [p28<=1 & 1<=p28]]] | [[p39<=1 & 1<=p39] & [p23<=1 & 1<=p23]]]]]] & [EX [[[[[[[[p34<=0 & 0<=p34] | [p8<=0 & 0<=p8]] & [[[p33<=0 & 0<=p33] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p12<=0 & 0<=p12]]]] & [[[[p35<=0 & 0<=p35] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p8<=0 & 0<=p8]]] & [[p36<=0 & 0<=p36] | [p7<=0 & 0<=p7]]]] & [[[[[p32<=0 & 0<=p32] | [p7<=0 & 0<=p7]] & [[p34<=0 & 0<=p34] | [p7<=0 & 0<=p7]]] & [[p36<=0 & 0<=p36] | [p8<=0 & 0<=p8]]] & [[[p36<=0 & 0<=p36] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p6<=0 & 0<=p6]]]]] & [[[[[[p35<=0 & 0<=p35] | [p9<=0 & 0<=p9]] & [[p32<=0 & 0<=p32] | [p6<=0 & 0<=p6]]] & [[p37<=0 & 0<=p37] | [p9<=0 & 0<=p9]]] & [[[p33<=0 & 0<=p33] | [p11<=0 & 0<=p11]] & [[p35<=0 & 0<=p35] | [p11<=0 & 0<=p11]]]] & [[[[[p33<=0 & 0<=p33] | [p9<=0 & 0<=p9]] & [[p37<=0 & 0<=p37] | [p11<=0 & 0<=p11]]] & [[p37<=0 & 0<=p37] | [p10<=0 & 0<=p10]]] & [[[p35<=0 & 0<=p35] | [p10<=0 & 0<=p10]] & [[p33<=0 & 0<=p33] | [p10<=0 & 0<=p10]]]]]] & [[[[[[p6<=0 & 0<=p6] | [p37<=0 & 0<=p37]] & [[[p32<=0 & 0<=p32] | [p9<=0 & 0<=p9]] & [[p36<=0 & 0<=p36] | [p11<=0 & 0<=p11]]]] & [[[p36<=0 & 0<=p36] | [p10<=0 & 0<=p10]] & [[p10<=0 & 0<=p10] | [p34<=0 & 0<=p34]]]] & [[[[[p33<=0 & 0<=p33] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p9<=0 & 0<=p9]]] & [[p36<=0 & 0<=p36] | [p9<=0 & 0<=p9]]] & [[[p32<=0 & 0<=p32] | [p11<=0 & 0<=p11]] & [[p34<=0 & 0<=p34] | [p11<=0 & 0<=p11]]]]] & [[[[[[p34<=0 & 0<=p34] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p12<=0 & 0<=p12]]] & [[p33<=0 & 0<=p33] | [p8<=0 & 0<=p8]]] & [[[[p36<=0 & 0<=p36] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p7<=0 & 0<=p7]]] & [[p33<=0 & 0<=p33] | [p7<=0 & 0<=p7]]]] & [[[[[p35<=0 & 0<=p35] | [p7<=0 & 0<=p7]] & [[p37<=0 & 0<=p37] | [p8<=0 & 0<=p8]]] & [[p35<=0 & 0<=p35] | [p8<=0 & 0<=p8]]] & [[[p32<=0 & 0<=p32] | [p10<=0 & 0<=p10]] & [[p35<=0 & 0<=p35] | [p6<=0 & 0<=p6]]]]]]]] | [[[[[[[p68<=0 & 0<=p68] & [p69<=0 & 0<=p69]] & [p72<=0 & 0<=p72]] & [[[p73<=0 & 0<=p73] & [p70<=0 & 0<=p70]] & [p71<=0 & 0<=p71]]] & [[[[[p164<=0 & 0<=p164] | [p18<=0 & 0<=p18]] & [[p165<=0 & 0<=p165] | [p14<=0 & 0<=p14]]] & [[p167<=0 & 0<=p167] | [p14<=0 & 0<=p14]]] & [[[[p166<=0 & 0<=p166] | [p17<=0 & 0<=p17]] & [[p168<=0 & 0<=p168] | [p17<=0 & 0<=p17]]] & [[p168<=0 & 0<=p168] | [p16<=0 & 0<=p16]]]]] & [[[[[[p167<=0 & 0<=p167] | [p15<=0 & 0<=p15]] & [[p165<=0 & 0<=p165] | [p15<=0 & 0<=p15]]] & [[p168<=0 & 0<=p168] | [p15<=0 & 0<=p15]]] & [[[[p165<=0 & 0<=p165] | [p16<=0 & 0<=p16]] & [[p169<=0 & 0<=p169] | [p19<=0 & 0<=p19]]] & [[p165<=0 & 0<=p165] | [p19<=0 & 0<=p19]]]] & [[[[[p167<=0 & 0<=p167] | [p19<=0 & 0<=p19]] & [[p165<=0 & 0<=p165] | [p17<=0 & 0<=p17]]] & [[p164<=0 & 0<=p164] | [p13<=0 & 0<=p13]]] & [[[[p167<=0 & 0<=p167] | [p18<=0 & 0<=p18]] & [[p165<=0 & 0<=p165] | [p18<=0 & 0<=p18]]] & [[p168<=0 & 0<=p168] | [p13<=0 & 0<=p13]]]]]] & [[[[[[[p166<=0 & 0<=p166] | [p13<=0 & 0<=p13]] & [[p169<=0 & 0<=p169] | [p18<=0 & 0<=p18]]] & [[p167<=0 & 0<=p167] | [p17<=0 & 0<=p17]]] & [[[[p166<=0 & 0<=p166] | [p14<=0 & 0<=p14]] & [[p169<=0 & 0<=p169] | [p17<=0 & 0<=p17]]] & [[p168<=0 & 0<=p168] | [p14<=0 & 0<=p14]]]] & [[[[[p164<=0 & 0<=p164] | [p14<=0 & 0<=p14]] & [[p167<=0 & 0<=p167] | [p16<=0 & 0<=p16]]] & [[p166<=0 & 0<=p166] | [p15<=0 & 0<=p15]]] & [[[[p169<=0 & 0<=p169] | [p16<=0 & 0<=p16]] & [[p164<=0 & 0<=p164] | [p15<=0 & 0<=p15]]] & [[p164<=0 & 0<=p164] | [p16<=0 & 0<=p16]]]]] & [[[[[[p169<=0 & 0<=p169] | [p15<=0 & 0<=p15]] & [[p166<=0 & 0<=p166] | [p16<=0 & 0<=p16]]] & [[p168<=0 & 0<=p168] | [p19<=0 & 0<=p19]]] & [[[[p164<=0 & 0<=p164] | [p19<=0 & 0<=p19]] & [[p166<=0 & 0<=p166] | [p19<=0 & 0<=p19]]] & [[p169<=0 & 0<=p169] | [p14<=0 & 0<=p14]]]] & [[[[[p164<=0 & 0<=p164] | [p17<=0 & 0<=p17]] & [[p168<=0 & 0<=p168] | [p18<=0 & 0<=p18]]] & [[p165<=0 & 0<=p165] | [p13<=0 & 0<=p13]]] & [[[[p166<=0 & 0<=p166] | [p18<=0 & 0<=p18]] & [[p169<=0 & 0<=p169] | [p13<=0 & 0<=p13]]] & [[p167<=0 & 0<=p167] | [p13<=0 & 0<=p13]]]]]]]]]]]]] | ~ [E [true U EG [~ [E [[[[[[[[[p155<=1 & 1<=p155] & [p14<=1 & 1<=p14]] | [[p156<=1 & 1<=p156] & [p14<=1 & 1<=p14]]] | [[p157<=1 & 1<=p157] & [p14<=1 & 1<=p14]]] | [[[p155<=1 & 1<=p155] & [p18<=1 & 1<=p18]] | [[p152<=1 & 1<=p152] & [p15<=1 & 1<=p15]]]] | [[[[p157<=1 & 1<=p157] & [p18<=1 & 1<=p18]] | [[p152<=1 & 1<=p152] & [p18<=1 & 1<=p18]]] | [[[p153<=1 & 1<=p153] & [p18<=1 & 1<=p18]] | [[p154<=1 & 1<=p154] & [p18<=1 & 1<=p18]]]]] | [[[[[[p156<=1 & 1<=p156] & [p15<=1 & 1<=p15]] | [[p157<=1 & 1<=p157] & [p15<=1 & 1<=p15]]] | [[p154<=1 & 1<=p154] & [p15<=1 & 1<=p15]]] | [[[p155<=1 & 1<=p155] & [p15<=1 & 1<=p15]] | [[p156<=1 & 1<=p156] & [p19<=1 & 1<=p19]]]] | [[[[p154<=1 & 1<=p154] & [p19<=1 & 1<=p19]] | [[p153<=1 & 1<=p153] & [p14<=1 & 1<=p14]]] | [[[p155<=1 & 1<=p155] & [p19<=1 & 1<=p19]] | [[p154<=1 & 1<=p154] & [p14<=1 & 1<=p14]]]]]] | [[[[[[[p152<=1 & 1<=p152] & [p19<=1 & 1<=p19]] | [[p153<=1 & 1<=p153] & [p19<=1 & 1<=p19]]] | [[p153<=1 & 1<=p153] & [p16<=1 & 1<=p16]]] | [[[p155<=1 & 1<=p155] & [p16<=1 & 1<=p16]] | [[p156<=1 & 1<=p156] & [p16<=1 & 1<=p16]]]] | [[[[p157<=1 & 1<=p157] & [p16<=1 & 1<=p16]] | [[p154<=1 & 1<=p154] & [p13<=1 & 1<=p13]]] | [[[p155<=1 & 1<=p155] & [p13<=1 & 1<=p13]] | [[p152<=1 & 1<=p152] & [p13<=1 & 1<=p13]]]]] | [[[[[[p153<=1 & 1<=p153] & [p13<=1 & 1<=p13]] | [[p156<=1 & 1<=p156] & [p13<=1 & 1<=p13]]] | [[p157<=1 & 1<=p157] & [p13<=1 & 1<=p13]]] | [[[p152<=1 & 1<=p152] & [p16<=1 & 1<=p16]] | [[p154<=1 & 1<=p154] & [p17<=1 & 1<=p17]]]] | [[[[p152<=1 & 1<=p152] & [p17<=1 & 1<=p17]] | [[p153<=1 & 1<=p153] & [p17<=1 & 1<=p17]]] | [[[p156<=1 & 1<=p156] & [p17<=1 & 1<=p17]] | [[p157<=1 & 1<=p157] & [p17<=1 & 1<=p17]]]]]]] U [[[[[[[[p51<=1 & 1<=p51] & [p19<=1 & 1<=p19]] | [[p50<=1 & 1<=p50] & [p15<=1 & 1<=p15]]] | [[p52<=1 & 1<=p52] & [p15<=1 & 1<=p15]]] | [[[[p54<=1 & 1<=p54] & [p15<=1 & 1<=p15]] | [[p55<=1 & 1<=p55] & [p18<=1 & 1<=p18]]] | [[p53<=1 & 1<=p53] & [p18<=1 & 1<=p18]]]] | [[[[[p51<=1 & 1<=p51] & [p18<=1 & 1<=p18]] | [[p54<=1 & 1<=p54] & [p14<=1 & 1<=p14]]] | [[p52<=1 & 1<=p52] & [p14<=1 & 1<=p14]]] | [[[p55<=1 & 1<=p55] & [p19<=1 & 1<=p19]] | [[p50<=1 & 1<=p50] & [p14<=1 & 1<=p14]]]]] | [[[[[[p53<=1 & 1<=p53] & [p19<=1 & 1<=p19]] | [[p52<=1 & 1<=p52] & [p17<=1 & 1<=p17]]] | [[p54<=1 & 1<=p54] & [p17<=1 & 1<=p17]]] | [[[p50<=1 & 1<=p50] & [p17<=1 & 1<=p17]] | [[p55<=1 & 1<=p55] & [p13<=1 & 1<=p13]]]] | [[[[[p51<=1 & 1<=p51] & [p13<=1 & 1<=p13]] | [[p53<=1 & 1<=p53] & [p13<=1 & 1<=p13]]] | [[p50<=1 & 1<=p50] & [p16<=1 & 1<=p16]]] | [[[p54<=1 & 1<=p54] & [p16<=1 & 1<=p16]] | [[p52<=1 & 1<=p52] & [p16<=1 & 1<=p16]]]]]] | [[[[[[[p52<=1 & 1<=p52] & [p19<=1 & 1<=p19]] | [[p51<=1 & 1<=p51] & [p15<=1 & 1<=p15]]] | [[p53<=1 & 1<=p53] & [p15<=1 & 1<=p15]]] | [[[[p55<=1 & 1<=p55] & [p15<=1 & 1<=p15]] | [[p54<=1 & 1<=p54] & [p18<=1 & 1<=p18]]] | [[p52<=1 & 1<=p52] & [p18<=1 & 1<=p18]]]] | [[[[[p50<=1 & 1<=p50] & [p18<=1 & 1<=p18]] | [[p55<=1 & 1<=p55] & [p14<=1 & 1<=p14]]] | [[p53<=1 & 1<=p53] & [p14<=1 & 1<=p14]]] | [[[p50<=1 & 1<=p50] & [p19<=1 & 1<=p19]] | [[p54<=1 & 1<=p54] & [p19<=1 & 1<=p19]]]]] | [[[[[[p51<=1 & 1<=p51] & [p14<=1 & 1<=p14]] | [[p51<=1 & 1<=p51] & [p17<=1 & 1<=p17]]] | [[p53<=1 & 1<=p53] & [p17<=1 & 1<=p17]]] | [[[p50<=1 & 1<=p50] & [p13<=1 & 1<=p13]] | [[p52<=1 & 1<=p52] & [p13<=1 & 1<=p13]]]] | [[[[[p54<=1 & 1<=p54] & [p13<=1 & 1<=p13]] | [[p51<=1 & 1<=p51] & [p16<=1 & 1<=p16]]] | [[p55<=1 & 1<=p55] & [p16<=1 & 1<=p16]]] | [[[p53<=1 & 1<=p53] & [p16<=1 & 1<=p16]] | [[p55<=1 & 1<=p55] & [p17<=1 & 1<=p17]]]]]]]]]]]]]
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (p53<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (p55<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (p54<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (p52<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (p50<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (p51<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (p17<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (p13<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (p16<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (p19<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (p154<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (p153<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (p15<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (p152<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (p18<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (p157<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (p156<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (p14<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (p155<=1)
states: 547,231,759,144 (11)
MC time: 1m 3.026sec
checking: AG [[[[[[AF [E [[AG [[[[[[[[p10<=1 & 1<=p10] & [p33<=1 & 1<=p33]] | [[p10<=1 & 1<=p10] & [p35<=1 & 1<=p35]]] | [[[p10<=1 & 1<=p10] & [p37<=1 & 1<=p37]] | [[[p11<=1 & 1<=p11] & [p37<=1 & 1<=p37]] | [[p9<=1 & 1<=p9] & [p33<=1 & 1<=p33]]]]] | [[[[p11<=1 & 1<=p11] & [p35<=1 & 1<=p35]] | [[p11<=1 & 1<=p11] & [p33<=1 & 1<=p33]]] | [[[p9<=1 & 1<=p9] & [p37<=1 & 1<=p37]] | [[[p6<=1 & 1<=p6] & [p32<=1 & 1<=p32]] | [[p9<=1 & 1<=p9] & [p35<=1 & 1<=p35]]]]]] | [[[[[p6<=1 & 1<=p6] & [p34<=1 & 1<=p34]] | [[p6<=1 & 1<=p6] & [p36<=1 & 1<=p36]]] | [[[p8<=1 & 1<=p8] & [p36<=1 & 1<=p36]] | [[[p7<=1 & 1<=p7] & [p34<=1 & 1<=p34]] | [[p7<=1 & 1<=p7] & [p32<=1 & 1<=p32]]]]] | [[[[p7<=1 & 1<=p7] & [p36<=1 & 1<=p36]] | [[[p8<=1 & 1<=p8] & [p32<=1 & 1<=p32]] | [[p12<=1 & 1<=p12] & [p35<=1 & 1<=p35]]]] | [[[p8<=1 & 1<=p8] & [p34<=1 & 1<=p34]] | [[[p12<=1 & 1<=p12] & [p37<=1 & 1<=p37]] | [[p12<=1 & 1<=p12] & [p33<=1 & 1<=p33]]]]]]] | [[[[[[p10<=1 & 1<=p10] & [p34<=1 & 1<=p34]] | [[p10<=1 & 1<=p10] & [p36<=1 & 1<=p36]]] | [[[p6<=1 & 1<=p6] & [p37<=1 & 1<=p37]] | [[[p11<=1 & 1<=p11] & [p36<=1 & 1<=p36]] | [[p9<=1 & 1<=p9] & [p32<=1 & 1<=p32]]]]] | [[[[p11<=1 & 1<=p11] & [p34<=1 & 1<=p34]] | [[p11<=1 & 1<=p11] & [p32<=1 & 1<=p32]]] | [[[p9<=1 & 1<=p9] & [p36<=1 & 1<=p36]] | [[[p9<=1 & 1<=p9] & [p34<=1 & 1<=p34]] | [[p6<=1 & 1<=p6] & [p33<=1 & 1<=p33]]]]]] | [[[[[p6<=1 & 1<=p6] & [p35<=1 & 1<=p35]] | [[p10<=1 & 1<=p10] & [p32<=1 & 1<=p32]]] | [[[p8<=1 & 1<=p8] & [p35<=1 & 1<=p35]] | [[[p8<=1 & 1<=p8] & [p37<=1 & 1<=p37]] | [[p7<=1 & 1<=p7] & [p35<=1 & 1<=p35]]]]] | [[[[p7<=1 & 1<=p7] & [p33<=1 & 1<=p33]] | [[[p7<=1 & 1<=p7] & [p37<=1 & 1<=p37]] | [[p12<=1 & 1<=p12] & [p36<=1 & 1<=p36]]]] | [[[p8<=1 & 1<=p8] & [p33<=1 & 1<=p33]] | [[[p12<=1 & 1<=p12] & [p32<=1 & 1<=p32]] | [[p12<=1 & 1<=p12] & [p34<=1 & 1<=p34]]]]]]]]] & [[[[p13<=1 & 1<=p13] & [p163<=1 & 1<=p163]] | [[[p13<=1 & 1<=p13] & [p160<=1 & 1<=p160]] | [[p13<=1 & 1<=p13] & [p159<=1 & 1<=p159]]]] | [[[p13<=1 & 1<=p13] & [p162<=1 & 1<=p162]] | [[[p13<=1 & 1<=p13] & [p161<=1 & 1<=p161]] | [[p13<=1 & 1<=p13] & [p158<=1 & 1<=p158]]]]]] U EX [[[[[[[[p12<=1 & 1<=p12] & [p56<=1 & 1<=p56]] | [[p12<=1 & 1<=p12] & [p58<=1 & 1<=p58]]] | [[[p12<=1 & 1<=p12] & [p57<=1 & 1<=p57]] | [[p7<=1 & 1<=p7] & [p61<=1 & 1<=p61]]]] | [[[[p7<=1 & 1<=p7] & [p60<=1 & 1<=p60]] | [[p7<=1 & 1<=p7] & [p59<=1 & 1<=p59]]] | [[[p7<=1 & 1<=p7] & [p58<=1 & 1<=p58]] | [[[p7<=1 & 1<=p7] & [p57<=1 & 1<=p57]] | [[p8<=1 & 1<=p8] & [p60<=1 & 1<=p60]]]]]] | [[[[[p8<=1 & 1<=p8] & [p59<=1 & 1<=p59]] | [[p8<=1 & 1<=p8] & [p61<=1 & 1<=p61]]] | [[[p8<=1 & 1<=p8] & [p56<=1 & 1<=p56]] | [[p12<=1 & 1<=p12] & [p60<=1 & 1<=p60]]]] | [[[[p12<=1 & 1<=p12] & [p59<=1 & 1<=p59]] | [[p8<=1 & 1<=p8] & [p58<=1 & 1<=p58]]] | [[[p10<=1 & 1<=p10] & [p61<=1 & 1<=p61]] | [[[p9<=1 & 1<=p9] & [p57<=1 & 1<=p57]] | [[p9<=1 & 1<=p9] & [p56<=1 & 1<=p56]]]]]]] | [[[[[[p9<=1 & 1<=p9] & [p61<=1 & 1<=p61]] | [[p9<=1 & 1<=p9] & [p60<=1 & 1<=p60]]] | [[[p9<=1 & 1<=p9] & [p59<=1 & 1<=p59]] | [[p11<=1 & 1<=p11] & [p61<=1 & 1<=p61]]]] | [[[[p6<=1 & 1<=p6] & [p57<=1 & 1<=p57]] | [[p11<=1 & 1<=p11] & [p59<=1 & 1<=p59]]] | [[[p6<=1 & 1<=p6] & [p58<=1 & 1<=p58]] | [[[p11<=1 & 1<=p11] & [p58<=1 & 1<=p58]] | [[p11<=1 & 1<=p11] & [p57<=1 & 1<=p57]]]]]] | [[[[[p6<=1 & 1<=p6] & [p59<=1 & 1<=p59]] | [[p11<=1 & 1<=p11] & [p56<=1 & 1<=p56]]] | [[[p6<=1 & 1<=p6] & [p60<=1 & 1<=p60]] | [[p6<=1 & 1<=p6] & [p61<=1 & 1<=p61]]]] | [[[[p10<=1 & 1<=p10] & [p56<=1 & 1<=p56]] | [[p10<=1 & 1<=p10] & [p58<=1 & 1<=p58]]] | [[[p10<=1 & 1<=p10] & [p57<=1 & 1<=p57]] | [[[p10<=1 & 1<=p10] & [p60<=1 & 1<=p60]] | [[p6<=1 & 1<=p6] & [p56<=1 & 1<=p56]]]]]]]]]]] | [E [[[[[[p13<=1 & 1<=p13] & [p47<=1 & 1<=p47]] | [[[p13<=1 & 1<=p13] & [p46<=1 & 1<=p46]] | [[p13<=1 & 1<=p13] & [p45<=1 & 1<=p45]]]] | [[[p13<=1 & 1<=p13] & [p44<=1 & 1<=p44]] | [[[p13<=1 & 1<=p13] & [p49<=1 & 1<=p49]] | [[p13<=1 & 1<=p13] & [p48<=1 & 1<=p48]]]]] & [[[[[p28<=1 & 1<=p28] & [p66<=1 & 1<=p66]] | [[[p20<=1 & 1<=p20] & [p62<=1 & 1<=p62]] | [[p25<=1 & 1<=p25] & [p64<=1 & 1<=p64]]]] | [[[p23<=1 & 1<=p23] & [p63<=1 & 1<=p63]] | [[[p26<=1 & 1<=p26] & [p65<=1 & 1<=p65]] | [[p30<=1 & 1<=p30] & [p67<=1 & 1<=p67]]]]] | [[[[p29<=1 & 1<=p29] & [p66<=1 & 1<=p66]] | [[[p27<=1 & 1<=p27] & [p65<=1 & 1<=p65]] | [[p24<=1 & 1<=p24] & [p64<=1 & 1<=p64]]]] | [[[p21<=1 & 1<=p21] & [p62<=1 & 1<=p62]] | [[[p22<=1 & 1<=p22] & [p63<=1 & 1<=p63]] | [[p31<=1 & 1<=p31] & [p67<=1 & 1<=p67]]]]]]] U ~ [[[[[[[[p13<=1 & 1<=p13] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p169<=1 & 1<=p169]]] | [[[p18<=1 & 1<=p18] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p168<=1 & 1<=p168]]]]] | [[[[p17<=1 & 1<=p17] & [p164<=1 & 1<=p164]] | [[p14<=1 & 1<=p14] & [p169<=1 & 1<=p169]]] | [[[p19<=1 & 1<=p19] & [p166<=1 & 1<=p166]] | [[[p19<=1 & 1<=p19] & [p164<=1 & 1<=p164]] | [[p19<=1 & 1<=p19] & [p168<=1 & 1<=p168]]]]]] | [[[[[p16<=1 & 1<=p16] & [p166<=1 & 1<=p166]] | [[p15<=1 & 1<=p15] & [p169<=1 & 1<=p169]]] | [[[p16<=1 & 1<=p16] & [p164<=1 & 1<=p164]] | [[[p15<=1 & 1<=p15] & [p164<=1 & 1<=p164]] | [[p16<=1 & 1<=p16] & [p169<=1 & 1<=p169]]]]] | [[[[p15<=1 & 1<=p15] & [p166<=1 & 1<=p166]] | [[[p16<=1 & 1<=p16] & [p167<=1 & 1<=p167]] | [[p14<=1 & 1<=p14] & [p164<=1 & 1<=p164]]]] | [[[p14<=1 & 1<=p14] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p169<=1 & 1<=p169]] | [[p14<=1 & 1<=p14] & [p166<=1 & 1<=p166]]]]]]] | [[[[[[p17<=1 & 1<=p17] & [p167<=1 & 1<=p167]] | [[p18<=1 & 1<=p18] & [p169<=1 & 1<=p169]]] | [[[p13<=1 & 1<=p13] & [p166<=1 & 1<=p166]] | [[[p13<=1 & 1<=p13] & [p168<=1 & 1<=p168]] | [[p18<=1 & 1<=p18] & [p165<=1 & 1<=p165]]]]] | [[[[p18<=1 & 1<=p18] & [p167<=1 & 1<=p167]] | [[p13<=1 & 1<=p13] & [p164<=1 & 1<=p164]]] | [[[p17<=1 & 1<=p17] & [p165<=1 & 1<=p165]] | [[[p19<=1 & 1<=p19] & [p167<=1 & 1<=p167]] | [[1<=p19 & p19<=1] & [p165<=1 & 1<=p165]]]]]] | [[[[[p19<=1 & 1<=p19] & [p169<=1 & 1<=p169]] | [[p16<=1 & 1<=p16] & [p165<=1 & 1<=p165]]] | [[[p15<=1 & 1<=p15] & [p168<=1 & 1<=p168]] | [[[p15<=1 & 1<=p15] & [p165<=1 & 1<=p165]] | [[p15<=1 & 1<=p15] & [p167<=1 & 1<=p167]]]]] | [[[[p16<=1 & 1<=p16] & [p168<=1 & 1<=p168]] | [[[p17<=1 & 1<=p17] & [p168<=1 & 1<=p168]] | [[p17<=1 & 1<=p17] & [p166<=1 & 1<=p166]]]] | [[[p14<=1 & 1<=p14] & [p167<=1 & 1<=p167]] | [[[p14<=1 & 1<=p14] & [p165<=1 & 1<=p165]] | [[p18<=1 & 1<=p18] & [p164<=1 & 1<=p164]]]]]]]]]] & [AX [AF [[[[[[[[p12<=1 & 1<=p12] & [p56<=1 & 1<=p56]] | [[p12<=1 & 1<=p12] & [p58<=1 & 1<=p58]]] | [[[p12<=1 & 1<=p12] & [p57<=1 & 1<=p57]] | [[p7<=1 & 1<=p7] & [p61<=1 & 1<=p61]]]] | [[[[p7<=1 & 1<=p7] & [p60<=1 & 1<=p60]] | [[p7<=1 & 1<=p7] & [p59<=1 & 1<=p59]]] | [[[p7<=1 & 1<=p7] & [p58<=1 & 1<=p58]] | [[[p7<=1 & 1<=p7] & [p57<=1 & 1<=p57]] | [[p8<=1 & 1<=p8] & [p60<=1 & 1<=p60]]]]]] | [[[[[p8<=1 & 1<=p8] & [p59<=1 & 1<=p59]] | [[p8<=1 & 1<=p8] & [p61<=1 & 1<=p61]]] | [[[p8<=1 & 1<=p8] & [p56<=1 & 1<=p56]] | [[p12<=1 & 1<=p12] & [p60<=1 & 1<=p60]]]] | [[[[p12<=1 & 1<=p12] & [p59<=1 & 1<=p59]] | [[p8<=1 & 1<=p8] & [p58<=1 & 1<=p58]]] | [[[p10<=1 & 1<=p10] & [p61<=1 & 1<=p61]] | [[[p9<=1 & 1<=p9] & [p57<=1 & 1<=p57]] | [[p9<=1 & 1<=p9] & [p56<=1 & 1<=p56]]]]]]] | [[[[[[p9<=1 & 1<=p9] & [p61<=1 & 1<=p61]] | [[p9<=1 & 1<=p9] & [p60<=1 & 1<=p60]]] | [[[p9<=1 & 1<=p9] & [p59<=1 & 1<=p59]] | [[p11<=1 & 1<=p11] & [p61<=1 & 1<=p61]]]] | [[[[p6<=1 & 1<=p6] & [p57<=1 & 1<=p57]] | [[p11<=1 & 1<=p11] & [p59<=1 & 1<=p59]]] | [[[p6<=1 & 1<=p6] & [p58<=1 & 1<=p58]] | [[[p11<=1 & 1<=p11] & [p58<=1 & 1<=p58]] | [[p11<=1 & 1<=p11] & [p57<=1 & 1<=p57]]]]]] | [[[[[p6<=1 & 1<=p6] & [p59<=1 & 1<=p59]] | [[p11<=1 & 1<=p11] & [p56<=1 & 1<=p56]]] | [[[p6<=1 & 1<=p6] & [p60<=1 & 1<=p60]] | [[p6<=1 & 1<=p6] & [p61<=1 & 1<=p61]]]] | [[[[p10<=1 & 1<=p10] & [p56<=1 & 1<=p56]] | [[p10<=1 & 1<=p10] & [p58<=1 & 1<=p58]]] | [[[p10<=1 & 1<=p10] & [p57<=1 & 1<=p57]] | [[[p10<=1 & 1<=p10] & [p60<=1 & 1<=p60]] | [[p6<=1 & 1<=p6] & [p56<=1 & 1<=p56]]]]]]]]]] & [[[AF [[[[[[p28<=1 & 1<=p28] & [p66<=1 & 1<=p66]] | [[[p20<=1 & 1<=p20] & [p62<=1 & 1<=p62]] | [[p25<=1 & 1<=p25] & [p64<=1 & 1<=p64]]]] | [[[p23<=1 & 1<=p23] & [p63<=1 & 1<=p63]] | [[[p26<=1 & 1<=p26] & [p65<=1 & 1<=p65]] | [[p30<=1 & 1<=p30] & [p67<=1 & 1<=p67]]]]] | [[[[p29<=1 & 1<=p29] & [p66<=1 & 1<=p66]] | [[[p27<=1 & 1<=p27] & [p65<=1 & 1<=p65]] | [[p24<=1 & 1<=p24] & [p64<=1 & 1<=p64]]]] | [[[p21<=1 & 1<=p21] & [p62<=1 & 1<=p62]] | [[[p22<=1 & 1<=p22] & [p63<=1 & 1<=p63]] | [[p31<=1 & 1<=p31] & [p67<=1 & 1<=p67]]]]]]] | EF [[[[[[p21<=1 & 1<=p21] & [p170<=1 & 1<=p170]] | [[[p26<=1 & 1<=p26] & [p173<=1 & 1<=p173]] | [[p24<=1 & 1<=p24] & [p172<=1 & 1<=p172]]]] | [[[p23<=1 & 1<=p23] & [p171<=1 & 1<=p171]] | [[[p27<=1 & 1<=p27] & [p173<=1 & 1<=p173]] | [[p29<=1 & 1<=p29] & [p174<=1 & 1<=p174]]]]] | [[[[p31<=1 & 1<=p31] & [p175<=1 & 1<=p175]] | [[[p30<=1 & 1<=p30] & [p175<=1 & 1<=p175]] | [[p25<=1 & 1<=p25] & [p172<=1 & 1<=p172]]]] | [[[p22<=1 & 1<=p22] & [p171<=1 & 1<=p171]] | [[[p20<=1 & 1<=p20] & [p170<=1 & 1<=p170]] | [[p28<=1 & 1<=p28] & [p174<=1 & 1<=p174]]]]]]]] | [[p71<=1 & 1<=p71] | [p70<=1 & 1<=p70]]] | [[[p73<=1 & 1<=p73] | [p72<=1 & 1<=p72]] | [[p69<=1 & 1<=p69] | [p68<=1 & 1<=p68]]]]]]] | [[[p17<=1 & 1<=p17] & [p157<=1 & 1<=p157]] | [[p17<=1 & 1<=p17] & [p156<=1 & 1<=p156]]]] | [[[[p17<=1 & 1<=p17] & [p153<=1 & 1<=p153]] | [[p17<=1 & 1<=p17] & [p152<=1 & 1<=p152]]] | [[[p17<=1 & 1<=p17] & [p154<=1 & 1<=p154]] | [[[p16<=1 & 1<=p16] & [p152<=1 & 1<=p152]] | [[p13<=1 & 1<=p13] & [p157<=1 & 1<=p157]]]]]] | [[[[[p13<=1 & 1<=p13] & [p156<=1 & 1<=p156]] | [[p13<=1 & 1<=p13] & [p153<=1 & 1<=p153]]] | [[[p13<=1 & 1<=p13] & [p152<=1 & 1<=p152]] | [[[p13<=1 & 1<=p13] & [p155<=1 & 1<=p155]] | [[p13<=1 & 1<=p13] & [p154<=1 & 1<=p154]]]]] | [[[[p16<=1 & 1<=p16] & [p157<=1 & 1<=p157]] | [[p16<=1 & 1<=p16] & [p156<=1 & 1<=p156]]] | [[[p16<=1 & 1<=p16] & [p155<=1 & 1<=p155]] | [[[p16<=1 & 1<=p16] & [p153<=1 & 1<=p153]] | [[p19<=1 & 1<=p19] & [p153<=1 & 1<=p153]]]]]]] | [[[[[[p19<=1 & 1<=p19] & [p152<=1 & 1<=p152]] | [[p14<=1 & 1<=p14] & [p154<=1 & 1<=p154]]] | [[[p19<=1 & 1<=p19] & [p155<=1 & 1<=p155]] | [[p14<=1 & 1<=p14] & [p153<=1 & 1<=p153]]]] | [[[[p19<=1 & 1<=p19] & [p154<=1 & 1<=p154]] | [[p19<=1 & 1<=p19] & [p156<=1 & 1<=p156]]] | [[[p15<=1 & 1<=p15] & [p155<=1 & 1<=p155]] | [[[p15<=1 & 1<=p15] & [p154<=1 & 1<=p154]] | [[p15<=1 & 1<=p15] & [p157<=1 & 1<=p157]]]]]] | [[[[[p15<=1 & 1<=p15] & [p156<=1 & 1<=p156]] | [[p18<=1 & 1<=p18] & [p154<=1 & 1<=p154]]] | [[[p18<=1 & 1<=p18] & [p153<=1 & 1<=p153]] | [[[p18<=1 & 1<=p18] & [p152<=1 & 1<=p152]] | [[p18<=1 & 1<=p18] & [p157<=1 & 1<=p157]]]]] | [[[[p15<=1 & 1<=p15] & [p152<=1 & 1<=p152]] | [[p18<=1 & 1<=p18] & [p155<=1 & 1<=p155]]] | [[[p14<=1 & 1<=p14] & [p157<=1 & 1<=p157]] | [[[p14<=1 & 1<=p14] & [p156<=1 & 1<=p156]] | [[p14<=1 & 1<=p14] & [p155<=1 & 1<=p155]]]]]]]]]
normalized: ~ [E [true U ~ [[[[[[[[p156<=1 & 1<=p156] & [p19<=1 & 1<=p19]] | [[p154<=1 & 1<=p154] & [p19<=1 & 1<=p19]]] | [[[[p157<=1 & 1<=p157] & [p15<=1 & 1<=p15]] | [[p154<=1 & 1<=p154] & [p15<=1 & 1<=p15]]] | [[p155<=1 & 1<=p155] & [p15<=1 & 1<=p15]]]] | [[[[p153<=1 & 1<=p153] & [p14<=1 & 1<=p14]] | [[p155<=1 & 1<=p155] & [p19<=1 & 1<=p19]]] | [[[p154<=1 & 1<=p154] & [p14<=1 & 1<=p14]] | [[p152<=1 & 1<=p152] & [p19<=1 & 1<=p19]]]]] | [[[[[[p14<=1 & 1<=p14] & [p155<=1 & 1<=p155]] | [[p156<=1 & 1<=p156] & [p14<=1 & 1<=p14]]] | [[p157<=1 & 1<=p157] & [p14<=1 & 1<=p14]]] | [[[p155<=1 & 1<=p155] & [p18<=1 & 1<=p18]] | [[p152<=1 & 1<=p152] & [p15<=1 & 1<=p15]]]] | [[[[[p157<=1 & 1<=p157] & [p18<=1 & 1<=p18]] | [[p152<=1 & 1<=p152] & [p18<=1 & 1<=p18]]] | [[p153<=1 & 1<=p153] & [p18<=1 & 1<=p18]]] | [[[p154<=1 & 1<=p154] & [p18<=1 & 1<=p18]] | [[p156<=1 & 1<=p156] & [p15<=1 & 1<=p15]]]]]] | [[[[[[[p153<=1 & 1<=p153] & [p19<=1 & 1<=p19]] | [[p153<=1 & 1<=p153] & [p16<=1 & 1<=p16]]] | [[p155<=1 & 1<=p155] & [p16<=1 & 1<=p16]]] | [[[p156<=1 & 1<=p156] & [p16<=1 & 1<=p16]] | [[p157<=1 & 1<=p157] & [p16<=1 & 1<=p16]]]] | [[[[[p154<=1 & 1<=p154] & [p13<=1 & 1<=p13]] | [[p155<=1 & 1<=p155] & [p13<=1 & 1<=p13]]] | [[p152<=1 & 1<=p152] & [p13<=1 & 1<=p13]]] | [[[p153<=1 & 1<=p153] & [p13<=1 & 1<=p13]] | [[p156<=1 & 1<=p156] & [p13<=1 & 1<=p13]]]]] | [[[[[[p157<=1 & 1<=p157] & [p13<=1 & 1<=p13]] | [[p152<=1 & 1<=p152] & [p16<=1 & 1<=p16]]] | [[p154<=1 & 1<=p154] & [p17<=1 & 1<=p17]]] | [[[p152<=1 & 1<=p152] & [p17<=1 & 1<=p17]] | [[p153<=1 & 1<=p153] & [p17<=1 & 1<=p17]]]] | [[[[p156<=1 & 1<=p156] & [p17<=1 & 1<=p17]] | [[p157<=1 & 1<=p157] & [p17<=1 & 1<=p17]]] | [[[[[[[p68<=1 & 1<=p68] | [p69<=1 & 1<=p69]] | [[p72<=1 & 1<=p72] | [p73<=1 & 1<=p73]]] | [[[p70<=1 & 1<=p70] | [p71<=1 & 1<=p71]] | [E [true U [[[[[[p174<=1 & 1<=p174] & [p28<=1 & 1<=p28]] | [[p170<=1 & 1<=p170] & [p20<=1 & 1<=p20]]] | [[p171<=1 & 1<=p171] & [p22<=1 & 1<=p22]]] | [[[[p172<=1 & 1<=p172] & [p25<=1 & 1<=p25]] | [[p175<=1 & 1<=p175] & [p30<=1 & 1<=p30]]] | [[p175<=1 & 1<=p175] & [p31<=1 & 1<=p31]]]] | [[[[[p174<=1 & 1<=p174] & [p29<=1 & 1<=p29]] | [[p173<=1 & 1<=p173] & [p27<=1 & 1<=p27]]] | [[p171<=1 & 1<=p171] & [p23<=1 & 1<=p23]]] | [[[[p172<=1 & 1<=p172] & [p24<=1 & 1<=p24]] | [[p173<=1 & 1<=p173] & [p26<=1 & 1<=p26]]] | [[p170<=1 & 1<=p170] & [p21<=1 & 1<=p21]]]]]] | ~ [EG [~ [[[[[[[p67<=1 & 1<=p67] & [p31<=1 & 1<=p31]] | [[p63<=1 & 1<=p63] & [p22<=1 & 1<=p22]]] | [[p62<=1 & 1<=p62] & [p21<=1 & 1<=p21]]] | [[[[p64<=1 & 1<=p64] & [p24<=1 & 1<=p24]] | [[p65<=1 & 1<=p65] & [p27<=1 & 1<=p27]]] | [[p66<=1 & 1<=p66] & [p29<=1 & 1<=p29]]]] | [[[[[p67<=1 & 1<=p67] & [p30<=1 & 1<=p30]] | [[p65<=1 & 1<=p65] & [p26<=1 & 1<=p26]]] | [[p63<=1 & 1<=p63] & [p23<=1 & 1<=p23]]] | [[[[p64<=1 & 1<=p64] & [p25<=1 & 1<=p25]] | [[p62<=1 & 1<=p62] & [p20<=1 & 1<=p20]]] | [[p66<=1 & 1<=p66] & [p28<=1 & 1<=p28]]]]]]]]]]] & ~ [EX [EG [~ [[[[[[[[[p56<=1 & 1<=p56] & [p6<=1 & 1<=p6]] | [[p60<=1 & 1<=p60] & [p10<=1 & 1<=p10]]] | [[p57<=1 & 1<=p57] & [p10<=1 & 1<=p10]]] | [[[p58<=1 & 1<=p58] & [p10<=1 & 1<=p10]] | [[p56<=1 & 1<=p56] & [p10<=1 & 1<=p10]]]] | [[[[p61<=1 & 1<=p61] & [p6<=1 & 1<=p6]] | [[p60<=1 & 1<=p60] & [p6<=1 & 1<=p6]]] | [[[p56<=1 & 1<=p56] & [p11<=1 & 1<=p11]] | [[p59<=1 & 1<=p59] & [p6<=1 & 1<=p6]]]]] | [[[[[[p57<=1 & 1<=p57] & [p11<=1 & 1<=p11]] | [[p58<=1 & 1<=p58] & [p11<=1 & 1<=p11]]] | [[p58<=1 & 1<=p58] & [p6<=1 & 1<=p6]]] | [[[p59<=1 & 1<=p59] & [p11<=1 & 1<=p11]] | [[p57<=1 & 1<=p57] & [p6<=1 & 1<=p6]]]] | [[[[p61<=1 & 1<=p61] & [p11<=1 & 1<=p11]] | [[p59<=1 & 1<=p59] & [p9<=1 & 1<=p9]]] | [[[p60<=1 & 1<=p60] & [p9<=1 & 1<=p9]] | [[p61<=1 & 1<=p61] & [p9<=1 & 1<=p9]]]]]] | [[[[[[[p56<=1 & 1<=p56] & [p9<=1 & 1<=p9]] | [[p57<=1 & 1<=p57] & [p9<=1 & 1<=p9]]] | [[p61<=1 & 1<=p61] & [p10<=1 & 1<=p10]]] | [[[p58<=1 & 1<=p58] & [p8<=1 & 1<=p8]] | [[p59<=1 & 1<=p59] & [p12<=1 & 1<=p12]]]] | [[[[p60<=1 & 1<=p60] & [p12<=1 & 1<=p12]] | [[p56<=1 & 1<=p56] & [p8<=1 & 1<=p8]]] | [[[p61<=1 & 1<=p61] & [p8<=1 & 1<=p8]] | [[p59<=1 & 1<=p59] & [p8<=1 & 1<=p8]]]]] | [[[[[[p60<=1 & 1<=p60] & [p8<=1 & 1<=p8]] | [[p57<=1 & 1<=p57] & [p7<=1 & 1<=p7]]] | [[p58<=1 & 1<=p58] & [p7<=1 & 1<=p7]]] | [[[p59<=1 & 1<=p59] & [p7<=1 & 1<=p7]] | [[p60<=1 & 1<=p60] & [p7<=1 & 1<=p7]]]] | [[[[p61<=1 & 1<=p61] & [p7<=1 & 1<=p7]] | [[p57<=1 & 1<=p57] & [p12<=1 & 1<=p12]]] | [[[p58<=1 & 1<=p58] & [p12<=1 & 1<=p12]] | [[p56<=1 & 1<=p56] & [p12<=1 & 1<=p12]]]]]]]]]]]] & E [[[[[[[[p67<=1 & 1<=p67] & [p31<=1 & 1<=p31]] | [[p63<=1 & 1<=p63] & [p22<=1 & 1<=p22]]] | [[p62<=1 & 1<=p62] & [p21<=1 & 1<=p21]]] | [[[[p64<=1 & 1<=p64] & [p24<=1 & 1<=p24]] | [[p65<=1 & 1<=p65] & [p27<=1 & 1<=p27]]] | [[p66<=1 & 1<=p66] & [p29<=1 & 1<=p29]]]] | [[[[[p67<=1 & 1<=p67] & [p30<=1 & 1<=p30]] | [[p65<=1 & 1<=p65] & [p26<=1 & 1<=p26]]] | [[p63<=1 & 1<=p63] & [p23<=1 & 1<=p23]]] | [[[[p64<=1 & 1<=p64] & [p25<=1 & 1<=p25]] | [[p62<=1 & 1<=p62] & [p20<=1 & 1<=p20]]] | [[p66<=1 & 1<=p66] & [p28<=1 & 1<=p28]]]]] & [[[[[p48<=1 & 1<=p48] & [p13<=1 & 1<=p13]] | [[p49<=1 & 1<=p49] & [p13<=1 & 1<=p13]]] | [[p44<=1 & 1<=p44] & [p13<=1 & 1<=p13]]] | [[[[p45<=1 & 1<=p45] & [p13<=1 & 1<=p13]] | [[p46<=1 & 1<=p46] & [p13<=1 & 1<=p13]]] | [[p47<=1 & 1<=p47] & [p13<=1 & 1<=p13]]]]] U ~ [[[[[[[[[p164<=1 & 1<=p164] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p14<=1 & 1<=p14]]] | [[p167<=1 & 1<=p167] & [p14<=1 & 1<=p14]]] | [[[[p166<=1 & 1<=p166] & [p17<=1 & 1<=p17]] | [[p168<=1 & 1<=p168] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p16<=1 & 1<=p16]]]] | [[[[[p167<=1 & 1<=p167] & [p15<=1 & 1<=p15]] | [[p165<=1 & 1<=p165] & [p15<=1 & 1<=p15]]] | [[p168<=1 & 1<=p168] & [p15<=1 & 1<=p15]]] | [[[p165<=1 & 1<=p165] & [p16<=1 & 1<=p16]] | [[p169<=1 & 1<=p169] & [p19<=1 & 1<=p19]]]]] | [[[[[[p165<=1 & 1<=p165] & [1<=p19 & p19<=1]] | [[p167<=1 & 1<=p167] & [p19<=1 & 1<=p19]]] | [[p165<=1 & 1<=p165] & [p17<=1 & 1<=p17]]] | [[[p164<=1 & 1<=p164] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p18<=1 & 1<=p18]]]] | [[[[[p165<=1 & 1<=p165] & [p18<=1 & 1<=p18]] | [[p168<=1 & 1<=p168] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p13<=1 & 1<=p13]]] | [[[p169<=1 & 1<=p169] & [p18<=1 & 1<=p18]] | [[p167<=1 & 1<=p167] & [p17<=1 & 1<=p17]]]]]] | [[[[[[[p166<=1 & 1<=p166] & [p14<=1 & 1<=p14]] | [[p169<=1 & 1<=p169] & [p17<=1 & 1<=p17]]] | [[p168<=1 & 1<=p168] & [p14<=1 & 1<=p14]]] | [[[[p164<=1 & 1<=p164] & [p14<=1 & 1<=p14]] | [[p167<=1 & 1<=p167] & [p16<=1 & 1<=p16]]] | [[p166<=1 & 1<=p166] & [p15<=1 & 1<=p15]]]] | [[[[[p169<=1 & 1<=p169] & [p16<=1 & 1<=p16]] | [[p164<=1 & 1<=p164] & [p15<=1 & 1<=p15]]] | [[p164<=1 & 1<=p164] & [p16<=1 & 1<=p16]]] | [[[p169<=1 & 1<=p169] & [p15<=1 & 1<=p15]] | [[p166<=1 & 1<=p166] & [p16<=1 & 1<=p16]]]]] | [[[[[[p168<=1 & 1<=p168] & [p19<=1 & 1<=p19]] | [[p164<=1 & 1<=p164] & [p19<=1 & 1<=p19]]] | [[p166<=1 & 1<=p166] & [p19<=1 & 1<=p19]]] | [[[p169<=1 & 1<=p169] & [p14<=1 & 1<=p14]] | [[p164<=1 & 1<=p164] & [p17<=1 & 1<=p17]]]] | [[[[[p168<=1 & 1<=p168] & [p18<=1 & 1<=p18]] | [[p165<=1 & 1<=p165] & [p13<=1 & 1<=p13]]] | [[p166<=1 & 1<=p166] & [p18<=1 & 1<=p18]]] | [[[p169<=1 & 1<=p169] & [p13<=1 & 1<=p13]] | [[p167<=1 & 1<=p167] & [p13<=1 & 1<=p13]]]]]]]]]] | ~ [EG [~ [E [[[[[[[p158<=1 & 1<=p158] & [p13<=1 & 1<=p13]] | [[p161<=1 & 1<=p161] & [p13<=1 & 1<=p13]]] | [[p162<=1 & 1<=p162] & [p13<=1 & 1<=p13]]] | [[[[p159<=1 & 1<=p159] & [p13<=1 & 1<=p13]] | [[p160<=1 & 1<=p160] & [p13<=1 & 1<=p13]]] | [[p163<=1 & 1<=p163] & [p13<=1 & 1<=p13]]]] & ~ [E [true U ~ [[[[[[[[[p34<=1 & 1<=p34] & [p12<=1 & 1<=p12]] | [[p32<=1 & 1<=p32] & [p12<=1 & 1<=p12]]] | [[p33<=1 & 1<=p33] & [p8<=1 & 1<=p8]]] | [[[[p36<=1 & 1<=p36] & [p12<=1 & 1<=p12]] | [[p37<=1 & 1<=p37] & [p7<=1 & 1<=p7]]] | [[p33<=1 & 1<=p33] & [p7<=1 & 1<=p7]]]] | [[[[[p35<=1 & 1<=p35] & [p7<=1 & 1<=p7]] | [[p37<=1 & 1<=p37] & [p8<=1 & 1<=p8]]] | [[p35<=1 & 1<=p35] & [p8<=1 & 1<=p8]]] | [[[p32<=1 & 1<=p32] & [p10<=1 & 1<=p10]] | [[p35<=1 & 1<=p35] & [p6<=1 & 1<=p6]]]]] | [[[[[[p33<=1 & 1<=p33] & [p6<=1 & 1<=p6]] | [[p34<=1 & 1<=p34] & [p9<=1 & 1<=p9]]] | [[p36<=1 & 1<=p36] & [p9<=1 & 1<=p9]]] | [[[p32<=1 & 1<=p32] & [p11<=1 & 1<=p11]] | [[p34<=1 & 1<=p34] & [p11<=1 & 1<=p11]]]] | [[[[[p32<=1 & 1<=p32] & [p9<=1 & 1<=p9]] | [[p36<=1 & 1<=p36] & [p11<=1 & 1<=p11]]] | [[p37<=1 & 1<=p37] & [p6<=1 & 1<=p6]]] | [[[p36<=1 & 1<=p36] & [p10<=1 & 1<=p10]] | [[p34<=1 & 1<=p34] & [p10<=1 & 1<=p10]]]]]] | [[[[[[[p33<=1 & 1<=p33] & [p12<=1 & 1<=p12]] | [[p37<=1 & 1<=p37] & [p12<=1 & 1<=p12]]] | [[p34<=1 & 1<=p34] & [p8<=1 & 1<=p8]]] | [[[[p35<=1 & 1<=p35] & [p12<=1 & 1<=p12]] | [[p32<=1 & 1<=p32] & [p8<=1 & 1<=p8]]] | [[p36<=1 & 1<=p36] & [p7<=1 & 1<=p7]]]] | [[[[[p32<=1 & 1<=p32] & [p7<=1 & 1<=p7]] | [[p34<=1 & 1<=p34] & [p7<=1 & 1<=p7]]] | [[p36<=1 & 1<=p36] & [p8<=1 & 1<=p8]]] | [[[p36<=1 & 1<=p36] & [p6<=1 & 1<=p6]] | [[p34<=1 & 1<=p34] & [p6<=1 & 1<=p6]]]]] | [[[[[[p35<=1 & 1<=p35] & [p9<=1 & 1<=p9]] | [[p32<=1 & 1<=p32] & [p6<=1 & 1<=p6]]] | [[p37<=1 & 1<=p37] & [p9<=1 & 1<=p9]]] | [[[p33<=1 & 1<=p33] & [p11<=1 & 1<=p11]] | [[p35<=1 & 1<=p35] & [p11<=1 & 1<=p11]]]] | [[[[[p33<=1 & 1<=p33] & [p9<=1 & 1<=p9]] | [[p37<=1 & 1<=p37] & [p11<=1 & 1<=p11]]] | [[p37<=1 & 1<=p37] & [p10<=1 & 1<=p10]]] | [[[p35<=1 & 1<=p35] & [p10<=1 & 1<=p10]] | [[p33<=1 & 1<=p33] & [p10<=1 & 1<=p10]]]]]]]]]]] U EX [[[[[[[[[p56<=1 & 1<=p56] & [p6<=1 & 1<=p6]] | [[p60<=1 & 1<=p60] & [p10<=1 & 1<=p10]]] | [[p57<=1 & 1<=p57] & [p10<=1 & 1<=p10]]] | [[[p58<=1 & 1<=p58] & [p10<=1 & 1<=p10]] | [[p56<=1 & 1<=p56] & [p10<=1 & 1<=p10]]]] | [[[[p61<=1 & 1<=p61] & [p6<=1 & 1<=p6]] | [[p60<=1 & 1<=p60] & [p6<=1 & 1<=p6]]] | [[[p56<=1 & 1<=p56] & [p11<=1 & 1<=p11]] | [[p59<=1 & 1<=p59] & [p6<=1 & 1<=p6]]]]] | [[[[[[p57<=1 & 1<=p57] & [p11<=1 & 1<=p11]] | [[p58<=1 & 1<=p58] & [p11<=1 & 1<=p11]]] | [[p58<=1 & 1<=p58] & [p6<=1 & 1<=p6]]] | [[[p59<=1 & 1<=p59] & [p11<=1 & 1<=p11]] | [[p57<=1 & 1<=p57] & [p6<=1 & 1<=p6]]]] | [[[[p61<=1 & 1<=p61] & [p11<=1 & 1<=p11]] | [[p59<=1 & 1<=p59] & [p9<=1 & 1<=p9]]] | [[[p60<=1 & 1<=p60] & [p9<=1 & 1<=p9]] | [[p61<=1 & 1<=p61] & [p9<=1 & 1<=p9]]]]]] | [[[[[[[p56<=1 & 1<=p56] & [p9<=1 & 1<=p9]] | [[p57<=1 & 1<=p57] & [p9<=1 & 1<=p9]]] | [[p61<=1 & 1<=p61] & [p10<=1 & 1<=p10]]] | [[[p58<=1 & 1<=p58] & [p8<=1 & 1<=p8]] | [[p59<=1 & 1<=p59] & [p12<=1 & 1<=p12]]]] | [[[[p60<=1 & 1<=p60] & [p12<=1 & 1<=p12]] | [[p56<=1 & 1<=p56] & [p8<=1 & 1<=p8]]] | [[[p61<=1 & 1<=p61] & [p8<=1 & 1<=p8]] | [[p59<=1 & 1<=p59] & [p8<=1 & 1<=p8]]]]] | [[[[[[p60<=1 & 1<=p60] & [p8<=1 & 1<=p8]] | [[p57<=1 & 1<=p57] & [p7<=1 & 1<=p7]]] | [[p58<=1 & 1<=p58] & [p7<=1 & 1<=p7]]] | [[[p59<=1 & 1<=p59] & [p7<=1 & 1<=p7]] | [[p60<=1 & 1<=p60] & [p7<=1 & 1<=p7]]]] | [[[[p61<=1 & 1<=p61] & [p7<=1 & 1<=p7]] | [[p57<=1 & 1<=p57] & [p12<=1 & 1<=p12]]] | [[[p58<=1 & 1<=p58] & [p12<=1 & 1<=p12]] | [[p56<=1 & 1<=p56] & [p12<=1 & 1<=p12]]]]]]]]]]]]]]]]]]]]
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (p7<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p12<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (p8<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (p9<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (p59<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (p61<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (p58<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (p57<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (p10<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (p60<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p6)
states: 64
abstracting: (p6<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 6497614
after gc: idd nodes used:28743594, unused:35256406; list nodes free:161487541
MC time: 0m59.143sec
checking: [EG [AF [[E [[[[[[[p21<=1 & 1<=p21] & [p170<=1 & 1<=p170]] | [[[p5<=1 & 1<=p5] & [p31<=1 & 1<=p31]] | [[p26<=1 & 1<=p26] & [p173<=1 & 1<=p173]]]] | [[[p27<=1 & 1<=p27] & [p173<=1 & 1<=p173]] | [[[p5<=1 & 1<=p5] & [p30<=1 & 1<=p30]] | [[p31<=1 & 1<=p31] & [p175<=1 & 1<=p175]]]]] | [[[[p30<=1 & 1<=p30] & [p175<=1 & 1<=p175]] | [[[p25<=1 & 1<=p25] & [p172<=1 & 1<=p172]] | [[p22<=1 & 1<=p22] & [p171<=1 & 1<=p171]]]] | [[[p2<=1 & 1<=p2] & [p25<=1 & 1<=p25]] | [[[p2<=1 & 1<=p2] & [p24<=1 & 1<=p24]] | [[p24<=1 & 1<=p24] & [p172<=1 & 1<=p172]]]]]] | [[[[[p23<=1 & 1<=p23] & [p171<=1 & 1<=p171]] | [[[p1<=1 & 1<=p1] & [p22<=1 & 1<=p22]] | [[p3<=1 & 1<=p3] & [p27<=1 & 1<=p27]]]] | [[[p29<=1 & 1<=p29] & [p174<=1 & 1<=p174]] | [[[p1<=1 & 1<=p1] & [p23<=1 & 1<=p23]] | [[p3<=1 & 1<=p3] & [p26<=1 & 1<=p26]]]]] | [[[[p20<=1 & 1<=p20] & [p170<=1 & 1<=p170]] | [[[p4<=1 & 1<=p4] & [p28<=1 & 1<=p28]] | [[p4<=1 & 1<=p4] & [p29<=1 & 1<=p29]]]] | [[[p0<=1 & 1<=p0] & [p21<=1 & 1<=p21]] | [[[p0<=1 & 1<=p0] & [p20<=1 & 1<=p20]] | [[p28<=1 & 1<=p28] & [p174<=1 & 1<=p174]]]]]]] U [[[[[[[p26<=1 & 1<=p26] & [[p83<=1 & 1<=p83] & [p111<=1 & 1<=p111]]] | [[p24<=1 & 1<=p24] & [[p100<=1 & 1<=p100] & [p114<=1 & 1<=p114]]]] | [[[p22<=1 & 1<=p22] & [[p93<=1 & 1<=p93] & [p113<=1 & 1<=p113]]] | [[p30<=1 & 1<=p30] & [[p103<=1 & 1<=p103] & [p114<=1 & 1<=p114]]]]] | [[[[p28<=1 & 1<=p28] & [[p90<=1 & 1<=p90] & [p112<=1 & 1<=p112]]] | [[p20<=1 & 1<=p20] & [[p86<=1 & 1<=p86] & [p112<=1 & 1<=p112]]]] | [[[p30<=1 & 1<=p30] & [[p79<=1 & 1<=p79] & [p110<=1 & 1<=p110]]] | [[[p24<=1 & 1<=p24] & [[p106<=1 & 1<=p106] & [p115<=1 & 1<=p115]]] | [[p20<=1 & 1<=p20] & [[p74<=1 & 1<=p74] & [p110<=1 & 1<=p110]]]]]]] | [[[[[p22<=1 & 1<=p22] & [[p99<=1 & 1<=p99] & [p114<=1 & 1<=p114]]] | [[p30<=1 & 1<=p30] & [[p97<=1 & 1<=p97] & [p113<=1 & 1<=p113]]]] | [[[p20<=1 & 1<=p20] & [[p104<=1 & 1<=p104] & [p115<=1 & 1<=p115]]] | [[p24<=1 & 1<=p24] & [[p82<=1 & 1<=p82] & [p111<=1 & 1<=p111]]]]] | [[[[p30<=1 & 1<=p30] & [[p85<=1 & 1<=p85] & [p111<=1 & 1<=p111]]] | [[p28<=1 & 1<=p28] & [[p96<=1 & 1<=p96] & [p113<=1 & 1<=p113]]]] | [[[p26<=1 & 1<=p26] & [[p89<=1 & 1<=p89] & [p112<=1 & 1<=p112]]] | [[[p26<=1 & 1<=p26] & [[p107<=1 & 1<=p107] & [p115<=1 & 1<=p115]]] | [[p28<=1 & 1<=p28] & [[p108<=1 & 1<=p108] & [p115<=1 & 1<=p115]]]]]]]] | [[[[[[p22<=1 & 1<=p22] & [[p105<=1 & 1<=p105] & [p115<=1 & 1<=p115]]] | [[p28<=1 & 1<=p28] & [[p78<=1 & 1<=p78] & [p110<=1 & 1<=p110]]]] | [[[p22<=1 & 1<=p22] & [[p75<=1 & 1<=p75] & [p110<=1 & 1<=p110]]] | [[p26<=1 & 1<=p26] & [[p101<=1 & 1<=p101] & [p114<=1 & 1<=p114]]]]] | [[[[p22<=1 & 1<=p22] & [[p81<=1 & 1<=p81] & [p111<=1 & 1<=p111]]] | [[p20<=1 & 1<=p20] & [[p92<=1 & 1<=p92] & [p113<=1 & 1<=p113]]]] | [[[p26<=1 & 1<=p26] & [[p95<=1 & 1<=p95] & [p113<=1 & 1<=p113]]] | [[[p24<=1 & 1<=p24] & [[p88<=1 & 1<=p88] & [p112<=1 & 1<=p112]]] | [[p24<=1 & 1<=p24] & [[p94<=1 & 1<=p94] & [p113<=1 & 1<=p113]]]]]]] | [[[[[p26<=1 & 1<=p26] & [[p77<=1 & 1<=p77] & [p110<=1 & 1<=p110]]] | [[p28<=1 & 1<=p28] & [[p84<=1 & 1<=p84] & [p111<=1 & 1<=p111]]]] | [[[p28<=1 & 1<=p28] & [[p102<=1 & 1<=p102] & [p114<=1 & 1<=p114]]] | [[p24<=1 & 1<=p24] & [[p76<=1 & 1<=p76] & [p110<=1 & 1<=p110]]]]] | [[[[p22<=1 & 1<=p22] & [[p87<=1 & 1<=p87] & [p112<=1 & 1<=p112]]] | [[p30<=1 & 1<=p30] & [[p91<=1 & 1<=p91] & [p112<=1 & 1<=p112]]]] | [[[p30<=1 & 1<=p30] & [[p109<=1 & 1<=p109] & [p115<=1 & 1<=p115]]] | [[[p20<=1 & 1<=p20] & [[p80<=1 & 1<=p80] & [p111<=1 & 1<=p111]]] | [[p20<=1 & 1<=p20] & [[p98<=1 & 1<=p98] & [p114<=1 & 1<=p114]]]]]]]]]] & [[[[[[[[p16<=1 & 1<=p16] & [p46<=1 & 1<=p46]] | [[p16<=1 & 1<=p16] & [p45<=1 & 1<=p45]]] | [[[p16<=1 & 1<=p16] & [p48<=1 & 1<=p48]] | [[p16<=1 & 1<=p16] & [p47<=1 & 1<=p47]]]] | [[[[p16<=1 & 1<=p16] & [p44<=1 & 1<=p44]] | [[p16<=1 & 1<=p16] & [p49<=1 & 1<=p49]]] | [[[p17<=1 & 1<=p17] & [p47<=1 & 1<=p47]] | [[[p17<=1 & 1<=p17] & [p46<=1 & 1<=p46]] | [[p17<=1 & 1<=p17] & [p45<=1 & 1<=p45]]]]]] | [[[[[p17<=1 & 1<=p17] & [p44<=1 & 1<=p44]] | [[p17<=1 & 1<=p17] & [p49<=1 & 1<=p49]]] | [[[p17<=1 & 1<=p17] & [p48<=1 & 1<=p48]] | [[p18<=1 & 1<=p18] & [p44<=1 & 1<=p44]]]] | [[[[p19<=1 & 1<=p19] & [p49<=1 & 1<=p49]] | [[p19<=1 & 1<=p19] & [p48<=1 & 1<=p48]]] | [[[p18<=1 & 1<=p18] & [p46<=1 & 1<=p46]] | [[[p19<=1 & 1<=p19] & [p47<=1 & 1<=p47]] | [[p18<=1 & 1<=p18] & [p45<=1 & 1<=p45]]]]]]] | [[[[[[p19<=1 & 1<=p19] & [p46<=1 & 1<=p46]] | [[p14<=1 & 1<=p14] & [p44<=1 & 1<=p44]]] | [[[p19<=1 & 1<=p19] & [p45<=1 & 1<=p45]] | [[p18<=1 & 1<=p18] & [p48<=1 & 1<=p48]]]] | [[[[p19<=1 & 1<=p19] & [p44<=1 & 1<=p44]] | [[p18<=1 & 1<=p18] & [p47<=1 & 1<=p47]]] | [[[p14<=1 & 1<=p14] & [p46<=1 & 1<=p46]] | [[[p14<=1 & 1<=p14] & [p45<=1 & 1<=p45]] | [[p18<=1 & 1<=p18] & [p49<=1 & 1<=p49]]]]]] | [[[[[p14<=1 & 1<=p14] & [p48<=1 & 1<=p48]] | [[p14<=1 & 1<=p14] & [p47<=1 & 1<=p47]]] | [[[p14<=1 & 1<=p14] & [p49<=1 & 1<=p49]] | [[p15<=1 & 1<=p15] & [p49<=1 & 1<=p49]]]] | [[[[p15<=1 & 1<=p15] & [p48<=1 & 1<=p48]] | [[p15<=1 & 1<=p15] & [p47<=1 & 1<=p47]]] | [[[p15<=1 & 1<=p15] & [p46<=1 & 1<=p46]] | [[[p15<=1 & 1<=p15] & [p45<=1 & 1<=p45]] | [[p15<=1 & 1<=p15] & [p44<=1 & 1<=p44]]]]]]]] & [[[[[p21<=1 & 1<=p21] & [p170<=1 & 1<=p170]] | [[[p26<=1 & 1<=p26] & [p173<=1 & 1<=p173]] | [[p24<=1 & 1<=p24] & [p172<=1 & 1<=p172]]]] | [[[p23<=1 & 1<=p23] & [p171<=1 & 1<=p171]] | [[[p173<=1 & 1<=p173] & [p27<=1 & 1<=p27]] | [[p29<=1 & 1<=p29] & [p174<=1 & 1<=p174]]]]] | [[[[p31<=1 & 1<=p31] & [p175<=1 & 1<=p175]] | [[[p30<=1 & 1<=p30] & [p175<=1 & 1<=p175]] | [[p25<=1 & 1<=p25] & [p172<=1 & 1<=p172]]]] | [[[p22<=1 & 1<=p22] & [p171<=1 & 1<=p171]] | [[[p20<=1 & 1<=p20] & [p170<=1 & 1<=p170]] | [[p28<=1 & 1<=p28] & [p174<=1 & 1<=p174]]]]]]]]]] | [AF [[EG [[[[[[[[p17<=0 & 0<=p17] | [p55<=0 & 0<=p55]] & [[[p16<=0 & 0<=p16] | [p53<=0 & 0<=p53]] & [[p16<=0 & 0<=p16] | [p55<=0 & 0<=p55]]]] & [[[p16<=0 & 0<=p16] | [p51<=0 & 0<=p51]] & [[[p13<=0 & 0<=p13] | [p54<=0 & 0<=p54]] & [[p13<=0 & 0<=p13] | [p52<=0 & 0<=p52]]]]] & [[[[p13<=0 & 0<=p13] | [p50<=0 & 0<=p50]] & [[[p17<=0 & 0<=p17] | [p53<=0 & 0<=p53]] & [[p17<=0 & 0<=p17] | [p51<=0 & 0<=p51]]]] & [[[p14<=0 & 0<=p14] | [p51<=0 & 0<=p51]] & [[[p19<=0 & 0<=p19] | [p54<=0 & 0<=p54]] & [[p19<=0 & 0<=p19] | [p50<=0 & 0<=p50]]]]]] & [[[[[p14<=0 & 0<=p14] | [p53<=0 & 0<=p53]] & [[[p14<=0 & 0<=p14] | [p55<=0 & 0<=p55]] & [[p18<=0 & 0<=p18] | [p50<=0 & 0<=p50]]]] & [[[p18<=0 & 0<=p18] | [p52<=0 & 0<=p52]] & [[[p18<=0 & 0<=p18] | [p54<=0 & 0<=p54]] & [[p15<=0 & 0<=p15] | [p55<=0 & 0<=p55]]]]] & [[[[p15<=0 & 0<=p15] | [p53<=0 & 0<=p53]] & [[[p15<=0 & 0<=p15] | [p51<=0 & 0<=p51]] & [[p19<=0 & 0<=p19] | [p52<=0 & 0<=p52]]]] & [[[p16<=0 & 0<=p16] | [p52<=0 & 0<=p52]] & [[[p16<=0 & 0<=p16] | [p54<=0 & 0<=p54]] & [[p16<=0 & 0<=p16] | [p50<=0 & 0<=p50]]]]]]] & [[[[[[p13<=0 & 0<=p13] | [p53<=0 & 0<=p53]] & [[[p13<=0 & 0<=p13] | [p51<=0 & 0<=p51]] & [[p13<=0 & 0<=p13] | [p55<=0 & 0<=p55]]]] & [[[p17<=0 & 0<=p17] | [p50<=0 & 0<=p50]] & [[[p17<=0 & 0<=p17] | [p54<=0 & 0<=p54]] & [[p17<=0 & 0<=p17] | [p52<=0 & 0<=p52]]]]] & [[[[p19<=0 & 0<=p19] | [p53<=0 & 0<=p53]] & [[[p14<=0 & 0<=p14] | [p50<=0 & 0<=p50]] & [[p19<=0 & 0<=p19] | [p55<=0 & 0<=p55]]]] & [[[p14<=0 & 0<=p14] | [p52<=0 & 0<=p52]] & [[[p14<=0 & 0<=p14] | [p54<=0 & 0<=p54]] & [[p18<=0 & 0<=p18] | [p51<=0 & 0<=p51]]]]]] & [[[[[p18<=0 & 0<=p18] | [p53<=0 & 0<=p53]] & [[[p18<=0 & 0<=p18] | [p55<=0 & 0<=p55]] & [[p15<=0 & 0<=p15] | [p54<=0 & 0<=p54]]]] & [[[p15<=0 & 0<=p15] | [p52<=0 & 0<=p52]] & [[[p15<=0 & 0<=p15] | [p50<=0 & 0<=p50]] & [[p19<=0 & 0<=p19] | [p51<=0 & 0<=p51]]]]] & [[[[p7<=0 & 0<=p7] | [p56<=0 & 0<=p56]] & [[[p8<=0 & 0<=p8] | [p57<=0 & 0<=p57]] & [[p9<=0 & 0<=p9] | [p58<=0 & 0<=p58]]]] & [[[p10<=0 & 0<=p10] | [p59<=0 & 0<=p59]] & [[[p11<=0 & 0<=p11] | [p60<=0 & 0<=p60]] & [[p12<=0 & 0<=p12] | [p61<=0 & 0<=p61]]]]]]]]] & [EF [[[[[[[[p10<=0 & 0<=p10] | [p33<=0 & 0<=p33]] & [[p10<=0 & 0<=p10] | [p35<=0 & 0<=p35]]] & [[[p10<=0 & 0<=p10] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p37<=0 & 0<=p37]] & [[p9<=0 & 0<=p9] | [p33<=0 & 0<=p33]]]]] & [[[[p11<=0 & 0<=p11] | [p35<=0 & 0<=p35]] & [[p11<=0 & 0<=p11] | [p33<=0 & 0<=p33]]] & [[[p9<=0 & 0<=p9] | [p37<=0 & 0<=p37]] & [[[p6<=0 & 0<=p6] | [p32<=0 & 0<=p32]] & [[p9<=0 & 0<=p9] | [p35<=0 & 0<=p35]]]]]] & [[[[[p6<=0 & 0<=p6] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p36<=0 & 0<=p36]]] & [[[p8<=0 & 0<=p8] | [p36<=0 & 0<=p36]] & [[[p7<=0 & 0<=p7] | [p34<=0 & 0<=p34]] & [[p7<=0 & 0<=p7] | [p32<=0 & 0<=p32]]]]] & [[[[p7<=0 & 0<=p7] | [p36<=0 & 0<=p36]] & [[[p8<=0 & 0<=p8] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p35<=0 & 0<=p35]]]] & [[[p8<=0 & 0<=p8] | [p34<=0 & 0<=p34]] & [[[p12<=0 & 0<=p12] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p33<=0 & 0<=p33]]]]]]] & [[[[[[p10<=0 & 0<=p10] | [p34<=0 & 0<=p34]] & [[p10<=0 & 0<=p10] | [p36<=0 & 0<=p36]]] & [[[p6<=0 & 0<=p6] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p36<=0 & 0<=p36]] & [[p9<=0 & 0<=p9] | [p32<=0 & 0<=p32]]]]] & [[[[p11<=0 & 0<=p11] | [p34<=0 & 0<=p34]] & [[p11<=0 & 0<=p11] | [p32<=0 & 0<=p32]]] & [[[p9<=0 & 0<=p9] | [p36<=0 & 0<=p36]] & [[[p9<=0 & 0<=p9] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p33<=0 & 0<=p33]]]]]] & [[[[[p6<=0 & 0<=p6] | [p35<=0 & 0<=p35]] & [[p10<=0 & 0<=p10] | [p32<=0 & 0<=p32]]] & [[[p8<=0 & 0<=p8] | [p35<=0 & 0<=p35]] & [[[p8<=0 & 0<=p8] | [p37<=0 & 0<=p37]] & [[p7<=0 & 0<=p7] | [p35<=0 & 0<=p35]]]]] & [[[[p7<=0 & 0<=p7] | [p33<=0 & 0<=p33]] & [[[p7<=0 & 0<=p7] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p36<=0 & 0<=p36]]]] & [[[p8<=0 & 0<=p8] | [p33<=0 & 0<=p33]] & [[[p12<=0 & 0<=p12] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p34<=0 & 0<=p34]]]]]]]]] & AG [[[[[[[[p10<=0 & 0<=p10] | [p33<=0 & 0<=p33]] & [[p10<=0 & 0<=p10] | [p35<=0 & 0<=p35]]] & [[[p10<=0 & 0<=p10] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p37<=0 & 0<=p37]] & [[p9<=0 & 0<=p9] | [p33<=0 & 0<=p33]]]]] & [[[[p11<=0 & 0<=p11] | [p35<=0 & 0<=p35]] & [[p11<=0 & 0<=p11] | [p33<=0 & 0<=p33]]] & [[[p9<=0 & 0<=p9] | [p37<=0 & 0<=p37]] & [[[p6<=0 & 0<=p6] | [p32<=0 & 0<=p32]] & [[p9<=0 & 0<=p9] | [p35<=0 & 0<=p35]]]]]] & [[[[[p6<=0 & 0<=p6] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p36<=0 & 0<=p36]]] & [[[p8<=0 & 0<=p8] | [p36<=0 & 0<=p36]] & [[[p7<=0 & 0<=p7] | [p34<=0 & 0<=p34]] & [[p7<=0 & 0<=p7] | [p32<=0 & 0<=p32]]]]] & [[[[p7<=0 & 0<=p7] | [p36<=0 & 0<=p36]] & [[[p8<=0 & 0<=p8] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p35<=0 & 0<=p35]]]] & [[[p8<=0 & 0<=p8] | [p34<=0 & 0<=p34]] & [[[p12<=0 & 0<=p12] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p33<=0 & 0<=p33]]]]]]] & [[[[[[p10<=0 & 0<=p10] | [p34<=0 & 0<=p34]] & [[p10<=0 & 0<=p10] | [p36<=0 & 0<=p36]]] & [[[p6<=0 & 0<=p6] | [p37<=0 & 0<=p37]] & [[[p11<=0 & 0<=p11] | [p36<=0 & 0<=p36]] & [[p9<=0 & 0<=p9] | [p32<=0 & 0<=p32]]]]] & [[[[p11<=0 & 0<=p11] | [p34<=0 & 0<=p34]] & [[p11<=0 & 0<=p11] | [p32<=0 & 0<=p32]]] & [[[p9<=0 & 0<=p9] | [p36<=0 & 0<=p36]] & [[[p9<=0 & 0<=p9] | [p34<=0 & 0<=p34]] & [[p6<=0 & 0<=p6] | [p33<=0 & 0<=p33]]]]]] & [[[[[p6<=0 & 0<=p6] | [p35<=0 & 0<=p35]] & [[p10<=0 & 0<=p10] | [p32<=0 & 0<=p32]]] & [[[p8<=0 & 0<=p8] | [p35<=0 & 0<=p35]] & [[[p8<=0 & 0<=p8] | [p37<=0 & 0<=p37]] & [[p7<=0 & 0<=p7] | [p35<=0 & 0<=p35]]]]] & [[[[p7<=0 & 0<=p7] | [p33<=0 & 0<=p33]] & [[[p7<=0 & 0<=p7] | [p37<=0 & 0<=p37]] & [[p12<=0 & 0<=p12] | [p36<=0 & 0<=p36]]]] & [[[p8<=0 & 0<=p8] | [p33<=0 & 0<=p33]] & [[[p12<=0 & 0<=p12] | [p32<=0 & 0<=p32]] & [[p12<=0 & 0<=p12] | [p34<=0 & 0<=p34]]]]]]]]]]]] & EG [AF [[[[[[p23<=0 & 0<=p23] | [p39<=0 & 0<=p39]] & [[[p28<=0 & 0<=p28] | [p42<=0 & 0<=p42]] & [[p26<=0 & 0<=p26] | [p41<=0 & 0<=p41]]]] & [[[p31<=0 & 0<=p31] | [p43<=0 & 0<=p43]] & [[[p25<=0 & 0<=p25] | [p40<=0 & 0<=p40]] & [[p21<=0 & 0<=p21] | [p38<=0 & 0<=p38]]]]] & [[[[p27<=0 & 0<=p27] | [p41<=0 & 0<=p41]] & [[[p22<=0 & 0<=p22] | [p39<=0 & 0<=p39]] & [[p30<=0 & 0<=p30] | [p43<=0 & 0<=p43]]]] & [[[[p29<=0 & 0<=p29] | [p42<=0 & 0<=p42]] & [[p20<=0 & 0<=p20] | [p38<=0 & 0<=p38]]] & [[[p24<=0 & 0<=p24] | [p40<=0 & 0<=p40]] & [[[[[[p21<=1 & 1<=p21] & [p170<=1 & 1<=p170]] | [[[p5<=1 & 1<=p5] & [p31<=1 & 1<=p31]] | [[p26<=1 & 1<=p26] & [p173<=1 & 1<=p173]]]] | [[[p27<=1 & 1<=p27] & [p173<=1 & 1<=p173]] | [[[p5<=1 & 1<=p5] & [p30<=1 & 1<=p30]] | [[p31<=1 & 1<=p31] & [p175<=1 & 1<=p175]]]]] | [[[[p30<=1 & 1<=p30] & [p175<=1 & 1<=p175]] | [[[p25<=1 & 1<=p25] & [p172<=1 & 1<=p172]] | [[p22<=1 & 1<=p22] & [p171<=1 & 1<=p171]]]] | [[[p2<=1 & 1<=p2] & [p25<=1 & 1<=p25]] | [[[p2<=1 & 1<=p2] & [p24<=1 & 1<=p24]] | [[p24<=1 & 1<=p24] & [p172<=1 & 1<=p172]]]]]] | [[[[[p23<=1 & 1<=p23] & [p171<=1 & 1<=p171]] | [[[p1<=1 & 1<=p1] & [p22<=1 & 1<=p22]] | [[p3<=1 & 1<=p3] & [p27<=1 & 1<=p27]]]] | [[[p29<=1 & 1<=p29] & [p174<=1 & 1<=p174]] | [[[p1<=1 & 1<=p1] & [p23<=1 & 1<=p23]] | [[p3<=1 & 1<=p3] & [p26<=1 & 1<=p26]]]]] | [[[[p20<=1 & 1<=p20] & [p170<=1 & 1<=p170]] | [[[p4<=1 & 1<=p4] & [p28<=1 & 1<=p28]] | [[p4<=1 & 1<=p4] & [p29<=1 & 1<=p29]]]] | [[[p0<=1 & 1<=p0] & [p21<=1 & 1<=p21]] | [[[p0<=1 & 1<=p0] & [p20<=1 & 1<=p20]] | [[p28<=1 & 1<=p28] & [p174<=1 & 1<=p174]]]]]]]]]]]]]]]
normalized: [[EG [~ [EG [~ [[[[[[[[[[[[p174<=1 & 1<=p174] & [p28<=1 & 1<=p28]] | [[p20<=1 & 1<=p20] & [p0<=1 & 1<=p0]]] | [[p21<=1 & 1<=p21] & [p0<=1 & 1<=p0]]] | [[[[p29<=1 & 1<=p29] & [p4<=1 & 1<=p4]] | [[p28<=1 & 1<=p28] & [p4<=1 & 1<=p4]]] | [[p170<=1 & 1<=p170] & [p20<=1 & 1<=p20]]]] | [[[[[p26<=1 & 1<=p26] & [p3<=1 & 1<=p3]] | [[p23<=1 & 1<=p23] & [p1<=1 & 1<=p1]]] | [[p174<=1 & 1<=p174] & [p29<=1 & 1<=p29]]] | [[[[p27<=1 & 1<=p27] & [p3<=1 & 1<=p3]] | [[p22<=1 & 1<=p22] & [p1<=1 & 1<=p1]]] | [[p171<=1 & 1<=p171] & [p23<=1 & 1<=p23]]]]] | [[[[[[p172<=1 & 1<=p172] & [p24<=1 & 1<=p24]] | [[p24<=1 & 1<=p24] & [p2<=1 & 1<=p2]]] | [[p25<=1 & 1<=p25] & [p2<=1 & 1<=p2]]] | [[[[p171<=1 & 1<=p171] & [p22<=1 & 1<=p22]] | [[p172<=1 & 1<=p172] & [p25<=1 & 1<=p25]]] | [[p175<=1 & 1<=p175] & [p30<=1 & 1<=p30]]]] | [[[[[p175<=1 & 1<=p175] & [p31<=1 & 1<=p31]] | [[p30<=1 & 1<=p30] & [p5<=1 & 1<=p5]]] | [[p173<=1 & 1<=p173] & [p27<=1 & 1<=p27]]] | [[[[p173<=1 & 1<=p173] & [p26<=1 & 1<=p26]] | [[p31<=1 & 1<=p31] & [p5<=1 & 1<=p5]]] | [[p170<=1 & 1<=p170] & [p21<=1 & 1<=p21]]]]]] & [[p40<=0 & 0<=p40] | [p24<=0 & 0<=p24]]] & [[[p38<=0 & 0<=p38] | [p20<=0 & 0<=p20]] & [[p42<=0 & 0<=p42] | [p29<=0 & 0<=p29]]]] & [[[[p43<=0 & 0<=p43] | [p30<=0 & 0<=p30]] & [[p39<=0 & 0<=p39] | [p22<=0 & 0<=p22]]] & [[p41<=0 & 0<=p41] | [p27<=0 & 0<=p27]]]] & [[[[[p38<=0 & 0<=p38] | [p21<=0 & 0<=p21]] & [[p40<=0 & 0<=p40] | [p25<=0 & 0<=p25]]] & [[p43<=0 & 0<=p43] | [p31<=0 & 0<=p31]]] & [[[[p41<=0 & 0<=p41] | [p26<=0 & 0<=p26]] & [[p42<=0 & 0<=p42] | [p28<=0 & 0<=p28]]] & [[p39<=0 & 0<=p39] | [p23<=0 & 0<=p23]]]]]]]]] & ~ [EG [~ [[[E [true U [[[[[[[[p33<=0 & 0<=p33] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p12<=0 & 0<=p12]]] & [[p34<=0 & 0<=p34] | [p8<=0 & 0<=p8]]] & [[[[p35<=0 & 0<=p35] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p8<=0 & 0<=p8]]] & [[p36<=0 & 0<=p36] | [p7<=0 & 0<=p7]]]] & [[[[[p32<=0 & 0<=p32] | [p7<=0 & 0<=p7]] & [[p34<=0 & 0<=p34] | [p7<=0 & 0<=p7]]] & [[p36<=0 & 0<=p36] | [p8<=0 & 0<=p8]]] & [[[p36<=0 & 0<=p36] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p6<=0 & 0<=p6]]]]] & [[[[[[p35<=0 & 0<=p35] | [p9<=0 & 0<=p9]] & [[p32<=0 & 0<=p32] | [p6<=0 & 0<=p6]]] & [[p37<=0 & 0<=p37] | [p9<=0 & 0<=p9]]] & [[[p33<=0 & 0<=p33] | [p11<=0 & 0<=p11]] & [[p35<=0 & 0<=p35] | [p11<=0 & 0<=p11]]]] & [[[[[p33<=0 & 0<=p33] | [p9<=0 & 0<=p9]] & [[p37<=0 & 0<=p37] | [p11<=0 & 0<=p11]]] & [[p37<=0 & 0<=p37] | [p10<=0 & 0<=p10]]] & [[[p35<=0 & 0<=p35] | [p10<=0 & 0<=p10]] & [[p33<=0 & 0<=p33] | [p10<=0 & 0<=p10]]]]]] & [[[[[[[p34<=0 & 0<=p34] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p12<=0 & 0<=p12]]] & [[p33<=0 & 0<=p33] | [p8<=0 & 0<=p8]]] & [[[[p36<=0 & 0<=p36] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p7<=0 & 0<=p7]]] & [[p33<=0 & 0<=p33] | [p7<=0 & 0<=p7]]]] & [[[[[p35<=0 & 0<=p35] | [p7<=0 & 0<=p7]] & [[p37<=0 & 0<=p37] | [p8<=0 & 0<=p8]]] & [[p35<=0 & 0<=p35] | [p8<=0 & 0<=p8]]] & [[[p32<=0 & 0<=p32] | [p10<=0 & 0<=p10]] & [[p35<=0 & 0<=p35] | [p6<=0 & 0<=p6]]]]] & [[[[[[p33<=0 & 0<=p33] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p9<=0 & 0<=p9]]] & [[p36<=0 & 0<=p36] | [p9<=0 & 0<=p9]]] & [[[p32<=0 & 0<=p32] | [p11<=0 & 0<=p11]] & [[p34<=0 & 0<=p34] | [p11<=0 & 0<=p11]]]] & [[[[[p32<=0 & 0<=p32] | [p9<=0 & 0<=p9]] & [[p36<=0 & 0<=p36] | [p11<=0 & 0<=p11]]] & [[p37<=0 & 0<=p37] | [p6<=0 & 0<=p6]]] & [[[p36<=0 & 0<=p36] | [p10<=0 & 0<=p10]] & [[p34<=0 & 0<=p34] | [p10<=0 & 0<=p10]]]]]]]] & ~ [E [true U ~ [[[[[[[[[p34<=0 & 0<=p34] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p12<=0 & 0<=p12]]] & [[p33<=0 & 0<=p33] | [p8<=0 & 0<=p8]]] & [[[[p36<=0 & 0<=p36] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p7<=0 & 0<=p7]]] & [[p33<=0 & 0<=p33] | [p7<=0 & 0<=p7]]]] & [[[[[p35<=0 & 0<=p35] | [p7<=0 & 0<=p7]] & [[p37<=0 & 0<=p37] | [p8<=0 & 0<=p8]]] & [[p35<=0 & 0<=p35] | [p8<=0 & 0<=p8]]] & [[[p32<=0 & 0<=p32] | [p10<=0 & 0<=p10]] & [[p35<=0 & 0<=p35] | [p6<=0 & 0<=p6]]]]] & [[[[[[p33<=0 & 0<=p33] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p9<=0 & 0<=p9]]] & [[p36<=0 & 0<=p36] | [p9<=0 & 0<=p9]]] & [[[p32<=0 & 0<=p32] | [p11<=0 & 0<=p11]] & [[p34<=0 & 0<=p34] | [p11<=0 & 0<=p11]]]] & [[[[[p32<=0 & 0<=p32] | [p9<=0 & 0<=p9]] & [[p36<=0 & 0<=p36] | [p11<=0 & 0<=p11]]] & [[p37<=0 & 0<=p37] | [p6<=0 & 0<=p6]]] & [[[p36<=0 & 0<=p36] | [p10<=0 & 0<=p10]] & [[p34<=0 & 0<=p34] | [p10<=0 & 0<=p10]]]]]] & [[[[[[[p33<=0 & 0<=p33] | [p12<=0 & 0<=p12]] & [[p37<=0 & 0<=p37] | [p12<=0 & 0<=p12]]] & [[p34<=0 & 0<=p34] | [p8<=0 & 0<=p8]]] & [[[[p35<=0 & 0<=p35] | [p12<=0 & 0<=p12]] & [[p32<=0 & 0<=p32] | [p8<=0 & 0<=p8]]] & [[p36<=0 & 0<=p36] | [p7<=0 & 0<=p7]]]] & [[[[[p32<=0 & 0<=p32] | [p7<=0 & 0<=p7]] & [[p34<=0 & 0<=p34] | [p7<=0 & 0<=p7]]] & [[p36<=0 & 0<=p36] | [p8<=0 & 0<=p8]]] & [[[p36<=0 & 0<=p36] | [p6<=0 & 0<=p6]] & [[p34<=0 & 0<=p34] | [p6<=0 & 0<=p6]]]]] & [[[[[[p35<=0 & 0<=p35] | [p9<=0 & 0<=p9]] & [[p32<=0 & 0<=p32] | [p6<=0 & 0<=p6]]] & [[p37<=0 & 0<=p37] | [p9<=0 & 0<=p9]]] & [[[p33<=0 & 0<=p33] | [p11<=0 & 0<=p11]] & [[p35<=0 & 0<=p35] | [p11<=0 & 0<=p11]]]] & [[[[[p33<=0 & 0<=p33] | [p9<=0 & 0<=p9]] & [[p37<=0 & 0<=p37] | [p11<=0 & 0<=p11]]] & [[p37<=0 & 0<=p37] | [p10<=0 & 0<=p10]]] & [[[p35<=0 & 0<=p35] | [p10<=0 & 0<=p10]] & [[p33<=0 & 0<=p33] | [p10<=0 & 0<=p10]]]]]]]]]]] & EG [[[[[[[[[p58<=0 & 0<=p58] | [p9<=0 & 0<=p9]] & [[p57<=0 & 0<=p57] | [p8<=0 & 0<=p8]]] & [[p56<=0 & 0<=p56] | [p7<=0 & 0<=p7]]] & [[[[p61<=0 & 0<=p61] | [p12<=0 & 0<=p12]] & [[p60<=0 & 0<=p60] | [p11<=0 & 0<=p11]]] & [[p59<=0 & 0<=p59] | [p10<=0 & 0<=p10]]]] & [[[[[p51<=0 & 0<=p51] | [p19<=0 & 0<=p19]] & [[p50<=0 & 0<=p50] | [p15<=0 & 0<=p15]]] & [[p52<=0 & 0<=p52] | [p15<=0 & 0<=p15]]] & [[[[p54<=0 & 0<=p54] | [p15<=0 & 0<=p15]] & [[p55<=0 & 0<=p55] | [p18<=0 & 0<=p18]]] & [[p53<=0 & 0<=p53] | [p18<=0 & 0<=p18]]]]] & [[[[[[p51<=0 & 0<=p51] | [p18<=0 & 0<=p18]] & [[p54<=0 & 0<=p54] | [p14<=0 & 0<=p14]]] & [[p52<=0 & 0<=p52] | [p14<=0 & 0<=p14]]] & [[[[p55<=0 & 0<=p55] | [p19<=0 & 0<=p19]] & [[p50<=0 & 0<=p50] | [p14<=0 & 0<=p14]]] & [[p53<=0 & 0<=p53] | [p19<=0 & 0<=p19]]]] & [[[[[p52<=0 & 0<=p52] | [p17<=0 & 0<=p17]] & [[p54<=0 & 0<=p54] | [p17<=0 & 0<=p17]]] & [[p50<=0 & 0<=p50] | [p17<=0 & 0<=p17]]] & [[[[p55<=0 & 0<=p55] | [p13<=0 & 0<=p13]] & [[p51<=0 & 0<=p51] | [p13<=0 & 0<=p13]]] & [[p53<=0 & 0<=p53] | [p13<=0 & 0<=p13]]]]]] & [[[[[[[p50<=0 & 0<=p50] | [p16<=0 & 0<=p16]] & [[p54<=0 & 0<=p54] | [p16<=0 & 0<=p16]]] & [[p52<=0 & 0<=p52] | [p16<=0 & 0<=p16]]] & [[[[p52<=0 & 0<=p52] | [p19<=0 & 0<=p19]] & [[p51<=0 & 0<=p51] | [p15<=0 & 0<=p15]]] & [[p53<=0 & 0<=p53] | [p15<=0 & 0<=p15]]]] & [[[[[p55<=0 & 0<=p55] | [p15<=0 & 0<=p15]] & [[p54<=0 & 0<=p54] | [p18<=0 & 0<=p18]]] & [[p52<=0 & 0<=p52] | [p18<=0 & 0<=p18]]] & [[[[p50<=0 & 0<=p50] | [p18<=0 & 0<=p18]] & [[p55<=0 & 0<=p55] | [p14<=0 & 0<=p14]]] & [[p53<=0 & 0<=p53] | [p14<=0 & 0<=p14]]]]] & [[[[[[p50<=0 & 0<=p50] | [p19<=0 & 0<=p19]] & [[p54<=0 & 0<=p54] | [p19<=0 & 0<=p19]]] & [[p51<=0 & 0<=p51] | [p14<=0 & 0<=p14]]] & [[[[p51<=0 & 0<=p51] | [p17<=0 & 0<=p17]] & [[p53<=0 & 0<=p53] | [p17<=0 & 0<=p17]]] & [[p50<=0 & 0<=p50] | [p13<=0 & 0<=p13]]]] & [[[[[p52<=0 & 0<=p52] | [p13<=0 & 0<=p13]] & [[p54<=0 & 0<=p54] | [p13<=0 & 0<=p13]]] & [[p51<=0 & 0<=p51] | [p16<=0 & 0<=p16]]] & [[[[p55<=0 & 0<=p55] | [p16<=0 & 0<=p16]] & [[p53<=0 & 0<=p53] | [p16<=0 & 0<=p16]]] & [[p55<=0 & 0<=p55] | [p17<=0 & 0<=p17]]]]]]]]]]]]] | EG [~ [EG [~ [[[[[[[[[p174<=1 & 1<=p174] & [p28<=1 & 1<=p28]] | [[p170<=1 & 1<=p170] & [p20<=1 & 1<=p20]]] | [[p171<=1 & 1<=p171] & [p22<=1 & 1<=p22]]] | [[[[p172<=1 & 1<=p172] & [p25<=1 & 1<=p25]] | [[p175<=1 & 1<=p175] & [p30<=1 & 1<=p30]]] | [[p175<=1 & 1<=p175] & [p31<=1 & 1<=p31]]]] | [[[[[p174<=1 & 1<=p174] & [p29<=1 & 1<=p29]] | [[p27<=1 & 1<=p27] & [p173<=1 & 1<=p173]]] | [[p171<=1 & 1<=p171] & [p23<=1 & 1<=p23]]] | [[[[p172<=1 & 1<=p172] & [p24<=1 & 1<=p24]] | [[p173<=1 & 1<=p173] & [p26<=1 & 1<=p26]]] | [[p170<=1 & 1<=p170] & [p21<=1 & 1<=p21]]]]] & [[[[[[[[p44<=1 & 1<=p44] & [p15<=1 & 1<=p15]] | [[p45<=1 & 1<=p45] & [p15<=1 & 1<=p15]]] | [[p46<=1 & 1<=p46] & [p15<=1 & 1<=p15]]] | [[[p47<=1 & 1<=p47] & [p15<=1 & 1<=p15]] | [[p48<=1 & 1<=p48] & [p15<=1 & 1<=p15]]]] | [[[[p49<=1 & 1<=p49] & [p15<=1 & 1<=p15]] | [[p49<=1 & 1<=p49] & [p14<=1 & 1<=p14]]] | [[[p47<=1 & 1<=p47] & [p14<=1 & 1<=p14]] | [[p48<=1 & 1<=p48] & [p14<=1 & 1<=p14]]]]] | [[[[[[p49<=1 & 1<=p49] & [p18<=1 & 1<=p18]] | [[p45<=1 & 1<=p45] & [p14<=1 & 1<=p14]]] | [[p46<=1 & 1<=p46] & [p14<=1 & 1<=p14]]] | [[[p47<=1 & 1<=p47] & [p18<=1 & 1<=p18]] | [[p44<=1 & 1<=p44] & [p19<=1 & 1<=p19]]]] | [[[[p48<=1 & 1<=p48] & [p18<=1 & 1<=p18]] | [[p45<=1 & 1<=p45] & [p19<=1 & 1<=p19]]] | [[[p44<=1 & 1<=p44] & [p14<=1 & 1<=p14]] | [[p46<=1 & 1<=p46] & [p19<=1 & 1<=p19]]]]]] | [[[[[[[p45<=1 & 1<=p45] & [p18<=1 & 1<=p18]] | [[p47<=1 & 1<=p47] & [p19<=1 & 1<=p19]]] | [[p46<=1 & 1<=p46] & [p18<=1 & 1<=p18]]] | [[[p48<=1 & 1<=p48] & [p19<=1 & 1<=p19]] | [[p49<=1 & 1<=p49] & [p19<=1 & 1<=p19]]]] | [[[[p44<=1 & 1<=p44] & [p18<=1 & 1<=p18]] | [[p48<=1 & 1<=p48] & [p17<=1 & 1<=p17]]] | [[[p49<=1 & 1<=p49] & [p17<=1 & 1<=p17]] | [[p44<=1 & 1<=p44] & [p17<=1 & 1<=p17]]]]] | [[[[[[p45<=1 & 1<=p45] & [p17<=1 & 1<=p17]] | [[p46<=1 & 1<=p46] & [p17<=1 & 1<=p17]]] | [[p47<=1 & 1<=p47] & [p17<=1 & 1<=p17]]] | [[[p49<=1 & 1<=p49] & [p16<=1 & 1<=p16]] | [[p44<=1 & 1<=p44] & [p16<=1 & 1<=p16]]]] | [[[[p47<=1 & 1<=p47] & [p16<=1 & 1<=p16]] | [[p48<=1 & 1<=p48] & [p16<=1 & 1<=p16]]] | [[[p45<=1 & 1<=p45] & [p16<=1 & 1<=p16]] | [[p46<=1 & 1<=p46] & [p16<=1 & 1<=p16]]]]]]]] & E [[[[[[[[p174<=1 & 1<=p174] & [p28<=1 & 1<=p28]] | [[p20<=1 & 1<=p20] & [p0<=1 & 1<=p0]]] | [[p21<=1 & 1<=p21] & [p0<=1 & 1<=p0]]] | [[[[p29<=1 & 1<=p29] & [p4<=1 & 1<=p4]] | [[p28<=1 & 1<=p28] & [p4<=1 & 1<=p4]]] | [[p170<=1 & 1<=p170] & [p20<=1 & 1<=p20]]]] | [[[[[p26<=1 & 1<=p26] & [p3<=1 & 1<=p3]] | [[p23<=1 & 1<=p23] & [p1<=1 & 1<=p1]]] | [[p174<=1 & 1<=p174] & [p29<=1 & 1<=p29]]] | [[[[p27<=1 & 1<=p27] & [p3<=1 & 1<=p3]] | [[p22<=1 & 1<=p22] & [p1<=1 & 1<=p1]]] | [[p171<=1 & 1<=p171] & [p23<=1 & 1<=p23]]]]] | [[[[[[p172<=1 & 1<=p172] & [p24<=1 & 1<=p24]] | [[p24<=1 & 1<=p24] & [p2<=1 & 1<=p2]]] | [[p25<=1 & 1<=p25] & [p2<=1 & 1<=p2]]] | [[[[p171<=1 & 1<=p171] & [p22<=1 & 1<=p22]] | [[p172<=1 & 1<=p172] & [p25<=1 & 1<=p25]]] | [[p175<=1 & 1<=p175] & [p30<=1 & 1<=p30]]]] | [[[[[p175<=1 & 1<=p175] & [p31<=1 & 1<=p31]] | [[p30<=1 & 1<=p30] & [p5<=1 & 1<=p5]]] | [[p173<=1 & 1<=p173] & [p27<=1 & 1<=p27]]] | [[[[p173<=1 & 1<=p173] & [p26<=1 & 1<=p26]] | [[p31<=1 & 1<=p31] & [p5<=1 & 1<=p5]]] | [[p170<=1 & 1<=p170] & [p21<=1 & 1<=p21]]]]]] U [[[[[[[[[p114<=1 & 1<=p114] & [p98<=1 & 1<=p98]] & [p20<=1 & 1<=p20]] | [[[p111<=1 & 1<=p111] & [p80<=1 & 1<=p80]] & [p20<=1 & 1<=p20]]] | [[[p115<=1 & 1<=p115] & [p109<=1 & 1<=p109]] & [p30<=1 & 1<=p30]]] | [[[[p112<=1 & 1<=p112] & [p91<=1 & 1<=p91]] & [p30<=1 & 1<=p30]] | [[[p112<=1 & 1<=p112] & [p87<=1 & 1<=p87]] & [p22<=1 & 1<=p22]]]] | [[[[[p110<=1 & 1<=p110] & [p76<=1 & 1<=p76]] & [p24<=1 & 1<=p24]] | [[[p114<=1 & 1<=p114] & [p102<=1 & 1<=p102]] & [p28<=1 & 1<=p28]]] | [[[[p111<=1 & 1<=p111] & [p84<=1 & 1<=p84]] & [p28<=1 & 1<=p28]] | [[[p110<=1 & 1<=p110] & [p77<=1 & 1<=p77]] & [p26<=1 & 1<=p26]]]]] | [[[[[[[p113<=1 & 1<=p113] & [p94<=1 & 1<=p94]] & [p24<=1 & 1<=p24]] | [[[p112<=1 & 1<=p112] & [p88<=1 & 1<=p88]] & [p24<=1 & 1<=p24]]] | [[[p113<=1 & 1<=p113] & [p95<=1 & 1<=p95]] & [p26<=1 & 1<=p26]]] | [[[[p113<=1 & 1<=p113] & [p92<=1 & 1<=p92]] & [p20<=1 & 1<=p20]] | [[[p111<=1 & 1<=p111] & [p81<=1 & 1<=p81]] & [p22<=1 & 1<=p22]]]] | [[[[[p114<=1 & 1<=p114] & [p101<=1 & 1<=p101]] & [p26<=1 & 1<=p26]] | [[[p110<=1 & 1<=p110] & [p75<=1 & 1<=p75]] & [p22<=1 & 1<=p22]]] | [[[[p110<=1 & 1<=p110] & [p78<=1 & 1<=p78]] & [p28<=1 & 1<=p28]] | [[[p115<=1 & 1<=p115] & [p105<=1 & 1<=p105]] & [p22<=1 & 1<=p22]]]]]] | [[[[[[[[p115<=1 & 1<=p115] & [p108<=1 & 1<=p108]] & [p28<=1 & 1<=p28]] | [[[p115<=1 & 1<=p115] & [p107<=1 & 1<=p107]] & [p26<=1 & 1<=p26]]] | [[[p112<=1 & 1<=p112] & [p89<=1 & 1<=p89]] & [p26<=1 & 1<=p26]]] | [[[[p113<=1 & 1<=p113] & [p96<=1 & 1<=p96]] & [p28<=1 & 1<=p28]] | [[[p111<=1 & 1<=p111] & [p85<=1 & 1<=p85]] & [p30<=1 & 1<=p30]]]] | [[[[[p111<=1 & 1<=p111] & [p82<=1 & 1<=p82]] & [p24<=1 & 1<=p24]] | [[[p115<=1 & 1<=p115] & [p104<=1 & 1<=p104]] & [p20<=1 & 1<=p20]]] | [[[[p113<=1 & 1<=p113] & [p97<=1 & 1<=p97]] & [p30<=1 & 1<=p30]] | [[[p114<=1 & 1<=p114] & [p99<=1 & 1<=p99]] & [p22<=1 & 1<=p22]]]]] | [[[[[[[p110<=1 & 1<=p110] & [p74<=1 & 1<=p74]] & [p20<=1 & 1<=p20]] | [[[p115<=1 & 1<=p115] & [p106<=1 & 1<=p106]] & [p24<=1 & 1<=p24]]] | [[[p110<=1 & 1<=p110] & [p79<=1 & 1<=p79]] & [p30<=1 & 1<=p30]]] | [[[[p112<=1 & 1<=p112] & [p86<=1 & 1<=p86]] & [p20<=1 & 1<=p20]] | [[[p112<=1 & 1<=p112] & [p90<=1 & 1<=p90]] & [p28<=1 & 1<=p28]]]] | [[[[[p114<=1 & 1<=p114] & [p103<=1 & 1<=p103]] & [p30<=1 & 1<=p30]] | [[[p113<=1 & 1<=p113] & [p93<=1 & 1<=p93]] & [p22<=1 & 1<=p22]]] | [[[[p114<=1 & 1<=p114] & [p100<=1 & 1<=p100]] & [p24<=1 & 1<=p24]] | [[[p111<=1 & 1<=p111] & [p83<=1 & 1<=p83]] & [p26<=1 & 1<=p26]]]]]]]]]]]]]]
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p83)
states: 200,549,728,448 (11)
abstracting: (p83<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p100)
states: 200,549,728,448 (11)
abstracting: (p100<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p93)
states: 200,549,728,448 (11)
abstracting: (p93<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p103)
states: 200,549,728,448 (11)
abstracting: (p103<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p90)
states: 200,549,728,448 (11)
abstracting: (p90<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p86)
states: 200,549,728,448 (11)
abstracting: (p86<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p79)
states: 200,549,728,448 (11)
abstracting: (p79<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p106)
states: 200,549,728,448 (11)
abstracting: (p106<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p74)
states: 197,739,387,520 (11)
abstracting: (p74<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p99)
states: 200,549,728,448 (11)
abstracting: (p99<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p97)
states: 200,549,728,448 (11)
abstracting: (p97<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p104)
states: 200,549,728,448 (11)
abstracting: (p104<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p82)
states: 200,549,728,448 (11)
abstracting: (p82<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p85)
states: 200,549,728,448 (11)
abstracting: (p85<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p96)
states: 200,549,728,448 (11)
abstracting: (p96<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p89)
states: 200,549,728,448 (11)
abstracting: (p89<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p107)
states: 200,549,728,448 (11)
abstracting: (p107<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p108)
states: 200,549,728,448 (11)
abstracting: (p108<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
before gc: list nodes free: 7455735
after gc: idd nodes used:32655560, unused:31344440; list nodes free:144387472
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p105)
states: 200,549,728,448 (11)
abstracting: (p105<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p78)
states: 200,549,728,448 (11)
abstracting: (p78<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p75)
states: 200,549,728,448 (11)
abstracting: (p75<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p101)
states: 200,549,728,448 (11)
abstracting: (p101<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p81)
states: 197,739,387,520 (11)
abstracting: (p81<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p92)
states: 200,549,728,448 (11)
abstracting: (p92<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p95)
states: 197,739,387,520 (11)
abstracting: (p95<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p88)
states: 197,739,387,520 (11)
abstracting: (p88<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p94)
states: 200,549,728,448 (11)
abstracting: (p94<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (p113<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p77)
states: 200,549,728,448 (11)
abstracting: (p77<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p84)
states: 200,549,728,448 (11)
abstracting: (p84<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p102)
states: 197,739,387,520 (11)
abstracting: (p102<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p76)
states: 200,549,728,448 (11)
abstracting: (p76<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (p110<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p87)
states: 200,549,728,448 (11)
abstracting: (p87<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p91)
states: 200,549,728,448 (11)
abstracting: (p91<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (p112<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p109)
states: 197,739,387,520 (11)
abstracting: (p109<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (p115<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p80)
states: 200,549,728,448 (11)
abstracting: (p80<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (p111<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p98)
states: 200,549,728,448 (11)
abstracting: (p98<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (p114<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p21)
states: 98,914,841,322 (10)
abstracting: (p21<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p170)
states: 16,526,699,296 (10)
abstracting: (p170<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p5)
states: 17,782,896,448 (10)
abstracting: (p5<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p31)
states: 98,914,841,322 (10)
abstracting: (p31<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p173)
states: 16,526,699,296 (10)
abstracting: (p173<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p27)
states: 98,914,841,322 (10)
abstracting: (p27<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p173)
states: 16,526,699,296 (10)
abstracting: (p173<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p5)
states: 17,782,896,448 (10)
abstracting: (p5<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p31)
states: 98,914,841,322 (10)
abstracting: (p31<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p175)
states: 16,526,699,296 (10)
abstracting: (p175<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (p30<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p175)
states: 16,526,699,296 (10)
abstracting: (p175<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p25)
states: 98,914,841,322 (10)
abstracting: (p25<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p172)
states: 16,526,699,296 (10)
abstracting: (p172<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p171)
states: 16,526,699,296 (10)
abstracting: (p171<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p2)
states: 17,782,896,448 (10)
abstracting: (p2<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p25)
states: 98,914,841,322 (10)
abstracting: (p25<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p2)
states: 17,782,896,448 (10)
abstracting: (p2<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (p24<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p172)
states: 16,526,699,296 (10)
abstracting: (p172<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p23)
states: 98,914,841,322 (10)
abstracting: (p23<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p171)
states: 16,526,699,296 (10)
abstracting: (p171<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p1)
states: 17,782,896,448 (10)
abstracting: (p1<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (p22<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p3)
states: 17,782,896,448 (10)
abstracting: (p3<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p27)
states: 98,914,841,322 (10)
abstracting: (p27<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p29)
states: 98,914,841,322 (10)
abstracting: (p29<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p174)
states: 16,526,699,296 (10)
abstracting: (p174<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p1)
states: 17,782,896,448 (10)
abstracting: (p1<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p23)
states: 98,914,841,322 (10)
abstracting: (p23<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p3)
states: 17,782,896,448 (10)
abstracting: (p3<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (p26<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p170)
states: 16,526,699,296 (10)
abstracting: (p170<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p4)
states: 17,782,896,448 (10)
abstracting: (p4<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p4)
states: 17,782,896,448 (10)
abstracting: (p4<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p29)
states: 98,914,841,322 (10)
abstracting: (p29<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p0)
states: 17,782,896,448 (10)
abstracting: (p0<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p21)
states: 98,914,841,322 (10)
abstracting: (p21<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p0)
states: 17,782,896,448 (10)
abstracting: (p0<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (p20<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (p28<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p174)
states: 16,526,699,296 (10)
abstracting: (p174<=1)
states: 547,231,759,144 (11)
MC time: 1m31.668sec
checking: AG [[EF [EX [0<=0]] | [[p11<=1 & 1<=p11] & [p56<=1 & 1<=p56]]]]
normalized: ~ [E [true U ~ [[[[p56<=1 & 1<=p56] & [p11<=1 & 1<=p11]] | E [true U EX [0<=0]]]]]]
abstracting: (0<=0)
states: 547,231,759,144 (11)
before gc: list nodes free: 7639604
after gc: idd nodes used:39016226, unused:24983774; list nodes free:116529308
before gc: list nodes free: 7328011
after gc: idd nodes used:39424301, unused:24575699; list nodes free:114520230
.
before gc: list nodes free: 4691999
after gc: idd nodes used:38335038, unused:25664962; list nodes free:119524494
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (p11<=1)
states: 547,231,759,144 (11)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (p56<=1)
states: 547,231,759,144 (11)
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-6-CTLFireability-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
TIME LIMIT: Killed by timeout after 3600 seconds
MemTotal: 16393216 kB
MemFree: 5959504 kB
After kill :
MemTotal: 16393216 kB
MemFree: 16094716 kB
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
17406 42594 80908 97493 104734 106984 98428 113376 122843 186762 321066 311846 297312 302898 591222 635250 743412 780462 769232 795640 858564 832386 704655 702524 718554
iterations count:2573905 (7270), effective:37534 (106)
initing FirstDep: 0m 0.000sec
sat_reach.icc:155: Timeout: after 140 sec
sat_reach.icc:155: Timeout: after 131 sec
sat_reach.icc:155: Timeout: after 122 sec
sat_reach.icc:155: Timeout: after 113 sec
net_ddint.h:442: Timeout: after 105 sec
sat_reach.icc:155: Timeout: after 98 sec
net_ddint.h:600: Timeout: after 91 sec
net_ddint.h:600: Timeout: after 84 sec
sat_reach.icc:155: Timeout: after 78 sec
sat_reach.icc:155: Timeout: after 72 sec
sat_reach.icc:155: Timeout: after 67 sec
sat_reach.icc:155: Timeout: after 62 sec
net_ddint.h:600: Timeout: after 58 sec
sat_reach.icc:155: Timeout: after 53 sec
iterations count:354 (1), effective:0 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="LamportFastMutEx-PT-6"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is LamportFastMutEx-PT-6, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r234-tall-167856420300426"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/LamportFastMutEx-PT-6.tgz
mv LamportFastMutEx-PT-6 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

