About the Execution of Marcie+red for LamportFastMutEx-COL-6
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 10116.859 | 3600000.00 | 3649786.00 | 8645.10 | ?????????????T?? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
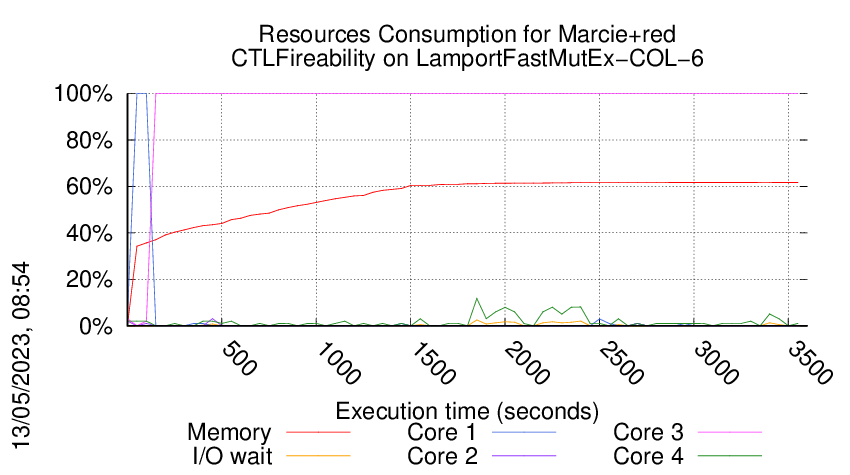
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r234-tall-167856420200370.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is LamportFastMutEx-COL-6, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r234-tall-167856420200370
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 484K
-rw-r--r-- 1 mcc users 7.1K Feb 25 13:41 CTLCardinality.txt
-rw-r--r-- 1 mcc users 70K Feb 25 13:41 CTLCardinality.xml
-rw-r--r-- 1 mcc users 6.1K Feb 25 13:40 CTLFireability.txt
-rw-r--r-- 1 mcc users 50K Feb 25 13:40 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.6K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 4.1K Feb 25 16:20 LTLCardinality.txt
-rw-r--r-- 1 mcc users 28K Feb 25 16:20 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.5K Feb 25 16:20 LTLFireability.txt
-rw-r--r-- 1 mcc users 17K Feb 25 16:20 LTLFireability.xml
-rw-r--r-- 1 mcc users 8.2K Feb 25 13:44 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 73K Feb 25 13:44 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 13K Feb 25 13:43 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 97K Feb 25 13:43 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.8K Feb 25 16:20 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Feb 25 16:20 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 equiv_pt
-rw-r--r-- 1 mcc users 2 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 iscolored
-rw-r--r-- 1 mcc users 42K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-00
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-01
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-02
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-03
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-04
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-05
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-06
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-07
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-08
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-09
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-10
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-11
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-12
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-13
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-14
FORMULA_NAME LamportFastMutEx-COL-6-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1679483715935
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=LamportFastMutEx-COL-6
Applying reductions before tool marcie
Invoking reducer
Running Version 202303021504
[2023-03-22 11:15:17] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2023-03-22 11:15:17] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-22 11:15:17] [INFO ] Detected file is not PT type :http://www.pnml.org/version-2009/grammar/symmetricnet
log4j:WARN No appenders could be found for logger (org.apache.axiom.locator.DefaultOMMetaFactoryLocator).
log4j:WARN Please initialize the log4j system properly.
log4j:WARN See http://logging.apache.org/log4j/1.2/faq.html#noconfig for more info.
[2023-03-22 11:15:17] [WARNING] Using fallBack plugin, rng conformance not checked
[2023-03-22 11:15:18] [INFO ] Load time of PNML (colored model parsed with PNMLFW) : 620 ms
[2023-03-22 11:15:18] [INFO ] Imported 18 HL places and 17 HL transitions for a total of 217 PT places and 525.0 transition bindings in 16 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 14 ms.
[2023-03-22 11:15:18] [INFO ] Built PT skeleton of HLPN with 18 places and 17 transitions 68 arcs in 4 ms.
[2023-03-22 11:15:18] [INFO ] Skeletonized 4 HLPN properties in 1 ms. Removed 12 properties that had guard overlaps.
Computed a total of 3 stabilizing places and 0 stable transitions
Remains 4 properties that can be checked using skeleton over-approximation.
Reduce places removed 3 places and 0 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Finished random walk after 171 steps, including 0 resets, run visited all 11 properties in 19 ms. (steps per millisecond=9 )
[2023-03-22 11:15:18] [INFO ] Flatten gal took : 13 ms
[2023-03-22 11:15:18] [INFO ] Flatten gal took : 2 ms
Domain [pid(7), pid(7)] of place P_wait breaks symmetries in sort pid
Symmetric sort wr.t. initial and guards and successors and join/free detected :P_bool
Arc [3:1*[$i, 1]] contains constants of sort P_bool
Transition T_setbi_2 : constants on arcs in [[3:1*[$i, 1]]] introduces in P_bool(2) partition with 1 elements that refines current partition to 2 subsets.
[2023-03-22 11:15:18] [INFO ] Unfolded HLPN to a Petri net with 217 places and 420 transitions 1834 arcs in 19 ms.
[2023-03-22 11:15:18] [INFO ] Unfolded 16 HLPN properties in 1 ms.
Deduced a syphon composed of 41 places in 2 ms
Reduce places removed 41 places and 66 transitions.
Support contains 176 out of 176 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 9 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
[2023-03-22 11:15:18] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
// Phase 1: matrix 264 rows 176 cols
[2023-03-22 11:15:18] [INFO ] Computed 50 place invariants in 18 ms
[2023-03-22 11:15:18] [INFO ] Implicit Places using invariants in 199 ms returned []
[2023-03-22 11:15:18] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 11:15:18] [INFO ] Invariant cache hit.
[2023-03-22 11:15:18] [INFO ] State equation strengthened by 72 read => feed constraints.
[2023-03-22 11:15:18] [INFO ] Implicit Places using invariants and state equation in 134 ms returned []
Implicit Place search using SMT with State Equation took 357 ms to find 0 implicit places.
[2023-03-22 11:15:18] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 11:15:18] [INFO ] Invariant cache hit.
[2023-03-22 11:15:18] [INFO ] Dead Transitions using invariants and state equation in 179 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 548 ms. Remains : 176/176 places, 354/354 transitions.
Support contains 176 out of 176 places after structural reductions.
[2023-03-22 11:15:18] [INFO ] Flatten gal took : 52 ms
[2023-03-22 11:15:19] [INFO ] Flatten gal took : 55 ms
[2023-03-22 11:15:19] [INFO ] Input system was already deterministic with 354 transitions.
Incomplete random walk after 10000 steps, including 2 resets, run finished after 238 ms. (steps per millisecond=42 ) properties (out of 42) seen :40
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 72 ms. (steps per millisecond=138 ) properties (out of 2) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 23 ms. (steps per millisecond=434 ) properties (out of 2) seen :1
Running SMT prover for 1 properties.
[2023-03-22 11:15:19] [INFO ] Flow matrix only has 264 transitions (discarded 90 similar events)
[2023-03-22 11:15:19] [INFO ] Invariant cache hit.
[2023-03-22 11:15:19] [INFO ] [Real]Absence check using 50 positive place invariants in 14 ms returned sat
[2023-03-22 11:15:19] [INFO ] After 76ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:1
[2023-03-22 11:15:20] [INFO ] [Nat]Absence check using 50 positive place invariants in 10 ms returned sat
[2023-03-22 11:15:20] [INFO ] After 127ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :1
[2023-03-22 11:15:20] [INFO ] State equation strengthened by 72 read => feed constraints.
[2023-03-22 11:15:20] [INFO ] After 89ms SMT Verify possible using 72 Read/Feed constraints in natural domain returned unsat :0 sat :1
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 8 places in 80 ms of which 5 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 18 places in 86 ms of which 0 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 8 places in 68 ms of which 1 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 15 places in 78 ms of which 8 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 16 places in 67 ms of which 1 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 9 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 9 places in 57 ms of which 1 ms to minimize.
[2023-03-22 11:15:20] [INFO ] Deduced a trap composed of 20 places in 62 ms of which 1 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 16 places in 78 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 15 places in 69 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 28 places in 56 ms of which 1 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 28 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 13 places in 52 ms of which 1 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 48 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 26 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 39 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 24 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 25 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 20 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 15 places in 59 ms of which 1 ms to minimize.
[2023-03-22 11:15:21] [INFO ] Deduced a trap composed of 30 places in 61 ms of which 2 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 36 places in 67 ms of which 1 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 30 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 9 places in 58 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 24 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 24 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 16 places in 60 ms of which 1 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 27 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 8 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 19 places in 56 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 25 places in 61 ms of which 1 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 20 places in 54 ms of which 1 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 16 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:22] [INFO ] Deduced a trap composed of 20 places in 65 ms of which 1 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 21 places in 64 ms of which 4 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 23 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 29 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 23 places in 64 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 21 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 16 places in 63 ms of which 2 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 21 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 9 places in 43 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 9 places in 38 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 35 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 19 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 9 places in 28 ms of which 0 ms to minimize.
[2023-03-22 11:15:23] [INFO ] Deduced a trap composed of 25 places in 56 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 18 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 22 places in 56 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 28 places in 64 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 30 places in 64 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 21 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 27 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 16 places in 62 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 29 places in 60 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 28 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 22 places in 57 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 23 places in 64 ms of which 0 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 19 places in 57 ms of which 1 ms to minimize.
[2023-03-22 11:15:24] [INFO ] Deduced a trap composed of 27 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 17 places in 69 ms of which 1 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 24 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 15 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 34 places in 63 ms of which 1 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 17 places in 64 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 17 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 26 places in 55 ms of which 1 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 25 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 41 places in 58 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 21 places in 53 ms of which 1 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 17 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 26 places in 59 ms of which 1 ms to minimize.
[2023-03-22 11:15:25] [INFO ] Deduced a trap composed of 18 places in 53 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 18 places in 66 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 9 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 15 places in 54 ms of which 1 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 9 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 24 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 21 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 23 places in 50 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 23 places in 59 ms of which 1 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 15 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 23 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 16 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 16 places in 56 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 20 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:26] [INFO ] Deduced a trap composed of 21 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 33 places in 55 ms of which 1 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 15 places in 56 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 18 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 15 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 19 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 15 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 29 places in 56 ms of which 1 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 22 places in 56 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 22 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 21 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 19 places in 67 ms of which 1 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 20 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 21 places in 54 ms of which 1 ms to minimize.
[2023-03-22 11:15:27] [INFO ] Deduced a trap composed of 21 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 19 places in 53 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 15 places in 52 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 20 places in 53 ms of which 1 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 18 places in 53 ms of which 1 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 9 places in 49 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 22 places in 58 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 29 places in 61 ms of which 1 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 15 places in 72 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 23 places in 59 ms of which 1 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 22 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 19 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 20 places in 56 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 19 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:28] [INFO ] Deduced a trap composed of 17 places in 65 ms of which 1 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 25 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 17 places in 67 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 15 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 22 places in 52 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 22 places in 49 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 21 places in 47 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 23 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 18 places in 62 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 16 places in 63 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 27 places in 60 ms of which 1 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 30 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 46 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 48 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:29] [INFO ] Deduced a trap composed of 17 places in 61 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 18 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 9 places in 60 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 26 places in 62 ms of which 1 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 19 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 35 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 15 places in 58 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 26 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 15 places in 65 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 19 places in 58 ms of which 1 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 26 places in 56 ms of which 1 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 15 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 40 places in 58 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 15 places in 59 ms of which 0 ms to minimize.
[2023-03-22 11:15:30] [INFO ] Deduced a trap composed of 25 places in 57 ms of which 2 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Deduced a trap composed of 22 places in 55 ms of which 0 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Deduced a trap composed of 22 places in 50 ms of which 0 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Deduced a trap composed of 19 places in 52 ms of which 1 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Deduced a trap composed of 46 places in 54 ms of which 0 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Deduced a trap composed of 17 places in 57 ms of which 0 ms to minimize.
[2023-03-22 11:15:31] [INFO ] Trap strengthening procedure managed to obtain unsat after adding 148 trap constraints in 10974 ms
[2023-03-22 11:15:31] [INFO ] After 11145ms SMT Verify possible using trap constraints in natural domain returned unsat :1 sat :0
[2023-03-22 11:15:31] [INFO ] After 11332ms SMT Verify possible using all constraints in natural domain returned unsat :1 sat :0
Fused 1 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 0 ms.
Successfully simplified 1 atomic propositions for a total of 16 simplifications.
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 31 ms
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 36 ms
[2023-03-22 11:15:31] [INFO ] Input system was already deterministic with 354 transitions.
Computed a total of 1 stabilizing places and 6 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 7 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 7 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 16 ms
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 16 ms
[2023-03-22 11:15:31] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 3 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 3 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 14 ms
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 15 ms
[2023-03-22 11:15:31] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 15 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 16 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 14 ms
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 14 ms
[2023-03-22 11:15:31] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 3 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 3 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:31] [INFO ] Flatten gal took : 12 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 13 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 4 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 12 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 13 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 11 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 11 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 13 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 14 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 5 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 5 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 13 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 1 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 1 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 12 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in LTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 2 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 11 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 10 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 10 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Finished random walk after 139 steps, including 0 resets, run visited all 1 properties in 2 ms. (steps per millisecond=69 )
FORMULA LamportFastMutEx-COL-6-CTLFireability-13 TRUE TECHNIQUES TOPOLOGICAL RANDOM_WALK
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 10 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 10 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 9 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 176/176 places, 354/354 transitions.
Applied a total of 0 rules in 9 ms. Remains 176 /176 variables (removed 0) and now considering 354/354 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 9 ms. Remains : 176/176 places, 354/354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 9 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 10 ms
[2023-03-22 11:15:32] [INFO ] Input system was already deterministic with 354 transitions.
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 25 ms
[2023-03-22 11:15:32] [INFO ] Flatten gal took : 28 ms
[2023-03-22 11:15:33] [INFO ] Export to MCC of 15 properties in file /home/mcc/execution/CTLFireability.sr.xml took 19 ms.
[2023-03-22 11:15:33] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 176 places, 354 transitions and 1536 arcs took 2 ms.
Total runtime 15660 ms.
There are residual formulas that ITS could not solve within timeout
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLFireability.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Petri
(NrP: 176 NrTr: 354 NrArc: 1536)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.008sec
net check time: 0m 0.000sec
init dd package: 0m 2.839sec
RS generation: 24m25.675sec
-> reachability set: #nodes 706675 (7.1e+05) #states 547,231,759,144 (11)
starting MCC model checker
--------------------------
checking: AF [[AG [[[p71<=0 & [p70<=0 & p73<=0]] & [p72<=0 & [p69<=0 & p68<=0]]]] & EX [0<=0]]]
normalized: ~ [EG [~ [[EX [0<=0] & ~ [E [true U ~ [[[[p70<=0 & p73<=0] & p71<=0] & [[p69<=0 & p68<=0] & p72<=0]]]]]]]]]
abstracting: (p72<=0)
states: 540,554,686,984 (11)
abstracting: (p68<=0)
states: 540,554,686,984 (11)
abstracting: (p69<=0)
states: 540,554,686,984 (11)
abstracting: (p71<=0)
states: 540,554,686,984 (11)
abstracting: (p73<=0)
states: 540,554,686,984 (11)
abstracting: (p70<=0)
states: 540,554,686,984 (11)
before gc: list nodes free: 1569457
after gc: idd nodes used:2570521, unused:61429479; list nodes free:271870982
MC time: 2m23.477sec
checking: EF [EG [[A [AF [[[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]] U ~ [[[[[[[p13<=0 | p167<=0] & [p13<=0 | p169<=0]] & [[p18<=0 | p166<=0] & [[p13<=0 | p165<=0] & [p18<=0 | p168<=0]]]] & [[[p14<=0 | p169<=0] & [p17<=0 | p164<=0]] & [[p19<=0 | p166<=0] & [[p19<=0 | p164<=0] & [p19<=0 | p168<=0]]]]] & [[[[p15<=0 | p169<=0] & [p16<=0 | p166<=0]] & [[p16<=0 | p164<=0] & [[p15<=0 | p164<=0] & [p16<=0 | p169<=0]]]] & [[[p15<=0 | p166<=0] & [[p16<=0 | p167<=0] & [p14<=0 | p164<=0]]] & [[p14<=0 | p168<=0] & [[p17<=0 | p169<=0] & [p14<=0 | p166<=0]]]]]] & [[[[[p17<=0 | p167<=0] & [p18<=0 | p169<=0]] & [[p13<=0 | p166<=0] & [[p13<=0 | p168<=0] & [p18<=0 | p165<=0]]]] & [[[p18<=0 | p167<=0] & [p13<=0 | p164<=0]] & [[p17<=0 | p165<=0] & [[p19<=0 | p167<=0] & [p19<=0 | p165<=0]]]]] & [[[[p19<=0 | p169<=0] & [p15<=0 | p168<=0]] & [[p16<=0 | p165<=0] & [[p15<=0 | p165<=0] & [p15<=0 | p167<=0]]]] & [[[p16<=0 | p168<=0] & [[p17<=0 | p168<=0] & [p14<=0 | p167<=0]]] & [[p17<=0 | p166<=0] & [[p14<=0 | p165<=0] & [p18<=0 | p164<=0]]]]]]]]] | EF [[[[1<=p13 & 1<=p163] | [[1<=p13 & 1<=p160] | [1<=p13 & 1<=p159]]] | [[1<=p13 & 1<=p162] | [[1<=p13 & 1<=p161] | [1<=p13 & 1<=p158]]]]]]]]
normalized: E [true U EG [[E [true U [[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]] | [1<=p13 & 1<=p163]]]] | [~ [EG [[[[[[[[p18<=0 | p164<=0] & [p14<=0 | p165<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]] & [[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[p15<=0 | p168<=0] & [p19<=0 | p169<=0]]]] & [[[[[p19<=0 | p165<=0] & [p19<=0 | p167<=0]] & [p17<=0 | p165<=0]] & [[p13<=0 | p164<=0] & [p18<=0 | p167<=0]]] & [[[[p18<=0 | p165<=0] & [p13<=0 | p168<=0]] & [p13<=0 | p166<=0]] & [[p18<=0 | p169<=0] & [p17<=0 | p167<=0]]]]] & [[[[[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]] & [[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]]] & [[[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]] & [[p16<=0 | p166<=0] & [p15<=0 | p169<=0]]]] & [[[[[p19<=0 | p168<=0] & [p19<=0 | p164<=0]] & [p19<=0 | p166<=0]] & [[p17<=0 | p164<=0] & [p14<=0 | p169<=0]]] & [[[[p18<=0 | p168<=0] & [p13<=0 | p165<=0]] & [p18<=0 | p166<=0]] & [[p13<=0 | p169<=0] & [p13<=0 | p167<=0]]]]]]]] & ~ [E [[[[[[[[p18<=0 | p164<=0] & [p14<=0 | p165<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]] & [[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[p15<=0 | p168<=0] & [p19<=0 | p169<=0]]]] & [[[[[p19<=0 | p165<=0] & [p19<=0 | p167<=0]] & [p17<=0 | p165<=0]] & [[p13<=0 | p164<=0] & [p18<=0 | p167<=0]]] & [[[[p18<=0 | p165<=0] & [p13<=0 | p168<=0]] & [p13<=0 | p166<=0]] & [[p18<=0 | p169<=0] & [p17<=0 | p167<=0]]]]] & [[[[[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]] & [[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]]] & [[[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]] & [[p16<=0 | p166<=0] & [p15<=0 | p169<=0]]]] & [[[[[p19<=0 | p168<=0] & [p19<=0 | p164<=0]] & [p19<=0 | p166<=0]] & [[p17<=0 | p164<=0] & [p14<=0 | p169<=0]]] & [[[[p18<=0 | p168<=0] & [p13<=0 | p165<=0]] & [p18<=0 | p166<=0]] & [[p13<=0 | p169<=0] & [p13<=0 | p167<=0]]]]]] U [EG [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]] & [[[[[[[p18<=0 | p164<=0] & [p14<=0 | p165<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]] & [[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[p15<=0 | p168<=0] & [p19<=0 | p169<=0]]]] & [[[[[p19<=0 | p165<=0] & [p19<=0 | p167<=0]] & [p17<=0 | p165<=0]] & [[p13<=0 | p164<=0] & [p18<=0 | p167<=0]]] & [[[[p18<=0 | p165<=0] & [p13<=0 | p168<=0]] & [p13<=0 | p166<=0]] & [[p18<=0 | p169<=0] & [p17<=0 | p167<=0]]]]] & [[[[[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]] & [[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]]] & [[[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]] & [[p16<=0 | p166<=0] & [p15<=0 | p169<=0]]]] & [[[[[p19<=0 | p168<=0] & [p19<=0 | p164<=0]] & [p19<=0 | p166<=0]] & [[p17<=0 | p164<=0] & [p14<=0 | p169<=0]]] & [[[[p18<=0 | p168<=0] & [p13<=0 | p165<=0]] & [p18<=0 | p166<=0]] & [[p13<=0 | p169<=0] & [p13<=0 | p167<=0]]]]]]]]]]]]]
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
before gc: list nodes free: 2341703
after gc: idd nodes used:5692752, unused:58307248; list nodes free:258333964
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p169<=0)
states: 537,651,396,328 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p168<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p167<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p166<=0)
states: 537,651,396,328 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p165<=0)
states: 537,651,396,328 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p164<=0)
states: 537,651,396,328 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (1<=p73)
states: 6,677,072,160 (9)
abstracting: (1<=p70)
states: 6,677,072,160 (9)
abstracting: (1<=p71)
states: 6,677,072,160 (9)
abstracting: (1<=p68)
states: 6,677,072,160 (9)
abstracting: (1<=p69)
states: 6,677,072,160 (9)
abstracting: (1<=p72)
states: 6,677,072,160 (9)
.
before gc: list nodes free: 650402
after gc: idd nodes used:7996660, unused:56003340; list nodes free:248190574
MC time: 2m13.147sec
checking: EG [[[AX [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]] | AX [AX [[[[p13<=0 | p47<=0] & [[p13<=0 | p46<=0] & [p13<=0 | p45<=0]]] & [[p13<=0 | p44<=0] & [[p13<=0 | p49<=0] & [p13<=0 | p48<=0]]]]]]] | [EG [[[[[p110<=0 | [p116<=0 | p117<=0]] | [[p118<=0 | p119<=0] | [p120<=0 | p121<=0]]] & [[[p114<=0 | [p140<=0 | p141<=0]] | [[p142<=0 | p143<=0] | [p144<=0 | p145<=0]]] & [[p111<=0 | [p122<=0 | p123<=0]] | [[p124<=0 | p125<=0] | [p126<=0 | p127<=0]]]]] & [[[p115<=0 | [p146<=0 | p147<=0]] | [[p148<=0 | p149<=0] | [p150<=0 | p151<=0]]] & [[[p113<=0 | [p134<=0 | p135<=0]] | [[p136<=0 | p137<=0] | [p138<=0 | p139<=0]]] & [[p112<=0 | [p128<=0 | p129<=0]] | [[p130<=0 | p131<=0] | [p132<=0 | p133<=0]]]]]]] | [[[[[[p13<=0 | p167<=0] & [p13<=0 | p169<=0]] & [[p18<=0 | p166<=0] & [[p13<=0 | p165<=0] & [p18<=0 | p168<=0]]]] & [[[p14<=0 | p169<=0] & [p17<=0 | p164<=0]] & [[p19<=0 | p166<=0] & [[p19<=0 | p164<=0] & [p19<=0 | p168<=0]]]]] & [[[[p15<=0 | p169<=0] & [p16<=0 | p166<=0]] & [[p16<=0 | p164<=0] & [[p15<=0 | p164<=0] & [p16<=0 | p169<=0]]]] & [[[p15<=0 | p166<=0] & [[p16<=0 | p167<=0] & [p14<=0 | p164<=0]]] & [[p14<=0 | p168<=0] & [[p17<=0 | p169<=0] & [p14<=0 | p166<=0]]]]]] & [[[[[p17<=0 | p167<=0] & [p18<=0 | p169<=0]] & [[p13<=0 | p166<=0] & [[p13<=0 | p168<=0] & [p18<=0 | p165<=0]]]] & [[[p18<=0 | p167<=0] & [p13<=0 | p164<=0]] & [[p17<=0 | p165<=0] & [[p19<=0 | p167<=0] & [p19<=0 | p165<=0]]]]] & [[[[p19<=0 | p169<=0] & [p15<=0 | p168<=0]] & [[p16<=0 | p165<=0] & [[p15<=0 | p165<=0] & [p15<=0 | p167<=0]]]] & [[[p16<=0 | p168<=0] & [[p17<=0 | p168<=0] & [p14<=0 | p167<=0]]] & [[p17<=0 | p166<=0] & [[p14<=0 | p165<=0] & [p18<=0 | p164<=0]]]]]]]]]]
normalized: EG [[[[[[[[[p13<=0 | p164<=0] & [p18<=0 | p167<=0]] & [[[p19<=0 | p165<=0] & [p19<=0 | p167<=0]] & [p17<=0 | p165<=0]]] & [[[[p18<=0 | p165<=0] & [p13<=0 | p168<=0]] & [p13<=0 | p166<=0]] & [[p18<=0 | p169<=0] & [p17<=0 | p167<=0]]]] & [[[[[p14<=0 | p165<=0] & [p18<=0 | p164<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]] & [[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[p15<=0 | p168<=0] & [p19<=0 | p169<=0]]]]] & [[[[[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]] & [[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]]] & [[[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]] & [[p16<=0 | p166<=0] & [p15<=0 | p169<=0]]]] & [[[[[p19<=0 | p168<=0] & [p19<=0 | p164<=0]] & [p19<=0 | p166<=0]] & [[p17<=0 | p164<=0] & [p14<=0 | p169<=0]]] & [[[[p18<=0 | p168<=0] & [p13<=0 | p165<=0]] & [p18<=0 | p166<=0]] & [[p13<=0 | p169<=0] & [p13<=0 | p167<=0]]]]]] | EG [[[[[[[p132<=0 | p133<=0] | [p130<=0 | p131<=0]] | [p112<=0 | [p128<=0 | p129<=0]]] & [[[p138<=0 | p139<=0] | [p136<=0 | p137<=0]] | [p113<=0 | [p134<=0 | p135<=0]]]] & [[[p150<=0 | p151<=0] | [p148<=0 | p149<=0]] | [p115<=0 | [p146<=0 | p147<=0]]]] & [[[[[p126<=0 | p127<=0] | [p124<=0 | p125<=0]] | [p111<=0 | [p122<=0 | p123<=0]]] & [[[p144<=0 | p145<=0] | [p142<=0 | p143<=0]] | [p114<=0 | [p140<=0 | p141<=0]]]] & [[[p120<=0 | p121<=0] | [p118<=0 | p119<=0]] | [p110<=0 | [p116<=0 | p117<=0]]]]]]] | [~ [EX [EX [~ [[[[[p13<=0 | p48<=0] & [p13<=0 | p49<=0]] & [p13<=0 | p44<=0]] & [[[p13<=0 | p45<=0] & [p13<=0 | p46<=0]] & [p13<=0 | p47<=0]]]]]]] | ~ [EX [~ [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]]]]]]]
abstracting: (p163<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p160<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p159<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p162<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p161<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p158<=0)
states: 530,678,972,010 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
.abstracting: (p47<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p46<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p45<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p44<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p49<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
abstracting: (p48<=0)
states: 529,752,753,288 (11)
abstracting: (p13<=0)
states: 464,134,200,192 (11)
.
before gc: list nodes free: 2555656
after gc: idd nodes used:10992370, unused:53007630; list nodes free:234938623
MC time: 2m 4.058sec
checking: EF [EG [[A [[[[[[[1<=p12 & 1<=p56] | [1<=p12 & 1<=p58]] | [[1<=p12 & 1<=p57] | [1<=p7 & 1<=p61]]] | [[[1<=p7 & 1<=p60] | [1<=p7 & 1<=p59]] | [[1<=p7 & 1<=p58] | [[1<=p7 & 1<=p57] | [1<=p8 & 1<=p60]]]]] | [[[[1<=p8 & 1<=p59] | [1<=p8 & 1<=p61]] | [[1<=p8 & 1<=p56] | [1<=p12 & 1<=p60]]] | [[[1<=p12 & 1<=p59] | [1<=p8 & 1<=p58]] | [[1<=p10 & 1<=p61] | [[1<=p9 & 1<=p57] | [1<=p9 & 1<=p56]]]]]] | [[[[[1<=p9 & 1<=p61] | [1<=p9 & 1<=p60]] | [[1<=p9 & 1<=p59] | [1<=p11 & 1<=p61]]] | [[[1<=p6 & 1<=p57] | [1<=p11 & 1<=p59]] | [[1<=p6 & 1<=p58] | [[1<=p11 & 1<=p58] | [1<=p6 & 1<=p59]]]]] | [[[[1<=p11 & 1<=p57] | [1<=p6 & 1<=p60]] | [[1<=p11 & 1<=p56] | [1<=p6 & 1<=p61]]] | [[[1<=p10 & 1<=p56] | [1<=p10 & 1<=p58]] | [[1<=p10 & 1<=p57] | [[1<=p10 & 1<=p60] | [1<=p6 & 1<=p56]]]]]]] U [[[[[[1<=p17 & 1<=p157] | [1<=p17 & 1<=p156]] | [[1<=p17 & 1<=p153] | [1<=p17 & 1<=p152]]] | [[[1<=p17 & 1<=p154] | [1<=p16 & 1<=p152]] | [[1<=p13 & 1<=p157] | [[1<=p13 & 1<=p156] | [1<=p13 & 1<=p153]]]]] | [[[[1<=p13 & 1<=p152] | [1<=p13 & 1<=p155]] | [[1<=p13 & 1<=p154] | [1<=p16 & 1<=p157]]] | [[[1<=p16 & 1<=p156] | [1<=p16 & 1<=p155]] | [[1<=p16 & 1<=p153] | [[1<=p19 & 1<=p153] | [1<=p19 & 1<=p152]]]]]] | [[[[[1<=p14 & 1<=p154] | [1<=p19 & 1<=p155]] | [[1<=p14 & 1<=p153] | [1<=p19 & 1<=p154]]] | [[[1<=p19 & 1<=p156] | [1<=p15 & 1<=p155]] | [[1<=p15 & 1<=p154] | [[1<=p15 & 1<=p157] | [1<=p15 & 1<=p156]]]]] | [[[[1<=p18 & 1<=p154] | [1<=p18 & 1<=p153]] | [[1<=p18 & 1<=p152] | [1<=p18 & 1<=p157]]] | [[[1<=p15 & 1<=p152] | [1<=p18 & 1<=p155]] | [[1<=p14 & 1<=p157] | [[1<=p14 & 1<=p156] | [1<=p14 & 1<=p155]]]]]]]] | EX [[[[1<=p19 & 1<=p157] | [[1<=p14 & 1<=p152] | [1<=p15 & 1<=p153]]] | [[1<=p16 & 1<=p154] | [[1<=p17 & 1<=p155] | [1<=p18 & 1<=p156]]]]]]]]
normalized: E [true U EG [[EX [[[[[1<=p18 & 1<=p156] | [1<=p17 & 1<=p155]] | [1<=p16 & 1<=p154]] | [[[1<=p15 & 1<=p153] | [1<=p14 & 1<=p152]] | [1<=p19 & 1<=p157]]]] | [~ [EG [~ [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]]]]] & ~ [E [~ [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]]] U [~ [[[[[[[[1<=p6 & 1<=p56] | [1<=p10 & 1<=p60]] | [1<=p10 & 1<=p57]] | [[1<=p10 & 1<=p58] | [1<=p10 & 1<=p56]]] | [[[1<=p6 & 1<=p61] | [1<=p11 & 1<=p56]] | [[1<=p6 & 1<=p60] | [1<=p11 & 1<=p57]]]] | [[[[[1<=p6 & 1<=p59] | [1<=p11 & 1<=p58]] | [1<=p6 & 1<=p58]] | [[1<=p11 & 1<=p59] | [1<=p6 & 1<=p57]]] | [[[1<=p11 & 1<=p61] | [1<=p9 & 1<=p59]] | [[1<=p9 & 1<=p60] | [1<=p9 & 1<=p61]]]]] | [[[[[[1<=p9 & 1<=p56] | [1<=p9 & 1<=p57]] | [1<=p10 & 1<=p61]] | [[1<=p8 & 1<=p58] | [1<=p12 & 1<=p59]]] | [[[1<=p12 & 1<=p60] | [1<=p8 & 1<=p56]] | [[1<=p8 & 1<=p61] | [1<=p8 & 1<=p59]]]] | [[[[[1<=p8 & 1<=p60] | [1<=p7 & 1<=p57]] | [1<=p7 & 1<=p58]] | [[1<=p7 & 1<=p59] | [1<=p7 & 1<=p60]]] | [[[1<=p7 & 1<=p61] | [1<=p12 & 1<=p57]] | [[1<=p12 & 1<=p58] | [1<=p12 & 1<=p56]]]]]]] & ~ [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]]]]]]]]]]
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
before gc: list nodes free: 2772316
after gc: idd nodes used:13623547, unused:50376453; list nodes free:223500124
MC time: 1m56.176sec
checking: [E [~ [EF [[[[[1<=p73 | 1<=p70] | 1<=p71] | [1<=p72 | [1<=p69 | 1<=p68]]] | [[[1<=p13 & 1<=p163] | [[1<=p13 & 1<=p160] | [1<=p13 & 1<=p159]]] | [[1<=p13 & 1<=p162] | [[1<=p13 & 1<=p161] | [1<=p13 & 1<=p158]]]]]]] U [[[[[[1<=p17 & 1<=p55] | [1<=p16 & 1<=p53]] | [[1<=p16 & 1<=p55] | [[1<=p16 & 1<=p51] | [1<=p13 & 1<=p54]]]] | [[[1<=p13 & 1<=p52] | [1<=p13 & 1<=p50]] | [[1<=p17 & 1<=p53] | [[1<=p17 & 1<=p51] | [1<=p14 & 1<=p51]]]]] | [[[[1<=p19 & 1<=p54] | [1<=p14 & 1<=p53]] | [[1<=p19 & 1<=p50] | [[1<=p14 & 1<=p55] | [1<=p18 & 1<=p50]]]] | [[[1<=p18 & 1<=p52] | [[1<=p18 & 1<=p54] | [1<=p15 & 1<=p55]]] | [[1<=p15 & 1<=p53] | [[1<=p15 & 1<=p51] | [1<=p19 & 1<=p52]]]]]] | [[[[[1<=p16 & 1<=p52] | [1<=p16 & 1<=p54]] | [[1<=p16 & 1<=p50] | [[1<=p13 & 1<=p53] | [1<=p13 & 1<=p51]]]] | [[[1<=p13 & 1<=p55] | [1<=p17 & 1<=p50]] | [[1<=p17 & 1<=p54] | [[1<=p17 & 1<=p52] | [1<=p19 & 1<=p53]]]]] | [[[[1<=p14 & 1<=p50] | [1<=p19 & 1<=p55]] | [[1<=p14 & 1<=p52] | [[1<=p14 & 1<=p54] | [1<=p18 & 1<=p51]]]] | [[[1<=p18 & 1<=p53] | [[1<=p18 & 1<=p55] | [1<=p15 & 1<=p54]]] | [[1<=p15 & 1<=p52] | [[1<=p15 & 1<=p50] | [1<=p19 & 1<=p51]]]]]]]] | [AF [AX [EG [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]]]] | AG [AX [[EG [[[[[p21<=0 | p170<=0] & [[p26<=0 | p173<=0] & [p24<=0 | p172<=0]]] & [[p23<=0 | p171<=0] & [[p27<=0 | p173<=0] & [p29<=0 | p174<=0]]]] & [[[p31<=0 | p175<=0] & [[p30<=0 | p175<=0] & [p25<=0 | p172<=0]]] & [[p22<=0 | p171<=0] & [[p20<=0 | p170<=0] & [p28<=0 | p174<=0]]]]]] & [[AX [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]]] | [1<=p71 | 1<=p70]] | [[1<=p73 | 1<=p72] | [1<=p69 | 1<=p68]]]]]]]]
normalized: [[~ [E [true U EX [~ [[[[[1<=p69 | 1<=p68] | [1<=p73 | 1<=p72]] | [[1<=p71 | 1<=p70] | ~ [EX [~ [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]]]] & EG [[[[[[p28<=0 | p174<=0] & [p20<=0 | p170<=0]] & [p22<=0 | p171<=0]] & [[[p25<=0 | p172<=0] & [p30<=0 | p175<=0]] & [p31<=0 | p175<=0]]] & [[[[p29<=0 | p174<=0] & [p27<=0 | p173<=0]] & [p23<=0 | p171<=0]] & [[[p24<=0 | p172<=0] & [p26<=0 | p173<=0]] & [p21<=0 | p170<=0]]]]]]]]]] | ~ [EG [EX [~ [EG [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]]]]]]] | E [~ [E [true U [[[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]] | [1<=p13 & 1<=p163]]] | [[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p73 | 1<=p70]]]]]] U [[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]]] | [[[[1<=p13 & 1<=p51] | [1<=p13 & 1<=p53]] | [1<=p16 & 1<=p50]] | [[1<=p16 & 1<=p54] | [1<=p16 & 1<=p52]]]]] | [[[[[[1<=p19 & 1<=p52] | [1<=p15 & 1<=p51]] | [1<=p15 & 1<=p53]] | [[[1<=p15 & 1<=p55] | [1<=p18 & 1<=p54]] | [1<=p18 & 1<=p52]]] | [[[[1<=p18 & 1<=p50] | [1<=p14 & 1<=p55]] | [1<=p19 & 1<=p50]] | [[1<=p14 & 1<=p53] | [1<=p19 & 1<=p54]]]] | [[[[[1<=p14 & 1<=p51] | [1<=p17 & 1<=p51]] | [1<=p17 & 1<=p53]] | [[1<=p13 & 1<=p50] | [1<=p13 & 1<=p52]]] | [[[[1<=p13 & 1<=p54] | [1<=p16 & 1<=p51]] | [1<=p16 & 1<=p55]] | [[1<=p16 & 1<=p53] | [1<=p17 & 1<=p55]]]]]]]]
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p70)
states: 6,677,072,160 (9)
abstracting: (1<=p73)
states: 6,677,072,160 (9)
abstracting: (1<=p71)
states: 6,677,072,160 (9)
abstracting: (1<=p68)
states: 6,677,072,160 (9)
abstracting: (1<=p69)
states: 6,677,072,160 (9)
abstracting: (1<=p72)
states: 6,677,072,160 (9)
abstracting: (1<=p163)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p160)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p159)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p162)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p161)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p158)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
before gc: list nodes free: 3341749
after gc: idd nodes used:16028219, unused:47971781; list nodes free:212938512
MC time: 1m48.155sec
checking: EF [AG [[[[AG [[[[[[[1<=p16 & 1<=p46] | [1<=p16 & 1<=p45]] | [[1<=p16 & 1<=p48] | [1<=p16 & 1<=p47]]] | [[[1<=p16 & 1<=p44] | [1<=p16 & 1<=p49]] | [[1<=p17 & 1<=p47] | [[1<=p17 & 1<=p46] | [1<=p17 & 1<=p45]]]]] | [[[[1<=p17 & 1<=p44] | [1<=p17 & 1<=p49]] | [[1<=p17 & 1<=p48] | [1<=p18 & 1<=p44]]] | [[[1<=p19 & 1<=p49] | [1<=p19 & 1<=p48]] | [[1<=p18 & 1<=p46] | [[1<=p19 & 1<=p47] | [1<=p18 & 1<=p45]]]]]] | [[[[[1<=p18 & 1<=p48] | [1<=p19 & 1<=p45]] | [[1<=p19 & 1<=p46] | [1<=p14 & 1<=p44]]] | [[[1<=p18 & 1<=p47] | [1<=p19 & 1<=p44]] | [[1<=p14 & 1<=p46] | [[1<=p14 & 1<=p45] | [1<=p18 & 1<=p49]]]]] | [[[[1<=p14 & 1<=p48] | [1<=p14 & 1<=p47]] | [[1<=p14 & 1<=p49] | [1<=p15 & 1<=p49]]] | [[[1<=p15 & 1<=p48] | [1<=p15 & 1<=p47]] | [[1<=p15 & 1<=p46] | [[1<=p15 & 1<=p45] | [1<=p15 & 1<=p44]]]]]]]] | 1<=p71] | [1<=p70 | 1<=p73]] | [[1<=p72 | 1<=p69] | [1<=p68 | [[[[[[[p17<=0 | p157<=0] & [p17<=0 | p156<=0]] & [[p17<=0 | p153<=0] & [p17<=0 | p152<=0]]] & [[[p17<=0 | p154<=0] & [p16<=0 | p152<=0]] & [[p13<=0 | p157<=0] & [[p13<=0 | p156<=0] & [p13<=0 | p153<=0]]]]] & [[[[p13<=0 | p152<=0] & [p13<=0 | p155<=0]] & [[p13<=0 | p154<=0] & [p16<=0 | p157<=0]]] & [[[p16<=0 | p156<=0] & [p16<=0 | p155<=0]] & [[p16<=0 | p153<=0] & [[p19<=0 | p153<=0] & [p19<=0 | p152<=0]]]]]] & [[[[[p14<=0 | p154<=0] & [p19<=0 | p155<=0]] & [[p14<=0 | p153<=0] & [p19<=0 | p154<=0]]] & [[[p19<=0 | p156<=0] & [p15<=0 | p155<=0]] & [[p15<=0 | p154<=0] & [[p15<=0 | p157<=0] & [p15<=0 | p156<=0]]]]] & [[[[p18<=0 | p154<=0] & [p18<=0 | p153<=0]] & [[p18<=0 | p152<=0] & [p18<=0 | p157<=0]]] & [[[p15<=0 | p152<=0] & [p18<=0 | p155<=0]] & [[p14<=0 | p157<=0] & [[p14<=0 | p156<=0] & [p14<=0 | p155<=0]]]]]]] | [[[[p2<=0 | p24<=0] & [[p5<=0 | p31<=0] & [p1<=0 | p22<=0]]] & [[p3<=0 | p27<=0] & [[p5<=0 | p30<=0] & [p1<=0 | p23<=0]]]] & [[[p3<=0 | p26<=0] & [[p4<=0 | p28<=0] & [p4<=0 | p29<=0]]] & [[p0<=0 | p21<=0] & [[p0<=0 | p20<=0] & [p2<=0 | p25<=0]]]]]]]]]]]
normalized: E [true U ~ [E [true U ~ [[[[1<=p68 | [[[[[[p2<=0 | p25<=0] & [p0<=0 | p20<=0]] & [p0<=0 | p21<=0]] & [[[p4<=0 | p29<=0] & [p4<=0 | p28<=0]] & [p3<=0 | p26<=0]]] & [[[[p1<=0 | p23<=0] & [p5<=0 | p30<=0]] & [p3<=0 | p27<=0]] & [[[p1<=0 | p22<=0] & [p5<=0 | p31<=0]] & [p2<=0 | p24<=0]]]] | [[[[[[[p14<=0 | p155<=0] & [p14<=0 | p156<=0]] & [p14<=0 | p157<=0]] & [[p18<=0 | p155<=0] & [p15<=0 | p152<=0]]] & [[[p18<=0 | p157<=0] & [p18<=0 | p152<=0]] & [[p18<=0 | p153<=0] & [p18<=0 | p154<=0]]]] & [[[[[p15<=0 | p156<=0] & [p15<=0 | p157<=0]] & [p15<=0 | p154<=0]] & [[p15<=0 | p155<=0] & [p19<=0 | p156<=0]]] & [[[p19<=0 | p154<=0] & [p14<=0 | p153<=0]] & [[p19<=0 | p155<=0] & [p14<=0 | p154<=0]]]]] & [[[[[[p19<=0 | p152<=0] & [p19<=0 | p153<=0]] & [p16<=0 | p153<=0]] & [[p16<=0 | p155<=0] & [p16<=0 | p156<=0]]] & [[[p16<=0 | p157<=0] & [p13<=0 | p154<=0]] & [[p13<=0 | p155<=0] & [p13<=0 | p152<=0]]]] & [[[[[p13<=0 | p153<=0] & [p13<=0 | p156<=0]] & [p13<=0 | p157<=0]] & [[p16<=0 | p152<=0] & [p17<=0 | p154<=0]]] & [[[p17<=0 | p152<=0] & [p17<=0 | p153<=0]] & [[p17<=0 | p156<=0] & [p17<=0 | p157<=0]]]]]]]] | [1<=p72 | 1<=p69]] | [[1<=p70 | 1<=p73] | [1<=p71 | ~ [E [true U ~ [[[[[[[[1<=p15 & 1<=p44] | [1<=p15 & 1<=p45]] | [1<=p15 & 1<=p46]] | [[1<=p15 & 1<=p47] | [1<=p15 & 1<=p48]]] | [[[1<=p15 & 1<=p49] | [1<=p14 & 1<=p49]] | [[1<=p14 & 1<=p47] | [1<=p14 & 1<=p48]]]] | [[[[[1<=p18 & 1<=p49] | [1<=p14 & 1<=p45]] | [1<=p14 & 1<=p46]] | [[1<=p19 & 1<=p44] | [1<=p18 & 1<=p47]]] | [[[1<=p14 & 1<=p44] | [1<=p19 & 1<=p46]] | [[1<=p19 & 1<=p45] | [1<=p18 & 1<=p48]]]]] | [[[[[[1<=p18 & 1<=p45] | [1<=p19 & 1<=p47]] | [1<=p18 & 1<=p46]] | [[1<=p19 & 1<=p48] | [1<=p19 & 1<=p49]]] | [[[1<=p18 & 1<=p44] | [1<=p17 & 1<=p48]] | [[1<=p17 & 1<=p49] | [1<=p17 & 1<=p44]]]] | [[[[[1<=p17 & 1<=p45] | [1<=p17 & 1<=p46]] | [1<=p17 & 1<=p47]] | [[1<=p16 & 1<=p49] | [1<=p16 & 1<=p44]]] | [[[1<=p16 & 1<=p47] | [1<=p16 & 1<=p48]] | [[1<=p16 & 1<=p45] | [1<=p16 & 1<=p46]]]]]]]]]]]]]]]]
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p49)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p48)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p47)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p46)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p45)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p44)
states: 17,479,005,856 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
before gc: list nodes free: 3169384
after gc: idd nodes used:16519703, unused:47480297; list nodes free:210842401
MC time: 1m41.097sec
checking: AG [[~ [A [AF [AX [[[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]]] U [EG [[[[[[[1<=p10 & 1<=p33] | [1<=p10 & 1<=p35]] | [[1<=p10 & 1<=p37] | [[1<=p11 & 1<=p37] | [1<=p9 & 1<=p33]]]] | [[[1<=p11 & 1<=p35] | [1<=p11 & 1<=p33]] | [[1<=p9 & 1<=p37] | [[1<=p6 & 1<=p32] | [1<=p9 & 1<=p35]]]]] | [[[[1<=p6 & 1<=p34] | [1<=p6 & 1<=p36]] | [[1<=p8 & 1<=p36] | [[1<=p7 & 1<=p34] | [1<=p7 & 1<=p32]]]] | [[[1<=p7 & 1<=p36] | [[1<=p8 & 1<=p32] | [1<=p12 & 1<=p35]]] | [[[1<=p12 & 1<=p37] | [1<=p12 & 1<=p33]] | [1<=p8 & 1<=p34]]]]] | [[[[[1<=p10 & 1<=p34] | [1<=p10 & 1<=p36]] | [[1<=p6 & 1<=p37] | [[1<=p11 & 1<=p36] | [1<=p9 & 1<=p32]]]] | [[[1<=p11 & 1<=p34] | [1<=p11 & 1<=p32]] | [[1<=p9 & 1<=p36] | [[1<=p9 & 1<=p34] | [1<=p6 & 1<=p33]]]]] | [[[[1<=p6 & 1<=p35] | [1<=p10 & 1<=p32]] | [[1<=p8 & 1<=p35] | [[1<=p8 & 1<=p37] | [1<=p7 & 1<=p35]]]] | [[[1<=p7 & 1<=p33] | [[1<=p7 & 1<=p37] | [1<=p12 & 1<=p36]]] | [[1<=p8 & 1<=p33] | [[1<=p12 & 1<=p32] | [1<=p12 & 1<=p34]]]]]]]] & [[[[1<=p13 & 1<=p163] | [[1<=p13 & 1<=p160] | [1<=p13 & 1<=p159]]] | [[1<=p13 & 1<=p162] | [[1<=p13 & 1<=p161] | [1<=p13 & 1<=p158]]]] & ~ [[[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]] & [[[[1<=p21 & 1<=p170] | [[1<=p26 & 1<=p173] | [1<=p24 & 1<=p172]]] | [[1<=p23 & 1<=p171] | [[1<=p27 & 1<=p173] | [1<=p29 & 1<=p174]]]] | [[[1<=p31 & 1<=p175] | [[1<=p30 & 1<=p175] | [1<=p25 & 1<=p172]]] | [[1<=p22 & 1<=p171] | [[1<=p20 & 1<=p170] | [1<=p28 & 1<=p174]]]]]]]]]]] | EG [AG [[[[[[[p10<=0 | p33<=0] & [[p10<=0 | p35<=0] & [p10<=0 | p37<=0]]] & [[p11<=0 | p37<=0] & [[p9<=0 | p33<=0] & [p11<=0 | p35<=0]]]] & [[[p11<=0 | p33<=0] & [[p9<=0 | p37<=0] & [p6<=0 | p32<=0]]] & [[[p9<=0 | p35<=0] & [p6<=0 | p34<=0]] & [[p6<=0 | p36<=0] & [p8<=0 | p36<=0]]]]] & [[[[p7<=0 | p34<=0] & [[p7<=0 | p32<=0] & [p7<=0 | p36<=0]]] & [[[p8<=0 | p32<=0] & [p12<=0 | p35<=0]] & [[p8<=0 | p34<=0] & [p12<=0 | p37<=0]]]] & [[[p12<=0 | p33<=0] & [[p10<=0 | p34<=0] & [p10<=0 | p36<=0]]] & [[[p6<=0 | p37<=0] & [p11<=0 | p36<=0]] & [[p9<=0 | p32<=0] & [p11<=0 | p34<=0]]]]]] & [[[[[p11<=0 | p32<=0] & [[p9<=0 | p36<=0] & [p9<=0 | p34<=0]]] & [[p6<=0 | p33<=0] & [[p6<=0 | p35<=0] & [p10<=0 | p32<=0]]]] & [[[p8<=0 | p35<=0] & [[p8<=0 | p37<=0] & [p7<=0 | p35<=0]]] & [[[p7<=0 | p33<=0] & [p7<=0 | p37<=0]] & [[p12<=0 | p36<=0] & [p8<=0 | p33<=0]]]]] & [[[[p12<=0 | p32<=0] & [[p12<=0 | p34<=0] & [p28<=0 | p66<=0]]] & [[[p20<=0 | p62<=0] & [p25<=0 | p64<=0]] & [[p23<=0 | p63<=0] & [p26<=0 | p65<=0]]]] & [[[p30<=0 | p67<=0] & [[p29<=0 | p66<=0] & [p27<=0 | p65<=0]]] & [[[p24<=0 | p64<=0] & [p22<=0 | p63<=0]] & [[p21<=0 | p62<=0] & [p31<=0 | p67<=0]]]]]]]]]]]
normalized: ~ [E [true U ~ [[EG [~ [E [true U ~ [[[[[[[[p31<=0 | p67<=0] & [p21<=0 | p62<=0]] & [[p22<=0 | p63<=0] & [p24<=0 | p64<=0]]] & [[[p27<=0 | p65<=0] & [p29<=0 | p66<=0]] & [p30<=0 | p67<=0]]] & [[[[p26<=0 | p65<=0] & [p23<=0 | p63<=0]] & [[p25<=0 | p64<=0] & [p20<=0 | p62<=0]]] & [[[p28<=0 | p66<=0] & [p12<=0 | p34<=0]] & [p12<=0 | p32<=0]]]] & [[[[[p8<=0 | p33<=0] & [p12<=0 | p36<=0]] & [[p7<=0 | p37<=0] & [p7<=0 | p33<=0]]] & [[[p7<=0 | p35<=0] & [p8<=0 | p37<=0]] & [p8<=0 | p35<=0]]] & [[[[p10<=0 | p32<=0] & [p6<=0 | p35<=0]] & [p6<=0 | p33<=0]] & [[[p9<=0 | p34<=0] & [p9<=0 | p36<=0]] & [p11<=0 | p32<=0]]]]] & [[[[[[p11<=0 | p34<=0] & [p9<=0 | p32<=0]] & [[p11<=0 | p36<=0] & [p6<=0 | p37<=0]]] & [[[p10<=0 | p36<=0] & [p10<=0 | p34<=0]] & [p12<=0 | p33<=0]]] & [[[[p12<=0 | p37<=0] & [p8<=0 | p34<=0]] & [[p12<=0 | p35<=0] & [p8<=0 | p32<=0]]] & [[[p7<=0 | p36<=0] & [p7<=0 | p32<=0]] & [p7<=0 | p34<=0]]]] & [[[[[p8<=0 | p36<=0] & [p6<=0 | p36<=0]] & [[p6<=0 | p34<=0] & [p9<=0 | p35<=0]]] & [[[p6<=0 | p32<=0] & [p9<=0 | p37<=0]] & [p11<=0 | p33<=0]]] & [[[[p11<=0 | p35<=0] & [p9<=0 | p33<=0]] & [p11<=0 | p37<=0]] & [[[p10<=0 | p37<=0] & [p10<=0 | p35<=0]] & [p10<=0 | p33<=0]]]]]]]]]] | ~ [[~ [EG [~ [[[~ [[[[[[[1<=p28 & 1<=p174] | [1<=p20 & 1<=p170]] | [1<=p22 & 1<=p171]] | [[[1<=p25 & 1<=p172] | [1<=p30 & 1<=p175]] | [1<=p31 & 1<=p175]]] | [[[[1<=p29 & 1<=p174] | [1<=p27 & 1<=p173]] | [1<=p23 & 1<=p171]] | [[[1<=p24 & 1<=p172] | [1<=p26 & 1<=p173]] | [1<=p21 & 1<=p170]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]] & [[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]] | [1<=p13 & 1<=p163]]]] & EG [[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]]]]]]] & ~ [E [~ [[[~ [[[[[[[1<=p28 & 1<=p174] | [1<=p20 & 1<=p170]] | [1<=p22 & 1<=p171]] | [[[1<=p25 & 1<=p172] | [1<=p30 & 1<=p175]] | [1<=p31 & 1<=p175]]] | [[[[1<=p29 & 1<=p174] | [1<=p27 & 1<=p173]] | [1<=p23 & 1<=p171]] | [[[1<=p24 & 1<=p172] | [1<=p26 & 1<=p173]] | [1<=p21 & 1<=p170]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]] & [[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]] | [1<=p13 & 1<=p163]]]] & EG [[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]]]]] U [EG [EX [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]]] & ~ [[[~ [[[[[[[1<=p28 & 1<=p174] | [1<=p20 & 1<=p170]] | [1<=p22 & 1<=p171]] | [[[1<=p25 & 1<=p172] | [1<=p30 & 1<=p175]] | [1<=p31 & 1<=p175]]] | [[[[1<=p29 & 1<=p174] | [1<=p27 & 1<=p173]] | [1<=p23 & 1<=p171]] | [[[1<=p24 & 1<=p172] | [1<=p26 & 1<=p173]] | [1<=p21 & 1<=p170]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]] & [[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]] | [1<=p13 & 1<=p163]]]] & EG [[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]]]]]]]]]]]]]]
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
before gc: list nodes free: 4075305
after gc: idd nodes used:18156424, unused:45843576; list nodes free:203446401
MC time: 1m34.676sec
checking: EG [AF [[AF [AG [[[[[1<=p110 & [1<=p116 & 1<=p117]] & [[1<=p118 & 1<=p119] & [1<=p120 & 1<=p121]]] | [[[1<=p114 & [1<=p140 & 1<=p141]] & [[1<=p142 & 1<=p143] & [1<=p144 & 1<=p145]]] | [[1<=p111 & [1<=p122 & 1<=p123]] & [[1<=p124 & 1<=p125] & [1<=p126 & 1<=p127]]]]] | [[[1<=p115 & [1<=p146 & 1<=p147]] & [[1<=p148 & 1<=p149] & [1<=p150 & 1<=p151]]] | [[[1<=p113 & [1<=p134 & 1<=p135]] & [[1<=p136 & 1<=p137] & [1<=p138 & 1<=p139]]] | [[1<=p112 & [1<=p128 & 1<=p129]] & [[1<=p130 & 1<=p131] & [1<=p132 & 1<=p133]]]]]]]] | [AG [[[[[[[1<=p26 & [1<=p83 & 1<=p111]] | [1<=p24 & [1<=p100 & 1<=p114]]] | [[1<=p22 & [1<=p93 & 1<=p113]] | [1<=p30 & [1<=p103 & 1<=p114]]]] | [[[1<=p28 & [1<=p90 & 1<=p112]] | [1<=p20 & [1<=p86 & 1<=p112]]] | [[1<=p30 & [1<=p79 & 1<=p110]] | [[1<=p24 & [1<=p106 & 1<=p115]] | [1<=p20 & [1<=p74 & 1<=p110]]]]]] | [[[[1<=p22 & [1<=p99 & 1<=p114]] | [1<=p20 & [1<=p104 & 1<=p115]]] | [[1<=p30 & [1<=p97 & 1<=p113]] | [1<=p24 & [1<=p82 & 1<=p111]]]] | [[[1<=p30 & [1<=p85 & 1<=p111]] | [1<=p28 & [1<=p96 & 1<=p113]]] | [[1<=p26 & [1<=p89 & 1<=p112]] | [[1<=p26 & [1<=p107 & 1<=p115]] | [1<=p28 & [1<=p108 & 1<=p115]]]]]]] | [[[[[1<=p22 & [1<=p105 & 1<=p115]] | [1<=p28 & [1<=p78 & 1<=p110]]] | [[1<=p22 & [1<=p75 & 1<=p110]] | [1<=p26 & [1<=p101 & 1<=p114]]]] | [[[1<=p20 & [1<=p92 & 1<=p113]] | [1<=p22 & [1<=p81 & 1<=p111]]] | [[1<=p26 & [1<=p95 & 1<=p113]] | [[1<=p24 & [1<=p88 & 1<=p112]] | [1<=p24 & [1<=p94 & 1<=p113]]]]]] | [[[[1<=p26 & [1<=p77 & 1<=p110]] | [1<=p28 & [1<=p84 & 1<=p111]]] | [[1<=p28 & [1<=p102 & 1<=p114]] | [1<=p24 & [1<=p76 & 1<=p110]]]] | [[[1<=p22 & [1<=p87 & 1<=p112]] | [1<=p30 & [1<=p91 & 1<=p112]]] | [[1<=p30 & [1<=p109 & 1<=p115]] | [[1<=p20 & [1<=p80 & 1<=p111]] | [1<=p20 & [1<=p98 & 1<=p114]]]]]]]]] & [[[[[[EF [[[[[[[1<=p13 & 1<=p167] | [1<=p13 & 1<=p169]] | [[1<=p18 & 1<=p166] | [[1<=p13 & 1<=p165] | [1<=p18 & 1<=p168]]]] | [[[1<=p14 & 1<=p169] | [1<=p17 & 1<=p164]] | [[1<=p19 & 1<=p166] | [[1<=p19 & 1<=p164] | [1<=p19 & 1<=p168]]]]] | [[[[1<=p15 & 1<=p169] | [1<=p16 & 1<=p166]] | [[1<=p16 & 1<=p164] | [[1<=p15 & 1<=p164] | [1<=p16 & 1<=p169]]]] | [[[1<=p15 & 1<=p166] | [[1<=p16 & 1<=p167] | [1<=p14 & 1<=p164]]] | [[1<=p14 & 1<=p168] | [[1<=p17 & 1<=p169] | [1<=p14 & 1<=p166]]]]]] | [[[[[1<=p17 & 1<=p167] | [1<=p18 & 1<=p169]] | [[1<=p13 & 1<=p166] | [[1<=p13 & 1<=p168] | [1<=p18 & 1<=p165]]]] | [[[1<=p18 & 1<=p167] | [1<=p13 & 1<=p164]] | [[1<=p17 & 1<=p165] | [[1<=p19 & 1<=p167] | [1<=p19 & 1<=p165]]]]] | [[[[1<=p19 & 1<=p169] | [1<=p15 & 1<=p168]] | [[1<=p16 & 1<=p165] | [[1<=p15 & 1<=p165] | [1<=p15 & 1<=p167]]]] | [[[1<=p16 & 1<=p168] | [[1<=p17 & 1<=p168] | [1<=p14 & 1<=p167]]] | [[1<=p17 & 1<=p166] | [[1<=p14 & 1<=p165] | [1<=p18 & 1<=p164]]]]]]]] & [[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]] | [1<=p16 & 1<=p46]] | [[1<=p16 & 1<=p45] | [1<=p16 & 1<=p48]]] | [[[1<=p16 & 1<=p47] | [1<=p16 & 1<=p44]] | [[1<=p16 & 1<=p49] | [[1<=p17 & 1<=p47] | [1<=p17 & 1<=p46]]]]] | [[[[1<=p17 & 1<=p45] | [1<=p17 & 1<=p44]] | [[1<=p17 & 1<=p49] | [1<=p17 & 1<=p48]]] | [[[1<=p18 & 1<=p44] | [1<=p19 & 1<=p49]] | [[1<=p19 & 1<=p48] | [[1<=p18 & 1<=p46] | [1<=p19 & 1<=p47]]]]]] | [[[[[1<=p18 & 1<=p45] | [1<=p19 & 1<=p46]] | [[1<=p14 & 1<=p44] | [1<=p18 & 1<=p48]]] | [[[1<=p19 & 1<=p45] | [1<=p18 & 1<=p47]] | [[1<=p19 & 1<=p44] | [[1<=p14 & 1<=p46] | [1<=p14 & 1<=p45]]]]] | [[[[1<=p18 & 1<=p49] | [1<=p14 & 1<=p48]] | [[1<=p14 & 1<=p47] | [[1<=p14 & 1<=p49] | [1<=p15 & 1<=p49]]]] | [[[1<=p15 & 1<=p48] | [1<=p15 & 1<=p47]] | [[1<=p15 & 1<=p46] | [[1<=p15 & 1<=p45] | [1<=p15 & 1<=p44]]]]]]]]]]]
normalized: EG [~ [EG [~ [[[[[[[[[1<=p17 & 1<=p44] | [1<=p17 & 1<=p45]] | [[1<=p17 & 1<=p48] | [1<=p17 & 1<=p49]]] | [[[[1<=p19 & 1<=p47] | [1<=p18 & 1<=p46]] | [1<=p19 & 1<=p48]] | [[1<=p19 & 1<=p49] | [1<=p18 & 1<=p44]]]] | [[[[[1<=p17 & 1<=p46] | [1<=p17 & 1<=p47]] | [1<=p16 & 1<=p49]] | [[1<=p16 & 1<=p44] | [1<=p16 & 1<=p47]]] | [[[1<=p16 & 1<=p48] | [1<=p16 & 1<=p45]] | [[1<=p16 & 1<=p46] | [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]] & E [true U [[[[[[[1<=p18 & 1<=p164] | [1<=p14 & 1<=p165]] | [1<=p17 & 1<=p166]] | [[[1<=p14 & 1<=p167] | [1<=p17 & 1<=p168]] | [1<=p16 & 1<=p168]]] | [[[[1<=p15 & 1<=p167] | [1<=p15 & 1<=p165]] | [1<=p16 & 1<=p165]] | [[1<=p15 & 1<=p168] | [1<=p19 & 1<=p169]]]] | [[[[[1<=p19 & 1<=p165] | [1<=p19 & 1<=p167]] | [1<=p17 & 1<=p165]] | [[1<=p13 & 1<=p164] | [1<=p18 & 1<=p167]]] | [[[[1<=p18 & 1<=p165] | [1<=p13 & 1<=p168]] | [1<=p13 & 1<=p166]] | [[1<=p18 & 1<=p169] | [1<=p17 & 1<=p167]]]]] | [[[[[[1<=p14 & 1<=p166] | [1<=p17 & 1<=p169]] | [1<=p14 & 1<=p168]] | [[[1<=p14 & 1<=p164] | [1<=p16 & 1<=p167]] | [1<=p15 & 1<=p166]]] | [[[[1<=p16 & 1<=p169] | [1<=p15 & 1<=p164]] | [1<=p16 & 1<=p164]] | [[1<=p16 & 1<=p166] | [1<=p15 & 1<=p169]]]] | [[[[[1<=p19 & 1<=p168] | [1<=p19 & 1<=p164]] | [1<=p19 & 1<=p166]] | [[1<=p17 & 1<=p164] | [1<=p14 & 1<=p169]]] | [[[[1<=p18 & 1<=p168] | [1<=p13 & 1<=p165]] | [1<=p18 & 1<=p166]] | [[1<=p13 & 1<=p169] | [1<=p13 & 1<=p167]]]]]]]]]]]] | [[[[[[1<=p15 & 1<=p44] | [1<=p15 & 1<=p45]] | [1<=p15 & 1<=p46]] | [[1<=p15 & 1<=p47] | [1<=p15 & 1<=p48]]] | [[[[1<=p15 & 1<=p49] | [1<=p14 & 1<=p49]] | [1<=p14 & 1<=p47]] | [[1<=p14 & 1<=p48] | [1<=p18 & 1<=p49]]]] | [[[[[1<=p14 & 1<=p45] | [1<=p14 & 1<=p46]] | [1<=p19 & 1<=p44]] | [[1<=p18 & 1<=p47] | [1<=p19 & 1<=p45]]] | [[[1<=p18 & 1<=p48] | [1<=p14 & 1<=p44]] | [[1<=p19 & 1<=p46] | [1<=p18 & 1<=p45]]]]]] & ~ [E [true U ~ [[[[[[[[1<=p20 & [1<=p98 & 1<=p114]] | [1<=p20 & [1<=p80 & 1<=p111]]] | [1<=p30 & [1<=p109 & 1<=p115]]] | [[1<=p30 & [1<=p91 & 1<=p112]] | [1<=p22 & [1<=p87 & 1<=p112]]]] | [[[1<=p24 & [1<=p76 & 1<=p110]] | [1<=p28 & [1<=p102 & 1<=p114]]] | [[1<=p28 & [1<=p84 & 1<=p111]] | [1<=p26 & [1<=p77 & 1<=p110]]]]] | [[[[[1<=p24 & [1<=p94 & 1<=p113]] | [1<=p24 & [1<=p88 & 1<=p112]]] | [1<=p26 & [1<=p95 & 1<=p113]]] | [[1<=p22 & [1<=p81 & 1<=p111]] | [1<=p20 & [1<=p92 & 1<=p113]]]] | [[[1<=p26 & [1<=p101 & 1<=p114]] | [1<=p22 & [1<=p75 & 1<=p110]]] | [[1<=p28 & [1<=p78 & 1<=p110]] | [1<=p22 & [1<=p105 & 1<=p115]]]]]] | [[[[[[1<=p28 & [1<=p108 & 1<=p115]] | [1<=p26 & [1<=p107 & 1<=p115]]] | [1<=p26 & [1<=p89 & 1<=p112]]] | [[1<=p28 & [1<=p96 & 1<=p113]] | [1<=p30 & [1<=p85 & 1<=p111]]]] | [[[1<=p24 & [1<=p82 & 1<=p111]] | [1<=p30 & [1<=p97 & 1<=p113]]] | [[1<=p20 & [1<=p104 & 1<=p115]] | [1<=p22 & [1<=p99 & 1<=p114]]]]] | [[[[[1<=p20 & [1<=p74 & 1<=p110]] | [1<=p24 & [1<=p106 & 1<=p115]]] | [1<=p30 & [1<=p79 & 1<=p110]]] | [[1<=p20 & [1<=p86 & 1<=p112]] | [1<=p28 & [1<=p90 & 1<=p112]]]] | [[[1<=p30 & [1<=p103 & 1<=p114]] | [1<=p22 & [1<=p93 & 1<=p113]]] | [[1<=p24 & [1<=p100 & 1<=p114]] | [1<=p26 & [1<=p83 & 1<=p111]]]]]]]]]]] | ~ [EG [E [true U ~ [[[[[[[1<=p132 & 1<=p133] & [1<=p130 & 1<=p131]] & [1<=p112 & [1<=p128 & 1<=p129]]] | [[[1<=p138 & 1<=p139] & [1<=p136 & 1<=p137]] & [1<=p113 & [1<=p134 & 1<=p135]]]] | [[[1<=p150 & 1<=p151] & [1<=p148 & 1<=p149]] & [1<=p115 & [1<=p146 & 1<=p147]]]] | [[[[[1<=p126 & 1<=p127] & [1<=p124 & 1<=p125]] & [1<=p111 & [1<=p122 & 1<=p123]]] | [[[1<=p144 & 1<=p145] & [1<=p142 & 1<=p143]] & [1<=p114 & [1<=p140 & 1<=p141]]]] | [[[1<=p120 & 1<=p121] & [1<=p118 & 1<=p119]] & [1<=p110 & [1<=p116 & 1<=p117]]]]]]]]]]]]]]
abstracting: (1<=p117)
states: 194,929,046,592 (11)
abstracting: (1<=p116)
states: 197,739,387,520 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p119)
states: 194,929,046,592 (11)
abstracting: (1<=p118)
states: 194,929,046,592 (11)
abstracting: (1<=p121)
states: 194,929,046,592 (11)
abstracting: (1<=p120)
states: 194,929,046,592 (11)
abstracting: (1<=p141)
states: 194,929,046,592 (11)
abstracting: (1<=p140)
states: 194,929,046,592 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p143)
states: 194,929,046,592 (11)
abstracting: (1<=p142)
states: 194,929,046,592 (11)
abstracting: (1<=p145)
states: 194,929,046,592 (11)
abstracting: (1<=p144)
states: 197,739,387,520 (11)
abstracting: (1<=p123)
states: 197,739,387,520 (11)
abstracting: (1<=p122)
states: 194,929,046,592 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p125)
states: 194,929,046,592 (11)
abstracting: (1<=p124)
states: 194,929,046,592 (11)
abstracting: (1<=p127)
states: 194,929,046,592 (11)
abstracting: (1<=p126)
states: 194,929,046,592 (11)
abstracting: (1<=p147)
states: 194,929,046,592 (11)
abstracting: (1<=p146)
states: 194,929,046,592 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p149)
states: 194,929,046,592 (11)
abstracting: (1<=p148)
states: 194,929,046,592 (11)
abstracting: (1<=p151)
states: 197,739,387,520 (11)
abstracting: (1<=p150)
states: 194,929,046,592 (11)
abstracting: (1<=p135)
states: 194,929,046,592 (11)
abstracting: (1<=p134)
states: 194,929,046,592 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p137)
states: 197,739,387,520 (11)
abstracting: (1<=p136)
states: 194,929,046,592 (11)
abstracting: (1<=p139)
states: 194,929,046,592 (11)
abstracting: (1<=p138)
states: 194,929,046,592 (11)
abstracting: (1<=p129)
states: 194,929,046,592 (11)
abstracting: (1<=p128)
states: 194,929,046,592 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p131)
states: 194,929,046,592 (11)
abstracting: (1<=p130)
states: 197,739,387,520 (11)
abstracting: (1<=p133)
states: 194,929,046,592 (11)
abstracting: (1<=p132)
states: 194,929,046,592 (11)
before gc: list nodes free: 1563743
after gc: idd nodes used:27232600, unused:36767400; list nodes free:163801303
MC time: 1m28.484sec
checking: [EF [[[[[[[[1<=p10 & 1<=p33] | [1<=p10 & 1<=p35]] | [[1<=p10 & 1<=p37] | [[1<=p11 & 1<=p37] | [1<=p9 & 1<=p33]]]] | [[[1<=p11 & 1<=p35] | [1<=p11 & 1<=p33]] | [[1<=p9 & 1<=p37] | [[1<=p6 & 1<=p32] | [1<=p9 & 1<=p35]]]]] | [[[[1<=p6 & 1<=p34] | [1<=p6 & 1<=p36]] | [[1<=p8 & 1<=p36] | [[1<=p7 & 1<=p34] | [1<=p7 & 1<=p32]]]] | [[[1<=p7 & 1<=p36] | [[1<=p8 & 1<=p32] | [1<=p12 & 1<=p35]]] | [[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p37] | [1<=p12 & 1<=p33]]]]]] | [[[[[1<=p10 & 1<=p34] | [1<=p10 & 1<=p36]] | [[1<=p6 & 1<=p37] | [[1<=p11 & 1<=p36] | [1<=p9 & 1<=p32]]]] | [[[1<=p11 & 1<=p34] | [1<=p11 & 1<=p32]] | [[1<=p9 & 1<=p36] | [[1<=p9 & 1<=p34] | [1<=p6 & 1<=p33]]]]] | [[[[1<=p6 & 1<=p35] | [1<=p10 & 1<=p32]] | [[1<=p8 & 1<=p35] | [[1<=p8 & 1<=p37] | [1<=p7 & 1<=p35]]]] | [[[1<=p7 & 1<=p33] | [[1<=p7 & 1<=p37] | [1<=p12 & 1<=p36]]] | [[1<=p8 & 1<=p33] | [[1<=p12 & 1<=p32] | [1<=p12 & 1<=p34]]]]]]] & [AG [[[[[p19<=0 | p157<=0] & [[p14<=0 | p152<=0] & [p15<=0 | p153<=0]]] & [[p16<=0 | p154<=0] & [[p17<=0 | p155<=0] & [p18<=0 | p156<=0]]]] | [[[[p21<=0 | p170<=0] & [[p26<=0 | p173<=0] & [p24<=0 | p172<=0]]] & [[p23<=0 | p171<=0] & [[p27<=0 | p173<=0] & [p29<=0 | p174<=0]]]] & [[[p31<=0 | p175<=0] & [[p30<=0 | p175<=0] & [p25<=0 | p172<=0]]] & [[p22<=0 | p171<=0] & [[p20<=0 | p170<=0] & [p28<=0 | p174<=0]]]]]]] | [[[[p7<=0 | p56<=0] & [[p8<=0 | p57<=0] & [p9<=0 | p58<=0]]] & [[p10<=0 | p59<=0] & [[p11<=0 | p60<=0] & [p12<=0 | p61<=0]]]] | [[[[[[p16<=0 | p46<=0] & [p16<=0 | p45<=0]] & [[p16<=0 | p48<=0] & [p16<=0 | p47<=0]]] & [[[p16<=0 | p44<=0] & [p16<=0 | p49<=0]] & [[p17<=0 | p47<=0] & [[p17<=0 | p46<=0] & [p17<=0 | p45<=0]]]]] & [[[[p17<=0 | p44<=0] & [p17<=0 | p49<=0]] & [[p17<=0 | p48<=0] & [p18<=0 | p44<=0]]] & [[[p19<=0 | p49<=0] & [p19<=0 | p48<=0]] & [[p18<=0 | p46<=0] & [[p19<=0 | p47<=0] & [p18<=0 | p45<=0]]]]]] & [[[[[p19<=0 | p46<=0] & [p14<=0 | p44<=0]] & [[p18<=0 | p48<=0] & [p19<=0 | p45<=0]]] & [[[p18<=0 | p47<=0] & [p19<=0 | p44<=0]] & [[p14<=0 | p46<=0] & [[p14<=0 | p45<=0] & [p18<=0 | p49<=0]]]]] & [[[[p14<=0 | p48<=0] & [p14<=0 | p47<=0]] & [[p14<=0 | p49<=0] & [p15<=0 | p49<=0]]] & [[[p15<=0 | p48<=0] & [p15<=0 | p47<=0]] & [[p15<=0 | p46<=0] & [[p15<=0 | p45<=0] & [p15<=0 | p44<=0]]]]]]]]]]] & EX [EX [[[[[[EG [[[[1<=p19 & 1<=p157] | [[1<=p14 & 1<=p152] | [1<=p15 & 1<=p153]]] | [[1<=p16 & 1<=p154] | [[1<=p18 & 1<=p156] | [1<=p17 & 1<=p155]]]]] | AX [[[[[1<=p28 & 1<=p66] | [[1<=p20 & 1<=p62] | [1<=p25 & 1<=p64]]] | [[1<=p23 & 1<=p63] | [[1<=p26 & 1<=p65] | [1<=p30 & 1<=p67]]]] | [[[1<=p29 & 1<=p66] | [[1<=p27 & 1<=p65] | [1<=p24 & 1<=p64]]] | [[1<=p22 & 1<=p63] | [[1<=p21 & 1<=p62] | [1<=p31 & 1<=p67]]]]]]] | [EG [EF [[[[1<=p13 & 1<=p47] | [[1<=p13 & 1<=p46] | [1<=p13 & 1<=p45]]] | [[1<=p13 & 1<=p44] | [[1<=p13 & 1<=p49] | [1<=p13 & 1<=p48]]]]]] | [[1<=p13 & 1<=p167] | [1<=p13 & 1<=p169]]]] | [[[1<=p18 & 1<=p166] | [[1<=p13 & 1<=p165] | [1<=p18 & 1<=p168]]] | [[1<=p14 & 1<=p169] | [[1<=p17 & 1<=p164] | [1<=p19 & 1<=p166]]]]] | [[[[1<=p19 & 1<=p164] | [1<=p19 & 1<=p168]] | [[1<=p15 & 1<=p169] | [[1<=p16 & 1<=p166] | [1<=p16 & 1<=p164]]]] | [[[1<=p15 & 1<=p164] | [[1<=p16 & 1<=p169] | [1<=p15 & 1<=p166]]] | [[1<=p16 & 1<=p167] | [[1<=p14 & 1<=p164] | [1<=p14 & 1<=p168]]]]]] | [[[[[1<=p17 & 1<=p169] | [1<=p14 & 1<=p166]] | [[1<=p17 & 1<=p167] | [[1<=p18 & 1<=p169] | [1<=p13 & 1<=p166]]]] | [[[1<=p13 & 1<=p168] | [[1<=p18 & 1<=p165] | [1<=p18 & 1<=p167]]] | [[1<=p13 & 1<=p164] | [[1<=p17 & 1<=p165] | [1<=p19 & 1<=p167]]]]] | [[[[1<=p19 & 1<=p165] | [[1<=p19 & 1<=p169] | [1<=p15 & 1<=p168]]] | [[1<=p16 & 1<=p165] | [[1<=p15 & 1<=p165] | [1<=p15 & 1<=p167]]]] | [[[1<=p16 & 1<=p168] | [[1<=p17 & 1<=p168] | [1<=p14 & 1<=p167]]] | [[1<=p17 & 1<=p166] | [[1<=p14 & 1<=p165] | [1<=p18 & 1<=p164]]]]]]]]]]
normalized: [EX [EX [[[[[[[[1<=p18 & 1<=p164] | [1<=p14 & 1<=p165]] | [1<=p17 & 1<=p166]] | [[[1<=p14 & 1<=p167] | [1<=p17 & 1<=p168]] | [1<=p16 & 1<=p168]]] | [[[[1<=p15 & 1<=p167] | [1<=p15 & 1<=p165]] | [1<=p16 & 1<=p165]] | [[[1<=p15 & 1<=p168] | [1<=p19 & 1<=p169]] | [1<=p19 & 1<=p165]]]] | [[[[[1<=p19 & 1<=p167] | [1<=p17 & 1<=p165]] | [1<=p13 & 1<=p164]] | [[[1<=p18 & 1<=p167] | [1<=p18 & 1<=p165]] | [1<=p13 & 1<=p168]]] | [[[[1<=p13 & 1<=p166] | [1<=p18 & 1<=p169]] | [1<=p17 & 1<=p167]] | [[1<=p14 & 1<=p166] | [1<=p17 & 1<=p169]]]]] | [[[[[[1<=p14 & 1<=p168] | [1<=p14 & 1<=p164]] | [1<=p16 & 1<=p167]] | [[[1<=p15 & 1<=p166] | [1<=p16 & 1<=p169]] | [1<=p15 & 1<=p164]]] | [[[[1<=p16 & 1<=p164] | [1<=p16 & 1<=p166]] | [1<=p15 & 1<=p169]] | [[1<=p19 & 1<=p168] | [1<=p19 & 1<=p164]]]] | [[[[[1<=p19 & 1<=p166] | [1<=p17 & 1<=p164]] | [1<=p14 & 1<=p169]] | [[[1<=p18 & 1<=p168] | [1<=p13 & 1<=p165]] | [1<=p18 & 1<=p166]]] | [[[[1<=p13 & 1<=p169] | [1<=p13 & 1<=p167]] | EG [E [true U [[[[1<=p13 & 1<=p48] | [1<=p13 & 1<=p49]] | [1<=p13 & 1<=p44]] | [[[1<=p13 & 1<=p45] | [1<=p13 & 1<=p46]] | [1<=p13 & 1<=p47]]]]]] | [~ [EX [~ [[[[[[1<=p31 & 1<=p67] | [1<=p21 & 1<=p62]] | [1<=p22 & 1<=p63]] | [[[1<=p24 & 1<=p64] | [1<=p27 & 1<=p65]] | [1<=p29 & 1<=p66]]] | [[[[1<=p30 & 1<=p67] | [1<=p26 & 1<=p65]] | [1<=p23 & 1<=p63]] | [[[1<=p25 & 1<=p64] | [1<=p20 & 1<=p62]] | [1<=p28 & 1<=p66]]]]]]] | EG [[[[[1<=p17 & 1<=p155] | [1<=p18 & 1<=p156]] | [1<=p16 & 1<=p154]] | [[[1<=p15 & 1<=p153] | [1<=p14 & 1<=p152]] | [1<=p19 & 1<=p157]]]]]]]]]]] & E [true U [[[[[[[[[[p15<=0 | p44<=0] & [p15<=0 | p45<=0]] & [p15<=0 | p46<=0]] & [[p15<=0 | p47<=0] & [p15<=0 | p48<=0]]] & [[[p15<=0 | p49<=0] & [p14<=0 | p49<=0]] & [[p14<=0 | p47<=0] & [p14<=0 | p48<=0]]]] & [[[[[p18<=0 | p49<=0] & [p14<=0 | p45<=0]] & [p14<=0 | p46<=0]] & [[p19<=0 | p44<=0] & [p18<=0 | p47<=0]]] & [[[p19<=0 | p45<=0] & [p18<=0 | p48<=0]] & [[p14<=0 | p44<=0] & [p19<=0 | p46<=0]]]]] & [[[[[[p18<=0 | p45<=0] & [p19<=0 | p47<=0]] & [p18<=0 | p46<=0]] & [[p19<=0 | p48<=0] & [p19<=0 | p49<=0]]] & [[[p18<=0 | p44<=0] & [p17<=0 | p48<=0]] & [[p17<=0 | p49<=0] & [p17<=0 | p44<=0]]]] & [[[[[p17<=0 | p45<=0] & [p17<=0 | p46<=0]] & [p17<=0 | p47<=0]] & [[p16<=0 | p49<=0] & [p16<=0 | p44<=0]]] & [[[p16<=0 | p47<=0] & [p16<=0 | p48<=0]] & [[p16<=0 | p45<=0] & [p16<=0 | p46<=0]]]]]] | [[[[p12<=0 | p61<=0] & [p11<=0 | p60<=0]] & [p10<=0 | p59<=0]] & [[[p9<=0 | p58<=0] & [p8<=0 | p57<=0]] & [p7<=0 | p56<=0]]]] | ~ [E [true U ~ [[[[[[[p28<=0 | p174<=0] & [p20<=0 | p170<=0]] & [p22<=0 | p171<=0]] & [[[p25<=0 | p172<=0] & [p30<=0 | p175<=0]] & [p31<=0 | p175<=0]]] & [[[[p29<=0 | p174<=0] & [p27<=0 | p173<=0]] & [p23<=0 | p171<=0]] & [[[p24<=0 | p172<=0] & [p26<=0 | p173<=0]] & [p21<=0 | p170<=0]]]] | [[[[p18<=0 | p156<=0] & [p17<=0 | p155<=0]] & [p16<=0 | p154<=0]] & [[[p15<=0 | p153<=0] & [p14<=0 | p152<=0]] & [p19<=0 | p157<=0]]]]]]]] & [[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]]]]]
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p35)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p37)
states: 17,782,896,448 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p36)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p33)
states: 17,782,896,448 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p32)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p34)
states: 17,782,896,448 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (p157<=0)
states: 541,439,115,624 (11)
abstracting: (p19<=0)
states: 469,876,059,112 (11)
abstracting: (p152<=0)
states: 541,439,115,624 (11)
abstracting: (p14<=0)
states: 469,876,059,112 (11)
abstracting: (p153<=0)
states: 541,439,115,624 (11)
abstracting: (p15<=0)
states: 469,876,059,112 (11)
abstracting: (p154<=0)
states: 541,439,115,624 (11)
abstracting: (p16<=0)
states: 469,876,059,112 (11)
abstracting: (p155<=0)
states: 541,439,115,624 (11)
abstracting: (p17<=0)
states: 469,876,059,112 (11)
abstracting: (p156<=0)
states: 541,439,115,624 (11)
abstracting: (p18<=0)
states: 469,876,059,112 (11)
abstracting: (p170<=0)
states: 530,705,059,848 (11)
abstracting: (p21<=0)
states: 448,316,917,822 (11)
abstracting: (p173<=0)
states: 530,705,059,848 (11)
abstracting: (p26<=0)
states: 98,914,841,322 (10)
abstracting: (p172<=0)
states: 530,705,059,848 (11)
abstracting: (p24<=0)
states: 98,914,841,322 (10)
abstracting: (p171<=0)
states: 530,705,059,848 (11)
abstracting: (p23<=0)
states: 448,316,917,822 (11)
abstracting: (p173<=0)
states: 530,705,059,848 (11)
abstracting: (p27<=0)
states: 448,316,917,822 (11)
abstracting: (p174<=0)
states: 530,705,059,848 (11)
abstracting: (p29<=0)
states: 448,316,917,822 (11)
abstracting: (p175<=0)
states: 530,705,059,848 (11)
abstracting: (p31<=0)
states: 448,316,917,822 (11)
abstracting: (p175<=0)
states: 530,705,059,848 (11)
abstracting: (p30<=0)
states: 98,914,841,322 (10)
abstracting: (p172<=0)
states: 530,705,059,848 (11)
abstracting: (p25<=0)
states: 448,316,917,822 (11)
abstracting: (p171<=0)
states: 530,705,059,848 (11)
abstracting: (p22<=0)
states: 98,914,841,322 (10)
abstracting: (p170<=0)
states: 530,705,059,848 (11)
abstracting: (p20<=0)
states: 98,914,841,322 (10)
abstracting: (p174<=0)
states: 530,705,059,848 (11)
abstracting: (p28<=0)
states: 98,914,841,322 (10)
MC time: 1m22.014sec
checking: E [[EG [~ [[[[[[[[1<=p12 & 1<=p56] | [1<=p12 & 1<=p58]] | [[1<=p12 & 1<=p57] | [1<=p7 & 1<=p61]]] | [[[1<=p7 & 1<=p60] | [1<=p7 & 1<=p59]] | [[1<=p7 & 1<=p58] | [[1<=p7 & 1<=p57] | [1<=p8 & 1<=p60]]]]] | [[[[1<=p8 & 1<=p59] | [1<=p8 & 1<=p61]] | [[1<=p8 & 1<=p56] | [1<=p12 & 1<=p60]]] | [[[1<=p12 & 1<=p59] | [1<=p8 & 1<=p58]] | [[1<=p10 & 1<=p61] | [[1<=p9 & 1<=p57] | [1<=p9 & 1<=p56]]]]]] | [[[[[1<=p9 & 1<=p61] | [1<=p9 & 1<=p60]] | [[1<=p9 & 1<=p59] | [1<=p11 & 1<=p61]]] | [[[1<=p6 & 1<=p57] | [1<=p11 & 1<=p59]] | [[1<=p6 & 1<=p58] | [[1<=p11 & 1<=p58] | [1<=p6 & 1<=p59]]]]] | [[[[1<=p11 & 1<=p57] | [1<=p6 & 1<=p60]] | [[1<=p11 & 1<=p56] | [1<=p6 & 1<=p61]]] | [[[1<=p10 & 1<=p56] | [1<=p10 & 1<=p58]] | [[1<=p10 & 1<=p57] | [[1<=p10 & 1<=p60] | [1<=p6 & 1<=p56]]]]]]] & [[[1<=p7 & 1<=p56] | [[1<=p57 & 1<=p8] | [1<=p9 & 1<=p58]]] | [[1<=p10 & 1<=p59] | [[1<=p11 & 1<=p60] | [1<=p12 & 1<=p61]]]]]]] & EX [~ [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]]]]] U [E [~ [E [~ [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]] U [[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]]] U E [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]] U [[[[[1<=p23 & 1<=p39] | [1<=p28 & 1<=p42]] | [[1<=p26 & 1<=p41] | [1<=p31 & 1<=p43]]] | [[[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]] | [[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]]]] | [[[[1<=p29 & 1<=p42] | [1<=p20 & 1<=p38]] | [[1<=p24 & 1<=p40] | [1<=p13 & 1<=p163]]] | [[[1<=p13 & 1<=p160] | [1<=p13 & 1<=p159]] | [[1<=p13 & 1<=p162] | [[1<=p13 & 1<=p161] | [1<=p13 & 1<=p158]]]]]]]] & [~ [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]] & [[A [[AF [[[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]] | EX [[[[[[[1<=p12 & 1<=p56] | [1<=p12 & 1<=p58]] | [[1<=p12 & 1<=p57] | [1<=p7 & 1<=p61]]] | [[[1<=p7 & 1<=p60] | [1<=p7 & 1<=p59]] | [[1<=p7 & 1<=p58] | [[1<=p7 & 1<=p57] | [1<=p8 & 1<=p60]]]]] | [[[[1<=p8 & 1<=p59] | [1<=p8 & 1<=p61]] | [[1<=p8 & 1<=p56] | [1<=p12 & 1<=p60]]] | [[[1<=p12 & 1<=p59] | [1<=p8 & 1<=p58]] | [[1<=p10 & 1<=p61] | [[1<=p9 & 1<=p57] | [1<=p9 & 1<=p56]]]]]] | [[[[[1<=p9 & 1<=p61] | [1<=p9 & 1<=p60]] | [[1<=p9 & 1<=p59] | [1<=p11 & 1<=p61]]] | [[[1<=p6 & 1<=p57] | [1<=p11 & 1<=p59]] | [[1<=p6 & 1<=p58] | [[1<=p11 & 1<=p58] | [1<=p6 & 1<=p59]]]]] | [[[[1<=p11 & 1<=p57] | [1<=p6 & 1<=p60]] | [[1<=p11 & 1<=p56] | [1<=p6 & 1<=p61]]] | [[[1<=p10 & 1<=p56] | [1<=p10 & 1<=p58]] | [[1<=p10 & 1<=p57] | [[1<=p10 & 1<=p60] | [1<=p6 & 1<=p56]]]]]]]]] U [[[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]] & [[[[[[1<=p17 & 1<=p157] | [1<=p17 & 1<=p156]] | [[1<=p17 & 1<=p153] | [1<=p17 & 1<=p152]]] | [[[1<=p17 & 1<=p154] | [1<=p16 & 1<=p152]] | [[1<=p13 & 1<=p157] | [[1<=p13 & 1<=p156] | [1<=p13 & 1<=p153]]]]] | [[[[1<=p13 & 1<=p152] | [1<=p13 & 1<=p155]] | [[1<=p13 & 1<=p154] | [1<=p16 & 1<=p157]]] | [[[1<=p16 & 1<=p156] | [1<=p16 & 1<=p155]] | [[1<=p16 & 1<=p153] | [[1<=p19 & 1<=p153] | [1<=p19 & 1<=p152]]]]]] | [[[[[1<=p14 & 1<=p154] | [1<=p19 & 1<=p155]] | [[1<=p14 & 1<=p153] | [1<=p19 & 1<=p154]]] | [[[1<=p19 & 1<=p156] | [1<=p15 & 1<=p155]] | [[1<=p15 & 1<=p154] | [[1<=p15 & 1<=p157] | [1<=p15 & 1<=p156]]]]] | [[[[1<=p18 & 1<=p154] | [1<=p18 & 1<=p153]] | [[1<=p18 & 1<=p152] | [1<=p18 & 1<=p157]]] | [[[1<=p15 & 1<=p152] | [1<=p18 & 1<=p155]] | [[1<=p14 & 1<=p157] | [[1<=p14 & 1<=p156] | [1<=p14 & 1<=p155]]]]]]]] | AX [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]]]]] | [[1<=p19 & 1<=p157] | [1<=p14 & 1<=p152]]] | [[[1<=p15 & 1<=p153] | [1<=p16 & 1<=p154]] | [[1<=p17 & 1<=p155] | [1<=p18 & 1<=p156]]]]]]]
normalized: E [[EX [~ [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]] & EG [~ [[[[[[1<=p12 & 1<=p61] | [1<=p11 & 1<=p60]] | [1<=p10 & 1<=p59]] | [[[1<=p9 & 1<=p58] | [1<=p57 & 1<=p8]] | [1<=p7 & 1<=p56]]] & [[[[[[[1<=p6 & 1<=p56] | [1<=p10 & 1<=p60]] | [1<=p10 & 1<=p57]] | [[1<=p10 & 1<=p58] | [1<=p10 & 1<=p56]]] | [[[1<=p6 & 1<=p61] | [1<=p11 & 1<=p56]] | [[1<=p6 & 1<=p60] | [1<=p11 & 1<=p57]]]] | [[[[[1<=p6 & 1<=p59] | [1<=p11 & 1<=p58]] | [1<=p6 & 1<=p58]] | [[1<=p11 & 1<=p59] | [1<=p6 & 1<=p57]]] | [[[1<=p11 & 1<=p61] | [1<=p9 & 1<=p59]] | [[1<=p9 & 1<=p60] | [1<=p9 & 1<=p61]]]]] | [[[[[[1<=p9 & 1<=p56] | [1<=p9 & 1<=p57]] | [1<=p10 & 1<=p61]] | [[1<=p8 & 1<=p58] | [1<=p12 & 1<=p59]]] | [[[1<=p12 & 1<=p60] | [1<=p8 & 1<=p56]] | [[1<=p8 & 1<=p61] | [1<=p8 & 1<=p59]]]] | [[[[[1<=p8 & 1<=p60] | [1<=p7 & 1<=p57]] | [1<=p7 & 1<=p58]] | [[1<=p7 & 1<=p59] | [1<=p7 & 1<=p60]]] | [[[1<=p7 & 1<=p61] | [1<=p12 & 1<=p57]] | [[1<=p12 & 1<=p58] | [1<=p12 & 1<=p56]]]]]]]]]] U [[[[[~ [EG [~ [[~ [EX [~ [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]] | [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]]]] & ~ [E [~ [[~ [EX [~ [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]] | [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]] U [~ [[EX [[[[[[[[1<=p6 & 1<=p59] | [1<=p11 & 1<=p58]] | [1<=p6 & 1<=p58]] | [[1<=p11 & 1<=p59] | [1<=p6 & 1<=p57]]] | [[[1<=p11 & 1<=p61] | [1<=p9 & 1<=p59]] | [[1<=p9 & 1<=p60] | [1<=p9 & 1<=p61]]]] | [[[[[1<=p6 & 1<=p56] | [1<=p10 & 1<=p60]] | [1<=p10 & 1<=p57]] | [[1<=p10 & 1<=p58] | [1<=p10 & 1<=p56]]] | [[[1<=p6 & 1<=p61] | [1<=p11 & 1<=p56]] | [[1<=p6 & 1<=p60] | [1<=p11 & 1<=p57]]]]] | [[[[[[1<=p9 & 1<=p56] | [1<=p9 & 1<=p57]] | [1<=p10 & 1<=p61]] | [[1<=p8 & 1<=p58] | [1<=p12 & 1<=p59]]] | [[[1<=p12 & 1<=p60] | [1<=p8 & 1<=p56]] | [[1<=p8 & 1<=p61] | [1<=p8 & 1<=p59]]]] | [[[[[1<=p8 & 1<=p60] | [1<=p7 & 1<=p57]] | [1<=p7 & 1<=p58]] | [[1<=p7 & 1<=p59] | [1<=p7 & 1<=p60]]] | [[[1<=p7 & 1<=p61] | [1<=p12 & 1<=p57]] | [[1<=p12 & 1<=p58] | [1<=p12 & 1<=p56]]]]]]] | ~ [EG [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]]]]] & ~ [[~ [EX [~ [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]] | [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]]]]]] | [[1<=p14 & 1<=p152] | [1<=p19 & 1<=p157]]] | [[[1<=p16 & 1<=p154] | [1<=p15 & 1<=p153]] | [[1<=p18 & 1<=p156] | [1<=p17 & 1<=p155]]]] & ~ [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]]] & E [~ [E [~ [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]] U [[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]] U E [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]] U [[[[[[1<=p13 & 1<=p158] | [1<=p13 & 1<=p161]] | [1<=p13 & 1<=p162]] | [[1<=p13 & 1<=p159] | [1<=p13 & 1<=p160]]] | [[[1<=p13 & 1<=p163] | [1<=p24 & 1<=p40]] | [[1<=p20 & 1<=p38] | [1<=p29 & 1<=p42]]]] | [[[[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]] | [[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]]] | [[[1<=p31 & 1<=p43] | [1<=p26 & 1<=p41]] | [[1<=p28 & 1<=p42] | [1<=p23 & 1<=p39]]]]]]]]]
abstracting: (1<=p39)
states: 15,529,463,614 (10)
abstracting: (1<=p23)
states: 98,914,841,322 (10)
abstracting: (1<=p42)
states: 15,529,463,614 (10)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p41)
states: 15,529,463,614 (10)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p43)
states: 15,529,463,614 (10)
abstracting: (1<=p31)
states: 98,914,841,322 (10)
abstracting: (1<=p40)
states: 15,529,463,614 (10)
abstracting: (1<=p25)
states: 98,914,841,322 (10)
abstracting: (1<=p38)
states: 15,529,463,614 (10)
abstracting: (1<=p21)
states: 98,914,841,322 (10)
abstracting: (1<=p41)
states: 15,529,463,614 (10)
abstracting: (1<=p27)
states: 98,914,841,322 (10)
abstracting: (1<=p39)
states: 15,529,463,614 (10)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p43)
states: 15,529,463,614 (10)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p42)
states: 15,529,463,614 (10)
abstracting: (1<=p29)
states: 98,914,841,322 (10)
abstracting: (1<=p38)
states: 15,529,463,614 (10)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p40)
states: 15,529,463,614 (10)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p163)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p160)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p159)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p162)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p161)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p158)
states: 16,552,787,134 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p39)
states: 15,529,463,614 (10)
abstracting: (1<=p23)
states: 98,914,841,322 (10)
abstracting: (1<=p42)
states: 15,529,463,614 (10)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p41)
states: 15,529,463,614 (10)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p43)
states: 15,529,463,614 (10)
abstracting: (1<=p31)
states: 98,914,841,322 (10)
abstracting: (1<=p40)
states: 15,529,463,614 (10)
abstracting: (1<=p25)
states: 98,914,841,322 (10)
abstracting: (1<=p38)
states: 15,529,463,614 (10)
abstracting: (1<=p21)
states: 98,914,841,322 (10)
abstracting: (1<=p41)
states: 15,529,463,614 (10)
abstracting: (1<=p27)
states: 98,914,841,322 (10)
abstracting: (1<=p39)
states: 15,529,463,614 (10)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p43)
states: 15,529,463,614 (10)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p42)
states: 15,529,463,614 (10)
abstracting: (1<=p29)
states: 98,914,841,322 (10)
abstracting: (1<=p38)
states: 15,529,463,614 (10)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p40)
states: 15,529,463,614 (10)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
before gc: list nodes free: 1595169
after gc: idd nodes used:33006015, unused:30993985; list nodes free:138584222
MC time: 1m17.176sec
checking: A [[~ [EX [[E [[[[[[[1<=p10 & 1<=p33] | [1<=p10 & 1<=p35]] | [[1<=p10 & 1<=p37] | [[1<=p11 & 1<=p37] | [1<=p9 & 1<=p33]]]] | [[[1<=p11 & 1<=p35] | [1<=p11 & 1<=p33]] | [[1<=p9 & 1<=p37] | [[1<=p6 & 1<=p32] | [1<=p9 & 1<=p35]]]]] | [[[[1<=p6 & 1<=p34] | [1<=p6 & 1<=p36]] | [[1<=p8 & 1<=p36] | [[1<=p7 & 1<=p34] | [1<=p7 & 1<=p32]]]] | [[[1<=p7 & 1<=p36] | [[1<=p8 & 1<=p32] | [1<=p12 & 1<=p35]]] | [[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p37] | [1<=p12 & 1<=p33]]]]]] | [[[[[1<=p10 & 1<=p34] | [1<=p10 & 1<=p36]] | [[1<=p6 & 1<=p37] | [[1<=p11 & 1<=p36] | [1<=p9 & 1<=p32]]]] | [[[1<=p11 & 1<=p34] | [1<=p11 & 1<=p32]] | [[1<=p9 & 1<=p36] | [[1<=p9 & 1<=p34] | [1<=p6 & 1<=p33]]]]] | [[[[1<=p6 & 1<=p35] | [1<=p10 & 1<=p32]] | [[1<=p8 & 1<=p35] | [[1<=p8 & 1<=p37] | [1<=p7 & 1<=p35]]]] | [[[1<=p7 & 1<=p33] | [[1<=p7 & 1<=p37] | [1<=p12 & 1<=p36]]] | [[1<=p8 & 1<=p33] | [[1<=p12 & 1<=p32] | [1<=p12 & 1<=p34]]]]]]] U [[[[[[1<=p16 & 1<=p46] | [1<=p16 & 1<=p45]] | [[1<=p16 & 1<=p48] | [1<=p16 & 1<=p47]]] | [[[1<=p16 & 1<=p44] | [1<=p16 & 1<=p49]] | [[1<=p17 & 1<=p47] | [[1<=p17 & 1<=p46] | [1<=p17 & 1<=p45]]]]] | [[[[1<=p17 & 1<=p44] | [1<=p17 & 1<=p49]] | [[1<=p17 & 1<=p48] | [1<=p18 & 1<=p44]]] | [[[1<=p19 & 1<=p49] | [1<=p19 & 1<=p48]] | [[1<=p18 & 1<=p46] | [[1<=p19 & 1<=p47] | [1<=p18 & 1<=p45]]]]]] | [[[[[1<=p19 & 1<=p46] | [1<=p14 & 1<=p44]] | [[1<=p18 & 1<=p48] | [1<=p19 & 1<=p45]]] | [[[1<=p18 & 1<=p47] | [1<=p19 & 1<=p44]] | [[1<=p14 & 1<=p46] | [[1<=p14 & 1<=p45] | [1<=p18 & 1<=p49]]]]] | [[[[1<=p14 & 1<=p48] | [1<=p14 & 1<=p47]] | [[1<=p14 & 1<=p49] | [1<=p15 & 1<=p49]]] | [[[1<=p15 & 1<=p48] | [1<=p15 & 1<=p47]] | [[1<=p15 & 1<=p46] | [[1<=p15 & 1<=p45] | [1<=p15 & 1<=p44]]]]]]]] & [[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]]]]] & AF [E [[[[[[[1<=p26 & [1<=p83 & 1<=p111]] | [1<=p24 & [1<=p100 & 1<=p114]]] | [[1<=p22 & [1<=p93 & 1<=p113]] | [1<=p30 & [1<=p103 & 1<=p114]]]] | [[[1<=p28 & [1<=p90 & 1<=p112]] | [1<=p20 & [1<=p86 & 1<=p112]]] | [[1<=p30 & [1<=p79 & 1<=p110]] | [[1<=p24 & [1<=p106 & 1<=p115]] | [1<=p20 & [1<=p74 & 1<=p110]]]]]] | [[[[1<=p22 & [1<=p99 & 1<=p114]] | [1<=p20 & [1<=p104 & 1<=p115]]] | [[1<=p30 & [1<=p97 & 1<=p113]] | [1<=p24 & [1<=p82 & 1<=p111]]]] | [[[1<=p30 & [1<=p85 & 1<=p111]] | [1<=p28 & [1<=p96 & 1<=p113]]] | [[1<=p26 & [1<=p89 & 1<=p112]] | [[1<=p26 & [1<=p107 & 1<=p115]] | [1<=p28 & [1<=p108 & 1<=p115]]]]]]] | [[[[[1<=p22 & [1<=p105 & 1<=p115]] | [1<=p28 & [1<=p78 & 1<=p110]]] | [[1<=p22 & [1<=p75 & 1<=p110]] | [1<=p26 & [1<=p101 & 1<=p114]]]] | [[[1<=p20 & [1<=p92 & 1<=p113]] | [1<=p22 & [1<=p81 & 1<=p111]]] | [[1<=p26 & [1<=p95 & 1<=p113]] | [[1<=p24 & [1<=p88 & 1<=p112]] | [1<=p24 & [1<=p94 & 1<=p113]]]]]] | [[[[1<=p26 & [1<=p77 & 1<=p110]] | [1<=p28 & [1<=p84 & 1<=p111]]] | [[1<=p28 & [1<=p102 & 1<=p114]] | [1<=p24 & [1<=p76 & 1<=p110]]]] | [[[1<=p22 & [1<=p87 & 1<=p112]] | [1<=p30 & [1<=p91 & 1<=p112]]] | [[1<=p30 & [1<=p109 & 1<=p115]] | [[1<=p20 & [1<=p80 & 1<=p111]] | [1<=p20 & [1<=p98 & 1<=p114]]]]]]]] U [[[[[EX [~ [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]]] | [[[1<=p110 & [1<=p116 & 1<=p117]] & [[1<=p118 & 1<=p119] & [1<=p120 & 1<=p121]]] | [[1<=p114 & [1<=p140 & 1<=p141]] & [[1<=p142 & 1<=p143] & [1<=p144 & 1<=p145]]]]] | [[[1<=p111 & [1<=p122 & 1<=p123]] & [[1<=p124 & 1<=p125] & [1<=p126 & 1<=p127]]] | [[[1<=p115 & [1<=p146 & 1<=p147]] & [[1<=p148 & 1<=p149] & [1<=p150 & 1<=p151]]] | [[1<=p113 & [1<=p134 & 1<=p135]] & [[1<=p136 & 1<=p137] & [1<=p138 & 1<=p139]]]]]] | [[[[1<=p112 & [1<=p128 & 1<=p129]] & [[1<=p130 & 1<=p131] & [1<=p132 & 1<=p133]]] | [[1<=p13 & 1<=p167] | [1<=p13 & 1<=p169]]] | [[1<=p18 & 1<=p166] | [[1<=p13 & 1<=p165] | [1<=p18 & 1<=p168]]]]] | [[[[1<=p14 & 1<=p169] | [[1<=p17 & 1<=p164] | [1<=p19 & 1<=p166]]] | [[1<=p19 & 1<=p164] | [[1<=p19 & 1<=p168] | [1<=p15 & 1<=p169]]]] | [[[1<=p16 & 1<=p166] | [[1<=p16 & 1<=p164] | [1<=p15 & 1<=p164]]] | [[1<=p16 & 1<=p169] | [[1<=p15 & 1<=p166] | [1<=p16 & 1<=p167]]]]]] | [[[[[1<=p14 & 1<=p164] | [[1<=p14 & 1<=p168] | [1<=p17 & 1<=p169]]] | [[1<=p14 & 1<=p166] | [[1<=p17 & 1<=p167] | [1<=p18 & 1<=p169]]]] | [[[1<=p13 & 1<=p166] | [[1<=p13 & 1<=p168] | [1<=p18 & 1<=p165]]] | [[1<=p18 & 1<=p167] | [[1<=p13 & 1<=p164] | [1<=p17 & 1<=p165]]]]] | [[[[1<=p19 & 1<=p167] | [[1<=p19 & 1<=p165] | [1<=p19 & 1<=p169]]] | [[1<=p15 & 1<=p168] | [[1<=p16 & 1<=p165] | [1<=p15 & 1<=p165]]]] | [[[1<=p15 & 1<=p167] | [[1<=p16 & 1<=p168] | [1<=p17 & 1<=p168]]] | [[[1<=p14 & 1<=p167] | [1<=p17 & 1<=p166]] | [[1<=p14 & 1<=p165] | [1<=p18 & 1<=p164]]]]]]]]]] U AX [[[1<=p71 | [1<=p70 | 1<=p73]] | [1<=p72 | [1<=p69 | 1<=p68]]]]]
normalized: [~ [EG [EX [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]]]] & ~ [E [EX [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]] U [~ [[~ [EG [~ [E [[[[[[[[1<=p20 & [1<=p98 & 1<=p114]] | [1<=p20 & [1<=p80 & 1<=p111]]] | [1<=p30 & [1<=p109 & 1<=p115]]] | [[1<=p30 & [1<=p91 & 1<=p112]] | [1<=p22 & [1<=p87 & 1<=p112]]]] | [[[1<=p24 & [1<=p76 & 1<=p110]] | [1<=p28 & [1<=p102 & 1<=p114]]] | [[1<=p28 & [1<=p84 & 1<=p111]] | [1<=p26 & [1<=p77 & 1<=p110]]]]] | [[[[[1<=p24 & [1<=p94 & 1<=p113]] | [1<=p24 & [1<=p88 & 1<=p112]]] | [1<=p26 & [1<=p95 & 1<=p113]]] | [[1<=p22 & [1<=p81 & 1<=p111]] | [1<=p20 & [1<=p92 & 1<=p113]]]] | [[[1<=p26 & [1<=p101 & 1<=p114]] | [1<=p22 & [1<=p75 & 1<=p110]]] | [[1<=p28 & [1<=p78 & 1<=p110]] | [1<=p22 & [1<=p105 & 1<=p115]]]]]] | [[[[[[1<=p28 & [1<=p108 & 1<=p115]] | [1<=p26 & [1<=p107 & 1<=p115]]] | [1<=p26 & [1<=p89 & 1<=p112]]] | [[1<=p28 & [1<=p96 & 1<=p113]] | [1<=p30 & [1<=p85 & 1<=p111]]]] | [[[1<=p24 & [1<=p82 & 1<=p111]] | [1<=p30 & [1<=p97 & 1<=p113]]] | [[1<=p20 & [1<=p104 & 1<=p115]] | [1<=p22 & [1<=p99 & 1<=p114]]]]] | [[[[[1<=p20 & [1<=p74 & 1<=p110]] | [1<=p24 & [1<=p106 & 1<=p115]]] | [1<=p30 & [1<=p79 & 1<=p110]]] | [[1<=p20 & [1<=p86 & 1<=p112]] | [1<=p28 & [1<=p90 & 1<=p112]]]] | [[[1<=p30 & [1<=p103 & 1<=p114]] | [1<=p22 & [1<=p93 & 1<=p113]]] | [[1<=p24 & [1<=p100 & 1<=p114]] | [1<=p26 & [1<=p83 & 1<=p111]]]]]]] U [[[[[[[1<=p18 & 1<=p164] | [1<=p14 & 1<=p165]] | [[1<=p17 & 1<=p166] | [1<=p14 & 1<=p167]]] | [[[1<=p17 & 1<=p168] | [1<=p16 & 1<=p168]] | [1<=p15 & 1<=p167]]] | [[[[1<=p15 & 1<=p165] | [1<=p16 & 1<=p165]] | [1<=p15 & 1<=p168]] | [[[1<=p19 & 1<=p169] | [1<=p19 & 1<=p165]] | [1<=p19 & 1<=p167]]]] | [[[[[1<=p17 & 1<=p165] | [1<=p13 & 1<=p164]] | [1<=p18 & 1<=p167]] | [[[1<=p18 & 1<=p165] | [1<=p13 & 1<=p168]] | [1<=p13 & 1<=p166]]] | [[[[1<=p18 & 1<=p169] | [1<=p17 & 1<=p167]] | [1<=p14 & 1<=p166]] | [[[1<=p17 & 1<=p169] | [1<=p14 & 1<=p168]] | [1<=p14 & 1<=p164]]]]] | [[[[[[1<=p16 & 1<=p167] | [1<=p15 & 1<=p166]] | [1<=p16 & 1<=p169]] | [[[1<=p15 & 1<=p164] | [1<=p16 & 1<=p164]] | [1<=p16 & 1<=p166]]] | [[[[1<=p15 & 1<=p169] | [1<=p19 & 1<=p168]] | [1<=p19 & 1<=p164]] | [[[1<=p19 & 1<=p166] | [1<=p17 & 1<=p164]] | [1<=p14 & 1<=p169]]]] | [[[[[1<=p18 & 1<=p168] | [1<=p13 & 1<=p165]] | [1<=p18 & 1<=p166]] | [[[1<=p13 & 1<=p169] | [1<=p13 & 1<=p167]] | [[[1<=p132 & 1<=p133] & [1<=p130 & 1<=p131]] & [1<=p112 & [1<=p128 & 1<=p129]]]]] | [[[[[[1<=p138 & 1<=p139] & [1<=p136 & 1<=p137]] & [1<=p113 & [1<=p134 & 1<=p135]]] | [[[1<=p150 & 1<=p151] & [1<=p148 & 1<=p149]] & [1<=p115 & [1<=p146 & 1<=p147]]]] | [[[1<=p126 & 1<=p127] & [1<=p124 & 1<=p125]] & [1<=p111 & [1<=p122 & 1<=p123]]]] | [[[[[1<=p144 & 1<=p145] & [1<=p142 & 1<=p143]] & [1<=p114 & [1<=p140 & 1<=p141]]] | [[[1<=p120 & 1<=p121] & [1<=p118 & 1<=p119]] & [1<=p110 & [1<=p116 & 1<=p117]]]] | EX [~ [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]]]]]]]]]]]] & ~ [EX [[[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]] & E [[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]] U [[[[[[[1<=p15 & 1<=p44] | [1<=p15 & 1<=p45]] | [1<=p15 & 1<=p46]] | [[1<=p15 & 1<=p47] | [1<=p15 & 1<=p48]]] | [[[1<=p15 & 1<=p49] | [1<=p14 & 1<=p49]] | [[1<=p14 & 1<=p47] | [1<=p14 & 1<=p48]]]] | [[[[[1<=p18 & 1<=p49] | [1<=p14 & 1<=p45]] | [1<=p14 & 1<=p46]] | [[1<=p19 & 1<=p44] | [1<=p18 & 1<=p47]]] | [[[1<=p19 & 1<=p45] | [1<=p18 & 1<=p48]] | [[1<=p14 & 1<=p44] | [1<=p19 & 1<=p46]]]]] | [[[[[[1<=p18 & 1<=p45] | [1<=p19 & 1<=p47]] | [1<=p18 & 1<=p46]] | [[1<=p19 & 1<=p48] | [1<=p19 & 1<=p49]]] | [[[1<=p18 & 1<=p44] | [1<=p17 & 1<=p48]] | [[1<=p17 & 1<=p49] | [1<=p17 & 1<=p44]]]] | [[[[[1<=p17 & 1<=p45] | [1<=p17 & 1<=p46]] | [1<=p17 & 1<=p47]] | [[1<=p16 & 1<=p49] | [1<=p16 & 1<=p44]]] | [[[1<=p16 & 1<=p47] | [1<=p16 & 1<=p48]] | [[1<=p16 & 1<=p45] | [1<=p16 & 1<=p46]]]]]]]]]]]] & EX [~ [[[1<=p72 | [1<=p69 | 1<=p68]] | [1<=p71 | [1<=p70 | 1<=p73]]]]]]]]]
abstracting: (1<=p73)
states: 6,677,072,160 (9)
abstracting: (1<=p70)
states: 6,677,072,160 (9)
abstracting: (1<=p71)
states: 6,677,072,160 (9)
abstracting: (1<=p68)
states: 6,677,072,160 (9)
abstracting: (1<=p69)
states: 6,677,072,160 (9)
abstracting: (1<=p72)
states: 6,677,072,160 (9)
before gc: list nodes free: 3218524
after gc: idd nodes used:33231313, unused:30768687; list nodes free:137556284
MC time: 1m11.201sec
checking: [AG [AF [E [[[[[[[1<=p17 & 1<=p157] | [1<=p17 & 1<=p156]] | [[1<=p17 & 1<=p153] | [1<=p17 & 1<=p152]]] | [[[1<=p17 & 1<=p154] | [1<=p16 & 1<=p152]] | [[1<=p13 & 1<=p157] | [[1<=p13 & 1<=p156] | [1<=p13 & 1<=p153]]]]] | [[[[1<=p13 & 1<=p152] | [1<=p13 & 1<=p155]] | [[1<=p13 & 1<=p154] | [1<=p16 & 1<=p157]]] | [[[1<=p16 & 1<=p156] | [1<=p16 & 1<=p155]] | [[1<=p16 & 1<=p153] | [[1<=p19 & 1<=p153] | [1<=p19 & 1<=p152]]]]]] | [[[[[1<=p14 & 1<=p154] | [1<=p19 & 1<=p155]] | [[1<=p14 & 1<=p153] | [1<=p19 & 1<=p154]]] | [[[1<=p19 & 1<=p156] | [1<=p15 & 1<=p155]] | [[1<=p15 & 1<=p154] | [[1<=p15 & 1<=p157] | [1<=p15 & 1<=p156]]]]] | [[[[1<=p18 & 1<=p154] | [1<=p18 & 1<=p153]] | [[1<=p18 & 1<=p152] | [1<=p18 & 1<=p157]]] | [[[1<=p15 & 1<=p152] | [1<=p18 & 1<=p155]] | [[1<=p14 & 1<=p157] | [[1<=p14 & 1<=p156] | [1<=p14 & 1<=p155]]]]]]] U [[[[[[1<=p17 & 1<=p55] | [1<=p16 & 1<=p53]] | [[1<=p16 & 1<=p55] | [[1<=p16 & 1<=p51] | [1<=p13 & 1<=p54]]]] | [[[1<=p13 & 1<=p52] | [1<=p13 & 1<=p50]] | [[1<=p17 & 1<=p53] | [[1<=p17 & 1<=p51] | [1<=p14 & 1<=p51]]]]] | [[[[1<=p19 & 1<=p54] | [1<=p14 & 1<=p53]] | [[1<=p19 & 1<=p50] | [[1<=p14 & 1<=p55] | [1<=p18 & 1<=p50]]]] | [[[1<=p18 & 1<=p52] | [[1<=p18 & 1<=p54] | [1<=p15 & 1<=p55]]] | [[1<=p15 & 1<=p53] | [[1<=p15 & 1<=p51] | [1<=p19 & 1<=p52]]]]]] | [[[[[1<=p16 & 1<=p52] | [1<=p16 & 1<=p54]] | [[1<=p16 & 1<=p50] | [[1<=p13 & 1<=p53] | [1<=p13 & 1<=p51]]]] | [[[1<=p13 & 1<=p55] | [1<=p17 & 1<=p50]] | [[1<=p17 & 1<=p54] | [[1<=p17 & 1<=p52] | [1<=p19 & 1<=p53]]]]] | [[[[1<=p14 & 1<=p50] | [1<=p19 & 1<=p55]] | [[1<=p14 & 1<=p52] | [[1<=p14 & 1<=p54] | [1<=p18 & 1<=p51]]]] | [[[1<=p18 & 1<=p53] | [[1<=p18 & 1<=p55] | [1<=p15 & 1<=p54]]] | [[1<=p15 & 1<=p52] | [[1<=p15 & 1<=p50] | [1<=p19 & 1<=p51]]]]]]]]]] | EG [AX [[[[[[[[[p13<=0 | p167<=0] & [[p13<=0 | p169<=0] & [p18<=0 | p166<=0]]] & [[p13<=0 | p165<=0] & [[p18<=0 | p168<=0] & [p14<=0 | p169<=0]]]] & [[[p17<=0 | p164<=0] & [[p19<=0 | p166<=0] & [p19<=0 | p164<=0]]] & [[p19<=0 | p168<=0] & [[p15<=0 | p169<=0] & [p16<=0 | p166<=0]]]]] & [[[[p16<=0 | p164<=0] & [[p15<=0 | p164<=0] & [p16<=0 | p169<=0]]] & [[p15<=0 | p166<=0] & [[p16<=0 | p167<=0] & [p14<=0 | p164<=0]]]] & [[[p14<=0 | p168<=0] & [[p17<=0 | p169<=0] & [p14<=0 | p166<=0]]] & [[p17<=0 | p167<=0] & [[p18<=0 | p169<=0] & [p13<=0 | p166<=0]]]]]] & [[[[[p13<=0 | p168<=0] & [[p18<=0 | p165<=0] & [p18<=0 | p167<=0]]] & [[p13<=0 | p164<=0] & [[p17<=0 | p165<=0] & [p19<=0 | p167<=0]]]] & [[[p19<=0 | p165<=0] & [[p19<=0 | p169<=0] & [p15<=0 | p168<=0]]] & [[p16<=0 | p165<=0] & [[p15<=0 | p165<=0] & [p15<=0 | p167<=0]]]]] & [[[[p16<=0 | p168<=0] & [[p17<=0 | p168<=0] & [p14<=0 | p167<=0]]] & [[p17<=0 | p166<=0] & [[p14<=0 | p165<=0] & [p18<=0 | p164<=0]]]] & [[p71<=0 & [p70<=0 & p73<=0]] & [p72<=0 & [p69<=0 & p68<=0]]]]]] | EX [[[[[[[p10<=0 | p33<=0] & [p10<=0 | p35<=0]] & [[p10<=0 | p37<=0] & [[p11<=0 | p37<=0] & [p9<=0 | p33<=0]]]] & [[[p11<=0 | p35<=0] & [p11<=0 | p33<=0]] & [[p9<=0 | p37<=0] & [[p6<=0 | p32<=0] & [p9<=0 | p35<=0]]]]] & [[[[p6<=0 | p34<=0] & [p6<=0 | p36<=0]] & [[p8<=0 | p36<=0] & [[p7<=0 | p34<=0] & [p7<=0 | p32<=0]]]] & [[[p7<=0 | p36<=0] & [[p8<=0 | p32<=0] & [p12<=0 | p35<=0]]] & [[p8<=0 | p34<=0] & [[p12<=0 | p37<=0] & [p12<=0 | p33<=0]]]]]] & [[[[[p10<=0 | p34<=0] & [p10<=0 | p36<=0]] & [[p6<=0 | p37<=0] & [[p11<=0 | p36<=0] & [p9<=0 | p32<=0]]]] & [[[p11<=0 | p34<=0] & [p11<=0 | p32<=0]] & [[p9<=0 | p36<=0] & [[p9<=0 | p34<=0] & [p6<=0 | p33<=0]]]]] & [[[[p6<=0 | p35<=0] & [p10<=0 | p32<=0]] & [[p8<=0 | p35<=0] & [[p8<=0 | p37<=0] & [p7<=0 | p35<=0]]]] & [[[p7<=0 | p33<=0] & [[p7<=0 | p37<=0] & [p12<=0 | p36<=0]]] & [[p8<=0 | p33<=0] & [[p12<=0 | p32<=0] & [p12<=0 | p34<=0]]]]]]]]] & [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]] & [[[[[[1<=p13 & 1<=p167] | [1<=p13 & 1<=p169]] | [[1<=p18 & 1<=p166] | [[1<=p13 & 1<=p165] | [1<=p18 & 1<=p168]]]] | [[[1<=p14 & 1<=p169] | [1<=p17 & 1<=p164]] | [[1<=p19 & 1<=p166] | [[1<=p19 & 1<=p164] | [1<=p19 & 1<=p168]]]]] | [[[[1<=p15 & 1<=p169] | [1<=p16 & 1<=p166]] | [[1<=p16 & 1<=p164] | [[1<=p15 & 1<=p164] | [1<=p16 & 1<=p169]]]] | [[[1<=p15 & 1<=p166] | [[1<=p16 & 1<=p167] | [1<=p14 & 1<=p164]]] | [[1<=p14 & 1<=p168] | [[1<=p17 & 1<=p169] | [1<=p14 & 1<=p166]]]]]] | [[[[[1<=p17 & 1<=p167] | [1<=p18 & 1<=p169]] | [[1<=p13 & 1<=p166] | [[1<=p13 & 1<=p168] | [1<=p18 & 1<=p165]]]] | [[[1<=p18 & 1<=p167] | [1<=p13 & 1<=p164]] | [[1<=p17 & 1<=p165] | [[1<=p19 & 1<=p167] | [1<=p19 & 1<=p165]]]]] | [[[[1<=p19 & 1<=p169] | [1<=p15 & 1<=p168]] | [[1<=p16 & 1<=p165] | [[1<=p15 & 1<=p165] | [1<=p15 & 1<=p167]]]] | [[[1<=p16 & 1<=p168] | [[1<=p17 & 1<=p168] | [1<=p14 & 1<=p167]]] | [[1<=p17 & 1<=p166] | [[1<=p14 & 1<=p165] | [1<=p18 & 1<=p164]]]]]]]]]]]]
normalized: [EG [~ [EX [~ [[[[[[[[[1<=p17 & 1<=p164] | [1<=p14 & 1<=p169]] | [[[1<=p19 & 1<=p168] | [1<=p19 & 1<=p164]] | [1<=p19 & 1<=p166]]] | [[[[1<=p18 & 1<=p168] | [1<=p13 & 1<=p165]] | [1<=p18 & 1<=p166]] | [[1<=p13 & 1<=p169] | [1<=p13 & 1<=p167]]]] | [[[[[1<=p14 & 1<=p166] | [1<=p17 & 1<=p169]] | [1<=p14 & 1<=p168]] | [[[1<=p14 & 1<=p164] | [1<=p16 & 1<=p167]] | [1<=p15 & 1<=p166]]] | [[[[1<=p16 & 1<=p169] | [1<=p15 & 1<=p164]] | [1<=p16 & 1<=p164]] | [[1<=p16 & 1<=p166] | [1<=p15 & 1<=p169]]]]] | [[[[[[1<=p18 & 1<=p164] | [1<=p14 & 1<=p165]] | [1<=p17 & 1<=p166]] | [[[1<=p14 & 1<=p167] | [1<=p17 & 1<=p168]] | [1<=p16 & 1<=p168]]] | [[[[1<=p15 & 1<=p167] | [1<=p15 & 1<=p165]] | [1<=p16 & 1<=p165]] | [[1<=p15 & 1<=p168] | [1<=p19 & 1<=p169]]]] | [[[[[1<=p19 & 1<=p165] | [1<=p19 & 1<=p167]] | [1<=p17 & 1<=p165]] | [[1<=p13 & 1<=p164] | [1<=p18 & 1<=p167]]] | [[[[1<=p18 & 1<=p165] | [1<=p13 & 1<=p168]] | [1<=p13 & 1<=p166]] | [[1<=p18 & 1<=p169] | [1<=p17 & 1<=p167]]]]]] & [[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]] & [EX [[[[[[[[p12<=0 | p34<=0] & [p12<=0 | p32<=0]] & [p8<=0 | p33<=0]] & [[[p12<=0 | p36<=0] & [p7<=0 | p37<=0]] & [p7<=0 | p33<=0]]] & [[[[p7<=0 | p35<=0] & [p8<=0 | p37<=0]] & [p8<=0 | p35<=0]] & [[p10<=0 | p32<=0] & [p6<=0 | p35<=0]]]] & [[[[[p6<=0 | p33<=0] & [p9<=0 | p34<=0]] & [p9<=0 | p36<=0]] & [[p11<=0 | p32<=0] & [p11<=0 | p34<=0]]] & [[[[p9<=0 | p32<=0] & [p11<=0 | p36<=0]] & [p6<=0 | p37<=0]] & [[p10<=0 | p36<=0] & [p10<=0 | p34<=0]]]]] & [[[[[[p12<=0 | p33<=0] & [p12<=0 | p37<=0]] & [p8<=0 | p34<=0]] & [[[p12<=0 | p35<=0] & [p8<=0 | p32<=0]] & [p7<=0 | p36<=0]]] & [[[[p7<=0 | p32<=0] & [p7<=0 | p34<=0]] & [p8<=0 | p36<=0]] & [[p6<=0 | p36<=0] & [p6<=0 | p34<=0]]]] & [[[[[p9<=0 | p35<=0] & [p6<=0 | p32<=0]] & [p9<=0 | p37<=0]] & [[p11<=0 | p33<=0] & [p11<=0 | p35<=0]]] & [[[[p9<=0 | p33<=0] & [p11<=0 | p37<=0]] & [p10<=0 | p37<=0]] & [[p10<=0 | p35<=0] & [p10<=0 | p33<=0]]]]]]] | [[[[[p72<=0 & [p69<=0 & p68<=0]] & [p71<=0 & [p70<=0 & p73<=0]]] & [[[[p18<=0 | p164<=0] & [p14<=0 | p165<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]]] & [[[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[[p15<=0 | p168<=0] & [p19<=0 | p169<=0]] & [p19<=0 | p165<=0]]] & [[[[p19<=0 | p167<=0] & [p17<=0 | p165<=0]] & [p13<=0 | p164<=0]] & [[[p18<=0 | p167<=0] & [p18<=0 | p165<=0]] & [p13<=0 | p168<=0]]]]] & [[[[[[p13<=0 | p166<=0] & [p18<=0 | p169<=0]] & [p17<=0 | p167<=0]] & [[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]]] & [[[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]] & [[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]]]] & [[[[[p16<=0 | p166<=0] & [p15<=0 | p169<=0]] & [p19<=0 | p168<=0]] & [[[p19<=0 | p164<=0] & [p19<=0 | p166<=0]] & [p17<=0 | p164<=0]]] & [[[[p14<=0 | p169<=0] & [p18<=0 | p168<=0]] & [p13<=0 | p165<=0]] & [[[p18<=0 | p166<=0] & [p13<=0 | p169<=0]] & [p13<=0 | p167<=0]]]]]]]]]]]] | ~ [E [true U EG [~ [E [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [[1<=p18 & 1<=p153] | [1<=p18 & 1<=p154]]]] | [[[[[1<=p15 & 1<=p156] | [1<=p15 & 1<=p157]] | [1<=p15 & 1<=p154]] | [[1<=p15 & 1<=p155] | [1<=p19 & 1<=p156]]] | [[[1<=p19 & 1<=p154] | [1<=p14 & 1<=p153]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p154]]]]] | [[[[[[1<=p19 & 1<=p152] | [1<=p19 & 1<=p153]] | [1<=p16 & 1<=p153]] | [[1<=p16 & 1<=p155] | [1<=p16 & 1<=p156]]] | [[[1<=p16 & 1<=p157] | [1<=p13 & 1<=p154]] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p152]]]] | [[[[[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]] | [1<=p13 & 1<=p157]] | [[1<=p16 & 1<=p152] | [1<=p17 & 1<=p154]]] | [[[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]] | [[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]]]]]] U [[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]]] | [[[[1<=p13 & 1<=p51] | [1<=p13 & 1<=p53]] | [1<=p16 & 1<=p50]] | [[1<=p16 & 1<=p54] | [1<=p16 & 1<=p52]]]]] | [[[[[[1<=p19 & 1<=p52] | [1<=p15 & 1<=p51]] | [1<=p15 & 1<=p53]] | [[[1<=p15 & 1<=p55] | [1<=p18 & 1<=p54]] | [1<=p18 & 1<=p52]]] | [[[[1<=p18 & 1<=p50] | [1<=p14 & 1<=p55]] | [1<=p19 & 1<=p50]] | [[1<=p14 & 1<=p53] | [1<=p19 & 1<=p54]]]] | [[[[[1<=p14 & 1<=p51] | [1<=p17 & 1<=p51]] | [1<=p17 & 1<=p53]] | [[1<=p13 & 1<=p50] | [1<=p13 & 1<=p52]]] | [[[[1<=p13 & 1<=p54] | [1<=p16 & 1<=p51]] | [1<=p16 & 1<=p55]] | [[1<=p16 & 1<=p53] | [1<=p17 & 1<=p55]]]]]]]]]]]]
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p154)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p153)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p152)
states: 5,792,643,520 (9)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p157)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p156)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p155)
states: 5,792,643,520 (9)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
before gc: list nodes free: 1631794
after gc: idd nodes used:33506125, unused:30493875; list nodes free:136446383
MC time: 1m 7.180sec
checking: [A [AG [~ [[[[[[~ [EG [[[[[1<=p23 & 1<=p39] | [[1<=p28 & 1<=p42] | [1<=p26 & 1<=p41]]] | [[1<=p31 & 1<=p43] | [[1<=p25 & 1<=p40] | [1<=p21 & 1<=p38]]]] | [[[1<=p27 & 1<=p41] | [[1<=p22 & 1<=p39] | [1<=p30 & 1<=p43]]] | [[1<=p29 & 1<=p42] | [[1<=p20 & 1<=p38] | [1<=p24 & 1<=p40]]]]]]] | [1<=p17 & 1<=p55]] | [[1<=p16 & 1<=p53] | [[1<=p16 & 1<=p55] | [1<=p16 & 1<=p51]]]] | [[[1<=p13 & 1<=p54] | [1<=p13 & 1<=p52]] | [[1<=p13 & 1<=p50] | [[1<=p17 & 1<=p53] | [1<=p17 & 1<=p51]]]]] | [[[[1<=p14 & 1<=p51] | [1<=p19 & 1<=p54]] | [[1<=p14 & 1<=p53] | [[1<=p19 & 1<=p50] | [1<=p14 & 1<=p55]]]] | [[[1<=p18 & 1<=p50] | [[1<=p18 & 1<=p52] | [1<=p18 & 1<=p54]]] | [[1<=p15 & 1<=p55] | [[1<=p15 & 1<=p53] | [1<=p15 & 1<=p51]]]]]] | [[[[[1<=p19 & 1<=p52] | [1<=p16 & 1<=p52]] | [[1<=p16 & 1<=p54] | [[1<=p16 & 1<=p50] | [1<=p13 & 1<=p53]]]] | [[[1<=p13 & 1<=p51] | [[1<=p13 & 1<=p55] | [1<=p17 & 1<=p50]]] | [[1<=p17 & 1<=p54] | [[1<=p17 & 1<=p52] | [1<=p19 & 1<=p53]]]]] | [[[[1<=p14 & 1<=p50] | [1<=p19 & 1<=p55]] | [[1<=p14 & 1<=p52] | [[1<=p14 & 1<=p54] | [1<=p18 & 1<=p51]]]] | [[[1<=p18 & 1<=p53] | [[1<=p18 & 1<=p55] | [1<=p15 & 1<=p54]]] | [[1<=p15 & 1<=p52] | [[1<=p15 & 1<=p50] | [1<=p19 & 1<=p51]]]]]]]]] U [AX [~ [EX [[[[[[[1<=p17 & 1<=p55] | [1<=p16 & 1<=p53]] | [[1<=p16 & 1<=p55] | [[1<=p16 & 1<=p51] | [1<=p13 & 1<=p54]]]] | [[[1<=p13 & 1<=p52] | [1<=p13 & 1<=p50]] | [[1<=p17 & 1<=p53] | [[1<=p17 & 1<=p51] | [1<=p14 & 1<=p51]]]]] | [[[[1<=p19 & 1<=p54] | [1<=p14 & 1<=p53]] | [[1<=p19 & 1<=p50] | [[1<=p14 & 1<=p55] | [1<=p18 & 1<=p50]]]] | [[[1<=p18 & 1<=p52] | [[1<=p18 & 1<=p54] | [1<=p15 & 1<=p55]]] | [[1<=p15 & 1<=p53] | [[1<=p15 & 1<=p51] | [1<=p19 & 1<=p52]]]]]] | [[[[[1<=p16 & 1<=p52] | [1<=p16 & 1<=p54]] | [[1<=p16 & 1<=p50] | [[1<=p13 & 1<=p53] | [1<=p13 & 1<=p51]]]] | [[[1<=p13 & 1<=p55] | [1<=p17 & 1<=p50]] | [[1<=p17 & 1<=p54] | [[1<=p17 & 1<=p52] | [1<=p19 & 1<=p53]]]]] | [[[[1<=p14 & 1<=p50] | [1<=p19 & 1<=p55]] | [[1<=p14 & 1<=p52] | [[1<=p14 & 1<=p54] | [1<=p18 & 1<=p51]]]] | [[[1<=p18 & 1<=p53] | [[1<=p18 & 1<=p55] | [1<=p15 & 1<=p54]]] | [[1<=p15 & 1<=p52] | [[1<=p15 & 1<=p50] | [1<=p19 & 1<=p51]]]]]]]]]] & [[[[[[1<=p10 & 1<=p33] | [1<=p10 & 1<=p35]] | [[1<=p10 & 1<=p37] | [[1<=p11 & 1<=p37] | [1<=p9 & 1<=p33]]]] | [[[1<=p11 & 1<=p35] | [1<=p11 & 1<=p33]] | [[1<=p9 & 1<=p37] | [[1<=p6 & 1<=p32] | [1<=p9 & 1<=p35]]]]] | [[[[1<=p6 & 1<=p34] | [1<=p6 & 1<=p36]] | [[1<=p8 & 1<=p36] | [[1<=p7 & 1<=p34] | [1<=p7 & 1<=p32]]]] | [[[1<=p7 & 1<=p36] | [[1<=p8 & 1<=p32] | [1<=p12 & 1<=p35]]] | [[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p37] | [1<=p12 & 1<=p33]]]]]] | [[[[[1<=p10 & 1<=p34] | [1<=p10 & 1<=p36]] | [[1<=p6 & 1<=p37] | [[1<=p11 & 1<=p36] | [1<=p9 & 1<=p32]]]] | [[[1<=p11 & 1<=p34] | [1<=p11 & 1<=p32]] | [[1<=p9 & 1<=p36] | [[1<=p9 & 1<=p34] | [1<=p6 & 1<=p33]]]]] | [[[[1<=p6 & 1<=p35] | [1<=p10 & 1<=p32]] | [[1<=p8 & 1<=p35] | [[1<=p8 & 1<=p37] | [1<=p7 & 1<=p35]]]] | [[[1<=p7 & 1<=p33] | [[1<=p7 & 1<=p37] | [1<=p12 & 1<=p36]]] | [[1<=p8 & 1<=p33] | [[1<=p12 & 1<=p32] | [1<=p12 & 1<=p34]]]]]]]]] | EG [E [[~ [[[[1<=p19 & 1<=p157] | [[1<=p14 & 1<=p152] | [1<=p15 & 1<=p153]]] | [[1<=p16 & 1<=p154] | [[1<=p17 & 1<=p155] | [1<=p18 & 1<=p156]]]]] | AX [[[[[[[1<=p26 & [1<=p83 & 1<=p111]] | [1<=p24 & [1<=p100 & 1<=p114]]] | [[1<=p22 & [1<=p93 & 1<=p113]] | [1<=p30 & [1<=p103 & 1<=p114]]]] | [[[1<=p28 & [1<=p90 & 1<=p112]] | [1<=p20 & [1<=p86 & 1<=p112]]] | [[1<=p30 & [1<=p79 & 1<=p110]] | [[1<=p24 & [1<=p106 & 1<=p115]] | [1<=p20 & [1<=p74 & 1<=p110]]]]]] | [[[[1<=p22 & [1<=p99 & 1<=p114]] | [1<=p20 & [1<=p104 & 1<=p115]]] | [[1<=p30 & [1<=p97 & 1<=p113]] | [1<=p24 & [1<=p82 & 1<=p111]]]] | [[[1<=p26 & [1<=p89 & 1<=p112]] | [[1<=p26 & [1<=p107 & 1<=p115]] | [1<=p28 & [1<=p108 & 1<=p115]]]] | [[1<=p30 & [1<=p85 & 1<=p111]] | [1<=p28 & [1<=p96 & 1<=p113]]]]]] | [[[[[1<=p22 & [1<=p105 & 1<=p115]] | [1<=p28 & [1<=p78 & 1<=p110]]] | [[1<=p22 & [1<=p75 & 1<=p110]] | [1<=p26 & [1<=p101 & 1<=p114]]]] | [[[1<=p20 & [1<=p92 & 1<=p113]] | [1<=p22 & [1<=p81 & 1<=p111]]] | [[1<=p26 & [1<=p95 & 1<=p113]] | [[1<=p24 & [1<=p88 & 1<=p112]] | [1<=p24 & [1<=p94 & 1<=p113]]]]]] | [[[[1<=p26 & [1<=p77 & 1<=p110]] | [1<=p28 & [1<=p84 & 1<=p111]]] | [[1<=p28 & [1<=p102 & 1<=p114]] | [1<=p24 & [1<=p76 & 1<=p110]]]] | [[[1<=p22 & [1<=p87 & 1<=p112]] | [1<=p30 & [1<=p91 & 1<=p112]]] | [[1<=p30 & [1<=p109 & 1<=p115]] | [[1<=p20 & [1<=p80 & 1<=p111]] | [1<=p20 & [1<=p98 & 1<=p114]]]]]]]]]] U EX [[[[[AF [~ [[[[p13<=0 | p47<=0] & [[p13<=0 | p46<=0] & [p13<=0 | p45<=0]]] & [[p13<=0 | p44<=0] & [[p13<=0 | p49<=0] & [p13<=0 | p48<=0]]]]]] | [1<=p13 & 1<=p47]] | [[1<=p13 & 1<=p46] | [1<=p13 & 1<=p45]]] | [[[1<=p13 & 1<=p44] | [1<=p13 & 1<=p49]] | [[1<=p13 & 1<=p48] | [[1<=p2 & 1<=p24] | [1<=p5 & 1<=p31]]]]] | [[[[1<=p1 & 1<=p22] | [1<=p3 & 1<=p27]] | [[1<=p5 & 1<=p30] | [[1<=p1 & 1<=p23] | [1<=p3 & 1<=p26]]]] | [[[1<=p4 & 1<=p28] | [1<=p4 & 1<=p29]] | [[1<=p0 & 1<=p21] | [[1<=p0 & 1<=p20] | [1<=p2 & 1<=p25]]]]]]]]]]
normalized: [EG [E [[~ [EX [~ [[[[[[[[1<=p20 & [1<=p98 & 1<=p114]] | [1<=p20 & [1<=p80 & 1<=p111]]] | [1<=p30 & [1<=p109 & 1<=p115]]] | [[1<=p30 & [1<=p91 & 1<=p112]] | [1<=p22 & [1<=p87 & 1<=p112]]]] | [[[1<=p24 & [1<=p76 & 1<=p110]] | [1<=p28 & [1<=p102 & 1<=p114]]] | [[1<=p28 & [1<=p84 & 1<=p111]] | [1<=p26 & [1<=p77 & 1<=p110]]]]] | [[[[[1<=p24 & [1<=p94 & 1<=p113]] | [1<=p24 & [1<=p88 & 1<=p112]]] | [1<=p26 & [1<=p95 & 1<=p113]]] | [[1<=p22 & [1<=p81 & 1<=p111]] | [1<=p20 & [1<=p92 & 1<=p113]]]] | [[[1<=p26 & [1<=p101 & 1<=p114]] | [1<=p22 & [1<=p75 & 1<=p110]]] | [[1<=p28 & [1<=p78 & 1<=p110]] | [1<=p22 & [1<=p105 & 1<=p115]]]]]] | [[[[[1<=p28 & [1<=p96 & 1<=p113]] | [1<=p30 & [1<=p85 & 1<=p111]]] | [[[1<=p28 & [1<=p108 & 1<=p115]] | [1<=p26 & [1<=p107 & 1<=p115]]] | [1<=p26 & [1<=p89 & 1<=p112]]]] | [[[1<=p24 & [1<=p82 & 1<=p111]] | [1<=p30 & [1<=p97 & 1<=p113]]] | [[1<=p20 & [1<=p104 & 1<=p115]] | [1<=p22 & [1<=p99 & 1<=p114]]]]] | [[[[[1<=p20 & [1<=p74 & 1<=p110]] | [1<=p24 & [1<=p106 & 1<=p115]]] | [1<=p30 & [1<=p79 & 1<=p110]]] | [[1<=p20 & [1<=p86 & 1<=p112]] | [1<=p28 & [1<=p90 & 1<=p112]]]] | [[[1<=p30 & [1<=p103 & 1<=p114]] | [1<=p22 & [1<=p93 & 1<=p113]]] | [[1<=p24 & [1<=p100 & 1<=p114]] | [1<=p26 & [1<=p83 & 1<=p111]]]]]]]]]] | ~ [[[[[1<=p18 & 1<=p156] | [1<=p17 & 1<=p155]] | [1<=p16 & 1<=p154]] | [[[1<=p15 & 1<=p153] | [1<=p14 & 1<=p152]] | [1<=p19 & 1<=p157]]]]] U EX [[[[[[[1<=p0 & 1<=p20] | [1<=p2 & 1<=p25]] | [1<=p0 & 1<=p21]] | [[1<=p4 & 1<=p29] | [1<=p4 & 1<=p28]]] | [[[[1<=p3 & 1<=p26] | [1<=p1 & 1<=p23]] | [1<=p5 & 1<=p30]] | [[1<=p3 & 1<=p27] | [1<=p1 & 1<=p22]]]] | [[[[[1<=p5 & 1<=p31] | [1<=p2 & 1<=p24]] | [1<=p13 & 1<=p48]] | [[1<=p13 & 1<=p49] | [1<=p13 & 1<=p44]]] | [[[1<=p13 & 1<=p45] | [1<=p13 & 1<=p46]] | [[1<=p13 & 1<=p47] | ~ [EG [[[[[p13<=0 | p48<=0] & [p13<=0 | p49<=0]] & [p13<=0 | p44<=0]] & [[[p13<=0 | p45<=0] & [p13<=0 | p46<=0]] & [p13<=0 | p47<=0]]]]]]]]]]]] | [~ [EG [~ [[[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]] & ~ [EX [EX [[[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]]] | [[[[1<=p13 & 1<=p51] | [1<=p13 & 1<=p53]] | [1<=p16 & 1<=p50]] | [[1<=p16 & 1<=p54] | [1<=p16 & 1<=p52]]]]] | [[[[[[1<=p19 & 1<=p52] | [1<=p15 & 1<=p51]] | [1<=p15 & 1<=p53]] | [[[1<=p15 & 1<=p55] | [1<=p18 & 1<=p54]] | [1<=p18 & 1<=p52]]] | [[[[1<=p18 & 1<=p50] | [1<=p14 & 1<=p55]] | [1<=p19 & 1<=p50]] | [[1<=p14 & 1<=p53] | [1<=p19 & 1<=p54]]]] | [[[[[1<=p14 & 1<=p51] | [1<=p17 & 1<=p51]] | [1<=p17 & 1<=p53]] | [[1<=p13 & 1<=p50] | [1<=p13 & 1<=p52]]] | [[[[1<=p13 & 1<=p54] | [1<=p16 & 1<=p51]] | [1<=p16 & 1<=p55]] | [[1<=p16 & 1<=p53] | [1<=p17 & 1<=p55]]]]]]]]]]]]] & ~ [E [~ [[[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]] & ~ [EX [EX [[[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]]] | [[[[1<=p13 & 1<=p51] | [1<=p13 & 1<=p53]] | [1<=p16 & 1<=p50]] | [[1<=p16 & 1<=p54] | [1<=p16 & 1<=p52]]]]] | [[[[[[1<=p19 & 1<=p52] | [1<=p15 & 1<=p51]] | [1<=p15 & 1<=p53]] | [[[1<=p15 & 1<=p55] | [1<=p18 & 1<=p54]] | [1<=p18 & 1<=p52]]] | [[[[1<=p18 & 1<=p50] | [1<=p14 & 1<=p55]] | [1<=p19 & 1<=p50]] | [[1<=p14 & 1<=p53] | [1<=p19 & 1<=p54]]]] | [[[[[1<=p14 & 1<=p51] | [1<=p17 & 1<=p51]] | [1<=p17 & 1<=p53]] | [[1<=p13 & 1<=p50] | [1<=p13 & 1<=p52]]] | [[[[1<=p13 & 1<=p54] | [1<=p16 & 1<=p51]] | [1<=p16 & 1<=p55]] | [[1<=p16 & 1<=p53] | [1<=p17 & 1<=p55]]]]]]]]]]] U [E [true U [[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]] | [1<=p13 & 1<=p51]]] | [[[[1<=p13 & 1<=p53] | [1<=p16 & 1<=p50]] | [1<=p16 & 1<=p54]] | [[1<=p16 & 1<=p52] | [1<=p19 & 1<=p52]]]]] | [[[[[[1<=p15 & 1<=p51] | [1<=p15 & 1<=p53]] | [1<=p15 & 1<=p55]] | [[[1<=p18 & 1<=p54] | [1<=p18 & 1<=p52]] | [1<=p18 & 1<=p50]]] | [[[[1<=p14 & 1<=p55] | [1<=p19 & 1<=p50]] | [1<=p14 & 1<=p53]] | [[1<=p19 & 1<=p54] | [1<=p14 & 1<=p51]]]] | [[[[[1<=p17 & 1<=p51] | [1<=p17 & 1<=p53]] | [1<=p13 & 1<=p50]] | [[1<=p13 & 1<=p52] | [1<=p13 & 1<=p54]]] | [[[[1<=p16 & 1<=p51] | [1<=p16 & 1<=p55]] | [1<=p16 & 1<=p53]] | [[1<=p17 & 1<=p55] | ~ [EG [[[[[[1<=p24 & 1<=p40] | [1<=p20 & 1<=p38]] | [1<=p29 & 1<=p42]] | [[[1<=p30 & 1<=p43] | [1<=p22 & 1<=p39]] | [1<=p27 & 1<=p41]]] | [[[[1<=p21 & 1<=p38] | [1<=p25 & 1<=p40]] | [1<=p31 & 1<=p43]] | [[[1<=p26 & 1<=p41] | [1<=p28 & 1<=p42]] | [1<=p23 & 1<=p39]]]]]]]]]]]] & ~ [[[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]] & ~ [EX [EX [[[[[[[[1<=p19 & 1<=p51] | [1<=p15 & 1<=p50]] | [1<=p15 & 1<=p52]] | [[[1<=p15 & 1<=p54] | [1<=p18 & 1<=p55]] | [1<=p18 & 1<=p53]]] | [[[[1<=p18 & 1<=p51] | [1<=p14 & 1<=p54]] | [1<=p14 & 1<=p52]] | [[1<=p19 & 1<=p55] | [1<=p14 & 1<=p50]]]] | [[[[[1<=p19 & 1<=p53] | [1<=p17 & 1<=p52]] | [1<=p17 & 1<=p54]] | [[1<=p17 & 1<=p50] | [1<=p13 & 1<=p55]]] | [[[[1<=p13 & 1<=p51] | [1<=p13 & 1<=p53]] | [1<=p16 & 1<=p50]] | [[1<=p16 & 1<=p54] | [1<=p16 & 1<=p52]]]]] | [[[[[[1<=p19 & 1<=p52] | [1<=p15 & 1<=p51]] | [1<=p15 & 1<=p53]] | [[[1<=p15 & 1<=p55] | [1<=p18 & 1<=p54]] | [1<=p18 & 1<=p52]]] | [[[[1<=p18 & 1<=p50] | [1<=p14 & 1<=p55]] | [1<=p19 & 1<=p50]] | [[1<=p14 & 1<=p53] | [1<=p19 & 1<=p54]]]] | [[[[[1<=p14 & 1<=p51] | [1<=p17 & 1<=p51]] | [1<=p17 & 1<=p53]] | [[1<=p13 & 1<=p50] | [1<=p13 & 1<=p52]]] | [[[[1<=p13 & 1<=p54] | [1<=p16 & 1<=p51]] | [1<=p16 & 1<=p55]] | [[1<=p16 & 1<=p53] | [1<=p17 & 1<=p55]]]]]]]]]]]]]]]]
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p16)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p13)
states: 83,097,558,952 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p17)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p14)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p53)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p55)
states: 10,867,198,016 (10)
abstracting: (1<=p18)
states: 77,355,700,032 (10)
abstracting: (1<=p54)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p52)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p50)
states: 10,867,198,016 (10)
abstracting: (1<=p15)
states: 77,355,700,032 (10)
abstracting: (1<=p51)
states: 10,867,198,016 (10)
abstracting: (1<=p19)
states: 77,355,700,032 (10)
before gc: list nodes free: 3200751
after gc: idd nodes used:33244886, unused:30755114; list nodes free:137513758
MC time: 1m 2.032sec
checking: AG [[[[[[AF [E [[AG [[[[[[[1<=p10 & 1<=p33] | [1<=p10 & 1<=p35]] | [[1<=p10 & 1<=p37] | [[1<=p11 & 1<=p37] | [1<=p9 & 1<=p33]]]] | [[[1<=p11 & 1<=p35] | [1<=p11 & 1<=p33]] | [[1<=p9 & 1<=p37] | [[1<=p6 & 1<=p32] | [1<=p9 & 1<=p35]]]]] | [[[[1<=p6 & 1<=p34] | [1<=p6 & 1<=p36]] | [[1<=p8 & 1<=p36] | [[1<=p7 & 1<=p34] | [1<=p7 & 1<=p32]]]] | [[[1<=p7 & 1<=p36] | [[1<=p8 & 1<=p32] | [1<=p12 & 1<=p35]]] | [[1<=p8 & 1<=p34] | [[1<=p12 & 1<=p37] | [1<=p12 & 1<=p33]]]]]] | [[[[[1<=p10 & 1<=p34] | [1<=p10 & 1<=p36]] | [[1<=p6 & 1<=p37] | [[1<=p11 & 1<=p36] | [1<=p9 & 1<=p32]]]] | [[[1<=p11 & 1<=p34] | [1<=p11 & 1<=p32]] | [[1<=p9 & 1<=p36] | [[1<=p9 & 1<=p34] | [1<=p6 & 1<=p33]]]]] | [[[[1<=p6 & 1<=p35] | [1<=p10 & 1<=p32]] | [[1<=p8 & 1<=p35] | [[1<=p8 & 1<=p37] | [1<=p7 & 1<=p35]]]] | [[[1<=p7 & 1<=p33] | [[1<=p7 & 1<=p37] | [1<=p12 & 1<=p36]]] | [[1<=p8 & 1<=p33] | [[1<=p12 & 1<=p32] | [1<=p12 & 1<=p34]]]]]]]] & ~ [[[[p13<=0 | p163<=0] & [[p13<=0 | p160<=0] & [p13<=0 | p159<=0]]] & [[p13<=0 | p162<=0] & [[p13<=0 | p161<=0] & [p13<=0 | p158<=0]]]]]] U EX [[[[[[[1<=p12 & 1<=p56] | [1<=p12 & 1<=p58]] | [[1<=p12 & 1<=p57] | [1<=p7 & 1<=p61]]] | [[[1<=p7 & 1<=p60] | [1<=p7 & 1<=p59]] | [[1<=p7 & 1<=p58] | [[1<=p7 & 1<=p57] | [1<=p8 & 1<=p60]]]]] | [[[[1<=p8 & 1<=p59] | [1<=p8 & 1<=p61]] | [[1<=p8 & 1<=p56] | [1<=p12 & 1<=p60]]] | [[[1<=p12 & 1<=p59] | [1<=p8 & 1<=p58]] | [[1<=p10 & 1<=p61] | [[1<=p9 & 1<=p57] | [1<=p9 & 1<=p56]]]]]] | [[[[[1<=p9 & 1<=p61] | [1<=p9 & 1<=p60]] | [[1<=p9 & 1<=p59] | [1<=p11 & 1<=p61]]] | [[[1<=p6 & 1<=p57] | [1<=p11 & 1<=p59]] | [[1<=p6 & 1<=p58] | [[1<=p11 & 1<=p58] | [1<=p6 & 1<=p59]]]]] | [[[[1<=p11 & 1<=p57] | [1<=p6 & 1<=p60]] | [[1<=p11 & 1<=p56] | [1<=p6 & 1<=p61]]] | [[[1<=p10 & 1<=p56] | [1<=p10 & 1<=p58]] | [[1<=p10 & 1<=p57] | [[1<=p10 & 1<=p60] | [1<=p6 & 1<=p56]]]]]]]]]] | [E [[[[[1<=p13 & 1<=p47] | [[1<=p13 & 1<=p46] | [1<=p13 & 1<=p45]]] | [[1<=p13 & 1<=p44] | [[1<=p13 & 1<=p49] | [1<=p13 & 1<=p48]]]] & [[[[1<=p28 & 1<=p66] | [[1<=p20 & 1<=p62] | [1<=p25 & 1<=p64]]] | [[1<=p23 & 1<=p63] | [[1<=p26 & 1<=p65] | [1<=p30 & 1<=p67]]]] | [[[1<=p29 & 1<=p66] | [[1<=p27 & 1<=p65] | [1<=p24 & 1<=p64]]] | [[1<=p22 & 1<=p63] | [[1<=p21 & 1<=p62] | [1<=p31 & 1<=p67]]]]]] U [[[[[[p13<=0 | p167<=0] & [p13<=0 | p169<=0]] & [[p18<=0 | p166<=0] & [[p13<=0 | p165<=0] & [p18<=0 | p168<=0]]]] & [[[p14<=0 | p169<=0] & [p17<=0 | p164<=0]] & [[p19<=0 | p166<=0] & [[p19<=0 | p164<=0] & [p19<=0 | p168<=0]]]]] & [[[[p15<=0 | p169<=0] & [p16<=0 | p166<=0]] & [[p16<=0 | p164<=0] & [[p15<=0 | p164<=0] & [p16<=0 | p169<=0]]]] & [[[p15<=0 | p166<=0] & [[p16<=0 | p167<=0] & [p14<=0 | p164<=0]]] & [[p14<=0 | p168<=0] & [[p17<=0 | p169<=0] & [p14<=0 | p166<=0]]]]]] & [[[[[p17<=0 | p167<=0] & [p18<=0 | p169<=0]] & [[p13<=0 | p166<=0] & [[p13<=0 | p168<=0] & [p18<=0 | p165<=0]]]] & [[[p18<=0 | p167<=0] & [p13<=0 | p164<=0]] & [[p17<=0 | p165<=0] & [[p19<=0 | p167<=0] & [p19<=0 | p165<=0]]]]] & [[[[p19<=0 | p169<=0] & [p15<=0 | p168<=0]] & [[p16<=0 | p165<=0] & [[p15<=0 | p165<=0] & [p15<=0 | p167<=0]]]] & [[[p16<=0 | p168<=0] & [[p17<=0 | p168<=0] & [p14<=0 | p167<=0]]] & [[p17<=0 | p166<=0] & [[p14<=0 | p165<=0] & [p18<=0 | p164<=0]]]]]]]] & [AX [AF [[[[[[[1<=p12 & 1<=p56] | [1<=p12 & 1<=p58]] | [[1<=p12 & 1<=p57] | [1<=p7 & 1<=p61]]] | [[[1<=p7 & 1<=p60] | [1<=p7 & 1<=p59]] | [[1<=p7 & 1<=p58] | [[1<=p7 & 1<=p57] | [1<=p8 & 1<=p60]]]]] | [[[[1<=p8 & 1<=p59] | [1<=p8 & 1<=p61]] | [[1<=p8 & 1<=p56] | [1<=p12 & 1<=p60]]] | [[[1<=p12 & 1<=p59] | [1<=p8 & 1<=p58]] | [[1<=p10 & 1<=p61] | [[1<=p9 & 1<=p57] | [1<=p9 & 1<=p56]]]]]] | [[[[[1<=p9 & 1<=p61] | [1<=p9 & 1<=p60]] | [[1<=p9 & 1<=p59] | [1<=p11 & 1<=p61]]] | [[[1<=p6 & 1<=p57] | [1<=p11 & 1<=p59]] | [[1<=p6 & 1<=p58] | [[1<=p11 & 1<=p58] | [1<=p6 & 1<=p59]]]]] | [[[[1<=p11 & 1<=p57] | [1<=p6 & 1<=p60]] | [[1<=p11 & 1<=p56] | [1<=p6 & 1<=p61]]] | [[[1<=p10 & 1<=p56] | [1<=p10 & 1<=p58]] | [[1<=p10 & 1<=p57] | [[1<=p10 & 1<=p60] | [1<=p6 & 1<=p56]]]]]]]]] & [[[AF [[[[[1<=p28 & 1<=p66] | [[1<=p20 & 1<=p62] | [1<=p25 & 1<=p64]]] | [[1<=p23 & 1<=p63] | [[1<=p26 & 1<=p65] | [1<=p30 & 1<=p67]]]] | [[[1<=p29 & 1<=p66] | [[1<=p27 & 1<=p65] | [1<=p24 & 1<=p64]]] | [[1<=p22 & 1<=p63] | [[1<=p21 & 1<=p62] | [1<=p31 & 1<=p67]]]]]] | EF [[[[[1<=p21 & 1<=p170] | [[1<=p26 & 1<=p173] | [1<=p24 & 1<=p172]]] | [[1<=p23 & 1<=p171] | [[1<=p27 & 1<=p173] | [1<=p29 & 1<=p174]]]] | [[[1<=p31 & 1<=p175] | [[1<=p30 & 1<=p175] | [1<=p25 & 1<=p172]]] | [[1<=p22 & 1<=p171] | [[1<=p20 & 1<=p170] | [1<=p28 & 1<=p174]]]]]]] | [1<=p71 | 1<=p70]] | [[1<=p73 | 1<=p72] | [1<=p69 | 1<=p68]]]]]] | [[1<=p17 & 1<=p157] | [1<=p17 & 1<=p156]]] | [[[1<=p17 & 1<=p153] | [1<=p17 & 1<=p152]] | [[1<=p17 & 1<=p154] | [[1<=p16 & 1<=p152] | [1<=p13 & 1<=p157]]]]] | [[[[1<=p13 & 1<=p156] | [1<=p13 & 1<=p153]] | [[1<=p13 & 1<=p152] | [[1<=p13 & 1<=p155] | [1<=p13 & 1<=p154]]]] | [[[1<=p16 & 1<=p157] | [1<=p16 & 1<=p156]] | [[1<=p16 & 1<=p155] | [[1<=p16 & 1<=p153] | [1<=p19 & 1<=p153]]]]]] | [[[[[1<=p19 & 1<=p152] | [1<=p14 & 1<=p154]] | [[1<=p19 & 1<=p155] | [1<=p14 & 1<=p153]]] | [[[1<=p19 & 1<=p154] | [1<=p19 & 1<=p156]] | [[1<=p15 & 1<=p155] | [[1<=p15 & 1<=p154] | [1<=p15 & 1<=p157]]]]] | [[[[1<=p15 & 1<=p156] | [1<=p18 & 1<=p154]] | [[1<=p18 & 1<=p153] | [[1<=p18 & 1<=p152] | [1<=p18 & 1<=p157]]]] | [[[1<=p15 & 1<=p152] | [1<=p18 & 1<=p155]] | [[1<=p14 & 1<=p157] | [[1<=p14 & 1<=p156] | [1<=p14 & 1<=p155]]]]]]]]
normalized: ~ [E [true U ~ [[[[[[[[1<=p14 & 1<=p155] | [1<=p14 & 1<=p156]] | [1<=p14 & 1<=p157]] | [[1<=p18 & 1<=p155] | [1<=p15 & 1<=p152]]] | [[[[1<=p18 & 1<=p157] | [1<=p18 & 1<=p152]] | [1<=p18 & 1<=p153]] | [[1<=p18 & 1<=p154] | [1<=p15 & 1<=p156]]]] | [[[[[1<=p15 & 1<=p157] | [1<=p15 & 1<=p154]] | [1<=p15 & 1<=p155]] | [[1<=p19 & 1<=p156] | [1<=p19 & 1<=p154]]] | [[[1<=p14 & 1<=p153] | [1<=p19 & 1<=p155]] | [[1<=p14 & 1<=p154] | [1<=p19 & 1<=p152]]]]] | [[[[[[1<=p19 & 1<=p153] | [1<=p16 & 1<=p153]] | [1<=p16 & 1<=p155]] | [[1<=p16 & 1<=p156] | [1<=p16 & 1<=p157]]] | [[[[1<=p13 & 1<=p154] | [1<=p13 & 1<=p155]] | [1<=p13 & 1<=p152]] | [[1<=p13 & 1<=p153] | [1<=p13 & 1<=p156]]]] | [[[[[1<=p13 & 1<=p157] | [1<=p16 & 1<=p152]] | [1<=p17 & 1<=p154]] | [[1<=p17 & 1<=p152] | [1<=p17 & 1<=p153]]] | [[[1<=p17 & 1<=p156] | [1<=p17 & 1<=p157]] | [[[[[[1<=p69 | 1<=p68] | [1<=p73 | 1<=p72]] | [[1<=p71 | 1<=p70] | [E [true U [[[[[1<=p28 & 1<=p174] | [1<=p20 & 1<=p170]] | [1<=p22 & 1<=p171]] | [[[1<=p25 & 1<=p172] | [1<=p30 & 1<=p175]] | [1<=p31 & 1<=p175]]] | [[[[1<=p29 & 1<=p174] | [1<=p27 & 1<=p173]] | [1<=p23 & 1<=p171]] | [[[1<=p24 & 1<=p172] | [1<=p26 & 1<=p173]] | [1<=p21 & 1<=p170]]]]] | ~ [EG [~ [[[[[[1<=p31 & 1<=p67] | [1<=p21 & 1<=p62]] | [1<=p22 & 1<=p63]] | [[[1<=p24 & 1<=p64] | [1<=p27 & 1<=p65]] | [1<=p29 & 1<=p66]]] | [[[[1<=p30 & 1<=p67] | [1<=p26 & 1<=p65]] | [1<=p23 & 1<=p63]] | [[[1<=p25 & 1<=p64] | [1<=p20 & 1<=p62]] | [1<=p28 & 1<=p66]]]]]]]]]] & ~ [EX [EG [~ [[[[[[[[1<=p6 & 1<=p56] | [1<=p10 & 1<=p60]] | [1<=p10 & 1<=p57]] | [[1<=p10 & 1<=p58] | [1<=p10 & 1<=p56]]] | [[[1<=p6 & 1<=p61] | [1<=p11 & 1<=p56]] | [[1<=p6 & 1<=p60] | [1<=p11 & 1<=p57]]]] | [[[[[1<=p6 & 1<=p59] | [1<=p11 & 1<=p58]] | [1<=p6 & 1<=p58]] | [[1<=p11 & 1<=p59] | [1<=p6 & 1<=p57]]] | [[[1<=p11 & 1<=p61] | [1<=p9 & 1<=p59]] | [[1<=p9 & 1<=p60] | [1<=p9 & 1<=p61]]]]] | [[[[[[1<=p9 & 1<=p56] | [1<=p9 & 1<=p57]] | [1<=p10 & 1<=p61]] | [[1<=p8 & 1<=p58] | [1<=p12 & 1<=p59]]] | [[[1<=p12 & 1<=p60] | [1<=p8 & 1<=p56]] | [[1<=p8 & 1<=p61] | [1<=p8 & 1<=p59]]]] | [[[[[1<=p8 & 1<=p60] | [1<=p7 & 1<=p57]] | [1<=p7 & 1<=p58]] | [[1<=p7 & 1<=p59] | [1<=p7 & 1<=p60]]] | [[[1<=p7 & 1<=p61] | [1<=p12 & 1<=p57]] | [[1<=p12 & 1<=p58] | [1<=p12 & 1<=p56]]]]]]]]]]] & E [[[[[[[1<=p31 & 1<=p67] | [1<=p21 & 1<=p62]] | [1<=p22 & 1<=p63]] | [[[1<=p24 & 1<=p64] | [1<=p27 & 1<=p65]] | [1<=p29 & 1<=p66]]] | [[[[1<=p30 & 1<=p67] | [1<=p26 & 1<=p65]] | [1<=p23 & 1<=p63]] | [[[1<=p25 & 1<=p64] | [1<=p20 & 1<=p62]] | [1<=p28 & 1<=p66]]]] & [[[[1<=p13 & 1<=p48] | [1<=p13 & 1<=p49]] | [1<=p13 & 1<=p44]] | [[[1<=p13 & 1<=p45] | [1<=p13 & 1<=p46]] | [1<=p13 & 1<=p47]]]] U [[[[[[[p18<=0 | p164<=0] & [p14<=0 | p165<=0]] & [p17<=0 | p166<=0]] & [[[p14<=0 | p167<=0] & [p17<=0 | p168<=0]] & [p16<=0 | p168<=0]]] & [[[[p15<=0 | p167<=0] & [p15<=0 | p165<=0]] & [p16<=0 | p165<=0]] & [[p15<=0 | p168<=0] & [p19<=0 | p169<=0]]]] & [[[[[p19<=0 | p165<=0] & [p19<=0 | p167<=0]] & [p17<=0 | p165<=0]] & [[p13<=0 | p164<=0] & [p18<=0 | p167<=0]]] & [[[[p18<=0 | p165<=0] & [p13<=0 | p168<=0]] & [p13<=0 | p166<=0]] & [[p18<=0 | p169<=0] & [p17<=0 | p167<=0]]]]] & [[[[[[p14<=0 | p166<=0] & [p17<=0 | p169<=0]] & [p14<=0 | p168<=0]] & [[[p14<=0 | p164<=0] & [p16<=0 | p167<=0]] & [p15<=0 | p166<=0]]] & [[[[p16<=0 | p169<=0] & [p15<=0 | p164<=0]] & [p16<=0 | p164<=0]] & [[p16<=0 | p166<=0] & [p15<=0 | p169<=0]]]] & [[[[[p19<=0 | p168<=0] & [p19<=0 | p164<=0]] & [p19<=0 | p166<=0]] & [[p17<=0 | p164<=0] & [p14<=0 | p169<=0]]] & [[[[p18<=0 | p168<=0] & [p13<=0 | p165<=0]] & [p18<=0 | p166<=0]] & [[p13<=0 | p169<=0] & [p13<=0 | p167<=0]]]]]]]] | ~ [EG [~ [E [[~ [[[[[p13<=0 | p158<=0] & [p13<=0 | p161<=0]] & [p13<=0 | p162<=0]] & [[[p13<=0 | p159<=0] & [p13<=0 | p160<=0]] & [p13<=0 | p163<=0]]]] & ~ [E [true U ~ [[[[[[[[1<=p12 & 1<=p34] | [1<=p12 & 1<=p32]] | [1<=p8 & 1<=p33]] | [[[1<=p12 & 1<=p36] | [1<=p7 & 1<=p37]] | [1<=p7 & 1<=p33]]] | [[[[1<=p7 & 1<=p35] | [1<=p8 & 1<=p37]] | [1<=p8 & 1<=p35]] | [[1<=p10 & 1<=p32] | [1<=p6 & 1<=p35]]]] | [[[[[1<=p6 & 1<=p33] | [1<=p9 & 1<=p34]] | [1<=p9 & 1<=p36]] | [[1<=p11 & 1<=p32] | [1<=p11 & 1<=p34]]] | [[[[1<=p9 & 1<=p32] | [1<=p11 & 1<=p36]] | [1<=p6 & 1<=p37]] | [[1<=p10 & 1<=p36] | [1<=p10 & 1<=p34]]]]] | [[[[[[1<=p12 & 1<=p33] | [1<=p12 & 1<=p37]] | [1<=p8 & 1<=p34]] | [[[1<=p12 & 1<=p35] | [1<=p8 & 1<=p32]] | [1<=p7 & 1<=p36]]] | [[[[1<=p7 & 1<=p32] | [1<=p7 & 1<=p34]] | [1<=p8 & 1<=p36]] | [[1<=p6 & 1<=p36] | [1<=p6 & 1<=p34]]]] | [[[[[1<=p9 & 1<=p35] | [1<=p6 & 1<=p32]] | [1<=p9 & 1<=p37]] | [[1<=p11 & 1<=p33] | [1<=p11 & 1<=p35]]] | [[[[1<=p9 & 1<=p33] | [1<=p11 & 1<=p37]] | [1<=p10 & 1<=p37]] | [[1<=p10 & 1<=p35] | [1<=p10 & 1<=p33]]]]]]]]]] U EX [[[[[[[[1<=p6 & 1<=p56] | [1<=p10 & 1<=p60]] | [1<=p10 & 1<=p57]] | [[1<=p10 & 1<=p58] | [1<=p10 & 1<=p56]]] | [[[1<=p6 & 1<=p61] | [1<=p11 & 1<=p56]] | [[1<=p6 & 1<=p60] | [1<=p11 & 1<=p57]]]] | [[[[[1<=p6 & 1<=p59] | [1<=p11 & 1<=p58]] | [1<=p6 & 1<=p58]] | [[1<=p11 & 1<=p59] | [1<=p6 & 1<=p57]]] | [[[1<=p11 & 1<=p61] | [1<=p9 & 1<=p59]] | [[1<=p9 & 1<=p60] | [1<=p9 & 1<=p61]]]]] | [[[[[[1<=p9 & 1<=p56] | [1<=p9 & 1<=p57]] | [1<=p10 & 1<=p61]] | [[1<=p8 & 1<=p58] | [1<=p12 & 1<=p59]]] | [[[1<=p12 & 1<=p60] | [1<=p8 & 1<=p56]] | [[1<=p8 & 1<=p61] | [1<=p8 & 1<=p59]]]] | [[[[[1<=p8 & 1<=p60] | [1<=p7 & 1<=p57]] | [1<=p7 & 1<=p58]] | [[1<=p7 & 1<=p59] | [1<=p7 & 1<=p60]]] | [[[1<=p7 & 1<=p61] | [1<=p12 & 1<=p57]] | [[1<=p12 & 1<=p58] | [1<=p12 & 1<=p56]]]]]]]]]]]]]]]]]]]
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p7)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p12)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p8)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p9)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p59)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p11)
states: 91,205,293,180 (10)
abstracting: (1<=p61)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p58)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p57)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p60)
states: 12,380,817,686 (10)
abstracting: (1<=p10)
states: 91,205,293,180 (10)
abstracting: (1<=p56)
states: 12,380,817,686 (10)
abstracting: (1<=p6)
states: 64
before gc: list nodes free: 3250237
after gc: idd nodes used:33172264, unused:30827736; list nodes free:137839305
MC time: 0m58.016sec
checking: [EG [AF [[E [[[[[1<=p2 & 1<=p24] | [[1<=p5 & 1<=p31] | [1<=p1 & 1<=p22]]] | [[1<=p3 & 1<=p27] | [[1<=p5 & 1<=p30] | [1<=p1 & 1<=p23]]]] | [[[1<=p3 & 1<=p26] | [[1<=p4 & 1<=p28] | [1<=p4 & 1<=p29]]] | [[1<=p0 & 1<=p21] | [[1<=p0 & 1<=p20] | [1<=p2 & 1<=p25]]]]] U [[[[[[1<=p26 & [1<=p83 & 1<=p111]] | [1<=p24 & [1<=p100 & 1<=p114]]] | [[1<=p22 & [1<=p93 & 1<=p113]] | [1<=p30 & [1<=p103 & 1<=p114]]]] | [[[1<=p28 & [1<=p90 & 1<=p112]] | [1<=p20 & [1<=p86 & 1<=p112]]] | [[1<=p30 & [1<=p79 & 1<=p110]] | [[1<=p24 & [1<=p106 & 1<=p115]] | [1<=p20 & [1<=p74 & 1<=p110]]]]]] | [[[[1<=p22 & [1<=p99 & 1<=p114]] | [1<=p20 & [1<=p104 & 1<=p115]]] | [[1<=p30 & [1<=p97 & 1<=p113]] | [1<=p24 & [1<=p82 & 1<=p111]]]] | [[[1<=p30 & [1<=p85 & 1<=p111]] | [1<=p28 & [1<=p96 & 1<=p113]]] | [[1<=p26 & [1<=p89 & 1<=p112]] | [[1<=p26 & [1<=p107 & 1<=p115]] | [1<=p28 & [1<=p108 & 1<=p115]]]]]]] | [[[[[1<=p22 & [1<=p105 & 1<=p115]] | [1<=p28 & [1<=p78 & 1<=p110]]] | [[1<=p22 & [1<=p75 & 1<=p110]] | [1<=p26 & [1<=p101 & 1<=p114]]]] | [[[1<=p20 & [1<=p92 & 1<=p113]] | [1<=p22 & [1<=p81 & 1<=p111]]] | [[1<=p26 & [1<=p95 & 1<=p113]] | [[1<=p24 & [1<=p88 & 1<=p112]] | [1<=p24 & [1<=p94 & 1<=p113]]]]]] | [[[[1<=p26 & [1<=p77 & 1<=p110]] | [1<=p28 & [1<=p84 & 1<=p111]]] | [[1<=p28 & [1<=p102 & 1<=p114]] | [1<=p24 & [1<=p76 & 1<=p110]]]] | [[[1<=p22 & [1<=p87 & 1<=p112]] | [1<=p30 & [1<=p91 & 1<=p112]]] | [[1<=p30 & [1<=p109 & 1<=p115]] | [[1<=p20 & [1<=p80 & 1<=p111]] | [1<=p20 & [1<=p98 & 1<=p114]]]]]]]]] & [[[[[[[1<=p16 & 1<=p46] | [1<=p16 & 1<=p45]] | [[1<=p16 & 1<=p48] | [1<=p16 & 1<=p47]]] | [[[1<=p16 & 1<=p44] | [1<=p16 & 1<=p49]] | [[1<=p17 & 1<=p47] | [[1<=p17 & 1<=p46] | [1<=p17 & 1<=p45]]]]] | [[[[1<=p17 & 1<=p44] | [1<=p17 & 1<=p49]] | [[1<=p17 & 1<=p48] | [1<=p18 & 1<=p44]]] | [[[1<=p19 & 1<=p49] | [1<=p19 & 1<=p48]] | [[1<=p18 & 1<=p46] | [[1<=p19 & 1<=p47] | [1<=p18 & 1<=p45]]]]]] | [[[[[1<=p19 & 1<=p46] | [1<=p14 & 1<=p44]] | [[1<=p18 & 1<=p48] | [1<=p19 & 1<=p45]]] | [[[1<=p18 & 1<=p47] | [1<=p19 & 1<=p44]] | [[1<=p14 & 1<=p46] | [[1<=p14 & 1<=p45] | [1<=p18 & 1<=p49]]]]] | [[[[1<=p14 & 1<=p48] | [1<=p14 & 1<=p47]] | [[1<=p14 & 1<=p49] | [1<=p15 & 1<=p49]]] | [[[1<=p15 & 1<=p48] | [1<=p15 & 1<=p47]] | [[1<=p15 & 1<=p46] | [[1<=p15 & 1<=p45] | [1<=p15 & 1<=p44]]]]]]] & [[[[1<=p21 & 1<=p170] | [[1<=p26 & 1<=p173] | [1<=p24 & 1<=p172]]] | [[1<=p23 & 1<=p171] | [[1<=p27 & 1<=p173] | [1<=p29 & 1<=p174]]]] | [[[1<=p31 & 1<=p175] | [[1<=p30 & 1<=p175] | [1<=p25 & 1<=p172]]] | [[1<=p22 & 1<=p171] | [[1<=p20 & 1<=p170] | [1<=p28 & 1<=p174]]]]]]]]] | [AF [[EG [[[[[[[p17<=0 | p55<=0] & [[p16<=0 | p53<=0] & [p16<=0 | p55<=0]]] & [[p16<=0 | p51<=0] & [[p13<=0 | p54<=0] & [p13<=0 | p52<=0]]]] & [[[p13<=0 | p50<=0] & [[p17<=0 | p53<=0] & [p17<=0 | p51<=0]]] & [[p14<=0 | p51<=0] & [[p19<=0 | p54<=0] & [p14<=0 | p53<=0]]]]] & [[[[p19<=0 | p50<=0] & [[p14<=0 | p55<=0] & [p18<=0 | p50<=0]]] & [[p18<=0 | p52<=0] & [[p18<=0 | p54<=0] & [p15<=0 | p55<=0]]]] & [[[p15<=0 | p53<=0] & [[p15<=0 | p51<=0] & [p19<=0 | p52<=0]]] & [[p16<=0 | p52<=0] & [[p16<=0 | p54<=0] & [p16<=0 | p50<=0]]]]]] & [[[[[p13<=0 | p53<=0] & [[p13<=0 | p51<=0] & [p13<=0 | p55<=0]]] & [[p17<=0 | p50<=0] & [[p17<=0 | p54<=0] & [p17<=0 | p52<=0]]]] & [[[p19<=0 | p53<=0] & [[p14<=0 | p50<=0] & [p19<=0 | p55<=0]]] & [[p14<=0 | p52<=0] & [[p14<=0 | p54<=0] & [p18<=0 | p51<=0]]]]] & [[[[p18<=0 | p53<=0] & [[p18<=0 | p55<=0] & [p15<=0 | p54<=0]]] & [[p15<=0 | p52<=0] & [[p15<=0 | p50<=0] & [p19<=0 | p51<=0]]]] & [[[p7<=0 | p56<=0] & [[p8<=0 | p57<=0] & [p9<=0 | p58<=0]]] & [[p10<=0 | p59<=0] & [[p11<=0 | p60<=0] & [p12<=0 | p61<=0]]]]]]]] & [EF [[[[[[[p10<=0 | p33<=0] & [p10<=0 | p35<=0]] & [[p10<=0 | p37<=0] & [[p11<=0 | p37<=0] & [p9<=0 | p33<=0]]]] & [[[p11<=0 | p35<=0] & [p11<=0 | p33<=0]] & [[p9<=0 | p37<=0] & [[p6<=0 | p32<=0] & [p9<=0 | p35<=0]]]]] & [[[[p6<=0 | p34<=0] & [p6<=0 | p36<=0]] & [[p8<=0 | p36<=0] & [[p7<=0 | p34<=0] & [p7<=0 | p32<=0]]]] & [[[p7<=0 | p36<=0] & [[p8<=0 | p32<=0] & [p12<=0 | p35<=0]]] & [[p8<=0 | p34<=0] & [[p12<=0 | p37<=0] & [p12<=0 | p33<=0]]]]]] & [[[[[p10<=0 | p34<=0] & [p10<=0 | p36<=0]] & [[p6<=0 | p37<=0] & [[p11<=0 | p36<=0] & [p9<=0 | p32<=0]]]] & [[[p11<=0 | p34<=0] & [p11<=0 | p32<=0]] & [[p9<=0 | p36<=0] & [[p9<=0 | p34<=0] & [p6<=0 | p33<=0]]]]] & [[[[p6<=0 | p35<=0] & [p10<=0 | p32<=0]] & [[p8<=0 | p35<=0] & [[p8<=0 | p37<=0] & [p7<=0 | p35<=0]]]] & [[[p7<=0 | p33<=0] & [[p7<=0 | p37<=0] & [p12<=0 | p36<=0]]] & [[p8<=0 | p33<=0] & [[p12<=0 | p32<=0] & [p12<=0 | p34<=0]]]]]]]] & AG [[[[[[[p10<=0 | p33<=0] & [p10<=0 | p35<=0]] & [[p10<=0 | p37<=0] & [[p11<=0 | p37<=0] & [p9<=0 | p33<=0]]]] & [[[p11<=0 | p35<=0] & [p11<=0 | p33<=0]] & [[p9<=0 | p37<=0] & [[p6<=0 | p32<=0] & [p9<=0 | p35<=0]]]]] & [[[[p6<=0 | p34<=0] & [p6<=0 | p36<=0]] & [[p8<=0 | p36<=0] & [[p7<=0 | p34<=0] & [p7<=0 | p32<=0]]]] & [[[p7<=0 | p36<=0] & [[p8<=0 | p32<=0] & [p12<=0 | p35<=0]]] & [[p8<=0 | p34<=0] & [[p12<=0 | p37<=0] & [p12<=0 | p33<=0]]]]]] & [[[[[p10<=0 | p34<=0] & [p10<=0 | p36<=0]] & [[p6<=0 | p37<=0] & [[p11<=0 | p36<=0] & [p9<=0 | p32<=0]]]] & [[[p11<=0 | p34<=0] & [p11<=0 | p32<=0]] & [[p9<=0 | p36<=0] & [[p9<=0 | p34<=0] & [p6<=0 | p33<=0]]]]] & [[[[p6<=0 | p35<=0] & [p10<=0 | p32<=0]] & [[p8<=0 | p35<=0] & [[p8<=0 | p37<=0] & [p7<=0 | p35<=0]]]] & [[[p7<=0 | p33<=0] & [[p7<=0 | p37<=0] & [p12<=0 | p36<=0]]] & [[p8<=0 | p33<=0] & [[p12<=0 | p32<=0] & [p12<=0 | p34<=0]]]]]]]]]]] & EG [AF [[[[[p23<=0 | p39<=0] & [[p28<=0 | p42<=0] & [p26<=0 | p41<=0]]] & [[p31<=0 | p43<=0] & [[p25<=0 | p40<=0] & [p21<=0 | p38<=0]]]] & [[[p27<=0 | p41<=0] & [[p22<=0 | p39<=0] & [p30<=0 | p43<=0]]] & [[[p29<=0 | p42<=0] & [p20<=0 | p38<=0]] & [[p24<=0 | p40<=0] & [[[[1<=p2 & 1<=p24] | [[1<=p5 & 1<=p31] | [1<=p1 & 1<=p22]]] | [[1<=p3 & 1<=p27] | [[1<=p5 & 1<=p30] | [1<=p1 & 1<=p23]]]] | [[[1<=p3 & 1<=p26] | [[1<=p4 & 1<=p28] | [1<=p4 & 1<=p29]]] | [[1<=p0 & 1<=p21] | [[1<=p0 & 1<=p20] | [1<=p2 & 1<=p25]]]]]]]]]]]]]
normalized: [[EG [~ [EG [~ [[[[[[[[[[1<=p2 & 1<=p25] | [1<=p0 & 1<=p20]] | [1<=p0 & 1<=p21]] | [[[1<=p4 & 1<=p29] | [1<=p4 & 1<=p28]] | [1<=p3 & 1<=p26]]] | [[[[1<=p1 & 1<=p23] | [1<=p5 & 1<=p30]] | [1<=p3 & 1<=p27]] | [[[1<=p1 & 1<=p22] | [1<=p5 & 1<=p31]] | [1<=p2 & 1<=p24]]]] & [p24<=0 | p40<=0]] & [[p20<=0 | p38<=0] & [p29<=0 | p42<=0]]] & [[[p30<=0 | p43<=0] & [p22<=0 | p39<=0]] & [p27<=0 | p41<=0]]] & [[[[p21<=0 | p38<=0] & [p25<=0 | p40<=0]] & [p31<=0 | p43<=0]] & [[[p26<=0 | p41<=0] & [p28<=0 | p42<=0]] & [p23<=0 | p39<=0]]]]]]]] & ~ [EG [~ [[[~ [E [true U ~ [[[[[[[[p12<=0 | p34<=0] & [p12<=0 | p32<=0]] & [p8<=0 | p33<=0]] & [[[p12<=0 | p36<=0] & [p7<=0 | p37<=0]] & [p7<=0 | p33<=0]]] & [[[[p7<=0 | p35<=0] & [p8<=0 | p37<=0]] & [p8<=0 | p35<=0]] & [[p10<=0 | p32<=0] & [p6<=0 | p35<=0]]]] & [[[[[p6<=0 | p33<=0] & [p9<=0 | p34<=0]] & [p9<=0 | p36<=0]] & [[p11<=0 | p32<=0] & [p11<=0 | p34<=0]]] & [[[[p9<=0 | p32<=0] & [p11<=0 | p36<=0]] & [p6<=0 | p37<=0]] & [[p10<=0 | p36<=0] & [p10<=0 | p34<=0]]]]] & [[[[[[p12<=0 | p33<=0] & [p12<=0 | p37<=0]] & [p8<=0 | p34<=0]] & [[[p12<=0 | p35<=0] & [p8<=0 | p32<=0]] & [p7<=0 | p36<=0]]] & [[[[p7<=0 | p32<=0] & [p7<=0 | p34<=0]] & [p8<=0 | p36<=0]] & [[p6<=0 | p36<=0] & [p6<=0 | p34<=0]]]] & [[[[[p9<=0 | p35<=0] & [p6<=0 | p32<=0]] & [p9<=0 | p37<=0]] & [[p11<=0 | p33<=0] & [p11<=0 | p35<=0]]] & [[[[p9<=0 | p33<=0] & [p11<=0 | p37<=0]] & [p10<=0 | p37<=0]] & [[p10<=0 | p35<=0] & [p10<=0 | p33<=0]]]]]]]]] & E [true U [[[[[[[p12<=0 | p34<=0] & [p12<=0 | p32<=0]] & [p8<=0 | p33<=0]] & [[[p12<=0 | p36<=0] & [p7<=0 | p37<=0]] & [p7<=0 | p33<=0]]] & [[[[p7<=0 | p35<=0] & [p8<=0 | p37<=0]] & [p8<=0 | p35<=0]] & [[p10<=0 | p32<=0] & [p6<=0 | p35<=0]]]] & [[[[[p6<=0 | p33<=0] & [p9<=0 | p34<=0]] & [p9<=0 | p36<=0]] & [[p11<=0 | p32<=0] & [p11<=0 | p34<=0]]] & [[[[p9<=0 | p32<=0] & [p11<=0 | p36<=0]] & [p6<=0 | p37<=0]] & [[p10<=0 | p36<=0] & [p10<=0 | p34<=0]]]]] & [[[[[[p12<=0 | p33<=0] & [p12<=0 | p37<=0]] & [p8<=0 | p34<=0]] & [[[p12<=0 | p35<=0] & [p8<=0 | p32<=0]] & [p7<=0 | p36<=0]]] & [[[[p7<=0 | p32<=0] & [p7<=0 | p34<=0]] & [p8<=0 | p36<=0]] & [[p6<=0 | p36<=0] & [p6<=0 | p34<=0]]]] & [[[[[p9<=0 | p35<=0] & [p6<=0 | p32<=0]] & [p9<=0 | p37<=0]] & [[p11<=0 | p33<=0] & [p11<=0 | p35<=0]]] & [[[[p9<=0 | p33<=0] & [p11<=0 | p37<=0]] & [p10<=0 | p37<=0]] & [[p10<=0 | p35<=0] & [p10<=0 | p33<=0]]]]]]]] & EG [[[[[[[[p12<=0 | p61<=0] & [p11<=0 | p60<=0]] & [p10<=0 | p59<=0]] & [[[p9<=0 | p58<=0] & [p8<=0 | p57<=0]] & [p7<=0 | p56<=0]]] & [[[[p19<=0 | p51<=0] & [p15<=0 | p50<=0]] & [p15<=0 | p52<=0]] & [[[p15<=0 | p54<=0] & [p18<=0 | p55<=0]] & [p18<=0 | p53<=0]]]] & [[[[[p18<=0 | p51<=0] & [p14<=0 | p54<=0]] & [p14<=0 | p52<=0]] & [[[p19<=0 | p55<=0] & [p14<=0 | p50<=0]] & [p19<=0 | p53<=0]]] & [[[[p17<=0 | p52<=0] & [p17<=0 | p54<=0]] & [p17<=0 | p50<=0]] & [[[p13<=0 | p55<=0] & [p13<=0 | p51<=0]] & [p13<=0 | p53<=0]]]]] & [[[[[[p16<=0 | p50<=0] & [p16<=0 | p54<=0]] & [p16<=0 | p52<=0]] & [[[p19<=0 | p52<=0] & [p15<=0 | p51<=0]] & [p15<=0 | p53<=0]]] & [[[[p15<=0 | p55<=0] & [p18<=0 | p54<=0]] & [p18<=0 | p52<=0]] & [[[p18<=0 | p50<=0] & [p14<=0 | p55<=0]] & [p19<=0 | p50<=0]]]] & [[[[[p14<=0 | p53<=0] & [p19<=0 | p54<=0]] & [p14<=0 | p51<=0]] & [[[p17<=0 | p51<=0] & [p17<=0 | p53<=0]] & [p13<=0 | p50<=0]]] & [[[[p13<=0 | p52<=0] & [p13<=0 | p54<=0]] & [p16<=0 | p51<=0]] & [[[p16<=0 | p55<=0] & [p16<=0 | p53<=0]] & [p17<=0 | p55<=0]]]]]]]]]]]] | EG [~ [EG [~ [[[[[[[[1<=p28 & 1<=p174] | [1<=p20 & 1<=p170]] | [1<=p22 & 1<=p171]] | [[[1<=p25 & 1<=p172] | [1<=p30 & 1<=p175]] | [1<=p31 & 1<=p175]]] | [[[[1<=p29 & 1<=p174] | [1<=p27 & 1<=p173]] | [1<=p23 & 1<=p171]] | [[[1<=p24 & 1<=p172] | [1<=p26 & 1<=p173]] | [1<=p21 & 1<=p170]]]] & [[[[[[[1<=p15 & 1<=p44] | [1<=p15 & 1<=p45]] | [1<=p15 & 1<=p46]] | [[1<=p15 & 1<=p47] | [1<=p15 & 1<=p48]]] | [[[1<=p15 & 1<=p49] | [1<=p14 & 1<=p49]] | [[1<=p14 & 1<=p47] | [1<=p14 & 1<=p48]]]] | [[[[[1<=p18 & 1<=p49] | [1<=p14 & 1<=p45]] | [1<=p14 & 1<=p46]] | [[1<=p19 & 1<=p44] | [1<=p18 & 1<=p47]]] | [[[1<=p19 & 1<=p45] | [1<=p18 & 1<=p48]] | [[1<=p14 & 1<=p44] | [1<=p19 & 1<=p46]]]]] | [[[[[[1<=p18 & 1<=p45] | [1<=p19 & 1<=p47]] | [1<=p18 & 1<=p46]] | [[1<=p19 & 1<=p48] | [1<=p19 & 1<=p49]]] | [[[1<=p18 & 1<=p44] | [1<=p17 & 1<=p48]] | [[1<=p17 & 1<=p49] | [1<=p17 & 1<=p44]]]] | [[[[[1<=p17 & 1<=p45] | [1<=p17 & 1<=p46]] | [1<=p17 & 1<=p47]] | [[1<=p16 & 1<=p49] | [1<=p16 & 1<=p44]]] | [[[1<=p16 & 1<=p47] | [1<=p16 & 1<=p48]] | [[1<=p16 & 1<=p45] | [1<=p16 & 1<=p46]]]]]]] & E [[[[[[1<=p2 & 1<=p25] | [1<=p0 & 1<=p20]] | [1<=p0 & 1<=p21]] | [[[1<=p4 & 1<=p29] | [1<=p4 & 1<=p28]] | [1<=p3 & 1<=p26]]] | [[[[1<=p1 & 1<=p23] | [1<=p5 & 1<=p30]] | [1<=p3 & 1<=p27]] | [[[1<=p1 & 1<=p22] | [1<=p5 & 1<=p31]] | [1<=p2 & 1<=p24]]]] U [[[[[[[1<=p20 & [1<=p98 & 1<=p114]] | [1<=p20 & [1<=p80 & 1<=p111]]] | [1<=p30 & [1<=p109 & 1<=p115]]] | [[1<=p30 & [1<=p91 & 1<=p112]] | [1<=p22 & [1<=p87 & 1<=p112]]]] | [[[1<=p24 & [1<=p76 & 1<=p110]] | [1<=p28 & [1<=p102 & 1<=p114]]] | [[1<=p28 & [1<=p84 & 1<=p111]] | [1<=p26 & [1<=p77 & 1<=p110]]]]] | [[[[[1<=p24 & [1<=p94 & 1<=p113]] | [1<=p24 & [1<=p88 & 1<=p112]]] | [1<=p26 & [1<=p95 & 1<=p113]]] | [[1<=p22 & [1<=p81 & 1<=p111]] | [1<=p20 & [1<=p92 & 1<=p113]]]] | [[[1<=p26 & [1<=p101 & 1<=p114]] | [1<=p22 & [1<=p75 & 1<=p110]]] | [[1<=p28 & [1<=p78 & 1<=p110]] | [1<=p22 & [1<=p105 & 1<=p115]]]]]] | [[[[[[1<=p28 & [1<=p108 & 1<=p115]] | [1<=p26 & [1<=p107 & 1<=p115]]] | [1<=p26 & [1<=p89 & 1<=p112]]] | [[1<=p28 & [1<=p96 & 1<=p113]] | [1<=p30 & [1<=p85 & 1<=p111]]]] | [[[1<=p24 & [1<=p82 & 1<=p111]] | [1<=p30 & [1<=p97 & 1<=p113]]] | [[1<=p20 & [1<=p104 & 1<=p115]] | [1<=p22 & [1<=p99 & 1<=p114]]]]] | [[[[[1<=p20 & [1<=p74 & 1<=p110]] | [1<=p24 & [1<=p106 & 1<=p115]]] | [1<=p30 & [1<=p79 & 1<=p110]]] | [[1<=p20 & [1<=p86 & 1<=p112]] | [1<=p28 & [1<=p90 & 1<=p112]]]] | [[[1<=p30 & [1<=p103 & 1<=p114]] | [1<=p22 & [1<=p93 & 1<=p113]]] | [[1<=p24 & [1<=p100 & 1<=p114]] | [1<=p26 & [1<=p83 & 1<=p111]]]]]]]]]]]]]]
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p83)
states: 200,549,728,448 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p100)
states: 200,549,728,448 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p93)
states: 200,549,728,448 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p103)
states: 200,549,728,448 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p90)
states: 200,549,728,448 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p86)
states: 200,549,728,448 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p79)
states: 200,549,728,448 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p106)
states: 200,549,728,448 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p74)
states: 197,739,387,520 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p99)
states: 200,549,728,448 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p104)
states: 200,549,728,448 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p97)
states: 200,549,728,448 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p82)
states: 200,549,728,448 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p85)
states: 200,549,728,448 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p96)
states: 200,549,728,448 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p89)
states: 200,549,728,448 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p107)
states: 200,549,728,448 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p108)
states: 200,549,728,448 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p105)
states: 200,549,728,448 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p78)
states: 200,549,728,448 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p75)
states: 200,549,728,448 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p101)
states: 200,549,728,448 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p92)
states: 200,549,728,448 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p81)
states: 197,739,387,520 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p95)
states: 197,739,387,520 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p88)
states: 197,739,387,520 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p113)
states: 395,478,775,040 (11)
abstracting: (1<=p94)
states: 200,549,728,448 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p77)
states: 200,549,728,448 (11)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p84)
states: 200,549,728,448 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p102)
states: 197,739,387,520 (11)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p110)
states: 395,478,775,040 (11)
abstracting: (1<=p76)
states: 200,549,728,448 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p87)
states: 200,549,728,448 (11)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p112)
states: 395,478,775,040 (11)
abstracting: (1<=p91)
states: 200,549,728,448 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p115)
states: 395,478,775,040 (11)
abstracting: (1<=p109)
states: 197,739,387,520 (11)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p111)
states: 395,478,775,040 (11)
abstracting: (1<=p80)
before gc: list nodes free: 3032113
after gc: idd nodes used:41154577, unused:22845423; list nodes free:102995308
states: 200,549,728,448 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p114)
states: 395,478,775,040 (11)
abstracting: (1<=p98)
states: 200,549,728,448 (11)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p24)
states: 448,316,917,822 (11)
abstracting: (1<=p2)
states: 17,782,896,448 (10)
abstracting: (1<=p31)
states: 98,914,841,322 (10)
abstracting: (1<=p5)
states: 17,782,896,448 (10)
abstracting: (1<=p22)
states: 448,316,917,822 (11)
abstracting: (1<=p1)
states: 17,782,896,448 (10)
abstracting: (1<=p27)
states: 98,914,841,322 (10)
abstracting: (1<=p3)
states: 17,782,896,448 (10)
abstracting: (1<=p30)
states: 448,316,917,822 (11)
abstracting: (1<=p5)
states: 17,782,896,448 (10)
abstracting: (1<=p23)
states: 98,914,841,322 (10)
abstracting: (1<=p1)
states: 17,782,896,448 (10)
abstracting: (1<=p26)
states: 448,316,917,822 (11)
abstracting: (1<=p3)
states: 17,782,896,448 (10)
abstracting: (1<=p28)
states: 448,316,917,822 (11)
abstracting: (1<=p4)
states: 17,782,896,448 (10)
abstracting: (1<=p29)
states: 98,914,841,322 (10)
abstracting: (1<=p4)
states: 17,782,896,448 (10)
abstracting: (1<=p21)
states: 98,914,841,322 (10)
abstracting: (1<=p0)
states: 17,782,896,448 (10)
abstracting: (1<=p20)
states: 448,316,917,822 (11)
abstracting: (1<=p0)
states: 17,782,896,448 (10)
abstracting: (1<=p25)
states: 98,914,841,322 (10)
abstracting: (1<=p2)
states: 17,782,896,448 (10)
TIME LIMIT: Killed by timeout after 3600 seconds
MemTotal: 16393232 kB
MemFree: 6026124 kB
After kill :
MemTotal: 16393232 kB
MemFree: 16094736 kB
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.003sec
17406 42594 80908 97493 104734 106984 98428 113376 122843 186762 321066 311846 297312 302898 591222 635250 743412 780462 769232 795640 858564 832386 704655 702524 718554
iterations count:2573905 (7270), effective:37534 (106)
initing FirstDep: 0m 0.000sec
sat_reach.icc:155: Timeout: after 142 sec
net_ddint.h:442: Timeout: after 132 sec
net_ddint.h:600: Timeout: after 123 sec
sat_reach.icc:155: Timeout: after 115 sec
sat_reach.icc:155: Timeout: after 107 sec
sat_reach.icc:155: Timeout: after 100 sec
net_ddint.h:600: Timeout: after 93 sec
sat_reach.icc:155: Timeout: after 87 sec
sat_reach.icc:155: Timeout: after 81 sec
sat_reach.icc:155: Timeout: after 76 sec
net_ddint.h:600: Timeout: after 70 sec
sat_reach.icc:155: Timeout: after 66 sec
net_ddint.h:600: Timeout: after 61 sec
net_ddint.h:600: Timeout: after 57 sec
sat_reach.icc:155: Timeout: after 53 sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="LamportFastMutEx-COL-6"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is LamportFastMutEx-COL-6, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r234-tall-167856420200370"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/LamportFastMutEx-COL-6.tgz
mv LamportFastMutEx-COL-6 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

