About the Execution of Marcie for LamportFastMutEx-PT-2
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5449.411 | 6764.00 | 6929.00 | 70.50 | TFTFTFFFTFTFTTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
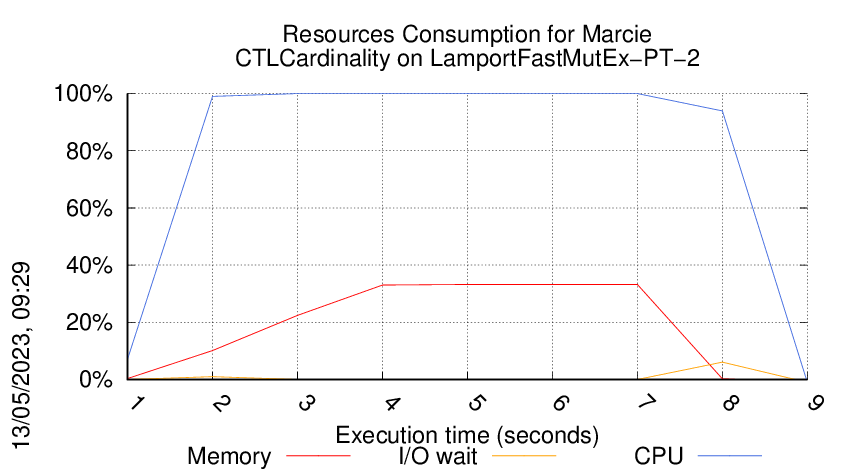
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r225-tall-167856407500393.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marcie
Input is LamportFastMutEx-PT-2, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r225-tall-167856407500393
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 708K
-rw-r--r-- 1 mcc users 13K Feb 25 13:42 CTLCardinality.txt
-rw-r--r-- 1 mcc users 103K Feb 25 13:42 CTLCardinality.xml
-rw-r--r-- 1 mcc users 12K Feb 25 13:42 CTLFireability.txt
-rw-r--r-- 1 mcc users 75K Feb 25 13:42 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.6K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 5.7K Feb 25 16:20 LTLCardinality.txt
-rw-r--r-- 1 mcc users 31K Feb 25 16:20 LTLCardinality.xml
-rw-r--r-- 1 mcc users 4.9K Feb 25 16:20 LTLFireability.txt
-rw-r--r-- 1 mcc users 26K Feb 25 16:20 LTLFireability.xml
-rw-r--r-- 1 mcc users 20K Feb 25 13:43 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 154K Feb 25 13:43 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 21K Feb 25 13:42 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 133K Feb 25 13:42 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 2.2K Feb 25 16:20 UpperBounds.txt
-rw-r--r-- 1 mcc users 4.8K Feb 25 16:20 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 equiv_col
-rw-r--r-- 1 mcc users 2 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 iscolored
-rw-r--r-- 1 mcc users 48K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-00
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-01
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-02
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-03
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-04
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-05
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-06
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-07
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-08
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-09
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-10
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-11
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-12
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-13
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-14
FORMULA_NAME LamportFastMutEx-PT-2-CTLCardinality-15
=== Now, execution of the tool begins
BK_START 1678622423588
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marcie
BK_EXAMINATION=CTLCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=LamportFastMutEx-PT-2
Not applying reductions.
Model is PT
CTLCardinality PT
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: LamportFastMutEx_PT_2
(NrP: 69 NrTr: 96 NrArc: 402)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 2.899sec
RS generation: 0m 0.018sec
-> reachability set: #nodes 687 (6.9e+02) #states 380
starting MCC model checker
--------------------------
checking: EF [P_wait_2_0<=0]
normalized: E [true U P_wait_2_0<=0]
abstracting: (P_wait_2_0<=0)
states: 380
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.012sec
checking: ~ [AG [~ [sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=67]]]
normalized: E [true U sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=67]
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=67)
states: 380
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-00 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.022sec
checking: EX [~ [AX [EF [~ [22<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]]]]]
normalized: EX [EX [~ [E [true U ~ [22<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]]]]]
abstracting: (22<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0))
states: 0
..-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-05 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.022sec
checking: EF [A [P_awaity_1<=1 U EF [[~ [1<=P_start_1_1] & A [1<=P_await_13_2 U 1<=P_setbi_5_1]]]]]
normalized: E [true U [~ [EG [~ [E [true U [[~ [EG [~ [1<=P_setbi_5_1]]] & ~ [E [~ [1<=P_setbi_5_1] U [~ [1<=P_await_13_2] & ~ [1<=P_setbi_5_1]]]]] & ~ [1<=P_start_1_1]]]]]] & ~ [E [~ [E [true U [[~ [EG [~ [1<=P_setbi_5_1]]] & ~ [E [~ [1<=P_setbi_5_1] U [~ [1<=P_await_13_2] & ~ [1<=P_setbi_5_1]]]]] & ~ [1<=P_start_1_1]]]] U [~ [P_awaity_1<=1] & ~ [E [true U [[~ [EG [~ [1<=P_setbi_5_1]]] & ~ [E [~ [1<=P_setbi_5_1] U [~ [1<=P_await_13_2] & ~ [1<=P_setbi_5_1]]]]] & ~ [1<=P_start_1_1]]]]]]]]]
abstracting: (1<=P_start_1_1)
states: 36
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_await_13_2)
states: 56
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_setbi_5_1)
states: 21
.......
EG iterations: 7
abstracting: (P_awaity_1<=1)
states: 380
abstracting: (1<=P_start_1_1)
states: 36
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_await_13_2)
states: 56
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_setbi_5_1)
states: 21
.......
EG iterations: 7
abstracting: (1<=P_start_1_1)
states: 36
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_await_13_2)
states: 56
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (1<=P_setbi_5_1)
states: 21
.......
EG iterations: 7
.
EG iterations: 1
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.061sec
checking: AG [E [EX [1<=P_fordo_12_1] U E [EX [P_CS_21_0<=P_wait_2_0] U A [~ [1<=P_b_2_false] U EG [P_setbi_5_2<=1]]]]]
normalized: ~ [E [true U ~ [E [EX [1<=P_fordo_12_1] U E [EX [P_CS_21_0<=P_wait_2_0] U [~ [EG [~ [EG [P_setbi_5_2<=1]]]] & ~ [E [~ [EG [P_setbi_5_2<=1]] U [~ [EG [P_setbi_5_2<=1]] & 1<=P_b_2_false]]]]]]]]]
abstracting: (1<=P_b_2_false)
states: 155
abstracting: (P_setbi_5_2<=1)
states: 380
EG iterations: 0
abstracting: (P_setbi_5_2<=1)
states: 380
EG iterations: 0
abstracting: (P_setbi_5_2<=1)
states: 380
EG iterations: 0
.
EG iterations: 1
abstracting: (P_CS_21_0<=P_wait_2_0)
states: 380
.abstracting: (1<=P_fordo_12_1)
states: 16
.-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-08 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.003sec
checking: E [EX [AF [P_wait_0_1<=P_awaity_1]] U EX [AG [AG [[P_wait_2_1<=P_wait_0_2 & 1<=P_ifyi_15_1]]]]]
normalized: E [EX [~ [EG [~ [P_wait_0_1<=P_awaity_1]]]] U EX [~ [E [true U E [true U ~ [[P_wait_2_1<=P_wait_0_2 & 1<=P_ifyi_15_1]]]]]]]
abstracting: (1<=P_ifyi_15_1)
states: 12
abstracting: (P_wait_2_1<=P_wait_0_2)
states: 348
.abstracting: (P_wait_0_1<=P_awaity_1)
states: 380
.
EG iterations: 1
.-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.003sec
checking: E [1<=P_CS_21_0 U ~ [[AG [[EG [P_fordo_12_1<=P_wait_2_0] | EG [P_b_0_true<=0]]] & [EF [~ [[P_start_1_0<=0 & P_done_0_0<=0]]] | EF [AX [1<=P_setx_3_0]]]]]]
normalized: E [1<=P_CS_21_0 U ~ [[[E [true U ~ [EX [~ [1<=P_setx_3_0]]]] | E [true U ~ [[P_start_1_0<=0 & P_done_0_0<=0]]]] & ~ [E [true U ~ [[EG [P_b_0_true<=0] | EG [P_fordo_12_1<=P_wait_2_0]]]]]]]]
abstracting: (P_fordo_12_1<=P_wait_2_0)
states: 364
........
EG iterations: 8
abstracting: (P_b_0_true<=0)
states: 380
EG iterations: 0
abstracting: (P_done_0_0<=0)
states: 380
abstracting: (P_start_1_0<=0)
states: 380
abstracting: (1<=P_setx_3_0)
states: 0
.abstracting: (1<=P_CS_21_0)
states: 0
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.014sec
checking: EX [EX [[[AG [P_fordo_12_2<=P_sety_9_1] | AX [[1<=P_sety_9_0 & P_done_2_1<=P_awaity_2]]] & P_awaity_0<=P_setbi_11_0]]]
normalized: EX [EX [[[~ [EX [~ [[1<=P_sety_9_0 & P_done_2_1<=P_awaity_2]]]] | ~ [E [true U ~ [P_fordo_12_2<=P_sety_9_1]]]] & P_awaity_0<=P_setbi_11_0]]]
abstracting: (P_awaity_0<=P_setbi_11_0)
states: 380
abstracting: (P_fordo_12_2<=P_sety_9_1)
states: 366
abstracting: (P_done_2_1<=P_awaity_2)
states: 356
abstracting: (1<=P_sety_9_0)
states: 0
...-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-15 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.019sec
checking: AX [[[[AX [[EX [P_setbi_11_0<=P_setbi_5_2] | A [P_ifyi_15_1<=P_CS_21_0 U P_ifyi_15_0<=x_2]]] | AF [P_setx_3_2<=P_ifxi_10_2]] | E [[EF [1<=P_b_2_true] | AF [P_ify0_4_2<=1]] U [P_ify0_4_1<=P_ify0_4_0 & ~ [EX [x_0<=P_setbi_24_1]]]]] & ~ [A [AX [P_fordo_12_1<=0] U ~ [P_start_1_1<=0]]]]]
normalized: ~ [EX [~ [[~ [[~ [EG [P_start_1_1<=0]] & ~ [E [P_start_1_1<=0 U [EX [~ [P_fordo_12_1<=0]] & P_start_1_1<=0]]]]] & [E [[~ [EG [~ [P_ify0_4_2<=1]]] | E [true U 1<=P_b_2_true]] U [~ [EX [x_0<=P_setbi_24_1]] & P_ify0_4_1<=P_ify0_4_0]] | [~ [EG [~ [P_setx_3_2<=P_ifxi_10_2]]] | ~ [EX [~ [[[~ [EG [~ [P_ifyi_15_0<=x_2]]] & ~ [E [~ [P_ifyi_15_0<=x_2] U [~ [P_ifyi_15_1<=P_CS_21_0] & ~ [P_ifyi_15_0<=x_2]]]]] | EX [P_setbi_11_0<=P_setbi_5_2]]]]]]]]]]]
abstracting: (P_setbi_11_0<=P_setbi_5_2)
states: 380
.abstracting: (P_ifyi_15_0<=x_2)
states: 380
abstracting: (P_ifyi_15_1<=P_CS_21_0)
states: 368
abstracting: (P_ifyi_15_0<=x_2)
states: 380
abstracting: (P_ifyi_15_0<=x_2)
states: 380
.
EG iterations: 1
.abstracting: (P_setx_3_2<=P_ifxi_10_2)
states: 344
........
EG iterations: 8
abstracting: (P_ify0_4_1<=P_ify0_4_0)
states: 347
abstracting: (x_0<=P_setbi_24_1)
states: 376
.abstracting: (1<=P_b_2_true)
states: 225
abstracting: (P_ify0_4_2<=1)
states: 380
.
EG iterations: 1
abstracting: (P_start_1_1<=0)
states: 344
abstracting: (P_fordo_12_1<=0)
states: 364
.abstracting: (P_start_1_1<=0)
states: 344
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
.-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-09 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.046sec
checking: EG [A [EX [[~ [sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)] | sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]] U 65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]
normalized: EG [[~ [EG [~ [65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]] & ~ [E [~ [65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)] U [~ [EX [[~ [sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)] | sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]] & ~ [65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]]]
abstracting: (65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 352
abstracting: (sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0))
states: 306
.abstracting: (65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
abstracting: (65<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
EG iterations: 0
.
EG iterations: 1
-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-03 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.081sec
checking: EF [[EG [[AG [E [30<=sum(y_2, y_1, y_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)]] & sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=6]] | AF [A [EF [10<=sum(P_start_1_2, P_start_1_1, P_start_1_0)] U ~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58]]]]]
normalized: E [true U [~ [EG [~ [[~ [EG [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58]] & ~ [E [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58 U [~ [E [true U 10<=sum(P_start_1_2, P_start_1_1, P_start_1_0)]] & sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58]]]]]]] | EG [[~ [E [true U ~ [E [30<=sum(y_2, y_1, y_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)]]]] & sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=6]]]]
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=6)
states: 380
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0))
states: 340
abstracting: (30<=sum(y_2, y_1, y_0))
states: 0
.
EG iterations: 1
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58)
states: 380
abstracting: (10<=sum(P_start_1_2, P_start_1_1, P_start_1_0))
states: 0
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58)
states: 380
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=58)
states: 380
EG iterations: 0
EG iterations: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-01 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.131sec
checking: A [[[[[P_done_0_2<=0 | ~ [[P_done_0_1<=1 & ~ [1<=P_setbi_5_1]]]] | A [[EG [P_b_0_false<=P_wait_2_1] | EG [1<=P_done_0_1]] U [E [P_setbi_24_2<=0 U P_ifxi_10_2<=1] | EG [P_done_2_2<=P_setbi_5_1]]]] & [AF [[[1<=P_setbi_24_2 & P_await_13_2<=1] & [P_ifxi_10_1<=P_b_2_true & 1<=P_sety_9_2]]] & [EF [~ [1<=P_start_1_2]] | [~ [AX [P_ify0_4_0<=P_await_13_0]] & P_ifxi_10_0<=P_wait_1_2]]]] | P_ifxi_10_0<=0] U [A [EF [~ [[P_b_2_true<=1 & 1<=P_start_1_2]]] U EF [1<=P_awaity_2]] | [E [P_setx_3_1<=1 U P_setbi_24_0<=0] & A [1<=P_done_0_1 U [1<=P_awaity_1 | EG [P_start_1_1<=0]]]]]]
normalized: [~ [EG [~ [[[[~ [EG [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]] & ~ [E [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]] U [~ [1<=P_done_0_1] & ~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]]]] & E [P_setx_3_1<=1 U P_setbi_24_0<=0]] | [~ [EG [~ [E [true U 1<=P_awaity_2]]]] & ~ [E [~ [E [true U 1<=P_awaity_2]] U [~ [E [true U ~ [[P_b_2_true<=1 & 1<=P_start_1_2]]]] & ~ [E [true U 1<=P_awaity_2]]]]]]]]]] & ~ [E [~ [[[[~ [EG [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]] & ~ [E [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]] U [~ [1<=P_done_0_1] & ~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]]]] & E [P_setx_3_1<=1 U P_setbi_24_0<=0]] | [~ [EG [~ [E [true U 1<=P_awaity_2]]]] & ~ [E [~ [E [true U 1<=P_awaity_2]] U [~ [E [true U ~ [[P_b_2_true<=1 & 1<=P_start_1_2]]]] & ~ [E [true U 1<=P_awaity_2]]]]]]]] U [~ [[[[[[EX [~ [P_ify0_4_0<=P_await_13_0]] & P_ifxi_10_0<=P_wait_1_2] | E [true U ~ [1<=P_start_1_2]]] & ~ [EG [~ [[[P_ifxi_10_1<=P_b_2_true & 1<=P_sety_9_2] & [1<=P_setbi_24_2 & P_await_13_2<=1]]]]]] & [[~ [EG [~ [[EG [P_done_2_2<=P_setbi_5_1] | E [P_setbi_24_2<=0 U P_ifxi_10_2<=1]]]]] & ~ [E [~ [[EG [P_done_2_2<=P_setbi_5_1] | E [P_setbi_24_2<=0 U P_ifxi_10_2<=1]]] U [~ [[EG [1<=P_done_0_1] | EG [P_b_0_false<=P_wait_2_1]]] & ~ [[EG [P_done_2_2<=P_setbi_5_1] | E [P_setbi_24_2<=0 U P_ifxi_10_2<=1]]]]]]] | [~ [[~ [1<=P_setbi_5_1] & P_done_0_1<=1]] | P_done_0_2<=0]]] | P_ifxi_10_0<=0]] & ~ [[[[~ [EG [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]] & ~ [E [~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]] U [~ [1<=P_done_0_1] & ~ [[EG [P_start_1_1<=0] | 1<=P_awaity_1]]]]]] & E [P_setx_3_1<=1 U P_setbi_24_0<=0]] | [~ [EG [~ [E [true U 1<=P_awaity_2]]]] & ~ [E [~ [E [true U 1<=P_awaity_2]] U [~ [E [true U ~ [[P_b_2_true<=1 & 1<=P_start_1_2]]]] & ~ [E [true U 1<=P_awaity_2]]]]]]]]]]]]
abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_start_1_2)
states: 36
abstracting: (P_b_2_true<=1)
states: 380
abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_awaity_2)
states: 21
.
EG iterations: 1
abstracting: (P_setbi_24_0<=0)
states: 380
abstracting: (P_setx_3_1<=1)
states: 380
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_done_0_1)
states: 0
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
.
EG iterations: 1
abstracting: (P_ifxi_10_0<=0)
states: 380
abstracting: (P_done_0_2<=0)
states: 380
abstracting: (P_done_0_1<=1)
states: 380
abstracting: (1<=P_setbi_5_1)
states: 21
abstracting: (P_ifxi_10_2<=1)
states: 380
abstracting: (P_setbi_24_2<=0)
states: 341
abstracting: (P_done_2_2<=P_setbi_5_1)
states: 354
.........
EG iterations: 9
abstracting: (P_b_0_false<=P_wait_2_1)
states: 380
EG iterations: 0
abstracting: (1<=P_done_0_1)
states: 0
.
EG iterations: 1
abstracting: (P_ifxi_10_2<=1)
states: 380
abstracting: (P_setbi_24_2<=0)
states: 341
abstracting: (P_done_2_2<=P_setbi_5_1)
states: 354
.........
EG iterations: 9
abstracting: (P_ifxi_10_2<=1)
states: 380
abstracting: (P_setbi_24_2<=0)
states: 341
abstracting: (P_done_2_2<=P_setbi_5_1)
states: 354
.........
EG iterations: 9
.
EG iterations: 1
abstracting: (P_await_13_2<=1)
states: 380
abstracting: (1<=P_setbi_24_2)
states: 39
abstracting: (1<=P_sety_9_2)
states: 28
abstracting: (P_ifxi_10_1<=P_b_2_true)
states: 365
EG iterations: 0
abstracting: (1<=P_start_1_2)
states: 36
abstracting: (P_ifxi_10_0<=P_wait_1_2)
states: 380
abstracting: (P_ify0_4_0<=P_await_13_0)
states: 380
.abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_start_1_2)
states: 36
abstracting: (P_b_2_true<=1)
states: 380
abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_awaity_2)
states: 21
.
EG iterations: 1
abstracting: (P_setbi_24_0<=0)
states: 380
abstracting: (P_setx_3_1<=1)
states: 380
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_done_0_1)
states: 0
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
.
EG iterations: 1
abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_start_1_2)
states: 36
abstracting: (P_b_2_true<=1)
states: 380
abstracting: (1<=P_awaity_2)
states: 21
abstracting: (1<=P_awaity_2)
states: 21
.
EG iterations: 1
abstracting: (P_setbi_24_0<=0)
states: 380
abstracting: (P_setx_3_1<=1)
states: 380
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_done_0_1)
states: 0
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
abstracting: (1<=P_awaity_1)
states: 21
abstracting: (P_start_1_1<=0)
states: 344
...........
EG iterations: 11
.
EG iterations: 1
.
EG iterations: 1
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.089sec
checking: AG [[[E [A [[sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=100 & sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] U [40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(x_2, x_1, x_0)<=69]] U [~ [[sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=69 & sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]] | [AX [21<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)] & [sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0) | 13<=sum(P_await_13_2, P_await_13_1, P_await_13_0)]]]] & EG [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]] & 23<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]]
normalized: ~ [E [true U ~ [[[EG [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] & E [[~ [EG [~ [[40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(x_2, x_1, x_0)<=69]]]] & ~ [E [~ [[40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(x_2, x_1, x_0)<=69]] U [~ [[sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=100 & sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]] & ~ [[40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(x_2, x_1, x_0)<=69]]]]]] U [[[sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0) | 13<=sum(P_await_13_2, P_await_13_1, P_await_13_0)] & ~ [EX [~ [21<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]] | ~ [[sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=69 & sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]]]] & 23<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]]]]
abstracting: (23<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0))
states: 0
abstracting: (sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 380
abstracting: (sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)<=69)
states: 380
abstracting: (21<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
.abstracting: (13<=sum(P_await_13_2, P_await_13_1, P_await_13_0))
states: 0
abstracting: (sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0))
states: 58
abstracting: (sum(x_2, x_1, x_0)<=69)
states: 380
abstracting: (40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0))
states: 0
abstracting: (sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 0
abstracting: (sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=100)
states: 380
abstracting: (sum(x_2, x_1, x_0)<=69)
states: 380
abstracting: (40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0))
states: 0
abstracting: (sum(x_2, x_1, x_0)<=69)
states: 380
abstracting: (40<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0))
states: 0
EG iterations: 0
abstracting: (sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 318
..................
EG iterations: 18
-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-06 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.308sec
checking: [~ [AF [33<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]] | [[[AF [~ [AG [19<=sum(P_awaity_2, P_awaity_1, P_awaity_0)]]] | A [[74<=sum(x_2, x_1, x_0) & ~ [39<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)]] U EG [E [73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0)]]]] | AG [E [[sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false) | ~ [sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_start_1_2, P_start_1_1, P_start_1_0)]] U sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=91]]] & [[EF [AF [AF [97<=sum(P_start_1_2, P_start_1_1, P_start_1_0)]]] | EG [~ [sum(x_2, x_1, x_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)]]] & ~ [[EF [60<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)] | EG [[[sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=14 | 89<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] & [sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | 43<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]]]]]]]]
normalized: [[[~ [[EG [[[sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=14 | 89<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] & [sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | 43<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]]] | E [true U 60<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]] & [EG [~ [sum(x_2, x_1, x_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)]] | E [true U ~ [EG [EG [~ [97<=sum(P_start_1_2, P_start_1_1, P_start_1_0)]]]]]]] & [~ [E [true U ~ [E [[sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false) | ~ [sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_start_1_2, P_start_1_1, P_start_1_0)]] U sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=91]]]] | [[~ [EG [~ [EG [E [73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0)]]]]] & ~ [E [~ [EG [E [73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0)]]] U [~ [[74<=sum(x_2, x_1, x_0) & ~ [39<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)]]] & ~ [EG [E [73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) U sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0)]]]]]]] | ~ [EG [~ [E [true U ~ [19<=sum(P_awaity_2, P_awaity_1, P_awaity_0)]]]]]]]] | EG [~ [33<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]]]
abstracting: (33<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0))
states: 0
EG iterations: 0
abstracting: (19<=sum(P_awaity_2, P_awaity_1, P_awaity_0))
states: 0
.
EG iterations: 1
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0))
states: 380
abstracting: (73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0))
states: 0
EG iterations: 0
abstracting: (39<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0))
states: 0
abstracting: (74<=sum(x_2, x_1, x_0))
states: 0
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0))
states: 380
abstracting: (73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0))
states: 0
EG iterations: 0
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(x_2, x_1, x_0))
states: 380
abstracting: (73<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0))
states: 0
EG iterations: 0
.
EG iterations: 1
abstracting: (sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=91)
states: 380
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_start_1_2, P_start_1_1, P_start_1_0))
states: 342
abstracting: (sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 380
abstracting: (97<=sum(P_start_1_2, P_start_1_1, P_start_1_0))
states: 0
EG iterations: 0
EG iterations: 0
abstracting: (sum(x_2, x_1, x_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0))
states: 69
..................
EG iterations: 18
abstracting: (60<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
abstracting: (43<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0))
states: 0
abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0))
states: 380
abstracting: (89<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 0
abstracting: (sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=14)
states: 380
EG iterations: 0
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-04 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.379sec
checking: [[A [EX [[sum(P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) & [~ [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=30] & [sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) & sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=77]]]] U [AX [AG [33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]] | [~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28] | [~ [AX [54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]] & sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96]]]] & EF [[[sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & AG [~ [sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=11]]] | ~ [AF [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]]]]] & EF [~ [[A [[EG [52<=sum(x_2, x_1, x_0)] & ~ [sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=1]] U ~ [73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]] & ~ [[sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=7]]]]]]
normalized: [E [true U ~ [[~ [[sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=7]] & [~ [EG [73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]] & ~ [E [73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) U [73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) & ~ [[~ [sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=1] & EG [52<=sum(x_2, x_1, x_0)]]]]]]]]]] & [E [true U [EG [~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)]] | [sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & ~ [E [true U sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=11]]]]] & [~ [EG [~ [[[[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96 & EX [~ [54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]] | ~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28]] | ~ [EX [E [true U ~ [33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]]]]]]] & ~ [E [~ [[[[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96 & EX [~ [54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]] | ~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28]] | ~ [EX [E [true U ~ [33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]]]]] U [~ [EX [[sum(P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) & [[sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) & sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=77] & ~ [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=30]]]]] & ~ [[[[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96 & EX [~ [54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]] | ~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28]] | ~ [EX [E [true U ~ [33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]]]]]]]]]]]
abstracting: (33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 0
.abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28)
states: 380
abstracting: (54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 0
.abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96)
states: 380
abstracting: (sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=30)
states: 380
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=77)
states: 380
abstracting: (sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0))
states: 308
abstracting: (sum(P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0))
states: 315
.abstracting: (33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 0
.abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28)
states: 380
abstracting: (54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 0
.abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96)
states: 380
abstracting: (33<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 0
.abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=28)
states: 380
abstracting: (54<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 0
.abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=96)
states: 380
.
EG iterations: 1
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=11)
states: 380
abstracting: (sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 315
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0))
states: 298
........
EG iterations: 8
abstracting: (52<=sum(x_2, x_1, x_0))
states: 0
.
EG iterations: 1
abstracting: (sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=1)
states: 376
abstracting: (73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 0
abstracting: (73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 0
abstracting: (73<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 0
.
EG iterations: 1
abstracting: (sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=7)
states: 380
abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 314
-> the formula is TRUE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-02 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.415sec
checking: [[[AX [[E [[69<=sum(P_start_1_2, P_start_1_1, P_start_1_0) & sum(x_2, x_1, x_0)<=10] U [sum(P_await_13_2, P_await_13_1, P_await_13_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0) & sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=33]] | EX [[sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) | sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]] & E [[EG [[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0) | sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=66]] & ~ [[[65<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 4<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)] | [74<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) | sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=1]]]] U 49<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]] | ~ [[EG [[76<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) | ~ [A [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(y_2, y_1, y_0) U sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29]]]] & A [~ [85<=sum(x_2, x_1, x_0)] U EF [43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]] & A [~ [[EX [EF [sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)]] & EF [[AX [72<=sum(y_2, y_1, y_0)] & EG [64<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]] U AX [~ [[sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31 & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53]]]]]
normalized: [[~ [EG [EX [[sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31 & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53]]]] & ~ [E [EX [[sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31 & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53]] U [[E [true U [EG [64<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)] & ~ [EX [~ [72<=sum(y_2, y_1, y_0)]]]]] & EX [E [true U sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)]]] & EX [[sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31 & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53]]]]]] & [~ [[[~ [EG [~ [E [true U 43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]] & ~ [E [~ [E [true U 43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]] U [85<=sum(x_2, x_1, x_0) & ~ [E [true U 43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]]] & EG [[76<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) | ~ [[~ [EG [~ [sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29]]] & ~ [E [~ [sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29] U [~ [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(y_2, y_1, y_0)] & ~ [sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29]]]]]]]]]] | [E [[~ [[[74<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) | sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=1] | [65<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 4<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]] & EG [[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0) | sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=66]]] U 49<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)] & ~ [EX [~ [[EX [[sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) | sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]] | E [[69<=sum(P_start_1_2, P_start_1_1, P_start_1_0) & sum(x_2, x_1, x_0)<=10] U [sum(P_await_13_2, P_await_13_1, P_await_13_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0) & sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=33]]]]]]]]]
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=33)
states: 380
abstracting: (sum(P_await_13_2, P_await_13_1, P_await_13_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0))
states: 356
abstracting: (sum(x_2, x_1, x_0)<=10)
states: 380
abstracting: (69<=sum(P_start_1_2, P_start_1_1, P_start_1_0))
states: 0
abstracting: (sum(P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0))
states: 338
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0))
states: 334
..abstracting: (49<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0))
states: 0
abstracting: (sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=66)
states: 380
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 352
EG iterations: 0
abstracting: (4<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false))
states: 0
abstracting: (65<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0))
states: 0
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=1)
states: 380
abstracting: (74<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0))
states: 0
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29)
states: 380
abstracting: (sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(y_2, y_1, y_0))
states: 378
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29)
states: 380
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=29)
states: 380
.
EG iterations: 1
abstracting: (76<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0))
states: 0
.
EG iterations: 1
abstracting: (43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
abstracting: (85<=sum(x_2, x_1, x_0))
states: 0
abstracting: (43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
abstracting: (43<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
EG iterations: 0
abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53)
states: 380
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31)
states: 380
.abstracting: (sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0))
states: 360
.abstracting: (72<=sum(y_2, y_1, y_0))
states: 0
.abstracting: (64<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0))
states: 0
.
EG iterations: 1
abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53)
states: 380
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31)
states: 380
.abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=53)
states: 380
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=31)
states: 380
.
EG iterations: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-PT-2-CTLCardinality-07 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.495sec
totally nodes used: 169569 (1.7e+05)
number of garbage collections: 0
fire ops cache: hits/miss/sum: 274142 961323 1235465
used/not used/entry size/cache size: 1120587 65988277 16 1024MB
basic ops cache: hits/miss/sum: 67409 154398 221807
used/not used/entry size/cache size: 261130 16516086 12 192MB
unary ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 8 128MB
abstract ops cache: hits/miss/sum: 0 4166 4166
used/not used/entry size/cache size: 1 16777215 12 192MB
state nr cache: hits/miss/sum: 1146 4007 5153
used/not used/entry size/cache size: 4007 8384601 32 256MB
max state cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 8388608 32 256MB
uniqueHash elements/entry size/size: 67108864 4 256MB
0 66949897
1 149186
2 9011
3 719
4 51
5 0
6 0
7 0
8 0
9 0
>= 10 0
Total processing time: 0m 6.715sec
BK_STOP 1678622430352
--------------------
content from stderr:
check for maximal unmarked siphon
found
The net has a maximal unmarked siphon:
P_wait_0_1
P_wait_0_2
P_awaity_0
P_setbi_24_0
P_CS_21_0
P_await_13_0
P_done_0_2
P_done_1_0
P_wait_1_0
P_wait_2_0
P_done_0_0
P_done_0_1
P_done_2_0
P_ifyi_15_0
P_fordo_12_0
P_ify0_4_0
P_setx_3_0
P_ifxi_10_0
P_b_0_false
P_b_0_true
P_sety_9_0
P_wait_0_0
P_setbi_5_0
P_setbi_11_0
P_start_1_0
The net has transition(s) that can never fire:
T_setx_3_3
T_yeq0_4_1
T_sety_9_3
T_sety_9_2
T_setbi_5_1
T_setbi_5_2
T_forod_13_1
T_yne0_4_3
T_await_13_7
T_xnei_10_2
T_xnei_10_3
T_awaity_1
T_ynei_15_2
T_ynei_15_3
T_yeqi_15_1
T_sety_9_1
T_xeqi_10_1
T_sety0_23_1
T_sety0_23_2
T_sety0_23_3
T_yne0_4_2
T_setbi_11_1
T_setbi_11_2
T_fordo_12_1
T_await_13_1
T_await_13_2
T_await_13_3
T_await_13_4
T_setbi_2_1
T_setx_3_1
T_setbi_24_1
T_setbi_24_2
T_setbi_2_2
T_setx_3_2
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:1779 (18), effective:98 (1)
initing FirstDep: 0m 0.000sec
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:261 (2), effective:11 (0)
iterations count:1560 (16), effective:78 (0)
iterations count:261 (2), effective:11 (0)
iterations count:1560 (16), effective:78 (0)
iterations count:261 (2), effective:11 (0)
iterations count:1560 (16), effective:78 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:145 (1), effective:4 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:1684 (17), effective:85 (0)
iterations count:825 (8), effective:37 (0)
iterations count:96 (1), effective:0 (0)
iterations count:646 (6), effective:26 (0)
iterations count:1752 (18), effective:85 (0)
iterations count:96 (1), effective:0 (0)
iterations count:1287 (13), effective:65 (0)
iterations count:96 (1), effective:0 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:129 (1), effective:1 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:129 (1), effective:1 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:129 (1), effective:1 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:129 (1), effective:1 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:1599 (16), effective:78 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:96 (1), effective:0 (0)
iterations count:2245 (23), effective:106 (1)
iterations count:187 (1), effective:4 (0)
iterations count:96 (1), effective:0 (0)
iterations count:208 (2), effective:8 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="LamportFastMutEx-PT-2"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marcie"
echo " Input is LamportFastMutEx-PT-2, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r225-tall-167856407500393"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/LamportFastMutEx-PT-2.tgz
mv LamportFastMutEx-PT-2 execution
cd execution
if [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "UpperBounds" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] || [ "CTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

