About the Execution of ITS-Tools for HexagonalGrid-PT-110
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 238.863 | 11626.00 | 21392.00 | 353.40 | FFFTTFFTFFFTTTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
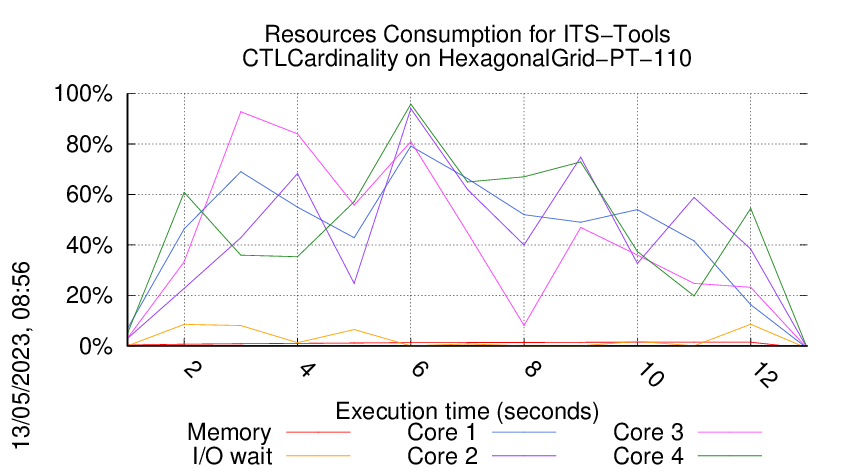
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r197-smll-167840344100369.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
..........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool itstools
Input is HexagonalGrid-PT-110, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r197-smll-167840344100369
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 456K
-rw-r--r-- 1 mcc users 5.7K Feb 26 17:02 CTLCardinality.txt
-rw-r--r-- 1 mcc users 55K Feb 26 17:02 CTLCardinality.xml
-rw-r--r-- 1 mcc users 5.4K Feb 26 17:00 CTLFireability.txt
-rw-r--r-- 1 mcc users 46K Feb 26 17:00 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.4K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 3.6K Feb 25 16:14 LTLCardinality.txt
-rw-r--r-- 1 mcc users 23K Feb 25 16:14 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.5K Feb 25 16:14 LTLFireability.txt
-rw-r--r-- 1 mcc users 18K Feb 25 16:14 LTLFireability.xml
-rw-r--r-- 1 mcc users 11K Feb 26 17:04 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 99K Feb 26 17:04 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 12K Feb 26 17:03 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 90K Feb 26 17:03 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.7K Feb 25 16:14 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Feb 25 16:14 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 equiv_col
-rw-r--r-- 1 mcc users 4 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 iscolored
-rwxr-xr-x 1 mcc users 29K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-00
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-01
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-02
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-03
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-04
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-05
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-06
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-07
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-08
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-09
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-10
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-11
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-12
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-13
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-14
FORMULA_NAME HexagonalGrid-PT-110-CTLCardinality-15
=== Now, execution of the tool begins
BK_START 1678522953813
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=itstools
BK_EXAMINATION=CTLCardinality
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=HexagonalGrid-PT-110
Not applying reductions.
Model is PT
CTLCardinality PT
Running Version 202303021504
[2023-03-11 08:22:36] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLCardinality, -its, -ltsmin, -greatspnpath, /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/, -order, META, -manyOrder, -smt, -timeout, 3600]
[2023-03-11 08:22:36] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-11 08:22:36] [INFO ] Load time of PNML (sax parser for PT used): 43 ms
[2023-03-11 08:22:36] [INFO ] Transformed 31 places.
[2023-03-11 08:22:36] [INFO ] Transformed 42 transitions.
[2023-03-11 08:22:36] [INFO ] Parsed PT model containing 31 places and 42 transitions and 168 arcs in 143 ms.
Parsed 16 properties from file /home/mcc/execution/CTLCardinality.xml in 17 ms.
Initial state reduction rules removed 2 formulas.
FORMULA HexagonalGrid-PT-110-CTLCardinality-12 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA HexagonalGrid-PT-110-CTLCardinality-14 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Support contains 29 out of 31 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 114 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
// Phase 1: matrix 42 rows 31 cols
[2023-03-11 08:22:37] [INFO ] Computed 14 place invariants in 10 ms
[2023-03-11 08:22:37] [INFO ] Implicit Places using invariants in 231 ms returned []
[2023-03-11 08:22:37] [INFO ] Invariant cache hit.
[2023-03-11 08:22:37] [INFO ] Implicit Places using invariants and state equation in 102 ms returned []
Implicit Place search using SMT with State Equation took 375 ms to find 0 implicit places.
[2023-03-11 08:22:37] [INFO ] Invariant cache hit.
[2023-03-11 08:22:37] [INFO ] Dead Transitions using invariants and state equation in 96 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 589 ms. Remains : 31/31 places, 42/42 transitions.
Support contains 29 out of 31 places after structural reductions.
[2023-03-11 08:22:37] [INFO ] Flatten gal took : 45 ms
[2023-03-11 08:22:37] [INFO ] Flatten gal took : 21 ms
[2023-03-11 08:22:37] [INFO ] Input system was already deterministic with 42 transitions.
Incomplete random walk after 10000 steps, including 2 resets, run finished after 822 ms. (steps per millisecond=12 ) properties (out of 47) seen :42
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 85 ms. (steps per millisecond=117 ) properties (out of 5) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 73 ms. (steps per millisecond=137 ) properties (out of 5) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 56 ms. (steps per millisecond=178 ) properties (out of 5) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 40 ms. (steps per millisecond=250 ) properties (out of 5) seen :0
Incomplete Best-First random walk after 10001 steps, including 2 resets, run finished after 47 ms. (steps per millisecond=212 ) properties (out of 5) seen :0
Running SMT prover for 5 properties.
[2023-03-11 08:22:39] [INFO ] Invariant cache hit.
[2023-03-11 08:22:39] [INFO ] [Real]Absence check using 13 positive place invariants in 4 ms returned sat
[2023-03-11 08:22:39] [INFO ] [Real]Absence check using 13 positive and 1 generalized place invariants in 1 ms returned sat
[2023-03-11 08:22:39] [INFO ] After 87ms SMT Verify possible using all constraints in real domain returned unsat :4 sat :0 real:1
[2023-03-11 08:22:39] [INFO ] [Nat]Absence check using 13 positive place invariants in 6 ms returned sat
[2023-03-11 08:22:39] [INFO ] [Nat]Absence check using 13 positive and 1 generalized place invariants in 2 ms returned sat
[2023-03-11 08:22:39] [INFO ] After 55ms SMT Verify possible using all constraints in natural domain returned unsat :5 sat :0
Fused 5 Parikh solutions to 0 different solutions.
Parikh walk visited 0 properties in 1 ms.
Successfully simplified 5 atomic propositions for a total of 14 simplifications.
[2023-03-11 08:22:39] [INFO ] Initial state reduction rules for CTL removed 1 formulas.
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 8 ms
FORMULA HexagonalGrid-PT-110-CTLCardinality-02 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 8 ms
[2023-03-11 08:22:39] [INFO ] Input system was already deterministic with 42 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:39] [INFO ] Invariant cache hit.
[2023-03-11 08:22:39] [INFO ] Implicit Places using invariants in 77 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 81 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 84 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:39] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:39] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:39] [INFO ] Time to serialize gal into /tmp/CTLCardinality5502771721253970836.gal : 3 ms
[2023-03-11 08:22:39] [INFO ] Time to serialize properties into /tmp/CTLCardinality11623301138083034238.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality5502771721253970836.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality11623301138083034238.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.049801,4616,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: EF(AG((((po5_1_1<1) + AX((pil3_1_1>0))) * ((A((pol1_1_1<=pb1_1_1) U (pb5_1_1<=pol1_1_1)) + AG((pol5_1_1<=pi4_1_1))) + AG(((pb3_1_1<=1)||(...173
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(E(TRUE U !((((po5_1_1<1) + !(EX(!((pil3_1_1>0))))) * ((!((E(!((pb5_1_1<=pol1_1_1)) U (!((p...334
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Hit Full ! (commute/partial/dont) 34/0/8
(forward)formula 0,0,0.474382,13320,1,0,18,57593,35,5,889,50396,20
FORMULA HexagonalGrid-PT-110-CTLCardinality-00 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:40] [INFO ] Invariant cache hit.
[2023-03-11 08:22:40] [INFO ] Implicit Places using invariants in 77 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 78 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 83 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:40] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:40] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:40] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:40] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:40] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:40] [INFO ] Time to serialize gal into /tmp/CTLCardinality659117431884468014.gal : 2 ms
[2023-03-11 08:22:40] [INFO ] Time to serialize properties into /tmp/CTLCardinality10761624290284417728.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality659117431884468014.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality10761624290284417728.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.059677,4432,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: AF(((EX(A(AX((pi6_1_1<=pi2_1_1)) U A((pi4_1_1>=1) U (pil5_1_1<=pi2_1_1)))) + (po2_1_1>=1)) + ((A((po1_1_1<=0) U ((po6_1_1>0)||((po3_1_1<=...237
=> equivalent forward existential formula: [FwdG(Init,!(((EX(!((E(!(!((E(!((pil5_1_1<=pi2_1_1)) U (!((pi4_1_1>=1)) * !((pil5_1_1<=pi2_1_1)))) + EG(!((pil5_...713
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Hit Full ! (commute/partial/dont) 30/0/12
Using saturation style SCC detection
Hit Full ! (commute/partial/dont) 34/0/8
Hit Full ! (commute/partial/dont) 32/10/10
(forward)formula 0,0,0.546216,13144,1,0,69,57135,62,46,1027,54672,67
FORMULA HexagonalGrid-PT-110-CTLCardinality-01 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in SI_CTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 10 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:40] [INFO ] Invariant cache hit.
[2023-03-11 08:22:40] [INFO ] Implicit Places using invariants in 93 ms returned []
[2023-03-11 08:22:40] [INFO ] Invariant cache hit.
[2023-03-11 08:22:40] [INFO ] Implicit Places using invariants and state equation in 109 ms returned []
Implicit Place search using SMT with State Equation took 207 ms to find 0 implicit places.
[2023-03-11 08:22:40] [INFO ] Redundant transitions in 2 ms returned []
[2023-03-11 08:22:40] [INFO ] Invariant cache hit.
[2023-03-11 08:22:41] [INFO ] Dead Transitions using invariants and state equation in 77 ms found 0 transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 304 ms. Remains : 31/31 places, 42/42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:41] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize gal into /tmp/CTLCardinality11310444791901930962.gal : 2 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize properties into /tmp/CTLCardinality4964885092901973473.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality11310444791901930962.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality4964885092901973473.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.049554,5064,2,377,5,8491,6,0,169,8100,0
Converting to forward existential form...Done !
original formula: EF(AG(EF((pbl_1_1>pol4_1_1))))
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(E(TRUE U !(E(TRUE U (pbl_1_1>pol4_1_1))))))] != FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,1,0.115423,6120,1,0,6,13940,14,0,902,12774,5
FORMULA HexagonalGrid-PT-110-CTLCardinality-03 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:41] [INFO ] Invariant cache hit.
[2023-03-11 08:22:41] [INFO ] Implicit Places using invariants in 62 ms returned []
[2023-03-11 08:22:41] [INFO ] Invariant cache hit.
[2023-03-11 08:22:41] [INFO ] Implicit Places using invariants and state equation in 90 ms returned []
Implicit Place search using SMT with State Equation took 154 ms to find 0 implicit places.
[2023-03-11 08:22:41] [INFO ] Invariant cache hit.
[2023-03-11 08:22:41] [INFO ] Dead Transitions using invariants and state equation in 80 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 236 ms. Remains : 31/31 places, 42/42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:41] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 6 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize gal into /tmp/CTLCardinality7297004642093804442.gal : 2 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize properties into /tmp/CTLCardinality969594823167063428.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality7297004642093804442.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality969594823167063428.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...282
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.050573,5068,2,377,5,8491,6,0,169,8100,0
Converting to forward existential form...Done !
original formula: AG((AG(AF((pbl_1_1>=1))) + (AX((pol3_1_1>pol5_1_1)) * (EG((pb4_1_1<=po6_1_1)) + (po2_1_1>=1)))))
=> equivalent forward existential formula: ([(EY((FwdU(Init,TRUE) * !(!(E(TRUE U !(!(EG(!((pbl_1_1>=1)))))))))) * !((pol3_1_1>pol5_1_1)))] = FALSE * [(((Fw...271
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,1,0.11957,6652,1,0,13,14876,33,3,964,14443,9
FORMULA HexagonalGrid-PT-110-CTLCardinality-04 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:41] [INFO ] Invariant cache hit.
[2023-03-11 08:22:41] [INFO ] Implicit Places using invariants in 73 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 75 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 77 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:41] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:41] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize gal into /tmp/CTLCardinality13762525245458312334.gal : 1 ms
[2023-03-11 08:22:41] [INFO ] Time to serialize properties into /tmp/CTLCardinality10523125051439944999.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality13762525245458312334.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality10523125051439944999.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...285
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.058516,4428,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: A(AX(A(((po4_1_1<=po5_1_1) + EX(TRUE)) U AX(((pol4_1_1>=1)&&(pb4_1_1>=1))))) U EF((AX(AG((pil3_1_1<=pil2_1_1))) * !(((!((pi1_1_1<=0)||(po...185
=> equivalent forward existential formula: [((Init * !(EG(!(E(TRUE U (!(EX(!(!(E(TRUE U !((pil3_1_1<=pil2_1_1))))))) * !(((!((pi1_1_1<=0)||(po5_1_1>=1)))&&...627
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Using saturation style SCC detection
(forward)formula 0,0,0.175829,6276,1,0,14,16261,27,3,886,13193,15
FORMULA HexagonalGrid-PT-110-CTLCardinality-05 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:41] [INFO ] Invariant cache hit.
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants in 97 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 100 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 103 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize gal into /tmp/CTLCardinality4342948824980500143.gal : 1 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize properties into /tmp/CTLCardinality2470496305728748262.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality4342948824980500143.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality2470496305728748262.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.061108,4428,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: EX(EF(AG(AF((pb4_1_1>0)))))
=> equivalent forward existential formula: [(FwdU(EY(Init),TRUE) * !(E(TRUE U !(!(EG(!((pb4_1_1>0))))))))] != FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,0,0.15027,5748,1,0,6,12907,23,0,839,11206,8
FORMULA HexagonalGrid-PT-110-CTLCardinality-06 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in SI_CTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 4 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:42] [INFO ] Invariant cache hit.
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants in 77 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 81 ms to find 1 implicit places.
Starting structural reductions in SI_CTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Performed 5 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 5 Pre rules applied. Total rules applied 0 place count 30 transition count 37
Deduced a syphon composed of 5 places in 1 ms
Reduce places removed 10 places and 0 transitions.
Iterating global reduction 0 with 15 rules applied. Total rules applied 15 place count 20 transition count 37
Performed 3 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 0 with 3 Pre rules applied. Total rules applied 15 place count 20 transition count 34
Deduced a syphon composed of 3 places in 0 ms
Reduce places removed 6 places and 0 transitions.
Iterating global reduction 0 with 9 rules applied. Total rules applied 24 place count 14 transition count 34
Graph (trivial) has 15 edges and 14 vertex of which 3 / 14 are part of one of the 1 SCC in 4 ms
Free SCC test removed 2 places
Iterating global reduction 0 with 1 rules applied. Total rules applied 25 place count 12 transition count 34
Ensure Unique test removed 17 transitions
Reduce isomorphic transitions removed 17 transitions.
Iterating post reduction 0 with 17 rules applied. Total rules applied 42 place count 12 transition count 17
Drop transitions removed 6 transitions
Redundant transition composition rules discarded 6 transitions
Iterating global reduction 1 with 6 rules applied. Total rules applied 48 place count 12 transition count 11
Applied a total of 48 rules in 23 ms. Remains 12 /30 variables (removed 18) and now considering 11/42 (removed 31) transitions.
// Phase 1: matrix 11 rows 12 cols
[2023-03-11 08:22:42] [INFO ] Computed 5 place invariants in 1 ms
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants in 38 ms returned []
[2023-03-11 08:22:42] [INFO ] Invariant cache hit.
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants and state equation in 44 ms returned []
Implicit Place search using SMT with State Equation took 85 ms to find 0 implicit places.
Starting structural reductions in SI_CTL mode, iteration 2 : 12/31 places, 11/42 transitions.
Finished structural reductions in SI_CTL mode , in 2 iterations and 194 ms. Remains : 12/31 places, 11/42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 2 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 1 ms
[2023-03-11 08:22:42] [INFO ] Input system was already deterministic with 11 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 1 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 2 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize gal into /tmp/CTLCardinality7144223039860389019.gal : 2 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize properties into /tmp/CTLCardinality16715486419215453776.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality7144223039860389019.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality16715486419215453776.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,608,0.007623,3360,2,74,5,407,6,0,61,330,0
Converting to forward existential form...Done !
original formula: EG(AG(EF((((pol1_1_1<=pi1_1_1)||(pi4_1_1<1))||(pi5_1_1>0)))))
=> equivalent forward existential formula: [FwdG(Init,!(E(TRUE U !(E(TRUE U (((pol1_1_1<=pi1_1_1)||(pi4_1_1<1))||(pi5_1_1>0)))))))] != FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,1,0.0176,3676,1,0,6,968,18,1,314,783,10
FORMULA HexagonalGrid-PT-110-CTLCardinality-07 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
// Phase 1: matrix 42 rows 31 cols
[2023-03-11 08:22:42] [INFO ] Computed 14 place invariants in 4 ms
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants in 103 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 104 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 106 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize gal into /tmp/CTLCardinality17196997939149490611.gal : 1 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize properties into /tmp/CTLCardinality6138295334014699285.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality17196997939149490611.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality6138295334014699285.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.035446,4428,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: (EF(AG(AF((pi1_1_1<=pil1_1_1)))) + (AF(AX(AX((pb5_1_1<=pil4_1_1)))) * A(A(((po5_1_1>=1)&&(pol1_1_1>=1)) U ((pil2_1_1<=pi1_1_1)||(pb3_1_1<...213
=> equivalent forward existential formula: ([FwdG((Init * !(E(TRUE U !(E(TRUE U !(!(EG(!((pi1_1_1<=pil1_1_1)))))))))),!(!(EX(!(!(EX(!((pb5_1_1<=pil4_1_1)))...1322
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Hit Full ! (commute/partial/dont) 34/0/8
(forward)formula 0,0,0.206221,9444,1,0,10,33174,38,2,931,30366,18
FORMULA HexagonalGrid-PT-110-CTLCardinality-08 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:42] [INFO ] Invariant cache hit.
[2023-03-11 08:22:42] [INFO ] Implicit Places using invariants in 87 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 89 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 91 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize gal into /tmp/CTLCardinality18040618997667943567.gal : 1 ms
[2023-03-11 08:22:42] [INFO ] Time to serialize properties into /tmp/CTLCardinality2546253669711884536.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality18040618997667943567.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality2546253669711884536.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.059791,4428,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: EF(EX((((EF((pb5_1_1<=1)) * EG((pil1_1_1<1))) * (EX((pb2_1_1<=pil5_1_1)) * (pol2_1_1>pi1_1_1))) * (po1_1_1<=0))))
=> equivalent forward existential formula: [(EY((((EY(FwdU(Init,TRUE)) * (po1_1_1<=0)) * (E(TRUE U (pb5_1_1<=1)) * EG((pil1_1_1<1)))) * (pol2_1_1>pi1_1_1))...189
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,0,0.154277,6012,1,0,13,13573,26,4,850,11857,13
FORMULA HexagonalGrid-PT-110-CTLCardinality-09 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:43] [INFO ] Invariant cache hit.
[2023-03-11 08:22:43] [INFO ] Implicit Places using invariants in 90 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 93 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 96 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize gal into /tmp/CTLCardinality1363118857331883812.gal : 2 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize properties into /tmp/CTLCardinality14805090908490158113.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality1363118857331883812.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality14805090908490158113.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.059294,4432,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: EF(AG(EX((pi2_1_1>=1))))
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(E(TRUE U !(EX((pi2_1_1>=1))))))] != FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,0,0.11415,5224,1,0,8,10145,14,1,781,7685,6
FORMULA HexagonalGrid-PT-110-CTLCardinality-10 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:43] [INFO ] Invariant cache hit.
[2023-03-11 08:22:43] [INFO ] Implicit Places using invariants in 68 ms returned []
[2023-03-11 08:22:43] [INFO ] Invariant cache hit.
[2023-03-11 08:22:43] [INFO ] Implicit Places using invariants and state equation in 106 ms returned []
Implicit Place search using SMT with State Equation took 177 ms to find 0 implicit places.
[2023-03-11 08:22:43] [INFO ] Invariant cache hit.
[2023-03-11 08:22:43] [INFO ] Dead Transitions using invariants and state equation in 82 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 263 ms. Remains : 31/31 places, 42/42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 5 ms
[2023-03-11 08:22:43] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize gal into /tmp/CTLCardinality2079007045558939998.gal : 1 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize properties into /tmp/CTLCardinality1946037928644047288.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality2079007045558939998.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality1946037928644047288.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.081228,5068,2,377,5,8491,6,0,169,8100,0
Converting to forward existential form...Done !
original formula: EG(AF(EX((pbl_1_1>1))))
=> equivalent forward existential formula: [FwdG(Init,!(EG(!(EX((pbl_1_1>1))))))] != FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Using saturation style SCC detection
(forward)formula 0,1,0.230362,7180,1,0,8,18246,19,2,1001,16956,9
FORMULA HexagonalGrid-PT-110-CTLCardinality-11 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:43] [INFO ] Invariant cache hit.
[2023-03-11 08:22:43] [INFO ] Implicit Places using invariants in 73 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 74 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 77 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:43] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:43] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize gal into /tmp/CTLCardinality7888740363996832940.gal : 1 ms
[2023-03-11 08:22:43] [INFO ] Time to serialize properties into /tmp/CTLCardinality7944846683914187283.ctl : 1 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality7888740363996832940.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality7944846683914187283.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...283
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.059099,4424,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: E((pb6_1_1<=1) U A(AG(!(((pb4_1_1>1)&&(po5_1_1<1)))) U ((AX((pi3_1_1<1)) + EF(!(AX((pi6_1_1>=1))))) + ((pi5_1_1>=1)&&(pi3_1_1<=0)))))
=> equivalent forward existential formula: [((FwdU(Init,(pb6_1_1<=1)) * !(EG(!(((!(EX(!((pi3_1_1<1)))) + E(TRUE U !(!(EX(!((pi6_1_1>=1))))))) + ((pi5_1_1>=...447
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
Hit Full ! (commute/partial/dont) 36/0/6
(forward)formula 0,1,0.173157,6272,1,0,13,15834,33,4,886,14557,14
FORMULA HexagonalGrid-PT-110-CTLCardinality-13 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Starting structural reductions in LTL mode, iteration 0 : 31/31 places, 42/42 transitions.
Applied a total of 0 rules in 1 ms. Remains 31 /31 variables (removed 0) and now considering 42/42 (removed 0) transitions.
[2023-03-11 08:22:44] [INFO ] Invariant cache hit.
[2023-03-11 08:22:44] [INFO ] Implicit Places using invariants in 80 ms returned [6]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 81 ms to find 1 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 30/31 places, 42/42 transitions.
Applied a total of 0 rules in 2 ms. Remains 30 /30 variables (removed 0) and now considering 42/42 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 84 ms. Remains : 30/31 places, 42/42 transitions.
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:44] [INFO ] Input system was already deterministic with 42 transitions.
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 3 ms
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:44] [INFO ] Time to serialize gal into /tmp/CTLCardinality17590947324157489404.gal : 1 ms
[2023-03-11 08:22:44] [INFO ] Time to serialize properties into /tmp/CTLCardinality8267646928739434144.ctl : 0 ms
Invoking ITS tools like this :cd /home/mcc/execution;'/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64' '--gc-threshold' '2000000' '--quiet' '-i' '/tmp/CTLCardinality17590947324157489404.gal' '-t' 'CGAL' '-ctl' '/tmp/CTLCardinality8267646928739434144.ctl' '--gen-order' 'FOLLOW'
its-ctl command run as :
/home/mcc/BenchKit/itstools/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202303021504/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -...284
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,40193,0.060079,4432,2,210,5,6578,6,0,165,5448,0
Converting to forward existential form...Done !
original formula: AG(EX((po2_1_1>=1)))
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(EX((po2_1_1>=1))))] = FALSE
Reverse transition relation is exact ! Faster fixpoint algorithm enabled.
(forward)formula 0,0,0.087788,4696,1,0,8,6578,10,2,749,5448,4
FORMULA HexagonalGrid-PT-110-CTLCardinality-15 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 4 ms
[2023-03-11 08:22:44] [INFO ] Flatten gal took : 5 ms
Total runtime 7671 ms.
BK_STOP 1678522965439
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
+ BINDIR=/home/mcc/BenchKit/bin//../itstools/bin//../
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ CTLCardinality = StateSpace ]]
+ /home/mcc/BenchKit/bin//../itstools/bin//..//runeclipse.sh /home/mcc/execution CTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../itstools/bin//..//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLCardinality -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//../itstools/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="HexagonalGrid-PT-110"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool itstools"
echo " Input is HexagonalGrid-PT-110, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r197-smll-167840344100369"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/HexagonalGrid-PT-110.tgz
mv HexagonalGrid-PT-110 execution
cd execution
if [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "UpperBounds" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] || [ "CTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLCardinality" = "ReachabilityDeadlock" ] || [ "CTLCardinality" = "QuasiLiveness" ] || [ "CTLCardinality" = "StableMarking" ] || [ "CTLCardinality" = "Liveness" ] || [ "CTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

