About the Execution of Marcie+red for DatabaseWithMutex-COL-04
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 10152.491 | 3600000.00 | 3629566.00 | 9181.20 | TFFFF?F?FF?????? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
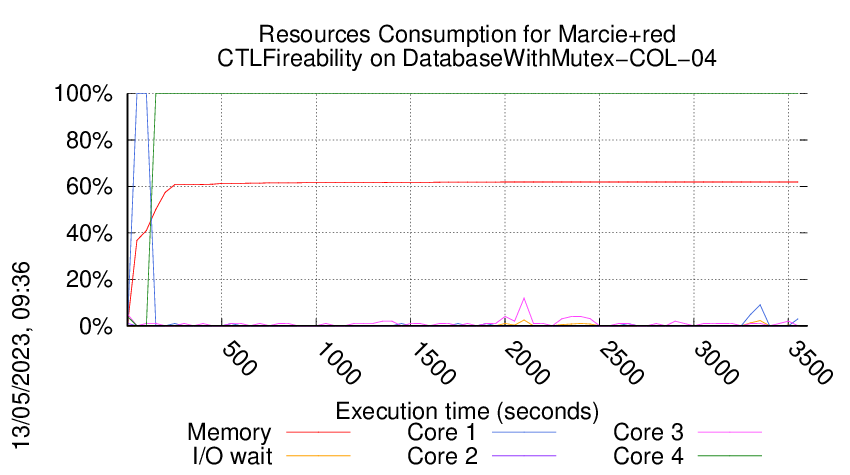
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r106-tall-167814483501026.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
..........................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is DatabaseWithMutex-COL-04, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r106-tall-167814483501026
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 488K
-rw-r--r-- 1 mcc users 8.3K Feb 25 13:17 CTLCardinality.txt
-rw-r--r-- 1 mcc users 82K Feb 25 13:17 CTLCardinality.xml
-rw-r--r-- 1 mcc users 5.2K Feb 25 13:16 CTLFireability.txt
-rw-r--r-- 1 mcc users 40K Feb 25 13:16 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Jan 29 11:40 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.7K Jan 29 11:40 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 4.0K Feb 25 15:56 LTLCardinality.txt
-rw-r--r-- 1 mcc users 24K Feb 25 15:56 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.4K Feb 25 15:56 LTLFireability.txt
-rw-r--r-- 1 mcc users 17K Feb 25 15:56 LTLFireability.xml
-rw-r--r-- 1 mcc users 10K Feb 25 13:21 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 90K Feb 25 13:21 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 14K Feb 25 13:20 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 112K Feb 25 13:20 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.8K Feb 25 15:56 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Feb 25 15:56 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 equiv_pt
-rw-r--r-- 1 mcc users 3 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 5 Mar 5 18:22 iscolored
-rw-r--r-- 1 mcc users 21K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-00
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-01
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-02
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-03
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-04
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-05
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-06
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-07
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-08
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-09
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-10
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-11
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-12
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-13
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-14
FORMULA_NAME DatabaseWithMutex-COL-04-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1678515445071
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=DatabaseWithMutex-COL-04
Applying reductions before tool marcie
Invoking reducer
Running Version 202303021504
[2023-03-11 06:17:26] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2023-03-11 06:17:26] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-11 06:17:26] [INFO ] Detected file is not PT type :http://www.pnml.org/version-2009/grammar/symmetricnet
log4j:WARN No appenders could be found for logger (org.apache.axiom.locator.DefaultOMMetaFactoryLocator).
log4j:WARN Please initialize the log4j system properly.
log4j:WARN See http://logging.apache.org/log4j/1.2/faq.html#noconfig for more info.
[2023-03-11 06:17:26] [WARNING] Using fallBack plugin, rng conformance not checked
[2023-03-11 06:17:27] [INFO ] Load time of PNML (colored model parsed with PNMLFW) : 653 ms
[2023-03-11 06:17:27] [INFO ] Imported 11 HL places and 8 HL transitions for a total of 140 PT places and 128.0 transition bindings in 11 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 12 ms.
[2023-03-11 06:17:27] [INFO ] Built PT skeleton of HLPN with 11 places and 8 transitions 22 arcs in 4 ms.
[2023-03-11 06:17:27] [INFO ] Skeletonized 16 HLPN properties in 2 ms.
Computed a total of 0 stabilizing places and 0 stable transitions
Remains 8 properties that can be checked using skeleton over-approximation.
Computed a total of 0 stabilizing places and 0 stable transitions
Finished random walk after 98 steps, including 0 resets, run visited all 12 properties in 14 ms. (steps per millisecond=7 )
[2023-03-11 06:17:27] [INFO ] Flatten gal took : 36 ms
[2023-03-11 06:17:27] [INFO ] Flatten gal took : 4 ms
Transition Release forces synchronizations/join behavior on parameter s of sort site
Transition Acquire forces synchronizations/join behavior on parameter f of sort file
[2023-03-11 06:17:27] [INFO ] Unfolded HLPN to a Petri net with 140 places and 128 transitions 416 arcs in 12 ms.
[2023-03-11 06:17:27] [INFO ] Unfolded 16 HLPN properties in 1 ms.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
[2023-03-11 06:17:27] [INFO ] Reduced 12 identical enabling conditions.
Support contains 140 out of 140 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 7 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
// Phase 1: matrix 128 rows 140 cols
[2023-03-11 06:17:27] [INFO ] Computed 28 place invariants in 7 ms
[2023-03-11 06:17:27] [INFO ] Implicit Places using invariants in 164 ms returned []
[2023-03-11 06:17:27] [INFO ] Invariant cache hit.
[2023-03-11 06:17:27] [INFO ] Implicit Places using invariants and state equation in 102 ms returned []
Implicit Place search using SMT with State Equation took 405 ms to find 0 implicit places.
[2023-03-11 06:17:27] [INFO ] Invariant cache hit.
[2023-03-11 06:17:27] [INFO ] Dead Transitions using invariants and state equation in 105 ms found 0 transitions.
Finished structural reductions in LTL mode , in 1 iterations and 518 ms. Remains : 140/140 places, 128/128 transitions.
Support contains 140 out of 140 places after structural reductions.
[2023-03-11 06:17:27] [INFO ] Flatten gal took : 21 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 28 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Finished random walk after 43 steps, including 0 resets, run visited all 26 properties in 20 ms. (steps per millisecond=2 )
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 14 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 24 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Computed a total of 0 stabilizing places and 0 stable transitions
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 0 with 16 rules applied. Total rules applied 16 place count 140 transition count 112
Reduce places removed 20 places and 0 transitions.
Drop transitions removed 32 transitions
Trivial Post-agglo rules discarded 32 transitions
Performed 32 trivial Post agglomeration. Transition count delta: 32
Iterating post reduction 1 with 52 rules applied. Total rules applied 68 place count 120 transition count 80
Reduce places removed 32 places and 0 transitions.
Iterating post reduction 2 with 32 rules applied. Total rules applied 100 place count 88 transition count 80
Performed 16 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 16 Pre rules applied. Total rules applied 100 place count 88 transition count 64
Deduced a syphon composed of 16 places in 1 ms
Reduce places removed 16 places and 0 transitions.
Iterating global reduction 3 with 32 rules applied. Total rules applied 132 place count 72 transition count 64
Applied a total of 132 rules in 16 ms. Remains 72 /140 variables (removed 68) and now considering 64/128 (removed 64) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 16 ms. Remains : 72/140 places, 64/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 64 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 2 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 8 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 9 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 4 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 7 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 3 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 3 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 7 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 0 with 16 rules applied. Total rules applied 16 place count 140 transition count 112
Reduce places removed 16 places and 0 transitions.
Iterating post reduction 1 with 16 rules applied. Total rules applied 32 place count 124 transition count 112
Performed 16 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 16 Pre rules applied. Total rules applied 32 place count 124 transition count 96
Deduced a syphon composed of 16 places in 0 ms
Reduce places removed 16 places and 0 transitions.
Iterating global reduction 2 with 32 rules applied. Total rules applied 64 place count 108 transition count 96
Applied a total of 64 rules in 10 ms. Remains 108 /140 variables (removed 32) and now considering 96/128 (removed 32) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 10 ms. Remains : 108/140 places, 96/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 96 transitions.
Finished random walk after 9 steps, including 0 resets, run visited all 1 properties in 1 ms. (steps per millisecond=9 )
FORMULA DatabaseWithMutex-COL-04-CTLFireability-04 FALSE TECHNIQUES TOPOLOGICAL RANDOM_WALK
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 2 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 32 transitions
Trivial Post-agglo rules discarded 32 transitions
Performed 32 trivial Post agglomeration. Transition count delta: 32
Iterating post reduction 0 with 32 rules applied. Total rules applied 32 place count 140 transition count 96
Reduce places removed 36 places and 0 transitions.
Drop transitions removed 32 transitions
Trivial Post-agglo rules discarded 32 transitions
Performed 32 trivial Post agglomeration. Transition count delta: 32
Iterating post reduction 1 with 68 rules applied. Total rules applied 100 place count 104 transition count 64
Reduce places removed 32 places and 0 transitions.
Iterating post reduction 2 with 32 rules applied. Total rules applied 132 place count 72 transition count 64
Performed 16 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 16 Pre rules applied. Total rules applied 132 place count 72 transition count 48
Deduced a syphon composed of 16 places in 0 ms
Reduce places removed 16 places and 0 transitions.
Iterating global reduction 3 with 32 rules applied. Total rules applied 164 place count 56 transition count 48
Applied a total of 164 rules in 7 ms. Remains 56 /140 variables (removed 84) and now considering 48/128 (removed 80) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 7 ms. Remains : 56/140 places, 48/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 3 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 48 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 0 with 16 rules applied. Total rules applied 16 place count 140 transition count 112
Reduce places removed 20 places and 0 transitions.
Performed 16 Post agglomeration using F-continuation condition.Transition count delta: 16
Iterating post reduction 1 with 36 rules applied. Total rules applied 52 place count 120 transition count 96
Reduce places removed 16 places and 0 transitions.
Iterating post reduction 2 with 16 rules applied. Total rules applied 68 place count 104 transition count 96
Applied a total of 68 rules in 7 ms. Remains 104 /140 variables (removed 36) and now considering 96/128 (removed 32) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 7 ms. Remains : 104/140 places, 96/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 96 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 4 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 10 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 0 with 16 rules applied. Total rules applied 16 place count 140 transition count 112
Reduce places removed 20 places and 0 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 1 with 36 rules applied. Total rules applied 52 place count 120 transition count 96
Reduce places removed 16 places and 0 transitions.
Iterating post reduction 2 with 16 rules applied. Total rules applied 68 place count 104 transition count 96
Performed 16 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 16 Pre rules applied. Total rules applied 68 place count 104 transition count 80
Deduced a syphon composed of 16 places in 0 ms
Reduce places removed 16 places and 0 transitions.
Iterating global reduction 3 with 32 rules applied. Total rules applied 100 place count 88 transition count 80
Applied a total of 100 rules in 7 ms. Remains 88 /140 variables (removed 52) and now considering 80/128 (removed 48) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 7 ms. Remains : 88/140 places, 80/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 80 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 4 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 4 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 7 ms
[2023-03-11 06:17:28] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 0 with 16 rules applied. Total rules applied 16 place count 140 transition count 112
Reduce places removed 20 places and 0 transitions.
Drop transitions removed 16 transitions
Trivial Post-agglo rules discarded 16 transitions
Performed 16 trivial Post agglomeration. Transition count delta: 16
Iterating post reduction 1 with 36 rules applied. Total rules applied 52 place count 120 transition count 96
Reduce places removed 16 places and 0 transitions.
Iterating post reduction 2 with 16 rules applied. Total rules applied 68 place count 104 transition count 96
Performed 16 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 16 Pre rules applied. Total rules applied 68 place count 104 transition count 80
Deduced a syphon composed of 16 places in 0 ms
Reduce places removed 16 places and 0 transitions.
Iterating global reduction 3 with 32 rules applied. Total rules applied 100 place count 88 transition count 80
Applied a total of 100 rules in 6 ms. Remains 88 /140 variables (removed 52) and now considering 80/128 (removed 48) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 7 ms. Remains : 88/140 places, 80/128 transitions.
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:28] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Input system was already deterministic with 80 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 3 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 3 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 7 ms
[2023-03-11 06:17:29] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 2 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 2 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in LTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 1 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 1 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 4 ms
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Input system was already deterministic with 128 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 140/140 places, 128/128 transitions.
Applied a total of 0 rules in 3 ms. Remains 140 /140 variables (removed 0) and now considering 128/128 (removed 0) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 3 ms. Remains : 140/140 places, 128/128 transitions.
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 5 ms
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 6 ms
[2023-03-11 06:17:29] [INFO ] Input system was already deterministic with 128 transitions.
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 14 ms
[2023-03-11 06:17:29] [INFO ] Flatten gal took : 14 ms
[2023-03-11 06:17:29] [INFO ] Export to MCC of 15 properties in file /home/mcc/execution/CTLFireability.sr.xml took 14 ms.
[2023-03-11 06:17:29] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 140 places, 128 transitions and 416 arcs took 1 ms.
Total runtime 2860 ms.
There are residual formulas that ITS could not solve within timeout
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLFireability.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Petri
(NrP: 140 NrTr: 128 NrArc: 416)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.003sec
net check time: 0m 0.000sec
init dd package: 0m 2.742sec
RS generation: 0m12.512sec
-> reachability set: #nodes 327920 (3.3e+05) #states 4,717,886,881 (9)
starting MCC model checker
--------------------------
checking: EF [EG [AG [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]]]
normalized: E [true U EG [~ [E [true U ~ [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]]]]]
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
.
EG iterations: 1
-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-06 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m26.149sec
checking: EG [EF [[[[[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]]
normalized: EG [E [true U [[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]]]]]]
abstracting: (1<=p66)
states: 10,898,249 (7)
abstracting: (1<=p67)
states: 10,898,249 (7)
abstracting: (1<=p64)
states: 10,898,249 (7)
abstracting: (1<=p65)
states: 10,898,249 (7)
abstracting: (1<=p68)
states: 10,898,249 (7)
abstracting: (1<=p69)
states: 10,898,249 (7)
abstracting: (1<=p70)
states: 10,898,249 (7)
abstracting: (1<=p71)
states: 10,898,249 (7)
abstracting: (1<=p56)
states: 10,898,249 (7)
abstracting: (1<=p57)
states: 10,898,249 (7)
abstracting: (1<=p58)
states: 10,898,249 (7)
abstracting: (1<=p59)
states: 10,898,249 (7)
abstracting: (1<=p60)
states: 10,898,249 (7)
abstracting: (1<=p61)
states: 10,898,249 (7)
abstracting: (1<=p62)
states: 10,898,249 (7)
abstracting: (1<=p63)
states: 10,898,249 (7)
EG iterations: 0
-> the formula is TRUE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-00 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m39.588sec
checking: AF [AX [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]]
normalized: ~ [EG [EX [~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]]
abstracting: (1<=p64)
states: 10,898,249 (7)
abstracting: (1<=p65)
states: 10,898,249 (7)
abstracting: (1<=p66)
states: 10,898,249 (7)
abstracting: (1<=p67)
states: 10,898,249 (7)
abstracting: (1<=p68)
states: 10,898,249 (7)
abstracting: (1<=p69)
states: 10,898,249 (7)
abstracting: (1<=p70)
states: 10,898,249 (7)
abstracting: (1<=p71)
states: 10,898,249 (7)
abstracting: (1<=p56)
states: 10,898,249 (7)
abstracting: (1<=p57)
states: 10,898,249 (7)
abstracting: (1<=p58)
states: 10,898,249 (7)
abstracting: (1<=p59)
states: 10,898,249 (7)
abstracting: (1<=p60)
states: 10,898,249 (7)
abstracting: (1<=p61)
states: 10,898,249 (7)
abstracting: (1<=p62)
states: 10,898,249 (7)
abstracting: (1<=p63)
states: 10,898,249 (7)
..
EG iterations: 1
-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-08 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m10.620sec
checking: EG [[AF [[[[[p73<=0 & p72<=0] & [p75<=0 & p74<=0]] & [[p77<=0 & p76<=0] & [p79<=0 & p78<=0]]] & [[[p81<=0 & p80<=0] & [p83<=0 & p82<=0]] & [[p85<=0 & p84<=0] & [p87<=0 & p86<=0]]]]] & [AF [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]] | EX [[[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]]]]]]
normalized: EG [[[EX [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]] | ~ [EG [~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]] & ~ [EG [~ [[[[[p87<=0 & p86<=0] & [p85<=0 & p84<=0]] & [[p83<=0 & p82<=0] & [p81<=0 & p80<=0]]] & [[[p79<=0 & p78<=0] & [p77<=0 & p76<=0]] & [[p75<=0 & p74<=0] & [p73<=0 & p72<=0]]]]]]]]]
abstracting: (p72<=0)
states: 4,001,663,527 (9)
abstracting: (p73<=0)
states: 4,001,663,527 (9)
abstracting: (p74<=0)
states: 4,001,663,527 (9)
abstracting: (p75<=0)
states: 4,001,663,527 (9)
abstracting: (p76<=0)
states: 4,001,663,527 (9)
abstracting: (p77<=0)
states: 4,001,663,527 (9)
abstracting: (p78<=0)
states: 4,001,663,527 (9)
abstracting: (p79<=0)
states: 4,001,663,527 (9)
abstracting: (p80<=0)
states: 4,001,663,527 (9)
abstracting: (p81<=0)
states: 4,001,663,527 (9)
abstracting: (p82<=0)
states: 4,001,663,527 (9)
abstracting: (p83<=0)
states: 4,001,663,527 (9)
abstracting: (p84<=0)
states: 4,001,663,527 (9)
abstracting: (p85<=0)
states: 4,001,663,527 (9)
abstracting: (p86<=0)
states: 4,001,663,527 (9)
abstracting: (p87<=0)
states: 4,001,663,527 (9)
..........
EG iterations: 10
abstracting: (1<=p64)
states: 10,898,249 (7)
abstracting: (1<=p65)
states: 10,898,249 (7)
abstracting: (1<=p66)
states: 10,898,249 (7)
abstracting: (1<=p67)
states: 10,898,249 (7)
abstracting: (1<=p68)
states: 10,898,249 (7)
abstracting: (1<=p69)
states: 10,898,249 (7)
abstracting: (1<=p70)
states: 10,898,249 (7)
abstracting: (1<=p71)
states: 10,898,249 (7)
abstracting: (1<=p56)
states: 10,898,249 (7)
abstracting: (1<=p57)
states: 10,898,249 (7)
abstracting: (1<=p58)
states: 10,898,249 (7)
abstracting: (1<=p59)
states: 10,898,249 (7)
abstracting: (1<=p60)
states: 10,898,249 (7)
abstracting: (1<=p61)
states: 10,898,249 (7)
abstracting: (1<=p62)
states: 10,898,249 (7)
abstracting: (1<=p63)
states: 10,898,249 (7)
........................
before gc: list nodes free: 18570
after gc: idd nodes used:6002877, unused:57997123; list nodes free:258791301
.........MC time: 4m53.013sec
checking: AX [[[[[AF [EX [[AX [[[[[[1<=p37 & 1<=p125] | [1<=p38 & 1<=p134]] | [[1<=p37 & 1<=p129] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p133] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p137] | [1<=p39 & 1<=p139]]]] | [[[[1<=p36 & 1<=p124] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p128] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p132] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]] & [[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]]]]] | 1<=p110] | [1<=p111 | 1<=p108]] | [[1<=p109 | 1<=p114] | [1<=p115 | 1<=p112]]] | [[[1<=p113 | 1<=p118] | [1<=p119 | 1<=p116]] | [[1<=p117 | 1<=p122] | [1<=p123 | [1<=p120 | 1<=p121]]]]]]
normalized: ~ [EX [~ [[[[[1<=p123 | [1<=p120 | 1<=p121]] | [1<=p117 | 1<=p122]] | [[1<=p119 | 1<=p116] | [1<=p113 | 1<=p118]]] | [[[1<=p115 | 1<=p112] | [1<=p109 | 1<=p114]] | [[1<=p111 | 1<=p108] | [1<=p110 | ~ [EG [~ [EX [[[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]] & ~ [EX [~ [[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]]]]]]]]]]]]]]]]
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
.abstracting: (1<=p111)
states: 487,527,594 (8)
abstracting: (1<=p110)
states: 487,527,594 (8)
abstracting: (1<=p109)
states: 487,527,594 (8)
abstracting: (1<=p108)
states: 487,527,594 (8)
abstracting: (1<=p115)
states: 487,527,594 (8)
abstracting: (1<=p114)
states: 487,527,594 (8)
abstracting: (1<=p113)
states: 487,527,594 (8)
abstracting: (1<=p112)
states: 487,527,594 (8)
abstracting: (1<=p119)
states: 487,527,594 (8)
abstracting: (1<=p118)
states: 487,527,594 (8)
abstracting: (1<=p117)
states: 487,527,594 (8)
abstracting: (1<=p116)
states: 487,527,594 (8)
abstracting: (1<=p123)
states: 487,527,594 (8)
abstracting: (1<=p122)
states: 487,527,594 (8)
abstracting: (1<=p121)
states: 487,527,594 (8)
abstracting: (1<=p120)
states: 487,527,594 (8)
..
EG iterations: 1
abstracting: (1<=p110)
states: 487,527,594 (8)
abstracting: (1<=p108)
states: 487,527,594 (8)
abstracting: (1<=p111)
states: 487,527,594 (8)
abstracting: (1<=p114)
states: 487,527,594 (8)
abstracting: (1<=p109)
states: 487,527,594 (8)
abstracting: (1<=p112)
states: 487,527,594 (8)
abstracting: (1<=p115)
states: 487,527,594 (8)
abstracting: (1<=p118)
states: 487,527,594 (8)
abstracting: (1<=p113)
states: 487,527,594 (8)
abstracting: (1<=p116)
states: 487,527,594 (8)
abstracting: (1<=p119)
states: 487,527,594 (8)
abstracting: (1<=p122)
states: 487,527,594 (8)
abstracting: (1<=p117)
states: 487,527,594 (8)
abstracting: (1<=p121)
states: 487,527,594 (8)
abstracting: (1<=p120)
states: 487,527,594 (8)
abstracting: (1<=p123)
states: 487,527,594 (8)
.-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-02 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m46.593sec
checking: [AG [EF [[[[[p65<=0 & p64<=0] & [p67<=0 & p66<=0]] & [[p69<=0 & p68<=0] & [p71<=0 & p70<=0]]] & [[[p57<=0 & p56<=0] & [p59<=0 & p58<=0]] & [[p61<=0 & p60<=0] & [p63<=0 & p62<=0]]]]]] & AF [EG [AG [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]]]]]
normalized: [~ [EG [~ [EG [~ [E [true U ~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]]]] & ~ [E [true U ~ [E [true U [[[[p63<=0 & p62<=0] & [p61<=0 & p60<=0]] & [[p59<=0 & p58<=0] & [p57<=0 & p56<=0]]] & [[[p71<=0 & p70<=0] & [p69<=0 & p68<=0]] & [[p67<=0 & p66<=0] & [p65<=0 & p64<=0]]]]]]]]]
abstracting: (p64<=0)
states: 4,706,988,632 (9)
abstracting: (p65<=0)
states: 4,706,988,632 (9)
abstracting: (p66<=0)
states: 4,706,988,632 (9)
abstracting: (p67<=0)
states: 4,706,988,632 (9)
abstracting: (p68<=0)
states: 4,706,988,632 (9)
abstracting: (p69<=0)
states: 4,706,988,632 (9)
abstracting: (p70<=0)
states: 4,706,988,632 (9)
abstracting: (p71<=0)
states: 4,706,988,632 (9)
abstracting: (p56<=0)
states: 4,706,988,632 (9)
abstracting: (p57<=0)
states: 4,706,988,632 (9)
abstracting: (p58<=0)
states: 4,706,988,632 (9)
abstracting: (p59<=0)
states: 4,706,988,632 (9)
abstracting: (p60<=0)
states: 4,706,988,632 (9)
abstracting: (p61<=0)
states: 4,706,988,632 (9)
abstracting: (p62<=0)
states: 4,706,988,632 (9)
abstracting: (p63<=0)
states: 4,706,988,632 (9)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
before gc: list nodes free: 1288597
after gc: idd nodes used:6334436, unused:57665564; list nodes free:256649574
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
.
EG iterations: 1
EG iterations: 0
-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-09 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m50.870sec
checking: AF [[E [[[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]] & [[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]] U EG [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]] & [AX [[[[[p65<=0 & p64<=0] & [p67<=0 & p66<=0]] & [[p69<=0 & p68<=0] & [p71<=0 & p70<=0]]] & [[[p57<=0 & p56<=0] & [p59<=0 & p58<=0]] & [[p61<=0 & p60<=0] & [p63<=0 & p62<=0]]]]] & AX [[[[[p110<=0 & p111<=0] & [p108<=0 & p109<=0]] & [[p114<=0 & p115<=0] & [p112<=0 & p113<=0]]] & [[[p118<=0 & p119<=0] & [p116<=0 & p117<=0]] & [[p122<=0 & p123<=0] & [p120<=0 & p121<=0]]]]]]]]
normalized: ~ [EG [~ [[[~ [EX [~ [[[[[p120<=0 & p121<=0] & [p122<=0 & p123<=0]] & [[p116<=0 & p117<=0] & [p118<=0 & p119<=0]]] & [[[p112<=0 & p113<=0] & [p114<=0 & p115<=0]] & [[p108<=0 & p109<=0] & [p110<=0 & p111<=0]]]]]]] & ~ [EX [~ [[[[[p63<=0 & p62<=0] & [p61<=0 & p60<=0]] & [[p59<=0 & p58<=0] & [p57<=0 & p56<=0]]] & [[[p71<=0 & p70<=0] & [p69<=0 & p68<=0]] & [[p67<=0 & p66<=0] & [p65<=0 & p64<=0]]]]]]]] & E [[[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]] & [[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]] U EG [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]]]]
abstracting: (1<=p64)
states: 10,898,249 (7)
abstracting: (1<=p65)
states: 10,898,249 (7)
abstracting: (1<=p66)
states: 10,898,249 (7)
abstracting: (1<=p67)
states: 10,898,249 (7)
abstracting: (1<=p68)
states: 10,898,249 (7)
abstracting: (1<=p69)
states: 10,898,249 (7)
abstracting: (1<=p70)
states: 10,898,249 (7)
abstracting: (1<=p71)
states: 10,898,249 (7)
abstracting: (1<=p56)
states: 10,898,249 (7)
abstracting: (1<=p57)
states: 10,898,249 (7)
abstracting: (1<=p58)
states: 10,898,249 (7)
abstracting: (1<=p59)
states: 10,898,249 (7)
abstracting: (1<=p60)
states: 10,898,249 (7)
abstracting: (1<=p61)
states: 10,898,249 (7)
abstracting: (1<=p62)
states: 10,898,249 (7)
abstracting: (1<=p63)
states: 10,898,249 (7)
..
EG iterations: 2
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p4)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p6)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p11)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p14)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p9)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p12)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p7)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p3)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p1)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p15)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p5)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p8)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p13)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p10)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p2)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p0)
states: 716,223,354 (8)
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
abstracting: (p64<=0)
states: 4,706,988,632 (9)
abstracting: (p65<=0)
states: 4,706,988,632 (9)
abstracting: (p66<=0)
states: 4,706,988,632 (9)
abstracting: (p67<=0)
states: 4,706,988,632 (9)
abstracting: (p68<=0)
states: 4,706,988,632 (9)
abstracting: (p69<=0)
states: 4,706,988,632 (9)
abstracting: (p70<=0)
states: 4,706,988,632 (9)
abstracting: (p71<=0)
states: 4,706,988,632 (9)
abstracting: (p56<=0)
states: 4,706,988,632 (9)
abstracting: (p57<=0)
states: 4,706,988,632 (9)
abstracting: (p58<=0)
states: 4,706,988,632 (9)
abstracting: (p59<=0)
states: 4,706,988,632 (9)
abstracting: (p60<=0)
states: 4,706,988,632 (9)
abstracting: (p61<=0)
states: 4,706,988,632 (9)
abstracting: (p62<=0)
states: 4,706,988,632 (9)
abstracting: (p63<=0)
states: 4,706,988,632 (9)
.abstracting: (p111<=0)
states: 4,230,359,287 (9)
abstracting: (p110<=0)
states: 4,230,359,287 (9)
abstracting: (p109<=0)
states: 4,230,359,287 (9)
abstracting: (p108<=0)
states: 4,230,359,287 (9)
abstracting: (p115<=0)
states: 4,230,359,287 (9)
abstracting: (p114<=0)
states: 4,230,359,287 (9)
abstracting: (p113<=0)
states: 4,230,359,287 (9)
abstracting: (p112<=0)
states: 4,230,359,287 (9)
abstracting: (p119<=0)
states: 4,230,359,287 (9)
abstracting: (p118<=0)
states: 4,230,359,287 (9)
abstracting: (p117<=0)
states: 4,230,359,287 (9)
abstracting: (p116<=0)
states: 4,230,359,287 (9)
abstracting: (p123<=0)
states: 4,230,359,287 (9)
abstracting: (p122<=0)
states: 4,230,359,287 (9)
abstracting: (p121<=0)
states: 4,230,359,287 (9)
abstracting: (p120<=0)
states: 4,230,359,287 (9)
.
EG iterations: 0
-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-03 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 2m28.402sec
checking: EF [[EX [AG [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]]] & [EG [[[[[[1<=p37 & 1<=p125] | [1<=p38 & 1<=p134]] | [[1<=p37 & 1<=p129] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p133] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p137] | [1<=p39 & 1<=p139]]]] | [[[[1<=p36 & 1<=p124] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p128] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p132] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]] & A [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]] U ~ [AG [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]]]]]]
normalized: E [true U [[[~ [EG [~ [E [true U ~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]]]] & ~ [E [~ [E [true U ~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]] U [~ [[[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]] & ~ [E [true U ~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]]]]]] & EG [[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]]] & EX [~ [E [true U ~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]]]
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
.abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
..
EG iterations: 2
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p4)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p6)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p11)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p14)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p9)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p12)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p7)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p3)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p1)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p15)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p5)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p8)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p13)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p10)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p2)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p0)
states: 716,223,354 (8)
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
.
EG iterations: 1
-> the formula is FALSE
FORMULA DatabaseWithMutex-COL-04-CTLFireability-01 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m35.752sec
checking: [AF [[[[[EG [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]] | [[[[p110<=0 & p111<=0] & [p108<=0 & p109<=0]] & [[p114<=0 & p115<=0] & [p112<=0 & p113<=0]]] & [[[p118<=0 & p119<=0] & [p116<=0 & p117<=0]] & [[p122<=0 & p123<=0] & [p120<=0 & p121<=0]]]]]]]]]] | 1<=p110] | [1<=p111 | 1<=p108]] | [[1<=p109 | 1<=p114] | [1<=p115 | 1<=p112]]] | [[[1<=p113 | 1<=p118] | [1<=p119 | 1<=p116]] | [[1<=p117 | 1<=p122] | [1<=p123 | [1<=p120 | 1<=p121]]]]]] & EX [AX [[AF [[[[[p41<=0 & p40<=0] & [p43<=0 & p42<=0]] & [[p45<=0 & p44<=0] & [p47<=0 & p46<=0]]] & [[[p49<=0 & p48<=0] & [p51<=0 & p50<=0]] & [[p53<=0 & p52<=0] & [p55<=0 & p54<=0]]]]] & ~ [E [[[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]] U [[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]]]]]]]
normalized: [EX [~ [EX [~ [[~ [E [[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]] U [[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]]] & ~ [EG [~ [[[[[p55<=0 & p54<=0] & [p53<=0 & p52<=0]] & [[p51<=0 & p50<=0] & [p49<=0 & p48<=0]]] & [[[p47<=0 & p46<=0] & [p45<=0 & p44<=0]] & [[p43<=0 & p42<=0] & [p41<=0 & p40<=0]]]]]]]]]]]] & ~ [EG [~ [[[[[1<=p123 | [1<=p120 | 1<=p121]] | [1<=p117 | 1<=p122]] | [[1<=p119 | 1<=p116] | [1<=p113 | 1<=p118]]] | [[[1<=p115 | 1<=p112] | [1<=p109 | 1<=p114]] | [[1<=p111 | 1<=p108] | [1<=p110 | EG [[[[[[[[[[p120<=0 & p121<=0] & [p122<=0 & p123<=0]] & [[p116<=0 & p117<=0] & [p118<=0 & p119<=0]]] & [[[p112<=0 & p113<=0] & [p114<=0 & p115<=0]] & [[p108<=0 & p109<=0] & [p110<=0 & p111<=0]]]] | [[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]]]]]]
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (p111<=0)
states: 4,230,359,287 (9)
abstracting: (p110<=0)
states: 4,230,359,287 (9)
abstracting: (p109<=0)
states: 4,230,359,287 (9)
abstracting: (p108<=0)
states: 4,230,359,287 (9)
abstracting: (p115<=0)
states: 4,230,359,287 (9)
abstracting: (p114<=0)
states: 4,230,359,287 (9)
abstracting: (p113<=0)
states: 4,230,359,287 (9)
abstracting: (p112<=0)
states: 4,230,359,287 (9)
abstracting: (p119<=0)
states: 4,230,359,287 (9)
abstracting: (p118<=0)
states: 4,230,359,287 (9)
abstracting: (p117<=0)
states: 4,230,359,287 (9)
abstracting: (p116<=0)
states: 4,230,359,287 (9)
abstracting: (p123<=0)
states: 4,230,359,287 (9)
abstracting: (p122<=0)
states: 4,230,359,287 (9)
abstracting: (p121<=0)
states: 4,230,359,287 (9)
abstracting: (p120<=0)
states: 4,230,359,287 (9)
...
before gc: list nodes free: 160230
after gc: idd nodes used:10733705, unused:53266295; list nodes free:239373860
.......................
EG iterations: 26
abstracting: (1<=p110)
states: 487,527,594 (8)
abstracting: (1<=p108)
states: 487,527,594 (8)
abstracting: (1<=p111)
states: 487,527,594 (8)
abstracting: (1<=p114)
states: 487,527,594 (8)
abstracting: (1<=p109)
states: 487,527,594 (8)
abstracting: (1<=p112)
states: 487,527,594 (8)
abstracting: (1<=p115)
states: 487,527,594 (8)
abstracting: (1<=p118)
states: 487,527,594 (8)
abstracting: (1<=p113)
states: 487,527,594 (8)
abstracting: (1<=p116)
states: 487,527,594 (8)
abstracting: (1<=p119)
states: 487,527,594 (8)
abstracting: (1<=p122)
states: 487,527,594 (8)
abstracting: (1<=p117)
states: 487,527,594 (8)
abstracting: (1<=p121)
states: 487,527,594 (8)
abstracting: (1<=p120)
states: 487,527,594 (8)
abstracting: (1<=p123)
states: 487,527,594 (8)
......
before gc: list nodes free: 2206282
after gc: idd nodes used:10636254, unused:53363746; list nodes free:239810537
....................
EG iterations: 26
abstracting: (p40<=0)
states: 4,001,663,527 (9)
abstracting: (p41<=0)
states: 4,001,663,527 (9)
abstracting: (p42<=0)
states: 4,001,663,527 (9)
abstracting: (p43<=0)
states: 4,001,663,527 (9)
abstracting: (p44<=0)
states: 4,001,663,527 (9)
abstracting: (p45<=0)
states: 4,001,663,527 (9)
abstracting: (p46<=0)
states: 4,001,663,527 (9)
abstracting: (p47<=0)
states: 4,001,663,527 (9)
abstracting: (p48<=0)
states: 4,001,663,527 (9)
abstracting: (p49<=0)
states: 4,001,663,527 (9)
abstracting: (p50<=0)
states: 4,001,663,527 (9)
abstracting: (p51<=0)
states: 4,001,663,527 (9)
abstracting: (p52<=0)
states: 4,001,663,527 (9)
abstracting: (p53<=0)
states: 4,001,663,527 (9)
abstracting: (p54<=0)
states: 4,001,663,527 (9)
abstracting: (p55<=0)
states: 4,001,663,527 (9)
..........
EG iterations: 10
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p4)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p6)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p11)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p14)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p9)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p12)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p7)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p3)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p1)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p15)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p5)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p8)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p13)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p10)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p2)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p0)
states: 716,223,354 (8)
abstracting: (1<=p111)
states: 487,527,594 (8)
abstracting: (1<=p110)
states: 487,527,594 (8)
abstracting: (1<=p109)
states: 487,527,594 (8)
abstracting: (1<=p108)
states: 487,527,594 (8)
abstracting: (1<=p115)
states: 487,527,594 (8)
abstracting: (1<=p114)
states: 487,527,594 (8)
abstracting: (1<=p113)
states: 487,527,594 (8)
abstracting: (1<=p112)
states: 487,527,594 (8)
abstracting: (1<=p119)
states: 487,527,594 (8)
abstracting: (1<=p118)
states: 487,527,594 (8)
abstracting: (1<=p117)
states: 487,527,594 (8)
abstracting: (1<=p116)
states: 487,527,594 (8)
abstracting: (1<=p123)
states: 487,527,594 (8)
abstracting: (1<=p122)
states: 487,527,594 (8)
abstracting: (1<=p121)
states: 487,527,594 (8)
abstracting: (1<=p120)
states: 487,527,594 (8)
MC time: 6m 7.020sec
checking: AF [[EX [[EG [[[[[p41<=0 & p40<=0] & [p43<=0 & p42<=0]] & [[p45<=0 & p44<=0] & [p47<=0 & p46<=0]]] & [[[p49<=0 & p48<=0] & [p51<=0 & p50<=0]] & [[p53<=0 & p52<=0] & [p55<=0 & p54<=0]]]]] & ~ [A [[[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]] U [[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]]]]]] & [[EG [[[[[p41<=0 & p40<=0] & [p43<=0 & p42<=0]] & [[p45<=0 & p44<=0] & [p47<=0 & p46<=0]]] & [[[p49<=0 & p48<=0] & [p51<=0 & p50<=0]] & [[p53<=0 & p52<=0] & [p55<=0 & p54<=0]]]]] | A [EF [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]] U ~ [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]]] & [AG [[[[[[p4<=0 | p105<=0] & [p6<=0 | p105<=0]] & [[p11<=0 | p106<=0] & [p14<=0 | p107<=0]]] & [[[p9<=0 | p106<=0] & [p12<=0 | p107<=0]] & [[p7<=0 | p105<=0] & [p3<=0 | p104<=0]]]] & [[[[p1<=0 | p104<=0] & [p15<=0 | p107<=0]] & [[p5<=0 | p105<=0] & [p8<=0 | p106<=0]]] & [[[p13<=0 | p107<=0] & [p10<=0 | p106<=0]] & [[p2<=0 | p104<=0] & [p0<=0 | p104<=0]]]]]] | [AF [[[[[p73<=0 & p72<=0] & [p75<=0 & p74<=0]] & [[p77<=0 & p76<=0] & [p79<=0 & p78<=0]]] & [[[p81<=0 & p80<=0] & [p83<=0 & p82<=0]] & [[p85<=0 & p84<=0] & [p87<=0 & p86<=0]]]]] | [[[[p73<=0 & p72<=0] & [p75<=0 & p74<=0]] & [[p77<=0 & p76<=0] & [p79<=0 & p78<=0]]] & [[[p81<=0 & p80<=0] & [p83<=0 & p82<=0]] & [[p85<=0 & p84<=0] & [p87<=0 & p86<=0]]]]]]]]]
normalized: ~ [EG [~ [[[[~ [E [true U ~ [[[[[[p0<=0 | p104<=0] & [p2<=0 | p104<=0]] & [[p10<=0 | p106<=0] & [p13<=0 | p107<=0]]] & [[[p8<=0 | p106<=0] & [p5<=0 | p105<=0]] & [[p15<=0 | p107<=0] & [p1<=0 | p104<=0]]]] & [[[[p3<=0 | p104<=0] & [p7<=0 | p105<=0]] & [[p12<=0 | p107<=0] & [p9<=0 | p106<=0]]] & [[[p14<=0 | p107<=0] & [p11<=0 | p106<=0]] & [[p6<=0 | p105<=0] & [p4<=0 | p105<=0]]]]]]]] | [[[[[p87<=0 & p86<=0] & [p85<=0 & p84<=0]] & [[p83<=0 & p82<=0] & [p81<=0 & p80<=0]]] & [[[p79<=0 & p78<=0] & [p77<=0 & p76<=0]] & [[p75<=0 & p74<=0] & [p73<=0 & p72<=0]]]] | ~ [EG [~ [[[[[p87<=0 & p86<=0] & [p85<=0 & p84<=0]] & [[p83<=0 & p82<=0] & [p81<=0 & p80<=0]]] & [[[p79<=0 & p78<=0] & [p77<=0 & p76<=0]] & [[p75<=0 & p74<=0] & [p73<=0 & p72<=0]]]]]]]]] & [[~ [EG [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]] & ~ [E [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]] U [~ [E [true U [[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]]] & [[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]]] | EG [[[[[p55<=0 & p54<=0] & [p53<=0 & p52<=0]] & [[p51<=0 & p50<=0] & [p49<=0 & p48<=0]]] & [[[p47<=0 & p46<=0] & [p45<=0 & p44<=0]] & [[p43<=0 & p42<=0] & [p41<=0 & p40<=0]]]]]]] & EX [[~ [[~ [EG [~ [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]]]] & ~ [E [~ [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]] U [~ [[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]]] & ~ [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]]]]]]] & EG [[[[[p55<=0 & p54<=0] & [p53<=0 & p52<=0]] & [[p51<=0 & p50<=0] & [p49<=0 & p48<=0]]] & [[[p47<=0 & p46<=0] & [p45<=0 & p44<=0]] & [[p43<=0 & p42<=0] & [p41<=0 & p40<=0]]]]]]]]]]]
abstracting: (p40<=0)
states: 4,001,663,527 (9)
abstracting: (p41<=0)
states: 4,001,663,527 (9)
abstracting: (p42<=0)
states: 4,001,663,527 (9)
abstracting: (p43<=0)
states: 4,001,663,527 (9)
abstracting: (p44<=0)
states: 4,001,663,527 (9)
abstracting: (p45<=0)
states: 4,001,663,527 (9)
abstracting: (p46<=0)
states: 4,001,663,527 (9)
abstracting: (p47<=0)
states: 4,001,663,527 (9)
abstracting: (p48<=0)
states: 4,001,663,527 (9)
abstracting: (p49<=0)
states: 4,001,663,527 (9)
abstracting: (p50<=0)
states: 4,001,663,527 (9)
abstracting: (p51<=0)
states: 4,001,663,527 (9)
abstracting: (p52<=0)
states: 4,001,663,527 (9)
abstracting: (p53<=0)
states: 4,001,663,527 (9)
abstracting: (p54<=0)
states: 4,001,663,527 (9)
abstracting: (p55<=0)
states: 4,001,663,527 (9)
...........
before gc: list nodes free: 4492683
after gc: idd nodes used:12127103, unused:51872897; list nodes free:233320432
...............
before gc: list nodes free: 4617213
after gc: idd nodes used:13498825, unused:50501175; list nodes free:227378571
..MC time: 5m21.092sec
checking: AG [~ [A [[[EF [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]] & A [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]] U [[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]]] | AF [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]] U EG [[[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p88 & 1<=p32] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]] & [[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]]]]]]]
normalized: ~ [E [true U [~ [EG [~ [EG [[[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]] & [[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p88 & 1<=p32]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]] & ~ [E [~ [EG [[[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]] & [[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p88 & 1<=p32]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]] U [~ [[~ [EG [~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]] | [[~ [EG [~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]] & ~ [E [~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]] U [~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]] & ~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]] & E [true U [[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]] & ~ [EG [[[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]] & [[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p88 & 1<=p32]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]]]]]]
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p40)
states: 716,223,354 (8)
abstracting: (1<=p41)
states: 716,223,354 (8)
abstracting: (1<=p42)
states: 716,223,354 (8)
abstracting: (1<=p43)
states: 716,223,354 (8)
abstracting: (1<=p44)
states: 716,223,354 (8)
abstracting: (1<=p45)
states: 716,223,354 (8)
abstracting: (1<=p46)
states: 716,223,354 (8)
abstracting: (1<=p47)
states: 716,223,354 (8)
abstracting: (1<=p48)
states: 716,223,354 (8)
abstracting: (1<=p49)
states: 716,223,354 (8)
abstracting: (1<=p50)
states: 716,223,354 (8)
abstracting: (1<=p51)
states: 716,223,354 (8)
abstracting: (1<=p52)
states: 716,223,354 (8)
abstracting: (1<=p53)
states: 716,223,354 (8)
abstracting: (1<=p54)
states: 716,223,354 (8)
abstracting: (1<=p55)
states: 716,223,354 (8)
..........
EG iterations: 10
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p17)
states: 40,879,841 (7)
abstracting: (1<=p16)
states: 40,879,841 (7)
abstracting: (1<=p19)
states: 40,879,841 (7)
abstracting: (1<=p18)
states: 40,879,841 (7)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
.....
before gc: list nodes free: 4130272
after gc: idd nodes used:14335501, unused:49664499; list nodes free:223427142
......MC time: 4m41.090sec
checking: AF [[[[[p65<=0 & p64<=0] & [p67<=0 & p66<=0]] & [[p69<=0 & p68<=0] & [p71<=0 & [p70<=0 & p57<=0]]]] & [[[p56<=0 & p59<=0] & [p58<=0 & [p61<=0 & p60<=0]]] & [[p63<=0 & p62<=0] & [EG [[[[[[[[p21<=0 | p93<=0] | [p97<=0 | p101<=0]] & [[p27<=0 | p91<=0] | [p99<=0 | p103<=0]]] & [[[p28<=0 | p88<=0] | [p92<=0 | p100<=0]] & [[p33<=0 | p89<=0] | [p93<=0 | p97<=0]]]] & [[[[p25<=0 | p89<=0] | [p97<=0 | p101<=0]] & [[p34<=0 | p90<=0] | [p94<=0 | p98<=0]]] & [[[p23<=0 | p95<=0] | [p99<=0 | p103<=0]] & [[p24<=0 | p88<=0] | [p96<=0 | p100<=0]]]]] & [[[[[p22<=0 | p94<=0] | [p98<=0 | p102<=0]] & [[p35<=0 | p91<=0] | [p95<=0 | p99<=0]]] & [[[p32<=0 | p88<=0] | [p92<=0 | p96<=0]] & [[p29<=0 | p89<=0] | [p93<=0 | p101<=0]]]] & [[[[p20<=0 | p92<=0] | [p96<=0 | p100<=0]] & [[p26<=0 | p90<=0] | [p98<=0 | p102<=0]]] & [[[p31<=0 | p91<=0] | [p95<=0 | p103<=0]] & [[p30<=0 | p90<=0] | [p94<=0 | p102<=0]]]]]] & [[[[[p4<=0 | p105<=0] & [p6<=0 | p105<=0]] & [[p11<=0 | p106<=0] & [p14<=0 | p107<=0]]] & [[[p9<=0 | p106<=0] & [p12<=0 | p107<=0]] & [[p7<=0 | p105<=0] & [p3<=0 | p104<=0]]]] & [[[[p1<=0 | p104<=0] & [p15<=0 | p107<=0]] & [[p5<=0 | p105<=0] & [p8<=0 | p106<=0]]] & [[[p13<=0 | p107<=0] & [p10<=0 | p106<=0]] & [[p2<=0 | p104<=0] & [p0<=0 | p104<=0]]]]]]] & [A [[E [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]] U [[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]] & [[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]] U ~ [EF [[[[[[1<=p37 & 1<=p125] | [1<=p134 & 1<=p38]] | [[1<=p37 & 1<=p129] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p133] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p137] | [1<=p39 & 1<=p139]]]] | [[[[1<=p36 & 1<=p124] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p128] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p132] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]]]] & [[[[[p41<=0 & p40<=0] & [p43<=0 & p42<=0]] & [[p45<=0 & p44<=0] & [p47<=0 & p46<=0]]] & [[[p49<=0 & p48<=0] & [p51<=0 & p50<=0]] & [[p53<=0 & p52<=0] & [p55<=0 & p54<=0]]]] | [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]] & [[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]]]]]]]]
normalized: ~ [EG [~ [[[[[[[[[[[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]] | [[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]]] & [[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]] | [[[[p55<=0 & p54<=0] & [p53<=0 & p52<=0]] & [[p51<=0 & p50<=0] & [p49<=0 & p48<=0]]] & [[[p47<=0 & p46<=0] & [p45<=0 & p44<=0]] & [[p43<=0 & p42<=0] & [p41<=0 & p40<=0]]]]] & [~ [EG [E [true U [[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p134 & 1<=p38] | [1<=p37 & 1<=p125]]]]]]]] & ~ [E [E [true U [[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p134 & 1<=p38] | [1<=p37 & 1<=p125]]]]]] U [~ [[[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]] & E [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]] U [[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]] & E [true U [[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p134 & 1<=p38] | [1<=p37 & 1<=p125]]]]]]]]]]] & EG [[[[[[[p0<=0 | p104<=0] & [p2<=0 | p104<=0]] & [[p10<=0 | p106<=0] & [p13<=0 | p107<=0]]] & [[[p8<=0 | p106<=0] & [p5<=0 | p105<=0]] & [[p15<=0 | p107<=0] & [p1<=0 | p104<=0]]]] & [[[[p3<=0 | p104<=0] & [p7<=0 | p105<=0]] & [[p12<=0 | p107<=0] & [p9<=0 | p106<=0]]] & [[[p14<=0 | p107<=0] & [p11<=0 | p106<=0]] & [[p6<=0 | p105<=0] & [p4<=0 | p105<=0]]]]] & [[[[[[p94<=0 | p102<=0] | [p30<=0 | p90<=0]] & [[p95<=0 | p103<=0] | [p31<=0 | p91<=0]]] & [[[p98<=0 | p102<=0] | [p26<=0 | p90<=0]] & [[p96<=0 | p100<=0] | [p20<=0 | p92<=0]]]] & [[[[p93<=0 | p101<=0] | [p29<=0 | p89<=0]] & [[p92<=0 | p96<=0] | [p32<=0 | p88<=0]]] & [[[p95<=0 | p99<=0] | [p35<=0 | p91<=0]] & [[p98<=0 | p102<=0] | [p22<=0 | p94<=0]]]]] & [[[[[p96<=0 | p100<=0] | [p24<=0 | p88<=0]] & [[p99<=0 | p103<=0] | [p23<=0 | p95<=0]]] & [[[p94<=0 | p98<=0] | [p34<=0 | p90<=0]] & [[p97<=0 | p101<=0] | [p25<=0 | p89<=0]]]] & [[[[p93<=0 | p97<=0] | [p33<=0 | p89<=0]] & [[p92<=0 | p100<=0] | [p28<=0 | p88<=0]]] & [[[p99<=0 | p103<=0] | [p27<=0 | p91<=0]] & [[p97<=0 | p101<=0] | [p21<=0 | p93<=0]]]]]]]]] & [p63<=0 & p62<=0]] & [[p58<=0 & [p61<=0 & p60<=0]] & [p56<=0 & p59<=0]]] & [[[p71<=0 & [p70<=0 & p57<=0]] & [p69<=0 & p68<=0]] & [[p67<=0 & p66<=0] & [p65<=0 & p64<=0]]]]]]]
abstracting: (p64<=0)
states: 4,706,988,632 (9)
abstracting: (p65<=0)
states: 4,706,988,632 (9)
abstracting: (p66<=0)
states: 4,706,988,632 (9)
abstracting: (p67<=0)
states: 4,706,988,632 (9)
abstracting: (p68<=0)
states: 4,706,988,632 (9)
abstracting: (p69<=0)
states: 4,706,988,632 (9)
abstracting: (p57<=0)
states: 4,706,988,632 (9)
abstracting: (p70<=0)
states: 4,706,988,632 (9)
abstracting: (p71<=0)
states: 4,706,988,632 (9)
abstracting: (p59<=0)
states: 4,706,988,632 (9)
abstracting: (p56<=0)
states: 4,706,988,632 (9)
abstracting: (p60<=0)
states: 4,706,988,632 (9)
abstracting: (p61<=0)
states: 4,706,988,632 (9)
abstracting: (p58<=0)
states: 4,706,988,632 (9)
abstracting: (p62<=0)
states: 4,706,988,632 (9)
abstracting: (p63<=0)
states: 4,706,988,632 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p21<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p27<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p28<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p33<=0)
states: 3,600,413,211 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p25<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p34<=0)
states: 3,600,413,211 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p23<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p24<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
abstracting: (p22<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p35<=0)
states: 3,600,413,211 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p32<=0)
states: 3,600,413,211 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p29<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p20<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p26<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p31<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p30<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
abstracting: (p105<=0)
states: 1,950,110,376 (9)
abstracting: (p4<=0)
states: 4,001,663,527 (9)
abstracting: (p105<=0)
states: 1,950,110,376 (9)
abstracting: (p6<=0)
states: 4,001,663,527 (9)
abstracting: (p106<=0)
states: 1,950,110,376 (9)
abstracting: (p11<=0)
states: 4,001,663,527 (9)
abstracting: (p107<=0)
states: 1,950,110,376 (9)
abstracting: (p14<=0)
states: 4,001,663,527 (9)
abstracting: (p106<=0)
states: 1,950,110,376 (9)
abstracting: (p9<=0)
states: 4,001,663,527 (9)
abstracting: (p107<=0)
states: 1,950,110,376 (9)
abstracting: (p12<=0)
states: 4,001,663,527 (9)
abstracting: (p105<=0)
states: 1,950,110,376 (9)
abstracting: (p7<=0)
states: 4,001,663,527 (9)
abstracting: (p104<=0)
states: 1,950,110,376 (9)
abstracting: (p3<=0)
states: 4,001,663,527 (9)
abstracting: (p104<=0)
states: 1,950,110,376 (9)
abstracting: (p1<=0)
states: 4,001,663,527 (9)
abstracting: (p107<=0)
states: 1,950,110,376 (9)
abstracting: (p15<=0)
states: 4,001,663,527 (9)
abstracting: (p105<=0)
states: 1,950,110,376 (9)
abstracting: (p5<=0)
states: 4,001,663,527 (9)
abstracting: (p106<=0)
states: 1,950,110,376 (9)
abstracting: (p8<=0)
states: 4,001,663,527 (9)
abstracting: (p107<=0)
states: 1,950,110,376 (9)
abstracting: (p13<=0)
states: 4,001,663,527 (9)
abstracting: (p106<=0)
states: 1,950,110,376 (9)
abstracting: (p10<=0)
states: 4,001,663,527 (9)
abstracting: (p104<=0)
states: 1,950,110,376 (9)
abstracting: (p2<=0)
states: 4,001,663,527 (9)
abstracting: (p104<=0)
states: 1,950,110,376 (9)
abstracting: (p0<=0)
states: 4,001,663,527 (9)
before gc: list nodes free: 1910673
after gc: idd nodes used:17786502, unused:46213498; list nodes free:208343119
..
before gc: list nodes free: 5407656
after gc: idd nodes used:22232722, unused:41767278; list nodes free:188949981
.MC time: 4m 8.267sec
checking: [[AG [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]] | AG [[[[[[[p16<=0 & p17<=0] & [p18<=0 & [p19<=0 & ~ [E [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]] U [[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]]]]]] | [1<=p37 & 1<=p125]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p129]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p133]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p137]]]] | [[[[1<=p39 & 1<=p139] | [1<=p36 & 1<=p124]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p128]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p132]] | [[1<=p39 & 1<=p127] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]]]] | [EF [EG [[[[[[p37<=0 | p125<=0] & [p38<=0 | p134<=0]] & [[p37<=0 | p129<=0] & [p38<=0 | p130<=0]]] & [[[p37<=0 | p133<=0] & [p38<=0 | p126<=0]] & [[p37<=0 | p137<=0] & [p39<=0 | p139<=0]]]] & [[[[p36<=0 | p124<=0] & [p39<=0 | p135<=0]] & [[p36<=0 | p128<=0] & [p39<=0 | p131<=0]]] & [[[p36<=0 | p132<=0] & [p39<=0 | p127<=0]] & [[p36<=0 | p136<=0] & [p38<=0 | p138<=0]]]]]]] | EG [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]] | AF [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]]]]]]]]]
normalized: [[EG [[[[[[~ [EG [~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]] | [[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]] | E [true U EG [[[[[[p38<=0 | p138<=0] & [p36<=0 | p136<=0]] & [[p39<=0 | p127<=0] & [p36<=0 | p132<=0]]] & [[[p39<=0 | p131<=0] & [p36<=0 | p128<=0]] & [[p39<=0 | p135<=0] & [p36<=0 | p124<=0]]]] & [[[[p39<=0 | p139<=0] & [p37<=0 | p137<=0]] & [[p38<=0 | p126<=0] & [p37<=0 | p133<=0]]] & [[[p38<=0 | p130<=0] & [p37<=0 | p129<=0]] & [[p38<=0 | p134<=0] & [p37<=0 | p125<=0]]]]]]]] | [~ [E [true U ~ [[[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p132] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p128] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p124] | [1<=p39 & 1<=p139]]]] | [[[[1<=p37 & 1<=p137] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p133] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p129] | [1<=p38 & 1<=p134]] | [[1<=p37 & 1<=p125] | [[p18<=0 & [p19<=0 & ~ [E [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]] U [[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]] & [p16<=0 & p17<=0]]]]]]]]] | ~ [E [true U ~ [[[[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]]]]]]]
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (p17<=0)
states: 4,677,007,040 (9)
abstracting: (p16<=0)
states: 4,677,007,040 (9)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (p19<=0)
states: 4,677,007,040 (9)
abstracting: (p18<=0)
states: 4,677,007,040 (9)
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (p125<=0)
states: 4,677,007,040 (9)
abstracting: (p37<=0)
states: 4,513,487,676 (9)
abstracting: (p134<=0)
states: 4,677,007,040 (9)
abstracting: (p38<=0)
states: 4,513,487,676 (9)
abstracting: (p129<=0)
states: 4,677,007,040 (9)
abstracting: (p37<=0)
states: 4,513,487,676 (9)
abstracting: (p130<=0)
states: 4,677,007,040 (9)
abstracting: (p38<=0)
states: 4,513,487,676 (9)
abstracting: (p133<=0)
states: 4,677,007,040 (9)
abstracting: (p37<=0)
states: 4,513,487,676 (9)
abstracting: (p126<=0)
states: 4,677,007,040 (9)
abstracting: (p38<=0)
states: 4,513,487,676 (9)
abstracting: (p137<=0)
states: 4,677,007,040 (9)
abstracting: (p37<=0)
states: 4,513,487,676 (9)
abstracting: (p139<=0)
states: 4,677,007,040 (9)
abstracting: (p39<=0)
states: 4,513,487,676 (9)
abstracting: (p124<=0)
states: 4,677,007,040 (9)
abstracting: (p36<=0)
states: 4,513,487,676 (9)
abstracting: (p135<=0)
states: 4,677,007,040 (9)
abstracting: (p39<=0)
states: 4,513,487,676 (9)
abstracting: (p128<=0)
states: 4,677,007,040 (9)
abstracting: (p36<=0)
states: 4,513,487,676 (9)
abstracting: (p131<=0)
states: 4,677,007,040 (9)
abstracting: (p39<=0)
states: 4,513,487,676 (9)
abstracting: (p132<=0)
states: 4,677,007,040 (9)
abstracting: (p36<=0)
states: 4,513,487,676 (9)
abstracting: (p127<=0)
states: 4,677,007,040 (9)
abstracting: (p39<=0)
states: 4,513,487,676 (9)
abstracting: (p136<=0)
states: 4,677,007,040 (9)
abstracting: (p36<=0)
states: 4,513,487,676 (9)
abstracting: (p138<=0)
states: 4,677,007,040 (9)
abstracting: (p38<=0)
states: 4,513,487,676 (9)
......
before gc: list nodes free: 5425730
after gc: idd nodes used:18194847, unused:45805153; list nodes free:206439616
........MC time: 3m35.117sec
checking: E [[~ [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]] | [[~ [[[A [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]] U [[[[[1<=p37 & 1<=p125] | [1<=p38 & 1<=p134]] | [[1<=p37 & 1<=p129] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p133] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p137] | [1<=p39 & 1<=p139]]]] | [[[[1<=p36 & 1<=p124] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p128] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p132] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]] | [[[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]] & [[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]]] & ~ [[[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]]]]] & [EF [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]] | AG [[[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]] & [[[[1<=p73 | 1<=p72] | [1<=p75 | 1<=p74]] | [[1<=p77 | 1<=p76] | [1<=p79 | 1<=p78]]] | [[[1<=p81 | 1<=p80] | [1<=p83 | 1<=p82]] | [[1<=p85 | 1<=p84] | [1<=p87 | 1<=p86]]]]]]]] | [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]] & [[[[1<=p73 | 1<=p72] | [1<=p75 | 1<=p74]] | [[1<=p77 | 1<=p76] | [1<=p79 | 1<=p78]]] | [[[1<=p81 | 1<=p80] | [1<=p83 | 1<=p82]] | [[1<=p85 | 1<=p84] | [1<=p87 | 1<=p86]]]]]]] U [EF [[[[[[1<=p37 & 1<=p125] | [1<=p38 & 1<=p134]] | [[1<=p37 & 1<=p129] | [1<=p38 & 1<=p130]]] | [[[1<=p37 & 1<=p133] | [1<=p38 & 1<=p126]] | [[1<=p37 & 1<=p137] | [1<=p39 & 1<=p139]]]] | [[[[1<=p36 & 1<=p124] | [1<=p39 & 1<=p135]] | [[1<=p36 & 1<=p128] | [1<=p39 & 1<=p131]]] | [[[1<=p36 & 1<=p132] | [1<=p39 & 1<=p127]] | [[1<=p36 & 1<=p136] | [1<=p38 & 1<=p138]]]]]] & [[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]] | [[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]]]]]]
normalized: E [[[[[[[[1<=p87 | 1<=p86] | [1<=p85 | 1<=p84]] | [[1<=p83 | 1<=p82] | [1<=p81 | 1<=p80]]] | [[[1<=p79 | 1<=p78] | [1<=p77 | 1<=p76]] | [[1<=p75 | 1<=p74] | [1<=p73 | 1<=p72]]]] & [[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]] | [[~ [E [true U ~ [[[[[[1<=p87 | 1<=p86] | [1<=p85 | 1<=p84]] | [[1<=p83 | 1<=p82] | [1<=p81 | 1<=p80]]] | [[[1<=p79 | 1<=p78] | [1<=p77 | 1<=p76]] | [[1<=p75 | 1<=p74] | [1<=p73 | 1<=p72]]]] & [[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]] | E [true U [[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]]] & ~ [[~ [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]] & [[[[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]] & [[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]] | [~ [EG [~ [[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]]]] & ~ [E [~ [[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]] U [~ [[[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]] & ~ [[[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]]]]]]]]]]] | ~ [[[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]]]] U [[[[[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]] | [[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]]] | [[[[[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]] | [[1<=p99 & 1<=p103] & [1<=p23 & 1<=p95]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]]] & E [true U [[[[[1<=p38 & 1<=p138] | [1<=p36 & 1<=p136]] | [[1<=p39 & 1<=p127] | [1<=p36 & 1<=p132]]] | [[[1<=p39 & 1<=p131] | [1<=p36 & 1<=p128]] | [[1<=p39 & 1<=p135] | [1<=p36 & 1<=p124]]]] | [[[[1<=p39 & 1<=p139] | [1<=p37 & 1<=p137]] | [[1<=p38 & 1<=p126] | [1<=p37 & 1<=p133]]] | [[[1<=p38 & 1<=p130] | [1<=p37 & 1<=p129]] | [[1<=p38 & 1<=p134] | [1<=p37 & 1<=p125]]]]]]]]
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p21)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p27)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p33)
states: 1,117,473,670 (9)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p28)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p25)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p97)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p34)
states: 1,117,473,670 (9)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p23)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p24)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p20)
states: 1,117,473,670 (9)
abstracting: (1<=p100)
states: 716,223,354 (8)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p26)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p31)
states: 1,117,473,670 (9)
abstracting: (1<=p103)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p90)
states: 716,223,354 (8)
abstracting: (1<=p30)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p94)
states: 716,223,354 (8)
abstracting: (1<=p22)
states: 1,117,473,670 (9)
abstracting: (1<=p102)
states: 716,223,354 (8)
abstracting: (1<=p98)
states: 716,223,354 (8)
abstracting: (1<=p91)
states: 716,223,354 (8)
abstracting: (1<=p35)
states: 1,117,473,670 (9)
abstracting: (1<=p99)
states: 716,223,354 (8)
abstracting: (1<=p95)
states: 716,223,354 (8)
abstracting: (1<=p88)
states: 716,223,354 (8)
abstracting: (1<=p32)
states: 1,117,473,670 (9)
abstracting: (1<=p96)
states: 716,223,354 (8)
abstracting: (1<=p92)
states: 716,223,354 (8)
abstracting: (1<=p89)
states: 716,223,354 (8)
abstracting: (1<=p29)
states: 1,117,473,670 (9)
abstracting: (1<=p101)
states: 716,223,354 (8)
abstracting: (1<=p93)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p4)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p6)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p11)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p14)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p9)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p12)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p7)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p3)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p1)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p15)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p5)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p8)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p13)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p10)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p2)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p0)
states: 716,223,354 (8)
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p4)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p6)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p11)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p14)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p9)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p12)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p7)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p3)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p1)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p15)
states: 716,223,354 (8)
abstracting: (1<=p105)
states: 2,767,776,505 (9)
abstracting: (1<=p5)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p8)
states: 716,223,354 (8)
abstracting: (1<=p107)
states: 2,767,776,505 (9)
abstracting: (1<=p13)
states: 716,223,354 (8)
abstracting: (1<=p106)
states: 2,767,776,505 (9)
abstracting: (1<=p10)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p2)
states: 716,223,354 (8)
abstracting: (1<=p104)
states: 2,767,776,505 (9)
abstracting: (1<=p0)
states: 716,223,354 (8)
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p125)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p134)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p129)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p130)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p133)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p126)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
abstracting: (1<=p137)
states: 40,879,841 (7)
abstracting: (1<=p37)
states: 204,399,205 (8)
abstracting: (1<=p139)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p124)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p135)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p128)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p131)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p132)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p127)
states: 40,879,841 (7)
abstracting: (1<=p39)
states: 204,399,205 (8)
abstracting: (1<=p136)
states: 40,879,841 (7)
abstracting: (1<=p36)
states: 204,399,205 (8)
abstracting: (1<=p138)
states: 40,879,841 (7)
abstracting: (1<=p38)
states: 204,399,205 (8)
........MC time: 3m 8.027sec
checking: EF [[[[[p16<=0 & p17<=0] & [p18<=0 & [p19<=0 & EG [[[[[[p73<=0 & p72<=0] & [p75<=0 & p74<=0]] & [[p77<=0 & p76<=0] & [p79<=0 & p78<=0]]] & [[[p81<=0 & p80<=0] & [p83<=0 & p82<=0]] & [[p85<=0 & p84<=0] & [p87<=0 & p86<=0]]]] | [[[[[[p21<=0 | p93<=0] | [p97<=0 | p101<=0]] & [[p27<=0 | p91<=0] | [p99<=0 | p103<=0]]] & [[[p33<=0 | p89<=0] | [p93<=0 | p97<=0]] & [[p28<=0 | p88<=0] | [p92<=0 | p100<=0]]]] & [[[[p25<=0 | p89<=0] | [p97<=0 | p101<=0]] & [[p94<=0 | p98<=0] | [p34<=0 | p90<=0]]] & [[[p23<=0 | p95<=0] | [p99<=0 | p103<=0]] & [[p24<=0 | p88<=0] | [p96<=0 | p100<=0]]]]] & [[[[[p22<=0 | p94<=0] | [p98<=0 | p102<=0]] & [[p35<=0 | p91<=0] | [p95<=0 | p99<=0]]] & [[[p32<=0 | p88<=0] | [p92<=0 | p96<=0]] & [[p29<=0 | p89<=0] | [p93<=0 | p101<=0]]]] & [[[[p20<=0 | p92<=0] | [p96<=0 | p100<=0]] & [[p26<=0 | p90<=0] | [p98<=0 | p102<=0]]] & [[[p31<=0 | p91<=0] | [p95<=0 | p103<=0]] & [[p30<=0 | p90<=0] | [p94<=0 | p102<=0]]]]]]]]]]] & [[[[p21<=0 | p93<=0] | [p97<=0 | p101<=0]] & [[[p27<=0 | p91<=0] | [p99<=0 | p103<=0]] & [[p33<=0 | p89<=0] | [p93<=0 | p97<=0]]]] & [[[p28<=0 | p88<=0] | [p92<=0 | p100<=0]] & [[[p25<=0 | p89<=0] | [p97<=0 | p101<=0]] & [[p34<=0 | p90<=0] | [p94<=0 | p98<=0]]]]]] & [[[[[p23<=0 | p95<=0] | [p99<=0 | p103<=0]] & [[[p24<=0 | p88<=0] | [p96<=0 | p100<=0]] & [[p22<=0 | p94<=0] | [p98<=0 | p102<=0]]]] & [[[p35<=0 | p91<=0] | [p95<=0 | p99<=0]] & [[[p32<=0 | p88<=0] | [p92<=0 | p96<=0]] & [[p29<=0 | p89<=0] | [p93<=0 | p101<=0]]]]] & [[[[p20<=0 | p92<=0] | [p96<=0 | p100<=0]] & [[[p26<=0 | p90<=0] | [p98<=0 | p102<=0]] & [[p31<=0 | p91<=0] | [p95<=0 | p103<=0]]]] & [[[p30<=0 | p90<=0] | [p94<=0 | p102<=0]] & [[[[[EF [[[[[p65<=0 & p64<=0] & [p67<=0 & p66<=0]] & [[p69<=0 & p68<=0] & [p71<=0 & p70<=0]]] & [[[p57<=0 & p56<=0] & [p59<=0 & p58<=0]] & [[p61<=0 & p60<=0] & [p63<=0 & p62<=0]]]]] | 1<=p110] | [1<=p111 | [1<=p108 | 1<=p109]]] | [[1<=p114 | 1<=p115] | [1<=p112 | [1<=p113 | 1<=p118]]]] | [[[1<=p119 | 1<=p116] | [1<=p117 | [1<=p122 | 1<=p123]]] | [[1<=p120 | [1<=p121 | AG [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]]]] | [EF [[[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]]] | [[[[[p65<=0 & p64<=0] & [p67<=0 & p66<=0]] & [[p69<=0 & p68<=0] & [p71<=0 & p70<=0]]] & [[[p57<=0 & p56<=0] & [p59<=0 & p58<=0]] & [[p61<=0 & p60<=0] & [p63<=0 & p62<=0]]]] | [[[[[p4<=0 | p105<=0] & [p6<=0 | p105<=0]] & [[p11<=0 | p106<=0] & [p14<=0 | p107<=0]]] & [[[p9<=0 | p106<=0] & [p12<=0 | p107<=0]] & [[p7<=0 | p105<=0] & [p3<=0 | p104<=0]]]] & [[[[p1<=0 | p104<=0] & [p15<=0 | p107<=0]] & [[p5<=0 | p105<=0] & [p8<=0 | p106<=0]]] & [[[p13<=0 | p107<=0] & [p10<=0 | p106<=0]] & [[p2<=0 | p104<=0] & [p0<=0 | p104<=0]]]]]]]]]] & [A [[~ [[[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]]] & ~ [[[[[[[1<=p21 & 1<=p93] & [1<=p97 & 1<=p101]] | [[1<=p27 & 1<=p91] & [1<=p99 & 1<=p103]]] | [[[1<=p33 & 1<=p89] & [1<=p93 & 1<=p97]] | [[1<=p28 & 1<=p88] & [1<=p92 & 1<=p100]]]] | [[[[1<=p25 & 1<=p89] & [1<=p97 & 1<=p101]] | [[1<=p34 & 1<=p90] & [1<=p94 & 1<=p98]]] | [[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p24 & 1<=p88] & [1<=p96 & 1<=p100]]]]] | [[[[[1<=p22 & 1<=p94] & [1<=p98 & 1<=p102]] | [[1<=p35 & 1<=p91] & [1<=p95 & 1<=p99]]] | [[[1<=p32 & 1<=p88] & [1<=p92 & 1<=p96]] | [[1<=p29 & 1<=p89] & [1<=p93 & 1<=p101]]]] | [[[[1<=p20 & 1<=p92] & [1<=p96 & 1<=p100]] | [[1<=p26 & 1<=p90] & [1<=p98 & 1<=p102]]] | [[[1<=p31 & 1<=p91] & [1<=p95 & 1<=p103]] | [[1<=p30 & 1<=p90] & [1<=p94 & 1<=p102]]]]]]]] U AF [[[1<=p16 | 1<=p17] | [1<=p18 | 1<=p19]]]] | ~ [A [~ [[[[[[1<=p4 & 1<=p105] | [1<=p6 & 1<=p105]] | [[1<=p11 & 1<=p106] | [1<=p14 & 1<=p107]]] | [[[1<=p9 & 1<=p106] | [1<=p12 & 1<=p107]] | [[1<=p7 & 1<=p105] | [1<=p3 & 1<=p104]]]] | [[[[1<=p1 & 1<=p104] | [1<=p15 & 1<=p107]] | [[1<=p5 & 1<=p105] | [1<=p8 & 1<=p106]]] | [[[1<=p13 & 1<=p107] | [1<=p10 & 1<=p106]] | [[1<=p2 & 1<=p104] | [1<=p0 & 1<=p104]]]]]] U [[[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]] | [[[[1<=p110 | 1<=p111] | [1<=p108 | 1<=p109]] | [[1<=p114 | 1<=p115] | [1<=p112 | 1<=p113]]] | [[[1<=p118 | 1<=p119] | [1<=p116 | 1<=p117]] | [[1<=p122 | 1<=p123] | [1<=p120 | 1<=p121]]]]]]]]]]]]]]
normalized: E [true U [[[[[[[~ [EG [EG [~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]]] & ~ [E [EG [~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]] U [~ [[~ [[[[[[[1<=p23 & 1<=p95] & [1<=p99 & 1<=p103]] | [[1<=p96 & 1<=p100] & [1<=p24 & 1<=p88]]] | [[[1<=p94 & 1<=p98] & [1<=p34 & 1<=p90]] | [[1<=p97 & 1<=p101] & [1<=p25 & 1<=p89]]]] | [[[[1<=p92 & 1<=p100] & [1<=p28 & 1<=p88]] | [[1<=p93 & 1<=p97] & [1<=p33 & 1<=p89]]] | [[[1<=p99 & 1<=p103] & [1<=p27 & 1<=p91]] | [[1<=p97 & 1<=p101] & [1<=p21 & 1<=p93]]]]] | [[[[[1<=p94 & 1<=p102] & [1<=p30 & 1<=p90]] | [[1<=p95 & 1<=p103] & [1<=p31 & 1<=p91]]] | [[[1<=p98 & 1<=p102] & [1<=p26 & 1<=p90]] | [[1<=p96 & 1<=p100] & [1<=p20 & 1<=p92]]]] | [[[[1<=p93 & 1<=p101] & [1<=p29 & 1<=p89]] | [[1<=p92 & 1<=p96] & [1<=p32 & 1<=p88]]] | [[[1<=p95 & 1<=p99] & [1<=p35 & 1<=p91]] | [[1<=p98 & 1<=p102] & [1<=p22 & 1<=p94]]]]]]] & ~ [[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]]]]] & EG [~ [[[1<=p18 | 1<=p19] | [1<=p16 | 1<=p17]]]]]]]] | ~ [[~ [EG [~ [[[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]] | [[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]]]]] & ~ [E [~ [[[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]] | [[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]]] U [[[[[[1<=p0 & 1<=p104] | [1<=p2 & 1<=p104]] | [[1<=p10 & 1<=p106] | [1<=p13 & 1<=p107]]] | [[[1<=p8 & 1<=p106] | [1<=p5 & 1<=p105]] | [[1<=p15 & 1<=p107] | [1<=p1 & 1<=p104]]]] | [[[[1<=p3 & 1<=p104] | [1<=p7 & 1<=p105]] | [[1<=p12 & 1<=p107] | [1<=p9 & 1<=p106]]] | [[[1<=p14 & 1<=p107] | [1<=p11 & 1<=p106]] | [[1<=p6 & 1<=p105] | [1<=p4 & 1<=p105]]]]] & ~ [[[[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]] | [[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]]]]]]]]] & [[[[[[[[[[p0<=0 | p104<=0] & [p2<=0 | p104<=0]] & [[p10<=0 | p106<=0] & [p13<=0 | p107<=0]]] & [[[p8<=0 | p106<=0] & [p5<=0 | p105<=0]] & [[p15<=0 | p107<=0] & [p1<=0 | p104<=0]]]] & [[[[p3<=0 | p104<=0] & [p7<=0 | p105<=0]] & [[p12<=0 | p107<=0] & [p9<=0 | p106<=0]]] & [[[p14<=0 | p107<=0] & [p11<=0 | p106<=0]] & [[p6<=0 | p105<=0] & [p4<=0 | p105<=0]]]]] | [[[[p63<=0 & p62<=0] & [p61<=0 & p60<=0]] & [[p59<=0 & p58<=0] & [p57<=0 & p56<=0]]] & [[[p71<=0 & p70<=0] & [p69<=0 & p68<=0]] & [[p67<=0 & p66<=0] & [p65<=0 & p64<=0]]]]] | E [true U [[[[1<=p120 | 1<=p121] | [1<=p122 | 1<=p123]] | [[1<=p116 | 1<=p117] | [1<=p118 | 1<=p119]]] | [[[1<=p112 | 1<=p113] | [1<=p114 | 1<=p115]] | [[1<=p108 | 1<=p109] | [1<=p110 | 1<=p111]]]]]] | [1<=p120 | [1<=p121 | ~ [E [true U ~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]]]] | [[1<=p117 | [1<=p122 | 1<=p123]] | [1<=p119 | 1<=p116]]] | [[[1<=p112 | [1<=p113 | 1<=p118]] | [1<=p114 | 1<=p115]] | [[1<=p111 | [1<=p108 | 1<=p109]] | [1<=p110 | E [true U [[[[p63<=0 & p62<=0] & [p61<=0 & p60<=0]] & [[p59<=0 & p58<=0] & [p57<=0 & p56<=0]]] & [[[p71<=0 & p70<=0] & [p69<=0 & p68<=0]] & [[p67<=0 & p66<=0] & [p65<=0 & p64<=0]]]]]]]]]] & [[p94<=0 | p102<=0] | [p30<=0 | p90<=0]]] & [[[[p95<=0 | p103<=0] | [p31<=0 | p91<=0]] & [[p98<=0 | p102<=0] | [p26<=0 | p90<=0]]] & [[p96<=0 | p100<=0] | [p20<=0 | p92<=0]]]] & [[[[[p93<=0 | p101<=0] | [p29<=0 | p89<=0]] & [[p92<=0 | p96<=0] | [p32<=0 | p88<=0]]] & [[p95<=0 | p99<=0] | [p35<=0 | p91<=0]]] & [[[[p98<=0 | p102<=0] | [p22<=0 | p94<=0]] & [[p96<=0 | p100<=0] | [p24<=0 | p88<=0]]] & [[p99<=0 | p103<=0] | [p23<=0 | p95<=0]]]]] & [[[[[[p94<=0 | p98<=0] | [p34<=0 | p90<=0]] & [[p97<=0 | p101<=0] | [p25<=0 | p89<=0]]] & [[p92<=0 | p100<=0] | [p28<=0 | p88<=0]]] & [[[[p93<=0 | p97<=0] | [p33<=0 | p89<=0]] & [[p99<=0 | p103<=0] | [p27<=0 | p91<=0]]] & [[p97<=0 | p101<=0] | [p21<=0 | p93<=0]]]] & [[p18<=0 & [p19<=0 & EG [[[[[[[[p94<=0 | p102<=0] | [p30<=0 | p90<=0]] & [[p95<=0 | p103<=0] | [p31<=0 | p91<=0]]] & [[[p98<=0 | p102<=0] | [p26<=0 | p90<=0]] & [[p96<=0 | p100<=0] | [p20<=0 | p92<=0]]]] & [[[[p93<=0 | p101<=0] | [p29<=0 | p89<=0]] & [[p92<=0 | p96<=0] | [p32<=0 | p88<=0]]] & [[[p95<=0 | p99<=0] | [p35<=0 | p91<=0]] & [[p98<=0 | p102<=0] | [p22<=0 | p94<=0]]]]] & [[[[[p96<=0 | p100<=0] | [p24<=0 | p88<=0]] & [[p99<=0 | p103<=0] | [p23<=0 | p95<=0]]] & [[[p34<=0 | p90<=0] | [p94<=0 | p98<=0]] & [[p97<=0 | p101<=0] | [p25<=0 | p89<=0]]]] & [[[[p92<=0 | p100<=0] | [p28<=0 | p88<=0]] & [[p93<=0 | p97<=0] | [p33<=0 | p89<=0]]] & [[[p99<=0 | p103<=0] | [p27<=0 | p91<=0]] & [[p97<=0 | p101<=0] | [p21<=0 | p93<=0]]]]]] | [[[[p87<=0 & p86<=0] & [p85<=0 & p84<=0]] & [[p83<=0 & p82<=0] & [p81<=0 & p80<=0]]] & [[[p79<=0 & p78<=0] & [p77<=0 & p76<=0]] & [[p75<=0 & p74<=0] & [p73<=0 & p72<=0]]]]]]]] & [p16<=0 & p17<=0]]]]]
abstracting: (p17<=0)
states: 4,677,007,040 (9)
abstracting: (p16<=0)
states: 4,677,007,040 (9)
abstracting: (p72<=0)
states: 4,001,663,527 (9)
abstracting: (p73<=0)
states: 4,001,663,527 (9)
abstracting: (p74<=0)
states: 4,001,663,527 (9)
abstracting: (p75<=0)
states: 4,001,663,527 (9)
abstracting: (p76<=0)
states: 4,001,663,527 (9)
abstracting: (p77<=0)
states: 4,001,663,527 (9)
abstracting: (p78<=0)
states: 4,001,663,527 (9)
abstracting: (p79<=0)
states: 4,001,663,527 (9)
abstracting: (p80<=0)
states: 4,001,663,527 (9)
abstracting: (p81<=0)
states: 4,001,663,527 (9)
abstracting: (p82<=0)
states: 4,001,663,527 (9)
abstracting: (p83<=0)
states: 4,001,663,527 (9)
abstracting: (p84<=0)
states: 4,001,663,527 (9)
abstracting: (p85<=0)
states: 4,001,663,527 (9)
abstracting: (p86<=0)
states: 4,001,663,527 (9)
abstracting: (p87<=0)
states: 4,001,663,527 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p21<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p27<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p33<=0)
states: 3,600,413,211 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p28<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p25<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p97<=0)
states: 4,001,663,527 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p34<=0)
states: 3,600,413,211 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p23<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p24<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
abstracting: (p22<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p35<=0)
states: 3,600,413,211 (9)
abstracting: (p99<=0)
states: 4,001,663,527 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p88<=0)
states: 4,001,663,527 (9)
abstracting: (p32<=0)
states: 3,600,413,211 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p89<=0)
states: 4,001,663,527 (9)
abstracting: (p29<=0)
states: 3,600,413,211 (9)
abstracting: (p101<=0)
states: 4,001,663,527 (9)
abstracting: (p93<=0)
states: 4,001,663,527 (9)
abstracting: (p92<=0)
states: 4,001,663,527 (9)
abstracting: (p20<=0)
states: 3,600,413,211 (9)
abstracting: (p100<=0)
states: 4,001,663,527 (9)
abstracting: (p96<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p26<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p98<=0)
states: 4,001,663,527 (9)
abstracting: (p91<=0)
states: 4,001,663,527 (9)
abstracting: (p31<=0)
states: 3,600,413,211 (9)
abstracting: (p103<=0)
states: 4,001,663,527 (9)
abstracting: (p95<=0)
states: 4,001,663,527 (9)
abstracting: (p90<=0)
states: 4,001,663,527 (9)
abstracting: (p30<=0)
states: 3,600,413,211 (9)
abstracting: (p102<=0)
states: 4,001,663,527 (9)
abstracting: (p94<=0)
states: 4,001,663,527 (9)
before gc: list nodes free: 1096670
after gc: idd nodes used:18384200, unused:45615800; list nodes free:205595933
.............
before gc: list nodes free: 2078128
after gc: idd nodes used:20071048, unused:43928952; list nodes free:198228800
MC time: 2m52.904sec
checking: EG [[AF [[[[[p73<=0 & p72<=0] & [p75<=0 & p74<=0]] & [[p77<=0 & p76<=0] & [p79<=0 & p78<=0]]] & [[[p81<=0 & p80<=0] & [p83<=0 & p82<=0]] & [[p85<=0 & p84<=0] & [p87<=0 & p86<=0]]]]] & [AF [[[[[1<=p65 | 1<=p64] | [1<=p67 | 1<=p66]] | [[1<=p69 | 1<=p68] | [1<=p71 | 1<=p70]]] | [[[1<=p57 | 1<=p56] | [1<=p59 | 1<=p58]] | [[1<=p61 | 1<=p60] | [1<=p63 | 1<=p62]]]]] | EX [[[[[1<=p41 | 1<=p40] | [1<=p43 | 1<=p42]] | [[1<=p45 | 1<=p44] | [1<=p47 | 1<=p46]]] | [[[1<=p49 | 1<=p48] | [1<=p51 | 1<=p50]] | [[1<=p53 | 1<=p52] | [1<=p55 | 1<=p54]]]]]]]]
normalized: EG [[[EX [[[[[1<=p55 | 1<=p54] | [1<=p53 | 1<=p52]] | [[1<=p51 | 1<=p50] | [1<=p49 | 1<=p48]]] | [[[1<=p47 | 1<=p46] | [1<=p45 | 1<=p44]] | [[1<=p43 | 1<=p42] | [1<=p41 | 1<=p40]]]]] | ~ [EG [~ [[[[[1<=p63 | 1<=p62] | [1<=p61 | 1<=p60]] | [[1<=p59 | 1<=p58] | [1<=p57 | 1<=p56]]] | [[[1<=p71 | 1<=p70] | [1<=p69 | 1<=p68]] | [[1<=p67 | 1<=p66] | [1<=p65 | 1<=p64]]]]]]]] & ~ [EG [~ [[[[[p87<=0 & p86<=0] & [p85<=0 & p84<=0]] & [[p83<=0 & p82<=0] & [p81<=0 & p80<=0]]] & [[[p79<=0 & p78<=0] & [p77<=0 & p76<=0]] & [[p75<=0 & p74<=0] & [p73<=0 & p72<=0]]]]]]]]]
abstracting: (p72<=0)
states: 4,001,663,527 (9)
abstracting: (p73<=0)
states: 4,001,663,527 (9)
abstracting: (p74<=0)
states: 4,001,663,527 (9)
abstracting: (p75<=0)
states: 4,001,663,527 (9)
abstracting: (p76<=0)
states: 4,001,663,527 (9)
abstracting: (p77<=0)
states: 4,001,663,527 (9)
abstracting: (p78<=0)
states: 4,001,663,527 (9)
abstracting: (p79<=0)
states: 4,001,663,527 (9)
abstracting: (p80<=0)
states: 4,001,663,527 (9)
abstracting: (p81<=0)
states: 4,001,663,527 (9)
abstracting: (p82<=0)
states: 4,001,663,527 (9)
abstracting: (p83<=0)
states: 4,001,663,527 (9)
abstracting: (p84<=0)
states: 4,001,663,527 (9)
abstracting: (p85<=0)
states: 4,001,663,527 (9)
abstracting: (p86<=0)
states: 4,001,663,527 (9)
abstracting: (p87<=0)
states: 4,001,663,527 (9)
..........
EG iterations: 10
abstracting: (1<=p64)
states: 10,898,249 (7)
abstracting: (1<=p65)
states: 10,898,249 (7)
abstracting: (1<=p66)
states: 10,898,249 (7)
abstracting: (1<=p67)
states: 10,898,249 (7)
abstracting: (1<=p68)
states: 10,898,249 (7)
abstracting: (1<=p69)
states: 10,898,249 (7)
abstracting: (1<=p70)
states: 10,898,249 (7)
abstracting: (1<=p71)
states: 10,898,249 (7)
abstracting: (1<=p56)
states: 10,898,249 (7)
abstracting: (1<=p57)
states: 10,898,249 (7)
abstracting: (1<=p58)
states: 10,898,249 (7)
abstracting: (1<=p59)
states: 10,898,249 (7)
abstracting: (1<=p60)
states: 10,898,249 (7)
abstracting: (1<=p61)
states: 10,898,249 (7)
abstracting: (1<=p62)
states: 10,898,249 (7)
abstracting: (1<=p63)
states: 10,898,249 (7)
.....................
before gc: list nodes free: 2383925
after gc: idd nodes used:20551316, unused:43448684; list nodes free:196219391
...........
before gc: list nodes free: 4176830
after gc: idd nodes used:20335021, unused:43664979; list nodes free:197232768
..........................
EG iterations: 58
abstracting: (1<=p40)
states: 716,223,354 (8)
abstracting: (1<=p41)
states: 716,223,354 (8)
abstracting: (1<=p42)
states: 716,223,354 (8)
abstracting: (1<=p43)
states: 716,223,354 (8)
abstracting: (1<=p44)
states: 716,223,354 (8)
abstracting: (1<=p45)
states: 716,223,354 (8)
abstracting: (1<=p46)
states: 716,223,354 (8)
abstracting: (1<=p47)
states: 716,223,354 (8)
abstracting: (1<=p48)
states: 716,223,354 (8)
abstracting: (1<=p49)
states: 716,223,354 (8)
abstracting: (1<=p50)
states: 716,223,354 (8)
abstracting: (1<=p51)
states: 716,223,354 (8)
abstracting: (1<=p52)
states: 716,223,354 (8)
abstracting: (1<=p53)
states: 716,223,354 (8)
abstracting: (1<=p54)
states: 716,223,354 (8)
abstracting: (1<=p55)
states: 716,223,354 (8)
..
before gc: list nodes free: 5605249
after gc: idd nodes used:19001274, unused:44998726; list nodes free:202930007
.....
before gc: list nodes free: 3676194
after gc: idd nodes used:22109928, unused:41890072; list nodes free:189273226
....
before gc: list nodes free: 4621044
TIME LIMIT: Killed by timeout after 3600 seconds
MemTotal: 16393216 kB
MemFree: 5995512 kB
After kill :
MemTotal: 16393216 kB
MemFree: 16098020 kB
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ perl -pe 's/.*\.//g'
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:4924 (38), effective:213 (1)
initing FirstDep: 0m 0.000sec
iterations count:211 (1), effective:4 (0)
iterations count:7288 (56), effective:420 (3)
net_ddint.h:600: Timeout: after 292 sec
iterations count:832 (6), effective:16 (0)
iterations count:528 (4), effective:16 (0)
iterations count:10237 (79), effective:540 (4)
iterations count:528 (4), effective:16 (0)
iterations count:211 (1), effective:4 (0)
iterations count:211 (1), effective:4 (0)
iterations count:211 (1), effective:4 (0)
sat_reach.icc:155: Timeout: after 366 sec
net_ddint.h:600: Timeout: after 320 sec
iterations count:3565 (27), effective:125 (0)
iterations count:211 (1), effective:4 (0)
net_ddint.h:600: Timeout: after 280 sec
net_ddint.h:600: Timeout: after 245 sec
iterations count:528 (4), effective:16 (0)
iterations count:128 (1), effective:0 (0)
iterations count:6234 (48), effective:312 (2)
net_ddint.h:600: Timeout: after 214 sec
iterations count:7097 (55), effective:380 (2)
iterations count:1390 (10), effective:48 (0)
net_ddint.h:600: Timeout: after 187 sec
net_ddint.h:600: Timeout: after 164 sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="DatabaseWithMutex-COL-04"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is DatabaseWithMutex-COL-04, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r106-tall-167814483501026"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/DatabaseWithMutex-COL-04.tgz
mv DatabaseWithMutex-COL-04 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

