About the Execution of Marcie+red for AutonomousCar-PT-09a
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 10315.012 | 3600000.00 | 3702003.00 | 160.70 | T?T????F?FF????? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
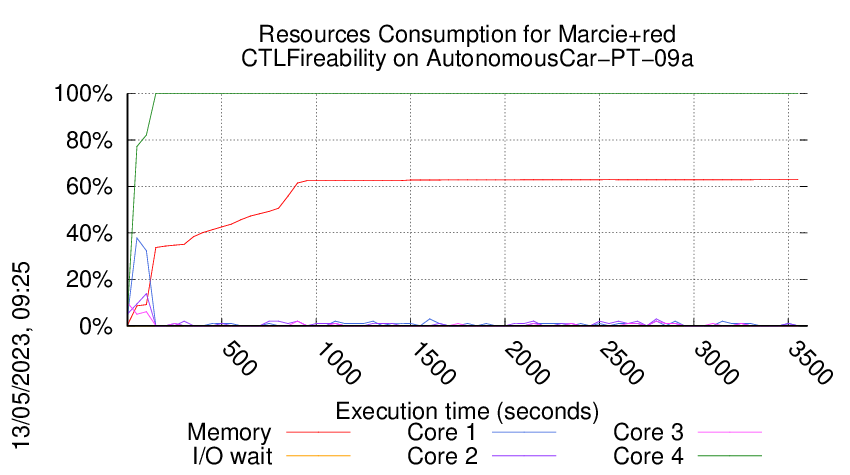
Trace from the execution
Formatting '/data/fkordon/mcc2023-input.r010-oct2-167813599400658.qcow2', fmt=qcow2 cluster_size=65536 extended_l2=off compression_type=zlib size=4294967296 backing_file=/data/fkordon/mcc2023-input.qcow2 backing_fmt=qcow2 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-5348
Executing tool marciexred
Input is AutonomousCar-PT-09a, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r010-oct2-167813599400658
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 1.2M
-rw-r--r-- 1 mcc users 5.8K Feb 25 12:53 CTLCardinality.txt
-rw-r--r-- 1 mcc users 61K Feb 25 12:53 CTLCardinality.xml
-rw-r--r-- 1 mcc users 4.8K Feb 25 12:52 CTLFireability.txt
-rw-r--r-- 1 mcc users 41K Feb 25 12:52 CTLFireability.xml
-rw-r--r-- 1 mcc users 3.7K Feb 25 15:34 LTLCardinality.txt
-rw-r--r-- 1 mcc users 26K Feb 25 15:34 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.2K Feb 25 15:34 LTLFireability.txt
-rw-r--r-- 1 mcc users 16K Feb 25 15:34 LTLFireability.xml
-rw-r--r-- 1 mcc users 7.7K Feb 25 12:54 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 77K Feb 25 12:54 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 6.8K Feb 25 12:53 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 54K Feb 25 12:53 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.7K Feb 25 15:34 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.7K Feb 25 15:34 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 equiv_col
-rw-r--r-- 1 mcc users 4 Mar 5 18:22 instance
-rw-r--r-- 1 mcc users 6 Mar 5 18:22 iscolored
-rw-r--r-- 1 mcc users 781K Mar 5 18:22 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-00
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-01
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-02
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-03
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-04
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-05
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-06
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-07
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-08
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-09
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-10
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-11
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-12
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-13
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-14
FORMULA_NAME AutonomousCar-PT-09a-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1678701575908
bash -c /home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n "BK_STOP " ; date -u +%s%3N
Invoking MCC driver with
BK_TOOL=marciexred
BK_EXAMINATION=CTLFireability
BK_BIN_PATH=/home/mcc/BenchKit/bin/
BK_TIME_CONFINEMENT=3600
BK_INPUT=AutonomousCar-PT-09a
Applying reductions before tool marcie
Invoking reducer
Running Version 202303021504
[2023-03-13 09:59:38] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -timeout, 360, -rebuildPNML]
[2023-03-13 09:59:38] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2023-03-13 09:59:38] [INFO ] Load time of PNML (sax parser for PT used): 139 ms
[2023-03-13 09:59:38] [INFO ] Transformed 89 places.
[2023-03-13 09:59:38] [INFO ] Transformed 1249 transitions.
[2023-03-13 09:59:38] [INFO ] Found NUPN structural information;
[2023-03-13 09:59:38] [INFO ] Parsed PT model containing 89 places and 1249 transitions and 15631 arcs in 239 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 8 ms.
Ensure Unique test removed 345 transitions
Reduce redundant transitions removed 345 transitions.
Support contains 60 out of 89 places. Attempting structural reductions.
Starting structural reductions in LTL mode, iteration 0 : 89/89 places, 904/904 transitions.
Discarding 2 places :
Symmetric choice reduction at 0 with 2 rule applications. Total rules 2 place count 87 transition count 893
Iterating global reduction 0 with 2 rules applied. Total rules applied 4 place count 87 transition count 893
Applied a total of 4 rules in 26 ms. Remains 87 /89 variables (removed 2) and now considering 893/904 (removed 11) transitions.
// Phase 1: matrix 893 rows 87 cols
[2023-03-13 09:59:38] [INFO ] Computed 13 place invariants in 19 ms
[2023-03-13 09:59:38] [INFO ] Implicit Places using invariants in 209 ms returned []
[2023-03-13 09:59:38] [INFO ] Invariant cache hit.
[2023-03-13 09:59:39] [INFO ] State equation strengthened by 318 read => feed constraints.
[2023-03-13 09:59:39] [INFO ] Implicit Places using invariants and state equation in 551 ms returned [83, 85]
Discarding 2 places :
Implicit Place search using SMT with State Equation took 804 ms to find 2 implicit places.
Starting structural reductions in LTL mode, iteration 1 : 85/89 places, 893/904 transitions.
Applied a total of 0 rules in 6 ms. Remains 85 /85 variables (removed 0) and now considering 893/893 (removed 0) transitions.
Finished structural reductions in LTL mode , in 2 iterations and 837 ms. Remains : 85/89 places, 893/904 transitions.
Support contains 60 out of 85 places after structural reductions.
[2023-03-13 09:59:39] [INFO ] Flatten gal took : 277 ms
[2023-03-13 09:59:40] [INFO ] Flatten gal took : 129 ms
[2023-03-13 09:59:40] [INFO ] Input system was already deterministic with 893 transitions.
Incomplete random walk after 10000 steps, including 486 resets, run finished after 632 ms. (steps per millisecond=15 ) properties (out of 69) seen :20
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1000 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 49) seen :0
Incomplete Best-First random walk after 1000 steps, including 2 resets, run finished after 7 ms. (steps per millisecond=142 ) properties (out of 49) seen :2
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 9 ms. (steps per millisecond=111 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 8 ms. (steps per millisecond=125 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 47) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=142 ) properties (out of 47) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 46) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 46) seen :2
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 44) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 44) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 44) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 44) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 44) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 44) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 8 ms. (steps per millisecond=125 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 43) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 43) seen :0
Running SMT prover for 43 properties.
// Phase 1: matrix 893 rows 85 cols
[2023-03-13 09:59:41] [INFO ] Computed 11 place invariants in 6 ms
[2023-03-13 09:59:42] [INFO ] [Real]Absence check using 11 positive place invariants in 2 ms returned sat
[2023-03-13 09:59:42] [INFO ] After 388ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:43
[2023-03-13 09:59:43] [INFO ] [Nat]Absence check using 11 positive place invariants in 2 ms returned sat
[2023-03-13 09:59:49] [INFO ] After 5707ms SMT Verify possible using state equation in natural domain returned unsat :4 sat :39
[2023-03-13 09:59:49] [INFO ] State equation strengthened by 318 read => feed constraints.
[2023-03-13 09:59:53] [INFO ] After 4794ms SMT Verify possible using 318 Read/Feed constraints in natural domain returned unsat :4 sat :39
[2023-03-13 10:00:00] [INFO ] After 11044ms SMT Verify possible using trap constraints in natural domain returned unsat :4 sat :39
Attempting to minimize the solution found.
Minimization took 4898 ms.
[2023-03-13 10:00:05] [INFO ] After 22151ms SMT Verify possible using all constraints in natural domain returned unsat :4 sat :39
Fused 43 Parikh solutions to 39 different solutions.
Parikh walk visited 0 properties in 872 ms.
Support contains 45 out of 85 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 85/85 places, 893/893 transitions.
Graph (complete) has 1023 edges and 85 vertex of which 84 are kept as prefixes of interest. Removing 1 places using SCC suffix rule.10 ms
Discarding 1 places :
Also discarding 1 output transitions
Drop transitions removed 1 transitions
Drop transitions removed 3 transitions
Reduce isomorphic transitions removed 3 transitions.
Drop transitions removed 1 transitions
Trivial Post-agglo rules discarded 1 transitions
Performed 1 trivial Post agglomeration. Transition count delta: 1
Iterating post reduction 0 with 4 rules applied. Total rules applied 5 place count 84 transition count 888
Reduce places removed 1 places and 0 transitions.
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Iterating post reduction 1 with 3 rules applied. Total rules applied 8 place count 83 transition count 886
Reduce places removed 2 places and 0 transitions.
Iterating post reduction 2 with 2 rules applied. Total rules applied 10 place count 81 transition count 886
Performed 3 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 3 Pre rules applied. Total rules applied 10 place count 81 transition count 883
Deduced a syphon composed of 3 places in 0 ms
Reduce places removed 3 places and 0 transitions.
Iterating global reduction 3 with 6 rules applied. Total rules applied 16 place count 78 transition count 883
Discarding 4 places :
Symmetric choice reduction at 3 with 4 rule applications. Total rules 20 place count 74 transition count 852
Iterating global reduction 3 with 4 rules applied. Total rules applied 24 place count 74 transition count 852
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Deduced a syphon composed of 1 places in 1 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 3 with 2 rules applied. Total rules applied 26 place count 73 transition count 851
Free-agglomeration rule applied 4 times.
Iterating global reduction 3 with 4 rules applied. Total rules applied 30 place count 73 transition count 847
Reduce places removed 4 places and 0 transitions.
Ensure Unique test removed 9 transitions
Reduce isomorphic transitions removed 9 transitions.
Iterating post reduction 3 with 13 rules applied. Total rules applied 43 place count 69 transition count 838
Applied a total of 43 rules in 191 ms. Remains 69 /85 variables (removed 16) and now considering 838/893 (removed 55) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 192 ms. Remains : 69/85 places, 838/893 transitions.
Incomplete random walk after 10000 steps, including 405 resets, run finished after 370 ms. (steps per millisecond=27 ) properties (out of 39) seen :1
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 38) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 38) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 38) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 38) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 37) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 37) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 37) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 37) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 37) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 37) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 2 ms. (steps per millisecond=500 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1000 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 36) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 36) seen :1
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 35) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 35) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 35) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 35) seen :1
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 34) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 34) seen :0
Running SMT prover for 34 properties.
// Phase 1: matrix 838 rows 69 cols
[2023-03-13 10:00:06] [INFO ] Computed 13 place invariants in 5 ms
[2023-03-13 10:00:07] [INFO ] [Real]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:00:08] [INFO ] After 1133ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:34
[2023-03-13 10:00:08] [INFO ] [Nat]Absence check using 13 positive place invariants in 2 ms returned sat
[2023-03-13 10:00:12] [INFO ] After 3759ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :34
[2023-03-13 10:00:12] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:00:16] [INFO ] After 4093ms SMT Verify possible using 280 Read/Feed constraints in natural domain returned unsat :0 sat :34
[2023-03-13 10:00:21] [INFO ] After 9423ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :34
Attempting to minimize the solution found.
Minimization took 4038 ms.
[2023-03-13 10:00:25] [INFO ] After 17530ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :34
Parikh walk visited 1 properties in 310 ms.
Support contains 44 out of 69 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 69/69 places, 838/838 transitions.
Applied a total of 0 rules in 35 ms. Remains 69 /69 variables (removed 0) and now considering 838/838 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 36 ms. Remains : 69/69 places, 838/838 transitions.
Incomplete random walk after 10000 steps, including 314 resets, run finished after 464 ms. (steps per millisecond=21 ) properties (out of 33) seen :1
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1000 steps, including 4 resets, run finished after 7 ms. (steps per millisecond=142 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 8 ms. (steps per millisecond=125 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 2 ms. (steps per millisecond=500 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 18 ms. (steps per millisecond=55 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 32) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 32) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 31) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 31) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 30) seen :0
Interrupted probabilistic random walk after 357146 steps, run timeout after 3001 ms. (steps per millisecond=119 ) properties seen :{}
Probabilistic random walk after 357146 steps, saw 61541 distinct states, run finished after 3002 ms. (steps per millisecond=118 ) properties seen :0
Running SMT prover for 30 properties.
[2023-03-13 10:00:29] [INFO ] Invariant cache hit.
[2023-03-13 10:00:30] [INFO ] [Real]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:00:31] [INFO ] After 945ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:30
[2023-03-13 10:00:31] [INFO ] [Nat]Absence check using 13 positive place invariants in 2 ms returned sat
[2023-03-13 10:00:34] [INFO ] After 3321ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :30
[2023-03-13 10:00:34] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:00:37] [INFO ] After 3209ms SMT Verify possible using 280 Read/Feed constraints in natural domain returned unsat :0 sat :30
[2023-03-13 10:00:42] [INFO ] After 7444ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :30
Attempting to minimize the solution found.
Minimization took 3261 ms.
[2023-03-13 10:00:45] [INFO ] After 14256ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :30
Parikh walk visited 1 properties in 583 ms.
Support contains 44 out of 69 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 69/69 places, 838/838 transitions.
Applied a total of 0 rules in 40 ms. Remains 69 /69 variables (removed 0) and now considering 838/838 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 40 ms. Remains : 69/69 places, 838/838 transitions.
Incomplete random walk after 10000 steps, including 141 resets, run finished after 490 ms. (steps per millisecond=20 ) properties (out of 29) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 16 ms. (steps per millisecond=62 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 23 ms. (steps per millisecond=43 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1000 steps, including 2 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 8 ms. (steps per millisecond=125 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 7 ms. (steps per millisecond=143 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 13 ms. (steps per millisecond=77 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 10 ms. (steps per millisecond=100 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 8 ms. (steps per millisecond=125 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 28) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 6 ms. (steps per millisecond=166 ) properties (out of 28) seen :0
Interrupted probabilistic random walk after 394310 steps, run timeout after 3001 ms. (steps per millisecond=131 ) properties seen :{}
Probabilistic random walk after 394310 steps, saw 67063 distinct states, run finished after 3001 ms. (steps per millisecond=131 ) properties seen :0
Running SMT prover for 28 properties.
[2023-03-13 10:00:49] [INFO ] Invariant cache hit.
[2023-03-13 10:00:50] [INFO ] [Real]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:00:51] [INFO ] After 908ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:28
[2023-03-13 10:00:51] [INFO ] [Nat]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:00:54] [INFO ] After 2833ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :28
[2023-03-13 10:00:54] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:00:56] [INFO ] After 2800ms SMT Verify possible using 280 Read/Feed constraints in natural domain returned unsat :0 sat :28
[2023-03-13 10:01:00] [INFO ] After 6677ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :28
Attempting to minimize the solution found.
Minimization took 3362 ms.
[2023-03-13 10:01:04] [INFO ] After 13158ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :28
Parikh walk visited 0 properties in 315 ms.
Support contains 44 out of 69 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 69/69 places, 838/838 transitions.
Applied a total of 0 rules in 46 ms. Remains 69 /69 variables (removed 0) and now considering 838/838 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 46 ms. Remains : 69/69 places, 838/838 transitions.
Incomplete random walk after 10000 steps, including 513 resets, run finished after 409 ms. (steps per millisecond=24 ) properties (out of 28) seen :2
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 26) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 26) seen :1
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1000 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1000 steps, including 5 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 25) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 25) seen :0
Running SMT prover for 25 properties.
[2023-03-13 10:01:05] [INFO ] Invariant cache hit.
[2023-03-13 10:01:05] [INFO ] [Real]Absence check using 13 positive place invariants in 13 ms returned sat
[2023-03-13 10:01:06] [INFO ] After 896ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:25
[2023-03-13 10:01:06] [INFO ] [Nat]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:01:09] [INFO ] After 2602ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :25
[2023-03-13 10:01:09] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:01:11] [INFO ] After 2541ms SMT Verify possible using 280 Read/Feed constraints in natural domain returned unsat :0 sat :25
[2023-03-13 10:01:14] [INFO ] After 5700ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :25
Attempting to minimize the solution found.
Minimization took 2689 ms.
[2023-03-13 10:01:17] [INFO ] After 11151ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :25
Parikh walk visited 3 properties in 422 ms.
Support contains 40 out of 69 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 69/69 places, 838/838 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 0 with 1 rules applied. Total rules applied 1 place count 69 transition count 837
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 1 with 1 rules applied. Total rules applied 2 place count 68 transition count 837
Free-agglomeration rule applied 2 times.
Iterating global reduction 2 with 2 rules applied. Total rules applied 4 place count 68 transition count 835
Reduce places removed 2 places and 0 transitions.
Iterating post reduction 2 with 2 rules applied. Total rules applied 6 place count 66 transition count 835
Applied a total of 6 rules in 83 ms. Remains 66 /69 variables (removed 3) and now considering 835/838 (removed 3) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 83 ms. Remains : 66/69 places, 835/838 transitions.
Incomplete random walk after 10000 steps, including 71 resets, run finished after 296 ms. (steps per millisecond=33 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 2 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 5 resets, run finished after 5 ms. (steps per millisecond=200 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1000 steps, including 3 resets, run finished after 3 ms. (steps per millisecond=333 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 3 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Incomplete Best-First random walk after 1001 steps, including 4 resets, run finished after 4 ms. (steps per millisecond=250 ) properties (out of 22) seen :0
Interrupted probabilistic random walk after 413753 steps, run timeout after 3001 ms. (steps per millisecond=137 ) properties seen :{}
Probabilistic random walk after 413753 steps, saw 68071 distinct states, run finished after 3001 ms. (steps per millisecond=137 ) properties seen :0
Running SMT prover for 22 properties.
// Phase 1: matrix 835 rows 66 cols
[2023-03-13 10:01:21] [INFO ] Computed 13 place invariants in 5 ms
[2023-03-13 10:01:21] [INFO ] [Real]Absence check using 13 positive place invariants in 2 ms returned sat
[2023-03-13 10:01:22] [INFO ] After 712ms SMT Verify possible using all constraints in real domain returned unsat :0 sat :0 real:22
[2023-03-13 10:01:22] [INFO ] [Nat]Absence check using 13 positive place invariants in 3 ms returned sat
[2023-03-13 10:01:25] [INFO ] After 2446ms SMT Verify possible using state equation in natural domain returned unsat :0 sat :22
[2023-03-13 10:01:25] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:01:27] [INFO ] After 2284ms SMT Verify possible using 280 Read/Feed constraints in natural domain returned unsat :0 sat :22
[2023-03-13 10:01:30] [INFO ] After 5103ms SMT Verify possible using trap constraints in natural domain returned unsat :0 sat :22
Attempting to minimize the solution found.
Minimization took 2669 ms.
[2023-03-13 10:01:32] [INFO ] After 10461ms SMT Verify possible using all constraints in natural domain returned unsat :0 sat :22
Parikh walk visited 0 properties in 919 ms.
Support contains 40 out of 66 places. Attempting structural reductions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 66/66 places, 835/835 transitions.
Applied a total of 0 rules in 37 ms. Remains 66 /66 variables (removed 0) and now considering 835/835 (removed 0) transitions.
Finished structural reductions in REACHABILITY mode , in 1 iterations and 37 ms. Remains : 66/66 places, 835/835 transitions.
Starting structural reductions in REACHABILITY mode, iteration 0 : 66/66 places, 835/835 transitions.
Applied a total of 0 rules in 39 ms. Remains 66 /66 variables (removed 0) and now considering 835/835 (removed 0) transitions.
[2023-03-13 10:01:33] [INFO ] Invariant cache hit.
[2023-03-13 10:01:33] [INFO ] Implicit Places using invariants in 52 ms returned [65]
Discarding 1 places :
Implicit Place search using SMT only with invariants took 59 ms to find 1 implicit places.
Starting structural reductions in REACHABILITY mode, iteration 1 : 65/66 places, 835/835 transitions.
Discarding 1 places :
Symmetric choice reduction at 0 with 1 rule applications. Total rules 1 place count 64 transition count 834
Iterating global reduction 0 with 1 rules applied. Total rules applied 2 place count 64 transition count 834
Applied a total of 2 rules in 41 ms. Remains 64 /65 variables (removed 1) and now considering 834/835 (removed 1) transitions.
// Phase 1: matrix 834 rows 64 cols
[2023-03-13 10:01:34] [INFO ] Computed 12 place invariants in 6 ms
[2023-03-13 10:01:34] [INFO ] Implicit Places using invariants in 52 ms returned []
[2023-03-13 10:01:34] [INFO ] Invariant cache hit.
[2023-03-13 10:01:34] [INFO ] State equation strengthened by 280 read => feed constraints.
[2023-03-13 10:01:34] [INFO ] Implicit Places using invariants and state equation in 287 ms returned []
Implicit Place search using SMT with State Equation took 358 ms to find 0 implicit places.
Starting structural reductions in REACHABILITY mode, iteration 2 : 64/66 places, 834/835 transitions.
Finished structural reductions in REACHABILITY mode , in 2 iterations and 497 ms. Remains : 64/66 places, 834/835 transitions.
Successfully simplified 4 atomic propositions for a total of 16 simplifications.
[2023-03-13 10:01:34] [INFO ] Flatten gal took : 123 ms
[2023-03-13 10:01:34] [INFO ] Flatten gal took : 105 ms
[2023-03-13 10:01:34] [INFO ] Input system was already deterministic with 893 transitions.
Computed a total of 3 stabilizing places and 2 stable transitions
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 6 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 7 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 74 ms
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 101 ms
[2023-03-13 10:01:35] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 5 places :
Symmetric choice reduction at 0 with 5 rule applications. Total rules 5 place count 80 transition count 843
Iterating global reduction 0 with 5 rules applied. Total rules applied 10 place count 80 transition count 843
Applied a total of 10 rules in 6 ms. Remains 80 /85 variables (removed 5) and now considering 843/893 (removed 50) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 7 ms. Remains : 80/85 places, 843/893 transitions.
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 79 ms
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 81 ms
[2023-03-13 10:01:35] [INFO ] Input system was already deterministic with 843 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 5 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 6 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 69 ms
[2023-03-13 10:01:35] [INFO ] Flatten gal took : 71 ms
[2023-03-13 10:01:36] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 11 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 11 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:36] [INFO ] Flatten gal took : 128 ms
[2023-03-13 10:01:36] [INFO ] Flatten gal took : 82 ms
[2023-03-13 10:01:36] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Drop transitions removed 9 transitions
Trivial Post-agglo rules discarded 9 transitions
Performed 9 trivial Post agglomeration. Transition count delta: 9
Iterating post reduction 0 with 9 rules applied. Total rules applied 9 place count 85 transition count 884
Reduce places removed 9 places and 0 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 1 with 10 rules applied. Total rules applied 19 place count 76 transition count 883
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 2 with 1 rules applied. Total rules applied 20 place count 75 transition count 883
Performed 1 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 1 Pre rules applied. Total rules applied 20 place count 75 transition count 882
Deduced a syphon composed of 1 places in 1 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 3 with 2 rules applied. Total rules applied 22 place count 74 transition count 882
Discarding 8 places :
Symmetric choice reduction at 3 with 8 rule applications. Total rules 30 place count 66 transition count 802
Iterating global reduction 3 with 8 rules applied. Total rules applied 38 place count 66 transition count 802
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 3 with 4 rules applied. Total rules applied 42 place count 64 transition count 800
Applied a total of 42 rules in 195 ms. Remains 64 /85 variables (removed 21) and now considering 800/893 (removed 93) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 196 ms. Remains : 64/85 places, 800/893 transitions.
[2023-03-13 10:01:36] [INFO ] Flatten gal took : 95 ms
[2023-03-13 10:01:36] [INFO ] Flatten gal took : 99 ms
[2023-03-13 10:01:37] [INFO ] Input system was already deterministic with 800 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 6 places :
Symmetric choice reduction at 0 with 6 rule applications. Total rules 6 place count 79 transition count 833
Iterating global reduction 0 with 6 rules applied. Total rules applied 12 place count 79 transition count 833
Applied a total of 12 rules in 8 ms. Remains 79 /85 variables (removed 6) and now considering 833/893 (removed 60) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 8 ms. Remains : 79/85 places, 833/893 transitions.
[2023-03-13 10:01:37] [INFO ] Flatten gal took : 71 ms
[2023-03-13 10:01:37] [INFO ] Flatten gal took : 76 ms
[2023-03-13 10:01:37] [INFO ] Input system was already deterministic with 833 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Drop transitions removed 9 transitions
Trivial Post-agglo rules discarded 9 transitions
Performed 9 trivial Post agglomeration. Transition count delta: 9
Iterating post reduction 0 with 9 rules applied. Total rules applied 9 place count 85 transition count 884
Reduce places removed 9 places and 0 transitions.
Iterating post reduction 1 with 9 rules applied. Total rules applied 18 place count 76 transition count 884
Performed 2 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 2 Pre rules applied. Total rules applied 18 place count 76 transition count 882
Deduced a syphon composed of 2 places in 1 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 2 with 4 rules applied. Total rules applied 22 place count 74 transition count 882
Discarding 7 places :
Symmetric choice reduction at 2 with 7 rule applications. Total rules 29 place count 67 transition count 812
Iterating global reduction 2 with 7 rules applied. Total rules applied 36 place count 67 transition count 812
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Deduced a syphon composed of 1 places in 0 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 2 with 2 rules applied. Total rules applied 38 place count 66 transition count 811
Applied a total of 38 rules in 75 ms. Remains 66 /85 variables (removed 19) and now considering 811/893 (removed 82) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 76 ms. Remains : 66/85 places, 811/893 transitions.
[2023-03-13 10:01:37] [INFO ] Flatten gal took : 89 ms
[2023-03-13 10:01:37] [INFO ] Flatten gal took : 92 ms
[2023-03-13 10:01:37] [INFO ] Input system was already deterministic with 811 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Reduce places removed 1 places and 1 transitions.
Reduce places removed 1 places and 0 transitions.
Drop transitions removed 10 transitions
Trivial Post-agglo rules discarded 10 transitions
Performed 10 trivial Post agglomeration. Transition count delta: 10
Iterating post reduction 0 with 11 rules applied. Total rules applied 11 place count 83 transition count 882
Reduce places removed 10 places and 0 transitions.
Iterating post reduction 1 with 10 rules applied. Total rules applied 21 place count 73 transition count 882
Performed 1 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 2 with 1 Pre rules applied. Total rules applied 21 place count 73 transition count 881
Deduced a syphon composed of 1 places in 0 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 2 with 2 rules applied. Total rules applied 23 place count 72 transition count 881
Discarding 8 places :
Symmetric choice reduction at 2 with 8 rule applications. Total rules 31 place count 64 transition count 801
Iterating global reduction 2 with 8 rules applied. Total rules applied 39 place count 64 transition count 801
Performed 2 Post agglomeration using F-continuation condition.Transition count delta: 2
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 2 with 4 rules applied. Total rules applied 43 place count 62 transition count 799
Applied a total of 43 rules in 89 ms. Remains 62 /85 variables (removed 23) and now considering 799/893 (removed 94) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 90 ms. Remains : 62/85 places, 799/893 transitions.
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 90 ms
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 95 ms
[2023-03-13 10:01:38] [INFO ] Input system was already deterministic with 799 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 7 places :
Symmetric choice reduction at 0 with 7 rule applications. Total rules 7 place count 78 transition count 823
Iterating global reduction 0 with 7 rules applied. Total rules applied 14 place count 78 transition count 823
Applied a total of 14 rules in 4 ms. Remains 78 /85 variables (removed 7) and now considering 823/893 (removed 70) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 78/85 places, 823/893 transitions.
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 66 ms
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 73 ms
[2023-03-13 10:01:38] [INFO ] Input system was already deterministic with 823 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 18 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 18 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 72 ms
[2023-03-13 10:01:38] [INFO ] Flatten gal took : 72 ms
[2023-03-13 10:01:38] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Drop transitions removed 8 transitions
Trivial Post-agglo rules discarded 8 transitions
Performed 8 trivial Post agglomeration. Transition count delta: 8
Iterating post reduction 0 with 8 rules applied. Total rules applied 8 place count 85 transition count 885
Reduce places removed 8 places and 0 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 1 with 9 rules applied. Total rules applied 17 place count 77 transition count 884
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 2 with 1 rules applied. Total rules applied 18 place count 76 transition count 884
Performed 2 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 2 Pre rules applied. Total rules applied 18 place count 76 transition count 882
Deduced a syphon composed of 2 places in 4 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 3 with 4 rules applied. Total rules applied 22 place count 74 transition count 882
Discarding 8 places :
Symmetric choice reduction at 3 with 8 rule applications. Total rules 30 place count 66 transition count 802
Iterating global reduction 3 with 8 rules applied. Total rules applied 38 place count 66 transition count 802
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Deduced a syphon composed of 1 places in 0 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 3 with 2 rules applied. Total rules applied 40 place count 65 transition count 801
Applied a total of 40 rules in 105 ms. Remains 65 /85 variables (removed 20) and now considering 801/893 (removed 92) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 105 ms. Remains : 65/85 places, 801/893 transitions.
[2023-03-13 10:01:39] [INFO ] Flatten gal took : 106 ms
[2023-03-13 10:01:39] [INFO ] Flatten gal took : 128 ms
[2023-03-13 10:01:39] [INFO ] Input system was already deterministic with 801 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Drop transitions removed 8 transitions
Trivial Post-agglo rules discarded 8 transitions
Performed 8 trivial Post agglomeration. Transition count delta: 8
Iterating post reduction 0 with 8 rules applied. Total rules applied 8 place count 85 transition count 885
Reduce places removed 8 places and 0 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 1 with 9 rules applied. Total rules applied 17 place count 77 transition count 884
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 2 with 1 rules applied. Total rules applied 18 place count 76 transition count 884
Performed 2 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 2 Pre rules applied. Total rules applied 18 place count 76 transition count 882
Deduced a syphon composed of 2 places in 0 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 3 with 4 rules applied. Total rules applied 22 place count 74 transition count 882
Discarding 6 places :
Symmetric choice reduction at 3 with 6 rule applications. Total rules 28 place count 68 transition count 822
Iterating global reduction 3 with 6 rules applied. Total rules applied 34 place count 68 transition count 822
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Deduced a syphon composed of 1 places in 0 ms
Reduce places removed 1 places and 0 transitions.
Iterating global reduction 3 with 2 rules applied. Total rules applied 36 place count 67 transition count 821
Applied a total of 36 rules in 58 ms. Remains 67 /85 variables (removed 18) and now considering 821/893 (removed 72) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 58 ms. Remains : 67/85 places, 821/893 transitions.
[2023-03-13 10:01:39] [INFO ] Flatten gal took : 90 ms
[2023-03-13 10:01:39] [INFO ] Flatten gal took : 91 ms
[2023-03-13 10:01:39] [INFO ] Input system was already deterministic with 821 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 5 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 5 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 73 ms
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 74 ms
[2023-03-13 10:01:40] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 8 places :
Symmetric choice reduction at 0 with 8 rule applications. Total rules 8 place count 77 transition count 813
Iterating global reduction 0 with 8 rules applied. Total rules applied 16 place count 77 transition count 813
Applied a total of 16 rules in 4 ms. Remains 77 /85 variables (removed 8) and now considering 813/893 (removed 80) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 4 ms. Remains : 77/85 places, 813/893 transitions.
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 67 ms
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 132 ms
[2023-03-13 10:01:40] [INFO ] Input system was already deterministic with 813 transitions.
Starting structural reductions in SI_CTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Drop transitions removed 8 transitions
Trivial Post-agglo rules discarded 8 transitions
Performed 8 trivial Post agglomeration. Transition count delta: 8
Iterating post reduction 0 with 8 rules applied. Total rules applied 8 place count 85 transition count 885
Reduce places removed 8 places and 0 transitions.
Performed 1 Post agglomeration using F-continuation condition.Transition count delta: 1
Iterating post reduction 1 with 9 rules applied. Total rules applied 17 place count 77 transition count 884
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 2 with 1 rules applied. Total rules applied 18 place count 76 transition count 884
Performed 2 Pre agglomeration using Quasi-Persistent + Divergent Free condition..
Pre-agglomeration after 3 with 2 Pre rules applied. Total rules applied 18 place count 76 transition count 882
Deduced a syphon composed of 2 places in 1 ms
Reduce places removed 2 places and 0 transitions.
Iterating global reduction 3 with 4 rules applied. Total rules applied 22 place count 74 transition count 882
Discarding 4 places :
Symmetric choice reduction at 3 with 4 rule applications. Total rules 26 place count 70 transition count 842
Iterating global reduction 3 with 4 rules applied. Total rules applied 30 place count 70 transition count 842
Applied a total of 30 rules in 64 ms. Remains 70 /85 variables (removed 15) and now considering 842/893 (removed 51) transitions.
Finished structural reductions in SI_CTL mode , in 1 iterations and 64 ms. Remains : 70/85 places, 842/893 transitions.
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 92 ms
[2023-03-13 10:01:40] [INFO ] Flatten gal took : 106 ms
[2023-03-13 10:01:41] [INFO ] Input system was already deterministic with 842 transitions.
Starting structural reductions in LTL mode, iteration 0 : 85/85 places, 893/893 transitions.
Discarding 5 places :
Symmetric choice reduction at 0 with 5 rule applications. Total rules 5 place count 80 transition count 843
Iterating global reduction 0 with 5 rules applied. Total rules applied 10 place count 80 transition count 843
Applied a total of 10 rules in 11 ms. Remains 80 /85 variables (removed 5) and now considering 843/893 (removed 50) transitions.
Finished structural reductions in LTL mode , in 1 iterations and 11 ms. Remains : 80/85 places, 843/893 transitions.
[2023-03-13 10:01:41] [INFO ] Flatten gal took : 70 ms
[2023-03-13 10:01:41] [INFO ] Flatten gal took : 73 ms
[2023-03-13 10:01:41] [INFO ] Input system was already deterministic with 843 transitions.
[2023-03-13 10:01:41] [INFO ] Flatten gal took : 84 ms
[2023-03-13 10:01:41] [INFO ] Flatten gal took : 86 ms
[2023-03-13 10:01:41] [INFO ] Export to MCC of 16 properties in file /home/mcc/execution/CTLFireability.sr.xml took 7 ms.
[2023-03-13 10:01:41] [INFO ] Export to PNML in file /home/mcc/execution/model.sr.pnml of net with 85 places, 893 transitions and 12914 arcs took 8 ms.
Total runtime 123521 ms.
There are residual formulas that ITS could not solve within timeout
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie built on Linux at 2019-11-18.
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: /home/mcc/BenchKit/bin//../reducer/bin//../../marcie/bin/marcie --net-file=model.pnml --mcc-file=CTLFireability.xml --memory=6 --mcc-mode
parse successfull
net created successfully
Net: Petri
(NrP: 85 NrTr: 893 NrArc: 12914)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.030sec
net check time: 0m 0.001sec
init dd package: 0m 3.033sec
RS generation: 3m 3.189sec
-> reachability set: #nodes 206846 (2.1e+05) #states 6,716,446,748 (9)
starting MCC model checker
--------------------------
checking: EF [AG [[p70<=1 & 1<=p70]]]
normalized: E [true U ~ [E [true U ~ [[p70<=1 & 1<=p70]]]]]
abstracting: (1<=p70)
states: 1,102,154,755 (9)
abstracting: (p70<=1)
states: 6,716,446,748 (9)
-> the formula is FALSE
FORMULA AutonomousCar-PT-09a-CTLFireability-07 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m18.792sec
checking: AX [EG [AG [AF [[[[0<=p80 & p80<=0] | [0<=p69 & p69<=0]] | [[0<=p10 & p10<=0] | [0<=p1 & p1<=0]]]]]]]
normalized: ~ [EX [~ [EG [~ [E [true U EG [~ [[[[0<=p1 & p1<=0] | [0<=p10 & p10<=0]] | [[0<=p69 & p69<=0] | [0<=p80 & p80<=0]]]]]]]]]]]
abstracting: (p80<=0)
states: 4,873,162,334 (9)
abstracting: (0<=p80)
states: 6,716,446,748 (9)
abstracting: (p69<=0)
states: 5,614,291,993 (9)
abstracting: (0<=p69)
states: 6,716,446,748 (9)
abstracting: (p10<=0)
states: 6,048,108,128 (9)
abstracting: (0<=p10)
states: 6,716,446,748 (9)
abstracting: (p1<=0)
states: 1
abstracting: (0<=p1)
states: 6,716,446,748 (9)
..................
EG iterations: 18
MC time: 3m47.015sec
checking: A [[[[1<=p80 & p80<=1] & [1<=p46 & p46<=1]] & [[1<=p12 & p12<=1] & [p1<=1 & 1<=p1]]] U AG [AF [~ [[[[1<=p80 & p80<=1] & [p48<=1 & 1<=p48]] & [[1<=p1 & p1<=1] & [1<=p12 & p12<=1]]]]]]]
normalized: [~ [EG [E [true U EG [[[[1<=p1 & p1<=1] & [1<=p12 & p12<=1]] & [[p48<=1 & 1<=p48] & [1<=p80 & p80<=1]]]]]]] & ~ [E [E [true U EG [[[[1<=p1 & p1<=1] & [1<=p12 & p12<=1]] & [[p48<=1 & 1<=p48] & [1<=p80 & p80<=1]]]]] U [E [true U EG [[[[1<=p1 & p1<=1] & [1<=p12 & p12<=1]] & [[p48<=1 & 1<=p48] & [1<=p80 & p80<=1]]]]] & ~ [[[[p1<=1 & 1<=p1] & [1<=p12 & p12<=1]] & [[1<=p46 & p46<=1] & [1<=p80 & p80<=1]]]]]]]]
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p46<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p46)
states: 948,582,198 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p48)
states: 948,582,198 (8)
abstracting: (p48<=1)
states: 6,716,446,748 (9)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
..................
EG iterations: 18
MC time: 3m32.000sec
checking: AF [AX [[AG [[[[[p19<=0 & 0<=p19] | [p23<=0 & 0<=p23]] | [[p33<=0 & 0<=p33] | [[p40<=0 & 0<=p40] | [p47<=0 & 0<=p47]]]] | [[[p51<=0 & 0<=p51] | [p58<=0 & 0<=p58]] | [[p65<=0 & 0<=p65] | [[p72<=0 & 0<=p72] | [p81<=0 & 0<=p81]]]]]] & EG [AX [[p60<=0 & 0<=p60]]]]]]
normalized: ~ [EG [EX [~ [[~ [E [true U ~ [[[[[[p81<=0 & 0<=p81] | [p72<=0 & 0<=p72]] | [p65<=0 & 0<=p65]] | [[p58<=0 & 0<=p58] | [p51<=0 & 0<=p51]]] | [[[[p47<=0 & 0<=p47] | [p40<=0 & 0<=p40]] | [p33<=0 & 0<=p33]] | [[p23<=0 & 0<=p23] | [p19<=0 & 0<=p19]]]]]]] & EG [~ [EX [~ [[p60<=0 & 0<=p60]]]]]]]]]]
abstracting: (0<=p60)
states: 6,716,446,748 (9)
abstracting: (p60<=0)
states: 5,767,864,550 (9)
............
EG iterations: 11
abstracting: (0<=p19)
states: 6,716,446,748 (9)
abstracting: (p19<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p23)
states: 6,716,446,748 (9)
abstracting: (p23<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p33)
states: 6,716,446,748 (9)
abstracting: (p33<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p40)
states: 6,716,446,748 (9)
abstracting: (p40<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p47)
states: 6,716,446,748 (9)
abstracting: (p47<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p51)
states: 6,716,446,748 (9)
abstracting: (p51<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p58)
states: 6,716,446,748 (9)
abstracting: (p58<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p65)
states: 6,716,446,748 (9)
abstracting: (p65<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p72)
states: 6,716,446,748 (9)
abstracting: (p72<=0)
states: 5,562,532,885 (9)
abstracting: (0<=p81)
states: 6,716,446,748 (9)
abstracting: (p81<=0)
states: 4,976,763,283 (9)
....
before gc: list nodes free: 1648323
after gc: idd nodes used:1761325, unused:62238675; list nodes free:298039446
.MC time: 3m18.022sec
checking: EG [[AF [AG [[[[[[0<=p81 & p81<=0] | [0<=p74 & p74<=0]] | [p65<=0 & 0<=p65]] | [[p61<=0 & 0<=p61] | [0<=p51 & p51<=0]]] | [[[[p47<=0 & 0<=p47] | [0<=p40 & p40<=0]] | [0<=p30 & p30<=0]] | [[p26<=0 & 0<=p26] | [0<=p19 & p19<=0]]]]]] & EF [AG [EF [[[[p8<=1 & 1<=p8] & [1<=p1 & p1<=1]] & [[1<=p80 & p80<=1] & [p15<=1 & 1<=p15]]]]]]]]
normalized: EG [[~ [EG [E [true U ~ [[[[[p61<=0 & 0<=p61] | [0<=p51 & p51<=0]] | [[p65<=0 & 0<=p65] | [[0<=p74 & p74<=0] | [0<=p81 & p81<=0]]]] | [[[0<=p19 & p19<=0] | [p26<=0 & 0<=p26]] | [[0<=p30 & p30<=0] | [[0<=p40 & p40<=0] | [p47<=0 & 0<=p47]]]]]]]]] & E [true U ~ [E [true U ~ [E [true U [[[p15<=1 & 1<=p15] & [1<=p80 & p80<=1]] & [[1<=p1 & p1<=1] & [p8<=1 & 1<=p8]]]]]]]]]]
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p15)
states: 942,060,342 (8)
abstracting: (p15<=1)
states: 6,716,446,748 (9)
MC time: 3m 3.999sec
checking: EF [AX [EF [[[[[[[p47<=1 & 1<=p47] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]]] & [[[p51<=1 & 1<=p51] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]]] | [[[p1<=1 & 1<=p1] & [p7<=1 & 1<=p7]] & [[p60<=1 & 1<=p60] & [p80<=1 & 1<=p80]]]]]]]
normalized: E [true U ~ [EX [~ [E [true U [[[[p80<=1 & 1<=p80] & [p60<=1 & 1<=p60]] & [[p7<=1 & 1<=p7] & [p1<=1 & 1<=p1]]] | [[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p51<=1 & 1<=p51]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p47<=1 & 1<=p47]]]]]]]]]]]
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p7)
states: 668,338,620 (8)
abstracting: (p7<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p60)
states: 948,582,198 (8)
abstracting: (p60<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
MC time: 2m52.001sec
checking: ~ [A [AX [~ [AF [E [[p32<=1 & 1<=p32] U [[[[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [p47<=1 & 1<=p47]]]] & [[[p51<=1 & 1<=p51] & [p61<=1 & 1<=p61]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]] U EG [~ [EX [[[[p1<=1 & 1<=p1] & [p5<=1 & 1<=p5]] & [[p32<=1 & 1<=p32] & [p80<=1 & 1<=p80]]]]]]]]
normalized: ~ [[~ [EG [~ [EG [~ [EX [[[[p80<=1 & 1<=p80] & [p32<=1 & 1<=p32]] & [[p5<=1 & 1<=p5] & [p1<=1 & 1<=p1]]]]]]]]] & ~ [E [~ [EG [~ [EX [[[[p80<=1 & 1<=p80] & [p32<=1 & 1<=p32]] & [[p5<=1 & 1<=p5] & [p1<=1 & 1<=p1]]]]]]] U [EX [~ [EG [~ [E [[p32<=1 & 1<=p32] U [[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]]] & [[[[p47<=1 & 1<=p47] & [p37<=1 & 1<=p37]] & [p33<=1 & 1<=p33]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]]]]]]] & ~ [EG [~ [EX [[[[p80<=1 & 1<=p80] & [p32<=1 & 1<=p32]] & [[p5<=1 & 1<=p5] & [p1<=1 & 1<=p1]]]]]]]]]]]]
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p5)
states: 668,338,620 (8)
abstracting: (p5<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p32)
states: 948,582,198 (8)
abstracting: (p32<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
............
EG iterations: 11
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p32)
states: 948,582,198 (8)
abstracting: (p32<=1)
states: 6,716,446,748 (9)
........
EG iterations: 8
.abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p5)
states: 668,338,620 (8)
abstracting: (p5<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p32)
states: 948,582,198 (8)
abstracting: (p32<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
............
EG iterations: 11
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p5)
states: 668,338,620 (8)
abstracting: (p5<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p32)
states: 948,582,198 (8)
abstracting: (p32<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
............
EG iterations: 11
......................
EG iterations: 22
-> the formula is FALSE
FORMULA AutonomousCar-PT-09a-CTLFireability-09 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m51.030sec
checking: AG [[[[[[p16<=0 & 0<=p16] | [p26<=0 & 0<=p26]] | [[p33<=0 & 0<=p33] | [[p40<=0 & 0<=p40] | [p47<=0 & 0<=p47]]]] | [[[p51<=0 & 0<=p51] | [p61<=0 & 0<=p61]] | [[p65<=0 & 0<=p65] | [[p72<=0 & 0<=p72] | [p81<=0 & 0<=p81]]]]] & [AF [AG [[p53<=1 & 1<=p53]]] | [[[[p19<=1 & 1<=p19] & [p23<=1 & 1<=p23]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p47<=1 & 1<=p47]]]] & [[[p51<=1 & 1<=p51] & [p61<=1 & 1<=p61]] & [[p68<=1 & 1<=p68] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]
normalized: ~ [E [true U ~ [[[[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]]] & [[[[p47<=1 & 1<=p47] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]] | ~ [EG [E [true U ~ [[p53<=1 & 1<=p53]]]]]] & [[[[[p81<=0 & 0<=p81] | [p72<=0 & 0<=p72]] | [p65<=0 & 0<=p65]] | [[p61<=0 & 0<=p61] | [p51<=0 & 0<=p51]]] | [[[[p47<=0 & 0<=p47] | [p40<=0 & 0<=p40]] | [p33<=0 & 0<=p33]] | [[p26<=0 & 0<=p26] | [p16<=0 & 0<=p16]]]]]]]]
abstracting: (0<=p16)
states: 6,716,446,748 (9)
abstracting: (p16<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p26)
states: 6,716,446,748 (9)
abstracting: (p26<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p33)
states: 6,716,446,748 (9)
abstracting: (p33<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p40)
states: 6,716,446,748 (9)
abstracting: (p40<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p47)
states: 6,716,446,748 (9)
abstracting: (p47<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p51)
states: 6,716,446,748 (9)
abstracting: (p51<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p61)
states: 6,716,446,748 (9)
abstracting: (p61<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p65)
states: 6,716,446,748 (9)
abstracting: (p65<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p72)
states: 6,716,446,748 (9)
abstracting: (p72<=0)
states: 5,562,532,885 (9)
abstracting: (0<=p81)
states: 6,716,446,748 (9)
abstracting: (p81<=0)
states: 4,976,763,283 (9)
abstracting: (1<=p53)
states: 948,582,198 (8)
abstracting: (p53<=1)
states: 6,716,446,748 (9)
EG iterations: 0
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
-> the formula is FALSE
FORMULA AutonomousCar-PT-09a-CTLFireability-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m22.940sec
checking: E [AX [~ [[~ [[[[1<=p80 & p80<=1] & [1<=p48 & p48<=1]] & [[1<=p9 & p9<=1] & [1<=p1 & p1<=1]]]] & AF [[[[[[1<=p81 & p81<=1] & [1<=p72 & p72<=1]] & [1<=p68 & p68<=1]] & [[1<=p58 & p58<=1] & [1<=p54 & p54<=1]]] & [[[p16<=1 & 1<=p16] & [p23<=1 & 1<=p23]] & [[p30<=1 & 1<=p30] & [[p37<=1 & 1<=p37] & [1<=p47 & p47<=1]]]]]]]]] U EG [~ [[[[[[1<=p40 & p40<=1] & [1<=p44 & p44<=1]] & [1<=p33 & p33<=1]] & [[1<=p23 & p23<=1] & [1<=p19 & p19<=1]]] & [[[1<=p58 & p58<=1] & [1<=p54 & p54<=1]] & [[1<=p65 & p65<=1] & [[1<=p72 & p72<=1] & [p81<=1 & 1<=p81]]]]]]]]
normalized: E [~ [EX [[~ [EG [~ [[[[[[1<=p47 & p47<=1] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]] & [[[1<=p54 & p54<=1] & [1<=p58 & p58<=1]] & [[1<=p68 & p68<=1] & [[1<=p72 & p72<=1] & [1<=p81 & p81<=1]]]]]]]] & ~ [[[[1<=p1 & p1<=1] & [1<=p9 & p9<=1]] & [[1<=p48 & p48<=1] & [1<=p80 & p80<=1]]]]]]] U EG [~ [[[[[[p81<=1 & 1<=p81] & [1<=p72 & p72<=1]] & [1<=p65 & p65<=1]] & [[1<=p54 & p54<=1] & [1<=p58 & p58<=1]]] & [[[1<=p19 & p19<=1] & [1<=p23 & p23<=1]] & [[1<=p33 & p33<=1] & [[1<=p44 & p44<=1] & [1<=p40 & p40<=1]]]]]]]]
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
........
EG iterations: 8
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p48<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p48)
states: 948,582,198 (8)
abstracting: (p9<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p9)
states: 668,338,620 (8)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
.........
EG iterations: 9
.-> the formula is TRUE
FORMULA AutonomousCar-PT-09a-CTLFireability-00 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m19.641sec
checking: EX [EG [AF [[[[[[[p81<=0 & 0<=p81] | [0<=p72 & p72<=0]] | [0<=p68 & p68<=0]] | [[[0<=p58 & p58<=0] | [0<=p54 & p54<=0]] | [p47<=0 & 0<=p47]]] | [[[[0<=p40 & p40<=0] | [0<=p33 & p33<=0]] | [p26<=0 & 0<=p26]] | [EX [[[[p1<=1 & 1<=p1] & [p10<=1 & 1<=p10]] & [[p25<=1 & 1<=p25] & [p80<=1 & 1<=p80]]]] | [p19<=0 & 0<=p19]]]] & [[[[[p16<=0 & 0<=p16] | [p23<=0 & 0<=p23]] | [[p30<=0 & 0<=p30] | [[p40<=0 & 0<=p40] | [p47<=0 & 0<=p47]]]] | [[[p51<=0 & 0<=p51] | [p58<=0 & 0<=p58]] | [[p68<=0 & 0<=p68] | [[p72<=0 & 0<=p72] | [p81<=0 & 0<=p81]]]]] & [[[p1<=0 & 0<=p1] | [p10<=0 & 0<=p10]] | [[p60<=0 & 0<=p60] | [p80<=0 & 0<=p80]]]]]]]]
normalized: EX [EG [~ [EG [~ [[[[[[p80<=0 & 0<=p80] | [p60<=0 & 0<=p60]] | [[p10<=0 & 0<=p10] | [p1<=0 & 0<=p1]]] & [[[[[p81<=0 & 0<=p81] | [p72<=0 & 0<=p72]] | [p68<=0 & 0<=p68]] | [[p58<=0 & 0<=p58] | [p51<=0 & 0<=p51]]] | [[[[p47<=0 & 0<=p47] | [p40<=0 & 0<=p40]] | [p30<=0 & 0<=p30]] | [[p23<=0 & 0<=p23] | [p16<=0 & 0<=p16]]]]] & [[[[p19<=0 & 0<=p19] | EX [[[[p80<=1 & 1<=p80] & [p25<=1 & 1<=p25]] & [[p10<=1 & 1<=p10] & [p1<=1 & 1<=p1]]]]] | [[p26<=0 & 0<=p26] | [[0<=p33 & p33<=0] | [0<=p40 & p40<=0]]]] | [[[p47<=0 & 0<=p47] | [[0<=p54 & p54<=0] | [0<=p58 & p58<=0]]] | [[0<=p68 & p68<=0] | [[0<=p72 & p72<=0] | [p81<=0 & 0<=p81]]]]]]]]]]]
abstracting: (0<=p81)
states: 6,716,446,748 (9)
abstracting: (p81<=0)
states: 4,976,763,283 (9)
abstracting: (p72<=0)
states: 5,562,532,885 (9)
abstracting: (0<=p72)
states: 6,716,446,748 (9)
abstracting: (p68<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p68)
states: 6,716,446,748 (9)
abstracting: (p58<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p58)
states: 6,716,446,748 (9)
abstracting: (p54<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p54)
states: 6,716,446,748 (9)
abstracting: (0<=p47)
states: 6,716,446,748 (9)
abstracting: (p47<=0)
states: 5,726,417,941 (9)
abstracting: (p40<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p40)
states: 6,716,446,748 (9)
abstracting: (p33<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p33)
states: 6,716,446,748 (9)
abstracting: (0<=p26)
states: 6,716,446,748 (9)
abstracting: (p26<=0)
states: 5,726,417,941 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p10)
states: 668,338,620 (8)
abstracting: (p10<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p25)
states: 948,582,198 (8)
abstracting: (p25<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
.abstracting: (0<=p19)
states: 6,716,446,748 (9)
abstracting: (p19<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p16)
states: 6,716,446,748 (9)
abstracting: (p16<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p23)
states: 6,716,446,748 (9)
abstracting: (p23<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p30)
states: 6,716,446,748 (9)
abstracting: (p30<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p40)
states: 6,716,446,748 (9)
abstracting: (p40<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p47)
states: 6,716,446,748 (9)
abstracting: (p47<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p51)
states: 6,716,446,748 (9)
abstracting: (p51<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p58)
states: 6,716,446,748 (9)
abstracting: (p58<=0)
states: 5,726,417,942 (9)
abstracting: (0<=p68)
states: 6,716,446,748 (9)
abstracting: (p68<=0)
states: 5,726,417,941 (9)
abstracting: (0<=p72)
states: 6,716,446,748 (9)
abstracting: (p72<=0)
states: 5,562,532,885 (9)
abstracting: (0<=p81)
states: 6,716,446,748 (9)
abstracting: (p81<=0)
states: 4,976,763,283 (9)
abstracting: (0<=p1)
states: 6,716,446,748 (9)
abstracting: (p1<=0)
states: 1
abstracting: (0<=p10)
states: 6,716,446,748 (9)
abstracting: (p10<=0)
states: 6,048,108,128 (9)
abstracting: (0<=p60)
states: 6,716,446,748 (9)
abstracting: (p60<=0)
states: 5,767,864,550 (9)
abstracting: (0<=p80)
states: 6,716,446,748 (9)
abstracting: (p80<=0)
states: 4,873,162,334 (9)
..................
EG iterations: 18
before gc: list nodes free: 2058586
after gc: idd nodes used:1744244, unused:62255756; list nodes free:300070902
...
EG iterations: 3
.-> the formula is TRUE
FORMULA AutonomousCar-PT-09a-CTLFireability-02 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m47.292sec
checking: AG [E [[[~ [EX [[[[p1<=1 & 1<=p1] & [p6<=1 & 1<=p6]] & [[p45<=1 & 1<=p45] & [p80<=1 & 1<=p80]]]]] & AX [AX [[[[p1<=1 & 1<=p1] & [p6<=1 & 1<=p6]] & [[p52<=1 & 1<=p52] & [p80<=1 & 1<=p80]]]]]] | [[[[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]] & [[p30<=1 & 1<=p30] & [[p40<=1 & 1<=p40] & [p47<=1 & 1<=p47]]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]] U E [EG [[p17<=1 & 1<=p17]] U ~ [A [[[[p1<=1 & 1<=p1] & [p8<=1 & 1<=p8]] & [[p20<=1 & 1<=p20] & [p80<=1 & 1<=p80]]] U [[[[p19<=1 & 1<=p19] & [p23<=1 & 1<=p23]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p44<=1 & 1<=p44]]]] & [[[p54<=1 & 1<=p54] & [p61<=1 & 1<=p61]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]]]
normalized: ~ [E [true U ~ [E [[[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [p40<=1 & 1<=p40]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]] | [~ [EX [EX [~ [[[[p80<=1 & 1<=p80] & [p52<=1 & 1<=p52]] & [[p6<=1 & 1<=p6] & [p1<=1 & 1<=p1]]]]]]] & ~ [EX [[[[p80<=1 & 1<=p80] & [p45<=1 & 1<=p45]] & [[p6<=1 & 1<=p6] & [p1<=1 & 1<=p1]]]]]]] U E [EG [[p17<=1 & 1<=p17]] U ~ [[~ [EG [~ [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]]]]] & ~ [E [~ [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]]] U [~ [[[[p80<=1 & 1<=p80] & [p20<=1 & 1<=p20]] & [[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]]]] & ~ [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]]]]]]]]]]]]]
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p20)
states: 948,582,198 (8)
abstracting: (p20<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
.......
EG iterations: 7
abstracting: (1<=p17)
states: 948,582,198 (8)
abstracting: (p17<=1)
states: 6,716,446,748 (9)
......................
EG iterations: 22
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p6)
states: 668,338,620 (8)
abstracting: (p6<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p45)
states: 948,582,198 (8)
abstracting: (p45<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p6)
states: 668,338,620 (8)
abstracting: (p6<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p52)
states: 948,582,198 (8)
abstracting: (p52<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
.MC time: 3m21.035sec
checking: [~ [A [AF [[[[[[p1<=1 & 1<=p1] & [p9<=1 & 1<=p9]] & [[p15<=1 & 1<=p15] & [p80<=1 & 1<=p80]]] | [[[p1<=1 & 1<=p1] & [p7<=1 & 1<=p7]] & [[p31<=1 & 1<=p31] & [p80<=1 & 1<=p80]]]] | [[[[p1<=1 & 1<=p1] & [p7<=1 & 1<=p7]] & [[p64<=1 & 1<=p64] & [p80<=1 & 1<=p80]]] | ~ [[[[p1<=1 & 1<=p1] & [p2<=1 & 1<=p2]] & [[p67<=1 & 1<=p67] & [p80<=1 & 1<=p80]]]]]]] U EG [EF [[[[[p1<=1 & 1<=p1] & [p8<=1 & 1<=p8]] & [[p50<=1 & 1<=p50] & [p80<=1 & 1<=p80]]] | [[[[p16<=1 & 1<=p16] & [p23<=1 & 1<=p23]] & [[p30<=1 & 1<=p30] & [[p37<=1 & 1<=p37] & [p47<=1 & 1<=p47]]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p68<=1 & 1<=p68] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]]] & EG [AF [[[[[p16<=0 & 0<=p16] | [p26<=0 & 0<=p26]] | [[p33<=0 & 0<=p33] | [[p40<=0 & 0<=p40] | [p44<=0 & 0<=p44]]]] | [[[p51<=0 & 0<=p51] | [p61<=0 & 0<=p61]] | [[p68<=0 & 0<=p68] | [[p72<=0 & 0<=p72] | [p81<=0 & 0<=p81]]]]]]]]
normalized: [EG [~ [EG [~ [[[[[[p81<=0 & 0<=p81] | [p72<=0 & 0<=p72]] | [p68<=0 & 0<=p68]] | [[p61<=0 & 0<=p61] | [p51<=0 & 0<=p51]]] | [[[[p44<=0 & 0<=p44] | [p40<=0 & 0<=p40]] | [p33<=0 & 0<=p33]] | [[p26<=0 & 0<=p26] | [p16<=0 & 0<=p16]]]]]]]] & ~ [[~ [EG [~ [EG [E [true U [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]]] | [[[p80<=1 & 1<=p80] & [p50<=1 & 1<=p50]] & [[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]]]]]]]]] & ~ [E [~ [EG [E [true U [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]]] | [[[p80<=1 & 1<=p80] & [p50<=1 & 1<=p50]] & [[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]]]]]]] U [EG [~ [[[~ [[[[p80<=1 & 1<=p80] & [p67<=1 & 1<=p67]] & [[p2<=1 & 1<=p2] & [p1<=1 & 1<=p1]]]] | [[[p80<=1 & 1<=p80] & [p64<=1 & 1<=p64]] & [[p7<=1 & 1<=p7] & [p1<=1 & 1<=p1]]]] | [[[[p80<=1 & 1<=p80] & [p31<=1 & 1<=p31]] & [[p7<=1 & 1<=p7] & [p1<=1 & 1<=p1]]] | [[[p80<=1 & 1<=p80] & [p15<=1 & 1<=p15]] & [[p9<=1 & 1<=p9] & [p1<=1 & 1<=p1]]]]]]] & ~ [EG [E [true U [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]]] | [[[p80<=1 & 1<=p80] & [p50<=1 & 1<=p50]] & [[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]]]]]]]]]]]]]
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p50)
states: 942,060,342 (8)
abstracting: (p50<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
MC time: 3m 1.999sec
checking: E [[[[[[1<=p62 & p62<=1] & [1<=p2 & p2<=1]] & [[[~ [[[[[[1<=p81 & p81<=1] & [1<=p74 & p74<=1]] & [p68<=1 & 1<=p68]] & [[p51<=1 & 1<=p51] & [p58<=1 & 1<=p58]]] & [[[p16<=1 & 1<=p16] & [p23<=1 & 1<=p23]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p47<=1 & 1<=p47]]]]]] & ~ [[1<=p57 & p57<=1]]] | EX [[[[p80<=1 & 1<=p80] & [1<=p64 & p64<=1]] & [[p1<=1 & 1<=p1] & [p9<=1 & 1<=p9]]]]] & [p80<=1 & 1<=p80]]] & [[EG [[~ [[[[1<=p80 & p80<=1] & [1<=p69 & p69<=1]] & [[1<=p9 & p9<=1] & [1<=p1 & p1<=1]]]] | EG [[[[1<=p6 & p6<=1] & [1<=p1 & p1<=1]] & [[1<=p27 & p27<=1] & [1<=p80 & p80<=1]]]]]] & [1<=p1 & p1<=1]] & ~ [AG [[[[[[1<=p81 & p81<=1] & [1<=p74 & p74<=1]] & [1<=p65 & p65<=1]] & [[1<=p61 & p61<=1] & [1<=p54 & p54<=1]]] & [[[[1<=p37 & p37<=1] & [1<=p44 & p44<=1]] & [1<=p30 & p30<=1]] & [[1<=p16 & p16<=1] & [1<=p26 & p26<=1]]]]]]]] | EF [~ [AF [[1<=p18 & p18<=1]]]]] U EF [AG [EF [[[[1<=p80 & p80<=1] & [p24<=1 & 1<=p24]] & [[1<=p1 & p1<=1] & [p9<=1 & 1<=p9]]]]]]]
normalized: E [[E [true U EG [~ [[1<=p18 & p18<=1]]]] | [[E [true U ~ [[[[[1<=p26 & p26<=1] & [1<=p16 & p16<=1]] & [[1<=p30 & p30<=1] & [[1<=p44 & p44<=1] & [1<=p37 & p37<=1]]]] & [[[1<=p54 & p54<=1] & [1<=p61 & p61<=1]] & [[1<=p65 & p65<=1] & [[1<=p74 & p74<=1] & [1<=p81 & p81<=1]]]]]]] & [[1<=p1 & p1<=1] & EG [[EG [[[[1<=p80 & p80<=1] & [1<=p27 & p27<=1]] & [[1<=p1 & p1<=1] & [1<=p6 & p6<=1]]]] | ~ [[[[1<=p1 & p1<=1] & [1<=p9 & p9<=1]] & [[1<=p69 & p69<=1] & [1<=p80 & p80<=1]]]]]]]] & [[[p80<=1 & 1<=p80] & [EX [[[[p9<=1 & 1<=p9] & [p1<=1 & 1<=p1]] & [[1<=p64 & p64<=1] & [p80<=1 & 1<=p80]]]] | [~ [[1<=p57 & p57<=1]] & ~ [[[[[[p47<=1 & 1<=p47] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]] & [[[p58<=1 & 1<=p58] & [p51<=1 & 1<=p51]] & [[p68<=1 & 1<=p68] & [[1<=p74 & p74<=1] & [1<=p81 & p81<=1]]]]]]]]] & [[1<=p2 & p2<=1] & [1<=p62 & p62<=1]]]]] U E [true U ~ [E [true U ~ [E [true U [[[p9<=1 & 1<=p9] & [1<=p1 & p1<=1]] & [[p24<=1 & 1<=p24] & [1<=p80 & p80<=1]]]]]]]]]
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p24)
states: 948,582,198 (8)
abstracting: (p24<=1)
states: 6,716,446,748 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (1<=p9)
states: 668,338,620 (8)
abstracting: (p9<=1)
states: 6,716,446,748 (9)
MC time: 2m45.999sec
checking: AX [[[[[[p80<=1 & 1<=p80] & [1<=p46 & p46<=1]] & [1<=p7 & p7<=1]] & [[p1<=1 & 1<=p1] & AX [[[[[0<=p80 & p80<=0] | [0<=p22 & p22<=0]] | [p11<=0 & 0<=p11]] | [AX [[[[[p16<=1 & 1<=p16] & [p23<=1 & 1<=p23]] & [[p30<=1 & 1<=p30] & [[p40<=1 & 1<=p40] & [p44<=1 & 1<=p44]]]] & [[[p54<=1 & 1<=p54] & [p61<=1 & 1<=p61]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]] | [p1<=0 & 0<=p1]]]]]] | EG [[[[AX [[[[[[p81<=1 & 1<=p81] & [1<=p72 & p72<=1]] & [1<=p68 & p68<=1]] & [[1<=p58 & p58<=1] & [1<=p51 & p51<=1]]] & [[[[1<=p44 & p44<=1] & [p40<=1 & 1<=p40]] & [1<=p30 & p30<=1]] & [[1<=p23 & p23<=1] & [p19<=1 & 1<=p19]]]]] | [[[[1<=p23 & p23<=1] & [p16<=1 & 1<=p16]] & [[1<=p33 & p33<=1] & [[1<=p40 & p40<=1] & [p47<=1 & 1<=p47]]]] & [[[p54<=1 & 1<=p54] & [[p58<=1 & 1<=p58] & [p65<=1 & 1<=p65]]] & [[p74<=1 & 1<=p74] & [[p81<=1 & 1<=p81] & [p36<=1 & 1<=p36]]]]]] | [AF [[[[[[1<=p37 & p37<=1] & [p47<=1 & 1<=p47]] & [1<=p33 & p33<=1]] & [[p23<=1 & 1<=p23] & [1<=p19 & p19<=1]]] & [[[p54<=1 & 1<=p54] & [1<=p61 & p61<=1]] & [[p68<=1 & 1<=p68] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]] & [EF [[p21<=1 & 1<=p21]] & [[[0<=p8 & p8<=0] | [p1<=0 & 0<=p1]] | [[0<=p80 & p80<=0] | [p62<=0 & 0<=p62]]]]]] | [[[p1<=0 & 0<=p1] | [p12<=0 & 0<=p12]] | [[p69<=0 & 0<=p69] | [p80<=0 & 0<=p80]]]]]]]
normalized: ~ [EX [~ [[EG [[[[[[[[p62<=0 & 0<=p62] | [0<=p80 & p80<=0]] | [[p1<=0 & 0<=p1] | [0<=p8 & p8<=0]]] & E [true U [p21<=1 & 1<=p21]]] & ~ [EG [~ [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[1<=p61 & p61<=1] & [p54<=1 & 1<=p54]]] & [[[1<=p19 & p19<=1] & [p23<=1 & 1<=p23]] & [[1<=p33 & p33<=1] & [[p47<=1 & 1<=p47] & [1<=p37 & p37<=1]]]]]]]]] | [[[[[[p36<=1 & 1<=p36] & [p81<=1 & 1<=p81]] & [p74<=1 & 1<=p74]] & [[[p65<=1 & 1<=p65] & [p58<=1 & 1<=p58]] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [1<=p40 & p40<=1]] & [1<=p33 & p33<=1]] & [[p16<=1 & 1<=p16] & [1<=p23 & p23<=1]]]] | ~ [EX [~ [[[[[p19<=1 & 1<=p19] & [1<=p23 & p23<=1]] & [[1<=p30 & p30<=1] & [[p40<=1 & 1<=p40] & [1<=p44 & p44<=1]]]] & [[[1<=p51 & p51<=1] & [1<=p58 & p58<=1]] & [[1<=p68 & p68<=1] & [[1<=p72 & p72<=1] & [p81<=1 & 1<=p81]]]]]]]]]] | [[[p80<=0 & 0<=p80] | [p69<=0 & 0<=p69]] | [[p12<=0 & 0<=p12] | [p1<=0 & 0<=p1]]]]] | [[~ [EX [~ [[[[p1<=0 & 0<=p1] | ~ [EX [~ [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p30<=1 & 1<=p30]] & [[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]]]]]]]] | [[p11<=0 & 0<=p11] | [[0<=p22 & p22<=0] | [0<=p80 & p80<=0]]]]]]] & [p1<=1 & 1<=p1]] & [[1<=p7 & p7<=1] & [[1<=p46 & p46<=1] & [p80<=1 & 1<=p80]]]]]]]]
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (p46<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p46)
states: 948,582,198 (8)
abstracting: (p7<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p7)
states: 668,338,620 (8)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (p80<=0)
states: 4,873,162,334 (9)
abstracting: (0<=p80)
states: 6,716,446,748 (9)
abstracting: (p22<=0)
states: 5,774,386,406 (9)
abstracting: (0<=p22)
states: 6,716,446,748 (9)
abstracting: (0<=p11)
states: 6,716,446,748 (9)
abstracting: (p11<=0)
states: 6,048,108,128 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
.abstracting: (0<=p1)
states: 6,716,446,748 (9)
abstracting: (p1<=0)
states: 1
.abstracting: (0<=p1)
states: 6,716,446,748 (9)
abstracting: (p1<=0)
states: 1
abstracting: (0<=p12)
states: 6,716,446,748 (9)
abstracting: (p12<=0)
states: 6,117,740,390 (9)
abstracting: (0<=p69)
states: 6,716,446,748 (9)
abstracting: (p69<=0)
states: 5,614,291,993 (9)
abstracting: (0<=p80)
states: 6,716,446,748 (9)
abstracting: (p80<=0)
states: 4,873,162,334 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
.abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p36)
states: 942,060,342 (8)
abstracting: (p36<=1)
states: 6,716,446,748 (9)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
......
EG iterations: 6
abstracting: (1<=p21)
states: 948,582,198 (8)
abstracting: (p21<=1)
states: 6,716,446,748 (9)
MC time: 2m30.999sec
checking: EG [[[[[[[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [p33<=1 & 1<=p33]] & [[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p68<=1 & 1<=p68] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]] | [[[[p19<=1 & 1<=p19] & [p23<=1 & 1<=p23]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p47<=1 & 1<=p47]]]] & [[[p54<=1 & 1<=p54] & [p61<=1 & 1<=p61]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]] | AF [[[[[[p1<=1 & 1<=p1] & [p12<=1 & 1<=p12]] & [[p24<=1 & 1<=p24] & [p80<=1 & 1<=p80]]] & [[[p1<=1 & 1<=p1] & [p12<=1 & 1<=p12]] & [[p67<=1 & 1<=p67] & [p80<=1 & 1<=p80]]]] | EF [[[[[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]] & [[p30<=1 & 1<=p30] & [[p37<=1 & 1<=p37] & [p47<=1 & 1<=p47]]]] & [[[p51<=1 & 1<=p51] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]] & EG [[[AG [[[[p36<=0 & 0<=p36] | [p80<=0 & 0<=p80]] | [[p1<=0 & 0<=p1] | [p7<=0 & 0<=p7]]]] & AF [[[[[p16<=0 & 0<=p16] | [p23<=0 & 0<=p23]] | [[p33<=0 & 0<=p33] | [[p40<=0 & 0<=p40] | [p44<=0 & 0<=p44]]]] | [[[p54<=0 & 0<=p54] | [p61<=0 & 0<=p61]] | [[p65<=0 & 0<=p65] | [[p72<=0 & 0<=p72] | [p81<=0 & 0<=p81]]]]]]] | [[[[p19<=1 & 1<=p19] & [p23<=1 & 1<=p23]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [p44<=1 & 1<=p44]]]] & [[[p51<=1 & 1<=p51] & [p61<=1 & 1<=p61]] & [[p65<=1 & 1<=p65] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]]]]]]]
normalized: EG [[EG [[[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]]] & [[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]] | [~ [EG [~ [[[[[[p81<=0 & 0<=p81] | [p72<=0 & 0<=p72]] | [p65<=0 & 0<=p65]] | [[p61<=0 & 0<=p61] | [p54<=0 & 0<=p54]]] | [[[[p44<=0 & 0<=p44] | [p40<=0 & 0<=p40]] | [p33<=0 & 0<=p33]] | [[p23<=0 & 0<=p23] | [p16<=0 & 0<=p16]]]]]]] & ~ [E [true U ~ [[[[p7<=0 & 0<=p7] | [p1<=0 & 0<=p1]] | [[p80<=0 & 0<=p80] | [p36<=0 & 0<=p36]]]]]]]]] & [~ [EG [~ [[E [true U [[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p51<=1 & 1<=p51]]] & [[[[p47<=1 & 1<=p47] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]]] | [[[[p80<=1 & 1<=p80] & [p67<=1 & 1<=p67]] & [[p12<=1 & 1<=p12] & [p1<=1 & 1<=p1]]] & [[[p80<=1 & 1<=p80] & [p24<=1 & 1<=p24]] & [[p12<=1 & 1<=p12] & [p1<=1 & 1<=p1]]]]]]]] | [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[[p47<=1 & 1<=p47] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]]]] | [[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p68<=1 & 1<=p68]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [p44<=1 & 1<=p44]]]]]]]]]
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p24)
states: 948,582,198 (8)
abstracting: (p24<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p67)
states: 948,582,198 (8)
abstracting: (p67<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
before gc: list nodes free: 2764229
after gc: idd nodes used:2201554, unused:61798446; list nodes free:297942734
MC time: 2m16.999sec
checking: [EG [A [[[[[[p37<=1 & 1<=p37] & [p44<=1 & 1<=p44]] & [1<=p33 & p33<=1]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]] & [[[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]] & [[[1<=p74 & p74<=1] & [p81<=1 & 1<=p81]] & [p68<=1 & 1<=p68]]]] U [[[[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p51<=1 & 1<=p51] & [p61<=1 & 1<=p61]]] & [[[p19<=1 & 1<=p19] & [p26<=1 & 1<=p26]] & [[p33<=1 & 1<=p33] & [[p40<=1 & 1<=p40] & [p44<=1 & 1<=p44]]]]] | [[[p1<=1 & 1<=p1] & [p12<=1 & 1<=p12]] & [[p46<=1 & 1<=p46] & [p80<=1 & 1<=p80]]]] | EX [[[[1<=p80 & p80<=1] & [p18<=1 & 1<=p18]] & [[p1<=1 & 1<=p1] & [p8<=1 & 1<=p8]]]]] | [[[[[[[p9<=1 & 1<=p9] & [p1<=1 & 1<=p1]] & [[p25<=1 & 1<=p25] & [p80<=1 & 1<=p80]]] & [[[p1<=1 & 1<=p1] & [p10<=1 & 1<=p10]] & [[p55<=1 & 1<=p55] & [p80<=1 & 1<=p80]]]] | [[[[[p40<=1 & 1<=p40] & [p44<=1 & 1<=p44]] & [p30<=1 & 1<=p30]] & [[p19<=1 & 1<=p19] & [p23<=1 & 1<=p23]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]] & [~ [[[[[[1<=p47 & p47<=1] & [p37<=1 & 1<=p37]] & [p33<=1 & 1<=p33]] & [[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]]] & [[[p54<=1 & 1<=p54] & [p61<=1 & 1<=p61]] & [[p68<=1 & 1<=p68] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]]]] | AX [[[[[p19<=1 & 1<=p19] & [p26<=1 & 1<=p26]] & [[p30<=1 & 1<=p30] & [[p37<=1 & 1<=p37] & [p44<=1 & 1<=p44]]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]]]]]] | AF [[[[[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]] & [[p30<=1 & 1<=p30] & [[p40<=1 & 1<=p40] & [p44<=1 & 1<=p44]]]] & [[[p54<=1 & 1<=p54] & [p58<=1 & 1<=p58]] & [[p65<=1 & 1<=p65] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]]]]]]]] | EG [[~ [E [EF [[[[[1<=p61 & p61<=1] & [p51<=1 & 1<=p51]] & [[1<=p68 & p68<=1] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]] & [[[p30<=1 & 1<=p30] & [[1<=p44 & p44<=1] & [p40<=1 & 1<=p40]]] & [[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]]]]] U EF [[[[[1<=p58 & p58<=1] & [p54<=1 & 1<=p54]] & [[p68<=1 & 1<=p68] & [[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]]]] & [[[[1<=p47 & p47<=1] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p16<=1 & 1<=p16] & [p23<=1 & 1<=p23]]]]]]] & [[p83<=0 & 0<=p83] & [[[p1<=0 & 0<=p1] | [p11<=0 & 0<=p11]] | [[p38<=0 & 0<=p38] | [p80<=0 & 0<=p80]]]]]]]
normalized: [EG [[~ [E [E [true U [[[[[p74<=1 & 1<=p74] & [p81<=1 & 1<=p81]] & [1<=p68 & p68<=1]] & [[p51<=1 & 1<=p51] & [1<=p61 & p61<=1]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[[p40<=1 & 1<=p40] & [1<=p44 & p44<=1]] & [p30<=1 & 1<=p30]]]]] U E [true U [[[[p23<=1 & 1<=p23] & [p16<=1 & 1<=p16]] & [[p30<=1 & 1<=p30] & [[p37<=1 & 1<=p37] & [1<=p47 & p47<=1]]]] & [[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p68<=1 & 1<=p68]] & [[p54<=1 & 1<=p54] & [1<=p58 & p58<=1]]]]]]] & [[[[p80<=0 & 0<=p80] | [p38<=0 & 0<=p38]] | [[p11<=0 & 0<=p11] | [p1<=0 & 0<=p1]]] & [p83<=0 & 0<=p83]]]] | EG [[~ [EG [~ [[[~ [EG [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]]]]] | [[~ [EX [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]]]]]] | ~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p68<=1 & 1<=p68]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [1<=p47 & p47<=1]]]]]]] & [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]] & [[p30<=1 & 1<=p30] & [[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]]]]] | [[[[p80<=1 & 1<=p80] & [p55<=1 & 1<=p55]] & [[p10<=1 & 1<=p10] & [p1<=1 & 1<=p1]]] & [[[p80<=1 & 1<=p80] & [p25<=1 & 1<=p25]] & [[p1<=1 & 1<=p1] & [p9<=1 & 1<=p9]]]]]]] | [EX [[[[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]] & [[p18<=1 & 1<=p18] & [1<=p80 & p80<=1]]]] | [[[[p80<=1 & 1<=p80] & [p46<=1 & 1<=p46]] & [[p12<=1 & 1<=p12] & [p1<=1 & 1<=p1]]] | [[[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]] & [[[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]]]] & ~ [E [~ [[[~ [EG [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]]]]] | [[~ [EX [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]]]]]] | ~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p68<=1 & 1<=p68]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [1<=p47 & p47<=1]]]]]]] & [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]] & [[p30<=1 & 1<=p30] & [[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]]]]] | [[[[p80<=1 & 1<=p80] & [p55<=1 & 1<=p55]] & [[p10<=1 & 1<=p10] & [p1<=1 & 1<=p1]]] & [[[p80<=1 & 1<=p80] & [p25<=1 & 1<=p25]] & [[p1<=1 & 1<=p1] & [p9<=1 & 1<=p9]]]]]]] | [EX [[[[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]] & [[p18<=1 & 1<=p18] & [1<=p80 & p80<=1]]]] | [[[[p80<=1 & 1<=p80] & [p46<=1 & 1<=p46]] & [[p12<=1 & 1<=p12] & [p1<=1 & 1<=p1]]] | [[[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]] & [[[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]] U [~ [[[[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [1<=p33 & p33<=1]] & [[p16<=1 & 1<=p16] & [p26<=1 & 1<=p26]]] & [[[[p81<=1 & 1<=p81] & [1<=p74 & p74<=1]] & [p68<=1 & 1<=p68]] & [[p54<=1 & 1<=p54] & [p61<=1 & 1<=p61]]]]] & ~ [[[~ [EG [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]]]]]]] | [[~ [EX [~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[[p44<=1 & 1<=p44] & [p37<=1 & 1<=p37]] & [p30<=1 & 1<=p30]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]]]]]] | ~ [[[[[[p81<=1 & 1<=p81] & [p74<=1 & 1<=p74]] & [p68<=1 & 1<=p68]] & [[p61<=1 & 1<=p61] & [p54<=1 & 1<=p54]]] & [[[p26<=1 & 1<=p26] & [p16<=1 & 1<=p16]] & [[p33<=1 & 1<=p33] & [[p37<=1 & 1<=p37] & [1<=p47 & p47<=1]]]]]]] & [[[[[[p81<=1 & 1<=p81] & [p72<=1 & 1<=p72]] & [p65<=1 & 1<=p65]] & [[p58<=1 & 1<=p58] & [p54<=1 & 1<=p54]]] & [[[p23<=1 & 1<=p23] & [p19<=1 & 1<=p19]] & [[p30<=1 & 1<=p30] & [[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]]]]] | [[[[p80<=1 & 1<=p80] & [p55<=1 & 1<=p55]] & [[p10<=1 & 1<=p10] & [p1<=1 & 1<=p1]]] & [[[p80<=1 & 1<=p80] & [p25<=1 & 1<=p25]] & [[p1<=1 & 1<=p1] & [p9<=1 & 1<=p9]]]]]]] | [EX [[[[p8<=1 & 1<=p8] & [p1<=1 & 1<=p1]] & [[p18<=1 & 1<=p18] & [1<=p80 & p80<=1]]]] | [[[[p80<=1 & 1<=p80] & [p46<=1 & 1<=p46]] & [[p12<=1 & 1<=p12] & [p1<=1 & 1<=p1]]] | [[[[[p44<=1 & 1<=p44] & [p40<=1 & 1<=p40]] & [p33<=1 & 1<=p33]] & [[p26<=1 & 1<=p26] & [p19<=1 & 1<=p19]]] & [[[p61<=1 & 1<=p61] & [p51<=1 & 1<=p51]] & [[p65<=1 & 1<=p65] & [[p72<=1 & 1<=p72] & [p81<=1 & 1<=p81]]]]]]]]]]]]]]]
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p46)
states: 948,582,198 (8)
abstracting: (p46<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p18)
states: 948,582,198 (8)
abstracting: (p18<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p9)
states: 668,338,620 (8)
abstracting: (p9<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p25)
states: 948,582,198 (8)
abstracting: (p25<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p10)
states: 668,338,620 (8)
abstracting: (p10<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p55)
states: 948,582,198 (8)
abstracting: (p55<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
........
EG iterations: 8
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p46)
states: 948,582,198 (8)
abstracting: (p46<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p18)
states: 948,582,198 (8)
abstracting: (p18<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p9)
states: 668,338,620 (8)
abstracting: (p9<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p25)
states: 948,582,198 (8)
abstracting: (p25<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p10)
states: 668,338,620 (8)
abstracting: (p10<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p55)
states: 948,582,198 (8)
abstracting: (p55<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
........
EG iterations: 8
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p51)
states: 990,028,806 (8)
abstracting: (p51<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p12)
states: 598,706,358 (8)
abstracting: (p12<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p46)
states: 948,582,198 (8)
abstracting: (p46<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (1<=p18)
states: 948,582,198 (8)
abstracting: (p18<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p8)
states: 668,338,620 (8)
abstracting: (p8<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p9)
states: 668,338,620 (8)
abstracting: (p9<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p25)
states: 948,582,198 (8)
abstracting: (p25<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p1)
states: 6,716,446,747 (9)
abstracting: (p1<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p10)
states: 668,338,620 (8)
abstracting: (p10<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p55)
states: 948,582,198 (8)
abstracting: (p55<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p80)
states: 1,843,284,414 (9)
abstracting: (p80<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p23)
states: 990,028,806 (8)
abstracting: (p23<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p72)
states: 1,153,913,863 (9)
abstracting: (p72<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (p47<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p47)
states: 990,028,807 (8)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p33)
states: 990,028,807 (8)
abstracting: (p33<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p61)
states: 990,028,807 (8)
abstracting: (p61<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p68)
states: 990,028,807 (8)
abstracting: (p68<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p19)
states: 990,028,807 (8)
abstracting: (p19<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p37)
states: 990,028,806 (8)
abstracting: (p37<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
.abstracting: (1<=p16)
states: 990,028,806 (8)
abstracting: (p16<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p26)
states: 990,028,807 (8)
abstracting: (p26<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p30)
states: 990,028,806 (8)
abstracting: (p30<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p40)
states: 990,028,807 (8)
abstracting: (p40<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p44)
states: 990,028,806 (8)
abstracting: (p44<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p54)
states: 990,028,807 (8)
abstracting: (p54<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p58)
states: 990,028,806 (8)
abstracting: (p58<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p65)
states: 990,028,806 (8)
abstracting: (p65<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p74)
states: 1,153,913,864 (9)
abstracting: (p74<=1)
states: 6,716,446,748 (9)
abstracting: (1<=p81)
states: 1,739,683,465 (9)
abstracting: (p81<=1)
states: 6,716,446,748 (9)
........
EG iterations: 8
.......MC time: 2m 5.005sec
checking: AX [EG [AG [AF [[[[0<=p80 & p80<=0] | [0<=p69 & p69<=0]] | [[0<=p10 & p10<=0] | [0<=p1 & p1<=0]]]]]]]
normalized: ~ [EX [~ [EG [~ [E [true U EG [~ [[[[0<=p1 & p1<=0] | [0<=p10 & p10<=0]] | [[0<=p69 & p69<=0] | [0<=p80 & p80<=0]]]]]]]]]]]
abstracting: (p80<=0)
states: 4,873,162,334 (9)
abstracting: (0<=p80)
states: 6,716,446,748 (9)
abstracting: (p69<=0)
states: 5,614,291,993 (9)
abstracting: (0<=p69)
states: 6,716,446,748 (9)
abstracting: (p10<=0)
states: 6,048,108,128 (9)
abstracting: (0<=p10)
states: 6,716,446,748 (9)
abstracting: (p1<=0)
states: 1
abstracting: (0<=p1)
states: 6,716,446,748 (9)
..................
EG iterations: 18
before gc: list nodes free: 4456826
after gc: idd nodes used:2400867, unused:61599133; list nodes free:297014737
TIME LIMIT: Killed by timeout after 3600 seconds
MemTotal: 16393220 kB
MemFree: 5829692 kB
After kill :
MemTotal: 16393220 kB
MemFree: 16094548 kB
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ export PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ PYTHONPATH=/home/mcc/BenchKit/itstools/pylibs
+ export LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
+ LD_LIBRARY_PATH=/home/mcc/BenchKit/itstools/pylibs:
++ sed s/.jar//
++ ls /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202303021504.jar
++ perl -pe 's/.*\.//g'
+ VERSION=202303021504
+ echo 'Running Version 202303021504'
+ /home/mcc/BenchKit/bin//../reducer/bin//../../itstools//itstools/its-tools -pnfolder /home/mcc/execution -examination CTLFireability -timeout 360 -rebuildPNML
check for maximal unmarked siphon
ok
check for constant places
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.002sec
154442 160206 161416 162826 164244 164727 166157 164969 165089 171744 166062 167508 180769 181061 180017 182325 181581 181281 181009 181026 183025 183683 183897 186468 185432 184198 183826 184730 201675 201295 201398 201918 201963 205543 203537 202527 205825 202773 203897 203235 203513 203361 204973 204237 204221 203875 205699 205307 205751 205471 205945 211490 205895 206388 207686 209602 206326 207292 208532 207226 206817 207276
iterations count:6212155 (6956), effective:59216 (66)
initing FirstDep: 0m 0.001sec
iterations count:894 (1), effective:1 (0)
32781 34924 37366 40567 41309 42826 44312 46324 47900 52569 53949 53489 46500 56607 57763 58561 56205 63720 68468 65975 73525 69124 64683 65727 66128 62110 70774 69975 85112 77204 71906 76360 77746
sat_reach.icc:155: Timeout: after 226 sec
31458 35479 36582 36612 39848 41210 42436 42815 44139 39060 47892 46972 48568 51461 54151 53475 53293 55071 52558 53833 42557 62530 61275 57217 54088 58981 62526 68202 74091 74788 74967 71160 72741 73704 73773 69976 71369 77475 74923 75439 75637 65378 66825
sat_reach.icc:155: Timeout: after 211 sec
7106 7981 10983 10228 11719 10428 10203 9809 8294 14163 13963 13502 15348
iterations count:1321405 (1479), effective:13790 (15)
net_ddint.h:600: Timeout: after 197 sec
20089 23250 24519 26184 27961 31160 29486 33137 29496 31047 36201 38232 39558 40806 39276 46187 42888 43412 43303 38075 47443 54309 52953 54860 53444 59353 60060 56642 54388 53494 58945 67079 65230 64170 65118 65533 64026 59824 56473 55285 54859 69058
sat_reach.icc:155: Timeout: after 183 sec
21384 24329 27088 30004 30384 35768 35021 34745 37320 32874 34547 35333 45666 53916 53555 53100 56015 57540 55647 59886 56743 56780 48392 57440 73255 71092 71142 70560 69704 70395 71857 76587 69550 72886 68652
sat_reach.icc:155: Timeout: after 171 sec
iterations count:38216 (42), effective:228 (0)
iterations count:3676 (4), effective:29 (0)
iterations count:1007 (1), effective:1 (0)
iterations count:1462 (1), effective:1 (0)
iterations count:5652 (6), effective:89 (0)
iterations count:940 (1), effective:3 (0)
iterations count:893 (1), effective:0 (0)
net_ddint.h:600: Timeout: after 200 sec
22135 27279 30256 34252 39333 43595 40034 44046 48848 47427 54372 60720 64861 50141 52733 50805 50739 54515 55241 56679 61691 59076 58947 63895 61360 62592 62297 68762 56958 55866 55362 60446 68610
sat_reach.icc:155: Timeout: after 181 sec
23685 27456 28624 29453 30852 33656 33924 35225 32615 37007 40956 40431 43328 39974 45826 49154 45955 44734 43636 40144 48290 59980 53962 55674 56620 60683 57019 52644 51031 56550 60347 73485 61374 62263 58925 66945 62541 58674 55240 53986
sat_reach.icc:155: Timeout: after 165 sec
179986 181572 180662 183082 184679 185633 184305 186762 188275 190541 188950 189918 189745 189756 187780 192573 194130 196161 199511 196927 197903 198514 197389 197535 198606 198304 199834 193658 194935 194522 194766 189374
sat_reach.icc:155: Timeout: after 150 sec
14103 16368 17993 19051 19621 22488 21780 22584 24494 23539 26477 33862 28613 29364 29085 31829 28863 26093 26232 29318 34258 31942 36870 28820 34689 31703 31816 35042 29632 37265 31433 32557 35906 30044
sat_reach.icc:155: Timeout: after 136 sec
iterations count:1603 (1), effective:1 (0)
net_ddint.h:600: Timeout: after 124 sec
32781 34924 37366 40567 41309 42826 44312 46324 47900 52569 53949 53489 46500 56607 57763 58561 56205 63720 68468 65975 73525 69124 64683 65727 66128 62110 70774 69975 85112 77204 71906 76360 77746 74307 71261 76890 84828 88414 87224 88592 92146 104619 105691 113409 96190 98198 84868 90860 93560 91760 92336 93361 94614 93573 87766 84912 77952 97589 104202 99336 101984 106800 114065 119180 115543 113413 111297 110092 111898 110640 112087 112433 118548 108863 106315 98761 100124 100155 113363 110683 124366 128319 133004 119689 124477 128304 126832 128601 127860 132925 134469 154159 143912 154804 152707
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="AutonomousCar-PT-09a"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="marciexred"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-5348"
echo " Executing tool marciexred"
echo " Input is AutonomousCar-PT-09a, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r010-oct2-167813599400658"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/AutonomousCar-PT-09a.tgz
mv AutonomousCar-PT-09a execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

