About the Execution of ITS-Tools for Angiogenesis-PT-05
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 7167.880 | 2282954.00 | 2233721.00 | 15315.80 | TFTTFTFFFTFFTTFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
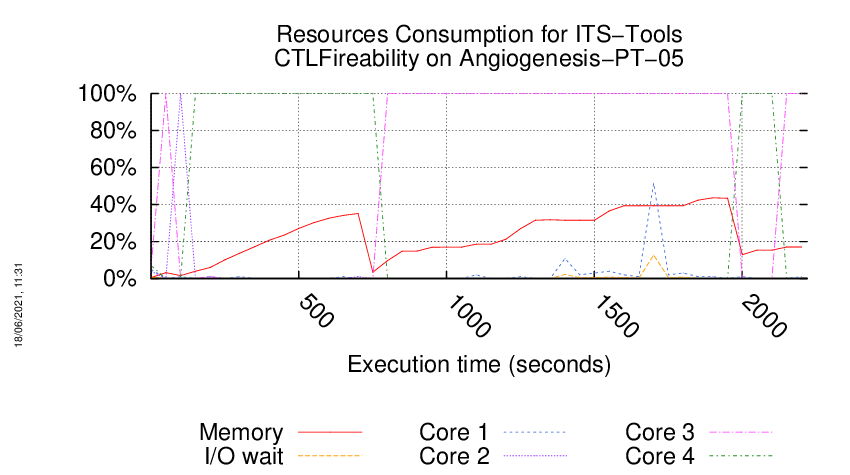
Trace from the execution
Formatting '/data/fkordon/mcc2021-input.r007-tall-162037989800324.qcow2', fmt=qcow2 size=4294967296 backing_file='/data/fkordon/mcc2021-input.qcow2' encryption=off cluster_size=65536 lazy_refcounts=off
Waiting for the VM to be ready (probing ssh)
...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-4028
Executing tool itstools
Input is Angiogenesis-PT-05, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r007-tall-162037989800324
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 404K
-rw-r--r-- 1 mcc users 16K May 5 16:58 CTLCardinality.txt
-rw-r--r-- 1 mcc users 107K May 10 09:42 CTLCardinality.xml
-rw-r--r-- 1 mcc users 9.1K May 5 16:58 CTLFireability.txt
-rw-r--r-- 1 mcc users 89K May 10 09:42 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K May 6 14:48 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.5K May 6 14:48 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 4.0K Apr 26 07:40 LTLCardinality.txt
-rw-r--r-- 1 mcc users 25K Apr 26 07:40 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.0K Apr 26 07:40 LTLFireability.txt
-rw-r--r-- 1 mcc users 18K Apr 26 07:40 LTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K Mar 23 01:45 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 18K Mar 23 01:45 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 2.7K Mar 22 10:14 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 17K Mar 22 10:14 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.7K Mar 22 09:09 UpperBounds.txt
-rw-r--r-- 1 mcc users 3.8K Mar 22 09:09 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 May 5 16:51 equiv_col
-rw-r--r-- 1 mcc users 3 May 5 16:51 instance
-rw-r--r-- 1 mcc users 6 May 5 16:51 iscolored
-rw-r--r-- 1 mcc users 33K May 5 16:51 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-00
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-01
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-02
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-03
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-04
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-05
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-06
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-07
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-08
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-09
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-10
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-11
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-12
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-13
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-14
FORMULA_NAME Angiogenesis-PT-05-CTLFireability-15
=== Now, execution of the tool begins
BK_START 1620741760931
Running Version 0
[2021-05-11 14:02:42] [INFO ] Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, CTLFireability, -spotpath, /home/mcc/BenchKit/bin//..//ltlfilt, -z3path, /home/mcc/BenchKit/bin//..//z3/bin/z3, -yices2path, /home/mcc/BenchKit/bin//..//yices/bin/yices, -its, -ltsmin, -greatspnpath, /home/mcc/BenchKit/bin//..//greatspn/, -order, META, -manyOrder, -smt, -timeout, 3600]
[2021-05-11 14:02:42] [INFO ] Parsing pnml file : /home/mcc/execution/model.pnml
[2021-05-11 14:02:42] [INFO ] Load time of PNML (sax parser for PT used): 33 ms
[2021-05-11 14:02:42] [INFO ] Transformed 39 places.
[2021-05-11 14:02:42] [INFO ] Transformed 64 transitions.
[2021-05-11 14:02:42] [INFO ] Parsed PT model containing 39 places and 64 transitions in 69 ms.
Parsed 16 properties from file /home/mcc/execution/CTLFireability.xml in 15 ms.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 2 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 2 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
[2021-05-11 14:02:42] [INFO ] Reduced 1 identical enabling conditions.
Support contains 38 out of 39 places. Attempting structural reductions.
Starting structural reductions, iteration 0 : 39/39 places, 64/64 transitions.
Reduce places removed 1 places and 0 transitions.
Iterating post reduction 0 with 1 rules applied. Total rules applied 1 place count 38 transition count 64
Applied a total of 1 rules in 9 ms. Remains 38 /39 variables (removed 1) and now considering 64/64 (removed 0) transitions.
// Phase 1: matrix 64 rows 38 cols
[2021-05-11 14:02:42] [INFO ] Computed 7 place invariants in 7 ms
[2021-05-11 14:02:42] [INFO ] Implicit Places using invariants in 77 ms returned []
// Phase 1: matrix 64 rows 38 cols
[2021-05-11 14:02:42] [INFO ] Computed 7 place invariants in 4 ms
[2021-05-11 14:02:42] [INFO ] Implicit Places using invariants and state equation in 56 ms returned []
Implicit Place search using SMT with State Equation took 158 ms to find 0 implicit places.
// Phase 1: matrix 64 rows 38 cols
[2021-05-11 14:02:42] [INFO ] Computed 7 place invariants in 2 ms
[2021-05-11 14:02:42] [INFO ] Dead Transitions using invariants and state equation in 56 ms returned []
Finished structural reductions, in 1 iterations. Remains : 38/39 places, 64/64 transitions.
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 34 ms
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 12 ms
[2021-05-11 14:02:43] [INFO ] Input system was already deterministic with 64 transitions.
Finished random walk after 5997 steps, including 0 resets, run visited all 86 properties in 22 ms. (steps per millisecond=272 )
Partial Post-agglomeration rule applied 1 times.
Drop transitions removed 1 transitions
Iterating global reduction 0 with 1 rules applied. Total rules applied 1 place count 38 transition count 64
Applied a total of 1 rules in 12 ms. Remains 38 /38 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 6 ms
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 5 ms
[2021-05-11 14:02:43] [INFO ] Input system was already deterministic with 64 transitions.
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:02:43] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:02:43] [INFO ] Time to serialize gal into /tmp/CTLFireability9882013813927186832.gal : 2 ms
[2021-05-11 14:02:43] [INFO ] Time to serialize properties into /tmp/CTLFireability9347449141874687938.ctl : 0 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability9882013813927186832.gal, -t, CGAL, -ctl, /tmp/CTLFireability9347449141874687938.ctl, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability9882013813927186832.gal -t CGAL -ctl /tmp/CTLFireability9347449141874687938.ctl --gen-order FOLLOW
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,0.990205,33420,2,11188,5,155361,6,0,219,155961,0
Converting to forward existential form...Done !
original formula: EF(AG((E(A((((((GStarP3>=1)&&(KdStar>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(KdStarG>=1))||(KdStarGStarP3>=1)) U ((DAGE>=1)||(PtP3P2>=1))) U E((((DAGE>=1)||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1)) U (((((((KdStarGStarP3kP3>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1))||((KdStar>=1)&&(Pg>=1))))) + (((((((AktP3<1)&&(PtP3<1))&&((KdStarGStarP3kStar<1)||(Pip2<1)))&&((GStarP3<1)||(KdStar<1)))&&((KdStarGStar<1)||(Pg<1)))&&((Pip3<1)||(Pten<1)))&&((KdStarGStarPgStarP3<1)||(Pip2<1))))))
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(E(TRUE U !((E(!((E(!(((DAGE>=1)||(PtP3P2>=1))) U (!((((((GStarP3>=1)&&(KdStar>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(KdStarG>=1))||(KdStarGStarP3>=1))) * !(((DAGE>=1)||(PtP3P2>=1))))) + EG(!(((DAGE>=1)||(PtP3P2>=1)))))) U E((((DAGE>=1)||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1)) U (((((((KdStarGStarP3kP3>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1))||((KdStar>=1)&&(Pg>=1))))) + (((((((AktP3<1)&&(PtP3<1))&&((KdStarGStarP3kStar<1)||(Pip2<1)))&&((GStarP3<1)||(KdStar<1)))&&((KdStarGStar<1)||(Pg<1)))&&((Pip3<1)||(Pten<1)))&&((KdStarGStarPgStarP3<1)||(Pip2<1))))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t50, t56, t60, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
(forward)formula 0,1,26.8911,666300,1,0,475,4.23477e+06,169,278,1672,3.58259e+06,583
FORMULA Angiogenesis-PT-05-CTLFireability-03 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
Partial Post-agglomeration rule applied 2 times.
Drop transitions removed 2 transitions
Iterating global reduction 0 with 2 rules applied. Total rules applied 2 place count 38 transition count 64
Applied a total of 2 rules in 4 ms. Remains 38 /38 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2021-05-11 14:03:10] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:03:10] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:03:10] [INFO ] Input system was already deterministic with 64 transitions.
[2021-05-11 14:03:10] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:03:10] [INFO ] Flatten gal took : 7 ms
[2021-05-11 14:03:10] [INFO ] Time to serialize gal into /tmp/CTLFireability15936090225652389152.gal : 1 ms
[2021-05-11 14:03:10] [INFO ] Time to serialize properties into /tmp/CTLFireability18395700549999431287.ctl : 0 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability15936090225652389152.gal, -t, CGAL, -ctl, /tmp/CTLFireability18395700549999431287.ctl, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability15936090225652389152.gal -t CGAL -ctl /tmp/CTLFireability18395700549999431287.ctl --gen-order FOLLOW
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,1.22997,42036,2,13683,5,194422,6,0,219,202741,0
Converting to forward existential form...Done !
original formula: AF(AG((EF((((((((((AktP3<1)&&((KdStarGStar<1)||(P3k<1)))&&(PtP3<1))&&(DAGE<1))&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&((Gab1<1)||(KdStar<1)))&&(KdStarG<1)) * AG(((GP3>=1)||((KdStar>=1)&&(Pg>=1)))))) + ((((((((((KdStarGStarP3k<1)&&(AktP3<1))&&(DAGE<1))&&(PtP2<1))&&(PtP3P2<1))&&((KdStarGStarPgStar<1)||(Pip2<1)))&&((Pip3<1)||(Pten<1)))&&((GStarP3<1)||(P3k<1)))&&((KdStarGStarPgStarP2>=1)||(KdStarPg>=1)))&&(((((((DAGE>=1)||(GP3>=1))||(KdStarG>=1))||(KdStarPgStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||((Pip3>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))))))
=> equivalent forward existential formula: [FwdG(Init,!(!(E(TRUE U !((E(TRUE U (((((((((AktP3<1)&&((KdStarGStar<1)||(P3k<1)))&&(PtP3<1))&&(DAGE<1))&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&((Gab1<1)||(KdStar<1)))&&(KdStarG<1)) * !(E(TRUE U !(((GP3>=1)||((KdStar>=1)&&(Pg>=1)))))))) + ((((((((((KdStarGStarP3k<1)&&(AktP3<1))&&(DAGE<1))&&(PtP2<1))&&(PtP3P2<1))&&((KdStarGStarPgStar<1)||(Pip2<1)))&&((Pip3<1)||(Pten<1)))&&((GStarP3<1)||(P3k<1)))&&((KdStarGStarPgStarP2>=1)||(KdStarPg>=1)))&&(((((((DAGE>=1)||(GP3>=1))||(KdStarG>=1))||(KdStarPgStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||((Pip3>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1))))))))))] = FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t50, t56, t63, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
(forward)formula 0,0,8.63553,204520,1,0,83,1.0109e+06,156,57,1707,918732,146
FORMULA Angiogenesis-PT-05-CTLFireability-04 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
Applied a total of 0 rules in 2 ms. Remains 38 /38 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2021-05-11 14:03:19] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:03:19] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:03:19] [INFO ] Input system was already deterministic with 64 transitions.
[2021-05-11 14:03:19] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:03:19] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:03:19] [INFO ] Time to serialize gal into /tmp/CTLFireability17984489294694045358.gal : 1 ms
[2021-05-11 14:03:19] [INFO ] Time to serialize properties into /tmp/CTLFireability5548939250865149776.ctl : 1 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability17984489294694045358.gal, -t, CGAL, -ctl, /tmp/CTLFireability5548939250865149776.ctl, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability17984489294694045358.gal -t CGAL -ctl /tmp/CTLFireability5548939250865149776.ctl --gen-order FOLLOW
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,0.953527,35268,2,11096,5,168402,6,0,219,163574,0
Converting to forward existential form...Done !
original formula: EF(((AG(((((KdStarGStarPg<1)&&((Gab1<1)||(KdStar<1)))&&((((((((((((((KdStarGStarP3kP3>=1)||(PtP2>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3k>=1))||(DAGE>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarPgStarP2>=1))) * E((((((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgP3>=1))||((Pip2>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)) U ((((((((KdStarGStarP3kP3>=1)||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||(DAGE>=1))||(GP3>=1))||(GStarP3kP3>=1))||(KdStarG>=1))))) * AF(((((((KdStarGStarPg<1)&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))||(((((((((GStarP3kP3<1)||(KdStar<1))&&(KdStarGStarP3kP3<1))&&(PtP3<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarG<1))&&((Gab1<1)||(Pip3<1))))&&((((((((KdStarGStarP3kP3>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(GP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))))) * ((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3>=1))||((Akt>=1)&&(Pip3>=1)))||((GP3>=1)&&(KdStar>=1)))))
=> equivalent forward existential formula: [(((FwdU(Init,TRUE) * ((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3>=1))||((Akt>=1)&&(Pip3>=1)))||((GP3>=1)&&(KdStar>=1)))) * !(E(TRUE U !(((((KdStarGStarPg<1)&&((Gab1<1)||(KdStar<1)))&&((((((((((((((KdStarGStarP3kP3>=1)||(PtP2>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3k>=1))||(DAGE>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarPgStarP2>=1))) * E((((((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgP3>=1))||((Pip2>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)) U ((((((((KdStarGStarP3kP3>=1)||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||(DAGE>=1))||(GP3>=1))||(GStarP3kP3>=1))||(KdStarG>=1)))))))) * !(EG(!(((((((KdStarGStarPg<1)&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))||(((((((((GStarP3kP3<1)||(KdStar<1))&&(KdStarGStarP3kP3<1))&&(PtP3<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarG<1))&&((Gab1<1)||(Pip3<1))))&&((((((((KdStarGStarP3kP3>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(GP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t51, t57, t61, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
Detected timeout of ITS tools.
[2021-05-11 14:03:49] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:03:49] [INFO ] Applying decomposition
[2021-05-11 14:03:49] [INFO ] Flatten gal took : 4 ms
Converted graph to binary with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/convert-linux64, -i, /tmp/graph5795892336531665550.txt, -o, /tmp/graph5795892336531665550.bin, -w, /tmp/graph5795892336531665550.weights], workingDir=null]
Built communities with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/louvain-linux64, /tmp/graph5795892336531665550.bin, -l, -1, -v, -w, /tmp/graph5795892336531665550.weights, -q, 0, -e, 0.001], workingDir=null]
[2021-05-11 14:03:49] [INFO ] Decomposing Gal with order
[2021-05-11 14:03:49] [INFO ] Rewriting arrays to variables to allow decomposition.
[2021-05-11 14:03:49] [INFO ] Removed a total of 39 redundant transitions.
[2021-05-11 14:03:49] [INFO ] Flatten gal took : 65 ms
[2021-05-11 14:03:49] [INFO ] Fuse similar labels procedure discarded/fused a total of 6 labels/synchronizations in 3 ms.
[2021-05-11 14:03:49] [INFO ] Time to serialize gal into /tmp/CTLFireability13562220174217022498.gal : 2 ms
[2021-05-11 14:03:49] [INFO ] Time to serialize properties into /tmp/CTLFireability2744870517192873348.ctl : 1 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability13562220174217022498.gal, -t, CGAL, -ctl, /tmp/CTLFireability2744870517192873348.ctl], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability13562220174217022498.gal -t CGAL -ctl /tmp/CTLFireability2744870517192873348.ctl
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,4.39084,95156,2574,218,175598,3667,213,206135,41,22341,0
Converting to forward existential form...Done !
original formula: EF(((AG(((((i2.u9.KdStarGStarPg<1)&&((i0.u2.Gab1<1)||(i4.u8.KdStar<1)))&&((((((((((((((i4.u3.KdStarGStarP3kP3>=1)||(i6.u13.PtP2>=1))||((i1.u1.DAG>=1)&&(i1.u1.Enz>=1)))||(i6.u13.PtP3P2>=1))||((i4.u8.KdStarGStarP3>=1)&&(i5.u4.Pg>=1)))||((i4.u8.KdStarGStarP3>=1)&&(i4.u3.P3k>=1)))||(i2.u9.KdStarGStarPgStarP2>=1))||((i0.u2.GP3>=1)&&(i4.u8.KdStar>=1)))||(i1.u11.KdStarPgStarP2>=1))||(u6.KdStarGStarP3k>=1))||(i1.u1.DAGE>=1))||((i0.u0.Pip3>=1)&&(i6.u12.Pten>=1)))||(i1.u11.KdStarPg>=1))||(i1.u11.KdStarPgStarP2>=1))) * E((((((((u6.KdStarGStarP3kStarP2>=1)||(i4.u7.KdStarGStarP3kStarP3P2>=1))||(i5.u4.KdStarGStarPgP3>=1))||((i6.u13.Pip2>=1)&&(i6.u12.Pten>=1)))||((i4.u7.KdStarGStarP3kStarP3>=1)&&(i6.u13.Pip2>=1)))||((i0.u2.Gab1>=1)&&(i0.u0.Pip3>=1)))||(i1.u11.KdStarPgStarP2>=1)) U ((((((((i4.u3.KdStarGStarP3kP3>=1)||(i0.u0.AktP3>=1))||((i1.u11.KdStarPgStar>=1)&&(i6.u13.Pip2>=1)))||(i6.u12.PtP3>=1))||(i1.u1.DAGE>=1))||(i0.u2.GP3>=1))||(i4.u3.GStarP3kP3>=1))||(i2.u5.KdStarG>=1))))) * AF(((((((i2.u9.KdStarGStarPg<1)&&((i4.u8.KdStarGStarP3<1)||(i5.u4.Pg<1)))&&(i2.u9.KdStarGStarPgStarP2<1))&&((i5.u10.KdStarGStarPgStarP3<1)||(i6.u13.Pip2<1)))||(((((((((i4.u3.GStarP3kP3<1)||(i4.u8.KdStar<1))&&(i4.u3.KdStarGStarP3kP3<1))&&(i6.u12.PtP3<1))&&((i4.u3.GStarP3<1)||(i4.u8.KdStar<1)))&&(i5.u4.KdStarGStarPgP3<1))&&((i0.u0.Pip3<1)||(i6.u12.Pten<1)))&&(i2.u5.KdStarG<1))&&((i0.u2.Gab1<1)||(i0.u0.Pip3<1))))&&((((((((i4.u3.KdStarGStarP3kP3>=1)||((u6.KdStarGStarP3kStar>=1)&&(i6.u13.Pip2>=1)))||(i0.u2.GP3>=1))||(i2.u9.KdStarGStarPgStarP2>=1))||(i1.u11.KdStarPg>=1))||((i4.u3.GStarP3>=1)&&(i5.u4.Pg>=1)))||((i0.u2.Gab1>=1)&&(i0.u0.Pip3>=1)))||(i1.u11.KdStarPgStarP2>=1))))) * ((((u6.KdStarGStarP3kStarP2>=1)||(i4.u8.KdStarGStarP3>=1))||((i0.u0.Akt>=1)&&(i0.u0.Pip3>=1)))||((i0.u2.GP3>=1)&&(i4.u8.KdStar>=1)))))
=> equivalent forward existential formula: [(((FwdU(Init,TRUE) * ((((u6.KdStarGStarP3kStarP2>=1)||(i4.u8.KdStarGStarP3>=1))||((i0.u0.Akt>=1)&&(i0.u0.Pip3>=1)))||((i0.u2.GP3>=1)&&(i4.u8.KdStar>=1)))) * !(E(TRUE U !(((((i2.u9.KdStarGStarPg<1)&&((i0.u2.Gab1<1)||(i4.u8.KdStar<1)))&&((((((((((((((i4.u3.KdStarGStarP3kP3>=1)||(i6.u13.PtP2>=1))||((i1.u1.DAG>=1)&&(i1.u1.Enz>=1)))||(i6.u13.PtP3P2>=1))||((i4.u8.KdStarGStarP3>=1)&&(i5.u4.Pg>=1)))||((i4.u8.KdStarGStarP3>=1)&&(i4.u3.P3k>=1)))||(i2.u9.KdStarGStarPgStarP2>=1))||((i0.u2.GP3>=1)&&(i4.u8.KdStar>=1)))||(i1.u11.KdStarPgStarP2>=1))||(u6.KdStarGStarP3k>=1))||(i1.u1.DAGE>=1))||((i0.u0.Pip3>=1)&&(i6.u12.Pten>=1)))||(i1.u11.KdStarPg>=1))||(i1.u11.KdStarPgStarP2>=1))) * E((((((((u6.KdStarGStarP3kStarP2>=1)||(i4.u7.KdStarGStarP3kStarP3P2>=1))||(i5.u4.KdStarGStarPgP3>=1))||((i6.u13.Pip2>=1)&&(i6.u12.Pten>=1)))||((i4.u7.KdStarGStarP3kStarP3>=1)&&(i6.u13.Pip2>=1)))||((i0.u2.Gab1>=1)&&(i0.u0.Pip3>=1)))||(i1.u11.KdStarPgStarP2>=1)) U ((((((((i4.u3.KdStarGStarP3kP3>=1)||(i0.u0.AktP3>=1))||((i1.u11.KdStarPgStar>=1)&&(i6.u13.Pip2>=1)))||(i6.u12.PtP3>=1))||(i1.u1.DAGE>=1))||(i0.u2.GP3>=1))||(i4.u3.GStarP3kP3>=1))||(i2.u5.KdStarG>=1)))))))) * !(EG(!(((((((i2.u9.KdStarGStarPg<1)&&((i4.u8.KdStarGStarP3<1)||(i5.u4.Pg<1)))&&(i2.u9.KdStarGStarPgStarP2<1))&&((i5.u10.KdStarGStarPgStarP3<1)||(i6.u13.Pip2<1)))||(((((((((i4.u3.GStarP3kP3<1)||(i4.u8.KdStar<1))&&(i4.u3.KdStarGStarP3kP3<1))&&(i6.u12.PtP3<1))&&((i4.u3.GStarP3<1)||(i4.u8.KdStar<1)))&&(i5.u4.KdStarGStarPgP3<1))&&((i0.u0.Pip3<1)||(i6.u12.Pten<1)))&&(i2.u5.KdStarG<1))&&((i0.u2.Gab1<1)||(i0.u0.Pip3<1))))&&((((((((i4.u3.KdStarGStarP3kP3>=1)||((u6.KdStarGStarP3kStar>=1)&&(i6.u13.Pip2>=1)))||(i0.u2.GP3>=1))||(i2.u9.KdStarGStarPgStarP2>=1))||(i1.u11.KdStarPg>=1))||((i4.u3.GStarP3>=1)&&(i5.u4.Pg>=1)))||((i0.u2.Gab1>=1)&&(i0.u0.Pip3>=1)))||(i1.u11.KdStarPgStarP2>=1)))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions i0.u0.t24, i2.u5.t12, i4.u8.t61, i6.t51, i6.u13.t57, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/56/5/61
Detected timeout of ITS tools.
Partial Post-agglomeration rule applied 1 times.
Drop transitions removed 1 transitions
Iterating global reduction 0 with 1 rules applied. Total rules applied 1 place count 38 transition count 64
Applied a total of 1 rules in 4 ms. Remains 38 /38 variables (removed 0) and now considering 64/64 (removed 0) transitions.
[2021-05-11 14:04:19] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:04:19] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:04:19] [INFO ] Input system was already deterministic with 64 transitions.
[2021-05-11 14:04:19] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:04:19] [INFO ] Flatten gal took : 4 ms
[2021-05-11 14:04:19] [INFO ] Time to serialize gal into /tmp/CTLFireability14201114582229959311.gal : 1 ms
[2021-05-11 14:04:19] [INFO ] Time to serialize properties into /tmp/CTLFireability1132081404458676401.ctl : 0 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability14201114582229959311.gal, -t, CGAL, -ctl, /tmp/CTLFireability1132081404458676401.ctl, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability14201114582229959311.gal -t CGAL -ctl /tmp/CTLFireability1132081404458676401.ctl --gen-order FOLLOW
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,1.27737,41784,2,13121,5,195389,6,0,219,202984,0
Converting to forward existential form...Done !
original formula: AF(((((((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(PtP2<1))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgP3<1))&&(GStarPgP3<1))&&((KdStarGStarPg>=1)||(KdStarPgStarP2>=1)))&&(((((((((KdStarGStarP3k>=1)||(AktP3>=1))||(DAGE>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarPgStarP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||((DAG>=1)&&(Enz>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||((KdStar>=1)&&(Pg>=1))))&&((KdStarPgStar<1)||(Pip2<1))) * (((PtP2>=1) + EF(((((((((AktP3>=1)||(KdStarGStarP3kP3>=1))||(PtP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarG>=1)))) + ((GStarP3>=1)&&(KdStar>=1)))))
=> equivalent forward existential formula: [FwdG(Init,!(((((((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(PtP2<1))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgP3<1))&&(GStarPgP3<1))&&((KdStarGStarPg>=1)||(KdStarPgStarP2>=1)))&&(((((((((KdStarGStarP3k>=1)||(AktP3>=1))||(DAGE>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarPgStarP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||((DAG>=1)&&(Enz>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||((KdStar>=1)&&(Pg>=1))))&&((KdStarPgStar<1)||(Pip2<1))) * (((PtP2>=1) + E(TRUE U ((((((((AktP3>=1)||(KdStarGStarP3kP3>=1))||(PtP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarG>=1)))) + ((GStarP3>=1)&&(KdStar>=1))))))] = FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t51, t57, t63, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
Detected timeout of ITS tools.
[2021-05-11 14:04:49] [INFO ] Flatten gal took : 3 ms
[2021-05-11 14:04:49] [INFO ] Applying decomposition
[2021-05-11 14:04:49] [INFO ] Flatten gal took : 3 ms
Converted graph to binary with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/convert-linux64, -i, /tmp/graph15966868053175359958.txt, -o, /tmp/graph15966868053175359958.bin, -w, /tmp/graph15966868053175359958.weights], workingDir=null]
Built communities with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/louvain-linux64, /tmp/graph15966868053175359958.bin, -l, -1, -v, -w, /tmp/graph15966868053175359958.weights, -q, 0, -e, 0.001], workingDir=null]
[2021-05-11 14:04:49] [INFO ] Decomposing Gal with order
[2021-05-11 14:04:49] [INFO ] Rewriting arrays to variables to allow decomposition.
[2021-05-11 14:04:49] [INFO ] Removed a total of 35 redundant transitions.
[2021-05-11 14:04:49] [INFO ] Flatten gal took : 24 ms
[2021-05-11 14:04:49] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 17 ms.
[2021-05-11 14:04:49] [INFO ] Time to serialize gal into /tmp/CTLFireability11678305859362044280.gal : 2 ms
[2021-05-11 14:04:49] [INFO ] Time to serialize properties into /tmp/CTLFireability6241117804476976067.ctl : 0 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability11678305859362044280.gal, -t, CGAL, -ctl, /tmp/CTLFireability6241117804476976067.ctl], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability11678305859362044280.gal -t CGAL -ctl /tmp/CTLFireability6241117804476976067.ctl
No direction supplied, using forward translation only.
Parsed 1 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,1.95421,50632,2488,383,67191,5092,210,222994,52,62031,0
Converting to forward existential form...Done !
original formula: AF(((((((((((i2.u5.KdStarGStarP3kP3<1)&&(i5.u12.PtP3<1))&&(i5.u11.PtP2<1))&&(i2.u7.KdStarGStarP3kStarP3P2<1))&&(i1.u4.KdStarGStarPgP3<1))&&(i1.u4.GStarPgP3<1))&&((i3.u8.KdStarGStarPg>=1)||(u10.KdStarPgStarP2>=1)))&&(((((((((i0.u6.KdStarGStarP3k>=1)||(i5.u0.AktP3>=1))||(i3.u1.DAGE>=1))||(i2.u7.KdStarGStarP3kStarP3P2>=1))||(u10.KdStarPgStarP2>=1))||((i0.u2.KdStarGStar>=1)&&(i2.u5.P3k>=1)))||((i3.u1.DAG>=1)&&(i3.u1.Enz>=1)))||((i0.u2.KdStarGStar>=1)&&(i1.u4.Pg>=1)))||((i2.u5.KdStar>=1)&&(i1.u4.Pg>=1))))&&((u10.KdStarPgStar<1)||(i5.u11.Pip2<1))) * (((i5.u11.PtP2>=1) + EF(((((((((i5.u0.AktP3>=1)||(i2.u5.KdStarGStarP3kP3>=1))||(i5.u11.PtP2>=1))||((i0.u2.KdStarGStar>=1)&&(i2.u5.P3k>=1)))||(i3.u1.DAGE>=1))||(i3.u8.KdStarGStarPgStarP2>=1))||((i0.u3.Gab1>=1)&&(i5.u0.Pip3>=1)))||(i0.u2.KdStarG>=1)))) + ((i2.u5.GStarP3>=1)&&(i2.u5.KdStar>=1)))))
=> equivalent forward existential formula: [FwdG(Init,!(((((((((((i2.u5.KdStarGStarP3kP3<1)&&(i5.u12.PtP3<1))&&(i5.u11.PtP2<1))&&(i2.u7.KdStarGStarP3kStarP3P2<1))&&(i1.u4.KdStarGStarPgP3<1))&&(i1.u4.GStarPgP3<1))&&((i3.u8.KdStarGStarPg>=1)||(u10.KdStarPgStarP2>=1)))&&(((((((((i0.u6.KdStarGStarP3k>=1)||(i5.u0.AktP3>=1))||(i3.u1.DAGE>=1))||(i2.u7.KdStarGStarP3kStarP3P2>=1))||(u10.KdStarPgStarP2>=1))||((i0.u2.KdStarGStar>=1)&&(i2.u5.P3k>=1)))||((i3.u1.DAG>=1)&&(i3.u1.Enz>=1)))||((i0.u2.KdStarGStar>=1)&&(i1.u4.Pg>=1)))||((i2.u5.KdStar>=1)&&(i1.u4.Pg>=1))))&&((u10.KdStarPgStar<1)||(i5.u11.Pip2<1))) * (((i5.u11.PtP2>=1) + E(TRUE U ((((((((i5.u0.AktP3>=1)||(i2.u5.KdStarGStarP3kP3>=1))||(i5.u11.PtP2>=1))||((i0.u2.KdStarGStar>=1)&&(i2.u5.P3k>=1)))||(i3.u1.DAGE>=1))||(i3.u8.KdStarGStarPgStarP2>=1))||((i0.u3.Gab1>=1)&&(i5.u0.Pip3>=1)))||(i0.u2.KdStarG>=1)))) + ((i2.u5.GStarP3>=1)&&(i2.u5.KdStar>=1))))))] = FALSE
Reverse transition relation is NOT exact ! Due to transitions t63, i0.u2.t12, i5.t51, i5.u0.t24, i5.u11.t57, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/57/5/62
Fast SCC detection found an SCC at level 1
Fast SCC detection found a local SCC at level 2
Fast SCC detection found an SCC at level 3
Fast SCC detection found an SCC at level 4
Fast SCC detection found an SCC at level 5
Detected timeout of ITS tools.
[2021-05-11 14:05:19] [INFO ] Flatten gal took : 6 ms
[2021-05-11 14:05:19] [INFO ] Flatten gal took : 5 ms
[2021-05-11 14:05:19] [INFO ] Applying decomposition
[2021-05-11 14:05:19] [INFO ] Flatten gal took : 5 ms
Converted graph to binary with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/convert-linux64, -i, /tmp/graph8134712060245812566.txt, -o, /tmp/graph8134712060245812566.bin, -w, /tmp/graph8134712060245812566.weights], workingDir=null]
Built communities with : CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.louvain.binaries_1.0.0.202104292328/bin/louvain-linux64, /tmp/graph8134712060245812566.bin, -l, -1, -v, -w, /tmp/graph8134712060245812566.weights, -q, 0, -e, 0.001], workingDir=null]
[2021-05-11 14:05:19] [INFO ] Decomposing Gal with order
[2021-05-11 14:05:19] [INFO ] Rewriting arrays to variables to allow decomposition.
[2021-05-11 14:05:19] [INFO ] Removed a total of 39 redundant transitions.
[2021-05-11 14:05:19] [INFO ] Flatten gal took : 40 ms
[2021-05-11 14:05:19] [INFO ] Fuse similar labels procedure discarded/fused a total of 4 labels/synchronizations in 1 ms.
[2021-05-11 14:05:19] [INFO ] Time to serialize gal into /tmp/CTLFireability4223032353383367267.gal : 2 ms
[2021-05-11 14:05:19] [INFO ] Time to serialize properties into /tmp/CTLFireability4610049497393254548.ctl : 5 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability4223032353383367267.gal, -t, CGAL, -ctl, /tmp/CTLFireability4610049497393254548.ctl], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability4223032353383367267.gal -t CGAL -ctl /tmp/CTLFireability4610049497393254548.ctl
No direction supplied, using forward translation only.
Parsed 14 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,1.44652,39756,1669,219,45729,2808,212,205259,41,15603,0
Converting to forward existential form...Done !
original formula: E(((((AX(!(A(((i3.u8.KdStarGStarPgStarP3P2>=1)||(i1.u5.KdStarGStarP3kStarP2>=1)) U (((((i4.u12.PtP3>=1)||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1)))||(i2.u7.KdStarGStarPgStarP2>=1))||(i0.u4.KdStarGStarP3>=1))&&(((i0.u2.KdStarGStarP3kP3>=1)||(i4.u13.PtP3P2>=1))||((i0.u4.KdStar>=1)&&(i3.u11.Pg>=1))))))) + (i2.u0.DAGE>=1)) + (i3.u11.KdStarGStarPgP3>=1)) + ((i1.u1.GP3>=1)&&(i0.u4.KdStar>=1))) + ((i4.u10.Pip3>=1)&&(i4.u12.Pten>=1))) U !(EX((!(AX((i3.u11.KdStarGStarPgP3>=1))) * (!(AG((((i1.u5.KdStarGStarP3kStarP2>=1)||(i4.u12.PtP3>=1))||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1))))) + !(AX((((((i2.u7.KdStarGStarPg>=1)||(i1.u1.GP3>=1))||((i0.u4.KdStarGStarP3>=1)&&(i0.u2.P3k>=1)))||(i3.u8.KdStarGStarPgStarP3P2>=1))||(u9.KdStarPgStarP2>=1)))))))))
=> equivalent forward existential formula: [(FwdU(Init,((((!(EX(!(!(!((E(!((((((i4.u12.PtP3>=1)||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1)))||(i2.u7.KdStarGStarPgStarP2>=1))||(i0.u4.KdStarGStarP3>=1))&&(((i0.u2.KdStarGStarP3kP3>=1)||(i4.u13.PtP3P2>=1))||((i0.u4.KdStar>=1)&&(i3.u11.Pg>=1))))) U (!(((i3.u8.KdStarGStarPgStarP3P2>=1)||(i1.u5.KdStarGStarP3kStarP2>=1))) * !((((((i4.u12.PtP3>=1)||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1)))||(i2.u7.KdStarGStarPgStarP2>=1))||(i0.u4.KdStarGStarP3>=1))&&(((i0.u2.KdStarGStarP3kP3>=1)||(i4.u13.PtP3P2>=1))||((i0.u4.KdStar>=1)&&(i3.u11.Pg>=1))))))) + EG(!((((((i4.u12.PtP3>=1)||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1)))||(i2.u7.KdStarGStarPgStarP2>=1))||(i0.u4.KdStarGStarP3>=1))&&(((i0.u2.KdStarGStarP3kP3>=1)||(i4.u13.PtP3P2>=1))||((i0.u4.KdStar>=1)&&(i3.u11.Pg>=1)))))))))))) + (i2.u0.DAGE>=1)) + (i3.u11.KdStarGStarPgP3>=1)) + ((i1.u1.GP3>=1)&&(i0.u4.KdStar>=1))) + ((i4.u10.Pip3>=1)&&(i4.u12.Pten>=1)))) * !(EX((!(!(EX(!((i3.u11.KdStarGStarPgP3>=1))))) * (!(!(E(TRUE U !((((i1.u5.KdStarGStarP3kStarP2>=1)||(i4.u12.PtP3>=1))||((i4.u10.Akt>=1)&&(i4.u10.Pip3>=1))))))) + !(!(EX(!((((((i2.u7.KdStarGStarPg>=1)||(i1.u1.GP3>=1))||((i0.u4.KdStarGStarP3>=1)&&(i0.u2.P3k>=1)))||(i3.u8.KdStarGStarPgStarP3P2>=1))||(u9.KdStarPgStarP2>=1)))))))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions i0.u4.t61, i1.u3.t12, i4.t51, i4.u10.t24, i4.u13.t57, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/57/5/62
ITS-tools command line returned an error code 139
[2021-05-11 14:14:56] [INFO ] Flatten gal took : 6 ms
[2021-05-11 14:14:56] [INFO ] Time to serialize gal into /tmp/CTLFireability6266312663724803433.gal : 1 ms
[2021-05-11 14:14:56] [INFO ] Time to serialize properties into /tmp/CTLFireability14118927611937519327.ctl : 3 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability6266312663724803433.gal, -t, CGAL, -ctl, /tmp/CTLFireability14118927611937519327.ctl, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability6266312663724803433.gal -t CGAL -ctl /tmp/CTLFireability14118927611937519327.ctl --gen-order FOLLOW
No direction supplied, using forward translation only.
Parsed 14 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,0.987822,35428,2,11096,5,168402,6,0,219,163574,0
Converting to forward existential form...Done !
original formula: E(((((AX(!(A(((KdStarGStarPgStarP3P2>=1)||(KdStarGStarP3kStarP2>=1)) U (((((PtP3>=1)||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3>=1))&&(((KdStarGStarP3kP3>=1)||(PtP3P2>=1))||((KdStar>=1)&&(Pg>=1))))))) + (DAGE>=1)) + (KdStarGStarPgP3>=1)) + ((GP3>=1)&&(KdStar>=1))) + ((Pip3>=1)&&(Pten>=1))) U !(EX((!(AX((KdStarGStarPgP3>=1))) * (!(AG((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||((Akt>=1)&&(Pip3>=1))))) + !(AX((((((KdStarGStarPg>=1)||(GP3>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPgStarP2>=1)))))))))
=> equivalent forward existential formula: [(FwdU(Init,((((!(EX(!(!(!((E(!((((((PtP3>=1)||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3>=1))&&(((KdStarGStarP3kP3>=1)||(PtP3P2>=1))||((KdStar>=1)&&(Pg>=1))))) U (!(((KdStarGStarPgStarP3P2>=1)||(KdStarGStarP3kStarP2>=1))) * !((((((PtP3>=1)||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3>=1))&&(((KdStarGStarP3kP3>=1)||(PtP3P2>=1))||((KdStar>=1)&&(Pg>=1))))))) + EG(!((((((PtP3>=1)||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3>=1))&&(((KdStarGStarP3kP3>=1)||(PtP3P2>=1))||((KdStar>=1)&&(Pg>=1)))))))))))) + (DAGE>=1)) + (KdStarGStarPgP3>=1)) + ((GP3>=1)&&(KdStar>=1))) + ((Pip3>=1)&&(Pten>=1)))) * !(EX((!(!(EX(!((KdStarGStarPgP3>=1))))) * (!(!(E(TRUE U !((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||((Akt>=1)&&(Pip3>=1))))))) + !(!(EX(!((((((KdStarGStarPg>=1)||(GP3>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPgStarP2>=1)))))))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t51, t57, t61, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
(forward)formula 0,1,282.568,2565436,1,0,367,1.38454e+07,12,201,763,1.85565e+07,81
FORMULA Angiogenesis-PT-05-CTLFireability-00 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: ((EF(((((KdStarGStarPgP3>=1)||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1))||(KdStarGStarP3>=1))) * AX(AG(EF(((((((((((KdStarGStarP3kP3<1)&&((Pip2<1)||(Pten<1)))&&((KdStarGStarP3<1)||(Pg<1)))&&(GStarP3kP3<1))&&((KdStarGStar<1)||(Pg<1)))&&(KdStarG<1))&&(KdStarPg<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))&&(KdStarPgStarP2<1))&&((GStarP3<1)||(P3k<1))))))) * EX(AX(((((A(((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(GP3<1))&&(KdStarGStarPgStarP2<1))&&((KdStarGStar<1)||(Pg<1)))&&((GStarP3<1)||(Pg<1))) U ((((KdStarGStarP3kStarP2<1)&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarPg<1))) + ((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kP3<1))&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&(KdStarG<1))) + AG((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((GStarP3>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pip3>=1)))||((Akt>=1)&&(Pip3>=1)))||((KdStarGStarP3>=1)&&(P3k>=1))))) + (GStarPgP3>=1)) + ((((((KdStarGStarP3kStar<1)||(Pip2<1))&&((DAG<1)||(Enz<1)))&&(KdStarGStarPgStarP2<1))&&(KdStarG<1))&&((GStarP3<1)||(P3k<1)))))))
=> equivalent forward existential formula: (([(Init * !(E(TRUE U ((((KdStarGStarPgP3>=1)||(KdStarGStarPgStarP3P2>=1))||(KdStarG>=1))||(KdStarGStarP3>=1)))))] = FALSE * [(FwdU(EY(Init),TRUE) * !(E(TRUE U ((((((((((KdStarGStarP3kP3<1)&&((Pip2<1)||(Pten<1)))&&((KdStarGStarP3<1)||(Pg<1)))&&(GStarP3kP3<1))&&((KdStarGStar<1)||(Pg<1)))&&(KdStarG<1))&&(KdStarPg<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))&&(KdStarPgStarP2<1))&&((GStarP3<1)||(P3k<1))))))] = FALSE) * [(Init * !(EX(!(EX(!(((((!((E(!(((((KdStarGStarP3kStarP2<1)&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarPg<1))) U (!(((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(GP3<1))&&(KdStarGStarPgStarP2<1))&&((KdStarGStar<1)||(Pg<1)))&&((GStarP3<1)||(Pg<1)))) * !(((((KdStarGStarP3kStarP2<1)&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarPg<1))))) + EG(!(((((KdStarGStarP3kStarP2<1)&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarPg<1)))))) + ((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kP3<1))&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&(KdStarG<1))) + !(E(TRUE U !((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((GStarP3>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pip3>=1)))||((Akt>=1)&&(Pip3>=1)))||((KdStarGStarP3>=1)&&(P3k>=1))))))) + (GStarPgP3>=1)) + ((((((KdStarGStarP3kStar<1)||(Pip2<1))&&((DAG<1)||(Enz<1)))&&(KdStarGStarPgStarP2<1))&&(KdStarG<1))&&((GStarP3<1)||(P3k<1))))))))))] = FALSE)
(forward)formula 1,0,303.616,2565436,1,0,367,1.38454e+07,37,201,1063,1.85565e+07,178
FORMULA Angiogenesis-PT-05-CTLFireability-01 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: (EG(EX(EF((((((KdStarGStar>=1)&&(P3k>=1))||(KdStarGStarP3kStarP3P2>=1))||((GStarP3>=1)&&(Pg>=1)))||(KdStarGStarP3>=1))))) * (EG((((((AktP3>=1)||(PtP3>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||((GStarP3>=1)&&(P3k>=1)))) + EF(AX(AG((((((((((AktP3<1)&&(KdStarGStarP3kStarP2<1))&&(PtP3<1))&&((KdStarGStar<1)||(P3k<1)))&&(KdStarGStarP3kStarP3P2<1))&&(GP3<1))&&(GStarP3kP3<1))&&(KdStarGStarPgStarP2<1))&&(KdStarPgStarP2<1)))))))
=> equivalent forward existential formula: ([FwdG((Init * EG(EX(E(TRUE U (((((KdStarGStar>=1)&&(P3k>=1))||(KdStarGStarP3kStarP3P2>=1))||((GStarP3>=1)&&(Pg>=1)))||(KdStarGStarP3>=1)))))),(((((AktP3>=1)||(PtP3>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||((GStarP3>=1)&&(P3k>=1))))] != FALSE + [(FwdU((Init * EG(EX(E(TRUE U (((((KdStarGStar>=1)&&(P3k>=1))||(KdStarGStarP3kStarP3P2>=1))||((GStarP3>=1)&&(Pg>=1)))||(KdStarGStarP3>=1)))))),TRUE) * !(EX(!(!(E(TRUE U !((((((((((AktP3<1)&&(KdStarGStarP3kStarP2<1))&&(PtP3<1))&&((KdStarGStar<1)||(P3k<1)))&&(KdStarGStarP3kStarP3P2<1))&&(GP3<1))&&(GStarP3kP3<1))&&(KdStarGStarPgStarP2<1))&&(KdStarPgStarP2<1)))))))))] != FALSE)
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
(forward)formula 2,1,306.625,2565436,1,0,367,1.38454e+07,54,201,1126,1.85565e+07,205
FORMULA Angiogenesis-PT-05-CTLFireability-02 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: (E((((((PtP2>=1)||(KdStarGStarPgStarP2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||((Gab1>=1)&&(KdStar>=1)))&&((((((PtP3>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPg>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(P3k>=1)))) U A(!(EF((((((((((GStarP3kP3>=1)&&(KdStar>=1))||(PtP3>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarGP3>=1))||(KdStarGStarP3>=1)))) U (EF((((KdStarGStarP3kStarP3>=1)&&(Pip2>=1))&&(((PtP3>=1)||(KdStarGStarPgP3>=1))||(KdStarPgStarP2>=1)))) + A((((((((((DAGE>=1)||(KdStarGStarPg>=1))||(PtP3P2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarGStarP3>=1))&&(((((((KdStarGStarP3kP3>=1)||(DAGE>=1))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||(GStarP3kP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))) U AX(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1))))))) * AX((((((((((((KdStarGStarP3kP3>=1)||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((GStarP3>=1)&&(KdStar>=1)))||(PtP3P2>=1))||((DAG>=1)&&(Enz>=1)))||((Pip2>=1)&&(Pten>=1)))||((Gab1>=1)&&(KdStar>=1)))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(((GStarPgP3<1)||(KdStar<1))&&(KdStarG<1)))))
=> equivalent forward existential formula: ([(Init * !(E((((((PtP2>=1)||(KdStarGStarPgStarP2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||((Gab1>=1)&&(KdStar>=1)))&&((((((PtP3>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPg>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(P3k>=1)))) U !((E(!((E(TRUE U (((KdStarGStarP3kStarP3>=1)&&(Pip2>=1))&&(((PtP3>=1)||(KdStarGStarPgP3>=1))||(KdStarPgStarP2>=1)))) + !((E(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))) U (!((((((((((DAGE>=1)||(KdStarGStarPg>=1))||(PtP3P2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarGStarP3>=1))&&(((((((KdStarGStarP3kP3>=1)||(DAGE>=1))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||(GStarP3kP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1)))) * !(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))))) + EG(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1))))))))))) U (!(!(E(TRUE U (((((((((GStarP3kP3>=1)&&(KdStar>=1))||(PtP3>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarGP3>=1))||(KdStarGStarP3>=1))))) * !((E(TRUE U (((KdStarGStarP3kStarP3>=1)&&(Pip2>=1))&&(((PtP3>=1)||(KdStarGStarPgP3>=1))||(KdStarPgStarP2>=1)))) + !((E(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))) U (!((((((((((DAGE>=1)||(KdStarGStarPg>=1))||(PtP3P2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarGStarP3>=1))&&(((((((KdStarGStarP3kP3>=1)||(DAGE>=1))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||(GStarP3kP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1)))) * !(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))))) + EG(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1))))))))))))) + EG(!((E(TRUE U (((KdStarGStarP3kStarP3>=1)&&(Pip2>=1))&&(((PtP3>=1)||(KdStarGStarPgP3>=1))||(KdStarPgStarP2>=1)))) + !((E(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))) U (!((((((((((DAGE>=1)||(KdStarGStarPg>=1))||(PtP3P2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarGStarP3>=1))&&(((((((KdStarGStarP3kP3>=1)||(DAGE>=1))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||(GStarP3kP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1)))) * !(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))))) + EG(!(!(EX(!(((KdStarGStarP3k>=1)||(KdStarGStarPgP3>=1)))))))))))))))))] = FALSE * [(EY(Init) * !((((((((((((KdStarGStarP3kP3>=1)||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((GStarP3>=1)&&(KdStar>=1)))||(PtP3P2>=1))||((DAG>=1)&&(Enz>=1)))||((Pip2>=1)&&(Pten>=1)))||((Gab1>=1)&&(KdStar>=1)))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(((GStarPgP3<1)||(KdStar<1))&&(KdStarG<1)))))] = FALSE)
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
(forward)formula 3,1,317.657,2565436,1,0,367,1.38454e+07,72,201,1204,1.85565e+07,306
FORMULA Angiogenesis-PT-05-CTLFireability-05 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: (A((KdStarGStarPg<1) U EG((E(((((((KdStarGStarP3k<1)&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&(KdStarGStarPgStarP3P2<1))&&((Pip3<1)||(PtP2<1)))&&(KdStarPgStarP2<1)) U AG(((((((((((GStarP3kP3>=1)&&(KdStar>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarP3kStarP3P2>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPg>=1))||(KdStarPgStarP2>=1)))) * A((KdStarGStarP3kP3<1) U E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1))))))) * E(A(AX((((((((((KdStarGStarP3k>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(KdStarGStarPgP3>=1))||(PtP3P2>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(PtP2>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))&&(((((((((((((((AktP3>=1)||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarG>=1))||((GStarP3>=1)&&(Pg>=1)))||(KdStarGP3>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(GStarPgP3>=1))||((Gab1>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pg>=1))))) U !(AF(((((((GStarP3>=1)&&(KdStar>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))) U ((((KdStarGStar>=1)&&(P3k>=1))||((Pip3>=1)&&(Pten>=1)))||((Gab1>=1)&&(Pip3>=1)))))
=> equivalent forward existential formula: [(FwdU((Init * !((E(!(EG((E(((((((KdStarGStarP3k<1)&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&(KdStarGStarPgStarP3P2<1))&&((Pip3<1)||(PtP2<1)))&&(KdStarPgStarP2<1)) U !(E(TRUE U !(((((((((((GStarP3kP3>=1)&&(KdStar>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarP3kStarP3P2>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPg>=1))||(KdStarPgStarP2>=1)))))) * !((E(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))) U (!((KdStarGStarP3kP3<1)) * !(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))) + EG(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))))))) U (!((KdStarGStarPg<1)) * !(EG((E(((((((KdStarGStarP3k<1)&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&(KdStarGStarPgStarP3P2<1))&&((Pip3<1)||(PtP2<1)))&&(KdStarPgStarP2<1)) U !(E(TRUE U !(((((((((((GStarP3kP3>=1)&&(KdStar>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarP3kStarP3P2>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPg>=1))||(KdStarPgStarP2>=1)))))) * !((E(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))) U (!((KdStarGStarP3kP3<1)) * !(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))) + EG(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))))))))) + EG(!(EG((E(((((((KdStarGStarP3k<1)&&(KdStarGStarP3kStarP3P2<1))&&((GP3<1)||(KdStar<1)))&&(KdStarGStarPgStarP3P2<1))&&((Pip3<1)||(PtP2<1)))&&(KdStarPgStarP2<1)) U !(E(TRUE U !(((((((((((GStarP3kP3>=1)&&(KdStar>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarP3kStarP3P2>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP3P2>=1))||(KdStarPg>=1))||(KdStarPgStarP2>=1)))))) * !((E(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))) U (!((KdStarGStarP3kP3<1)) * !(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))) + EG(!(E(((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(DAGE>=1))||((KdStarGStar>=1)&&(Pip3>=1)))||(KdStarGStarPg>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))||(KdStarG>=1)) U ((((((KdStarGStarP3kStar>=1)&&(Pip2>=1))||(PtP2>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3>=1)))))))))))))),!((E(!(!(!(EG(!(((((((GStarP3>=1)&&(KdStar>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))))) U (!(!(EX(!((((((((((KdStarGStarP3k>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(KdStarGStarPgP3>=1))||(PtP3P2>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(PtP2>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))&&(((((((((((((((AktP3>=1)||(KdStarGStarP3kStarP2>=1))||(PtP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarG>=1))||((GStarP3>=1)&&(Pg>=1)))||(KdStarGP3>=1))||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(GStarPgP3>=1))||((Gab1>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pg>=1)))))))) * !(!(!(EG(!(((((((GStarP3>=1)&&(KdStar>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))))))) + EG(!(!(!(EG(!(((((((GStarP3>=1)&&(KdStar>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))))))))) * ((((KdStarGStar>=1)&&(P3k>=1))||((Pip3>=1)&&(Pten>=1)))||((Gab1>=1)&&(Pip3>=1))))] != FALSE
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
(forward)formula 4,0,396.364,2834420,1,0,590,1.54734e+07,52,351,1023,1.91705e+07,693
FORMULA Angiogenesis-PT-05-CTLFireability-06 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: EG(!(EX(EF(EG((KdStarGStarPgStarP3P2>=1))))))
=> equivalent forward existential formula: [FwdG(Init,!(EX(E(TRUE U EG((KdStarGStarPgStarP3P2>=1))))))] != FALSE
(forward)formula 5,0,399.338,2834420,1,0,606,1.54734e+07,62,364,1025,1.91705e+07,725
FORMULA Angiogenesis-PT-05-CTLFireability-07 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: EF(((AG(((((KdStarGStarPg<1)&&((Gab1<1)||(KdStar<1)))&&((((((((((((((KdStarGStarP3kP3>=1)||(PtP2>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3k>=1))||(DAGE>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarPgStarP2>=1))) * E((((((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgP3>=1))||((Pip2>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)) U ((((((((KdStarGStarP3kP3>=1)||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||(DAGE>=1))||(GP3>=1))||(GStarP3kP3>=1))||(KdStarG>=1))))) * AF(((((((KdStarGStarPg<1)&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))||(((((((((GStarP3kP3<1)||(KdStar<1))&&(KdStarGStarP3kP3<1))&&(PtP3<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarG<1))&&((Gab1<1)||(Pip3<1))))&&((((((((KdStarGStarP3kP3>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(GP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))))) * ((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3>=1))||((Akt>=1)&&(Pip3>=1)))||((GP3>=1)&&(KdStar>=1)))))
=> equivalent forward existential formula: [(((FwdU(Init,TRUE) * ((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3>=1))||((Akt>=1)&&(Pip3>=1)))||((GP3>=1)&&(KdStar>=1)))) * !(E(TRUE U !(((((KdStarGStarPg<1)&&((Gab1<1)||(KdStar<1)))&&((((((((((((((KdStarGStarP3kP3>=1)||(PtP2>=1))||((DAG>=1)&&(Enz>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((GP3>=1)&&(KdStar>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3k>=1))||(DAGE>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarPg>=1))||(KdStarPgStarP2>=1))) * E((((((((KdStarGStarP3kStarP2>=1)||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgP3>=1))||((Pip2>=1)&&(Pten>=1)))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)) U ((((((((KdStarGStarP3kP3>=1)||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||(DAGE>=1))||(GP3>=1))||(GStarP3kP3>=1))||(KdStarG>=1)))))))) * !(EG(!(((((((KdStarGStarPg<1)&&((KdStarGStarP3<1)||(Pg<1)))&&(KdStarGStarPgStarP2<1))&&((KdStarGStarPgStarP3<1)||(Pip2<1)))||(((((((((GStarP3kP3<1)||(KdStar<1))&&(KdStarGStarP3kP3<1))&&(PtP3<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarPgP3<1))&&((Pip3<1)||(Pten<1)))&&(KdStarG<1))&&((Gab1<1)||(Pip3<1))))&&((((((((KdStarGStarP3kP3>=1)||((KdStarGStarP3kStar>=1)&&(Pip2>=1)))||(GP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarPg>=1))||((GStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)))))))] != FALSE
(forward)formula 6,0,626.988,4949112,1,0,1021,3.15212e+07,22,572,945,3.07933e+07,60
FORMULA Angiogenesis-PT-05-CTLFireability-08 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: AF(!(E(((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1)) U !(EF(AX((KdStarGStarP3kStarP2>=1)))))))
=> equivalent forward existential formula: [FwdG(Init,!(!(E(((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1)) U !(E(TRUE U !(EX(!((KdStarGStarP3kStarP2>=1))))))))))] = FALSE
(forward)formula 7,1,633.354,4949112,1,0,1021,3.15212e+07,33,572,953,3.07933e+07,98
FORMULA Angiogenesis-PT-05-CTLFireability-09 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: EX(AG(EF((((((AktP3>=1)||(KdStarPg>=1)) + AF((KdStarGStarPgStarP3P2>=1))) + ((KdStarGStarP3>=1)&&(P3k>=1))) + ((GStarP3>=1)&&(P3k>=1))))))
=> equivalent forward existential formula: [(EY(Init) * !(E(TRUE U !(E(TRUE U (((((AktP3>=1)||(KdStarPg>=1)) + !(EG(!((KdStarGStarPgStarP3P2>=1))))) + ((KdStarGStarP3>=1)&&(P3k>=1))) + ((GStarP3>=1)&&(P3k>=1))))))))] != FALSE
(forward)formula 8,0,674.641,4949112,1,0,1021,3.15212e+07,42,572,1028,3.07933e+07,619
FORMULA Angiogenesis-PT-05-CTLFireability-10 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: ((A(((((((((((((PtP2>=1)||((Akt>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(AktP3>=1))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(GStarP3kP3>=1))||((Gab1>=1)&&(Pip3>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1))) U ((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))) + !(EF(EG((((KdStarGStar>=1)&&(Pip3>=1))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1))))))) + (!(EF(((((((((((((((((KdStarGStarP3k<1)&&(KdStarGStarP3kP3<1))&&((KdStarGStar<1)||(P3k<1)))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPg<1))&&(GP3<1))&&((KdStarGStarP3<1)||(P3k<1)))&&((Gab1<1)||(KdStar<1)))&&(KdStarG<1))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPg>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgP3>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1))))) * !(AX(((((Gab1>=1)&&(Pip3>=1))||(KdStarPgStarP2>=1)) + AX((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarP3kP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))))))))
=> equivalent forward existential formula: ([(FwdU((Init * !((!((E(!(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))) U (!(((((((((((((PtP2>=1)||((Akt>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(AktP3>=1))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(GStarP3kP3>=1))||((Gab1>=1)&&(Pip3>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))) * !(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))))) + EG(!(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1)))))) + !(E(TRUE U EG((((KdStarGStar>=1)&&(Pip3>=1))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1))))))))),TRUE) * ((((((((((((((((KdStarGStarP3k<1)&&(KdStarGStarP3kP3<1))&&((KdStarGStar<1)||(P3k<1)))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPg<1))&&(GP3<1))&&((KdStarGStarP3<1)||(P3k<1)))&&((Gab1<1)||(KdStar<1)))&&(KdStarG<1))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPg>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgP3>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1))))] = FALSE * [((Init * !((!((E(!(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))) U (!(((((((((((((PtP2>=1)||((Akt>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(AktP3>=1))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(GStarP3kP3>=1))||((Gab1>=1)&&(Pip3>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))) * !(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1))))) + EG(!(((((KdStarGStarP3kStarP2>=1)||(PtP3>=1))||(KdStarGStarPgStarP3P2>=1))||(KdStarGP3>=1)))))) + !(E(TRUE U EG((((KdStarGStar>=1)&&(Pip3>=1))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1))))))))) * !(EX(!(((((Gab1>=1)&&(Pip3>=1))||(KdStarPgStarP2>=1)) + !(EX(!((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarP3kP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))))))))))] = FALSE)
(forward)formula 9,0,790.319,5275732,1,0,1083,3.44274e+07,60,576,1077,3.23449e+07,1189
FORMULA Angiogenesis-PT-05-CTLFireability-11 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: A((((((AktP3<1)&&(KdStarG<1)) * EF(((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(DAGE<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgStarP2<1))&&(KdStarGP3<1))&&(KdStarPgStarP2<1)))) * A((((DAGE>=1)||(KdStarGStarP3kStarP3P2>=1))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||((GStarP3>=1)&&(KdStar>=1)))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarGStarPgStarP3P2>=1))) U ((((((((((KdStarGStarP3kP3>=1)||(KdStarGStarPgP3>=1))||(GP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarG>=1))||(KdStarGP3>=1))||(KdStarGStarP3>=1))||((DAG>=1)&&(Enz>=1))))) * ((GStarP3<1)||(P3k<1))) U (((AF(EX(((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))) + AF((AG((((((DAGE>=1)||(KdStarGStarPg>=1))||(KdStarPg>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))) + (((KdStarGStarP3kStarP2<1)&&((Akt<1)||(Pip3<1))) * AG(((((((KdStarGStarP3k>=1)||(KdStarGStarP3kStarP2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(Pg>=1)))))))) + EG((((((((((((((((KdStarGStarP3k<1)&&((KdStarGStarPgStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP3P2<1))&&((Akt<1)||(Pip3<1)))&&(KdStarGStarPgP3<1))&&((GP3<1)||(KdStar<1)))&&(GStarPgP3<1))&&((Gab1<1)||(Pip3<1)))&&(KdStarPgStarP2<1))||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStar>=1)&&(Pg>=1)))||((GStarP3>=1)&&(P3k>=1))))) + (((((((((AktP3>=1)||(PtP3>=1))||(DAGE>=1))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarG>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((GStarP3>=1)&&(Pg>=1))) * ((((((((((AG(((GStarP3>=1)&&(P3k>=1))) + (KdStarGStarP3kP3>=1)) + (KdStarGStarP3kStarP2>=1)) + (GP3>=1)) + (KdStarGStarPgStarP3P2>=1)) + (KdStarGStarPg>=1)) + (KdStarGStarPgStarP2>=1)) + ((KdStarGStar>=1)&&(Pip3>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + ((((((((((KdStarGStarP3k>=1)||(DAGE>=1))||(PtP2>=1))||(KdStarGStarPgP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1)))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||(PtP3P2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1))))))))
=> equivalent forward existential formula: [((Init * !(EG(!((((!(EG(!(EX(((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))))) + !(EG(!((!(E(TRUE U !((((((DAGE>=1)||(KdStarGStarPg>=1))||(KdStarPg>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))) + (((KdStarGStarP3kStarP2<1)&&((Akt<1)||(Pip3<1))) * !(E(TRUE U !(((((((KdStarGStarP3k>=1)||(KdStarGStarP3kStarP2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(Pg>=1)))))))))))) + EG((((((((((((((((KdStarGStarP3k<1)&&((KdStarGStarPgStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP3P2<1))&&((Akt<1)||(Pip3<1)))&&(KdStarGStarPgP3<1))&&((GP3<1)||(KdStar<1)))&&(GStarPgP3<1))&&((Gab1<1)||(Pip3<1)))&&(KdStarPgStarP2<1))||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStar>=1)&&(Pg>=1)))||((GStarP3>=1)&&(P3k>=1))))) + (((((((((AktP3>=1)||(PtP3>=1))||(DAGE>=1))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarG>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((GStarP3>=1)&&(Pg>=1))) * ((((((((((!(E(TRUE U !(((GStarP3>=1)&&(P3k>=1))))) + (KdStarGStarP3kP3>=1)) + (KdStarGStarP3kStarP2>=1)) + (GP3>=1)) + (KdStarGStarPgStarP3P2>=1)) + (KdStarGStarPg>=1)) + (KdStarGStarPgStarP2>=1)) + ((KdStarGStar>=1)&&(Pip3>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + ((((((((((KdStarGStarP3k>=1)||(DAGE>=1))||(PtP2>=1))||(KdStarGStarPgP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1)))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||(PtP3P2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1))))))))))) * !(E(!((((!(EG(!(EX(((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))))) + !(EG(!((!(E(TRUE U !((((((DAGE>=1)||(KdStarGStarPg>=1))||(KdStarPg>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))) + (((KdStarGStarP3kStarP2<1)&&((Akt<1)||(Pip3<1))) * !(E(TRUE U !(((((((KdStarGStarP3k>=1)||(KdStarGStarP3kStarP2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(Pg>=1)))))))))))) + EG((((((((((((((((KdStarGStarP3k<1)&&((KdStarGStarPgStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP3P2<1))&&((Akt<1)||(Pip3<1)))&&(KdStarGStarPgP3<1))&&((GP3<1)||(KdStar<1)))&&(GStarPgP3<1))&&((Gab1<1)||(Pip3<1)))&&(KdStarPgStarP2<1))||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStar>=1)&&(Pg>=1)))||((GStarP3>=1)&&(P3k>=1))))) + (((((((((AktP3>=1)||(PtP3>=1))||(DAGE>=1))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarG>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((GStarP3>=1)&&(Pg>=1))) * ((((((((((!(E(TRUE U !(((GStarP3>=1)&&(P3k>=1))))) + (KdStarGStarP3kP3>=1)) + (KdStarGStarP3kStarP2>=1)) + (GP3>=1)) + (KdStarGStarPgStarP3P2>=1)) + (KdStarGStarPg>=1)) + (KdStarGStarPgStarP2>=1)) + ((KdStarGStar>=1)&&(Pip3>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + ((((((((((KdStarGStarP3k>=1)||(DAGE>=1))||(PtP2>=1))||(KdStarGStarPgP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1)))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||(PtP3P2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1)))))))) U (!((((((AktP3<1)&&(KdStarG<1)) * E(TRUE U ((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(DAGE<1))&&((GStarP3<1)||(KdStar<1)))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgStarP2<1))&&(KdStarGP3<1))&&(KdStarPgStarP2<1)))) * !((E(!(((((((((((KdStarGStarP3kP3>=1)||(KdStarGStarPgP3>=1))||(GP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarG>=1))||(KdStarGP3>=1))||(KdStarGStarP3>=1))||((DAG>=1)&&(Enz>=1)))) U (!((((DAGE>=1)||(KdStarGStarP3kStarP3P2>=1))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||((GStarP3>=1)&&(KdStar>=1)))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarGStarPgStarP3P2>=1)))) * !(((((((((((KdStarGStarP3kP3>=1)||(KdStarGStarPgP3>=1))||(GP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarG>=1))||(KdStarGP3>=1))||(KdStarGStarP3>=1))||((DAG>=1)&&(Enz>=1)))))) + EG(!(((((((((((KdStarGStarP3kP3>=1)||(KdStarGStarPgP3>=1))||(GP3>=1))||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarG>=1))||(KdStarGP3>=1))||(KdStarGStarP3>=1))||((DAG>=1)&&(Enz>=1)))))))) * ((GStarP3<1)||(P3k<1)))) * !((((!(EG(!(EX(((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))))) + !(EG(!((!(E(TRUE U !((((((DAGE>=1)||(KdStarGStarPg>=1))||(KdStarPg>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))))) + (((KdStarGStarP3kStarP2<1)&&((Akt<1)||(Pip3<1))) * !(E(TRUE U !(((((((KdStarGStarP3k>=1)||(KdStarGStarP3kStarP2>=1))||(KdStarGStarPgP3>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||((GStarP3>=1)&&(Pg>=1)))))))))))) + EG((((((((((((((((KdStarGStarP3k<1)&&((KdStarGStarPgStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP3P2<1))&&((Akt<1)||(Pip3<1)))&&(KdStarGStarPgP3<1))&&((GP3<1)||(KdStar<1)))&&(GStarPgP3<1))&&((Gab1<1)||(Pip3<1)))&&(KdStarPgStarP2<1))||(AktP3>=1))||((KdStarPgStar>=1)&&(Pip2>=1)))||(PtP3P2>=1))||(KdStarGStarPgP3>=1))||((KdStar>=1)&&(Pg>=1)))||((GStarP3>=1)&&(P3k>=1))))) + (((((((((AktP3>=1)||(PtP3>=1))||(DAGE>=1))||(GStarP3kP3>=1))||(GStarPgP3>=1))||(KdStarG>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((GStarP3>=1)&&(Pg>=1))) * ((((((((((!(E(TRUE U !(((GStarP3>=1)&&(P3k>=1))))) + (KdStarGStarP3kP3>=1)) + (KdStarGStarP3kStarP2>=1)) + (GP3>=1)) + (KdStarGStarPgStarP3P2>=1)) + (KdStarGStarPg>=1)) + (KdStarGStarPgStarP2>=1)) + ((KdStarGStar>=1)&&(Pip3>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + ((((((((((KdStarGStarP3k>=1)||(DAGE>=1))||(PtP2>=1))||(KdStarGStarPgP3>=1))||(KdStarGStarPgStarP2>=1))||(KdStarGP3>=1))||(KdStarPgStarP2>=1))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1)))&&((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||(PtP3P2>=1))||((GStarP3kP3>=1)&&(KdStar>=1)))||((DAG>=1)&&(Enz>=1)))||((GStarP3>=1)&&(P3k>=1))))))))))))] != FALSE
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
Using saturation style SCC detection
Fast SCC detection found a local SCC at level 0
(forward)formula 10,1,1039.98,6234444,1,0,1502,4.06052e+07,59,880,1037,3.8288e+07,1198
FORMULA Angiogenesis-PT-05-CTLFireability-12 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: (AX((!(EX(AF((((KdStarGStarP3kP3>=1)||(PtP3>=1))||((GStarP3>=1)&&(Pg>=1)))))) * ((((((((AX(((((((KdStarGStarPg>=1)||(KdStarGStarPgP3>=1))||(PtP3P2>=1))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarGStarP3>=1))) * EG((((((((KdStarGStarP3k>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarGStarPgStarP3P2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPg>=1))||((Pip3>=1)&&(PtP2>=1))))) * (((DAGE>=1)||((GStarP3>=1)&&(Pg>=1))) + E(((((KdStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarPg>=1))||(KdStarPgStarP2>=1)) U ((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||((KdStar>=1)&&(Pg>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))||(KdStarGStarP3>=1))||((GStarP3>=1)&&(P3k>=1)))))) * E((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(AktP3>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgStarP2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarG>=1))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||(KdStarGP3>=1)) U E(((((((((((DAGE>=1)||(PtP3>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarG>=1))||(KdStarGP3>=1)) U ((((((KdStarPgStar>=1)&&(Pip2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarGP3>=1))))) + ((KdStar>=1)&&(Pg>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + (KdStarGStarPgP3>=1)) + (KdStarGStarPgStarP2>=1)))) + AF((A(!(E(((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(GStarPgP3>=1)) U (((((((((KdStarGStarP3k>=1)||((GStarP3kP3>=1)&&(KdStar>=1)))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1)))) U (((((((((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kStarP2<1))&&(KdStarGStarP3kStarP3P2<1))&&((GStarPgP3<1)||(KdStar<1)))&&((KdStarGStarP3<1)||(P3k<1)))&&(GStarPgP3<1))&&(KdStarG<1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(DAGE>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1)))) * (((((KdStarGStarP3kStarP3P2>=1)||((GStarPgP3>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarPgStarP2>=1)) + AX((((((((((KdStarGStarP3kP3<1)&&((KdStarGStarP3kStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP2<1))&&(PtP2<1))&&(KdStarGStarPgP3<1))&&(GStarP3kP3<1))&&((GStarP3<1)||(Pg<1)))&&(KdStarPgStarP2<1))||((((((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||((Gab1>=1)&&(KdStar>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarGP3>=1))&&((((KdStarGStarP3kStarP2>=1)||(KdStarGStarPgP3>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarPgStarP2>=1)))))))))
=> equivalent forward existential formula: [FwdG((Init * !(!(EX(!((!(EX(!(EG(!((((KdStarGStarP3kP3>=1)||(PtP3>=1))||((GStarP3>=1)&&(Pg>=1)))))))) * ((((((((!(EX(!(((((((KdStarGStarPg>=1)||(KdStarGStarPgP3>=1))||(PtP3P2>=1))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarGStarP3>=1))))) * EG((((((((KdStarGStarP3k>=1)||((KdStarGStar>=1)&&(Pip3>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarGStarPgStarP3P2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPg>=1))||((Pip3>=1)&&(PtP2>=1))))) * (((DAGE>=1)||((GStarP3>=1)&&(Pg>=1))) + E(((((KdStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarPg>=1))||(KdStarPgStarP2>=1)) U ((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP2>=1))||((KdStar>=1)&&(Pg>=1)))||((KdStarGStarPgStarP3>=1)&&(Pip2>=1)))||(KdStarGStarP3>=1))||((GStarP3>=1)&&(P3k>=1)))))) * E((((((((((KdStarGStarPgStar>=1)&&(Pip2>=1))||(AktP3>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarGStarPgStarP2>=1))||((KdStarGStarP3>=1)&&(P3k>=1)))||(KdStarG>=1))||((KdStarGStarP3kStarP3>=1)&&(Pip2>=1)))||(KdStarGP3>=1)) U E(((((((((((DAGE>=1)||(PtP3>=1))||((GStarPgP3>=1)&&(KdStar>=1)))||(PtP3P2>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarG>=1))||(KdStarGP3>=1)) U ((((((KdStarPgStar>=1)&&(Pip2>=1))||((Pip2>=1)&&(Pten>=1)))||(KdStarGStarPgStarP2>=1))||((Pip3>=1)&&(Pten>=1)))||(KdStarGP3>=1))))) + ((KdStar>=1)&&(Pg>=1))) + ((KdStarPgStar>=1)&&(Pip2>=1))) + ((GStarP3>=1)&&(KdStar>=1))) + (KdStarGStarPgP3>=1)) + (KdStarGStarPgStarP2>=1)))))))),!((!((E(!((((((((((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kStarP2<1))&&(KdStarGStarP3kStarP3P2<1))&&((GStarPgP3<1)||(KdStar<1)))&&((KdStarGStarP3<1)||(P3k<1)))&&(GStarPgP3<1))&&(KdStarG<1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(DAGE>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1)))) U (!(!(E(((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarP3>=1)&&(Pg>=1)))||(GStarPgP3>=1)) U (((((((((KdStarGStarP3k>=1)||((GStarP3kP3>=1)&&(KdStar>=1)))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(PtP3>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(KdStarGStarPgStarP2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarPgStarP2>=1))))) * !((((((((((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kStarP2<1))&&(KdStarGStarP3kStarP3P2<1))&&((GStarPgP3<1)||(KdStar<1)))&&((KdStarGStarP3<1)||(P3k<1)))&&(GStarPgP3<1))&&(KdStarG<1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(DAGE>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1)))))) + EG(!((((((((((((((((KdStarGStarPgStar<1)||(Pip2<1))&&(KdStarGStarP3kStarP2<1))&&(KdStarGStarP3kStarP3P2<1))&&((GStarPgP3<1)||(KdStar<1)))&&((KdStarGStarP3<1)||(P3k<1)))&&(GStarPgP3<1))&&(KdStarG<1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||(DAGE>=1))||(KdStarGStarPgP3>=1))||((DAG>=1)&&(Enz>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStar>=1)&&(Pg>=1))))))) * (((((KdStarGStarP3kStarP3P2>=1)||((GStarPgP3>=1)&&(KdStar>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarPgStarP2>=1)) + !(EX(!((((((((((KdStarGStarP3kP3<1)&&((KdStarGStarP3kStar<1)||(Pip2<1)))&&(KdStarGStarP3kStarP2<1))&&(PtP2<1))&&(KdStarGStarPgP3<1))&&(GStarP3kP3<1))&&((GStarP3<1)||(Pg<1)))&&(KdStarPgStarP2<1))||((((((((((KdStarGStarP3k>=1)||(KdStarGStarP3kP3>=1))||((Akt>=1)&&(Pip3>=1)))||(KdStarGStarPgStarP2>=1))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||((Gab1>=1)&&(KdStar>=1)))||((Gab1>=1)&&(Pip3>=1)))||(KdStarGP3>=1))&&((((KdStarGStarP3kStarP2>=1)||(KdStarGStarPgP3>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarPgStarP2>=1)))))))))))] = FALSE
(forward)formula 11,1,1121.01,6835828,1,0,1835,4.46401e+07,108,1061,1167,4.31053e+07,1878
FORMULA Angiogenesis-PT-05-CTLFireability-13 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
Detected timeout of ITS tools.
[2021-05-11 14:35:48] [INFO ] Flatten gal took : 6 ms
[2021-05-11 14:35:48] [INFO ] Input system was already deterministic with 64 transitions.
[2021-05-11 14:35:48] [INFO ] Transformed 38 places.
[2021-05-11 14:35:48] [INFO ] Transformed 64 transitions.
Running greatSPN : CommandLine [args=[/home/mcc/BenchKit/bin//..//greatspn//bin/pinvar, /home/mcc/execution/gspn], workingDir=/home/mcc/execution]
Run of greatSPN captured in /home/mcc/execution/outPut.txt
Running greatSPN : CommandLine [args=[/home/mcc/BenchKit/bin//..//greatspn//bin/RGMEDD2, /home/mcc/execution/gspn, -META, -varord-only], workingDir=/home/mcc/execution]
Run of greatSPN captured in /home/mcc/execution/outPut.txt
Using order generated by GreatSPN with heuristic : META
[2021-05-11 14:35:48] [INFO ] Time to serialize gal into /tmp/CTLFireability6450284047541642320.gal : 1 ms
[2021-05-11 14:35:48] [INFO ] Time to serialize properties into /tmp/CTLFireability5814524505083513920.ctl : 1 ms
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64, --gc-threshold, 2000000, --quiet, -i, /tmp/CTLFireability6450284047541642320.gal, -t, CGAL, -ctl, /tmp/CTLFireability5814524505083513920.ctl, --load-order, /home/mcc/execution/model.ord, --gen-order, FOLLOW], workingDir=/home/mcc/execution]
its-ctl command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.202104292328/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /tmp/CTLFireability6450284047541642320.gal -t CGAL -ctl /tmp/CTLFireability5814524505083513920.ctl --load-order /home/mcc/execution/model.ord --gen-order FOLLOW
Successfully loaded order from file /home/mcc/execution/model.ord
No direction supplied, using forward translation only.
Parsed 2 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,4.27349e+07,1.12647,37148,2,6159,5,168551,6,0,219,173293,0
Converting to forward existential form...Done !
original formula: A(AX(!(A((((KdStarGStarPg>=1)||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1)) U (((((((((((KdStarGStarPgP3>=1)||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarG>=1))||((GStarP3>=1)&&(P3k>=1)))||(PtP3>=1))||((GStarP3>=1)&&(P3k>=1)))&&((((((((((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(KdStarGStarP3kStarP2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||(GStarPgP3>=1))||(KdStarPg>=1))||(KdStarGStarP3>=1)))))) U AG((((AktP3>=1)||(PtP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))))
=> equivalent forward existential formula: [((Init * !(EG(!(!(E(TRUE U !((((AktP3>=1)||(PtP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))))))))) * !(E(!(!(E(TRUE U !((((AktP3>=1)||(PtP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1))))))) U (!(!(EX(!(!(!((E(!((((((((((((KdStarGStarPgP3>=1)||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarG>=1))||((GStarP3>=1)&&(P3k>=1)))||(PtP3>=1))||((GStarP3>=1)&&(P3k>=1)))&&((((((((((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(KdStarGStarP3kStarP2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||(GStarPgP3>=1))||(KdStarPg>=1))||(KdStarGStarP3>=1)))) U (!((((KdStarGStarPg>=1)||((DAG>=1)&&(Enz>=1)))||(KdStarPg>=1))) * !((((((((((((KdStarGStarPgP3>=1)||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarG>=1))||((GStarP3>=1)&&(P3k>=1)))||(PtP3>=1))||((GStarP3>=1)&&(P3k>=1)))&&((((((((((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(KdStarGStarP3kStarP2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||(GStarPgP3>=1))||(KdStarPg>=1))||(KdStarGStarP3>=1)))))) + EG(!((((((((((((KdStarGStarPgP3>=1)||((Pip2>=1)&&(Pten>=1)))||((GP3>=1)&&(KdStar>=1)))||((Gab1>=1)&&(KdStar>=1)))||(KdStarGStarPgStarP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))||(KdStarG>=1))||((GStarP3>=1)&&(P3k>=1)))||(PtP3>=1))||((GStarP3>=1)&&(P3k>=1)))&&((((((((((((GStarP3kP3>=1)&&(KdStar>=1))||((KdStarGStarPgStar>=1)&&(Pip2>=1)))||(KdStarGStarP3kStarP2>=1))||((Pip3>=1)&&(PtP2>=1)))||(KdStarPgStarP2>=1))||(KdStarGStarP3kP3>=1))||(KdStarGStarP3kStarP2>=1))||((Akt>=1)&&(Pip3>=1)))||(GStarPgP3>=1))||(KdStarPg>=1))||(KdStarGStarP3>=1)))))))))))) * !(!(E(TRUE U !((((AktP3>=1)||(PtP3P2>=1))||((KdStarGStar>=1)&&(Pg>=1)))))))))))] != FALSE
Reverse transition relation is NOT exact ! Due to transitions t12, t24, t51, t57, t61, Intersection with reachable at each step enabled. (destroyed/reverse/intersect/total) :0/59/5/64
(forward)formula 0,0,265.156,2572964,1,0,325,1.47067e+07,23,178,982,1.72411e+07,373
FORMULA Angiogenesis-PT-05-CTLFireability-14 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: AF(((((((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(PtP2<1))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgP3<1))&&(GStarPgP3<1))&&((KdStarGStarPg>=1)||(KdStarPgStarP2>=1)))&&(((((((((KdStarGStarP3k>=1)||(AktP3>=1))||(DAGE>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarPgStarP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||((DAG>=1)&&(Enz>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||((KdStar>=1)&&(Pg>=1))))&&((KdStarPgStar<1)||(Pip2<1))) * (((PtP2>=1) + EF(((((((((AktP3>=1)||(KdStarGStarP3kP3>=1))||(PtP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarG>=1)))) + ((GStarP3>=1)&&(KdStar>=1)))))
=> equivalent forward existential formula: [FwdG(Init,!(((((((((((KdStarGStarP3kP3<1)&&(PtP3<1))&&(PtP2<1))&&(KdStarGStarP3kStarP3P2<1))&&(KdStarGStarPgP3<1))&&(GStarPgP3<1))&&((KdStarGStarPg>=1)||(KdStarPgStarP2>=1)))&&(((((((((KdStarGStarP3k>=1)||(AktP3>=1))||(DAGE>=1))||(KdStarGStarP3kStarP3P2>=1))||(KdStarPgStarP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||((DAG>=1)&&(Enz>=1)))||((KdStarGStar>=1)&&(Pg>=1)))||((KdStar>=1)&&(Pg>=1))))&&((KdStarPgStar<1)||(Pip2<1))) * (((PtP2>=1) + E(TRUE U ((((((((AktP3>=1)||(KdStarGStarP3kP3>=1))||(PtP2>=1))||((KdStarGStar>=1)&&(P3k>=1)))||(DAGE>=1))||(KdStarGStarPgStarP2>=1))||((Gab1>=1)&&(Pip3>=1)))||(KdStarG>=1)))) + ((GStarP3>=1)&&(KdStar>=1))))))] = FALSE
(forward)formula 1,0,293.158,2572964,1,0,453,1.47067e+07,31,297,1014,1.72411e+07,515
FORMULA Angiogenesis-PT-05-CTLFireability-15 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
BK_STOP 1620744043885
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/bin//../
+ BINDIR=/home/mcc/BenchKit/bin//../
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ CTLFireability = StateSpace ]]
+ /home/mcc/BenchKit/bin//..//runeclipse.sh /home/mcc/execution CTLFireability -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
++ cut -d . -f 9
++ ls /home/mcc/BenchKit/bin//..//itstools/plugins/fr.lip6.move.gal.application.pnmcc_1.0.0.202104292328.jar
+ VERSION=0
+ echo 'Running Version 0'
+ /home/mcc/BenchKit/bin//..//itstools/its-tools -data /home/mcc/execution/workspace -pnfolder /home/mcc/execution -examination CTLFireability -spotpath /home/mcc/BenchKit/bin//..//ltlfilt -z3path /home/mcc/BenchKit/bin//..//z3/bin/z3 -yices2path /home/mcc/BenchKit/bin//..//yices/bin/yices -its -ltsmin -greatspnpath /home/mcc/BenchKit/bin//..//greatspn/ -order META -manyOrder -smt -timeout 3600 -vmargs -Dosgi.locking=none -Declipse.stateSaveDelayInterval=-1 -Dosgi.configuration.area=/tmp/.eclipse -Xss128m -Xms40m -Xmx16000m
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="Angiogenesis-PT-05"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
export BK_BIN_PATH="/home/mcc/BenchKit/bin/"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-4028"
echo " Executing tool itstools"
echo " Input is Angiogenesis-PT-05, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r007-tall-162037989800324"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/Angiogenesis-PT-05.tgz
mv Angiogenesis-PT-05 execution
cd execution
if [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "UpperBounds" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] || [ "CTLFireability" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "CTLFireability" = "ReachabilityDeadlock" ] || [ "CTLFireability" = "QuasiLiveness" ] || [ "CTLFireability" = "StableMarking" ] || [ "CTLFireability" = "Liveness" ] || [ "CTLFireability" = "OneSafe" ] ; then
echo "FORMULA_NAME CTLFireability"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

