About the Execution of 2019-Gold for NeoElection-PT-2
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 4273.190 | 5587.00 | 6254.00 | 10.00 | TTTTTTFFFFTFFFFT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
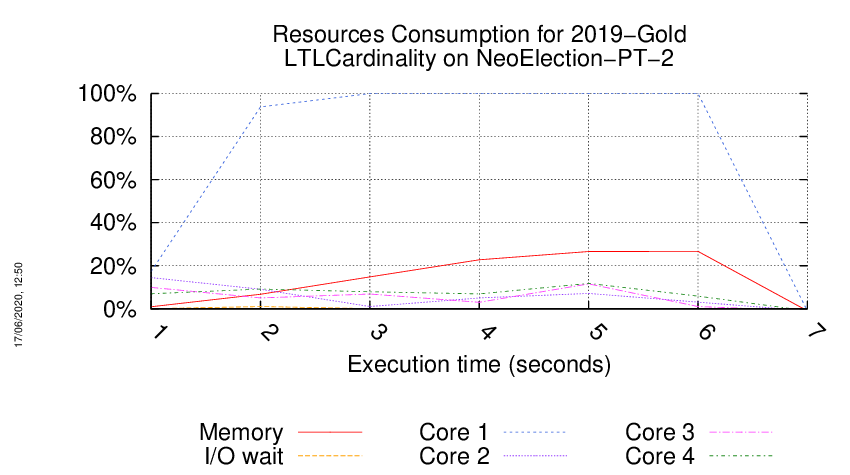
Trace from the execution
Formatting '/local/x2003239/mcc2020-input.r120-csrt-158961292500069.qcow2', fmt=qcow2 size=4294967296 backing_file=/local/x2003239/mcc2020-input.qcow2 encryption=off cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
=====================================================================
Generated by BenchKit 2-4028
Executing tool win2019
Input is NeoElection-PT-2, examination is LTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r120-csrt-158961292500069
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 856K
-rw-r--r-- 1 mcc users 18K Apr 30 13:04 CTLCardinality.txt
-rw-r--r-- 1 mcc users 50K Apr 30 13:04 CTLCardinality.xml
-rw-r--r-- 1 mcc users 15K Apr 30 13:04 CTLFireability.txt
-rw-r--r-- 1 mcc users 50K Apr 30 13:04 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K Apr 30 13:04 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K Apr 30 13:04 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 31K Apr 30 13:04 LTLCardinality.txt
-rw-r--r-- 1 mcc users 94K Apr 30 13:04 LTLCardinality.xml
-rw-r--r-- 1 mcc users 7.8K Apr 30 13:04 LTLFireability.txt
-rw-r--r-- 1 mcc users 33K Apr 30 13:04 LTLFireability.xml
-rw-r--r-- 1 mcc users 27K Apr 30 13:04 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 73K Apr 30 13:04 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 13K Apr 30 13:04 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 41K Apr 30 13:04 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 11K Apr 30 13:04 UpperBounds.txt
-rw-r--r-- 1 mcc users 21K Apr 30 13:04 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 Apr 30 13:04 equiv_col
-rw-r--r-- 1 mcc users 2 Apr 30 13:04 instance
-rw-r--r-- 1 mcc users 6 Apr 30 13:04 iscolored
-rw-r--r-- 1 mcc users 320K Apr 30 13:04 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-2-00
FORMULA_NAME NeoElection-PT-2-01
FORMULA_NAME NeoElection-PT-2-02
FORMULA_NAME NeoElection-PT-2-03
FORMULA_NAME NeoElection-PT-2-04
FORMULA_NAME NeoElection-PT-2-05
FORMULA_NAME NeoElection-PT-2-06
FORMULA_NAME NeoElection-PT-2-07
FORMULA_NAME NeoElection-PT-2-08
FORMULA_NAME NeoElection-PT-2-09
FORMULA_NAME NeoElection-PT-2-10
FORMULA_NAME NeoElection-PT-2-11
FORMULA_NAME NeoElection-PT-2-12
FORMULA_NAME NeoElection-PT-2-13
FORMULA_NAME NeoElection-PT-2-14
FORMULA_NAME NeoElection-PT-2-15
=== Now, execution of the tool begins
BK_START 1590337617485
info: Time: 3600 - MCC
vrfy: Checking LTLCardinality @ NeoElection-PT-2 @ 3570 seconds
FORMULA NeoElection-PT-2-00 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-01 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-03 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-06 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-07 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-08 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-11 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-12 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-14 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-15 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-09 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-10 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-04 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-05 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-13 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
FORMULA NeoElection-PT-2-02 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
vrfy: finished
info: timeLeft: 3564
rslt: Output for LTLCardinality @ NeoElection-PT-2
{
"build":
{
"architecture": 64,
"assertions": false,
"build_hostname": "mcc2019",
"build_system": "x86_64-unknown-linux-gnu",
"optimizations": true,
"package_version": "2.0",
"svn_version": "3189M"
},
"call":
{
"exec_host": "mcc2019",
"markinglimit": null,
"parameters":
[
"--pnmlnet",
"model.pnml",
"--xmlformula",
"--formula=LTLCardinality.xml",
"--mcc",
"--donotcomputecapacities",
"--encoder=simplecompressed",
"--safe",
"--check=modelchecking",
"--stubborn=deletion",
"--stateequation=par",
"--timelimit=3570",
"--localtimelimit=0",
"--preference=force_ltl",
"--json=LTLCardinality.json",
"--jsoninclude=formula,formulastat,net"
],
"starttime": "Sun May 24 16:26:57 2020
",
"timelimit": 3570
},
"child":
[
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 222
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "TRUE",
"processed_size": 4,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": true
},
"task":
{
"compoundnumber": 0,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 237
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "TRUE",
"processed_size": 4,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": true
},
"task":
{
"compoundnumber": 1,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 254
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 1,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 72,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 72,
"visible_transitions": 0
},
"processed": "(P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 <= 0)",
"processed_size": 1606,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": true
},
"task":
{
"compoundnumber": 2,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 274
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 3,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 297
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 4,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 324
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 5,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 356
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 6,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 396
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 7,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 445
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "FALSE",
"processed_size": 5,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": false
},
"task":
{
"compoundnumber": 8,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 509
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "TRUE",
"processed_size": 4,
"rewrites": 166
},
"result":
{
"edges": 0,
"markings": 0,
"produced_by": "preprocessing",
"value": true
},
"task":
{
"compoundnumber": 9,
"type": "initial_satisfaction",
"workflow": "preprocessing"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 594
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 1,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 1,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 1,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 2,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 2,
"visible_transitions": 0
},
"processed": "A (X ((P-startNeg__broadcasting_1_1 <= P-polling_1)))",
"processed_size": 53,
"rewrites": 166
},
"result":
{
"edges": 34,
"markings": 34,
"produced_by": "LTL model checker",
"value": false
},
"task":
{
"buchi":
{
"states": 3
},
"compoundnumber": 10,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "no (formula contains X operator)"
},
"type": "product automaton/dfs"
},
"type": "LTL",
"workflow": "product automaton"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 713
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 1,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 1,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "A (X (TRUE))",
"processed_size": 12,
"rewrites": 166
},
"result":
{
"edges": 2,
"markings": 3,
"produced_by": "LTL model checker",
"value": true
},
"task":
{
"buchi":
{
"states": 3
},
"compoundnumber": 11,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "no (formula contains X operator)"
},
"type": "product automaton/dfs"
},
"type": "LTL",
"workflow": "product automaton"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 891
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 1,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 1,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 0,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 0,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 0,
"visible_transitions": 0
},
"processed": "A (X (TRUE))",
"processed_size": 12,
"rewrites": 166
},
"result":
{
"edges": 2,
"markings": 3,
"produced_by": "LTL model checker",
"value": true
},
"task":
{
"buchi":
{
"states": 3
},
"compoundnumber": 12,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "no (formula contains X operator)"
},
"type": "product automaton/dfs"
},
"type": "LTL",
"workflow": "product automaton"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 1188
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 0,
"E": 0,
"F": 0,
"G": 0,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 1,
"comp": 1,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 6,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 6,
"visible_transitions": 0
},
"processed": "(P-electionInit_0 + P-electionInit_1 + P-electionInit_2 <= P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0)",
"processed_size": 117,
"rewrites": 168
},
"result":
{
"edges": 0,
"markings": 1,
"produced_by": "state space / EG",
"value": true
},
"task":
{
"compoundnumber": 13,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "reachability preserving/insertion",
"visible": 312
},
"threads": 1,
"type": "dfs"
},
"type": "eventual_occurrence"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 1782
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 1,
"E": 0,
"F": 1,
"G": 1,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 0,
"comp": 1,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 1,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 1,
"visible_transitions": 0
},
"processed": "A (G (F ((P-poll__handlingMessage_2 <= 0))))",
"processed_size": 44,
"rewrites": 166
},
"result":
{
"edges": 65,
"markings": 56,
"produced_by": "LTL model checker",
"value": false
},
"task":
{
"buchi":
{
"states": 2
},
"compoundnumber": 14,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "ltl preserving/insertion"
},
"type": "product automaton/dfs"
},
"type": "LTL",
"workflow": "product automaton"
}
},
{
"call":
{
"dynamic_timelimit": true,
"localtimelimit": 3564
},
"exit":
{
"localtimelimitreached": false
},
"formula":
{
"count":
{
"A": 1,
"E": 0,
"F": 1,
"G": 1,
"U": 0,
"X": 0,
"aconj": 0,
"adisj": 0,
"aneg": 1,
"comp": 1,
"cont": 0,
"dl": 0,
"fir": 0,
"nodl": 0,
"place_references": 3,
"taut": 0,
"tconj": 0,
"tdisj": 0,
"tneg": 0,
"transition_references": 0,
"unfir": 0,
"visible_places": 3,
"visible_transitions": 0
},
"processed": "A (F (G ((P-polling_0 + P-polling_1 + P-polling_2 <= 1))))",
"processed_size": 58,
"rewrites": 166
},
"result":
{
"edges": 565,
"markings": 279,
"produced_by": "LTL model checker",
"value": true
},
"task":
{
"buchi":
{
"states": 2
},
"compoundnumber": 15,
"search":
{
"store":
{
"encoder": "simple compression",
"type": "prefix"
},
"stubborn":
{
"type": "ltl preserving/insertion"
},
"type": "product automaton/dfs"
},
"type": "LTL",
"workflow": "product automaton"
}
}
],
"exit":
{
"error": null,
"memory": 22832,
"runtime": 6.000000,
"signal": null,
"timelimitreached": false
},
"files":
{
"formula": "LTLCardinality.xml",
"net": "model.pnml"
},
"formula":
{
"skeleton": "TRUE : TRUE : A(F(G(*))) : ** : A(X(TRUE)) : A(F(**)) : FALSE : FALSE : FALSE : A(X(**)) : A(X(TRUE)) : FALSE : FALSE : A(G(F(**))) : FALSE : TRUE"
},
"net":
{
"arcs": 1998,
"conflict_clusters": 288,
"places": 438,
"places_significant": 153,
"singleton_clusters": 0,
"transitions": 357
},
"result":
{
"preliminary_value": "yes yes yes yes yes yes no no no no yes no no no no yes ",
"value": "yes yes yes yes yes yes no no no no yes no no no no yes "
},
"task":
{
"type": "compound"
}
}
lola: LoLA will run for 3570 seconds at most (--timelimit)
lola: NET
lola: input: PNML file (--pnml)
lola: reading net from model.pnml
lola: reading pnml
lola: PNML file contains place/transition net
lola: finished parsing
lola: closed net file model.pnml
lola: 795/268435456 symbol table entries, 0 collisions
lola: preprocessing...
lola: Size of bit vector: 438
lola: finding significant places
lola: 438 places, 357 transitions, 153 significant places
lola: compute conflict clusters
lola: computed conflict clusters
lola: Computing conflicting sets
lola: Computing back conflicting sets
lola: TASK
lola: Reading formula in XML format (--xmlformula)
lola: reading pnml
lola: reading formula from LTLCardinality.xml
lola: place invariant simplifies atomic proposition
lola: before: (2 <= P-electionFailed_2 + P-electionFailed_1 + P-electionFailed_0)
lola: after: (2 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (2 <= P-electionFailed_2 + P-electionFailed_1 + P-electionFailed_0)
lola: after: (2 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-negotiation_2_0_NONE + P-negotiation_0_1_NONE + P-negotiation_2_1_CO + P-negotiation_1_1_DONE + P-negotiation_1_0_DONE + P-negotiation_2_0_CO + P-negotiation_2_2_DONE + P-negotiation_1_1_NONE + P-negotiation_0_2_CO + P-negotiation_1_2_NONE + P-negotiation_0_0_DONE + P-negotiation_1_2_DONE + P-negotiation_0_1_CO + P-negotiation_2_1_DONE + P-negotiation_0_2_DONE + P-negotiation_0_0_CO + P-negotiation_2_1_NONE + P-negotiation_0_2_NONE + P-negotiation_1_2_CO + P-negotiation_0_0_NONE + P-negotiation_1_1_CO + P-negotiation_2_2_NONE + P-negotiation_1_0_CO + P-negotiation_1_0_NONE + P-negotiation_2_0_DONE + P-negotiation_0_1_DONE + P-negotiation_2_2_CO)
lola: after: (0 <= 1)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-negotiation_2_0_NONE + P-negotiation_0_1_NONE + P-negotiation_2_1_CO + P-negotiation_1_1_DONE + P-negotiation_1_0_DONE + P-negotiation_2_0_CO + P-negotiation_2_2_DONE + P-negotiation_1_1_NONE + P-negotiation_0_2_CO + P-negotiation_1_2_NONE + P-negotiation_0_0_DONE + P-negotiation_1_2_DONE + P-negotiation_0_1_CO + P-negotiation_2_1_DONE + P-negotiation_0_2_DONE + P-negotiation_0_0_CO + P-negotiation_2_1_NONE + P-negotiation_0_2_NONE + P-negotiation_1_2_CO + P-negotiation_0_0_NONE + P-negotiation_1_1_CO + P-negotiation_2_2_NONE + P-negotiation_1_0_CO + P-negotiation_1_0_NONE + P-negotiation_2_0_DONE + P-negotiation_0_1_DONE + P-negotiation_2_2_CO)
lola: after: (0 <= 1)
lola: place invariant simplifies atomic proposition
lola: before: (P-crashed_0 + P-crashed_1 + P-crashed_2 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2)
lola: after: (0 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-dead_2 + P-dead_1 + P-dead_0)
lola: after: (3 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-crashed_0 + P-crashed_1 + P-crashed_2 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2)
lola: after: (0 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-polling_0 + P-polling_1 + P-polling_2 <= P-masterList_1_2_2 + P-masterList_1_2_1 + P-masterList_1_2_0 + P-masterList_1_1_2 + P-masterList_1_1_1 + P-masterList_1_1_0 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0)
lola: after: (P-polling_0 + P-polling_1 + P-polling_2 <= 2)
lola: LP says that atomic proposition is always true: (P-polling_0 + P-polling_1 + P-polling_2 <= 2)
lola: place invariant simplifies atomic proposition
lola: before: (P-masterList_1_2_2 + P-masterList_1_2_1 + P-masterList_1_2_0 + P-masterList_1_1_2 + P-masterList_1_1_1 + P-masterList_1_1_0 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 <= P-polling_0 + P-polling_1 + P-polling_2)
lola: after: (2 <= P-polling_0 + P-polling_1 + P-polling_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_1 + P-network_0_0_AI_1 + P-network_0_0_AI_2 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_2_AI_2 + P-network_1_2_AI_1 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_1_AnnP_2 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_1_1_AnnP_1 + P-network_2_2_AI_1 + P-network_2_2_AI_2 + P-network_2_2_AnnP_1 + P-network_2_2_AnnP_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_2_0_AskP_1 + P-network_2_0_AskP_2 + P-network_0_1_AskP_1 + P-network_0_1_AskP_2 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_2_0_AnnP_2 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_2_0_AnnP_1 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_0_2_AI_2 + P-network_0_2_AI_1 + P-network_2_1_RP_1 + P-network_2_1_RP_2 + P-network_0_2_RP_1 + P-network_0_2_RP_2 + P-network_2_1_AI_2 + P-network_2_1_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_1 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_2_2_AskP_2 + P-network_2_2_AskP_1 + P-network_1_1_AI_1 + P-network_1_1_AI_2 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_2_2_RI_1 + P-network_2_2_RI_2 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_0_0_RP_2 + P-network_0_0_AnnP_1 + P-network_0_0_AnnP_2 + P-network_0_0_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2 <= P-electionFailed_2 + P-electionFailed_1 + P-electionFailed_0)
lola: after: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_1 + P-network_0_0_AI_1 + P-network_0_0_AI_2 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_2_AI_2 + P-network_1_2_AI_1 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_1_AnnP_2 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_1_1_AnnP_1 + P-network_2_2_AI_1 + P-network_2_2_AI_2 + P-network_2_2_AnnP_1 + P-network_2_2_AnnP_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_2_0_AskP_1 + P-network_2_0_AskP_2 + P-network_0_1_AskP_1 + P-network_0_1_AskP_2 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_2_0_AnnP_2 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_2_0_AnnP_1 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_0_2_AI_2 + P-network_0_2_AI_1 + P-network_2_1_RP_1 + P-network_2_1_RP_2 + P-network_0_2_RP_1 + P-network_0_2_RP_2 + P-network_2_1_AI_2 + P-network_2_1_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_1 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_2_2_AskP_2 + P-network_2_2_AskP_1 + P-network_1_1_AI_1 + P-network_1_1_AI_2 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_2_2_RI_1 + P-network_2_2_RI_2 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_0_0_RP_2 + P-network_0_0_AnnP_1 + P-network_0_0_AnnP_2 + P-network_0_0_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2 <= P-electionFailed_2 + P-electionFailed_1 + P-electionFailed_0)
lola: after: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 <= 0)
lola: LP says that atomic proposition is always false: (2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: place invariant simplifies atomic proposition
lola: before: (P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= P-stage_2_PRIM + P-stage_0_NEG + P-stage_1_PRIM + P-stage_1_NEG + P-stage_0_SEC + P-stage_1_SEC + P-stage_2_NEG + P-stage_0_PRIM + P-stage_2_SEC)
lola: after: (P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= 2)
lola: LP says that atomic proposition is always true: (P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= 2)
lola: place invariant simplifies atomic proposition
lola: before: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_1 + P-network_0_0_AI_1 + P-network_0_0_AI_2 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_2_AI_2 + P-network_1_2_AI_1 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_1_AnnP_2 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_1_1_AnnP_1 + P-network_2_2_AI_1 + P-network_2_2_AI_2 + P-network_2_2_AnnP_1 + P-network_2_2_AnnP_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_2_0_AskP_1 + P-network_2_0_AskP_2 + P-network_0_1_AskP_1 + P-network_0_1_AskP_2 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_2_0_AnnP_2 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_2_0_AnnP_1 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_0_2_AI_2 + P-network_0_2_AI_1 + P-network_2_1_RP_1 + P-network_2_1_RP_2 + P-network_0_2_RP_1 + P-network_0_2_RP_2 + P-network_2_1_AI_2 + P-network_2_1_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_1 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_2_2_AskP_2 + P-network_2_2_AskP_1 + P-network_1_1_AI_1 + P-network_1_1_AI_2 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_2_2_RI_1 + P-network_2_2_RI_2 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_0_0_RP_2 + P-network_0_0_AnnP_1 + P-network_0_0_AnnP_2 + P-network_0_0_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2)
lola: after: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0)
lola: LP says that atomic proposition is always true: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0)
lola: place invariant simplifies atomic proposition
lola: before: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_1 + P-network_0_0_AI_1 + P-network_0_0_AI_2 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_2_AI_2 + P-network_1_2_AI_1 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_1_AnnP_2 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_1_1_AnnP_1 + P-network_2_2_AI_1 + P-network_2_2_AI_2 + P-network_2_2_AnnP_1 + P-network_2_2_AnnP_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_2_0_AskP_1 + P-network_2_0_AskP_2 + P-network_0_1_AskP_1 + P-network_0_1_AskP_2 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_2_0_AnnP_2 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_2_0_AnnP_1 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_0_2_AI_2 + P-network_0_2_AI_1 + P-network_2_1_RP_1 + P-network_2_1_RP_2 + P-network_0_2_RP_1 + P-network_0_2_RP_2 + P-network_2_1_AI_2 + P-network_2_1_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_1 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_2_2_AskP_2 + P-network_2_2_AskP_1 + P-network_1_1_AI_1 + P-network_1_1_AI_2 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_2_2_RI_1 + P-network_2_2_RI_2 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_0_0_RP_2 + P-network_0_0_AnnP_1 + P-network_0_0_AnnP_2 + P-network_0_0_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2)
lola: after: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0)
lola: LP says that atomic proposition is always true: (P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0)
lola: place invariant simplifies atomic proposition
lola: before: (P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2 <= P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_1_T_2 + P-masterState_2_T_2 + P-masterState_0_F_2)
lola: after: (P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2 <= 2)
lola: LP says that atomic proposition is always true: (P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2 <= 2)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_0 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_2_1_RP_0 + P-poll__networl_2_1_RP_1 + P-poll__networl_2_1_RP_2 + P-poll__networl_0_2_RP_0 + P-poll__networl_0_2_RP_1 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_0_RI_0 + P-poll__networl_0_0_RI_1 + P-poll__networl_0_0_RI_2 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_0_2_RI_0 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_0 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_0 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_1_1_AI_0 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_2 + P-poll__networl_2_2_RI_0 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_2_2_AI_2 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_0_0_AskP_0 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_0 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_2_AskP_1 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_0_2_AskP_0 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_2_1_AskP_2 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_0)
lola: after: (3 <= P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_2_2_AnsP_2)
lola: LP says that atomic proposition is always false: (3 <= P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_2_2_AnsP_2)
lola: place invariant simplifies atomic proposition
lola: before: (1 <= P-stage_2_PRIM + P-stage_0_NEG + P-stage_1_PRIM + P-stage_1_NEG + P-stage_0_SEC + P-stage_1_SEC + P-stage_2_NEG + P-stage_0_PRIM + P-stage_2_SEC)
lola: after: (0 <= 1)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-crashed_0 + P-crashed_1 + P-crashed_2)
lola: after: (3 <= 0)
lola: LP says that atomic proposition is always false: (3 <= P-electionInit_0 + P-electionInit_1 + P-electionInit_2)
lola: place invariant simplifies atomic proposition
lola: before: (2 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_1 + P-network_0_0_AI_1 + P-network_0_0_AI_2 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_2_AI_2 + P-network_1_2_AI_1 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_1_AnnP_2 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_1_1_AnnP_1 + P-network_2_2_AI_1 + P-network_2_2_AI_2 + P-network_2_2_AnnP_1 + P-network_2_2_AnnP_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_2_0_AskP_1 + P-network_2_0_AskP_2 + P-network_0_1_AskP_1 + P-network_0_1_AskP_2 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_2_0_AnnP_2 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_2_0_AnnP_1 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_0_2_AI_2 + P-network_0_2_AI_1 + P-network_2_1_RP_1 + P-network_2_1_RP_2 + P-network_0_2_RP_1 + P-network_0_2_RP_2 + P-network_2_1_AI_2 + P-network_2_1_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_1 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_2_2_AskP_2 + P-network_2_2_AskP_1 + P-network_1_1_AI_1 + P-network_1_1_AI_2 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_2_2_RI_1 + P-network_2_2_RI_2 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_0_0_RP_2 + P-network_0_0_AnnP_1 + P-network_0_0_AnnP_2 + P-network_0_0_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2)
lola: after: (2 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0)
lola: place invariant simplifies atomic proposition
lola: before: (P-masterList_1_2_2 + P-masterList_1_2_1 + P-masterList_1_2_0 + P-masterList_1_1_2 + P-masterList_1_1_1 + P-masterList_1_1_0 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: after: (2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: LP says that atomic proposition is always false: (2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: place invariant simplifies atomic proposition
lola: before: (P-electionInit_0 + P-electionInit_1 + P-electionInit_2 <= P-dead_2 + P-dead_1 + P-dead_0)
lola: after: (P-electionInit_0 + P-electionInit_1 + P-electionInit_2 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-masterList_1_2_2 + P-masterList_1_2_1 + P-masterList_1_2_0 + P-masterList_1_1_2 + P-masterList_1_1_1 + P-masterList_1_1_0 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: after: (2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: LP says that atomic proposition is always false: (2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)
lola: place invariant simplifies atomic proposition
lola: before: (P-stage_2_PRIM + P-stage_0_NEG + P-stage_1_PRIM + P-stage_1_NEG + P-stage_0_SEC + P-stage_1_SEC + P-stage_2_NEG + P-stage_0_PRIM + P-stage_2_SEC <= P-poll__waitingMessage_2 + P-poll__waitingMessage_0 + P-poll__waitingMessage_1)
lola: after: (2 <= P-poll__waitingMessage_2 + P-poll__waitingMessage_0 + P-poll__waitingMessage_1)
lola: LP says that atomic proposition is always false: (2 <= P-poll__waitingMessage_2 + P-poll__waitingMessage_0 + P-poll__waitingMessage_1)
lola: LP says that atomic proposition is always true: (P-sendAnnPs__broadcasting_1_1 <= P-masterState_1_F_0)
lola: place invariant simplifies atomic proposition
lola: before: (P-crashed_0 <= P-electedPrimary_0)
lola: after: (0 <= P-electedPrimary_0)
lola: place invariant simplifies atomic proposition
lola: before: (P-masterList_1_1_0 <= P-negotiation_2_0_NONE)
lola: after: (0 <= P-negotiation_2_0_NONE)
lola: LP says that atomic proposition is always false: (1 <= P-negotiation_2_2_CO)
lola: LP says that atomic proposition is always true: (P-poll__pollEnd_0 <= P-sendAnnPs__broadcasting_1_2)
lola: LP says that atomic proposition is always false: (3 <= P-polling_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-dead_1 <= P-sendAnnPs__broadcasting_2_2)
lola: after: (0 <= P-sendAnnPs__broadcasting_2_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-dead_1 <= P-sendAnnPs__broadcasting_2_2)
lola: after: (0 <= P-sendAnnPs__broadcasting_2_2)
lola: place invariant simplifies atomic proposition
lola: before: (0 <= P-dead_0)
lola: after: (0 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (0 <= P-dead_0)
lola: after: (0 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (1 <= P-network_0_2_AnnP_1)
lola: after: (1 <= 0)
lola: LP says that atomic proposition is always true: (P-stage_0_NEG <= P-poll__pollEnd_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__pollEnd_2 <= P-dead_1)
lola: after: (P-poll__pollEnd_2 <= 0)
lola: LP says that atomic proposition is always false: (3 <= P-electedSecondary_1)
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__pollEnd_2 <= P-dead_1)
lola: after: (P-poll__pollEnd_2 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-crashed_1 <= P-polling_1)
lola: after: (0 <= P-polling_1)
lola: place invariant simplifies atomic proposition
lola: before: (P-stage_0_PRIM <= P-dead_1)
lola: after: (P-stage_0_PRIM <= 0)
lola: LP says that atomic proposition is always true: (P-stage_0_PRIM <= 0)
lola: LP says that atomic proposition is always false: (1 <= P-masterState_2_F_1)
lola: place invariant simplifies atomic proposition
lola: before: (1 <= P-masterList_1_1_2)
lola: after: (0 <= 0)
lola: LP says that atomic proposition is always true: (P-network_0_1_AnsP_1 <= P-electedPrimary_2)
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__handlingMessage_2 <= P-poll__networl_0_1_AI_2)
lola: after: (P-poll__handlingMessage_2 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-crashed_0)
lola: after: (3 <= 0)
lola: LP says that atomic proposition is always false: (1 <= P-negotiation_0_0_DONE)
lola: place invariant simplifies atomic proposition
lola: before: (3 <= P-crashed_0)
lola: after: (3 <= 0)
lola: LP says that atomic proposition is always false: (1 <= P-negotiation_0_0_DONE)
lola: LP says that atomic proposition is always false: (1 <= P-masterState_0_F_2)
lola: place invariant simplifies atomic proposition
lola: before: (2 <= P-crashed_1)
lola: after: (2 <= 0)
lola: A ((X ((G ((2 <= 0)) OR F ((0 <= P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0)))) U (() OR F ((0 <= 1))))) : A ((NOT(G (NOT(((0 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2) OR X ((3 <= 0)))))) OR (F (X ((0 <= P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2))) AND NOT(F ((1 <= P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0)))))) : A (NOT(((P-polling_0 + P-polling_1 + P-polling_2 <= 2) AND F (NOT(F (NOT(F (G (F ((2 <= P-polling_0 + P-polling_1 + P-polling_2))))))))))) : A (((P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 <= 0) AND NOT((X ((P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 <= 0)) AND G ((2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)))))) : A (F (X ((X (G ((P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= 2))) OR F (X (((P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0) AND F ((P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0 + 1 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1))))))))) : A ((NOT((G ((P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_0_2 <= 2)) U (3 <= P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_2_2_AnsP_2))) AND F ((P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0 + 1 <= P-electionInit_0 + P-electionInit_1 + P-electionInit_2)))) : A (NOT(F (()))) : A (F (X (((2 <= P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP_0 + P-network_1_0_AnnP_0 + P-network_2_1_AskP_0 + P-network_0_0_RI_0 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_1_1_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_RP_0 + P-network_2_1_RP_0 + P-network_0_2_AI_0 + P-network_2_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_1_AskP_0 + P-network_0_1_AI_0 + P-network_2_0_AI_0 + P-network_2_2_RP_0 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_0_1_AnsP_0 + P-network_0_1_AnnP_0 + P-network_2_0_RI_0 + P-network_2_0_AnsP_2 + P-network_0_1_RI_0 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_0_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_1_RP_0 + P-network_0_2_RI_0 + P-network_1_0_AskP_0 + P-network_2_1_RI_0 + P-network_1_0_AI_0 + P-network_2_2_AnnP_0 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_0 + P-network_2_2_AI_0 + P-network_1_1_AnnP_0 + P-network_0_0_AskP_0 + P-network_1_2_AnnP_0 + P-network_0_1_RP_0 + P-network_2_0_RP_0 + P-network_1_2_AI_0 + P-network_1_1_RI_0 + P-network_0_2_AnnP_0 + P-network_0_0_AI_0 + P-network_2_1_AnnP_0) AND (G ((2 <= P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)) OR ((P-electionInit_0 + P-electionInit_1 + P-electionInit_2 <= 0) U ())))))) : A (NOT(F (((P-sendAnnPs__broadcasting_1_1 <= P-masterState_1_F_0) AND X ((G ((0 <= P-electedPrimary_0)) OR F (G (F ((0 <= P-negotiation_2_0_NONE)))))))))) : A ((X ((P-startNeg__broadcasting_1_1 <= P-polling_1)) OR G ((F ((NOT(X (((1 <= P-negotiation_2_2_CO) U (P-poll__pollEnd_0 <= P-sendAnnPs__broadcasting_1_2)))) U (P-polling_1 + 1 <= P-startNeg__broadcasting_1_1))) U (3 <= P-polling_2))))) : A (((X ((0 <= P-sendAnnPs__broadcasting_2_2)) OR NOT(G ((0 <= P-sendAnnPs__broadcasting_2_2)))) U G (X (G (((0 <= 0) OR G ((0 <= 0)))))))) : A (F (((1 <= 0) AND G (((0 <= P-sendAnnPs__broadcasting_2_2) U (P-stage_0_NEG <= P-poll__pollEnd_2)))))) : A ((((P-poll__pollEnd_2 <= 0) OR G ((3 <= P-electedSecondary_1))) U (((P-poll__pollEnd_2 <= 0) AND F (X (((0 <= P-polling_1) AND G ((P-stage_0_PRIM <= 0)))))) U (1 <= P-masterState_2_F_1)))) : A (F (X (((0 <= 0) AND F (((P-network_0_1_AnsP_1 <= P-electedPrimary_2) AND F (G (F (X (F ((P-poll__handlingMessage_2 <= 0)))))))))))) : A (G ((() AND X (((1 <= P-negotiation_0_0_DONE) OR ((P-masterState_0_F_2 <= 0) AND X ((0 <= P-poll__waitingMessage_0)))))))) : A (NOT(F ((2 <= 0))))
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:122
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:124
lola: rewrite Frontend/Parser/formula_rewrite.k:166
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:145
lola: rewrite Frontend/Parser/formula_rewrite.k:124
lola: rewrite Frontend/Parser/formula_rewrite.k:279
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:282
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:356
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:332
lola: rewrite Frontend/Parser/formula_rewrite.k:297
lola: rewrite Frontend/Parser/formula_rewrite.k:124
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:371
lola: rewrite Frontend/Parser/formula_rewrite.k:329
lola: rewrite Frontend/Parser/formula_rewrite.k:332
lola: rewrite Frontend/Parser/formula_rewrite.k:297
lola: rewrite Frontend/Parser/formula_rewrite.k:347
lola: rewrite Frontend/Parser/formula_rewrite.k:332
lola: rewrite Frontend/Parser/formula_rewrite.k:329
lola: rewrite Frontend/Parser/formula_rewrite.k:300
lola: rewrite Frontend/Parser/formula_rewrite.k:371
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:329
lola: rewrite Frontend/Parser/formula_rewrite.k:332
lola: rewrite Frontend/Parser/formula_rewrite.k:297
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:117
lola: rewrite Frontend/Parser/formula_rewrite.k:282
lola: rewrite Frontend/Parser/formula_rewrite.k:115
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:145
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:121
lola: rewrite Frontend/Parser/formula_rewrite.k:142
lola: rewrite Frontend/Parser/formula_rewrite.k:356
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:169
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:282
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:279
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:180
lola: rewrite Frontend/Parser/formula_rewrite.k:122
lola: rewrite Frontend/Parser/formula_rewrite.k:117
lola: rewrite Frontend/Parser/formula_rewrite.k:145
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:124
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:356
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:335
lola: rewrite Frontend/Parser/formula_rewrite.k:279
lola: rewrite Frontend/Parser/formula_rewrite.k:145
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:185
lola: rewrite Frontend/Parser/formula_rewrite.k:335
lola: rewrite Frontend/Parser/formula_rewrite.k:279
lola: rewrite Frontend/Parser/formula_rewrite.k:145
lola: rewrite Frontend/Parser/formula_rewrite.k:185
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:180
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:121
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:279
lola: rewrite Frontend/Parser/formula_rewrite.k:121
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:124
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:353
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:410
lola: rewrite Frontend/Parser/formula_rewrite.k:169
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:169
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:118
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:121
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:160
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:356
lola: rewrite Frontend/Parser/formula_rewrite.k:154
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:180
lola: rewrite Frontend/Parser/formula_rewrite.k:180
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:356
lola: rewrite Frontend/Parser/formula_rewrite.k:347
lola: rewrite Frontend/Parser/formula_rewrite.k:353
lola: rewrite Frontend/Parser/formula_rewrite.k:377
lola: rewrite Frontend/Parser/formula_rewrite.k:371
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:371
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:377
lola: rewrite Frontend/Parser/formula_rewrite.k:371
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:100
lola: rewrite Frontend/Parser/formula_rewrite.k:116
lola: rewrite Frontend/Parser/formula_rewrite.k:122
lola: rewrite Frontend/Parser/formula_rewrite.k:142
lola: rewrite Frontend/Parser/formula_rewrite.k:118
lola: rewrite Frontend/Parser/formula_rewrite.k:163
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: rewrite Frontend/Parser/formula_rewrite.k:98
lola: rewrite Frontend/Parser/formula_rewrite.k:157
lola: rewrite Frontend/Parser/formula_rewrite.k:282
lola: rewrite Frontend/Parser/formula_rewrite.k:151
lola: computing a collection of formulas
lola: RUNNING
lola: subprocess 0 will run for 222 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: TRUE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: TRUE
lola: processed formula length: 4
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: preprocessing
lola: The net satisfies the property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 1 will run for 237 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: TRUE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: TRUE
lola: processed formula length: 4
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: preprocessing
lola: The net satisfies the property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 2 will run for 254 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: (P-network_1_0_RI_0 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_0_0_RP_0 + P-network_1_2_AnsP_0 + P-network_0_0_AnnP_0 + P-network_1_2_RP_0 + P-network_2_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AI_0 + P-network_2_2_AskP_0 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_0_2_AskP... (shortened)
lola: processed formula length: 1606
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 1 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: preprocessing
lola: The net satisfies the property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 3 will run for 274 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 4 will run for 297 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 5 will run for 324 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 6 will run for 356 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 7 will run for 396 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 8 will run for 445 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: FALSE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 9 will run for 509 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: TRUE
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: TRUE
lola: processed formula length: 4
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: preprocessing
lola: The net satisfies the property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 10 will run for 594 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (X ((P-startNeg__broadcasting_1_1 <= P-polling_1)))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a Büchi-Automaton
lola: processed formula: A (X ((P-startNeg__broadcasting_1_1 <= P-polling_1)))
lola: processed formula length: 53
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: the resulting Büchi automaton has 3 states
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: Formula contains X operator; stubborn sets not applicable
lola: Formula contains X operator; stubborn sets not applicable
lola: SEARCH
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: LTL model checker
lola: The net does not satisfy the given formula (language of the product automaton is nonempty).
lola: 34 markings, 34 edges
lola: ========================================
lola: subprocess 11 will run for 713 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (X (TRUE))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a Büchi-Automaton
lola: processed formula: A (X (TRUE))
lola: processed formula length: 12
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: the resulting Büchi automaton has 3 states
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: Formula contains X operator; stubborn sets not applicable
lola: Formula contains X operator; stubborn sets not applicable
lola: SEARCH
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: LTL model checker
lola: The net satisfies the given formula (language of the product automaton is empty).
lola: 3 markings, 2 edges
lola: ========================================
lola: subprocess 12 will run for 891 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (X (TRUE))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a Büchi-Automaton
lola: processed formula: A (X (TRUE))
lola: processed formula length: 12
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: the resulting Büchi automaton has 3 states
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: Formula contains X operator; stubborn sets not applicable
lola: Formula contains X operator; stubborn sets not applicable
lola: SEARCH
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: LTL model checker
lola: The net satisfies the given formula (language of the product automaton is empty).
lola: 3 markings, 2 edges
lola: ========================================
lola: subprocess 13 will run for 1188 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (F ((P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0 + 1 <= P-electionInit_0 + P-electionInit_1 + P-electionInit_2)))
lola: ========================================
lola: SUBTASK
lola: checking eventual occurrence
lola: rewrite Frontend/Parser/formula_rewrite.k:749
lola: rewrite Frontend/Parser/formula_rewrite.k:787
lola: processed formula: (P-electionInit_0 + P-electionInit_1 + P-electionInit_2 <= P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0)
lola: processed formula length: 117
lola: 168 rewrites
lola: closed formula file LTLCardinality.xml
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space / EG)
lola: state space: using search routine for EG formula (--search=depth)
lola: state space: using EG preserving stubborn set method (--stubborn=tarjan)
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: state space / EG
lola: The predicate eventually occurs.
lola: 1 markings, 0 edges
lola: ========================================
lola: subprocess 14 will run for 1782 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (G (F ((P-poll__handlingMessage_2 <= 0))))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a Büchi-Automaton
lola: processed formula: A (G (F ((P-poll__handlingMessage_2 <= 0))))
lola: processed formula length: 44
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: the resulting Büchi automaton has 2 states
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: using ltl preserving stubborn set method with deletion algorithm (--stubborn=deletion)
lola: using ltl preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: SEARCH
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: LTL model checker
lola: The net does not satisfy the given formula (language of the product automaton is nonempty).
lola: 56 markings, 65 edges
lola: ========================================
lola: subprocess 15 will run for 3564 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: A (F (G ((P-polling_0 + P-polling_1 + P-polling_2 <= 1))))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a Büchi-Automaton
lola: processed formula: A (F (G ((P-polling_0 + P-polling_1 + P-polling_2 <= 1))))
lola: processed formula length: 58
lola: 166 rewrites
lola: closed formula file LTLCardinality.xml
lola: the resulting Büchi automaton has 2 states
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: using ltl preserving stubborn set method with deletion algorithm (--stubborn=deletion)
lola: using ltl preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: SEARCH
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: LTL model checker
lola: The net satisfies the given formula (language of the product automaton is empty).
lola: 279 markings, 565 edges
lola: ========================================
lola: RESULT
lola:
SUMMARY: yes yes yes yes yes yes no no no no yes no no no no yes
lola:
preliminary result: yes yes yes yes yes yes no no no no yes no no no no yes
lola: memory consumption: 22832 KB
lola: time consumption: 6 seconds
lola: print data as JSON (--json)
lola: writing JSON to LTLCardinality.json
lola: closed JSON file LTLCardinality.json
rslt: finished
BK_STOP 1590337623072
--------------------
content from stderr:
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-2"
export BK_EXAMINATION="LTLCardinality"
export BK_TOOL="win2019"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-4028"
echo " Executing tool win2019"
echo " Input is NeoElection-PT-2, examination is LTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r120-csrt-158961292500069"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-2.tgz
mv NeoElection-PT-2 execution
cd execution
if [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "UpperBounds" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] || [ "LTLCardinality" = "StateSpace" ]; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
elif [ "LTLCardinality" = "ReachabilityDeadlock" ] || [ "LTLCardinality" = "QuasiLiveness" ] || [ "LTLCardinality" = "StableMarking" ] || [ "LTLCardinality" = "Liveness" ] || [ "LTLCardinality" = "OneSafe" ] ; then
echo "FORMULA_NAME LTLCardinality"
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

