About the Execution of ITS-Tools for PhaseVariation-PT-D30CS010
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 15918.950 | 3600000.00 | 12978445.00 | 1550.30 | T?FTF??????????? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
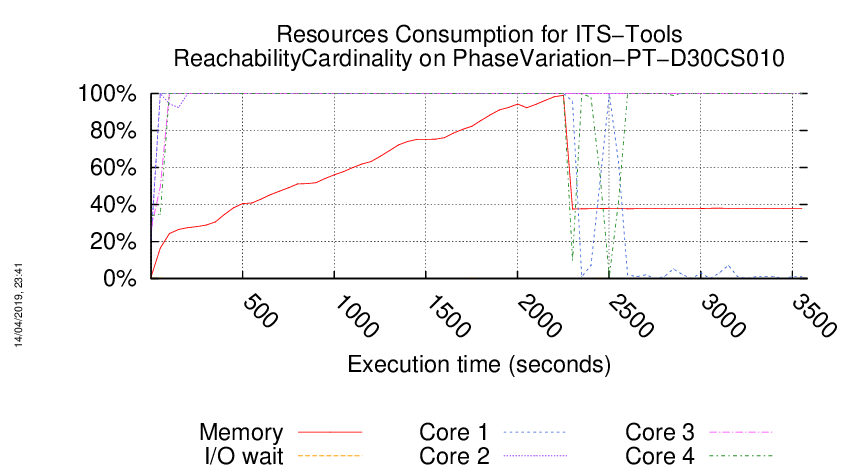
Trace from the execution
Formatting '/data/fko/mcc2019-input.r107-oct2-155272231300656.qcow2', fmt=qcow2 size=4294967296 backing_file=/data/fko/mcc2019-input.qcow2 cluster_size=65536 lazy_refcounts=off refcount_bits=16
Waiting for the VM to be ready (probing ssh)
.............................................................
=====================================================================
Generated by BenchKit 2-3954
Executing tool itstools
Input is PhaseVariation-PT-D30CS010, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r107-oct2-155272231300656
=====================================================================
--------------------
preparation of the directory to be used:
/home/mcc/execution
total 30M
-rw-r--r-- 1 mcc users 4.1K Feb 12 04:32 CTLCardinality.txt
-rw-r--r-- 1 mcc users 19K Feb 12 04:32 CTLCardinality.xml
-rw-r--r-- 1 mcc users 3.8K Feb 8 03:45 CTLFireability.txt
-rw-r--r-- 1 mcc users 17K Feb 8 03:45 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K Mar 10 17:31 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 5.6K Mar 10 17:31 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 113 Feb 24 15:05 GlobalProperties.txt
-rw-r--r-- 1 mcc users 351 Feb 24 15:05 GlobalProperties.xml
-rw-r--r-- 1 mcc users 2.7K Feb 5 00:27 LTLCardinality.txt
-rw-r--r-- 1 mcc users 9.9K Feb 5 00:27 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.6K Feb 4 22:37 LTLFireability.txt
-rw-r--r-- 1 mcc users 9.5K Feb 4 22:37 LTLFireability.xml
-rw-r--r-- 1 mcc users 4.2K Feb 4 08:17 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 18K Feb 4 08:17 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 3.4K Feb 1 02:42 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 12K Feb 1 02:42 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 1.9K Feb 4 22:22 UpperBounds.txt
-rw-r--r-- 1 mcc users 4.0K Feb 4 22:22 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 Jan 29 09:34 equiv_col
-rw-r--r-- 1 mcc users 9 Jan 29 09:34 instance
-rw-r--r-- 1 mcc users 6 Jan 29 09:34 iscolored
-rw-r--r-- 1 mcc users 30M Mar 10 17:31 model.pnml
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-00
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-01
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-02
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-03
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-04
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-05
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-06
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-07
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-08
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-09
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-10
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-11
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-12
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-13
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-14
FORMULA_NAME PhaseVariation-PT-D30CS010-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1552946501802
Working with output stream class java.io.PrintStream
Using solver Z3 to compute partial order matrices.
Built C files in :
/home/mcc/execution
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201903111103/bin/its-reach-linux64, --gc-threshold, 2000000, --quiet, -i, /home/mcc/execution/ReachabilityCardinality.pnml.gal, -t, CGAL, -reachable-file, ReachabilityCardinality.prop, --nowitness], workingDir=/home/mcc/execution]
its-reach command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201903111103/bin/its-reach-linux64 --gc-threshold 2000000 --quiet -i /home/mcc/execution/ReachabilityCardinality.pnml.gal -t CGAL -reachable-file ReachabilityCardinality.prop --nowitness
Running compilation step : CommandLine [args=[gcc, -c, -I/home/mcc/BenchKit//lts_install_dir//include, -I., -std=c99, -fPIC, -O2, model.c], workingDir=/home/mcc/execution]
Loading property file ReachabilityCardinality.prop.
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-00 with value :(!((!(cell___8_28__A_<=pool__29_16_))&&(pool__8_16_>=2)))
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-01 with value :(cell___6_6__A_<=cell___27_2__B_)
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-02 with value :(cell___17_2__A_>=3)
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-03 with value :((((cell___2_21__A_>=3)&&(pool__24_15_>=3))||(!(cell___3_4__B_>=3)))||(((pool__20_7_<=pool__20_17_)||(cell___9_13__B_>=2))||(cell___26_6__A_>=1)))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-04 with value :((((cell___11_2__A_>=2)||(cell___4_4__A_>=3))&&(!(pool__10_7_>=1)))&&(cell___29_2__B_<=cell___20_6__A_))
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-05 with value :(cell___18_8__B_<=pool__11_26_)
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-06 with value :(!(cell___19_15__B_<=cell___27_11__B_))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-07 with value :(!(((cell___18_10__A_>=3)&&(cell___16_4__B_<=pool__25_22_))||(pool__29_6_>=1)))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-08 with value :((((cell___23_26__B_<=pool__8_19_)||(pool__2_12_>=1))&&(!(cell___6_16__A_<=pool__9_6_)))&&(cell___9_4__A_>=1))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-09 with value :(((cell___15_4__B_<=cell___16_15__A_)||(cell___15_14__B_>=1))&&(!((cell___19_1__A_<=cell___28_3__B_)||(cell___7_13__A_<=cell___16_28__B_))))
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-10 with value :(!(cell___5_23__B_>=2))
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-11 with value :((cell___7_20__A_<=cell___28_4__B_)&&(((cell___6_3__B_>=1)||(cell___12_20__B_>=3))||(!(cell___15_12__A_>=2))))
Read [invariant] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-12 with value :(!(((cell___25_18__A_>=2)||(cell___12_22__B_<=pool__23_24_))&&((cell___24_28__A_<=cell___19_21__B_)&&(cell___23_30__B_>=2))))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-13 with value :((cell___9_30__B_>=1)&&(((pool__1_3_>=1)||(pool__29_8_<=pool__27_18_))||((cell___5_6__B_>=3)||(cell___4_22__A_>=1))))
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-14 with value :(cell___21_9__B_>=1)
Read [reachable] property : PhaseVariation-PT-D30CS010-ReachabilityCardinality-15 with value :(((cell___15_3__A_<=pool__3_17_)||((cell___25_24__B_>=3)||(cell___25_6__A_<=cell___28_27__B_)))&&(cell___27_2__B_>=1))
Presburger conditions satisfied. Using coverability to approximate state space in K-Induction.
Normalized transition count is 1801
// Phase 1: matrix 1801 rows 2702 cols
invariant :cell___21_7__A_ + cell___21_7__B_ + pool__21_7_ = 1
invariant :cell___25_7__A_ + cell___25_7__B_ + pool__25_7_ = 1
invariant :cell___8_4__A_ + cell___8_4__B_ + pool__8_4_ = 1
invariant :cell___25_4__A_ + cell___25_4__B_ + pool__25_4_ = 1
invariant :cell___9_9__A_ + cell___9_9__B_ + pool__9_9_ = 1
invariant :cell___19_30__A_ + cell___19_30__B_ + pool__19_30_ = 1
invariant :cell___1_5__A_ + cell___1_5__B_ + pool__1_5_ = 1
invariant :cell___10_12__A_ + cell___10_12__B_ + pool__10_12_ = 1
invariant :cell___16_1__A_ + cell___16_1__B_ + pool__16_1_ = 1
invariant :cell___30_24__A_ + cell___30_24__B_ + pool__30_24_ = 1
invariant :cell___24_13__A_ + cell___24_13__B_ + pool__24_13_ = 1
invariant :cell___6_12__A_ + cell___6_12__B_ + pool__6_12_ = 1
invariant :cell___13_23__A_ + cell___13_23__B_ + pool__13_23_ = 1
invariant :cell___29_12__A_ + cell___29_12__B_ + pool__29_12_ = 1
invariant :cell___16_30__A_ + cell___16_30__B_ + pool__16_30_ = 1
invariant :cell___28_3__A_ + cell___28_3__B_ + pool__28_3_ = 1
invariant :cell___1_26__A_ + cell___1_26__B_ + pool__1_26_ = 1
invariant :cell___20_29__A_ + cell___20_29__B_ + pool__20_29_ = 1
invariant :cell___22_6__A_ + cell___22_6__B_ + pool__22_6_ = 1
invariant :cell___11_25__A_ + cell___11_25__B_ + pool__11_25_ = 1
invariant :cell___3_2__A_ + cell___3_2__B_ + pool__3_2_ = 1
invariant :cell___21_9__A_ + cell___21_9__B_ + pool__21_9_ = 1
invariant :cell___24_3__A_ + cell___24_3__B_ + pool__24_3_ = 1
invariant :cell___7_6__A_ + cell___7_6__B_ + pool__7_6_ = 1
invariant :cell___11_2__A_ + cell___11_2__B_ + pool__11_2_ = 1
invariant :cell___17_21__A_ + cell___17_21__B_ + pool__17_21_ = 1
invariant :cell___29_9__A_ + cell___29_9__B_ + pool__29_9_ = 1
invariant :cell___19_27__A_ + cell___19_27__B_ + pool__19_27_ = 1
invariant :cell___27_11__A_ + cell___27_11__B_ + pool__27_11_ = 1
invariant :cell___1_23__A_ + cell___1_23__B_ + pool__1_23_ = 1
invariant :cell___23_13__A_ + cell___23_13__B_ + pool__23_13_ = 1
invariant :cell___8_10__A_ + cell___8_10__B_ + pool__8_10_ = 1
invariant :cell___2_9__A_ + cell___2_9__B_ + pool__2_9_ = 1
invariant :cell___9_21__A_ + cell___9_21__B_ + pool__9_21_ = 1
invariant :cell___11_24__A_ + cell___11_24__B_ + pool__11_24_ = 1
invariant :cell___28_17__A_ + cell___28_17__B_ + pool__28_17_ = 1
invariant :cell___30_10__A_ + cell___30_10__B_ + pool__30_10_ = 1
invariant :cell___19_10__A_ + cell___19_10__B_ + pool__19_10_ = 1
invariant :cell___20_30__A_ + cell___20_30__B_ + pool__20_30_ = 1
invariant :cell___7_11__A_ + cell___7_11__B_ + pool__7_11_ = 1
invariant :cell___24_25__A_ + cell___24_25__B_ + pool__24_25_ = 1
invariant :cell___3_23__A_ + cell___3_23__B_ + pool__3_23_ = 1
invariant :cell___24_1__A_ + cell___24_1__B_ + pool__24_1_ = 1
invariant :cell___3_3__A_ + cell___3_3__B_ + pool__3_3_ = 1
invariant :cell___28_5__A_ + cell___28_5__B_ + pool__28_5_ = 1
invariant :cell___15_30__A_ + cell___15_30__B_ + pool__15_30_ = 1
invariant :cell___6_14__A_ + cell___6_14__B_ + pool__6_14_ = 1
invariant :cell___8_6__A_ + cell___8_6__B_ + pool__8_6_ = 1
invariant :cell___15_3__A_ + cell___15_3__B_ + pool__15_3_ = 1
invariant :cell___2_16__A_ + cell___2_16__B_ + pool__2_16_ = 1
invariant :cell___20_1__A_ + cell___20_1__B_ + pool__20_1_ = 1
invariant :cell___18_20__A_ + cell___18_20__B_ + pool__18_20_ = 1
invariant :cell___19_23__A_ + cell___19_23__B_ + pool__19_23_ = 1
invariant :cell___10_18__A_ + cell___10_18__B_ + pool__10_18_ = 1
invariant :cell___25_1__A_ + cell___25_1__B_ + pool__25_1_ = 1
invariant :cell___3_26__A_ + cell___3_26__B_ + pool__3_26_ = 1
invariant :cell___30_19__A_ + cell___30_19__B_ + pool__30_19_ = 1
invariant :cell___18_29__A_ + cell___18_29__B_ + pool__18_29_ = 1
invariant :cell___1_9__A_ + cell___1_9__B_ + pool__1_9_ = 1
invariant :cell___8_13__A_ + cell___8_13__B_ + pool__8_13_ = 1
invariant :cell___8_21__A_ + cell___8_21__B_ + pool__8_21_ = 1
invariant :cell___27_19__A_ + cell___27_19__B_ + pool__27_19_ = 1
invariant :cell___15_11__A_ + cell___15_11__B_ + pool__15_11_ = 1
invariant :cell___20_27__A_ + cell___20_27__B_ + pool__20_27_ = 1
invariant :cell___18_18__A_ + cell___18_18__B_ + pool__18_18_ = 1
invariant :cell___16_7__A_ + cell___16_7__B_ + pool__16_7_ = 1
invariant :cell___27_7__A_ + cell___27_7__B_ + pool__27_7_ = 1
invariant :cell___3_19__A_ + cell___3_19__B_ + pool__3_19_ = 1
invariant :cell___14_2__A_ + cell___14_2__B_ + pool__14_2_ = 1
invariant :cell___9_11__A_ + cell___9_11__B_ + pool__9_11_ = 1
invariant :cell___1_4__A_ + cell___1_4__B_ + pool__1_4_ = 1
invariant :cell___6_26__A_ + cell___6_26__B_ + pool__6_26_ = 1
invariant :cell___13_7__A_ + cell___13_7__B_ + pool__13_7_ = 1
invariant :cell___18_2__A_ + cell___18_2__B_ + pool__18_2_ = 1
invariant :cell___15_24__A_ + cell___15_24__B_ + pool__15_24_ = 1
invariant :cell___13_30__A_ + cell___13_30__B_ + pool__13_30_ = 1
invariant :cell___17_19__A_ + cell___17_19__B_ + pool__17_19_ = 1
invariant :cell___26_17__A_ + cell___26_17__B_ + pool__26_17_ = 1
invariant :cell___8_26__A_ + cell___8_26__B_ + pool__8_26_ = 1
invariant :cell___22_7__A_ + cell___22_7__B_ + pool__22_7_ = 1
invariant :cell___4_13__A_ + cell___4_13__B_ + pool__4_13_ = 1
invariant :cell___12_30__A_ + cell___12_30__B_ + pool__12_30_ = 1
invariant :cell___1_11__A_ + cell___1_11__B_ + pool__1_11_ = 1
invariant :cell___26_5__A_ + cell___26_5__B_ + pool__26_5_ = 1
invariant :cell___29_28__A_ + cell___29_28__B_ + pool__29_28_ = 1
invariant :cell___10_2__A_ + cell___10_2__B_ + pool__10_2_ = 1
invariant :cell___1_27__A_ + cell___1_27__B_ + pool__1_27_ = 1
invariant :cell___3_22__A_ + cell___3_22__B_ + pool__3_22_ = 1
invariant :cell___19_8__A_ + cell___19_8__B_ + pool__19_8_ = 1
invariant :cell___27_20__A_ + cell___27_20__B_ + pool__27_20_ = 1
invariant :cell___21_25__A_ + cell___21_25__B_ + pool__21_25_ = 1
invariant :cell___24_18__A_ + cell___24_18__B_ + pool__24_18_ = 1
invariant :cell___1_7__A_ + cell___1_7__B_ + pool__1_7_ = 1
invariant :cell___24_29__A_ + cell___24_29__B_ + pool__24_29_ = 1
invariant :cell___10_6__A_ + cell___10_6__B_ + pool__10_6_ = 1
invariant :cell___1_19__A_ + cell___1_19__B_ + pool__1_19_ = 1
invariant :cell___2_23__A_ + cell___2_23__B_ + pool__2_23_ = 1
invariant :cell___1_6__A_ + cell___1_6__B_ + pool__1_6_ = 1
invariant :cell___2_18__A_ + cell___2_18__B_ + pool__2_18_ = 1
invariant :cell___27_29__A_ + cell___27_29__B_ + pool__27_29_ = 1
invariant :cell___25_23__A_ + cell___25_23__B_ + pool__25_23_ = 1
invariant :cell___4_24__A_ + cell___4_24__B_ + pool__4_24_ = 1
invariant :cell___18_17__A_ + cell___18_17__B_ + pool__18_17_ = 1
invariant :cell___1_1__A_ + cell___1_1__B_ + pool__1_1_ = 1
invariant :cell___29_29__A_ + cell___29_29__B_ + pool__29_29_ = 1
invariant :cell___17_6__A_ + cell___17_6__B_ + pool__17_6_ = 1
invariant :cell___26_11__A_ + cell___26_11__B_ + pool__26_11_ = 1
invariant :cell___26_2__A_ + cell___26_2__B_ + pool__26_2_ = 1
invariant :cell___8_15__A_ + cell___8_15__B_ + pool__8_15_ = 1
invariant :cell___15_5__A_ + cell___15_5__B_ + pool__15_5_ = 1
invariant :cell___2_28__A_ + cell___2_28__B_ + pool__2_28_ = 1
invariant :cell___21_5__A_ + cell___21_5__B_ + pool__21_5_ = 1
invariant :cell___22_24__A_ + cell___22_24__B_ + pool__22_24_ = 1
invariant :cell___1_17__A_ + cell___1_17__B_ + pool__1_17_ = 1
invariant :cell___2_27__A_ + cell___2_27__B_ + pool__2_27_ = 1
invariant :cell___14_19__A_ + cell___14_19__B_ + pool__14_19_ = 1
invariant :cell___1_25__A_ + cell___1_25__B_ + pool__1_25_ = 1
invariant :cell___15_20__A_ + cell___15_20__B_ + pool__15_20_ = 1
invariant :cell___3_16__A_ + cell___3_16__B_ + pool__3_16_ = 1
invariant :cell___16_26__A_ + cell___16_26__B_ + pool__16_26_ = 1
invariant :cell___7_29__A_ + cell___7_29__B_ + pool__7_29_ = 1
invariant :cell___8_24__A_ + cell___8_24__B_ + pool__8_24_ = 1
invariant :cell___6_16__A_ + cell___6_16__B_ + pool__6_16_ = 1
invariant :cell___15_25__A_ + cell___15_25__B_ + pool__15_25_ = 1
invariant :cell___28_20__A_ + cell___28_20__B_ + pool__28_20_ = 1
invariant :cell___27_14__A_ + cell___27_14__B_ + pool__27_14_ = 1
invariant :cell___24_8__A_ + cell___24_8__B_ + pool__24_8_ = 1
invariant :cell___8_19__A_ + cell___8_19__B_ + pool__8_19_ = 1
invariant :cell___30_9__A_ + cell___30_9__B_ + pool__30_9_ = 1
invariant :cell___25_29__A_ + cell___25_29__B_ + pool__25_29_ = 1
invariant :cell___7_25__A_ + cell___7_25__B_ + pool__7_25_ = 1
invariant :cell___10_14__A_ + cell___10_14__B_ + pool__10_14_ = 1
invariant :cell___13_22__A_ + cell___13_22__B_ + pool__13_22_ = 1
invariant :cell___25_12__A_ + cell___25_12__B_ + pool__25_12_ = 1
invariant :cell___5_21__A_ + cell___5_21__B_ + pool__5_21_ = 1
invariant :cell___15_23__A_ + cell___15_23__B_ + pool__15_23_ = 1
invariant :cell___6_17__A_ + cell___6_17__B_ + pool__6_17_ = 1
invariant :cell___17_18__A_ + cell___17_18__B_ + pool__17_18_ = 1
invariant :cell___25_18__A_ + cell___25_18__B_ + pool__25_18_ = 1
invariant :cell___1_10__A_ + cell___1_10__B_ + pool__1_10_ = 1
invariant :cell___12_5__A_ + cell___12_5__B_ + pool__12_5_ = 1
invariant :cell___12_11__A_ + cell___12_11__B_ + pool__12_11_ = 1
invariant :cell___26_8__A_ + cell___26_8__B_ + pool__26_8_ = 1
invariant :cell___28_28__A_ + cell___28_28__B_ + pool__28_28_ = 1
invariant :cell___14_30__A_ + cell___14_30__B_ + pool__14_30_ = 1
invariant :cell___19_16__A_ + cell___19_16__B_ + pool__19_16_ = 1
invariant :cell___17_10__A_ + cell___17_10__B_ + pool__17_10_ = 1
invariant :cell___9_12__A_ + cell___9_12__B_ + pool__9_12_ = 1
invariant :cell___11_16__A_ + cell___11_16__B_ + pool__11_16_ = 1
invariant :cell___30_18__A_ + cell___30_18__B_ + pool__30_18_ = 1
invariant :cell___14_21__A_ + cell___14_21__B_ + pool__14_21_ = 1
invariant :cell___24_21__A_ + cell___24_21__B_ + pool__24_21_ = 1
invariant :cell___29_7__A_ + cell___29_7__B_ + pool__29_7_ = 1
invariant :cell___3_24__A_ + cell___3_24__B_ + pool__3_24_ = 1
invariant :cell___7_3__A_ + cell___7_3__B_ + pool__7_3_ = 1
invariant :cell___11_8__A_ + cell___11_8__B_ + pool__11_8_ = 1
invariant :cell___20_18__A_ + cell___20_18__B_ + pool__20_18_ = 1
invariant :cell___15_1__A_ + cell___15_1__B_ + pool__15_1_ = 1
invariant :cell___23_12__A_ + cell___23_12__B_ + pool__23_12_ = 1
invariant :cell___3_25__A_ + cell___3_25__B_ + pool__3_25_ = 1
invariant :cell___12_18__A_ + cell___12_18__B_ + pool__12_18_ = 1
invariant :cell___8_29__A_ + cell___8_29__B_ + pool__8_29_ = 1
invariant :cell___13_1__A_ + cell___13_1__B_ + pool__13_1_ = 1
invariant :cell___9_18__A_ + cell___9_18__B_ + pool__9_18_ = 1
invariant :cell___15_17__A_ + cell___15_17__B_ + pool__15_17_ = 1
invariant :cell___9_29__A_ + cell___9_29__B_ + pool__9_29_ = 1
invariant :cell___12_12__A_ + cell___12_12__B_ + pool__12_12_ = 1
invariant :cell___24_11__A_ + cell___24_11__B_ + pool__24_11_ = 1
invariant :cell___19_14__A_ + cell___19_14__B_ + pool__19_14_ = 1
invariant :cell___3_18__A_ + cell___3_18__B_ + pool__3_18_ = 1
invariant :cell___25_20__A_ + cell___25_20__B_ + pool__25_20_ = 1
invariant :cell___25_30__A_ + cell___25_30__B_ + pool__25_30_ = 1
invariant :cell___25_24__A_ + cell___25_24__B_ + pool__25_24_ = 1
invariant :cell___19_19__A_ + cell___19_19__B_ + pool__19_19_ = 1
invariant :cell___19_5__A_ + cell___19_5__B_ + pool__19_5_ = 1
invariant :cell___17_30__A_ + cell___17_30__B_ + pool__17_30_ = 1
invariant :cell___5_7__A_ + cell___5_7__B_ + pool__5_7_ = 1
invariant :cell___24_26__A_ + cell___24_26__B_ + pool__24_26_ = 1
invariant :cell___21_2__A_ + cell___21_2__B_ + pool__21_2_ = 1
invariant :cell___30_26__A_ + cell___30_26__B_ + pool__30_26_ = 1
invariant :cell___7_26__A_ + cell___7_26__B_ + pool__7_26_ = 1
invariant :cell___18_5__A_ + cell___18_5__B_ + pool__18_5_ = 1
invariant :cell___17_5__A_ + cell___17_5__B_ + pool__17_5_ = 1
invariant :cell___22_9__A_ + cell___22_9__B_ + pool__22_9_ = 1
invariant :cell___30_28__A_ + cell___30_28__B_ + pool__30_28_ = 1
invariant :cell___25_22__A_ + cell___25_22__B_ + pool__25_22_ = 1
invariant :cell___8_20__A_ + cell___8_20__B_ + pool__8_20_ = 1
invariant :cell___30_1__A_ + cell___30_1__B_ + pool__30_1_ = 1
invariant :cell___16_6__A_ + cell___16_6__B_ + pool__16_6_ = 1
invariant :cell___7_10__A_ + cell___7_10__B_ + pool__7_10_ = 1
invariant :cell___5_16__A_ + cell___5_16__B_ + pool__5_16_ = 1
invariant :cell___5_8__A_ + cell___5_8__B_ + pool__5_8_ = 1
invariant :cell___11_27__A_ + cell___11_27__B_ + pool__11_27_ = 1
invariant :cell___26_6__A_ + cell___26_6__B_ + pool__26_6_ = 1
invariant :cell___21_26__A_ + cell___21_26__B_ + pool__21_26_ = 1
invariant :cell___26_14__A_ + cell___26_14__B_ + pool__26_14_ = 1
invariant :cell___15_12__A_ + cell___15_12__B_ + pool__15_12_ = 1
invariant :cell___20_14__A_ + cell___20_14__B_ + pool__20_14_ = 1
invariant :cell___17_27__A_ + cell___17_27__B_ + pool__17_27_ = 1
invariant :cell___25_10__A_ + cell___25_10__B_ + pool__25_10_ = 1
invariant :cell___4_9__A_ + cell___4_9__B_ + pool__4_9_ = 1
invariant :cell___11_7__A_ + cell___11_7__B_ + pool__11_7_ = 1
invariant :cell___18_1__A_ + cell___18_1__B_ + pool__18_1_ = 1
invariant :cell___26_23__A_ + cell___26_23__B_ + pool__26_23_ = 1
invariant :cell___13_5__A_ + cell___13_5__B_ + pool__13_5_ = 1
invariant :cell___6_9__A_ + cell___6_9__B_ + pool__6_9_ = 1
invariant :cell___13_14__A_ + cell___13_14__B_ + pool__13_14_ = 1
invariant :cell___18_6__A_ + cell___18_6__B_ + pool__18_6_ = 1
invariant :cell___2_13__A_ + cell___2_13__B_ + pool__2_13_ = 1
invariant :cell___17_14__A_ + cell___17_14__B_ + pool__17_14_ = 1
invariant :cell___30_30__A_ + cell___30_30__B_ + pool__30_30_ = 1
invariant :cell___5_5__A_ + cell___5_5__B_ + pool__5_5_ = 1
invariant :cell___21_10__A_ + cell___21_10__B_ + pool__21_10_ = 1
invariant :cell___24_5__A_ + cell___24_5__B_ + pool__24_5_ = 1
invariant :cell___12_3__A_ + cell___12_3__B_ + pool__12_3_ = 1
invariant :cell___28_2__A_ + cell___28_2__B_ + pool__28_2_ = 1
invariant :cell___14_6__A_ + cell___14_6__B_ + pool__14_6_ = 1
invariant :cell___22_18__A_ + cell___22_18__B_ + pool__22_18_ = 1
invariant :cell___6_19__A_ + cell___6_19__B_ + pool__6_19_ = 1
invariant :cell___17_23__A_ + cell___17_23__B_ + pool__17_23_ = 1
invariant :cell___29_4__A_ + cell___29_4__B_ + pool__29_4_ = 1
invariant :cell___5_15__A_ + cell___5_15__B_ + pool__5_15_ = 1
invariant :cell___27_5__A_ + cell___27_5__B_ + pool__27_5_ = 1
invariant :cell___29_21__A_ + cell___29_21__B_ + pool__29_21_ = 1
invariant :cell___18_3__A_ + cell___18_3__B_ + pool__18_3_ = 1
invariant :cell___2_14__A_ + cell___2_14__B_ + pool__2_14_ = 1
invariant :cell___27_27__A_ + cell___27_27__B_ + pool__27_27_ = 1
invariant :cell___22_21__A_ + cell___22_21__B_ + pool__22_21_ = 1
invariant :cell___27_30__A_ + cell___27_30__B_ + pool__27_30_ = 1
invariant :cell___23_6__A_ + cell___23_6__B_ + pool__23_6_ = 1
invariant :cell___21_29__A_ + cell___21_29__B_ + pool__21_29_ = 1
invariant :cell___16_25__A_ + cell___16_25__B_ + pool__16_25_ = 1
invariant :cell___25_11__A_ + cell___25_11__B_ + pool__25_11_ = 1
invariant :cell___1_20__A_ + cell___1_20__B_ + pool__1_20_ = 1
invariant :cell___18_10__A_ + cell___18_10__B_ + pool__18_10_ = 1
invariant :cell___7_18__A_ + cell___7_18__B_ + pool__7_18_ = 1
invariant :cell___14_20__A_ + cell___14_20__B_ + pool__14_20_ = 1
invariant :cell___8_17__A_ + cell___8_17__B_ + pool__8_17_ = 1
invariant :cell___22_22__A_ + cell___22_22__B_ + pool__22_22_ = 1
invariant :cell___28_23__A_ + cell___28_23__B_ + pool__28_23_ = 1
invariant :cell___2_22__A_ + cell___2_22__B_ + pool__2_22_ = 1
invariant :cell___6_30__A_ + cell___6_30__B_ + pool__6_30_ = 1
invariant :cell___21_24__A_ + cell___21_24__B_ + pool__21_24_ = 1
invariant :cell___22_19__A_ + cell___22_19__B_ + pool__22_19_ = 1
invariant :cell___23_21__A_ + cell___23_21__B_ + pool__23_21_ = 1
invariant :cell___13_4__A_ + cell___13_4__B_ + pool__13_4_ = 1
invariant :cell___9_5__A_ + cell___9_5__B_ + pool__9_5_ = 1
invariant :cell___5_6__A_ + cell___5_6__B_ + pool__5_6_ = 1
invariant :cell___3_1__A_ + cell___3_1__B_ + pool__3_1_ = 1
invariant :cell___9_15__A_ + cell___9_15__B_ + pool__9_15_ = 1
invariant :cell___24_4__A_ + cell___24_4__B_ + pool__24_4_ = 1
invariant :cell___14_3__A_ + cell___14_3__B_ + pool__14_3_ = 1
invariant :cell___14_9__A_ + cell___14_9__B_ + pool__14_9_ = 1
invariant :cell___26_7__A_ + cell___26_7__B_ + pool__26_7_ = 1
invariant :cell___2_11__A_ + cell___2_11__B_ + pool__2_11_ = 1
invariant :cell___23_23__A_ + cell___23_23__B_ + pool__23_23_ = 1
invariant :cell___25_28__A_ + cell___25_28__B_ + pool__25_28_ = 1
invariant :cell___29_18__A_ + cell___29_18__B_ + pool__29_18_ = 1
invariant :cell___16_23__A_ + cell___16_23__B_ + pool__16_23_ = 1
invariant :cell___3_9__A_ + cell___3_9__B_ + pool__3_9_ = 1
invariant :cell___27_9__A_ + cell___27_9__B_ + pool__27_9_ = 1
invariant :cell___10_29__A_ + cell___10_29__B_ + pool__10_29_ = 1
invariant :cell___14_8__A_ + cell___14_8__B_ + pool__14_8_ = 1
invariant :cell___24_24__A_ + cell___24_24__B_ + pool__24_24_ = 1
invariant :cell___17_8__A_ + cell___17_8__B_ + pool__17_8_ = 1
invariant :cell___29_27__A_ + cell___29_27__B_ + pool__29_27_ = 1
invariant :cell___1_14__A_ + cell___1_14__B_ + pool__1_14_ = 1
invariant :cell___4_18__A_ + cell___4_18__B_ + pool__4_18_ = 1
invariant :cell___1_12__A_ + cell___1_12__B_ + pool__1_12_ = 1
invariant :cell___21_18__A_ + cell___21_18__B_ + pool__21_18_ = 1
invariant :cell___7_13__A_ + cell___7_13__B_ + pool__7_13_ = 1
invariant :cell___11_11__A_ + cell___11_11__B_ + pool__11_11_ = 1
invariant :cell___22_8__A_ + cell___22_8__B_ + pool__22_8_ = 1
invariant :cell___11_6__A_ + cell___11_6__B_ + pool__11_6_ = 1
invariant :cell___23_9__A_ + cell___23_9__B_ + pool__23_9_ = 1
invariant :cell___4_28__A_ + cell___4_28__B_ + pool__4_28_ = 1
invariant :cell___12_4__A_ + cell___12_4__B_ + pool__12_4_ = 1
invariant :cell___22_30__A_ + cell___22_30__B_ + pool__22_30_ = 1
invariant :cell___23_15__A_ + cell___23_15__B_ + pool__23_15_ = 1
invariant :cell___15_13__A_ + cell___15_13__B_ + pool__15_13_ = 1
invariant :cell___22_14__A_ + cell___22_14__B_ + pool__22_14_ = 1
invariant :cell___10_20__A_ + cell___10_20__B_ + pool__10_20_ = 1
invariant :cell___12_17__A_ + cell___12_17__B_ + pool__12_17_ = 1
invariant :cell___16_24__A_ + cell___16_24__B_ + pool__16_24_ = 1
invariant :cell___2_19__A_ + cell___2_19__B_ + pool__2_19_ = 1
invariant :cell___27_22__A_ + cell___27_22__B_ + pool__27_22_ = 1
invariant :cell___3_8__A_ + cell___3_8__B_ + pool__3_8_ = 1
invariant :cell___8_30__A_ + cell___8_30__B_ + pool__8_30_ = 1
invariant :cell___28_6__A_ + cell___28_6__B_ + pool__28_6_ = 1
invariant :cell___17_2__A_ + cell___17_2__B_ + pool__17_2_ = 1
invariant :cell___13_16__A_ + cell___13_16__B_ + pool__13_16_ = 1
invariant :cell___24_9__A_ + cell___24_9__B_ + pool__24_9_ = 1
invariant :cell___27_28__A_ + cell___27_28__B_ + pool__27_28_ = 1
invariant :cell___15_21__A_ + cell___15_21__B_ + pool__15_21_ = 1
invariant :cell___10_13__A_ + cell___10_13__B_ + pool__10_13_ = 1
invariant :cell___24_10__A_ + cell___24_10__B_ + pool__24_10_ = 1
invariant :cell___13_17__A_ + cell___13_17__B_ + pool__13_17_ = 1
invariant :cell___29_3__A_ + cell___29_3__B_ + pool__29_3_ = 1
invariant :cell___18_28__A_ + cell___18_28__B_ + pool__18_28_ = 1
invariant :cell___24_2__A_ + cell___24_2__B_ + pool__24_2_ = 1
invariant :cell___5_9__A_ + cell___5_9__B_ + pool__5_9_ = 1
invariant :cell___13_15__A_ + cell___13_15__B_ + pool__13_15_ = 1
invariant :cell___29_5__A_ + cell___29_5__B_ + pool__29_5_ = 1
invariant :cell___3_27__A_ + cell___3_27__B_ + pool__3_27_ = 1
invariant :cell___9_13__A_ + cell___9_13__B_ + pool__9_13_ = 1
invariant :cell___25_2__A_ + cell___25_2__B_ + pool__25_2_ = 1
invariant :cell___12_9__A_ + cell___12_9__B_ + pool__12_9_ = 1
invariant :cell___8_28__A_ + cell___8_28__B_ + pool__8_28_ = 1
invariant :cell___24_28__A_ + cell___24_28__B_ + pool__24_28_ = 1
invariant :cell___2_10__A_ + cell___2_10__B_ + pool__2_10_ = 1
invariant :cell___22_16__A_ + cell___22_16__B_ + pool__22_16_ = 1
invariant :cell___11_22__A_ + cell___11_22__B_ + pool__11_22_ = 1
invariant :cell___14_27__A_ + cell___14_27__B_ + pool__14_27_ = 1
invariant :cell___12_2__A_ + cell___12_2__B_ + pool__12_2_ = 1
invariant :cell___22_27__A_ + cell___22_27__B_ + pool__22_27_ = 1
invariant :cell___28_10__A_ + cell___28_10__B_ + pool__28_10_ = 1
invariant :cell___23_4__A_ + cell___23_4__B_ + pool__23_4_ = 1
invariant :cell___19_1__A_ + cell___19_1__B_ + pool__19_1_ = 1
invariant :cell___22_5__A_ + cell___22_5__B_ + pool__22_5_ = 1
invariant :cell___17_9__A_ + cell___17_9__B_ + pool__17_9_ = 1
invariant :cell___30_11__A_ + cell___30_11__B_ + pool__30_11_ = 1
invariant :cell___4_19__A_ + cell___4_19__B_ + pool__4_19_ = 1
invariant :cell___5_27__A_ + cell___5_27__B_ + pool__5_27_ = 1
invariant :cell___9_20__A_ + cell___9_20__B_ + pool__9_20_ = 1
invariant :cell___9_30__A_ + cell___9_30__B_ + pool__9_30_ = 1
invariant :cell___25_13__A_ + cell___25_13__B_ + pool__25_13_ = 1
invariant :cell___2_7__A_ + cell___2_7__B_ + pool__2_7_ = 1
invariant :cell___11_29__A_ + cell___11_29__B_ + pool__11_29_ = 1
invariant :cell___2_25__A_ + cell___2_25__B_ + pool__2_25_ = 1
invariant :cell___28_8__A_ + cell___28_8__B_ + pool__28_8_ = 1
invariant :cell___6_20__A_ + cell___6_20__B_ + pool__6_20_ = 1
invariant :cell___1_28__A_ + cell___1_28__B_ + pool__1_28_ = 1
invariant :cell___21_13__A_ + cell___21_13__B_ + pool__21_13_ = 1
invariant :cell___17_12__A_ + cell___17_12__B_ + pool__17_12_ = 1
invariant :cell___16_20__A_ + cell___16_20__B_ + pool__16_20_ = 1
invariant :cell___27_25__A_ + cell___27_25__B_ + pool__27_25_ = 1
invariant :cell___6_28__A_ + cell___6_28__B_ + pool__6_28_ = 1
invariant :cell___28_11__A_ + cell___28_11__B_ + pool__28_11_ = 1
invariant :cell___7_7__A_ + cell___7_7__B_ + pool__7_7_ = 1
invariant :cell___28_25__A_ + cell___28_25__B_ + pool__28_25_ = 1
invariant :cell___18_16__A_ + cell___18_16__B_ + pool__18_16_ = 1
invariant :cell___6_24__A_ + cell___6_24__B_ + pool__6_24_ = 1
invariant :cell___18_30__A_ + cell___18_30__B_ + pool__18_30_ = 1
invariant :cell___25_27__A_ + cell___25_27__B_ + pool__25_27_ = 1
invariant :cell___10_5__A_ + cell___10_5__B_ + pool__10_5_ = 1
invariant :cell___16_15__A_ + cell___16_15__B_ + pool__16_15_ = 1
invariant :cell___23_10__A_ + cell___23_10__B_ + pool__23_10_ = 1
invariant :cell___13_21__A_ + cell___13_21__B_ + pool__13_21_ = 1
invariant :cell___30_21__A_ + cell___30_21__B_ + pool__30_21_ = 1
invariant :cell___7_30__A_ + cell___7_30__B_ + pool__7_30_ = 1
invariant :cell___15_19__A_ + cell___15_19__B_ + pool__15_19_ = 1
invariant :cell___29_16__A_ + cell___29_16__B_ + pool__29_16_ = 1
invariant :cell___12_7__A_ + cell___12_7__B_ + pool__12_7_ = 1
invariant :cell___29_1__A_ + cell___29_1__B_ + pool__29_1_ = 1
invariant :cell___15_22__A_ + cell___15_22__B_ + pool__15_22_ = 1
invariant :cell___9_22__A_ + cell___9_22__B_ + pool__9_22_ = 1
invariant :cell___5_25__A_ + cell___5_25__B_ + pool__5_25_ = 1
invariant :cell___7_14__A_ + cell___7_14__B_ + pool__7_14_ = 1
invariant :cell___22_13__A_ + cell___22_13__B_ + pool__22_13_ = 1
invariant :cell___30_7__A_ + cell___30_7__B_ + pool__30_7_ = 1
invariant :cell___19_7__A_ + cell___19_7__B_ + pool__19_7_ = 1
invariant :cell___20_19__A_ + cell___20_19__B_ + pool__20_19_ = 1
invariant :cell___17_20__A_ + cell___17_20__B_ + pool__17_20_ = 1
invariant :cell___17_13__A_ + cell___17_13__B_ + pool__17_13_ = 1
invariant :cell___12_1__A_ + cell___12_1__B_ + pool__12_1_ = 1
invariant :cell___23_1__A_ + cell___23_1__B_ + pool__23_1_ = 1
invariant :cell___1_22__A_ + cell___1_22__B_ + pool__1_22_ = 1
invariant :cell___20_6__A_ + cell___20_6__B_ + pool__20_6_ = 1
invariant :cell___28_22__A_ + cell___28_22__B_ + pool__28_22_ = 1
invariant :cell___5_11__A_ + cell___5_11__B_ + pool__5_11_ = 1
invariant :cell___3_12__A_ + cell___3_12__B_ + pool__3_12_ = 1
invariant :cell___9_25__A_ + cell___9_25__B_ + pool__9_25_ = 1
invariant :cell___7_15__A_ + cell___7_15__B_ + pool__7_15_ = 1
invariant :cell___16_29__A_ + cell___16_29__B_ + pool__16_29_ = 1
invariant :cell___6_8__A_ + cell___6_8__B_ + pool__6_8_ = 1
invariant :cell___17_4__A_ + cell___17_4__B_ + pool__17_4_ = 1
invariant :cell___23_11__A_ + cell___23_11__B_ + pool__23_11_ = 1
invariant :cell___20_2__A_ + cell___20_2__B_ + pool__20_2_ = 1
invariant :cell___20_3__A_ + cell___20_3__B_ + pool__20_3_ = 1
invariant :cell___20_8__A_ + cell___20_8__B_ + pool__20_8_ = 1
invariant :cell___22_29__A_ + cell___22_29__B_ + pool__22_29_ = 1
invariant :cell___3_29__A_ + cell___3_29__B_ + pool__3_29_ = 1
invariant :cell___27_8__A_ + cell___27_8__B_ + pool__27_8_ = 1
invariant :cell___28_24__A_ + cell___28_24__B_ + pool__28_24_ = 1
invariant :cell___2_26__A_ + cell___2_26__B_ + pool__2_26_ = 1
invariant :cell___4_2__A_ + cell___4_2__B_ + pool__4_2_ = 1
invariant :cell___11_15__A_ + cell___11_15__B_ + pool__11_15_ = 1
invariant :cell___18_15__A_ + cell___18_15__B_ + pool__18_15_ = 1
invariant :cell___15_14__A_ + cell___15_14__B_ + pool__15_14_ = 1
invariant :cell___6_18__A_ + cell___6_18__B_ + pool__6_18_ = 1
invariant :cell___16_22__A_ + cell___16_22__B_ + pool__16_22_ = 1
invariant :cell___18_12__A_ + cell___18_12__B_ + pool__18_12_ = 1
invariant :cell___11_12__A_ + cell___11_12__B_ + pool__11_12_ = 1
invariant :cell___1_16__A_ + cell___1_16__B_ + pool__1_16_ = 1
invariant :cell___26_20__A_ + cell___26_20__B_ + pool__26_20_ = 1
invariant :cell___7_8__A_ + cell___7_8__B_ + pool__7_8_ = 1
invariant :cell___3_5__A_ + cell___3_5__B_ + pool__3_5_ = 1
invariant :cell___20_17__A_ + cell___20_17__B_ + pool__20_17_ = 1
invariant :cell___1_3__A_ + cell___1_3__B_ + pool__1_3_ = 1
invariant :cell___4_12__A_ + cell___4_12__B_ + pool__4_12_ = 1
invariant :cell___24_16__A_ + cell___24_16__B_ + pool__24_16_ = 1
invariant :cell___15_10__A_ + cell___15_10__B_ + pool__15_10_ = 1
invariant :cell___22_11__A_ + cell___22_11__B_ + pool__22_11_ = 1
invariant :cell___22_25__A_ + cell___22_25__B_ + pool__22_25_ = 1
invariant :cell___5_4__A_ + cell___5_4__B_ + pool__5_4_ = 1
invariant :cell___13_29__A_ + cell___13_29__B_ + pool__13_29_ = 1
invariant :cell___24_17__A_ + cell___24_17__B_ + pool__24_17_ = 1
invariant :cell___15_6__A_ + cell___15_6__B_ + pool__15_6_ = 1
invariant :cell___9_19__A_ + cell___9_19__B_ + pool__9_19_ = 1
invariant :cell___13_24__A_ + cell___13_24__B_ + pool__13_24_ = 1
invariant :cell___3_6__A_ + cell___3_6__B_ + pool__3_6_ = 1
invariant :cell___5_1__A_ + cell___5_1__B_ + pool__5_1_ = 1
invariant :cell___9_1__A_ + cell___9_1__B_ + pool__9_1_ = 1
invariant :cell___10_7__A_ + cell___10_7__B_ + pool__10_7_ = 1
invariant :cell___30_3__A_ + cell___30_3__B_ + pool__30_3_ = 1
invariant :cell___7_12__A_ + cell___7_12__B_ + pool__7_12_ = 1
invariant :cell___29_25__A_ + cell___29_25__B_ + pool__29_25_ = 1
invariant :cell___11_23__A_ + cell___11_23__B_ + pool__11_23_ = 1
invariant :cell___21_20__A_ + cell___21_20__B_ + pool__21_20_ = 1
invariant :cell___16_9__A_ + cell___16_9__B_ + pool__16_9_ = 1
invariant :cell___17_17__A_ + cell___17_17__B_ + pool__17_17_ = 1
invariant :cell___21_8__A_ + cell___21_8__B_ + pool__21_8_ = 1
invariant :cell___13_27__A_ + cell___13_27__B_ + pool__13_27_ = 1
invariant :cell___21_16__A_ + cell___21_16__B_ + pool__21_16_ = 1
invariant :cell___10_17__A_ + cell___10_17__B_ + pool__10_17_ = 1
invariant :cell___11_3__A_ + cell___11_3__B_ + pool__11_3_ = 1
invariant :cell___22_2__A_ + cell___22_2__B_ + pool__22_2_ = 1
invariant :cell___15_8__A_ + cell___15_8__B_ + pool__15_8_ = 1
invariant :cell___25_25__A_ + cell___25_25__B_ + pool__25_25_ = 1
invariant :cell___23_25__A_ + cell___23_25__B_ + pool__23_25_ = 1
invariant :cell___7_22__A_ + cell___7_22__B_ + pool__7_22_ = 1
invariant :cell___28_14__A_ + cell___28_14__B_ + pool__28_14_ = 1
invariant :cell___21_1__A_ + cell___21_1__B_ + pool__21_1_ = 1
invariant :cell___23_27__A_ + cell___23_27__B_ + pool__23_27_ = 1
invariant :cell___10_19__A_ + cell___10_19__B_ + pool__10_19_ = 1
invariant :cell___9_8__A_ + cell___9_8__B_ + pool__9_8_ = 1
invariant :cell___25_6__A_ + cell___25_6__B_ + pool__25_6_ = 1
invariant :cell___8_8__A_ + cell___8_8__B_ + pool__8_8_ = 1
invariant :cell___12_28__A_ + cell___12_28__B_ + pool__12_28_ = 1
invariant :cell___30_2__A_ + cell___30_2__B_ + pool__30_2_ = 1
invariant :cell___30_25__A_ + cell___30_25__B_ + pool__30_25_ = 1
invariant :cell___6_11__A_ + cell___6_11__B_ + pool__6_11_ = 1
invariant :cell___21_15__A_ + cell___21_15__B_ + pool__21_15_ = 1
invariant :cell___17_22__A_ + cell___17_22__B_ + pool__17_22_ = 1
invariant :cell___27_2__A_ + cell___27_2__B_ + pool__27_2_ = 1
invariant :cell___22_3__A_ + cell___22_3__B_ + pool__22_3_ = 1
invariant :cell___18_22__A_ + cell___18_22__B_ + pool__18_22_ = 1
invariant :cell___19_2__A_ + cell___19_2__B_ + pool__19_2_ = 1
invariant :cell___1_8__A_ + cell___1_8__B_ + pool__1_8_ = 1
invariant :cell___4_16__A_ + cell___4_16__B_ + pool__4_16_ = 1
invariant :cell___11_26__A_ + cell___11_26__B_ + pool__11_26_ = 1
invariant :cell___15_9__A_ + cell___15_9__B_ + pool__15_9_ = 1
invariant :cell___24_15__A_ + cell___24_15__B_ + pool__24_15_ = 1
invariant :cell___8_23__A_ + cell___8_23__B_ + pool__8_23_ = 1
invariant :cell___26_24__A_ + cell___26_24__B_ + pool__26_24_ = 1
invariant :cell___1_30__A_ + cell___1_30__B_ + pool__1_30_ = 1
invariant :cell___4_17__A_ + cell___4_17__B_ + pool__4_17_ = 1
invariant :cell___2_21__A_ + cell___2_21__B_ + pool__2_21_ = 1
invariant :cell___27_26__A_ + cell___27_26__B_ + pool__27_26_ = 1
invariant :cell___4_21__A_ + cell___4_21__B_ + pool__4_21_ = 1
invariant :cell___11_19__A_ + cell___11_19__B_ + pool__11_19_ = 1
invariant :cell___19_29__A_ + cell___19_29__B_ + pool__19_29_ = 1
invariant :cell___5_18__A_ + cell___5_18__B_ + pool__5_18_ = 1
invariant :cell___9_23__A_ + cell___9_23__B_ + pool__9_23_ = 1
invariant :cell___19_3__A_ + cell___19_3__B_ + pool__19_3_ = 1
invariant :cell___24_6__A_ + cell___24_6__B_ + pool__24_6_ = 1
invariant :cell___4_10__A_ + cell___4_10__B_ + pool__4_10_ = 1
invariant :cell___26_19__A_ + cell___26_19__B_ + pool__26_19_ = 1
invariant :cell___15_4__A_ + cell___15_4__B_ + pool__15_4_ = 1
invariant :cell___1_24__A_ + cell___1_24__B_ + pool__1_24_ = 1
invariant :cell___19_26__A_ + cell___19_26__B_ + pool__19_26_ = 1
invariant :cell___29_23__A_ + cell___29_23__B_ + pool__29_23_ = 1
invariant :cell___5_14__A_ + cell___5_14__B_ + pool__5_14_ = 1
invariant :cell___16_16__A_ + cell___16_16__B_ + pool__16_16_ = 1
invariant :cell___29_24__A_ + cell___29_24__B_ + pool__29_24_ = 1
invariant :cell___17_3__A_ + cell___17_3__B_ + pool__17_3_ = 1
invariant :cell___16_14__A_ + cell___16_14__B_ + pool__16_14_ = 1
invariant :cell___6_27__A_ + cell___6_27__B_ + pool__6_27_ = 1
invariant :cell___10_1__A_ + cell___10_1__B_ + pool__10_1_ = 1
invariant :cell___18_25__A_ + cell___18_25__B_ + pool__18_25_ = 1
invariant :cell___29_11__A_ + cell___29_11__B_ + pool__29_11_ = 1
invariant :cell___8_3__A_ + cell___8_3__B_ + pool__8_3_ = 1
invariant :cell___25_5__A_ + cell___25_5__B_ + pool__25_5_ = 1
invariant :cell___16_12__A_ + cell___16_12__B_ + pool__16_12_ = 1
invariant :cell___24_20__A_ + cell___24_20__B_ + pool__24_20_ = 1
invariant :cell___4_22__A_ + cell___4_22__B_ + pool__4_22_ = 1
invariant :cell___5_22__A_ + cell___5_22__B_ + pool__5_22_ = 1
invariant :cell___10_16__A_ + cell___10_16__B_ + pool__10_16_ = 1
invariant :cell___16_4__A_ + cell___16_4__B_ + pool__16_4_ = 1
invariant :cell___25_8__A_ + cell___25_8__B_ + pool__25_8_ = 1
invariant :cell___17_7__A_ + cell___17_7__B_ + pool__17_7_ = 1
invariant :cell___8_5__A_ + cell___8_5__B_ + pool__8_5_ = 1
invariant :cell___20_10__A_ + cell___20_10__B_ + pool__20_10_ = 1
invariant :cell___30_22__A_ + cell___30_22__B_ + pool__30_22_ = 1
invariant :cell___12_29__A_ + cell___12_29__B_ + pool__12_29_ = 1
invariant :cell___27_16__A_ + cell___27_16__B_ + pool__27_16_ = 1
invariant :cell___2_2__A_ + cell___2_2__B_ + pool__2_2_ = 1
invariant :cell___16_27__A_ + cell___16_27__B_ + pool__16_27_ = 1
invariant :cell___30_17__A_ + cell___30_17__B_ + pool__30_17_ = 1
invariant :cell___22_4__A_ + cell___22_4__B_ + pool__22_4_ = 1
invariant :cell___15_2__A_ + cell___15_2__B_ + pool__15_2_ = 1
invariant :cell___21_4__A_ + cell___21_4__B_ + pool__21_4_ = 1
invariant :cell___26_30__A_ + cell___26_30__B_ + pool__26_30_ = 1
invariant :cell___27_17__A_ + cell___27_17__B_ + pool__27_17_ = 1
invariant :cell___1_29__A_ + cell___1_29__B_ + pool__1_29_ = 1
invariant :cell___4_29__A_ + cell___4_29__B_ + pool__4_29_ = 1
invariant :cell___15_18__A_ + cell___15_18__B_ + pool__15_18_ = 1
invariant :cell___28_19__A_ + cell___28_19__B_ + pool__28_19_ = 1
invariant :cell___30_13__A_ + cell___30_13__B_ + pool__30_13_ = 1
invariant :cell___10_28__A_ + cell___10_28__B_ + pool__10_28_ = 1
invariant :cell___28_30__A_ + cell___28_30__B_ + pool__28_30_ = 1
invariant :cell___10_21__A_ + cell___10_21__B_ + pool__10_21_ = 1
invariant :cell___4_26__A_ + cell___4_26__B_ + pool__4_26_ = 1
invariant :cell___17_28__A_ + cell___17_28__B_ + pool__17_28_ = 1
invariant :cell___6_2__A_ + cell___6_2__B_ + pool__6_2_ = 1
invariant :cell___17_15__A_ + cell___17_15__B_ + pool__17_15_ = 1
invariant :cell___29_15__A_ + cell___29_15__B_ + pool__29_15_ = 1
invariant :cell___4_27__A_ + cell___4_27__B_ + pool__4_27_ = 1
invariant :cell___27_21__A_ + cell___27_21__B_ + pool__27_21_ = 1
invariant :cell___21_30__A_ + cell___21_30__B_ + pool__21_30_ = 1
invariant :cell___29_22__A_ + cell___29_22__B_ + pool__29_22_ = 1
invariant :cell___19_20__A_ + cell___19_20__B_ + pool__19_20_ = 1
invariant :cell___23_29__A_ + cell___23_29__B_ + pool__23_29_ = 1
invariant :cell___1_13__A_ + cell___1_13__B_ + pool__1_13_ = 1
invariant :cell___20_5__A_ + cell___20_5__B_ + pool__20_5_ = 1
invariant :cell___19_17__A_ + cell___19_17__B_ + pool__19_17_ = 1
invariant :cell___30_27__A_ + cell___30_27__B_ + pool__30_27_ = 1
invariant :cell___25_21__A_ + cell___25_21__B_ + pool__25_21_ = 1
invariant :cell___9_17__A_ + cell___9_17__B_ + pool__9_17_ = 1
invariant :cell___5_23__A_ + cell___5_23__B_ + pool__5_23_ = 1
invariant :cell___18_8__A_ + cell___18_8__B_ + pool__18_8_ = 1
invariant :cell___10_15__A_ + cell___10_15__B_ + pool__10_15_ = 1
invariant :cell___19_15__A_ + cell___19_15__B_ + pool__19_15_ = 1
invariant :cell___6_21__A_ + cell___6_21__B_ + pool__6_21_ = 1
invariant :cell___15_26__A_ + cell___15_26__B_ + pool__15_26_ = 1
invariant :cell___28_18__A_ + cell___28_18__B_ + pool__28_18_ = 1
invariant :cell___26_18__A_ + cell___26_18__B_ + pool__26_18_ = 1
invariant :cell___26_16__A_ + cell___26_16__B_ + pool__26_16_ = 1
invariant :cell___5_3__A_ + cell___5_3__B_ + pool__5_3_ = 1
invariant :cell___24_7__A_ + cell___24_7__B_ + pool__24_7_ = 1
invariant :cell___30_6__A_ + cell___30_6__B_ + pool__30_6_ = 1
invariant :cell___23_26__A_ + cell___23_26__B_ + pool__23_26_ = 1
invariant :cell___25_17__A_ + cell___25_17__B_ + pool__25_17_ = 1
invariant :cell___6_5__A_ + cell___6_5__B_ + pool__6_5_ = 1
invariant :cell___18_23__A_ + cell___18_23__B_ + pool__18_23_ = 1
invariant :cell___1_21__A_ + cell___1_21__B_ + pool__1_21_ = 1
invariant :cell___29_10__A_ + cell___29_10__B_ + pool__29_10_ = 1
invariant :cell___12_24__A_ + cell___12_24__B_ + pool__12_24_ = 1
invariant :cell___12_6__A_ + cell___12_6__B_ + pool__12_6_ = 1
invariant :cell___19_25__A_ + cell___19_25__B_ + pool__19_25_ = 1
invariant :cell___6_3__A_ + cell___6_3__B_ + pool__6_3_ = 1
invariant :cell___22_26__A_ + cell___22_26__B_ + pool__22_26_ = 1
invariant :cell___12_8__A_ + cell___12_8__B_ + pool__12_8_ = 1
invariant :cell___21_21__A_ + cell___21_21__B_ + pool__21_21_ = 1
invariant :cell___11_9__A_ + cell___11_9__B_ + pool__11_9_ = 1
invariant :cell___15_27__A_ + cell___15_27__B_ + pool__15_27_ = 1
invariant :cell___20_15__A_ + cell___20_15__B_ + pool__20_15_ = 1
invariant :cell___23_28__A_ + cell___23_28__B_ + pool__23_28_ = 1
invariant :cell___9_7__A_ + cell___9_7__B_ + pool__9_7_ = 1
invariant :cell___4_4__A_ + cell___4_4__B_ + pool__4_4_ = 1
invariant :cell___26_26__A_ + cell___26_26__B_ + pool__26_26_ = 1
invariant :cell___2_20__A_ + cell___2_20__B_ + pool__2_20_ = 1
invariant :cell___25_26__A_ + cell___25_26__B_ + pool__25_26_ = 1
invariant :cell___23_30__A_ + cell___23_30__B_ + pool__23_30_ = 1
invariant :cell___7_2__A_ + cell___7_2__B_ + pool__7_2_ = 1
invariant :cell___4_5__A_ + cell___4_5__B_ + pool__4_5_ = 1
invariant :cell___12_23__A_ + cell___12_23__B_ + pool__12_23_ = 1
invariant :cell___5_10__A_ + cell___5_10__B_ + pool__5_10_ = 1
invariant :cell___12_16__A_ + cell___12_16__B_ + pool__12_16_ = 1
invariant :cell___19_9__A_ + cell___19_9__B_ + pool__19_9_ = 1
invariant :cell___10_25__A_ + cell___10_25__B_ + pool__10_25_ = 1
invariant :cell___28_26__A_ + cell___28_26__B_ + pool__28_26_ = 1
invariant :cell___8_14__A_ + cell___8_14__B_ + pool__8_14_ = 1
invariant :cell___3_7__A_ + cell___3_7__B_ + pool__3_7_ = 1
invariant :cell___12_13__A_ + cell___12_13__B_ + pool__12_13_ = 1
invariant :cell___23_17__A_ + cell___23_17__B_ + pool__23_17_ = 1
invariant :cell___20_25__A_ + cell___20_25__B_ + pool__20_25_ = 1
invariant :cell___16_19__A_ + cell___16_19__B_ + pool__16_19_ = 1
invariant :cell___29_2__A_ + cell___29_2__B_ + pool__29_2_ = 1
invariant :cell___7_17__A_ + cell___7_17__B_ + pool__7_17_ = 1
invariant :cell___4_8__A_ + cell___4_8__B_ + pool__4_8_ = 1
invariant :cell___4_11__A_ + cell___4_11__B_ + pool__4_11_ = 1
invariant :cell___20_24__A_ + cell___20_24__B_ + pool__20_24_ = 1
invariant :cell___22_17__A_ + cell___22_17__B_ + pool__22_17_ = 1
invariant :cell___9_10__A_ + cell___9_10__B_ + pool__9_10_ = 1
invariant :cell___24_12__A_ + cell___24_12__B_ + pool__24_12_ = 1
invariant :cell___10_24__A_ + cell___10_24__B_ + pool__10_24_ = 1
invariant :cell___11_28__A_ + cell___11_28__B_ + pool__11_28_ = 1
invariant :cell___27_10__A_ + cell___27_10__B_ + pool__27_10_ = 1
invariant :cell___4_3__A_ + cell___4_3__B_ + pool__4_3_ = 1
invariant :cell___8_22__A_ + cell___8_22__B_ + pool__8_22_ = 1
invariant :cell___2_6__A_ + cell___2_6__B_ + pool__2_6_ = 1
invariant :cell___7_24__A_ + cell___7_24__B_ + pool__7_24_ = 1
invariant :cell___26_3__A_ + cell___26_3__B_ + pool__26_3_ = 1
invariant :cell___3_21__A_ + cell___3_21__B_ + pool__3_21_ = 1
invariant :cell___3_11__A_ + cell___3_11__B_ + pool__3_11_ = 1
invariant :cell___9_2__A_ + cell___9_2__B_ + pool__9_2_ = 1
invariant :cell___4_30__A_ + cell___4_30__B_ + pool__4_30_ = 1
invariant :cell___29_8__A_ + cell___29_8__B_ + pool__29_8_ = 1
invariant :cell___5_28__A_ + cell___5_28__B_ + pool__5_28_ = 1
invariant :cell___7_5__A_ + cell___7_5__B_ + pool__7_5_ = 1
invariant :cell___15_29__A_ + cell___15_29__B_ + pool__15_29_ = 1
invariant :cell___26_12__A_ + cell___26_12__B_ + pool__26_12_ = 1
invariant :cell___6_6__A_ + cell___6_6__B_ + pool__6_6_ = 1
invariant :cell___26_28__A_ + cell___26_28__B_ + pool__26_28_ = 1
invariant :cell___27_13__A_ + cell___27_13__B_ + pool__27_13_ = 1
invariant :cell___18_26__A_ + cell___18_26__B_ + pool__18_26_ = 1
invariant :cell___4_20__A_ + cell___4_20__B_ + pool__4_20_ = 1
invariant :cell___15_15__A_ + cell___15_15__B_ + pool__15_15_ = 1
invariant :cell___7_16__A_ + cell___7_16__B_ + pool__7_16_ = 1
invariant :cell___7_4__A_ + cell___7_4__B_ + pool__7_4_ = 1
invariant :cell___19_28__A_ + cell___19_28__B_ + pool__19_28_ = 1
invariant :cell___2_4__A_ + cell___2_4__B_ + pool__2_4_ = 1
invariant :cell___2_8__A_ + cell___2_8__B_ + pool__2_8_ = 1
invariant :cell___25_14__A_ + cell___25_14__B_ + pool__25_14_ = 1
invariant :cell___19_24__A_ + cell___19_24__B_ + pool__19_24_ = 1
invariant :cell___12_22__A_ + cell___12_22__B_ + pool__12_22_ = 1
invariant :cell___21_28__A_ + cell___21_28__B_ + pool__21_28_ = 1
invariant :cell___11_14__A_ + cell___11_14__B_ + pool__11_14_ = 1
invariant :cell___12_21__A_ + cell___12_21__B_ + pool__12_21_ = 1
invariant :cell___8_12__A_ + cell___8_12__B_ + pool__8_12_ = 1
invariant :cell___4_25__A_ + cell___4_25__B_ + pool__4_25_ = 1
invariant :cell___13_28__A_ + cell___13_28__B_ + pool__13_28_ = 1
invariant :cell___14_16__A_ + cell___14_16__B_ + pool__14_16_ = 1
invariant :cell___14_11__A_ + cell___14_11__B_ + pool__14_11_ = 1
invariant :cell___4_6__A_ + cell___4_6__B_ + pool__4_6_ = 1
invariant :cell___23_16__A_ + cell___23_16__B_ + pool__23_16_ = 1
invariant :cell___23_14__A_ + cell___23_14__B_ + pool__23_14_ = 1
invariant :cell___28_21__A_ + cell___28_21__B_ + pool__28_21_ = 1
invariant :cell___16_21__A_ + cell___16_21__B_ + pool__16_21_ = 1
invariant :pool__10_10_ + pool__10_11_ + pool__10_12_ + pool__10_13_ + pool__10_14_ + pool__10_15_ + pool__10_16_ + pool__10_17_ + pool__10_18_ + pool__10_19_ + pool__10_1_ + pool__10_20_ + pool__10_21_ + pool__10_22_ + pool__10_23_ + pool__10_24_ + pool__10_25_ + pool__10_26_ + pool__10_27_ + pool__10_28_ + pool__10_29_ + pool__10_2_ + pool__10_30_ + pool__10_3_ + pool__10_4_ + pool__10_5_ + pool__10_6_ + pool__10_7_ + pool__10_8_ + pool__10_9_ + pool__11_10_ + pool__11_11_ + pool__11_12_ + pool__11_13_ + pool__11_14_ + pool__11_15_ + pool__11_16_ + pool__11_17_ + pool__11_18_ + pool__11_19_ + pool__11_1_ + pool__11_20_ + pool__11_21_ + pool__11_22_ + pool__11_23_ + pool__11_24_ + pool__11_25_ + pool__11_26_ + pool__11_27_ + pool__11_28_ + pool__11_29_ + pool__11_2_ + pool__11_30_ + pool__11_3_ + pool__11_4_ + pool__11_5_ + pool__11_6_ + pool__11_7_ + pool__11_8_ + pool__11_9_ + pool__12_10_ + pool__12_11_ + pool__12_12_ + pool__12_13_ + pool__12_14_ + pool__12_15_ + pool__12_16_ + pool__12_17_ + pool__12_18_ + pool__12_19_ + pool__12_1_ + pool__12_20_ + pool__12_21_ + pool__12_22_ + pool__12_23_ + pool__12_24_ + pool__12_25_ + pool__12_26_ + pool__12_27_ + pool__12_28_ + pool__12_29_ + pool__12_2_ + pool__12_30_ + pool__12_3_ + pool__12_4_ + pool__12_5_ + pool__12_6_ + pool__12_7_ + pool__12_8_ + pool__12_9_ + pool__13_10_ + pool__13_11_ + pool__13_12_ + pool__13_13_ + pool__13_14_ + pool__13_15_ + pool__13_16_ + pool__13_17_ + pool__13_18_ + pool__13_19_ + pool__13_1_ + pool__13_20_ + pool__13_21_ + pool__13_22_ + pool__13_23_ + pool__13_24_ + pool__13_25_ + pool__13_26_ + pool__13_27_ + pool__13_28_ + pool__13_29_ + pool__13_2_ + pool__13_30_ + pool__13_3_ + pool__13_4_ + pool__13_5_ + pool__13_6_ + pool__13_7_ + pool__13_8_ + pool__13_9_ + pool__14_10_ + pool__14_11_ + pool__14_12_ + pool__14_13_ + pool__14_14_ + pool__14_15_ + pool__14_16_ + pool__14_17_ + pool__14_18_ + pool__14_19_ + pool__14_1_ + pool__14_20_ + pool__14_21_ + pool__14_22_ + pool__14_23_ + pool__14_24_ + pool__14_25_ + pool__14_26_ + pool__14_27_ + pool__14_28_ + pool__14_29_ + pool__14_2_ + pool__14_30_ + pool__14_3_ + pool__14_4_ + pool__14_5_ + pool__14_6_ + pool__14_7_ + pool__14_8_ + pool__14_9_ + pool__15_10_ + pool__15_11_ + pool__15_12_ + pool__15_13_ + pool__15_14_ + pool__15_15_ + pool__15_16_ + pool__15_17_ + pool__15_18_ + pool__15_19_ + pool__15_1_ + pool__15_20_ + pool__15_21_ + pool__15_22_ + pool__15_23_ + pool__15_24_ + pool__15_25_ + pool__15_26_ + pool__15_27_ + pool__15_28_ + pool__15_29_ + pool__15_2_ + pool__15_30_ + pool__15_3_ + pool__15_4_ + pool__15_5_ + pool__15_6_ + pool__15_7_ + pool__15_8_ + pool__15_9_ + pool__16_10_ + pool__16_11_ + pool__16_12_ + pool__16_13_ + pool__16_14_ + pool__16_15_ + pool__16_16_ + pool__16_17_ + pool__16_18_ + pool__16_19_ + pool__16_1_ + pool__16_20_ + pool__16_21_ + pool__16_22_ + pool__16_23_ + pool__16_24_ + pool__16_25_ + pool__16_26_ + pool__16_27_ + pool__16_28_ + pool__16_29_ + pool__16_2_ + pool__16_30_ + pool__16_3_ + pool__16_4_ + pool__16_5_ + pool__16_6_ + pool__16_7_ + pool__16_8_ + pool__16_9_ + pool__17_10_ + pool__17_11_ + pool__17_12_ + pool__17_13_ + pool__17_14_ + pool__17_15_ + pool__17_16_ + pool__17_17_ + pool__17_18_ + pool__17_19_ + pool__17_1_ + pool__17_20_ + pool__17_21_ + pool__17_22_ + pool__17_23_ + pool__17_24_ + pool__17_25_ + pool__17_26_ + pool__17_27_ + pool__17_28_ + pool__17_29_ + pool__17_2_ + pool__17_30_ + pool__17_3_ + pool__17_4_ + pool__17_5_ + pool__17_6_ + pool__17_7_ + pool__17_8_ + pool__17_9_ + pool__18_10_ + pool__18_11_ + pool__18_12_ + pool__18_13_ + pool__18_14_ + pool__18_15_ + pool__18_16_ + pool__18_17_ + pool__18_18_ + pool__18_19_ + pool__18_1_ + pool__18_20_ + pool__18_21_ + pool__18_22_ + pool__18_23_ + pool__18_24_ + pool__18_25_ + pool__18_26_ + pool__18_27_ + pool__18_28_ + pool__18_29_ + pool__18_2_ + pool__18_30_ + pool__18_3_ + pool__18_4_ + pool__18_5_ + pool__18_6_ + pool__18_7_ + pool__18_8_ + pool__18_9_ + pool__19_10_ + pool__19_11_ + pool__19_12_ + pool__19_13_ + pool__19_14_ + pool__19_15_ + pool__19_16_ + pool__19_17_ + pool__19_18_ + pool__19_19_ + pool__19_1_ + pool__19_20_ + pool__19_21_ + pool__19_22_ + pool__19_23_ + pool__19_24_ + pool__19_25_ + pool__19_26_ + pool__19_27_ + pool__19_28_ + pool__19_29_ + pool__19_2_ + pool__19_30_ + pool__19_3_ + pool__19_4_ + pool__19_5_ + pool__19_6_ + pool__19_7_ + pool__19_8_ + pool__19_9_ + pool__1_10_ + pool__1_11_ + pool__1_12_ + pool__1_13_ + pool__1_14_ + pool__1_15_ + pool__1_16_ + pool__1_17_ + pool__1_18_ + pool__1_19_ + pool__1_1_ + pool__1_20_ + pool__1_21_ + pool__1_22_ + pool__1_23_ + pool__1_24_ + pool__1_25_ + pool__1_26_ + pool__1_27_ + pool__1_28_ + pool__1_29_ + pool__1_2_ + pool__1_30_ + pool__1_3_ + pool__1_4_ + pool__1_5_ + pool__1_6_ + pool__1_7_ + pool__1_8_ + pool__1_9_ + pool__20_10_ + pool__20_11_ + pool__20_12_ + pool__20_13_ + pool__20_14_ + pool__20_15_ + pool__20_16_ + pool__20_17_ + pool__20_18_ + pool__20_19_ + pool__20_1_ + pool__20_20_ + pool__20_21_ + pool__20_22_ + pool__20_23_ + pool__20_24_ + pool__20_25_ + pool__20_26_ + pool__20_27_ + pool__20_28_ + pool__20_29_ + pool__20_2_ + pool__20_30_ + pool__20_3_ + pool__20_4_ + pool__20_5_ + pool__20_6_ + pool__20_7_ + pool__20_8_ + pool__20_9_ + pool__21_10_ + pool__21_11_ + pool__21_12_ + pool__21_13_ + pool__21_14_ + pool__21_15_ + pool__21_16_ + pool__21_17_ + pool__21_18_ + pool__21_19_ + pool__21_1_ + pool__21_20_ + pool__21_21_ + pool__21_22_ + pool__21_23_ + pool__21_24_ + pool__21_25_ + pool__21_26_ + pool__21_27_ + pool__21_28_ + pool__21_29_ + pool__21_2_ + pool__21_30_ + pool__21_3_ + pool__21_4_ + pool__21_5_ + pool__21_6_ + pool__21_7_ + pool__21_8_ + pool__21_9_ + pool__22_10_ + pool__22_11_ + pool__22_12_ + pool__22_13_ + pool__22_14_ + pool__22_15_ + pool__22_16_ + pool__22_17_ + pool__22_18_ + pool__22_19_ + pool__22_1_ + pool__22_20_ + pool__22_21_ + pool__22_22_ + pool__22_23_ + pool__22_24_ + pool__22_25_ + pool__22_26_ + pool__22_27_ + pool__22_28_ + pool__22_29_ + pool__22_2_ + pool__22_30_ + pool__22_3_ + pool__22_4_ + pool__22_5_ + pool__22_6_ + pool__22_7_ + pool__22_8_ + pool__22_9_ + pool__23_10_ + pool__23_11_ + pool__23_12_ + pool__23_13_ + pool__23_14_ + pool__23_15_ + pool__23_16_ + pool__23_17_ + pool__23_18_ + pool__23_19_ + pool__23_1_ + pool__23_20_ + pool__23_21_ + pool__23_22_ + pool__23_23_ + pool__23_24_ + pool__23_25_ + pool__23_26_ + pool__23_27_ + pool__23_28_ + pool__23_29_ + pool__23_2_ + pool__23_30_ + pool__23_3_ + pool__23_4_ + pool__23_5_ + pool__23_6_ + pool__23_7_ + pool__23_8_ + pool__23_9_ + pool__24_10_ + pool__24_11_ + pool__24_12_ + pool__24_13_ + pool__24_14_ + pool__24_15_ + pool__24_16_ + pool__24_17_ + pool__24_18_ + pool__24_19_ + pool__24_1_ + pool__24_20_ + pool__24_21_ + pool__24_22_ + pool__24_23_ + pool__24_24_ + pool__24_25_ + pool__24_26_ + pool__24_27_ + pool__24_28_ + pool__24_29_ + pool__24_2_ + pool__24_30_ + pool__24_3_ + pool__24_4_ + pool__24_5_ + pool__24_6_ + pool__24_7_ + pool__24_8_ + pool__24_9_ + pool__25_10_ + pool__25_11_ + pool__25_12_ + pool__25_13_ + pool__25_14_ + pool__25_15_ + pool__25_16_ + pool__25_17_ + pool__25_18_ + pool__25_19_ + pool__25_1_ + pool__25_20_ + pool__25_21_ + pool__25_22_ + pool__25_23_ + pool__25_24_ + pool__25_25_ + pool__25_26_ + pool__25_27_ + pool__25_28_ + pool__25_29_ + pool__25_2_ + pool__25_30_ + pool__25_3_ + pool__25_4_ + pool__25_5_ + pool__25_6_ + pool__25_7_ + pool__25_8_ + pool__25_9_ + pool__26_10_ + pool__26_11_ + pool__26_12_ + pool__26_13_ + pool__26_14_ + pool__26_15_ + pool__26_16_ + pool__26_17_ + pool__26_18_ + pool__26_19_ + pool__26_1_ + pool__26_20_ + pool__26_21_ + pool__26_22_ + pool__26_23_ + pool__26_24_ + pool__26_25_ + pool__26_26_ + pool__26_27_ + pool__26_28_ + pool__26_29_ + pool__26_2_ + pool__26_30_ + pool__26_3_ + pool__26_4_ + pool__26_5_ + pool__26_6_ + pool__26_7_ + pool__26_8_ + pool__26_9_ + pool__27_10_ + pool__27_11_ + pool__27_12_ + pool__27_13_ + pool__27_14_ + pool__27_15_ + pool__27_16_ + pool__27_17_ + pool__27_18_ + pool__27_19_ + pool__27_1_ + pool__27_20_ + pool__27_21_ + pool__27_22_ + pool__27_23_ + pool__27_24_ + pool__27_25_ + pool__27_26_ + pool__27_27_ + pool__27_28_ + pool__27_29_ + pool__27_2_ + pool__27_30_ + pool__27_3_ + pool__27_4_ + pool__27_5_ + pool__27_6_ + pool__27_7_ + pool__27_8_ + pool__27_9_ + pool__28_10_ + pool__28_11_ + pool__28_12_ + pool__28_13_ + pool__28_14_ + pool__28_15_ + pool__28_16_ + pool__28_17_ + pool__28_18_ + pool__28_19_ + pool__28_1_ + pool__28_20_ + pool__28_21_ + pool__28_22_ + pool__28_23_ + pool__28_24_ + pool__28_25_ + pool__28_26_ + pool__28_27_ + pool__28_28_ + pool__28_29_ + pool__28_2_ + pool__28_30_ + pool__28_3_ + pool__28_4_ + pool__28_5_ + pool__28_6_ + pool__28_7_ + pool__28_8_ + pool__28_9_ + pool__29_10_ + pool__29_11_ + pool__29_12_ + pool__29_13_ + pool__29_14_ + pool__29_15_ + pool__29_16_ + pool__29_17_ + pool__29_18_ + pool__29_19_ + pool__29_1_ + pool__29_20_ + pool__29_21_ + pool__29_22_ + pool__29_23_ + pool__29_24_ + pool__29_25_ + pool__29_26_ + pool__29_27_ + pool__29_28_ + pool__29_29_ + pool__29_2_ + pool__29_30_ + pool__29_3_ + pool__29_4_ + pool__29_5_ + pool__29_6_ + pool__29_7_ + pool__29_8_ + pool__29_9_ + pool__2_10_ + pool__2_11_ + pool__2_12_ + pool__2_13_ + pool__2_14_ + pool__2_15_ + pool__2_16_ + pool__2_17_ + pool__2_18_ + pool__2_19_ + pool__2_1_ + pool__2_20_ + pool__2_21_ + pool__2_22_ + pool__2_23_ + pool__2_24_ + pool__2_25_ + pool__2_26_ + pool__2_27_ + pool__2_28_ + pool__2_29_ + pool__2_2_ + pool__2_30_ + pool__2_3_ + pool__2_4_ + pool__2_5_ + pool__2_6_ + pool__2_7_ + pool__2_8_ + pool__2_9_ + pool__30_10_ + pool__30_11_ + pool__30_12_ + pool__30_13_ + pool__30_14_ + pool__30_15_ + pool__30_16_ + pool__30_17_ + pool__30_18_ + pool__30_19_ + pool__30_1_ + pool__30_20_ + pool__30_21_ + pool__30_22_ + pool__30_23_ + pool__30_24_ + pool__30_25_ + pool__30_26_ + pool__30_27_ + pool__30_28_ + pool__30_29_ + pool__30_2_ + pool__30_30_ + pool__30_3_ + pool__30_4_ + pool__30_5_ + pool__30_6_ + pool__30_7_ + pool__30_8_ + pool__30_9_ + pool__3_10_ + pool__3_11_ + pool__3_12_ + pool__3_13_ + pool__3_14_ + pool__3_15_ + pool__3_16_ + pool__3_17_ + pool__3_18_ + pool__3_19_ + pool__3_1_ + pool__3_20_ + pool__3_21_ + pool__3_22_ + pool__3_23_ + pool__3_24_ + pool__3_25_ + pool__3_26_ + pool__3_27_ + pool__3_28_ + pool__3_29_ + pool__3_2_ + pool__3_30_ + pool__3_3_ + pool__3_4_ + pool__3_5_ + pool__3_6_ + pool__3_7_ + pool__3_8_ + pool__3_9_ + pool__4_10_ + pool__4_11_ + pool__4_12_ + pool__4_13_ + pool__4_14_ + pool__4_15_ + pool__4_16_ + pool__4_17_ + pool__4_18_ + pool__4_19_ + pool__4_1_ + pool__4_20_ + pool__4_21_ + pool__4_22_ + pool__4_23_ + pool__4_24_ + pool__4_25_ + pool__4_26_ + pool__4_27_ + pool__4_28_ + pool__4_29_ + pool__4_2_ + pool__4_30_ + pool__4_3_ + pool__4_4_ + pool__4_5_ + pool__4_6_ + pool__4_7_ + pool__4_8_ + pool__4_9_ + pool__5_10_ + pool__5_11_ + pool__5_12_ + pool__5_13_ + pool__5_14_ + pool__5_15_ + pool__5_16_ + pool__5_17_ + pool__5_18_ + pool__5_19_ + pool__5_1_ + pool__5_20_ + pool__5_21_ + pool__5_22_ + pool__5_23_ + pool__5_24_ + pool__5_25_ + pool__5_26_ + pool__5_27_ + pool__5_28_ + pool__5_29_ + pool__5_2_ + pool__5_30_ + pool__5_3_ + pool__5_4_ + pool__5_5_ + pool__5_6_ + pool__5_7_ + pool__5_8_ + pool__5_9_ + pool__6_10_ + pool__6_11_ + pool__6_12_ + pool__6_13_ + pool__6_14_ + pool__6_15_ + pool__6_16_ + pool__6_17_ + pool__6_18_ + pool__6_19_ + pool__6_1_ + pool__6_20_ + pool__6_21_ + pool__6_22_ + pool__6_23_ + pool__6_24_ + pool__6_25_ + pool__6_26_ + pool__6_27_ + pool__6_28_ + pool__6_29_ + pool__6_2_ + pool__6_30_ + pool__6_3_ + pool__6_4_ + pool__6_5_ + pool__6_6_ + pool__6_7_ + pool__6_8_ + pool__6_9_ + pool__7_10_ + pool__7_11_ + pool__7_12_ + pool__7_13_ + pool__7_14_ + pool__7_15_ + pool__7_16_ + pool__7_17_ + pool__7_18_ + pool__7_19_ + pool__7_1_ + pool__7_20_ + pool__7_21_ + pool__7_22_ + pool__7_23_ + pool__7_24_ + pool__7_25_ + pool__7_26_ + pool__7_27_ + pool__7_28_ + pool__7_29_ + pool__7_2_ + pool__7_30_ + pool__7_3_ + pool__7_4_ + pool__7_5_ + pool__7_6_ + pool__7_7_ + pool__7_8_ + pool__7_9_ + pool__8_10_ + pool__8_11_ + pool__8_12_ + pool__8_13_ + pool__8_14_ + pool__8_15_ + pool__8_16_ + pool__8_17_ + pool__8_18_ + pool__8_19_ + pool__8_1_ + pool__8_20_ + pool__8_21_ + pool__8_22_ + pool__8_23_ + pool__8_24_ + pool__8_25_ + pool__8_26_ + pool__8_27_ + pool__8_28_ + pool__8_29_ + pool__8_2_ + pool__8_30_ + pool__8_3_ + pool__8_4_ + pool__8_5_ + pool__8_6_ + pool__8_7_ + pool__8_8_ + pool__8_9_ + pool__9_10_ + pool__9_11_ + pool__9_12_ + pool__9_13_ + pool__9_14_ + pool__9_15_ + pool__9_16_ + pool__9_17_ + pool__9_18_ + pool__9_19_ + pool__9_1_ + pool__9_20_ + pool__9_21_ + pool__9_22_ + pool__9_23_ + pool__9_24_ + pool__9_25_ + pool__9_26_ + pool__9_27_ + pool__9_28_ + pool__9_29_ + pool__9_2_ + pool__9_30_ + pool__9_3_ + pool__9_4_ + pool__9_5_ + pool__9_6_ + pool__9_7_ + pool__9_8_ + pool__9_9_ + size_dot = 900
invariant :cell___13_8__A_ + cell___13_8__B_ + pool__13_8_ = 1
invariant :cell___23_22__A_ + cell___23_22__B_ + pool__23_22_ = 1
invariant :cell___13_20__A_ + cell___13_20__B_ + pool__13_20_ = 1
invariant :cell___11_20__A_ + cell___11_20__B_ + pool__11_20_ = 1
invariant :cell___20_9__A_ + cell___20_9__B_ + pool__20_9_ = 1
invariant :cell___16_11__A_ + cell___16_11__B_ + pool__16_11_ = 1
invariant :cell___27_3__A_ + cell___27_3__B_ + pool__27_3_ = 1
invariant :cell___3_15__A_ + cell___3_15__B_ + pool__3_15_ = 1
invariant :cell___7_23__A_ + cell___7_23__B_ + pool__7_23_ = 1
invariant :cell___19_6__A_ + cell___19_6__B_ + pool__19_6_ = 1
invariant :cell___20_12__A_ + cell___20_12__B_ + pool__20_12_ = 1
invariant :cell___23_7__A_ + cell___23_7__B_ + pool__23_7_ = 1
invariant :cell___20_21__A_ + cell___20_21__B_ + pool__20_21_ = 1
invariant :cell___2_30__A_ + cell___2_30__B_ + pool__2_30_ = 1
invariant :cell___1_18__A_ + cell___1_18__B_ + pool__1_18_ = 1
invariant :cell___20_26__A_ + cell___20_26__B_ + pool__20_26_ = 1
invariant :cell___10_9__A_ + cell___10_9__B_ + pool__10_9_ = 1
invariant :cell___9_28__A_ + cell___9_28__B_ + pool__9_28_ = 1
invariant :cell___10_30__A_ + cell___10_30__B_ + pool__10_30_ = 1
invariant :cell___19_4__A_ + cell___19_4__B_ + pool__19_4_ = 1
invariant :cell___26_4__A_ + cell___26_4__B_ + pool__26_4_ = 1
invariant :cell___9_14__A_ + cell___9_14__B_ + pool__9_14_ = 1
invariant :cell___14_28__A_ + cell___14_28__B_ + pool__14_28_ = 1
invariant :cell___27_24__A_ + cell___27_24__B_ + pool__27_24_ = 1
invariant :cell___12_20__A_ + cell___12_20__B_ + pool__12_20_ = 1
invariant :cell___23_8__A_ + cell___23_8__B_ + pool__23_8_ = 1
invariant :cell___6_22__A_ + cell___6_22__B_ + pool__6_22_ = 1
invariant :cell___3_4__A_ + cell___3_4__B_ + pool__3_4_ = 1
invariant :cell___10_26__A_ + cell___10_26__B_ + pool__10_26_ = 1
invariant :cell___18_19__A_ + cell___18_19__B_ + pool__18_19_ = 1
invariant :cell___23_2__A_ + cell___23_2__B_ + pool__23_2_ = 1
invariant :cell___8_9__A_ + cell___8_9__B_ + pool__8_9_ = 1
invariant :cell___21_6__A_ + cell___21_6__B_ + pool__21_6_ = 1
invariant :cell___22_10__A_ + cell___22_10__B_ + pool__22_10_ = 1
invariant :cell___2_29__A_ + cell___2_29__B_ + pool__2_29_ = 1
invariant :cell___29_20__A_ + cell___29_20__B_ + pool__29_20_ = 1
invariant :cell___16_10__A_ + cell___16_10__B_ + pool__16_10_ = 1
invariant :cell___13_3__A_ + cell___13_3__B_ + pool__13_3_ = 1
invariant :cell___25_16__A_ + cell___25_16__B_ + pool__25_16_ = 1
invariant :cell___8_11__A_ + cell___8_11__B_ + pool__8_11_ = 1
invariant :cell___14_22__A_ + cell___14_22__B_ + pool__14_22_ = 1
invariant :cell___21_23__A_ + cell___21_23__B_ + pool__21_23_ = 1
invariant :cell___30_20__A_ + cell___30_20__B_ + pool__30_20_ = 1
invariant :cell___19_12__A_ + cell___19_12__B_ + pool__19_12_ = 1
invariant :cell___19_22__A_ + cell___19_22__B_ + pool__19_22_ = 1
invariant :cell___20_11__A_ + cell___20_11__B_ + pool__20_11_ = 1
invariant :cell___11_5__A_ + cell___11_5__B_ + pool__11_5_ = 1
invariant :cell___29_26__A_ + cell___29_26__B_ + pool__29_26_ = 1
invariant :cell___7_20__A_ + cell___7_20__B_ + pool__7_20_ = 1
invariant :cell___7_9__A_ + cell___7_9__B_ + pool__7_9_ = 1
invariant :cell___27_12__A_ + cell___27_12__B_ + pool__27_12_ = 1
invariant :cell___13_10__A_ + cell___13_10__B_ + pool__13_10_ = 1
invariant :cell___17_11__A_ + cell___17_11__B_ + pool__17_11_ = 1
invariant :cell___29_30__A_ + cell___29_30__B_ + pool__29_30_ = 1
invariant :cell___22_1__A_ + cell___22_1__B_ + pool__22_1_ = 1
invariant :cell___20_4__A_ + cell___20_4__B_ + pool__20_4_ = 1
invariant :cell___2_24__A_ + cell___2_24__B_ + pool__2_24_ = 1
invariant :cell___6_25__A_ + cell___6_25__B_ + pool__6_25_ = 1
invariant :cell___24_19__A_ + cell___24_19__B_ + pool__24_19_ = 1
invariant :cell___21_14__A_ + cell___21_14__B_ + pool__21_14_ = 1
invariant :cell___13_11__A_ + cell___13_11__B_ + pool__13_11_ = 1
invariant :cell___14_17__A_ + cell___14_17__B_ + pool__14_17_ = 1
invariant :cell___13_9__A_ + cell___13_9__B_ + pool__13_9_ = 1
invariant :cell___2_12__A_ + cell___2_12__B_ + pool__2_12_ = 1
invariant :cell___9_24__A_ + cell___9_24__B_ + pool__9_24_ = 1
invariant :cell___18_7__A_ + cell___18_7__B_ + pool__18_7_ = 1
invariant :cell___2_5__A_ + cell___2_5__B_ + pool__2_5_ = 1
invariant :cell___14_23__A_ + cell___14_23__B_ + pool__14_23_ = 1
invariant :cell___26_9__A_ + cell___26_9__B_ + pool__26_9_ = 1
invariant :cell___11_30__A_ + cell___11_30__B_ + pool__11_30_ = 1
invariant :cell___24_30__A_ + cell___24_30__B_ + pool__24_30_ = 1
invariant :cell___13_6__A_ + cell___13_6__B_ + pool__13_6_ = 1
invariant :cell___20_16__A_ + cell___20_16__B_ + pool__20_16_ = 1
invariant :cell___17_16__A_ + cell___17_16__B_ + pool__17_16_ = 1
invariant :cell___6_7__A_ + cell___6_7__B_ + pool__6_7_ = 1
invariant :cell___20_13__A_ + cell___20_13__B_ + pool__20_13_ = 1
invariant :cell___21_19__A_ + cell___21_19__B_ + pool__21_19_ = 1
invariant :cell___12_15__A_ + cell___12_15__B_ + pool__12_15_ = 1
invariant :cell___23_5__A_ + cell___23_5__B_ + pool__23_5_ = 1
invariant :cell___30_29__A_ + cell___30_29__B_ + pool__30_29_ = 1
invariant :cell___28_4__A_ + cell___28_4__B_ + pool__28_4_ = 1
invariant :cell___13_2__A_ + cell___13_2__B_ + pool__13_2_ = 1
invariant :cell___16_2__A_ + cell___16_2__B_ + pool__16_2_ = 1
invariant :cell___18_13__A_ + cell___18_13__B_ + pool__18_13_ = 1
invariant :cell___28_12__A_ + cell___28_12__B_ + pool__28_12_ = 1
invariant :cell___25_19__A_ + cell___25_19__B_ + pool__25_19_ = 1
invariant :cell___15_7__A_ + cell___15_7__B_ + pool__15_7_ = 1
invariant :cell___27_6__A_ + cell___27_6__B_ + pool__27_6_ = 1
invariant :cell___4_15__A_ + cell___4_15__B_ + pool__4_15_ = 1
invariant :cell___21_3__A_ + cell___21_3__B_ + pool__21_3_ = 1
invariant :cell___26_25__A_ + cell___26_25__B_ + pool__26_25_ = 1
invariant :cell___5_20__A_ + cell___5_20__B_ + pool__5_20_ = 1
invariant :cell___7_19__A_ + cell___7_19__B_ + pool__7_19_ = 1
invariant :cell___21_27__A_ + cell___21_27__B_ + pool__21_27_ = 1
invariant :cell___4_23__A_ + cell___4_23__B_ + pool__4_23_ = 1
invariant :cell___7_28__A_ + cell___7_28__B_ + pool__7_28_ = 1
invariant :cell___8_16__A_ + cell___8_16__B_ + pool__8_16_ = 1
invariant :cell___14_25__A_ + cell___14_25__B_ + pool__14_25_ = 1
invariant :cell___1_15__A_ + cell___1_15__B_ + pool__1_15_ = 1
invariant :cell___26_15__A_ + cell___26_15__B_ + pool__26_15_ = 1
invariant :cell___8_18__A_ + cell___8_18__B_ + pool__8_18_ = 1
invariant :cell___14_12__A_ + cell___14_12__B_ + pool__14_12_ = 1
invariant :cell___5_2__A_ + cell___5_2__B_ + pool__5_2_ = 1
invariant :cell___14_14__A_ + cell___14_14__B_ + pool__14_14_ = 1
invariant :cell___9_3__A_ + cell___9_3__B_ + pool__9_3_ = 1
invariant :cell___9_16__A_ + cell___9_16__B_ + pool__9_16_ = 1
invariant :cell___11_21__A_ + cell___11_21__B_ + pool__11_21_ = 1
invariant :cell___12_10__A_ + cell___12_10__B_ + pool__12_10_ = 1
invariant :cell___12_27__A_ + cell___12_27__B_ + pool__12_27_ = 1
invariant :cell___18_14__A_ + cell___18_14__B_ + pool__18_14_ = 1
invariant :cell___13_12__A_ + cell___13_12__B_ + pool__13_12_ = 1
invariant :cell___23_24__A_ + cell___23_24__B_ + pool__23_24_ = 1
invariant :cell___5_26__A_ + cell___5_26__B_ + pool__5_26_ = 1
invariant :cell___30_23__A_ + cell___30_23__B_ + pool__30_23_ = 1
invariant :cell___6_4__A_ + cell___6_4__B_ + pool__6_4_ = 1
invariant :cell___26_22__A_ + cell___26_22__B_ + pool__26_22_ = 1
invariant :cell___28_16__A_ + cell___28_16__B_ + pool__28_16_ = 1
invariant :cell___26_10__A_ + cell___26_10__B_ + pool__26_10_ = 1
invariant :cell___30_8__A_ + cell___30_8__B_ + pool__30_8_ = 1
invariant :cell___30_4__A_ + cell___30_4__B_ + pool__30_4_ = 1
invariant :cell___19_11__A_ + cell___19_11__B_ + pool__19_11_ = 1
invariant :cell___18_11__A_ + cell___18_11__B_ + pool__18_11_ = 1
invariant :cell___14_1__A_ + cell___14_1__B_ + pool__14_1_ = 1
invariant :cell___3_10__A_ + cell___3_10__B_ + pool__3_10_ = 1
invariant :cell___25_3__A_ + cell___25_3__B_ + pool__25_3_ = 1
invariant :cell___15_28__A_ + cell___15_28__B_ + pool__15_28_ = 1
invariant :cell___16_28__A_ + cell___16_28__B_ + pool__16_28_ = 1
invariant :cell___8_25__A_ + cell___8_25__B_ + pool__8_25_ = 1
invariant :cell___19_21__A_ + cell___19_21__B_ + pool__19_21_ = 1
invariant :cell___20_28__A_ + cell___20_28__B_ + pool__20_28_ = 1
invariant :cell___16_17__A_ + cell___16_17__B_ + pool__16_17_ = 1
invariant :cell___23_19__A_ + cell___23_19__B_ + pool__23_19_ = 1
invariant :cell___4_7__A_ + cell___4_7__B_ + pool__4_7_ = 1
invariant :cell___10_10__A_ + cell___10_10__B_ + -1'pool__10_11_ + -1'pool__10_12_ + -1'pool__10_13_ + -1'pool__10_14_ + -1'pool__10_15_ + -1'pool__10_16_ + -1'pool__10_17_ + -1'pool__10_18_ + -1'pool__10_19_ + -1'pool__10_1_ + -1'pool__10_20_ + -1'pool__10_21_ + -1'pool__10_22_ + -1'pool__10_23_ + -1'pool__10_24_ + -1'pool__10_25_ + -1'pool__10_26_ + -1'pool__10_27_ + -1'pool__10_28_ + -1'pool__10_29_ + -1'pool__10_2_ + -1'pool__10_30_ + -1'pool__10_3_ + -1'pool__10_4_ + -1'pool__10_5_ + -1'pool__10_6_ + -1'pool__10_7_ + -1'pool__10_8_ + -1'pool__10_9_ + -1'pool__11_10_ + -1'pool__11_11_ + -1'pool__11_12_ + -1'pool__11_13_ + -1'pool__11_14_ + -1'pool__11_15_ + -1'pool__11_16_ + -1'pool__11_17_ + -1'pool__11_18_ + -1'pool__11_19_ + -1'pool__11_1_ + -1'pool__11_20_ + -1'pool__11_21_ + -1'pool__11_22_ + -1'pool__11_23_ + -1'pool__11_24_ + -1'pool__11_25_ + -1'pool__11_26_ + -1'pool__11_27_ + -1'pool__11_28_ + -1'pool__11_29_ + -1'pool__11_2_ + -1'pool__11_30_ + -1'pool__11_3_ + -1'pool__11_4_ + -1'pool__11_5_ + -1'pool__11_6_ + -1'pool__11_7_ + -1'pool__11_8_ + -1'pool__11_9_ + -1'pool__12_10_ + -1'pool__12_11_ + -1'pool__12_12_ + -1'pool__12_13_ + -1'pool__12_14_ + -1'pool__12_15_ + -1'pool__12_16_ + -1'pool__12_17_ + -1'pool__12_18_ + -1'pool__12_19_ + -1'pool__12_1_ + -1'pool__12_20_ + -1'pool__12_21_ + -1'pool__12_22_ + -1'pool__12_23_ + -1'pool__12_24_ + -1'pool__12_25_ + -1'pool__12_26_ + -1'pool__12_27_ + -1'pool__12_28_ + -1'pool__12_29_ + -1'pool__12_2_ + -1'pool__12_30_ + -1'pool__12_3_ + -1'pool__12_4_ + -1'pool__12_5_ + -1'pool__12_6_ + -1'pool__12_7_ + -1'pool__12_8_ + -1'pool__12_9_ + -1'pool__13_10_ + -1'pool__13_11_ + -1'pool__13_12_ + -1'pool__13_13_ + -1'pool__13_14_ + -1'pool__13_15_ + -1'pool__13_16_ + -1'pool__13_17_ + -1'pool__13_18_ + -1'pool__13_19_ + -1'pool__13_1_ + -1'pool__13_20_ + -1'pool__13_21_ + -1'pool__13_22_ + -1'pool__13_23_ + -1'pool__13_24_ + -1'pool__13_25_ + -1'pool__13_26_ + -1'pool__13_27_ + -1'pool__13_28_ + -1'pool__13_29_ + -1'pool__13_2_ + -1'pool__13_30_ + -1'pool__13_3_ + -1'pool__13_4_ + -1'pool__13_5_ + -1'pool__13_6_ + -1'pool__13_7_ + -1'pool__13_8_ + -1'pool__13_9_ + -1'pool__14_10_ + -1'pool__14_11_ + -1'pool__14_12_ + -1'pool__14_13_ + -1'pool__14_14_ + -1'pool__14_15_ + -1'pool__14_16_ + -1'pool__14_17_ + -1'pool__14_18_ + -1'pool__14_19_ + -1'pool__14_1_ + -1'pool__14_20_ + -1'pool__14_21_ + -1'pool__14_22_ + -1'pool__14_23_ + -1'pool__14_24_ + -1'pool__14_25_ + -1'pool__14_26_ + -1'pool__14_27_ + -1'pool__14_28_ + -1'pool__14_29_ + -1'pool__14_2_ + -1'pool__14_30_ + -1'pool__14_3_ + -1'pool__14_4_ + -1'pool__14_5_ + -1'pool__14_6_ + -1'pool__14_7_ + -1'pool__14_8_ + -1'pool__14_9_ + -1'pool__15_10_ + -1'pool__15_11_ + -1'pool__15_12_ + -1'pool__15_13_ + -1'pool__15_14_ + -1'pool__15_15_ + -1'pool__15_16_ + -1'pool__15_17_ + -1'pool__15_18_ + -1'pool__15_19_ + -1'pool__15_1_ + -1'pool__15_20_ + -1'pool__15_21_ + -1'pool__15_22_ + -1'pool__15_23_ + -1'pool__15_24_ + -1'pool__15_25_ + -1'pool__15_26_ + -1'pool__15_27_ + -1'pool__15_28_ + -1'pool__15_29_ + -1'pool__15_2_ + -1'pool__15_30_ + -1'pool__15_3_ + -1'pool__15_4_ + -1'pool__15_5_ + -1'pool__15_6_ + -1'pool__15_7_ + -1'pool__15_8_ + -1'pool__15_9_ + -1'pool__16_10_ + -1'pool__16_11_ + -1'pool__16_12_ + -1'pool__16_13_ + -1'pool__16_14_ + -1'pool__16_15_ + -1'pool__16_16_ + -1'pool__16_17_ + -1'pool__16_18_ + -1'pool__16_19_ + -1'pool__16_1_ + -1'pool__16_20_ + -1'pool__16_21_ + -1'pool__16_22_ + -1'pool__16_23_ + -1'pool__16_24_ + -1'pool__16_25_ + -1'pool__16_26_ + -1'pool__16_27_ + -1'pool__16_28_ + -1'pool__16_29_ + -1'pool__16_2_ + -1'pool__16_30_ + -1'pool__16_3_ + -1'pool__16_4_ + -1'pool__16_5_ + -1'pool__16_6_ + -1'pool__16_7_ + -1'pool__16_8_ + -1'pool__16_9_ + -1'pool__17_10_ + -1'pool__17_11_ + -1'pool__17_12_ + -1'pool__17_13_ + -1'pool__17_14_ + -1'pool__17_15_ + -1'pool__17_16_ + -1'pool__17_17_ + -1'pool__17_18_ + -1'pool__17_19_ + -1'pool__17_1_ + -1'pool__17_20_ + -1'pool__17_21_ + -1'pool__17_22_ + -1'pool__17_23_ + -1'pool__17_24_ + -1'pool__17_25_ + -1'pool__17_26_ + -1'pool__17_27_ + -1'pool__17_28_ + -1'pool__17_29_ + -1'pool__17_2_ + -1'pool__17_30_ + -1'pool__17_3_ + -1'pool__17_4_ + -1'pool__17_5_ + -1'pool__17_6_ + -1'pool__17_7_ + -1'pool__17_8_ + -1'pool__17_9_ + -1'pool__18_10_ + -1'pool__18_11_ + -1'pool__18_12_ + -1'pool__18_13_ + -1'pool__18_14_ + -1'pool__18_15_ + -1'pool__18_16_ + -1'pool__18_17_ + -1'pool__18_18_ + -1'pool__18_19_ + -1'pool__18_1_ + -1'pool__18_20_ + -1'pool__18_21_ + -1'pool__18_22_ + -1'pool__18_23_ + -1'pool__18_24_ + -1'pool__18_25_ + -1'pool__18_26_ + -1'pool__18_27_ + -1'pool__18_28_ + -1'pool__18_29_ + -1'pool__18_2_ + -1'pool__18_30_ + -1'pool__18_3_ + -1'pool__18_4_ + -1'pool__18_5_ + -1'pool__18_6_ + -1'pool__18_7_ + -1'pool__18_8_ + -1'pool__18_9_ + -1'pool__19_10_ + -1'pool__19_11_ + -1'pool__19_12_ + -1'pool__19_13_ + -1'pool__19_14_ + -1'pool__19_15_ + -1'pool__19_16_ + -1'pool__19_17_ + -1'pool__19_18_ + -1'pool__19_19_ + -1'pool__19_1_ + -1'pool__19_20_ + -1'pool__19_21_ + -1'pool__19_22_ + -1'pool__19_23_ + -1'pool__19_24_ + -1'pool__19_25_ + -1'pool__19_26_ + -1'pool__19_27_ + -1'pool__19_28_ + -1'pool__19_29_ + -1'pool__19_2_ + -1'pool__19_30_ + -1'pool__19_3_ + -1'pool__19_4_ + -1'pool__19_5_ + -1'pool__19_6_ + -1'pool__19_7_ + -1'pool__19_8_ + -1'pool__19_9_ + -1'pool__1_10_ + -1'pool__1_11_ + -1'pool__1_12_ + -1'pool__1_13_ + -1'pool__1_14_ + -1'pool__1_15_ + -1'pool__1_16_ + -1'pool__1_17_ + -1'pool__1_18_ + -1'pool__1_19_ + -1'pool__1_1_ + -1'pool__1_20_ + -1'pool__1_21_ + -1'pool__1_22_ + -1'pool__1_23_ + -1'pool__1_24_ + -1'pool__1_25_ + -1'pool__1_26_ + -1'pool__1_27_ + -1'pool__1_28_ + -1'pool__1_29_ + -1'pool__1_2_ + -1'pool__1_30_ + -1'pool__1_3_ + -1'pool__1_4_ + -1'pool__1_5_ + -1'pool__1_6_ + -1'pool__1_7_ + -1'pool__1_8_ + -1'pool__1_9_ + -1'pool__20_10_ + -1'pool__20_11_ + -1'pool__20_12_ + -1'pool__20_13_ + -1'pool__20_14_ + -1'pool__20_15_ + -1'pool__20_16_ + -1'pool__20_17_ + -1'pool__20_18_ + -1'pool__20_19_ + -1'pool__20_1_ + -1'pool__20_20_ + -1'pool__20_21_ + -1'pool__20_22_ + -1'pool__20_23_ + -1'pool__20_24_ + -1'pool__20_25_ + -1'pool__20_26_ + -1'pool__20_27_ + -1'pool__20_28_ + -1'pool__20_29_ + -1'pool__20_2_ + -1'pool__20_30_ + -1'pool__20_3_ + -1'pool__20_4_ + -1'pool__20_5_ + -1'pool__20_6_ + -1'pool__20_7_ + -1'pool__20_8_ + -1'pool__20_9_ + -1'pool__21_10_ + -1'pool__21_11_ + -1'pool__21_12_ + -1'pool__21_13_ + -1'pool__21_14_ + -1'pool__21_15_ + -1'pool__21_16_ + -1'pool__21_17_ + -1'pool__21_18_ + -1'pool__21_19_ + -1'pool__21_1_ + -1'pool__21_20_ + -1'pool__21_21_ + -1'pool__21_22_ + -1'pool__21_23_ + -1'pool__21_24_ + -1'pool__21_25_ + -1'pool__21_26_ + -1'pool__21_27_ + -1'pool__21_28_ + -1'pool__21_29_ + -1'pool__21_2_ + -1'pool__21_30_ + -1'pool__21_3_ + -1'pool__21_4_ + -1'pool__21_5_ + -1'pool__21_6_ + -1'pool__21_7_ + -1'pool__21_8_ + -1'pool__21_9_ + -1'pool__22_10_ + -1'pool__22_11_ + -1'pool__22_12_ + -1'pool__22_13_ + -1'pool__22_14_ + -1'pool__22_15_ + -1'pool__22_16_ + -1'pool__22_17_ + -1'pool__22_18_ + -1'pool__22_19_ + -1'pool__22_1_ + -1'pool__22_20_ + -1'pool__22_21_ + -1'pool__22_22_ + -1'pool__22_23_ + -1'pool__22_24_ + -1'pool__22_25_ + -1'pool__22_26_ + -1'pool__22_27_ + -1'pool__22_28_ + -1'pool__22_29_ + -1'pool__22_2_ + -1'pool__22_30_ + -1'pool__22_3_ + -1'pool__22_4_ + -1'pool__22_5_ + -1'pool__22_6_ + -1'pool__22_7_ + -1'pool__22_8_ + -1'pool__22_9_ + -1'pool__23_10_ + -1'pool__23_11_ + -1'pool__23_12_ + -1'pool__23_13_ + -1'pool__23_14_ + -1'pool__23_15_ + -1'pool__23_16_ + -1'pool__23_17_ + -1'pool__23_18_ + -1'pool__23_19_ + -1'pool__23_1_ + -1'pool__23_20_ + -1'pool__23_21_ + -1'pool__23_22_ + -1'pool__23_23_ + -1'pool__23_24_ + -1'pool__23_25_ + -1'pool__23_26_ + -1'pool__23_27_ + -1'pool__23_28_ + -1'pool__23_29_ + -1'pool__23_2_ + -1'pool__23_30_ + -1'pool__23_3_ + -1'pool__23_4_ + -1'pool__23_5_ + -1'pool__23_6_ + -1'pool__23_7_ + -1'pool__23_8_ + -1'pool__23_9_ + -1'pool__24_10_ + -1'pool__24_11_ + -1'pool__24_12_ + -1'pool__24_13_ + -1'pool__24_14_ + -1'pool__24_15_ + -1'pool__24_16_ + -1'pool__24_17_ + -1'pool__24_18_ + -1'pool__24_19_ + -1'pool__24_1_ + -1'pool__24_20_ + -1'pool__24_21_ + -1'pool__24_22_ + -1'pool__24_23_ + -1'pool__24_24_ + -1'pool__24_25_ + -1'pool__24_26_ + -1'pool__24_27_ + -1'pool__24_28_ + -1'pool__24_29_ + -1'pool__24_2_ + -1'pool__24_30_ + -1'pool__24_3_ + -1'pool__24_4_ + -1'pool__24_5_ + -1'pool__24_6_ + -1'pool__24_7_ + -1'pool__24_8_ + -1'pool__24_9_ + -1'pool__25_10_ + -1'pool__25_11_ + -1'pool__25_12_ + -1'pool__25_13_ + -1'pool__25_14_ + -1'pool__25_15_ + -1'pool__25_16_ + -1'pool__25_17_ + -1'pool__25_18_ + -1'pool__25_19_ + -1'pool__25_1_ + -1'pool__25_20_ + -1'pool__25_21_ + -1'pool__25_22_ + -1'pool__25_23_ + -1'pool__25_24_ + -1'pool__25_25_ + -1'pool__25_26_ + -1'pool__25_27_ + -1'pool__25_28_ + -1'pool__25_29_ + -1'pool__25_2_ + -1'pool__25_30_ + -1'pool__25_3_ + -1'pool__25_4_ + -1'pool__25_5_ + -1'pool__25_6_ + -1'pool__25_7_ + -1'pool__25_8_ + -1'pool__25_9_ + -1'pool__26_10_ + -1'pool__26_11_ + -1'pool__26_12_ + -1'pool__26_13_ + -1'pool__26_14_ + -1'pool__26_15_ + -1'pool__26_16_ + -1'pool__26_17_ + -1'pool__26_18_ + -1'pool__26_19_ + -1'pool__26_1_ + -1'pool__26_20_ + -1'pool__26_21_ + -1'pool__26_22_ + -1'pool__26_23_ + -1'pool__26_24_ + -1'pool__26_25_ + -1'pool__26_26_ + -1'pool__26_27_ + -1'pool__26_28_ + -1'pool__26_29_ + -1'pool__26_2_ + -1'pool__26_30_ + -1'pool__26_3_ + -1'pool__26_4_ + -1'pool__26_5_ + -1'pool__26_6_ + -1'pool__26_7_ + -1'pool__26_8_ + -1'pool__26_9_ + -1'pool__27_10_ + -1'pool__27_11_ + -1'pool__27_12_ + -1'pool__27_13_ + -1'pool__27_14_ + -1'pool__27_15_ + -1'pool__27_16_ + -1'pool__27_17_ + -1'pool__27_18_ + -1'pool__27_19_ + -1'pool__27_1_ + -1'pool__27_20_ + -1'pool__27_21_ + -1'pool__27_22_ + -1'pool__27_23_ + -1'pool__27_24_ + -1'pool__27_25_ + -1'pool__27_26_ + -1'pool__27_27_ + -1'pool__27_28_ + -1'pool__27_29_ + -1'pool__27_2_ + -1'pool__27_30_ + -1'pool__27_3_ + -1'pool__27_4_ + -1'pool__27_5_ + -1'pool__27_6_ + -1'pool__27_7_ + -1'pool__27_8_ + -1'pool__27_9_ + -1'pool__28_10_ + -1'pool__28_11_ + -1'pool__28_12_ + -1'pool__28_13_ + -1'pool__28_14_ + -1'pool__28_15_ + -1'pool__28_16_ + -1'pool__28_17_ + -1'pool__28_18_ + -1'pool__28_19_ + -1'pool__28_1_ + -1'pool__28_20_ + -1'pool__28_21_ + -1'pool__28_22_ + -1'pool__28_23_ + -1'pool__28_24_ + -1'pool__28_25_ + -1'pool__28_26_ + -1'pool__28_27_ + -1'pool__28_28_ + -1'pool__28_29_ + -1'pool__28_2_ + -1'pool__28_30_ + -1'pool__28_3_ + -1'pool__28_4_ + -1'pool__28_5_ + -1'pool__28_6_ + -1'pool__28_7_ + -1'pool__28_8_ + -1'pool__28_9_ + -1'pool__29_10_ + -1'pool__29_11_ + -1'pool__29_12_ + -1'pool__29_13_ + -1'pool__29_14_ + -1'pool__29_15_ + -1'pool__29_16_ + -1'pool__29_17_ + -1'pool__29_18_ + -1'pool__29_19_ + -1'pool__29_1_ + -1'pool__29_20_ + -1'pool__29_21_ + -1'pool__29_22_ + -1'pool__29_23_ + -1'pool__29_24_ + -1'pool__29_25_ + -1'pool__29_26_ + -1'pool__29_27_ + -1'pool__29_28_ + -1'pool__29_29_ + -1'pool__29_2_ + -1'pool__29_30_ + -1'pool__29_3_ + -1'pool__29_4_ + -1'pool__29_5_ + -1'pool__29_6_ + -1'pool__29_7_ + -1'pool__29_8_ + -1'pool__29_9_ + -1'pool__2_10_ + -1'pool__2_11_ + -1'pool__2_12_ + -1'pool__2_13_ + -1'pool__2_14_ + -1'pool__2_15_ + -1'pool__2_16_ + -1'pool__2_17_ + -1'pool__2_18_ + -1'pool__2_19_ + -1'pool__2_1_ + -1'pool__2_20_ + -1'pool__2_21_ + -1'pool__2_22_ + -1'pool__2_23_ + -1'pool__2_24_ + -1'pool__2_25_ + -1'pool__2_26_ + -1'pool__2_27_ + -1'pool__2_28_ + -1'pool__2_29_ + -1'pool__2_2_ + -1'pool__2_30_ + -1'pool__2_3_ + -1'pool__2_4_ + -1'pool__2_5_ + -1'pool__2_6_ + -1'pool__2_7_ + -1'pool__2_8_ + -1'pool__2_9_ + -1'pool__30_10_ + -1'pool__30_11_ + -1'pool__30_12_ + -1'pool__30_13_ + -1'pool__30_14_ + -1'pool__30_15_ + -1'pool__30_16_ + -1'pool__30_17_ + -1'pool__30_18_ + -1'pool__30_19_ + -1'pool__30_1_ + -1'pool__30_20_ + -1'pool__30_21_ + -1'pool__30_22_ + -1'pool__30_23_ + -1'pool__30_24_ + -1'pool__30_25_ + -1'pool__30_26_ + -1'pool__30_27_ + -1'pool__30_28_ + -1'pool__30_29_ + -1'pool__30_2_ + -1'pool__30_30_ + -1'pool__30_3_ + -1'pool__30_4_ + -1'pool__30_5_ + -1'pool__30_6_ + -1'pool__30_7_ + -1'pool__30_8_ + -1'pool__30_9_ + -1'pool__3_10_ + -1'pool__3_11_ + -1'pool__3_12_ + -1'pool__3_13_ + -1'pool__3_14_ + -1'pool__3_15_ + -1'pool__3_16_ + -1'pool__3_17_ + -1'pool__3_18_ + -1'pool__3_19_ + -1'pool__3_1_ + -1'pool__3_20_ + -1'pool__3_21_ + -1'pool__3_22_ + -1'pool__3_23_ + -1'pool__3_24_ + -1'pool__3_25_ + -1'pool__3_26_ + -1'pool__3_27_ + -1'pool__3_28_ + -1'pool__3_29_ + -1'pool__3_2_ + -1'pool__3_30_ + -1'pool__3_3_ + -1'pool__3_4_ + -1'pool__3_5_ + -1'pool__3_6_ + -1'pool__3_7_ + -1'pool__3_8_ + -1'pool__3_9_ + -1'pool__4_10_ + -1'pool__4_11_ + -1'pool__4_12_ + -1'pool__4_13_ + -1'pool__4_14_ + -1'pool__4_15_ + -1'pool__4_16_ + -1'pool__4_17_ + -1'pool__4_18_ + -1'pool__4_19_ + -1'pool__4_1_ + -1'pool__4_20_ + -1'pool__4_21_ + -1'pool__4_22_ + -1'pool__4_23_ + -1'pool__4_24_ + -1'pool__4_25_ + -1'pool__4_26_ + -1'pool__4_27_ + -1'pool__4_28_ + -1'pool__4_29_ + -1'pool__4_2_ + -1'pool__4_30_ + -1'pool__4_3_ + -1'pool__4_4_ + -1'pool__4_5_ + -1'pool__4_6_ + -1'pool__4_7_ + -1'pool__4_8_ + -1'pool__4_9_ + -1'pool__5_10_ + -1'pool__5_11_ + -1'pool__5_12_ + -1'pool__5_13_ + -1'pool__5_14_ + -1'pool__5_15_ + -1'pool__5_16_ + -1'pool__5_17_ + -1'pool__5_18_ + -1'pool__5_19_ + -1'pool__5_1_ + -1'pool__5_20_ + -1'pool__5_21_ + -1'pool__5_22_ + -1'pool__5_23_ + -1'pool__5_24_ + -1'pool__5_25_ + -1'pool__5_26_ + -1'pool__5_27_ + -1'pool__5_28_ + -1'pool__5_29_ + -1'pool__5_2_ + -1'pool__5_30_ + -1'pool__5_3_ + -1'pool__5_4_ + -1'pool__5_5_ + -1'pool__5_6_ + -1'pool__5_7_ + -1'pool__5_8_ + -1'pool__5_9_ + -1'pool__6_10_ + -1'pool__6_11_ + -1'pool__6_12_ + -1'pool__6_13_ + -1'pool__6_14_ + -1'pool__6_15_ + -1'pool__6_16_ + -1'pool__6_17_ + -1'pool__6_18_ + -1'pool__6_19_ + -1'pool__6_1_ + -1'pool__6_20_ + -1'pool__6_21_ + -1'pool__6_22_ + -1'pool__6_23_ + -1'pool__6_24_ + -1'pool__6_25_ + -1'pool__6_26_ + -1'pool__6_27_ + -1'pool__6_28_ + -1'pool__6_29_ + -1'pool__6_2_ + -1'pool__6_30_ + -1'pool__6_3_ + -1'pool__6_4_ + -1'pool__6_5_ + -1'pool__6_6_ + -1'pool__6_7_ + -1'pool__6_8_ + -1'pool__6_9_ + -1'pool__7_10_ + -1'pool__7_11_ + -1'pool__7_12_ + -1'pool__7_13_ + -1'pool__7_14_ + -1'pool__7_15_ + -1'pool__7_16_ + -1'pool__7_17_ + -1'pool__7_18_ + -1'pool__7_19_ + -1'pool__7_1_ + -1'pool__7_20_ + -1'pool__7_21_ + -1'pool__7_22_ + -1'pool__7_23_ + -1'pool__7_24_ + -1'pool__7_25_ + -1'pool__7_26_ + -1'pool__7_27_ + -1'pool__7_28_ + -1'pool__7_29_ + -1'pool__7_2_ + -1'pool__7_30_ + -1'pool__7_3_ + -1'pool__7_4_ + -1'pool__7_5_ + -1'pool__7_6_ + -1'pool__7_7_ + -1'pool__7_8_ + -1'pool__7_9_ + -1'pool__8_10_ + -1'pool__8_11_ + -1'pool__8_12_ + -1'pool__8_13_ + -1'pool__8_14_ + -1'pool__8_15_ + -1'pool__8_16_ + -1'pool__8_17_ + -1'pool__8_18_ + -1'pool__8_19_ + -1'pool__8_1_ + -1'pool__8_20_ + -1'pool__8_21_ + -1'pool__8_22_ + -1'pool__8_23_ + -1'pool__8_24_ + -1'pool__8_25_ + -1'pool__8_26_ + -1'pool__8_27_ + -1'pool__8_28_ + -1'pool__8_29_ + -1'pool__8_2_ + -1'pool__8_30_ + -1'pool__8_3_ + -1'pool__8_4_ + -1'pool__8_5_ + -1'pool__8_6_ + -1'pool__8_7_ + -1'pool__8_8_ + -1'pool__8_9_ + -1'pool__9_10_ + -1'pool__9_11_ + -1'pool__9_12_ + -1'pool__9_13_ + -1'pool__9_14_ + -1'pool__9_15_ + -1'pool__9_16_ + -1'pool__9_17_ + -1'pool__9_18_ + -1'pool__9_19_ + -1'pool__9_1_ + -1'pool__9_20_ + -1'pool__9_21_ + -1'pool__9_22_ + -1'pool__9_23_ + -1'pool__9_24_ + -1'pool__9_25_ + -1'pool__9_26_ + -1'pool__9_27_ + -1'pool__9_28_ + -1'pool__9_29_ + -1'pool__9_2_ + -1'pool__9_30_ + -1'pool__9_3_ + -1'pool__9_4_ + -1'pool__9_5_ + -1'pool__9_6_ + -1'pool__9_7_ + -1'pool__9_8_ + -1'pool__9_9_ + -1'size_dot = -899
invariant :cell___20_23__A_ + cell___20_23__B_ + pool__20_23_ = 1
invariant :cell___21_17__A_ + cell___21_17__B_ + pool__21_17_ = 1
invariant :cell___26_1__A_ + cell___26_1__B_ + pool__26_1_ = 1
invariant :cell___6_13__A_ + cell___6_13__B_ + pool__6_13_ = 1
invariant :cell___5_17__A_ + cell___5_17__B_ + pool__5_17_ = 1
invariant :cell___16_3__A_ + cell___16_3__B_ + pool__16_3_ = 1
invariant :cell___24_27__A_ + cell___24_27__B_ + pool__24_27_ = 1
invariant :cell___13_18__A_ + cell___13_18__B_ + pool__13_18_ = 1
invariant :cell___28_1__A_ + cell___28_1__B_ + pool__28_1_ = 1
invariant :cell___6_10__A_ + cell___6_10__B_ + pool__6_10_ = 1
invariant :cell___14_18__A_ + cell___14_18__B_ + pool__14_18_ = 1
invariant :cell___7_1__A_ + cell___7_1__B_ + pool__7_1_ = 1
invariant :cell___11_10__A_ + cell___11_10__B_ + pool__11_10_ = 1
invariant :cell___28_9__A_ + cell___28_9__B_ + pool__28_9_ = 1
invariant :cell___4_14__A_ + cell___4_14__B_ + pool__4_14_ = 1
invariant :cell___21_22__A_ + cell___21_22__B_ + pool__21_22_ = 1
invariant :cell___27_15__A_ + cell___27_15__B_ + pool__27_15_ = 1
invariant :cell___9_26__A_ + cell___9_26__B_ + pool__9_26_ = 1
invariant :cell___9_6__A_ + cell___9_6__B_ + pool__9_6_ = 1
invariant :cell___18_24__A_ + cell___18_24__B_ + pool__18_24_ = 1
invariant :cell___20_20__A_ + cell___20_20__B_ + pool__20_20_ = 1
invariant :cell___12_19__A_ + cell___12_19__B_ + pool__12_19_ = 1
invariant :cell___5_30__A_ + cell___5_30__B_ + pool__5_30_ = 1
invariant :cell___10_22__A_ + cell___10_22__B_ + pool__10_22_ = 1
invariant :cell___29_13__A_ + cell___29_13__B_ + pool__29_13_ = 1
invariant :cell___11_1__A_ + cell___11_1__B_ + pool__11_1_ = 1
invariant :cell___5_29__A_ + cell___5_29__B_ + pool__5_29_ = 1
invariant :cell___8_27__A_ + cell___8_27__B_ + pool__8_27_ = 1
invariant :cell___13_19__A_ + cell___13_19__B_ + pool__13_19_ = 1
invariant :cell___23_18__A_ + cell___23_18__B_ + pool__23_18_ = 1
invariant :cell___17_1__A_ + cell___17_1__B_ + pool__17_1_ = 1
invariant :cell___3_13__A_ + cell___3_13__B_ + pool__3_13_ = 1
invariant :cell___4_1__A_ + cell___4_1__B_ + pool__4_1_ = 1
invariant :cell___21_12__A_ + cell___21_12__B_ + pool__21_12_ = 1
invariant :cell___22_20__A_ + cell___22_20__B_ + pool__22_20_ = 1
invariant :cell___3_28__A_ + cell___3_28__B_ + pool__3_28_ = 1
invariant :cell___5_24__A_ + cell___5_24__B_ + pool__5_24_ = 1
invariant :cell___8_2__A_ + cell___8_2__B_ + pool__8_2_ = 1
invariant :cell___14_4__A_ + cell___14_4__B_ + pool__14_4_ = 1
invariant :cell___13_13__A_ + cell___13_13__B_ + pool__13_13_ = 1
invariant :cell___3_17__A_ + cell___3_17__B_ + pool__3_17_ = 1
invariant :cell___2_3__A_ + cell___2_3__B_ + pool__2_3_ = 1
invariant :cell___3_14__A_ + cell___3_14__B_ + pool__3_14_ = 1
invariant :cell___6_23__A_ + cell___6_23__B_ + pool__6_23_ = 1
invariant :cell___5_13__A_ + cell___5_13__B_ + pool__5_13_ = 1
invariant :cell___6_15__A_ + cell___6_15__B_ + pool__6_15_ = 1
invariant :cell___27_1__A_ + cell___27_1__B_ + pool__27_1_ = 1
invariant :cell___20_7__A_ + cell___20_7__B_ + pool__20_7_ = 1
invariant :cell___5_12__A_ + cell___5_12__B_ + pool__5_12_ = 1
invariant :cell___30_5__A_ + cell___30_5__B_ + pool__30_5_ = 1
invariant :cell___29_6__A_ + cell___29_6__B_ + pool__29_6_ = 1
invariant :cell___14_26__A_ + cell___14_26__B_ + pool__14_26_ = 1
invariant :cell___9_4__A_ + cell___9_4__B_ + pool__9_4_ = 1
invariant :cell___16_5__A_ + cell___16_5__B_ + pool__16_5_ = 1
invariant :cell___22_23__A_ + cell___22_23__B_ + pool__22_23_ = 1
invariant :cell___26_27__A_ + cell___26_27__B_ + pool__26_27_ = 1
invariant :cell___3_20__A_ + cell___3_20__B_ + pool__3_20_ = 1
invariant :cell___16_18__A_ + cell___16_18__B_ + pool__16_18_ = 1
invariant :cell___5_19__A_ + cell___5_19__B_ + pool__5_19_ = 1
invariant :cell___28_13__A_ + cell___28_13__B_ + pool__28_13_ = 1
invariant :cell___17_26__A_ + cell___17_26__B_ + pool__17_26_ = 1
invariant :cell___14_10__A_ + cell___14_10__B_ + pool__14_10_ = 1
invariant :cell___10_27__A_ + cell___10_27__B_ + pool__10_27_ = 1
invariant :cell___1_2__A_ + cell___1_2__B_ + pool__1_2_ = 1
invariant :cell___14_15__A_ + cell___14_15__B_ + pool__14_15_ = 1
invariant :cell___14_5__A_ + cell___14_5__B_ + pool__14_5_ = 1
invariant :cell___28_29__A_ + cell___28_29__B_ + pool__28_29_ = 1
invariant :cell___14_24__A_ + cell___14_24__B_ + pool__14_24_ = 1
invariant :cell___27_4__A_ + cell___27_4__B_ + pool__27_4_ = 1
invariant :cell___11_4__A_ + cell___11_4__B_ + pool__11_4_ = 1
invariant :cell___12_26__A_ + cell___12_26__B_ + pool__12_26_ = 1
invariant :cell___11_17__A_ + cell___11_17__B_ + pool__11_17_ = 1
invariant :cell___2_17__A_ + cell___2_17__B_ + pool__2_17_ = 1
invariant :cell___29_14__A_ + cell___29_14__B_ + pool__29_14_ = 1
invariant :cell___8_1__A_ + cell___8_1__B_ + pool__8_1_ = 1
invariant :cell___15_16__A_ + cell___15_16__B_ + pool__15_16_ = 1
invariant :cell___26_13__A_ + cell___26_13__B_ + pool__26_13_ = 1
invariant :cell___30_12__A_ + cell___30_12__B_ + pool__30_12_ = 1
invariant :cell___27_23__A_ + cell___27_23__B_ + pool__27_23_ = 1
invariant :cell___26_29__A_ + cell___26_29__B_ + pool__26_29_ = 1
invariant :cell___13_26__A_ + cell___13_26__B_ + pool__13_26_ = 1
invariant :cell___17_24__A_ + cell___17_24__B_ + pool__17_24_ = 1
invariant :cell___10_8__A_ + cell___10_8__B_ + pool__10_8_ = 1
invariant :cell___10_11__A_ + cell___10_11__B_ + pool__10_11_ = 1
invariant :cell___14_29__A_ + cell___14_29__B_ + pool__14_29_ = 1
invariant :cell___28_7__A_ + cell___28_7__B_ + pool__28_7_ = 1
invariant :cell___8_7__A_ + cell___8_7__B_ + pool__8_7_ = 1
invariant :cell___30_15__A_ + cell___30_15__B_ + pool__30_15_ = 1
invariant :cell___12_25__A_ + cell___12_25__B_ + pool__12_25_ = 1
invariant :cell___2_1__A_ + cell___2_1__B_ + pool__2_1_ = 1
invariant :cell___18_4__A_ + cell___18_4__B_ + pool__18_4_ = 1
invariant :cell___20_22__A_ + cell___20_22__B_ + pool__20_22_ = 1
invariant :cell___23_20__A_ + cell___23_20__B_ + pool__23_20_ = 1
invariant :cell___3_30__A_ + cell___3_30__B_ + pool__3_30_ = 1
invariant :cell___30_14__A_ + cell___30_14__B_ + pool__30_14_ = 1
invariant :cell___11_18__A_ + cell___11_18__B_ + pool__11_18_ = 1
invariant :cell___29_17__A_ + cell___29_17__B_ + pool__29_17_ = 1
invariant :cell___10_23__A_ + cell___10_23__B_ + pool__10_23_ = 1
invariant :cell___30_16__A_ + cell___30_16__B_ + pool__30_16_ = 1
invariant :cell___29_19__A_ + cell___29_19__B_ + pool__29_19_ = 1
invariant :cell___19_13__A_ + cell___19_13__B_ + pool__19_13_ = 1
invariant :cell___10_4__A_ + cell___10_4__B_ + pool__10_4_ = 1
invariant :cell___2_15__A_ + cell___2_15__B_ + pool__2_15_ = 1
invariant :cell___9_27__A_ + cell___9_27__B_ + pool__9_27_ = 1
invariant :cell___22_12__A_ + cell___22_12__B_ + pool__22_12_ = 1
invariant :cell___11_13__A_ + cell___11_13__B_ + pool__11_13_ = 1
invariant :cell___18_21__A_ + cell___18_21__B_ + pool__18_21_ = 1
invariant :cell___24_22__A_ + cell___24_22__B_ + pool__24_22_ = 1
invariant :cell___14_7__A_ + cell___14_7__B_ + pool__14_7_ = 1
invariant :cell___16_8__A_ + cell___16_8__B_ + pool__16_8_ = 1
invariant :cell___28_15__A_ + cell___28_15__B_ + pool__28_15_ = 1
invariant :cell___7_27__A_ + cell___7_27__B_ + pool__7_27_ = 1
invariant :cell___17_25__A_ + cell___17_25__B_ + pool__17_25_ = 1
invariant :cell___22_15__A_ + cell___22_15__B_ + pool__22_15_ = 1
invariant :cell___16_13__A_ + cell___16_13__B_ + pool__16_13_ = 1
invariant :cell___10_3__A_ + cell___10_3__B_ + pool__10_3_ = 1
invariant :cell___27_18__A_ + cell___27_18__B_ + pool__27_18_ = 1
invariant :cell___21_11__A_ + cell___21_11__B_ + pool__21_11_ = 1
invariant :cell___17_29__A_ + cell___17_29__B_ + pool__17_29_ = 1
invariant :cell___13_25__A_ + cell___13_25__B_ + pool__13_25_ = 1
invariant :cell___24_23__A_ + cell___24_23__B_ + pool__24_23_ = 1
invariant :cell___18_27__A_ + cell___18_27__B_ + pool__18_27_ = 1
invariant :cell___18_9__A_ + cell___18_9__B_ + pool__18_9_ = 1
invariant :cell___28_27__A_ + cell___28_27__B_ + pool__28_27_ = 1
invariant :cell___7_21__A_ + cell___7_21__B_ + pool__7_21_ = 1
invariant :cell___23_3__A_ + cell___23_3__B_ + pool__23_3_ = 1
invariant :cell___6_29__A_ + cell___6_29__B_ + pool__6_29_ = 1
invariant :cell___19_18__A_ + cell___19_18__B_ + pool__19_18_ = 1
invariant :cell___6_1__A_ + cell___6_1__B_ + pool__6_1_ = 1
invariant :cell___12_14__A_ + cell___12_14__B_ + pool__12_14_ = 1
invariant :cell___22_28__A_ + cell___22_28__B_ + pool__22_28_ = 1
invariant :cell___14_13__A_ + cell___14_13__B_ + pool__14_13_ = 1
invariant :cell___25_9__A_ + cell___25_9__B_ + pool__25_9_ = 1
invariant :cell___26_21__A_ + cell___26_21__B_ + pool__26_21_ = 1
invariant :cell___25_15__A_ + cell___25_15__B_ + pool__25_15_ = 1
invariant :cell___24_14__A_ + cell___24_14__B_ + pool__24_14_ = 1
FORMULA PhaseVariation-PT-D30CS010-ReachabilityCardinality-00 TRUE TECHNIQUES SAT_SMT K_INDUCTION(0)
WARNING : LTS min runner thread failed on error :java.lang.RuntimeException: Compilation or link of executable timed out.java.util.concurrent.TimeoutException: Subprocess running CommandLine [args=[gcc, -c, -I/home/mcc/BenchKit//lts_install_dir//include, -I., -std=c99, -fPIC, -O2, model.c], workingDir=/home/mcc/execution] killed by timeout after 400 SECONDS
FORMULA PhaseVariation-PT-D30CS010-ReachabilityCardinality-02 FALSE TECHNIQUES SAT_SMT K_INDUCTION(0)
FORMULA PhaseVariation-PT-D30CS010-ReachabilityCardinality-03 TRUE TECHNIQUES SAT_SMT K_INDUCTION(0)
FORMULA PhaseVariation-PT-D30CS010-ReachabilityCardinality-04 FALSE TECHNIQUES SAT_SMT K_INDUCTION(0)
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/
+ BINDIR=/home/mcc/BenchKit/
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ ReachabilityCardinality = StateSpace ]]
+ /home/mcc/BenchKit//runeclipse.sh /home/mcc/execution ReachabilityCardinality -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ /home/mcc/BenchKit//itstools/its-tools -data /home/mcc/execution/workspace -pnfolder /home/mcc/execution -examination ReachabilityCardinality -z3path /home/mcc/BenchKit//z3/bin/z3 -yices2path /home/mcc/BenchKit//yices/bin/yices -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt -vmargs -Dosgi.locking=none -Declipse.stateSaveDelayInterval=-1 -Dosgi.configuration.area=/tmp/.eclipse -Xss8m -Xms40m -Xmx8192m -Dfile.encoding=UTF-8 -Dosgi.requiredJavaVersion=1.6
Mar 18, 2019 10:01:43 PM fr.lip6.move.gal.application.Application start
INFO: Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, ReachabilityCardinality, -z3path, /home/mcc/BenchKit//z3/bin/z3, -yices2path, /home/mcc/BenchKit//yices/bin/yices, -its, -ltsminpath, /home/mcc/BenchKit//lts_install_dir/, -smt]
Mar 18, 2019 10:01:43 PM fr.lip6.move.gal.application.MccTranslator transformPNML
INFO: Parsing pnml file : /home/mcc/execution/model.pnml
Mar 18, 2019 10:01:44 PM fr.lip6.move.gal.nupn.PTNetReader loadFromXML
INFO: Load time of PNML (sax parser for PT used): 1090 ms
Mar 18, 2019 10:01:44 PM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 2702 places.
Mar 18, 2019 10:01:46 PM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 30977 transitions.
Mar 18, 2019 10:01:52 PM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 5273 ms
Mar 18, 2019 10:02:00 PM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 30977 transitions.
Mar 18, 2019 10:02:00 PM fr.lip6.move.gal.gal2pins.Gal2PinsTransformerNext transform
INFO: Too many transitions (30977) to apply POR reductions. Disabling POR matrices.
Mar 18, 2019 10:02:02 PM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 9741 ms
Mar 18, 2019 10:02:05 PM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 10139 ms
Mar 18, 2019 10:02:05 PM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 30977 transitions.
Mar 18, 2019 10:02:05 PM fr.lip6.move.serialization.SerializationUtil systemToFile
INFO: Time to serialize gal into /home/mcc/execution/ReachabilityCardinality.pnml.gal : 503 ms
Mar 18, 2019 10:02:06 PM fr.lip6.move.serialization.SerializationUtil serializePropertiesForITSTools
INFO: Time to serialize properties into /home/mcc/execution/ReachabilityCardinality.prop : 49 ms
Mar 18, 2019 10:02:07 PM fr.lip6.move.gal.gal2pins.Gal2PinsTransformerNext transform
INFO: Built C files in 11642ms conformant to PINS in folder :/home/mcc/execution
Mar 18, 2019 10:02:34 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd checkProperties
INFO: Ran tautology test, simplified 0 / 16 in 32192 ms.
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-00(UNSAT) depth K=0 took 425 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-01(UNSAT) depth K=0 took 48 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-02(UNSAT) depth K=0 took 67 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-03(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-04(UNSAT) depth K=0 took 84 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-05(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-06(UNSAT) depth K=0 took 34 ms
Mar 18, 2019 10:02:35 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-07(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-08(UNSAT) depth K=0 took 48 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-09(UNSAT) depth K=0 took 469 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-10(UNSAT) depth K=0 took 21 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-11(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-12(UNSAT) depth K=0 took 41 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-13(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-14(UNSAT) depth K=0 took 34 ms
Mar 18, 2019 10:02:36 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-15(UNSAT) depth K=0 took 7 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-00(UNSAT) depth K=1 took 30 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-01(UNSAT) depth K=1 took 20 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-02(UNSAT) depth K=1 took 43 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-03(UNSAT) depth K=1 took 28 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-04(UNSAT) depth K=1 took 35 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-05(UNSAT) depth K=1 took 31 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-06(UNSAT) depth K=1 took 56 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-07(UNSAT) depth K=1 took 21 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-08(UNSAT) depth K=1 took 28 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-09(UNSAT) depth K=1 took 7 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-10(UNSAT) depth K=1 took 35 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-11(UNSAT) depth K=1 took 28 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-12(UNSAT) depth K=1 took 290 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-13(UNSAT) depth K=1 took 44 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-14(UNSAT) depth K=1 took 33 ms
Mar 18, 2019 10:02:37 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-15(UNSAT) depth K=1 took 23 ms
Mar 18, 2019 10:02:40 PM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 30977 transitions.
Mar 18, 2019 10:03:13 PM fr.lip6.move.gal.gal2smt.bmc.KInductionSolver computeAndDeclareInvariants
INFO: Computed 901 place invariants in 5031 ms
Mar 18, 2019 10:05:23 PM fr.lip6.move.gal.gal2smt.bmc.KInductionSolver init
INFO: Proved 2702 variables to be positive in 135749 ms
Mar 18, 2019 10:06:20 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, proved invariant PhaseVariation-PT-D30CS010-ReachabilityCardinality-00
Mar 18, 2019 10:06:20 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, successfully proved induction at step 0 for PhaseVariation-PT-D30CS010-ReachabilityCardinality-00
Mar 18, 2019 10:06:20 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-00(TRUE) depth K=0 took 56652 ms
java.lang.RuntimeException: Compilation or link of executable timed out.java.util.concurrent.TimeoutException: Subprocess running CommandLine [args=[gcc, -c, -I/home/mcc/BenchKit//lts_install_dir//include, -I., -std=c99, -fPIC, -O2, model.c], workingDir=/home/mcc/execution] killed by timeout after 400 SECONDS
at fr.lip6.move.gal.application.LTSminRunner$1.run(LTSminRunner.java:78)
at java.lang.Thread.run(Thread.java:748)
Mar 18, 2019 10:09:16 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-00(UNSAT) depth K=2 took 397903 ms
Mar 18, 2019 10:10:15 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-01(UNSAT) depth K=2 took 59411 ms
Mar 18, 2019 10:22:57 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is SAT, non conclusive we might be starting from unreachable statesPhaseVariation-PT-D30CS010-ReachabilityCardinality-01
Mar 18, 2019 10:22:57 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-01(SAT) depth K=0 took 997118 ms
Mar 18, 2019 10:25:13 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, proved UNreachability of reachability predicate PhaseVariation-PT-D30CS010-ReachabilityCardinality-02
Mar 18, 2019 10:25:13 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, successfully proved induction at step 0 for PhaseVariation-PT-D30CS010-ReachabilityCardinality-02
Mar 18, 2019 10:25:13 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-02(FALSE) depth K=0 took 135750 ms
Mar 18, 2019 10:26:46 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, proved invariant PhaseVariation-PT-D30CS010-ReachabilityCardinality-03
Mar 18, 2019 10:26:46 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, successfully proved induction at step 0 for PhaseVariation-PT-D30CS010-ReachabilityCardinality-03
Mar 18, 2019 10:26:46 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-03(TRUE) depth K=0 took 93491 ms
Mar 18, 2019 10:29:07 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, proved UNreachability of reachability predicate PhaseVariation-PT-D30CS010-ReachabilityCardinality-04
Mar 18, 2019 10:29:07 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is UNSAT, successfully proved induction at step 0 for PhaseVariation-PT-D30CS010-ReachabilityCardinality-04
Mar 18, 2019 10:29:07 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-04(FALSE) depth K=0 took 140701 ms
Mar 18, 2019 10:31:34 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-02(UNSAT) depth K=2 took 1278791 ms
ITS-tools command line returned an error code 137
Mar 18, 2019 10:41:01 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-03(UNSAT) depth K=2 took 566327 ms
Mar 18, 2019 10:41:49 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-04(UNSAT) depth K=2 took 48531 ms
Mar 18, 2019 10:42:33 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-05(UNSAT) depth K=2 took 43678 ms
Mar 18, 2019 10:44:53 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is SAT, non conclusive we might be starting from unreachable statesPhaseVariation-PT-D30CS010-ReachabilityCardinality-05
Mar 18, 2019 10:44:53 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-05(SAT) depth K=0 took 946445 ms
Mar 18, 2019 10:45:55 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-06(UNSAT) depth K=2 took 202277 ms
Mar 18, 2019 10:47:09 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-07(UNSAT) depth K=2 took 73592 ms
Mar 18, 2019 10:47:25 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-08(UNSAT) depth K=2 took 16081 ms
Mar 18, 2019 10:48:56 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-09(UNSAT) depth K=2 took 91014 ms
Mar 18, 2019 10:49:25 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-10(UNSAT) depth K=2 took 29353 ms
Mar 18, 2019 10:53:56 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: Induction result is SAT, non conclusive we might be starting from unreachable statesPhaseVariation-PT-D30CS010-ReachabilityCardinality-06
Mar 18, 2019 10:53:56 PM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
INFO: KInduction solution for property PhaseVariation-PT-D30CS010-ReachabilityCardinality-06(SAT) depth K=0 took 542221 ms
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="PhaseVariation-PT-D30CS010"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-3954"
echo " Executing tool itstools"
echo " Input is PhaseVariation-PT-D30CS010, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r107-oct2-155272231300656"
echo "====================================================================="
echo
echo "--------------------"
echo "preparation of the directory to be used:"
tar xzf /home/mcc/BenchKit/INPUTS/PhaseVariation-PT-D30CS010.tgz
mv PhaseVariation-PT-D30CS010 execution
cd execution
if [ "ReachabilityCardinality" = "GlobalProperties" ] ; then
rm -f GenericPropertiesVerdict.xml
fi
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
rm -f GenericPropertiesVerdict.xml
fi
pwd
ls -lh
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

