About the Execution of M4M.struct for NeoElection-PT-8
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 617.840 | 242856.00 | 253108.00 | 288.40 | ???????????????? | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
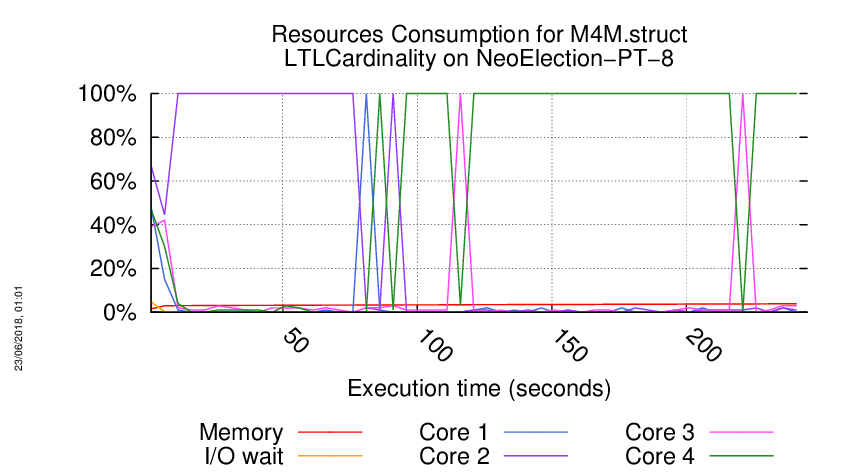
Trace from the execution
Waiting for the VM to be ready (probing ssh)
.......................................................................................
/home/mcc/execution
total 26M
-rw-r--r-- 1 mcc users 273K May 15 18:54 CTLCardinality.txt
-rw-r--r-- 1 mcc users 718K May 15 18:54 CTLCardinality.xml
-rw-r--r-- 1 mcc users 594K May 15 18:54 CTLFireability.txt
-rw-r--r-- 1 mcc users 1.6M May 15 18:54 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K May 15 18:50 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K May 15 18:50 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 261K May 26 09:26 LTLCardinality.txt
-rw-r--r-- 1 mcc users 591K May 26 09:26 LTLCardinality.xml
-rw-r--r-- 1 mcc users 213K May 26 09:26 LTLFireability.txt
-rw-r--r-- 1 mcc users 545K May 26 09:26 LTLFireability.xml
-rw-r--r-- 1 mcc users 235K May 15 18:54 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 581K May 15 18:54 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 107 May 15 18:54 ReachabilityDeadlock.txt
-rw-r--r-- 1 mcc users 345 May 15 18:54 ReachabilityDeadlock.xml
-rw-r--r-- 1 mcc users 116K May 15 18:54 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 327K May 15 18:54 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 213K May 15 18:54 UpperBounds.txt
-rw-r--r-- 1 mcc users 409K May 15 18:54 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 May 15 18:50 equiv_col
-rw-r--r-- 1 mcc users 2 May 15 18:50 instance
-rw-r--r-- 1 mcc users 6 May 15 18:50 iscolored
-rw-r--r-- 1 mcc users 20M May 15 18:50 model.pnml
=====================================================================
Generated by BenchKit 2-3637
Executing tool mcc4mcc-structural
Input is NeoElection-PT-8, examination is LTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r263-csrt-152732587400095
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-8-LTLCardinality-00
FORMULA_NAME NeoElection-PT-8-LTLCardinality-01
FORMULA_NAME NeoElection-PT-8-LTLCardinality-02
FORMULA_NAME NeoElection-PT-8-LTLCardinality-03
FORMULA_NAME NeoElection-PT-8-LTLCardinality-04
FORMULA_NAME NeoElection-PT-8-LTLCardinality-05
FORMULA_NAME NeoElection-PT-8-LTLCardinality-06
FORMULA_NAME NeoElection-PT-8-LTLCardinality-07
FORMULA_NAME NeoElection-PT-8-LTLCardinality-08
FORMULA_NAME NeoElection-PT-8-LTLCardinality-09
FORMULA_NAME NeoElection-PT-8-LTLCardinality-10
FORMULA_NAME NeoElection-PT-8-LTLCardinality-11
FORMULA_NAME NeoElection-PT-8-LTLCardinality-12
FORMULA_NAME NeoElection-PT-8-LTLCardinality-13
FORMULA_NAME NeoElection-PT-8-LTLCardinality-14
FORMULA_NAME NeoElection-PT-8-LTLCardinality-15
=== Now, execution of the tool begins
BK_START 1527830855579
BK_STOP 1527831098435
--------------------
content from stderr:
Prefix is 75f5f979.
Reading known information in /usr/share/mcc4mcc/75f5f979-known.json.
Reading learned information in /usr/share/mcc4mcc/75f5f979-learned.json.
Reading value translations in /usr/share/mcc4mcc/75f5f979-values.json.
Using directory /home/mcc/execution for input, as it contains a model.pnml file.
Using NeoElection-PT-8 as instance name.
Using NeoElection as model name.
Using algorithm or tool bmdt.
Model characteristics are: {'Examination': 'LTLCardinality', 'Place/Transition': True, 'Colored': True, 'Relative-Time': 1, 'Relative-Memory': 1, 'Ordinary': True, 'Simple Free Choice': False, 'Extended Free Choice': False, 'State Machine': False, 'Marked Graph': False, 'Connected': False, 'Strongly Connected': False, 'Source Place': True, 'Sink Place': True, 'Source Transition': False, 'Sink Transition': False, 'Loop Free': False, 'Conservative': False, 'Sub-Conservative': False, 'Nested Units': False, 'Safe': True, 'Deadlock': True, 'Reversible': False, 'Quasi Live': False, 'Live': False}.
Known tools are: [{'Time': 2425434, 'Memory': 2163.1, 'Tool': 'lola'}, {'Time': 2425532, 'Memory': 14399.37, 'Tool': 'lola'}].
Learned tools are: [{'Tool': 'lola'}].
Learned tool lola is 1.0x far from the best tool lola.
LTLCardinality lola NeoElection-PT-8...
Time: 3600 - MCC
----- Start make prepare stdout -----
----- Start make prepare stderr -----
===========================================================================================
NeoElection-PT-8: translating PT Petri net model.pnml into LoLA format
===========================================================================================
translating PT Petri net complete
checking for too many tokens
===========================================================================================
NeoElection-PT-8: translating PT formula LTLCardinality into LoLA format
===========================================================================================
translating formula complete
touch formulae;
----- Start make result stderr -----
----- Start make result stdout -----
LTLCardinality @ NeoElection-PT-8 @ 3540 seconds
Makefile:222: recipe for target 'verify' failed
make: [verify] Error 134 (ignored)
----- Start make result stdout -----
----- Start make result stderr -----
lola: LoLA will run for 3540 seconds at most (--timelimit)
lola: NET
lola: reading net from model.pnml.lola
lola: finished parsing
lola: closed net file model.pnml.lola
lola: 32328/65536 symbol table entries, 8032 collisions
lola: preprocessing...
lola: finding significant places
lola: 10062 places, 22266 transitions, 2295 significant places
lola: computing forward-conflicting sets
lola: computing back-conflicting sets
lola: 5067 transition conflict sets
lola: TASK
lola: reading formula from NeoElection-PT-8-LTLCardinality.task
lola: A ((2 <= P-sendAnnPs__broadcasting_8_8 + P-sendAnnPs__broadcasting_8_7 + P-sendAnnPs__broadcasting_8_6 + P-sendAnnPs__broadcasting_8_5 + P-sendAnnPs__broadcasting_8_4 + P-sendAnnPs__broadcasting_8_3 + P-sendAnnPs__broadcasting_8_2 + P-sendAnnPs__broadcasting_8_1 + P-sendAnnPs__broadcasting_7_8 + P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_8 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_8 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_8 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_8 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_8 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_8 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_8 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1)) : A (F (G (G (G ((P-electedSecondary_8 + P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 + P-polling_8)))))) : A ((F ((3 <= P-poll__networl_7_4_AnsP_8 + P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_8 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_2_8_AnsP_8 + P-poll__networl_2_8_AnsP_7 + P-poll__networl_2_8_AnsP_6 + P-poll__networl_2_8_AnsP_5 + P-poll__networl_2_8_AnsP_4 + P-poll__networl_2_8_AnsP_3 + P-poll__networl_2_8_AnsP_2 + P-poll__networl_2_8_AnsP_1 + P-poll__networl_8_0_AnsP_8 + P-poll__networl_8_0_AnsP_7 + P-poll__networl_8_0_AnsP_6 + P-poll__networl_8_0_AnsP_5 + P-poll__networl_8_0_AnsP_4 + P-poll__networl_8_0_AnsP_3 + P-poll__networl_8_0_AnsP_2 + P-poll__networl_8_0_AnsP_1 + P-poll__networl_6_8_AnsP_1 + P-poll__networl_6_8_AnsP_2 + P-poll__networl_6_8_AnsP_3 + P-poll__networl_6_8_AnsP_4 + P-poll__networl_6_8_AnsP_5 + P-poll__networl_6_8_AnsP_6 + P-poll__networl_6_8_AnsP_7 + P-poll__networl_6_8_AnsP_8 + P-poll__networl_3_4_AnsP_8 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_8 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_8 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_4_3_AnsP_8 + P-poll__networl_7_1_AnsP_8 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_8 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_8 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_8 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_5_6_AnsP_8 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_3_7_AnsP_8 + P-poll__networl_6_2_AnsP_8 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_8_7_AnsP_8 + P-poll__networl_8_7_AnsP_7 + P-poll__networl_8_7_AnsP_6 + P-poll__networl_8_7_AnsP_5 + P-poll__networl_8_7_AnsP_4 + P-poll__networl_8_7_AnsP_3 + P-poll__networl_8_7_AnsP_2 + P-poll__networl_8_7_AnsP_1 + P-poll__networl_1_6_AnsP_8 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_2_AnsP_8 + P-poll__networl_2_2_AnsP_8 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_8_3_AnsP_1 + P-poll__networl_8_3_AnsP_2 + P-poll__networl_8_3_AnsP_3 + P-poll__networl_8_3_AnsP_4 + P-poll__networl_8_3_AnsP_5 + P-poll__networl_8_3_AnsP_6 + P-poll__networl_8_3_AnsP_7 + P-poll__networl_8_3_AnsP_8 + P-poll__networl_4_7_AnsP_8 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_8 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_7_8_AnsP_8 + P-poll__networl_7_8_AnsP_7 + P-poll__networl_7_8_AnsP_6 + P-poll__networl_7_8_AnsP_5 + P-poll__networl_7_8_AnsP_4 + P-poll__networl_7_8_AnsP_3 + P-poll__networl_7_8_AnsP_2 + P-poll__networl_7_8_AnsP_1 + P-poll__networl_0_7_AnsP_8 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_8_4_AnsP_8 + P-poll__networl_8_4_AnsP_7 + P-poll__networl_8_4_AnsP_6 + P-poll__networl_8_4_AnsP_5 + P-poll__networl_8_4_AnsP_4 + P-poll__networl_8_4_AnsP_3 + P-poll__networl_8_4_AnsP_2 + P-poll__networl_8_4_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_1_3_AnsP_8 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_6_AnsP_8 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_3_8_AnsP_8 + P-poll__networl_3_8_AnsP_7 + P-poll__networl_3_8_AnsP_6 + P-poll__networl_3_8_AnsP_5 + P-poll__networl_3_8_AnsP_4 + P-poll__networl_3_8_AnsP_3 + P-poll__networl_3_8_AnsP_2 + P-poll__networl_3_8_AnsP_1 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_7_7_AnsP_8 + P-poll__networl_4_4_AnsP_8 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_0_AnsP_8 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_2_AnsP_8 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_8 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_8 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_8_1_AnsP_8 + P-poll__networl_8_1_AnsP_7 + P-poll__networl_8_1_AnsP_6 + P-poll__networl_8_1_AnsP_5 + P-poll__networl_8_1_AnsP_4 + P-poll__networl_8_1_AnsP_3 + P-poll__networl_8_1_AnsP_2 + P-poll__networl_8_1_AnsP_1 + P-poll__networl_1_0_AnsP_8 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_8 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_1_AnsP_8 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_6_AnsP_8 + P-poll__networl_6_6_AnsP_8 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_2_1_AnsP_8 + P-poll__networl_7_2_AnsP_8 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_8 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_8 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_3_2_AnsP_8 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_8 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_8 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_1_5_AnsP_8 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_8_8_AnsP_8 + P-poll__networl_8_8_AnsP_7 + P-poll__networl_8_8_AnsP_6 + P-poll__networl_8_8_AnsP_5 + P-poll__networl_8_8_AnsP_4 + P-poll__networl_8_8_AnsP_3 + P-poll__networl_8_8_AnsP_2 + P-poll__networl_8_8_AnsP_1 + P-poll__networl_1_7_AnsP_8 + P-poll__networl_8_6_AnsP_1 + P-poll__networl_8_6_AnsP_2 + P-poll__networl_8_6_AnsP_3 + P-poll__networl_8_6_AnsP_4 + P-poll__networl_8_6_AnsP_5 + P-poll__networl_8_6_AnsP_6 + P-poll__networl_8_6_AnsP_7 + P-poll__networl_8_6_AnsP_8 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_8 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_4_8_AnsP_8 + P-poll__networl_4_8_AnsP_7 + P-poll__networl_4_8_AnsP_6 + P-poll__networl_4_8_AnsP_5 + P-poll__networl_4_8_AnsP_4 + P-poll__networl_4_8_AnsP_3 + P-poll__networl_4_8_AnsP_2 + P-poll__networl_4_8_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_6_1_AnsP_8 + P-poll__networl_5_4_AnsP_8 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_0_8_AnsP_8 + P-poll__networl_0_8_AnsP_7 + P-poll__networl_0_8_AnsP_6 + P-poll__networl_0_8_AnsP_5 + P-poll__networl_0_8_AnsP_4 + P-poll__networl_0_8_AnsP_3 + P-poll__networl_0_8_AnsP_2 + P-poll__networl_0_8_AnsP_1 + P-poll__networl_6_0_AnsP_8 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_8_5_AnsP_8 + P-poll__networl_8_5_AnsP_7 + P-poll__networl_8_5_AnsP_6 + P-poll__networl_8_5_AnsP_5 + P-poll__networl_8_5_AnsP_4 + P-poll__networl_8_5_AnsP_3 + P-poll__networl_8_5_AnsP_2 + P-poll__networl_8_5_AnsP_1 + P-po
ll__networl_1_4_AnsP_8 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_2_0_AnsP_8 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_5_5_AnsP_8 + P-poll__networl_4_5_AnsP_8 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_8 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_3_0_AnsP_8 + P-poll__networl_7_6_AnsP_8 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_8 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_8_2_AnsP_8 + P-poll__networl_8_2_AnsP_7 + P-poll__networl_8_2_AnsP_6 + P-poll__networl_8_2_AnsP_5 + P-poll__networl_8_2_AnsP_4 + P-poll__networl_8_2_AnsP_3 + P-poll__networl_8_2_AnsP_2 + P-poll__networl_8_2_AnsP_1 + P-poll__networl_1_1_AnsP_8 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_3_6_AnsP_8 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_8 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_2_4_AnsP_8 + P-poll__networl_6_7_AnsP_8 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_3_AnsP_8 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_8 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_8 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_0_AnsP_8 + P-poll__networl_3_3_AnsP_8 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_1_8_AnsP_1 + P-poll__networl_1_8_AnsP_2 + P-poll__networl_1_8_AnsP_3 + P-poll__networl_1_8_AnsP_4 + P-poll__networl_1_8_AnsP_5 + P-poll__networl_1_8_AnsP_6 + P-poll__networl_1_8_AnsP_7 + P-poll__networl_1_8_AnsP_8 + P-poll__networl_5_8_AnsP_8 + P-poll__networl_5_8_AnsP_7 + P-poll__networl_5_8_AnsP_6 + P-poll__networl_5_8_AnsP_5 + P-poll__networl_5_8_AnsP_4 + P-poll__networl_5_8_AnsP_3 + P-poll__networl_5_8_AnsP_2 + P-poll__networl_5_8_AnsP_1 + P-poll__networl_6_4_AnsP_8 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_8_4_AI_7 + P-poll__networl_8_4_AI_8 + P-poll__networl_1_1_AI_0 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_3 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_8 + P-poll__networl_8_4_AI_6 + P-poll__networl_8_7_RI_0 + P-poll__networl_8_7_RI_1 + P-poll__networl_8_7_RI_2 + P-poll__networl_8_7_RI_3 + P-poll__networl_8_7_RI_4 + P-poll__networl_8_7_RI_5 + P-poll__networl_8_7_RI_6 + P-poll__networl_8_7_RI_7 + P-poll__networl_8_7_RI_8 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_8 + P-poll__networl_8_4_AI_5 + P-poll__networl_8_4_AI_4 + P-poll__networl_8_4_AI_3 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_8_4_AI_2 + P-poll__networl_8_4_AI_1 + P-poll__networl_8_4_AI_0 + P-poll__networl_3_0_AI_0 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_4 + P-poll__networl_3_0_AI_5 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_7 + P-poll__networl_3_0_AI_8 + P-poll__networl_0_0_AskP_0 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_0_0_AskP_8 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_3_3_RI_8 + P-poll__networl_2_5_AskP_8 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_6_7_AnnP_8 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_2_5_AskP_0 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_7_1_AskP_8 + P-poll__networl_7_3_AnnP_8 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_5_2_RI_8 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_4_2_AnnP_8 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_5_8_AnsP_0 + P-poll__networl_6_8_RI_8 + P-poll__networl_6_8_RI_7 + P-poll__networl_6_8_RI_6 + P-poll__networl_6_8_RI_5 + P-poll__networl_6_8_RI_4 + P-poll__networl_6_8_RI_3 + P-poll__networl_6_8_RI_2 + P-poll__networl_6_8_RI_1 + P-poll__networl_6_8_RI_0 + P-poll__networl_6_5_AI_8 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_4_8_RP_0 + P-poll__networl_7_1_RI_3 + P-poll__networl_4_8_RP_1 + P-poll__networl_7_1_RI_4 + P-poll__networl_4_8_RP_2 + P-poll__networl_7_1_RI_5 + P-poll__networl_4_8_RP_3 + P-poll__networl_7_1_RI_6 + P-poll__networl_4_8_RP_4 + P-poll__networl_7_1_RI_7 + P-poll__networl_4_8_RP_5 + P-poll__networl_7_1_RI_8 + P-poll__networl_4_8_RP_6 + P-poll__networl_4_8_RP_7 + P-poll__networl_4_8_RP_8 + P-poll__networl_6_5_AI_0 + P-poll__networl_1_8_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_6_5_AskP_8 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_4_0_RP_8 + P-poll__networl_4_0_RP_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_8 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_6_7_RP_8 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_3_6_AnnP_8 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_4_0_AskP_8 + P-poll__networl_8_6_RP_0 + P-poll__networl_8_6_RP_1 + P-poll__networl_8_6_RP_2 + P-poll__networl_8_6_RP_3 + P-poll__networl_8_6_RP_4 + P-poll__networl_8_6_RP_5 + P-poll__networl_8_6_RP_6 + P-poll__networl_8_6_RP_7 + P-poll__networl_8_6_RP_8 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_1_3_RP_8 + P-poll__networl_3_8_AI_0 + P-poll__networl_3_8_AI_1 + P-poll__networl_3_8_AI_2 + P-poll__networl_3_8_AI_3 + P-poll__networl_3_8_AI_4 + P-poll__networl_3_8_AI_5 + P-poll__networl_3_8_AI_6 + P-poll__networl_3_8_AI_7 + P-poll__networl_3_8_AI_8 + P-poll__networl_4_6_AI_8 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_1_1_AnnP_8 + P-poll__networl_4_6_AI_3 + P-poll__networl_4_6_AI_2 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_3_2_RP_8 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_5_7_AI_8 + P-poll__networl_8_2_AnnP_0 + P-poll__networl_8_2_AnnP_1 + P-poll__networl_8_2_AnnP_2 + P-poll__networl_8_2_AnnP_3 + P-poll__networl_8_2_AnnP_4 + P-poll__networl_8_2_AnnP_5 + P-poll__networl_8_2_AnnP_6 + P-poll__networl_8_2_AnnP_7 + P-poll__networl_8_2_AnnP_8 + P-poll__networl_2_1_RP_8 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_2_1_RP_0 + P-poll__networl_3_1_AskP_8 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_3_4_AskP_8 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_5_1_RP_8 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_7_6_AI_8 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_0_3_AI_4 + P-poll__networl_3_1_AskP_1 + P-poll__networl_0_3_AI_5 + P-poll__networl_3_1_AskP_0 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_0_3_AI_8 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_0_6_RI_8 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_2_7_AnnP_8 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_0_5_AnnP_8 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_7_0_RP_8 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_2_2_AI_0 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_2_AI_8 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_2_5_RI_8 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_6_AnnP_8 + P-poll__networl_8_0_AskP_0 + P-poll__networl_8_0_AskP_
1 + P-poll__networl_8_0_AskP_2 + P-poll__networl_8_0_AskP_3 + P-poll__networl_8_0_AskP_4 + P-poll__networl_8_0_AskP_5 + P-poll__networl_8_0_AskP_6 + P-poll__networl_8_0_AskP_7 + P-poll__networl_8_0_AskP_8 + P-poll__networl_2_8_AskP_0 + P-poll__networl_2_8_AskP_1 + P-poll__networl_2_8_AskP_2 + P-poll__networl_2_8_AskP_3 + P-poll__networl_2_8_AskP_4 + P-poll__networl_2_8_AskP_5 + P-poll__networl_2_8_AskP_6 + P-poll__networl_2_8_AskP_7 + P-poll__networl_2_8_AskP_8 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_1_AI_8 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_4_4_RI_8 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_5_1_AnnP_8 + P-poll__networl_2_7_AI_8 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_7_AI_2 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_6_0_AI_7 + P-poll__networl_6_0_AI_8 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_8 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_0_3_AskP_8 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_6_3_RI_8 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_0_2_RP_0 + P-poll__networl_7_5_RP_8 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_7_4_AskP_8 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_8_2_RI_0 + P-poll__networl_8_2_RI_1 + P-poll__networl_8_2_RI_2 + P-poll__networl_8_2_RI_3 + P-poll__networl_8_2_RI_4 + P-poll__networl_8_2_RI_5 + P-poll__networl_8_2_RI_6 + P-poll__networl_8_2_RI_7 + P-poll__networl_8_2_RI_8 + P-poll__networl_5_6_AskP_8 + P-poll__networl_5_6_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_5_6_AskP_3 + P-poll__networl_5_6_AskP_2 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_4_5_AnnP_8 + P-poll__networl_5_6_AskP_1 + P-poll__networl_5_6_AskP_0 + P-poll__networl_7_8_RP_0 + P-poll__networl_7_8_RP_1 + P-poll__networl_7_8_RP_2 + P-poll__networl_7_8_RP_3 + P-poll__networl_7_8_RP_4 + P-poll__networl_7_8_RP_5 + P-poll__networl_7_8_RP_6 + P-poll__networl_7_8_RP_7 + P-poll__networl_7_8_RP_8 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_0_5_RP_8 + P-poll__networl_0_8_AI_8 + P-poll__networl_0_8_AI_7 + P-poll__networl_0_8_AI_6 + P-poll__networl_0_8_AI_5 + P-poll__networl_0_8_AI_4 + P-poll__networl_6_8_AskP_0 + P-poll__networl_6_8_AskP_1 + P-poll__networl_6_8_AskP_2 + P-poll__networl_6_8_AskP_3 + P-poll__networl_6_8_AskP_4 + P-poll__networl_6_8_AskP_5 + P-poll__networl_6_8_AskP_6 + P-poll__networl_6_8_AskP_7 + P-poll__networl_6_8_AskP_8 + P-poll__networl_0_8_AI_3 + P-poll__networl_0_8_AI_2 + P-poll__networl_0_8_AI_1 + P-poll__networl_0_8_AI_0 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_0_AnnP_8 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_5_6_RP_8 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_RP_8 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_4_3_AskP_8 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_4_3_RP_8 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_6_8_AI_0 + P-poll__networl_6_8_AI_1 + P-poll__networl_6_8_AI_2 + P-poll__networl_6_8_AI_3 + P-poll__networl_6_8_AI_4 + P-poll__networl_6_8_AI_5 + P-poll__networl_6_8_AI_6 + P-poll__networl_6_8_AI_7 + P-poll__networl_6_8_AI_8 + P-poll__networl_8_2_AnsP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_1_4_AnnP_8 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_6_2_RP_8 + P-poll__networl_8_7_AI_0 + P-poll__networl_8_7_AI_1 + P-poll__networl_8_7_AI_2 + P-poll__networl_8_7_AI_3 + P-poll__networl_8_7_AI_4 + P-poll__networl_8_7_AI_5 + P-poll__networl_8_7_AI_6 + P-poll__networl_8_7_AI_7 + P-poll__networl_8_7_AI_8 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_4_AI_8 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_1_7_RI_8 + P-poll__networl_8_5_AnnP_0 + P-poll__networl_8_5_AnnP_1 + P-poll__networl_8_5_AnnP_2 + P-poll__networl_8_5_AnnP_3 + P-poll__networl_8_5_AnnP_4 + P-poll__networl_8_5_AnnP_5 + P-poll__networl_8_5_AnnP_6 + P-poll__networl_8_5_AnnP_7 + P-poll__networl_8_5_AnnP_8 + P-poll__networl_3_3_AnnP_8 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_3_7_AskP_8 + P-poll__networl_8_1_RP_0 + P-poll__networl_8_1_RP_1 + P-poll__networl_8_1_RP_2 + P-poll__networl_8_1_RP_3 + P-poll__networl_8_1_RP_4 + P-poll__networl_8_1_RP_5 + P-poll__networl_8_1_RP_6 + P-poll__networl_8_1_RP_7 + P-poll__networl_8_1_RP_8 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_3_3_AI_5 + P-poll__networl_3_3_AI_6 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_3_AI_8 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_3_6_RI_8 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_6_0_AnnP_8 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_3_7_RP_8 + P-poll__networl_3_7_RP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_0_8_AnnP_0 + P-poll__networl_0_8_AnnP_1 + P-poll__networl_0_8_AnnP_2 + P-poll__networl_0_8_AnnP_3 + P-poll__networl_0_8_AnnP_4 + P-poll__networl_0_8_AnnP_5 + P-poll__networl_0_8_AnnP_6 + P-poll__networl_0_8_AnnP_7 + P-poll__networl_0_8_AnnP_8 + P-poll__networl_6_0_RI_8 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_1_2_AskP_8 + P-poll__networl_3_7_RP_0 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_2_AI_8 + P-poll__networl_6_0_RI_2 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_5_RI_8 + P-poll__networl_6_0_RI_1 + P-poll__networl_6_0_RI_0 + P-poll__networl_8_3_AskP_0 + P-poll__networl_8_3_AskP_1 + P-poll__networl_8_3_AskP_2 + P-poll__networl_8_3_AskP_3 + P-poll__networl_8_3_AskP_4 + P-poll__networl_8_3_AskP_5 + P-poll__networl_8_3_AskP_6 + P-poll__networl_8_3_AskP_7 + P-poll__networl_8_3_AskP_8 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_6_2_AskP_8 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_1_AI_8 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_7_4_RI_8 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_0_1_RI_8 + P-poll__networl_6_2_AskP_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_5_4_AnnP_8 + P-poll__networl_6_2_AskP_6 + P-poll__networl_6_2_AskP_5 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_0_6_AskP_8 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_2_0_RI_8 + P-poll__networl_6_2_AskP_0 + P-poll__networl_5_8_AnnP_8 + P-poll__networl_5_8_AnnP_7 + P-poll__networl_5_8_AnnP_6 + P-poll__networl_5_8_AnnP_5 + P-poll__networl_5_8_AnnP_4 + P-poll__networl_5_8_AnnP_3 + P-poll__networl_5_8_AnnP_2 + P-poll__networl_5_8_AnnP_1 + P-poll__networl_5_8_AnnP_0 + P-poll__networl_1_8_RP_8 + P-poll__networl_1_8_RP_7 + P-poll__networl_1_8_RP_6 + P-poll__networl_4_1_RI_8 + P-poll__networl_1_8_RP_5 + P-poll__networl_4_1_RI_7 + P-poll__networl_1_8_RP_4 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_7_7_AskP_8 + P-poll__networl_4_1_RI_6 + P-poll__networl_1_8_RP_3 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_1_8_RP_2 + P-poll__networl_4_1_RI_4 + P-poll__networl_1_8_RP_1 + P-poll__networl_4_1_RI_3 + P-poll__networl_1_8_RP_0 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_1_6_RP_8 + P-poll__networl_4_8_AnnP_0 + P-poll__networl_4_8_AnnP_1 + P-poll__networl_4_8_AnnP_2 + P-poll__networl_4_8_AnnP_3 + P-poll__networl_4_8_AnnP_4 + P-poll__networl_4_8_AnnP_5 + P-poll__networl_4_8_AnnP_6 + P-poll__networl_4_8_AnnP_7 + P-poll__networl_4_8_AnnP_8 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_5_2_AskP_8 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_3_5_RP_8 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_2_3_AnnP_8 + P-poll__networl_8_7_AskP_8 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_5_4_RP_8 + P-poll__networl_8_7_AskP_7 + P-poll__networl_8_7_AskP_6 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_0_6_AI_8 + P-poll__networl_8_7_AskP_5 + P-poll__networl_8_7_AskP_4 + P-poll__networl_8_7_AskP_3 + P-poll__networl_8_7_AskP_2 + P-poll__networl_8_7_AskP_1 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_4_6_AskP_8 + P-poll__networl_7_3_RP_0 + P-poll_
_networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_7_3_RP_8 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_0_0_RP_8 + P-poll__networl_8_7_AskP_0 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_2_5_AI_0 + P-poll__networl_2_2_RI_8 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_2_5_AI_8 + P-poll__networl_2_8_RI_0 + P-poll__networl_2_8_RI_1 + P-poll__networl_2_8_RI_2 + P-poll__networl_2_8_RI_3 + P-poll__networl_2_8_RI_4 + P-poll__networl_2_8_RI_5 + P-poll__networl_2_8_RI_6 + P-poll__networl_2_8_RI_7 + P-poll__networl_2_8_RI_8 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_8_5_AnsP_0 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_8 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_1_7_AnnP_8 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_2_1_AskP_8 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_4_AI_8 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_4_7_RI_8 + P-poll__networl_8_8_AnnP_0 + P-poll__networl_8_8_AnnP_1 + P-poll__networl_8_8_AnnP_2 + P-poll__networl_8_8_AnnP_3 + P-poll__networl_8_8_AnnP_4 + P-poll__networl_8_8_AnnP_5 + P-poll__networl_8_8_AnnP_6 + P-poll__networl_8_8_AnnP_7 + P-poll__networl_8_8_AnnP_8 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_0_8_AnsP_0 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_3_AI_8 + P-poll__networl_6_4_AnnP_8 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_6_6_RI_8 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_6_3_AnnP_8 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_8 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_8 + P-poll__networl_7_6_RI_7 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_1_5_AskP_8 + P-poll__networl_7_6_RI_2 + P-poll__networl_8_2_AI_0 + P-poll__networl_8_2_AI_1 + P-poll__networl_8_2_AI_2 + P-poll__networl_8_2_AI_3 + P-poll__networl_8_2_AI_4 + P-poll__networl_8_2_AI_5 + P-poll__networl_8_2_AI_6 + P-poll__networl_8_2_AI_7 + P-poll__networl_8_2_AI_8 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_8 + P-poll__networl_0_0_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_0_0_AI_4 + P-poll__networl_0_0_AI_3 + P-poll__networl_8_5_RI_0 + P-poll__networl_8_5_RI_1 + P-poll__networl_8_5_RI_2 + P-poll__networl_8_5_RI_3 + P-poll__networl_8_5_RI_4 + P-poll__networl_8_5_RI_5 + P-poll__networl_8_5_RI_6 + P-poll__networl_8_5_RI_7 + P-poll__networl_8_5_RI_8 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_2_RI_8 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_8_6_AskP_0 + P-poll__networl_8_6_AskP_1 + P-poll__networl_8_6_AskP_2 + P-poll__networl_8_6_AskP_3 + P-poll__networl_8_6_AskP_4 + P-poll__networl_8_6_AskP_5 + P-poll__networl_8_6_AskP_6 + P-poll__networl_8_6_AskP_7 + P-poll__networl_8_6_AskP_8 + P-poll__networl_0_0_AI_0 + P-poll__networl_7_3_AI_8 + P-poll__networl_7_3_AI_7 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_0_8_RP_0 + P-poll__networl_3_1_RI_3 + P-poll__networl_0_8_RP_1 + P-poll__networl_3_1_RI_4 + P-poll__networl_0_8_RP_2 + P-poll__networl_3_1_RI_5 + P-poll__networl_0_8_RP_3 + P-poll__networl_3_1_RI_6 + P-poll__networl_0_8_RP_4 + P-poll__networl_3_1_RI_7 + P-poll__networl_0_8_RP_5 + P-poll__networl_3_1_RI_8 + P-poll__networl_0_8_RP_6 + P-poll__networl_0_8_RP_7 + P-poll__networl_0_8_RP_8 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_5_7_AnnP_8 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_1_AskP_8 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_5_0_RI_8 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_2_7_RP_8 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_3_2_AnnP_8 + P-poll__networl_4_8_AnsP_0 + P-poll__networl_5_7_RI_8 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_4_6_RP_8 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_8 + P-poll__networl_5_4_AI_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_5_5_AskP_8 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_6_5_RP_8 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_2_2_AskP_8 + P-poll__networl_2_2_AskP_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_1_7_AI_8 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_2_6_AnnP_8 + P-poll__networl_2_2_AskP_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_3_0_AskP_8 + P-poll__networl_8_4_RP_0 + P-poll__networl_8_4_RP_1 + P-poll__networl_8_4_RP_2 + P-poll__networl_8_4_RP_3 + P-poll__networl_8_4_RP_4 + P-poll__networl_8_4_RP_5 + P-poll__networl_8_4_RP_6 + P-poll__networl_8_4_RP_7 + P-poll__networl_8_4_RP_8 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_1_1_RP_8 + P-poll__networl_2_2_AskP_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_3_6_AI_8 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_1_8_AnnP_8 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_0_1_AnnP_8 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_3_0_RP_8 + P-poll__networl_1_8_AnnP_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_1_8_AnnP_6 + P-poll__networl_1_8_AnnP_5 + P-poll__networl_1_8_AnnP_4 + P-poll__networl_1_8_AnnP_3 + P-poll__networl_1_8_AnnP_2 + P-poll__networl_1_8_AnnP_1 + P-poll__networl_1_8_AnnP_0 + P-poll__networl_8_6_AnsP_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_5_5_AI_8 + P-poll__networl_5_8_RI_0 + P-poll__networl_5_8_RI_1 + P-poll__networl_5_8_RI_2 + P-poll__networl_5_8_RI_3 + P-poll__networl_5_8_RI_4 + P-poll__networl_5_8_RI_5 + P-poll__networl_5_8_RI_6 + P-poll__networl_5_8_RI_7 + P-poll__networl_5_8_RI_8 + P-poll__networl_7_0_AnnP_8 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_7_2_AnnP_8 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_8_8_AnsP_0 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_8_RI_8 + P-poll__networl_3_8_RI_7 + P-poll__networl_3_8_RI_6 + P-poll__networl_3_8_RI_5 + P-poll__networl_3_8_RI_4 + P-poll__networl_3_8_RI_3 + P-poll__networl_3_8_RI_2 + P-poll__networl_3_8_RI_1 + P-poll__networl_3_8_RI_0 + P-poll__networl_3_5_AI_8 + P-poll__networl_3_5_AI_7 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_2_4_AskP_8 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_7_4_AI_8 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_0_1_AI_8 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_7_7_RI_8 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_0_4_RI_8 + P-poll__networl_3_5_AI_3 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_0_AI_8 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_2_3_RI_8 + P-poll__networl_1_0_RP_8 + P-poll__networl_1_0_RP_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_6_6_AnnP_8 + P-poll__networl_1_0_RP_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_7_0_AskP_8 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_8_3_RP_8 + P-poll__networl_8_3_RP_7 + P-poll__networl_8_3_RP_6 + P-poll__networl_8_3_RP_5 + P-poll__networl_8_3_RP_4 + P-poll__networl_1_8_AskP_0 + P-poll__networl_1_8_AskP_1 + P-poll__networl_1_8_AskP_2 + P-poll__networl_1_8_AskP_3 + P-poll__networl_1_8_AskP_4 + P-poll__networl_1_8_AskP_5 + P-poll__networl_1_8_AskP_6 + P-poll__networl_1_8_AskP_7 + P-poll__networl_1_8_AskP_8 + P-poll__networl_8_3_RP_3 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2
_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_2_RI_8 + P-poll__networl_8_3_RP_2 + P-poll__networl_8_3_RP_1 + P-poll__networl_8_3_RP_0 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_4_1_AnnP_8 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_4_7_AskP_8 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_3_8_RP_0 + P-poll__networl_6_1_RI_3 + P-poll__networl_3_8_RP_1 + P-poll__networl_6_1_RI_4 + P-poll__networl_3_8_RP_2 + P-poll__networl_6_1_RI_5 + P-poll__networl_3_8_RP_3 + P-poll__networl_6_1_RI_6 + P-poll__networl_3_8_RP_4 + P-poll__networl_6_1_RI_7 + P-poll__networl_3_8_RP_5 + P-poll__networl_6_1_RI_8 + P-poll__networl_3_8_RP_6 + P-poll__networl_3_8_RP_7 + P-poll__networl_3_8_RP_8 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_6_4_AskP_8 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_1_6_AI_8 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_8_0_RI_0 + P-poll__networl_8_0_RI_1 + P-poll__networl_8_0_RI_2 + P-poll__networl_5_7_RP_0 + P-poll__networl_8_0_RI_3 + P-poll__networl_5_7_RP_1 + P-poll__networl_8_0_RI_4 + P-poll__networl_5_7_RP_2 + P-poll__networl_8_0_RI_5 + P-poll__networl_5_7_RP_3 + P-poll__networl_8_0_RI_6 + P-poll__networl_5_7_RP_4 + P-poll__networl_8_0_RI_7 + P-poll__networl_5_7_RP_5 + P-poll__networl_8_0_RI_8 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_5_7_RP_8 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_1_6_AI_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_3_5_AnnP_8 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_7_6_RP_8 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_0_3_RP_8 + P-poll__networl_2_8_AI_0 + P-poll__networl_2_8_AI_1 + P-poll__networl_2_8_AI_2 + P-poll__networl_2_8_AI_3 + P-poll__networl_2_8_AI_4 + P-poll__networl_2_8_AI_5 + P-poll__networl_2_8_AI_6 + P-poll__networl_2_8_AI_7 + P-poll__networl_2_8_AI_8 + P-poll__networl_6_4_RP_8 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_5_8_AskP_0 + P-poll__networl_5_8_AskP_1 + P-poll__networl_5_8_AskP_2 + P-poll__networl_5_8_AskP_3 + P-poll__networl_5_8_AskP_4 + P-poll__networl_5_8_AskP_5 + P-poll__networl_5_8_AskP_6 + P-poll__networl_5_8_AskP_7 + P-poll__networl_5_8_AskP_8 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_1_0_AnnP_8 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_2_RP_8 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_4_7_AI_8 + P-poll__networl_8_1_AnnP_0 + P-poll__networl_8_1_AnnP_1 + P-poll__networl_8_1_AnnP_2 + P-poll__networl_8_1_AnnP_3 + P-poll__networl_8_1_AnnP_4 + P-poll__networl_8_1_AnnP_5 + P-poll__networl_8_1_AnnP_6 + P-poll__networl_8_1_AnnP_7 + P-poll__networl_8_1_AnnP_8 + P-poll__networl_2_4_AnnP_8 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_3_3_AskP_8 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_4_1_RP_8 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_6_6_AI_8 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_0_4_AnnP_8 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_6_0_RP_8 + P-poll__networl_8_5_AI_0 + P-poll__networl_8_5_AI_1 + P-poll__networl_8_5_AI_2 + P-poll__networl_8_5_AI_3 + P-poll__networl_8_5_AI_4 + P-poll__networl_8_5_AI_5 + P-poll__networl_8_5_AI_6 + P-poll__networl_8_5_AI_7 + P-poll__networl_8_5_AI_8 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_2_AI_8 + P-poll__networl_8_8_RI_0 + P-poll__networl_8_8_RI_1 + P-poll__networl_8_8_RI_2 + P-poll__networl_8_8_RI_3 + P-poll__networl_8_8_RI_4 + P-poll__networl_8_8_RI_5 + P-poll__networl_8_8_RI_6 + P-poll__networl_8_8_RI_7 + P-poll__networl_8_8_RI_8 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_1_5_RI_8 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_7_5_AnnP_8 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_8 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_7_AskP_8 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_1_AI_8 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_3_4_RI_8 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_5_0_AnnP_8 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_5_3_AskP_8 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_3_AskP_0 + P-poll__networl_5_0_AI_7 + P-poll__networl_5_0_AI_8 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_0_2_AskP_8 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_5_3_RI_8 + P-poll__networl_2_6_RP_8 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_7_3_AskP_8 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_7_2_RI_8 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_4_4_AnnP_8 + P-poll__networl_3_0_AnnP_8 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_7_8_AskP_8 + P-poll__networl_7_8_AskP_7 + P-poll__networl_7_8_AskP_6 + P-poll__networl_7_8_AskP_5 + P-poll__networl_6_8_RP_0 + P-poll__networl_6_8_RP_1 + P-poll__networl_6_8_RP_2 + P-poll__networl_6_8_RP_3 + P-poll__networl_6_8_RP_4 + P-poll__networl_6_8_RP_5 + P-poll__networl_6_8_RP_6 + P-poll__networl_6_8_RP_7 + P-poll__networl_6_8_RP_8 + P-poll__networl_7_8_AskP_4 + P-poll__networl_7_8_AskP_3 + P-poll__networl_7_8_AskP_2 + P-poll__networl_7_8_AskP_1 + P-poll__networl_7_8_AskP_0 + P-poll__networl_0_7_RP_8 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_3_0_RI_8 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_6_7_AskP_8 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_8_7_RP_0 + P-poll__networl_8_7_RP_1 + P-poll__networl_8_7_RP_2 + P-poll__networl_8_7_RP_3 + P-poll__networl_8_7_RP_4 + P-poll__networl_8_7_RP_5 + P-poll__networl_8_7_RP_6 + P-poll__networl_8_7_RP_7 + P-poll__networl_8_7_RP_8 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_1_4_RP_8 + P-poll__networl_3_8_AnnP_0 + P-poll__networl_3_8_AnnP_1 + P-poll__networl_3_8_AnnP_2 + P-poll__networl_3_8_AnnP_3 + P-poll__networl_3_8_AnnP_4 + P-poll__networl_3_8_AnnP_5 + P-poll__networl_3_8_AnnP_6 + P-poll__networl_3_8_AnnP_7 + P-poll__networl_3_8_AnnP_8 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_4_2_AskP_8 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_3_3_RP_8 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_AskP_8 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_5_8_AI_0 + P-poll__networl_5_8_AI_1 + P-poll__networl_5_8_AI_2 + P-poll__networl_5_8_AI_3 + P-poll__networl_5_8_AI_4 + P-poll__networl_5_8_AI_5 + P-poll__networl_5_8_AI_6 + P-poll__networl_5_8_AI_7 + P-poll__networl_5_8_AI_8 + P-poll__networl_0_7_AskP_3 + P-poll__networl_8_1_AnsP_0 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_1_3_AnnP_8 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_5_2_RP_8 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_7_7_AI_8 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_4_AI_8 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RI_8 + P-poll__networl_8_4_AnnP_0 + P-poll__networl_8_4_AnnP_1 + P-poll__networl_8_4_AnnP_2 + P-poll__networl_8_4_AnnP_3 + P-poll__networl_8_4_AnnP_4 + P-poll__networl_8_4_AnnP_5 + P-poll__networl_8_4_AnnP_6 + P-poll__networl_8_4_AnnP_7 + P-poll__networl_8_4_AnnP_8 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_3_6_AskP_8 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_7_1_RP_8 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__
networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_3_AI_8 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_2_6_RI_8 + P-poll__networl_5_5_AnnP_8 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_8 + P-poll__networl_1_1_RI_7 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_1_1_RI_6 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_8_4_RI_8 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_0_7_AnnP_8 + P-poll__networl_8_4_RI_7 + P-poll__networl_8_4_RI_6 + P-poll__networl_8_4_RI_5 + P-poll__networl_8_4_RI_4 + P-poll__networl_8_4_RI_3 + P-poll__networl_8_4_RI_2 + P-poll__networl_8_4_RI_1 + P-poll__networl_8_4_RI_0 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_1_1_AskP_8 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_2_AI_8 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_4_5_RI_8 + P-poll__networl_7_8_AnnP_0 + P-poll__networl_7_8_AnnP_1 + P-poll__networl_7_8_AnnP_2 + P-poll__networl_7_8_AnnP_3 + P-poll__networl_7_8_AnnP_4 + P-poll__networl_7_8_AnnP_5 + P-poll__networl_7_8_AnnP_6 + P-poll__networl_7_8_AnnP_7 + P-poll__networl_7_8_AnnP_8 + P-poll__networl_8_1_AI_8 + P-poll__networl_8_1_AI_7 + P-poll__networl_8_1_AI_6 + P-poll__networl_8_1_AI_5 + P-poll__networl_8_1_AI_4 + P-poll__networl_8_1_AI_3 + P-poll__networl_8_2_AskP_0 + P-poll__networl_8_2_AskP_1 + P-poll__networl_8_2_AskP_2 + P-poll__networl_8_2_AskP_3 + P-poll__networl_8_2_AskP_4 + P-poll__networl_8_2_AskP_5 + P-poll__networl_8_2_AskP_6 + P-poll__networl_8_2_AskP_7 + P-poll__networl_8_2_AskP_8 + P-poll__networl_8_1_AI_2 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_8_1_AI_1 + P-poll__networl_8_1_AI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_1_AI_8 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_6_4_RI_8 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_5_3_AnnP_8 + P-poll__networl_8_4_AskP_8 + P-poll__networl_8_4_AskP_7 + P-poll__networl_8_0_AI_0 + P-poll__networl_8_0_AI_1 + P-poll__networl_8_0_AI_2 + P-poll__networl_8_0_AI_3 + P-poll__networl_8_0_AI_4 + P-poll__networl_8_0_AI_5 + P-poll__networl_8_0_AI_6 + P-poll__networl_8_0_AI_7 + P-poll__networl_8_4_AskP_6 + P-poll__networl_8_0_AI_8 + P-poll__networl_8_4_AskP_5 + P-poll__networl_8_4_AskP_4 + P-poll__networl_8_4_AskP_3 + P-poll__networl_8_4_AskP_2 + P-poll__networl_8_4_AskP_1 + P-poll__networl_0_5_AskP_0 + P-poll__networl_8_4_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_0_5_AskP_8 + P-poll__networl_8_3_RI_0 + P-poll__networl_8_3_RI_1 + P-poll__networl_8_3_RI_2 + P-poll__networl_8_3_RI_3 + P-poll__networl_8_3_RI_4 + P-poll__networl_8_3_RI_5 + P-poll__networl_8_3_RI_6 + P-poll__networl_8_3_RI_7 + P-poll__networl_8_3_RI_8 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_1_0_RI_8 + P-poll__networl_6_5_RI_8 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_6_5_RI_4 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_7_6_AskP_8 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_8 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_0_6_RP_8 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_8 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_4_7_AnnP_8 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_1_3_AskP_2 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_5_1_AskP_8 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_2_5_RP_8 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_2_2_AnnP_8 + P-poll__networl_3_8_AnsP_0 + P-poll__networl_6_1_AnnP_8 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_4_RP_8 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_4_6_RI_8 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_4_5_AskP_8 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_6_3_RP_8 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_8 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_8_8_AI_0 + P-poll__networl_8_8_AI_1 + P-poll__networl_8_8_AI_2 + P-poll__networl_8_8_AI_3 + P-poll__networl_8_8_AI_4 + P-poll__networl_8_8_AI_5 + P-poll__networl_8_8_AI_6 + P-poll__networl_8_8_AI_7 + P-poll__networl_8_8_AI_8 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_5_AI_8 + P-poll__networl_4_3_AI_4 + P-poll__networl_1_8_RI_0 + P-poll__networl_1_8_RI_1 + P-poll__networl_1_8_RI_2 + P-poll__networl_1_8_RI_3 + P-poll__networl_1_8_RI_4 + P-poll__networl_1_8_RI_5 + P-poll__networl_1_8_RI_6 + P-poll__networl_1_8_RI_7 + P-poll__networl_1_8_RI_8 + P-poll__networl_4_3_AI_3 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_8_4_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_1_6_AnnP_8 + P-poll__networl_8_2_RP_0 + P-poll__networl_8_2_RP_1 + P-poll__networl_8_2_RP_2 + P-poll__networl_8_2_RP_3 + P-poll__networl_8_2_RP_4 + P-poll__networl_8_2_RP_5 + P-poll__networl_8_2_RP_6 + P-poll__networl_8_2_RP_7 + P-poll__networl_8_2_RP_8 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_2_0_AskP_8 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_4_AI_8 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_3_7_RI_8 + P-poll__networl_8_7_AnnP_0 + P-poll__networl_8_7_AnnP_1 + P-poll__networl_8_7_AnnP_2 + P-poll__networl_8_7_AnnP_3 + P-poll__networl_8_7_AnnP_4 + P-poll__networl_8_7_AnnP_5 + P-poll__networl_8_7_AnnP_6 + P-poll__networl_8_7_AnnP_7 + P-poll__networl_8_7_AnnP_8 + P-poll__networl_3_8_AskP_8 + P-poll__networl_3_8_AskP_7 + P-poll__networl_3_8_AskP_6 + P-poll__networl_3_8_AskP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_3_8_AskP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_3_8_AskP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_3_8_AskP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_3_8_AskP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_3_8_AskP_0 + P-poll__networl_5_3_AI_8 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_5_6_RI_8 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_6_2_AnnP_8 + P-poll__networl_7_8_AnsP_0 + P-poll__networl_8_6_AnnP_8 + P-poll__networl_8_6_AnnP_7 + P-poll__networl_8_6_AnnP_6 + P-poll__networl_8_6_AnnP_5 + P-poll__networl_8_6_AnnP_4 + P-poll__networl_8_6_AnnP_3 + P-poll__networl_8_6_AnnP_2 + P-poll__networl_8_6_AnnP_1 + P-poll__networl_8_6_AnnP_0 + P-poll__networl_2_7_RI_8 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_1_4_AskP_8 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_2_AI_8 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_7_5_RI_8 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_2_RI_8 + P-poll__networl_2_7_RI_2 + P-poll__networl_2_7_RI_1 + P-poll__networl_8_5_AskP_0 + P-poll__networl_8_5_AskP_1 + P-poll__networl_8_5_AskP_2 + P-poll__networl_8_5_AskP_3 + P-poll__networl_8_5_AskP_4 + P-poll__networl_8_5_AskP_5 + P-poll__networl_8_5_AskP_6 + P-poll__networl_8_5_AskP_7 + P-poll__networl_8_5_AskP_8 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_8 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_2_1_RI_8 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_5_6_AnnP_8 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_6_0_AskP_8 + P-poll__networl_7_2_RP_8 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_0_8_AskP_0 + P-poll__networl_0_8_AskP_1 + P-poll__networl_0_8_AskP_2 + P-poll__networl_0_8_AskP_3 + P-poll__networl_0_8_AskP_4 + P-poll__networl_0_8_AskP_5 + P-poll__networl_0_8_AskP_6 + P-poll__networl_0_8_AskP_7 + P-poll__networl_0_8_AskP_8 + P-poll__networl_7_2_RP_1 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_4_0_RI_8 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_1_7_RP_8 + P-poll__networl_7_2_RP_0 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_3_1_AnnP_8 + P-poll__networl_4_7_AnsP_0 + P-
poll__networl_1_5_AnnP_8 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_8_3_AnsP_0 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_3_6_RP_8 + P-poll__networl_0_8_RI_8 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_5_4_AskP_8 + P-poll__networl_0_8_RI_7 + P-poll__networl_0_8_RI_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_5_5_RP_8 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_0_8_RI_5 + P-poll__networl_0_8_RI_4 + P-poll__networl_0_8_RI_3 + P-poll__networl_0_8_RI_2 + P-poll__networl_0_8_RI_1 + P-poll__networl_0_8_RI_0 + P-poll__networl_0_5_AI_8 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_0_7_AI_8 + P-poll__networl_0_5_AI_4 + P-poll__networl_0_5_AI_3 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_2_5_AnnP_8 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_7_4_RP_8 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_0_1_RP_8 + P-poll__networl_0_5_AI_0 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_2_6_AI_8 + P-poll__networl_7_8_AI_8 + P-poll__networl_7_8_AI_7 + P-poll__networl_7_8_AI_6 + P-poll__networl_7_8_AI_5 + P-poll__networl_7_8_AI_4 + P-poll__networl_7_8_AI_3 + P-poll__networl_7_8_AI_2 + P-poll__networl_7_8_AI_1 + P-poll__networl_7_8_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_8_AskP_0 + P-poll__networl_4_8_AskP_1 + P-poll__networl_4_8_AskP_2 + P-poll__networl_4_8_AskP_3 + P-poll__networl_4_8_AskP_4 + P-poll__networl_4_8_AskP_5 + P-poll__networl_4_8_AskP_6 + P-poll__networl_4_8_AskP_7 + P-poll__networl_4_8_AskP_8 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_0_0_AnnP_8 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_2_0_RP_8 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_5_3_RP_8 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_4_5_AI_8 + P-poll__networl_4_8_RI_0 + P-poll__networl_4_8_RI_1 + P-poll__networl_4_8_RI_2 + P-poll__networl_4_8_RI_3 + P-poll__networl_4_8_RI_4 + P-poll__networl_4_8_RI_5 + P-poll__networl_4_8_RI_6 + P-poll__networl_4_8_RI_7 + P-poll__networl_4_8_RI_8 + P-poll__networl_5_3_RP_5 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_7_1_AnnP_8 + P-poll__networl_5_3_RP_4 + P-poll__networl_8_7_AnsP_0 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_5_3_RP_1 + P-poll__networl_5_3_RP_0 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_2_3_AskP_8 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_6_4_AI_8 + P-poll__networl_4_4_AskP_8 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_6_7_RI_8 + P-poll__networl_4_4_AskP_2 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_4_4_AskP_1 + P-poll__networl_4_4_AskP_0 + P-poll__networl_8_3_AI_0 + P-poll__networl_8_3_AI_1 + P-poll__networl_8_3_AI_2 + P-poll__networl_8_3_AI_3 + P-poll__networl_8_3_AI_4 + P-poll__networl_8_3_AI_5 + P-poll__networl_8_3_AI_6 + P-poll__networl_8_3_AI_7 + P-poll__networl_8_3_AI_8 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_0_AI_8 + P-poll__networl_8_6_RI_0 + P-poll__networl_8_6_RI_1 + P-poll__networl_8_6_RI_2 + P-poll__networl_8_6_RI_3 + P-poll__networl_8_6_RI_4 + P-poll__networl_8_6_RI_5 + P-poll__networl_8_6_RI_6 + P-poll__networl_8_6_RI_7 + P-poll__networl_8_6_RI_8 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_1_3_RI_8 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_6_5_AnnP_8 + P-poll__networl_3_4_RP_8 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_1_7_AskP_8 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_3_2_RI_8 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_8_8_AskP_0 + P-poll__networl_8_8_AskP_1 + P-poll__networl_8_8_AskP_2 + P-poll__networl_8_8_AskP_3 + P-poll__networl_8_8_AskP_4 + P-poll__networl_8_8_AskP_5 + P-poll__networl_8_8_AskP_6 + P-poll__networl_8_8_AskP_7 + P-poll__networl_8_8_AskP_8 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_0_AnnP_8 + P-poll__networl_3_4_RP_0 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_2_1_AnnP_8 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_2_8_RP_0 + P-poll__networl_5_1_RI_3 + P-poll__networl_2_8_RP_1 + P-poll__networl_5_1_RI_4 + P-poll__networl_2_8_RP_2 + P-poll__networl_5_1_RI_5 + P-poll__networl_2_8_RP_3 + P-poll__networl_5_1_RI_6 + P-poll__networl_2_8_RP_4 + P-poll__networl_5_1_RI_7 + P-poll__networl_2_8_RP_5 + P-poll__networl_5_1_RI_8 + P-poll__networl_2_8_RP_6 + P-poll__networl_2_8_RP_7 + P-poll__networl_2_8_RP_8 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_6_3_AskP_8 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_7_0_RI_8 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_4_7_RP_8 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_3_4_AnnP_8 + P-poll__networl_1_5_RP_8 + P-poll__networl_1_5_RP_7 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_6_6_RP_8 + P-poll__networl_1_5_RP_6 + P-poll__networl_1_8_AI_0 + P-poll__networl_1_8_AI_1 + P-poll__networl_1_8_AI_2 + P-poll__networl_1_8_AI_3 + P-poll__networl_1_8_AI_4 + P-poll__networl_1_8_AI_5 + P-poll__networl_1_8_AI_6 + P-poll__networl_1_8_AI_7 + P-poll__networl_1_8_AI_8 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_8_8_RP_8 + P-poll__networl_8_8_RP_7 + P-poll__networl_8_8_RP_6 + P-poll__networl_8_8_RP_5 + P-poll__networl_8_8_RP_4 + P-poll__networl_8_8_RP_3 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_5_7_AskP_8 + P-poll__networl_8_8_RP_2 + P-poll__networl_8_8_RP_1 + P-poll__networl_8_5_RP_0 + P-poll__networl_8_5_RP_1 + P-poll__networl_8_5_RP_2 + P-poll__networl_8_5_RP_3 + P-poll__networl_8_5_RP_4 + P-poll__networl_8_5_RP_5 + P-poll__networl_8_5_RP_6 + P-poll__networl_8_5_RP_7 + P-poll__networl_8_5_RP_8 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_1_2_RP_8 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_8_8_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_3_7_AI_8 + P-poll__networl_8_0_AnnP_0 + P-poll__networl_8_0_AnnP_1 + P-poll__networl_8_0_AnnP_2 + P-poll__networl_8_0_AnnP_3 + P-poll__networl_8_0_AnnP_4 + P-poll__networl_8_0_AnnP_5 + P-poll__networl_8_0_AnnP_6 + P-poll__networl_8_0_AnnP_7 + P-poll__networl_8_0_AnnP_8 + P-poll__networl_5_0_AskP_8 + P-poll__networl_5_0_AskP_7 + P-poll__networl_2_8_AnnP_0 + P-poll__networl_2_8_AnnP_1 + P-poll__networl_2_8_AnnP_2 + P-poll__networl_2_8_AnnP_3 + P-poll__networl_2_8_AnnP_4 + P-poll__networl_2_8_AnnP_5 + P-poll__networl_2_8_AnnP_6 + P-poll__networl_2_8_AnnP_7 + P-poll__networl_2_8_AnnP_8 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_5_0_AskP_0 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_2_AskP_8 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_3_1_RP_8 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_5_6_AI_8 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_8 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_0_3_AnnP_8 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_5_0_RP_8 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_7_5_AI_8 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_2_AI_8 + P-poll__networl_7_8_RI_0 + P-poll__networl_7_8_RI_1 + P-poll__networl_7_8_RI_2 + P-poll__networl_7_8_RI_3 + P-poll__networl_7_8_RI_4 + P-poll__networl_7_8_RI_5 + P-poll__networl_7_8_RI_6 + P-poll__networl_7_8_RI_7 + P-poll__networl_7_8_RI_8 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_0_5_RI_8 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_7_4_AnnP_8 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_6_AskP_8 + P-poll__networl_2_1_AI_0 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_1_AI_8 + P-poll__networl_2_4_RI_0
+ P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_2_4_RI_8 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_4_0_AI_8 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_0_1_AskP_8 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_4_3_RI_8 + P-poll__networl_6_8_AnnP_0 + P-poll__networl_6_8_AnnP_1 + P-poll__networl_6_8_AnnP_2 + P-poll__networl_6_8_AnnP_3 + P-poll__networl_6_8_AnnP_4 + P-poll__networl_6_8_AnnP_5 + P-poll__networl_6_8_AnnP_6 + P-poll__networl_6_8_AnnP_7 + P-poll__networl_6_8_AnnP_8 + P-poll__networl_7_5_AskP_8 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_2_AskP_8 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_4 + P-poll__networl_7_5_AskP_3 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_6_2_RI_8 + P-poll__networl_7_5_AskP_0 + P-poll__networl_0_0_RI_8 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_4_3_AnnP_8 + P-poll__networl_0_0_RI_1 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_8 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_8 + P-poll__networl_0_4_AskP_7 + P-poll__networl_8_1_RI_0 + P-poll__networl_8_1_RI_1 + P-poll__networl_8_1_RI_2 + P-poll__networl_5_8_RP_0 + P-poll__networl_8_1_RI_3 + P-poll__networl_5_8_RP_1 + P-poll__networl_8_1_RI_4 + P-poll__networl_5_8_RP_2 + P-poll__networl_8_1_RI_5 + P-poll__networl_5_8_RP_3 + P-poll__networl_8_1_RI_6 + P-poll__networl_5_8_RP_4 + P-poll__networl_8_1_RI_7 + P-poll__networl_5_8_RP_5 + P-poll__networl_8_1_RI_8 + P-poll__networl_5_8_RP_6 + P-poll__networl_5_8_RP_7 + P-poll__networl_5_8_RP_8 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_8 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_6_6_AskP_8 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_7_7_RP_8 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_0_4_RP_8 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_3_7_AnnP_8 + P-poll__networl_6_8_AnsP_0 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_4_1_AskP_8 + P-poll__networl_5_2_AnnP_8 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_2_3_RP_8 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_4_8_AI_0 + P-poll__networl_4_8_AI_1 + P-poll__networl_4_8_AI_2 + P-poll__networl_4_8_AI_3 + P-poll__networl_4_8_AI_4 + P-poll__networl_4_8_AI_5 + P-poll__networl_4_8_AI_6 + P-poll__networl_4_8_AI_7 + P-poll__networl_4_8_AI_8 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_8_0_AnsP_0 + P-poll__networl_5_4_RI_8 + P-poll__networl_5_4_RI_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_1_2_AnnP_8 + P-poll__networl_5_4_RI_0 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_2_8_AnsP_0 + P-poll__networl_4_2_RP_8 + P-poll__networl_5_1_AI_8 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_6_7_AI_8 + P-poll__networl_8_3_AnnP_0 + P-poll__networl_8_3_AnnP_1 + P-poll__networl_8_3_AnnP_2 + P-poll__networl_8_3_AnnP_3 + P-poll__networl_8_3_AnnP_4 + P-poll__networl_8_3_AnnP_5 + P-poll__networl_8_3_AnnP_6 + P-poll__networl_8_3_AnnP_7 + P-poll__networl_8_3_AnnP_8 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_5_1_AI_4 + P-poll__networl_5_1_AI_3 + P-poll__networl_5_1_AI_2 + P-poll__networl_5_1_AI_1 + P-poll__networl_5_1_AI_0 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_3_5_AskP_8 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_6_1_RP_8 + P-poll__networl_8_6_AI_0 + P-poll__networl_8_6_AI_1 + P-poll__networl_8_6_AI_2 + P-poll__networl_8_6_AI_3 + P-poll__networl_8_6_AI_4 + P-poll__networl_8_6_AI_5 + P-poll__networl_8_6_AI_6 + P-poll__networl_8_6_AI_7 + P-poll__networl_8_6_AI_8 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_1_3_AI_5 + P-poll__networl_1_3_AI_6 + P-poll__networl_8_1_AskP_8 + P-poll__networl_1_3_AI_7 + P-poll__networl_8_1_AskP_7 + P-poll__networl_1_3_AI_8 + P-poll__networl_8_1_AskP_6 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_1_6_RI_8 + P-poll__networl_8_1_AskP_5 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_8_1_AskP_4 + P-poll__networl_8_1_AskP_3 + P-poll__networl_8_1_AskP_2 + P-poll__networl_8_1_AskP_1 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_0_6_AnnP_8 + P-poll__networl_8_0_RP_0 + P-poll__networl_8_0_RP_1 + P-poll__networl_8_0_RP_2 + P-poll__networl_8_0_RP_3 + P-poll__networl_8_0_RP_4 + P-poll__networl_8_0_RP_5 + P-poll__networl_8_0_RP_6 + P-poll__networl_8_0_RP_7 + P-poll__networl_8_0_RP_8 + P-poll__networl_8_1_AskP_0 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_1_0_AskP_8 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_2_AI_8 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_3_5_RI_8 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7 + P-poll__networl_7_7_AnnP_8)) U F (F ((2 <= P-startNeg__broadcasting_1_6 + P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_6 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_2_3 + P-startNeg__broadcasting_2_4 + P-startNeg__broadcasting_2_5 + P-startNeg__broadcasting_2_6 + P-startNeg__broadcasting_2_7 + P-startNeg__broadcasting_2_8 + P-startNeg__broadcasting_3_1 + P-startNeg__broadcasting_3_2 + P-startNeg__broadcasting_3_3 + P-startNeg__broadcasting_3_4 + P-startNeg__broadcasting_3_5 + P-startNeg__broadcasting_3_6 + P-startNeg__broadcasting_3_7 + P-startNeg__broadcasting_3_8 + P-startNeg__broadcasting_4_1 + P-startNeg__broadcasting_4_2 + P-startNeg__broadcasting_4_3 + P-startNeg__broadcasting_4_4 + P-startNeg__broadcasting_4_5 + P-startNeg__broadcasting_4_6 + P-startNeg__broadcasting_4_7 + P-startNeg__broadcasting_4_8 + P-startNeg__broadcasting_8_8 + P-startNeg__broadcasting_8_7 + P-startNeg__broadcasting_8_6 + P-startNeg__broadcasting_8_5 + P-startNeg__broadcasting_8_4 + P-startNeg__broadcasting_8_3 + P-startNeg__broadcasting_8_2 + P-startNeg__broadcasting_8_1 + P-startNeg__broadcasting_7_8 + P-startNeg__broadcasting_7_7 + P-startNeg__broadcasting_7_6 + P-startNeg__broadcasting_7_5 + P-startNeg__broadcasting_7_4 + P-startNeg__broadcasting_7_3 + P-startNeg__broadcasting_7_2 + P-startNeg__broadcasting_7_1 + P-startNeg__broadcasting_6_8 + P-startNeg__broadcasting_6_7 + P-startNeg__broadcasting_6_6 + P-startNeg__broadcasting_5_1 + P-startNeg__broadcasting_5_2 + P-startNeg__broadcasting_5_3 + P-startNeg__broadcasting_5_4 + P-startNeg__broadcasting_5_5 + P-startNeg__broadcasting_5_6 + P-startNeg__broadcasting_5_7 + P-startNeg__broadcasting_5_8 + P-startNeg__broadcasting_6_5 + P-startNeg__broadcasting_6_4 + P-startNeg__broadcasting_6_3 + P-startNeg__broadcasting_6_2 + P-startNeg__broadcasting_6_1 + P-startNeg__broadcasting_0_7 + P-startNeg__broadcasting_0_8 + P-startNeg__broadcasting_1_7 + P-startNeg__broadcasting_1_8))))) : A ((G (F ((P-poll__networl_7_4_AnsP_8 + P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_8 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_2_8_AnsP_8 + P-poll__networl_2_8_AnsP_7 + P-poll__networl_2_8_AnsP_6 + P-poll__networl_2_8_AnsP_5 + P-poll__networl_2_8_AnsP_4 + P-poll__networl_2_8_AnsP_3 + P-poll__networl_2_8_AnsP_2 + P-poll__networl_2_8_AnsP_1 + P-poll__networl_8_0_AnsP_8 + P-poll__networl_8_0_AnsP_7 + P-poll__networl_8_0_AnsP_6 + P-poll__networl_8_0_AnsP_5 + P-poll__networl_8_0_AnsP_4 + P-poll__networl_8_0_AnsP_3 + P-poll__networl_8_0_AnsP_2 + P-poll__networl_8_0_AnsP_1 + P-poll__networl_6_8_AnsP_1 + P-poll__networl_6_8_AnsP_2 + P-poll__networl_6_8_AnsP_3 + P-poll__networl_6_8_AnsP_4 + P-poll__networl_6_8_AnsP_5 + P-poll__networl_6_8_AnsP_6 + P-poll__networl_6_8_AnsP_7 + P-poll__networl_6_8_AnsP_8 + P-poll__networl_3_4_AnsP_8 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_8 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_8 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_4_3_AnsP_8 + P-poll__networl_7_1_AnsP_8 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_8 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_8 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_8 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_5_6_AnsP_8 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_3_7_AnsP_8 + P-poll__networl_6_2_AnsP_8 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_A
nsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_8_7_AnsP_8 + P-poll__networl_8_7_AnsP_7 + P-poll__networl_8_7_AnsP_6 + P-poll__networl_8_7_AnsP_5 + P-poll__networl_8_7_AnsP_4 + P-poll__networl_8_7_AnsP_3 + P-poll__networl_8_7_AnsP_2 + P-poll__networl_8_7_AnsP_1 + P-poll__networl_1_6_AnsP_8 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_2_AnsP_8 + P-poll__networl_2_2_AnsP_8 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_8_3_AnsP_1 + P-poll__networl_8_3_AnsP_2 + P-poll__networl_8_3_AnsP_3 + P-poll__networl_8_3_AnsP_4 + P-poll__networl_8_3_AnsP_5 + P-poll__networl_8_3_AnsP_6 + P-poll__networl_8_3_AnsP_7 + P-poll__networl_8_3_AnsP_8 + P-poll__networl_4_7_AnsP_8 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_8 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_7_8_AnsP_8 + P-poll__networl_7_8_AnsP_7 + P-poll__networl_7_8_AnsP_6 + P-poll__networl_7_8_AnsP_5 + P-poll__networl_7_8_AnsP_4 + P-poll__networl_7_8_AnsP_3 + P-poll__networl_7_8_AnsP_2 + P-poll__networl_7_8_AnsP_1 + P-poll__networl_0_7_AnsP_8 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_8_4_AnsP_8 + P-poll__networl_8_4_AnsP_7 + P-poll__networl_8_4_AnsP_6 + P-poll__networl_8_4_AnsP_5 + P-poll__networl_8_4_AnsP_4 + P-poll__networl_8_4_AnsP_3 + P-poll__networl_8_4_AnsP_2 + P-poll__networl_8_4_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_1_3_AnsP_8 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_6_AnsP_8 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_3_8_AnsP_8 + P-poll__networl_3_8_AnsP_7 + P-poll__networl_3_8_AnsP_6 + P-poll__networl_3_8_AnsP_5 + P-poll__networl_3_8_AnsP_4 + P-poll__networl_3_8_AnsP_3 + P-poll__networl_3_8_AnsP_2 + P-poll__networl_3_8_AnsP_1 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_7_7_AnsP_8 + P-poll__networl_4_4_AnsP_8 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_0_AnsP_8 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_2_AnsP_8 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_8 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_8 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_8_1_AnsP_8 + P-poll__networl_8_1_AnsP_7 + P-poll__networl_8_1_AnsP_6 + P-poll__networl_8_1_AnsP_5 + P-poll__networl_8_1_AnsP_4 + P-poll__networl_8_1_AnsP_3 + P-poll__networl_8_1_AnsP_2 + P-poll__networl_8_1_AnsP_1 + P-poll__networl_1_0_AnsP_8 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_8 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_1_AnsP_8 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_6_AnsP_8 + P-poll__networl_6_6_AnsP_8 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_2_1_AnsP_8 + P-poll__networl_7_2_AnsP_8 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_8 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_8 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_3_2_AnsP_8 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_8 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_8 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_1_5_AnsP_8 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_8_8_AnsP_8 + P-poll__networl_8_8_AnsP_7 + P-poll__networl_8_8_AnsP_6 + P-poll__networl_8_8_AnsP_5 + P-poll__networl_8_8_AnsP_4 + P-poll__networl_8_8_AnsP_3 + P-poll__networl_8_8_AnsP_2 + P-poll__networl_8_8_AnsP_1 + P-poll__networl_1_7_AnsP_8 + P-poll__networl_8_6_AnsP_1 + P-poll__networl_8_6_AnsP_2 + P-poll__networl_8_6_AnsP_3 + P-poll__networl_8_6_AnsP_4 + P-poll__networl_8_6_AnsP_5 + P-poll__networl_8_6_AnsP_6 + P-poll__networl_8_6_AnsP_7 + P-poll__networl_8_6_AnsP_8 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_8 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_4_8_AnsP_8 + P-poll__networl_4_8_AnsP_7 + P-poll__networl_4_8_AnsP_6 + P-poll__networl_4_8_AnsP_5 + P-poll__networl_4_8_AnsP_4 + P-poll__networl_4_8_AnsP_3 + P-poll__networl_4_8_AnsP_2 + P-poll__networl_4_8_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_6_1_AnsP_8 + P-poll__networl_5_4_AnsP_8 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_0_8_AnsP_8 + P-poll__networl_0_8_AnsP_7 + P-poll__networl_0_8_AnsP_6 + P-poll__networl_0_8_AnsP_5 + P-poll__networl_0_8_AnsP_4 + P-poll__networl_0_8_AnsP_3 + P-poll__networl_0_8_AnsP_2 + P-poll__networl_0_8_AnsP_1 + P-poll__networl_6_0_AnsP_8 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_8_5_AnsP_8 + P-poll__networl_8_5_AnsP_7 + P-poll__networl_8_5_AnsP_6 + P-poll__networl_8_5_AnsP_5 + P-poll__networl_8_5_AnsP_4 + P-poll__networl_8_5_AnsP_3 + P-poll__networl_8_5_AnsP_2 + P-poll__networl_8_5_AnsP_1 + P-poll__networl_1_4_AnsP_8 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_2_0_AnsP_8 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_5_5_AnsP_8 + P-poll__networl_4_5_AnsP_8 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_8 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_3_0_AnsP_8 + P-poll__networl_7_6_AnsP_8 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_8 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_8_2_AnsP_8 + P-poll__networl_8_2_AnsP_7 + P-poll__networl_8_2_AnsP_6 + P-poll__networl_8_2_AnsP_5 + P-poll__networl_8_2_AnsP_4 + P-poll__networl_8_2_AnsP_3 + P-poll__networl_8_2_AnsP_2 + P-poll__networl_8_2_AnsP_1 + P-poll__networl_1_1_AnsP_8 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_3_6_AnsP_8 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_8 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_2_4_AnsP_8 + P-poll__networl_6_7_AnsP_8 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_3_AnsP_8 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_8 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_8 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_0_AnsP_8 + P-poll__networl_3_3_AnsP_8 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_1_8_AnsP_1 + P-poll__networl_1_8_AnsP_2 + P-poll__networl_1_8_AnsP_3 + P-poll__networl_1_8_AnsP_4 + P-poll__networl_1_8_AnsP_5 + P-poll__networl_1_8_AnsP_6 + P-poll__networl_1_8_AnsP_7 + P-poll__networl_1_8_AnsP_8 + P-poll__networl_5_8_AnsP_8 + P-poll__networl_5_8_AnsP_7 + P-poll__networl_5_8_AnsP_6 + P-poll__networl_5_8_AnsP_5 + P-poll__networl_5_8_AnsP_4 + P-poll__networl_5_8_AnsP_3 + P-poll__networl_5_8_AnsP_2 + P-poll__networl_5_8_AnsP_1 + P-poll__networl_6_4_AnsP_8 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_8_4_AI_7 + P-poll__networl_8_4_AI_8 + P-poll__networl_1_1_AI_0 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_3 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_8 + P-poll__networl_8_4_AI_6 + P-poll__networl_8_7_RI_0 + P-poll__networl_8_7_RI_1 + P-poll__networl_8_7_RI_2 + P-poll__networl_8_7_RI_3 + P-poll__networl_8_7_RI_4 + P-poll__networl_8_7_RI_5 + P-poll__networl_8_7_RI_6 + P-poll__networl_8_7_RI_7 + P-poll__networl_8_7_RI_8 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_8 + P-poll__networl_8_4_AI_5 + P-poll__networl_8_4_AI_4 + P-poll__networl_8_4_AI_3 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_8_4_AI_2 + P-poll__networl_8_4_AI_1 + P-poll__networl_8_4_AI_0 + P-poll__networl_3_0_AI_0 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_4 + P-poll__networl_3_0_AI_5 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_7 + P-poll__networl_3_0_A
I_8 + P-poll__networl_0_0_AskP_0 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_0_0_AskP_8 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_3_3_RI_8 + P-poll__networl_2_5_AskP_8 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_6_7_AnnP_8 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_2_5_AskP_0 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_7_1_AskP_8 + P-poll__networl_7_3_AnnP_8 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_5_2_RI_8 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_4_2_AnnP_8 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_5_8_AnsP_0 + P-poll__networl_6_8_RI_8 + P-poll__networl_6_8_RI_7 + P-poll__networl_6_8_RI_6 + P-poll__networl_6_8_RI_5 + P-poll__networl_6_8_RI_4 + P-poll__networl_6_8_RI_3 + P-poll__networl_6_8_RI_2 + P-poll__networl_6_8_RI_1 + P-poll__networl_6_8_RI_0 + P-poll__networl_6_5_AI_8 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_4_8_RP_0 + P-poll__networl_7_1_RI_3 + P-poll__networl_4_8_RP_1 + P-poll__networl_7_1_RI_4 + P-poll__networl_4_8_RP_2 + P-poll__networl_7_1_RI_5 + P-poll__networl_4_8_RP_3 + P-poll__networl_7_1_RI_6 + P-poll__networl_4_8_RP_4 + P-poll__networl_7_1_RI_7 + P-poll__networl_4_8_RP_5 + P-poll__networl_7_1_RI_8 + P-poll__networl_4_8_RP_6 + P-poll__networl_4_8_RP_7 + P-poll__networl_4_8_RP_8 + P-poll__networl_6_5_AI_0 + P-poll__networl_1_8_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_6_5_AskP_8 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_4_0_RP_8 + P-poll__networl_4_0_RP_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_8 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_6_7_RP_8 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_3_6_AnnP_8 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_4_0_AskP_8 + P-poll__networl_8_6_RP_0 + P-poll__networl_8_6_RP_1 + P-poll__networl_8_6_RP_2 + P-poll__networl_8_6_RP_3 + P-poll__networl_8_6_RP_4 + P-poll__networl_8_6_RP_5 + P-poll__networl_8_6_RP_6 + P-poll__networl_8_6_RP_7 + P-poll__networl_8_6_RP_8 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_1_3_RP_8 + P-poll__networl_3_8_AI_0 + P-poll__networl_3_8_AI_1 + P-poll__networl_3_8_AI_2 + P-poll__networl_3_8_AI_3 + P-poll__networl_3_8_AI_4 + P-poll__networl_3_8_AI_5 + P-poll__networl_3_8_AI_6 + P-poll__networl_3_8_AI_7 + P-poll__networl_3_8_AI_8 + P-poll__networl_4_6_AI_8 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_1_1_AnnP_8 + P-poll__networl_4_6_AI_3 + P-poll__networl_4_6_AI_2 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_3_2_RP_8 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_5_7_AI_8 + P-poll__networl_8_2_AnnP_0 + P-poll__networl_8_2_AnnP_1 + P-poll__networl_8_2_AnnP_2 + P-poll__networl_8_2_AnnP_3 + P-poll__networl_8_2_AnnP_4 + P-poll__networl_8_2_AnnP_5 + P-poll__networl_8_2_AnnP_6 + P-poll__networl_8_2_AnnP_7 + P-poll__networl_8_2_AnnP_8 + P-poll__networl_2_1_RP_8 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_2_1_RP_0 + P-poll__networl_3_1_AskP_8 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_3_4_AskP_8 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_5_1_RP_8 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_7_6_AI_8 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_0_3_AI_4 + P-poll__networl_3_1_AskP_1 + P-poll__networl_0_3_AI_5 + P-poll__networl_3_1_AskP_0 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_0_3_AI_8 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_0_6_RI_8 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_2_7_AnnP_8 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_0_5_AnnP_8 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_7_0_RP_8 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_2_2_AI_0 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_2_AI_8 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_2_5_RI_8 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_6_AnnP_8 + P-poll__networl_8_0_AskP_0 + P-poll__networl_8_0_AskP_1 + P-poll__networl_8_0_AskP_2 + P-poll__networl_8_0_AskP_3 + P-poll__networl_8_0_AskP_4 + P-poll__networl_8_0_AskP_5 + P-poll__networl_8_0_AskP_6 + P-poll__networl_8_0_AskP_7 + P-poll__networl_8_0_AskP_8 + P-poll__networl_2_8_AskP_0 + P-poll__networl_2_8_AskP_1 + P-poll__networl_2_8_AskP_2 + P-poll__networl_2_8_AskP_3 + P-poll__networl_2_8_AskP_4 + P-poll__networl_2_8_AskP_5 + P-poll__networl_2_8_AskP_6 + P-poll__networl_2_8_AskP_7 + P-poll__networl_2_8_AskP_8 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_1_AI_8 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_4_4_RI_8 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_5_1_AnnP_8 + P-poll__networl_2_7_AI_8 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_7_AI_2 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_6_0_AI_7 + P-poll__networl_6_0_AI_8 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_8 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_0_3_AskP_8 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_6_3_RI_8 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_0_2_RP_0 + P-poll__networl_7_5_RP_8 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_7_4_AskP_8 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_8_2_RI_0 + P-poll__networl_8_2_RI_1 + P-poll__networl_8_2_RI_2 + P-poll__networl_8_2_RI_3 + P-poll__networl_8_2_RI_4 + P-poll__networl_8_2_RI_5 + P-poll__networl_8_2_RI_6 + P-poll__networl_8_2_RI_7 + P-poll__networl_8_2_RI_8 + P-poll__networl_5_6_AskP_8 + P-poll__networl_5_6_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_5_6_AskP_3 + P-poll__networl_5_6_AskP_2 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_4_5_AnnP_8 + P-poll__networl_5_6_AskP_1 + P-poll__networl_5_6_AskP_0 + P-poll__networl_7_8_RP_0 + P-poll__networl_7_8_RP_1 + P-poll__networl_7_8_RP_2 + P-poll__networl_7_8_RP_3 + P-poll__networl_7_8_RP_4 + P-poll__networl_7_8_RP_5 + P-poll__networl_7_8_RP_6 + P-poll__networl_7_8_RP_7 + P-poll__networl_7_8_RP_8 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_0_5_RP_8 + P-poll__networl_0_8_AI_8 + P-poll__networl_0_8_AI_7 + P-poll__networl_0_8_AI_6 + P-poll__networl_0_8_AI_5 + P-poll__networl_0_8_AI_4 + P-poll__networl_6_8_AskP_0 + P-poll__networl_6_8_AskP_1 + P-poll__networl_6_8_AskP_2 + P-poll__networl_6_8_AskP_3 + P-poll__networl_6_8_AskP_4 + P-poll__networl_6_8_AskP_5 + P-poll__networl_6_8_AskP_6 + P-poll__networl_6_8_AskP_7 + P-poll__networl_6_8_AskP_8 + P-poll__networl_0_8_AI_3 + P-poll__networl_0_8_AI_2 + P-poll__networl_0_8_AI_1 + P-poll__networl_0_8_AI_0 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_0_AnnP_8 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_5_6_RP_8 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_RP_8 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_4_3_AskP_8 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_4_3_RP_8 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_6_8_AI_0 + P-poll__networl_6_8_AI_1 + P-poll__networl_6_8_AI_2 + P-poll__networl_6_8_AI_3 + P-poll__networl_6_8_AI_4 + P-poll__networl_6_8_AI_5 + P-poll__networl_6_8_AI_6 + P-poll__networl_6_8_AI_7 + P-poll__networl_6_8
_AI_8 + P-poll__networl_8_2_AnsP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_1_4_AnnP_8 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_6_2_RP_8 + P-poll__networl_8_7_AI_0 + P-poll__networl_8_7_AI_1 + P-poll__networl_8_7_AI_2 + P-poll__networl_8_7_AI_3 + P-poll__networl_8_7_AI_4 + P-poll__networl_8_7_AI_5 + P-poll__networl_8_7_AI_6 + P-poll__networl_8_7_AI_7 + P-poll__networl_8_7_AI_8 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_4_AI_8 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_1_7_RI_8 + P-poll__networl_8_5_AnnP_0 + P-poll__networl_8_5_AnnP_1 + P-poll__networl_8_5_AnnP_2 + P-poll__networl_8_5_AnnP_3 + P-poll__networl_8_5_AnnP_4 + P-poll__networl_8_5_AnnP_5 + P-poll__networl_8_5_AnnP_6 + P-poll__networl_8_5_AnnP_7 + P-poll__networl_8_5_AnnP_8 + P-poll__networl_3_3_AnnP_8 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_3_7_AskP_8 + P-poll__networl_8_1_RP_0 + P-poll__networl_8_1_RP_1 + P-poll__networl_8_1_RP_2 + P-poll__networl_8_1_RP_3 + P-poll__networl_8_1_RP_4 + P-poll__networl_8_1_RP_5 + P-poll__networl_8_1_RP_6 + P-poll__networl_8_1_RP_7 + P-poll__networl_8_1_RP_8 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_3_3_AI_5 + P-poll__networl_3_3_AI_6 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_3_AI_8 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_3_6_RI_8 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_6_0_AnnP_8 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_3_7_RP_8 + P-poll__networl_3_7_RP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_0_8_AnnP_0 + P-poll__networl_0_8_AnnP_1 + P-poll__networl_0_8_AnnP_2 + P-poll__networl_0_8_AnnP_3 + P-poll__networl_0_8_AnnP_4 + P-poll__networl_0_8_AnnP_5 + P-poll__networl_0_8_AnnP_6 + P-poll__networl_0_8_AnnP_7 + P-poll__networl_0_8_AnnP_8 + P-poll__networl_6_0_RI_8 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_1_2_AskP_8 + P-poll__networl_3_7_RP_0 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_2_AI_8 + P-poll__networl_6_0_RI_2 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_5_RI_8 + P-poll__networl_6_0_RI_1 + P-poll__networl_6_0_RI_0 + P-poll__networl_8_3_AskP_0 + P-poll__networl_8_3_AskP_1 + P-poll__networl_8_3_AskP_2 + P-poll__networl_8_3_AskP_3 + P-poll__networl_8_3_AskP_4 + P-poll__networl_8_3_AskP_5 + P-poll__networl_8_3_AskP_6 + P-poll__networl_8_3_AskP_7 + P-poll__networl_8_3_AskP_8 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_6_2_AskP_8 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_1_AI_8 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_7_4_RI_8 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_0_1_RI_8 + P-poll__networl_6_2_AskP_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_5_4_AnnP_8 + P-poll__networl_6_2_AskP_6 + P-poll__networl_6_2_AskP_5 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_0_6_AskP_8 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_2_0_RI_8 + P-poll__networl_6_2_AskP_0 + P-poll__networl_5_8_AnnP_8 + P-poll__networl_5_8_AnnP_7 + P-poll__networl_5_8_AnnP_6 + P-poll__networl_5_8_AnnP_5 + P-poll__networl_5_8_AnnP_4 + P-poll__networl_5_8_AnnP_3 + P-poll__networl_5_8_AnnP_2 + P-poll__networl_5_8_AnnP_1 + P-poll__networl_5_8_AnnP_0 + P-poll__networl_1_8_RP_8 + P-poll__networl_1_8_RP_7 + P-poll__networl_1_8_RP_6 + P-poll__networl_4_1_RI_8 + P-poll__networl_1_8_RP_5 + P-poll__networl_4_1_RI_7 + P-poll__networl_1_8_RP_4 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_7_7_AskP_8 + P-poll__networl_4_1_RI_6 + P-poll__networl_1_8_RP_3 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_1_8_RP_2 + P-poll__networl_4_1_RI_4 + P-poll__networl_1_8_RP_1 + P-poll__networl_4_1_RI_3 + P-poll__networl_1_8_RP_0 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_1_6_RP_8 + P-poll__networl_4_8_AnnP_0 + P-poll__networl_4_8_AnnP_1 + P-poll__networl_4_8_AnnP_2 + P-poll__networl_4_8_AnnP_3 + P-poll__networl_4_8_AnnP_4 + P-poll__networl_4_8_AnnP_5 + P-poll__networl_4_8_AnnP_6 + P-poll__networl_4_8_AnnP_7 + P-poll__networl_4_8_AnnP_8 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_5_2_AskP_8 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_3_5_RP_8 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_2_3_AnnP_8 + P-poll__networl_8_7_AskP_8 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_5_4_RP_8 + P-poll__networl_8_7_AskP_7 + P-poll__networl_8_7_AskP_6 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_0_6_AI_8 + P-poll__networl_8_7_AskP_5 + P-poll__networl_8_7_AskP_4 + P-poll__networl_8_7_AskP_3 + P-poll__networl_8_7_AskP_2 + P-poll__networl_8_7_AskP_1 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_4_6_AskP_8 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_7_3_RP_8 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_0_0_RP_8 + P-poll__networl_8_7_AskP_0 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_2_5_AI_0 + P-poll__networl_2_2_RI_8 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_2_5_AI_8 + P-poll__networl_2_8_RI_0 + P-poll__networl_2_8_RI_1 + P-poll__networl_2_8_RI_2 + P-poll__networl_2_8_RI_3 + P-poll__networl_2_8_RI_4 + P-poll__networl_2_8_RI_5 + P-poll__networl_2_8_RI_6 + P-poll__networl_2_8_RI_7 + P-poll__networl_2_8_RI_8 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_8_5_AnsP_0 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_8 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_1_7_AnnP_8 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_2_1_AskP_8 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_4_AI_8 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_4_7_RI_8 + P-poll__networl_8_8_AnnP_0 + P-poll__networl_8_8_AnnP_1 + P-poll__networl_8_8_AnnP_2 + P-poll__networl_8_8_AnnP_3 + P-poll__networl_8_8_AnnP_4 + P-poll__networl_8_8_AnnP_5 + P-poll__networl_8_8_AnnP_6 + P-poll__networl_8_8_AnnP_7 + P-poll__networl_8_8_AnnP_8 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_0_8_AnsP_0 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_3_AI_8 + P-poll__networl_6_4_AnnP_8 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_6_6_RI_8 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_6_3_AnnP_8 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_8 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_8 + P-poll__networl_7_6_RI_7 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_1_5_AskP_8 + P-poll__networl_7_6_RI_2 + P-poll__networl_8_2_AI_0 + P-poll__networl_8_2_AI_1 + P-poll__networl_8_2_AI_2 + P-poll__networl_8_2_AI_3 + P-poll__networl_8_2_AI_4 + P-poll__networl_8_2_AI_5 + P-poll__networl_8_2_AI_6 + P-poll__networl_8_2_AI_7 + P-poll__networl_8_2_AI_8 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_8 + P-poll__networl_0_0_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_0_0_AI_4 + P-poll__networl_0_0_AI_3 + P-poll__networl_8_5_RI_0 + P-poll__networl_8_5_RI_1 + P-poll__networl_8_5_RI_2 + P-poll__networl_8_5_RI_3 + P-poll__networl_8_5_RI_4 + P-poll__networl_8_5_RI_5 + P-poll__networl_8_5_RI_6 + P-poll__networl_8_5_RI_7 + P-poll__networl_8_5_RI_8 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_2_RI_8 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_8_6_AskP_0 + P-poll__networl_8_6_AskP_1 + P-poll__networl_8_6_AskP_2 + P-poll__networl_8_6_AskP_3 + P-poll__networl_8_6_AskP_4 + P-poll__networl_8_6_AskP_5 + P-poll__networl_8_6_AskP_6 + P-poll__networl_8_6_AskP_7 + P-poll__networl_8_6_AskP_8 + P-poll__networl_0_0_AI_0 + P-poll__networl_7_3_AI_8 + P-poll__networl_7_3_AI_7 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_0_8_RP_0 + P-poll__networl_3_1_RI_3 + P-poll__networl_0_8_RP_1 + P-poll__networl_3_1_RI_4 + P-poll__networl_0_8_RP_2 + P-poll
__networl_3_1_RI_5 + P-poll__networl_0_8_RP_3 + P-poll__networl_3_1_RI_6 + P-poll__networl_0_8_RP_4 + P-poll__networl_3_1_RI_7 + P-poll__networl_0_8_RP_5 + P-poll__networl_3_1_RI_8 + P-poll__networl_0_8_RP_6 + P-poll__networl_0_8_RP_7 + P-poll__networl_0_8_RP_8 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_5_7_AnnP_8 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_1_AskP_8 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_5_0_RI_8 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_2_7_RP_8 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_3_2_AnnP_8 + P-poll__networl_4_8_AnsP_0 + P-poll__networl_5_7_RI_8 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_4_6_RP_8 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_8 + P-poll__networl_5_4_AI_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_5_5_AskP_8 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_6_5_RP_8 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_2_2_AskP_8 + P-poll__networl_2_2_AskP_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_1_7_AI_8 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_2_6_AnnP_8 + P-poll__networl_2_2_AskP_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_3_0_AskP_8 + P-poll__networl_8_4_RP_0 + P-poll__networl_8_4_RP_1 + P-poll__networl_8_4_RP_2 + P-poll__networl_8_4_RP_3 + P-poll__networl_8_4_RP_4 + P-poll__networl_8_4_RP_5 + P-poll__networl_8_4_RP_6 + P-poll__networl_8_4_RP_7 + P-poll__networl_8_4_RP_8 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_1_1_RP_8 + P-poll__networl_2_2_AskP_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_3_6_AI_8 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_1_8_AnnP_8 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_0_1_AnnP_8 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_3_0_RP_8 + P-poll__networl_1_8_AnnP_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_1_8_AnnP_6 + P-poll__networl_1_8_AnnP_5 + P-poll__networl_1_8_AnnP_4 + P-poll__networl_1_8_AnnP_3 + P-poll__networl_1_8_AnnP_2 + P-poll__networl_1_8_AnnP_1 + P-poll__networl_1_8_AnnP_0 + P-poll__networl_8_6_AnsP_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_5_5_AI_8 + P-poll__networl_5_8_RI_0 + P-poll__networl_5_8_RI_1 + P-poll__networl_5_8_RI_2 + P-poll__networl_5_8_RI_3 + P-poll__networl_5_8_RI_4 + P-poll__networl_5_8_RI_5 + P-poll__networl_5_8_RI_6 + P-poll__networl_5_8_RI_7 + P-poll__networl_5_8_RI_8 + P-poll__networl_7_0_AnnP_8 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_7_2_AnnP_8 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_8_8_AnsP_0 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_8_RI_8 + P-poll__networl_3_8_RI_7 + P-poll__networl_3_8_RI_6 + P-poll__networl_3_8_RI_5 + P-poll__networl_3_8_RI_4 + P-poll__networl_3_8_RI_3 + P-poll__networl_3_8_RI_2 + P-poll__networl_3_8_RI_1 + P-poll__networl_3_8_RI_0 + P-poll__networl_3_5_AI_8 + P-poll__networl_3_5_AI_7 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_2_4_AskP_8 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_7_4_AI_8 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_0_1_AI_8 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_7_7_RI_8 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_0_4_RI_8 + P-poll__networl_3_5_AI_3 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_0_AI_8 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_2_3_RI_8 + P-poll__networl_1_0_RP_8 + P-poll__networl_1_0_RP_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_6_6_AnnP_8 + P-poll__networl_1_0_RP_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_7_0_AskP_8 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_8_3_RP_8 + P-poll__networl_8_3_RP_7 + P-poll__networl_8_3_RP_6 + P-poll__networl_8_3_RP_5 + P-poll__networl_8_3_RP_4 + P-poll__networl_1_8_AskP_0 + P-poll__networl_1_8_AskP_1 + P-poll__networl_1_8_AskP_2 + P-poll__networl_1_8_AskP_3 + P-poll__networl_1_8_AskP_4 + P-poll__networl_1_8_AskP_5 + P-poll__networl_1_8_AskP_6 + P-poll__networl_1_8_AskP_7 + P-poll__networl_1_8_AskP_8 + P-poll__networl_8_3_RP_3 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_2_RI_8 + P-poll__networl_8_3_RP_2 + P-poll__networl_8_3_RP_1 + P-poll__networl_8_3_RP_0 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_4_1_AnnP_8 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_4_7_AskP_8 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_3_8_RP_0 + P-poll__networl_6_1_RI_3 + P-poll__networl_3_8_RP_1 + P-poll__networl_6_1_RI_4 + P-poll__networl_3_8_RP_2 + P-poll__networl_6_1_RI_5 + P-poll__networl_3_8_RP_3 + P-poll__networl_6_1_RI_6 + P-poll__networl_3_8_RP_4 + P-poll__networl_6_1_RI_7 + P-poll__networl_3_8_RP_5 + P-poll__networl_6_1_RI_8 + P-poll__networl_3_8_RP_6 + P-poll__networl_3_8_RP_7 + P-poll__networl_3_8_RP_8 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_6_4_AskP_8 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_1_6_AI_8 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_8_0_RI_0 + P-poll__networl_8_0_RI_1 + P-poll__networl_8_0_RI_2 + P-poll__networl_5_7_RP_0 + P-poll__networl_8_0_RI_3 + P-poll__networl_5_7_RP_1 + P-poll__networl_8_0_RI_4 + P-poll__networl_5_7_RP_2 + P-poll__networl_8_0_RI_5 + P-poll__networl_5_7_RP_3 + P-poll__networl_8_0_RI_6 + P-poll__networl_5_7_RP_4 + P-poll__networl_8_0_RI_7 + P-poll__networl_5_7_RP_5 + P-poll__networl_8_0_RI_8 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_5_7_RP_8 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_1_6_AI_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_3_5_AnnP_8 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_7_6_RP_8 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_0_3_RP_8 + P-poll__networl_2_8_AI_0 + P-poll__networl_2_8_AI_1 + P-poll__networl_2_8_AI_2 + P-poll__networl_2_8_AI_3 + P-poll__networl_2_8_AI_4 + P-poll__networl_2_8_AI_5 + P-poll__networl_2_8_AI_6 + P-poll__networl_2_8_AI_7 + P-poll__networl_2_8_AI_8 + P-poll__networl_6_4_RP_8 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_5_8_AskP_0 + P-poll__networl_5_8_AskP_1 + P-poll__networl_5_8_AskP_2 + P-poll__networl_5_8_AskP_3 + P-poll__networl_5_8_AskP_4 + P-poll__networl_5_8_AskP_5 + P-poll__networl_5_8_AskP_6 + P-poll__networl_5_8_AskP_7 + P-poll__networl_5_8_AskP_8 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_1_0_AnnP_8 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_2_RP_8 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_4_7_AI_8 + P-poll__networl_8_1_AnnP_0 + P-poll__networl_8_1_AnnP_1 + P-poll__networl_8_1_AnnP_2 + P-poll__networl_8_1_AnnP_3 + P-poll__networl_8_1_AnnP_4 + P-poll__networl_8_1_AnnP_5 + P-poll__networl_8_1_AnnP_6 + P-poll__networl_8_1_AnnP_7 + P-poll__networl_8_1_AnnP_8 + P-poll__networl_2_4_AnnP_8 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_3_3_AskP_8 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_4_1_RP_8 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_6_6_AI_8 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_0_4_AnnP_8 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__net
worl_6_0_RP_8 + P-poll__networl_8_5_AI_0 + P-poll__networl_8_5_AI_1 + P-poll__networl_8_5_AI_2 + P-poll__networl_8_5_AI_3 + P-poll__networl_8_5_AI_4 + P-poll__networl_8_5_AI_5 + P-poll__networl_8_5_AI_6 + P-poll__networl_8_5_AI_7 + P-poll__networl_8_5_AI_8 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_2_AI_8 + P-poll__networl_8_8_RI_0 + P-poll__networl_8_8_RI_1 + P-poll__networl_8_8_RI_2 + P-poll__networl_8_8_RI_3 + P-poll__networl_8_8_RI_4 + P-poll__networl_8_8_RI_5 + P-poll__networl_8_8_RI_6 + P-poll__networl_8_8_RI_7 + P-poll__networl_8_8_RI_8 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_1_5_RI_8 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_7_5_AnnP_8 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_8 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_7_AskP_8 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_1_AI_8 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_3_4_RI_8 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_5_0_AnnP_8 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_5_3_AskP_8 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_3_AskP_0 + P-poll__networl_5_0_AI_7 + P-poll__networl_5_0_AI_8 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_0_2_AskP_8 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_5_3_RI_8 + P-poll__networl_2_6_RP_8 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_7_3_AskP_8 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_7_2_RI_8 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_4_4_AnnP_8 + P-poll__networl_3_0_AnnP_8 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_7_8_AskP_8 + P-poll__networl_7_8_AskP_7 + P-poll__networl_7_8_AskP_6 + P-poll__networl_7_8_AskP_5 + P-poll__networl_6_8_RP_0 + P-poll__networl_6_8_RP_1 + P-poll__networl_6_8_RP_2 + P-poll__networl_6_8_RP_3 + P-poll__networl_6_8_RP_4 + P-poll__networl_6_8_RP_5 + P-poll__networl_6_8_RP_6 + P-poll__networl_6_8_RP_7 + P-poll__networl_6_8_RP_8 + P-poll__networl_7_8_AskP_4 + P-poll__networl_7_8_AskP_3 + P-poll__networl_7_8_AskP_2 + P-poll__networl_7_8_AskP_1 + P-poll__networl_7_8_AskP_0 + P-poll__networl_0_7_RP_8 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_3_0_RI_8 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_6_7_AskP_8 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_8_7_RP_0 + P-poll__networl_8_7_RP_1 + P-poll__networl_8_7_RP_2 + P-poll__networl_8_7_RP_3 + P-poll__networl_8_7_RP_4 + P-poll__networl_8_7_RP_5 + P-poll__networl_8_7_RP_6 + P-poll__networl_8_7_RP_7 + P-poll__networl_8_7_RP_8 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_1_4_RP_8 + P-poll__networl_3_8_AnnP_0 + P-poll__networl_3_8_AnnP_1 + P-poll__networl_3_8_AnnP_2 + P-poll__networl_3_8_AnnP_3 + P-poll__networl_3_8_AnnP_4 + P-poll__networl_3_8_AnnP_5 + P-poll__networl_3_8_AnnP_6 + P-poll__networl_3_8_AnnP_7 + P-poll__networl_3_8_AnnP_8 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_4_2_AskP_8 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_3_3_RP_8 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_AskP_8 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_5_8_AI_0 + P-poll__networl_5_8_AI_1 + P-poll__networl_5_8_AI_2 + P-poll__networl_5_8_AI_3 + P-poll__networl_5_8_AI_4 + P-poll__networl_5_8_AI_5 + P-poll__networl_5_8_AI_6 + P-poll__networl_5_8_AI_7 + P-poll__networl_5_8_AI_8 + P-poll__networl_0_7_AskP_3 + P-poll__networl_8_1_AnsP_0 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_1_3_AnnP_8 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_5_2_RP_8 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_7_7_AI_8 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_4_AI_8 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RI_8 + P-poll__networl_8_4_AnnP_0 + P-poll__networl_8_4_AnnP_1 + P-poll__networl_8_4_AnnP_2 + P-poll__networl_8_4_AnnP_3 + P-poll__networl_8_4_AnnP_4 + P-poll__networl_8_4_AnnP_5 + P-poll__networl_8_4_AnnP_6 + P-poll__networl_8_4_AnnP_7 + P-poll__networl_8_4_AnnP_8 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_3_6_AskP_8 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_7_1_RP_8 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_3_AI_8 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_2_6_RI_8 + P-poll__networl_5_5_AnnP_8 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_8 + P-poll__networl_1_1_RI_7 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_1_1_RI_6 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_8_4_RI_8 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_0_7_AnnP_8 + P-poll__networl_8_4_RI_7 + P-poll__networl_8_4_RI_6 + P-poll__networl_8_4_RI_5 + P-poll__networl_8_4_RI_4 + P-poll__networl_8_4_RI_3 + P-poll__networl_8_4_RI_2 + P-poll__networl_8_4_RI_1 + P-poll__networl_8_4_RI_0 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_1_1_AskP_8 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_2_AI_8 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_4_5_RI_8 + P-poll__networl_7_8_AnnP_0 + P-poll__networl_7_8_AnnP_1 + P-poll__networl_7_8_AnnP_2 + P-poll__networl_7_8_AnnP_3 + P-poll__networl_7_8_AnnP_4 + P-poll__networl_7_8_AnnP_5 + P-poll__networl_7_8_AnnP_6 + P-poll__networl_7_8_AnnP_7 + P-poll__networl_7_8_AnnP_8 + P-poll__networl_8_1_AI_8 + P-poll__networl_8_1_AI_7 + P-poll__networl_8_1_AI_6 + P-poll__networl_8_1_AI_5 + P-poll__networl_8_1_AI_4 + P-poll__networl_8_1_AI_3 + P-poll__networl_8_2_AskP_0 + P-poll__networl_8_2_AskP_1 + P-poll__networl_8_2_AskP_2 + P-poll__networl_8_2_AskP_3 + P-poll__networl_8_2_AskP_4 + P-poll__networl_8_2_AskP_5 + P-poll__networl_8_2_AskP_6 + P-poll__networl_8_2_AskP_7 + P-poll__networl_8_2_AskP_8 + P-poll__networl_8_1_AI_2 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_8_1_AI_1 + P-poll__networl_8_1_AI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_1_AI_8 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_6_4_RI_8 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_5_3_AnnP_8 + P-poll__networl_8_4_AskP_8 + P-poll__networl_8_4_AskP_7 + P-poll__networl_8_0_AI_0 + P-poll__networl_8_0_AI_1 + P-poll__networl_8_0_AI_2 + P-poll__networl_8_0_AI_3 + P-poll__networl_8_0_AI_4 + P-poll__networl_8_0_AI_5 + P-poll__networl_8_0_AI_6 + P-poll__networl_8_0_AI_7 + P-poll__networl_8_4_AskP_6 + P-poll__networl_8_0_AI_8 + P-poll__networl_8_4_AskP_5 + P-poll__networl_8_4_AskP_4 + P-poll__networl_8_4_AskP_3 + P-poll__networl_8_4_AskP_2 + P-poll__networl_8_4_AskP_1 + P-poll__networl_0_5_AskP_0 + P-poll__networl_8_4_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_0_5_AskP_8 + P-poll__networl_8_3_RI_0 + P-poll__networl_8_3_RI_1 + P-poll__networl_8_3_RI_2 + P-poll__networl_8_3_RI_3 + P-poll__networl_8_3_RI_4 + P-poll__networl_8_3_RI_5 + P-poll__networl_8_3_RI_6 + P-poll__networl_8_3_RI_7 + P-poll__networl_8_3_RI_8 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_1_0_RI_8 + P-poll__networl_6_5_RI_8 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_6_5_RI_4 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_7_6_AskP_8 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_8 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_0_6_RP_8 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_8 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 +
P-poll__networl_4_7_AnnP_8 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_1_3_AskP_2 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_5_1_AskP_8 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_2_5_RP_8 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_2_2_AnnP_8 + P-poll__networl_3_8_AnsP_0 + P-poll__networl_6_1_AnnP_8 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_4_RP_8 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_4_6_RI_8 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_4_5_AskP_8 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_6_3_RP_8 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_8 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_8_8_AI_0 + P-poll__networl_8_8_AI_1 + P-poll__networl_8_8_AI_2 + P-poll__networl_8_8_AI_3 + P-poll__networl_8_8_AI_4 + P-poll__networl_8_8_AI_5 + P-poll__networl_8_8_AI_6 + P-poll__networl_8_8_AI_7 + P-poll__networl_8_8_AI_8 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_5_AI_8 + P-poll__networl_4_3_AI_4 + P-poll__networl_1_8_RI_0 + P-poll__networl_1_8_RI_1 + P-poll__networl_1_8_RI_2 + P-poll__networl_1_8_RI_3 + P-poll__networl_1_8_RI_4 + P-poll__networl_1_8_RI_5 + P-poll__networl_1_8_RI_6 + P-poll__networl_1_8_RI_7 + P-poll__networl_1_8_RI_8 + P-poll__networl_4_3_AI_3 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_8_4_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_1_6_AnnP_8 + P-poll__networl_8_2_RP_0 + P-poll__networl_8_2_RP_1 + P-poll__networl_8_2_RP_2 + P-poll__networl_8_2_RP_3 + P-poll__networl_8_2_RP_4 + P-poll__networl_8_2_RP_5 + P-poll__networl_8_2_RP_6 + P-poll__networl_8_2_RP_7 + P-poll__networl_8_2_RP_8 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_2_0_AskP_8 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_4_AI_8 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_3_7_RI_8 + P-poll__networl_8_7_AnnP_0 + P-poll__networl_8_7_AnnP_1 + P-poll__networl_8_7_AnnP_2 + P-poll__networl_8_7_AnnP_3 + P-poll__networl_8_7_AnnP_4 + P-poll__networl_8_7_AnnP_5 + P-poll__networl_8_7_AnnP_6 + P-poll__networl_8_7_AnnP_7 + P-poll__networl_8_7_AnnP_8 + P-poll__networl_3_8_AskP_8 + P-poll__networl_3_8_AskP_7 + P-poll__networl_3_8_AskP_6 + P-poll__networl_3_8_AskP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_3_8_AskP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_3_8_AskP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_3_8_AskP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_3_8_AskP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_3_8_AskP_0 + P-poll__networl_5_3_AI_8 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_5_6_RI_8 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_6_2_AnnP_8 + P-poll__networl_7_8_AnsP_0 + P-poll__networl_8_6_AnnP_8 + P-poll__networl_8_6_AnnP_7 + P-poll__networl_8_6_AnnP_6 + P-poll__networl_8_6_AnnP_5 + P-poll__networl_8_6_AnnP_4 + P-poll__networl_8_6_AnnP_3 + P-poll__networl_8_6_AnnP_2 + P-poll__networl_8_6_AnnP_1 + P-poll__networl_8_6_AnnP_0 + P-poll__networl_2_7_RI_8 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_1_4_AskP_8 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_2_AI_8 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_7_5_RI_8 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_2_RI_8 + P-poll__networl_2_7_RI_2 + P-poll__networl_2_7_RI_1 + P-poll__networl_8_5_AskP_0 + P-poll__networl_8_5_AskP_1 + P-poll__networl_8_5_AskP_2 + P-poll__networl_8_5_AskP_3 + P-poll__networl_8_5_AskP_4 + P-poll__networl_8_5_AskP_5 + P-poll__networl_8_5_AskP_6 + P-poll__networl_8_5_AskP_7 + P-poll__networl_8_5_AskP_8 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_8 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_2_1_RI_8 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_5_6_AnnP_8 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_6_0_AskP_8 + P-poll__networl_7_2_RP_8 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_0_8_AskP_0 + P-poll__networl_0_8_AskP_1 + P-poll__networl_0_8_AskP_2 + P-poll__networl_0_8_AskP_3 + P-poll__networl_0_8_AskP_4 + P-poll__networl_0_8_AskP_5 + P-poll__networl_0_8_AskP_6 + P-poll__networl_0_8_AskP_7 + P-poll__networl_0_8_AskP_8 + P-poll__networl_7_2_RP_1 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_4_0_RI_8 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_1_7_RP_8 + P-poll__networl_7_2_RP_0 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_3_1_AnnP_8 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_1_5_AnnP_8 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_8_3_AnsP_0 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_3_6_RP_8 + P-poll__networl_0_8_RI_8 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_5_4_AskP_8 + P-poll__networl_0_8_RI_7 + P-poll__networl_0_8_RI_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_5_5_RP_8 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_0_8_RI_5 + P-poll__networl_0_8_RI_4 + P-poll__networl_0_8_RI_3 + P-poll__networl_0_8_RI_2 + P-poll__networl_0_8_RI_1 + P-poll__networl_0_8_RI_0 + P-poll__networl_0_5_AI_8 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_0_7_AI_8 + P-poll__networl_0_5_AI_4 + P-poll__networl_0_5_AI_3 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_2_5_AnnP_8 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_7_4_RP_8 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_0_1_RP_8 + P-poll__networl_0_5_AI_0 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_2_6_AI_8 + P-poll__networl_7_8_AI_8 + P-poll__networl_7_8_AI_7 + P-poll__networl_7_8_AI_6 + P-poll__networl_7_8_AI_5 + P-poll__networl_7_8_AI_4 + P-poll__networl_7_8_AI_3 + P-poll__networl_7_8_AI_2 + P-poll__networl_7_8_AI_1 + P-poll__networl_7_8_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_8_AskP_0 + P-poll__networl_4_8_AskP_1 + P-poll__networl_4_8_AskP_2 + P-poll__networl_4_8_AskP_3 + P-poll__networl_4_8_AskP_4 + P-poll__networl_4_8_AskP_5 + P-poll__networl_4_8_AskP_6 + P-poll__networl_4_8_AskP_7 + P-poll__networl_4_8_AskP_8 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_0_0_AnnP_8 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_2_0_RP_8 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_5_3_RP_8 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_4_5_AI_8 + P-poll__networl_4_8_RI_0 + P-poll__networl_4_8_RI_1 + P-poll__networl_4_8_RI_2 + P-poll__networl_4_8_RI_3 + P-poll__networl_4_8_RI_4 + P-poll__networl_4_8_RI_5 + P-poll__networl_4_8_RI_6 + P-poll__networl_4_8_RI_7 + P-poll__networl_4_8_RI_8 + P-poll__networl_5_3_RP_5 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_7_1_AnnP_8 + P-poll__networl_5_3_RP_4 + P-poll__networl_8_7_AnsP_0 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_5_3_RP_1 + P-poll__networl_5_3_RP_0 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_2_3_AskP_8 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_6_4_AI_8 + P-poll__networl_4_4_AskP_8 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_6_7_RI_8 + P-poll__networl_4_4_AskP_2 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_4_4_AskP_1 + P-poll__networl_4_4_AskP_0 + P-poll__networl_8_3_AI_0 + P-poll__networl_8_3_AI_1 + P-poll__networl_8_3_AI_2 + P-poll__networl_8_3_AI_3 + P-poll__networl_8_3_AI_4 + P-poll__networl_8_3_AI_5 + P-poll__networl_8_3_AI_6 + P-poll__networl_8_3_AI_7 + P-poll__networl_8_3_AI_8 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P
-poll__networl_1_0_AI_7 + P-poll__networl_1_0_AI_8 + P-poll__networl_8_6_RI_0 + P-poll__networl_8_6_RI_1 + P-poll__networl_8_6_RI_2 + P-poll__networl_8_6_RI_3 + P-poll__networl_8_6_RI_4 + P-poll__networl_8_6_RI_5 + P-poll__networl_8_6_RI_6 + P-poll__networl_8_6_RI_7 + P-poll__networl_8_6_RI_8 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_1_3_RI_8 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_6_5_AnnP_8 + P-poll__networl_3_4_RP_8 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_1_7_AskP_8 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_3_2_RI_8 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_8_8_AskP_0 + P-poll__networl_8_8_AskP_1 + P-poll__networl_8_8_AskP_2 + P-poll__networl_8_8_AskP_3 + P-poll__networl_8_8_AskP_4 + P-poll__networl_8_8_AskP_5 + P-poll__networl_8_8_AskP_6 + P-poll__networl_8_8_AskP_7 + P-poll__networl_8_8_AskP_8 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_0_AnnP_8 + P-poll__networl_3_4_RP_0 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_2_1_AnnP_8 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_2_8_RP_0 + P-poll__networl_5_1_RI_3 + P-poll__networl_2_8_RP_1 + P-poll__networl_5_1_RI_4 + P-poll__networl_2_8_RP_2 + P-poll__networl_5_1_RI_5 + P-poll__networl_2_8_RP_3 + P-poll__networl_5_1_RI_6 + P-poll__networl_2_8_RP_4 + P-poll__networl_5_1_RI_7 + P-poll__networl_2_8_RP_5 + P-poll__networl_5_1_RI_8 + P-poll__networl_2_8_RP_6 + P-poll__networl_2_8_RP_7 + P-poll__networl_2_8_RP_8 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_6_3_AskP_8 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_7_0_RI_8 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_4_7_RP_8 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_3_4_AnnP_8 + P-poll__networl_1_5_RP_8 + P-poll__networl_1_5_RP_7 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_6_6_RP_8 + P-poll__networl_1_5_RP_6 + P-poll__networl_1_8_AI_0 + P-poll__networl_1_8_AI_1 + P-poll__networl_1_8_AI_2 + P-poll__networl_1_8_AI_3 + P-poll__networl_1_8_AI_4 + P-poll__networl_1_8_AI_5 + P-poll__networl_1_8_AI_6 + P-poll__networl_1_8_AI_7 + P-poll__networl_1_8_AI_8 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_8_8_RP_8 + P-poll__networl_8_8_RP_7 + P-poll__networl_8_8_RP_6 + P-poll__networl_8_8_RP_5 + P-poll__networl_8_8_RP_4 + P-poll__networl_8_8_RP_3 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_5_7_AskP_8 + P-poll__networl_8_8_RP_2 + P-poll__networl_8_8_RP_1 + P-poll__networl_8_5_RP_0 + P-poll__networl_8_5_RP_1 + P-poll__networl_8_5_RP_2 + P-poll__networl_8_5_RP_3 + P-poll__networl_8_5_RP_4 + P-poll__networl_8_5_RP_5 + P-poll__networl_8_5_RP_6 + P-poll__networl_8_5_RP_7 + P-poll__networl_8_5_RP_8 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_1_2_RP_8 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_8_8_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_3_7_AI_8 + P-poll__networl_8_0_AnnP_0 + P-poll__networl_8_0_AnnP_1 + P-poll__networl_8_0_AnnP_2 + P-poll__networl_8_0_AnnP_3 + P-poll__networl_8_0_AnnP_4 + P-poll__networl_8_0_AnnP_5 + P-poll__networl_8_0_AnnP_6 + P-poll__networl_8_0_AnnP_7 + P-poll__networl_8_0_AnnP_8 + P-poll__networl_5_0_AskP_8 + P-poll__networl_5_0_AskP_7 + P-poll__networl_2_8_AnnP_0 + P-poll__networl_2_8_AnnP_1 + P-poll__networl_2_8_AnnP_2 + P-poll__networl_2_8_AnnP_3 + P-poll__networl_2_8_AnnP_4 + P-poll__networl_2_8_AnnP_5 + P-poll__networl_2_8_AnnP_6 + P-poll__networl_2_8_AnnP_7 + P-poll__networl_2_8_AnnP_8 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_5_0_AskP_0 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_2_AskP_8 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_3_1_RP_8 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_5_6_AI_8 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_8 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_0_3_AnnP_8 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_5_0_RP_8 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_7_5_AI_8 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_2_AI_8 + P-poll__networl_7_8_RI_0 + P-poll__networl_7_8_RI_1 + P-poll__networl_7_8_RI_2 + P-poll__networl_7_8_RI_3 + P-poll__networl_7_8_RI_4 + P-poll__networl_7_8_RI_5 + P-poll__networl_7_8_RI_6 + P-poll__networl_7_8_RI_7 + P-poll__networl_7_8_RI_8 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_0_5_RI_8 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_7_4_AnnP_8 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_6_AskP_8 + P-poll__networl_2_1_AI_0 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_1_AI_8 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_2_4_RI_8 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_4_0_AI_8 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_0_1_AskP_8 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_4_3_RI_8 + P-poll__networl_6_8_AnnP_0 + P-poll__networl_6_8_AnnP_1 + P-poll__networl_6_8_AnnP_2 + P-poll__networl_6_8_AnnP_3 + P-poll__networl_6_8_AnnP_4 + P-poll__networl_6_8_AnnP_5 + P-poll__networl_6_8_AnnP_6 + P-poll__networl_6_8_AnnP_7 + P-poll__networl_6_8_AnnP_8 + P-poll__networl_7_5_AskP_8 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_2_AskP_8 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_4 + P-poll__networl_7_5_AskP_3 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_6_2_RI_8 + P-poll__networl_7_5_AskP_0 + P-poll__networl_0_0_RI_8 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_4_3_AnnP_8 + P-poll__networl_0_0_RI_1 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_8 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_8 + P-poll__networl_0_4_AskP_7 + P-poll__networl_8_1_RI_0 + P-poll__networl_8_1_RI_1 + P-poll__networl_8_1_RI_2 + P-poll__networl_5_8_RP_0 + P-poll__networl_8_1_RI_3 + P-poll__networl_5_8_RP_1 + P-poll__networl_8_1_RI_4 + P-poll__networl_5_8_RP_2 + P-poll__networl_8_1_RI_5 + P-poll__networl_5_8_RP_3 + P-poll__networl_8_1_RI_6 + P-poll__networl_5_8_RP_4 + P-poll__networl_8_1_RI_7 + P-poll__networl_5_8_RP_5 + P-poll__networl_8_1_RI_8 + P-poll__networl_5_8_RP_6 + P-poll__networl_5_8_RP_7 + P-poll__networl_5_8_RP_8 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_8 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_6_6_AskP_8 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_7_7_RP_8 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_0_4_RP_8 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_3_7_AnnP_8 + P-poll__networl_6_8_AnsP_0 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_4_1_AskP_8 + P-poll__networl_5_2_AnnP_8 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_2_3_RP_8 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_4_8_AI_0 + P-poll__networl_4_8_AI_1 + P-poll__networl_4_8_AI_2 + P-poll__networl_4_8_AI_3 + P-poll__networl_4_8_AI_4 + P-poll__networl_4_8_AI_5 + P-poll__networl_4_8_AI_6 + P-poll__networl_4_8_AI_7 + P-poll__networl_4_8_AI_8 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_8_0_AnsP_0 + P-poll__networl_5_4_RI_8 + P-poll__networl_5_4_RI_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P
-poll__networl_1_2_AnnP_8 + P-poll__networl_5_4_RI_0 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_2_8_AnsP_0 + P-poll__networl_4_2_RP_8 + P-poll__networl_5_1_AI_8 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_6_7_AI_8 + P-poll__networl_8_3_AnnP_0 + P-poll__networl_8_3_AnnP_1 + P-poll__networl_8_3_AnnP_2 + P-poll__networl_8_3_AnnP_3 + P-poll__networl_8_3_AnnP_4 + P-poll__networl_8_3_AnnP_5 + P-poll__networl_8_3_AnnP_6 + P-poll__networl_8_3_AnnP_7 + P-poll__networl_8_3_AnnP_8 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_5_1_AI_4 + P-poll__networl_5_1_AI_3 + P-poll__networl_5_1_AI_2 + P-poll__networl_5_1_AI_1 + P-poll__networl_5_1_AI_0 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_3_5_AskP_8 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_6_1_RP_8 + P-poll__networl_8_6_AI_0 + P-poll__networl_8_6_AI_1 + P-poll__networl_8_6_AI_2 + P-poll__networl_8_6_AI_3 + P-poll__networl_8_6_AI_4 + P-poll__networl_8_6_AI_5 + P-poll__networl_8_6_AI_6 + P-poll__networl_8_6_AI_7 + P-poll__networl_8_6_AI_8 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_1_3_AI_5 + P-poll__networl_1_3_AI_6 + P-poll__networl_8_1_AskP_8 + P-poll__networl_1_3_AI_7 + P-poll__networl_8_1_AskP_7 + P-poll__networl_1_3_AI_8 + P-poll__networl_8_1_AskP_6 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_1_6_RI_8 + P-poll__networl_8_1_AskP_5 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_8_1_AskP_4 + P-poll__networl_8_1_AskP_3 + P-poll__networl_8_1_AskP_2 + P-poll__networl_8_1_AskP_1 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_0_6_AnnP_8 + P-poll__networl_8_0_RP_0 + P-poll__networl_8_0_RP_1 + P-poll__networl_8_0_RP_2 + P-poll__networl_8_0_RP_3 + P-poll__networl_8_0_RP_4 + P-poll__networl_8_0_RP_5 + P-poll__networl_8_0_RP_6 + P-poll__networl_8_0_RP_7 + P-poll__networl_8_0_RP_8 + P-poll__networl_8_1_AskP_0 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_1_0_AskP_8 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_2_AI_8 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_3_5_RI_8 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7 + P-poll__networl_7_7_AnnP_8 <= P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3 + P-poll__handlingMessage_4 + P-poll__handlingMessage_5 + P-poll__handlingMessage_6 + P-poll__handlingMessage_7 + P-poll__handlingMessage_8))) U G (G ((3 <= P-crashed_8 + P-crashed_7 + P-crashed_6 + P-crashed_5 + P-crashed_4 + P-crashed_3 + P-crashed_2 + P-crashed_1 + P-crashed_0))))) : A ((G (F ((2 <= P-masterList_8_4_0 + P-masterList_8_4_1 + P-masterList_8_4_2 + P-masterList_8_4_3 + P-masterList_8_4_4 + P-masterList_8_4_5 + P-masterList_8_4_6 + P-masterList_8_4_7 + P-masterList_8_4_8 + P-masterList_0_3_8 + P-masterList_0_3_7 + P-masterList_0_3_6 + P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_5_6_8 + P-masterList_0_3_5 + P-masterList_0_3_4 + P-masterList_0_3_3 + P-masterList_0_3_2 + P-masterList_0_3_1 + P-masterList_0_3_0 + P-masterList_2_8_0 + P-masterList_2_8_1 + P-masterList_2_8_2 + P-masterList_2_8_3 + P-masterList_2_8_4 + P-masterList_2_8_5 + P-masterList_2_8_6 + P-masterList_2_8_7 + P-masterList_2_8_8 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_3_2_8 + P-masterList_3_1_8 + P-masterList_3_1_7 + P-masterList_3_1_6 + P-masterList_3_1_5 + P-masterList_3_1_4 + P-masterList_3_1_3 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterList_0_4_2 + P-masterList_0_4_3 + P-masterList_0_4_4 + P-masterList_0_4_5 + P-masterList_3_1_2 + P-masterList_0_4_6 + P-masterList_3_1_1 + P-masterList_0_4_7 + P-masterList_3_1_0 + P-masterList_0_4_8 + P-masterList_8_5_0 + P-masterList_8_5_1 + P-masterList_8_5_2 + P-masterList_8_5_3 + P-masterList_2_7_8 + P-masterList_8_5_4 + P-masterList_2_7_7 + P-masterList_8_5_5 + P-masterList_2_7_6 + P-masterList_8_5_6 + P-masterList_2_7_5 + P-masterList_8_5_7 + P-masterList_2_7_4 + P-masterList_8_5_8 + P-masterList_2_7_3 + P-masterList_2_7_2 + P-masterList_2_7_1 + P-masterList_2_7_0 + P-masterList_5_7_0 + P-masterList_5_7_1 + P-masterList_5_7_2 + P-masterList_5_7_3 + P-masterList_5_7_4 + P-masterList_5_7_5 + P-masterList_5_7_6 + P-masterList_5_7_7 + P-masterList_5_7_8 + P-masterList_6_1_0 + P-masterList_6_1_1 + P-masterList_6_1_2 + P-masterList_6_1_3 + P-masterList_6_1_4 + P-masterList_6_1_5 + P-masterList_6_1_6 + P-masterList_6_1_7 + P-masterList_6_1_8 + P-masterList_3_3_0 + P-masterList_3_3_1 + P-masterList_3_3_2 + P-masterList_3_3_3 + P-masterList_3_3_4 + P-masterList_3_3_5 + P-masterList_3_3_6 + P-masterList_3_3_7 + P-masterList_3_3_8 + P-masterList_5_5_8 + P-masterList_5_5_7 + P-masterList_5_5_6 + P-masterList_5_5_5 + P-masterList_0_5_0 + P-masterList_0_5_1 + P-masterList_0_5_2 + P-masterList_0_5_3 + P-masterList_0_5_4 + P-masterList_0_5_5 + P-masterList_0_5_6 + P-masterList_0_5_7 + P-masterList_0_5_8 + P-masterList_5_5_4 + P-masterList_5_5_3 + P-masterList_5_5_2 + P-masterList_5_5_1 + P-masterList_5_5_0 + P-masterList_8_3_8 + P-masterList_8_3_7 + P-masterList_8_3_6 + P-masterList_8_3_5 + P-masterList_8_3_4 + P-masterList_8_3_3 + P-masterList_8_3_2 + P-masterList_8_3_1 + P-masterList_8_6_0 + P-masterList_8_6_1 + P-masterList_8_6_2 + P-masterList_8_6_3 + P-masterList_8_6_4 + P-masterList_8_6_5 + P-masterList_8_6_6 + P-masterList_8_6_7 + P-masterList_8_6_8 + P-masterList_8_3_0 + P-masterList_5_8_0 + P-masterList_5_8_1 + P-masterList_5_8_2 + P-masterList_5_8_3 + P-masterList_5_8_4 + P-masterList_5_8_5 + P-masterList_5_8_6 + P-masterList_5_8_7 + P-masterList_5_8_8 + P-masterList_6_2_0 + P-masterList_6_2_1 + P-masterList_6_2_2 + P-masterList_6_2_3 + P-masterList_6_2_4 + P-masterList_6_2_5 + P-masterList_6_2_6 + P-masterList_6_2_7 + P-masterList_6_2_8 + P-masterList_3_4_0 + P-masterList_3_4_1 + P-masterList_3_4_2 + P-masterList_3_4_3 + P-masterList_3_4_4 + P-masterList_3_4_5 + P-masterList_3_4_6 + P-masterList_3_4_7 + P-masterList_3_4_8 + P-masterList_0_6_0 + P-masterList_0_6_1 + P-masterList_0_6_2 + P-masterList_0_6_3 + P-masterList_0_6_4 + P-masterList_0_6_5 + P-masterList_0_6_6 + P-masterList_0_6_7 + P-masterList_0_6_8 + P-masterList_8_7_0 + P-masterList_8_7_1 + P-masterList_8_7_2 + P-masterList_8_7_3 + P-masterList_8_7_4 + P-masterList_8_7_5 + P-masterList_8_7_6 + P-masterList_8_7_7 + P-masterList_8_7_8 + P-masterList_6_3_0 + P-masterList_6_3_1 + P-masterList_6_3_2 + P-masterList_6_3_3 + P-masterList_6_3_4 + P-masterList_6_3_5 + P-masterList_6_3_6 + P-masterList_6_3_7 + P-masterList_6_3_8 + P-masterList_3_5_0 + P-masterList_3_5_1 + P-masterList_3_5_2 + P-masterList_3_5_3 + P-masterList_3_5_4 + P-masterList_3_5_5 + P-masterList_3_5_6 + P-masterList_3_5_7 + P-masterList_3_5_8 + P-masterList_0_2_8 + P-masterList_0_2_7 + P-masterList_0_2_6 + P-masterList_0_2_5 + P-masterList_0_2_4 + P-masterList_0_2_3 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_0_7_0 + P-masterList_0_7_1 + P-masterList_0_7_2 + P-masterList_0_7_3 + P-masterList_0_7_4 + P-masterList_0_7_5 + P-masterList_0_7_6 + P-masterList_0_7_7 + P-masterList_0_7_8 + P-masterList_1_1_0 + P-masterList_1_1_1 + P-masterList_1_1_2 + P-masterList_1_1_3 + P-masterList_1_1_4 + P-masterList_1_1_5 + P-masterList_1_1_6 + P-masterList_1_1_7 + P-masterList_1_1_8 + P-masterList_8_8_0 + P-masterList_8_8_1 + P-masterList_8_8_2 + P-masterList_8_8_3 + P-masterList_8_8_4 + P-masterList_8_8_5 + P-masterList_8_8_6 + P-masterList_8_8_7 + P-masterList_8_8_8 + P-masterList_6_4_0 + P-masterList_6_4_1 + P-masterList_6_4_2 + P-masterList_6_4_3 + P-masterList_6_4_4 + P-masterList_6_4_5 + P-masterList_6_4_6 + P-masterList_6_4_7 + P-masterList_6_4_8 + P-masterList_3_6_0 + P-masterList_3_6_1 + P-masterList_3_6_2 + P-masterList_3_6_3 + P-masterList_3_6_4 + P-masterList_3_6_5 + P-masterList_3_6_6 + P-masterList_3_6_7 + P-masterList_3_6_8 + P-masterList_2_6_8 + P-masterList_2_6_7 + P-masterList_2_6_6 + P-masterList_2_6_5 + P-masterList_2_6_4 + P-masterList_2_6_3 + P-masterList_2_6_2 + P-masterList_2_6_1 + P-masterList_2_6_0 + P-masterList_0_8_0 + P-masterList_0_8_1 + P-masterList_0_8_2 + P-masterList_0_8_3 + P-masterList_0_8_4 + P-masterList_0_8_5 + P-masterList_0_8_6 + P-masterList_0_8_7 + P-masterList_0_8_8 + P-masterList_1_2_0 + P-masterList_1_2_1 + P-masterList_1_2_2 + P-masterList_1_2_3 + P-masterList_1_2_4 + P-masterList_1_2_5 + P-masterList_1_2_6 + P-masterList_1_2_7 + P-masterList_1_2_8 + P-masterList_5_4_8 + P-masterList_5_4_7 + P-masterList_5_4_6 + P-masterList_5_4_5 + P-masterList_5_4_4 + P-masterList_5_4_3 + P-masterList_5_4_2 + P-masterList_5_4_1 + P-masterList_5_4_0 + P-masterList_6_5_0 + P-masterList_6_5_1 + P-masterList_6_5_2 + P-masterList_6_5_3 + P-masterList_6_5_4 + P-masterList_6_5_5 + P-masterList_6_5_6 + P-masterList_6_5_7 + P-masterList_6_5_8 + P-masterList_8_2_8 + P-masterList_8_2_7 + P-masterList_8_2_6 + P-masterList_8_2_5 + P-masterList_8_2_4 + P-masterList_8_2_3 + P-masterList_8_2_2 + P-masterList_8_2_1 + P-masterList_8_2_0 + P-masterList_3_7_0 + P-masterList_3_7_1 + P-masterList_3_7_2 + P-masterList_3_7_3 + P-masterList_3_7_4 + P-masterList_3_7_5 + P-masterList_3_7_6 + P-masterList_3_7_7 + P-masterList_3_7_8 + P-masterList_4_1_0 + P-masterList_4_1_1 + P-masterList_4_1_2 + P-masterList_4_1_3 + P-masterList_4_1_4 + P-masterList_4_1_5 + P-masterList_4_1_6 + P-masterList_4_1_7 + P-masterList_4_1_8 + P-masterList_1_3_0 + P-masterList_1_3_1 + P-masterList_1_3_2 + P-masterList_1_3_3 + P-masterList_1_3_4 + P-masterList_1_3_5 + P-masterList_1_3_6 + P-masterList_1_3_7 + P-masterList_1_3_8 + P-masterList_7_8_8 + P-masterList_7_8_7 + P-masterList_7_8_6 + P-masterList_7_8_5 + P-masterList_7_8_4 + P-masterList_7_8_3 + P-masterList_7_8_2 + P-masterList_7_8_1 + P-masterList_7_8_0 + P-masterList_6_6_0 + P-masterList_6_6_1 + P-masterList_6_6_2 + P-masterList_6_6_3 + P-masterList_6_6_4 + P-masterList_6_6_5 + P-masterList_6_6_6 + P-masterList_6_6_7 + P-masterList_6_6_8 + P-masterList_3_8_0 + P-masterList_3_8_1 + P-masterList_3_8_2 + P-masterList_3_8_3 + P-masterList_3_8_4 + P-masterList_3_8_5 + P-masterList_3_8_6 + P-masterList_3_8_7 + P-masterList_3_8_8 + P-masterList_4_2_0 + P-masterList_4_2_1 + P-masterList_4_2_2 + P-masterList_4_2_3 + P-masterList_4_2_4 + P-masterList_4_2_5 + P-masterList_4_2_6 + P-masterList_4_2_7 + P-masterList_4_2_8 + P-masterList_1_4_0 + P-masterList_1_4_1 + P-masterList_1_4_2 + P-masterList_1_4_3 + P-masterList_1_4_4 + P-masterList_1_4_5 + P-masterList_1_4_6 + P-masterList_1_4_7 + P-masterList_1_4_8 + P-masterList_0_1_8 + P-masterList_0_1_7 + P-masterList_0_1_6 + P-masterList_0_1_5 + P-masterList_0_1_4 + P-masterList_0_1_3 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 + P-masterList_6_7_0 + P-masterList_6_7_1 + P-masterList_6_7_2 + P-masterList_6_7_3 + P-masterList_6_7_4 + P-masterList_6_7_5 + P-masterList_6_7_6 + P-masterList_6_7_7 + P-masterList_6_7_8 + P-masterList_7_1_0 + P-masterList_7_1_1 + P-masterList_7_1_2 + P-masterList_7_1_3 + P-masterList_7_1_4 + P-masterList_7_1_5 + P-masterList_7_1_6 + P-masterList_7_1_7 + P-masterList_7_1_8 + P-masterList_4_3_0 + P-masterList_4_3_1 + P-masterList_4_3_2 + P-masterList_4_3_3 + P-masterList_4_3_4 + P-masterList_4_3_5 + P-masterList_4_3_6 + P-masterList_4_3_7 + P-masterList_4_3_8 + P-masterList_2_5_8 + P-masterList_2_5_7 + P-masterList_2_5_6 + P-masterList_2_5_5 + P-masterList_1_5_0 + P-masterList_1_5_1 + P-masterList_1_5_2 + P-masterList_1_5_3 + P-masterList_1_5_4 + P-masterList_1_5_5 + P-masterList_1_5_6 + P-masterList_1_5_7 + P-masterList_1_5_8 + P-masterList_2_5_4 + P-masterList_2_5_3 + P-masterList_2_5_2 + P-masterList_2_5_1 + P-masterList_2_5_0 + P-masterList_5_3_8 + P-masterList_5_3_7 + P-masterList_5_3_6 + P-masterList_5_3_5 + P-masterList_5_3_4 + P-masterList_5_3_3 + P-masterList_5_3_2 + P-masterList_5_3_1 + P-masterList_5_3_0 + P-masterList_6_8_0 + P-masterList_6_8_1 + P-masterList_6_8_2 + P-masterList_6_8_3 + P-masterList_6_8_4 + P-masterList_6_8_5 + P-masterList_6_8_6 + P-masterList_6_8_7 + P-masterList_6_8_8 + P-masterList_7_2_0 + P-masterList_7_2_1 + P-masterList_7_2_2 + P-masterList_7_2_3 + P-masterList_7_2_4 + P-masterList_7_2_5 + P-masterList_7_2_6 + P-masterList_7_2_7 + P-masterList_7_2_8 + P-masterList_4_4_0 + P-masterList_4_4_1 + P-masterList_4_4_2 + P-masterList_4_4_3 + P-masterList_4_4_4 + P-masterList_4_4_5 + P-masterList_4_4_6 + P-masterList_4_4_7 + P-masterList_4_4_8 + P-masterList_8_1_8 + P-masterList_8_1_7 + P-masterList_8_1_6 + P-masterList_8_1_5 + P-masterList_8_1_4 + P-masterList_8_1_3 + P-masterList_8_1_2 + P-masterList_8_1_1 + P-masterList_8_1_0 + P-masterList_1_6_0 + P-masterList_1_6_1 + P-masterList_1_6_2 + P-masterList_1_6_3 + P-masterList_1_6_4 + P-masterList_1_6_5 + P-masterList_1_6_6 + P-masterList_1_6_7 + P-masterList_1_6_8 + P-masterList_7_7_8 + P-masterList_7_7_7 + P-masterList_7_7_6 + P-masterList_7_7_5 + P-masterList_7_7_4 + P-masterList_7_7_3 + P-masterList_7_7_2 + P-masterList_7_7_1 + P-masterList_7_7_0 + P-masterList_7_3_0 + P-masterList_7_3_1 + P-masterList_7_3_2 + P-masterList_7_3_3 + P-masterList_7_3_4 + P-masterList_7_3_5 + P-masterList_7_3_6 + P-masterList_7_3_7 + P-masterList_7_3_8 + P-masterList_4_5_0 + P-masterList_4_5_1 + P-masterList_4_5_2 + P-masterList_4_5_3 + P-masterList_4_5_4 + P-masterList_4_5_5 + P-masterList_4_5_6 + P-masterList_4_5_7 + P-masterList_4_5_8 + P-masterList_1_7_0 + P-masterList_1_7_1 + P-masterList_1_7_2 + P-masterList_1_7_3 + P-masterList_1_7_4 + P-masterList_1_7_5 + P-masterList_1_7_6 + P-masterList_1_7_7 + P-masterList_1_7_8 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_1_3 + P-masterList_2_1_4 + P-masterList_2_1_5 + P-masterList_2_1_6 + P-masterList_2_1_7 + P-masterList_2_1_8 + P-masterList_7_4_0 + P-masterList_7_4_1 + P-masterList_7_4_2 + P-masterList_7_4_3 + P-masterList_7_4_4 + P-masterList_7_4_5 + P-masterList_7_4_6 + P-masterList_7_4_7 + P-masterList_7_4_8 + P-masterList_4_6_0 + P-masterList_4_6_1 + P-masterList_4_6_2 + P-masterList_4_6_3 + P-masterList_4_6_4 + P-masterList_4_6_5 + P-masterList_4_6_6 + P-masterList_4_6_7 + P-masterList_4_6_8 + P-masterList_1_8_0 + P-masterList_1_8_1 + P-masterList_1_8_2 + P-masterList_1_8_3 + P-masterList_1_8_4 + P-master
List_1_8_5 + P-masterList_1_8_6 + P-masterList_1_8_7 + P-masterList_1_8_8 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_2_2_3 + P-masterList_2_2_4 + P-masterList_2_2_5 + P-masterList_2_2_6 + P-masterList_2_2_7 + P-masterList_2_2_8 + P-masterList_2_4_8 + P-masterList_2_4_7 + P-masterList_2_4_6 + P-masterList_2_4_5 + P-masterList_2_4_4 + P-masterList_2_4_3 + P-masterList_2_4_2 + P-masterList_2_4_1 + P-masterList_2_4_0 + P-masterList_7_5_0 + P-masterList_7_5_1 + P-masterList_7_5_2 + P-masterList_7_5_3 + P-masterList_7_5_4 + P-masterList_7_5_5 + P-masterList_7_5_6 + P-masterList_7_5_7 + P-masterList_7_5_8 + P-masterList_4_7_0 + P-masterList_4_7_1 + P-masterList_4_7_2 + P-masterList_4_7_3 + P-masterList_4_7_4 + P-masterList_4_7_5 + P-masterList_4_7_6 + P-masterList_4_7_7 + P-masterList_4_7_8 + P-masterList_5_1_0 + P-masterList_5_1_1 + P-masterList_5_1_2 + P-masterList_5_1_3 + P-masterList_5_1_4 + P-masterList_5_1_5 + P-masterList_5_1_6 + P-masterList_5_1_7 + P-masterList_5_1_8 + P-masterList_5_2_8 + P-masterList_5_2_7 + P-masterList_5_2_6 + P-masterList_5_2_5 + P-masterList_5_2_4 + P-masterList_5_2_3 + P-masterList_5_2_2 + P-masterList_5_2_1 + P-masterList_5_2_0 + P-masterList_2_3_0 + P-masterList_2_3_1 + P-masterList_2_3_2 + P-masterList_2_3_3 + P-masterList_2_3_4 + P-masterList_2_3_5 + P-masterList_2_3_6 + P-masterList_2_3_7 + P-masterList_2_3_8 + P-masterList_4_8_8 + P-masterList_4_8_7 + P-masterList_4_8_6 + P-masterList_4_8_5 + P-masterList_4_8_4 + P-masterList_4_8_3 + P-masterList_4_8_2 + P-masterList_4_8_1 + P-masterList_4_8_0 + P-masterList_7_6_0 + P-masterList_7_6_1 + P-masterList_7_6_2 + P-masterList_7_6_3 + P-masterList_7_6_4 + P-masterList_7_6_5 + P-masterList_7_6_6 + P-masterList_7_6_7 + P-masterList_7_6_8))) U X (G ((2 <= P-electedPrimary_8 + P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0))))) : A (X (X (X (F ((2 <= P-electionFailed_0 + P-electionFailed_1 + P-electionFailed_2 + P-electionFailed_3 + P-electionFailed_4 + P-electionFailed_5 + P-electionFailed_6 + P-electionFailed_7 + P-electionFailed_8)))))) : A ((P-sendAnnPs__broadcasting_8_8 + P-sendAnnPs__broadcasting_8_7 + P-sendAnnPs__broadcasting_8_6 + P-sendAnnPs__broadcasting_8_5 + P-sendAnnPs__broadcasting_8_4 + P-sendAnnPs__broadcasting_8_3 + P-sendAnnPs__broadcasting_8_2 + P-sendAnnPs__broadcasting_8_1 + P-sendAnnPs__broadcasting_7_8 + P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_8 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_8 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_8 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_8 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_8 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_8 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_8 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-electionInit_4 + P-electionInit_2 + P-electionInit_1 + P-electionInit_0 + P-electionInit_3 + P-electionInit_5 + P-electionInit_6 + P-electionInit_7 + P-electionInit_8)) : A ((G (G ((3 <= P-masterState_6_F_7 + P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_7 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_7 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_6_T_8 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_4_T_8 + P-masterState_0_F_7 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_8_F_7 + P-masterState_8_F_6 + P-masterState_8_F_5 + P-masterState_8_F_4 + P-masterState_8_F_3 + P-masterState_8_F_2 + P-masterState_8_F_1 + P-masterState_8_F_0 + P-masterState_3_T_8 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_1_F_8 + P-masterState_5_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_8 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_8_T_8 + P-masterState_8_T_7 + P-masterState_8_T_6 + P-masterState_8_T_5 + P-masterState_8_T_4 + P-masterState_8_T_3 + P-masterState_8_T_2 + P-masterState_8_T_1 + P-masterState_8_T_0 + P-masterState_2_F_7 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_5_T_8 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_7_T_8 + P-masterState_7_F_7 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_2_T_8 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_4_F_7 + P-masterState_4_F_8 + P-masterState_7_F_8 + P-masterState_2_F_8 + P-masterState_5_F_8 + P-masterState_8_F_8 + P-masterState_0_F_8 + P-masterState_3_F_8 + P-masterState_1_T_8 + P-masterState_6_F_8))) U (P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3 + P-poll__handlingMessage_4 + P-poll__handlingMessage_5 + P-poll__handlingMessage_6 + P-poll__handlingMessage_7 + P-poll__handlingMessage_8 <= P-masterState_6_F_7 + P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_7 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_7 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_6_T_8 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_4_T_8 + P-masterState_0_F_7 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_8_F_7 + P-masterState_8_F_6 + P-masterState_8_F_5 + P-masterState_8_F_4 + P-masterState_8_F_3 + P-masterState_8_F_2 + P-masterState_8_F_1 + P-masterState_8_F_0 + P-masterState_3_T_8 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_1_F_8 + P-masterState_5_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_8 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_8_T_8 + P-masterState_8_T_7 + P-masterState_8_T_6 + P-masterState_8_T_5 + P-masterState_8_T_4 + P-masterState_8_T_3 + P-masterState_8_T_2 + P-masterState_8_T_1 + P-masterState_8_T_0 + P-masterState_2_F_7 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_5_T_8 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_7_T_8 + P-masterState_7_F_7 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_2_T_8 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_4_F_7 + P-masterState_4_F_8 + P-masterState_7_F_8 + P-masterState_2_F_8 + P-masterState_5_F_8 + P-masterState_8_F_8 + P-masterState_0_F_8 + P-masterState_3_F_8 + P-masterState_1_T_8 + P-masterState_6_F_8))) : A (F (G (G ((P-network_1_0_AnsP_6 <= P-network_1_7_RI_5))))) : A (G (X (((P-network_5_1_AskP_2 <= P-network_2_8_AI_1) U (P-masterList_1_2_6 <= P-network_8_1_RP_1))))) : A (G (((P-poll__networl_4_8_RI_5 <= P-poll__networl_8_1_AI_7) U F ((P-network_7_4_AnnP_4 <= P-poll__networl_3_4_AnsP_7))))) : A ((P-network_7_8_AskP_0 <= P-network_8_7_AskP_2)) : A (F (X (F (X ((P-network_6_6_RP_1 <= P-network_8_0_RP_6)))))) : A (G (((P-network_8_1_AnnP_0 <= P-network_4_5_RI_8) U F ((P-network_5_7_RP_6 <= P-network_2_4_RI_6))))) : A ((P-poll__networl_7_1_AskP_2 <= P-network_7_4_RI_0)) : A ((P-network_2_1_RP_7 <= P-poll__networl_1_4_RI_5))
lola: computing a collection of formulas
lola: RUNNING
lola: subprocess 0 will run for 221 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A ((2 <= P-sendAnnPs__broadcasting_8_8 + P-sendAnnPs__broadcasting_8_7 + P-sendAnnPs__broadcasting_8_6 + P-sendAnnPs__broadcasting_8_5 + P-sendAnnPs__broadcasting_8_4 + P-sendAnnPs__broadcasting_8_3 + P-sendAnnPs__broadcasting_8_2 + P-sendAnnPs__broadcasting_8_1 + P-sendAnnPs__broadcasting_7_8 + P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendA... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: (2 <= P-sendAnnPs__broadcasting_8_8 + P-sendAnnPs__broadcasting_8_7 + P-sendAnnPs__broadcasting_8_6 + P-sendAnnPs__broadcasting_8_5 + P-sendAnnPs__broadcasting_8_4 + P-sendAnnPs__broadcasting_8_3 + P-sendAnnPs__broadcasting_8_2 + P-sendAnnPs__broadcasting_8_1 + P-sendAnnPs__broadcasting_7_8 + P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnP... (shortened)
lola: processed formula length: 2308
lola: 1 rewrites
lola: formula mentions 0 of 10062 places; total mentions: 0
lola: closed formula file NeoElection-PT-8-LTLCardinality.task
lola: processed formula with 1 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: 0 markings, 0 edges
lola: ========================================
lola: subprocess 1 will run for 235 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (F (G (G (G ((P-electedSecondary_8 + P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 + P-polling_8))))))
lola: ========================================
lola: SUBTASK
lola: checking LTL
lola: transforming LTL-Formula into a B\xfcchi-Automaton
lola: processed formula: A (F (G (G (G ((P-electedSecondary_8 + P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 + P-polling_8))))))
lola: processed formula: A (F (G (G (G ((P-electedSecondary_8 + P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 + P-polling_8))))))
lola: processed formula length: 353
lola: 0 rewrites
lola: formula mentions 0 of 10062 places; total mentions: 0
lola: closed formula file NeoElection-PT-8-LTLCardinality.task
lola: the resulting B\xfcchi automaton has 2 states
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 288 bytes per marking, with 7 unused bits
lola: using a prefix tree store (--store=prefix)
lola: using ltl preserving stubborn set method (--stubborn)
lola: SEARCH
lola: RUNNING
lola: 2275 markings, 4832 edges, 455 markings/sec, 0 secs
lola: 22899 markings, 81201 edges, 4125 markings/sec, 5 secs
lola: 40904 markings, 148224 edges, 3601 markings/sec, 10 secs
lola: 54432 markings, 199198 edges, 2706 markings/sec, 15 secs
lola: 72915 markings, 274879 edges, 3697 markings/sec, 20 secs
lola: 90139 markings, 344276 edges, 3445 markings/sec, 25 secs
lola: 103457 markings, 394008 edges, 2664 markings/sec, 30 secs
lola: 122946 markings, 475289 edges, 3898 markings/sec, 35 secs
lola: 138125 markings, 536597 edges, 3036 markings/sec, 40 secs
lola: 153002 markings, 594702 edges, 2975 markings/sec, 45 secs
lola: 175522 markings, 685183 edges, 4504 markings/sec, 50 secs
lola: 188502 markings, 738722 edges, 2596 markings/sec, 55 secs
lola: 203613 markings, 796877 edges, 3022 markings/sec, 60 secs
lola: 221289 markings, 868905 edges, 3535 markings/sec, 65 secs
lola: 241094 markings, 949100 edges, 3961 markings/sec, 70 secs
lola: 259392 markings, 1016915 edges, 3660 markings/sec, 75 secs
lola: 275990 markings, 1079866 edges, 3320 markings/sec, 80 secs
lola: 294770 markings, 1154557 edges, 3756 markings/sec, 85 secs
lola: 312193 markings, 1226512 edges, 3485 markings/sec, 90 secs
lola: 324969 markings, 1276608 edges, 2555 markings/sec, 95 secs
lola: 342290 markings, 1348705 edges, 3464 markings/sec, 100 secs
lola: 360000 markings, 1420332 edges, 3542 markings/sec, 105 secs
lola: 376506 markings, 1489338 edges, 3301 markings/sec, 110 secs
lola: 392238 markings, 1552803 edges, 3146 markings/sec, 115 secs
lola: 409816 markings, 1625166 edges, 3516 markings/sec, 120 secs
lola: 424996 markings, 1687396 edges, 3036 markings/sec, 125 secs
lola: 435655 markings, 1726614 edges, 2132 markings/sec, 130 secs
lola: 453428 markings, 1806999 edges, 3555 markings/sec, 135 secs
lola: 468565 markings, 1870853 edges, 3027 markings/sec, 140 secs
lola: 483310 markings, 1935088 edges, 2949 markings/sec, 145 secs
lola: 492830 markings, 1977701 edges, 1904 markings/sec, 150 secs
lola: 511479 markings, 2064536 edges, 3730 markings/sec, 155 secs
lola: 528121 markings, 2139752 edges, 3328 markings/sec, 160 secs
lola: 539340 markings, 2188241 edges, 2244 markings/sec, 165 secs
lola: 554055 markings, 2257048 edges, 2943 markings/sec, 170 secs
lola: 568676 markings, 2326460 edges, 2924 markings/sec, 175 secs
lola: 582828 markings, 2391575 edges, 2830 markings/sec, 180 secs
lola: 599409 markings, 2465813 edges, 3316 markings/sec, 185 secs
lola: 607751 markings, 2503848 edges, 1668 markings/sec, 190 secs
lola: 626823 markings, 2591369 edges, 3814 markings/sec, 195 secs
lola: 640322 markings, 2652867 edges, 2700 markings/sec, 200 secs
lola: 652038 markings, 2707197 edges, 2343 markings/sec, 205 secs
lola: 663273 markings, 2755779 edges, 2247 markings/sec, 210 secs
lola: 678988 markings, 2831434 edges, 3143 markings/sec, 215 secs
lola: 693708 markings, 2898381 edges, 2944 markings/sec, 220 secs
lola: 708871 markings, 2966830 edges, 3033 markings/sec, 225 secs
lola: local time limit reached - aborting
lola: Child process aborted or communication problem between parent and child process
terminate called after throwing an instance of 'std::runtime_error'
what(): parse error at position 0: unexpected character, last read: '
'
Aborted (core dumped)
FORMULA NeoElection-PT-8-LTLCardinality-0 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-1 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-2 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-3 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-4 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-5 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-6 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-7 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-8 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-9 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-10 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-11 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-12 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-13 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-14 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-PT-8-LTLCardinality-15 CANNOT_COMPUTE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
----- Kill lola and sara stdout -----
----- Kill lola and sara stderr -----
----- Finished stdout -----
----- Finished stderr -----
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-8"
export BK_EXAMINATION="LTLCardinality"
export BK_TOOL="mcc4mcc-structural"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-8.tgz
mv NeoElection-PT-8 execution
cd execution
pwd
ls -lh
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-3637"
echo " Executing tool mcc4mcc-structural"
echo " Input is NeoElection-PT-8, examination is LTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r263-csrt-152732587400095"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

