About the Execution of M4M.full for NeoElection-PT-6
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 15901.640 | 3600000.00 | 8138640.00 | 871.40 | ???????FF?T??F?T | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
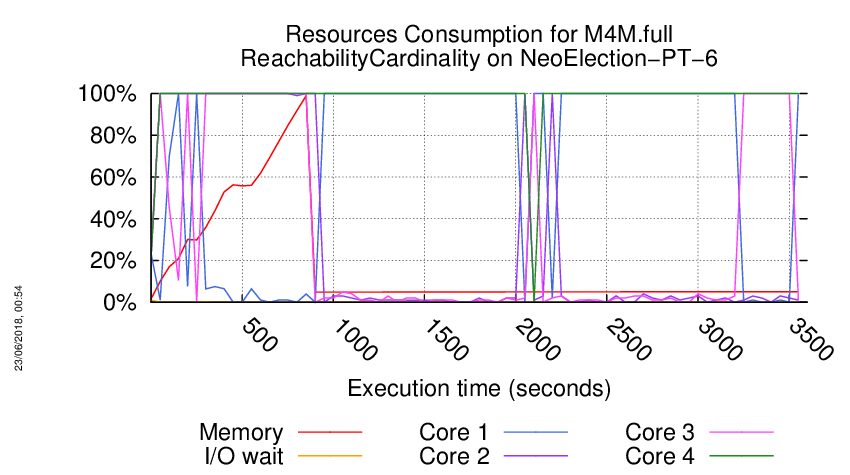
Trace from the execution
Waiting for the VM to be ready (probing ssh)
...................
/home/mcc/execution
total 13M
-rw-r--r-- 1 mcc users 164K May 15 18:54 CTLCardinality.txt
-rw-r--r-- 1 mcc users 400K May 15 18:54 CTLCardinality.xml
-rw-r--r-- 1 mcc users 321K May 15 18:54 CTLFireability.txt
-rw-r--r-- 1 mcc users 880K May 15 18:54 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K May 15 18:50 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K May 15 18:50 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 129K May 15 18:54 LTLCardinality.txt
-rw-r--r-- 1 mcc users 300K May 15 18:54 LTLCardinality.xml
-rw-r--r-- 1 mcc users 18K May 15 18:54 LTLFireability.txt
-rw-r--r-- 1 mcc users 56K May 15 18:54 LTLFireability.xml
-rw-r--r-- 1 mcc users 296K May 15 18:54 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 667K May 15 18:54 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 107 May 15 18:54 ReachabilityDeadlock.txt
-rw-r--r-- 1 mcc users 345 May 15 18:54 ReachabilityDeadlock.xml
-rw-r--r-- 1 mcc users 451K May 15 18:54 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 1.3M May 15 18:54 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 106K May 15 18:54 UpperBounds.txt
-rw-r--r-- 1 mcc users 202K May 15 18:54 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 May 15 18:50 equiv_col
-rw-r--r-- 1 mcc users 2 May 15 18:50 instance
-rw-r--r-- 1 mcc users 6 May 15 18:50 iscolored
-rw-r--r-- 1 mcc users 7.3M May 15 18:50 model.pnml
=====================================================================
Generated by BenchKit 2-3637
Executing tool mcc4mcc-full
Input is NeoElection-PT-6, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r118-csrt-152666478300320
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-00
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-01
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-02
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-03
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-04
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-05
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-06
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-07
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-08
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-09
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-10
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-11
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-12
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-13
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-14
FORMULA_NAME NeoElection-PT-6-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1527293507561
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
Prefix is 65b80f64.
Reading known information in /usr/share/mcc4mcc/65b80f64-known.json.
Reading learned information in /usr/share/mcc4mcc/65b80f64-learned.json.
Reading value translations in /usr/share/mcc4mcc/65b80f64-values.json.
Using directory /home/mcc/execution for input, as it contains a model.pnml file.
Using NeoElection-PT-6 as instance name.
Using NeoElection as model name.
Using algorithm or tool bmdt.
Model characteristics are: {'Examination': 'ReachabilityCardinality', 'Place/Transition': True, 'Colored': True, 'Relative-Time': 1, 'Relative-Memory': 1, 'Ordinary': True, 'Simple Free Choice': False, 'Extended Free Choice': False, 'State Machine': False, 'Marked Graph': False, 'Connected': False, 'Strongly Connected': False, 'Source Place': True, 'Sink Place': True, 'Source Transition': False, 'Sink Transition': False, 'Loop Free': False, 'Conservative': False, 'Sub-Conservative': False, 'Nested Units': False, 'Safe': True, 'Deadlock': True, 'Reversible': False, 'Quasi Live': False, 'Live': False}.
Known tools are: [{'Time': 83929, 'Memory': 364.71, 'Tool': 'lola'}, {'Time': 87315, 'Memory': 449.41, 'Tool': 'lola'}].
Learned tools are: [{'Tool': 'itstools'}].
ReachabilityCardinality itstools NeoElection-PT-6...
May 26, 2018 12:11:54 AM fr.lip6.move.gal.application.Application start
INFO: Running its-tools with arguments : [-z3path, /usr/bin/z3, -yices2path, /usr/bin/yices, -ltsminpath, /usr/bin, -smt, -its, -pnfolder, /mcc-data, -examination, ReachabilityCardinality]
May 26, 2018 12:11:54 AM fr.lip6.move.gal.application.MccTranslator transformPNML
INFO: Parsing pnml file : /mcc-data/model.pnml
May 26, 2018 12:11:55 AM fr.lip6.move.gal.nupn.PTNetReader loadFromXML
INFO: Load time of PNML (sax parser for PT used): 367 ms
May 26, 2018 12:11:55 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 4830 places.
May 26, 2018 12:11:55 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 8435 transitions.
May 26, 2018 12:11:57 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 3304 fixed domain variables (out of 4830 variables) in GAL type NeoElection_PT_6
May 26, 2018 12:11:57 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 3304 constant array cells/variables (out of 4830 variables) in type NeoElection_PT_6
May 26, 2018 12:11:57 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_network_2_0_RI_3,P_poll__networl_1_6_RP_0,P_poll__networl_6_3_AskP_1,P_poll__networl_1_2_RP_1,P_poll__networl_1_0_RI_3,P_network_5_2_RP_4,P_poll__networl_2_2_RI_1,P_network_5_3_AskP_3,P_network_0_4_AskP_2,P_poll__networl_1_1_AskP_3,P_masterList_2_6_1,P_poll__networl_0_0_AnnP_4,P_poll__networl_4_6_RI_5,P_poll__networl_6_0_AnnP_6,P_poll__networl_5_4_AskP_6,P_network_3_1_AI_5,P_network_2_1_RI_6,P_poll__networl_2_0_AI_2,P_network_3_2_AnnP_1,P_network_2_2_AskP_2,P_poll__networl_6_4_RI_1,P_poll__networl_4_4_RP_2,P_poll__networl_2_5_AI_1,P_poll__networl_5_2_RI_3,P_network_6_5_AI_5,P_poll__networl_2_0_AnnP_2,P_poll__networl_1_1_RI_6,P_poll__networl_4_5_AnsP_0,P_network_3_6_AnnP_3,P_network_0_3_AI_4,P_poll__networl_0_5_RI_6,P_network_5_3_AI_2,P_crashed_5,P_poll__networl_5_3_RI_6,P_poll__networl_5_1_AI_4,P_poll__networl_4_3_AskP_0,P_network_3_2_AnnP_6,P_network_4_4_RI_1,P_poll__networl_1_3_AI_6,P_network_1_5_RI_2,P_network_5_4_AskP_3,P_network_6_0_AI_3,P_network_1_0_AI_2,P_masterList_1_6_0,P_network_4_3_AI_5,P_poll__networl_0_5_AnnP_1,P_poll__networl_6_6_AskP_0,P_poll__networl_6_4_AnnP_5,P_poll__networl_0_3_AskP_6,P_network_0_2_AnnP_2,P_network_3_4_RI_2,P_poll__networl_3_5_AI_3,P_poll__networl_5_5_RI_5,P_network_2_0_AskP_1,P_network_6_2_AnnP_3,P_poll__networl_2_4_RI_1,P_network_6_4_AskP_5,P_poll__networl_1_0_AskP_6,P_poll__networl_4_0_AnsP_0,P_network_0_2_RP_4,P_network_5_4_AI_2,P_network_5_5_AnnP_5,P_network_4_0_AI_4,P_poll__networl_5_1_AskP_2,P_network_1_3_RP_3,P_network_5_0_AnnP_1,P_poll__networl_2_6_RI_5,P_network_6_5_AskP_5,P_dead_3,P_network_4_5_RP_6,P_poll__networl_2_5_AnnP_3,P_network_0_0_RI_2,P_masterList_4_6_4,P_poll__networl_6_0_RP_0,P_poll__networl_4_2_AnnP_1,P_network_1_0_AnnP_3,P_poll__networl_6_0_AskP_0,P_poll__networl_6_1_RI_2,P_poll__networl_6_3_AI_0,P_network_0_0_AskP_1,P_network_0_0_AskP_4,P_network_5_1_RI_6,P_network_1_6_AskP_6,P_poll__networl_1_5_AI_0,P_poll__networl_6_4_AI_2,P_poll__networl_6_1_AnnP_2,P_network_2_0_AI_5,P_network_6_6_RI_4,P_poll__networl_2_1_AI_2,P_poll__networl_3_4_RI_2,P_network_1_3_AnnP_2,P_poll__networl_3_4_RP_0,P_network_2_3_AskP_5,P_network_1_4_AnnP_5,P_network_6_4_RP_3,P_poll__networl_4_6_AskP_0,P_network_1_4_RP_1,P_masterList_5_6_1,P_poll__networl_5_0_AnnP_1,P_poll__networl_1_2_RP_2,P_poll__networl_3_3_AskP_2,P_poll__networl_2_6_AnnP_6,P_poll__networl_3_6_AI_0,P_network_0_1_AskP_6,P_poll__networl_0_3_RI_5,P_poll__networl_2_0_RP_5,P_poll__networl_1_2_RI_6,P_poll__networl_1_0_AskP_3,P_poll__networl_3_4_AI_4,P_network_1_0_RP_4,P_poll__networl_0_5_RP_3,P_poll__networl_6_1_AI_6,P_network_5_2_AI_2,P_poll__networl_1_5_AnnP_4,P_network_2_5_RI_5,P_poll__networl_3_6_AI_2,P_poll__networl_0_6_AI_1,P_poll__networl_6_6_AskP_3,P_poll__networl_0_2_RI_5,P_poll__networl_0_0_AnnP_3,P_poll__networl_0_3_AI_5,P_poll__networl_2_6_AI_2,P_network_5_6_AskP_3,P_poll__networl_1_0_AnnP_3,P_poll__networl_6_6_AnnP_5,P_network_5_3_RP_2,P_poll__networl_0_0_AskP_0,P_network_0_4_AnnP_3,P_network_4_2_AskP_3,P_poll__networl_3_6_AI_5,P_network_1_0_AnnP_2,P_masterList_4_6_0,P_poll__networl_5_0_AI_3,P_poll__networl_3_3_AI_5,P_poll__networl_6_1_AI_2,P_poll__networl_5_1_AnnP_2,P_poll__networl_2_6_AnnP_5,P_network_4_1_RP_3,P_network_5_4_AskP_5,P_poll__networl_5_0_RP_4,P_network_2_1_AskP_4,P_network_4_0_RP_5,P_network_4_6_AnnP_3,P_poll__networl_3_6_AI_1,P_network_1_6_AskP_5,P_poll__networl_6_5_AI_6,P_poll__networl_6_0_RI_4,P_poll__networl_1_4_AskP_1,P_poll__networl_4_0_AI_0,P_network_4_2_RP_3,P_network_5_5_AI_5,P_poll__networl_4_4_RP_0,P_network_2_0_RI_5,P_poll__networl_3_2_RI_5,P_poll__networl_1_5_AI_1,P_network_3_4_RP_5,P_poll__networl_3_0_RP_2,P_poll__networl_5_0_AskP_5,P_poll__networl_6_3_AnnP_5,P_network_3_0_AnnP_5,P_network_5_4_AI_6,P_network_2_6_AI_3,P_poll__networl_1_1_AI_2,P_network_2_3_AskP_6,P_network_2_6_RP_4,P_poll__networl_4_5_RP_0,P_network_2_3_RI_2,P_poll__networl_6_0_AskP_3,P_poll__networl_0_0_AI_0,P_poll__networl_4_2_RI_2,P_poll__networl_2_5_AskP_5,P_network_6_3_RP_2,P_network_6_5_AnnP_2,P_poll__networl_5_0_RP_0,P_poll__networl_5_5_AskP_3,P_poll__networl_1_2_RI_3,P_poll__networl_6_2_RI_5,P_network_0_1_AI_2,P_poll__networl_6_3_RI_3,P_poll__networl_6_0_AI_3,P_network_3_4_RP_4,P_network_6_6_AI_2,P_poll__networl_5_1_RP_5,P_network_0_2_RI_5,P_poll__networl_5_1_RP_1,P_network_1_0_AskP_3,P_poll__networl_4_6_AI_0,P_poll__networl_3_3_AI_2,P_poll__networl_6_4_RP_0,P_network_5_3_RI_6,P_poll__networl_1_5_AskP_3,P_poll__networl_1_1_RI_2,P_poll__networl_2_1_AnnP_5,P_poll__networl_3_5_RP_3,P_poll__networl_6_1_AskP_0,P_network_3_3_RP_4,P_poll__networl_4_5_RI_5,P_poll__networl_3_2_RI_4,P_network_2_4_AskP_4,P_poll__networl_6_5_AI_5,P_network_0_4_AI_2,P_poll__networl_2_3_RI_2,P_poll__networl_2_4_RI_3,P_poll__networl_1_4_AI_3,P_poll__networl_6_4_AI_4,P_poll__networl_0_0_AnnP_0,P_poll__networl_0_6_AnsP_0,P_network_6_6_RI_5,P_poll__networl_0_3_RP_3,P_network_1_6_AskP_2,P_network_2_2_AI_4,P_network_0_0_AnnP_2,P_network_5_3_AnnP_1,P_poll__networl_3_1_RP_5,P_poll__networl_6_2_AnnP_2,P_poll__networl_2_4_AI_2,P_network_2_4_AskP_2,P_network_6_4_RI_6,P_poll__networl_2_2_RP_0,P_network_6_3_AskP_2,P_poll__networl_1_3_AI_5,P_network_1_1_AI_6,P_poll__networl_0_0_RI_0,P_poll__networl_2_4_AI_6,P_poll__networl_2_6_AnsP_0,P_poll__networl_5_2_AI_1,P_poll__networl_6_5_RI_1,P_poll__networl_6_6_AI_0,P_poll__networl_4_3_AI_4,P_network_4_3_AI_1,P_network_3_0_AI_6,P_poll__networl_6_0_AnnP_5,P_poll__networl_4_6_AskP_5,P_poll__networl_3_5_RI_4,P_poll__networl_1_2_AnsP_0,P_network_4_6_RP_5,P_poll__networl_6_1_RP_6,P_poll__networl_6_4_AnnP_4,P_masterList_2_6_0,P_network_1_1_AI_4,P_poll__networl_5_3_RI_2,P_network_2_5_RI_4,P_network_4_2_RP_1,P_poll__networl_0_4_AI_2,P_network_5_0_RP_2,P_poll__networl_2_4_AskP_0,P_poll__networl_2_4_AnnP_4,P_network_6_1_RP_6,P_network_2_3_RI_5,P_poll__networl_0_0_AI_6,P_poll__networl_3_0_AnnP_1,P_poll__networl_0_3_AskP_0,P_network_1_4_AskP_6,P_network_1_6_RP_3,P_poll__networl_1_6_AskP_0,P_network_2_1_RP_4,P_poll__networl_5_2_AI_5,P_poll__networl_6_4_RI_6,P_poll__networl_2_5_RP_1,P_network_2_2_AI_1,P_poll__networl_1_6_RI_2,P_network_0_3_AnnP_3,P_network_2_4_AnnP_1,P_network_2_3_AnnP_3,P_poll__networl_5_0_RI_3,P_poll__networl_1_6_RI_0,P_poll__networl_1_6_AskP_4,P_poll__networl_4_4_AskP_2,P_network_0_6_AI_3,P_poll__networl_2_2_AnnP_6,P_poll__networl_5_5_AI_4,P_network_2_0_AI_3,P_poll__networl_3_6_AI_4,P_network_1_1_AnnP_6,P_network_5_3_RP_5,P_network_0_4_RP_3,P_poll__networl_1_5_RI_1,P_poll__networl_6_5_RI_2,P_poll__networl_6_3_AskP_3,P_network_3_5_RI_6,P_network_6_3_AnnP_6,P_poll__networl_2_4_AI_5,P_network_1_3_AskP_4,P_poll__networl_4_1_RI_6,P_poll__networl_6_2_AnnP_4,P_network_0_4_RI_3,P_electionFailed_5,P_poll__networl_2_6_AskP_4,P_network_5_5_RI_4,P_masterList_0_6_1,P_network_0_6_AI_4,P_network_2_5_AskP_1,P_network_6_0_RI_2,P_poll__networl_3_6_RI_5,P_network_3_5_RP_2,P_network_6_1_RP_2,P_network_5_6_AI_4,P_poll__networl_2_5_RI_6,P_poll__networl_1_0_AI_1,P_poll__networl_4_3_AI_5,P_poll__networl_1_4_AI_2,P_poll__networl_5_6_AnnP_6,P_network_1_2_RP_3,P_poll__networl_5_5_AnnP_0,P_poll__networl_6_6_RP_0,P_poll__networl_0_4_AskP_6,P_network_3_2_RP_6,P_network_4_5_AskP_1,P_poll__networl_1_3_AnnP_4,P_network_2_1_AnnP_1,P_network_0_4_AskP_3,P_poll__networl_3_5_AI_1,P_network_6_6_RP_4,P_network_3_6_AnnP_5,P_poll__networl_2_3_AnsP_0,P_network_3_4_AI_6,P_poll__networl_4_0_RP_6,P_poll__networl_4_2_AI_5,P_poll__networl_6_1_AnsP_0,P_poll__networl_3_5_AI_2,P_poll__networl_3_5_RI_0,P_network_1_0_RP_1,P_masterList_2_6_3,P_poll__networl_4_5_AnnP_2,P_network_5_2_AskP_6,P_poll__networl_0_1_RP_0,P_network_4_4_AI_3,P_network_1_0_RP_3,P_poll__networl_2_2_AnnP_3,P_network_4_0_RI_2,P_network_3_5_RP_3,P_network_2_4_AskP_5,P_network_1_6_AnnP_4,P_network_3_0_AI_1,P_network_4_5_AnnP_3,P_network_6_2_AnnP_5,P_poll__networl_3_5_AI_4,P_poll__networl_1_2_AskP_3,P_poll__networl_4_6_RP_1,P_poll__networl_5_2_AnnP_0,P_network_0_6_RI_6,P_poll__networl_0_5_AnnP_2,P_network_1_4_RI_6,P_network_5_5_AI_3,P_network_2_4_RP_2,P_poll__networl_2_6_RI_2,P_poll__networl_2_3_RI_1,P_network_4_4_AnnP_6,P_poll__networl_2_4_RP_0,P_poll__networl_5_2_RI_2,P_network_0_0_AskP_6,P_poll__networl_0_3_AskP_1,P_poll__networl_5_0_RP_1,P_network_5_4_RI_6,P_poll__networl_6_3_AnnP_6,P_network_0_1_AnnP_5,P_network_4_3_AI_2,P_network_2_4_AnnP_3,P_network_6_5_AnnP_4,P_poll__networl_3_2_AI_6,P_network_4_1_AI_2,P_network_3_2_RP_4,P_network_4_3_AnnP_2,P_poll__networl_5_2_RI_4,P_network_5_0_AskP_2,P_poll__networl_3_3_AI_1,P_crashed_1,P_poll__networl_0_4_RI_2,P_network_0_4_AI_6,P_network_5_5_AskP_1,P_poll__networl_1_0_RP_4,P_poll__networl_3_4_AnnP_5,P_poll__networl_5_2_RP_1,P_poll__networl_1_0_RP_3,P_poll__networl_2_4_RI_6,P_poll__networl_5_5_RP_5,P_poll__networl_3_4_AnnP_4,P_poll__networl_0_1_AskP_4,P_poll__networl_3_4_AI_0,P_poll__networl_4_0_RI_0,P_poll__networl_1_1_RP_1,P_network_0_3_AskP_6,P_poll__networl_0_3_RI_6,P_poll__networl_6_1_AskP_2,P_network_2_3_RI_1,P_network_0_6_AskP_6,P_network_3_5_RP_4,P_network_4_1_AnnP_2,P_poll__networl_4_6_RP_6,P_poll__networl_6_3_AnnP_4,P_poll__networl_3_1_AI_3,P_poll__networl_6_5_RP_4,P_network_6_5_AI_1,P_poll__networl_6_0_RI_2,P_poll__networl_1_1_RP_0,P_network_5_4_AnnP_6,P_poll__networl_0_1_AnnP_6,P_poll__networl_3_1_AI_1,P_poll__networl_1_2_AnnP_5,P_poll__networl_6_0_AnsP_0,P_network_4_6_RI_5,P_poll__networl_6_3_AskP_4,P_network_0_6_AI_1,P_network_2_5_AskP_5,P_network_1_4_AskP_3,P_network_5_0_AI_6,P_network_1_6_RI_6,P_network_5_6_AnnP_2,P_network_6_0_AnnP_5,P_poll__networl_1_3_AnnP_1,P_network_6_2_AnnP_6,P_poll__networl_4_6_RI_3,P_poll__networl_0_2_AI_1,P_poll__networl_3_0_AnsP_0,P_poll__networl_5_4_RI_1,P_network_3_0_RI_5,P_poll__networl_0_6_RI_2,P_poll__networl_2_6_AskP_5,P_network_6_3_AskP_1,P_poll__networl_0_5_AI_4,P_network_2_3_AI_3,P_poll__networl_0_1_AnsP_0,P_network_3_5_AI_4,P_poll__networl_0_2_RI_6,P_network_6_1_AI_1,P_poll__networl_5_6_RP_0,P_poll__networl_2_3_RP_4,P_poll__networl_4_3_AnnP_1,P_poll__networl_4_4_AskP_4,P_network_5_5_AskP_5,P_network_6_3_RP_1,P_network_0_5_AI_6,P_network_0_5_AskP_4,P_poll__networl_1_0_RI_0,P_poll__networl_3_2_AnnP_6,P_poll__networl_2_6_RP_2,P_network_2_4_AI_1,P_network_6_4_AskP_6,P_network_6_2_AskP_1,P_poll__networl_4_3_AI_6,P_network_4_5_RP_3,P_poll__networl_2_3_AskP_0,P_network_3_3_AI_3,P_network_3_0_AskP_6,P_poll__networl_3_4_AskP_3,P_poll__networl_5_5_AnnP_2,P_poll__networl_5_5_AnnP_1,P_poll__networl_4_4_AskP_3,P_poll__networl_4_3_RP_5,P_network_4_4_AnnP_5,P_poll__networl_1_6_RI_4,P_dead_5,P_poll__networl_0_3_AskP_4,P_poll__networl_1_4_AnnP_6,P_poll__networl_3_5_AI_6,P_network_1_2_AI_5,P_poll__networl_6_5_AnnP_4,P_poll__networl_1_4_RI_3,P_network_0_4_AnnP_4,P_poll__networl_4_4_AnnP_2,P_poll__networl_5_1_AnnP_5,P_poll__networl_0_5_AskP_3,P_network_1_1_AskP_3,P_poll__networl_4_0_RI_6,P_poll__networl_0_2_RI_1,P_poll__networl_2_6_RP_0,P_poll__networl_6_4_AskP_2,P_network_6_2_RI_5,P_network_1_1_AskP_2,P_network_5_4_AnnP_3,P_poll__networl_5_0_RI_5,P_network_1_1_RI_2,P_poll__networl_2_4_AnsP_0,P_poll__networl_6_4_RP_4,P_poll__networl_5_0_AI_2,P_poll__networl_5_2_AskP_6,P_network_0_2_RP_2,P_network_2_4_RP_6,P_poll__networl_2_0_AskP_0,P_network_3_0_AI_2,P_poll__networl_0_1_AI_3,P_network_0_2_RP_3,P_poll__networl_3_3_AskP_1,P_network_1_0_AnnP_1,P_poll__networl_3_5_AI_5,P_poll__networl_5_5_RI_4,P_network_0_6_AI_6,P_network_3_6_RP_1,P_network_2_4_AI_5,P_network_1_0_AI_1,P_network_2_0_RP_4,P_poll__networl_6_2_AnnP_1,P_network_3_1_AnnP_4,P_poll__networl_6_2_AskP_3,P_poll__networl_0_2_AI_2,P_network_1_3_RI_5,P_network_2_3_RP_6,P_poll__networl_4_1_AI_6,P_poll__networl_1_0_AI_5,P_masterList_6_6_0,P_network_4_2_AnnP_6,P_network_1_1_RP_3,P_network_2_5_RP_2,P_network_4_5_AskP_5,P_poll__networl_2_1_AI_4,P_poll__networl_5_4_AnnP_2,P_network_2_6_AskP_6,P_poll__networl_4_3_AnnP_3,P_poll__networl_4_0_AnnP_0,P_poll__networl_5_6_RP_3,P_poll__networl_5_0_RI_4,P_poll__networl_3_4_RP_5,P_poll__networl_5_2_AnnP_3,P_network_2_5_AskP_2,P_network_4_1_AnnP_3,P_network_4_2_AskP_1,P_network_4_1_AI_3,P_poll__networl_0_4_AskP_5,P_poll__networl_1_6_AI_3,P_poll__networl_5_1_RI_6,P_network_2_5_AnnP_3,P_poll__networl_1_4_AskP_3,P_poll__networl_0_3_RP_4,P_network_4_6_RP_3,P_poll__networl_0_0_AnsP_0,P_poll__networl_4_0_AskP_2,P_network_5_0_AnnP_5,P_masterList_5_6_2,P_poll__networl_1_2_AI_3,P_network_0_1_AI_3,P_poll__networl_2_1_RP_2,P_network_3_4_AnnP_1,P_poll__networl_1_2_AskP_5,P_network_2_1_AnnP_5,P_poll__networl_5_3_AnnP_3,P_poll__networl_0_2_AnnP_1,P_poll__networl_4_6_AnnP_1,P_poll__networl_3_5_RP_6,P_poll__networl_1_5_AskP_2,P_network_3_3_AnnP_3,P_poll__networl_4_6_RI_4,P_network_6_2_AskP_3,P_poll__networl_5_4_AnnP_0,P_network_2_6_AnnP_2,P_network_4_5_RP_5,P_poll__networl_6_0_AnnP_0,P_poll__networl_1_2_AI_0,P_poll__networl_3_0_RP_3,P_poll__networl_2_6_AI_3,P_poll__networl_6_0_RP_6,P_poll__networl_4_0_AskP_0,P_network_4_5_AnnP_4,P_poll__networl_2_3_RP_5,P_network_4_2_AskP_4,P_poll__networl_0_3_RI_0,P_poll__networl_3_0_AI_4,P_network_1_6_RP_6,P_poll__networl_2_0_AskP_6,P_network_2_4_RI_5,P_poll__networl_3_6_AskP_2,P_poll__networl_4_1_AnnP_0,P_poll__networl_3_3_AskP_4,P_poll__networl_1_0_RI_6,P_network_1_5_RP_6,P_network_4_1_AskP_2,P_network_4_3_AnnP_5,P_network_0_2_AnnP_3,P_poll__networl_2_2_RI_5,P_network_4_3_RI_3,P_poll__networl_2_3_AnnP_1,P_network_2_5_AI_3,P_network_6_5_RP_1,P_poll__networl_1_5_AnnP_5,P_network_5_0_RP_5,P_poll__networl_0_2_AskP_1,P_poll__networl_2_0_AnnP_5,P_poll__networl_6_4_RP_2,P_network_3_0_AI_5,P_network_2_6_RP_5,P_poll__networl_6_4_AI_0,P_poll__networl_2_4_AnnP_3,P_network_6_1_AI_3,P_poll__networl_6_2_RP_3,P_poll__networl_6_3_RI_1,P_network_4_6_AI_1,P_poll__networl_4_4_RI_0,P_network_5_1_RP_5,P_poll__networl_4_1_RI_5,P_poll__networl_2_4_AskP_2,P_poll__networl_4_4_AnnP_6,P_network_4_3_AskP_5,P_network_1_6_AI_4,P_poll__networl_3_2_RP_5,P_network_0_5_RP_2,P_network_0_2_RI_4,P_network_3_6_RP_5,P_masterList_6_6_3,P_poll__networl_1_5_RP_5,P_poll__networl_3_2_AI_2,P_network_0_1_RP_3,P_poll__networl_2_2_AskP_1,P_network_3_2_AskP_3,P_poll__networl_3_3_AI_3,P_poll__networl_0_6_AskP_0,P_network_5_2_RI_2,P_poll__networl_4_3_RP_3,P_network_6_6_RP_2,P_network_1_5_AnnP_5,P_poll__networl_1_6_AI_2,P_poll__networl_3_5_AskP_1,P_poll__networl_4_1_AI_2,P_network_1_1_RI_3,P_poll__networl_1_6_RP_5,P_poll__networl_5_6_AI_5,P_network_3_2_AskP_1,P_poll__networl_3_0_RI_2,P_network_0_3_AnnP_5,P_network_6_4_AnnP_3,P_poll__networl_1_1_RI_0,P_poll__networl_2_2_AskP_6,P_network_4_6_AI_4,P_poll__networl_1_5_RI_3,P_network_3_0_RI_3,P_network_5_0_AI_1,P_network_4_3_RP_5,P_network_5_6_RI_6,P_poll__networl_4_3_AI_2,P_poll__networl_4_6_AskP_2,P_network_2_2_RI_1,P_network_2_1_AnnP_6,P_poll__networl_2_0_AI_5,P_network_3_2_AskP_2,P_poll__networl_6_3_AskP_0,P_network_4_6_RP_6,P_network_1_1_RI_1,P_poll__networl_0_0_AskP_3,P_poll__networl_5_4_RP_4,P_network_5_1_RI_5,P_network_1_4_AskP_5,P_poll__networl_6_2_RI_0,P_network_4_6_AskP_5,P_poll__networl_3_3_RP_6,P_poll__networl_5_3_AskP_1,P_poll__networl_6_0_RI_1,P_poll__networl_6_6_RP_2,P_network_1_4_RI_2,P_poll__networl_4_4_RI_1,P_network_0_5_RI_1,P_network_2_1_RI_4,P_poll__networl_3_1_RI_5,P_poll__networl_0_6_RI_3,P_poll__networl_4_6_RI_6,P_poll__networl_3_6_RI_0,P_poll__networl_3_0_AskP_2,P_network_6_2_AI_6,P_network_2_3_AI_1,P_network_3_6_AnnP_2,P_poll__networl_2_1_AskP_5,P_poll__networl_5_0_RP_5,P_network_0_1_AnnP_4,P_network_3_4_RI_4,P_poll__networl_0_4_RI_6,P_poll__networl_2_6_RI_6,P_poll__networl_5_5_AskP_2,P_network_3_3_AnnP_1,P_poll__networl_3_0_RI_5,P_poll__networl_5_0_RI_6,P_poll__networl_0_6_RI_5,P_poll__networl_0_6_AskP_2,P_poll__networl_5_6_AnnP_4,P_network_2_4_RI_2,P_poll__networl_5_0_AI_1,P_network_3_4_RI_6,P_network_2_3_RP_5,P_network_6_5_AI_4,P_poll__networl_0_1_RI_0,P_network_4_2_RI_5,P_network_1_2_AskP_1,P_poll__networl_5_6_AI_6,P_poll__networl_3_1_AskP_5,P_poll__networl_4_6_RI_0,P_poll__networl_1_6_RI_5,P_network_6_1_RI_5,P_poll__networl_1_0_RP_0,P_poll__networl_4_2_AnnP_4,P_poll__networl_0_4_AnnP_4,P_network_4_5_AskP_4,P_poll__networl_4_1_AskP_2,P_poll__networl_4_1_RI_0,P_network_0_0_AI_3,P_network_6_6_AI_6,P_network_4_4_RP_3,P_network_1_5_RI_5,P_poll__networl_6_5_AskP_1,P_poll__networl_2_4_AI_0,P_network_0_2_AskP_5,P_poll__networl_0_4_RP_5,P_poll__networl_5_2_AI_4,P_poll__networl_0_3_AnnP_0,P_network_0_3_AI_5,P_poll__networl_0_0_AskP_4,P_poll__networl_6_6_RI_6,P_network_1_5_AnnP_6,P_poll__networl_0_3_AI_6,P_poll__networl_5_4_RI_4,P_network_1_1_AnnP_1,P_network_1_6_RP_5,P_network_1_0_AI_6,P_poll__networl_0_2_AnnP_0,P_poll__networl_2_0_AnnP_6,
P_network_3_3_AskP_3,P_network_4_6_AnnP_1,P_network_2_5_AI_4,P_poll__networl_4_5_AnnP_4,P_poll__networl_5_2_AnsP_0,P_poll__networl_1_1_RI_5,P_poll__networl_0_6_AnnP_1,P_poll__networl_0_6_RI_6,P_network_4_0_AnnP_3,P_poll__networl_1_4_RP_1,P_poll__networl_5_2_RI_6,P_network_3_5_AI_1,P_network_1_4_RP_2,P_poll__networl_0_1_RP_3,P_network_0_4_RI_2,P_poll__networl_6_1_RI_6,P_poll__networl_3_2_AskP_0,P_masterList_3_6_0,P_network_6_2_RI_4,P_network_3_2_AskP_6,P_masterList_1_6_6,P_network_5_1_AnnP_2,P_poll__networl_5_2_AskP_3,P_poll__networl_2_3_AI_1,P_poll__networl_3_1_AnnP_0,P_network_2_2_AI_5,P_network_4_4_AskP_6,P_poll__networl_2_0_RP_2,P_poll__networl_2_5_RI_0,P_poll__networl_5_5_AnnP_4,P_network_0_3_AskP_1,P_poll__networl_5_2_AskP_1,P_network_3_5_RI_1,P_poll__networl_3_2_RI_3,P_network_0_3_RP_6,P_network_4_6_RI_6,P_poll__networl_2_4_AI_4,P_network_5_6_AskP_4,P_poll__networl_1_1_AI_4,P_network_3_4_RP_3,P_network_5_6_RI_2,P_network_1_5_AskP_4,P_poll__networl_4_4_AnnP_4,P_poll__networl_0_0_RI_4,P_network_5_5_AnnP_3,P_network_3_5_RP_1,P_poll__networl_6_5_AskP_5,P_poll__networl_2_3_RI_0,P_poll__networl_3_3_RP_4,P_network_4_4_RI_5,P_poll__networl_0_1_AI_4,P_network_6_1_AI_6,P_network_3_2_AI_5,P_network_6_2_AI_5,P_poll__networl_4_4_RI_4,P_poll__networl_1_0_RI_2,P_poll__networl_0_1_AI_6,P_poll__networl_4_6_AnnP_2,P_network_5_3_AI_5,P_network_2_4_AskP_6,P_network_3_1_AskP_3,P_poll__networl_1_1_AI_1,P_poll__networl_3_5_AI_0,P_network_1_5_RI_4,P_poll__networl_3_2_AnsP_0,P_network_5_4_AskP_1,P_network_0_2_AskP_6,P_poll__networl_4_3_AnnP_2,P_poll__networl_5_0_AskP_0,P_poll__networl_5_4_RI_0,P_network_0_4_RI_4,P_network_4_1_AI_1,P_network_6_0_RI_1,P_poll__networl_3_0_AnnP_2,P_poll__networl_6_3_AnnP_0,P_poll__networl_2_6_AI_1,P_poll__networl_0_5_RP_1,P_network_6_6_RP_5,P_poll__networl_6_3_AnnP_2,P_network_1_3_AskP_2,P_poll__networl_3_4_AnnP_2,P_poll__networl_5_4_RP_1,P_poll__networl_6_5_RI_3,P_poll__networl_1_3_RI_3,P_poll__networl_1_1_RI_3,P_network_5_1_AskP_4,P_network_3_1_RP_5,P_poll__networl_3_0_AskP_1,P_network_0_4_AskP_6,P_network_3_6_AI_6,P_poll__networl_4_2_AnnP_3,P_network_3_4_AnnP_2,P_poll__networl_4_0_RP_2,P_network_2_1_RP_5,P_poll__networl_6_3_RP_6,P_poll__networl_5_6_AskP_0,P_poll__networl_5_0_AnsP_0,P_poll__networl_5_1_RI_5,P_network_5_6_RP_4,P_poll__networl_1_4_RP_4,P_network_4_1_RI_2,P_network_1_2_AI_6,P_poll__networl_0_0_AskP_6,P_poll__networl_3_1_AskP_6,P_poll__networl_2_0_AI_4,P_poll__networl_2_2_AnnP_1,P_poll__networl_5_0_AskP_2,P_poll__networl_2_0_AskP_1,P_network_6_1_RI_6,P_network_0_1_AskP_3,P_network_1_6_RI_5,P_poll__networl_6_4_AI_3,P_poll__networl_0_0_AI_1,P_network_3_4_AskP_2,P_poll__networl_5_6_RP_1,P_network_0_5_AI_4,P_poll__networl_6_2_RI_4,P_network_3_5_AskP_3,P_network_1_2_AnnP_5,P_poll__networl_0_3_AnnP_4,P_network_5_5_RI_5,P_network_5_4_AnnP_1,P_poll__networl_6_4_AnnP_3,P_poll__networl_3_6_RP_5,P_poll__networl_0_2_AskP_4,P_poll__networl_5_3_AnnP_5,P_network_2_5_RI_1,P_poll__networl_0_5_RI_0,P_network_4_6_RI_1,P_network_5_0_AI_3,P_network_0_1_RP_4,P_network_2_4_RP_5,P_network_3_3_RP_3,P_network_4_6_RP_4,P_network_6_0_AI_1,P_poll__networl_0_5_AskP_2,P_network_1_2_AskP_3,P_network_6_3_RP_6,P_network_3_3_AskP_6,P_poll__networl_4_5_AI_4,P_poll__networl_1_4_AskP_0,P_network_6_6_AI_5,P_poll__networl_3_3_RI_5,P_poll__networl_2_2_AI_5,P_network_0_2_AnnP_1,P_poll__networl_0_2_AskP_6,P_poll__networl_6_2_AI_5,P_network_0_6_AskP_1,P_network_1_2_AI_3,P_network_2_5_AnnP_1,P_network_4_3_AnnP_1,P_network_1_2_RP_2,P_poll__networl_2_1_RP_6,P_poll__networl_4_2_AskP_0,P_network_1_5_RP_3,P_poll__networl_1_6_RI_3,P_network_2_3_AnnP_4,P_poll__networl_2_6_AI_4,P_network_5_2_AskP_1,P_network_5_0_RP_6,P_poll__networl_4_3_AskP_1,P_poll__networl_2_5_RP_3,P_poll__networl_4_0_RI_5,P_network_2_2_AnnP_6,P_poll__networl_1_1_AnnP_3,P_network_5_0_AskP_5,P_poll__networl_2_5_RI_5,P_network_6_5_RI_1,P_network_4_5_AI_4,P_network_6_5_AnnP_1,P_poll__networl_0_0_RI_3,P_poll__networl_6_5_AskP_3,P_poll__networl_0_4_AI_3,P_network_5_2_AI_5,P_network_0_5_AskP_6,P_network_5_6_AnnP_4,P_network_6_1_AI_4,P_network_5_0_AskP_6,P_poll__networl_6_3_AI_2,P_network_1_6_AnnP_6,P_poll__networl_5_5_RP_2,P_network_5_1_AnnP_1,P_poll__networl_2_1_RP_0,P_poll__networl_4_0_AnnP_4,P_poll__networl_4_1_RP_3,P_poll__networl_6_6_AI_1,P_network_6_0_AskP_1,P_network_2_2_RI_3,P_poll__networl_6_6_RI_0,P_poll__networl_1_6_RI_1,P_poll__networl_2_1_RP_1,P_network_6_1_AnnP_2,P_network_5_0_AI_5,P_poll__networl_3_0_RP_1,P_network_0_2_AI_6,P_network_4_1_RI_3,P_poll__networl_5_3_RP_1,P_poll__networl_1_5_RI_5,P_network_4_4_RP_4,P_network_6_6_AI_3,P_network_3_1_RI_5,P_network_2_3_AnnP_6,P_network_1_3_AnnP_3,P_network_5_2_AI_6,P_network_5_6_RP_3,P_network_1_4_AnnP_2,P_network_5_1_RI_3,P_network_1_0_AnnP_5,P_network_0_6_AskP_2,P_poll__networl_5_0_AnnP_3,P_poll__networl_0_2_RI_4,P_poll__networl_6_0_AskP_4,P_network_2_2_RP_4,P_poll__networl_0_3_AskP_5,P_network_0_0_AI_1,P_network_2_3_AnnP_5,P_poll__networl_1_3_RP_2,P_network_2_1_RI_1,P_poll__networl_3_1_RI_1,P_network_3_5_AnnP_5,P_network_4_5_AnnP_1,P_network_5_6_AskP_6,P_poll__networl_4_0_RP_5,P_network_6_0_RI_3,P_network_3_5_RP_5,P_network_0_5_RP_4,P_network_3_3_RI_5,P_poll__networl_3_0_RP_0,P_network_6_0_RI_5,P_poll__networl_0_2_AnnP_6,P_network_4_2_RI_4,P_poll__networl_5_4_RP_0,P_poll__networl_2_5_AI_5,P_poll__networl_4_4_AnnP_3,P_poll__networl_0_6_AskP_5,P_network_5_2_AnnP_5,P_poll__networl_5_4_AskP_2,P_network_2_2_AnnP_4,P_poll__networl_2_3_AskP_2,P_network_5_0_AnnP_6,P_poll__networl_3_1_AI_2,P_network_0_1_RP_2,P_network_5_1_RP_1,P_network_3_0_AnnP_1,P_network_4_2_AnnP_5,P_network_6_4_RI_5,P_poll__networl_6_6_AI_3,P_network_5_2_AI_1,P_poll__networl_1_4_RI_1,P_network_5_1_AnnP_4,P_network_6_0_RP_2,P_poll__networl_2_6_AskP_0,P_poll__networl_5_4_RP_3,P_poll__networl_0_4_RP_6,P_network_6_0_AI_6,P_poll__networl_4_5_AskP_2,P_network_3_5_AI_3,P_poll__networl_1_1_AskP_2,P_poll__networl_1_2_AskP_4,P_poll__networl_3_0_AnnP_5,P_network_0_5_RI_2,P_network_6_3_AI_2,P_network_3_3_AI_4,P_network_4_1_AI_4,P_masterList_5_6_5,P_network_0_6_AnnP_6,P_network_6_0_RP_6,P_poll__networl_1_1_RP_3,P_poll__networl_6_1_RI_4,P_poll__networl_2_4_RP_1,P_network_1_4_RP_3,P_network_2_0_AnnP_2,P_poll__networl_2_4_AskP_3,P_network_5_1_AI_1,P_network_6_3_AskP_6,P_poll__networl_5_6_AnnP_3,P_dead_2,P_poll__networl_4_6_AI_4,P_poll__networl_2_0_AnnP_3,P_network_3_3_AskP_2,P_poll__networl_5_5_AI_3,P_poll__networl_5_6_RI_1,P_poll__networl_6_6_RI_4,P_poll__networl_2_6_AskP_3,P_poll__networl_4_3_RI_0,P_network_0_1_AI_1,P_network_4_3_AskP_1,P_poll__networl_4_3_RI_6,P_network_2_4_RP_3,P_poll__networl_4_1_AskP_3,P_network_1_2_RI_1,P_poll__networl_2_1_RI_2,P_poll__networl_0_6_AI_2,P_poll__networl_2_3_AskP_4,P_poll__networl_4_0_RP_1,P_poll__networl_0_2_RP_6,P_network_0_5_AnnP_2,P_network_4_6_AI_3,P_network_4_5_AskP_2,P_network_0_0_RP_6,P_network_2_6_AnnP_4,P_network_1_4_AskP_4,P_poll__networl_5_1_RP_4,P_network_6_0_RP_1,P_poll__networl_1_5_AI_2,P_network_3_6_AI_4,P_poll__networl_4_0_AI_4,P_network_1_5_RP_5,P_network_1_5_AskP_5,P_poll__networl_6_0_AskP_5,P_poll__networl_5_4_AI_0,P_poll__networl_1_2_RP_4,P_poll__networl_5_1_AskP_4,P_network_2_4_AnnP_6,P_network_5_3_AnnP_3,P_poll__networl_6_4_RP_3,P_poll__networl_2_3_AI_0,P_poll__networl_2_1_AI_3,P_poll__networl_5_4_RI_3,P_network_6_4_RP_2,P_poll__networl_5_1_RI_2,P_poll__networl_1_3_RI_2,P_masterList_1_6_1,P_poll__networl_0_5_AI_2,P_network_0_2_RI_3,P_poll__networl_3_2_AskP_4,P_poll__networl_5_5_AI_1,P_network_4_0_RI_1,P_poll__networl_3_3_RI_0,P_poll__networl_1_5_AnnP_6,P_poll__networl_4_5_AnnP_5,P_poll__networl_3_4_RP_6,P_poll__networl_4_5_RP_1,P_poll__networl_5_4_AI_5,P_network_0_0_AnnP_6,P_network_6_6_RI_6,P_network_1_5_RI_6,P_network_1_4_AnnP_4,P_poll__networl_4_2_AskP_5,P_network_6_4_RI_4,P_poll__networl_1_3_AskP_0,P_poll__networl_3_5_AnnP_5,P_network_2_6_RI_3,P_poll__networl_1_6_AI_6,P_network_6_4_AnnP_4,P_network_2_2_AskP_1,P_poll__networl_1_1_AskP_1,P_poll__networl_6_3_AI_3,P_network_3_4_AskP_6,P_poll__networl_2_2_RP_5,P_network_5_2_AnnP_4,P_poll__networl_1_6_AnnP_5,P_network_5_1_AnnP_3,P_poll__networl_2_0_RI_4,P_poll__networl_3_0_AI_3,P_poll__networl_4_2_RP_2,P_poll__networl_5_3_AnsP_0,P_poll__networl_5_1_AskP_3,P_poll__networl_0_3_AnnP_2,P_network_0_1_AnnP_2,P_network_4_1_RI_4,P_masterList_4_6_1,P_poll__networl_2_0_RP_1,P_poll__networl_4_2_AnsP_0,P_network_5_4_RP_5,P_network_4_1_RI_6,P_poll__networl_1_3_RP_4,P_network_3_2_RI_5,P_poll__networl_1_4_RP_5,P_poll__networl_1_2_AnnP_3,P_poll__networl_5_6_RI_3,P_poll__networl_1_0_AnnP_4,P_network_5_4_AnnP_4,P_network_6_5_RP_4,P_poll__networl_0_0_RI_6,P_poll__networl_1_4_RP_3,P_poll__networl_1_0_AI_0,P_poll__networl_3_0_AskP_3,P_network_5_2_RI_3,P_poll__networl_1_6_RP_2,P_poll__networl_4_0_AskP_1,P_network_3_2_RI_1,P_poll__networl_5_3_AskP_6,P_network_2_2_RI_2,P_network_1_4_RP_4,P_network_0_5_RP_3,P_network_4_3_AI_4,P_poll__networl_0_6_AnnP_6,P_network_2_2_AI_6,P_network_5_5_AnnP_4,P_poll__networl_2_4_AnnP_5,P_poll__networl_6_4_RI_5,P_poll__networl_5_3_AI_3,P_poll__networl_1_1_AskP_6,P_poll__networl_6_5_AnnP_6,P_network_0_5_AI_2,P_network_4_2_RP_4,P_network_6_5_RP_2,P_poll__networl_4_4_AskP_0,P_network_3_4_AnnP_4,P_poll__networl_3_3_AskP_5,P_poll__networl_4_2_RI_3,P_network_0_6_AI_2,P_network_4_0_RI_3,P_poll__networl_2_5_AnnP_6,P_poll__networl_3_0_AnnP_3,P_network_4_4_RI_2,P_poll__networl_4_2_AI_3,P_poll__networl_6_1_AI_3,P_network_5_6_RI_3,P_poll__networl_1_6_AnnP_3,P_poll__networl_6_3_RI_6,P_electionFailed_2,P_poll__networl_6_1_RP_2,P_network_0_2_AI_5,P_poll__networl_2_6_AnnP_1,P_poll__networl_3_3_AnnP_3,P_poll__networl_1_1_RI_1,P_network_3_6_RP_6,P_poll__networl_1_2_AnnP_2,P_network_3_3_RI_3,P_network_6_5_AskP_4,P_poll__networl_3_3_RP_1,P_network_6_5_RI_5,P_network_5_0_AnnP_3,P_network_4_4_AskP_3,P_poll__networl_0_5_RI_1,P_poll__networl_1_0_AI_3,P_network_5_2_RI_4,P_network_2_4_RI_6,P_poll__networl_5_1_RI_4,P_masterList_1_6_4,P_poll__networl_2_5_AI_3,P_poll__networl_6_6_RI_5,P_poll__networl_1_1_AnsP_0,P_poll__networl_5_3_RP_3,P_network_4_0_RI_4,P_network_0_4_AskP_5,P_network_0_2_AI_3,P_network_1_1_RP_6,P_poll__networl_5_6_RP_6,P_network_4_5_AI_3,P_network_1_5_AnnP_2,P_poll__networl_2_2_AskP_0,P_network_1_2_RI_2,P_network_6_2_AnnP_4,P_poll__networl_4_3_AnsP_0,P_poll__networl_3_6_AskP_0,P_network_5_6_RP_5,P_poll__networl_3_2_AI_5,P_poll__networl_3_1_RP_2,P_poll__networl_1_3_AskP_1,P_network_6_3_AskP_4,P_poll__networl_0_5_RP_4,P_poll__networl_1_2_RI_1,P_poll__networl_2_3_AnnP_6,P_network_1_5_AskP_3,P_network_2_1_AnnP_3,P_network_1_2_AnnP_2,P_network_4_1_AskP_1,P_poll__networl_2_1_AI_1,P_poll__networl_6_0_AskP_6,P_poll__networl_2_1_AskP_6,P_poll__networl_3_6_AskP_6,P_network_1_4_RP_6,P_poll__networl_4_2_RI_5,P_poll__networl_5_0_AI_6,P_network_0_4_AnnP_5,P_network_0_1_RI_2,P_network_4_4_AskP_1,P_network_2_5_AnnP_6,P_poll__networl_3_2_RP_0,P_network_5_0_RP_4,P_network_3_5_AnnP_3,P_network_5_5_AI_6,P_network_0_1_AnnP_3,P_masterList_4_6_3,P_network_2_6_AnnP_5,P_poll__networl_5_2_AskP_0,P_network_3_1_RI_2,P_poll__networl_5_3_AI_6,P_network_2_4_AI_2,P_masterList_0_6_5,P_network_1_2_RI_4,P_network_4_5_RI_3,P_network_6_5_AI_2,P_poll__networl_6_4_AnnP_2,P_network_5_1_AskP_5,P_network_0_1_AskP_1,P_poll__networl_2_2_AnnP_5,P_poll__networl_4_3_AI_3,P_poll__networl_4_4_AskP_5,P_poll__networl_1_3_AskP_6,P_network_2_3_RI_6,P_network_5_5_RP_3,P_poll__networl_6_6_RI_2,P_poll__networl_4_2_AskP_1,P_network_0_5_AnnP_5,P_network_2_3_AI_4,P_poll__networl_6_5_RP_2,P_poll__networl_6_6_AI_2,P_poll__networl_0_3_AI_3,P_poll__networl_3_1_AI_6,P_network_1_2_AskP_4,P_network_2_3_AI_6,P_network_3_4_AskP_4,P_poll__networl_1_3_AnsP_0,P_poll__networl_1_3_AI_3,P_network_1_1_RI_6,P_poll__networl_0_3_AnnP_6,P_poll__networl_5_1_RI_3,P_network_6_0_AnnP_2,P_network_6_0_AskP_5,P_network_1_2_RI_5,P_poll__networl_5_2_AnnP_6,P_poll__networl_3_5_AskP_5,P_poll__networl_4_5_AI_0,P_network_3_6_AskP_6,P_network_6_0_AI_2,P_poll__networl_0_0_RI_5,P_poll__networl_2_2_RP_4,P_poll__networl_1_0_AnnP_6,P_network_1_3_RI_3,P_network_6_3_RI_4,P_poll__networl_0_3_RP_6,P_poll__networl_3_6_RP_4,P_poll__networl_1_3_AnnP_3,P_network_3_6_RP_3,P_network_2_6_RP_6,P_network_3_4_AskP_3,P_network_1_2_RI_3,P_network_6_3_AI_5,P_network_1_6_RI_3,P_poll__networl_6_2_AskP_6,P_poll__networl_1_2_AnnP_0,P_network_1_1_AnnP_5,P_poll__networl_3_2_RP_4,P_poll__networl_3_5_RI_5,P_network_2_5_AI_6,P_poll__networl_1_6_RP_3,P_network_6_1_AnnP_3,P_poll__networl_0_6_AnnP_2,P_poll__networl_6_4_AnnP_0,P_poll__networl_6_3_AnnP_1,P_masterList_1_6_2,P_poll__networl_5_3_AskP_0,P_poll__networl_1_4_AI_6,P_poll__networl_3_4_AskP_0,P_poll__networl_2_0_RI_0,P_poll__networl_1_6_AnnP_6,P_network_1_3_RP_4,P_poll__networl_5_1_AI_0,P_poll__networl_2_5_AskP_3,P_poll__networl_5_2_RP_4,P_poll__networl_3_4_RP_1,P_poll__networl_4_1_AnnP_3,P_network_2_1_AskP_3,P_poll__networl_0_4_AI_5,P_poll__networl_5_5_AskP_4,P_poll__networl_2_0_AnnP_1,P_poll__networl_6_6_RP_3,P_network_6_4_AnnP_5,P_poll__networl_1_3_RP_5,P_network_2_1_AI_3,P_network_0_4_AI_4,P_network_0_2_AI_2,P_poll__networl_3_6_AskP_4,P_poll__networl_3_5_RI_2,P_network_2_6_AI_2,P_network_5_6_RI_4,P_poll__networl_4_4_AI_2,P_network_1_0_AskP_1,P_poll__networl_0_2_AnnP_2,P_poll__networl_3_2_RI_2,P_poll__networl_1_2_RI_2,P_poll__networl_0_5_AI_3,P_network_4_1_RI_1,P_poll__networl_3_5_RP_0,P_network_5_2_AI_4,P_poll__networl_2_1_AskP_2,P_network_6_6_AskP_6,P_poll__networl_2_0_RP_0,P_poll__networl_6_5_AnnP_1,P_network_5_6_RP_1,P_poll__networl_3_4_AI_5,P_poll__networl_4_6_RP_3,P_network_6_1_RP_5,P_network_6_3_AnnP_2,P_poll__networl_2_6_RP_5,P_network_3_4_RI_1,P_network_1_4_AI_3,P_poll__networl_0_5_AskP_5,P_poll__networl_6_5_AnsP_0,P_network_3_1_RP_2,P_network_1_5_AI_1,P_poll__networl_5_1_RP_3,P_masterList_1_6_5,P_network_4_6_AI_2,P_poll__networl_2_4_AskP_1,P_network_4_2_AI_4,P_network_1_1_RI_4,P_poll__networl_3_0_AskP_0,P_network_1_2_AskP_5,P_poll__networl_5_6_AskP_1,P_network_1_0_AI_5,P_network_0_5_AI_1,P_poll__networl_4_3_AI_0,P_poll__networl_4_6_AnnP_4,P_network_3_0_AskP_1,P_network_5_5_AnnP_2,P_poll__networl_5_4_RP_5,P_poll__networl_2_0_AskP_4,P_network_1_1_AI_5,P_poll__networl_3_0_RP_4,P_poll__networl_5_1_AI_3,P_poll__networl_4_1_AnnP_1,P_poll__networl_1_5_AskP_5,P_poll__networl_3_4_AI_1,P_poll__networl_1_1_AnnP_5,P_poll__networl_1_4_AnnP_0,P_poll__networl_3_3_AnnP_2,P_poll__networl_4_1_AnnP_6,P_network_1_0_AI_3,P_poll__networl_2_5_RI_3,P_network_5_2_RP_3,P_poll__networl_3_6_RI_3,P_poll__networl_1_6_AI_4,P_poll__networl_2_2_AI_3,P_poll__networl_5_2_RI_5,P_network_1_1_AI_2,P_network_3_0_AI_3,P_dead_6,P_network_6_6_RI_3,P_network_4_6_RP_1,P_network_1_5_RI_3,P_poll__networl_0_1_AnnP_4,P_network_4_1_AskP_3,P_network_0_3_AskP_2,P_poll__networl_0_1_AnnP_3,P_poll__networl_2_1_AnnP_3,P_poll__networl_2_1_RP_4,P_network_4_1_RP_1,P_network_0_0_RI_1,P_network_2_1_AskP_2,P_network_4_4_AI_2,P_poll__networl_5_6_RP_2,P_poll__networl_6_5_RI_4,P_network_6_4_AI_5,P_poll__networl_0_0_AI_4,P_poll__networl_1_2_AI_4,P_network_3_2_RI_3,P_poll__networl_6_0_AskP_1,P_poll__networl_6_4_AskP_1,P_network_5_3_AnnP_5,P_network_0_3_AskP_3,P_poll__networl_6_2_AskP_4,P_network_6_5_AI_3,P_network_0_0_AI_5,P_network_2_0_RP_5,P_network_0_6_RP_6,P_poll__networl_3_5_RP_4,P_poll__networl_6_2_RI_6,P_network_1_4_AI_4,P_poll__networl_1_3_RP_6,P_poll__networl_3_4_AI_2,P_poll__networl_4_6_AnnP_6,P_network_2_6_AnnP_1,P_network_0_4_RP_2,P_network_4_6_RP_2,P_poll__networl_6_4_AskP_0,P_network_0_3_RP_3,P_network_4_3_AskP_4,P_network_6_6_AskP_3,P_network_4_0_AI_5,P_poll__networl_5_0_RP_2,P_poll__networl_3_6_AnnP_5,P_network_3_2_RP_2,P_network_6_0_AskP_3,P_poll__networl_0_3_RP_2,P_poll__networl_5_0_RP_3,P_poll__networl_2_3_RI_5,P_network_1_1_AnnP_4,P_poll__networl_2_0_RP_3,P_network_2_5_AnnP_4,P_poll__networl_3_4_AnnP_3,P_masterList_0_6_3,P_network_1_4_RP_5,P_poll__networl_3_5_RI_6,P_network_0_5_AI_5,P_poll__networl_0_6_RP_0,P_network_1_1_RP_5,P_poll__networl_2_4_AnnP_2,P_poll__networl_4_6_AnnP_3,P_network_6_3_RI_6,P_poll__networl_0_6_AI_4,P_network_6_5_RP_6,P_poll__networl_0_4_AskP_0,P_poll__networl_6_0_RI_3,P_network_4_5_RI_4,P_network_1_0_AskP_2,P_poll__networl_1_5_RI_4,P_poll__networl_3_5_RI_3,P_poll__networl_0_2_AnnP_3,P_network_3_0_AnnP_4,P_poll__networl_3_4_RP_2,P_network_4_3_AI_6,P_poll__networl_2_2_RI_2,P_network_0_2_AnnP_5,P_poll__networl_3_6_RP_2,P_network_1_5_RP_2,P_poll__networl_6_6_AnnP_3,P_poll__networl_3_2_AskP_5,P_poll__networl_3_6_AskP_5,P_poll__networl_0_0_RP_1,P_poll__networl_0_5_AI_6,P_poll__networl_3_0_AI_1,P_poll__ne
tworl_4_0_AskP_6,P_poll__networl_2_4_AnnP_6,P_network_2_3_AnnP_1,P_poll__networl_0_6_AskP_6,P_poll__networl_6_6_AnnP_6,P_poll__networl_1_5_AnnP_1,P_poll__networl_6_2_AskP_2,P_network_6_1_AI_5,P_poll__networl_4_6_AnnP_5,P_network_3_2_AskP_5,P_network_4_0_AskP_6,P_network_2_0_AskP_4,P_poll__networl_2_4_RP_6,P_network_0_0_AnnP_5,P_network_0_5_AskP_5,P_poll__networl_2_0_AI_0,P_poll__networl_2_3_AskP_1,P_poll__networl_4_1_RP_6,P_network_0_1_RI_5,P_network_5_3_AnnP_2,P_poll__networl_0_3_AI_2,P_network_0_1_AskP_5,P_network_4_2_AI_3,P_poll__networl_1_6_RI_6,P_network_1_2_RP_5,P_network_2_2_RI_5,P_network_6_6_AnnP_5,P_network_3_4_RP_6,P_crashed_3,P_network_6_4_AI_2,P_network_0_3_AskP_4,P_network_0_2_AnnP_4,P_poll__networl_3_2_AskP_1,P_network_5_4_RI_1,P_poll__networl_5_3_RI_5,P_network_2_4_AnnP_2,P_poll__networl_4_4_RI_3,P_poll__networl_6_2_AskP_1,P_network_6_1_RP_4,P_poll__networl_2_5_AI_0,P_network_1_0_RI_5,P_poll__networl_4_5_AI_2,P_network_0_2_AI_1,P_network_4_0_AnnP_1,P_poll__networl_3_0_AI_5,P_poll__networl_3_6_AnnP_0,P_network_0_6_RP_3,P_poll__networl_2_0_AI_1,P_poll__networl_1_5_AskP_1,P_poll__networl_6_0_AnnP_4,P_poll__networl_3_3_RI_6,P_poll__networl_6_2_RP_6,P_network_3_6_AskP_2,P_poll__networl_5_1_AI_1,P_poll__networl_5_5_AnsP_0,P_network_2_1_RI_3,P_poll__networl_4_0_RI_3,P_poll__networl_1_1_RP_2,P_poll__networl_5_5_RP_3,P_network_0_5_RI_6,P_poll__networl_4_1_AI_1,P_poll__networl_3_2_RI_0,P_network_6_0_RP_5,P_network_6_2_AskP_2,P_network_6_2_AI_3,P_network_3_6_AI_1,P_masterList_3_6_2,P_poll__networl_5_1_AskP_0,P_poll__networl_5_1_RP_6,P_network_0_1_RI_1,P_poll__networl_4_5_RP_5,P_poll__networl_3_6_AnsP_0,P_network_0_3_RI_1,P_poll__networl_3_5_AnnP_2,P_network_0_4_AI_5,P_network_0_1_AskP_2,P_poll__networl_5_3_RI_3,P_network_6_1_AskP_3,P_poll__networl_1_6_AnnP_0,P_poll__networl_6_3_AskP_6,P_poll__networl_1_0_RP_2,P_poll__networl_4_5_AskP_0,P_poll__networl_6_5_RP_3,P_poll__networl_3_4_AnnP_1,P_masterList_5_6_4,P_poll__networl_1_5_RP_6,P_network_3_1_RI_3,P_poll__networl_1_5_RP_4,P_poll__networl_6_6_RP_1,P_poll__networl_4_2_RP_1,P_network_4_6_AI_5,P_poll__networl_0_6_AI_6,P_network_6_0_AskP_2,P_network_2_5_RI_3,P_poll__networl_1_5_AI_4,P_network_2_0_AI_6,P_network_2_2_AI_3,P_network_3_3_RI_4,P_network_5_1_RI_2,P_poll__networl_5_6_AnsP_0,P_poll__networl_3_2_AI_4,P_network_3_2_AnnP_2,P_network_3_4_AskP_1,P_poll__networl_2_2_AI_2,P_network_6_1_AskP_1,P_network_6_6_RP_6,P_poll__networl_5_4_AnnP_5,P_poll__networl_6_5_RP_6,P_network_1_2_AskP_2,P_network_1_5_AnnP_3,P_poll__networl_5_6_RP_5,P_network_0_2_AskP_2,P_poll__networl_2_3_AskP_5,P_poll__networl_5_5_AskP_0,P_poll__networl_6_6_AskP_4,P_network_4_5_RI_5,P_poll__networl_2_2_RP_3,P_network_4_4_RP_1,P_poll__networl_3_4_RP_4,P_poll__networl_2_6_RI_1,P_poll__networl_0_6_RP_3,P_network_6_4_AskP_4,P_poll__networl_4_5_RI_0,P_poll__networl_5_3_AI_5,P_poll__networl_0_0_RP_2,P_poll__networl_4_5_AskP_1,P_network_0_1_RP_1,P_network_2_5_AI_1,P_poll__networl_3_2_RI_1,P_network_1_3_RP_2,P_poll__networl_2_6_AI_0,P_poll__networl_2_3_RI_6,P_poll__networl_3_4_AI_6,P_poll__networl_6_4_RI_4,P_network_1_2_RP_6,P_poll__networl_5_5_AskP_1,P_network_3_4_AI_1,P_poll__networl_1_3_RP_1,P_poll__networl_4_5_AI_3,P_poll__networl_3_2_AI_3,P_poll__networl_0_0_RP_5,P_poll__networl_3_1_AskP_0,P_poll__networl_1_0_AI_6,P_poll__networl_2_3_RP_6,P_poll__networl_2_1_RI_1,P_network_4_4_AskP_2,P_poll__networl_0_6_RP_6,P_network_6_2_AskP_5,P_network_1_0_RP_5,P_network_1_1_RP_4,P_network_0_4_RI_6,P_poll__networl_0_3_AnnP_1,P_poll__networl_0_4_RP_3,P_poll__networl_3_5_AskP_4,P_network_2_5_RI_2,P_poll__networl_2_0_RP_4,P_poll__networl_4_6_RI_2,P_poll__networl_6_0_AI_2,P_network_5_4_AskP_6,P_poll__networl_3_2_AskP_2,P_network_0_6_AnnP_5,P_network_6_0_AskP_4,P_network_4_0_RP_4,P_poll__networl_0_6_AnnP_4,P_network_0_5_AI_3,P_poll__networl_0_3_RI_4,P_poll__networl_6_4_AskP_3,P_network_3_6_RP_2,P_poll__networl_0_0_AskP_2,P_network_6_5_RI_2,P_network_4_4_AnnP_2,P_poll__networl_0_5_AskP_6,P_poll__networl_1_2_RP_6,P_poll__networl_6_1_AI_0,P_poll__networl_3_0_AI_6,P_network_4_0_AnnP_4,P_poll__networl_0_1_RP_6,P_poll__networl_6_1_AnnP_0,P_poll__networl_6_1_RP_5,P_network_2_4_AnnP_5,P_poll__networl_3_1_RI_6,P_poll__networl_3_2_RP_2,P_network_5_0_AskP_4,P_poll__networl_0_3_AI_4,P_masterList_3_6_3,P_network_3_5_RI_4,P_poll__networl_0_5_AnnP_6,P_network_3_1_AskP_1,P_network_5_1_RI_4,P_poll__networl_3_6_RP_0,P_network_5_4_AI_5,P_network_1_2_AnnP_1,P_network_2_1_AI_4,P_network_4_2_RP_6,P_network_5_6_AnnP_6,P_poll__networl_5_3_AnnP_1,P_poll__networl_2_1_RI_6,P_network_3_0_AskP_4,P_network_3_4_AskP_5,P_poll__networl_5_1_AnnP_0,P_network_3_1_AI_6,P_poll__networl_1_0_AnnP_0,P_poll__networl_6_4_RP_5,P_poll__networl_6_3_RI_4,P_network_6_4_AnnP_1,P_poll__networl_1_4_RI_0,P_network_1_1_AskP_4,P_network_2_4_RI_4,P_poll__networl_4_5_AskP_6,P_network_6_5_RP_3,P_poll__networl_4_3_AnnP_6,P_network_1_3_RI_2,P_poll__networl_4_3_AnnP_5,P_network_0_4_AnnP_2,P_poll__networl_1_5_AnnP_0,P_network_2_3_AskP_1,P_poll__networl_0_4_RP_4,P_poll__networl_0_1_AI_2,P_network_3_2_RP_5,P_network_0_3_RI_3,P_network_2_6_RI_5,P_poll__networl_0_1_AskP_0,P_poll__networl_0_1_AI_0,P_masterList_6_6_4,P_network_2_2_RP_3,P_masterList_2_6_2,P_network_3_6_AskP_4,P_poll__networl_4_3_RP_6,P_network_2_5_AskP_4,P_network_0_1_RI_4,P_poll__networl_3_5_AnnP_3,P_network_1_0_RI_1,P_network_5_2_AnnP_3,P_network_4_2_AI_2,P_network_3_1_AskP_2,P_poll__networl_1_4_AI_4,P_poll__networl_3_6_RI_1,P_network_0_0_RI_6,P_poll__networl_4_3_RP_0,P_poll__networl_6_4_AskP_5,P_network_4_6_AnnP_4,P_network_4_3_RI_2,P_poll__networl_4_5_RI_3,P_network_4_6_AI_6,P_poll__networl_1_0_AskP_4,P_poll__networl_4_6_AI_5,P_network_1_3_RP_5,P_network_0_6_AskP_4,P_network_6_4_AnnP_2,P_poll__networl_1_5_AskP_0,P_network_5_6_AskP_2,P_network_3_0_AnnP_2,P_network_5_2_AskP_3,P_network_3_5_AI_5,P_poll__networl_1_4_RI_4,P_poll__networl_4_0_RP_0,P_poll__networl_1_1_AI_3,P_network_0_4_AskP_4,P_network_6_5_AI_6,P_poll__networl_4_1_AskP_0,P_network_3_2_RI_6,P_poll__networl_3_4_AnnP_0,P_network_6_4_RI_1,P_network_0_3_RP_4,P_network_5_6_RI_1,P_poll__networl_5_3_RP_2,P_network_0_2_AskP_4,P_poll__networl_5_3_AskP_5,P_poll__networl_1_2_RI_5,P_poll__networl_6_5_AnnP_2,P_network_6_5_RP_5,P_network_6_6_RP_1,P_poll__networl_3_6_AskP_1,P_poll__networl_3_0_RI_0,P_poll__networl_2_4_AskP_5,P_poll__networl_0_4_AI_1,P_poll__networl_3_2_RP_3,P_network_3_6_AnnP_4,P_network_2_5_RI_6,P_poll__networl_4_6_AI_3,P_network_2_1_AskP_1,P_poll__networl_1_5_RP_2,P_poll__networl_5_0_AskP_4,P_poll__networl_6_6_AnnP_0,P_poll__networl_3_5_RI_1,P_poll__networl_6_5_AI_1,P_network_4_2_RI_2,P_poll__networl_4_6_RP_0,P_network_1_3_AnnP_4,P_poll__networl_5_5_AI_5,P_poll__networl_6_0_RI_6,P_network_2_6_AskP_1,P_poll__networl_6_3_RP_2,P_poll__networl_4_2_RP_5,P_network_3_6_RI_5,P_network_2_2_AskP_5,P_network_6_4_AI_6,P_network_0_6_RP_1,P_poll__networl_2_2_RI_4,P_poll__networl_6_2_AnnP_0,P_network_5_0_AskP_3,P_poll__networl_1_1_RI_4,P_network_4_0_RI_5,P_poll__networl_3_0_AnnP_0,P_electionFailed_1,P_poll__networl_3_5_AskP_6,P_network_3_0_RI_6,P_poll__networl_1_3_RI_4,P_poll__networl_5_3_AskP_2,P_poll__networl_6_2_AI_4,P_network_5_3_RI_3,P_poll__networl_6_1_AskP_5,P_network_4_2_AnnP_4,P_poll__networl_3_3_RI_2,P_poll__networl_2_6_RP_4,P_network_3_3_AI_6,P_network_1_3_AI_5,P_network_4_3_RP_6,P_network_3_3_AskP_1,P_network_2_3_RI_4,P_network_2_0_RP_2,P_network_1_6_AI_1,P_poll__networl_6_3_RP_5,P_network_0_6_RP_4,P_network_5_3_RI_2,P_poll__networl_6_3_AskP_5,P_poll__networl_4_0_RP_3,P_network_5_6_RI_5,P_poll__networl_0_5_RI_4,P_poll__networl_5_3_AnnP_0,P_poll__networl_1_1_AnnP_0,P_poll__networl_6_6_RI_3,P_poll__networl_0_2_AI_3,P_poll__networl_4_6_AnnP_0,P_poll__networl_1_6_AskP_2,P_poll__networl_0_1_AskP_5,P_poll__networl_0_1_AI_1,P_network_3_3_RP_1,P_poll__networl_4_2_AI_2,P_network_1_6_AskP_1,P_network_0_3_RP_2,P_poll__networl_3_0_AskP_4,P_network_1_4_AskP_1,P_poll__networl_4_1_AnnP_4,P_network_2_3_RP_1,P_network_4_3_RP_4,P_poll__networl_2_0_AnnP_4,P_poll__networl_4_2_AI_0,P_network_5_4_RP_6,P_poll__networl_2_0_RI_2,P_network_4_5_AnnP_2,P_poll__networl_5_4_RI_5,P_network_4_0_AskP_2,P_poll__networl_2_1_AskP_4,P_network_0_3_RI_4,P_network_1_0_RP_2,P_network_5_3_AnnP_6,P_poll__networl_3_1_AnnP_2,P_network_6_4_AI_4,P_poll__networl_0_4_AskP_3,P_network_1_5_RP_4,P_network_0_1_AskP_4,P_network_5_4_AI_3,P_network_4_5_RP_4,P_poll__networl_3_4_RI_4,P_poll__networl_4_4_AnsP_0,P_poll__networl_0_2_RP_2,P_poll__networl_5_0_AI_0,P_poll__networl_2_5_AnnP_5,P_network_1_3_RI_4,P_network_5_2_RP_6,P_network_6_1_RP_3,P_poll__networl_2_5_RI_1,P_poll__networl_0_0_RP_4,P_network_2_0_AnnP_6,P_poll__networl_0_5_AskP_4,P_network_3_1_RP_3,P_poll__networl_6_2_AnnP_6,P_network_6_4_RI_2,P_poll__networl_1_0_RP_1,P_network_4_4_AnnP_4,P_poll__networl_5_1_AskP_1,P_network_4_4_RP_5,P_network_3_6_AskP_3,P_network_3_0_RI_4,P_poll__networl_0_0_RP_0,P_network_1_2_AskP_6,P_poll__networl_5_6_AI_0,P_network_5_1_RP_4,P_poll__networl_3_5_AnnP_6,P_poll__networl_6_4_AI_5,P_network_3_4_AnnP_5,P_network_2_5_RP_3,P_network_6_3_AI_3,P_poll__networl_3_3_RI_3,P_network_0_6_RI_3,P_poll__networl_5_5_RI_1,P_network_5_3_RP_1,P_masterList_3_6_6,P_poll__networl_3_1_AI_0,P_network_2_0_AnnP_4,P_poll__networl_5_3_AnnP_6,P_network_4_0_AskP_4,P_poll__networl_5_3_RP_4,P_network_6_1_RI_4,P_poll__networl_6_0_RP_3,P_network_3_1_RI_4,P_poll__networl_4_2_RI_0,P_poll__networl_5_2_RP_5,P_network_5_3_RP_3,P_network_1_6_AnnP_5,P_network_2_2_AskP_6,P_poll__networl_5_6_AskP_2,P_network_4_3_AskP_3,P_poll__networl_5_5_RP_6,P_poll__networl_6_3_RP_0,P_network_2_6_RI_1,P_poll__networl_1_0_AskP_2,P_network_2_0_AnnP_3,P_poll__networl_0_1_AnnP_1,P_poll__networl_2_2_AskP_5,P_poll__networl_5_3_AnnP_2,P_network_4_3_RI_5,P_poll__networl_4_5_AnnP_3,P_network_2_6_RI_6,P_network_5_6_AnnP_5,P_poll__networl_6_2_AnsP_0,P_network_4_2_AskP_2,P_poll__networl_3_1_AskP_1,P_network_0_3_RI_5,P_poll__networl_4_0_RI_4,P_poll__networl_6_1_AnnP_4,P_network_3_5_AnnP_4,P_network_0_1_AnnP_1,P_network_2_3_AskP_4,P_network_0_2_AnnP_6,P_poll__networl_0_1_AskP_6,P_poll__networl_3_4_AnnP_6,P_poll__networl_6_6_AI_5,P_poll__networl_4_0_AnnP_5,P_network_4_6_AnnP_6,P_poll__networl_0_0_AI_5,P_network_6_6_AnnP_6,P_poll__networl_0_6_AnnP_5,P_poll__networl_6_2_AI_2,P_network_5_6_AI_5,P_network_1_3_AskP_3,P_poll__networl_1_4_RP_2,P_poll__networl_5_3_AI_4,P_poll__networl_2_2_AnnP_0,P_poll__networl_5_4_AI_4,P_poll__networl_2_4_RI_2,P_poll__networl_4_2_AskP_6,P_network_1_0_AnnP_6,P_poll__networl_3_6_RP_6,P_poll__networl_3_3_AnnP_6,P_poll__networl_1_4_AI_0,P_poll__networl_4_2_AI_6,P_poll__networl_3_5_RP_5,P_poll__networl_4_4_AskP_1,P_poll__networl_1_6_AI_0,P_masterList_0_6_2,P_network_1_2_AI_2,P_poll__networl_0_4_RI_0,P_poll__networl_4_5_AskP_3,P_poll__networl_2_3_RP_3,P_poll__networl_1_3_AskP_2,P_network_2_6_AI_4,P_poll__networl_0_2_RP_3,P_poll__networl_1_1_AI_6,P_poll__networl_0_0_AnnP_1,P_poll__networl_4_4_AI_1,P_network_3_0_RP_2,P_poll__networl_1_5_RI_6,P_poll__networl_1_6_AskP_6,P_network_2_3_RP_2,P_poll__networl_6_1_RP_1,P_network_3_1_AI_1,P_poll__networl_1_5_AnnP_2,P_poll__networl_5_4_AI_1,P_network_2_1_AI_6,P_network_6_2_RP_1,P_network_0_2_AI_4,P_poll__networl_1_0_RI_4,P_network_0_2_AskP_3,P_poll__networl_5_5_AnnP_3,P_poll__networl_3_1_RP_3,P_network_5_1_AskP_3,P_masterList_3_6_4,P_network_3_3_AskP_5,P_poll__networl_2_0_AnsP_0,P_poll__networl_6_2_RP_2,P_poll__networl_2_4_AskP_4,P_network_1_1_AnnP_2,P_network_4_5_RI_6,P_poll__networl_3_1_AI_5,P_poll__networl_3_3_AnsP_0,P_poll__networl_4_5_RP_4,P_poll__networl_4_1_RP_1,P_poll__networl_0_2_RI_0,P_poll__networl_6_4_RP_1,P_network_6_3_RP_3,P_poll__networl_3_6_AnnP_6,P_poll__networl_5_5_AI_2,P_poll__networl_2_3_AskP_6,P_network_2_3_AI_5,P_network_3_1_AnnP_1,P_poll__networl_2_5_AskP_0,P_dead_0,P_poll__networl_2_1_RI_5,P_poll__networl_4_4_AskP_6,P_poll__networl_3_3_RP_2,P_network_5_1_AskP_1,P_network_6_2_RI_1,P_poll__networl_1_3_AnnP_5,P_poll__networl_6_1_AnnP_3,P_poll__networl_1_3_AnnP_6,P_network_4_0_RP_3,P_network_3_4_RI_5,P_network_5_1_AnnP_5,P_poll__networl_3_0_RI_6,P_network_1_0_AI_4,P_poll__networl_0_1_RI_2,P_network_1_3_AskP_5,P_poll__networl_6_1_RI_5,P_network_5_6_AI_3,P_network_2_0_RI_4,P_poll__networl_3_6_AI_6,P_network_0_6_AskP_5,P_poll__networl_6_0_AnnP_3,P_poll__networl_6_1_RI_3,P_network_1_5_AI_2,P_poll__networl_6_3_AI_6,P_poll__networl_6_5_AI_4,P_network_1_0_RI_3,P_poll__networl_5_0_AskP_1,P_poll__networl_4_4_RP_6,P_poll__networl_5_3_RI_1,P_poll__networl_6_3_AskP_2,P_poll__networl_4_2_RI_4,P_poll__networl_6_1_AskP_3,P_poll__networl_0_2_RI_2,P_network_4_6_AnnP_5,P_poll__networl_1_3_AI_0,P_poll__networl_4_5_RI_4,P_poll__networl_5_3_AI_2,P_poll__networl_1_4_AnsP_0,P_network_2_5_AnnP_5,P_poll__networl_3_4_RI_5,P_poll__networl_4_0_AI_3,P_network_6_2_AI_2,P_poll__networl_4_5_RP_6,P_poll__networl_6_3_AnnP_3,P_poll__networl_2_5_AskP_2,P_poll__networl_0_3_AnnP_3,P_network_1_2_AnnP_3,P_network_6_1_RI_1,P_network_6_4_AI_1,P_network_4_0_AskP_3,P_poll__networl_2_2_AskP_2,P_poll__networl_0_1_AnnP_5,P_network_4_6_AskP_4,P_poll__networl_2_1_AnnP_6,P_poll__networl_4_2_RP_4,P_poll__networl_4_5_AnnP_0,P_poll__networl_4_6_AskP_4,P_poll__networl_0_6_RI_0,P_poll__networl_4_2_RI_1,P_poll__networl_6_2_RP_0,P_poll__networl_2_1_AnnP_2,P_poll__networl_5_2_RP_3,P_network_0_0_AI_6,P_network_4_3_AskP_2,P_network_3_5_RP_6,P_network_6_2_RI_6,P_network_1_3_AI_6,P_poll__networl_6_2_RI_1,P_poll__networl_0_6_RP_1,P_poll__networl_0_5_AnsP_0,P_poll__networl_5_0_AnnP_5,P_poll__networl_1_0_AI_2,P_poll__networl_0_2_RP_0,P_network_2_0_AskP_3,P_network_4_4_AI_1,P_network_3_2_AI_2,P_poll__networl_5_5_RP_4,P_masterList_4_6_5,P_network_6_3_AnnP_1,P_network_5_0_RI_6,P_network_2_6_AnnP_6,P_poll__networl_3_0_RI_4,P_poll__networl_0_2_AskP_2,P_poll__networl_3_4_AI_3,P_network_2_6_AskP_4,P_network_3_2_AnnP_3,P_network_5_2_AskP_2,P_poll__networl_1_1_AI_5,P_network_4_2_AnnP_2,P_poll__networl_6_4_RI_0,P_poll__networl_3_3_RP_0,P_poll__networl_5_6_AnnP_0,P_poll__networl_2_5_AnnP_1,P_poll__networl_5_6_AskP_6,P_network_3_1_AnnP_5,P_poll__networl_1_6_AnnP_4,P_network_3_5_AskP_2,P_network_0_0_AI_4,P_network_5_5_RI_3,P_network_4_2_RI_3,P_network_0_6_AskP_3,P_network_3_4_AnnP_3,P_network_5_3_AI_6,P_network_3_2_AI_3,P_network_2_0_RP_3,P_poll__networl_0_1_RP_2,P_masterList_2_6_4,P_poll__networl_3_4_AskP_2,P_network_1_3_AI_2,P_network_6_3_RI_1,P_network_3_3_RP_6,P_network_2_2_AnnP_3,P_poll__networl_3_6_RI_6,P_network_6_2_AI_4,P_poll__networl_2_0_AI_3,P_network_4_4_AskP_5,P_poll__networl_4_0_AskP_3,P_network_0_1_AI_4,P_poll__networl_1_6_RP_4,P_poll__networl_4_2_AskP_2,P_network_4_2_RI_1,P_poll__networl_0_2_RP_1,P_network_6_3_AskP_5,P_network_1_0_RI_6,P_network_2_3_RI_3,P_network_2_6_RI_4,P_poll__networl_5_0_AskP_3,P_network_2_1_AI_1,P_poll__networl_1_4_RI_5,P_network_2_4_AskP_1,P_poll__networl_1_0_RP_5,P_poll__networl_2_5_RI_4,P_masterList_4_6_2,P_network_1_1_RP_2,P_network_0_6_RI_4,P_network_5_1_RI_1,P_network_2_0_RP_1,P_poll__networl_3_4_RI_3,P_network_1_3_AskP_1,P_poll__networl_3_1_AnnP_4,P_poll__networl_2_0_AskP_3,P_poll__networl_4_3_AnnP_0,P_network_0_2_RP_1,P_poll__networl_5_2_AI_3,P_network_5_1_AI_4,P_network_5_2_RP_2,P_network_0_3_AnnP_1,P_network_0_4_RI_1,P_poll__networl_5_4_AI_2,P_network_6_5_RI_3,P_poll__networl_5_4_AnnP_1,P_poll__networl_4_3_AskP_4,P_poll__networl_2_3_RI_3,P_poll__networl_4_5_AskP_4,P_poll__networl_4_6_AskP_3,P_poll__networl_6_0_RI_5,P_network_4_1_RI_5,P_network_2_6_AI_1,P_network_5_2_RI_1,P_poll__networl_2_2_AI_0,P_network_5_6_AI_6,P_network_1_5_AnnP_1,P_network_1_6_RP_1,P_network_2_2_RP_6,P_network_2_3_RP_3,P_network_4_1_AnnP_1,P_poll__networl_6_6_AnsP_0,P_poll__networl_3_2_RP_6,P_network_2_1_RI_5,P_network_6_1_AskP_2,P_network_0_6_AI_5,P_network_5_1_AI_3,P_network_4_6_AskP_1,P_network_0_4_RP_6,P_poll__networl_2_1_AnnP_1,P_network_5_6_RP_2,P_poll__networl_6_0_AskP_2,P_poll__networl_5_0_RI_2,P_network_3_3_RP_5,P_network_3_5_AskP_1,P_poll__networl_1_6_AnnP_1,P_poll__networl_6_2_RP_5,P_poll__networl_3_1_AnsP_0,P_network_4_6_AskP_6,P_network_3_3_RI_6,P_poll__networl_2_4_AskP_6,P_network_0_4_RP_5,P_network_5_0_RP_1,P_poll__networl_6_1_RP_3,P_poll__networl_3_5_AnsP_0,P_poll__networl_4_1_AI_0,P_poll__networl_1_0_RI_1,P_poll__networl_5_2_RP_6,P_poll__networl_6_1_AnnP_5,P_poll__networl_0_4_AnnP_2,P_network_3_0_AskP_3,P_poll__networl_1_2_AskP_1,P_network_3_4_RP_1,P_poll__networl_5_4_AnsP_0,P_network_3_1_AnnP_6,P_poll__networl_6_3_AnsP_0,P_network_5_4_RP_2,P_network_3_0_AskP_2,P_poll__networl_3_6_AI_3,P_poll__networl_3_3_RP
_5,P_poll__networl_5_6_RI_6,P_poll__networl_2_2_AI_6,P_network_6_0_RI_6,P_network_3_3_AnnP_6,P_poll__networl_3_3_AnnP_0,P_network_2_2_AI_2,P_poll__networl_1_6_AI_1,P_network_5_1_AI_6,P_network_0_0_AskP_2,P_poll__networl_3_4_AskP_4,P_network_0_6_RI_2,P_poll__networl_5_6_RI_0,P_poll__networl_5_0_AnnP_4,P_network_3_6_AnnP_6,P_network_6_2_RP_4,P_poll__networl_0_2_AI_5,P_poll__networl_5_4_RI_2,P_network_0_5_AnnP_1,P_network_4_3_AnnP_6,P_poll__networl_0_6_RI_1,P_poll__networl_2_0_RI_1,P_poll__networl_2_1_AI_0,P_network_3_1_RP_4,P_poll__networl_0_0_AskP_1,P_poll__networl_0_2_RP_4,P_poll__networl_3_4_RI_6,P_poll__networl_3_1_AnnP_6,P_poll__networl_4_4_RP_5,P_network_6_3_AskP_3,P_poll__networl_6_3_RP_3,P_poll__networl_6_5_AnnP_0,P_network_5_0_AnnP_2,P_poll__networl_4_1_AskP_6,P_poll__networl_0_6_RP_5,P_poll__networl_6_2_AI_0,P_poll__networl_5_0_AI_5,P_poll__networl_5_4_RI_6,P_poll__networl_0_2_AskP_3,P_network_3_3_RI_1,P_network_1_4_AI_5,P_poll__networl_2_3_RP_2,P_poll__networl_6_6_RP_5,P_poll__networl_0_5_RP_6,P_network_1_1_RP_1,P_masterList_5_6_0,P_network_1_1_AskP_5,P_network_4_5_AI_2,P_poll__networl_4_3_AskP_3,P_poll__networl_1_5_RP_3,P_poll__networl_6_3_RI_5,P_network_2_2_AnnP_1,P_poll__networl_0_6_RI_4,P_poll__networl_5_2_AI_0,P_poll__networl_5_4_RP_6,P_network_0_5_AskP_3,P_poll__networl_5_3_AskP_3,P_poll__networl_1_5_AskP_6,P_poll__networl_5_6_RI_4,P_poll__networl_3_4_RP_3,P_network_4_5_AI_1,P_poll__networl_1_4_AI_1,P_network_6_2_RI_3,P_poll__networl_2_1_RI_0,P_poll__networl_4_3_AskP_6,P_poll__networl_6_5_AskP_4,P_poll__networl_1_3_RP_0,P_network_6_2_RP_6,P_poll__networl_0_5_AI_0,P_poll__networl_6_6_AI_6,P_network_3_0_RP_4,P_network_4_0_AnnP_6,P_network_0_6_RI_5,P_poll__networl_1_3_AskP_4,P_network_4_5_AskP_3,P_network_6_5_AskP_2,P_poll__networl_6_2_AI_1,P_poll__networl_2_4_RP_3,P_poll__networl_2_5_AI_2,P_poll__networl_6_5_AskP_2,P_network_3_6_AskP_5,P_network_1_2_RP_1,P_poll__networl_4_6_AskP_1,P_poll__networl_6_5_AI_0,P_network_0_1_RI_6,P_network_4_1_AskP_5,P_network_0_3_AI_3,P_poll__networl_4_3_RI_3,P_network_0_5_RP_6,P_network_3_0_AskP_5,P_network_4_1_AskP_4,P_poll__networl_1_5_RP_0,P_poll__networl_5_5_RI_0,P_network_0_1_RP_5,P_poll__networl_5_1_AI_2,P_poll__networl_5_3_RP_5,P_network_1_0_AskP_6,P_network_0_2_RI_6,P_network_5_3_AI_3,P_network_3_0_AnnP_3,P_network_1_6_AnnP_2,P_network_4_0_RP_6,P_network_0_0_AskP_3,P_poll__networl_1_3_AI_4,P_network_4_0_AI_3,P_poll__networl_4_0_AI_2,P_poll__networl_2_6_AskP_1,P_poll__networl_0_5_RI_3,P_network_1_2_AnnP_4,P_poll__networl_6_2_AI_3,P_network_5_0_RI_5,P_poll__networl_1_2_AI_1,P_network_6_4_RP_5,P_poll__networl_4_2_RP_0,P_network_0_5_AskP_2,P_poll__networl_2_1_RP_3,P_network_6_5_AskP_6,P_poll__networl_4_4_RI_5,P_network_5_1_AskP_6,P_poll__networl_3_5_AskP_3,P_network_1_3_AnnP_6,P_poll__networl_2_5_RI_2,P_poll__networl_0_3_AI_1,P_network_1_4_AnnP_3,P_poll__networl_2_0_AskP_5,P_network_3_6_RI_3,P_poll__networl_6_5_RI_5,P_poll__networl_3_6_RI_2,P_crashed_4,P_network_5_5_AskP_3,P_poll__networl_1_0_RP_6,P_poll__networl_0_0_AnnP_2,P_poll__networl_6_5_RP_0,P_network_0_0_AI_2,P_network_4_3_RI_6,P_poll__networl_3_0_RP_5,P_network_6_0_AnnP_1,P_poll__networl_3_2_AnnP_5,P_poll__networl_5_6_AskP_3,P_poll__networl_3_2_AskP_6,P_network_2_6_RI_2,P_poll__networl_1_3_RI_5,P_network_6_3_AnnP_5,P_poll__networl_0_4_RI_1,P_poll__networl_1_0_AskP_0,P_poll__networl_2_3_AI_4,P_network_5_4_RP_4,P_poll__networl_2_1_AnsP_0,P_poll__networl_1_2_RI_4,P_poll__networl_1_3_AnnP_0,P_network_5_0_RI_2,P_network_1_3_AnnP_5,P_poll__networl_5_4_AskP_0,P_network_3_1_AskP_5,P_poll__networl_5_6_AnnP_1,P_network_0_5_RI_5,P_poll__networl_1_6_AskP_5,P_poll__networl_6_1_RP_0,P_poll__networl_5_1_AskP_5,P_poll__networl_4_2_RP_3,P_poll__networl_6_3_RI_2,P_network_4_0_AI_2,P_poll__networl_1_2_RI_0,P_network_5_6_AnnP_3,P_electionFailed_0,P_poll__networl_3_1_AnnP_5,P_network_5_2_RI_5,P_poll__networl_5_4_AI_3,P_poll__networl_1_4_AskP_4,P_network_1_3_RI_6,P_masterList_6_6_1,P_poll__networl_2_1_AskP_3,P_network_5_5_AskP_4,P_poll__networl_3_0_AskP_5,P_poll__networl_5_4_AnnP_6,P_masterList_0_6_6,P_network_6_1_AnnP_6,P_poll__networl_1_5_RP_1,P_network_4_4_RP_2,P_network_1_1_AI_1,P_network_2_1_RP_6,P_network_0_3_AI_2,P_network_1_2_RP_4,P_poll__networl_3_5_AskP_2,P_poll__networl_1_0_AnnP_2,P_network_1_2_AnnP_6,P_network_2_4_AI_6,P_network_5_2_AI_3,P_poll__networl_6_4_AskP_4,P_network_3_6_RI_1,P_poll__networl_4_6_RP_5,P_network_5_3_RI_1,P_electionFailed_4,P_poll__networl_3_3_AskP_6,P_network_4_3_AI_3,P_poll__networl_2_6_AnnP_0,P_poll__networl_3_5_AnnP_1,P_network_5_2_AnnP_2,P_network_5_6_AskP_1,P_poll__networl_0_3_AskP_2,P_poll__networl_0_2_RP_5,P_poll__networl_0_5_AskP_0,P_network_6_2_AskP_6,P_masterList_6_6_6,P_network_4_5_AI_5,P_poll__networl_2_2_RP_6,P_poll__networl_6_2_AskP_0,P_poll__networl_6_6_RP_4,P_network_0_1_RI_3,P_poll__networl_6_2_RP_1,P_network_4_0_RI_6,P_network_2_5_AI_2,P_network_1_3_AI_1,P_poll__networl_1_2_AnnP_6,P_network_6_2_RP_2,P_poll__networl_2_2_RI_0,P_poll__networl_4_1_RP_2,P_network_6_2_AnnP_2,P_poll__networl_0_0_RI_1,P_network_6_3_AI_6,P_poll__networl_0_5_AnnP_0,P_network_1_3_AnnP_1,P_poll__networl_2_4_RI_0,P_poll__networl_2_3_RP_1,P_poll__networl_5_1_AnsP_0,P_poll__networl_6_1_RI_0,P_network_3_2_AnnP_4,P_network_5_4_AI_1,P_network_5_5_AnnP_6,P_poll__networl_1_4_AI_5,P_network_3_1_AskP_4,P_poll__networl_3_1_RI_3,P_network_1_3_AI_3,P_network_5_2_RP_5,P_network_2_1_AnnP_4,P_poll__networl_5_5_RI_6,P_network_5_3_RI_4,P_poll__networl_5_1_AnnP_3,P_poll__networl_3_3_AnnP_4,P_poll__networl_0_6_AskP_3,P_poll__networl_4_3_RI_1,P_poll__networl_4_0_AnnP_2,P_poll__networl_3_2_AnnP_1,P_poll__networl_6_0_AI_1,P_network_6_3_RP_5,P_network_1_6_RP_2,P_poll__networl_6_5_RI_0,P_network_0_6_RP_5,P_poll__networl_3_0_AnnP_4,P_poll__networl_0_6_AskP_4,P_network_0_2_RI_2,P_poll__networl_0_1_RP_1,P_network_3_5_AI_2,P_poll__networl_3_1_AskP_3,P_poll__networl_2_0_AI_6,P_poll__networl_5_2_AskP_2,P_network_0_2_RP_5,P_poll__networl_2_6_AnnP_4,P_network_3_5_AnnP_1,P_poll__networl_0_5_AI_1,P_network_2_1_AI_2,P_network_6_4_RP_6,P_poll__networl_2_4_AI_3,P_network_5_6_AnnP_1,P_poll__networl_6_6_AnnP_2,P_network_2_6_RP_3,P_poll__networl_4_3_RP_1,P_poll__networl_5_1_AnnP_4,P_masterList_2_6_6,P_network_0_0_AskP_5,P_poll__networl_1_4_RP_6,P_poll__networl_4_4_RP_4,P_poll__networl_2_5_AskP_1,P_electionFailed_6,P_poll__networl_4_5_AskP_5,P_poll__networl_2_3_AnnP_4,P_network_0_5_RP_5,P_poll__networl_4_0_AI_1,P_network_6_0_RP_4,P_network_0_5_AnnP_6,P_poll__networl_5_0_RI_1,P_poll__networl_6_4_RP_6,P_dead_4,P_network_2_6_AskP_2,P_network_5_1_RP_2,P_network_1_6_RI_4,P_poll__networl_3_2_AI_0,P_network_4_6_RI_4,P_poll__networl_6_6_AnnP_4,P_network_5_0_AskP_1,P_poll__networl_0_5_RP_5,P_poll__networl_1_1_AnnP_2,P_network_6_6_AnnP_4,P_network_0_2_AskP_1,P_poll__networl_3_1_AskP_2,P_network_1_4_AskP_2,P_poll__networl_3_3_AskP_0,P_network_4_4_AI_4,P_network_6_5_AnnP_6,P_poll__networl_4_6_AI_6,P_poll__networl_1_6_AskP_1,P_poll__networl_5_2_RP_2,P_poll__networl_5_1_RP_2,P_poll__networl_1_1_AnnP_6,P_poll__networl_2_0_RP_6,P_network_4_1_AI_6,P_poll__networl_6_1_AI_5,P_network_1_0_AnnP_4,P_network_6_3_AI_1,P_poll__networl_6_1_RP_4,P_network_1_2_AI_4,P_poll__networl_1_5_AI_3,P_poll__networl_3_0_AI_0,P_poll__networl_6_4_AnnP_6,P_network_5_3_AskP_2,P_poll__networl_2_1_RP_5,P_poll__networl_0_1_AskP_3,P_network_1_5_AI_4,P_network_1_0_RP_6,P_poll__networl_5_0_AnnP_0,P_network_3_0_RP_5,P_poll__networl_0_1_AskP_1,P_poll__networl_6_5_RI_6,P_poll__networl_2_2_AnsP_0,P_network_2_6_RP_1,P_network_3_3_RI_2,P_network_4_2_RP_5,P_poll__networl_0_0_AI_2,P_poll__networl_6_1_AskP_1,P_network_4_2_AnnP_3,P_network_3_2_RP_3,P_poll__networl_6_1_AI_1,P_network_4_4_RP_6,P_poll__networl_3_2_AnnP_3,P_network_6_6_AskP_5,P_poll__networl_6_6_AskP_6,P_poll__networl_2_1_AnnP_4,P_poll__networl_3_5_AnnP_0,P_poll__networl_3_6_AnnP_2,P_network_4_3_RI_1,P_poll__networl_5_5_AnnP_6,P_network_0_3_RI_6,P_poll__networl_5_5_AI_0,P_poll__networl_5_5_RI_3,P_poll__networl_6_1_RI_1,P_network_5_5_RP_6,P_poll__networl_1_6_AnsP_0,P_network_1_6_AI_3,P_network_5_1_AnnP_6,P_poll__networl_0_6_AskP_1,P_network_5_2_AnnP_6,P_poll__networl_3_6_RI_4,P_poll__networl_1_5_AI_6,P_network_2_2_AskP_3,P_network_6_6_RI_2,P_network_6_0_AskP_6,P_network_5_5_RP_2,P_network_1_2_AI_1,P_poll__networl_2_4_AI_1,P_poll__networl_6_0_AnnP_1,P_network_0_5_AnnP_4,P_poll__networl_1_2_AskP_6,P_poll__networl_0_5_RP_0,P_network_4_5_AskP_6,P_poll__networl_3_1_AnnP_1,P_poll__networl_4_4_RP_3,P_poll__networl_5_2_RP_0,P_poll__networl_4_0_AnnP_3,P_poll__networl_4_5_AnnP_6,P_network_0_1_AnnP_6,P_poll__networl_2_2_AnnP_4,P_poll__networl_4_3_AskP_2,P_network_6_5_RI_4,P_poll__networl_6_3_AI_4,P_poll__networl_0_0_AI_3,P_poll__networl_0_4_AnsP_0,P_network_4_5_RP_1,P_poll__networl_3_3_AI_4,P_network_6_6_AI_1,P_poll__networl_2_0_RI_6,P_poll__networl_5_1_AI_5,P_poll__networl_5_5_AnnP_5,P_poll__networl_2_5_RP_6,P_poll__networl_6_4_RI_3,P_network_2_1_RP_3,P_poll__networl_5_1_AnnP_1,P_network_4_1_AskP_6,P_poll__networl_4_0_AskP_4,P_poll__networl_1_4_AnnP_3,P_poll__networl_5_6_AskP_4,P_poll__networl_1_0_AskP_5,P_network_5_0_RI_1,P_network_4_2_AI_1,P_poll__networl_4_1_RI_1,P_poll__networl_0_5_AI_5,P_poll__networl_0_0_RI_2,P_poll__networl_3_3_AI_6,P_network_1_5_AnnP_4,P_poll__networl_0_1_RI_5,P_poll__networl_3_5_RP_2,P_network_2_4_AskP_3,P_poll__networl_3_2_RP_1,P_poll__networl_6_4_AnnP_1,P_poll__networl_0_2_AI_6,P_poll__networl_4_4_AI_3,P_network_2_5_RP_6,P_poll__networl_2_1_AI_5,P_network_4_1_RP_4,P_network_3_2_AI_6,P_poll__networl_3_0_RP_6,P_network_3_0_RI_1,P_poll__networl_1_1_AnnP_4,P_poll__networl_2_3_AskP_3,P_poll__networl_5_3_AI_1,P_network_1_0_AskP_5,P_poll__networl_0_1_AskP_2,P_network_6_3_RI_2,P_poll__networl_1_5_RI_2,P_poll__networl_1_1_AI_0,P_network_5_3_AI_4,P_poll__networl_1_6_AskP_3,P_poll__networl_2_6_RP_3,P_network_4_0_AI_1,P_poll__networl_0_4_AI_6,P_poll__networl_2_0_AnnP_0,P_poll__networl_3_1_AnnP_3,P_network_0_0_RP_2,P_poll__networl_0_0_RP_3,P_poll__networl_5_5_AskP_6,P_poll__networl_0_0_AnnP_6,P_network_5_3_RI_5,P_poll__networl_3_5_AnnP_4,P_poll__networl_0_2_RI_3,P_poll__networl_0_4_AnnP_5,P_poll__networl_6_2_AnnP_3,P_poll__networl_6_0_AnnP_2,P_crashed_0,P_poll__networl_3_0_AnnP_6,P_poll__networl_2_4_RP_4,P_poll__networl_3_2_AI_1,P_poll__networl_6_1_AskP_6,P_poll__networl_6_6_AskP_1,P_poll__networl_6_6_AnnP_1,P_poll__networl_0_5_AnnP_5,P_network_5_4_RI_2,P_poll__networl_5_4_AI_6,P_network_4_1_AnnP_4,P_network_5_4_AskP_4,P_poll__networl_5_6_AI_3,P_poll__networl_4_0_RP_4,P_network_3_2_RP_1,P_masterList_4_6_6,P_network_2_5_AI_5,P_network_3_1_RP_6,P_network_3_5_RI_5,P_poll__networl_4_3_RP_2,P_poll__networl_0_4_RI_3,P_poll__networl_4_5_RI_6,P_poll__networl_5_0_AnnP_2,P_poll__networl_6_4_AI_1,P_network_0_0_RI_5,P_poll__networl_6_0_AI_5,P_network_5_1_AI_5,P_network_2_1_AnnP_2,P_network_3_3_RP_2,P_network_2_1_AskP_5,P_poll__networl_5_4_AnnP_3,P_poll__networl_6_3_AI_1,P_network_5_3_AskP_5,P_poll__networl_0_6_RP_2,P_network_2_0_RI_6,P_network_3_1_AI_4,P_network_4_3_RP_1,P_network_0_4_AI_1,P_poll__networl_6_3_RP_4,P_poll__networl_4_4_AI_0,P_network_5_5_RP_5,P_network_0_4_RP_4,P_network_2_2_AskP_4,P_network_5_2_RP_1,P_network_3_1_AskP_6,P_network_3_5_RI_3,P_poll__networl_5_1_AnnP_6,P_network_4_1_RP_5,P_poll__networl_4_4_AnnP_1,P_poll__networl_4_2_AI_1,P_poll__networl_3_4_RI_0,P_network_1_4_AI_6,P_network_4_5_AnnP_6,P_poll__networl_1_5_AI_5,P_poll__networl_2_2_AI_1,P_poll__networl_0_1_RI_4,P_network_1_0_AskP_4,P_network_3_6_AnnP_1,P_network_3_4_AI_5,P_poll__networl_2_1_AI_6,P_network_1_5_AI_6,P_network_0_3_AnnP_2,P_network_1_2_RI_6,P_poll__networl_0_4_RI_4,P_network_6_2_RP_3,P_network_5_4_RP_1,P_poll__networl_0_5_RP_2,P_poll__networl_0_1_AI_5,P_network_5_2_RI_6,P_poll__networl_6_1_AskP_4,P_poll__networl_1_1_AskP_0,P_network_0_3_RP_5,P_poll__networl_2_3_AnnP_3,P_poll__networl_3_1_RI_4,P_network_0_4_AskP_1,P_network_3_0_RI_2,P_poll__networl_6_0_RP_2,P_poll__networl_5_4_AskP_3,P_poll__networl_4_1_AI_5,P_network_1_0_RI_4,P_network_1_6_AnnP_3,P_network_3_2_AskP_4,P_poll__networl_4_0_AskP_5,P_poll__networl_5_6_AskP_5,P_poll__networl_6_5_AnnP_3,P_network_5_0_RI_4,P_network_0_0_RP_3,P_network_1_1_RI_5,P_poll__networl_2_3_AI_5,P_poll__networl_4_2_AnnP_5,P_network_0_0_AnnP_4,P_poll__networl_0_3_AnnP_5,P_network_6_2_AskP_4,P_network_6_4_AskP_3,P_network_3_1_RI_1,P_network_6_6_AI_4,P_network_0_3_AI_6,P_network_4_3_AnnP_3,P_network_5_4_AnnP_2,P_network_6_1_AnnP_1,P_poll__networl_3_6_RP_3,P_network_4_6_AskP_3,P_network_6_4_RP_4,P_network_4_0_RP_2,P_network_2_5_AskP_3,P_poll__networl_3_1_RP_0,P_poll__networl_2_4_RP_2,P_poll__networl_0_3_RI_2,P_network_6_6_AskP_2,P_network_4_4_AI_6,P_poll__networl_4_2_AnnP_2,P_network_5_0_AI_4,P_network_0_3_RP_1,P_network_3_3_AnnP_5,P_network_6_1_RI_3,P_network_0_0_RP_5,P_network_0_4_RP_1,P_poll__networl_2_6_AskP_2,P_network_1_6_AI_6,P_poll__networl_5_3_RI_0,P_network_3_1_RI_6,P_network_4_2_AnnP_1,P_network_5_1_AskP_2,P_poll__networl_3_0_AskP_6,P_poll__networl_5_2_AnnP_5,P_network_2_6_AskP_5,P_network_4_2_AskP_6,P_network_5_6_AskP_5,P_network_0_4_RI_5,P_network_4_2_AI_6,P_poll__networl_4_5_RP_3,P_network_2_0_RI_1,P_poll__networl_2_0_RI_3,P_network_0_1_AI_6,P_poll__networl_4_4_RI_2,P_poll__networl_4_0_RI_2,P_network_6_0_AnnP_6,P_network_6_4_RI_3,P_network_0_3_AI_1,P_network_3_5_RI_2,P_poll__networl_6_4_RI_2,P_network_5_1_RP_3,P_network_6_0_AnnP_3,P_poll__networl_3_4_AskP_6,P_poll__networl_4_3_RI_4,P_poll__networl_3_2_AnnP_4,P_poll__networl_0_2_AnnP_5,P_poll__networl_5_1_AskP_6,P_poll__networl_1_5_RI_0,P_poll__networl_2_6_RI_4,P_poll__networl_6_4_AI_6,P_poll__networl_6_5_RP_5,P_poll__networl_4_1_AI_3,P_poll__networl_3_4_RI_1,P_network_3_0_RP_6,P_poll__networl_4_5_AI_1,P_poll__networl_3_3_RI_1,P_poll__networl_0_4_AskP_4,P_network_6_3_RP_4,P_network_1_5_AI_3,P_poll__networl_4_1_RP_0,P_poll__networl_2_4_AnnP_1,P_poll__networl_3_5_AskP_0,P_poll__networl_3_2_RI_6,P_poll__networl_5_2_AI_6,P_network_2_4_AI_3,P_poll__networl_6_1_AnnP_6,P_network_3_0_AnnP_6,P_poll__networl_0_1_AnnP_2,P_poll__networl_4_1_AnsP_0,P_poll__networl_5_4_AskP_5,P_network_4_0_AnnP_2,P_poll__networl_6_5_AnnP_5,P_network_3_6_RP_4,P_poll__networl_2_1_RI_3,P_network_6_1_RP_1,P_poll__networl_2_6_AskP_6,P_network_6_3_AI_4,P_network_0_1_RP_6,P_poll__networl_6_0_RP_1,P_poll__networl_6_2_AnnP_5,P_network_0_0_AnnP_3,P_poll__networl_1_2_AnnP_4,P_poll__networl_2_5_AI_6,P_poll__networl_0_0_RP_6,P_network_4_0_AI_6,P_network_2_0_AI_1,P_poll__networl_0_1_RP_4,P_network_3_4_AI_4,P_poll__networl_3_6_AskP_3,P_poll__networl_1_0_AnnP_1,P_poll__networl_4_1_RI_3,P_network_5_4_RP_3,P_poll__networl_4_5_AI_6,P_network_1_5_AI_5,P_network_2_4_RI_1,P_network_3_6_AI_5,P_network_3_5_AI_6,P_crashed_6,P_poll__networl_2_0_RI_5,P_poll__networl_2_5_AI_4,P_network_0_4_AnnP_1,P_poll__networl_4_1_AnnP_5,P_network_6_3_RI_3,P_poll__networl_1_5_AskP_4,P_network_4_4_AnnP_3,P_poll__networl_0_0_AnnP_5,P_poll__networl_0_0_AskP_5,P_poll__networl_1_3_AnnP_2,P_network_5_5_RP_4,P_network_1_3_RP_6,P_network_2_4_RP_4,P_network_4_1_RP_2,P_poll__networl_1_3_AI_1,P_masterList_1_6_3,P_poll__networl_1_3_AskP_5,P_poll__networl_3_1_RI_0,P_poll__networl_4_1_RI_2,P_poll__networl_6_3_RI_0,P_poll__networl_5_6_RI_5,P_network_6_0_RI_4,P_poll__networl_4_3_AskP_5,P_network_5_5_RP_1,P_poll__networl_5_3_RP_0,P_poll__networl_5_2_RI_1,P_network_0_3_AnnP_6,P_poll__networl_0_3_RP_5,P_poll__networl_1_3_RI_6,P_poll__networl_5_2_AnnP_4,P_network_0_1_AI_5,P_network_5_6_RP_6,P_poll__networl_4_0_AnnP_6,P_network_2_6_AskP_3,P_network_3_1_AI_3,P_poll__networl_0_6_AI_0,P_poll__networl_5_4_AskP_4,P_network_6_6_AskP_4,P_poll__networl_0_5_RI_2,P_masterList_5_6_3,P_network_1_4_RI_5,P_network_2_0_AI_4,P_network_5_5_RI_6,P_network_3_3_AnnP_2,P_network_4_5_AnnP_5,P_network_2_6_RP_2,P_network_0_3_RI_2,P_poll__networl_0_1_RI_6,P_poll__networl_1_6_RP_6,P_network_4_2_RI_6,P_network_5_4_AI_4,P_network_6_5_AskP_3,P_network_5_2_AnnP_1,P_poll__networl_4_3_AI_1,P_poll__networl_6_3_RP_1,P_network_1_5_AskP_6,P_poll__networl_4_4_RP_1,P_poll__networl_2_4_RI_5,P_poll__networl_4_5_RI_1,P_network_1_4_AnnP_6,P_poll__networl_0_4_AnnP_6,P_poll__networl_0_6_AnnP_0,P_poll__networl_1_4_AskP_2,P_poll__networl_3_4_AskP_5,P_network_1_4_AI_1,P_network_6_4_AskP_1,P_network_1_6_RI_1,P_poll__networl_2_5_RP_0,P_poll__networl_6_4_AnsP_0,P_network_5_3_AskP_4,P_poll__networl_0_2_AnsP_0,P_poll__networl_3_1_RI_2,P_poll__networl_2_5_AskP_6,P_network_1_5_RP_1,P_network_5_5_AskP_2,P_poll__networl_4_5_RI_2,P_poll__networl_5_2_AnnP_2,P_poll__networl_4_1
_AI_4,P_network_3_0_RP_1,P_network_6_0_AnnP_4,P_poll__networl_1_0_AnsP_0,P_poll__networl_6_0_RP_4,P_poll__networl_4_0_AI_6,P_poll__networl_5_0_AnnP_6,P_poll__networl_3_4_AskP_1,P_network_4_4_RI_6,P_network_5_3_AskP_1,P_poll__networl_2_3_RI_4,P_poll__networl_6_1_AnnP_1,P_poll__networl_2_5_AnnP_4,P_network_5_3_AnnP_4,P_network_5_4_RI_3,P_network_5_6_AI_2,P_network_5_0_RP_3,P_poll__networl_0_6_AI_5,P_network_2_2_RP_5,P_network_2_4_RI_3,P_poll__networl_3_3_AnnP_1,P_poll__networl_3_2_AnnP_0,P_poll__networl_1_3_RI_1,P_poll__networl_1_3_RI_0,P_poll__networl_2_3_RP_0,P_network_3_0_AI_4,P_network_4_5_RI_1,P_poll__networl_0_2_AnnP_4,P_poll__networl_4_3_RI_5,P_network_5_3_RP_6,P_network_1_4_AnnP_1,P_network_4_5_RP_2,P_network_3_1_AnnP_2,P_poll__networl_1_2_AI_2,P_poll__networl_4_2_AnnP_0,P_poll__networl_4_3_RI_2,P_poll__networl_1_1_RP_4,P_poll__networl_6_6_AI_4,P_poll__networl_2_3_AnnP_5,P_network_4_3_AskP_6,P_poll__networl_1_2_AskP_0,P_poll__networl_0_3_RI_3,P_network_1_6_AnnP_1,P_poll__networl_2_5_RP_4,P_poll__networl_2_3_AnnP_2,P_poll__networl_4_2_RP_6,P_network_6_5_RI_6,P_network_3_3_AI_5,P_poll__networl_4_2_AnnP_6,P_network_6_2_RI_2,P_poll__networl_4_6_AskP_6,P_poll__networl_5_6_AI_4,P_network_1_3_RP_1,P_poll__networl_5_6_AI_2,P_network_5_5_AI_4,P_poll__networl_5_6_AnnP_5,P_poll__networl_0_4_AnnP_0,P_poll__networl_2_6_AnnP_3,P_poll__networl_5_2_AskP_4,P_network_2_0_AnnP_5,P_poll__networl_3_1_RP_6,P_poll__networl_0_4_RI_5,P_network_6_6_AnnP_1,P_network_0_6_AnnP_1,P_poll__networl_0_2_AI_4,P_network_3_5_AskP_6,P_network_5_6_AI_1,P_poll__networl_6_4_AskP_6,P_poll__networl_4_0_AnnP_1,P_network_6_6_RP_3,P_poll__networl_0_3_RP_0,P_network_1_1_AI_3,P_poll__networl_0_1_RI_1,P_poll__networl_2_0_AskP_2,P_network_3_2_RI_4,P_network_2_6_AnnP_3,P_poll__networl_3_5_RP_1,P_network_1_6_RP_4,P_network_2_3_AnnP_2,P_poll__networl_3_4_AnsP_0,P_poll__networl_6_5_AI_3,P_poll__networl_1_4_RI_6,P_network_3_3_AnnP_4,P_network_4_5_RI_2,P_poll__networl_0_4_RP_2,P_network_3_5_AskP_4,P_poll__networl_1_2_AI_6,P_network_3_2_AI_4,P_poll__networl_2_5_RP_2,P_poll__networl_3_1_RP_4,P_network_5_0_AnnP_4,P_poll__networl_4_3_AnnP_4,P_poll__networl_5_6_RP_4,P_network_1_4_AI_2,P_masterList_0_6_0,P_network_3_4_RP_2,P_poll__networl_1_4_AnnP_5,P_network_0_3_AskP_5,P_poll__networl_1_0_AI_4,P_poll__networl_4_4_AI_4,P_network_0_5_RP_1,P_network_2_4_RP_1,P_poll__networl_5_0_AI_4,P_network_1_1_AnnP_3,P_poll__networl_4_2_AI_4,P_network_3_3_AI_1,P_network_0_2_RP_6,P_poll__networl_3_6_RP_1,P_poll__networl_6_2_RI_3,P_poll__networl_4_6_AI_2,P_network_3_6_RI_2,P_network_6_1_RI_2,P_network_0_2_RI_1,P_network_6_0_AI_5,P_poll__networl_2_6_AnnP_2,P_network_4_4_AnnP_1,P_poll__networl_0_2_AskP_5,P_poll__networl_2_1_AskP_1,P_network_3_2_AnnP_5,P_network_0_6_AnnP_2,P_poll__networl_3_2_AnnP_2,P_network_0_4_AI_3,P_poll__networl_0_3_AskP_3,P_poll__networl_0_3_RI_1,P_network_0_0_AnnP_1,P_poll__networl_1_3_AskP_3,P_network_3_1_RP_1,P_network_3_5_AskP_5,P_poll__networl_0_1_RI_3,P_poll__networl_2_6_RI_3,P_network_0_5_AskP_1,P_network_0_6_RP_2,P_network_6_0_AI_4,P_network_6_6_AskP_1,P_poll__networl_6_0_AI_0,P_poll__networl_6_6_RP_6,P_masterList_3_6_5,P_poll__networl_1_4_AskP_5,P_poll__networl_2_1_AnnP_0,P_poll__networl_1_2_AskP_2,P_network_6_1_AI_2,P_network_1_3_AI_4,P_poll__networl_4_5_AI_5,P_network_2_5_AskP_6,P_poll__networl_6_3_AI_5,P_poll__networl_2_2_RP_2,P_poll__networl_0_4_AskP_2,P_poll__networl_0_1_AnnP_0,P_network_3_4_AnnP_6,P_network_6_1_AskP_5,P_poll__networl_3_0_AI_2,P_network_1_6_AI_5,P_network_6_1_AskP_6,P_poll__networl_2_1_RI_4,P_masterList_0_6_4,P_poll__networl_1_3_AI_2,P_crashed_2,P_network_5_3_RP_4,P_network_2_6_AI_5,P_network_0_5_RI_3,P_network_2_6_AI_6,P_network_2_0_RP_6,P_network_6_1_AskP_4,P_poll__networl_1_1_AskP_4,P_network_3_6_RI_6,P_network_2_4_AnnP_4,P_poll__networl_1_2_RP_5,P_poll__networl_6_0_AI_6,P_poll__networl_5_5_RI_2,P_poll__networl_2_5_AskP_4,P_network_2_0_AI_2,P_poll__networl_1_2_RP_3,P_network_0_4_AnnP_6,P_poll__networl_3_2_AskP_3,P_poll__networl_5_5_AI_6,P_network_6_4_AskP_2,P_network_2_1_RP_1,P_network_4_0_RP_1,P_poll__networl_5_0_RP_6,P_masterList_2_6_5,P_poll__networl_2_6_RP_1,P_network_3_5_AnnP_6,P_network_4_4_AI_5,P_network_3_3_AskP_4,P_network_5_5_AI_1,P_poll__networl_1_4_RI_2,P_network_6_3_AnnP_3,P_poll__networl_3_3_AskP_3,P_poll__networl_6_2_RP_4,P_poll__networl_2_4_AnnP_0,P_network_6_6_AnnP_2,P_poll__networl_1_0_AnnP_5,P_network_3_4_RI_3,P_poll__networl_0_4_AnnP_3,P_poll__networl_5_3_AskP_4,P_poll__networl_0_2_AI_0,P_poll__networl_6_1_AI_4,P_network_4_6_AnnP_2,P_poll__networl_5_2_AnnP_1,P_poll__networl_5_4_AnnP_4,P_poll__networl_1_3_RP_3,P_network_2_5_AnnP_2,P_poll__networl_0_3_RP_1,P_poll__networl_1_6_AI_5,P_network_4_4_RI_3,P_network_2_3_AI_2,P_network_5_0_RI_3,P_poll__networl_0_4_RP_0,P_poll__networl_2_5_AnsP_0,P_poll__networl_5_6_RI_2,P_masterList_3_6_1,P_network_0_3_AnnP_4,P_network_6_0_RP_3,P_poll__networl_2_6_AI_6,P_network_3_2_RI_2,P_poll__networl_5_1_RI_1,P_poll__networl_3_1_RP_1,P_network_2_0_AskP_5,P_poll__networl_5_4_AskP_1,P_poll__networl_6_5_RP_1,P_poll__networl_0_2_AskP_0,P_poll__networl_3_1_AskP_4,P_network_2_2_RP_1,P_poll__networl_0_1_RP_5,P_poll__networl_2_3_AI_3,P_network_2_1_RI_2,P_poll__networl_2_5_AnnP_0,P_poll__networl_2_2_RP_1,P_poll__networl_3_3_AnnP_5,P_poll__networl_4_5_AnnP_1,P_network_5_5_RI_1,P_network_6_6_RI_1,P_network_1_6_AskP_3,P_network_0_0_RI_4,P_poll__networl_5_5_RP_1,P_network_3_4_AI_2,P_network_6_1_AnnP_4,P_poll__networl_4_4_RI_6,P_network_5_3_AI_1,P_poll__networl_1_4_AnnP_4,P_poll__networl_5_2_RI_0,P_poll__networl_0_5_RI_5,P_masterList_6_6_2,P_network_2_1_AI_5,P_network_2_3_RP_4,P_masterList_5_6_6,P_poll__networl_1_4_AnnP_1,P_network_2_3_AskP_3,P_network_5_1_AI_2,P_network_2_2_AnnP_2,P_network_5_5_AnnP_1,P_poll__networl_4_4_AI_5,P_poll__networl_1_1_RP_5,P_network_0_5_RI_4,P_network_2_2_AnnP_5,P_poll__networl_2_6_AI_5,P_network_6_2_RP_5,P_poll__networl_6_6_AskP_5,P_network_2_2_RI_6,P_poll__networl_2_3_AnnP_0,P_network_2_4_AI_4,P_poll__networl_0_3_AnsP_0,P_network_5_2_AskP_4,P_poll__networl_5_1_AI_6,P_network_3_6_AI_2,P_poll__networl_4_6_AnsP_0,P_poll__networl_2_2_RI_3,P_poll__networl_0_4_AskP_1,P_poll__networl_4_2_AskP_3,P_network_4_2_RP_2,P_network_5_1_RP_6,P_network_5_3_AskP_6,P_poll__networl_0_4_AI_0,P_poll__networl_1_5_AnsP_0,P_network_6_4_AI_3,P_network_5_4_RI_5,P_network_6_5_AnnP_3,P_poll__networl_3_1_AI_4,P_network_5_5_RI_2,P_poll__networl_2_2_AskP_4,P_poll__networl_0_5_AnnP_3,P_poll__networl_4_4_AnnP_5,P_network_5_5_AskP_6,P_network_5_4_AnnP_5,P_poll__networl_3_3_RI_4,P_poll__networl_4_4_AnnP_0,P_poll__networl_4_2_RI_6,P_network_3_1_AI_2,P_poll__networl_0_6_RP_4,P_poll__networl_6_0_AI_4,P_poll__networl_5_6_AnnP_2,P_poll__networl_6_6_RI_1,P_poll__networl_5_3_RP_6,P_poll__networl_6_5_AskP_0,P_network_1_1_AskP_1,P_network_0_6_RI_1,P_network_1_3_RI_1,P_poll__networl_4_1_AskP_4,P_network_6_3_RI_5,P_poll__networl_3_0_RI_3,P_network_3_6_AskP_1,P_poll__networl_5_2_AI_2,P_network_4_2_AI_5,P_poll__networl_0_5_AnnP_4,P_poll__networl_4_1_RP_4,P_poll__networl_3_3_AI_0,P_network_5_0_AI_2,P_poll__networl_0_5_AskP_1,P_poll__networl_5_0_RI_0,P_poll__networl_5_5_RP_0,P_network_1_0_RI_2,P_network_0_0_RI_3,P_network_4_4_AskP_4,P_poll__networl_3_6_AnnP_1,P_network_1_3_AskP_6,P_poll__networl_4_0_RI_1,P_poll__networl_0_4_AI_4,P_poll__networl_6_2_AI_6,P_network_6_4_RP_1,P_poll__networl_1_1_AskP_5,P_network_4_6_AskP_2,P_network_4_0_AskP_1,P_network_5_5_AI_2,P_poll__networl_5_3_AnnP_4,P_network_0_0_RP_1,P_poll__networl_2_1_AskP_0,P_network_1_5_AskP_1,P_network_6_5_AnnP_5,P_network_6_5_AskP_1,P_electionFailed_3,P_poll__networl_4_0_AI_5,P_poll__networl_1_5_AnnP_3,P_dead_1,P_network_1_5_AskP_2,P_network_2_3_AskP_2,P_network_4_3_RP_2,P_poll__networl_6_2_RI_2,P_poll__networl_6_0_RI_0,P_network_4_3_RP_3,P_poll__networl_1_1_AnnP_1,P_masterList_6_6_5,P_network_3_5_AnnP_2,P_network_4_1_RP_6,P_poll__networl_4_6_RI_1,P_poll__networl_0_3_AI_0,P_poll__networl_1_2_RP_0,P_network_3_4_AI_3,P_poll__networl_2_2_AI_4,P_network_2_0_AnnP_1,P_network_4_6_RI_2,P_network_4_3_AnnP_4,P_network_2_5_RP_5,P_poll__networl_5_0_AskP_6,P_poll__networl_2_4_RP_5,P_network_6_2_AnnP_1,P_poll__networl_4_1_RP_5,P_poll__networl_5_2_AskP_5,P_poll__networl_6_0_RP_5,P_poll__networl_0_6_AnnP_3,P_poll__networl_5_4_RP_2,P_poll__networl_6_5_AI_2,P_network_4_5_AI_6,P_network_0_0_RP_4,P_poll__networl_4_1_AskP_5,P_network_6_6_AnnP_3,P_poll__networl_5_3_AI_0,P_poll__networl_6_6_AskP_2,P_poll__networl_3_3_RP_3,P_network_1_6_AI_2,P_poll__networl_4_5_RP_2,P_poll__networl_1_2_AI_5,P_network_1_4_RI_3,P_network_6_2_AI_1,P_network_1_6_AskP_4,P_network_2_5_RP_1,P_poll__networl_5_1_RI_0,P_poll__networl_5_5_AskP_5,P_poll__networl_1_4_AnnP_2,P_network_3_2_AI_1,P_network_2_0_RI_2,P_poll__networl_5_3_RI_4,P_poll__networl_2_4_RI_4,P_poll__networl_1_6_RP_1,P_poll__networl_2_6_RI_0,P_network_0_6_AnnP_3,P_network_0_6_AnnP_4,P_network_6_1_AnnP_5,P_poll__networl_4_2_AskP_4,P_network_1_1_AskP_6,P_poll__networl_5_1_RP_0,P_poll__networl_6_5_AskP_6,P_poll__networl_4_3_RP_4,P_poll__networl_4_4_AI_6,P_network_2_2_RP_2,P_poll__networl_3_0_RI_1,P_poll__networl_0_6_AI_3,P_poll__networl_4_1_AnnP_2,P_network_4_1_AI_5,P_network_4_0_AskP_5,P_poll__networl_4_6_AI_1,P_poll__networl_4_1_AskP_1,P_network_4_6_RI_3,P_poll__networl_1_4_RP_0,P_poll__networl_2_3_AI_2,P_network_6_4_AnnP_6,P_poll__networl_2_3_AI_6,P_network_1_5_RI_1,P_network_1_4_RI_1,P_poll__networl_1_0_AskP_1,P_poll__networl_1_1_RP_6,P_poll__networl_3_6_AnnP_4,P_poll__networl_1_6_AnnP_2,P_network_4_1_AnnP_5,P_poll__networl_2_2_AskP_3,P_network_2_1_RP_2,P_network_5_4_AskP_2,P_poll__networl_4_6_RP_2,P_network_3_0_RP_3,P_poll__networl_0_4_AnnP_1,P_poll__networl_1_4_AskP_6,P_network_5_2_AskP_5,P_network_2_0_AskP_6,P_network_4_3_RI_4,P_network_3_6_RI_4,P_network_6_3_AnnP_4,P_network_0_5_AnnP_3,P_poll__networl_4_1_RI_4,P_poll__networl_2_2_RI_6,P_network_2_0_AskP_2,P_network_1_6_RI_2,P_poll__networl_6_2_AskP_5,P_network_3_1_AnnP_3,P_network_5_4_RI_4,P_network_3_6_AI_3,P_network_4_4_RI_4,P_network_4_2_AskP_5,P_poll__networl_3_6_AnnP_3,P_network_2_1_AskP_6,P_poll__networl_1_2_AnnP_1,P_poll__networl_2_6_RP_6,P_poll__networl_5_6_AI_1,P_poll__networl_1_0_RI_5,P_network_2_5_RP_4,P_poll__networl_4_6_RP_4,P_network_1_4_RI_4,P_poll__networl_2_5_RP_5,P_poll__networl_2_5_AnnP_2,P_network_3_3_AI_2,P_poll__networl_0_4_RP_1,P_network_4_1_AnnP_6,P_network_2_2_RI_4,P_network_4_0_AnnP_5,P_poll__networl_2_2_AnnP_2,
May 26, 2018 12:11:58 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 3549 fixed domain variables (out of 4830 variables) in GAL type NeoElection_PT_6
May 26, 2018 12:11:58 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 3549 constant array cells/variables (out of 4830 variables) in type NeoElection_PT_6
May 26, 2018 12:11:58 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_network_2_0_RI_3,P_poll__networl_1_6_RP_0,P_poll__networl_6_3_AskP_1,P_poll__networl_1_2_RP_1,P_poll__networl_1_0_RI_3,P_network_5_2_RP_4,P_poll__networl_2_2_RI_1,P_network_5_3_AskP_3,P_network_0_4_AskP_2,P_poll__networl_1_1_AskP_3,P_masterList_2_6_1,P_poll__networl_0_0_AnnP_4,P_poll__networl_4_6_RI_5,P_poll__networl_6_0_AnnP_6,P_poll__networl_5_4_AskP_6,P_network_3_1_AI_5,P_network_2_1_RI_6,P_poll__networl_2_0_AI_2,P_network_3_2_AnnP_1,P_network_2_2_AskP_2,P_poll__networl_6_4_RI_1,P_poll__networl_4_4_RP_2,P_poll__networl_2_5_AI_1,P_poll__networl_5_2_RI_3,P_network_6_5_AI_5,P_poll__networl_2_0_AnnP_2,P_poll__networl_1_1_RI_6,P_poll__networl_4_5_AnsP_0,P_network_3_6_AnnP_3,P_network_0_3_AI_4,P_poll__networl_0_5_RI_6,P_network_5_3_AI_2,P_crashed_5,P_poll__networl_5_3_RI_6,P_poll__networl_5_1_AI_4,P_poll__networl_4_3_AskP_0,P_network_3_2_AnnP_6,P_network_4_4_RI_1,P_masterList_5_2_0,P_poll__networl_1_3_AI_6,P_network_1_5_RI_2,P_network_5_4_AskP_3,P_network_6_0_AI_3,P_network_1_0_AI_2,P_masterList_1_6_0,P_network_4_3_AI_5,P_poll__networl_0_5_AnnP_1,P_masterList_3_4_2,P_poll__networl_6_6_AskP_0,P_poll__networl_6_4_AnnP_5,P_poll__networl_0_3_AskP_6,P_network_0_2_AnnP_2,P_network_3_4_RI_2,P_poll__networl_3_5_AI_3,P_poll__networl_5_5_RI_5,P_network_2_0_AskP_1,P_network_6_2_AnnP_3,P_poll__networl_2_4_RI_1,P_network_6_4_AskP_5,P_poll__networl_1_0_AskP_6,P_poll__networl_4_0_AnsP_0,P_network_0_2_RP_4,P_network_5_4_AI_2,P_network_5_5_AnnP_5,P_network_4_0_AI_4,P_poll__networl_5_1_AskP_2,P_network_1_3_RP_3,P_network_5_0_AnnP_1,P_poll__networl_2_6_RI_5,P_network_6_5_AskP_5,P_dead_3,P_network_4_5_RP_6,P_poll__networl_2_5_AnnP_3,P_network_0_0_RI_2,P_masterList_4_6_4,P_poll__networl_6_0_RP_0,P_poll__networl_4_2_AnnP_1,P_network_1_0_AnnP_3,P_poll__networl_6_0_AskP_0,P_poll__networl_6_1_RI_2,P_masterList_1_5_6,P_poll__networl_6_3_AI_0,P_network_0_0_AskP_1,P_network_0_0_AskP_4,P_network_5_1_RI_6,P_network_1_6_AskP_6,P_poll__networl_1_5_AI_0,P_poll__networl_6_4_AI_2,P_poll__networl_6_1_AnnP_2,P_masterList_2_2_3,P_network_2_0_AI_5,P_network_6_6_RI_4,P_poll__networl_2_1_AI_2,P_poll__networl_3_4_RI_2,P_network_1_3_AnnP_2,P_poll__networl_3_4_RP_0,P_network_2_3_AskP_5,P_network_1_4_AnnP_5,P_network_6_4_RP_3,P_poll__networl_4_6_AskP_0,P_network_1_4_RP_1,P_masterList_0_3_5,P_masterList_5_6_1,P_poll__networl_5_0_AnnP_1,P_poll__networl_1_2_RP_2,P_poll__networl_3_3_AskP_2,P_poll__networl_2_6_AnnP_6,P_poll__networl_3_6_AI_0,P_masterList_6_3_3,P_network_0_1_AskP_6,P_poll__networl_0_3_RI_5,P_poll__networl_2_0_RP_5,P_poll__networl_1_2_RI_6,P_poll__networl_1_0_AskP_3,P_poll__networl_3_4_AI_4,P_network_1_0_RP_4,P_poll__networl_0_5_RP_3,P_poll__networl_6_1_AI_6,P_network_5_2_AI_2,P_poll__networl_1_5_AnnP_4,P_network_2_5_RI_5,P_poll__networl_3_6_AI_2,P_poll__networl_0_6_AI_1,P_poll__networl_6_6_AskP_3,P_poll__networl_0_2_RI_5,P_poll__networl_0_0_AnnP_3,P_poll__networl_0_3_AI_5,P_poll__networl_2_6_AI_2,P_network_5_6_AskP_3,P_poll__networl_1_0_AnnP_3,P_poll__networl_6_6_AnnP_5,P_network_5_3_RP_2,P_poll__networl_0_0_AskP_0,P_network_0_4_AnnP_3,P_network_4_2_AskP_3,P_poll__networl_3_6_AI_5,P_network_1_0_AnnP_2,P_masterList_4_6_0,P_poll__networl_5_0_AI_3,P_poll__networl_3_3_AI_5,P_poll__networl_6_1_AI_2,P_poll__networl_5_1_AnnP_2,P_poll__networl_2_6_AnnP_5,P_masterList_6_2_0,P_network_4_1_RP_3,P_network_5_4_AskP_5,P_poll__networl_5_0_RP_4,P_network_2_1_AskP_4,P_network_4_0_RP_5,P_network_4_6_AnnP_3,P_poll__networl_3_6_AI_1,P_network_1_6_AskP_5,P_poll__networl_6_5_AI_6,P_poll__networl_6_0_RI_4,P_poll__networl_1_4_AskP_1,P_poll__networl_4_0_AI_0,P_network_4_2_RP_3,P_masterList_2_1_4,P_network_5_5_AI_5,P_poll__networl_4_4_RP_0,P_network_2_0_RI_5,P_poll__networl_3_2_RI_5,P_masterList_0_1_3,P_poll__networl_1_5_AI_1,P_network_3_4_RP_5,P_masterList_3_1_5,P_poll__networl_3_0_RP_2,P_poll__networl_5_0_AskP_5,P_poll__networl_6_3_AnnP_5,P_network_3_0_AnnP_5,P_network_5_4_AI_6,P_network_2_6_AI_3,P_poll__networl_1_1_AI_2,P_masterList_1_3_4,P_network_2_3_AskP_6,P_network_2_6_RP_4,P_poll__networl_4_5_RP_0,P_network_2_3_RI_2,P_poll__networl_6_0_AskP_3,P_poll__networl_0_0_AI_0,P_poll__networl_4_2_RI_2,P_poll__networl_2_5_AskP_5,P_network_6_3_RP_2,P_network_6_5_AnnP_2,P_poll__networl_5_0_RP_0,P_poll__networl_5_5_AskP_3,P_poll__networl_1_2_RI_3,P_poll__networl_6_2_RI_5,P_network_0_1_AI_2,P_poll__networl_6_3_RI_3,P_poll__networl_6_0_AI_3,P_network_3_4_RP_4,P_network_6_6_AI_2,P_poll__networl_5_1_RP_5,P_network_0_2_RI_5,P_poll__networl_5_1_RP_1,P_network_1_0_AskP_3,P_poll__networl_4_6_AI_0,P_poll__networl_3_3_AI_2,P_poll__networl_6_4_RP_0,P_masterList_4_5_6,P_network_5_3_RI_6,P_poll__networl_1_5_AskP_3,P_poll__networl_1_1_RI_2,P_poll__networl_2_1_AnnP_5,P_poll__networl_3_5_RP_3,P_poll__networl_6_1_AskP_0,P_network_3_3_RP_4,P_poll__networl_4_5_RI_5,P_poll__networl_3_2_RI_4,P_network_2_4_AskP_4,P_poll__networl_6_5_AI_5,P_network_0_4_AI_2,P_poll__networl_2_3_RI_2,P_poll__networl_2_4_RI_3,P_poll__networl_1_4_AI_3,P_poll__networl_6_4_AI_4,P_poll__networl_0_0_AnnP_0,P_poll__networl_0_6_AnsP_0,P_network_6_6_RI_5,P_poll__networl_0_3_RP_3,P_masterList_1_2_4,P_network_1_6_AskP_2,P_network_2_2_AI_4,P_network_0_0_AnnP_2,P_network_5_3_AnnP_1,P_poll__networl_3_1_RP_5,P_poll__networl_6_2_AnnP_2,P_poll__networl_2_4_AI_2,P_masterList_1_2_6,P_network_2_4_AskP_2,P_network_6_4_RI_6,P_poll__networl_2_2_RP_0,P_network_6_3_AskP_2,P_poll__networl_1_3_AI_5,P_network_1_1_AI_6,P_poll__networl_0_0_RI_0,P_poll__networl_2_4_AI_6,P_poll__networl_2_6_AnsP_0,P_poll__networl_5_2_AI_1,P_poll__networl_6_5_RI_1,P_poll__networl_6_6_AI_0,P_poll__networl_4_3_AI_4,P_network_4_3_AI_1,P_network_3_0_AI_6,P_poll__networl_6_0_AnnP_5,P_poll__networl_4_6_AskP_5,P_poll__networl_3_5_RI_4,P_poll__networl_1_2_AnsP_0,P_network_4_6_RP_5,P_poll__networl_6_1_RP_6,P_poll__networl_6_4_AnnP_4,P_masterList_2_6_0,P_network_1_1_AI_4,P_masterList_2_1_3,P_masterList_2_3_4,P_poll__networl_5_3_RI_2,P_network_2_5_RI_4,P_network_4_2_RP_1,P_poll__networl_0_4_AI_2,P_network_5_0_RP_2,P_poll__networl_2_4_AskP_0,P_poll__networl_2_4_AnnP_4,P_network_6_1_RP_6,P_network_2_3_RI_5,P_poll__networl_0_0_AI_6,P_poll__networl_3_0_AnnP_1,P_poll__networl_0_3_AskP_0,P_network_1_4_AskP_6,P_network_1_6_RP_3,P_poll__networl_1_6_AskP_0,P_network_2_1_RP_4,P_masterList_1_1_2,P_poll__networl_5_2_AI_5,P_poll__networl_6_4_RI_6,P_poll__networl_2_5_RP_1,P_network_2_2_AI_1,P_poll__networl_1_6_RI_2,P_masterList_4_3_5,P_network_0_3_AnnP_3,P_network_2_4_AnnP_1,P_network_2_3_AnnP_3,P_poll__networl_5_0_RI_3,P_poll__networl_1_6_RI_0,P_poll__networl_1_6_AskP_4,P_masterList_2_3_6,P_poll__networl_4_4_AskP_2,P_network_0_6_AI_3,P_poll__networl_2_2_AnnP_6,P_poll__networl_5_5_AI_4,P_network_2_0_AI_3,P_poll__networl_3_6_AI_4,P_network_1_1_AnnP_6,P_network_5_3_RP_5,P_network_0_4_RP_3,P_poll__networl_1_5_RI_1,P_poll__networl_6_5_RI_2,P_poll__networl_6_3_AskP_3,P_network_3_5_RI_6,P_network_6_3_AnnP_6,P_poll__networl_2_4_AI_5,P_network_1_3_AskP_4,P_poll__networl_4_1_RI_6,P_poll__networl_6_2_AnnP_4,P_network_0_4_RI_3,P_electionFailed_5,P_poll__networl_2_6_AskP_4,P_masterList_2_1_6,P_network_5_5_RI_4,P_masterList_0_6_1,P_network_0_6_AI_4,P_network_2_5_AskP_1,P_network_6_0_RI_2,P_poll__networl_3_6_RI_5,P_network_3_5_RP_2,P_masterList_0_1_6,P_network_6_1_RP_2,P_network_5_6_AI_4,P_poll__networl_2_5_RI_6,P_poll__networl_1_0_AI_1,P_poll__networl_4_3_AI_5,P_poll__networl_1_4_AI_2,P_poll__networl_5_6_AnnP_6,P_network_1_2_RP_3,P_poll__networl_5_5_AnnP_0,P_poll__networl_6_6_RP_0,P_masterList_6_5_1,P_poll__networl_0_4_AskP_6,P_network_3_2_RP_6,P_network_4_5_AskP_1,P_poll__networl_1_3_AnnP_4,P_network_2_1_AnnP_1,P_network_0_4_AskP_3,P_poll__networl_3_5_AI_1,P_network_6_6_RP_4,P_network_3_6_AnnP_5,P_poll__networl_2_3_AnsP_0,P_network_3_4_AI_6,P_poll__networl_4_0_RP_6,P_poll__networl_4_2_AI_5,P_poll__networl_6_1_AnsP_0,P_poll__networl_3_5_AI_2,P_masterList_2_2_1,P_poll__networl_3_5_RI_0,P_network_1_0_RP_1,P_masterList_2_6_3,P_masterList_6_1_3,P_poll__networl_4_5_AnnP_2,P_network_5_2_AskP_6,P_poll__networl_0_1_RP_0,P_network_4_4_AI_3,P_network_1_0_RP_3,P_poll__networl_2_2_AnnP_3,P_masterList_2_4_4,P_network_4_0_RI_2,P_network_3_5_RP_3,P_network_2_4_AskP_5,P_network_1_6_AnnP_4,P_network_3_0_AI_1,P_network_4_5_AnnP_3,P_network_6_2_AnnP_5,P_poll__networl_3_5_AI_4,P_poll__networl_1_2_AskP_3,P_poll__networl_4_6_RP_1,P_poll__networl_5_2_AnnP_0,P_network_0_6_RI_6,P_poll__networl_0_5_AnnP_2,P_network_1_4_RI_6,P_network_5_5_AI_3,P_network_2_4_RP_2,P_poll__networl_2_6_RI_2,P_poll__networl_2_3_RI_1,P_network_4_4_AnnP_6,P_poll__networl_2_4_RP_0,P_masterList_2_4_1,P_poll__networl_5_2_RI_2,P_network_0_0_AskP_6,P_poll__networl_0_3_AskP_1,P_poll__networl_5_0_RP_1,P_network_5_4_RI_6,P_poll__networl_6_3_AnnP_6,P_network_0_1_AnnP_5,P_network_4_3_AI_2,P_masterList_4_3_1,P_network_2_4_AnnP_3,P_network_6_5_AnnP_4,P_poll__networl_3_2_AI_6,P_network_4_1_AI_2,P_network_3_2_RP_4,P_network_4_3_AnnP_2,P_poll__networl_5_2_RI_4,P_network_5_0_AskP_2,P_poll__networl_3_3_AI_1,P_crashed_1,P_poll__networl_0_4_RI_2,P_network_0_4_AI_6,P_network_5_5_AskP_1,P_poll__networl_1_0_RP_4,P_poll__networl_3_4_AnnP_5,P_poll__networl_5_2_RP_1,P_poll__networl_1_0_RP_3,P_poll__networl_2_4_RI_6,P_poll__networl_5_5_RP_5,P_poll__networl_3_4_AnnP_4,P_poll__networl_0_1_AskP_4,P_poll__networl_3_4_AI_0,P_poll__networl_4_0_RI_0,P_poll__networl_1_1_RP_1,P_network_0_3_AskP_6,P_poll__networl_0_3_RI_6,P_poll__networl_6_1_AskP_2,P_network_2_3_RI_1,P_network_0_6_AskP_6,P_network_3_5_RP_4,P_network_4_1_AnnP_2,P_poll__networl_4_6_RP_6,P_masterList_5_4_1,P_poll__networl_6_3_AnnP_4,P_poll__networl_3_1_AI_3,P_poll__networl_6_5_RP_4,P_network_6_5_AI_1,P_poll__networl_6_0_RI_2,P_poll__networl_1_1_RP_0,P_network_5_4_AnnP_6,P_poll__networl_0_1_AnnP_6,P_poll__networl_3_1_AI_1,P_masterList_2_1_5,P_poll__networl_1_2_AnnP_5,P_poll__networl_6_0_AnsP_0,P_network_4_6_RI_5,P_poll__networl_6_3_AskP_4,P_network_0_6_AI_1,P_network_2_5_AskP_5,P_network_1_4_AskP_3,P_network_5_0_AI_6,P_masterList_6_2_4,P_network_1_6_RI_6,P_network_5_6_AnnP_2,P_network_6_0_AnnP_5,P_poll__networl_1_3_AnnP_1,P_network_6_2_AnnP_6,P_poll__networl_4_6_RI_3,P_poll__networl_0_2_AI_1,P_poll__networl_3_0_AnsP_0,P_poll__networl_5_4_RI_1,P_network_3_0_RI_5,P_poll__networl_0_6_RI_2,P_poll__networl_2_6_AskP_5,P_network_6_3_AskP_1,P_poll__networl_0_5_AI_4,P_network_2_3_AI_3,P_poll__networl_0_1_AnsP_0,P_network_3_5_AI_4,P_poll__networl_0_2_RI_6,P_network_6_1_AI_1,P_poll__networl_5_6_RP_0,P_poll__networl_2_3_RP_4,P_poll__networl_4_3_AnnP_1,P_poll__networl_4_4_AskP_4,P_network_5_5_AskP_5,P_network_6_3_RP_1,P_network_0_5_AI_6,P_network_0_5_AskP_4,P_poll__networl_1_0_RI_0,P_poll__networl_3_2_AnnP_6,P_poll__networl_2_6_RP_2,P_network_2_4_AI_1,P_network_6_4_AskP_6,P_network_6_2_AskP_1,P_poll__networl_4_3_AI_6,P_network_4_5_RP_3,P_poll__networl_2_3_AskP_0,P_network_3_3_AI_3,P_network_3_0_AskP_6,P_masterList_3_3_6,P_poll__networl_3_4_AskP_3,P_poll__networl_5_5_AnnP_2,P_poll__networl_5_5_AnnP_1,P_poll__networl_4_4_AskP_3,P_poll__networl_4_3_RP_5,P_network_4_4_AnnP_5,P_poll__networl_1_6_RI_4,P_dead_5,P_poll__networl_0_3_AskP_4,P_poll__networl_1_4_AnnP_6,P_poll__networl_3_5_AI_6,P_network_1_2_AI_5,P_poll__networl_6_5_AnnP_4,P_poll__networl_1_4_RI_3,P_network_0_4_AnnP_4,P_masterList_2_5_6,P_poll__networl_4_4_AnnP_2,P_poll__networl_5_1_AnnP_5,P_poll__networl_0_5_AskP_3,P_network_1_1_AskP_3,P_poll__networl_4_0_RI_6,P_poll__networl_0_2_RI_1,P_poll__networl_2_6_RP_0,P_poll__networl_6_4_AskP_2,P_network_6_2_RI_5,P_network_1_1_AskP_2,P_network_5_4_AnnP_3,P_poll__networl_5_0_RI_5,P_network_1_1_RI_2,P_poll__networl_2_4_AnsP_0,P_poll__networl_6_4_RP_4,P_poll__networl_5_0_AI_2,P_poll__networl_5_2_AskP_6,P_masterList_6_1_2,P_network_0_2_RP_2,P_network_2_4_RP_6,P_poll__networl_2_0_AskP_0,P_network_3_0_AI_2,P_poll__networl_0_1_AI_3,P_network_0_2_RP_3,P_poll__networl_3_3_AskP_1,P_network_1_0_AnnP_1,P_poll__networl_3_5_AI_5,P_poll__networl_5_5_RI_4,P_network_0_6_AI_6,P_network_3_6_RP_1,P_network_2_4_AI_5,P_network_1_0_AI_1,P_network_2_0_RP_4,P_poll__networl_6_2_AnnP_1,P_network_3_1_AnnP_4,P_poll__networl_6_2_AskP_3,P_poll__networl_0_2_AI_2,P_network_1_3_RI_5,P_network_2_3_RP_6,P_poll__networl_4_1_AI_6,P_poll__networl_1_0_AI_5,P_masterList_6_6_0,P_network_4_2_AnnP_6,P_network_1_1_RP_3,P_network_2_5_RP_2,P_network_4_5_AskP_5,P_poll__networl_2_1_AI_4,P_poll__networl_5_4_AnnP_2,P_network_2_6_AskP_6,P_poll__networl_4_3_AnnP_3,P_poll__networl_4_0_AnnP_0,P_poll__networl_5_6_RP_3,P_poll__networl_5_0_RI_4,P_poll__networl_3_4_RP_5,P_poll__networl_5_2_AnnP_3,P_network_2_5_AskP_2,P_network_4_1_AnnP_3,P_network_4_2_AskP_1,P_network_4_1_AI_3,P_poll__networl_0_4_AskP_5,P_poll__networl_1_6_AI_3,P_poll__networl_5_1_RI_6,P_network_2_5_AnnP_3,P_masterList_6_2_1,P_poll__networl_1_4_AskP_3,P_poll__networl_0_3_RP_4,P_network_4_6_RP_3,P_masterList_2_3_3,P_poll__networl_0_0_AnsP_0,P_poll__networl_4_0_AskP_2,P_network_5_0_AnnP_5,P_masterList_5_6_2,P_poll__networl_1_2_AI_3,P_network_0_1_AI_3,P_poll__networl_2_1_RP_2,P_network_3_4_AnnP_1,P_poll__networl_1_2_AskP_5,P_network_2_1_AnnP_5,P_poll__networl_5_3_AnnP_3,P_poll__networl_0_2_AnnP_1,P_poll__networl_4_6_AnnP_1,P_poll__networl_3_5_RP_6,P_poll__networl_1_5_AskP_2,P_network_3_3_AnnP_3,P_poll__networl_4_6_RI_4,P_network_6_2_AskP_3,P_masterList_3_3_0,P_poll__networl_5_4_AnnP_0,P_network_2_6_AnnP_2,P_network_4_5_RP_5,P_poll__networl_6_0_AnnP_0,P_poll__networl_1_2_AI_0,P_poll__networl_3_0_RP_3,P_poll__networl_2_6_AI_3,P_poll__networl_6_0_RP_6,P_poll__networl_4_0_AskP_0,P_network_4_5_AnnP_4,P_poll__networl_2_3_RP_5,P_network_4_2_AskP_4,P_poll__networl_0_3_RI_0,P_poll__networl_3_0_AI_4,P_network_1_6_RP_6,P_poll__networl_2_0_AskP_6,P_network_2_4_RI_5,P_poll__networl_3_6_AskP_2,P_poll__networl_4_1_AnnP_0,P_poll__networl_3_3_AskP_4,P_poll__networl_1_0_RI_6,P_network_1_5_RP_6,P_network_4_1_AskP_2,P_network_4_3_AnnP_5,P_network_0_2_AnnP_3,P_poll__networl_2_2_RI_5,P_network_4_3_RI_3,P_poll__networl_2_3_AnnP_1,P_network_2_5_AI_3,P_network_6_5_RP_1,P_poll__networl_1_5_AnnP_5,P_network_5_0_RP_5,P_poll__networl_0_2_AskP_1,P_poll__networl_2_0_AnnP_5,P_poll__networl_6_4_RP_2,P_network_3_0_AI_5,P_network_2_6_RP_5,P_poll__networl_6_4_AI_0,P_poll__networl_2_4_AnnP_3,P_network_6_1_AI_3,P_poll__networl_6_2_RP_3,P_poll__networl_6_3_RI_1,P_network_4_6_AI_1,P_poll__networl_4_4_RI_0,P_network_5_1_RP_5,P_poll__networl_4_1_RI_5,P_poll__networl_2_4_AskP_2,P_poll__networl_4_4_AnnP_6,P_network_4_3_AskP_5,P_network_1_6_AI_4,P_poll__networl_3_2_RP_5,P_network_0_5_RP_2,P_network_0_2_RI_4,P_network_3_6_RP_5,P_masterList_2_3_0,P_masterList_6_6_3,P_masterList_3_2_6,P_poll__networl_1_5_RP_5,P_poll__networl_3_2_AI_2,P_masterList_5_1_6,P_network_0_1_RP_3,P_poll__networl_2_2_AskP_1,P_network_3_2_AskP_3,P_masterList_0_5_2,P_poll__networl_3_3_AI_3,P_poll__networl_0_6_AskP_0,P_network_5_2_RI_2,P_poll__networl_4_3_RP_3,P_network_6_6_RP_2,P_masterList_6_4_2,P_network_1_5_AnnP_5,P_poll__networl_1_6_AI_2,P_poll__networl_3_5_AskP_1,P_poll__networl_4_1_AI_2,P_network_1_1_RI_3,P_poll__networl_1_6_RP_5,P_poll__networl_5_6_AI_5,P_network_3_2_AskP_1,P_poll__networl_3_0_RI_2,P_masterList_4_5_4,P_network_0_3_AnnP_5,P_masterList_0_4_1,P_network_6_4_AnnP_3,P_poll__networl_1_1_RI_0,P_poll__networl_2_2_AskP_6,P_network_4_6_AI_4,P_poll__networl_1_5_RI_3,P_network_3_0_RI_3,P_network_5_0_AI_1,P_network_4_3_RP_5,P_network_5_6_RI_6,P_poll__networl_4_3_AI_2,P_poll__networl_4_6_AskP_2,P_network_2_2_RI_1,P_network_2_1_AnnP_6,P_poll__networl_2_0_AI_5,P_network_3_2_AskP_2,P_poll__networl_6_3_AskP_0,P_network_4_6_RP_6,P_network_1_1_RI_1,P_masterList_3_1_2,P_masterList_1_5_3,P_poll__networl_0_0_AskP_3,P_poll__networl_5_4_RP_4,P_network_5_1_RI_5,P_network_1_4_AskP_5,P_poll__networl_6_2_RI_0,P_network_4_6_AskP_5,P_poll__networl_3_3_RP_6,P_poll__networl_5_3_AskP_1,P_poll__networl_6_0_RI_1,P_poll__networl_6_6_RP_2,P_network_1_4_RI_2,P_poll__networl_4_4_RI_1,P_network_0_5_RI_1,P_network_2_1_RI_4,P_poll__networl_3_1_RI_5,P_poll__networl_0_6_RI_3,P_poll__networl_4_6_RI_6,P_poll__networl_3_6_RI_0,P_masterList_4_4_0,P_poll__networl_3_0_AskP_2,P_network_6_2_AI_6,P_masterList_1_4_6,P_network_2_3_AI_1,P_network_3_6_AnnP_2,P_poll__networl_2_1_AskP_5,P_poll__networl_5_0_RP_5,P_network_0_1_AnnP_4,P_network_3_4_RI_4,P_poll__networl_0_4_RI_6,P_poll__networl_2_6_RI_6,P_poll__networl_5_5_AskP_2,P_network_3_3_AnnP_1,P_poll__networl_3_0_RI_5,P_poll__networl_5_0_RI_6,P_poll__networl_0_6_RI_5,P_poll__networl_0_6_AskP_2,P_poll__networl_5_6_AnnP_4,P_network_2_4_RI_2,P_poll__
networl_5_0_AI_1,P_network_3_4_RI_6,P_network_2_3_RP_5,P_network_6_5_AI_4,P_poll__networl_0_1_RI_0,P_network_4_2_RI_5,P_network_1_2_AskP_1,P_poll__networl_5_6_AI_6,P_poll__networl_3_1_AskP_5,P_poll__networl_4_6_RI_0,P_poll__networl_1_6_RI_5,P_network_6_1_RI_5,P_poll__networl_1_0_RP_0,P_poll__networl_4_2_AnnP_4,P_poll__networl_0_4_AnnP_4,P_masterList_4_4_4,P_network_4_5_AskP_4,P_poll__networl_4_1_AskP_2,P_poll__networl_4_1_RI_0,P_network_0_0_AI_3,P_network_6_6_AI_6,P_network_4_4_RP_3,P_network_1_5_RI_5,P_poll__networl_6_5_AskP_1,P_poll__networl_2_4_AI_0,P_masterList_0_4_2,P_network_0_2_AskP_5,P_poll__networl_0_4_RP_5,P_poll__networl_5_2_AI_4,P_poll__networl_0_3_AnnP_0,P_network_0_3_AI_5,P_poll__networl_0_0_AskP_4,P_poll__networl_6_6_RI_6,P_network_1_5_AnnP_6,P_poll__networl_0_3_AI_6,P_poll__networl_5_4_RI_4,P_network_1_1_AnnP_1,P_network_1_6_RP_5,P_network_1_0_AI_6,P_masterList_4_5_1,P_masterList_5_4_3,P_poll__networl_0_2_AnnP_0,P_poll__networl_2_0_AnnP_6,P_network_3_3_AskP_3,P_network_4_6_AnnP_1,P_network_2_5_AI_4,P_poll__networl_4_5_AnnP_4,P_poll__networl_5_2_AnsP_0,P_poll__networl_1_1_RI_5,P_poll__networl_0_6_AnnP_1,P_masterList_6_1_4,P_poll__networl_0_6_RI_6,P_network_4_0_AnnP_3,P_poll__networl_1_4_RP_1,P_poll__networl_5_2_RI_6,P_network_3_5_AI_1,P_network_1_4_RP_2,P_poll__networl_0_1_RP_3,P_network_0_4_RI_2,P_masterList_4_3_0,P_poll__networl_6_1_RI_6,P_poll__networl_3_2_AskP_0,P_masterList_3_6_0,P_network_6_2_RI_4,P_network_3_2_AskP_6,P_masterList_1_6_6,P_network_5_1_AnnP_2,P_poll__networl_5_2_AskP_3,P_masterList_4_1_5,P_poll__networl_2_3_AI_1,P_poll__networl_3_1_AnnP_0,P_network_2_2_AI_5,P_network_4_4_AskP_6,P_poll__networl_2_0_RP_2,P_poll__networl_2_5_RI_0,P_poll__networl_5_5_AnnP_4,P_network_0_3_AskP_1,P_poll__networl_5_2_AskP_1,P_network_3_5_RI_1,P_poll__networl_3_2_RI_3,P_network_0_3_RP_6,P_network_4_6_RI_6,P_poll__networl_2_4_AI_4,P_network_5_6_AskP_4,P_poll__networl_1_1_AI_4,P_network_3_4_RP_3,P_network_5_6_RI_2,P_network_1_5_AskP_4,P_poll__networl_4_4_AnnP_4,P_poll__networl_0_0_RI_4,P_network_5_5_AnnP_3,P_network_3_5_RP_1,P_poll__networl_6_5_AskP_5,P_poll__networl_2_3_RI_0,P_poll__networl_3_3_RP_4,P_network_4_4_RI_5,P_poll__networl_0_1_AI_4,P_network_6_1_AI_6,P_network_3_2_AI_5,P_network_6_2_AI_5,P_poll__networl_4_4_RI_4,P_poll__networl_1_0_RI_2,P_poll__networl_0_1_AI_6,P_masterList_6_3_0,P_poll__networl_4_6_AnnP_2,P_network_5_3_AI_5,P_network_2_4_AskP_6,P_network_3_1_AskP_3,P_masterList_0_5_4,P_poll__networl_1_1_AI_1,P_poll__networl_3_5_AI_0,P_network_1_5_RI_4,P_poll__networl_3_2_AnsP_0,P_network_5_4_AskP_1,P_network_0_2_AskP_6,P_poll__networl_4_3_AnnP_2,P_poll__networl_5_0_AskP_0,P_poll__networl_5_4_RI_0,P_network_0_4_RI_4,P_network_4_1_AI_1,P_network_6_0_RI_1,P_poll__networl_3_0_AnnP_2,P_poll__networl_6_3_AnnP_0,P_poll__networl_2_6_AI_1,P_poll__networl_0_5_RP_1,P_masterList_5_4_5,P_network_6_6_RP_5,P_poll__networl_6_3_AnnP_2,P_network_1_3_AskP_2,P_poll__networl_3_4_AnnP_2,P_poll__networl_5_4_RP_1,P_poll__networl_6_5_RI_3,P_poll__networl_1_3_RI_3,P_poll__networl_1_1_RI_3,P_network_5_1_AskP_4,P_network_3_1_RP_5,P_poll__networl_3_0_AskP_1,P_network_0_4_AskP_6,P_network_3_6_AI_6,P_poll__networl_4_2_AnnP_3,P_network_3_4_AnnP_2,P_poll__networl_4_0_RP_2,P_network_2_1_RP_5,P_poll__networl_6_3_RP_6,P_poll__networl_5_6_AskP_0,P_poll__networl_5_0_AnsP_0,P_poll__networl_5_1_RI_5,P_network_5_6_RP_4,P_poll__networl_1_4_RP_4,P_network_4_1_RI_2,P_network_1_2_AI_6,P_poll__networl_0_0_AskP_6,P_poll__networl_3_1_AskP_6,P_poll__networl_2_0_AI_4,P_poll__networl_2_2_AnnP_1,P_poll__networl_5_0_AskP_2,P_poll__networl_2_0_AskP_1,P_network_6_1_RI_6,P_network_0_1_AskP_3,P_network_1_6_RI_5,P_poll__networl_6_4_AI_3,P_poll__networl_0_0_AI_1,P_masterList_0_5_5,P_network_3_4_AskP_2,P_poll__networl_5_6_RP_1,P_network_0_5_AI_4,P_poll__networl_6_2_RI_4,P_network_3_5_AskP_3,P_network_1_2_AnnP_5,P_poll__networl_0_3_AnnP_4,P_network_5_5_RI_5,P_network_5_4_AnnP_1,P_poll__networl_6_4_AnnP_3,P_poll__networl_3_6_RP_5,P_poll__networl_0_2_AskP_4,P_poll__networl_5_3_AnnP_5,P_network_2_5_RI_1,P_poll__networl_0_5_RI_0,P_network_4_6_RI_1,P_network_5_0_AI_3,P_network_0_1_RP_4,P_network_2_4_RP_5,P_network_3_3_RP_3,P_network_4_6_RP_4,P_network_6_0_AI_1,P_poll__networl_0_5_AskP_2,P_network_1_2_AskP_3,P_network_6_3_RP_6,P_network_3_3_AskP_6,P_poll__networl_4_5_AI_4,P_poll__networl_1_4_AskP_0,P_network_6_6_AI_5,P_poll__networl_3_3_RI_5,P_poll__networl_2_2_AI_5,P_network_0_2_AnnP_1,P_poll__networl_0_2_AskP_6,P_poll__networl_6_2_AI_5,P_network_0_6_AskP_1,P_network_1_2_AI_3,P_network_2_5_AnnP_1,P_network_4_3_AnnP_1,P_network_1_2_RP_2,P_poll__networl_2_1_RP_6,P_poll__networl_4_2_AskP_0,P_network_1_5_RP_3,P_poll__networl_1_6_RI_3,P_network_2_3_AnnP_4,P_poll__networl_2_6_AI_4,P_network_5_2_AskP_1,P_network_5_0_RP_6,P_poll__networl_4_3_AskP_1,P_poll__networl_2_5_RP_3,P_poll__networl_4_0_RI_5,P_network_2_2_AnnP_6,P_poll__networl_1_1_AnnP_3,P_network_5_0_AskP_5,P_poll__networl_2_5_RI_5,P_network_6_5_RI_1,P_network_4_5_AI_4,P_network_6_5_AnnP_1,P_poll__networl_0_0_RI_3,P_poll__networl_6_5_AskP_3,P_poll__networl_0_4_AI_3,P_network_5_2_AI_5,P_network_0_5_AskP_6,P_network_5_6_AnnP_4,P_network_6_1_AI_4,P_network_5_0_AskP_6,P_poll__networl_6_3_AI_2,P_network_1_6_AnnP_6,P_poll__networl_5_5_RP_2,P_network_5_1_AnnP_1,P_poll__networl_2_1_RP_0,P_poll__networl_4_0_AnnP_4,P_poll__networl_4_1_RP_3,P_poll__networl_6_6_AI_1,P_network_6_0_AskP_1,P_network_2_2_RI_3,P_poll__networl_6_6_RI_0,P_poll__networl_1_6_RI_1,P_poll__networl_2_1_RP_1,P_network_6_1_AnnP_2,P_network_5_0_AI_5,P_poll__networl_3_0_RP_1,P_network_0_2_AI_6,P_network_4_1_RI_3,P_poll__networl_5_3_RP_1,P_poll__networl_1_5_RI_5,P_network_4_4_RP_4,P_network_6_6_AI_3,P_network_3_1_RI_5,P_network_2_3_AnnP_6,P_network_1_3_AnnP_3,P_network_5_2_AI_6,P_network_5_6_RP_3,P_masterList_5_3_4,P_network_1_4_AnnP_2,P_network_5_1_RI_3,P_network_1_0_AnnP_5,P_network_0_6_AskP_2,P_poll__networl_5_0_AnnP_3,P_masterList_0_3_3,P_poll__networl_0_2_RI_4,P_poll__networl_6_0_AskP_4,P_network_2_2_RP_4,P_poll__networl_0_3_AskP_5,P_network_0_0_AI_1,P_network_2_3_AnnP_5,P_poll__networl_1_3_RP_2,P_network_2_1_RI_1,P_poll__networl_3_1_RI_1,P_network_3_5_AnnP_5,P_network_4_5_AnnP_1,P_network_5_6_AskP_6,P_poll__networl_4_0_RP_5,P_network_6_0_RI_3,P_network_3_5_RP_5,P_network_0_5_RP_4,P_network_3_3_RI_5,P_poll__networl_3_0_RP_0,P_network_6_0_RI_5,P_poll__networl_0_2_AnnP_6,P_network_4_2_RI_4,P_poll__networl_5_4_RP_0,P_poll__networl_2_5_AI_5,P_poll__networl_4_4_AnnP_3,P_masterList_5_5_4,P_poll__networl_0_6_AskP_5,P_network_5_2_AnnP_5,P_poll__networl_5_4_AskP_2,P_network_2_2_AnnP_4,P_poll__networl_2_3_AskP_2,P_network_5_0_AnnP_6,P_poll__networl_3_1_AI_2,P_network_0_1_RP_2,P_network_5_1_RP_1,P_network_3_0_AnnP_1,P_network_4_2_AnnP_5,P_network_6_4_RI_5,P_poll__networl_6_6_AI_3,P_network_5_2_AI_1,P_poll__networl_1_4_RI_1,P_masterList_5_3_1,P_network_5_1_AnnP_4,P_network_6_0_RP_2,P_poll__networl_2_6_AskP_0,P_poll__networl_5_4_RP_3,P_poll__networl_0_4_RP_6,P_network_6_0_AI_6,P_masterList_3_5_6,P_poll__networl_4_5_AskP_2,P_network_3_5_AI_3,P_poll__networl_1_1_AskP_2,P_poll__networl_1_2_AskP_4,P_poll__networl_3_0_AnnP_5,P_network_0_5_RI_2,P_network_6_3_AI_2,P_network_3_3_AI_4,P_network_4_1_AI_4,P_masterList_5_6_5,P_network_0_6_AnnP_6,P_masterList_4_5_3,P_network_6_0_RP_6,P_poll__networl_1_1_RP_3,P_poll__networl_6_1_RI_4,P_poll__networl_2_4_RP_1,P_network_1_4_RP_3,P_network_2_0_AnnP_2,P_poll__networl_2_4_AskP_3,P_network_5_1_AI_1,P_network_6_3_AskP_6,P_poll__networl_5_6_AnnP_3,P_dead_2,P_poll__networl_4_6_AI_4,P_poll__networl_2_0_AnnP_3,P_network_3_3_AskP_2,P_poll__networl_5_5_AI_3,P_poll__networl_5_6_RI_1,P_poll__networl_6_6_RI_4,P_poll__networl_2_6_AskP_3,P_poll__networl_4_3_RI_0,P_network_0_1_AI_1,P_network_4_3_AskP_1,P_poll__networl_4_3_RI_6,P_network_2_4_RP_3,P_poll__networl_4_1_AskP_3,P_network_1_2_RI_1,P_poll__networl_2_1_RI_2,P_poll__networl_0_6_AI_2,P_poll__networl_2_3_AskP_4,P_poll__networl_4_0_RP_1,P_poll__networl_0_2_RP_6,P_network_0_5_AnnP_2,P_network_4_6_AI_3,P_masterList_3_2_2,P_masterList_6_1_5,P_network_4_5_AskP_2,P_network_0_0_RP_6,P_network_2_6_AnnP_4,P_network_1_4_AskP_4,P_poll__networl_5_1_RP_4,P_network_6_0_RP_1,P_poll__networl_1_5_AI_2,P_network_3_6_AI_4,P_poll__networl_4_0_AI_4,P_network_1_5_RP_5,P_network_1_5_AskP_5,P_poll__networl_6_0_AskP_5,P_masterList_3_5_5,P_poll__networl_5_4_AI_0,P_poll__networl_1_2_RP_4,P_poll__networl_5_1_AskP_4,P_network_2_4_AnnP_6,P_network_5_3_AnnP_3,P_masterList_2_3_2,P_poll__networl_6_4_RP_3,P_poll__networl_2_3_AI_0,P_poll__networl_2_1_AI_3,P_poll__networl_5_4_RI_3,P_network_6_4_RP_2,P_poll__networl_5_1_RI_2,P_poll__networl_1_3_RI_2,P_masterList_1_6_1,P_poll__networl_0_5_AI_2,P_masterList_5_5_5,P_network_0_2_RI_3,P_poll__networl_3_2_AskP_4,P_poll__networl_5_5_AI_1,P_network_4_0_RI_1,P_poll__networl_3_3_RI_0,P_poll__networl_1_5_AnnP_6,P_poll__networl_4_5_AnnP_5,P_poll__networl_3_4_RP_6,P_poll__networl_4_5_RP_1,P_poll__networl_5_4_AI_5,P_network_0_0_AnnP_6,P_network_6_6_RI_6,P_network_1_5_RI_6,P_network_1_4_AnnP_4,P_poll__networl_4_2_AskP_5,P_network_6_4_RI_4,P_poll__networl_1_3_AskP_0,P_poll__networl_3_5_AnnP_5,P_network_2_6_RI_3,P_poll__networl_1_6_AI_6,P_network_6_4_AnnP_4,P_network_2_2_AskP_1,P_poll__networl_1_1_AskP_1,P_poll__networl_6_3_AI_3,P_network_3_4_AskP_6,P_poll__networl_2_2_RP_5,P_masterList_3_5_2,P_network_5_2_AnnP_4,P_poll__networl_1_6_AnnP_5,P_network_5_1_AnnP_3,P_poll__networl_2_0_RI_4,P_poll__networl_3_0_AI_3,P_poll__networl_4_2_RP_2,P_masterList_4_1_2,P_poll__networl_5_3_AnsP_0,P_poll__networl_5_1_AskP_3,P_poll__networl_0_3_AnnP_2,P_network_0_1_AnnP_2,P_network_4_1_RI_4,P_masterList_4_6_1,P_poll__networl_2_0_RP_1,P_poll__networl_4_2_AnsP_0,P_network_5_4_RP_5,P_network_4_1_RI_6,P_masterList_3_3_3,P_poll__networl_1_3_RP_4,P_masterList_4_5_2,P_network_3_2_RI_5,P_poll__networl_1_4_RP_5,P_poll__networl_1_2_AnnP_3,P_poll__networl_5_6_RI_3,P_poll__networl_1_0_AnnP_4,P_network_5_4_AnnP_4,P_network_6_5_RP_4,P_poll__networl_0_0_RI_6,P_poll__networl_1_4_RP_3,P_poll__networl_1_0_AI_0,P_poll__networl_3_0_AskP_3,P_network_5_2_RI_3,P_poll__networl_1_6_RP_2,P_poll__networl_4_0_AskP_1,P_network_3_2_RI_1,P_poll__networl_5_3_AskP_6,P_network_2_2_RI_2,P_network_1_4_RP_4,P_network_0_5_RP_3,P_network_4_3_AI_4,P_poll__networl_0_6_AnnP_6,P_masterList_0_4_6,P_network_2_2_AI_6,P_network_5_5_AnnP_4,P_poll__networl_2_4_AnnP_5,P_poll__networl_6_4_RI_5,P_poll__networl_5_3_AI_3,P_poll__networl_1_1_AskP_6,P_poll__networl_6_5_AnnP_6,P_network_0_5_AI_2,P_network_4_2_RP_4,P_network_6_5_RP_2,P_poll__networl_4_4_AskP_0,P_network_3_4_AnnP_4,P_poll__networl_3_3_AskP_5,P_poll__networl_4_2_RI_3,P_network_0_6_AI_2,P_network_4_0_RI_3,P_poll__networl_2_5_AnnP_6,P_poll__networl_3_0_AnnP_3,P_network_4_4_RI_2,P_poll__networl_4_2_AI_3,P_poll__networl_6_1_AI_3,P_network_5_6_RI_3,P_poll__networl_1_6_AnnP_3,P_poll__networl_6_3_RI_6,P_electionFailed_2,P_poll__networl_6_1_RP_2,P_network_0_2_AI_5,P_poll__networl_2_6_AnnP_1,P_poll__networl_3_3_AnnP_3,P_poll__networl_1_1_RI_1,P_network_3_6_RP_6,P_poll__networl_1_2_AnnP_2,P_network_3_3_RI_3,P_network_6_5_AskP_4,P_poll__networl_3_3_RP_1,P_network_6_5_RI_5,P_network_5_0_AnnP_3,P_network_4_4_AskP_3,P_poll__networl_0_5_RI_1,P_poll__networl_1_0_AI_3,P_network_5_2_RI_4,P_network_2_4_RI_6,P_poll__networl_5_1_RI_4,P_masterList_1_6_4,P_poll__networl_2_5_AI_3,P_poll__networl_6_6_RI_5,P_poll__networl_1_1_AnsP_0,P_poll__networl_5_3_RP_3,P_network_4_0_RI_4,P_network_0_4_AskP_5,P_network_0_2_AI_3,P_network_1_1_RP_6,P_poll__networl_5_6_RP_6,P_network_4_5_AI_3,P_network_1_5_AnnP_2,P_poll__networl_2_2_AskP_0,P_network_1_2_RI_2,P_network_6_2_AnnP_4,P_poll__networl_4_3_AnsP_0,P_masterList_5_1_0,P_poll__networl_3_6_AskP_0,P_network_5_6_RP_5,P_poll__networl_3_2_AI_5,P_poll__networl_3_1_RP_2,P_poll__networl_1_3_AskP_1,P_network_6_3_AskP_4,P_poll__networl_0_5_RP_4,P_poll__networl_1_2_RI_1,P_poll__networl_2_3_AnnP_6,P_masterList_1_3_5,P_network_1_5_AskP_3,P_network_2_1_AnnP_3,P_masterList_0_2_5,P_masterList_6_2_3,P_network_1_2_AnnP_2,P_network_4_1_AskP_1,P_poll__networl_2_1_AI_1,P_poll__networl_6_0_AskP_6,P_poll__networl_2_1_AskP_6,P_poll__networl_3_6_AskP_6,P_network_1_4_RP_6,P_poll__networl_4_2_RI_5,P_poll__networl_5_0_AI_6,P_network_0_4_AnnP_5,P_network_0_1_RI_2,P_network_4_4_AskP_1,P_network_2_5_AnnP_6,P_poll__networl_3_2_RP_0,P_network_5_0_RP_4,P_network_3_5_AnnP_3,P_network_5_5_AI_6,P_masterList_5_4_4,P_network_0_1_AnnP_3,P_masterList_4_6_3,P_network_2_6_AnnP_5,P_poll__networl_5_2_AskP_0,P_masterList_0_3_6,P_network_3_1_RI_2,P_poll__networl_5_3_AI_6,P_network_2_4_AI_2,P_masterList_0_6_5,P_network_1_2_RI_4,P_network_4_5_RI_3,P_network_6_5_AI_2,P_poll__networl_6_4_AnnP_2,P_network_5_1_AskP_5,P_network_0_1_AskP_1,P_poll__networl_2_2_AnnP_5,P_poll__networl_4_3_AI_3,P_poll__networl_4_4_AskP_5,P_poll__networl_1_3_AskP_6,P_network_2_3_RI_6,P_network_5_5_RP_3,P_poll__networl_6_6_RI_2,P_masterList_2_5_2,P_masterList_2_4_6,P_poll__networl_4_2_AskP_1,P_network_0_5_AnnP_5,P_network_2_3_AI_4,P_poll__networl_6_5_RP_2,P_poll__networl_6_6_AI_2,P_masterList_0_5_1,P_poll__networl_0_3_AI_3,P_poll__networl_3_1_AI_6,P_network_1_2_AskP_4,P_network_2_3_AI_6,P_network_3_4_AskP_4,P_poll__networl_1_3_AnsP_0,P_poll__networl_1_3_AI_3,P_network_1_1_RI_6,P_poll__networl_0_3_AnnP_6,P_poll__networl_5_1_RI_3,P_network_6_0_AnnP_2,P_network_6_0_AskP_5,P_network_1_2_RI_5,P_poll__networl_5_2_AnnP_6,P_poll__networl_3_5_AskP_5,P_poll__networl_4_5_AI_0,P_masterList_0_2_6,P_network_3_6_AskP_6,P_network_6_0_AI_2,P_poll__networl_0_0_RI_5,P_poll__networl_2_2_RP_4,P_poll__networl_1_0_AnnP_6,P_network_1_3_RI_3,P_network_6_3_RI_4,P_poll__networl_0_3_RP_6,P_poll__networl_3_6_RP_4,P_poll__networl_1_3_AnnP_3,P_network_3_6_RP_3,P_masterList_1_1_3,P_network_2_6_RP_6,P_network_3_4_AskP_3,P_network_1_2_RI_3,P_masterList_5_2_3,P_network_6_3_AI_5,P_network_1_6_RI_3,P_poll__networl_6_2_AskP_6,P_masterList_2_3_5,P_poll__networl_1_2_AnnP_0,P_network_1_1_AnnP_5,P_poll__networl_3_2_RP_4,P_poll__networl_3_5_RI_5,P_network_2_5_AI_6,P_poll__networl_1_6_RP_3,P_network_6_1_AnnP_3,P_poll__networl_0_6_AnnP_2,P_masterList_5_4_6,P_poll__networl_6_4_AnnP_0,P_poll__networl_6_3_AnnP_1,P_masterList_1_4_2,P_masterList_1_6_2,P_masterList_3_5_4,P_poll__networl_5_3_AskP_0,P_poll__networl_1_4_AI_6,P_poll__networl_3_4_AskP_0,P_poll__networl_2_0_RI_0,P_poll__networl_1_6_AnnP_6,P_network_1_3_RP_4,P_poll__networl_5_1_AI_0,P_poll__networl_2_5_AskP_3,P_poll__networl_5_2_RP_4,P_poll__networl_3_4_RP_1,P_poll__networl_4_1_AnnP_3,P_masterList_6_3_2,P_network_2_1_AskP_3,P_poll__networl_0_4_AI_5,P_poll__networl_5_5_AskP_4,P_poll__networl_2_0_AnnP_1,P_poll__networl_6_6_RP_3,P_network_6_4_AnnP_5,P_poll__networl_1_3_RP_5,P_network_2_1_AI_3,P_network_0_4_AI_4,P_network_0_2_AI_2,P_poll__networl_3_6_AskP_4,P_poll__networl_3_5_RI_2,P_network_2_6_AI_2,P_network_5_6_RI_4,P_poll__networl_4_4_AI_2,P_network_1_0_AskP_1,P_poll__networl_0_2_AnnP_2,P_poll__networl_3_2_RI_2,P_masterList_1_2_3,P_poll__networl_1_2_RI_2,P_poll__networl_0_5_AI_3,P_network_4_1_RI_1,P_poll__networl_3_5_RP_0,P_network_5_2_AI_4,P_poll__networl_2_1_AskP_2,P_network_6_6_AskP_6,P_poll__networl_2_0_RP_0,P_poll__networl_6_5_AnnP_1,P_network_5_6_RP_1,P_poll__networl_3_4_AI_5,P_poll__networl_4_6_RP_3,P_network_6_1_RP_5,P_network_6_3_AnnP_2,P_poll__networl_2_6_RP_5,P_network_3_4_RI_1,P_network_1_4_AI_3,P_poll__networl_0_5_AskP_5,P_poll__networl_6_5_AnsP_0,P_network_3_1_RP_2,P_masterList_1_1_1,P_network_1_5_AI_1,P_masterList_6_4_6,P_masterList_1_5_5,P_poll__networl_5_1_RP_3,P_masterList_1_6_5,P_network_4_6_AI_2,P_poll__networl_2_4_AskP_1,P_network_4_2_AI_4,P_network_1_1_RI_4,P_poll__networl_3_0_AskP_0,P_masterList_1_5_0,P_network_1_2_AskP_5,P_poll__networl_5_6_AskP_1,P_network_1_0_AI_5,P_network_0_5_AI_1,P_poll__networl_4_3_AI_0,P_poll__networl_4_6_AnnP_4,P_network_3_0_AskP_1,P_network_5_5_AnnP_2,P_poll__networl_5_4_RP_5,P_poll__networl_2_0_AskP_4,P_network_1_1_AI_5,P_poll__networl_3_0_RP_4,P_poll__networl_5_1_AI_3,P_poll__networl_4_1_AnnP_1,P_poll__networl_1_5_AskP_5,P_poll__networl_3_4_AI_1,P_poll__networl_1_1_AnnP_5,P_poll__networl_1_4_AnnP_0,P_poll__networl_3_3_AnnP_2,P_poll__networl_4_1_AnnP_6,P_network_1_0_AI_3,P_poll__networl_2_5_RI_3,P_network_5_2_RP_3,P_poll__networl_3_6_RI_3,P_poll__networl_1_6_AI_4,P_poll__networl_2_2_AI_3,P_poll__networl_5_2_RI_5,P_network_1_1_AI_2,P_network_3_0_AI_3,P_dead_6,P_network_6_6_RI_3,P_network_4_6_RP_1,P_network_1_5_RI_3,P_poll__networl_0_1_AnnP_4,P_network_4_1_AskP
_3,P_network_0_3_AskP_2,P_poll__networl_0_1_AnnP_3,P_poll__networl_2_1_AnnP_3,P_poll__networl_2_1_RP_4,P_network_4_1_RP_1,P_masterList_5_4_2,P_network_0_0_RI_1,P_network_2_1_AskP_2,P_network_4_4_AI_2,P_poll__networl_5_6_RP_2,P_poll__networl_6_5_RI_4,P_network_6_4_AI_5,P_poll__networl_0_0_AI_4,P_poll__networl_1_2_AI_4,P_network_3_2_RI_3,P_poll__networl_6_0_AskP_1,P_poll__networl_6_4_AskP_1,P_network_5_3_AnnP_5,P_network_0_3_AskP_3,P_poll__networl_6_2_AskP_4,P_network_6_5_AI_3,P_network_0_0_AI_5,P_network_2_0_RP_5,P_network_0_6_RP_6,P_poll__networl_3_5_RP_4,P_poll__networl_6_2_RI_6,P_network_1_4_AI_4,P_poll__networl_1_3_RP_6,P_poll__networl_3_4_AI_2,P_poll__networl_4_6_AnnP_6,P_network_2_6_AnnP_1,P_network_0_4_RP_2,P_network_4_6_RP_2,P_poll__networl_6_4_AskP_0,P_network_0_3_RP_3,P_network_4_3_AskP_4,P_network_6_6_AskP_3,P_network_4_0_AI_5,P_poll__networl_5_0_RP_2,P_poll__networl_3_6_AnnP_5,P_network_3_2_RP_2,P_network_6_0_AskP_3,P_poll__networl_0_3_RP_2,P_masterList_4_1_0,P_poll__networl_5_0_RP_3,P_masterList_0_2_4,P_poll__networl_2_3_RI_5,P_network_1_1_AnnP_4,P_poll__networl_2_0_RP_3,P_network_2_5_AnnP_4,P_poll__networl_3_4_AnnP_3,P_masterList_0_6_3,P_network_1_4_RP_5,P_poll__networl_3_5_RI_6,P_network_0_5_AI_5,P_poll__networl_0_6_RP_0,P_network_1_1_RP_5,P_poll__networl_2_4_AnnP_2,P_poll__networl_4_6_AnnP_3,P_network_6_3_RI_6,P_poll__networl_0_6_AI_4,P_masterList_4_2_3,P_network_6_5_RP_6,P_poll__networl_0_4_AskP_0,P_poll__networl_6_0_RI_3,P_network_4_5_RI_4,P_masterList_0_3_4,P_network_1_0_AskP_2,P_poll__networl_1_5_RI_4,P_poll__networl_3_5_RI_3,P_poll__networl_0_2_AnnP_3,P_network_3_0_AnnP_4,P_poll__networl_3_4_RP_2,P_network_4_3_AI_6,P_poll__networl_2_2_RI_2,P_network_0_2_AnnP_5,P_poll__networl_3_6_RP_2,P_network_1_5_RP_2,P_poll__networl_6_6_AnnP_3,P_poll__networl_3_2_AskP_5,P_poll__networl_3_6_AskP_5,P_poll__networl_0_0_RP_1,P_poll__networl_0_5_AI_6,P_poll__networl_3_0_AI_1,P_poll__networl_4_0_AskP_6,P_poll__networl_2_4_AnnP_6,P_network_2_3_AnnP_1,P_poll__networl_0_6_AskP_6,P_poll__networl_6_6_AnnP_6,P_poll__networl_1_5_AnnP_1,P_poll__networl_6_2_AskP_2,P_network_6_1_AI_5,P_poll__networl_4_6_AnnP_5,P_network_3_2_AskP_5,P_network_4_0_AskP_6,P_network_2_0_AskP_4,P_poll__networl_2_4_RP_6,P_network_0_0_AnnP_5,P_network_0_5_AskP_5,P_poll__networl_2_0_AI_0,P_poll__networl_2_3_AskP_1,P_poll__networl_4_1_RP_6,P_network_0_1_RI_5,P_network_5_3_AnnP_2,P_poll__networl_0_3_AI_2,P_network_0_1_AskP_5,P_network_4_2_AI_3,P_poll__networl_1_6_RI_6,P_masterList_4_2_6,P_network_1_2_RP_5,P_network_2_2_RI_5,P_network_6_6_AnnP_5,P_network_3_4_RP_6,P_crashed_3,P_network_6_4_AI_2,P_masterList_1_2_5,P_network_0_3_AskP_4,P_masterList_3_1_0,P_network_0_2_AnnP_4,P_poll__networl_3_2_AskP_1,P_network_5_4_RI_1,P_poll__networl_5_3_RI_5,P_network_2_4_AnnP_2,P_poll__networl_4_4_RI_3,P_poll__networl_6_2_AskP_1,P_network_6_1_RP_4,P_poll__networl_2_5_AI_0,P_network_1_0_RI_5,P_poll__networl_4_5_AI_2,P_network_0_2_AI_1,P_network_4_0_AnnP_1,P_poll__networl_3_0_AI_5,P_poll__networl_3_6_AnnP_0,P_network_0_6_RP_3,P_poll__networl_2_0_AI_1,P_masterList_4_1_4,P_poll__networl_1_5_AskP_1,P_masterList_3_1_1,P_poll__networl_6_0_AnnP_4,P_poll__networl_3_3_RI_6,P_poll__networl_6_2_RP_6,P_network_3_6_AskP_2,P_poll__networl_5_1_AI_1,P_poll__networl_5_5_AnsP_0,P_network_2_1_RI_3,P_poll__networl_4_0_RI_3,P_poll__networl_1_1_RP_2,P_poll__networl_5_5_RP_3,P_network_0_5_RI_6,P_masterList_1_5_1,P_poll__networl_4_1_AI_1,P_masterList_4_3_4,P_masterList_1_1_0,P_poll__networl_3_2_RI_0,P_network_6_0_RP_5,P_masterList_6_4_1,P_network_6_2_AskP_2,P_network_6_2_AI_3,P_network_3_6_AI_1,P_masterList_3_6_2,P_poll__networl_5_1_AskP_0,P_poll__networl_5_1_RP_6,P_network_0_1_RI_1,P_poll__networl_4_5_RP_5,P_poll__networl_3_6_AnsP_0,P_network_0_3_RI_1,P_poll__networl_3_5_AnnP_2,P_network_0_4_AI_5,P_masterList_1_4_3,P_network_0_1_AskP_2,P_poll__networl_5_3_RI_3,P_network_6_1_AskP_3,P_poll__networl_1_6_AnnP_0,P_poll__networl_6_3_AskP_6,P_poll__networl_1_0_RP_2,P_poll__networl_4_5_AskP_0,P_poll__networl_6_5_RP_3,P_masterList_1_3_6,P_poll__networl_3_4_AnnP_1,P_masterList_5_6_4,P_poll__networl_1_5_RP_6,P_masterList_3_4_3,P_network_3_1_RI_3,P_poll__networl_1_5_RP_4,P_poll__networl_6_6_RP_1,P_poll__networl_4_2_RP_1,P_network_4_6_AI_5,P_poll__networl_0_6_AI_6,P_network_6_0_AskP_2,P_network_2_5_RI_3,P_poll__networl_1_5_AI_4,P_network_2_0_AI_6,P_network_2_2_AI_3,P_network_3_3_RI_4,P_network_5_1_RI_2,P_poll__networl_5_6_AnsP_0,P_poll__networl_3_2_AI_4,P_network_3_2_AnnP_2,P_network_3_4_AskP_1,P_poll__networl_2_2_AI_2,P_network_6_1_AskP_1,P_network_6_6_RP_6,P_poll__networl_5_4_AnnP_5,P_poll__networl_6_5_RP_6,P_network_1_2_AskP_2,P_network_1_5_AnnP_3,P_poll__networl_5_6_RP_5,P_network_0_2_AskP_2,P_poll__networl_2_3_AskP_5,P_poll__networl_5_5_AskP_0,P_poll__networl_6_6_AskP_4,P_network_4_5_RI_5,P_poll__networl_2_2_RP_3,P_network_4_4_RP_1,P_poll__networl_3_4_RP_4,P_poll__networl_2_6_RI_1,P_poll__networl_0_6_RP_3,P_network_6_4_AskP_4,P_poll__networl_4_5_RI_0,P_poll__networl_5_3_AI_5,P_poll__networl_0_0_RP_2,P_poll__networl_4_5_AskP_1,P_network_0_1_RP_1,P_network_2_5_AI_1,P_poll__networl_3_2_RI_1,P_masterList_1_3_2,P_network_1_3_RP_2,P_poll__networl_2_6_AI_0,P_poll__networl_2_3_RI_6,P_poll__networl_3_4_AI_6,P_poll__networl_6_4_RI_4,P_network_1_2_RP_6,P_poll__networl_5_5_AskP_1,P_network_3_4_AI_1,P_poll__networl_1_3_RP_1,P_poll__networl_4_5_AI_3,P_poll__networl_3_2_AI_3,P_poll__networl_0_0_RP_5,P_poll__networl_3_1_AskP_0,P_poll__networl_1_0_AI_6,P_poll__networl_2_3_RP_6,P_poll__networl_2_1_RI_1,P_network_4_4_AskP_2,P_poll__networl_0_6_RP_6,P_network_6_2_AskP_5,P_network_1_0_RP_5,P_network_1_1_RP_4,P_network_0_4_RI_6,P_masterList_3_5_1,P_poll__networl_0_3_AnnP_1,P_poll__networl_0_4_RP_3,P_poll__networl_3_5_AskP_4,P_network_2_5_RI_2,P_poll__networl_2_0_RP_4,P_poll__networl_4_6_RI_2,P_poll__networl_6_0_AI_2,P_network_5_4_AskP_6,P_poll__networl_3_2_AskP_2,P_network_0_6_AnnP_5,P_network_6_0_AskP_4,P_network_4_0_RP_4,P_poll__networl_0_6_AnnP_4,P_network_0_5_AI_3,P_poll__networl_0_3_RI_4,P_poll__networl_6_4_AskP_3,P_network_3_6_RP_2,P_poll__networl_0_0_AskP_2,P_network_6_5_RI_2,P_network_4_4_AnnP_2,P_poll__networl_0_5_AskP_6,P_poll__networl_1_2_RP_6,P_poll__networl_6_1_AI_0,P_poll__networl_3_0_AI_6,P_network_4_0_AnnP_4,P_poll__networl_0_1_RP_6,P_poll__networl_6_1_AnnP_0,P_poll__networl_6_1_RP_5,P_network_2_4_AnnP_5,P_poll__networl_3_1_RI_6,P_poll__networl_3_2_RP_2,P_network_5_0_AskP_4,P_poll__networl_0_3_AI_4,P_masterList_3_6_3,P_network_3_5_RI_4,P_poll__networl_0_5_AnnP_6,P_network_3_1_AskP_1,P_network_5_1_RI_4,P_poll__networl_3_6_RP_0,P_network_5_4_AI_5,P_network_1_2_AnnP_1,P_network_2_1_AI_4,P_network_4_2_RP_6,P_network_5_6_AnnP_6,P_poll__networl_5_3_AnnP_1,P_poll__networl_2_1_RI_6,P_masterList_4_4_3,P_network_3_0_AskP_4,P_network_3_4_AskP_5,P_masterList_6_1_1,P_poll__networl_5_1_AnnP_0,P_network_3_1_AI_6,P_poll__networl_1_0_AnnP_0,P_poll__networl_6_4_RP_5,P_masterList_3_4_5,P_poll__networl_6_3_RI_4,P_network_6_4_AnnP_1,P_poll__networl_1_4_RI_0,P_network_1_1_AskP_4,P_network_2_4_RI_4,P_poll__networl_4_5_AskP_6,P_network_6_5_RP_3,P_poll__networl_4_3_AnnP_6,P_network_1_3_RI_2,P_poll__networl_4_3_AnnP_5,P_network_0_4_AnnP_2,P_poll__networl_1_5_AnnP_0,P_masterList_0_5_6,P_network_2_3_AskP_1,P_poll__networl_0_4_RP_4,P_poll__networl_0_1_AI_2,P_network_3_2_RP_5,P_network_0_3_RI_3,P_network_2_6_RI_5,P_masterList_0_4_0,P_poll__networl_0_1_AskP_0,P_poll__networl_0_1_AI_0,P_masterList_6_6_4,P_network_2_2_RP_3,P_masterList_2_6_2,P_network_3_6_AskP_4,P_poll__networl_4_3_RP_6,P_network_2_5_AskP_4,P_network_0_1_RI_4,P_poll__networl_3_5_AnnP_3,P_network_1_0_RI_1,P_network_5_2_AnnP_3,P_network_4_2_AI_2,P_network_3_1_AskP_2,P_poll__networl_1_4_AI_4,P_poll__networl_3_6_RI_1,P_network_0_0_RI_6,P_poll__networl_4_3_RP_0,P_poll__networl_6_4_AskP_5,P_masterList_6_5_6,P_network_4_6_AnnP_4,P_network_4_3_RI_2,P_poll__networl_4_5_RI_3,P_network_4_6_AI_6,P_poll__networl_1_0_AskP_4,P_poll__networl_4_6_AI_5,P_network_1_3_RP_5,P_network_0_6_AskP_4,P_network_6_4_AnnP_2,P_poll__networl_1_5_AskP_0,P_network_5_6_AskP_2,P_network_3_0_AnnP_2,P_network_5_2_AskP_3,P_network_3_5_AI_5,P_poll__networl_1_4_RI_4,P_poll__networl_4_0_RP_0,P_poll__networl_1_1_AI_3,P_network_0_4_AskP_4,P_network_6_5_AI_6,P_poll__networl_4_1_AskP_0,P_network_3_2_RI_6,P_poll__networl_3_4_AnnP_0,P_masterList_0_1_1,P_network_6_4_RI_1,P_network_0_3_RP_4,P_network_5_6_RI_1,P_poll__networl_5_3_RP_2,P_network_0_2_AskP_4,P_poll__networl_5_3_AskP_5,P_poll__networl_1_2_RI_5,P_poll__networl_6_5_AnnP_2,P_network_6_5_RP_5,P_network_6_6_RP_1,P_poll__networl_3_6_AskP_1,P_poll__networl_3_0_RI_0,P_poll__networl_2_4_AskP_5,P_masterList_5_2_5,P_poll__networl_0_4_AI_1,P_poll__networl_3_2_RP_3,P_network_3_6_AnnP_4,P_network_2_5_RI_6,P_poll__networl_4_6_AI_3,P_network_2_1_AskP_1,P_poll__networl_1_5_RP_2,P_poll__networl_5_0_AskP_4,P_poll__networl_6_6_AnnP_0,P_poll__networl_3_5_RI_1,P_poll__networl_6_5_AI_1,P_network_4_2_RI_2,P_masterList_0_1_5,P_poll__networl_4_6_RP_0,P_network_1_3_AnnP_4,P_poll__networl_5_5_AI_5,P_poll__networl_6_0_RI_6,P_network_2_6_AskP_1,P_poll__networl_6_3_RP_2,P_poll__networl_4_2_RP_5,P_network_3_6_RI_5,P_masterList_3_1_4,P_network_2_2_AskP_5,P_network_6_4_AI_6,P_network_0_6_RP_1,P_poll__networl_2_2_RI_4,P_poll__networl_6_2_AnnP_0,P_network_5_0_AskP_3,P_poll__networl_1_1_RI_4,P_network_4_0_RI_5,P_poll__networl_3_0_AnnP_0,P_electionFailed_1,P_poll__networl_3_5_AskP_6,P_network_3_0_RI_6,P_poll__networl_1_3_RI_4,P_poll__networl_5_3_AskP_2,P_poll__networl_6_2_AI_4,P_network_5_3_RI_3,P_poll__networl_6_1_AskP_5,P_network_4_2_AnnP_4,P_poll__networl_3_3_RI_2,P_poll__networl_2_6_RP_4,P_masterList_2_5_3,P_network_3_3_AI_6,P_network_1_3_AI_5,P_network_4_3_RP_6,P_network_3_3_AskP_1,P_network_2_3_RI_4,P_network_2_0_RP_2,P_masterList_6_4_4,P_network_1_6_AI_1,P_poll__networl_6_3_RP_5,P_network_0_6_RP_4,P_network_5_3_RI_2,P_poll__networl_6_3_AskP_5,P_poll__networl_4_0_RP_3,P_network_5_6_RI_5,P_poll__networl_0_5_RI_4,P_poll__networl_5_3_AnnP_0,P_poll__networl_1_1_AnnP_0,P_poll__networl_6_6_RI_3,P_poll__networl_0_2_AI_3,P_poll__networl_4_6_AnnP_0,P_poll__networl_1_6_AskP_2,P_poll__networl_0_1_AskP_5,P_poll__networl_0_1_AI_1,P_network_3_3_RP_1,P_poll__networl_4_2_AI_2,P_network_1_6_AskP_1,P_network_0_3_RP_2,P_poll__networl_3_0_AskP_4,P_network_1_4_AskP_1,P_poll__networl_4_1_AnnP_4,P_network_2_3_RP_1,P_network_4_3_RP_4,P_poll__networl_2_0_AnnP_4,P_poll__networl_4_2_AI_0,P_network_5_4_RP_6,P_poll__networl_2_0_RI_2,P_network_4_5_AnnP_2,P_masterList_1_2_0,P_poll__networl_5_4_RI_5,P_network_4_0_AskP_2,P_poll__networl_2_1_AskP_4,P_network_0_3_RI_4,P_network_1_0_RP_2,P_network_5_3_AnnP_6,P_poll__networl_3_1_AnnP_2,P_network_6_4_AI_4,P_masterList_2_4_5,P_poll__networl_0_4_AskP_3,P_network_1_5_RP_4,P_masterList_6_5_3,P_network_0_1_AskP_4,P_network_5_4_AI_3,P_network_4_5_RP_4,P_masterList_1_2_2,P_poll__networl_3_4_RI_4,P_poll__networl_4_4_AnsP_0,P_poll__networl_0_2_RP_2,P_poll__networl_5_0_AI_0,P_poll__networl_2_5_AnnP_5,P_network_1_3_RI_4,P_network_5_2_RP_6,P_masterList_4_1_6,P_network_6_1_RP_3,P_masterList_3_3_2,P_poll__networl_2_5_RI_1,P_poll__networl_0_0_RP_4,P_network_2_0_AnnP_6,P_poll__networl_0_5_AskP_4,P_network_3_1_RP_3,P_poll__networl_6_2_AnnP_6,P_network_6_4_RI_2,P_poll__networl_1_0_RP_1,P_network_4_4_AnnP_4,P_poll__networl_5_1_AskP_1,P_network_4_4_RP_5,P_network_3_6_AskP_3,P_network_3_0_RI_4,P_poll__networl_0_0_RP_0,P_network_1_2_AskP_6,P_poll__networl_5_6_AI_0,P_network_5_1_RP_4,P_poll__networl_3_5_AnnP_6,P_poll__networl_6_4_AI_5,P_network_3_4_AnnP_5,P_network_2_5_RP_3,P_network_6_3_AI_3,P_poll__networl_3_3_RI_3,P_network_0_6_RI_3,P_poll__networl_5_5_RI_1,P_network_5_3_RP_1,P_masterList_3_6_6,P_poll__networl_3_1_AI_0,P_network_2_0_AnnP_4,P_poll__networl_5_3_AnnP_6,P_network_4_0_AskP_4,P_poll__networl_5_3_RP_4,P_masterList_4_3_2,P_network_6_1_RI_4,P_poll__networl_6_0_RP_3,P_network_3_1_RI_4,P_poll__networl_4_2_RI_0,P_poll__networl_5_2_RP_5,P_network_5_3_RP_3,P_network_1_6_AnnP_5,P_network_2_2_AskP_6,P_masterList_1_4_5,P_poll__networl_5_6_AskP_2,P_network_4_3_AskP_3,P_poll__networl_5_5_RP_6,P_poll__networl_6_3_RP_0,P_network_2_6_RI_1,P_poll__networl_1_0_AskP_2,P_network_2_0_AnnP_3,P_masterList_3_1_3,P_poll__networl_0_1_AnnP_1,P_poll__networl_2_2_AskP_5,P_poll__networl_5_3_AnnP_2,P_network_4_3_RI_5,P_poll__networl_4_5_AnnP_3,P_masterList_4_5_5,P_network_2_6_RI_6,P_network_5_6_AnnP_5,P_poll__networl_6_2_AnsP_0,P_network_4_2_AskP_2,P_poll__networl_3_1_AskP_1,P_network_0_3_RI_5,P_poll__networl_4_0_RI_4,P_poll__networl_6_1_AnnP_4,P_network_3_5_AnnP_4,P_network_0_1_AnnP_1,P_network_2_3_AskP_4,P_masterList_0_3_1,P_network_0_2_AnnP_6,P_poll__networl_0_1_AskP_6,P_poll__networl_3_4_AnnP_6,P_masterList_1_3_1,P_poll__networl_6_6_AI_5,P_poll__networl_4_0_AnnP_5,P_network_4_6_AnnP_6,P_poll__networl_0_0_AI_5,P_network_6_6_AnnP_6,P_poll__networl_0_6_AnnP_5,P_poll__networl_6_2_AI_2,P_network_5_6_AI_5,P_network_1_3_AskP_3,P_poll__networl_1_4_RP_2,P_poll__networl_5_3_AI_4,P_poll__networl_2_2_AnnP_0,P_poll__networl_5_4_AI_4,P_poll__networl_2_4_RI_2,P_poll__networl_4_2_AskP_6,P_network_1_0_AnnP_6,P_poll__networl_3_6_RP_6,P_poll__networl_3_3_AnnP_6,P_poll__networl_1_4_AI_0,P_poll__networl_4_2_AI_6,P_poll__networl_3_5_RP_5,P_poll__networl_4_4_AskP_1,P_poll__networl_1_6_AI_0,P_masterList_0_4_5,P_masterList_0_6_2,P_network_1_2_AI_2,P_poll__networl_0_4_RI_0,P_poll__networl_4_5_AskP_3,P_poll__networl_2_3_RP_3,P_poll__networl_1_3_AskP_2,P_network_2_6_AI_4,P_masterList_2_4_2,P_poll__networl_0_2_RP_3,P_poll__networl_1_1_AI_6,P_poll__networl_0_0_AnnP_1,P_poll__networl_4_4_AI_1,P_network_3_0_RP_2,P_poll__networl_1_5_RI_6,P_poll__networl_1_6_AskP_6,P_network_2_3_RP_2,P_poll__networl_6_1_RP_1,P_network_3_1_AI_1,P_poll__networl_1_5_AnnP_2,P_poll__networl_5_4_AI_1,P_network_2_1_AI_6,P_network_6_2_RP_1,P_masterList_1_5_2,P_network_0_2_AI_4,P_poll__networl_1_0_RI_4,P_network_0_2_AskP_3,P_poll__networl_5_5_AnnP_3,P_poll__networl_3_1_RP_3,P_network_5_1_AskP_3,P_masterList_3_6_4,P_network_3_3_AskP_5,P_poll__networl_2_0_AnsP_0,P_poll__networl_6_2_RP_2,P_masterList_5_3_6,P_poll__networl_2_4_AskP_4,P_network_1_1_AnnP_2,P_network_4_5_RI_6,P_poll__networl_3_1_AI_5,P_poll__networl_3_3_AnsP_0,P_poll__networl_4_5_RP_4,P_poll__networl_4_1_RP_1,P_poll__networl_0_2_RI_0,P_masterList_3_2_0,P_poll__networl_6_4_RP_1,P_network_6_3_RP_3,P_poll__networl_3_6_AnnP_6,P_poll__networl_5_5_AI_2,P_poll__networl_2_3_AskP_6,P_network_2_3_AI_5,P_masterList_4_2_0,P_network_3_1_AnnP_1,P_poll__networl_2_5_AskP_0,P_dead_0,P_poll__networl_2_1_RI_5,P_poll__networl_4_4_AskP_6,P_poll__networl_3_3_RP_2,P_network_5_1_AskP_1,P_network_6_2_RI_1,P_poll__networl_1_3_AnnP_5,P_poll__networl_6_1_AnnP_3,P_poll__networl_1_3_AnnP_6,P_network_4_0_RP_3,P_masterList_5_1_3,P_network_3_4_RI_5,P_network_5_1_AnnP_5,P_poll__networl_3_0_RI_6,P_network_1_0_AI_4,P_masterList_4_5_0,P_poll__networl_0_1_RI_2,P_network_1_3_AskP_5,P_poll__networl_6_1_RI_5,P_network_5_6_AI_3,P_network_2_0_RI_4,P_poll__networl_3_6_AI_6,P_network_0_6_AskP_5,P_poll__networl_6_0_AnnP_3,P_poll__networl_6_1_RI_3,P_network_1_5_AI_2,P_poll__networl_6_3_AI_6,P_poll__networl_6_5_AI_4,P_network_1_0_RI_3,P_poll__networl_5_0_AskP_1,P_poll__networl_4_4_RP_6,P_poll__networl_5_3_RI_1,P_poll__networl_6_3_AskP_2,P_poll__networl_4_2_RI_4,P_poll__networl_6_1_AskP_3,P_poll__networl_0_2_RI_2,P_network_4_6_AnnP_5,P_poll__networl_1_3_AI_0,P_masterList_5_2_6,P_poll__networl_4_5_RI_4,P_poll__networl_5_3_AI_2,P_poll__networl_1_4_AnsP_0,P_network_2_5_AnnP_5,P_poll__networl_3_4_RI_5,P_poll__networl_4_0_AI_3,P_network_6_2_AI_2,P_poll__networl_4_5_RP_6,P_poll__networl_6_3_AnnP_3,P_poll__networl_2_5_AskP_2,P_poll__networl_0_3_AnnP_3,P_network_1_2_AnnP_3,P_network_6_1_RI_1,P_network_6_4_AI_1,P_masterList_2_5_1,P_network_4_0_AskP_3,P_masterList_0_5_3,P_poll__networl_2_2_AskP_2,P_masterList_6_2_5,P_poll__networl_0_1_AnnP_5,P_network_4_6_AskP_4,P_poll__networl_2_1_AnnP_6,P_poll__networl_4_2_RP_4,P_poll__networl_4_5_AnnP_0,P_poll__networl_4_6_AskP_4,P_poll__networl_0_6_RI_0,P_poll__networl_4_2_RI_1,P_poll__networl_6_2_RP_0,P_poll__networl_2_1_AnnP_2,P_poll__networl_5_2_RP_3,P_network_0_0_AI_6,P_network_4_3_AskP_2,P_network_3_5_RP_6,P_network_6_2_RI_6,P_network_1_3_AI_6,P_poll__networl_6_2_RI_1,P_poll__networl_0_6_RP_1,P_poll__networl_0_5_AnsP_0,P_poll__networl_5_0_AnnP_5,P_masterList_0_3_0,P_poll__networl_1_0_AI_2,P_masterList_6_1_6,P_poll__networl_0_2_RP_0,P_network_2_0_AskP_3,P_network_4_4_AI_1,P_networ
k_3_2_AI_2,P_poll__networl_5_5_RP_4,P_masterList_4_6_5,P_network_6_3_AnnP_1,P_masterList_4_3_6,P_network_5_0_RI_6,P_network_2_6_AnnP_6,P_poll__networl_3_0_RI_4,P_poll__networl_0_2_AskP_2,P_poll__networl_3_4_AI_3,P_network_2_6_AskP_4,P_network_3_2_AnnP_3,P_network_5_2_AskP_2,P_poll__networl_1_1_AI_5,P_network_4_2_AnnP_2,P_poll__networl_6_4_RI_0,P_poll__networl_3_3_RP_0,P_poll__networl_5_6_AnnP_0,P_poll__networl_2_5_AnnP_1,P_poll__networl_5_6_AskP_6,P_network_3_1_AnnP_5,P_poll__networl_1_6_AnnP_4,P_network_3_5_AskP_2,P_network_0_0_AI_4,P_network_5_5_RI_3,P_network_4_2_RI_3,P_network_0_6_AskP_3,P_network_3_4_AnnP_3,P_network_5_3_AI_6,P_network_3_2_AI_3,P_network_2_0_RP_3,P_poll__networl_0_1_RP_2,P_masterList_2_6_4,P_poll__networl_3_4_AskP_2,P_network_1_3_AI_2,P_network_6_3_RI_1,P_network_3_3_RP_6,P_network_2_2_AnnP_3,P_poll__networl_3_6_RI_6,P_masterList_5_4_0,P_network_6_2_AI_4,P_poll__networl_2_0_AI_3,P_network_4_4_AskP_5,P_poll__networl_4_0_AskP_3,P_network_0_1_AI_4,P_poll__networl_1_6_RP_4,P_poll__networl_4_2_AskP_2,P_masterList_3_3_1,P_network_4_2_RI_1,P_poll__networl_0_2_RP_1,P_network_6_3_AskP_5,P_network_1_0_RI_6,P_network_2_3_RI_3,P_network_2_6_RI_4,P_poll__networl_5_0_AskP_3,P_network_2_1_AI_1,P_masterList_2_3_1,P_masterList_2_2_5,P_poll__networl_1_4_RI_5,P_network_2_4_AskP_1,P_poll__networl_1_0_RP_5,P_poll__networl_2_5_RI_4,P_masterList_4_6_2,P_network_1_1_RP_2,P_network_0_6_RI_4,P_network_5_1_RI_1,P_network_2_0_RP_1,P_poll__networl_3_4_RI_3,P_masterList_5_3_3,P_masterList_6_3_4,P_network_1_3_AskP_1,P_poll__networl_3_1_AnnP_4,P_poll__networl_2_0_AskP_3,P_poll__networl_4_3_AnnP_0,P_network_0_2_RP_1,P_poll__networl_5_2_AI_3,P_network_5_1_AI_4,P_network_5_2_RP_2,P_network_0_3_AnnP_1,P_network_0_4_RI_1,P_poll__networl_5_4_AI_2,P_network_6_5_RI_3,P_poll__networl_5_4_AnnP_1,P_poll__networl_4_3_AskP_4,P_poll__networl_2_3_RI_3,P_poll__networl_4_5_AskP_4,P_poll__networl_4_6_AskP_3,P_poll__networl_6_0_RI_5,P_network_4_1_RI_5,P_network_2_6_AI_1,P_network_5_2_RI_1,P_masterList_1_1_6,P_poll__networl_2_2_AI_0,P_network_5_6_AI_6,P_masterList_0_1_0,P_masterList_5_5_1,P_network_1_5_AnnP_1,P_network_1_6_RP_1,P_network_2_2_RP_6,P_network_2_3_RP_3,P_network_4_1_AnnP_1,P_poll__networl_6_6_AnsP_0,P_poll__networl_3_2_RP_6,P_network_2_1_RI_5,P_network_6_1_AskP_2,P_network_0_6_AI_5,P_network_5_1_AI_3,P_masterList_5_2_1,P_masterList_2_1_0,P_network_4_6_AskP_1,P_network_0_4_RP_6,P_poll__networl_2_1_AnnP_1,P_network_5_6_RP_2,P_poll__networl_6_0_AskP_2,P_poll__networl_5_0_RI_2,P_network_3_3_RP_5,P_network_3_5_AskP_1,P_poll__networl_1_6_AnnP_1,P_poll__networl_6_2_RP_5,P_poll__networl_3_1_AnsP_0,P_network_4_6_AskP_6,P_network_3_3_RI_6,P_poll__networl_2_4_AskP_6,P_network_0_4_RP_5,P_network_5_0_RP_1,P_poll__networl_6_1_RP_3,P_poll__networl_3_5_AnsP_0,P_poll__networl_4_1_AI_0,P_poll__networl_1_0_RI_1,P_masterList_1_4_0,P_poll__networl_5_2_RP_6,P_poll__networl_6_1_AnnP_5,P_poll__networl_0_4_AnnP_2,P_network_3_0_AskP_3,P_poll__networl_1_2_AskP_1,P_network_3_4_RP_1,P_poll__networl_5_4_AnsP_0,P_network_3_1_AnnP_6,P_poll__networl_6_3_AnsP_0,P_network_5_4_RP_2,P_network_3_0_AskP_2,P_poll__networl_3_6_AI_3,P_poll__networl_3_3_RP_5,P_poll__networl_5_6_RI_6,P_poll__networl_2_2_AI_6,P_network_6_0_RI_6,P_network_3_3_AnnP_6,P_poll__networl_3_3_AnnP_0,P_network_2_2_AI_2,P_poll__networl_1_6_AI_1,P_network_5_1_AI_6,P_network_0_0_AskP_2,P_poll__networl_3_4_AskP_4,P_network_0_6_RI_2,P_poll__networl_5_6_RI_0,P_poll__networl_5_0_AnnP_4,P_network_3_6_AnnP_6,P_network_6_2_RP_4,P_poll__networl_0_2_AI_5,P_poll__networl_5_4_RI_2,P_network_0_5_AnnP_1,P_network_4_3_AnnP_6,P_poll__networl_0_6_RI_1,P_poll__networl_2_0_RI_1,P_poll__networl_2_1_AI_0,P_network_3_1_RP_4,P_poll__networl_0_0_AskP_1,P_poll__networl_0_2_RP_4,P_poll__networl_3_4_RI_6,P_poll__networl_3_1_AnnP_6,P_poll__networl_4_4_RP_5,P_network_6_3_AskP_3,P_poll__networl_6_3_RP_3,P_poll__networl_6_5_AnnP_0,P_masterList_4_4_5,P_network_5_0_AnnP_2,P_poll__networl_4_1_AskP_6,P_poll__networl_0_6_RP_5,P_poll__networl_6_2_AI_0,P_poll__networl_5_0_AI_5,P_poll__networl_5_4_RI_6,P_poll__networl_0_2_AskP_3,P_network_3_3_RI_1,P_network_1_4_AI_5,P_poll__networl_2_3_RP_2,P_poll__networl_6_6_RP_5,P_poll__networl_0_5_RP_6,P_masterList_6_5_5,P_network_1_1_RP_1,P_masterList_4_2_1,P_masterList_5_6_0,P_network_1_1_AskP_5,P_network_4_5_AI_2,P_poll__networl_4_3_AskP_3,P_poll__networl_1_5_RP_3,P_poll__networl_6_3_RI_5,P_masterList_1_4_1,P_network_2_2_AnnP_1,P_poll__networl_0_6_RI_4,P_poll__networl_5_2_AI_0,P_poll__networl_5_4_RP_6,P_network_0_5_AskP_3,P_poll__networl_5_3_AskP_3,P_poll__networl_1_5_AskP_6,P_poll__networl_5_6_RI_4,P_poll__networl_3_4_RP_3,P_network_4_5_AI_1,P_poll__networl_1_4_AI_1,P_masterList_0_2_1,P_network_6_2_RI_3,P_poll__networl_2_1_RI_0,P_poll__networl_4_3_AskP_6,P_poll__networl_6_5_AskP_4,P_poll__networl_1_3_RP_0,P_network_6_2_RP_6,P_poll__networl_0_5_AI_0,P_masterList_2_4_0,P_poll__networl_6_6_AI_6,P_network_3_0_RP_4,P_network_4_0_AnnP_6,P_network_0_6_RI_5,P_poll__networl_1_3_AskP_4,P_network_4_5_AskP_3,P_network_6_5_AskP_2,P_poll__networl_6_2_AI_1,P_poll__networl_2_4_RP_3,P_poll__networl_2_5_AI_2,P_poll__networl_6_5_AskP_2,P_network_3_6_AskP_5,P_network_1_2_RP_1,P_poll__networl_4_6_AskP_1,P_poll__networl_6_5_AI_0,P_network_0_1_RI_6,P_network_4_1_AskP_5,P_network_0_3_AI_3,P_poll__networl_4_3_RI_3,P_network_0_5_RP_6,P_network_3_0_AskP_5,P_network_4_1_AskP_4,P_poll__networl_1_5_RP_0,P_poll__networl_5_5_RI_0,P_network_0_1_RP_5,P_poll__networl_5_1_AI_2,P_poll__networl_5_3_RP_5,P_network_1_0_AskP_6,P_network_0_2_RI_6,P_network_5_3_AI_3,P_network_3_0_AnnP_3,P_network_1_6_AnnP_2,P_network_4_0_RP_6,P_network_0_0_AskP_3,P_poll__networl_1_3_AI_4,P_network_4_0_AI_3,P_poll__networl_4_0_AI_2,P_poll__networl_2_6_AskP_1,P_poll__networl_0_5_RI_3,P_network_1_2_AnnP_4,P_poll__networl_6_2_AI_3,P_network_5_0_RI_5,P_poll__networl_1_2_AI_1,P_network_6_4_RP_5,P_poll__networl_4_2_RP_0,P_network_0_5_AskP_2,P_poll__networl_2_1_RP_3,P_masterList_0_3_2,P_masterList_2_2_4,P_network_6_5_AskP_6,P_poll__networl_4_4_RI_5,P_network_5_1_AskP_6,P_poll__networl_3_5_AskP_3,P_network_1_3_AnnP_6,P_poll__networl_2_5_RI_2,P_poll__networl_0_3_AI_1,P_network_1_4_AnnP_3,P_poll__networl_2_0_AskP_5,P_masterList_6_5_0,P_network_3_6_RI_3,P_poll__networl_6_5_RI_5,P_poll__networl_3_6_RI_2,P_crashed_4,P_network_5_5_AskP_3,P_poll__networl_1_0_RP_6,P_masterList_5_5_0,P_poll__networl_0_0_AnnP_2,P_poll__networl_6_5_RP_0,P_network_0_0_AI_2,P_network_4_3_RI_6,P_poll__networl_3_0_RP_5,P_network_6_0_AnnP_1,P_masterList_4_4_6,P_poll__networl_3_2_AnnP_5,P_poll__networl_5_6_AskP_3,P_poll__networl_3_2_AskP_6,P_network_2_6_RI_2,P_masterList_3_3_5,P_poll__networl_1_3_RI_5,P_network_6_3_AnnP_5,P_poll__networl_0_4_RI_1,P_poll__networl_1_0_AskP_0,P_poll__networl_2_3_AI_4,P_network_5_4_RP_4,P_poll__networl_2_1_AnsP_0,P_poll__networl_1_2_RI_4,P_poll__networl_1_3_AnnP_0,P_network_5_0_RI_2,P_network_1_3_AnnP_5,P_poll__networl_5_4_AskP_0,P_network_3_1_AskP_5,P_poll__networl_5_6_AnnP_1,P_network_0_5_RI_5,P_poll__networl_1_6_AskP_5,P_poll__networl_6_1_RP_0,P_poll__networl_5_1_AskP_5,P_poll__networl_4_2_RP_3,P_poll__networl_6_3_RI_2,P_network_4_0_AI_2,P_poll__networl_1_2_RI_0,P_network_5_6_AnnP_3,P_electionFailed_0,P_poll__networl_3_1_AnnP_5,P_network_5_2_RI_5,P_poll__networl_5_4_AI_3,P_poll__networl_1_4_AskP_4,P_network_1_3_RI_6,P_masterList_6_6_1,P_poll__networl_2_1_AskP_3,P_network_5_5_AskP_4,P_poll__networl_3_0_AskP_5,P_poll__networl_5_4_AnnP_6,P_masterList_0_6_6,P_network_6_1_AnnP_6,P_poll__networl_1_5_RP_1,P_network_4_4_RP_2,P_network_1_1_AI_1,P_network_2_1_RP_6,P_network_0_3_AI_2,P_network_1_2_RP_4,P_poll__networl_3_5_AskP_2,P_poll__networl_1_0_AnnP_2,P_network_1_2_AnnP_6,P_network_2_4_AI_6,P_network_5_2_AI_3,P_poll__networl_6_4_AskP_4,P_network_3_6_RI_1,P_poll__networl_4_6_RP_5,P_network_5_3_RI_1,P_masterList_0_2_0,P_electionFailed_4,P_poll__networl_3_3_AskP_6,P_network_4_3_AI_3,P_poll__networl_2_6_AnnP_0,P_poll__networl_3_5_AnnP_1,P_network_5_2_AnnP_2,P_network_5_6_AskP_1,P_poll__networl_0_3_AskP_2,P_poll__networl_0_2_RP_5,P_poll__networl_0_5_AskP_0,P_network_6_2_AskP_6,P_masterList_6_6_6,P_network_4_5_AI_5,P_poll__networl_2_2_RP_6,P_poll__networl_6_2_AskP_0,P_poll__networl_6_6_RP_4,P_network_0_1_RI_3,P_poll__networl_6_2_RP_1,P_network_4_0_RI_6,P_network_2_5_AI_2,P_network_1_3_AI_1,P_poll__networl_1_2_AnnP_6,P_network_6_2_RP_2,P_poll__networl_2_2_RI_0,P_poll__networl_4_1_RP_2,P_network_6_2_AnnP_2,P_poll__networl_0_0_RI_1,P_network_6_3_AI_6,P_poll__networl_0_5_AnnP_0,P_network_1_3_AnnP_1,P_poll__networl_2_4_RI_0,P_masterList_4_3_3,P_poll__networl_2_3_RP_1,P_poll__networl_5_1_AnsP_0,P_poll__networl_6_1_RI_0,P_network_3_2_AnnP_4,P_network_5_4_AI_1,P_network_5_5_AnnP_6,P_poll__networl_1_4_AI_5,P_network_3_1_AskP_4,P_poll__networl_3_1_RI_3,P_network_1_3_AI_3,P_network_5_2_RP_5,P_network_2_1_AnnP_4,P_poll__networl_5_5_RI_6,P_network_5_3_RI_4,P_poll__networl_5_1_AnnP_3,P_poll__networl_3_3_AnnP_4,P_poll__networl_0_6_AskP_3,P_poll__networl_4_3_RI_1,P_poll__networl_4_0_AnnP_2,P_poll__networl_3_2_AnnP_1,P_poll__networl_6_0_AI_1,P_network_6_3_RP_5,P_network_1_6_RP_2,P_poll__networl_6_5_RI_0,P_network_0_6_RP_5,P_poll__networl_3_0_AnnP_4,P_poll__networl_0_6_AskP_4,P_masterList_1_1_4,P_network_0_2_RI_2,P_poll__networl_0_1_RP_1,P_masterList_5_5_3,P_network_3_5_AI_2,P_poll__networl_3_1_AskP_3,P_poll__networl_2_0_AI_6,P_poll__networl_5_2_AskP_2,P_network_0_2_RP_5,P_poll__networl_2_6_AnnP_4,P_network_3_5_AnnP_1,P_poll__networl_0_5_AI_1,P_network_2_1_AI_2,P_network_6_4_RP_6,P_poll__networl_2_4_AI_3,P_network_5_6_AnnP_1,P_poll__networl_6_6_AnnP_2,P_network_2_6_RP_3,P_poll__networl_4_3_RP_1,P_poll__networl_5_1_AnnP_4,P_masterList_2_6_6,P_network_0_0_AskP_5,P_poll__networl_1_4_RP_6,P_poll__networl_4_4_RP_4,P_poll__networl_2_5_AskP_1,P_electionFailed_6,P_poll__networl_4_5_AskP_5,P_poll__networl_2_3_AnnP_4,P_network_0_5_RP_5,P_poll__networl_4_0_AI_1,P_network_6_0_RP_4,P_network_0_5_AnnP_6,P_masterList_2_2_2,P_poll__networl_5_0_RI_1,P_poll__networl_6_4_RP_6,P_dead_4,P_network_2_6_AskP_2,P_network_5_1_RP_2,P_network_1_6_RI_4,P_poll__networl_3_2_AI_0,P_network_4_6_RI_4,P_poll__networl_6_6_AnnP_4,P_network_5_0_AskP_1,P_poll__networl_0_5_RP_5,P_poll__networl_1_1_AnnP_2,P_network_6_6_AnnP_4,P_network_0_2_AskP_1,P_poll__networl_3_1_AskP_2,P_network_1_4_AskP_2,P_masterList_3_2_5,P_poll__networl_3_3_AskP_0,P_network_4_4_AI_4,P_network_6_5_AnnP_6,P_poll__networl_4_6_AI_6,P_poll__networl_1_6_AskP_1,P_poll__networl_5_2_RP_2,P_masterList_6_3_6,P_poll__networl_5_1_RP_2,P_poll__networl_1_1_AnnP_6,P_poll__networl_2_0_RP_6,P_network_4_1_AI_6,P_poll__networl_6_1_AI_5,P_network_1_0_AnnP_4,P_network_6_3_AI_1,P_poll__networl_6_1_RP_4,P_network_1_2_AI_4,P_poll__networl_1_5_AI_3,P_poll__networl_3_0_AI_0,P_poll__networl_6_4_AnnP_6,P_network_5_3_AskP_2,P_poll__networl_2_1_RP_5,P_poll__networl_0_1_AskP_3,P_network_1_5_AI_4,P_masterList_1_1_5,P_network_1_0_RP_6,P_poll__networl_5_0_AnnP_0,P_network_3_0_RP_5,P_poll__networl_0_1_AskP_1,P_poll__networl_6_5_RI_6,P_poll__networl_2_2_AnsP_0,P_network_2_6_RP_1,P_network_3_3_RI_2,P_network_4_2_RP_5,P_poll__networl_0_0_AI_2,P_poll__networl_6_1_AskP_1,P_network_4_2_AnnP_3,P_network_3_2_RP_3,P_poll__networl_6_1_AI_1,P_masterList_2_1_2,P_network_4_4_RP_6,P_poll__networl_3_2_AnnP_3,P_network_6_6_AskP_5,P_poll__networl_6_6_AskP_6,P_poll__networl_2_1_AnnP_4,P_poll__networl_3_5_AnnP_0,P_poll__networl_3_6_AnnP_2,P_network_4_3_RI_1,P_poll__networl_5_5_AnnP_6,P_network_0_3_RI_6,P_poll__networl_5_5_AI_0,P_poll__networl_5_5_RI_3,P_poll__networl_6_1_RI_1,P_network_5_5_RP_6,P_poll__networl_1_6_AnsP_0,P_masterList_4_1_3,P_network_1_6_AI_3,P_network_5_1_AnnP_6,P_poll__networl_0_6_AskP_1,P_network_5_2_AnnP_6,P_poll__networl_3_6_RI_4,P_poll__networl_1_5_AI_6,P_network_2_2_AskP_3,P_network_6_6_RI_2,P_network_6_0_AskP_6,P_network_5_5_RP_2,P_network_1_2_AI_1,P_poll__networl_2_4_AI_1,P_poll__networl_6_0_AnnP_1,P_network_0_5_AnnP_4,P_poll__networl_1_2_AskP_6,P_poll__networl_0_5_RP_0,P_network_4_5_AskP_6,P_poll__networl_3_1_AnnP_1,P_poll__networl_4_4_RP_3,P_poll__networl_5_2_RP_0,P_poll__networl_4_0_AnnP_3,P_poll__networl_4_5_AnnP_6,P_network_0_1_AnnP_6,P_masterList_1_3_3,P_poll__networl_2_2_AnnP_4,P_poll__networl_4_3_AskP_2,P_network_6_5_RI_4,P_poll__networl_6_3_AI_4,P_poll__networl_0_0_AI_3,P_poll__networl_0_4_AnsP_0,P_network_4_5_RP_1,P_poll__networl_3_3_AI_4,P_network_6_6_AI_1,P_poll__networl_2_0_RI_6,P_poll__networl_5_1_AI_5,P_poll__networl_5_5_AnnP_5,P_poll__networl_2_5_RP_6,P_poll__networl_6_4_RI_3,P_network_2_1_RP_3,P_poll__networl_5_1_AnnP_1,P_network_4_1_AskP_6,P_poll__networl_4_0_AskP_4,P_poll__networl_1_4_AnnP_3,P_poll__networl_5_6_AskP_4,P_poll__networl_1_0_AskP_5,P_network_5_0_RI_1,P_network_4_2_AI_1,P_poll__networl_4_1_RI_1,P_poll__networl_0_5_AI_5,P_poll__networl_0_0_RI_2,P_poll__networl_3_3_AI_6,P_network_1_5_AnnP_4,P_poll__networl_0_1_RI_5,P_poll__networl_3_5_RP_2,P_network_2_4_AskP_3,P_poll__networl_3_2_RP_1,P_poll__networl_6_4_AnnP_1,P_poll__networl_0_2_AI_6,P_poll__networl_4_4_AI_3,P_masterList_0_5_0,P_network_2_5_RP_6,P_poll__networl_2_1_AI_5,P_network_4_1_RP_4,P_network_3_2_AI_6,P_poll__networl_3_0_RP_6,P_network_3_0_RI_1,P_poll__networl_1_1_AnnP_4,P_poll__networl_2_3_AskP_3,P_poll__networl_5_3_AI_1,P_network_1_0_AskP_5,P_poll__networl_0_1_AskP_2,P_masterList_1_4_4,P_network_6_3_RI_2,P_poll__networl_1_5_RI_2,P_poll__networl_1_1_AI_0,P_network_5_3_AI_4,P_poll__networl_1_6_AskP_3,P_poll__networl_2_6_RP_3,P_network_4_0_AI_1,P_poll__networl_0_4_AI_6,P_poll__networl_2_0_AnnP_0,P_poll__networl_3_1_AnnP_3,P_network_0_0_RP_2,P_poll__networl_0_0_RP_3,P_poll__networl_5_5_AskP_6,P_poll__networl_0_0_AnnP_6,P_network_5_3_RI_5,P_poll__networl_3_5_AnnP_4,P_poll__networl_0_2_RI_3,P_poll__networl_0_4_AnnP_5,P_poll__networl_6_2_AnnP_3,P_poll__networl_6_0_AnnP_2,P_crashed_0,P_poll__networl_3_0_AnnP_6,P_poll__networl_2_4_RP_4,P_poll__networl_3_2_AI_1,P_poll__networl_6_1_AskP_6,P_masterList_3_3_4,P_poll__networl_6_6_AskP_1,P_poll__networl_6_6_AnnP_1,P_poll__networl_0_5_AnnP_5,P_masterList_6_2_6,P_network_5_4_RI_2,P_poll__networl_5_4_AI_6,P_network_4_1_AnnP_4,P_network_5_4_AskP_4,P_poll__networl_5_6_AI_3,P_poll__networl_4_0_RP_4,P_network_3_2_RP_1,P_masterList_4_6_6,P_network_2_5_AI_5,P_network_3_1_RP_6,P_network_3_5_RI_5,P_masterList_3_2_3,P_poll__networl_4_3_RP_2,P_poll__networl_0_4_RI_3,P_poll__networl_4_5_RI_6,P_poll__networl_5_0_AnnP_2,P_poll__networl_6_4_AI_1,P_network_0_0_RI_5,P_poll__networl_6_0_AI_5,P_network_5_1_AI_5,P_network_2_1_AnnP_2,P_network_3_3_RP_2,P_network_2_1_AskP_5,P_poll__networl_5_4_AnnP_3,P_poll__networl_6_3_AI_1,P_network_5_3_AskP_5,P_poll__networl_0_6_RP_2,P_network_2_0_RI_6,P_network_3_1_AI_4,P_network_4_3_RP_1,P_network_0_4_AI_1,P_poll__networl_6_3_RP_4,P_poll__networl_4_4_AI_0,P_network_5_5_RP_5,P_network_0_4_RP_4,P_network_2_2_AskP_4,P_network_5_2_RP_1,P_masterList_3_4_0,P_network_3_1_AskP_6,P_network_3_5_RI_3,P_poll__networl_5_1_AnnP_6,P_network_4_1_RP_5,P_poll__networl_4_4_AnnP_1,P_poll__networl_4_2_AI_1,P_masterList_0_2_2,P_poll__networl_3_4_RI_0,P_network_1_4_AI_6,P_network_4_5_AnnP_6,P_poll__networl_1_5_AI_5,P_poll__networl_2_2_AI_1,P_poll__networl_0_1_RI_4,P_network_1_0_AskP_4,P_network_3_6_AnnP_1,P_network_3_4_AI_5,P_masterList_3_1_6,P_poll__networl_2_1_AI_6,P_masterList_3_2_1,P_masterList_5_1_1,P_network_1_5_AI_6,P_network_0_3_AnnP_2,P_network_1_2_RI_6,P_poll__networl_0_4_RI_4,P_network_6_2_RP_3,P_network_5_4_RP_1,P_poll__networl_0_5_RP_2,P_poll__networl_0_1_AI_5,P_network_5_2_RI_6,P_poll__networl_6_1_AskP_4,P_poll__networl_1_1_AskP_0,P_network_0_3_RP_5,P_poll__networl_2_3_AnnP_3,P_poll__networl_3_1_RI_4,P_network_0_4_AskP_1,P_network_3_0_RI_2,P_poll__networl_6_0_RP_2,P_poll__networl_5_4_AskP_3,P_poll__networl_4_1_AI_5,P_network_1_0_RI_4,P_network_1_6_AnnP_3,P_network_3_2_AskP_4,P_poll__networl_4_0_AskP_5,P_poll__networl_5_6_AskP_5,P_poll__networl_6_5_AnnP_3,P_network_5_0_RI_4,P_network_0_0_RP_3,P_network_1_1_RI_5,P_poll__networl_2_3_AI_5,P_poll__networl_4_2_AnnP_5,P_network_0_0_AnnP_4,P_masterList_6_1_0,P_poll__networl_0_3_AnnP_5,P_network_6_2_AskP_4,P_network_6_4_AskP_3,P_network_3_1_RI_1,P_masterList_1_3_0,P_network_6_6_AI_4,P_masterList_4_2_5,P_network_0_3_AI_6,P_network_4_3_AnnP_3,P_network_5_4_AnnP_2,P_network_6_1_AnnP_1,P_poll__networl_3_6_RP_3,P_network_4_6_AskP_3,P_network_6_4_RP_4,P_network_4_0_RP_2,P_network_2_5_AskP_3,P_poll__networl_3_1_RP_0,P_poll__networl_2_4_RP_2,P_poll__networl_0_3_RI_2,P_network_6_6_AskP
_2,P_network_4_4_AI_6,P_poll__networl_4_2_AnnP_2,P_network_5_0_AI_4,P_network_0_3_RP_1,P_network_3_3_AnnP_5,P_network_6_1_RI_3,P_network_0_0_RP_5,P_network_0_4_RP_1,P_poll__networl_2_6_AskP_2,P_network_1_6_AI_6,P_poll__networl_5_3_RI_0,P_network_3_1_RI_6,P_network_4_2_AnnP_1,P_network_5_1_AskP_2,P_poll__networl_3_0_AskP_6,P_poll__networl_5_2_AnnP_5,P_network_2_6_AskP_5,P_network_4_2_AskP_6,P_network_5_6_AskP_5,P_masterList_6_3_5,P_network_0_4_RI_5,P_network_4_2_AI_6,P_poll__networl_4_5_RP_3,P_network_2_0_RI_1,P_poll__networl_2_0_RI_3,P_network_0_1_AI_6,P_poll__networl_4_4_RI_2,P_poll__networl_4_0_RI_2,P_network_6_0_AnnP_6,P_network_6_4_RI_3,P_network_0_3_AI_1,P_network_3_5_RI_2,P_poll__networl_6_4_RI_2,P_network_5_1_RP_3,P_network_6_0_AnnP_3,P_masterList_2_4_3,P_poll__networl_3_4_AskP_6,P_poll__networl_4_3_RI_4,P_poll__networl_3_2_AnnP_4,P_poll__networl_0_2_AnnP_5,P_poll__networl_5_1_AskP_6,P_poll__networl_1_5_RI_0,P_poll__networl_2_6_RI_4,P_poll__networl_6_4_AI_6,P_poll__networl_6_5_RP_5,P_masterList_5_3_5,P_poll__networl_4_1_AI_3,P_masterList_3_4_4,P_poll__networl_3_4_RI_1,P_network_3_0_RP_6,P_poll__networl_4_5_AI_1,P_poll__networl_3_3_RI_1,P_poll__networl_0_4_AskP_4,P_network_6_3_RP_4,P_network_1_5_AI_3,P_poll__networl_4_1_RP_0,P_poll__networl_2_4_AnnP_1,P_poll__networl_3_5_AskP_0,P_poll__networl_3_2_RI_6,P_poll__networl_5_2_AI_6,P_network_2_4_AI_3,P_poll__networl_6_1_AnnP_6,P_network_3_0_AnnP_6,P_poll__networl_0_1_AnnP_2,P_poll__networl_4_1_AnsP_0,P_poll__networl_5_4_AskP_5,P_network_4_0_AnnP_2,P_poll__networl_6_5_AnnP_5,P_network_3_6_RP_4,P_poll__networl_2_1_RI_3,P_network_6_1_RP_1,P_poll__networl_2_6_AskP_6,P_network_6_3_AI_4,P_network_0_1_RP_6,P_poll__networl_6_0_RP_1,P_poll__networl_6_2_AnnP_5,P_network_0_0_AnnP_3,P_poll__networl_1_2_AnnP_4,P_poll__networl_2_5_AI_6,P_poll__networl_0_0_RP_6,P_network_4_0_AI_6,P_network_2_0_AI_1,P_poll__networl_0_1_RP_4,P_network_3_4_AI_4,P_poll__networl_3_6_AskP_3,P_masterList_0_4_4,P_poll__networl_1_0_AnnP_1,P_masterList_6_4_3,P_poll__networl_4_1_RI_3,P_network_5_4_RP_3,P_poll__networl_4_5_AI_6,P_network_1_5_AI_5,P_network_2_4_RI_1,P_network_3_6_AI_5,P_network_3_5_AI_6,P_crashed_6,P_poll__networl_2_0_RI_5,P_poll__networl_2_5_AI_4,P_masterList_6_2_2,P_network_0_4_AnnP_1,P_poll__networl_4_1_AnnP_5,P_network_6_3_RI_3,P_poll__networl_1_5_AskP_4,P_network_4_4_AnnP_3,P_poll__networl_0_0_AnnP_5,P_poll__networl_0_0_AskP_5,P_poll__networl_1_3_AnnP_2,P_network_5_5_RP_4,P_network_1_3_RP_6,P_network_2_4_RP_4,P_network_4_1_RP_2,P_poll__networl_1_3_AI_1,P_masterList_1_6_3,P_poll__networl_1_3_AskP_5,P_poll__networl_3_1_RI_0,P_poll__networl_4_1_RI_2,P_poll__networl_6_3_RI_0,P_poll__networl_5_6_RI_5,P_network_6_0_RI_4,P_poll__networl_4_3_AskP_5,P_network_5_5_RP_1,P_poll__networl_5_3_RP_0,P_poll__networl_5_2_RI_1,P_network_0_3_AnnP_6,P_poll__networl_0_3_RP_5,P_poll__networl_1_3_RI_6,P_poll__networl_5_2_AnnP_4,P_network_0_1_AI_5,P_network_5_6_RP_6,P_poll__networl_4_0_AnnP_6,P_network_2_6_AskP_3,P_network_3_1_AI_3,P_poll__networl_0_6_AI_0,P_poll__networl_5_4_AskP_4,P_network_6_6_AskP_4,P_poll__networl_0_5_RI_2,P_masterList_5_6_3,P_network_1_4_RI_5,P_network_2_0_AI_4,P_masterList_3_4_1,P_network_5_5_RI_6,P_network_3_3_AnnP_2,P_network_4_5_AnnP_5,P_network_2_6_RP_2,P_network_0_3_RI_2,P_poll__networl_0_1_RI_6,P_poll__networl_1_6_RP_6,P_network_4_2_RI_6,P_network_5_4_AI_4,P_network_6_5_AskP_3,P_network_5_2_AnnP_1,P_poll__networl_4_3_AI_1,P_poll__networl_6_3_RP_1,P_network_1_5_AskP_6,P_poll__networl_4_4_RP_1,P_poll__networl_2_4_RI_5,P_poll__networl_4_5_RI_1,P_network_1_4_AnnP_6,P_poll__networl_0_4_AnnP_6,P_poll__networl_0_6_AnnP_0,P_poll__networl_1_4_AskP_2,P_poll__networl_3_4_AskP_5,P_network_1_4_AI_1,P_network_6_4_AskP_1,P_masterList_5_5_2,P_network_1_6_RI_1,P_poll__networl_2_5_RP_0,P_poll__networl_6_4_AnsP_0,P_network_5_3_AskP_4,P_poll__networl_0_2_AnsP_0,P_poll__networl_3_1_RI_2,P_poll__networl_2_5_AskP_6,P_network_1_5_RP_1,P_network_5_5_AskP_2,P_poll__networl_4_5_RI_2,P_poll__networl_5_2_AnnP_2,P_poll__networl_4_1_AI_4,P_network_3_0_RP_1,P_network_6_0_AnnP_4,P_poll__networl_1_0_AnsP_0,P_poll__networl_6_0_RP_4,P_masterList_3_5_0,P_poll__networl_4_0_AI_6,P_poll__networl_5_0_AnnP_6,P_masterList_5_3_2,P_poll__networl_3_4_AskP_1,P_network_4_4_RI_6,P_network_5_3_AskP_1,P_poll__networl_2_3_RI_4,P_poll__networl_6_1_AnnP_1,P_poll__networl_2_5_AnnP_4,P_network_5_3_AnnP_4,P_network_5_4_RI_3,P_network_5_6_AI_2,P_network_5_0_RP_3,P_poll__networl_0_6_AI_5,P_network_2_2_RP_5,P_network_2_4_RI_3,P_poll__networl_3_3_AnnP_1,P_poll__networl_3_2_AnnP_0,P_poll__networl_1_3_RI_1,P_poll__networl_1_3_RI_0,P_poll__networl_2_3_RP_0,P_network_3_0_AI_4,P_network_4_5_RI_1,P_poll__networl_0_2_AnnP_4,P_poll__networl_4_3_RI_5,P_network_5_3_RP_6,P_network_1_4_AnnP_1,P_network_4_5_RP_2,P_network_3_1_AnnP_2,P_poll__networl_1_2_AI_2,P_poll__networl_4_2_AnnP_0,P_poll__networl_4_3_RI_2,P_poll__networl_1_1_RP_4,P_poll__networl_6_6_AI_4,P_masterList_2_5_0,P_poll__networl_2_3_AnnP_5,P_network_4_3_AskP_6,P_poll__networl_1_2_AskP_0,P_poll__networl_0_3_RI_3,P_network_1_6_AnnP_1,P_poll__networl_2_5_RP_4,P_poll__networl_2_3_AnnP_2,P_poll__networl_4_2_RP_6,P_network_6_5_RI_6,P_network_3_3_AI_5,P_poll__networl_4_2_AnnP_6,P_network_6_2_RI_2,P_poll__networl_4_6_AskP_6,P_poll__networl_5_6_AI_4,P_network_1_3_RP_1,P_poll__networl_5_6_AI_2,P_network_5_5_AI_4,P_poll__networl_5_6_AnnP_5,P_poll__networl_0_4_AnnP_0,P_poll__networl_2_6_AnnP_3,P_poll__networl_5_2_AskP_4,P_network_2_0_AnnP_5,P_poll__networl_3_1_RP_6,P_masterList_6_4_5,P_poll__networl_0_4_RI_5,P_network_6_6_AnnP_1,P_network_0_6_AnnP_1,P_poll__networl_0_2_AI_4,P_network_3_5_AskP_6,P_network_5_6_AI_1,P_poll__networl_6_4_AskP_6,P_masterList_4_4_1,P_poll__networl_4_0_AnnP_1,P_network_6_6_RP_3,P_poll__networl_0_3_RP_0,P_network_1_1_AI_3,P_poll__networl_0_1_RI_1,P_poll__networl_2_0_AskP_2,P_network_3_2_RI_4,P_network_2_6_AnnP_3,P_masterList_0_2_3,P_poll__networl_3_5_RP_1,P_network_1_6_RP_4,P_network_2_3_AnnP_2,P_poll__networl_3_4_AnsP_0,P_poll__networl_6_5_AI_3,P_poll__networl_1_4_RI_6,P_network_3_3_AnnP_4,P_network_4_5_RI_2,P_poll__networl_0_4_RP_2,P_network_3_5_AskP_4,P_poll__networl_1_2_AI_6,P_network_3_2_AI_4,P_poll__networl_2_5_RP_2,P_poll__networl_3_1_RP_4,P_network_5_0_AnnP_4,P_poll__networl_4_3_AnnP_4,P_poll__networl_5_6_RP_4,P_masterList_6_5_2,P_network_1_4_AI_2,P_masterList_0_6_0,P_network_3_4_RP_2,P_masterList_1_5_4,P_poll__networl_1_4_AnnP_5,P_masterList_5_5_6,P_network_0_3_AskP_5,P_poll__networl_1_0_AI_4,P_poll__networl_4_4_AI_4,P_network_0_5_RP_1,P_network_2_4_RP_1,P_poll__networl_5_0_AI_4,P_network_1_1_AnnP_3,P_poll__networl_4_2_AI_4,P_network_3_3_AI_1,P_network_0_2_RP_6,P_poll__networl_3_6_RP_1,P_masterList_1_2_1,P_poll__networl_6_2_RI_3,P_poll__networl_4_6_AI_2,P_network_3_6_RI_2,P_network_6_1_RI_2,P_network_0_2_RI_1,P_network_6_0_AI_5,P_poll__networl_2_6_AnnP_2,P_network_4_4_AnnP_1,P_poll__networl_0_2_AskP_5,P_poll__networl_2_1_AskP_1,P_network_3_2_AnnP_5,P_network_0_6_AnnP_2,P_masterList_2_1_1,P_poll__networl_3_2_AnnP_2,P_network_0_4_AI_3,P_poll__networl_0_3_AskP_3,P_poll__networl_0_3_RI_1,P_network_0_0_AnnP_1,P_masterList_3_4_6,P_poll__networl_1_3_AskP_3,P_network_3_1_RP_1,P_masterList_4_2_4,P_network_3_5_AskP_5,P_poll__networl_0_1_RI_3,P_poll__networl_2_6_RI_3,P_network_0_5_AskP_1,P_network_0_6_RP_2,P_network_6_0_AI_4,P_network_6_6_AskP_1,P_poll__networl_6_0_AI_0,P_poll__networl_6_6_RP_6,P_masterList_3_6_5,P_poll__networl_1_4_AskP_5,P_poll__networl_2_1_AnnP_0,P_poll__networl_1_2_AskP_2,P_network_6_1_AI_2,P_network_1_3_AI_4,P_poll__networl_4_5_AI_5,P_network_2_5_AskP_6,P_poll__networl_6_3_AI_5,P_poll__networl_2_2_RP_2,P_poll__networl_0_4_AskP_2,P_poll__networl_0_1_AnnP_0,P_network_3_4_AnnP_6,P_network_6_1_AskP_5,P_poll__networl_3_0_AI_2,P_network_1_6_AI_5,P_network_6_1_AskP_6,P_poll__networl_2_1_RI_4,P_masterList_0_6_4,P_poll__networl_1_3_AI_2,P_crashed_2,P_network_5_3_RP_4,P_network_2_6_AI_5,P_masterList_6_3_1,P_network_0_5_RI_3,P_network_2_6_AI_6,P_network_2_0_RP_6,P_network_6_1_AskP_4,P_poll__networl_1_1_AskP_4,P_network_3_6_RI_6,P_network_2_4_AnnP_4,P_poll__networl_1_2_RP_5,P_poll__networl_6_0_AI_6,P_poll__networl_5_5_RI_2,P_poll__networl_2_5_AskP_4,P_masterList_2_2_0,P_network_2_0_AI_2,P_poll__networl_1_2_RP_3,P_masterList_5_1_2,P_network_0_4_AnnP_6,P_poll__networl_3_2_AskP_3,P_poll__networl_5_5_AI_6,P_network_6_4_AskP_2,P_network_2_1_RP_1,P_masterList_5_1_5,P_network_4_0_RP_1,P_poll__networl_5_0_RP_6,P_masterList_2_6_5,P_poll__networl_2_6_RP_1,P_network_3_5_AnnP_6,P_network_4_4_AI_5,P_masterList_0_4_3,P_masterList_2_5_4,P_network_3_3_AskP_4,P_masterList_4_4_2,P_network_5_5_AI_1,P_poll__networl_1_4_RI_2,P_network_6_3_AnnP_3,P_poll__networl_3_3_AskP_3,P_poll__networl_6_2_RP_4,P_poll__networl_2_4_AnnP_0,P_network_6_6_AnnP_2,P_poll__networl_1_0_AnnP_5,P_network_3_4_RI_3,P_poll__networl_0_4_AnnP_3,P_poll__networl_5_3_AskP_4,P_poll__networl_0_2_AI_0,P_poll__networl_6_1_AI_4,P_network_4_6_AnnP_2,P_poll__networl_5_2_AnnP_1,P_poll__networl_5_4_AnnP_4,P_poll__networl_1_3_RP_3,P_network_2_5_AnnP_2,P_poll__networl_0_3_RP_1,P_poll__networl_1_6_AI_5,P_network_4_4_RI_3,P_network_2_3_AI_2,P_network_5_0_RI_3,P_poll__networl_0_4_RP_0,P_poll__networl_2_5_AnsP_0,P_poll__networl_5_6_RI_2,P_masterList_3_6_1,P_network_0_3_AnnP_4,P_network_6_0_RP_3,P_poll__networl_2_6_AI_6,P_network_3_2_RI_2,P_poll__networl_5_1_RI_1,P_masterList_4_1_1,P_poll__networl_3_1_RP_1,P_network_2_0_AskP_5,P_poll__networl_5_4_AskP_1,P_poll__networl_6_5_RP_1,P_poll__networl_0_2_AskP_0,P_poll__networl_3_1_AskP_4,P_network_2_2_RP_1,P_poll__networl_0_1_RP_5,P_poll__networl_2_3_AI_3,P_masterList_6_4_0,P_network_2_1_RI_2,P_masterList_6_5_4,P_poll__networl_2_5_AnnP_0,P_poll__networl_2_2_RP_1,P_poll__networl_3_3_AnnP_5,P_poll__networl_4_5_AnnP_1,P_network_5_5_RI_1,P_network_6_6_RI_1,P_network_1_6_AskP_3,P_network_0_0_RI_4,P_poll__networl_5_5_RP_1,P_network_3_4_AI_2,P_network_6_1_AnnP_4,P_poll__networl_4_4_RI_6,P_network_5_3_AI_1,P_poll__networl_1_4_AnnP_4,P_poll__networl_5_2_RI_0,P_poll__networl_0_5_RI_5,P_masterList_6_6_2,P_network_2_1_AI_5,P_network_2_3_RP_4,P_masterList_5_6_6,P_poll__networl_1_4_AnnP_1,P_network_2_3_AskP_3,P_network_5_1_AI_2,P_masterList_0_1_2,P_masterList_4_2_2,P_network_2_2_AnnP_2,P_network_5_5_AnnP_1,P_poll__networl_4_4_AI_5,P_poll__networl_1_1_RP_5,P_network_0_5_RI_4,P_network_2_2_AnnP_5,P_poll__networl_2_6_AI_5,P_network_6_2_RP_5,P_poll__networl_6_6_AskP_5,P_network_2_2_RI_6,P_poll__networl_2_3_AnnP_0,P_network_2_4_AI_4,P_poll__networl_0_3_AnsP_0,P_network_5_2_AskP_4,P_poll__networl_5_1_AI_6,P_network_3_6_AI_2,P_poll__networl_4_6_AnsP_0,P_poll__networl_2_2_RI_3,P_poll__networl_0_4_AskP_1,P_poll__networl_4_2_AskP_3,P_network_4_2_RP_2,P_masterList_5_2_2,P_network_5_1_RP_6,P_network_5_3_AskP_6,P_poll__networl_0_4_AI_0,P_poll__networl_1_5_AnsP_0,P_network_6_4_AI_3,P_network_5_4_RI_5,P_network_6_5_AnnP_3,P_poll__networl_3_1_AI_4,P_network_5_5_RI_2,P_poll__networl_2_2_AskP_4,P_poll__networl_0_5_AnnP_3,P_poll__networl_4_4_AnnP_5,P_network_5_5_AskP_6,P_network_5_4_AnnP_5,P_poll__networl_3_3_RI_4,P_poll__networl_4_4_AnnP_0,P_poll__networl_4_2_RI_6,P_network_3_1_AI_2,P_poll__networl_0_6_RP_4,P_poll__networl_6_0_AI_4,P_poll__networl_5_6_AnnP_2,P_poll__networl_6_6_RI_1,P_poll__networl_5_3_RP_6,P_poll__networl_6_5_AskP_0,P_network_1_1_AskP_1,P_network_0_6_RI_1,P_network_1_3_RI_1,P_poll__networl_4_1_AskP_4,P_network_6_3_RI_5,P_poll__networl_3_0_RI_3,P_masterList_5_3_0,P_network_3_6_AskP_1,P_poll__networl_5_2_AI_2,P_network_4_2_AI_5,P_poll__networl_0_5_AnnP_4,P_poll__networl_4_1_RP_4,P_poll__networl_3_3_AI_0,P_network_5_0_AI_2,P_poll__networl_0_5_AskP_1,P_poll__networl_5_0_RI_0,P_poll__networl_5_5_RP_0,P_masterList_2_5_5,P_network_1_0_RI_2,P_network_0_0_RI_3,P_network_4_4_AskP_4,P_poll__networl_3_6_AnnP_1,P_network_1_3_AskP_6,P_poll__networl_4_0_RI_1,P_poll__networl_0_4_AI_4,P_poll__networl_6_2_AI_6,P_network_6_4_RP_1,P_poll__networl_1_1_AskP_5,P_network_4_6_AskP_2,P_network_4_0_AskP_1,P_network_5_5_AI_2,P_poll__networl_5_3_AnnP_4,P_network_0_0_RP_1,P_poll__networl_2_1_AskP_0,P_network_1_5_AskP_1,P_network_6_5_AnnP_5,P_network_6_5_AskP_1,P_electionFailed_3,P_poll__networl_4_0_AI_5,P_poll__networl_1_5_AnnP_3,P_dead_1,P_network_1_5_AskP_2,P_network_2_3_AskP_2,P_network_4_3_RP_2,P_poll__networl_6_2_RI_2,P_poll__networl_6_0_RI_0,P_network_4_3_RP_3,P_poll__networl_1_1_AnnP_1,P_masterList_6_6_5,P_network_3_5_AnnP_2,P_network_4_1_RP_6,P_poll__networl_4_6_RI_1,P_poll__networl_0_3_AI_0,P_poll__networl_1_2_RP_0,P_network_3_4_AI_3,P_poll__networl_2_2_AI_4,P_network_2_0_AnnP_1,P_network_4_6_RI_2,P_network_4_3_AnnP_4,P_network_2_5_RP_5,P_poll__networl_5_0_AskP_6,P_poll__networl_2_4_RP_5,P_network_6_2_AnnP_1,P_poll__networl_4_1_RP_5,P_poll__networl_5_2_AskP_5,P_poll__networl_6_0_RP_5,P_poll__networl_0_6_AnnP_3,P_poll__networl_5_4_RP_2,P_poll__networl_6_5_AI_2,P_network_4_5_AI_6,P_network_0_0_RP_4,P_poll__networl_4_1_AskP_5,P_network_6_6_AnnP_3,P_poll__networl_5_3_AI_0,P_poll__networl_6_6_AskP_2,P_poll__networl_3_3_RP_3,P_network_1_6_AI_2,P_poll__networl_4_5_RP_2,P_poll__networl_1_2_AI_5,P_network_1_4_RI_3,P_network_6_2_AI_1,P_network_1_6_AskP_4,P_network_2_5_RP_1,P_poll__networl_5_1_RI_0,P_poll__networl_5_5_AskP_5,P_poll__networl_1_4_AnnP_2,P_network_3_2_AI_1,P_network_2_0_RI_2,P_poll__networl_5_3_RI_4,P_masterList_0_1_4,P_poll__networl_2_4_RI_4,P_poll__networl_1_6_RP_1,P_poll__networl_2_6_RI_0,P_network_0_6_AnnP_3,P_network_0_6_AnnP_4,P_network_6_1_AnnP_5,P_poll__networl_4_2_AskP_4,P_network_1_1_AskP_6,P_poll__networl_5_1_RP_0,P_poll__networl_6_5_AskP_6,P_poll__networl_4_3_RP_4,P_poll__networl_4_4_AI_6,P_network_2_2_RP_2,P_poll__networl_3_0_RI_1,P_poll__networl_0_6_AI_3,P_poll__networl_4_1_AnnP_2,P_network_4_1_AI_5,P_network_4_0_AskP_5,P_poll__networl_4_6_AI_1,P_poll__networl_4_1_AskP_1,P_network_4_6_RI_3,P_masterList_3_5_3,P_poll__networl_1_4_RP_0,P_poll__networl_2_3_AI_2,P_network_6_4_AnnP_6,P_poll__networl_2_3_AI_6,P_network_1_5_RI_1,P_network_1_4_RI_1,P_poll__networl_1_0_AskP_1,P_masterList_3_2_4,P_poll__networl_1_1_RP_6,P_poll__networl_3_6_AnnP_4,P_poll__networl_1_6_AnnP_2,P_network_4_1_AnnP_5,P_poll__networl_2_2_AskP_3,P_network_2_1_RP_2,P_network_5_4_AskP_2,P_poll__networl_4_6_RP_2,P_network_3_0_RP_3,P_poll__networl_0_4_AnnP_1,P_poll__networl_1_4_AskP_6,P_network_5_2_AskP_5,P_network_2_0_AskP_6,P_network_4_3_RI_4,P_network_3_6_RI_4,P_network_6_3_AnnP_4,P_network_0_5_AnnP_3,P_poll__networl_4_1_RI_4,P_masterList_2_2_6,P_masterList_5_2_4,P_poll__networl_2_2_RI_6,P_network_2_0_AskP_2,P_masterList_5_1_4,P_network_1_6_RI_2,P_poll__networl_6_2_AskP_5,P_network_3_1_AnnP_3,P_network_5_4_RI_4,P_network_3_6_AI_3,P_network_4_4_RI_4,P_network_4_2_AskP_5,P_poll__networl_3_6_AnnP_3,P_network_2_1_AskP_6,P_poll__networl_1_2_AnnP_1,P_poll__networl_2_6_RP_6,P_poll__networl_5_6_AI_1,P_poll__networl_1_0_RI_5,P_network_2_5_RP_4,P_poll__networl_4_6_RP_4,P_network_1_4_RI_4,P_poll__networl_2_5_RP_5,P_poll__networl_2_5_AnnP_2,P_network_3_3_AI_2,P_poll__networl_0_4_RP_1,P_network_4_1_AnnP_6,P_network_2_2_RI_4,P_network_4_0_AnnP_5,P_poll__networl_2_2_AnnP_2,
May 26, 2018 12:11:59 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Removed 3549 constant variables :P_network_2_0_RI_3=0, P_poll__networl_1_6_RP_0=0, P_poll__networl_6_3_AskP_1=0, P_poll__networl_1_2_RP_1=0, P_poll__networl_1_0_RI_3=0, P_network_5_2_RP_4=0, P_poll__networl_2_2_RI_1=0, P_network_5_3_AskP_3=0, P_network_0_4_AskP_2=0, P_poll__networl_1_1_AskP_3=0, P_masterList_2_6_1=0, P_poll__networl_0_0_AnnP_4=0, P_poll__networl_4_6_RI_5=0, P_poll__networl_6_0_AnnP_6=0, P_poll__networl_5_4_AskP_6=0, P_network_3_1_AI_5=0, P_network_2_1_RI_6=0, P_poll__networl_2_0_AI_2=0, P_network_3_2_AnnP_1=0, P_network_2_2_AskP_2=0, P_poll__networl_6_4_RI_1=0, P_poll__networl_4_4_RP_2=0, P_poll__networl_2_5_AI_1=0, P_poll__networl_5_2_RI_3=0, P_network_6_5_AI_5=0, P_poll__networl_2_0_AnnP_2=0, P_poll__networl_1_1_RI_6=0, P_poll__networl_4_5_AnsP_0=0, P_network_3_6_AnnP_3=0, P_network_0_3_AI_4=0, P_poll__networl_0_5_RI_6=0, P_network_5_3_AI_2=0, P_crashed_5=0, P_poll__networl_5_3_RI_6=0, P_poll__networl_5_1_AI_4=0, P_poll__networl_4_3_AskP_0=0, P_network_3_2_AnnP_6=0, P_network_4_4_RI_1=0, P_masterList_5_2_0=0, P_poll__networl_1_3_AI_6=0, P_network_1_5_RI_2=0, P_network_5_4_AskP_3=0, P_network_6_0_AI_3=0, P_network_1_0_AI_2=0, P_masterList_1_6_0=0, P_network_4_3_AI_5=0, P_poll__networl_0_5_AnnP_1=0, P_masterList_3_4_2=0, P_poll__networl_6_6_AskP_0=0, P_poll__networl_6_4_AnnP_5=0, P_poll__networl_0_3_AskP_6=0, P_network_0_2_AnnP_2=0, P_network_3_4_RI_2=0, P_poll__networl_3_5_AI_3=0, P_poll__networl_5_5_RI_5=0, P_network_2_0_AskP_1=0, P_network_6_2_AnnP_3=0, P_poll__networl_2_4_RI_1=0, P_network_6_4_AskP_5=0, P_poll__networl_1_0_AskP_6=0, P_poll__networl_4_0_AnsP_0=0, P_network_0_2_RP_4=0, P_network_5_4_AI_2=0, P_network_5_5_AnnP_5=0, P_network_4_0_AI_4=0, P_poll__networl_5_1_AskP_2=0, P_network_1_3_RP_3=0, P_network_5_0_AnnP_1=0, P_poll__networl_2_6_RI_5=0, P_network_6_5_AskP_5=0, P_dead_3=0, P_network_4_5_RP_6=0, P_poll__networl_2_5_AnnP_3=0, P_network_0_0_RI_2=0, P_masterList_4_6_4=0, P_poll__networl_6_0_RP_0=0, P_poll__networl_4_2_AnnP_1=0, P_network_1_0_AnnP_3=0, P_poll__networl_6_0_AskP_0=0, P_poll__networl_6_1_RI_2=0, P_masterList_1_5_6=1, P_poll__networl_6_3_AI_0=0, P_network_0_0_AskP_1=0, P_network_0_0_AskP_4=0, P_network_5_1_RI_6=0, P_network_1_6_AskP_6=0, P_poll__networl_1_5_AI_0=0, P_poll__networl_6_4_AI_2=0, P_poll__networl_6_1_AnnP_2=0, P_masterList_2_2_3=1, P_network_2_0_AI_5=0, P_network_6_6_RI_4=0, P_poll__networl_2_1_AI_2=0, P_poll__networl_3_4_RI_2=0, P_network_1_3_AnnP_2=0, P_poll__networl_3_4_RP_0=0, P_network_2_3_AskP_5=0, P_network_1_4_AnnP_5=0, P_network_6_4_RP_3=0, P_poll__networl_4_6_AskP_0=0, P_network_1_4_RP_1=0, P_masterList_0_3_5=0, P_masterList_5_6_1=0, P_poll__networl_5_0_AnnP_1=0, P_poll__networl_1_2_RP_2=0, P_poll__networl_3_3_AskP_2=0, P_poll__networl_2_6_AnnP_6=0, P_poll__networl_3_6_AI_0=0, P_masterList_6_3_3=1, P_network_0_1_AskP_6=0, P_poll__networl_0_3_RI_5=0, P_poll__networl_2_0_RP_5=0, P_poll__networl_1_2_RI_6=0, P_poll__networl_1_0_AskP_3=0, P_poll__networl_3_4_AI_4=0, P_network_1_0_RP_4=0, P_poll__networl_0_5_RP_3=0, P_poll__networl_6_1_AI_6=0, P_network_5_2_AI_2=0, P_poll__networl_1_5_AnnP_4=0, P_network_2_5_RI_5=0, P_poll__networl_3_6_AI_2=0, P_poll__networl_0_6_AI_1=0, P_poll__networl_6_6_AskP_3=0, P_poll__networl_0_2_RI_5=0, P_poll__networl_0_0_AnnP_3=0, P_poll__networl_0_3_AI_5=0, P_poll__networl_2_6_AI_2=0, P_network_5_6_AskP_3=0, P_poll__networl_1_0_AnnP_3=0, P_poll__networl_6_6_AnnP_5=0, P_network_5_3_RP_2=0, P_poll__networl_0_0_AskP_0=0, P_network_0_4_AnnP_3=0, P_network_4_2_AskP_3=0, P_poll__networl_3_6_AI_5=0, P_network_1_0_AnnP_2=0, P_masterList_4_6_0=0, P_poll__networl_5_0_AI_3=0, P_poll__networl_3_3_AI_5=0, P_poll__networl_6_1_AI_2=0, P_poll__networl_5_1_AnnP_2=0, P_poll__networl_2_6_AnnP_5=0, P_masterList_6_2_0=0, P_network_4_1_RP_3=0, P_network_5_4_AskP_5=0, P_poll__networl_5_0_RP_4=0, P_network_2_1_AskP_4=0, P_network_4_0_RP_5=0, P_network_4_6_AnnP_3=0, P_poll__networl_3_6_AI_1=0, P_network_1_6_AskP_5=0, P_poll__networl_6_5_AI_6=0, P_poll__networl_6_0_RI_4=0, P_poll__networl_1_4_AskP_1=0, P_poll__networl_4_0_AI_0=0, P_network_4_2_RP_3=0, P_masterList_2_1_4=0, P_network_5_5_AI_5=0, P_poll__networl_4_4_RP_0=0, P_network_2_0_RI_5=0, P_poll__networl_3_2_RI_5=0, P_masterList_0_1_3=0, P_poll__networl_1_5_AI_1=0, P_network_3_4_RP_5=0, P_masterList_3_1_5=0, P_poll__networl_3_0_RP_2=0, P_poll__networl_5_0_AskP_5=0, P_poll__networl_6_3_AnnP_5=0, P_network_3_0_AnnP_5=0, P_network_5_4_AI_6=0, P_network_2_6_AI_3=0, P_poll__networl_1_1_AI_2=0, P_masterList_1_3_4=1, P_network_2_3_AskP_6=0, P_network_2_6_RP_4=0, P_poll__networl_4_5_RP_0=0, P_network_2_3_RI_2=0, P_poll__networl_6_0_AskP_3=0, P_poll__networl_0_0_AI_0=0, P_poll__networl_4_2_RI_2=0, P_poll__networl_2_5_AskP_5=0, P_network_6_3_RP_2=0, P_network_6_5_AnnP_2=0, P_poll__networl_5_0_RP_0=0, P_poll__networl_5_5_AskP_3=0, P_poll__networl_1_2_RI_3=0, P_poll__networl_6_2_RI_5=0, P_network_0_1_AI_2=0, P_poll__networl_6_3_RI_3=0, P_poll__networl_6_0_AI_3=0, P_network_3_4_RP_4=0, P_network_6_6_AI_2=0, P_poll__networl_5_1_RP_5=0, P_network_0_2_RI_5=0, P_poll__networl_5_1_RP_1=0, P_network_1_0_AskP_3=0, P_poll__networl_4_6_AI_0=0, P_poll__networl_3_3_AI_2=0, P_poll__networl_6_4_RP_0=0, P_masterList_4_5_6=1, P_network_5_3_RI_6=0, P_poll__networl_1_5_AskP_3=0, P_poll__networl_1_1_RI_2=0, P_poll__networl_2_1_AnnP_5=0, P_poll__networl_3_5_RP_3=0, P_poll__networl_6_1_AskP_0=0, P_network_3_3_RP_4=0, P_poll__networl_4_5_RI_5=0, P_poll__networl_3_2_RI_4=0, P_network_2_4_AskP_4=0, P_poll__networl_6_5_AI_5=0, P_network_0_4_AI_2=0, P_poll__networl_2_3_RI_2=0, P_poll__networl_2_4_RI_3=0, P_poll__networl_1_4_AI_3=0, P_poll__networl_6_4_AI_4=0, P_poll__networl_0_0_AnnP_0=0, P_poll__networl_0_6_AnsP_0=0, P_network_6_6_RI_5=0, P_poll__networl_0_3_RP_3=0, P_masterList_1_2_4=0, P_network_1_6_AskP_2=0, P_network_2_2_AI_4=0, P_network_0_0_AnnP_2=0, P_network_5_3_AnnP_1=0, P_poll__networl_3_1_RP_5=0, P_poll__networl_6_2_AnnP_2=0, P_poll__networl_2_4_AI_2=0, P_masterList_1_2_6=0, P_network_2_4_AskP_2=0, P_network_6_4_RI_6=0, P_poll__networl_2_2_RP_0=0, P_network_6_3_AskP_2=0, P_poll__networl_1_3_AI_5=0, P_network_1_1_AI_6=0, P_poll__networl_0_0_RI_0=0, P_poll__networl_2_4_AI_6=0, P_poll__networl_2_6_AnsP_0=0, P_poll__networl_5_2_AI_1=0, P_poll__networl_6_5_RI_1=0, P_poll__networl_6_6_AI_0=0, P_poll__networl_4_3_AI_4=0, P_network_4_3_AI_1=0, P_network_3_0_AI_6=0, P_poll__networl_6_0_AnnP_5=0, P_poll__networl_4_6_AskP_5=0, P_poll__networl_3_5_RI_4=0, P_poll__networl_1_2_AnsP_0=0, P_network_4_6_RP_5=0, P_poll__networl_6_1_RP_6=0, P_poll__networl_6_4_AnnP_4=0, P_masterList_2_6_0=0, P_network_1_1_AI_4=0, P_masterList_2_1_3=0, P_masterList_2_3_4=1, P_poll__networl_5_3_RI_2=0, P_network_2_5_RI_4=0, P_network_4_2_RP_1=0, P_poll__networl_0_4_AI_2=0, P_network_5_0_RP_2=0, P_poll__networl_2_4_AskP_0=0, P_poll__networl_2_4_AnnP_4=0, P_network_6_1_RP_6=0, P_network_2_3_RI_5=0, P_poll__networl_0_0_AI_6=0, P_poll__networl_3_0_AnnP_1=0, P_poll__networl_0_3_AskP_0=0, P_network_1_4_AskP_6=0, P_network_1_6_RP_3=0, P_poll__networl_1_6_AskP_0=0, P_network_2_1_RP_4=0, P_masterList_1_1_2=1, P_poll__networl_5_2_AI_5=0, P_poll__networl_6_4_RI_6=0, P_poll__networl_2_5_RP_1=0, P_network_2_2_AI_1=0, P_poll__networl_1_6_RI_2=0, P_masterList_4_3_5=0, P_network_0_3_AnnP_3=0, P_network_2_4_AnnP_1=0, P_network_2_3_AnnP_3=0, P_poll__networl_5_0_RI_3=0, P_poll__networl_1_6_RI_0=0, P_poll__networl_1_6_AskP_4=0, P_masterList_2_3_6=0, P_poll__networl_4_4_AskP_2=0, P_network_0_6_AI_3=0, P_poll__networl_2_2_AnnP_6=0, P_poll__networl_5_5_AI_4=0, P_network_2_0_AI_3=0, P_poll__networl_3_6_AI_4=0, P_network_1_1_AnnP_6=0, P_network_5_3_RP_5=0, P_network_0_4_RP_3=0, P_poll__networl_1_5_RI_1=0, P_poll__networl_6_5_RI_2=0, P_poll__networl_6_3_AskP_3=0, P_network_3_5_RI_6=0, P_network_6_3_AnnP_6=0, P_poll__networl_2_4_AI_5=0, P_network_1_3_AskP_4=0, P_poll__networl_4_1_RI_6=0, P_poll__networl_6_2_AnnP_4=0, P_network_0_4_RI_3=0, P_electionFailed_5=0, P_poll__networl_2_6_AskP_4=0, P_masterList_2_1_6=0, P_network_5_5_RI_4=0, P_masterList_0_6_1=0, P_network_0_6_AI_4=0, P_network_2_5_AskP_1=0, P_network_6_0_RI_2=0, P_poll__networl_3_6_RI_5=0, P_network_3_5_RP_2=0, P_masterList_0_1_6=0, P_network_6_1_RP_2=0, P_network_5_6_AI_4=0, P_poll__networl_2_5_RI_6=0, P_poll__networl_1_0_AI_1=0, P_poll__networl_4_3_AI_5=0, P_poll__networl_1_4_AI_2=0, P_poll__networl_5_6_AnnP_6=0, P_network_1_2_RP_3=0, P_poll__networl_5_5_AnnP_0=0, P_poll__networl_6_6_RP_0=0, P_masterList_6_5_1=0, P_poll__networl_0_4_AskP_6=0, P_network_3_2_RP_6=0, P_network_4_5_AskP_1=0, P_poll__networl_1_3_AnnP_4=0, P_network_2_1_AnnP_1=0, P_network_0_4_AskP_3=0, P_poll__networl_3_5_AI_1=0, P_network_6_6_RP_4=0, P_network_3_6_AnnP_5=0, P_poll__networl_2_3_AnsP_0=0, P_network_3_4_AI_6=0, P_poll__networl_4_0_RP_6=0, P_poll__networl_4_2_AI_5=0, P_poll__networl_6_1_AnsP_0=0, P_poll__networl_3_5_AI_2=0, P_masterList_2_2_1=0, P_poll__networl_3_5_RI_0=0, P_network_1_0_RP_1=0, P_masterList_2_6_3=0, P_masterList_6_1_3=0, P_poll__networl_4_5_AnnP_2=0, P_network_5_2_AskP_6=0, P_poll__networl_0_1_RP_0=0, P_network_4_4_AI_3=0, P_network_1_0_RP_3=0, P_poll__networl_2_2_AnnP_3=0, P_masterList_2_4_4=0, P_network_4_0_RI_2=0, P_network_3_5_RP_3=0, P_network_2_4_AskP_5=0, P_network_1_6_AnnP_4=0, P_network_3_0_AI_1=0, P_network_4_5_AnnP_3=0, P_network_6_2_AnnP_5=0, P_poll__networl_3_5_AI_4=0, P_poll__networl_1_2_AskP_3=0, P_poll__networl_4_6_RP_1=0, P_poll__networl_5_2_AnnP_0=0, P_network_0_6_RI_6=0, P_poll__networl_0_5_AnnP_2=0, P_network_1_4_RI_6=0, P_network_5_5_AI_3=0, P_network_2_4_RP_2=0, P_poll__networl_2_6_RI_2=0, P_poll__networl_2_3_RI_1=0, P_network_4_4_AnnP_6=0, P_poll__networl_2_4_RP_0=0, P_masterList_2_4_1=0, P_poll__networl_5_2_RI_2=0, P_network_0_0_AskP_6=0, P_poll__networl_0_3_AskP_1=0, P_poll__networl_5_0_RP_1=0, P_network_5_4_RI_6=0, P_poll__networl_6_3_AnnP_6=0, P_network_0_1_AnnP_5=0, P_network_4_3_AI_2=0, P_masterList_4_3_1=0, P_network_2_4_AnnP_3=0, P_network_6_5_AnnP_4=0, P_poll__networl_3_2_AI_6=0, P_network_4_1_AI_2=0, P_network_3_2_RP_4=0, P_network_4_3_AnnP_2=0, P_poll__networl_5_2_RI_4=0, P_network_5_0_AskP_2=0, P_poll__networl_3_3_AI_1=0, P_crashed_1=0, P_poll__networl_0_4_RI_2=0, P_network_0_4_AI_6=0, P_network_5_5_AskP_1=0, P_poll__networl_1_0_RP_4=0, P_poll__networl_3_4_AnnP_5=0, P_poll__networl_5_2_RP_1=0, P_poll__networl_1_0_RP_3=0, P_poll__networl_2_4_RI_6=0, P_poll__networl_5_5_RP_5=0, P_poll__networl_3_4_AnnP_4=0, P_poll__networl_0_1_AskP_4=0, P_poll__networl_3_4_AI_0=0, P_poll__networl_4_0_RI_0=0, P_poll__networl_1_1_RP_1=0, P_network_0_3_AskP_6=0, P_poll__networl_0_3_RI_6=0, P_poll__networl_6_1_AskP_2=0, P_network_2_3_RI_1=0, P_network_0_6_AskP_6=0, P_network_3_5_RP_4=0, P_network_4_1_AnnP_2=0, P_poll__networl_4_6_RP_6=0, P_masterList_5_4_1=0, P_poll__networl_6_3_AnnP_4=0, P_poll__networl_3_1_AI_3=0, P_poll__networl_6_5_RP_4=0, P_network_6_5_AI_1=0, P_poll__networl_6_0_RI_2=0, P_poll__networl_1_1_RP_0=0, P_network_5_4_AnnP_6=0, P_poll__networl_0_1_AnnP_6=0, P_poll__networl_3_1_AI_1=0, P_masterList_2_1_5=0, P_poll__networl_1_2_AnnP_5=0, P_poll__networl_6_0_AnsP_0=0, P_network_4_6_RI_5=0, P_poll__networl_6_3_AskP_4=0, P_network_0_6_AI_1=0, P_network_2_5_AskP_5=0, P_network_1_4_AskP_3=0, P_network_5_0_AI_6=0, P_masterList_6_2_4=0, P_network_1_6_RI_6=0, P_network_5_6_AnnP_2=0, P_network_6_0_AnnP_5=0, P_poll__networl_1_3_AnnP_1=0, P_network_6_2_AnnP_6=0, P_poll__networl_4_6_RI_3=0, P_poll__networl_0_2_AI_1=0, P_poll__networl_3_0_AnsP_0=0, P_poll__networl_5_4_RI_1=0, P_network_3_0_RI_5=0, P_poll__networl_0_6_RI_2=0, P_poll__networl_2_6_AskP_5=0, P_network_6_3_AskP_1=0, P_poll__networl_0_5_AI_4=0, P_network_2_3_AI_3=0, P_poll__networl_0_1_AnsP_0=0, P_network_3_5_AI_4=0, P_poll__networl_0_2_RI_6=0, P_network_6_1_AI_1=0, P_poll__networl_5_6_RP_0=0, P_poll__networl_2_3_RP_4=0, P_poll__networl_4_3_AnnP_1=0, P_poll__networl_4_4_AskP_4=0, P_network_5_5_AskP_5=0, P_network_6_3_RP_1=0, P_network_0_5_AI_6=0, P_network_0_5_AskP_4=0, P_poll__networl_1_0_RI_0=0, P_poll__networl_3_2_AnnP_6=0, P_poll__networl_2_6_RP_2=0, P_network_2_4_AI_1=0, P_network_6_4_AskP_6=0, P_network_6_2_AskP_1=0, P_poll__networl_4_3_AI_6=0, P_network_4_5_RP_3=0, P_poll__networl_2_3_AskP_0=0, P_network_3_3_AI_3=0, P_network_3_0_AskP_6=0, P_masterList_3_3_6=0, P_poll__networl_3_4_AskP_3=0, P_poll__networl_5_5_AnnP_2=0, P_poll__networl_5_5_AnnP_1=0, P_poll__networl_4_4_AskP_3=0, P_poll__networl_4_3_RP_5=0, P_network_4_4_AnnP_5=0, P_poll__networl_1_6_RI_4=0, P_dead_5=0, P_poll__networl_0_3_AskP_4=0, P_poll__networl_1_4_AnnP_6=0, P_poll__networl_3_5_AI_6=0, P_network_1_2_AI_5=0, P_poll__networl_6_5_AnnP_4=0, P_poll__networl_1_4_RI_3=0, P_network_0_4_AnnP_4=0, P_masterList_2_5_6=1, P_poll__networl_4_4_AnnP_2=0, P_poll__networl_5_1_AnnP_5=0, P_poll__networl_0_5_AskP_3=0, P_network_1_1_AskP_3=0, P_poll__networl_4_0_RI_6=0, P_poll__networl_0_2_RI_1=0, P_poll__networl_2_6_RP_0=0, P_poll__networl_6_4_AskP_2=0, P_network_6_2_RI_5=0, P_network_1_1_AskP_2=0, P_network_5_4_AnnP_3=0, P_poll__networl_5_0_RI_5=0, P_network_1_1_RI_2=0, P_poll__networl_2_4_AnsP_0=0, P_poll__networl_6_4_RP_4=0, P_poll__networl_5_0_AI_2=0, P_poll__networl_5_2_AskP_6=0, P_masterList_6_1_2=0, P_network_0_2_RP_2=0, P_network_2_4_RP_6=0, P_poll__networl_2_0_AskP_0=0, P_network_3_0_AI_2=0, P_poll__networl_0_1_AI_3=0, P_network_0_2_RP_3=0, P_poll__networl_3_3_AskP_1=0, P_network_1_0_AnnP_1=0, P_poll__networl_3_5_AI_5=0, P_poll__networl_5_5_RI_4=0, P_network_0_6_AI_6=0, P_network_3_6_RP_1=0, P_network_2_4_AI_5=0, P_network_1_0_AI_1=0, P_network_2_0_RP_4=0, P_poll__networl_6_2_AnnP_1=0, P_network_3_1_AnnP_4=0, P_poll__networl_6_2_AskP_3=0, P_poll__networl_0_2_AI_2=0, P_network_1_3_RI_5=0, P_network_2_3_RP_6=0, P_poll__networl_4_1_AI_6=0, P_poll__networl_1_0_AI_5=0, P_masterList_6_6_0=0, P_network_4_2_AnnP_6=0, P_network_1_1_RP_3=0, P_network_2_5_RP_2=0, P_network_4_5_AskP_5=0, P_poll__networl_2_1_AI_4=0, P_poll__networl_5_4_AnnP_2=0, P_network_2_6_AskP_6=0, P_poll__networl_4_3_AnnP_3=0, P_poll__networl_4_0_AnnP_0=0, P_poll__networl_5_6_RP_3=0, P_poll__networl_5_0_RI_4=0, P_poll__networl_3_4_RP_5=0, P_poll__networl_5_2_AnnP_3=0, P_network_2_5_AskP_2=0, P_network_4_1_AnnP_3=0, P_network_4_2_AskP_1=0, P_network_4_1_AI_3=0, P_poll__networl_0_4_AskP_5=0, P_poll__networl_1_6_AI_3=0, P_poll__networl_5_1_RI_6=0, P_network_2_5_AnnP_3=0, P_masterList_6_2_1=0, P_poll__networl_1_4_AskP_3=0, P_poll__networl_0_3_RP_4=0, P_network_4_6_RP_3=0, P_masterList_2_3_3=0, P_poll__networl_0_0_AnsP_0=0, P_poll__networl_4_0_AskP_2=0, P_network_5_0_AnnP_5=0, P_masterList_5_6_2=0, P_poll__networl_1_2_AI_3=0, P_network_0_1_AI_3=0, P_poll__networl_2_1_RP_2=0, P_network_3_4_AnnP_1=0, P_poll__networl_1_2_AskP_5=0, P_network_2_1_AnnP_5=0, P_poll__networl_5_3_AnnP_3=0, P_poll__networl_0_2_AnnP_1=0, P_poll__networl_4_6_AnnP_1=0, P_poll__networl_3_5_RP_6=0, P_poll__networl_1_5_AskP_2=0, P_network_3_3_AnnP_3=0, P_poll__networl_4_6_RI_4=0, P_network_6_2_AskP_3=0, P_masterList_3_3_0=0, P_poll__networl_5_4_AnnP_0=0, P_network_2_6_AnnP_2=0, P_network_4_5_RP_5=0, P_poll__networl_6_0_AnnP_0=0, P_poll__networl_1_2_AI_0=0, P_poll__networl_3_0_RP_3=0, P_poll__networl_2_6_AI_3=0, P_poll__networl_6_0_RP_6=0, P_poll__networl_4_0_AskP_0=0, P_network_4_5_AnnP_4=0, P_poll__networl_2_3_RP_5=0, P_network_4_2_AskP_4=0, P_poll__networl_0_3_RI_0=0, P_poll__networl_3_0_AI_4=0, P_network_1_6_RP_6=0, P_poll__networl_2_0_AskP_6=0, P_network_2_4_RI_5=0, P_poll__networl_3_6_AskP_2=0, P_poll__networl_4_1_AnnP_0=0, P_poll__networl_3_3_AskP_4=0, P_poll__networl_1_0_RI_6=0, P_network_1_5_RP_6=0, P_network_4_1_AskP_2=0, P_network_4_3_AnnP_5=0, P_network_0_2_AnnP_3=0, P_poll__networl_2_2_RI_5=0, P_network_4_3_RI_3=0, P_poll__networl_2_3_AnnP_1=0, P_network_2_5_AI_3=0, P_network_6_5_RP_1=0, P_poll__networl_1_5_AnnP_5=0, P_network_5_0_RP_5=0, P_poll__networl_0_2_AskP_1=0, P_poll__networl_2_0_AnnP_5=0, P_poll__networl_6_4_RP_2=0, P_network_3_0_AI_5=0, P_network_2_6_RP_5=0, P_poll__networl_6_4_AI_0=0, P_poll__networl_2_4_AnnP_3=0, P_network_6_1_AI_3=0, P_poll__networl_6_2_RP_3=0, P_poll__networl_6_3_RI_1=0, P_network_4_6_AI_1=0, P_poll__networl_4_4_RI_0=0, P_network_5_1_RP_5=0, P_poll__networl_4_1_RI_5=0, P_poll__networl_2_4_AskP_2=0, P_poll__networl_4_4_AnnP_6=0, P_network_4_3_AskP_5=0, P_network_1_6_AI_4=0, P_poll__networl_3_2_RP_5=0, P_network_0_5_RP_2=0, P_network_0_2_RI_4=0, P_network_3_6_RP_5=0, P_masterList_2_
3_0=0, P_masterList_6_6_3=0, P_masterList_3_2_6=0, P_poll__networl_1_5_RP_5=0, P_poll__networl_3_2_AI_2=0, P_masterList_5_1_6=0, P_network_0_1_RP_3=0, P_poll__networl_2_2_AskP_1=0, P_network_3_2_AskP_3=0, P_masterList_0_5_2=0, P_poll__networl_3_3_AI_3=0, P_poll__networl_0_6_AskP_0=0, P_network_5_2_RI_2=0, P_poll__networl_4_3_RP_3=0, P_network_6_6_RP_2=0, P_masterList_6_4_2=0, P_network_1_5_AnnP_5=0, P_poll__networl_1_6_AI_2=0, P_poll__networl_3_5_AskP_1=0, P_poll__networl_4_1_AI_2=0, P_network_1_1_RI_3=0, P_poll__networl_1_6_RP_5=0, P_poll__networl_5_6_AI_5=0, P_network_3_2_AskP_1=0, P_poll__networl_3_0_RI_2=0, P_masterList_4_5_4=0, P_network_0_3_AnnP_5=0, P_masterList_0_4_1=0, P_network_6_4_AnnP_3=0, P_poll__networl_1_1_RI_0=0, P_poll__networl_2_2_AskP_6=0, P_network_4_6_AI_4=0, P_poll__networl_1_5_RI_3=0, P_network_3_0_RI_3=0, P_network_5_0_AI_1=0, P_network_4_3_RP_5=0, P_network_5_6_RI_6=0, P_poll__networl_4_3_AI_2=0, P_poll__networl_4_6_AskP_2=0, P_network_2_2_RI_1=0, P_network_2_1_AnnP_6=0, P_poll__networl_2_0_AI_5=0, P_network_3_2_AskP_2=0, P_poll__networl_6_3_AskP_0=0, P_network_4_6_RP_6=0, P_network_1_1_RI_1=0, P_masterList_3_1_2=0, P_masterList_1_5_3=0, P_poll__networl_0_0_AskP_3=0, P_poll__networl_5_4_RP_4=0, P_network_5_1_RI_5=0, P_network_1_4_AskP_5=0, P_poll__networl_6_2_RI_0=0, P_network_4_6_AskP_5=0, P_poll__networl_3_3_RP_6=0, P_poll__networl_5_3_AskP_1=0, P_poll__networl_6_0_RI_1=0, P_poll__networl_6_6_RP_2=0, P_network_1_4_RI_2=0, P_poll__networl_4_4_RI_1=0, P_network_0_5_RI_1=0, P_network_2_1_RI_4=0, P_poll__networl_3_1_RI_5=0, P_poll__networl_0_6_RI_3=0, P_poll__networl_4_6_RI_6=0, P_poll__networl_3_6_RI_0=0, P_masterList_4_4_0=0, P_poll__networl_3_0_AskP_2=0, P_network_6_2_AI_6=0, P_masterList_1_4_6=0, P_network_2_3_AI_1=0, P_network_3_6_AnnP_2=0, P_poll__networl_2_1_AskP_5=0, P_poll__networl_5_0_RP_5=0, P_network_0_1_AnnP_4=0, P_network_3_4_RI_4=0, P_poll__networl_0_4_RI_6=0, P_poll__networl_2_6_RI_6=0, P_poll__networl_5_5_AskP_2=0, P_network_3_3_AnnP_1=0, P_poll__networl_3_0_RI_5=0, P_poll__networl_5_0_RI_6=0, P_poll__networl_0_6_RI_5=0, P_poll__networl_0_6_AskP_2=0, P_poll__networl_5_6_AnnP_4=0, P_network_2_4_RI_2=0, P_poll__networl_5_0_AI_1=0, P_network_3_4_RI_6=0, P_network_2_3_RP_5=0, P_network_6_5_AI_4=0, P_poll__networl_0_1_RI_0=0, P_network_4_2_RI_5=0, P_network_1_2_AskP_1=0, P_poll__networl_5_6_AI_6=0, P_poll__networl_3_1_AskP_5=0, P_poll__networl_4_6_RI_0=0, P_poll__networl_1_6_RI_5=0, P_network_6_1_RI_5=0, P_poll__networl_1_0_RP_0=0, P_poll__networl_4_2_AnnP_4=0, P_poll__networl_0_4_AnnP_4=0, P_masterList_4_4_4=0, P_network_4_5_AskP_4=0, P_poll__networl_4_1_AskP_2=0, P_poll__networl_4_1_RI_0=0, P_network_0_0_AI_3=0, P_network_6_6_AI_6=0, P_network_4_4_RP_3=0, P_network_1_5_RI_5=0, P_poll__networl_6_5_AskP_1=0, P_poll__networl_2_4_AI_0=0, P_masterList_0_4_2=0, P_network_0_2_AskP_5=0, P_poll__networl_0_4_RP_5=0, P_poll__networl_5_2_AI_4=0, P_poll__networl_0_3_AnnP_0=0, P_network_0_3_AI_5=0, P_poll__networl_0_0_AskP_4=0, P_poll__networl_6_6_RI_6=0, P_network_1_5_AnnP_6=0, P_poll__networl_0_3_AI_6=0, P_poll__networl_5_4_RI_4=0, P_network_1_1_AnnP_1=0, P_network_1_6_RP_5=0, P_network_1_0_AI_6=0, P_masterList_4_5_1=0, P_masterList_5_4_3=0, P_poll__networl_0_2_AnnP_0=0, P_poll__networl_2_0_AnnP_6=0, P_network_3_3_AskP_3=0, P_network_4_6_AnnP_1=0, P_network_2_5_AI_4=0, P_poll__networl_4_5_AnnP_4=0, P_poll__networl_5_2_AnsP_0=0, P_poll__networl_1_1_RI_5=0, P_poll__networl_0_6_AnnP_1=0, P_masterList_6_1_4=0, P_poll__networl_0_6_RI_6=0, P_network_4_0_AnnP_3=0, P_poll__networl_1_4_RP_1=0, P_poll__networl_5_2_RI_6=0, P_network_3_5_AI_1=0, P_network_1_4_RP_2=0, P_poll__networl_0_1_RP_3=0, P_network_0_4_RI_2=0, P_masterList_4_3_0=0, P_poll__networl_6_1_RI_6=0, P_poll__networl_3_2_AskP_0=0, P_masterList_3_6_0=0, P_network_6_2_RI_4=0, P_network_3_2_AskP_6=0, P_masterList_1_6_6=0, P_network_5_1_AnnP_2=0, P_poll__networl_5_2_AskP_3=0, P_masterList_4_1_5=0, P_poll__networl_2_3_AI_1=0, P_poll__networl_3_1_AnnP_0=0, P_network_2_2_AI_5=0, P_network_4_4_AskP_6=0, P_poll__networl_2_0_RP_2=0, P_poll__networl_2_5_RI_0=0, P_poll__networl_5_5_AnnP_4=0, P_network_0_3_AskP_1=0, P_poll__networl_5_2_AskP_1=0, P_network_3_5_RI_1=0, P_poll__networl_3_2_RI_3=0, P_network_0_3_RP_6=0, P_network_4_6_RI_6=0, P_poll__networl_2_4_AI_4=0, P_network_5_6_AskP_4=0, P_poll__networl_1_1_AI_4=0, P_network_3_4_RP_3=0, P_network_5_6_RI_2=0, P_network_1_5_AskP_4=0, P_poll__networl_4_4_AnnP_4=0, P_poll__networl_0_0_RI_4=0, P_network_5_5_AnnP_3=0, P_network_3_5_RP_1=0, P_poll__networl_6_5_AskP_5=0, P_poll__networl_2_3_RI_0=0, P_poll__networl_3_3_RP_4=0, P_network_4_4_RI_5=0, P_poll__networl_0_1_AI_4=0, P_network_6_1_AI_6=0, P_network_3_2_AI_5=0, P_network_6_2_AI_5=0, P_poll__networl_4_4_RI_4=0, P_poll__networl_1_0_RI_2=0, P_poll__networl_0_1_AI_6=0, P_masterList_6_3_0=0, P_poll__networl_4_6_AnnP_2=0, P_network_5_3_AI_5=0, P_network_2_4_AskP_6=0, P_network_3_1_AskP_3=0, P_masterList_0_5_4=0, P_poll__networl_1_1_AI_1=0, P_poll__networl_3_5_AI_0=0, P_network_1_5_RI_4=0, P_poll__networl_3_2_AnsP_0=0, P_network_5_4_AskP_1=0, P_network_0_2_AskP_6=0, P_poll__networl_4_3_AnnP_2=0, P_poll__networl_5_0_AskP_0=0, P_poll__networl_5_4_RI_0=0, P_network_0_4_RI_4=0, P_network_4_1_AI_1=0, P_network_6_0_RI_1=0, P_poll__networl_3_0_AnnP_2=0, P_poll__networl_6_3_AnnP_0=0, P_poll__networl_2_6_AI_1=0, P_poll__networl_0_5_RP_1=0, P_masterList_5_4_5=0, P_network_6_6_RP_5=0, P_poll__networl_6_3_AnnP_2=0, P_network_1_3_AskP_2=0, P_poll__networl_3_4_AnnP_2=0, P_poll__networl_5_4_RP_1=0, P_poll__networl_6_5_RI_3=0, P_poll__networl_1_3_RI_3=0, P_poll__networl_1_1_RI_3=0, P_network_5_1_AskP_4=0, P_network_3_1_RP_5=0, P_poll__networl_3_0_AskP_1=0, P_network_0_4_AskP_6=0, P_network_3_6_AI_6=0, P_poll__networl_4_2_AnnP_3=0, P_network_3_4_AnnP_2=0, P_poll__networl_4_0_RP_2=0, P_network_2_1_RP_5=0, P_poll__networl_6_3_RP_6=0, P_poll__networl_5_6_AskP_0=0, P_poll__networl_5_0_AnsP_0=0, P_poll__networl_5_1_RI_5=0, P_network_5_6_RP_4=0, P_poll__networl_1_4_RP_4=0, P_network_4_1_RI_2=0, P_network_1_2_AI_6=0, P_poll__networl_0_0_AskP_6=0, P_poll__networl_3_1_AskP_6=0, P_poll__networl_2_0_AI_4=0, P_poll__networl_2_2_AnnP_1=0, P_poll__networl_5_0_AskP_2=0, P_poll__networl_2_0_AskP_1=0, P_network_6_1_RI_6=0, P_network_0_1_AskP_3=0, P_network_1_6_RI_5=0, P_poll__networl_6_4_AI_3=0, P_poll__networl_0_0_AI_1=0, P_masterList_0_5_5=0, P_network_3_4_AskP_2=0, P_poll__networl_5_6_RP_1=0, P_network_0_5_AI_4=0, P_poll__networl_6_2_RI_4=0, P_network_3_5_AskP_3=0, P_network_1_2_AnnP_5=0, P_poll__networl_0_3_AnnP_4=0, P_network_5_5_RI_5=0, P_network_5_4_AnnP_1=0, P_poll__networl_6_4_AnnP_3=0, P_poll__networl_3_6_RP_5=0, P_poll__networl_0_2_AskP_4=0, P_poll__networl_5_3_AnnP_5=0, P_network_2_5_RI_1=0, P_poll__networl_0_5_RI_0=0, P_network_4_6_RI_1=0, P_network_5_0_AI_3=0, P_network_0_1_RP_4=0, P_network_2_4_RP_5=0, P_network_3_3_RP_3=0, P_network_4_6_RP_4=0, P_network_6_0_AI_1=0, P_poll__networl_0_5_AskP_2=0, P_network_1_2_AskP_3=0, P_network_6_3_RP_6=0, P_network_3_3_AskP_6=0, P_poll__networl_4_5_AI_4=0, P_poll__networl_1_4_AskP_0=0, P_network_6_6_AI_5=0, P_poll__networl_3_3_RI_5=0, P_poll__networl_2_2_AI_5=0, P_network_0_2_AnnP_1=0, P_poll__networl_0_2_AskP_6=0, P_poll__networl_6_2_AI_5=0, P_network_0_6_AskP_1=0, P_network_1_2_AI_3=0, P_network_2_5_AnnP_1=0, P_network_4_3_AnnP_1=0, P_network_1_2_RP_2=0, P_poll__networl_2_1_RP_6=0, P_poll__networl_4_2_AskP_0=0, P_network_1_5_RP_3=0, P_poll__networl_1_6_RI_3=0, P_network_2_3_AnnP_4=0, P_poll__networl_2_6_AI_4=0, P_network_5_2_AskP_1=0, P_network_5_0_RP_6=0, P_poll__networl_4_3_AskP_1=0, P_poll__networl_2_5_RP_3=0, P_poll__networl_4_0_RI_5=0, P_network_2_2_AnnP_6=0, P_poll__networl_1_1_AnnP_3=0, P_network_5_0_AskP_5=0, P_poll__networl_2_5_RI_5=0, P_network_6_5_RI_1=0, P_network_4_5_AI_4=0, P_network_6_5_AnnP_1=0, P_poll__networl_0_0_RI_3=0, P_poll__networl_6_5_AskP_3=0, P_poll__networl_0_4_AI_3=0, P_network_5_2_AI_5=0, P_network_0_5_AskP_6=0, P_network_5_6_AnnP_4=0, P_network_6_1_AI_4=0, P_network_5_0_AskP_6=0, P_poll__networl_6_3_AI_2=0, P_network_1_6_AnnP_6=0, P_poll__networl_5_5_RP_2=0, P_network_5_1_AnnP_1=0, P_poll__networl_2_1_RP_0=0, P_poll__networl_4_0_AnnP_4=0, P_poll__networl_4_1_RP_3=0, P_poll__networl_6_6_AI_1=0, P_network_6_0_AskP_1=0, P_network_2_2_RI_3=0, P_poll__networl_6_6_RI_0=0, P_poll__networl_1_6_RI_1=0, P_poll__networl_2_1_RP_1=0, P_network_6_1_AnnP_2=0, P_network_5_0_AI_5=0, P_poll__networl_3_0_RP_1=0, P_network_0_2_AI_6=0, P_network_4_1_RI_3=0, P_poll__networl_5_3_RP_1=0, P_poll__networl_1_5_RI_5=0, P_network_4_4_RP_4=0, P_network_6_6_AI_3=0, P_network_3_1_RI_5=0, P_network_2_3_AnnP_6=0, P_network_1_3_AnnP_3=0, P_network_5_2_AI_6=0, P_network_5_6_RP_3=0, P_masterList_5_3_4=0, P_network_1_4_AnnP_2=0, P_network_5_1_RI_3=0, P_network_1_0_AnnP_5=0, P_network_0_6_AskP_2=0, P_poll__networl_5_0_AnnP_3=0, P_masterList_0_3_3=0, P_poll__networl_0_2_RI_4=0, P_poll__networl_6_0_AskP_4=0, P_network_2_2_RP_4=0, P_poll__networl_0_3_AskP_5=0, P_network_0_0_AI_1=0, P_network_2_3_AnnP_5=0, P_poll__networl_1_3_RP_2=0, P_network_2_1_RI_1=0, P_poll__networl_3_1_RI_1=0, P_network_3_5_AnnP_5=0, P_network_4_5_AnnP_1=0, P_network_5_6_AskP_6=0, P_poll__networl_4_0_RP_5=0, P_network_6_0_RI_3=0, P_network_3_5_RP_5=0, P_network_0_5_RP_4=0, P_network_3_3_RI_5=0, P_poll__networl_3_0_RP_0=0, P_network_6_0_RI_5=0, P_poll__networl_0_2_AnnP_6=0, P_network_4_2_RI_4=0, P_poll__networl_5_4_RP_0=0, P_poll__networl_2_5_AI_5=0, P_poll__networl_4_4_AnnP_3=0, P_masterList_5_5_4=0, P_poll__networl_0_6_AskP_5=0, P_network_5_2_AnnP_5=0, P_poll__networl_5_4_AskP_2=0, P_network_2_2_AnnP_4=0, P_poll__networl_2_3_AskP_2=0, P_network_5_0_AnnP_6=0, P_poll__networl_3_1_AI_2=0, P_network_0_1_RP_2=0, P_network_5_1_RP_1=0, P_network_3_0_AnnP_1=0, P_network_4_2_AnnP_5=0, P_network_6_4_RI_5=0, P_poll__networl_6_6_AI_3=0, P_network_5_2_AI_1=0, P_poll__networl_1_4_RI_1=0, P_masterList_5_3_1=0, P_network_5_1_AnnP_4=0, P_network_6_0_RP_2=0, P_poll__networl_2_6_AskP_0=0, P_poll__networl_5_4_RP_3=0, P_poll__networl_0_4_RP_6=0, P_network_6_0_AI_6=0, P_masterList_3_5_6=1, P_poll__networl_4_5_AskP_2=0, P_network_3_5_AI_3=0, P_poll__networl_1_1_AskP_2=0, P_poll__networl_1_2_AskP_4=0, P_poll__networl_3_0_AnnP_5=0, P_network_0_5_RI_2=0, P_network_6_3_AI_2=0, P_network_3_3_AI_4=0, P_network_4_1_AI_4=0, P_masterList_5_6_5=0, P_network_0_6_AnnP_6=0, P_masterList_4_5_3=0, P_network_6_0_RP_6=0, P_poll__networl_1_1_RP_3=0, P_poll__networl_6_1_RI_4=0, P_poll__networl_2_4_RP_1=0, P_network_1_4_RP_3=0, P_network_2_0_AnnP_2=0, P_poll__networl_2_4_AskP_3=0, P_network_5_1_AI_1=0, P_network_6_3_AskP_6=0, P_poll__networl_5_6_AnnP_3=0, P_dead_2=0, P_poll__networl_4_6_AI_4=0, P_poll__networl_2_0_AnnP_3=0, P_network_3_3_AskP_2=0, P_poll__networl_5_5_AI_3=0, P_poll__networl_5_6_RI_1=0, P_poll__networl_6_6_RI_4=0, P_poll__networl_2_6_AskP_3=0, P_poll__networl_4_3_RI_0=0, P_network_0_1_AI_1=0, P_network_4_3_AskP_1=0, P_poll__networl_4_3_RI_6=0, P_network_2_4_RP_3=0, P_poll__networl_4_1_AskP_3=0, P_network_1_2_RI_1=0, P_poll__networl_2_1_RI_2=0, P_poll__networl_0_6_AI_2=0, P_poll__networl_2_3_AskP_4=0, P_poll__networl_4_0_RP_1=0, P_poll__networl_0_2_RP_6=0, P_network_0_5_AnnP_2=0, P_network_4_6_AI_3=0, P_masterList_3_2_2=1, P_masterList_6_1_5=0, P_network_4_5_AskP_2=0, P_network_0_0_RP_6=0, P_network_2_6_AnnP_4=0, P_network_1_4_AskP_4=0, P_poll__networl_5_1_RP_4=0, P_network_6_0_RP_1=0, P_poll__networl_1_5_AI_2=0, P_network_3_6_AI_4=0, P_poll__networl_4_0_AI_4=0, P_network_1_5_RP_5=0, P_network_1_5_AskP_5=0, P_poll__networl_6_0_AskP_5=0, P_masterList_3_5_5=0, P_poll__networl_5_4_AI_0=0, P_poll__networl_1_2_RP_4=0, P_poll__networl_5_1_AskP_4=0, P_network_2_4_AnnP_6=0, P_network_5_3_AnnP_3=0, P_masterList_2_3_2=0, P_poll__networl_6_4_RP_3=0, P_poll__networl_2_3_AI_0=0, P_poll__networl_2_1_AI_3=0, P_poll__networl_5_4_RI_3=0, P_network_6_4_RP_2=0, P_poll__networl_5_1_RI_2=0, P_poll__networl_1_3_RI_2=0, P_masterList_1_6_1=0, P_poll__networl_0_5_AI_2=0, P_masterList_5_5_5=0, P_network_0_2_RI_3=0, P_poll__networl_3_2_AskP_4=0, P_poll__networl_5_5_AI_1=0, P_network_4_0_RI_1=0, P_poll__networl_3_3_RI_0=0, P_poll__networl_1_5_AnnP_6=0, P_poll__networl_4_5_AnnP_5=0, P_poll__networl_3_4_RP_6=0, P_poll__networl_4_5_RP_1=0, P_poll__networl_5_4_AI_5=0, P_network_0_0_AnnP_6=0, P_network_6_6_RI_6=0, P_network_1_5_RI_6=0, P_network_1_4_AnnP_4=0, P_poll__networl_4_2_AskP_5=0, P_network_6_4_RI_4=0, P_poll__networl_1_3_AskP_0=0, P_poll__networl_3_5_AnnP_5=0, P_network_2_6_RI_3=0, P_poll__networl_1_6_AI_6=0, P_network_6_4_AnnP_4=0, P_network_2_2_AskP_1=0, P_poll__networl_1_1_AskP_1=0, P_poll__networl_6_3_AI_3=0, P_network_3_4_AskP_6=0, P_poll__networl_2_2_RP_5=0, P_masterList_3_5_2=0, P_network_5_2_AnnP_4=0, P_poll__networl_1_6_AnnP_5=0, P_network_5_1_AnnP_3=0, P_poll__networl_2_0_RI_4=0, P_poll__networl_3_0_AI_3=0, P_poll__networl_4_2_RP_2=0, P_masterList_4_1_2=0, P_poll__networl_5_3_AnsP_0=0, P_poll__networl_5_1_AskP_3=0, P_poll__networl_0_3_AnnP_2=0, P_network_0_1_AnnP_2=0, P_network_4_1_RI_4=0, P_masterList_4_6_1=0, P_poll__networl_2_0_RP_1=0, P_poll__networl_4_2_AnsP_0=0, P_network_5_4_RP_5=0, P_network_4_1_RI_6=0, P_masterList_3_3_3=0, P_poll__networl_1_3_RP_4=0, P_masterList_4_5_2=0, P_network_3_2_RI_5=0, P_poll__networl_1_4_RP_5=0, P_poll__networl_1_2_AnnP_3=0, P_poll__networl_5_6_RI_3=0, P_poll__networl_1_0_AnnP_4=0, P_network_5_4_AnnP_4=0, P_network_6_5_RP_4=0, P_poll__networl_0_0_RI_6=0, P_poll__networl_1_4_RP_3=0, P_poll__networl_1_0_AI_0=0, P_poll__networl_3_0_AskP_3=0, P_network_5_2_RI_3=0, P_poll__networl_1_6_RP_2=0, P_poll__networl_4_0_AskP_1=0, P_network_3_2_RI_1=0, P_poll__networl_5_3_AskP_6=0, P_network_2_2_RI_2=0, P_network_1_4_RP_4=0, P_network_0_5_RP_3=0, P_network_4_3_AI_4=0, P_poll__networl_0_6_AnnP_6=0, P_masterList_0_4_6=0, P_network_2_2_AI_6=0, P_network_5_5_AnnP_4=0, P_poll__networl_2_4_AnnP_5=0, P_poll__networl_6_4_RI_5=0, P_poll__networl_5_3_AI_3=0, P_poll__networl_1_1_AskP_6=0, P_poll__networl_6_5_AnnP_6=0, P_network_0_5_AI_2=0, P_network_4_2_RP_4=0, P_network_6_5_RP_2=0, P_poll__networl_4_4_AskP_0=0, P_network_3_4_AnnP_4=0, P_poll__networl_3_3_AskP_5=0, P_poll__networl_4_2_RI_3=0, P_network_0_6_AI_2=0, P_network_4_0_RI_3=0, P_poll__networl_2_5_AnnP_6=0, P_poll__networl_3_0_AnnP_3=0, P_network_4_4_RI_2=0, P_poll__networl_4_2_AI_3=0, P_poll__networl_6_1_AI_3=0, P_network_5_6_RI_3=0, P_poll__networl_1_6_AnnP_3=0, P_poll__networl_6_3_RI_6=0, P_electionFailed_2=0, P_poll__networl_6_1_RP_2=0, P_network_0_2_AI_5=0, P_poll__networl_2_6_AnnP_1=0, P_poll__networl_3_3_AnnP_3=0, P_poll__networl_1_1_RI_1=0, P_network_3_6_RP_6=0, P_poll__networl_1_2_AnnP_2=0, P_network_3_3_RI_3=0, P_network_6_5_AskP_4=0, P_poll__networl_3_3_RP_1=0, P_network_6_5_RI_5=0, P_network_5_0_AnnP_3=0, P_network_4_4_AskP_3=0, P_poll__networl_0_5_RI_1=0, P_poll__networl_1_0_AI_3=0, P_network_5_2_RI_4=0, P_network_2_4_RI_6=0, P_poll__networl_5_1_RI_4=0, P_masterList_1_6_4=0, P_poll__networl_2_5_AI_3=0, P_poll__networl_6_6_RI_5=0, P_poll__networl_1_1_AnsP_0=0, P_poll__networl_5_3_RP_3=0, P_network_4_0_RI_4=0, P_network_0_4_AskP_5=0, P_network_0_2_AI_3=0, P_network_1_1_RP_6=0, P_poll__networl_5_6_RP_6=0, P_network_4_5_AI_3=0, P_network_1_5_AnnP_2=0, P_poll__networl_2_2_AskP_0=0, P_network_1_2_RI_2=0, P_network_6_2_AnnP_4=0, P_poll__networl_4_3_AnsP_0=0, P_masterList_5_1_0=0, P_poll__networl_3_6_AskP_0=0, P_network_5_6_RP_5=0, P_poll__networl_3_2_AI_5=0, P_poll__networl_3_1_RP_2=0, P_poll__networl_1_3_AskP_1=0, P_network_6_3_AskP_4=0, P_poll__networl_0_5_RP_4=0, P_poll__networl_1_2_RI_1=0, P_poll__networl_2_3_AnnP_6=0, P_masterList_1_3_5=0, P_network_1_5_AskP_3=0, P_network_2_1_AnnP_3=0, P_masterList_0_2_5=0, P_masterList_6_2_3=0, P_network_1_2_AnnP_2=0, P_network_4_1_AskP_1=0, P_poll__networl_2_1_AI_1=0, P_poll__networl_6_0_AskP_6=0, P_poll__networl_2_1_AskP_6=0, P_poll__networl_3_6_AskP_6=0, P_network_1_4_RP_6=0, P_poll__networl_4_2_RI_5=0, P_poll__networl_5_0_AI_6=0, P_network_0_4_AnnP_5=0, P_network_0_1_RI_2=0, P_network_4_4_AskP_1=0, P_network_2_5_AnnP_6=0, P_poll__networl_3_2_RP_0=0, P_network_5_0_RP_4=0, P_network_3_5_AnnP_3=0, P_network_5_5_AI_6=0, P_masterList_5_4_4=1, P_network_0_1_AnnP_3=0, P_masterList_4_6_3=0, P_network_2_6_AnnP_5=0, P_poll__networl_5_2_AskP_0=0, P_masterList_0_3_6=0, P_network_3_1_RI_2=0, P_poll__networl_5_3_AI_6=0, P_network_2_4_AI_2=0, P_masterList_0_6_5=0, P_n
etwork_1_2_RI_4=0, P_network_4_5_RI_3=0, P_network_6_5_AI_2=0, P_poll__networl_6_4_AnnP_2=0, P_network_5_1_AskP_5=0, P_network_0_1_AskP_1=0, P_poll__networl_2_2_AnnP_5=0, P_poll__networl_4_3_AI_3=0, P_poll__networl_4_4_AskP_5=0, P_poll__networl_1_3_AskP_6=0, P_network_2_3_RI_6=0, P_network_5_5_RP_3=0, P_poll__networl_6_6_RI_2=0, P_masterList_2_5_2=0, P_masterList_2_4_6=0, P_poll__networl_4_2_AskP_1=0, P_network_0_5_AnnP_5=0, P_network_2_3_AI_4=0, P_poll__networl_6_5_RP_2=0, P_poll__networl_6_6_AI_2=0, P_masterList_0_5_1=0, P_poll__networl_0_3_AI_3=0, P_poll__networl_3_1_AI_6=0, P_network_1_2_AskP_4=0, P_network_2_3_AI_6=0, P_network_3_4_AskP_4=0, P_poll__networl_1_3_AnsP_0=0, P_poll__networl_1_3_AI_3=0, P_network_1_1_RI_6=0, P_poll__networl_0_3_AnnP_6=0, P_poll__networl_5_1_RI_3=0, P_network_6_0_AnnP_2=0, P_network_6_0_AskP_5=0, P_network_1_2_RI_5=0, P_poll__networl_5_2_AnnP_6=0, P_poll__networl_3_5_AskP_5=0, P_poll__networl_4_5_AI_0=0, P_masterList_0_2_6=0, P_network_3_6_AskP_6=0, P_network_6_0_AI_2=0, P_poll__networl_0_0_RI_5=0, P_poll__networl_2_2_RP_4=0, P_poll__networl_1_0_AnnP_6=0, P_network_1_3_RI_3=0, P_network_6_3_RI_4=0, P_poll__networl_0_3_RP_6=0, P_poll__networl_3_6_RP_4=0, P_poll__networl_1_3_AnnP_3=0, P_network_3_6_RP_3=0, P_masterList_1_1_3=0, P_network_2_6_RP_6=0, P_network_3_4_AskP_3=0, P_network_1_2_RI_3=0, P_masterList_5_2_3=0, P_network_6_3_AI_5=0, P_network_1_6_RI_3=0, P_poll__networl_6_2_AskP_6=0, P_masterList_2_3_5=0, P_poll__networl_1_2_AnnP_0=0, P_network_1_1_AnnP_5=0, P_poll__networl_3_2_RP_4=0, P_poll__networl_3_5_RI_5=0, P_network_2_5_AI_6=0, P_poll__networl_1_6_RP_3=0, P_network_6_1_AnnP_3=0, P_poll__networl_0_6_AnnP_2=0, P_masterList_5_4_6=0, P_poll__networl_6_4_AnnP_0=0, P_poll__networl_6_3_AnnP_1=0, P_masterList_1_4_2=0, P_masterList_1_6_2=0, P_masterList_3_5_4=0, P_poll__networl_5_3_AskP_0=0, P_poll__networl_1_4_AI_6=0, P_poll__networl_3_4_AskP_0=0, P_poll__networl_2_0_RI_0=0, P_poll__networl_1_6_AnnP_6=0, P_network_1_3_RP_4=0, P_poll__networl_5_1_AI_0=0, P_poll__networl_2_5_AskP_3=0, P_poll__networl_5_2_RP_4=0, P_poll__networl_3_4_RP_1=0, P_poll__networl_4_1_AnnP_3=0, P_masterList_6_3_2=0, P_network_2_1_AskP_3=0, P_poll__networl_0_4_AI_5=0, P_poll__networl_5_5_AskP_4=0, P_poll__networl_2_0_AnnP_1=0, P_poll__networl_6_6_RP_3=0, P_network_6_4_AnnP_5=0, P_poll__networl_1_3_RP_5=0, P_network_2_1_AI_3=0, P_network_0_4_AI_4=0, P_network_0_2_AI_2=0, P_poll__networl_3_6_AskP_4=0, P_poll__networl_3_5_RI_2=0, P_network_2_6_AI_2=0, P_network_5_6_RI_4=0, P_poll__networl_4_4_AI_2=0, P_network_1_0_AskP_1=0, P_poll__networl_0_2_AnnP_2=0, P_poll__networl_3_2_RI_2=0, P_masterList_1_2_3=1, P_poll__networl_1_2_RI_2=0, P_poll__networl_0_5_AI_3=0, P_network_4_1_RI_1=0, P_poll__networl_3_5_RP_0=0, P_network_5_2_AI_4=0, P_poll__networl_2_1_AskP_2=0, P_network_6_6_AskP_6=0, P_poll__networl_2_0_RP_0=0, P_poll__networl_6_5_AnnP_1=0, P_network_5_6_RP_1=0, P_poll__networl_3_4_AI_5=0, P_poll__networl_4_6_RP_3=0, P_network_6_1_RP_5=0, P_network_6_3_AnnP_2=0, P_poll__networl_2_6_RP_5=0, P_network_3_4_RI_1=0, P_network_1_4_AI_3=0, P_poll__networl_0_5_AskP_5=0, P_poll__networl_6_5_AnsP_0=0, P_network_3_1_RP_2=0, P_masterList_1_1_1=0, P_network_1_5_AI_1=0, P_masterList_6_4_6=0, P_masterList_1_5_5=0, P_poll__networl_5_1_RP_3=0, P_masterList_1_6_5=0, P_network_4_6_AI_2=0, P_poll__networl_2_4_AskP_1=0, P_network_4_2_AI_4=0, P_network_1_1_RI_4=0, P_poll__networl_3_0_AskP_0=0, P_masterList_1_5_0=0, P_network_1_2_AskP_5=0, P_poll__networl_5_6_AskP_1=0, P_network_1_0_AI_5=0, P_network_0_5_AI_1=0, P_poll__networl_4_3_AI_0=0, P_poll__networl_4_6_AnnP_4=0, P_network_3_0_AskP_1=0, P_network_5_5_AnnP_2=0, P_poll__networl_5_4_RP_5=0, P_poll__networl_2_0_AskP_4=0, P_network_1_1_AI_5=0, P_poll__networl_3_0_RP_4=0, P_poll__networl_5_1_AI_3=0, P_poll__networl_4_1_AnnP_1=0, P_poll__networl_1_5_AskP_5=0, P_poll__networl_3_4_AI_1=0, P_poll__networl_1_1_AnnP_5=0, P_poll__networl_1_4_AnnP_0=0, P_poll__networl_3_3_AnnP_2=0, P_poll__networl_4_1_AnnP_6=0, P_network_1_0_AI_3=0, P_poll__networl_2_5_RI_3=0, P_network_5_2_RP_3=0, P_poll__networl_3_6_RI_3=0, P_poll__networl_1_6_AI_4=0, P_poll__networl_2_2_AI_3=0, P_poll__networl_5_2_RI_5=0, P_network_1_1_AI_2=0, P_network_3_0_AI_3=0, P_dead_6=0, P_network_6_6_RI_3=0, P_network_4_6_RP_1=0, P_network_1_5_RI_3=0, P_poll__networl_0_1_AnnP_4=0, P_network_4_1_AskP_3=0, P_network_0_3_AskP_2=0, P_poll__networl_0_1_AnnP_3=0, P_poll__networl_2_1_AnnP_3=0, P_poll__networl_2_1_RP_4=0, P_network_4_1_RP_1=0, P_masterList_5_4_2=0, P_network_0_0_RI_1=0, P_network_2_1_AskP_2=0, P_network_4_4_AI_2=0, P_poll__networl_5_6_RP_2=0, P_poll__networl_6_5_RI_4=0, P_network_6_4_AI_5=0, P_poll__networl_0_0_AI_4=0, P_poll__networl_1_2_AI_4=0, P_network_3_2_RI_3=0, P_poll__networl_6_0_AskP_1=0, P_poll__networl_6_4_AskP_1=0, P_network_5_3_AnnP_5=0, P_network_0_3_AskP_3=0, P_poll__networl_6_2_AskP_4=0, P_network_6_5_AI_3=0, P_network_0_0_AI_5=0, P_network_2_0_RP_5=0, P_network_0_6_RP_6=0, P_poll__networl_3_5_RP_4=0, P_poll__networl_6_2_RI_6=0, P_network_1_4_AI_4=0, P_poll__networl_1_3_RP_6=0, P_poll__networl_3_4_AI_2=0, P_poll__networl_4_6_AnnP_6=0, P_network_2_6_AnnP_1=0, P_network_0_4_RP_2=0, P_network_4_6_RP_2=0, P_poll__networl_6_4_AskP_0=0, P_network_0_3_RP_3=0, P_network_4_3_AskP_4=0, P_network_6_6_AskP_3=0, P_network_4_0_AI_5=0, P_poll__networl_5_0_RP_2=0, P_poll__networl_3_6_AnnP_5=0, P_network_3_2_RP_2=0, P_network_6_0_AskP_3=0, P_poll__networl_0_3_RP_2=0, P_masterList_4_1_0=0, P_poll__networl_5_0_RP_3=0, P_masterList_0_2_4=0, P_poll__networl_2_3_RI_5=0, P_network_1_1_AnnP_4=0, P_poll__networl_2_0_RP_3=0, P_network_2_5_AnnP_4=0, P_poll__networl_3_4_AnnP_3=0, P_masterList_0_6_3=0, P_network_1_4_RP_5=0, P_poll__networl_3_5_RI_6=0, P_network_0_5_AI_5=0, P_poll__networl_0_6_RP_0=0, P_network_1_1_RP_5=0, P_poll__networl_2_4_AnnP_2=0, P_poll__networl_4_6_AnnP_3=0, P_network_6_3_RI_6=0, P_poll__networl_0_6_AI_4=0, P_masterList_4_2_3=0, P_network_6_5_RP_6=0, P_poll__networl_0_4_AskP_0=0, P_poll__networl_6_0_RI_3=0, P_network_4_5_RI_4=0, P_masterList_0_3_4=0, P_network_1_0_AskP_2=0, P_poll__networl_1_5_RI_4=0, P_poll__networl_3_5_RI_3=0, P_poll__networl_0_2_AnnP_3=0, P_network_3_0_AnnP_4=0, P_poll__networl_3_4_RP_2=0, P_network_4_3_AI_6=0, P_poll__networl_2_2_RI_2=0, P_network_0_2_AnnP_5=0, P_poll__networl_3_6_RP_2=0, P_network_1_5_RP_2=0, P_poll__networl_6_6_AnnP_3=0, P_poll__networl_3_2_AskP_5=0, P_poll__networl_3_6_AskP_5=0, P_poll__networl_0_0_RP_1=0, P_poll__networl_0_5_AI_6=0, P_poll__networl_3_0_AI_1=0, P_poll__networl_4_0_AskP_6=0, P_poll__networl_2_4_AnnP_6=0, P_network_2_3_AnnP_1=0, P_poll__networl_0_6_AskP_6=0, P_poll__networl_6_6_AnnP_6=0, P_poll__networl_1_5_AnnP_1=0, P_poll__networl_6_2_AskP_2=0, P_network_6_1_AI_5=0, P_poll__networl_4_6_AnnP_5=0, P_network_3_2_AskP_5=0, P_network_4_0_AskP_6=0, P_network_2_0_AskP_4=0, P_poll__networl_2_4_RP_6=0, P_network_0_0_AnnP_5=0, P_network_0_5_AskP_5=0, P_poll__networl_2_0_AI_0=0, P_poll__networl_2_3_AskP_1=0, P_poll__networl_4_1_RP_6=0, P_network_0_1_RI_5=0, P_network_5_3_AnnP_2=0, P_poll__networl_0_3_AI_2=0, P_network_0_1_AskP_5=0, P_network_4_2_AI_3=0, P_poll__networl_1_6_RI_6=0, P_masterList_4_2_6=0, P_network_1_2_RP_5=0, P_network_2_2_RI_5=0, P_network_6_6_AnnP_5=0, P_network_3_4_RP_6=0, P_crashed_3=0, P_network_6_4_AI_2=0, P_masterList_1_2_5=0, P_network_0_3_AskP_4=0, P_masterList_3_1_0=0, P_network_0_2_AnnP_4=0, P_poll__networl_3_2_AskP_1=0, P_network_5_4_RI_1=0, P_poll__networl_5_3_RI_5=0, P_network_2_4_AnnP_2=0, P_poll__networl_4_4_RI_3=0, P_poll__networl_6_2_AskP_1=0, P_network_6_1_RP_4=0, P_poll__networl_2_5_AI_0=0, P_network_1_0_RI_5=0, P_poll__networl_4_5_AI_2=0, P_network_0_2_AI_1=0, P_network_4_0_AnnP_1=0, P_poll__networl_3_0_AI_5=0, P_poll__networl_3_6_AnnP_0=0, P_network_0_6_RP_3=0, P_poll__networl_2_0_AI_1=0, P_masterList_4_1_4=0, P_poll__networl_1_5_AskP_1=0, P_masterList_3_1_1=1, P_poll__networl_6_0_AnnP_4=0, P_poll__networl_3_3_RI_6=0, P_poll__networl_6_2_RP_6=0, P_network_3_6_AskP_2=0, P_poll__networl_5_1_AI_1=0, P_poll__networl_5_5_AnsP_0=0, P_network_2_1_RI_3=0, P_poll__networl_4_0_RI_3=0, P_poll__networl_1_1_RP_2=0, P_poll__networl_5_5_RP_3=0, P_network_0_5_RI_6=0, P_masterList_1_5_1=0, P_poll__networl_4_1_AI_1=0, P_masterList_4_3_4=0, P_masterList_1_1_0=0, P_poll__networl_3_2_RI_0=0, P_network_6_0_RP_5=0, P_masterList_6_4_1=0, P_network_6_2_AskP_2=0, P_network_6_2_AI_3=0, P_network_3_6_AI_1=0, P_masterList_3_6_2=0, P_poll__networl_5_1_AskP_0=0, P_poll__networl_5_1_RP_6=0, P_network_0_1_RI_1=0, P_poll__networl_4_5_RP_5=0, P_poll__networl_3_6_AnsP_0=0, P_network_0_3_RI_1=0, P_poll__networl_3_5_AnnP_2=0, P_network_0_4_AI_5=0, P_masterList_1_4_3=0, P_network_0_1_AskP_2=0, P_poll__networl_5_3_RI_3=0, P_network_6_1_AskP_3=0, P_poll__networl_1_6_AnnP_0=0, P_poll__networl_6_3_AskP_6=0, P_poll__networl_1_0_RP_2=0, P_poll__networl_4_5_AskP_0=0, P_poll__networl_6_5_RP_3=0, P_masterList_1_3_6=0, P_poll__networl_3_4_AnnP_1=0, P_masterList_5_6_4=0, P_poll__networl_1_5_RP_6=0, P_masterList_3_4_3=0, P_network_3_1_RI_3=0, P_poll__networl_1_5_RP_4=0, P_poll__networl_6_6_RP_1=0, P_poll__networl_4_2_RP_1=0, P_network_4_6_AI_5=0, P_poll__networl_0_6_AI_6=0, P_network_6_0_AskP_2=0, P_network_2_5_RI_3=0, P_poll__networl_1_5_AI_4=0, P_network_2_0_AI_6=0, P_network_2_2_AI_3=0, P_network_3_3_RI_4=0, P_network_5_1_RI_2=0, P_poll__networl_5_6_AnsP_0=0, P_poll__networl_3_2_AI_4=0, P_network_3_2_AnnP_2=0, P_network_3_4_AskP_1=0, P_poll__networl_2_2_AI_2=0, P_network_6_1_AskP_1=0, P_network_6_6_RP_6=0, P_poll__networl_5_4_AnnP_5=0, P_poll__networl_6_5_RP_6=0, P_network_1_2_AskP_2=0, P_network_1_5_AnnP_3=0, P_poll__networl_5_6_RP_5=0, P_network_0_2_AskP_2=0, P_poll__networl_2_3_AskP_5=0, P_poll__networl_5_5_AskP_0=0, P_poll__networl_6_6_AskP_4=0, P_network_4_5_RI_5=0, P_poll__networl_2_2_RP_3=0, P_network_4_4_RP_1=0, P_poll__networl_3_4_RP_4=0, P_poll__networl_2_6_RI_1=0, P_poll__networl_0_6_RP_3=0, P_network_6_4_AskP_4=0, P_poll__networl_4_5_RI_0=0, P_poll__networl_5_3_AI_5=0, P_poll__networl_0_0_RP_2=0, P_poll__networl_4_5_AskP_1=0, P_network_0_1_RP_1=0, P_network_2_5_AI_1=0, P_poll__networl_3_2_RI_1=0, P_masterList_1_3_2=0, P_network_1_3_RP_2=0, P_poll__networl_2_6_AI_0=0, P_poll__networl_2_3_RI_6=0, P_poll__networl_3_4_AI_6=0, P_poll__networl_6_4_RI_4=0, P_network_1_2_RP_6=0, P_poll__networl_5_5_AskP_1=0, P_network_3_4_AI_1=0, P_poll__networl_1_3_RP_1=0, P_poll__networl_4_5_AI_3=0, P_poll__networl_3_2_AI_3=0, P_poll__networl_0_0_RP_5=0, P_poll__networl_3_1_AskP_0=0, P_poll__networl_1_0_AI_6=0, P_poll__networl_2_3_RP_6=0, P_poll__networl_2_1_RI_1=0, P_network_4_4_AskP_2=0, P_poll__networl_0_6_RP_6=0, P_network_6_2_AskP_5=0, P_network_1_0_RP_5=0, P_network_1_1_RP_4=0, P_network_0_4_RI_6=0, P_masterList_3_5_1=0, P_poll__networl_0_3_AnnP_1=0, P_poll__networl_0_4_RP_3=0, P_poll__networl_3_5_AskP_4=0, P_network_2_5_RI_2=0, P_poll__networl_2_0_RP_4=0, P_poll__networl_4_6_RI_2=0, P_poll__networl_6_0_AI_2=0, P_network_5_4_AskP_6=0, P_poll__networl_3_2_AskP_2=0, P_network_0_6_AnnP_5=0, P_network_6_0_AskP_4=0, P_network_4_0_RP_4=0, P_poll__networl_0_6_AnnP_4=0, P_network_0_5_AI_3=0, P_poll__networl_0_3_RI_4=0, P_poll__networl_6_4_AskP_3=0, P_network_3_6_RP_2=0, P_poll__networl_0_0_AskP_2=0, P_network_6_5_RI_2=0, P_network_4_4_AnnP_2=0, P_poll__networl_0_5_AskP_6=0, P_poll__networl_1_2_RP_6=0, P_poll__networl_6_1_AI_0=0, P_poll__networl_3_0_AI_6=0, P_network_4_0_AnnP_4=0, P_poll__networl_0_1_RP_6=0, P_poll__networl_6_1_AnnP_0=0, P_poll__networl_6_1_RP_5=0, P_network_2_4_AnnP_5=0, P_poll__networl_3_1_RI_6=0, P_poll__networl_3_2_RP_2=0, P_network_5_0_AskP_4=0, P_poll__networl_0_3_AI_4=0, P_masterList_3_6_3=0, P_network_3_5_RI_4=0, P_poll__networl_0_5_AnnP_6=0, P_network_3_1_AskP_1=0, P_network_5_1_RI_4=0, P_poll__networl_3_6_RP_0=0, P_network_5_4_AI_5=0, P_network_1_2_AnnP_1=0, P_network_2_1_AI_4=0, P_network_4_2_RP_6=0, P_network_5_6_AnnP_6=0, P_poll__networl_5_3_AnnP_1=0, P_poll__networl_2_1_RI_6=0, P_masterList_4_4_3=0, P_network_3_0_AskP_4=0, P_network_3_4_AskP_5=0, P_masterList_6_1_1=1, P_poll__networl_5_1_AnnP_0=0, P_network_3_1_AI_6=0, P_poll__networl_1_0_AnnP_0=0, P_poll__networl_6_4_RP_5=0, P_masterList_3_4_5=1, P_poll__networl_6_3_RI_4=0, P_network_6_4_AnnP_1=0, P_poll__networl_1_4_RI_0=0, P_network_1_1_AskP_4=0, P_network_2_4_RI_4=0, P_poll__networl_4_5_AskP_6=0, P_network_6_5_RP_3=0, P_poll__networl_4_3_AnnP_6=0, P_network_1_3_RI_2=0, P_poll__networl_4_3_AnnP_5=0, P_network_0_4_AnnP_2=0, P_poll__networl_1_5_AnnP_0=0, P_masterList_0_5_6=0, P_network_2_3_AskP_1=0, P_poll__networl_0_4_RP_4=0, P_poll__networl_0_1_AI_2=0, P_network_3_2_RP_5=0, P_network_0_3_RI_3=0, P_network_2_6_RI_5=0, P_masterList_0_4_0=0, P_poll__networl_0_1_AskP_0=0, P_poll__networl_0_1_AI_0=0, P_masterList_6_6_4=0, P_network_2_2_RP_3=0, P_masterList_2_6_2=0, P_network_3_6_AskP_4=0, P_poll__networl_4_3_RP_6=0, P_network_2_5_AskP_4=0, P_network_0_1_RI_4=0, P_poll__networl_3_5_AnnP_3=0, P_network_1_0_RI_1=0, P_network_5_2_AnnP_3=0, P_network_4_2_AI_2=0, P_network_3_1_AskP_2=0, P_poll__networl_1_4_AI_4=0, P_poll__networl_3_6_RI_1=0, P_network_0_0_RI_6=0, P_poll__networl_4_3_RP_0=0, P_poll__networl_6_4_AskP_5=0, P_masterList_6_5_6=0, P_network_4_6_AnnP_4=0, P_network_4_3_RI_2=0, P_poll__networl_4_5_RI_3=0, P_network_4_6_AI_6=0, P_poll__networl_1_0_AskP_4=0, P_poll__networl_4_6_AI_5=0, P_network_1_3_RP_5=0, P_network_0_6_AskP_4=0, P_network_6_4_AnnP_2=0, P_poll__networl_1_5_AskP_0=0, P_network_5_6_AskP_2=0, P_network_3_0_AnnP_2=0, P_network_5_2_AskP_3=0, P_network_3_5_AI_5=0, P_poll__networl_1_4_RI_4=0, P_poll__networl_4_0_RP_0=0, P_poll__networl_1_1_AI_3=0, P_network_0_4_AskP_4=0, P_network_6_5_AI_6=0, P_poll__networl_4_1_AskP_0=0, P_network_3_2_RI_6=0, P_poll__networl_3_4_AnnP_0=0, P_masterList_0_1_1=0, P_network_6_4_RI_1=0, P_network_0_3_RP_4=0, P_network_5_6_RI_1=0, P_poll__networl_5_3_RP_2=0, P_network_0_2_AskP_4=0, P_poll__networl_5_3_AskP_5=0, P_poll__networl_1_2_RI_5=0, P_poll__networl_6_5_AnnP_2=0, P_network_6_5_RP_5=0, P_network_6_6_RP_1=0, P_poll__networl_3_6_AskP_1=0, P_poll__networl_3_0_RI_0=0, P_poll__networl_2_4_AskP_5=0, P_masterList_5_2_5=0, P_poll__networl_0_4_AI_1=0, P_poll__networl_3_2_RP_3=0, P_network_3_6_AnnP_4=0, P_network_2_5_RI_6=0, P_poll__networl_4_6_AI_3=0, P_network_2_1_AskP_1=0, P_poll__networl_1_5_RP_2=0, P_poll__networl_5_0_AskP_4=0, P_poll__networl_6_6_AnnP_0=0, P_poll__networl_3_5_RI_1=0, P_poll__networl_6_5_AI_1=0, P_network_4_2_RI_2=0, P_masterList_0_1_5=0, P_poll__networl_4_6_RP_0=0, P_network_1_3_AnnP_4=0, P_poll__networl_5_5_AI_5=0, P_poll__networl_6_0_RI_6=0, P_network_2_6_AskP_1=0, P_poll__networl_6_3_RP_2=0, P_poll__networl_4_2_RP_5=0, P_network_3_6_RI_5=0, P_masterList_3_1_4=0, P_network_2_2_AskP_5=0, P_network_6_4_AI_6=0, P_network_0_6_RP_1=0, P_poll__networl_2_2_RI_4=0, P_poll__networl_6_2_AnnP_0=0, P_network_5_0_AskP_3=0, P_poll__networl_1_1_RI_4=0, P_network_4_0_RI_5=0, P_poll__networl_3_0_AnnP_0=0, P_electionFailed_1=0, P_poll__networl_3_5_AskP_6=0, P_network_3_0_RI_6=0, P_poll__networl_1_3_RI_4=0, P_poll__networl_5_3_AskP_2=0, P_poll__networl_6_2_AI_4=0, P_network_5_3_RI_3=0, P_poll__networl_6_1_AskP_5=0, P_network_4_2_AnnP_4=0, P_poll__networl_3_3_RI_2=0, P_poll__networl_2_6_RP_4=0, P_masterList_2_5_3=0, P_network_3_3_AI_6=0, P_network_1_3_AI_5=0, P_network_4_3_RP_6=0, P_network_3_3_AskP_1=0, P_network_2_3_RI_4=0, P_network_2_0_RP_2=0, P_masterList_6_4_4=1, P_network_1_6_AI_1=0, P_poll__networl_6_3_RP_5=0, P_network_0_6_RP_4=0, P_network_5_3_RI_2=0, P_poll__networl_6_3_AskP_5=0, P_poll__networl_4_0_RP_3=0, P_network_5_6_RI_5=0, P_poll__networl_0_5_RI_4=0, P_poll__networl_5_3_AnnP_0=0, P_poll__networl_1_1_AnnP_0=0, P_poll__networl_6_6_RI_3=0, P_poll__networl_0_2_AI_3=0, P_poll__networl_4_6_AnnP_0=0, P_poll__networl_1_6_AskP_2=0, P_poll__networl_0_1_AskP_5=0, P_poll__networl_0_1_AI_1=0, P_network_3_3_RP_1=0, P_poll__networl_4_2_AI_2=0, P_network_1_6_AskP_1=0, P_network_0_3_RP_2=0, P_poll__networl_3_0_AskP_4=0, P_network_1_4_AskP_1=0, P_poll__networl_4_1_AnnP_4=0, P_network_2_3_RP_1=0, P_network_4_3_RP_4=0, P_poll__networl_2_0_AnnP_4=0, P_poll__networl_4_2_AI_0=0, P_network_5_4_RP_6=0, P_poll__networl_2_0_RI_2=0, P_network_4_5_AnnP_2=0, P_masterList_1_2_0=0, P_poll__networl_5_4_RI_5=0, P_network_4_0_AskP_2=0, P_poll__networl_2_1_AskP_4=0, P_network_0_3_RI_4=0, P_network_1_0_RP_2=0, P_network_5_3_AnnP_6=0, P_poll__networl_
3_1_AnnP_2=0, P_network_6_4_AI_4=0, P_masterList_2_4_5=1, P_poll__networl_0_4_AskP_3=0, P_network_1_5_RP_4=0, P_masterList_6_5_3=0, P_network_0_1_AskP_4=0, P_network_5_4_AI_3=0, P_network_4_5_RP_4=0, P_masterList_1_2_2=0, P_poll__networl_3_4_RI_4=0, P_poll__networl_4_4_AnsP_0=0, P_poll__networl_0_2_RP_2=0, P_poll__networl_5_0_AI_0=0, P_poll__networl_2_5_AnnP_5=0, P_network_1_3_RI_4=0, P_network_5_2_RP_6=0, P_masterList_4_1_6=0, P_network_6_1_RP_3=0, P_masterList_3_3_2=0, P_poll__networl_2_5_RI_1=0, P_poll__networl_0_0_RP_4=0, P_network_2_0_AnnP_6=0, P_poll__networl_0_5_AskP_4=0, P_network_3_1_RP_3=0, P_poll__networl_6_2_AnnP_6=0, P_network_6_4_RI_2=0, P_poll__networl_1_0_RP_1=0, P_network_4_4_AnnP_4=0, P_poll__networl_5_1_AskP_1=0, P_network_4_4_RP_5=0, P_network_3_6_AskP_3=0, P_network_3_0_RI_4=0, P_poll__networl_0_0_RP_0=0, P_network_1_2_AskP_6=0, P_poll__networl_5_6_AI_0=0, P_network_5_1_RP_4=0, P_poll__networl_3_5_AnnP_6=0, P_poll__networl_6_4_AI_5=0, P_network_3_4_AnnP_5=0, P_network_2_5_RP_3=0, P_network_6_3_AI_3=0, P_poll__networl_3_3_RI_3=0, P_network_0_6_RI_3=0, P_poll__networl_5_5_RI_1=0, P_network_5_3_RP_1=0, P_masterList_3_6_6=0, P_poll__networl_3_1_AI_0=0, P_network_2_0_AnnP_4=0, P_poll__networl_5_3_AnnP_6=0, P_network_4_0_AskP_4=0, P_poll__networl_5_3_RP_4=0, P_masterList_4_3_2=0, P_network_6_1_RI_4=0, P_poll__networl_6_0_RP_3=0, P_network_3_1_RI_4=0, P_poll__networl_4_2_RI_0=0, P_poll__networl_5_2_RP_5=0, P_network_5_3_RP_3=0, P_network_1_6_AnnP_5=0, P_network_2_2_AskP_6=0, P_masterList_1_4_5=1, P_poll__networl_5_6_AskP_2=0, P_network_4_3_AskP_3=0, P_poll__networl_5_5_RP_6=0, P_poll__networl_6_3_RP_0=0, P_network_2_6_RI_1=0, P_poll__networl_1_0_AskP_2=0, P_network_2_0_AnnP_3=0, P_masterList_3_1_3=0, P_poll__networl_0_1_AnnP_1=0, P_poll__networl_2_2_AskP_5=0, P_poll__networl_5_3_AnnP_2=0, P_network_4_3_RI_5=0, P_poll__networl_4_5_AnnP_3=0, P_masterList_4_5_5=0, P_network_2_6_RI_6=0, P_network_5_6_AnnP_5=0, P_poll__networl_6_2_AnsP_0=0, P_network_4_2_AskP_2=0, P_poll__networl_3_1_AskP_1=0, P_network_0_3_RI_5=0, P_poll__networl_4_0_RI_4=0, P_poll__networl_6_1_AnnP_4=0, P_network_3_5_AnnP_4=0, P_network_0_1_AnnP_1=0, P_network_2_3_AskP_4=0, P_masterList_0_3_1=0, P_network_0_2_AnnP_6=0, P_poll__networl_0_1_AskP_6=0, P_poll__networl_3_4_AnnP_6=0, P_masterList_1_3_1=0, P_poll__networl_6_6_AI_5=0, P_poll__networl_4_0_AnnP_5=0, P_network_4_6_AnnP_6=0, P_poll__networl_0_0_AI_5=0, P_network_6_6_AnnP_6=0, P_poll__networl_0_6_AnnP_5=0, P_poll__networl_6_2_AI_2=0, P_network_5_6_AI_5=0, P_network_1_3_AskP_3=0, P_poll__networl_1_4_RP_2=0, P_poll__networl_5_3_AI_4=0, P_poll__networl_2_2_AnnP_0=0, P_poll__networl_5_4_AI_4=0, P_poll__networl_2_4_RI_2=0, P_poll__networl_4_2_AskP_6=0, P_network_1_0_AnnP_6=0, P_poll__networl_3_6_RP_6=0, P_poll__networl_3_3_AnnP_6=0, P_poll__networl_1_4_AI_0=0, P_poll__networl_4_2_AI_6=0, P_poll__networl_3_5_RP_5=0, P_poll__networl_4_4_AskP_1=0, P_poll__networl_1_6_AI_0=0, P_masterList_0_4_5=0, P_masterList_0_6_2=0, P_network_1_2_AI_2=0, P_poll__networl_0_4_RI_0=0, P_poll__networl_4_5_AskP_3=0, P_poll__networl_2_3_RP_3=0, P_poll__networl_1_3_AskP_2=0, P_network_2_6_AI_4=0, P_masterList_2_4_2=0, P_poll__networl_0_2_RP_3=0, P_poll__networl_1_1_AI_6=0, P_poll__networl_0_0_AnnP_1=0, P_poll__networl_4_4_AI_1=0, P_network_3_0_RP_2=0, P_poll__networl_1_5_RI_6=0, P_poll__networl_1_6_AskP_6=0, P_network_2_3_RP_2=0, P_poll__networl_6_1_RP_1=0, P_network_3_1_AI_1=0, P_poll__networl_1_5_AnnP_2=0, P_poll__networl_5_4_AI_1=0, P_network_2_1_AI_6=0, P_network_6_2_RP_1=0, P_masterList_1_5_2=0, P_network_0_2_AI_4=0, P_poll__networl_1_0_RI_4=0, P_network_0_2_AskP_3=0, P_poll__networl_5_5_AnnP_3=0, P_poll__networl_3_1_RP_3=0, P_network_5_1_AskP_3=0, P_masterList_3_6_4=0, P_network_3_3_AskP_5=0, P_poll__networl_2_0_AnsP_0=0, P_poll__networl_6_2_RP_2=0, P_masterList_5_3_6=0, P_poll__networl_2_4_AskP_4=0, P_network_1_1_AnnP_2=0, P_network_4_5_RI_6=0, P_poll__networl_3_1_AI_5=0, P_poll__networl_3_3_AnsP_0=0, P_poll__networl_4_5_RP_4=0, P_poll__networl_4_1_RP_1=0, P_poll__networl_0_2_RI_0=0, P_masterList_3_2_0=0, P_poll__networl_6_4_RP_1=0, P_network_6_3_RP_3=0, P_poll__networl_3_6_AnnP_6=0, P_poll__networl_5_5_AI_2=0, P_poll__networl_2_3_AskP_6=0, P_network_2_3_AI_5=0, P_masterList_4_2_0=0, P_network_3_1_AnnP_1=0, P_poll__networl_2_5_AskP_0=0, P_dead_0=0, P_poll__networl_2_1_RI_5=0, P_poll__networl_4_4_AskP_6=0, P_poll__networl_3_3_RP_2=0, P_network_5_1_AskP_1=0, P_network_6_2_RI_1=0, P_poll__networl_1_3_AnnP_5=0, P_poll__networl_6_1_AnnP_3=0, P_poll__networl_1_3_AnnP_6=0, P_network_4_0_RP_3=0, P_masterList_5_1_3=0, P_network_3_4_RI_5=0, P_network_5_1_AnnP_5=0, P_poll__networl_3_0_RI_6=0, P_network_1_0_AI_4=0, P_masterList_4_5_0=0, P_poll__networl_0_1_RI_2=0, P_network_1_3_AskP_5=0, P_poll__networl_6_1_RI_5=0, P_network_5_6_AI_3=0, P_network_2_0_RI_4=0, P_poll__networl_3_6_AI_6=0, P_network_0_6_AskP_5=0, P_poll__networl_6_0_AnnP_3=0, P_poll__networl_6_1_RI_3=0, P_network_1_5_AI_2=0, P_poll__networl_6_3_AI_6=0, P_poll__networl_6_5_AI_4=0, P_network_1_0_RI_3=0, P_poll__networl_5_0_AskP_1=0, P_poll__networl_4_4_RP_6=0, P_poll__networl_5_3_RI_1=0, P_poll__networl_6_3_AskP_2=0, P_poll__networl_4_2_RI_4=0, P_poll__networl_6_1_AskP_3=0, P_poll__networl_0_2_RI_2=0, P_network_4_6_AnnP_5=0, P_poll__networl_1_3_AI_0=0, P_masterList_5_2_6=0, P_poll__networl_4_5_RI_4=0, P_poll__networl_5_3_AI_2=0, P_poll__networl_1_4_AnsP_0=0, P_network_2_5_AnnP_5=0, P_poll__networl_3_4_RI_5=0, P_poll__networl_4_0_AI_3=0, P_network_6_2_AI_2=0, P_poll__networl_4_5_RP_6=0, P_poll__networl_6_3_AnnP_3=0, P_poll__networl_2_5_AskP_2=0, P_poll__networl_0_3_AnnP_3=0, P_network_1_2_AnnP_3=0, P_network_6_1_RI_1=0, P_network_6_4_AI_1=0, P_masterList_2_5_1=0, P_network_4_0_AskP_3=0, P_masterList_0_5_3=0, P_poll__networl_2_2_AskP_2=0, P_masterList_6_2_5=0, P_poll__networl_0_1_AnnP_5=0, P_network_4_6_AskP_4=0, P_poll__networl_2_1_AnnP_6=0, P_poll__networl_4_2_RP_4=0, P_poll__networl_4_5_AnnP_0=0, P_poll__networl_4_6_AskP_4=0, P_poll__networl_0_6_RI_0=0, P_poll__networl_4_2_RI_1=0, P_poll__networl_6_2_RP_0=0, P_poll__networl_2_1_AnnP_2=0, P_poll__networl_5_2_RP_3=0, P_network_0_0_AI_6=0, P_network_4_3_AskP_2=0, P_network_3_5_RP_6=0, P_network_6_2_RI_6=0, P_network_1_3_AI_6=0, P_poll__networl_6_2_RI_1=0, P_poll__networl_0_6_RP_1=0, P_poll__networl_0_5_AnsP_0=0, P_poll__networl_5_0_AnnP_5=0, P_masterList_0_3_0=0, P_poll__networl_1_0_AI_2=0, P_masterList_6_1_6=0, P_poll__networl_0_2_RP_0=0, P_network_2_0_AskP_3=0, P_network_4_4_AI_1=0, P_network_3_2_AI_2=0, P_poll__networl_5_5_RP_4=0, P_masterList_4_6_5=0, P_network_6_3_AnnP_1=0, P_masterList_4_3_6=0, P_network_5_0_RI_6=0, P_network_2_6_AnnP_6=0, P_poll__networl_3_0_RI_4=0, P_poll__networl_0_2_AskP_2=0, P_poll__networl_3_4_AI_3=0, P_network_2_6_AskP_4=0, P_network_3_2_AnnP_3=0, P_network_5_2_AskP_2=0, P_poll__networl_1_1_AI_5=0, P_network_4_2_AnnP_2=0, P_poll__networl_6_4_RI_0=0, P_poll__networl_3_3_RP_0=0, P_poll__networl_5_6_AnnP_0=0, P_poll__networl_2_5_AnnP_1=0, P_poll__networl_5_6_AskP_6=0, P_network_3_1_AnnP_5=0, P_poll__networl_1_6_AnnP_4=0, P_network_3_5_AskP_2=0, P_network_0_0_AI_4=0, P_network_5_5_RI_3=0, P_network_4_2_RI_3=0, P_network_0_6_AskP_3=0, P_network_3_4_AnnP_3=0, P_network_5_3_AI_6=0, P_network_3_2_AI_3=0, P_network_2_0_RP_3=0, P_poll__networl_0_1_RP_2=0, P_masterList_2_6_4=0, P_poll__networl_3_4_AskP_2=0, P_network_1_3_AI_2=0, P_network_6_3_RI_1=0, P_network_3_3_RP_6=0, P_network_2_2_AnnP_3=0, P_poll__networl_3_6_RI_6=0, P_masterList_5_4_0=0, P_network_6_2_AI_4=0, P_poll__networl_2_0_AI_3=0, P_network_4_4_AskP_5=0, P_poll__networl_4_0_AskP_3=0, P_network_0_1_AI_4=0, P_poll__networl_1_6_RP_4=0, P_poll__networl_4_2_AskP_2=0, P_masterList_3_3_1=0, P_network_4_2_RI_1=0, P_poll__networl_0_2_RP_1=0, P_network_6_3_AskP_5=0, P_network_1_0_RI_6=0, P_network_2_3_RI_3=0, P_network_2_6_RI_4=0, P_poll__networl_5_0_AskP_3=0, P_network_2_1_AI_1=0, P_masterList_2_3_1=0, P_masterList_2_2_5=0, P_poll__networl_1_4_RI_5=0, P_network_2_4_AskP_1=0, P_poll__networl_1_0_RP_5=0, P_poll__networl_2_5_RI_4=0, P_masterList_4_6_2=0, P_network_1_1_RP_2=0, P_network_0_6_RI_4=0, P_network_5_1_RI_1=0, P_network_2_0_RP_1=0, P_poll__networl_3_4_RI_3=0, P_masterList_5_3_3=1, P_masterList_6_3_4=0, P_network_1_3_AskP_1=0, P_poll__networl_3_1_AnnP_4=0, P_poll__networl_2_0_AskP_3=0, P_poll__networl_4_3_AnnP_0=0, P_network_0_2_RP_1=0, P_poll__networl_5_2_AI_3=0, P_network_5_1_AI_4=0, P_network_5_2_RP_2=0, P_network_0_3_AnnP_1=0, P_network_0_4_RI_1=0, P_poll__networl_5_4_AI_2=0, P_network_6_5_RI_3=0, P_poll__networl_5_4_AnnP_1=0, P_poll__networl_4_3_AskP_4=0, P_poll__networl_2_3_RI_3=0, P_poll__networl_4_5_AskP_4=0, P_poll__networl_4_6_AskP_3=0, P_poll__networl_6_0_RI_5=0, P_network_4_1_RI_5=0, P_network_2_6_AI_1=0, P_network_5_2_RI_1=0, P_masterList_1_1_6=0, P_poll__networl_2_2_AI_0=0, P_network_5_6_AI_6=0, P_masterList_0_1_0=0, P_masterList_5_5_1=0, P_network_1_5_AnnP_1=0, P_network_1_6_RP_1=0, P_network_2_2_RP_6=0, P_network_2_3_RP_3=0, P_network_4_1_AnnP_1=0, P_poll__networl_6_6_AnsP_0=0, P_poll__networl_3_2_RP_6=0, P_network_2_1_RI_5=0, P_network_6_1_AskP_2=0, P_network_0_6_AI_5=0, P_network_5_1_AI_3=0, P_masterList_5_2_1=0, P_masterList_2_1_0=0, P_network_4_6_AskP_1=0, P_network_0_4_RP_6=0, P_poll__networl_2_1_AnnP_1=0, P_network_5_6_RP_2=0, P_poll__networl_6_0_AskP_2=0, P_poll__networl_5_0_RI_2=0, P_network_3_3_RP_5=0, P_network_3_5_AskP_1=0, P_poll__networl_1_6_AnnP_1=0, P_poll__networl_6_2_RP_5=0, P_poll__networl_3_1_AnsP_0=0, P_network_4_6_AskP_6=0, P_network_3_3_RI_6=0, P_poll__networl_2_4_AskP_6=0, P_network_0_4_RP_5=0, P_network_5_0_RP_1=0, P_poll__networl_6_1_RP_3=0, P_poll__networl_3_5_AnsP_0=0, P_poll__networl_4_1_AI_0=0, P_poll__networl_1_0_RI_1=0, P_masterList_1_4_0=0, P_poll__networl_5_2_RP_6=0, P_poll__networl_6_1_AnnP_5=0, P_poll__networl_0_4_AnnP_2=0, P_network_3_0_AskP_3=0, P_poll__networl_1_2_AskP_1=0, P_network_3_4_RP_1=0, P_poll__networl_5_4_AnsP_0=0, P_network_3_1_AnnP_6=0, P_poll__networl_6_3_AnsP_0=0, P_network_5_4_RP_2=0, P_network_3_0_AskP_2=0, P_poll__networl_3_6_AI_3=0, P_poll__networl_3_3_RP_5=0, P_poll__networl_5_6_RI_6=0, P_poll__networl_2_2_AI_6=0, P_network_6_0_RI_6=0, P_network_3_3_AnnP_6=0, P_poll__networl_3_3_AnnP_0=0, P_network_2_2_AI_2=0, P_poll__networl_1_6_AI_1=0, P_network_5_1_AI_6=0, P_network_0_0_AskP_2=0, P_poll__networl_3_4_AskP_4=0, P_network_0_6_RI_2=0, P_poll__networl_5_6_RI_0=0, P_poll__networl_5_0_AnnP_4=0, P_network_3_6_AnnP_6=0, P_network_6_2_RP_4=0, P_poll__networl_0_2_AI_5=0, P_poll__networl_5_4_RI_2=0, P_network_0_5_AnnP_1=0, P_network_4_3_AnnP_6=0, P_poll__networl_0_6_RI_1=0, P_poll__networl_2_0_RI_1=0, P_poll__networl_2_1_AI_0=0, P_network_3_1_RP_4=0, P_poll__networl_0_0_AskP_1=0, P_poll__networl_0_2_RP_4=0, P_poll__networl_3_4_RI_6=0, P_poll__networl_3_1_AnnP_6=0, P_poll__networl_4_4_RP_5=0, P_network_6_3_AskP_3=0, P_poll__networl_6_3_RP_3=0, P_poll__networl_6_5_AnnP_0=0, P_masterList_4_4_5=1, P_network_5_0_AnnP_2=0, P_poll__networl_4_1_AskP_6=0, P_poll__networl_0_6_RP_5=0, P_poll__networl_6_2_AI_0=0, P_poll__networl_5_0_AI_5=0, P_poll__networl_5_4_RI_6=0, P_poll__networl_0_2_AskP_3=0, P_network_3_3_RI_1=0, P_network_1_4_AI_5=0, P_poll__networl_2_3_RP_2=0, P_poll__networl_6_6_RP_5=0, P_poll__networl_0_5_RP_6=0, P_masterList_6_5_5=1, P_network_1_1_RP_1=0, P_masterList_4_2_1=0, P_masterList_5_6_0=0, P_network_1_1_AskP_5=0, P_network_4_5_AI_2=0, P_poll__networl_4_3_AskP_3=0, P_poll__networl_1_5_RP_3=0, P_poll__networl_6_3_RI_5=0, P_masterList_1_4_1=0, P_network_2_2_AnnP_1=0, P_poll__networl_0_6_RI_4=0, P_poll__networl_5_2_AI_0=0, P_poll__networl_5_4_RP_6=0, P_network_0_5_AskP_3=0, P_poll__networl_5_3_AskP_3=0, P_poll__networl_1_5_AskP_6=0, P_poll__networl_5_6_RI_4=0, P_poll__networl_3_4_RP_3=0, P_network_4_5_AI_1=0, P_poll__networl_1_4_AI_1=0, P_masterList_0_2_1=0, P_network_6_2_RI_3=0, P_poll__networl_2_1_RI_0=0, P_poll__networl_4_3_AskP_6=0, P_poll__networl_6_5_AskP_4=0, P_poll__networl_1_3_RP_0=0, P_network_6_2_RP_6=0, P_poll__networl_0_5_AI_0=0, P_masterList_2_4_0=0, P_poll__networl_6_6_AI_6=0, P_network_3_0_RP_4=0, P_network_4_0_AnnP_6=0, P_network_0_6_RI_5=0, P_poll__networl_1_3_AskP_4=0, P_network_4_5_AskP_3=0, P_network_6_5_AskP_2=0, P_poll__networl_6_2_AI_1=0, P_poll__networl_2_4_RP_3=0, P_poll__networl_2_5_AI_2=0, P_poll__networl_6_5_AskP_2=0, P_network_3_6_AskP_5=0, P_network_1_2_RP_1=0, P_poll__networl_4_6_AskP_1=0, P_poll__networl_6_5_AI_0=0, P_network_0_1_RI_6=0, P_network_4_1_AskP_5=0, P_network_0_3_AI_3=0, P_poll__networl_4_3_RI_3=0, P_network_0_5_RP_6=0, P_network_3_0_AskP_5=0, P_network_4_1_AskP_4=0, P_poll__networl_1_5_RP_0=0, P_poll__networl_5_5_RI_0=0, P_network_0_1_RP_5=0, P_poll__networl_5_1_AI_2=0, P_poll__networl_5_3_RP_5=0, P_network_1_0_AskP_6=0, P_network_0_2_RI_6=0, P_network_5_3_AI_3=0, P_network_3_0_AnnP_3=0, P_network_1_6_AnnP_2=0, P_network_4_0_RP_6=0, P_network_0_0_AskP_3=0, P_poll__networl_1_3_AI_4=0, P_network_4_0_AI_3=0, P_poll__networl_4_0_AI_2=0, P_poll__networl_2_6_AskP_1=0, P_poll__networl_0_5_RI_3=0, P_network_1_2_AnnP_4=0, P_poll__networl_6_2_AI_3=0, P_network_5_0_RI_5=0, P_poll__networl_1_2_AI_1=0, P_network_6_4_RP_5=0, P_poll__networl_4_2_RP_0=0, P_network_0_5_AskP_2=0, P_poll__networl_2_1_RP_3=0, P_masterList_0_3_2=0, P_masterList_2_2_4=0, P_network_6_5_AskP_6=0, P_poll__networl_4_4_RI_5=0, P_network_5_1_AskP_6=0, P_poll__networl_3_5_AskP_3=0, P_network_1_3_AnnP_6=0, P_poll__networl_2_5_RI_2=0, P_poll__networl_0_3_AI_1=0, P_network_1_4_AnnP_3=0, P_poll__networl_2_0_AskP_5=0, P_masterList_6_5_0=0, P_network_3_6_RI_3=0, P_poll__networl_6_5_RI_5=0, P_poll__networl_3_6_RI_2=0, P_crashed_4=0, P_network_5_5_AskP_3=0, P_poll__networl_1_0_RP_6=0, P_masterList_5_5_0=0, P_poll__networl_0_0_AnnP_2=0, P_poll__networl_6_5_RP_0=0, P_network_0_0_AI_2=0, P_network_4_3_RI_6=0, P_poll__networl_3_0_RP_5=0, P_network_6_0_AnnP_1=0, P_masterList_4_4_6=0, P_poll__networl_3_2_AnnP_5=0, P_poll__networl_5_6_AskP_3=0, P_poll__networl_3_2_AskP_6=0, P_network_2_6_RI_2=0, P_masterList_3_3_5=0, P_poll__networl_1_3_RI_5=0, P_network_6_3_AnnP_5=0, P_poll__networl_0_4_RI_1=0, P_poll__networl_1_0_AskP_0=0, P_poll__networl_2_3_AI_4=0, P_network_5_4_RP_4=0, P_poll__networl_2_1_AnsP_0=0, P_poll__networl_1_2_RI_4=0, P_poll__networl_1_3_AnnP_0=0, P_network_5_0_RI_2=0, P_network_1_3_AnnP_5=0, P_poll__networl_5_4_AskP_0=0, P_network_3_1_AskP_5=0, P_poll__networl_5_6_AnnP_1=0, P_network_0_5_RI_5=0, P_poll__networl_1_6_AskP_5=0, P_poll__networl_6_1_RP_0=0, P_poll__networl_5_1_AskP_5=0, P_poll__networl_4_2_RP_3=0, P_poll__networl_6_3_RI_2=0, P_network_4_0_AI_2=0, P_poll__networl_1_2_RI_0=0, P_network_5_6_AnnP_3=0, P_electionFailed_0=0, P_poll__networl_3_1_AnnP_5=0, P_network_5_2_RI_5=0, P_poll__networl_5_4_AI_3=0, P_poll__networl_1_4_AskP_4=0, P_network_1_3_RI_6=0, P_masterList_6_6_1=0, P_poll__networl_2_1_AskP_3=0, P_network_5_5_AskP_4=0, P_poll__networl_3_0_AskP_5=0, P_poll__networl_5_4_AnnP_6=0, P_masterList_0_6_6=0, P_network_6_1_AnnP_6=0, P_poll__networl_1_5_RP_1=0, P_network_4_4_RP_2=0, P_network_1_1_AI_1=0, P_network_2_1_RP_6=0, P_network_0_3_AI_2=0, P_network_1_2_RP_4=0, P_poll__networl_3_5_AskP_2=0, P_poll__networl_1_0_AnnP_2=0, P_network_1_2_AnnP_6=0, P_network_2_4_AI_6=0, P_network_5_2_AI_3=0, P_poll__networl_6_4_AskP_4=0, P_network_3_6_RI_1=0, P_poll__networl_4_6_RP_5=0, P_network_5_3_RI_1=0, P_masterList_0_2_0=0, P_electionFailed_4=0, P_poll__networl_3_3_AskP_6=0, P_network_4_3_AI_3=0, P_poll__networl_2_6_AnnP_0=0, P_poll__networl_3_5_AnnP_1=0, P_network_5_2_AnnP_2=0, P_network_5_6_AskP_1=0, P_poll__networl_0_3_AskP_2=0, P_poll__networl_0_2_RP_5=0, P_poll__networl_0_5_AskP_0=0, P_network_6_2_AskP_6=0, P_masterList_6_6_6=0, P_network_4_5_AI_5=0, P_poll__networl_2_2_RP_6=0, P_poll__networl_6_2_AskP_0=0, P_poll__networl_6_6_RP_4=0, P_network_0_1_RI_3=0, P_poll__networl_6_2_RP_1=0, P_network_4_0_RI_6=0, P_network_2_5_AI_2=0, P_network_1_3_AI_1=0, P_poll__networl_1_2_AnnP_6=0, P_network_6_2_RP_2=0, P_poll__networl_2_2_RI_0=0, P_poll__networl_4_1_RP_2=0, P_network_6_2_AnnP_2=0, P_poll__networl_0_0_RI_1=0, P_network_6_3_AI_6=0, P_poll__networl_0_5_AnnP_0=0, P_network_1_3_AnnP_1=0, P_poll__networl_2_4_RI_0=0, P_masterList_4_3_3=1, P_poll__networl_2_3_RP_1=0, P_poll__networl_5_1_AnsP_0=0, P_poll__networl_6_1_RI_0=0, P_network_3_2_AnnP_4=0, P_network_5_4_AI_1=0, P_network_5_5_AnnP_6=0, P_poll__networl_1_4_AI_5=0, P_netwo
rk_3_1_AskP_4=0, P_poll__networl_3_1_RI_3=0, P_network_1_3_AI_3=0, P_network_5_2_RP_5=0, P_network_2_1_AnnP_4=0, P_poll__networl_5_5_RI_6=0, P_network_5_3_RI_4=0, P_poll__networl_5_1_AnnP_3=0, P_poll__networl_3_3_AnnP_4=0, P_poll__networl_0_6_AskP_3=0, P_poll__networl_4_3_RI_1=0, P_poll__networl_4_0_AnnP_2=0, P_poll__networl_3_2_AnnP_1=0, P_poll__networl_6_0_AI_1=0, P_network_6_3_RP_5=0, P_network_1_6_RP_2=0, P_poll__networl_6_5_RI_0=0, P_network_0_6_RP_5=0, P_poll__networl_3_0_AnnP_4=0, P_poll__networl_0_6_AskP_4=0, P_masterList_1_1_4=0, P_network_0_2_RI_2=0, P_poll__networl_0_1_RP_1=0, P_masterList_5_5_3=0, P_network_3_5_AI_2=0, P_poll__networl_3_1_AskP_3=0, P_poll__networl_2_0_AI_6=0, P_poll__networl_5_2_AskP_2=0, P_network_0_2_RP_5=0, P_poll__networl_2_6_AnnP_4=0, P_network_3_5_AnnP_1=0, P_poll__networl_0_5_AI_1=0, P_network_2_1_AI_2=0, P_network_6_4_RP_6=0, P_poll__networl_2_4_AI_3=0, P_network_5_6_AnnP_1=0, P_poll__networl_6_6_AnnP_2=0, P_network_2_6_RP_3=0, P_poll__networl_4_3_RP_1=0, P_poll__networl_5_1_AnnP_4=0, P_masterList_2_6_6=0, P_network_0_0_AskP_5=0, P_poll__networl_1_4_RP_6=0, P_poll__networl_4_4_RP_4=0, P_poll__networl_2_5_AskP_1=0, P_electionFailed_6=0, P_poll__networl_4_5_AskP_5=0, P_poll__networl_2_3_AnnP_4=0, P_network_0_5_RP_5=0, P_poll__networl_4_0_AI_1=0, P_network_6_0_RP_4=0, P_network_0_5_AnnP_6=0, P_masterList_2_2_2=0, P_poll__networl_5_0_RI_1=0, P_poll__networl_6_4_RP_6=0, P_dead_4=0, P_network_2_6_AskP_2=0, P_network_5_1_RP_2=0, P_network_1_6_RI_4=0, P_poll__networl_3_2_AI_0=0, P_network_4_6_RI_4=0, P_poll__networl_6_6_AnnP_4=0, P_network_5_0_AskP_1=0, P_poll__networl_0_5_RP_5=0, P_poll__networl_1_1_AnnP_2=0, P_network_6_6_AnnP_4=0, P_network_0_2_AskP_1=0, P_poll__networl_3_1_AskP_2=0, P_network_1_4_AskP_2=0, P_masterList_3_2_5=0, P_poll__networl_3_3_AskP_0=0, P_network_4_4_AI_4=0, P_network_6_5_AnnP_6=0, P_poll__networl_4_6_AI_6=0, P_poll__networl_1_6_AskP_1=0, P_poll__networl_5_2_RP_2=0, P_masterList_6_3_6=0, P_poll__networl_5_1_RP_2=0, P_poll__networl_1_1_AnnP_6=0, P_poll__networl_2_0_RP_6=0, P_network_4_1_AI_6=0, P_poll__networl_6_1_AI_5=0, P_network_1_0_AnnP_4=0, P_network_6_3_AI_1=0, P_poll__networl_6_1_RP_4=0, P_network_1_2_AI_4=0, P_poll__networl_1_5_AI_3=0, P_poll__networl_3_0_AI_0=0, P_poll__networl_6_4_AnnP_6=0, P_network_5_3_AskP_2=0, P_poll__networl_2_1_RP_5=0, P_poll__networl_0_1_AskP_3=0, P_network_1_5_AI_4=0, P_masterList_1_1_5=0, P_network_1_0_RP_6=0, P_poll__networl_5_0_AnnP_0=0, P_network_3_0_RP_5=0, P_poll__networl_0_1_AskP_1=0, P_poll__networl_6_5_RI_6=0, P_poll__networl_2_2_AnsP_0=0, P_network_2_6_RP_1=0, P_network_3_3_RI_2=0, P_network_4_2_RP_5=0, P_poll__networl_0_0_AI_2=0, P_poll__networl_6_1_AskP_1=0, P_network_4_2_AnnP_3=0, P_network_3_2_RP_3=0, P_poll__networl_6_1_AI_1=0, P_masterList_2_1_2=0, P_network_4_4_RP_6=0, P_poll__networl_3_2_AnnP_3=0, P_network_6_6_AskP_5=0, P_poll__networl_6_6_AskP_6=0, P_poll__networl_2_1_AnnP_4=0, P_poll__networl_3_5_AnnP_0=0, P_poll__networl_3_6_AnnP_2=0, P_network_4_3_RI_1=0, P_poll__networl_5_5_AnnP_6=0, P_network_0_3_RI_6=0, P_poll__networl_5_5_AI_0=0, P_poll__networl_5_5_RI_3=0, P_poll__networl_6_1_RI_1=0, P_network_5_5_RP_6=0, P_poll__networl_1_6_AnsP_0=0, P_masterList_4_1_3=0, P_network_1_6_AI_3=0, P_network_5_1_AnnP_6=0, P_poll__networl_0_6_AskP_1=0, P_network_5_2_AnnP_6=0, P_poll__networl_3_6_RI_4=0, P_poll__networl_1_5_AI_6=0, P_network_2_2_AskP_3=0, P_network_6_6_RI_2=0, P_network_6_0_AskP_6=0, P_network_5_5_RP_2=0, P_network_1_2_AI_1=0, P_poll__networl_2_4_AI_1=0, P_poll__networl_6_0_AnnP_1=0, P_network_0_5_AnnP_4=0, P_poll__networl_1_2_AskP_6=0, P_poll__networl_0_5_RP_0=0, P_network_4_5_AskP_6=0, P_poll__networl_3_1_AnnP_1=0, P_poll__networl_4_4_RP_3=0, P_poll__networl_5_2_RP_0=0, P_poll__networl_4_0_AnnP_3=0, P_poll__networl_4_5_AnnP_6=0, P_network_0_1_AnnP_6=0, P_masterList_1_3_3=0, P_poll__networl_2_2_AnnP_4=0, P_poll__networl_4_3_AskP_2=0, P_network_6_5_RI_4=0, P_poll__networl_6_3_AI_4=0, P_poll__networl_0_0_AI_3=0, P_poll__networl_0_4_AnsP_0=0, P_network_4_5_RP_1=0, P_poll__networl_3_3_AI_4=0, P_network_6_6_AI_1=0, P_poll__networl_2_0_RI_6=0, P_poll__networl_5_1_AI_5=0, P_poll__networl_5_5_AnnP_5=0, P_poll__networl_2_5_RP_6=0, P_poll__networl_6_4_RI_3=0, P_network_2_1_RP_3=0, P_poll__networl_5_1_AnnP_1=0, P_network_4_1_AskP_6=0, P_poll__networl_4_0_AskP_4=0, P_poll__networl_1_4_AnnP_3=0, P_poll__networl_5_6_AskP_4=0, P_poll__networl_1_0_AskP_5=0, P_network_5_0_RI_1=0, P_network_4_2_AI_1=0, P_poll__networl_4_1_RI_1=0, P_poll__networl_0_5_AI_5=0, P_poll__networl_0_0_RI_2=0, P_poll__networl_3_3_AI_6=0, P_network_1_5_AnnP_4=0, P_poll__networl_0_1_RI_5=0, P_poll__networl_3_5_RP_2=0, P_network_2_4_AskP_3=0, P_poll__networl_3_2_RP_1=0, P_poll__networl_6_4_AnnP_1=0, P_poll__networl_0_2_AI_6=0, P_poll__networl_4_4_AI_3=0, P_masterList_0_5_0=0, P_network_2_5_RP_6=0, P_poll__networl_2_1_AI_5=0, P_network_4_1_RP_4=0, P_network_3_2_AI_6=0, P_poll__networl_3_0_RP_6=0, P_network_3_0_RI_1=0, P_poll__networl_1_1_AnnP_4=0, P_poll__networl_2_3_AskP_3=0, P_poll__networl_5_3_AI_1=0, P_network_1_0_AskP_5=0, P_poll__networl_0_1_AskP_2=0, P_masterList_1_4_4=0, P_network_6_3_RI_2=0, P_poll__networl_1_5_RI_2=0, P_poll__networl_1_1_AI_0=0, P_network_5_3_AI_4=0, P_poll__networl_1_6_AskP_3=0, P_poll__networl_2_6_RP_3=0, P_network_4_0_AI_1=0, P_poll__networl_0_4_AI_6=0, P_poll__networl_2_0_AnnP_0=0, P_poll__networl_3_1_AnnP_3=0, P_network_0_0_RP_2=0, P_poll__networl_0_0_RP_3=0, P_poll__networl_5_5_AskP_6=0, P_poll__networl_0_0_AnnP_6=0, P_network_5_3_RI_5=0, P_poll__networl_3_5_AnnP_4=0, P_poll__networl_0_2_RI_3=0, P_poll__networl_0_4_AnnP_5=0, P_poll__networl_6_2_AnnP_3=0, P_poll__networl_6_0_AnnP_2=0, P_crashed_0=0, P_poll__networl_3_0_AnnP_6=0, P_poll__networl_2_4_RP_4=0, P_poll__networl_3_2_AI_1=0, P_poll__networl_6_1_AskP_6=0, P_masterList_3_3_4=1, P_poll__networl_6_6_AskP_1=0, P_poll__networl_6_6_AnnP_1=0, P_poll__networl_0_5_AnnP_5=0, P_masterList_6_2_6=0, P_network_5_4_RI_2=0, P_poll__networl_5_4_AI_6=0, P_network_4_1_AnnP_4=0, P_network_5_4_AskP_4=0, P_poll__networl_5_6_AI_3=0, P_poll__networl_4_0_RP_4=0, P_network_3_2_RP_1=0, P_masterList_4_6_6=0, P_network_2_5_AI_5=0, P_network_3_1_RP_6=0, P_network_3_5_RI_5=0, P_masterList_3_2_3=0, P_poll__networl_4_3_RP_2=0, P_poll__networl_0_4_RI_3=0, P_poll__networl_4_5_RI_6=0, P_poll__networl_5_0_AnnP_2=0, P_poll__networl_6_4_AI_1=0, P_network_0_0_RI_5=0, P_poll__networl_6_0_AI_5=0, P_network_5_1_AI_5=0, P_network_2_1_AnnP_2=0, P_network_3_3_RP_2=0, P_network_2_1_AskP_5=0, P_poll__networl_5_4_AnnP_3=0, P_poll__networl_6_3_AI_1=0, P_network_5_3_AskP_5=0, P_poll__networl_0_6_RP_2=0, P_network_2_0_RI_6=0, P_network_3_1_AI_4=0, P_network_4_3_RP_1=0, P_network_0_4_AI_1=0, P_poll__networl_6_3_RP_4=0, P_poll__networl_4_4_AI_0=0, P_network_5_5_RP_5=0, P_network_0_4_RP_4=0, P_network_2_2_AskP_4=0, P_network_5_2_RP_1=0, P_masterList_3_4_0=0, P_network_3_1_AskP_6=0, P_network_3_5_RI_3=0, P_poll__networl_5_1_AnnP_6=0, P_network_4_1_RP_5=0, P_poll__networl_4_4_AnnP_1=0, P_poll__networl_4_2_AI_1=0, P_masterList_0_2_2=0, P_poll__networl_3_4_RI_0=0, P_network_1_4_AI_6=0, P_network_4_5_AnnP_6=0, P_poll__networl_1_5_AI_5=0, P_poll__networl_2_2_AI_1=0, P_poll__networl_0_1_RI_4=0, P_network_1_0_AskP_4=0, P_network_3_6_AnnP_1=0, P_network_3_4_AI_5=0, P_masterList_3_1_6=0, P_poll__networl_2_1_AI_6=0, P_masterList_3_2_1=0, P_masterList_5_1_1=1, P_network_1_5_AI_6=0, P_network_0_3_AnnP_2=0, P_network_1_2_RI_6=0, P_poll__networl_0_4_RI_4=0, P_network_6_2_RP_3=0, P_network_5_4_RP_1=0, P_poll__networl_0_5_RP_2=0, P_poll__networl_0_1_AI_5=0, P_network_5_2_RI_6=0, P_poll__networl_6_1_AskP_4=0, P_poll__networl_1_1_AskP_0=0, P_network_0_3_RP_5=0, P_poll__networl_2_3_AnnP_3=0, P_poll__networl_3_1_RI_4=0, P_network_0_4_AskP_1=0, P_network_3_0_RI_2=0, P_poll__networl_6_0_RP_2=0, P_poll__networl_5_4_AskP_3=0, P_poll__networl_4_1_AI_5=0, P_network_1_0_RI_4=0, P_network_1_6_AnnP_3=0, P_network_3_2_AskP_4=0, P_poll__networl_4_0_AskP_5=0, P_poll__networl_5_6_AskP_5=0, P_poll__networl_6_5_AnnP_3=0, P_network_5_0_RI_4=0, P_network_0_0_RP_3=0, P_network_1_1_RI_5=0, P_poll__networl_2_3_AI_5=0, P_poll__networl_4_2_AnnP_5=0, P_network_0_0_AnnP_4=0, P_masterList_6_1_0=0, P_poll__networl_0_3_AnnP_5=0, P_network_6_2_AskP_4=0, P_network_6_4_AskP_3=0, P_network_3_1_RI_1=0, P_masterList_1_3_0=0, P_network_6_6_AI_4=0, P_masterList_4_2_5=0, P_network_0_3_AI_6=0, P_network_4_3_AnnP_3=0, P_network_5_4_AnnP_2=0, P_network_6_1_AnnP_1=0, P_poll__networl_3_6_RP_3=0, P_network_4_6_AskP_3=0, P_network_6_4_RP_4=0, P_network_4_0_RP_2=0, P_network_2_5_AskP_3=0, P_poll__networl_3_1_RP_0=0, P_poll__networl_2_4_RP_2=0, P_poll__networl_0_3_RI_2=0, P_network_6_6_AskP_2=0, P_network_4_4_AI_6=0, P_poll__networl_4_2_AnnP_2=0, P_network_5_0_AI_4=0, P_network_0_3_RP_1=0, P_network_3_3_AnnP_5=0, P_network_6_1_RI_3=0, P_network_0_0_RP_5=0, P_network_0_4_RP_1=0, P_poll__networl_2_6_AskP_2=0, P_network_1_6_AI_6=0, P_poll__networl_5_3_RI_0=0, P_network_3_1_RI_6=0, P_network_4_2_AnnP_1=0, P_network_5_1_AskP_2=0, P_poll__networl_3_0_AskP_6=0, P_poll__networl_5_2_AnnP_5=0, P_network_2_6_AskP_5=0, P_network_4_2_AskP_6=0, P_network_5_6_AskP_5=0, P_masterList_6_3_5=0, P_network_0_4_RI_5=0, P_network_4_2_AI_6=0, P_poll__networl_4_5_RP_3=0, P_network_2_0_RI_1=0, P_poll__networl_2_0_RI_3=0, P_network_0_1_AI_6=0, P_poll__networl_4_4_RI_2=0, P_poll__networl_4_0_RI_2=0, P_network_6_0_AnnP_6=0, P_network_6_4_RI_3=0, P_network_0_3_AI_1=0, P_network_3_5_RI_2=0, P_poll__networl_6_4_RI_2=0, P_network_5_1_RP_3=0, P_network_6_0_AnnP_3=0, P_masterList_2_4_3=0, P_poll__networl_3_4_AskP_6=0, P_poll__networl_4_3_RI_4=0, P_poll__networl_3_2_AnnP_4=0, P_poll__networl_0_2_AnnP_5=0, P_poll__networl_5_1_AskP_6=0, P_poll__networl_1_5_RI_0=0, P_poll__networl_2_6_RI_4=0, P_poll__networl_6_4_AI_6=0, P_poll__networl_6_5_RP_5=0, P_masterList_5_3_5=0, P_poll__networl_4_1_AI_3=0, P_masterList_3_4_4=0, P_poll__networl_3_4_RI_1=0, P_network_3_0_RP_6=0, P_poll__networl_4_5_AI_1=0, P_poll__networl_3_3_RI_1=0, P_poll__networl_0_4_AskP_4=0, P_network_6_3_RP_4=0, P_network_1_5_AI_3=0, P_poll__networl_4_1_RP_0=0, P_poll__networl_2_4_AnnP_1=0, P_poll__networl_3_5_AskP_0=0, P_poll__networl_3_2_RI_6=0, P_poll__networl_5_2_AI_6=0, P_network_2_4_AI_3=0, P_poll__networl_6_1_AnnP_6=0, P_network_3_0_AnnP_6=0, P_poll__networl_0_1_AnnP_2=0, P_poll__networl_4_1_AnsP_0=0, P_poll__networl_5_4_AskP_5=0, P_network_4_0_AnnP_2=0, P_poll__networl_6_5_AnnP_5=0, P_network_3_6_RP_4=0, P_poll__networl_2_1_RI_3=0, P_network_6_1_RP_1=0, P_poll__networl_2_6_AskP_6=0, P_network_6_3_AI_4=0, P_network_0_1_RP_6=0, P_poll__networl_6_0_RP_1=0, P_poll__networl_6_2_AnnP_5=0, P_network_0_0_AnnP_3=0, P_poll__networl_1_2_AnnP_4=0, P_poll__networl_2_5_AI_6=0, P_poll__networl_0_0_RP_6=0, P_network_4_0_AI_6=0, P_network_2_0_AI_1=0, P_poll__networl_0_1_RP_4=0, P_network_3_4_AI_4=0, P_poll__networl_3_6_AskP_3=0, P_masterList_0_4_4=0, P_poll__networl_1_0_AnnP_1=0, P_masterList_6_4_3=0, P_poll__networl_4_1_RI_3=0, P_network_5_4_RP_3=0, P_poll__networl_4_5_AI_6=0, P_network_1_5_AI_5=0, P_network_2_4_RI_1=0, P_network_3_6_AI_5=0, P_network_3_5_AI_6=0, P_crashed_6=0, P_poll__networl_2_0_RI_5=0, P_poll__networl_2_5_AI_4=0, P_masterList_6_2_2=1, P_network_0_4_AnnP_1=0, P_poll__networl_4_1_AnnP_5=0, P_network_6_3_RI_3=0, P_poll__networl_1_5_AskP_4=0, P_network_4_4_AnnP_3=0, P_poll__networl_0_0_AnnP_5=0, P_poll__networl_0_0_AskP_5=0, P_poll__networl_1_3_AnnP_2=0, P_network_5_5_RP_4=0, P_network_1_3_RP_6=0, P_network_2_4_RP_4=0, P_network_4_1_RP_2=0, P_poll__networl_1_3_AI_1=0, P_masterList_1_6_3=0, P_poll__networl_1_3_AskP_5=0, P_poll__networl_3_1_RI_0=0, P_poll__networl_4_1_RI_2=0, P_poll__networl_6_3_RI_0=0, P_poll__networl_5_6_RI_5=0, P_network_6_0_RI_4=0, P_poll__networl_4_3_AskP_5=0, P_network_5_5_RP_1=0, P_poll__networl_5_3_RP_0=0, P_poll__networl_5_2_RI_1=0, P_network_0_3_AnnP_6=0, P_poll__networl_0_3_RP_5=0, P_poll__networl_1_3_RI_6=0, P_poll__networl_5_2_AnnP_4=0, P_network_0_1_AI_5=0, P_network_5_6_RP_6=0, P_poll__networl_4_0_AnnP_6=0, P_network_2_6_AskP_3=0, P_network_3_1_AI_3=0, P_poll__networl_0_6_AI_0=0, P_poll__networl_5_4_AskP_4=0, P_network_6_6_AskP_4=0, P_poll__networl_0_5_RI_2=0, P_masterList_5_6_3=0, P_network_1_4_RI_5=0, P_network_2_0_AI_4=0, P_masterList_3_4_1=0, P_network_5_5_RI_6=0, P_network_3_3_AnnP_2=0, P_network_4_5_AnnP_5=0, P_network_2_6_RP_2=0, P_network_0_3_RI_2=0, P_poll__networl_0_1_RI_6=0, P_poll__networl_1_6_RP_6=0, P_network_4_2_RI_6=0, P_network_5_4_AI_4=0, P_network_6_5_AskP_3=0, P_network_5_2_AnnP_1=0, P_poll__networl_4_3_AI_1=0, P_poll__networl_6_3_RP_1=0, P_network_1_5_AskP_6=0, P_poll__networl_4_4_RP_1=0, P_poll__networl_2_4_RI_5=0, P_poll__networl_4_5_RI_1=0, P_network_1_4_AnnP_6=0, P_poll__networl_0_4_AnnP_6=0, P_poll__networl_0_6_AnnP_0=0, P_poll__networl_1_4_AskP_2=0, P_poll__networl_3_4_AskP_5=0, P_network_1_4_AI_1=0, P_network_6_4_AskP_1=0, P_masterList_5_5_2=0, P_network_1_6_RI_1=0, P_poll__networl_2_5_RP_0=0, P_poll__networl_6_4_AnsP_0=0, P_network_5_3_AskP_4=0, P_poll__networl_0_2_AnsP_0=0, P_poll__networl_3_1_RI_2=0, P_poll__networl_2_5_AskP_6=0, P_network_1_5_RP_1=0, P_network_5_5_AskP_2=0, P_poll__networl_4_5_RI_2=0, P_poll__networl_5_2_AnnP_2=0, P_poll__networl_4_1_AI_4=0, P_network_3_0_RP_1=0, P_network_6_0_AnnP_4=0, P_poll__networl_1_0_AnsP_0=0, P_poll__networl_6_0_RP_4=0, P_masterList_3_5_0=0, P_poll__networl_4_0_AI_6=0, P_poll__networl_5_0_AnnP_6=0, P_masterList_5_3_2=0, P_poll__networl_3_4_AskP_1=0, P_network_4_4_RI_6=0, P_network_5_3_AskP_1=0, P_poll__networl_2_3_RI_4=0, P_poll__networl_6_1_AnnP_1=0, P_poll__networl_2_5_AnnP_4=0, P_network_5_3_AnnP_4=0, P_network_5_4_RI_3=0, P_network_5_6_AI_2=0, P_network_5_0_RP_3=0, P_poll__networl_0_6_AI_5=0, P_network_2_2_RP_5=0, P_network_2_4_RI_3=0, P_poll__networl_3_3_AnnP_1=0, P_poll__networl_3_2_AnnP_0=0, P_poll__networl_1_3_RI_1=0, P_poll__networl_1_3_RI_0=0, P_poll__networl_2_3_RP_0=0, P_network_3_0_AI_4=0, P_network_4_5_RI_1=0, P_poll__networl_0_2_AnnP_4=0, P_poll__networl_4_3_RI_5=0, P_network_5_3_RP_6=0, P_network_1_4_AnnP_1=0, P_network_4_5_RP_2=0, P_network_3_1_AnnP_2=0, P_poll__networl_1_2_AI_2=0, P_poll__networl_4_2_AnnP_0=0, P_poll__networl_4_3_RI_2=0, P_poll__networl_1_1_RP_4=0, P_poll__networl_6_6_AI_4=0, P_masterList_2_5_0=0, P_poll__networl_2_3_AnnP_5=0, P_network_4_3_AskP_6=0, P_poll__networl_1_2_AskP_0=0, P_poll__networl_0_3_RI_3=0, P_network_1_6_AnnP_1=0, P_poll__networl_2_5_RP_4=0, P_poll__networl_2_3_AnnP_2=0, P_poll__networl_4_2_RP_6=0, P_network_6_5_RI_6=0, P_network_3_3_AI_5=0, P_poll__networl_4_2_AnnP_6=0, P_network_6_2_RI_2=0, P_poll__networl_4_6_AskP_6=0, P_poll__networl_5_6_AI_4=0, P_network_1_3_RP_1=0, P_poll__networl_5_6_AI_2=0, P_network_5_5_AI_4=0, P_poll__networl_5_6_AnnP_5=0, P_poll__networl_0_4_AnnP_0=0, P_poll__networl_2_6_AnnP_3=0, P_poll__networl_5_2_AskP_4=0, P_network_2_0_AnnP_5=0, P_poll__networl_3_1_RP_6=0, P_masterList_6_4_5=0, P_poll__networl_0_4_RI_5=0, P_network_6_6_AnnP_1=0, P_network_0_6_AnnP_1=0, P_poll__networl_0_2_AI_4=0, P_network_3_5_AskP_6=0, P_network_5_6_AI_1=0, P_poll__networl_6_4_AskP_6=0, P_masterList_4_4_1=0, P_poll__networl_4_0_AnnP_1=0, P_network_6_6_RP_3=0, P_poll__networl_0_3_RP_0=0, P_network_1_1_AI_3=0, P_poll__networl_0_1_RI_1=0, P_poll__networl_2_0_AskP_2=0, P_network_3_2_RI_4=0, P_network_2_6_AnnP_3=0, P_masterList_0_2_3=0, P_poll__networl_3_5_RP_1=0, P_network_1_6_RP_4=0, P_network_2_3_AnnP_2=0, P_poll__networl_3_4_AnsP_0=0, P_poll__networl_6_5_AI_3=0, P_poll__networl_1_4_RI_6=0, P_network_3_3_AnnP_4=0, P_network_4_5_RI_2=0, P_poll__networl_0_4_RP_2=0, P_network_3_5_AskP_4=0, P_poll__networl_1_2_AI_6=0, P_network_3_2_AI_4=0, P_poll__networl_2_5_RP_2=0, P_poll__networl_3_1_RP_4=0, P_network_5_0_AnnP_4=0, P_poll__networl_4_3_AnnP_4=0, P_poll__networl_5_6_RP_4=0, P_masterList_6_5_2=0, P_network_1_4_AI_2=0, P_masterList_0_6_0=0, P_network_3_4_RP_2=0, P_masterList_1_5_4=0, P_poll__networl_1_4_AnnP_5=0, P_masterList_5_5_6=1, P_network_0_3_AskP_5=0, P_poll__networl_1_0_AI_4=0, P_poll__networl_4_4_AI_4=0, P_network_0_5_RP_1=0, P_network_2_4_RP_1=0, P_poll__networl_5_0_AI_4=0, P_network_1_1_AnnP_3=0, P_poll__networl_4_2_AI_4=0, P_network_3_3_AI_1=0, P_network_0_2_RP_6=0, P_poll__networl_3_6_RP_1=0, P_masterList_1_2_1=0, P_poll__networl_6_2_RI_3=0, P_poll__networl_4_6_AI_2=0, P_network_3_6_RI_2=0, P_network_6_1_RI_2=0, P_network_0_2_RI_1=0, P_network_6_0
_AI_5=0, P_poll__networl_2_6_AnnP_2=0, P_network_4_4_AnnP_1=0, P_poll__networl_0_2_AskP_5=0, P_poll__networl_2_1_AskP_1=0, P_network_3_2_AnnP_5=0, P_network_0_6_AnnP_2=0, P_masterList_2_1_1=1, P_poll__networl_3_2_AnnP_2=0, P_network_0_4_AI_3=0, P_poll__networl_0_3_AskP_3=0, P_poll__networl_0_3_RI_1=0, P_network_0_0_AnnP_1=0, P_masterList_3_4_6=0, P_poll__networl_1_3_AskP_3=0, P_network_3_1_RP_1=0, P_masterList_4_2_4=0, P_network_3_5_AskP_5=0, P_poll__networl_0_1_RI_3=0, P_poll__networl_2_6_RI_3=0, P_network_0_5_AskP_1=0, P_network_0_6_RP_2=0, P_network_6_0_AI_4=0, P_network_6_6_AskP_1=0, P_poll__networl_6_0_AI_0=0, P_poll__networl_6_6_RP_6=0, P_masterList_3_6_5=0, P_poll__networl_1_4_AskP_5=0, P_poll__networl_2_1_AnnP_0=0, P_poll__networl_1_2_AskP_2=0, P_network_6_1_AI_2=0, P_network_1_3_AI_4=0, P_poll__networl_4_5_AI_5=0, P_network_2_5_AskP_6=0, P_poll__networl_6_3_AI_5=0, P_poll__networl_2_2_RP_2=0, P_poll__networl_0_4_AskP_2=0, P_poll__networl_0_1_AnnP_0=0, P_network_3_4_AnnP_6=0, P_network_6_1_AskP_5=0, P_poll__networl_3_0_AI_2=0, P_network_1_6_AI_5=0, P_network_6_1_AskP_6=0, P_poll__networl_2_1_RI_4=0, P_masterList_0_6_4=0, P_poll__networl_1_3_AI_2=0, P_crashed_2=0, P_network_5_3_RP_4=0, P_network_2_6_AI_5=0, P_masterList_6_3_1=0, P_network_0_5_RI_3=0, P_network_2_6_AI_6=0, P_network_2_0_RP_6=0, P_network_6_1_AskP_4=0, P_poll__networl_1_1_AskP_4=0, P_network_3_6_RI_6=0, P_network_2_4_AnnP_4=0, P_poll__networl_1_2_RP_5=0, P_poll__networl_6_0_AI_6=0, P_poll__networl_5_5_RI_2=0, P_poll__networl_2_5_AskP_4=0, P_masterList_2_2_0=0, P_network_2_0_AI_2=0, P_poll__networl_1_2_RP_3=0, P_masterList_5_1_2=0, P_network_0_4_AnnP_6=0, P_poll__networl_3_2_AskP_3=0, P_poll__networl_5_5_AI_6=0, P_network_6_4_AskP_2=0, P_network_2_1_RP_1=0, P_masterList_5_1_5=0, P_network_4_0_RP_1=0, P_poll__networl_5_0_RP_6=0, P_masterList_2_6_5=0, P_poll__networl_2_6_RP_1=0, P_network_3_5_AnnP_6=0, P_network_4_4_AI_5=0, P_masterList_0_4_3=0, P_masterList_2_5_4=0, P_network_3_3_AskP_4=0, P_masterList_4_4_2=0, P_network_5_5_AI_1=0, P_poll__networl_1_4_RI_2=0, P_network_6_3_AnnP_3=0, P_poll__networl_3_3_AskP_3=0, P_poll__networl_6_2_RP_4=0, P_poll__networl_2_4_AnnP_0=0, P_network_6_6_AnnP_2=0, P_poll__networl_1_0_AnnP_5=0, P_network_3_4_RI_3=0, P_poll__networl_0_4_AnnP_3=0, P_poll__networl_5_3_AskP_4=0, P_poll__networl_0_2_AI_0=0, P_poll__networl_6_1_AI_4=0, P_network_4_6_AnnP_2=0, P_poll__networl_5_2_AnnP_1=0, P_poll__networl_5_4_AnnP_4=0, P_poll__networl_1_3_RP_3=0, P_network_2_5_AnnP_2=0, P_poll__networl_0_3_RP_1=0, P_poll__networl_1_6_AI_5=0, P_network_4_4_RI_3=0, P_network_2_3_AI_2=0, P_network_5_0_RI_3=0, P_poll__networl_0_4_RP_0=0, P_poll__networl_2_5_AnsP_0=0, P_poll__networl_5_6_RI_2=0, P_masterList_3_6_1=0, P_network_0_3_AnnP_4=0, P_network_6_0_RP_3=0, P_poll__networl_2_6_AI_6=0, P_network_3_2_RI_2=0, P_poll__networl_5_1_RI_1=0, P_masterList_4_1_1=1, P_poll__networl_3_1_RP_1=0, P_network_2_0_AskP_5=0, P_poll__networl_5_4_AskP_1=0, P_poll__networl_6_5_RP_1=0, P_poll__networl_0_2_AskP_0=0, P_poll__networl_3_1_AskP_4=0, P_network_2_2_RP_1=0, P_poll__networl_0_1_RP_5=0, P_poll__networl_2_3_AI_3=0, P_masterList_6_4_0=0, P_network_2_1_RI_2=0, P_masterList_6_5_4=0, P_poll__networl_2_5_AnnP_0=0, P_poll__networl_2_2_RP_1=0, P_poll__networl_3_3_AnnP_5=0, P_poll__networl_4_5_AnnP_1=0, P_network_5_5_RI_1=0, P_network_6_6_RI_1=0, P_network_1_6_AskP_3=0, P_network_0_0_RI_4=0, P_poll__networl_5_5_RP_1=0, P_network_3_4_AI_2=0, P_network_6_1_AnnP_4=0, P_poll__networl_4_4_RI_6=0, P_network_5_3_AI_1=0, P_poll__networl_1_4_AnnP_4=0, P_poll__networl_5_2_RI_0=0, P_poll__networl_0_5_RI_5=0, P_masterList_6_6_2=0, P_network_2_1_AI_5=0, P_network_2_3_RP_4=0, P_masterList_5_6_6=0, P_poll__networl_1_4_AnnP_1=0, P_network_2_3_AskP_3=0, P_network_5_1_AI_2=0, P_masterList_0_1_2=0, P_masterList_4_2_2=1, P_network_2_2_AnnP_2=0, P_network_5_5_AnnP_1=0, P_poll__networl_4_4_AI_5=0, P_poll__networl_1_1_RP_5=0, P_network_0_5_RI_4=0, P_network_2_2_AnnP_5=0, P_poll__networl_2_6_AI_5=0, P_network_6_2_RP_5=0, P_poll__networl_6_6_AskP_5=0, P_network_2_2_RI_6=0, P_poll__networl_2_3_AnnP_0=0, P_network_2_4_AI_4=0, P_poll__networl_0_3_AnsP_0=0, P_network_5_2_AskP_4=0, P_poll__networl_5_1_AI_6=0, P_network_3_6_AI_2=0, P_poll__networl_4_6_AnsP_0=0, P_poll__networl_2_2_RI_3=0, P_poll__networl_0_4_AskP_1=0, P_poll__networl_4_2_AskP_3=0, P_network_4_2_RP_2=0, P_masterList_5_2_2=1, P_network_5_1_RP_6=0, P_network_5_3_AskP_6=0, P_poll__networl_0_4_AI_0=0, P_poll__networl_1_5_AnsP_0=0, P_network_6_4_AI_3=0, P_network_5_4_RI_5=0, P_network_6_5_AnnP_3=0, P_poll__networl_3_1_AI_4=0, P_network_5_5_RI_2=0, P_poll__networl_2_2_AskP_4=0, P_poll__networl_0_5_AnnP_3=0, P_poll__networl_4_4_AnnP_5=0, P_network_5_5_AskP_6=0, P_network_5_4_AnnP_5=0, P_poll__networl_3_3_RI_4=0, P_poll__networl_4_4_AnnP_0=0, P_poll__networl_4_2_RI_6=0, P_network_3_1_AI_2=0, P_poll__networl_0_6_RP_4=0, P_poll__networl_6_0_AI_4=0, P_poll__networl_5_6_AnnP_2=0, P_poll__networl_6_6_RI_1=0, P_poll__networl_5_3_RP_6=0, P_poll__networl_6_5_AskP_0=0, P_network_1_1_AskP_1=0, P_network_0_6_RI_1=0, P_network_1_3_RI_1=0, P_poll__networl_4_1_AskP_4=0, P_network_6_3_RI_5=0, P_poll__networl_3_0_RI_3=0, P_masterList_5_3_0=0, P_network_3_6_AskP_1=0, P_poll__networl_5_2_AI_2=0, P_network_4_2_AI_5=0, P_poll__networl_0_5_AnnP_4=0, P_poll__networl_4_1_RP_4=0, P_poll__networl_3_3_AI_0=0, P_network_5_0_AI_2=0, P_poll__networl_0_5_AskP_1=0, P_poll__networl_5_0_RI_0=0, P_poll__networl_5_5_RP_0=0, P_masterList_2_5_5=0, P_network_1_0_RI_2=0, P_network_0_0_RI_3=0, P_network_4_4_AskP_4=0, P_poll__networl_3_6_AnnP_1=0, P_network_1_3_AskP_6=0, P_poll__networl_4_0_RI_1=0, P_poll__networl_0_4_AI_4=0, P_poll__networl_6_2_AI_6=0, P_network_6_4_RP_1=0, P_poll__networl_1_1_AskP_5=0, P_network_4_6_AskP_2=0, P_network_4_0_AskP_1=0, P_network_5_5_AI_2=0, P_poll__networl_5_3_AnnP_4=0, P_network_0_0_RP_1=0, P_poll__networl_2_1_AskP_0=0, P_network_1_5_AskP_1=0, P_network_6_5_AnnP_5=0, P_network_6_5_AskP_1=0, P_electionFailed_3=0, P_poll__networl_4_0_AI_5=0, P_poll__networl_1_5_AnnP_3=0, P_dead_1=0, P_network_1_5_AskP_2=0, P_network_2_3_AskP_2=0, P_network_4_3_RP_2=0, P_poll__networl_6_2_RI_2=0, P_poll__networl_6_0_RI_0=0, P_network_4_3_RP_3=0, P_poll__networl_1_1_AnnP_1=0, P_masterList_6_6_5=0, P_network_3_5_AnnP_2=0, P_network_4_1_RP_6=0, P_poll__networl_4_6_RI_1=0, P_poll__networl_0_3_AI_0=0, P_poll__networl_1_2_RP_0=0, P_network_3_4_AI_3=0, P_poll__networl_2_2_AI_4=0, P_network_2_0_AnnP_1=0, P_network_4_6_RI_2=0, P_network_4_3_AnnP_4=0, P_network_2_5_RP_5=0, P_poll__networl_5_0_AskP_6=0, P_poll__networl_2_4_RP_5=0, P_network_6_2_AnnP_1=0, P_poll__networl_4_1_RP_5=0, P_poll__networl_5_2_AskP_5=0, P_poll__networl_6_0_RP_5=0, P_poll__networl_0_6_AnnP_3=0, P_poll__networl_5_4_RP_2=0, P_poll__networl_6_5_AI_2=0, P_network_4_5_AI_6=0, P_network_0_0_RP_4=0, P_poll__networl_4_1_AskP_5=0, P_network_6_6_AnnP_3=0, P_poll__networl_5_3_AI_0=0, P_poll__networl_6_6_AskP_2=0, P_poll__networl_3_3_RP_3=0, P_network_1_6_AI_2=0, P_poll__networl_4_5_RP_2=0, P_poll__networl_1_2_AI_5=0, P_network_1_4_RI_3=0, P_network_6_2_AI_1=0, P_network_1_6_AskP_4=0, P_network_2_5_RP_1=0, P_poll__networl_5_1_RI_0=0, P_poll__networl_5_5_AskP_5=0, P_poll__networl_1_4_AnnP_2=0, P_network_3_2_AI_1=0, P_network_2_0_RI_2=0, P_poll__networl_5_3_RI_4=0, P_masterList_0_1_4=0, P_poll__networl_2_4_RI_4=0, P_poll__networl_1_6_RP_1=0, P_poll__networl_2_6_RI_0=0, P_network_0_6_AnnP_3=0, P_network_0_6_AnnP_4=0, P_network_6_1_AnnP_5=0, P_poll__networl_4_2_AskP_4=0, P_network_1_1_AskP_6=0, P_poll__networl_5_1_RP_0=0, P_poll__networl_6_5_AskP_6=0, P_poll__networl_4_3_RP_4=0, P_poll__networl_4_4_AI_6=0, P_network_2_2_RP_2=0, P_poll__networl_3_0_RI_1=0, P_poll__networl_0_6_AI_3=0, P_poll__networl_4_1_AnnP_2=0, P_network_4_1_AI_5=0, P_network_4_0_AskP_5=0, P_poll__networl_4_6_AI_1=0, P_poll__networl_4_1_AskP_1=0, P_network_4_6_RI_3=0, P_masterList_3_5_3=0, P_poll__networl_1_4_RP_0=0, P_poll__networl_2_3_AI_2=0, P_network_6_4_AnnP_6=0, P_poll__networl_2_3_AI_6=0, P_network_1_5_RI_1=0, P_network_1_4_RI_1=0, P_poll__networl_1_0_AskP_1=0, P_masterList_3_2_4=0, P_poll__networl_1_1_RP_6=0, P_poll__networl_3_6_AnnP_4=0, P_poll__networl_1_6_AnnP_2=0, P_network_4_1_AnnP_5=0, P_poll__networl_2_2_AskP_3=0, P_network_2_1_RP_2=0, P_network_5_4_AskP_2=0, P_poll__networl_4_6_RP_2=0, P_network_3_0_RP_3=0, P_poll__networl_0_4_AnnP_1=0, P_poll__networl_1_4_AskP_6=0, P_network_5_2_AskP_5=0, P_network_2_0_AskP_6=0, P_network_4_3_RI_4=0, P_network_3_6_RI_4=0, P_network_6_3_AnnP_4=0, P_network_0_5_AnnP_3=0, P_poll__networl_4_1_RI_4=0, P_masterList_2_2_6=0, P_masterList_5_2_4=0, P_poll__networl_2_2_RI_6=0, P_network_2_0_AskP_2=0, P_masterList_5_1_4=0, P_network_1_6_RI_2=0, P_poll__networl_6_2_AskP_5=0, P_network_3_1_AnnP_3=0, P_network_5_4_RI_4=0, P_network_3_6_AI_3=0, P_network_4_4_RI_4=0, P_network_4_2_AskP_5=0, P_poll__networl_3_6_AnnP_3=0, P_network_2_1_AskP_6=0, P_poll__networl_1_2_AnnP_1=0, P_poll__networl_2_6_RP_6=0, P_poll__networl_5_6_AI_1=0, P_poll__networl_1_0_RI_5=0, P_network_2_5_RP_4=0, P_poll__networl_4_6_RP_4=0, P_network_1_4_RI_4=0, P_poll__networl_2_5_RP_5=0, P_poll__networl_2_5_AnnP_2=0, P_network_3_3_AI_2=0, P_poll__networl_0_4_RP_1=0, P_network_4_1_AnnP_6=0, P_network_2_2_RI_4=0, P_network_4_0_AnnP_5=0, P_poll__networl_2_2_AnnP_2=0
May 26, 2018 12:11:59 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Simplified 9400 expressions due to constant valuations.
May 26, 2018 12:11:59 AM fr.lip6.move.gal.instantiate.Simplifier simplifyFalseTransitions
INFO: Removed 430 false transitions.
May 26, 2018 12:11:59 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
May 26, 2018 12:11:59 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 2772 ms
FORMULA NeoElection-PT-6-ReachabilityCardinality-15 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-ReachabilityCardinality-13 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-ReachabilityCardinality-10 TRUE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-ReachabilityCardinality-08 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
FORMULA NeoElection-PT-6-ReachabilityCardinality-07 FALSE TECHNIQUES TOPOLOGICAL INITIAL_STATE
Using solver Z3 to compute partial order matrices.
Built C files in :
/mcc-data
May 26, 2018 12:12:00 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
May 26, 2018 12:12:00 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 27 constant array cells/variables (out of 1281 variables) in type NeoElection_PT_6_flat
May 26, 2018 12:12:00 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_negotiation_3_0_NONE,P_negotiation_0_3_NONE,P_negotiation_0_0_NONE,P_sendAnnPs__broadcasting_0_2,P_negotiation_0_4_NONE,P_sendAnnPs__broadcasting_0_5,P_negotiation_0_5_NONE,P_negotiation_1_0_NONE,P_startNeg__broadcasting_0_4,P_negotiation_4_0_NONE,P_startNeg__broadcasting_0_2,P_negotiation_6_0_NONE,P_negotiation_0_1_NONE,P_negotiation_0_2_NONE,P_negotiation_4_4_NONE,P_startNeg__broadcasting_0_3,P_negotiation_5_5_NONE,P_sendAnnPs__broadcasting_0_3,P_negotiation_0_6_NONE,P_startNeg__broadcasting_0_5,P_negotiation_6_6_NONE,P_negotiation_5_0_NONE,P_negotiation_1_1_NONE,P_sendAnnPs__broadcasting_0_4,P_negotiation_3_3_NONE,P_negotiation_2_2_NONE,P_negotiation_2_0_NONE,
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 27 constant array cells/variables (out of 1281 variables) in type NeoElection_PT_6_flat
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_negotiation_0_2_NONE,P_negotiation_0_5_NONE,P_negotiation_2_0_NONE,P_negotiation_1_1_NONE,P_negotiation_0_3_NONE,P_sendAnnPs__broadcasting_0_3,P_startNeg__broadcasting_0_5,P_negotiation_1_0_NONE,P_negotiation_0_1_NONE,P_negotiation_5_5_NONE,P_negotiation_5_0_NONE,P_negotiation_4_4_NONE,P_startNeg__broadcasting_0_2,P_negotiation_0_0_NONE,P_negotiation_4_0_NONE,P_negotiation_0_6_NONE,P_negotiation_6_6_NONE,P_negotiation_3_3_NONE,P_sendAnnPs__broadcasting_0_4,P_startNeg__broadcasting_0_3,P_negotiation_2_2_NONE,P_startNeg__broadcasting_0_4,P_sendAnnPs__broadcasting_0_2,P_negotiation_3_0_NONE,P_sendAnnPs__broadcasting_0_5,P_negotiation_6_0_NONE,P_negotiation_0_4_NONE,
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 27 constant array cells/variables (out of 1281 variables) in type NeoElection_PT_6_flat
May 26, 2018 12:12:01 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_negotiation_3_0_NONE,P_negotiation_0_3_NONE,P_negotiation_0_0_NONE,P_sendAnnPs__broadcasting_0_2,P_negotiation_0_4_NONE,P_sendAnnPs__broadcasting_0_5,P_negotiation_0_5_NONE,P_negotiation_1_0_NONE,P_startNeg__broadcasting_0_4,P_negotiation_4_0_NONE,P_startNeg__broadcasting_0_2,P_negotiation_6_0_NONE,P_negotiation_0_1_NONE,P_negotiation_0_2_NONE,P_negotiation_4_4_NONE,P_startNeg__broadcasting_0_3,P_negotiation_5_5_NONE,P_sendAnnPs__broadcasting_0_3,P_negotiation_0_6_NONE,P_startNeg__broadcasting_0_5,P_negotiation_6_6_NONE,P_negotiation_5_0_NONE,P_negotiation_1_1_NONE,P_sendAnnPs__broadcasting_0_4,P_negotiation_3_3_NONE,P_negotiation_2_2_NONE,P_negotiation_2_0_NONE,
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: Found a total of 27 constant array cells/variables (out of 1281 variables) in type NeoElection_PT_6_flat
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier printConstantVars
INFO: P_negotiation_0_2_NONE,P_negotiation_0_5_NONE,P_negotiation_2_0_NONE,P_negotiation_1_1_NONE,P_negotiation_0_3_NONE,P_sendAnnPs__broadcasting_0_3,P_startNeg__broadcasting_0_5,P_negotiation_1_0_NONE,P_negotiation_0_1_NONE,P_negotiation_5_5_NONE,P_negotiation_5_0_NONE,P_negotiation_4_4_NONE,P_startNeg__broadcasting_0_2,P_negotiation_0_0_NONE,P_negotiation_4_0_NONE,P_negotiation_0_6_NONE,P_negotiation_6_6_NONE,P_negotiation_3_3_NONE,P_sendAnnPs__broadcasting_0_4,P_startNeg__broadcasting_0_3,P_negotiation_2_2_NONE,P_startNeg__broadcasting_0_4,P_sendAnnPs__broadcasting_0_2,P_negotiation_3_0_NONE,P_sendAnnPs__broadcasting_0_5,P_negotiation_6_0_NONE,P_negotiation_0_4_NONE,
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Removed 27 constant variables :P_negotiation_3_0_NONE=0, P_negotiation_0_3_NONE=0, P_negotiation_0_0_NONE=0, P_sendAnnPs__broadcasting_0_2=0, P_negotiation_0_4_NONE=0, P_sendAnnPs__broadcasting_0_5=0, P_negotiation_0_5_NONE=0, P_negotiation_1_0_NONE=0, P_startNeg__broadcasting_0_4=0, P_negotiation_4_0_NONE=0, P_startNeg__broadcasting_0_2=0, P_negotiation_6_0_NONE=0, P_negotiation_0_1_NONE=0, P_negotiation_0_2_NONE=0, P_negotiation_4_4_NONE=0, P_startNeg__broadcasting_0_3=0, P_negotiation_5_5_NONE=0, P_sendAnnPs__broadcasting_0_3=0, P_negotiation_0_6_NONE=0, P_startNeg__broadcasting_0_5=0, P_negotiation_6_6_NONE=0, P_negotiation_5_0_NONE=0, P_negotiation_1_1_NONE=0, P_sendAnnPs__broadcasting_0_4=0, P_negotiation_3_3_NONE=0, P_negotiation_2_2_NONE=0, P_negotiation_2_0_NONE=0
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Simplified 46 expressions due to constant valuations.
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Removed 27 constant variables :P_negotiation_0_2_NONE=0, P_negotiation_0_5_NONE=0, P_negotiation_2_0_NONE=0, P_negotiation_1_1_NONE=0, P_negotiation_0_3_NONE=0, P_sendAnnPs__broadcasting_0_3=0, P_startNeg__broadcasting_0_5=0, P_negotiation_1_0_NONE=0, P_negotiation_0_1_NONE=0, P_negotiation_5_5_NONE=0, P_negotiation_5_0_NONE=0, P_negotiation_4_4_NONE=0, P_startNeg__broadcasting_0_2=0, P_negotiation_0_0_NONE=0, P_negotiation_4_0_NONE=0, P_negotiation_0_6_NONE=0, P_negotiation_6_6_NONE=0, P_negotiation_3_3_NONE=0, P_sendAnnPs__broadcasting_0_4=0, P_startNeg__broadcasting_0_3=0, P_negotiation_2_2_NONE=0, P_startNeg__broadcasting_0_4=0, P_sendAnnPs__broadcasting_0_2=0, P_negotiation_3_0_NONE=0, P_sendAnnPs__broadcasting_0_5=0, P_negotiation_6_0_NONE=0, P_negotiation_0_4_NONE=0
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Simplified 46 expressions due to constant valuations.
May 26, 2018 12:12:02 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 2752 ms
May 26, 2018 12:12:03 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 2311 ms
May 26, 2018 12:12:03 AM fr.lip6.move.serialization.SerializationUtil systemToFile
INFO: Time to serialize gal into /mcc-data/ReachabilityCardinality.pnml.gal : 186 ms
May 26, 2018 12:12:03 AM fr.lip6.move.serialization.SerializationUtil serializePropertiesForITSTools
INFO: Time to serialize properties into /mcc-data/ReachabilityCardinality.prop : 54 ms
Invoking ITS tools like this :CommandLine [args=[/usr/share/itscl/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201804131302/bin/its-reach-linux64, --gc-threshold, 2000000, --quiet, -i, /mcc-data/ReachabilityCardinality.pnml.gal, -t, CGAL, -reachable-file, ReachabilityCardinality.prop, --nowitness], workingDir=/mcc-data]
its-reach command run as :
/usr/share/itscl/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201804131302/bin/its-reach-linux64 --gc-threshold 2000000 --quiet -i /mcc-data/ReachabilityCardinality.pnml.gal -t CGAL -reachable-file ReachabilityCardinality.prop --nowitness
Loading property file ReachabilityCardinality.prop.
Read [invariant] property : NeoElection-PT-6-ReachabilityCardinality-00 with value :((((((((P_poll__pollEnd_0+P_poll__pollEnd_1)+P_poll__pollEnd_2)+P_poll__pollEnd_3)+P_poll__pollEnd_4)+P_poll__pollEnd_5)+P_poll__pollEnd_6)<=(((((((((((((((((((((((((((((((((((((P_sendAnnPs__broadcasting_0_1+P_sendAnnPs__broadcasting_0_6)+P_sendAnnPs__broadcasting_1_1)+P_sendAnnPs__broadcasting_1_2)+P_sendAnnPs__broadcasting_1_3)+P_sendAnnPs__broadcasting_1_4)+P_sendAnnPs__broadcasting_1_5)+P_sendAnnPs__broadcasting_1_6)+P_sendAnnPs__broadcasting_2_1)+P_sendAnnPs__broadcasting_2_2)+P_sendAnnPs__broadcasting_2_3)+P_sendAnnPs__broadcasting_2_4)+P_sendAnnPs__broadcasting_2_5)+P_sendAnnPs__broadcasting_2_6)+P_sendAnnPs__broadcasting_3_1)+P_sendAnnPs__broadcasting_3_2)+P_sendAnnPs__broadcasting_3_3)+P_sendAnnPs__broadcasting_3_4)+P_sendAnnPs__broadcasting_3_5)+P_sendAnnPs__broadcasting_3_6)+P_sendAnnPs__broadcasting_4_1)+P_sendAnnPs__broadcasting_4_2)+P_sendAnnPs__broadcasting_4_3)+P_sendAnnPs__broadcasting_4_4)+P_sendAnnPs__broadcasting_4_5)+P_sendAnnPs__broadcasting_4_6)+P_sendAnnPs__broadcasting_5_1)+P_sendAnnPs__broadcasting_5_2)+P_sendAnnPs__broadcasting_5_3)+P_sendAnnPs__broadcasting_5_4)+P_sendAnnPs__broadcasting_5_5)+P_sendAnnPs__broadcasting_5_6)+P_sendAnnPs__broadcasting_6_1)+P_sendAnnPs__broadcasting_6_2)+P_sendAnnPs__broadcasting_6_3)+P_sendAnnPs__broadcasting_6_4)+P_sendAnnPs__broadcasting_6_5)+P_sendAnnPs__broadcasting_6_6))||(!(((((((P_electedPrimary_0+P_electedPrimary_1)+P_electedPrimary_2)+P_electedPrimary_3)+P_electedPrimary_4)+P_electedPrimary_5)+P_electedPrimary_6)<=((((((P_poll__pollEnd_0+P_poll__pollEnd_1)+P_poll__pollEnd_2)+P_poll__pollEnd_3)+P_poll__pollEnd_4)+P_poll__pollEnd_5)+P_poll__pollEnd_6))))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-01 with value :(!((!((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_poll__networl_0_0_AnsP_1+P_poll__networl_0_0_AnsP_2)+P_poll__networl_0_0_AnsP_3)+P_poll__networl_0_0_AnsP_4)+P_poll__networl_0_0_AnsP_5)+P_poll__networl_0_0_AnsP_6)+P_poll__networl_0_1_AnsP_1)+P_poll__networl_0_1_AnsP_2)+P_poll__networl_0_1_AnsP_3)+P_poll__networl_0_1_AnsP_4)+P_poll__networl_0_1_AnsP_5)+P_poll__networl_0_1_AnsP_6)+P_poll__networl_0_2_AnsP_1)+P_poll__networl_0_2_AnsP_2)+P_poll__networl_0_2_AnsP_3)+P_poll__networl_0_2_AnsP_4)+P_poll__networl_0_2_AnsP_5)+P_poll__networl_0_2_AnsP_6)+P_poll__networl_0_3_AnsP_1)+P_poll__networl_0_3_AnsP_2)+P_poll__networl_0_3_AnsP_3)+P_poll__networl_0_3_AnsP_4)+P_poll__networl_0_3_AnsP_5)+P_poll__networl_0_3_AnsP_6)+P_poll__networl_0_4_AnsP_1)+P_poll__networl_0_4_AnsP_2)+P_poll__networl_0_4_AnsP_3)+P_poll__networl_0_4_AnsP_4)+P_poll__networl_0_4_AnsP_5)+P_poll__networl_0_4_AnsP_6)+P_poll__networl_0_5_AnsP_1)+P_poll__networl_0_5_AnsP_2)+P_poll__networl_0_5_AnsP_3)+P_poll__networl_0_5_AnsP_4)+P_poll__networl_0_5_AnsP_5)+P_poll__networl_0_5_AnsP_6)+P_poll__networl_0_6_AnsP_1)+P_poll__networl_0_6_AnsP_2)+P_poll__networl_0_6_AnsP_3)+P_poll__networl_0_6_AnsP_4)+P_poll__networl_0_6_AnsP_5)+P_poll__networl_0_6_AnsP_6)+P_poll__networl_1_0_AnsP_1)+P_poll__networl_1_0_AnsP_2)+P_poll__networl_1_0_AnsP_3)+P_poll__networl_1_0_AnsP_4)+P_poll__networl_1_0_AnsP_5)+P_poll__networl_1_0_AnsP_6)+P_poll__networl_1_1_AnsP_1)+P_poll__networl_1_1_AnsP_2)+P_poll__networl_1_1_AnsP_3)+P_poll__networl_1_1_AnsP_4)+P_poll__networl_1_1_AnsP_5)+P_poll__networl_1_1_AnsP_6)+P_poll__networl_1_2_AnsP_1)+P_poll__networl_1_2_AnsP_2)+P_poll__networl_1_2_AnsP_3)+P_poll__networl_1_2_AnsP_4)+P_poll__networl_1_2_AnsP_5)+P_poll__networl_1_2_AnsP_6)+P_poll__networl_1_3_AnsP_1)+P_poll__networl_1_3_AnsP_2)+P_poll__networl_1_3_AnsP_3)+P_poll__networl_1_3_AnsP_4)+P_poll__networl_1_3_AnsP_5)+P_poll__networl_1_3_AnsP_6)+P_poll__networl_1_4_AnsP_1)+P_poll__networl_1_4_AnsP_2)+P_poll__networl_1_4_AnsP_3)+P_poll__networl_1_4_AnsP_4)+P_poll__networl_1_4_AnsP_5)+P_poll__networl_1_4_AnsP_6)+P_poll__networl_1_5_AnsP_1)+P_poll__networl_1_5_AnsP_2)+P_poll__networl_1_5_AnsP_3)+P_poll__networl_1_5_AnsP_4)+P_poll__networl_1_5_AnsP_5)+P_poll__networl_1_5_AnsP_6)+P_poll__networl_1_6_AnsP_1)+P_poll__networl_1_6_AnsP_2)+P_poll__networl_1_6_AnsP_3)+P_poll__networl_1_6_AnsP_4)+P_poll__networl_1_6_AnsP_5)+P_poll__networl_1_6_AnsP_6)+P_poll__networl_2_0_AnsP_1)+P_poll__networl_2_0_AnsP_2)+P_poll__networl_2_0_AnsP_3)+P_poll__networl_2_0_AnsP_4)+P_poll__networl_2_0_AnsP_5)+P_poll__networl_2_0_AnsP_6)+P_poll__networl_2_1_AnsP_1)+P_poll__networl_2_1_AnsP_2)+P_poll__networl_2_1_AnsP_3)+P_poll__networl_2_1_AnsP_4)+P_poll__networl_2_1_AnsP_5)+P_poll__networl_2_1_AnsP_6)+P_poll__networl_2_2_AnsP_1)+P_poll__networl_2_2_AnsP_2)+P_poll__networl_2_2_AnsP_3)+P_poll__networl_2_2_AnsP_4)+P_poll__networl_2_2_AnsP_5)+P_poll__networl_2_2_AnsP_6)+P_poll__networl_2_3_AnsP_1)+P_poll__networl_2_3_AnsP_2)+P_poll__networl_2_3_AnsP_3)+P_poll__networl_2_3_AnsP_4)+P_poll__networl_2_3_AnsP_5)+P_poll__networl_2_3_AnsP_6)+P_poll__networl_2_4_AnsP_1)+P_poll__networl_2_4_AnsP_2)+P_poll__networl_2_4_AnsP_3)+P_poll__networl_2_4_AnsP_4)+P_poll__networl_2_4_AnsP_5)+P_poll__networl_2_4_AnsP_6)+P_poll__networl_2_5_AnsP_1)+P_poll__networl_2_5_AnsP_2)+P_poll__networl_2_5_AnsP_3)+P_poll__networl_2_5_AnsP_4)+P_poll__networl_2_5_AnsP_5)+P_poll__networl_2_5_AnsP_6)+P_poll__networl_2_6_AnsP_1)+P_poll__networl_2_6_AnsP_2)+P_poll__networl_2_6_AnsP_3)+P_poll__networl_2_6_AnsP_4)+P_poll__networl_2_6_AnsP_5)+P_poll__networl_2_6_AnsP_6)+P_poll__networl_3_0_AnsP_1)+P_poll__networl_3_0_AnsP_2)+P_poll__networl_3_0_AnsP_3)+P_poll__networl_3_0_AnsP_4)+P_poll__networl_3_0_AnsP_5)+P_poll__networl_3_0_AnsP_6)+P_poll__networl_3_1_AnsP_1)+P_poll__networl_3_1_AnsP_2)+P_poll__networl_3_1_AnsP_3)+P_poll__networl_3_1_AnsP_4)+P_poll__networl_3_1_AnsP_5)+P_poll__networl_3_1_AnsP_6)+P_poll__networl_3_2_AnsP_1)+P_poll__networl_3_2_AnsP_2)+P_poll__networl_3_2_AnsP_3)+P_poll__networl_3_2_AnsP_4)+P_poll__networl_3_2_AnsP_5)+P_poll__networl_3_2_AnsP_6)+P_poll__networl_3_3_AnsP_1)+P_poll__networl_3_3_AnsP_2)+P_poll__networl_3_3_AnsP_3)+P_poll__networl_3_3_AnsP_4)+P_poll__networl_3_3_AnsP_5)+P_poll__networl_3_3_AnsP_6)+P_poll__networl_3_4_AnsP_1)+P_poll__networl_3_4_AnsP_2)+P_poll__networl_3_4_AnsP_3)+P_poll__networl_3_4_AnsP_4)+P_poll__networl_3_4_AnsP_5)+P_poll__networl_3_4_AnsP_6)+P_poll__networl_3_5_AnsP_1)+P_poll__networl_3_5_AnsP_2)+P_poll__networl_3_5_AnsP_3)+P_poll__networl_3_5_AnsP_4)+P_poll__networl_3_5_AnsP_5)+P_poll__networl_3_5_AnsP_6)+P_poll__networl_3_6_AnsP_1)+P_poll__networl_3_6_AnsP_2)+P_poll__networl_3_6_AnsP_3)+P_poll__networl_3_6_AnsP_4)+P_poll__networl_3_6_AnsP_5)+P_poll__networl_3_6_AnsP_6)+P_poll__networl_4_0_AnsP_1)+P_poll__networl_4_0_AnsP_2)+P_poll__networl_4_0_AnsP_3)+P_poll__networl_4_0_AnsP_4)+P_poll__networl_4_0_AnsP_5)+P_poll__networl_4_0_AnsP_6)+P_poll__networl_4_1_AnsP_1)+P_poll__networl_4_1_AnsP_2)+P_poll__networl_4_1_AnsP_3)+P_poll__networl_4_1_AnsP_4)+P_poll__networl_4_1_AnsP_5)+P_poll__networl_4_1_AnsP_6)+P_poll__networl_4_2_AnsP_1)+P_poll__networl_4_2_AnsP_2)+P_poll__networl_4_2_AnsP_3)+P_poll__networl_4_2_AnsP_4)+P_poll__networl_4_2_AnsP_5)+P_poll__networl_4_2_AnsP_6)+P_poll__networl_4_3_AnsP_1)+P_poll__networl_4_3_AnsP_2)+P_poll__networl_4_3_AnsP_3)+P_poll__networl_4_3_AnsP_4)+P_poll__networl_4_3_AnsP_5)+P_poll__networl_4_3_AnsP_6)+P_poll__networl_4_4_AnsP_1)+P_poll__networl_4_4_AnsP_2)+P_poll__networl_4_4_AnsP_3)+P_poll__networl_4_4_AnsP_4)+P_poll__networl_4_4_AnsP_5)+P_poll__networl_4_4_AnsP_6)+P_poll__networl_4_5_AnsP_1)+P_poll__networl_4_5_AnsP_2)+P_poll__networl_4_5_AnsP_3)+P_poll__networl_4_5_AnsP_4)+P_poll__networl_4_5_AnsP_5)+P_poll__networl_4_5_AnsP_6)+P_poll__networl_4_6_AnsP_1)+P_poll__networl_4_6_AnsP_2)+P_poll__networl_4_6_AnsP_3)+P_poll__networl_4_6_AnsP_4)+P_poll__networl_4_6_AnsP_5)+P_poll__networl_4_6_AnsP_6)+P_poll__networl_5_0_AnsP_1)+P_poll__networl_5_0_AnsP_2)+P_poll__networl_5_0_AnsP_3)+P_poll__networl_5_0_AnsP_4)+P_poll__networl_5_0_AnsP_5)+P_poll__networl_5_0_AnsP_6)+P_poll__networl_5_1_AnsP_1)+P_poll__networl_5_1_AnsP_2)+P_poll__networl_5_1_AnsP_3)+P_poll__networl_5_1_AnsP_4)+P_poll__networl_5_1_AnsP_5)+P_poll__networl_5_1_AnsP_6)+P_poll__networl_5_2_AnsP_1)+P_poll__networl_5_2_AnsP_2)+P_poll__networl_5_2_AnsP_3)+P_poll__networl_5_2_AnsP_4)+P_poll__networl_5_2_AnsP_5)+P_poll__networl_5_2_AnsP_6)+P_poll__networl_5_3_AnsP_1)+P_poll__networl_5_3_AnsP_2)+P_poll__networl_5_3_AnsP_3)+P_poll__networl_5_3_AnsP_4)+P_poll__networl_5_3_AnsP_5)+P_poll__networl_5_3_AnsP_6)+P_poll__networl_5_4_AnsP_1)+P_poll__networl_5_4_AnsP_2)+P_poll__networl_5_4_AnsP_3)+P_poll__networl_5_4_AnsP_4)+P_poll__networl_5_4_AnsP_5)+P_poll__networl_5_4_AnsP_6)+P_poll__networl_5_5_AnsP_1)+P_poll__networl_5_5_AnsP_2)+P_poll__networl_5_5_AnsP_3)+P_poll__networl_5_5_AnsP_4)+P_poll__networl_5_5_AnsP_5)+P_poll__networl_5_5_AnsP_6)+P_poll__networl_5_6_AnsP_1)+P_poll__networl_5_6_AnsP_2)+P_poll__networl_5_6_AnsP_3)+P_poll__networl_5_6_AnsP_4)+P_poll__networl_5_6_AnsP_5)+P_poll__networl_5_6_AnsP_6)+P_poll__networl_6_0_AnsP_1)+P_poll__networl_6_0_AnsP_2)+P_poll__networl_6_0_AnsP_3)+P_poll__networl_6_0_AnsP_4)+P_poll__networl_6_0_AnsP_5)+P_poll__networl_6_0_AnsP_6)+P_poll__networl_6_1_AnsP_1)+P_poll__networl_6_1_AnsP_2)+P_poll__networl_6_1_AnsP_3)+P_poll__networl_6_1_AnsP_4)+P_poll__networl_6_1_AnsP_5)+P_poll__networl_6_1_AnsP_6)+P_poll__networl_6_2_AnsP_1)+P_poll__networl_6_2_AnsP_2)+P_poll__networl_6_2_AnsP_3)+P_poll__networl_6_2_AnsP_4)+P_poll__networl_6_2_AnsP_5)+P_poll__networl_6_2_AnsP_6)+P_poll__networl_6_3_AnsP_1)+P_poll__networl_6_3_AnsP_2)+P_poll__networl_6_3_AnsP_3)+P_poll__networl_6_3_AnsP_4)+P_poll__networl_6_3_AnsP_5)+P_poll__networl_6_3_AnsP_6)+P_poll__networl_6_4_AnsP_1)+P_poll__networl_6_4_AnsP_2)+P_poll__networl_6_4_AnsP_3)+P_poll__networl_6_4_AnsP_4)+P_poll__networl_6_4_AnsP_5)+P_poll__networl_6_4_AnsP_6)+P_poll__networl_6_5_AnsP_1)+P_poll__networl_6_5_AnsP_2)+P_poll__networl_6_5_AnsP_3)+P_poll__networl_6_5_AnsP_4)+P_poll__networl_6_5_AnsP_5)+P_poll__networl_6_5_AnsP_6)+P_poll__networl_6_6_AnsP_1)+P_poll__networl_6_6_AnsP_2)+P_poll__networl_6_6_AnsP_3)+P_poll__networl_6_6_AnsP_4)+P_poll__networl_6_6_AnsP_5)+P_poll__networl_6_6_AnsP_6)>=1))||((((((((P_poll__handlingMessage_0+P_poll__handlingMessage_1)+P_poll__handlingMessage_2)+P_poll__handlingMessage_3)+P_poll__handlingMessage_4)+P_poll__handlingMessage_5)+P_poll__handlingMessage_6)<=(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_masterState_0_F_0+P_masterState_0_F_1)+P_masterState_0_F_2)+P_masterState_0_F_3)+P_masterState_0_F_4)+P_masterState_0_F_5)+P_masterState_0_F_6)+P_masterState_0_T_0)+P_masterState_0_T_1)+P_masterState_0_T_2)+P_masterState_0_T_3)+P_masterState_0_T_4)+P_masterState_0_T_5)+P_masterState_0_T_6)+P_masterState_1_F_0)+P_masterState_1_F_1)+P_masterState_1_F_2)+P_masterState_1_F_3)+P_masterState_1_F_4)+P_masterState_1_F_5)+P_masterState_1_F_6)+P_masterState_1_T_0)+P_masterState_1_T_1)+P_masterState_1_T_2)+P_masterState_1_T_3)+P_masterState_1_T_4)+P_masterState_1_T_5)+P_masterState_1_T_6)+P_masterState_2_F_0)+P_masterState_2_F_1)+P_masterState_2_F_2)+P_masterState_2_F_3)+P_masterState_2_F_4)+P_masterState_2_F_5)+P_masterState_2_F_6)+P_masterState_2_T_0)+P_masterState_2_T_1)+P_masterState_2_T_2)+P_masterState_2_T_3)+P_masterState_2_T_4)+P_masterState_2_T_5)+P_masterState_2_T_6)+P_masterState_3_F_0)+P_masterState_3_F_1)+P_masterState_3_F_2)+P_masterState_3_F_3)+P_masterState_3_F_4)+P_masterState_3_F_5)+P_masterState_3_F_6)+P_masterState_3_T_0)+P_masterState_3_T_1)+P_masterState_3_T_2)+P_masterState_3_T_3)+P_masterState_3_T_4)+P_masterState_3_T_5)+P_masterState_3_T_6)+P_masterState_4_F_0)+P_masterState_4_F_1)+P_masterState_4_F_2)+P_masterState_4_F_3)+P_masterState_4_F_4)+P_masterState_4_F_5)+P_masterState_4_F_6)+P_masterState_4_T_0)+P_masterState_4_T_1)+P_masterState_4_T_2)+P_masterState_4_T_3)+P_masterState_4_T_4)+P_masterState_4_T_5)+P_masterState_4_T_6)+P_masterState_5_F_0)+P_masterState_5_F_1)+P_masterState_5_F_2)+P_masterState_5_F_3)+P_masterState_5_F_4)+P_masterState_5_F_5)+P_masterState_5_F_6)+P_masterState_5_T_0)+P_masterState_5_T_1)+P_masterState_5_T_2)+P_masterState_5_T_3)+P_masterState_5_T_4)+P_masterState_5_T_5)+P_masterState_5_T_6)+P_masterState_6_F_0)+P_masterState_6_F_1)+P_masterState_6_F_2)+P_masterState_6_F_3)+P_masterState_6_F_4)+P_masterState_6_F_5)+P_masterState_6_F_6)+P_masterState_6_T_0)+P_masterState_6_T_1)+P_masterState_6_T_2)+P_masterState_6_T_3)+P_masterState_6_T_4)+P_masterState_6_T_5)+P_masterState_6_T_6))&&((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_negotiation_0_0_CO+P_negotiation_0_0_DONE)+P_negotiation_0_1_CO)+P_negotiation_0_1_DONE)+P_negotiation_0_2_CO)+P_negotiation_0_2_DONE)+P_negotiation_0_3_CO)+P_negotiation_0_3_DONE)+P_negotiation_0_4_CO)+P_negotiation_0_4_DONE)+P_negotiation_0_5_CO)+P_negotiation_0_5_DONE)+P_negotiation_0_6_CO)+P_negotiation_0_6_DONE)+P_negotiation_1_0_CO)+P_negotiation_1_0_DONE)+P_negotiation_1_1_CO)+P_negotiation_1_1_DONE)+P_negotiation_1_2_NONE)+P_negotiation_1_2_CO)+P_negotiation_1_2_DONE)+P_negotiation_1_3_NONE)+P_negotiation_1_3_CO)+P_negotiation_1_3_DONE)+P_negotiation_1_4_NONE)+P_negotiation_1_4_CO)+P_negotiation_1_4_DONE)+P_negotiation_1_5_NONE)+P_negotiation_1_5_CO)+P_negotiation_1_5_DONE)+P_negotiation_1_6_NONE)+P_negotiation_1_6_CO)+P_negotiation_1_6_DONE)+P_negotiation_2_0_CO)+P_negotiation_2_0_DONE)+P_negotiation_2_1_NONE)+P_negotiation_2_1_CO)+P_negotiation_2_1_DONE)+P_negotiation_2_2_CO)+P_negotiation_2_2_DONE)+P_negotiation_2_3_NONE)+P_negotiation_2_3_CO)+P_negotiation_2_3_DONE)+P_negotiation_2_4_NONE)+P_negotiation_2_4_CO)+P_negotiation_2_4_DONE)+P_negotiation_2_5_NONE)+P_negotiation_2_5_CO)+P_negotiation_2_5_DONE)+P_negotiation_2_6_NONE)+P_negotiation_2_6_CO)+P_negotiation_2_6_DONE)+P_negotiation_3_0_CO)+P_negotiation_3_0_DONE)+P_negotiation_3_1_NONE)+P_negotiation_3_1_CO)+P_negotiation_3_1_DONE)+P_negotiation_3_2_NONE)+P_negotiation_3_2_CO)+P_negotiation_3_2_DONE)+P_negotiation_3_3_CO)+P_negotiation_3_3_DONE)+P_negotiation_3_4_NONE)+P_negotiation_3_4_CO)+P_negotiation_3_4_DONE)+P_negotiation_3_5_NONE)+P_negotiation_3_5_CO)+P_negotiation_3_5_DONE)+P_negotiation_3_6_NONE)+P_negotiation_3_6_CO)+P_negotiation_3_6_DONE)+P_negotiation_4_0_CO)+P_negotiation_4_0_DONE)+P_negotiation_4_1_NONE)+P_negotiation_4_1_CO)+P_negotiation_4_1_DONE)+P_negotiation_4_2_NONE)+P_negotiation_4_2_CO)+P_negotiation_4_2_DONE)+P_negotiation_4_3_NONE)+P_negotiation_4_3_CO)+P_negotiation_4_3_DONE)+P_negotiation_4_4_CO)+P_negotiation_4_4_DONE)+P_negotiation_4_5_NONE)+P_negotiation_4_5_CO)+P_negotiation_4_5_DONE)+P_negotiation_4_6_NONE)+P_negotiation_4_6_CO)+P_negotiation_4_6_DONE)+P_negotiation_5_0_CO)+P_negotiation_5_0_DONE)+P_negotiation_5_1_NONE)+P_negotiation_5_1_CO)+P_negotiation_5_1_DONE)+P_negotiation_5_2_NONE)+P_negotiation_5_2_CO)+P_negotiation_5_2_DONE)+P_negotiation_5_3_NONE)+P_negotiation_5_3_CO)+P_negotiation_5_3_DONE)+P_negotiation_5_4_NONE)+P_negotiation_5_4_CO)+P_negotiation_5_4_DONE)+P_negotiation_5_5_CO)+P_negotiation_5_5_DONE)+P_negotiation_5_6_NONE)+P_negotiation_5_6_CO)+P_negotiation_5_6_DONE)+P_negotiation_6_0_CO)+P_negotiation_6_0_DONE)+P_negotiation_6_1_NONE)+P_negotiation_6_1_CO)+P_negotiation_6_1_DONE)+P_negotiation_6_2_NONE)+P_negotiation_6_2_CO)+P_negotiation_6_2_DONE)+P_negotiation_6_3_NONE)+P_negotiation_6_3_CO)+P_negotiation_6_3_DONE)+P_negotiation_6_4_NONE)+P_negotiation_6_4_CO)+P_negotiation_6_4_DONE)+P_negotiation_6_5_NONE)+P_negotiation_6_5_CO)+P_negotiation_6_5_DONE)+P_negotiation_6_6_CO)+P_negotiation_6_6_DONE)<=((((((P_poll__handlingMessage_0+P_poll__handlingMessage_1)+P_poll__handlingMessage_2)+P_poll__handlingMessage_3)+P_poll__handlingMessage_4)+P_poll__handlingMessage_5)+P_poll__handlingMessage_6)))))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-02 with value :(!((((((((P_electedPrimary_0+P_electedPrimary_1)+P_electedPrimary_2)+P_electedPrimary_3)+P_electedPrimary_4)+P_electedPrimary_5)+P_electedPrimary_6)>=0)||(!((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_masterState_0_F_0+P_masterState_0_F_1)+P_masterState_0_F_2)+P_masterState_0_F_3)+P_masterState_0_F_4)+P_masterState_0_F_5)+P_masterState_0_F_6)+P_masterState_0_T_0)+P_masterState_0_T_1)+P_masterState_0_T_2)+P_masterState_0_T_3)+P_masterState_0_T_4)+P_masterState_0_T_5)+P_masterState_0_T_6)+P_masterState_1_F_0)+P_masterState_1_F_1)+P_masterState_1_F_2)+P_masterState_1_F_3)+P_masterState_1_F_4)+P_masterState_1_F_5)+P_masterState_1_F_6)+P_masterState_1_T_0)+P_masterState_1_T_1)+P_masterState_1_T_2)+P_masterState_1_T_3)+P_masterState_1_T_4)+P_masterState_1_T_5)+P_masterState_1_T_6)+P_masterState_2_F_0)+P_masterState_2_F_1)+P_masterState_2_F_2)+P_masterState_2_F_3)+P_masterState_2_F_4)+P_masterState_2_F_5)+P_masterState_2_F_6)+P_masterState_2_T_0)+P_masterState_2_T_1)+P_masterState_2_T_2)+P_masterState_2_T_3)+P_masterState_2_T_4)+P_masterState_2_T_5)+P_masterState_2_T_6)+P_masterState_3_F_0)+P_masterState_3_F_1)+P_masterState_3_F_2)+P_masterState_3_F_3)+P_masterState_3_F_4)+P_masterState_3_F_5)+P_masterState_3_F_6)+P_masterState_3_T_0)+P_masterState_3_T_1)+P_masterState_3_T_2)+P_masterState_3_T_3)+P_masterState_3_T_4)+P_masterState_3_T_5)+P_masterState_3_T_6)+P_masterState_4_F_0)+P_masterState_4_F_1)+P_masterState_4_F_2)+P_masterState_4_F_3)+P_masterState_4_F_4)+P_masterState_4_F_5)+P_masterState_4_F_6)+P_masterState_4_T_0)+P_masterState_4_T_1)+P_masterState_4_T_2)+P_masterState_4_T_3)+P_masterState_4_T_4)+P_masterState_4_T_5)+P_masterState_4_T_6)+P_masterState_5_F_0)+P_masterState_5_F_1)+P_masterState_5_F_2)+P_masterState_5_F_3)+P_masterState_5_F_4)+P_masterState_5_F_5)+P_masterState_5_F_6)+P_masterState_5_T_0)+P_masterState_5_T_1)+P_masterState_5_T_2)+P_masterState_5_T_3)+P_masterState_5_T_4)+P_masterState_5_T_5)+P_masterState_5_T_6)+P_masterState_6_F_0)+P_masterState_6_F_1)+P_masterState_6_F_2)+P_masterState_6_F_3)+P_masterState_6_F_4)+P_masterState_6_F_5)+P_masterState_6_F_6)+P_masterState_6_T_0)+P_masterState_6_T_1)+P_masterState_6_T_2)+P_masterState_6_T_3)+P_masterState_6_T_4)+P_masterState_6_T_5)+P_masterState_6_T_6)<=((((((P_electionInit_0+P_electionInit_1)+P_electionInit_2)+P_electionInit_3)+P_electionInit_4)+P_electionInit_5)+P_electionInit_6)))))
Read [invariant] property : NeoElection-PT-6-ReachabilityCardinality-03 with value :(((((((P_electedSecondary_0+P_electedSecondary_1)+P_electedSecondary_2)+P_electedSecondary_3)+P_electedSecondary_4)+P_electedSecondary_5)+P_electedSecondary_6)<=((((((((((((((((((((P_stage_0_NEG+P_stage_0_PRIM)+P_stage_0_SEC)+P_stage_1_NEG)+P_stage_1_PRIM)+P_stage_1_SEC)+P_stage_2_NEG)+P_stage_2_PRIM)+P_stage_2_SEC)+P_stage_3_NEG)+P_stage_3_PRIM)+P_stage_3_SEC)+P_stage_4_NEG)+P_stage_4_PRIM)+P_stage_4_SEC)+P_stage_5_NEG)+P_stage_5_PRIM)+P_stage_5_SEC)+P_stage_6_NEG)+P_stage_6_PRIM)+P_stage_6_SEC))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-04 with value :((!((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_negotiation_0_0_CO+P_negotiation_0_0_DONE)+P_negotiation_0_1_CO)+P_negotiation_0_1_DONE)+P_negotiation_0_2_CO)+P_negotiation_0_2_DONE)+P_negotiation_0_3_CO)+P_negotiation_0_3_DONE)+P_negotiation_0_4_CO)+P_negotiation_0_4_DONE)+P_negotiation_0_5_CO)+P_negotiation_0_5_DONE)+P_negotiation_0_6_CO)+P_negotiation_0_6_DONE)+P_negotiation_1_0_CO)+P_negotiation_1_0_DONE)+P_negotiation_1_1_CO)+P_negotiation_1_1_DONE)+P_negotiation_1_2_NONE)+P_negotiation_1_2_CO)+P_negotiation_1_2_DONE)+P_negotiation_1_3_NONE)+P_negotiation_1_3_CO)+P_negotiation_1_3_DONE)+P_negotiation_1_4_NONE)+P_negotiation_1_4_CO)+P_negotiation_1_4_DONE)+P_negotiation_1_5_NONE)+P_negotiation_1_5_CO)+P_negotiation_1_5_DONE)+P_negotiation_1_6_NONE)+P_negotiation_1_6_CO)+P_negotiation_1_6_DONE)+P_negotiation_2_0_CO)+P_negotiation_2_0_DONE)+P_negotiation_2_1_NONE)+P_negotiation_2_1_CO)+P_negotiation_2_1_DONE)+P_negotiation_2_2_CO)+P_negotiation_2_2_DONE)+P_negotiation_2_3_NONE)+P_negotiation_2_3_CO)+P_negotiation_2_3_DONE)+P_negotiation_2_4_NONE)+P_negotiation_2_4_CO)+P_negotiation_2_4_DONE)+P_negotiation_2_5_NONE)+P_negotiation_2_5_CO)+P_negotiation_2_5_DONE)+P_negotiation_2_6_NONE)+P_negotiation_2_6_CO)+P_negotiation_2_6_DONE)+P_negotiation_3_0_CO)+P_negotiation_3_0_DONE)+P_negotiation_3_1_NONE)+P_negotiation_3_1_CO)+P_negotiation_3_1_DONE)+P_negotiation_3_2_NONE)+P_negotiation_3_2_CO)+P_negotiation_3_2_DONE)+P_negotiation_3_3_CO)+P_negotiation_3_3_DONE)+P_negotiation_3_4_NONE)+P_negotiation_3_4_CO)+P_negotiation_3_4_DONE)+P_negotiation_3_5_NONE)+P_negotiation_3_5_CO)+P_negotiation_3_5_DONE)+P_negotiation_3_6_NONE)+P_negotiation_3_6_CO)+P_negotiation_3_6_DONE)+P_negotiation_4_0_CO)+P_negotiation_4_0_DONE)+P_negotiation_4_1_NONE)+P_negotiation_4_1_CO)+P_negotiation_4_1_DONE)+P_negotiation_4_2_NONE)+P_negotiation_4_2_CO)+P_negotiation_4_2_DONE)+P_negotiation_4_3_NONE)+P_negotiation_4_3_CO)+P_negotiation_4_3_DONE)+P_negotiation_4_4_CO)+P_negotiation_4_4_DONE)+P_negotiation_4_5_NONE)+P_negotiation_4_5_CO)+P_negotiation_4_5_DONE)+P_negotiation_4_6_NONE)+P_negotiation_4_6_CO)+P_negotiation_4_6_DONE)+P_negotiation_5_0_CO)+P_negotiation_5_0_DONE)+P_negotiation_5_1_NONE)+P_negotiation_5_1_CO)+P_negotiation_5_1_DONE)+P_negotiation_5_2_NONE)+P_negotiation_5_2_CO)+P_negotiation_5_2_DONE)+P_negotiation_5_3_NONE)+P_negotiation_5_3_CO)+P_negotiation_5_3_DONE)+P_negotiation_5_4_NONE)+P_negotiation_5_4_CO)+P_negotiation_5_4_DONE)+P_negotiation_5_5_CO)+P_negotiation_5_5_DONE)+P_negotiation_5_6_NONE)+P_negotiation_5_6_CO)+P_negotiation_5_6_DONE)+P_negotiation_6_0_CO)+P_negotiation_6_0_DONE)+P_negotiation_6_1_NONE)+P_negotiation_6_1_CO)+P_negotiation_6_1_DONE)+P_negotiation_6_2_NONE)+P_negotiation_6_2_CO)+P_negotiation_6_2_DONE)+P_negotiation_6_3_NONE)+P_negotiation_6_3_CO)+P_negotiation_6_3_DONE)+P_negotiation_6_4_NONE)+P_negotiation_6_4_CO)+P_negotiation_6_4_DONE)+P_negotiation_6_5_NONE)+P_negotiation_6_5_CO)+P_negotiation_6_5_DONE)+P_negotiation_6_6_CO)+P_negotiation_6_6_DONE)>=2))&&((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_poll__networl_0_0_AnsP_1+P_poll__networl_0_0_AnsP_2)+P_poll__networl_0_0_AnsP_3)+P_poll__networl_0_0_AnsP_4)+P_poll__networl_0_0_AnsP_5)+P_poll__networl_0_0_AnsP_6)+P_poll__networl_0_1_AnsP_1)+P_poll__networl_0_1_AnsP_2)+P_poll__networl_0_1_AnsP_3)+P_poll__networl_0_1_AnsP_4)+P_poll__networl_0_1_AnsP_5)+P_poll__networl_0_1_AnsP_6)+P_poll__networl_0_2_AnsP_1)+P_poll__networl_0_2_AnsP_2)+P_poll__networl_0_2_AnsP_3)+P_poll__networl_0_2_AnsP_4)+P_poll__networl_0_2_AnsP_5)+P_poll__networl_0_2_AnsP_6)+P_poll__networl_0_3_AnsP_1)+P_poll__networl_0_3_AnsP_2)+P_poll__networl_0_3_AnsP_3)+P_poll__networl_0_3_AnsP_4)+P_poll__networl_0_3_AnsP_5)+P_poll__networl_0_3_AnsP_6)+P_poll__networl_0_4_AnsP_1)+P_poll__networl_0_4_AnsP_2)+P_poll__networl_0_4_AnsP_3)+P_poll__networl_0_4_AnsP_4)+P_poll__networl_0_4_AnsP_5)+P_poll__networl_0_4_AnsP_6)+P_poll__networl_0_5_AnsP_1)+P_poll__networl_0_5_AnsP_2)+P_poll__networl_0_5_AnsP_3)+P_poll__networl_0_5_AnsP_4)+P_poll__networl_0_5_AnsP_5)+P_poll__networl_0_5_AnsP_6)+P_poll__networl_0_6_AnsP_1)+P_poll__networl_0_6_AnsP_2)+P_poll__networl_0_6_AnsP_3)+P_poll__networl_0_6_AnsP_4)+P_poll__networl_0_6_AnsP_5)+P_poll__networl_0_6_AnsP_6)+P_poll__networl_1_0_AnsP_1)+P_poll__networl_1_0_AnsP_2)+P_poll__networl_1_0_AnsP_3)+P_poll__networl_1_0_AnsP_4)+P_poll__networl_1_0_AnsP_5)+P_poll__networl_1_0_AnsP_6)+P_poll__networl_1_1_AnsP_1)+P_poll__networl_1_1_AnsP_2)+P_poll__networl_1_1_AnsP_3)+P_poll__networl_1_1_AnsP_4)+P_poll__networl_1_1_AnsP_5)+P_poll__networl_1_1_AnsP_6)+P_poll__networl_1_2_AnsP_1)+P_poll__networl_1_2_AnsP_2)+P_poll__networl_1_2_AnsP_3)+P_poll__networl_1_2_AnsP_4)+P_poll__networl_1_2_AnsP_5)+P_poll__networl_1_2_AnsP_6)+P_poll__networl_1_3_AnsP_1)+P_poll__networl_1_3_AnsP_2)+P_poll__networl_1_3_AnsP_3)+P_poll__networl_1_3_AnsP_4)+P_poll__networl_1_3_AnsP_5)+P_poll__networl_1_3_AnsP_6)+P_poll__networl_1_4_AnsP_1)+P_poll__networl_1_4_AnsP_2)+P_poll__networl_1_4_AnsP_3)+P_poll__networl_1_4_AnsP_4)+P_poll__networl_1_4_AnsP_5)+P_poll__networl_1_4_AnsP_6)+P_poll__networl_1_5_AnsP_1)+P_poll__networl_1_5_AnsP_2)+P_poll__networl_1_5_AnsP_3)+P_poll__networl_1_5_AnsP_4)+P_poll__networl_1_5_AnsP_5)+P_poll__networl_1_5_AnsP_6)+P_poll__networl_1_6_AnsP_1)+P_poll__networl_1_6_AnsP_2)+P_poll__networl_1_6_AnsP_3)+P_poll__networl_1_6_AnsP_4)+P_poll__networl_1_6_AnsP_5)+P_poll__networl_1_6_AnsP_6)+P_poll__networl_2_0_AnsP_1)+P_poll__networl_2_0_AnsP_2)+P_poll__networl_2_0_AnsP_3)+P_poll__networl_2_0_AnsP_4)+P_poll__networl_2_0_AnsP_5)+P_poll__networl_2_0_AnsP_6)+P_poll__networl_2_1_AnsP_1)+P_poll__networl_2_1_AnsP_2)+P_poll__networl_2_1_AnsP_3)+P_poll__networl_2_1_AnsP_4)+P_poll__networl_2_1_AnsP_5)+P_poll__networl_2_1_AnsP_6)+P_poll__networl_2_2_AnsP_1)+P_poll__networl_2_2_AnsP_2)+P_poll__networl_2_2_AnsP_3)+P_poll__networl_2_2_AnsP_4)+P_poll__networl_2_2_AnsP_5)+P_poll__networl_2_2_AnsP_6)+P_poll__networl_2_3_AnsP_1)+P_poll__networl_2_3_AnsP_2)+P_poll__networl_2_3_AnsP_3)+P_poll__networl_2_3_AnsP_4)+P_poll__networl_2_3_AnsP_5)+P_poll__networl_2_3_AnsP_6)+P_poll__networl_2_4_AnsP_1)+P_poll__networl_2_4_AnsP_2)+P_poll__networl_2_4_AnsP_3)+P_poll__networl_2_4_AnsP_4)+P_poll__networl_2_4_AnsP_5)+P_poll__networl_2_4_AnsP_6)+P_poll__networl_2_5_AnsP_1)+P_poll__networl_2_5_AnsP_2)+P_poll__networl_2_5_AnsP_3)+P_poll__networl_2_5_AnsP_4)+P_poll__networl_2_5_AnsP_5)+P_poll__networl_2_5_AnsP_6)+P_poll__networl_2_6_AnsP_1)+P_poll__networl_2_6_AnsP_2)+P_poll__networl_2_6_AnsP_3)+P_poll__networl_2_6_AnsP_4)+P_poll__networl_2_6_AnsP_5)+P_poll__networl_2_6_AnsP_6)+P_poll__networl_3_0_AnsP_1)+P_poll__networl_3_0_AnsP_2)+P_poll__networl_3_0_AnsP_3)+P_poll__networl_3_0_AnsP_4)+P_poll__networl_3_0_AnsP_5)+P_poll__networl_3_0_AnsP_6)+P_poll__networl_3_1_AnsP_1)+P_poll__networl_3_1_AnsP_2)+P_poll__networl_3_1_AnsP_3)+P_poll__networl_3_1_AnsP_4)+P_poll__networl_3_1_AnsP_5)+P_poll__networl_3_1_AnsP_6)+P_poll__networl_3_2_AnsP_1)+P_poll__networl_3_2_AnsP_2)+P_poll__networl_3_2_AnsP_3)+P_poll__networl_3_2_AnsP_4)+P_poll__networl_3_2_AnsP_5)+P_poll__networl_3_2_AnsP_6)+P_poll__networl_3_3_AnsP_1)+P_poll__networl_3_3_AnsP_2)+P_poll__networl_3_3_AnsP_3)+P_poll__networl_3_3_AnsP_4)+P_poll__networl_3_3_AnsP_5)+P_poll__networl_3_3_AnsP_6)+P_poll__networl_3_4_AnsP_1)+P_poll__networl_3_4_AnsP_2)+P_poll__networl_3_4_AnsP_3)+P_poll__networl_3_4_AnsP_4)+P_poll__networl_3_4_AnsP_5)+P_poll__networl_3_4_AnsP_6)+P_poll__networl_3_5_AnsP_1)+P_poll__networl_3_5_AnsP_2)+P_poll__networl_3_5_AnsP_3)+P_poll__networl_3_5_AnsP_4)+P_poll__networl_3_5_AnsP_5)+P_poll__networl_3_5_AnsP_6)+P_poll__networl_3_6_AnsP_1)+P_poll__networl_3_6_AnsP_2)+P_poll__networl_3_6_AnsP_3)+P_poll__networl_3_6_AnsP_4)+P_poll__networl_3_6_AnsP_5)+P_poll__networl_3_6_AnsP_6)+P_poll__networl_4_0_AnsP_1)+P_poll__networl_4_0_AnsP_2)+P_poll__networl_4_0_AnsP_3)+P_poll__networl_4_0_AnsP_4)+P_poll__networl_4_0_AnsP_5)+P_poll__networl_4_0_AnsP_6)+P_poll__networl_4_1_AnsP_1)+P_poll__networl_4_1_AnsP_2)+P_poll__networl_4_1_AnsP_3)+P_poll__networl_4_1_AnsP_4)+P_poll__networl_4_1_AnsP_5)+P_poll__networl_4_1_AnsP_6)+P_poll__networl_4_2_AnsP_1)+P_poll__networl_4_2_AnsP_2)+P_poll__networl_4_2_AnsP_3)+P_poll__networl_4_2_AnsP_4)+P_poll__networl_4_2_AnsP_5)+P_poll__networl_4_2_AnsP_6)+P_poll__networl_4_3_AnsP_1)+P_poll__networl_4_3_AnsP_2)+P_poll__networl_4_3_AnsP_3)+P_poll__networl_4_3_AnsP_4)+P_poll__networl_4_3_AnsP_5)+P_poll__networl_4_3_AnsP_6)+P_poll__networl_4_4_AnsP_1)+P_poll__networl_4_4_AnsP_2)+P_poll__networl_4_4_AnsP_3)+P_poll__networl_4_4_AnsP_4)+P_poll__networl_4_4_AnsP_5)+P_poll__networl_4_4_AnsP_6)+P_poll__networl_4_5_AnsP_1)+P_poll__networl_4_5_AnsP_2)+P_poll__networl_4_5_AnsP_3)+P_poll__networl_4_5_AnsP_4)+P_poll__networl_4_5_AnsP_5)+P_poll__networl_4_5_AnsP_6)+P_poll__networl_4_6_AnsP_1)+P_poll__networl_4_6_AnsP_2)+P_poll__networl_4_6_AnsP_3)+P_poll__networl_4_6_AnsP_4)+P_poll__networl_4_6_AnsP_5)+P_poll__networl_4_6_AnsP_6)+P_poll__networl_5_0_AnsP_1)+P_poll__networl_5_0_AnsP_2)+P_poll__networl_5_0_AnsP_3)+P_poll__networl_5_0_AnsP_4)+P_poll__networl_5_0_AnsP_5)+P_poll__networl_5_0_AnsP_6)+P_poll__networl_5_1_AnsP_1)+P_poll__networl_5_1_AnsP_2)+P_poll__networl_5_1_AnsP_3)+P_poll__networl_5_1_AnsP_4)+P_poll__networl_5_1_AnsP_5)+P_poll__networl_5_1_AnsP_6)+P_poll__networl_5_2_AnsP_1)+P_poll__networl_5_2_AnsP_2)+P_poll__networl_5_2_AnsP_3)+P_poll__networl_5_2_AnsP_4)+P_poll__networl_5_2_AnsP_5)+P_poll__networl_5_2_AnsP_6)+P_poll__networl_5_3_AnsP_1)+P_poll__networl_5_3_AnsP_2)+P_poll__networl_5_3_AnsP_3)+P_poll__networl_5_3_AnsP_4)+P_poll__networl_5_3_AnsP_5)+P_poll__networl_5_3_AnsP_6)+P_poll__networl_5_4_AnsP_1)+P_poll__networl_5_4_AnsP_2)+P_poll__networl_5_4_AnsP_3)+P_poll__networl_5_4_AnsP_4)+P_poll__networl_5_4_AnsP_5)+P_poll__networl_5_4_AnsP_6)+P_poll__networl_5_5_AnsP_1)+P_poll__networl_5_5_AnsP_2)+P_poll__networl_5_5_AnsP_3)+P_poll__networl_5_5_AnsP_4)+P_poll__networl_5_5_AnsP_5)+P_poll__networl_5_5_AnsP_6)+P_poll__networl_5_6_AnsP_1)+P_poll__networl_5_6_AnsP_2)+P_poll__networl_5_6_AnsP_3)+P_poll__networl_5_6_AnsP_4)+P_poll__networl_5_6_AnsP_5)+P_poll__networl_5_6_AnsP_6)+P_poll__networl_6_0_AnsP_1)+P_poll__networl_6_0_AnsP_2)+P_poll__networl_6_0_AnsP_3)+P_poll__networl_6_0_AnsP_4)+P_poll__networl_6_0_AnsP_5)+P_poll__networl_6_0_AnsP_6)+P_poll__networl_6_1_AnsP_1)+P_poll__networl_6_1_AnsP_2)+P_poll__networl_6_1_AnsP_3)+P_poll__networl_6_1_AnsP_4)+P_poll__networl_6_1_AnsP_5)+P_poll__networl_6_1_AnsP_6)+P_poll__networl_6_2_AnsP_1)+P_poll__networl_6_2_AnsP_2)+P_poll__networl_6_2_AnsP_3)+P_poll__networl_6_2_AnsP_4)+P_poll__networl_6_2_AnsP_5)+P_poll__networl_6_2_AnsP_6)+P_poll__networl_6_3_AnsP_1)+P_poll__networl_6_3_AnsP_2)+P_poll__networl_6_3_AnsP_3)+P_poll__networl_6_3_AnsP_4)+P_poll__networl_6_3_AnsP_5)+P_poll__networl_6_3_AnsP_6)+P_poll__networl_6_4_AnsP_1)+P_poll__networl_6_4_AnsP_2)+P_poll__networl_6_4_AnsP_3)+P_poll__networl_6_4_AnsP_4)+P_poll__networl_6_4_AnsP_5)+P_poll__networl_6_4_AnsP_6)+P_poll__networl_6_5_AnsP_1)+P_poll__networl_6_5_AnsP_2)+P_poll__networl_6_5_AnsP_3)+P_poll__networl_6_5_AnsP_4)+P_poll__networl_6_5_AnsP_5)+P_poll__networl_6_5_AnsP_6)+P_poll__networl_6_6_AnsP_1)+P_poll__networl_6_6_AnsP_2)+P_poll__networl_6_6_AnsP_3)+P_poll__networl_6_6_AnsP_4)+P_poll__networl_6_6_AnsP_5)+P_poll__networl_6_6_AnsP_6)>=1))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-05 with value :(!((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_poll__networl_0_0_AnsP_1+P_poll__networl_0_0_AnsP_2)+P_poll__networl_0_0_AnsP_3)+P_poll__networl_0_0_AnsP_4)+P_poll__networl_0_0_AnsP_5)+P_poll__networl_0_0_AnsP_6)+P_poll__networl_0_1_AnsP_1)+P_poll__networl_0_1_AnsP_2)+P_poll__networl_0_1_AnsP_3)+P_poll__networl_0_1_AnsP_4)+P_poll__networl_0_1_AnsP_5)+P_poll__networl_0_1_AnsP_6)+P_poll__networl_0_2_AnsP_1)+P_poll__networl_0_2_AnsP_2)+P_poll__networl_0_2_AnsP_3)+P_poll__networl_0_2_AnsP_4)+P_poll__networl_0_2_AnsP_5)+P_poll__networl_0_2_AnsP_6)+P_poll__networl_0_3_AnsP_1)+P_poll__networl_0_3_AnsP_2)+P_poll__networl_0_3_AnsP_3)+P_poll__networl_0_3_AnsP_4)+P_poll__networl_0_3_AnsP_5)+P_poll__networl_0_3_AnsP_6)+P_poll__networl_0_4_AnsP_1)+P_poll__networl_0_4_AnsP_2)+P_poll__networl_0_4_AnsP_3)+P_poll__networl_0_4_AnsP_4)+P_poll__networl_0_4_AnsP_5)+P_poll__networl_0_4_AnsP_6)+P_poll__networl_0_5_AnsP_1)+P_poll__networl_0_5_AnsP_2)+P_poll__networl_0_5_AnsP_3)+P_poll__networl_0_5_AnsP_4)+P_poll__networl_0_5_AnsP_5)+P_poll__networl_0_5_AnsP_6)+P_poll__networl_0_6_AnsP_1)+P_poll__networl_0_6_AnsP_2)+P_poll__networl_0_6_AnsP_3)+P_poll__networl_0_6_AnsP_4)+P_poll__networl_0_6_AnsP_5)+P_poll__networl_0_6_AnsP_6)+P_poll__networl_1_0_AnsP_1)+P_poll__networl_1_0_AnsP_2)+P_poll__networl_1_0_AnsP_3)+P_poll__networl_1_0_AnsP_4)+P_poll__networl_1_0_AnsP_5)+P_poll__networl_1_0_AnsP_6)+P_poll__networl_1_1_AnsP_1)+P_poll__networl_1_1_AnsP_2)+P_poll__networl_1_1_AnsP_3)+P_poll__networl_1_1_AnsP_4)+P_poll__networl_1_1_AnsP_5)+P_poll__networl_1_1_AnsP_6)+P_poll__networl_1_2_AnsP_1)+P_poll__networl_1_2_AnsP_2)+P_poll__networl_1_2_AnsP_3)+P_poll__networl_1_2_AnsP_4)+P_poll__networl_1_2_AnsP_5)+P_poll__networl_1_2_AnsP_6)+P_poll__networl_1_3_AnsP_1)+P_poll__networl_1_3_AnsP_2)+P_poll__networl_1_3_AnsP_3)+P_poll__networl_1_3_AnsP_4)+P_poll__networl_1_3_AnsP_5)+P_poll__networl_1_3_AnsP_6)+P_poll__networl_1_4_AnsP_1)+P_poll__networl_1_4_AnsP_2)+P_poll__networl_1_4_AnsP_3)+P_poll__networl_1_4_AnsP_4)+P_poll__networl_1_4_AnsP_5)+P_poll__networl_1_4_AnsP_6)+P_poll__networl_1_5_AnsP_1)+P_poll__networl_1_5_AnsP_2)+P_poll__networl_1_5_AnsP_3)+P_poll__networl_1_5_AnsP_4)+P_poll__networl_1_5_AnsP_5)+P_poll__networl_1_5_AnsP_6)+P_poll__networl_1_6_AnsP_1)+P_poll__networl_1_6_AnsP_2)+P_poll__networl_1_6_AnsP_3)+P_poll__networl_1_6_AnsP_4)+P_poll__networl_1_6_AnsP_5)+P_poll__networl_1_6_AnsP_6)+P_poll__networl_2_0_AnsP_1)+P_poll__networl_2_0_AnsP_2)+P_poll__networl_2_0_AnsP_3)+P_poll__networl_2_0_AnsP_4)+P_poll__networl_2_0_AnsP_5)+P_poll__networl_2_0_AnsP_6)+P_poll__networl_2_1_AnsP_1)+P_poll__networl_2_1_AnsP_2)+P_poll__networl_2_1_AnsP_3)+P_poll__networl_2_1_AnsP_4)+P_poll__networl_2_1_AnsP_5)+P_poll__networl_2_1_AnsP_6)+P_poll__networl_2_2_AnsP_1)+P_poll__networl_2_2_AnsP_2)+P_poll__networl_2_2_AnsP_3)+P_poll__networl_2_2_AnsP_4)+P_poll__networl_2_2_AnsP_5)+P_poll__networl_2_2_AnsP_6)+P_poll__networl_2_3_AnsP_1)+P_poll__networl_2_3_AnsP_2)+P_poll__networl_2_3_AnsP_3)+P_poll__networl_2_3_AnsP_4)+P_poll__networl_2_3_AnsP_5)+P_poll__networl_2_3_AnsP_6)+P_poll__networl_2_4_AnsP_1)+P_poll__networl_2_4_AnsP_2)+P_poll__networl_2_4_AnsP_3)+P_poll__networl_2_4_AnsP_4)+P_poll__networl_2_4_AnsP_5)+P_poll__networl_2_4_AnsP_6)+P_poll__networl_2_5_AnsP_1)+P_poll__networl_2_5_AnsP_2)+P_poll__networl_2_5_AnsP_3)+P_poll__networl_2_5_AnsP_4)+P_poll__networl_2_5_AnsP_5)+P_poll__networl_2_5_AnsP_6)+P_poll__networl_2_6_AnsP_1)+P_poll__networl_2_6_AnsP_2)+P_poll__networl_2_6_AnsP_3)+P_poll__networl_2_6_AnsP_4)+P_poll__networl_2_6_AnsP_5)+P_poll__networl_2_6_AnsP_6)+P_poll__networl_3_0_AnsP_1)+P_poll__networl_3_0_AnsP_2)+P_poll__networl_3_0_AnsP_3)+P_poll__networl_3_0_AnsP_4)+P_poll__networl_3_0_AnsP_5)+P_poll__networl_3_0_AnsP_6)+P_poll__networl_3_1_AnsP_1)+P_poll__networl_3_1_AnsP_2)+P_poll__networl_3_1_AnsP_3)+P_poll__networl_3_1_AnsP_4)+P_poll__networl_3_1_AnsP_5)+P_poll__networl_3_1_AnsP_6)+P_poll__networl_3_2_AnsP_1)+P_poll__networl_3_2_AnsP_2)+P_poll__networl_3_2_AnsP_3)+P_poll__networl_3_2_AnsP_4)+P_poll__networl_3_2_AnsP_5)+P_poll__networl_3_2_AnsP_6)+P_poll__networl_3_3_AnsP_1)+P_poll__networl_3_3_AnsP_2)+P_poll__networl_3_3_AnsP_3)+P_poll__networl_3_3_AnsP_4)+P_poll__networl_3_3_AnsP_5)+P_poll__networl_3_3_AnsP_6)+P_poll__networl_3_4_AnsP_1)+P_poll__networl_3_4_AnsP_2)+P_poll__networl_3_4_AnsP_3)+P_poll__networl_3_4_AnsP_4)+P_poll__networl_3_4_AnsP_5)+P_poll__networl_3_4_AnsP_6)+P_poll__networl_3_5_AnsP_1)+P_poll__networl_3_5_AnsP_2)+P_poll__networl_3_5_AnsP_3)+P_poll__networl_3_5_AnsP_4)+P_poll__networl_3_5_AnsP_5)+P_poll__networl_3_5_AnsP_6)+P_poll__networl_3_6_AnsP_1)+P_poll__networl_3_6_AnsP_2)+P_poll__networl_3_6_AnsP_3)+P_poll__networl_3_6_AnsP_4)+P_poll__networl_3_6_AnsP_5)+P_poll__networl_3_6_AnsP_6)+P_poll__networl_4_0_AnsP_1)+P_poll__networl_4_0_AnsP_2)+P_poll__networl_4_0_AnsP_3)+P_poll__networl_4_0_AnsP_4)+P_poll__networl_4_0_AnsP_5)+P_poll__networl_4_0_AnsP_6)+P_poll__networl_4_1_AnsP_1)+P_poll__networl_4_1_AnsP_2)+P_poll__networl_4_1_AnsP_3)+P_poll__networl_4_1_AnsP_4)+P_poll__networl_4_1_AnsP_5)+P_poll__networl_4_1_AnsP_6)+P_poll__networl_4_2_AnsP_1)+P_poll__networl_4_2_AnsP_2)+P_poll__networl_4_2_AnsP_3)+P_poll__networl_4_2_AnsP_4)+P_poll__networl_4_2_AnsP_5)+P_poll__networl_4_2_AnsP_6)+P_poll__networl_4_3_AnsP_1)+P_poll__networl_4_3_AnsP_2)+P_poll__networl_4_3_AnsP_3)+P_poll__networl_4_3_AnsP_4)+P_poll__networl_4_3_AnsP_5)+P_poll__networl_4_3_AnsP_6)+P_poll__networl_4_4_AnsP_1)+P_poll__networl_4_4_AnsP_2)+P_poll__networl_4_4_AnsP_3)+P_poll__networl_4_4_AnsP_4)+P_poll__networl_4_4_AnsP_5)+P_poll__networl_4_4_AnsP_6)+P_poll__networl_4_5_AnsP_1)+P_poll__networl_4_5_AnsP_2)+P_poll__networl_4_5_AnsP_3)+P_poll__networl_4_5_AnsP_4)+P_poll__networl_4_5_AnsP_5)+P_poll__networl_4_5_AnsP_6)+P_poll__networl_4_6_AnsP_1)+P_poll__networl_4_6_AnsP_2)+P_poll__networl_4_6_AnsP_3)+P_poll__networl_4_6_AnsP_4)+P_poll__networl_4_6_AnsP_5)+P_poll__networl_4_6_AnsP_6)+P_poll__networl_5_0_AnsP_1)+P_poll__networl_5_0_AnsP_2)+P_poll__networl_5_0_AnsP_3)+P_poll__networl_5_0_AnsP_4)+P_poll__networl_5_0_AnsP_5)+P_poll__networl_5_0_AnsP_6)+P_poll__networl_5_1_AnsP_1)+P_poll__networl_5_1_AnsP_2)+P_poll__networl_5_1_AnsP_3)+P_poll__networl_5_1_AnsP_4)+P_poll__networl_5_1_AnsP_5)+P_poll__networl_5_1_AnsP_6)+P_poll__networl_5_2_AnsP_1)+P_poll__networl_5_2_AnsP_2)+P_poll__networl_5_2_AnsP_3)+P_poll__networl_5_2_AnsP_4)+P_poll__networl_5_2_AnsP_5)+P_poll__networl_5_2_AnsP_6)+P_poll__networl_5_3_AnsP_1)+P_poll__networl_5_3_AnsP_2)+P_poll__networl_5_3_AnsP_3)+P_poll__networl_5_3_AnsP_4)+P_poll__networl_5_3_AnsP_5)+P_poll__networl_5_3_AnsP_6)+P_poll__networl_5_4_AnsP_1)+P_poll__networl_5_4_AnsP_2)+P_poll__networl_5_4_AnsP_3)+P_poll__networl_5_4_AnsP_4)+P_poll__networl_5_4_AnsP_5)+P_poll__networl_5_4_AnsP_6)+P_poll__networl_5_5_AnsP_1)+P_poll__networl_5_5_AnsP_2)+P_poll__networl_5_5_AnsP_3)+P_poll__networl_5_5_AnsP_4)+P_poll__networl_5_5_AnsP_5)+P_poll__networl_5_5_AnsP_6)+P_poll__networl_5_6_AnsP_1)+P_poll__networl_5_6_AnsP_2)+P_poll__networl_5_6_AnsP_3)+P_poll__networl_5_6_AnsP_4)+P_poll__networl_5_6_AnsP_5)+P_poll__networl_5_6_AnsP_6)+P_poll__networl_6_0_AnsP_1)+P_poll__networl_6_0_AnsP_2)+P_poll__networl_6_0_AnsP_3)+P_poll__networl_6_0_AnsP_4)+P_poll__networl_6_0_AnsP_5)+P_poll__networl_6_0_AnsP_6)+P_poll__networl_6_1_AnsP_1)+P_poll__networl_6_1_AnsP_2)+P_poll__networl_6_1_AnsP_3)+P_poll__networl_6_1_AnsP_4)+P_poll__networl_6_1_AnsP_5)+P_poll__networl_6_1_AnsP_6)+P_poll__networl_6_2_AnsP_1)+P_poll__networl_6_2_AnsP_2)+P_poll__networl_6_2_AnsP_3)+P_poll__networl_6_2_AnsP_4)+P_poll__networl_6_2_AnsP_5)+P_poll__networl_6_2_AnsP_6)+P_poll__networl_6_3_AnsP_1)+P_poll__networl_6_3_AnsP_2)+P_poll__networl_6_3_AnsP_3)+P_poll__networl_6_3_AnsP_4)+P_poll__networl_6_3_AnsP_5)+P_poll__networl_6_3_AnsP_6)+P_poll__networl_6_4_AnsP_1)+P_poll__networl_6_4_AnsP_2)+P_poll__networl_6_4_AnsP_3)+P_poll__networl_6_4_AnsP_4)+P_poll__networl_6_4_AnsP_5)+P_poll__networl_6_4_AnsP_6)+P_poll__networl_6_5_AnsP_1)+P_poll__networl_6_5_AnsP_2)+P_poll__networl_6_5_AnsP_3)+P_poll__networl_6_5_AnsP_4)+P_poll__networl_6_5_AnsP_5)+P_poll__networl_6_5_AnsP_6)+P_poll__networl_6_6_AnsP_1)+P_poll__networl_6_6_AnsP_2)+P_poll__networl_6_6_AnsP_3)+P_poll__networl_6_6_AnsP_4)+P_poll__networl_6_6_AnsP_5)+P_poll__networl_6_6_AnsP_6)>=0))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-06 with value :((((((((P_poll__handlingMessage_0+P_poll__handlingMessage_1)+P_poll__handlingMessage_2)+P_poll__handlingMessage_3)+P_poll__handlingMessage_4)+P_poll__handlingMessage_5)+P_poll__handlingMessage_6)<=0)&&(!(((((((((((((((((((((((((((((((((((((((P_startNeg__broadcasting_0_1+P_startNeg__broadcasting_0_6)+P_startNeg__broadcasting_1_1)+P_startNeg__broadcasting_1_2)+P_startNeg__broadcasting_1_3)+P_startNeg__broadcasting_1_4)+P_startNeg__broadcasting_1_5)+P_startNeg__broadcasting_1_6)+P_startNeg__broadcasting_2_1)+P_startNeg__broadcasting_2_2)+P_startNeg__broadcasting_2_3)+P_startNeg__broadcasting_2_4)+P_startNeg__broadcasting_2_5)+P_startNeg__broadcasting_2_6)+P_startNeg__broadcasting_3_1)+P_startNeg__broadcasting_3_2)+P_startNeg__broadcasting_3_3)+P_startNeg__broadcasting_3_4)+P_startNeg__broadcasting_3_5)+P_startNeg__broadcasting_3_6)+P_startNeg__broadcasting_4_1)+P_startNeg__broadcasting_4_2)+P_startNeg__broadcasting_4_3)+P_startNeg__broadcasting_4_4)+P_startNeg__broadcasting_4_5)+P_startNeg__broadcasting_4_6)+P_startNeg__broadcasting_5_1)+P_startNeg__broadcasting_5_2)+P_startNeg__broadcasting_5_3)+P_startNeg__broadcasting_5_4)+P_startNeg__broadcasting_5_5)+P_startNeg__broadcasting_5_6)+P_startNeg__broadcasting_6_1)+P_startNeg__broadcasting_6_2)+P_startNeg__broadcasting_6_3)+P_startNeg__broadcasting_6_4)+P_startNeg__broadcasting_6_5)+P_startNeg__broadcasting_6_6)>=0)&&((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((P_poll__networl_0_0_AnsP_1+P_poll__networl_0_0_AnsP_2)+P_poll__networl_0_0_AnsP_3)+P_poll__networl_0_0_AnsP_4)+P_poll__networl_0_0_AnsP_5)+P_poll__networl_0_0_AnsP_6)+P_poll__networl_0_1_AnsP_1)+P_poll__networl_0_1_AnsP_2)+P_poll__networl_0_1_AnsP_3)+P_poll__networl_0_1_AnsP_4)+P_poll__networl_0_1_AnsP_5)+P_poll__networl_0_1_AnsP_6)+P_poll__networl_0_2_AnsP_1)+P_poll__networl_0_2_AnsP_2)+P_poll__networl_0_2_AnsP_3)+P_poll__networl_0_2_AnsP_4)+P_poll__networl_0_2_AnsP_5)+P_poll__networl_0_2_AnsP_6)+P_poll__networl_0_3_AnsP_1)+P_poll__networl_0_3_AnsP_2)+P_poll__networl_0_3_AnsP_3)+P_poll__networl_0_3_AnsP_4)+P_poll__networl_0_3_AnsP_5)+P_poll__networl_0_3_AnsP_6)+P_poll__networl_0_4_AnsP_1)+P_poll__networl_0_4_AnsP_2)+P_poll__networl_0_4_AnsP_3)+P_poll__networl_0_4_AnsP_4)+P_poll__networl_0_4_AnsP_5)+P_poll__networl_0_4_AnsP_6)+P_poll__networl_0_5_AnsP_1)+P_poll__networl_0_5_AnsP_2)+P_poll__networl_0_5_AnsP_3)+P_poll__networl_0_5_AnsP_4)+P_poll__networl_0_5_AnsP_5)+P_poll__networl_0_5_AnsP_6)+P_poll__networl_0_6_AnsP_1)+P_poll__networl_0_6_AnsP_2)+P_poll__networl_0_6_AnsP_3)+P_poll__networl_0_6_AnsP_4)+P_poll__networl_0_6_AnsP_5)+P_poll__networl_0_6_AnsP_6)+P_poll__networl_1_0_AnsP_1)+P_poll__networl_1_0_AnsP_2)+P_poll__networl_1_0_AnsP_3)+P_poll__networl_1_0_AnsP_4)+P_poll__networl_1_0_AnsP_5)+P_poll__networl_1_0_AnsP_6)+P_poll__networl_1_1_AnsP_1)+P_poll__networl_1_1_AnsP_2)+P_poll__networl_1_1_AnsP_3)+P_poll__networl_1_1_AnsP_4)+P_poll__networl_1_1_AnsP_5)+P_poll__networl_1_1_AnsP_6)+P_poll__networl_1_2_AnsP_1)+P_poll__networl_1_2_AnsP_2)+P_poll__networl_1_2_AnsP_3)+P_poll__networl_1_2_AnsP_4)+P_poll__networl_1_2_AnsP_5)+P_poll__networl_1_2_AnsP_6)+P_poll__networl_1_3_AnsP_1)+P_poll__networl_1_3_AnsP_2)+P_poll__networl_1_3_AnsP_3)+P_poll__networl_1_3_AnsP_4)+P_poll__networl_1_3_AnsP_5)+P_poll__networl_1_3_AnsP_6)+P_poll__networl_1_4_AnsP_1)+P_poll__networl_1_4_AnsP_2)+P_poll__networl_1_4_AnsP_3)+P_poll__networl_1_4_AnsP_4)+P_poll__networl_1_4_AnsP_5)+P_poll__networl_1_4_AnsP_6)+P_poll__networl_1_5_AnsP_1)+P_poll__networl_1_5_AnsP_2)+P_poll__networl_1_5_AnsP_3)+P_poll__networl_1_5_AnsP_4)+P_poll__networl_1_5_AnsP_5)+P_poll__networl_1_5_AnsP_6)+P_poll__networl_1_6_AnsP_1)+P_poll__networl_1_6_AnsP_2)+P_poll__networl_1_6_AnsP_3)+P_poll__networl_1_6_AnsP_4)+P_poll__networl_1_6_AnsP_5)+P_poll__networl_1_6_AnsP_6)+P_poll__networl_2_0_AnsP_1)+P_poll__networl_2_0_AnsP_2)+P_poll__networl_2_0_AnsP_3)+P_poll__networl_2_0_AnsP_4)+P_poll__networl_2_0_AnsP_5)+P_poll__networl_2_0_AnsP_6)+P_poll__networl_2_1_AnsP_1)+P_poll__networl_2_1_AnsP_2)+P_poll__networl_2_1_AnsP_3)+P_poll__networl_2_1_AnsP_4)+P_poll__networl_2_1_AnsP_5)+P_poll__networl_2_1_AnsP_6)+P_poll__networl_2_2_AnsP_1)+P_poll__networl_2_2_AnsP_2)+P_poll__networl_2_2_AnsP_3)+P_poll__networl_2_2_AnsP_4)+P_poll__networl_2_2_AnsP_5)+P_poll__networl_2_2_AnsP_6)+P_poll__networl_2_3_AnsP_1)+P_poll__networl_2_3_AnsP_2)+P_poll__networl_2_3_AnsP_3)+P_poll__networl_2_3_AnsP_4)+P_poll__networl_2_3_AnsP_5)+P_poll__networl_2_3_AnsP_6)+P_poll__networl_2_4_AnsP_1)+P_poll__networl_2_4_AnsP_2)+P_poll__networl_2_4_AnsP_3)+P_poll__networl_2_4_AnsP_4)+P_poll__networl_2_4_AnsP_5)+P_poll__networl_2_4_AnsP_6)+P_poll__networl_2_5_AnsP_1)+P_poll__networl_2_5_AnsP_2)+P_poll__networl_2_5_AnsP_3)+P_poll__networl_2_5_AnsP_4)+P_poll__networl_2_5_AnsP_5)+P_poll__networl_2_5_AnsP_6)+P_poll__networl_2_6_AnsP_1)+P_poll__networl_2_6_AnsP_2)+P_poll__networl_2_6_AnsP_3)+P_poll__networl_2_6_AnsP_4)+P_poll__networl_2_6_AnsP_5)+P_poll__networl_2_6_AnsP_6)+P_poll__networl_3_0_AnsP_1)+P_poll__networl_3_0_AnsP_2)+P_poll__networl_3_0_AnsP_3)+P_poll__networl_3_0_AnsP_4)+P_poll__networl_3_0_AnsP_5)+P_poll__networl_3_0_AnsP_6)+P_poll__networl_3_1_AnsP_1)+P_poll__networl_3_1_AnsP_2)+P_poll__networl_3_1_AnsP_3)+P_poll__networl_3_1_AnsP_4)+P_poll__networl_3_1_AnsP_5)+P_poll__networl_3_1_AnsP_6)+P_poll__networl_3_2_AnsP_1)+P_poll__networl_3_2_AnsP_2)+P_poll__networl_3_2_AnsP_3)+P_poll__networl_3_2_AnsP_4)+P_poll__networl_3_2_AnsP_5)+P_poll__networl_3_2_AnsP_6)+P_poll__networl_3_3_AnsP_1)+P_poll__networl_3_3_AnsP_2)+P_poll__networl_3_3_AnsP_3)+P_poll__networl_3_3_AnsP_4)+P_poll__networl_3_3_AnsP_5)+P_poll__networl_3_3_AnsP_6)+P_poll__networl_3_4_AnsP_1)+P_poll__networl_3_4_AnsP_2)+P_poll__networl_3_4_AnsP_3)+P_poll__networl_3_4_AnsP_4)+P_poll__networl_3_4_AnsP_5)+P_poll__networl_3_4_AnsP_6)+P_poll__networl_3_5_AnsP_1)+P_poll__networl_3_5_AnsP_2)+P_poll__networl_3_5_AnsP_3)+P_poll__networl_3_5_AnsP_4)+P_poll__networl_3_5_AnsP_5)+P_poll__networl_3_5_AnsP_6)+P_poll__networl_3_6_AnsP_1)+P_poll__networl_3_6_AnsP_2)+P_poll__networl_3_6_AnsP_3)+P_poll__networl_3_6_AnsP_4)+P_poll__networl_3_6_AnsP_5)+P_poll__networl_3_6_AnsP_6)+P_poll__networl_4_0_AnsP_1)+P_poll__networl_4_0_AnsP_2)+P_poll__networl_4_0_AnsP_3)+P_poll__networl_4_0_AnsP_4)+P_poll__networl_4_0_AnsP_5)+P_poll__networl_4_0_AnsP_6)+P_poll__networl_4_1_AnsP_1)+P_poll__networl_4_1_AnsP_2)+P_poll__networl_4_1_AnsP_3)+P_poll__networl_4_1_AnsP_4)+P_poll__networl_4_1_AnsP_5)+P_poll__networl_4_1_AnsP_6)+P_poll__networl_4_2_AnsP_1)+P_poll__networl_4_2_AnsP_2)+P_poll__networl_4_2_AnsP_3)+P_poll__networl_4_2_AnsP_4)+P_poll__networl_4_2_AnsP_5)+P_poll__networl_4_2_AnsP_6)+P_poll__networl_4_3_AnsP_1)+P_poll__networl_4_3_AnsP_2)+P_poll__networl_4_3_AnsP_3)+P_poll__networl_4_3_AnsP_4)+P_poll__networl_4_3_AnsP_5)+P_poll__networl_4_3_AnsP_6)+P_poll__networl_4_4_AnsP_1)+P_poll__networl_4_4_AnsP_2)+P_poll__networl_4_4_AnsP_3)+P_poll__networl_4_4_AnsP_4)+P_poll__networl_4_4_AnsP_5)+P_poll__networl_4_4_AnsP_6)+P_poll__networl_4_5_AnsP_1)+P_poll__networl_4_5_AnsP_2)+P_poll__networl_4_5_AnsP_3)+P_poll__networl_4_5_AnsP_4)+P_poll__networl_4_5_AnsP_5)+P_poll__networl_4_5_AnsP_6)+P_poll__networl_4_6_AnsP_1)+P_poll__networl_4_6_AnsP_2)+P_poll__networl_4_6_AnsP_3)+P_poll__networl_4_6_AnsP_4)+P_poll__networl_4_6_AnsP_5)+P_poll__networl_4_6_AnsP_6)+P_poll__networl_5_0_AnsP_1)+P_poll__networl_5_0_AnsP_2)+P_poll__networl_5_0_AnsP_3)+P_poll__networl_5_0_AnsP_4)+P_poll__networl_5_0_AnsP_5)+P_poll__networl_5_0_AnsP_6)+P_poll__networl_5_1_AnsP_1)+P_poll__networl_5_1_AnsP_2)+P_poll__networl_5_1_AnsP_3)+P_poll__networl_5_1_AnsP_4)+P_poll__networl_5_1_AnsP_5)+P_poll__networl_5_1_AnsP_6)+P_poll__networl_5_2_AnsP_1)+P_poll__networl_5_2_AnsP_2)+P_poll__networl_5_2_AnsP_3)+P_poll__networl_5_2_AnsP_4)+P_poll__networl_5_2_AnsP_5)+P_poll__networl_5_2_AnsP_6)+P_poll__networl_5_3_AnsP_1)+P_poll__networl_5_3_AnsP_2)+P_poll__networl_5_3_AnsP_3)+P_poll__networl_5_3_AnsP_4)+P_poll__networl_5_3_AnsP_5)+P_poll__networl_5_3_AnsP_6)+P_poll__networl_5_4_AnsP_1)+P_poll__networl_5_4_AnsP_2)+P_poll__networl_5_4_AnsP_3)+P_poll__networl_5_4_AnsP_4)+P_poll__networl_5_4_AnsP_5)+P_poll__networl_5_4_AnsP_6)+P_poll__networl_5_5_AnsP_1)+P_poll__networl_5_5_AnsP_2)+P_poll__networl_5_5_AnsP_3)+P_poll__networl_5_5_AnsP_4)+P_poll__networl_5_5_AnsP_5)+P_poll__networl_5_5_AnsP_6)+P_poll__networl_5_6_AnsP_1)+P_poll__networl_5_6_AnsP_2)+P_poll__networl_5_6_AnsP_3)+P_poll__networl_5_6_AnsP_4)+P_poll__networl_5_6_AnsP_5)+P_poll__networl_5_6_AnsP_6)+P_poll__networl_6_0_AnsP_1)+P_poll__networl_6_0_AnsP_2)+P_poll__networl_6_0_AnsP_3)+P_poll__networl_6_0_AnsP_4)+P_poll__networl_6_0_AnsP_5)+P_poll__networl_6_0_AnsP_6)+P_poll__networl_6_1_AnsP_1)+P_poll__networl_6_1_AnsP_2)+P_poll__networl_6_1_AnsP_3)+P_poll__networl_6_1_AnsP_4)+P_poll__networl_6_1_AnsP_5)+P_poll__networl_6_1_AnsP_6)+P_poll__networl_6_2_AnsP_1)+P_poll__networl_6_2_AnsP_2)+P_poll__networl_6_2_AnsP_3)+P_poll__networl_6_2_AnsP_4)+P_poll__networl_6_2_AnsP_5)+P_poll__networl_6_2_AnsP_6)+P_poll__networl_6_3_AnsP_1)+P_poll__networl_6_3_AnsP_2)+P_poll__networl_6_3_AnsP_3)+P_poll__networl_6_3_AnsP_4)+P_poll__networl_6_3_AnsP_5)+P_poll__networl_6_3_AnsP_6)+P_poll__networl_6_4_AnsP_1)+P_poll__networl_6_4_AnsP_2)+P_poll__networl_6_4_AnsP_3)+P_poll__networl_6_4_AnsP_4)+P_poll__networl_6_4_AnsP_5)+P_poll__networl_6_4_AnsP_6)+P_poll__networl_6_5_AnsP_1)+P_poll__networl_6_5_AnsP_2)+P_poll__networl_6_5_AnsP_3)+P_poll__networl_6_5_AnsP_4)+P_poll__networl_6_5_AnsP_5)+P_poll__networl_6_5_AnsP_6)+P_poll__networl_6_6_AnsP_1)+P_poll__networl_6_6_AnsP_2)+P_poll__networl_6_6_AnsP_3)+P_poll__networl_6_6_AnsP_4)+P_poll__networl_6_6_AnsP_5)+P_poll__networl_6_6_AnsP_6)<=((((((P_poll__pollEnd_0+P_poll__pollEnd_1)+P_poll__pollEnd_2)+P_poll__pollEnd_3)+P_poll__pollEnd_4)+P_poll__pollEnd_5)+P_poll__pollEnd_6)))))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-09 with value :(!(P_masterState_3_T_0>=1))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-11 with value :(P_negotiation_5_4_NONE>=3)
Read [invariant] property : NeoElection-PT-6-ReachabilityCardinality-12 with value :((!((P_poll__networl_5_4_AnsP_2<=P_negotiation_1_0_CO)||(P_network_0_0_AskP_0<=P_sendAnnPs__broadcasting_3_3)))||(P_network_6_1_RP_0>=0))
Read [reachable] property : NeoElection-PT-6-ReachabilityCardinality-14 with value :(((P_poll__networl_2_2_AnsP_3>=2)&&(P_network_4_4_AnnP_0>=0))&&(P_poll__networl_6_2_AnsP_3>=3))
ITS-tools command line returned an error code 137
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-6"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="mcc4mcc-full"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-6.tgz
mv NeoElection-PT-6 execution
cd execution
pwd
ls -lh
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-3637"
echo " Executing tool mcc4mcc-full"
echo " Input is NeoElection-PT-6, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r118-csrt-152666478300320"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

