About the Execution of LoLA for NeoElection-PT-3
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 171.230 | 1268.00 | 1530.00 | 19.50 | 0 3 9 0 6 3 0 3 0 0 0 0 0 0 0 0 | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
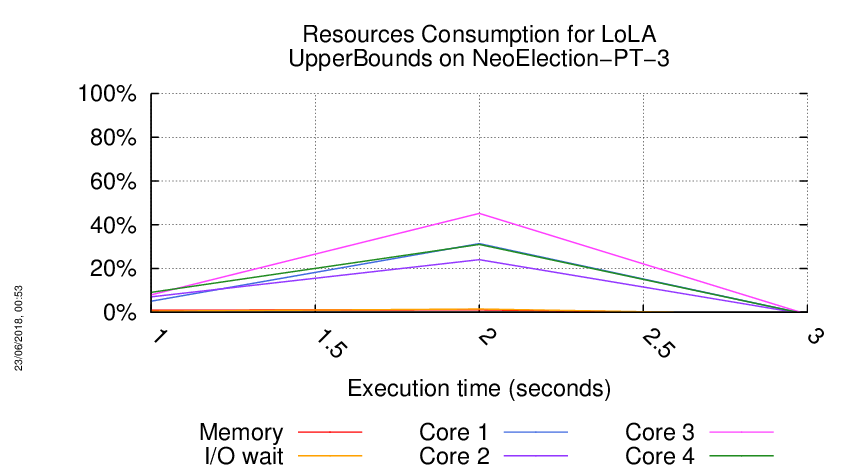
Trace from the execution
Waiting for the VM to be ready (probing ssh)
..................
/home/mcc/execution
total 1.9M
-rw-r--r-- 1 mcc users 37K May 15 18:54 CTLCardinality.txt
-rw-r--r-- 1 mcc users 101K May 15 18:54 CTLCardinality.xml
-rw-r--r-- 1 mcc users 25K May 15 18:54 CTLFireability.txt
-rw-r--r-- 1 mcc users 75K May 15 18:54 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K May 15 18:50 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 6.1K May 15 18:50 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 46K May 15 18:54 LTLCardinality.txt
-rw-r--r-- 1 mcc users 113K May 15 18:54 LTLCardinality.xml
-rw-r--r-- 1 mcc users 19K May 15 18:54 LTLFireability.txt
-rw-r--r-- 1 mcc users 56K May 15 18:54 LTLFireability.xml
-rw-r--r-- 1 mcc users 64K May 15 18:54 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 157K May 15 18:54 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 107 May 15 18:54 ReachabilityDeadlock.txt
-rw-r--r-- 1 mcc users 345 May 15 18:54 ReachabilityDeadlock.xml
-rw-r--r-- 1 mcc users 35K May 15 18:54 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 101K May 15 18:54 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 33K May 15 18:54 UpperBounds.txt
-rw-r--r-- 1 mcc users 62K May 15 18:54 UpperBounds.xml
-rw-r--r-- 1 mcc users 5 May 15 18:50 equiv_col
-rw-r--r-- 1 mcc users 2 May 15 18:50 instance
-rw-r--r-- 1 mcc users 6 May 15 18:50 iscolored
-rw-r--r-- 1 mcc users 911K May 15 18:50 model.pnml
=====================================================================
Generated by BenchKit 2-3637
Executing tool lola
Input is NeoElection-PT-3, examination is UpperBounds
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r112-csrt-152666469300296
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of positive values
NUM_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-PT-3-UpperBounds-00
FORMULA_NAME NeoElection-PT-3-UpperBounds-01
FORMULA_NAME NeoElection-PT-3-UpperBounds-02
FORMULA_NAME NeoElection-PT-3-UpperBounds-03
FORMULA_NAME NeoElection-PT-3-UpperBounds-04
FORMULA_NAME NeoElection-PT-3-UpperBounds-05
FORMULA_NAME NeoElection-PT-3-UpperBounds-06
FORMULA_NAME NeoElection-PT-3-UpperBounds-07
FORMULA_NAME NeoElection-PT-3-UpperBounds-08
FORMULA_NAME NeoElection-PT-3-UpperBounds-09
FORMULA_NAME NeoElection-PT-3-UpperBounds-10
FORMULA_NAME NeoElection-PT-3-UpperBounds-11
FORMULA_NAME NeoElection-PT-3-UpperBounds-12
FORMULA_NAME NeoElection-PT-3-UpperBounds-13
FORMULA_NAME NeoElection-PT-3-UpperBounds-14
FORMULA_NAME NeoElection-PT-3-UpperBounds-15
=== Now, execution of the tool begins
BK_START 1527027004660
info: Time: 3600 - MCC
===========================================================================================
prep: translating NeoElection-PT-3 Petri net model.pnml into LoLA format
===========================================================================================
prep: translating PT Petri net complete
prep: added safe information to the net based on GenericPropertiesVerdict
prep: check for too many tokens
===========================================================================================
prep: translating NeoElection-PT-3 formula UpperBounds into LoLA format
===========================================================================================
prep: translating PT formula complete
vrfy: Checking UpperBounds @ NeoElection-PT-3 @ 3570 seconds
lola: LoLA will run for 3570 seconds at most (--timelimit)
lola: NET
lola: reading net from model.pnml.lola
lola: finished parsing
lola: closed net file model.pnml.lola
lola: 1988/65536 symbol table entries, 6 collisions
lola: preprocessing...
lola: Size of bit vector: 972
lola: finding significant places
lola: 972 places, 1016 transitions, 300 significant places
lola: computing forward-conflicting sets
lola: computing back-conflicting sets
lola: 472 transition conflict sets
lola: TASK
lola: reading formula from NeoElection-PT-3-UpperBounds.task
lola: place invariant simplifies atomic proposition
lola: before: (P-crashed_3 + P-crashed_2 + P-crashed_1 + P-crashed_0 <= 0)
lola: after: (0 <= 0)
lola: always true
lola: place invariant simplifies atomic proposition
lola: before: (P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_2_F_3 + P-masterState_0_F_3 + P-masterState_3_F_3 + P-masterState_1_T_3 <= 0)
lola: after: (3 <= 0)
lola: always false
lola: place invariant simplifies atomic proposition
lola: before: (P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_1_3_CO + P-negotiation_3_1_CO + P-negotiation_0_2_NONE + P-negotiation_2_1_NONE + P-negotiation_0_0_CO + P-negotiation_1_2_CO + P-negotiation_0_2_CO + P-negotiation_2_0_NONE + P-negotiation_0_1_NONE + P-negotiation_2_3_DONE + P-negotiation_1_3_NONE + P-negotiation_2_1_CO + P-negotiation_3_2_NONE + P-negotiation_3_1_DONE + P-negotiation_0_0_DONE + P-negotiation_1_2_DONE + P-negotiation_2_0_DONE + P-negotiation_0_1_DONE + P-negotiation_3_3_NONE + P-negotiation_1_0_CO + P-negotiation_2_2_NONE + P-negotiation_0_3_NONE + P-negotiation_3_0_CO + P-negotiation_3_3_DONE + P-negotiation_1_1_DONE + P-negotiation_3_0_DONE + P-negotiation_2_2_DONE + P-negotiation_0_3_DONE + P-negotiation_2_3_CO + P-negotiation_1_1_CO + P-negotiation_0_0_NONE + P-negotiation_1_1_NONE + P-negotiation_3_0_NONE + P-negotiation_2_2_CO + P-negotiation_0_3_CO + P-negotiation_3_3_CO + P-negotiation_1_2_NONE + P-negotiation_3_1_NONE + P-negotiation_2_3_NONE + P-negotiation_2_0_CO + P-negotiation_1_0_DONE + P-negotiation_3_2_CO + P-negotiation_0_1_CO + P-negotiation_0_2_DONE + P-negotiation_2_1_DONE + P-negotiation_1_3_DONE <= 0)
lola: after: (9 <= 0)
lola: always false
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_0 + P-poll__networl_2_2_AI_0 + P-poll__networl_3_2_RP_3 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_0 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_3_3_AI_3 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_2 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_3_3_RI_1 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_3_3_RI_0 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_0 + P-poll__networl_3_0_AI_3 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_1_1_AI_3 + P-poll__networl_1_1_AI_2 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_2_1_RP_0 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_3_1_AskP_0 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_0_2_RP_0 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_2_2_RI_1 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_2_2_RI_0 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_3_RI_1 + P-poll__networl_0_3_RI_0 + P-poll__networl_0_0_AI_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_3_0_RI_3 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_0_RI_0 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_1_RI_1 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_1_1_RI_0 + P-poll__networl_1_3_AskP_3 + P-poll__networl_1_3_AskP_2 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_0_RI_3 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_0_0_RI_1 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_0_0_RI_0 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 <= 0)
lola: after: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 <= 0)
lola: LP says that atomic proposition is always true: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-network_2_2_AnnP_0 + P-network_3_0_RI_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_1_RI_0 + P-network_1_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_0_0_RI_0 + P-network_0_0_AI_0 + P-network_0_3_RI_0 + P-network_0_2_AskP_0 + P-network_3_2_AI_0 + P-network_1_3_AI_0 + P-network_2_2_RI_0 + P-network_3_1_AnnP_0 + P-network_0_1_AnsP_3 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_2_2_AnsP_3 + P-network_0_1_AnsP_0 + P-network_2_3_RP_0 + P-network_3_3_AskP_0 + P-network_1_0_AnnP_0 + P-network_0_0_AnnP_0 + P-network_3_2_AnsP_3 + P-network_3_2_AnsP_2 + P-network_0_2_RP_0 + P-network_3_2_AnsP_1 + P-network_3_2_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_AI_0 + P-network_3_1_RP_0 + P-network_1_2_RP_0 + P-network_0_1_AnnP_0 + P-network_3_0_AskP_0 + P-network_2_3_AnsP_3 + P-network_2_3_AnsP_2 + P-network_2_1_RP_0 + P-network_2_3_AnsP_1 + P-network_2_3_AnsP_0 + P-network_3_2_AnnP_0 + P-network_2_3_AskP_0 + P-network_3_2_RI_0 + P-network_1_1_AI_0 + P-network_1_3_RI_0 + P-network_1_0_AI_0 + P-network_3_0_AI_0 + P-network_2_0_RP_0 + P-network_2_1_AskP_0 + P-network_0_1_RP_0 + P-network_3_3_RI_0 + P-network_2_3_AnnP_0 + P-network_3_1_AnsP_0 + P-network_3_1_AnsP_1 + P-network_3_1_AnsP_2 + P-network_3_1_AnsP_3 + P-network_2_0_AnsP_3 + P-network_2_0_AnsP_2 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_2_1_RI_0 + P-network_0_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AnsP_3 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_3_2_AskP_0 + P-network_1_1_AnsP_0 + P-network_2_0_AnnP_0 + P-network_1_3_RP_0 + P-network_1_0_RI_0 + P-network_0_0_AnsP_0 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_3 + P-network_0_3_AnnP_0 + P-network_0_3_AskP_0 + P-network_2_3_AI_0 + P-network_3_2_RP_0 + P-network_0_2_AnsP_3 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_3_3_RP_0 + P-network_0_3_AI_0 + P-network_1_1_AnnP_0 + P-network_2_2_AI_0 + P-network_3_3_AnsP_3 + P-network_3_3_AnsP_2 + P-network_3_3_AnsP_1 + P-network_0_1_AskP_0 + P-network_3_3_AnsP_0 + P-network_3_1_AI_0 + P-network_0_0_AskP_0 + P-network_1_2_AI_0 + P-network_2_2_RP_0 + P-network_0_2_AnnP_0 + P-network_0_3_RP_0 + P-network_3_1_AskP_0 + P-network_3_3_AnnP_0 + P-network_3_0_AnsP_3 + P-network_3_0_AnsP_2 + P-network_3_0_AnsP_1 + P-network_3_0_AnsP_0 + P-network_2_3_RI_0 + P-network_2_0_AI_0 + P-network_0_1_AI_0 + P-network_3_0_RP_0 + P-network_2_2_AskP_0 + P-network_1_1_RP_0 + P-network_2_1_AnsP_3 + P-network_2_1_AnsP_2 + P-network_1_2_AnnP_0 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_3_1_RI_0 + P-network_0_3_AnsP_0 + P-network_0_3_AnsP_1 + P-network_0_3_AnsP_2 + P-network_0_3_AnsP_3 + P-network_1_0_AskP_0 + P-network_3_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_3_AskP_0 + P-network_3_3_AI_0 + P-network_0_0_RP_0 + P-network_1_2_AnsP_3 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_1_2_AnsP_0 + P-network_2_1_AnnP_0 + P-network_0_1_RI_0 + P-network_2_0_RI_0 + P-network_0_1_RI_3 + P-network_0_1_RI_2 + P-network_0_1_RI_1 + P-network_2_0_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_3 + P-network_2_1_AnnP_1 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_3 + P-network_3_3_AI_3 + P-network_0_0_RP_1 + P-network_0_0_RP_2 + P-network_0_0_RP_3 + P-network_3_3_AI_2 + P-network_3_3_AI_1 + P-network_1_3_AskP_1 + P-network_1_3_AskP_2 + P-network_1_3_AskP_3 + P-network_1_0_AskP_3 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_1_2_RI_3 + P-network_1_0_AskP_2 + P-network_3_0_AnnP_1 + P-network_3_0_AnnP_2 + P-network_3_0_AnnP_3 + P-network_1_0_AskP_1 + P-network_1_2_AnnP_3 + P-network_3_1_RI_1 + P-network_3_1_RI_2 + P-network_3_1_RI_3 + P-network_1_2_AnnP_2 + P-network_1_2_AnnP_1 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_1_RP_3 + P-network_2_2_AskP_1 + P-network_2_2_AskP_2 + P-network_2_2_AskP_3 + P-network_3_0_RP_1 + P-network_3_0_RP_2 + P-network_3_0_RP_3 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_0_1_AI_3 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_2_0_AI_3 + P-network_2_3_RI_1 + P-network_2_3_RI_2 + P-network_2_3_RI_3 + P-network_3_3_AnnP_1 + P-network_3_3_AnnP_2 + P-network_3_3_AnnP_3 + P-network_3_1_AskP_1 + P-network_3_1_AskP_2 + P-network_3_1_AskP_3 + P-network_0_3_RP_1 + P-network_0_3_RP_2 + P-network_0_3_RP_3 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_0_2_AnnP_3 + P-network_2_2_RP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_3 + P-network_1_2_AI_1 + P-network_1_2_AI_2 + P-network_1_2_AI_3 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_0_0_AskP_3 + P-network_3_1_AI_1 + P-network_3_1_AI_2 + P-network_3_1_AI_3 + P-network_0_1_AskP_3 + P-network_0_1_AskP_2 + P-network_0_1_AskP_1 + P-network_2_2_AI_3 + P-network_2_2_AI_2 + P-network_2_2_AI_1 + P-network_0_3_AI_3 + P-network_0_3_AI_2 + P-network_0_3_AI_1 + P-network_1_1_AnnP_1 + P-network_1_1_AnnP_2 + P-network_1_1_AnnP_3 + P-network_3_3_RP_1 + P-network_3_3_RP_2 + P-network_3_3_RP_3 + P-network_3_2_RP_3 + P-network_3_2_RP_2 + P-network_3_2_RP_1 + P-network_0_3_AnnP_3 + P-network_0_3_AnnP_2 + P-network_2_3_AI_1 + P-network_2_3_AI_2 + P-network_2_3_AI_3 + P-network_0_3_AnnP_1 + P-network_0_3_AskP_1 + P-network_0_3_AskP_2 + P-network_0_3_AskP_3 + P-network_1_3_RP_3 + P-network_1_3_RP_2 + P-network_1_3_RP_1 + P-network_1_0_RI_1 + P-network_1_0_RI_2 + P-network_1_0_RI_3 + P-network_3_2_AskP_3 + P-network_2_0_AnnP_1 + P-network_2_0_AnnP_2 + P-network_2_0_AnnP_3 + P-network_3_2_AskP_2 + P-network_3_2_AskP_1 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_1_2_AskP_3 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_0_2_RI_3 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_2_1_RI_3 + P-network_3_3_RI_3 + P-network_3_3_RI_2 + P-network_2_3_AnnP_1 + P-network_2_3_AnnP_2 + P-network_2_3_AnnP_3 + P-network_3_3_RI_1 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_0_1_RP_3 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_2_1_AskP_3 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_2_0_RP_3 + P-network_3_0_AI_3 + P-network_3_0_AI_2 + P-network_3_0_AI_1 + P-network_1_1_AI_3 + P-network_1_1_AI_2 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_1_0_AI_3 + P-network_1_1_AI_1 + P-network_1_3_RI_1 + P-network_1_3_RI_2 + P-network_1_3_RI_3 + P-network_2_3_AskP_3 + P-network_2_3_AskP_2 + P-network_2_3_AskP_1 + P-network_3_2_RI_1 + P-network_3_2_RI_2 + P-network_3_2_RI_3 + P-network_2_1_RP_3 + P-network_3_2_AnnP_1 + P-network_3_2_AnnP_2 + P-network_3_2_AnnP_3 + P-network_2_1_RP_2 + P-network_2_1_RP_1 + P-network_3_0_AskP_1 + P-network_3_0_AskP_2 + P-network_3_0_AskP_3 + P-network_0_1_AnnP_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_3 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_1_2_RP_3 + P-network_3_1_RP_1 + P-network_3_1_RP_2 + P-network_3_1_RP_3 + P-network_0_2_AI_1 + P-network_0_2_AI_2 + P-network_0_2_AI_3 + P-network_0_2_RP_3 + P-network_2_1_AI_1 + P-network_2_1_AI_2 + P-network_2_1_AI_3 + P-network_0_2_RP_2 + P-network_0_2_RP_1 + P-network_0_0_AnnP_3 + P-network_0_0_AnnP_2 + P-network_0_0_AnnP_1 + P-network_1_0_AnnP_1 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_3 + P-network_3_3_AskP_1 + P-network_3_3_AskP_2 + P-network_3_3_AskP_3 + P-network_2_3_RP_1 + P-network_2_3_RP_2 + P-network_2_3_RP_3 + P-network_3_1_AnnP_3 + P-network_3_1_AnnP_2 + P-network_3_1_AnnP_1 + P-network_2_2_RI_3 + P-network_2_2_RI_2 + P-network_2_2_RI_1 + P-network_1_3_AI_1 + P-network_1_3_AI_2 + P-network_1_3_AI_3 + P-network_0_3_RI_3 + P-network_3_2_AI_1 + P-network_3_2_AI_2 + P-network_3_2_AI_3 + P-network_0_3_RI_2 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_0_2_AskP_3 + P-network_0_3_RI_1 + P-network_0_0_AI_3 + P-network_0_0_AI_2 + P-network_0_0_AI_1 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_0_0_RI_3 + P-network_1_0_RP_3 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_1_3_AnnP_1 + P-network_1_3_AnnP_2 + P-network_1_3_AnnP_3 + P-network_2_0_AskP_3 + P-network_2_0_AskP_2 + P-network_2_0_AskP_1 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_1_1_AskP_3 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_1_RI_3 + P-network_2_2_AnnP_3 + P-network_2_2_AnnP_2 + P-network_2_2_AnnP_1 + P-network_3_0_RI_1 + P-network_3_0_RI_2 + P-network_3_0_RI_3 <= 0)
lola: after: (P-network_2_2_AnnP_0 + P-network_3_0_RI_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_1_RI_0 + P-network_1_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_0_0_RI_0 + P-network_0_0_AI_0 + P-network_0_3_RI_0 + P-network_0_2_AskP_0 + P-network_3_2_AI_0 + P-network_1_3_AI_0 + P-network_2_2_RI_0 + P-network_3_1_AnnP_0 + P-network_0_1_AnsP_3 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_2_2_AnsP_3 + P-network_0_1_AnsP_0 + P-network_2_3_RP_0 + P-network_3_3_AskP_0 + P-network_1_0_AnnP_0 + P-network_0_0_AnnP_0 + P-network_3_2_AnsP_3 + P-network_3_2_AnsP_2 + P-network_0_2_RP_0 + P-network_3_2_AnsP_1 + P-network_3_2_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_AI_0 + P-network_3_1_RP_0 + P-network_1_2_RP_0 + P-network_0_1_AnnP_0 + P-network_3_0_AskP_0 + P-network_2_3_AnsP_3 + P-network_2_3_AnsP_2 + P-network_2_1_RP_0 + P-network_2_3_AnsP_1 + P-network_2_3_AnsP_0 + P-network_3_2_AnnP_0 + P-network_2_3_AskP_0 + P-network_3_2_RI_0 + P-network_1_1_AI_0 + P-network_1_3_RI_0 + P-network_1_0_AI_0 + P-network_3_0_AI_0 + P-network_2_0_RP_0 + P-network_2_1_AskP_0 + P-network_0_1_RP_0 + P-network_3_3_RI_0 + P-network_2_3_AnnP_0 + P-network_3_1_AnsP_0 + P-network_3_1_AnsP_1 + P-network_3_1_AnsP_2 + P-network_3_1_AnsP_3 + P-network_2_0_AnsP_3 + P-network_2_0_AnsP_2 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_2_1_RI_0 + P-network_0_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AnsP_3 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_3_2_AskP_0 + P-network_1_1_AnsP_0 + P-network_2_0_AnnP_0 + P-network_1_3_RP_0 + P-network_1_0_RI_0 + P-network_0_0_AnsP_0 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_3 + P-network_0_3_AnnP_0 + P-network_0_3_AskP_0 + P-network_2_3_AI_0 + P-network_3_2_RP_0 + P-network_0_2_AnsP_3 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_3_3_RP_0 + P-network_0_3_AI_0 + P-network_1_1_AnnP_0 + P-network_2_2_AI_0 + P-network_3_3_AnsP_3 + P-network_3_3_AnsP_2 + P-network_3_3_AnsP_1 + P-network_0_1_AskP_0 + P-network_3_3_AnsP_0 + P-network_3_1_AI_0 + P-network_0_0_AskP_0 + P-network_1_2_AI_0 + P-network_2_2_RP_0 + P-network_0_2_AnnP_0 + P-network_0_3_RP_0 + P-network_3_1_AskP_0 + P-network_3_3_AnnP_0 + P-network_3_0_AnsP_3 + P-network_3_0_AnsP_2 + P-network_3_0_AnsP_1 + P-network_3_0_AnsP_0 + P-network_2_3_RI_0 + P-network_2_0_AI_0 + P-network_0_1_AI_0 + P-network_3_0_RP_0 + P-network_2_2_AskP_0 + P-network_1_1_RP_0 + P-network_2_1_AnsP_3 + P-network_2_1_AnsP_2 + P-network_1_2_AnnP_0 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_3_1_RI_0 + P-network_0_3_AnsP_0 + P-network_0_3_AnsP_1 + P-network_0_3_AnsP_2 + P-network_0_3_AnsP_3 + P-network_1_0_AskP_0 + P-network_3_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_3_AskP_0 + P-network_3_3_AI_0 + P-network_0_0_RP_0 + P-network_1_2_AnsP_3 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_1_2_AnsP_0 + P-network_2_1_AnnP_0 + P-network_0_1_RI_0 + P-network_2_0_RI_0 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_2_F_3 + P-masterState_0_F_3 + P-masterState_3_F_3 + P-masterState_1_T_3 <= 0)
lola: after: (3 <= 0)
lola: always false
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_0 + P-poll__networl_2_2_AI_0 + P-poll__networl_3_2_RP_3 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_0 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_3_3_AI_3 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_2 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_3_3_RI_1 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_3_3_RI_0 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_0 + P-poll__networl_3_0_AI_3 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_1_1_AI_3 + P-poll__networl_1_1_AI_2 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_2_1_RP_0 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_3_1_AskP_0 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_0_2_RP_0 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_2_2_RI_1 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_2_2_RI_0 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_3_RI_1 + P-poll__networl_0_3_RI_0 + P-poll__networl_0_0_AI_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_3_0_RI_3 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_0_RI_0 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_1_RI_1 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_1_1_RI_0 + P-poll__networl_1_3_AskP_3 + P-poll__networl_1_3_AskP_2 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_0_RI_3 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_0_0_RI_1 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_0_0_RI_0 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 <= 0)
lola: after: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 <= 0)
lola: LP says that atomic proposition is always true: (P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_2_1_AI_3 <= 0)
lola: after: (0 <= 0)
lola: always true
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_2_1_AI_1 <= 0)
lola: after: (0 <= 0)
lola: always true
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_3_3_AnnP_2 <= 0)
lola: after: (0 <= 0)
lola: always true
lola: LP says that atomic proposition is always true: (P-sendAnnPs__broadcasting_1_2 <= 0)
lola: LP says that atomic proposition is always true: (P-network_0_0_AskP_0 <= 0)
lola: place invariant simplifies atomic proposition
lola: before: (P-poll__networl_3_1_RI_1 <= 0)
lola: after: (0 <= 0)
lola: always true
lola: LP says that atomic proposition is always true: (P-network_1_0_RP_0 <= 0)
lola: LP says that atomic proposition is always true: (P-negotiation_3_3_CO <= 0)
lola: MAX(0) : MAX(0) : MAX(0) : MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1) : MAX(P-network_2_2_AnnP_0 + P-network_3_0_RI_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_1_RI_0 + P-network_1_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_0_0_RI_0 + P-network_0_0_AI_0 + P-network_0_3_RI_0 + P-network_0_2_AskP_0 + P-network_3_2_AI_0 + P-network_1_3_AI_0 + P-network_2_2_RI_0 + P-network_3_1_AnnP_0 + P-network_0_1_AnsP_3 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_2_2_AnsP_3 + P-network_0_1_AnsP_0 + P-network_2_3_RP_0 + P-network_3_3_AskP_0 + P-network_1_0_AnnP_0 + P-network_0_0_AnnP_0 + P-network_3_2_AnsP_3 + P-network_3_2_AnsP_2 + P-network_0_2_RP_0 + P-network_3_2_AnsP_1 + P-network_3_2_AnsP_0 + P-network_2_1_AI_0 + P-network_0_2_AI_0 + P-network_3_1_RP_0 + P-network_1_2_RP_0 + P-network_0_1_AnnP_0 + P-network_3_0_AskP_0 + P-network_2_3_AnsP_3 + P-network_2_3_AnsP_2 + P-network_2_1_RP_0 + P-network_2_3_AnsP_1 + P-network_2_3_AnsP_0 + P-network_3_2_AnnP_0 + P-network_2_3_AskP_0 + P-network_3_2_RI_0 + P-network_1_1_AI_0 + P-network_1_3_RI_0 + P-network_1_0_AI_0 + P-network_3_0_AI_0 + P-network_2_0_RP_0 + P-network_2_1_AskP_0 + P-network_0_1_RP_0 + P-network_3_3_RI_0 + P-network_2_3_AnnP_0 + P-network_3_1_AnsP_0 + P-network_3_1_AnsP_1 + P-network_3_1_AnsP_2 + P-network_3_1_AnsP_3 + P-network_2_0_AnsP_3 + P-network_2_0_AnsP_2 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_2_1_RI_0 + P-network_0_2_RI_0 + P-network_1_2_AskP_0 + P-network_1_1_AnsP_3 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_3_2_AskP_0 + P-network_1_1_AnsP_0 + P-network_2_0_AnnP_0 + P-network_1_3_RP_0 + P-network_1_0_RI_0 + P-network_0_0_AnsP_0 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_3 + P-network_0_3_AnnP_0 + P-network_0_3_AskP_0 + P-network_2_3_AI_0 + P-network_3_2_RP_0 + P-network_0_2_AnsP_3 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_3_3_RP_0 + P-network_0_3_AI_0 + P-network_1_1_AnnP_0 + P-network_2_2_AI_0 + P-network_3_3_AnsP_3 + P-network_3_3_AnsP_2 + P-network_3_3_AnsP_1 + P-network_0_1_AskP_0 + P-network_3_3_AnsP_0 + P-network_3_1_AI_0 + P-network_0_0_AskP_0 + P-network_1_2_AI_0 + P-network_2_2_RP_0 + P-network_0_2_AnnP_0 + P-network_0_3_RP_0 + P-network_3_1_AskP_0 + P-network_3_3_AnnP_0 + P-network_3_0_AnsP_3 + P-network_3_0_AnsP_2 + P-network_3_0_AnsP_1 + P-network_3_0_AnsP_0 + P-network_2_3_RI_0 + P-network_2_0_AI_0 + P-network_0_1_AI_0 + P-network_3_0_RP_0 + P-network_2_2_AskP_0 + P-network_1_1_RP_0 + P-network_2_1_AnsP_3 + P-network_2_1_AnsP_2 + P-network_1_2_AnnP_0 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_3_1_RI_0 + P-network_0_3_AnsP_0 + P-network_0_3_AnsP_1 + P-network_0_3_AnsP_2 + P-network_0_3_AnsP_3 + P-network_1_0_AskP_0 + P-network_3_0_AnnP_0 + P-network_1_2_RI_0 + P-network_1_3_AskP_0 + P-network_3_3_AI_0 + P-network_0_0_RP_0 + P-network_1_2_AnsP_3 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_1_2_AnsP_0 + P-network_2_1_AnnP_0 + P-network_0_1_RI_0 + P-network_2_0_RI_0) : MAX(0) : MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1) : MAX(P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3) : MAX(0) : MAX(0) : MAX(0) : MAX(P-sendAnnPs__broadcasting_1_2) : MAX(P-network_0_0_AskP_0) : MAX(0) : MAX(P-network_1_0_RP_0) : MAX(P-negotiation_3_3_CO)
lola: computing a collection of formulas
lola: RUNNING
lola: subprocess 0 will run for 223 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
FORMULA NeoElection-PT-3-UpperBounds-0 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 1 will run for 237 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 3
lola: SUBRESULT
lola: result: 3
lola: produced by: state space
lola: The maximum value of the given expression is 3
lola: 0 markings, 0 edges
FORMULA NeoElection-PT-3-UpperBounds-1 3 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: ========================================
lola: subprocess 2 will run for 254 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: ========================================
lola: Structural Bound: 9
lola: SUBRESULT
lola: result: 9
lola: produced by: state space
lola: The maximum value of the given expression is 9
lola: 0 markings, 0 edges
FORMULA NeoElection-PT-3-UpperBounds-2 9 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: ========================================
lola: subprocess 3 will run for 274 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2... (shortened)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2... (shortened)
lola: processed formula length: 1394
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola:
FORMULA NeoElection-PT-3-UpperBounds-3 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
========================================
lola: subprocess 4 will run for 297 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 3
lola: SUBRESULT
lola: result: 3
lola: produced by: state space
lola: The maximum value of the given expression is 3
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-5 3 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 5 will run for 324 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2... (shortened)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2... (shortened)
lola: processed formula length: 1394
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-6 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 6 will run for 356 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-8 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 7 will run for 396 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
FORMULA NeoElection-PT-3-UpperBounds-9 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: lola: ========================================
subprocess 8 will run for 446 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-10 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 9 will run for 509 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-sendAnnPs__broadcasting_1_2)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-sendAnnPs__broadcasting_1_2)
lola: processed formula length: 34
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-11 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 10 will run for 594 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-network_0_0_AskP_0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-network_0_0_AskP_0)
lola: processed formula length: 25
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
FORMULA NeoElection-PT-3-UpperBounds-12 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: ========================================
lola: subprocess 11 will run for 713 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(0)
lola: processed formula length: 6
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-13 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 12 will run for 892 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-network_1_0_RP_0)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-network_1_0_RP_0)
lola: processed formula length: 23
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-14 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 13 will run for 1189 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-negotiation_3_3_CO)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-negotiation_3_3_CO)
lola: processed formula length: 25
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 0
lola: SUBRESULT
lola: result: 0
lola: produced by: state space
lola: The maximum value of the given expression is 0
lola: 0 markings, 0 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-15 0 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 14 will run for 1784 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3)
lola: processed formula length: 114
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 3
lola: SUBRESULT
lola: result: 3
lola: produced by: state space
lola: The maximum value of the given expression is 3
lola: 43 markings, 42 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-7 3 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: subprocess 15 will run for 3569 seconds at most (--localtimelimit=0)
lola: ========================================
lola: ...considering subproblem: MAX(P-network_2_2_AnnP_0 + P-network_3_0_RI_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_1_RI_0 + P-network_1_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_0_0_RI_0 + P-network_0_0_AI_0 + P-network_0_3_R... (shortened)
lola: ========================================
lola: SUBTASK
lola: computing bound of an expression
lola: processed formula: MAX(P-network_2_2_AnnP_0 + P-network_3_0_RI_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_1_RI_0 + P-network_1_1_AskP_0 + P-network_2_0_AskP_0 + P-network_1_0_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_0_0_RI_0 + P-network_0_0_AI_0 + P-network_0_3_R... (shortened)
lola: processed formula length: 3218
lola: 0 rewrites
lola: closed formula file NeoElection-PT-3-UpperBounds.task
lola: STORE
lola: using a simple compression encoder (--encoder=simplecompressed)
lola: using a prefix tree store (--store=prefix)
lola: SEARCH
lola: using bound preserving stubborn set method with insertion algorithm(--stubborn=tarjan)
lola: RUNNING
lola: Structural Bound: 6
lola: SUBRESULT
lola: result: 6
lola: produced by: state space
lola: The maximum value of the given expression is 6
lola: 10 markings, 9 edges
lola: ========================================
FORMULA NeoElection-PT-3-UpperBounds-4 6 TECHNIQUES COLLATERAL_PROCESSING EXPLICIT TOPOLOGICAL STATE_COMPRESSION STUBBORN_SETS USE_NUPN UNFOLDING_TO_PT
lola: RESULT
lola:
SUMMARY: 0 3 9 0 6 3 0 3 0 0 0 0 0 0 0 0
lola:
preliminary result: 0 3 9 0 6 3 0 3 0 0 0 0 0 0 0 0
lola: memory consumption: 18404 KB
lola: time consumption: 1 seconds
BK_STOP 1527027005928
--------------------
content from stderr:
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-3"
export BK_EXAMINATION="UpperBounds"
export BK_TOOL="lola"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-3.tgz
mv NeoElection-PT-3 execution
cd execution
pwd
ls -lh
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-3637"
echo " Executing tool lola"
echo " Input is NeoElection-PT-3, examination is UpperBounds"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r112-csrt-152666469300296"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "UpperBounds" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "UpperBounds" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "UpperBounds.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property UpperBounds.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "UpperBounds.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

