About the Execution of ITS-Tools for HypercubeGrid-PT-C4K3P3B12
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 15752.390 | 3600000.00 | 6094316.00 | 7994.70 | [undef] | Time out reached |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
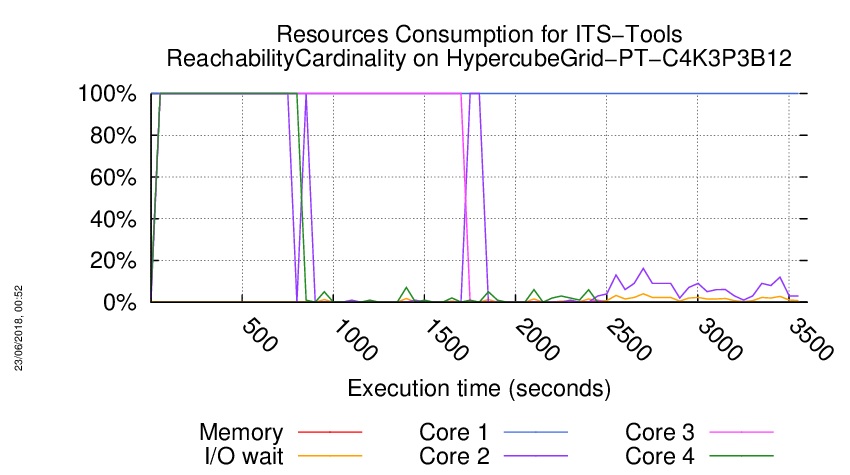
Trace from the execution
Waiting for the VM to be ready (probing ssh)
......................
/home/mcc/execution
total 3.1M
-rw-r--r-- 1 mcc users 4.7K May 15 18:54 CTLCardinality.txt
-rw-r--r-- 1 mcc users 23K May 15 18:54 CTLCardinality.xml
-rw-r--r-- 1 mcc users 3.0K May 15 18:54 CTLFireability.txt
-rw-r--r-- 1 mcc users 14K May 15 18:54 CTLFireability.xml
-rw-r--r-- 1 mcc users 4.0K May 15 18:50 GenericPropertiesDefinition.xml
-rw-r--r-- 1 mcc users 5.9K May 15 18:50 GenericPropertiesVerdict.xml
-rw-r--r-- 1 mcc users 2.9K May 15 18:54 LTLCardinality.txt
-rw-r--r-- 1 mcc users 12K May 15 18:54 LTLCardinality.xml
-rw-r--r-- 1 mcc users 2.6K May 15 18:54 LTLFireability.txt
-rw-r--r-- 1 mcc users 11K May 15 18:54 LTLFireability.xml
-rw-r--r-- 1 mcc users 5.0K May 15 18:54 ReachabilityCardinality.txt
-rw-r--r-- 1 mcc users 22K May 15 18:54 ReachabilityCardinality.xml
-rw-r--r-- 1 mcc users 117 May 15 18:54 ReachabilityDeadlock.txt
-rw-r--r-- 1 mcc users 355 May 15 18:54 ReachabilityDeadlock.xml
-rw-r--r-- 1 mcc users 3.7K May 15 18:54 ReachabilityFireability.txt
-rw-r--r-- 1 mcc users 15K May 15 18:54 ReachabilityFireability.xml
-rw-r--r-- 1 mcc users 2.0K May 15 18:54 UpperBounds.txt
-rw-r--r-- 1 mcc users 4.0K May 15 18:54 UpperBounds.xml
-rw-r--r-- 1 mcc users 6 May 15 18:50 equiv_col
-rw-r--r-- 1 mcc users 10 May 15 18:50 instance
-rw-r--r-- 1 mcc users 6 May 15 18:50 iscolored
-rwxr-xr-x 1 mcc users 3.0M May 15 18:50 model.pnml
=====================================================================
Generated by BenchKit 2-3637
Executing tool itstools
Input is HypercubeGrid-PT-C4K3P3B12, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r104-smll-152658634200117
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-00
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-01
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-02
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-03
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-04
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-05
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-06
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-07
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-08
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-09
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-10
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-11
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-12
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-13
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-14
FORMULA_NAME HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-15
=== Now, execution of the tool begins
BK_START 1526784284031
Using solver Z3 to compute partial order matrices.
Built C files in :
/home/mcc/execution
Invoking ITS tools like this :CommandLine [args=[/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201805151631/bin/its-reach-linux64, --gc-threshold, 2000000, --quiet, -i, /home/mcc/execution/ReachabilityCardinality.pnml.gal, -t, CGAL, -reachable-file, ReachabilityCardinality.prop, --nowitness], workingDir=/home/mcc/execution]
its-reach command run as :
/home/mcc/BenchKit/itstools/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201805151631/bin/its-reach-linux64 --gc-threshold 2000000 --quiet -i /home/mcc/execution/ReachabilityCardinality.pnml.gal -t CGAL -reachable-file ReachabilityCardinality.prop --nowitness
Running compilation step : CommandLine [args=[gcc, -c, -I/home/mcc/BenchKit//lts_install_dir//include, -I., -std=c99, -fPIC, -O3, model.c], workingDir=/home/mcc/execution]
Loading property file ReachabilityCardinality.prop.
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-00 with value :(pi_d3_n1_1_2_1_1<=pi_d2_n1_3_2_1_2)
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-01 with value :((((pil_d3_n1_2_2_1_1>=1)||(pb_d3_n1_3_2_3_3<=pol_d2_n1_1_1_1_3))&&(!(po_d2_n1_3_1_2_2<=pol_d1_n1_3_3_2_1)))||(!((pi_d3_n1_1_1_1_3<=pi_d1_n1_4_2_2_1)||(pb_d1_n1_3_1_3_2<=pol_d4_n1_1_2_1_3))))
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-02 with value :((((pol_d2_n1_3_3_2_3<=pb_d1_n2_3_3_3_3)&&(po_d1_n1_4_3_1_2<=pb_d1_n2_1_2_1_2))&&(pil_d1_n1_2_2_2_2<=pol_d3_n1_3_1_2_1))||((!(pi_d4_n1_2_2_1_2<=pb_d1_n1_2_3_2_1))||(pb_d1_n2_2_3_3_2>=2)))
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-03 with value :((((pil_d2_n1_2_2_1_3>=2)&&(po_d4_n1_3_1_2_3<=pil_d2_n1_1_4_1_3))||(pol_d4_n1_3_1_2_2<=po_d1_n1_2_3_1_3))||(((po_d1_n1_4_3_1_1<=po_d2_n1_1_1_1_3)||(pb_d3_n2_1_2_2_3<=pi_d3_n1_1_3_4_1))||((pil_d3_n1_1_3_4_3>=1)&&(pil_d2_n1_3_3_3_1>=1))))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-04 with value :((!((pol_d2_n1_3_2_3_1<=pb_d2_n1_3_3_1_1)&&(pil_d3_n1_1_2_1_1<=pol_d3_n1_3_3_1_1)))&&(!((pb_d2_n1_3_1_1_1>=1)&&(pb_d3_n2_3_3_3_2>=1))))
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-05 with value :(!((!(pbl_3_1_2_1<=po_d2_n1_3_2_2_2))&&((po_d3_n1_3_3_1_2<=pil_d1_n1_4_2_3_2)&&(pil_d4_n1_1_1_2_3>=3))))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-06 with value :(po_d3_n1_1_3_2_3>=3)
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-07 with value :(!((!(pi_d3_n1_3_1_3_2>=2))||((pil_d3_n1_3_3_3_2>=1)&&(pb_d1_n1_1_1_1_2<=pb_d3_n1_2_2_1_3))))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-08 with value :(!(po_d4_n1_3_1_2_2<=pil_d1_n1_1_2_3_2))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-09 with value :((!((pil_d1_n1_3_2_2_1>=3)||(pol_d3_n1_3_2_4_2>=2)))&&(pil_d2_n1_2_1_2_1>=3))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-10 with value :((pb_d4_n2_2_3_1_1<=pb_d3_n2_1_3_2_3)&&(pil_d1_n1_1_3_1_2>=2))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-11 with value :(((pb_d4_n1_2_1_3_1>=2)&&((pb_d3_n2_1_1_2_3>=2)&&(pil_d2_n1_2_4_2_3>=3)))&&(!(pb_d1_n1_2_2_3_1<=po_d3_n1_3_2_1_3)))
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-12 with value :((((pi_d2_n1_3_4_1_3<=pi_d4_n1_1_1_1_2)&&(pb_d1_n2_2_1_3_3>=1))||(pol_d2_n1_2_3_3_3<=po_d1_n1_2_1_2_3))||(((pol_d3_n1_2_2_2_2<=pol_d4_n1_2_3_1_2)&&(pil_d1_n1_3_2_3_2>=1))||((pol_d1_n1_3_3_2_2>=2)||(pol_d2_n1_2_3_1_2>=2))))
Read [invariant] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-13 with value :(pb_d1_n1_3_3_2_2>=2)
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-14 with value :(!(((pil_d1_n1_1_1_3_2>=1)||(po_d2_n1_1_4_2_2<=pil_d1_n1_4_1_3_2))||(!(po_d4_n1_3_2_2_3>=3))))
Read [reachable] property : HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-15 with value :((((pb_d1_n1_1_2_3_2>=1)||(pil_d4_n1_2_1_3_2>=2))&&((pb_d2_n2_2_3_2_1>=1)&&(pil_d3_n1_2_1_3_3>=2)))||((pil_d1_n1_1_2_3_3>=3)&&((pol_d1_n1_4_1_2_3>=2)||(po_d3_n1_3_2_2_2<=pol_d4_n1_2_2_2_2))))
Presburger conditions satisfied. Using coverability to approximate state space in K-Induction.
// Phase 1: matrix 5400 rows 2457 cols
invariant :po_d2_n1_3_1_1_1 + pol_d2_n1_3_1_1_1 = 1
invariant :pi_d3_n1_1_1_1_2 + pil_d3_n1_1_1_1_2 = 1
invariant :po_d3_n1_3_3_4_2 + pol_d3_n1_3_3_4_2 = 1
invariant :pi_d1_n1_2_1_1_1 + pil_d1_n1_2_1_1_1 = 1
invariant :pi_d3_n1_3_3_1_2 + pil_d3_n1_3_3_1_2 = 1
invariant :po_d4_n1_1_1_2_3 + pol_d4_n1_1_1_2_3 = 1
invariant :pi_d4_n1_1_1_2_1 + pil_d4_n1_1_1_2_1 = 1
invariant :po_d4_n1_1_1_2_1 + pol_d4_n1_1_1_2_1 = 1
invariant :po_d3_n1_2_2_3_1 + pol_d3_n1_2_2_3_1 = 1
invariant :pb_d1_n1_1_2_2_2 + pb_d1_n2_1_2_2_2 + pb_d2_n1_1_2_2_2 + pb_d2_n2_1_2_2_2 + pb_d3_n1_1_2_2_2 + pb_d3_n2_1_2_2_2 + pb_d4_n1_1_2_2_2 + pb_d4_n2_1_2_2_2 + pbl_1_2_2_2 = 36
invariant :pi_d2_n1_2_3_1_2 + pil_d2_n1_2_3_1_2 = 1
invariant :pi_d3_n1_1_3_2_3 + pil_d3_n1_1_3_2_3 = 1
invariant :pi_d1_n1_3_1_1_1 + pil_d1_n1_3_1_1_1 = 1
invariant :pi_d4_n1_2_1_2_3 + pil_d4_n1_2_1_2_3 = 1
invariant :pi_d3_n1_3_1_2_3 + pil_d3_n1_3_1_2_3 = 1
invariant :po_d1_n1_4_3_2_3 + pol_d1_n1_4_3_2_3 = 1
invariant :po_d4_n1_3_3_3_2 + pol_d4_n1_3_3_3_2 = 1
invariant :po_d1_n1_2_2_1_1 + pol_d1_n1_2_2_1_1 = 1
invariant :pb_d1_n1_3_1_1_2 + pb_d1_n2_3_1_1_2 + pb_d2_n1_3_1_1_2 + pb_d2_n2_3_1_1_2 + pb_d3_n1_3_1_1_2 + pb_d3_n2_3_1_1_2 + pb_d4_n1_3_1_1_2 + pb_d4_n2_3_1_1_2 + pbl_3_1_1_2 = 36
invariant :pi_d2_n1_3_3_1_1 + pil_d2_n1_3_3_1_1 = 1
invariant :po_d2_n1_2_4_2_3 + pol_d2_n1_2_4_2_3 = 1
invariant :po_d1_n1_2_2_3_2 + pol_d1_n1_2_2_3_2 = 1
invariant :po_d2_n1_3_2_1_1 + pol_d2_n1_3_2_1_1 = 1
invariant :pi_d4_n1_1_3_2_2 + pil_d4_n1_1_3_2_2 = 1
invariant :po_d3_n1_2_1_4_1 + pol_d3_n1_2_1_4_1 = 1
invariant :po_d3_n1_3_1_1_1 + pol_d3_n1_3_1_1_1 = 1
invariant :po_d1_n1_2_2_1_3 + pol_d1_n1_2_2_1_3 = 1
invariant :pi_d2_n1_2_2_3_2 + pil_d2_n1_2_2_3_2 = 1
invariant :pi_d1_n1_1_3_1_3 + pil_d1_n1_1_3_1_3 = 1
invariant :pi_d4_n1_1_2_3_2 + pil_d4_n1_1_2_3_2 = 1
invariant :pi_d4_n1_2_1_3_1 + pil_d4_n1_2_1_3_1 = 1
invariant :po_d1_n1_3_1_3_1 + pol_d1_n1_3_1_3_1 = 1
invariant :po_d2_n1_1_1_3_2 + pol_d2_n1_1_1_3_2 = 1
invariant :po_d3_n1_3_1_2_1 + pol_d3_n1_3_1_2_1 = 1
invariant :po_d3_n1_3_1_4_3 + pol_d3_n1_3_1_4_3 = 1
invariant :pi_d2_n1_2_4_1_1 + pil_d2_n1_2_4_1_1 = 1
invariant :po_d1_n1_2_1_1_2 + pol_d1_n1_2_1_1_2 = 1
invariant :po_d1_n1_4_2_2_3 + pol_d1_n1_4_2_2_3 = 1
invariant :pi_d4_n1_3_3_3_1 + pil_d4_n1_3_3_3_1 = 1
invariant :pi_d1_n1_2_3_2_3 + pil_d1_n1_2_3_2_3 = 1
invariant :pi_d4_n1_2_3_3_1 + pil_d4_n1_2_3_3_1 = 1
invariant :pi_d2_n1_3_4_3_3 + pil_d2_n1_3_4_3_3 = 1
invariant :pi_d3_n1_3_3_1_3 + pil_d3_n1_3_3_1_3 = 1
invariant :po_d3_n1_3_2_4_1 + pol_d3_n1_3_2_4_1 = 1
invariant :po_d4_n1_2_2_3_4 + pol_d4_n1_2_2_3_4 = 1
invariant :pi_d2_n1_1_4_2_3 + pil_d2_n1_1_4_2_3 = 1
invariant :pi_d3_n1_2_1_1_3 + pil_d3_n1_2_1_1_3 = 1
invariant :pi_d2_n1_3_1_2_3 + pil_d2_n1_3_1_2_3 = 1
invariant :po_d3_n1_2_3_2_2 + pol_d3_n1_2_3_2_2 = 1
invariant :pb_d1_n1_2_3_1_2 + pb_d1_n2_2_3_1_2 + pb_d2_n1_2_3_1_2 + pb_d2_n2_2_3_1_2 + pb_d3_n1_2_3_1_2 + pb_d3_n2_2_3_1_2 + pb_d4_n1_2_3_1_2 + pb_d4_n2_2_3_1_2 + pbl_2_3_1_2 = 36
invariant :po_d1_n1_2_1_3_3 + pol_d1_n1_2_1_3_3 = 1
invariant :pb_d1_n1_2_3_3_3 + pb_d1_n2_2_3_3_3 + pb_d2_n1_2_3_3_3 + pb_d2_n2_2_3_3_3 + pb_d3_n1_2_3_3_3 + pb_d3_n2_2_3_3_3 + pb_d4_n1_2_3_3_3 + pb_d4_n2_2_3_3_3 + pbl_2_3_3_3 = 36
invariant :pb_d1_n1_2_1_1_3 + pb_d1_n2_2_1_1_3 + pb_d2_n1_2_1_1_3 + pb_d2_n2_2_1_1_3 + pb_d3_n1_2_1_1_3 + pb_d3_n2_2_1_1_3 + pb_d4_n1_2_1_1_3 + pb_d4_n2_2_1_1_3 + pbl_2_1_1_3 = 36
invariant :po_d4_n1_1_2_1_2 + pol_d4_n1_1_2_1_2 = 1
invariant :po_d4_n1_3_1_2_3 + pol_d4_n1_3_1_2_3 = 1
invariant :po_d1_n1_1_2_1_3 + pol_d1_n1_1_2_1_3 = 1
invariant :pb_d1_n1_3_2_1_3 + pb_d1_n2_3_2_1_3 + pb_d2_n1_3_2_1_3 + pb_d2_n2_3_2_1_3 + pb_d3_n1_3_2_1_3 + pb_d3_n2_3_2_1_3 + pb_d4_n1_3_2_1_3 + pb_d4_n2_3_2_1_3 + pbl_3_2_1_3 = 36
invariant :pi_d1_n1_4_3_1_2 + pil_d1_n1_4_3_1_2 = 1
invariant :pi_d2_n1_1_3_2_3 + pil_d2_n1_1_3_2_3 = 1
invariant :pi_d2_n1_1_4_2_1 + pil_d2_n1_1_4_2_1 = 1
invariant :po_d2_n1_2_2_1_3 + pol_d2_n1_2_2_1_3 = 1
invariant :po_d2_n1_3_4_3_1 + pol_d2_n1_3_4_3_1 = 1
invariant :po_d4_n1_1_1_1_1 + pol_d4_n1_1_1_1_1 = 1
invariant :po_d4_n1_3_1_2_4 + pol_d4_n1_3_1_2_4 = 1
invariant :pi_d2_n1_3_2_3_3 + pil_d2_n1_3_2_3_3 = 1
invariant :po_d2_n1_3_1_2_1 + pol_d2_n1_3_1_2_1 = 1
invariant :pi_d2_n1_2_4_3_2 + pil_d2_n1_2_4_3_2 = 1
invariant :po_d4_n1_3_2_1_3 + pol_d4_n1_3_2_1_3 = 1
invariant :po_d2_n1_3_2_1_3 + pol_d2_n1_3_2_1_3 = 1
invariant :pi_d4_n1_2_3_1_1 + pil_d4_n1_2_3_1_1 = 1
invariant :pi_d4_n1_3_3_1_2 + pil_d4_n1_3_3_1_2 = 1
invariant :pi_d3_n1_2_2_1_1 + pil_d3_n1_2_2_1_1 = 1
invariant :pi_d4_n1_1_3_3_2 + pil_d4_n1_1_3_3_2 = 1
invariant :pi_d1_n1_2_1_3_2 + pil_d1_n1_2_1_3_2 = 1
invariant :po_d2_n1_3_3_1_2 + pol_d2_n1_3_3_1_2 = 1
invariant :po_d3_n1_2_1_1_2 + pol_d3_n1_2_1_1_2 = 1
invariant :po_d4_n1_1_3_3_2 + pol_d4_n1_1_3_3_2 = 1
invariant :pi_d1_n1_4_2_1_2 + pil_d1_n1_4_2_1_2 = 1
invariant :pi_d4_n1_1_3_3_3 + pil_d4_n1_1_3_3_3 = 1
invariant :pb_d1_n1_3_3_2_1 + pb_d1_n2_3_3_2_1 + pb_d2_n1_3_3_2_1 + pb_d2_n2_3_3_2_1 + pb_d3_n1_3_3_2_1 + pb_d3_n2_3_3_2_1 + pb_d4_n1_3_3_2_1 + pb_d4_n2_3_3_2_1 + pbl_3_3_2_1 = 36
invariant :pi_d4_n1_2_3_1_4 + pil_d4_n1_2_3_1_4 = 1
invariant :pi_d3_n1_3_1_1_3 + pil_d3_n1_3_1_1_3 = 1
invariant :po_d4_n1_2_2_3_2 + pol_d4_n1_2_2_3_2 = 1
invariant :pi_d1_n1_1_2_3_2 + pil_d1_n1_1_2_3_2 = 1
invariant :pi_d3_n1_1_3_1_2 + pil_d3_n1_1_3_1_2 = 1
invariant :po_d1_n1_4_2_2_1 + pol_d1_n1_4_2_2_1 = 1
invariant :pi_d2_n1_1_2_1_3 + pil_d2_n1_1_2_1_3 = 1
invariant :pi_d4_n1_2_3_2_4 + pil_d4_n1_2_3_2_4 = 1
invariant :pb_d1_n1_3_1_1_1 + pb_d1_n2_3_1_1_1 + pb_d2_n1_3_1_1_1 + pb_d2_n2_3_1_1_1 + pb_d3_n1_3_1_1_1 + pb_d3_n2_3_1_1_1 + pb_d4_n1_3_1_1_1 + pb_d4_n2_3_1_1_1 + pbl_3_1_1_1 = 36
invariant :po_d3_n1_3_1_3_3 + pol_d3_n1_3_1_3_3 = 1
invariant :po_d1_n1_2_2_2_1 + pol_d1_n1_2_2_2_1 = 1
invariant :pi_d4_n1_1_3_3_4 + pil_d4_n1_1_3_3_4 = 1
invariant :pi_d2_n1_1_2_3_2 + pil_d2_n1_1_2_3_2 = 1
invariant :pi_d3_n1_1_1_2_2 + pil_d3_n1_1_1_2_2 = 1
invariant :po_d1_n1_1_2_2_2 + pol_d1_n1_1_2_2_2 = 1
invariant :po_d2_n1_3_3_2_1 + pol_d2_n1_3_3_2_1 = 1
invariant :po_d1_n1_4_2_1_3 + pol_d1_n1_4_2_1_3 = 1
invariant :pi_d4_n1_1_2_1_3 + pil_d4_n1_1_2_1_3 = 1
invariant :po_d2_n1_2_4_1_3 + pol_d2_n1_2_4_1_3 = 1
invariant :po_d3_n1_2_1_1_3 + pol_d3_n1_2_1_1_3 = 1
invariant :po_d3_n1_2_1_3_2 + pol_d3_n1_2_1_3_2 = 1
invariant :pi_d3_n1_2_1_2_2 + pil_d3_n1_2_1_2_2 = 1
invariant :po_d3_n1_1_1_2_1 + pol_d3_n1_1_1_2_1 = 1
invariant :pi_d3_n1_3_3_3_2 + pil_d3_n1_3_3_3_2 = 1
invariant :po_d2_n1_1_2_2_2 + pol_d2_n1_1_2_2_2 = 1
invariant :po_d4_n1_1_2_1_4 + pol_d4_n1_1_2_1_4 = 1
invariant :po_d3_n1_3_2_1_3 + pol_d3_n1_3_2_1_3 = 1
invariant :pi_d4_n1_3_2_3_4 + pil_d4_n1_3_2_3_4 = 1
invariant :pi_d3_n1_2_2_4_3 + pil_d3_n1_2_2_4_3 = 1
invariant :po_d2_n1_2_3_2_2 + pol_d2_n1_2_3_2_2 = 1
invariant :pi_d2_n1_3_3_1_2 + pil_d2_n1_3_3_1_2 = 1
invariant :po_d3_n1_2_3_3_1 + pol_d3_n1_2_3_3_1 = 1
invariant :po_d2_n1_1_2_3_3 + pol_d2_n1_1_2_3_3 = 1
invariant :pi_d3_n1_2_3_2_1 + pil_d3_n1_2_3_2_1 = 1
invariant :pi_d1_n1_3_1_2_2 + pil_d1_n1_3_1_2_2 = 1
invariant :pi_d2_n1_1_1_3_3 + pil_d2_n1_1_1_3_3 = 1
invariant :po_d3_n1_2_2_4_2 + pol_d3_n1_2_2_4_2 = 1
invariant :po_d2_n1_2_4_2_2 + pol_d2_n1_2_4_2_2 = 1
invariant :pi_d4_n1_1_2_1_2 + pil_d4_n1_1_2_1_2 = 1
invariant :po_d4_n1_1_3_3_4 + pol_d4_n1_1_3_3_4 = 1
invariant :pi_d3_n1_3_2_2_1 + pil_d3_n1_3_2_2_1 = 1
invariant :pi_d4_n1_1_2_3_3 + pil_d4_n1_1_2_3_3 = 1
invariant :po_d1_n1_1_1_3_2 + pol_d1_n1_1_1_3_2 = 1
invariant :po_d4_n1_3_1_1_4 + pol_d4_n1_3_1_1_4 = 1
invariant :pi_d3_n1_3_1_4_2 + pil_d3_n1_3_1_4_2 = 1
invariant :po_d1_n1_3_2_3_3 + pol_d1_n1_3_2_3_3 = 1
invariant :po_d1_n1_4_2_1_2 + pol_d1_n1_4_2_1_2 = 1
invariant :pi_d3_n1_1_2_1_2 + pil_d3_n1_1_2_1_2 = 1
invariant :po_d3_n1_3_2_2_3 + pol_d3_n1_3_2_2_3 = 1
invariant :pi_d4_n1_1_1_2_4 + pil_d4_n1_1_1_2_4 = 1
invariant :pb_d1_n1_3_3_1_3 + pb_d1_n2_3_3_1_3 + pb_d2_n1_3_3_1_3 + pb_d2_n2_3_3_1_3 + pb_d3_n1_3_3_1_3 + pb_d3_n2_3_3_1_3 + pb_d4_n1_3_3_1_3 + pb_d4_n2_3_3_1_3 + pbl_3_3_1_3 = 36
invariant :pi_d2_n1_3_1_2_1 + pil_d2_n1_3_1_2_1 = 1
invariant :po_d3_n1_3_3_1_2 + pol_d3_n1_3_3_1_2 = 1
invariant :po_d4_n1_2_3_3_1 + pol_d4_n1_2_3_3_1 = 1
invariant :pi_d1_n1_3_2_1_1 + pil_d1_n1_3_2_1_1 = 1
invariant :pi_d4_n1_1_3_1_3 + pil_d4_n1_1_3_1_3 = 1
invariant :pi_d4_n1_3_3_2_4 + pil_d4_n1_3_3_2_4 = 1
invariant :po_d1_n1_3_2_3_1 + pol_d1_n1_3_2_3_1 = 1
invariant :pb_d1_n1_1_3_3_3 + pb_d1_n2_1_3_3_3 + pb_d2_n1_1_3_3_3 + pb_d2_n2_1_3_3_3 + pb_d3_n1_1_3_3_3 + pb_d3_n2_1_3_3_3 + pb_d4_n1_1_3_3_3 + pb_d4_n2_1_3_3_3 + pbl_1_3_3_3 = 36
invariant :po_d2_n1_2_1_2_2 + pol_d2_n1_2_1_2_2 = 1
invariant :pi_d1_n1_1_3_3_2 + pil_d1_n1_1_3_3_2 = 1
invariant :pi_d4_n1_2_3_2_3 + pil_d4_n1_2_3_2_3 = 1
invariant :po_d4_n1_2_2_3_1 + pol_d4_n1_2_2_3_1 = 1
invariant :pb_d1_n1_3_1_2_3 + pb_d1_n2_3_1_2_3 + pb_d2_n1_3_1_2_3 + pb_d2_n2_3_1_2_3 + pb_d3_n1_3_1_2_3 + pb_d3_n2_3_1_2_3 + pb_d4_n1_3_1_2_3 + pb_d4_n2_3_1_2_3 + pbl_3_1_2_3 = 36
invariant :po_d2_n1_2_3_1_1 + pol_d2_n1_2_3_1_1 = 1
invariant :pi_d2_n1_2_2_1_3 + pil_d2_n1_2_2_1_3 = 1
invariant :po_d1_n1_3_1_1_2 + pol_d1_n1_3_1_1_2 = 1
invariant :po_d4_n1_3_3_3_4 + pol_d4_n1_3_3_3_4 = 1
invariant :pi_d2_n1_1_3_3_2 + pil_d2_n1_1_3_3_2 = 1
invariant :pi_d4_n1_1_2_1_4 + pil_d4_n1_1_2_1_4 = 1
invariant :po_d2_n1_1_1_3_1 + pol_d2_n1_1_1_3_1 = 1
invariant :po_d1_n1_1_2_1_1 + pol_d1_n1_1_2_1_1 = 1
invariant :po_d2_n1_1_2_3_2 + pol_d2_n1_1_2_3_2 = 1
invariant :po_d4_n1_2_3_1_2 + pol_d4_n1_2_3_1_2 = 1
invariant :pi_d2_n1_3_4_2_2 + pil_d2_n1_3_4_2_2 = 1
invariant :po_d3_n1_2_1_2_2 + pol_d3_n1_2_1_2_2 = 1
invariant :po_d2_n1_1_2_2_3 + pol_d2_n1_1_2_2_3 = 1
invariant :po_d3_n1_3_1_2_3 + pol_d3_n1_3_1_2_3 = 1
invariant :po_d2_n1_2_3_3_3 + pol_d2_n1_2_3_3_3 = 1
invariant :po_d3_n1_2_3_1_2 + pol_d3_n1_2_3_1_2 = 1
invariant :pi_d1_n1_1_3_3_1 + pil_d1_n1_1_3_3_1 = 1
invariant :pi_d3_n1_1_2_1_3 + pil_d3_n1_1_2_1_3 = 1
invariant :po_d1_n1_2_2_3_3 + pol_d1_n1_2_2_3_3 = 1
invariant :pi_d4_n1_3_2_2_2 + pil_d4_n1_3_2_2_2 = 1
invariant :pi_d4_n1_2_1_2_2 + pil_d4_n1_2_1_2_2 = 1
invariant :pi_d4_n1_2_1_3_3 + pil_d4_n1_2_1_3_3 = 1
invariant :po_d3_n1_1_3_3_1 + pol_d3_n1_1_3_3_1 = 1
invariant :po_d4_n1_3_3_1_3 + pol_d4_n1_3_3_1_3 = 1
invariant :pi_d4_n1_1_3_1_4 + pil_d4_n1_1_3_1_4 = 1
invariant :pi_d3_n1_3_3_2_3 + pil_d3_n1_3_3_2_3 = 1
invariant :po_d3_n1_2_3_4_2 + pol_d3_n1_2_3_4_2 = 1
invariant :pi_d1_n1_3_2_2_3 + pil_d1_n1_3_2_2_3 = 1
invariant :pi_d3_n1_2_1_2_1 + pil_d3_n1_2_1_2_1 = 1
invariant :pb_d1_n1_2_2_1_3 + pb_d1_n2_2_2_1_3 + pb_d2_n1_2_2_1_3 + pb_d2_n2_2_2_1_3 + pb_d3_n1_2_2_1_3 + pb_d3_n2_2_2_1_3 + pb_d4_n1_2_2_1_3 + pb_d4_n2_2_2_1_3 + pbl_2_2_1_3 = 36
invariant :pi_d1_n1_4_1_2_3 + pil_d1_n1_4_1_2_3 = 1
invariant :pi_d2_n1_2_2_2_3 + pil_d2_n1_2_2_2_3 = 1
invariant :pi_d2_n1_2_3_1_1 + pil_d2_n1_2_3_1_1 = 1
invariant :po_d4_n1_1_2_3_2 + pol_d4_n1_1_2_3_2 = 1
invariant :po_d4_n1_2_1_2_1 + pol_d4_n1_2_1_2_1 = 1
invariant :po_d1_n1_2_3_2_2 + pol_d1_n1_2_3_2_2 = 1
invariant :pb_d1_n1_2_2_1_2 + pb_d1_n2_2_2_1_2 + pb_d2_n1_2_2_1_2 + pb_d2_n2_2_2_1_2 + pb_d3_n1_2_2_1_2 + pb_d3_n2_2_2_1_2 + pb_d4_n1_2_2_1_2 + pb_d4_n2_2_2_1_2 + pbl_2_2_1_2 = 36
invariant :po_d2_n1_2_3_3_2 + pol_d2_n1_2_3_3_2 = 1
invariant :pi_d1_n1_3_3_3_1 + pil_d1_n1_3_3_3_1 = 1
invariant :pi_d2_n1_3_4_1_2 + pil_d2_n1_3_4_1_2 = 1
invariant :po_d3_n1_2_3_3_2 + pol_d3_n1_2_3_3_2 = 1
invariant :po_d2_n1_1_4_1_1 + pol_d2_n1_1_4_1_1 = 1
invariant :po_d2_n1_3_1_2_2 + pol_d2_n1_3_1_2_2 = 1
invariant :po_d1_n1_4_3_2_1 + pol_d1_n1_4_3_2_1 = 1
invariant :pi_d1_n1_1_1_1_1 + pil_d1_n1_1_1_1_1 = 1
invariant :po_d1_n1_4_3_1_1 + pol_d1_n1_4_3_1_1 = 1
invariant :po_d4_n1_2_1_1_1 + pol_d4_n1_2_1_1_1 = 1
invariant :po_d1_n1_4_1_3_1 + pol_d1_n1_4_1_3_1 = 1
invariant :pi_d1_n1_4_3_2_3 + pil_d1_n1_4_3_2_3 = 1
invariant :pi_d2_n1_2_4_1_2 + pil_d2_n1_2_4_1_2 = 1
invariant :po_d3_n1_2_2_2_2 + pol_d3_n1_2_2_2_2 = 1
invariant :pi_d2_n1_3_4_3_1 + pil_d2_n1_3_4_3_1 = 1
invariant :po_d1_n1_2_1_1_1 + pol_d1_n1_2_1_1_1 = 1
invariant :pi_d3_n1_2_1_2_3 + pil_d3_n1_2_1_2_3 = 1
invariant :pi_d3_n1_3_3_2_2 + pil_d3_n1_3_3_2_2 = 1
invariant :po_d4_n1_1_1_1_3 + pol_d4_n1_1_1_1_3 = 1
invariant :po_d3_n1_3_3_3_2 + pol_d3_n1_3_3_3_2 = 1
invariant :po_d4_n1_3_3_2_3 + pol_d4_n1_3_3_2_3 = 1
invariant :po_d3_n1_2_1_2_1 + pol_d3_n1_2_1_2_1 = 1
invariant :po_d1_n1_1_1_2_1 + pol_d1_n1_1_1_2_1 = 1
invariant :pi_d2_n1_2_1_2_1 + pil_d2_n1_2_1_2_1 = 1
invariant :pb_d1_n1_1_2_3_2 + pb_d1_n2_1_2_3_2 + pb_d2_n1_1_2_3_2 + pb_d2_n2_1_2_3_2 + pb_d3_n1_1_2_3_2 + pb_d3_n2_1_2_3_2 + pb_d4_n1_1_2_3_2 + pb_d4_n2_1_2_3_2 + pbl_1_2_3_2 = 36
invariant :pi_d2_n1_2_3_2_3 + pil_d2_n1_2_3_2_3 = 1
invariant :pi_d3_n1_3_2_4_2 + pil_d3_n1_3_2_4_2 = 1
invariant :po_d2_n1_1_4_3_3 + pol_d2_n1_1_4_3_3 = 1
invariant :po_d2_n1_2_2_1_1 + pol_d2_n1_2_2_1_1 = 1
invariant :pb_d1_n1_1_3_3_2 + pb_d1_n2_1_3_3_2 + pb_d2_n1_1_3_3_2 + pb_d2_n2_1_3_3_2 + pb_d3_n1_1_3_3_2 + pb_d3_n2_1_3_3_2 + pb_d4_n1_1_3_3_2 + pb_d4_n2_1_3_3_2 + pbl_1_3_3_2 = 36
invariant :pi_d2_n1_3_1_3_1 + pil_d2_n1_3_1_3_1 = 1
invariant :po_d2_n1_2_3_1_3 + pol_d2_n1_2_3_1_3 = 1
invariant :pb_d1_n1_2_3_1_1 + pb_d1_n2_2_3_1_1 + pb_d2_n1_2_3_1_1 + pb_d2_n2_2_3_1_1 + pb_d3_n1_2_3_1_1 + pb_d3_n2_2_3_1_1 + pb_d4_n1_2_3_1_1 + pb_d4_n2_2_3_1_1 + pbl_2_3_1_1 = 36
invariant :po_d1_n1_4_1_3_2 + pol_d1_n1_4_1_3_2 = 1
invariant :po_d4_n1_3_2_3_3 + pol_d4_n1_3_2_3_3 = 1
invariant :po_d2_n1_2_2_2_1 + pol_d2_n1_2_2_2_1 = 1
invariant :pi_d4_n1_1_1_3_1 + pil_d4_n1_1_1_3_1 = 1
invariant :pi_d1_n1_2_1_1_2 + pil_d1_n1_2_1_1_2 = 1
invariant :pi_d3_n1_1_1_1_1 + pil_d3_n1_1_1_1_1 = 1
invariant :po_d3_n1_3_1_1_3 + pol_d3_n1_3_1_1_3 = 1
invariant :pi_d1_n1_3_3_2_2 + pil_d1_n1_3_3_2_2 = 1
invariant :pb_d1_n1_2_1_3_3 + pb_d1_n2_2_1_3_3 + pb_d2_n1_2_1_3_3 + pb_d2_n2_2_1_3_3 + pb_d3_n1_2_1_3_3 + pb_d3_n2_2_1_3_3 + pb_d4_n1_2_1_3_3 + pb_d4_n2_2_1_3_3 + pbl_2_1_3_3 = 36
invariant :pi_d3_n1_2_2_2_2 + pil_d3_n1_2_2_2_2 = 1
invariant :po_d1_n1_2_3_2_1 + pol_d1_n1_2_3_2_1 = 1
invariant :pb_d1_n1_2_1_2_3 + pb_d1_n2_2_1_2_3 + pb_d2_n1_2_1_2_3 + pb_d2_n2_2_1_2_3 + pb_d3_n1_2_1_2_3 + pb_d3_n2_2_1_2_3 + pb_d4_n1_2_1_2_3 + pb_d4_n2_2_1_2_3 + pbl_2_1_2_3 = 36
invariant :po_d3_n1_1_3_1_2 + pol_d3_n1_1_3_1_2 = 1
invariant :pi_d2_n1_2_4_1_3 + pil_d2_n1_2_4_1_3 = 1
invariant :pi_d4_n1_3_1_1_1 + pil_d4_n1_3_1_1_1 = 1
invariant :po_d4_n1_3_3_3_3 + pol_d4_n1_3_3_3_3 = 1
invariant :po_d2_n1_1_1_2_3 + pol_d2_n1_1_1_2_3 = 1
invariant :po_d4_n1_3_1_3_2 + pol_d4_n1_3_1_3_2 = 1
invariant :po_d4_n1_3_2_3_1 + pol_d4_n1_3_2_3_1 = 1
invariant :po_d2_n1_2_2_2_3 + pol_d2_n1_2_2_2_3 = 1
invariant :pi_d4_n1_1_2_2_1 + pil_d4_n1_1_2_2_1 = 1
invariant :pi_d2_n1_2_4_2_3 + pil_d2_n1_2_4_2_3 = 1
invariant :po_d1_n1_2_1_2_2 + pol_d1_n1_2_1_2_2 = 1
invariant :po_d1_n1_2_3_1_3 + pol_d1_n1_2_3_1_3 = 1
invariant :po_d2_n1_3_1_3_1 + pol_d2_n1_3_1_3_1 = 1
invariant :pb_d1_n1_1_3_1_2 + pb_d1_n2_1_3_1_2 + pb_d2_n1_1_3_1_2 + pb_d2_n2_1_3_1_2 + pb_d3_n1_1_3_1_2 + pb_d3_n2_1_3_1_2 + pb_d4_n1_1_3_1_2 + pb_d4_n2_1_3_1_2 + pbl_1_3_1_2 = 36
invariant :pi_d1_n1_4_2_3_1 + pil_d1_n1_4_2_3_1 = 1
invariant :pi_d3_n1_1_2_3_1 + pil_d3_n1_1_2_3_1 = 1
invariant :po_d3_n1_1_3_3_2 + pol_d3_n1_1_3_3_2 = 1
invariant :pi_d4_n1_3_2_1_4 + pil_d4_n1_3_2_1_4 = 1
invariant :po_d2_n1_1_3_2_2 + pol_d2_n1_1_3_2_2 = 1
invariant :pi_d4_n1_2_1_1_4 + pil_d4_n1_2_1_1_4 = 1
invariant :po_d3_n1_3_2_4_2 + pol_d3_n1_3_2_4_2 = 1
invariant :po_d4_n1_2_3_3_4 + pol_d4_n1_2_3_3_4 = 1
invariant :pi_d4_n1_1_2_1_1 + pil_d4_n1_1_2_1_1 = 1
invariant :pi_d1_n1_1_2_1_1 + pil_d1_n1_1_2_1_1 = 1
invariant :pi_d2_n1_3_3_3_2 + pil_d2_n1_3_3_3_2 = 1
invariant :pi_d2_n1_2_1_3_1 + pil_d2_n1_2_1_3_1 = 1
invariant :pi_d4_n1_3_1_3_4 + pil_d4_n1_3_1_3_4 = 1
invariant :pb_d1_n1_2_3_3_2 + pb_d1_n2_2_3_3_2 + pb_d2_n1_2_3_3_2 + pb_d2_n2_2_3_3_2 + pb_d3_n1_2_3_3_2 + pb_d3_n2_2_3_3_2 + pb_d4_n1_2_3_3_2 + pb_d4_n2_2_3_3_2 + pbl_2_3_3_2 = 36
invariant :po_d1_n1_1_3_2_2 + pol_d1_n1_1_3_2_2 = 1
invariant :po_d4_n1_1_1_3_4 + pol_d4_n1_1_1_3_4 = 1
invariant :po_d1_n1_4_1_2_3 + pol_d1_n1_4_1_2_3 = 1
invariant :po_d3_n1_1_3_2_3 + pol_d3_n1_1_3_2_3 = 1
invariant :pi_d3_n1_2_1_4_1 + pil_d3_n1_2_1_4_1 = 1
invariant :po_d1_n1_3_1_2_1 + pol_d1_n1_3_1_2_1 = 1
invariant :pi_d3_n1_3_3_4_2 + pil_d3_n1_3_3_4_2 = 1
invariant :po_d3_n1_1_2_3_1 + pol_d3_n1_1_2_3_1 = 1
invariant :pb_d1_n1_1_1_1_1 + pb_d1_n2_1_1_1_1 + pb_d2_n1_1_1_1_1 + pb_d2_n2_1_1_1_1 + pb_d3_n1_1_1_1_1 + pb_d3_n2_1_1_1_1 + pb_d4_n1_1_1_1_1 + pb_d4_n2_1_1_1_1 + pbl_1_1_1_1 = 36
invariant :po_d3_n1_1_2_1_3 + pol_d3_n1_1_2_1_3 = 1
invariant :po_d2_n1_1_2_2_1 + pol_d2_n1_1_2_2_1 = 1
invariant :po_d2_n1_2_4_2_1 + pol_d2_n1_2_4_2_1 = 1
invariant :po_d4_n1_2_1_1_3 + pol_d4_n1_2_1_1_3 = 1
invariant :pb_d1_n1_1_1_3_2 + pb_d1_n2_1_1_3_2 + pb_d2_n1_1_1_3_2 + pb_d2_n2_1_1_3_2 + pb_d3_n1_1_1_3_2 + pb_d3_n2_1_1_3_2 + pb_d4_n1_1_1_3_2 + pb_d4_n2_1_1_3_2 + pbl_1_1_3_2 = 36
invariant :pi_d1_n1_3_1_2_3 + pil_d1_n1_3_1_2_3 = 1
invariant :po_d4_n1_3_3_1_2 + pol_d4_n1_3_3_1_2 = 1
invariant :po_d1_n1_3_2_2_3 + pol_d1_n1_3_2_2_3 = 1
invariant :pb_d1_n1_3_2_3_1 + pb_d1_n2_3_2_3_1 + pb_d2_n1_3_2_3_1 + pb_d2_n2_3_2_3_1 + pb_d3_n1_3_2_3_1 + pb_d3_n2_3_2_3_1 + pb_d4_n1_3_2_3_1 + pb_d4_n2_3_2_3_1 + pbl_3_2_3_1 = 36
invariant :pi_d4_n1_3_3_2_3 + pil_d4_n1_3_3_2_3 = 1
invariant :po_d3_n1_1_1_3_3 + pol_d3_n1_1_1_3_3 = 1
invariant :pi_d1_n1_3_3_2_3 + pil_d1_n1_3_3_2_3 = 1
invariant :pi_d2_n1_2_4_3_1 + pil_d2_n1_2_4_3_1 = 1
invariant :pi_d4_n1_3_1_3_1 + pil_d4_n1_3_1_3_1 = 1
invariant :po_d1_n1_4_1_1_2 + pol_d1_n1_4_1_1_2 = 1
invariant :po_d2_n1_2_4_3_3 + pol_d2_n1_2_4_3_3 = 1
invariant :po_d4_n1_2_2_2_1 + pol_d4_n1_2_2_2_1 = 1
invariant :pi_d3_n1_2_1_1_1 + pil_d3_n1_2_1_1_1 = 1
invariant :pi_d4_n1_2_2_3_2 + pil_d4_n1_2_2_3_2 = 1
invariant :pi_d4_n1_3_1_1_2 + pil_d4_n1_3_1_1_2 = 1
invariant :po_d2_n1_2_3_2_1 + pol_d2_n1_2_3_2_1 = 1
invariant :po_d3_n1_2_2_1_2 + pol_d3_n1_2_2_1_2 = 1
invariant :pi_d3_n1_2_3_1_1 + pil_d3_n1_2_3_1_1 = 1
invariant :pb_d1_n1_2_2_3_2 + pb_d1_n2_2_2_3_2 + pb_d2_n1_2_2_3_2 + pb_d2_n2_2_2_3_2 + pb_d3_n1_2_2_3_2 + pb_d3_n2_2_2_3_2 + pb_d4_n1_2_2_3_2 + pb_d4_n2_2_2_3_2 + pbl_2_2_3_2 = 36
invariant :po_d3_n1_1_1_1_1 + pol_d3_n1_1_1_1_1 = 1
invariant :po_d2_n1_3_2_3_1 + pol_d2_n1_3_2_3_1 = 1
invariant :po_d3_n1_2_1_3_3 + pol_d3_n1_2_1_3_3 = 1
invariant :po_d4_n1_3_1_3_1 + pol_d4_n1_3_1_3_1 = 1
invariant :po_d2_n1_2_2_3_3 + pol_d2_n1_2_2_3_3 = 1
invariant :po_d4_n1_1_1_1_2 + pol_d4_n1_1_1_1_2 = 1
invariant :pi_d2_n1_3_1_1_2 + pil_d2_n1_3_1_1_2 = 1
invariant :pi_d1_n1_1_3_3_3 + pil_d1_n1_1_3_3_3 = 1
invariant :po_d3_n1_3_3_2_2 + pol_d3_n1_3_3_2_2 = 1
invariant :pi_d4_n1_3_3_3_4 + pil_d4_n1_3_3_3_4 = 1
invariant :po_d1_n1_1_2_1_2 + pol_d1_n1_1_2_1_2 = 1
invariant :pi_d1_n1_1_3_2_3 + pil_d1_n1_1_3_2_3 = 1
invariant :pi_d2_n1_3_1_2_2 + pil_d2_n1_3_1_2_2 = 1
invariant :po_d4_n1_1_2_3_4 + pol_d4_n1_1_2_3_4 = 1
invariant :po_d4_n1_2_1_2_4 + pol_d4_n1_2_1_2_4 = 1
invariant :po_d4_n1_2_1_3_1 + pol_d4_n1_2_1_3_1 = 1
invariant :po_d2_n1_1_3_1_1 + pol_d2_n1_1_3_1_1 = 1
invariant :po_d2_n1_3_1_3_2 + pol_d2_n1_3_1_3_2 = 1
invariant :pi_d1_n1_3_1_3_1 + pil_d1_n1_3_1_3_1 = 1
invariant :pi_d4_n1_1_1_1_2 + pil_d4_n1_1_1_1_2 = 1
invariant :pi_d4_n1_3_2_3_1 + pil_d4_n1_3_2_3_1 = 1
invariant :po_d1_n1_2_1_1_3 + pol_d1_n1_2_1_1_3 = 1
invariant :pi_d3_n1_2_3_3_1 + pil_d3_n1_2_3_3_1 = 1
invariant :pi_d2_n1_1_2_1_2 + pil_d2_n1_1_2_1_2 = 1
invariant :po_d3_n1_1_2_4_3 + pol_d3_n1_1_2_4_3 = 1
invariant :pi_d1_n1_4_2_3_2 + pil_d1_n1_4_2_3_2 = 1
invariant :po_d4_n1_2_3_2_4 + pol_d4_n1_2_3_2_4 = 1
invariant :po_d2_n1_1_4_2_3 + pol_d2_n1_1_4_2_3 = 1
invariant :pi_d4_n1_2_2_3_4 + pil_d4_n1_2_2_3_4 = 1
invariant :pi_d4_n1_3_1_2_3 + pil_d4_n1_3_1_2_3 = 1
invariant :pi_d4_n1_1_2_2_4 + pil_d4_n1_1_2_2_4 = 1
invariant :po_d2_n1_1_1_1_3 + pol_d2_n1_1_1_1_3 = 1
invariant :pi_d1_n1_2_1_2_1 + pil_d1_n1_2_1_2_1 = 1
invariant :pi_d3_n1_3_1_1_1 + pil_d3_n1_3_1_1_1 = 1
invariant :pi_d4_n1_2_2_2_4 + pil_d4_n1_2_2_2_4 = 1
invariant :pb_d1_n1_3_1_3_3 + pb_d1_n2_3_1_3_3 + pb_d2_n1_3_1_3_3 + pb_d2_n2_3_1_3_3 + pb_d3_n1_3_1_3_3 + pb_d3_n2_3_1_3_3 + pb_d4_n1_3_1_3_3 + pb_d4_n2_3_1_3_3 + pbl_3_1_3_3 = 36
invariant :pi_d3_n1_1_1_2_1 + pil_d3_n1_1_1_2_1 = 1
invariant :po_d1_n1_1_3_2_1 + pol_d1_n1_1_3_2_1 = 1
invariant :pb_d1_n1_3_3_3_1 + pb_d1_n2_3_3_3_1 + pb_d2_n1_3_3_3_1 + pb_d2_n2_3_3_3_1 + pb_d3_n1_3_3_3_1 + pb_d3_n2_3_3_3_1 + pb_d4_n1_3_3_3_1 + pb_d4_n2_3_3_3_1 + pbl_3_3_3_1 = 36
invariant :po_d2_n1_2_1_1_2 + pol_d2_n1_2_1_1_2 = 1
invariant :po_d2_n1_1_1_2_2 + pol_d2_n1_1_1_2_2 = 1
invariant :po_d2_n1_1_1_3_3 + pol_d2_n1_1_1_3_3 = 1
invariant :pi_d1_n1_3_3_2_1 + pil_d1_n1_3_3_2_1 = 1
invariant :po_d2_n1_1_3_3_2 + pol_d2_n1_1_3_3_2 = 1
invariant :pi_d2_n1_3_4_2_1 + pil_d2_n1_3_4_2_1 = 1
invariant :pi_d4_n1_3_1_1_3 + pil_d4_n1_3_1_1_3 = 1
invariant :pb_d1_n1_2_3_2_1 + pb_d1_n2_2_3_2_1 + pb_d2_n1_2_3_2_1 + pb_d2_n2_2_3_2_1 + pb_d3_n1_2_3_2_1 + pb_d3_n2_2_3_2_1 + pb_d4_n1_2_3_2_1 + pb_d4_n2_2_3_2_1 + pbl_2_3_2_1 = 36
invariant :pi_d2_n1_1_2_3_1 + pil_d2_n1_1_2_3_1 = 1
invariant :po_d4_n1_3_1_3_3 + pol_d4_n1_3_1_3_3 = 1
invariant :pi_d1_n1_4_1_1_2 + pil_d1_n1_4_1_1_2 = 1
invariant :po_d1_n1_4_1_2_2 + pol_d1_n1_4_1_2_2 = 1
invariant :po_d3_n1_2_3_2_1 + pol_d3_n1_2_3_2_1 = 1
invariant :pi_d2_n1_1_4_1_2 + pil_d2_n1_1_4_1_2 = 1
invariant :pi_d3_n1_2_2_2_1 + pil_d3_n1_2_2_2_1 = 1
invariant :pi_d2_n1_3_2_1_2 + pil_d2_n1_3_2_1_2 = 1
invariant :po_d3_n1_1_2_2_2 + pol_d3_n1_1_2_2_2 = 1
invariant :pb_d1_n1_1_1_3_3 + pb_d1_n2_1_1_3_3 + pb_d2_n1_1_1_3_3 + pb_d2_n2_1_1_3_3 + pb_d3_n1_1_1_3_3 + pb_d3_n2_1_1_3_3 + pb_d4_n1_1_1_3_3 + pb_d4_n2_1_1_3_3 + pbl_1_1_3_3 = 36
invariant :po_d2_n1_1_2_3_1 + pol_d2_n1_1_2_3_1 = 1
invariant :pi_d1_n1_2_2_1_1 + pil_d1_n1_2_2_1_1 = 1
invariant :pi_d1_n1_4_3_3_2 + pil_d1_n1_4_3_3_2 = 1
invariant :pi_d3_n1_2_3_4_2 + pil_d3_n1_2_3_4_2 = 1
invariant :po_d1_n1_3_3_2_3 + pol_d1_n1_3_3_2_3 = 1
invariant :po_d2_n1_3_4_1_1 + pol_d2_n1_3_4_1_1 = 1
invariant :po_d4_n1_2_2_1_1 + pol_d4_n1_2_2_1_1 = 1
invariant :pb_d1_n1_2_2_1_1 + pb_d1_n2_2_2_1_1 + pb_d2_n1_2_2_1_1 + pb_d2_n2_2_2_1_1 + pb_d3_n1_2_2_1_1 + pb_d3_n2_2_2_1_1 + pb_d4_n1_2_2_1_1 + pb_d4_n2_2_2_1_1 + pbl_2_2_1_1 = 36
invariant :po_d3_n1_2_2_3_3 + pol_d3_n1_2_2_3_3 = 1
invariant :po_d2_n1_1_4_3_2 + pol_d2_n1_1_4_3_2 = 1
invariant :po_d3_n1_3_3_1_3 + pol_d3_n1_3_3_1_3 = 1
invariant :po_d3_n1_1_3_4_3 + pol_d3_n1_1_3_4_3 = 1
invariant :pi_d1_n1_3_2_2_1 + pil_d1_n1_3_2_2_1 = 1
invariant :pi_d2_n1_3_4_2_3 + pil_d2_n1_3_4_2_3 = 1
invariant :pi_d4_n1_1_2_3_1 + pil_d4_n1_1_2_3_1 = 1
invariant :po_d3_n1_1_2_4_1 + pol_d3_n1_1_2_4_1 = 1
invariant :pb_d1_n1_1_1_2_2 + pb_d1_n2_1_1_2_2 + pb_d2_n1_1_1_2_2 + pb_d2_n2_1_1_2_2 + pb_d3_n1_1_1_2_2 + pb_d3_n2_1_1_2_2 + pb_d4_n1_1_1_2_2 + pb_d4_n2_1_1_2_2 + pbl_1_1_2_2 = 36
invariant :pi_d4_n1_1_1_1_4 + pil_d4_n1_1_1_1_4 = 1
invariant :pi_d2_n1_1_1_1_1 + pil_d2_n1_1_1_1_1 = 1
invariant :po_d4_n1_3_3_1_1 + pol_d4_n1_3_3_1_1 = 1
invariant :pi_d1_n1_1_1_3_1 + pil_d1_n1_1_1_3_1 = 1
invariant :po_d4_n1_3_2_3_4 + pol_d4_n1_3_2_3_4 = 1
invariant :pi_d3_n1_3_3_1_1 + pil_d3_n1_3_3_1_1 = 1
invariant :pi_d2_n1_2_4_2_1 + pil_d2_n1_2_4_2_1 = 1
invariant :pi_d4_n1_1_3_2_3 + pil_d4_n1_1_3_2_3 = 1
invariant :pi_d4_n1_2_2_2_1 + pil_d4_n1_2_2_2_1 = 1
invariant :po_d4_n1_3_1_1_1 + pol_d4_n1_3_1_1_1 = 1
invariant :pi_d2_n1_1_2_2_2 + pil_d2_n1_1_2_2_2 = 1
invariant :pi_d1_n1_4_3_3_3 + pil_d1_n1_4_3_3_3 = 1
invariant :pi_d1_n1_2_3_3_2 + pil_d1_n1_2_3_3_2 = 1
invariant :po_d4_n1_2_1_2_2 + pol_d4_n1_2_1_2_2 = 1
invariant :po_d3_n1_1_2_2_3 + pol_d3_n1_1_2_2_3 = 1
invariant :po_d3_n1_3_2_1_1 + pol_d3_n1_3_2_1_1 = 1
invariant :pb_d1_n1_2_3_2_3 + pb_d1_n2_2_3_2_3 + pb_d2_n1_2_3_2_3 + pb_d2_n2_2_3_2_3 + pb_d3_n1_2_3_2_3 + pb_d3_n2_2_3_2_3 + pb_d4_n1_2_3_2_3 + pb_d4_n2_2_3_2_3 + pbl_2_3_2_3 = 36
invariant :pi_d3_n1_2_2_3_1 + pil_d3_n1_2_2_3_1 = 1
invariant :pi_d1_n1_2_2_1_2 + pil_d1_n1_2_2_1_2 = 1
invariant :pi_d3_n1_3_3_4_1 + pil_d3_n1_3_3_4_1 = 1
invariant :pi_d1_n1_2_1_3_1 + pil_d1_n1_2_1_3_1 = 1
invariant :pi_d4_n1_1_2_2_2 + pil_d4_n1_1_2_2_2 = 1
invariant :po_d1_n1_4_1_3_3 + pol_d1_n1_4_1_3_3 = 1
invariant :po_d3_n1_1_1_3_1 + pol_d3_n1_1_1_3_1 = 1
invariant :po_d4_n1_1_2_2_4 + pol_d4_n1_1_2_2_4 = 1
invariant :pi_d2_n1_3_3_1_3 + pil_d2_n1_3_3_1_3 = 1
invariant :pi_d3_n1_2_3_2_2 + pil_d3_n1_2_3_2_2 = 1
invariant :po_d1_n1_3_1_2_3 + pol_d1_n1_3_1_2_3 = 1
invariant :po_d1_n1_4_3_3_3 + pol_d1_n1_4_3_3_3 = 1
invariant :po_d4_n1_1_2_2_1 + pol_d4_n1_1_2_2_1 = 1
invariant :po_d3_n1_1_3_1_3 + pol_d3_n1_1_3_1_3 = 1
invariant :pi_d4_n1_3_2_1_1 + pil_d4_n1_3_2_1_1 = 1
invariant :pi_d4_n1_3_3_1_3 + pil_d4_n1_3_3_1_3 = 1
invariant :po_d3_n1_1_2_4_2 + pol_d3_n1_1_2_4_2 = 1
invariant :pi_d1_n1_3_3_3_2 + pil_d1_n1_3_3_3_2 = 1
invariant :po_d3_n1_1_2_3_2 + pol_d3_n1_1_2_3_2 = 1
invariant :po_d2_n1_3_2_2_1 + pol_d2_n1_3_2_2_1 = 1
invariant :pi_d3_n1_3_1_3_2 + pil_d3_n1_3_1_3_2 = 1
invariant :po_d1_n1_2_3_2_3 + pol_d1_n1_2_3_2_3 = 1
invariant :po_d2_n1_3_3_2_3 + pol_d2_n1_3_3_2_3 = 1
invariant :po_d4_n1_2_3_2_3 + pol_d4_n1_2_3_2_3 = 1
invariant :po_d4_n1_2_3_1_4 + pol_d4_n1_2_3_1_4 = 1
invariant :pi_d4_n1_3_2_1_2 + pil_d4_n1_3_2_1_2 = 1
invariant :pi_d2_n1_1_1_2_1 + pil_d2_n1_1_1_2_1 = 1
invariant :po_d4_n1_3_3_2_4 + pol_d4_n1_3_3_2_4 = 1
invariant :pi_d1_n1_1_2_2_3 + pil_d1_n1_1_2_2_3 = 1
invariant :po_d4_n1_1_1_2_2 + pol_d4_n1_1_1_2_2 = 1
invariant :po_d4_n1_2_1_3_3 + pol_d4_n1_2_1_3_3 = 1
invariant :pi_d3_n1_2_1_3_2 + pil_d3_n1_2_1_3_2 = 1
invariant :po_d2_n1_2_2_1_2 + pol_d2_n1_2_2_1_2 = 1
invariant :po_d1_n1_3_3_1_1 + pol_d1_n1_3_3_1_1 = 1
invariant :pi_d1_n1_2_3_2_2 + pil_d1_n1_2_3_2_2 = 1
invariant :pi_d4_n1_1_2_2_3 + pil_d4_n1_1_2_2_3 = 1
invariant :pi_d3_n1_1_3_3_2 + pil_d3_n1_1_3_3_2 = 1
invariant :pi_d3_n1_1_3_3_3 + pil_d3_n1_1_3_3_3 = 1
invariant :pi_d3_n1_2_1_4_2 + pil_d3_n1_2_1_4_2 = 1
invariant :pi_d3_n1_3_1_2_1 + pil_d3_n1_3_1_2_1 = 1
invariant :po_d1_n1_3_3_2_1 + pol_d1_n1_3_3_2_1 = 1
invariant :pi_d1_n1_3_3_1_2 + pil_d1_n1_3_3_1_2 = 1
invariant :pi_d2_n1_2_2_1_2 + pil_d2_n1_2_2_1_2 = 1
invariant :pi_d2_n1_2_2_1_1 + pil_d2_n1_2_2_1_1 = 1
invariant :po_d1_n1_2_3_1_1 + pol_d1_n1_2_3_1_1 = 1
invariant :po_d1_n1_4_1_1_3 + pol_d1_n1_4_1_1_3 = 1
invariant :pi_d1_n1_2_2_2_2 + pil_d1_n1_2_2_2_2 = 1
invariant :pi_d2_n1_2_1_2_3 + pil_d2_n1_2_1_2_3 = 1
invariant :pi_d3_n1_2_2_1_3 + pil_d3_n1_2_2_1_3 = 1
invariant :pi_d1_n1_1_1_2_3 + pil_d1_n1_1_1_2_3 = 1
invariant :po_d2_n1_3_2_1_2 + pol_d2_n1_3_2_1_2 = 1
invariant :pi_d4_n1_3_1_1_4 + pil_d4_n1_3_1_1_4 = 1
invariant :po_d2_n1_1_3_1_2 + pol_d2_n1_1_3_1_2 = 1
invariant :pi_d4_n1_3_2_2_4 + pil_d4_n1_3_2_2_4 = 1
invariant :pb_d1_n1_1_2_1_2 + pb_d1_n2_1_2_1_2 + pb_d2_n1_1_2_1_2 + pb_d2_n2_1_2_1_2 + pb_d3_n1_1_2_1_2 + pb_d3_n2_1_2_1_2 + pb_d4_n1_1_2_1_2 + pb_d4_n2_1_2_1_2 + pbl_1_2_1_2 = 36
invariant :pi_d2_n1_3_4_1_1 + pil_d2_n1_3_4_1_1 = 1
invariant :po_d2_n1_2_1_2_3 + pol_d2_n1_2_1_2_3 = 1
invariant :pi_d1_n1_2_3_1_1 + pil_d1_n1_2_3_1_1 = 1
invariant :pi_d1_n1_4_2_2_2 + pil_d1_n1_4_2_2_2 = 1
invariant :po_d1_n1_4_2_3_3 + pol_d1_n1_4_2_3_3 = 1
invariant :po_d4_n1_2_3_3_2 + pol_d4_n1_2_3_3_2 = 1
invariant :pi_d3_n1_2_2_4_1 + pil_d3_n1_2_2_4_1 = 1
invariant :pi_d1_n1_4_1_1_1 + pil_d1_n1_4_1_1_1 = 1
invariant :pi_d1_n1_1_2_1_2 + pil_d1_n1_1_2_1_2 = 1
invariant :pb_d1_n1_1_2_2_3 + pb_d1_n2_1_2_2_3 + pb_d2_n1_1_2_2_3 + pb_d2_n2_1_2_2_3 + pb_d3_n1_1_2_2_3 + pb_d3_n2_1_2_2_3 + pb_d4_n1_1_2_2_3 + pb_d4_n2_1_2_2_3 + pbl_1_2_2_3 = 36
invariant :pb_d1_n1_2_1_3_2 + pb_d1_n2_2_1_3_2 + pb_d2_n1_2_1_3_2 + pb_d2_n2_2_1_3_2 + pb_d3_n1_2_1_3_2 + pb_d3_n2_2_1_3_2 + pb_d4_n1_2_1_3_2 + pb_d4_n2_2_1_3_2 + pbl_2_1_3_2 = 36
invariant :pb_d1_n1_1_2_1_3 + pb_d1_n2_1_2_1_3 + pb_d2_n1_1_2_1_3 + pb_d2_n2_1_2_1_3 + pb_d3_n1_1_2_1_3 + pb_d3_n2_1_2_1_3 + pb_d4_n1_1_2_1_3 + pb_d4_n2_1_2_1_3 + pbl_1_2_1_3 = 36
invariant :pi_d3_n1_3_2_1_1 + pil_d3_n1_3_2_1_1 = 1
invariant :pi_d3_n1_1_2_4_3 + pil_d3_n1_1_2_4_3 = 1
invariant :pi_d4_n1_2_2_3_3 + pil_d4_n1_2_2_3_3 = 1
invariant :po_d2_n1_3_3_3_1 + pol_d2_n1_3_3_3_1 = 1
invariant :po_d2_n1_2_1_3_1 + pol_d2_n1_2_1_3_1 = 1
invariant :pi_d1_n1_4_3_2_2 + pil_d1_n1_4_3_2_2 = 1
invariant :pi_d4_n1_2_2_1_2 + pil_d4_n1_2_2_1_2 = 1
invariant :po_d3_n1_2_2_2_3 + pol_d3_n1_2_2_2_3 = 1
invariant :po_d4_n1_1_3_1_1 + pol_d4_n1_1_3_1_1 = 1
invariant :po_d1_n1_3_1_3_2 + pol_d1_n1_3_1_3_2 = 1
invariant :pi_d2_n1_3_2_2_1 + pil_d2_n1_3_2_2_1 = 1
invariant :pi_d2_n1_3_2_2_3 + pil_d2_n1_3_2_2_3 = 1
invariant :po_d2_n1_3_3_3_3 + pol_d2_n1_3_3_3_3 = 1
invariant :pi_d4_n1_2_2_2_2 + pil_d4_n1_2_2_2_2 = 1
invariant :po_d3_n1_2_2_1_1 + pol_d3_n1_2_2_1_1 = 1
invariant :pi_d4_n1_1_3_1_1 + pil_d4_n1_1_3_1_1 = 1
invariant :po_d2_n1_3_3_2_2 + pol_d2_n1_3_3_2_2 = 1
invariant :pi_d3_n1_3_1_4_3 + pil_d3_n1_3_1_4_3 = 1
invariant :pi_d4_n1_3_2_2_1 + pil_d4_n1_3_2_2_1 = 1
invariant :po_d2_n1_1_3_1_3 + pol_d2_n1_1_3_1_3 = 1
invariant :pi_d4_n1_1_3_2_4 + pil_d4_n1_1_3_2_4 = 1
invariant :pi_d2_n1_1_2_2_1 + pil_d2_n1_1_2_2_1 = 1
invariant :pi_d4_n1_2_1_1_1 + pil_d4_n1_2_1_1_1 = 1
invariant :po_d3_n1_1_3_4_1 + pol_d3_n1_1_3_4_1 = 1
invariant :pb_d1_n1_3_2_1_2 + pb_d1_n2_3_2_1_2 + pb_d2_n1_3_2_1_2 + pb_d2_n2_3_2_1_2 + pb_d3_n1_3_2_1_2 + pb_d3_n2_3_2_1_2 + pb_d4_n1_3_2_1_2 + pb_d4_n2_3_2_1_2 + pbl_3_2_1_2 = 36
invariant :pi_d3_n1_3_1_3_1 + pil_d3_n1_3_1_3_1 = 1
invariant :pb_d1_n1_2_2_2_1 + pb_d1_n2_2_2_2_1 + pb_d2_n1_2_2_2_1 + pb_d2_n2_2_2_2_1 + pb_d3_n1_2_2_2_1 + pb_d3_n2_2_2_2_1 + pb_d4_n1_2_2_2_1 + pb_d4_n2_2_2_2_1 + pbl_2_2_2_1 = 36
invariant :pi_d3_n1_1_3_1_3 + pil_d3_n1_1_3_1_3 = 1
invariant :po_d4_n1_3_1_2_1 + pol_d4_n1_3_1_2_1 = 1
invariant :po_d2_n1_1_2_1_1 + pol_d2_n1_1_2_1_1 = 1
invariant :po_d2_n1_2_1_3_2 + pol_d2_n1_2_1_3_2 = 1
invariant :pb_d1_n1_3_3_3_2 + pb_d1_n2_3_3_3_2 + pb_d2_n1_3_3_3_2 + pb_d2_n2_3_3_3_2 + pb_d3_n1_3_3_3_2 + pb_d3_n2_3_3_3_2 + pb_d4_n1_3_3_3_2 + pb_d4_n2_3_3_3_2 + pbl_3_3_3_2 = 36
invariant :pi_d3_n1_1_3_4_1 + pil_d3_n1_1_3_4_1 = 1
invariant :pi_d3_n1_2_3_2_3 + pil_d3_n1_2_3_2_3 = 1
invariant :po_d3_n1_3_3_2_1 + pol_d3_n1_3_3_2_1 = 1
invariant :po_d4_n1_1_1_1_4 + pol_d4_n1_1_1_1_4 = 1
invariant :pi_d1_n1_4_1_3_1 + pil_d1_n1_4_1_3_1 = 1
invariant :pi_d1_n1_3_3_1_3 + pil_d1_n1_3_3_1_3 = 1
invariant :pi_d3_n1_2_3_3_3 + pil_d3_n1_2_3_3_3 = 1
invariant :po_d1_n1_1_3_3_3 + pol_d1_n1_1_3_3_3 = 1
invariant :po_d3_n1_3_2_3_3 + pol_d3_n1_3_2_3_3 = 1
invariant :po_d4_n1_1_3_3_1 + pol_d4_n1_1_3_3_1 = 1
invariant :pi_d1_n1_1_1_2_2 + pil_d1_n1_1_1_2_2 = 1
invariant :pi_d4_n1_2_3_1_3 + pil_d4_n1_2_3_1_3 = 1
invariant :pi_d2_n1_3_1_3_2 + pil_d2_n1_3_1_3_2 = 1
invariant :po_d2_n1_1_4_3_1 + pol_d2_n1_1_4_3_1 = 1
invariant :pi_d2_n1_3_3_3_3 + pil_d2_n1_3_3_3_3 = 1
invariant :po_d2_n1_1_3_2_3 + pol_d2_n1_1_3_2_3 = 1
invariant :pi_d2_n1_2_1_2_2 + pil_d2_n1_2_1_2_2 = 1
invariant :po_d2_n1_3_2_2_2 + pol_d2_n1_3_2_2_2 = 1
invariant :po_d2_n1_1_1_2_1 + pol_d2_n1_1_1_2_1 = 1
invariant :po_d1_n1_3_2_3_2 + pol_d1_n1_3_2_3_2 = 1
invariant :pi_d3_n1_3_3_3_3 + pil_d3_n1_3_3_3_3 = 1
invariant :pi_d4_n1_2_1_1_3 + pil_d4_n1_2_1_1_3 = 1
invariant :pi_d4_n1_2_2_1_4 + pil_d4_n1_2_2_1_4 = 1
invariant :po_d4_n1_2_3_1_1 + pol_d4_n1_2_3_1_1 = 1
invariant :po_d1_n1_4_1_2_1 + pol_d1_n1_4_1_2_1 = 1
invariant :po_d2_n1_1_3_2_1 + pol_d2_n1_1_3_2_1 = 1
invariant :pi_d2_n1_1_1_3_2 + pil_d2_n1_1_1_3_2 = 1
invariant :pb_d1_n1_3_1_3_2 + pb_d1_n2_3_1_3_2 + pb_d2_n1_3_1_3_2 + pb_d2_n2_3_1_3_2 + pb_d3_n1_3_1_3_2 + pb_d3_n2_3_1_3_2 + pb_d4_n1_3_1_3_2 + pb_d4_n2_3_1_3_2 + pbl_3_1_3_2 = 36
invariant :pi_d1_n1_2_2_2_1 + pil_d1_n1_2_2_2_1 = 1
invariant :po_d4_n1_2_3_1_3 + pol_d4_n1_2_3_1_3 = 1
invariant :pi_d4_n1_2_2_1_3 + pil_d4_n1_2_2_1_3 = 1
invariant :pi_d3_n1_3_2_2_2 + pil_d3_n1_3_2_2_2 = 1
invariant :po_d4_n1_1_3_2_2 + pol_d4_n1_1_3_2_2 = 1
invariant :po_d3_n1_2_2_1_3 + pol_d3_n1_2_2_1_3 = 1
invariant :po_d1_n1_3_3_1_2 + pol_d1_n1_3_3_1_2 = 1
invariant :pi_d1_n1_2_1_2_3 + pil_d1_n1_2_1_2_3 = 1
invariant :pi_d3_n1_3_1_3_3 + pil_d3_n1_3_1_3_3 = 1
invariant :po_d3_n1_2_1_3_1 + pol_d3_n1_2_1_3_1 = 1
invariant :po_d4_n1_1_1_3_1 + pol_d4_n1_1_1_3_1 = 1
invariant :pi_d1_n1_3_2_3_2 + pil_d1_n1_3_2_3_2 = 1
invariant :po_d4_n1_3_2_1_4 + pol_d4_n1_3_2_1_4 = 1
invariant :po_d1_n1_1_3_1_1 + pol_d1_n1_1_3_1_1 = 1
invariant :po_d3_n1_2_1_1_1 + pol_d3_n1_2_1_1_1 = 1
invariant :po_d4_n1_2_1_3_2 + pol_d4_n1_2_1_3_2 = 1
invariant :pb_d1_n1_3_2_1_1 + pb_d1_n2_3_2_1_1 + pb_d2_n1_3_2_1_1 + pb_d2_n2_3_2_1_1 + pb_d3_n1_3_2_1_1 + pb_d3_n2_3_2_1_1 + pb_d4_n1_3_2_1_1 + pb_d4_n2_3_2_1_1 + pbl_3_2_1_1 = 36
invariant :po_d1_n1_4_3_1_2 + pol_d1_n1_4_3_1_2 = 1
invariant :po_d3_n1_1_1_1_3 + pol_d3_n1_1_1_1_3 = 1
invariant :po_d3_n1_1_3_2_1 + pol_d3_n1_1_3_2_1 = 1
invariant :pi_d1_n1_2_2_1_3 + pil_d1_n1_2_2_1_3 = 1
invariant :po_d1_n1_2_2_2_3 + pol_d1_n1_2_2_2_3 = 1
invariant :pi_d2_n1_1_3_1_1 + pil_d2_n1_1_3_1_1 = 1
invariant :pi_d3_n1_2_3_1_2 + pil_d3_n1_2_3_1_2 = 1
invariant :pb_d1_n1_1_1_1_3 + pb_d1_n2_1_1_1_3 + pb_d2_n1_1_1_1_3 + pb_d2_n2_1_1_1_3 + pb_d3_n1_1_1_1_3 + pb_d3_n2_1_1_1_3 + pb_d4_n1_1_1_1_3 + pb_d4_n2_1_1_1_3 + pbl_1_1_1_3 = 36
invariant :pb_d1_n1_2_3_2_2 + pb_d1_n2_2_3_2_2 + pb_d2_n1_2_3_2_2 + pb_d2_n2_2_3_2_2 + pb_d3_n1_2_3_2_2 + pb_d3_n2_2_3_2_2 + pb_d4_n1_2_3_2_2 + pb_d4_n2_2_3_2_2 + pbl_2_3_2_2 = 36
invariant :pi_d1_n1_2_2_2_3 + pil_d1_n1_2_2_2_3 = 1
invariant :po_d2_n1_3_2_3_2 + pol_d2_n1_3_2_3_2 = 1
invariant :pi_d1_n1_1_2_2_1 + pil_d1_n1_1_2_2_1 = 1
invariant :pi_d2_n1_3_1_1_3 + pil_d2_n1_3_1_1_3 = 1
invariant :pi_d2_n1_1_2_1_1 + pil_d2_n1_1_2_1_1 = 1
invariant :pi_d3_n1_1_2_3_3 + pil_d3_n1_1_2_3_3 = 1
invariant :po_d3_n1_2_3_2_3 + pol_d3_n1_2_3_2_3 = 1
invariant :pi_d4_n1_3_3_2_1 + pil_d4_n1_3_3_2_1 = 1
invariant :pi_d4_n1_2_3_3_2 + pil_d4_n1_2_3_3_2 = 1
invariant :po_d1_n1_3_3_1_3 + pol_d1_n1_3_3_1_3 = 1
invariant :po_d3_n1_1_2_1_2 + pol_d3_n1_1_2_1_2 = 1
invariant :po_d4_n1_3_1_1_2 + pol_d4_n1_3_1_1_2 = 1
invariant :pi_d4_n1_2_1_2_4 + pil_d4_n1_2_1_2_4 = 1
invariant :pi_d1_n1_3_3_1_1 + pil_d1_n1_3_3_1_1 = 1
invariant :po_d2_n1_3_4_1_2 + pol_d2_n1_3_4_1_2 = 1
invariant :pi_d1_n1_4_2_2_3 + pil_d1_n1_4_2_2_3 = 1
invariant :po_d3_n1_3_1_3_1 + pol_d3_n1_3_1_3_1 = 1
invariant :pi_d3_n1_1_2_2_2 + pil_d3_n1_1_2_2_2 = 1
invariant :pi_d2_n1_1_4_1_1 + pil_d2_n1_1_4_1_1 = 1
invariant :po_d3_n1_2_3_1_1 + pol_d3_n1_2_3_1_1 = 1
invariant :pb_d1_n1_1_1_2_3 + pb_d1_n2_1_1_2_3 + pb_d2_n1_1_1_2_3 + pb_d2_n2_1_1_2_3 + pb_d3_n1_1_1_2_3 + pb_d3_n2_1_1_2_3 + pb_d4_n1_1_1_2_3 + pb_d4_n2_1_1_2_3 + pbl_1_1_2_3 = 36
invariant :po_d4_n1_2_2_3_3 + pol_d4_n1_2_2_3_3 = 1
invariant :po_d2_n1_3_4_3_2 + pol_d2_n1_3_4_3_2 = 1
invariant :pi_d4_n1_3_3_3_3 + pil_d4_n1_3_3_3_3 = 1
invariant :pb_d1_n1_1_3_2_2 + pb_d1_n2_1_3_2_2 + pb_d2_n1_1_3_2_2 + pb_d2_n2_1_3_2_2 + pb_d3_n1_1_3_2_2 + pb_d3_n2_1_3_2_2 + pb_d4_n1_1_3_2_2 + pb_d4_n2_1_3_2_2 + pbl_1_3_2_2 = 36
invariant :pi_d3_n1_1_1_4_1 + pil_d3_n1_1_1_4_1 = 1
invariant :po_d1_n1_1_3_3_2 + pol_d1_n1_1_3_3_2 = 1
invariant :pi_d2_n1_1_3_2_1 + pil_d2_n1_1_3_2_1 = 1
invariant :pi_d2_n1_3_3_2_3 + pil_d2_n1_3_3_2_3 = 1
invariant :po_d3_n1_3_1_3_2 + pol_d3_n1_3_1_3_2 = 1
invariant :pi_d4_n1_3_3_1_4 + pil_d4_n1_3_3_1_4 = 1
invariant :pi_d1_n1_1_3_1_2 + pil_d1_n1_1_3_1_2 = 1
invariant :po_d2_n1_2_2_3_2 + pol_d2_n1_2_2_3_2 = 1
invariant :po_d2_n1_3_4_2_1 + pol_d2_n1_3_4_2_1 = 1
invariant :pi_d1_n1_3_2_3_1 + pil_d1_n1_3_2_3_1 = 1
invariant :pi_d2_n1_1_1_3_1 + pil_d2_n1_1_1_3_1 = 1
invariant :po_d3_n1_3_1_4_1 + pol_d3_n1_3_1_4_1 = 1
invariant :po_d1_n1_3_2_2_1 + pol_d1_n1_3_2_2_1 = 1
invariant :pi_d3_n1_2_3_3_2 + pil_d3_n1_2_3_3_2 = 1
invariant :pi_d2_n1_2_1_1_1 + pil_d2_n1_2_1_1_1 = 1
invariant :pi_d4_n1_2_3_1_2 + pil_d4_n1_2_3_1_2 = 1
invariant :pi_d3_n1_3_2_1_2 + pil_d3_n1_3_2_1_2 = 1
invariant :pi_d3_n1_3_2_4_3 + pil_d3_n1_3_2_4_3 = 1
invariant :pi_d2_n1_2_2_3_1 + pil_d2_n1_2_2_3_1 = 1
invariant :po_d2_n1_2_1_3_3 + pol_d2_n1_2_1_3_3 = 1
invariant :po_d4_n1_1_1_2_4 + pol_d4_n1_1_1_2_4 = 1
invariant :pi_d2_n1_3_3_2_2 + pil_d2_n1_3_3_2_2 = 1
invariant :pb_d1_n1_3_3_2_2 + pb_d1_n2_3_3_2_2 + pb_d2_n1_3_3_2_2 + pb_d2_n2_3_3_2_2 + pb_d3_n1_3_3_2_2 + pb_d3_n2_3_3_2_2 + pb_d4_n1_3_3_2_2 + pb_d4_n2_3_3_2_2 + pbl_3_3_2_2 = 36
invariant :pb_d1_n1_2_1_3_1 + pb_d1_n2_2_1_3_1 + pb_d2_n1_2_1_3_1 + pb_d2_n2_2_1_3_1 + pb_d3_n1_2_1_3_1 + pb_d3_n2_2_1_3_1 + pb_d4_n1_2_1_3_1 + pb_d4_n2_2_1_3_1 + -1'pbl_1_1_1_1 + -1'pbl_1_1_1_2 + -1'pbl_1_1_1_3 + -1'pbl_1_1_2_1 + -1'pbl_1_1_2_2 + -1'pbl_1_1_2_3 + -1'pbl_1_1_3_1 + -1'pbl_1_1_3_2 + -1'pbl_1_1_3_3 + -1'pbl_1_2_1_1 + -1'pbl_1_2_1_2 + -1'pbl_1_2_1_3 + -1'pbl_1_2_2_1 + -1'pbl_1_2_2_2 + -1'pbl_1_2_2_3 + -1'pbl_1_2_3_1 + -1'pbl_1_2_3_2 + -1'pbl_1_2_3_3 + -1'pbl_1_3_1_1 + -1'pbl_1_3_1_2 + -1'pbl_1_3_1_3 + -1'pbl_1_3_2_1 + -1'pbl_1_3_2_2 + -1'pbl_1_3_2_3 + -1'pbl_1_3_3_1 + -1'pbl_1_3_3_2 + -1'pbl_1_3_3_3 + -1'pbl_2_1_1_1 + -1'pbl_2_1_1_2 + -1'pbl_2_1_1_3 + -1'pbl_2_1_2_1 + -1'pbl_2_1_2_2 + -1'pbl_2_1_2_3 + -1'pbl_2_1_3_2 + -1'pbl_2_1_3_3 + -1'pbl_2_2_1_1 + -1'pbl_2_2_1_2 + -1'pbl_2_2_1_3 + -1'pbl_2_2_2_1 + -1'pbl_2_2_2_2 + -1'pbl_2_2_2_3 + -1'pbl_2_2_3_1 + -1'pbl_2_2_3_2 + -1'pbl_2_2_3_3 + -1'pbl_2_3_1_1 + -1'pbl_2_3_1_2 + -1'pbl_2_3_1_3 + -1'pbl_2_3_2_1 + -1'pbl_2_3_2_2 + -1'pbl_2_3_2_3 + -1'pbl_2_3_3_1 + -1'pbl_2_3_3_2 + -1'pbl_2_3_3_3 + -1'pbl_3_1_1_1 + -1'pbl_3_1_1_2 + -1'pbl_3_1_1_3 + -1'pbl_3_1_2_1 + -1'pbl_3_1_2_2 + -1'pbl_3_1_2_3 + -1'pbl_3_1_3_1 + -1'pbl_3_1_3_2 + -1'pbl_3_1_3_3 + -1'pbl_3_2_1_1 + -1'pbl_3_2_1_2 + -1'pbl_3_2_1_3 + -1'pbl_3_2_2_1 + -1'pbl_3_2_2_2 + -1'pbl_3_2_2_3 + -1'pbl_3_2_3_1 + -1'pbl_3_2_3_2 + -1'pbl_3_2_3_3 + -1'pbl_3_3_1_1 + -1'pbl_3_3_1_2 + -1'pbl_3_3_1_3 + -1'pbl_3_3_2_1 + -1'pbl_3_3_2_2 + -1'pbl_3_3_2_3 + -1'pbl_3_3_3_1 + -1'pbl_3_3_3_2 + -1'pbl_3_3_3_3 + -1'pil_d1_n1_1_1_1_1 + -1'pil_d1_n1_1_1_1_2 + -1'pil_d1_n1_1_1_1_3 + -1'pil_d1_n1_1_1_2_1 + -1'pil_d1_n1_1_1_2_2 + -1'pil_d1_n1_1_1_2_3 + -1'pil_d1_n1_1_1_3_1 + -1'pil_d1_n1_1_1_3_2 + -1'pil_d1_n1_1_1_3_3 + -1'pil_d1_n1_1_2_1_1 + -1'pil_d1_n1_1_2_1_2 + -1'pil_d1_n1_1_2_1_3 + -1'pil_d1_n1_1_2_2_1 + -1'pil_d1_n1_1_2_2_2 + -1'pil_d1_n1_1_2_2_3 + -1'pil_d1_n1_1_2_3_1 + -1'pil_d1_n1_1_2_3_2 + -1'pil_d1_n1_1_2_3_3 + -1'pil_d1_n1_1_3_1_1 + -1'pil_d1_n1_1_3_1_2 + -1'pil_d1_n1_1_3_1_3 + -1'pil_d1_n1_1_3_2_1 + -1'pil_d1_n1_1_3_2_2 + -1'pil_d1_n1_1_3_2_3 + -1'pil_d1_n1_1_3_3_1 + -1'pil_d1_n1_1_3_3_2 + -1'pil_d1_n1_1_3_3_3 + -1'pil_d1_n1_2_1_1_1 + -1'pil_d1_n1_2_1_1_2 + -1'pil_d1_n1_2_1_1_3 + -1'pil_d1_n1_2_1_2_1 + -1'pil_d1_n1_2_1_2_2 + -1'pil_d1_n1_2_1_2_3 + -1'pil_d1_n1_2_1_3_1 + -1'pil_d1_n1_2_1_3_2 + -1'pil_d1_n1_2_1_3_3 + -1'pil_d1_n1_2_2_1_1 + -1'pil_d1_n1_2_2_1_2 + -1'pil_d1_n1_2_2_1_3 + -1'pil_d1_n1_2_2_2_1 + -1'pil_d1_n1_2_2_2_2 + -1'pil_d1_n1_2_2_2_3 + -1'pil_d1_n1_2_2_3_1 + -1'pil_d1_n1_2_2_3_2 + -1'pil_d1_n1_2_2_3_3 + -1'pil_d1_n1_2_3_1_1 + -1'pil_d1_n1_2_3_1_2 + -1'pil_d1_n1_2_3_1_3 + -1'pil_d1_n1_2_3_2_1 + -1'pil_d1_n1_2_3_2_2 + -1'pil_d1_n1_2_3_2_3 + -1'pil_d1_n1_2_3_3_1 + -1'pil_d1_n1_2_3_3_2 + -1'pil_d1_n1_2_3_3_3 + -1'pil_d1_n1_3_1_1_1 + -1'pil_d1_n1_3_1_1_2 + -1'pil_d1_n1_3_1_1_3 + -1'pil_d1_n1_3_1_2_1 + -1'pil_d1_n1_3_1_2_2 + -1'pil_d1_n1_3_1_2_3 + -1'pil_d1_n1_3_1_3_1 + -1'pil_d1_n1_3_1_3_2 + -1'pil_d1_n1_3_1_3_3 + -1'pil_d1_n1_3_2_1_1 + -1'pil_d1_n1_3_2_1_2 + -1'pil_d1_n1_3_2_1_3 + -1'pil_d1_n1_3_2_2_1 + -1'pil_d1_n1_3_2_2_2 + -1'pil_d1_n1_3_2_2_3 + -1'pil_d1_n1_3_2_3_1 + -1'pil_d1_n1_3_2_3_2 + -1'pil_d1_n1_3_2_3_3 + -1'pil_d1_n1_3_3_1_1 + -1'pil_d1_n1_3_3_1_2 + -1'pil_d1_n1_3_3_1_3 + -1'pil_d1_n1_3_3_2_1 + -1'pil_d1_n1_3_3_2_2 + -1'pil_d1_n1_3_3_2_3 + -1'pil_d1_n1_3_3_3_1 + -1'pil_d1_n1_3_3_3_2 + -1'pil_d1_n1_3_3_3_3 + -1'pil_d1_n1_4_1_1_1 + -1'pil_d1_n1_4_1_1_2 + -1'pil_d1_n1_4_1_1_3 + -1'pil_d1_n1_4_1_2_1 + -1'pil_d1_n1_4_1_2_2 + -1'pil_d1_n1_4_1_2_3 + -1'pil_d1_n1_4_1_3_1 + -1'pil_d1_n1_4_1_3_2 + -1'pil_d1_n1_4_1_3_3 + -1'pil_d1_n1_4_2_1_1 + -1'pil_d1_n1_4_2_1_2 + -1'pil_d1_n1_4_2_1_3 + -1'pil_d1_n1_4_2_2_1 + -1'pil_d1_n1_4_2_2_2 + -1'pil_d1_n1_4_2_2_3 + -1'pil_d1_n1_4_2_3_1 + -1'pil_d1_n1_4_2_3_2 + -1'pil_d1_n1_4_2_3_3 + -1'pil_d1_n1_4_3_1_1 + -1'pil_d1_n1_4_3_1_2 + -1'pil_d1_n1_4_3_1_3 + -1'pil_d1_n1_4_3_2_1 + -1'pil_d1_n1_4_3_2_2 + -1'pil_d1_n1_4_3_2_3 + -1'pil_d1_n1_4_3_3_1 + -1'pil_d1_n1_4_3_3_2 + -1'pil_d1_n1_4_3_3_3 + -1'pil_d2_n1_1_1_1_1 + -1'pil_d2_n1_1_1_1_2 + -1'pil_d2_n1_1_1_1_3 + -1'pil_d2_n1_1_1_2_1 + -1'pil_d2_n1_1_1_2_2 + -1'pil_d2_n1_1_1_2_3 + -1'pil_d2_n1_1_1_3_1 + -1'pil_d2_n1_1_1_3_2 + -1'pil_d2_n1_1_1_3_3 + -1'pil_d2_n1_1_2_1_1 + -1'pil_d2_n1_1_2_1_2 + -1'pil_d2_n1_1_2_1_3 + -1'pil_d2_n1_1_2_2_1 + -1'pil_d2_n1_1_2_2_2 + -1'pil_d2_n1_1_2_2_3 + -1'pil_d2_n1_1_2_3_1 + -1'pil_d2_n1_1_2_3_2 + -1'pil_d2_n1_1_2_3_3 + -1'pil_d2_n1_1_3_1_1 + -1'pil_d2_n1_1_3_1_2 + -1'pil_d2_n1_1_3_1_3 + -1'pil_d2_n1_1_3_2_1 + -1'pil_d2_n1_1_3_2_2 + -1'pil_d2_n1_1_3_2_3 + -1'pil_d2_n1_1_3_3_1 + -1'pil_d2_n1_1_3_3_2 + -1'pil_d2_n1_1_3_3_3 + -1'pil_d2_n1_1_4_1_1 + -1'pil_d2_n1_1_4_1_2 + -1'pil_d2_n1_1_4_1_3 + -1'pil_d2_n1_1_4_2_1 + -1'pil_d2_n1_1_4_2_2 + -1'pil_d2_n1_1_4_2_3 + -1'pil_d2_n1_1_4_3_1 + -1'pil_d2_n1_1_4_3_2 + -1'pil_d2_n1_1_4_3_3 + -1'pil_d2_n1_2_1_1_1 + -1'pil_d2_n1_2_1_1_2 + -1'pil_d2_n1_2_1_1_3 + -1'pil_d2_n1_2_1_2_1 + -1'pil_d2_n1_2_1_2_2 + -1'pil_d2_n1_2_1_2_3 + -1'pil_d2_n1_2_1_3_1 + -1'pil_d2_n1_2_1_3_2 + -1'pil_d2_n1_2_1_3_3 + -1'pil_d2_n1_2_2_1_1 + -1'pil_d2_n1_2_2_1_2 + -1'pil_d2_n1_2_2_1_3 + -1'pil_d2_n1_2_2_2_1 + -1'pil_d2_n1_2_2_2_2 + -1'pil_d2_n1_2_2_2_3 + -1'pil_d2_n1_2_2_3_1 + -1'pil_d2_n1_2_2_3_2 + -1'pil_d2_n1_2_2_3_3 + -1'pil_d2_n1_2_3_1_1 + -1'pil_d2_n1_2_3_1_2 + -1'pil_d2_n1_2_3_1_3 + -1'pil_d2_n1_2_3_2_1 + -1'pil_d2_n1_2_3_2_2 + -1'pil_d2_n1_2_3_2_3 + -1'pil_d2_n1_2_3_3_1 + -1'pil_d2_n1_2_3_3_2 + -1'pil_d2_n1_2_3_3_3 + -1'pil_d2_n1_2_4_1_1 + -1'pil_d2_n1_2_4_1_2 + -1'pil_d2_n1_2_4_1_3 + -1'pil_d2_n1_2_4_2_1 + -1'pil_d2_n1_2_4_2_2 + -1'pil_d2_n1_2_4_2_3 + -1'pil_d2_n1_2_4_3_1 + -1'pil_d2_n1_2_4_3_2 + -1'pil_d2_n1_2_4_3_3 + -1'pil_d2_n1_3_1_1_1 + -1'pil_d2_n1_3_1_1_2 + -1'pil_d2_n1_3_1_1_3 + -1'pil_d2_n1_3_1_2_1 + -1'pil_d2_n1_3_1_2_2 + -1'pil_d2_n1_3_1_2_3 + -1'pil_d2_n1_3_1_3_1 + -1'pil_d2_n1_3_1_3_2 + -1'pil_d2_n1_3_1_3_3 + -1'pil_d2_n1_3_2_1_1 + -1'pil_d2_n1_3_2_1_2 + -1'pil_d2_n1_3_2_1_3 + -1'pil_d2_n1_3_2_2_1 + -1'pil_d2_n1_3_2_2_2 + -1'pil_d2_n1_3_2_2_3 + -1'pil_d2_n1_3_2_3_1 + -1'pil_d2_n1_3_2_3_2 + -1'pil_d2_n1_3_2_3_3 + -1'pil_d2_n1_3_3_1_1 + -1'pil_d2_n1_3_3_1_2 + -1'pil_d2_n1_3_3_1_3 + -1'pil_d2_n1_3_3_2_1 + -1'pil_d2_n1_3_3_2_2 + -1'pil_d2_n1_3_3_2_3 + -1'pil_d2_n1_3_3_3_1 + -1'pil_d2_n1_3_3_3_2 + -1'pil_d2_n1_3_3_3_3 + -1'pil_d2_n1_3_4_1_1 + -1'pil_d2_n1_3_4_1_2 + -1'pil_d2_n1_3_4_1_3 + -1'pil_d2_n1_3_4_2_1 + -1'pil_d2_n1_3_4_2_2 + -1'pil_d2_n1_3_4_2_3 + -1'pil_d2_n1_3_4_3_1 + -1'pil_d2_n1_3_4_3_2 + -1'pil_d2_n1_3_4_3_3 + -1'pil_d3_n1_1_1_1_1 + -1'pil_d3_n1_1_1_1_2 + -1'pil_d3_n1_1_1_1_3 + -1'pil_d3_n1_1_1_2_1 + -1'pil_d3_n1_1_1_2_2 + -1'pil_d3_n1_1_1_2_3 + -1'pil_d3_n1_1_1_3_1 + -1'pil_d3_n1_1_1_3_2 + -1'pil_d3_n1_1_1_3_3 + -1'pil_d3_n1_1_1_4_1 + -1'pil_d3_n1_1_1_4_2 + -1'pil_d3_n1_1_1_4_3 + -1'pil_d3_n1_1_2_1_1 + -1'pil_d3_n1_1_2_1_2 + -1'pil_d3_n1_1_2_1_3 + -1'pil_d3_n1_1_2_2_1 + -1'pil_d3_n1_1_2_2_2 + -1'pil_d3_n1_1_2_2_3 + -1'pil_d3_n1_1_2_3_1 + -1'pil_d3_n1_1_2_3_2 + -1'pil_d3_n1_1_2_3_3 + -1'pil_d3_n1_1_2_4_1 + -1'pil_d3_n1_1_2_4_2 + -1'pil_d3_n1_1_2_4_3 + -1'pil_d3_n1_1_3_1_1 + -1'pil_d3_n1_1_3_1_2 + -1'pil_d3_n1_1_3_1_3 + -1'pil_d3_n1_1_3_2_1 + -1'pil_d3_n1_1_3_2_2 + -1'pil_d3_n1_1_3_2_3 + -1'pil_d3_n1_1_3_3_1 + -1'pil_d3_n1_1_3_3_2 + -1'pil_d3_n1_1_3_3_3 + -1'pil_d3_n1_1_3_4_1 + -1'pil_d3_n1_1_3_4_2 + -1'pil_d3_n1_1_3_4_3 + -1'pil_d3_n1_2_1_1_1 + -1'pil_d3_n1_2_1_1_2 + -1'pil_d3_n1_2_1_1_3 + -1'pil_d3_n1_2_1_2_1 + -1'pil_d3_n1_2_1_2_2 + -1'pil_d3_n1_2_1_2_3 + -1'pil_d3_n1_2_1_3_1 + -1'pil_d3_n1_2_1_3_2 + -1'pil_d3_n1_2_1_3_3 + -1'pil_d3_n1_2_1_4_1 + -1'pil_d3_n1_2_1_4_2 + -1'pil_d3_n1_2_1_4_3 + -1'pil_d3_n1_2_2_1_1 + -1'pil_d3_n1_2_2_1_2 + -1'pil_d3_n1_2_2_1_3 + -1'pil_d3_n1_2_2_2_1 + -1'pil_d3_n1_2_2_2_2 + -1'pil_d3_n1_2_2_2_3 + -1'pil_d3_n1_2_2_3_1 + -1'pil_d3_n1_2_2_3_2 + -1'pil_d3_n1_2_2_3_3 + -1'pil_d3_n1_2_2_4_1 + -1'pil_d3_n1_2_2_4_2 + -1'pil_d3_n1_2_2_4_3 + -1'pil_d3_n1_2_3_1_1 + -1'pil_d3_n1_2_3_1_2 + -1'pil_d3_n1_2_3_1_3 + -1'pil_d3_n1_2_3_2_1 + -1'pil_d3_n1_2_3_2_2 + -1'pil_d3_n1_2_3_2_3 + -1'pil_d3_n1_2_3_3_1 + -1'pil_d3_n1_2_3_3_2 + -1'pil_d3_n1_2_3_3_3 + -1'pil_d3_n1_2_3_4_1 + -1'pil_d3_n1_2_3_4_2 + -1'pil_d3_n1_2_3_4_3 + -1'pil_d3_n1_3_1_1_1 + -1'pil_d3_n1_3_1_1_2 + -1'pil_d3_n1_3_1_1_3 + -1'pil_d3_n1_3_1_2_1 + -1'pil_d3_n1_3_1_2_2 + -1'pil_d3_n1_3_1_2_3 + -1'pil_d3_n1_3_1_3_1 + -1'pil_d3_n1_3_1_3_2 + -1'pil_d3_n1_3_1_3_3 + -1'pil_d3_n1_3_1_4_1 + -1'pil_d3_n1_3_1_4_2 + -1'pil_d3_n1_3_1_4_3 + -1'pil_d3_n1_3_2_1_1 + -1'pil_d3_n1_3_2_1_2 + -1'pil_d3_n1_3_2_1_3 + -1'pil_d3_n1_3_2_2_1 + -1'pil_d3_n1_3_2_2_2 + -1'pil_d3_n1_3_2_2_3 + -1'pil_d3_n1_3_2_3_1 + -1'pil_d3_n1_3_2_3_2 + -1'pil_d3_n1_3_2_3_3 + -1'pil_d3_n1_3_2_4_1 + -1'pil_d3_n1_3_2_4_2 + -1'pil_d3_n1_3_2_4_3 + -1'pil_d3_n1_3_3_1_1 + -1'pil_d3_n1_3_3_1_2 + -1'pil_d3_n1_3_3_1_3 + -1'pil_d3_n1_3_3_2_1 + -1'pil_d3_n1_3_3_2_2 + -1'pil_d3_n1_3_3_2_3 + -1'pil_d3_n1_3_3_3_1 + -1'pil_d3_n1_3_3_3_2 + -1'pil_d3_n1_3_3_3_3 + -1'pil_d3_n1_3_3_4_1 + -1'pil_d3_n1_3_3_4_2 + -1'pil_d3_n1_3_3_4_3 + -1'pil_d4_n1_1_1_1_1 + -1'pil_d4_n1_1_1_1_2 + -1'pil_d4_n1_1_1_1_3 + -1'pil_d4_n1_1_1_1_4 + -1'pil_d4_n1_1_1_2_1 + -1'pil_d4_n1_1_1_2_2 + -1'pil_d4_n1_1_1_2_3 + -1'pil_d4_n1_1_1_2_4 + -1'pil_d4_n1_1_1_3_1 + -1'pil_d4_n1_1_1_3_2 + -1'pil_d4_n1_1_1_3_3 + -1'pil_d4_n1_1_1_3_4 + -1'pil_d4_n1_1_2_1_1 + -1'pil_d4_n1_1_2_1_2 + -1'pil_d4_n1_1_2_1_3 + -1'pil_d4_n1_1_2_1_4 + -1'pil_d4_n1_1_2_2_1 + -1'pil_d4_n1_1_2_2_2 + -1'pil_d4_n1_1_2_2_3 + -1'pil_d4_n1_1_2_2_4 + -1'pil_d4_n1_1_2_3_1 + -1'pil_d4_n1_1_2_3_2 + -1'pil_d4_n1_1_2_3_3 + -1'pil_d4_n1_1_2_3_4 + -1'pil_d4_n1_1_3_1_1 + -1'pil_d4_n1_1_3_1_2 + -1'pil_d4_n1_1_3_1_3 + -1'pil_d4_n1_1_3_1_4 + -1'pil_d4_n1_1_3_2_1 + -1'pil_d4_n1_1_3_2_2 + -1'pil_d4_n1_1_3_2_3 + -1'pil_d4_n1_1_3_2_4 + -1'pil_d4_n1_1_3_3_1 + -1'pil_d4_n1_1_3_3_2 + -1'pil_d4_n1_1_3_3_3 + -1'pil_d4_n1_1_3_3_4 + -1'pil_d4_n1_2_1_1_1 + -1'pil_d4_n1_2_1_1_2 + -1'pil_d4_n1_2_1_1_3 + -1'pil_d4_n1_2_1_1_4 + -1'pil_d4_n1_2_1_2_1 + -1'pil_d4_n1_2_1_2_2 + -1'pil_d4_n1_2_1_2_3 + -1'pil_d4_n1_2_1_2_4 + -1'pil_d4_n1_2_1_3_1 + -1'pil_d4_n1_2_1_3_2 + -1'pil_d4_n1_2_1_3_3 + -1'pil_d4_n1_2_1_3_4 + -1'pil_d4_n1_2_2_1_1 + -1'pil_d4_n1_2_2_1_2 + -1'pil_d4_n1_2_2_1_3 + -1'pil_d4_n1_2_2_1_4 + -1'pil_d4_n1_2_2_2_1 + -1'pil_d4_n1_2_2_2_2 + -1'pil_d4_n1_2_2_2_3 + -1'pil_d4_n1_2_2_2_4 + -1'pil_d4_n1_2_2_3_1 + -1'pil_d4_n1_2_2_3_2 + -1'pil_d4_n1_2_2_3_3 + -1'pil_d4_n1_2_2_3_4 + -1'pil_d4_n1_2_3_1_1 + -1'pil_d4_n1_2_3_1_2 + -1'pil_d4_n1_2_3_1_3 + -1'pil_d4_n1_2_3_1_4 + -1'pil_d4_n1_2_3_2_1 + -1'pil_d4_n1_2_3_2_2 + -1'pil_d4_n1_2_3_2_3 + -1'pil_d4_n1_2_3_2_4 + -1'pil_d4_n1_2_3_3_1 + -1'pil_d4_n1_2_3_3_2 + -1'pil_d4_n1_2_3_3_3 + -1'pil_d4_n1_2_3_3_4 + -1'pil_d4_n1_3_1_1_1 + -1'pil_d4_n1_3_1_1_2 + -1'pil_d4_n1_3_1_1_3 + -1'pil_d4_n1_3_1_1_4 + -1'pil_d4_n1_3_1_2_1 + -1'pil_d4_n1_3_1_2_2 + -1'pil_d4_n1_3_1_2_3 + -1'pil_d4_n1_3_1_2_4 + -1'pil_d4_n1_3_1_3_1 + -1'pil_d4_n1_3_1_3_2 + -1'pil_d4_n1_3_1_3_3 + -1'pil_d4_n1_3_1_3_4 + -1'pil_d4_n1_3_2_1_1 + -1'pil_d4_n1_3_2_1_2 + -1'pil_d4_n1_3_2_1_3 + -1'pil_d4_n1_3_2_1_4 + -1'pil_d4_n1_3_2_2_1 + -1'pil_d4_n1_3_2_2_2 + -1'pil_d4_n1_3_2_2_3 + -1'pil_d4_n1_3_2_2_4 + -1'pil_d4_n1_3_2_3_1 + -1'pil_d4_n1_3_2_3_2 + -1'pil_d4_n1_3_2_3_3 + -1'pil_d4_n1_3_2_3_4 + -1'pil_d4_n1_3_3_1_1 + -1'pil_d4_n1_3_3_1_2 + -1'pil_d4_n1_3_3_1_3 + -1'pil_d4_n1_3_3_1_4 + -1'pil_d4_n1_3_3_2_1 + -1'pil_d4_n1_3_3_2_2 + -1'pil_d4_n1_3_3_2_3 + -1'pil_d4_n1_3_3_2_4 + -1'pil_d4_n1_3_3_3_1 + -1'pil_d4_n1_3_3_3_2 + -1'pil_d4_n1_3_3_3_3 + -1'pil_d4_n1_3_3_3_4 + -1'pol_d1_n1_1_1_1_1 + -1'pol_d1_n1_1_1_1_2 + -1'pol_d1_n1_1_1_1_3 + -1'pol_d1_n1_1_1_2_1 + -1'pol_d1_n1_1_1_2_2 + -1'pol_d1_n1_1_1_2_3 + -1'pol_d1_n1_1_1_3_1 + -1'pol_d1_n1_1_1_3_2 + -1'pol_d1_n1_1_1_3_3 + -1'pol_d1_n1_1_2_1_1 + -1'pol_d1_n1_1_2_1_2 + -1'pol_d1_n1_1_2_1_3 + -1'pol_d1_n1_1_2_2_1 + -1'pol_d1_n1_1_2_2_2 + -1'pol_d1_n1_1_2_2_3 + -1'pol_d1_n1_1_2_3_1 + -1'pol_d1_n1_1_2_3_2 + -1'pol_d1_n1_1_2_3_3 + -1'pol_d1_n1_1_3_1_1 + -1'pol_d1_n1_1_3_1_2 + -1'pol_d1_n1_1_3_1_3 + -1'pol_d1_n1_1_3_2_1 + -1'pol_d1_n1_1_3_2_2 + -1'pol_d1_n1_1_3_2_3 + -1'pol_d1_n1_1_3_3_1 + -1'pol_d1_n1_1_3_3_2 + -1'pol_d1_n1_1_3_3_3 + -1'pol_d1_n1_2_1_1_1 + -1'pol_d1_n1_2_1_1_2 + -1'pol_d1_n1_2_1_1_3 + -1'pol_d1_n1_2_1_2_1 + -1'pol_d1_n1_2_1_2_2 + -1'pol_d1_n1_2_1_2_3 + -1'pol_d1_n1_2_1_3_1 + -1'pol_d1_n1_2_1_3_2 + -1'pol_d1_n1_2_1_3_3 + -1'pol_d1_n1_2_2_1_1 + -1'pol_d1_n1_2_2_1_2 + -1'pol_d1_n1_2_2_1_3 + -1'pol_d1_n1_2_2_2_1 + -1'pol_d1_n1_2_2_2_2 + -1'pol_d1_n1_2_2_2_3 + -1'pol_d1_n1_2_2_3_1 + -1'pol_d1_n1_2_2_3_2 + -1'pol_d1_n1_2_2_3_3 + -1'pol_d1_n1_2_3_1_1 + -1'pol_d1_n1_2_3_1_2 + -1'pol_d1_n1_2_3_1_3 + -1'pol_d1_n1_2_3_2_1 + -1'pol_d1_n1_2_3_2_2 + -1'pol_d1_n1_2_3_2_3 + -1'pol_d1_n1_2_3_3_1 + -1'pol_d1_n1_2_3_3_2 + -1'pol_d1_n1_2_3_3_3 + -1'pol_d1_n1_3_1_1_1 + -1'pol_d1_n1_3_1_1_2 + -1'pol_d1_n1_3_1_1_3 + -1'pol_d1_n1_3_1_2_1 + -1'pol_d1_n1_3_1_2_2 + -1'pol_d1_n1_3_1_2_3 + -1'pol_d1_n1_3_1_3_1 + -1'pol_d1_n1_3_1_3_2 + -1'pol_d1_n1_3_1_3_3 + -1'pol_d1_n1_3_2_1_1 + -1'pol_d1_n1_3_2_1_2 + -1'pol_d1_n1_3_2_1_3 + -1'pol_d1_n1_3_2_2_1 + -1'pol_d1_n1_3_2_2_2 + -1'pol_d1_n1_3_2_2_3 + -1'pol_d1_n1_3_2_3_1 + -1'pol_d1_n1_3_2_3_2 + -1'pol_d1_n1_3_2_3_3 + -1'pol_d1_n1_3_3_1_1 + -1'pol_d1_n1_3_3_1_2 + -1'pol_d1_n1_3_3_1_3 + -1'pol_d1_n1_3_3_2_1 + -1'pol_d1_n1_3_3_2_2 + -1'pol_d1_n1_3_3_2_3 + -1'pol_d1_n1_3_3_3_1 + -1'pol_d1_n1_3_3_3_2 + -1'pol_d1_n1_3_3_3_3 + -1'pol_d1_n1_4_1_1_1 + -1'pol_d1_n1_4_1_1_2 + -1'pol_d1_n1_4_1_1_3 + -1'pol_d1_n1_4_1_2_1 + -1'pol_d1_n1_4_1_2_2 + -1'pol_d1_n1_4_1_2_3 + -1'pol_d1_n1_4_1_3_1 + -1'pol_d1_n1_4_1_3_2 + -1'pol_d1_n1_4_1_3_3 + -1'pol_d1_n1_4_2_1_1 + -1'pol_d1_n1_4_2_1_2 + -1'pol_d1_n1_4_2_1_3 + -1'pol_d1_n1_4_2_2_1 + -1'pol_d1_n1_4_2_2_2 + -1'pol_d1_n1_4_2_2_3 + -1'pol_d1_n1_4_2_3_1 + -1'pol_d1_n1_4_2_3_2 + -1'pol_d1_n1_4_2_3_3 + -1'pol_d1_n1_4_3_1_1 + -1'pol_d1_n1_4_3_1_2 + -1'pol_d1_n1_4_3_1_3 + -1'pol_d1_n1_4_3_2_1 + -1'pol_d1_n1_4_3_2_2 + -1'pol_d1_n1_4_3_2_3 + -1'pol_d1_n1_4_3_3_1 + -1'pol_d1_n1_4_3_3_2 + -1'pol_d1_n1_4_3_3_3 + -1'pol_d2_n1_1_1_1_1 + -1'pol_d2_n1_1_1_1_2 + -1'pol_d2_n1_1_1_1_3 + -1'pol_d2_n1_1_1_2_1 + -1'pol_d2_n1_1_1_2_2 + -1'pol_d2_n1_1_1_2_3 + -1'pol_d2_n1_1_1_3_1 + -1'pol_d2_n1_1_1_3_2 + -1'pol_d2_n1_1_1_3_3 + -1'pol_d2_n1_1_2_1_1 + -1'pol_d2_n1_1_2_1_2 + -1'pol_d2_n1_1_2_1_3 + -1'pol_d2_n1_1_2_2_1 + -1'pol_d2_n1_1_2_2_2 + -1'pol_d2_n1_1_2_2_3 + -1'pol_d2_n1_1_2_3_1 + -1'pol_d2_n1_1_2_3_2 + -1'pol_d2_n1_1_2_3_3 + -1'pol_d2_n1_1_3_1_1 + -1'pol_d2_n1_1_3_1_2 + -1'pol_d2_n1_1_3_1_3 + -1'pol_d2_n1_1_3_2_1 + -1'pol_d2_n1_1_3_2_2 + -1'pol_d2_n1_1_3_2_3 + -1'pol_d2_n1_1_3_3_1 + -1'pol_d2_n1_1_3_3_2 + -1'pol_d2_n1_1_3_3_3 + -1'pol_d2_n1_1_4_1_1 + -1'pol_d2_n1_1_4_1_2 + -1'pol_d2_n1_1_4_1_3 + -1'pol_d2_n1_1_4_2_1 + -1'pol_d2_n1_1_4_2_2 + -1'pol_d2_n1_1_4_2_3 + -1'pol_d2_n1_1_4_3_1 + -1'pol_d2_n1_1_4_3_2 + -1'pol_d2_n1_1_4_3_3 + -1'pol_d2_n1_2_1_1_1 + -1'pol_d2_n1_2_1_1_2 + -1'pol_d2_n1_2_1_1_3 + -1'pol_d2_n1_2_1_2_1 + -1'pol_d2_n1_2_1_2_2 + -1'pol_d2_n1_2_1_2_3 + -1'pol_d2_n1_2_1_3_1 + -1'pol_d2_n1_2_1_3_2 + -1'pol_d2_n1_2_1_3_3 + -1'pol_d2_n1_2_2_1_1 + -1'pol_d2_n1_2_2_1_2 + -1'pol_d2_n1_2_2_1_3 + -1'pol_d2_n1_2_2_2_1 + -1'pol_d2_n1_2_2_2_2 + -1'pol_d2_n1_2_2_2_3 + -1'pol_d2_n1_2_2_3_1 + -1'pol_d2_n1_2_2_3_2 + -1'pol_d2_n1_2_2_3_3 + -1'pol_d2_n1_2_3_1_1 + -1'pol_d2_n1_2_3_1_2 + -1'pol_d2_n1_2_3_1_3 + -1'pol_d2_n1_2_3_2_1 + -1'pol_d2_n1_2_3_2_2 + -1'pol_d2_n1_2_3_2_3 + -1'pol_d2_n1_2_3_3_1 + -1'pol_d2_n1_2_3_3_2 + -1'pol_d2_n1_2_3_3_3 + -1'pol_d2_n1_2_4_1_1 + -1'pol_d2_n1_2_4_1_2 + -1'pol_d2_n1_2_4_1_3 + -1'pol_d2_n1_2_4_2_1 + -1'pol_d2_n1_2_4_2_2 + -1'pol_d2_n1_2_4_2_3 + -1'pol_d2_n1_2_4_3_1 + -1'pol_d2_n1_2_4_3_2 + -1'pol_d2_n1_2_4_3_3 + -1'pol_d2_n1_3_1_1_1 + -1'pol_d2_n1_3_1_1_2 + -1'pol_d2_n1_3_1_1_3 + -1'pol_d2_n1_3_1_2_1 + -1'pol_d2_n1_3_1_2_2 + -1'pol_d2_n1_3_1_2_3 + -1'pol_d2_n1_3_1_3_1 + -1'pol_d2_n1_3_1_3_2 + -1'pol_d2_n1_3_1_3_3 + -1'pol_d2_n1_3_2_1_1 + -1'pol_d2_n1_3_2_1_2 + -1'pol_d2_n1_3_2_1_3 + -1'pol_d2_n1_3_2_2_1 + -1'pol_d2_n1_3_2_2_2 + -1'pol_d2_n1_3_2_2_3 + -1'pol_d2_n1_3_2_3_1 + -1'pol_d2_n1_3_2_3_2 + -1'pol_d2_n1_3_2_3_3 + -1'pol_d2_n1_3_3_1_1 + -1'pol_d2_n1_3_3_1_2 + -1'pol_d2_n1_3_3_1_3 + -1'pol_d2_n1_3_3_2_1 + -1'pol_d2_n1_3_3_2_2 + -1'pol_d2_n1_3_3_2_3 + -1'pol_d2_n1_3_3_3_1 + -1'pol_d2_n1_3_3_3_2 + -1'pol_d2_n1_3_3_3_3 + -1'pol_d2_n1_3_4_1_1 + -1'pol_d2_n1_3_4_1_2 + -1'pol_d2_n1_3_4_1_3 + -1'pol_d2_n1_3_4_2_1 + -1'pol_d2_n1_3_4_2_2 + -1'pol_d2_n1_3_4_2_3 + -1'pol_d2_n1_3_4_3_1 + -1'pol_d2_n1_3_4_3_2 + -1'pol_d2_n1_3_4_3_3 + -1'pol_d3_n1_1_1_1_1 + -1'pol_d3_n1_1_1_1_2 + -1'pol_d3_n1_1_1_1_3 + -1'pol_d3_n1_1_1_2_1 + -1'pol_d3_n1_1_1_2_2 + -1'pol_d3_n1_1_1_2_3 + -1'pol_d3_n1_1_1_3_1 + -1'pol_d3_n1_1_1_3_2 + -1'pol_d3_n1_1_1_3_3 + -1'pol_d3_n1_1_1_4_1 + -1'pol_d3_n1_1_1_4_2 + -1'pol_d3_n1_1_1_4_3 + -1'pol_d3_n1_1_2_1_1 + -1'pol_d3_n1_1_2_1_2 + -1'pol_d3_n1_1_2_1_3 + -1'pol_d3_n1_1_2_2_1 + -1'pol_d3_n1_1_2_2_2 + -1'pol_d3_n1_1_2_2_3 + -1'pol_d3_n1_1_2_3_1 + -1'pol_d3_n1_1_2_3_2 + -1'pol_d3_n1_1_2_3_3 + -1'pol_d3_n1_1_2_4_1 + -1'pol_d3_n1_1_2_4_2 + -1'pol_d3_n1_1_2_4_3 + -1'pol_d3_n1_1_3_1_1 + -1'pol_d3_n1_1_3_1_2 + -1'pol_d3_n1_1_3_1_3 + -1'pol_d3_n1_1_3_2_1 + -1'pol_d3_n1_1_3_2_2 + -1'pol_d3_n1_1_3_2_3 + -1'pol_d3_n1_1_3_3_1 + -1'pol_d3_n1_1_3_3_2 + -1'pol_d3_n1_1_3_3_3 + -1'pol_d3_n1_1_3_4_1 + -1'pol_d3_n1_1_3_4_2 + -1'pol_d3_n1_1_3_4_3 + -1'pol_d3_n1_2_1_1_1 + -1'pol_d3_n1_2_1_1_2 + -1'pol_d3_n1_2_1_1_3 + -1'pol_d3_n1_2_1_2_1 + -1'pol_d3_n1_2_1_2_2 + -1'pol_d3_n1_2_1_2_3 + -1'pol_d3_n1_2_1_3_1 + -1'pol_d3_n1_2_1_3_2 + -1'pol_d3_n1_2_1_3_3 + -1'pol_d3_n1_2_1_4_1 + -1'pol_d3_n1_2_1_4_2 + -1'pol_d3_n1_2_1_4_3 + -1'pol_d3_n1_2_2_1_1 + -1'pol_d3_n1_2_2_1_2 + -1'pol_d3_n1_2_2_1_3 + -1'pol_d3_n1_2_2_2_1 + -1'pol_d3_n1_2_2_2_2 + -1'pol_d3_n1_2_2_2_3 + -1'pol_d3_n1_2_2_3_1 + -1'pol_d3_n1_2_2_3_2 + -1'pol_d3_n1_2_2_3_3 + -1'pol_d3_n1_2_2_4_1 + -1'pol_d3_n1_2_2_4_2 + -1'pol_d3_n1_2_2_4_3 + -1'pol_d3_n1_2_3_1_1 + -1'pol_d3_n1_2_3_1_2 + -1'pol_d3_n1_2_3_1_3 + -1'pol_d3_n1_2_3_2_1 + -1'pol_d3_n1_2_3_2_2 + -1'pol_d3_n1_2_3_2_3 + -1'pol_d3_n1_2_3_3_1 + -1'pol_d3_n1_2_3_3_2 + -1'pol_d3_n1_2_3_3_3 + -1'pol_d3_n1_2_3_4_1 + -1'pol_d3_n1_2_3_4_2 + -1'pol_d3_n1_2_3_4_3 + -1'pol_d3_n1_3_1_1_1 + -1'pol_d3_n1_3_1_1_2 + -1'pol_d3_n1_3_1_1_3 + -1'pol_d3_n1_3_1_2_1 + -1'pol_d3_n1_3_1_2_2 + -1'pol_d3_n1_3_1_2_3 + -1'pol_d3_n1_3_1_3_1 + -1'pol_d3_n1_3_1_3_2 + -1'pol_d3_n1_3_1_3_3 + -1'pol_d3_n1_3_1_4_1 + -1'pol_d3_n1_3_1_4_2 + -1'pol_d3_n1_3_1_4_3 + -1'pol_d3_n1_3_2_1_1 + -1'pol_d3_n1_3_2_1_2 + -1'pol_d3_n1_3_2_1_3 + -1'pol_d3_n1_3_2_2_1 + -1'pol_d3_n1_3_2_2_2 + -1'pol_d3_n1_3_2_2_3 + -1'pol_d3_n1_3_2_3_1 + -1'pol_d3_n1_3_2_3_2 + -1'pol_d3_n1_3_2_3_3 + -1'pol_d3_n1_3_2_4_1 + -1'pol_d3_n1_3_2_4_2 + -1'pol_d3_n1_3_2_4_3 + -1'pol_d3_n1_3_3_1_1 + -1'pol_d3_n1_3_3_1_2 + -1'pol_d3_n1_3_3_1_3 + -1'pol_d3_n1_3_3_2_1 + -1'pol_d3_n1_3_3_2_2 + -1'pol_d3_n1_3_3_2_3 + -1'pol_d3_n1_3_3_3_1 + -1'pol_d3_n1_3_3_3_2 + -1'pol_d3_n1_3_3_3_3 + -1'pol_d3_n1_3_3_4_1 + -1'pol_d3_n1_3_3_4_2 + -1'pol_d3_n1_3_3_4_3 + -1'pol_d4_n1_1_1_1_1 + -1'pol_d4_n1_1_1_1_2 + -1'pol_d4_n1_1_1_1_3 + -1'pol_d4_n1_1_1_1_4 + -1'pol_d4_n1_1_1_2_1 + -1'pol_d4_n1_1_1_2_2 + -1'pol_d4_n1_1_1_2_3 + -1'pol_d4_n1_1_1_2_4 + -1'pol_d4_n1_1_1_3_1 + -1'pol_d4_n1_1_1_3_2 + -1'pol_d4_n1_1_1_3_3 + -1'pol_d4_n1_1_1_3_4 + -1'pol_d4_n1_1_2_1_1 + -1'pol_d4_n1_1_2_1_2 + -1'pol_d4_n1_1_2_1_3 + -1'pol_d4_n1_1_2_1_4 + -1'pol_d4_n1_1_2_2_1 + -1'pol_d4_n1_1_2_2_2 + -1'pol_d4_n1_1_2_2_3 + -1'pol_d4_n1_1_2_2_4 + -1'pol_d4_n1_1_2_3_1 + -1'pol_d4_n1_1_2_3_2 + -1'pol_d4_n1_1_2_3_3 + -1'pol_d4_n1_1_2_3_4 + -1'pol_d4_n1_1_3_1_1 + -1'pol_d4_n1_1_3_1_2 + -1'pol_d4_n1_1_3_1_3 + -1'pol_d4_n1_1_3_1_4 + -1'pol_d4_n1_1_3_2_1 + -1'pol_d4_n1_1_3_2_2 + -1'pol_d4_n1_1_3_2_3 + -1'pol_d4_n1_1_3_2_4 + -1'pol_d4_n1_1_3_3_1 + -1'pol_d4_n1_1_3_3_2 + -1'pol_d4_n1_1_3_3_3 + -1'pol_d4_n1_1_3_3_4 + -1'pol_d4_n1_2_1_1_1 + -1'pol_d4_n1_2_1_1_2 + -1'pol_d4_n1_2_1_1_3 + -1'pol_d4_n1_2_1_1_4 + -1'pol_d4_n1_2_1_2_1 + -1'pol_d4_n1_2_1_2_2 + -1'pol_d4_n1_2_1_2_3 + -1'pol_d4_n1_2_1_2_4 + -1'pol_d4_n1_2_1_3_1 + -1'pol_d4_n1_2_1_3_2 + -1'pol_d4_n1_2_1_3_3 + -1'pol_d4_n1_2_1_3_4 + -1'pol_d4_n1_2_2_1_1 + -1'pol_d4_n1_2_2_1_2 + -1'pol_d4_n1_2_2_1_3 + -1'pol_d4_n1_2_2_1_4 + -1'pol_d4_n1_2_2_2_1 + -1'pol_d4_n1_2_2_2_2 + -1'pol_d4_n1_2_2_2_3 + -1'pol_d4_n1_2_2_2_4 + -1'pol_d4_n1_2_2_3_1 + -1'pol_d4_n1_2_2_3_2 + -1'pol_d4_n1_2_2_3_3 + -1'pol_d4_n1_2_2_3_4 + -1'pol_d4_n1_2_3_1_1 + -1'pol_d4_n1_2_3_1_2 + -1'pol_d4_n1_2_3_1_3 + -1'pol_d4_n1_2_3_1_4 + -1'pol_d4_n1_2_3_2_1 + -1'pol_d4_n1_2_3_2_2 + -1'pol_d4_n1_2_3_2_3 + -1'pol_d4_n1_2_3_2_4 + -1'pol_d4_n1_2_3_3_1 + -1'pol_d4_n1_2_3_3_2 + -1'pol_d4_n1_2_3_3_3 + -1'pol_d4_n1_2_3_3_4 + -1'pol_d4_n1_3_1_1_1 + -1'pol_d4_n1_3_1_1_2 + -1'pol_d4_n1_3_1_1_3 + -1'pol_d4_n1_3_1_1_4 + -1'pol_d4_n1_3_1_2_1 + -1'pol_d4_n1_3_1_2_2 + -1'pol_d4_n1_3_1_2_3 + -1'pol_d4_n1_3_1_2_4 + -1'pol_d4_n1_3_1_3_1 + -1'pol_d4_n1_3_1_3_2 + -1'pol_d4_n1_3_1_3_3 + -1'pol_d4_n1_3_1_3_4 + -1'pol_d4_n1_3_2_1_1 + -1'pol_d4_n1_3_2_1_2 + -1'pol_d4_n1_3_2_1_3 + -1'pol_d4_n1_3_2_1_4 + -1'pol_d4_n1_3_2_2_1 + -1'pol_d4_n1_3_2_2_2 + -1'pol_d4_n1_3_2_2_3 + -1'pol_d4_n1_3_2_2_4 + -1'pol_d4_n1_3_2_3_1 + -1'pol_d4_n1_3_2_3_2 + -1'pol_d4_n1_3_2_3_3 + -1'pol_d4_n1_3_2_3_4 + -1'pol_d4_n1_3_3_1_1 + -1'pol_d4_n1_3_3_1_2 + -1'pol_d4_n1_3_3_1_3 + -1'pol_d4_n1_3_3_1_4 + -1'pol_d4_n1_3_3_2_1 + -1'pol_d4_n1_3_3_2_2 + -1'pol_d4_n1_3_3_2_3 + -1'pol_d4_n1_3_3_2_4 + -1'pol_d4_n1_3_3_3_1 + -1'pol_d4_n1_3_3_3_2 + -1'pol_d4_n1_3_3_3_3 + -1'pol_d4_n1_3_3_3_4 = -1800
invariant :pi_d1_n1_2_3_1_2 + pil_d1_n1_2_3_1_2 = 1
invariant :po_d4_n1_3_3_3_1 + pol_d4_n1_3_3_3_1 = 1
invariant :po_d1_n1_2_3_3_3 + pol_d1_n1_2_3_3_3 = 1
invariant :po_d3_n1_1_2_3_3 + pol_d3_n1_1_2_3_3 = 1
invariant :pi_d1_n1_3_2_3_3 + pil_d1_n1_3_2_3_3 = 1
invariant :po_d4_n1_1_2_1_3 + pol_d4_n1_1_2_1_3 = 1
invariant :pi_d4_n1_2_3_2_1 + pil_d4_n1_2_3_2_1 = 1
invariant :po_d1_n1_1_2_2_1 + pol_d1_n1_1_2_2_1 = 1
invariant :po_d4_n1_1_2_3_3 + pol_d4_n1_1_2_3_3 = 1
invariant :pi_d2_n1_1_3_1_3 + pil_d2_n1_1_3_1_3 = 1
invariant :po_d3_n1_1_2_2_1 + pol_d3_n1_1_2_2_1 = 1
invariant :po_d1_n1_1_2_3_3 + pol_d1_n1_1_2_3_3 = 1
invariant :pi_d3_n1_3_1_2_2 + pil_d3_n1_3_1_2_2 = 1
invariant :po_d1_n1_1_1_1_1 + pol_d1_n1_1_1_1_1 = 1
invariant :pb_d1_n1_3_3_1_2 + pb_d1_n2_3_3_1_2 + pb_d2_n1_3_3_1_2 + pb_d2_n2_3_3_1_2 + pb_d3_n1_3_3_1_2 + pb_d3_n2_3_3_1_2 + pb_d4_n1_3_3_1_2 + pb_d4_n2_3_3_1_2 + pbl_3_3_1_2 = 36
invariant :pi_d3_n1_1_1_4_2 + pil_d3_n1_1_1_4_2 = 1
invariant :po_d2_n1_1_1_1_2 + pol_d2_n1_1_1_1_2 = 1
invariant :po_d4_n1_2_1_1_2 + pol_d4_n1_2_1_1_2 = 1
invariant :pi_d4_n1_3_2_3_3 + pil_d4_n1_3_2_3_3 = 1
invariant :pi_d1_n1_1_1_1_2 + pil_d1_n1_1_1_1_2 = 1
invariant :pi_d2_n1_3_4_1_3 + pil_d2_n1_3_4_1_3 = 1
invariant :pi_d1_n1_4_3_2_1 + pil_d1_n1_4_3_2_1 = 1
invariant :pi_d3_n1_1_1_2_3 + pil_d3_n1_1_1_2_3 = 1
invariant :po_d1_n1_2_1_2_3 + pol_d1_n1_2_1_2_3 = 1
invariant :po_d2_n1_3_1_1_2 + pol_d2_n1_3_1_1_2 = 1
invariant :pi_d4_n1_1_1_1_1 + pil_d4_n1_1_1_1_1 = 1
invariant :pi_d4_n1_1_3_3_1 + pil_d4_n1_1_3_3_1 = 1
invariant :po_d1_n1_1_2_3_1 + pol_d1_n1_1_2_3_1 = 1
invariant :po_d1_n1_3_2_1_1 + pol_d1_n1_3_2_1_1 = 1
invariant :po_d1_n1_2_3_1_2 + pol_d1_n1_2_3_1_2 = 1
invariant :po_d1_n1_3_1_3_3 + pol_d1_n1_3_1_3_3 = 1
invariant :po_d1_n1_2_2_2_2 + pol_d1_n1_2_2_2_2 = 1
invariant :po_d1_n1_1_1_2_3 + pol_d1_n1_1_1_2_3 = 1
invariant :po_d1_n1_3_3_3_1 + pol_d1_n1_3_3_3_1 = 1
invariant :po_d1_n1_2_1_2_1 + pol_d1_n1_2_1_2_1 = 1
invariant :po_d2_n1_2_1_1_1 + pol_d2_n1_2_1_1_1 = 1
invariant :po_d3_n1_2_3_1_3 + pol_d3_n1_2_3_1_3 = 1
invariant :pi_d4_n1_2_3_2_2 + pil_d4_n1_2_3_2_2 = 1
invariant :po_d3_n1_2_3_3_3 + pol_d3_n1_2_3_3_3 = 1
invariant :po_d3_n1_2_3_4_1 + pol_d3_n1_2_3_4_1 = 1
invariant :po_d4_n1_2_2_2_4 + pol_d4_n1_2_2_2_4 = 1
invariant :po_d1_n1_2_1_3_1 + pol_d1_n1_2_1_3_1 = 1
invariant :pi_d2_n1_1_4_1_3 + pil_d2_n1_1_4_1_3 = 1
invariant :pi_d4_n1_3_3_1_1 + pil_d4_n1_3_3_1_1 = 1
invariant :po_d3_n1_3_1_2_2 + pol_d3_n1_3_1_2_2 = 1
invariant :po_d1_n1_1_3_2_3 + pol_d1_n1_1_3_2_3 = 1
invariant :po_d1_n1_4_2_2_2 + pol_d1_n1_4_2_2_2 = 1
invariant :po_d1_n1_1_2_2_3 + pol_d1_n1_1_2_2_3 = 1
invariant :pi_d1_n1_3_2_1_3 + pil_d1_n1_3_2_1_3 = 1
invariant :pi_d3_n1_1_1_3_3 + pil_d3_n1_1_1_3_3 = 1
invariant :pi_d1_n1_2_2_3_3 + pil_d1_n1_2_2_3_3 = 1
invariant :pi_d1_n1_4_3_1_1 + pil_d1_n1_4_3_1_1 = 1
invariant :pi_d2_n1_1_1_1_3 + pil_d2_n1_1_1_1_3 = 1
invariant :po_d3_n1_3_1_1_2 + pol_d3_n1_3_1_1_2 = 1
invariant :po_d4_n1_3_2_2_3 + pol_d4_n1_3_2_2_3 = 1
invariant :pi_d1_n1_2_1_1_3 + pil_d1_n1_2_1_1_3 = 1
invariant :pi_d1_n1_3_1_1_2 + pil_d1_n1_3_1_1_2 = 1
invariant :pi_d3_n1_1_3_4_2 + pil_d3_n1_1_3_4_2 = 1
invariant :po_d1_n1_3_2_1_2 + pol_d1_n1_3_2_1_2 = 1
invariant :pi_d4_n1_2_3_3_3 + pil_d4_n1_2_3_3_3 = 1
invariant :po_d1_n1_1_3_3_1 + pol_d1_n1_1_3_3_1 = 1
invariant :pi_d4_n1_3_2_3_2 + pil_d4_n1_3_2_3_2 = 1
invariant :po_d2_n1_2_1_2_1 + pol_d2_n1_2_1_2_1 = 1
invariant :po_d1_n1_2_2_1_2 + pol_d1_n1_2_2_1_2 = 1
invariant :pb_d1_n1_1_2_1_1 + pb_d1_n2_1_2_1_1 + pb_d2_n1_1_2_1_1 + pb_d2_n2_1_2_1_1 + pb_d3_n1_1_2_1_1 + pb_d3_n2_1_2_1_1 + pb_d4_n1_1_2_1_1 + pb_d4_n2_1_2_1_1 + pbl_1_2_1_1 = 36
invariant :pi_d2_n1_2_1_3_3 + pil_d2_n1_2_1_3_3 = 1
invariant :po_d1_n1_3_3_2_2 + pol_d1_n1_3_3_2_2 = 1
invariant :po_d4_n1_2_2_1_3 + pol_d4_n1_2_2_1_3 = 1
invariant :pi_d1_n1_4_1_2_2 + pil_d1_n1_4_1_2_2 = 1
invariant :pi_d2_n1_1_1_2_2 + pil_d2_n1_1_1_2_2 = 1
invariant :pi_d2_n1_2_2_2_2 + pil_d2_n1_2_2_2_2 = 1
invariant :po_d1_n1_4_2_3_2 + pol_d1_n1_4_2_3_2 = 1
invariant :po_d1_n1_4_2_3_1 + pol_d1_n1_4_2_3_1 = 1
invariant :pi_d2_n1_3_4_3_2 + pil_d2_n1_3_4_3_2 = 1
invariant :pi_d1_n1_4_2_2_1 + pil_d1_n1_4_2_2_1 = 1
invariant :pb_d1_n1_1_3_1_3 + pb_d1_n2_1_3_1_3 + pb_d2_n1_1_3_1_3 + pb_d2_n2_1_3_1_3 + pb_d3_n1_1_3_1_3 + pb_d3_n2_1_3_1_3 + pb_d4_n1_1_3_1_3 + pb_d4_n2_1_3_1_3 + pbl_1_3_1_3 = 36
invariant :pi_d2_n1_1_2_2_3 + pil_d2_n1_1_2_2_3 = 1
invariant :pi_d4_n1_1_1_3_4 + pil_d4_n1_1_1_3_4 = 1
invariant :pi_d2_n1_3_3_2_1 + pil_d2_n1_3_3_2_1 = 1
invariant :pi_d3_n1_2_2_1_2 + pil_d3_n1_2_2_1_2 = 1
invariant :pi_d3_n1_2_1_3_3 + pil_d3_n1_2_1_3_3 = 1
invariant :pi_d2_n1_2_2_3_3 + pil_d2_n1_2_2_3_3 = 1
invariant :pi_d4_n1_1_1_3_2 + pil_d4_n1_1_1_3_2 = 1
invariant :po_d1_n1_1_1_3_1 + pol_d1_n1_1_1_3_1 = 1
invariant :po_d3_n1_1_1_4_3 + pol_d3_n1_1_1_4_3 = 1
invariant :po_d1_n1_2_2_3_1 + pol_d1_n1_2_2_3_1 = 1
invariant :po_d3_n1_3_3_1_1 + pol_d3_n1_3_3_1_1 = 1
invariant :po_d4_n1_2_1_1_4 + pol_d4_n1_2_1_1_4 = 1
invariant :po_d3_n1_2_2_4_1 + pol_d3_n1_2_2_4_1 = 1
invariant :pb_d1_n1_1_3_2_1 + pb_d1_n2_1_3_2_1 + pb_d2_n1_1_3_2_1 + pb_d2_n2_1_3_2_1 + pb_d3_n1_1_3_2_1 + pb_d3_n2_1_3_2_1 + pb_d4_n1_1_3_2_1 + pb_d4_n2_1_3_2_1 + pbl_1_3_2_1 = 36
invariant :pi_d1_n1_4_3_1_3 + pil_d1_n1_4_3_1_3 = 1
invariant :po_d3_n1_1_1_4_2 + pol_d3_n1_1_1_4_2 = 1
invariant :pb_d1_n1_3_1_2_1 + pb_d1_n2_3_1_2_1 + pb_d2_n1_3_1_2_1 + pb_d2_n2_3_1_2_1 + pb_d3_n1_3_1_2_1 + pb_d3_n2_3_1_2_1 + pb_d4_n1_3_1_2_1 + pb_d4_n2_3_1_2_1 + pbl_3_1_2_1 = 36
invariant :pi_d1_n1_3_1_2_1 + pil_d1_n1_3_1_2_1 = 1
invariant :po_d3_n1_1_1_4_1 + pol_d3_n1_1_1_4_1 = 1
invariant :po_d4_n1_3_1_1_3 + pol_d4_n1_3_1_1_3 = 1
invariant :pi_d3_n1_3_2_1_3 + pil_d3_n1_3_2_1_3 = 1
invariant :pi_d3_n1_2_2_4_2 + pil_d3_n1_2_2_4_2 = 1
invariant :pi_d3_n1_1_2_1_1 + pil_d3_n1_1_2_1_1 = 1
invariant :pi_d4_n1_3_2_2_3 + pil_d4_n1_3_2_2_3 = 1
invariant :pi_d4_n1_2_2_3_1 + pil_d4_n1_2_2_3_1 = 1
invariant :po_d2_n1_3_3_1_3 + pol_d2_n1_3_3_1_3 = 1
invariant :pb_d1_n1_1_2_3_3 + pb_d1_n2_1_2_3_3 + pb_d2_n1_1_2_3_3 + pb_d2_n2_1_2_3_3 + pb_d3_n1_1_2_3_3 + pb_d3_n2_1_2_3_3 + pb_d4_n1_1_2_3_3 + pb_d4_n2_1_2_3_3 + pbl_1_2_3_3 = 36
invariant :po_d1_n1_1_1_2_2 + pol_d1_n1_1_1_2_2 = 1
invariant :pb_d1_n1_3_3_3_3 + pb_d1_n2_3_3_3_3 + pb_d2_n1_3_3_3_3 + pb_d2_n2_3_3_3_3 + pb_d3_n1_3_3_3_3 + pb_d3_n2_3_3_3_3 + pb_d4_n1_3_3_3_3 + pb_d4_n2_3_3_3_3 + pbl_3_3_3_3 = 36
invariant :pi_d2_n1_2_2_2_1 + pil_d2_n1_2_2_2_1 = 1
invariant :pi_d1_n1_3_2_2_2 + pil_d1_n1_3_2_2_2 = 1
invariant :po_d3_n1_3_2_2_2 + pol_d3_n1_3_2_2_2 = 1
invariant :po_d3_n1_3_2_4_3 + pol_d3_n1_3_2_4_3 = 1
invariant :pi_d1_n1_1_3_1_1 + pil_d1_n1_1_3_1_1 = 1
invariant :po_d4_n1_3_1_3_4 + pol_d4_n1_3_1_3_4 = 1
invariant :pi_d3_n1_1_3_4_3 + pil_d3_n1_1_3_4_3 = 1
invariant :pi_d4_n1_1_1_2_2 + pil_d4_n1_1_1_2_2 = 1
invariant :po_d2_n1_1_3_3_3 + pol_d2_n1_1_3_3_3 = 1
invariant :pi_d3_n1_1_2_3_2 + pil_d3_n1_1_2_3_2 = 1
invariant :po_d1_n1_2_1_3_2 + pol_d1_n1_2_1_3_2 = 1
invariant :po_d4_n1_3_3_2_2 + pol_d4_n1_3_3_2_2 = 1
invariant :po_d3_n1_1_3_2_2 + pol_d3_n1_1_3_2_2 = 1
invariant :po_d2_n1_1_2_1_3 + pol_d2_n1_1_2_1_3 = 1
invariant :po_d4_n1_2_3_2_2 + pol_d4_n1_2_3_2_2 = 1
invariant :pi_d1_n1_4_2_3_3 + pil_d1_n1_4_2_3_3 = 1
invariant :pi_d1_n1_2_3_3_1 + pil_d1_n1_2_3_3_1 = 1
invariant :pi_d2_n1_1_4_3_1 + pil_d2_n1_1_4_3_1 = 1
invariant :pi_d4_n1_2_2_1_1 + pil_d4_n1_2_2_1_1 = 1
invariant :po_d3_n1_3_1_4_2 + pol_d3_n1_3_1_4_2 = 1
invariant :pi_d1_n1_4_1_2_1 + pil_d1_n1_4_1_2_1 = 1
invariant :pi_d2_n1_1_1_1_2 + pil_d2_n1_1_1_1_2 = 1
invariant :po_d1_n1_2_3_3_2 + pol_d1_n1_2_3_3_2 = 1
invariant :pi_d1_n1_1_2_3_1 + pil_d1_n1_1_2_3_1 = 1
invariant :pi_d1_n1_3_1_3_3 + pil_d1_n1_3_1_3_3 = 1
invariant :po_d4_n1_1_1_3_3 + pol_d4_n1_1_1_3_3 = 1
invariant :pi_d1_n1_3_1_1_3 + pil_d1_n1_3_1_1_3 = 1
invariant :pb_d1_n1_3_1_2_2 + pb_d1_n2_3_1_2_2 + pb_d2_n1_3_1_2_2 + pb_d2_n2_3_1_2_2 + pb_d3_n1_3_1_2_2 + pb_d3_n2_3_1_2_2 + pb_d4_n1_3_1_2_2 + pb_d4_n2_3_1_2_2 + pbl_3_1_2_2 = 36
invariant :pi_d3_n1_3_2_3_3 + pil_d3_n1_3_2_3_3 = 1
invariant :po_d3_n1_1_1_3_2 + pol_d3_n1_1_1_3_2 = 1
invariant :pi_d2_n1_1_4_3_2 + pil_d2_n1_1_4_3_2 = 1
invariant :po_d4_n1_3_2_3_2 + pol_d4_n1_3_2_3_2 = 1
invariant :pi_d3_n1_2_3_4_3 + pil_d3_n1_2_3_4_3 = 1
invariant :po_d2_n1_2_4_3_2 + pol_d2_n1_2_4_3_2 = 1
invariant :pb_d1_n1_2_1_1_2 + pb_d1_n2_2_1_1_2 + pb_d2_n1_2_1_1_2 + pb_d2_n2_2_1_1_2 + pb_d3_n1_2_1_1_2 + pb_d3_n2_2_1_1_2 + pb_d4_n1_2_1_1_2 + pb_d4_n2_2_1_1_2 + pbl_2_1_1_2 = 36
invariant :pi_d4_n1_1_1_3_3 + pil_d4_n1_1_1_3_3 = 1
invariant :pi_d2_n1_2_3_3_1 + pil_d2_n1_2_3_3_1 = 1
invariant :pi_d3_n1_2_3_4_1 + pil_d3_n1_2_3_4_1 = 1
invariant :pi_d3_n1_1_3_3_1 + pil_d3_n1_1_3_3_1 = 1
invariant :pi_d1_n1_4_3_3_1 + pil_d1_n1_4_3_3_1 = 1
invariant :po_d2_n1_1_1_1_1 + pol_d2_n1_1_1_1_1 = 1
invariant :po_d4_n1_1_3_3_3 + pol_d4_n1_1_3_3_3 = 1
invariant :po_d3_n1_2_2_4_3 + pol_d3_n1_2_2_4_3 = 1
invariant :pi_d1_n1_1_1_1_3 + pil_d1_n1_1_1_1_3 = 1
invariant :po_d1_n1_1_1_1_2 + pol_d1_n1_1_1_1_2 = 1
invariant :po_d1_n1_1_2_3_2 + pol_d1_n1_1_2_3_2 = 1
invariant :po_d3_n1_2_1_4_3 + pol_d3_n1_2_1_4_3 = 1
invariant :pi_d4_n1_3_1_2_2 + pil_d4_n1_3_1_2_2 = 1
invariant :po_d4_n1_1_3_1_4 + pol_d4_n1_1_3_1_4 = 1
invariant :po_d1_n1_4_2_1_1 + pol_d1_n1_4_2_1_1 = 1
invariant :pi_d4_n1_3_3_2_2 + pil_d4_n1_3_3_2_2 = 1
invariant :pb_d1_n1_1_2_2_1 + pb_d1_n2_1_2_2_1 + pb_d2_n1_1_2_2_1 + pb_d2_n2_1_2_2_1 + pb_d3_n1_1_2_2_1 + pb_d3_n2_1_2_2_1 + pb_d4_n1_1_2_2_1 + pb_d4_n2_1_2_2_1 + pbl_1_2_2_1 = 36
invariant :po_d3_n1_2_2_3_2 + pol_d3_n1_2_2_3_2 = 1
invariant :po_d1_n1_3_1_1_1 + pol_d1_n1_3_1_1_1 = 1
invariant :pb_d1_n1_3_2_2_2 + pb_d1_n2_3_2_2_2 + pb_d2_n1_3_2_2_2 + pb_d2_n2_3_2_2_2 + pb_d3_n1_3_2_2_2 + pb_d3_n2_3_2_2_2 + pb_d4_n1_3_2_2_2 + pb_d4_n2_3_2_2_2 + pbl_3_2_2_2 = 36
invariant :pi_d2_n1_3_2_3_2 + pil_d2_n1_3_2_3_2 = 1
invariant :pb_d1_n1_2_1_2_2 + pb_d1_n2_2_1_2_2 + pb_d2_n1_2_1_2_2 + pb_d2_n2_2_1_2_2 + pb_d3_n1_2_1_2_2 + pb_d3_n2_2_1_2_2 + pb_d4_n1_2_1_2_2 + pb_d4_n2_2_1_2_2 + pbl_2_1_2_2 = 36
invariant :pi_d4_n1_1_3_2_1 + pil_d4_n1_1_3_2_1 = 1
invariant :pi_d1_n1_2_2_3_1 + pil_d1_n1_2_2_3_1 = 1
invariant :pi_d3_n1_2_2_3_2 + pil_d3_n1_2_2_3_2 = 1
invariant :pi_d4_n1_3_1_3_3 + pil_d4_n1_3_1_3_3 = 1
invariant :po_d4_n1_2_2_2_2 + pol_d4_n1_2_2_2_2 = 1
invariant :pi_d3_n1_1_2_2_1 + pil_d3_n1_1_2_2_1 = 1
invariant :po_d1_n1_3_3_3_3 + pol_d1_n1_3_3_3_3 = 1
invariant :pb_d1_n1_3_1_1_3 + pb_d1_n2_3_1_1_3 + pb_d2_n1_3_1_1_3 + pb_d2_n2_3_1_1_3 + pb_d3_n1_3_1_1_3 + pb_d3_n2_3_1_1_3 + pb_d4_n1_3_1_1_3 + pb_d4_n2_3_1_1_3 + pbl_3_1_1_3 = 36
invariant :pb_d1_n1_2_2_2_2 + pb_d1_n2_2_2_2_2 + pb_d2_n1_2_2_2_2 + pb_d2_n2_2_2_2_2 + pb_d3_n1_2_2_2_2 + pb_d3_n2_2_2_2_2 + pb_d4_n1_2_2_2_2 + pb_d4_n2_2_2_2_2 + pbl_2_2_2_2 = 36
invariant :po_d4_n1_1_3_2_3 + pol_d4_n1_1_3_2_3 = 1
invariant :pb_d1_n1_2_3_1_3 + pb_d1_n2_2_3_1_3 + pb_d2_n1_2_3_1_3 + pb_d2_n2_2_3_1_3 + pb_d3_n1_2_3_1_3 + pb_d3_n2_2_3_1_3 + pb_d4_n1_2_3_1_3 + pb_d4_n2_2_3_1_3 + pbl_2_3_1_3 = 36
invariant :pb_d1_n1_2_3_3_1 + pb_d1_n2_2_3_3_1 + pb_d2_n1_2_3_3_1 + pb_d2_n2_2_3_3_1 + pb_d3_n1_2_3_3_1 + pb_d3_n2_2_3_3_1 + pb_d4_n1_2_3_3_1 + pb_d4_n2_2_3_3_1 + pbl_2_3_3_1 = 36
invariant :po_d4_n1_3_2_2_2 + pol_d4_n1_3_2_2_2 = 1
invariant :po_d1_n1_4_1_1_1 + pol_d1_n1_4_1_1_1 = 1
invariant :po_d4_n1_3_2_1_2 + pol_d4_n1_3_2_1_2 = 1
invariant :pi_d4_n1_3_1_2_4 + pil_d4_n1_3_1_2_4 = 1
invariant :po_d3_n1_3_2_2_1 + pol_d3_n1_3_2_2_1 = 1
invariant :po_d4_n1_2_2_1_4 + pol_d4_n1_2_2_1_4 = 1
invariant :pb_d1_n1_1_3_2_3 + pb_d1_n2_1_3_2_3 + pb_d2_n1_1_3_2_3 + pb_d2_n2_1_3_2_3 + pb_d3_n1_1_3_2_3 + pb_d3_n2_1_3_2_3 + pb_d4_n1_1_3_2_3 + pb_d4_n2_1_3_2_3 + pbl_1_3_2_3 = 36
invariant :po_d3_n1_3_3_3_1 + pol_d3_n1_3_3_3_1 = 1
invariant :po_d1_n1_1_3_1_2 + pol_d1_n1_1_3_1_2 = 1
invariant :po_d2_n1_3_3_1_1 + pol_d2_n1_3_3_1_1 = 1
invariant :pi_d3_n1_1_2_4_2 + pil_d3_n1_1_2_4_2 = 1
invariant :pi_d4_n1_1_1_2_3 + pil_d4_n1_1_1_2_3 = 1
invariant :pi_d3_n1_1_3_2_2 + pil_d3_n1_1_3_2_2 = 1
invariant :pb_d1_n1_3_2_3_2 + pb_d1_n2_3_2_3_2 + pb_d2_n1_3_2_3_2 + pb_d2_n2_3_2_3_2 + pb_d3_n1_3_2_3_2 + pb_d3_n2_3_2_3_2 + pb_d4_n1_3_2_3_2 + pb_d4_n2_3_2_3_2 + pbl_3_2_3_2 = 36
invariant :pi_d2_n1_2_1_1_3 + pil_d2_n1_2_1_1_3 = 1
invariant :pi_d1_n1_2_2_3_2 + pil_d1_n1_2_2_3_2 = 1
invariant :pi_d2_n1_2_3_3_3 + pil_d2_n1_2_3_3_3 = 1
invariant :po_d4_n1_3_3_2_1 + pol_d4_n1_3_3_2_1 = 1
invariant :pi_d3_n1_2_2_3_3 + pil_d3_n1_2_2_3_3 = 1
invariant :pi_d2_n1_2_1_1_2 + pil_d2_n1_2_1_1_2 = 1
invariant :po_d4_n1_3_2_2_4 + pol_d4_n1_3_2_2_4 = 1
invariant :pb_d1_n1_1_1_3_1 + pb_d1_n2_1_1_3_1 + pb_d2_n1_1_1_3_1 + pb_d2_n2_1_1_3_1 + pb_d3_n1_1_1_3_1 + pb_d3_n2_1_1_3_1 + pb_d4_n1_1_1_3_1 + pb_d4_n2_1_1_3_1 + pbl_1_1_3_1 = 36
invariant :po_d2_n1_1_4_1_2 + pol_d2_n1_1_4_1_2 = 1
invariant :po_d2_n1_3_1_3_3 + pol_d2_n1_3_1_3_3 = 1
invariant :pb_d1_n1_2_2_3_3 + pb_d1_n2_2_2_3_3 + pb_d2_n1_2_2_3_3 + pb_d2_n2_2_2_3_3 + pb_d3_n1_2_2_3_3 + pb_d3_n2_2_2_3_3 + pb_d4_n1_2_2_3_3 + pb_d4_n2_2_2_3_3 + pbl_2_2_3_3 = 36
invariant :pb_d1_n1_3_2_2_3 + pb_d1_n2_3_2_2_3 + pb_d2_n1_3_2_2_3 + pb_d2_n2_3_2_2_3 + pb_d3_n1_3_2_2_3 + pb_d3_n2_3_2_2_3 + pb_d4_n1_3_2_2_3 + pb_d4_n2_3_2_2_3 + pbl_3_2_2_3 = 36
invariant :pi_d1_n1_3_3_3_3 + pil_d1_n1_3_3_3_3 = 1
invariant :pi_d4_n1_3_1_2_1 + pil_d4_n1_3_1_2_1 = 1
invariant :po_d1_n1_4_3_1_3 + pol_d1_n1_4_3_1_3 = 1
invariant :pi_d1_n1_1_2_1_3 + pil_d1_n1_1_2_1_3 = 1
invariant :po_d4_n1_1_3_1_2 + pol_d4_n1_1_3_1_2 = 1
invariant :po_d2_n1_2_4_3_1 + pol_d2_n1_2_4_3_1 = 1
invariant :pi_d1_n1_2_3_3_3 + pil_d1_n1_2_3_3_3 = 1
invariant :po_d1_n1_3_2_2_2 + pol_d1_n1_3_2_2_2 = 1
invariant :pi_d3_n1_3_1_1_2 + pil_d3_n1_3_1_1_2 = 1
invariant :pb_d1_n1_3_2_3_3 + pb_d1_n2_3_2_3_3 + pb_d2_n1_3_2_3_3 + pb_d2_n2_3_2_3_3 + pb_d3_n1_3_2_3_3 + pb_d3_n2_3_2_3_3 + pb_d4_n1_3_2_3_3 + pb_d4_n2_3_2_3_3 + pbl_3_2_3_3 = 36
invariant :po_d2_n1_3_4_2_3 + pol_d2_n1_3_4_2_3 = 1
invariant :po_d2_n1_1_4_2_1 + pol_d2_n1_1_4_2_1 = 1
invariant :po_d1_n1_1_1_1_3 + pol_d1_n1_1_1_1_3 = 1
invariant :pi_d2_n1_1_3_3_3 + pil_d2_n1_1_3_3_3 = 1
invariant :pi_d1_n1_1_1_3_3 + pil_d1_n1_1_1_3_3 = 1
invariant :po_d2_n1_2_2_3_1 + pol_d2_n1_2_2_3_1 = 1
invariant :pi_d2_n1_3_2_1_3 + pil_d2_n1_3_2_1_3 = 1
invariant :po_d2_n1_3_4_1_3 + pol_d2_n1_3_4_1_3 = 1
invariant :po_d4_n1_1_3_2_1 + pol_d4_n1_1_3_2_1 = 1
invariant :pi_d3_n1_3_2_2_3 + pil_d3_n1_3_2_2_3 = 1
invariant :po_d2_n1_3_1_2_3 + pol_d2_n1_3_1_2_3 = 1
invariant :po_d3_n1_1_1_2_3 + pol_d3_n1_1_1_2_3 = 1
invariant :pi_d2_n1_1_3_1_2 + pil_d2_n1_1_3_1_2 = 1
invariant :pi_d1_n1_2_1_3_3 + pil_d1_n1_2_1_3_3 = 1
invariant :po_d2_n1_1_4_1_3 + pol_d2_n1_1_4_1_3 = 1
invariant :pb_d1_n1_1_1_1_2 + pb_d1_n2_1_1_1_2 + pb_d2_n1_1_1_1_2 + pb_d2_n2_1_1_1_2 + pb_d3_n1_1_1_1_2 + pb_d3_n2_1_1_1_2 + pb_d4_n1_1_1_1_2 + pb_d4_n2_1_1_1_2 + pbl_1_1_1_2 = 36
invariant :pi_d4_n1_1_1_1_3 + pil_d4_n1_1_1_1_3 = 1
invariant :po_d3_n1_3_3_4_1 + pol_d3_n1_3_3_4_1 = 1
invariant :pb_d1_n1_1_3_1_1 + pb_d1_n2_1_3_1_1 + pb_d2_n1_1_3_1_1 + pb_d2_n2_1_3_1_1 + pb_d3_n1_1_3_1_1 + pb_d3_n2_1_3_1_1 + pb_d4_n1_1_3_1_1 + pb_d4_n2_1_3_1_1 + pbl_1_3_1_1 = 36
invariant :pi_d1_n1_4_1_3_3 + pil_d1_n1_4_1_3_3 = 1
invariant :pi_d4_n1_2_2_2_3 + pil_d4_n1_2_2_2_3 = 1
invariant :po_d4_n1_1_2_3_1 + pol_d4_n1_1_2_3_1 = 1
invariant :po_d4_n1_2_1_3_4 + pol_d4_n1_2_1_3_4 = 1
invariant :pi_d1_n1_3_2_1_2 + pil_d1_n1_3_2_1_2 = 1
invariant :po_d3_n1_3_2_3_1 + pol_d3_n1_3_2_3_1 = 1
invariant :po_d1_n1_2_3_3_1 + pol_d1_n1_2_3_3_1 = 1
invariant :pi_d3_n1_1_3_2_1 + pil_d3_n1_1_3_2_1 = 1
invariant :pi_d3_n1_3_2_3_1 + pil_d3_n1_3_2_3_1 = 1
invariant :po_d2_n1_2_3_3_1 + pol_d2_n1_2_3_3_1 = 1
invariant :po_d2_n1_1_3_3_1 + pol_d2_n1_1_3_3_1 = 1
invariant :pi_d2_n1_3_2_2_2 + pil_d2_n1_3_2_2_2 = 1
invariant :pb_d1_n1_3_2_2_1 + pb_d1_n2_3_2_2_1 + pb_d2_n1_3_2_2_1 + pb_d2_n2_3_2_2_1 + pb_d3_n1_3_2_2_1 + pb_d3_n2_3_2_2_1 + pb_d4_n1_3_2_2_1 + pb_d4_n2_3_2_2_1 + pbl_3_2_2_1 = 36
invariant :po_d1_n1_3_3_3_2 + pol_d1_n1_3_3_3_2 = 1
invariant :po_d2_n1_2_4_1_1 + pol_d2_n1_2_4_1_1 = 1
invariant :pi_d4_n1_1_2_3_4 + pil_d4_n1_1_2_3_4 = 1
invariant :po_d2_n1_2_4_1_2 + pol_d2_n1_2_4_1_2 = 1
invariant :po_d1_n1_4_3_2_2 + pol_d1_n1_4_3_2_2 = 1
invariant :po_d4_n1_3_1_2_2 + pol_d4_n1_3_1_2_2 = 1
invariant :pi_d3_n1_2_2_2_3 + pil_d3_n1_2_2_2_3 = 1
invariant :po_d2_n1_1_4_2_2 + pol_d2_n1_1_4_2_2 = 1
invariant :pi_d2_n1_1_1_2_3 + pil_d2_n1_1_1_2_3 = 1
invariant :pi_d2_n1_3_3_3_1 + pil_d2_n1_3_3_3_1 = 1
invariant :pb_d1_n1_2_1_1_1 + pb_d1_n2_2_1_1_1 + pb_d2_n1_2_1_1_1 + pb_d2_n2_2_1_1_1 + pb_d3_n1_2_1_1_1 + pb_d3_n2_2_1_1_1 + pb_d4_n1_2_1_1_1 + pb_d4_n2_2_1_1_1 + pbl_2_1_1_1 = 36
invariant :pi_d3_n1_1_1_3_1 + pil_d3_n1_1_1_3_1 = 1
invariant :po_d1_n1_3_1_2_2 + pol_d1_n1_3_1_2_2 = 1
invariant :po_d3_n1_2_1_4_2 + pol_d3_n1_2_1_4_2 = 1
invariant :po_d4_n1_3_2_2_1 + pol_d4_n1_3_2_2_1 = 1
invariant :po_d4_n1_1_1_3_2 + pol_d4_n1_1_1_3_2 = 1
invariant :pi_d1_n1_1_2_2_2 + pil_d1_n1_1_2_2_2 = 1
invariant :pi_d3_n1_1_3_1_1 + pil_d3_n1_1_3_1_1 = 1
invariant :pi_d2_n1_2_3_1_3 + pil_d2_n1_2_3_1_3 = 1
invariant :pi_d2_n1_2_3_3_2 + pil_d2_n1_2_3_3_2 = 1
invariant :pi_d1_n1_4_1_3_2 + pil_d1_n1_4_1_3_2 = 1
invariant :pi_d4_n1_2_1_1_2 + pil_d4_n1_2_1_1_2 = 1
invariant :pi_d1_n1_4_1_1_3 + pil_d1_n1_4_1_1_3 = 1
invariant :pi_d2_n1_2_4_2_2 + pil_d2_n1_2_4_2_2 = 1
invariant :po_d3_n1_1_2_1_1 + pol_d3_n1_1_2_1_1 = 1
invariant :pb_d1_n1_2_1_2_1 + pb_d1_n2_2_1_2_1 + pb_d2_n1_2_1_2_1 + pb_d2_n2_2_1_2_1 + pb_d3_n1_2_1_2_1 + pb_d3_n2_2_1_2_1 + pb_d4_n1_2_1_2_1 + pb_d4_n2_2_1_2_1 + pbl_2_1_2_1 = 36
invariant :pi_d3_n1_2_1_3_1 + pil_d3_n1_2_1_3_1 = 1
invariant :po_d3_n1_1_1_2_2 + pol_d3_n1_1_1_2_2 = 1
invariant :pi_d3_n1_3_3_3_1 + pil_d3_n1_3_3_3_1 = 1
invariant :po_d2_n1_3_1_1_3 + pol_d2_n1_3_1_1_3 = 1
invariant :pi_d4_n1_3_3_3_2 + pil_d4_n1_3_3_3_2 = 1
invariant :pb_d1_n1_2_2_2_3 + pb_d1_n2_2_2_2_3 + pb_d2_n1_2_2_2_3 + pb_d2_n2_2_2_2_3 + pb_d3_n1_2_2_2_3 + pb_d3_n2_2_2_2_3 + pb_d4_n1_2_2_2_3 + pb_d4_n2_2_2_2_3 + pbl_2_2_2_3 = 36
invariant :po_d4_n1_2_2_2_3 + pol_d4_n1_2_2_2_3 = 1
invariant :po_d2_n1_3_3_3_2 + pol_d2_n1_3_3_3_2 = 1
invariant :pi_d3_n1_2_3_1_3 + pil_d3_n1_2_3_1_3 = 1
invariant :po_d2_n1_3_4_2_2 + pol_d2_n1_3_4_2_2 = 1
invariant :pi_d4_n1_1_3_1_2 + pil_d4_n1_1_3_1_2 = 1
invariant :pi_d1_n1_1_3_2_2 + pil_d1_n1_1_3_2_2 = 1
invariant :pi_d1_n1_2_1_2_2 + pil_d1_n1_2_1_2_2 = 1
invariant :po_d4_n1_1_2_2_2 + pol_d4_n1_1_2_2_2 = 1
invariant :po_d4_n1_1_2_2_3 + pol_d4_n1_1_2_2_3 = 1
invariant :pb_d1_n1_3_1_3_1 + pb_d1_n2_3_1_3_1 + pb_d2_n1_3_1_3_1 + pb_d2_n2_3_1_3_1 + pb_d3_n1_3_1_3_1 + pb_d3_n2_3_1_3_1 + pb_d4_n1_3_1_3_1 + pb_d4_n2_3_1_3_1 + pbl_3_1_3_1 = 36
invariant :po_d3_n1_3_3_2_3 + pol_d3_n1_3_3_2_3 = 1
invariant :pi_d3_n1_2_1_1_2 + pil_d3_n1_2_1_1_2 = 1
invariant :po_d4_n1_1_3_2_4 + pol_d4_n1_1_3_2_4 = 1
invariant :po_d1_n1_1_1_3_3 + pol_d1_n1_1_1_3_3 = 1
invariant :pi_d3_n1_3_2_3_2 + pil_d3_n1_3_2_3_2 = 1
invariant :pi_d3_n1_1_1_3_2 + pil_d3_n1_1_1_3_2 = 1
invariant :pi_d1_n1_1_3_2_1 + pil_d1_n1_1_3_2_1 = 1
invariant :pi_d2_n1_3_1_3_3 + pil_d2_n1_3_1_3_3 = 1
invariant :po_d3_n1_1_3_3_3 + pol_d3_n1_1_3_3_3 = 1
invariant :po_d4_n1_1_2_1_1 + pol_d4_n1_1_2_1_1 = 1
invariant :pi_d2_n1_1_4_3_3 + pil_d2_n1_1_4_3_3 = 1
invariant :pb_d1_n1_2_2_3_1 + pb_d1_n2_2_2_3_1 + pb_d2_n1_2_2_3_1 + pb_d2_n2_2_2_3_1 + pb_d3_n1_2_2_3_1 + pb_d3_n2_2_2_3_1 + pb_d4_n1_2_2_3_1 + pb_d4_n2_2_2_3_1 + pbl_2_2_3_1 = 36
invariant :po_d4_n1_2_1_2_3 + pol_d4_n1_2_1_2_3 = 1
invariant :po_d2_n1_2_3_1_2 + pol_d2_n1_2_3_1_2 = 1
invariant :po_d3_n1_1_3_4_2 + pol_d3_n1_1_3_4_2 = 1
invariant :pi_d3_n1_3_2_4_1 + pil_d3_n1_3_2_4_1 = 1
invariant :po_d2_n1_3_4_3_3 + pol_d2_n1_3_4_3_3 = 1
invariant :pi_d2_n1_1_2_3_3 + pil_d2_n1_1_2_3_3 = 1
invariant :po_d2_n1_1_2_1_2 + pol_d2_n1_1_2_1_2 = 1
invariant :pi_d1_n1_4_2_1_3 + pil_d1_n1_4_2_1_3 = 1
invariant :po_d1_n1_4_3_3_2 + pol_d1_n1_4_3_3_2 = 1
invariant :pi_d2_n1_1_4_2_2 + pil_d2_n1_1_4_2_2 = 1
invariant :po_d4_n1_2_2_1_2 + pol_d4_n1_2_2_1_2 = 1
invariant :pi_d2_n1_3_1_1_1 + pil_d2_n1_3_1_1_1 = 1
invariant :pi_d1_n1_2_3_2_1 + pil_d1_n1_2_3_2_1 = 1
invariant :pi_d2_n1_1_3_2_2 + pil_d2_n1_1_3_2_2 = 1
invariant :pi_d3_n1_1_1_4_3 + pil_d3_n1_1_1_4_3 = 1
invariant :po_d4_n1_1_3_1_3 + pol_d4_n1_1_3_1_3 = 1
invariant :pi_d1_n1_1_1_2_1 + pil_d1_n1_1_1_2_1 = 1
invariant :po_d1_n1_3_1_1_3 + pol_d1_n1_3_1_1_3 = 1
invariant :po_d3_n1_3_2_3_2 + pol_d3_n1_3_2_3_2 = 1
invariant :po_d4_n1_2_3_3_3 + pol_d4_n1_2_3_3_3 = 1
invariant :pi_d1_n1_1_2_3_3 + pil_d1_n1_1_2_3_3 = 1
invariant :pi_d3_n1_1_2_2_3 + pil_d3_n1_1_2_2_3 = 1
invariant :pi_d2_n1_2_3_2_1 + pil_d2_n1_2_3_2_1 = 1
invariant :pi_d2_n1_2_4_3_3 + pil_d2_n1_2_4_3_3 = 1
invariant :pi_d4_n1_2_1_3_2 + pil_d4_n1_2_1_3_2 = 1
invariant :pb_d1_n1_1_2_3_1 + pb_d1_n2_1_2_3_1 + pb_d2_n1_1_2_3_1 + pb_d2_n2_1_2_3_1 + pb_d3_n1_1_2_3_1 + pb_d3_n2_1_2_3_1 + pb_d4_n1_1_2_3_1 + pb_d4_n2_1_2_3_1 + pbl_1_2_3_1 = 36
invariant :pi_d3_n1_3_1_4_1 + pil_d3_n1_3_1_4_1 = 1
invariant :po_d2_n1_2_2_2_2 + pol_d2_n1_2_2_2_2 = 1
invariant :po_d4_n1_2_3_2_1 + pol_d4_n1_2_3_2_1 = 1
invariant :po_d3_n1_3_3_3_3 + pol_d3_n1_3_3_3_3 = 1
invariant :po_d4_n1_3_2_1_1 + pol_d4_n1_3_2_1_1 = 1
invariant :po_d2_n1_3_2_3_3 + pol_d2_n1_3_2_3_3 = 1
invariant :pi_d1_n1_1_1_3_2 + pil_d1_n1_1_1_3_2 = 1
invariant :po_d3_n1_1_1_1_2 + pol_d3_n1_1_1_1_2 = 1
invariant :pb_d1_n1_3_3_2_3 + pb_d1_n2_3_3_2_3 + pb_d2_n1_3_3_2_3 + pb_d2_n2_3_3_2_3 + pb_d3_n1_3_3_2_3 + pb_d3_n2_3_3_2_3 + pb_d4_n1_3_3_2_3 + pb_d4_n2_3_3_2_3 + pbl_3_3_2_3 = 36
invariant :pi_d1_n1_4_2_1_1 + pil_d1_n1_4_2_1_1 = 1
invariant :pi_d3_n1_2_1_4_3 + pil_d3_n1_2_1_4_3 = 1
invariant :pi_d2_n1_3_2_3_1 + pil_d2_n1_3_2_3_1 = 1
invariant :pi_d2_n1_2_1_3_2 + pil_d2_n1_2_1_3_2 = 1
invariant :pi_d3_n1_3_3_2_1 + pil_d3_n1_3_3_2_1 = 1
invariant :po_d3_n1_3_2_1_2 + pol_d3_n1_3_2_1_2 = 1
invariant :po_d2_n1_3_2_2_3 + pol_d2_n1_3_2_2_3 = 1
invariant :pi_d1_n1_3_1_3_2 + pil_d1_n1_3_1_3_2 = 1
invariant :pi_d4_n1_3_1_3_2 + pil_d4_n1_3_1_3_2 = 1
invariant :pi_d2_n1_2_3_2_2 + pil_d2_n1_2_3_2_2 = 1
invariant :po_d1_n1_4_3_3_1 + pol_d1_n1_4_3_3_1 = 1
invariant :po_d2_n1_2_3_2_3 + pol_d2_n1_2_3_2_3 = 1
invariant :pi_d3_n1_1_1_1_3 + pil_d3_n1_1_1_1_3 = 1
invariant :po_d4_n1_3_3_1_4 + pol_d4_n1_3_3_1_4 = 1
invariant :po_d1_n1_1_3_1_3 + pol_d1_n1_1_3_1_3 = 1
invariant :po_d1_n1_3_2_1_3 + pol_d1_n1_3_2_1_3 = 1
invariant :pi_d1_n1_2_3_1_3 + pil_d1_n1_2_3_1_3 = 1
invariant :pi_d3_n1_1_2_4_1 + pil_d3_n1_1_2_4_1 = 1
invariant :pb_d1_n1_3_3_1_1 + pb_d1_n2_3_3_1_1 + pb_d2_n1_3_3_1_1 + pb_d2_n2_3_3_1_1 + pb_d3_n1_3_3_1_1 + pb_d3_n2_3_3_1_1 + pb_d4_n1_3_3_1_1 + pb_d4_n2_3_3_1_1 + pbl_3_3_1_1 = 36
invariant :pb_d1_n1_1_3_3_1 + pb_d1_n2_1_3_3_1 + pb_d2_n1_1_3_3_1 + pb_d2_n2_1_3_3_1 + pb_d3_n1_1_3_3_1 + pb_d3_n2_1_3_3_1 + pb_d4_n1_1_3_3_1 + pb_d4_n2_1_3_3_1 + pbl_1_3_3_1 = 36
invariant :pb_d1_n1_1_1_2_1 + pb_d1_n2_1_1_2_1 + pb_d2_n1_1_1_2_1 + pb_d2_n2_1_1_2_1 + pb_d3_n1_1_1_2_1 + pb_d3_n2_1_1_2_1 + pb_d4_n1_1_1_2_1 + pb_d4_n2_1_1_2_1 + pbl_1_1_2_1 = 36
invariant :pi_d2_n1_1_3_3_1 + pil_d2_n1_1_3_3_1 = 1
invariant :po_d3_n1_1_3_1_1 + pol_d3_n1_1_3_1_1 = 1
invariant :po_d2_n1_2_1_1_3 + pol_d2_n1_2_1_1_3 = 1
invariant :po_d3_n1_3_3_4_3 + pol_d3_n1_3_3_4_3 = 1
invariant :pi_d2_n1_3_2_1_1 + pil_d2_n1_3_2_1_1 = 1
invariant :pi_d4_n1_3_2_1_3 + pil_d4_n1_3_2_1_3 = 1
invariant :po_d3_n1_2_2_2_1 + pol_d3_n1_2_2_2_1 = 1
invariant :pi_d4_n1_2_3_3_4 + pil_d4_n1_2_3_3_4 = 1
invariant :pi_d4_n1_2_1_3_4 + pil_d4_n1_2_1_3_4 = 1
invariant :po_d3_n1_2_3_4_3 + pol_d3_n1_2_3_4_3 = 1
invariant :pi_d3_n1_3_3_4_3 + pil_d3_n1_3_3_4_3 = 1
invariant :pbl_1_1_1_1 + pbl_1_1_1_2 + pbl_1_1_1_3 + pbl_1_1_2_1 + pbl_1_1_2_2 + pbl_1_1_2_3 + pbl_1_1_3_1 + pbl_1_1_3_2 + pbl_1_1_3_3 + pbl_1_2_1_1 + pbl_1_2_1_2 + pbl_1_2_1_3 + pbl_1_2_2_1 + pbl_1_2_2_2 + pbl_1_2_2_3 + pbl_1_2_3_1 + pbl_1_2_3_2 + pbl_1_2_3_3 + pbl_1_3_1_1 + pbl_1_3_1_2 + pbl_1_3_1_3 + pbl_1_3_2_1 + pbl_1_3_2_2 + pbl_1_3_2_3 + pbl_1_3_3_1 + pbl_1_3_3_2 + pbl_1_3_3_3 + pbl_2_1_1_1 + pbl_2_1_1_2 + pbl_2_1_1_3 + pbl_2_1_2_1 + pbl_2_1_2_2 + pbl_2_1_2_3 + pbl_2_1_3_1 + pbl_2_1_3_2 + pbl_2_1_3_3 + pbl_2_2_1_1 + pbl_2_2_1_2 + pbl_2_2_1_3 + pbl_2_2_2_1 + pbl_2_2_2_2 + pbl_2_2_2_3 + pbl_2_2_3_1 + pbl_2_2_3_2 + pbl_2_2_3_3 + pbl_2_3_1_1 + pbl_2_3_1_2 + pbl_2_3_1_3 + pbl_2_3_2_1 + pbl_2_3_2_2 + pbl_2_3_2_3 + pbl_2_3_3_1 + pbl_2_3_3_2 + pbl_2_3_3_3 + pbl_3_1_1_1 + pbl_3_1_1_2 + pbl_3_1_1_3 + pbl_3_1_2_1 + pbl_3_1_2_2 + pbl_3_1_2_3 + pbl_3_1_3_1 + pbl_3_1_3_2 + pbl_3_1_3_3 + pbl_3_2_1_1 + pbl_3_2_1_2 + pbl_3_2_1_3 + pbl_3_2_2_1 + pbl_3_2_2_2 + pbl_3_2_2_3 + pbl_3_2_3_1 + pbl_3_2_3_2 + pbl_3_2_3_3 + pbl_3_3_1_1 + pbl_3_3_1_2 + pbl_3_3_1_3 + pbl_3_3_2_1 + pbl_3_3_2_2 + pbl_3_3_2_3 + pbl_3_3_3_1 + pbl_3_3_3_2 + pbl_3_3_3_3 + pil_d1_n1_1_1_1_1 + pil_d1_n1_1_1_1_2 + pil_d1_n1_1_1_1_3 + pil_d1_n1_1_1_2_1 + pil_d1_n1_1_1_2_2 + pil_d1_n1_1_1_2_3 + pil_d1_n1_1_1_3_1 + pil_d1_n1_1_1_3_2 + pil_d1_n1_1_1_3_3 + pil_d1_n1_1_2_1_1 + pil_d1_n1_1_2_1_2 + pil_d1_n1_1_2_1_3 + pil_d1_n1_1_2_2_1 + pil_d1_n1_1_2_2_2 + pil_d1_n1_1_2_2_3 + pil_d1_n1_1_2_3_1 + pil_d1_n1_1_2_3_2 + pil_d1_n1_1_2_3_3 + pil_d1_n1_1_3_1_1 + pil_d1_n1_1_3_1_2 + pil_d1_n1_1_3_1_3 + pil_d1_n1_1_3_2_1 + pil_d1_n1_1_3_2_2 + pil_d1_n1_1_3_2_3 + pil_d1_n1_1_3_3_1 + pil_d1_n1_1_3_3_2 + pil_d1_n1_1_3_3_3 + pil_d1_n1_2_1_1_1 + pil_d1_n1_2_1_1_2 + pil_d1_n1_2_1_1_3 + pil_d1_n1_2_1_2_1 + pil_d1_n1_2_1_2_2 + pil_d1_n1_2_1_2_3 + pil_d1_n1_2_1_3_1 + pil_d1_n1_2_1_3_2 + pil_d1_n1_2_1_3_3 + pil_d1_n1_2_2_1_1 + pil_d1_n1_2_2_1_2 + pil_d1_n1_2_2_1_3 + pil_d1_n1_2_2_2_1 + pil_d1_n1_2_2_2_2 + pil_d1_n1_2_2_2_3 + pil_d1_n1_2_2_3_1 + pil_d1_n1_2_2_3_2 + pil_d1_n1_2_2_3_3 + pil_d1_n1_2_3_1_1 + pil_d1_n1_2_3_1_2 + pil_d1_n1_2_3_1_3 + pil_d1_n1_2_3_2_1 + pil_d1_n1_2_3_2_2 + pil_d1_n1_2_3_2_3 + pil_d1_n1_2_3_3_1 + pil_d1_n1_2_3_3_2 + pil_d1_n1_2_3_3_3 + pil_d1_n1_3_1_1_1 + pil_d1_n1_3_1_1_2 + pil_d1_n1_3_1_1_3 + pil_d1_n1_3_1_2_1 + pil_d1_n1_3_1_2_2 + pil_d1_n1_3_1_2_3 + pil_d1_n1_3_1_3_1 + pil_d1_n1_3_1_3_2 + pil_d1_n1_3_1_3_3 + pil_d1_n1_3_2_1_1 + pil_d1_n1_3_2_1_2 + pil_d1_n1_3_2_1_3 + pil_d1_n1_3_2_2_1 + pil_d1_n1_3_2_2_2 + pil_d1_n1_3_2_2_3 + pil_d1_n1_3_2_3_1 + pil_d1_n1_3_2_3_2 + pil_d1_n1_3_2_3_3 + pil_d1_n1_3_3_1_1 + pil_d1_n1_3_3_1_2 + pil_d1_n1_3_3_1_3 + pil_d1_n1_3_3_2_1 + pil_d1_n1_3_3_2_2 + pil_d1_n1_3_3_2_3 + pil_d1_n1_3_3_3_1 + pil_d1_n1_3_3_3_2 + pil_d1_n1_3_3_3_3 + pil_d1_n1_4_1_1_1 + pil_d1_n1_4_1_1_2 + pil_d1_n1_4_1_1_3 + pil_d1_n1_4_1_2_1 + pil_d1_n1_4_1_2_2 + pil_d1_n1_4_1_2_3 + pil_d1_n1_4_1_3_1 + pil_d1_n1_4_1_3_2 + pil_d1_n1_4_1_3_3 + pil_d1_n1_4_2_1_1 + pil_d1_n1_4_2_1_2 + pil_d1_n1_4_2_1_3 + pil_d1_n1_4_2_2_1 + pil_d1_n1_4_2_2_2 + pil_d1_n1_4_2_2_3 + pil_d1_n1_4_2_3_1 + pil_d1_n1_4_2_3_2 + pil_d1_n1_4_2_3_3 + pil_d1_n1_4_3_1_1 + pil_d1_n1_4_3_1_2 + pil_d1_n1_4_3_1_3 + pil_d1_n1_4_3_2_1 + pil_d1_n1_4_3_2_2 + pil_d1_n1_4_3_2_3 + pil_d1_n1_4_3_3_1 + pil_d1_n1_4_3_3_2 + pil_d1_n1_4_3_3_3 + pil_d2_n1_1_1_1_1 + pil_d2_n1_1_1_1_2 + pil_d2_n1_1_1_1_3 + pil_d2_n1_1_1_2_1 + pil_d2_n1_1_1_2_2 + pil_d2_n1_1_1_2_3 + pil_d2_n1_1_1_3_1 + pil_d2_n1_1_1_3_2 + pil_d2_n1_1_1_3_3 + pil_d2_n1_1_2_1_1 + pil_d2_n1_1_2_1_2 + pil_d2_n1_1_2_1_3 + pil_d2_n1_1_2_2_1 + pil_d2_n1_1_2_2_2 + pil_d2_n1_1_2_2_3 + pil_d2_n1_1_2_3_1 + pil_d2_n1_1_2_3_2 + pil_d2_n1_1_2_3_3 + pil_d2_n1_1_3_1_1 + pil_d2_n1_1_3_1_2 + pil_d2_n1_1_3_1_3 + pil_d2_n1_1_3_2_1 + pil_d2_n1_1_3_2_2 + pil_d2_n1_1_3_2_3 + pil_d2_n1_1_3_3_1 + pil_d2_n1_1_3_3_2 + pil_d2_n1_1_3_3_3 + pil_d2_n1_1_4_1_1 + pil_d2_n1_1_4_1_2 + pil_d2_n1_1_4_1_3 + pil_d2_n1_1_4_2_1 + pil_d2_n1_1_4_2_2 + pil_d2_n1_1_4_2_3 + pil_d2_n1_1_4_3_1 + pil_d2_n1_1_4_3_2 + pil_d2_n1_1_4_3_3 + pil_d2_n1_2_1_1_1 + pil_d2_n1_2_1_1_2 + pil_d2_n1_2_1_1_3 + pil_d2_n1_2_1_2_1 + pil_d2_n1_2_1_2_2 + pil_d2_n1_2_1_2_3 + pil_d2_n1_2_1_3_1 + pil_d2_n1_2_1_3_2 + pil_d2_n1_2_1_3_3 + pil_d2_n1_2_2_1_1 + pil_d2_n1_2_2_1_2 + pil_d2_n1_2_2_1_3 + pil_d2_n1_2_2_2_1 + pil_d2_n1_2_2_2_2 + pil_d2_n1_2_2_2_3 + pil_d2_n1_2_2_3_1 + pil_d2_n1_2_2_3_2 + pil_d2_n1_2_2_3_3 + pil_d2_n1_2_3_1_1 + pil_d2_n1_2_3_1_2 + pil_d2_n1_2_3_1_3 + pil_d2_n1_2_3_2_1 + pil_d2_n1_2_3_2_2 + pil_d2_n1_2_3_2_3 + pil_d2_n1_2_3_3_1 + pil_d2_n1_2_3_3_2 + pil_d2_n1_2_3_3_3 + pil_d2_n1_2_4_1_1 + pil_d2_n1_2_4_1_2 + pil_d2_n1_2_4_1_3 + pil_d2_n1_2_4_2_1 + pil_d2_n1_2_4_2_2 + pil_d2_n1_2_4_2_3 + pil_d2_n1_2_4_3_1 + pil_d2_n1_2_4_3_2 + pil_d2_n1_2_4_3_3 + pil_d2_n1_3_1_1_1 + pil_d2_n1_3_1_1_2 + pil_d2_n1_3_1_1_3 + pil_d2_n1_3_1_2_1 + pil_d2_n1_3_1_2_2 + pil_d2_n1_3_1_2_3 + pil_d2_n1_3_1_3_1 + pil_d2_n1_3_1_3_2 + pil_d2_n1_3_1_3_3 + pil_d2_n1_3_2_1_1 + pil_d2_n1_3_2_1_2 + pil_d2_n1_3_2_1_3 + pil_d2_n1_3_2_2_1 + pil_d2_n1_3_2_2_2 + pil_d2_n1_3_2_2_3 + pil_d2_n1_3_2_3_1 + pil_d2_n1_3_2_3_2 + pil_d2_n1_3_2_3_3 + pil_d2_n1_3_3_1_1 + pil_d2_n1_3_3_1_2 + pil_d2_n1_3_3_1_3 + pil_d2_n1_3_3_2_1 + pil_d2_n1_3_3_2_2 + pil_d2_n1_3_3_2_3 + pil_d2_n1_3_3_3_1 + pil_d2_n1_3_3_3_2 + pil_d2_n1_3_3_3_3 + pil_d2_n1_3_4_1_1 + pil_d2_n1_3_4_1_2 + pil_d2_n1_3_4_1_3 + pil_d2_n1_3_4_2_1 + pil_d2_n1_3_4_2_2 + pil_d2_n1_3_4_2_3 + pil_d2_n1_3_4_3_1 + pil_d2_n1_3_4_3_2 + pil_d2_n1_3_4_3_3 + pil_d3_n1_1_1_1_1 + pil_d3_n1_1_1_1_2 + pil_d3_n1_1_1_1_3 + pil_d3_n1_1_1_2_1 + pil_d3_n1_1_1_2_2 + pil_d3_n1_1_1_2_3 + pil_d3_n1_1_1_3_1 + pil_d3_n1_1_1_3_2 + pil_d3_n1_1_1_3_3 + pil_d3_n1_1_1_4_1 + pil_d3_n1_1_1_4_2 + pil_d3_n1_1_1_4_3 + pil_d3_n1_1_2_1_1 + pil_d3_n1_1_2_1_2 + pil_d3_n1_1_2_1_3 + pil_d3_n1_1_2_2_1 + pil_d3_n1_1_2_2_2 + pil_d3_n1_1_2_2_3 + pil_d3_n1_1_2_3_1 + pil_d3_n1_1_2_3_2 + pil_d3_n1_1_2_3_3 + pil_d3_n1_1_2_4_1 + pil_d3_n1_1_2_4_2 + pil_d3_n1_1_2_4_3 + pil_d3_n1_1_3_1_1 + pil_d3_n1_1_3_1_2 + pil_d3_n1_1_3_1_3 + pil_d3_n1_1_3_2_1 + pil_d3_n1_1_3_2_2 + pil_d3_n1_1_3_2_3 + pil_d3_n1_1_3_3_1 + pil_d3_n1_1_3_3_2 + pil_d3_n1_1_3_3_3 + pil_d3_n1_1_3_4_1 + pil_d3_n1_1_3_4_2 + pil_d3_n1_1_3_4_3 + pil_d3_n1_2_1_1_1 + pil_d3_n1_2_1_1_2 + pil_d3_n1_2_1_1_3 + pil_d3_n1_2_1_2_1 + pil_d3_n1_2_1_2_2 + pil_d3_n1_2_1_2_3 + pil_d3_n1_2_1_3_1 + pil_d3_n1_2_1_3_2 + pil_d3_n1_2_1_3_3 + pil_d3_n1_2_1_4_1 + pil_d3_n1_2_1_4_2 + pil_d3_n1_2_1_4_3 + pil_d3_n1_2_2_1_1 + pil_d3_n1_2_2_1_2 + pil_d3_n1_2_2_1_3 + pil_d3_n1_2_2_2_1 + pil_d3_n1_2_2_2_2 + pil_d3_n1_2_2_2_3 + pil_d3_n1_2_2_3_1 + pil_d3_n1_2_2_3_2 + pil_d3_n1_2_2_3_3 + pil_d3_n1_2_2_4_1 + pil_d3_n1_2_2_4_2 + pil_d3_n1_2_2_4_3 + pil_d3_n1_2_3_1_1 + pil_d3_n1_2_3_1_2 + pil_d3_n1_2_3_1_3 + pil_d3_n1_2_3_2_1 + pil_d3_n1_2_3_2_2 + pil_d3_n1_2_3_2_3 + pil_d3_n1_2_3_3_1 + pil_d3_n1_2_3_3_2 + pil_d3_n1_2_3_3_3 + pil_d3_n1_2_3_4_1 + pil_d3_n1_2_3_4_2 + pil_d3_n1_2_3_4_3 + pil_d3_n1_3_1_1_1 + pil_d3_n1_3_1_1_2 + pil_d3_n1_3_1_1_3 + pil_d3_n1_3_1_2_1 + pil_d3_n1_3_1_2_2 + pil_d3_n1_3_1_2_3 + pil_d3_n1_3_1_3_1 + pil_d3_n1_3_1_3_2 + pil_d3_n1_3_1_3_3 + pil_d3_n1_3_1_4_1 + pil_d3_n1_3_1_4_2 + pil_d3_n1_3_1_4_3 + pil_d3_n1_3_2_1_1 + pil_d3_n1_3_2_1_2 + pil_d3_n1_3_2_1_3 + pil_d3_n1_3_2_2_1 + pil_d3_n1_3_2_2_2 + pil_d3_n1_3_2_2_3 + pil_d3_n1_3_2_3_1 + pil_d3_n1_3_2_3_2 + pil_d3_n1_3_2_3_3 + pil_d3_n1_3_2_4_1 + pil_d3_n1_3_2_4_2 + pil_d3_n1_3_2_4_3 + pil_d3_n1_3_3_1_1 + pil_d3_n1_3_3_1_2 + pil_d3_n1_3_3_1_3 + pil_d3_n1_3_3_2_1 + pil_d3_n1_3_3_2_2 + pil_d3_n1_3_3_2_3 + pil_d3_n1_3_3_3_1 + pil_d3_n1_3_3_3_2 + pil_d3_n1_3_3_3_3 + pil_d3_n1_3_3_4_1 + pil_d3_n1_3_3_4_2 + pil_d3_n1_3_3_4_3 + pil_d4_n1_1_1_1_1 + pil_d4_n1_1_1_1_2 + pil_d4_n1_1_1_1_3 + pil_d4_n1_1_1_1_4 + pil_d4_n1_1_1_2_1 + pil_d4_n1_1_1_2_2 + pil_d4_n1_1_1_2_3 + pil_d4_n1_1_1_2_4 + pil_d4_n1_1_1_3_1 + pil_d4_n1_1_1_3_2 + pil_d4_n1_1_1_3_3 + pil_d4_n1_1_1_3_4 + pil_d4_n1_1_2_1_1 + pil_d4_n1_1_2_1_2 + pil_d4_n1_1_2_1_3 + pil_d4_n1_1_2_1_4 + pil_d4_n1_1_2_2_1 + pil_d4_n1_1_2_2_2 + pil_d4_n1_1_2_2_3 + pil_d4_n1_1_2_2_4 + pil_d4_n1_1_2_3_1 + pil_d4_n1_1_2_3_2 + pil_d4_n1_1_2_3_3 + pil_d4_n1_1_2_3_4 + pil_d4_n1_1_3_1_1 + pil_d4_n1_1_3_1_2 + pil_d4_n1_1_3_1_3 + pil_d4_n1_1_3_1_4 + pil_d4_n1_1_3_2_1 + pil_d4_n1_1_3_2_2 + pil_d4_n1_1_3_2_3 + pil_d4_n1_1_3_2_4 + pil_d4_n1_1_3_3_1 + pil_d4_n1_1_3_3_2 + pil_d4_n1_1_3_3_3 + pil_d4_n1_1_3_3_4 + pil_d4_n1_2_1_1_1 + pil_d4_n1_2_1_1_2 + pil_d4_n1_2_1_1_3 + pil_d4_n1_2_1_1_4 + pil_d4_n1_2_1_2_1 + pil_d4_n1_2_1_2_2 + pil_d4_n1_2_1_2_3 + pil_d4_n1_2_1_2_4 + pil_d4_n1_2_1_3_1 + pil_d4_n1_2_1_3_2 + pil_d4_n1_2_1_3_3 + pil_d4_n1_2_1_3_4 + pil_d4_n1_2_2_1_1 + pil_d4_n1_2_2_1_2 + pil_d4_n1_2_2_1_3 + pil_d4_n1_2_2_1_4 + pil_d4_n1_2_2_2_1 + pil_d4_n1_2_2_2_2 + pil_d4_n1_2_2_2_3 + pil_d4_n1_2_2_2_4 + pil_d4_n1_2_2_3_1 + pil_d4_n1_2_2_3_2 + pil_d4_n1_2_2_3_3 + pil_d4_n1_2_2_3_4 + pil_d4_n1_2_3_1_1 + pil_d4_n1_2_3_1_2 + pil_d4_n1_2_3_1_3 + pil_d4_n1_2_3_1_4 + pil_d4_n1_2_3_2_1 + pil_d4_n1_2_3_2_2 + pil_d4_n1_2_3_2_3 + pil_d4_n1_2_3_2_4 + pil_d4_n1_2_3_3_1 + pil_d4_n1_2_3_3_2 + pil_d4_n1_2_3_3_3 + pil_d4_n1_2_3_3_4 + pil_d4_n1_3_1_1_1 + pil_d4_n1_3_1_1_2 + pil_d4_n1_3_1_1_3 + pil_d4_n1_3_1_1_4 + pil_d4_n1_3_1_2_1 + pil_d4_n1_3_1_2_2 + pil_d4_n1_3_1_2_3 + pil_d4_n1_3_1_2_4 + pil_d4_n1_3_1_3_1 + pil_d4_n1_3_1_3_2 + pil_d4_n1_3_1_3_3 + pil_d4_n1_3_1_3_4 + pil_d4_n1_3_2_1_1 + pil_d4_n1_3_2_1_2 + pil_d4_n1_3_2_1_3 + pil_d4_n1_3_2_1_4 + pil_d4_n1_3_2_2_1 + pil_d4_n1_3_2_2_2 + pil_d4_n1_3_2_2_3 + pil_d4_n1_3_2_2_4 + pil_d4_n1_3_2_3_1 + pil_d4_n1_3_2_3_2 + pil_d4_n1_3_2_3_3 + pil_d4_n1_3_2_3_4 + pil_d4_n1_3_3_1_1 + pil_d4_n1_3_3_1_2 + pil_d4_n1_3_3_1_3 + pil_d4_n1_3_3_1_4 + pil_d4_n1_3_3_2_1 + pil_d4_n1_3_3_2_2 + pil_d4_n1_3_3_2_3 + pil_d4_n1_3_3_2_4 + pil_d4_n1_3_3_3_1 + pil_d4_n1_3_3_3_2 + pil_d4_n1_3_3_3_3 + pil_d4_n1_3_3_3_4 + pol_d1_n1_1_1_1_1 + pol_d1_n1_1_1_1_2 + pol_d1_n1_1_1_1_3 + pol_d1_n1_1_1_2_1 + pol_d1_n1_1_1_2_2 + pol_d1_n1_1_1_2_3 + pol_d1_n1_1_1_3_1 + pol_d1_n1_1_1_3_2 + pol_d1_n1_1_1_3_3 + pol_d1_n1_1_2_1_1 + pol_d1_n1_1_2_1_2 + pol_d1_n1_1_2_1_3 + pol_d1_n1_1_2_2_1 + pol_d1_n1_1_2_2_2 + pol_d1_n1_1_2_2_3 + pol_d1_n1_1_2_3_1 + pol_d1_n1_1_2_3_2 + pol_d1_n1_1_2_3_3 + pol_d1_n1_1_3_1_1 + pol_d1_n1_1_3_1_2 + pol_d1_n1_1_3_1_3 + pol_d1_n1_1_3_2_1 + pol_d1_n1_1_3_2_2 + pol_d1_n1_1_3_2_3 + pol_d1_n1_1_3_3_1 + pol_d1_n1_1_3_3_2 + pol_d1_n1_1_3_3_3 + pol_d1_n1_2_1_1_1 + pol_d1_n1_2_1_1_2 + pol_d1_n1_2_1_1_3 + pol_d1_n1_2_1_2_1 + pol_d1_n1_2_1_2_2 + pol_d1_n1_2_1_2_3 + pol_d1_n1_2_1_3_1 + pol_d1_n1_2_1_3_2 + pol_d1_n1_2_1_3_3 + pol_d1_n1_2_2_1_1 + pol_d1_n1_2_2_1_2 + pol_d1_n1_2_2_1_3 + pol_d1_n1_2_2_2_1 + pol_d1_n1_2_2_2_2 + pol_d1_n1_2_2_2_3 + pol_d1_n1_2_2_3_1 + pol_d1_n1_2_2_3_2 + pol_d1_n1_2_2_3_3 + pol_d1_n1_2_3_1_1 + pol_d1_n1_2_3_1_2 + pol_d1_n1_2_3_1_3 + pol_d1_n1_2_3_2_1 + pol_d1_n1_2_3_2_2 + pol_d1_n1_2_3_2_3 + pol_d1_n1_2_3_3_1 + pol_d1_n1_2_3_3_2 + pol_d1_n1_2_3_3_3 + pol_d1_n1_3_1_1_1 + pol_d1_n1_3_1_1_2 + pol_d1_n1_3_1_1_3 + pol_d1_n1_3_1_2_1 + pol_d1_n1_3_1_2_2 + pol_d1_n1_3_1_2_3 + pol_d1_n1_3_1_3_1 + pol_d1_n1_3_1_3_2 + pol_d1_n1_3_1_3_3 + pol_d1_n1_3_2_1_1 + pol_d1_n1_3_2_1_2 + pol_d1_n1_3_2_1_3 + pol_d1_n1_3_2_2_1 + pol_d1_n1_3_2_2_2 + pol_d1_n1_3_2_2_3 + pol_d1_n1_3_2_3_1 + pol_d1_n1_3_2_3_2 + pol_d1_n1_3_2_3_3 + pol_d1_n1_3_3_1_1 + pol_d1_n1_3_3_1_2 + pol_d1_n1_3_3_1_3 + pol_d1_n1_3_3_2_1 + pol_d1_n1_3_3_2_2 + pol_d1_n1_3_3_2_3 + pol_d1_n1_3_3_3_1 + pol_d1_n1_3_3_3_2 + pol_d1_n1_3_3_3_3 + pol_d1_n1_4_1_1_1 + pol_d1_n1_4_1_1_2 + pol_d1_n1_4_1_1_3 + pol_d1_n1_4_1_2_1 + pol_d1_n1_4_1_2_2 + pol_d1_n1_4_1_2_3 + pol_d1_n1_4_1_3_1 + pol_d1_n1_4_1_3_2 + pol_d1_n1_4_1_3_3 + pol_d1_n1_4_2_1_1 + pol_d1_n1_4_2_1_2 + pol_d1_n1_4_2_1_3 + pol_d1_n1_4_2_2_1 + pol_d1_n1_4_2_2_2 + pol_d1_n1_4_2_2_3 + pol_d1_n1_4_2_3_1 + pol_d1_n1_4_2_3_2 + pol_d1_n1_4_2_3_3 + pol_d1_n1_4_3_1_1 + pol_d1_n1_4_3_1_2 + pol_d1_n1_4_3_1_3 + pol_d1_n1_4_3_2_1 + pol_d1_n1_4_3_2_2 + pol_d1_n1_4_3_2_3 + pol_d1_n1_4_3_3_1 + pol_d1_n1_4_3_3_2 + pol_d1_n1_4_3_3_3 + pol_d2_n1_1_1_1_1 + pol_d2_n1_1_1_1_2 + pol_d2_n1_1_1_1_3 + pol_d2_n1_1_1_2_1 + pol_d2_n1_1_1_2_2 + pol_d2_n1_1_1_2_3 + pol_d2_n1_1_1_3_1 + pol_d2_n1_1_1_3_2 + pol_d2_n1_1_1_3_3 + pol_d2_n1_1_2_1_1 + pol_d2_n1_1_2_1_2 + pol_d2_n1_1_2_1_3 + pol_d2_n1_1_2_2_1 + pol_d2_n1_1_2_2_2 + pol_d2_n1_1_2_2_3 + pol_d2_n1_1_2_3_1 + pol_d2_n1_1_2_3_2 + pol_d2_n1_1_2_3_3 + pol_d2_n1_1_3_1_1 + pol_d2_n1_1_3_1_2 + pol_d2_n1_1_3_1_3 + pol_d2_n1_1_3_2_1 + pol_d2_n1_1_3_2_2 + pol_d2_n1_1_3_2_3 + pol_d2_n1_1_3_3_1 + pol_d2_n1_1_3_3_2 + pol_d2_n1_1_3_3_3 + pol_d2_n1_1_4_1_1 + pol_d2_n1_1_4_1_2 + pol_d2_n1_1_4_1_3 + pol_d2_n1_1_4_2_1 + pol_d2_n1_1_4_2_2 + pol_d2_n1_1_4_2_3 + pol_d2_n1_1_4_3_1 + pol_d2_n1_1_4_3_2 + pol_d2_n1_1_4_3_3 + pol_d2_n1_2_1_1_1 + pol_d2_n1_2_1_1_2 + pol_d2_n1_2_1_1_3 + pol_d2_n1_2_1_2_1 + pol_d2_n1_2_1_2_2 + pol_d2_n1_2_1_2_3 + pol_d2_n1_2_1_3_1 + pol_d2_n1_2_1_3_2 + pol_d2_n1_2_1_3_3 + pol_d2_n1_2_2_1_1 + pol_d2_n1_2_2_1_2 + pol_d2_n1_2_2_1_3 + pol_d2_n1_2_2_2_1 + pol_d2_n1_2_2_2_2 + pol_d2_n1_2_2_2_3 + pol_d2_n1_2_2_3_1 + pol_d2_n1_2_2_3_2 + pol_d2_n1_2_2_3_3 + pol_d2_n1_2_3_1_1 + pol_d2_n1_2_3_1_2 + pol_d2_n1_2_3_1_3 + pol_d2_n1_2_3_2_1 + pol_d2_n1_2_3_2_2 + pol_d2_n1_2_3_2_3 + pol_d2_n1_2_3_3_1 + pol_d2_n1_2_3_3_2 + pol_d2_n1_2_3_3_3 + pol_d2_n1_2_4_1_1 + pol_d2_n1_2_4_1_2 + pol_d2_n1_2_4_1_3 + pol_d2_n1_2_4_2_1 + pol_d2_n1_2_4_2_2 + pol_d2_n1_2_4_2_3 + pol_d2_n1_2_4_3_1 + pol_d2_n1_2_4_3_2 + pol_d2_n1_2_4_3_3 + pol_d2_n1_3_1_1_1 + pol_d2_n1_3_1_1_2 + pol_d2_n1_3_1_1_3 + pol_d2_n1_3_1_2_1 + pol_d2_n1_3_1_2_2 + pol_d2_n1_3_1_2_3 + pol_d2_n1_3_1_3_1 + pol_d2_n1_3_1_3_2 + pol_d2_n1_3_1_3_3 + pol_d2_n1_3_2_1_1 + pol_d2_n1_3_2_1_2 + pol_d2_n1_3_2_1_3 + pol_d2_n1_3_2_2_1 + pol_d2_n1_3_2_2_2 + pol_d2_n1_3_2_2_3 + pol_d2_n1_3_2_3_1 + pol_d2_n1_3_2_3_2 + pol_d2_n1_3_2_3_3 + pol_d2_n1_3_3_1_1 + pol_d2_n1_3_3_1_2 + pol_d2_n1_3_3_1_3 + pol_d2_n1_3_3_2_1 + pol_d2_n1_3_3_2_2 + pol_d2_n1_3_3_2_3 + pol_d2_n1_3_3_3_1 + pol_d2_n1_3_3_3_2 + pol_d2_n1_3_3_3_3 + pol_d2_n1_3_4_1_1 + pol_d2_n1_3_4_1_2 + pol_d2_n1_3_4_1_3 + pol_d2_n1_3_4_2_1 + pol_d2_n1_3_4_2_2 + pol_d2_n1_3_4_2_3 + pol_d2_n1_3_4_3_1 + pol_d2_n1_3_4_3_2 + pol_d2_n1_3_4_3_3 + pol_d3_n1_1_1_1_1 + pol_d3_n1_1_1_1_2 + pol_d3_n1_1_1_1_3 + pol_d3_n1_1_1_2_1 + pol_d3_n1_1_1_2_2 + pol_d3_n1_1_1_2_3 + pol_d3_n1_1_1_3_1 + pol_d3_n1_1_1_3_2 + pol_d3_n1_1_1_3_3 + pol_d3_n1_1_1_4_1 + pol_d3_n1_1_1_4_2 + pol_d3_n1_1_1_4_3 + pol_d3_n1_1_2_1_1 + pol_d3_n1_1_2_1_2 + pol_d3_n1_1_2_1_3 + pol_d3_n1_1_2_2_1 + pol_d3_n1_1_2_2_2 + pol_d3_n1_1_2_2_3 + pol_d3_n1_1_2_3_1 + pol_d3_n1_1_2_3_2 + pol_d3_n1_1_2_3_3 + pol_d3_n1_1_2_4_1 + pol_d3_n1_1_2_4_2 + pol_d3_n1_1_2_4_3 + pol_d3_n1_1_3_1_1 + pol_d3_n1_1_3_1_2 + pol_d3_n1_1_3_1_3 + pol_d3_n1_1_3_2_1 + pol_d3_n1_1_3_2_2 + pol_d3_n1_1_3_2_3 + pol_d3_n1_1_3_3_1 + pol_d3_n1_1_3_3_2 + pol_d3_n1_1_3_3_3 + pol_d3_n1_1_3_4_1 + pol_d3_n1_1_3_4_2 + pol_d3_n1_1_3_4_3 + pol_d3_n1_2_1_1_1 + pol_d3_n1_2_1_1_2 + pol_d3_n1_2_1_1_3 + pol_d3_n1_2_1_2_1 + pol_d3_n1_2_1_2_2 + pol_d3_n1_2_1_2_3 + pol_d3_n1_2_1_3_1 + pol_d3_n1_2_1_3_2 + pol_d3_n1_2_1_3_3 + pol_d3_n1_2_1_4_1 + pol_d3_n1_2_1_4_2 + pol_d3_n1_2_1_4_3 + pol_d3_n1_2_2_1_1 + pol_d3_n1_2_2_1_2 + pol_d3_n1_2_2_1_3 + pol_d3_n1_2_2_2_1 + pol_d3_n1_2_2_2_2 + pol_d3_n1_2_2_2_3 + pol_d3_n1_2_2_3_1 + pol_d3_n1_2_2_3_2 + pol_d3_n1_2_2_3_3 + pol_d3_n1_2_2_4_1 + pol_d3_n1_2_2_4_2 + pol_d3_n1_2_2_4_3 + pol_d3_n1_2_3_1_1 + pol_d3_n1_2_3_1_2 + pol_d3_n1_2_3_1_3 + pol_d3_n1_2_3_2_1 + pol_d3_n1_2_3_2_2 + pol_d3_n1_2_3_2_3 + pol_d3_n1_2_3_3_1 + pol_d3_n1_2_3_3_2 + pol_d3_n1_2_3_3_3 + pol_d3_n1_2_3_4_1 + pol_d3_n1_2_3_4_2 + pol_d3_n1_2_3_4_3 + pol_d3_n1_3_1_1_1 + pol_d3_n1_3_1_1_2 + pol_d3_n1_3_1_1_3 + pol_d3_n1_3_1_2_1 + pol_d3_n1_3_1_2_2 + pol_d3_n1_3_1_2_3 + pol_d3_n1_3_1_3_1 + pol_d3_n1_3_1_3_2 + pol_d3_n1_3_1_3_3 + pol_d3_n1_3_1_4_1 + pol_d3_n1_3_1_4_2 + pol_d3_n1_3_1_4_3 + pol_d3_n1_3_2_1_1 + pol_d3_n1_3_2_1_2 + pol_d3_n1_3_2_1_3 + pol_d3_n1_3_2_2_1 + pol_d3_n1_3_2_2_2 + pol_d3_n1_3_2_2_3 + pol_d3_n1_3_2_3_1 + pol_d3_n1_3_2_3_2 + pol_d3_n1_3_2_3_3 + pol_d3_n1_3_2_4_1 + pol_d3_n1_3_2_4_2 + pol_d3_n1_3_2_4_3 + pol_d3_n1_3_3_1_1 + pol_d3_n1_3_3_1_2 + pol_d3_n1_3_3_1_3 + pol_d3_n1_3_3_2_1 + pol_d3_n1_3_3_2_2 + pol_d3_n1_3_3_2_3 + pol_d3_n1_3_3_3_1 + pol_d3_n1_3_3_3_2 + pol_d3_n1_3_3_3_3 + pol_d3_n1_3_3_4_1 + pol_d3_n1_3_3_4_2 + pol_d3_n1_3_3_4_3 + pol_d4_n1_1_1_1_1 + pol_d4_n1_1_1_1_2 + pol_d4_n1_1_1_1_3 + pol_d4_n1_1_1_1_4 + pol_d4_n1_1_1_2_1 + pol_d4_n1_1_1_2_2 + pol_d4_n1_1_1_2_3 + pol_d4_n1_1_1_2_4 + pol_d4_n1_1_1_3_1 + pol_d4_n1_1_1_3_2 + pol_d4_n1_1_1_3_3 + pol_d4_n1_1_1_3_4 + pol_d4_n1_1_2_1_1 + pol_d4_n1_1_2_1_2 + pol_d4_n1_1_2_1_3 + pol_d4_n1_1_2_1_4 + pol_d4_n1_1_2_2_1 + pol_d4_n1_1_2_2_2 + pol_d4_n1_1_2_2_3 + pol_d4_n1_1_2_2_4 + pol_d4_n1_1_2_3_1 + pol_d4_n1_1_2_3_2 + pol_d4_n1_1_2_3_3 + pol_d4_n1_1_2_3_4 + pol_d4_n1_1_3_1_1 + pol_d4_n1_1_3_1_2 + pol_d4_n1_1_3_1_3 + pol_d4_n1_1_3_1_4 + pol_d4_n1_1_3_2_1 + pol_d4_n1_1_3_2_2 + pol_d4_n1_1_3_2_3 + pol_d4_n1_1_3_2_4 + pol_d4_n1_1_3_3_1 + pol_d4_n1_1_3_3_2 + pol_d4_n1_1_3_3_3 + pol_d4_n1_1_3_3_4 + pol_d4_n1_2_1_1_1 + pol_d4_n1_2_1_1_2 + pol_d4_n1_2_1_1_3 + pol_d4_n1_2_1_1_4 + pol_d4_n1_2_1_2_1 + pol_d4_n1_2_1_2_2 + pol_d4_n1_2_1_2_3 + pol_d4_n1_2_1_2_4 + pol_d4_n1_2_1_3_1 + pol_d4_n1_2_1_3_2 + pol_d4_n1_2_1_3_3 + pol_d4_n1_2_1_3_4 + pol_d4_n1_2_2_1_1 + pol_d4_n1_2_2_1_2 + pol_d4_n1_2_2_1_3 + pol_d4_n1_2_2_1_4 + pol_d4_n1_2_2_2_1 + pol_d4_n1_2_2_2_2 + pol_d4_n1_2_2_2_3 + pol_d4_n1_2_2_2_4 + pol_d4_n1_2_2_3_1 + pol_d4_n1_2_2_3_2 + pol_d4_n1_2_2_3_3 + pol_d4_n1_2_2_3_4 + pol_d4_n1_2_3_1_1 + pol_d4_n1_2_3_1_2 + pol_d4_n1_2_3_1_3 + pol_d4_n1_2_3_1_4 + pol_d4_n1_2_3_2_1 + pol_d4_n1_2_3_2_2 + pol_d4_n1_2_3_2_3 + pol_d4_n1_2_3_2_4 + pol_d4_n1_2_3_3_1 + pol_d4_n1_2_3_3_2 + pol_d4_n1_2_3_3_3 + pol_d4_n1_2_3_3_4 + pol_d4_n1_3_1_1_1 + pol_d4_n1_3_1_1_2 + pol_d4_n1_3_1_1_3 + pol_d4_n1_3_1_1_4 + pol_d4_n1_3_1_2_1 + pol_d4_n1_3_1_2_2 + pol_d4_n1_3_1_2_3 + pol_d4_n1_3_1_2_4 + pol_d4_n1_3_1_3_1 + pol_d4_n1_3_1_3_2 + pol_d4_n1_3_1_3_3 + pol_d4_n1_3_1_3_4 + pol_d4_n1_3_2_1_1 + pol_d4_n1_3_2_1_2 + pol_d4_n1_3_2_1_3 + pol_d4_n1_3_2_1_4 + pol_d4_n1_3_2_2_1 + pol_d4_n1_3_2_2_2 + pol_d4_n1_3_2_2_3 + pol_d4_n1_3_2_2_4 + pol_d4_n1_3_2_3_1 + pol_d4_n1_3_2_3_2 + pol_d4_n1_3_2_3_3 + pol_d4_n1_3_2_3_4 + pol_d4_n1_3_3_1_1 + pol_d4_n1_3_3_1_2 + pol_d4_n1_3_3_1_3 + pol_d4_n1_3_3_1_4 + pol_d4_n1_3_3_2_1 + pol_d4_n1_3_3_2_2 + pol_d4_n1_3_3_2_3 + pol_d4_n1_3_3_2_4 + pol_d4_n1_3_3_3_1 + pol_d4_n1_3_3_3_2 + pol_d4_n1_3_3_3_3 + pol_d4_n1_3_3_3_4 = 1836
invariant :pi_d4_n1_2_1_2_1 + pil_d4_n1_2_1_2_1 = 1
invariant :po_d3_n1_2_1_2_3 + pol_d3_n1_2_1_2_3 = 1
Compilation finished in 98994 ms.
Running link step : CommandLine [args=[gcc, -shared, -o, gal.so, model.o], workingDir=/home/mcc/execution]
Link finished in 158 ms.
Running LTSmin : CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality00==true], workingDir=/home/mcc/execution]
WARNING : LTSmin timed out (>225 s) on command CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality00==true], workingDir=/home/mcc/execution]
Running LTSmin : CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality01==true], workingDir=/home/mcc/execution]
WARNING : LTSmin timed out (>225 s) on command CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality01==true], workingDir=/home/mcc/execution]
Running LTSmin : CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality02==true], workingDir=/home/mcc/execution]
WARNING : LTSmin timed out (>225 s) on command CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality02==true], workingDir=/home/mcc/execution]
Running LTSmin : CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality03==true], workingDir=/home/mcc/execution]
WARNING : LTS min runner thread failed on error :java.lang.RuntimeException: Unexpected exception when executing ltsmin :CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality03==true], workingDir=/home/mcc/execution]
255
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/
+ BINDIR=/home/mcc/BenchKit/
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ /home/mcc/BenchKit//runeclipse.sh /home/mcc/execution ReachabilityCardinality -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt
+ ulimit -s 65536
+ [[ -z '' ]]
+ export LTSMIN_MEM_SIZE=8589934592
+ LTSMIN_MEM_SIZE=8589934592
+ /home/mcc/BenchKit//itstools/its-tools -consoleLog -data /home/mcc/execution/workspace -pnfolder /home/mcc/execution -examination ReachabilityCardinality -z3path /home/mcc/BenchKit//z3/bin/z3 -yices2path /home/mcc/BenchKit//yices/bin/yices -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt -vmargs -Dosgi.locking=none -Declipse.stateSaveDelayInterval=-1 -Dosgi.configuration.area=/tmp/.eclipse -Xss8m -Xms40m -Xmx8192m -Dfile.encoding=UTF-8 -Dosgi.requiredJavaVersion=1.6
May 20, 2018 2:44:46 AM fr.lip6.move.gal.application.Application start
INFO: Running its-tools with arguments : [-pnfolder, /home/mcc/execution, -examination, ReachabilityCardinality, -z3path, /home/mcc/BenchKit//z3/bin/z3, -yices2path, /home/mcc/BenchKit//yices/bin/yices, -its, -ltsminpath, /home/mcc/BenchKit//lts_install_dir/, -smt]
May 20, 2018 2:44:46 AM fr.lip6.move.gal.application.MccTranslator transformPNML
INFO: Parsing pnml file : /home/mcc/execution/model.pnml
May 20, 2018 2:44:47 AM fr.lip6.move.gal.nupn.PTNetReader loadFromXML
INFO: Load time of PNML (sax parser for PT used): 465 ms
May 20, 2018 2:44:47 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 2457 places.
May 20, 2018 2:44:47 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 5400 transitions.
May 20, 2018 2:44:49 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 1580 ms
May 20, 2018 2:44:50 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 1077 ms
May 20, 2018 2:44:50 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 1004 ms
May 20, 2018 2:44:50 AM fr.lip6.move.serialization.SerializationUtil systemToFile
INFO: Time to serialize gal into /home/mcc/execution/ReachabilityCardinality.pnml.gal : 245 ms
May 20, 2018 2:44:50 AM fr.lip6.move.serialization.SerializationUtil serializePropertiesForITSTools
INFO: Time to serialize properties into /home/mcc/execution/ReachabilityCardinality.prop : 1 ms
May 20, 2018 2:44:51 AM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 5400 transitions.
May 20, 2018 2:44:51 AM fr.lip6.move.gal.gal2pins.Gal2PinsTransformerNext transform
INFO: Too many transitions (5400) to apply POR reductions. Disabling POR matrices.
May 20, 2018 2:44:51 AM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 5400 transitions.
May 20, 2018 2:44:52 AM fr.lip6.move.gal.gal2pins.Gal2PinsTransformerNext transform
INFO: Built C files in 2267ms conformant to PINS in folder :/home/mcc/execution
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd checkProperties
INFO: Ran tautology test, simplified 0 / 16 in 4425 ms.
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-00(UNSAT) depth K=0 took 38 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-01(UNSAT) depth K=0 took 9 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-02(UNSAT) depth K=0 took 7 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-03(UNSAT) depth K=0 took 7 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-04(UNSAT) depth K=0 took 15 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-05(UNSAT) depth K=0 took 7 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-06(UNSAT) depth K=0 took 13 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-07(UNSAT) depth K=0 took 6 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-08(UNSAT) depth K=0 took 12 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-09(UNSAT) depth K=0 took 6 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-10(UNSAT) depth K=0 took 20 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-11(UNSAT) depth K=0 took 23 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-12(UNSAT) depth K=0 took 15 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-13(UNSAT) depth K=0 took 15 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-14(UNSAT) depth K=0 took 16 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-15(UNSAT) depth K=0 took 11 ms
May 20, 2018 2:44:55 AM fr.lip6.move.gal.semantics.DeterministicNextBuilder getDeterministicNext
INFO: Input system was already deterministic with 5400 transitions.
May 20, 2018 2:44:57 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-00(UNSAT) depth K=1 took 1696 ms
May 20, 2018 2:45:00 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-01(UNSAT) depth K=1 took 3574 ms
May 20, 2018 2:45:01 AM fr.lip6.move.gal.gal2smt.bmc.KInductionSolver computeAndDeclareInvariants
INFO: Computed 946 place invariants in 3626 ms
May 20, 2018 2:45:02 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-02(UNSAT) depth K=1 took 1648 ms
May 20, 2018 2:45:07 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-03(UNSAT) depth K=1 took 4580 ms
May 20, 2018 2:45:10 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-04(UNSAT) depth K=1 took 3515 ms
May 20, 2018 2:45:12 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-05(UNSAT) depth K=1 took 1619 ms
May 20, 2018 2:45:14 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-06(UNSAT) depth K=1 took 1753 ms
May 20, 2018 2:45:15 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-07(UNSAT) depth K=1 took 1830 ms
May 20, 2018 2:45:17 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-08(UNSAT) depth K=1 took 1935 ms
May 20, 2018 2:45:19 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-09(UNSAT) depth K=1 took 1570 ms
May 20, 2018 2:45:20 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-10(UNSAT) depth K=1 took 1544 ms
May 20, 2018 2:45:22 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-11(UNSAT) depth K=1 took 1588 ms
May 20, 2018 2:45:24 AM fr.lip6.move.gal.gal2smt.bmc.KInductionSolver init
INFO: Proved 2457 variables to be positive in 26657 ms
May 20, 2018 2:45:26 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-12(UNSAT) depth K=1 took 4275 ms
May 20, 2018 2:45:28 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-13(UNSAT) depth K=1 took 1548 ms
May 20, 2018 2:45:29 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-14(UNSAT) depth K=1 took 1519 ms
May 20, 2018 2:45:32 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runBMC
INFO: BMC solution for property HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-15(UNSAT) depth K=1 took 3086 ms
pins2lts-mc, 0.000: Registering PINS so language module
pins2lts-mc, 0.000, ** error **: out of memory trying to get 4294967296
java.lang.RuntimeException: Unexpected exception when executing ltsmin :CommandLine [args=[/home/mcc/BenchKit//lts_install_dir//bin/pins2lts-mc, ./gal.so, --threads=1, -p, --pins-guards, --when, -i, HypercubeGridPTC4K3P3B12ReachabilityCardinality03==true], workingDir=/home/mcc/execution]
255
at fr.lip6.move.gal.application.LTSminRunner.checkProperty(LTSminRunner.java:167)
at fr.lip6.move.gal.application.LTSminRunner.access$9(LTSminRunner.java:122)
at fr.lip6.move.gal.application.LTSminRunner$1.run(LTSminRunner.java:91)
at java.lang.Thread.run(Thread.java:748)
java.lang.RuntimeException: SMT solver raised an exception or timeout :(error "Solver has unexpectedly terminated")
at fr.lip6.move.gal.gal2smt.bmc.NextBMCSolver.checkSat(NextBMCSolver.java:297)
at fr.lip6.move.gal.gal2smt.bmc.KInductionSolver.verify(KInductionSolver.java:573)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd.runKInduction(Gal2SMTFrontEnd.java:301)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd.access$1(Gal2SMTFrontEnd.java:274)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd$2.run(Gal2SMTFrontEnd.java:166)
at java.lang.Thread.run(Thread.java:748)
May 20, 2018 2:59:00 AM fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd runKInduction
WARNING: Unexpected error occurred while running SMT. Was verifying HypercubeGrid-PT-C4K3P3B12-ReachabilityCardinality-00 K-induction depth 0
Exception in thread "Thread-8" java.lang.RuntimeException: java.lang.RuntimeException: SMT solver raised an exception or timeout :(error "Solver has unexpectedly terminated")
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd.runKInduction(Gal2SMTFrontEnd.java:336)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd.access$1(Gal2SMTFrontEnd.java:274)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd$2.run(Gal2SMTFrontEnd.java:166)
at java.lang.Thread.run(Thread.java:748)
Caused by: java.lang.RuntimeException: SMT solver raised an exception or timeout :(error "Solver has unexpectedly terminated")
at fr.lip6.move.gal.gal2smt.bmc.NextBMCSolver.checkSat(NextBMCSolver.java:297)
at fr.lip6.move.gal.gal2smt.bmc.KInductionSolver.verify(KInductionSolver.java:573)
at fr.lip6.move.gal.gal2smt.Gal2SMTFrontEnd.runKInduction(Gal2SMTFrontEnd.java:301)
... 3 more
ITS-tools command line returned an error code 137
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="HypercubeGrid-PT-C4K3P3B12"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/HypercubeGrid-PT-C4K3P3B12.tgz
mv HypercubeGrid-PT-C4K3P3B12 execution
cd execution
pwd
ls -lh
# this is for BenchKit: explicit launching of the test
echo "====================================================================="
echo " Generated by BenchKit 2-3637"
echo " Executing tool itstools"
echo " Input is HypercubeGrid-PT-C4K3P3B12, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r104-smll-152658634200117"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

