Introduction
This page presents how GreatSPN do cope efficiently with the StateSpace examination face to the other participating tools. In this page, we consider «Surprise» models.
The next sections will show chart comparing performances in terms of both memory and execution time.The x-axis corresponds to the challenging tool where the y-axes represents GreatSPN' performances. Thus, points below the diagonal of a chart denote comparisons favorables to the tool while others corresponds to situations where the challenging tool performs better.
You might also find plots out of the range that denote the case were at least one tool could not answer appropriately (error, time-out, could not compute or did not competed).
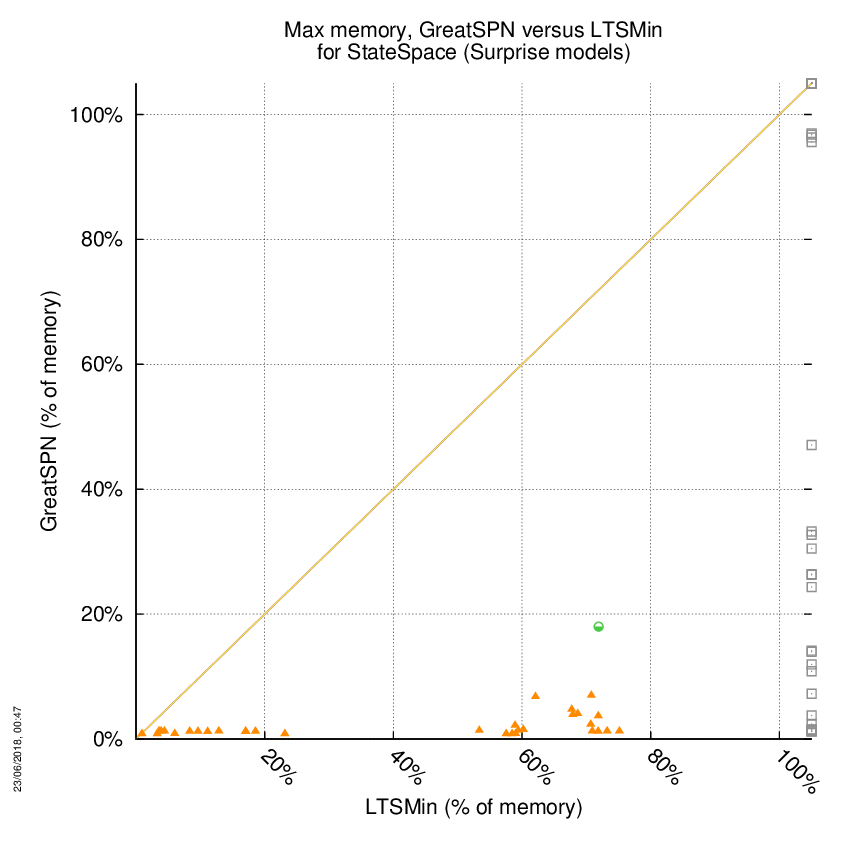
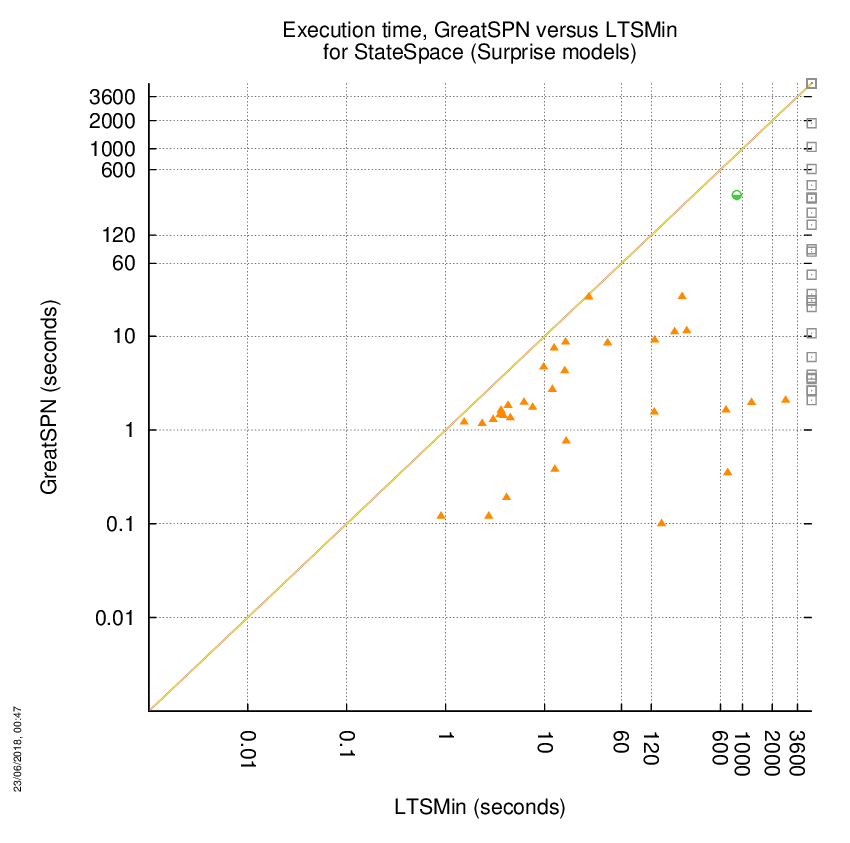
GreatSPN versus LTSMin
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for LTSMin, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to LTSMin are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | LTSMin | Both tools | GreatSPN | LTSMin | ||
| All computed OK | 24 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = LTSMin | — | — | 1 | Times tool wins | 57 | 0 |
| GreatSPN > LTSMin | — | — | 32 | Shortest Execution Time | ||
| GreatSPN < LTSMin | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 24 | 82 | |||
On the chart below, 
denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than LTSMin,
denote cases where GreatSPN
computed less values than LTSMin,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and 
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, LTSMin wins when points are above the diagonal.
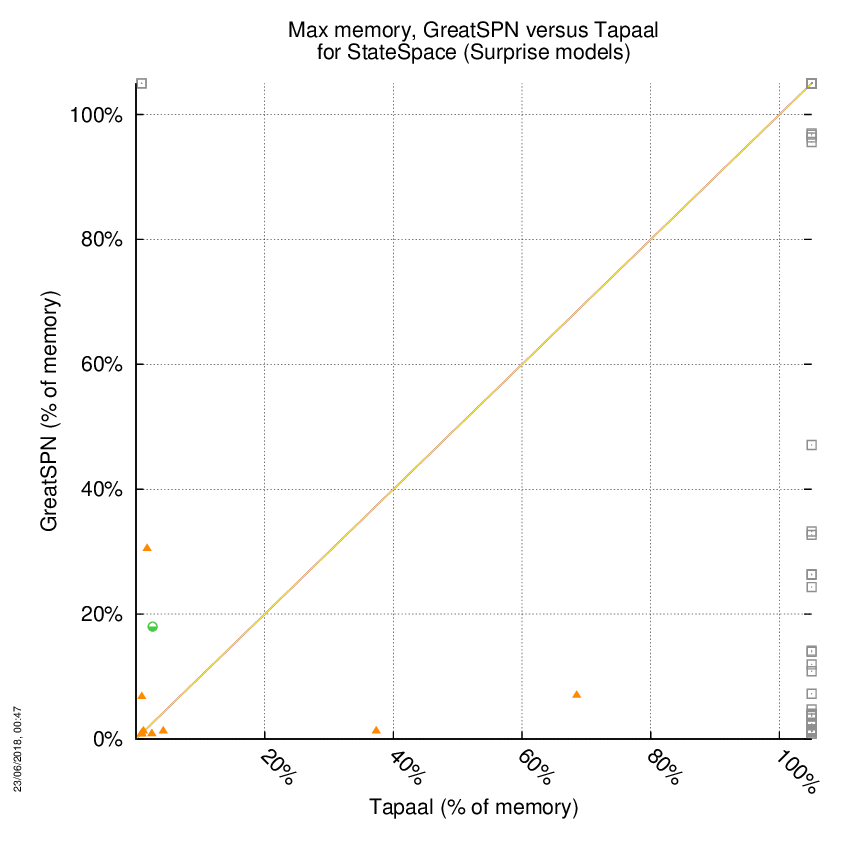
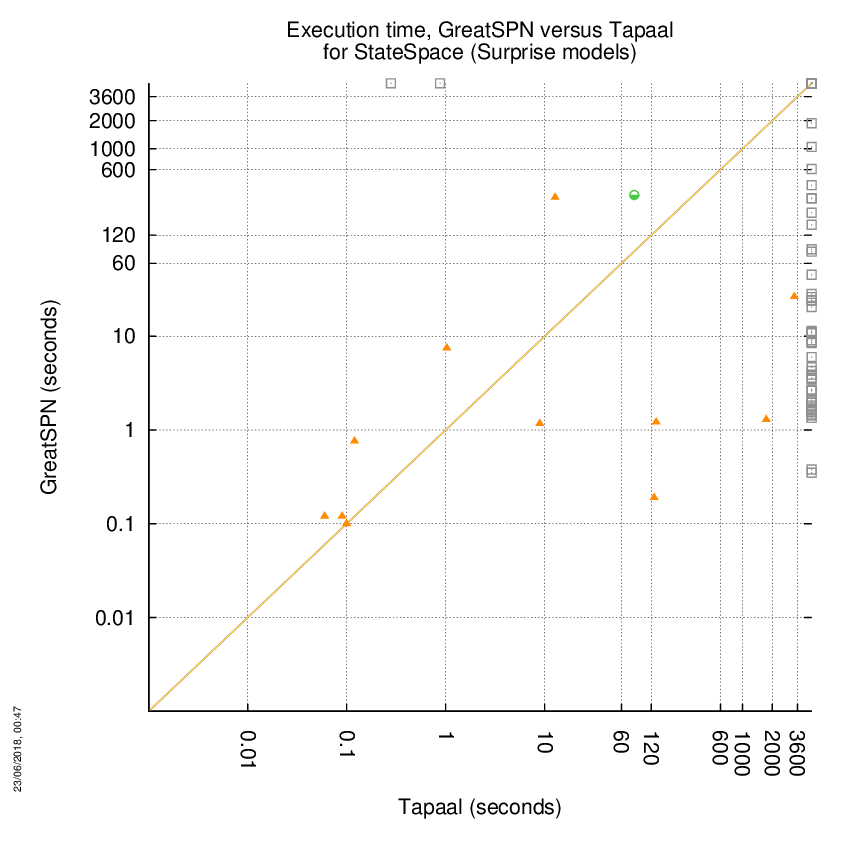
GreatSPN versus Tapaal
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for Tapaal, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to Tapaal are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | Tapaal | Both tools | GreatSPN | Tapaal | ||
| All computed OK | 45 | 2 | 0 | Smallest Memory Footprint | ||
| GreatSPN = Tapaal | — | — | 1 | Times tool wins | 53 | 6 |
| GreatSPN > Tapaal | — | — | 11 | Shortest Execution Time | ||
| GreatSPN < Tapaal | — | — | 0 | Times tool wins | 50 | 9 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 2 | 45 | 80 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than Tapaal,
denote cases where GreatSPN
computed less values than Tapaal,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, Tapaal wins when points are above the diagonal.
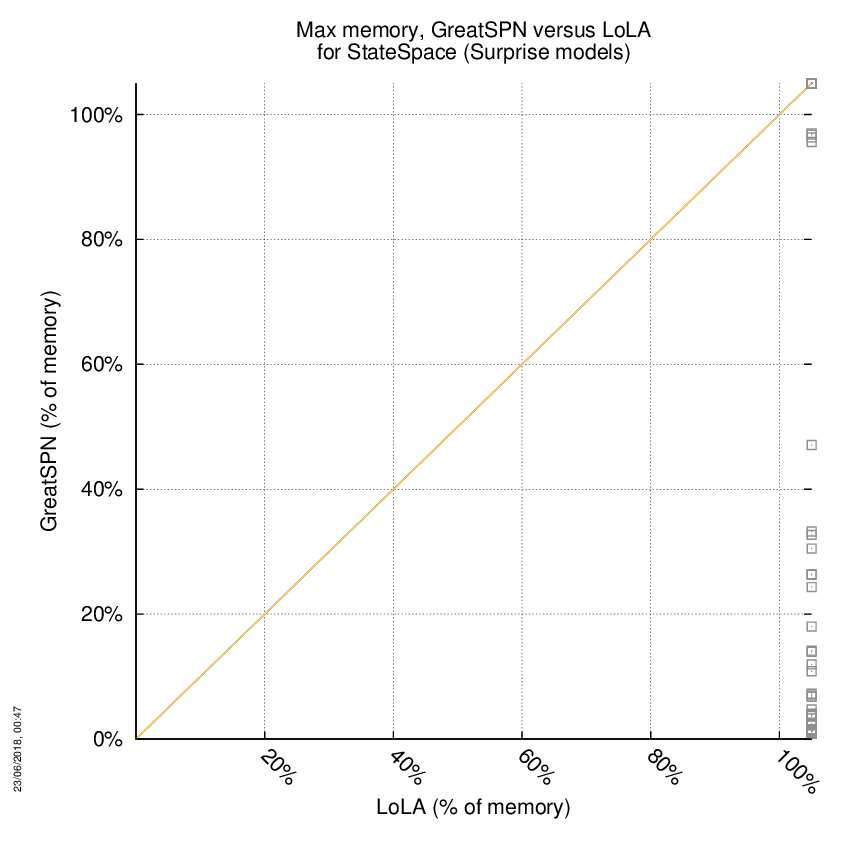
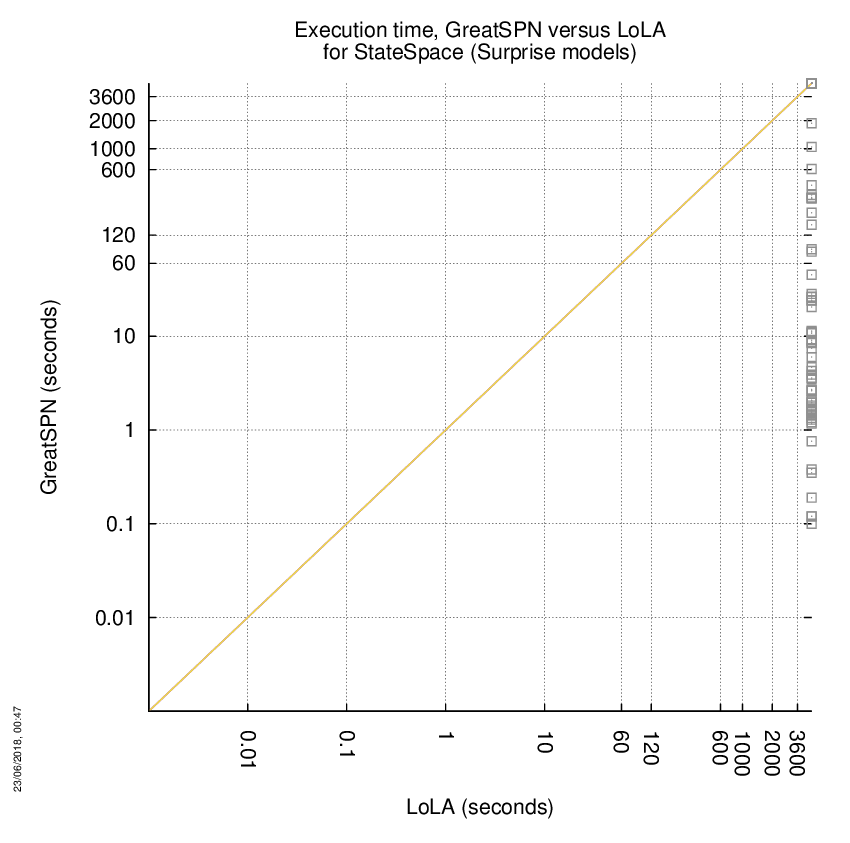
GreatSPN versus LoLA
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for LoLA, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to LoLA are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | LoLA | Both tools | GreatSPN | LoLA | ||
| All computed OK | 57 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = LoLA | — | — | 0 | Times tool wins | 57 | 0 |
| GreatSPN > LoLA | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < LoLA | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 57 | 82 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than LoLA,
denote cases where GreatSPN
computed less values than LoLA,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, LoLA wins when points are above the diagonal.
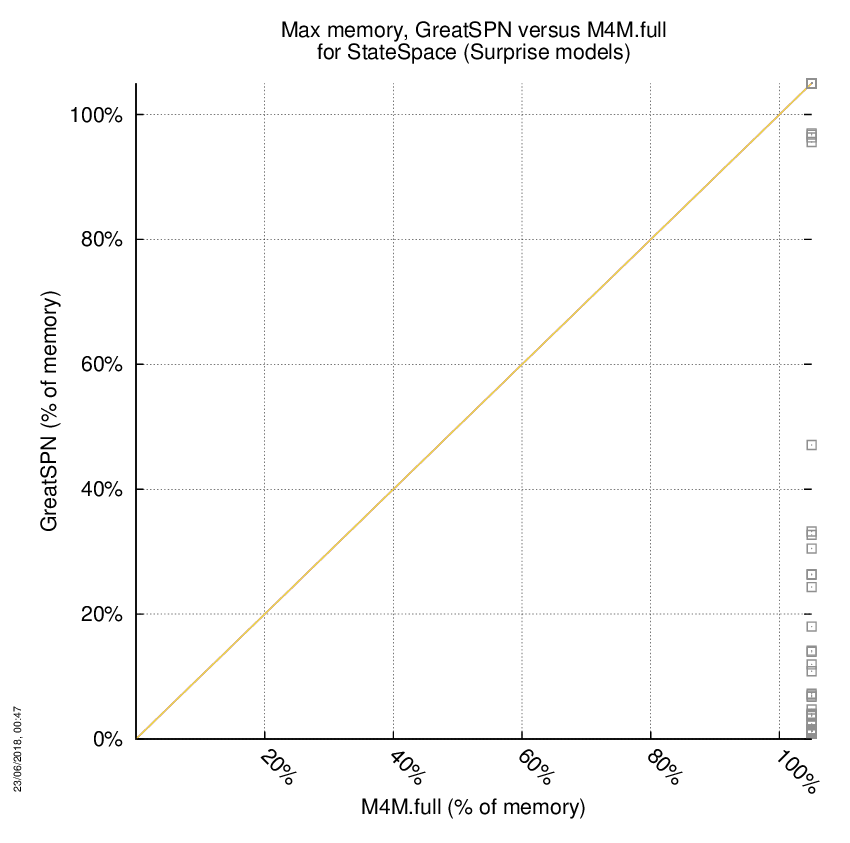
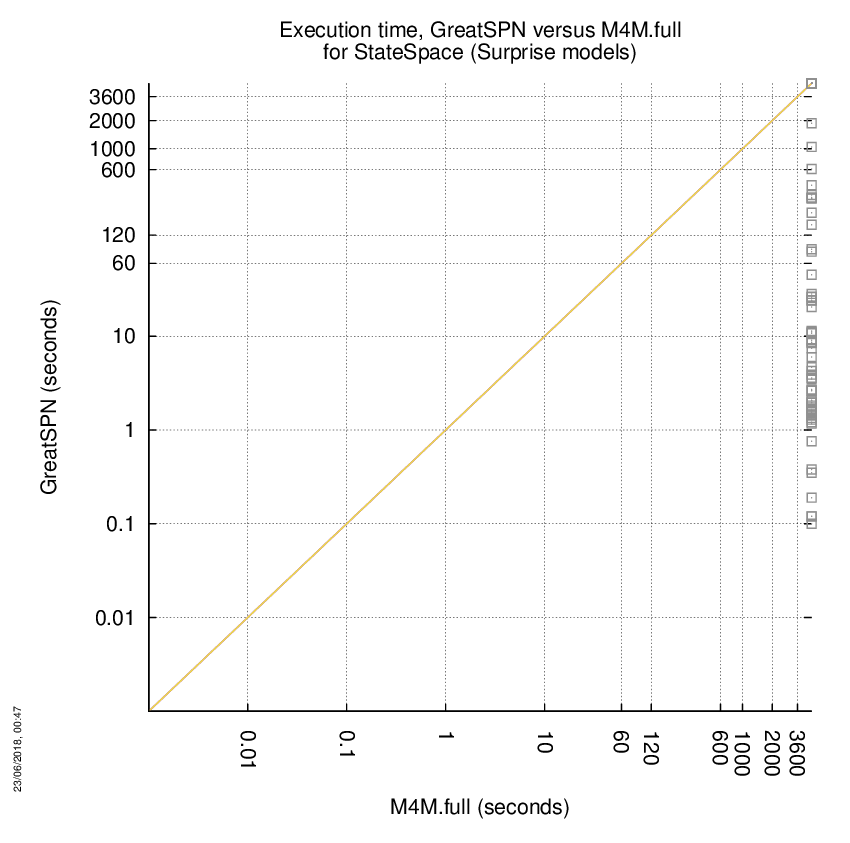
GreatSPN versus M4M.full
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for M4M.full, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to M4M.full are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | M4M.full | Both tools | GreatSPN | M4M.full | ||
| All computed OK | 57 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = M4M.full | — | — | 0 | Times tool wins | 57 | 0 |
| GreatSPN > M4M.full | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < M4M.full | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 57 | 82 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than M4M.full,
denote cases where GreatSPN
computed less values than M4M.full,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, M4M.full wins when points are above the diagonal.
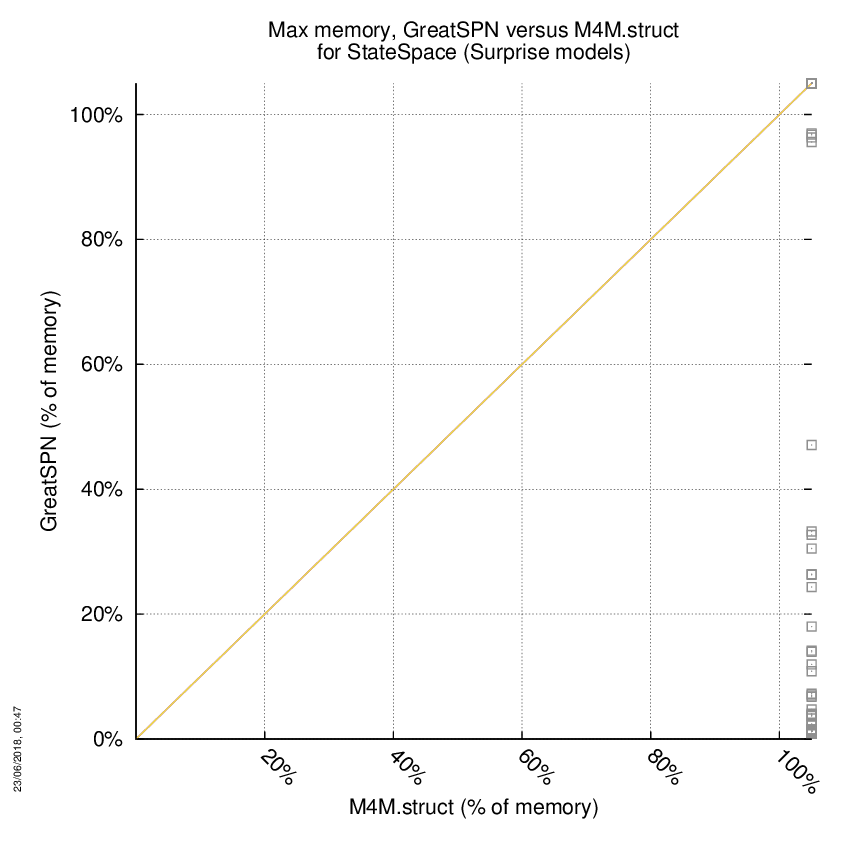
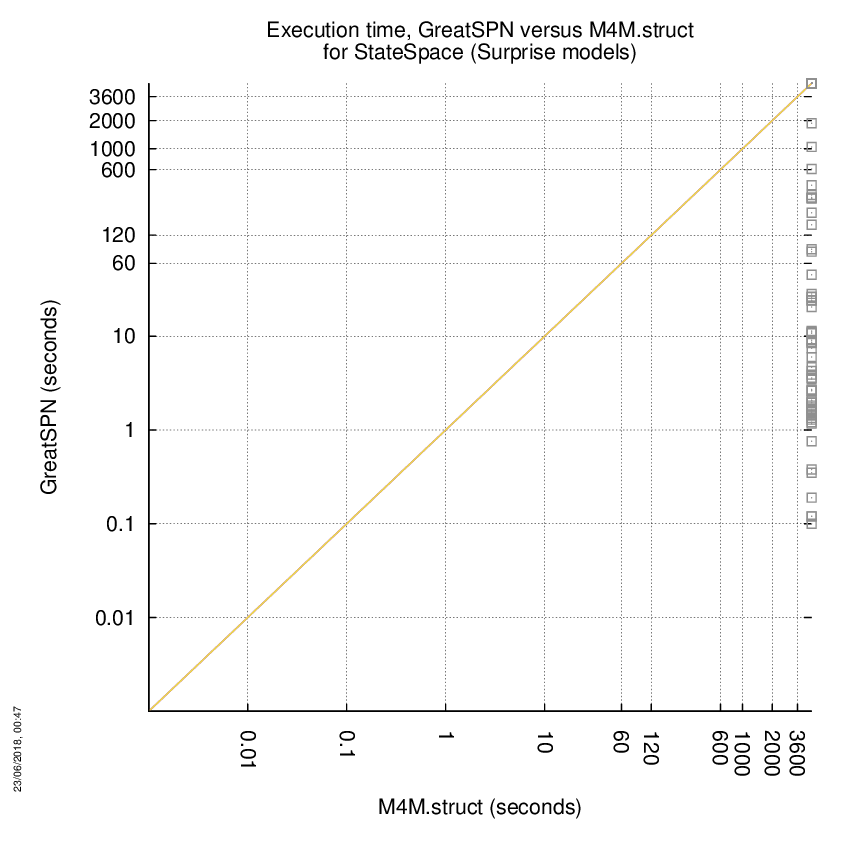
GreatSPN versus M4M.struct
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for M4M.struct, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to M4M.struct are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | M4M.struct | Both tools | GreatSPN | M4M.struct | ||
| All computed OK | 57 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = M4M.struct | — | — | 0 | Times tool wins | 57 | 0 |
| GreatSPN > M4M.struct | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < M4M.struct | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 57 | 82 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than M4M.struct,
denote cases where GreatSPN
computed less values than M4M.struct,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, M4M.struct wins when points are above the diagonal.
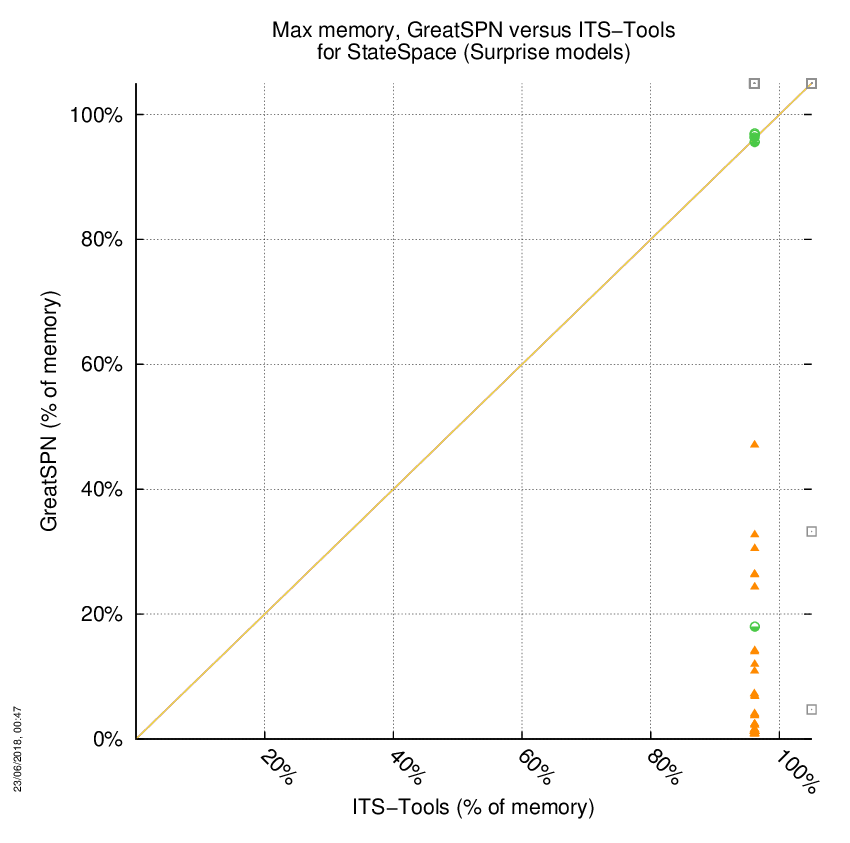
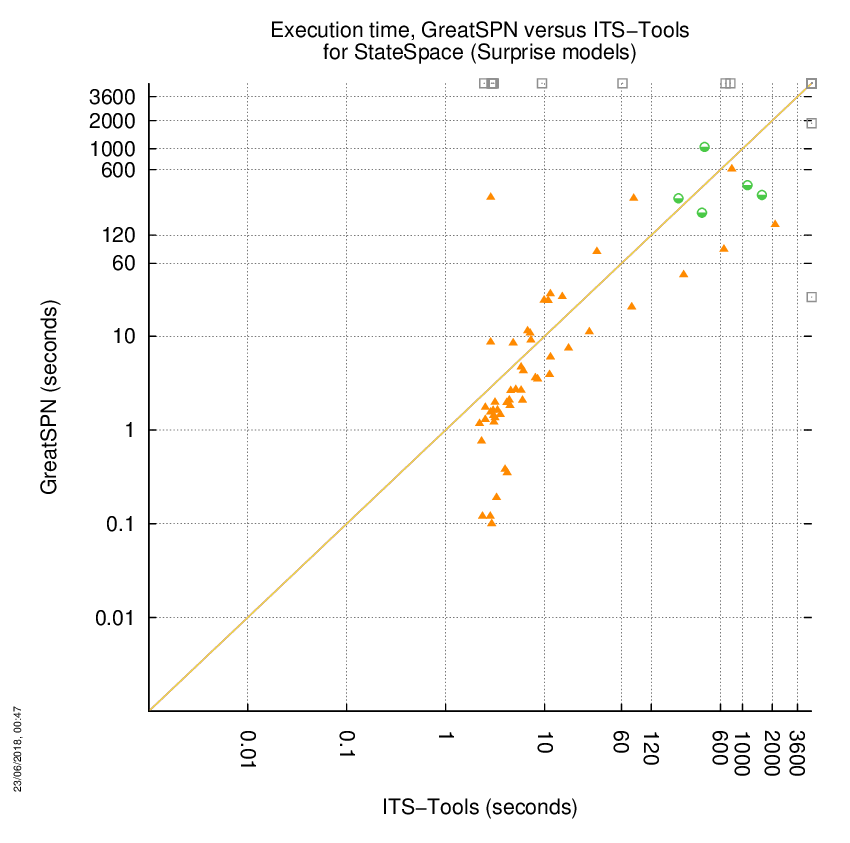
GreatSPN versus ITS-Tools
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for ITS-Tools, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to ITS-Tools are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | ITS-Tools | Both tools | GreatSPN | ITS-Tools | ||
| All computed OK | 2 | 9 | 0 | Smallest Memory Footprint | ||
| GreatSPN = ITS-Tools | — | — | 5 | Times tool wins | 54 | 12 |
| GreatSPN > ITS-Tools | — | — | 50 | Shortest Execution Time | ||
| GreatSPN < ITS-Tools | — | — | 0 | Times tool wins | 43 | 23 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 9 | 2 | 73 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than ITS-Tools,
denote cases where GreatSPN
computed less values than ITS-Tools,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, ITS-Tools wins when points are above the diagonal.
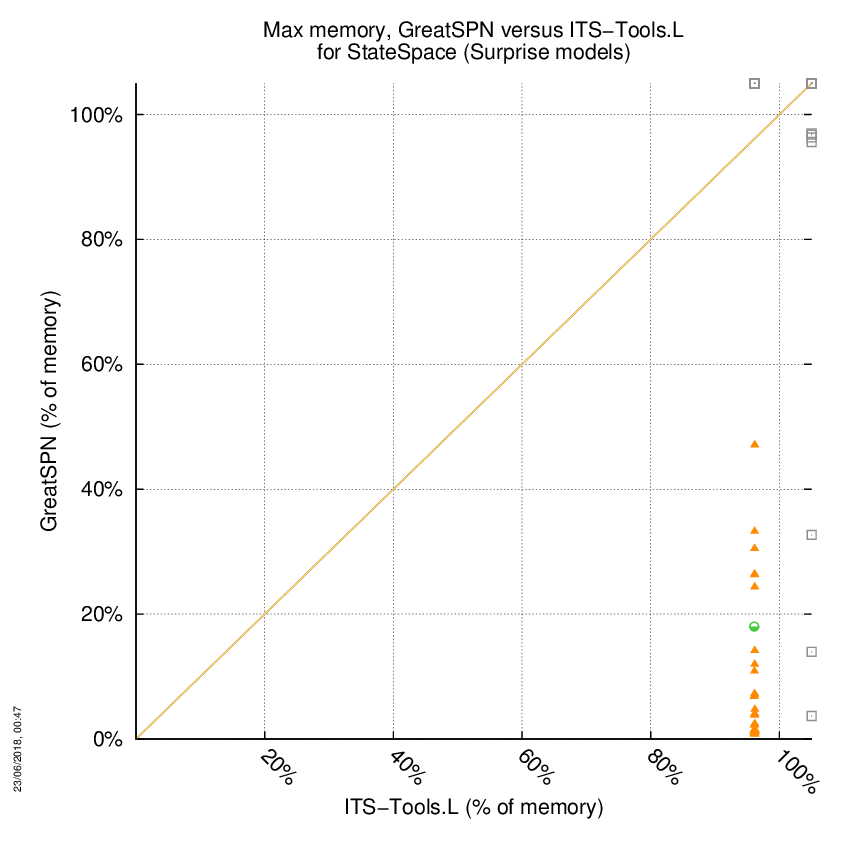
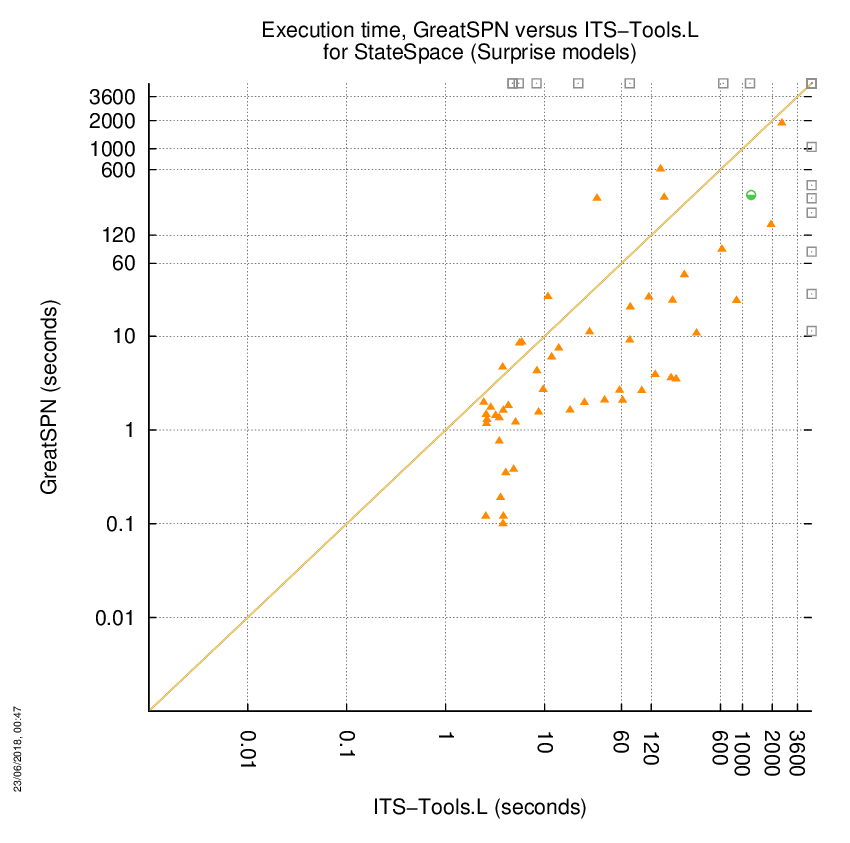
GreatSPN versus ITS-Tools.L
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for ITS-Tools.L, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to ITS-Tools.L are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | ITS-Tools.L | Both tools | GreatSPN | ITS-Tools.L | ||
| All computed OK | 7 | 8 | 0 | Smallest Memory Footprint | ||
| GreatSPN = ITS-Tools.L | — | — | 1 | Times tool wins | 57 | 8 |
| GreatSPN > ITS-Tools.L | — | — | 49 | Shortest Execution Time | ||
| GreatSPN < ITS-Tools.L | — | — | 0 | Times tool wins | 50 | 15 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 8 | 7 | 74 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than ITS-Tools.L,
denote cases where GreatSPN
computed less values than ITS-Tools.L,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, ITS-Tools.L wins when points are above the diagonal.
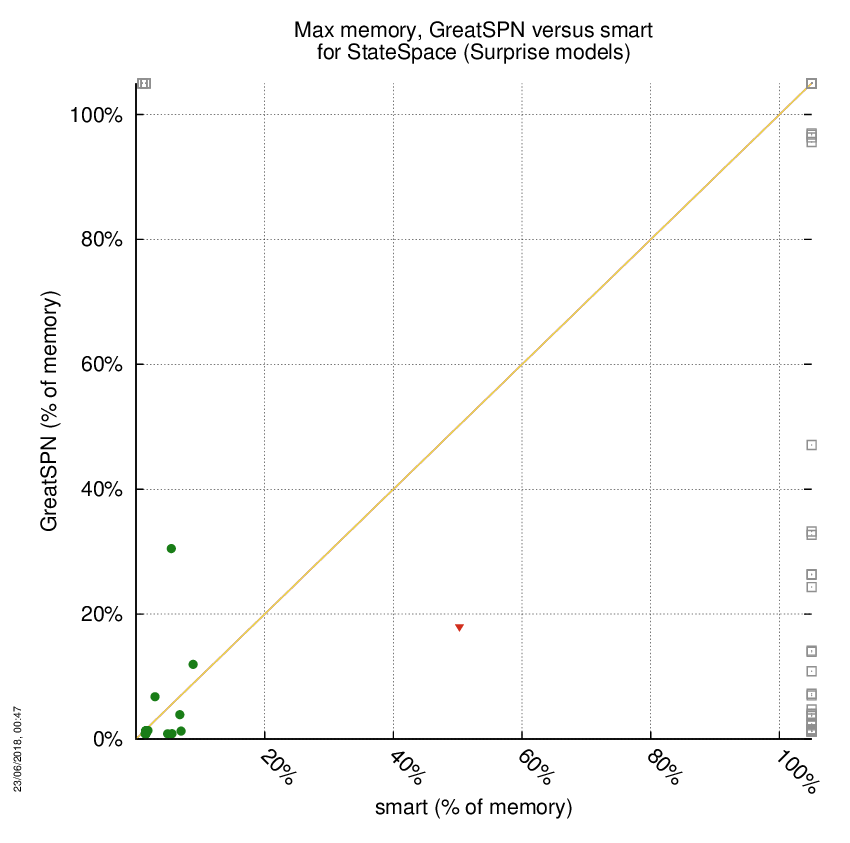
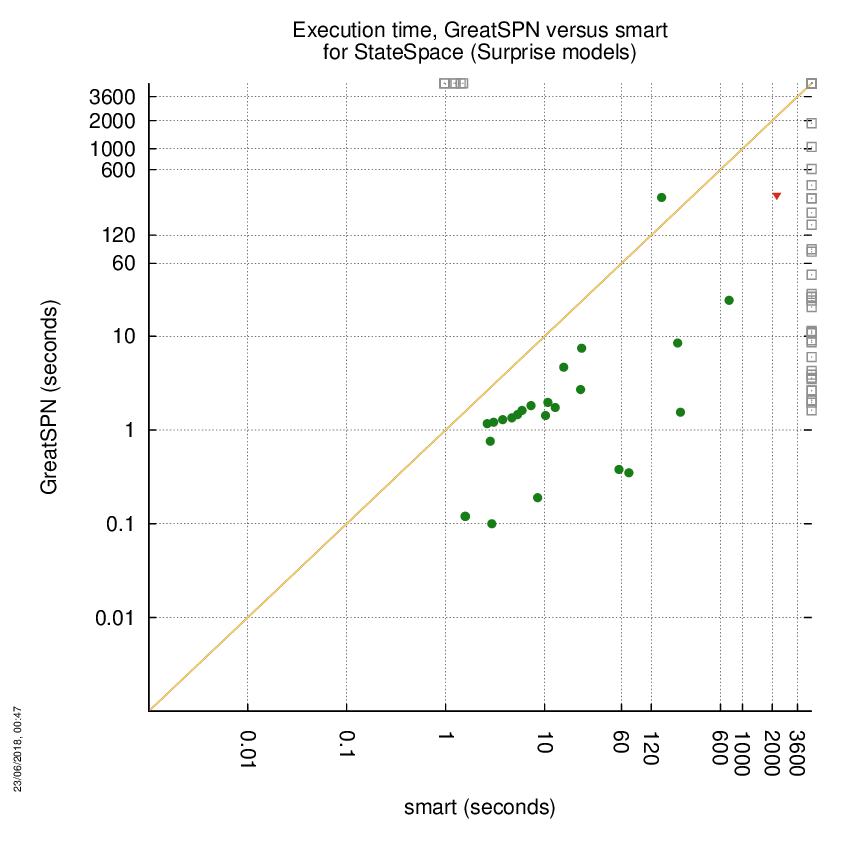
GreatSPN versus smart
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for smart, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to smart are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | smart | Both tools | GreatSPN | smart | ||
| All computed OK | 32 | 6 | 24 | Smallest Memory Footprint | ||
| GreatSPN = smart | — | — | 0 | Times tool wins | 54 | 9 |
| GreatSPN > smart | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < smart | — | — | 1 | Times tool wins | 56 | 7 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 6 | 32 | 76 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than smart,
denote cases where GreatSPN
computed less values than smart,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, smart wins when points are above the diagonal.
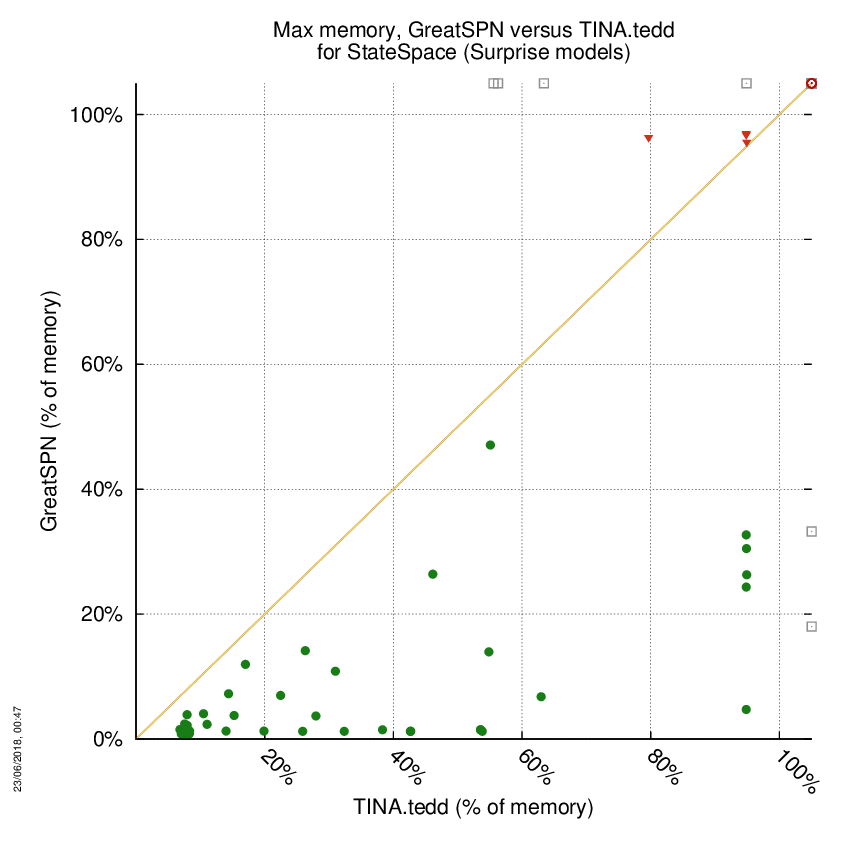
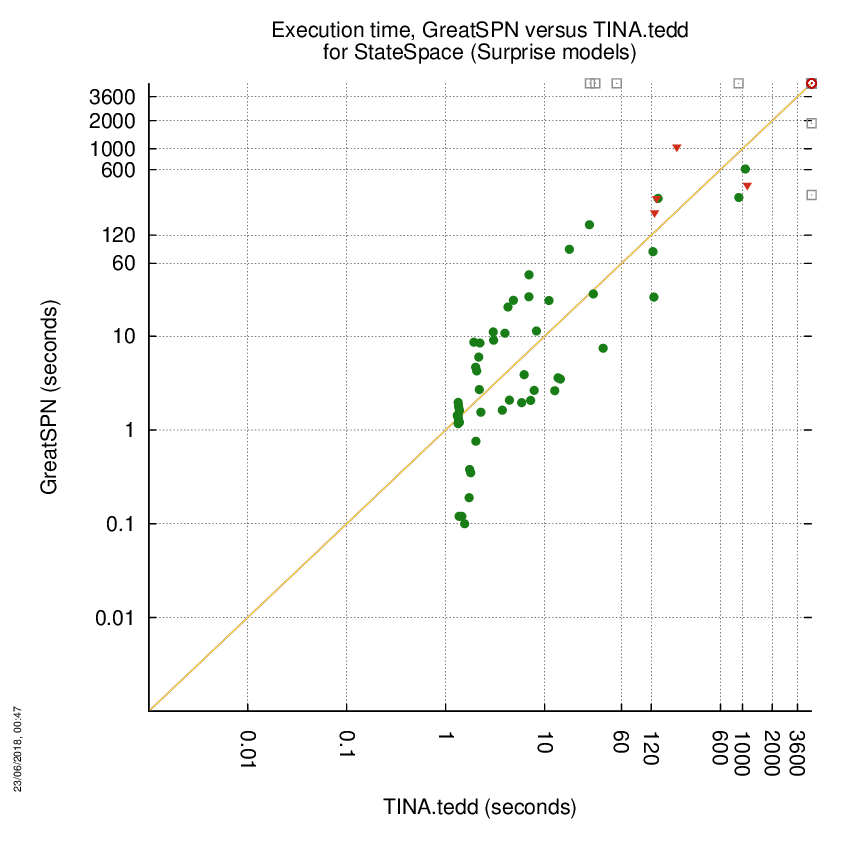
GreatSPN versus TINA.tedd
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for TINA.tedd, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to TINA.tedd are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | TINA.tedd | Both tools | GreatSPN | TINA.tedd | ||
| All computed OK | 2 | 4 | 51 | Smallest Memory Footprint | ||
| GreatSPN = TINA.tedd | — | — | 0 | Times tool wins | 53 | 8 |
| GreatSPN > TINA.tedd | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < TINA.tedd | — | — | 4 | Times tool wins | 29 | 32 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 6 | 0 | |||
| Cannot Compute + Time-out | 10 | 2 | 72 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than TINA.tedd,
denote cases where GreatSPN
computed less values than TINA.tedd,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, TINA.tedd wins when points are above the diagonal.
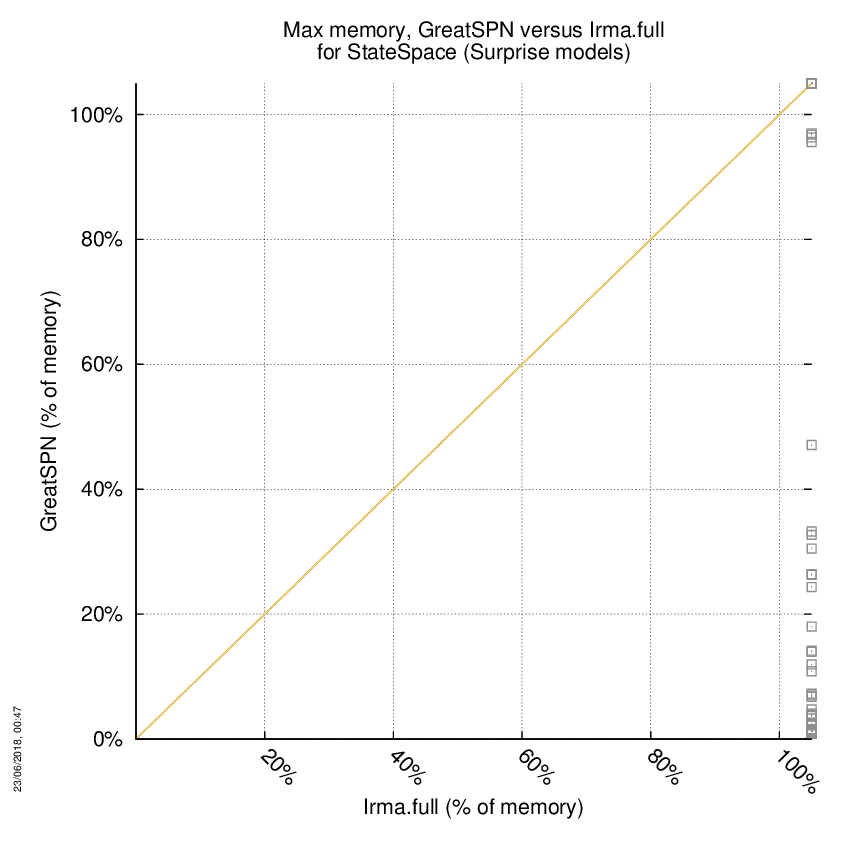
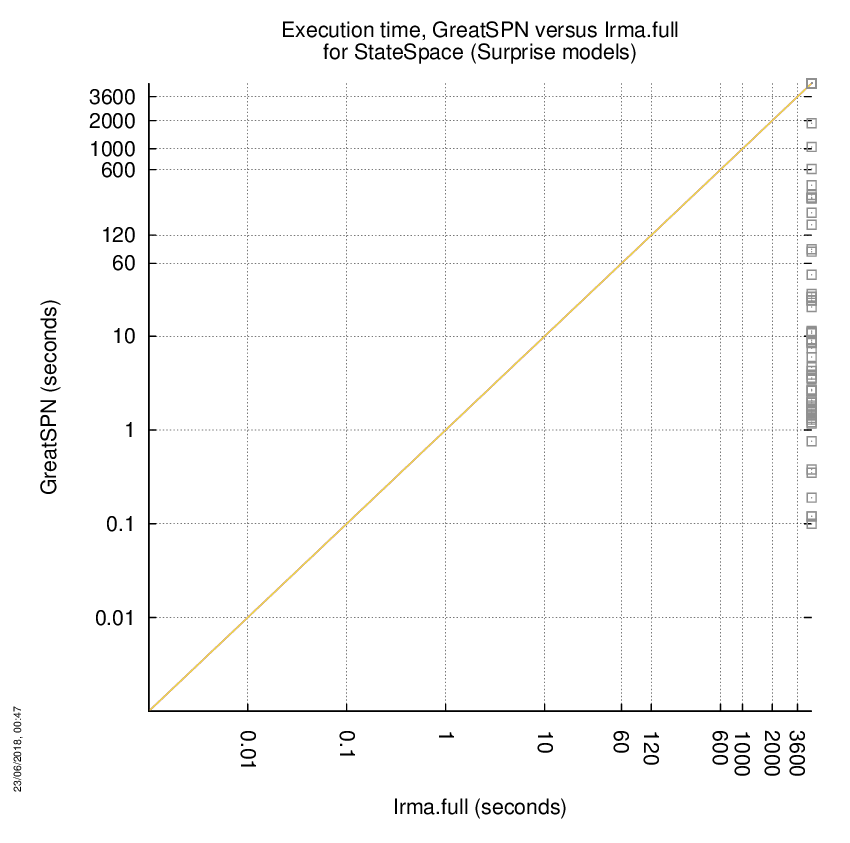
GreatSPN versus Irma.full
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for Irma.full, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to Irma.full are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | Irma.full | Both tools | GreatSPN | Irma.full | ||
| All computed OK | 57 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = Irma.full | — | — | 0 | Times tool wins | 57 | 0 |
| GreatSPN > Irma.full | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < Irma.full | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 57 | 82 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than Irma.full,
denote cases where GreatSPN
computed less values than Irma.full,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, Irma.full wins when points are above the diagonal.
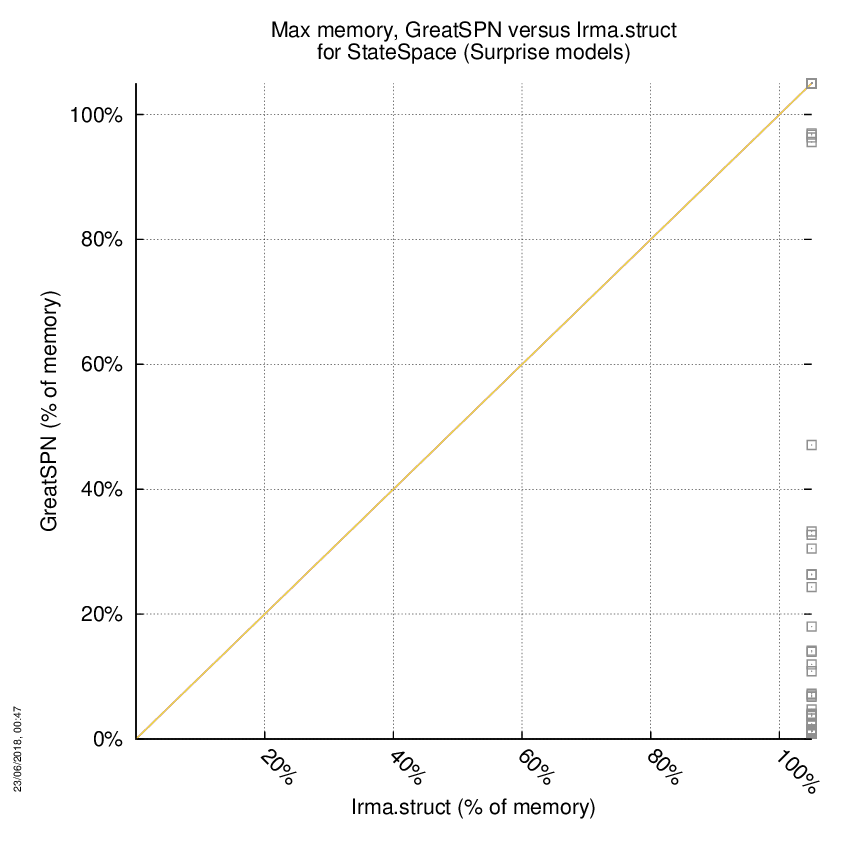
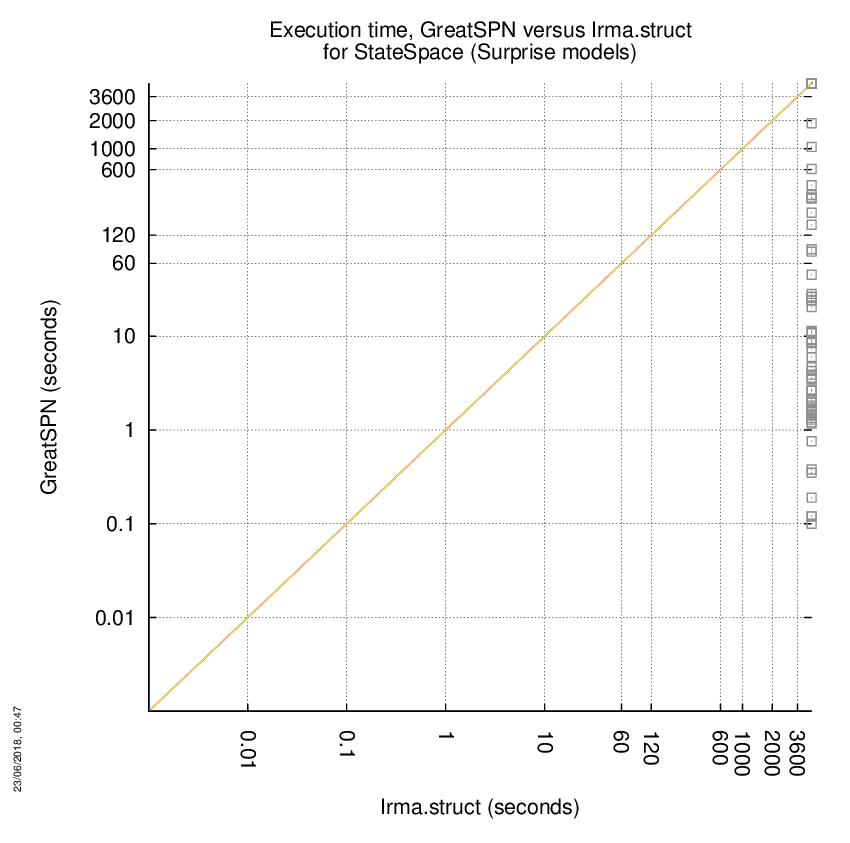
GreatSPN versus Irma.struct
Some statistics are displayed below, based on 278 runs (139 for GreatSPN and 139 for Irma.struct, so there are 139 plots on each of the two charts). Each execution was allowed 1 hour and 16 GByte of memory. Then performance charts comparing GreatSPN to Irma.struct are shown (you may click on one graph to enlarge it).
| Statistics on the executions | ||||||
| GreatSPN | Irma.struct | Both tools | GreatSPN | Irma.struct | ||
| All computed OK | 57 | 0 | 0 | Smallest Memory Footprint | ||
| GreatSPN = Irma.struct | — | — | 0 | Times tool wins | 57 | 0 |
| GreatSPN > Irma.struct | — | — | 0 | Shortest Execution Time | ||
| GreatSPN < Irma.struct | — | — | 0 | Times tool wins | 57 | 0 |
| Do not compete | 0 | 0 | 0 | |||
| Error detected | 0 | 0 | 0 | |||
| Cannot Compute + Time-out | 0 | 57 | 82 | |||
On the chart below, denote cases where
the two tools did computed all results without error,
denote cases where the two tool did computed the
same number of values (but not al values in the examination),
denote cases where GreatSPN
computed more values than Irma.struct,
denote cases where GreatSPN
computed less values than Irma.struct,
denote the cases where at least one tool did not competed,
denote the cases where at least one
tool computed a bad value and
denote the cases where at least one tool stated it could not compute a result or timed-out.
GreatSPN wins when points are below the diagonal, Irma.struct wins when points are above the diagonal.
