About the Execution of MARCIE for JoinFreeModules-PT-0010
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 11528.140 | 89836.00 | 89029.00 | 20.10 | TFFTTFFTFFTFTTTT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
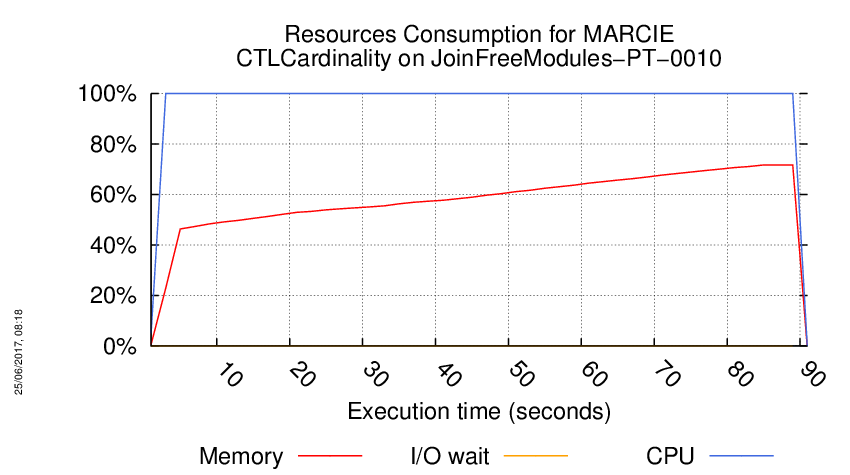
Trace from the execution
Waiting for the VM to be ready (probing ssh)
............
=====================================================================
Generated by BenchKit 2-3254
Executing tool marcie
Input is JoinFreeModules-PT-0010, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r191-blw7-149581061600030
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-0
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-1
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-10
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-11
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-12
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-13
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-14
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-15
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-2
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-3
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-4
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-5
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-6
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-7
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-8
FORMULA_NAME JoinFreeModules-PT-0010-CTLCardinality-9
=== Now, execution of the tool begins
BK_START 1496737800819
timeout --kill-after=10s --signal=SIGINT 1m for testing only
Marcie rev. 8852M (built: crohr on 2017-05-03)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --memory=6
parse successfull
net created successfully
Net: JoinFreeModules_PT_0010
(NrP: 51 NrTr: 81 NrArc: 232)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 1.021sec
parse successfull
net created successfully
Net: JoinFreeModules_PT_0010
(NrP: 51 NrTr: 81 NrArc: 232)
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
net check time: 0m 0.000sec
init dd package: 0m 3.223sec
RS generation: 0m 0.087sec
-> reachability set: #nodes 1422 (1.4e+03) #states 1,590,240,687,854,486,655,624,010,000,000,000 (33)
starting MCC model checker
--------------------------
checking: ~ [EF [AX [3<=p29]]]
normalized: ~ [E [true U ~ [EX [~ [3<=p29]]]]]
abstracting: (3<=p29)
states: 753,271,904,773,177,889,506,110,000,000,000 (32)
.-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.338sec
checking: ~ [~ [EG [1<=p33]]]
normalized: EG [1<=p33]
abstracting: (1<=p33)
states: 1,193,060,956,246,811,041,157,152,000,000,000 (33)
.
EG iterations: 1
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.132sec
checking: ~ [~ [~ [AF [p1<=p25]]]]
normalized: EG [~ [p1<=p25]]
abstracting: (p1<=p25)
states: 880,863,226,829,074,489,445,797,000,000,000 (32)
.
EG iterations: 1
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-9 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.176sec
checking: AG [AF [[1<=p25 | 2<=p8]]]
normalized: ~ [E [true U EG [~ [[1<=p25 | 2<=p8]]]]]
abstracting: (2<=p8)
states: 865,121,369,421,316,424,614,593,000,000,000 (32)
abstracting: (1<=p25)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
.
EG iterations: 1
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.388sec
checking: AX [EG [p39<=p22]]
normalized: ~ [EX [~ [EG [p39<=p22]]]]
abstracting: (p39<=p22)
states: 836,612,734,595,074,090,183,466,200,000,000 (32)
.
EG iterations: 1
.-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.410sec
checking: AG [AF [[p49<=p14 | 2<=p2]]]
normalized: ~ [E [true U EG [~ [[p49<=p14 | 2<=p2]]]]]
abstracting: (2<=p2)
states: 874,251,937,964,021,611,154,061,000,000,000 (32)
abstracting: (p49<=p14)
states: 904,579,769,401,424,145,630,551,500,000,000 (32)
.
EG iterations: 1
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-3 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.813sec
checking: EX [E [p7<=p25 U 3<=p4]]
normalized: EX [E [p7<=p25 U 3<=p4]]
abstracting: (3<=p4)
states: 753,271,904,773,177,889,506,110,000,000,000 (32)
abstracting: (p7<=p25)
states: 980,188,012,467,058,059,142,903,700,000,000 (32)
.-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.603sec
checking: AF [[AG [1<=p5] & ~ [[1<=p9 | p25<=p49]]]]
normalized: ~ [EG [~ [[~ [[1<=p9 | p25<=p49]] & ~ [E [true U ~ [1<=p5]]]]]]]
abstracting: (1<=p5)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
abstracting: (p25<=p49)
states: 912,119,041,488,779,875,616,430,400,000,000 (32)
abstracting: (1<=p9)
states: 1,240,996,441,096,013,270,489,359,000,000,000 (33)
EG iterations: 0
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.403sec
checking: E [[~ [1<=p41] | [p32<=p12 | p48<=p8]] U 3<=p25]
normalized: E [[[p32<=p12 | p48<=p8] | ~ [1<=p41]] U 3<=p25]
abstracting: (3<=p25)
states: 715,988,749,890,465,044,469,949,000,000,000 (32)
abstracting: (1<=p41)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
abstracting: (p48<=p8)
states: 925,130,465,719,891,652,606,884,400,000,000 (32)
abstracting: (p32<=p12)
states: 923,006,188,708,460,840,666,780,900,000,000 (32)
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.578sec
checking: A [EX [p15<=p37] U [3<=p26 & [p44<=p34 | 3<=p18]]]
normalized: [~ [EG [~ [[3<=p26 & [p44<=p34 | 3<=p18]]]]] & ~ [E [~ [[3<=p26 & [p44<=p34 | 3<=p18]]] U [~ [EX [p15<=p37]] & ~ [[3<=p26 & [p44<=p34 | 3<=p18]]]]]]]
abstracting: (3<=p18)
states: 606,421,927,378,002,805,996,333,000,000,000 (32)
abstracting: (p44<=p34)
states: 904,579,769,401,424,145,630,551,500,000,000 (32)
abstracting: (3<=p26)
states: 753,271,904,773,177,889,506,110,000,000,000 (32)
abstracting: (p15<=p37)
states: 846,585,732,787,213,878,064,733,600,000,000 (32)
.abstracting: (3<=p18)
states: 606,421,927,378,002,805,996,333,000,000,000 (32)
abstracting: (p44<=p34)
states: 904,579,769,401,424,145,630,551,500,000,000 (32)
abstracting: (3<=p26)
states: 753,271,904,773,177,889,506,110,000,000,000 (32)
abstracting: (3<=p18)
states: 606,421,927,378,002,805,996,333,000,000,000 (32)
abstracting: (p44<=p34)
states: 904,579,769,401,424,145,630,551,500,000,000 (32)
abstracting: (3<=p26)
states: 753,271,904,773,177,889,506,110,000,000,000 (32)
.
EG iterations: 1
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-5 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m20.460sec
checking: [[EX [[2<=p1 | 1<=p43]] & [AG [2<=p23] & 1<=p48]] | A [~ [p2<=p12] U ~ [1<=p41]]]
normalized: [[~ [EG [1<=p41]] & ~ [E [1<=p41 U [p2<=p12 & 1<=p41]]]] | [[1<=p48 & ~ [E [true U ~ [2<=p23]]]] & EX [[2<=p1 | 1<=p43]]]]
abstracting: (1<=p43)
states: 1,193,060,956,246,811,041,157,152,000,000,000 (33)
abstracting: (2<=p1)
states: 1,020,341,034,647,304,595,785,549,000,000,000 (33)
.abstracting: (2<=p23)
states: 865,121,369,421,316,424,614,593,000,000,000 (32)
abstracting: (1<=p48)
states: 1,193,060,956,246,811,041,157,152,000,000,000 (33)
abstracting: (1<=p41)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
abstracting: (p2<=p12)
states: 923,006,188,708,460,840,666,780,900,000,000 (32)
abstracting: (1<=p41)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
abstracting: (1<=p41)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
.
EG iterations: 1
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-1 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.526sec
checking: [p3<=p1 | [~ [~ [p6<=p17]] | EG [[p24<=p4 | 1<=p45]]]]
normalized: [p3<=p1 | [p6<=p17 | EG [[p24<=p4 | 1<=p45]]]]
abstracting: (1<=p45)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
abstracting: (p24<=p4)
states: 904,579,769,401,424,145,630,551,500,000,000 (32)
.
EG iterations: 1
abstracting: (p6<=p17)
states: 818,259,854,954,928,401,833,081,000,000,000 (32)
abstracting: (p3<=p1)
states: 984,579,641,188,375,948,505,966,000,000,000 (32)
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.316sec
checking: [[AF [~ [2<=p27]] & ~ [EG [1<=p6]]] | [[1<=p50 | 3<=p40] | [EF [p48<=p3] & EG [p48<=p28]]]]
normalized: [[[EG [p48<=p28] & E [true U p48<=p3]] | [1<=p50 | 3<=p40]] | [~ [EG [1<=p6]] & ~ [EG [2<=p27]]]]
abstracting: (2<=p27)
states: 874,251,937,964,021,611,154,061,000,000,000 (32)
.
EG iterations: 1
abstracting: (1<=p6)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
.
EG iterations: 1
abstracting: (3<=p40)
states: 715,988,749,890,465,044,469,949,000,000,000 (32)
abstracting: (1<=p50)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
abstracting: (p48<=p3)
states: 925,130,465,719,891,652,606,884,400,000,000 (32)
abstracting: (p48<=p28)
states: 925,130,465,719,891,652,606,884,400,000,000 (32)
.
EG iterations: 1
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 3.546sec
checking: [E [p7<=p48 U ~ [p37<=p28]] | [AG [[p14<=p | 1<=p38]] | A [p38<=p24 U 2<=p40]]]
normalized: [[[~ [E [~ [2<=p40] U [~ [2<=p40] & ~ [p38<=p24]]]] & ~ [EG [~ [2<=p40]]]] | ~ [E [true U ~ [[p14<=p | 1<=p38]]]]] | E [p7<=p48 U ~ [p37<=p28]]]
abstracting: (p37<=p28)
states: 916,214,691,253,749,307,377,555,400,000,000 (32)
abstracting: (p7<=p48)
states: 916,214,691,253,749,307,377,555,400,000,000 (32)
abstracting: (1<=p38)
states: 1,193,060,956,246,811,041,157,152,000,000,000 (33)
abstracting: (p14<=p)
states: 624,683,064,463,413,179,075,269,000,000,000 (32)
abstracting: (2<=p40)
states: 942,731,202,034,310,510,200,071,000,000,000 (32)
.
EG iterations: 1
abstracting: (p38<=p24)
states: 996,908,093,067,569,267,364,520,400,000,000 (32)
abstracting: (2<=p40)
states: 942,731,202,034,310,510,200,071,000,000,000 (32)
abstracting: (2<=p40)
states: 942,731,202,034,310,510,200,071,000,000,000 (32)
-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-4 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.473sec
checking: [EF [[p40<=p10 & [p17<=p46 | 2<=p32]]] & [A [2<=p36 U 1<=p36] & [[2<=p27 | [1<=p45 & 2<=p14]] | AG [p37<=p33]]]]
normalized: [[[~ [E [true U ~ [p37<=p33]]] | [2<=p27 | [1<=p45 & 2<=p14]]] & [~ [EG [~ [1<=p36]]] & ~ [E [~ [1<=p36] U [~ [2<=p36] & ~ [1<=p36]]]]]] & E [true U [p40<=p10 & [p17<=p46 | 2<=p32]]]]
abstracting: (2<=p32)
states: 874,251,937,964,021,611,154,061,000,000,000 (32)
abstracting: (p17<=p46)
states: 1,003,146,222,731,813,819,651,353,900,000,000 (33)
abstracting: (p40<=p10)
states: 905,712,353,083,097,025,826,894,600,000,000 (32)
abstracting: (1<=p36)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
abstracting: (2<=p36)
states: 1,020,341,034,647,304,595,785,549,000,000,000 (33)
abstracting: (1<=p36)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
abstracting: (1<=p36)
states: 1,269,909,908,147,913,027,864,341,000,000,000 (33)
.
EG iterations: 1
abstracting: (2<=p14)
states: 965,557,623,391,073,476,548,741,000,000,000 (32)
abstracting: (1<=p45)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
abstracting: (2<=p27)
states: 874,251,937,964,021,611,154,061,000,000,000 (32)
abstracting: (p37<=p33)
states: 916,214,691,253,749,307,377,555,400,000,000 (32)
-> the formula is FALSE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m44.122sec
checking: [[[[[3<=p32 & p48<=p25] & p16<=p3] & AX [p27<=p32]] | A [1<=p40 U p8<=p2]] | [[EF [p13<=p12] & AX [2<=p23]] | AX [p13<=p6]]]
normalized: [[~ [EX [~ [p13<=p6]]] | [~ [EX [~ [2<=p23]]] & E [true U p13<=p12]]] | [[~ [EG [~ [p8<=p2]]] & ~ [E [~ [p8<=p2] U [~ [1<=p40] & ~ [p8<=p2]]]]] | [~ [EX [~ [p27<=p32]]] & [p16<=p3 & [3<=p32 & p48<=p25]]]]]
abstracting: (p48<=p25)
states: 988,800,526,821,714,223,336,053,400,000,000 (32)
abstracting: (3<=p32)
states: 615,552,495,920,707,992,535,801,000,000,000 (32)
abstracting: (p16<=p3)
states: 811,244,461,979,731,872,940,914,000,000,000 (32)
abstracting: (p27<=p32)
states: 923,006,188,708,460,840,666,780,900,000,000 (32)
.abstracting: (p8<=p2)
states: 931,890,654,207,510,975,128,869,300,000,000 (32)
abstracting: (1<=p40)
states: 1,234,148,514,688,984,380,584,758,000,000,000 (33)
abstracting: (p8<=p2)
states: 931,890,654,207,510,975,128,869,300,000,000 (32)
abstracting: (p8<=p2)
states: 931,890,654,207,510,975,128,869,300,000,000 (32)
.
EG iterations: 1
abstracting: (p13<=p12)
states: 906,969,808,575,381,862,920,488,000,000,000 (32)
abstracting: (2<=p23)
states: 865,121,369,421,316,424,614,593,000,000,000 (32)
.abstracting: (p13<=p6)
states: 1,011,782,764,898,424,471,177,502,200,000,000 (33)
.-> the formula is TRUE
FORMULA JoinFreeModules-PT-0010-CTLCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.225sec
totally nodes used: 29119937 (2.9e+07)
number of garbage collections: 0
fire ops cache: hits/miss/sum: 147469763 31846602 179316365
used/not used/entry size/cache size: 38228278 28880586 16 1024MB
basic ops cache: hits/miss/sum: 105295931 22355086 127651017
used/not used/entry size/cache size: 15689709 1087507 12 192MB
unary ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 8 128MB
abstract ops cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 16777216 12 192MB
state nr cache: hits/miss/sum: 638825 128972 767797
used/not used/entry size/cache size: 127994 8260614 32 256MB
max state cache: hits/miss/sum: 0 0 0
used/not used/entry size/cache size: 0 8388608 32 256MB
uniqueHash elements/entry size/size: 67108864 4 256MB
0 43783517
1 18663451
2 3986627
3 573296
4 65452
5 8890
6 3575
7 3264
8 2953
9 2846
>= 10 14993
Total processing time: 1m29.610sec
BK_STOP 1496737890655
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check for constant places
p
found 1 constant places
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
ptnet_zbdd.cc:255: Boundedness exception: net is not 1-bounded!
check for maximal unmarked siphon
ok
check for constant places
p
found 1 constant places
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:4865 (60), effective:1313 (16)
initing FirstDep: 0m 0.000sec
iterations count:181 (2), effective:51 (0)
iterations count:219 (2), effective:52 (0)
iterations count:315 (3), effective:44 (0)
iterations count:106 (1), effective:11 (0)
iterations count:233 (2), effective:46 (0)
iterations count:159 (1), effective:29 (0)
iterations count:1262 (15), effective:433 (5)
iterations count:90 (1), effective:9 (0)
iterations count:114 (1), effective:11 (0)
iterations count:1144 (14), effective:331 (4)
iterations count:108 (1), effective:15 (0)
iterations count:122 (1), effective:23 (0)
iterations count:172 (2), effective:30 (0)
iterations count:1290 (15), effective:444 (5)
iterations count:81 (1), effective:0 (0)
iterations count:108 (1), effective:15 (0)
iterations count:210 (2), effective:43 (0)
iterations count:86 (1), effective:5 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="JoinFreeModules-PT-0010"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/JoinFreeModules-PT-0010.tgz
mv JoinFreeModules-PT-0010 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-3254"
echo " Executing tool marcie"
echo " Input is JoinFreeModules-PT-0010, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r191-blw7-149581061600030"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

