About the Execution of LoLA for S_QuasiCertifProtocol-PT-32
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 792.180 | 33597.00 | 67376.00 | 127.80 | TTFFTFTFFTFTTTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
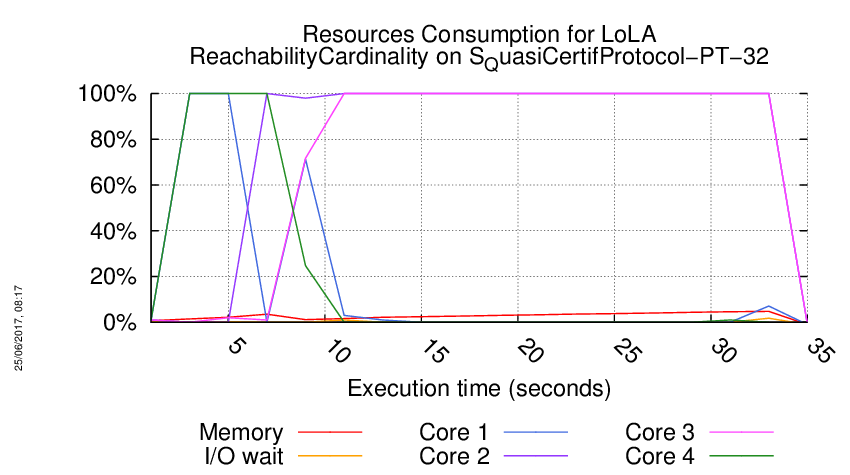
Trace from the execution
Waiting for the VM to be ready (probing ssh)
..............
=====================================================================
Generated by BenchKit 2-3254
Executing tool lola
Input is S_QuasiCertifProtocol-PT-32, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r138-smll-149479231800295
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-0
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-1
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-10
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-11
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-12
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-13
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-14
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-15
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-2
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-3
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-4
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-5
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-6
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-7
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-8
FORMULA_NAME QuasiCertifProtocol-COL-32-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1496398446781
Time: 3600 - MCC
----- Start make prepare stdout -----
===========================================================================================
S_QuasiCertifProtocol-PT-32: translating PT Petri net model.pnml into LoLA format
===========================================================================================
translating PT Petri net complete
checking for too many tokens
===========================================================================================
S_QuasiCertifProtocol-PT-32: translating PT formula ReachabilityCardinality into LoLA format
===========================================================================================
translating formula complete
touch formulae;
----- Start make result stdout -----
ReachabilityCardinality @ S_QuasiCertifProtocol-PT-32 @ 3540 seconds
----- Start make result stdout -----
lola: LoLA will run for 3540 seconds at most (--timelimit)
lola: NET
lola: reading net from model.pnml.lola
lola: finished parsing
lola: closed net file model.pnml.lola
lola: 4312/65536 symbol table entries, 134 collisions
lola: preprocessing...
lola: finding significant places
lola: 3806 places, 506 transitions, 505 significant places
lola: computing forward-conflicting sets
lola: computing back-conflicting sets
lola: 671 transition conflict sets
lola: TASK
lola: reading formula from QuasiCertifProtocol-COL-32-ReachabilityCardinality.task
lola: E (F ((n2_32 + n2_31 + n2_30 + n2_29 + n2_28 + n2_27 + n2_26 + n2_25 + n2_24 + n2_23 + n2_22 + n2_21 + n2_20 + n2_19 + n2_18 + n2_17 + n2_16 + n2_15 + n2_14 + n2_13 + n2_12 + n2_11 + n2_10 + n2_0 + n2_1 + n2_2 + n2_3 + n2_4 + n2_5 + n2_6 + n2_7 + n2_8 + n2_9 + 1 <= AstopOK))) : E (F ((3 <= CstopAbort))) : A (G (((a2 <= n7_17_0 + n7_17_1 + n7_17_2 + n7_17_3 + n7_17_4 + n7_17_5 + n7_17_6 + n7_17_7 + n7_17_8 + n7_17_9 + n7_21_10 + n7_21_11 + n7_21_12 + n7_21_13 + n7_21_14 + n7_21_15 + n7_21_16 + n7_21_17 + n7_21_18 + n7_21_19 + n7_21_20 + n7_21_21 + n7_21_22 + n7_21_23 + n7_21_24 + n7_21_25 + n7_21_26 + n7_21_27 + n7_21_28 + n7_21_29 + n7_3_10 + n7_21_30 + n7_21_31 + n7_21_32 + n7_15_0 + n7_6_0 + n7_4_10 + n7_27_0 + n7_28_10 + n7_16_10 + n7_5_10 + n7_11_10 + n7_10_0 + n7_23_0 + n7_0_10 + n7_29_10 + n7_22_0 + n7_18_0 + n7_24_10 + n7_12_10 + n7_7_0 + n7_1_10 + n7_14_10 + n7_25_10 + n7_31_0 + n7_13_10 + n7_26_10 + n7_30_0 + n7_9_0 + n7_32_10 + n7_2_10 + n7_20_10 + n7_8_10 + n7_19_0 + n7_8_32 + n7_8_31 + n7_8_30 + n7_8_29 + n7_8_28 + n7_8_27 + n7_8_26 + n7_8_25 + n7_8_24 + n7_8_23 + n7_19_1 + n7_19_2 + n7_19_3 + n7_19_4 + n7_19_5 + n7_19_6 + n7_19_7 + n7_19_8 + n7_19_9 + n7_8_22 + n7_8_21 + n7_8_20 + n7_8_19 + n7_26_32 + n7_8_18 + n7_26_31 + n7_8_17 + n7_26_30 + n7_8_16 + n7_8_15 + n7_8_14 + n7_8_13 + n7_8_0 + n7_8_1 + n7_8_2 + n7_8_3 + n7_8_4 + n7_8_5 + n7_8_6 + n7_8_7 + n7_8_8 + n7_8_9 + n7_8_12 + n7_8_11 + n7_26_29 + n7_19_10 + n7_19_11 + n7_19_12 + n7_19_13 + n7_19_14 + n7_19_15 + n7_19_16 + n7_19_17 + n7_19_18 + n7_19_19 + n7_19_20 + n7_19_21 + n7_19_22 + n7_19_23 + n7_19_24 + n7_19_25 + n7_19_26 + n7_19_27 + n7_19_28 + n7_19_29 + n7_19_30 + n7_19_31 + n7_19_32 + n7_26_28 + n7_26_27 + n7_20_11 + n7_20_12 + n7_20_13 + n7_20_14 + n7_20_15 + n7_20_16 + n7_20_17 + n7_20_18 + n7_20_19 + n7_20_20 + n7_20_21 + n7_20_22 + n7_20_23 + n7_20_24 + n7_20_25 + n7_20_26 + n7_20_27 + n7_20_28 + n7_20_29 + n7_26_26 + n7_2_11 + n7_2_12 + n7_2_13 + n7_2_14 + n7_2_15 + n7_2_16 + n7_20_30 + n7_26_25 + n7_2_17 + n7_20_31 + n7_32_11 + n7_2_18 + n7_20_32 + n7_32_12 + n7_2_19 + n7_32_13 + n7_32_14 + n7_32_15 + n7_32_16 + n7_32_17 + n7_32_18 + n7_32_19 + n7_2_20 + n7_2_21 + n7_2_22 + n7_2_23 + n7_2_24 + n7_2_25 + n7_2_26 + n7_2_27 + n7_32_20 + n7_2_28 + n7_32_21 + n7_32_22 + n7_2_29 + n7_32_23 + n7_32_24 + n7_32_25 + n7_32_26 + n7_32_27 + n7_32_28 + n7_32_29 + n7_26_24 + n7_2_30 + n7_2_31 + n7_2_32 + n7_32_30 + n7_32_31 + n7_32_32 + n7_26_23 + n7_9_1 + n7_9_2 + n7_9_3 + n7_9_4 + n7_9_5 + n7_9_6 + n7_9_7 + n7_9_8 + n7_9_9 + n7_26_22 + n7_26_21 + n7_26_20 + n7_26_19 + n7_30_1 + n7_30_2 + n7_30_3 + n7_30_4 + n7_30_5 + n7_30_6 + n7_30_7 + n7_30_8 + n7_30_9 + n7_26_18 + n7_26_17 + n7_26_16 + n7_26_15 + n7_26_14 + n7_26_13 + n7_26_12 + n7_14_32 + n7_26_11 + n7_14_31 + n7_14_30 + n7_14_29 + n7_14_28 + n7_14_27 + n7_14_26 + n7_14_25 + n7_14_24 + n7_14_23 + n7_14_22 + n7_14_21 + n7_14_20 + n7_13_11 + n7_13_12 + n7_13_13 + n7_13_14 + n7_13_15 + n7_13_16 + n7_13_17 + n7_13_18 + n7_13_19 + n7_31_1 + n7_31_2 + n7_31_3 + n7_31_4 + n7_31_5 + n7_31_6 + n7_31_7 + n7_31_8 + n7_31_9 + n7_13_20 + n7_13_21 + n7_13_22 + n7_13_23 + n7_13_24 + n7_13_25 + n7_13_26 + n7_13_27 + n7_13_28 + n7_13_29 + n7_13_30 + n7_13_31 + n7_25_11 + n7_13_32 + n7_25_12 + n7_25_13 + n7_25_14 + n7_25_15 + n7_25_16 + n7_25_17 + n7_25_18 + n7_25_19 + n7_25_20 + n7_25_21 + n7_25_22 + n7_25_23 + n7_25_24 + n7_25_25 + n7_25_26 + n7_25_27 + n7_25_28 + n7_25_29 + n7_7_10 + n7_7_11 + n7_7_12 + n7_7_13 + n7_7_14 + n7_7_15 + n7_7_16 + n7_25_30 + n7_7_17 + n7_25_31 + n7_7_18 + n7_25_32 + n7_7_19 + n7_7_20 + n7_7_21 + n7_7_22 + n7_7_23 + n7_7_24 + n7_7_25 + n7_7_26 + n7_7_27 + n7_7_28 + n7_7_29 + n7_7_30 + n7_7_31 + n7_7_32 + n7_14_19 + n7_14_18 + n7_14_17 + n7_14_16 + n7_14_15 + n7_14_14 + n7_14_13 + n7_14_12 + n7_14_11 + n7_32_0 + n7_32_1 + n7_32_2 + n7_32_3 + n7_32_4 + n7_32_5 + n7_32_6 + n7_32_7 + n7_32_8 + n7_32_9 + n7_18_10 + n7_18_11 + n7_18_12 + n7_18_13 + n7_18_14 + n7_18_15 + n7_18_16 + n7_18_17 + n7_18_18 + n7_18_19 + n7_18_20 + n7_18_21 + n7_18_22 + n7_18_23 + n7_18_24 + n7_18_25 + n7_18_26 + n7_18_27 + n7_18_28 + n7_18_29 + n7_18_30 + n7_18_31 + n7_18_32 + n7_1_11 + n7_1_12 + n7_1_13 + n7_1_14 + n7_1_15 + n7_1_16 + n7_31_10 + n7_1_17 + n7_31_11 + n7_1_18 + n7_31_12 + n7_1_19 + n7_31_13 + n7_31_14 + n7_31_15 + n7_31_16 + n7_31_17 + n7_31_18 + n7_31_19 + n7_1_20 + n7_1_21 + n7_1_22 + n7_1_23 + n7_1_24 + n7_1_25 + n7_1_26 + n7_1_27 + n7_31_20 + n7_1_28 + n7_31_21 + n7_31_22 + n7_1_29 + n7_31_23 + n7_31_24 + n7_31_25 + n7_31_26 + n7_31_27 + n7_31_28 + n7_31_29 + n7_1_30 + n7_1_31 + n7_1_32 + n7_31_30 + n7_31_31 + n7_31_32 + n7_7_9 + n7_7_8 + n7_7_7 + n7_7_6 + n7_7_5 + n7_7_4 + n7_7_3 + n7_7_2 + n7_7_1 + n7_18_9 + n7_20_0 + n7_20_1 + n7_20_2 + n7_20_3 + n7_20_4 + n7_20_5 + n7_20_6 + n7_20_7 + n7_20_8 + n7_20_9 + n7_18_8 + n7_18_7 + n7_12_11 + n7_12_12 + n7_12_13 + n7_12_14 + n7_12_15 + n7_12_16 + n7_12_17 + n7_12_18 + n7_12_19 + n7_21_0 + n7_21_1 + n7_21_2 + n7_21_3 + n7_21_4 + n7_21_5 + n7_21_6 + n7_21_7 + n7_21_8 + n7_21_9 + n7_12_20 + n7_12_21 + n7_12_22 + n7_12_23 + n7_12_24 + n7_12_25 + n7_12_26 + n7_12_27 + n7_12_28 + n7_12_29 + n7_12_30 + n7_18_6 + n7_12_31 + n7_24_11 + n7_12_32 + n7_24_12 + n7_24_13 + n7_24_14 + n7_24_15 + n7_24_16 + n7_24_17 + n7_24_18 + n7_24_19 + n7_24_20 + n7_24_21 + n7_24_22 + n7_24_23 + n7_24_24 + n7_24_25 + n7_24_26 + n7_24_27 + n7_24_28 + n7_24_29 + n7_6_10 + n7_6_11 + n7_6_12 + n7_6_13 + n7_6_14 + n7_6_15 + n7_6_16 + n7_24_30 + n7_6_17 + n7_24_31 + n7_6_18 + n7_24_32 + n7_6_19 + n7_6_20 + n7_6_21 + n7_6_22 + n7_6_23 + n7_6_24 + n7_6_25 + n7_6_26 + n7_6_27 + n7_6_28 + n7_6_29 + n7_6_30 + n7_6_31 + n7_6_32 + n7_18_5 + n7_18_4 + n7_18_3 + n7_18_2 + n7_18_1 + n7_22_1 + n7_22_2 + n7_22_3 + n7_22_4 + n7_22_5 + n7_22_6 + n7_22_7 + n7_22_8 + n7_22_9 + n7_17_10 + n7_17_11 + n7_17_12 + n7_17_13 + n7_17_14 + n7_17_15 + n7_17_16 + n7_17_17 + n7_17_18 + n7_17_19 + n7_17_20 + n7_17_21 + n7_17_22 + n7_17_23 + n7_17_24 + n7_17_25 + n7_17_26 + n7_17_27 + n7_17_28 + n7_17_29 + n7_17_30 + n7_17_31 + n7_29_11 + n7_17_32 + n7_29_12 + n7_29_13 + n7_29_14 + n7_29_15 + n7_29_16 + n7_29_17 + n7_29_18 + n7_29_19 + n7_29_20 + n7_29_21 + n7_29_22 + n7_29_23 + n7_29_24 + n7_29_25 + n7_29_26 + n7_29_27 + n7_29_28 + n7_29_29 + n7_29_30 + n7_29_31 + n7_29_32 + n7_0_11 + n7_0_12 + n7_0_13 + n7_0_14 + n7_0_15 + n7_0_16 + n7_30_10 + n7_0_17 + n7_30_11 + n7_0_18 + n7_30_12 + n7_0_19 + n7_30_13 + n7_30_14 + n7_30_15 + n7_30_16 + n7_30_17 + n7_30_18 + n7_30_19 + n7_0_20 + n7_0_21 + n7_0_22 + n7_0_23 + n7_0_24 + n7_0_25 + n7_0_26 + n7_0_27 + n7_30_20 + n7_0_28 + n7_30_21 + n7_30_22 + n7_0_29 + n7_30_23 + n7_30_24 + n7_30_25 + n7_30_26 + n7_30_27 + n7_30_28 + n7_30_29 + n7_0_30 + n7_0_31 + n7_0_32 + n7_30_30 + n7_30_31 + n7_30_32 + n7_23_1 + n7_23_2 + n7_23_3 + n7_23_4 + n7_23_5 + n7_23_6 + n7_23_7 + n7_23_8 + n7_23_9 + n7_10_1 + n7_10_2 + n7_10_3 + n7_10_4 + n7_10_5 + n7_10_6 + n7_10_7 + n7_10_8 + n7_10_9 + n7_24_0 + n7_24_1 + n7_24_2 + n7_24_3 + n7_24_4 + n7_24_5 + n7_24_6 + n7_24_7 + n7_24_8 + n7_24_9 + n7_11_11 + n7_11_12 + n7_11_13 + n7_11_14 + n7_11_15 + n7_11_16 + n7_11_17 + n7_11_18 + n7_11_19 + n7_11_0 + n7_11_1 + n7_11_2 + n7_11_3 + n7_11_4 + n7_11_5 + n7_11_6 + n7_11_7 + n7_11_8 + n7_11_9 + n7_11_20 + n7_11_21 + n7_11_22 + n7_11_23 + n7_11_24 + n7_11_25 + n7_11_26 + n7_11_27 + n7_11_28 + n7_11_29 + n7_11_30 + n7_23_10 + n7_11_31 + n7_23_11 + n7_11_32 + n7_23_12 + n7_23_13 + n7_23_14 + n7_23_15 + n7_23_16 + n7_23_17 + n7_23_18 + n7_23_19 + n7_23_20 + n7_23_21 + n7_23_22 + n7_23_23 + n7_23_24 + n7_23_25 + n7_23_26 + n7_23_27 + n7_23_28 + n7_23_29 + n7_5_11 + n7_5_12 + n7_5_13 + n7_5_14 + n7_5_15 + n7_5_16 + n7_23_30 + n7_5_17 + n7_23_31 + n7_5_18 + n7_23_32 + n7_5_19 + n7_5_20 + n7_5_21 + n7_5_22 + n7_5_23 + n7_5_24 + n7_5_25 + n7_5_26 + n7_5_27 + n7_5_28 + n7_5_29 + n7_5_30 + n7_5_31 + n7_5_32 + n7_0_0 + n7_0_1 + n7_0_2 + n7_0_3 + n7_0_4 + n7_0_5 + n7_0_6 + n7_0_7 + n7_0_8 + n7_0_9 + n7_25_0 + n7_25_1 + n7_25_2 + n7_25_3 + n7_25_4 + n7_25_5 + n7_25_6 + n7_25_7 + n7_25_8 + n7_25_9 + n7_12_0 + n7_12_1 + n7_12_2 + n7_12_3 + n7_12_4 + n7_12_5 + n7_12_6 + n7_12_7 + n7_12_8 + n7_12_9 + n7_1_0 + n7_1_1 + n7_1_2 + n7_1_3 + n7_1_4 + n7_1_5 + n7_1_6 + n7_1_7 + n7_1_8 + n7_1_9 + n7_16_11 + n7_16_12 + n7_16_13 + n7_16_14 + n7_16_15 + n7_16_16 + n7_16_17 + n7_16_18 + n7_16_19 + n7_16_20 + n7_16_21 + n7_16_22 + n7_16_23 + n7_16_24 + n7_16_25 + n7_16_26 + n7_16_27 + n7_16_28 + n7_16_29 + n7_16_30 + n7_16_31 + n7_28_11 + n7_16_32 + n7_28_12 + n7_28_13 + n7_28_14 + n7_28_15 + n7_28_16 + n7_28_17 + n7_28_18 + n7_28_19 + n7_28_20 + n7_28_21 + n7_28_22 + n7_28_23 + n7_28_24 + n7_28_25 + n7_28_26 + n7_28_27 + n7_28_28 + n7_28_29 + n7_28_30 + n7_28_31 + n7_28_32 + n7_26_0 + n7_26_1 + n7_26_2 + n7_26_3 + n7_26_4 + n7_26_5 + n7_26_6 + n7_26_7 + n7_26_8 + n7_26_9 + n7_13_0 + n7_13_1 + n7_13_2 + n7_13_3 + n7_13_4 + n7_13_5 + n7_13_6 + n7_13_7 + n7_13_8 + n7_13_9 + n7_2_0 + n7_2_1 + n7_2_2 + n7_2_3 + n7_2_4 + n7_2_5 + n7_2_6 + n7_2_7 + n7_2_8 + n7_2_9 + n7_27_1 + n7_27_2 + n7_27_3 + n7_27_4 + n7_27_5 + n7_27_6 + n7_27_7 + n7_27_8 + n7_27_9 + n7_14_0 + n7_14_1 + n7_14_2 + n7_14_3 + n7_14_4 + n7_14_5 + n7_14_6 + n7_14_7 + n7_14_8 + n7_14_9 + n7_10_10 + n7_10_11 + n7_10_12 + n7_10_13 + n7_10_14 + n7_10_15 + n7_10_16 + n7_10_17 + n7_10_18 + n7_10_19 + n7_10_20 + n7_10_21 + n7_10_22 + n7_10_23 + n7_10_24 + n7_10_25 + n7_10_26 + n7_10_27 + n7_10_28 + n7_10_29 + n7_10_30 + n7_22_10 + n7_10_31 + n7_22_11 + n7_10_32 + n7_22_12 + n7_22_13 + n7_22_14 + n7_22_15 + n7_22_16 + n7_22_17 + n7_22_18 + n7_22_19 + n7_22_20 + n7_22_21 + n7_22_22 + n7_22_23 + n7_22_24 + n7_22_25 + n7_22_26 + n7_22_27 + n7_22_28 + n7_22_29 + n7_4_11 + n7_4_12 + n7_4_13 + n7_4_14 + n7_4_15 + n7_4_16 + n7_22_30 + n7_4_17 + n7_22_31 + n7_4_18 + n7_22_32 + n7_4_19 + n7_4_20 + n7_4_21 + n7_4_22 + n7_4_23 + n7_4_24 + n7_4_25 + n7_4_26 + n7_4_27 + n7_4_28 + n7_4_29 + n7_4_30 + n7_4_31 + n7_4_32 + n7_3_0 + n7_3_1 + n7_3_2 + n7_3_3 + n7_3_4 + n7_3_5 + n7_3_6 + n7_3_7 + n7_3_8 + n7_3_9 + n7_6_9 + n7_6_8 + n7_6_7 + n7_6_6 + n7_6_5 + n7_6_4 + n7_6_3 + n7_6_2 + n7_6_1 + n7_28_0 + n7_28_1 + n7_28_2 + n7_28_3 + n7_28_4 + n7_28_5 + n7_28_6 + n7_28_7 + n7_28_8 + n7_28_9 + n7_15_1 + n7_15_2 + n7_15_3 + n7_15_4 + n7_15_5 + n7_15_6 + n7_15_7 + n7_15_8 + n7_15_9 + n7_3_32 + n7_3_31 + n7_3_30 + n7_4_0 + n7_4_1 + n7_4_2 + n7_4_3 + n7_4_4 + n7_4_5 + n7_4_6 + n7_4_7 + n7_4_8 + n7_4_9 + n7_3_29 + n7_3_28 + n7_3_27 + n7_3_26 + n7_3_25 + n7_3_24 + n7_3_23 + n7_3_22 + n7_3_21 + n7_3_20 + n7_15_10 + n7_15_11 + n7_15_12 + n7_15_13 + n7_15_14 + n7_15_15 + n7_15_16 + n7_15_17 + n7_15_18 + n7_15_19 + n7_15_20 + n7_15_21 + n7_15_22 + n7_15_23 + n7_15_24 + n7_15_25 + n7_15_26 + n7_15_27 + n7_15_28 + n7_15_29 + n7_15_30 + n7_27_10 + n7_15_31 + n7_27_11 + n7_15_32 + n7_27_12 + n7_27_13 + n7_27_14 + n7_27_15 + n7_27_16 + n7_27_17 + n7_27_18 + n7_27_19 + n7_27_20 + n7_27_21 + n7_27_22 + n7_27_23 + n7_27_24 + n7_27_25 + n7_27_26 + n7_27_27 + n7_27_28 + n7_27_29 + n7_9_10 + n7_9_11 + n7_9_12 + n7_9_13 + n7_9_14 + n7_9_15 + n7_9_16 + n7_27_30 + n7_9_17 + n7_27_31 + n7_9_18 + n7_27_32 + n7_9_19 + n7_9_20 + n7_9_21 + n7_9_22 + n7_9_23 + n7_9_24 + n7_9_25 + n7_9_26 + n7_9_27 + n7_9_28 + n7_9_29 + n7_9_30 + n7_9_31 + n7_9_32 + n7_29_0 + n7_29_1 + n7_29_2 + n7_29_3 + n7_29_4 + n7_29_5 + n7_29_6 + n7_29_7 + n7_29_8 + n7_29_9 + n7_16_0 + n7_16_1 + n7_16_2 + n7_16_3 + n7_16_4 + n7_16_5 + n7_16_6 + n7_16_7 + n7_16_8 + n7_16_9 + n7_3_19 + n7_3_18 + n7_3_17 + n7_3_16 + n7_3_15 + n7_3_14 + n7_3_13 + n7_3_12 + n7_3_11 + n7_5_0 + n7_5_1 + n7_5_2 + n7_5_3 + n7_5_4 + n7_5_5 + n7_5_6 + n7_5_7 + n7_5_8 + n7_5_9) AND ((n2_32 + n2_31 + n2_30 + n2_29 + n2_28 + n2_27 + n2_26 + n2_25 + n2_24 + n2_23 + n2_22 + n2_21 + n2_20 + n2_19 + n2_18 + n2_17 + n2_16 + n2_15 + n2_14 + n2_13 + n2_12 + n2_11 + n2_10 + n2_0 + n2_1 + n2_2 + n2_3 + n2_4 + n2_5 + n2_6 + n2_7 + n2_8 + n2_9 <= CstopOK_0 + CstopOK_1 + CstopOK_2 + CstopOK_3 + CstopOK_4 + CstopOK_5 + CstopOK_6 + CstopOK_7 + CstopOK_8 + CstopOK_9 + CstopOK_10 + CstopOK_11 + CstopOK_12 + CstopOK_13 + CstopOK_14 + CstopOK_15 + CstopOK_16 + CstopOK_17 + CstopOK_18 + CstopOK_19 + CstopOK_20 + CstopOK_21 + CstopOK_22 + CstopOK_23 + CstopOK_24 + CstopOK_25 + CstopOK_26 + CstopOK_27 + CstopOK_28 + CstopOK_29 + CstopOK_30 + CstopOK_31 + CstopOK_32) OR (3 <= SstopAbort) OR (n3_9 + n3_8 + n3_7 + n3_6 + n3_5 + n3_4 + n3_3 + n3_2 + n3_1 + n3_0 + n3_10 + n3_11 + n3_12 + n3_13 + n3_14 + n3_15 + n3_16 + n3_17 + n3_18 + n3_19 + n3_20 + n3_21 + n3_22 + n3_23 + n3_24 + n3_25 + n3_26 + n3_27 + n3_28 + n3_29 + n3_30 + n3_31 + n3_32 <= 1))))) : E (F ((((3 <= CstopOK_0 + CstopOK_1 + CstopOK_2 + CstopOK_3 + CstopOK_4 + CstopOK_5 + CstopOK_6 + CstopOK_7 + CstopOK_8 + CstopOK_9 + CstopOK_10 + CstopOK_11 + CstopOK_12 + CstopOK_13 + CstopOK_14 + CstopOK_15 + CstopOK_16 + CstopOK_17 + CstopOK_18 + CstopOK_19 + CstopOK_20 + CstopOK_21 + CstopOK_22 + CstopOK_23 + CstopOK_24 + CstopOK_25 + CstopOK_26 + CstopOK_27 + CstopOK_28 + CstopOK_29 + CstopOK_30 + CstopOK_31 + CstopOK_32) AND (2 <= CstopAbort) AND (a1 + 1 <= n6_32 + n6_31 + n6_30 + n6_29 + n6_28 + n6_27 + n6_26 + n6_25 + n6_24 + n6_23 + n6_22 + n6_21 + n6_20 + n6_19 + n6_18 + n6_17 + n6_16 + n6_15 + n6_14 + n6_13 + n6_12 + n6_11 + n6_10 + n6_0 + n6_1 + n6_2 + n6_3 + n6_4 + n6_5 + n6_6 + n6_7 + n6_8 + n6_9)) OR ((a3 <= s5_32 + s5_31 + s5_30 + s5_29 + s5_28 + s5_27 + s5_26 + s5_25 + s5_24 + s5_23 + s5_22 + s5_21 + s5_20 + s5_19 + s5_18 + s5_17 + s5_16 + s5_15 + s5_14 + s5_13 + s5_12 + s5_11 + s5_10 + s5_0 + s5_1 + s5_2 + s5_3 + s5_4 + s5_5 + s5_6 + s5_7 + s5_8 + s5_9) AND (Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9 <= 0))))) : E (F ((3 <= AstopAbort))) : E (F (((3 <= n9_19_10 + n9_19_11 + n9_19_12 + n9_19_13 + n9_19_14 + n9_19_15 + n9_19_16 + n9_19_17 + n9_19_18 + n9_19_19 + n9_19_20 + n9_19_21 + n9_19_22 + n9_19_23 + n9_19_24 + n9_19_25 + n9_19_26 + n9_19_27 + n9_19_28 + n9_19_29 + n9_19_30 + n9_19_31 + n9_19_32 + n9_31_0 + n9_31_1 + n9_31_2 + n9_31_3 + n9_31_4 + n9_31_5 + n9_31_6 + n9_31_7 + n9_31_8 + n9_31_9 + n9_7_10 + n9_20_10 + n9_32_10 + n9_6_10 + n9_1_10 + n9_32_0 + n9_32_9 + n9_32_8 + n9_32_7 + n9_32_6 + n9_32_5 + n9_32_4 + n9_32_3 + n9_32_2 + n9_32_1 + n9_13_10 + n9_13_11 + n9_13_12 + n9_13_13 + n9_13_14 + n9_13_15 + n9_13_16 + n9_13_17 + n9_13_18 + n9_13_19 + n9_13_20 + n9_13_21 + n9_13_22 + n9_13_23 + n9_13_24 + n9_13_25 + n9_13_26 + n9_13_27 + n9_13_28 + n9_13_29 + n9_13_30 + n9_25_10 + n9_13_31 + n9_25_11 + n9_13_32 + n9_25_12 + n9_25_13 + n9_25_14 + n9_25_15 + n9_25_16 + n9_25_17 + n9_25_18 + n9_25_19 + n9_25_20 + n9_25_21 + n9_25_22 + n9_25_23 + n9_25_24 + n9_25_25 + n9_25_26 + n9_25_27 + n9_25_28 + n9_25_29 + n9_25_30 + n9_25_31 + n9_25_32 + n9_1_11 + n9_1_12 + n9_1_13 + n9_1_14 + n9_1_15 + n9_1_16 + n9_1_17 + n9_1_18 + n9_1_19 + n9_1_20 + n9_1_21 + n9_1_22 + n9_1_23 + n9_1_24 + n9_1_25 + n9_1_26 + n9_1_27 + n9_1_28 + n9_1_29 + n9_1_30 + n9_1_31 + n9_1_32 + n9_20_0 + n9_20_1 + n9_20_2 + n9_20_3 + n9_20_4 + n9_20_5 + n9_20_6 + n9_20_7 + n9_20_8 + n9_20_9 + n9_18_10 + n9_18_11 + n9_18_12 + n9_18_13 + n9_18_14 + n9_18_15 + n9_18_16 + n9_18_17 + n9_18_18 + n9_18_19 + n9_18_20 + n9_18_21 + n9_18_22 + n9_18_23 + n9_18_24 + n9_18_25 + n9_18_26 + n9_18_27 + n9_18_28 + n9_18_29 + n9_18_30 + n9_18_31 + n9_18_32 + n9_21_0 + n9_21_1 + n9_21_2 + n9_21_3 + n9_21_4 + n9_21_5 + n9_21_6 + n9_21_7 + n9_21_8 + n9_21_9 + n9_6_11 + n9_6_12 + n9_6_13 + n9_6_14 + n9_6_15 + n9_6_16 + n9_6_17 + n9_6_18 + n9_6_19 + n9_6_20 + n9_6_21 + n9_6_22 + n9_6_23 + n9_6_24 + n9_6_25 + n9_6_26 + n9_6_27 + n9_6_28 + n9_6_29 + n9_6_30 + n9_6_31 + n9_6_32 + n9_31_10 + n9_31_11 + n9_31_12 + n9_31_13 + n9_31_14 + n9_31_15 + n9_31_16 + n9_31_17 + n9_31_18 + n9_31_19 + n9_31_20 + n9_31_21 + n9_31_22 + n9_31_23 + n9_31_24 + n9_31_25 + n9_31_26 + n9_31_27 + n9_31_28 + n9_31_29 + n9_31_30 + n9_31_31 + n9_31_32 + n9_22_0 + n9_22_1 + n9_22_2 + n9_22_3 + n9_22_4 + n9_22_5 + n9_22_6 + n9_22_7 + n9_22_8 + n9_22_9 + n9_12_10 + n9_12_11 + n9_12_12 + n9_12_13 + n9_12_14 + n9_12_15 + n9_12_16 + n9_12_17 + n9_12_18 + n9_12_19 + n9_12_20 + n9_12_21 + n9_12_22 + n9_12_23 + n9_12_24 + n9_12_25 + n9_12_26 + n9_12_27 + n9_12_28 + n9_12_29 + n9_12_30 + n9_24_10 + n9_12_31 + n9_24_11 + n9_12_32 + n9_24_12 + n9_24_13 + n9_24_14 + n9_24_15 + n9_24_16 + n9_24_17 + n9_24_18 + n9_24_19 + n9_24_20 + n9_24_21 + n9_24_22 + n9_24_23 + n9_24_24 + n9_24_25 + n9_24_26 + n9_24_27 + n9_24_28 + n9_24_29 + n9_24_30 + n9_24_31 + n9_24_32 + n9_0_10 + n9_0_11 + n9_0_12 + n9_0_13 + n9_0_14 + n9_0_15 + n9_0_16 + n9_0_17 + n9_0_18 + n9_0_19 + n9_0_20 + n9_0_21 + n9_0_22 + n9_0_23 + n9_0_24 + n9_0_25 + n9_0_26 + n9_0_27 + n9_0_28 + n9_0_29 + n9_0_30 + n9_0_31 + n9_0_32 + n9_23_0 + n9_23_1 + n9_23_2 + n9_23_3 + n9_23_4 + n9_23_5 + n9_23_6 + n9_23_7 + n9_23_8 + n9_23_9 + n9_10_0 + n9_10_1 + n9_10_2 + n9_10_3 + n9_10_4 + n9_10_5 + n9_10_6 + n9_10_7 + n9_10_8 + n9_10_9 + n9_17_10 + n9_17_11 + n9_17_12 + n9_17_13 + n9_17_14 + n9_17_15 + n9_17_16 + n9_17_17 + n9_17_18 + n9_17_19 + n9_17_20 + n9_17_21 + n9_17_22 + n9_17_23 + n9_17_24 + n9_17_25 + n9_17_26 + n9_17_27 + n9_17_28 + n9_17_29 + n9_24_0 + n9_24_1 + n9_24_2 + n9_24_3 + n9_24_4 + n9_24_5 + n9_0_0 + n9_24_6 + n9_0_1 + n9_24_7 + n9_0_2 + n9_24_8 + n9_0_3 + n9_24_9 + n9_0_4 + n9_0_5 + n9_0_6 + n9_0_7 + n9_0_8 + n9_0_9 + n9_17_30 + n9_29_10 + n9_17_31 + n9_29_11 + n9_17_32 + n9_29_12 + n9_29_13 + n9_29_14 + n9_29_15 + n9_29_16 + n9_29_17 + n9_29_18 + n9_29_19 + n9_29_20 + n9_29_21 + n9_29_22 + n9_29_23 + n9_29_24 + n9_29_25 + n9_29_26 + n9_29_27 + n9_29_28 + n9_29_29 + n9_29_30 + n9_29_31 + n9_29_32 + n9_11_0 + n9_11_1 + n9_11_2 + n9_11_3 + n9_11_4 + n9_11_5 + n9_11_6 + n9_11_7 + n9_11_8 + n9_11_9 + n9_5_10 + n9_5_11 + n9_5_12 + n9_5_13 + n9_5_14 + n9_5_15 + n9_5_16 + n9_5_17 + n9_5_18 + n9_5_19 + n9_5_20 + n9_5_21 + n9_5_22 + n9_5_23 + n9_5_24 + n9_5_25 + n9_5_26 + n9_5_27 + n9_5_28 + n9_5_29 + n9_5_30 + n9_5_31 + n9_5_32 + n9_30_10 + n9_30_11 + n9_30_12 + n9_30_13 + n9_30_14 + n9_30_15 + n9_30_16 + n9_30_17 + n9_30_18 + n9_30_19 + n9_30_20 + n9_30_21 + n9_30_22 + n9_30_23 + n9_30_24 + n9_30_25 + n9_30_26 + n9_30_27 + n9_30_28 + n9_30_29 + n9_30_30 + n9_30_31 + n9_30_32 + n9_25_0 + n9_25_1 + n9_25_2 + n9_25_3 + n9_25_4 + n9_25_5 + n9_1_0 + n9_25_6 + n9_1_1 + n9_25_7 + n9_1_2 + n9_25_8 + n9_1_3 + n9_25_9 + n9_1_4 + n9_1_5 + n9_1_6 + n9_1_7 + n9_1_8 + n9_1_9 + n9_12_0 + n9_12_1 + n9_12_2 + n9_12_3 + n9_12_4 + n9_12_5 + n9_12_6 + n9_12_7 + n9_12_8 + n9_12_9 + n9_32_32 + n9_32_31 + n9_32_30 + n9_32_29 + n9_32_28 + n9_32_27 + n9_32_26 + n9_32_25 + n9_32_24 + n9_32_23 + n9_32_22 + n9_32_21 + n9_32_20 + n9_32_19 + n9_32_18 + n9_32_17 + n9_32_16 + n9_32_15 + n9_32_14 + n9_32_13 + n9_11_10 + n9_11_11 + n9_11_12 + n9_11_13 + n9_11_14 + n9_11_15 + n9_11_16 + n9_11_17 + n9_11_18 + n9_11_19 + n9_11_20 + n9_11_21 + n9_11_22 + n9_11_23 + n9_11_24 + n9_11_25 + n9_11_26 + n9_11_27 + n9_11_28 + n9_11_29 + n9_11_30 + n9_23_10 + n9_11_31 + n9_23_11 + n9_11_32 + n9_23_12 + n9_23_13 + n9_23_14 + n9_23_15 + n9_23_16 + n9_23_17 + n9_23_18 + n9_23_19 + n9_23_20 + n9_23_21 + n9_23_22 + n9_23_23 + n9_23_24 + n9_23_25 + n9_23_26 + n9_23_27 + n9_23_28 + n9_23_29 + n9_32_12 + n9_20_32 + n9_32_11 + n9_20_31 + n9_20_30 + n9_20_29 + n9_20_28 + n9_20_27 + n9_20_26 + n9_20_25 + n9_23_30 + n9_23_31 + n9_23_32 + n9_20_24 + n9_20_23 + n9_20_22 + n9_20_21 + n9_20_20 + n9_20_19 + n9_20_18 + n9_20_17 + n9_20_16 + n9_20_15 + n9_20_14 + n9_20_13 + n9_20_12 + n9_20_11 + n9_26_0 + n9_26_1 + n9_26_2 + n9_26_3 + n9_26_4 + n9_26_5 + n9_2_0 + n9_26_6 + n9_2_1 + n9_26_7 + n9_2_2 + n9_26_8 + n9_2_3 + n9_26_9 + n9_2_4 + n9_2_5 + n9_2_6 + n9_2_7 + n9_2_8 + n9_2_9 + n9_13_0 + n9_13_1 + n9_13_2 + n9_13_3 + n9_13_4 + n9_13_5 + n9_13_6 + n9_13_7 + n9_13_8 + n9_13_9 + n9_7_32 + n9_7_31 + n9_7_30 + n9_7_29 + n9_7_28 + n9_7_27 + n9_27_0 + n9_27_1 + n9_27_2 + n9_27_3 + n9_27_4 + n9_27_5 + n9_3_0 + n9_27_6 + n9_3_1 + n9_27_7 + n9_3_2 + n9_27_8 + n9_3_3 + n9_27_9 + n9_3_4 + n9_3_5 + n9_3_6 + n9_3_7 + n9_3_8 + n9_3_9 + n9_7_26 + n9_16_10 + n9_16_11 + n9_16_12 + n9_16_13 + n9_16_14 + n9_16_15 + n9_16_16 + n9_16_17 + n9_16_18 + n9_16_19 + n9_16_20 + n9_16_21 + n9_16_22 + n9_16_23 + n9_16_24 + n9_16_25 + n9_16_26 + n9_16_27 + n9_16_28 + n9_16_29 + n9_14_0 + n9_14_1 + n9_14_2 + n9_14_3 + n9_14_4 + n9_14_5 + n9_14_6 + n9_14_7 + n9_14_8 + n9_14_9 + n9_16_30 + n9_28_10 + n9_16_31 + n9_28_11 + n9_16_32 + n9_28_12 + n9_28_13 + n9_28_14 + n9_28_15 + n9_28_16 + n9_28_17 + n9_28_18 + n9_28_19 + n9_28_20 + n9_28_21 + n9_28_22 + n9_28_23 + n9_28_24 + n9_28_25 + n9_28_26 + n9_28_27 + n9_28_28 + n9_28_29 + n9_28_30 + n9_28_31 + n9_28_32 + n9_4_10 + n9_4_11 + n9_4_12 + n9_4_13 + n9_4_14 + n9_4_15 + n9_4_16 + n9_4_17 + n9_4_18 + n9_4_19 + n9_4_20 + n9_4_21 + n9_4_22 + n9_4_23 + n9_4_24 + n9_4_25 + n9_4_26 + n9_4_27 + n9_4_28 + n9_4_29 + n9_4_30 + n9_4_31 + n9_4_32 + n9_28_0 + n9_28_1 + n9_28_2 + n9_28_3 + n9_28_4 + n9_28_5 + n9_4_0 + n9_28_6 + n9_4_1 + n9_28_7 + n9_4_2 + n9_28_8 + n9_4_3 + n9_28_9 + n9_4_4 + n9_4_5 + n9_4_6 + n9_4_7 + n9_4_8 + n9_4_9 + n9_7_25 + n9_15_0 + n9_15_1 + n9_15_2 + n9_15_3 + n9_15_4 + n9_15_5 + n9_15_6 + n9_15_7 + n9_15_8 + n9_15_9 + n9_7_24 + n9_7_23 + n9_7_22 + n9_7_21 + n9_7_20 + n9_7_19 + n9_7_18 + n9_7_17 + n9_7_16 + n9_7_15 + n9_7_14 + n9_7_13 + n9_7_12 + n9_7_11 + n9_9_10 + n9_9_11 + n9_9_12 + n9_9_13 + n9_9_14 + n9_9_15 + n9_9_16 + n9_9_17 + n9_9_18 + n9_9_19 + n9_9_20 + n9_9_21 + n9_9_22 + n9_9_23 + n9_9_24 + n9_9_25 + n9_9_26 + n9_9_27 + n9_9_28 + n9_9_29 + n9_9_30 + n9_9_31 + n9_9_32 + n9_10_10 + n9_10_11 + n9_10_12 + n9_10_13 + n9_10_14 + n9_10_15 + n9_10_16 + n9_10_17 + n9_10_18 + n9_10_19 + n9_10_20 + n9_10_21 + n9_10_22 + n9_10_23 + n9_10_24 + n9_10_25 + n9_10_26 + n9_10_27 + n9_10_28 + n9_10_29 + n9_10_30 + n9_22_10 + n9_10_31 + n9_22_11 + n9_10_32 + n9_22_12 + n9_22_13 + n9_22_14 + n9_22_15 + n9_22_16 + n9_22_17 + n9_22_18 + n9_22_19 + n9_22_20 + n9_22_21 + n9_22_22 + n9_22_23 + n9_22_24 + n9_22_25 + n9_22_26 + n9_22_27 + n9_22_28 + n9_22_29 + n9_22_30 + n9_22_31 + n9_22_32 + n9_29_0 + n9_29_1 + n9_29_2 + n9_29_3 + n9_29_4 + n9_29_5 + n9_5_0 + n9_29_6 + n9_5_1 + n9_29_7 + n9_5_2 + n9_29_8 + n9_5_3 + n9_29_9 + n9_5_4 + n9_5_5 + n9_5_6 + n9_5_7 + n9_5_8 + n9_5_9 + n9_16_0 + n9_16_1 + n9_16_2 + n9_16_3 + n9_16_4 + n9_16_5 + n9_16_6 + n9_16_7 + n9_16_8 + n9_16_9 + n9_6_0 + n9_6_1 + n9_6_2 + n9_6_3 + n9_6_4 + n9_6_5 + n9_6_6 + n9_6_7 + n9_6_8 + n9_6_9 + n9_17_0 + n9_17_1 + n9_17_2 + n9_17_3 + n9_17_4 + n9_17_5 + n9_17_6 + n9_17_7 + n9_17_8 + n9_17_9 + n9_15_10 + n9_15_11 + n9_15_12 + n9_15_13 + n9_15_14 + n9_15_15 + n9_15_16 + n9_15_17 + n9_15_18 + n9_15_19 + n9_15_20 + n9_15_21 + n9_15_22 + n9_15_23 + n9_15_24 + n9_15_25 + n9_15_26 + n9_15_27 + n9_15_28 + n9_15_29 + n9_15_30 + n9_27_10 + n9_15_31 + n9_27_11 + n9_15_32 + n9_27_12 + n9_27_13 + n9_27_14 + n9_27_15 + n9_27_16 + n9_27_17 + n9_27_18 + n9_27_19 + n9_27_20 + n9_27_21 + n9_27_22 + n9_27_23 + n9_27_24 + n9_27_25 + n9_27_26 + n9_27_27 + n9_27_28 + n9_27_29 + n9_27_30 + n9_27_31 + n9_27_32 + n9_3_10 + n9_3_11 + n9_3_12 + n9_3_13 + n9_3_14 + n9_3_15 + n9_3_16 + n9_3_17 + n9_3_18 + n9_3_19 + n9_3_20 + n9_3_21 + n9_3_22 + n9_3_23 + n9_3_24 + n9_3_25 + n9_3_26 + n9_3_27 + n9_3_28 + n9_3_29 + n9_3_30 + n9_3_31 + n9_3_32 + n9_7_0 + n9_7_1 + n9_7_2 + n9_7_3 + n9_7_4 + n9_7_5 + n9_7_6 + n9_7_7 + n9_7_8 + n9_7_9 + n9_18_0 + n9_18_1 + n9_18_2 + n9_18_3 + n9_18_4 + n9_18_5 + n9_18_6 + n9_18_7 + n9_18_8 + n9_18_9 + n9_8_10 + n9_8_11 + n9_8_12 + n9_8_13 + n9_8_14 + n9_8_15 + n9_8_16 + n9_8_17 + n9_8_18 + n9_8_19 + n9_8_20 + n9_8_21 + n9_8_22 + n9_8_23 + n9_8_24 + n9_8_25 + n9_8_26 + n9_8_27 + n9_8_28 + n9_8_29 + n9_8_30 + n9_8_31 + n9_8_32 + n9_21_10 + n9_21_11 + n9_21_12 + n9_21_13 + n9_21_14 + n9_21_15 + n9_21_16 + n9_21_17 + n9_21_18 + n9_21_19 + n9_21_20 + n9_21_21 + n9_21_22 + n9_21_23 + n9_21_24 + n9_21_25 + n9_21_26 + n9_21_27 + n9_21_28 + n9_21_29 + n9_21_30 + n9_21_31 + n9_21_32 + n9_8_0 + n9_8_1 + n9_8_2 + n9_8_3 + n9_8_4 + n9_8_5 + n9_8_6 + n9_8_7 + n9_8_8 + n9_8_9 + n9_19_0 + n9_19_1 + n9_19_2 + n9_19_3 + n9_19_4 + n9_19_5 + n9_19_6 + n9_19_7 + n9_19_8 + n9_19_9 + n9_9_0 + n9_9_1 + n9_9_2 + n9_9_3 + n9_9_4 + n9_9_5 + n9_9_6 + n9_9_7 + n9_9_8 + n9_9_9 + n9_14_10 + n9_14_11 + n9_14_12 + n9_14_13 + n9_14_14 + n9_14_15 + n9_14_16 + n9_14_17 + n9_14_18 + n9_14_19 + n9_14_20 + n9_14_21 + n9_14_22 + n9_14_23 + n9_14_24 + n9_14_25 + n9_14_26 + n9_14_27 + n9_14_28 + n9_14_29 + n9_14_30 + n9_26_10 + n9_14_31 + n9_26_11 + n9_14_32 + n9_26_12 + n9_26_13 + n9_26_14 + n9_26_15 + n9_26_16 + n9_26_17 + n9_26_18 + n9_26_19 + n9_26_20 + n9_26_21 + n9_26_22 + n9_26_23 + n9_26_24 + n9_26_25 + n9_26_26 + n9_26_27 + n9_26_28 + n9_26_29 + n9_26_30 + n9_26_31 + n9_26_32 + n9_2_10 + n9_2_11 + n9_2_12 + n9_2_13 + n9_2_14 + n9_2_15 + n9_2_16 + n9_2_17 + n9_2_18 + n9_2_19 + n9_2_20 + n9_2_21 + n9_2_22 + n9_2_23 + n9_2_24 + n9_2_25 + n9_2_26 + n9_2_27 + n9_2_28 + n9_2_29 + n9_2_30 + n9_2_31 + n9_2_32 + n9_30_0 + n9_30_1 + n9_30_2 + n9_30_3 + n9_30_4 + n9_30_5 + n9_30_6 + n9_30_7 + n9_30_8 + n9_30_9) AND ((s5_32 + s5_31 + s5_30 + s5_29 + s5_28 + s5_27 + s5_26 + s5_25 + s5_24 + s5_23 + s5_22 + s5_21 + s5_20 + s5_19 + s5_18 + s5_17 + s5_16 + s5_15 + s5_14 + s5_13 + s5_12 + s5_11 + s5_10 + s5_0 + s5_1 + s5_2 + s5_3 + s5_4 + s5_5 + s5_6 + s5_7 + s5_8 + s5_9 <= 1) OR (CstopOK_0 + CstopOK_1 + CstopOK_2 + CstopOK_3 + CstopOK_4 + CstopOK_5 + CstopOK_6 + CstopOK_7 + CstopOK_8 + CstopOK_9 + CstopOK_10 + CstopOK_11 + CstopOK_12 + CstopOK_13 + CstopOK_14 + CstopOK_15 + CstopOK_16 + CstopOK_17 + CstopOK_18 + CstopOK_19 + CstopOK_20 + CstopOK_21 + CstopOK_22 + CstopOK_23 + CstopOK_24 + CstopOK_25 + CstopOK_26 + CstopOK_27 + CstopOK_28 + CstopOK_29 + CstopOK_30 + CstopOK_31 + CstopOK_32 + 1 <= s6_32 + s6_31 + s6_30 + s6_29 + s6_28 + s6_27 + s6_26 + s6_25 + s6_24 + s6_23 + s6_22 + s6_21 + s6_20 + s6_19 + s6_18 + s6_17 + s6_16 + s6_15 + s6_14 + s6_13 + s6_12 + s6_11 + s6_10 + s6_9 + s6_8 + s6_7 + s6_6 + s6_5 + s6_4 + s6_3 + s6_2 + s6_1 + s6_0))))) : A (G (())) : A (G ((Astart <= 1))) : E (F ((Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9 <= malicious_reservoir))) : A (G ((n5_10 + n5_11 + n5_12 + n5_13 + n5_14 + n5_15 + n5_16 + n5_17 + n5_18 + n5_19 + n5_20 + n5_21 + n5_22 + n5_23 + n5_24 + n5_25 + n5_26 + n5_27 + n5_28 + n5_29 + n5_30 + n5_31 + n5_32 + n5_0 + n5_1 + n5_2 + n5_3 + n5_4 + n5_5 + n5_6 + n5_7 + n5_8 + n5_9 <= a5))) : A (G (((1 <= Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9) OR (((2 <= SstopAbort) OR (3 <= n4_10 + n4_11 + n4_12 + n4_13 + n4_14 + n4_15 + n4_16 + n4_17 + n4_18 + n4_19 + n4_20 + n4_21 + n4_22 + n4_23 + n4_24 + n4_25 + n4_26 + n4_27 + n4_28 + n4_29 + n4_30 + n4_31 + n4_32 + n4_0 + n4_1 + n4_2 + n4_3 + n4_4 + n4_5 + n4_6 + n4_7 + n4_8 + n4_9)) AND ((2 <= Astart) OR (3 <= s2_9 + s2_8 + s2_7 + s2_6 + s2_5 + s2_4 + s2_3 + s2_2 + s2_1 + s2_0 + s2_32 + s2_31 + s2_30 + s2_29 + s2_28 + s2_27 + s2_26 + s2_25 + s2_24 + s2_23 + s2_22 + s2_21 + s2_20 + s2_19 + s2_18 + s2_17 + s2_16 + s2_15 + s2_14 + s2_13 + s2_12 + s2_11 + s2_10)))))) : A (G ((((n6_32 + n6_31 + n6_30 + n6_29 + n6_28 + n6_27 + n6_26 + n6_25 + n6_24 + n6_23 + n6_22 + n6_21 + n6_20 + n6_19 + n6_18 + n6_17 + n6_16 + n6_15 + n6_14 + n6_13 + n6_12 + n6_11 + n6_10 + n6_0 + n6_1 + n6_2 + n6_3 + n6_4 + n6_5 + n6_6 + n6_7 + n6_8 + n6_9 <= 0) OR (n9_19_10 + n9_19_11 + n9_19_12 + n9_19_13 + n9_19_14 + n9_19_15 + n9_19_16 + n9_19_17 + n9_19_18 + n9_19_19 + n9_19_20 + n9_19_21 + n9_19_22 + n9_19_23 + n9_19_24 + n9_19_25 + n9_19_26 + n9_19_27 + n9_19_28 + n9_19_29 + n9_19_30 + n9_19_31 + n9_19_32 + n9_31_0 + n9_31_1 + n9_31_2 + n9_31_3 + n9_31_4 + n9_31_5 + n9_31_6 + n9_31_7 + n9_31_8 + n9_31_9 + n9_7_10 + n9_20_10 + n9_32_10 + n9_6_10 + n9_1_10 + n9_32_0 + n9_32_9 + n9_32_8 + n9_32_7 + n9_32_6 + n9_32_5 + n9_32_4 + n9_32_3 + n9_32_2 + n9_32_1 + n9_13_10 + n9_13_11 + n9_13_12 + n9_13_13 + n9_13_14 + n9_13_15 + n9_13_16 + n9_13_17 + n9_13_18 + n9_13_19 + n9_13_20 + n9_13_21 + n9_13_22 + n9_13_23 + n9_13_24 + n9_13_25 + n9_13_26 + n9_13_27 + n9_13_28 + n9_13_29 + n9_13_30 + n9_25_10 + n9_13_31 + n9_25_11 + n9_13_32 + n9_25_12 + n9_25_13 + n9_25_14 + n9_25_15 + n9_25_16 + n9_25_17 + n9_25_18 + n9_25_19 + n9_25_20 + n9_25_21 + n9_25_22 + n9_25_23 + n9_25_24 + n9_25_25 + n9_25_26 + n9_25_27 + n9_25_28 + n9_25_29 + n9_25_30 + n9_25_31 + n9_25_32 + n9_1_11 + n9_1_12 + n9_1_13 + n9_1_14 + n9_1_15 + n9_1_16 + n9_1_17 + n9_1_18 + n9_1_19 + n9_1_20 + n9_1_21 + n9_1_22 + n9_1_23 + n9_1_24 + n9_1_25 + n9_1_26 + n9_1_27 + n9_1_28 + n9_1_29 + n9_1_30 + n9_1_31 + n9_1_32 + n9_20_0 + n9_20_1 + n9_20_2 + n9_20_3 + n9_20_4 + n9_20_5 + n9_20_6 + n9_20_7 + n9_20_8 + n9_20_9 + n9_18_10 + n9_18_11 + n9_18_12 + n9_18_13 + n9_18_14 + n9_18_15 + n9_18_16 + n9_18_17 + n9_18_18 + n9_18_19 + n9_18_20 + n9_18_21 + n9_18_22 + n9_18_23 + n9_18_24 + n9_18_25 + n9_18_26 + n9_18_27 + n9_18_28 + n9_18_29 + n9_18_30 + n9_18_31 + n9_18_32 + n9_21_0 + n9_21_1 + n9_21_2 + n9_21_3 + n9_21_4 + n9_21_5 + n9_21_6 + n9_21_7 + n9_21_8 + n9_21_9 + n9_6_11 + n9_6_12 + n9_6_13 + n9_6_14 + n9_6_15 + n9_6_16 + n9_6_17 + n9_6_18 + n9_6_19 + n9_6_20 + n9_6_21 + n9_6_22 + n9_6_23 + n9_6_24 + n9_6_25 + n9_6_26 + n9_6_27 + n9_6_28 + n9_6_29 + n9_6_30 + n9_6_31 + n9_6_32 + n9_31_10 + n9_31_11 + n9_31_12 + n9_31_13 + n9_31_14 + n9_31_15 + n9_31_16 + n9_31_17 + n9_31_18 + n9_31_19 + n9_31_20 + n9_31_21 + n9_31_22 + n9_31_23 + n9_31_24 + n9_31_25 + n9_31_26 + n9_31_27 + n9_31_28 + n9_31_29 + n9_31_30 + n9_31_31 + n9_31_32 + n9_22_0 + n9_22_1 + n9_22_2 + n9_22_3 + n9_22_4 + n9_22_5 + n9_22_6 + n9_22_7 + n9_22_8 + n9_22_9 + n9_12_10 + n9_12_11 + n9_12_12 + n9_12_13 + n9_12_14 + n9_12_15 + n9_12_16 + n9_12_17 + n9_12_18 + n9_12_19 + n9_12_20 + n9_12_21 + n9_12_22 + n9_12_23 + n9_12_24 + n9_12_25 + n9_12_26 + n9_12_27 + n9_12_28 + n9_12_29 + n9_12_30 + n9_24_10 + n9_12_31 + n9_24_11 + n9_12_32 + n9_24_12 + n9_24_13 + n9_24_14 + n9_24_15 + n9_24_16 + n9_24_17 + n9_24_18 + n9_24_19 + n9_24_20 + n9_24_21 + n9_24_22 + n9_24_23 + n9_24_24 + n9_24_25 + n9_24_26 + n9_24_27 + n9_24_28 + n9_24_29 + n9_24_30 + n9_24_31 + n9_24_32 + n9_0_10 + n9_0_11 + n9_0_12 + n9_0_13 + n9_0_14 + n9_0_15 + n9_0_16 + n9_0_17 + n9_0_18 + n9_0_19 + n9_0_20 + n9_0_21 + n9_0_22 + n9_0_23 + n9_0_24 + n9_0_25 + n9_0_26 + n9_0_27 + n9_0_28 + n9_0_29 + n9_0_30 + n9_0_31 + n9_0_32 + n9_23_0 + n9_23_1 + n9_23_2 + n9_23_3 + n9_23_4 + n9_23_5 + n9_23_6 + n9_23_7 + n9_23_8 + n9_23_9 + n9_10_0 + n9_10_1 + n9_10_2 + n9_10_3 + n9_10_4 + n9_10_5 + n9_10_6 + n9_10_7 + n9_10_8 + n9_10_9 + n9_17_10 + n9_17_11 + n9_17_12 + n9_17_13 + n9_17_14 + n9_17_15 + n9_17_16 + n9_17_17 + n9_17_18 + n9_17_19 + n9_17_20 + n9_17_21 + n9_17_22 + n9_17_23 + n9_17_24 + n9_17_25 + n9_17_26 + n9_17_27 + n9_17_28 + n9_17_29 + n9_24_0 + n9_24_1 + n9_24_2 + n9_24_3 + n9_24_4 + n9_24_5 + n9_0_0 + n9_24_6 + n9_0_1 + n9_24_7 + n9_0_2 + n9_24_8 + n9_0_3 + n9_24_9 + n9_0_4 + n9_0_5 + n9_0_6 + n9_0_7 + n9_0_8 + n9_0_9 + n9_17_30 + n9_29_10 + n9_17_31 + n9_29_11 + n9_17_32 + n9_29_12 + n9_29_13 + n9_29_14 + n9_29_15 + n9_29_16 + n9_29_17 + n9_29_18 + n9_29_19 + n9_29_20 + n9_29_21 + n9_29_22 + n9_29_23 + n9_29_24 + n9_29_25 + n9_29_26 + n9_29_27 + n9_29_28 + n9_29_29 + n9_29_30 + n9_29_31 + n9_29_32 + n9_11_0 + n9_11_1 + n9_11_2 + n9_11_3 + n9_11_4 + n9_11_5 + n9_11_6 + n9_11_7 + n9_11_8 + n9_11_9 + n9_5_10 + n9_5_11 + n9_5_12 + n9_5_13 + n9_5_14 + n9_5_15 + n9_5_16 + n9_5_17 + n9_5_18 + n9_5_19 + n9_5_20 + n9_5_21 + n9_5_22 + n9_5_23 + n9_5_24 + n9_5_25 + n9_5_26 + n9_5_27 + n9_5_28 + n9_5_29 + n9_5_30 + n9_5_31 + n9_5_32 + n9_30_10 + n9_30_11 + n9_30_12 + n9_30_13 + n9_30_14 + n9_30_15 + n9_30_16 + n9_30_17 + n9_30_18 + n9_30_19 + n9_30_20 + n9_30_21 + n9_30_22 + n9_30_23 + n9_30_24 + n9_30_25 + n9_30_26 + n9_30_27 + n9_30_28 + n9_30_29 + n9_30_30 + n9_30_31 + n9_30_32 + n9_25_0 + n9_25_1 + n9_25_2 + n9_25_3 + n9_25_4 + n9_25_5 + n9_1_0 + n9_25_6 + n9_1_1 + n9_25_7 + n9_1_2 + n9_25_8 + n9_1_3 + n9_25_9 + n9_1_4 + n9_1_5 + n9_1_6 + n9_1_7 + n9_1_8 + n9_1_9 + n9_12_0 + n9_12_1 + n9_12_2 + n9_12_3 + n9_12_4 + n9_12_5 + n9_12_6 + n9_12_7 + n9_12_8 + n9_12_9 + n9_32_32 + n9_32_31 + n9_32_30 + n9_32_29 + n9_32_28 + n9_32_27 + n9_32_26 + n9_32_25 + n9_32_24 + n9_32_23 + n9_32_22 + n9_32_21 + n9_32_20 + n9_32_19 + n9_32_18 + n9_32_17 + n9_32_16 + n9_32_15 + n9_32_14 + n9_32_13 + n9_11_10 + n9_11_11 + n9_11_12 + n9_11_13 + n9_11_14 + n9_11_15 + n9_11_16 + n9_11_17 + n9_11_18 + n9_11_19 + n9_11_20 + n9_11_21 + n9_11_22 + n9_11_23 + n9_11_24 + n9_11_25 + n9_11_26 + n9_11_27 + n9_11_28 + n9_11_29 + n9_11_30 + n9_23_10 + n9_11_31 + n9_23_11 + n9_11_32 + n9_23_12 + n9_23_13 + n9_23_14 + n9_23_15 + n9_23_16 + n9_23_17 + n9_23_18 + n9_23_19 + n9_23_20 + n9_23_21 + n9_23_22 + n9_23_23 + n9_23_24 + n9_23_25 + n9_23_26 + n9_23_27 + n9_23_28 + n9_23_29 + n9_32_12 + n9_20_32 + n9_32_11 + n9_20_31 + n9_20_30 + n9_20_29 + n9_20_28 + n9_20_27 + n9_20_26 + n9_20_25 + n9_23_30 + n9_23_31 + n9_23_32 + n9_20_24 + n9_20_23 + n9_20_22 + n9_20_21 + n9_20_20 + n9_20_19 + n9_20_18 + n9_20_17 + n9_20_16 + n9_20_15 + n9_20_14 + n9_20_13 + n9_20_12 + n9_20_11 + n9_26_0 + n9_26_1 + n9_26_2 + n9_26_3 + n9_26_4 + n9_26_5 + n9_2_0 + n9_26_6 + n9_2_1 + n9_26_7 + n9_2_2 + n9_26_8 + n9_2_3 + n9_26_9 + n9_2_4 + n9_2_5 + n9_2_6 + n9_2_7 + n9_2_8 + n9_2_9 + n9_13_0 + n9_13_1 + n9_13_2 + n9_13_3 + n9_13_4 + n9_13_5 + n9_13_6 + n9_13_7 + n9_13_8 + n9_13_9 + n9_7_32 + n9_7_31 + n9_7_30 + n9_7_29 + n9_7_28 + n9_7_27 + n9_27_0 + n9_27_1 + n9_27_2 + n9_27_3 + n9_27_4 + n9_27_5 + n9_3_0 + n9_27_6 + n9_3_1 + n9_27_7 + n9_3_2 + n9_27_8 + n9_3_3 + n9_27_9 + n9_3_4 + n9_3_5 + n9_3_6 + n9_3_7 + n9_3_8 + n9_3_9 + n9_7_26 + n9_16_10 + n9_16_11 + n9_16_12 + n9_16_13 + n9_16_14 + n9_16_15 + n9_16_16 + n9_16_17 + n9_16_18 + n9_16_19 + n9_16_20 + n9_16_21 + n9_16_22 + n9_16_23 + n9_16_24 + n9_16_25 + n9_16_26 + n9_16_27 + n9_16_28 + n9_16_29 + n9_14_0 + n9_14_1 + n9_14_2 + n9_14_3 + n9_14_4 + n9_14_5 + n9_14_6 + n9_14_7 + n9_14_8 + n9_14_9 + n9_16_30 + n9_28_10 + n9_16_31 + n9_28_11 + n9_16_32 + n9_28_12 + n9_28_13 + n9_28_14 + n9_28_15 + n9_28_16 + n9_28_17 + n9_28_18 + n9_28_19 + n9_28_20 + n9_28_21 + n9_28_22 + n9_28_23 + n9_28_24 + n9_28_25 + n9_28_26 + n9_28_27 + n9_28_28 + n9_28_29 + n9_28_30 + n9_28_31 + n9_28_32 + n9_4_10 + n9_4_11 + n9_4_12 + n9_4_13 + n9_4_14 + n9_4_15 + n9_4_16 + n9_4_17 + n9_4_18 + n9_4_19 + n9_4_20 + n9_4_21 + n9_4_22 + n9_4_23 + n9_4_24 + n9_4_25 + n9_4_26 + n9_4_27 + n9_4_28 + n9_4_29 + n9_4_30 + n9_4_31 + n9_4_32 + n9_28_0 + n9_28_1 + n9_28_2 + n9_28_3 + n9_28_4 + n9_28_5 + n9_4_0 + n9_28_6 + n9_4_1 + n9_28_7 + n9_4_2 + n9_28_8 + n9_4_3 + n9_28_9 + n9_4_4 + n9_4_5 + n9_4_6 + n9_4_7 + n9_4_8 + n9_4_9 + n9_7_25 + n9_15_0 + n9_15_1 + n9_15_2 + n9_15_3 + n9_15_4 + n9_15_5 + n9_15_6 + n9_15_7 + n9_15_8 + n9_15_9 + n9_7_24 + n9_7_23 + n9_7_22 + n9_7_21 + n9_7_20 + n9_7_19 + n9_7_18 + n9_7_17 + n9_7_16 + n9_7_15 + n9_7_14 + n9_7_13 + n9_7_12 + n9_7_11 + n9_9_10 + n9_9_11 + n9_9_12 + n9_9_13 + n9_9_14 + n9_9_15 + n9_9_16 + n9_9_17 + n9_9_18 + n9_9_19 + n9_9_20 + n9_9_21 + n9_9_22 + n9_9_23 + n9_9_24 + n9_9_25 + n9_9_26 + n9_9_27 + n9_9_28 + n9_9_29 + n9_9_30 + n9_9_31 + n9_9_32 + n9_10_10 + n9_10_11 + n9_10_12 + n9_10_13 + n9_10_14 + n9_10_15 + n9_10_16 + n9_10_17 + n9_10_18 + n9_10_19 + n9_10_20 + n9_10_21 + n9_10_22 + n9_10_23 + n9_10_24 + n9_10_25 + n9_10_26 + n9_10_27 + n9_10_28 + n9_10_29 + n9_10_30 + n9_22_10 + n9_10_31 + n9_22_11 + n9_10_32 + n9_22_12 + n9_22_13 + n9_22_14 + n9_22_15 + n9_22_16 + n9_22_17 + n9_22_18 + n9_22_19 + n9_22_20 + n9_22_21 + n9_22_22 + n9_22_23 + n9_22_24 + n9_22_25 + n9_22_26 + n9_22_27 + n9_22_28 + n9_22_29 + n9_22_30 + n9_22_31 + n9_22_32 + n9_29_0 + n9_29_1 + n9_29_2 + n9_29_3 + n9_29_4 + n9_29_5 + n9_5_0 + n9_29_6 + n9_5_1 + n9_29_7 + n9_5_2 + n9_29_8 + n9_5_3 + n9_29_9 + n9_5_4 + n9_5_5 + n9_5_6 + n9_5_7 + n9_5_8 + n9_5_9 + n9_16_0 + n9_16_1 + n9_16_2 + n9_16_3 + n9_16_4 + n9_16_5 + n9_16_6 + n9_16_7 + n9_16_8 + n9_16_9 + n9_6_0 + n9_6_1 + n9_6_2 + n9_6_3 + n9_6_4 + n9_6_5 + n9_6_6 + n9_6_7 + n9_6_8 + n9_6_9 + n9_17_0 + n9_17_1 + n9_17_2 + n9_17_3 + n9_17_4 + n9_17_5 + n9_17_6 + n9_17_7 + n9_17_8 + n9_17_9 + n9_15_10 + n9_15_11 + n9_15_12 + n9_15_13 + n9_15_14 + n9_15_15 + n9_15_16 + n9_15_17 + n9_15_18 + n9_15_19 + n9_15_20 + n9_15_21 + n9_15_22 + n9_15_23 + n9_15_24 + n9_15_25 + n9_15_26 + n9_15_27 + n9_15_28 + n9_15_29 + n9_15_30 + n9_27_10 + n9_15_31 + n9_27_11 + n9_15_32 + n9_27_12 + n9_27_13 + n9_27_14 + n9_27_15 + n9_27_16 + n9_27_17 + n9_27_18 + n9_27_19 + n9_27_20 + n9_27_21 + n9_27_22 + n9_27_23 + n9_27_24 + n9_27_25 + n9_27_26 + n9_27_27 + n9_27_28 + n9_27_29 + n9_27_30 + n9_27_31 + n9_27_32 + n9_3_10 + n9_3_11 + n9_3_12 + n9_3_13 + n9_3_14 + n9_3_15 + n9_3_16 + n9_3_17 + n9_3_18 + n9_3_19 + n9_3_20 + n9_3_21 + n9_3_22 + n9_3_23 + n9_3_24 + n9_3_25 + n9_3_26 + n9_3_27 + n9_3_28 + n9_3_29 + n9_3_30 + n9_3_31 + n9_3_32 + n9_7_0 + n9_7_1 + n9_7_2 + n9_7_3 + n9_7_4 + n9_7_5 + n9_7_6 + n9_7_7 + n9_7_8 + n9_7_9 + n9_18_0 + n9_18_1 + n9_18_2 + n9_18_3 + n9_18_4 + n9_18_5 + n9_18_6 + n9_18_7 + n9_18_8 + n9_18_9 + n9_8_10 + n9_8_11 + n9_8_12 + n9_8_13 + n9_8_14 + n9_8_15 + n9_8_16 + n9_8_17 + n9_8_18 + n9_8_19 + n9_8_20 + n9_8_21 + n9_8_22 + n9_8_23 + n9_8_24 + n9_8_25 + n9_8_26 + n9_8_27 + n9_8_28 + n9_8_29 + n9_8_30 + n9_8_31 + n9_8_32 + n9_21_10 + n9_21_11 + n9_21_12 + n9_21_13 + n9_21_14 + n9_21_15 + n9_21_16 + n9_21_17 + n9_21_18 + n9_21_19 + n9_21_20 + n9_21_21 + n9_21_22 + n9_21_23 + n9_21_24 + n9_21_25 + n9_21_26 + n9_21_27 + n9_21_28 + n9_21_29 + n9_21_30 + n9_21_31 + n9_21_32 + n9_8_0 + n9_8_1 + n9_8_2 + n9_8_3 + n9_8_4 + n9_8_5 + n9_8_6 + n9_8_7 + n9_8_8 + n9_8_9 + n9_19_0 + n9_19_1 + n9_19_2 + n9_19_3 + n9_19_4 + n9_19_5 + n9_19_6 + n9_19_7 + n9_19_8 + n9_19_9 + n9_9_0 + n9_9_1 + n9_9_2 + n9_9_3 + n9_9_4 + n9_9_5 + n9_9_6 + n9_9_7 + n9_9_8 + n9_9_9 + n9_14_10 + n9_14_11 + n9_14_12 + n9_14_13 + n9_14_14 + n9_14_15 + n9_14_16 + n9_14_17 + n9_14_18 + n9_14_19 + n9_14_20 + n9_14_21 + n9_14_22 + n9_14_23 + n9_14_24 + n9_14_25 + n9_14_26 + n9_14_27 + n9_14_28 + n9_14_29 + n9_14_30 + n9_26_10 + n9_14_31 + n9_26_11 + n9_14_32 + n9_26_12 + n9_26_13 + n9_26_14 + n9_26_15 + n9_26_16 + n9_26_17 + n9_26_18 + n9_26_19 + n9_26_20 + n9_26_21 + n9_26_22 + n9_26_23 + n9_26_24 + n9_26_25 + n9_26_26 + n9_26_27 + n9_26_28 + n9_26_29 + n9_26_30 + n9_26_31 + n9_26_32 + n9_2_10 + n9_2_11 + n9_2_12 + n9_2_13 + n9_2_14 + n9_2_15 + n9_2_16 + n9_2_17 + n9_2_18 + n9_2_19 + n9_2_20 + n9_2_21 + n9_2_22 + n9_2_23 + n9_2_24 + n9_2_25 + n9_2_26 + n9_2_27 + n9_2_28 + n9_2_29 + n9_2_30 + n9_2_31 + n9_2_32 + n9_30_0 + n9_30_1 + n9_30_2 + n9_30_3 + n9_30_4 + n9_30_5 + n9_30_6 + n9_30_7 + n9_30_8 + n9_30_9 + 1 <= s4_0 + s4_1 + s4_2 + s4_3 + s4_4 + s4_5 + s4_6 + s4_7 + s4_8 + s4_9 + s4_32 + s4_31 + s4_30 + s4_29 + s4_28 + s4_27 + s4_26 + s4_25 + s4_24 + s4_23 + s4_22 + s4_21 + s4_20 + s4_19 + s4_18 + s4_17 + s4_16 + s4_15 + s4_14 + s4_13 + s4_12 + s4_11 + s4_10)) AND (n7_17_0 + n7_17_1 + n7_17_2 + n7_17_3 + n7_17_4 + n7_17_5 + n7_17_6 + n7_17_7 + n7_17_8 + n7_17_9 + n7_21_10 + n7_21_11 + n7_21_12 + n7_21_13 + n7_21_14 + n7_21_15 + n7_21_16 + n7_21_17 + n7_21_18 + n7_21_19 + n7_21_20 + n7_21_21 + n7_21_22 + n7_21_23 + n7_21_24 + n7_21_25 + n7_21_26 + n7_21_27 + n7_21_28 + n7_21_29 + n7_3_10 + n7_21_30 + n7_21_31 + n7_21_32 + n7_15_0 + n7_6_0 + n7_4_10 + n7_27_0 + n7_28_10 + n7_16_10 + n7_5_10 + n7_11_10 + n7_10_0 + n7_23_0 + n7_0_10 + n7_29_10 + n7_22_0 + n7_18_0 + n7_24_10 + n7_12_10 + n7_7_0 + n7_1_10 + n7_14_10 + n7_25_10 + n7_31_0 + n7_13_10 + n7_26_10 + n7_30_0 + n7_9_0 + n7_32_10 + n7_2_10 + n7_20_10 + n7_8_10 + n7_19_0 + n7_8_32 + n7_8_31 + n7_8_30 + n7_8_29 + n7_8_28 + n7_8_27 + n7_8_26 + n7_8_25 + n7_8_24 + n7_8_23 + n7_19_1 + n7_19_2 + n7_19_3 + n7_19_4 + n7_19_5 + n7_19_6 + n7_19_7 + n7_19_8 + n7_19_9 + n7_8_22 + n7_8_21 + n7_8_20 + n7_8_19 + n7_26_32 + n7_8_18 + n7_26_31 + n7_8_17 + n7_26_30 + n7_8_16 + n7_8_15 + n7_8_14 + n7_8_13 + n7_8_0 + n7_8_1 + n7_8_2 + n7_8_3 + n7_8_4 + n7_8_5 + n7_8_6 + n7_8_7 + n7_8_8 + n7_8_9 + n7_8_12 + n7_8_11 + n7_26_29 + n7_19_10 + n7_19_11 + n7_19_12 + n7_19_13 + n7_19_14 + n7_19_15 + n7_19_16 + n7_19_17 + n7_19_18 + n7_19_19 + n7_19_20 + n7_19_21 + n7_19_22 + n7_19_23 + n7_19_24 + n7_19_25 + n7_19_26 + n7_19_27 + n7_19_28 + n7_19_29 + n7_19_30 + n7_19_31 + n7_19_32 + n7_26_28 + n7_26_27 + n7_20_11 + n7_20_12 + n7_20_13 + n7_20_14 + n7_20_15 + n7_20_16 + n7_20_17 + n7_20_18 + n7_20_19 + n7_20_20 + n7_20_21 + n7_20_22 + n7_20_23 + n7_20_24 + n7_20_25 + n7_20_26 + n7_20_27 + n7_20_28 + n7_20_29 + n7_26_26 + n7_2_11 + n7_2_12 + n7_2_13 + n7_2_14 + n7_2_15 + n7_2_16 + n7_20_30 + n7_26_25 + n7_2_17 + n7_20_31 + n7_32_11 + n7_2_18 + n7_20_32 + n7_32_12 + n7_2_19 + n7_32_13 + n7_32_14 + n7_32_15 + n7_32_16 + n7_32_17 + n7_32_18 + n7_32_19 + n7_2_20 + n7_2_21 + n7_2_22 + n7_2_23 + n7_2_24 + n7_2_25 + n7_2_26 + n7_2_27 + n7_32_20 + n7_2_28 + n7_32_21 + n7_32_22 + n7_2_29 + n7_32_23 + n7_32_24 + n7_32_25 + n7_32_26 + n7_32_27 + n7_32_28 + n7_32_29 + n7_26_24 + n7_2_30 + n7_2_31 + n7_2_32 + n7_32_30 + n7_32_31 + n7_32_32 + n7_26_23 + n7_9_1 + n7_9_2 + n7_9_3 + n7_9_4 + n7_9_5 + n7_9_6 + n7_9_7 + n7_9_8 + n7_9_9 + n7_26_22 + n7_26_21 + n7_26_20 + n7_26_19 + n7_30_1 + n7_30_2 + n7_30_3 + n7_30_4 + n7_30_5 + n7_30_6 + n7_30_7 + n7_30_8 + n7_30_9 + n7_26_18 + n7_26_17 + n7_26_16 + n7_26_15 + n7_26_14 + n7_26_13 + n7_26_12 + n7_14_32 + n7_26_11 + n7_14_31 + n7_14_30 + n7_14_29 + n7_14_28 + n7_14_27 + n7_14_26 + n7_14_25 + n7_14_24 + n7_14_23 + n7_14_22 + n7_14_21 + n7_14_20 + n7_13_11 + n7_13_12 + n7_13_13 + n7_13_14 + n7_13_15 + n7_13_16 + n7_13_17 + n7_13_18 + n7_13_19 + n7_31_1 + n7_31_2 + n7_31_3 + n7_31_4 + n7_31_5 + n7_31_6 + n7_31_7 + n7_31_8 + n7_31_9 + n7_13_20 + n7_13_21 + n7_13_22 + n7_13_23 + n7_13_24 + n7_13_25 + n7_13_26 + n7_13_27 + n7_13_28 + n7_13_29 + n7_13_30 + n7_13_31 + n7_25_11 + n7_13_32 + n7_25_12 + n7_25_13 + n7_25_14 + n7_25_15 + n7_25_16 + n7_25_17 + n7_25_18 + n7_25_19 + n7_25_20 + n7_25_21 + n7_25_22 + n7_25_23 + n7_25_24 + n7_25_25 + n7_25_26 + n7_25_27 + n7_25_28 + n7_25_29 + n7_7_10 + n7_7_11 + n7_7_12 + n7_7_13 + n7_7_14 + n7_7_15 + n7_7_16 + n7_25_30 + n7_7_17 + n7_25_31 + n7_7_18 + n7_25_32 + n7_7_19 + n7_7_20 + n7_7_21 + n7_7_22 + n7_7_23 + n7_7_24 + n7_7_25 + n7_7_26 + n7_7_27 + n7_7_28 + n7_7_29 + n7_7_30 + n7_7_31 + n7_7_32 + n7_14_19 + n7_14_18 + n7_14_17 + n7_14_16 + n7_14_15 + n7_14_14 + n7_14_13 + n7_14_12 + n7_14_11 + n7_32_0 + n7_32_1 + n7_32_2 + n7_32_3 + n7_32_4 + n7_32_5 + n7_32_6 + n7_32_7 + n7_32_8 + n7_32_9 + n7_18_10 + n7_18_11 + n7_18_12 + n7_18_13 + n7_18_14 + n7_18_15 + n7_18_16 + n7_18_17 + n7_18_18 + n7_18_19 + n7_18_20 + n7_18_21 + n7_18_22 + n7_18_23 + n7_18_24 + n7_18_25 + n7_18_26 + n7_18_27 + n7_18_28 + n7_18_29 + n7_18_30 + n7_18_31 + n7_18_32 + n7_1_11 + n7_1_12 + n7_1_13 + n7_1_14 + n7_1_15 + n7_1_16 + n7_31_10 + n7_1_17 + n7_31_11 + n7_1_18 + n7_31_12 + n7_1_19 + n7_31_13 + n7_31_14 + n7_31_15 + n7_31_16 + n7_31_17 + n7_31_18 + n7_31_19 + n7_1_20 + n7_1_21 + n7_1_22 + n7_1_23 + n7_1_24 + n7_1_25 + n7_1_26 + n7_1_27 + n7_31_20 + n7_1_28 + n7_31_21 + n7_31_22 + n7_1_29 + n7_31_23 + n7_31_24 + n7_31_25 + n7_31_26 + n7_31_27 + n7_31_28 + n7_31_29 + n7_1_30 + n7_1_31 + n7_1_32 + n7_31_30 + n7_31_31 + n7_31_32 + n7_7_9 + n7_7_8 + n7_7_7 + n7_7_6 + n7_7_5 + n7_7_4 + n7_7_3 + n7_7_2 + n7_7_1 + n7_18_9 + n7_20_0 + n7_20_1 + n7_20_2 + n7_20_3 + n7_20_4 + n7_20_5 + n7_20_6 + n7_20_7 + n7_20_8 + n7_20_9 + n7_18_8 + n7_18_7 + n7_12_11 + n7_12_12 + n7_12_13 + n7_12_14 + n7_12_15 + n7_12_16 + n7_12_17 + n7_12_18 + n7_12_19 + n7_21_0 + n7_21_1 + n7_21_2 + n7_21_3 + n7_21_4 + n7_21_5 + n7_21_6 + n7_21_7 + n7_21_8 + n7_21_9 + n7_12_20 + n7_12_21 + n7_12_22 + n7_12_23 + n7_12_24 + n7_12_25 + n7_12_26 + n7_12_27 + n7_12_28 + n7_12_29 + n7_12_30 + n7_18_6 + n7_12_31 + n7_24_11 + n7_12_32 + n7_24_12 + n7_24_13 + n7_24_14 + n7_24_15 + n7_24_16 + n7_24_17 + n7_24_18 + n7_24_19 + n7_24_20 + n7_24_21 + n7_24_22 + n7_24_23 + n7_24_24 + n7_24_25 + n7_24_26 + n7_24_27 + n7_24_28 + n7_24_29 + n7_6_10 + n7_6_11 + n7_6_12 + n7_6_13 + n7_6_14 + n7_6_15 + n7_6_16 + n7_24_30 + n7_6_17 + n7_24_31 + n7_6_18 + n7_24_32 + n7_6_19 + n7_6_20 + n7_6_21 + n7_6_22 + n7_6_23 + n7_6_24 + n7_6_25 + n7_6_26 + n7_6_27 + n7_6_28 + n7_6_29 + n7_6_30 + n7_6_31 + n7_6_32 + n7_18_5 + n7_18_4 + n7_18_3 + n7_18_2 + n7_18_1 + n7_22_1 + n7_22_2 + n7_22_3 + n7_22_4 + n7_22_5 + n7_22_6 + n7_22_7 + n7_22_8 + n7_22_9 + n7_17_10 + n7_17_11 + n7_17_12 + n7_17_13 + n7_17_14 + n7_17_15 + n7_17_16 + n7_17_17 + n7_17_18 + n7_17_19 + n7_17_20 + n7_17_21 + n7_17_22 + n7_17_23 + n7_17_24 + n7_17_25 + n7_17_26 + n7_17_27 + n7_17_28 + n7_17_29 + n7_17_30 + n7_17_31 + n7_29_11 + n7_17_32 + n7_29_12 + n7_29_13 + n7_29_14 + n7_29_15 + n7_29_16 + n7_29_17 + n7_29_18 + n7_29_19 + n7_29_20 + n7_29_21 + n7_29_22 + n7_29_23 + n7_29_24 + n7_29_25 + n7_29_26 + n7_29_27 + n7_29_28 + n7_29_29 + n7_29_30 + n7_29_31 + n7_29_32 + n7_0_11 + n7_0_12 + n7_0_13 + n7_0_14 + n7_0_15 + n7_0_16 + n7_30_10 + n7_0_17 + n7_30_11 + n7_0_18 + n7_30_12 + n7_0_19 + n7_30_13 + n7_30_14 + n7_30_15 + n7_30_16 + n7_30_17 + n7_30_18 + n7_30_19 + n7_0_20 + n7_0_21 + n7_0_22 + n7_0_23 + n7_0_24 + n7_0_25 + n7_0_26 + n7_0_27 + n7_30_20 + n7_0_28 + n7_30_21 + n7_30_22 + n7_0_29 + n7_30_23 + n7_30_24 + n7_30_25 + n7_30_26 + n7_30_27 + n7_30_28 + n7_30_29 + n7_0_30 + n7_0_31 + n7_0_32 + n7_30_30 + n7_30_31 + n7_30_32 + n7_23_1 + n7_23_2 + n7_23_3 + n7_23_4 + n7_23_5 + n7_23_6 + n7_23_7 + n7_23_8 + n7_23_9 + n7_10_1 + n7_10_2 + n7_10_3 + n7_10_4 + n7_10_5 + n7_10_6 + n7_10_7 + n7_10_8 + n7_10_9 + n7_24_0 + n7_24_1 + n7_24_2 + n7_24_3 + n7_24_4 + n7_24_5 + n7_24_6 + n7_24_7 + n7_24_8 + n7_24_9 + n7_11_11 + n7_11_12 + n7_11_13 + n7_11_14 + n7_11_15 + n7_11_16 + n7_11_17 + n7_11_18 + n7_11_19 + n7_11_0 + n7_11_1 + n7_11_2 + n7_11_3 + n7_11_4 + n7_11_5 + n7_11_6 + n7_11_7 + n7_11_8 + n7_11_9 + n7_11_20 + n7_11_21 + n7_11_22 + n7_11_23 + n7_11_24 + n7_11_25 + n7_11_26 + n7_11_27 + n7_11_28 + n7_11_29 + n7_11_30 + n7_23_10 + n7_11_31 + n7_23_11 + n7_11_32 + n7_23_12 + n7_23_13 + n7_23_14 + n7_23_15 + n7_23_16 + n7_23_17 + n7_23_18 + n7_23_19 + n7_23_20 + n7_23_21 + n7_23_22 + n7_23_23 + n7_23_24 + n7_23_25 + n7_23_26 + n7_23_27 + n7_23_28 + n7_23_29 + n7_5_11 + n7_5_12 + n7_5_13 + n7_5_14 + n7_5_15 + n7_5_16 + n7_23_30 + n7_5_17 + n7_23_31 + n7_5_18 + n7_23_32 + n7_5_19 + n7_5_20 + n7_5_21 + n7_5_22 + n7_5_23 + n7_5_24 + n7_5_25 + n7_5_26 + n7_5_27 + n7_5_28 + n7_5_29 + n7_5_30 + n7_5_31 + n7_5_32 + n7_0_0 + n7_0_1 + n7_0_2 + n7_0_3 + n7_0_4 + n7_0_5 + n7_0_6 + n7_0_7 + n7_0_8 + n7_0_9 + n7_25_0 + n7_25_1 + n7_25_2 + n7_25_3 + n7_25_4 + n7_25_5 + n7_25_6 + n7_25_7 + n7_25_8 + n7_25_9 + n7_12_0 + n7_12_1 + n7_12_2 + n7_12_3 + n7_12_4 + n7_12_5 + n7_12_6 + n7_12_7 + n7_12_8 + n7_12_9 + n7_1_0 + n7_1_1 + n7_1_2 + n7_1_3 + n7_1_4 + n7_1_5 + n7_1_6 + n7_1_7 + n7_1_8 + n7_1_9 + n7_16_11 + n7_16_12 + n7_16_13 + n7_16_14 + n7_16_15 + n7_16_16 + n7_16_17 + n7_16_18 + n7_16_19 + n7_16_20 + n7_16_21 + n7_16_22 + n7_16_23 + n7_16_24 + n7_16_25 + n7_16_26 + n7_16_27 + n7_16_28 + n7_16_29 + n7_16_30 + n7_16_31 + n7_28_11 + n7_16_32 + n7_28_12 + n7_28_13 + n7_28_14 + n7_28_15 + n7_28_16 + n7_28_17 + n7_28_18 + n7_28_19 + n7_28_20 + n7_28_21 + n7_28_22 + n7_28_23 + n7_28_24 + n7_28_25 + n7_28_26 + n7_28_27 + n7_28_28 + n7_28_29 + n7_28_30 + n7_28_31 + n7_28_32 + n7_26_0 + n7_26_1 + n7_26_2 + n7_26_3 + n7_26_4 + n7_26_5 + n7_26_6 + n7_26_7 + n7_26_8 + n7_26_9 + n7_13_0 + n7_13_1 + n7_13_2 + n7_13_3 + n7_13_4 + n7_13_5 + n7_13_6 + n7_13_7 + n7_13_8 + n7_13_9 + n7_2_0 + n7_2_1 + n7_2_2 + n7_2_3 + n7_2_4 + n7_2_5 + n7_2_6 + n7_2_7 + n7_2_8 + n7_2_9 + n7_27_1 + n7_27_2 + n7_27_3 + n7_27_4 + n7_27_5 + n7_27_6 + n7_27_7 + n7_27_8 + n7_27_9 + n7_14_0 + n7_14_1 + n7_14_2 + n7_14_3 + n7_14_4 + n7_14_5 + n7_14_6 + n7_14_7 + n7_14_8 + n7_14_9 + n7_10_10 + n7_10_11 + n7_10_12 + n7_10_13 + n7_10_14 + n7_10_15 + n7_10_16 + n7_10_17 + n7_10_18 + n7_10_19 + n7_10_20 + n7_10_21 + n7_10_22 + n7_10_23 + n7_10_24 + n7_10_25 + n7_10_26 + n7_10_27 + n7_10_28 + n7_10_29 + n7_10_30 + n7_22_10 + n7_10_31 + n7_22_11 + n7_10_32 + n7_22_12 + n7_22_13 + n7_22_14 + n7_22_15 + n7_22_16 + n7_22_17 + n7_22_18 + n7_22_19 + n7_22_20 + n7_22_21 + n7_22_22 + n7_22_23 + n7_22_24 + n7_22_25 + n7_22_26 + n7_22_27 + n7_22_28 + n7_22_29 + n7_4_11 + n7_4_12 + n7_4_13 + n7_4_14 + n7_4_15 + n7_4_16 + n7_22_30 + n7_4_17 + n7_22_31 + n7_4_18 + n7_22_32 + n7_4_19 + n7_4_20 + n7_4_21 + n7_4_22 + n7_4_23 + n7_4_24 + n7_4_25 + n7_4_26 + n7_4_27 + n7_4_28 + n7_4_29 + n7_4_30 + n7_4_31 + n7_4_32 + n7_3_0 + n7_3_1 + n7_3_2 + n7_3_3 + n7_3_4 + n7_3_5 + n7_3_6 + n7_3_7 + n7_3_8 + n7_3_9 + n7_6_9 + n7_6_8 + n7_6_7 + n7_6_6 + n7_6_5 + n7_6_4 + n7_6_3 + n7_6_2 + n7_6_1 + n7_28_0 + n7_28_1 + n7_28_2 + n7_28_3 + n7_28_4 + n7_28_5 + n7_28_6 + n7_28_7 + n7_28_8 + n7_28_9 + n7_15_1 + n7_15_2 + n7_15_3 + n7_15_4 + n7_15_5 + n7_15_6 + n7_15_7 + n7_15_8 + n7_15_9 + n7_3_32 + n7_3_31 + n7_3_30 + n7_4_0 + n7_4_1 + n7_4_2 + n7_4_3 + n7_4_4 + n7_4_5 + n7_4_6 + n7_4_7 + n7_4_8 + n7_4_9 + n7_3_29 + n7_3_28 + n7_3_27 + n7_3_26 + n7_3_25 + n7_3_24 + n7_3_23 + n7_3_22 + n7_3_21 + n7_3_20 + n7_15_10 + n7_15_11 + n7_15_12 + n7_15_13 + n7_15_14 + n7_15_15 + n7_15_16 + n7_15_17 + n7_15_18 + n7_15_19 + n7_15_20 + n7_15_21 + n7_15_22 + n7_15_23 + n7_15_24 + n7_15_25 + n7_15_26 + n7_15_27 + n7_15_28 + n7_15_29 + n7_15_30 + n7_27_10 + n7_15_31 + n7_27_11 + n7_15_32 + n7_27_12 + n7_27_13 + n7_27_14 + n7_27_15 + n7_27_16 + n7_27_17 + n7_27_18 + n7_27_19 + n7_27_20 + n7_27_21 + n7_27_22 + n7_27_23 + n7_27_24 + n7_27_25 + n7_27_26 + n7_27_27 + n7_27_28 + n7_27_29 + n7_9_10 + n7_9_11 + n7_9_12 + n7_9_13 + n7_9_14 + n7_9_15 + n7_9_16 + n7_27_30 + n7_9_17 + n7_27_31 + n7_9_18 + n7_27_32 + n7_9_19 + n7_9_20 + n7_9_21 + n7_9_22 + n7_9_23 + n7_9_24 + n7_9_25 + n7_9_26 + n7_9_27 + n7_9_28 + n7_9_29 + n7_9_30 + n7_9_31 + n7_9_32 + n7_29_0 + n7_29_1 + n7_29_2 + n7_29_3 + n7_29_4 + n7_29_5 + n7_29_6 + n7_29_7 + n7_29_8 + n7_29_9 + n7_16_0 + n7_16_1 + n7_16_2 + n7_16_3 + n7_16_4 + n7_16_5 + n7_16_6 + n7_16_7 + n7_16_8 + n7_16_9 + n7_3_19 + n7_3_18 + n7_3_17 + n7_3_16 + n7_3_15 + n7_3_14 + n7_3_13 + n7_3_12 + n7_3_11 + n7_5_0 + n7_5_1 + n7_5_2 + n7_5_3 + n7_5_4 + n7_5_5 + n7_5_6 + n7_5_7 + n7_5_8 + n7_5_9 <= 1)))) : E (F ((2 <= s2_9 + s2_8 + s2_7 + s2_6 + s2_5 + s2_4 + s2_3 + s2_2 + s2_1 + s2_0 + s2_32 + s2_31 + s2_30 + s2_29 + s2_28 + s2_27 + s2_26 + s2_25 + s2_24 + s2_23 + s2_22 + s2_21 + s2_20 + s2_19 + s2_18 + s2_17 + s2_16 + s2_15 + s2_14 + s2_13 + s2_12 + s2_11 + s2_10))) : A (G ((2 <= Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9))) : E (F ((s4_0 + s4_1 + s4_2 + s4_3 + s4_4 + s4_5 + s4_6 + s4_7 + s4_8 + s4_9 + s4_32 + s4_31 + s4_30 + s4_29 + s4_28 + s4_27 + s4_26 + s4_25 + s4_24 + s4_23 + s4_22 + s4_21 + s4_20 + s4_19 + s4_18 + s4_17 + s4_16 + s4_15 + s4_14 + s4_13 + s4_12 + s4_11 + s4_10 + 1 <= a3))) : E (F (((2 <= n4_10 + n4_11 + n4_12 + n4_13 + n4_14 + n4_15 + n4_16 + n4_17 + n4_18 + n4_19 + n4_20 + n4_21 + n4_22 + n4_23 + n4_24 + n4_25 + n4_26 + n4_27 + n4_28 + n4_29 + n4_30 + n4_31 + n4_32 + n4_0 + n4_1 + n4_2 + n4_3 + n4_4 + n4_5 + n4_6 + n4_7 + n4_8 + n4_9) AND (2 <= n3_9 + n3_8 + n3_7 + n3_6 + n3_5 + n3_4 + n3_3 + n3_2 + n3_1 + n3_0 + n3_10 + n3_11 + n3_12 + n3_13 + n3_14 + n3_15 + n3_16 + n3_17 + n3_18 + n3_19 + n3_20 + n3_21 + n3_22 + n3_23 + n3_24 + n3_25 + n3_26 + n3_27 + n3_28 + n3_29 + n3_30 + n3_31 + n3_32) AND ((1 <= SstopOK_9 + SstopOK_8 + SstopOK_5 + SstopOK_4 + SstopOK_3 + SstopOK_2 + SstopOK_0 + SstopOK_30 + SstopOK_29 + SstopOK_28 + SstopOK_27 + SstopOK_26 + SstopOK_25 + SstopOK_24 + SstopOK_23 + SstopOK_22 + SstopOK_21 + SstopOK_19 + SstopOK_18 + SstopOK_17 + SstopOK_16 + SstopOK_15 + SstopOK_14 + SstopOK_13 + SstopOK_12 + SstopOK_11 + SstopOK_10 + SstopOK_20 + SstopOK_31 + SstopOK_32 + SstopOK_1 + SstopOK_6 + SstopOK_7) OR (1 <= Sstart_9 + Sstart_8 + Sstart_7 + Sstart_6 + Sstart_5 + Sstart_4 + Sstart_3 + Sstart_2 + Sstart_1 + Sstart_0 + Sstart_10 + Sstart_11 + Sstart_12 + Sstart_13 + Sstart_14 + Sstart_15 + Sstart_16 + Sstart_17 + Sstart_18 + Sstart_19 + Sstart_20 + Sstart_21 + Sstart_22 + Sstart_23 + Sstart_24 + Sstart_25 + Sstart_26 + Sstart_27 + Sstart_28 + Sstart_29 + Sstart_30 + Sstart_31 + Sstart_32)) AND (2 <= AstopAbort) AND (3 <= s2_9 + s2_8 + s2_7 + s2_6 + s2_5 + s2_4 + s2_3 + s2_2 + s2_1 + s2_0 + s2_32 + s2_31 + s2_30 + s2_29 + s2_28 + s2_27 + s2_26 + s2_25 + s2_24 + s2_23 + s2_22 + s2_21 + s2_20 + s2_19 + s2_18 + s2_17 + s2_16 + s2_15 + s2_14 + s2_13 + s2_12 + s2_11 + s2_10) AND ((a4 <= s3_8 + s3_7 + s3_6 + s3_5 + s3_4 + s3_3 + s3_2 + s3_1 + s3_0 + s3_10 + s3_11 + s3_12 + s3_13 + s3_14 + s3_15 + s3_16 + s3_17 + s3_18 + s3_19 + s3_20 + s3_21 + s3_22 + s3_23 + s3_24 + s3_25 + s3_26 + s3_27 + s3_28 + s3_29 + s3_30 + s3_31 + s3_32 + s3_9) OR (3 <= s4_0 + s4_1 + s4_2 + s4_3 + s4_4 + s4_5 + s4_6 + s4_7 + s4_8 + s4_9 + s4_32 + s4_31 + s4_30 + s4_29 + s4_28 + s4_27 + s4_26 + s4_25 + s4_24 + s4_23 + s4_22 + s4_21 + s4_20 + s4_19 + s4_18 + s4_17 + s4_16 + s4_15 + s4_14 + s4_13 + s4_12 + s4_11 + s4_10)))))
lola: computing a collection of formulas
lola: RUNNING
lola: subprocess 0 will run for 221 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((n2_32 + n2_31 + n2_30 + n2_29 + n2_28 + n2_27 + n2_26 + n2_25 + n2_24 + n2_23 + n2_22 + n2_21 + n2_20 + n2_19 + n2_18 + n2_17 + n2_16 + n2_15 + n2_14 + n2_13 + n2_12 + n2_11 + n2_10 + n2_0 + n2_1 + n2_2 + n2_3 + n2_4 + n2_5 + n2_6 + n2_7 + n2_8 + n2_9 + 1 <= AstopOK)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality.sara
lola: state equation: calling and running sara
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 1 will run for 235 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((3 <= CstopAbort)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality.sara
lola: state equation: calling and running sara
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 2 will run for 252 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (((a2 <= n7_17_0 + n7_17_1 + n7_17_2 + n7_17_3 + n7_17_4 + n7_17_5 + n7_17_6 + n7_17_7 + n7_17_8 + n7_17_9 + n7_21_10 + n7_21_11 + n7_21_12 + n7_21_13 + n7_21_14 + n7_21_15 + n7_21_16 + n7_21_17 + n7_21_18 + n7_21_19 + n7_21_20 + n7_21_21 + n7_21_22 + n7_21_23 + n7_21_24 + n7_21_25 + n7_21_26 + n7_21_27 + n7_21_28 + n7_21_29 + n7_3_10 + n7_21_30 + n7_21_31 + n7_21_32 + n7_15_0 + n7_6_0 + n7_4... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 4 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-2.sara
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is not invariant.
lola: ========================================
lola: subprocess 3 will run for 272 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((((3 <= CstopOK_0 + CstopOK_1 + CstopOK_2 + CstopOK_3 + CstopOK_4 + CstopOK_5 + CstopOK_6 + CstopOK_7 + CstopOK_8 + CstopOK_9 + CstopOK_10 + CstopOK_11 + CstopOK_12 + CstopOK_13 + CstopOK_14 + CstopOK_15 + CstopOK_16 + CstopOK_17 + CstopOK_18 + CstopOK_19 + CstopOK_20 + CstopOK_21 + CstopOK_22 + CstopOK_23 + CstopOK_24 + CstopOK_25 + CstopOK_26 + CstopOK_27 + CstopOK_28 + CstopOK_29 + CstopO... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 5 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-3.sara
lola: state equation: calling and running sara
sara: try reading problem file QuasiCertifProtocol-COL-32-ReachabilityCardinality-3.sara.
sara: place or transition ordering is non-deterministic
lola: state equation: solution produced
lola: SUBRESULT
lola: result: yes
lola: produced by: state equation
lola: The predicate is reachable.
lola: subprocess 4 will run for 294 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((3 <= AstopAbort)))
lola: ========================================
lola: SUBTASK
lola: ========================================
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-4.sara
lola: state equation: calling and running sara
sara: try reading problem file QuasiCertifProtocol-COL-32-ReachabilityCardinality-4.sara.
sara: place or transition ordering is non-deterministic
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: no
lola: produced by: state equation
lola: The predicate is unreachable.
lola: ========================================
lola: subprocess 5 will run for 321 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F (((3 <= n9_19_10 + n9_19_11 + n9_19_12 + n9_19_13 + n9_19_14 + n9_19_15 + n9_19_16 + n9_19_17 + n9_19_18 + n9_19_19 + n9_19_20 + n9_19_21 + n9_19_22 + n9_19_23 + n9_19_24 + n9_19_25 + n9_19_26 + n9_19_27 + n9_19_28 + n9_19_29 + n9_19_30 + n9_19_31 + n9_19_32 + n9_31_0 + n9_31_1 + n9_31_2 + n9_31_3 + n9_31_4 + n9_31_5 + n9_31_6 + n9_31_7 + n9_31_8 + n9_31_9 + n9_7_10 + n9_20_10 + n9_32_10 + n9... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 4 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-5.sara
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 6 will run for 353 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (()))
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: processed formula: TRUE
lola: processed formula length: 4
lola: 3 rewrites
lola: formula mentions 0 of 3806 places; total mentions: 0
lola: closed formula file QuasiCertifProtocol-COL-32-ReachabilityCardinality.task
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: preprocessing
lola: The net satisfies the property already in its initial state.
lola: ========================================
lola: subprocess 7 will run for 392 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((Astart <= 1)))
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is invariant.
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: ========================================
lola: subprocess 8 will run for 441 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9 <= malici... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-8.sara
lola: state equation: calling and running sara
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 9 will run for 504 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((n5_10 + n5_11 + n5_12 + n5_13 + n5_14 + n5_15 + n5_16 + n5_17 + n5_18 + n5_19 + n5_20 + n5_21 + n5_22 + n5_23 + n5_24 + n5_25 + n5_26 + n5_27 + n5_28 + n5_29 + n5_30 + n5_31 + n5_32 + n5_0 + n5_1 + n5_2 + n5_3 + n5_4 + n5_5 + n5_6 + n5_7 + n5_8 + n5_9 <= a5)))
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-9.sara
lola: state equation: calling and running sara
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is not invariant.
lola: ========================================
lola: subprocess 10 will run for 588 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (((1 <= Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9) OR... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 6 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-10.sara
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is not invariant.
lola: ========================================
lola: subprocess 11 will run for 706 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((((n6_32 + n6_31 + n6_30 + n6_29 + n6_28 + n6_27 + n6_26 + n6_25 + n6_24 + n6_23 + n6_22 + n6_21 + n6_20 + n6_19 + n6_18 + n6_17 + n6_16 + n6_15 + n6_14 + n6_13 + n6_12 + n6_11 + n6_10 + n6_0 + n6_1 + n6_2 + n6_3 + n6_4 + n6_5 + n6_6 + n6_7 + n6_8 + n6_9 <= 0) OR (n9_19_10 + n9_19_11 + n9_19_12 + n9_19_13 + n9_19_14 + n9_19_15 + n9_19_16 + n9_19_17 + n9_19_18 + n9_19_19 + n9_19_20 + n9_19_2... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 3 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-11.sara
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is not invariant.
lola: ========================================
lola: subprocess 12 will run for 883 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((2 <= s2_9 + s2_8 + s2_7 + s2_6 + s2_5 + s2_4 + s2_3 + s2_2 + s2_1 + s2_0 + s2_32 + s2_31 + s2_30 + s2_29 + s2_28 + s2_27 + s2_26 + s2_25 + s2_24 + s2_23 + s2_22 + s2_21 + s2_20 + s2_19 + s2_18 + s2_17 + s2_16 + s2_15 + s2_14 + s2_13 + s2_12 + s2_11 + s2_10)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-12.sara
lola: lola: SUBRESULT
state equation: calling and running sara
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 13 will run for 1177 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((2 <= Cstart_10 + Cstart_11 + Cstart_12 + Cstart_13 + Cstart_14 + Cstart_15 + Cstart_16 + Cstart_17 + Cstart_18 + Cstart_19 + Cstart_20 + Cstart_21 + Cstart_22 + Cstart_23 + Cstart_24 + Cstart_25 + Cstart_26 + Cstart_27 + Cstart_28 + Cstart_29 + Cstart_30 + Cstart_31 + Cstart_32 + Cstart_0 + Cstart_1 + Cstart_2 + Cstart_3 + Cstart_4 + Cstart_5 + Cstart_6 + Cstart_7 + Cstart_8 + Cstart_9)))
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
sara: try reading problem file QuasiCertifProtocol-COL-32-ReachabilityCardinality-12.sara.
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-13.sara
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is not invariant.
lola: ========================================
lola: subprocess 14 will run for 1766 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((s4_0 + s4_1 + s4_2 + s4_3 + s4_4 + s4_5 + s4_6 + s4_7 + s4_8 + s4_9 + s4_32 + s4_31 + s4_30 + s4_29 + s4_28 + s4_27 + s4_26 + s4_25 + s4_24 + s4_23 + s4_22 + s4_21 + s4_20 + s4_19 + s4_18 + s4_17 + s4_16 + s4_15 + s4_14 + s4_13 + s4_12 + s4_11 + s4_10 + 1 <= a3)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-14.sara
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 15 will run for 3532 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F (((2 <= n4_10 + n4_11 + n4_12 + n4_13 + n4_14 + n4_15 + n4_16 + n4_17 + n4_18 + n4_19 + n4_20 + n4_21 + n4_22 + n4_23 + n4_24 + n4_25 + n4_26 + n4_27 + n4_28 + n4_29 + n4_30 + n4_31 + n4_32 + n4_0 + n4_1 + n4_2 + n4_3 + n4_4 + n4_5 + n4_6 + n4_7 + n4_8 + n4_9) AND (2 <= n3_9 + n3_8 + n3_7 + n3_6 + n3_5 + n3_4 + n3_3 + n3_2 + n3_1 + n3_0 + n3_10 + n3_11 + n3_12 + n3_13 + n3_14 + n3_15 + n3_16 ... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 2020 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 24 literals and 4 conjunctive subformulas
lola: state equation: write sara problem file to QuasiCertifProtocol-COL-32-ReachabilityCardinality-15.sara
lola: state equation: calling and running sara
sara: try reading problem file QuasiCertifProtocol-COL-32-ReachabilityCardinality-15.sara.
sara: place or transition ordering is non-deterministic
sara: place or transition ordering is non-deterministic
lola: sara is running 0 secs || 542192 markings, 1184928 edges, 108438 markings/sec, 0 secs
lola: sara is running 5 secs || 854448 markings, 1926375 edges, 62451 markings/sec, 5 secs
lola: sara is running 10 secs || 1176252 markings, 2658058 edges, 64361 markings/sec, 10 secs
lola: sara is running 15 secs || 1482694 markings, 3389049 edges, 61288 markings/sec, 15 secs
lola: sara is running 20 secs || 1787011 markings, 4124148 edges, 60863 markings/sec, 20 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: no
lola: produced by: state equation
lola: The predicate is unreachable.
lola: ========================================
lola: RESULT
lola:
SUMMARY: yes yes no yes no yes yes yes yes no no no yes no yes no
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-0 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-1 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-2 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-3 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-4 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-5 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-6 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-7 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-8 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-9 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-10 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-11 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-12 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-13 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-14 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA QuasiCertifProtocol-COL-32-ReachabilityCardinality-15 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
----- Kill lola and sara stdout -----
----- Finished stdout -----
BK_STOP 1496398480378
--------------------
content from stderr:
----- Start make prepare stderr -----
----- Start make result stderr -----
----- Start make result stderr -----
----- Kill lola and sara stderr -----
----- Finished stderr -----
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_QuasiCertifProtocol-PT-32"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="lola"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_QuasiCertifProtocol-PT-32.tgz
mv S_QuasiCertifProtocol-PT-32 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-3254"
echo " Executing tool lola"
echo " Input is S_QuasiCertifProtocol-PT-32, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r138-smll-149479231800295"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

