About the Execution of ITS-Tools for S_NeoElection-PT-6
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 15938.740 | 3600000.00 | 4333272.00 | 516.20 | [undef] | Time out reached |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
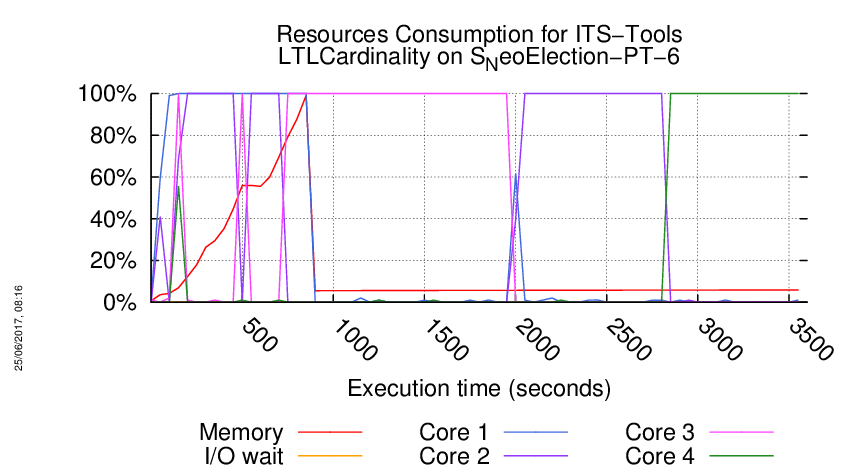
Trace from the execution
Waiting for the VM to be ready (probing ssh)
......
=====================================================================
Generated by BenchKit 2-3254
Executing tool itstools
Input is S_NeoElection-PT-6, examination is LTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r120-blw7-149441652000275
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-COL-6-LTLCardinality-0
FORMULA_NAME NeoElection-COL-6-LTLCardinality-1
FORMULA_NAME NeoElection-COL-6-LTLCardinality-10
FORMULA_NAME NeoElection-COL-6-LTLCardinality-11
FORMULA_NAME NeoElection-COL-6-LTLCardinality-12
FORMULA_NAME NeoElection-COL-6-LTLCardinality-13
FORMULA_NAME NeoElection-COL-6-LTLCardinality-14
FORMULA_NAME NeoElection-COL-6-LTLCardinality-15
FORMULA_NAME NeoElection-COL-6-LTLCardinality-2
FORMULA_NAME NeoElection-COL-6-LTLCardinality-3
FORMULA_NAME NeoElection-COL-6-LTLCardinality-4
FORMULA_NAME NeoElection-COL-6-LTLCardinality-5
FORMULA_NAME NeoElection-COL-6-LTLCardinality-6
FORMULA_NAME NeoElection-COL-6-LTLCardinality-7
FORMULA_NAME NeoElection-COL-6-LTLCardinality-8
FORMULA_NAME NeoElection-COL-6-LTLCardinality-9
=== Now, execution of the tool begins
BK_START 1496444827492
Using solver YICES2 to compute partial order matrices.
Built C files in :
/home/mcc/execution
its-ltl command run as :
/home/mcc/BenchKit/eclipse/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201705302212/bin/its-ltl-linux64 --gc-threshold 2000000 -i /home/mcc/execution/LTLCardinality.pnml.gal -t CGAL -LTL /home/mcc/execution/LTLCardinality.ltl -c -stutter-deadlock
Read 16 LTL properties
Checking formula 0 : !((true))
Formula 0 simplified : 0
Presburger conditions satisfied. Using coverability to approximate state space in K-Induction.
// Phase 1: matrix 8005 rows 1281 cols
invariant : 1'P_negotiation_5_0_CO + 1'P_negotiation_5_0_DONE= 0
invariant : 1'P_negotiation_4_6_NONE + 1'P_negotiation_4_6_CO + 1'P_negotiation_4_6_DONE= 1
invariant : 1'P_negotiation_5_0_NONE= 0
invariant : 1'P_sendAnnPs__broadcasting_0_4= 0
invariant : 1'P_electionInit_0 + 1'P_startNeg__broadcasting_0_1= 0
invariant : 1'P_negotiation_2_0_NONE= 0
invariant : 1'P_negotiation_0_0_CO + 1'P_negotiation_0_0_DONE= 0
invariant : 1'P_negotiation_0_0_NONE= 0
invariant : 1'P_negotiation_5_3_NONE + -1'P_negotiation_5_4_NONE + 1'P_startNeg__broadcasting_5_4= 0
invariant : 1'P_startNeg__broadcasting_0_4= 0
invariant : 1'P_negotiation_3_4_NONE + -1'P_negotiation_3_5_NONE + 1'P_startNeg__broadcasting_3_4= 0
invariant : -1'P_poll__waitingMessage_4 + 1'P_stage_4_NEG= 1
invariant : 1'P_masterState_5_F_0 + 1'P_masterState_5_F_1 + 1'P_masterState_5_F_2 + 1'P_masterState_5_F_3 + 1'P_masterState_5_F_4 + 1'P_masterState_5_F_5 + 1'P_masterState_5_F_6 + 1'P_masterState_5_T_0 + 1'P_masterState_5_T_1 + 1'P_masterState_5_T_2 + 1'P_masterState_5_T_3 + 1'P_masterState_5_T_4 + 1'P_masterState_5_T_5 + 1'P_masterState_5_T_6= 1
invariant : 1'P_negotiation_6_5_NONE + 1'P_negotiation_6_5_CO + 1'P_negotiation_6_5_DONE= 1
invariant : -1'P_poll__waitingMessage_3 + 1'P_stage_3_NEG= 1
invariant : 1'P_negotiation_4_3_NONE + 1'P_negotiation_4_3_CO + 1'P_negotiation_4_3_DONE= 1
invariant : 1'P_poll__waitingMessage_1 + 1'P_stage_1_PRIM + 1'P_stage_1_SEC= 0
invariant : 1'P_negotiation_1_4_NONE + -1'P_negotiation_1_5_NONE + 1'P_startNeg__broadcasting_1_4= 0
invariant : 1'P_negotiation_6_4_NONE + 1'P_negotiation_6_4_CO + 1'P_negotiation_6_4_DONE= 1
invariant : 1'P_negotiation_1_5_NONE + -1'P_negotiation_1_6_NONE + 1'P_startNeg__broadcasting_1_5= 0
invariant : 1'P_negotiation_5_5_CO + 1'P_negotiation_5_5_DONE= 1
invariant : 1'P_negotiation_1_3_NONE + -1'P_negotiation_1_4_NONE + 1'P_startNeg__broadcasting_1_3= 0
invariant : -1'P_poll__waitingMessage_2 + 1'P_stage_2_NEG= 1
invariant : 1'P_electionInit_5 + -1'P_negotiation_5_1_NONE + 1'P_startNeg__broadcasting_5_1= 0
invariant : 1'P_electedPrimary_2 + 1'P_electedSecondary_2 + 1'P_negotiation_2_6_NONE + 1'P_poll__handlingMessage_2 + 1'P_poll__pollEnd_2 + 1'P_poll__waitingMessage_2 + 1'P_polling_2 + 1'P_sendAnnPs__broadcasting_2_1 + 1'P_sendAnnPs__broadcasting_2_2 + 1'P_sendAnnPs__broadcasting_2_3 + 1'P_sendAnnPs__broadcasting_2_4 + 1'P_sendAnnPs__broadcasting_2_5 + 1'P_sendAnnPs__broadcasting_2_6 + 1'P_startNeg__broadcasting_2_6= 1
invariant : 1'P_negotiation_6_3_NONE + -1'P_negotiation_6_4_NONE + 1'P_startNeg__broadcasting_6_4= 0
invariant : 1'P_negotiation_1_0_CO + 1'P_negotiation_1_0_DONE= 0
invariant : 1'P_electedPrimary_0 + 1'P_poll__waitingMessage_0 + 1'P_sendAnnPs__broadcasting_0_1 + 1'P_stage_0_SEC= 0
invariant : 1'P_negotiation_6_1_NONE + -1'P_negotiation_6_2_NONE + 1'P_startNeg__broadcasting_6_2= 0
invariant : 1'P_electedPrimary_3 + 1'P_electedSecondary_3 + 1'P_negotiation_3_6_NONE + 1'P_poll__handlingMessage_3 + 1'P_poll__pollEnd_3 + 1'P_poll__waitingMessage_3 + 1'P_polling_3 + 1'P_sendAnnPs__broadcasting_3_1 + 1'P_sendAnnPs__broadcasting_3_2 + 1'P_sendAnnPs__broadcasting_3_3 + 1'P_sendAnnPs__broadcasting_3_4 + 1'P_sendAnnPs__broadcasting_3_5 + 1'P_sendAnnPs__broadcasting_3_6 + 1'P_startNeg__broadcasting_3_6= 1
invariant : 1'P_negotiation_3_3_CO + 1'P_negotiation_3_3_DONE= 1
invariant : 1'P_negotiation_3_0_NONE= 0
invariant : 1'P_negotiation_3_0_CO + 1'P_negotiation_3_0_DONE= 0
invariant : 1'P_negotiation_2_2_NONE= 0
invariant : 1'P_masterState_0_F_0 + 1'P_masterState_0_F_1 + 1'P_masterState_0_F_2 + 1'P_masterState_0_F_3 + 1'P_masterState_0_F_4 + 1'P_masterState_0_F_5 + 1'P_masterState_0_F_6 + 1'P_masterState_0_T_0 + 1'P_masterState_0_T_1 + 1'P_masterState_0_T_2 + 1'P_masterState_0_T_3 + 1'P_masterState_0_T_4 + 1'P_masterState_0_T_5 + 1'P_masterState_0_T_6= 0
invariant : 1'P_negotiation_0_5_CO + 1'P_negotiation_0_5_DONE= 0
invariant : 1'P_poll__waitingMessage_2 + 1'P_stage_2_PRIM + 1'P_stage_2_SEC= 0
invariant : 1'P_negotiation_2_0_CO + 1'P_negotiation_2_0_DONE= 0
invariant : 1'P_negotiation_1_4_NONE + 1'P_negotiation_1_4_CO + 1'P_negotiation_1_4_DONE= 1
invariant : 1'P_negotiation_4_0_NONE= 0
invariant : 1'P_electionInit_6 + -1'P_negotiation_6_1_NONE + 1'P_startNeg__broadcasting_6_1= 0
invariant : 1'P_negotiation_5_6_NONE + 1'P_negotiation_5_6_CO + 1'P_negotiation_5_6_DONE= 1
invariant : 1'P_electionInit_3 + -1'P_negotiation_3_1_NONE + 1'P_startNeg__broadcasting_3_1= 0
invariant : -1'P_electedPrimary_0 + -1'P_sendAnnPs__broadcasting_0_1 + 1'P_stage_0_PRIM= 0
invariant : 1'P_poll__waitingMessage_5 + 1'P_stage_5_PRIM + 1'P_stage_5_SEC= 0
invariant : 1'P_negotiation_2_4_NONE + -1'P_negotiation_2_5_NONE + 1'P_startNeg__broadcasting_2_4= 0
invariant : 1'P_negotiation_6_4_NONE + -1'P_negotiation_6_5_NONE + 1'P_startNeg__broadcasting_6_5= 0
invariant : 1'P_negotiation_5_1_NONE + 1'P_negotiation_5_1_CO + 1'P_negotiation_5_1_DONE= 1
invariant : 1'P_electedPrimary_0 + 1'P_electedSecondary_0 + 1'P_poll__handlingMessage_0 + 1'P_poll__pollEnd_0 + 1'P_poll__waitingMessage_0 + 1'P_polling_0 + 1'P_sendAnnPs__broadcasting_0_1 + 1'P_sendAnnPs__broadcasting_0_6 + 1'P_startNeg__broadcasting_0_6= 0
invariant : 1'P_negotiation_0_2_CO + 1'P_negotiation_0_2_DONE= 0
invariant : 1'P_negotiation_1_6_NONE + 1'P_negotiation_1_6_CO + 1'P_negotiation_1_6_DONE= 1
invariant : 1'P_sendAnnPs__broadcasting_0_5= 0
invariant : -1'P_poll__waitingMessage_0 + 1'P_stage_0_NEG= 0
invariant : 1'P_poll__waitingMessage_4 + 1'P_stage_4_PRIM + 1'P_stage_4_SEC= 0
invariant : 1'P_masterState_6_F_0 + 1'P_masterState_6_F_1 + 1'P_masterState_6_F_2 + 1'P_masterState_6_F_3 + 1'P_masterState_6_F_4 + 1'P_masterState_6_F_5 + 1'P_masterState_6_F_6 + 1'P_masterState_6_T_0 + 1'P_masterState_6_T_1 + 1'P_masterState_6_T_2 + 1'P_masterState_6_T_3 + 1'P_masterState_6_T_4 + 1'P_masterState_6_T_5 + 1'P_masterState_6_T_6= 1
invariant : 1'P_negotiation_2_1_NONE + -1'P_negotiation_2_3_NONE + 1'P_startNeg__broadcasting_2_2= 0
invariant : 1'P_negotiation_3_1_NONE + 1'P_negotiation_3_1_CO + 1'P_negotiation_3_1_DONE= 1
invariant : 1'P_negotiation_1_2_NONE + 1'P_negotiation_1_2_CO + 1'P_negotiation_1_2_DONE= 1
invariant : 1'P_negotiation_5_2_NONE + -1'P_negotiation_5_3_NONE + 1'P_startNeg__broadcasting_5_3= 0
invariant : 1'P_electedPrimary_5 + 1'P_electedSecondary_5 + 1'P_negotiation_5_6_NONE + 1'P_poll__handlingMessage_5 + 1'P_poll__pollEnd_5 + 1'P_poll__waitingMessage_5 + 1'P_polling_5 + 1'P_sendAnnPs__broadcasting_5_1 + 1'P_sendAnnPs__broadcasting_5_2 + 1'P_sendAnnPs__broadcasting_5_3 + 1'P_sendAnnPs__broadcasting_5_4 + 1'P_sendAnnPs__broadcasting_5_5 + 1'P_sendAnnPs__broadcasting_5_6 + 1'P_startNeg__broadcasting_5_6= 1
invariant : 1'P_negotiation_3_5_NONE + -1'P_negotiation_3_6_NONE + 1'P_startNeg__broadcasting_3_5= 0
invariant : 1'P_negotiation_4_5_NONE + -1'P_negotiation_4_6_NONE + 1'P_startNeg__broadcasting_4_5= 0
invariant : 1'P_negotiation_2_6_NONE + 1'P_negotiation_2_6_CO + 1'P_negotiation_2_6_DONE= 1
invariant : 1'P_negotiation_0_3_CO + 1'P_negotiation_0_3_DONE= 0
invariant : 1'P_negotiation_4_5_NONE + 1'P_negotiation_4_5_CO + 1'P_negotiation_4_5_DONE= 1
invariant : 1'P_negotiation_4_4_CO + 1'P_negotiation_4_4_DONE= 1
invariant : 1'P_negotiation_4_1_NONE + 1'P_negotiation_4_1_CO + 1'P_negotiation_4_1_DONE= 1
invariant : 1'P_sendAnnPs__broadcasting_0_3= 0
invariant : 1'P_negotiation_5_5_NONE= 0
invariant : 1'P_negotiation_5_4_NONE + -1'P_negotiation_5_6_NONE + 1'P_startNeg__broadcasting_5_5= 0
invariant : 1'P_negotiation_4_2_NONE + -1'P_negotiation_4_3_NONE + 1'P_startNeg__broadcasting_4_3= 0
invariant : 1'P_negotiation_2_3_NONE + 1'P_negotiation_2_3_CO + 1'P_negotiation_2_3_DONE= 1
invariant : 1'P_negotiation_2_4_NONE + 1'P_negotiation_2_4_CO + 1'P_negotiation_2_4_DONE= 1
invariant : 1'P_negotiation_5_2_NONE + 1'P_negotiation_5_2_CO + 1'P_negotiation_5_2_DONE= 1
invariant : 1'P_negotiation_2_1_NONE + 1'P_negotiation_2_1_CO + 1'P_negotiation_2_1_DONE= 1
invariant : 1'P_negotiation_3_5_NONE + 1'P_negotiation_3_5_CO + 1'P_negotiation_3_5_DONE= 1
invariant : 1'P_negotiation_0_4_NONE= 0
invariant : 1'P_negotiation_3_2_NONE + 1'P_negotiation_3_2_CO + 1'P_negotiation_3_2_DONE= 1
invariant : 1'P_negotiation_6_6_CO + 1'P_negotiation_6_6_DONE= 1
invariant : 1'P_negotiation_3_2_NONE + -1'P_negotiation_3_4_NONE + 1'P_startNeg__broadcasting_3_3= 0
invariant : 1'P_masterState_2_F_0 + 1'P_masterState_2_F_1 + 1'P_masterState_2_F_2 + 1'P_masterState_2_F_3 + 1'P_masterState_2_F_4 + 1'P_masterState_2_F_5 + 1'P_masterState_2_F_6 + 1'P_masterState_2_T_0 + 1'P_masterState_2_T_1 + 1'P_masterState_2_T_2 + 1'P_masterState_2_T_3 + 1'P_masterState_2_T_4 + 1'P_masterState_2_T_5 + 1'P_masterState_2_T_6= 1
invariant : 1'P_negotiation_4_4_NONE= 0
invariant : 1'P_negotiation_1_1_CO + 1'P_negotiation_1_1_DONE= 1
invariant : 1'P_negotiation_1_3_NONE + 1'P_negotiation_1_3_CO + 1'P_negotiation_1_3_DONE= 1
invariant : 1'P_startNeg__broadcasting_0_5= 0
invariant : 1'P_negotiation_6_0_NONE= 0
invariant : 1'P_negotiation_6_3_NONE + 1'P_negotiation_6_3_CO + 1'P_negotiation_6_3_DONE= 1
invariant : 1'P_poll__waitingMessage_3 + 1'P_stage_3_PRIM + 1'P_stage_3_SEC= 0
invariant : 1'P_negotiation_5_3_NONE + 1'P_negotiation_5_3_CO + 1'P_negotiation_5_3_DONE= 1
invariant : 1'P_electedPrimary_6 + 1'P_electedSecondary_6 + 1'P_negotiation_6_5_NONE + 1'P_poll__handlingMessage_6 + 1'P_poll__pollEnd_6 + 1'P_poll__waitingMessage_6 + 1'P_polling_6 + 1'P_sendAnnPs__broadcasting_6_1 + 1'P_sendAnnPs__broadcasting_6_2 + 1'P_sendAnnPs__broadcasting_6_3 + 1'P_sendAnnPs__broadcasting_6_4 + 1'P_sendAnnPs__broadcasting_6_5 + 1'P_sendAnnPs__broadcasting_6_6 + 1'P_startNeg__broadcasting_6_6= 1
invariant : 1'P_negotiation_2_2_CO + 1'P_negotiation_2_2_DONE= 1
invariant : 1'P_electedPrimary_4 + 1'P_electedSecondary_4 + 1'P_negotiation_4_6_NONE + 1'P_poll__handlingMessage_4 + 1'P_poll__pollEnd_4 + 1'P_poll__waitingMessage_4 + 1'P_polling_4 + 1'P_sendAnnPs__broadcasting_4_1 + 1'P_sendAnnPs__broadcasting_4_2 + 1'P_sendAnnPs__broadcasting_4_3 + 1'P_sendAnnPs__broadcasting_4_4 + 1'P_sendAnnPs__broadcasting_4_5 + 1'P_sendAnnPs__broadcasting_4_6 + 1'P_startNeg__broadcasting_4_6= 1
invariant : 1'P_negotiation_6_6_NONE= 0
invariant : 1'P_negotiation_6_2_NONE + 1'P_negotiation_6_2_CO + 1'P_negotiation_6_2_DONE= 1
invariant : 1'P_negotiation_0_1_NONE= 0
invariant : 1'P_negotiation_3_3_NONE= 0
invariant : 1'P_sendAnnPs__broadcasting_0_2= 0
invariant : 1'P_negotiation_1_5_NONE + 1'P_negotiation_1_5_CO + 1'P_negotiation_1_5_DONE= 1
invariant : 1'P_negotiation_2_3_NONE + -1'P_negotiation_2_4_NONE + 1'P_startNeg__broadcasting_2_3= 0
invariant : 1'P_negotiation_3_1_NONE + -1'P_negotiation_3_2_NONE + 1'P_startNeg__broadcasting_3_2= 0
invariant : 1'P_negotiation_5_4_NONE + 1'P_negotiation_5_4_CO + 1'P_negotiation_5_4_DONE= 1
invariant : 1'P_negotiation_1_2_NONE + -1'P_negotiation_1_3_NONE + 1'P_startNeg__broadcasting_1_2= 0
invariant : -1'P_poll__waitingMessage_5 + 1'P_stage_5_NEG= 1
invariant : 1'P_negotiation_6_0_CO + 1'P_negotiation_6_0_DONE= 0
invariant : 1'P_negotiation_0_4_CO + 1'P_negotiation_0_4_DONE= 0
invariant : 1'P_negotiation_0_5_NONE= 0
invariant : 1'P_poll__waitingMessage_6 + 1'P_stage_6_PRIM + 1'P_stage_6_SEC= 0
invariant : 1'P_negotiation_4_1_NONE + -1'P_negotiation_4_2_NONE + 1'P_startNeg__broadcasting_4_2= 0
invariant : 1'P_negotiation_4_0_CO + 1'P_negotiation_4_0_DONE= 0
invariant : 1'P_negotiation_5_1_NONE + -1'P_negotiation_5_2_NONE + 1'P_startNeg__broadcasting_5_2= 0
invariant : 1'P_startNeg__broadcasting_0_3= 0
invariant : 1'P_electionInit_2 + -1'P_negotiation_2_1_NONE + 1'P_startNeg__broadcasting_2_1= 0
invariant : 1'P_negotiation_4_3_NONE + -1'P_negotiation_4_5_NONE + 1'P_startNeg__broadcasting_4_4= 0
invariant : 1'P_negotiation_1_0_NONE= 0
invariant : 1'P_negotiation_0_6_NONE= 0
invariant : 1'P_negotiation_3_4_NONE + 1'P_negotiation_3_4_CO + 1'P_negotiation_3_4_DONE= 1
invariant : -1'P_poll__waitingMessage_6 + 1'P_stage_6_NEG= 1
invariant : 1'P_electionInit_4 + -1'P_negotiation_4_1_NONE + 1'P_startNeg__broadcasting_4_1= 0
invariant : 1'P_negotiation_4_2_NONE + 1'P_negotiation_4_2_CO + 1'P_negotiation_4_2_DONE= 1
invariant : 1'P_electionInit_1 + -1'P_negotiation_1_2_NONE + 1'P_startNeg__broadcasting_1_1= 0
invariant : 1'P_negotiation_0_3_NONE= 0
invariant : 1'P_negotiation_6_2_NONE + -1'P_negotiation_6_3_NONE + 1'P_startNeg__broadcasting_6_3= 0
invariant : 1'P_negotiation_0_2_NONE= 0
invariant : 1'P_negotiation_0_6_CO + 1'P_negotiation_0_6_DONE= 0
invariant : 1'P_masterState_1_F_0 + 1'P_masterState_1_F_1 + 1'P_masterState_1_F_2 + 1'P_masterState_1_F_3 + 1'P_masterState_1_F_4 + 1'P_masterState_1_F_5 + 1'P_masterState_1_F_6 + 1'P_masterState_1_T_0 + 1'P_masterState_1_T_1 + 1'P_masterState_1_T_2 + 1'P_masterState_1_T_3 + 1'P_masterState_1_T_4 + 1'P_masterState_1_T_5 + 1'P_masterState_1_T_6= 1
invariant : 1'P_masterState_4_F_0 + 1'P_masterState_4_F_1 + 1'P_masterState_4_F_2 + 1'P_masterState_4_F_3 + 1'P_masterState_4_F_4 + 1'P_masterState_4_F_5 + 1'P_masterState_4_F_6 + 1'P_masterState_4_T_0 + 1'P_masterState_4_T_1 + 1'P_masterState_4_T_2 + 1'P_masterState_4_T_3 + 1'P_masterState_4_T_4 + 1'P_masterState_4_T_5 + 1'P_masterState_4_T_6= 1
invariant : 1'P_negotiation_1_1_NONE= 0
invariant : 1'P_negotiation_2_5_NONE + -1'P_negotiation_2_6_NONE + 1'P_startNeg__broadcasting_2_5= 0
invariant : 1'P_negotiation_6_1_NONE + 1'P_negotiation_6_1_CO + 1'P_negotiation_6_1_DONE= 1
invariant : 1'P_negotiation_2_5_NONE + 1'P_negotiation_2_5_CO + 1'P_negotiation_2_5_DONE= 1
invariant : 1'P_startNeg__broadcasting_0_2= 0
invariant : 1'P_masterState_3_F_0 + 1'P_masterState_3_F_1 + 1'P_masterState_3_F_2 + 1'P_masterState_3_F_3 + 1'P_masterState_3_F_4 + 1'P_masterState_3_F_5 + 1'P_masterState_3_F_6 + 1'P_masterState_3_T_0 + 1'P_masterState_3_T_1 + 1'P_masterState_3_T_2 + 1'P_masterState_3_T_3 + 1'P_masterState_3_T_4 + 1'P_masterState_3_T_5 + 1'P_masterState_3_T_6= 1
invariant : 1'P_negotiation_0_1_CO + 1'P_negotiation_0_1_DONE= 0
invariant : 1'P_negotiation_3_6_NONE + 1'P_negotiation_3_6_CO + 1'P_negotiation_3_6_DONE= 1
invariant : -1'P_poll__waitingMessage_1 + 1'P_stage_1_NEG= 1
invariant : 1'P_electedPrimary_1 + 1'P_electedSecondary_1 + 1'P_negotiation_1_6_NONE + 1'P_poll__handlingMessage_1 + 1'P_poll__pollEnd_1 + 1'P_poll__waitingMessage_1 + 1'P_polling_1 + 1'P_sendAnnPs__broadcasting_1_1 + 1'P_sendAnnPs__broadcasting_1_2 + 1'P_sendAnnPs__broadcasting_1_3 + 1'P_sendAnnPs__broadcasting_1_4 + 1'P_sendAnnPs__broadcasting_1_5 + 1'P_sendAnnPs__broadcasting_1_6 + 1'P_startNeg__broadcasting_1_6= 1
Exit code :137
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/
+ BINDIR=/home/mcc/BenchKit/
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ LTLCardinality = StateSpace ]]
+ /home/mcc/BenchKit//runeclipse.sh /home/mcc/execution LTLCardinality -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt
+ ulimit -s 65536
+ java -Dosgi.requiredJavaVersion=1.6 -Xss8m -Xms40m -Xmx8192m -Declipse.pde.launch=true -Dfile.encoding=UTF-8 -classpath /home/mcc/BenchKit//eclipse/plugins/org.eclipse.equinox.launcher_1.3.201.v20161025-1711.jar org.eclipse.equinox.launcher.Main -application fr.lip6.move.gal.application.pnmcc -data /home/mcc/BenchKit//workspace -os linux -ws gtk -arch x86_64 -nl en_US -consoleLog -pnfolder /home/mcc/execution -examination LTLCardinality -yices2path /home/mcc/BenchKit//yices/bin/yices -its -ltsminpath /home/mcc/BenchKit//lts_install_dir/ -smt
Jun 02, 2017 11:07:08 PM fr.lip6.move.gal.application.MccTranslator transformPNML
INFO: Parsing pnml file : /home/mcc/execution/model.pnml
Jun 02, 2017 11:07:09 PM fr.lip6.move.gal.nupn.PTNetReader loadFromXML
INFO: Load time of PNML (sax parser for PT used): 519 ms
Jun 02, 2017 11:07:09 PM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 4830 places.
Jun 02, 2017 11:07:09 PM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 8435 transitions.
Jun 02, 2017 11:07:11 PM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 3549 fixed domain variables (out of 4830 variables) in GAL type NeoElection_PT_6
Jun 02, 2017 11:07:11 PM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Found a total of 3549 constant array cells/variables (out of 4830 variables) in type NeoElection_PT_6
Jun 02, 2017 11:07:11 PM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: P_network_6_5_RP_3,P_masterList_3_5_4,P_network_1_2_AI_3,P_poll__networl_2_1_AskP_0,P_poll__networl_1_2_RP_5,P_poll__networl_2_4_RI_1,P_poll__networl_4_3_RP_3,P_network_6_2_AnnP_6,P_network_5_6_AnnP_6,P_poll__networl_3_0_AskP_4,P_poll__networl_5_2_AnnP_4,P_masterList_4_6_4,P_poll__networl_4_5_RP_0,P_masterList_0_2_4,P_poll__networl_3_4_RI_4,P_poll__networl_6_0_AnnP_1,P_poll__networl_1_2_RI_0,P_poll__networl_1_3_AI_2,P_network_1_3_AI_2,P_poll__networl_0_3_AI_6,P_masterList_4_4_6,P_network_5_5_RI_3,P_poll__networl_6_1_AI_6,P_network_5_2_RP_4,P_network_4_1_AI_3,P_poll__networl_3_6_AI_5,P_poll__networl_5_0_AskP_6,P_network_3_5_AskP_1,P_poll__networl_1_0_RI_3,P_network_5_2_AnnP_1,P_poll__networl_3_6_AskP_1,P_poll__networl_2_3_RP_1,P_poll__networl_6_3_AskP_6,P_network_2_1_AI_5,P_network_4_5_AnnP_1,P_poll__networl_0_0_AnnP_5,P_network_3_4_RI_1,P_network_4_3_AI_5,P_poll__networl_6_4_RP_1,P_poll__networl_5_0_AnsP_0,P_poll__networl_3_0_AskP_0,P_network_4_2_AI_1,P_masterList_4_1_6,P_poll__networl_6_6_AnnP_6,P_network_4_0_AnnP_3,P_network_3_5_RP_4,P_network_2_6_AnnP_4,P_network_4_0_RI_3,P_poll__networl_0_3_AnnP_0,P_network_6_2_RI_6,P_poll__networl_0_6_AskP_6,P_poll__networl_2_3_RI_3,P_network_3_4_RP_2,P_network_4_2_RP_1,P_poll__networl_3_5_AnnP_3,P_poll__networl_3_6_RP_1,P_poll__networl_3_3_RP_2,P_network_4_4_RP_3,P_network_3_6_AnnP_6,P_network_0_2_RP_3,P_poll__networl_6_4_AnnP_1,P_poll__networl_0_1_RP_5,P_network_5_2_AskP_2,P_network_0_0_AnnP_6,P_network_2_5_AnnP_4,P_poll__networl_1_6_AskP_6,P_masterList_2_4_0,P_poll__networl_4_4_AskP_2,P_poll__networl_6_4_RP_0,P_masterList_4_1_1,P_network_6_1_AskP_2,P_poll__networl_4_6_AnsP_0,P_masterList_0_5_1,P_network_4_0_RI_5,P_network_0_6_AI_4,P_poll__networl_2_0_RI_1,P_poll__networl_4_3_RI_6,P_network_0_1_AnnP_6,P_poll__networl_2_1_AskP_6,P_poll__networl_2_2_AnnP_0,P_poll__networl_5_1_AnnP_3,P_network_6_1_RP_4,P_network_4_0_AskP_5,P_network_1_0_AskP_5,P_poll__networl_3_2_RP_2,P_poll__networl_2_3_AI_1,P_masterList_4_2_6,P_network_6_1_RI_3,P_network_3_2_RI_5,P_network_1_3_AI_3,P_poll__networl_3_4_AskP_6,P_network_2_5_AskP_4,P_network_0_3_AI_5,P_poll__networl_5_0_AnnP_0,P_poll__networl_4_4_AnnP_0,P_poll__networl_6_5_AskP_0,P_poll__networl_6_5_RI_1,P_poll__networl_3_6_AnnP_5,P_poll__networl_6_0_RI_2,P_poll__networl_6_3_RP_2,P_network_5_2_RI_3,P_poll__networl_0_2_RI_5,P_network_3_4_AskP_1,P_poll__networl_5_1_RI_6,P_network_4_6_AskP_5,P_masterList_1_2_4,P_poll__networl_3_4_AskP_0,P_poll__networl_5_6_RI_4,P_network_6_1_AI_6,P_network_3_4_AnnP_6,P_network_2_2_AnnP_5,P_masterList_2_4_2,P_network_5_0_AnnP_2,P_network_2_5_RI_5,P_network_0_4_AnnP_1,P_network_1_6_RP_2,P_poll__networl_5_5_RP_0,P_network_1_0_AnnP_5,P_masterList_0_3_5,P_poll__networl_5_5_AskP_3,P_poll__networl_3_1_AI_1,P_poll__networl_4_3_AskP_5,P_poll__networl_2_3_RP_4,P_poll__networl_1_6_AskP_1,P_masterList_1_2_6,P_network_3_1_RI_5,P_poll__networl_1_3_RP_4,P_network_6_6_AI_2,P_network_4_6_RP_1,P_network_1_1_AI_2,P_network_5_2_AnnP_6,P_poll__networl_2_2_AnnP_6,P_poll__networl_0_2_AskP_5,P_poll__networl_0_2_RI_2,P_masterList_2_2_1,P_poll__networl_1_4_AI_3,P_poll__networl_0_6_AskP_0,P_poll__networl_4_6_RI_2,P_poll__networl_4_6_RI_3,P_network_6_1_RI_6,P_poll__networl_1_5_RI_4,P_poll__networl_1_2_AnnP_5,P_poll__networl_4_5_AnsP_0,P_network_0_2_AnnP_2,P_poll__networl_0_4_RI_3,P_poll__networl_4_6_RP_4,P_poll__networl_0_6_RI_5,P_network_4_6_RP_6,P_poll__networl_0_5_RI_5,P_poll__networl_4_1_AskP_5,P_poll__networl_4_5_RP_3,P_network_0_0_AskP_2,P_network_4_2_RI_3,P_poll__networl_6_0_AskP_4,P_poll__networl_0_2_AI_6,P_poll__networl_2_0_RI_2,P_network_1_4_AnnP_2,P_network_0_2_AI_2,P_poll__networl_0_5_RP_1,P_poll__networl_1_4_RI_6,P_poll__networl_3_4_AnnP_2,P_network_3_3_AnnP_4,P_network_3_2_AnnP_6,P_network_0_5_AskP_3,P_poll__networl_1_0_AI_6,P_network_5_4_RP_6,P_poll__networl_2_1_RP_3,P_masterList_1_4_3,P_network_1_3_AskP_1,P_poll__networl_5_0_AI_6,P_network_1_5_RP_1,P_network_3_0_AskP_3,P_poll__networl_2_2_RI_0,P_network_5_0_AskP_6,P_network_5_3_AnnP_6,P_poll__networl_1_4_AnnP_0,P_poll__networl_1_5_RI_1,P_network_0_6_RI_2,P_network_0_5_AskP_2,P_network_2_6_AskP_4,P_masterList_5_4_1,P_network_3_5_AskP_4,P_masterList_3_1_6,P_poll__networl_3_0_RP_5,P_masterList_0_6_2,P_poll__networl_5_5_AI_4,P_poll__networl_5_2_AnnP_0,P_network_2_6_RP_3,P_network_3_5_RP_3,P_poll__networl_1_0_AskP_1,P_poll__networl_1_5_RP_3,P_poll__networl_0_5_RP_3,P_poll__networl_1_3_AI_5,P_poll__networl_5_4_RP_1,P_network_2_5_AskP_2,P_poll__networl_6_3_RP_4,P_network_2_1_AskP_1,P_network_6_2_RI_5,P_poll__networl_0_3_RP_6,P_poll__networl_0_4_RI_2,P_poll__networl_1_1_AskP_2,P_masterList_6_2_2,P_network_2_2_AskP_2,P_network_4_5_RI_5,P_network_2_3_AskP_2,P_poll__networl_2_2_AnnP_4,P_masterList_6_5_5,P_poll__networl_2_6_RI_4,P_poll__networl_2_0_RP_0,P_network_0_4_RP_6,P_network_6_0_AnnP_1,P_network_6_4_RI_5,P_network_3_2_AskP_6,P_network_0_6_AskP_1,P_network_5_3_AskP_5,P_poll__networl_5_3_RP_3,P_network_2_2_RI_3,P_poll__networl_0_1_AnnP_2,P_poll__networl_4_6_AnnP_2,P_network_3_0_AskP_5,P_poll__networl_4_6_AskP_3,P_network_1_6_AnnP_1,P_poll__networl_4_4_RI_0,P_poll__networl_4_4_AI_1,P_network_5_6_RI_2,P_network_6_0_RP_6,P_poll__networl_4_0_RI_1,P_poll__networl_4_0_AI_5,P_network_4_0_AnnP_5,P_poll__networl_6_3_AI_5,P_network_3_1_RP_5,P_network_2_1_RI_3,P_network_1_5_RI_3,P_network_6_1_AnnP_3,P_network_0_6_RP_5,P_network_5_2_AskP_4,P_network_3_5_AI_5,P_network_1_3_AI_5,P_network_3_2_AnnP_4,P_poll__networl_4_2_AskP_1,P_poll__networl_5_2_AI_4,P_network_1_5_AI_1,P_network_2_2_AnnP_1,P_network_4_0_RI_1,P_poll__networl_0_2_RP_4,P_poll__networl_2_2_RP_0,P_network_3_5_AnnP_3,P_network_4_0_AskP_1,P_network_1_3_AskP_6,P_poll__networl_4_6_RP_1,P_poll__networl_6_2_AskP_6,P_poll__networl_2_5_AI_1,P_poll__networl_3_3_AskP_4,P_network_1_4_AskP_5,P_poll__networl_4_1_AI_1,P_network_1_6_AI_3,P_network_3_3_AskP_3,P_poll__networl_6_2_RI_5,P_network_2_2_RI_1,P_poll__networl_3_5_AskP_5,P_poll__networl_5_2_AnnP_1,P_network_3_6_AI_5,P_poll__networl_0_6_RP_4,P_network_1_0_AnnP_6,P_masterList_2_5_1,P_network_1_1_RI_5,P_poll__networl_3_6_RI_2,P_network_5_5_RI_4,P_poll__networl_4_1_RI_6,P_network_3_5_RI_4,P_poll__networl_4_2_RI_3,P_masterList_4_6_0,P_network_6_0_RP_1,P_network_5_4_AskP_5,P_poll__networl_0_3_RI_1,P_network_2_2_AI_1,P_poll__networl_3_0_RI_1,P_poll__networl_6_6_RI_0,P_network_2_3_AnnP_6,P_network_0_5_AI_1,P_network_1_5_AnnP_2,P_poll__networl_1_3_AskP_5,P_poll__networl_1_4_RP_1,P_network_4_2_RI_1,P_network_5_3_AskP_6,P_poll__networl_1_0_RP_6,P_network_4_3_AskP_1,P_masterList_2_1_5,P_network_5_6_AskP_2,P_poll__networl_2_5_RI_0,P_poll__networl_6_5_RP_0,P_network_1_3_AnnP_3,P_poll__networl_0_3_AnnP_2,P_poll__networl_6_4_RP_5,P_poll__networl_6_1_RP_2,P_poll__networl_2_2_AskP_6,P_poll__networl_4_0_AI_3,P_poll__networl_1_5_AnnP_6,P_poll__networl_1_6_RI_6,P_network_1_3_AskP_2,P_poll__networl_1_0_AskP_6,P_poll__networl_2_2_AI_6,P_network_3_0_AnnP_6,P_poll__networl_2_2_RP_2,P_network_0_5_RI_3,P_network_3_3_AI_6,P_network_4_6_AI_1,P_poll__networl_1_4_RP_6,P_poll__networl_2_1_RP_2,P_network_4_2_AskP_2,P_network_5_2_AnnP_5,P_network_0_1_AI_1,P_network_2_3_AI_3,P_poll__networl_4_0_RP_2,P_network_3_2_AnnP_5,P_network_1_4_RI_6,P_network_4_3_AnnP_2,P_poll__networl_2_6_RI_0,P_network_5_0_AI_2,P_poll__networl_0_4_AnnP_2,P_poll__networl_2_3_RP_5,P_poll__networl_3_2_AI_0,P_network_0_3_RP_3,P_network_2_6_RI_5,P_network_0_1_AI_6,P_network_2_0_AskP_1,P_network_3_0_AI_3,P_poll__networl_4_1_RI_5,P_network_1_5_RP_2,P_poll__networl_4_4_AskP_4,P_masterList_5_2_3,P_network_6_3_AskP_4,P_poll__networl_2_5_RP_6,P_poll__networl_0_2_AnsP_0,P_poll__networl_4_0_AnnP_1,P_network_5_4_RP_2,P_network_1_2_RI_1,P_network_6_0_AnnP_5,P_poll__networl_3_1_RP_1,P_poll__networl_6_3_AnnP_3,P_poll__networl_6_5_RI_4,P_network_4_3_AnnP_4,P_poll__networl_6_3_AskP_0,P_masterList_2_5_5,P_network_5_6_AI_3,P_network_0_0_RP_2,P_masterList_4_3_4,P_network_5_1_AI_4,P_network_2_0_RP_6,P_network_0_1_AnnP_1,P_network_3_6_AnnP_2,P_masterList_5_5_3,P_masterList_1_2_1,P_network_2_5_AI_4,P_masterList_6_4_4,P_poll__networl_5_3_AnnP_3,P_poll__networl_1_4_AnnP_5,P_poll__networl_2_5_RP_2,P_masterList_2_1_1,P_poll__networl_2_5_AnnP_4,P_poll__networl_1_1_AI_2,P_poll__networl_3_1_AskP_0,P_poll__networl_6_6_RP_6,P_network_2_6_AskP_6,P_poll__networl_3_3_AnnP_2,P_network_1_2_AskP_4,P_network_2_3_AnnP_2,P_network_0_4_AskP_4,P_network_2_3_RP_1,P_network_0_3_RI_6,P_poll__networl_0_4_RI_4,P_poll__networl_2_2_AskP_2,P_network_4_0_RP_6,P_poll__networl_3_0_AnnP_0,P_network_2_5_AskP_6,P_poll__networl_4_4_RI_2,P_network_6_2_AI_2,P_network_4_6_AnnP_5,P_network_3_4_RI_5,P_poll__networl_3_0_RI_4,P_masterList_4_1_3,P_masterList_5_2_1,P_poll__networl_4_1_AskP_6,P_poll__networl_1_2_AI_1,P_poll__networl_1_5_AI_6,P_poll__networl_3_0_AI_0,P_network_6_5_AnnP_2,P_poll__networl_1_3_AI_3,P_network_0_0_AI_6,P_network_5_0_AnnP_5,P_poll__networl_1_3_RI_5,P_poll__networl_0_6_AI_5,P_poll__networl_6_5_AI_1,P_network_1_0_AnnP_4,P_network_3_5_RI_6,P_poll__networl_2_6_RI_5,P_poll__networl_0_1_AnnP_6,P_poll__networl_2_0_AskP_3,P_poll__networl_0_3_AskP_6,P_poll__networl_3_6_RI_6,P_network_2_1_RI_5,P_poll__networl_3_4_RI_0,P_dead_1,P_poll__networl_1_1_RI_2,P_poll__networl_6_2_RI_2,P_poll__networl_0_1_AskP_2,P_poll__networl_6_4_AI_4,P_network_1_6_RP_1,P_poll__networl_1_2_AskP_6,P_poll__networl_3_0_AI_5,P_poll__networl_0_5_AnnP_1,P_poll__networl_6_0_AnnP_4,P_network_0_5_AnnP_5,P_poll__networl_5_1_RP_0,P_network_6_6_AskP_1,P_network_3_0_AI_5,P_poll__networl_5_5_AskP_5,P_poll__networl_2_3_AskP_3,P_poll__networl_4_6_RP_3,P_poll__networl_3_5_AI_5,P_network_6_5_AI_6,P_poll__networl_3_0_AskP_5,P_poll__networl_6_2_AI_0,P_poll__networl_5_3_AI_1,P_poll__networl_6_6_RI_2,P_network_5_6_AskP_6,P_masterList_0_3_4,P_masterList_4_3_0,P_network_0_2_RP_6,P_poll__networl_0_2_RP_1,P_network_5_0_RI_6,P_network_1_1_AI_6,P_poll__networl_4_2_AskP_4,P_network_3_5_RI_2,P_network_4_3_AskP_2,P_poll__networl_3_2_RP_1,P_poll__networl_6_5_RP_2,P_poll__networl_3_5_RP_4,P_network_5_6_RI_6,P_network_4_4_AI_6,P_poll__networl_4_0_AskP_4,P_poll__networl_4_3_AI_4,P_poll__networl_5_3_RP_2,P_network_0_5_AI_6,P_poll__networl_0_1_RI_1,P_network_6_1_RP_5,P_network_6_1_AnnP_5,P_network_6_0_AI_5,P_poll__networl_6_0_RP_0,P_poll__networl_1_4_RP_0,P_network_6_2_RI_2,P_network_2_6_RI_2,P_masterList_2_3_3,P_network_2_0_RP_5,P_masterList_5_3_6,P_poll__networl_1_1_RI_1,P_masterList_5_3_0,P_network_3_6_AI_3,P_network_4_2_AskP_4,P_network_4_4_AskP_6,P_poll__networl_3_0_AnnP_2,P_poll__networl_5_2_AI_0,P_network_3_0_RI_3,P_network_2_3_RI_1,P_masterList_5_6_4,P_poll__networl_3_0_RI_5,P_poll__networl_6_6_AI_2,P_poll__networl_4_5_AskP_1,P_poll__networl_2_2_AnsP_0,P_network_2_1_AI_1,P_poll__networl_2_0_AnnP_4,P_poll__networl_2_4_AnnP_1,P_network_3_1_AskP_6,P_network_1_6_AI_5,P_poll__networl_3_3_AskP_1,P_network_6_3_RI_6,P_network_1_3_AI_6,P_network_4_2_AskP_1,P_poll__networl_3_0_RI_6,P_network_3_0_AnnP_3,P_network_5_4_AI_5,P_network_2_3_AskP_4,P_poll__networl_0_6_AI_2,P_network_0_3_AI_6,P_network_1_0_AI_6,P_network_2_2_AskP_6,P_poll__networl_6_1_AnnP_1,P_poll__networl_6_2_RI_0,P_poll__networl_5_1_RP_1,P_poll__networl_4_3_AnnP_2,P_network_0_0_AI_4,P_network_0_5_RI_2,P_network_1_2_AskP_3,P_network_0_2_AI_6,P_network_0_4_AnnP_3,P_poll__networl_2_1_RI_2,P_poll__networl_5_6_AI_1,P_network_5_2_AI_1,P_network_4_4_RP_2,P_poll__networl_3_3_RP_4,P_masterList_4_6_2,P_masterList_6_4_6,P_network_4_3_RP_4,P_network_0_0_RI_4,P_network_2_3_RP_6,P_network_0_4_AI_4,P_network_0_1_RI_1,P_poll__networl_5_5_RP_6,P_poll__networl_2_0_AI_5,P_masterList_0_2_1,P_poll__networl_2_4_RP_3,P_poll__networl_4_2_RI_5,P_poll__networl_0_0_RP_6,P_network_6_1_RP_2,P_network_3_3_AI_2,P_poll__networl_4_1_AnsP_0,P_poll__networl_6_1_AI_0,P_poll__networl_3_6_AI_0,P_network_5_4_RP_1,P_network_6_6_AnnP_3,P_poll__networl_5_6_RI_3,P_poll__networl_6_3_AI_4,P_poll__networl_1_0_RP_1,P_poll__networl_0_4_AskP_5,P_network_5_5_AnnP_5,P_poll__networl_2_4_AskP_4,P_poll__networl_4_1_RP_4,P_masterList_6_5_3,P_network_3_6_RP_4,P_network_5_6_RP_1,P_poll__networl_0_0_AI_2,P_network_0_1_RP_5,P_masterList_5_2_6,P_network_0_6_AskP_5,P_poll__networl_5_1_AskP_5,P_poll__networl_0_5_AnnP_0,P_network_2_1_AnnP_5,P_network_5_1_AnnP_3,P_network_3_1_RP_4,P_poll__networl_3_4_AI_5,P_poll__networl_5_4_AI_0,P_poll__networl_4_2_RI_0,P_network_0_4_RI_5,P_poll__networl_0_6_RI_4,P_masterList_1_3_6,P_poll__networl_4_6_AI_2,P_masterList_6_4_3,P_poll__networl_3_4_RI_3,P_network_3_2_AI_4,P_poll__networl_4_3_AI_1,P_poll__networl_6_0_RP_2,P_network_0_6_AnnP_6,P_poll__networl_1_4_AskP_1,P_poll__networl_4_4_AI_2,P_masterList_2_5_3,P_poll__networl_5_5_RP_4,P_masterList_0_1_0,P_network_5_3_RI_2,P_poll__networl_3_6_AnnP_2,P_poll__networl_4_3_RP_2,P_poll__networl_4_6_AI_5,P_poll__networl_5_6_AI_5,P_network_4_1_RI_3,P_network_6_3_AI_1,P_network_3_1_RP_2,P_poll__networl_5_5_RI_0,P_network_3_2_AI_6,P_poll__networl_5_3_RP_5,P_poll__networl_1_4_AI_5,P_poll__networl_3_3_RP_3,P_network_1_0_AI_3,P_poll__networl_1_4_RP_4,P_poll__networl_2_5_AI_5,P_poll__networl_0_3_AI_4,P_network_0_2_AnnP_3,P_poll__networl_4_1_RI_0,P_poll__networl_3_2_AnnP_0,P_masterList_1_3_3,P_poll__networl_0_6_AskP_1,P_network_1_3_RI_6,P_network_4_5_AnnP_6,P_poll__networl_1_5_AnnP_2,P_network_2_0_AskP_3,P_poll__networl_1_1_AI_1,P_network_0_0_RP_5,P_network_3_4_AskP_3,P_poll__networl_2_4_AI_5,P_network_0_4_AI_2,P_poll__networl_6_0_AI_6,P_network_0_4_AskP_6,P_poll__networl_1_3_RI_3,P_poll__networl_3_2_RP_0,P_network_0_2_AskP_1,P_poll__networl_3_1_RI_2,P_network_2_3_RP_5,P_poll__networl_1_0_AnnP_0,P_poll__networl_1_6_RI_4,P_masterList_3_6_6,P_poll__networl_6_2_RP_5,P_network_1_3_AnnP_1,P_masterList_6_5_1,P_poll__networl_2_6_RP_0,P_poll__networl_1_6_RP_4,P_poll__networl_5_6_RI_5,P_network_2_5_RI_2,P_poll__networl_5_6_AI_4,P_network_1_4_RI_4,P_poll__networl_3_6_RP_5,P_network_5_2_RP_3,P_poll__networl_1_2_AskP_5,P_network_6_0_RP_5,P_poll__networl_1_0_RP_5,P_masterList_1_3_0,P_masterList_4_4_0,P_poll__networl_1_3_RI_4,P_network_0_4_RI_4,P_dead_3,P_network_5_4_AnnP_6,P_network_6_0_AskP_4,P_masterList_4_2_4,P_network_6_6_AI_3,P_network_1_4_AskP_1,P_masterList_2_1_4,P_network_0_2_RI_3,P_poll__networl_5_3_RI_4,P_masterList_5_2_2,P_network_4_2_AnnP_5,P_poll__networl_5_6_AI_2,P_network_1_4_AnnP_6,P_network_2_1_RP_3,P_poll__networl_3_4_RP_5,P_poll__networl_2_0_RI_0,P_poll__networl_3_4_RP_4,P_network_6_4_AI_6,P_network_5_1_AskP_1,P_network_2_3_RI_4,P_network_4_6_AnnP_6,P_poll__networl_3_1_AnnP_1,P_network_1_2_RP_3,P_masterList_5_5_4,P_network_6_1_AI_2,P_network_5_4_RI_1,P_poll__networl_3_3_AskP_2,P_network_5_5_RI_6,P_network_1_6_RP_5,P_masterList_4_1_5,P_poll__networl_0_4_AnnP_3,P_poll__networl_6_2_RP_6,P_network_0_3_RI_3,P_network_5_4_RI_4,P_network_0_0_AI_1,P_network_1_6_AskP_4,P_poll__networl_4_6_AnnP_5,P_masterList_5_1_4,P_poll__networl_6_4_AskP_2,P_network_3_5_AskP_2,P_poll__networl_0_3_AskP_4,P_network_4_6_AI_3,P_poll__networl_4_3_AskP_4,P_poll__networl_0_6_AI_4,P_poll__networl_1_4_AnnP_4,P_network_5_5_RI_1,P_poll__networl_6_1_RI_2,P_network_5_1_AskP_5,P_poll__networl_1_4_AnnP_2,P_poll__networl_6_4_RP_4,P_network_6_2_AnnP_4,P_network_4_2_AskP_6,P_network_1_0_AnnP_2,P_network_6_1_AI_5,P_poll__networl_2_1_AnnP_4,P_poll__networl_5_6_RI_0,P_poll__networl_0_5_AnnP_6,P_network_4_3_RP_3,P_network_4_0_AskP_4,P_poll__networl_4_2_AI_3,P_poll__networl_5_0_AI_0,P_poll__networl_4_5_RP_4,P_masterList_5_5_5,P_masterList_1_2_3,P_network_6_5_AskP_2,P_poll__networl_2_5_RP_3,P_network_0_4_RI_2,P_poll__networl_4_0_AI_0,P_network_1_1_AskP_2,P_network_2_2_AnnP_2,P_poll__networl_3_5_RI_1,P_poll__networl_5_2_AnnP_2,P_network_0_2_RI_5,P_masterList_4_6_6,P_network_5_5_AskP_6,P_poll__networl_3_1_AskP_6,P_poll__networl_5_4_AskP_6,P_network_3_2_AskP_2,P_network_0_5_AI_5,P_poll__networl_3_1_RP_6,P_poll__networl_3_3_AI_2,P_poll__networl_5_6_AskP_4,P_network_0_3_RI_4,P_network_5_6_RP_3,P_network_0_0_AskP_5,P_network_5_5_AskP_5,P_network_1_3_AskP_3,P_network_6_5_RI_5,P_masterList_2_4_1,P_network_2_4_AskP_2,P_masterList_4_2_5,P_poll__networl_6_4_AI_5,P_poll__networl_6_0_AnsP_0,P_poll__networl_3_1_RP_5,P_network_0_0_AnnP_1,P_network_0_4_AskP_5,P_network_0_6_AnnP_5,P_network_6_5_AnnP_4,P_masterList_3_2_5,P_electionFailed_1,P_network_3_3_RI_3,P_poll__networl_4_1_AnnP_1,P_network_0_4_AskP_1,P_network_2_3_RI_5,P_poll__networl_0_2_AI_4,P_poll__networl_1_5_AnnP_0,P_poll__networl_0_4_AI_1,P_poll__networl_4_6_AnnP_1,P_masterList_0_6_1,P_masterList_6_2_3,P_network_4_0_RP_4,P_network_2_0_AI_4,P_network_3_4_RP_3,P_network_1_6_RI_4,P_poll__networl_1_1_AI_3,P_poll__networl_4_1_AI_5,P_poll__networl_5_4_AI_5,P_network_0_4_RP_1,P_network_6_3_AskP_5,P_poll__networl_1_4_AskP_3,P_masterList_1_5_4,P_network_3_5_AskP_3,P_poll__networl_2_6_AnnP_1,P_poll__networl_5_1_AskP_4,P_network_0_3_RI_2,P_network_4_4_RI_3,P_masterList_1_4_4,P_network_0_1_AnnP_4,P_poll__networl_4_4_AskP_5,P_network_3_4_AnnP_1,P_poll__networl_5_3_AnsP_0,P_network_3_2_RI_6,P_poll__networl_1_1_RP_5,P_network_3_3_RI_1,P_poll__networl_5_3_AI_4,P_network_0_0_AI_5,P_network_4_6_AnnP_2,P_poll__networl_5_3_AI_3,P_poll__networl_3_2_AskP_0,P_masterList_3_5_2,P_poll__networl_3_5_RI_6,P_network_6_2_AskP_5,P_poll__networl_1_4_AskP_0,P_poll__networl_0_3_RI_4,P_poll__networl_0_1_AskP_4,P_masterList_2_6_0,P_network_3_6_AskP_5,P_network_5_2_RP_1,P_network_4_2_AnnP_2,P_network_1_0_AskP_1,P_network_0_2_AnnP_6,P_poll__networl_2_3_AI_0,P_poll__networl_3_1_RP_0,P_poll__networl_0_1_RI_5,P_masterList_6_3_2,P_network_3_1_AnnP_2,P_poll__networl_6_2_AI_1,P_network_3_1_AskP_1,P_network_3_4_RI_3,P_poll__networl_1_3_AnsP_0,P_network_2_0_AskP_6,P_poll__networl_3_3_RP_0,P_poll__networl_6_4_RI_4,P_network_1_5_AI_3,P_electionFailed_6,P_network_3_6_AskP_1,P_network_1_2_RP_1,P_poll__networl_0_2_RP_5,P_poll__networl_0_0_AI_6,P_poll__networl_3_2_AskP_2,P_poll__networl_2_0_RP_1,P_poll__networl_2_1_AI_3,P_network_2_6_AskP_1,P_poll__networl_6_6_RI_3,P_poll__networl_5_4_RI_3,P_network_2_1_AI_6,P_poll__networl_4_5_AnnP_4,P_masterList_4_2_0,P_network_0_2_RP_2,P_poll__networl_2_1_RI_4,P_poll__networl_5_2_AskP_1,P_network_6_3_RI_4,P_network_0_3_RP_5,P_network_5_1_AskP_2,P_network_1_1_RP_5,P_masterList_0_4_4,P_poll__networl_1_2_AskP_0,P_network_6_0_AI_4,P_poll__networl_3_5_RP_1,P_poll__networl_0_0_RI_2,P_network_1_0_AI_1,P_poll__networl_1_1_RP_6,P_poll__networl_6_2_RP_0,P_network_2_3_AI_5,P_network_4_0_RP_2,P_poll__networl_0_1_AI_3,P_network_0_0_AI_3,P_poll__networl_1_1_RI_4,P_poll__networl_1_2_AskP_4,P_network_0_1_AI_4,P_poll__networl_6_5_AnnP_4,P_poll__networl_0_1_AI_0,P_poll__networl_6_5_AskP_1,P_network_3_5_RP_2,P_network_1_5_AskP_2,P_poll__networl_0_1_AI_4,P_poll__networl_1_1_RI_3,P_network_0_3_AI_4,P_network_0_6_AI_3,P_poll__networl_1_0_AnnP_2,P_network_2_6_RI_4,P_poll__networl_0_4_RP_6,P_poll__networl_2_6_RP_6,P_network_5_5_AskP_3,P_network_5_4_AskP_6,P_network_2_2_RP_6,P_poll__networl_0_5_RI_3,P_network_2_2_AnnP_4,P_poll__networl_6_3_RP_1,P_network_1_6_AI_6,P_poll__networl_6_1_AI_5,P_network_3_3_AnnP_5,P_poll__networl_6_2_AnnP_1,P_network_1_2_AnnP_3,P_network_2_6_AnnP_6,P_network_3_3_AI_1,P_poll__networl_5_6_RI_1,P_poll__networl_2_2_AskP_3,P_poll__networl_5_5_AnnP_1,P_network_2_5_AnnP_6,P_poll__networl_3_3_AskP_0,P_poll__networl_4_0_RP_1,P_poll__networl_2_4_AI_6,P_poll__networl_3_5_RI_4,P_masterList_3_2_6,P_poll__networl_2_4_AnsP_0,P_network_3_2_AnnP_1,P_poll__networl_2_1_AI_0,P_poll__networl_4_1_AI_6,P_network_6_6_AI_4,P_poll__networl_0_6_AI_0,P_network_0_5_RI_6,P_poll__networl_1_6_AI_4,P_poll__networl_5_1_AI_5,P_masterList_4_2_3,P_masterList_6_3_4,P_network_6_6_AnnP_4,P_poll__networl_3_3_AI_6,P_poll__networl_6_6_AskP_4,P_poll__networl_3_0_RP_1,P_network_0_5_RP_4,P_network_1_3_RP_5,P_network_1_5_RP_5,P_poll__networl_4_6_RP_0,P_network_1_3_RP_1,P_poll__networl_1_1_AnnP_2,P_network_1_4_AnnP_3,P_poll__networl_1_3_AskP_1,P_poll__networl_6_3_RI_5,P_masterList_6_5_2,P_masterList_3_2_3,P_poll__networl_0_3_RP_0,P_poll__networl_1_3_AskP_4,P_masterList_3_3_4,P_poll__networl_4_5_AI_3,P_network_4_1_AskP_4,P_poll__networl_1_5_AskP_4,P_network_6_5_AI_4,P_network_1_0_RP_5,P_network_5_3_AnnP_1,P_poll__networl_3_6_RP_2,P_network_0_5_RI_5,P_network_5_2_AI_2,P_network_4_4_AI_2,P_network_4_3_AI_4,P_poll__networl_4_4_AnsP_0,P_network_2_0_AnnP_4,P_poll__networl_3_4_RP_6,P_poll__networl_1_2_AnnP_2,P_network_5_4_RI_3,P_network_0_5_RI_1,P_poll__networl_4_5_AnnP_6,P_poll__networl_2_6_RP_3,P_network_0_3_AskP_6,P_poll__networl_1_1_AnnP_3,P_poll__networl_3_4_RP_3,P_network_2_2_AnnP_3,P_poll__networl_5_5_RP_5,P_network_1_0_AnnP_1,P_network_1_2_RI_4,P_masterList_5_5_6,P_poll__networl_1_0_AskP_2,P_network_2_0_AI_3,P_network_3_0_AI_4,P_network_3_6_RI_2,P_network_0_2_AskP_2,P_poll__networl_4_1_AskP_4,P_network_0_4_AI_6,P_poll__networl_6_5_AI_2,P_network_5_1_AnnP_4,P_network_3_1_RI_1,P_poll__networl_0_0_AI_3,P_network_3_0_AnnP_4,P_poll__networl_3_1_AnnP_5,P_poll__networl_2_5_AI_4,P_poll__networl_3_3_AI_1,P_network_1_2_AskP_2,P_poll__networl_0_0_AskP_4,P_poll__networl_4_3_AskP_0,P_poll__networl_0_0_AskP_0,P_network_1_3_AnnP_5,P_network_6_0_RP_3,P_poll__networl_3_1_RI_4,P_masterList_6_5_6,P_network_6_1_AskP_4,P_poll__networl_2_2_AskP_4,P_poll__networl_6_2_AnnP_6,P_poll__networl_1_2_AI_2,P_network_4_0_AnnP_4,P_masterList_0_2_0,P_poll__networl_5_6_RI_6,P_poll__networl_2_2_AnnP_3,P_poll__networl_5_4_AI_4,P_network_5_1_RI_4,P_poll__networl_6_6_AskP_6,P_masterList_0_5_3,P_poll__networl_0_3_RP_4,P_network_1_1_AskP_1,P_network_1_4_AI_6,P_network_4_4_AskP_4,P_network_5_4_RI_6,P_poll__networl_2_2_AskP_1,P_network_0_5_AI_3,P_masterList_6_2_0,P_network_3_0_RI_1,P_network_3_3_RI_2,P_network_0_3_RI_1,P_poll__networl_4_1_AnnP_2,P_network_4_3_RI_4,P_network_2_3_RP_3,P_poll__networl_0_4_RI_1,P_poll__networl_2_1_AI_4,P_network_5_5_AI_2,P_masterList_2_3_5,P_network_0_4_AskP_2,P_network_4_4_AnnP_4,P_poll__networl_4_2_AnnP_3,P_poll__networl_0_4_RI_5,P_poll__networl_2_5_RI_6,P_poll__networl_1_6_AnnP_3,P_poll__networl_2_4_RI_5,P_network_4_3_RI_5,P_network_3_5_AskP_6,P_network_4_0_RP_3,P_poll__networl_5_2_AskP_2,P_poll__networl_6_0_RP_6,P_poll__networl_2_5_AI_3,P_network_2_3_AI_1,P_poll__networl_2_5_AI_6,P_masterList_6_2_5,P_network_3_6_RI_3,P_poll__networl_2_0_AI_0,P_poll__networl_0_4_AskP_2,P_poll__networl_5_5_RI_5,P_poll__networl_6_1_AnnP_6,P_masterList_2_1_3,P_network_0_1_RI_4,P_poll__networl_2_2_RI_5,P_network_0_3_AI_2,P_network_3_1_AI_2,P_network_5_4_AskP_4,P_network_2_4_AI_4,P_masterList_0_4_1,P_poll__networl_6_5_AnnP_5,P_masterList_6_6_5,P_poll__networl_5_1_RI_0,P_poll__networl_3_3_AnnP_0,P_network_5_1_RP_3,P_poll__networl_1_4_RP_3,P_poll__networl_5_1_RI_4,P_poll__networl_1_0_AI_4,P_poll__networl_5_5_AI_0,P_network_5_4_RP_5,P_poll__networl_6_3_RI_2,P_network_5_5_RP_5,P_poll__networl_3_1_AnnP_4,P_network_3_2_RI_4,P_network_6_0_AnnP_6,P_poll__networl_3_2_RI_4,P_poll__networl_6_5_AnnP_1,P_poll__networl_3_5_AskP_6,P_poll__networl_6_6_RP_2,P_masterList_5_3_4,P_poll__networl_3_3_AskP_5,P_masterList_0_2_6,P_poll__networl_4_2_RP_2,P_network_6_3_AI_3,P_poll__networl_2_6_RI_2,P_masterList_0_3_1,P_masterList_1_4_6,P_network_2_2_RP_4,P_poll__networl_4_1_AskP_0,P_network_1_2_AskP_5,P_network_6_3_RP_5,P_network_0_1_RP_3,P_poll__networl_5_2_RP_2,P_poll__networl_4_6_RI_4,P_network_5_5_RI_5,P_network_6_6_RI_6,P_poll__networl_1_6_RP_2,P_network_1_5_RI_5,P_masterList_3_3_1,P_network_1_5_AskP_3,P_network_1_3_RP_3,P_network_3_0_AI_2,P_network_1_6_AskP_5,P_poll__networl_3_0_AI_6,P_poll__networl_2_0_AskP_4,P_network_4_4_RI_5,P_network_6_1_AI_4,P_network_0_2_AskP_5,P_poll__networl_5_3_AI_5,P_masterList_0_4_3,P_network_0_2_RP_5,P_network_1_3_RP_2,P_poll__networl_0_2_RP_3,P_network_3_1_AnnP_6,P_network_1_1_AskP_3,P_network_2_4_AnnP_1,P_network_5_2_AI_3,P_poll__networl_2_6_AskP_2,P_network_2_3_AskP_5,P_poll__networl_4_2_AnnP_1,P_poll__networl_1_3_AnnP_4,P_network_6_4_AskP_2,P_network_0_4_RI_1,P_poll__networl_2_0_AnsP_0,P_masterList_0_5_2,P_network_6_3_RP_6,P_poll__networl_5_0_AskP_5,P_poll__networl_2_6_AI_3,P_network_1_3_AI_4,P_network_4_1_AI_5,P_poll__networl_1_2_AI_4,P_network_4_5_RP_6,P_network_0_6_RP_1,P_poll__networl_5_0_AskP_4,P_poll__networl_2_4_RP_1,P_network_5_3_AnnP_4,P_network_1_3_RI_1,P_network_4_2_AskP_3,P_poll__networl_0_6_AskP_3,P_poll__networl_3_4_AnnP_5,P_network_6_5_AskP_3,P_network_5_3_RP_6,P_network_6_3_RP_1,P_poll__networl_4_2_RP_1,P_network_3_2_AnnP_2,P_poll__networl_1_0_AI_5,P_network_6_6_RP_6,P_network_5_3_RI_3,P_poll__networl_4_1_AI_0,P_network_6_4_AI_4,P_poll__networl_5_1_AnnP_4,P_network_4_5_AI_5,P_network_6_3_RI_5,P_poll__networl_0_0_RI_1,P_poll__networl_4_6_AskP_5,P_network_2_1_RP_5,P_network_2_5_RP_4,P_poll__networl_4_6_AI_6,P_network_2_1_RI_4,P_poll__networl_1_3_AskP_3,P_network_4_3_RP_1,P_network_6_5_AnnP_6,P_poll__networl_3_6_AI_6,P_poll__networl_3_6_RI_5,P_network_6_2_AI_6,P_masterList_1_6_1,P_poll__networl_6_6_AI_1,P_network_2_1_RP_2,P_electionFailed_4,P_network_0_0_AnnP_3,P_network_1_5_AI_6,P_poll__networl_1_4_RI_0,P_network_4_1_RP_5,P_network_2_0_AnnP_5,P_network_2_5_AI_5,P_poll__networl_0_1_AI_5,P_network_1_2_RP_2,P_masterList_3_6_0,P_poll__networl_6_5_AI_5,P_network_3_5_AskP_5,P_poll__networl_4_5_AskP_0,P_network_5_5_AskP_4,P_network_6_6_AnnP_6,P_poll__networl_6_4_RI_5,P_network_0_6_RI_5,P_network_6_4_RI_3,P_poll__networl_5_2_RP_6,P_poll__networl_2_4_AnnP_3,P_network_5_1_RI_1,P_poll__networl_4_5_RI_1,P_poll__networl_1_6_RI_5,P_network_1_4_AI_3,P_network_5_3_AnnP_3,P_poll__networl_5_1_RP_6,P_network_5_6_AnnP_3,P_network_4_6_RP_3,P_network_0_6_AskP_6,P_network_2_3_AskP_3,P_network_1_6_RI_3,P_poll__networl_3_5_RP_0,P_poll__networl_5_1_RP_4,P_poll__networl_4_1_RI_3,P_masterList_2_1_2,P_network_1_3_AnnP_4,P_poll__networl_6_3_AnnP_1,P_poll__networl_1_1_AnnP_5,P_masterList_2_2_4,P_poll__networl_0_6_AnnP_5,P_network_5_4_RI_2,P_poll__networl_4_5_AnnP_5,P_poll__networl_4_4_RI_1,P_masterList_3_1_3,P_poll__networl_3_5_AnnP_2,P_poll__networl_2_1_AskP_5,P_poll__networl_0_4_RI_6,P_network_6_4_AskP_6,P_poll__networl_4_3_AI_3,P_network_2_2_RP_5,P_network_5_2_RP_6,P_network_6_4_RP_2,P_poll__networl_0_2_AnnP_6,P_poll__networl_6_1_RI_0,P_poll__networl_0_0_RI_0,P_masterList_1_5_2,P_network_6_5_RI_1,P_network_6_3_AskP_2,P_poll__networl_3_0_AnnP_6,P_poll__networl_5_6_AskP_2,P_poll__networl_2_5_RP_0,P_poll__networl_4_1_RP_1,P_network_1_0_AI_2,P_poll__networl_5_3_AskP_2,P_network_1_6_AnnP_6,P_network_4_6_AnnP_3,P_poll__networl_6_4_AI_3,P_poll__networl_2_0_RP_3,P_poll__networl_4_1_AskP_2,P_poll__networl_4_6_AskP_2,P_poll__networl_3_0_AnnP_1,P_poll__networl_5_5_AI_5,P_network_6_3_AskP_6,P_poll__networl_3_4_AI_2,P_network_1_2_AnnP_5,P_network_4_6_AI_5,P_poll__networl_5_3_AI_2,P_network_5_1_RP_5,P_network_6_2_RI_3,P_poll__networl_1_5_AI_1,P_poll__networl_6_1_AnnP_4,P_poll__networl_2_0_RI_6,P_poll__networl_0_5_AnnP_3,P_poll__networl_3_4_RI_5,P_poll__networl_4_1_AnnP_5,P_network_4_5_AskP_5,P_poll__networl_2_0_AnnP_2,P_masterList_5_6_0,P_poll__networl_3_0_RI_2,P_poll__networl_3_1_AskP_2,P_network_5_6_RP_6,P_poll__networl_3_2_AskP_5,P_network_6_0_RP_2,P_poll__networl_0_5_RI_0,P_poll__networl_0_0_AskP_6,P_network_4_5_RP_3,P_network_2_4_AI_2,P_poll__networl_3_6_AI_4,P_network_6_1_AnnP_4,P_poll__networl_0_3_AnnP_3,P_network_1_2_RI_5,P_poll__networl_2_2_AnnP_1,P_poll__networl_2_4_AnnP_0,P_network_0_0_RI_2,P_poll__networl_0_1_AnnP_0,P_poll__networl_6_0_RI_0,P_masterList_1_1_6,P_network_4_2_RP_5,P_poll__networl_0_1_AI_2,P_electionFailed_0,P_network_4_1_AI_4,P_poll__networl_6_6_AskP_0,P_network_3_0_AI_6,P_poll__networl_6_2_AnnP_2,P_poll__networl_5_0_AnnP_6,P_network_3_6_AskP_6,P_poll__networl_3_2_RP_6,P_network_3_4_AskP_4,P_poll__networl_6_0_RI_3,P_network_4_2_AI_4,P_poll__networl_0_6_AnnP_6,P_network_0_4_RI_6,P_poll__networl_6_2_AI_5,P_poll__networl_2_3_RP_0,P_poll__networl_1_5_AnnP_4,P_poll__networl_2_6_AI_0,P_poll__networl_6_0_AnnP_5,P_poll__networl_2_6_AskP_0,P_poll__networl_6_5_AI_0,P_network_0_2_AskP_4,P_network_5_5_AI_4,P_poll__networl_5_0_RP_0,P_poll__networl_4_4_RP_1,P_network_0_1_AI_5,P_poll__networl_0_5_RP_4,P_poll__networl_4_0_AI_2,P_poll__networl_5_4_RI_6,P_masterList_1_5_0,P_network_5_1_AnnP_2,P_network_3_2_RP_1,P_poll__networl_0_0_AI_5,P_network_2_0_AnnP_1,P_poll__networl_1_1_AskP_5,P_poll__networl_5_4_AI_1,P_poll__networl_4_2_RI_2,P_masterList_1_4_5,P_network_6_0_AskP_3,P_poll__networl_1_6_AI_1,P_poll__networl_3_5_RI_0,P_masterList_4_1_4,P_poll__networl_5_5_AnnP_5,P_network_4_1_AnnP_3,P_network_6_1_RP_1,P_poll__networl_3_4_AskP_2,P_poll__networl_3_2_AI_5,P_network_6_1_AnnP_2,P_network_0_3_AnnP_4,P_network_5_0_AskP_4,P_poll__networl_3_1_AskP_5,P_poll__networl_1_1_AnsP_0,P_poll__networl_2_5_AI_0,P_network_3_6_RI_5,P_poll__networl_1_6_AI_0,P_network_6_3_AI_5,P_masterList_6_1_3,P_network_3_3_RI_5,P_poll__networl_3_6_RI_3,P_poll__networl_5_4_RP_2,P_network_3_4_AnnP_2,P_poll__networl_5_3_AskP_1,P_poll__networl_4_0_AI_4,P_poll__networl_5_3_AnnP_0,P_poll__networl_6_2_AnnP_0,P_poll__networl_1_2_RI_5,P_poll__networl_3_6_AnsP_0,P_poll__networl_5_1_AskP_3,P_network_4_4_RI_4,P_poll__networl_0_0_RI_3,P_poll__networl_1_5_AI_2,P_masterList_1_5_5,P_network_3_2_AskP_1,P_masterList_2_5_6,P_poll__networl_2_2_AI_5,P_poll__networl_4_1_RP_6,P_network_6_0_RI_2,P_poll__networl_0_2_AI_2,P_network_1_4_RP_5,P_poll__networl_3_6_RI_0,P_poll__networl_0_3_AskP_3,P_network_0_3_AskP_2,P_poll__networl_0_4_RP_1,P_masterList_3_2_0,P_network_5_4_AI_4,P_poll__networl_6_1_AskP_0,P_masterList_1_6_4,P_network_6_0_AI_6,P_network_2_1_AnnP_4,P_poll__networl_3_5_AI_1,P_poll__networl_1_6_AI_3,P_network_1_4_AI_5,P_network_5_2_AI_6,P_poll__networl_5_1_AI_3,P_masterList_5_2_5,P_poll__networl_2_3_AskP_6,P_network_0_1_AskP_3,P_poll__networl_6_2_AnnP_3,P_network_5_1_AnnP_1,P_network_0_3_RP_6,P_poll__networl_0_4_AskP_6,P_poll__networl_2_1_RP_5,P_network_1_1_AI_5,P_poll__networl_6_5_RP_6,P_network_6_3_AI_6,P_network_4_4_AskP_2,P_network_6_2_AskP_3,P_poll__networl_0_3_RP_2,P_network_6_4_AskP_1,P_network_6_3_AskP_3,P_network_3_1_AI_6,P_poll__networl_2_0_AskP_0,P_network_5_1_AnnP_6,P_network_5_2_AI_5,P_poll__networl_6_5_RP_5,P_network_4_0_AskP_3,P_poll__networl_5_2_AskP_4,P_network_4_3_AnnP_5,P_network_0_4_AnnP_4,P_poll__networl_5_1_AskP_6,P_network_3_6_AI_1,P_masterList_5_1_2,P_network_5_3_RI_6,P_network_6_0_AskP_2,P_poll__networl_5_3_RI_5,P_network_0_5_AskP_6,P_network_1_6_AnnP_5,P_network_3_4_AskP_5,P_poll__networl_4_5_AnnP_0,P_poll__networl_1_3_RP_6,P_network_2_4_RP_6,P_poll__networl_1_2_AI_5,P_network_0_1_AnnP_5,P_network_3_6_RI_1,P_masterList_3_3_5,P_network_4_1_AskP_2,P_network_6_2_AI_1,P_poll__networl_0_0_AnnP_0,P_poll__networl_2_6_AskP_5,P_poll__networl_4_6_AnnP_3,P_poll__networl_6_6_AskP_5,P_poll__networl_4_3_AskP_2,P_poll__networl_5_2_AskP_0,P_network_0_2_AI_5,P_network_4_0_RP_1,P_poll__networl_2_6_AskP_4,P_network_6_0_AI_2,P_poll__networl_2_5_AnnP_5,P_poll__networl_0_1_RP_0,P_poll__networl_4_4_RI_5,P_poll__networl_2_6_RI_3,P_masterList_6_3_5,P_poll__networl_1_3_AI_1,P_network_0_5_AnnP_3,P_network_0_5_AnnP_6,P_network_5_0_RP_1,P_network_3_5_RI_1,P_network_4_1_RI_5,P_network_3_1_RP_6,P_poll__networl_6_6_RI_1,P_poll__networl_6_2_AI_6,P_network_2_4_AskP_3,P_network_3_1_AnnP_3,P_poll__networl_0_1_AskP_0,P_network_6_1_RP_3,P_network_2_0_RP_3,P_network_3_1_AI_1,P_masterList_3_5_3,P_masterList_3_5_6,P_masterList_2_3_6,P_poll__networl_3_4_AnsP_0,P_poll__networl_2_2_AI_1,P_network_0_4_AI_3,P_network_6_4_AI_1,P_poll__networl_0_0_RP_3,P_network_4_1_AskP_1,P_poll__networl_5_4_AI_6,P_network_0_1_AskP_6,P_network_4_0_AI_6,P_network_6_5_RI_3,P_poll__networl_6_5_RI_2,P_poll__networl_0_4_AnnP_5,P_network_1_2_AskP_1,P_poll__networl_5_2_AnnP_6,P_poll__networl_5_5_AskP_4,P_network_4_3_AI_1,P_network_6_5_AI_3,P_poll__networl_4_1_RP_2,P_network_3_6_RP_2,P_masterList_4_6_1,P_masterList_5_2_4,P_network_4_0_AnnP_6,P_poll__networl_3_5_AnnP_4,P_poll__networl_4_5_AI_6,P_poll__networl_1_5_AnnP_1,P_network_5_3_RI_1,P_network_2_6_AskP_5,P_poll__networl_5_0_RI_4,P_poll__networl_6_3_AnnP_5,P_network_3_4_RI_6,P_poll__networl_2_3_AnnP_6,P_masterList_5_6_5,P_poll__networl_4_0_AskP_5,P_poll__networl_5_0_AnnP_1,P_poll__networl_2_4_RP_2,P_masterList_1_1_5,P_network_4_3_AskP_6,P_poll__networl_3_0_RI_3,P_network_4_1_AnnP_6,P_masterList_3_2_1,P_poll__networl_1_1_AI_6,P_poll__networl_0_0_AnsP_0,P_masterList_5_2_0,P_network_5_1_RI_6,P_poll__networl_0_4_AnnP_4,P_network_6_4_AnnP_3,P_network_1_1_RI_1,P_poll__networl_2_5_AnsP_0,P_network_5_5_RP_1,P_masterList_3_4_4,P_network_0_3_RP_1,P_poll__networl_5_6_AnnP_3,P_network_3_6_RP_1,P_masterList_0_5_0,P_poll__networl_4_2_RI_6,P_poll__networl_4_5_AI_1,P_network_2_2_AskP_5,P_network_5_5_RI_2,P_network_1_0_RI_5,P_poll__networl_5_2_RI_2,P_poll__networl_4_5_AI_5,P_network_4_1_RP_6,P_masterList_6_4_1,P_poll__networl_5_0_AskP_3,P_poll__networl_4_5_AnnP_2,P_network_3_6_RI_6,P_poll__networl_3_2_RI_0,P_masterList_2_6_1,P_poll__networl_6_0_AI_2,P_masterList_6_1_6,P_network_5_6_AI_2,P_network_5_1_RI_3,P_poll__networl_3_6_AI_1,P_poll__networl_4_2_AskP_0,P_network_6_0_AnnP_3,P_poll__networl_6_4_AskP_0,P_masterList_6_5_4,P_poll__networl_5_0_AI_5,P_masterList_3_3_6,P_poll__networl_1_0_RP_2,P_poll__networl_4_4_RP_3,P_network_0_3_RI_5,P_network_4_5_AskP_2,P_network_2_5_AnnP_2,P_poll__networl_0_5_RI_2,P_network_0_6_RI_4,P_poll__networl_0_5_RI_1,P_poll__networl_4_4_AI_4,P_network_0_3_AnnP_5,P_network_3_0_RP_3,P_poll__networl_5_4_RP_3,P_poll__networl_0_5_AskP_2,P_poll__networl_6_0_AskP_0,P_network_1_1_RP_4,P_network_5_6_AnnP_2,P_masterList_0_3_3,P_network_5_6_RI_1,P_network_3_2_RI_2,P_poll__networl_6_5_AskP_2,P_network_3_0_AskP_1,P_dead_4,P_crashed_3,P_poll__networl_4_3_AnnP_5,P_poll__networl_4_6_RI_5,P_poll__networl_0_4_RP_2,P_network_6_6_AnnP_2,P_network_5_4_AI_2,P_poll__networl_2_4_RI_6,P_network_6_0_AnnP_4,P_poll__networl_1_2_AnnP_4,P_network_4_6_AI_2,P_masterList_4_5_6,P_masterList_1_5_6,P_poll__networl_4_4_RI_4,P_network_2_3_AnnP_3,P_masterList_4_3_5,P_network_2_0_RI_1,P_poll__networl_3_5_AnnP_6,P_poll__networl_5_6_AnnP_2,P_poll__networl_6_1_RP_1,P_poll__networl_0_6_RI_6,P_network_1_6_AskP_1,P_masterList_6_2_6,P_network_3_4_AnnP_4,P_poll__networl_0_1_RI_3,P_network_4_1_RP_4,P_network_4_2_RP_2,P_poll__networl_5_4_RP_5,P_network_0_6_AI_2,P_masterList_3_2_2,P_poll__networl_1_6_AskP_3,P_masterList_3_1_0,P_poll__networl_1_3_AnnP_3,P_poll__networl_2_6_RP_2,P_poll__networl_4_5_RI_3,P_masterList_6_1_5,P_poll__networl_4_3_RI_4,P_poll__networl_5_0_RI_6,P_poll__networl_2_0_AnnP_5,P_masterList_2_6_5,P_poll__networl_2_0_RP_5,P_network_6_5_AI_2,P_poll__networl_3_4_RP_2,P_poll__networl_3_3_AI_0,P_network_5_1_AI_3,P_network_0_5_RP_3,P_poll__networl_4_3_RP_0,P_poll__networl_5_4_RI_5,P_poll__networl_0_3_AI_1,P_network_0_1_AskP_4,P_poll__networl_5_0_RP_3,P_poll__networl_4_6_AnnP_4,P_network_6_6_AI_1,P_poll__networl_6_0_AskP_1,P_masterList_4_3_6,P_network_4_2_AnnP_6,P_network_0_1_AskP_1,P_poll__networl_4_3_RI_0,P_poll__networl_0_5_AnnP_5,P_poll__networl_5_5_RP_2,P_poll__networl_1_0_AnnP_3,P_poll__networl_1_0_RI_0,P_masterList_3_2_4,P_poll__networl_0_4_AI_2,P_crashed_2,P_poll__networl_0_2_AskP_2,P_network_6_2_AnnP_2,P_poll__networl_5_1_RP_3,P_poll__networl_3_5_AskP_4,P_network_1_4_RP_4,P_network_3_2_RP_2,P_network_1_4_AI_4,P_poll__networl_0_6_AskP_4,P_poll__networl_5_4_RI_0,P_poll__networl_2_2_RI_4,P_network_3_1_RP_1,P_poll__networl_2_2_RI_6,P_poll__networl_3_0_RP_6,P_network_4_2_RP_3,P_network_6_4_AnnP_4,P_network_2_6_AI_1,P_network_4_2_AI_6,P_poll__networl_1_3_AnnP_2,P_masterList_3_6_1,P_poll__networl_4_5_RI_5,P_poll__networl_4_2_AI_2,P_poll__networl_4_4_AnnP_1,P_poll__networl_3_2_AskP_6,P_poll__networl_5_2_AskP_6,P_poll__networl_5_6_AnnP_4,P_poll__networl_5_6_AnnP_1,P_network_1_0_AskP_4,P_network_1_5_RI_6,P_masterList_5_1_1,P_network_0_5_AskP_4,P_poll__networl_1_6_RP_5,P_masterList_5_4_2,P_network_3_1_RI_6,P_poll__networl_1_4_AI_2,P_poll__networl_2_4_RP_4,P_masterList_6_3_1,P_masterList_4_4_5,P_poll__networl_5_0_RP_4,P_network_1_0_RI_4,P_network_4_0_RI_6,P_network_0_1_RI_5,P_network_0_2_AskP_6,P_poll__networl_6_6_RP_5,P_network_2_6_AnnP_3,P_masterList_5_6_3,P_network_4_4_AnnP_2,P_network_2_1_AskP_4,P_network_2_4_RI_4,P_network_3_0_RI_5,P_poll__networl_6_6_AnnP_2,P_network_0_4_AnnP_6,P_poll__networl_3_1_RI_6,P_poll__networl_3_4_AnnP_0,P_network_0_2_RI_6,P_poll__networl_1_5_RI_6,P_poll__networl_3_4_RI_6,P_poll__networl_2_1_RP_0,P_network_1_1_AnnP_1,P_poll__networl_4_6_RP_2,P_network_6_4_RP_5,P_masterList_5_1_3,P_network_5_4_AskP_2,P_poll__networl_6_4_AskP_4,P_network_1_4_AnnP_4,P_poll__networl_3_4_AI_6,P_poll__networl_5_6_RP_4,P_poll__networl_4_1_RI_1,P_network_1_4_AnnP_1,P_poll__networl_6_4_AI_2,P_poll__networl_4_6_RP_5,P_poll__networl_6_2_RI_4,P_masterList_2_3_1,P_network_5_0_RI_5,P_poll__networl_0_5_AskP_5,P_network_5_6_AI_5,P_network_5_2_AnnP_4,P_network_4_6_AskP_1,P_poll__networl_5_2_RI_4,P_poll__networl_1_0_AnnP_6,P_masterList_3_1_4,P_poll__networl_0_3_AskP_1,P_poll__networl_0_6_AI_1,P_masterList_2_4_3,P_poll__networl_5_3_AskP_6,P_network_5_5_AnnP_6,P_network_2_2_AskP_1,P_poll__networl_5_2_RP_4,P_network_5_5_AnnP_2,P_poll__networl_0_3_AskP_5,P_poll__networl_0_2_RI_0,P_network_3_5_RI_3,P_network_0_0_AnnP_4,P_network_5_6_RI_4,P_network_4_5_AI_6,P_poll__networl_5_4_RP_4,P_poll__networl_6_1_AskP_1,P_poll__networl_0_4_AI_5,P_poll__networl_2_1_AI_5,P_poll__networl_5_0_AskP_1,P_network_3_3_AskP_1,P_poll__networl_3_0_AskP_3,P_poll__networl_5_4_AnnP_5,P_network_1_6_RI_6,P_poll__networl_6_0_AI_5,P_poll__networl_5_5_AskP_2,P_poll__networl_3_0_AskP_6,P_network_3_6_AI_4,P_poll__networl_6_0_AI_1,P_network_0_5_RP_1,P_poll__networl_4_0_AnnP_2,P_poll__networl_0_1_AnnP_1,P_poll__networl_6_3_RI_6,P_poll__networl_6_5_AskP_5,P_network_2_2_RI_5,P_poll__networl_1_6_AnnP_5,P_poll__networl_2_2_AnnP_5,P_poll__networl_6_5_AnsP_0,P_network_3_0_AnnP_2,P_poll__networl_6_1_AnnP_5,P_network_4_4_RI_2,P_network_3_6_AnnP_1,P_network_2_2_AskP_4,P_poll__networl_2_3_RI_5,P_poll__networl_0_6_RP_0,P_poll__networl_1_5_RI_0,P_network_0_5_RP_2,P_network_2_6_AskP_2,P_poll__networl_5_3_RI_0,P_masterList_2_5_2,P_network_4_1_RI_6,P_poll__networl_6_0_AskP_5,P_network_0_6_RI_3,P_masterList_6_5_0,P_poll__networl_6_4_RI_3,P_poll__networl_2_1_AskP_1,P_poll__networl_3_2_AnsP_0,P_network_2_2_RP_2,P_network_3_1_AI_4,P_network_6_5_AskP_4,P_network_4_1_RP_2,P_network_6_6_RI_2,P_network_5_0_RP_5,P_network_6_3_AI_2,P_poll__networl_6_4_AI_0,P_poll__networl_4_2_RP_4,P_network_6_3_AnnP_4,P_poll__networl_2_1_AskP_4,P_poll__networl_5_0_AI_2,P_poll__networl_6_2_AnnP_5,P_network_2_3_AI_6,P_network_4_5_AskP_6,P_poll__networl_6_1_RP_6,P_poll__networl_6_5_RI_3,P_network_0_5_AI_4,P_poll__networl_1_6_RI_1,P_poll__networl_2_3_AI_4,P_network_3_4_RP_6,P_poll__networl_1_1_AskP_6,P_network_0_0_AnnP_5,P_poll__networl_3_5_AI_0,P_masterList_3_5_5,P_network_2_3_AI_4,P_network_4_4_AnnP_6,P_poll__networl_1_0_AI_2,P_network_3_6_AskP_3,P_network_1_6_AI_2,P_network_1_5_AI_4,P_network_4_0_AskP_2,P_network_6_3_AnnP_2,P_poll__networl_3_0_AskP_2,P_poll__networl_5_2_AskP_3,P_poll__networl_6_5_AI_6,P_network_2_1_RI_6,P_poll__networl_0_2_RI_1,P_network_0_2_RI_4,P_network_3_5_AI_3,P_network_0_3_RP_2,P_network_1_0_RI_1,P_network_4_6_RI_2,P_network_1_0_RI_3,P_poll__networl_6_1_AnnP_2,P_network_3_4_AnnP_3,P_poll__networl_3_0_AI_3,P_network_6_6_AnnP_5,P_poll__networl_2_2_RI_1,P_network_5_1_RP_1,P_network_6_1_AskP_3,P_poll__networl_2_6_RP_5,P_poll__networl_3_1_RI_0,P_poll__networl_6_2_RP_4,P_network_2_6_AI_5,P_network_2_0_AI_5,P_network_4_4_RI_6,P_network_5_4_AnnP_5,P_poll__networl_6_6_AI_0,P_poll__networl_1_0_RP_3,P_network_1_5_AnnP_6,P_network_4_5_RP_4,P_network_4_6_RI_5,P_poll__networl_0_2_AnnP_5,P_poll__networl_4_4_AI_0,P_network_0_4_AnnP_5,P_network_6_4_RP_4,P_masterList_1_6_3,P_network_6_5_RI_6,P_network_1_3_RI_4,P_poll__networl_0_3_RI_5,P_poll__networl_2_1_AskP_3,P_poll__networl_3_6_AnnP_4,P_poll__networl_5_4_AskP_4,P_network_2_6_AnnP_2,P_poll__networl_2_5_AskP_1,P_network_5_1_RP_2,P_poll__networl_0_3_AI_3,P_poll__networl_4_5_AskP_4,P_poll__networl_0_3_RP_3,P_network_1_1_RP_2,P_network_5_1_AI_5,P_network_3_3_AI_5,P_network_6_1_AskP_6,P_masterList_2_2_5,P_masterList_3_3_2,P_poll__networl_5_4_AnnP_1,P_network_0_6_RP_2,P_poll__networl_6_1_RP_4,P_poll__networl_6_3_AI_3,P_poll__networl_3_4_AskP_1,P_network_6_2_AI_5,P_network_1_4_AI_1,P_poll__networl_1_1_AnnP_4,P_network_5_0_AI_6,P_network_6_4_RI_2,P_poll__networl_2_0_AnnP_6,P_network_4_1_RI_1,P_poll__networl_1_6_RI_3,P_masterList_6_1_4,P_network_2_6_AnnP_5,P_poll__networl_6_4_RI_2,P_network_6_2_RP_6,P_network_4_5_AI_3,P_network_4_0_RI_4,P_masterList_2_3_0,P_poll__networl_2_3_AnnP_3,P_poll__networl_1_4_RP_5,P_poll__networl_2_5_RI_4,P_network_1_5_RP_3,P_poll__networl_0_1_RP_2,P_network_1_4_RI_3,P_masterList_0_5_6,P_masterList_0_6_3,P_network_1_5_RI_1,P_poll__networl_6_6_RI_6,P_network_6_5_RP_6,P_poll__networl_5_4_AskP_1,P_poll__networl_0_2_RI_3,P_poll__networl_6_6_AskP_3,P_network_0_0_RP_3,P_poll__networl_4_1_AI_2,P_poll__networl_6_4_AI_6,P_poll__networl_6_0_RI_6,P_poll__networl_0_0_AI_0,P_poll__networl_1_2_RP_1,P_network_2_4_RI_2,P_network_5_4_AnnP_1,P_poll__networl_3_0_RP_4,P_network_5_1_AI_2,P_poll__networl_2_3_AI_6,P_poll__networl_5_4_AskP_2,P_poll__networl_3_1_RI_5,P_poll__networl_4_2_AI_6,P_network_4_0_AskP_6,P_poll__networl_5_4_AnnP_2,P_network_4_6_RI_4,P_poll__networl_5_4_AskP_0,P_poll__networl_3_2_RI_3,P_network_2_0_AI_1,P_poll__networl_1_5_AskP_5,P_poll__networl_0_1_RI_2,P_network_1_5_AskP_5,P_network_6_0_AI_3,P_network_1_0_RP_2,P_poll__networl_5_5_AnnP_2,P_network_6_5_AnnP_1,P_network_2_2_RI_6,P_poll__networl_4_5_RI_6,P_network_2_4_AskP_1,P_network_4_0_RI_2,P_poll__networl_3_1_RI_1,P_network_0_4_RP_2,P_poll__networl_5_1_AI_4,P_poll__networl_3_4_RP_0,P_masterList_3_5_1,P_poll__networl_0_5_AskP_4,P_poll__networl_6_5_RP_3,P_poll__networl_6_6_AskP_2,P_poll__networl_3_4_AskP_3,P_poll__networl_0_1_RP_4,P_poll__networl_6_6_RI_4,P_poll__networl_5_2_RP_0,P_poll__networl_2_3_RP_3,P_network_3_5_AI_4,P_masterList_1_4_0,P_masterList_6_2_1,P_poll__networl_6_5_AskP_6,P_poll__networl_0_0_RI_5,P_network_4_6_RP_5,P_masterList_2_6_6,P_network_6_4_AI_3,P_poll__networl_3_5_RP_6,P_network_2_1_AnnP_1,P_network_5_3_RP_1,P_poll__networl_4_0_AnsP_0,P_network_1_1_AnnP_4,P_network_4_4_RP_6,P_network_3_2_AnnP_3,P_network_5_0_RP_4,P_network_5_3_AnnP_2,P_network_6_0_AskP_1,P_network_2_6_RI_3,P_network_6_3_AnnP_5,P_poll__networl_3_0_RP_3,P_poll__networl_2_0_AI_3,P_network_3_6_RP_6,P_masterList_0_2_2,P_network_5_4_AskP_3,P_network_2_3_AnnP_4,P_electionFailed_5,P_poll__networl_5_2_RI_5,P_network_3_3_RI_6,P_network_0_6_AnnP_4,P_network_3_5_RI_5,P_network_0_0_AskP_1,P_poll__networl_0_5_AskP_1,P_poll__networl_4_3_RP_6,P_network_1_4_AnnP_5,P_network_3_4_AI_4,P_network_0_6_AnnP_1,P_crashed_5,P_network_6_5_AnnP_3,P_network_1_1_AI_4,P_poll__networl_1_5_RP_4,P_poll__networl_2_4_RI_2,P_poll__networl_1_2_AnnP_0,P_poll__networl_2_6_AI_1,P_network_4_0_AI_1,P_poll__networl_3_1_AI_5,P_network_2_5_AskP_3,P_network_3_4_AskP_6,P_poll__networl_5_3_RI_3,P_crashed_0,P_network_0_6_AskP_2,P_poll__networl_2_2_AskP_0,P_poll__networl_6_0_RP_1,P_poll__networl_6_0_AI_3,P_network_6_4_RP_6,P_poll__networl_5_4_AI_2,P_poll__networl_2_2_RP_5,P_poll__networl_0_0_AskP_1,P_network_2_6_AI_6,P_poll__networl_4_2_AI_4,P_network_4_5_RI_2,P_network_2_4_RP_2,P_poll__networl_4_0_AskP_3,P_poll__networl_6_5_AskP_3,P_network_5_5_AskP_2,P_poll__networl_1_3_AnnP_0,P_poll__networl_4_4_AnnP_5,P_network_0_5_AnnP_4,P_poll__networl_5_6_AskP_5,P_network_4_6_AnnP_4,P_poll__networl_0_5_RI_6,P_poll__networl_0_5_RP_6,P_network_3_0_AnnP_1,P_poll__networl_1_2_RP_4,P_poll__networl_2_3_RI_0,P_network_2_0_RP_4,P_poll__networl_2_3_AskP_2,P_masterList_6_6_0,P_poll__networl_2_4_AskP_2,P_poll__networl_4_0_RP_3,P_poll__networl_3_2_AnnP_6,P_network_4_6_RP_4,P_poll__networl_6_4_RI_6,P_network_3_6_AnnP_3,P_network_6_2_RI_4,P_poll__networl_3_5_AnnP_0,P_poll__networl_2_5_AskP_4,P_poll__networl_0_4_RP_5,P_poll__networl_2_3_AskP_0,P_poll__networl_1_3_AI_4,P_poll__networl_4_1_RP_0,P_masterList_5_1_6,P_network_1_5_RI_2,P_network_0_0_AskP_4,P_network_0_4_AI_1,P_poll__networl_3_3_AnnP_5,P_network_6_6_AskP_3,P_network_4_5_RI_6,P_network_6_0_RI_5,P_network_3_4_AI_1,P_network_1_2_AnnP_4,P_network_5_0_AskP_3,P_poll__networl_1_2_RP_0,P_poll__networl_1_2_RP_6,P_network_4_4_AI_1,P_poll__networl_3_4_AI_3,P_poll__networl_0_2_RP_0,P_poll__networl_3_1_AskP_4,P_poll__networl_5_5_AnnP_3,P_poll__networl_3_0_AskP_1,P_poll__networl_0_4_RP_4,P_poll__networl_2_1_AnnP_6,P_poll__networl_5_4_AskP_3,P_poll__networl_0_5_AI_6,P_poll__networl_2_5_AskP_2,P_network_1_2_RI_3,P_network_5_0_RP_3,P_network_6_4_RP_3,P_poll__networl_5_1_RI_1,P_network_2_3_RI_3,P_network_6_4_AnnP_5,P_network_1_1_AI_1,P_poll__networl_0_2_AskP_0,P_network_1_2_AI_2,P_network_2_6_RI_6,P_poll__networl_6_3_AnnP_0,P_poll__networl_0_3_RI_3,P_network_2_4_AnnP_6,P_poll__networl_6_0_AI_0,P_masterList_0_4_5,P_poll__networl_5_1_AnnP_1,P_poll__networl_5_0_RI_3,P_poll__networl_5_3_AnnP_5,P_poll__networl_4_4_RP_6,P_masterList_0_6_5,P_poll__networl_5_5_AI_1,P_network_2_3_AnnP_5,P_poll__networl_0_0_RI_4,P_poll__networl_4_1_AnnP_0,P_poll__networl_3_1_AI_6,P_poll__networl_4_6_AskP_6,P_masterList_1_3_2,P_crashed_6,P_network_5_3_AnnP_5,P_network_3_4_RP_1,P_poll__networl_2_5_RI_1,P_poll__networl_0_3_AI_2,P_poll__networl_3_4_AI_1,P_network_0_4_RP_4,P_network_0_3_AI_1,P_network_5_5_AnnP_4,P_poll__networl_4_2_AnnP_4,P_poll__networl_2_0_RI_4,P_poll__networl_5_6_AI_3,P_network_5_1_RI_2,P_network_2_2_RI_2,P_poll__networl_4_0_AskP_0,P_poll__networl_5_3_RP_1,P_network_6_5_AI_1,P_network_2_4_RI_5,P_network_5_1_AnnP_5,P_network_6_5_AI_5,P_poll__networl_3_4_RP_1,P_network_3_3_RP_2,P_poll__networl_6_3_RP_0,P_network_2_6_RP_6,P_network_4_2_AI_2,P_masterList_5_4_4,P_poll__networl_6_6_RP_0,P_network_2_3_RI_2,P_network_1_0_AskP_2,P_network_6_2_AskP_2,P_network_2_1_AnnP_3,P_network_5_2_RP_5,P_poll__networl_2_1_AI_2,P_poll__networl_3_5_AskP_3,P_poll__networl_0_6_AnsP_0,P_network_3_4_RP_5,P_poll__networl_4_2_AnsP_0,P_poll__networl_4_2_AI_5,P_poll__networl_4_4_AnnP_4,P_poll__networl_6_2_RP_3,P_network_6_1_AskP_5,P_poll__networl_3_1_AI_0,P_network_0_6_AnnP_2,P_masterList_6_6_2,P_network_5_2_AskP_1,P_poll__networl_2_3_AnnP_4,P_network_0_6_AskP_3,P_poll__networl_3_0_AI_4,P_network_2_5_AnnP_1,P_poll__networl_2_6_RI_6,P_network_1_1_AnnP_3,P_poll__networl_1_6_RP_1,P_poll__networl_4_6_AI_0,P_poll__networl_1_6_AnnP_4,P_network_4_2_AI_3,P_poll__networl_0_2_AnnP_3,P_network_0_2_AnnP_4,P_network_5_0_AskP_1,P_network_6_5_AskP_1,P_poll__networl_6_3_AskP_2,P_network_6_6_AskP_4,P_poll__networl_1_4_RI_3,P_poll__networl_2_0_AskP_2,P_poll__networl_0_0_RP_2,P_masterList_4_2_2,P_poll__networl_1_4_AnnP_6,P_poll__networl_5_0_RP_1,P_poll__networl_1_6_RP_6,P_poll__networl_5_2_RI_6,P_network_3_5_AnnP_4,P_masterList_5_4_0,P_network_4_0_AnnP_2,P_poll__networl_5_2_AI_6,P_poll__networl_2_4_AI_4,P_poll__networl_5_0_AI_3,P_network_1_5_AI_5,P_network_2_1_AskP_3,P_network_5_3_RP_2,P_poll__networl_2_1_RI_5,P_poll__networl_6_5_AnnP_6,P_network_4_3_AskP_4,P_masterList_4_3_1,P_poll__networl_0_1_AskP_6,P_poll__networl_3_0_AI_2,P_network_2_5_RP_3,P_network_4_4_RP_4,P_poll__networl_6_4_AskP_6,P_network_1_0_AskP_3,P_network_1_4_AskP_3,P_network_3_3_RP_4,P_network_3_0_RP_2,P_poll__networl_2_6_AnsP_0,P_network_2_1_AI_3,P_poll__networl_4_3_AnsP_0,P_network_1_6_AI_4,P_masterList_0_4_0,P_poll__networl_4_4_RP_4,P_poll__networl_6_1_AI_3,P_poll__networl_0_2_AI_3,P_poll__networl_1_2_AI_6,P_network_3_4_AI_2,P_network_5_6_AI_6,P_network_2_1_AnnP_6,P_network_2_3_RP_2,P_poll__networl_4_4_AnnP_2,P_network_2_4_RP_4,P_network_5_3_RP_5,P_poll__networl_0_2_RI_4,P_poll__networl_2_3_RI_4,P_network_5_2_RI_5,P_network_3_0_RP_4,P_poll__networl_2_3_AskP_5,P_network_0_3_AnnP_6,P_network_5_0_RI_1,P_poll__networl_6_0_AI_4,P_network_2_6_AI_2,P_poll__networl_1_5_AI_0,P_poll__networl_0_6_AI_3,P_poll__networl_6_3_AI_1,P_poll__networl_4_5_RP_6,P_network_1_0_RP_6,P_network_6_5_RP_2,P_masterList_2_4_6,P_poll__networl_5_1_AskP_0,P_masterList_2_6_3,P_poll__networl_1_6_AskP_2,P_poll__networl_3_2_AskP_4,P_poll__networl_2_6_RP_1,P_poll__networl_5_3_AskP_5,P_poll__networl_6_6_RP_3,P_network_3_2_RP_4,P_poll__networl_2_6_AI_4,P_poll__networl_3_6_AskP_0,P_poll__networl_5_0_RI_5,P_network_5_3_AskP_4,P_network_3_1_AnnP_4,P_poll__networl_5_4_AnnP_3,P_poll__networl_0_6_RP_6,P_masterList_3_4_6,P_poll__networl_5_2_RP_5,P_masterList_4_2_1,P_network_0_5_RP_5,P_poll__networl_6_1_AnnP_0,P_poll__networl_0_5_RP_2,P_network_6_6_RP_2,P_network_4_5_AnnP_2,P_poll__networl_4_2_AI_0,P_poll__networl_2_4_RI_3,P_network_2_0_AI_2,P_poll__networl_5_5_RI_6,P_network_1_4_AskP_6,P_poll__networl_3_3_AnnP_4,P_network_6_3_AskP_1,P_poll__networl_3_2_AI_3,P_network_3_6_AI_6,P_poll__networl_0_0_RI_6,P_poll__networl_2_5_RP_1,P_poll__networl_6_2_RI_1,P_poll__networl_2_4_AnnP_6,P_poll__networl_6_1_AnsP_0,P_poll__networl_3_3_RP_6,P_masterList_4_6_5,P_masterList_1_2_2,P_masterList_5_4_3,P_poll__networl_5_3_RI_6,P_poll__networl_5_1_AnnP_6,P_poll__networl_0_5_AI_2,P_network_4_2_AskP_5,P_poll__networl_2_5_RP_4,P_poll__networl_6_2_AskP_5,P_poll__networl_6_6_RP_4,P_masterList_3_6_4,P_network_5_1_RP_6,P_network_3_1_AskP_3,P_poll__networl_6_0_AnnP_2,P_network_1_3_AnnP_2,P_network_6_6_RI_3,P_network_5_6_AskP_3,P_poll__networl_1_2_RI_1,P_poll__networl_2_1_RI_3,P_poll__networl_4_6_RI_1,P_poll__networl_1_4_AskP_6,P_poll__networl_6_4_AnnP_3,P_poll__networl_6_6_AnnP_0,P_poll__networl_0_2_AI_5,P_poll__networl_2_1_AskP_2,P_masterList_4_5_2,P_poll__networl_5_6_AskP_6,P_network_4_5_RI_3,P_poll__networl_2_0_AI_2,P_poll__networl_3_4_RI_2,P_masterList_2_2_2,P_poll__networl_1_5_AskP_3,P_poll__networl_1_5_AnsP_0,P_poll__networl_2_4_RP_0,P_poll__networl_3_6_RP_0,P_poll__networl_3_3_AskP_6,P_poll__networl_6_1_RP_3,P_network_0_0_AskP_3,P_network_1_6_RI_1,P_network_3_0_AnnP_5,P_network_5_0_RI_4,P_network_1_4_RP_3,P_network_1_1_AskP_5,P_network_2_0_AskP_5,P_network_5_2_AnnP_3,P_network_1_1_AnnP_5,P_network_6_0_AnnP_2,P_poll__networl_1_5_AnnP_3,P_poll__networl_1_4_RI_5,P_poll__networl_0_4_AskP_3,P_network_6_6_RP_5,P_poll__networl_5_6_RP_2,P_poll__networl_5_3_AnnP_1,P_poll__networl_6_5_RI_5,P_network_6_2_AI_4,P_network_1_6_AnnP_2,P_network_6_3_AI_4,P_poll__networl_1_4_AI_0,P_poll__networl_4_5_AskP_5,P_network_2_2_RI_4,P_poll__networl_4_2_AnnP_5,P_network_5_5_AnnP_3,P_network_2_6_RP_4,P_poll__networl_2_5_AnnP_1,P_poll__networl_5_0_AI_4,P_poll__networl_3_3_AnnP_6,P_network_3_1_RI_4,P_poll__networl_0_4_AskP_0,P_masterList_2_4_4,P_network_0_2_RI_1,P_network_6_5_RP_1,P_poll__networl_2_5_RP_5,P_network_5_4_AskP_1,P_poll__networl_3_0_AnsP_0,P_network_2_6_AI_3,P_masterList_6_6_3,P_network_2_1_AskP_5,P_poll__networl_2_4_AnnP_2,P_network_2_5_RP_6,P_poll__networl_0_5_RI_4,P_poll__networl_6_1_AskP_6,P_network_4_5_AnnP_4,P_poll__networl_0_2_AskP_4,P_network_5_5_RP_2,P_poll__networl_4_4_AI_3,P_poll__networl_1_5_RI_2,P_poll__networl_3_4_AskP_5,P_poll__networl_5_0_RP_5,P_poll__networl_5_6_RP_6,P_masterList_3_4_5,P_poll__networl_3_2_RI_6,P_poll__networl_2_1_AnnP_1,P_network_3_1_RI_2,P_poll__networl_6_1_AI_2,P_poll__networl_1_4_AI_6,P_poll__networl_6_6_AnsP_0,P_poll__networl_4_6_RI_6,P_masterList_0_3_0,P_poll__networl_1_2_RI_6,P_poll__networl_6_2_AskP_2,P_network_4_1_RI_2,P_network_4_3_AskP_3,P_poll__networl_0_0_RP_5,P_poll__networl_2_3_RI_1,P_network_4_5_AskP_1,P_network_3_4_RI_4,P_poll__networl_4_2_RP_0,P_network_2_5_AnnP_5,P_network_5_3_RP_3,P_poll__networl_5_1_RP_2,P_network_3_5_AI_1,P_poll__networl_0_1_RP_1,P_poll__networl_3_4_AnnP_4,P_poll__networl_2_6_AnnP_5,P_poll__networl_0_0_RP_0,P_poll__networl_2_3_RP_2,P_poll__networl_4_5_RI_0,P_network_4_2_AnnP_1,P_poll__networl_1_1_AskP_3,P_network_0_2_AI_4,P_poll__networl_6_6_AskP_1,P_network_1_0_RP_1,P_poll__networl_5_2_RI_3,P_poll__networl_5_6_AnnP_6,P_network_4_4_AnnP_1,P_network_5_1_AskP_4,P_network_2_2_AskP_3,P_poll__networl_5_1_RI_2,P_network_0_6_AI_1,P_poll__networl_4_3_RI_3,P_network_6_2_RI_1,P_network_0_4_RP_3,P_masterList_2_5_0,P_poll__networl_1_4_AnsP_0,P_network_1_5_AI_2,P_masterList_1_4_2,P_poll__networl_3_6_RP_6,P_network_5_2_RI_6,P_poll__networl_4_3_RI_2,P_poll__networl_4_6_AnnP_6,P_network_1_5_AskP_4,P_poll__networl_0_2_AnnP_4,P_network_5_4_AI_1,P_poll__networl_0_3_RI_0,P_poll__networl_3_5_RP_2,P_network_1_5_AnnP_1,P_poll__networl_2_4_AnnP_4,P_poll__networl_1_6_RI_0,P_network_0_6_RP_3,P_network_6_3_AnnP_6,P_network_5_0_RP_6,P_poll__networl_6_4_AnnP_2,P_poll__networl_0_0_AskP_2,P_poll__networl_4_5_AskP_2,P_poll__networl_6_3_AI_6,P_poll__networl_1_1_AI_5,P_network_0_1_AnnP_3,P_poll__networl_5_1_AnnP_0,P_network_2_1_AnnP_2,P_poll__networl_5_1_AI_1,P_poll__networl_5_4_RI_1,P_network_1_5_AnnP_3,P_poll__networl_6_5_RI_0,P_poll__networl_4_0_AnnP_0,P_poll__networl_5_3_RP_0,P_network_4_3_RI_6,P_network_6_0_RI_6,P_network_4_1_AI_6,P_network_0_1_RP_4,P_poll__networl_5_5_RI_4,P_network_1_1_AnnP_2,P_network_6_3_RP_4,P_network_3_6_AskP_4,P_poll__networl_0_3_AI_5,P_poll__networl_4_0_AskP_6,P_poll__networl_0_6_RP_5,P_network_3_0_RI_6,P_poll__networl_6_0_AnnP_3,P_poll__networl_3_2_RP_4,P_poll__networl_3_5_AI_3,P_network_1_2_RP_6,P_network_0_5_AnnP_2,P_poll__networl_6_3_RI_0,P_network_4_5_AI_1,P_masterList_6_1_1,P_poll__networl_2_1_RP_4,P_poll__networl_3_2_RP_5,P_network_5_0_AI_5,P_network_5_5_AnnP_1,P_poll__networl_4_3_AskP_3,P_poll__networl_4_0_AI_1,P_masterList_5_6_1,P_poll__networl_0_3_RI_6,P_poll__networl_6_4_AnsP_0,P_network_3_3_AskP_5,P_poll__networl_0_1_RI_6,P_network_3_4_RP_4,P_poll__networl_6_2_AI_2,P_network_4_4_AskP_3,P_network_2_0_AnnP_6,P_network_5_4_AnnP_4,P_network_3_3_RP_5,P_network_1_4_AI_2,P_masterList_0_1_4,P_poll__networl_2_0_RP_4,P_network_6_2_RP_2,P_poll__networl_2_2_RI_2,P_network_4_2_RI_6,P_poll__networl_6_2_AskP_0,P_masterList_2_3_2,P_network_2_2_AI_3,P_poll__networl_1_5_AI_5,P_poll__networl_3_6_AskP_3,P_poll__networl_3_0_RI_0,P_network_6_1_AnnP_6,P_poll__networl_2_4_AI_1,P_poll__networl_0_1_AI_6,P_poll__networl_6_0_RP_5,P_poll__networl_1_3_AI_6,P_network_4_5_RI_4,P_poll__networl_6_2_RI_6,P_poll__networl_0_4_AnnP_1,P_poll__networl_5_4_AskP_5,P_poll__networl_0_6_AI_6,P_network_4_0_RP_5,P_network_3_6_AskP_2,P_network_4_5_RP_5,P_poll__networl_2_3_AI_3,P_network_5_1_RI_5,P_masterList_1_2_5,P_poll__networl_6_1_RI_1,P_network_0_2_AI_3,P_poll__networl_2_3_RI_6,P_poll__networl_2_1_RP_1,P_network_2_3_RI_6,P_poll__networl_5_2_RP_3,P_network_4_3_AskP_5,P_poll__networl_6_1_RI_6,P_poll__networl_1_2_AskP_3,P_poll__networl_5_1_AnnP_2,P_poll__networl_4_1_RI_2,P_masterList_6_1_0,P_poll__networl_4_2_AnnP_6,P_network_1_5_RP_6,P_poll__networl_3_6_AskP_5,P_poll__networl_1_2_RI_2,P_poll__networl_2_2_AI_2,P_network_6_2_RP_4,P_network_2_1_RI_1,P_network_3_1_AI_5,P_network_2_5_RP_5,P_poll__networl_4_5_RP_5,P_network_4_6_AnnP_1,P_poll__networl_1_0_RI_4,P_network_6_3_RI_2,P_network_2_0_RP_2,P_poll__networl_5_3_AnnP_4,P_network_1_3_AI_1,P_network_4_6_RI_1,P_network_1_1_AskP_6,P_poll__networl_0_6_RI_2,P_network_6_6_RI_4,P_network_5_6_AskP_1,P_poll__networl_5_1_AI_6,P_poll__networl_6_3_AnnP_6,P_masterList_5_1_5,P_masterList_2_2_0,P_network_1_2_AI_6,P_network_0_2_RP_1,P_poll__networl_6_6_RP_1,P_network_0_2_RI_2,P_poll__networl_0_2_AnnP_2,P_network_1_4_RI_2,P_network_5_2_AI_4,P_masterList_4_5_5,P_poll__networl_6_0_AskP_3,P_poll__networl_6_3_RI_4,P_network_2_1_AskP_2,P_poll__networl_2_1_RI_0,P_network_3_3_AnnP_2,P_poll__networl_3_5_RI_2,P_poll__networl_1_2_AI_0,P_masterList_3_3_3,P_poll__networl_2_4_AI_3,P_poll__networl_4_4_RP_2,P_poll__networl_1_4_RP_2,P_network_5_0_RI_2,P_poll__networl_0_1_RP_6,P_poll__networl_2_1_RI_6,P_poll__networl_0_1_AskP_1,P_masterList_4_3_3,P_poll__networl_2_6_RI_1,P_poll__networl_4_0_RI_2,P_poll__networl_5_0_RI_0,P_poll__networl_6_3_AskP_4,P_poll__networl_4_4_AnnP_3,P_network_2_4_AnnP_3,P_network_4_2_AnnP_3,P_poll__networl_2_3_AskP_1,P_poll__networl_4_6_AskP_4,P_poll__networl_3_3_RP_5,P_network_4_6_AskP_4,P_poll__networl_6_3_AskP_1,P_masterList_4_5_0,P_masterList_2_6_4,P_network_4_2_RI_2,P_network_3_2_RI_3,P_network_0_1_AI_2,P_poll__networl_0_0_AskP_5,P_poll__networl_6_4_RI_0,P_network_3_3_AnnP_1,P_poll__networl_2_2_AnnP_2,P_poll__networl_5_5_AskP_1,P_network_6_0_AskP_6,P_poll__networl_5_5_AnsP_0,P_poll__networl_0_5_AnnP_2,P_poll__networl_4_5_RI_2,P_masterList_6_6_1,P_poll__networl_4_1_AskP_3,P_poll__networl_5_2_AI_5,P_network_5_2_AnnP_2,P_poll__networl_4_5_AnnP_1,P_network_6_4_AI_5,P_poll__networl_2_0_RI_3,P_masterList_6_2_4,P_network_5_0_AI_3,P_network_3_6_AnnP_5,P_network_2_1_RP_1,P_network_6_2_AskP_4,P_network_5_3_AskP_1,P_poll__networl_6_4_AnnP_0,P_poll__networl_3_2_AI_6,P_poll__networl_1_1_RP_0,P_network_2_6_AskP_3,P_network_0_6_AI_6,P_network_0_0_AnnP_2,P_network_1_4_RP_2,P_poll__networl_4_1_AnnP_6,P_network_4_4_AI_4,P_poll__networl_4_6_AI_1,P_masterList_4_5_3,P_poll__networl_4_4_RP_5,P_poll__networl_3_4_RI_1,P_network_5_4_RP_4,P_poll__networl_5_2_AI_1,P_masterList_6_3_0,P_network_1_4_RI_1,P_poll__networl_2_1_AI_1,P_network_3_3_AnnP_3,P_network_6_5_RI_4,P_poll__networl_2_5_AnnP_6,P_poll__networl_3_2_AnnP_5,P_poll__networl_6_4_RP_6,P_network_2_5_AI_2,P_network_1_4_RP_6,P_network_2_3_RP_4,P_poll__networl_1_1_AnnP_0,P_poll__networl_1_5_RI_5,P_poll__networl_5_1_AI_2,P_poll__networl_4_1_AnnP_3,P_network_0_1_RI_2,P_network_4_5_AI_2,P_poll__networl_3_1_AskP_1,P_poll__networl_6_0_AskP_2,P_network_3_3_RP_1,P_poll__networl_1_2_AnnP_1,P_poll__networl_3_5_AnnP_5,P_poll__networl_0_0_AI_4,P_network_1_0_RP_4,P_network_4_4_AI_3,P_network_1_3_RP_6,P_poll__networl_1_6_AnnP_6,P_network_6_0_RI_3,P_network_3_2_RP_6,P_network_6_6_AI_6,P_poll__networl_3_2_RI_1,P_poll__networl_0_3_AnnP_5,P_network_1_1_RP_6,P_poll__networl_1_6_AskP_0,P_poll__networl_2_1_AI_6,P_dead_0,P_network_5_4_AnnP_3,P_network_6_6_RP_4,P_poll__networl_5_3_RI_1,P_network_5_6_AskP_5,P_network_5_0_RP_2,P_poll__networl_4_0_RP_6,P_poll__networl_5_5_RI_3,P_network_4_6_AskP_2,P_network_5_2_AskP_3,P_poll__networl_5_2_AI_3,P_network_4_1_AnnP_4,P_network_2_5_AI_3,P_poll__networl_1_2_AnnP_3,P_poll__networl_4_6_AI_3,P_network_1_5_AskP_1,P_network_6_6_AI_5,P_poll__networl_2_4_RP_6,P_poll__networl_4_3_RI_1,P_poll__networl_5_4_RP_6,P_network_3_5_AI_6,P_poll__networl_1_4_RI_2,P_network_5_6_RP_5,P_poll__networl_4_5_RP_1,P_network_4_4_AskP_1,P_network_1_3_RI_3,P_poll__networl_2_5_RI_2,P_poll__networl_2_6_AskP_1,P_network_5_4_RP_3,P_network_0_3_AskP_5,P_network_6_0_RI_1,P_network_3_2_RI_1,P_network_6_2_RP_3,P_network_4_3_RP_2,P_network_5_1_AI_6,P_poll__networl_5_3_AskP_0,P_network_2_5_AskP_1,P_network_6_4_RP_1,P_poll__networl_2_1_AnsP_0,P_poll__networl_4_5_AI_0,P_poll__networl_3_0_AI_1,P_poll__networl_4_3_AI_5,P_network_1_3_RI_2,P_network_5_6_AskP_4,P_poll__networl_4_3_AnnP_3,P_network_6_6_AskP_6,P_poll__networl_2_6_AskP_3,P_poll__networl_4_5_AI_2,P_poll__networl_2_1_RP_6,P_poll__networl_6_6_AI_3,P_network_0_3_AnnP_3,P_poll__networl_5_1_AnnP_5,P_network_1_3_RI_5,P_poll__networl_4_3_RI_5,P_poll__networl_2_3_AnnP_0,P_poll__networl_5_0_RP_2,P_poll__networl_5_2_AnsP_0,P_network_3_2_RP_3,P_poll__networl_1_5_AI_3,P_poll__networl_0_3_RP_5,P_poll__networl_6_1_RP_5,P_network_2_5_AskP_5,P_poll__networl_1_2_RP_2,P_network_3_5_AI_2,P_poll__networl_5_3_AnnP_2,P_poll__networl_4_0_RP_0,P_poll__networl_5_3_AskP_3,P_poll__networl_2_2_RP_6,P_masterList_6_3_3,P_masterList_4_4_2,P_poll__networl_0_6_AskP_2,P_poll__networl_1_6_AnnP_1,P_poll__networl_6_2_AskP_1,P_poll__networl_0_4_RP_3,P_poll__networl_2_6_AI_5,P_poll__networl_6_1_RI_5,P_network_4_1_AnnP_5,P_network_2_6_AnnP_1,P_network_1_2_RP_4,P_poll__networl_4_0_RI_0,P_poll__networl_4_3_AnnP_1,P_poll__networl_1_1_RI_0,P_poll__networl_1_1_RI_5,P_poll__networl_3_1_AI_3,P_poll__networl_3_3_AnnP_3,P_poll__networl_1_5_RP_6,P_poll__networl_4_6_RI_0,P_network_6_6_RI_5,P_poll__networl_0_6_AnnP_4,P_network_5_3_AskP_3,P_network_1_5_AskP_6,P_poll__networl_2_5_AskP_3,P_network_0_1_RP_1,P_network_5_4_AnnP_2,P_poll__networl_5_6_RP_1,P_network_4_0_AI_2,P_poll__networl_0_0_AnnP_2,P_poll__networl_3_2_AskP_1,P_network_4_0_AI_3,P_network_4_1_AnnP_2,P_poll__networl_4_1_AI_3,P_poll__networl_6_6_AnnP_4,P_network_2_1_RI_2,P_network_3_2_AI_5,P_network_0_3_AnnP_1,P_network_4_5_AskP_3,P_masterList_3_4_3,P_masterList_5_3_5,P_network_1_3_AskP_4,P_network_3_0_RI_4,P_poll__networl_1_6_AI_2,P_poll__networl_6_0_RI_5,P_network_3_1_AskP_2,P_poll__networl_2_1_AnnP_0,P_network_2_4_RI_6,P_poll__networl_1_6_AI_5,P_poll__networl_3_5_RI_5,P_poll__networl_2_4_RP_5,P_network_2_5_RP_2,P_poll__networl_4_3_RP_1,P_network_1_6_AskP_6,P_poll__networl_4_3_AI_2,P_poll__networl_2_5_AskP_5,P_network_2_1_AskP_6,P_network_2_5_RI_1,P_network_1_6_AskP_2,P_poll__networl_0_5_AI_3,P_poll__networl_0_2_AnnP_0,P_network_2_2_AI_4,P_network_4_1_RI_4,P_network_5_3_AI_3,P_poll__networl_2_6_AnnP_4,P_poll__networl_2_4_AI_2,P_poll__networl_5_0_AnnP_4,P_network_3_2_AI_2,P_network_5_2_AskP_6,P_poll__networl_6_1_AnnP_3,P_poll__networl_0_4_AnnP_0,P_poll__networl_1_4_AI_1,P_poll__networl_5_5_AI_3,P_poll__networl_0_1_AI_1,P_network_3_5_RP_5,P_poll__networl_4_0_RP_5,P_poll__networl_6_5_AnnP_0,P_poll__networl_6_5_AnnP_3,P_network_1_5_AnnP_4,P_poll__networl_4_0_RI_5,P_network_1_0_RP_3,P_network_6_2_AskP_6,P_poll__networl_6_3_AI_0,P_poll__networl_1_0_AnsP_0,P_poll__networl_4_1_AI_4,P_network_5_0_AI_4,P_network_1_4_RI_5,P_network_2_4_RP_1,P_poll__networl_3_0_AnnP_3,P_network_3_6_AnnP_4,P_poll__networl_3_6_AnnP_6,P_poll__networl_6_5_AnnP_2,P_poll__networl_4_6_AnnP_0,P_poll__networl_5_3_RI_2,P_network_1_5_AnnP_5,P_masterList_1_5_1,P_network_1_2_RP_5,P_poll__networl_4_4_AI_6,P_network_2_1_AI_2,P_poll__networl_2_4_AskP_6,P_poll__networl_3_3_AskP_3,P_poll__networl_3_5_AskP_2,P_poll__networl_1_0_AskP_4,P_poll__networl_0_3_AskP_0,P_poll__networl_4_2_AnnP_2,P_poll__networl_2_1_AnnP_3,P_network_2_5_RP_1,P_poll__networl_4_2_AskP_3,P_poll__networl_3_6_AnnP_0,P_poll__networl_2_5_AnnP_3,P_masterList_4_4_1,P_poll__networl_5_6_AskP_3,P_network_6_6_AskP_5,P_poll__networl_1_0_AI_3,P_network_0_5_AskP_5,P_network_1_6_AnnP_4,P_network_3_4_RI_2,P_poll__networl_2_4_AskP_1,P_poll__networl_0_1_RI_4,P_poll__networl_2_0_AI_1,P_network_4_5_AnnP_5,P_dead_2,P_network_1_4_AskP_4,P_poll__networl_1_3_RI_1,P_poll__networl_4_2_AskP_6,P_poll__networl_5_4_AnsP_0,P_poll__networl_4_0_AI_6,P_poll__networl_4_0_AskP_2,P_poll__networl_5_6_AskP_0,P_poll__networl_5_0_AnnP_2,P_poll__networl_1_3_AskP_0,P_network_1_2_AnnP_1,P_network_5_5_RP_6,P_poll__networl_5_2_AI_2,P_network_1_2_AnnP_2,P_masterList_1_3_1,P_poll__networl_4_4_AskP_0,P_masterList_6_1_2,P_network_5_4_AI_3,P_poll__networl_1_2_AI_3,P_masterList_1_3_5,P_poll__networl_0_3_AI_0,P_network_6_1_AnnP_1,P_poll__networl_2_2_RP_1,P_poll__networl_5_6_RI_2,P_network_1_2_AI_1,P_poll__networl_3_2_AnnP_1,P_masterList_4_1_0,P_masterList_0_6_4,P_poll__networl_3_5_AskP_1,P_poll__networl_2_6_AnnP_2,P_network_3_3_AskP_4,P_poll__networl_3_1_RI_3,P_masterList_3_1_5,P_network_0_0_RP_4,P_poll__networl_6_3_AI_2,P_network_3_5_AnnP_2,P_poll__networl_6_0_AskP_6,P_electionFailed_3,P_masterList_1_3_4,P_poll__networl_0_3_AnnP_6,P_masterList_6_3_6,P_network_4_6_AI_6,P_poll__networl_6_4_AskP_5,P_network_0_2_AnnP_1,P_network_6_4_AnnP_2,P_poll__networl_1_3_RI_2,P_network_1_3_AnnP_6,P_network_2_3_AskP_6,P_poll__networl_0_4_AI_0,P_network_0_0_RP_6,P_network_6_2_AnnP_3,P_poll__networl_4_6_AI_4,P_masterList_0_6_0,P_poll__networl_5_5_RP_3,P_poll__networl_4_1_RP_5,P_poll__networl_6_3_AnnP_2,P_poll__networl_6_4_RI_1,P_network_1_1_RI_4,P_network_3_4_AI_6,P_network_1_1_RI_2,P_poll__networl_5_0_RI_1,P_network_5_3_AI_6,P_poll__networl_2_0_AnnP_0,P_poll__networl_3_4_AI_4,P_poll__networl_2_2_AI_4,P_poll__networl_1_5_AI_4,P_network_2_4_AskP_4,P_poll__networl_2_3_AnnP_1,P_poll__networl_5_4_AnnP_0,P_network_3_5_AnnP_6,P_poll__networl_5_1_AI_0,P_poll__networl_3_2_RI_2,P_masterList_2_3_4,P_network_0_6_AnnP_3,P_poll__networl_0_6_RP_3,P_poll__networl_0_4_AskP_4,P_poll__networl_2_0_AI_4,P_poll__networl_2_4_AskP_3,P_poll__networl_2_5_AnnP_0,P_poll__networl_1_0_AI_1,P_network_4_4_AskP_5,P_network_6_2_AI_3,P_poll__networl_3_4_AskP_4,P_poll__networl_5_5_AskP_6,P_network_2_3_AskP_1,P_poll__networl_1_4_AskP_4,P_poll__networl_3_6_AnnP_3,P_network_3_6_AI_2,P_network_4_1_AnnP_1,P_poll__networl_6_4_AI_1,P_network_4_4_RP_5,P_network_6_5_RI_2,P_poll__networl_5_5_AI_6,P_network_1_3_AskP_5,P_network_5_5_AI_1,P_poll__networl_1_1_AI_0,P_poll__networl_4_2_AI_1,P_poll__networl_6_3_AnsP_0,P_masterList_0_3_2,P_poll__networl_3_5_AI_4,P_network_5_0_AI_1,P_poll__networl_1_1_AI_4,P_poll__networl_1_3_AnnP_6,P_poll__networl_1_0_AskP_5,P_poll__networl_3_1_AnnP_6,P_poll__networl_5_2_RI_0,P_network_3_2_AI_1,P_poll__networl_4_1_AnnP_4,P_network_5_3_AskP_2,P_masterList_5_6_6,P_network_4_3_AI_3,P_network_1_2_AnnP_6,P_poll__networl_2_3_AI_2,P_poll__networl_0_0_AnnP_1,P_poll__networl_2_0_AnnP_1,P_poll__networl_1_0_RI_2,P_network_5_0_AskP_5,P_network_2_0_AnnP_2,P_network_3_4_AskP_2,P_poll__networl_1_6_AskP_4,P_network_0_2_AskP_3,P_masterList_3_4_1,P_network_6_3_RI_3,P_poll__networl_2_4_RI_0,P_poll__networl_6_2_AskP_3,P_masterList_1_6_6,P_poll__networl_2_3_RP_6,P_network_4_0_AI_4,P_network_3_0_AskP_4,P_poll__networl_6_6_AnnP_3,P_poll__networl_1_0_AnnP_5,P_network_0_5_AI_2,P_poll__networl_5_0_AI_1,P_network_1_3_RP_4,P_network_1_1_RI_3,P_poll__networl_0_5_RP_5,P_poll__networl_3_1_RP_3,P_poll__networl_0_2_AnnP_1,P_masterList_0_2_3,P_network_3_0_AI_1,P_poll__networl_0_6_AnnP_0,P_masterList_0_1_5,P_network_5_2_RP_2,P_poll__networl_4_3_AnnP_6,P_network_2_4_AnnP_5,P_network_3_3_AnnP_6,P_poll__networl_2_5_AskP_6,P_poll__networl_6_2_AskP_4,P_poll__networl_0_4_AnnP_6,P_poll__networl_1_3_RP_1,P_network_6_5_RP_5,P_masterList_3_1_1,P_masterList_3_5_0,P_poll__networl_3_1_AI_2,P_network_6_5_AnnP_5,P_poll__networl_3_1_RP_2,P_poll__networl_5_5_RP_1,P_network_0_1_AI_3,P_poll__networl_6_4_RP_2,P_masterList_2_1_0,P_poll__networl_0_3_RI_2,P_masterList_5_3_1,P_network_6_3_RP_3,P_poll__networl_3_1_AnnP_2,P_poll__networl_0_5_AnnP_4,P_poll__networl_6_5_AskP_4,P_poll__networl_6_6_AI_5,P_masterList_2_2_6,P_network_4_5_AI_4,P_masterList_4_5_1,P_network_5_1_AskP_3,P_network_0_4_AI_5,P_poll__networl_3_3_RI_2,P_poll__networl_4_3_AskP_6,P_poll__networl_0_4_AI_4,P_poll__networl_1_6_AI_6,P_network_5_5_RP_4,P_poll__networl_5_6_RP_3,P_poll__networl_4_4_RI_6,P_masterList_5_4_6,P_poll__networl_0_0_RP_4,P_poll__networl_3_3_RP_1,P_poll__networl_2_2_AI_3,P_poll__networl_2_4_AnnP_5,P_poll__networl_3_3_RI_6,P_poll__networl_0_2_AI_0,P_poll__networl_0_4_RP_0,P_poll__networl_3_5_RI_3,P_poll__networl_6_6_AI_6,P_masterList_1_1_4,P_poll__networl_1_6_AnnP_0,P_network_4_5_RI_1,P_network_5_2_AskP_5,P_poll__networl_1_2_RI_4,P_poll__networl_0_2_AskP_3,P_network_0_5_RP_6,P_poll__networl_2_6_AI_2,P_network_6_1_RI_4,P_poll__networl_4_0_RI_3,P_network_1_1_RP_1,P_poll__networl_3_1_RP_4,P_network_5_5_AI_5,P_network_2_6_AI_4,P_poll__networl_0_1_AskP_3,P_poll__networl_5_3_AnnP_6,P_poll__networl_6_0_RI_4,P_network_3_4_AI_5,P_poll__networl_2_5_AnnP_2,P_poll__networl_2_6_AnnP_0,P_network_5_6_AI_4,P_poll__networl_1_0_AnnP_4,P_poll__networl_3_3_AI_4,P_poll__networl_1_3_AnnP_5,P_network_4_2_RP_6,P_network_6_2_RP_1,P_poll__networl_6_6_AnnP_1,P_network_3_0_AskP_6,P_poll__networl_1_0_RI_1,P_poll__networl_6_0_RI_1,P_network_0_5_AskP_1,P_network_6_0_RI_4,P_poll__networl_3_6_AnnP_1,P_poll__networl_4_5_AI_4,P_network_0_3_AskP_3,P_network_5_3_AI_5,P_network_4_1_AI_2,P_poll__networl_0_1_AnnP_5,P_poll__networl_1_1_AnnP_1,P_poll__networl_5_1_AskP_2,P_network_4_2_RP_4,P_network_4_3_AI_6,P_network_0_0_AskP_6,P_poll__networl_2_3_AskP_4,P_network_0_0_RI_5,P_poll__networl_0_6_AnnP_3,P_poll__networl_2_2_AskP_5,P_network_1_5_RP_4,P_network_1_1_RI_6,P_poll__networl_4_6_AskP_1,P_poll__networl_1_5_RP_2,P_poll__networl_5_6_AI_6,P_network_5_0_AnnP_4,P_network_6_4_AskP_4,P_poll__networl_0_1_AskP_5,P_poll__networl_3_4_AI_0,P_masterList_0_5_5,P_network_6_4_AskP_5,P_network_3_1_AnnP_1,P_poll__networl_3_5_AnnP_1,P_network_4_4_AI_5,P_poll__networl_6_6_AI_4,P_network_5_3_AI_4,P_masterList_5_5_2,P_poll__networl_6_3_RI_3,P_network_0_6_RP_6,P_poll__networl_5_6_AskP_1,P_poll__networl_2_6_AnnP_6,P_network_0_1_RP_2,P_network_3_4_AI_3,P_masterList_5_6_2,P_poll__networl_2_3_AnnP_2,P_poll__networl_4_5_RP_2,P_network_4_6_RI_3,P_network_3_1_AnnP_5,P_network_6_1_AI_3,P_poll__networl_1_1_AskP_4,P_network_2_4_AskP_5,P_poll__networl_1_6_RP_0,P_network_3_1_RI_3,P_poll__networl_0_6_RP_1,P_poll__networl_4_0_AnnP_4,P_poll__networl_2_5_AskP_0,P_network_5_3_AI_1,P_poll__networl_5_0_AnnP_3,P_network_6_1_AI_1,P_poll__networl_0_5_AskP_6,P_masterList_6_6_6,P_network_0_0_RI_3,P_network_5_4_RI_5,P_network_1_0_AI_5,P_poll__networl_4_4_AskP_6,P_poll__networl_5_3_RP_6,P_poll__networl_3_2_AI_2,P_masterList_0_3_6,P_masterList_4_1_2,P_network_6_4_RI_4,P_poll__networl_4_1_RP_3,P_network_4_6_AskP_6,P_poll__networl_0_5_AskP_3,P_poll__networl_0_3_AnsP_0,P_network_6_2_AskP_1,P_poll__networl_2_4_AI_0,P_poll__networl_3_6_RP_4,P_network_0_3_AI_3,P_poll__networl_3_3_AI_5,P_poll__networl_5_2_RI_1,P_network_1_6_RP_6,P_masterList_3_1_2,P_poll__networl_4_0_RI_6,P_poll__networl_5_5_AnnP_0,P_poll__networl_4_3_RP_5,P_masterList_5_3_2,P_network_4_1_AskP_3,P_network_3_3_RP_6,P_poll__networl_0_6_AskP_5,P_network_0_1_AskP_2,P_network_6_4_AskP_3,P_network_6_4_AI_2,P_poll__networl_1_1_RP_2,P_poll__networl_5_0_RP_6,P_network_6_4_RI_6,P_masterList_1_1_0,P_network_0_1_RP_6,P_network_5_5_AI_6,P_poll__networl_6_4_AnnP_4,P_poll__networl_2_0_AskP_6,P_poll__networl_6_1_AskP_5,P_masterList_3_4_2,P_poll__networl_3_5_RP_3,P_poll__networl_0_5_AI_0,P_poll__networl_3_4_AnnP_3,P_poll__networl_4_4_AskP_1,P_poll__networl_4_3_AI_0,P_poll__networl_1_4_AskP_2,P_network_2_3_AI_2,P_poll__networl_5_6_AnnP_5,P_masterList_1_6_0,P_poll__networl_5_2_AnnP_5,P_poll__networl_0_2_AskP_6,P_network_2_1_AI_4,P_network_4_3_AnnP_3,P_poll__networl_1_5_RI_3,P_network_0_3_AskP_4,P_poll__networl_1_4_AskP_5,P_poll__networl_5_2_AskP_5,P_poll__networl_5_3_AskP_4,P_network_1_5_RI_4,P_poll__networl_1_3_AnnP_1,P_network_5_0_AnnP_1,P_poll__networl_2_0_RP_2,P_network_1_0_AskP_6,P_network_4_3_RI_1,P_poll__networl_5_2_RP_1,P_poll__networl_2_3_AI_5,P_poll__networl_4_1_RI_4,P_masterList_0_2_5,P_network_1_6_RP_3,P_poll__networl_6_4_AnnP_5,P_network_1_2_AI_4,P_network_2_6_RP_5,P_network_5_6_AI_1,P_poll__networl_5_1_RI_3,P_poll__networl_5_6_RP_5,P_poll__networl_1_1_RP_1,P_network_4_2_RI_5,P_poll__networl_0_6_RI_0,P_poll__networl_1_4_AnnP_1,P_poll__networl_6_1_AI_4,P_network_5_1_AI_1,P_masterList_2_6_2,P_network_6_5_AskP_5,P_network_2_2_AI_2,P_network_4_3_RI_3,P_masterList_0_5_4,P_masterList_1_1_3,P_electionFailed_2,P_masterList_6_4_5,P_poll__networl_6_1_AskP_4,P_poll__networl_5_0_AskP_0,P_poll__networl_6_0_AnnP_6,P_poll__networl_6_3_RP_6,P_masterList_3_6_3,P_poll__networl_4_2_RI_1,P_network_3_3_AskP_6,P_network_2_0_AI_6,P_network_4_5_RP_1,P_network_4_3_RP_5,P_masterList_2_1_6,P_poll__networl_5_1_AskP_1,P_poll__networl_5_5_RI_1,P_poll__networl_1_5_AskP_1,P_network_6_3_RP_2,P_masterList_5_4_5,P_poll__networl_3_5_AskP_0,P_dead_6,P_poll__networl_6_2_RP_2,P_masterList_1_1_1,P_network_5_1_RP_4,P_poll__networl_2_3_AnsP_0,P_poll__networl_3_1_AI_4,P_poll__networl_6_1_AskP_2,P_poll__networl_2_6_RP_4,P_poll__networl_5_0_AskP_2,P_network_0_1_RI_3,P_poll__networl_3_1_AnsP_0,P_masterList_4_5_4,P_network_0_3_RP_4,P_poll__networl_0_2_RP_6,P_poll__networl_1_0_RP_4,P_poll__networl_0_0_AnnP_6,P_poll__networl_5_5_AnnP_4,P_poll__networl_5_6_AI_0,P_poll__networl_2_5_RI_5,P_poll__networl_4_0_RP_4,P_masterList_4_4_4,P_network_3_3_RI_4,P_network_4_2_RI_4,P_poll__networl_4_4_AnnP_6,P_masterList_2_4_5,P_poll__networl_2_0_AskP_1,P_poll__networl_3_3_AI_3,P_poll__networl_2_1_AnnP_5,P_network_2_4_AI_1,P_masterList_0_1_6,P_poll__networl_0_1_AnnP_4,P_poll__networl_0_5_AnsP_0,P_poll__networl_6_6_AnnP_5,P_network_2_2_AI_6,P_network_2_4_RP_3,P_network_2_0_RI_3,P_poll__networl_0_3_AnnP_4,P_poll__networl_4_4_AI_5,P_poll__networl_1_3_RP_5,P_network_3_5_RP_1,P_poll__networl_1_0_RI_5,P_poll__networl_6_5_AI_3,P_poll__networl_1_3_AskP_6,P_network_2_5_RI_6,P_poll__networl_5_5_RI_2,P_network_4_1_RP_3,P_network_4_4_AnnP_5,P_network_4_1_AskP_6,P_poll__networl_1_4_AI_4,P_masterList_4_4_3,P_poll__networl_6_5_RI_6,P_network_0_3_AnnP_2,P_network_0_0_RI_1,P_poll__networl_2_6_AI_6,P_poll__networl_6_3_RP_3,P_poll__networl_1_0_AI_0,P_poll__networl_6_0_AnnP_0,P_network_5_5_AskP_1,P_network_4_2_AI_5,P_poll__networl_6_3_RI_1,P_network_6_1_RI_2,P_network_2_4_RP_5,P_network_3_6_RI_4,P_poll__networl_4_2_RP_3,P_poll__networl_3_0_AnnP_5,P_network_2_6_RI_1,P_poll__networl_1_6_AnsP_0,P_poll__networl_3_2_AnnP_3,P_network_3_6_RP_3,P_poll__networl_1_2_AskP_1,P_poll__networl_5_6_RP_0,P_poll__networl_6_2_RP_1,P_network_6_1_RP_6,P_network_5_4_AI_6,P_poll__networl_4_4_RP_0,P_network_3_2_AskP_5,P_poll__networl_6_0_RP_4,P_network_6_0_RP_4,P_poll__networl_2_0_AI_6,P_masterList_5_3_3,P_network_2_6_RP_1,P_masterList_1_1_2,P_network_0_1_RI_6,P_poll__networl_6_5_AI_4,P_network_5_5_RP_3,P_network_2_2_AI_5,P_poll__networl_3_6_AskP_4,P_network_2_4_AI_3,P_poll__networl_1_6_RI_2,P_poll__networl_5_3_AI_6,P_poll__networl_4_1_AskP_1,P_poll__networl_6_3_AskP_5,P_poll__networl_1_4_AnnP_3,P_poll__networl_4_2_RP_6,P_poll__networl_6_2_AI_4,P_poll__networl_1_5_AskP_6,P_network_6_4_RI_1,P_poll__networl_2_1_AnnP_2,P_poll__networl_0_2_AI_1,P_network_4_4_RI_1,P_network_3_2_AskP_3,P_network_0_6_AI_5,P_network_6_1_RI_1,P_poll__networl_2_2_RP_3,P_poll__networl_5_5_AnnP_6,P_network_5_6_AnnP_1,P_poll__networl_1_0_RP_0,P_poll__networl_5_6_AnnP_0,P_poll__networl_1_6_RP_3,P_poll__networl_4_3_AnnP_4,P_poll__networl_2_5_AI_2,P_poll__networl_2_0_AskP_5,P_masterList_1_2_0,P_network_4_0_AI_5,P_poll__networl_0_5_AskP_0,P_poll__networl_0_2_AskP_1,P_poll__networl_3_0_RP_0,P_poll__networl_3_3_AnnP_1,P_network_2_1_RP_4,P_poll__networl_0_4_AnsP_0,P_network_5_2_RI_2,P_network_5_5_AI_3,P_poll__networl_3_3_RI_0,P_network_6_6_RI_1,P_poll__networl_5_0_RI_2,P_network_5_2_RI_4,P_poll__networl_3_6_AI_2,P_poll__networl_1_5_RP_1,P_masterList_6_4_2,P_network_4_1_RP_1,P_poll__networl_0_0_RP_1,P_poll__networl_5_3_RP_4,P_poll__networl_3_6_AI_3,P_masterList_3_6_2,P_network_1_2_AI_5,P_network_1_6_RP_4,P_masterList_0_4_6,P_network_6_2_AnnP_1,P_network_2_4_RI_3,P_poll__networl_0_1_AnsP_0,P_poll__networl_2_4_RI_4,P_network_0_2_RP_4,P_poll__networl_2_1_RI_1,P_poll__networl_0_6_RP_2,P_poll__networl_6_6_RI_5,P_network_4_1_AI_1,P_poll__networl_3_6_AskP_2,P_poll__networl_6_4_AnnP_6,P_masterList_3_4_0,P_poll__networl_1_2_AnsP_0,P_poll__networl_3_2_AskP_3,P_network_1_0_AnnP_3,P_network_3_6_RP_5,P_poll__networl_5_4_AI_3,P_network_0_6_RP_4,P_poll__networl_1_0_AnnP_1,P_poll__networl_1_3_RP_0,P_poll__networl_1_4_RI_4,P_network_0_5_RI_4,P_network_6_3_AnnP_3,P_network_1_0_AI_4,P_poll__networl_1_1_RP_4,P_network_3_3_AI_3,P_network_0_1_AskP_5,P_masterList_1_6_5,P_poll__networl_1_3_RP_3,P_network_2_4_AI_6,P_network_6_6_RP_1,P_network_4_2_AnnP_4,P_poll__networl_0_3_AnnP_1,P_poll__networl_3_0_RP_2,P_poll__networl_0_5_AI_4,P_network_2_0_RP_1,P_poll__networl_3_1_AskP_3,P_poll__networl_3_1_AnnP_0,P_poll__networl_4_3_AI_6,P_network_6_4_AnnP_1,P_masterList_2_2_3,P_poll__networl_4_2_AskP_5,P_poll__networl_1_5_AnnP_5,P_masterList_1_5_3,P_poll__networl_3_5_AI_2,P_poll__networl_0_0_AI_1,P_network_2_1_RP_6,P_poll__networl_2_2_RI_3,P_poll__networl_2_0_RP_6,P_poll__networl_4_6_RP_6,P_network_6_4_AnnP_6,P_poll__networl_3_4_AnnP_1,P_poll__networl_6_3_RP_5,P_poll__networl_1_2_RP_3,P_poll__networl_0_5_AI_5,P_network_1_1_AskP_4,P_network_2_6_RP_2,P_network_4_6_RI_6,P_poll__networl_5_3_AI_0,P_poll__networl_6_3_AnnP_4,P_network_4_3_AI_2,P_masterList_3_6_5,P_network_1_2_RI_2,P_poll__networl_4_5_RI_4,P_masterList_0_1_2,P_network_3_1_AskP_5,P_poll__networl_0_5_RP_0,P_dead_5,P_poll__networl_1_4_RI_1,P_crashed_1,P_network_4_4_AnnP_3,P_poll__networl_3_2_RP_3,P_poll__networl_4_2_AskP_2,P_poll__networl_3_1_AnnP_3,P_network_3_2_RP_5,P_poll__networl_4_3_RP_4,P_network_4_5_AnnP_3,P_poll__networl_5_1_RP_5,P_network_3_5_AnnP_5,P_poll__networl_1_3_RI_0,P_poll__networl_3_2_AI_4,P_network_3_1_AskP_4,P_masterList_0_1_3,P_poll__networl_3_3_AnsP_0,P_network_2_0_AnnP_3,P_network_4_3_AnnP_6,P_network_1_6_AI_1,P_poll__networl_1_1_RI_6,P_poll__networl_1_1_RP_3,P_poll__networl_4_5_AskP_3,P_poll__networl_2_2_RP_4,P_poll__networl_4_3_AnnP_0,P_poll__networl_6_0_RP_3,P_poll__networl_6_5_RP_4,P_poll__networl_0_0_AnnP_3,P_poll__networl_6_4_AskP_3,P_poll__networl_0_4_AskP_1,P_poll__networl_1_6_AskP_5,P_poll__networl_1_6_AnnP_2,P_poll__networl_5_4_RI_4,P_poll__networl_0_2_RI_6,P_poll__networl_1_0_AskP_0,P_network_5_3_RI_4,P_poll__networl_5_1_AnsP_0,P_poll__networl_4_2_AnnP_0,P_poll__networl_3_6_RI_4,P_poll__networl_1_2_RI_3,P_poll__networl_6_1_RP_0,P_poll__networl_3_5_RP_5,P_network_3_1_AI_3,P_network_1_1_AnnP_6,P_network_5_0_AnnP_3,P_poll__networl_4_0_AnnP_5,P_network_6_3_AnnP_1,P_network_6_5_AskP_6,P_network_6_1_AskP_1,P_network_2_0_RI_6,P_poll__networl_0_6_RI_1,P_poll__networl_2_6_AnnP_3,P_network_1_6_AskP_3,P_network_3_0_AskP_2,P_network_6_6_AnnP_1,P_network_0_6_RI_1,P_poll__networl_1_3_AI_0,P_poll__networl_2_2_AI_0,P_network_3_3_AskP_2,P_network_5_6_RP_4,P_network_6_3_RI_1,P_poll__networl_6_4_RP_3,P_poll__networl_3_6_AskP_6,P_network_5_6_AnnP_5,P_poll__networl_4_4_AskP_3,P_network_4_5_RP_2,P_masterList_4_3_2,P_network_3_4_AnnP_5,P_poll__networl_6_2_AnnP_4,P_network_1_6_AnnP_3,P_network_5_6_RP_2,P_network_3_3_AI_4,P_poll__networl_1_1_AskP_0,P_masterList_4_6_3,P_network_1_2_AskP_6,P_network_4_0_AnnP_1,P_network_2_4_RI_1,P_poll__networl_3_2_AI_1,P_network_0_6_RI_6,P_network_1_0_RI_2,P_poll__networl_2_3_RI_2,P_network_5_2_RI_1,P_masterList_6_6_4,P_network_6_0_AskP_5,P_network_3_3_RP_3,P_poll__networl_3_6_RI_1,P_poll__networl_0_5_AI_1,P_poll__networl_1_1_AnnP_6,P_masterList_5_1_0,P_poll__networl_4_5_AskP_6,P_poll__networl_1_5_RP_0,P_network_4_3_RP_6,P_poll__networl_1_3_AskP_2,P_network_6_1_RI_5,P_poll__networl_6_2_RI_3,P_network_4_4_RP_1,P_poll__networl_0_6_AnnP_2,P_poll__networl_6_1_AI_1,P_poll__networl_6_3_AskP_3,P_network_2_2_RP_1,P_poll__networl_0_1_RI_0,P_poll__networl_4_6_AskP_0,P_masterList_2_5_4,P_poll__networl_4_3_AskP_1,P_poll__networl_6_4_AskP_1,P_network_3_0_RI_2,P_poll__networl_4_2_RP_5,P_network_2_4_AnnP_2,P_network_5_0_AnnP_6,P_network_2_0_RI_5,P_poll__networl_3_3_RI_5,P_masterList_0_6_6,P_network_1_1_AI_3,P_poll__networl_4_0_RI_4,P_poll__networl_1_0_RI_6,P_poll__networl_0_3_RP_1,P_poll__networl_3_0_AnnP_4,P_network_2_2_RP_3,P_network_3_0_RP_1,P_network_3_2_AskP_4,P_poll__networl_1_2_AnnP_6,P_poll__networl_5_4_AnnP_4,P_poll__networl_5_5_AI_2,P_network_2_4_AI_5,P_network_0_0_RP_1,P_network_4_3_RI_2,P_poll__networl_5_4_AnnP_6,P_network_6_5_RP_4,P_poll__networl_3_5_AnsP_0,P_network_0_4_AnnP_2,P_poll__networl_2_0_RI_5,P_poll__networl_2_0_AnnP_3,P_poll__networl_2_5_RI_3,P_poll__networl_3_3_RI_3,P_network_0_0_AI_2,P_poll__networl_1_3_RI_6,P_network_5_3_RI_5,P_masterList_0_4_2,P_network_0_0_RI_6,P_poll__networl_6_1_RI_3,P_poll__networl_5_6_AnsP_0,P_network_3_5_AnnP_1,P_poll__networl_6_2_AnsP_0,P_network_4_3_AnnP_1,P_network_2_5_RI_4,P_network_4_6_AskP_3,P_poll__networl_3_2_AnnP_2,P_poll__networl_0_4_RI_0,P_network_5_3_RP_4,P_network_3_5_RP_6,P_network_2_5_AnnP_3,P_network_5_6_RI_3,P_poll__networl_3_2_RI_5,P_poll__networl_0_0_AnnP_4,P_masterList_1_6_2,P_poll__networl_3_6_RP_3,P_network_1_2_RI_6,P_poll__networl_0_2_RP_2,P_network_2_5_RI_3,P_network_1_1_RP_3,P_network_5_0_RI_3,P_network_0_1_AnnP_2,P_network_0_2_AI_1,P_poll__networl_0_4_AI_3,P_network_2_0_AskP_2,P_poll__networl_4_0_AnnP_6,P_poll__networl_4_0_AskP_1,P_network_5_3_AI_2,P_poll__networl_3_3_RI_1,P_network_6_2_RP_5,P_poll__networl_5_2_AnnP_3,P_masterList_6_4_0,P_network_5_6_AnnP_4,P_network_6_6_AskP_2,P_poll__networl_2_4_AskP_0,P_poll__networl_4_2_RI_4,P_poll__networl_6_2_AI_3,P_masterList_0_1_1,P_network_0_4_RP_5,P_network_6_0_AI_1,P_poll__networl_6_5_RP_1,P_masterList_3_3_0,P_poll__networl_0_6_RI_3,P_network_2_0_RI_4,P_poll__networl_0_1_RP_3,P_network_0_6_AskP_4,P_network_1_4_AskP_2,P_network_3_0_RP_5,P_poll__networl_5_5_AskP_0,P_network_0_2_AnnP_5,P_network_4_6_AI_4,P_network_6_2_AnnP_5,P_poll__networl_1_1_AskP_1,P_poll__networl_0_6_AnnP_1,P_masterList_5_5_0,P_network_0_4_AskP_3,P_poll__networl_0_4_AI_6,P_network_2_3_AnnP_1,P_network_2_5_AI_6,P_poll__networl_1_3_RP_2,P_masterList_1_4_1,P_network_5_0_AskP_2,P_poll__networl_4_5_AnnP_3,P_poll__networl_2_4_AskP_5,P_poll__networl_1_2_AskP_2,P_poll__networl_1_5_RP_5,P_poll__networl_5_4_RI_2,P_network_0_4_RI_3,P_poll__networl_5_0_AnnP_5,P_poll__networl_5_4_RP_0,P_network_1_4_RP_1,P_poll__networl_0_3_AskP_2,P_network_2_5_AI_1,P_poll__networl_0_0_AskP_3,P_poll__networl_3_5_AI_6,P_crashed_4,P_network_3_1_RP_3,P_network_4_6_RP_2,P_network_4_1_AskP_5,P_network_2_4_AskP_6,P_network_2_0_AskP_4,P_masterList_5_5_1,P_network_0_3_AskP_1,P_poll__networl_4_4_RI_3,P_network_3_2_AI_3,P_network_6_6_RP_3,P_network_2_2_AnnP_6,P_network_1_6_RI_5,P_poll__networl_1_0_AskP_3,P_poll__networl_3_4_AnnP_6,P_network_1_6_RI_2,P_poll__networl_5_1_RI_5,P_network_5_1_AskP_6,P_poll__networl_1_5_AskP_0,P_poll__networl_0_1_AnnP_3,P_network_1_0_RI_6,P_poll__networl_6_1_RI_4,P_network_4_5_AskP_4,P_poll__networl_2_3_AnnP_5,P_poll__networl_6_1_AskP_3,P_network_5_6_RI_5,P_network_2_0_RI_2,P_network_0_5_AnnP_1,P_network_2_4_AnnP_4,P_poll__networl_4_0_AnnP_3,P_network_3_0_RP_6,P_poll__networl_2_6_AskP_6,P_poll__networl_1_5_AskP_2,P_poll__networl_3_3_RI_4,P_poll__networl_3_2_AnnP_4,
Jun 02, 2017 11:09:32 PM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Removed 3549 constant variables :P_network_6_5_RP_3, P_masterList_3_5_4, P_network_1_2_AI_3, P_poll__networl_2_1_AskP_0, P_poll__networl_1_2_RP_5, P_poll__networl_2_4_RI_1, P_poll__networl_4_3_RP_3, P_network_6_2_AnnP_6, P_network_5_6_AnnP_6, P_poll__networl_3_0_AskP_4, P_poll__networl_5_2_AnnP_4, P_masterList_4_6_4, P_poll__networl_4_5_RP_0, P_masterList_0_2_4, P_poll__networl_3_4_RI_4, P_poll__networl_6_0_AnnP_1, P_poll__networl_1_2_RI_0, P_poll__networl_1_3_AI_2, P_network_1_3_AI_2, P_poll__networl_0_3_AI_6, P_masterList_4_4_6, P_network_5_5_RI_3, P_poll__networl_6_1_AI_6, P_network_5_2_RP_4, P_network_4_1_AI_3, P_poll__networl_3_6_AI_5, P_poll__networl_5_0_AskP_6, P_network_3_5_AskP_1, P_poll__networl_1_0_RI_3, P_network_5_2_AnnP_1, P_poll__networl_3_6_AskP_1, P_poll__networl_2_3_RP_1, P_poll__networl_6_3_AskP_6, P_network_2_1_AI_5, P_network_4_5_AnnP_1, P_poll__networl_0_0_AnnP_5, P_network_3_4_RI_1, P_network_4_3_AI_5, P_poll__networl_6_4_RP_1, P_poll__networl_5_0_AnsP_0, P_poll__networl_3_0_AskP_0, P_network_4_2_AI_1, P_masterList_4_1_6, P_poll__networl_6_6_AnnP_6, P_network_4_0_AnnP_3, P_network_3_5_RP_4, P_network_2_6_AnnP_4, P_network_4_0_RI_3, P_poll__networl_0_3_AnnP_0, P_network_6_2_RI_6, P_poll__networl_0_6_AskP_6, P_poll__networl_2_3_RI_3, P_network_3_4_RP_2, P_network_4_2_RP_1, P_poll__networl_3_5_AnnP_3, P_poll__networl_3_6_RP_1, P_poll__networl_3_3_RP_2, P_network_4_4_RP_3, P_network_3_6_AnnP_6, P_network_0_2_RP_3, P_poll__networl_6_4_AnnP_1, P_poll__networl_0_1_RP_5, P_network_5_2_AskP_2, P_network_0_0_AnnP_6, P_network_2_5_AnnP_4, P_poll__networl_1_6_AskP_6, P_masterList_2_4_0, P_poll__networl_4_4_AskP_2, P_poll__networl_6_4_RP_0, P_masterList_4_1_1, P_network_6_1_AskP_2, P_poll__networl_4_6_AnsP_0, P_masterList_0_5_1, P_network_4_0_RI_5, P_network_0_6_AI_4, P_poll__networl_2_0_RI_1, P_poll__networl_4_3_RI_6, P_network_0_1_AnnP_6, P_poll__networl_2_1_AskP_6, P_poll__networl_2_2_AnnP_0, P_poll__networl_5_1_AnnP_3, P_network_6_1_RP_4, P_network_4_0_AskP_5, P_network_1_0_AskP_5, P_poll__networl_3_2_RP_2, P_poll__networl_2_3_AI_1, P_masterList_4_2_6, P_network_6_1_RI_3, P_network_3_2_RI_5, P_network_1_3_AI_3, P_poll__networl_3_4_AskP_6, P_network_2_5_AskP_4, P_network_0_3_AI_5, P_poll__networl_5_0_AnnP_0, P_poll__networl_4_4_AnnP_0, P_poll__networl_6_5_AskP_0, P_poll__networl_6_5_RI_1, P_poll__networl_3_6_AnnP_5, P_poll__networl_6_0_RI_2, P_poll__networl_6_3_RP_2, P_network_5_2_RI_3, P_poll__networl_0_2_RI_5, P_network_3_4_AskP_1, P_poll__networl_5_1_RI_6, P_network_4_6_AskP_5, P_masterList_1_2_4, P_poll__networl_3_4_AskP_0, P_poll__networl_5_6_RI_4, P_network_6_1_AI_6, P_network_3_4_AnnP_6, P_network_2_2_AnnP_5, P_masterList_2_4_2, P_network_5_0_AnnP_2, P_network_2_5_RI_5, P_network_0_4_AnnP_1, P_network_1_6_RP_2, P_poll__networl_5_5_RP_0, P_network_1_0_AnnP_5, P_masterList_0_3_5, P_poll__networl_5_5_AskP_3, P_poll__networl_3_1_AI_1, P_poll__networl_4_3_AskP_5, P_poll__networl_2_3_RP_4, P_poll__networl_1_6_AskP_1, P_masterList_1_2_6, P_network_3_1_RI_5, P_poll__networl_1_3_RP_4, P_network_6_6_AI_2, P_network_4_6_RP_1, P_network_1_1_AI_2, P_network_5_2_AnnP_6, P_poll__networl_2_2_AnnP_6, P_poll__networl_0_2_AskP_5, P_poll__networl_0_2_RI_2, P_masterList_2_2_1, P_poll__networl_1_4_AI_3, P_poll__networl_0_6_AskP_0, P_poll__networl_4_6_RI_2, P_poll__networl_4_6_RI_3, P_network_6_1_RI_6, P_poll__networl_1_5_RI_4, P_poll__networl_1_2_AnnP_5, P_poll__networl_4_5_AnsP_0, P_network_0_2_AnnP_2, P_poll__networl_0_4_RI_3, P_poll__networl_4_6_RP_4, P_poll__networl_0_6_RI_5, P_network_4_6_RP_6, P_poll__networl_0_5_RI_5, P_poll__networl_4_1_AskP_5, P_poll__networl_4_5_RP_3, P_network_0_0_AskP_2, P_network_4_2_RI_3, P_poll__networl_6_0_AskP_4, P_poll__networl_0_2_AI_6, P_poll__networl_2_0_RI_2, P_network_1_4_AnnP_2, P_network_0_2_AI_2, P_poll__networl_0_5_RP_1, P_poll__networl_1_4_RI_6, P_poll__networl_3_4_AnnP_2, P_network_3_3_AnnP_4, P_network_3_2_AnnP_6, P_network_0_5_AskP_3, P_poll__networl_1_0_AI_6, P_network_5_4_RP_6, P_poll__networl_2_1_RP_3, P_masterList_1_4_3, P_network_1_3_AskP_1, P_poll__networl_5_0_AI_6, P_network_1_5_RP_1, P_network_3_0_AskP_3, P_poll__networl_2_2_RI_0, P_network_5_0_AskP_6, P_network_5_3_AnnP_6, P_poll__networl_1_4_AnnP_0, P_poll__networl_1_5_RI_1, P_network_0_6_RI_2, P_network_0_5_AskP_2, P_network_2_6_AskP_4, P_masterList_5_4_1, P_network_3_5_AskP_4, P_masterList_3_1_6, P_poll__networl_3_0_RP_5, P_masterList_0_6_2, P_poll__networl_5_5_AI_4, P_poll__networl_5_2_AnnP_0, P_network_2_6_RP_3, P_network_3_5_RP_3, P_poll__networl_1_0_AskP_1, P_poll__networl_1_5_RP_3, P_poll__networl_0_5_RP_3, P_poll__networl_1_3_AI_5, P_poll__networl_5_4_RP_1, P_network_2_5_AskP_2, P_poll__networl_6_3_RP_4, P_network_2_1_AskP_1, P_network_6_2_RI_5, P_poll__networl_0_3_RP_6, P_poll__networl_0_4_RI_2, P_poll__networl_1_1_AskP_2, P_masterList_6_2_2, P_network_2_2_AskP_2, P_network_4_5_RI_5, P_network_2_3_AskP_2, P_poll__networl_2_2_AnnP_4, P_masterList_6_5_5, P_poll__networl_2_6_RI_4, P_poll__networl_2_0_RP_0, P_network_0_4_RP_6, P_network_6_0_AnnP_1, P_network_6_4_RI_5, P_network_3_2_AskP_6, P_network_0_6_AskP_1, P_network_5_3_AskP_5, P_poll__networl_5_3_RP_3, P_network_2_2_RI_3, P_poll__networl_0_1_AnnP_2, P_poll__networl_4_6_AnnP_2, P_network_3_0_AskP_5, P_poll__networl_4_6_AskP_3, P_network_1_6_AnnP_1, P_poll__networl_4_4_RI_0, P_poll__networl_4_4_AI_1, P_network_5_6_RI_2, P_network_6_0_RP_6, P_poll__networl_4_0_RI_1, P_poll__networl_4_0_AI_5, P_network_4_0_AnnP_5, P_poll__networl_6_3_AI_5, P_network_3_1_RP_5, P_network_2_1_RI_3, P_network_1_5_RI_3, P_network_6_1_AnnP_3, P_network_0_6_RP_5, P_network_5_2_AskP_4, P_network_3_5_AI_5, P_network_1_3_AI_5, P_network_3_2_AnnP_4, P_poll__networl_4_2_AskP_1, P_poll__networl_5_2_AI_4, P_network_1_5_AI_1, P_network_2_2_AnnP_1, P_network_4_0_RI_1, P_poll__networl_0_2_RP_4, P_poll__networl_2_2_RP_0, P_network_3_5_AnnP_3, P_network_4_0_AskP_1, P_network_1_3_AskP_6, P_poll__networl_4_6_RP_1, P_poll__networl_6_2_AskP_6, P_poll__networl_2_5_AI_1, P_poll__networl_3_3_AskP_4, P_network_1_4_AskP_5, P_poll__networl_4_1_AI_1, P_network_1_6_AI_3, P_network_3_3_AskP_3, P_poll__networl_6_2_RI_5, P_network_2_2_RI_1, P_poll__networl_3_5_AskP_5, P_poll__networl_5_2_AnnP_1, P_network_3_6_AI_5, P_poll__networl_0_6_RP_4, P_network_1_0_AnnP_6, P_masterList_2_5_1, P_network_1_1_RI_5, P_poll__networl_3_6_RI_2, P_network_5_5_RI_4, P_poll__networl_4_1_RI_6, P_network_3_5_RI_4, P_poll__networl_4_2_RI_3, P_masterList_4_6_0, P_network_6_0_RP_1, P_network_5_4_AskP_5, P_poll__networl_0_3_RI_1, P_network_2_2_AI_1, P_poll__networl_3_0_RI_1, P_poll__networl_6_6_RI_0, P_network_2_3_AnnP_6, P_network_0_5_AI_1, P_network_1_5_AnnP_2, P_poll__networl_1_3_AskP_5, P_poll__networl_1_4_RP_1, P_network_4_2_RI_1, P_network_5_3_AskP_6, P_poll__networl_1_0_RP_6, P_network_4_3_AskP_1, P_masterList_2_1_5, P_network_5_6_AskP_2, P_poll__networl_2_5_RI_0, P_poll__networl_6_5_RP_0, P_network_1_3_AnnP_3, P_poll__networl_0_3_AnnP_2, P_poll__networl_6_4_RP_5, P_poll__networl_6_1_RP_2, P_poll__networl_2_2_AskP_6, P_poll__networl_4_0_AI_3, P_poll__networl_1_5_AnnP_6, P_poll__networl_1_6_RI_6, P_network_1_3_AskP_2, P_poll__networl_1_0_AskP_6, P_poll__networl_2_2_AI_6, P_network_3_0_AnnP_6, P_poll__networl_2_2_RP_2, P_network_0_5_RI_3, P_network_3_3_AI_6, P_network_4_6_AI_1, P_poll__networl_1_4_RP_6, P_poll__networl_2_1_RP_2, P_network_4_2_AskP_2, P_network_5_2_AnnP_5, P_network_0_1_AI_1, P_network_2_3_AI_3, P_poll__networl_4_0_RP_2, P_network_3_2_AnnP_5, P_network_1_4_RI_6, P_network_4_3_AnnP_2, P_poll__networl_2_6_RI_0, P_network_5_0_AI_2, P_poll__networl_0_4_AnnP_2, P_poll__networl_2_3_RP_5, P_poll__networl_3_2_AI_0, P_network_0_3_RP_3, P_network_2_6_RI_5, P_network_0_1_AI_6, P_network_2_0_AskP_1, P_network_3_0_AI_3, P_poll__networl_4_1_RI_5, P_network_1_5_RP_2, P_poll__networl_4_4_AskP_4, P_masterList_5_2_3, P_network_6_3_AskP_4, P_poll__networl_2_5_RP_6, P_poll__networl_0_2_AnsP_0, P_poll__networl_4_0_AnnP_1, P_network_5_4_RP_2, P_network_1_2_RI_1, P_network_6_0_AnnP_5, P_poll__networl_3_1_RP_1, P_poll__networl_6_3_AnnP_3, P_poll__networl_6_5_RI_4, P_network_4_3_AnnP_4, P_poll__networl_6_3_AskP_0, P_masterList_2_5_5, P_network_5_6_AI_3, P_network_0_0_RP_2, P_masterList_4_3_4, P_network_5_1_AI_4, P_network_2_0_RP_6, P_network_0_1_AnnP_1, P_network_3_6_AnnP_2, P_masterList_5_5_3, P_masterList_1_2_1, P_network_2_5_AI_4, P_masterList_6_4_4, P_poll__networl_5_3_AnnP_3, P_poll__networl_1_4_AnnP_5, P_poll__networl_2_5_RP_2, P_masterList_2_1_1, P_poll__networl_2_5_AnnP_4, P_poll__networl_1_1_AI_2, P_poll__networl_3_1_AskP_0, P_poll__networl_6_6_RP_6, P_network_2_6_AskP_6, P_poll__networl_3_3_AnnP_2, P_network_1_2_AskP_4, P_network_2_3_AnnP_2, P_network_0_4_AskP_4, P_network_2_3_RP_1, P_network_0_3_RI_6, P_poll__networl_0_4_RI_4, P_poll__networl_2_2_AskP_2, P_network_4_0_RP_6, P_poll__networl_3_0_AnnP_0, P_network_2_5_AskP_6, P_poll__networl_4_4_RI_2, P_network_6_2_AI_2, P_network_4_6_AnnP_5, P_network_3_4_RI_5, P_poll__networl_3_0_RI_4, P_masterList_4_1_3, P_masterList_5_2_1, P_poll__networl_4_1_AskP_6, P_poll__networl_1_2_AI_1, P_poll__networl_1_5_AI_6, P_poll__networl_3_0_AI_0, P_network_6_5_AnnP_2, P_poll__networl_1_3_AI_3, P_network_0_0_AI_6, P_network_5_0_AnnP_5, P_poll__networl_1_3_RI_5, P_poll__networl_0_6_AI_5, P_poll__networl_6_5_AI_1, P_network_1_0_AnnP_4, P_network_3_5_RI_6, P_poll__networl_2_6_RI_5, P_poll__networl_0_1_AnnP_6, P_poll__networl_2_0_AskP_3, P_poll__networl_0_3_AskP_6, P_poll__networl_3_6_RI_6, P_network_2_1_RI_5, P_poll__networl_3_4_RI_0, P_dead_1, P_poll__networl_1_1_RI_2, P_poll__networl_6_2_RI_2, P_poll__networl_0_1_AskP_2, P_poll__networl_6_4_AI_4, P_network_1_6_RP_1, P_poll__networl_1_2_AskP_6, P_poll__networl_3_0_AI_5, P_poll__networl_0_5_AnnP_1, P_poll__networl_6_0_AnnP_4, P_network_0_5_AnnP_5, P_poll__networl_5_1_RP_0, P_network_6_6_AskP_1, P_network_3_0_AI_5, P_poll__networl_5_5_AskP_5, P_poll__networl_2_3_AskP_3, P_poll__networl_4_6_RP_3, P_poll__networl_3_5_AI_5, P_network_6_5_AI_6, P_poll__networl_3_0_AskP_5, P_poll__networl_6_2_AI_0, P_poll__networl_5_3_AI_1, P_poll__networl_6_6_RI_2, P_network_5_6_AskP_6, P_masterList_0_3_4, P_masterList_4_3_0, P_network_0_2_RP_6, P_poll__networl_0_2_RP_1, P_network_5_0_RI_6, P_network_1_1_AI_6, P_poll__networl_4_2_AskP_4, P_network_3_5_RI_2, P_network_4_3_AskP_2, P_poll__networl_3_2_RP_1, P_poll__networl_6_5_RP_2, P_poll__networl_3_5_RP_4, P_network_5_6_RI_6, P_network_4_4_AI_6, P_poll__networl_4_0_AskP_4, P_poll__networl_4_3_AI_4, P_poll__networl_5_3_RP_2, P_network_0_5_AI_6, P_poll__networl_0_1_RI_1, P_network_6_1_RP_5, P_network_6_1_AnnP_5, P_network_6_0_AI_5, P_poll__networl_6_0_RP_0, P_poll__networl_1_4_RP_0, P_network_6_2_RI_2, P_network_2_6_RI_2, P_masterList_2_3_3, P_network_2_0_RP_5, P_masterList_5_3_6, P_poll__networl_1_1_RI_1, P_masterList_5_3_0, P_network_3_6_AI_3, P_network_4_2_AskP_4, P_network_4_4_AskP_6, P_poll__networl_3_0_AnnP_2, P_poll__networl_5_2_AI_0, P_network_3_0_RI_3, P_network_2_3_RI_1, P_masterList_5_6_4, P_poll__networl_3_0_RI_5, P_poll__networl_6_6_AI_2, P_poll__networl_4_5_AskP_1, P_poll__networl_2_2_AnsP_0, P_network_2_1_AI_1, P_poll__networl_2_0_AnnP_4, P_poll__networl_2_4_AnnP_1, P_network_3_1_AskP_6, P_network_1_6_AI_5, P_poll__networl_3_3_AskP_1, P_network_6_3_RI_6, P_network_1_3_AI_6, P_network_4_2_AskP_1, P_poll__networl_3_0_RI_6, P_network_3_0_AnnP_3, P_network_5_4_AI_5, P_network_2_3_AskP_4, P_poll__networl_0_6_AI_2, P_network_0_3_AI_6, P_network_1_0_AI_6, P_network_2_2_AskP_6, P_poll__networl_6_1_AnnP_1, P_poll__networl_6_2_RI_0, P_poll__networl_5_1_RP_1, P_poll__networl_4_3_AnnP_2, P_network_0_0_AI_4, P_network_0_5_RI_2, P_network_1_2_AskP_3, P_network_0_2_AI_6, P_network_0_4_AnnP_3, P_poll__networl_2_1_RI_2, P_poll__networl_5_6_AI_1, P_network_5_2_AI_1, P_network_4_4_RP_2, P_poll__networl_3_3_RP_4, P_masterList_4_6_2, P_masterList_6_4_6, P_network_4_3_RP_4, P_network_0_0_RI_4, P_network_2_3_RP_6, P_network_0_4_AI_4, P_network_0_1_RI_1, P_poll__networl_5_5_RP_6, P_poll__networl_2_0_AI_5, P_masterList_0_2_1, P_poll__networl_2_4_RP_3, P_poll__networl_4_2_RI_5, P_poll__networl_0_0_RP_6, P_network_6_1_RP_2, P_network_3_3_AI_2, P_poll__networl_4_1_AnsP_0, P_poll__networl_6_1_AI_0, P_poll__networl_3_6_AI_0, P_network_5_4_RP_1, P_network_6_6_AnnP_3, P_poll__networl_5_6_RI_3, P_poll__networl_6_3_AI_4, P_poll__networl_1_0_RP_1, P_poll__networl_0_4_AskP_5, P_network_5_5_AnnP_5, P_poll__networl_2_4_AskP_4, P_poll__networl_4_1_RP_4, P_masterList_6_5_3, P_network_3_6_RP_4, P_network_5_6_RP_1, P_poll__networl_0_0_AI_2, P_network_0_1_RP_5, P_masterList_5_2_6, P_network_0_6_AskP_5, P_poll__networl_5_1_AskP_5, P_poll__networl_0_5_AnnP_0, P_network_2_1_AnnP_5, P_network_5_1_AnnP_3, P_network_3_1_RP_4, P_poll__networl_3_4_AI_5, P_poll__networl_5_4_AI_0, P_poll__networl_4_2_RI_0, P_network_0_4_RI_5, P_poll__networl_0_6_RI_4, P_masterList_1_3_6, P_poll__networl_4_6_AI_2, P_masterList_6_4_3, P_poll__networl_3_4_RI_3, P_network_3_2_AI_4, P_poll__networl_4_3_AI_1, P_poll__networl_6_0_RP_2, P_network_0_6_AnnP_6, P_poll__networl_1_4_AskP_1, P_poll__networl_4_4_AI_2, P_masterList_2_5_3, P_poll__networl_5_5_RP_4, P_masterList_0_1_0, P_network_5_3_RI_2, P_poll__networl_3_6_AnnP_2, P_poll__networl_4_3_RP_2, P_poll__networl_4_6_AI_5, P_poll__networl_5_6_AI_5, P_network_4_1_RI_3, P_network_6_3_AI_1, P_network_3_1_RP_2, P_poll__networl_5_5_RI_0, P_network_3_2_AI_6, P_poll__networl_5_3_RP_5, P_poll__networl_1_4_AI_5, P_poll__networl_3_3_RP_3, P_network_1_0_AI_3, P_poll__networl_1_4_RP_4, P_poll__networl_2_5_AI_5, P_poll__networl_0_3_AI_4, P_network_0_2_AnnP_3, P_poll__networl_4_1_RI_0, P_poll__networl_3_2_AnnP_0, P_masterList_1_3_3, P_poll__networl_0_6_AskP_1, P_network_1_3_RI_6, P_network_4_5_AnnP_6, P_poll__networl_1_5_AnnP_2, P_network_2_0_AskP_3, P_poll__networl_1_1_AI_1, P_network_0_0_RP_5, P_network_3_4_AskP_3, P_poll__networl_2_4_AI_5, P_network_0_4_AI_2, P_poll__networl_6_0_AI_6, P_network_0_4_AskP_6, P_poll__networl_1_3_RI_3, P_poll__networl_3_2_RP_0, P_network_0_2_AskP_1, P_poll__networl_3_1_RI_2, P_network_2_3_RP_5, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_6_RI_4, P_masterList_3_6_6, P_poll__networl_6_2_RP_5, P_network_1_3_AnnP_1, P_masterList_6_5_1, P_poll__networl_2_6_RP_0, P_poll__networl_1_6_RP_4, P_poll__networl_5_6_RI_5, P_network_2_5_RI_2, P_poll__networl_5_6_AI_4, P_network_1_4_RI_4, P_poll__networl_3_6_RP_5, P_network_5_2_RP_3, P_poll__networl_1_2_AskP_5, P_network_6_0_RP_5, P_poll__networl_1_0_RP_5, P_masterList_1_3_0, P_masterList_4_4_0, P_poll__networl_1_3_RI_4, P_network_0_4_RI_4, P_dead_3, P_network_5_4_AnnP_6, P_network_6_0_AskP_4, P_masterList_4_2_4, P_network_6_6_AI_3, P_network_1_4_AskP_1, P_masterList_2_1_4, P_network_0_2_RI_3, P_poll__networl_5_3_RI_4, P_masterList_5_2_2, P_network_4_2_AnnP_5, P_poll__networl_5_6_AI_2, P_network_1_4_AnnP_6, P_network_2_1_RP_3, P_poll__networl_3_4_RP_5, P_poll__networl_2_0_RI_0, P_poll__networl_3_4_RP_4, P_network_6_4_AI_6, P_network_5_1_AskP_1, P_network_2_3_RI_4, P_network_4_6_AnnP_6, P_poll__networl_3_1_AnnP_1, P_network_1_2_RP_3, P_masterList_5_5_4, P_network_6_1_AI_2, P_network_5_4_RI_1, P_poll__networl_3_3_AskP_2, P_network_5_5_RI_6, P_network_1_6_RP_5, P_masterList_4_1_5, P_poll__networl_0_4_AnnP_3, P_poll__networl_6_2_RP_6, P_network_0_3_RI_3, P_network_5_4_RI_4, P_network_0_0_AI_1, P_network_1_6_AskP_4, P_poll__networl_4_6_AnnP_5, P_masterList_5_1_4, P_poll__networl_6_4_AskP_2, P_network_3_5_AskP_2, P_poll__networl_0_3_AskP_4, P_network_4_6_AI_3, P_poll__networl_4_3_AskP_4, P_poll__networl_0_6_AI_4, P_poll__networl_1_4_AnnP_4, P_network_5_5_RI_1, P_poll__networl_6_1_RI_2, P_network_5_1_AskP_5, P_poll__networl_1_4_AnnP_2, P_poll__networl_6_4_RP_4, P_network_6_2_AnnP_4, P_network_4_2_AskP_6, P_network_1_0_AnnP_2, P_network_6_1_AI_5, P_poll__networl_2_1_AnnP_4, P_poll__networl_5_6_RI_0, P_poll__networl_0_5_AnnP_6, P_network_4_3_RP_3, P_network_4_0_AskP_4, P_poll__networl_4_2_AI_3, P_poll__networl_5_0_AI_0, P_poll__networl_4_5_RP_4, P_masterList_5_5_5, P_masterList_1_2_3, P_network_6_5_AskP_2, P_poll__networl_2_5_RP_3, P_network_0_4_RI_2, P_poll__networl_4_0_AI_0, P_network_1_1_AskP_2, P_network_2_2_AnnP_2, P_poll__networl_3_5_RI_1, P_poll__networl_5_2_AnnP_2, P_network_0_2_RI_5, P_masterList_4_6_6, P_network_5_5_AskP_6, P_poll__networl_3_1_AskP_6, P_poll__networl_5_4_AskP_6, P_network_3_2_AskP_2, P_network_0_5_AI_5, P_poll__networl_3_1_RP_6, P_poll__networl_3_3_AI_2, P_poll__networl_5_6_AskP_4, P_network_0_3_RI_4, P_network_5_6_RP_3, P_network_0_0_AskP_5, P_network_5_5_AskP_5, P_network_1_3_AskP_3, P_network_6_5_RI_5, P_masterList_2_4_1, P_network_2_4_AskP_2, P_masterList_4_2_5, P_poll__networl_6_4_AI_5, P_poll__networl_6_0_AnsP_0, P_poll__networl_3_1_RP_5, P_network_0_0_AnnP_1, P_network_0_4_AskP_5, P_network_0_6_AnnP_5, P_network_6_5_AnnP_4, P_masterList_3_2_5, P_electionFailed_1, P_network_3_3_RI_3, P_poll__networl_4_1_AnnP_1, P_network_0_4_AskP_1, P_network_2_3_RI_5, P_poll__networl_0_2_AI_4, P_poll__networl_1_5_AnnP_0, P_poll__networl_0_4_AI_1, P_poll__networl_4_6_AnnP_1, P_masterList_0_6_1, P_masterList_6_2_3, P_network_4_0_RP_4, P_network_2_0_AI_4, P_network_3_4_RP_3, P_network_1_6_RI_4, P_poll__networl_1_1_AI_3, P_poll__networl_4_1_AI_5, P_poll__networl_5_4_AI_5, P_network_0_4_RP_1, P_network_6_3_AskP_5, P_poll__networl_1_4_AskP_3, P_masterList_1_5_4, P_network_3_5_AskP_3, P_poll__networl_2_6_AnnP_1, P_poll__networl_5_1_AskP_4, P_network_0_3_RI_2, P_network_4_4_RI_3, P_masterList_1_4_4, P_network_0_1_AnnP_4, P_poll__networl_4_4_AskP_5, P_network_3_4_AnnP_1, P_poll__networl_5_3_AnsP_0, P_network_3_2_RI_6, P_poll__networl_1_1_RP_5, P_network_3_3_RI_1, P_poll__networl_5_3_AI_4, P_network_0_0_AI_5, P_network_4_6_AnnP_2, P_poll__networl_5_3_AI_3, P_poll__networl_3_2_AskP_0, P_masterList_3_5_2, P_poll__networl_3_5_RI_6, P_network_6_2_AskP_5, P_poll__networl_1_4_AskP_0, P_poll__networl_0_3_RI_4, P_poll__networl_0_1_AskP_4, P_masterList_2_6_0, P_network_3_6_AskP_5, P_network_5_2_RP_1, P_network_4_2_AnnP_2, P_network_1_0_AskP_1, P_network_0_2_AnnP_6, P_poll__networl_2_3_AI_0, P_poll__networl_3_1_RP_0, P_poll__networl_0_1_RI_5, P_masterList_6_3_2, P_network_3_1_AnnP_2, P_poll__networl_6_2_AI_1, P_network_3_1_AskP_1, P_network_3_4_RI_3, P_poll__networl_1_3_AnsP_0, P_network_2_0_AskP_6, P_poll__networl_3_3_RP_0, P_poll__networl_6_4_RI_4, P_network_1_5_AI_3, P_electionFailed_6, P_network_3_6_AskP_1, P_network_1_2_RP_1, P_poll__networl_0_2_RP_5, P_poll__networl_0_0_AI_6, P_poll__networl_3_2_AskP_2, P_poll__networl_2_0_RP_1, P_poll__networl_2_1_AI_3, P_network_2_6_AskP_1, P_poll__networl_6_6_RI_3, P_poll__networl_5_4_RI_3, P_network_2_1_AI_6, P_poll__networl_4_5_AnnP_4, P_masterList_4_2_0, P_network_0_2_RP_2, P_poll__networl_2_1_RI_4, P_poll__networl_5_2_AskP_1, P_network_6_3_RI_4, P_network_0_3_RP_5, P_network_5_1_AskP_2, P_network_1_1_RP_5, P_masterList_0_4_4, P_poll__networl_1_2_AskP_0, P_network_6_0_AI_4, P_poll__networl_3_5_RP_1, P_poll__networl_0_0_RI_2, P_network_1_0_AI_1, P_poll__networl_1_1_RP_6, P_poll__networl_6_2_RP_0, P_network_2_3_AI_5, P_network_4_0_RP_2, P_poll__networl_0_1_AI_3, P_network_0_0_AI_3, P_poll__networl_1_1_RI_4, P_poll__networl_1_2_AskP_4, P_network_0_1_AI_4, P_poll__networl_6_5_AnnP_4, P_poll__networl_0_1_AI_0, P_poll__networl_6_5_AskP_1, P_network_3_5_RP_2, P_network_1_5_AskP_2, P_poll__networl_0_1_AI_4, P_poll__networl_1_1_RI_3, P_network_0_3_AI_4, P_network_0_6_AI_3, P_poll__networl_1_0_AnnP_2, P_network_2_6_RI_4, P_poll__networl_0_4_RP_6, P_poll__networl_2_6_RP_6, P_network_5_5_AskP_3, P_network_5_4_AskP_6, P_network_2_2_RP_6, P_poll__networl_0_5_RI_3, P_network_2_2_AnnP_4, P_poll__networl_6_3_RP_1, P_network_1_6_AI_6, P_poll__networl_6_1_AI_5, P_network_3_3_AnnP_5, P_poll__networl_6_2_AnnP_1, P_network_1_2_AnnP_3, P_network_2_6_AnnP_6, P_network_3_3_AI_1, P_poll__networl_5_6_RI_1, P_poll__networl_2_2_AskP_3, P_poll__networl_5_5_AnnP_1, P_network_2_5_AnnP_6, P_poll__networl_3_3_AskP_0, P_poll__networl_4_0_RP_1, P_poll__networl_2_4_AI_6, P_poll__networl_3_5_RI_4, P_masterList_3_2_6, P_poll__networl_2_4_AnsP_0, P_network_3_2_AnnP_1, P_poll__networl_2_1_AI_0, P_poll__networl_4_1_AI_6, P_network_6_6_AI_4, P_poll__networl_0_6_AI_0, P_network_0_5_RI_6, P_poll__networl_1_6_AI_4, P_poll__networl_5_1_AI_5, P_masterList_4_2_3, P_masterList_6_3_4, P_network_6_6_AnnP_4, P_poll__networl_3_3_AI_6, P_poll__networl_6_6_AskP_4, P_poll__networl_3_0_RP_1, P_network_0_5_RP_4, P_network_1_3_RP_5, P_network_1_5_RP_5, P_poll__networl_4_6_RP_0, P_network_1_3_RP_1, P_poll__networl_1_1_AnnP_2, P_network_1_4_AnnP_3, P_poll__networl_1_3_AskP_1, P_poll__networl_6_3_RI_5, P_masterList_6_5_2, P_masterList_3_2_3, P_poll__networl_0_3_RP_0, P_poll__networl_1_3_AskP_4, P_masterList_3_3_4, P_poll__networl_4_5_AI_3, P_network_4_1_AskP_4, P_poll__networl_1_5_AskP_4, P_network_6_5_AI_4, P_network_1_0_RP_5, P_network_5_3_AnnP_1, P_poll__networl_3_6_RP_2, P_network_0_5_RI_5, P_network_5_2_AI_2, P_network_4_4_AI_2, P_network_4_3_AI_4, P_poll__networl_4_4_AnsP_0, P_network_2_0_AnnP_4, P_poll__networl_3_4_RP_6, P_poll__networl_1_2_AnnP_2, P_network_5_4_RI_3, P_network_0_5_RI_1, P_poll__networl_4_5_AnnP_6, P_poll__networl_2_6_RP_3, P_network_0_3_AskP_6, P_poll__networl_1_1_AnnP_3, P_poll__networl_3_4_RP_3, P_network_2_2_AnnP_3, P_poll__networl_5_5_RP_5, P_network_1_0_AnnP_1, P_network_1_2_RI_4, P_masterList_5_5_6, P_poll__networl_1_0_AskP_2, P_network_2_0_AI_3, P_network_3_0_AI_4, P_network_3_6_RI_2, P_network_0_2_AskP_2, P_poll__networl_4_1_AskP_4, P_network_0_4_AI_6, P_poll__networl_6_5_AI_2, P_network_5_1_AnnP_4, P_network_3_1_RI_1, P_poll__networl_0_0_AI_3, P_network_3_0_AnnP_4, P_poll__networl_3_1_AnnP_5, P_poll__networl_2_5_AI_4, P_poll__networl_3_3_AI_1, P_network_1_2_AskP_2, P_poll__networl_0_0_AskP_4, P_poll__networl_4_3_AskP_0, P_poll__networl_0_0_AskP_0, P_network_1_3_AnnP_5, P_network_6_0_RP_3, P_poll__networl_3_1_RI_4, P_masterList_6_5_6, P_network_6_1_AskP_4, P_poll__networl_2_2_AskP_4, P_poll__networl_6_2_AnnP_6, P_poll__networl_1_2_AI_2, P_network_4_0_AnnP_4, P_masterList_0_2_0, P_poll__networl_5_6_RI_6, P_poll__networl_2_2_AnnP_3, P_poll__networl_5_4_AI_4, P_network_5_1_RI_4, P_poll__networl_6_6_AskP_6, P_masterList_0_5_3, P_poll__networl_0_3_RP_4, P_network_1_1_AskP_1, P_network_1_4_AI_6, P_network_4_4_AskP_4, P_network_5_4_RI_6, P_poll__networl_2_2_AskP_1, P_network_0_5_AI_3, P_masterList_6_2_0, P_network_3_0_RI_1, P_network_3_3_RI_2, P_network_0_3_RI_1, P_poll__networl_4_1_AnnP_2, P_network_4_3_RI_4, P_network_2_3_RP_3, P_poll__networl_0_4_RI_1, P_poll__networl_2_1_AI_4, P_network_5_5_AI_2, P_masterList_2_3_5, P_network_0_4_AskP_2, P_network_4_4_AnnP_4, P_poll__networl_4_2_AnnP_3, P_poll__networl_0_4_RI_5, P_poll__networl_2_5_RI_6, P_poll__networl_1_6_AnnP_3, P_poll__networl_2_4_RI_5, P_network_4_3_RI_5, P_network_3_5_AskP_6, P_network_4_0_RP_3, P_poll__networl_5_2_AskP_2, P_poll__networl_6_0_RP_6, P_poll__networl_2_5_AI_3, P_network_2_3_AI_1, P_poll__networl_2_5_AI_6, P_masterList_6_2_5, P_network_3_6_RI_3, P_poll__networl_2_0_AI_0, P_poll__networl_0_4_AskP_2, P_poll__networl_5_5_RI_5, P_poll__networl_6_1_AnnP_6, P_masterList_2_1_3, P_network_0_1_RI_4, P_poll__networl_2_2_RI_5, P_network_0_3_AI_2, P_network_3_1_AI_2, P_network_5_4_AskP_4, P_network_2_4_AI_4, P_masterList_0_4_1, P_poll__networl_6_5_AnnP_5, P_masterList_6_6_5, P_poll__networl_5_1_RI_0, P_poll__networl_3_3_AnnP_0, P_network_5_1_RP_3, P_poll__networl_1_4_RP_3, P_poll__networl_5_1_RI_4, P_poll__networl_1_0_AI_4, P_poll__networl_5_5_AI_0, P_network_5_4_RP_5, P_poll__networl_6_3_RI_2, P_network_5_5_RP_5, P_poll__networl_3_1_AnnP_4, P_network_3_2_RI_4, P_network_6_0_AnnP_6, P_poll__networl_3_2_RI_4, P_poll__networl_6_5_AnnP_1, P_poll__networl_3_5_AskP_6, P_poll__networl_6_6_RP_2, P_masterList_5_3_4, P_poll__networl_3_3_AskP_5, P_masterList_0_2_6, P_poll__networl_4_2_RP_2, P_network_6_3_AI_3, P_poll__networl_2_6_RI_2, P_masterList_0_3_1, P_masterList_1_4_6, P_network_2_2_RP_4, P_poll__networl_4_1_AskP_0, P_network_1_2_AskP_5, P_network_6_3_RP_5, P_network_0_1_RP_3, P_poll__networl_5_2_RP_2, P_poll__networl_4_6_RI_4, P_network_5_5_RI_5, P_network_6_6_RI_6, P_poll__networl_1_6_RP_2, P_network_1_5_RI_5, P_masterList_3_3_1, P_network_1_5_AskP_3, P_network_1_3_RP_3, P_network_3_0_AI_2, P_network_1_6_AskP_5, P_poll__networl_3_0_AI_6, P_poll__networl_2_0_AskP_4, P_network_4_4_RI_5, P_network_6_1_AI_4, P_network_0_2_AskP_5, P_poll__networl_5_3_AI_5, P_masterList_0_4_3, P_network_0_2_RP_5, P_network_1_3_RP_2, P_poll__networl_0_2_RP_3, P_network_3_1_AnnP_6, P_network_1_1_AskP_3, P_network_2_4_AnnP_1, P_network_5_2_AI_3, P_poll__networl_2_6_AskP_2, P_network_2_3_AskP_5, P_poll__networl_4_2_AnnP_1, P_poll__networl_1_3_AnnP_4, P_network_6_4_AskP_2, P_network_0_4_RI_1, P_poll__networl_2_0_AnsP_0, P_masterList_0_5_2, P_network_6_3_RP_6, P_poll__networl_5_0_AskP_5, P_poll__networl_2_6_AI_3, P_network_1_3_AI_4, P_network_4_1_AI_5, P_poll__networl_1_2_AI_4, P_network_4_5_RP_6, P_network_0_6_RP_1, P_poll__networl_5_0_AskP_4, P_poll__networl_2_4_RP_1, P_network_5_3_AnnP_4, P_network_1_3_RI_1, P_network_4_2_AskP_3, P_poll__networl_0_6_AskP_3, P_poll__networl_3_4_AnnP_5, P_network_6_5_AskP_3, P_network_5_3_RP_6, P_network_6_3_RP_1, P_poll__networl_4_2_RP_1, P_network_3_2_AnnP_2, P_poll__networl_1_0_AI_5, P_network_6_6_RP_6, P_network_5_3_RI_3, P_poll__networl_4_1_AI_0, P_network_6_4_AI_4, P_poll__networl_5_1_AnnP_4, P_network_4_5_AI_5, P_network_6_3_RI_5, P_poll__networl_0_0_RI_1, P_poll__networl_4_6_AskP_5, P_network_2_1_RP_5, P_network_2_5_RP_4, P_poll__networl_4_6_AI_6, P_network_2_1_RI_4, P_poll__networl_1_3_AskP_3, P_network_4_3_RP_1, P_network_6_5_AnnP_6, P_poll__networl_3_6_AI_6, P_poll__networl_3_6_RI_5, P_network_6_2_AI_6, P_masterList_1_6_1, P_poll__networl_6_6_AI_1, P_network_2_1_RP_2, P_electionFailed_4, P_network_0_0_AnnP_3, P_network_1_5_AI_6, P_poll__networl_1_4_RI_0, P_network_4_1_RP_5, P_network_2_0_AnnP_5, P_network_2_5_AI_5, P_poll__networl_0_1_AI_5, P_network_1_2_RP_2, P_masterList_3_6_0, P_poll__networl_6_5_AI_5, P_network_3_5_AskP_5, P_poll__networl_4_5_AskP_0, P_network_5_5_AskP_4, P_network_6_6_AnnP_6, P_poll__networl_6_4_RI_5, P_network_0_6_RI_5, P_network_6_4_RI_3, P_poll__networl_5_2_RP_6, P_poll__networl_2_4_AnnP_3, P_network_5_1_RI_1, P_poll__networl_4_5_RI_1, P_poll__networl_1_6_RI_5, P_network_1_4_AI_3, P_network_5_3_AnnP_3, P_poll__networl_5_1_RP_6, P_network_5_6_AnnP_3, P_network_4_6_RP_3, P_network_0_6_AskP_6, P_network_2_3_AskP_3, P_network_1_6_RI_3, P_poll__networl_3_5_RP_0, P_poll__networl_5_1_RP_4, P_poll__networl_4_1_RI_3, P_masterList_2_1_2, P_network_1_3_AnnP_4, P_poll__networl_6_3_AnnP_1, P_poll__networl_1_1_AnnP_5, P_masterList_2_2_4, P_poll__networl_0_6_AnnP_5, P_network_5_4_RI_2, P_poll__networl_4_5_AnnP_5, P_poll__networl_4_4_RI_1, P_masterList_3_1_3, P_poll__networl_3_5_AnnP_2, P_poll__networl_2_1_AskP_5, P_poll__networl_0_4_RI_6, P_network_6_4_AskP_6, P_poll__networl_4_3_AI_3, P_network_2_2_RP_5, P_network_5_2_RP_6, P_network_6_4_RP_2, P_poll__networl_0_2_AnnP_6, P_poll__networl_6_1_RI_0, P_poll__networl_0_0_RI_0, P_masterList_1_5_2, P_network_6_5_RI_1, P_network_6_3_AskP_2, P_poll__networl_3_0_AnnP_6, P_poll__networl_5_6_AskP_2, P_poll__networl_2_5_RP_0, P_poll__networl_4_1_RP_1, P_network_1_0_AI_2, P_poll__networl_5_3_AskP_2, P_network_1_6_AnnP_6, P_network_4_6_AnnP_3, P_poll__networl_6_4_AI_3, P_poll__networl_2_0_RP_3, P_poll__networl_4_1_AskP_2, P_poll__networl_4_6_AskP_2, P_poll__networl_3_0_AnnP_1, P_poll__networl_5_5_AI_5, P_network_6_3_AskP_6, P_poll__networl_3_4_AI_2, P_network_1_2_AnnP_5, P_network_4_6_AI_5, P_poll__networl_5_3_AI_2, P_network_5_1_RP_5, P_network_6_2_RI_3, P_poll__networl_1_5_AI_1, P_poll__networl_6_1_AnnP_4, P_poll__networl_2_0_RI_6, P_poll__networl_0_5_AnnP_3, P_poll__networl_3_4_RI_5, P_poll__networl_4_1_AnnP_5, P_network_4_5_AskP_5, P_poll__networl_2_0_AnnP_2, P_masterList_5_6_0, P_poll__networl_3_0_RI_2, P_poll__networl_3_1_AskP_2, P_network_5_6_RP_6, P_poll__networl_3_2_AskP_5, P_network_6_0_RP_2, P_poll__networl_0_5_RI_0, P_poll__networl_0_0_AskP_6, P_network_4_5_RP_3, P_network_2_4_AI_2, P_poll__networl_3_6_AI_4, P_network_6_1_AnnP_4, P_poll__networl_0_3_AnnP_3, P_network_1_2_RI_5, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_4_AnnP_0, P_network_0_0_RI_2, P_poll__networl_0_1_AnnP_0, P_poll__networl_6_0_RI_0, P_masterList_1_1_6, P_network_4_2_RP_5, P_poll__networl_0_1_AI_2, P_electionFailed_0, P_network_4_1_AI_4, P_poll__networl_6_6_AskP_0, P_network_3_0_AI_6, P_poll__networl_6_2_AnnP_2, P_poll__networl_5_0_AnnP_6, P_network_3_6_AskP_6, P_poll__networl_3_2_RP_6, P_network_3_4_AskP_4, P_poll__networl_6_0_RI_3, P_network_4_2_AI_4, P_poll__networl_0_6_AnnP_6, P_network_0_4_RI_6, P_poll__networl_6_2_AI_5, P_poll__networl_2_3_RP_0, P_poll__networl_1_5_AnnP_4, P_poll__networl_2_6_AI_0, P_poll__networl_6_0_AnnP_5, P_poll__networl_2_6_AskP_0, P_poll__networl_6_5_AI_0, P_network_0_2_AskP_4, P_network_5_5_AI_4, P_poll__networl_5_0_RP_0, P_poll__networl_4_4_RP_1, P_network_0_1_AI_5, P_poll__networl_0_5_RP_4, P_poll__networl_4_0_AI_2, P_poll__networl_5_4_RI_6, P_masterList_1_5_0, P_network_5_1_AnnP_2, P_network_3_2_RP_1, P_poll__networl_0_0_AI_5, P_network_2_0_AnnP_1, P_poll__networl_1_1_AskP_5, P_poll__networl_5_4_AI_1, P_poll__networl_4_2_RI_2, P_masterList_1_4_5, P_network_6_0_AskP_3, P_poll__networl_1_6_AI_1, P_poll__networl_3_5_RI_0, P_masterList_4_1_4, P_poll__networl_5_5_AnnP_5, P_network_4_1_AnnP_3, P_network_6_1_RP_1, P_poll__networl_3_4_AskP_2, P_poll__networl_3_2_AI_5, P_network_6_1_AnnP_2, P_network_0_3_AnnP_4, P_network_5_0_AskP_4, P_poll__networl_3_1_AskP_5, P_poll__networl_1_1_AnsP_0, P_poll__networl_2_5_AI_0, P_network_3_6_RI_5, P_poll__networl_1_6_AI_0, P_network_6_3_AI_5, P_masterList_6_1_3, P_network_3_3_RI_5, P_poll__networl_3_6_RI_3, P_poll__networl_5_4_RP_2, P_network_3_4_AnnP_2, P_poll__networl_5_3_AskP_1, P_poll__networl_4_0_AI_4, P_poll__networl_5_3_AnnP_0, P_poll__networl_6_2_AnnP_0, P_poll__networl_1_2_RI_5, P_poll__networl_3_6_AnsP_0, P_poll__networl_5_1_AskP_3, P_network_4_4_RI_4, P_poll__networl_0_0_RI_3, P_poll__networl_1_5_AI_2, P_masterList_1_5_5, P_network_3_2_AskP_1, P_masterList_2_5_6, P_poll__networl_2_2_AI_5, P_poll__networl_4_1_RP_6, P_network_6_0_RI_2, P_poll__networl_0_2_AI_2, P_network_1_4_RP_5, P_poll__networl_3_6_RI_0, P_poll__networl_0_3_AskP_3, P_network_0_3_AskP_2, P_poll__networl_0_4_RP_1, P_masterList_3_2_0, P_network_5_4_AI_4, P_poll__networl_6_1_AskP_0, P_masterList_1_6_4, P_network_6_0_AI_6, P_network_2_1_AnnP_4, P_poll__networl_3_5_AI_1, P_poll__networl_1_6_AI_3, P_network_1_4_AI_5, P_network_5_2_AI_6, P_poll__networl_5_1_AI_3, P_masterList_5_2_5, P_poll__networl_2_3_AskP_6, P_network_0_1_AskP_3, P_poll__networl_6_2_AnnP_3, P_network_5_1_AnnP_1, P_network_0_3_RP_6, P_poll__networl_0_4_AskP_6, P_poll__networl_2_1_RP_5, P_network_1_1_AI_5, P_poll__networl_6_5_RP_6, P_network_6_3_AI_6, P_network_4_4_AskP_2, P_network_6_2_AskP_3, P_poll__networl_0_3_RP_2, P_network_6_4_AskP_1, P_network_6_3_AskP_3, P_network_3_1_AI_6, P_poll__networl_2_0_AskP_0, P_network_5_1_AnnP_6, P_network_5_2_AI_5, P_poll__networl_6_5_RP_5, P_network_4_0_AskP_3, P_poll__networl_5_2_AskP_4, P_network_4_3_AnnP_5, P_network_0_4_AnnP_4, P_poll__networl_5_1_AskP_6, P_network_3_6_AI_1, P_masterList_5_1_2, P_network_5_3_RI_6, P_network_6_0_AskP_2, P_poll__networl_5_3_RI_5, P_network_0_5_AskP_6, P_network_1_6_AnnP_5, P_network_3_4_AskP_5, P_poll__networl_4_5_AnnP_0, P_poll__networl_1_3_RP_6, P_network_2_4_RP_6, P_poll__networl_1_2_AI_5, P_network_0_1_AnnP_5, P_network_3_6_RI_1, P_masterList_3_3_5, P_network_4_1_AskP_2, P_network_6_2_AI_1, P_poll__networl_0_0_AnnP_0, P_poll__networl_2_6_AskP_5, P_poll__networl_4_6_AnnP_3, P_poll__networl_6_6_AskP_5, P_poll__networl_4_3_AskP_2, P_poll__networl_5_2_AskP_0, P_network_0_2_AI_5, P_network_4_0_RP_1, P_poll__networl_2_6_AskP_4, P_network_6_0_AI_2, P_poll__networl_2_5_AnnP_5, P_poll__networl_0_1_RP_0, P_poll__networl_4_4_RI_5, P_poll__networl_2_6_RI_3, P_masterList_6_3_5, P_poll__networl_1_3_AI_1, P_network_0_5_AnnP_3, P_network_0_5_AnnP_6, P_network_5_0_RP_1, P_network_3_5_RI_1, P_network_4_1_RI_5, P_network_3_1_RP_6, P_poll__networl_6_6_RI_1, P_poll__networl_6_2_AI_6, P_network_2_4_AskP_3, P_network_3_1_AnnP_3, P_poll__networl_0_1_AskP_0, P_network_6_1_RP_3, P_network_2_0_RP_3, P_network_3_1_AI_1, P_masterList_3_5_3, P_masterList_3_5_6, P_masterList_2_3_6, P_poll__networl_3_4_AnsP_0, P_poll__networl_2_2_AI_1, P_network_0_4_AI_3, P_network_6_4_AI_1, P_poll__networl_0_0_RP_3, P_network_4_1_AskP_1, P_poll__networl_5_4_AI_6, P_network_0_1_AskP_6, P_network_4_0_AI_6, P_network_6_5_RI_3, P_poll__networl_6_5_RI_2, P_poll__networl_0_4_AnnP_5, P_network_1_2_AskP_1, P_poll__networl_5_2_AnnP_6, P_poll__networl_5_5_AskP_4, P_network_4_3_AI_1, P_network_6_5_AI_3, P_poll__networl_4_1_RP_2, P_network_3_6_RP_2, P_masterList_4_6_1, P_masterList_5_2_4, P_network_4_0_AnnP_6, P_poll__networl_3_5_AnnP_4, P_poll__networl_4_5_AI_6, P_poll__networl_1_5_AnnP_1, P_network_5_3_RI_1, P_network_2_6_AskP_5, P_poll__networl_5_0_RI_4, P_poll__networl_6_3_AnnP_5, P_network_3_4_RI_6, P_poll__networl_2_3_AnnP_6, P_masterList_5_6_5, P_poll__networl_4_0_AskP_5, P_poll__networl_5_0_AnnP_1, P_poll__networl_2_4_RP_2, P_masterList_1_1_5, P_network_4_3_AskP_6, P_poll__networl_3_0_RI_3, P_network_4_1_AnnP_6, P_masterList_3_2_1, P_poll__networl_1_1_AI_6, P_poll__networl_0_0_AnsP_0, P_masterList_5_2_0, P_network_5_1_RI_6, P_poll__networl_0_4_AnnP_4, P_network_6_4_AnnP_3, P_network_1_1_RI_1, P_poll__networl_2_5_AnsP_0, P_network_5_5_RP_1, P_masterList_3_4_4, P_network_0_3_RP_1, P_poll__networl_5_6_AnnP_3, P_network_3_6_RP_1, P_masterList_0_5_0, P_poll__networl_4_2_RI_6, P_poll__networl_4_5_AI_1, P_network_2_2_AskP_5, P_network_5_5_RI_2, P_network_1_0_RI_5, P_poll__networl_5_2_RI_2, P_poll__networl_4_5_AI_5, P_network_4_1_RP_6, P_masterList_6_4_1, P_poll__networl_5_0_AskP_3, P_poll__networl_4_5_AnnP_2, P_network_3_6_RI_6, P_poll__networl_3_2_RI_0, P_masterList_2_6_1, P_poll__networl_6_0_AI_2, P_masterList_6_1_6, P_network_5_6_AI_2, P_network_5_1_RI_3, P_poll__networl_3_6_AI_1, P_poll__networl_4_2_AskP_0, P_network_6_0_AnnP_3, P_poll__networl_6_4_AskP_0, P_masterList_6_5_4, P_poll__networl_5_0_AI_5, P_masterList_3_3_6, P_poll__networl_1_0_RP_2, P_poll__networl_4_4_RP_3, P_network_0_3_RI_5, P_network_4_5_AskP_2, P_network_2_5_AnnP_2, P_poll__networl_0_5_RI_2, P_network_0_6_RI_4, P_poll__networl_0_5_RI_1, P_poll__networl_4_4_AI_4, P_network_0_3_AnnP_5, P_network_3_0_RP_3, P_poll__networl_5_4_RP_3, P_poll__networl_0_5_AskP_2, P_poll__networl_6_0_AskP_0, P_network_1_1_RP_4, P_network_5_6_AnnP_2, P_masterList_0_3_3, P_network_5_6_RI_1, P_network_3_2_RI_2, P_poll__networl_6_5_AskP_2, P_network_3_0_AskP_1, P_dead_4, P_crashed_3, P_poll__networl_4_3_AnnP_5, P_poll__networl_4_6_RI_5, P_poll__networl_0_4_RP_2, P_network_6_6_AnnP_2, P_network_5_4_AI_2, P_poll__networl_2_4_RI_6, P_network_6_0_AnnP_4, P_poll__networl_1_2_AnnP_4, P_network_4_6_AI_2, P_masterList_4_5_6, P_masterList_1_5_6, P_poll__networl_4_4_RI_4, P_network_2_3_AnnP_3, P_masterList_4_3_5, P_network_2_0_RI_1, P_poll__networl_3_5_AnnP_6, P_poll__networl_5_6_AnnP_2, P_poll__networl_6_1_RP_1, P_poll__networl_0_6_RI_6, P_network_1_6_AskP_1, P_masterList_6_2_6, P_network_3_4_AnnP_4, P_poll__networl_0_1_RI_3, P_network_4_1_RP_4, P_network_4_2_RP_2, P_poll__networl_5_4_RP_5, P_network_0_6_AI_2, P_masterList_3_2_2, P_poll__networl_1_6_AskP_3, P_masterList_3_1_0, P_poll__networl_1_3_AnnP_3, P_poll__networl_2_6_RP_2, P_poll__networl_4_5_RI_3, P_masterList_6_1_5, P_poll__networl_4_3_RI_4, P_poll__networl_5_0_RI_6, P_poll__networl_2_0_AnnP_5, P_masterList_2_6_5, P_poll__networl_2_0_RP_5, P_network_6_5_AI_2, P_poll__networl_3_4_RP_2, P_poll__networl_3_3_AI_0, P_network_5_1_AI_3, P_network_0_5_RP_3, P_poll__networl_4_3_RP_0, P_poll__networl_5_4_RI_5, P_poll__networl_0_3_AI_1, P_network_0_1_AskP_4, P_poll__networl_5_0_RP_3, P_poll__networl_4_6_AnnP_4, P_network_6_6_AI_1, P_poll__networl_6_0_AskP_1, P_masterList_4_3_6, P_network_4_2_AnnP_6, P_network_0_1_AskP_1, P_poll__networl_4_3_RI_0, P_poll__networl_0_5_AnnP_5, P_poll__networl_5_5_RP_2, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_RI_0, P_masterList_3_2_4, P_poll__networl_0_4_AI_2, P_crashed_2, P_poll__networl_0_2_AskP_2, P_network_6_2_AnnP_2, P_poll__networl_5_1_RP_3, P_poll__networl_3_5_AskP_4, P_network_1_4_RP_4, P_network_3_2_RP_2, P_network_1_4_AI_4, P_poll__networl_0_6_AskP_4, P_poll__networl_5_4_RI_0, P_poll__networl_2_2_RI_4, P_network_3_1_RP_1, P_poll__networl_2_2_RI_6, P_poll__networl_3_0_RP_6, P_network_4_2_RP_3, P_network_6_4_AnnP_4, P_network_2_6_AI_1, P_network_4_2_AI_6, P_poll__networl_1_3_AnnP_2, P_masterList_3_6_1, P_poll__networl_4_5_RI_5, P_poll__networl_4_2_AI_2, P_poll__networl_4_4_AnnP_1, P_poll__networl_3_2_AskP_6, P_poll__networl_5_2_AskP_6, P_poll__networl_5_6_AnnP_4, P_poll__networl_5_6_AnnP_1, P_network_1_0_AskP_4, P_network_1_5_RI_6, P_masterList_5_1_1, P_network_0_5_AskP_4, P_poll__networl_1_6_RP_5, P_masterList_5_4_2, P_network_3_1_RI_6, P_poll__networl_1_4_AI_2, P_poll__networl_2_4_RP_4, P_masterList_6_3_1, P_masterList_4_4_5, P_poll__networl_5_0_RP_4, P_network_1_0_RI_4, P_network_4_0_RI_6, P_network_0_1_RI_5, P_network_0_2_AskP_6, P_poll__networl_6_6_RP_5, P_network_2_6_AnnP_3, P_masterList_5_6_3, P_network_4_4_AnnP_2, P_network_2_1_AskP_4, P_network_2_4_RI_4, P_network_3_0_RI_5, P_poll__networl_6_6_AnnP_2, P_network_0_4_AnnP_6, P_poll__networl_3_1_RI_6, P_poll__networl_3_4_AnnP_0, P_network_0_2_RI_6, P_poll__networl_1_5_RI_6, P_poll__networl_3_4_RI_6, P_poll__networl_2_1_RP_0, P_network_1_1_AnnP_1, P_poll__networl_4_6_RP_2, P_network_6_4_RP_5, P_masterList_5_1_3, P_network_5_4_AskP_2, P_poll__networl_6_4_AskP_4, P_network_1_4_AnnP_4, P_poll__networl_3_4_AI_6, P_poll__networl_5_6_RP_4, P_poll__networl_4_1_RI_1, P_network_1_4_AnnP_1, P_poll__networl_6_4_AI_2, P_poll__networl_4_6_RP_5, P_poll__networl_6_2_RI_4, P_masterList_2_3_1, P_network_5_0_RI_5, P_poll__networl_0_5_AskP_5, P_network_5_6_AI_5, P_network_5_2_AnnP_4, P_network_4_6_AskP_1, P_poll__networl_5_2_RI_4, P_poll__networl_1_0_AnnP_6, P_masterList_3_1_4, P_poll__networl_0_3_AskP_1, P_poll__networl_0_6_AI_1, P_masterList_2_4_3, P_poll__networl_5_3_AskP_6, P_network_5_5_AnnP_6, P_network_2_2_AskP_1, P_poll__networl_5_2_RP_4, P_network_5_5_AnnP_2, P_poll__networl_0_3_AskP_5, P_poll__networl_0_2_RI_0, P_network_3_5_RI_3, P_network_0_0_AnnP_4, P_network_5_6_RI_4, P_network_4_5_AI_6, P_poll__networl_5_4_RP_4, P_poll__networl_6_1_AskP_1, P_poll__networl_0_4_AI_5, P_poll__networl_2_1_AI_5, P_poll__networl_5_0_AskP_1, P_network_3_3_AskP_1, P_poll__networl_3_0_AskP_3, P_poll__networl_5_4_AnnP_5, P_network_1_6_RI_6, P_poll__networl_6_0_AI_5, P_poll__networl_5_5_AskP_2, P_poll__networl_3_0_AskP_6, P_network_3_6_AI_4, P_poll__networl_6_0_AI_1, P_network_0_5_RP_1, P_poll__networl_4_0_AnnP_2, P_poll__networl_0_1_AnnP_1, P_poll__networl_6_3_RI_6, P_poll__networl_6_5_AskP_5, P_network_2_2_RI_5, P_poll__networl_1_6_AnnP_5, P_poll__networl_2_2_AnnP_5, P_poll__networl_6_5_AnsP_0, P_network_3_0_AnnP_2, P_poll__networl_6_1_AnnP_5, P_network_4_4_RI_2, P_network_3_6_AnnP_1, P_network_2_2_AskP_4, P_poll__networl_2_3_RI_5, P_poll__networl_0_6_RP_0, P_poll__networl_1_5_RI_0, P_network_0_5_RP_2, P_network_2_6_AskP_2, P_poll__networl_5_3_RI_0, P_masterList_2_5_2, P_network_4_1_RI_6, P_poll__networl_6_0_AskP_5, P_network_0_6_RI_3, P_masterList_6_5_0, P_poll__networl_6_4_RI_3, P_poll__networl_2_1_AskP_1, P_poll__networl_3_2_AnsP_0, P_network_2_2_RP_2, P_network_3_1_AI_4, P_network_6_5_AskP_4, P_network_4_1_RP_2, P_network_6_6_RI_2, P_network_5_0_RP_5, P_network_6_3_AI_2, P_poll__networl_6_4_AI_0, P_poll__networl_4_2_RP_4, P_network_6_3_AnnP_4, P_poll__networl_2_1_AskP_4, P_poll__networl_5_0_AI_2, P_poll__networl_6_2_AnnP_5, P_network_2_3_AI_6, P_network_4_5_AskP_6, P_poll__networl_6_1_RP_6, P_poll__networl_6_5_RI_3, P_network_0_5_AI_4, P_poll__networl_1_6_RI_1, P_poll__networl_2_3_AI_4, P_network_3_4_RP_6, P_poll__networl_1_1_AskP_6, P_network_0_0_AnnP_5, P_poll__networl_3_5_AI_0, P_masterList_3_5_5, P_network_2_3_AI_4, P_network_4_4_AnnP_6, P_poll__networl_1_0_AI_2, P_network_3_6_AskP_3, P_network_1_6_AI_2, P_network_1_5_AI_4, P_network_4_0_AskP_2, P_network_6_3_AnnP_2, P_poll__networl_3_0_AskP_2, P_poll__networl_5_2_AskP_3, P_poll__networl_6_5_AI_6, P_network_2_1_RI_6, P_poll__networl_0_2_RI_1, P_network_0_2_RI_4, P_network_3_5_AI_3, P_network_0_3_RP_2, P_network_1_0_RI_1, P_network_4_6_RI_2, P_network_1_0_RI_3, P_poll__networl_6_1_AnnP_2, P_network_3_4_AnnP_3, P_poll__networl_3_0_AI_3, P_network_6_6_AnnP_5, P_poll__networl_2_2_RI_1, P_network_5_1_RP_1, P_network_6_1_AskP_3, P_poll__networl_2_6_RP_5, P_poll__networl_3_1_RI_0, P_poll__networl_6_2_RP_4, P_network_2_6_AI_5, P_network_2_0_AI_5, P_network_4_4_RI_6, P_network_5_4_AnnP_5, P_poll__networl_6_6_AI_0, P_poll__networl_1_0_RP_3, P_network_1_5_AnnP_6, P_network_4_5_RP_4, P_network_4_6_RI_5, P_poll__networl_0_2_AnnP_5, P_poll__networl_4_4_AI_0, P_network_0_4_AnnP_5, P_network_6_4_RP_4, P_masterList_1_6_3, P_network_6_5_RI_6, P_network_1_3_RI_4, P_poll__networl_0_3_RI_5, P_poll__networl_2_1_AskP_3, P_poll__networl_3_6_AnnP_4, P_poll__networl_5_4_AskP_4, P_network_2_6_AnnP_2, P_poll__networl_2_5_AskP_1, P_network_5_1_RP_2, P_poll__networl_0_3_AI_3, P_poll__networl_4_5_AskP_4, P_poll__networl_0_3_RP_3, P_network_1_1_RP_2, P_network_5_1_AI_5, P_network_3_3_AI_5, P_network_6_1_AskP_6, P_masterList_2_2_5, P_masterList_3_3_2, P_poll__networl_5_4_AnnP_1, P_network_0_6_RP_2, P_poll__networl_6_1_RP_4, P_poll__networl_6_3_AI_3, P_poll__networl_3_4_AskP_1, P_network_6_2_AI_5, P_network_1_4_AI_1, P_poll__networl_1_1_AnnP_4, P_network_5_0_AI_6, P_network_6_4_RI_2, P_poll__networl_2_0_AnnP_6, P_network_4_1_RI_1, P_poll__networl_1_6_RI_3, P_masterList_6_1_4, P_network_2_6_AnnP_5, P_poll__networl_6_4_RI_2, P_network_6_2_RP_6, P_network_4_5_AI_3, P_network_4_0_RI_4, P_masterList_2_3_0, P_poll__networl_2_3_AnnP_3, P_poll__networl_1_4_RP_5, P_poll__networl_2_5_RI_4, P_network_1_5_RP_3, P_poll__networl_0_1_RP_2, P_network_1_4_RI_3, P_masterList_0_5_6, P_masterList_0_6_3, P_network_1_5_RI_1, P_poll__networl_6_6_RI_6, P_network_6_5_RP_6, P_poll__networl_5_4_AskP_1, P_poll__networl_0_2_RI_3, P_poll__networl_6_6_AskP_3, P_network_0_0_RP_3, P_poll__networl_4_1_AI_2, P_poll__networl_6_4_AI_6, P_poll__networl_6_0_RI_6, P_poll__networl_0_0_AI_0, P_poll__networl_1_2_RP_1, P_network_2_4_RI_2, P_network_5_4_AnnP_1, P_poll__networl_3_0_RP_4, P_network_5_1_AI_2, P_poll__networl_2_3_AI_6, P_poll__networl_5_4_AskP_2, P_poll__networl_3_1_RI_5, P_poll__networl_4_2_AI_6, P_network_4_0_AskP_6, P_poll__networl_5_4_AnnP_2, P_network_4_6_RI_4, P_poll__networl_5_4_AskP_0, P_poll__networl_3_2_RI_3, P_network_2_0_AI_1, P_poll__networl_1_5_AskP_5, P_poll__networl_0_1_RI_2, P_network_1_5_AskP_5, P_network_6_0_AI_3, P_network_1_0_RP_2, P_poll__networl_5_5_AnnP_2, P_network_6_5_AnnP_1, P_network_2_2_RI_6, P_poll__networl_4_5_RI_6, P_network_2_4_AskP_1, P_network_4_0_RI_2, P_poll__networl_3_1_RI_1, P_network_0_4_RP_2, P_poll__networl_5_1_AI_4, P_poll__networl_3_4_RP_0, P_masterList_3_5_1, P_poll__networl_0_5_AskP_4, P_poll__networl_6_5_RP_3, P_poll__networl_6_6_AskP_2, P_poll__networl_3_4_AskP_3, P_poll__networl_0_1_RP_4, P_poll__networl_6_6_RI_4, P_poll__networl_5_2_RP_0, P_poll__networl_2_3_RP_3, P_network_3_5_AI_4, P_masterList_1_4_0, P_masterList_6_2_1, P_poll__networl_6_5_AskP_6, P_poll__networl_0_0_RI_5, P_network_4_6_RP_5, P_masterList_2_6_6, P_network_6_4_AI_3, P_poll__networl_3_5_RP_6, P_network_2_1_AnnP_1, P_network_5_3_RP_1, P_poll__networl_4_0_AnsP_0, P_network_1_1_AnnP_4, P_network_4_4_RP_6, P_network_3_2_AnnP_3, P_network_5_0_RP_4, P_network_5_3_AnnP_2, P_network_6_0_AskP_1, P_network_2_6_RI_3, P_network_6_3_AnnP_5, P_poll__networl_3_0_RP_3, P_poll__networl_2_0_AI_3, P_network_3_6_RP_6, P_masterList_0_2_2, P_network_5_4_AskP_3, P_network_2_3_AnnP_4, P_electionFailed_5, P_poll__networl_5_2_RI_5, P_network_3_3_RI_6, P_network_0_6_AnnP_4, P_network_3_5_RI_5, P_network_0_0_AskP_1, P_poll__networl_0_5_AskP_1, P_poll__networl_4_3_RP_6, P_network_1_4_AnnP_5, P_network_3_4_AI_4, P_network_0_6_AnnP_1, P_crashed_5, P_network_6_5_AnnP_3, P_network_1_1_AI_4, P_poll__networl_1_5_RP_4, P_poll__networl_2_4_RI_2, P_poll__networl_1_2_AnnP_0, P_poll__networl_2_6_AI_1, P_network_4_0_AI_1, P_poll__networl_3_1_AI_5, P_network_2_5_AskP_3, P_network_3_4_AskP_6, P_poll__networl_5_3_RI_3, P_crashed_0, P_network_0_6_AskP_2, P_poll__networl_2_2_AskP_0, P_poll__networl_6_0_RP_1, P_poll__networl_6_0_AI_3, P_network_6_4_RP_6, P_poll__networl_5_4_AI_2, P_poll__networl_2_2_RP_5, P_poll__networl_0_0_AskP_1, P_network_2_6_AI_6, P_poll__networl_4_2_AI_4, P_network_4_5_RI_2, P_network_2_4_RP_2, P_poll__networl_4_0_AskP_3, P_poll__networl_6_5_AskP_3, P_network_5_5_AskP_2, P_poll__networl_1_3_AnnP_0, P_poll__networl_4_4_AnnP_5, P_network_0_5_AnnP_4, P_poll__networl_5_6_AskP_5, P_network_4_6_AnnP_4, P_poll__networl_0_5_RI_6, P_poll__networl_0_5_RP_6, P_network_3_0_AnnP_1, P_poll__networl_1_2_RP_4, P_poll__networl_2_3_RI_0, P_network_2_0_RP_4, P_poll__networl_2_3_AskP_2, P_masterList_6_6_0, P_poll__networl_2_4_AskP_2, P_poll__networl_4_0_RP_3, P_poll__networl_3_2_AnnP_6, P_network_4_6_RP_4, P_poll__networl_6_4_RI_6, P_network_3_6_AnnP_3, P_network_6_2_RI_4, P_poll__networl_3_5_AnnP_0, P_poll__networl_2_5_AskP_4, P_poll__networl_0_4_RP_5, P_poll__networl_2_3_AskP_0, P_poll__networl_1_3_AI_4, P_poll__networl_4_1_RP_0, P_masterList_5_1_6, P_network_1_5_RI_2, P_network_0_0_AskP_4, P_network_0_4_AI_1, P_poll__networl_3_3_AnnP_5, P_network_6_6_AskP_3, P_network_4_5_RI_6, P_network_6_0_RI_5, P_network_3_4_AI_1, P_network_1_2_AnnP_4, P_network_5_0_AskP_3, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_RP_6, P_network_4_4_AI_1, P_poll__networl_3_4_AI_3, P_poll__networl_0_2_RP_0, P_poll__networl_3_1_AskP_4, P_poll__networl_5_5_AnnP_3, P_poll__networl_3_0_AskP_1, P_poll__networl_0_4_RP_4, P_poll__networl_2_1_AnnP_6, P_poll__networl_5_4_AskP_3, P_poll__networl_0_5_AI_6, P_poll__networl_2_5_AskP_2, P_network_1_2_RI_3, P_network_5_0_RP_3, P_network_6_4_RP_3, P_poll__networl_5_1_RI_1, P_network_2_3_RI_3, P_network_6_4_AnnP_5, P_network_1_1_AI_1, P_poll__networl_0_2_AskP_0, P_network_1_2_AI_2, P_network_2_6_RI_6, P_poll__networl_6_3_AnnP_0, P_poll__networl_0_3_RI_3, P_network_2_4_AnnP_6, P_poll__networl_6_0_AI_0, P_masterList_0_4_5, P_poll__networl_5_1_AnnP_1, P_poll__networl_5_0_RI_3, P_poll__networl_5_3_AnnP_5, P_poll__networl_4_4_RP_6, P_masterList_0_6_5, P_poll__networl_5_5_AI_1, P_network_2_3_AnnP_5, P_poll__networl_0_0_RI_4, P_poll__networl_4_1_AnnP_0, P_poll__networl_3_1_AI_6, P_poll__networl_4_6_AskP_6, P_masterList_1_3_2, P_crashed_6, P_network_5_3_AnnP_5, P_network_3_4_RP_1, P_poll__networl_2_5_RI_1, P_poll__networl_0_3_AI_2, P_poll__networl_3_4_AI_1, P_network_0_4_RP_4, P_network_0_3_AI_1, P_network_5_5_AnnP_4, P_poll__networl_4_2_AnnP_4, P_poll__networl_2_0_RI_4, P_poll__networl_5_6_AI_3, P_network_5_1_RI_2, P_network_2_2_RI_2, P_poll__networl_4_0_AskP_0, P_poll__networl_5_3_RP_1, P_network_6_5_AI_1, P_network_2_4_RI_5, P_network_5_1_AnnP_5, P_network_6_5_AI_5, P_poll__networl_3_4_RP_1, P_network_3_3_RP_2, P_poll__networl_6_3_RP_0, P_network_2_6_RP_6, P_network_4_2_AI_2, P_masterList_5_4_4, P_poll__networl_6_6_RP_0, P_network_2_3_RI_2, P_network_1_0_AskP_2, P_network_6_2_AskP_2, P_network_2_1_AnnP_3, P_network_5_2_RP_5, P_poll__networl_2_1_AI_2, P_poll__networl_3_5_AskP_3, P_poll__networl_0_6_AnsP_0, P_network_3_4_RP_5, P_poll__networl_4_2_AnsP_0, P_poll__networl_4_2_AI_5, P_poll__networl_4_4_AnnP_4, P_poll__networl_6_2_RP_3, P_network_6_1_AskP_5, P_poll__networl_3_1_AI_0, P_network_0_6_AnnP_2, P_masterList_6_6_2, P_network_5_2_AskP_1, P_poll__networl_2_3_AnnP_4, P_network_0_6_AskP_3, P_poll__networl_3_0_AI_4, P_network_2_5_AnnP_1, P_poll__networl_2_6_RI_6, P_network_1_1_AnnP_3, P_poll__networl_1_6_RP_1, P_poll__networl_4_6_AI_0, P_poll__networl_1_6_AnnP_4, P_network_4_2_AI_3, P_poll__networl_0_2_AnnP_3, P_network_0_2_AnnP_4, P_network_5_0_AskP_1, P_network_6_5_AskP_1, P_poll__networl_6_3_AskP_2, P_network_6_6_AskP_4, P_poll__networl_1_4_RI_3, P_poll__networl_2_0_AskP_2, P_poll__networl_0_0_RP_2, P_masterList_4_2_2, P_poll__networl_1_4_AnnP_6, P_poll__networl_5_0_RP_1, P_poll__networl_1_6_RP_6, P_poll__networl_5_2_RI_6, P_network_3_5_AnnP_4, P_masterList_5_4_0, P_network_4_0_AnnP_2, P_poll__networl_5_2_AI_6, P_poll__networl_2_4_AI_4, P_poll__networl_5_0_AI_3, P_network_1_5_AI_5, P_network_2_1_AskP_3, P_network_5_3_RP_2, P_poll__networl_2_1_RI_5, P_poll__networl_6_5_AnnP_6, P_network_4_3_AskP_4, P_masterList_4_3_1, P_poll__networl_0_1_AskP_6, P_poll__networl_3_0_AI_2, P_network_2_5_RP_3, P_network_4_4_RP_4, P_poll__networl_6_4_AskP_6, P_network_1_0_AskP_3, P_network_1_4_AskP_3, P_network_3_3_RP_4, P_network_3_0_RP_2, P_poll__networl_2_6_AnsP_0, P_network_2_1_AI_3, P_poll__networl_4_3_AnsP_0, P_network_1_6_AI_4, P_masterList_0_4_0, P_poll__networl_4_4_RP_4, P_poll__networl_6_1_AI_3, P_poll__networl_0_2_AI_3, P_poll__networl_1_2_AI_6, P_network_3_4_AI_2, P_network_5_6_AI_6, P_network_2_1_AnnP_6, P_network_2_3_RP_2, P_poll__networl_4_4_AnnP_2, P_network_2_4_RP_4, P_network_5_3_RP_5, P_poll__networl_0_2_RI_4, P_poll__networl_2_3_RI_4, P_network_5_2_RI_5, P_network_3_0_RP_4, P_poll__networl_2_3_AskP_5, P_network_0_3_AnnP_6, P_network_5_0_RI_1, P_poll__networl_6_0_AI_4, P_network_2_6_AI_2, P_poll__networl_1_5_AI_0, P_poll__networl_0_6_AI_3, P_poll__networl_6_3_AI_1, P_poll__networl_4_5_RP_6, P_network_1_0_RP_6, P_network_6_5_RP_2, P_masterList_2_4_6, P_poll__networl_5_1_AskP_0, P_masterList_2_6_3, P_poll__networl_1_6_AskP_2, P_poll__networl_3_2_AskP_4, P_poll__networl_2_6_RP_1, P_poll__networl_5_3_AskP_5, P_poll__networl_6_6_RP_3, P_network_3_2_RP_4, P_poll__networl_2_6_AI_4, P_poll__networl_3_6_AskP_0, P_poll__networl_5_0_RI_5, P_network_5_3_AskP_4, P_network_3_1_AnnP_4, P_poll__networl_5_4_AnnP_3, P_poll__networl_0_6_RP_6, P_masterList_3_4_6, P_poll__networl_5_2_RP_5, P_masterList_4_2_1, P_network_0_5_RP_5, P_poll__networl_6_1_AnnP_0, P_poll__networl_0_5_RP_2, P_network_6_6_RP_2, P_network_4_5_AnnP_2, P_poll__networl_4_2_AI_0, P_poll__networl_2_4_RI_3, P_network_2_0_AI_2, P_poll__networl_5_5_RI_6, P_network_1_4_AskP_6, P_poll__networl_3_3_AnnP_4, P_network_6_3_AskP_1, P_poll__networl_3_2_AI_3, P_network_3_6_AI_6, P_poll__networl_0_0_RI_6, P_poll__networl_2_5_RP_1, P_poll__networl_6_2_RI_1, P_poll__networl_2_4_AnnP_6, P_poll__networl_6_1_AnsP_0, P_poll__networl_3_3_RP_6, P_masterList_4_6_5, P_masterList_1_2_2, P_masterList_5_4_3, P_poll__networl_5_3_RI_6, P_poll__networl_5_1_AnnP_6, P_poll__networl_0_5_AI_2, P_network_4_2_AskP_5, P_poll__networl_2_5_RP_4, P_poll__networl_6_2_AskP_5, P_poll__networl_6_6_RP_4, P_masterList_3_6_4, P_network_5_1_RP_6, P_network_3_1_AskP_3, P_poll__networl_6_0_AnnP_2, P_network_1_3_AnnP_2, P_network_6_6_RI_3, P_network_5_6_AskP_3, P_poll__networl_1_2_RI_1, P_poll__networl_2_1_RI_3, P_poll__networl_4_6_RI_1, P_poll__networl_1_4_AskP_6, P_poll__networl_6_4_AnnP_3, P_poll__networl_6_6_AnnP_0, P_poll__networl_0_2_AI_5, P_poll__networl_2_1_AskP_2, P_masterList_4_5_2, P_poll__networl_5_6_AskP_6, P_network_4_5_RI_3, P_poll__networl_2_0_AI_2, P_poll__networl_3_4_RI_2, P_masterList_2_2_2, P_poll__networl_1_5_AskP_3, P_poll__networl_1_5_AnsP_0, P_poll__networl_2_4_RP_0, P_poll__networl_3_6_RP_0, P_poll__networl_3_3_AskP_6, P_poll__networl_6_1_RP_3, P_network_0_0_AskP_3, P_network_1_6_RI_1, P_network_3_0_AnnP_5, P_network_5_0_RI_4, P_network_1_4_RP_3, P_network_1_1_AskP_5, P_network_2_0_AskP_5, P_network_5_2_AnnP_3, P_network_1_1_AnnP_5, P_network_6_0_AnnP_2, P_poll__networl_1_5_AnnP_3, P_poll__networl_1_4_RI_5, P_poll__networl_0_4_AskP_3, P_network_6_6_RP_5, P_poll__networl_5_6_RP_2, P_poll__networl_5_3_AnnP_1, P_poll__networl_6_5_RI_5, P_network_6_2_AI_4, P_network_1_6_AnnP_2, P_network_6_3_AI_4, P_poll__networl_1_4_AI_0, P_poll__networl_4_5_AskP_5, P_network_2_2_RI_4, P_poll__networl_4_2_AnnP_5, P_network_5_5_AnnP_3, P_network_2_6_RP_4, P_poll__networl_2_5_AnnP_1, P_poll__networl_5_0_AI_4, P_poll__networl_3_3_AnnP_6, P_network_3_1_RI_4, P_poll__networl_0_4_AskP_0, P_masterList_2_4_4, P_network_0_2_RI_1, P_network_6_5_RP_1, P_poll__networl_2_5_RP_5, P_network_5_4_AskP_1, P_poll__networl_3_0_AnsP_0, P_network_2_6_AI_3, P_masterList_6_6_3, P_network_2_1_AskP_5, P_poll__networl_2_4_AnnP_2, P_network_2_5_RP_6, P_poll__networl_0_5_RI_4, P_poll__networl_6_1_AskP_6, P_network_4_5_AnnP_4, P_poll__networl_0_2_AskP_4, P_network_5_5_RP_2, P_poll__networl_4_4_AI_3, P_poll__networl_1_5_RI_2, P_poll__networl_3_4_AskP_5, P_poll__networl_5_0_RP_5, P_poll__networl_5_6_RP_6, P_masterList_3_4_5, P_poll__networl_3_2_RI_6, P_poll__networl_2_1_AnnP_1, P_network_3_1_RI_2, P_poll__networl_6_1_AI_2, P_poll__networl_1_4_AI_6, P_poll__networl_6_6_AnsP_0, P_poll__networl_4_6_RI_6, P_masterList_0_3_0, P_poll__networl_1_2_RI_6, P_poll__networl_6_2_AskP_2, P_network_4_1_RI_2, P_network_4_3_AskP_3, P_poll__networl_0_0_RP_5, P_poll__networl_2_3_RI_1, P_network_4_5_AskP_1, P_network_3_4_RI_4, P_poll__networl_4_2_RP_0, P_network_2_5_AnnP_5, P_network_5_3_RP_3, P_poll__networl_5_1_RP_2, P_network_3_5_AI_1, P_poll__networl_0_1_RP_1, P_poll__networl_3_4_AnnP_4, P_poll__networl_2_6_AnnP_5, P_poll__networl_0_0_RP_0, P_poll__networl_2_3_RP_2, P_poll__networl_4_5_RI_0, P_network_4_2_AnnP_1, P_poll__networl_1_1_AskP_3, P_network_0_2_AI_4, P_poll__networl_6_6_AskP_1, P_network_1_0_RP_1, P_poll__networl_5_2_RI_3, P_poll__networl_5_6_AnnP_6, P_network_4_4_AnnP_1, P_network_5_1_AskP_4, P_network_2_2_AskP_3, P_poll__networl_5_1_RI_2, P_network_0_6_AI_1, P_poll__networl_4_3_RI_3, P_network_6_2_RI_1, P_network_0_4_RP_3, P_masterList_2_5_0, P_poll__networl_1_4_AnsP_0, P_network_1_5_AI_2, P_masterList_1_4_2, P_poll__networl_3_6_RP_6, P_network_5_2_RI_6, P_poll__networl_4_3_RI_2, P_poll__networl_4_6_AnnP_6, P_network_1_5_AskP_4, P_poll__networl_0_2_AnnP_4, P_network_5_4_AI_1, P_poll__networl_0_3_RI_0, P_poll__networl_3_5_RP_2, P_network_1_5_AnnP_1, P_poll__networl_2_4_AnnP_4, P_poll__networl_1_6_RI_0, P_network_0_6_RP_3, P_network_6_3_AnnP_6, P_network_5_0_RP_6, P_poll__networl_6_4_AnnP_2, P_poll__networl_0_0_AskP_2, P_poll__networl_4_5_AskP_2, P_poll__networl_6_3_AI_6, P_poll__networl_1_1_AI_5, P_network_0_1_AnnP_3, P_poll__networl_5_1_AnnP_0, P_network_2_1_AnnP_2, P_poll__networl_5_1_AI_1, P_poll__networl_5_4_RI_1, P_network_1_5_AnnP_3, P_poll__networl_6_5_RI_0, P_poll__networl_4_0_AnnP_0, P_poll__networl_5_3_RP_0, P_network_4_3_RI_6, P_network_6_0_RI_6, P_network_4_1_AI_6, P_network_0_1_RP_4, P_poll__networl_5_5_RI_4, P_network_1_1_AnnP_2, P_network_6_3_RP_4, P_network_3_6_AskP_4, P_poll__networl_0_3_AI_5, P_poll__networl_4_0_AskP_6, P_poll__networl_0_6_RP_5, P_network_3_0_RI_6, P_poll__networl_6_0_AnnP_3, P_poll__networl_3_2_RP_4, P_poll__networl_3_5_AI_3, P_network_1_2_RP_6, P_network_0_5_AnnP_2, P_poll__networl_6_3_RI_0, P_network_4_5_AI_1, P_masterList_6_1_1, P_poll__networl_2_1_RP_4, P_poll__networl_3_2_RP_5, P_network_5_0_AI_5, P_network_5_5_AnnP_1, P_poll__networl_4_3_AskP_3, P_poll__networl_4_0_AI_1, P_masterList_5_6_1, P_poll__networl_0_3_RI_6, P_poll__networl_6_4_AnsP_0, P_network_3_3_AskP_5, P_poll__networl_0_1_RI_6, P_network_3_4_RP_4, P_poll__networl_6_2_AI_2, P_network_4_4_AskP_3, P_network_2_0_AnnP_6, P_network_5_4_AnnP_4, P_network_3_3_RP_5, P_network_1_4_AI_2, P_masterList_0_1_4, P_poll__networl_2_0_RP_4, P_network_6_2_RP_2, P_poll__networl_2_2_RI_2, P_network_4_2_RI_6, P_poll__networl_6_2_AskP_0, P_masterList_2_3_2, P_network_2_2_AI_3, P_poll__networl_1_5_AI_5, P_poll__networl_3_6_AskP_3, P_poll__networl_3_0_RI_0, P_network_6_1_AnnP_6, P_poll__networl_2_4_AI_1, P_poll__networl_0_1_AI_6, P_poll__networl_6_0_RP_5, P_poll__networl_1_3_AI_6, P_network_4_5_RI_4, P_poll__networl_6_2_RI_6, P_poll__networl_0_4_AnnP_1, P_poll__networl_5_4_AskP_5, P_poll__networl_0_6_AI_6, P_network_4_0_RP_5, P_network_3_6_AskP_2, P_network_4_5_RP_5, P_poll__networl_2_3_AI_3, P_network_5_1_RI_5, P_masterList_1_2_5, P_poll__networl_6_1_RI_1, P_network_0_2_AI_3, P_poll__networl_2_3_RI_6, P_poll__networl_2_1_RP_1, P_network_2_3_RI_6, P_poll__networl_5_2_RP_3, P_network_4_3_AskP_5, P_poll__networl_6_1_RI_6, P_poll__networl_1_2_AskP_3, P_poll__networl_5_1_AnnP_2, P_poll__networl_4_1_RI_2, P_masterList_6_1_0, P_poll__networl_4_2_AnnP_6, P_network_1_5_RP_6, P_poll__networl_3_6_AskP_5, P_poll__networl_1_2_RI_2, P_poll__networl_2_2_AI_2, P_network_6_2_RP_4, P_network_2_1_RI_1, P_network_3_1_AI_5, P_network_2_5_RP_5, P_poll__networl_4_5_RP_5, P_network_4_6_AnnP_1, P_poll__networl_1_0_RI_4, P_network_6_3_RI_2, P_network_2_0_RP_2, P_poll__networl_5_3_AnnP_4, P_network_1_3_AI_1, P_network_4_6_RI_1, P_network_1_1_AskP_6, P_poll__networl_0_6_RI_2, P_network_6_6_RI_4, P_network_5_6_AskP_1, P_poll__networl_5_1_AI_6, P_poll__networl_6_3_AnnP_6, P_masterList_5_1_5, P_masterList_2_2_0, P_network_1_2_AI_6, P_network_0_2_RP_1, P_poll__networl_6_6_RP_1, P_network_0_2_RI_2, P_poll__networl_0_2_AnnP_2, P_network_1_4_RI_2, P_network_5_2_AI_4, P_masterList_4_5_5, P_poll__networl_6_0_AskP_3, P_poll__networl_6_3_RI_4, P_network_2_1_AskP_2, P_poll__networl_2_1_RI_0, P_network_3_3_AnnP_2, P_poll__networl_3_5_RI_2, P_poll__networl_1_2_AI_0, P_masterList_3_3_3, P_poll__networl_2_4_AI_3, P_poll__networl_4_4_RP_2, P_poll__networl_1_4_RP_2, P_network_5_0_RI_2, P_poll__networl_0_1_RP_6, P_poll__networl_2_1_RI_6, P_poll__networl_0_1_AskP_1, P_masterList_4_3_3, P_poll__networl_2_6_RI_1, P_poll__networl_4_0_RI_2, P_poll__networl_5_0_RI_0, P_poll__networl_6_3_AskP_4, P_poll__networl_4_4_AnnP_3, P_network_2_4_AnnP_3, P_network_4_2_AnnP_3, P_poll__networl_2_3_AskP_1, P_poll__networl_4_6_AskP_4, P_poll__networl_3_3_RP_5, P_network_4_6_AskP_4, P_poll__networl_6_3_AskP_1, P_masterList_4_5_0, P_masterList_2_6_4, P_network_4_2_RI_2, P_network_3_2_RI_3, P_network_0_1_AI_2, P_poll__networl_0_0_AskP_5, P_poll__networl_6_4_RI_0, P_network_3_3_AnnP_1, P_poll__networl_2_2_AnnP_2, P_poll__networl_5_5_AskP_1, P_network_6_0_AskP_6, P_poll__networl_5_5_AnsP_0, P_poll__networl_0_5_AnnP_2, P_poll__networl_4_5_RI_2, P_masterList_6_6_1, P_poll__networl_4_1_AskP_3, P_poll__networl_5_2_AI_5, P_network_5_2_AnnP_2, P_poll__networl_4_5_AnnP_1, P_network_6_4_AI_5, P_poll__networl_2_0_RI_3, P_masterList_6_2_4, P_network_5_0_AI_3, P_network_3_6_AnnP_5, P_network_2_1_RP_1, P_network_6_2_AskP_4, P_network_5_3_AskP_1, P_poll__networl_6_4_AnnP_0, P_poll__networl_3_2_AI_6, P_poll__networl_1_1_RP_0, P_network_2_6_AskP_3, P_network_0_6_AI_6, P_network_0_0_AnnP_2, P_network_1_4_RP_2, P_poll__networl_4_1_AnnP_6, P_network_4_4_AI_4, P_poll__networl_4_6_AI_1, P_masterList_4_5_3, P_poll__networl_4_4_RP_5, P_poll__networl_3_4_RI_1, P_network_5_4_RP_4, P_poll__networl_5_2_AI_1, P_masterList_6_3_0, P_network_1_4_RI_1, P_poll__networl_2_1_AI_1, P_network_3_3_AnnP_3, P_network_6_5_RI_4, P_poll__networl_2_5_AnnP_6, P_poll__networl_3_2_AnnP_5, P_poll__networl_6_4_RP_6, P_network_2_5_AI_2, P_network_1_4_RP_6, P_network_2_3_RP_4, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_5_RI_5, P_poll__networl_5_1_AI_2, P_poll__networl_4_1_AnnP_3, P_network_0_1_RI_2, P_network_4_5_AI_2, P_poll__networl_3_1_AskP_1, P_poll__networl_6_0_AskP_2, P_network_3_3_RP_1, P_poll__networl_1_2_AnnP_1, P_poll__networl_3_5_AnnP_5, P_poll__networl_0_0_AI_4, P_network_1_0_RP_4, P_network_4_4_AI_3, P_network_1_3_RP_6, P_poll__networl_1_6_AnnP_6, P_network_6_0_RI_3, P_network_3_2_RP_6, P_network_6_6_AI_6, P_poll__networl_3_2_RI_1, P_poll__networl_0_3_AnnP_5, P_network_1_1_RP_6, P_poll__networl_1_6_AskP_0, P_poll__networl_2_1_AI_6, P_dead_0, P_network_5_4_AnnP_3, P_network_6_6_RP_4, P_poll__networl_5_3_RI_1, P_network_5_6_AskP_5, P_network_5_0_RP_2, P_poll__networl_4_0_RP_6, P_poll__networl_5_5_RI_3, P_network_4_6_AskP_2, P_network_5_2_AskP_3, P_poll__networl_5_2_AI_3, P_network_4_1_AnnP_4, P_network_2_5_AI_3, P_poll__networl_1_2_AnnP_3, P_poll__networl_4_6_AI_3, P_network_1_5_AskP_1, P_network_6_6_AI_5, P_poll__networl_2_4_RP_6, P_poll__networl_4_3_RI_1, P_poll__networl_5_4_RP_6, P_network_3_5_AI_6, P_poll__networl_1_4_RI_2, P_network_5_6_RP_5, P_poll__networl_4_5_RP_1, P_network_4_4_AskP_1, P_network_1_3_RI_3, P_poll__networl_2_5_RI_2, P_poll__networl_2_6_AskP_1, P_network_5_4_RP_3, P_network_0_3_AskP_5, P_network_6_0_RI_1, P_network_3_2_RI_1, P_network_6_2_RP_3, P_network_4_3_RP_2, P_network_5_1_AI_6, P_poll__networl_5_3_AskP_0, P_network_2_5_AskP_1, P_network_6_4_RP_1, P_poll__networl_2_1_AnsP_0, P_poll__networl_4_5_AI_0, P_poll__networl_3_0_AI_1, P_poll__networl_4_3_AI_5, P_network_1_3_RI_2, P_network_5_6_AskP_4, P_poll__networl_4_3_AnnP_3, P_network_6_6_AskP_6, P_poll__networl_2_6_AskP_3, P_poll__networl_4_5_AI_2, P_poll__networl_2_1_RP_6, P_poll__networl_6_6_AI_3, P_network_0_3_AnnP_3, P_poll__networl_5_1_AnnP_5, P_network_1_3_RI_5, P_poll__networl_4_3_RI_5, P_poll__networl_2_3_AnnP_0, P_poll__networl_5_0_RP_2, P_poll__networl_5_2_AnsP_0, P_network_3_2_RP_3, P_poll__networl_1_5_AI_3, P_poll__networl_0_3_RP_5, P_poll__networl_6_1_RP_5, P_network_2_5_AskP_5, P_poll__networl_1_2_RP_2, P_network_3_5_AI_2, P_poll__networl_5_3_AnnP_2, P_poll__networl_4_0_RP_0, P_poll__networl_5_3_AskP_3, P_poll__networl_2_2_RP_6, P_masterList_6_3_3, P_masterList_4_4_2, P_poll__networl_0_6_AskP_2, P_poll__networl_1_6_AnnP_1, P_poll__networl_6_2_AskP_1, P_poll__networl_0_4_RP_3, P_poll__networl_2_6_AI_5, P_poll__networl_6_1_RI_5, P_network_4_1_AnnP_5, P_network_2_6_AnnP_1, P_network_1_2_RP_4, P_poll__networl_4_0_RI_0, P_poll__networl_4_3_AnnP_1, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_RI_5, P_poll__networl_3_1_AI_3, P_poll__networl_3_3_AnnP_3, P_poll__networl_1_5_RP_6, P_poll__networl_4_6_RI_0, P_network_6_6_RI_5, P_poll__networl_0_6_AnnP_4, P_network_5_3_AskP_3, P_network_1_5_AskP_6, P_poll__networl_2_5_AskP_3, P_network_0_1_RP_1, P_network_5_4_AnnP_2, P_poll__networl_5_6_RP_1, P_network_4_0_AI_2, P_poll__networl_0_0_AnnP_2, P_poll__networl_3_2_AskP_1, P_network_4_0_AI_3, P_network_4_1_AnnP_2, P_poll__networl_4_1_AI_3, P_poll__networl_6_6_AnnP_4, P_network_2_1_RI_2, P_network_3_2_AI_5, P_network_0_3_AnnP_1, P_network_4_5_AskP_3, P_masterList_3_4_3, P_masterList_5_3_5, P_network_1_3_AskP_4, P_network_3_0_RI_4, P_poll__networl_1_6_AI_2, P_poll__networl_6_0_RI_5, P_network_3_1_AskP_2, P_poll__networl_2_1_AnnP_0, P_network_2_4_RI_6, P_poll__networl_1_6_AI_5, P_poll__networl_3_5_RI_5, P_poll__networl_2_4_RP_5, P_network_2_5_RP_2, P_poll__networl_4_3_RP_1, P_network_1_6_AskP_6, P_poll__networl_4_3_AI_2, P_poll__networl_2_5_AskP_5, P_network_2_1_AskP_6, P_network_2_5_RI_1, P_network_1_6_AskP_2, P_poll__networl_0_5_AI_3, P_poll__networl_0_2_AnnP_0, P_network_2_2_AI_4, P_network_4_1_RI_4, P_network_5_3_AI_3, P_poll__networl_2_6_AnnP_4, P_poll__networl_2_4_AI_2, P_poll__networl_5_0_AnnP_4, P_network_3_2_AI_2, P_network_5_2_AskP_6, P_poll__networl_6_1_AnnP_3, P_poll__networl_0_4_AnnP_0, P_poll__networl_1_4_AI_1, P_poll__networl_5_5_AI_3, P_poll__networl_0_1_AI_1, P_network_3_5_RP_5, P_poll__networl_4_0_RP_5, P_poll__networl_6_5_AnnP_0, P_poll__networl_6_5_AnnP_3, P_network_1_5_AnnP_4, P_poll__networl_4_0_RI_5, P_network_1_0_RP_3, P_network_6_2_AskP_6, P_poll__networl_6_3_AI_0, P_poll__networl_1_0_AnsP_0, P_poll__networl_4_1_AI_4, P_network_5_0_AI_4, P_network_1_4_RI_5, P_network_2_4_RP_1, P_poll__networl_3_0_AnnP_3, P_network_3_6_AnnP_4, P_poll__networl_3_6_AnnP_6, P_poll__networl_6_5_AnnP_2, P_poll__networl_4_6_AnnP_0, P_poll__networl_5_3_RI_2, P_network_1_5_AnnP_5, P_masterList_1_5_1, P_network_1_2_RP_5, P_poll__networl_4_4_AI_6, P_network_2_1_AI_2, P_poll__networl_2_4_AskP_6, P_poll__networl_3_3_AskP_3, P_poll__networl_3_5_AskP_2, P_poll__networl_1_0_AskP_4, P_poll__networl_0_3_AskP_0, P_poll__networl_4_2_AnnP_2, P_poll__networl_2_1_AnnP_3, P_network_2_5_RP_1, P_poll__networl_4_2_AskP_3, P_poll__networl_3_6_AnnP_0, P_poll__networl_2_5_AnnP_3, P_masterList_4_4_1, P_poll__networl_5_6_AskP_3, P_network_6_6_AskP_5, P_poll__networl_1_0_AI_3, P_network_0_5_AskP_5, P_network_1_6_AnnP_4, P_network_3_4_RI_2, P_poll__networl_2_4_AskP_1, P_poll__networl_0_1_RI_4, P_poll__networl_2_0_AI_1, P_network_4_5_AnnP_5, P_dead_2, P_network_1_4_AskP_4, P_poll__networl_1_3_RI_1, P_poll__networl_4_2_AskP_6, P_poll__networl_5_4_AnsP_0, P_poll__networl_4_0_AI_6, P_poll__networl_4_0_AskP_2, P_poll__networl_5_6_AskP_0, P_poll__networl_5_0_AnnP_2, P_poll__networl_1_3_AskP_0, P_network_1_2_AnnP_1, P_network_5_5_RP_6, P_poll__networl_5_2_AI_2, P_network_1_2_AnnP_2, P_masterList_1_3_1, P_poll__networl_4_4_AskP_0, P_masterList_6_1_2, P_network_5_4_AI_3, P_poll__networl_1_2_AI_3, P_masterList_1_3_5, P_poll__networl_0_3_AI_0, P_network_6_1_AnnP_1, P_poll__networl_2_2_RP_1, P_poll__networl_5_6_RI_2, P_network_1_2_AI_1, P_poll__networl_3_2_AnnP_1, P_masterList_4_1_0, P_masterList_0_6_4, P_poll__networl_3_5_AskP_1, P_poll__networl_2_6_AnnP_2, P_network_3_3_AskP_4, P_poll__networl_3_1_RI_3, P_masterList_3_1_5, P_network_0_0_RP_4, P_poll__networl_6_3_AI_2, P_network_3_5_AnnP_2, P_poll__networl_6_0_AskP_6, P_electionFailed_3, P_masterList_1_3_4, P_poll__networl_0_3_AnnP_6, P_masterList_6_3_6, P_network_4_6_AI_6, P_poll__networl_6_4_AskP_5, P_network_0_2_AnnP_1, P_network_6_4_AnnP_2, P_poll__networl_1_3_RI_2, P_network_1_3_AnnP_6, P_network_2_3_AskP_6, P_poll__networl_0_4_AI_0, P_network_0_0_RP_6, P_network_6_2_AnnP_3, P_poll__networl_4_6_AI_4, P_masterList_0_6_0, P_poll__networl_5_5_RP_3, P_poll__networl_4_1_RP_5, P_poll__networl_6_3_AnnP_2, P_poll__networl_6_4_RI_1, P_network_1_1_RI_4, P_network_3_4_AI_6, P_network_1_1_RI_2, P_poll__networl_5_0_RI_1, P_network_5_3_AI_6, P_poll__networl_2_0_AnnP_0, P_poll__networl_3_4_AI_4, P_poll__networl_2_2_AI_4, P_poll__networl_1_5_AI_4, P_network_2_4_AskP_4, P_poll__networl_2_3_AnnP_1, P_poll__networl_5_4_AnnP_0, P_network_3_5_AnnP_6, P_poll__networl_5_1_AI_0, P_poll__networl_3_2_RI_2, P_masterList_2_3_4, P_network_0_6_AnnP_3, P_poll__networl_0_6_RP_3, P_poll__networl_0_4_AskP_4, P_poll__networl_2_0_AI_4, P_poll__networl_2_4_AskP_3, P_poll__networl_2_5_AnnP_0, P_poll__networl_1_0_AI_1, P_network_4_4_AskP_5, P_network_6_2_AI_3, P_poll__networl_3_4_AskP_4, P_poll__networl_5_5_AskP_6, P_network_2_3_AskP_1, P_poll__networl_1_4_AskP_4, P_poll__networl_3_6_AnnP_3, P_network_3_6_AI_2, P_network_4_1_AnnP_1, P_poll__networl_6_4_AI_1, P_network_4_4_RP_5, P_network_6_5_RI_2, P_poll__networl_5_5_AI_6, P_network_1_3_AskP_5, P_network_5_5_AI_1, P_poll__networl_1_1_AI_0, P_poll__networl_4_2_AI_1, P_poll__networl_6_3_AnsP_0, P_masterList_0_3_2, P_poll__networl_3_5_AI_4, P_network_5_0_AI_1, P_poll__networl_1_1_AI_4, P_poll__networl_1_3_AnnP_6, P_poll__networl_1_0_AskP_5, P_poll__networl_3_1_AnnP_6, P_poll__networl_5_2_RI_0, P_network_3_2_AI_1, P_poll__networl_4_1_AnnP_4, P_network_5_3_AskP_2, P_masterList_5_6_6, P_network_4_3_AI_3, P_network_1_2_AnnP_6, P_poll__networl_2_3_AI_2, P_poll__networl_0_0_AnnP_1, P_poll__networl_2_0_AnnP_1, P_poll__networl_1_0_RI_2, P_network_5_0_AskP_5, P_network_2_0_AnnP_2, P_network_3_4_AskP_2, P_poll__networl_1_6_AskP_4, P_network_0_2_AskP_3, P_masterList_3_4_1, P_network_6_3_RI_3, P_poll__networl_2_4_RI_0, P_poll__networl_6_2_AskP_3, P_masterList_1_6_6, P_poll__networl_2_3_RP_6, P_network_4_0_AI_4, P_network_3_0_AskP_4, P_poll__networl_6_6_AnnP_3, P_poll__networl_1_0_AnnP_5, P_network_0_5_AI_2, P_poll__networl_5_0_AI_1, P_network_1_3_RP_4, P_network_1_1_RI_3, P_poll__networl_0_5_RP_5, P_poll__networl_3_1_RP_3, P_poll__networl_0_2_AnnP_1, P_masterList_0_2_3, P_network_3_0_AI_1, P_poll__networl_0_6_AnnP_0, P_masterList_0_1_5, P_network_5_2_RP_2, P_poll__networl_4_3_AnnP_6, P_network_2_4_AnnP_5, P_network_3_3_AnnP_6, P_poll__networl_2_5_AskP_6, P_poll__networl_6_2_AskP_4, P_poll__networl_0_4_AnnP_6, P_poll__networl_1_3_RP_1, P_network_6_5_RP_5, P_masterList_3_1_1, P_masterList_3_5_0, P_poll__networl_3_1_AI_2, P_network_6_5_AnnP_5, P_poll__networl_3_1_RP_2, P_poll__networl_5_5_RP_1, P_network_0_1_AI_3, P_poll__networl_6_4_RP_2, P_masterList_2_1_0, P_poll__networl_0_3_RI_2, P_masterList_5_3_1, P_network_6_3_RP_3, P_poll__networl_3_1_AnnP_2, P_poll__networl_0_5_AnnP_4, P_poll__networl_6_5_AskP_4, P_poll__networl_6_6_AI_5, P_masterList_2_2_6, P_network_4_5_AI_4, P_masterList_4_5_1, P_network_5_1_AskP_3, P_network_0_4_AI_5, P_poll__networl_3_3_RI_2, P_poll__networl_4_3_AskP_6, P_poll__networl_0_4_AI_4, P_poll__networl_1_6_AI_6, P_network_5_5_RP_4, P_poll__networl_5_6_RP_3, P_poll__networl_4_4_RI_6, P_masterList_5_4_6, P_poll__networl_0_0_RP_4, P_poll__networl_3_3_RP_1, P_poll__networl_2_2_AI_3, P_poll__networl_2_4_AnnP_5, P_poll__networl_3_3_RI_6, P_poll__networl_0_2_AI_0, P_poll__networl_0_4_RP_0, P_poll__networl_3_5_RI_3, P_poll__networl_6_6_AI_6, P_masterList_1_1_4, P_poll__networl_1_6_AnnP_0, P_network_4_5_RI_1, P_network_5_2_AskP_5, P_poll__networl_1_2_RI_4, P_poll__networl_0_2_AskP_3, P_network_0_5_RP_6, P_poll__networl_2_6_AI_2, P_network_6_1_RI_4, P_poll__networl_4_0_RI_3, P_network_1_1_RP_1, P_poll__networl_3_1_RP_4, P_network_5_5_AI_5, P_network_2_6_AI_4, P_poll__networl_0_1_AskP_3, P_poll__networl_5_3_AnnP_6, P_poll__networl_6_0_RI_4, P_network_3_4_AI_5, P_poll__networl_2_5_AnnP_2, P_poll__networl_2_6_AnnP_0, P_network_5_6_AI_4, P_poll__networl_1_0_AnnP_4, P_poll__networl_3_3_AI_4, P_poll__networl_1_3_AnnP_5, P_network_4_2_RP_6, P_network_6_2_RP_1, P_poll__networl_6_6_AnnP_1, P_network_3_0_AskP_6, P_poll__networl_1_0_RI_1, P_poll__networl_6_0_RI_1, P_network_0_5_AskP_1, P_network_6_0_RI_4, P_poll__networl_3_6_AnnP_1, P_poll__networl_4_5_AI_4, P_network_0_3_AskP_3, P_network_5_3_AI_5, P_network_4_1_AI_2, P_poll__networl_0_1_AnnP_5, P_poll__networl_1_1_AnnP_1, P_poll__networl_5_1_AskP_2, P_network_4_2_RP_4, P_network_4_3_AI_6, P_network_0_0_AskP_6, P_poll__networl_2_3_AskP_4, P_network_0_0_RI_5, P_poll__networl_0_6_AnnP_3, P_poll__networl_2_2_AskP_5, P_network_1_5_RP_4, P_network_1_1_RI_6, P_poll__networl_4_6_AskP_1, P_poll__networl_1_5_RP_2, P_poll__networl_5_6_AI_6, P_network_5_0_AnnP_4, P_network_6_4_AskP_4, P_poll__networl_0_1_AskP_5, P_poll__networl_3_4_AI_0, P_masterList_0_5_5, P_network_6_4_AskP_5, P_network_3_1_AnnP_1, P_poll__networl_3_5_AnnP_1, P_network_4_4_AI_5, P_poll__networl_6_6_AI_4, P_network_5_3_AI_4, P_masterList_5_5_2, P_poll__networl_6_3_RI_3, P_network_0_6_RP_6, P_poll__networl_5_6_AskP_1, P_poll__networl_2_6_AnnP_6, P_network_0_1_RP_2, P_network_3_4_AI_3, P_masterList_5_6_2, P_poll__networl_2_3_AnnP_2, P_poll__networl_4_5_RP_2, P_network_4_6_RI_3, P_network_3_1_AnnP_5, P_network_6_1_AI_3, P_poll__networl_1_1_AskP_4, P_network_2_4_AskP_5, P_poll__networl_1_6_RP_0, P_network_3_1_RI_3, P_poll__networl_0_6_RP_1, P_poll__networl_4_0_AnnP_4, P_poll__networl_2_5_AskP_0, P_network_5_3_AI_1, P_poll__networl_5_0_AnnP_3, P_network_6_1_AI_1, P_poll__networl_0_5_AskP_6, P_masterList_6_6_6, P_network_0_0_RI_3, P_network_5_4_RI_5, P_network_1_0_AI_5, P_poll__networl_4_4_AskP_6, P_poll__networl_5_3_RP_6, P_poll__networl_3_2_AI_2, P_masterList_0_3_6, P_masterList_4_1_2, P_network_6_4_RI_4, P_poll__networl_4_1_RP_3, P_network_4_6_AskP_6, P_poll__networl_0_5_AskP_3, P_poll__networl_0_3_AnsP_0, P_network_6_2_AskP_1, P_poll__networl_2_4_AI_0, P_poll__networl_3_6_RP_4, P_network_0_3_AI_3, P_poll__networl_3_3_AI_5, P_poll__networl_5_2_RI_1, P_network_1_6_RP_6, P_masterList_3_1_2, P_poll__networl_4_0_RI_6, P_poll__networl_5_5_AnnP_0, P_poll__networl_4_3_RP_5, P_masterList_5_3_2, P_network_4_1_AskP_3, P_network_3_3_RP_6, P_poll__networl_0_6_AskP_5, P_network_0_1_AskP_2, P_network_6_4_AskP_3, P_network_6_4_AI_2, P_poll__networl_1_1_RP_2, P_poll__networl_5_0_RP_6, P_network_6_4_RI_6, P_masterList_1_1_0, P_network_0_1_RP_6, P_network_5_5_AI_6, P_poll__networl_6_4_AnnP_4, P_poll__networl_2_0_AskP_6, P_poll__networl_6_1_AskP_5, P_masterList_3_4_2, P_poll__networl_3_5_RP_3, P_poll__networl_0_5_AI_0, P_poll__networl_3_4_AnnP_3, P_poll__networl_4_4_AskP_1, P_poll__networl_4_3_AI_0, P_poll__networl_1_4_AskP_2, P_network_2_3_AI_2, P_poll__networl_5_6_AnnP_5, P_masterList_1_6_0, P_poll__networl_5_2_AnnP_5, P_poll__networl_0_2_AskP_6, P_network_2_1_AI_4, P_network_4_3_AnnP_3, P_poll__networl_1_5_RI_3, P_network_0_3_AskP_4, P_poll__networl_1_4_AskP_5, P_poll__networl_5_2_AskP_5, P_poll__networl_5_3_AskP_4, P_network_1_5_RI_4, P_poll__networl_1_3_AnnP_1, P_network_5_0_AnnP_1, P_poll__networl_2_0_RP_2, P_network_1_0_AskP_6, P_network_4_3_RI_1, P_poll__networl_5_2_RP_1, P_poll__networl_2_3_AI_5, P_poll__networl_4_1_RI_4, P_masterList_0_2_5, P_network_1_6_RP_3, P_poll__networl_6_4_AnnP_5, P_network_1_2_AI_4, P_network_2_6_RP_5, P_network_5_6_AI_1, P_poll__networl_5_1_RI_3, P_poll__networl_5_6_RP_5, P_poll__networl_1_1_RP_1, P_network_4_2_RI_5, P_poll__networl_0_6_RI_0, P_poll__networl_1_4_AnnP_1, P_poll__networl_6_1_AI_4, P_network_5_1_AI_1, P_masterList_2_6_2, P_network_6_5_AskP_5, P_network_2_2_AI_2, P_network_4_3_RI_3, P_masterList_0_5_4, P_masterList_1_1_3, P_electionFailed_2, P_masterList_6_4_5, P_poll__networl_6_1_AskP_4, P_poll__networl_5_0_AskP_0, P_poll__networl_6_0_AnnP_6, P_poll__networl_6_3_RP_6, P_masterList_3_6_3, P_poll__networl_4_2_RI_1, P_network_3_3_AskP_6, P_network_2_0_AI_6, P_network_4_5_RP_1, P_network_4_3_RP_5, P_masterList_2_1_6, P_poll__networl_5_1_AskP_1, P_poll__networl_5_5_RI_1, P_poll__networl_1_5_AskP_1, P_network_6_3_RP_2, P_masterList_5_4_5, P_poll__networl_3_5_AskP_0, P_dead_6, P_poll__networl_6_2_RP_2, P_masterList_1_1_1, P_network_5_1_RP_4, P_poll__networl_2_3_AnsP_0, P_poll__networl_3_1_AI_4, P_poll__networl_6_1_AskP_2, P_poll__networl_2_6_RP_4, P_poll__networl_5_0_AskP_2, P_network_0_1_RI_3, P_poll__networl_3_1_AnsP_0, P_masterList_4_5_4, P_network_0_3_RP_4, P_poll__networl_0_2_RP_6, P_poll__networl_1_0_RP_4, P_poll__networl_0_0_AnnP_6, P_poll__networl_5_5_AnnP_4, P_poll__networl_5_6_AI_0, P_poll__networl_2_5_RI_5, P_poll__networl_4_0_RP_4, P_masterList_4_4_4, P_network_3_3_RI_4, P_network_4_2_RI_4, P_poll__networl_4_4_AnnP_6, P_masterList_2_4_5, P_poll__networl_2_0_AskP_1, P_poll__networl_3_3_AI_3, P_poll__networl_2_1_AnnP_5, P_network_2_4_AI_1, P_masterList_0_1_6, P_poll__networl_0_1_AnnP_4, P_poll__networl_0_5_AnsP_0, P_poll__networl_6_6_AnnP_5, P_network_2_2_AI_6, P_network_2_4_RP_3, P_network_2_0_RI_3, P_poll__networl_0_3_AnnP_4, P_poll__networl_4_4_AI_5, P_poll__networl_1_3_RP_5, P_network_3_5_RP_1, P_poll__networl_1_0_RI_5, P_poll__networl_6_5_AI_3, P_poll__networl_1_3_AskP_6, P_network_2_5_RI_6, P_poll__networl_5_5_RI_2, P_network_4_1_RP_3, P_network_4_4_AnnP_5, P_network_4_1_AskP_6, P_poll__networl_1_4_AI_4, P_masterList_4_4_3, P_poll__networl_6_5_RI_6, P_network_0_3_AnnP_2, P_network_0_0_RI_1, P_poll__networl_2_6_AI_6, P_poll__networl_6_3_RP_3, P_poll__networl_1_0_AI_0, P_poll__networl_6_0_AnnP_0, P_network_5_5_AskP_1, P_network_4_2_AI_5, P_poll__networl_6_3_RI_1, P_network_6_1_RI_2, P_network_2_4_RP_5, P_network_3_6_RI_4, P_poll__networl_4_2_RP_3, P_poll__networl_3_0_AnnP_5, P_network_2_6_RI_1, P_poll__networl_1_6_AnsP_0, P_poll__networl_3_2_AnnP_3, P_network_3_6_RP_3, P_poll__networl_1_2_AskP_1, P_poll__networl_5_6_RP_0, P_poll__networl_6_2_RP_1, P_network_6_1_RP_6, P_network_5_4_AI_6, P_poll__networl_4_4_RP_0, P_network_3_2_AskP_5, P_poll__networl_6_0_RP_4, P_network_6_0_RP_4, P_poll__networl_2_0_AI_6, P_masterList_5_3_3, P_network_2_6_RP_1, P_masterList_1_1_2, P_network_0_1_RI_6, P_poll__networl_6_5_AI_4, P_network_5_5_RP_3, P_network_2_2_AI_5, P_poll__networl_3_6_AskP_4, P_network_2_4_AI_3, P_poll__networl_1_6_RI_2, P_poll__networl_5_3_AI_6, P_poll__networl_4_1_AskP_1, P_poll__networl_6_3_AskP_5, P_poll__networl_1_4_AnnP_3, P_poll__networl_4_2_RP_6, P_poll__networl_6_2_AI_4, P_poll__networl_1_5_AskP_6, P_network_6_4_RI_1, P_poll__networl_2_1_AnnP_2, P_poll__networl_0_2_AI_1, P_network_4_4_RI_1, P_network_3_2_AskP_3, P_network_0_6_AI_5, P_network_6_1_RI_1, P_poll__networl_2_2_RP_3, P_poll__networl_5_5_AnnP_6, P_network_5_6_AnnP_1, P_poll__networl_1_0_RP_0, P_poll__networl_5_6_AnnP_0, P_poll__networl_1_6_RP_3, P_poll__networl_4_3_AnnP_4, P_poll__networl_2_5_AI_2, P_poll__networl_2_0_AskP_5, P_masterList_1_2_0, P_network_4_0_AI_5, P_poll__networl_0_5_AskP_0, P_poll__networl_0_2_AskP_1, P_poll__networl_3_0_RP_0, P_poll__networl_3_3_AnnP_1, P_network_2_1_RP_4, P_poll__networl_0_4_AnsP_0, P_network_5_2_RI_2, P_network_5_5_AI_3, P_poll__networl_3_3_RI_0, P_network_6_6_RI_1, P_poll__networl_5_0_RI_2, P_network_5_2_RI_4, P_poll__networl_3_6_AI_2, P_poll__networl_1_5_RP_1, P_masterList_6_4_2, P_network_4_1_RP_1, P_poll__networl_0_0_RP_1, P_poll__networl_5_3_RP_4, P_poll__networl_3_6_AI_3, P_masterList_3_6_2, P_network_1_2_AI_5, P_network_1_6_RP_4, P_masterList_0_4_6, P_network_6_2_AnnP_1, P_network_2_4_RI_3, P_poll__networl_0_1_AnsP_0, P_poll__networl_2_4_RI_4, P_network_0_2_RP_4, P_poll__networl_2_1_RI_1, P_poll__networl_0_6_RP_2, P_poll__networl_6_6_RI_5, P_network_4_1_AI_1, P_poll__networl_3_6_AskP_2, P_poll__networl_6_4_AnnP_6, P_masterList_3_4_0, P_poll__networl_1_2_AnsP_0, P_poll__networl_3_2_AskP_3, P_network_1_0_AnnP_3, P_network_3_6_RP_5, P_poll__networl_5_4_AI_3, P_network_0_6_RP_4, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_3_RP_0, P_poll__networl_1_4_RI_4, P_network_0_5_RI_4, P_network_6_3_AnnP_3, P_network_1_0_AI_4, P_poll__networl_1_1_RP_4, P_network_3_3_AI_3, P_network_0_1_AskP_5, P_masterList_1_6_5, P_poll__networl_1_3_RP_3, P_network_2_4_AI_6, P_network_6_6_RP_1, P_network_4_2_AnnP_4, P_poll__networl_0_3_AnnP_1, P_poll__networl_3_0_RP_2, P_poll__networl_0_5_AI_4, P_network_2_0_RP_1, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AnnP_0, P_poll__networl_4_3_AI_6, P_network_6_4_AnnP_1, P_masterList_2_2_3, P_poll__networl_4_2_AskP_5, P_poll__networl_1_5_AnnP_5, P_masterList_1_5_3, P_poll__networl_3_5_AI_2, P_poll__networl_0_0_AI_1, P_network_2_1_RP_6, P_poll__networl_2_2_RI_3, P_poll__networl_2_0_RP_6, P_poll__networl_4_6_RP_6, P_network_6_4_AnnP_6, P_poll__networl_3_4_AnnP_1, P_poll__networl_6_3_RP_5, P_poll__networl_1_2_RP_3, P_poll__networl_0_5_AI_5, P_network_1_1_AskP_4, P_network_2_6_RP_2, P_network_4_6_RI_6, P_poll__networl_5_3_AI_0, P_poll__networl_6_3_AnnP_4, P_network_4_3_AI_2, P_masterList_3_6_5, P_network_1_2_RI_2, P_poll__networl_4_5_RI_4, P_masterList_0_1_2, P_network_3_1_AskP_5, P_poll__networl_0_5_RP_0, P_dead_5, P_poll__networl_1_4_RI_1, P_crashed_1, P_network_4_4_AnnP_3, P_poll__networl_3_2_RP_3, P_poll__networl_4_2_AskP_2, P_poll__networl_3_1_AnnP_3, P_network_3_2_RP_5, P_poll__networl_4_3_RP_4, P_network_4_5_AnnP_3, P_poll__networl_5_1_RP_5, P_network_3_5_AnnP_5, P_poll__networl_1_3_RI_0, P_poll__networl_3_2_AI_4, P_network_3_1_AskP_4, P_masterList_0_1_3, P_poll__networl_3_3_AnsP_0, P_network_2_0_AnnP_3, P_network_4_3_AnnP_6, P_network_1_6_AI_1, P_poll__networl_1_1_RI_6, P_poll__networl_1_1_RP_3, P_poll__networl_4_5_AskP_3, P_poll__networl_2_2_RP_4, P_poll__networl_4_3_AnnP_0, P_poll__networl_6_0_RP_3, P_poll__networl_6_5_RP_4, P_poll__networl_0_0_AnnP_3, P_poll__networl_6_4_AskP_3, P_poll__networl_0_4_AskP_1, P_poll__networl_1_6_AskP_5, P_poll__networl_1_6_AnnP_2, P_poll__networl_5_4_RI_4, P_poll__networl_0_2_RI_6, P_poll__networl_1_0_AskP_0, P_network_5_3_RI_4, P_poll__networl_5_1_AnsP_0, P_poll__networl_4_2_AnnP_0, P_poll__networl_3_6_RI_4, P_poll__networl_1_2_RI_3, P_poll__networl_6_1_RP_0, P_poll__networl_3_5_RP_5, P_network_3_1_AI_3, P_network_1_1_AnnP_6, P_network_5_0_AnnP_3, P_poll__networl_4_0_AnnP_5, P_network_6_3_AnnP_1, P_network_6_5_AskP_6, P_network_6_1_AskP_1, P_network_2_0_RI_6, P_poll__networl_0_6_RI_1, P_poll__networl_2_6_AnnP_3, P_network_1_6_AskP_3, P_network_3_0_AskP_2, P_network_6_6_AnnP_1, P_network_0_6_RI_1, P_poll__networl_1_3_AI_0, P_poll__networl_2_2_AI_0, P_network_3_3_AskP_2, P_network_5_6_RP_4, P_network_6_3_RI_1, P_poll__networl_6_4_RP_3, P_poll__networl_3_6_AskP_6, P_network_5_6_AnnP_5, P_poll__networl_4_4_AskP_3, P_network_4_5_RP_2, P_masterList_4_3_2, P_network_3_4_AnnP_5, P_poll__networl_6_2_AnnP_4, P_network_1_6_AnnP_3, P_network_5_6_RP_2, P_network_3_3_AI_4, P_poll__networl_1_1_AskP_0, P_masterList_4_6_3, P_network_1_2_AskP_6, P_network_4_0_AnnP_1, P_network_2_4_RI_1, P_poll__networl_3_2_AI_1, P_network_0_6_RI_6, P_network_1_0_RI_2, P_poll__networl_2_3_RI_2, P_network_5_2_RI_1, P_masterList_6_6_4, P_network_6_0_AskP_5, P_network_3_3_RP_3, P_poll__networl_3_6_RI_1, P_poll__networl_0_5_AI_1, P_poll__networl_1_1_AnnP_6, P_masterList_5_1_0, P_poll__networl_4_5_AskP_6, P_poll__networl_1_5_RP_0, P_network_4_3_RP_6, P_poll__networl_1_3_AskP_2, P_network_6_1_RI_5, P_poll__networl_6_2_RI_3, P_network_4_4_RP_1, P_poll__networl_0_6_AnnP_2, P_poll__networl_6_1_AI_1, P_poll__networl_6_3_AskP_3, P_network_2_2_RP_1, P_poll__networl_0_1_RI_0, P_poll__networl_4_6_AskP_0, P_masterList_2_5_4, P_poll__networl_4_3_AskP_1, P_poll__networl_6_4_AskP_1, P_network_3_0_RI_2, P_poll__networl_4_2_RP_5, P_network_2_4_AnnP_2, P_network_5_0_AnnP_6, P_network_2_0_RI_5, P_poll__networl_3_3_RI_5, P_masterList_0_6_6, P_network_1_1_AI_3, P_poll__networl_4_0_RI_4, P_poll__networl_1_0_RI_6, P_poll__networl_0_3_RP_1, P_poll__networl_3_0_AnnP_4, P_network_2_2_RP_3, P_network_3_0_RP_1, P_network_3_2_AskP_4, P_poll__networl_1_2_AnnP_6, P_poll__networl_5_4_AnnP_4, P_poll__networl_5_5_AI_2, P_network_2_4_AI_5, P_network_0_0_RP_1, P_network_4_3_RI_2, P_poll__networl_5_4_AnnP_6, P_network_6_5_RP_4, P_poll__networl_3_5_AnsP_0, P_network_0_4_AnnP_2, P_poll__networl_2_0_RI_5, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_5_RI_3, P_poll__networl_3_3_RI_3, P_network_0_0_AI_2, P_poll__networl_1_3_RI_6, P_network_5_3_RI_5, P_masterList_0_4_2, P_network_0_0_RI_6, P_poll__networl_6_1_RI_3, P_poll__networl_5_6_AnsP_0, P_network_3_5_AnnP_1, P_poll__networl_6_2_AnsP_0, P_network_4_3_AnnP_1, P_network_2_5_RI_4, P_network_4_6_AskP_3, P_poll__networl_3_2_AnnP_2, P_poll__networl_0_4_RI_0, P_network_5_3_RP_4, P_network_3_5_RP_6, P_network_2_5_AnnP_3, P_network_5_6_RI_3, P_poll__networl_3_2_RI_5, P_poll__networl_0_0_AnnP_4, P_masterList_1_6_2, P_poll__networl_3_6_RP_3, P_network_1_2_RI_6, P_poll__networl_0_2_RP_2, P_network_2_5_RI_3, P_network_1_1_RP_3, P_network_5_0_RI_3, P_network_0_1_AnnP_2, P_network_0_2_AI_1, P_poll__networl_0_4_AI_3, P_network_2_0_AskP_2, P_poll__networl_4_0_AnnP_6, P_poll__networl_4_0_AskP_1, P_network_5_3_AI_2, P_poll__networl_3_3_RI_1, P_network_6_2_RP_5, P_poll__networl_5_2_AnnP_3, P_masterList_6_4_0, P_network_5_6_AnnP_4, P_network_6_6_AskP_2, P_poll__networl_2_4_AskP_0, P_poll__networl_4_2_RI_4, P_poll__networl_6_2_AI_3, P_masterList_0_1_1, P_network_0_4_RP_5, P_network_6_0_AI_1, P_poll__networl_6_5_RP_1, P_masterList_3_3_0, P_poll__networl_0_6_RI_3, P_network_2_0_RI_4, P_poll__networl_0_1_RP_3, P_network_0_6_AskP_4, P_network_1_4_AskP_2, P_network_3_0_RP_5, P_poll__networl_5_5_AskP_0, P_network_0_2_AnnP_5, P_network_4_6_AI_4, P_network_6_2_AnnP_5, P_poll__networl_1_1_AskP_1, P_poll__networl_0_6_AnnP_1, P_masterList_5_5_0, P_network_0_4_AskP_3, P_poll__networl_0_4_AI_6, P_network_2_3_AnnP_1, P_network_2_5_AI_6, P_poll__networl_1_3_RP_2, P_masterList_1_4_1, P_network_5_0_AskP_2, P_poll__networl_4_5_AnnP_3, P_poll__networl_2_4_AskP_5, P_poll__networl_1_2_AskP_2, P_poll__networl_1_5_RP_5, P_poll__networl_5_4_RI_2, P_network_0_4_RI_3, P_poll__networl_5_0_AnnP_5, P_poll__networl_5_4_RP_0, P_network_1_4_RP_1, P_poll__networl_0_3_AskP_2, P_network_2_5_AI_1, P_poll__networl_0_0_AskP_3, P_poll__networl_3_5_AI_6, P_crashed_4, P_network_3_1_RP_3, P_network_4_6_RP_2, P_network_4_1_AskP_5, P_network_2_4_AskP_6, P_network_2_0_AskP_4, P_masterList_5_5_1, P_network_0_3_AskP_1, P_poll__networl_4_4_RI_3, P_network_3_2_AI_3, P_network_6_6_RP_3, P_network_2_2_AnnP_6, P_network_1_6_RI_5, P_poll__networl_1_0_AskP_3, P_poll__networl_3_4_AnnP_6, P_network_1_6_RI_2, P_poll__networl_5_1_RI_5, P_network_5_1_AskP_6, P_poll__networl_1_5_AskP_0, P_poll__networl_0_1_AnnP_3, P_network_1_0_RI_6, P_poll__networl_6_1_RI_4, P_network_4_5_AskP_4, P_poll__networl_2_3_AnnP_5, P_poll__networl_6_1_AskP_3, P_network_5_6_RI_5, P_network_2_0_RI_2, P_network_0_5_AnnP_1, P_network_2_4_AnnP_4, P_poll__networl_4_0_AnnP_3, P_network_3_0_RP_6, P_poll__networl_2_6_AskP_6, P_poll__networl_1_5_AskP_2, P_poll__networl_3_3_RI_4, P_poll__networl_3_2_AnnP_4
Jun 02, 2017 11:09:32 PM fr.lip6.move.gal.instantiate.Simplifier simplifyConstantVariables
INFO: Simplified 2604 expressions due to constant valuations.
Jun 02, 2017 11:09:32 PM fr.lip6.move.gal.instantiate.Simplifier simplifyFalseTransitions
INFO: Removed 430 false transitions.
Jun 02, 2017 11:09:33 PM fr.lip6.move.gal.instantiate.DomainAnalyzer computeVariableDomains
INFO: Found a total of 27 fixed domain variables (out of 1281 variables) in GAL type NeoElection_PT_6_flat
Jun 02, 2017 11:09:33 PM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 143024 ms
Jun 02, 2017 11:09:33 PM fr.lip6.move.serialization.SerializationUtil systemToFile
INFO: Time to serialize gal into /home/mcc/execution/LTLCardinality.pnml.gal : 92 ms
Jun 02, 2017 11:09:33 PM fr.lip6.move.serialization.SerializationUtil serializePropertiesForITSLTLTools
INFO: Time to serialize properties into /home/mcc/execution/LTLCardinality.ltl : 2 ms
Jun 02, 2017 11:09:39 PM fr.lip6.move.gal.gal2smt.bmc.KInductionSolver computeAndDeclareInvariants
INFO: Computed 136 place invariants in 2429 ms
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_NeoElection-PT-6"
export BK_EXAMINATION="LTLCardinality"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_NeoElection-PT-6.tgz
mv S_NeoElection-PT-6 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-3254"
echo " Executing tool itstools"
echo " Input is S_NeoElection-PT-6, examination is LTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r120-blw7-149441652000275"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "LTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "LTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "LTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property LTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "LTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

