About the Execution of LoLA for S_NeoElection-PT-7
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 707.370 | 290346.00 | 736290.00 | 37.60 | TTFFFFFTTTTTFTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
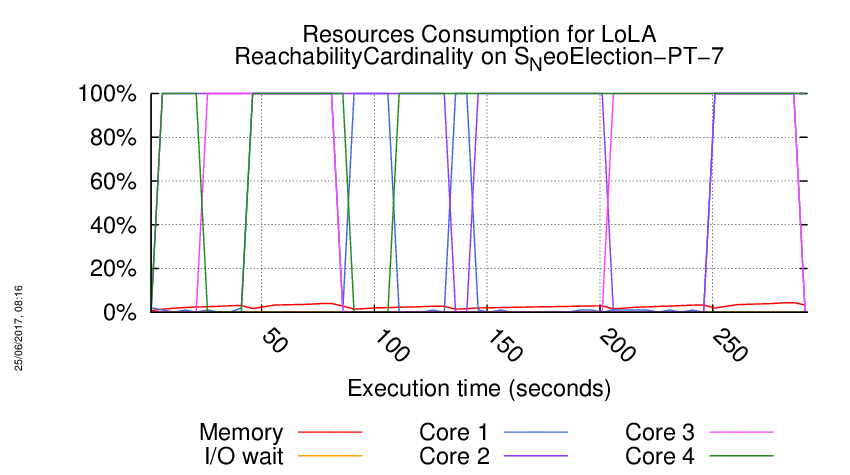
Trace from the execution
Waiting for the VM to be ready (probing ssh)
......
=====================================================================
Generated by BenchKit 2-3254
Executing tool lola
Input is S_NeoElection-PT-7, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r118-blw7-149441650100286
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-0
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-1
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-10
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-11
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-12
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-13
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-14
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-15
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-2
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-3
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-4
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-5
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-6
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-7
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-8
FORMULA_NAME NeoElection-COL-7-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1496372236191
Time: 3600 - MCC
----- Start make prepare stdout -----
===========================================================================================
S_NeoElection-PT-7: translating PT Petri net model.pnml into LoLA format
===========================================================================================
translating PT Petri net complete
checking for too many tokens
===========================================================================================
S_NeoElection-PT-7: translating PT formula ReachabilityCardinality into LoLA format
===========================================================================================
translating formula complete
touch formulae;
----- Start make result stdout -----
ReachabilityCardinality @ S_NeoElection-PT-7 @ 3540 seconds
----- Start make result stdout -----
lola: LoLA will run for 3540 seconds at most (--timelimit)
lola: NET
lola: reading net from model.pnml.lola
lola: finished parsing
lola: closed net file model.pnml.lola
lola: 21240/65536 symbol table entries, 3557 collisions
lola: preprocessing...
lola: finding significant places
lola: 7128 places, 14112 transitions, 1688 significant places
lola: computing forward-conflicting sets
lola: computing back-conflicting sets
lola: 3568 transition conflict sets
lola: TASK
lola: reading formula from NeoElection-COL-7-ReachabilityCardinality.task
lola: A (G (((P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_7 + P-masterState_7_F_7 + P-masterState_2_F_7 + P-masterState_5_F_7 + P-masterState_0_F_7 + P-masterState_3_F_7 + P-masterState_1_T_7 + P-masterState_6_F_7 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7) OR (P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-crashed_7 + P-crashed_6 + P-crashed_5 + P-crashed_4 + P-crashed_3 + P-crashed_2 + P-crashed_1 + P-crashed_0) OR (P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3 + P-poll__handlingMessage_4 + P-poll__handlingMessage_5 + P-poll__handlingMessage_6 + P-poll__handlingMessage_7) OR (P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterList_0_4_2 + P-masterList_0_4_3 + P-masterList_0_4_4 + P-masterList_0_4_5 + P-masterList_0_4_6 + P-masterList_0_4_7 + P-masterList_0_3_7 + P-masterList_0_3_6 + P-masterList_0_3_5 + P-masterList_0_3_4 + P-masterList_0_3_3 + P-masterList_0_3_2 + P-masterList_0_3_1 + P-masterList_0_3_0 + P-masterList_3_1_7 + P-masterList_3_1_6 + P-masterList_3_1_5 + P-masterList_3_1_4 + P-masterList_5_7_0 + P-masterList_5_7_1 + P-masterList_5_7_2 + P-masterList_5_7_3 + P-masterList_5_7_4 + P-masterList_5_7_5 + P-masterList_5_7_6 + P-masterList_5_7_7 + P-masterList_3_1_3 + P-masterList_3_1_2 + P-masterList_3_1_1 + P-masterList_3_1_0 + P-masterList_6_1_0 + P-masterList_6_1_1 + P-masterList_6_1_2 + P-masterList_6_1_3 + P-masterList_6_1_4 + P-masterList_6_1_5 + P-masterList_6_1_6 + P-masterList_6_1_7 + P-masterList_3_3_0 + P-masterList_3_3_1 + P-masterList_3_3_2 + P-masterList_3_3_3 + P-masterList_3_3_4 + P-masterList_3_3_5 + P-masterList_3_3_6 + P-masterList_3_3_7 + P-masterList_0_5_0 + P-masterList_0_5_1 + P-masterList_0_5_2 + P-masterList_0_5_3 + P-masterList_0_5_4 + P-masterList_0_5_5 + P-masterList_0_5_6 + P-masterList_0_5_7 + P-masterList_2_7_7 + P-masterList_2_7_6 + P-masterList_2_7_5 + P-masterList_2_7_4 + P-masterList_2_7_3 + P-masterList_2_7_2 + P-masterList_2_7_1 + P-masterList_2_7_0 + P-masterList_5_5_7 + P-masterList_5_5_6 + P-masterList_5_5_5 + P-masterList_5_5_4 + P-masterList_5_5_3 + P-masterList_5_5_2 + P-masterList_5_5_1 + P-masterList_5_5_0 + P-masterList_6_2_0 + P-masterList_6_2_1 + P-masterList_6_2_2 + P-masterList_6_2_3 + P-masterList_6_2_4 + P-masterList_6_2_5 + P-masterList_6_2_6 + P-masterList_6_2_7 + P-masterList_3_4_0 + P-masterList_3_4_1 + P-masterList_3_4_2 + P-masterList_3_4_3 + P-masterList_3_4_4 + P-masterList_3_4_5 + P-masterList_3_4_6 + P-masterList_3_4_7 + P-masterList_0_6_0 + P-masterList_0_6_1 + P-masterList_0_6_2 + P-masterList_0_6_3 + P-masterList_0_6_4 + P-masterList_0_6_5 + P-masterList_0_6_6 + P-masterList_0_6_7 + P-masterList_6_3_0 + P-masterList_6_3_1 + P-masterList_6_3_2 + P-masterList_6_3_3 + P-masterList_6_3_4 + P-masterList_6_3_5 + P-masterList_6_3_6 + P-masterList_6_3_7 + P-masterList_3_5_0 + P-masterList_3_5_1 + P-masterList_3_5_2 + P-masterList_3_5_3 + P-masterList_3_5_4 + P-masterList_3_5_5 + P-masterList_3_5_6 + P-masterList_3_5_7 + P-masterList_0_7_0 + P-masterList_0_7_1 + P-masterList_0_7_2 + P-masterList_0_7_3 + P-masterList_0_7_4 + P-masterList_0_7_5 + P-masterList_0_7_6 + P-masterList_0_7_7 + P-masterList_1_1_0 + P-masterList_1_1_1 + P-masterList_1_1_2 + P-masterList_1_1_3 + P-masterList_1_1_4 + P-masterList_1_1_5 + P-masterList_1_1_6 + P-masterList_1_1_7 + P-masterList_0_2_7 + P-masterList_0_2_6 + P-masterList_0_2_5 + P-masterList_0_2_4 + P-masterList_0_2_3 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_6_4_0 + P-masterList_6_4_1 + P-masterList_6_4_2 + P-masterList_6_4_3 + P-masterList_6_4_4 + P-masterList_6_4_5 + P-masterList_6_4_6 + P-masterList_6_4_7 + P-masterList_3_6_0 + P-masterList_3_6_1 + P-masterList_3_6_2 + P-masterList_3_6_3 + P-masterList_3_6_4 + P-masterList_3_6_5 + P-masterList_3_6_6 + P-masterList_3_6_7 + P-masterList_1_2_0 + P-masterList_1_2_1 + P-masterList_1_2_2 + P-masterList_1_2_3 + P-masterList_1_2_4 + P-masterList_1_2_5 + P-masterList_1_2_6 + P-masterList_1_2_7 + P-masterList_2_6_7 + P-masterList_2_6_6 + P-masterList_2_6_5 + P-masterList_2_6_4 + P-masterList_2_6_3 + P-masterList_2_6_2 + P-masterList_2_6_1 + P-masterList_2_6_0 + P-masterList_6_5_0 + P-masterList_6_5_1 + P-masterList_6_5_2 + P-masterList_6_5_3 + P-masterList_6_5_4 + P-masterList_6_5_5 + P-masterList_6_5_6 + P-masterList_6_5_7 + P-masterList_5_4_7 + P-masterList_5_4_6 + P-masterList_5_4_5 + P-masterList_5_4_4 + P-masterList_5_4_3 + P-masterList_5_4_2 + P-masterList_3_7_0 + P-masterList_3_7_1 + P-masterList_3_7_2 + P-masterList_3_7_3 + P-masterList_3_7_4 + P-masterList_3_7_5 + P-masterList_3_7_6 + P-masterList_3_7_7 + P-masterList_5_4_1 + P-masterList_5_4_0 + P-masterList_4_1_0 + P-masterList_4_1_1 + P-masterList_4_1_2 + P-masterList_4_1_3 + P-masterList_4_1_4 + P-masterList_4_1_5 + P-masterList_4_1_6 + P-masterList_4_1_7 + P-masterList_1_3_0 + P-masterList_1_3_1 + P-masterList_1_3_2 + P-masterList_1_3_3 + P-masterList_1_3_4 + P-masterList_1_3_5 + P-masterList_1_3_6 + P-masterList_1_3_7 + P-masterList_6_6_0 + P-masterList_6_6_1 + P-masterList_6_6_2 + P-masterList_6_6_3 + P-masterList_6_6_4 + P-masterList_6_6_5 + P-masterList_6_6_6 + P-masterList_6_6_7 + P-masterList_4_2_0 + P-masterList_4_2_1 + P-masterList_4_2_2 + P-masterList_4_2_3 + P-masterList_4_2_4 + P-masterList_4_2_5 + P-masterList_4_2_6 + P-masterList_4_2_7 + P-masterList_1_4_0 + P-masterList_1_4_1 + P-masterList_1_4_2 + P-masterList_1_4_3 + P-masterList_1_4_4 + P-masterList_1_4_5 + P-masterList_1_4_6 + P-masterList_1_4_7 + P-masterList_0_1_7 + P-masterList_0_1_6 + P-masterList_0_1_5 + P-masterList_0_1_4 + P-masterList_0_1_3 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 + P-masterList_6_7_0 + P-masterList_6_7_1 + P-masterList_6_7_2 + P-masterList_6_7_3 + P-masterList_6_7_4 + P-masterList_6_7_5 + P-masterList_6_7_6 + P-masterList_6_7_7 + P-masterList_7_1_0 + P-masterList_7_1_1 + P-masterList_7_1_2 + P-masterList_7_1_3 + P-masterList_7_1_4 + P-masterList_7_1_5 + P-masterList_7_1_6 + P-masterList_7_1_7 + P-masterList_4_3_0 + P-masterList_4_3_1 + P-masterList_4_3_2 + P-masterList_4_3_3 + P-masterList_4_3_4 + P-masterList_4_3_5 + P-masterList_4_3_6 + P-masterList_4_3_7 + P-masterList_1_5_0 + P-masterList_1_5_1 + P-masterList_1_5_2 + P-masterList_1_5_3 + P-masterList_1_5_4 + P-masterList_1_5_5 + P-masterList_1_5_6 + P-masterList_1_5_7 + P-masterList_2_5_7 + P-masterList_2_5_6 + P-masterList_2_5_5 + P-masterList_2_5_4 + P-masterList_2_5_3 + P-masterList_2_5_2 + P-masterList_2_5_1 + P-masterList_2_5_0 + P-masterList_7_2_0 + P-masterList_7_2_1 + P-masterList_7_2_2 + P-masterList_7_2_3 + P-masterList_7_2_4 + P-masterList_7_2_5 + P-masterList_7_2_6 + P-masterList_7_2_7 + P-masterList_4_4_0 + P-masterList_4_4_1 + P-masterList_4_4_2 + P-masterList_4_4_3 + P-masterList_4_4_4 + P-masterList_4_4_5 + P-masterList_4_4_6 + P-masterList_4_4_7 + P-masterList_5_3_7 + P-masterList_5_3_6 + P-masterList_5_3_5 + P-masterList_5_3_4 + P-masterList_5_3_3 + P-masterList_5_3_2 + P-masterList_5_3_1 + P-masterList_5_3_0 + P-masterList_1_6_0 + P-masterList_1_6_1 + P-masterList_1_6_2 + P-masterList_1_6_3 + P-masterList_1_6_4 + P-masterList_1_6_5 + P-masterList_1_6_6 + P-masterList_1_6_7 + P-masterList_7_7_7 + P-masterList_7_7_6 + P-masterList_7_7_5 + P-masterList_7_7_4 + P-masterList_7_7_3 + P-masterList_7_7_2 + P-masterList_7_7_1 + P-masterList_7_7_0 + P-masterList_7_3_0 + P-masterList_7_3_1 + P-masterList_7_3_2 + P-masterList_7_3_3 + P-masterList_7_3_4 + P-masterList_7_3_5 + P-masterList_7_3_6 + P-masterList_7_3_7 + P-masterList_4_5_0 + P-masterList_4_5_1 + P-masterList_4_5_2 + P-masterList_4_5_3 + P-masterList_4_5_4 + P-masterList_4_5_5 + P-masterList_4_5_6 + P-masterList_4_5_7 + P-masterList_1_7_0 + P-masterList_1_7_1 + P-masterList_1_7_2 + P-masterList_1_7_3 + P-masterList_1_7_4 + P-masterList_1_7_5 + P-masterList_1_7_6 + P-masterList_1_7_7 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_1_3 + P-masterList_2_1_4 + P-masterList_2_1_5 + P-masterList_2_1_6 + P-masterList_2_1_7 + P-masterList_7_4_0 + P-masterList_7_4_1 + P-masterList_7_4_2 + P-masterList_7_4_3 + P-masterList_7_4_4 + P-masterList_7_4_5 + P-masterList_7_4_6 + P-masterList_7_4_7 + P-masterList_4_6_0 + P-masterList_4_6_1 + P-masterList_4_6_2 + P-masterList_4_6_3 + P-masterList_4_6_4 + P-masterList_4_6_5 + P-masterList_4_6_6 + P-masterList_4_6_7 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_2_2_3 + P-masterList_2_2_4 + P-masterList_2_2_5 + P-masterList_2_2_6 + P-masterList_2_2_7 + P-masterList_2_4_7 + P-masterList_2_4_6 + P-masterList_2_4_5 + P-masterList_2_4_4 + P-masterList_2_4_3 + P-masterList_2_4_2 + P-masterList_2_4_1 + P-masterList_2_4_0 + P-masterList_7_5_0 + P-masterList_7_5_1 + P-masterList_7_5_2 + P-masterList_7_5_3 + P-masterList_7_5_4 + P-masterList_7_5_5 + P-masterList_7_5_6 + P-masterList_7_5_7 + P-masterList_4_7_0 + P-masterList_4_7_1 + P-masterList_4_7_2 + P-masterList_4_7_3 + P-masterList_4_7_4 + P-masterList_4_7_5 + P-masterList_4_7_6 + P-masterList_4_7_7 + P-masterList_5_1_0 + P-masterList_5_1_1 + P-masterList_5_1_2 + P-masterList_5_1_3 + P-masterList_5_1_4 + P-masterList_5_1_5 + P-masterList_5_1_6 + P-masterList_5_1_7 + P-masterList_5_2_7 + P-masterList_5_2_6 + P-masterList_5_2_5 + P-masterList_5_2_4 + P-masterList_5_2_3 + P-masterList_5_2_2 + P-masterList_5_2_1 + P-masterList_5_2_0 + P-masterList_2_3_0 + P-masterList_2_3_1 + P-masterList_2_3_2 + P-masterList_2_3_3 + P-masterList_2_3_4 + P-masterList_2_3_5 + P-masterList_2_3_6 + P-masterList_2_3_7 + P-masterList_7_6_0 + P-masterList_7_6_1 + P-masterList_7_6_2 + P-masterList_7_6_3 + P-masterList_7_6_4 + P-masterList_7_6_5 + P-masterList_7_6_6 + P-masterList_7_6_7)))) : A (G ((3 <= P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterList_0_4_2 + P-masterList_0_4_3 + P-masterList_0_4_4 + P-masterList_0_4_5 + P-masterList_0_4_6 + P-masterList_0_4_7 + P-masterList_0_3_7 + P-masterList_0_3_6 + P-masterList_0_3_5 + P-masterList_0_3_4 + P-masterList_0_3_3 + P-masterList_0_3_2 + P-masterList_0_3_1 + P-masterList_0_3_0 + P-masterList_3_1_7 + P-masterList_3_1_6 + P-masterList_3_1_5 + P-masterList_3_1_4 + P-masterList_5_7_0 + P-masterList_5_7_1 + P-masterList_5_7_2 + P-masterList_5_7_3 + P-masterList_5_7_4 + P-masterList_5_7_5 + P-masterList_5_7_6 + P-masterList_5_7_7 + P-masterList_3_1_3 + P-masterList_3_1_2 + P-masterList_3_1_1 + P-masterList_3_1_0 + P-masterList_6_1_0 + P-masterList_6_1_1 + P-masterList_6_1_2 + P-masterList_6_1_3 + P-masterList_6_1_4 + P-masterList_6_1_5 + P-masterList_6_1_6 + P-masterList_6_1_7 + P-masterList_3_3_0 + P-masterList_3_3_1 + P-masterList_3_3_2 + P-masterList_3_3_3 + P-masterList_3_3_4 + P-masterList_3_3_5 + P-masterList_3_3_6 + P-masterList_3_3_7 + P-masterList_0_5_0 + P-masterList_0_5_1 + P-masterList_0_5_2 + P-masterList_0_5_3 + P-masterList_0_5_4 + P-masterList_0_5_5 + P-masterList_0_5_6 + P-masterList_0_5_7 + P-masterList_2_7_7 + P-masterList_2_7_6 + P-masterList_2_7_5 + P-masterList_2_7_4 + P-masterList_2_7_3 + P-masterList_2_7_2 + P-masterList_2_7_1 + P-masterList_2_7_0 + P-masterList_5_5_7 + P-masterList_5_5_6 + P-masterList_5_5_5 + P-masterList_5_5_4 + P-masterList_5_5_3 + P-masterList_5_5_2 + P-masterList_5_5_1 + P-masterList_5_5_0 + P-masterList_6_2_0 + P-masterList_6_2_1 + P-masterList_6_2_2 + P-masterList_6_2_3 + P-masterList_6_2_4 + P-masterList_6_2_5 + P-masterList_6_2_6 + P-masterList_6_2_7 + P-masterList_3_4_0 + P-masterList_3_4_1 + P-masterList_3_4_2 + P-masterList_3_4_3 + P-masterList_3_4_4 + P-masterList_3_4_5 + P-masterList_3_4_6 + P-masterList_3_4_7 + P-masterList_0_6_0 + P-masterList_0_6_1 + P-masterList_0_6_2 + P-masterList_0_6_3 + P-masterList_0_6_4 + P-masterList_0_6_5 + P-masterList_0_6_6 + P-masterList_0_6_7 + P-masterList_6_3_0 + P-masterList_6_3_1 + P-masterList_6_3_2 + P-masterList_6_3_3 + P-masterList_6_3_4 + P-masterList_6_3_5 + P-masterList_6_3_6 + P-masterList_6_3_7 + P-masterList_3_5_0 + P-masterList_3_5_1 + P-masterList_3_5_2 + P-masterList_3_5_3 + P-masterList_3_5_4 + P-masterList_3_5_5 + P-masterList_3_5_6 + P-masterList_3_5_7 + P-masterList_0_7_0 + P-masterList_0_7_1 + P-masterList_0_7_2 + P-masterList_0_7_3 + P-masterList_0_7_4 + P-masterList_0_7_5 + P-masterList_0_7_6 + P-masterList_0_7_7 + P-masterList_1_1_0 + P-masterList_1_1_1 + P-masterList_1_1_2 + P-masterList_1_1_3 + P-masterList_1_1_4 + P-masterList_1_1_5 + P-masterList_1_1_6 + P-masterList_1_1_7 + P-masterList_0_2_7 + P-masterList_0_2_6 + P-masterList_0_2_5 + P-masterList_0_2_4 + P-masterList_0_2_3 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_6_4_0 + P-masterList_6_4_1 + P-masterList_6_4_2 + P-masterList_6_4_3 + P-masterList_6_4_4 + P-masterList_6_4_5 + P-masterList_6_4_6 + P-masterList_6_4_7 + P-masterList_3_6_0 + P-masterList_3_6_1 + P-masterList_3_6_2 + P-masterList_3_6_3 + P-masterList_3_6_4 + P-masterList_3_6_5 + P-masterList_3_6_6 + P-masterList_3_6_7 + P-masterList_1_2_0 + P-masterList_1_2_1 + P-masterList_1_2_2 + P-masterList_1_2_3 + P-masterList_1_2_4 + P-masterList_1_2_5 + P-masterList_1_2_6 + P-masterList_1_2_7 + P-masterList_2_6_7 + P-masterList_2_6_6 + P-masterList_2_6_5 + P-masterList_2_6_4 + P-masterList_2_6_3 + P-masterList_2_6_2 + P-masterList_2_6_1 + P-masterList_2_6_0 + P-masterList_6_5_0 + P-masterList_6_5_1 + P-masterList_6_5_2 + P-masterList_6_5_3 + P-masterList_6_5_4 + P-masterList_6_5_5 + P-masterList_6_5_6 + P-masterList_6_5_7 + P-masterList_5_4_7 + P-masterList_5_4_6 + P-masterList_5_4_5 + P-masterList_5_4_4 + P-masterList_5_4_3 + P-masterList_5_4_2 + P-masterList_3_7_0 + P-masterList_3_7_1 + P-masterList_3_7_2 + P-masterList_3_7_3 + P-masterList_3_7_4 + P-masterList_3_7_5 + P-masterList_3_7_6 + P-masterList_3_7_7 + P-masterList_5_4_1 + P-masterList_5_4_0 + P-masterList_4_1_0 + P-masterList_4_1_1 + P-masterList_4_1_2 + P-masterList_4_1_3 + P-masterList_4_1_4 + P-masterList_4_1_5 + P-masterList_4_1_6 + P-masterList_4_1_7 + P-masterList_1_3_0 + P-masterList_1_3_1 + P-masterList_1_3_2 + P-masterList_1_3_3 + P-masterList_1_3_4 + P-masterList_1_3_5 + P-masterList_1_3_6 + P-masterList_1_3_7 + P-masterList_6_6_0 + P-masterList_6_6_1 + P-masterList_6_6_2 + P-masterList_6_6_3 + P-masterList_6_6_4 + P-masterList_6_6_5 + P-masterList_6_6_6 + P-masterList_6_6_7 + P-masterList_4_2_0 + P-masterList_4_2_1 + P-masterList_4_2_2 + P-masterList_4_2_3 + P-masterList_4_2_4 + P-masterList_4_2_5 + P-masterList_4_2_6 + P-masterList_4_2_7 + P-masterList_1_4_0 + P-masterList_1_4_1 + P-masterList_1_4_2 + P-masterList_1_4_3 + P-masterList_1_4_4 + P-masterList_1_4_5 + P-masterList_1_4_6 + P-masterList_1_4_7 + P-masterList_0_1_7 + P-masterList_0_1_6 + P-masterList_0_1_5 + P-masterList_0_1_4 + P-masterList_0_1_3 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 + P-masterList_6_7_0 + P-masterList_6_7_1 + P-masterList_6_7_2 + P-masterList_6_7_3 + P-masterList_6_7_4 + P-masterList_6_7_5 + P-masterList_6_7_6 + P-masterList_6_7_7 + P-masterList_7_1_0 + P-masterList_7_1_1 + P-masterList_7_1_2 + P-masterList_7_1_3 + P-masterList_7_1_4 + P-masterList_7_1_5 + P-masterList_7_1_6 + P-masterList_7_1_7 + P-masterList_4_3_0 + P-masterList_4_3_1 + P-masterList_4_3_2 + P-masterList_4_3_3 + P-masterList_4_3_4 + P-masterList_4_3_5 + P-masterList_4_3_6 + P-masterList_4_3_7 + P-masterList_1_5_0 + P-masterList_1_5_1 + P-masterList_1_5_2 + P-masterList_1_5_3 + P-masterList_1_5_4 + P-masterList_1_5_5 + P-masterList_1_5_6 + P-masterList_1_5_7 + P-masterList_2_5_7 + P-masterList_2_5_6 + P-masterList_2_5_5 + P-masterList_2_5_4 + P-masterList_2_5_3 + P-masterList_2_5_2 + P-masterList_2_5_1 + P-masterList_2_5_0 + P-masterList_7_2_0 + P-masterList_7_2_1 + P-masterList_7_2_2 + P-masterList_7_2_3 + P-masterList_7_2_4 + P-masterList_7_2_5 + P-masterList_7_2_6 + P-masterList_7_2_7 + P-masterList_4_4_0 + P-masterList_4_4_1 + P-masterList_4_4_2 + P-masterList_4_4_3 + P-masterList_4_4_4 + P-masterList_4_4_5 + P-masterList_4_4_6 + P-masterList_4_4_7 + P-masterList_5_3_7 + P-masterList_5_3_6 + P-masterList_5_3_5 + P-masterList_5_3_4 + P-masterList_5_3_3 + P-masterList_5_3_2 + P-masterList_5_3_1 + P-masterList_5_3_0 + P-masterList_1_6_0 + P-masterList_1_6_1 + P-masterList_1_6_2 + P-masterList_1_6_3 + P-masterList_1_6_4 + P-masterList_1_6_5 + P-masterList_1_6_6 + P-masterList_1_6_7 + P-masterList_7_7_7 + P-masterList_7_7_6 + P-masterList_7_7_5 + P-masterList_7_7_4 + P-masterList_7_7_3 + P-masterList_7_7_2 + P-masterList_7_7_1 + P-masterList_7_7_0 + P-masterList_7_3_0 + P-masterList_7_3_1 + P-masterList_7_3_2 + P-masterList_7_3_3 + P-masterList_7_3_4 + P-masterList_7_3_5 + P-masterList_7_3_6 + P-masterList_7_3_7 + P-masterList_4_5_0 + P-masterList_4_5_1 + P-masterList_4_5_2 + P-masterList_4_5_3 + P-masterList_4_5_4 + P-masterList_4_5_5 + P-masterList_4_5_6 + P-masterList_4_5_7 + P-masterList_1_7_0 + P-masterList_1_7_1 + P-masterList_1_7_2 + P-masterList_1_7_3 + P-masterList_1_7_4 + P-masterList_1_7_5 + P-masterList_1_7_6 + P-masterList_1_7_7 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_1_3 + P-masterList_2_1_4 + P-masterList_2_1_5 + P-masterList_2_1_6 + P-masterList_2_1_7 + P-masterList_7_4_0 + P-masterList_7_4_1 + P-masterList_7_4_2 + P-masterList_7_4_3 + P-masterList_7_4_4 + P-masterList_7_4_5 + P-masterList_7_4_6 + P-masterList_7_4_7 + P-masterList_4_6_0 + P-masterList_4_6_1 + P-masterList_4_6_2 + P-masterList_4_6_3 + P-masterList_4_6_4 + P-masterList_4_6_5 + P-masterList_4_6_6 + P-masterList_4_6_7 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_2_2_3 + P-masterList_2_2_4 + P-masterList_2_2_5 + P-masterList_2_2_6 + P-masterList_2_2_7 + P-masterList_2_4_7 + P-masterList_2_4_6 + P-masterList_2_4_5 + P-masterList_2_4_4 + P-masterList_2_4_3 + P-masterList_2_4_2 + P-masterList_2_4_1 + P-masterList_2_4_0 + P-masterList_7_5_0 + P-masterList_7_5_1 + P-masterList_7_5_2 + P-masterList_7_5_3 + P-masterList_7_5_4 + P-masterList_7_5_5 + P-masterList_7_5_6 + P-masterList_7_5_7 + P-masterList_4_7_0 + P-masterList_4_7_1 + P-masterList_4_7_2 + P-masterList_4_7_3 + P-masterList_4_7_4 + P-masterList_4_7_5 + P-masterList_4_7_6 + P-masterList_4_7_7 + P-masterList_5_1_0 + P-masterList_5_1_1 + P-masterList_5_1_2 + P-masterList_5_1_3 + P-masterList_5_1_4 + P-masterList_5_1_5 + P-masterList_5_1_6 + P-masterList_5_1_7 + P-masterList_5_2_7 + P-masterList_5_2_6 + P-masterList_5_2_5 + P-masterList_5_2_4 + P-masterList_5_2_3 + P-masterList_5_2_2 + P-masterList_5_2_1 + P-masterList_5_2_0 + P-masterList_2_3_0 + P-masterList_2_3_1 + P-masterList_2_3_2 + P-masterList_2_3_3 + P-masterList_2_3_4 + P-masterList_2_3_5 + P-masterList_2_3_6 + P-masterList_2_3_7 + P-masterList_7_6_0 + P-masterList_7_6_1 + P-masterList_7_6_2 + P-masterList_7_6_3 + P-masterList_7_6_4 + P-masterList_7_6_5 + P-masterList_7_6_6 + P-masterList_7_6_7))) : E (F ((P-poll__pollEnd_7 + P-poll__pollEnd_6 + P-poll__pollEnd_5 + P-poll__pollEnd_4 + P-poll__pollEnd_3 + P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0 + 1 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7))) : A (G ((P-poll__waitingMessage_0 + P-poll__waitingMessage_1 + P-poll__waitingMessage_2 + P-poll__waitingMessage_4 + P-poll__waitingMessage_5 + P-poll__waitingMessage_6 + P-poll__waitingMessage_7 + P-poll__waitingMessage_3 <= P-dead_7 + P-dead_6 + P-dead_5 + P-dead_4 + P-dead_3 + P-dead_2 + P-dead_1 + P-dead_0))) : E (F ((1 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7))) : A (G (((P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_2_3 + P-startNeg__broadcasting_2_4 + P-startNeg__broadcasting_2_5 + P-startNeg__broadcasting_2_6 + P-startNeg__broadcasting_2_7 + P-startNeg__broadcasting_3_1 + P-startNeg__broadcasting_3_2 + P-startNeg__broadcasting_3_3 + P-startNeg__broadcasting_3_4 + P-startNeg__broadcasting_3_5 + P-startNeg__broadcasting_3_6 + P-startNeg__broadcasting_3_7 + P-startNeg__broadcasting_4_1 + P-startNeg__broadcasting_4_2 + P-startNeg__broadcasting_4_3 + P-startNeg__broadcasting_4_4 + P-startNeg__broadcasting_4_5 + P-startNeg__broadcasting_4_6 + P-startNeg__broadcasting_4_7 + P-startNeg__broadcasting_7_7 + P-startNeg__broadcasting_7_6 + P-startNeg__broadcasting_7_5 + P-startNeg__broadcasting_7_4 + P-startNeg__broadcasting_7_3 + P-startNeg__broadcasting_7_2 + P-startNeg__broadcasting_7_1 + P-startNeg__broadcasting_5_1 + P-startNeg__broadcasting_5_2 + P-startNeg__broadcasting_5_3 + P-startNeg__broadcasting_5_4 + P-startNeg__broadcasting_5_5 + P-startNeg__broadcasting_5_6 + P-startNeg__broadcasting_5_7 + P-startNeg__broadcasting_6_7 + P-startNeg__broadcasting_6_6 + P-startNeg__broadcasting_6_5 + P-startNeg__broadcasting_6_4 + P-startNeg__broadcasting_6_3 + P-startNeg__broadcasting_6_2 + P-startNeg__broadcasting_6_1 + P-startNeg__broadcasting_0_6 + P-startNeg__broadcasting_0_7 + P-startNeg__broadcasting_1_6 + P-startNeg__broadcasting_1_7 + 1 <= P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0) OR (P-dead_7 + P-dead_6 + P-dead_5 + P-dead_4 + P-dead_3 + P-dead_2 + P-dead_1 + P-dead_0 + 1 <= P-stage_2_SEC + P-stage_3_NEG + P-stage_5_SEC + P-stage_4_PRIM + P-stage_1_SEC + P-stage_6_SEC + P-stage_3_SEC + P-stage_0_SEC + P-stage_7_PRIM + P-stage_1_NEG + P-stage_2_PRIM + P-stage_6_NEG + P-stage_4_NEG + P-stage_5_PRIM + P-stage_7_NEG + P-stage_0_PRIM + P-stage_2_NEG + P-stage_3_PRIM + P-stage_4_SEC + P-stage_5_NEG + P-stage_7_SEC + P-stage_6_PRIM + P-stage_0_NEG + P-stage_1_PRIM) OR (2 <= P-network_2_2_AnnP_0 + P-network_0_7_RP_0 + P-network_3_0_RI_0 + P-network_2_6_RP_0 + P-network_5_1_AskP_0 + P-network_4_7_AnnP_0 + P-network_1_1_RI_0 + P-network_4_4_AnsP_7 + P-network_4_4_AnsP_6 + P-network_4_4_AnsP_5 + P-network_4_4_AnsP_4 + P-network_4_4_AnsP_3 + P-network_4_4_AnsP_2 + P-network_4_4_AnsP_1 + P-network_4_4_AnsP_0 + P-network_7_6_AskP_0 + P-network_6_5_RI_0 + P-network_0_5_AskP_0 + P-network_6_2_AI_0 + P-network_5_3_AnnP_0 + P-network_4_6_RI_0 + P-network_4_5_AskP_0 + P-network_4_3_AI_0 + P-network_5_0_AnsP_7 + P-network_5_0_AnsP_6 + P-network_5_0_AnsP_5 + P-network_5_0_AnsP_4 + P-network_5_0_AnsP_3 + P-network_5_0_AnsP_2 + P-network_4_5_RP_0 + P-network_5_0_AnsP_1 + P-network_5_0_AnsP_0 + P-network_2_7_RI_0 + P-network_2_4_AI_0 + P-network_1_1_AskP_0 + P-network_7_2_RP_0 + P-network_0_7_AnnP_0 + P-network_7_5_AnsP_7 + P-network_7_5_AnsP_6 + P-network_7_5_AnsP_5 + P-network_7_5_AnsP_4 + P-network_7_5_AnsP_3 + P-network_7_5_AnsP_2 + P-network_7_5_AnsP_1 + P-network_7_5_AnsP_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_3_AnsP_4 + P-network_1_3_AnsP_5 + P-network_1_3_AnsP_6 + P-network_1_3_AnsP_7 + P-network_0_4_AnsP_7 + P-network_0_4_AnsP_6 + P-network_0_4_AnsP_5 + P-network_0_4_AnsP_4 + P-network_0_4_AnsP_3 + P-network_0_4_AnsP_2 + P-network_0_4_AnsP_1 + P-network_0_4_AnsP_0 + P-network_0_5_AI_0 + P-network_5_3_RP_0 + P-network_3_6_AskP_0 + P-network_1_6_AnnP_0 + P-network_3_4_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_7 + P-network_1_0_AnsP_6 + P-network_1_0_AnsP_5 + P-network_1_0_AnsP_4 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_6_4_RP_0 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_5_RP_0 + P-network_4_2_AskP_0 + P-network_3_5_AnsP_7 + P-network_3_5_AnsP_6 + P-network_3_5_AnsP_5 + P-network_2_0_AskP_0 + P-network_3_5_AnsP_4 + P-network_3_5_AnsP_3 + P-network_3_5_AnsP_2 + P-network_3_5_AnsP_1 + P-network_3_5_AnsP_0 + P-network_6_7_AskP_0 + P-network_0_0_RI_0 + P-network_7_3_RI_0 + P-network_1_6_AI_0 + P-network_7_0_AI_0 + P-network_4_4_AnnP_0 + P-network_1_0_RP_0 + P-network_5_4_RI_0 + P-network_4_1_AnsP_7 + P-network_4_1_AnsP_6 + P-network_4_1_AnsP_5 + P-network_4_1_AnsP_4 + P-network_4_1_AnsP_3 + P-network_4_1_AnsP_2 + P-network_4_1_AnsP_1 + P-network_3_5_AI_0 + P-network_4_1_AnsP_0 + P-network_5_1_AI_0 + P-network_0_7_AnsP_0 + P-network_7_3_AskP_0 + P-network_0_7_AnsP_1 + P-network_3_5_RI_0 + P-network_0_7_AnsP_2 + P-network_0_7_AnsP_3 + P-network_0_7_AnsP_4 + P-network_0_7_AnsP_5 + P-network_0_7_AnsP_6 + P-network_0_7_AnsP_7 + P-network_0_2_AskP_0 + P-network_3_2_AI_0 + P-network_6_6_AnsP_7 + P-network_6_6_AnsP_6 + P-network_6_2_AnnP_0 + P-network_6_6_AnsP_5 + P-network_6_6_AnsP_4 + P-network_6_6_AnsP_3 + P-network_6_6_AnsP_2 + P-network_6_6_AnsP_1 + P-network_6_6_AnsP_0 + P-network_5_0_AnnP_0 + P-network_1_6_RI_0 + P-network_1_3_AI_0 + P-network_2_7_AskP_0 + P-network_6_1_RP_0 + P-network_7_5_AnnP_0 + P-network_1_4_AskP_0 + P-network_6_7_AI_0 + P-network_4_2_RP_0 + P-network_0_4_AnnP_0 + P-network_5_4_AI_0 + P-network_7_2_AnsP_7 + P-network_7_2_AnsP_6 + P-network_7_2_AnsP_5 + P-network_7_2_AnsP_4 + P-network_7_2_AnsP_3 + P-network_7_2_AnsP_2 + P-network_7_2_AnsP_1 + P-network_7_2_AnsP_0 + P-network_0_1_AnsP_7 + P-network_0_1_AnsP_6 + P-network_0_1_AnsP_5 + P-network_0_1_AnsP_4 + P-network_0_1_AnsP_3 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_5_7_RI_0 + P-network_0_1_AnsP_0 + P-network_5_3_AnsP_0 + P-network_5_3_AnsP_1 + P-network_5_3_AnsP_2 + P-network_5_3_AnsP_3 + P-network_5_3_AnsP_4 + P-network_5_3_AnsP_5 + P-network_5_3_AnsP_6 + P-network_5_3_AnsP_7 + P-network_2_3_RP_0 + P-network_3_3_AskP_0 + P-network_2_6_AnsP_7 + P-network_2_6_AnsP_6 + P-network_2_6_AnsP_5 + P-network_7_3_AI_0 + P-network_2_6_AnsP_4 + P-network_2_6_AnsP_3 + P-network_2_6_AnsP_2 + P-network_2_6_AnsP_1 + P-network_2_6_AnsP_0 + P-network_0_4_RP_0 + P-network_7_7_RP_0 + P-network_0_0_AI_0 + P-network_1_0_AnnP_0 + P-network_3_5_AnnP_0 + P-network_7_6_RI_0 + P-network_6_2_RI_0 + P-network_3_2_AnsP_7 + P-network_3_2_AnsP_6 + P-network_3_2_AnsP_5 + P-network_3_2_AnsP_4 + P-network_3_2_AnsP_3 + P-network_0_3_RI_0 + P-network_3_2_AnsP_2 + P-network_3_2_AnsP_1 + P-network_3_2_AnsP_0 + P-network_6_4_AskP_0 + P-network_4_3_RI_0 + P-network_4_0_AI_0 + P-network_5_7_AnsP_7 + P-network_5_7_AnsP_6 + P-network_5_6_AnnP_0 + P-network_5_7_AnsP_5 + P-network_5_7_AnsP_4 + P-network_5_7_AnsP_3 + P-network_5_7_AnsP_2 + P-network_5_7_AnsP_1 + P-network_5_7_AnsP_0 + P-network_4_1_AnnP_0 + P-network_6_0_AskP_0 + P-network_2_4_RI_0 + P-network_2_1_AI_0 + P-network_7_0_AskP_0 + P-network_6_6_AnnP_0 + P-network_0_5_RI_0 + P-network_0_2_AI_0 + P-network_7_5_AI_0 + P-network_6_3_AnsP_7 + P-network_6_3_AnsP_6 + P-network_6_3_AnsP_5 + P-network_6_3_AnsP_4 + P-network_6_3_AnsP_3 + P-network_6_3_AnsP_2 + P-network_6_3_AnsP_1 + P-network_6_3_AnsP_0 + P-network_5_0_RP_0 + P-network_5_6_AI_0 + P-network_2_2_RI_0 + P-network_2_4_AskP_0 + P-network_3_1_RP_0 + P-network_7_2_AnnP_0 + P-network_3_7_AI_0 + P-network_1_7_AnsP_7 + P-network_1_7_AnsP_6 + P-network_1_7_AnsP_5 + P-network_1_7_AnsP_4 + P-network_1_7_AnsP_3 + P-network_3_1_AnnP_0 + P-network_1_7_AnsP_2 + P-network_1_7_AnsP_1 + P-network_1_7_AnsP_0 + P-network_1_2_RP_0 + P-network_0_1_AnnP_0 + P-network_4_7_AnsP_0 + P-network_4_7_AnsP_1 + P-network_4_7_AnsP_2 + P-network_4_7_AnsP_3 + P-network_4_7_AnsP_4 + P-network_4_7_AnsP_5 + P-network_4_7_AnsP_6 + P-network_4_7_AnsP_7 + P-network_4_1_RI_0 + P-network_6_6_RP_0 + P-network_3_0_AskP_0 + P-network_2_6_AnnP_0 + P-network_2_3_AnsP_7 + P-network_2_3_AnsP_6 + P-network_2_3_AnsP_5 + P-network_2_3_AnsP_4 + P-network_2_3_AnsP_3 + P-network_2_3_AnsP_2 + P-network_2_3_AnsP_1 + P-network_2_3_AnsP_0 + P-network_4_7_RP_0 + P-network_7_0_RI_0 + P-network_5_5_AskP_0 + P-network_5_1_RI_0 + P-network_3_2_AnnP_0 + P-network_5_4_AskP_0 + P-network_3_2_RI_0 + P-network_6_1_AskP_0 + P-network_5_7_AnnP_0 + P-network_6_0_RI_0 + P-network_3_7_RP_0 + P-network_1_3_RI_0 + P-network_1_0_AI_0 + P-network_5_4_AnsP_7 + P-network_5_4_AnsP_6 + P-network_5_4_AnsP_5 + P-network_5_4_AnsP_4 + P-network_5_4_AnsP_3 + P-network_5_4_AnsP_2 + P-network_5_4_AnsP_1 + P-network_5_4_AnsP_0 + P-network_6_7_RI_0 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_2_2_AnsP_3 + P-network_2_2_AnsP_4 + P-network_2_2_AnsP_5 + P-network_2_2_AnsP_6 + P-network_2_2_AnsP_7 + P-network_6_4_AI_0 + P-network_1_5_AskP_0 + P-network_6_3_AnnP_0 + P-network_4_5_AI_0 + P-network_6_0_AnsP_7 + P-network_6_0_AnsP_6 + P-network_6_0_AnsP_5 + P-network_6_0_AnsP_4 + P-network_6_0_AnsP_3 + P-network_6_0_AnsP_2 + P-network_6_0_AnsP_1 + P-network_6_0_AnsP_0 + P-network_2_0_RP_0 + P-network_2_6_AI_0 + P-network_2_1_AskP_0 + P-network_0_1_RP_0 + P-network_7_4_RP_0 + P-network_2_5_AnnP_0 + P-network_1_7_AnnP_0 + P-network_0_7_AI_0 + P-network_5_6_RP_0 + P-network_1_4_AnsP_7 + P-network_1_4_AnsP_6 + P-network_1_4_AnsP_5 + P-network_1_4_AnsP_4 + P-network_1_4_AnsP_3 + P-network_1_4_AnsP_2 + P-network_1_4_AnsP_1 + P-network_1_4_AnsP_0 + P-network_5_5_RP_0 + P-network_4_6_AskP_0 + P-network_3_6_RP_0 + P-network_0_0_AnnP_0 + P-network_2_3_AnnP_0 + P-network_2_0_AnsP_7 + P-network_2_0_AnsP_6 + P-network_2_0_AnsP_5 + P-network_2_0_AnsP_4 + P-network_7_5_RP_0 + P-network_2_0_AnsP_3 + P-network_2_0_AnsP_2 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_1_7_RP_0 + P-network_4_0_RI_0 + P-network_0_2_RP_0 + P-network_1_6_AnsP_0 + P-network_1_6_AnsP_1 + P-network_1_6_AnsP_2 + P-network_1_6_AnsP_3 + P-network_1_6_AnsP_4 + P-network_1_6_AnsP_5 + P-network_1_6_AnsP_6 + P-network_1_6_AnsP_7 + P-network_5_2_AskP_0 + P-network_2_7_AI_0 + P-network_2_1_RI_0 + P-network_4_5_AnsP_7 + P-network_4_5_AnsP_6 + P-network_4_5_AnsP_5 + P-network_4_5_AnsP_4 + P-network_4_5_AnsP_3 + P-network_4_5_AnsP_2 + P-network_4_5_AnsP_1 + P-network_4_5_AnsP_0 + P-network_7_7_AskP_0 + P-network_0_2_RI_0 + P-network_7_5_RI_0 + P-network_0_6_AskP_0 + P-network_7_2_AI_0 + P-network_5_4_AnnP_0 + P-network_7_1_AnnP_0 + P-network_5_6_RI_0 + P-network_5_3_AI_0 + P-network_5_1_AnsP_7 + P-network_5_1_AnsP_6 + P-network_5_1_AnsP_5 + P-network_5_1_AnsP_4 + P-network_5_1_AnsP_3 + P-network_5_1_AnsP_2 + P-network_5_1_AnsP_1 + P-network_5_1_AnsP_0 + P-network_3_7_RI_0 + P-network_2_1_RP_0 + P-network_3_4_AI_0 + P-network_1_2_AskP_0 + P-network_7_6_AnsP_7 + P-network_2_3_AskP_0 + P-network_7_6_AnsP_6 + P-network_7_6_AnsP_5 + P-network_7_6_AnsP_4 + P-network_7_6_AnsP_3 + P-network_7_6_AnsP_2 + P-network_7_6_AnsP_1 + P-network_7_6_AnsP_0 + P-network_4_6_AI_0 + P-network_6_0_AnnP_0 + P-network_0_5_AnsP_7 + P-network_0_5_AnsP_6 + P-network_0_5_AnsP_5 + P-network_0_5_AnsP_4 + P-network_0_5_AnsP_3 + P-network_0_5_AnsP_2 + P-network_0_5_AnsP_1 + P-network_0_5_AnsP_0 + P-network_4_0_RP_0 + P-network_1_5_AI_0 + P-network_6_3_RP_0 + P-network_3_7_AskP_0 + P-network_6_2_AnsP_0 + P-network_6_2_AnsP_1 + P-network_6_2_AnsP_2 + P-network_6_2_AnsP_3 + P-network_6_2_AnsP_4 + P-network_6_2_AnsP_5 + P-network_6_2_AnsP_6 + P-network_6_2_AnsP_7 + P-network_4_4_RP_0 + P-network_6_5_AI_0 + P-network_1_4_AnnP_0 + P-network_1_1_AnsP_7 + P-network_1_1_AnsP_6 + P-network_1_1_AnsP_5 + P-network_1_1_AnsP_4 + P-network_1_1_AnsP_3 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_6_5_AnnP_0 + P-network_1_1_AnsP_0 + P-network_2_5_RP_0 + P-network_4_3_AskP_0 + P-network_0_6_RP_0 + P-network_1_7_AskP_0 + P-network_3_6_AnsP_7 + P-network_3_6_AnsP_6 + P-network_3_6_AnsP_5 + P-network_3_6_AnsP_4 + P-network_3_6_AnsP_3 + P-network_3_6_AnsP_2 + P-network_3_6_AnsP_1 + P-network_1_1_AI_0 + P-network_3_6_AnsP_0 + P-network_2_0_AnnP_0 + P-network_1_0_RI_0 + P-network_4_5_AnnP_0 + P-network_1_4_RI_0 + P-network_6_4_RI_0 + P-network_4_2_AnsP_7 + P-network_4_2_AnsP_6 + P-network_4_2_AnsP_5 + P-network_4_2_AnsP_4 + P-network_4_2_AnsP_3 + P-network_4_2_AnsP_2 + P-network_4_2_AnsP_1 + P-network_4_0_AnnP_0 + P-network_4_2_AnsP_0 + P-network_6_1_AI_0 + P-network_7_4_AskP_0 + P-network_4_5_RI_0 + P-network_5_6_AnsP_0 + P-network_5_6_AnsP_1 + P-network_5_6_AnsP_2 + P-network_5_6_AnsP_3 + P-network_5_6_AnsP_4 + P-network_5_6_AnsP_5 + P-network_5_6_AnsP_6 + P-network_5_6_AnsP_7 + P-network_0_3_AskP_0 + P-network_3_0_AI_0 + P-network_4_2_AI_0 + P-network_6_7_AnsP_7 + P-network_6_7_AnsP_6 + P-network_6_7_AnsP_5 + P-network_6_7_AnsP_4 + P-network_6_7_AnsP_3 + P-network_6_7_AnsP_2 + P-network_6_7_AnsP_1 + P-network_6_7_AnsP_0 + P-network_5_1_AnnP_0 + P-network_3_3_RI_0 + P-network_2_6_RI_0 + P-network_2_3_AI_0 + P-network_7_1_RP_0 + P-network_7_6_AnnP_0 + P-network_0_7_RI_0 + P-network_0_4_AI_0 + P-network_7_7_AI_0 + P-network_5_2_RP_0 + P-network_0_5_AnnP_0 + P-network_7_3_AnsP_7 + P-network_7_3_AnsP_6 + P-network_6_3_AskP_0 + P-network_7_3_AnsP_5 + P-network_7_3_AnsP_4 + P-network_7_3_AnsP_3 + P-network_7_3_AnsP_2 + P-network_7_3_AnsP_1 + P-network_7_3_AnsP_0 + P-network_0_2_AnsP_7 + P-network_0_2_AnsP_6 + P-network_0_2_AnsP_5 + P-network_0_2_AnsP_4 + P-network_0_2_AnsP_3 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_3_1_AnsP_0 + P-network_3_1_AnsP_1 + P-network_3_1_AnsP_2 + P-network_3_1_AnsP_3 + P-network_3_1_AnsP_4 + P-network_3_1_AnsP_5 + P-network_3_1_AnsP_6 + P-network_3_1_AnsP_7 + P-network_3_3_RP_0 + P-network_5_2_RI_0 + P-network_3_4_AskP_0 + P-network_2_7_AnsP_7 + P-network_2_7_AnsP_6 + P-network_2_7_AnsP_5 + P-network_2_7_AnsP_4 + P-network_2_7_AnsP_3 + P-network_2_7_AnsP_2 + P-network_2_7_AnsP_1 + P-network_2_7_AnsP_0 + P-network_1_4_RP_0 + P-network_1_1_AnnP_0 + P-network_3_4_AnnP_0 + P-network_4_0_AskP_0 + P-network_3_6_AnnP_0 + P-network_7_2_RI_0 + P-network_3_3_AnsP_7 + P-network_3_3_AnsP_6 + P-network_7_1_RI_0 + P-network_3_3_AnsP_5 + P-network_3_3_AnsP_4 + P-network_3_3_AnsP_3 + P-network_3_3_AnsP_2 + P-network_3_3_AnsP_1 + P-network_3_3_AnsP_0 + P-network_6_5_AskP_0 + P-network_5_3_RI_0 + P-network_5_0_AI_0 + P-network_4_2_AnnP_0 + P-network_3_4_RI_0 + P-network_3_1_AI_0 + P-network_7_1_AskP_0 + P-network_6_7_AnnP_0 + P-network_1_5_RI_0 + P-network_0_0_AskP_0 + P-network_1_2_AI_0 + P-network_6_4_AnsP_7 + P-network_6_4_AnsP_6 + P-network_6_4_AnsP_5 + P-network_6_4_AnsP_4 + P-network_6_4_AnsP_3 + P-network_6_4_AnsP_2 + P-network_6_4_AnsP_1 + P-network_6_4_AnsP_0 + P-network_6_0_RP_0 + P-network_6_6_AI_0 + P-network_2_5_AskP_0 + P-network_4_1_RP_0 + P-network_7_3_AnnP_0 + P-network_4_7_AI_0 + P-network_2_2_RP_0 + P-network_0_2_AnnP_0 + P-network_7_0_AnsP_7 + P-network_7_0_AnsP_6 + P-network_7_0_AnsP_5 + P-network_7_0_AnsP_4 + P-network_7_0_AnsP_3 + P-network_5_7_AskP_0 + P-network_7_0_AnsP_2 + P-network_7_0_AnsP_1 + P-network_7_0_AnsP_0 + P-network_6_7_RP_0 + P-network_0_3_RP_0 + P-network_7_6_RP_0 + P-network_3_1_AskP_0 + P-network_2_5_AnsP_0 + P-network_2_5_AnsP_1 + P-network_2_5_AnsP_2 + P-network_2_5_AnsP_3 + P-network_2_5_AnsP_4 + P-network_2_5_AnsP_5 + P-network_2_5_AnsP_6 + P-network_2_5_AnsP_7 + P-network_2_7_AnnP_0 + P-network_2_4_AnsP_7 + P-network_2_4_AnsP_6 + P-network_2_4_AnsP_5 + P-network_2_4_AnsP_4 + P-network_2_4_AnsP_3 + P-network_2_4_AnsP_2 + P-network_3_2_AskP_0 + P-network_2_4_AnsP_1 + P-network_2_4_AnsP_0 + P-network_5_7_RP_0 + P-network_1_3_RP_0 + P-network_5_6_AskP_0 + P-network_0_0_AnsP_0 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_3 + P-network_0_0_AnsP_4 + P-network_0_0_AnsP_5 + P-network_0_0_AnsP_6 + P-network_0_0_AnsP_7 + P-network_6_1_RI_0 + P-network_3_3_AnnP_0 + P-network_7_1_AnsP_0 + P-network_7_1_AnsP_1 + P-network_7_1_AnsP_2 + P-network_7_1_AnsP_3 + P-network_7_1_AnsP_4 + P-network_7_1_AnsP_5 + P-network_7_1_AnsP_6 + P-network_7_1_AnsP_7 + P-network_0_3_AnnP_0 + P-network_4_2_RI_0 + P-network_3_0_AnsP_7 + P-network_3_0_AnsP_6 + P-network_3_0_AnsP_5 + P-network_3_0_AnsP_4 + P-network_3_0_AnsP_3 + P-network_3_0_AnsP_2 + P-network_3_0_AnsP_1 + P-network_3_0_AnsP_0 + P-network_6_2_AskP_0 + P-network_3_2_RP_0 + P-network_2_3_RI_0 + P-network_5_7_AI_0 + P-network_2_0_AI_0 + P-network_5_5_AnsP_7 + P-network_5_5_AnsP_6 + P-network_5_5_AnsP_5 + P-network_5_5_AnsP_4 + P-network_5_5_AnsP_3 + P-network_5_5_AnsP_2 + P-network_5_5_AnsP_1 + P-network_5_5_AnsP_0 + P-network_0_4_RI_0 + P-network_7_7_RI_0 + P-network_0_1_AI_0 + P-network_7_4_AI_0 + P-network_1_6_AskP_0 + P-network_6_4_AnnP_0 + P-network_5_5_AI_0 + P-network_6_1_AnsP_7 + P-network_7_4_AnnP_0 + P-network_6_1_AnsP_6 + P-network_6_1_AnsP_5 + P-network_6_1_AnsP_4 + P-network_6_1_AnsP_3 + P-network_6_1_AnsP_2 + P-network_6_1_AnsP_1 + P-network_6_1_AnsP_0 + P-network_3_0_RP_0 + P-network_3_6_AI_0 + P-network_5_1_RP_0 + P-network_2_2_AskP_0 + P-network_1_1_RP_0 + P-network_7_0_AnnP_0 + P-network_2_6_AskP_0 + P-network_1_7_AI_0 + P-network_1_5_AnsP_7 + P-network_7_6_AI_0 + P-network_1_5_AnsP_6 + P-network_1_5_AnsP_5 + P-network_1_5_AnsP_4 + P-network_1_5_AnsP_3 + P-network_1_5_AnsP_2 + P-network_1_5_AnsP_1 + P-network_1_5_AnsP_0 + P-network_0_3_AI_0 + P-network_6_5_RP_0 + P-network_4_7_AskP_0 + P-network_4_6_RP_0 + P-network_2_4_AnnP_0 + P-network_0_6_RI_0 + P-network_2_1_AnsP_7 + P-network_2_1_AnsP_6 + P-network_2_1_AnsP_5 + P-network_2_1_AnsP_4 + P-network_2_1_AnsP_3 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_2_7_RP_0 + P-network_5_0_RI_0 + P-network_7_0_RP_0 + P-network_5_3_AskP_0 + P-network_6_5_AnsP_0 + P-network_6_5_AnsP_1 + P-network_6_5_AnsP_2 + P-network_6_5_AnsP_3 + P-network_6_5_AnsP_4 + P-network_6_5_AnsP_5 + P-network_6_5_AnsP_6 + P-network_6_5_AnsP_7 + P-network_3_1_RI_0 + P-network_4_6_AnsP_7 + P-network_2_2_AI_0 + P-network_4_6_AnsP_6 + P-network_4_6_AnsP_5 + P-network_4_6_AnsP_4 + P-network_4_6_AnsP_3 + P-network_4_6_AnsP_2 + P-network_4_6_AnsP_1 + P-network_4_6_AnsP_0 + P-network_0_1_AskP_0 + P-network_3_0_AnnP_0 + P-network_1_2_RI_0 + P-network_0_7_AskP_0 + P-network_5_5_AnnP_0 + P-network_6_6_RI_0 + P-network_6_3_AI_0 + P-network_5_2_AnsP_7 + P-network_5_2_AnsP_6 + P-network_5_2_AnsP_5 + P-network_5_2_AnsP_4 + P-network_5_2_AnsP_3 + P-network_5_2_AnsP_2 + P-network_5_2_AnsP_1 + P-network_5_2_AnsP_0 + P-network_2_5_RI_0 + P-network_4_7_RI_0 + P-network_4_4_AI_0 + P-network_1_3_AskP_0 + P-network_7_7_AnsP_7 + P-network_7_7_AnsP_6 + P-network_7_7_AnsP_5 + P-network_7_7_AnsP_4 + P-network_7_7_AnsP_3 + P-network_7_7_AnsP_2 + P-network_7_2_AskP_0 + P-network_7_7_AnsP_1 + P-network_7_7_AnsP_0 + P-network_6_1_AnnP_0 + P-network_0_6_AnsP_7 + P-network_0_6_AnsP_6 + P-network_0_6_AnsP_5 + P-network_0_6_AnsP_4 + P-network_0_6_AnsP_3 + P-network_0_6_AnsP_2 + P-network_0_6_AnsP_1 + P-network_0_6_AnsP_0 + P-network_2_5_AI_0 + P-network_0_0_RP_0 + P-network_7_3_RP_0 + P-network_4_1_AI_0 + P-network_4_0_AnsP_0 + P-network_4_0_AnsP_1 + P-network_4_0_AnsP_2 + P-network_4_0_AnsP_3 + P-network_4_0_AnsP_4 + P-network_4_0_AnsP_5 + P-network_4_0_AnsP_6 + P-network_4_0_AnsP_7 + P-network_0_6_AI_0 + P-network_5_4_RP_0 + P-network_1_5_AnnP_0 + P-network_4_4_RI_0 + P-network_1_2_AnsP_7 + P-network_1_2_AnsP_6 + P-network_1_2_AnsP_5 + P-network_1_2_AnsP_4 + P-network_1_2_AnsP_3 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_1_2_AnsP_0 + P-network_3_5_RP_0 + P-network_4_4_AskP_0 + P-network_4_3_AnnP_0 + P-network_1_6_RP_0 + P-network_3_7_AnsP_7 + P-network_3_7_AnsP_6 + P-network_6_0_AI_0 + P-network_3_7_AnsP_5 + P-network_3_7_AnsP_4 + P-network_3_7_AnsP_3 + P-network_3_7_AnsP_2 + P-network_3_7_AnsP_1 + P-network_3_7_AnsP_0 + P-network_2_1_AnnP_0 + P-network_2_0_RI_0 + P-network_5_0_AskP_0 + P-network_4_6_AnnP_0 + P-network_6_3_RI_0 + P-network_0_1_RI_0 + P-network_7_4_RI_0 + P-network_4_3_AnsP_7 + P-network_4_3_AnsP_6 + P-network_4_3_AnsP_5 + P-network_4_3_AnsP_4 + P-network_4_3_AnsP_3 + P-network_4_3_AnsP_2 + P-network_4_3_AnsP_1 + P-network_4_3_AnsP_0 + P-network_7_1_AI_0 + P-network_7_5_AskP_0 + P-network_5_5_RI_0 + P-network_0_4_AskP_0 + P-network_5_2_AI_0 + P-network_5_2_AnnP_0 + P-network_3_6_RI_0 + P-network_6_6_AskP_0 + P-network_3_3_AI_0 + P-network_3_4_AnsP_0 + P-network_3_4_AnsP_1 + P-network_3_4_AnsP_2 + P-network_3_4_AnsP_3 + P-network_3_4_AnsP_4 + P-network_3_4_AnsP_5 + P-network_3_4_AnsP_6 + P-network_3_4_AnsP_7 + P-network_7_7_AnnP_0 + P-network_1_7_RI_0 + P-network_3_7_AnnP_0 + P-network_1_4_AI_0 + P-network_1_0_AskP_0 + P-network_6_2_RP_0 + P-network_0_6_AnnP_0 + P-network_7_4_AnsP_7 + P-network_4_1_AskP_0 + P-network_7_4_AnsP_6 + P-network_7_4_AnsP_5 + P-network_7_4_AnsP_4 + P-network_7_4_AnsP_3 + P-network_7_4_AnsP_2 + P-network_7_4_AnsP_1 + P-network_7_4_AnsP_0 + P-network_0_5_RP_0 + P-network_0_3_AnsP_7 + P-network_0_3_AnsP_6 + P-network_0_3_AnsP_5 + P-network_0_3_AnsP_4 + P-network_0_3_AnsP_3 + P-network_0_3_AnsP_2 + P-network_0_3_AnsP_1 + P-network_0_3_AnsP_0 + P-network_4_3_RP_0 + P-network_3_5_AskP_0 + P-network_2_4_RP_0 + P-network_1_2_AnnP_0 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_2_AnnP_3 + P-network_1_2_AnnP_4 + P-network_1_2_AnnP_5 + P-network_1_2_AnnP_6 + P-network_1_2_AnnP_7 + P-network_2_4_RP_1 + P-network_2_4_RP_2 + P-network_2_4_RP_3 + P-network_2_4_RP_4 + P-network_2_4_RP_5 + P-network_2_4_RP_6 + P-network_2_4_RP_7 + P-network_3_5_AskP_1 + P-network_3_5_AskP_2 + P-network_3_5_AskP_3 + P-network_3_5_AskP_4 + P-network_3_5_AskP_5 + P-network_3_5_AskP_6 + P-network_3_5_AskP_7 + P-network_4_3_RP_1 + P-network_4_3_RP_2 + P-network_4_3_RP_3 + P-network_4_3_RP_4 + P-network_4_3_RP_5 + P-network_4_3_RP_6 + P-network_4_3_RP_7 + P-network_0_5_RP_7 + P-network_0_5_RP_6 + P-network_0_5_RP_5 + P-network_0_5_RP_4 + P-network_0_5_RP_3 + P-network_0_5_RP_2 + P-network_0_5_RP_1 + P-network_4_1_AskP_7 + P-network_4_1_AskP_6 + P-network_4_1_AskP_5 + P-network_4_1_AskP_4 + P-network_4_1_AskP_3 + P-network_4_1_AskP_2 + P-network_4_1_AskP_1 + P-network_3_7_AnnP_7 + P-network_3_7_AnnP_6 + P-network_0_6_AnnP_1 + P-network_0_6_AnnP_2 + P-network_0_6_AnnP_3 + P-network_0_6_AnnP_4 + P-network_0_6_AnnP_5 + P-network_0_6_AnnP_6 + P-network_0_6_AnnP_7 + P-network_3_7_AnnP_5 + P-network_6_2_RP_1 + P-network_6_2_RP_2 + P-network_6_2_RP_3 + P-network_6_2_RP_4 + P-network_6_2_RP_5 + P-network_6_2_RP_6 + P-network_6_2_RP_7 + P-network_3_7_AnnP_4 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_1_0_AskP_3 + P-network_1_0_AskP_4 + P-network_1_0_AskP_5 + P-network_1_0_AskP_6 + P-network_1_0_AskP_7 + P-network_3_7_AnnP_3 + P-network_3_7_AnnP_2 + P-network_1_4_AI_1 + P-network_3_7_AnnP_1 + P-network_1_4_AI_2 + P-network_1_4_AI_3 + P-network_1_4_AI_4 + P-network_1_4_AI_5 + P-network_1_4_AI_6 + P-network_1_4_AI_7 + P-network_1_7_RI_1 + P-network_1_7_RI_2 + P-network_1_7_RI_3 + P-network_1_7_RI_4 + P-network_1_7_RI_5 + P-network_1_7_RI_6 + P-network_1_7_RI_7 + P-network_7_7_AnnP_1 + P-network_7_7_AnnP_2 + P-network_7_7_AnnP_3 + P-network_7_7_AnnP_4 + P-network_7_7_AnnP_5 + P-network_7_7_AnnP_6 + P-network_7_7_AnnP_7 + P-network_6_6_AskP_7 + P-network_6_6_AskP_6 + P-network_6_6_AskP_5 + P-network_6_6_AskP_4 + P-network_6_6_AskP_3 + P-network_6_6_AskP_2 + P-network_6_6_AskP_1 + P-network_3_3_AI_1 + P-network_3_3_AI_2 + P-network_3_3_AI_3 + P-network_3_3_AI_4 + P-network_3_3_AI_5 + P-network_3_3_AI_6 + P-network_3_3_AI_7 + P-network_3_6_RI_1 + P-network_3_6_RI_2 + P-network_3_6_RI_3 + P-network_3_6_RI_4 + P-network_3_6_RI_5 + P-network_3_6_RI_6 + P-network_3_6_RI_7 + P-network_5_2_AnnP_1 + P-network_5_2_AnnP_2 + P-network_5_2_AnnP_3 + P-network_5_2_AnnP_4 + P-network_5_2_AnnP_5 + P-network_5_2_AnnP_6 + P-network_5_2_AnnP_7 + P-network_5_2_AI_1 + P-network_5_2_AI_2 + P-network_5_2_AI_3 + P-network_5_2_AI_4 + P-network_5_2_AI_5 + P-network_5_2_AI_6 + P-network_5_2_AI_7 + P-network_0_4_AskP_1 + P-network_0_4_AskP_2 + P-network_0_4_AskP_3 + P-network_0_4_AskP_4 + P-network_0_4_AskP_5 + P-network_0_4_AskP_6 + P-network_0_4_AskP_7 + P-network_5_5_RI_1 + P-network_5_5_RI_2 + P-network_5_5_RI_3 + P-network_5_5_RI_4 + P-network_5_5_RI_5 + P-network_5_5_RI_6 + P-network_5_5_RI_7 + P-network_7_5_AskP_1 + P-network_7_5_AskP_2 + P-network_7_5_AskP_3 + P-network_7_5_AskP_4 + P-network_7_5_AskP_5 + P-network_7_5_AskP_6 + P-network_7_5_AskP_7 + P-network_7_1_AI_1 + P-network_7_1_AI_2 + P-network_7_1_AI_3 + P-network_7_1_AI_4 + P-network_7_1_AI_5 + P-network_7_1_AI_6 + P-network_7_1_AI_7 + P-network_7_4_RI_1 + P-network_7_4_RI_2 + P-network_7_4_RI_3 + P-network_7_4_RI_4 + P-network_7_4_RI_5 + P-network_7_4_RI_6 + P-network_7_4_RI_7 + P-network_0_1_RI_1 + P-network_0_1_RI_2 + P-network_0_1_RI_3 + P-network_0_1_RI_4 + P-network_0_1_RI_5 + P-network_0_1_RI_6 + P-network_0_1_RI_7 + P-network_6_3_RI_7 + P-network_6_3_RI_6 + P-network_6_3_RI_5 + P-network_6_3_RI_4 + P-network_6_3_RI_3 + P-network_6_3_RI_2 + P-network_6_3_RI_1 + P-network_4_6_AnnP_1 + P-network_4_6_AnnP_2 + P-network_4_6_AnnP_3 + P-network_4_6_AnnP_4 + P-network_4_6_AnnP_5 + P-network_4_6_AnnP_6 + P-network_4_6_AnnP_7 + P-network_5_0_AskP_1 + P-network_5_0_AskP_2 + P-network_5_0_AskP_3 + P-network_5_0_AskP_4 + P-network_5_0_AskP_5 + P-network_5_0_AskP_6 + P-network_5_0_AskP_7 + P-network_2_0_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_3 + P-network_2_0_RI_4 + P-network_2_0_RI_5 + P-network_2_0_RI_6 + P-network_2_0_RI_7 + P-network_6_0_AI_7 + P-network_2_1_AnnP_1 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_3 + P-network_2_1_AnnP_4 + P-network_2_1_AnnP_5 + P-network_2_1_AnnP_6 + P-network_2_1_AnnP_7 + P-network_6_0_AI_6 + P-network_6_0_AI_5 + P-network_6_0_AI_4 + P-network_6_0_AI_3 + P-network_6_0_AI_2 + P-network_6_0_AI_1 + P-network_4_3_AnnP_7 + P-network_4_3_AnnP_6 + P-network_1_6_RP_1 + P-network_1_6_RP_2 + P-network_1_6_RP_3 + P-network_1_6_RP_4 + P-network_1_6_RP_5 + P-network_1_6_RP_6 + P-network_1_6_RP_7 + P-network_4_3_AnnP_5 + P-network_4_3_AnnP_4 + P-network_4_3_AnnP_3 + P-network_4_3_AnnP_2 + P-network_4_3_AnnP_1 + P-network_4_4_AskP_1 + P-network_4_4_AskP_2 + P-network_4_4_AskP_3 + P-network_4_4_AskP_4 + P-network_4_4_AskP_5 + P-network_4_4_AskP_6 + P-network_4_4_AskP_7 + P-network_3_5_RP_1 + P-network_3_5_RP_2 + P-network_3_5_RP_3 + P-network_3_5_RP_4 + P-network_3_5_RP_5 + P-network_3_5_RP_6 + P-network_3_5_RP_7 + P-network_4_4_RI_7 + P-network_4_4_RI_6 + P-network_4_4_RI_5 + P-network_4_4_RI_4 + P-network_4_4_RI_3 + P-network_4_4_RI_2 + P-network_4_4_RI_1 + P-network_1_5_AnnP_1 + P-network_1_5_AnnP_2 + P-network_1_5_AnnP_3 + P-network_1_5_AnnP_4 + P-network_1_5_AnnP_5 + P-network_1_5_AnnP_6 + P-network_1_5_AnnP_7 + P-network_5_4_RP_1 + P-network_5_4_RP_2 + P-network_5_4_RP_3 + P-network_5_4_RP_4 + P-network_5_4_RP_5 + P-network_5_4_RP_6 + P-network_5_4_RP_7 + P-network_0_6_AI_1 + P-network_0_6_AI_2 + P-network_0_6_AI_3 + P-network_0_6_AI_4 + P-network_0_6_AI_5 + P-network_0_6_AI_6 + P-network_0_6_AI_7 + P-network_4_1_AI_7 + P-network_4_1_AI_6 + P-network_4_1_AI_5 + P-network_4_1_AI_4 + P-network_4_1_AI_3 + P-network_4_1_AI_2 + P-network_4_1_AI_1 + P-network_7_3_RP_1 + P-network_7_3_RP_2 + P-network_7_3_RP_3 + P-network_7_3_RP_4 + P-network_7_3_RP_5 + P-network_7_3_RP_6 + P-network_7_3_RP_7 + P-network_0_0_RP_1 + P-network_0_0_RP_2 + P-network_0_0_RP_3 + P-network_0_0_RP_4 + P-network_0_0_RP_5 + P-network_0_0_RP_6 + P-network_0_0_RP_7 + P-network_2_5_AI_1 + P-network_2_5_AI_2 + P-network_2_5_AI_3 + P-network_2_5_AI_4 + P-network_2_5_AI_5 + P-network_2_5_AI_6 + P-network_7_2_AskP_7 + P-network_2_5_AI_7 + P-network_7_2_AskP_6 + P-network_7_2_AskP_5 + P-network_7_2_AskP_4 + P-network_7_2_AskP_3 + P-network_6_1_AnnP_1 + P-network_6_1_AnnP_2 + P-network_6_1_AnnP_3 + P-network_6_1_AnnP_4 + P-network_6_1_AnnP_5 + P-network_6_1_AnnP_6 + P-network_6_1_AnnP_7 + P-network_7_2_AskP_2 + P-network_7_2_AskP_1 + P-network_1_3_AskP_1 + P-network_1_3_AskP_2 + P-network_1_3_AskP_3 + P-network_1_3_AskP_4 + P-network_1_3_AskP_5 + P-network_1_3_AskP_6 + P-network_1_3_AskP_7 + P-network_4_4_AI_1 + P-network_2_5_RI_7 + P-network_4_4_AI_2 + P-network_2_5_RI_6 + P-network_4_4_AI_3 + P-network_2_5_RI_5 + P-network_4_4_AI_4 + P-network_2_5_RI_4 + P-network_4_4_AI_5 + P-network_2_5_RI_3 + P-network_4_4_AI_6 + P-network_2_5_RI_2 + P-network_4_4_AI_7 + P-network_2_5_RI_1 + P-network_4_7_RI_1 + P-network_4_7_RI_2 + P-network_4_7_RI_3 + P-network_4_7_RI_4 + P-network_4_7_RI_5 + P-network_4_7_RI_6 + P-network_4_7_RI_7 + P-network_6_3_AI_1 + P-network_6_3_AI_2 + P-network_6_3_AI_3 + P-network_6_3_AI_4 + P-network_6_3_AI_5 + P-network_6_3_AI_6 + P-network_6_3_AI_7 + P-network_6_6_RI_1 + P-network_6_6_RI_2 + P-network_6_6_RI_3 + P-network_6_6_RI_4 + P-network_6_6_RI_5 + P-network_6_6_RI_6 + P-network_6_6_RI_7 + P-network_0_1_AskP_7 + P-network_0_1_AskP_6 + P-network_5_5_AnnP_1 + P-network_5_5_AnnP_2 + P-network_5_5_AnnP_3 + P-network_5_5_AnnP_4 + P-network_5_5_AnnP_5 + P-network_5_5_AnnP_6 + P-network_5_5_AnnP_7 + P-network_0_1_AskP_5 + P-network_0_7_AskP_1 + P-network_0_7_AskP_2 + P-network_0_7_AskP_3 + P-network_0_7_AskP_4 + P-network_0_7_AskP_5 + P-network_0_7_AskP_6 + P-network_0_7_AskP_7 + P-network_0_1_AskP_4 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_1_2_RI_3 + P-network_1_2_RI_4 + P-network_1_2_RI_5 + P-network_1_2_RI_6 + P-network_1_2_RI_7 + P-network_0_1_AskP_3 + P-network_0_1_AskP_2 + P-network_3_0_AnnP_1 + P-network_3_0_AnnP_2 + P-network_3_0_AnnP_3 + P-network_3_0_AnnP_4 + P-network_3_0_AnnP_5 + P-network_3_0_AnnP_6 + P-network_3_0_AnnP_7 + P-network_0_1_AskP_1 + P-network_2_2_AI_7 + P-network_2_2_AI_6 + P-network_2_2_AI_5 + P-network_2_2_AI_4 + P-network_2_2_AI_3 + P-network_2_2_AI_2 + P-network_2_2_AI_1 + P-network_3_1_RI_1 + P-network_3_1_RI_2 + P-network_3_1_RI_3 + P-network_3_1_RI_4 + P-network_3_1_RI_5 + P-network_3_1_RI_6 + P-network_3_1_RI_7 + P-network_7_0_RP_7 + P-network_7_0_RP_6 + P-network_7_0_RP_5 + P-network_7_0_RP_4 + P-network_7_0_RP_3 + P-network_5_3_AskP_1 + P-network_5_3_AskP_2 + P-network_5_3_AskP_3 + P-network_5_3_AskP_4 + P-network_5_3_AskP_5 + P-network_5_3_AskP_6 + P-network_5_3_AskP_7 + P-network_7_0_RP_2 + P-network_7_0_RP_1 + P-network_5_0_RI_1 + P-network_5_0_RI_2 + P-network_5_0_RI_3 + P-network_2_7_RP_1 + P-network_5_0_RI_4 + P-network_2_7_RP_2 + P-network_5_0_RI_5 + P-network_2_7_RP_3 + P-network_5_0_RI_6 + P-network_2_7_RP_4 + P-network_5_0_RI_7 + P-network_2_7_RP_5 + P-network_2_7_RP_6 + P-network_2_7_RP_7 + P-network_0_6_RI_7 + P-network_0_6_RI_6 + P-network_0_6_RI_5 + P-network_0_6_RI_4 + P-network_0_6_RI_3 + P-network_0_6_RI_2 + P-network_0_6_RI_1 + P-network_2_4_AnnP_1 + P-network_2_4_AnnP_2 + P-network_2_4_AnnP_3 + P-network_2_4_AnnP_4 + P-network_2_4_AnnP_5 + P-network_2_4_AnnP_6 + P-network_2_4_AnnP_7 + P-network_4_6_RP_1 + P-network_4_6_RP_2 + P-network_4_6_RP_3 + P-network_4_6_RP_4 + P-network_4_6_RP_5 + P-network_4_6_RP_6 + P-network_4_6_RP_7 + P-network_0_3_AI_7 + P-network_0_3_AI_6 + P-network_0_3_AI_5 + P-network_0_3_AI_4 + P-network_0_3_AI_3 + P-network_0_3_AI_2 + P-network_4_7_AskP_1 + P-network_4_7_AskP_2 + P-network_4_7_AskP_3 + P-network_4_7_AskP_4 + P-network_4_7_AskP_5 + P-network_4_7_AskP_6 + P-network_4_7_AskP_7 + P-network_0_3_AI_1 + P-network_6_5_RP_1 + P-network_6_5_RP_2 + P-network_6_5_RP_3 + P-network_6_5_RP_4 + P-network_6_5_RP_5 + P-network_6_5_RP_6 + P-network_6_5_RP_7 + P-network_7_6_AI_7 + P-network_7_6_AI_6 + P-network_7_6_AI_5 + P-network_7_6_AI_4 + P-network_7_6_AI_3 + P-network_7_6_AI_2 + P-network_7_6_AI_1 + P-network_2_6_AskP_7 + P-network_2_6_AskP_6 + P-network_1_7_AI_1 + P-network_1_7_AI_2 + P-network_1_7_AI_3 + P-network_1_7_AI_4 + P-network_1_7_AI_5 + P-network_1_7_AI_6 + P-network_1_7_AI_7 + P-network_2_6_AskP_5 + P-network_2_6_AskP_4 + P-network_2_6_AskP_3 + P-network_2_6_AskP_2 + P-network_2_6_AskP_1 + P-network_5_1_RP_7 + P-network_5_1_RP_6 + P-network_5_1_RP_5 + P-network_5_1_RP_4 + P-network_7_0_AnnP_1 + P-network_7_0_AnnP_2 + P-network_7_0_AnnP_3 + P-network_7_0_AnnP_4 + P-network_7_0_AnnP_5 + P-network_7_0_AnnP_6 + P-network_7_0_AnnP_7 + P-network_5_1_RP_3 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_1_RP_3 + P-network_1_1_RP_4 + P-network_1_1_RP_5 + P-network_1_1_RP_6 + P-network_1_1_RP_7 + P-network_5_1_RP_2 + P-network_2_2_AskP_1 + P-network_2_2_AskP_2 + P-network_2_2_AskP_3 + P-network_2_2_AskP_4 + P-network_2_2_AskP_5 + P-network_2_2_AskP_6 + P-network_2_2_AskP_7 + P-network_5_1_RP_1 + P-network_3_6_AI_1 + P-network_3_6_AI_2 + P-network_3_6_AI_3 + P-network_3_6_AI_4 + P-network_3_6_AI_5 + P-network_3_6_AI_6 + P-network_3_6_AI_7 + P-network_3_0_RP_1 + P-network_3_0_RP_2 + P-network_3_0_RP_3 + P-network_3_0_RP_4 + P-network_3_0_RP_5 + P-network_3_0_RP_6 + P-network_3_0_RP_7 + P-network_7_4_AnnP_7 + P-network_7_4_AnnP_6 + P-network_7_4_AnnP_5 + P-network_7_4_AnnP_4 + P-network_7_4_AnnP_3 + P-network_7_4_AnnP_2 + P-network_7_4_AnnP_1 + P-network_5_5_AI_1 + P-network_5_5_AI_2 + P-network_5_5_AI_3 + P-network_5_5_AI_4 + P-network_5_5_AI_5 + P-network_5_5_AI_6 + P-network_5_5_AI_7 + P-network_6_4_AnnP_1 + P-network_6_4_AnnP_2 + P-network_6_4_AnnP_3 + P-network_6_4_AnnP_4 + P-network_6_4_AnnP_5 + P-network_6_4_AnnP_6 + P-network_6_4_AnnP_7 + P-network_1_6_AskP_1 + P-network_1_6_AskP_2 + P-network_1_6_AskP_3 + P-network_1_6_AskP_4 + P-network_1_6_AskP_5 + P-network_1_6_AskP_6 + P-network_1_6_AskP_7 + P-network_7_4_AI_1 + P-network_7_4_AI_2 + P-network_7_4_AI_3 + P-network_7_4_AI_4 + P-network_7_4_AI_5 + P-network_7_4_AI_6 + P-network_7_4_AI_7 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_0_1_AI_3 + P-network_0_1_AI_4 + P-network_0_1_AI_5 + P-network_0_1_AI_6 + P-network_0_1_AI_7 + P-network_7_7_RI_1 + P-network_7_7_RI_2 + P-network_7_7_RI_3 + P-network_7_7_RI_4 + P-network_7_7_RI_5 + P-network_7_7_RI_6 + P-network_7_7_RI_7 + P-network_0_4_RI_1 + P-network_0_4_RI_2 + P-network_0_4_RI_3 + P-network_0_4_RI_4 + P-network_0_4_RI_5 + P-network_0_4_RI_6 + P-network_0_4_RI_7 + P-network_5_7_AI_7 + P-network_5_7_AI_6 + P-network_5_7_AI_5 + P-network_5_7_AI_4 + P-network_5_7_AI_3 + P-network_5_7_AI_2 + P-network_5_7_AI_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_2_0_AI_3 + P-network_2_0_AI_4 + P-network_2_0_AI_5 + P-network_2_0_AI_6 + P-network_2_0_AI_7 + P-network_3_2_RP_7 + P-network_2_3_RI_1 + P-network_2_3_RI_2 + P-network_2_3_RI_3 + P-network_2_3_RI_4 + P-network_2_3_RI_5 + P-network_2_3_RI_6 + P-network_2_3_RI_7 + P-network_3_2_RP_6 + P-network_3_2_RP_5 + P-network_3_2_RP_4 + P-network_3_2_RP_3 + P-network_3_2_RP_2 + P-network_3_2_RP_1 + P-network_0_3_AnnP_7 + P-network_6_2_AskP_1 + P-network_6_2_AskP_2 + P-network_6_2_AskP_3 + P-network_6_2_AskP_4 + P-network_6_2_AskP_5 + P-network_6_2_AskP_6 + P-network_6_2_AskP_7 + P-network_0_3_AnnP_6 + P-network_0_3_AnnP_5 + P-network_0_3_AnnP_4 + P-network_0_3_AnnP_3 + P-network_0_3_AnnP_2 + P-network_4_2_RI_1 + P-network_4_2_RI_2 + P-network_4_2_RI_3 + P-network_4_2_RI_4 + P-network_4_2_RI_5 + P-network_4_2_RI_6 + P-network_4_2_RI_7 + P-network_0_3_AnnP_1 + P-network_3_3_AnnP_1 + P-network_3_3_AnnP_2 + P-network_3_3_AnnP_3 + P-network_3_3_AnnP_4 + P-network_3_3_AnnP_5 + P-network_3_3_AnnP_6 + P-network_3_3_AnnP_7 + P-network_6_1_RI_1 + P-network_6_1_RI_2 + P-network_6_1_RI_3 + P-network_6_1_RI_4 + P-network_6_1_RI_5 + P-network_6_1_RI_6 + P-network_6_1_RI_7 + P-network_1_3_RP_7 + P-network_1_3_RP_6 + P-network_1_3_RP_5 + P-network_1_3_RP_4 + P-network_5_6_AskP_1 + P-network_5_6_AskP_2 + P-network_5_6_AskP_3 + P-network_5_6_AskP_4 + P-network_5_6_AskP_5 + P-network_5_6_AskP_6 + P-network_5_6_AskP_7 + P-network_1_3_RP_3 + P-network_1_3_RP_2 + P-network_1_3_RP_1 + P-network_3_2_AskP_7 + P-network_3_2_AskP_6 + P-network_3_2_AskP_5 + P-network_3_2_AskP_4 + P-network_3_2_AskP_3 + P-network_5_7_RP_1 + P-network_5_7_RP_2 + P-network_5_7_RP_3 + P-network_5_7_RP_4 + P-network_5_7_RP_5 + P-network_5_7_RP_6 + P-network_5_7_RP_7 + P-network_3_2_AskP_2 + P-network_3_2_AskP_1 + P-network_2_7_AnnP_1 + P-network_2_7_AnnP_2 + P-network_2_7_AnnP_3 + P-network_2_7_AnnP_4 + P-network_2_7_AnnP_5 + P-network_2_7_AnnP_6 + P-network_2_7_AnnP_7 + P-network_6_7_RP_7 + P-network_3_1_AskP_1 + P-network_3_1_AskP_2 + P-network_3_1_AskP_3 + P-network_3_1_AskP_4 + P-network_3_1_AskP_5 + P-network_3_1_AskP_6 + P-network_3_1_AskP_7 + P-network_6_7_RP_6 + P-network_7_6_RP_1 + P-network_7_6_RP_2 + P-network_7_6_RP_3 + P-network_7_6_RP_4 + P-network_7_6_RP_5 + P-network_7_6_RP_6 + P-network_7_6_RP_7 + P-network_6_7_RP_5 + P-network_0_3_RP_1 + P-network_0_3_RP_2 + P-network_0_3_RP_3 + P-network_0_3_RP_4 + P-network_0_3_RP_5 + P-network_6_7_RP_4 + P-network_0_3_RP_6 + P-network_6_7_RP_3 + P-network_0_3_RP_7 + P-network_6_7_RP_2 + P-network_6_7_RP_1 + P-network_5_7_AskP_7 + P-network_5_7_AskP_6 + P-network_5_7_AskP_5 + P-network_5_7_AskP_4 + P-network_5_7_AskP_3 + P-network_5_7_AskP_2 + P-network_5_7_AskP_1 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_0_2_AnnP_3 + P-network_0_2_AnnP_4 + P-network_0_2_AnnP_5 + P-network_0_2_AnnP_6 + P-network_0_2_AnnP_7 + P-network_2_2_RP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_3 + P-network_2_2_RP_4 + P-network_2_2_RP_5 + P-network_2_2_RP_6 + P-network_2_2_RP_7 + P-network_4_7_AI_1 + P-network_4_7_AI_2 + P-network_4_7_AI_3 + P-network_4_7_AI_4 + P-network_4_7_AI_5 + P-network_4_7_AI_6 + P-network_4_7_AI_7 + P-network_7_3_AnnP_1 + P-network_7_3_AnnP_2 + P-network_7_3_AnnP_3 + P-network_7_3_AnnP_4 + P-network_7_3_AnnP_5 + P-network_7_3_AnnP_6 + P-network_7_3_AnnP_7 + P-network_4_1_RP_1 + P-network_4_1_RP_2 + P-network_4_1_RP_3 + P-network_4_1_RP_4 + P-network_4_1_RP_5 + P-network_4_1_RP_6 + P-network_4_1_RP_7 + P-network_2_5_AskP_1 + P-network_2_5_AskP_2 + P-network_2_5_AskP_3 + P-network_2_5_AskP_4 + P-network_2_5_AskP_5 + P-network_2_5_AskP_6 + P-network_2_5_AskP_7 + P-network_6_6_AI_1 + P-network_6_6_AI_2 + P-network_6_6_AI_3 + P-network_6_6_AI_4 + P-network_6_6_AI_5 + P-network_6_6_AI_6 + P-network_6_6_AI_7 + P-network_6_0_RP_1 + P-network_6_0_RP_2 + P-network_6_0_RP_3 + P-network_6_0_RP_4 + P-network_6_0_RP_5 + P-network_6_0_RP_6 + P-network_6_0_RP_7 + P-network_1_2_AI_1 + P-network_1_2_AI_2 + P-network_1_2_AI_3 + P-network_1_2_AI_4 + P-network_1_2_AI_5 + P-network_1_2_AI_6 + P-network_1_2_AI_7 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_0_0_AskP_3 + P-network_0_0_AskP_4 + P-network_0_0_AskP_5 + P-network_0_0_AskP_6 + P-network_0_0_AskP_7 + P-network_1_5_RI_1 + P-network_1_5_RI_2 + P-network_1_5_RI_3 + P-network_1_5_RI_4 + P-network_1_5_RI_5 + P-network_1_5_RI_6 + P-network_1_5_RI_7 + P-network_6_7_AnnP_1 + P-network_6_7_AnnP_2 + P-network_6_7_AnnP_3 + P-network_6_7_AnnP_4 + P-network_6_7_AnnP_5 + P-network_6_7_AnnP_6 + P-network_6_7_AnnP_7 + P-network_7_1_AskP_1 + P-network_7_1_AskP_2 + P-network_7_1_AskP_3 + P-network_7_1_AskP_4 + P-network_7_1_AskP_5 + P-network_7_1_AskP_6 + P-network_7_1_AskP_7 + P-network_3_1_AI_1 + P-network_3_1_AI_2 + P-network_3_1_AI_3 + P-network_3_1_AI_4 + P-network_3_1_AI_5 + P-network_3_1_AI_6 + P-network_3_1_AI_7 + P-network_3_4_RI_1 + P-network_3_4_RI_2 + P-network_3_4_RI_3 + P-network_3_4_RI_4 + P-network_3_4_RI_5 + P-network_3_4_RI_6 + P-network_3_4_RI_7 + P-network_4_2_AnnP_1 + P-network_4_2_AnnP_2 + P-network_4_2_AnnP_3 + P-network_4_2_AnnP_4 + P-network_4_2_AnnP_5 + P-network_4_2_AnnP_6 + P-network_4_2_AnnP_7 + P-network_5_0_AI_1 + P-network_5_0_AI_2 + P-network_5_0_AI_3 + P-network_5_0_AI_4 + P-network_5_0_AI_5 + P-network_5_0_AI_6 + P-network_5_0_AI_7 + P-network_5_3_RI_1 + P-network_5_3_RI_2 + P-network_5_3_RI_3 + P-network_5_3_RI_4 + P-network_5_3_RI_5 + P-network_5_3_RI_6 + P-network_5_3_RI_7 + P-network_7_1_RI_7 + P-network_6_5_AskP_1 + P-network_6_5_AskP_2 + P-network_6_5_AskP_3 + P-network_6_5_AskP_4 + P-network_6_5_AskP_5 + P-network_6_5_AskP_6 + P-network_6_5_AskP_7 + P-network_7_1_RI_6 + P-network_7_1_RI_5 + P-network_7_1_RI_4 + P-network_7_1_RI_3 + P-network_7_1_RI_2 + P-network_7_1_RI_1 + P-network_3_4_AnnP_7 + P-network_3_4_AnnP_6 + P-network_7_2_RI_1 + P-network_7_2_RI_2 + P-network_7_2_RI_3 + P-network_7_2_RI_4 + P-network_7_2_RI_5 + P-network_7_2_RI_6 + P-network_7_2_RI_7 + P-network_3_4_AnnP_5 + P-network_3_4_AnnP_4 + P-network_3_4_AnnP_3 + P-network_3_6_AnnP_1 + P-network_3_6_AnnP_2 + P-network_3_6_AnnP_3 + P-network_3_6_AnnP_4 + P-network_3_6_AnnP_5 + P-network_3_6_AnnP_6 + P-network_3_6_AnnP_7 + P-network_3_4_AnnP_2 + P-network_4_0_AskP_1 + P-network_4_0_AskP_2 + P-network_4_0_AskP_3 + P-network_4_0_AskP_4 + P-network_4_0_AskP_5 + P-network_4_0_AskP_6 + P-network_4_0_AskP_7 + P-network_3_4_AnnP_1 + P-network_1_1_AnnP_1 + P-network_1_1_AnnP_2 + P-network_1_1_AnnP_3 + P-network_1_1_AnnP_4 + P-network_1_1_AnnP_5 + P-network_1_1_AnnP_6 + P-network_1_1_AnnP_7 + P-network_1_4_RP_1 + P-network_1_4_RP_2 + P-network_1_4_RP_3 + P-network_1_4_RP_4 + P-network_1_4_RP_5 + P-network_1_4_RP_6 + P-network_1_4_RP_7 + P-network_5_2_RI_7 + P-network_5_2_RI_6 + P-network_5_2_RI_5 + P-network_5_2_RI_4 + P-network_5_2_RI_3 + P-network_5_2_RI_2 + P-network_5_2_RI_1 + P-network_3_4_AskP_1 + P-network_3_4_AskP_2 + P-network_3_4_AskP_3 + P-network_3_4_AskP_4 + P-network_3_4_AskP_5 + P-network_3_4_AskP_6 + P-network_3_4_AskP_7 + P-network_3_3_RP_1 + P-network_3_3_RP_2 + P-network_3_3_RP_3 + P-network_3_3_RP_4 + P-network_3_3_RP_5 + P-network_3_3_RP_6 + P-network_3_3_RP_7 + P-network_6_3_AskP_7 + P-network_6_3_AskP_6 + P-network_6_3_AskP_5 + P-network_6_3_AskP_4 + P-network_6_3_AskP_3 + P-network_6_3_AskP_2 + P-network_6_3_AskP_1 + P-network_0_5_AnnP_1 + P-network_0_5_AnnP_2 + P-network_0_5_AnnP_3 + P-network_0_5_AnnP_4 + P-network_0_5_AnnP_5 + P-network_0_5_AnnP_6 + P-network_0_5_AnnP_7 + P-network_5_2_RP_1 + P-network_5_2_RP_2 + P-network_5_2_RP_3 + P-network_5_2_RP_4 + P-network_5_2_RP_5 + P-network_5_2_RP_6 + P-network_5_2_RP_7 + P-network_7_7_AI_1 + P-network_7_7_AI_2 + P-network_7_7_AI_3 + P-network_7_7_AI_4 + P-network_7_7_AI_5 + P-network_7_7_AI_6 + P-network_7_7_AI_7 + P-network_0_4_AI_1 + P-network_0_4_AI_2 + P-network_0_4_AI_3 + P-network_0_4_AI_4 + P-network_0_4_AI_5 + P-network_0_4_AI_6 + P-network_0_4_AI_7 + P-network_0_7_RI_1 + P-network_0_7_RI_2 + P-network_0_7_RI_3 + P-network_0_7_RI_4 + P-network_0_7_RI_5 + P-network_0_7_RI_6 + P-network_0_7_RI_7 + P-network_7_6_AnnP_1 + P-network_7_6_AnnP_2 + P-network_7_6_AnnP_3 + P-network_7_6_AnnP_4 + P-network_7_6_AnnP_5 + P-network_7_6_AnnP_6 + P-network_7_6_AnnP_7 + P-network_7_1_RP_1 + P-network_7_1_RP_2 + P-network_7_1_RP_3 + P-network_7_1_RP_4 + P-network_7_1_RP_5 + P-network_7_1_RP_6 + P-network_7_1_RP_7 + P-network_2_3_AI_1 + P-network_2_3_AI_2 + P-network_2_3_AI_3 + P-network_2_3_AI_4 + P-network_2_3_AI_5 + P-network_2_3_AI_6 + P-network_2_3_AI_7 + P-network_3_3_RI_7 + P-network_2_6_RI_1 + P-network_2_6_RI_2 + P-network_2_6_RI_3 + P-network_2_6_RI_4 + P-network_2_6_RI_5 + P-network_2_6_RI_6 + P-network_2_6_RI_7 + P-network_3_3_RI_6 + P-network_3_3_RI_5 + P-network_3_3_RI_4 + P-network_3_3_RI_3 + P-network_3_3_RI_2 + P-network_3_3_RI_1 + P-network_5_1_AnnP_1 + P-network_5_1_AnnP_2 + P-network_5_1_AnnP_3 + P-network_5_1_AnnP_4 + P-network_5_1_AnnP_5 + P-network_5_1_AnnP_6 + P-network_5_1_AnnP_7 + P-network_3_0_AI_7 + P-network_3_0_AI_6 + P-network_3_0_AI_5 + P-network_4_2_AI_1 + P-network_4_2_AI_2 + P-network_4_2_AI_3 + P-network_4_2_AI_4 + P-network_4_2_AI_5 + P-network_4_2_AI_6 + P-network_4_2_AI_7 + P-network_3_0_AI_4 + P-network_3_0_AI_3 + P-network_3_0_AI_2 + P-network_3_0_AI_1 + P-network_0_3_AskP_1 + P-network_0_3_AskP_2 + P-network_0_3_AskP_3 + P-network_0_3_AskP_4 + P-network_0_3_AskP_5 + P-network_0_3_AskP_6 + P-network_0_3_AskP_7 + P-network_4_0_AnnP_7 + P-network_4_0_AnnP_6 + P-network_4_0_AnnP_5 + P-network_4_0_AnnP_4 + P-network_4_5_RI_1 + P-network_4_5_RI_2 + P-network_4_5_RI_3 + P-network_4_5_RI_4 + P-network_4_5_RI_5 + P-network_4_5_RI_6 + P-network_4_5_RI_7 + P-network_4_0_AnnP_3 + P-network_7_4_AskP_1 + P-network_7_4_AskP_2 + P-network_7_4_AskP_3 + P-network_7_4_AskP_4 + P-network_7_4_AskP_5 + P-network_7_4_AskP_6 + P-network_7_4_AskP_7 + P-network_4_0_AnnP_2 + P-network_6_1_AI_1 + P-network_6_1_AI_2 + P-network_4_0_AnnP_1 + P-network_6_1_AI_3 + P-network_6_1_AI_4 + P-network_6_1_AI_5 + P-network_6_1_AI_6 + P-network_6_1_AI_7 + P-network_6_4_RI_1 + P-network_6_4_RI_2 + P-network_6_4_RI_3 + P-network_6_4_RI_4 + P-network_6_4_RI_5 + P-network_6_4_RI_6 + P-network_6_4_RI_7 + P-network_1_4_RI_7 + P-network_1_4_RI_6 + P-network_1_4_RI_5 + P-network_1_4_RI_4 + P-network_1_4_RI_3 + P-network_1_4_RI_2 + P-network_1_4_RI_1 + P-network_4_5_AnnP_1 + P-network_4_5_AnnP_2 + P-network_4_5_AnnP_3 + P-network_4_5_AnnP_4 + P-network_4_5_AnnP_5 + P-network_4_5_AnnP_6 + P-network_4_5_AnnP_7 + P-network_1_1_AI_7 + P-network_1_1_AI_6 + P-network_1_1_AI_5 + P-network_1_0_RI_1 + P-network_1_0_RI_2 + P-network_1_0_RI_3 + P-network_1_0_RI_4 + P-network_1_0_RI_5 + P-network_1_0_RI_6 + P-network_1_0_RI_7 + P-network_1_1_AI_4 + P-network_1_1_AI_3 + P-network_1_1_AI_2 + P-network_2_0_AnnP_1 + P-network_2_0_AnnP_2 + P-network_2_0_AnnP_3 + P-network_2_0_AnnP_4 + P-network_2_0_AnnP_5 + P-network_2_0_AnnP_6 + P-network_2_0_AnnP_7 + P-network_1_1_AI_1 + P-network_1_7_AskP_7 + P-network_1_7_AskP_6 + P-network_1_7_AskP_5 + P-network_1_7_AskP_4 + P-network_1_7_AskP_3 + P-network_1_7_AskP_2 + P-network_1_7_AskP_1 + P-network_0_6_RP_1 + P-network_0_6_RP_2 + P-network_0_6_RP_3 + P-network_0_6_RP_4 + P-network_0_6_RP_5 + P-network_0_6_RP_6 + P-network_0_6_RP_7 + P-network_4_3_AskP_1 + P-network_4_3_AskP_2 + P-network_4_3_AskP_3 + P-network_4_3_AskP_4 + P-network_4_3_AskP_5 + P-network_4_3_AskP_6 + P-network_4_3_AskP_7 + P-network_6_5_AnnP_7 + P-network_6_5_AnnP_6 + P-network_6_5_AnnP_5 + P-network_6_5_AnnP_4 + P-network_6_5_AnnP_3 + P-network_2_5_RP_1 + P-network_2_5_RP_2 + P-network_2_5_RP_3 + P-network_2_5_RP_4 + P-network_2_5_RP_5 + P-network_2_5_RP_6 + P-network_2_5_RP_7 + P-network_6_5_AnnP_2 + P-network_6_5_AnnP_1 + P-network_6_5_AI_7 + P-network_1_4_AnnP_1 + P-network_1_4_AnnP_2 + P-network_1_4_AnnP_3 + P-network_1_4_AnnP_4 + P-network_1_4_AnnP_5 + P-network_1_4_AnnP_6 + P-network_1_4_AnnP_7 + P-network_6_5_AI_6 + P-network_6_5_AI_5 + P-network_6_5_AI_4 + P-network_6_5_AI_3 + P-network_6_5_AI_2 + P-network_6_5_AI_1 + P-network_4_4_RP_1 + P-network_4_4_RP_2 + P-network_4_4_RP_3 + P-network_4_4_RP_4 + P-network_4_4_RP_5 + P-network_4_4_RP_6 + P-network_4_4_RP_7 + P-network_4_0_RP_7 + P-network_4_0_RP_6 + P-network_4_0_RP_5 + P-network_4_0_RP_4 + P-network_4_0_RP_3 + P-network_3_7_AskP_1 + P-network_3_7_AskP_2 + P-network_3_7_AskP_3 + P-network_3_7_AskP_4 + P-network_3_7_AskP_5 + P-network_3_7_AskP_6 + P-network_3_7_AskP_7 + P-network_4_0_RP_2 + P-network_6_3_RP_1 + P-network_6_3_RP_2 + P-network_6_3_RP_3 + P-network_6_3_RP_4 + P-network_6_3_RP_5 + P-network_6_3_RP_6 + P-network_6_3_RP_7 + P-network_4_0_RP_1 + P-network_1_5_AI_1 + P-network_1_5_AI_2 + P-network_1_5_AI_3 + P-network_1_5_AI_4 + P-network_1_5_AI_5 + P-network_1_5_AI_6 + P-network_1_5_AI_7 + P-network_4_6_AI_7 + P-network_6_0_AnnP_1 + P-network_6_0_AnnP_2 + P-network_4_6_AI_6 + P-network_6_0_AnnP_3 + P-network_4_6_AI_5 + P-network_6_0_AnnP_4 + P-network_4_6_AI_4 + P-network_6_0_AnnP_5 + P-network_4_6_AI_3 + P-network_6_0_AnnP_6 + P-network_4_6_AI_2 + P-network_6_0_AnnP_7 + P-network_4_6_AI_1 + P-network_2_3_AskP_7 + P-network_2_3_AskP_6 + P-network_2_3_AskP_5 + P-network_2_3_AskP_4 + P-network_2_3_AskP_3 + P-network_2_3_AskP_2 + P-network_2_3_AskP_1 + P-network_2_1_RP_7 + P-network_2_1_RP_6 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_1_2_AskP_3 + P-network_1_2_AskP_4 + P-network_1_2_AskP_5 + P-network_1_2_AskP_6 + P-network_1_2_AskP_7 + P-network_2_1_RP_5 + P-network_2_1_RP_4 + P-network_3_4_AI_1 + P-network_2_1_RP_3 + P-network_3_4_AI_2 + P-network_2_1_RP_2 + P-network_3_4_AI_3 + P-network_2_1_RP_1 + P-network_3_4_AI_4 + P-network_3_4_AI_5 + P-network_3_4_AI_6 + P-network_3_4_AI_7 + P-network_3_7_RI_1 + P-network_3_7_RI_2 + P-network_3_7_RI_3 + P-network_3_7_RI_4 + P-network_3_7_RI_5 + P-network_3_7_RI_6 + P-network_3_7_RI_7 + P-network_7_1_AnnP_7 + P-network_7_1_AnnP_6 + P-network_7_1_AnnP_5 + P-network_7_1_AnnP_4 + P-network_7_1_AnnP_3 + P-network_5_3_AI_1 + P-network_5_3_AI_2 + P-network_5_3_AI_3 + P-network_5_3_AI_4 + P-network_5_3_AI_5 + P-network_5_3_AI_6 + P-network_5_3_AI_7 + P-network_7_1_AnnP_2 + P-network_5_6_RI_1 + P-network_5_6_RI_2 + P-network_5_6_RI_3 + P-network_5_6_RI_4 + P-network_5_6_RI_5 + P-network_5_6_RI_6 + P-network_5_6_RI_7 + P-network_7_1_AnnP_1 + P-network_5_4_AnnP_1 + P-network_5_4_AnnP_2 + P-network_5_4_AnnP_3 + P-network_5_4_AnnP_4 + P-network_5_4_AnnP_5 + P-network_5_4_AnnP_6 + P-network_5_4_AnnP_7 + P-network_7_2_AI_1 + P-network_7_2_AI_2 + P-network_7_2_AI_3 + P-network_7_2_AI_4 + P-network_7_2_AI_5 + P-network_7_2_AI_6 + P-network_7_2_AI_7 + P-network_0_6_AskP_1 + P-network_0_6_AskP_2 + P-network_0_6_AskP_3 + P-network_0_6_AskP_4 + P-network_0_6_AskP_5 + P-network_0_6_AskP_6 + P-network_0_6_AskP_7 + P-network_7_5_RI_1 + P-network_7_5_RI_2 + P-network_7_5_RI_3 + P-network_7_5_RI_4 + P-network_7_5_RI_5 + P-network_7_5_RI_6 + P-network_7_5_RI_7 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_0_2_RI_3 + P-network_0_2_RI_4 + P-network_0_2_RI_5 + P-network_0_2_RI_6 + P-network_0_2_RI_7 + P-network_7_7_AskP_1 + P-network_7_7_AskP_2 + P-network_7_7_AskP_3 + P-network_7_7_AskP_4 + P-network_7_7_AskP_5 + P-network_7_7_AskP_6 + P-network_7_7_AskP_7 + P-network_2_7_AI_7 + P-network_2_7_AI_6 + P-network_2_7_AI_5 + P-network_2_7_AI_4 + P-network_2_7_AI_3 + P-network_2_7_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_2_1_RI_3 + P-network_2_1_RI_4 + P-network_2_1_RI_5 + P-network_2_1_RI_6 + P-network_2_1_RI_7 + P-network_2_7_AI_1 + P-network_5_2_AskP_1 + P-network_5_2_AskP_2 + P-network_5_2_AskP_3 + P-network_5_2_AskP_4 + P-network_5_2_AskP_5 + P-network_5_2_AskP_6 + P-network_5_2_AskP_7 + P-network_0_2_RP_7 + P-network_0_2_RP_6 + P-network_0_2_RP_5 + P-network_0_2_RP_4 + P-network_0_2_RP_3 + P-network_0_2_RP_2 + P-network_0_2_RP_1 + P-network_7_5_RP_7 + P-network_7_5_RP_6 + P-network_4_0_RI_1 + P-network_4_0_RI_2 + P-network_7_5_RP_5 + P-network_4_0_RI_3 + P-network_1_7_RP_1 + P-network_4_0_RI_4 + P-network_1_7_RP_2 + P-network_4_0_RI_5 + P-network_1_7_RP_3 + P-network_4_0_RI_6 + P-network_1_7_RP_4 + P-network_4_0_RI_7 + P-network_1_7_RP_5 + P-network_1_7_RP_6 + P-network_1_7_RP_7 + P-network_7_5_RP_4 + P-network_7_5_RP_3 + P-network_7_5_RP_2 + P-network_7_5_RP_1 + P-network_0_0_AnnP_7 + P-network_0_0_AnnP_6 + P-network_0_0_AnnP_5 + P-network_0_0_AnnP_4 + P-network_0_0_AnnP_3 + P-network_0_0_AnnP_2 + P-network_0_0_AnnP_1 + P-network_2_3_AnnP_1 + P-network_2_3_AnnP_2 + P-network_2_3_AnnP_3 + P-network_2_3_AnnP_4 + P-network_2_3_AnnP_5 + P-network_2_3_AnnP_6 + P-network_2_3_AnnP_7 + P-network_3_6_RP_1 + P-network_3_6_RP_2 + P-network_3_6_RP_3 + P-network_3_6_RP_4 + P-network_3_6_RP_5 + P-network_3_6_RP_6 + P-network_3_6_RP_7 + P-network_4_6_AskP_1 + P-network_4_6_AskP_2 + P-network_4_6_AskP_3 + P-network_4_6_AskP_4 + P-network_4_6_AskP_5 + P-network_4_6_AskP_6 + P-network_4_6_AskP_7 + P-network_5_5_RP_1 + P-network_5_5_RP_2 + P-network_5_5_RP_3 + P-network_5_5_RP_4 + P-network_5_5_RP_5 + P-network_5_5_RP_6 + P-network_5_5_RP_7 + P-network_5_6_RP_7 + P-network_5_6_RP_6 + P-network_5_6_RP_5 + P-network_5_6_RP_4 + P-network_5_6_RP_3 + P-network_5_6_RP_2 + P-network_5_6_RP_1 + P-network_2_5_AnnP_7 + P-network_2_5_AnnP_6 + P-network_2_5_AnnP_5 + P-network_2_5_AnnP_4 + P-network_2_5_AnnP_3 + P-network_0_7_AI_1 + P-network_0_7_AI_2 + P-network_0_7_AI_3 + P-network_0_7_AI_4 + P-network_0_7_AI_5 + P-network_0_7_AI_6 + P-network_0_7_AI_7 + P-network_2_5_AnnP_2 + P-network_2_5_AnnP_1 + P-network_1_7_AnnP_1 + P-network_1_7_AnnP_2 + P-network_1_7_AnnP_3 + P-network_1_7_AnnP_4 + P-network_1_7_AnnP_5 + P-network_1_7_AnnP_6 + P-network_1_7_AnnP_7 + P-network_7_4_RP_1 + P-network_7_4_RP_2 + P-network_7_4_RP_3 + P-network_7_4_RP_4 + P-network_7_4_RP_5 + P-network_7_4_RP_6 + P-network_7_4_RP_7 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_0_1_RP_3 + P-network_0_1_RP_4 + P-network_0_1_RP_5 + P-network_0_1_RP_6 + P-network_0_1_RP_7 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_2_1_AskP_3 + P-network_2_1_AskP_4 + P-network_2_1_AskP_5 + P-network_2_1_AskP_6 + P-network_2_1_AskP_7 + P-network_2_6_AI_1 + P-network_2_6_AI_2 + P-network_2_6_AI_3 + P-network_2_6_AI_4 + P-network_2_6_AI_5 + P-network_2_6_AI_6 + P-network_2_6_AI_7 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_2_0_RP_3 + P-network_2_0_RP_4 + P-network_2_0_RP_5 + P-network_2_0_RP_6 + P-network_2_0_RP_7 + P-network_4_5_AI_1 + P-network_4_5_AI_2 + P-network_4_5_AI_3 + P-network_4_5_AI_4 + P-network_4_5_AI_5 + P-network_4_5_AI_6 + P-network_4_5_AI_7 + P-network_6_3_AnnP_1 + P-network_6_3_AnnP_2 + P-network_6_3_AnnP_3 + P-network_6_3_AnnP_4 + P-network_6_3_AnnP_5 + P-network_6_3_AnnP_6 + P-network_6_3_AnnP_7 + P-network_1_5_AskP_1 + P-network_1_5_AskP_2 + P-network_1_5_AskP_3 + P-network_1_5_AskP_4 + P-network_1_5_AskP_5 + P-network_1_5_AskP_6 + P-network_1_5_AskP_7 + P-network_6_4_AI_1 + P-network_6_4_AI_2 + P-network_6_4_AI_3 + P-network_6_4_AI_4 + P-network_6_4_AI_5 + P-network_6_4_AI_6 + P-network_6_4_AI_7 + P-network_3_7_RP_7 + P-network_6_7_RI_1 + P-network_6_7_RI_2 + P-network_6_7_RI_3 + P-network_6_7_RI_4 + P-network_6_7_RI_5 + P-network_6_7_RI_6 + P-network_6_7_RI_7 + P-network_3_7_RP_6 + P-network_3_7_RP_5 + P-network_6_0_RI_7 + P-network_3_7_RP_4 + P-network_6_0_RI_6 + P-network_3_7_RP_3 + P-network_6_0_RI_5 + P-network_3_7_RP_2 + P-network_6_0_RI_4 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_1_0_AI_3 + P-network_1_0_AI_4 + P-network_1_0_AI_5 + P-network_1_0_AI_6 + P-network_1_0_AI_7 + P-network_3_7_RP_1 + P-network_1_3_RI_1 + P-network_1_3_RI_2 + P-network_1_3_RI_3 + P-network_1_3_RI_4 + P-network_1_3_RI_5 + P-network_1_3_RI_6 + P-network_1_3_RI_7 + P-network_6_0_RI_3 + P-network_6_0_RI_2 + P-network_6_0_RI_1 + P-network_5_4_AskP_7 + P-network_5_4_AskP_6 + P-network_5_4_AskP_5 + P-network_5_4_AskP_4 + P-network_5_4_AskP_3 + P-network_5_7_AnnP_1 + P-network_5_7_AnnP_2 + P-network_5_7_AnnP_3 + P-network_5_7_AnnP_4 + P-network_5_7_AnnP_5 + P-network_5_7_AnnP_6 + P-network_5_7_AnnP_7 + P-network_5_4_AskP_2 + P-network_6_1_AskP_1 + P-network_6_1_AskP_2 + P-network_6_1_AskP_3 + P-network_6_1_AskP_4 + P-network_6_1_AskP_5 + P-network_6_1_AskP_6 + P-network_6_1_AskP_7 + P-network_5_4_AskP_1 + P-network_3_2_RI_1 + P-network_3_2_RI_2 + P-network_3_2_RI_3 + P-network_3_2_RI_4 + P-network_3_2_RI_5 + P-network_3_2_RI_6 + P-network_3_2_RI_7 + P-network_3_2_AnnP_1 + P-network_3_2_AnnP_2 + P-network_3_2_AnnP_3 + P-network_3_2_AnnP_4 + P-network_3_2_AnnP_5 + P-network_3_2_AnnP_6 + P-network_3_2_AnnP_7 + P-network_5_1_RI_1 + P-network_5_1_RI_2 + P-network_5_1_RI_3 + P-network_5_1_RI_4 + P-network_5_1_RI_5 + P-network_5_1_RI_6 + P-network_5_1_RI_7 + P-network_5_5_AskP_1 + P-network_5_5_AskP_2 + P-network_5_5_AskP_3 + P-network_5_5_AskP_4 + P-network_5_5_AskP_5 + P-network_5_5_AskP_6 + P-network_5_5_AskP_7 + P-network_7_0_RI_1 + P-network_7_0_RI_2 + P-network_7_0_RI_3 + P-network_4_7_RP_1 + P-network_7_0_RI_4 + P-network_4_7_RP_2 + P-network_7_0_RI_5 + P-network_4_7_RP_3 + P-network_7_0_RI_6 + P-network_4_7_RP_4 + P-network_7_0_RI_7 + P-network_4_7_RP_5 + P-network_4_7_RP_6 + P-network_4_7_RP_7 + P-network_2_6_AnnP_1 + P-network_2_6_AnnP_2 + P-network_2_6_AnnP_3 + P-network_2_6_AnnP_4 + P-network_2_6_AnnP_5 + P-network_2_6_AnnP_6 + P-network_2_6_AnnP_7 + P-network_3_0_AskP_1 + P-network_3_0_AskP_2 + P-network_3_0_AskP_3 + P-network_3_0_AskP_4 + P-network_3_0_AskP_5 + P-network_3_0_AskP_6 + P-network_3_0_AskP_7 + P-network_6_6_RP_1 + P-network_6_6_RP_2 + P-network_6_6_RP_3 + P-network_6_6_RP_4 + P-network_6_6_RP_5 + P-network_6_6_RP_6 + P-network_6_6_RP_7 + P-network_4_1_RI_7 + P-network_4_1_RI_6 + P-network_4_1_RI_5 + P-network_4_1_RI_4 + P-network_4_1_RI_3 + P-network_4_1_RI_2 + P-network_4_1_RI_1 + P-network_3_1_AnnP_7 + P-network_3_1_AnnP_6 + P-network_0_1_AnnP_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_3 + P-network_0_1_AnnP_4 + P-network_0_1_AnnP_5 + P-network_0_1_AnnP_6 + P-network_0_1_AnnP_7 + P-network_3_1_AnnP_5 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_1_2_RP_3 + P-network_1_2_RP_4 + P-network_1_2_RP_5 + P-network_1_2_RP_6 + P-network_1_2_RP_7 + P-network_3_1_AnnP_4 + P-network_3_1_AnnP_3 + P-network_3_1_AnnP_2 + P-network_3_1_AnnP_1 + P-network_3_7_AI_1 + P-network_3_7_AI_2 + P-network_3_7_AI_3 + P-network_3_7_AI_4 + P-network_3_7_AI_5 + P-network_3_7_AI_6 + P-network_3_7_AI_7 + P-network_7_2_AnnP_1 + P-network_7_2_AnnP_2 + P-network_7_2_AnnP_3 + P-network_7_2_AnnP_4 + P-network_7_2_AnnP_5 + P-network_7_2_AnnP_6 + P-network_7_2_AnnP_7 + P-network_3_1_RP_1 + P-network_3_1_RP_2 + P-network_3_1_RP_3 + P-network_3_1_RP_4 + P-network_3_1_RP_5 + P-network_3_1_RP_6 + P-network_3_1_RP_7 + P-network_2_4_AskP_1 + P-network_2_4_AskP_2 + P-network_2_4_AskP_3 + P-network_2_4_AskP_4 + P-network_2_4_AskP_5 + P-network_2_4_AskP_6 + P-network_2_4_AskP_7 + P-network_2_2_RI_7 + P-network_2_2_RI_6 + P-network_2_2_RI_5 + P-network_2_2_RI_4 + P-network_2_2_RI_3 + P-network_2_2_RI_2 + P-network_2_2_RI_1 + P-network_5_6_AI_1 + P-network_5_6_AI_2 + P-network_5_6_AI_3 + P-network_5_6_AI_4 + P-network_5_6_AI_5 + P-network_5_6_AI_6 + P-network_5_6_AI_7 + P-network_5_0_RP_1 + P-network_5_0_RP_2 + P-network_5_0_RP_3 + P-network_5_0_RP_4 + P-network_5_0_RP_5 + P-network_5_0_RP_6 + P-network_5_0_RP_7 + P-network_7_5_AI_1 + P-network_7_5_AI_2 + P-network_7_5_AI_3 + P-network_7_5_AI_4 + P-network_7_5_AI_5 + P-network_7_5_AI_6 + P-network_7_5_AI_7 + P-network_0_2_AI_1 + P-network_0_2_AI_2 + P-network_0_2_AI_3 + P-network_0_2_AI_4 + P-network_0_2_AI_5 + P-network_0_2_AI_6 + P-network_0_2_AI_7 + P-network_6_0_AskP_7 + P-network_6_0_AskP_6 + P-network_0_5_RI_1 + P-network_0_5_RI_2 + P-network_0_5_RI_3 + P-network_0_5_RI_4 + P-network_0_5_RI_5 + P-network_0_5_RI_6 + P-network_0_5_RI_7 + P-network_6_0_AskP_5 + P-network_6_6_AnnP_1 + P-network_6_6_AnnP_2 + P-network_6_6_AnnP_3 + P-network_6_6_AnnP_4 + P-network_6_6_AnnP_5 + P-network_6_6_AnnP_6 + P-network_6_6_AnnP_7 + P-network_6_0_AskP_4 + P-network_7_0_AskP_1 + P-network_7_0_AskP_2 + P-network_7_0_AskP_3 + P-network_7_0_AskP_4 + P-network_7_0_AskP_5 + P-network_7_0_AskP_6 + P-network_7_0_AskP_7 + P-network_6_0_AskP_3 + P-network_2_1_AI_1 + P-network_2_1_AI_2 + P-network_2_1_AI_3 + P-network_2_1_AI_4 + P-network_2_1_AI_5 + P-network_2_1_AI_6 + P-network_2_1_AI_7 + P-network_6_0_AskP_2 + P-network_2_4_RI_1 + P-network_2_4_RI_2 + P-network_2_4_RI_3 + P-network_2_4_RI_4 + P-network_2_4_RI_5 + P-network_2_4_RI_6 + P-network_2_4_RI_7 + P-network_6_0_AskP_1 + P-network_5_6_AnnP_7 + P-network_4_1_AnnP_1 + P-network_4_1_AnnP_2 + P-network_4_1_AnnP_3 + P-network_4_1_AnnP_4 + P-network_4_1_AnnP_5 + P-network_4_1_AnnP_6 + P-network_4_1_AnnP_7 + P-network_5_6_AnnP_6 + P-network_5_6_AnnP_5 + P-network_5_6_AnnP_4 + P-network_5_6_AnnP_3 + P-network_5_6_AnnP_2 + P-network_5_6_AnnP_1 + P-network_4_0_AI_1 + P-network_4_0_AI_2 + P-network_4_0_AI_3 + P-network_4_0_AI_4 + P-network_4_0_AI_5 + P-network_4_0_AI_6 + P-network_4_0_AI_7 + P-network_4_3_RI_1 + P-network_4_3_RI_2 + P-network_4_3_RI_3 + P-network_4_3_RI_4 + P-network_4_3_RI_5 + P-network_4_3_RI_6 + P-network_4_3_RI_7 + P-network_0_3_RI_7 + P-network_0_3_RI_6 + P-network_0_3_RI_5 + P-network_0_3_RI_4 + P-network_6_4_AskP_1 + P-network_6_4_AskP_2 + P-network_6_4_AskP_3 + P-network_6_4_AskP_4 + P-network_6_4_AskP_5 + P-network_6_4_AskP_6 + P-network_6_4_AskP_7 + P-network_0_3_RI_3 + P-network_0_3_RI_2 + P-network_0_3_RI_1 + P-network_7_6_RI_7 + P-network_7_6_RI_6 + P-network_7_6_RI_5 + P-network_7_6_RI_4 + P-network_7_6_RI_3 + P-network_7_6_RI_2 + P-network_6_2_RI_1 + P-network_6_2_RI_2 + P-network_6_2_RI_3 + P-network_6_2_RI_4 + P-network_6_2_RI_5 + P-network_6_2_RI_6 + P-network_6_2_RI_7 + P-network_7_6_RI_1 + P-network_3_5_AnnP_1 + P-network_3_5_AnnP_2 + P-network_3_5_AnnP_3 + P-network_3_5_AnnP_4 + P-network_3_5_AnnP_5 + P-network_3_5_AnnP_6 + P-network_3_5_AnnP_7 + P-network_0_0_AI_7 + P-network_0_0_AI_6 + P-network_0_0_AI_5 + P-network_0_0_AI_4 + P-network_0_0_AI_3 + P-network_0_0_AI_2 + P-network_0_0_AI_1 + P-network_1_0_AnnP_1 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_3 + P-network_1_0_AnnP_4 + P-network_1_0_AnnP_5 + P-network_1_0_AnnP_6 + P-network_1_0_AnnP_7 + P-network_7_3_AI_7 + P-network_7_7_RP_1 + P-network_7_7_RP_2 + P-network_7_7_RP_3 + P-network_7_7_RP_4 + P-network_7_7_RP_5 + P-network_7_7_RP_6 + P-network_7_7_RP_7 + P-network_7_3_AI_6 + P-network_0_4_RP_1 + P-network_0_4_RP_2 + P-network_0_4_RP_3 + P-network_0_4_RP_4 + P-network_0_4_RP_5 + P-network_0_4_RP_6 + P-network_0_4_RP_7 + P-network_7_3_AI_5 + P-network_7_3_AI_4 + P-network_7_3_AI_3 + P-network_7_3_AI_2 + P-network_7_3_AI_1 + P-network_3_3_AskP_1 + P-network_3_3_AskP_2 + P-network_3_3_AskP_3 + P-network_3_3_AskP_4 + P-network_3_3_AskP_5 + P-network_3_3_AskP_6 + P-network_3_3_AskP_7 + P-network_2_3_RP_1 + P-network_2_3_RP_2 + P-network_2_3_RP_3 + P-network_2_3_RP_4 + P-network_2_3_RP_5 + P-network_2_3_RP_6 + P-network_5_7_RI_7 + P-network_2_3_RP_7 + P-network_5_7_RI_6 + P-network_5_7_RI_5 + P-network_5_7_RI_4 + P-network_5_7_RI_3 + P-network_5_7_RI_2 + P-network_5_7_RI_1 + P-network_5_4_AI_7 + P-network_5_4_AI_6 + P-network_5_4_AI_5 + P-network_5_4_AI_4 + P-network_5_4_AI_3 + P-network_5_4_AI_2 + P-network_5_4_AI_1 + P-network_0_4_AnnP_1 + P-network_0_4_AnnP_2 + P-network_0_4_AnnP_3 + P-network_0_4_AnnP_4 + P-network_0_4_AnnP_5 + P-network_0_4_AnnP_6 + P-network_0_4_AnnP_7 + P-network_1_4_AskP_7 + P-network_4_2_RP_1 + P-network_4_2_RP_2 + P-network_4_2_RP_3 + P-network_4_2_RP_4 + P-network_4_2_RP_5 + P-network_4_2_RP_6 + P-network_4_2_RP_7 + P-network_1_4_AskP_6 + P-network_6_7_AI_1 + P-network_6_7_AI_2 + P-network_6_7_AI_3 + P-network_6_7_AI_4 + P-network_6_7_AI_5 + P-network_6_7_AI_6 + P-network_6_7_AI_7 + P-network_1_4_AskP_5 + P-network_1_4_AskP_4 + P-network_1_4_AskP_3 + P-network_1_4_AskP_2 + P-network_1_4_AskP_1 + P-network_7_5_AnnP_1 + P-network_7_5_AnnP_2 + P-network_7_5_AnnP_3 + P-network_7_5_AnnP_4 + P-network_7_5_AnnP_5 + P-network_7_5_AnnP_6 + P-network_7_5_AnnP_7 + P-network_6_1_RP_1 + P-network_6_1_RP_2 + P-network_6_1_RP_3 + P-network_6_1_RP_4 + P-network_6_1_RP_5 + P-network_6_1_RP_6 + P-network_6_1_RP_7 + P-network_2_7_AskP_1 + P-network_2_7_AskP_2 + P-network_2_7_AskP_3 + P-network_2_7_AskP_4 + P-network_2_7_AskP_5 + P-network_2_7_AskP_6 + P-network_2_7_AskP_7 + P-network_1_3_AI_1 + P-network_1_3_AI_2 + P-network_1_3_AI_3 + P-network_1_3_AI_4 + P-network_1_3_AI_5 + P-network_1_3_AI_6 + P-network_1_3_AI_7 + P-network_1_6_RI_1 + P-network_1_6_RI_2 + P-network_1_6_RI_3 + P-network_1_6_RI_4 + P-network_1_6_RI_5 + P-network_1_6_RI_6 + P-network_1_6_RI_7 + P-network_6_2_AnnP_7 + P-network_5_0_AnnP_1 + P-network_5_0_AnnP_2 + P-network_5_0_AnnP_3 + P-network_5_0_AnnP_4 + P-network_5_0_AnnP_5 + P-network_5_0_AnnP_6 + P-network_5_0_AnnP_7 + P-network_6_2_AnnP_6 + P-network_6_2_AnnP_5 + P-network_6_2_AnnP_4 + P-network_6_2_AnnP_3 + P-network_6_2_AnnP_2 + P-network_6_2_AnnP_1 + P-network_3_2_AI_1 + P-network_3_2_AI_2 + P-network_3_2_AI_3 + P-network_3_2_AI_4 + P-network_3_2_AI_5 + P-network_3_2_AI_6 + P-network_3_2_AI_7 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_0_2_AskP_3 + P-network_0_2_AskP_4 + P-network_0_2_AskP_5 + P-network_0_2_AskP_6 + P-network_0_2_AskP_7 + P-network_3_5_AI_7 + P-network_3_5_AI_6 + P-network_3_5_AI_5 + P-network_3_5_AI_4 + P-network_3_5_RI_1 + P-network_3_5_RI_2 + P-network_3_5_RI_3 + P-network_3_5_RI_4 + P-network_3_5_RI_5 + P-network_3_5_RI_6 + P-network_3_5_RI_7 + P-network_3_5_AI_3 + P-network_7_3_AskP_1 + P-network_7_3_AskP_2 + P-network_7_3_AskP_3 + P-network_7_3_AskP_4 + P-network_7_3_AskP_5 + P-network_7_3_AskP_6 + P-network_7_3_AskP_7 + P-network_3_5_AI_2 + P-network_5_1_AI_1 + P-network_5_1_AI_2 + P-network_3_5_AI_1 + P-network_5_1_AI_3 + P-network_5_1_AI_4 + P-network_5_1_AI_5 + P-network_5_1_AI_6 + P-network_5_1_AI_7 + P-network_5_4_RI_1 + P-network_5_4_RI_2 + P-network_5_4_RI_3 + P-network_5_4_RI_4 + P-network_5_4_RI_5 + P-network_5_4_RI_6 + P-network_5_4_RI_7 + P-network_1_0_RP_7 + P-network_1_0_RP_6 + P-network_1_0_RP_5 + P-network_1_0_RP_4 + P-network_1_0_RP_3 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_4_4_AnnP_1 + P-network_4_4_AnnP_2 + P-network_4_4_AnnP_3 + P-network_4_4_AnnP_4 + P-network_4_4_AnnP_5 + P-network_4_4_AnnP_6 + P-network_4_4_AnnP_7 + P-network_1_6_AI_7 + P-network_7_0_AI_1 + P-network_1_6_AI_6 + P-network_7_0_AI_2 + P-network_1_6_AI_5 + P-network_7_0_AI_3 + P-network_1_6_AI_4 + P-network_7_0_AI_4 + P-network_1_6_AI_3 + P-network_7_0_AI_5 + P-network_1_6_AI_2 + P-network_7_0_AI_6 + P-network_1_6_AI_1 + P-network_7_0_AI_7 + P-network_7_3_RI_1 + P-network_7_3_RI_2 + P-network_7_3_RI_3 + P-network_7_3_RI_4 + P-network_7_3_RI_5 + P-network_7_3_RI_6 + P-network_7_3_RI_7 + P-network_2_0_AskP_7 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_0_0_RI_3 + P-network_0_0_RI_4 + P-network_0_0_RI_5 + P-network_0_0_RI_6 + P-network_0_0_RI_7 + P-network_2_0_AskP_6 + P-network_6_7_AskP_1 + P-network_6_7_AskP_2 + P-network_6_7_AskP_3 + P-network_6_7_AskP_4 + P-network_6_7_AskP_5 + P-network_6_7_AskP_6 + P-network_6_7_AskP_7 + P-network_2_0_AskP_5 + P-network_2_0_AskP_4 + P-network_2_0_AskP_3 + P-network_2_0_AskP_2 + P-network_2_0_AskP_1 + P-network_4_2_AskP_1 + P-network_4_2_AskP_2 + P-network_4_2_AskP_3 + P-network_4_2_AskP_4 + P-network_4_2_AskP_5 + P-network_4_2_AskP_6 + P-network_4_2_AskP_7 + P-network_6_4_RP_7 + P-network_6_4_RP_6 + P-network_6_4_RP_5 + P-network_6_4_RP_4 + P-network_6_4_RP_3 + P-network_1_5_RP_1 + P-network_1_5_RP_2 + P-network_1_5_RP_3 + P-network_1_5_RP_4 + P-network_1_5_RP_5 + P-network_1_5_RP_6 + P-network_1_5_RP_7 + P-network_6_4_RP_2 + P-network_6_4_RP_1 + P-network_1_6_AnnP_7 + P-network_1_6_AnnP_6 + P-network_1_6_AnnP_5 + P-network_1_3_AnnP_1 + P-network_1_3_AnnP_2 + P-network_1_3_AnnP_3 + P-network_1_3_AnnP_4 + P-network_1_3_AnnP_5 + P-network_1_3_AnnP_6 + P-network_1_3_AnnP_7 + P-network_3_4_RP_1 + P-network_3_4_RP_2 + P-network_3_4_RP_3 + P-network_3_4_RP_4 + P-network_3_4_RP_5 + P-network_3_4_RP_6 + P-network_3_4_RP_7 + P-network_1_6_AnnP_4 + P-network_1_6_AnnP_3 + P-network_1_6_AnnP_2 + P-network_1_6_AnnP_1 + P-network_3_6_AskP_1 + P-network_3_6_AskP_2 + P-network_3_6_AskP_3 + P-network_3_6_AskP_4 + P-network_3_6_AskP_5 + P-network_3_6_AskP_6 + P-network_3_6_AskP_7 + P-network_5_3_RP_1 + P-network_5_3_RP_2 + P-network_5_3_RP_3 + P-network_5_3_RP_4 + P-network_5_3_RP_5 + P-network_5_3_RP_6 + P-network_5_3_RP_7 + P-network_0_5_AI_1 + P-network_0_5_AI_2 + P-network_0_5_AI_3 + P-network_0_5_AI_4 + P-network_0_5_AI_5 + P-network_0_5_AI_6 + P-network_0_5_AI_7 + P-network_0_7_AnnP_1 + P-network_0_7_AnnP_2 + P-network_0_7_AnnP_3 + P-network_0_7_AnnP_4 + P-network_0_7_AnnP_5 + P-network_0_7_AnnP_6 + P-network_0_7_AnnP_7 + P-network_7_2_RP_1 + P-network_7_2_RP_2 + P-network_7_2_RP_3 + P-network_7_2_RP_4 + P-network_7_2_RP_5 + P-network_7_2_RP_6 + P-network_7_2_RP_7 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_1_1_AskP_3 + P-network_1_1_AskP_4 + P-network_1_1_AskP_5 + P-network_1_1_AskP_6 + P-network_1_1_AskP_7 + P-network_2_4_AI_1 + P-network_2_4_AI_2 + P-network_2_4_AI_3 + P-network_4_5_RP_7 + P-network_2_4_AI_4 + P-network_4_5_RP_6 + P-network_2_4_AI_5 + P-network_4_5_RP_5 + P-network_2_4_AI_6 + P-network_4_5_RP_4 + P-network_2_4_AI_7 + P-network_4_5_RP_3 + P-network_2_7_RI_1 + P-network_2_7_RI_2 + P-network_2_7_RI_3 + P-network_2_7_RI_4 + P-network_2_7_RI_5 + P-network_2_7_RI_6 + P-network_2_7_RI_7 + P-network_4_5_RP_2 + P-network_4_5_RP_1 + P-network_4_5_AskP_7 + P-network_4_5_AskP_6 + P-network_4_5_AskP_5 + P-network_4_5_AskP_4 + P-network_4_5_AskP_3 + P-network_4_5_AskP_2 + P-network_4_5_AskP_1 + P-network_4_3_AI_1 + P-network_4_3_AI_2 + P-network_4_3_AI_3 + P-network_4_3_AI_4 + P-network_4_3_AI_5 + P-network_4_3_AI_6 + P-network_4_3_AI_7 + P-network_4_6_RI_1 + P-network_4_6_RI_2 + P-network_4_6_RI_3 + P-network_4_6_RI_4 + P-network_4_6_RI_5 + P-network_4_6_RI_6 + P-network_4_6_RI_7 + P-network_5_3_AnnP_1 + P-network_5_3_AnnP_2 + P-network_5_3_AnnP_3 + P-network_5_3_AnnP_4 + P-network_5_3_AnnP_5 + P-network_5_3_AnnP_6 + P-network_5_3_AnnP_7 + P-network_6_2_AI_1 + P-network_6_2_AI_2 + P-network_6_2_AI_3 + P-network_6_2_AI_4 + P-network_6_2_AI_5 + P-network_6_2_AI_6 + P-network_6_2_AI_7 + P-network_0_5_AskP_1 + P-network_0_5_AskP_2 + P-network_0_5_AskP_3 + P-network_0_5_AskP_4 + P-network_0_5_AskP_5 + P-network_0_5_AskP_6 + P-network_0_5_AskP_7 + P-network_6_5_RI_1 + P-network_6_5_RI_2 + P-network_6_5_RI_3 + P-network_6_5_RI_4 + P-network_6_5_RI_5 + P-network_6_5_RI_6 + P-network_6_5_RI_7 + P-network_7_6_AskP_1 + P-network_7_6_AskP_2 + P-network_7_6_AskP_3 + P-network_7_6_AskP_4 + P-network_7_6_AskP_5 + P-network_7_6_AskP_6 + P-network_7_6_AskP_7 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_1_RI_3 + P-network_1_1_RI_4 + P-network_1_1_RI_5 + P-network_1_1_RI_6 + P-network_1_1_RI_7 + P-network_2_6_RP_7 + P-network_2_6_RP_6 + P-network_2_6_RP_5 + P-network_2_6_RP_4 + P-network_4_7_AnnP_1 + P-network_4_7_AnnP_2 + P-network_4_7_AnnP_3 + P-network_4_7_AnnP_4 + P-network_4_7_AnnP_5 + P-network_4_7_AnnP_6 + P-network_4_7_AnnP_7 + P-network_2_6_RP_3 + P-network_5_1_AskP_1 + P-network_5_1_AskP_2 + P-network_5_1_AskP_3 + P-network_5_1_AskP_4 + P-network_5_1_AskP_5 + P-network_5_1_AskP_6 + P-network_5_1_AskP_7 + P-network_2_6_RP_2 + P-network_2_6_RP_1 + P-network_2_2_AnnP_7 + P-network_2_2_AnnP_6 + P-network_2_2_AnnP_5 + P-network_2_2_AnnP_4 + P-network_2_2_AnnP_3 + P-network_2_2_AnnP_2 + P-network_3_0_RI_1 + P-network_3_0_RI_2 + P-network_2_2_AnnP_1 + P-network_3_0_RI_3 + P-network_0_7_RP_1 + P-network_3_0_RI_4 + P-network_0_7_RP_2 + P-network_3_0_RI_5 + P-network_0_7_RP_3 + P-network_3_0_RI_6 + P-network_0_7_RP_4 + P-network_3_0_RI_7 + P-network_0_7_RP_5 + P-network_0_7_RP_6 + P-network_0_7_RP_7)))) : E (F ((((P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7) AND (P-poll__waitingMessage_0 + P-poll__waitingMessage_1 + P-poll__waitingMessage_2 + P-poll__waitingMessage_4 + P-poll__waitingMessage_5 + P-poll__waitingMessage_6 + P-poll__waitingMessage_7 + P-poll__waitingMessage_3 + 1 <= P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0)) OR ((1 <= P-crashed_7 + P-crashed_6 + P-crashed_5 + P-crashed_4 + P-crashed_3 + P-crashed_2 + P-crashed_1 + P-crashed_0) AND (2 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7) AND (P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 + 1 <= P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0))))) : A (G ((((P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1 <= 0) AND ((P-electionFailed_0 + P-electionFailed_1 + P-electionFailed_2 + P-electionFailed_3 + P-electionFailed_4 + P-electionFailed_5 + P-electionFailed_6 + P-electionFailed_7 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7) OR (2 <= P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0))) OR (1 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7)))) : A (G (((P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 <= P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_7 + P-masterState_7_F_7 + P-masterState_2_F_7 + P-masterState_5_F_7 + P-masterState_0_F_7 + P-masterState_3_F_7 + P-masterState_1_T_7 + P-masterState_6_F_7) OR (1 <= P-crashed_7 + P-crashed_6 + P-crashed_5 + P-crashed_4 + P-crashed_3 + P-crashed_2 + P-crashed_1 + P-crashed_0) OR ((P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_7 + P-masterState_7_F_7 + P-masterState_2_F_7 + P-masterState_5_F_7 + P-masterState_0_F_7 + P-masterState_3_F_7 + P-masterState_1_T_7 + P-masterState_6_F_7 <= P-poll__handlingMessage_1 + P-poll__handlingMessage_0 + P-poll__handlingMessage_2 + P-poll__handlingMessage_3 + P-poll__handlingMessage_4 + P-poll__handlingMessage_5 + P-poll__handlingMessage_6 + P-poll__handlingMessage_7) AND (P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_2_3 + P-startNeg__broadcasting_2_4 + P-startNeg__broadcasting_2_5 + P-startNeg__broadcasting_2_6 + P-startNeg__broadcasting_2_7 + P-startNeg__broadcasting_3_1 + P-startNeg__broadcasting_3_2 + P-startNeg__broadcasting_3_3 + P-startNeg__broadcasting_3_4 + P-startNeg__broadcasting_3_5 + P-startNeg__broadcasting_3_6 + P-startNeg__broadcasting_3_7 + P-startNeg__broadcasting_4_1 + P-startNeg__broadcasting_4_2 + P-startNeg__broadcasting_4_3 + P-startNeg__broadcasting_4_4 + P-startNeg__broadcasting_4_5 + P-startNeg__broadcasting_4_6 + P-startNeg__broadcasting_4_7 + P-startNeg__broadcasting_7_7 + P-startNeg__broadcasting_7_6 + P-startNeg__broadcasting_7_5 + P-startNeg__broadcasting_7_4 + P-startNeg__broadcasting_7_3 + P-startNeg__broadcasting_7_2 + P-startNeg__broadcasting_7_1 + P-startNeg__broadcasting_5_1 + P-startNeg__broadcasting_5_2 + P-startNeg__broadcasting_5_3 + P-startNeg__broadcasting_5_4 + P-startNeg__broadcasting_5_5 + P-startNeg__broadcasting_5_6 + P-startNeg__broadcasting_5_7 + P-startNeg__broadcasting_6_7 + P-startNeg__broadcasting_6_6 + P-startNeg__broadcasting_6_5 + P-startNeg__broadcasting_6_4 + P-startNeg__broadcasting_6_3 + P-startNeg__broadcasting_6_2 + P-startNeg__broadcasting_6_1 + P-startNeg__broadcasting_0_6 + P-startNeg__broadcasting_0_7 + P-startNeg__broadcasting_1_6 + P-startNeg__broadcasting_1_7 <= P-electionFailed_0 + P-electionFailed_1 + P-electionFailed_2 + P-electionFailed_3 + P-electionFailed_4 + P-electionFailed_5 + P-electionFailed_6 + P-electionFailed_7)) OR ((1 <= P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0) AND (1 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7) AND (P-stage_2_SEC + P-stage_3_NEG + P-stage_5_SEC + P-stage_4_PRIM + P-stage_1_SEC + P-stage_6_SEC + P-stage_3_SEC + P-stage_0_SEC + P-stage_7_PRIM + P-stage_1_NEG + P-stage_2_PRIM + P-stage_6_NEG + P-stage_4_NEG + P-stage_5_PRIM + P-stage_7_NEG + P-stage_0_PRIM + P-stage_2_NEG + P-stage_3_PRIM + P-stage_4_SEC + P-stage_5_NEG + P-stage_7_SEC + P-stage_6_PRIM + P-stage_0_NEG + P-stage_1_PRIM <= 2))))) : E (F (((P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_2_3 + P-startNeg__broadcasting_2_4 + P-startNeg__broadcasting_2_5 + P-startNeg__broadcasting_2_6 + P-startNeg__broadcasting_2_7 + P-startNeg__broadcasting_3_1 + P-startNeg__broadcasting_3_2 + P-startNeg__broadcasting_3_3 + P-startNeg__broadcasting_3_4 + P-startNeg__broadcasting_3_5 + P-startNeg__broadcasting_3_6 + P-startNeg__broadcasting_3_7 + P-startNeg__broadcasting_4_1 + P-startNeg__broadcasting_4_2 + P-startNeg__broadcasting_4_3 + P-startNeg__broadcasting_4_4 + P-startNeg__broadcasting_4_5 + P-startNeg__broadcasting_4_6 + P-startNeg__broadcasting_4_7 + P-startNeg__broadcasting_7_7 + P-startNeg__broadcasting_7_6 + P-startNeg__broadcasting_7_5 + P-startNeg__broadcasting_7_4 + P-startNeg__broadcasting_7_3 + P-startNeg__broadcasting_7_2 + P-startNeg__broadcasting_7_1 + P-startNeg__broadcasting_5_1 + P-startNeg__broadcasting_5_2 + P-startNeg__broadcasting_5_3 + P-startNeg__broadcasting_5_4 + P-startNeg__broadcasting_5_5 + P-startNeg__broadcasting_5_6 + P-startNeg__broadcasting_5_7 + P-startNeg__broadcasting_6_7 + P-startNeg__broadcasting_6_6 + P-startNeg__broadcasting_6_5 + P-startNeg__broadcasting_6_4 + P-startNeg__broadcasting_6_3 + P-startNeg__broadcasting_6_2 + P-startNeg__broadcasting_6_1 + P-startNeg__broadcasting_0_6 + P-startNeg__broadcasting_0_7 + P-startNeg__broadcasting_1_6 + P-startNeg__broadcasting_1_7) AND (1 <= P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0) AND (P-network_2_2_AnnP_0 + P-network_0_7_RP_0 + P-network_3_0_RI_0 + P-network_2_6_RP_0 + P-network_5_1_AskP_0 + P-network_4_7_AnnP_0 + P-network_1_1_RI_0 + P-network_4_4_AnsP_7 + P-network_4_4_AnsP_6 + P-network_4_4_AnsP_5 + P-network_4_4_AnsP_4 + P-network_4_4_AnsP_3 + P-network_4_4_AnsP_2 + P-network_4_4_AnsP_1 + P-network_4_4_AnsP_0 + P-network_7_6_AskP_0 + P-network_6_5_RI_0 + P-network_0_5_AskP_0 + P-network_6_2_AI_0 + P-network_5_3_AnnP_0 + P-network_4_6_RI_0 + P-network_4_5_AskP_0 + P-network_4_3_AI_0 + P-network_5_0_AnsP_7 + P-network_5_0_AnsP_6 + P-network_5_0_AnsP_5 + P-network_5_0_AnsP_4 + P-network_5_0_AnsP_3 + P-network_5_0_AnsP_2 + P-network_4_5_RP_0 + P-network_5_0_AnsP_1 + P-network_5_0_AnsP_0 + P-network_2_7_RI_0 + P-network_2_4_AI_0 + P-network_1_1_AskP_0 + P-network_7_2_RP_0 + P-network_0_7_AnnP_0 + P-network_7_5_AnsP_7 + P-network_7_5_AnsP_6 + P-network_7_5_AnsP_5 + P-network_7_5_AnsP_4 + P-network_7_5_AnsP_3 + P-network_7_5_AnsP_2 + P-network_7_5_AnsP_1 + P-network_7_5_AnsP_0 + P-network_1_3_AnsP_0 + P-network_1_3_AnsP_1 + P-network_1_3_AnsP_2 + P-network_1_3_AnsP_3 + P-network_1_3_AnsP_4 + P-network_1_3_AnsP_5 + P-network_1_3_AnsP_6 + P-network_1_3_AnsP_7 + P-network_0_4_AnsP_7 + P-network_0_4_AnsP_6 + P-network_0_4_AnsP_5 + P-network_0_4_AnsP_4 + P-network_0_4_AnsP_3 + P-network_0_4_AnsP_2 + P-network_0_4_AnsP_1 + P-network_0_4_AnsP_0 + P-network_0_5_AI_0 + P-network_5_3_RP_0 + P-network_3_6_AskP_0 + P-network_1_6_AnnP_0 + P-network_3_4_RP_0 + P-network_1_3_AnnP_0 + P-network_1_0_AnsP_7 + P-network_1_0_AnsP_6 + P-network_1_0_AnsP_5 + P-network_1_0_AnsP_4 + P-network_1_0_AnsP_3 + P-network_1_0_AnsP_2 + P-network_6_4_RP_0 + P-network_1_0_AnsP_1 + P-network_1_0_AnsP_0 + P-network_1_5_RP_0 + P-network_4_2_AskP_0 + P-network_3_5_AnsP_7 + P-network_3_5_AnsP_6 + P-network_3_5_AnsP_5 + P-network_2_0_AskP_0 + P-network_3_5_AnsP_4 + P-network_3_5_AnsP_3 + P-network_3_5_AnsP_2 + P-network_3_5_AnsP_1 + P-network_3_5_AnsP_0 + P-network_6_7_AskP_0 + P-network_0_0_RI_0 + P-network_7_3_RI_0 + P-network_1_6_AI_0 + P-network_7_0_AI_0 + P-network_4_4_AnnP_0 + P-network_1_0_RP_0 + P-network_5_4_RI_0 + P-network_4_1_AnsP_7 + P-network_4_1_AnsP_6 + P-network_4_1_AnsP_5 + P-network_4_1_AnsP_4 + P-network_4_1_AnsP_3 + P-network_4_1_AnsP_2 + P-network_4_1_AnsP_1 + P-network_3_5_AI_0 + P-network_4_1_AnsP_0 + P-network_5_1_AI_0 + P-network_0_7_AnsP_0 + P-network_7_3_AskP_0 + P-network_0_7_AnsP_1 + P-network_3_5_RI_0 + P-network_0_7_AnsP_2 + P-network_0_7_AnsP_3 + P-network_0_7_AnsP_4 + P-network_0_7_AnsP_5 + P-network_0_7_AnsP_6 + P-network_0_7_AnsP_7 + P-network_0_2_AskP_0 + P-network_3_2_AI_0 + P-network_6_6_AnsP_7 + P-network_6_6_AnsP_6 + P-network_6_2_AnnP_0 + P-network_6_6_AnsP_5 + P-network_6_6_AnsP_4 + P-network_6_6_AnsP_3 + P-network_6_6_AnsP_2 + P-network_6_6_AnsP_1 + P-network_6_6_AnsP_0 + P-network_5_0_AnnP_0 + P-network_1_6_RI_0 + P-network_1_3_AI_0 + P-network_2_7_AskP_0 + P-network_6_1_RP_0 + P-network_7_5_AnnP_0 + P-network_1_4_AskP_0 + P-network_6_7_AI_0 + P-network_4_2_RP_0 + P-network_0_4_AnnP_0 + P-network_5_4_AI_0 + P-network_7_2_AnsP_7 + P-network_7_2_AnsP_6 + P-network_7_2_AnsP_5 + P-network_7_2_AnsP_4 + P-network_7_2_AnsP_3 + P-network_7_2_AnsP_2 + P-network_7_2_AnsP_1 + P-network_7_2_AnsP_0 + P-network_0_1_AnsP_7 + P-network_0_1_AnsP_6 + P-network_0_1_AnsP_5 + P-network_0_1_AnsP_4 + P-network_0_1_AnsP_3 + P-network_0_1_AnsP_2 + P-network_0_1_AnsP_1 + P-network_5_7_RI_0 + P-network_0_1_AnsP_0 + P-network_5_3_AnsP_0 + P-network_5_3_AnsP_1 + P-network_5_3_AnsP_2 + P-network_5_3_AnsP_3 + P-network_5_3_AnsP_4 + P-network_5_3_AnsP_5 + P-network_5_3_AnsP_6 + P-network_5_3_AnsP_7 + P-network_2_3_RP_0 + P-network_3_3_AskP_0 + P-network_2_6_AnsP_7 + P-network_2_6_AnsP_6 + P-network_2_6_AnsP_5 + P-network_7_3_AI_0 + P-network_2_6_AnsP_4 + P-network_2_6_AnsP_3 + P-network_2_6_AnsP_2 + P-network_2_6_AnsP_1 + P-network_2_6_AnsP_0 + P-network_0_4_RP_0 + P-network_7_7_RP_0 + P-network_0_0_AI_0 + P-network_1_0_AnnP_0 + P-network_3_5_AnnP_0 + P-network_7_6_RI_0 + P-network_6_2_RI_0 + P-network_3_2_AnsP_7 + P-network_3_2_AnsP_6 + P-network_3_2_AnsP_5 + P-network_3_2_AnsP_4 + P-network_3_2_AnsP_3 + P-network_0_3_RI_0 + P-network_3_2_AnsP_2 + P-network_3_2_AnsP_1 + P-network_3_2_AnsP_0 + P-network_6_4_AskP_0 + P-network_4_3_RI_0 + P-network_4_0_AI_0 + P-network_5_7_AnsP_7 + P-network_5_7_AnsP_6 + P-network_5_6_AnnP_0 + P-network_5_7_AnsP_5 + P-network_5_7_AnsP_4 + P-network_5_7_AnsP_3 + P-network_5_7_AnsP_2 + P-network_5_7_AnsP_1 + P-network_5_7_AnsP_0 + P-network_4_1_AnnP_0 + P-network_6_0_AskP_0 + P-network_2_4_RI_0 + P-network_2_1_AI_0 + P-network_7_0_AskP_0 + P-network_6_6_AnnP_0 + P-network_0_5_RI_0 + P-network_0_2_AI_0 + P-network_7_5_AI_0 + P-network_6_3_AnsP_7 + P-network_6_3_AnsP_6 + P-network_6_3_AnsP_5 + P-network_6_3_AnsP_4 + P-network_6_3_AnsP_3 + P-network_6_3_AnsP_2 + P-network_6_3_AnsP_1 + P-network_6_3_AnsP_0 + P-network_5_0_RP_0 + P-network_5_6_AI_0 + P-network_2_2_RI_0 + P-network_2_4_AskP_0 + P-network_3_1_RP_0 + P-network_7_2_AnnP_0 + P-network_3_7_AI_0 + P-network_1_7_AnsP_7 + P-network_1_7_AnsP_6 + P-network_1_7_AnsP_5 + P-network_1_7_AnsP_4 + P-network_1_7_AnsP_3 + P-network_3_1_AnnP_0 + P-network_1_7_AnsP_2 + P-network_1_7_AnsP_1 + P-network_1_7_AnsP_0 + P-network_1_2_RP_0 + P-network_0_1_AnnP_0 + P-network_4_7_AnsP_0 + P-network_4_7_AnsP_1 + P-network_4_7_AnsP_2 + P-network_4_7_AnsP_3 + P-network_4_7_AnsP_4 + P-network_4_7_AnsP_5 + P-network_4_7_AnsP_6 + P-network_4_7_AnsP_7 + P-network_4_1_RI_0 + P-network_6_6_RP_0 + P-network_3_0_AskP_0 + P-network_2_6_AnnP_0 + P-network_2_3_AnsP_7 + P-network_2_3_AnsP_6 + P-network_2_3_AnsP_5 + P-network_2_3_AnsP_4 + P-network_2_3_AnsP_3 + P-network_2_3_AnsP_2 + P-network_2_3_AnsP_1 + P-network_2_3_AnsP_0 + P-network_4_7_RP_0 + P-network_7_0_RI_0 + P-network_5_5_AskP_0 + P-network_5_1_RI_0 + P-network_3_2_AnnP_0 + P-network_5_4_AskP_0 + P-network_3_2_RI_0 + P-network_6_1_AskP_0 + P-network_5_7_AnnP_0 + P-network_6_0_RI_0 + P-network_3_7_RP_0 + P-network_1_3_RI_0 + P-network_1_0_AI_0 + P-network_5_4_AnsP_7 + P-network_5_4_AnsP_6 + P-network_5_4_AnsP_5 + P-network_5_4_AnsP_4 + P-network_5_4_AnsP_3 + P-network_5_4_AnsP_2 + P-network_5_4_AnsP_1 + P-network_5_4_AnsP_0 + P-network_6_7_RI_0 + P-network_2_2_AnsP_0 + P-network_2_2_AnsP_1 + P-network_2_2_AnsP_2 + P-network_2_2_AnsP_3 + P-network_2_2_AnsP_4 + P-network_2_2_AnsP_5 + P-network_2_2_AnsP_6 + P-network_2_2_AnsP_7 + P-network_6_4_AI_0 + P-network_1_5_AskP_0 + P-network_6_3_AnnP_0 + P-network_4_5_AI_0 + P-network_6_0_AnsP_7 + P-network_6_0_AnsP_6 + P-network_6_0_AnsP_5 + P-network_6_0_AnsP_4 + P-network_6_0_AnsP_3 + P-network_6_0_AnsP_2 + P-network_6_0_AnsP_1 + P-network_6_0_AnsP_0 + P-network_2_0_RP_0 + P-network_2_6_AI_0 + P-network_2_1_AskP_0 + P-network_0_1_RP_0 + P-network_7_4_RP_0 + P-network_2_5_AnnP_0 + P-network_1_7_AnnP_0 + P-network_0_7_AI_0 + P-network_5_6_RP_0 + P-network_1_4_AnsP_7 + P-network_1_4_AnsP_6 + P-network_1_4_AnsP_5 + P-network_1_4_AnsP_4 + P-network_1_4_AnsP_3 + P-network_1_4_AnsP_2 + P-network_1_4_AnsP_1 + P-network_1_4_AnsP_0 + P-network_5_5_RP_0 + P-network_4_6_AskP_0 + P-network_3_6_RP_0 + P-network_0_0_AnnP_0 + P-network_2_3_AnnP_0 + P-network_2_0_AnsP_7 + P-network_2_0_AnsP_6 + P-network_2_0_AnsP_5 + P-network_2_0_AnsP_4 + P-network_7_5_RP_0 + P-network_2_0_AnsP_3 + P-network_2_0_AnsP_2 + P-network_2_0_AnsP_1 + P-network_2_0_AnsP_0 + P-network_1_7_RP_0 + P-network_4_0_RI_0 + P-network_0_2_RP_0 + P-network_1_6_AnsP_0 + P-network_1_6_AnsP_1 + P-network_1_6_AnsP_2 + P-network_1_6_AnsP_3 + P-network_1_6_AnsP_4 + P-network_1_6_AnsP_5 + P-network_1_6_AnsP_6 + P-network_1_6_AnsP_7 + P-network_5_2_AskP_0 + P-network_2_7_AI_0 + P-network_2_1_RI_0 + P-network_4_5_AnsP_7 + P-network_4_5_AnsP_6 + P-network_4_5_AnsP_5 + P-network_4_5_AnsP_4 + P-network_4_5_AnsP_3 + P-network_4_5_AnsP_2 + P-network_4_5_AnsP_1 + P-network_4_5_AnsP_0 + P-network_7_7_AskP_0 + P-network_0_2_RI_0 + P-network_7_5_RI_0 + P-network_0_6_AskP_0 + P-network_7_2_AI_0 + P-network_5_4_AnnP_0 + P-network_7_1_AnnP_0 + P-network_5_6_RI_0 + P-network_5_3_AI_0 + P-network_5_1_AnsP_7 + P-network_5_1_AnsP_6 + P-network_5_1_AnsP_5 + P-network_5_1_AnsP_4 + P-network_5_1_AnsP_3 + P-network_5_1_AnsP_2 + P-network_5_1_AnsP_1 + P-network_5_1_AnsP_0 + P-network_3_7_RI_0 + P-network_2_1_RP_0 + P-network_3_4_AI_0 + P-network_1_2_AskP_0 + P-network_7_6_AnsP_7 + P-network_2_3_AskP_0 + P-network_7_6_AnsP_6 + P-network_7_6_AnsP_5 + P-network_7_6_AnsP_4 + P-network_7_6_AnsP_3 + P-network_7_6_AnsP_2 + P-network_7_6_AnsP_1 + P-network_7_6_AnsP_0 + P-network_4_6_AI_0 + P-network_6_0_AnnP_0 + P-network_0_5_AnsP_7 + P-network_0_5_AnsP_6 + P-network_0_5_AnsP_5 + P-network_0_5_AnsP_4 + P-network_0_5_AnsP_3 + P-network_0_5_AnsP_2 + P-network_0_5_AnsP_1 + P-network_0_5_AnsP_0 + P-network_4_0_RP_0 + P-network_1_5_AI_0 + P-network_6_3_RP_0 + P-network_3_7_AskP_0 + P-network_6_2_AnsP_0 + P-network_6_2_AnsP_1 + P-network_6_2_AnsP_2 + P-network_6_2_AnsP_3 + P-network_6_2_AnsP_4 + P-network_6_2_AnsP_5 + P-network_6_2_AnsP_6 + P-network_6_2_AnsP_7 + P-network_4_4_RP_0 + P-network_6_5_AI_0 + P-network_1_4_AnnP_0 + P-network_1_1_AnsP_7 + P-network_1_1_AnsP_6 + P-network_1_1_AnsP_5 + P-network_1_1_AnsP_4 + P-network_1_1_AnsP_3 + P-network_1_1_AnsP_2 + P-network_1_1_AnsP_1 + P-network_6_5_AnnP_0 + P-network_1_1_AnsP_0 + P-network_2_5_RP_0 + P-network_4_3_AskP_0 + P-network_0_6_RP_0 + P-network_1_7_AskP_0 + P-network_3_6_AnsP_7 + P-network_3_6_AnsP_6 + P-network_3_6_AnsP_5 + P-network_3_6_AnsP_4 + P-network_3_6_AnsP_3 + P-network_3_6_AnsP_2 + P-network_3_6_AnsP_1 + P-network_1_1_AI_0 + P-network_3_6_AnsP_0 + P-network_2_0_AnnP_0 + P-network_1_0_RI_0 + P-network_4_5_AnnP_0 + P-network_1_4_RI_0 + P-network_6_4_RI_0 + P-network_4_2_AnsP_7 + P-network_4_2_AnsP_6 + P-network_4_2_AnsP_5 + P-network_4_2_AnsP_4 + P-network_4_2_AnsP_3 + P-network_4_2_AnsP_2 + P-network_4_2_AnsP_1 + P-network_4_0_AnnP_0 + P-network_4_2_AnsP_0 + P-network_6_1_AI_0 + P-network_7_4_AskP_0 + P-network_4_5_RI_0 + P-network_5_6_AnsP_0 + P-network_5_6_AnsP_1 + P-network_5_6_AnsP_2 + P-network_5_6_AnsP_3 + P-network_5_6_AnsP_4 + P-network_5_6_AnsP_5 + P-network_5_6_AnsP_6 + P-network_5_6_AnsP_7 + P-network_0_3_AskP_0 + P-network_3_0_AI_0 + P-network_4_2_AI_0 + P-network_6_7_AnsP_7 + P-network_6_7_AnsP_6 + P-network_6_7_AnsP_5 + P-network_6_7_AnsP_4 + P-network_6_7_AnsP_3 + P-network_6_7_AnsP_2 + P-network_6_7_AnsP_1 + P-network_6_7_AnsP_0 + P-network_5_1_AnnP_0 + P-network_3_3_RI_0 + P-network_2_6_RI_0 + P-network_2_3_AI_0 + P-network_7_1_RP_0 + P-network_7_6_AnnP_0 + P-network_0_7_RI_0 + P-network_0_4_AI_0 + P-network_7_7_AI_0 + P-network_5_2_RP_0 + P-network_0_5_AnnP_0 + P-network_7_3_AnsP_7 + P-network_7_3_AnsP_6 + P-network_6_3_AskP_0 + P-network_7_3_AnsP_5 + P-network_7_3_AnsP_4 + P-network_7_3_AnsP_3 + P-network_7_3_AnsP_2 + P-network_7_3_AnsP_1 + P-network_7_3_AnsP_0 + P-network_0_2_AnsP_7 + P-network_0_2_AnsP_6 + P-network_0_2_AnsP_5 + P-network_0_2_AnsP_4 + P-network_0_2_AnsP_3 + P-network_0_2_AnsP_2 + P-network_0_2_AnsP_1 + P-network_0_2_AnsP_0 + P-network_3_1_AnsP_0 + P-network_3_1_AnsP_1 + P-network_3_1_AnsP_2 + P-network_3_1_AnsP_3 + P-network_3_1_AnsP_4 + P-network_3_1_AnsP_5 + P-network_3_1_AnsP_6 + P-network_3_1_AnsP_7 + P-network_3_3_RP_0 + P-network_5_2_RI_0 + P-network_3_4_AskP_0 + P-network_2_7_AnsP_7 + P-network_2_7_AnsP_6 + P-network_2_7_AnsP_5 + P-network_2_7_AnsP_4 + P-network_2_7_AnsP_3 + P-network_2_7_AnsP_2 + P-network_2_7_AnsP_1 + P-network_2_7_AnsP_0 + P-network_1_4_RP_0 + P-network_1_1_AnnP_0 + P-network_3_4_AnnP_0 + P-network_4_0_AskP_0 + P-network_3_6_AnnP_0 + P-network_7_2_RI_0 + P-network_3_3_AnsP_7 + P-network_3_3_AnsP_6 + P-network_7_1_RI_0 + P-network_3_3_AnsP_5 + P-network_3_3_AnsP_4 + P-network_3_3_AnsP_3 + P-network_3_3_AnsP_2 + P-network_3_3_AnsP_1 + P-network_3_3_AnsP_0 + P-network_6_5_AskP_0 + P-network_5_3_RI_0 + P-network_5_0_AI_0 + P-network_4_2_AnnP_0 + P-network_3_4_RI_0 + P-network_3_1_AI_0 + P-network_7_1_AskP_0 + P-network_6_7_AnnP_0 + P-network_1_5_RI_0 + P-network_0_0_AskP_0 + P-network_1_2_AI_0 + P-network_6_4_AnsP_7 + P-network_6_4_AnsP_6 + P-network_6_4_AnsP_5 + P-network_6_4_AnsP_4 + P-network_6_4_AnsP_3 + P-network_6_4_AnsP_2 + P-network_6_4_AnsP_1 + P-network_6_4_AnsP_0 + P-network_6_0_RP_0 + P-network_6_6_AI_0 + P-network_2_5_AskP_0 + P-network_4_1_RP_0 + P-network_7_3_AnnP_0 + P-network_4_7_AI_0 + P-network_2_2_RP_0 + P-network_0_2_AnnP_0 + P-network_7_0_AnsP_7 + P-network_7_0_AnsP_6 + P-network_7_0_AnsP_5 + P-network_7_0_AnsP_4 + P-network_7_0_AnsP_3 + P-network_5_7_AskP_0 + P-network_7_0_AnsP_2 + P-network_7_0_AnsP_1 + P-network_7_0_AnsP_0 + P-network_6_7_RP_0 + P-network_0_3_RP_0 + P-network_7_6_RP_0 + P-network_3_1_AskP_0 + P-network_2_5_AnsP_0 + P-network_2_5_AnsP_1 + P-network_2_5_AnsP_2 + P-network_2_5_AnsP_3 + P-network_2_5_AnsP_4 + P-network_2_5_AnsP_5 + P-network_2_5_AnsP_6 + P-network_2_5_AnsP_7 + P-network_2_7_AnnP_0 + P-network_2_4_AnsP_7 + P-network_2_4_AnsP_6 + P-network_2_4_AnsP_5 + P-network_2_4_AnsP_4 + P-network_2_4_AnsP_3 + P-network_2_4_AnsP_2 + P-network_3_2_AskP_0 + P-network_2_4_AnsP_1 + P-network_2_4_AnsP_0 + P-network_5_7_RP_0 + P-network_1_3_RP_0 + P-network_5_6_AskP_0 + P-network_0_0_AnsP_0 + P-network_0_0_AnsP_1 + P-network_0_0_AnsP_2 + P-network_0_0_AnsP_3 + P-network_0_0_AnsP_4 + P-network_0_0_AnsP_5 + P-network_0_0_AnsP_6 + P-network_0_0_AnsP_7 + P-network_6_1_RI_0 + P-network_3_3_AnnP_0 + P-network_7_1_AnsP_0 + P-network_7_1_AnsP_1 + P-network_7_1_AnsP_2 + P-network_7_1_AnsP_3 + P-network_7_1_AnsP_4 + P-network_7_1_AnsP_5 + P-network_7_1_AnsP_6 + P-network_7_1_AnsP_7 + P-network_0_3_AnnP_0 + P-network_4_2_RI_0 + P-network_3_0_AnsP_7 + P-network_3_0_AnsP_6 + P-network_3_0_AnsP_5 + P-network_3_0_AnsP_4 + P-network_3_0_AnsP_3 + P-network_3_0_AnsP_2 + P-network_3_0_AnsP_1 + P-network_3_0_AnsP_0 + P-network_6_2_AskP_0 + P-network_3_2_RP_0 + P-network_2_3_RI_0 + P-network_5_7_AI_0 + P-network_2_0_AI_0 + P-network_5_5_AnsP_7 + P-network_5_5_AnsP_6 + P-network_5_5_AnsP_5 + P-network_5_5_AnsP_4 + P-network_5_5_AnsP_3 + P-network_5_5_AnsP_2 + P-network_5_5_AnsP_1 + P-network_5_5_AnsP_0 + P-network_0_4_RI_0 + P-network_7_7_RI_0 + P-network_0_1_AI_0 + P-network_7_4_AI_0 + P-network_1_6_AskP_0 + P-network_6_4_AnnP_0 + P-network_5_5_AI_0 + P-network_6_1_AnsP_7 + P-network_7_4_AnnP_0 + P-network_6_1_AnsP_6 + P-network_6_1_AnsP_5 + P-network_6_1_AnsP_4 + P-network_6_1_AnsP_3 + P-network_6_1_AnsP_2 + P-network_6_1_AnsP_1 + P-network_6_1_AnsP_0 + P-network_3_0_RP_0 + P-network_3_6_AI_0 + P-network_5_1_RP_0 + P-network_2_2_AskP_0 + P-network_1_1_RP_0 + P-network_7_0_AnnP_0 + P-network_2_6_AskP_0 + P-network_1_7_AI_0 + P-network_1_5_AnsP_7 + P-network_7_6_AI_0 + P-network_1_5_AnsP_6 + P-network_1_5_AnsP_5 + P-network_1_5_AnsP_4 + P-network_1_5_AnsP_3 + P-network_1_5_AnsP_2 + P-network_1_5_AnsP_1 + P-network_1_5_AnsP_0 + P-network_0_3_AI_0 + P-network_6_5_RP_0 + P-network_4_7_AskP_0 + P-network_4_6_RP_0 + P-network_2_4_AnnP_0 + P-network_0_6_RI_0 + P-network_2_1_AnsP_7 + P-network_2_1_AnsP_6 + P-network_2_1_AnsP_5 + P-network_2_1_AnsP_4 + P-network_2_1_AnsP_3 + P-network_2_1_AnsP_2 + P-network_2_1_AnsP_1 + P-network_2_1_AnsP_0 + P-network_2_7_RP_0 + P-network_5_0_RI_0 + P-network_7_0_RP_0 + P-network_5_3_AskP_0 + P-network_6_5_AnsP_0 + P-network_6_5_AnsP_1 + P-network_6_5_AnsP_2 + P-network_6_5_AnsP_3 + P-network_6_5_AnsP_4 + P-network_6_5_AnsP_5 + P-network_6_5_AnsP_6 + P-network_6_5_AnsP_7 + P-network_3_1_RI_0 + P-network_4_6_AnsP_7 + P-network_2_2_AI_0 + P-network_4_6_AnsP_6 + P-network_4_6_AnsP_5 + P-network_4_6_AnsP_4 + P-network_4_6_AnsP_3 + P-network_4_6_AnsP_2 + P-network_4_6_AnsP_1 + P-network_4_6_AnsP_0 + P-network_0_1_AskP_0 + P-network_3_0_AnnP_0 + P-network_1_2_RI_0 + P-network_0_7_AskP_0 + P-network_5_5_AnnP_0 + P-network_6_6_RI_0 + P-network_6_3_AI_0 + P-network_5_2_AnsP_7 + P-network_5_2_AnsP_6 + P-network_5_2_AnsP_5 + P-network_5_2_AnsP_4 + P-network_5_2_AnsP_3 + P-network_5_2_AnsP_2 + P-network_5_2_AnsP_1 + P-network_5_2_AnsP_0 + P-network_2_5_RI_0 + P-network_4_7_RI_0 + P-network_4_4_AI_0 + P-network_1_3_AskP_0 + P-network_7_7_AnsP_7 + P-network_7_7_AnsP_6 + P-network_7_7_AnsP_5 + P-network_7_7_AnsP_4 + P-network_7_7_AnsP_3 + P-network_7_7_AnsP_2 + P-network_7_2_AskP_0 + P-network_7_7_AnsP_1 + P-network_7_7_AnsP_0 + P-network_6_1_AnnP_0 + P-network_0_6_AnsP_7 + P-network_0_6_AnsP_6 + P-network_0_6_AnsP_5 + P-network_0_6_AnsP_4 + P-network_0_6_AnsP_3 + P-network_0_6_AnsP_2 + P-network_0_6_AnsP_1 + P-network_0_6_AnsP_0 + P-network_2_5_AI_0 + P-network_0_0_RP_0 + P-network_7_3_RP_0 + P-network_4_1_AI_0 + P-network_4_0_AnsP_0 + P-network_4_0_AnsP_1 + P-network_4_0_AnsP_2 + P-network_4_0_AnsP_3 + P-network_4_0_AnsP_4 + P-network_4_0_AnsP_5 + P-network_4_0_AnsP_6 + P-network_4_0_AnsP_7 + P-network_0_6_AI_0 + P-network_5_4_RP_0 + P-network_1_5_AnnP_0 + P-network_4_4_RI_0 + P-network_1_2_AnsP_7 + P-network_1_2_AnsP_6 + P-network_1_2_AnsP_5 + P-network_1_2_AnsP_4 + P-network_1_2_AnsP_3 + P-network_1_2_AnsP_2 + P-network_1_2_AnsP_1 + P-network_1_2_AnsP_0 + P-network_3_5_RP_0 + P-network_4_4_AskP_0 + P-network_4_3_AnnP_0 + P-network_1_6_RP_0 + P-network_3_7_AnsP_7 + P-network_3_7_AnsP_6 + P-network_6_0_AI_0 + P-network_3_7_AnsP_5 + P-network_3_7_AnsP_4 + P-network_3_7_AnsP_3 + P-network_3_7_AnsP_2 + P-network_3_7_AnsP_1 + P-network_3_7_AnsP_0 + P-network_2_1_AnnP_0 + P-network_2_0_RI_0 + P-network_5_0_AskP_0 + P-network_4_6_AnnP_0 + P-network_6_3_RI_0 + P-network_0_1_RI_0 + P-network_7_4_RI_0 + P-network_4_3_AnsP_7 + P-network_4_3_AnsP_6 + P-network_4_3_AnsP_5 + P-network_4_3_AnsP_4 + P-network_4_3_AnsP_3 + P-network_4_3_AnsP_2 + P-network_4_3_AnsP_1 + P-network_4_3_AnsP_0 + P-network_7_1_AI_0 + P-network_7_5_AskP_0 + P-network_5_5_RI_0 + P-network_0_4_AskP_0 + P-network_5_2_AI_0 + P-network_5_2_AnnP_0 + P-network_3_6_RI_0 + P-network_6_6_AskP_0 + P-network_3_3_AI_0 + P-network_3_4_AnsP_0 + P-network_3_4_AnsP_1 + P-network_3_4_AnsP_2 + P-network_3_4_AnsP_3 + P-network_3_4_AnsP_4 + P-network_3_4_AnsP_5 + P-network_3_4_AnsP_6 + P-network_3_4_AnsP_7 + P-network_7_7_AnnP_0 + P-network_1_7_RI_0 + P-network_3_7_AnnP_0 + P-network_1_4_AI_0 + P-network_1_0_AskP_0 + P-network_6_2_RP_0 + P-network_0_6_AnnP_0 + P-network_7_4_AnsP_7 + P-network_4_1_AskP_0 + P-network_7_4_AnsP_6 + P-network_7_4_AnsP_5 + P-network_7_4_AnsP_4 + P-network_7_4_AnsP_3 + P-network_7_4_AnsP_2 + P-network_7_4_AnsP_1 + P-network_7_4_AnsP_0 + P-network_0_5_RP_0 + P-network_0_3_AnsP_7 + P-network_0_3_AnsP_6 + P-network_0_3_AnsP_5 + P-network_0_3_AnsP_4 + P-network_0_3_AnsP_3 + P-network_0_3_AnsP_2 + P-network_0_3_AnsP_1 + P-network_0_3_AnsP_0 + P-network_4_3_RP_0 + P-network_3_5_AskP_0 + P-network_2_4_RP_0 + P-network_1_2_AnnP_0 + P-network_1_2_AnnP_1 + P-network_1_2_AnnP_2 + P-network_1_2_AnnP_3 + P-network_1_2_AnnP_4 + P-network_1_2_AnnP_5 + P-network_1_2_AnnP_6 + P-network_1_2_AnnP_7 + P-network_2_4_RP_1 + P-network_2_4_RP_2 + P-network_2_4_RP_3 + P-network_2_4_RP_4 + P-network_2_4_RP_5 + P-network_2_4_RP_6 + P-network_2_4_RP_7 + P-network_3_5_AskP_1 + P-network_3_5_AskP_2 + P-network_3_5_AskP_3 + P-network_3_5_AskP_4 + P-network_3_5_AskP_5 + P-network_3_5_AskP_6 + P-network_3_5_AskP_7 + P-network_4_3_RP_1 + P-network_4_3_RP_2 + P-network_4_3_RP_3 + P-network_4_3_RP_4 + P-network_4_3_RP_5 + P-network_4_3_RP_6 + P-network_4_3_RP_7 + P-network_0_5_RP_7 + P-network_0_5_RP_6 + P-network_0_5_RP_5 + P-network_0_5_RP_4 + P-network_0_5_RP_3 + P-network_0_5_RP_2 + P-network_0_5_RP_1 + P-network_4_1_AskP_7 + P-network_4_1_AskP_6 + P-network_4_1_AskP_5 + P-network_4_1_AskP_4 + P-network_4_1_AskP_3 + P-network_4_1_AskP_2 + P-network_4_1_AskP_1 + P-network_3_7_AnnP_7 + P-network_3_7_AnnP_6 + P-network_0_6_AnnP_1 + P-network_0_6_AnnP_2 + P-network_0_6_AnnP_3 + P-network_0_6_AnnP_4 + P-network_0_6_AnnP_5 + P-network_0_6_AnnP_6 + P-network_0_6_AnnP_7 + P-network_3_7_AnnP_5 + P-network_6_2_RP_1 + P-network_6_2_RP_2 + P-network_6_2_RP_3 + P-network_6_2_RP_4 + P-network_6_2_RP_5 + P-network_6_2_RP_6 + P-network_6_2_RP_7 + P-network_3_7_AnnP_4 + P-network_1_0_AskP_1 + P-network_1_0_AskP_2 + P-network_1_0_AskP_3 + P-network_1_0_AskP_4 + P-network_1_0_AskP_5 + P-network_1_0_AskP_6 + P-network_1_0_AskP_7 + P-network_3_7_AnnP_3 + P-network_3_7_AnnP_2 + P-network_1_4_AI_1 + P-network_3_7_AnnP_1 + P-network_1_4_AI_2 + P-network_1_4_AI_3 + P-network_1_4_AI_4 + P-network_1_4_AI_5 + P-network_1_4_AI_6 + P-network_1_4_AI_7 + P-network_1_7_RI_1 + P-network_1_7_RI_2 + P-network_1_7_RI_3 + P-network_1_7_RI_4 + P-network_1_7_RI_5 + P-network_1_7_RI_6 + P-network_1_7_RI_7 + P-network_7_7_AnnP_1 + P-network_7_7_AnnP_2 + P-network_7_7_AnnP_3 + P-network_7_7_AnnP_4 + P-network_7_7_AnnP_5 + P-network_7_7_AnnP_6 + P-network_7_7_AnnP_7 + P-network_6_6_AskP_7 + P-network_6_6_AskP_6 + P-network_6_6_AskP_5 + P-network_6_6_AskP_4 + P-network_6_6_AskP_3 + P-network_6_6_AskP_2 + P-network_6_6_AskP_1 + P-network_3_3_AI_1 + P-network_3_3_AI_2 + P-network_3_3_AI_3 + P-network_3_3_AI_4 + P-network_3_3_AI_5 + P-network_3_3_AI_6 + P-network_3_3_AI_7 + P-network_3_6_RI_1 + P-network_3_6_RI_2 + P-network_3_6_RI_3 + P-network_3_6_RI_4 + P-network_3_6_RI_5 + P-network_3_6_RI_6 + P-network_3_6_RI_7 + P-network_5_2_AnnP_1 + P-network_5_2_AnnP_2 + P-network_5_2_AnnP_3 + P-network_5_2_AnnP_4 + P-network_5_2_AnnP_5 + P-network_5_2_AnnP_6 + P-network_5_2_AnnP_7 + P-network_5_2_AI_1 + P-network_5_2_AI_2 + P-network_5_2_AI_3 + P-network_5_2_AI_4 + P-network_5_2_AI_5 + P-network_5_2_AI_6 + P-network_5_2_AI_7 + P-network_0_4_AskP_1 + P-network_0_4_AskP_2 + P-network_0_4_AskP_3 + P-network_0_4_AskP_4 + P-network_0_4_AskP_5 + P-network_0_4_AskP_6 + P-network_0_4_AskP_7 + P-network_5_5_RI_1 + P-network_5_5_RI_2 + P-network_5_5_RI_3 + P-network_5_5_RI_4 + P-network_5_5_RI_5 + P-network_5_5_RI_6 + P-network_5_5_RI_7 + P-network_7_5_AskP_1 + P-network_7_5_AskP_2 + P-network_7_5_AskP_3 + P-network_7_5_AskP_4 + P-network_7_5_AskP_5 + P-network_7_5_AskP_6 + P-network_7_5_AskP_7 + P-network_7_1_AI_1 + P-network_7_1_AI_2 + P-network_7_1_AI_3 + P-network_7_1_AI_4 + P-network_7_1_AI_5 + P-network_7_1_AI_6 + P-network_7_1_AI_7 + P-network_7_4_RI_1 + P-network_7_4_RI_2 + P-network_7_4_RI_3 + P-network_7_4_RI_4 + P-network_7_4_RI_5 + P-network_7_4_RI_6 + P-network_7_4_RI_7 + P-network_0_1_RI_1 + P-network_0_1_RI_2 + P-network_0_1_RI_3 + P-network_0_1_RI_4 + P-network_0_1_RI_5 + P-network_0_1_RI_6 + P-network_0_1_RI_7 + P-network_6_3_RI_7 + P-network_6_3_RI_6 + P-network_6_3_RI_5 + P-network_6_3_RI_4 + P-network_6_3_RI_3 + P-network_6_3_RI_2 + P-network_6_3_RI_1 + P-network_4_6_AnnP_1 + P-network_4_6_AnnP_2 + P-network_4_6_AnnP_3 + P-network_4_6_AnnP_4 + P-network_4_6_AnnP_5 + P-network_4_6_AnnP_6 + P-network_4_6_AnnP_7 + P-network_5_0_AskP_1 + P-network_5_0_AskP_2 + P-network_5_0_AskP_3 + P-network_5_0_AskP_4 + P-network_5_0_AskP_5 + P-network_5_0_AskP_6 + P-network_5_0_AskP_7 + P-network_2_0_RI_1 + P-network_2_0_RI_2 + P-network_2_0_RI_3 + P-network_2_0_RI_4 + P-network_2_0_RI_5 + P-network_2_0_RI_6 + P-network_2_0_RI_7 + P-network_6_0_AI_7 + P-network_2_1_AnnP_1 + P-network_2_1_AnnP_2 + P-network_2_1_AnnP_3 + P-network_2_1_AnnP_4 + P-network_2_1_AnnP_5 + P-network_2_1_AnnP_6 + P-network_2_1_AnnP_7 + P-network_6_0_AI_6 + P-network_6_0_AI_5 + P-network_6_0_AI_4 + P-network_6_0_AI_3 + P-network_6_0_AI_2 + P-network_6_0_AI_1 + P-network_4_3_AnnP_7 + P-network_4_3_AnnP_6 + P-network_1_6_RP_1 + P-network_1_6_RP_2 + P-network_1_6_RP_3 + P-network_1_6_RP_4 + P-network_1_6_RP_5 + P-network_1_6_RP_6 + P-network_1_6_RP_7 + P-network_4_3_AnnP_5 + P-network_4_3_AnnP_4 + P-network_4_3_AnnP_3 + P-network_4_3_AnnP_2 + P-network_4_3_AnnP_1 + P-network_4_4_AskP_1 + P-network_4_4_AskP_2 + P-network_4_4_AskP_3 + P-network_4_4_AskP_4 + P-network_4_4_AskP_5 + P-network_4_4_AskP_6 + P-network_4_4_AskP_7 + P-network_3_5_RP_1 + P-network_3_5_RP_2 + P-network_3_5_RP_3 + P-network_3_5_RP_4 + P-network_3_5_RP_5 + P-network_3_5_RP_6 + P-network_3_5_RP_7 + P-network_4_4_RI_7 + P-network_4_4_RI_6 + P-network_4_4_RI_5 + P-network_4_4_RI_4 + P-network_4_4_RI_3 + P-network_4_4_RI_2 + P-network_4_4_RI_1 + P-network_1_5_AnnP_1 + P-network_1_5_AnnP_2 + P-network_1_5_AnnP_3 + P-network_1_5_AnnP_4 + P-network_1_5_AnnP_5 + P-network_1_5_AnnP_6 + P-network_1_5_AnnP_7 + P-network_5_4_RP_1 + P-network_5_4_RP_2 + P-network_5_4_RP_3 + P-network_5_4_RP_4 + P-network_5_4_RP_5 + P-network_5_4_RP_6 + P-network_5_4_RP_7 + P-network_0_6_AI_1 + P-network_0_6_AI_2 + P-network_0_6_AI_3 + P-network_0_6_AI_4 + P-network_0_6_AI_5 + P-network_0_6_AI_6 + P-network_0_6_AI_7 + P-network_4_1_AI_7 + P-network_4_1_AI_6 + P-network_4_1_AI_5 + P-network_4_1_AI_4 + P-network_4_1_AI_3 + P-network_4_1_AI_2 + P-network_4_1_AI_1 + P-network_7_3_RP_1 + P-network_7_3_RP_2 + P-network_7_3_RP_3 + P-network_7_3_RP_4 + P-network_7_3_RP_5 + P-network_7_3_RP_6 + P-network_7_3_RP_7 + P-network_0_0_RP_1 + P-network_0_0_RP_2 + P-network_0_0_RP_3 + P-network_0_0_RP_4 + P-network_0_0_RP_5 + P-network_0_0_RP_6 + P-network_0_0_RP_7 + P-network_2_5_AI_1 + P-network_2_5_AI_2 + P-network_2_5_AI_3 + P-network_2_5_AI_4 + P-network_2_5_AI_5 + P-network_2_5_AI_6 + P-network_7_2_AskP_7 + P-network_2_5_AI_7 + P-network_7_2_AskP_6 + P-network_7_2_AskP_5 + P-network_7_2_AskP_4 + P-network_7_2_AskP_3 + P-network_6_1_AnnP_1 + P-network_6_1_AnnP_2 + P-network_6_1_AnnP_3 + P-network_6_1_AnnP_4 + P-network_6_1_AnnP_5 + P-network_6_1_AnnP_6 + P-network_6_1_AnnP_7 + P-network_7_2_AskP_2 + P-network_7_2_AskP_1 + P-network_1_3_AskP_1 + P-network_1_3_AskP_2 + P-network_1_3_AskP_3 + P-network_1_3_AskP_4 + P-network_1_3_AskP_5 + P-network_1_3_AskP_6 + P-network_1_3_AskP_7 + P-network_4_4_AI_1 + P-network_2_5_RI_7 + P-network_4_4_AI_2 + P-network_2_5_RI_6 + P-network_4_4_AI_3 + P-network_2_5_RI_5 + P-network_4_4_AI_4 + P-network_2_5_RI_4 + P-network_4_4_AI_5 + P-network_2_5_RI_3 + P-network_4_4_AI_6 + P-network_2_5_RI_2 + P-network_4_4_AI_7 + P-network_2_5_RI_1 + P-network_4_7_RI_1 + P-network_4_7_RI_2 + P-network_4_7_RI_3 + P-network_4_7_RI_4 + P-network_4_7_RI_5 + P-network_4_7_RI_6 + P-network_4_7_RI_7 + P-network_6_3_AI_1 + P-network_6_3_AI_2 + P-network_6_3_AI_3 + P-network_6_3_AI_4 + P-network_6_3_AI_5 + P-network_6_3_AI_6 + P-network_6_3_AI_7 + P-network_6_6_RI_1 + P-network_6_6_RI_2 + P-network_6_6_RI_3 + P-network_6_6_RI_4 + P-network_6_6_RI_5 + P-network_6_6_RI_6 + P-network_6_6_RI_7 + P-network_0_1_AskP_7 + P-network_0_1_AskP_6 + P-network_5_5_AnnP_1 + P-network_5_5_AnnP_2 + P-network_5_5_AnnP_3 + P-network_5_5_AnnP_4 + P-network_5_5_AnnP_5 + P-network_5_5_AnnP_6 + P-network_5_5_AnnP_7 + P-network_0_1_AskP_5 + P-network_0_7_AskP_1 + P-network_0_7_AskP_2 + P-network_0_7_AskP_3 + P-network_0_7_AskP_4 + P-network_0_7_AskP_5 + P-network_0_7_AskP_6 + P-network_0_7_AskP_7 + P-network_0_1_AskP_4 + P-network_1_2_RI_1 + P-network_1_2_RI_2 + P-network_1_2_RI_3 + P-network_1_2_RI_4 + P-network_1_2_RI_5 + P-network_1_2_RI_6 + P-network_1_2_RI_7 + P-network_0_1_AskP_3 + P-network_0_1_AskP_2 + P-network_3_0_AnnP_1 + P-network_3_0_AnnP_2 + P-network_3_0_AnnP_3 + P-network_3_0_AnnP_4 + P-network_3_0_AnnP_5 + P-network_3_0_AnnP_6 + P-network_3_0_AnnP_7 + P-network_0_1_AskP_1 + P-network_2_2_AI_7 + P-network_2_2_AI_6 + P-network_2_2_AI_5 + P-network_2_2_AI_4 + P-network_2_2_AI_3 + P-network_2_2_AI_2 + P-network_2_2_AI_1 + P-network_3_1_RI_1 + P-network_3_1_RI_2 + P-network_3_1_RI_3 + P-network_3_1_RI_4 + P-network_3_1_RI_5 + P-network_3_1_RI_6 + P-network_3_1_RI_7 + P-network_7_0_RP_7 + P-network_7_0_RP_6 + P-network_7_0_RP_5 + P-network_7_0_RP_4 + P-network_7_0_RP_3 + P-network_5_3_AskP_1 + P-network_5_3_AskP_2 + P-network_5_3_AskP_3 + P-network_5_3_AskP_4 + P-network_5_3_AskP_5 + P-network_5_3_AskP_6 + P-network_5_3_AskP_7 + P-network_7_0_RP_2 + P-network_7_0_RP_1 + P-network_5_0_RI_1 + P-network_5_0_RI_2 + P-network_5_0_RI_3 + P-network_2_7_RP_1 + P-network_5_0_RI_4 + P-network_2_7_RP_2 + P-network_5_0_RI_5 + P-network_2_7_RP_3 + P-network_5_0_RI_6 + P-network_2_7_RP_4 + P-network_5_0_RI_7 + P-network_2_7_RP_5 + P-network_2_7_RP_6 + P-network_2_7_RP_7 + P-network_0_6_RI_7 + P-network_0_6_RI_6 + P-network_0_6_RI_5 + P-network_0_6_RI_4 + P-network_0_6_RI_3 + P-network_0_6_RI_2 + P-network_0_6_RI_1 + P-network_2_4_AnnP_1 + P-network_2_4_AnnP_2 + P-network_2_4_AnnP_3 + P-network_2_4_AnnP_4 + P-network_2_4_AnnP_5 + P-network_2_4_AnnP_6 + P-network_2_4_AnnP_7 + P-network_4_6_RP_1 + P-network_4_6_RP_2 + P-network_4_6_RP_3 + P-network_4_6_RP_4 + P-network_4_6_RP_5 + P-network_4_6_RP_6 + P-network_4_6_RP_7 + P-network_0_3_AI_7 + P-network_0_3_AI_6 + P-network_0_3_AI_5 + P-network_0_3_AI_4 + P-network_0_3_AI_3 + P-network_0_3_AI_2 + P-network_4_7_AskP_1 + P-network_4_7_AskP_2 + P-network_4_7_AskP_3 + P-network_4_7_AskP_4 + P-network_4_7_AskP_5 + P-network_4_7_AskP_6 + P-network_4_7_AskP_7 + P-network_0_3_AI_1 + P-network_6_5_RP_1 + P-network_6_5_RP_2 + P-network_6_5_RP_3 + P-network_6_5_RP_4 + P-network_6_5_RP_5 + P-network_6_5_RP_6 + P-network_6_5_RP_7 + P-network_7_6_AI_7 + P-network_7_6_AI_6 + P-network_7_6_AI_5 + P-network_7_6_AI_4 + P-network_7_6_AI_3 + P-network_7_6_AI_2 + P-network_7_6_AI_1 + P-network_2_6_AskP_7 + P-network_2_6_AskP_6 + P-network_1_7_AI_1 + P-network_1_7_AI_2 + P-network_1_7_AI_3 + P-network_1_7_AI_4 + P-network_1_7_AI_5 + P-network_1_7_AI_6 + P-network_1_7_AI_7 + P-network_2_6_AskP_5 + P-network_2_6_AskP_4 + P-network_2_6_AskP_3 + P-network_2_6_AskP_2 + P-network_2_6_AskP_1 + P-network_5_1_RP_7 + P-network_5_1_RP_6 + P-network_5_1_RP_5 + P-network_5_1_RP_4 + P-network_7_0_AnnP_1 + P-network_7_0_AnnP_2 + P-network_7_0_AnnP_3 + P-network_7_0_AnnP_4 + P-network_7_0_AnnP_5 + P-network_7_0_AnnP_6 + P-network_7_0_AnnP_7 + P-network_5_1_RP_3 + P-network_1_1_RP_1 + P-network_1_1_RP_2 + P-network_1_1_RP_3 + P-network_1_1_RP_4 + P-network_1_1_RP_5 + P-network_1_1_RP_6 + P-network_1_1_RP_7 + P-network_5_1_RP_2 + P-network_2_2_AskP_1 + P-network_2_2_AskP_2 + P-network_2_2_AskP_3 + P-network_2_2_AskP_4 + P-network_2_2_AskP_5 + P-network_2_2_AskP_6 + P-network_2_2_AskP_7 + P-network_5_1_RP_1 + P-network_3_6_AI_1 + P-network_3_6_AI_2 + P-network_3_6_AI_3 + P-network_3_6_AI_4 + P-network_3_6_AI_5 + P-network_3_6_AI_6 + P-network_3_6_AI_7 + P-network_3_0_RP_1 + P-network_3_0_RP_2 + P-network_3_0_RP_3 + P-network_3_0_RP_4 + P-network_3_0_RP_5 + P-network_3_0_RP_6 + P-network_3_0_RP_7 + P-network_7_4_AnnP_7 + P-network_7_4_AnnP_6 + P-network_7_4_AnnP_5 + P-network_7_4_AnnP_4 + P-network_7_4_AnnP_3 + P-network_7_4_AnnP_2 + P-network_7_4_AnnP_1 + P-network_5_5_AI_1 + P-network_5_5_AI_2 + P-network_5_5_AI_3 + P-network_5_5_AI_4 + P-network_5_5_AI_5 + P-network_5_5_AI_6 + P-network_5_5_AI_7 + P-network_6_4_AnnP_1 + P-network_6_4_AnnP_2 + P-network_6_4_AnnP_3 + P-network_6_4_AnnP_4 + P-network_6_4_AnnP_5 + P-network_6_4_AnnP_6 + P-network_6_4_AnnP_7 + P-network_1_6_AskP_1 + P-network_1_6_AskP_2 + P-network_1_6_AskP_3 + P-network_1_6_AskP_4 + P-network_1_6_AskP_5 + P-network_1_6_AskP_6 + P-network_1_6_AskP_7 + P-network_7_4_AI_1 + P-network_7_4_AI_2 + P-network_7_4_AI_3 + P-network_7_4_AI_4 + P-network_7_4_AI_5 + P-network_7_4_AI_6 + P-network_7_4_AI_7 + P-network_0_1_AI_1 + P-network_0_1_AI_2 + P-network_0_1_AI_3 + P-network_0_1_AI_4 + P-network_0_1_AI_5 + P-network_0_1_AI_6 + P-network_0_1_AI_7 + P-network_7_7_RI_1 + P-network_7_7_RI_2 + P-network_7_7_RI_3 + P-network_7_7_RI_4 + P-network_7_7_RI_5 + P-network_7_7_RI_6 + P-network_7_7_RI_7 + P-network_0_4_RI_1 + P-network_0_4_RI_2 + P-network_0_4_RI_3 + P-network_0_4_RI_4 + P-network_0_4_RI_5 + P-network_0_4_RI_6 + P-network_0_4_RI_7 + P-network_5_7_AI_7 + P-network_5_7_AI_6 + P-network_5_7_AI_5 + P-network_5_7_AI_4 + P-network_5_7_AI_3 + P-network_5_7_AI_2 + P-network_5_7_AI_1 + P-network_2_0_AI_1 + P-network_2_0_AI_2 + P-network_2_0_AI_3 + P-network_2_0_AI_4 + P-network_2_0_AI_5 + P-network_2_0_AI_6 + P-network_2_0_AI_7 + P-network_3_2_RP_7 + P-network_2_3_RI_1 + P-network_2_3_RI_2 + P-network_2_3_RI_3 + P-network_2_3_RI_4 + P-network_2_3_RI_5 + P-network_2_3_RI_6 + P-network_2_3_RI_7 + P-network_3_2_RP_6 + P-network_3_2_RP_5 + P-network_3_2_RP_4 + P-network_3_2_RP_3 + P-network_3_2_RP_2 + P-network_3_2_RP_1 + P-network_0_3_AnnP_7 + P-network_6_2_AskP_1 + P-network_6_2_AskP_2 + P-network_6_2_AskP_3 + P-network_6_2_AskP_4 + P-network_6_2_AskP_5 + P-network_6_2_AskP_6 + P-network_6_2_AskP_7 + P-network_0_3_AnnP_6 + P-network_0_3_AnnP_5 + P-network_0_3_AnnP_4 + P-network_0_3_AnnP_3 + P-network_0_3_AnnP_2 + P-network_4_2_RI_1 + P-network_4_2_RI_2 + P-network_4_2_RI_3 + P-network_4_2_RI_4 + P-network_4_2_RI_5 + P-network_4_2_RI_6 + P-network_4_2_RI_7 + P-network_0_3_AnnP_1 + P-network_3_3_AnnP_1 + P-network_3_3_AnnP_2 + P-network_3_3_AnnP_3 + P-network_3_3_AnnP_4 + P-network_3_3_AnnP_5 + P-network_3_3_AnnP_6 + P-network_3_3_AnnP_7 + P-network_6_1_RI_1 + P-network_6_1_RI_2 + P-network_6_1_RI_3 + P-network_6_1_RI_4 + P-network_6_1_RI_5 + P-network_6_1_RI_6 + P-network_6_1_RI_7 + P-network_1_3_RP_7 + P-network_1_3_RP_6 + P-network_1_3_RP_5 + P-network_1_3_RP_4 + P-network_5_6_AskP_1 + P-network_5_6_AskP_2 + P-network_5_6_AskP_3 + P-network_5_6_AskP_4 + P-network_5_6_AskP_5 + P-network_5_6_AskP_6 + P-network_5_6_AskP_7 + P-network_1_3_RP_3 + P-network_1_3_RP_2 + P-network_1_3_RP_1 + P-network_3_2_AskP_7 + P-network_3_2_AskP_6 + P-network_3_2_AskP_5 + P-network_3_2_AskP_4 + P-network_3_2_AskP_3 + P-network_5_7_RP_1 + P-network_5_7_RP_2 + P-network_5_7_RP_3 + P-network_5_7_RP_4 + P-network_5_7_RP_5 + P-network_5_7_RP_6 + P-network_5_7_RP_7 + P-network_3_2_AskP_2 + P-network_3_2_AskP_1 + P-network_2_7_AnnP_1 + P-network_2_7_AnnP_2 + P-network_2_7_AnnP_3 + P-network_2_7_AnnP_4 + P-network_2_7_AnnP_5 + P-network_2_7_AnnP_6 + P-network_2_7_AnnP_7 + P-network_6_7_RP_7 + P-network_3_1_AskP_1 + P-network_3_1_AskP_2 + P-network_3_1_AskP_3 + P-network_3_1_AskP_4 + P-network_3_1_AskP_5 + P-network_3_1_AskP_6 + P-network_3_1_AskP_7 + P-network_6_7_RP_6 + P-network_7_6_RP_1 + P-network_7_6_RP_2 + P-network_7_6_RP_3 + P-network_7_6_RP_4 + P-network_7_6_RP_5 + P-network_7_6_RP_6 + P-network_7_6_RP_7 + P-network_6_7_RP_5 + P-network_0_3_RP_1 + P-network_0_3_RP_2 + P-network_0_3_RP_3 + P-network_0_3_RP_4 + P-network_0_3_RP_5 + P-network_6_7_RP_4 + P-network_0_3_RP_6 + P-network_6_7_RP_3 + P-network_0_3_RP_7 + P-network_6_7_RP_2 + P-network_6_7_RP_1 + P-network_5_7_AskP_7 + P-network_5_7_AskP_6 + P-network_5_7_AskP_5 + P-network_5_7_AskP_4 + P-network_5_7_AskP_3 + P-network_5_7_AskP_2 + P-network_5_7_AskP_1 + P-network_0_2_AnnP_1 + P-network_0_2_AnnP_2 + P-network_0_2_AnnP_3 + P-network_0_2_AnnP_4 + P-network_0_2_AnnP_5 + P-network_0_2_AnnP_6 + P-network_0_2_AnnP_7 + P-network_2_2_RP_1 + P-network_2_2_RP_2 + P-network_2_2_RP_3 + P-network_2_2_RP_4 + P-network_2_2_RP_5 + P-network_2_2_RP_6 + P-network_2_2_RP_7 + P-network_4_7_AI_1 + P-network_4_7_AI_2 + P-network_4_7_AI_3 + P-network_4_7_AI_4 + P-network_4_7_AI_5 + P-network_4_7_AI_6 + P-network_4_7_AI_7 + P-network_7_3_AnnP_1 + P-network_7_3_AnnP_2 + P-network_7_3_AnnP_3 + P-network_7_3_AnnP_4 + P-network_7_3_AnnP_5 + P-network_7_3_AnnP_6 + P-network_7_3_AnnP_7 + P-network_4_1_RP_1 + P-network_4_1_RP_2 + P-network_4_1_RP_3 + P-network_4_1_RP_4 + P-network_4_1_RP_5 + P-network_4_1_RP_6 + P-network_4_1_RP_7 + P-network_2_5_AskP_1 + P-network_2_5_AskP_2 + P-network_2_5_AskP_3 + P-network_2_5_AskP_4 + P-network_2_5_AskP_5 + P-network_2_5_AskP_6 + P-network_2_5_AskP_7 + P-network_6_6_AI_1 + P-network_6_6_AI_2 + P-network_6_6_AI_3 + P-network_6_6_AI_4 + P-network_6_6_AI_5 + P-network_6_6_AI_6 + P-network_6_6_AI_7 + P-network_6_0_RP_1 + P-network_6_0_RP_2 + P-network_6_0_RP_3 + P-network_6_0_RP_4 + P-network_6_0_RP_5 + P-network_6_0_RP_6 + P-network_6_0_RP_7 + P-network_1_2_AI_1 + P-network_1_2_AI_2 + P-network_1_2_AI_3 + P-network_1_2_AI_4 + P-network_1_2_AI_5 + P-network_1_2_AI_6 + P-network_1_2_AI_7 + P-network_0_0_AskP_1 + P-network_0_0_AskP_2 + P-network_0_0_AskP_3 + P-network_0_0_AskP_4 + P-network_0_0_AskP_5 + P-network_0_0_AskP_6 + P-network_0_0_AskP_7 + P-network_1_5_RI_1 + P-network_1_5_RI_2 + P-network_1_5_RI_3 + P-network_1_5_RI_4 + P-network_1_5_RI_5 + P-network_1_5_RI_6 + P-network_1_5_RI_7 + P-network_6_7_AnnP_1 + P-network_6_7_AnnP_2 + P-network_6_7_AnnP_3 + P-network_6_7_AnnP_4 + P-network_6_7_AnnP_5 + P-network_6_7_AnnP_6 + P-network_6_7_AnnP_7 + P-network_7_1_AskP_1 + P-network_7_1_AskP_2 + P-network_7_1_AskP_3 + P-network_7_1_AskP_4 + P-network_7_1_AskP_5 + P-network_7_1_AskP_6 + P-network_7_1_AskP_7 + P-network_3_1_AI_1 + P-network_3_1_AI_2 + P-network_3_1_AI_3 + P-network_3_1_AI_4 + P-network_3_1_AI_5 + P-network_3_1_AI_6 + P-network_3_1_AI_7 + P-network_3_4_RI_1 + P-network_3_4_RI_2 + P-network_3_4_RI_3 + P-network_3_4_RI_4 + P-network_3_4_RI_5 + P-network_3_4_RI_6 + P-network_3_4_RI_7 + P-network_4_2_AnnP_1 + P-network_4_2_AnnP_2 + P-network_4_2_AnnP_3 + P-network_4_2_AnnP_4 + P-network_4_2_AnnP_5 + P-network_4_2_AnnP_6 + P-network_4_2_AnnP_7 + P-network_5_0_AI_1 + P-network_5_0_AI_2 + P-network_5_0_AI_3 + P-network_5_0_AI_4 + P-network_5_0_AI_5 + P-network_5_0_AI_6 + P-network_5_0_AI_7 + P-network_5_3_RI_1 + P-network_5_3_RI_2 + P-network_5_3_RI_3 + P-network_5_3_RI_4 + P-network_5_3_RI_5 + P-network_5_3_RI_6 + P-network_5_3_RI_7 + P-network_7_1_RI_7 + P-network_6_5_AskP_1 + P-network_6_5_AskP_2 + P-network_6_5_AskP_3 + P-network_6_5_AskP_4 + P-network_6_5_AskP_5 + P-network_6_5_AskP_6 + P-network_6_5_AskP_7 + P-network_7_1_RI_6 + P-network_7_1_RI_5 + P-network_7_1_RI_4 + P-network_7_1_RI_3 + P-network_7_1_RI_2 + P-network_7_1_RI_1 + P-network_3_4_AnnP_7 + P-network_3_4_AnnP_6 + P-network_7_2_RI_1 + P-network_7_2_RI_2 + P-network_7_2_RI_3 + P-network_7_2_RI_4 + P-network_7_2_RI_5 + P-network_7_2_RI_6 + P-network_7_2_RI_7 + P-network_3_4_AnnP_5 + P-network_3_4_AnnP_4 + P-network_3_4_AnnP_3 + P-network_3_6_AnnP_1 + P-network_3_6_AnnP_2 + P-network_3_6_AnnP_3 + P-network_3_6_AnnP_4 + P-network_3_6_AnnP_5 + P-network_3_6_AnnP_6 + P-network_3_6_AnnP_7 + P-network_3_4_AnnP_2 + P-network_4_0_AskP_1 + P-network_4_0_AskP_2 + P-network_4_0_AskP_3 + P-network_4_0_AskP_4 + P-network_4_0_AskP_5 + P-network_4_0_AskP_6 + P-network_4_0_AskP_7 + P-network_3_4_AnnP_1 + P-network_1_1_AnnP_1 + P-network_1_1_AnnP_2 + P-network_1_1_AnnP_3 + P-network_1_1_AnnP_4 + P-network_1_1_AnnP_5 + P-network_1_1_AnnP_6 + P-network_1_1_AnnP_7 + P-network_1_4_RP_1 + P-network_1_4_RP_2 + P-network_1_4_RP_3 + P-network_1_4_RP_4 + P-network_1_4_RP_5 + P-network_1_4_RP_6 + P-network_1_4_RP_7 + P-network_5_2_RI_7 + P-network_5_2_RI_6 + P-network_5_2_RI_5 + P-network_5_2_RI_4 + P-network_5_2_RI_3 + P-network_5_2_RI_2 + P-network_5_2_RI_1 + P-network_3_4_AskP_1 + P-network_3_4_AskP_2 + P-network_3_4_AskP_3 + P-network_3_4_AskP_4 + P-network_3_4_AskP_5 + P-network_3_4_AskP_6 + P-network_3_4_AskP_7 + P-network_3_3_RP_1 + P-network_3_3_RP_2 + P-network_3_3_RP_3 + P-network_3_3_RP_4 + P-network_3_3_RP_5 + P-network_3_3_RP_6 + P-network_3_3_RP_7 + P-network_6_3_AskP_7 + P-network_6_3_AskP_6 + P-network_6_3_AskP_5 + P-network_6_3_AskP_4 + P-network_6_3_AskP_3 + P-network_6_3_AskP_2 + P-network_6_3_AskP_1 + P-network_0_5_AnnP_1 + P-network_0_5_AnnP_2 + P-network_0_5_AnnP_3 + P-network_0_5_AnnP_4 + P-network_0_5_AnnP_5 + P-network_0_5_AnnP_6 + P-network_0_5_AnnP_7 + P-network_5_2_RP_1 + P-network_5_2_RP_2 + P-network_5_2_RP_3 + P-network_5_2_RP_4 + P-network_5_2_RP_5 + P-network_5_2_RP_6 + P-network_5_2_RP_7 + P-network_7_7_AI_1 + P-network_7_7_AI_2 + P-network_7_7_AI_3 + P-network_7_7_AI_4 + P-network_7_7_AI_5 + P-network_7_7_AI_6 + P-network_7_7_AI_7 + P-network_0_4_AI_1 + P-network_0_4_AI_2 + P-network_0_4_AI_3 + P-network_0_4_AI_4 + P-network_0_4_AI_5 + P-network_0_4_AI_6 + P-network_0_4_AI_7 + P-network_0_7_RI_1 + P-network_0_7_RI_2 + P-network_0_7_RI_3 + P-network_0_7_RI_4 + P-network_0_7_RI_5 + P-network_0_7_RI_6 + P-network_0_7_RI_7 + P-network_7_6_AnnP_1 + P-network_7_6_AnnP_2 + P-network_7_6_AnnP_3 + P-network_7_6_AnnP_4 + P-network_7_6_AnnP_5 + P-network_7_6_AnnP_6 + P-network_7_6_AnnP_7 + P-network_7_1_RP_1 + P-network_7_1_RP_2 + P-network_7_1_RP_3 + P-network_7_1_RP_4 + P-network_7_1_RP_5 + P-network_7_1_RP_6 + P-network_7_1_RP_7 + P-network_2_3_AI_1 + P-network_2_3_AI_2 + P-network_2_3_AI_3 + P-network_2_3_AI_4 + P-network_2_3_AI_5 + P-network_2_3_AI_6 + P-network_2_3_AI_7 + P-network_3_3_RI_7 + P-network_2_6_RI_1 + P-network_2_6_RI_2 + P-network_2_6_RI_3 + P-network_2_6_RI_4 + P-network_2_6_RI_5 + P-network_2_6_RI_6 + P-network_2_6_RI_7 + P-network_3_3_RI_6 + P-network_3_3_RI_5 + P-network_3_3_RI_4 + P-network_3_3_RI_3 + P-network_3_3_RI_2 + P-network_3_3_RI_1 + P-network_5_1_AnnP_1 + P-network_5_1_AnnP_2 + P-network_5_1_AnnP_3 + P-network_5_1_AnnP_4 + P-network_5_1_AnnP_5 + P-network_5_1_AnnP_6 + P-network_5_1_AnnP_7 + P-network_3_0_AI_7 + P-network_3_0_AI_6 + P-network_3_0_AI_5 + P-network_4_2_AI_1 + P-network_4_2_AI_2 + P-network_4_2_AI_3 + P-network_4_2_AI_4 + P-network_4_2_AI_5 + P-network_4_2_AI_6 + P-network_4_2_AI_7 + P-network_3_0_AI_4 + P-network_3_0_AI_3 + P-network_3_0_AI_2 + P-network_3_0_AI_1 + P-network_0_3_AskP_1 + P-network_0_3_AskP_2 + P-network_0_3_AskP_3 + P-network_0_3_AskP_4 + P-network_0_3_AskP_5 + P-network_0_3_AskP_6 + P-network_0_3_AskP_7 + P-network_4_0_AnnP_7 + P-network_4_0_AnnP_6 + P-network_4_0_AnnP_5 + P-network_4_0_AnnP_4 + P-network_4_5_RI_1 + P-network_4_5_RI_2 + P-network_4_5_RI_3 + P-network_4_5_RI_4 + P-network_4_5_RI_5 + P-network_4_5_RI_6 + P-network_4_5_RI_7 + P-network_4_0_AnnP_3 + P-network_7_4_AskP_1 + P-network_7_4_AskP_2 + P-network_7_4_AskP_3 + P-network_7_4_AskP_4 + P-network_7_4_AskP_5 + P-network_7_4_AskP_6 + P-network_7_4_AskP_7 + P-network_4_0_AnnP_2 + P-network_6_1_AI_1 + P-network_6_1_AI_2 + P-network_4_0_AnnP_1 + P-network_6_1_AI_3 + P-network_6_1_AI_4 + P-network_6_1_AI_5 + P-network_6_1_AI_6 + P-network_6_1_AI_7 + P-network_6_4_RI_1 + P-network_6_4_RI_2 + P-network_6_4_RI_3 + P-network_6_4_RI_4 + P-network_6_4_RI_5 + P-network_6_4_RI_6 + P-network_6_4_RI_7 + P-network_1_4_RI_7 + P-network_1_4_RI_6 + P-network_1_4_RI_5 + P-network_1_4_RI_4 + P-network_1_4_RI_3 + P-network_1_4_RI_2 + P-network_1_4_RI_1 + P-network_4_5_AnnP_1 + P-network_4_5_AnnP_2 + P-network_4_5_AnnP_3 + P-network_4_5_AnnP_4 + P-network_4_5_AnnP_5 + P-network_4_5_AnnP_6 + P-network_4_5_AnnP_7 + P-network_1_1_AI_7 + P-network_1_1_AI_6 + P-network_1_1_AI_5 + P-network_1_0_RI_1 + P-network_1_0_RI_2 + P-network_1_0_RI_3 + P-network_1_0_RI_4 + P-network_1_0_RI_5 + P-network_1_0_RI_6 + P-network_1_0_RI_7 + P-network_1_1_AI_4 + P-network_1_1_AI_3 + P-network_1_1_AI_2 + P-network_2_0_AnnP_1 + P-network_2_0_AnnP_2 + P-network_2_0_AnnP_3 + P-network_2_0_AnnP_4 + P-network_2_0_AnnP_5 + P-network_2_0_AnnP_6 + P-network_2_0_AnnP_7 + P-network_1_1_AI_1 + P-network_1_7_AskP_7 + P-network_1_7_AskP_6 + P-network_1_7_AskP_5 + P-network_1_7_AskP_4 + P-network_1_7_AskP_3 + P-network_1_7_AskP_2 + P-network_1_7_AskP_1 + P-network_0_6_RP_1 + P-network_0_6_RP_2 + P-network_0_6_RP_3 + P-network_0_6_RP_4 + P-network_0_6_RP_5 + P-network_0_6_RP_6 + P-network_0_6_RP_7 + P-network_4_3_AskP_1 + P-network_4_3_AskP_2 + P-network_4_3_AskP_3 + P-network_4_3_AskP_4 + P-network_4_3_AskP_5 + P-network_4_3_AskP_6 + P-network_4_3_AskP_7 + P-network_6_5_AnnP_7 + P-network_6_5_AnnP_6 + P-network_6_5_AnnP_5 + P-network_6_5_AnnP_4 + P-network_6_5_AnnP_3 + P-network_2_5_RP_1 + P-network_2_5_RP_2 + P-network_2_5_RP_3 + P-network_2_5_RP_4 + P-network_2_5_RP_5 + P-network_2_5_RP_6 + P-network_2_5_RP_7 + P-network_6_5_AnnP_2 + P-network_6_5_AnnP_1 + P-network_6_5_AI_7 + P-network_1_4_AnnP_1 + P-network_1_4_AnnP_2 + P-network_1_4_AnnP_3 + P-network_1_4_AnnP_4 + P-network_1_4_AnnP_5 + P-network_1_4_AnnP_6 + P-network_1_4_AnnP_7 + P-network_6_5_AI_6 + P-network_6_5_AI_5 + P-network_6_5_AI_4 + P-network_6_5_AI_3 + P-network_6_5_AI_2 + P-network_6_5_AI_1 + P-network_4_4_RP_1 + P-network_4_4_RP_2 + P-network_4_4_RP_3 + P-network_4_4_RP_4 + P-network_4_4_RP_5 + P-network_4_4_RP_6 + P-network_4_4_RP_7 + P-network_4_0_RP_7 + P-network_4_0_RP_6 + P-network_4_0_RP_5 + P-network_4_0_RP_4 + P-network_4_0_RP_3 + P-network_3_7_AskP_1 + P-network_3_7_AskP_2 + P-network_3_7_AskP_3 + P-network_3_7_AskP_4 + P-network_3_7_AskP_5 + P-network_3_7_AskP_6 + P-network_3_7_AskP_7 + P-network_4_0_RP_2 + P-network_6_3_RP_1 + P-network_6_3_RP_2 + P-network_6_3_RP_3 + P-network_6_3_RP_4 + P-network_6_3_RP_5 + P-network_6_3_RP_6 + P-network_6_3_RP_7 + P-network_4_0_RP_1 + P-network_1_5_AI_1 + P-network_1_5_AI_2 + P-network_1_5_AI_3 + P-network_1_5_AI_4 + P-network_1_5_AI_5 + P-network_1_5_AI_6 + P-network_1_5_AI_7 + P-network_4_6_AI_7 + P-network_6_0_AnnP_1 + P-network_6_0_AnnP_2 + P-network_4_6_AI_6 + P-network_6_0_AnnP_3 + P-network_4_6_AI_5 + P-network_6_0_AnnP_4 + P-network_4_6_AI_4 + P-network_6_0_AnnP_5 + P-network_4_6_AI_3 + P-network_6_0_AnnP_6 + P-network_4_6_AI_2 + P-network_6_0_AnnP_7 + P-network_4_6_AI_1 + P-network_2_3_AskP_7 + P-network_2_3_AskP_6 + P-network_2_3_AskP_5 + P-network_2_3_AskP_4 + P-network_2_3_AskP_3 + P-network_2_3_AskP_2 + P-network_2_3_AskP_1 + P-network_2_1_RP_7 + P-network_2_1_RP_6 + P-network_1_2_AskP_1 + P-network_1_2_AskP_2 + P-network_1_2_AskP_3 + P-network_1_2_AskP_4 + P-network_1_2_AskP_5 + P-network_1_2_AskP_6 + P-network_1_2_AskP_7 + P-network_2_1_RP_5 + P-network_2_1_RP_4 + P-network_3_4_AI_1 + P-network_2_1_RP_3 + P-network_3_4_AI_2 + P-network_2_1_RP_2 + P-network_3_4_AI_3 + P-network_2_1_RP_1 + P-network_3_4_AI_4 + P-network_3_4_AI_5 + P-network_3_4_AI_6 + P-network_3_4_AI_7 + P-network_3_7_RI_1 + P-network_3_7_RI_2 + P-network_3_7_RI_3 + P-network_3_7_RI_4 + P-network_3_7_RI_5 + P-network_3_7_RI_6 + P-network_3_7_RI_7 + P-network_7_1_AnnP_7 + P-network_7_1_AnnP_6 + P-network_7_1_AnnP_5 + P-network_7_1_AnnP_4 + P-network_7_1_AnnP_3 + P-network_5_3_AI_1 + P-network_5_3_AI_2 + P-network_5_3_AI_3 + P-network_5_3_AI_4 + P-network_5_3_AI_5 + P-network_5_3_AI_6 + P-network_5_3_AI_7 + P-network_7_1_AnnP_2 + P-network_5_6_RI_1 + P-network_5_6_RI_2 + P-network_5_6_RI_3 + P-network_5_6_RI_4 + P-network_5_6_RI_5 + P-network_5_6_RI_6 + P-network_5_6_RI_7 + P-network_7_1_AnnP_1 + P-network_5_4_AnnP_1 + P-network_5_4_AnnP_2 + P-network_5_4_AnnP_3 + P-network_5_4_AnnP_4 + P-network_5_4_AnnP_5 + P-network_5_4_AnnP_6 + P-network_5_4_AnnP_7 + P-network_7_2_AI_1 + P-network_7_2_AI_2 + P-network_7_2_AI_3 + P-network_7_2_AI_4 + P-network_7_2_AI_5 + P-network_7_2_AI_6 + P-network_7_2_AI_7 + P-network_0_6_AskP_1 + P-network_0_6_AskP_2 + P-network_0_6_AskP_3 + P-network_0_6_AskP_4 + P-network_0_6_AskP_5 + P-network_0_6_AskP_6 + P-network_0_6_AskP_7 + P-network_7_5_RI_1 + P-network_7_5_RI_2 + P-network_7_5_RI_3 + P-network_7_5_RI_4 + P-network_7_5_RI_5 + P-network_7_5_RI_6 + P-network_7_5_RI_7 + P-network_0_2_RI_1 + P-network_0_2_RI_2 + P-network_0_2_RI_3 + P-network_0_2_RI_4 + P-network_0_2_RI_5 + P-network_0_2_RI_6 + P-network_0_2_RI_7 + P-network_7_7_AskP_1 + P-network_7_7_AskP_2 + P-network_7_7_AskP_3 + P-network_7_7_AskP_4 + P-network_7_7_AskP_5 + P-network_7_7_AskP_6 + P-network_7_7_AskP_7 + P-network_2_7_AI_7 + P-network_2_7_AI_6 + P-network_2_7_AI_5 + P-network_2_7_AI_4 + P-network_2_7_AI_3 + P-network_2_7_AI_2 + P-network_2_1_RI_1 + P-network_2_1_RI_2 + P-network_2_1_RI_3 + P-network_2_1_RI_4 + P-network_2_1_RI_5 + P-network_2_1_RI_6 + P-network_2_1_RI_7 + P-network_2_7_AI_1 + P-network_5_2_AskP_1 + P-network_5_2_AskP_2 + P-network_5_2_AskP_3 + P-network_5_2_AskP_4 + P-network_5_2_AskP_5 + P-network_5_2_AskP_6 + P-network_5_2_AskP_7 + P-network_0_2_RP_7 + P-network_0_2_RP_6 + P-network_0_2_RP_5 + P-network_0_2_RP_4 + P-network_0_2_RP_3 + P-network_0_2_RP_2 + P-network_0_2_RP_1 + P-network_7_5_RP_7 + P-network_7_5_RP_6 + P-network_4_0_RI_1 + P-network_4_0_RI_2 + P-network_7_5_RP_5 + P-network_4_0_RI_3 + P-network_1_7_RP_1 + P-network_4_0_RI_4 + P-network_1_7_RP_2 + P-network_4_0_RI_5 + P-network_1_7_RP_3 + P-network_4_0_RI_6 + P-network_1_7_RP_4 + P-network_4_0_RI_7 + P-network_1_7_RP_5 + P-network_1_7_RP_6 + P-network_1_7_RP_7 + P-network_7_5_RP_4 + P-network_7_5_RP_3 + P-network_7_5_RP_2 + P-network_7_5_RP_1 + P-network_0_0_AnnP_7 + P-network_0_0_AnnP_6 + P-network_0_0_AnnP_5 + P-network_0_0_AnnP_4 + P-network_0_0_AnnP_3 + P-network_0_0_AnnP_2 + P-network_0_0_AnnP_1 + P-network_2_3_AnnP_1 + P-network_2_3_AnnP_2 + P-network_2_3_AnnP_3 + P-network_2_3_AnnP_4 + P-network_2_3_AnnP_5 + P-network_2_3_AnnP_6 + P-network_2_3_AnnP_7 + P-network_3_6_RP_1 + P-network_3_6_RP_2 + P-network_3_6_RP_3 + P-network_3_6_RP_4 + P-network_3_6_RP_5 + P-network_3_6_RP_6 + P-network_3_6_RP_7 + P-network_4_6_AskP_1 + P-network_4_6_AskP_2 + P-network_4_6_AskP_3 + P-network_4_6_AskP_4 + P-network_4_6_AskP_5 + P-network_4_6_AskP_6 + P-network_4_6_AskP_7 + P-network_5_5_RP_1 + P-network_5_5_RP_2 + P-network_5_5_RP_3 + P-network_5_5_RP_4 + P-network_5_5_RP_5 + P-network_5_5_RP_6 + P-network_5_5_RP_7 + P-network_5_6_RP_7 + P-network_5_6_RP_6 + P-network_5_6_RP_5 + P-network_5_6_RP_4 + P-network_5_6_RP_3 + P-network_5_6_RP_2 + P-network_5_6_RP_1 + P-network_2_5_AnnP_7 + P-network_2_5_AnnP_6 + P-network_2_5_AnnP_5 + P-network_2_5_AnnP_4 + P-network_2_5_AnnP_3 + P-network_0_7_AI_1 + P-network_0_7_AI_2 + P-network_0_7_AI_3 + P-network_0_7_AI_4 + P-network_0_7_AI_5 + P-network_0_7_AI_6 + P-network_0_7_AI_7 + P-network_2_5_AnnP_2 + P-network_2_5_AnnP_1 + P-network_1_7_AnnP_1 + P-network_1_7_AnnP_2 + P-network_1_7_AnnP_3 + P-network_1_7_AnnP_4 + P-network_1_7_AnnP_5 + P-network_1_7_AnnP_6 + P-network_1_7_AnnP_7 + P-network_7_4_RP_1 + P-network_7_4_RP_2 + P-network_7_4_RP_3 + P-network_7_4_RP_4 + P-network_7_4_RP_5 + P-network_7_4_RP_6 + P-network_7_4_RP_7 + P-network_0_1_RP_1 + P-network_0_1_RP_2 + P-network_0_1_RP_3 + P-network_0_1_RP_4 + P-network_0_1_RP_5 + P-network_0_1_RP_6 + P-network_0_1_RP_7 + P-network_2_1_AskP_1 + P-network_2_1_AskP_2 + P-network_2_1_AskP_3 + P-network_2_1_AskP_4 + P-network_2_1_AskP_5 + P-network_2_1_AskP_6 + P-network_2_1_AskP_7 + P-network_2_6_AI_1 + P-network_2_6_AI_2 + P-network_2_6_AI_3 + P-network_2_6_AI_4 + P-network_2_6_AI_5 + P-network_2_6_AI_6 + P-network_2_6_AI_7 + P-network_2_0_RP_1 + P-network_2_0_RP_2 + P-network_2_0_RP_3 + P-network_2_0_RP_4 + P-network_2_0_RP_5 + P-network_2_0_RP_6 + P-network_2_0_RP_7 + P-network_4_5_AI_1 + P-network_4_5_AI_2 + P-network_4_5_AI_3 + P-network_4_5_AI_4 + P-network_4_5_AI_5 + P-network_4_5_AI_6 + P-network_4_5_AI_7 + P-network_6_3_AnnP_1 + P-network_6_3_AnnP_2 + P-network_6_3_AnnP_3 + P-network_6_3_AnnP_4 + P-network_6_3_AnnP_5 + P-network_6_3_AnnP_6 + P-network_6_3_AnnP_7 + P-network_1_5_AskP_1 + P-network_1_5_AskP_2 + P-network_1_5_AskP_3 + P-network_1_5_AskP_4 + P-network_1_5_AskP_5 + P-network_1_5_AskP_6 + P-network_1_5_AskP_7 + P-network_6_4_AI_1 + P-network_6_4_AI_2 + P-network_6_4_AI_3 + P-network_6_4_AI_4 + P-network_6_4_AI_5 + P-network_6_4_AI_6 + P-network_6_4_AI_7 + P-network_3_7_RP_7 + P-network_6_7_RI_1 + P-network_6_7_RI_2 + P-network_6_7_RI_3 + P-network_6_7_RI_4 + P-network_6_7_RI_5 + P-network_6_7_RI_6 + P-network_6_7_RI_7 + P-network_3_7_RP_6 + P-network_3_7_RP_5 + P-network_6_0_RI_7 + P-network_3_7_RP_4 + P-network_6_0_RI_6 + P-network_3_7_RP_3 + P-network_6_0_RI_5 + P-network_3_7_RP_2 + P-network_6_0_RI_4 + P-network_1_0_AI_1 + P-network_1_0_AI_2 + P-network_1_0_AI_3 + P-network_1_0_AI_4 + P-network_1_0_AI_5 + P-network_1_0_AI_6 + P-network_1_0_AI_7 + P-network_3_7_RP_1 + P-network_1_3_RI_1 + P-network_1_3_RI_2 + P-network_1_3_RI_3 + P-network_1_3_RI_4 + P-network_1_3_RI_5 + P-network_1_3_RI_6 + P-network_1_3_RI_7 + P-network_6_0_RI_3 + P-network_6_0_RI_2 + P-network_6_0_RI_1 + P-network_5_4_AskP_7 + P-network_5_4_AskP_6 + P-network_5_4_AskP_5 + P-network_5_4_AskP_4 + P-network_5_4_AskP_3 + P-network_5_7_AnnP_1 + P-network_5_7_AnnP_2 + P-network_5_7_AnnP_3 + P-network_5_7_AnnP_4 + P-network_5_7_AnnP_5 + P-network_5_7_AnnP_6 + P-network_5_7_AnnP_7 + P-network_5_4_AskP_2 + P-network_6_1_AskP_1 + P-network_6_1_AskP_2 + P-network_6_1_AskP_3 + P-network_6_1_AskP_4 + P-network_6_1_AskP_5 + P-network_6_1_AskP_6 + P-network_6_1_AskP_7 + P-network_5_4_AskP_1 + P-network_3_2_RI_1 + P-network_3_2_RI_2 + P-network_3_2_RI_3 + P-network_3_2_RI_4 + P-network_3_2_RI_5 + P-network_3_2_RI_6 + P-network_3_2_RI_7 + P-network_3_2_AnnP_1 + P-network_3_2_AnnP_2 + P-network_3_2_AnnP_3 + P-network_3_2_AnnP_4 + P-network_3_2_AnnP_5 + P-network_3_2_AnnP_6 + P-network_3_2_AnnP_7 + P-network_5_1_RI_1 + P-network_5_1_RI_2 + P-network_5_1_RI_3 + P-network_5_1_RI_4 + P-network_5_1_RI_5 + P-network_5_1_RI_6 + P-network_5_1_RI_7 + P-network_5_5_AskP_1 + P-network_5_5_AskP_2 + P-network_5_5_AskP_3 + P-network_5_5_AskP_4 + P-network_5_5_AskP_5 + P-network_5_5_AskP_6 + P-network_5_5_AskP_7 + P-network_7_0_RI_1 + P-network_7_0_RI_2 + P-network_7_0_RI_3 + P-network_4_7_RP_1 + P-network_7_0_RI_4 + P-network_4_7_RP_2 + P-network_7_0_RI_5 + P-network_4_7_RP_3 + P-network_7_0_RI_6 + P-network_4_7_RP_4 + P-network_7_0_RI_7 + P-network_4_7_RP_5 + P-network_4_7_RP_6 + P-network_4_7_RP_7 + P-network_2_6_AnnP_1 + P-network_2_6_AnnP_2 + P-network_2_6_AnnP_3 + P-network_2_6_AnnP_4 + P-network_2_6_AnnP_5 + P-network_2_6_AnnP_6 + P-network_2_6_AnnP_7 + P-network_3_0_AskP_1 + P-network_3_0_AskP_2 + P-network_3_0_AskP_3 + P-network_3_0_AskP_4 + P-network_3_0_AskP_5 + P-network_3_0_AskP_6 + P-network_3_0_AskP_7 + P-network_6_6_RP_1 + P-network_6_6_RP_2 + P-network_6_6_RP_3 + P-network_6_6_RP_4 + P-network_6_6_RP_5 + P-network_6_6_RP_6 + P-network_6_6_RP_7 + P-network_4_1_RI_7 + P-network_4_1_RI_6 + P-network_4_1_RI_5 + P-network_4_1_RI_4 + P-network_4_1_RI_3 + P-network_4_1_RI_2 + P-network_4_1_RI_1 + P-network_3_1_AnnP_7 + P-network_3_1_AnnP_6 + P-network_0_1_AnnP_1 + P-network_0_1_AnnP_2 + P-network_0_1_AnnP_3 + P-network_0_1_AnnP_4 + P-network_0_1_AnnP_5 + P-network_0_1_AnnP_6 + P-network_0_1_AnnP_7 + P-network_3_1_AnnP_5 + P-network_1_2_RP_1 + P-network_1_2_RP_2 + P-network_1_2_RP_3 + P-network_1_2_RP_4 + P-network_1_2_RP_5 + P-network_1_2_RP_6 + P-network_1_2_RP_7 + P-network_3_1_AnnP_4 + P-network_3_1_AnnP_3 + P-network_3_1_AnnP_2 + P-network_3_1_AnnP_1 + P-network_3_7_AI_1 + P-network_3_7_AI_2 + P-network_3_7_AI_3 + P-network_3_7_AI_4 + P-network_3_7_AI_5 + P-network_3_7_AI_6 + P-network_3_7_AI_7 + P-network_7_2_AnnP_1 + P-network_7_2_AnnP_2 + P-network_7_2_AnnP_3 + P-network_7_2_AnnP_4 + P-network_7_2_AnnP_5 + P-network_7_2_AnnP_6 + P-network_7_2_AnnP_7 + P-network_3_1_RP_1 + P-network_3_1_RP_2 + P-network_3_1_RP_3 + P-network_3_1_RP_4 + P-network_3_1_RP_5 + P-network_3_1_RP_6 + P-network_3_1_RP_7 + P-network_2_4_AskP_1 + P-network_2_4_AskP_2 + P-network_2_4_AskP_3 + P-network_2_4_AskP_4 + P-network_2_4_AskP_5 + P-network_2_4_AskP_6 + P-network_2_4_AskP_7 + P-network_2_2_RI_7 + P-network_2_2_RI_6 + P-network_2_2_RI_5 + P-network_2_2_RI_4 + P-network_2_2_RI_3 + P-network_2_2_RI_2 + P-network_2_2_RI_1 + P-network_5_6_AI_1 + P-network_5_6_AI_2 + P-network_5_6_AI_3 + P-network_5_6_AI_4 + P-network_5_6_AI_5 + P-network_5_6_AI_6 + P-network_5_6_AI_7 + P-network_5_0_RP_1 + P-network_5_0_RP_2 + P-network_5_0_RP_3 + P-network_5_0_RP_4 + P-network_5_0_RP_5 + P-network_5_0_RP_6 + P-network_5_0_RP_7 + P-network_7_5_AI_1 + P-network_7_5_AI_2 + P-network_7_5_AI_3 + P-network_7_5_AI_4 + P-network_7_5_AI_5 + P-network_7_5_AI_6 + P-network_7_5_AI_7 + P-network_0_2_AI_1 + P-network_0_2_AI_2 + P-network_0_2_AI_3 + P-network_0_2_AI_4 + P-network_0_2_AI_5 + P-network_0_2_AI_6 + P-network_0_2_AI_7 + P-network_6_0_AskP_7 + P-network_6_0_AskP_6 + P-network_0_5_RI_1 + P-network_0_5_RI_2 + P-network_0_5_RI_3 + P-network_0_5_RI_4 + P-network_0_5_RI_5 + P-network_0_5_RI_6 + P-network_0_5_RI_7 + P-network_6_0_AskP_5 + P-network_6_6_AnnP_1 + P-network_6_6_AnnP_2 + P-network_6_6_AnnP_3 + P-network_6_6_AnnP_4 + P-network_6_6_AnnP_5 + P-network_6_6_AnnP_6 + P-network_6_6_AnnP_7 + P-network_6_0_AskP_4 + P-network_7_0_AskP_1 + P-network_7_0_AskP_2 + P-network_7_0_AskP_3 + P-network_7_0_AskP_4 + P-network_7_0_AskP_5 + P-network_7_0_AskP_6 + P-network_7_0_AskP_7 + P-network_6_0_AskP_3 + P-network_2_1_AI_1 + P-network_2_1_AI_2 + P-network_2_1_AI_3 + P-network_2_1_AI_4 + P-network_2_1_AI_5 + P-network_2_1_AI_6 + P-network_2_1_AI_7 + P-network_6_0_AskP_2 + P-network_2_4_RI_1 + P-network_2_4_RI_2 + P-network_2_4_RI_3 + P-network_2_4_RI_4 + P-network_2_4_RI_5 + P-network_2_4_RI_6 + P-network_2_4_RI_7 + P-network_6_0_AskP_1 + P-network_5_6_AnnP_7 + P-network_4_1_AnnP_1 + P-network_4_1_AnnP_2 + P-network_4_1_AnnP_3 + P-network_4_1_AnnP_4 + P-network_4_1_AnnP_5 + P-network_4_1_AnnP_6 + P-network_4_1_AnnP_7 + P-network_5_6_AnnP_6 + P-network_5_6_AnnP_5 + P-network_5_6_AnnP_4 + P-network_5_6_AnnP_3 + P-network_5_6_AnnP_2 + P-network_5_6_AnnP_1 + P-network_4_0_AI_1 + P-network_4_0_AI_2 + P-network_4_0_AI_3 + P-network_4_0_AI_4 + P-network_4_0_AI_5 + P-network_4_0_AI_6 + P-network_4_0_AI_7 + P-network_4_3_RI_1 + P-network_4_3_RI_2 + P-network_4_3_RI_3 + P-network_4_3_RI_4 + P-network_4_3_RI_5 + P-network_4_3_RI_6 + P-network_4_3_RI_7 + P-network_0_3_RI_7 + P-network_0_3_RI_6 + P-network_0_3_RI_5 + P-network_0_3_RI_4 + P-network_6_4_AskP_1 + P-network_6_4_AskP_2 + P-network_6_4_AskP_3 + P-network_6_4_AskP_4 + P-network_6_4_AskP_5 + P-network_6_4_AskP_6 + P-network_6_4_AskP_7 + P-network_0_3_RI_3 + P-network_0_3_RI_2 + P-network_0_3_RI_1 + P-network_7_6_RI_7 + P-network_7_6_RI_6 + P-network_7_6_RI_5 + P-network_7_6_RI_4 + P-network_7_6_RI_3 + P-network_7_6_RI_2 + P-network_6_2_RI_1 + P-network_6_2_RI_2 + P-network_6_2_RI_3 + P-network_6_2_RI_4 + P-network_6_2_RI_5 + P-network_6_2_RI_6 + P-network_6_2_RI_7 + P-network_7_6_RI_1 + P-network_3_5_AnnP_1 + P-network_3_5_AnnP_2 + P-network_3_5_AnnP_3 + P-network_3_5_AnnP_4 + P-network_3_5_AnnP_5 + P-network_3_5_AnnP_6 + P-network_3_5_AnnP_7 + P-network_0_0_AI_7 + P-network_0_0_AI_6 + P-network_0_0_AI_5 + P-network_0_0_AI_4 + P-network_0_0_AI_3 + P-network_0_0_AI_2 + P-network_0_0_AI_1 + P-network_1_0_AnnP_1 + P-network_1_0_AnnP_2 + P-network_1_0_AnnP_3 + P-network_1_0_AnnP_4 + P-network_1_0_AnnP_5 + P-network_1_0_AnnP_6 + P-network_1_0_AnnP_7 + P-network_7_3_AI_7 + P-network_7_7_RP_1 + P-network_7_7_RP_2 + P-network_7_7_RP_3 + P-network_7_7_RP_4 + P-network_7_7_RP_5 + P-network_7_7_RP_6 + P-network_7_7_RP_7 + P-network_7_3_AI_6 + P-network_0_4_RP_1 + P-network_0_4_RP_2 + P-network_0_4_RP_3 + P-network_0_4_RP_4 + P-network_0_4_RP_5 + P-network_0_4_RP_6 + P-network_0_4_RP_7 + P-network_7_3_AI_5 + P-network_7_3_AI_4 + P-network_7_3_AI_3 + P-network_7_3_AI_2 + P-network_7_3_AI_1 + P-network_3_3_AskP_1 + P-network_3_3_AskP_2 + P-network_3_3_AskP_3 + P-network_3_3_AskP_4 + P-network_3_3_AskP_5 + P-network_3_3_AskP_6 + P-network_3_3_AskP_7 + P-network_2_3_RP_1 + P-network_2_3_RP_2 + P-network_2_3_RP_3 + P-network_2_3_RP_4 + P-network_2_3_RP_5 + P-network_2_3_RP_6 + P-network_5_7_RI_7 + P-network_2_3_RP_7 + P-network_5_7_RI_6 + P-network_5_7_RI_5 + P-network_5_7_RI_4 + P-network_5_7_RI_3 + P-network_5_7_RI_2 + P-network_5_7_RI_1 + P-network_5_4_AI_7 + P-network_5_4_AI_6 + P-network_5_4_AI_5 + P-network_5_4_AI_4 + P-network_5_4_AI_3 + P-network_5_4_AI_2 + P-network_5_4_AI_1 + P-network_0_4_AnnP_1 + P-network_0_4_AnnP_2 + P-network_0_4_AnnP_3 + P-network_0_4_AnnP_4 + P-network_0_4_AnnP_5 + P-network_0_4_AnnP_6 + P-network_0_4_AnnP_7 + P-network_1_4_AskP_7 + P-network_4_2_RP_1 + P-network_4_2_RP_2 + P-network_4_2_RP_3 + P-network_4_2_RP_4 + P-network_4_2_RP_5 + P-network_4_2_RP_6 + P-network_4_2_RP_7 + P-network_1_4_AskP_6 + P-network_6_7_AI_1 + P-network_6_7_AI_2 + P-network_6_7_AI_3 + P-network_6_7_AI_4 + P-network_6_7_AI_5 + P-network_6_7_AI_6 + P-network_6_7_AI_7 + P-network_1_4_AskP_5 + P-network_1_4_AskP_4 + P-network_1_4_AskP_3 + P-network_1_4_AskP_2 + P-network_1_4_AskP_1 + P-network_7_5_AnnP_1 + P-network_7_5_AnnP_2 + P-network_7_5_AnnP_3 + P-network_7_5_AnnP_4 + P-network_7_5_AnnP_5 + P-network_7_5_AnnP_6 + P-network_7_5_AnnP_7 + P-network_6_1_RP_1 + P-network_6_1_RP_2 + P-network_6_1_RP_3 + P-network_6_1_RP_4 + P-network_6_1_RP_5 + P-network_6_1_RP_6 + P-network_6_1_RP_7 + P-network_2_7_AskP_1 + P-network_2_7_AskP_2 + P-network_2_7_AskP_3 + P-network_2_7_AskP_4 + P-network_2_7_AskP_5 + P-network_2_7_AskP_6 + P-network_2_7_AskP_7 + P-network_1_3_AI_1 + P-network_1_3_AI_2 + P-network_1_3_AI_3 + P-network_1_3_AI_4 + P-network_1_3_AI_5 + P-network_1_3_AI_6 + P-network_1_3_AI_7 + P-network_1_6_RI_1 + P-network_1_6_RI_2 + P-network_1_6_RI_3 + P-network_1_6_RI_4 + P-network_1_6_RI_5 + P-network_1_6_RI_6 + P-network_1_6_RI_7 + P-network_6_2_AnnP_7 + P-network_5_0_AnnP_1 + P-network_5_0_AnnP_2 + P-network_5_0_AnnP_3 + P-network_5_0_AnnP_4 + P-network_5_0_AnnP_5 + P-network_5_0_AnnP_6 + P-network_5_0_AnnP_7 + P-network_6_2_AnnP_6 + P-network_6_2_AnnP_5 + P-network_6_2_AnnP_4 + P-network_6_2_AnnP_3 + P-network_6_2_AnnP_2 + P-network_6_2_AnnP_1 + P-network_3_2_AI_1 + P-network_3_2_AI_2 + P-network_3_2_AI_3 + P-network_3_2_AI_4 + P-network_3_2_AI_5 + P-network_3_2_AI_6 + P-network_3_2_AI_7 + P-network_0_2_AskP_1 + P-network_0_2_AskP_2 + P-network_0_2_AskP_3 + P-network_0_2_AskP_4 + P-network_0_2_AskP_5 + P-network_0_2_AskP_6 + P-network_0_2_AskP_7 + P-network_3_5_AI_7 + P-network_3_5_AI_6 + P-network_3_5_AI_5 + P-network_3_5_AI_4 + P-network_3_5_RI_1 + P-network_3_5_RI_2 + P-network_3_5_RI_3 + P-network_3_5_RI_4 + P-network_3_5_RI_5 + P-network_3_5_RI_6 + P-network_3_5_RI_7 + P-network_3_5_AI_3 + P-network_7_3_AskP_1 + P-network_7_3_AskP_2 + P-network_7_3_AskP_3 + P-network_7_3_AskP_4 + P-network_7_3_AskP_5 + P-network_7_3_AskP_6 + P-network_7_3_AskP_7 + P-network_3_5_AI_2 + P-network_5_1_AI_1 + P-network_5_1_AI_2 + P-network_3_5_AI_1 + P-network_5_1_AI_3 + P-network_5_1_AI_4 + P-network_5_1_AI_5 + P-network_5_1_AI_6 + P-network_5_1_AI_7 + P-network_5_4_RI_1 + P-network_5_4_RI_2 + P-network_5_4_RI_3 + P-network_5_4_RI_4 + P-network_5_4_RI_5 + P-network_5_4_RI_6 + P-network_5_4_RI_7 + P-network_1_0_RP_7 + P-network_1_0_RP_6 + P-network_1_0_RP_5 + P-network_1_0_RP_4 + P-network_1_0_RP_3 + P-network_1_0_RP_2 + P-network_1_0_RP_1 + P-network_4_4_AnnP_1 + P-network_4_4_AnnP_2 + P-network_4_4_AnnP_3 + P-network_4_4_AnnP_4 + P-network_4_4_AnnP_5 + P-network_4_4_AnnP_6 + P-network_4_4_AnnP_7 + P-network_1_6_AI_7 + P-network_7_0_AI_1 + P-network_1_6_AI_6 + P-network_7_0_AI_2 + P-network_1_6_AI_5 + P-network_7_0_AI_3 + P-network_1_6_AI_4 + P-network_7_0_AI_4 + P-network_1_6_AI_3 + P-network_7_0_AI_5 + P-network_1_6_AI_2 + P-network_7_0_AI_6 + P-network_1_6_AI_1 + P-network_7_0_AI_7 + P-network_7_3_RI_1 + P-network_7_3_RI_2 + P-network_7_3_RI_3 + P-network_7_3_RI_4 + P-network_7_3_RI_5 + P-network_7_3_RI_6 + P-network_7_3_RI_7 + P-network_2_0_AskP_7 + P-network_0_0_RI_1 + P-network_0_0_RI_2 + P-network_0_0_RI_3 + P-network_0_0_RI_4 + P-network_0_0_RI_5 + P-network_0_0_RI_6 + P-network_0_0_RI_7 + P-network_2_0_AskP_6 + P-network_6_7_AskP_1 + P-network_6_7_AskP_2 + P-network_6_7_AskP_3 + P-network_6_7_AskP_4 + P-network_6_7_AskP_5 + P-network_6_7_AskP_6 + P-network_6_7_AskP_7 + P-network_2_0_AskP_5 + P-network_2_0_AskP_4 + P-network_2_0_AskP_3 + P-network_2_0_AskP_2 + P-network_2_0_AskP_1 + P-network_4_2_AskP_1 + P-network_4_2_AskP_2 + P-network_4_2_AskP_3 + P-network_4_2_AskP_4 + P-network_4_2_AskP_5 + P-network_4_2_AskP_6 + P-network_4_2_AskP_7 + P-network_6_4_RP_7 + P-network_6_4_RP_6 + P-network_6_4_RP_5 + P-network_6_4_RP_4 + P-network_6_4_RP_3 + P-network_1_5_RP_1 + P-network_1_5_RP_2 + P-network_1_5_RP_3 + P-network_1_5_RP_4 + P-network_1_5_RP_5 + P-network_1_5_RP_6 + P-network_1_5_RP_7 + P-network_6_4_RP_2 + P-network_6_4_RP_1 + P-network_1_6_AnnP_7 + P-network_1_6_AnnP_6 + P-network_1_6_AnnP_5 + P-network_1_3_AnnP_1 + P-network_1_3_AnnP_2 + P-network_1_3_AnnP_3 + P-network_1_3_AnnP_4 + P-network_1_3_AnnP_5 + P-network_1_3_AnnP_6 + P-network_1_3_AnnP_7 + P-network_3_4_RP_1 + P-network_3_4_RP_2 + P-network_3_4_RP_3 + P-network_3_4_RP_4 + P-network_3_4_RP_5 + P-network_3_4_RP_6 + P-network_3_4_RP_7 + P-network_1_6_AnnP_4 + P-network_1_6_AnnP_3 + P-network_1_6_AnnP_2 + P-network_1_6_AnnP_1 + P-network_3_6_AskP_1 + P-network_3_6_AskP_2 + P-network_3_6_AskP_3 + P-network_3_6_AskP_4 + P-network_3_6_AskP_5 + P-network_3_6_AskP_6 + P-network_3_6_AskP_7 + P-network_5_3_RP_1 + P-network_5_3_RP_2 + P-network_5_3_RP_3 + P-network_5_3_RP_4 + P-network_5_3_RP_5 + P-network_5_3_RP_6 + P-network_5_3_RP_7 + P-network_0_5_AI_1 + P-network_0_5_AI_2 + P-network_0_5_AI_3 + P-network_0_5_AI_4 + P-network_0_5_AI_5 + P-network_0_5_AI_6 + P-network_0_5_AI_7 + P-network_0_7_AnnP_1 + P-network_0_7_AnnP_2 + P-network_0_7_AnnP_3 + P-network_0_7_AnnP_4 + P-network_0_7_AnnP_5 + P-network_0_7_AnnP_6 + P-network_0_7_AnnP_7 + P-network_7_2_RP_1 + P-network_7_2_RP_2 + P-network_7_2_RP_3 + P-network_7_2_RP_4 + P-network_7_2_RP_5 + P-network_7_2_RP_6 + P-network_7_2_RP_7 + P-network_1_1_AskP_1 + P-network_1_1_AskP_2 + P-network_1_1_AskP_3 + P-network_1_1_AskP_4 + P-network_1_1_AskP_5 + P-network_1_1_AskP_6 + P-network_1_1_AskP_7 + P-network_2_4_AI_1 + P-network_2_4_AI_2 + P-network_2_4_AI_3 + P-network_4_5_RP_7 + P-network_2_4_AI_4 + P-network_4_5_RP_6 + P-network_2_4_AI_5 + P-network_4_5_RP_5 + P-network_2_4_AI_6 + P-network_4_5_RP_4 + P-network_2_4_AI_7 + P-network_4_5_RP_3 + P-network_2_7_RI_1 + P-network_2_7_RI_2 + P-network_2_7_RI_3 + P-network_2_7_RI_4 + P-network_2_7_RI_5 + P-network_2_7_RI_6 + P-network_2_7_RI_7 + P-network_4_5_RP_2 + P-network_4_5_RP_1 + P-network_4_5_AskP_7 + P-network_4_5_AskP_6 + P-network_4_5_AskP_5 + P-network_4_5_AskP_4 + P-network_4_5_AskP_3 + P-network_4_5_AskP_2 + P-network_4_5_AskP_1 + P-network_4_3_AI_1 + P-network_4_3_AI_2 + P-network_4_3_AI_3 + P-network_4_3_AI_4 + P-network_4_3_AI_5 + P-network_4_3_AI_6 + P-network_4_3_AI_7 + P-network_4_6_RI_1 + P-network_4_6_RI_2 + P-network_4_6_RI_3 + P-network_4_6_RI_4 + P-network_4_6_RI_5 + P-network_4_6_RI_6 + P-network_4_6_RI_7 + P-network_5_3_AnnP_1 + P-network_5_3_AnnP_2 + P-network_5_3_AnnP_3 + P-network_5_3_AnnP_4 + P-network_5_3_AnnP_5 + P-network_5_3_AnnP_6 + P-network_5_3_AnnP_7 + P-network_6_2_AI_1 + P-network_6_2_AI_2 + P-network_6_2_AI_3 + P-network_6_2_AI_4 + P-network_6_2_AI_5 + P-network_6_2_AI_6 + P-network_6_2_AI_7 + P-network_0_5_AskP_1 + P-network_0_5_AskP_2 + P-network_0_5_AskP_3 + P-network_0_5_AskP_4 + P-network_0_5_AskP_5 + P-network_0_5_AskP_6 + P-network_0_5_AskP_7 + P-network_6_5_RI_1 + P-network_6_5_RI_2 + P-network_6_5_RI_3 + P-network_6_5_RI_4 + P-network_6_5_RI_5 + P-network_6_5_RI_6 + P-network_6_5_RI_7 + P-network_7_6_AskP_1 + P-network_7_6_AskP_2 + P-network_7_6_AskP_3 + P-network_7_6_AskP_4 + P-network_7_6_AskP_5 + P-network_7_6_AskP_6 + P-network_7_6_AskP_7 + P-network_1_1_RI_1 + P-network_1_1_RI_2 + P-network_1_1_RI_3 + P-network_1_1_RI_4 + P-network_1_1_RI_5 + P-network_1_1_RI_6 + P-network_1_1_RI_7 + P-network_2_6_RP_7 + P-network_2_6_RP_6 + P-network_2_6_RP_5 + P-network_2_6_RP_4 + P-network_4_7_AnnP_1 + P-network_4_7_AnnP_2 + P-network_4_7_AnnP_3 + P-network_4_7_AnnP_4 + P-network_4_7_AnnP_5 + P-network_4_7_AnnP_6 + P-network_4_7_AnnP_7 + P-network_2_6_RP_3 + P-network_5_1_AskP_1 + P-network_5_1_AskP_2 + P-network_5_1_AskP_3 + P-network_5_1_AskP_4 + P-network_5_1_AskP_5 + P-network_5_1_AskP_6 + P-network_5_1_AskP_7 + P-network_2_6_RP_2 + P-network_2_6_RP_1 + P-network_2_2_AnnP_7 + P-network_2_2_AnnP_6 + P-network_2_2_AnnP_5 + P-network_2_2_AnnP_4 + P-network_2_2_AnnP_3 + P-network_2_2_AnnP_2 + P-network_3_0_RI_1 + P-network_3_0_RI_2 + P-network_2_2_AnnP_1 + P-network_3_0_RI_3 + P-network_0_7_RP_1 + P-network_3_0_RI_4 + P-network_0_7_RP_2 + P-network_3_0_RI_5 + P-network_0_7_RP_3 + P-network_3_0_RI_6 + P-network_0_7_RP_4 + P-network_3_0_RI_7 + P-network_0_7_RP_5 + P-network_0_7_RP_6 + P-network_0_7_RP_7 + 1 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7) AND (1 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-poll__networl_0_3_AnsP_7 + P-poll__networl_0_3_AnsP_6 + P-poll__networl_0_3_AnsP_5 + P-poll__networl_0_3_AnsP_4 + P-poll__networl_0_3_AnsP_3 + P-poll__networl_0_3_AnsP_2 + P-poll__networl_0_3_AnsP_1 + P-poll__networl_3_4_AnsP_7 + P-poll__networl_3_4_AnsP_6 + P-poll__networl_3_4_AnsP_5 + P-poll__networl_3_4_AnsP_4 + P-poll__networl_3_4_AnsP_3 + P-poll__networl_3_4_AnsP_2 + P-poll__networl_3_4_AnsP_1 + P-poll__networl_4_0_AnsP_7 + P-poll__networl_4_0_AnsP_6 + P-poll__networl_4_0_AnsP_5 + P-poll__networl_4_0_AnsP_4 + P-poll__networl_4_0_AnsP_3 + P-poll__networl_4_0_AnsP_2 + P-poll__networl_4_0_AnsP_1 + P-poll__networl_6_5_AnsP_7 + P-poll__networl_6_5_AnsP_6 + P-poll__networl_6_5_AnsP_5 + P-poll__networl_6_5_AnsP_4 + P-poll__networl_6_5_AnsP_3 + P-poll__networl_6_5_AnsP_2 + P-poll__networl_6_5_AnsP_1 + P-poll__networl_4_3_AnsP_1 + P-poll__networl_4_3_AnsP_2 + P-poll__networl_4_3_AnsP_3 + P-poll__networl_4_3_AnsP_4 + P-poll__networl_4_3_AnsP_5 + P-poll__networl_4_3_AnsP_6 + P-poll__networl_4_3_AnsP_7 + P-poll__networl_7_1_AnsP_7 + P-poll__networl_7_1_AnsP_6 + P-poll__networl_7_1_AnsP_5 + P-poll__networl_7_1_AnsP_4 + P-poll__networl_7_1_AnsP_3 + P-poll__networl_7_1_AnsP_2 + P-poll__networl_7_1_AnsP_1 + P-poll__networl_0_0_AnsP_7 + P-poll__networl_0_0_AnsP_6 + P-poll__networl_0_0_AnsP_5 + P-poll__networl_0_0_AnsP_4 + P-poll__networl_0_0_AnsP_3 + P-poll__networl_0_0_AnsP_2 + P-poll__networl_0_0_AnsP_1 + P-poll__networl_2_5_AnsP_7 + P-poll__networl_2_5_AnsP_6 + P-poll__networl_2_5_AnsP_5 + P-poll__networl_2_5_AnsP_4 + P-poll__networl_2_5_AnsP_3 + P-poll__networl_2_5_AnsP_2 + P-poll__networl_2_5_AnsP_1 + P-poll__networl_3_1_AnsP_7 + P-poll__networl_3_1_AnsP_6 + P-poll__networl_3_1_AnsP_5 + P-poll__networl_3_1_AnsP_4 + P-poll__networl_3_1_AnsP_3 + P-poll__networl_3_1_AnsP_2 + P-poll__networl_3_1_AnsP_1 + P-poll__networl_3_7_AnsP_1 + P-poll__networl_3_7_AnsP_2 + P-poll__networl_3_7_AnsP_3 + P-poll__networl_3_7_AnsP_4 + P-poll__networl_3_7_AnsP_5 + P-poll__networl_3_7_AnsP_6 + P-poll__networl_3_7_AnsP_7 + P-poll__networl_5_6_AnsP_7 + P-poll__networl_5_6_AnsP_6 + P-poll__networl_5_6_AnsP_5 + P-poll__networl_5_6_AnsP_4 + P-poll__networl_5_6_AnsP_3 + P-poll__networl_5_6_AnsP_2 + P-poll__networl_5_6_AnsP_1 + P-poll__networl_6_2_AnsP_7 + P-poll__networl_6_2_AnsP_6 + P-poll__networl_6_2_AnsP_5 + P-poll__networl_6_2_AnsP_4 + P-poll__networl_6_2_AnsP_3 + P-poll__networl_6_2_AnsP_2 + P-poll__networl_6_2_AnsP_1 + P-poll__networl_1_6_AnsP_7 + P-poll__networl_1_6_AnsP_6 + P-poll__networl_1_6_AnsP_5 + P-poll__networl_1_2_AnsP_1 + P-poll__networl_1_2_AnsP_2 + P-poll__networl_1_2_AnsP_3 + P-poll__networl_1_2_AnsP_4 + P-poll__networl_1_2_AnsP_5 + P-poll__networl_1_2_AnsP_6 + P-poll__networl_1_2_AnsP_7 + P-poll__networl_1_6_AnsP_4 + P-poll__networl_1_6_AnsP_3 + P-poll__networl_1_6_AnsP_2 + P-poll__networl_1_6_AnsP_1 + P-poll__networl_2_2_AnsP_7 + P-poll__networl_2_2_AnsP_6 + P-poll__networl_2_2_AnsP_5 + P-poll__networl_2_2_AnsP_4 + P-poll__networl_2_2_AnsP_3 + P-poll__networl_2_2_AnsP_2 + P-poll__networl_2_2_AnsP_1 + P-poll__networl_4_7_AnsP_7 + P-poll__networl_4_7_AnsP_6 + P-poll__networl_4_7_AnsP_5 + P-poll__networl_4_7_AnsP_4 + P-poll__networl_4_7_AnsP_3 + P-poll__networl_4_7_AnsP_2 + P-poll__networl_4_7_AnsP_1 + P-poll__networl_5_3_AnsP_7 + P-poll__networl_5_3_AnsP_6 + P-poll__networl_5_3_AnsP_5 + P-poll__networl_5_3_AnsP_4 + P-poll__networl_5_3_AnsP_3 + P-poll__networl_5_3_AnsP_2 + P-poll__networl_5_3_AnsP_1 + P-poll__networl_0_6_AnsP_1 + P-poll__networl_0_6_AnsP_2 + P-poll__networl_0_6_AnsP_3 + P-poll__networl_0_6_AnsP_4 + P-poll__networl_0_6_AnsP_5 + P-poll__networl_0_6_AnsP_6 + P-poll__networl_0_6_AnsP_7 + P-poll__networl_0_7_AnsP_7 + P-poll__networl_0_7_AnsP_6 + P-poll__networl_0_7_AnsP_5 + P-poll__networl_0_7_AnsP_4 + P-poll__networl_0_7_AnsP_3 + P-poll__networl_0_7_AnsP_2 + P-poll__networl_0_7_AnsP_1 + P-poll__networl_1_3_AnsP_7 + P-poll__networl_1_3_AnsP_6 + P-poll__networl_1_3_AnsP_5 + P-poll__networl_1_3_AnsP_4 + P-poll__networl_7_7_AnsP_1 + P-poll__networl_7_7_AnsP_2 + P-poll__networl_7_7_AnsP_3 + P-poll__networl_7_7_AnsP_4 + P-poll__networl_7_7_AnsP_5 + P-poll__networl_7_7_AnsP_6 + P-poll__networl_7_7_AnsP_7 + P-poll__networl_1_3_AnsP_3 + P-poll__networl_1_3_AnsP_2 + P-poll__networl_1_3_AnsP_1 + P-poll__networl_4_4_AnsP_7 + P-poll__networl_4_4_AnsP_6 + P-poll__networl_4_4_AnsP_5 + P-poll__networl_4_4_AnsP_4 + P-poll__networl_4_4_AnsP_3 + P-poll__networl_4_4_AnsP_2 + P-poll__networl_4_4_AnsP_1 + P-poll__networl_5_2_AnsP_1 + P-poll__networl_5_2_AnsP_2 + P-poll__networl_5_2_AnsP_3 + P-poll__networl_5_2_AnsP_4 + P-poll__networl_5_2_AnsP_5 + P-poll__networl_5_2_AnsP_6 + P-poll__networl_5_2_AnsP_7 + P-poll__networl_5_0_AnsP_7 + P-poll__networl_5_0_AnsP_6 + P-poll__networl_5_0_AnsP_5 + P-poll__networl_5_0_AnsP_4 + P-poll__networl_5_0_AnsP_3 + P-poll__networl_5_0_AnsP_2 + P-poll__networl_5_0_AnsP_1 + P-poll__networl_7_5_AnsP_7 + P-poll__networl_7_5_AnsP_6 + P-poll__networl_7_5_AnsP_5 + P-poll__networl_7_5_AnsP_4 + P-poll__networl_7_5_AnsP_3 + P-poll__networl_7_5_AnsP_2 + P-poll__networl_7_5_AnsP_1 + P-poll__networl_0_4_AnsP_7 + P-poll__networl_0_4_AnsP_6 + P-poll__networl_0_4_AnsP_5 + P-poll__networl_0_4_AnsP_4 + P-poll__networl_0_4_AnsP_3 + P-poll__networl_0_4_AnsP_2 + P-poll__networl_0_4_AnsP_1 + P-poll__networl_1_0_AnsP_7 + P-poll__networl_1_0_AnsP_6 + P-poll__networl_1_0_AnsP_5 + P-poll__networl_1_0_AnsP_4 + P-poll__networl_1_0_AnsP_3 + P-poll__networl_1_0_AnsP_2 + P-poll__networl_1_0_AnsP_1 + P-poll__networl_3_5_AnsP_7 + P-poll__networl_3_5_AnsP_6 + P-poll__networl_3_5_AnsP_5 + P-poll__networl_3_5_AnsP_4 + P-poll__networl_3_5_AnsP_3 + P-poll__networl_3_5_AnsP_2 + P-poll__networl_3_5_AnsP_1 + P-poll__networl_4_6_AnsP_1 + P-poll__networl_4_6_AnsP_2 + P-poll__networl_4_6_AnsP_3 + P-poll__networl_4_6_AnsP_4 + P-poll__networl_4_6_AnsP_5 + P-poll__networl_4_6_AnsP_6 + P-poll__networl_4_6_AnsP_7 + P-poll__networl_4_1_AnsP_7 + P-poll__networl_4_1_AnsP_6 + P-poll__networl_4_1_AnsP_5 + P-poll__networl_4_1_AnsP_4 + P-poll__networl_4_1_AnsP_3 + P-poll__networl_4_1_AnsP_2 + P-poll__networl_4_1_AnsP_1 + P-poll__networl_2_1_AnsP_1 + P-poll__networl_2_1_AnsP_2 + P-poll__networl_2_1_AnsP_3 + P-poll__networl_2_1_AnsP_4 + P-poll__networl_2_1_AnsP_5 + P-poll__networl_2_1_AnsP_6 + P-poll__networl_2_1_AnsP_7 + P-poll__networl_6_6_AnsP_7 + P-poll__networl_6_6_AnsP_6 + P-poll__networl_6_6_AnsP_5 + P-poll__networl_6_6_AnsP_4 + P-poll__networl_6_6_AnsP_3 + P-poll__networl_6_6_AnsP_2 + P-poll__networl_6_6_AnsP_1 + P-poll__networl_7_2_AnsP_7 + P-poll__networl_7_2_AnsP_6 + P-poll__networl_7_2_AnsP_5 + P-poll__networl_7_2_AnsP_4 + P-poll__networl_7_2_AnsP_3 + P-poll__networl_7_2_AnsP_2 + P-poll__networl_7_2_AnsP_1 + P-poll__networl_0_1_AnsP_7 + P-poll__networl_0_1_AnsP_6 + P-poll__networl_0_1_AnsP_5 + P-poll__networl_0_1_AnsP_4 + P-poll__networl_0_1_AnsP_3 + P-poll__networl_0_1_AnsP_2 + P-poll__networl_0_1_AnsP_1 + P-poll__networl_2_6_AnsP_7 + P-poll__networl_2_6_AnsP_6 + P-poll__networl_2_6_AnsP_5 + P-poll__networl_2_6_AnsP_4 + P-poll__networl_2_6_AnsP_3 + P-poll__networl_2_6_AnsP_2 + P-poll__networl_2_6_AnsP_1 + P-poll__networl_1_5_AnsP_1 + P-poll__networl_1_5_AnsP_2 + P-poll__networl_1_5_AnsP_3 + P-poll__networl_1_5_AnsP_4 + P-poll__networl_1_5_AnsP_5 + P-poll__networl_1_5_AnsP_6 + P-poll__networl_1_5_AnsP_7 + P-poll__networl_3_2_AnsP_7 + P-poll__networl_3_2_AnsP_6 + P-poll__networl_3_2_AnsP_5 + P-poll__networl_3_2_AnsP_4 + P-poll__networl_3_2_AnsP_3 + P-poll__networl_3_2_AnsP_2 + P-poll__networl_3_2_AnsP_1 + P-poll__networl_5_7_AnsP_7 + P-poll__networl_5_7_AnsP_6 + P-poll__networl_5_7_AnsP_5 + P-poll__networl_5_7_AnsP_4 + P-poll__networl_5_7_AnsP_3 + P-poll__networl_5_7_AnsP_2 + P-poll__networl_5_7_AnsP_1 + P-poll__networl_6_3_AnsP_7 + P-poll__networl_6_3_AnsP_6 + P-poll__networl_6_3_AnsP_5 + P-poll__networl_6_3_AnsP_4 + P-poll__networl_6_3_AnsP_3 + P-poll__networl_6_3_AnsP_2 + P-poll__networl_6_3_AnsP_1 + P-poll__networl_6_1_AnsP_1 + P-poll__networl_6_1_AnsP_2 + P-poll__networl_6_1_AnsP_3 + P-poll__networl_6_1_AnsP_4 + P-poll__networl_6_1_AnsP_5 + P-poll__networl_6_1_AnsP_6 + P-poll__networl_6_1_AnsP_7 + P-poll__networl_1_7_AnsP_7 + P-poll__networl_1_7_AnsP_6 + P-poll__networl_1_7_AnsP_5 + P-poll__networl_1_7_AnsP_4 + P-poll__networl_1_7_AnsP_3 + P-poll__networl_1_7_AnsP_2 + P-poll__networl_1_7_AnsP_1 + P-poll__networl_2_3_AnsP_7 + P-poll__networl_2_3_AnsP_6 + P-poll__networl_2_3_AnsP_5 + P-poll__networl_2_3_AnsP_4 + P-poll__networl_2_3_AnsP_3 + P-poll__networl_2_3_AnsP_2 + P-poll__networl_2_3_AnsP_1 + P-poll__networl_5_4_AnsP_7 + P-poll__networl_5_4_AnsP_6 + P-poll__networl_5_4_AnsP_5 + P-poll__networl_5_4_AnsP_4 + P-poll__networl_5_4_AnsP_3 + P-poll__networl_5_4_AnsP_2 + P-poll__networl_5_4_AnsP_1 + P-poll__networl_5_5_AnsP_1 + P-poll__networl_5_5_AnsP_2 + P-poll__networl_5_5_AnsP_3 + P-poll__networl_5_5_AnsP_4 + P-poll__networl_5_5_AnsP_5 + P-poll__networl_5_5_AnsP_6 + P-poll__networl_5_5_AnsP_7 + P-poll__networl_6_0_AnsP_7 + P-poll__networl_6_0_AnsP_6 + P-poll__networl_6_0_AnsP_5 + P-poll__networl_6_0_AnsP_4 + P-poll__networl_6_0_AnsP_3 + P-poll__networl_6_0_AnsP_2 + P-poll__networl_6_0_AnsP_1 + P-poll__networl_1_4_AnsP_7 + P-poll__networl_1_4_AnsP_6 + P-poll__networl_1_4_AnsP_5 + P-poll__networl_1_4_AnsP_4 + P-poll__networl_1_4_AnsP_3 + P-poll__networl_1_4_AnsP_2 + P-poll__networl_1_4_AnsP_1 + P-poll__networl_3_0_AnsP_1 + P-poll__networl_3_0_AnsP_2 + P-poll__networl_3_0_AnsP_3 + P-poll__networl_3_0_AnsP_4 + P-poll__networl_3_0_AnsP_5 + P-poll__networl_3_0_AnsP_6 + P-poll__networl_3_0_AnsP_7 + P-poll__networl_2_0_AnsP_7 + P-poll__networl_2_0_AnsP_6 + P-poll__networl_2_0_AnsP_5 + P-poll__networl_2_0_AnsP_4 + P-poll__networl_2_0_AnsP_3 + P-poll__networl_2_0_AnsP_2 + P-poll__networl_2_0_AnsP_1 + P-poll__networl_4_5_AnsP_7 + P-poll__networl_4_5_AnsP_6 + P-poll__networl_4_5_AnsP_5 + P-poll__networl_4_5_AnsP_4 + P-poll__networl_4_5_AnsP_3 + P-poll__networl_4_5_AnsP_2 + P-poll__networl_4_5_AnsP_1 + P-poll__networl_5_1_AnsP_7 + P-poll__networl_5_1_AnsP_6 + P-poll__networl_5_1_AnsP_5 + P-poll__networl_5_1_AnsP_4 + P-poll__networl_5_1_AnsP_3 + P-poll__networl_5_1_AnsP_2 + P-poll__networl_5_1_AnsP_1 + P-poll__networl_7_6_AnsP_7 + P-poll__networl_7_6_AnsP_6 + P-poll__networl_7_6_AnsP_5 + P-poll__networl_7_6_AnsP_4 + P-poll__networl_7_6_AnsP_3 + P-poll__networl_7_6_AnsP_2 + P-poll__networl_7_6_AnsP_1 + P-poll__networl_0_5_AnsP_7 + P-poll__networl_0_5_AnsP_6 + P-poll__networl_0_5_AnsP_5 + P-poll__networl_0_5_AnsP_4 + P-poll__networl_0_5_AnsP_3 + P-poll__networl_0_5_AnsP_2 + P-poll__networl_0_5_AnsP_1 + P-poll__networl_1_1_AnsP_7 + P-poll__networl_1_1_AnsP_6 + P-poll__networl_1_1_AnsP_5 + P-poll__networl_1_1_AnsP_4 + P-poll__networl_1_1_AnsP_3 + P-poll__networl_1_1_AnsP_2 + P-poll__networl_1_1_AnsP_1 + P-poll__networl_2_4_AnsP_1 + P-poll__networl_2_4_AnsP_2 + P-poll__networl_2_4_AnsP_3 + P-poll__networl_2_4_AnsP_4 + P-poll__networl_2_4_AnsP_5 + P-poll__networl_2_4_AnsP_6 + P-poll__networl_2_4_AnsP_7 + P-poll__networl_3_6_AnsP_7 + P-poll__networl_3_6_AnsP_6 + P-poll__networl_3_6_AnsP_5 + P-poll__networl_3_6_AnsP_4 + P-poll__networl_3_6_AnsP_3 + P-poll__networl_3_6_AnsP_2 + P-poll__networl_3_6_AnsP_1 + P-poll__networl_4_2_AnsP_7 + P-poll__networl_4_2_AnsP_6 + P-poll__networl_4_2_AnsP_5 + P-poll__networl_4_2_AnsP_4 + P-poll__networl_4_2_AnsP_3 + P-poll__networl_4_2_AnsP_2 + P-poll__networl_4_2_AnsP_1 + P-poll__networl_6_7_AnsP_7 + P-poll__networl_6_7_AnsP_6 + P-poll__networl_6_7_AnsP_5 + P-poll__networl_6_7_AnsP_4 + P-poll__networl_6_7_AnsP_3 + P-poll__networl_6_7_AnsP_2 + P-poll__networl_6_7_AnsP_1 + P-poll__networl_7_0_AnsP_1 + P-poll__networl_7_0_AnsP_2 + P-poll__networl_7_0_AnsP_3 + P-poll__networl_7_0_AnsP_4 + P-poll__networl_7_0_AnsP_5 + P-poll__networl_7_0_AnsP_6 + P-poll__networl_7_0_AnsP_7 + P-poll__networl_7_3_AnsP_7 + P-poll__networl_7_3_AnsP_6 + P-poll__networl_7_3_AnsP_5 + P-poll__networl_7_3_AnsP_4 + P-poll__networl_7_3_AnsP_3 + P-poll__networl_7_3_AnsP_2 + P-poll__networl_7_3_AnsP_1 + P-poll__networl_0_2_AnsP_7 + P-poll__networl_0_2_AnsP_6 + P-poll__networl_0_2_AnsP_5 + P-poll__networl_0_2_AnsP_4 + P-poll__networl_0_2_AnsP_3 + P-poll__networl_0_2_AnsP_2 + P-poll__networl_0_2_AnsP_1 + P-poll__networl_2_7_AnsP_7 + P-poll__networl_2_7_AnsP_6 + P-poll__networl_2_7_AnsP_5 + P-poll__networl_2_7_AnsP_4 + P-poll__networl_2_7_AnsP_3 + P-poll__networl_2_7_AnsP_2 + P-poll__networl_2_7_AnsP_1 + P-poll__networl_3_3_AnsP_7 + P-poll__networl_3_3_AnsP_6 + P-poll__networl_3_3_AnsP_5 + P-poll__networl_3_3_AnsP_4 + P-poll__networl_3_3_AnsP_3 + P-poll__networl_3_3_AnsP_2 + P-poll__networl_3_3_AnsP_1 + P-poll__networl_6_4_AnsP_1 + P-poll__networl_6_4_AnsP_2 + P-poll__networl_6_4_AnsP_3 + P-poll__networl_6_4_AnsP_4 + P-poll__networl_6_4_AnsP_5 + P-poll__networl_6_4_AnsP_6 + P-poll__networl_6_4_AnsP_7 + P-poll__networl_0_0_AskP_1 + P-poll__networl_0_0_AskP_2 + P-poll__networl_0_0_AskP_3 + P-poll__networl_0_0_AskP_4 + P-poll__networl_0_0_AskP_5 + P-poll__networl_0_0_AskP_6 + P-poll__networl_0_0_AskP_7 + P-poll__networl_3_3_RI_0 + P-poll__networl_3_3_RI_1 + P-poll__networl_3_3_RI_2 + P-poll__networl_3_3_RI_3 + P-poll__networl_3_3_RI_4 + P-poll__networl_3_3_RI_5 + P-poll__networl_3_3_RI_6 + P-poll__networl_3_3_RI_7 + P-poll__networl_0_0_AskP_0 + P-poll__networl_6_7_AnnP_0 + P-poll__networl_6_7_AnnP_1 + P-poll__networl_6_7_AnnP_2 + P-poll__networl_6_7_AnnP_3 + P-poll__networl_6_7_AnnP_4 + P-poll__networl_6_7_AnnP_5 + P-poll__networl_6_7_AnnP_6 + P-poll__networl_6_7_AnnP_7 + P-poll__networl_3_0_AI_7 + P-poll__networl_7_1_AskP_0 + P-poll__networl_7_1_AskP_1 + P-poll__networl_7_1_AskP_2 + P-poll__networl_7_1_AskP_3 + P-poll__networl_7_1_AskP_4 + P-poll__networl_7_1_AskP_5 + P-poll__networl_7_1_AskP_6 + P-poll__networl_7_1_AskP_7 + P-poll__networl_3_0_AI_6 + P-poll__networl_3_0_AI_5 + P-poll__networl_5_2_RI_0 + P-poll__networl_5_2_RI_1 + P-poll__networl_5_2_RI_2 + P-poll__networl_5_2_RI_3 + P-poll__networl_5_2_RI_4 + P-poll__networl_5_2_RI_5 + P-poll__networl_5_2_RI_6 + P-poll__networl_5_2_RI_7 + P-poll__networl_3_0_AI_4 + P-poll__networl_4_2_AnnP_0 + P-poll__networl_4_2_AnnP_1 + P-poll__networl_4_2_AnnP_2 + P-poll__networl_4_2_AnnP_3 + P-poll__networl_4_2_AnnP_4 + P-poll__networl_4_2_AnnP_5 + P-poll__networl_4_2_AnnP_6 + P-poll__networl_4_2_AnnP_7 + P-poll__networl_3_0_AI_3 + P-poll__networl_3_0_AI_2 + P-poll__networl_3_0_AI_1 + P-poll__networl_3_0_AI_0 + P-poll__networl_7_1_RI_0 + P-poll__networl_7_1_RI_1 + P-poll__networl_7_1_RI_2 + P-poll__networl_7_1_RI_3 + P-poll__networl_7_1_RI_4 + P-poll__networl_7_1_RI_5 + P-poll__networl_7_1_RI_6 + P-poll__networl_7_1_RI_7 + P-poll__networl_6_4_AnsP_0 + P-poll__networl_6_5_AskP_0 + P-poll__networl_6_5_AskP_1 + P-poll__networl_6_5_AskP_2 + P-poll__networl_6_5_AskP_3 + P-poll__networl_6_5_AskP_4 + P-poll__networl_6_5_AskP_5 + P-poll__networl_6_5_AskP_6 + P-poll__networl_6_5_AskP_7 + P-poll__networl_3_3_AnsP_0 + P-poll__networl_1_4_RI_7 + P-poll__networl_1_4_RI_6 + P-poll__networl_1_4_RI_5 + P-poll__networl_1_4_RI_4 + P-poll__networl_1_4_RI_3 + P-poll__networl_1_4_RI_2 + P-poll__networl_1_4_RI_1 + P-poll__networl_1_4_RI_0 + P-poll__networl_1_1_AI_7 + P-poll__networl_1_1_AI_6 + P-poll__networl_1_1_AI_5 + P-poll__networl_1_1_AI_4 + P-poll__networl_1_1_AI_3 + P-poll__networl_6_7_RP_0 + P-poll__networl_6_7_RP_1 + P-poll__networl_6_7_RP_2 + P-poll__networl_6_7_RP_3 + P-poll__networl_6_7_RP_4 + P-poll__networl_6_7_RP_5 + P-poll__networl_6_7_RP_6 + P-poll__networl_6_7_RP_7 + P-poll__networl_1_1_AI_2 + P-poll__networl_1_1_AI_1 + P-poll__networl_1_1_AI_0 + P-poll__networl_3_6_AnnP_0 + P-poll__networl_3_6_AnnP_1 + P-poll__networl_3_6_AnnP_2 + P-poll__networl_3_6_AnnP_3 + P-poll__networl_3_6_AnnP_4 + P-poll__networl_3_6_AnnP_5 + P-poll__networl_3_6_AnnP_6 + P-poll__networl_3_6_AnnP_7 + P-poll__networl_2_5_AskP_7 + P-poll__networl_2_5_AskP_6 + P-poll__networl_2_5_AskP_5 + P-poll__networl_2_5_AskP_4 + P-poll__networl_2_5_AskP_3 + P-poll__networl_2_5_AskP_2 + P-poll__networl_2_5_AskP_1 + P-poll__networl_4_0_AskP_0 + P-poll__networl_4_0_AskP_1 + P-poll__networl_4_0_AskP_2 + P-poll__networl_4_0_AskP_3 + P-poll__networl_4_0_AskP_4 + P-poll__networl_4_0_AskP_5 + P-poll__networl_4_0_AskP_6 + P-poll__networl_4_0_AskP_7 + P-poll__networl_2_5_AskP_0 + P-poll__networl_1_3_RP_0 + P-poll__networl_1_3_RP_1 + P-poll__networl_1_3_RP_2 + P-poll__networl_1_3_RP_3 + P-poll__networl_1_3_RP_4 + P-poll__networl_1_3_RP_5 + P-poll__networl_1_3_RP_6 + P-poll__networl_1_3_RP_7 + P-poll__networl_7_3_AnnP_7 + P-poll__networl_7_3_AnnP_6 + P-poll__networl_1_1_AnnP_0 + P-poll__networl_1_1_AnnP_1 + P-poll__networl_1_1_AnnP_2 + P-poll__networl_1_1_AnnP_3 + P-poll__networl_1_1_AnnP_4 + P-poll__networl_1_1_AnnP_5 + P-poll__networl_1_1_AnnP_6 + P-poll__networl_1_1_AnnP_7 + P-poll__networl_7_3_AnnP_5 + P-poll__networl_7_3_AnnP_4 + P-poll__networl_3_2_RP_0 + P-poll__networl_3_2_RP_1 + P-poll__networl_3_2_RP_2 + P-poll__networl_3_2_RP_3 + P-poll__networl_3_2_RP_4 + P-poll__networl_3_2_RP_5 + P-poll__networl_3_2_RP_6 + P-poll__networl_3_2_RP_7 + P-poll__networl_2_7_AnsP_0 + P-poll__networl_7_3_AnnP_3 + P-poll__networl_7_3_AnnP_2 + P-poll__networl_7_3_AnnP_1 + P-poll__networl_7_3_AnnP_0 + P-poll__networl_6_5_AI_7 + P-poll__networl_6_5_AI_6 + P-poll__networl_6_5_AI_5 + P-poll__networl_6_5_AI_4 + P-poll__networl_5_7_AI_0 + P-poll__networl_5_7_AI_1 + P-poll__networl_5_7_AI_2 + P-poll__networl_5_7_AI_3 + P-poll__networl_5_7_AI_4 + P-poll__networl_5_7_AI_5 + P-poll__networl_5_7_AI_6 + P-poll__networl_5_7_AI_7 + P-poll__networl_6_5_AI_3 + P-poll__networl_6_5_AI_2 + P-poll__networl_6_5_AI_1 + P-poll__networl_6_5_AI_0 + P-poll__networl_3_4_AskP_0 + P-poll__networl_3_4_AskP_1 + P-poll__networl_3_4_AskP_2 + P-poll__networl_3_4_AskP_3 + P-poll__networl_3_4_AskP_4 + P-poll__networl_3_4_AskP_5 + P-poll__networl_3_4_AskP_6 + P-poll__networl_3_4_AskP_7 + P-poll__networl_5_1_RP_0 + P-poll__networl_5_1_RP_1 + P-poll__networl_5_1_RP_2 + P-poll__networl_5_1_RP_3 + P-poll__networl_5_1_RP_4 + P-poll__networl_5_1_RP_5 + P-poll__networl_5_1_RP_6 + P-poll__networl_5_1_RP_7 + P-poll__networl_7_6_AI_0 + P-poll__networl_7_6_AI_1 + P-poll__networl_7_6_AI_2 + P-poll__networl_7_6_AI_3 + P-poll__networl_7_6_AI_4 + P-poll__networl_7_6_AI_5 + P-poll__networl_7_6_AI_6 + P-poll__networl_7_6_AI_7 + P-poll__networl_0_3_AI_0 + P-poll__networl_0_3_AI_1 + P-poll__networl_0_3_AI_2 + P-poll__networl_0_2_AnsP_0 + P-poll__networl_0_3_AI_3 + P-poll__networl_0_3_AI_4 + P-poll__networl_0_3_AI_5 + P-poll__networl_0_3_AI_6 + P-poll__networl_0_3_AI_7 + P-poll__networl_4_0_RP_7 + P-poll__networl_0_6_RI_0 + P-poll__networl_0_6_RI_1 + P-poll__networl_0_6_RI_2 + P-poll__networl_0_6_RI_3 + P-poll__networl_0_6_RI_4 + P-poll__networl_0_6_RI_5 + P-poll__networl_0_6_RI_6 + P-poll__networl_0_6_RI_7 + P-poll__networl_4_0_RP_6 + P-poll__networl_4_0_RP_5 + P-poll__networl_4_0_RP_4 + P-poll__networl_7_3_AnsP_0 + P-poll__networl_4_0_RP_3 + P-poll__networl_4_0_RP_2 + P-poll__networl_4_0_RP_1 + P-poll__networl_4_0_RP_0 + P-poll__networl_0_2_AnnP_7 + P-poll__networl_0_2_AnnP_6 + P-poll__networl_0_2_AnnP_5 + P-poll__networl_0_5_AnnP_0 + P-poll__networl_0_5_AnnP_1 + P-poll__networl_0_5_AnnP_2 + P-poll__networl_0_5_AnnP_3 + P-poll__networl_0_5_AnnP_4 + P-poll__networl_0_5_AnnP_5 + P-poll__networl_0_5_AnnP_6 + P-poll__networl_0_5_AnnP_7 + P-poll__networl_7_0_RP_0 + P-poll__networl_7_0_RP_1 + P-poll__networl_7_0_RP_2 + P-poll__networl_7_0_RP_3 + P-poll__networl_7_0_RP_4 + P-poll__networl_7_0_RP_5 + P-poll__networl_7_0_RP_6 + P-poll__networl_7_0_RP_7 + P-poll__networl_0_2_AnnP_4 + P-poll__networl_0_2_AnnP_3 + P-poll__networl_2_2_AI_0 + P-poll__networl_0_2_AnnP_2 + P-poll__networl_2_2_AI_1 + P-poll__networl_2_2_AI_2 + P-poll__networl_2_2_AI_3 + P-poll__networl_2_2_AI_4 + P-poll__networl_2_2_AI_5 + P-poll__networl_2_2_AI_6 + P-poll__networl_2_2_AI_7 + P-poll__networl_2_5_RI_0 + P-poll__networl_2_5_RI_1 + P-poll__networl_2_5_RI_2 + P-poll__networl_2_5_RI_3 + P-poll__networl_2_5_RI_4 + P-poll__networl_2_5_RI_5 + P-poll__networl_2_5_RI_6 + P-poll__networl_2_5_RI_7 + P-poll__networl_0_2_AnnP_1 + P-poll__networl_0_2_AnnP_0 + P-poll__networl_7_6_AnnP_0 + P-poll__networl_7_6_AnnP_1 + P-poll__networl_7_6_AnnP_2 + P-poll__networl_7_6_AnnP_3 + P-poll__networl_7_6_AnnP_4 + P-poll__networl_7_6_AnnP_5 + P-poll__networl_7_6_AnnP_6 + P-poll__networl_7_6_AnnP_7 + P-poll__networl_7_0_AnsP_0 + P-poll__networl_4_1_AI_0 + P-poll__networl_4_1_AI_1 + P-poll__networl_4_1_AI_2 + P-poll__networl_4_1_AI_3 + P-poll__networl_4_1_AI_4 + P-poll__networl_4_1_AI_5 + P-poll__networl_4_1_AI_6 + P-poll__networl_4_1_AI_7 + P-poll__networl_4_4_RI_0 + P-poll__networl_4_4_RI_1 + P-poll__networl_4_4_RI_2 + P-poll__networl_4_4_RI_3 + P-poll__networl_4_4_RI_4 + P-poll__networl_4_4_RI_5 + P-poll__networl_4_4_RI_6 + P-poll__networl_4_4_RI_7 + P-poll__networl_5_1_AnnP_0 + P-poll__networl_5_1_AnnP_1 + P-poll__networl_5_1_AnnP_2 + P-poll__networl_5_1_AnnP_3 + P-poll__networl_5_1_AnnP_4 + P-poll__networl_5_1_AnnP_5 + P-poll__networl_5_1_AnnP_6 + P-poll__networl_5_1_AnnP_7 + P-poll__networl_6_7_AnsP_0 + P-poll__networl_4_6_AI_7 + P-poll__networl_4_6_AI_6 + P-poll__networl_4_6_AI_5 + P-poll__networl_4_6_AI_4 + P-poll__networl_6_0_AI_0 + P-poll__networl_6_0_AI_1 + P-poll__networl_6_0_AI_2 + P-poll__networl_6_0_AI_3 + P-poll__networl_6_0_AI_4 + P-poll__networl_6_0_AI_5 + P-poll__networl_6_0_AI_6 + P-poll__networl_4_6_AI_3 + P-poll__networl_6_0_AI_7 + P-poll__networl_4_6_AI_2 + P-poll__networl_4_6_AI_1 + P-poll__networl_4_6_AI_0 + P-poll__networl_0_3_AskP_0 + P-poll__networl_0_3_AskP_1 + P-poll__networl_0_3_AskP_2 + P-poll__networl_0_3_AskP_3 + P-poll__networl_0_3_AskP_4 + P-poll__networl_0_3_AskP_5 + P-poll__networl_0_3_AskP_6 + P-poll__networl_0_3_AskP_7 + P-poll__networl_6_3_RI_0 + P-poll__networl_6_3_RI_1 + P-poll__networl_6_3_RI_2 + P-poll__networl_6_3_RI_3 + P-poll__networl_6_3_RI_4 + P-poll__networl_6_3_RI_5 + P-poll__networl_6_3_RI_6 + P-poll__networl_6_3_RI_7 + P-poll__networl_2_1_RP_7 + P-poll__networl_2_1_RP_6 + P-poll__networl_2_1_RP_5 + P-poll__networl_2_1_RP_4 + P-poll__networl_2_1_RP_3 + P-poll__networl_2_1_RP_2 + P-poll__networl_2_1_RP_1 + P-poll__networl_7_4_AskP_0 + P-poll__networl_7_4_AskP_1 + P-poll__networl_7_4_AskP_2 + P-poll__networl_7_4_AskP_3 + P-poll__networl_7_4_AskP_4 + P-poll__networl_7_4_AskP_5 + P-poll__networl_7_4_AskP_6 + P-poll__networl_7_4_AskP_7 + P-poll__networl_2_1_RP_0 + P-poll__networl_4_2_AnsP_0 + P-poll__networl_3_1_AskP_7 + P-poll__networl_3_1_AskP_6 + P-poll__networl_3_1_AskP_5 + P-poll__networl_3_1_AskP_4 + P-poll__networl_3_1_AskP_3 + P-poll__networl_3_1_AskP_2 + P-poll__networl_3_1_AskP_1 + P-poll__networl_3_1_AskP_0 + P-poll__networl_2_7_AnnP_7 + P-poll__networl_4_5_AnnP_0 + P-poll__networl_4_5_AnnP_1 + P-poll__networl_4_5_AnnP_2 + P-poll__networl_4_5_AnnP_3 + P-poll__networl_4_5_AnnP_4 + P-poll__networl_4_5_AnnP_5 + P-poll__networl_4_5_AnnP_6 + P-poll__networl_4_5_AnnP_7 + P-poll__networl_2_7_AnnP_6 + P-poll__networl_2_7_AnnP_5 + P-poll__networl_2_7_AnnP_4 + P-poll__networl_2_7_AnnP_3 + P-poll__networl_2_7_AnnP_2 + P-poll__networl_2_7_AnnP_1 + P-poll__networl_2_7_AnnP_0 + P-poll__networl_0_5_RP_0 + P-poll__networl_0_5_RP_1 + P-poll__networl_0_5_RP_2 + P-poll__networl_0_5_RP_3 + P-poll__networl_0_5_RP_4 + P-poll__networl_0_5_RP_5 + P-poll__networl_0_5_RP_6 + P-poll__networl_0_5_RP_7 + P-poll__networl_2_7_AI_7 + P-poll__networl_2_7_AI_6 + P-poll__networl_2_7_AI_5 + P-poll__networl_2_0_AnnP_0 + P-poll__networl_2_7_AI_4 + P-poll__networl_2_0_AnnP_1 + P-poll__networl_2_7_AI_3 + P-poll__networl_2_0_AnnP_2 + P-poll__networl_2_0_AnnP_3 + P-poll__networl_2_0_AnnP_4 + P-poll__networl_2_0_AnnP_5 + P-poll__networl_2_0_AnnP_6 + P-poll__networl_2_0_AnnP_7 + P-poll__networl_2_7_AI_2 + P-poll__networl_3_6_AnsP_0 + P-poll__networl_2_7_AI_1 + P-poll__networl_2_7_AI_0 + P-poll__networl_2_4_RP_0 + P-poll__networl_2_4_RP_1 + P-poll__networl_2_4_RP_2 + P-poll__networl_2_4_RP_3 + P-poll__networl_2_4_RP_4 + P-poll__networl_2_4_RP_5 + P-poll__networl_2_4_RP_6 + P-poll__networl_2_4_RP_7 + P-poll__networl_2_4_AnsP_0 + P-poll__networl_0_2_RP_7 + P-poll__networl_0_2_RP_6 + P-poll__networl_0_2_RP_5 + P-poll__networl_0_2_RP_4 + P-poll__networl_0_2_RP_3 + P-poll__networl_0_2_RP_2 + P-poll__networl_0_2_RP_1 + P-poll__networl_4_3_AskP_0 + P-poll__networl_4_3_AskP_1 + P-poll__networl_4_3_AskP_2 + P-poll__networl_4_3_AskP_3 + P-poll__networl_4_3_AskP_4 + P-poll__networl_4_3_AskP_5 + P-poll__networl_4_3_AskP_6 + P-poll__networl_4_3_AskP_7 + P-poll__networl_0_2_RP_0 + P-poll__networl_4_3_RP_0 + P-poll__networl_4_3_RP_1 + P-poll__networl_4_3_RP_2 + P-poll__networl_4_3_RP_3 + P-poll__networl_4_3_RP_4 + P-poll__networl_4_3_RP_5 + P-poll__networl_4_3_RP_6 + P-poll__networl_4_3_RP_7 + P-poll__networl_7_5_RP_7 + P-poll__networl_7_5_RP_6 + P-poll__networl_1_1_AnsP_0 + P-poll__networl_7_5_RP_5 + P-poll__networl_7_5_RP_4 + P-poll__networl_7_5_RP_3 + P-poll__networl_7_5_RP_2 + P-poll__networl_7_5_RP_1 + P-poll__networl_7_5_RP_0 + P-poll__networl_1_4_AnnP_0 + P-poll__networl_1_4_AnnP_1 + P-poll__networl_1_4_AnnP_2 + P-poll__networl_1_4_AnnP_3 + P-poll__networl_1_4_AnnP_4 + P-poll__networl_1_4_AnnP_5 + P-poll__networl_1_4_AnnP_6 + P-poll__networl_1_4_AnnP_7 + P-poll__networl_6_2_RP_0 + P-poll__networl_6_2_RP_1 + P-poll__networl_6_2_RP_2 + P-poll__networl_6_2_RP_3 + P-poll__networl_6_2_RP_4 + P-poll__networl_6_2_RP_5 + P-poll__networl_6_2_RP_6 + P-poll__networl_6_2_RP_7 + P-poll__networl_1_4_AI_0 + P-poll__networl_1_4_AI_1 + P-poll__networl_1_4_AI_2 + P-poll__networl_1_4_AI_3 + P-poll__networl_1_4_AI_4 + P-poll__networl_1_4_AI_5 + P-poll__networl_1_4_AI_6 + P-poll__networl_1_4_AI_7 + P-poll__networl_1_7_RI_0 + P-poll__networl_1_7_RI_1 + P-poll__networl_1_7_RI_2 + P-poll__networl_1_7_RI_3 + P-poll__networl_1_7_RI_4 + P-poll__networl_1_7_RI_5 + P-poll__networl_1_7_RI_6 + P-poll__networl_1_7_RI_7 + P-poll__networl_5_6_AskP_7 + P-poll__networl_3_7_AskP_0 + P-poll__networl_3_7_AskP_1 + P-poll__networl_3_7_AskP_2 + P-poll__networl_3_7_AskP_3 + P-poll__networl_3_7_AskP_4 + P-poll__networl_3_7_AskP_5 + P-poll__networl_3_7_AskP_6 + P-poll__networl_3_7_AskP_7 + P-poll__networl_5_6_AskP_6 + P-poll__networl_5_6_AskP_5 + P-poll__networl_5_6_AskP_4 + P-poll__networl_3_3_AI_0 + P-poll__networl_3_3_AI_1 + P-poll__networl_3_3_AI_2 + P-poll__networl_0_5_AnsP_0 + P-poll__networl_3_3_AI_3 + P-poll__networl_5_6_AskP_3 + P-poll__networl_3_3_AI_4 + P-poll__networl_5_6_AskP_2 + P-poll__networl_3_3_AI_5 + P-poll__networl_5_6_AskP_1 + P-poll__networl_3_3_AI_6 + P-poll__networl_5_6_AskP_0 + P-poll__networl_3_3_AI_7 + P-poll__networl_3_6_RI_0 + P-poll__networl_3_6_RI_1 + P-poll__networl_3_6_RI_2 + P-poll__networl_3_6_RI_3 + P-poll__networl_3_6_RI_4 + P-poll__networl_3_6_RI_5 + P-poll__networl_3_6_RI_6 + P-poll__networl_3_6_RI_7 + P-poll__networl_6_0_AnnP_0 + P-poll__networl_6_0_AnnP_1 + P-poll__networl_6_0_AnnP_2 + P-poll__networl_6_0_AnnP_3 + P-poll__networl_6_0_AnnP_4 + P-poll__networl_6_0_AnnP_5 + P-poll__networl_6_0_AnnP_6 + P-poll__networl_6_0_AnnP_7 + P-poll__networl_7_6_AnsP_0 + P-poll__networl_1_2_AskP_0 + P-poll__networl_1_2_AskP_1 + P-poll__networl_1_2_AskP_2 + P-poll__networl_1_2_AskP_3 + P-poll__networl_1_2_AskP_4 + P-poll__networl_1_2_AskP_5 + P-poll__networl_1_2_AskP_6 + P-poll__networl_1_2_AskP_7 + P-poll__networl_5_6_RP_7 + P-poll__networl_5_2_AI_0 + P-poll__networl_5_2_AI_1 + P-poll__networl_5_2_AI_2 + P-poll__networl_5_2_AI_3 + P-poll__networl_5_2_AI_4 + P-poll__networl_5_2_AI_5 + P-poll__networl_5_2_AI_6 + P-poll__networl_5_2_AI_7 + P-poll__networl_5_6_RP_6 + P-poll__networl_5_5_RI_0 + P-poll__networl_5_5_RI_1 + P-poll__networl_5_5_RI_2 + P-poll__networl_5_5_RI_3 + P-poll__networl_5_5_RI_4 + P-poll__networl_5_5_RI_5 + P-poll__networl_5_5_RI_6 + P-poll__networl_5_5_RI_7 + P-poll__networl_5_6_RP_5 + P-poll__networl_5_6_RP_4 + P-poll__networl_5_6_RP_3 + P-poll__networl_5_1_AnsP_0 + P-poll__networl_5_6_RP_2 + P-poll__networl_5_6_RP_1 + P-poll__networl_5_6_RP_0 + P-poll__networl_7_1_AI_0 + P-poll__networl_7_1_AI_1 + P-poll__networl_7_1_AI_2 + P-poll__networl_7_1_AI_3 + P-poll__networl_7_1_AI_4 + P-poll__networl_7_1_AI_5 + P-poll__networl_7_1_AI_6 + P-poll__networl_7_1_AI_7 + P-poll__networl_7_4_RI_0 + P-poll__networl_7_4_RI_1 + P-poll__networl_7_4_RI_2 + P-poll__networl_7_4_RI_3 + P-poll__networl_7_4_RI_4 + P-poll__networl_7_4_RI_5 + P-poll__networl_7_4_RI_6 + P-poll__networl_7_4_RI_7 + P-poll__networl_0_1_RI_0 + P-poll__networl_0_1_RI_1 + P-poll__networl_0_1_RI_2 + P-poll__networl_0_1_RI_3 + P-poll__networl_0_1_RI_4 + P-poll__networl_0_1_RI_5 + P-poll__networl_0_1_RI_6 + P-poll__networl_0_1_RI_7 + P-poll__networl_5_4_AnnP_0 + P-poll__networl_5_4_AnnP_1 + P-poll__networl_5_4_AnnP_2 + P-poll__networl_5_4_AnnP_3 + P-poll__networl_5_4_AnnP_4 + P-poll__networl_5_4_AnnP_5 + P-poll__networl_5_4_AnnP_6 + P-poll__networl_5_4_AnnP_7 + P-poll__networl_0_6_AskP_0 + P-poll__networl_0_6_AskP_1 + P-poll__networl_0_6_AskP_2 + P-poll__networl_0_6_AskP_3 + P-poll__networl_0_6_AskP_4 + P-poll__networl_0_6_AskP_5 + P-poll__networl_0_6_AskP_6 + P-poll__networl_0_6_AskP_7 + P-poll__networl_2_0_RI_0 + P-poll__networl_2_0_RI_1 + P-poll__networl_2_0_RI_2 + P-poll__networl_2_0_RI_3 + P-poll__networl_2_0_RI_4 + P-poll__networl_2_0_RI_5 + P-poll__networl_2_0_RI_6 + P-poll__networl_2_0_RI_7 + P-poll__networl_7_7_AskP_0 + P-poll__networl_7_7_AskP_1 + P-poll__networl_7_7_AskP_2 + P-poll__networl_7_7_AskP_3 + P-poll__networl_7_7_AskP_4 + P-poll__networl_7_7_AskP_5 + P-poll__networl_7_7_AskP_6 + P-poll__networl_7_7_AskP_7 + P-poll__networl_4_5_AnsP_0 + P-poll__networl_3_3_AnnP_7 + P-poll__networl_3_3_AnnP_6 + P-poll__networl_3_3_AnnP_5 + P-poll__networl_3_3_AnnP_4 + P-poll__networl_3_3_AnnP_3 + P-poll__networl_3_3_AnnP_2 + P-poll__networl_3_3_AnnP_1 + P-poll__networl_1_6_RP_0 + P-poll__networl_1_6_RP_1 + P-poll__networl_1_6_RP_2 + P-poll__networl_1_6_RP_3 + P-poll__networl_1_6_RP_4 + P-poll__networl_1_6_RP_5 + P-poll__networl_1_6_RP_6 + P-poll__networl_1_6_RP_7 + P-poll__networl_3_3_AnnP_0 + P-poll__networl_5_2_AskP_0 + P-poll__networl_5_2_AskP_1 + P-poll__networl_5_2_AskP_2 + P-poll__networl_5_2_AskP_3 + P-poll__networl_5_2_AskP_4 + P-poll__networl_5_2_AskP_5 + P-poll__networl_5_2_AskP_6 + P-poll__networl_5_2_AskP_7 + P-poll__networl_3_5_RP_0 + P-poll__networl_3_5_RP_1 + P-poll__networl_3_5_RP_2 + P-poll__networl_3_5_RP_3 + P-poll__networl_3_5_RP_4 + P-poll__networl_3_5_RP_5 + P-poll__networl_3_5_RP_6 + P-poll__networl_3_5_RP_7 + P-poll__networl_2_0_AnsP_0 + P-poll__networl_3_7_RP_7 + P-poll__networl_2_3_AnnP_0 + P-poll__networl_2_3_AnnP_1 + P-poll__networl_2_3_AnnP_2 + P-poll__networl_2_3_AnnP_3 + P-poll__networl_2_3_AnnP_4 + P-poll__networl_2_3_AnnP_5 + P-poll__networl_2_3_AnnP_6 + P-poll__networl_2_3_AnnP_7 + P-poll__networl_3_7_RP_6 + P-poll__networl_3_7_RP_5 + P-poll__networl_6_0_RI_7 + P-poll__networl_3_7_RP_4 + P-poll__networl_6_0_RI_6 + P-poll__networl_3_7_RP_3 + P-poll__networl_6_0_RI_5 + P-poll__networl_3_7_RP_2 + P-poll__networl_6_0_RI_4 + P-poll__networl_3_7_RP_1 + P-poll__networl_6_0_RI_3 + P-poll__networl_5_4_RP_0 + P-poll__networl_5_4_RP_1 + P-poll__networl_5_4_RP_2 + P-poll__networl_5_4_RP_3 + P-poll__networl_5_4_RP_4 + P-poll__networl_5_4_RP_5 + P-poll__networl_5_4_RP_6 + P-poll__networl_5_4_RP_7 + P-poll__networl_3_7_RP_0 + P-poll__networl_6_0_RI_2 + P-poll__networl_6_0_RI_1 + P-poll__networl_0_6_AI_0 + P-poll__networl_0_6_AI_1 + P-poll__networl_0_6_AI_2 + P-poll__networl_0_6_AI_3 + P-poll__networl_0_6_AI_4 + P-poll__networl_0_6_AI_5 + P-poll__networl_0_6_AI_6 + P-poll__networl_0_6_AI_7 + P-poll__networl_6_0_RI_0 + P-poll__networl_3_0_AnsP_0 + P-poll__networl_4_6_AskP_0 + P-poll__networl_4_6_AskP_1 + P-poll__networl_4_6_AskP_2 + P-poll__networl_4_6_AskP_3 + P-poll__networl_4_6_AskP_4 + P-poll__networl_4_6_AskP_5 + P-poll__networl_4_6_AskP_6 + P-poll__networl_4_6_AskP_7 + P-poll__networl_7_3_RP_0 + P-poll__networl_7_3_RP_1 + P-poll__networl_7_3_RP_2 + P-poll__networl_7_3_RP_3 + P-poll__networl_7_3_RP_4 + P-poll__networl_7_3_RP_5 + P-poll__networl_7_3_RP_6 + P-poll__networl_7_3_RP_7 + P-poll__networl_0_0_RP_0 + P-poll__networl_0_0_RP_1 + P-poll__networl_0_0_RP_2 + P-poll__networl_0_0_RP_3 + P-poll__networl_0_0_RP_4 + P-poll__networl_0_0_RP_5 + P-poll__networl_0_0_RP_6 + P-poll__networl_0_0_RP_7 + P-poll__networl_1_4_AnsP_0 + P-poll__networl_6_2_AskP_7 + P-poll__networl_2_5_AI_0 + P-poll__networl_6_2_AskP_6 + P-poll__networl_2_5_AI_1 + P-poll__networl_2_5_AI_2 + P-poll__networl_2_5_AI_3 + P-poll__networl_2_5_AI_4 + P-poll__networl_2_5_AI_5 + P-poll__networl_2_5_AI_6 + P-poll__networl_2_5_AI_7 + P-poll__networl_6_2_AskP_5 + P-poll__networl_1_7_AnnP_0 + P-poll__networl_1_7_AnnP_1 + P-poll__networl_1_7_AnnP_2 + P-poll__networl_1_7_AnnP_3 + P-poll__networl_1_7_AnnP_4 + P-poll__networl_1_7_AnnP_5 + P-poll__networl_1_7_AnnP_6 + P-poll__networl_1_7_AnnP_7 + P-poll__networl_6_2_AskP_4 + P-poll__networl_6_2_AskP_3 + P-poll__networl_6_2_AskP_2 + P-poll__networl_6_2_AskP_1 + P-poll__networl_2_1_AskP_0 + P-poll__networl_2_1_AskP_1 + P-poll__networl_2_1_AskP_2 + P-poll__networl_2_1_AskP_3 + P-poll__networl_2_1_AskP_4 + P-poll__networl_2_1_AskP_5 + P-poll__networl_2_1_AskP_6 + P-poll__networl_2_1_AskP_7 + P-poll__networl_6_2_AskP_0 + P-poll__networl_4_4_AI_0 + P-poll__networl_4_4_AI_1 + P-poll__networl_4_4_AI_2 + P-poll__networl_4_4_AI_3 + P-poll__networl_4_4_AI_4 + P-poll__networl_4_4_AI_5 + P-poll__networl_4_4_AI_6 + P-poll__networl_4_4_AI_7 + P-poll__networl_4_7_RI_0 + P-poll__networl_4_7_RI_1 + P-poll__networl_4_7_RI_2 + P-poll__networl_4_7_RI_3 + P-poll__networl_4_7_RI_4 + P-poll__networl_4_7_RI_5 + P-poll__networl_4_7_RI_6 + P-poll__networl_4_7_RI_7 + P-poll__networl_6_0_AnsP_0 + P-poll__networl_4_1_RI_7 + P-poll__networl_4_1_RI_6 + P-poll__networl_4_1_RI_5 + P-poll__networl_4_1_RI_4 + P-poll__networl_4_1_RI_3 + P-poll__networl_4_1_RI_2 + P-poll__networl_4_1_RI_1 + P-poll__networl_4_1_RI_0 + P-poll__networl_6_3_AI_0 + P-poll__networl_6_3_AI_1 + P-poll__networl_6_3_AI_2 + P-poll__networl_6_3_AI_3 + P-poll__networl_6_3_AI_4 + P-poll__networl_6_3_AI_5 + P-poll__networl_6_3_AI_6 + P-poll__networl_6_3_AI_7 + P-poll__networl_6_6_RI_0 + P-poll__networl_6_6_RI_1 + P-poll__networl_6_6_RI_2 + P-poll__networl_6_6_RI_3 + P-poll__networl_6_6_RI_4 + P-poll__networl_6_6_RI_5 + P-poll__networl_6_6_RI_6 + P-poll__networl_6_6_RI_7 + P-poll__networl_5_5_AnsP_0 + P-poll__networl_6_3_AnnP_0 + P-poll__networl_6_3_AnnP_1 + P-poll__networl_6_3_AnnP_2 + P-poll__networl_6_3_AnnP_3 + P-poll__networl_6_3_AnnP_4 + P-poll__networl_6_3_AnnP_5 + P-poll__networl_6_3_AnnP_6 + P-poll__networl_6_3_AnnP_7 + P-poll__networl_2_2_RI_7 + P-poll__networl_2_2_RI_6 + P-poll__networl_2_2_RI_5 + P-poll__networl_2_2_RI_4 + P-poll__networl_2_2_RI_3 + P-poll__networl_2_2_RI_2 + P-poll__networl_1_5_AskP_0 + P-poll__networl_1_5_AskP_1 + P-poll__networl_1_5_AskP_2 + P-poll__networl_1_5_AskP_3 + P-poll__networl_1_5_AskP_4 + P-poll__networl_1_5_AskP_5 + P-poll__networl_1_5_AskP_6 + P-poll__networl_1_5_AskP_7 + P-poll__networl_2_2_RI_1 + P-poll__networl_2_2_RI_0 + P-poll__networl_1_6_AskP_7 + P-poll__networl_1_6_AskP_6 + P-poll__networl_1_6_AskP_5 + P-poll__networl_1_6_AskP_4 + P-poll__networl_1_6_AskP_3 + P-poll__networl_1_6_AskP_2 + P-poll__networl_1_2_RI_0 + P-poll__networl_1_2_RI_1 + P-poll__networl_1_2_RI_2 + P-poll__networl_1_2_RI_3 + P-poll__networl_1_2_RI_4 + P-poll__networl_1_2_RI_5 + P-poll__networl_1_2_RI_6 + P-poll__networl_1_2_RI_7 + P-poll__networl_1_6_AskP_1 + P-poll__networl_1_6_AskP_0 + P-poll__networl_5_4_AnsP_0 + P-poll__networl_3_1_RI_0 + P-poll__networl_3_1_RI_1 + P-poll__networl_3_1_RI_2 + P-poll__networl_3_1_RI_3 + P-poll__networl_3_1_RI_4 + P-poll__networl_3_1_RI_5 + P-poll__networl_3_1_RI_6 + P-poll__networl_3_1_RI_7 + P-poll__networl_5_7_AnnP_0 + P-poll__networl_5_7_AnnP_1 + P-poll__networl_5_7_AnnP_2 + P-poll__networl_5_7_AnnP_3 + P-poll__networl_5_7_AnnP_4 + P-poll__networl_5_7_AnnP_5 + P-poll__networl_5_7_AnnP_6 + P-poll__networl_5_7_AnnP_7 + P-poll__networl_6_1_AskP_0 + P-poll__networl_6_1_AskP_1 + P-poll__networl_6_1_AskP_2 + P-poll__networl_6_1_AskP_3 + P-poll__networl_6_1_AskP_4 + P-poll__networl_6_1_AskP_5 + P-poll__networl_6_1_AskP_6 + P-poll__networl_6_1_AskP_7 + P-poll__networl_6_4_AnnP_7 + P-poll__networl_5_0_RI_0 + P-poll__networl_5_0_RI_1 + P-poll__networl_5_0_RI_2 + P-poll__networl_2_7_RP_0 + P-poll__networl_5_0_RI_3 + P-poll__networl_2_7_RP_1 + P-poll__networl_5_0_RI_4 + P-poll__networl_2_7_RP_2 + P-poll__networl_5_0_RI_5 + P-poll__networl_2_7_RP_3 + P-poll__networl_5_0_RI_6 + P-poll__networl_2_7_RP_4 + P-poll__networl_5_0_RI_7 + P-poll__networl_2_7_RP_5 + P-poll__networl_2_7_RP_6 + P-poll__networl_2_7_RP_7 + P-poll__networl_6_4_AnnP_6 + P-poll__networl_3_2_AnnP_0 + P-poll__networl_3_2_AnnP_1 + P-poll__networl_3_2_AnnP_2 + P-poll__networl_3_2_AnnP_3 + P-poll__networl_3_2_AnnP_4 + P-poll__networl_3_2_AnnP_5 + P-poll__networl_3_2_AnnP_6 + P-poll__networl_3_2_AnnP_7 + P-poll__networl_6_4_AnnP_5 + P-poll__networl_6_4_AnnP_4 + P-poll__networl_6_4_AnnP_3 + P-poll__networl_4_6_RP_0 + P-poll__networl_4_6_RP_1 + P-poll__networl_4_6_RP_2 + P-poll__networl_4_6_RP_3 + P-poll__networl_4_6_RP_4 + P-poll__networl_4_6_RP_5 + P-poll__networl_4_6_RP_6 + P-poll__networl_4_6_RP_7 + P-poll__networl_6_4_AnnP_2 + P-poll__networl_6_4_AnnP_1 + P-poll__networl_6_4_AnnP_0 + P-poll__networl_0_3_RI_7 + P-poll__networl_0_3_RI_6 + P-poll__networl_0_3_RI_5 + P-poll__networl_0_3_RI_4 + P-poll__networl_0_3_RI_3 + P-poll__networl_0_3_RI_2 + P-poll__networl_0_3_RI_1 + P-poll__networl_5_5_AskP_0 + P-poll__networl_5_5_AskP_1 + P-poll__networl_5_5_AskP_2 + P-poll__networl_5_5_AskP_3 + P-poll__networl_5_5_AskP_4 + P-poll__networl_5_5_AskP_5 + P-poll__networl_5_5_AskP_6 + P-poll__networl_5_5_AskP_7 + P-poll__networl_0_3_RI_0 + P-poll__networl_7_6_RI_7 + P-poll__networl_6_5_RP_0 + P-poll__networl_6_5_RP_1 + P-poll__networl_6_5_RP_2 + P-poll__networl_6_5_RP_3 + P-poll__networl_6_5_RP_4 + P-poll__networl_6_5_RP_5 + P-poll__networl_6_5_RP_6 + P-poll__networl_6_5_RP_7 + P-poll__networl_2_3_AnsP_0 + P-poll__networl_7_6_RI_6 + P-poll__networl_7_6_RI_5 + P-poll__networl_7_6_RI_4 + P-poll__networl_7_6_RI_3 + P-poll__networl_7_6_RI_2 + P-poll__networl_7_6_RI_1 + P-poll__networl_7_6_RI_0 + P-poll__networl_0_0_AI_7 + P-poll__networl_1_7_AI_0 + P-poll__networl_1_7_AI_1 + P-poll__networl_1_7_AI_2 + P-poll__networl_1_7_AI_3 + P-poll__networl_1_7_AI_4 + P-poll__networl_1_7_AI_5 + P-poll__networl_1_7_AI_6 + P-poll__networl_1_7_AI_7 + P-poll__networl_0_0_AI_6 + P-poll__networl_0_0_AI_5 + P-poll__networl_2_6_AnnP_0 + P-poll__networl_2_6_AnnP_1 + P-poll__networl_2_6_AnnP_2 + P-poll__networl_2_6_AnnP_3 + P-poll__networl_2_6_AnnP_4 + P-poll__networl_2_6_AnnP_5 + P-poll__networl_2_6_AnnP_6 + P-poll__networl_2_6_AnnP_7 + P-poll__networl_0_0_AI_4 + P-poll__networl_3_0_AskP_0 + P-poll__networl_3_0_AskP_1 + P-poll__networl_3_0_AskP_2 + P-poll__networl_3_0_AskP_3 + P-poll__networl_3_0_AskP_4 + P-poll__networl_3_0_AskP_5 + P-poll__networl_3_0_AskP_6 + P-poll__networl_3_0_AskP_7 + P-poll__networl_1_1_RP_0 + P-poll__networl_1_1_RP_1 + P-poll__networl_1_1_RP_2 + P-poll__networl_1_1_RP_3 + P-poll__networl_1_1_RP_4 + P-poll__networl_1_1_RP_5 + P-poll__networl_1_1_RP_6 + P-poll__networl_1_1_RP_7 + P-poll__networl_0_0_AI_3 + P-poll__networl_3_6_AI_0 + P-poll__networl_3_6_AI_1 + P-poll__networl_3_6_AI_2 + P-poll__networl_3_6_AI_3 + P-poll__networl_3_6_AI_4 + P-poll__networl_3_6_AI_5 + P-poll__networl_3_6_AI_6 + P-poll__networl_3_6_AI_7 + P-poll__networl_0_0_AI_2 + P-poll__networl_0_0_AI_1 + P-poll__networl_0_0_AI_0 + P-poll__networl_0_1_AnnP_0 + P-poll__networl_0_1_AnnP_1 + P-poll__networl_0_1_AnnP_2 + P-poll__networl_0_1_AnnP_3 + P-poll__networl_0_1_AnnP_4 + P-poll__networl_0_1_AnnP_5 + P-poll__networl_0_1_AnnP_6 + P-poll__networl_0_1_AnnP_7 + P-poll__networl_3_0_RP_0 + P-poll__networl_3_0_RP_1 + P-poll__networl_3_0_RP_2 + P-poll__networl_3_0_RP_3 + P-poll__networl_3_0_RP_4 + P-poll__networl_3_0_RP_5 + P-poll__networl_3_0_RP_6 + P-poll__networl_3_0_RP_7 + P-poll__networl_7_3_AI_7 + P-poll__networl_1_7_AnsP_0 + P-poll__networl_7_3_AI_6 + P-poll__networl_7_3_AI_5 + P-poll__networl_7_3_AI_4 + P-poll__networl_7_3_AI_3 + P-poll__networl_7_3_AI_2 + P-poll__networl_7_3_AI_1 + P-poll__networl_7_3_AI_0 + P-poll__networl_5_5_AI_0 + P-poll__networl_5_5_AI_1 + P-poll__networl_5_5_AI_2 + P-poll__networl_5_5_AI_3 + P-poll__networl_5_5_AI_4 + P-poll__networl_5_5_AI_5 + P-poll__networl_5_5_AI_6 + P-poll__networl_5_5_AI_7 + P-poll__networl_7_2_AnnP_0 + P-poll__networl_7_2_AnnP_1 + P-poll__networl_7_2_AnnP_2 + P-poll__networl_7_2_AnnP_3 + P-poll__networl_7_2_AnnP_4 + P-poll__networl_7_2_AnnP_5 + P-poll__networl_7_2_AnnP_6 + P-poll__networl_7_2_AnnP_7 + P-poll__networl_6_1_AnsP_0 + P-poll__networl_2_4_AskP_0 + P-poll__networl_2_4_AskP_1 + P-poll__networl_2_4_AskP_2 + P-poll__networl_2_4_AskP_3 + P-poll__networl_2_4_AskP_4 + P-poll__networl_2_4_AskP_5 + P-poll__networl_2_4_AskP_6 + P-poll__networl_2_4_AskP_7 + P-poll__networl_7_4_AI_0 + P-poll__networl_7_4_AI_1 + P-poll__networl_7_4_AI_2 + P-poll__networl_7_4_AI_3 + P-poll__networl_7_4_AI_4 + P-poll__networl_7_4_AI_5 + P-poll__networl_7_4_AI_6 + P-poll__networl_7_4_AI_7 + P-poll__networl_0_1_AI_0 + P-poll__networl_0_1_AI_1 + P-poll__networl_0_1_AI_2 + P-poll__networl_0_1_AI_3 + P-poll__networl_0_1_AI_4 + P-poll__networl_0_1_AI_5 + P-poll__networl_0_1_AI_6 + P-poll__networl_0_1_AI_7 + P-poll__networl_7_7_RI_0 + P-poll__networl_7_7_RI_1 + P-poll__networl_7_7_RI_2 + P-poll__networl_7_7_RI_3 + P-poll__networl_7_7_RI_4 + P-poll__networl_7_7_RI_5 + P-poll__networl_7_7_RI_6 + P-poll__networl_7_7_RI_7 + P-poll__networl_0_4_RI_0 + P-poll__networl_0_4_RI_1 + P-poll__networl_0_4_RI_2 + P-poll__networl_0_4_RI_3 + P-poll__networl_0_4_RI_4 + P-poll__networl_0_4_RI_5 + P-poll__networl_0_4_RI_6 + P-poll__networl_0_4_RI_7 + P-poll__networl_6_3_AnsP_0 + P-poll__networl_5_7_RI_7 + P-poll__networl_5_7_RI_6 + P-poll__networl_5_7_RI_5 + P-poll__networl_5_7_RI_4 + P-poll__networl_5_7_RI_3 + P-poll__networl_5_7_RI_2 + P-poll__networl_5_7_RI_1 + P-poll__networl_2_0_AI_0 + P-poll__networl_2_0_AI_1 + P-poll__networl_2_0_AI_2 + P-poll__networl_2_0_AI_3 + P-poll__networl_2_0_AI_4 + P-poll__networl_2_0_AI_5 + P-poll__networl_2_0_AI_6 + P-poll__networl_2_0_AI_7 + P-poll__networl_2_3_RI_0 + P-poll__networl_2_3_RI_1 + P-poll__networl_2_3_RI_2 + P-poll__networl_2_3_RI_3 + P-poll__networl_2_3_RI_4 + P-poll__networl_2_3_RI_5 + P-poll__networl_2_3_RI_6 + P-poll__networl_2_3_RI_7 + P-poll__networl_5_7_RI_0 + P-poll__networl_5_4_AI_7 + P-poll__networl_6_6_AnnP_0 + P-poll__networl_6_6_AnnP_1 + P-poll__networl_6_6_AnnP_2 + P-poll__networl_6_6_AnnP_3 + P-poll__networl_6_6_AnnP_4 + P-poll__networl_6_6_AnnP_5 + P-poll__networl_6_6_AnnP_6 + P-poll__networl_6_6_AnnP_7 + P-poll__networl_5_4_AI_6 + P-poll__networl_7_0_AskP_0 + P-poll__networl_7_0_AskP_1 + P-poll__networl_7_0_AskP_2 + P-poll__networl_7_0_AskP_3 + P-poll__networl_7_0_AskP_4 + P-poll__networl_7_0_AskP_5 + P-poll__networl_7_0_AskP_6 + P-poll__networl_7_0_AskP_7 + P-poll__networl_5_4_AI_5 + P-poll__networl_5_4_AI_4 + P-poll__networl_5_4_AI_3 + P-poll__networl_5_4_AI_2 + P-poll__networl_5_4_AI_1 + P-poll__networl_5_4_AI_0 + P-poll__networl_4_2_RI_0 + P-poll__networl_4_2_RI_1 + P-poll__networl_4_2_RI_2 + P-poll__networl_4_2_RI_3 + P-poll__networl_4_2_RI_4 + P-poll__networl_4_2_RI_5 + P-poll__networl_4_2_RI_6 + P-poll__networl_4_2_RI_7 + P-poll__networl_4_1_AnnP_0 + P-poll__networl_4_1_AnnP_1 + P-poll__networl_4_1_AnnP_2 + P-poll__networl_4_1_AnnP_3 + P-poll__networl_4_1_AnnP_4 + P-poll__networl_4_1_AnnP_5 + P-poll__networl_4_1_AnnP_6 + P-poll__networl_4_1_AnnP_7 + P-poll__networl_2_2_AskP_7 + P-poll__networl_5_7_AnsP_0 + P-poll__networl_2_2_AskP_6 + P-poll__networl_2_2_AskP_5 + P-poll__networl_2_2_AskP_4 + P-poll__networl_2_2_AskP_3 + P-poll__networl_2_2_AskP_2 + P-poll__networl_2_2_AskP_1 + P-poll__networl_2_2_AskP_0 + P-poll__networl_6_1_RI_0 + P-poll__networl_6_1_RI_1 + P-poll__networl_6_1_RI_2 + P-poll__networl_6_1_RI_3 + P-poll__networl_6_1_RI_4 + P-poll__networl_6_1_RI_5 + P-poll__networl_6_1_RI_6 + P-poll__networl_6_1_RI_7 + P-poll__networl_7_0_AnnP_7 + P-poll__networl_7_0_AnnP_6 + P-poll__networl_7_0_AnnP_5 + P-poll__networl_6_4_AskP_0 + P-poll__networl_6_4_AskP_1 + P-poll__networl_6_4_AskP_2 + P-poll__networl_6_4_AskP_3 + P-poll__networl_6_4_AskP_4 + P-poll__networl_6_4_AskP_5 + P-poll__networl_6_4_AskP_6 + P-poll__networl_6_4_AskP_7 + P-poll__networl_7_0_AnnP_4 + P-poll__networl_7_0_AnnP_3 + P-poll__networl_3_2_AnsP_0 + P-poll__networl_7_0_AnnP_2 + P-poll__networl_7_0_AnnP_1 + P-poll__networl_7_0_AnnP_0 + P-poll__networl_3_5_AI_7 + P-poll__networl_3_5_AI_6 + P-poll__networl_3_5_AI_5 + P-poll__networl_3_5_AI_4 + P-poll__networl_3_5_AI_3 + P-poll__networl_5_7_RP_0 + P-poll__networl_5_7_RP_1 + P-poll__networl_5_7_RP_2 + P-poll__networl_5_7_RP_3 + P-poll__networl_5_7_RP_4 + P-poll__networl_5_7_RP_5 + P-poll__networl_5_7_RP_6 + P-poll__networl_5_7_RP_7 + P-poll__networl_3_5_AI_2 + P-poll__networl_3_5_AI_1 + P-poll__networl_3_5_AI_0 + P-poll__networl_1_5_AnsP_0 + P-poll__networl_3_5_AnnP_0 + P-poll__networl_3_5_AnnP_1 + P-poll__networl_3_5_AnnP_2 + P-poll__networl_3_5_AnnP_3 + P-poll__networl_3_5_AnnP_4 + P-poll__networl_3_5_AnnP_5 + P-poll__networl_3_5_AnnP_6 + P-poll__networl_3_5_AnnP_7 + P-poll__networl_7_6_RP_0 + P-poll__networl_7_6_RP_1 + P-poll__networl_7_6_RP_2 + P-poll__networl_7_6_RP_3 + P-poll__networl_7_6_RP_4 + P-poll__networl_7_6_RP_5 + P-poll__networl_7_6_RP_6 + P-poll__networl_7_6_RP_7 + P-poll__networl_0_3_RP_0 + P-poll__networl_0_3_RP_1 + P-poll__networl_0_3_RP_2 + P-poll__networl_0_3_RP_3 + P-poll__networl_0_3_RP_4 + P-poll__networl_0_3_RP_5 + P-poll__networl_0_3_RP_6 + P-poll__networl_0_3_RP_7 + P-poll__networl_1_0_RP_7 + P-poll__networl_1_0_RP_6 + P-poll__networl_1_0_RP_5 + P-poll__networl_1_0_RP_4 + P-poll__networl_1_0_RP_3 + P-poll__networl_1_0_RP_2 + P-poll__networl_1_0_RP_1 + P-poll__networl_1_0_RP_0 + P-poll__networl_1_0_AnnP_0 + P-poll__networl_1_0_AnnP_1 + P-poll__networl_1_0_AnnP_2 + P-poll__networl_1_0_AnnP_3 + P-poll__networl_1_0_AnnP_4 + P-poll__networl_1_0_AnnP_5 + P-poll__networl_1_0_AnnP_6 + P-poll__networl_1_0_AnnP_7 + P-poll__networl_4_7_AskP_7 + P-poll__networl_4_7_AskP_6 + P-poll__networl_4_7_AskP_5 + P-poll__networl_4_7_AskP_4 + P-poll__networl_2_2_RP_0 + P-poll__networl_2_2_RP_1 + P-poll__networl_2_2_RP_2 + P-poll__networl_2_2_RP_3 + P-poll__networl_2_2_RP_4 + P-poll__networl_2_2_RP_5 + P-poll__networl_2_2_RP_6 + P-poll__networl_2_2_RP_7 + P-poll__networl_2_6_AnsP_0 + P-poll__networl_4_7_AskP_3 + P-poll__networl_4_7_AskP_2 + P-poll__networl_4_7_AskP_1 + P-poll__networl_4_7_AskP_0 + P-poll__networl_4_7_AI_0 + P-poll__networl_4_7_AI_1 + P-poll__networl_4_7_AI_2 + P-poll__networl_4_7_AI_3 + P-poll__networl_4_7_AI_4 + P-poll__networl_4_7_AI_5 + P-poll__networl_4_7_AI_6 + P-poll__networl_4_7_AI_7 + P-poll__networl_1_6_AI_7 + P-poll__networl_1_6_AI_6 + P-poll__networl_1_6_AI_5 + P-poll__networl_1_6_AI_4 + P-poll__networl_1_6_AI_3 + P-poll__networl_1_6_AI_2 + P-poll__networl_1_6_AI_1 + P-poll__networl_3_3_AskP_0 + P-poll__networl_3_3_AskP_1 + P-poll__networl_3_3_AskP_2 + P-poll__networl_3_3_AskP_3 + P-poll__networl_3_3_AskP_4 + P-poll__networl_3_3_AskP_5 + P-poll__networl_3_3_AskP_6 + P-poll__networl_3_3_AskP_7 + P-poll__networl_4_1_RP_0 + P-poll__networl_4_1_RP_1 + P-poll__networl_4_1_RP_2 + P-poll__networl_4_1_RP_3 + P-poll__networl_4_1_RP_4 + P-poll__networl_4_1_RP_5 + P-poll__networl_4_1_RP_6 + P-poll__networl_4_1_RP_7 + P-poll__networl_1_6_AI_0 + P-poll__networl_6_6_AI_0 + P-poll__networl_6_6_AI_1 + P-poll__networl_6_6_AI_2 + P-poll__networl_6_6_AI_3 + P-poll__networl_6_6_AI_4 + P-poll__networl_6_6_AI_5 + P-poll__networl_6_6_AI_6 + P-poll__networl_6_6_AI_7 + P-poll__networl_0_1_AnsP_0 + P-poll__networl_6_4_RP_7 + P-poll__networl_6_4_RP_6 + P-poll__networl_6_4_RP_5 + P-poll__networl_7_2_AnsP_0 + P-poll__networl_6_4_RP_4 + P-poll__networl_6_4_RP_3 + P-poll__networl_6_4_RP_2 + P-poll__networl_6_4_RP_1 + P-poll__networl_6_4_RP_0 + P-poll__networl_0_4_AnnP_0 + P-poll__networl_0_4_AnnP_1 + P-poll__networl_0_4_AnnP_2 + P-poll__networl_0_4_AnnP_3 + P-poll__networl_0_4_AnnP_4 + P-poll__networl_0_4_AnnP_5 + P-poll__networl_0_4_AnnP_6 + P-poll__networl_0_4_AnnP_7 + P-poll__networl_6_0_RP_0 + P-poll__networl_6_0_RP_1 + P-poll__networl_6_0_RP_2 + P-poll__networl_6_0_RP_3 + P-poll__networl_6_0_RP_4 + P-poll__networl_6_0_RP_5 + P-poll__networl_6_0_RP_6 + P-poll__networl_6_0_RP_7 + P-poll__networl_1_2_AI_0 + P-poll__networl_1_2_AI_1 + P-poll__networl_1_2_AI_2 + P-poll__networl_1_2_AI_3 + P-poll__networl_1_2_AI_4 + P-poll__networl_1_2_AI_5 + P-poll__networl_1_2_AI_6 + P-poll__networl_1_2_AI_7 + P-poll__networl_1_5_RI_0 + P-poll__networl_1_5_RI_1 + P-poll__networl_1_5_RI_2 + P-poll__networl_1_5_RI_3 + P-poll__networl_1_5_RI_4 + P-poll__networl_1_5_RI_5 + P-poll__networl_1_5_RI_6 + P-poll__networl_1_5_RI_7 + P-poll__networl_7_5_AnnP_0 + P-poll__networl_7_5_AnnP_1 + P-poll__networl_7_5_AnnP_2 + P-poll__networl_7_5_AnnP_3 + P-poll__networl_7_5_AnnP_4 + P-poll__networl_7_5_AnnP_5 + P-poll__networl_7_5_AnnP_6 + P-poll__networl_7_5_AnnP_7 + P-poll__networl_2_7_AskP_0 + P-poll__networl_2_7_AskP_1 + P-poll__networl_2_7_AskP_2 + P-poll__networl_2_7_AskP_3 + P-poll__networl_2_7_AskP_4 + P-poll__networl_2_7_AskP_5 + P-poll__networl_2_7_AskP_6 + P-poll__networl_2_7_AskP_7 + P-poll__networl_2_4_AnnP_7 + P-poll__networl_2_4_AnnP_6 + P-poll__networl_2_4_AnnP_5 + P-poll__networl_3_1_AI_0 + P-poll__networl_3_1_AI_1 + P-poll__networl_3_1_AI_2 + P-poll__networl_3_1_AI_3 + P-poll__networl_3_1_AI_4 + P-poll__networl_3_1_AI_5 + P-poll__networl_3_1_AI_6 + P-poll__networl_3_1_AI_7 + P-poll__networl_3_4_RI_0 + P-poll__networl_3_4_RI_1 + P-poll__networl_3_4_RI_2 + P-poll__networl_3_4_RI_3 + P-poll__networl_3_4_RI_4 + P-poll__networl_3_4_RI_5 + P-poll__networl_3_4_RI_6 + P-poll__networl_3_4_RI_7 + P-poll__networl_2_4_AnnP_4 + P-poll__networl_5_0_AnnP_0 + P-poll__networl_5_0_AnnP_1 + P-poll__networl_5_0_AnnP_2 + P-poll__networl_5_0_AnnP_3 + P-poll__networl_5_0_AnnP_4 + P-poll__networl_5_0_AnnP_5 + P-poll__networl_5_0_AnnP_6 + P-poll__networl_5_0_AnnP_7 + P-poll__networl_2_4_AnnP_3 + P-poll__networl_6_6_AnsP_0 + P-poll__networl_2_4_AnnP_2 + P-poll__networl_2_4_AnnP_1 + P-poll__networl_2_4_AnnP_0 + P-poll__networl_5_0_AI_0 + P-poll__networl_5_0_AI_1 + P-poll__networl_5_0_AI_2 + P-poll__networl_5_0_AI_3 + P-poll__networl_5_0_AI_4 + P-poll__networl_5_0_AI_5 + P-poll__networl_5_0_AI_6 + P-poll__networl_5_0_AI_7 + P-poll__networl_2_1_AnsP_0 + P-poll__networl_4_5_RP_7 + P-poll__networl_4_5_RP_6 + P-poll__networl_4_5_RP_5 + P-poll__networl_4_5_RP_4 + P-poll__networl_4_5_RP_3 + P-poll__networl_4_5_RP_2 + P-poll__networl_0_2_AskP_0 + P-poll__networl_0_2_AskP_1 + P-poll__networl_0_2_AskP_2 + P-poll__networl_0_2_AskP_3 + P-poll__networl_0_2_AskP_4 + P-poll__networl_0_2_AskP_5 + P-poll__networl_0_2_AskP_6 + P-poll__networl_0_2_AskP_7 + P-poll__networl_5_3_RI_0 + P-poll__networl_5_3_RI_1 + P-poll__networl_5_3_RI_2 + P-poll__networl_5_3_RI_3 + P-poll__networl_5_3_RI_4 + P-poll__networl_5_3_RI_5 + P-poll__networl_5_3_RI_6 + P-poll__networl_5_3_RI_7 + P-poll__networl_4_5_RP_1 + P-poll__networl_4_5_RP_0 + P-poll__networl_7_3_AskP_0 + P-poll__networl_7_3_AskP_1 + P-poll__networl_7_3_AskP_2 + P-poll__networl_7_3_AskP_3 + P-poll__networl_7_3_AskP_4 + P-poll__networl_7_3_AskP_5 + P-poll__networl_7_3_AskP_6 + P-poll__networl_7_3_AskP_7 + P-poll__networl_5_3_AskP_7 + P-poll__networl_5_3_AskP_6 + P-poll__networl_5_3_AskP_5 + P-poll__networl_4_1_AnsP_0 + P-poll__networl_5_3_AskP_4 + P-poll__networl_5_3_AskP_3 + P-poll__networl_5_3_AskP_2 + P-poll__networl_5_3_AskP_1 + P-poll__networl_5_3_AskP_0 + P-poll__networl_7_2_RI_0 + P-poll__networl_7_2_RI_1 + P-poll__networl_7_2_RI_2 + P-poll__networl_7_2_RI_3 + P-poll__networl_7_2_RI_4 + P-poll__networl_7_2_RI_5 + P-poll__networl_7_2_RI_6 + P-poll__networl_7_2_RI_7 + P-poll__networl_4_4_AnnP_0 + P-poll__networl_4_4_AnnP_1 + P-poll__networl_4_4_AnnP_2 + P-poll__networl_4_4_AnnP_3 + P-poll__networl_4_4_AnnP_4 + P-poll__networl_4_4_AnnP_5 + P-poll__networl_4_4_AnnP_6 + P-poll__networl_4_4_AnnP_7 + P-poll__networl_2_6_RP_7 + P-poll__networl_2_6_RP_6 + P-poll__networl_2_6_RP_5 + P-poll__networl_2_6_RP_4 + P-poll__networl_2_6_RP_3 + P-poll__networl_2_6_RP_2 + P-poll__networl_2_6_RP_1 + P-poll__networl_2_6_RP_0 + P-poll__networl_4_6_AnsP_0 + P-poll__networl_6_7_AskP_0 + P-poll__networl_6_7_AskP_1 + P-poll__networl_6_7_AskP_2 + P-poll__networl_6_7_AskP_3 + P-poll__networl_6_7_AskP_4 + P-poll__networl_6_7_AskP_5 + P-poll__networl_6_7_AskP_6 + P-poll__networl_6_7_AskP_7 + P-poll__networl_3_5_AnsP_0 + P-poll__networl_3_0_AnnP_7 + P-poll__networl_3_0_AnnP_6 + P-poll__networl_3_0_AnnP_5 + P-poll__networl_1_4_RP_0 + P-poll__networl_1_4_RP_1 + P-poll__networl_1_4_RP_2 + P-poll__networl_1_4_RP_3 + P-poll__networl_1_4_RP_4 + P-poll__networl_1_4_RP_5 + P-poll__networl_1_4_RP_6 + P-poll__networl_1_4_RP_7 + P-poll__networl_3_0_AnnP_4 + P-poll__networl_3_0_AnnP_3 + P-poll__networl_3_0_AnnP_2 + P-poll__networl_3_0_AnnP_1 + P-poll__networl_3_0_AnnP_0 + P-poll__networl_4_2_AskP_0 + P-poll__networl_4_2_AskP_1 + P-poll__networl_4_2_AskP_2 + P-poll__networl_4_2_AskP_3 + P-poll__networl_4_2_AskP_4 + P-poll__networl_4_2_AskP_5 + P-poll__networl_4_2_AskP_6 + P-poll__networl_4_2_AskP_7 + P-poll__networl_3_3_RP_0 + P-poll__networl_3_3_RP_1 + P-poll__networl_3_3_RP_2 + P-poll__networl_3_3_RP_3 + P-poll__networl_3_3_RP_4 + P-poll__networl_3_3_RP_5 + P-poll__networl_3_3_RP_6 + P-poll__networl_3_3_RP_7 + P-poll__networl_1_0_AnsP_0 + P-poll__networl_0_7_RP_7 + P-poll__networl_0_7_RP_6 + P-poll__networl_0_7_RP_5 + P-poll__networl_3_0_RI_7 + P-poll__networl_0_7_RP_4 + P-poll__networl_3_0_RI_6 + P-poll__networl_0_7_RP_3 + P-poll__networl_1_3_AnnP_0 + P-poll__networl_1_3_AnnP_1 + P-poll__networl_1_3_AnnP_2 + P-poll__networl_1_3_AnnP_3 + P-poll__networl_1_3_AnnP_4 + P-poll__networl_1_3_AnnP_5 + P-poll__networl_1_3_AnnP_6 + P-poll__networl_1_3_AnnP_7 + P-poll__networl_3_0_RI_5 + P-poll__networl_0_7_RP_2 + P-poll__networl_5_2_RP_0 + P-poll__networl_5_2_RP_1 + P-poll__networl_5_2_RP_2 + P-poll__networl_5_2_RP_3 + P-poll__networl_5_2_RP_4 + P-poll__networl_5_2_RP_5 + P-poll__networl_5_2_RP_6 + P-poll__networl_5_2_RP_7 + P-poll__networl_3_0_RI_4 + P-poll__networl_0_7_RP_1 + P-poll__networl_3_0_RI_3 + P-poll__networl_7_7_AI_0 + P-poll__networl_7_7_AI_1 + P-poll__networl_7_7_AI_2 + P-poll__networl_7_7_AI_3 + P-poll__networl_7_7_AI_4 + P-poll__networl_7_7_AI_5 + P-poll__networl_7_7_AI_6 + P-poll__networl_7_7_AI_7 + P-poll__networl_0_4_AI_0 + P-poll__networl_0_4_AI_1 + P-poll__networl_0_4_AI_2 + P-poll__networl_0_4_AI_3 + P-poll__networl_0_4_AI_4 + P-poll__networl_0_4_AI_5 + P-poll__networl_0_4_AI_6 + P-poll__networl_0_4_AI_7 + P-poll__networl_0_7_RI_0 + P-poll__networl_0_7_RI_1 + P-poll__networl_0_7_RI_2 + P-poll__networl_0_7_RI_3 + P-poll__networl_0_7_RI_4 + P-poll__networl_0_7_RI_5 + P-poll__networl_0_7_RI_6 + P-poll__networl_0_7_RI_7 + P-poll__networl_0_7_RP_0 + P-poll__networl_3_0_RI_2 + P-poll__networl_3_0_RI_1 + P-poll__networl_3_0_RI_0 + P-poll__networl_3_6_AskP_0 + P-poll__networl_3_6_AskP_1 + P-poll__networl_3_6_AskP_2 + P-poll__networl_3_6_AskP_3 + P-poll__networl_3_6_AskP_4 + P-poll__networl_3_6_AskP_5 + P-poll__networl_3_6_AskP_6 + P-poll__networl_3_6_AskP_7 + P-poll__networl_7_1_RP_0 + P-poll__networl_7_1_RP_1 + P-poll__networl_7_1_RP_2 + P-poll__networl_7_1_RP_3 + P-poll__networl_7_1_RP_4 + P-poll__networl_7_1_RP_5 + P-poll__networl_7_1_RP_6 + P-poll__networl_7_1_RP_7 + P-poll__networl_2_3_AI_0 + P-poll__networl_2_3_AI_1 + P-poll__networl_2_3_AI_2 + P-poll__networl_0_4_AnsP_0 + P-poll__networl_2_3_AI_3 + P-poll__networl_2_3_AI_4 + P-poll__networl_2_3_AI_5 + P-poll__networl_2_3_AI_6 + P-poll__networl_2_3_AI_7 + P-poll__networl_2_6_RI_0 + P-poll__networl_2_6_RI_1 + P-poll__networl_2_6_RI_2 + P-poll__networl_2_6_RI_3 + P-poll__networl_2_6_RI_4 + P-poll__networl_2_6_RI_5 + P-poll__networl_2_6_RI_6 + P-poll__networl_2_6_RI_7 + P-poll__networl_0_7_AskP_7 + P-poll__networl_0_7_AskP_6 + P-poll__networl_0_7_AskP_5 + P-poll__networl_0_7_AskP_4 + P-poll__networl_0_7_AskP_3 + P-poll__networl_0_7_AskP_2 + P-poll__networl_0_7_AskP_1 + P-poll__networl_0_7_AskP_0 + P-poll__networl_7_5_AnsP_0 + P-poll__networl_0_7_AnnP_0 + P-poll__networl_0_7_AnnP_1 + P-poll__networl_0_7_AnnP_2 + P-poll__networl_0_7_AnnP_3 + P-poll__networl_0_7_AnnP_4 + P-poll__networl_0_7_AnnP_5 + P-poll__networl_0_7_AnnP_6 + P-poll__networl_0_7_AnnP_7 + P-poll__networl_1_1_AskP_0 + P-poll__networl_1_1_AskP_1 + P-poll__networl_1_1_AskP_2 + P-poll__networl_1_1_AskP_3 + P-poll__networl_1_1_AskP_4 + P-poll__networl_1_1_AskP_5 + P-poll__networl_1_1_AskP_6 + P-poll__networl_1_1_AskP_7 + P-poll__networl_4_2_AI_0 + P-poll__networl_4_2_AI_1 + P-poll__networl_4_2_AI_2 + P-poll__networl_4_2_AI_3 + P-poll__networl_4_2_AI_4 + P-poll__networl_4_2_AI_5 + P-poll__networl_4_2_AI_6 + P-poll__networl_4_2_AI_7 + P-poll__networl_4_5_RI_0 + P-poll__networl_4_5_RI_1 + P-poll__networl_4_5_RI_2 + P-poll__networl_4_5_RI_3 + P-poll__networl_4_5_RI_4 + P-poll__networl_4_5_RI_5 + P-poll__networl_4_5_RI_6 + P-poll__networl_4_5_RI_7 + P-poll__networl_5_5_AnnP_7 + P-poll__networl_5_0_AnsP_0 + P-poll__networl_5_5_AnnP_6 + P-poll__networl_5_5_AnnP_5 + P-poll__networl_5_5_AnnP_4 + P-poll__networl_5_5_AnnP_3 + P-poll__networl_5_5_AnnP_2 + P-poll__networl_5_5_AnnP_1 + P-poll__networl_5_5_AnnP_0 + P-poll__networl_1_1_RI_7 + P-poll__networl_6_1_AI_0 + P-poll__networl_6_1_AI_1 + P-poll__networl_6_1_AI_2 + P-poll__networl_6_1_AI_3 + P-poll__networl_6_1_AI_4 + P-poll__networl_6_1_AI_5 + P-poll__networl_6_1_AI_6 + P-poll__networl_6_1_AI_7 + P-poll__networl_6_4_RI_0 + P-poll__networl_6_4_RI_1 + P-poll__networl_6_4_RI_2 + P-poll__networl_6_4_RI_3 + P-poll__networl_6_4_RI_4 + P-poll__networl_6_4_RI_5 + P-poll__networl_6_4_RI_6 + P-poll__networl_6_4_RI_7 + P-poll__networl_1_1_RI_6 + P-poll__networl_5_3_AnnP_0 + P-poll__networl_5_3_AnnP_1 + P-poll__networl_5_3_AnnP_2 + P-poll__networl_5_3_AnnP_3 + P-poll__networl_5_3_AnnP_4 + P-poll__networl_5_3_AnnP_5 + P-poll__networl_5_3_AnnP_6 + P-poll__networl_5_3_AnnP_7 + P-poll__networl_1_1_RI_5 + P-poll__networl_1_1_RI_4 + P-poll__networl_1_1_RI_3 + P-poll__networl_1_1_RI_2 + P-poll__networl_1_1_RI_1 + P-poll__networl_1_1_RI_0 + P-poll__networl_5_2_AnsP_0 + P-poll__networl_0_5_AskP_0 + P-poll__networl_0_5_AskP_1 + P-poll__networl_0_5_AskP_2 + P-poll__networl_0_5_AskP_3 + P-poll__networl_0_5_AskP_4 + P-poll__networl_0_5_AskP_5 + P-poll__networl_0_5_AskP_6 + P-poll__networl_0_5_AskP_7 + P-poll__networl_1_0_RI_0 + P-poll__networl_1_0_RI_1 + P-poll__networl_1_0_RI_2 + P-poll__networl_1_0_RI_3 + P-poll__networl_1_0_RI_4 + P-poll__networl_1_0_RI_5 + P-poll__networl_1_0_RI_6 + P-poll__networl_1_0_RI_7 + P-poll__networl_7_6_AskP_0 + P-poll__networl_7_6_AskP_1 + P-poll__networl_7_6_AskP_2 + P-poll__networl_7_6_AskP_3 + P-poll__networl_7_6_AskP_4 + P-poll__networl_7_6_AskP_5 + P-poll__networl_7_6_AskP_6 + P-poll__networl_7_6_AskP_7 + P-poll__networl_4_4_AnsP_0 + P-poll__networl_6_5_RI_7 + P-poll__networl_6_5_RI_6 + P-poll__networl_6_5_RI_5 + P-poll__networl_0_6_RP_0 + P-poll__networl_0_6_RP_1 + P-poll__networl_0_6_RP_2 + P-poll__networl_0_6_RP_3 + P-poll__networl_0_6_RP_4 + P-poll__networl_0_6_RP_5 + P-poll__networl_0_6_RP_6 + P-poll__networl_0_6_RP_7 + P-poll__networl_4_7_AnnP_0 + P-poll__networl_4_7_AnnP_1 + P-poll__networl_4_7_AnnP_2 + P-poll__networl_4_7_AnnP_3 + P-poll__networl_4_7_AnnP_4 + P-poll__networl_4_7_AnnP_5 + P-poll__networl_4_7_AnnP_6 + P-poll__networl_4_7_AnnP_7 + P-poll__networl_6_5_RI_4 + P-poll__networl_6_5_RI_3 + P-poll__networl_6_5_RI_2 + P-poll__networl_6_5_RI_1 + P-poll__networl_6_5_RI_0 + P-poll__networl_6_2_AI_7 + P-poll__networl_6_2_AI_6 + P-poll__networl_6_2_AI_5 + P-poll__networl_6_2_AI_4 + P-poll__networl_5_1_AskP_0 + P-poll__networl_5_1_AskP_1 + P-poll__networl_5_1_AskP_2 + P-poll__networl_5_1_AskP_3 + P-poll__networl_5_1_AskP_4 + P-poll__networl_5_1_AskP_5 + P-poll__networl_5_1_AskP_6 + P-poll__networl_5_1_AskP_7 + P-poll__networl_6_2_AI_3 + P-poll__networl_6_2_AI_2 + P-poll__networl_6_2_AI_1 + P-poll__networl_6_2_AI_0 + P-poll__networl_1_3_AskP_7 + P-poll__networl_1_3_AskP_6 + P-poll__networl_1_3_AskP_5 + P-poll__networl_1_3_AskP_4 + P-poll__networl_1_3_AskP_3 + P-poll__networl_2_5_RP_0 + P-poll__networl_2_5_RP_1 + P-poll__networl_2_5_RP_2 + P-poll__networl_2_5_RP_3 + P-poll__networl_2_5_RP_4 + P-poll__networl_2_5_RP_5 + P-poll__networl_2_5_RP_6 + P-poll__networl_2_5_RP_7 + P-poll__networl_1_3_AskP_2 + P-poll__networl_2_2_AnnP_0 + P-poll__networl_2_2_AnnP_1 + P-poll__networl_2_2_AnnP_2 + P-poll__networl_2_2_AnnP_3 + P-poll__networl_2_2_AnnP_4 + P-poll__networl_2_2_AnnP_5 + P-poll__networl_2_2_AnnP_6 + P-poll__networl_2_2_AnnP_7 + P-poll__networl_1_3_AskP_1 + P-poll__networl_1_3_AskP_0 + P-poll__networl_4_4_RP_0 + P-poll__networl_4_4_RP_1 + P-poll__networl_4_4_RP_2 + P-poll__networl_4_4_RP_3 + P-poll__networl_4_4_RP_4 + P-poll__networl_4_4_RP_5 + P-poll__networl_4_4_RP_6 + P-poll__networl_4_4_RP_7 + P-poll__networl_4_5_AskP_0 + P-poll__networl_4_5_AskP_1 + P-poll__networl_4_5_AskP_2 + P-poll__networl_4_5_AskP_3 + P-poll__networl_4_5_AskP_4 + P-poll__networl_4_5_AskP_5 + P-poll__networl_4_5_AskP_6 + P-poll__networl_4_5_AskP_7 + P-poll__networl_6_3_RP_0 + P-poll__networl_6_3_RP_1 + P-poll__networl_6_3_RP_2 + P-poll__networl_6_3_RP_3 + P-poll__networl_6_3_RP_4 + P-poll__networl_6_3_RP_5 + P-poll__networl_6_3_RP_6 + P-poll__networl_6_3_RP_7 + P-poll__networl_1_3_AnsP_0 + P-poll__networl_7_7_AnsP_0 + P-poll__networl_1_5_AI_0 + P-poll__networl_1_5_AI_1 + P-poll__networl_1_5_AI_2 + P-poll__networl_1_5_AI_3 + P-poll__networl_1_5_AI_4 + P-poll__networl_1_5_AI_5 + P-poll__networl_1_5_AI_6 + P-poll__networl_1_5_AI_7 + P-poll__networl_1_6_AnnP_0 + P-poll__networl_1_6_AnnP_1 + P-poll__networl_1_6_AnnP_2 + P-poll__networl_1_6_AnnP_3 + P-poll__networl_1_6_AnnP_4 + P-poll__networl_1_6_AnnP_5 + P-poll__networl_1_6_AnnP_6 + P-poll__networl_1_6_AnnP_7 + P-poll__networl_2_0_AskP_0 + P-poll__networl_2_0_AskP_1 + P-poll__networl_2_0_AskP_2 + P-poll__networl_2_0_AskP_3 + P-poll__networl_2_0_AskP_4 + P-poll__networl_2_0_AskP_5 + P-poll__networl_2_0_AskP_6 + P-poll__networl_2_0_AskP_7 + P-poll__networl_3_4_AI_0 + P-poll__networl_3_4_AI_1 + P-poll__networl_3_4_AI_2 + P-poll__networl_3_4_AI_3 + P-poll__networl_3_4_AI_4 + P-poll__networl_3_4_AI_5 + P-poll__networl_3_4_AI_6 + P-poll__networl_3_4_AI_7 + P-poll__networl_3_7_RI_0 + P-poll__networl_3_7_RI_1 + P-poll__networl_3_7_RI_2 + P-poll__networl_3_7_RI_3 + P-poll__networl_3_7_RI_4 + P-poll__networl_3_7_RI_5 + P-poll__networl_3_7_RI_6 + P-poll__networl_3_7_RI_7 + P-poll__networl_6_1_AnnP_7 + P-poll__networl_6_1_AnnP_6 + P-poll__networl_6_1_AnnP_5 + P-poll__networl_5_3_AI_0 + P-poll__networl_5_3_AI_1 + P-poll__networl_5_3_AI_2 + P-poll__networl_0_7_AnsP_0 + P-poll__networl_5_3_AI_3 + P-poll__networl_6_1_AnnP_4 + P-poll__networl_5_3_AI_4 + P-poll__networl_6_1_AnnP_3 + P-poll__networl_5_3_AI_5 + P-poll__networl_6_1_AnnP_2 + P-poll__networl_5_3_AI_6 + P-poll__networl_6_1_AnnP_1 + P-poll__networl_5_3_AI_7 + P-poll__networl_6_1_AnnP_0 + P-poll__networl_5_6_RI_0 + P-poll__networl_5_6_RI_1 + P-poll__networl_5_6_RI_2 + P-poll__networl_5_6_RI_3 + P-poll__networl_5_6_RI_4 + P-poll__networl_5_6_RI_5 + P-poll__networl_5_6_RI_6 + P-poll__networl_5_6_RI_7 + P-poll__networl_6_2_AnnP_0 + P-poll__networl_6_2_AnnP_1 + P-poll__networl_6_2_AnnP_2 + P-poll__networl_6_2_AnnP_3 + P-poll__networl_6_2_AnnP_4 + P-poll__networl_6_2_AnnP_5 + P-poll__networl_6_2_AnnP_6 + P-poll__networl_6_2_AnnP_7 + P-poll__networl_4_6_RI_7 + P-poll__networl_4_6_RI_6 + P-poll__networl_4_6_RI_5 + P-poll__networl_4_6_RI_4 + P-poll__networl_4_6_RI_3 + P-poll__networl_4_6_RI_2 + P-poll__networl_4_6_RI_1 + P-poll__networl_4_6_RI_0 + P-poll__networl_4_3_AI_7 + P-poll__networl_4_3_AI_6 + P-poll__networl_4_3_AI_5 + P-poll__networl_4_3_AI_4 + P-poll__networl_4_3_AI_3 + P-poll__networl_1_4_AskP_0 + P-poll__networl_1_4_AskP_1 + P-poll__networl_1_4_AskP_2 + P-poll__networl_1_4_AskP_3 + P-poll__networl_1_4_AskP_4 + P-poll__networl_1_4_AskP_5 + P-poll__networl_1_4_AskP_6 + P-poll__networl_1_4_AskP_7 + P-poll__networl_7_2_AI_0 + P-poll__networl_7_2_AI_1 + P-poll__networl_7_2_AI_2 + P-poll__networl_7_2_AI_3 + P-poll__networl_7_2_AI_4 + P-poll__networl_7_2_AI_5 + P-poll__networl_7_2_AI_6 + P-poll__networl_7_2_AI_7 + P-poll__networl_7_5_RI_0 + P-poll__networl_7_5_RI_1 + P-poll__networl_7_5_RI_2 + P-poll__networl_7_5_RI_3 + P-poll__networl_7_5_RI_4 + P-poll__networl_7_5_RI_5 + P-poll__networl_7_5_RI_6 + P-poll__networl_7_5_RI_7 + P-poll__networl_0_2_RI_0 + P-poll__networl_0_2_RI_1 + P-poll__networl_0_2_RI_2 + P-poll__networl_0_2_RI_3 + P-poll__networl_0_2_RI_4 + P-poll__networl_0_2_RI_5 + P-poll__networl_0_2_RI_6 + P-poll__networl_0_2_RI_7 + P-poll__networl_0_6_AnsP_0 + P-poll__networl_4_3_AI_2 + P-poll__networl_4_3_AI_1 + P-poll__networl_4_3_AI_0 + P-poll__networl_5_3_AnsP_0 + P-poll__networl_2_1_RI_0 + P-poll__networl_2_1_RI_1 + P-poll__networl_2_1_RI_2 + P-poll__networl_2_1_RI_3 + P-poll__networl_2_1_RI_4 + P-poll__networl_2_1_RI_5 + P-poll__networl_2_1_RI_6 + P-poll__networl_2_1_RI_7 + P-poll__networl_5_6_AnnP_0 + P-poll__networl_5_6_AnnP_1 + P-poll__networl_5_6_AnnP_2 + P-poll__networl_5_6_AnnP_3 + P-poll__networl_5_6_AnnP_4 + P-poll__networl_5_6_AnnP_5 + P-poll__networl_5_6_AnnP_6 + P-poll__networl_5_6_AnnP_7 + P-poll__networl_6_0_AskP_0 + P-poll__networl_6_0_AskP_1 + P-poll__networl_6_0_AskP_2 + P-poll__networl_6_0_AskP_3 + P-poll__networl_6_0_AskP_4 + P-poll__networl_6_0_AskP_5 + P-poll__networl_6_0_AskP_6 + P-poll__networl_6_0_AskP_7 + P-poll__networl_2_7_RI_7 + P-poll__networl_2_7_RI_6 + P-poll__networl_2_7_RI_5 + P-poll__networl_2_7_RI_4 + P-poll__networl_2_7_RI_3 + P-poll__networl_2_7_RI_2 + P-poll__networl_4_0_RI_0 + P-poll__networl_4_0_RI_1 + P-poll__networl_4_0_RI_2 + P-poll__networl_1_7_RP_0 + P-poll__networl_4_0_RI_3 + P-poll__networl_1_7_RP_1 + P-poll__networl_4_0_RI_4 + P-poll__networl_1_7_RP_2 + P-poll__networl_4_0_RI_5 + P-poll__networl_1_7_RP_3 + P-poll__networl_4_0_RI_6 + P-poll__networl_1_7_RP_4 + P-poll__networl_4_0_RI_7 + P-poll__networl_1_7_RP_5 + P-poll__networl_1_7_RP_6 + P-poll__networl_1_7_RP_7 + P-poll__networl_2_7_RI_1 + P-poll__networl_2_7_RI_0 + P-poll__networl_2_4_AI_7 + P-poll__networl_2_4_AI_6 + P-poll__networl_2_4_AI_5 + P-poll__networl_3_1_AnnP_0 + P-poll__networl_3_1_AnnP_1 + P-poll__networl_3_1_AnnP_2 + P-poll__networl_3_1_AnnP_3 + P-poll__networl_3_1_AnnP_4 + P-poll__networl_3_1_AnnP_5 + P-poll__networl_3_1_AnnP_6 + P-poll__networl_3_1_AnnP_7 + P-poll__networl_2_4_AI_4 + P-poll__networl_2_4_AI_3 + P-poll__networl_4_7_AnsP_0 + P-poll__networl_2_4_AI_2 + P-poll__networl_2_4_AI_1 + P-poll__networl_2_4_AI_0 + P-poll__networl_7_2_RP_7 + P-poll__networl_7_2_RP_6 + P-poll__networl_7_2_RP_5 + P-poll__networl_7_2_RP_4 + P-poll__networl_7_2_RP_3 + P-poll__networl_7_2_RP_2 + P-poll__networl_3_6_RP_0 + P-poll__networl_3_6_RP_1 + P-poll__networl_3_6_RP_2 + P-poll__networl_3_6_RP_3 + P-poll__networl_3_6_RP_4 + P-poll__networl_3_6_RP_5 + P-poll__networl_3_6_RP_6 + P-poll__networl_3_6_RP_7 + P-poll__networl_7_2_RP_1 + P-poll__networl_7_2_RP_0 + P-poll__networl_5_4_AskP_0 + P-poll__networl_5_4_AskP_1 + P-poll__networl_5_4_AskP_2 + P-poll__networl_5_4_AskP_3 + P-poll__networl_5_4_AskP_4 + P-poll__networl_5_4_AskP_5 + P-poll__networl_5_4_AskP_6 + P-poll__networl_5_4_AskP_7 + P-poll__networl_1_5_AnnP_7 + P-poll__networl_1_5_AnnP_6 + P-poll__networl_5_5_RP_0 + P-poll__networl_5_5_RP_1 + P-poll__networl_5_5_RP_2 + P-poll__networl_5_5_RP_3 + P-poll__networl_5_5_RP_4 + P-poll__networl_5_5_RP_5 + P-poll__networl_5_5_RP_6 + P-poll__networl_5_5_RP_7 + P-poll__networl_2_2_AnsP_0 + P-poll__networl_1_5_AnnP_5 + P-poll__networl_1_5_AnnP_4 + P-poll__networl_1_5_AnnP_3 + P-poll__networl_1_5_AnnP_2 + P-poll__networl_1_5_AnnP_1 + P-poll__networl_1_5_AnnP_0 + P-poll__networl_0_7_AI_0 + P-poll__networl_0_7_AI_1 + P-poll__networl_0_7_AI_2 + P-poll__networl_0_7_AI_3 + P-poll__networl_0_7_AI_4 + P-poll__networl_0_7_AI_5 + P-poll__networl_0_7_AI_6 + P-poll__networl_0_7_AI_7 + P-poll__networl_2_5_AnnP_0 + P-poll__networl_2_5_AnnP_1 + P-poll__networl_2_5_AnnP_2 + P-poll__networl_2_5_AnnP_3 + P-poll__networl_2_5_AnnP_4 + P-poll__networl_2_5_AnnP_5 + P-poll__networl_2_5_AnnP_6 + P-poll__networl_2_5_AnnP_7 + P-poll__networl_7_4_RP_0 + P-poll__networl_7_4_RP_1 + P-poll__networl_7_4_RP_2 + P-poll__networl_7_4_RP_3 + P-poll__networl_7_4_RP_4 + P-poll__networl_7_4_RP_5 + P-poll__networl_7_4_RP_6 + P-poll__networl_7_4_RP_7 + P-poll__networl_0_1_RP_0 + P-poll__networl_0_1_RP_1 + P-poll__networl_0_1_RP_2 + P-poll__networl_0_1_RP_3 + P-poll__networl_0_1_RP_4 + P-poll__networl_0_1_RP_5 + P-poll__networl_0_1_RP_6 + P-poll__networl_0_1_RP_7 + P-poll__networl_2_6_AI_0 + P-poll__networl_2_6_AI_1 + P-poll__networl_2_6_AI_2 + P-poll__networl_2_6_AI_3 + P-poll__networl_2_6_AI_4 + P-poll__networl_2_6_AI_5 + P-poll__networl_2_6_AI_6 + P-poll__networl_2_6_AI_7 + P-poll__networl_0_5_AI_7 + P-poll__networl_0_5_AI_6 + P-poll__networl_0_5_AI_5 + P-poll__networl_0_0_AnnP_0 + P-poll__networl_0_0_AnnP_1 + P-poll__networl_0_0_AnnP_2 + P-poll__networl_0_0_AnnP_3 + P-poll__networl_0_0_AnnP_4 + P-poll__networl_0_0_AnnP_5 + P-poll__networl_0_0_AnnP_6 + P-poll__networl_0_0_AnnP_7 + P-poll__networl_2_0_RP_0 + P-poll__networl_2_0_RP_1 + P-poll__networl_2_0_RP_2 + P-poll__networl_2_0_RP_3 + P-poll__networl_2_0_RP_4 + P-poll__networl_2_0_RP_5 + P-poll__networl_2_0_RP_6 + P-poll__networl_2_0_RP_7 + P-poll__networl_0_5_AI_4 + P-poll__networl_1_6_AnsP_0 + P-poll__networl_0_5_AI_3 + P-poll__networl_0_5_AI_2 + P-poll__networl_0_5_AI_1 + P-poll__networl_0_5_AI_0 + P-poll__networl_1_2_AnsP_0 + P-poll__networl_4_5_AI_0 + P-poll__networl_4_5_AI_1 + P-poll__networl_4_5_AI_2 + P-poll__networl_4_5_AI_3 + P-poll__networl_4_5_AI_4 + P-poll__networl_4_5_AI_5 + P-poll__networl_4_5_AI_6 + P-poll__networl_4_5_AI_7 + P-poll__networl_7_1_AnnP_0 + P-poll__networl_7_1_AnnP_1 + P-poll__networl_7_1_AnnP_2 + P-poll__networl_7_1_AnnP_3 + P-poll__networl_7_1_AnnP_4 + P-poll__networl_7_1_AnnP_5 + P-poll__networl_7_1_AnnP_6 + P-poll__networl_7_1_AnnP_7 + P-poll__networl_2_3_AskP_0 + P-poll__networl_2_3_AskP_1 + P-poll__networl_2_3_AskP_2 + P-poll__networl_2_3_AskP_3 + P-poll__networl_2_3_AskP_4 + P-poll__networl_2_3_AskP_5 + P-poll__networl_2_3_AskP_6 + P-poll__networl_2_3_AskP_7 + P-poll__networl_6_4_AI_0 + P-poll__networl_6_4_AI_1 + P-poll__networl_6_4_AI_2 + P-poll__networl_6_4_AI_3 + P-poll__networl_6_4_AI_4 + P-poll__networl_6_4_AI_5 + P-poll__networl_6_4_AI_6 + P-poll__networl_6_4_AI_7 + P-poll__networl_5_3_RP_7 + P-poll__networl_5_3_RP_6 + P-poll__networl_5_3_RP_5 + P-poll__networl_5_3_RP_4 + P-poll__networl_5_3_RP_3 + P-poll__networl_5_3_RP_2 + P-poll__networl_6_7_RI_0 + P-poll__networl_6_7_RI_1 + P-poll__networl_6_7_RI_2 + P-poll__networl_6_7_RI_3 + P-poll__networl_6_7_RI_4 + P-poll__networl_6_7_RI_5 + P-poll__networl_6_7_RI_6 + P-poll__networl_6_7_RI_7 + P-poll__networl_5_3_RP_1 + P-poll__networl_6_2_AnsP_0 + P-poll__networl_5_3_RP_0 + P-poll__networl_1_0_AI_0 + P-poll__networl_1_0_AI_1 + P-poll__networl_1_0_AI_2 + P-poll__networl_1_0_AI_3 + P-poll__networl_1_0_AI_4 + P-poll__networl_1_0_AI_5 + P-poll__networl_1_0_AI_6 + P-poll__networl_1_0_AI_7 + P-poll__networl_1_3_RI_0 + P-poll__networl_1_3_RI_1 + P-poll__networl_1_3_RI_2 + P-poll__networl_1_3_RI_3 + P-poll__networl_1_3_RI_4 + P-poll__networl_1_3_RI_5 + P-poll__networl_1_3_RI_6 + P-poll__networl_1_3_RI_7 + P-poll__networl_6_5_AnnP_0 + P-poll__networl_6_5_AnnP_1 + P-poll__networl_6_5_AnnP_2 + P-poll__networl_6_5_AnnP_3 + P-poll__networl_6_5_AnnP_4 + P-poll__networl_6_5_AnnP_5 + P-poll__networl_6_5_AnnP_6 + P-poll__networl_6_5_AnnP_7 + P-poll__networl_4_4_AskP_7 + P-poll__networl_4_4_AskP_6 + P-poll__networl_4_4_AskP_5 + P-poll__networl_1_7_AskP_0 + P-poll__networl_1_7_AskP_1 + P-poll__networl_1_7_AskP_2 + P-poll__networl_1_7_AskP_3 + P-poll__networl_1_7_AskP_4 + P-poll__networl_1_7_AskP_5 + P-poll__networl_1_7_AskP_6 + P-poll__networl_1_7_AskP_7 + P-poll__networl_3_2_RI_0 + P-poll__networl_3_2_RI_1 + P-poll__networl_3_2_RI_2 + P-poll__networl_3_2_RI_3 + P-poll__networl_3_2_RI_4 + P-poll__networl_3_2_RI_5 + P-poll__networl_3_2_RI_6 + P-poll__networl_3_2_RI_7 + P-poll__networl_4_4_AskP_4 + P-poll__networl_4_4_AskP_3 + P-poll__networl_4_0_AnnP_0 + P-poll__networl_4_0_AnnP_1 + P-poll__networl_4_0_AnnP_2 + P-poll__networl_4_0_AnnP_3 + P-poll__networl_4_0_AnnP_4 + P-poll__networl_4_0_AnnP_5 + P-poll__networl_4_0_AnnP_6 + P-poll__networl_4_0_AnnP_7 + P-poll__networl_4_4_AskP_2 + P-poll__networl_4_4_AskP_1 + P-poll__networl_5_6_AnsP_0 + P-poll__networl_4_4_AskP_0 + P-poll__networl_3_4_RP_7 + P-poll__networl_3_4_RP_6 + P-poll__networl_3_4_RP_5 + P-poll__networl_3_4_RP_4 + P-poll__networl_3_4_RP_3 + P-poll__networl_3_4_RP_2 + P-poll__networl_3_4_RP_1 + P-poll__networl_5_1_RI_0 + P-poll__networl_5_1_RI_1 + P-poll__networl_5_1_RI_2 + P-poll__networl_5_1_RI_3 + P-poll__networl_5_1_RI_4 + P-poll__networl_5_1_RI_5 + P-poll__networl_5_1_RI_6 + P-poll__networl_5_1_RI_7 + P-poll__networl_3_4_RP_0 + P-poll__networl_3_7_AnsP_0 + P-poll__networl_6_3_AskP_0 + P-poll__networl_6_3_AskP_1 + P-poll__networl_6_3_AskP_2 + P-poll__networl_6_3_AskP_3 + P-poll__networl_6_3_AskP_4 + P-poll__networl_6_3_AskP_5 + P-poll__networl_6_3_AskP_6 + P-poll__networl_6_3_AskP_7 + P-poll__networl_3_1_AnsP_0 + P-poll__networl_2_1_AnnP_7 + P-poll__networl_2_1_AnnP_6 + P-poll__networl_7_0_RI_0 + P-poll__networl_7_0_RI_1 + P-poll__networl_7_0_RI_2 + P-poll__networl_4_7_RP_0 + P-poll__networl_7_0_RI_3 + P-poll__networl_4_7_RP_1 + P-poll__networl_7_0_RI_4 + P-poll__networl_4_7_RP_2 + P-poll__networl_7_0_RI_5 + P-poll__networl_4_7_RP_3 + P-poll__networl_7_0_RI_6 + P-poll__networl_4_7_RP_4 + P-poll__networl_7_0_RI_7 + P-poll__networl_4_7_RP_5 + P-poll__networl_4_7_RP_6 + P-poll__networl_4_7_RP_7 + P-poll__networl_2_1_AnnP_5 + P-poll__networl_3_4_AnnP_0 + P-poll__networl_3_4_AnnP_1 + P-poll__networl_3_4_AnnP_2 + P-poll__networl_3_4_AnnP_3 + P-poll__networl_3_4_AnnP_4 + P-poll__networl_3_4_AnnP_5 + P-poll__networl_3_4_AnnP_6 + P-poll__networl_3_4_AnnP_7 + P-poll__networl_2_1_AnnP_4 + P-poll__networl_2_1_AnnP_3 + P-poll__networl_2_1_AnnP_2 + P-poll__networl_6_6_RP_0 + P-poll__networl_6_6_RP_1 + P-poll__networl_6_6_RP_2 + P-poll__networl_6_6_RP_3 + P-poll__networl_6_6_RP_4 + P-poll__networl_6_6_RP_5 + P-poll__networl_6_6_RP_6 + P-poll__networl_6_6_RP_7 + P-poll__networl_2_1_AnnP_1 + P-poll__networl_2_1_AnnP_0 + P-poll__networl_1_5_RP_7 + P-poll__networl_1_5_RP_6 + P-poll__networl_5_7_AskP_0 + P-poll__networl_5_7_AskP_1 + P-poll__networl_5_7_AskP_2 + P-poll__networl_5_7_AskP_3 + P-poll__networl_5_7_AskP_4 + P-poll__networl_5_7_AskP_5 + P-poll__networl_5_7_AskP_6 + P-poll__networl_5_7_AskP_7 + P-poll__networl_1_5_RP_5 + P-poll__networl_1_5_RP_4 + P-poll__networl_1_2_RP_0 + P-poll__networl_1_2_RP_1 + P-poll__networl_1_2_RP_2 + P-poll__networl_1_2_RP_3 + P-poll__networl_1_2_RP_4 + P-poll__networl_1_2_RP_5 + P-poll__networl_1_2_RP_6 + P-poll__networl_1_2_RP_7 + P-poll__networl_2_5_AnsP_0 + P-poll__networl_1_5_RP_3 + P-poll__networl_1_5_RP_2 + P-poll__networl_1_5_RP_1 + P-poll__networl_1_5_RP_0 + P-poll__networl_3_7_AI_0 + P-poll__networl_3_7_AI_1 + P-poll__networl_3_7_AI_2 + P-poll__networl_3_7_AI_3 + P-poll__networl_3_7_AI_4 + P-poll__networl_3_7_AI_5 + P-poll__networl_3_7_AI_6 + P-poll__networl_3_7_AI_7 + P-poll__networl_5_0_AskP_7 + P-poll__networl_5_0_AskP_6 + P-poll__networl_5_0_AskP_5 + P-poll__networl_5_0_AskP_4 + P-poll__networl_5_0_AskP_3 + P-poll__networl_5_0_AskP_2 + P-poll__networl_5_0_AskP_1 + P-poll__networl_3_2_AskP_0 + P-poll__networl_3_2_AskP_1 + P-poll__networl_3_2_AskP_2 + P-poll__networl_3_2_AskP_3 + P-poll__networl_3_2_AskP_4 + P-poll__networl_3_2_AskP_5 + P-poll__networl_3_2_AskP_6 + P-poll__networl_3_2_AskP_7 + P-poll__networl_3_1_RP_0 + P-poll__networl_3_1_RP_1 + P-poll__networl_3_1_RP_2 + P-poll__networl_3_1_RP_3 + P-poll__networl_3_1_RP_4 + P-poll__networl_3_1_RP_5 + P-poll__networl_3_1_RP_6 + P-poll__networl_3_1_RP_7 + P-poll__networl_5_0_AskP_0 + P-poll__networl_5_6_AI_0 + P-poll__networl_5_6_AI_1 + P-poll__networl_5_6_AI_2 + P-poll__networl_5_6_AI_3 + P-poll__networl_5_6_AI_4 + P-poll__networl_5_6_AI_5 + P-poll__networl_5_6_AI_6 + P-poll__networl_5_6_AI_7 + P-poll__networl_0_0_AnsP_0 + P-poll__networl_4_6_AnnP_7 + P-poll__networl_4_6_AnnP_6 + P-poll__networl_4_6_AnnP_5 + P-poll__networl_4_6_AnnP_4 + P-poll__networl_4_6_AnnP_3 + P-poll__networl_4_6_AnnP_2 + P-poll__networl_4_6_AnnP_1 + P-poll__networl_7_1_AnsP_0 + P-poll__networl_4_6_AnnP_0 + P-poll__networl_0_3_AnnP_0 + P-poll__networl_0_3_AnnP_1 + P-poll__networl_0_3_AnnP_2 + P-poll__networl_0_3_AnnP_3 + P-poll__networl_0_3_AnnP_4 + P-poll__networl_0_3_AnnP_5 + P-poll__networl_0_3_AnnP_6 + P-poll__networl_0_3_AnnP_7 + P-poll__networl_5_0_RP_0 + P-poll__networl_5_0_RP_1 + P-poll__networl_5_0_RP_2 + P-poll__networl_5_0_RP_3 + P-poll__networl_5_0_RP_4 + P-poll__networl_5_0_RP_5 + P-poll__networl_5_0_RP_6 + P-poll__networl_5_0_RP_7 + P-poll__networl_4_3_AnsP_0 + P-poll__networl_7_5_AI_0 + P-poll__networl_7_5_AI_1 + P-poll__networl_7_5_AI_2 + P-poll__networl_7_5_AI_3 + P-poll__networl_7_5_AI_4 + P-poll__networl_7_5_AI_5 + P-poll__networl_7_5_AI_6 + P-poll__networl_7_5_AI_7 + P-poll__networl_0_2_AI_0 + P-poll__networl_0_2_AI_1 + P-poll__networl_0_2_AI_2 + P-poll__networl_0_2_AI_3 + P-poll__networl_0_2_AI_4 + P-poll__networl_0_2_AI_5 + P-poll__networl_0_2_AI_6 + P-poll__networl_0_2_AI_7 + P-poll__networl_0_5_RI_0 + P-poll__networl_0_5_RI_1 + P-poll__networl_0_5_RI_2 + P-poll__networl_0_5_RI_3 + P-poll__networl_0_5_RI_4 + P-poll__networl_0_5_RI_5 + P-poll__networl_0_5_RI_6 + P-poll__networl_0_5_RI_7 + P-poll__networl_7_4_AnnP_0 + P-poll__networl_7_4_AnnP_1 + P-poll__networl_7_4_AnnP_2 + P-poll__networl_7_4_AnnP_3 + P-poll__networl_7_4_AnnP_4 + P-poll__networl_7_4_AnnP_5 + P-poll__networl_7_4_AnnP_6 + P-poll__networl_7_4_AnnP_7 + P-poll__networl_2_6_AskP_0 + P-poll__networl_2_6_AskP_1 + P-poll__networl_2_6_AskP_2 + P-poll__networl_2_6_AskP_3 + P-poll__networl_2_6_AskP_4 + P-poll__networl_2_6_AskP_5 + P-poll__networl_2_6_AskP_6 + P-poll__networl_2_6_AskP_7 + P-poll__networl_2_1_AI_0 + P-poll__networl_2_1_AI_1 + P-poll__networl_2_1_AI_2 + P-poll__networl_2_1_AI_3 + P-poll__networl_2_1_AI_4 + P-poll__networl_2_1_AI_5 + P-poll__networl_2_1_AI_6 + P-poll__networl_2_1_AI_7 + P-poll__networl_2_4_RI_0 + P-poll__networl_2_4_RI_1 + P-poll__networl_2_4_RI_2 + P-poll__networl_2_4_RI_3 + P-poll__networl_2_4_RI_4 + P-poll__networl_2_4_RI_5 + P-poll__networl_2_4_RI_6 + P-poll__networl_2_4_RI_7 + P-poll__networl_6_5_AnsP_0 + P-poll__networl_4_0_AI_0 + P-poll__networl_4_0_AI_1 + P-poll__networl_4_0_AI_2 + P-poll__networl_4_0_AI_3 + P-poll__networl_4_0_AI_4 + P-poll__networl_4_0_AI_5 + P-poll__networl_4_0_AI_6 + P-poll__networl_4_0_AI_7 + P-poll__networl_7_5_AskP_7 + P-poll__networl_7_5_AskP_6 + P-poll__networl_7_5_AskP_5 + P-poll__networl_7_5_AskP_4 + P-poll__networl_0_1_AskP_0 + P-poll__networl_0_1_AskP_1 + P-poll__networl_0_1_AskP_2 + P-poll__networl_0_1_AskP_3 + P-poll__networl_0_1_AskP_4 + P-poll__networl_0_1_AskP_5 + P-poll__networl_0_1_AskP_6 + P-poll__networl_0_1_AskP_7 + P-poll__networl_4_3_RI_0 + P-poll__networl_4_3_RI_1 + P-poll__networl_4_3_RI_2 + P-poll__networl_4_3_RI_3 + P-poll__networl_4_3_RI_4 + P-poll__networl_4_3_RI_5 + P-poll__networl_4_3_RI_6 + P-poll__networl_4_3_RI_7 + P-poll__networl_7_2_AskP_0 + P-poll__networl_7_2_AskP_1 + P-poll__networl_7_2_AskP_2 + P-poll__networl_7_2_AskP_3 + P-poll__networl_7_2_AskP_4 + P-poll__networl_7_2_AskP_5 + P-poll__networl_7_2_AskP_6 + P-poll__networl_7_2_AskP_7 + P-poll__networl_7_5_AskP_3 + P-poll__networl_4_0_AnsP_0 + P-poll__networl_7_5_AskP_2 + P-poll__networl_7_5_AskP_1 + P-poll__networl_7_5_AskP_0 + P-poll__networl_6_2_RI_0 + P-poll__networl_6_2_RI_1 + P-poll__networl_6_2_RI_2 + P-poll__networl_6_2_RI_3 + P-poll__networl_6_2_RI_4 + P-poll__networl_6_2_RI_5 + P-poll__networl_6_2_RI_6 + P-poll__networl_6_2_RI_7 + P-poll__networl_0_0_RI_7 + P-poll__networl_0_0_RI_6 + P-poll__networl_0_0_RI_5 + P-poll__networl_0_0_RI_4 + P-poll__networl_0_0_RI_3 + P-poll__networl_0_0_RI_2 + P-poll__networl_0_0_RI_1 + P-poll__networl_4_3_AnnP_0 + P-poll__networl_4_3_AnnP_1 + P-poll__networl_4_3_AnnP_2 + P-poll__networl_4_3_AnnP_3 + P-poll__networl_4_3_AnnP_4 + P-poll__networl_4_3_AnnP_5 + P-poll__networl_4_3_AnnP_6 + P-poll__networl_4_3_AnnP_7 + P-poll__networl_0_0_RI_0 + P-poll__networl_7_3_RI_7 + P-poll__networl_7_3_RI_6 + P-poll__networl_7_3_RI_5 + P-poll__networl_7_3_RI_4 + P-poll__networl_7_3_RI_3 + P-poll__networl_7_3_RI_2 + P-poll__networl_7_3_RI_1 + P-poll__networl_7_3_RI_0 + P-poll__networl_0_4_AskP_7 + P-poll__networl_0_4_AskP_6 + P-poll__networl_0_4_AskP_5 + P-poll__networl_0_4_AskP_4 + P-poll__networl_0_4_AskP_3 + P-poll__networl_0_4_AskP_2 + P-poll__networl_0_4_AskP_1 + P-poll__networl_0_4_AskP_0 + P-poll__networl_7_0_AI_7 + P-poll__networl_7_0_AI_6 + P-poll__networl_7_0_AI_5 + P-poll__networl_7_0_AI_4 + P-poll__networl_7_0_AI_3 + P-poll__networl_7_0_AI_2 + P-poll__networl_7_0_AI_1 + P-poll__networl_7_0_AI_0 + P-poll__networl_6_6_AskP_0 + P-poll__networl_6_6_AskP_1 + P-poll__networl_6_6_AskP_2 + P-poll__networl_6_6_AskP_3 + P-poll__networl_6_6_AskP_4 + P-poll__networl_6_6_AskP_5 + P-poll__networl_6_6_AskP_6 + P-poll__networl_6_6_AskP_7 + P-poll__networl_3_4_AnsP_0 + P-poll__networl_7_7_RP_0 + P-poll__networl_7_7_RP_1 + P-poll__networl_7_7_RP_2 + P-poll__networl_7_7_RP_3 + P-poll__networl_7_7_RP_4 + P-poll__networl_7_7_RP_5 + P-poll__networl_7_7_RP_6 + P-poll__networl_7_7_RP_7 + P-poll__networl_0_4_RP_0 + P-poll__networl_0_4_RP_1 + P-poll__networl_0_4_RP_2 + P-poll__networl_0_4_RP_3 + P-poll__networl_0_4_RP_4 + P-poll__networl_0_4_RP_5 + P-poll__networl_0_4_RP_6 + P-poll__networl_0_4_RP_7 + P-poll__networl_3_7_AnnP_0 + P-poll__networl_3_7_AnnP_1 + P-poll__networl_3_7_AnnP_2 + P-poll__networl_3_7_AnnP_3 + P-poll__networl_3_7_AnnP_4 + P-poll__networl_3_7_AnnP_5 + P-poll__networl_3_7_AnnP_6 + P-poll__networl_3_7_AnnP_7 + P-poll__networl_4_1_AskP_0 + P-poll__networl_4_1_AskP_1 + P-poll__networl_4_1_AskP_2 + P-poll__networl_4_1_AskP_3 + P-poll__networl_4_1_AskP_4 + P-poll__networl_4_1_AskP_5 + P-poll__networl_4_1_AskP_6 + P-poll__networl_4_1_AskP_7 + P-poll__networl_2_3_RP_0 + P-poll__networl_2_3_RP_1 + P-poll__networl_2_3_RP_2 + P-poll__networl_2_3_RP_3 + P-poll__networl_2_3_RP_4 + P-poll__networl_2_3_RP_5 + P-poll__networl_2_3_RP_6 + P-poll__networl_2_3_RP_7 + P-poll__networl_5_2_AnnP_7 + P-poll__networl_5_2_AnnP_6 + P-poll__networl_5_2_AnnP_5 + P-poll__networl_5_2_AnnP_4 + P-poll__networl_5_2_AnnP_3 + P-poll__networl_5_2_AnnP_2 + P-poll__networl_5_2_AnnP_1 + P-poll__networl_1_2_AnnP_0 + P-poll__networl_1_2_AnnP_1 + P-poll__networl_1_2_AnnP_2 + P-poll__networl_1_2_AnnP_3 + P-poll__networl_1_2_AnnP_4 + P-poll__networl_1_2_AnnP_5 + P-poll__networl_1_2_AnnP_6 + P-poll__networl_1_2_AnnP_7 + P-poll__networl_5_2_AnnP_0 + P-poll__networl_5_4_RI_7 + P-poll__networl_4_2_RP_0 + P-poll__networl_4_2_RP_1 + P-poll__networl_4_2_RP_2 + P-poll__networl_4_2_RP_3 + P-poll__networl_4_2_RP_4 + P-poll__networl_4_2_RP_5 + P-poll__networl_4_2_RP_6 + P-poll__networl_4_2_RP_7 + P-poll__networl_5_4_RI_6 + P-poll__networl_6_7_AI_0 + P-poll__networl_6_7_AI_1 + P-poll__networl_6_7_AI_2 + P-poll__networl_6_7_AI_3 + P-poll__networl_6_7_AI_4 + P-poll__networl_6_7_AI_5 + P-poll__networl_6_7_AI_6 + P-poll__networl_6_7_AI_7 + P-poll__networl_5_4_RI_5 + P-poll__networl_5_4_RI_4 + P-poll__networl_5_4_RI_3 + P-poll__networl_5_4_RI_2 + P-poll__networl_5_4_RI_1 + P-poll__networl_5_4_RI_0 + P-poll__networl_5_1_AI_7 + P-poll__networl_5_1_AI_6 + P-poll__networl_5_1_AI_5 + P-poll__networl_3_5_AskP_0 + P-poll__networl_3_5_AskP_1 + P-poll__networl_3_5_AskP_2 + P-poll__networl_3_5_AskP_3 + P-poll__networl_3_5_AskP_4 + P-poll__networl_3_5_AskP_5 + P-poll__networl_3_5_AskP_6 + P-poll__networl_3_5_AskP_7 + P-poll__networl_6_1_RP_0 + P-poll__networl_6_1_RP_1 + P-poll__networl_6_1_RP_2 + P-poll__networl_6_1_RP_3 + P-poll__networl_6_1_RP_4 + P-poll__networl_6_1_RP_5 + P-poll__networl_6_1_RP_6 + P-poll__networl_6_1_RP_7 + P-poll__networl_5_1_AI_4 + P-poll__networl_1_3_AI_0 + P-poll__networl_1_3_AI_1 + P-poll__networl_1_3_AI_2 + P-poll__networl_0_3_AnsP_0 + P-poll__networl_1_3_AI_3 + P-poll__networl_5_1_AI_3 + P-poll__networl_1_3_AI_4 + P-poll__networl_5_1_AI_2 + P-poll__networl_1_3_AI_5 + P-poll__networl_5_1_AI_1 + P-poll__networl_1_3_AI_6 + P-poll__networl_5_1_AI_0 + P-poll__networl_1_3_AI_7 + P-poll__networl_1_6_RI_0 + P-poll__networl_1_6_RI_1 + P-poll__networl_1_6_RI_2 + P-poll__networl_1_6_RI_3 + P-poll__networl_1_6_RI_4 + P-poll__networl_1_6_RI_5 + P-poll__networl_1_6_RI_6 + P-poll__networl_1_6_RI_7 + P-poll__networl_7_4_AnsP_0 + P-poll__networl_0_6_AnnP_0 + P-poll__networl_0_6_AnnP_1 + P-poll__networl_0_6_AnnP_2 + P-poll__networl_0_6_AnnP_3 + P-poll__networl_0_6_AnnP_4 + P-poll__networl_0_6_AnnP_5 + P-poll__networl_0_6_AnnP_6 + P-poll__networl_0_6_AnnP_7 + P-poll__networl_1_0_AskP_0 + P-poll__networl_1_0_AskP_1 + P-poll__networl_1_0_AskP_2 + P-poll__networl_1_0_AskP_3 + P-poll__networl_1_0_AskP_4 + P-poll__networl_1_0_AskP_5 + P-poll__networl_1_0_AskP_6 + P-poll__networl_1_0_AskP_7 + P-poll__networl_3_2_AI_0 + P-poll__networl_3_2_AI_1 + P-poll__networl_3_2_AI_2 + P-poll__networl_3_2_AI_3 + P-poll__networl_3_2_AI_4 + P-poll__networl_3_2_AI_5 + P-poll__networl_3_2_AI_6 + P-poll__networl_3_2_AI_7 + P-poll__networl_3_5_RI_0 + P-poll__networl_3_5_RI_1 + P-poll__networl_3_5_RI_2 + P-poll__networl_3_5_RI_3 + P-poll__networl_3_5_RI_4 + P-poll__networl_3_5_RI_5 + P-poll__networl_3_5_RI_6 + P-poll__networl_3_5_RI_7 + P-poll__networl_7_7_AnnP_0 + P-poll__networl_7_7_AnnP_1 + P-poll__networl_7_7_AnnP_2 + P-poll__networl_7_7_AnnP_3 + P-poll__networl_7_7_AnnP_4 + P-poll__networl_7_7_AnnP_5 + P-poll__networl_7_7_AnnP_6 + P-poll__networl_7_7_AnnP_7)))) : E (F ((P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterList_0_4_2 + P-masterList_0_4_3 + P-masterList_0_4_4 + P-masterList_0_4_5 + P-masterList_0_4_6 + P-masterList_0_4_7 + P-masterList_0_3_7 + P-masterList_0_3_6 + P-masterList_0_3_5 + P-masterList_0_3_4 + P-masterList_0_3_3 + P-masterList_0_3_2 + P-masterList_0_3_1 + P-masterList_0_3_0 + P-masterList_3_1_7 + P-masterList_3_1_6 + P-masterList_3_1_5 + P-masterList_3_1_4 + P-masterList_5_7_0 + P-masterList_5_7_1 + P-masterList_5_7_2 + P-masterList_5_7_3 + P-masterList_5_7_4 + P-masterList_5_7_5 + P-masterList_5_7_6 + P-masterList_5_7_7 + P-masterList_3_1_3 + P-masterList_3_1_2 + P-masterList_3_1_1 + P-masterList_3_1_0 + P-masterList_6_1_0 + P-masterList_6_1_1 + P-masterList_6_1_2 + P-masterList_6_1_3 + P-masterList_6_1_4 + P-masterList_6_1_5 + P-masterList_6_1_6 + P-masterList_6_1_7 + P-masterList_3_3_0 + P-masterList_3_3_1 + P-masterList_3_3_2 + P-masterList_3_3_3 + P-masterList_3_3_4 + P-masterList_3_3_5 + P-masterList_3_3_6 + P-masterList_3_3_7 + P-masterList_0_5_0 + P-masterList_0_5_1 + P-masterList_0_5_2 + P-masterList_0_5_3 + P-masterList_0_5_4 + P-masterList_0_5_5 + P-masterList_0_5_6 + P-masterList_0_5_7 + P-masterList_2_7_7 + P-masterList_2_7_6 + P-masterList_2_7_5 + P-masterList_2_7_4 + P-masterList_2_7_3 + P-masterList_2_7_2 + P-masterList_2_7_1 + P-masterList_2_7_0 + P-masterList_5_5_7 + P-masterList_5_5_6 + P-masterList_5_5_5 + P-masterList_5_5_4 + P-masterList_5_5_3 + P-masterList_5_5_2 + P-masterList_5_5_1 + P-masterList_5_5_0 + P-masterList_6_2_0 + P-masterList_6_2_1 + P-masterList_6_2_2 + P-masterList_6_2_3 + P-masterList_6_2_4 + P-masterList_6_2_5 + P-masterList_6_2_6 + P-masterList_6_2_7 + P-masterList_3_4_0 + P-masterList_3_4_1 + P-masterList_3_4_2 + P-masterList_3_4_3 + P-masterList_3_4_4 + P-masterList_3_4_5 + P-masterList_3_4_6 + P-masterList_3_4_7 + P-masterList_0_6_0 + P-masterList_0_6_1 + P-masterList_0_6_2 + P-masterList_0_6_3 + P-masterList_0_6_4 + P-masterList_0_6_5 + P-masterList_0_6_6 + P-masterList_0_6_7 + P-masterList_6_3_0 + P-masterList_6_3_1 + P-masterList_6_3_2 + P-masterList_6_3_3 + P-masterList_6_3_4 + P-masterList_6_3_5 + P-masterList_6_3_6 + P-masterList_6_3_7 + P-masterList_3_5_0 + P-masterList_3_5_1 + P-masterList_3_5_2 + P-masterList_3_5_3 + P-masterList_3_5_4 + P-masterList_3_5_5 + P-masterList_3_5_6 + P-masterList_3_5_7 + P-masterList_0_7_0 + P-masterList_0_7_1 + P-masterList_0_7_2 + P-masterList_0_7_3 + P-masterList_0_7_4 + P-masterList_0_7_5 + P-masterList_0_7_6 + P-masterList_0_7_7 + P-masterList_1_1_0 + P-masterList_1_1_1 + P-masterList_1_1_2 + P-masterList_1_1_3 + P-masterList_1_1_4 + P-masterList_1_1_5 + P-masterList_1_1_6 + P-masterList_1_1_7 + P-masterList_0_2_7 + P-masterList_0_2_6 + P-masterList_0_2_5 + P-masterList_0_2_4 + P-masterList_0_2_3 + P-masterList_0_2_2 + P-masterList_0_2_1 + P-masterList_0_2_0 + P-masterList_6_4_0 + P-masterList_6_4_1 + P-masterList_6_4_2 + P-masterList_6_4_3 + P-masterList_6_4_4 + P-masterList_6_4_5 + P-masterList_6_4_6 + P-masterList_6_4_7 + P-masterList_3_6_0 + P-masterList_3_6_1 + P-masterList_3_6_2 + P-masterList_3_6_3 + P-masterList_3_6_4 + P-masterList_3_6_5 + P-masterList_3_6_6 + P-masterList_3_6_7 + P-masterList_1_2_0 + P-masterList_1_2_1 + P-masterList_1_2_2 + P-masterList_1_2_3 + P-masterList_1_2_4 + P-masterList_1_2_5 + P-masterList_1_2_6 + P-masterList_1_2_7 + P-masterList_2_6_7 + P-masterList_2_6_6 + P-masterList_2_6_5 + P-masterList_2_6_4 + P-masterList_2_6_3 + P-masterList_2_6_2 + P-masterList_2_6_1 + P-masterList_2_6_0 + P-masterList_6_5_0 + P-masterList_6_5_1 + P-masterList_6_5_2 + P-masterList_6_5_3 + P-masterList_6_5_4 + P-masterList_6_5_5 + P-masterList_6_5_6 + P-masterList_6_5_7 + P-masterList_5_4_7 + P-masterList_5_4_6 + P-masterList_5_4_5 + P-masterList_5_4_4 + P-masterList_5_4_3 + P-masterList_5_4_2 + P-masterList_3_7_0 + P-masterList_3_7_1 + P-masterList_3_7_2 + P-masterList_3_7_3 + P-masterList_3_7_4 + P-masterList_3_7_5 + P-masterList_3_7_6 + P-masterList_3_7_7 + P-masterList_5_4_1 + P-masterList_5_4_0 + P-masterList_4_1_0 + P-masterList_4_1_1 + P-masterList_4_1_2 + P-masterList_4_1_3 + P-masterList_4_1_4 + P-masterList_4_1_5 + P-masterList_4_1_6 + P-masterList_4_1_7 + P-masterList_1_3_0 + P-masterList_1_3_1 + P-masterList_1_3_2 + P-masterList_1_3_3 + P-masterList_1_3_4 + P-masterList_1_3_5 + P-masterList_1_3_6 + P-masterList_1_3_7 + P-masterList_6_6_0 + P-masterList_6_6_1 + P-masterList_6_6_2 + P-masterList_6_6_3 + P-masterList_6_6_4 + P-masterList_6_6_5 + P-masterList_6_6_6 + P-masterList_6_6_7 + P-masterList_4_2_0 + P-masterList_4_2_1 + P-masterList_4_2_2 + P-masterList_4_2_3 + P-masterList_4_2_4 + P-masterList_4_2_5 + P-masterList_4_2_6 + P-masterList_4_2_7 + P-masterList_1_4_0 + P-masterList_1_4_1 + P-masterList_1_4_2 + P-masterList_1_4_3 + P-masterList_1_4_4 + P-masterList_1_4_5 + P-masterList_1_4_6 + P-masterList_1_4_7 + P-masterList_0_1_7 + P-masterList_0_1_6 + P-masterList_0_1_5 + P-masterList_0_1_4 + P-masterList_0_1_3 + P-masterList_0_1_2 + P-masterList_0_1_1 + P-masterList_0_1_0 + P-masterList_6_7_0 + P-masterList_6_7_1 + P-masterList_6_7_2 + P-masterList_6_7_3 + P-masterList_6_7_4 + P-masterList_6_7_5 + P-masterList_6_7_6 + P-masterList_6_7_7 + P-masterList_7_1_0 + P-masterList_7_1_1 + P-masterList_7_1_2 + P-masterList_7_1_3 + P-masterList_7_1_4 + P-masterList_7_1_5 + P-masterList_7_1_6 + P-masterList_7_1_7 + P-masterList_4_3_0 + P-masterList_4_3_1 + P-masterList_4_3_2 + P-masterList_4_3_3 + P-masterList_4_3_4 + P-masterList_4_3_5 + P-masterList_4_3_6 + P-masterList_4_3_7 + P-masterList_1_5_0 + P-masterList_1_5_1 + P-masterList_1_5_2 + P-masterList_1_5_3 + P-masterList_1_5_4 + P-masterList_1_5_5 + P-masterList_1_5_6 + P-masterList_1_5_7 + P-masterList_2_5_7 + P-masterList_2_5_6 + P-masterList_2_5_5 + P-masterList_2_5_4 + P-masterList_2_5_3 + P-masterList_2_5_2 + P-masterList_2_5_1 + P-masterList_2_5_0 + P-masterList_7_2_0 + P-masterList_7_2_1 + P-masterList_7_2_2 + P-masterList_7_2_3 + P-masterList_7_2_4 + P-masterList_7_2_5 + P-masterList_7_2_6 + P-masterList_7_2_7 + P-masterList_4_4_0 + P-masterList_4_4_1 + P-masterList_4_4_2 + P-masterList_4_4_3 + P-masterList_4_4_4 + P-masterList_4_4_5 + P-masterList_4_4_6 + P-masterList_4_4_7 + P-masterList_5_3_7 + P-masterList_5_3_6 + P-masterList_5_3_5 + P-masterList_5_3_4 + P-masterList_5_3_3 + P-masterList_5_3_2 + P-masterList_5_3_1 + P-masterList_5_3_0 + P-masterList_1_6_0 + P-masterList_1_6_1 + P-masterList_1_6_2 + P-masterList_1_6_3 + P-masterList_1_6_4 + P-masterList_1_6_5 + P-masterList_1_6_6 + P-masterList_1_6_7 + P-masterList_7_7_7 + P-masterList_7_7_6 + P-masterList_7_7_5 + P-masterList_7_7_4 + P-masterList_7_7_3 + P-masterList_7_7_2 + P-masterList_7_7_1 + P-masterList_7_7_0 + P-masterList_7_3_0 + P-masterList_7_3_1 + P-masterList_7_3_2 + P-masterList_7_3_3 + P-masterList_7_3_4 + P-masterList_7_3_5 + P-masterList_7_3_6 + P-masterList_7_3_7 + P-masterList_4_5_0 + P-masterList_4_5_1 + P-masterList_4_5_2 + P-masterList_4_5_3 + P-masterList_4_5_4 + P-masterList_4_5_5 + P-masterList_4_5_6 + P-masterList_4_5_7 + P-masterList_1_7_0 + P-masterList_1_7_1 + P-masterList_1_7_2 + P-masterList_1_7_3 + P-masterList_1_7_4 + P-masterList_1_7_5 + P-masterList_1_7_6 + P-masterList_1_7_7 + P-masterList_2_1_0 + P-masterList_2_1_1 + P-masterList_2_1_2 + P-masterList_2_1_3 + P-masterList_2_1_4 + P-masterList_2_1_5 + P-masterList_2_1_6 + P-masterList_2_1_7 + P-masterList_7_4_0 + P-masterList_7_4_1 + P-masterList_7_4_2 + P-masterList_7_4_3 + P-masterList_7_4_4 + P-masterList_7_4_5 + P-masterList_7_4_6 + P-masterList_7_4_7 + P-masterList_4_6_0 + P-masterList_4_6_1 + P-masterList_4_6_2 + P-masterList_4_6_3 + P-masterList_4_6_4 + P-masterList_4_6_5 + P-masterList_4_6_6 + P-masterList_4_6_7 + P-masterList_2_2_0 + P-masterList_2_2_1 + P-masterList_2_2_2 + P-masterList_2_2_3 + P-masterList_2_2_4 + P-masterList_2_2_5 + P-masterList_2_2_6 + P-masterList_2_2_7 + P-masterList_2_4_7 + P-masterList_2_4_6 + P-masterList_2_4_5 + P-masterList_2_4_4 + P-masterList_2_4_3 + P-masterList_2_4_2 + P-masterList_2_4_1 + P-masterList_2_4_0 + P-masterList_7_5_0 + P-masterList_7_5_1 + P-masterList_7_5_2 + P-masterList_7_5_3 + P-masterList_7_5_4 + P-masterList_7_5_5 + P-masterList_7_5_6 + P-masterList_7_5_7 + P-masterList_4_7_0 + P-masterList_4_7_1 + P-masterList_4_7_2 + P-masterList_4_7_3 + P-masterList_4_7_4 + P-masterList_4_7_5 + P-masterList_4_7_6 + P-masterList_4_7_7 + P-masterList_5_1_0 + P-masterList_5_1_1 + P-masterList_5_1_2 + P-masterList_5_1_3 + P-masterList_5_1_4 + P-masterList_5_1_5 + P-masterList_5_1_6 + P-masterList_5_1_7 + P-masterList_5_2_7 + P-masterList_5_2_6 + P-masterList_5_2_5 + P-masterList_5_2_4 + P-masterList_5_2_3 + P-masterList_5_2_2 + P-masterList_5_2_1 + P-masterList_5_2_0 + P-masterList_2_3_0 + P-masterList_2_3_1 + P-masterList_2_3_2 + P-masterList_2_3_3 + P-masterList_2_3_4 + P-masterList_2_3_5 + P-masterList_2_3_6 + P-masterList_2_3_7 + P-masterList_7_6_0 + P-masterList_7_6_1 + P-masterList_7_6_2 + P-masterList_7_6_3 + P-masterList_7_6_4 + P-masterList_7_6_5 + P-masterList_7_6_6 + P-masterList_7_6_7 <= 0))) : E (F (FALSE)) : E (F (((P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 <= 2) AND (P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcasting_2_3 + P-startNeg__broadcasting_2_4 + P-startNeg__broadcasting_2_5 + P-startNeg__broadcasting_2_6 + P-startNeg__broadcasting_2_7 + P-startNeg__broadcasting_3_1 + P-startNeg__broadcasting_3_2 + P-startNeg__broadcasting_3_3 + P-startNeg__broadcasting_3_4 + P-startNeg__broadcasting_3_5 + P-startNeg__broadcasting_3_6 + P-startNeg__broadcasting_3_7 + P-startNeg__broadcasting_4_1 + P-startNeg__broadcasting_4_2 + P-startNeg__broadcasting_4_3 + P-startNeg__broadcasting_4_4 + P-startNeg__broadcasting_4_5 + P-startNeg__broadcasting_4_6 + P-startNeg__broadcasting_4_7 + P-startNeg__broadcasting_7_7 + P-startNeg__broadcasting_7_6 + P-startNeg__broadcasting_7_5 + P-startNeg__broadcasting_7_4 + P-startNeg__broadcasting_7_3 + P-startNeg__broadcasting_7_2 + P-startNeg__broadcasting_7_1 + P-startNeg__broadcasting_5_1 + P-startNeg__broadcasting_5_2 + P-startNeg__broadcasting_5_3 + P-startNeg__broadcasting_5_4 + P-startNeg__broadcasting_5_5 + P-startNeg__broadcasting_5_6 + P-startNeg__broadcasting_5_7 + P-startNeg__broadcasting_6_7 + P-startNeg__broadcasting_6_6 + P-startNeg__broadcasting_6_5 + P-startNeg__broadcasting_6_4 + P-startNeg__broadcasting_6_3 + P-startNeg__broadcasting_6_2 + P-startNeg__broadcasting_6_1 + P-startNeg__broadcasting_0_6 + P-startNeg__broadcasting_0_7 + P-startNeg__broadcasting_1_6 + P-startNeg__broadcasting_1_7 <= 1) AND (P-poll__pollEnd_7 + P-poll__pollEnd_6 + P-poll__pollEnd_5 + P-poll__pollEnd_4 + P-poll__pollEnd_3 + P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0 <= 2) AND (P-negotiation_6_4_NONE + P-negotiation_6_2_CO + P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_5_1_DONE + P-negotiation_7_4_CO + P-negotiation_1_3_CO + P-negotiation_7_0_DONE + P-negotiation_3_7_DONE + P-negotiation_5_6_CO + P-negotiation_3_1_CO + P-negotiation_7_5_CO + P-negotiation_0_7_DONE + P-negotiation_0_7_CO + P-negotiation_3_7_NONE + P-negotiation_4_3_CO + P-negotiation_0_5_DONE + P-negotiation_5_0_NONE + P-negotiation_7_2_DONE + P-negotiation_5_6_NONE + P-negotiation_5_3_DONE + P-negotiation_5_5_CO + P-negotiation_2_4_DONE + P-negotiation_3_4_DONE + P-negotiation_1_5_DONE + P-negotiation_2_6_CO + P-negotiation_0_2_CO + P-negotiation_7_5_NONE + P-negotiation_0_2_NONE + P-negotiation_4_3_DONE + P-negotiation_6_7_CO + P-negotiation_6_1_DONE + P-negotiation_2_1_NONE + P-negotiation_2_0_NONE + P-negotiation_4_2_DONE + P-negotiation_0_1_NONE + P-negotiation_6_2_DONE + P-negotiation_2_3_DONE + P-negotiation_4_5_CO + P-negotiation_0_0_CO + P-negotiation_4_0_NONE + P-negotiation_0_4_DONE + P-negotiation_7_7_DONE + P-negotiation_2_1_CO + P-negotiation_1_2_CO + P-negotiation_6_4_CO + P-negotiation_5_0_DONE + P-negotiation_3_1_DONE + P-negotiation_2_4_CO + P-negotiation_6_3_NONE + P-negotiation_1_2_DONE + P-negotiation_4_4_NONE + P-negotiation_4_0_CO + P-negotiation_6_6_DONE + P-negotiation_2_5_NONE + P-negotiation_4_7_DONE + P-negotiation_0_6_NONE + P-negotiation_3_6_CO + P-negotiation_1_6_DONE + P-negotiation_7_1_NONE + P-negotiation_2_0_DONE + P-negotiation_1_5_CO + P-negotiation_5_2_NONE + P-negotiation_6_7_NONE + P-negotiation_0_1_DONE + P-negotiation_7_4_DONE + P-negotiation_3_3_NONE + P-negotiation_3_5_DONE + P-negotiation_5_5_DONE + P-negotiation_1_4_NONE + P-negotiation_3_6_DONE + P-negotiation_1_3_NONE + P-negotiation_1_7_DONE + P-negotiation_5_4_DONE + P-negotiation_3_4_CO + P-negotiation_1_0_CO + P-negotiation_6_3_DONE + P-negotiation_3_2_NONE + P-negotiation_2_2_NONE + P-negotiation_7_3_DONE + P-negotiation_0_0_DONE + P-negotiation_7_7_CO + P-negotiation_4_4_DONE + P-negotiation_0_3_NONE + P-negotiation_7_6_NONE + P-negotiation_5_1_NONE + P-negotiation_0_5_CO + P-negotiation_2_5_DONE + P-negotiation_5_7_NONE + P-negotiation_0_6_DONE + P-negotiation_5_3_CO + P-negotiation_7_0_NONE + P-negotiation_4_1_CO + P-negotiation_1_7_CO + P-negotiation_7_1_DONE + P-negotiation_5_2_DONE + P-negotiation_3_3_DONE + P-negotiation_7_2_CO + P-negotiation_6_5_NONE + P-negotiation_6_1_CO + P-negotiation_1_4_DONE + P-negotiation_4_6_NONE + P-negotiation_6_0_CO + P-negotiation_2_7_NONE + P-negotiation_0_4_CO + P-negotiation_7_3_CO + P-negotiation_6_0_DONE + P-negotiation_4_7_CO + P-negotiation_4_1_DONE + P-negotiation_2_7_DONE + P-negotiation_2_2_DONE + P-negotiation_0_3_DONE + P-negotiation_7_6_DONE + P-negotiation_2_3_CO + P-negotiation_3_5_NONE + P-negotiation_5_7_DONE + P-negotiation_1_6_NONE + P-negotiation_1_1_CO + P-negotiation_4_6_DONE + P-negotiation_6_6_CO + P-negotiation_6_5_DONE + P-negotiation_5_4_CO + P-negotiation_3_0_CO + P-negotiation_3_0_DONE + P-negotiation_4_2_CO + P-negotiation_1_1_DONE + P-negotiation_6_2_NONE + P-negotiation_4_3_NONE + P-negotiation_2_4_NONE + P-negotiation_0_5_NONE + P-negotiation_5_4_NONE + P-negotiation_3_5_CO + P-negotiation_7_3_NONE + P-negotiation_0_0_NONE + P-negotiation_1_6_CO + P-negotiation_1_1_NONE + P-negotiation_3_0_NONE + P-negotiation_6_5_CO + P-negotiation_4_1_NONE + P-negotiation_6_0_NONE + P-negotiation_2_2_CO + P-negotiation_4_6_CO + P-negotiation_0_3_CO + P-negotiation_2_7_CO + P-negotiation_7_1_CO + P-negotiation_5_2_CO + P-negotiation_7_6_CO + P-negotiation_1_7_NONE + P-negotiation_3_6_NONE + P-negotiation_3_3_CO + P-negotiation_5_5_NONE + P-negotiation_7_4_NONE + P-negotiation_5_7_CO + P-negotiation_1_4_CO + P-negotiation_7_0_CO + P-negotiation_4_7_NONE + P-negotiation_6_6_NONE + P-negotiation_1_2_NONE + P-negotiation_3_1_NONE + P-negotiation_5_1_CO + P-negotiation_6_3_CO + P-negotiation_2_6_DONE + P-negotiation_7_7_NONE + P-negotiation_0_4_NONE + P-negotiation_4_5_DONE + P-negotiation_2_3_NONE + P-negotiation_6_4_DONE + P-negotiation_2_0_CO + P-negotiation_4_2_NONE + P-negotiation_1_0_DONE + P-negotiation_6_1_NONE + P-negotiation_3_2_CO + P-negotiation_4_4_CO + P-negotiation_0_1_CO + P-negotiation_1_5_NONE + P-negotiation_5_6_DONE + P-negotiation_3_4_NONE + P-negotiation_7_5_DONE + P-negotiation_0_2_DONE + P-negotiation_5_3_NONE + P-negotiation_2_5_CO + P-negotiation_2_1_DONE + P-negotiation_7_2_NONE + P-negotiation_4_0_DONE + P-negotiation_3_7_CO + P-negotiation_0_7_NONE + P-negotiation_2_6_NONE + P-negotiation_0_6_CO + P-negotiation_6_7_DONE + P-negotiation_5_0_CO + P-negotiation_4_5_NONE + P-negotiation_1_3_DONE <= 2)))) : E (F ((P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3 + P-masterState_3_F_2 + P-masterState_3_F_1 + P-masterState_3_F_0 + P-masterState_4_T_0 + P-masterState_4_T_1 + P-masterState_4_T_2 + P-masterState_4_T_3 + P-masterState_4_T_4 + P-masterState_4_T_5 + P-masterState_4_T_6 + P-masterState_4_T_7 + P-masterState_6_T_7 + P-masterState_6_T_6 + P-masterState_6_T_5 + P-masterState_6_T_4 + P-masterState_6_T_3 + P-masterState_6_T_2 + P-masterState_6_T_1 + P-masterState_6_T_0 + P-masterState_0_F_6 + P-masterState_0_F_5 + P-masterState_0_F_4 + P-masterState_0_F_3 + P-masterState_0_F_2 + P-masterState_0_F_1 + P-masterState_0_F_0 + P-masterState_3_T_7 + P-masterState_3_T_6 + P-masterState_3_T_5 + P-masterState_3_T_4 + P-masterState_3_T_3 + P-masterState_3_T_2 + P-masterState_3_T_1 + P-masterState_3_T_0 + P-masterState_1_F_0 + P-masterState_1_F_1 + P-masterState_1_F_2 + P-masterState_1_F_3 + P-masterState_1_F_4 + P-masterState_1_F_5 + P-masterState_1_F_6 + P-masterState_1_F_7 + P-masterState_5_F_6 + P-masterState_5_F_5 + P-masterState_5_F_4 + P-masterState_5_F_3 + P-masterState_5_F_2 + P-masterState_5_F_1 + P-masterState_5_F_0 + P-masterState_0_T_7 + P-masterState_0_T_6 + P-masterState_0_T_5 + P-masterState_0_T_4 + P-masterState_0_T_3 + P-masterState_0_T_2 + P-masterState_0_T_1 + P-masterState_0_T_0 + P-masterState_2_F_6 + P-masterState_2_F_5 + P-masterState_2_F_4 + P-masterState_2_F_3 + P-masterState_2_F_2 + P-masterState_2_F_1 + P-masterState_2_F_0 + P-masterState_7_T_0 + P-masterState_7_T_1 + P-masterState_7_T_2 + P-masterState_7_T_3 + P-masterState_7_T_4 + P-masterState_7_T_5 + P-masterState_7_T_6 + P-masterState_7_T_7 + P-masterState_5_T_7 + P-masterState_5_T_6 + P-masterState_5_T_5 + P-masterState_5_T_4 + P-masterState_5_T_3 + P-masterState_5_T_2 + P-masterState_5_T_1 + P-masterState_5_T_0 + P-masterState_7_F_6 + P-masterState_7_F_5 + P-masterState_7_F_4 + P-masterState_7_F_3 + P-masterState_7_F_2 + P-masterState_7_F_1 + P-masterState_7_F_0 + P-masterState_4_F_0 + P-masterState_4_F_1 + P-masterState_4_F_2 + P-masterState_4_F_3 + P-masterState_4_F_4 + P-masterState_4_F_5 + P-masterState_4_F_6 + P-masterState_2_T_7 + P-masterState_2_T_6 + P-masterState_2_T_5 + P-masterState_2_T_4 + P-masterState_2_T_3 + P-masterState_2_T_2 + P-masterState_2_T_1 + P-masterState_2_T_0 + P-masterState_4_F_7 + P-masterState_7_F_7 + P-masterState_2_F_7 + P-masterState_5_F_7 + P-masterState_0_F_7 + P-masterState_3_F_7 + P-masterState_1_T_7 + P-masterState_6_F_7 <= 0))) : E (F ((P-negotiation_6_4_NONE + P-negotiation_6_2_CO + P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_5_1_DONE + P-negotiation_7_4_CO + P-negotiation_1_3_CO + P-negotiation_7_0_DONE + P-negotiation_3_7_DONE + P-negotiation_5_6_CO + P-negotiation_3_1_CO + P-negotiation_7_5_CO + P-negotiation_0_7_DONE + P-negotiation_0_7_CO + P-negotiation_3_7_NONE + P-negotiation_4_3_CO + P-negotiation_0_5_DONE + P-negotiation_5_0_NONE + P-negotiation_7_2_DONE + P-negotiation_5_6_NONE + P-negotiation_5_3_DONE + P-negotiation_5_5_CO + P-negotiation_2_4_DONE + P-negotiation_3_4_DONE + P-negotiation_1_5_DONE + P-negotiation_2_6_CO + P-negotiation_0_2_CO + P-negotiation_7_5_NONE + P-negotiation_0_2_NONE + P-negotiation_4_3_DONE + P-negotiation_6_7_CO + P-negotiation_6_1_DONE + P-negotiation_2_1_NONE + P-negotiation_2_0_NONE + P-negotiation_4_2_DONE + P-negotiation_0_1_NONE + P-negotiation_6_2_DONE + P-negotiation_2_3_DONE + P-negotiation_4_5_CO + P-negotiation_0_0_CO + P-negotiation_4_0_NONE + P-negotiation_0_4_DONE + P-negotiation_7_7_DONE + P-negotiation_2_1_CO + P-negotiation_1_2_CO + P-negotiation_6_4_CO + P-negotiation_5_0_DONE + P-negotiation_3_1_DONE + P-negotiation_2_4_CO + P-negotiation_6_3_NONE + P-negotiation_1_2_DONE + P-negotiation_4_4_NONE + P-negotiation_4_0_CO + P-negotiation_6_6_DONE + P-negotiation_2_5_NONE + P-negotiation_4_7_DONE + P-negotiation_0_6_NONE + P-negotiation_3_6_CO + P-negotiation_1_6_DONE + P-negotiation_7_1_NONE + P-negotiation_2_0_DONE + P-negotiation_1_5_CO + P-negotiation_5_2_NONE + P-negotiation_6_7_NONE + P-negotiation_0_1_DONE + P-negotiation_7_4_DONE + P-negotiation_3_3_NONE + P-negotiation_3_5_DONE + P-negotiation_5_5_DONE + P-negotiation_1_4_NONE + P-negotiation_3_6_DONE + P-negotiation_1_3_NONE + P-negotiation_1_7_DONE + P-negotiation_5_4_DONE + P-negotiation_3_4_CO + P-negotiation_1_0_CO + P-negotiation_6_3_DONE + P-negotiation_3_2_NONE + P-negotiation_2_2_NONE + P-negotiation_7_3_DONE + P-negotiation_0_0_DONE + P-negotiation_7_7_CO + P-negotiation_4_4_DONE + P-negotiation_0_3_NONE + P-negotiation_7_6_NONE + P-negotiation_5_1_NONE + P-negotiation_0_5_CO + P-negotiation_2_5_DONE + P-negotiation_5_7_NONE + P-negotiation_0_6_DONE + P-negotiation_5_3_CO + P-negotiation_7_0_NONE + P-negotiation_4_1_CO + P-negotiation_1_7_CO + P-negotiation_7_1_DONE + P-negotiation_5_2_DONE + P-negotiation_3_3_DONE + P-negotiation_7_2_CO + P-negotiation_6_5_NONE + P-negotiation_6_1_CO + P-negotiation_1_4_DONE + P-negotiation_4_6_NONE + P-negotiation_6_0_CO + P-negotiation_2_7_NONE + P-negotiation_0_4_CO + P-negotiation_7_3_CO + P-negotiation_6_0_DONE + P-negotiation_4_7_CO + P-negotiation_4_1_DONE + P-negotiation_2_7_DONE + P-negotiation_2_2_DONE + P-negotiation_0_3_DONE + P-negotiation_7_6_DONE + P-negotiation_2_3_CO + P-negotiation_3_5_NONE + P-negotiation_5_7_DONE + P-negotiation_1_6_NONE + P-negotiation_1_1_CO + P-negotiation_4_6_DONE + P-negotiation_6_6_CO + P-negotiation_6_5_DONE + P-negotiation_5_4_CO + P-negotiation_3_0_CO + P-negotiation_3_0_DONE + P-negotiation_4_2_CO + P-negotiation_1_1_DONE + P-negotiation_6_2_NONE + P-negotiation_4_3_NONE + P-negotiation_2_4_NONE + P-negotiation_0_5_NONE + P-negotiation_5_4_NONE + P-negotiation_3_5_CO + P-negotiation_7_3_NONE + P-negotiation_0_0_NONE + P-negotiation_1_6_CO + P-negotiation_1_1_NONE + P-negotiation_3_0_NONE + P-negotiation_6_5_CO + P-negotiation_4_1_NONE + P-negotiation_6_0_NONE + P-negotiation_2_2_CO + P-negotiation_4_6_CO + P-negotiation_0_3_CO + P-negotiation_2_7_CO + P-negotiation_7_1_CO + P-negotiation_5_2_CO + P-negotiation_7_6_CO + P-negotiation_1_7_NONE + P-negotiation_3_6_NONE + P-negotiation_3_3_CO + P-negotiation_5_5_NONE + P-negotiation_7_4_NONE + P-negotiation_5_7_CO + P-negotiation_1_4_CO + P-negotiation_7_0_CO + P-negotiation_4_7_NONE + P-negotiation_6_6_NONE + P-negotiation_1_2_NONE + P-negotiation_3_1_NONE + P-negotiation_5_1_CO + P-negotiation_6_3_CO + P-negotiation_2_6_DONE + P-negotiation_7_7_NONE + P-negotiation_0_4_NONE + P-negotiation_4_5_DONE + P-negotiation_2_3_NONE + P-negotiation_6_4_DONE + P-negotiation_2_0_CO + P-negotiation_4_2_NONE + P-negotiation_1_0_DONE + P-negotiation_6_1_NONE + P-negotiation_3_2_CO + P-negotiation_4_4_CO + P-negotiation_0_1_CO + P-negotiation_1_5_NONE + P-negotiation_5_6_DONE + P-negotiation_3_4_NONE + P-negotiation_7_5_DONE + P-negotiation_0_2_DONE + P-negotiation_5_3_NONE + P-negotiation_2_5_CO + P-negotiation_2_1_DONE + P-negotiation_7_2_NONE + P-negotiation_4_0_DONE + P-negotiation_3_7_CO + P-negotiation_0_7_NONE + P-negotiation_2_6_NONE + P-negotiation_0_6_CO + P-negotiation_6_7_DONE + P-negotiation_5_0_CO + P-negotiation_4_5_NONE + P-negotiation_1_3_DONE + 1 <= P-stage_2_SEC + P-stage_3_NEG + P-stage_5_SEC + P-stage_4_PRIM + P-stage_1_SEC + P-stage_6_SEC + P-stage_3_SEC + P-stage_0_SEC + P-stage_7_PRIM + P-stage_1_NEG + P-stage_2_PRIM + P-stage_6_NEG + P-stage_4_NEG + P-stage_5_PRIM + P-stage_7_NEG + P-stage_0_PRIM + P-stage_2_NEG + P-stage_3_PRIM + P-stage_4_SEC + P-stage_5_NEG + P-stage_7_SEC + P-stage_6_PRIM + P-stage_0_NEG + P-stage_1_PRIM))) : A (G ((((P-negotiation_6_4_NONE + P-negotiation_6_2_CO + P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_5_1_DONE + P-negotiation_7_4_CO + P-negotiation_1_3_CO + P-negotiation_7_0_DONE + P-negotiation_3_7_DONE + P-negotiation_5_6_CO + P-negotiation_3_1_CO + P-negotiation_7_5_CO + P-negotiation_0_7_DONE + P-negotiation_0_7_CO + P-negotiation_3_7_NONE + P-negotiation_4_3_CO + P-negotiation_0_5_DONE + P-negotiation_5_0_NONE + P-negotiation_7_2_DONE + P-negotiation_5_6_NONE + P-negotiation_5_3_DONE + P-negotiation_5_5_CO + P-negotiation_2_4_DONE + P-negotiation_3_4_DONE + P-negotiation_1_5_DONE + P-negotiation_2_6_CO + P-negotiation_0_2_CO + P-negotiation_7_5_NONE + P-negotiation_0_2_NONE + P-negotiation_4_3_DONE + P-negotiation_6_7_CO + P-negotiation_6_1_DONE + P-negotiation_2_1_NONE + P-negotiation_2_0_NONE + P-negotiation_4_2_DONE + P-negotiation_0_1_NONE + P-negotiation_6_2_DONE + P-negotiation_2_3_DONE + P-negotiation_4_5_CO + P-negotiation_0_0_CO + P-negotiation_4_0_NONE + P-negotiation_0_4_DONE + P-negotiation_7_7_DONE + P-negotiation_2_1_CO + P-negotiation_1_2_CO + P-negotiation_6_4_CO + P-negotiation_5_0_DONE + P-negotiation_3_1_DONE + P-negotiation_2_4_CO + P-negotiation_6_3_NONE + P-negotiation_1_2_DONE + P-negotiation_4_4_NONE + P-negotiation_4_0_CO + P-negotiation_6_6_DONE + P-negotiation_2_5_NONE + P-negotiation_4_7_DONE + P-negotiation_0_6_NONE + P-negotiation_3_6_CO + P-negotiation_1_6_DONE + P-negotiation_7_1_NONE + P-negotiation_2_0_DONE + P-negotiation_1_5_CO + P-negotiation_5_2_NONE + P-negotiation_6_7_NONE + P-negotiation_0_1_DONE + P-negotiation_7_4_DONE + P-negotiation_3_3_NONE + P-negotiation_3_5_DONE + P-negotiation_5_5_DONE + P-negotiation_1_4_NONE + P-negotiation_3_6_DONE + P-negotiation_1_3_NONE + P-negotiation_1_7_DONE + P-negotiation_5_4_DONE + P-negotiation_3_4_CO + P-negotiation_1_0_CO + P-negotiation_6_3_DONE + P-negotiation_3_2_NONE + P-negotiation_2_2_NONE + P-negotiation_7_3_DONE + P-negotiation_0_0_DONE + P-negotiation_7_7_CO + P-negotiation_4_4_DONE + P-negotiation_0_3_NONE + P-negotiation_7_6_NONE + P-negotiation_5_1_NONE + P-negotiation_0_5_CO + P-negotiation_2_5_DONE + P-negotiation_5_7_NONE + P-negotiation_0_6_DONE + P-negotiation_5_3_CO + P-negotiation_7_0_NONE + P-negotiation_4_1_CO + P-negotiation_1_7_CO + P-negotiation_7_1_DONE + P-negotiation_5_2_DONE + P-negotiation_3_3_DONE + P-negotiation_7_2_CO + P-negotiation_6_5_NONE + P-negotiation_6_1_CO + P-negotiation_1_4_DONE + P-negotiation_4_6_NONE + P-negotiation_6_0_CO + P-negotiation_2_7_NONE + P-negotiation_0_4_CO + P-negotiation_7_3_CO + P-negotiation_6_0_DONE + P-negotiation_4_7_CO + P-negotiation_4_1_DONE + P-negotiation_2_7_DONE + P-negotiation_2_2_DONE + P-negotiation_0_3_DONE + P-negotiation_7_6_DONE + P-negotiation_2_3_CO + P-negotiation_3_5_NONE + P-negotiation_5_7_DONE + P-negotiation_1_6_NONE + P-negotiation_1_1_CO + P-negotiation_4_6_DONE + P-negotiation_6_6_CO + P-negotiation_6_5_DONE + P-negotiation_5_4_CO + P-negotiation_3_0_CO + P-negotiation_3_0_DONE + P-negotiation_4_2_CO + P-negotiation_1_1_DONE + P-negotiation_6_2_NONE + P-negotiation_4_3_NONE + P-negotiation_2_4_NONE + P-negotiation_0_5_NONE + P-negotiation_5_4_NONE + P-negotiation_3_5_CO + P-negotiation_7_3_NONE + P-negotiation_0_0_NONE + P-negotiation_1_6_CO + P-negotiation_1_1_NONE + P-negotiation_3_0_NONE + P-negotiation_6_5_CO + P-negotiation_4_1_NONE + P-negotiation_6_0_NONE + P-negotiation_2_2_CO + P-negotiation_4_6_CO + P-negotiation_0_3_CO + P-negotiation_2_7_CO + P-negotiation_7_1_CO + P-negotiation_5_2_CO + P-negotiation_7_6_CO + P-negotiation_1_7_NONE + P-negotiation_3_6_NONE + P-negotiation_3_3_CO + P-negotiation_5_5_NONE + P-negotiation_7_4_NONE + P-negotiation_5_7_CO + P-negotiation_1_4_CO + P-negotiation_7_0_CO + P-negotiation_4_7_NONE + P-negotiation_6_6_NONE + P-negotiation_1_2_NONE + P-negotiation_3_1_NONE + P-negotiation_5_1_CO + P-negotiation_6_3_CO + P-negotiation_2_6_DONE + P-negotiation_7_7_NONE + P-negotiation_0_4_NONE + P-negotiation_4_5_DONE + P-negotiation_2_3_NONE + P-negotiation_6_4_DONE + P-negotiation_2_0_CO + P-negotiation_4_2_NONE + P-negotiation_1_0_DONE + P-negotiation_6_1_NONE + P-negotiation_3_2_CO + P-negotiation_4_4_CO + P-negotiation_0_1_CO + P-negotiation_1_5_NONE + P-negotiation_5_6_DONE + P-negotiation_3_4_NONE + P-negotiation_7_5_DONE + P-negotiation_0_2_DONE + P-negotiation_5_3_NONE + P-negotiation_2_5_CO + P-negotiation_2_1_DONE + P-negotiation_7_2_NONE + P-negotiation_4_0_DONE + P-negotiation_3_7_CO + P-negotiation_0_7_NONE + P-negotiation_2_6_NONE + P-negotiation_0_6_CO + P-negotiation_6_7_DONE + P-negotiation_5_0_CO + P-negotiation_4_5_NONE + P-negotiation_1_3_DONE <= 1) OR (P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= 0)) AND (P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendAnnPs__broadcasting_6_2 + P-sendAnnPs__broadcasting_6_1 + P-sendAnnPs__broadcasting_5_7 + P-sendAnnPs__broadcasting_5_6 + P-sendAnnPs__broadcasting_5_5 + P-sendAnnPs__broadcasting_5_4 + P-sendAnnPs__broadcasting_5_3 + P-sendAnnPs__broadcasting_5_2 + P-sendAnnPs__broadcasting_5_1 + P-sendAnnPs__broadcasting_4_7 + P-sendAnnPs__broadcasting_4_6 + P-sendAnnPs__broadcasting_4_5 + P-sendAnnPs__broadcasting_4_4 + P-sendAnnPs__broadcasting_4_3 + P-sendAnnPs__broadcasting_4_2 + P-sendAnnPs__broadcasting_4_1 + P-sendAnnPs__broadcasting_3_7 + P-sendAnnPs__broadcasting_3_6 + P-sendAnnPs__broadcasting_3_5 + P-sendAnnPs__broadcasting_3_4 + P-sendAnnPs__broadcasting_3_3 + P-sendAnnPs__broadcasting_3_2 + P-sendAnnPs__broadcasting_3_1 + P-sendAnnPs__broadcasting_2_7 + P-sendAnnPs__broadcasting_2_6 + P-sendAnnPs__broadcasting_2_5 + P-sendAnnPs__broadcasting_2_4 + P-sendAnnPs__broadcasting_2_3 + P-sendAnnPs__broadcasting_2_2 + P-sendAnnPs__broadcasting_2_1 + P-sendAnnPs__broadcasting_1_7 + P-sendAnnPs__broadcasting_1_6 + P-sendAnnPs__broadcasting_1_5 + P-sendAnnPs__broadcasting_1_4 + P-sendAnnPs__broadcasting_1_3 + P-sendAnnPs__broadcasting_1_2 + P-sendAnnPs__broadcasting_1_1 + P-sendAnnPs__broadcasting_0_7 + P-sendAnnPs__broadcasting_0_6 + P-sendAnnPs__broadcasting_0_5 + P-sendAnnPs__broadcasting_0_4 + P-sendAnnPs__broadcasting_0_3 + P-sendAnnPs__broadcasting_0_2 + P-sendAnnPs__broadcasting_0_1))))
lola: computing a collection of formulas
lola: RUNNING
lola: subprocess 0 will run for 221 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (((P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 4 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality.sara.
lola: sara is running 0 secs || 15862 markings, 27603 edges, 3172 markings/sec, 0 secs
lola: sara is running 5 secs || 32494 markings, 59241 edges, 3326 markings/sec, 5 secs
lola: sara is running 10 secs || 49306 markings, 90801 edges, 3362 markings/sec, 10 secs
lola: sara is running 15 secs || 66350 markings, 123520 edges, 3409 markings/sec, 15 secs
lola: sara is running 20 secs || 83667 markings, 156610 edges, 3463 markings/sec, 20 secs
sara: place or transition ordering is non-deterministic
lola: sara is running 25 secs || 100916 markings, 189052 edges, 3450 markings/sec, 25 secs
lola: sara is running 30 secs || 118206 markings, 221952 edges, 3458 markings/sec, 30 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: yes
lola: produced by: state equation
lola: The predicate is invariant.
lola: ========================================
lola: subprocess 1 will run for 233 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((3 <= P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterLi... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is invariant.
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality.sara
lola: subprocess 2 will run for 249 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((P-poll__pollEnd_7 + P-poll__pollEnd_6 + P-poll__pollEnd_5 + P-poll__pollEnd_4 + P-poll__pollEnd_3 + P-poll__pollEnd_2 + P-poll__pollEnd_1 + P-poll__pollEnd_0 + 1 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: ========================================
lola: state equation: calling and running sara
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality.sara.
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-2.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-2.sara.
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 3 will run for 269 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((P-poll__waitingMessage_0 + P-poll__waitingMessage_1 + P-poll__waitingMessage_2 + P-poll__waitingMessage_4 + P-poll__waitingMessage_5 + P-poll__waitingMessage_6 + P-poll__waitingMessage_7 + P-poll__waitingMessage_3 <= P-dead_7 + P-dead_6 + P-dead_5 + P-dead_4 + P-dead_3 + P-dead_2 + P-dead_1 + P-dead_0)))
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is invariant.
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-3.sara
lola: subprocess 4 will run for 291 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((1 <= P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7)))
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: ========================================
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-3.sara.
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-4.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-4.sara.
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is reachable.
lola: ========================================
lola: subprocess 5 will run for 318 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (((P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcasting_0_2 + P-startNeg__broadcasting_0_1 + P-startNeg__broadcasting_2_1 + P-startNeg__broadcasting_2_2 + P-startNeg__broadcas... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 3 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: yes
lola: produced by: state space
lola: The predicate is invariant.
lola: ========================================
lola: subprocess 6 will run for 349 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((((P-electedSecondary_7 + P-electedSecondary_6 + P-electedSecondary_5 + P-electedSecondary_4 + P-electedSecondary_3 + P-electedSecondary_2 + P-electedSecondary_1 + P-electedSecondary_0 <= P-poll__networl_7_4_AnsP_7 + P-poll__networl_7_4_AnsP_6 + P-poll__networl_7_4_AnsP_5 + P-poll__networl_7_4_AnsP_4 + P-poll__networl_7_4_AnsP_3 + P-poll__networl_7_4_AnsP_2 + P-poll__networl_7_4_AnsP_1 + P-p... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 5 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-6.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-6.sara.
lola: sara is running 0 secs || 14551 markings, 33893 edges, 2910 markings/sec, 0 secs
lola: sara is running 5 secs || 29098 markings, 72367 edges, 2909 markings/sec, 5 secs
lola: sara is running 10 secs || 43920 markings, 113193 edges, 2964 markings/sec, 10 secs
lola: sara is running 15 secs || 58478 markings, 151502 edges, 2912 markings/sec, 15 secs
lola: sara is running 20 secs || 72916 markings, 189765 edges, 2888 markings/sec, 20 secs
sara: place or transition ordering is non-deterministic
sara: place or transition ordering is non-deterministic
sara: place or transition ordering is non-deterministic
lola: sara is running 25 secs || 87466 markings, 231032 edges, 2910 markings/sec, 25 secs
lola: sara is running 30 secs || 101741 markings, 270878 edges, 2855 markings/sec, 30 secs
lola: sara is running 35 secs || 115831 markings, 313348 edges, 2818 markings/sec, 35 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: no
lola: produced by: state equation
lola: The predicate is unreachable.
lola: ========================================
lola: subprocess 7 will run for 383 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((((P-sendAnnPs__broadcasting_7_7 + P-sendAnnPs__broadcasting_7_6 + P-sendAnnPs__broadcasting_7_5 + P-sendAnnPs__broadcasting_7_4 + P-sendAnnPs__broadcasting_7_3 + P-sendAnnPs__broadcasting_7_2 + P-sendAnnPs__broadcasting_7_1 + P-sendAnnPs__broadcasting_6_7 + P-sendAnnPs__broadcasting_6_6 + P-sendAnnPs__broadcasting_6_5 + P-sendAnnPs__broadcasting_6_4 + P-sendAnnPs__broadcasting_6_3 + P-sendA... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 5 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-7.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-7.sara.
lola: sara is running 0 secs || 10254 markings, 21085 edges, 2051 markings/sec, 0 secs
lola: sara is running 5 secs || 21652 markings, 45997 edges, 2280 markings/sec, 5 secs
lola: sara is running 10 secs || 33047 markings, 70917 edges, 2279 markings/sec, 10 secs
lola: sara is running 15 secs || 46844 markings, 110451 edges, 2759 markings/sec, 15 secs
lola: sara is running 20 secs || 62145 markings, 159285 edges, 3060 markings/sec, 20 secs
sara: place or transition ordering is non-deterministic
lola: sara is running 25 secs || 74250 markings, 188563 edges, 2421 markings/sec, 25 secs
lola: sara is running 30 secs || 86853 markings, 220929 edges, 2521 markings/sec, 30 secs
lola: sara is running 35 secs || 102149 markings, 269709 edges, 3059 markings/sec, 35 secs
lola: sara is running 40 secs || 115426 markings, 306130 edges, 2655 markings/sec, 40 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: yes
lola: produced by: state equation
lola: The predicate is invariant.
lola: ========================================
lola: subprocess 8 will run for 425 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G (((P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 <= P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 24 literals and 6 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-8.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-8.sara.
lola: sara is running 0 secs || 9494 markings, 32532 edges, 1899 markings/sec, 0 secs
lola: sara is running 5 secs || 19442 markings, 77451 edges, 1990 markings/sec, 5 secs
lola: sara is running 10 secs || 30790 markings, 133580 edges, 2270 markings/sec, 10 secs
lola: sara is running 15 secs || 42027 markings, 189544 edges, 2247 markings/sec, 15 secs
lola: sara is running 20 secs || 52002 markings, 230972 edges, 1995 markings/sec, 20 secs
lola: sara is running 25 secs || 62247 markings, 276352 edges, 2049 markings/sec, 25 secs
sara: place or transition ordering is non-deterministic
lola: sara is running 30 secs || 73588 markings, 336019 edges, 2268 markings/sec, 30 secs
lola: sara is running 35 secs || 83433 markings, 379587 edges, 1969 markings/sec, 35 secs
lola: sara is running 40 secs || 94060 markings, 435576 edges, 2125 markings/sec, 40 secs
lola: sara is running 45 secs || 104091 markings, 490651 edges, 2006 markings/sec, 45 secs
lola: sara is running 50 secs || 113959 markings, 535241 edges, 1974 markings/sec, 50 secs
lola: sara is running 55 secs || 123828 markings, 592717 edges, 1974 markings/sec, 55 secs
lola: sara is running 60 secs || 134668 markings, 652703 edges, 2168 markings/sec, 60 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: yes
lola: produced by: state equation
lola: The predicate is invariant.
lola: ========================================
lola: subprocess 9 will run for 477 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F (((P-electedPrimary_7 + P-electedPrimary_6 + P-electedPrimary_5 + P-electedPrimary_4 + P-electedPrimary_3 + P-electedPrimary_2 + P-electedPrimary_1 + P-electedPrimary_0 <= P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-star... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 4 literals and 1 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-9.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-9.sara.
lola: sara is running 0 secs || 16547 markings, 28672 edges, 3309 markings/sec, 0 secs
lola: sara is running 5 secs || 33884 markings, 61640 edges, 3467 markings/sec, 5 secs
lola: sara is running 10 secs || 51240 markings, 94793 edges, 3471 markings/sec, 10 secs
lola: sara is running 15 secs || 67708 markings, 126098 edges, 3294 markings/sec, 15 secs
lola: sara is running 20 secs || 83974 markings, 157084 edges, 3253 markings/sec, 20 secs
sara: place or transition ordering is non-deterministic
lola: sara is running 25 secs || 100990 markings, 189168 edges, 3403 markings/sec, 25 secs
lola: sara is running 30 secs || 118216 markings, 221976 edges, 3445 markings/sec, 30 secs
lola: sara is running 35 secs || 134546 markings, 253072 edges, 3266 markings/sec, 35 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: no
lola: produced by: state equation
lola: The predicate is unreachable.
lola: ========================================
lola: subprocess 10 will run for 549 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((P-masterList_5_6_0 + P-masterList_5_6_1 + P-masterList_5_6_2 + P-masterList_5_6_3 + P-masterList_5_6_4 + P-masterList_5_6_5 + P-masterList_5_6_6 + P-masterList_5_6_7 + P-masterList_3_2_0 + P-masterList_3_2_1 + P-masterList_3_2_2 + P-masterList_3_2_3 + P-masterList_3_2_4 + P-masterList_3_2_5 + P-masterList_3_2_6 + P-masterList_3_2_7 + P-masterList_0_4_0 + P-masterList_0_4_1 + P-masterList_0_... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: The predicate is unreachable.
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-10.sara
lola: subprocess 11 will run for 658 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F (FALSE))
lola: ========================================
lola: SUBTASK
lola: checking initial satisfaction
lola: ========================================
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-10.sara.
lola: processed formula: FALSE
lola: processed formula length: 5
lola: 3 rewrites
lola: formula mentions 0 of 7128 places; total mentions: 0
lola: closed formula file NeoElection-COL-7-ReachabilityCardinality.task
lola: processed formula with 0 atomic propositions
lola: RUNNING
lola: SUBRESULT
lola: result: no
lola: produced by: preprocessing
lola: The net violates the given property already in its initial state.
lola: ========================================
lola: subprocess 12 will run for 823 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F (((P-polling_0 + P-polling_1 + P-polling_2 + P-polling_3 + P-polling_4 + P-polling_5 + P-polling_6 + P-polling_7 <= 2) AND (P-startNeg__broadcasting_1_5 + P-startNeg__broadcasting_1_4 + P-startNeg__broadcasting_1_3 + P-startNeg__broadcasting_1_2 + P-startNeg__broadcasting_1_1 + P-startNeg__broadcasting_0_5 + P-startNeg__broadcasting_0_4 + P-startNeg__broadcasting_0_3 + P-startNeg__broadcastin... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 4 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is unreachable.
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-12.sara
lola: subprocess 13 will run for 1098 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ========================================lola:
state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-12.sara.
lola: ...considering subproblem: E (F ((P-masterState_6_F_6 + P-masterState_6_F_5 + P-masterState_6_F_4 + P-masterState_6_F_3 + P-masterState_6_F_2 + P-masterState_6_F_1 + P-masterState_6_F_0 + P-masterState_1_T_6 + P-masterState_1_T_5 + P-masterState_1_T_4 + P-masterState_1_T_3 + P-masterState_1_T_2 + P-masterState_1_T_1 + P-masterState_1_T_0 + P-masterState_3_F_6 + P-masterState_3_F_5 + P-masterState_3_F_4 + P-masterState_3_F_3... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is unreachable.
lola: ========================================
lola: subprocess 14 will run for 1647 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: E (F ((P-negotiation_6_4_NONE + P-negotiation_6_2_CO + P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_5_1_DONE + P-negotiation_7_4_CO + P-negotiation_1_3_CO + P-negotiation_7_0_DONE + P-negotiation_3_7_DONE + P-negotiation_5_6_CO + P-negotiation_3_1_CO + P-negotiation_7_5_CO + P-negotiation_0_7_DONE + P-negotiation_0_7_CO + P-negotiation_3_7_NONE + P-negotiation_4_3_CO + P-negotia... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking reachability
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 1 literals and 1 conjunctive subformulas
lola: SUBRESULT
lola: result: no
lola: produced by: state space
lola: The predicate is unreachable.
lola: ========================================
lola: subprocess 15 will run for 3294 seconds at most (--localtimelimit=-1)
lola: ========================================
lola: ...considering subproblem: A (G ((((P-negotiation_6_4_NONE + P-negotiation_6_2_CO + P-negotiation_3_2_DONE + P-negotiation_1_0_NONE + P-negotiation_5_1_DONE + P-negotiation_7_4_CO + P-negotiation_1_3_CO + P-negotiation_7_0_DONE + P-negotiation_3_7_DONE + P-negotiation_5_6_CO + P-negotiation_3_1_CO + P-negotiation_7_5_CO + P-negotiation_0_7_DONE + P-negotiation_0_7_CO + P-negotiation_3_7_NONE + P-negotiation_4_3_CO + P-negot... (shortened)
lola: ========================================
lola: SUBTASK
lola: checking invariance
lola: Planning: workflow for reachability check: stateequation||search (--findpath=off)
lola: STORE
lola: using a bit-perfect encoder (--encoder=bit)
lola: using 6752 bytes per marking, with 0 unused bits
lola: using a prefix tree store (--store=prefix)
lola: SEARCH (state space)
lola: state space: using reachability graph (--search=depth)
lola: state space: using reachability preserving stubborn set method with insertion algorithm (--stubborn=tarjan)
lola: RUNNING
lola: state equation: Generated DNF with 3 literals and 2 conjunctive subformulas
lola: state equation: write sara problem file to NeoElection-COL-7-ReachabilityCardinality-15.sara
lola: state equation: calling and running sara
sara: try reading problem file NeoElection-COL-7-ReachabilityCardinality-15.sara.
lola: sara is running 0 secs || 16107 markings, 27983 edges, 3221 markings/sec, 0 secs
lola: sara is running 5 secs || 32194 markings, 58746 edges, 3217 markings/sec, 5 secs
lola: sara is running 10 secs || 48352 markings, 89305 edges, 3232 markings/sec, 10 secs
lola: sara is running 15 secs || 65418 markings, 121921 edges, 3413 markings/sec, 15 secs
lola: sara is running 20 secs || 80578 markings, 150643 edges, 3032 markings/sec, 20 secs
sara: place or transition ordering is non-deterministic
sara: place or transition ordering is non-deterministic
lola: sara is running 25 secs || 96552 markings, 180652 edges, 3195 markings/sec, 25 secs
sara: place or transition ordering is non-deterministic
lola: sara is running 30 secs || 112510 markings, 211086 edges, 3192 markings/sec, 30 secs
lola: sara is running 35 secs || 129614 markings, 243761 edges, 3421 markings/sec, 35 secs
lola: state equation: solution impossible
lola: SUBRESULT
lola: result: yes
lola: produced by: state equation
lola: The predicate is invariant.
lola: ========================================
lola: RESULT
lola:
SUMMARY: yes yes yes yes yes yes no yes yes no no no no no no yes
FORMULA NeoElection-COL-7-ReachabilityCardinality-0 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-1 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-2 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-3 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-4 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-5 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-6 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-7 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-8 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-9 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-10 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-11 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-12 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-13 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-14 FALSE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
FORMULA NeoElection-COL-7-ReachabilityCardinality-15 TRUE TECHNIQUES COLLATERAL_PROCESSING EXPLICIT STATE_COMPRESSION STUBBORN_SETS TOPOLOGICAL USE_NUPN
----- Kill lola and sara stdout -----
----- Finished stdout -----
BK_STOP 1496372526537
--------------------
content from stderr:
----- Start make prepare stderr -----
----- Start make result stderr -----
----- Start make result stderr -----
----- Kill lola and sara stderr -----
----- Finished stderr -----
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_NeoElection-PT-7"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="lola"
export BK_RESULT_DIR="/tmp/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_NeoElection-PT-7.tgz
mv S_NeoElection-PT-7 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-3254"
echo " Executing tool lola"
echo " Input is S_NeoElection-PT-7, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r118-blw7-149441650100286"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

