About the Execution of Marcie for GPPP-PT-C0001N0000000100
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5543.950 | 9166.00 | 9010.00 | 201.70 | FTFTFTTFFFFFFTFT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
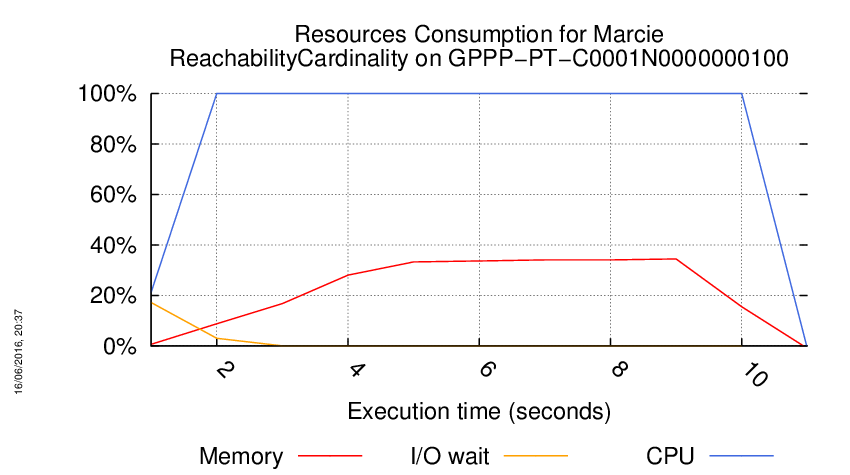
Trace from the execution
Waiting for the VM to be ready (probing ssh)
.................................................................
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is GPPP-PT-C0001N0000000100, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r221su-smll-146468027600457
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-0
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-1
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-10
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-11
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-12
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-13
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-14
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-15
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-2
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-3
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-4
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-5
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-6
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-7
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-8
FORMULA_NAME GPPP-PT-C0001N0000000100-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1465033967155
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: GPPP_PT_C0001N0000000100
(NrP: 33 NrTr: 22 NrArc: 83)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
init dd package: 0m 3.965sec
RS generation: 0m 0.151sec
-> reachability set: #nodes 1358 (1.4e+03) #states 145,476,966 (8)
starting MCC model checker
--------------------------
checking: AG [~ [~ [2<=NADPplus]]]
normalized: ~ [E [true U ~ [2<=NADPplus]]]
abstracting: (2<=NADPplus) states: 144,029,434 (8)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-0 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.273sec
checking: EF [3<=S7P]
normalized: E [true U 3<=S7P]
abstracting: (3<=S7P) states: 0
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.001sec
checking: EF [~ [c2<=c2]]
normalized: E [true U ~ [c2<=c2]]
abstracting: (c2<=c2) states: 145,476,966 (8)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-3 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: AG [PEP<=Ru5P]
normalized: ~ [E [true U ~ [PEP<=Ru5P]]]
abstracting: (PEP<=Ru5P) states: 85,913,832 (7)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.055sec
checking: AG [PEP<=c1]
normalized: ~ [E [true U ~ [PEP<=c1]]]
abstracting: (PEP<=c1) states: 145,476,966 (8)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.001sec
checking: EF [NADplus<=PEP]
normalized: E [true U NADplus<=PEP]
abstracting: (NADplus<=PEP) states: 0
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-8 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.032sec
checking: AG [~ [[~ [2<=NADPplus] & [3<=E4P | 1<=NADPH]]]]
normalized: ~ [E [true U [[3<=E4P | 1<=NADPH] & ~ [2<=NADPplus]]]]
abstracting: (2<=NADPplus) states: 144,029,434 (8)
abstracting: (1<=NADPH) states: 144,753,200 (8)
abstracting: (3<=E4P) states: 0
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-15 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.058sec
checking: AG [~ [[1<=Pyr & [3<=a2 | _1_3_BPG<=NADPH]]]]
normalized: ~ [E [true U [1<=Pyr & [3<=a2 | _1_3_BPG<=NADPH]]]]
abstracting: (_1_3_BPG<=NADPH) states: 144,985,702 (8)
abstracting: (3<=a2) states: 0
abstracting: (1<=Pyr) states: 61,552,632 (7)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-6 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.149sec
checking: EF [[start<=Xu5P & ~ [_3PG<=E4P]]]
normalized: E [true U [start<=Xu5P & ~ [_3PG<=E4P]]]
abstracting: (_3PG<=E4P) states: 91,882,326 (7)
abstracting: (start<=Xu5P) states: 145,456,665 (8)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-9 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.052sec
checking: AG [~ [[[S7P<=_1_3_BPG | GAP<=Ru5P] & 2<=PEP]]]
normalized: ~ [E [true U [2<=PEP & [S7P<=_1_3_BPG | GAP<=Ru5P]]]]
abstracting: (GAP<=Ru5P) states: 85,040,889 (7)
abstracting: (S7P<=_1_3_BPG) states: 144,827,334 (8)
abstracting: (2<=PEP) states: 24,523,608 (7)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-5 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.047sec
checking: EF [[2<=G6P & [[3<=_3PG | R5P<=a2] & 2<=_3PG]]]
normalized: E [true U [2<=G6P & [2<=_3PG & [3<=_3PG | R5P<=a2]]]]
abstracting: (R5P<=a2) states: 145,375,461 (8)
abstracting: (3<=_3PG) states: 8,871,537 (6)
abstracting: (2<=_3PG) states: 24,523,608 (7)
abstracting: (2<=G6P) states: 466,923 (5)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.004sec
checking: AG [[3<=ADP | [[PEP<=b2 | ATP<=NADPH] | ~ [_2PG<=b1]]]]
normalized: ~ [E [true U ~ [[3<=ADP | [~ [_2PG<=b1] | [PEP<=b2 | ATP<=NADPH]]]]]]
abstracting: (ATP<=NADPH) states: 0
abstracting: (PEP<=b2) states: 87,903,330 (7)
abstracting: (_2PG<=b1) states: 142,350,612 (8)
abstracting: (3<=ADP) states: 143,710,779 (8)
-> the formula is FALSE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.135sec
checking: AG [[[[1<=DHAP & 3<=NADPH] | [1<=b2 | DHAP<=NADPplus]] | c2<=c1]]
normalized: ~ [E [true U ~ [[c2<=c1 | [[1<=b2 | DHAP<=NADPplus] | [1<=DHAP & 3<=NADPH]]]]]]
abstracting: (3<=NADPH) states: 143,305,668 (8)
abstracting: (1<=DHAP) states: 62,770,692 (7)
abstracting: (DHAP<=NADPplus) states: 144,976,410 (8)
abstracting: (1<=b2) states: 18,392,706 (7)
abstracting: (c2<=c1) states: 93,912,426 (7)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.011sec
checking: EF [[[[2<=Pyr | a2<=a1] & ~ [1<=GSSG]] & [[1<=GSSG | Lac<=_2PG] & 2<=NADPH]]]
normalized: E [true U [[2<=NADPH & [1<=GSSG | Lac<=_2PG]] & [~ [1<=GSSG] & [2<=Pyr | a2<=a1]]]]
abstracting: (a2<=a1) states: 144,867,936 (8)
abstracting: (2<=Pyr) states: 24,523,608 (7)
abstracting: (1<=GSSG) states: 144,036,600 (8)
abstracting: (Lac<=_2PG) states: 101,789,214 (8)
abstracting: (1<=GSSG) states: 144,036,600 (8)
abstracting: (2<=NADPH) states: 144,029,434 (8)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.369sec
checking: AG [[[S7P<=b2 & 2<=b2] | [~ [1<=S7P] | [_1_3_BPG<=NADPplus & c2<=Gluc]]]]
normalized: ~ [E [true U ~ [[[[_1_3_BPG<=NADPplus & c2<=Gluc] | ~ [1<=S7P]] | [S7P<=b2 & 2<=b2]]]]]
abstracting: (2<=b2) states: 1,015,050 (6)
abstracting: (S7P<=b2) states: 145,152,150 (8)
abstracting: (1<=S7P) states: 649,632 (5)
abstracting: (c2<=Gluc) states: 18,879,930 (7)
abstracting: (_1_3_BPG<=NADPplus) states: 144,985,702 (8)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.007sec
checking: EF [[[[1<=Gluc | E4P<=GSH] | [3<=_2PG & 2<=a1]] & [~ [NADPplus<=NADplus] & [R5P<=S7P | 2<=b2]]]]
normalized: E [true U [[[R5P<=S7P | 2<=b2] & ~ [NADPplus<=NADplus]] & [[3<=_2PG & 2<=a1] | [1<=Gluc | E4P<=GSH]]]]
abstracting: (E4P<=GSH) states: 145,151,346 (8)
abstracting: (1<=Gluc) states: 9,480,567 (6)
abstracting: (2<=a1) states: 119,410,482 (8)
abstracting: (3<=_2PG) states: 8,871,537 (6)
abstracting: (NADPplus<=NADplus) states: 143,020,646 (8)
abstracting: (2<=b2) states: 1,015,050 (6)
abstracting: (R5P<=S7P) states: 144,461,916 (8)
-> the formula is TRUE
FORMULA GPPP-PT-C0001N0000000100-ReachabilityCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.325sec
Total processing time: 0m 9.127sec
BK_STOP 1465033976321
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
1092 1181 1384 1145 1128 1217 1330 1177 1171 1200 1709 1811 1769 1769 1783
iterations count:15790 (717), effective:3705 (168)
initing FirstDep: 0m 0.000sec
1188 1176 1208 1253 1233 1288 1223 1229 1226 1255 1256 1273 1287 1288 1307 1283 1296 1287 1322 1325 1346 1349 1342 1366 1347 1363 1354 1385
iterations count:28122 (1278), effective:7000 (318)
iterations count:200 (9), effective:45 (2)
1188 1176 1208 1253 1233 1288 1223 1229 1226 1255 1256 1273 1287 1288 1307 1283 1296 1287 1322 1325 1346 1349 1342 1366 1347 1363 1354 1385
iterations count:28122 (1278), effective:7000 (318)
iterations count:192 (8), effective:38 (1)
iterations count:236 (10), effective:55 (2)
iterations count:223 (10), effective:51 (2)
iterations count:352 (16), effective:82 (3)
1357 1380 1364 1393 1389 1400 1405 1432 1416 1416 1481 1401 1436 1411 1420 1411 1433 1417 1446 1442 1453 1458 1471 1469 1469 1480 1454 1489
iterations count:28753 (1306), effective:7214 (327)
2940
iterations count:1109 (50), effective:454 (20)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="GPPP-PT-C0001N0000000100"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/root/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/GPPP-PT-C0001N0000000100.tgz
mv GPPP-PT-C0001N0000000100 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is GPPP-PT-C0001N0000000100, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r221su-smll-146468027600457"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

