About the Execution of Marcie for S_QuasiCertifProtocol-PT-02
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5414.980 | 7021.00 | 7010.00 | 50.00 | TTFFTFFTFTFTFFTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
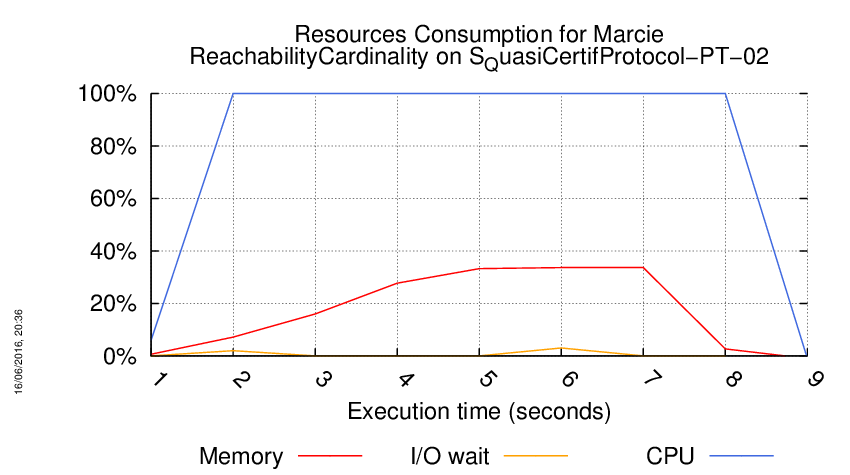
Trace from the execution
Waiting for the VM to be ready (probing ssh)
..............
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is S_QuasiCertifProtocol-PT-02, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r185kn-smll-146444127900079
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-0
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-1
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-10
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-11
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-12
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-13
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-14
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-15
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-2
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-3
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-4
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-5
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-6
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-7
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-8
FORMULA_NAME QuasiCertifProtocol-COL-02-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1464537489624
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: QuasiCertifProtocol_PT_02
(NrP: 86 NrTr: 56 NrArc: 223)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.001sec
init dd package: 0m 3.949sec
RS generation: 0m 0.036sec
-> reachability set: #nodes 1808 (1.8e+03) #states 1,029 (3)
starting MCC model checker
--------------------------
checking: EF [2<=Astart]
normalized: E [true U 2<=Astart]
abstracting: (2<=Astart) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.001sec
checking: EF [3<=a2]
normalized: E [true U 3<=a2]
abstracting: (3<=a2) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-7 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [3<=a3]
normalized: E [true U 3<=a3]
abstracting: (3<=a3) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [~ [~ [2<=AstopOK]]]
normalized: E [true U 2<=AstopOK]
abstracting: (2<=AstopOK) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.000sec
checking: EF [[~ [[3<=sum(n2_2, n2_1, n2_0) | 2<=a2]] & 2<=malicious_reservoir]]
normalized: E [true U [2<=malicious_reservoir & ~ [[3<=sum(n2_2, n2_1, n2_0) | 2<=a2]]]]
abstracting: (2<=a2) states: 0
abstracting: (3<=sum(n2_2, n2_1, n2_0)) states: 8
abstracting: (2<=malicious_reservoir) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.036sec
checking: AG [[sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1) | ~ [~ [3<=Astart]]]]
normalized: ~ [E [true U ~ [[sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1) | 3<=Astart]]]]
abstracting: (3<=Astart) states: 0
abstracting: (sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 1,029 (3)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.035sec
checking: AG [[~ [3<=sum(c1_2, c1_1, c1_0)] | Astart<=sum(n6_1, n6_2, n6_0)]]
normalized: ~ [E [true U ~ [[Astart<=sum(n6_1, n6_2, n6_0) | ~ [3<=sum(c1_2, c1_1, c1_0)]]]]]
abstracting: (3<=sum(c1_2, c1_1, c1_0)) states: 243
abstracting: (Astart<=sum(n6_1, n6_2, n6_0)) states: 1,025 (3)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.069sec
checking: EF [[[[1<=sum(n6_1, n6_2, n6_0) & 2<=a1] & 2<=sum(n3_2, n3_1, n3_0)] & 2<=sum(n5_2, n5_1, n5_0)]]
normalized: E [true U [2<=sum(n5_2, n5_1, n5_0) & [2<=sum(n3_2, n3_1, n3_0) & [1<=sum(n6_1, n6_2, n6_0) & 2<=a1]]]]
abstracting: (2<=a1) states: 0
abstracting: (1<=sum(n6_1, n6_2, n6_0)) states: 630
abstracting: (2<=sum(n3_2, n3_1, n3_0)) states: 32
abstracting: (2<=sum(n5_2, n5_1, n5_0)) states: 56
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-6 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.105sec
checking: AG [[[[3<=AstopOK & sum(SstopOK_2, SstopOK_0, SstopOK_1)<=sum(CstopOK_2, CstopOK_1, CstopOK_0)] | 3<=sum(Cstart_2, Cstart_0, Cstart_1)] | ~ [[2<=sum(n3_2, n3_1, n3_0) | 3<=sum(Cstart_2, Cstart_0, Cstart_1)]]]]
normalized: ~ [E [true U ~ [[~ [[2<=sum(n3_2, n3_1, n3_0) | 3<=sum(Cstart_2, Cstart_0, Cstart_1)]] | [3<=sum(Cstart_2, Cstart_0, Cstart_1) | [3<=AstopOK & sum(SstopOK_2, SstopOK_0, SstopOK_1)<=sum(CstopOK_2, CstopOK_1, CstopOK_0)]]]]]]
abstracting: (sum(SstopOK_2, SstopOK_0, SstopOK_1)<=sum(CstopOK_2, CstopOK_1, CstopOK_0)) states: 666
abstracting: (3<=AstopOK) states: 0
abstracting: (3<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 396
abstracting: (3<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 396
abstracting: (2<=sum(n3_2, n3_1, n3_0)) states: 32
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.136sec
checking: AG [~ [[1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0) & [1<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0) & 3<=a5]]]]
normalized: ~ [E [true U [1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0) & [1<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0) & 3<=a5]]]]
abstracting: (3<=a5) states: 0
abstracting: (1<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0)) states: 453
abstracting: (1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0)) states: 279
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.071sec
checking: AG [[[~ [sum(n3_2, n3_1, n3_0)<=a4] | [sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1) | sum(CstopOK_2, CstopOK_1, CstopOK_0)<=sum(n5_2, n5_1, n5_0)]] | ~ [sum(c1_2, c1_1, c1_0)<=sum(s5_2, s5_1, s5_0)]]]
normalized: ~ [E [true U ~ [[~ [sum(c1_2, c1_1, c1_0)<=sum(s5_2, s5_1, s5_0)] | [[sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1) | sum(CstopOK_2, CstopOK_1, CstopOK_0)<=sum(n5_2, n5_1, n5_0)] | ~ [sum(n3_2, n3_1, n3_0)<=a4]]]]]]
abstracting: (sum(n3_2, n3_1, n3_0)<=a4) states: 973
abstracting: (sum(CstopOK_2, CstopOK_1, CstopOK_0)<=sum(n5_2, n5_1, n5_0)) states: 981
abstracting: (sum(n4_0, n4_2, n4_1)<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 1,029 (3)
abstracting: (sum(c1_2, c1_1, c1_0)<=sum(s5_2, s5_1, s5_0)) states: 573
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.145sec
checking: EF [[[~ [sum(s3_2, s3_0, s3_1)<=sum(Cstart_2, Cstart_0, Cstart_1)] & [sum(s3_2, s3_0, s3_1)<=sum(s6_2, s6_1, s6_0) | sum(s4_1, s4_2, s4_0)<=a1]] & [sum(Sstart_2, Sstart_0, Sstart_1)<=sum(s2_1, s2_2, s2_0) & [1<=a2 | 1<=sum(s6_2, s6_1, s6_0)]]]]
normalized: E [true U [[sum(Sstart_2, Sstart_0, Sstart_1)<=sum(s2_1, s2_2, s2_0) & [1<=a2 | 1<=sum(s6_2, s6_1, s6_0)]] & [[sum(s3_2, s3_0, s3_1)<=sum(s6_2, s6_1, s6_0) | sum(s4_1, s4_2, s4_0)<=a1] & ~ [sum(s3_2, s3_0, s3_1)<=sum(Cstart_2, Cstart_0, Cstart_1)]]]]
abstracting: (sum(s3_2, s3_0, s3_1)<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 1,029 (3)
abstracting: (sum(s4_1, s4_2, s4_0)<=a1) states: 876
abstracting: (sum(s3_2, s3_0, s3_1)<=sum(s6_2, s6_1, s6_0)) states: 843
abstracting: (1<=sum(s6_2, s6_1, s6_0)) states: 318
abstracting: (1<=a2) states: 4
abstracting: (sum(Sstart_2, Sstart_0, Sstart_1)<=sum(s2_1, s2_2, s2_0)) states: 1,005 (3)
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.176sec
checking: EF [[[[sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0)<=sum(c1_2, c1_1, c1_0) | a1<=sum(CstopOK_2, CstopOK_1, CstopOK_0)] & [1<=a2 & sum(c1_2, c1_1, c1_0)<=sum(n1_1, n1_0, n1_2)]] & ~ [~ [1<=sum(Sstart_2, Sstart_0, Sstart_1)]]]]
normalized: E [true U [1<=sum(Sstart_2, Sstart_0, Sstart_1) & [[sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0)<=sum(c1_2, c1_1, c1_0) | a1<=sum(CstopOK_2, CstopOK_1, CstopOK_0)] & [1<=a2 & sum(c1_2, c1_1, c1_0)<=sum(n1_1, n1_0, n1_2)]]]]
abstracting: (sum(c1_2, c1_1, c1_0)<=sum(n1_1, n1_0, n1_2)) states: 417
abstracting: (1<=a2) states: 4
abstracting: (a1<=sum(CstopOK_2, CstopOK_1, CstopOK_0)) states: 997
abstracting: (sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0)<=sum(c1_2, c1_1, c1_0)) states: 684
abstracting: (1<=sum(Sstart_2, Sstart_0, Sstart_1)) states: 54
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.145sec
checking: EF [[~ [[AstopOK<=sum(c1_2, c1_1, c1_0) | sum(n2_2, n2_1, n2_0)<=Astart]] & [~ [sum(n5_2, n5_1, n5_0)<=sum(n3_2, n3_1, n3_0)] & [sum(s2_1, s2_2, s2_0)<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0) | a4<=sum(n3_2, n3_1, n3_0)]]]]
normalized: E [true U [[~ [sum(n5_2, n5_1, n5_0)<=sum(n3_2, n3_1, n3_0)] & [sum(s2_1, s2_2, s2_0)<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0) | a4<=sum(n3_2, n3_1, n3_0)]] & ~ [[AstopOK<=sum(c1_2, c1_1, c1_0) | sum(n2_2, n2_1, n2_0)<=Astart]]]]
abstracting: (sum(n2_2, n2_1, n2_0)<=Astart) states: 973
abstracting: (AstopOK<=sum(c1_2, c1_1, c1_0)) states: 990
abstracting: (a4<=sum(n3_2, n3_1, n3_0)) states: 1,025 (3)
abstracting: (sum(s2_1, s2_2, s2_0)<=sum(n8_2_2, n8_1_2, n8_0_1, n8_1_1, n8_2_1, n8_0_2, n8_0_0, n8_1_0, n8_2_0)) states: 921
abstracting: (sum(n5_2, n5_1, n5_0)<=sum(n3_2, n3_1, n3_0)) states: 877
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.180sec
checking: AG [[[[1<=sum(SstopOK_2, SstopOK_0, SstopOK_1) | 1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0)] & [3<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0) | 3<=a2]] | [[sum(n6_1, n6_2, n6_0)<=sum(n2_2, n2_1, n2_0) | 3<=sum(s2_1, s2_2, s2_0)] | ~ [2<=SstopAbort]]]]
normalized: ~ [E [true U ~ [[[[sum(n6_1, n6_2, n6_0)<=sum(n2_2, n2_1, n2_0) | 3<=sum(s2_1, s2_2, s2_0)] | ~ [2<=SstopAbort]] | [[1<=sum(SstopOK_2, SstopOK_0, SstopOK_1) | 1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0)] & [3<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0) | 3<=a2]]]]]]
abstracting: (3<=a2) states: 0
abstracting: (3<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0)) states: 363
abstracting: (1<=sum(n7_1_2, n7_2_2, n7_0_1, n7_1_1, n7_2_1, n7_0_2, n7_0_0, n7_2_0, n7_1_0)) states: 279
abstracting: (1<=sum(SstopOK_2, SstopOK_0, SstopOK_1)) states: 366
abstracting: (2<=SstopAbort) states: 0
abstracting: (3<=sum(s2_1, s2_2, s2_0)) states: 6
abstracting: (sum(n6_1, n6_2, n6_0)<=sum(n2_2, n2_1, n2_0)) states: 399
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.175sec
checking: AG [[[[1<=sum(Cstart_2, Cstart_0, Cstart_1) & AstopAbort<=sum(n2_2, n2_1, n2_0)] | [SstopAbort<=sum(n1_1, n1_0, n1_2) & sum(n6_1, n6_2, n6_0)<=CstopAbort]] | [[sum(s4_1, s4_2, s4_0)<=a4 | malicious_reservoir<=sum(Cstart_2, Cstart_0, Cstart_1)] | [sum(n2_2, n2_1, n2_0)<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0) | 2<=a2]]]]
normalized: ~ [E [true U ~ [[[[sum(n2_2, n2_1, n2_0)<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0) | 2<=a2] | [sum(s4_1, s4_2, s4_0)<=a4 | malicious_reservoir<=sum(Cstart_2, Cstart_0, Cstart_1)]] | [[SstopAbort<=sum(n1_1, n1_0, n1_2) & sum(n6_1, n6_2, n6_0)<=CstopAbort] | [1<=sum(Cstart_2, Cstart_0, Cstart_1) & AstopAbort<=sum(n2_2, n2_1, n2_0)]]]]]]
abstracting: (AstopAbort<=sum(n2_2, n2_1, n2_0)) states: 666
abstracting: (1<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 495
abstracting: (sum(n6_1, n6_2, n6_0)<=CstopAbort) states: 399
abstracting: (SstopAbort<=sum(n1_1, n1_0, n1_2)) states: 558
abstracting: (malicious_reservoir<=sum(Cstart_2, Cstart_0, Cstart_1)) states: 927
abstracting: (sum(s4_1, s4_2, s4_0)<=a4) states: 876
abstracting: (2<=a2) states: 0
abstracting: (sum(n2_2, n2_1, n2_0)<=sum(n9_2_2, n9_1_2, n9_1_1, n9_0_1, n9_0_2, n9_2_1, n9_0_0, n9_2_0, n9_1_0)) states: 973
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-02-ReachabilityCardinality-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.248sec
Total processing time: 0m 6.984sec
BK_STOP 1464537496645
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
iterations count:899 (16), effective:56 (1)
initing FirstDep: 0m 0.000sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_QuasiCertifProtocol-PT-02"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/root/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_QuasiCertifProtocol-PT-02.tgz
mv S_QuasiCertifProtocol-PT-02 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is S_QuasiCertifProtocol-PT-02, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r185kn-smll-146444127900079"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

