About the Execution of Marcie for S_PhilosophersDyn-PT-03
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5415.860 | 15047.00 | 15145.00 | 30.30 | TTFFTTFTFTFTTTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
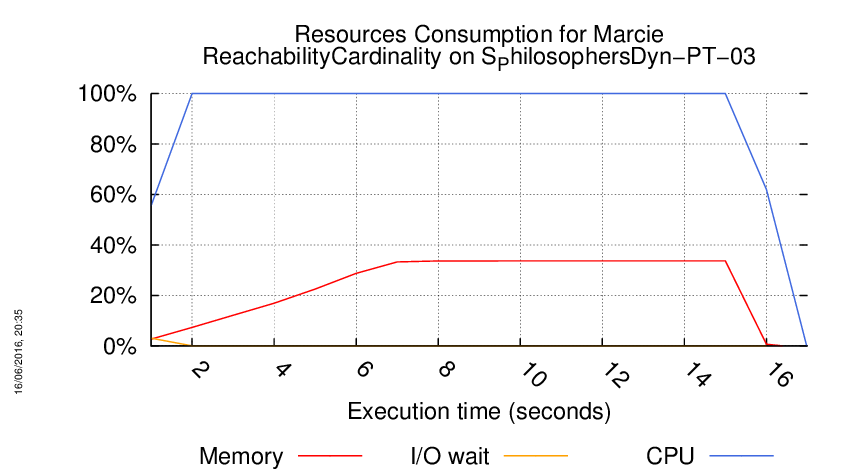
Trace from the execution
Waiting for the VM to be ready (probing ssh)
.................
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is S_PhilosophersDyn-PT-03, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r173kn-ebro-146433147001006
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-0
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-1
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-10
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-11
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-12
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-13
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-14
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-15
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-2
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-3
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-4
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-5
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-6
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-7
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-8
FORMULA_NAME PhilosophersDyn-COL-03-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1464816650791
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: PhilosophersDyn_PT_03
(NrP: 30 NrTr: 84 NrArc: 564)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.001sec
init dd package: 0m 7.304sec
RS generation: 0m 0.024sec
-> reachability set: #nodes 448 (4.5e+02) #states 325
starting MCC model checker
--------------------------
checking: AG [~ [3<=sum(HasRight_3, HasRight_1, HasRight_2)]]
normalized: ~ [E [true U 3<=sum(HasRight_3, HasRight_1, HasRight_2)]]
abstracting: (3<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 0
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.064sec
checking: AG [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]
normalized: ~ [E [true U ~ [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]]]
abstracting: (sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 271
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.107sec
checking: EF [[sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3) | sum(Think_1, Think_2, Think_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]
normalized: E [true U [sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3) | sum(Think_1, Think_2, Think_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 232
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)) states: 166
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.134sec
checking: EF [~ [~ [[3<=sum(HasLeft_1, HasLeft_3, HasLeft_2) & 1<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]]]]
normalized: E [true U [3<=sum(HasLeft_1, HasLeft_3, HasLeft_2) & 1<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]]
abstracting: (1<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)) states: 324
abstracting: (3<=sum(HasLeft_1, HasLeft_3, HasLeft_2)) states: 0
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.123sec
checking: AG [sum(Outside_1, Outside_2, Outside_3)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]
normalized: ~ [E [true U ~ [sum(Outside_1, Outside_2, Outside_3)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]]]
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)) states: 306
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.091sec
checking: EF [[~ [[sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) | sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] | ~ [~ [2<=sum(Think_1, Think_2, Think_3)]]]]
normalized: E [true U [2<=sum(Think_1, Think_2, Think_3) | ~ [[sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) | sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]]]
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 265
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 265
abstracting: (2<=sum(Think_1, Think_2, Think_3)) states: 63
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.203sec
checking: EF [[[3<=sum(Outside_1, Outside_2, Outside_3) | ~ [sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)]] | sum(Forks_3, Forks_2, Forks_1)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]]
normalized: E [true U [sum(Forks_3, Forks_2, Forks_1)<=sum(WaitRight_3, WaitRight_2, WaitRight_1) | [3<=sum(Outside_1, Outside_2, Outside_3) | ~ [sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)]]]]
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)) states: 261
abstracting: (3<=sum(Outside_1, Outside_2, Outside_3)) states: 1
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 265
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.186sec
checking: AG [[~ [[1<=sum(Think_1, Think_2, Think_3) | sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] | ~ [sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)]]]
normalized: ~ [E [true U ~ [[~ [[1<=sum(Think_1, Think_2, Think_3) | sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] | ~ [sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)]]]]]
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)) states: 166
abstracting: (sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 313
abstracting: (1<=sum(Think_1, Think_2, Think_3)) states: 213
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.196sec
checking: AG [[[[1<=sum(Think_1, Think_2, Think_3) | 1<=sum(HasRight_3, HasRight_1, HasRight_2)] & sum(HasLeft_1, HasLeft_3, HasLeft_2)<=sum(HasRight_3, HasRight_1, HasRight_2)] & sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(HasRight_3, HasRight_1, HasRight_2)]]
normalized: ~ [E [true U ~ [[sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(HasRight_3, HasRight_1, HasRight_2) & [sum(HasLeft_1, HasLeft_3, HasLeft_2)<=sum(HasRight_3, HasRight_1, HasRight_2) & [1<=sum(Think_1, Think_2, Think_3) | 1<=sum(HasRight_3, HasRight_1, HasRight_2)]]]]]]
abstracting: (1<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 138
abstracting: (1<=sum(Think_1, Think_2, Think_3)) states: 213
abstracting: (sum(HasLeft_1, HasLeft_3, HasLeft_2)<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 235
abstracting: (sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 136
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.261sec
checking: EF [[[[sum(HasRight_3, HasRight_1, HasRight_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2) | sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)] | 1<=sum(HasRight_3, HasRight_1, HasRight_2)] | 2<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]]
normalized: E [true U [2<=sum(WaitRight_3, WaitRight_2, WaitRight_1) | [1<=sum(HasRight_3, HasRight_1, HasRight_2) | [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2) | sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)]]]]
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)) states: 166
abstracting: (sum(HasRight_3, HasRight_1, HasRight_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)) states: 235
abstracting: (1<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 138
abstracting: (2<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 120
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.244sec
checking: EF [[[[sum(Think_1, Think_2, Think_3)<=sum(Forks_3, Forks_2, Forks_1) & 2<=sum(Outside_1, Outside_2, Outside_3)] & [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(Outside_1, Outside_2, Outside_3) | 2<=sum(HasRight_3, HasRight_1, HasRight_2)]] & sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)]]
normalized: E [true U [sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3) & [[sum(HasRight_3, HasRight_1, HasRight_2)<=sum(Outside_1, Outside_2, Outside_3) | 2<=sum(HasRight_3, HasRight_1, HasRight_2)] & [sum(Think_1, Think_2, Think_3)<=sum(Forks_3, Forks_2, Forks_1) & 2<=sum(Outside_1, Outside_2, Outside_3)]]]]
abstracting: (2<=sum(Outside_1, Outside_2, Outside_3)) states: 19
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(Forks_3, Forks_2, Forks_1)) states: 232
abstracting: (2<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 15
abstracting: (sum(HasRight_3, HasRight_1, HasRight_2)<=sum(Outside_1, Outside_2, Outside_3)) states: 226
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(Outside_1, Outside_2, Outside_3)) states: 166
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.327sec
checking: EF [[[~ [sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)<=sum(Forks_3, Forks_2, Forks_1)] & [2<=sum(HasRight_3, HasRight_1, HasRight_2) | sum(Think_1, Think_2, Think_3)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]] | [~ [2<=sum(HasLeft_1, HasLeft_3, HasLeft_2)] & sum(Think_1, Think_2, Think_3)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)]]]
normalized: E [true U [[sum(Think_1, Think_2, Think_3)<=sum(HasLeft_1, HasLeft_3, HasLeft_2) & ~ [2<=sum(HasLeft_1, HasLeft_3, HasLeft_2)]] | [~ [sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)<=sum(Forks_3, Forks_2, Forks_1)] & [2<=sum(HasRight_3, HasRight_1, HasRight_2) | sum(Think_1, Think_2, Think_3)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)]]]]
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 232
abstracting: (2<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 15
abstracting: (sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)<=sum(Forks_3, Forks_2, Forks_1)) states: 178
abstracting: (2<=sum(HasLeft_1, HasLeft_3, HasLeft_2)) states: 15
abstracting: (sum(Think_1, Think_2, Think_3)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)) states: 178
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.317sec
checking: EF [~ [[~ [3<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)] | sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]]]
normalized: E [true U ~ [[sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2) | ~ [3<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)]]]]
abstracting: (3<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)) states: 204
abstracting: (sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)) states: 325
-> the formula is FALSE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.120sec
checking: EF [[[sum(Outside_1, Outside_2, Outside_3)<=sum(HasRight_3, HasRight_1, HasRight_2) & [sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) & 1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] & [2<=sum(WaitRight_3, WaitRight_2, WaitRight_1) | [sum(Forks_3, Forks_2, Forks_1)<=sum(Forks_3, Forks_2, Forks_1) & sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]]]
normalized: E [true U [[2<=sum(WaitRight_3, WaitRight_2, WaitRight_1) | [sum(Forks_3, Forks_2, Forks_1)<=sum(Forks_3, Forks_2, Forks_1) & sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] & [sum(Outside_1, Outside_2, Outside_3)<=sum(HasRight_3, HasRight_1, HasRight_2) & [sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) & 1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]]]
abstracting: (1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 255
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 276
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(HasRight_3, HasRight_1, HasRight_2)) states: 243
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 276
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(Forks_3, Forks_2, Forks_1)) states: 325
abstracting: (2<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 120
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.380sec
checking: AG [[[~ [sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)] | [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) & sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] | ~ [[1<=sum(WaitRight_3, WaitRight_2, WaitRight_1) & sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)]]]]
normalized: ~ [E [true U ~ [[~ [[1<=sum(WaitRight_3, WaitRight_2, WaitRight_1) & sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)]] | [~ [sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)] | [sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) & sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]]]]]
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 276
abstracting: (sum(HasRight_3, HasRight_1, HasRight_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 313
abstracting: (sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 58
abstracting: (sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)<=sum(HasLeft_1, HasLeft_3, HasLeft_2)) states: 7
abstracting: (1<=sum(WaitRight_3, WaitRight_2, WaitRight_1)) states: 255
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.333sec
checking: EF [[[[1<=sum(Forks_3, Forks_2, Forks_1) & sum(Forks_3, Forks_2, Forks_1)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)] & [sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) | sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)]] | [[2<=sum(Forks_3, Forks_2, Forks_1) | sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)] | 1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]]]
normalized: E [true U [[1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) | [2<=sum(Forks_3, Forks_2, Forks_1) | sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)]] | [[1<=sum(Forks_3, Forks_2, Forks_1) & sum(Forks_3, Forks_2, Forks_1)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)] & [sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2) | sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)]]]]
abstracting: (sum(Outside_1, Outside_2, Outside_3)<=sum(Think_1, Think_2, Think_3)) states: 261
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 265
abstracting: (sum(Forks_3, Forks_2, Forks_1)<=sum(Neighbourhood_3_1, Neighbourhood_3_2, Neighbourhood_1_3, Neighbourhood_2_1, Neighbourhood_2_3, Neighbourhood_1_1, Neighbourhood_3_3, Neighbourhood_2_2, Neighbourhood_1_2)) states: 325
abstracting: (1<=sum(Forks_3, Forks_2, Forks_1)) states: 210
abstracting: (sum(WaitRight_3, WaitRight_2, WaitRight_1)<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 235
abstracting: (2<=sum(Forks_3, Forks_2, Forks_1)) states: 60
abstracting: (1<=sum(WaitLeft_1, WaitLeft_3, WaitLeft_2)) states: 255
-> the formula is TRUE
FORMULA PhilosophersDyn-COL-03-ReachabilityCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.448sec
Total processing time: 0m14.996sec
BK_STOP 1464816665838
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.000sec
291
iterations count:1658 (19), effective:60 (0)
initing FirstDep: 0m 0.001sec
616
iterations count:1779 (21), effective:50 (0)
iterations count:144 (1), effective:3 (0)
372
iterations count:1484 (17), effective:48 (0)
iterations count:695 (8), effective:18 (0)
iterations count:121 (1), effective:5 (0)
iterations count:676 (8), effective:25 (0)
iterations count:479 (5), effective:14 (0)
iterations count:84 (1), effective:0 (0)
384
iterations count:1544 (18), effective:51 (0)
iterations count:280 (3), effective:11 (0)
iterations count:603 (7), effective:19 (0)
iterations count:144 (1), effective:3 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_PhilosophersDyn-PT-03"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_PhilosophersDyn-PT-03.tgz
mv S_PhilosophersDyn-PT-03 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is S_PhilosophersDyn-PT-03, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r173kn-ebro-146433147001006"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

