About the Execution of Marcie for S_BridgeAndVehicles-PT-V10P10N10
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 8136.030 | 2115922.00 | 2115980.00 | 20.20 | TTTTTTTFTTFTTTFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
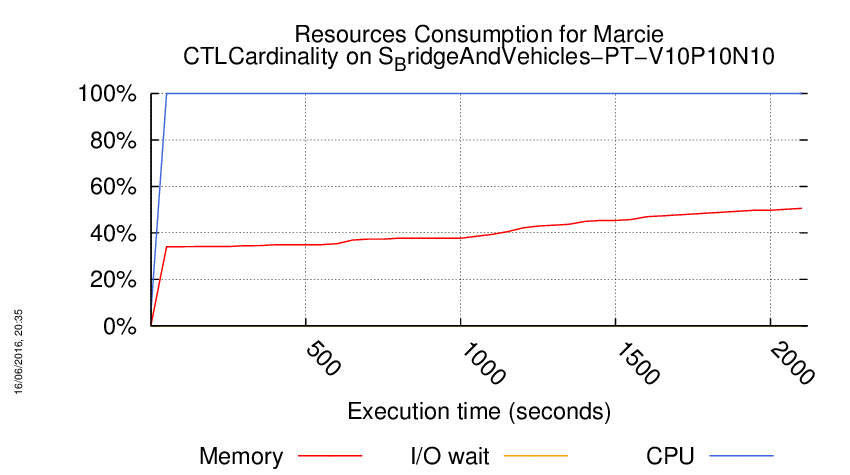
Trace from the execution
Waiting for the VM to be ready (probing ssh)
.....................
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is S_BridgeAndVehicles-PT-V10P10N10, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r173kn-ebro-146433145300264
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-0
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-1
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-10
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-11
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-12
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-13
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-14
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-15
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-2
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-3
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-4
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-5
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-6
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-7
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-8
FORMULA_NAME BridgeAndVehicles-COL-V10P10N10-CTLCardinality-9
=== Now, execution of the tool begins
BK_START 1464792419483
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: BridgeAndVehicles_PT_V10P10N10
(NrP: 48 NrTr: 288 NrArc: 2090)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.001sec
init dd package: 0m 9.464sec
RS generation: 0m 4.598sec
-> reachability set: #nodes 22599 (2.3e+04) #states 259,556 (5)
starting MCC model checker
--------------------------
checking: AG [3<=CAPACITE]
normalized: ~ [E [true U ~ [3<=CAPACITE]]]
abstracting: (3<=CAPACITE) states: 255,046 (5)
-> the formula is FALSE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 5m26.166sec
checking: AF [AG [ROUTE_A<=CAPACITE]]
normalized: ~ [EG [E [true U ~ [ROUTE_A<=CAPACITE]]]]
abstracting: (ROUTE_A<=CAPACITE) states: 250,998 (5)
....................................................................................
EG iterations: 84
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 5m 6.329sec
checking: ~ [EG [EF [sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CHOIX_2, CHOIX_1)]]]
normalized: ~ [EG [E [true U sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CHOIX_2, CHOIX_1)]]]
abstracting: (sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CHOIX_2, CHOIX_1)) states: 145,805 (5)
..............................................................................................................................................
EG iterations: 142
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-2 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 8m54.949sec
checking: AF [~ [[~ [1<=sum(VIDANGE_2, VIDANGE_1)] | ~ [3<=sum(CHOIX_2, CHOIX_1)]]]]
normalized: ~ [EG [[~ [1<=sum(VIDANGE_2, VIDANGE_1)] | ~ [3<=sum(CHOIX_2, CHOIX_1)]]]]
abstracting: (3<=sum(CHOIX_2, CHOIX_1)) states: 0
abstracting: (1<=sum(VIDANGE_2, VIDANGE_1)) states: 30,602 (4)
EG iterations: 0
-> the formula is FALSE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.401sec
checking: EG [[EF [sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(VIDANGE_2, VIDANGE_1)] | AX [2<=SORTI_B]]]
normalized: EG [[~ [EX [~ [2<=SORTI_B]]] | E [true U sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(VIDANGE_2, VIDANGE_1)]]]
abstracting: (sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(VIDANGE_2, VIDANGE_1)) states: 145,805 (5)
abstracting: (2<=SORTI_B) states: 200,614 (5)
.
EG iterations: 0
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.639sec
checking: [~ [~ [AF [1<=SORTI_A]]] | EG [[[2<=ATTENTE_B & 3<=ROUTE_A] & [SUR_PONT_A<=CAPACITE & 2<=ROUTE_B]]]]
normalized: [EG [[[SUR_PONT_A<=CAPACITE & 2<=ROUTE_B] & [2<=ATTENTE_B & 3<=ROUTE_A]]] | ~ [EG [~ [1<=SORTI_A]]]]
abstracting: (1<=SORTI_A) states: 238,962 (5)
..............................................................................
EG iterations: 78
abstracting: (3<=ROUTE_A) states: 111,708 (5)
abstracting: (2<=ATTENTE_B) states: 155,067 (5)
abstracting: (2<=ROUTE_B) states: 151,686 (5)
abstracting: (SUR_PONT_A<=CAPACITE) states: 249,436 (5)
..........................................................
EG iterations: 58
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m17.010sec
checking: ~ [EG [~ [[sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CONTROLEUR_2, CONTROLEUR_1) & 1<=sum(CONTROLEUR_2, CONTROLEUR_1)]]]]
normalized: ~ [EG [~ [[sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CONTROLEUR_2, CONTROLEUR_1) & 1<=sum(CONTROLEUR_2, CONTROLEUR_1)]]]]
abstracting: (1<=sum(CONTROLEUR_2, CONTROLEUR_1)) states: 113,751 (5)
abstracting: (sum(CONTROLEUR_2, CONTROLEUR_1)<=sum(CONTROLEUR_2, CONTROLEUR_1)) states: 259,556 (5)
........................
EG iterations: 24
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m30.189sec
checking: [~ [~ [[[1<=ATTENTE_B | 2<=ATTENTE_A] | ATTENTE_A<=SUR_PONT_A]]] & [A [2<=SUR_PONT_A U SUR_PONT_B<=ROUTE_A] & EG [[2<=ROUTE_A | 1<=ROUTE_B]]]]
normalized: [[ATTENTE_A<=SUR_PONT_A | [1<=ATTENTE_B | 2<=ATTENTE_A]] & [[~ [EG [~ [SUR_PONT_B<=ROUTE_A]]] & ~ [E [~ [SUR_PONT_B<=ROUTE_A] U [~ [SUR_PONT_B<=ROUTE_A] & ~ [2<=SUR_PONT_A]]]]] & EG [[2<=ROUTE_A | 1<=ROUTE_B]]]]
abstracting: (1<=ROUTE_B) states: 200,737 (5)
abstracting: (2<=ROUTE_A) states: 151,692 (5)
.....................................................................................................................................
EG iterations: 133
abstracting: (2<=SUR_PONT_A) states: 66,660 (4)
abstracting: (SUR_PONT_B<=ROUTE_A) states: 218,614 (5)
abstracting: (SUR_PONT_B<=ROUTE_A) states: 218,614 (5)
abstracting: (SUR_PONT_B<=ROUTE_A) states: 218,614 (5)
.......................................
EG iterations: 39
abstracting: (2<=ATTENTE_A) states: 155,040 (5)
abstracting: (1<=ATTENTE_B) states: 204,490 (5)
abstracting: (ATTENTE_A<=SUR_PONT_A) states: 94,861 (4)
-> the formula is FALSE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-8 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 2m52.353sec
checking: AF [sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=ATTENTE_A]
normalized: ~ [EG [~ [sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=ATTENTE_A]]]
abstracting: (sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=ATTENTE_A) states: 204,460 (5)
.........................................................
EG iterations: 57
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 2m39.936sec
checking: EX [E [3<=ROUTE_B U CAPACITE<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)]]
normalized: EX [E [3<=ROUTE_B U CAPACITE<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)]]
abstracting: (CAPACITE<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 1,496 (3)
abstracting: (3<=ROUTE_B) states: 111,699 (5)
.-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 6.804sec
checking: [~ [A [sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(CHOIX_2, CHOIX_1) U ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)]] | [AF [[1<=ROUTE_B & sum(CONTROLEUR_2, CONTROLEUR_1)<=SUR_PONT_B]] & ~ [EG [2<=ROUTE_B]]]]
normalized: [[~ [EG [2<=ROUTE_B]] & ~ [EG [~ [[1<=ROUTE_B & sum(CONTROLEUR_2, CONTROLEUR_1)<=SUR_PONT_B]]]]] | ~ [[~ [EG [~ [ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)]]] & ~ [E [~ [ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)] U [~ [sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(CHOIX_2, CHOIX_1)] & ~ [ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)]]]]]]]
abstracting: (ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)) states: 76,886 (4)
abstracting: (sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(CHOIX_2, CHOIX_1)) states: 115,203 (5)
abstracting: (ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)) states: 76,886 (4)
abstracting: (ATTENTE_A<=sum(CONTROLEUR_2, CONTROLEUR_1)) states: 76,886 (4)
................................................................................
EG iterations: 80
abstracting: (sum(CONTROLEUR_2, CONTROLEUR_1)<=SUR_PONT_B) states: 186,890 (5)
abstracting: (1<=ROUTE_B) states: 200,737 (5)
.
EG iterations: 1
abstracting: (2<=ROUTE_B) states: 151,686 (5)
...........................................................................................................................
EG iterations: 123
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m44.194sec
checking: [[[[[ROUTE_A<=sum(CHOIX_2, CHOIX_1) & sum(CHOIX_2, CHOIX_1)<=ROUTE_B] | [3<=ATTENTE_B & 3<=ROUTE_A]] | [[1<=SORTI_A | ROUTE_B<=sum(VIDANGE_2, VIDANGE_1)] & [SUR_PONT_B<=ATTENTE_A | 2<=sum(VIDANGE_2, VIDANGE_1)]]] | EG [[ROUTE_A<=SUR_PONT_B | ROUTE_A<=ROUTE_A]]] | ~ [EF [[2<=ATTENTE_B & ROUTE_A<=ROUTE_A]]]]
normalized: [[[[[SUR_PONT_B<=ATTENTE_A | 2<=sum(VIDANGE_2, VIDANGE_1)] & [1<=SORTI_A | ROUTE_B<=sum(VIDANGE_2, VIDANGE_1)]] | [[3<=ATTENTE_B & 3<=ROUTE_A] | [ROUTE_A<=sum(CHOIX_2, CHOIX_1) & sum(CHOIX_2, CHOIX_1)<=ROUTE_B]]] | EG [[ROUTE_A<=SUR_PONT_B | ROUTE_A<=ROUTE_A]]] | ~ [E [true U [2<=ATTENTE_B & ROUTE_A<=ROUTE_A]]]]
abstracting: (ROUTE_A<=ROUTE_A) states: 259,556 (5)
abstracting: (2<=ATTENTE_B) states: 155,067 (5)
abstracting: (ROUTE_A<=ROUTE_A) states: 259,556 (5)
abstracting: (ROUTE_A<=SUR_PONT_B) states: 95,094 (4)
EG iterations: 0
abstracting: (sum(CHOIX_2, CHOIX_1)<=ROUTE_B) states: 232,957 (5)
abstracting: (ROUTE_A<=sum(CHOIX_2, CHOIX_1)) states: 80,662 (4)
abstracting: (3<=ROUTE_A) states: 111,708 (5)
abstracting: (3<=ATTENTE_B) states: 114,708 (5)
abstracting: (ROUTE_B<=sum(VIDANGE_2, VIDANGE_1)) states: 64,286 (4)
abstracting: (1<=SORTI_A) states: 238,962 (5)
abstracting: (2<=sum(VIDANGE_2, VIDANGE_1)) states: 0
abstracting: (SUR_PONT_B<=ATTENTE_A) states: 220,264 (5)
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 3.535sec
checking: EF [E [ATTENTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) U 2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]
normalized: E [true U E [ATTENTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) U 2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]
abstracting: (2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (ATTENTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 104,489 (5)
-> the formula is FALSE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-15 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.346sec
checking: [A [[sum(VIDANGE_2, VIDANGE_1)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) | 2<=ROUTE_A] U ~ [3<=ROUTE_A]] & E [SORTI_A<=sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0) U [3<=ATTENTE_A | 2<=SORTI_B]]]
normalized: [[~ [E [3<=ROUTE_A U [3<=ROUTE_A & ~ [[sum(VIDANGE_2, VIDANGE_1)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) | 2<=ROUTE_A]]]]] & ~ [EG [3<=ROUTE_A]]] & E [SORTI_A<=sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0) U [3<=ATTENTE_A | 2<=SORTI_B]]]
abstracting: (2<=SORTI_B) states: 200,614 (5)
abstracting: (3<=ATTENTE_A) states: 114,684 (5)
abstracting: (SORTI_A<=sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)) states: 58,942 (4)
abstracting: (3<=ROUTE_A) states: 111,708 (5)
....................................................................................................................
EG iterations: 116
abstracting: (2<=ROUTE_A) states: 151,692 (5)
abstracting: (sum(VIDANGE_2, VIDANGE_1)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 259,556 (5)
abstracting: (3<=ROUTE_A) states: 111,708 (5)
abstracting: (3<=ROUTE_A) states: 111,708 (5)
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m21.535sec
checking: AF [EX [[ROUTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) & sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)]]]
normalized: ~ [EG [~ [EX [[ROUTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) & sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)]]]]]
abstracting: (sum(COMPTEUR_10, COMPTEUR_9, COMPTEUR_8, COMPTEUR_7, COMPTEUR_6, COMPTEUR_5, COMPTEUR_4, COMPTEUR_3, COMPTEUR_2, COMPTEUR_1, COMPTEUR_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 259,556 (5)
abstracting: (ROUTE_B<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 107,870 (5)
..................................................................................................................
EG iterations: 113
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m36.958sec
checking: A [[sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) | sum(VIDANGE_2, VIDANGE_1)<=SORTI_A] U [2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0) | [sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1) | 3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]]
normalized: [~ [EG [~ [[2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0) | [sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1) | 3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]]]] & ~ [E [~ [[2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0) | [sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1) | 3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]] U [~ [[sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0) | sum(VIDANGE_2, VIDANGE_1)<=SORTI_A]] & ~ [[2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0) | [sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1) | 3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)]]]]]]]
abstracting: (3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1)) states: 144,353 (5)
abstracting: (2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (sum(VIDANGE_2, VIDANGE_1)<=SORTI_A) states: 253,649 (5)
abstracting: (sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)<=sum(NB_ATTENTE_A_10, NB_ATTENTE_A_9, NB_ATTENTE_A_8, NB_ATTENTE_A_7, NB_ATTENTE_A_6, NB_ATTENTE_A_5, NB_ATTENTE_A_4, NB_ATTENTE_A_3, NB_ATTENTE_A_2, NB_ATTENTE_A_1, NB_ATTENTE_A_0)) states: 259,556 (5)
abstracting: (3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1)) states: 144,353 (5)
abstracting: (2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (3<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
abstracting: (sum(CHOIX_2, CHOIX_1)<=sum(VIDANGE_2, VIDANGE_1)) states: 144,353 (5)
abstracting: (2<=sum(NB_ATTENTE_B_10, NB_ATTENTE_B_9, NB_ATTENTE_B_8, NB_ATTENTE_B_7, NB_ATTENTE_B_6, NB_ATTENTE_B_5, NB_ATTENTE_B_4, NB_ATTENTE_B_3, NB_ATTENTE_B_2, NB_ATTENTE_B_1, NB_ATTENTE_B_0)) states: 0
......................
EG iterations: 22
-> the formula is TRUE
FORMULA BridgeAndVehicles-COL-V10P10N10-CTLCardinality-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 6.536sec
Total processing time: 35m15.661sec
BK_STOP 1464794535405
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.001sec
1721 2604 3092 3210 4515 5858 6294 6380 7131 6957 7531 7461 7953 8048 8604 8566 9016 10283 9873 9954 9706 11693 11308 11516 11418 12794 12803 13338 13315 14741 15608 15336 15426 15159 17870 17518 17750 17568 19738 19687 20262 20205 22126 22269 22529 22599
iterations count:46237 (160), effective:1794 (6)
initing FirstDep: 0m 0.001sec
4409 5899 6843 9175 9582 10865 12444 12470 12473 12501 12543 12694 12733 12764 12784 13040 13229 13430 13571 13780 13915 14521 15024 15333 16311 16686 17591 18207 18935 19775 20191 21170 22026 22407 23661 24404 24764 24896 24992 25028 28091 29195 30254 30074 30056 30062 29972 30027 29890 29706 29452 29135 28530 29731 29672 29685 29676 29625 29467 29535 29327 29096 28781 27924 28167 29093 29082 29097 29037 28903 28967 28761 28530 28208 27576 27611 28495 28497 28503 28437 28309 28373 28167 27954 27645 26739 28155 27876 27894 27906 27846 27685 27751 27575 27342 27031 26145 27329 27333 27300 27309 27219 27275 27135 26936 26699 26425 25548 26681 26706 26724 26706 26571 26650 26420 26260 26004 25665 25809 25707 25686 25698 25638 25477 25543 25365 25150 24875 23842
iterations count:129209 (448), effective:3925 (13)
8467 12329 16477 17734 17941 18137 18310 18583 18919 19060 19719 19979 20603 21033 21592 22276 22613 23508 24113 24873 25618 26139 27090 27767 28353 28402 28444 28465 40106 49419 53803
iterations count:31355 (108), effective:454 (1)
16477 16927 17188 17578 18057 17854 18485 19182 19745 19785 20638 20733 20938 21028 21251 21305 21558 21607 21856 21934 22194 22286 22488 22623 22822 22946 22984 23273 23385 23393 23451 23493
iterations count:32992 (114), effective:213 (0)
16477 16927 17188 17578 18057 17854 18485 19182 19745 19785 20638 20733 20938 21028 21251 21305 21558 21607 21856 21934 22194 22286 22488 22623 22822 22946 22984 23273 23385 23393 23451 23493
iterations count:32992 (114), effective:213 (0)
iterations count:288 (1), effective:0 (0)
2906 4335 4545 5570 6758 6357 7127 7281 7320 7355 7361 7517 7574 7872 8059 7865 7662 7361 7367 7699 7634 8118 7964 7751 7458 7357 7984 7487 8052 8023 7825 7575 7363 7880 7537 7870 8053 7859 7654 7355 7509 7578 7864 8076 7911 7685 7376 7526 7576 7868 8079 7909 7680 7398 7874 7544 7860 8050 7881 7678 7372 7925 7469 8004 8033 7842 7630 7344
iterations count:68307 (237), effective:2125 (7)
iterations count:937 (3), effective:21 (0)
iterations count:307 (1), effective:2 (0)
30776 30777 30784 30795 30828 30883 30929 30040
iterations count:8368 (29), effective:95 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_BridgeAndVehicles-PT-V10P10N10"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_BridgeAndVehicles-PT-V10P10N10.tgz
mv S_BridgeAndVehicles-PT-V10P10N10 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is S_BridgeAndVehicles-PT-V10P10N10, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r173kn-ebro-146433145300264"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

