About the Execution of Marcie for SquareGrid-PT-020102
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5671.790 | 53039.00 | 53069.00 | 30.20 | TTTFFTFTFFFTTTFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
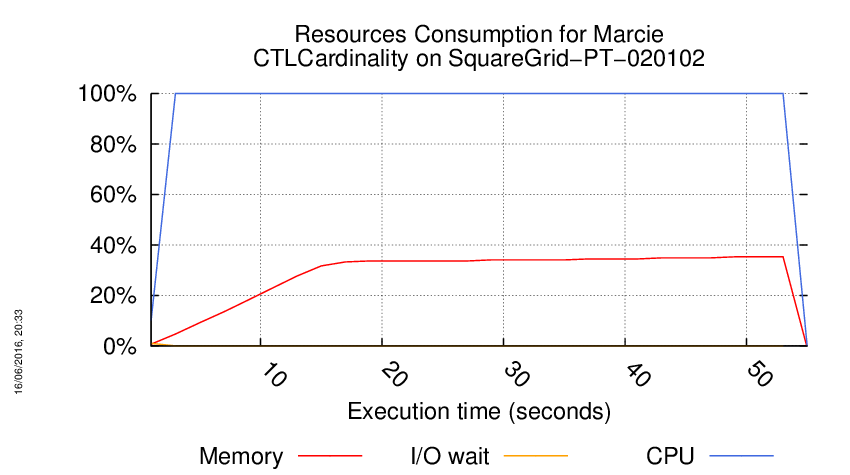
Trace from the execution
Waiting for the VM to be ready (probing ssh)
...........
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is SquareGrid-PT-020102, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r125kn-qhx2-146373371400318
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-0
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-1
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-10
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-11
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-12
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-13
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-14
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-15
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-2
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-3
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-4
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-5
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-6
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-7
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-8
FORMULA_NAME SquareGrid-PT-020102-CTLCardinality-9
=== Now, execution of the tool begins
BK_START 1464492711467
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: SquareGrid_PT_020102
(NrP: 68 NrTr: 72 NrArc: 288)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
init dd package: 0m16.815sec
RS generation: 0m 1.148sec
-> reachability set: #nodes 2034 (2.0e+03) #states 2,085,423,232,578 (12)
starting MCC model checker
--------------------------
checking: EF [AX [3<=pb3_2_2]]
normalized: E [true U ~ [EX [~ [3<=pb3_2_2]]]]
abstracting: (3<=pb3_2_2) states: 90,137,146,432 (10)
.-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m16.003sec
checking: ~ [AX [EG [p1i_1_2<=pb2_1_2]]]
normalized: EX [~ [EG [p1i_1_2<=pb2_1_2]]]
abstracting: (p1i_1_2<=pb2_1_2) states: 1,710,070,304,850 (12)
......
EG iterations: 6
.-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-3 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.637sec
checking: EF [AG [[1<=pb1_2_1 & 2<=p3ol_2_2]]]
normalized: E [true U ~ [E [true U ~ [[1<=pb1_2_1 & 2<=p3ol_2_2]]]]]
abstracting: (2<=p3ol_2_2) states: 0
abstracting: (1<=pb1_2_1) states: 794,343,606,432 (11)
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.010sec
checking: EG [A [1<=p4il_2_1 U p4il_2_2<=p1il_2_1]]
normalized: EG [[~ [EG [~ [p4il_2_2<=p1il_2_1]]] & ~ [E [~ [p4il_2_2<=p1il_2_1] U [~ [1<=p4il_2_1] & ~ [p4il_2_2<=p1il_2_1]]]]]]
abstracting: (p4il_2_2<=p1il_2_1) states: 1,656,051,315,618 (12)
abstracting: (1<=p4il_2_1) states: 1,493,062,557,126 (12)
abstracting: (p4il_2_2<=p1il_2_1) states: 1,656,051,315,618 (12)
abstracting: (p4il_2_2<=p1il_2_1) states: 1,656,051,315,618 (12)
......
EG iterations: 6
......
EG iterations: 6
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.665sec
checking: [~ [[2<=pb2_1_1 | EF [p2ol_1_2<=p2ol_2_2]]] | EF [~ [~ [2<=p1ol_1_1]]]]
normalized: [~ [[2<=pb2_1_1 | E [true U p2ol_1_2<=p2ol_2_2]]] | E [true U 2<=p1ol_1_1]]
abstracting: (2<=p1ol_1_1) states: 0
abstracting: (p2ol_1_2<=p2ol_2_2) states: 1,656,051,315,618 (12)
abstracting: (2<=pb2_1_1) states: 280,659,824,176 (11)
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.525sec
checking: EG [[[~ [1<=p2ol_2_2] & [1<=pb3_2_2 | 1<=p3o_2_1]] | EF [p2i_1_2<=p4ol_1_2]]]
normalized: EG [[E [true U p2i_1_2<=p4ol_1_2] | [[1<=pb3_2_2 | 1<=p3o_2_1] & ~ [1<=p2ol_2_2]]]]
abstracting: (1<=p2ol_2_2) states: 1,493,062,557,126 (12)
abstracting: (1<=p3o_2_1) states: 592,360,675,452 (11)
abstracting: (1<=pb3_2_2) states: 794,343,606,432 (11)
abstracting: (p2i_1_2<=p4ol_1_2) states: 1,922,434,474,086 (12)
...
EG iterations: 3
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.157sec
checking: AG [[[pb3_2_2<=p4o_1_1 | ~ [pb2_2_1<=p4i_2_1]] | AF [3<=p4il_2_1]]]
normalized: ~ [E [true U ~ [[~ [EG [~ [3<=p4il_2_1]]] | [pb3_2_2<=p4o_1_1 | ~ [pb2_2_1<=p4i_2_1]]]]]]
abstracting: (pb2_2_1<=p4i_2_1) states: 1,434,418,752,922 (12)
abstracting: (pb3_2_2<=p4o_1_1) states: 1,434,418,752,922 (12)
abstracting: (3<=p4il_2_1) states: 0
EG iterations: 0
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.467sec
checking: AF [[~ [~ [pb2_1_2<=p2il_2_2]] & ~ [[p4ol_2_2<=p4il_2_1 | 3<=p4o_2_2]]]]
normalized: ~ [EG [~ [[pb2_1_2<=p2il_2_2 & ~ [[p4ol_2_2<=p4il_2_1 | 3<=p4o_2_2]]]]]]
abstracting: (3<=p4o_2_2) states: 0
abstracting: (p4ol_2_2<=p4il_2_1) states: 1,656,051,315,618 (12)
abstracting: (pb2_1_2<=p2il_2_2) states: 1,661,424,281,626 (12)
......
EG iterations: 6
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-8 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.571sec
checking: ~ [[EG [[1<=p1o_2_1 | 1<=p4ol_1_2]] | [EX [2<=p4il_2_1] & AX [p1i_2_2<=pb4_2_1]]]]
normalized: ~ [[[~ [EX [~ [p1i_2_2<=pb4_2_1]]] & EX [2<=p4il_2_1]] | EG [[1<=p1o_2_1 | 1<=p4ol_1_2]]]]
abstracting: (1<=p4ol_1_2) states: 1,493,062,557,126 (12)
abstracting: (1<=p1o_2_1) states: 592,360,675,452 (11)
......
EG iterations: 6
abstracting: (2<=p4il_2_1) states: 0
.abstracting: (p1i_2_2<=pb4_2_1) states: 1,710,070,304,850 (12)
.-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.619sec
checking: E [[~ [1<=pbl_2_2] | ~ [p1o_1_1<=p1i_2_2]] U EG [p3o_2_2<=p4o_2_2]]
normalized: E [[~ [p1o_1_1<=p1i_2_2] | ~ [1<=pbl_2_2]] U EG [p3o_2_2<=p4o_2_2]]
abstracting: (p3o_2_2<=p4o_2_2) states: 1,656,051,315,618 (12)
.....
EG iterations: 5
abstracting: (1<=pbl_2_2) states: 2,019,114,033,090 (12)
abstracting: (p1o_1_1<=p1i_2_2) states: 1,656,051,315,618 (12)
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.398sec
checking: [EG [[[p2ol_2_2<=p1il_0 | p3i_2_2<=p4ol_2_1] & 2<=pbl_1_1]] | AG [3<=pb3_1_2]]
normalized: [~ [E [true U ~ [3<=pb3_1_2]]] | EG [[2<=pbl_1_1 & [p2ol_2_2<=p1il_0 | p3i_2_2<=p4ol_2_1]]]]
abstracting: (p3i_2_2<=p4ol_2_1) states: 1,922,434,474,086 (12)
abstracting: (p2ol_2_2<=p1il_0) states: 1,656,051,315,618 (12)
abstracting: (2<=pbl_1_1) states: 1,878,473,281,986 (12)
............
EG iterations: 12
abstracting: (3<=pb3_1_2) states: 90,137,146,432 (10)
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.840sec
checking: E [EG [1<=p2il_2_2] U [~ [3<=p3o_2_1] & [p3ol_2_2<=pb2_2_2 & p4il_2_2<=p1o_1_1]]]
normalized: E [EG [1<=p2il_2_2] U [[p3ol_2_2<=pb2_2_2 & p4il_2_2<=p1o_1_1] & ~ [3<=p3o_2_1]]]
abstracting: (3<=p3o_2_1) states: 0
abstracting: (p4il_2_2<=p1o_1_1) states: 1,021,732,592,412 (12)
abstracting: (p3ol_2_2<=pb2_2_2) states: 1,169,696,534,160 (12)
abstracting: (1<=p2il_2_2) states: 1,493,062,557,126 (12)
......
EG iterations: 6
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 2.068sec
checking: [EG [~ [[2<=p4ol_2_2 | 3<=p1i_1_2]]] & AF [[~ [p4ol_2_1<=p2ol_2_2] | ~ [pbl_1_2<=p3ol_2_2]]]]
normalized: [~ [EG [~ [[~ [p4ol_2_1<=p2ol_2_2] | ~ [pbl_1_2<=p3ol_2_2]]]]] & EG [~ [[2<=p4ol_2_2 | 3<=p1i_1_2]]]]
abstracting: (3<=p1i_1_2) states: 0
abstracting: (2<=p4ol_2_2) states: 0
EG iterations: 0
abstracting: (pbl_1_2<=p3ol_2_2) states: 172,760,362,096 (11)
abstracting: (p4ol_2_1<=p2ol_2_2) states: 1,656,051,315,618 (12)
......
EG iterations: 6
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.591sec
checking: E [~ [[2<=pb1_1_2 & pbl_1_2<=p3il_2_1]] U [~ [p4o_2_2<=p1ol_1_2] & [3<=p4il_1_2 & 1<=p4ol_1_1]]]
normalized: E [~ [[2<=pb1_1_2 & pbl_1_2<=p3il_2_1]] U [~ [p4o_2_2<=p1ol_1_2] & [3<=p4il_1_2 & 1<=p4ol_1_1]]]
abstracting: (1<=p4ol_1_1) states: 1,493,062,557,126 (12)
abstracting: (3<=p4il_1_2) states: 0
abstracting: (p4o_2_2<=p1ol_1_2) states: 1,922,434,474,086 (12)
abstracting: (pbl_1_2<=p3il_2_1) states: 172,760,362,096 (11)
abstracting: (2<=pb1_1_2) states: 280,659,824,176 (11)
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.018sec
checking: [~ [A [1<=p1ol_2_2 U 2<=pb1_1_2]] & AF [[[p2o_1_2<=p4il_2_2 & p1ol_2_2<=p1ol_1_1] & ~ [pb4_2_1<=p2ol_2_2]]]]
normalized: [~ [EG [~ [[~ [pb4_2_1<=p2ol_2_2] & [p2o_1_2<=p4il_2_2 & p1ol_2_2<=p1ol_1_1]]]]] & ~ [[~ [EG [~ [2<=pb1_1_2]]] & ~ [E [~ [2<=pb1_1_2] U [~ [1<=p1ol_2_2] & ~ [2<=pb1_1_2]]]]]]]
abstracting: (2<=pb1_1_2) states: 280,659,824,176 (11)
abstracting: (1<=p1ol_2_2) states: 1,493,062,557,126 (12)
abstracting: (2<=pb1_1_2) states: 280,659,824,176 (11)
abstracting: (2<=pb1_1_2) states: 280,659,824,176 (11)
.
EG iterations: 1
abstracting: (p1ol_2_2<=p1ol_1_1) states: 1,656,051,315,618 (12)
abstracting: (p2o_1_2<=p4il_2_2) states: 1,922,434,474,086 (12)
abstracting: (pb4_2_1<=p2ol_2_2) states: 1,661,424,281,626 (12)
.....
EG iterations: 5
-> the formula is FALSE
FORMULA SquareGrid-PT-020102-CTLCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.743sec
checking: [EG [[[p3ol_2_1<=p4il_1_1 & 1<=pb3_2_1] | [3<=p1il_1_2 & pbl_2_2<=p1o_1_1]]] | [~ [[~ [3<=p4o_2_2] | 3<=p2i_1_2]] | [[~ [p3ol_2_2<=p4i_1_1] & [2<=p4ol_2_1 | 2<=pb2_1_1]] | AF [3<=p3o_2_2]]]]
normalized: [[[~ [EG [~ [3<=p3o_2_2]]] | [[2<=p4ol_2_1 | 2<=pb2_1_1] & ~ [p3ol_2_2<=p4i_1_1]]] | ~ [[3<=p2i_1_2 | ~ [3<=p4o_2_2]]]] | EG [[[3<=p1il_1_2 & pbl_2_2<=p1o_1_1] | [p3ol_2_1<=p4il_1_1 & 1<=pb3_2_1]]]]
abstracting: (1<=pb3_2_1) states: 794,343,606,432 (11)
abstracting: (p3ol_2_1<=p4il_1_1) states: 1,656,051,315,618 (12)
abstracting: (pbl_2_2<=p1o_1_1) states: 100,498,787,984 (11)
abstracting: (3<=p1il_1_2) states: 0
......
EG iterations: 6
abstracting: (3<=p4o_2_2) states: 0
abstracting: (3<=p2i_1_2) states: 0
abstracting: (p3ol_2_2<=p4i_1_1) states: 1,021,732,592,412 (12)
abstracting: (2<=pb2_1_1) states: 280,659,824,176 (11)
abstracting: (2<=p4ol_2_1) states: 0
abstracting: (3<=p3o_2_2) states: 0
EG iterations: 0
-> the formula is TRUE
FORMULA SquareGrid-PT-020102-CTLCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.680sec
Total processing time: 0m52.968sec
BK_STOP 1464492764506
--------------------
content from stderr:
check for maximal unmarked siphon
ok
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.002sec
1016 1431 1226 1667 1244 2180 2341 1627 1794 2598 2198
iterations count:11383 (158), effective:1118 (15)
initing FirstDep: 0m 0.000sec
4350 4819 6999 5248 6493 6255 6811 6954 7250 9786 10236 6141 8873 9560 10494 11475 7598 8632 9901 8646 11371 11093 9604 10649 12551 13993 12823 2034
iterations count:28013 (389), effective:2814 (39)
iterations count:72 (1), effective:0 (0)
iterations count:979 (13), effective:85 (1)
2500
iterations count:1068 (14), effective:84 (1)
iterations count:307 (4), effective:22 (0)
5518 7159 7230
iterations count:3392 (47), effective:282 (3)
9656
iterations count:1417 (19), effective:116 (1)
2465
iterations count:1094 (15), effective:73 (1)
8269 10053
iterations count:2533 (35), effective:207 (2)
4224
iterations count:1480 (20), effective:123 (1)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="SquareGrid-PT-020102"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/home/fko/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/SquareGrid-PT-020102.tgz
mv SquareGrid-PT-020102 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is SquareGrid-PT-020102, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r125kn-qhx2-146373371400318"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

