About the Execution of ITS-Tools for PhilosophersDyn-PT-03
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 344.460 | 7511.00 | 16539.00 | 232.50 | TFTFFFTTTTFFFTFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
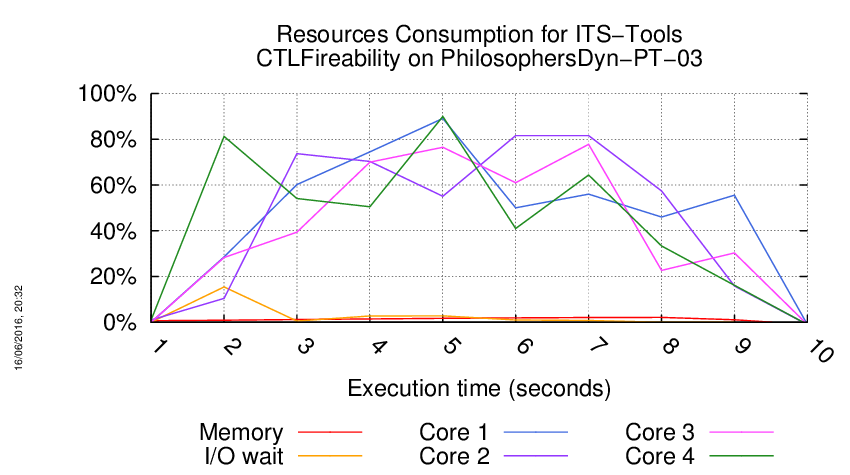
Trace from the execution
Waiting for the VM to be ready (probing ssh)
................
=====================================================================
Generated by BenchKit 2-2979
Executing tool itstools
Input is PhilosophersDyn-PT-03, examination is CTLFireability
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r085kn-ebro-146369085400463
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-0
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-1
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-10
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-11
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-12
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-13
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-14
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-15
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-2
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-3
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-4
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-5
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-6
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-7
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-8
FORMULA_NAME PhilosophersDyn-COL-03-CTLFireability-9
=== Now, execution of the tool begins
BK_START 1464063773633
its-ctl command run as :
/home/mcc/BenchKit/eclipse/plugins/fr.lip6.move.gal.itstools.binaries_1.0.0.201605191313/bin/its-ctl-linux64 --gc-threshold 2000000 --quiet -i /home/mcc/execution/CTLFireability.gal -t CGAL -ctl /home/mcc/execution/CTLFireability.ctl
No direction supplied, using forward translation only.
Parsed 16 CTL formulae.
Model ,|S| ,Time ,Mem(kb) ,fin. SDD ,fin. DDD ,peak SDD ,peak DDD ,SDD Hom ,SDD cache peak ,DDD Hom ,DDD cachepeak ,SHom cache
reachable,325,0.056952,5844,2,486,5,2123,6,0,221,1608,0
Converting to forward existential form...Done !
original formula: EG(E((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) U !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))
=> equivalent forward existential formula: [FwdG(Init,E((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) U !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))] != FALSE
Checking (exact) 0 :[FwdG(Init,E((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) U !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))] != FALSE
Checking (exact) 0 :FwdG(Init,E((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) U !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))
Checking (exact) 1 :Init
Checking (exact) 1 :E((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) U !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))
(forward)formula 0,1,0.303746,10072,1,0,124,19051,238,61,2475,16929,163
FORMULA PhilosophersDyn-COL-03-CTLFireability-0 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: AX(AF((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))
=> equivalent forward existential formula: [FwdG(EY(Init),!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))] = FALSE
Checking (exact) 0 :[FwdG(EY(Init),!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))] = FALSE
Checking (exact) 0 :FwdG(EY(Init),!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))
Checking (exact) 1 :EY(Init)
Checking (exact) 1 :Init
Hit Full ! (commute/partial/dont) 0/178/83
(forward)formula 1,0,0.358308,10824,1,0,125,21142,296,63,2674,19633,167
FORMULA PhilosophersDyn-COL-03-CTLFireability-1 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: !((EG(AF((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))) * (((!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + EX((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) * !((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))))
=> equivalent forward existential formula: ([(Init * !(EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))] != FALSE + [(((Init * !((!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) * !((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))) * !((!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))) * !(EX((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))] != FALSE)
Checking (exact) 0 :([(Init * !(EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))] != FALSE + [(((Init * !((!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) * !((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) + (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))) * !((!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))) * !(EX((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))] != FALSE)
Checking (exact) 0 :[(Init * !(EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))] != FALSE
Checking (exact) 0 :(Init * !(EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))
Checking (exact) 1 :!(EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :EG(!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))
Checking (exact) 1 :!(EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
Fast SCC detection found none.
Checking (exact) 1 :Init
(forward)formula 2,1,0.585175,15744,1,0,195,41526,317,104,2689,35250,276
FORMULA PhilosophersDyn-COL-03-CTLFireability-2 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: EG(!((((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) * ((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
=> equivalent forward existential formula: [FwdG(Init,!((((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) * ((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))] != FALSE
Checking (exact) 0 :[FwdG(Init,!((((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) * ((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))] != FALSE
Checking (exact) 0 :FwdG(Init,!((((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) * ((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) + ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :Init
Hit Full ! (commute/partial/dont) 0/0/83
(forward)formula 3,1,0.678105,17472,1,0,196,45494,328,106,2748,41112,280
FORMULA PhilosophersDyn-COL-03-CTLFireability-3 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: EG(AF(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
=> equivalent forward existential formula: [FwdG(Init,!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))] != FALSE
Checking (exact) 0 :[FwdG(Init,!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))] != FALSE
Checking (exact) 0 :FwdG(Init,!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :Init
Checking (exact) 1 :!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
(forward)formula 4,0,0.774618,19420,1,0,227,52738,336,127,2748,47636,349
FORMULA PhilosophersDyn-COL-03-CTLFireability-4 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: !((((EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) * ((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))) + (E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(AF(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
=> equivalent forward existential formula: (([((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))))] != FALSE + [((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE) + [((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))))] != FALSE)
Checking (exact) 0 :(([((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))))] != FALSE + [((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE) + [((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))))] != FALSE)
Checking (exact) 0 :([((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))))] != FALSE + [((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE)
Checking (exact) 0 :[((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))))] != FALSE
Checking (exact) 0 :((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))))
Checking (exact) 1 :!(EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))
Checking (exact) 1 :EX((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))
Checking (exact) 1 :(Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))))
Checking (exact) 1 :!((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))
Checking (exact) 1 :(E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))
Checking (exact) 1 :!(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :Init
Checking (exact) 0 :[((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE
Checking (exact) 0 :((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))
Checking (exact) 1 :!((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))
Checking (exact) 1 :(Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))))
Checking (exact) 1 :!((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))
Checking (exact) 1 :(E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))
Checking (exact) 1 :!(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :Init
Checking (exact) 0 :[((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))))] != FALSE
Checking (exact) 0 :((Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))) * !(((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))))))
Checking (exact) 1 :!(((!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) * !(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * ((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))))
Checking (exact) 1 :(Init * !((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))))
Checking (exact) 1 :!((E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))
Checking (exact) 1 :(E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + !(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :E((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) U (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))
Checking (exact) 1 :!(!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :Init
(forward)formula 5,0,1.05063,20312,1,0,236,53592,517,132,3013,49093,358
FORMULA PhilosophersDyn-COL-03-CTLFireability-5 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: ((AG(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) * A((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) U ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) + A(AF((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) U ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
=> equivalent forward existential formula: ([(FwdU((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),TRUE) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))] = FALSE * ([(FwdU((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) * (!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))] = FALSE * [FwdG((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE))
Checking (exact) 0 :([(FwdU((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),TRUE) * !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))))] = FALSE * ([(FwdU((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) * (!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))] = FALSE * [FwdG((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE))
Checking (exact) 1 :([(FwdU((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) * (!((((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))] = FALSE * [FwdG((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE)
Checking (exact) 1 :[FwdG((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE
Checking (exact) 0 :FwdG((Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))),!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Checking (exact) 1 :(Init * !(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))))
Checking (exact) 1 :!(!((E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))) + EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :(!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Checking (exact) 1 :!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))
Checking (exact) 1 :!(!(EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))
Checking (exact) 1 :EG(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :Init
Hit Full ! (commute/partial/dont) 3/147/80
(forward)formula 6,0,1.29509,24324,1,0,268,61972,698,154,3303,59014,422
FORMULA PhilosophersDyn-COL-03-CTLFireability-6 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: AF((!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
=> equivalent forward existential formula: [FwdG(Init,!((!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))] = FALSE
Checking (exact) 0 :[FwdG(Init,!((!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))] = FALSE
Checking (exact) 0 :FwdG(Init,!((!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :Init
Checking (exact) 1 :!((!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :(!((!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
(forward)formula 7,1,1.3469,24796,1,0,271,62254,707,157,3318,59608,423
FORMULA PhilosophersDyn-COL-03-CTLFireability-7 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: (((((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((Think_1>=1 + Think_3>=1) + Think_2>=1) + (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))) * AG(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))) * EF(!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))
=> equivalent forward existential formula: (([(Init * !((((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((Think_1>=1 + Think_3>=1) + Think_2>=1) + (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE * [(FwdU(Init,TRUE) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE) * [(Init * !(E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE)
Checking (exact) 0 :(([(Init * !((((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((Think_1>=1 + Think_3>=1) + Think_2>=1) + (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE * [(FwdU(Init,TRUE) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE) * [(Init * !(E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE)
Checking (exact) 1 :[(Init * !(E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE
Checking (exact) 0 :(Init * !(E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))
Checking (exact) 1 :!(E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)))))
Checking (exact) 1 :E(TRUE U !((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))
Checking (exact) 1 :([(Init * !((((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((Think_1>=1 + Think_3>=1) + Think_2>=1) + (((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))))] = FALSE * [(FwdU(Init,TRUE) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE)
Checking (exact) 1 :[(FwdU(Init,TRUE) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))] = FALSE
Checking (exact) 0 :(FwdU(Init,TRUE) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Checking (exact) 1 :!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))
Checking (exact) 1 :FwdU(Init,TRUE)
Checking (exact) 1 :Init
(forward)formula 8,0,1.4033,25608,1,0,273,63123,712,159,3342,60838,428
FORMULA PhilosophersDyn-COL-03-CTLFireability-8 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: (((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))
=> equivalent forward existential formula: [(Init * (((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))] != FALSE
Checking (exact) 0 :[(Init * (((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))] != FALSE
Checking (exact) 0 :(Init * (((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))
(forward)formula 9,0,1.40434,25612,1,0,273,63124,712,159,3343,60838,429
FORMULA PhilosophersDyn-COL-03-CTLFireability-9 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))
=> equivalent forward existential formula: [(Init * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))] != FALSE
Checking (exact) 0 :[(Init * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))] != FALSE
Checking (exact) 0 :(Init * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))
(forward)formula 10,1,1.40766,25612,1,0,273,63124,712,159,3343,60838,430
FORMULA PhilosophersDyn-COL-03-CTLFireability-10 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: A(AF(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))) U A(((Think_1>=1 + Think_3>=1) + Think_2>=1) U (((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
=> equivalent forward existential formula: [((Init * !(EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))) * !(E(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) U (!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))))] != FALSE
Checking (exact) 0 :[((Init * !(EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))) * !(E(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) U (!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))))] != FALSE
Checking (exact) 0 :((Init * !(EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))) * !(E(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) U (!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))))
Checking (exact) 1 :!(E(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) U (!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))))
Checking (exact) 1 :E(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) U (!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))
Checking (exact) 1 :!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :(E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
Fast SCC detection found none.
Checking (exact) 1 :(!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))) * !(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))
Checking (exact) 1 :!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :(E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
Fast SCC detection found none.
Checking (exact) 1 :!(!(EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :EG(!(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Fast SCC detection found none.
Checking (exact) 1 :(Init * !(EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))))
Checking (exact) 1 :!(EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))
Checking (exact) 1 :EG(!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))
Checking (exact) 1 :!(!((E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :(E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))) + EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :E(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))) U (!(((Think_1>=1 + Think_3>=1) + Think_2>=1)) * !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
Checking (exact) 1 :EG(!((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
Fast SCC detection found none.
Fast SCC detection found none.
Checking (exact) 1 :Init
(forward)formula 11,0,1.4736,26640,1,0,306,66243,721,198,3349,65591,510
FORMULA PhilosophersDyn-COL-03-CTLFireability-11 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: ((!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) + (A(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))) U ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
=> equivalent forward existential formula: ([(Init * (!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE + [(((Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * !(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))) * !(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))] != FALSE)
Checking (exact) 0 :([(Init * (!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE + [(((Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * !(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))) * !(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))] != FALSE)
Checking (exact) 0 :[(Init * (!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))] != FALSE
Checking (exact) 0 :(Init * (!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1))))
Checking (exact) 0 :[(((Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * !(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))) * !(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))] != FALSE
Checking (exact) 0 :(((Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * !(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))) * !(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))))
Checking (exact) 1 :!(E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :E(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) U (!(((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)) * (((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)))) * !(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :((Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))) * !(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))))
Checking (exact) 1 :!(EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))))
Checking (exact) 1 :EG(!(((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1))))
Fast SCC detection found none.
Checking (exact) 1 :(Init * ((((((((((HasRight_3>=1 * HasLeft_3>=1) * Neighbourhood_3_2>=1) + ((HasRight_1>=1 * Neighbourhood_1_3>=1) * HasLeft_1>=1)) + ((HasRight_1>=1 * HasLeft_1>=1) * Neighbourhood_1_2>=1)) + ((Neighbourhood_2_2>=1 * HasLeft_2>=1) * HasRight_2>=1)) + ((Neighbourhood_3_1>=1 * HasLeft_3>=1) * HasRight_3>=1)) + ((HasRight_2>=1 * HasLeft_2>=1) * Neighbourhood_2_1>=1)) + ((HasRight_2>=1 * Neighbourhood_2_3>=1) * HasLeft_2>=1)) + ((HasRight_1>=1 * Neighbourhood_1_1>=1) * HasLeft_1>=1)) + ((HasRight_3>=1 * Neighbourhood_3_3>=1) * HasLeft_3>=1)))
(forward)formula 12,0,1.57076,26900,1,0,310,66841,728,201,3356,66306,520
FORMULA PhilosophersDyn-COL-03-CTLFireability-12 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: AF(EG(EF((((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))
=> equivalent forward existential formula: [FwdG(Init,!(EG(E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))] = FALSE
Checking (exact) 0 :[FwdG(Init,!(EG(E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))] = FALSE
Checking (exact) 0 :FwdG(Init,!(EG(E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))))
Checking (exact) 1 :Init
Checking (exact) 1 :!(EG(E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))
Checking (exact) 1 :EG(E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1))))
Checking (exact) 1 :E(TRUE U (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))
Fast SCC detection found none.
(forward)formula 13,0,1.58778,26964,1,0,310,66963,732,205,3376,67119,528
FORMULA PhilosophersDyn-COL-03-CTLFireability-13 FALSE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is FALSE !
***************************************
original formula: (AF((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))) * AF((((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)) + !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + ((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))))
=> equivalent forward existential formula: ([FwdG(Init,!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))] = FALSE * [FwdG(Init,!((((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)) + !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + ((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))))] = FALSE)
Checking (exact) 0 :([FwdG(Init,!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))] = FALSE * [FwdG(Init,!((((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)) + !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + ((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))))] = FALSE)
Checking (exact) 1 :[FwdG(Init,!((((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)) + !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + ((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))))] = FALSE
Checking (exact) 0 :FwdG(Init,!((((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1)) + !(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1)))) + (!(((((((((((WaitRight_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=1) + ((Forks_3>=1 * Neighbourhood_2_3>=1) * WaitRight_2>=1)) + ((Neighbourhood_2_1>=1 * WaitRight_2>=1) * Forks_1>=1)) + ((Forks_1>=1 * Neighbourhood_3_1>=1) * WaitRight_3>=1)) + ((Neighbourhood_1_3>=1 * Forks_3>=1) * WaitRight_1>=1)) + ((WaitRight_3>=1 * Forks_2>=1) * Neighbourhood_3_2>=1)) + ((WaitRight_1>=1 * Neighbourhood_1_2>=1) * Forks_2>=1)) + ((Forks_2>=1 * Neighbourhood_2_2>=1) * WaitRight_2>=1)) + ((Neighbourhood_3_3>=1 * WaitRight_3>=1) * Forks_3>=1))) + ((((((((((((((((((((((((((((((Neighbourhood_1_2>=1 * Outside_2>=1) * Forks_2>=1) * Forks_1>=1) + ((Forks_1>=2 * Neighbourhood_1_1>=1) * Outside_2>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Forks_3>=1) * Outside_2>=1)) + (((Neighbourhood_1_2>=1 * Forks_2>=1) * Forks_1>=1) * Outside_1>=1)) + ((Forks_1>=2 * Outside_3>=1) * Neighbourhood_1_1>=1)) + (((Forks_2>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Outside_3>=1)) + (((Forks_2>=1 * Forks_1>=1) * Outside_1>=1) * Neighbourhood_2_1>=1)) + (((Outside_3>=1 * Neighbourhood_3_2>=1) * Forks_3>=1) * Forks_2>=1)) + (((Neighbourhood_3_1>=1 * Outside_3>=1) * Forks_3>=1) * Forks_1>=1)) + (((Forks_2>=1 * Outside_2>=1) * Neighbourhood_2_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Outside_2>=1) * Forks_3>=1) * Neighbourhood_3_1>=1)) + ((Neighbourhood_2_2>=1 * Forks_2>=2) * Outside_3>=1)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Outside_1>=1) * Forks_1>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_1>=1)) + (((Neighbourhood_3_2>=1 * Outside_1>=1) * Forks_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_2_2>=1) * Forks_2>=2)) + (((Forks_1>=1 * Outside_2>=1) * Neighbourhood_1_3>=1) * Forks_3>=1)) + (((Forks_1>=1 * Neighbourhood_2_1>=1) * Forks_2>=1) * Outside_3>=1)) + ((Forks_2>=2 * Neighbourhood_2_2>=1) * Outside_2>=1)) + ((Neighbourhood_3_3>=1 * Outside_2>=1) * Forks_3>=2)) + (((Neighbourhood_2_1>=1 * Forks_1>=1) * Forks_2>=1) * Outside_2>=1)) + (((Neighbourhood_1_3>=1 * Outside_1>=1) * Forks_1>=1) * Forks_3>=1)) + ((Neighbourhood_3_3>=1 * Forks_3>=2) * Outside_3>=1)) + (((Outside_1>=1 * Forks_3>=1) * Neighbourhood_2_3>=1) * Forks_2>=1)) + ((Outside_1>=1 * Neighbourhood_1_1>=1) * Forks_1>=2)) + (((Outside_3>=1 * Forks_1>=1) * Forks_3>=1) * Neighbourhood_1_3>=1)) + (((Forks_1>=1 * Forks_2>=1) * Neighbourhood_1_2>=1) * Outside_3>=1)) * (((((((Outside_3>=1 * Outside_1>=1) * Outside_2>=1) + ((Outside_1>=1 * Outside_2>=1) * Outside_3>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)) + ((Outside_2>=1 * Outside_1>=1) * Outside_3>=1)) + ((Outside_1>=1 * Outside_3>=1) * Outside_2>=1)) + ((Outside_3>=1 * Outside_2>=1) * Outside_1>=1)))))))
Checking (exact) 1 :Init
Checking (exact) 1 :[FwdG(Init,!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))] = FALSE
Checking (exact) 0 :FwdG(Init,!((((((((((((((((((((((((((((((Think_2>=1 * Neighbourhood_2_1>=1) * Neighbourhood_1_2>=1) * Forks_2>=1) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_3>=1) * Think_3>=1)) + (((Neighbourhood_1_1>=1 * Neighbourhood_1_2>=1) * Think_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1) * Think_3>=1)) + (((Forks_3>=1 * Neighbourhood_3_3>=1) * Think_3>=1) * Neighbourhood_3_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_1>=1) * Neighbourhood_2_1>=1)) + (((Neighbourhood_1_3>=1 * Think_1>=1) * Neighbourhood_1_1>=1) * Forks_1>=1)) + (((Neighbourhood_2_3>=1 * Neighbourhood_2_2>=1) * Forks_2>=1) * Think_2>=1)) + (((Neighbourhood_3_1>=1 * Neighbourhood_3_3>=1) * Forks_3>=1) * Think_3>=1)) + (((Neighbourhood_3_2>=1 * Forks_2>=1) * Think_2>=1) * Neighbourhood_2_3>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Neighbourhood_1_2>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Think_2>=1 * Forks_2>=1) * Neighbourhood_3_2>=1) * Neighbourhood_2_1>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_1>=1)) + (((Neighbourhood_2_2>=1 * Think_2>=1) * Forks_2>=1) * Neighbourhood_3_2>=1)) + (((Neighbourhood_1_1>=1 * Think_1>=1) * Neighbourhood_3_1>=1) * Forks_1>=1)) + (((Forks_3>=1 * Think_3>=1) * Neighbourhood_1_3>=1) * Neighbourhood_3_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_1>=1) * Think_1>=1) * Forks_1>=1)) + ((Think_3>=1 * Forks_3>=1) * Neighbourhood_3_3>=2)) + (((Neighbourhood_3_1>=1 * Forks_3>=1) * Think_3>=1) * Neighbourhood_2_3>=1)) + (((Neighbourhood_1_2>=1 * Neighbourhood_2_3>=1) * Think_2>=1) * Forks_2>=1)) + (((Forks_3>=1 * Neighbourhood_2_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=2)) + (((Neighbourhood_1_3>=1 * Forks_3>=1) * Neighbourhood_3_2>=1) * Think_3>=1)) + ((Neighbourhood_1_1>=2 * Think_1>=1) * Forks_1>=1)) + (((Forks_2>=1 * Think_2>=1) * Neighbourhood_2_2>=1) * Neighbourhood_1_2>=1)) + (((Think_1>=1 * Forks_1>=1) * Neighbourhood_2_1>=1) * Neighbourhood_1_3>=1))))
Checking (exact) 1 :Init
Hit Full ! (commute/partial/dont) 0/53/83
(forward)formula 14,1,1.77364,27588,1,0,311,67248,749,207,3501,67623,532
FORMULA PhilosophersDyn-COL-03-CTLFireability-14 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
original formula: EF(AX(AG((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))
=> equivalent forward existential formula: [(FwdU(Init,TRUE) * !(EX(!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))] != FALSE
Checking (exact) 0 :[(FwdU(Init,TRUE) * !(EX(!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))] != FALSE
Checking (exact) 0 :(FwdU(Init,TRUE) * !(EX(!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))))
Checking (exact) 1 :!(EX(!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))))
Checking (exact) 1 :EX(!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1)))))))
Checking (exact) 1 :!(!(E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))))
Checking (exact) 1 :E(TRUE U !((((Forks_3>=1 * WaitLeft_3>=1) + (WaitLeft_1>=1 * Forks_1>=1)) + (Forks_2>=1 * WaitLeft_2>=1))))
Checking (exact) 1 :FwdU(Init,TRUE)
Checking (exact) 1 :Init
(forward)formula 15,1,1.77763,27588,1,0,311,67269,749,207,3501,67670,534
FORMULA PhilosophersDyn-COL-03-CTLFireability-15 TRUE TECHNIQUES DECISION_DIAGRAMS TOPOLOGICAL
Formula is TRUE !
***************************************
BK_STOP 1464063781144
--------------------
content from stderr:
+ export BINDIR=/home/mcc/BenchKit/
+ BINDIR=/home/mcc/BenchKit/
++ pwd
+ export MODEL=/home/mcc/execution
+ MODEL=/home/mcc/execution
+ [[ CTLFireability = StateSpace ]]
+ /home/mcc/BenchKit//runeclipse.sh /home/mcc/execution CTLFireability -its
+ ulimit -s 65536
+ java -Dosgi.requiredJavaVersion=1.6 -XX:MaxPermSize=512m -Xss8m -Xms40m -Xmx8192m -Declipse.pde.launch=true -Dfile.encoding=UTF-8 -classpath /home/mcc/BenchKit//eclipse/plugins/org.eclipse.equinox.launcher_1.3.100.v20150511-1540.jar org.eclipse.equinox.launcher.Main -application fr.lip6.move.gal.application.pnmcc -data /home/mcc/BenchKit//workspace -os linux -ws gtk -arch x86_64 -nl en_US -consoleLog -pnfolder /home/mcc/execution -examination CTLFireability -z3path /home/mcc/BenchKit//z3/bin/z3 -yices2path /home/mcc/BenchKit//yices/bin/yices -its
Java HotSpot(TM) 64-Bit Server VM warning: ignoring option MaxPermSize=512m; support was removed in 8.0
May 24, 2016 4:22:57 AM fr.lip6.move.gal.application.Application transformPNML
INFO: Parsing pnml file : /home/mcc/execution/model.pnml
May 24, 2016 4:22:57 AM fr.lip6.move.gal.nupn.PTNetReader loadFromXML
INFO: Load time of PNML (sax parser for PT used): 81 ms
May 24, 2016 4:22:57 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 30 places.
May 24, 2016 4:22:58 AM fr.lip6.move.gal.pnml.togal.PTGALTransformer handlePage
INFO: Transformed 84 transitions.
May 24, 2016 4:22:58 AM fr.lip6.move.gal.instantiate.GALRewriter flatten
INFO: Flatten gal took : 87 ms
May 24, 2016 4:22:58 AM fr.lip6.move.serialization.SerializationUtil systemToFile
INFO: Time to serialize gal into /home/mcc/execution/CTLFireability.gal : 24 ms
May 24, 2016 4:22:58 AM fr.lip6.move.serialization.SerializationUtil serializePropertiesForITSCTLTools
INFO: Time to serialize properties into /home/mcc/execution/CTLFireability.ctl : 22 ms
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="PhilosophersDyn-PT-03"
export BK_EXAMINATION="CTLFireability"
export BK_TOOL="itstools"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/PhilosophersDyn-PT-03.tgz
mv PhilosophersDyn-PT-03 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool itstools"
echo " Input is PhilosophersDyn-PT-03, examination is CTLFireability"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r085kn-ebro-146369085400463"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLFireability" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLFireability" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLFireability.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLFireability.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLFireability.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

