About the Execution of Marcie for NeoElection-PT-3
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 9678.500 | 1304608.00 | 1304040.00 | 171.70 | FTFFFFTTFFFFFTTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
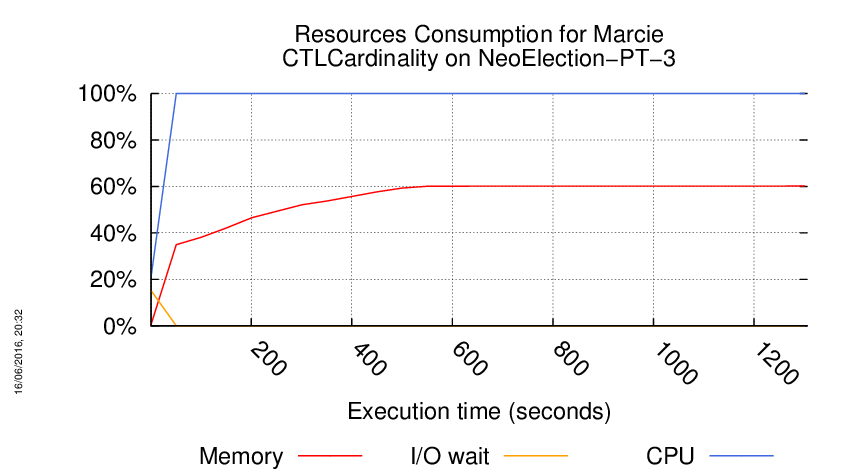
Trace from the execution
Waiting for the VM to be ready (probing ssh)
.................
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is NeoElection-PT-3, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r077kn-smll-146363815900084
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-COL-3-CTLCardinality-0
FORMULA_NAME NeoElection-COL-3-CTLCardinality-1
FORMULA_NAME NeoElection-COL-3-CTLCardinality-10
FORMULA_NAME NeoElection-COL-3-CTLCardinality-11
FORMULA_NAME NeoElection-COL-3-CTLCardinality-12
FORMULA_NAME NeoElection-COL-3-CTLCardinality-13
FORMULA_NAME NeoElection-COL-3-CTLCardinality-14
FORMULA_NAME NeoElection-COL-3-CTLCardinality-15
FORMULA_NAME NeoElection-COL-3-CTLCardinality-2
FORMULA_NAME NeoElection-COL-3-CTLCardinality-3
FORMULA_NAME NeoElection-COL-3-CTLCardinality-4
FORMULA_NAME NeoElection-COL-3-CTLCardinality-5
FORMULA_NAME NeoElection-COL-3-CTLCardinality-6
FORMULA_NAME NeoElection-COL-3-CTLCardinality-7
FORMULA_NAME NeoElection-COL-3-CTLCardinality-8
FORMULA_NAME NeoElection-COL-3-CTLCardinality-9
=== Now, execution of the tool begins
BK_START 1463690005710
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: NeoElection_PT_3
(NrP: 972 NrTr: 1016 NrArc: 5840)
net check time: 0m 0.002sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.157sec
init dd package: 0m 3.705sec
RS generation: 0m16.649sec
-> reachability set: #nodes 152061 (1.5e+05) #states 974,325 (5)
starting MCC model checker
--------------------------
checking: EF [3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)]
normalized: E [true U 3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)]
abstracting: (3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)) states: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-0 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.035sec
checking: AF [2<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)]
normalized: ~ [EG [~ [2<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)]]]
abstracting: (2<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)) states: 0
EG iterations: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.034sec
checking: AG [EF [[2<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & 1<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]
normalized: ~ [E [true U ~ [E [true U [2<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & 1<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]]]
abstracting: (1<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)) states: 0
abstracting: (2<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-3 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m47.407sec
checking: EG [EX [sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)]]
normalized: EG [EX [sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)]]
abstracting: (sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)<=sum(P_crashed_3, P_crashed_2, P_crashed_1, P_crashed_0)) states: 291,198 (5)
........................................
before gc: list nodes free: 1026559
after gc: idd nodes used:521906, unused:63478094; list nodes free:278778486
.................................................
EG iterations: 88
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 15m53.041sec
checking: EX [~ [EG [sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]
normalized: EX [~ [EG [sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]
abstracting: (sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 974,325 (5)
EG iterations: 0
.-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.319sec
checking: AF [AG [~ [2<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)]]]
normalized: ~ [EG [E [true U 2<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)]]]
abstracting: (2<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)) states: 974,325 (5)
before gc: list nodes free: 3621154
after gc: idd nodes used:153779, unused:63846221; list nodes free:280365479
EG iterations: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m23.908sec
checking: EG [AF [[3<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)]]]
normalized: EG [~ [EG [~ [[3<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)]]]]]
abstracting: (sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)) states: 974,325 (5)
abstracting: (3<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
EG iterations: 0
.
EG iterations: 1
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-5 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.369sec
checking: AG [AF [[2<=sum(P_sendAnnPs__broadcasting_3_3, P_sendAnnPs__broadcasting_3_2, P_sendAnnPs__broadcasting_3_1, P_sendAnnPs__broadcasting_2_3, P_sendAnnPs__broadcasting_2_2, P_sendAnnPs__broadcasting_2_1, P_sendAnnPs__broadcasting_1_3, P_sendAnnPs__broadcasting_1_2, P_sendAnnPs__broadcasting_1_1, P_sendAnnPs__broadcasting_0_3, P_sendAnnPs__broadcasting_0_2, P_sendAnnPs__broadcasting_0_1) & sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]
normalized: ~ [E [true U EG [~ [[2<=sum(P_sendAnnPs__broadcasting_3_3, P_sendAnnPs__broadcasting_3_2, P_sendAnnPs__broadcasting_3_1, P_sendAnnPs__broadcasting_2_3, P_sendAnnPs__broadcasting_2_2, P_sendAnnPs__broadcasting_2_1, P_sendAnnPs__broadcasting_1_3, P_sendAnnPs__broadcasting_1_2, P_sendAnnPs__broadcasting_1_1, P_sendAnnPs__broadcasting_0_3, P_sendAnnPs__broadcasting_0_2, P_sendAnnPs__broadcasting_0_1) & sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]]]
abstracting: (sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)) states: 974,325 (5)
abstracting: (2<=sum(P_sendAnnPs__broadcasting_3_3, P_sendAnnPs__broadcasting_3_2, P_sendAnnPs__broadcasting_3_1, P_sendAnnPs__broadcasting_2_3, P_sendAnnPs__broadcasting_2_2, P_sendAnnPs__broadcasting_2_1, P_sendAnnPs__broadcasting_1_3, P_sendAnnPs__broadcasting_1_2, P_sendAnnPs__broadcasting_1_1, P_sendAnnPs__broadcasting_0_3, P_sendAnnPs__broadcasting_0_2, P_sendAnnPs__broadcasting_0_1)) states: 0
EG iterations: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-6 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m 9.719sec
checking: EG [EF [~ [sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]
normalized: EG [E [true U ~ [sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)]]]
abstracting: (sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_dead_3, P_dead_2, P_dead_1, P_dead_0)) states: 0
EG iterations: 0
-> the formula is TRUE
FORMULA NeoElection-COL-3-CTLCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.268sec
checking: AF [A [3<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0) U 1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]
normalized: ~ [EG [~ [[~ [E [~ [1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)] U [~ [1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)] & ~ [3<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)]]]] & ~ [EG [~ [1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]]]]]
abstracting: (1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
EG iterations: 0
abstracting: (3<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)) states: 974,325 (5)
abstracting: (1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
abstracting: (1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
EG iterations: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.332sec
checking: EX [[2<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0) & AG [1<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)]]]
normalized: EX [[2<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0) & ~ [E [true U ~ [1<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)]]]]]
abstracting: (1<=sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)) states: 974,325 (5)
abstracting: (2<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0)) states: 16
.-> the formula is TRUE
FORMULA NeoElection-COL-3-CTLCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 1.052sec
checking: ~ [~ [EF [[sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & 1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]]
normalized: E [true U [sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) & 1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]
abstracting: (1<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
abstracting: (sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-2 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.188sec
checking: A [sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0) U EG [sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]
normalized: [~ [EG [~ [EG [sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]] & ~ [E [~ [EG [sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]] U [~ [EG [sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]] & ~ [sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)]]]]]
abstracting: (sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 0
abstracting: (sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 974,325 (5)
EG iterations: 0
abstracting: (sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 974,325 (5)
EG iterations: 0
abstracting: (sum(P_electionFailed_3, P_electionFailed_2, P_electionFailed_1, P_electionFailed_0)<=sum(P_poll__waitingMessage_3, P_poll__waitingMessage_2, P_poll__waitingMessage_1, P_poll__waitingMessage_0)) states: 974,325 (5)
EG iterations: 0
.
EG iterations: 1
-> the formula is TRUE
FORMULA NeoElection-COL-3-CTLCardinality-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m10.407sec
checking: [AF [AX [3<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)]] & [[AG [3<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)] | [sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0) & [2<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0) & sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)]]] | [EG [3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)] | EF [sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_polling_3, P_polling_2, P_polling_1, P_polling_0)]]]]
normalized: [~ [EG [EX [~ [3<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)]]]] & [[~ [E [true U ~ [3<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)]]] | [sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0) & [2<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0) & sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)]]] | [EG [3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)] | E [true U sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_polling_3, P_polling_2, P_polling_1, P_polling_0)]]]]
abstracting: (sum(P_masterList_3_3_3, P_masterList_3_3_2, P_masterList_3_3_1, P_masterList_3_3_0, P_masterList_3_2_3, P_masterList_3_2_2, P_masterList_3_2_1, P_masterList_3_2_0, P_masterList_3_1_3, P_masterList_3_1_2, P_masterList_3_1_1, P_masterList_3_1_0, P_masterList_2_3_3, P_masterList_2_3_2, P_masterList_2_3_1, P_masterList_2_3_0, P_masterList_2_2_3, P_masterList_2_2_2, P_masterList_2_2_1, P_masterList_2_2_0, P_masterList_2_1_3, P_masterList_2_1_2, P_masterList_2_1_1, P_masterList_2_1_0, P_masterList_1_3_3, P_masterList_1_3_2, P_masterList_1_3_1, P_masterList_1_3_0, P_masterList_1_2_3, P_masterList_1_2_2, P_masterList_1_2_1, P_masterList_1_2_0, P_masterList_1_1_3, P_masterList_1_1_2, P_masterList_1_1_1, P_masterList_1_1_0, P_masterList_0_3_3, P_masterList_0_3_2, P_masterList_0_3_1, P_masterList_0_3_0, P_masterList_0_2_3, P_masterList_0_2_2, P_masterList_0_2_1, P_masterList_0_2_0, P_masterList_0_1_3, P_masterList_0_1_2, P_masterList_0_1_1, P_masterList_0_1_0)<=sum(P_polling_3, P_polling_2, P_polling_1, P_polling_0)) states: 0
abstracting: (3<=sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)) states: 0
.
EG iterations: 1
abstracting: (sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)) states: 35,516 (4)
abstracting: (2<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)) states: 250,244 (5)
abstracting: (sum(P_electedSecondary_3, P_electedSecondary_2, P_electedSecondary_1, P_electedSecondary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0)) states: 974,325 (5)
abstracting: (3<=sum(P_poll__pollEnd_3, P_poll__pollEnd_2, P_poll__pollEnd_1, P_poll__pollEnd_0)) states: 35,516 (4)
abstracting: (3<=sum(P_stage_3_SEC, P_stage_3_PRIM, P_stage_3_NEG, P_stage_2_SEC, P_stage_2_PRIM, P_stage_2_NEG, P_stage_1_SEC, P_stage_1_PRIM, P_stage_1_NEG, P_stage_0_SEC, P_stage_0_PRIM, P_stage_0_NEG)) states: 974,325 (5)
..
EG iterations: 1
-> the formula is FALSE
FORMULA NeoElection-COL-3-CTLCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 5.625sec
checking: EX [EG [[sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE) | sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0)]]]
normalized: EX [EG [[sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE) | sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0)]]]
abstracting: (sum(P_electedPrimary_3, P_electedPrimary_2, P_electedPrimary_1, P_electedPrimary_0)<=sum(P_electionInit_3, P_electionInit_2, P_electionInit_1, P_electionInit_0)) states: 974,325 (5)
abstracting: (sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)<=sum(P_negotiation_3_3_DONE, P_negotiation_3_3_CO, P_negotiation_3_3_NONE, P_negotiation_3_2_DONE, P_negotiation_3_2_CO, P_negotiation_3_2_NONE, P_negotiation_3_1_DONE, P_negotiation_3_1_CO, P_negotiation_3_1_NONE, P_negotiation_3_0_DONE, P_negotiation_3_0_CO, P_negotiation_3_0_NONE, P_negotiation_2_3_DONE, P_negotiation_2_3_CO, P_negotiation_2_3_NONE, P_negotiation_2_2_DONE, P_negotiation_2_2_CO, P_negotiation_2_2_NONE, P_negotiation_2_1_DONE, P_negotiation_2_1_CO, P_negotiation_2_1_NONE, P_negotiation_2_0_DONE, P_negotiation_2_0_CO, P_negotiation_2_0_NONE, P_negotiation_1_3_DONE, P_negotiation_1_3_CO, P_negotiation_1_3_NONE, P_negotiation_1_2_DONE, P_negotiation_1_2_CO, P_negotiation_1_2_NONE, P_negotiation_1_1_DONE, P_negotiation_1_1_CO, P_negotiation_1_1_NONE, P_negotiation_1_0_DONE, P_negotiation_1_0_CO, P_negotiation_1_0_NONE, P_negotiation_0_3_DONE, P_negotiation_0_3_CO, P_negotiation_0_3_NONE, P_negotiation_0_2_DONE, P_negotiation_0_2_CO, P_negotiation_0_2_NONE, P_negotiation_0_1_DONE, P_negotiation_0_1_CO, P_negotiation_0_1_NONE, P_negotiation_0_0_DONE, P_negotiation_0_0_CO, P_negotiation_0_0_NONE)) states: 974,325 (5)
EG iterations: 0
.-> the formula is TRUE
FORMULA NeoElection-COL-3-CTLCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m 9.237sec
checking: EG [EF [~ [1<=sum(P_poll__networl_3_3_RP_3, P_poll__networl_3_3_RP_2, P_poll__networl_3_3_RP_1, P_poll__networl_3_3_RP_0, P_poll__networl_3_3_AnnP_3, P_poll__networl_3_3_AnnP_2, P_poll__networl_3_3_AnnP_1, P_poll__networl_3_3_AnnP_0, P_poll__networl_3_3_AI_3, P_poll__networl_3_3_AI_2, P_poll__networl_3_3_AI_1, P_poll__networl_3_3_AI_0, P_poll__networl_3_3_RI_3, P_poll__networl_3_3_RI_2, P_poll__networl_3_3_RI_1, P_poll__networl_3_3_RI_0, P_poll__networl_3_3_AnsP_3, P_poll__networl_3_3_AnsP_2, P_poll__networl_3_3_AnsP_1, P_poll__networl_3_3_AnsP_0, P_poll__networl_3_3_AskP_3, P_poll__networl_3_3_AskP_2, P_poll__networl_3_3_AskP_1, P_poll__networl_3_3_AskP_0, P_poll__networl_3_2_RP_3, P_poll__networl_3_2_RP_2, P_poll__networl_3_2_RP_1, P_poll__networl_3_2_RP_0, P_poll__networl_3_2_AnnP_3, P_poll__networl_3_2_AnnP_2, P_poll__networl_3_2_AnnP_1, P_poll__networl_3_2_AnnP_0, P_poll__networl_3_2_AI_3, P_poll__networl_3_2_AI_2, P_poll__networl_3_2_AI_1, P_poll__networl_3_2_AI_0, P_poll__networl_3_2_RI_3, P_poll__networl_3_2_RI_2, P_poll__networl_3_2_RI_1, P_poll__networl_3_2_RI_0, P_poll__networl_3_2_AnsP_3, P_poll__networl_3_2_AnsP_2, P_poll__networl_3_2_AnsP_1, P_poll__networl_3_2_AnsP_0, P_poll__networl_3_2_AskP_3, P_poll__networl_3_2_AskP_2, P_poll__networl_3_2_AskP_1, P_poll__networl_3_2_AskP_0, P_poll__networl_3_1_RP_3, P_poll__networl_3_1_RP_2, P_poll__networl_3_1_RP_1, P_poll__networl_3_1_RP_0, P_poll__networl_3_1_AnnP_3, P_poll__networl_3_1_AnnP_2, P_poll__networl_3_1_AnnP_1, P_poll__networl_3_1_AnnP_0, P_poll__networl_3_1_AI_3, P_poll__networl_3_1_AI_2, P_poll__networl_3_1_AI_1, P_poll__networl_3_1_AI_0, P_poll__networl_3_1_RI_3, P_poll__networl_3_1_RI_2, P_poll__networl_3_1_RI_1, P_poll__networl_3_1_RI_0, P_poll__networl_3_1_AnsP_3, P_poll__networl_3_1_AnsP_2, P_poll__networl_3_1_AnsP_1, P_poll__networl_3_1_AnsP_0, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AskP_2, P_poll__networl_3_1_AskP_1, P_poll__networl_3_1_AskP_0, P_poll__networl_3_0_RP_3, P_poll__networl_3_0_RP_2, P_poll__networl_3_0_RP_1, P_poll__networl_3_0_RP_0, P_poll__networl_3_0_AnnP_3, P_poll__networl_3_0_AnnP_2, P_poll__networl_3_0_AnnP_1, P_poll__networl_3_0_AnnP_0, P_poll__networl_3_0_AI_3, P_poll__networl_3_0_AI_2, P_poll__networl_3_0_AI_1, P_poll__networl_3_0_AI_0, P_poll__networl_3_0_RI_3, P_poll__networl_3_0_RI_2, P_poll__networl_3_0_RI_1, P_poll__networl_3_0_RI_0, P_poll__networl_3_0_AnsP_3, P_poll__networl_3_0_AnsP_2, P_poll__networl_3_0_AnsP_1, P_poll__networl_3_0_AnsP_0, P_poll__networl_3_0_AskP_3, P_poll__networl_3_0_AskP_2, P_poll__networl_3_0_AskP_1, P_poll__networl_3_0_AskP_0, P_poll__networl_2_3_RP_3, P_poll__networl_2_3_RP_2, P_poll__networl_2_3_RP_1, P_poll__networl_2_3_RP_0, P_poll__networl_2_3_AnnP_3, P_poll__networl_2_3_AnnP_2, P_poll__networl_2_3_AnnP_1, P_poll__networl_2_3_AnnP_0, P_poll__networl_2_3_AI_3, P_poll__networl_2_3_AI_2, P_poll__networl_2_3_AI_1, P_poll__networl_2_3_AI_0, P_poll__networl_2_3_RI_3, P_poll__networl_2_3_RI_2, P_poll__networl_2_3_RI_1, P_poll__networl_2_3_RI_0, P_poll__networl_2_3_AnsP_3, P_poll__networl_2_3_AnsP_2, P_poll__networl_2_3_AnsP_1, P_poll__networl_2_3_AnsP_0, P_poll__networl_2_3_AskP_3, P_poll__networl_2_3_AskP_2, P_poll__networl_2_3_AskP_1, P_poll__networl_2_3_AskP_0, P_poll__networl_2_2_RP_3, P_poll__networl_2_2_RP_2, P_poll__networl_2_2_RP_1, P_poll__networl_2_2_RP_0, P_poll__networl_2_2_AnnP_3, P_poll__networl_2_2_AnnP_2, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_2_AnnP_0, P_poll__networl_2_2_AI_3, P_poll__networl_2_2_AI_2, P_poll__networl_2_2_AI_1, P_poll__networl_2_2_AI_0, P_poll__networl_2_2_RI_3, P_poll__networl_2_2_RI_2, P_poll__networl_2_2_RI_1, P_poll__networl_2_2_RI_0, P_poll__networl_2_2_AnsP_3, P_poll__networl_2_2_AnsP_2, P_poll__networl_2_2_AnsP_1, P_poll__networl_2_2_AnsP_0, P_poll__networl_2_2_AskP_3, P_poll__networl_2_2_AskP_2, P_poll__networl_2_2_AskP_1, P_poll__networl_2_2_AskP_0, P_poll__networl_2_1_RP_3, P_poll__networl_2_1_RP_2, P_poll__networl_2_1_RP_1, P_poll__networl_2_1_RP_0, P_poll__networl_2_1_AnnP_3, P_poll__networl_2_1_AnnP_2, P_poll__networl_2_1_AnnP_1, P_poll__networl_2_1_AnnP_0, P_poll__networl_2_1_AI_3, P_poll__networl_2_1_AI_2, P_poll__networl_2_1_AI_1, P_poll__networl_2_1_AI_0, P_poll__networl_2_1_RI_3, P_poll__networl_2_1_RI_2, P_poll__networl_2_1_RI_1, P_poll__networl_2_1_RI_0, P_poll__networl_2_1_AnsP_3, P_poll__networl_2_1_AnsP_2, P_poll__networl_2_1_AnsP_1, P_poll__networl_2_1_AnsP_0, P_poll__networl_2_1_AskP_3, P_poll__networl_2_1_AskP_2, P_poll__networl_2_1_AskP_1, P_poll__networl_2_1_AskP_0, P_poll__networl_2_0_RP_3, P_poll__networl_2_0_RP_2, P_poll__networl_2_0_RP_1, P_poll__networl_2_0_RP_0, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_0_AnnP_2, P_poll__networl_2_0_AnnP_1, P_poll__networl_2_0_AnnP_0, P_poll__networl_2_0_AI_3, P_poll__networl_2_0_AI_2, P_poll__networl_2_0_AI_1, P_poll__networl_2_0_AI_0, P_poll__networl_2_0_RI_3, P_poll__networl_2_0_RI_2, P_poll__networl_2_0_RI_1, P_poll__networl_2_0_RI_0, P_poll__networl_2_0_AnsP_3, P_poll__networl_2_0_AnsP_2, P_poll__networl_2_0_AnsP_1, P_poll__networl_2_0_AnsP_0, P_poll__networl_2_0_AskP_3, P_poll__networl_2_0_AskP_2, P_poll__networl_2_0_AskP_1, P_poll__networl_2_0_AskP_0, P_poll__networl_1_3_RP_3, P_poll__networl_1_3_RP_2, P_poll__networl_1_3_RP_1, P_poll__networl_1_3_RP_0, P_poll__networl_1_3_AnnP_3, P_poll__networl_1_3_AnnP_2, P_poll__networl_1_3_AnnP_1, P_poll__networl_1_3_AnnP_0, P_poll__networl_1_3_AI_3, P_poll__networl_1_3_AI_2, P_poll__networl_1_3_AI_1, P_poll__networl_1_3_AI_0, P_poll__networl_1_3_RI_3, P_poll__networl_1_3_RI_2, P_poll__networl_1_3_RI_1, P_poll__networl_1_3_RI_0, P_poll__networl_1_3_AnsP_3, P_poll__networl_1_3_AnsP_2, P_poll__networl_1_3_AnsP_1, P_poll__networl_1_3_AnsP_0, P_poll__networl_1_3_AskP_3, P_poll__networl_1_3_AskP_2, P_poll__networl_1_3_AskP_1, P_poll__networl_1_3_AskP_0, P_poll__networl_1_2_RP_3, P_poll__networl_1_2_RP_2, P_poll__networl_1_2_RP_1, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_AnnP_3, P_poll__networl_1_2_AnnP_2, P_poll__networl_1_2_AnnP_1, P_poll__networl_1_2_AnnP_0, P_poll__networl_1_2_AI_3, P_poll__networl_1_2_AI_2, P_poll__networl_1_2_AI_1, P_poll__networl_1_2_AI_0, P_poll__networl_1_2_RI_3, P_poll__networl_1_2_RI_2, P_poll__networl_1_2_RI_1, P_poll__networl_1_2_RI_0, P_poll__networl_1_2_AnsP_3, P_poll__networl_1_2_AnsP_2, P_poll__networl_1_2_AnsP_1, P_poll__networl_1_2_AnsP_0, P_poll__networl_1_2_AskP_3, P_poll__networl_1_2_AskP_2, P_poll__networl_1_2_AskP_1, P_poll__networl_1_2_AskP_0, P_poll__networl_1_1_RP_3, P_poll__networl_1_1_RP_2, P_poll__networl_1_1_RP_1, P_poll__networl_1_1_RP_0, P_poll__networl_1_1_AnnP_3, P_poll__networl_1_1_AnnP_2, P_poll__networl_1_1_AnnP_1, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_1_AI_3, P_poll__networl_1_1_AI_2, P_poll__networl_1_1_AI_1, P_poll__networl_1_1_AI_0, P_poll__networl_1_1_RI_3, P_poll__networl_1_1_RI_2, P_poll__networl_1_1_RI_1, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_AnsP_3, P_poll__networl_1_1_AnsP_2, P_poll__networl_1_1_AnsP_1, P_poll__networl_1_1_AnsP_0, P_poll__networl_1_1_AskP_3, P_poll__networl_1_1_AskP_2, P_poll__networl_1_1_AskP_1, P_poll__networl_1_1_AskP_0, P_poll__networl_1_0_RP_3, P_poll__networl_1_0_RP_2, P_poll__networl_1_0_RP_1, P_poll__networl_1_0_RP_0, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_AnnP_2, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_0_AI_3, P_poll__networl_1_0_AI_2, P_poll__networl_1_0_AI_1, P_poll__networl_1_0_AI_0, P_poll__networl_1_0_RI_3, P_poll__networl_1_0_RI_2, P_poll__networl_1_0_RI_1, P_poll__networl_1_0_RI_0, P_poll__networl_1_0_AnsP_3, P_poll__networl_1_0_AnsP_2, P_poll__networl_1_0_AnsP_1, P_poll__networl_1_0_AnsP_0, P_poll__networl_1_0_AskP_3, P_poll__networl_1_0_AskP_2, P_poll__networl_1_0_AskP_1, P_poll__networl_1_0_AskP_0, P_poll__networl_0_3_RP_3, P_poll__networl_0_3_RP_2, P_poll__networl_0_3_RP_1, P_poll__networl_0_3_RP_0, P_poll__networl_0_3_AnnP_3, P_poll__networl_0_3_AnnP_2, P_poll__networl_0_3_AnnP_1, P_poll__networl_0_3_AnnP_0, P_poll__networl_0_3_AI_3, P_poll__networl_0_3_AI_2, P_poll__networl_0_3_AI_1, P_poll__networl_0_3_AI_0, P_poll__networl_0_3_RI_3, P_poll__networl_0_3_RI_2, P_poll__networl_0_3_RI_1, P_poll__networl_0_3_RI_0, P_poll__networl_0_3_AnsP_3, P_poll__networl_0_3_AnsP_2, P_poll__networl_0_3_AnsP_1, P_poll__networl_0_3_AnsP_0, P_poll__networl_0_3_AskP_3, P_poll__networl_0_3_AskP_2, P_poll__networl_0_3_AskP_1, P_poll__networl_0_3_AskP_0, P_poll__networl_0_2_RP_3, P_poll__networl_0_2_RP_2, P_poll__networl_0_2_RP_1, P_poll__networl_0_2_RP_0, P_poll__networl_0_2_AnnP_3, P_poll__networl_0_2_AnnP_2, P_poll__networl_0_2_AnnP_1, P_poll__networl_0_2_AnnP_0, P_poll__networl_0_2_AI_3, P_poll__networl_0_2_AI_2, P_poll__networl_0_2_AI_1, P_poll__networl_0_2_AI_0, P_poll__networl_0_2_RI_3, P_poll__networl_0_2_RI_2, P_poll__networl_0_2_RI_1, P_poll__networl_0_2_RI_0, P_poll__networl_0_2_AnsP_3, P_poll__networl_0_2_AnsP_2, P_poll__networl_0_2_AnsP_1, P_poll__networl_0_2_AnsP_0, P_poll__networl_0_2_AskP_3, P_poll__networl_0_2_AskP_2, P_poll__networl_0_2_AskP_1, P_poll__networl_0_2_AskP_0, P_poll__networl_0_1_RP_3, P_poll__networl_0_1_RP_2, P_poll__networl_0_1_RP_1, P_poll__networl_0_1_RP_0, P_poll__networl_0_1_AnnP_3, P_poll__networl_0_1_AnnP_2, P_poll__networl_0_1_AnnP_1, P_poll__networl_0_1_AnnP_0, P_poll__networl_0_1_AI_3, P_poll__networl_0_1_AI_2, P_poll__networl_0_1_AI_1, P_poll__networl_0_1_AI_0, P_poll__networl_0_1_RI_3, P_poll__networl_0_1_RI_2, P_poll__networl_0_1_RI_1, P_poll__networl_0_1_RI_0, P_poll__networl_0_1_AnsP_3, P_poll__networl_0_1_AnsP_2, P_poll__networl_0_1_AnsP_1, P_poll__networl_0_1_AnsP_0, P_poll__networl_0_1_AskP_3, P_poll__networl_0_1_AskP_2, P_poll__networl_0_1_AskP_1, P_poll__networl_0_1_AskP_0, P_poll__networl_0_0_RP_3, P_poll__networl_0_0_RP_2, P_poll__networl_0_0_RP_1, P_poll__networl_0_0_RP_0, P_poll__networl_0_0_AnnP_3, P_poll__networl_0_0_AnnP_2, P_poll__networl_0_0_AnnP_1, P_poll__networl_0_0_AnnP_0, P_poll__networl_0_0_AI_3, P_poll__networl_0_0_AI_2, P_poll__networl_0_0_AI_1, P_poll__networl_0_0_AI_0, P_poll__networl_0_0_RI_3, P_poll__networl_0_0_RI_2, P_poll__networl_0_0_RI_1, P_poll__networl_0_0_RI_0, P_poll__networl_0_0_AnsP_3, P_poll__networl_0_0_AnsP_2, P_poll__networl_0_0_AnsP_1, P_poll__networl_0_0_AnsP_0, P_poll__networl_0_0_AskP_3, P_poll__networl_0_0_AskP_2, P_poll__networl_0_0_AskP_1, P_poll__networl_0_0_AskP_0)]]]
normalized: EG [E [true U ~ [1<=sum(P_poll__networl_3_3_RP_3, P_poll__networl_3_3_RP_2, P_poll__networl_3_3_RP_1, P_poll__networl_3_3_RP_0, P_poll__networl_3_3_AnnP_3, P_poll__networl_3_3_AnnP_2, P_poll__networl_3_3_AnnP_1, P_poll__networl_3_3_AnnP_0, P_poll__networl_3_3_AI_3, P_poll__networl_3_3_AI_2, P_poll__networl_3_3_AI_1, P_poll__networl_3_3_AI_0, P_poll__networl_3_3_RI_3, P_poll__networl_3_3_RI_2, P_poll__networl_3_3_RI_1, P_poll__networl_3_3_RI_0, P_poll__networl_3_3_AnsP_3, P_poll__networl_3_3_AnsP_2, P_poll__networl_3_3_AnsP_1, P_poll__networl_3_3_AnsP_0, P_poll__networl_3_3_AskP_3, P_poll__networl_3_3_AskP_2, P_poll__networl_3_3_AskP_1, P_poll__networl_3_3_AskP_0, P_poll__networl_3_2_RP_3, P_poll__networl_3_2_RP_2, P_poll__networl_3_2_RP_1, P_poll__networl_3_2_RP_0, P_poll__networl_3_2_AnnP_3, P_poll__networl_3_2_AnnP_2, P_poll__networl_3_2_AnnP_1, P_poll__networl_3_2_AnnP_0, P_poll__networl_3_2_AI_3, P_poll__networl_3_2_AI_2, P_poll__networl_3_2_AI_1, P_poll__networl_3_2_AI_0, P_poll__networl_3_2_RI_3, P_poll__networl_3_2_RI_2, P_poll__networl_3_2_RI_1, P_poll__networl_3_2_RI_0, P_poll__networl_3_2_AnsP_3, P_poll__networl_3_2_AnsP_2, P_poll__networl_3_2_AnsP_1, P_poll__networl_3_2_AnsP_0, P_poll__networl_3_2_AskP_3, P_poll__networl_3_2_AskP_2, P_poll__networl_3_2_AskP_1, P_poll__networl_3_2_AskP_0, P_poll__networl_3_1_RP_3, P_poll__networl_3_1_RP_2, P_poll__networl_3_1_RP_1, P_poll__networl_3_1_RP_0, P_poll__networl_3_1_AnnP_3, P_poll__networl_3_1_AnnP_2, P_poll__networl_3_1_AnnP_1, P_poll__networl_3_1_AnnP_0, P_poll__networl_3_1_AI_3, P_poll__networl_3_1_AI_2, P_poll__networl_3_1_AI_1, P_poll__networl_3_1_AI_0, P_poll__networl_3_1_RI_3, P_poll__networl_3_1_RI_2, P_poll__networl_3_1_RI_1, P_poll__networl_3_1_RI_0, P_poll__networl_3_1_AnsP_3, P_poll__networl_3_1_AnsP_2, P_poll__networl_3_1_AnsP_1, P_poll__networl_3_1_AnsP_0, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AskP_2, P_poll__networl_3_1_AskP_1, P_poll__networl_3_1_AskP_0, P_poll__networl_3_0_RP_3, P_poll__networl_3_0_RP_2, P_poll__networl_3_0_RP_1, P_poll__networl_3_0_RP_0, P_poll__networl_3_0_AnnP_3, P_poll__networl_3_0_AnnP_2, P_poll__networl_3_0_AnnP_1, P_poll__networl_3_0_AnnP_0, P_poll__networl_3_0_AI_3, P_poll__networl_3_0_AI_2, P_poll__networl_3_0_AI_1, P_poll__networl_3_0_AI_0, P_poll__networl_3_0_RI_3, P_poll__networl_3_0_RI_2, P_poll__networl_3_0_RI_1, P_poll__networl_3_0_RI_0, P_poll__networl_3_0_AnsP_3, P_poll__networl_3_0_AnsP_2, P_poll__networl_3_0_AnsP_1, P_poll__networl_3_0_AnsP_0, P_poll__networl_3_0_AskP_3, P_poll__networl_3_0_AskP_2, P_poll__networl_3_0_AskP_1, P_poll__networl_3_0_AskP_0, P_poll__networl_2_3_RP_3, P_poll__networl_2_3_RP_2, P_poll__networl_2_3_RP_1, P_poll__networl_2_3_RP_0, P_poll__networl_2_3_AnnP_3, P_poll__networl_2_3_AnnP_2, P_poll__networl_2_3_AnnP_1, P_poll__networl_2_3_AnnP_0, P_poll__networl_2_3_AI_3, P_poll__networl_2_3_AI_2, P_poll__networl_2_3_AI_1, P_poll__networl_2_3_AI_0, P_poll__networl_2_3_RI_3, P_poll__networl_2_3_RI_2, P_poll__networl_2_3_RI_1, P_poll__networl_2_3_RI_0, P_poll__networl_2_3_AnsP_3, P_poll__networl_2_3_AnsP_2, P_poll__networl_2_3_AnsP_1, P_poll__networl_2_3_AnsP_0, P_poll__networl_2_3_AskP_3, P_poll__networl_2_3_AskP_2, P_poll__networl_2_3_AskP_1, P_poll__networl_2_3_AskP_0, P_poll__networl_2_2_RP_3, P_poll__networl_2_2_RP_2, P_poll__networl_2_2_RP_1, P_poll__networl_2_2_RP_0, P_poll__networl_2_2_AnnP_3, P_poll__networl_2_2_AnnP_2, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_2_AnnP_0, P_poll__networl_2_2_AI_3, P_poll__networl_2_2_AI_2, P_poll__networl_2_2_AI_1, P_poll__networl_2_2_AI_0, P_poll__networl_2_2_RI_3, P_poll__networl_2_2_RI_2, P_poll__networl_2_2_RI_1, P_poll__networl_2_2_RI_0, P_poll__networl_2_2_AnsP_3, P_poll__networl_2_2_AnsP_2, P_poll__networl_2_2_AnsP_1, P_poll__networl_2_2_AnsP_0, P_poll__networl_2_2_AskP_3, P_poll__networl_2_2_AskP_2, P_poll__networl_2_2_AskP_1, P_poll__networl_2_2_AskP_0, P_poll__networl_2_1_RP_3, P_poll__networl_2_1_RP_2, P_poll__networl_2_1_RP_1, P_poll__networl_2_1_RP_0, P_poll__networl_2_1_AnnP_3, P_poll__networl_2_1_AnnP_2, P_poll__networl_2_1_AnnP_1, P_poll__networl_2_1_AnnP_0, P_poll__networl_2_1_AI_3, P_poll__networl_2_1_AI_2, P_poll__networl_2_1_AI_1, P_poll__networl_2_1_AI_0, P_poll__networl_2_1_RI_3, P_poll__networl_2_1_RI_2, P_poll__networl_2_1_RI_1, P_poll__networl_2_1_RI_0, P_poll__networl_2_1_AnsP_3, P_poll__networl_2_1_AnsP_2, P_poll__networl_2_1_AnsP_1, P_poll__networl_2_1_AnsP_0, P_poll__networl_2_1_AskP_3, P_poll__networl_2_1_AskP_2, P_poll__networl_2_1_AskP_1, P_poll__networl_2_1_AskP_0, P_poll__networl_2_0_RP_3, P_poll__networl_2_0_RP_2, P_poll__networl_2_0_RP_1, P_poll__networl_2_0_RP_0, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_0_AnnP_2, P_poll__networl_2_0_AnnP_1, P_poll__networl_2_0_AnnP_0, P_poll__networl_2_0_AI_3, P_poll__networl_2_0_AI_2, P_poll__networl_2_0_AI_1, P_poll__networl_2_0_AI_0, P_poll__networl_2_0_RI_3, P_poll__networl_2_0_RI_2, P_poll__networl_2_0_RI_1, P_poll__networl_2_0_RI_0, P_poll__networl_2_0_AnsP_3, P_poll__networl_2_0_AnsP_2, P_poll__networl_2_0_AnsP_1, P_poll__networl_2_0_AnsP_0, P_poll__networl_2_0_AskP_3, P_poll__networl_2_0_AskP_2, P_poll__networl_2_0_AskP_1, P_poll__networl_2_0_AskP_0, P_poll__networl_1_3_RP_3, P_poll__networl_1_3_RP_2, P_poll__networl_1_3_RP_1, P_poll__networl_1_3_RP_0, P_poll__networl_1_3_AnnP_3, P_poll__networl_1_3_AnnP_2, P_poll__networl_1_3_AnnP_1, P_poll__networl_1_3_AnnP_0, P_poll__networl_1_3_AI_3, P_poll__networl_1_3_AI_2, P_poll__networl_1_3_AI_1, P_poll__networl_1_3_AI_0, P_poll__networl_1_3_RI_3, P_poll__networl_1_3_RI_2, P_poll__networl_1_3_RI_1, P_poll__networl_1_3_RI_0, P_poll__networl_1_3_AnsP_3, P_poll__networl_1_3_AnsP_2, P_poll__networl_1_3_AnsP_1, P_poll__networl_1_3_AnsP_0, P_poll__networl_1_3_AskP_3, P_poll__networl_1_3_AskP_2, P_poll__networl_1_3_AskP_1, P_poll__networl_1_3_AskP_0, P_poll__networl_1_2_RP_3, P_poll__networl_1_2_RP_2, P_poll__networl_1_2_RP_1, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_AnnP_3, P_poll__networl_1_2_AnnP_2, P_poll__networl_1_2_AnnP_1, P_poll__networl_1_2_AnnP_0, P_poll__networl_1_2_AI_3, P_poll__networl_1_2_AI_2, P_poll__networl_1_2_AI_1, P_poll__networl_1_2_AI_0, P_poll__networl_1_2_RI_3, P_poll__networl_1_2_RI_2, P_poll__networl_1_2_RI_1, P_poll__networl_1_2_RI_0, P_poll__networl_1_2_AnsP_3, P_poll__networl_1_2_AnsP_2, P_poll__networl_1_2_AnsP_1, P_poll__networl_1_2_AnsP_0, P_poll__networl_1_2_AskP_3, P_poll__networl_1_2_AskP_2, P_poll__networl_1_2_AskP_1, P_poll__networl_1_2_AskP_0, P_poll__networl_1_1_RP_3, P_poll__networl_1_1_RP_2, P_poll__networl_1_1_RP_1, P_poll__networl_1_1_RP_0, P_poll__networl_1_1_AnnP_3, P_poll__networl_1_1_AnnP_2, P_poll__networl_1_1_AnnP_1, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_1_AI_3, P_poll__networl_1_1_AI_2, P_poll__networl_1_1_AI_1, P_poll__networl_1_1_AI_0, P_poll__networl_1_1_RI_3, P_poll__networl_1_1_RI_2, P_poll__networl_1_1_RI_1, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_AnsP_3, P_poll__networl_1_1_AnsP_2, P_poll__networl_1_1_AnsP_1, P_poll__networl_1_1_AnsP_0, P_poll__networl_1_1_AskP_3, P_poll__networl_1_1_AskP_2, P_poll__networl_1_1_AskP_1, P_poll__networl_1_1_AskP_0, P_poll__networl_1_0_RP_3, P_poll__networl_1_0_RP_2, P_poll__networl_1_0_RP_1, P_poll__networl_1_0_RP_0, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_AnnP_2, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_0_AI_3, P_poll__networl_1_0_AI_2, P_poll__networl_1_0_AI_1, P_poll__networl_1_0_AI_0, P_poll__networl_1_0_RI_3, P_poll__networl_1_0_RI_2, P_poll__networl_1_0_RI_1, P_poll__networl_1_0_RI_0, P_poll__networl_1_0_AnsP_3, P_poll__networl_1_0_AnsP_2, P_poll__networl_1_0_AnsP_1, P_poll__networl_1_0_AnsP_0, P_poll__networl_1_0_AskP_3, P_poll__networl_1_0_AskP_2, P_poll__networl_1_0_AskP_1, P_poll__networl_1_0_AskP_0, P_poll__networl_0_3_RP_3, P_poll__networl_0_3_RP_2, P_poll__networl_0_3_RP_1, P_poll__networl_0_3_RP_0, P_poll__networl_0_3_AnnP_3, P_poll__networl_0_3_AnnP_2, P_poll__networl_0_3_AnnP_1, P_poll__networl_0_3_AnnP_0, P_poll__networl_0_3_AI_3, P_poll__networl_0_3_AI_2, P_poll__networl_0_3_AI_1, P_poll__networl_0_3_AI_0, P_poll__networl_0_3_RI_3, P_poll__networl_0_3_RI_2, P_poll__networl_0_3_RI_1, P_poll__networl_0_3_RI_0, P_poll__networl_0_3_AnsP_3, P_poll__networl_0_3_AnsP_2, P_poll__networl_0_3_AnsP_1, P_poll__networl_0_3_AnsP_0, P_poll__networl_0_3_AskP_3, P_poll__networl_0_3_AskP_2, P_poll__networl_0_3_AskP_1, P_poll__networl_0_3_AskP_0, P_poll__networl_0_2_RP_3, P_poll__networl_0_2_RP_2, P_poll__networl_0_2_RP_1, P_poll__networl_0_2_RP_0, P_poll__networl_0_2_AnnP_3, P_poll__networl_0_2_AnnP_2, P_poll__networl_0_2_AnnP_1, P_poll__networl_0_2_AnnP_0, P_poll__networl_0_2_AI_3, P_poll__networl_0_2_AI_2, P_poll__networl_0_2_AI_1, P_poll__networl_0_2_AI_0, P_poll__networl_0_2_RI_3, P_poll__networl_0_2_RI_2, P_poll__networl_0_2_RI_1, P_poll__networl_0_2_RI_0, P_poll__networl_0_2_AnsP_3, P_poll__networl_0_2_AnsP_2, P_poll__networl_0_2_AnsP_1, P_poll__networl_0_2_AnsP_0, P_poll__networl_0_2_AskP_3, P_poll__networl_0_2_AskP_2, P_poll__networl_0_2_AskP_1, P_poll__networl_0_2_AskP_0, P_poll__networl_0_1_RP_3, P_poll__networl_0_1_RP_2, P_poll__networl_0_1_RP_1, P_poll__networl_0_1_RP_0, P_poll__networl_0_1_AnnP_3, P_poll__networl_0_1_AnnP_2, P_poll__networl_0_1_AnnP_1, P_poll__networl_0_1_AnnP_0, P_poll__networl_0_1_AI_3, P_poll__networl_0_1_AI_2, P_poll__networl_0_1_AI_1, P_poll__networl_0_1_AI_0, P_poll__networl_0_1_RI_3, P_poll__networl_0_1_RI_2, P_poll__networl_0_1_RI_1, P_poll__networl_0_1_RI_0, P_poll__networl_0_1_AnsP_3, P_poll__networl_0_1_AnsP_2, P_poll__networl_0_1_AnsP_1, P_poll__networl_0_1_AnsP_0, P_poll__networl_0_1_AskP_3, P_poll__networl_0_1_AskP_2, P_poll__networl_0_1_AskP_1, P_poll__networl_0_1_AskP_0, P_poll__networl_0_0_RP_3, P_poll__networl_0_0_RP_2, P_poll__networl_0_0_RP_1, P_poll__networl_0_0_RP_0, P_poll__networl_0_0_AnnP_3, P_poll__networl_0_0_AnnP_2, P_poll__networl_0_0_AnnP_1, P_poll__networl_0_0_AnnP_0, P_poll__networl_0_0_AI_3, P_poll__networl_0_0_AI_2, P_poll__networl_0_0_AI_1, P_poll__networl_0_0_AI_0, P_poll__networl_0_0_RI_3, P_poll__networl_0_0_RI_2, P_poll__networl_0_0_RI_1, P_poll__networl_0_0_RI_0, P_poll__networl_0_0_AnsP_3, P_poll__networl_0_0_AnsP_2, P_poll__networl_0_0_AnsP_1, P_poll__networl_0_0_AnsP_0, P_poll__networl_0_0_AskP_3, P_poll__networl_0_0_AskP_2, P_poll__networl_0_0_AskP_1, P_poll__networl_0_0_AskP_0)]]]
abstracting: (1<=sum(P_poll__networl_3_3_RP_3, P_poll__networl_3_3_RP_2, P_poll__networl_3_3_RP_1, P_poll__networl_3_3_RP_0, P_poll__networl_3_3_AnnP_3, P_poll__networl_3_3_AnnP_2, P_poll__networl_3_3_AnnP_1, P_poll__networl_3_3_AnnP_0, P_poll__networl_3_3_AI_3, P_poll__networl_3_3_AI_2, P_poll__networl_3_3_AI_1, P_poll__networl_3_3_AI_0, P_poll__networl_3_3_RI_3, P_poll__networl_3_3_RI_2, P_poll__networl_3_3_RI_1, P_poll__networl_3_3_RI_0, P_poll__networl_3_3_AnsP_3, P_poll__networl_3_3_AnsP_2, P_poll__networl_3_3_AnsP_1, P_poll__networl_3_3_AnsP_0, P_poll__networl_3_3_AskP_3, P_poll__networl_3_3_AskP_2, P_poll__networl_3_3_AskP_1, P_poll__networl_3_3_AskP_0, P_poll__networl_3_2_RP_3, P_poll__networl_3_2_RP_2, P_poll__networl_3_2_RP_1, P_poll__networl_3_2_RP_0, P_poll__networl_3_2_AnnP_3, P_poll__networl_3_2_AnnP_2, P_poll__networl_3_2_AnnP_1, P_poll__networl_3_2_AnnP_0, P_poll__networl_3_2_AI_3, P_poll__networl_3_2_AI_2, P_poll__networl_3_2_AI_1, P_poll__networl_3_2_AI_0, P_poll__networl_3_2_RI_3, P_poll__networl_3_2_RI_2, P_poll__networl_3_2_RI_1, P_poll__networl_3_2_RI_0, P_poll__networl_3_2_AnsP_3, P_poll__networl_3_2_AnsP_2, P_poll__networl_3_2_AnsP_1, P_poll__networl_3_2_AnsP_0, P_poll__networl_3_2_AskP_3, P_poll__networl_3_2_AskP_2, P_poll__networl_3_2_AskP_1, P_poll__networl_3_2_AskP_0, P_poll__networl_3_1_RP_3, P_poll__networl_3_1_RP_2, P_poll__networl_3_1_RP_1, P_poll__networl_3_1_RP_0, P_poll__networl_3_1_AnnP_3, P_poll__networl_3_1_AnnP_2, P_poll__networl_3_1_AnnP_1, P_poll__networl_3_1_AnnP_0, P_poll__networl_3_1_AI_3, P_poll__networl_3_1_AI_2, P_poll__networl_3_1_AI_1, P_poll__networl_3_1_AI_0, P_poll__networl_3_1_RI_3, P_poll__networl_3_1_RI_2, P_poll__networl_3_1_RI_1, P_poll__networl_3_1_RI_0, P_poll__networl_3_1_AnsP_3, P_poll__networl_3_1_AnsP_2, P_poll__networl_3_1_AnsP_1, P_poll__networl_3_1_AnsP_0, P_poll__networl_3_1_AskP_3, P_poll__networl_3_1_AskP_2, P_poll__networl_3_1_AskP_1, P_poll__networl_3_1_AskP_0, P_poll__networl_3_0_RP_3, P_poll__networl_3_0_RP_2, P_poll__networl_3_0_RP_1, P_poll__networl_3_0_RP_0, P_poll__networl_3_0_AnnP_3, P_poll__networl_3_0_AnnP_2, P_poll__networl_3_0_AnnP_1, P_poll__networl_3_0_AnnP_0, P_poll__networl_3_0_AI_3, P_poll__networl_3_0_AI_2, P_poll__networl_3_0_AI_1, P_poll__networl_3_0_AI_0, P_poll__networl_3_0_RI_3, P_poll__networl_3_0_RI_2, P_poll__networl_3_0_RI_1, P_poll__networl_3_0_RI_0, P_poll__networl_3_0_AnsP_3, P_poll__networl_3_0_AnsP_2, P_poll__networl_3_0_AnsP_1, P_poll__networl_3_0_AnsP_0, P_poll__networl_3_0_AskP_3, P_poll__networl_3_0_AskP_2, P_poll__networl_3_0_AskP_1, P_poll__networl_3_0_AskP_0, P_poll__networl_2_3_RP_3, P_poll__networl_2_3_RP_2, P_poll__networl_2_3_RP_1, P_poll__networl_2_3_RP_0, P_poll__networl_2_3_AnnP_3, P_poll__networl_2_3_AnnP_2, P_poll__networl_2_3_AnnP_1, P_poll__networl_2_3_AnnP_0, P_poll__networl_2_3_AI_3, P_poll__networl_2_3_AI_2, P_poll__networl_2_3_AI_1, P_poll__networl_2_3_AI_0, P_poll__networl_2_3_RI_3, P_poll__networl_2_3_RI_2, P_poll__networl_2_3_RI_1, P_poll__networl_2_3_RI_0, P_poll__networl_2_3_AnsP_3, P_poll__networl_2_3_AnsP_2, P_poll__networl_2_3_AnsP_1, P_poll__networl_2_3_AnsP_0, P_poll__networl_2_3_AskP_3, P_poll__networl_2_3_AskP_2, P_poll__networl_2_3_AskP_1, P_poll__networl_2_3_AskP_0, P_poll__networl_2_2_RP_3, P_poll__networl_2_2_RP_2, P_poll__networl_2_2_RP_1, P_poll__networl_2_2_RP_0, P_poll__networl_2_2_AnnP_3, P_poll__networl_2_2_AnnP_2, P_poll__networl_2_2_AnnP_1, P_poll__networl_2_2_AnnP_0, P_poll__networl_2_2_AI_3, P_poll__networl_2_2_AI_2, P_poll__networl_2_2_AI_1, P_poll__networl_2_2_AI_0, P_poll__networl_2_2_RI_3, P_poll__networl_2_2_RI_2, P_poll__networl_2_2_RI_1, P_poll__networl_2_2_RI_0, P_poll__networl_2_2_AnsP_3, P_poll__networl_2_2_AnsP_2, P_poll__networl_2_2_AnsP_1, P_poll__networl_2_2_AnsP_0, P_poll__networl_2_2_AskP_3, P_poll__networl_2_2_AskP_2, P_poll__networl_2_2_AskP_1, P_poll__networl_2_2_AskP_0, P_poll__networl_2_1_RP_3, P_poll__networl_2_1_RP_2, P_poll__networl_2_1_RP_1, P_poll__networl_2_1_RP_0, P_poll__networl_2_1_AnnP_3, P_poll__networl_2_1_AnnP_2, P_poll__networl_2_1_AnnP_1, P_poll__networl_2_1_AnnP_0, P_poll__networl_2_1_AI_3, P_poll__networl_2_1_AI_2, P_poll__networl_2_1_AI_1, P_poll__networl_2_1_AI_0, P_poll__networl_2_1_RI_3, P_poll__networl_2_1_RI_2, P_poll__networl_2_1_RI_1, P_poll__networl_2_1_RI_0, P_poll__networl_2_1_AnsP_3, P_poll__networl_2_1_AnsP_2, P_poll__networl_2_1_AnsP_1, P_poll__networl_2_1_AnsP_0, P_poll__networl_2_1_AskP_3, P_poll__networl_2_1_AskP_2, P_poll__networl_2_1_AskP_1, P_poll__networl_2_1_AskP_0, P_poll__networl_2_0_RP_3, P_poll__networl_2_0_RP_2, P_poll__networl_2_0_RP_1, P_poll__networl_2_0_RP_0, P_poll__networl_2_0_AnnP_3, P_poll__networl_2_0_AnnP_2, P_poll__networl_2_0_AnnP_1, P_poll__networl_2_0_AnnP_0, P_poll__networl_2_0_AI_3, P_poll__networl_2_0_AI_2, P_poll__networl_2_0_AI_1, P_poll__networl_2_0_AI_0, P_poll__networl_2_0_RI_3, P_poll__networl_2_0_RI_2, P_poll__networl_2_0_RI_1, P_poll__networl_2_0_RI_0, P_poll__networl_2_0_AnsP_3, P_poll__networl_2_0_AnsP_2, P_poll__networl_2_0_AnsP_1, P_poll__networl_2_0_AnsP_0, P_poll__networl_2_0_AskP_3, P_poll__networl_2_0_AskP_2, P_poll__networl_2_0_AskP_1, P_poll__networl_2_0_AskP_0, P_poll__networl_1_3_RP_3, P_poll__networl_1_3_RP_2, P_poll__networl_1_3_RP_1, P_poll__networl_1_3_RP_0, P_poll__networl_1_3_AnnP_3, P_poll__networl_1_3_AnnP_2, P_poll__networl_1_3_AnnP_1, P_poll__networl_1_3_AnnP_0, P_poll__networl_1_3_AI_3, P_poll__networl_1_3_AI_2, P_poll__networl_1_3_AI_1, P_poll__networl_1_3_AI_0, P_poll__networl_1_3_RI_3, P_poll__networl_1_3_RI_2, P_poll__networl_1_3_RI_1, P_poll__networl_1_3_RI_0, P_poll__networl_1_3_AnsP_3, P_poll__networl_1_3_AnsP_2, P_poll__networl_1_3_AnsP_1, P_poll__networl_1_3_AnsP_0, P_poll__networl_1_3_AskP_3, P_poll__networl_1_3_AskP_2, P_poll__networl_1_3_AskP_1, P_poll__networl_1_3_AskP_0, P_poll__networl_1_2_RP_3, P_poll__networl_1_2_RP_2, P_poll__networl_1_2_RP_1, P_poll__networl_1_2_RP_0, P_poll__networl_1_2_AnnP_3, P_poll__networl_1_2_AnnP_2, P_poll__networl_1_2_AnnP_1, P_poll__networl_1_2_AnnP_0, P_poll__networl_1_2_AI_3, P_poll__networl_1_2_AI_2, P_poll__networl_1_2_AI_1, P_poll__networl_1_2_AI_0, P_poll__networl_1_2_RI_3, P_poll__networl_1_2_RI_2, P_poll__networl_1_2_RI_1, P_poll__networl_1_2_RI_0, P_poll__networl_1_2_AnsP_3, P_poll__networl_1_2_AnsP_2, P_poll__networl_1_2_AnsP_1, P_poll__networl_1_2_AnsP_0, P_poll__networl_1_2_AskP_3, P_poll__networl_1_2_AskP_2, P_poll__networl_1_2_AskP_1, P_poll__networl_1_2_AskP_0, P_poll__networl_1_1_RP_3, P_poll__networl_1_1_RP_2, P_poll__networl_1_1_RP_1, P_poll__networl_1_1_RP_0, P_poll__networl_1_1_AnnP_3, P_poll__networl_1_1_AnnP_2, P_poll__networl_1_1_AnnP_1, P_poll__networl_1_1_AnnP_0, P_poll__networl_1_1_AI_3, P_poll__networl_1_1_AI_2, P_poll__networl_1_1_AI_1, P_poll__networl_1_1_AI_0, P_poll__networl_1_1_RI_3, P_poll__networl_1_1_RI_2, P_poll__networl_1_1_RI_1, P_poll__networl_1_1_RI_0, P_poll__networl_1_1_AnsP_3, P_poll__networl_1_1_AnsP_2, P_poll__networl_1_1_AnsP_1, P_poll__networl_1_1_AnsP_0, P_poll__networl_1_1_AskP_3, P_poll__networl_1_1_AskP_2, P_poll__networl_1_1_AskP_1, P_poll__networl_1_1_AskP_0, P_poll__networl_1_0_RP_3, P_poll__networl_1_0_RP_2, P_poll__networl_1_0_RP_1, P_poll__networl_1_0_RP_0, P_poll__networl_1_0_AnnP_3, P_poll__networl_1_0_AnnP_2, P_poll__networl_1_0_AnnP_1, P_poll__networl_1_0_AnnP_0, P_poll__networl_1_0_AI_3, P_poll__networl_1_0_AI_2, P_poll__networl_1_0_AI_1, P_poll__networl_1_0_AI_0, P_poll__networl_1_0_RI_3, P_poll__networl_1_0_RI_2, P_poll__networl_1_0_RI_1, P_poll__networl_1_0_RI_0, P_poll__networl_1_0_AnsP_3, P_poll__networl_1_0_AnsP_2, P_poll__networl_1_0_AnsP_1, P_poll__networl_1_0_AnsP_0, P_poll__networl_1_0_AskP_3, P_poll__networl_1_0_AskP_2, P_poll__networl_1_0_AskP_1, P_poll__networl_1_0_AskP_0, P_poll__networl_0_3_RP_3, P_poll__networl_0_3_RP_2, P_poll__networl_0_3_RP_1, P_poll__networl_0_3_RP_0, P_poll__networl_0_3_AnnP_3, P_poll__networl_0_3_AnnP_2, P_poll__networl_0_3_AnnP_1, P_poll__networl_0_3_AnnP_0, P_poll__networl_0_3_AI_3, P_poll__networl_0_3_AI_2, P_poll__networl_0_3_AI_1, P_poll__networl_0_3_AI_0, P_poll__networl_0_3_RI_3, P_poll__networl_0_3_RI_2, P_poll__networl_0_3_RI_1, P_poll__networl_0_3_RI_0, P_poll__networl_0_3_AnsP_3, P_poll__networl_0_3_AnsP_2, P_poll__networl_0_3_AnsP_1, P_poll__networl_0_3_AnsP_0, P_poll__networl_0_3_AskP_3, P_poll__networl_0_3_AskP_2, P_poll__networl_0_3_AskP_1, P_poll__networl_0_3_AskP_0, P_poll__networl_0_2_RP_3, P_poll__networl_0_2_RP_2, P_poll__networl_0_2_RP_1, P_poll__networl_0_2_RP_0, P_poll__networl_0_2_AnnP_3, P_poll__networl_0_2_AnnP_2, P_poll__networl_0_2_AnnP_1, P_poll__networl_0_2_AnnP_0, P_poll__networl_0_2_AI_3, P_poll__networl_0_2_AI_2, P_poll__networl_0_2_AI_1, P_poll__networl_0_2_AI_0, P_poll__networl_0_2_RI_3, P_poll__networl_0_2_RI_2, P_poll__networl_0_2_RI_1, P_poll__networl_0_2_RI_0, P_poll__networl_0_2_AnsP_3, P_poll__networl_0_2_AnsP_2, P_poll__networl_0_2_AnsP_1, P_poll__networl_0_2_AnsP_0, P_poll__networl_0_2_AskP_3, P_poll__networl_0_2_AskP_2, P_poll__networl_0_2_AskP_1, P_poll__networl_0_2_AskP_0, P_poll__networl_0_1_RP_3, P_poll__networl_0_1_RP_2, P_poll__networl_0_1_RP_1, P_poll__networl_0_1_RP_0, P_poll__networl_0_1_AnnP_3, P_poll__networl_0_1_AnnP_2, P_poll__networl_0_1_AnnP_1, P_poll__networl_0_1_AnnP_0, P_poll__networl_0_1_AI_3, P_poll__networl_0_1_AI_2, P_poll__networl_0_1_AI_1, P_poll__networl_0_1_AI_0, P_poll__networl_0_1_RI_3, P_poll__networl_0_1_RI_2, P_poll__networl_0_1_RI_1, P_poll__networl_0_1_RI_0, P_poll__networl_0_1_AnsP_3, P_poll__networl_0_1_AnsP_2, P_poll__networl_0_1_AnsP_1, P_poll__networl_0_1_AnsP_0, P_poll__networl_0_1_AskP_3, P_poll__networl_0_1_AskP_2, P_poll__networl_0_1_AskP_1, P_poll__networl_0_1_AskP_0, P_poll__networl_0_0_RP_3, P_poll__networl_0_0_RP_2, P_poll__networl_0_0_RP_1, P_poll__networl_0_0_RP_0, P_poll__networl_0_0_AnnP_3, P_poll__networl_0_0_AnnP_2, P_poll__networl_0_0_AnnP_1, P_poll__networl_0_0_AnnP_0, P_poll__networl_0_0_AI_3, P_poll__networl_0_0_AI_2, P_poll__networl_0_0_AI_1, P_poll__networl_0_0_AI_0, P_poll__networl_0_0_RI_3, P_poll__networl_0_0_RI_2, P_poll__networl_0_0_RI_1, P_poll__networl_0_0_RI_0, P_poll__networl_0_0_AnsP_3, P_poll__networl_0_0_AnsP_2, P_poll__networl_0_0_AnsP_1, P_poll__networl_0_0_AnsP_0, P_poll__networl_0_0_AskP_3, P_poll__networl_0_0_AskP_2, P_poll__networl_0_0_AskP_1, P_poll__networl_0_0_AskP_0)) states: 0
EG iterations: 0
-> the formula is TRUE
FORMULA NeoElection-COL-3-CTLCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.179sec
Total processing time: 21m44.416sec
BK_STOP 1463691310318
--------------------
content from stderr:
check for maximal unmarked siphon
found
The net has a maximal unmarked siphon:
P_dead_0
P_electedPrimary_1
P_crashed_0
P_poll__networl_1_0_RI_1
P_poll__networl_1_0_RI_0
P_poll__networl_0_3_RP_0
P_poll__networl_0_3_RP_1
P_poll__networl_0_3_AnnP_2
P_poll__networl_0_3_AnnP_3
P_poll__networl_1_0_AskP_2
P_poll__networl_1_0_AskP_3
P_poll__networl_1_0_AskP_0
P_poll__networl_1_0_AskP_1
P_poll__networl_0_3_RP_2
P_poll__networl_0_3_RP_3
P_poll__networl_0_3_AnnP_0
P_poll__networl_0_3_AnnP_1
P_poll__networl_0_3_AI_2
P_poll__networl_0_3_AI_3
P_poll__networl_0_3_RI_0
P_poll__networl_0_3_AnsP_2
P_poll__networl_0_3_AnsP_3
P_poll__networl_0_3_AnsP_0
P_poll__networl_0_3_AnsP_1
P_poll__networl_0_3_AI_0
P_poll__networl_0_3_AI_1
P_poll__networl_0_3_RI_2
P_poll__networl_0_3_RI_3
P_poll__networl_0_3_RI_1
P_poll__networl_0_2_RP_0
P_poll__networl_0_2_RP_1
P_poll__networl_0_2_AnnP_2
P_poll__networl_0_2_AnnP_3
P_poll__networl_0_3_AskP_2
P_poll__networl_0_3_AskP_3
P_poll__networl_0_3_AskP_0
P_poll__networl_0_3_AskP_1
P_poll__networl_0_2_RP_2
P_poll__networl_0_2_RP_3
P_poll__networl_0_2_AnnP_1
P_poll__networl_0_0_AskP_0
P_poll__networl_0_0_AskP_1
P_poll__handlingMessage_0
P_network_3_3_RP_2
P_network_3_3_RP_0
P_network_3_3_RP_1
P_network_3_3_AnnP_2
P_network_3_3_AnnP_3
P_network_3_3_AnnP_0
P_network_3_3_AnnP_1
P_network_3_3_AI_2
P_network_3_3_AI_3
P_network_3_3_AI_0
P_network_3_3_AI_1
P_network_3_3_RI_2
P_network_3_3_RI_3
P_poll__networl_0_2_AnnP_0
P_network_3_3_RI_1
P_poll__networl_0_2_AI_2
P_poll__networl_0_2_AI_3
P_poll__networl_0_2_AI_0
P_poll__networl_0_2_AI_1
P_poll__networl_0_2_RI_2
P_poll__networl_0_2_RI_3
P_poll__networl_0_2_RI_0
P_poll__networl_0_2_RI_1
P_poll__networl_0_2_AnsP_2
P_poll__networl_0_2_AnsP_3
P_poll__networl_0_2_AnsP_0
P_poll__networl_0_2_AnsP_1
P_poll__networl_0_2_AskP_3
P_poll__networl_0_2_AskP_0
P_poll__networl_0_2_AskP_1
P_poll__networl_0_1_RP_2
P_poll__networl_0_1_RP_3
P_poll__networl_0_1_RP_0
P_poll__networl_0_1_RP_1
P_poll__networl_0_1_AnnP_2
P_poll__networl_0_1_AnnP_0
P_poll__networl_0_1_AnnP_1
P_poll__networl_0_1_AI_2
P_poll__networl_0_1_AI_3
P_poll__networl_0_1_AI_0
P_poll__networl_0_1_AI_1
P_poll__networl_0_1_RI_2
P_poll__networl_0_1_RI_3
P_poll__networl_0_1_RI_0
P_poll__networl_0_1_RI_1
P_poll__networl_0_1_AnsP_2
P_poll__networl_0_1_AnsP_3
P_poll__networl_0_1_AnsP_1
P_poll__networl_0_1_AskP_2
P_poll__networl_0_1_AskP_3
P_poll__networl_0_1_AskP_0
P_poll__networl_0_1_AskP_1
P_poll__networl_0_0_RP_2
P_poll__networl_0_0_RP_3
P_poll__networl_0_0_RP_0
P_poll__networl_0_0_AnnP_2
P_poll__networl_0_0_AnnP_3
P_poll__networl_0_0_AnnP_0
P_poll__networl_0_0_AnnP_1
P_poll__networl_0_0_AI_2
P_poll__networl_0_0_AI_3
P_poll__networl_0_0_AI_0
P_poll__networl_0_0_AI_1
P_poll__networl_0_0_RI_2
P_poll__networl_0_0_RI_3
P_poll__networl_0_0_RI_0
P_poll__networl_0_0_RI_1
P_poll__networl_0_0_AnsP_3
P_poll__networl_0_0_AnsP_0
P_poll__networl_0_0_AnsP_1
P_poll__networl_0_0_AskP_2
P_poll__networl_0_0_AskP_3
P_network_3_3_RP_3
P_network_3_3_RI_0
P_poll__networl_0_2_AskP_2
P_poll__networl_0_1_AnnP_3
P_poll__networl_0_1_AnsP_0
P_poll__networl_0_0_RP_1
P_poll__networl_0_0_AnsP_2
P_network_3_1_AnsP_3
P_network_3_1_AnsP_1
P_network_3_1_AnsP_2
P_network_3_1_AskP_1
P_network_3_1_AskP_2
P_network_3_0_RP_3
P_network_3_0_RP_2
P_network_3_0_AnnP_3
P_network_3_0_RP_0
P_network_3_0_AnnP_1
P_network_3_0_AnnP_2
P_network_3_0_AnnP_0
P_network_3_3_AnsP_2
P_network_3_3_AnsP_3
P_network_3_3_AnsP_0
P_network_3_3_AnsP_1
P_network_3_3_AskP_2
P_network_3_3_AskP_3
P_network_3_3_AskP_1
P_network_3_2_RP_3
P_network_3_3_AskP_0
P_network_3_2_RP_1
P_network_3_2_AnnP_3
P_network_3_2_RP_0
P_network_3_2_AnnP_1
P_network_3_2_AnnP_2
P_network_3_2_AI_3
P_network_3_2_AI_1
P_network_3_2_AI_2
P_network_3_2_RI_3
P_network_3_2_RI_1
P_network_3_2_AnsP_3
P_network_3_2_AnsP_1
P_network_3_2_AnsP_2
P_network_3_2_AskP_3
P_network_3_2_AskP_1
P_network_3_2_AskP_2
P_network_3_1_RP_1
P_network_3_1_RP_2
P_network_3_1_AnnP_3
P_network_3_1_RP_0
P_network_3_1_AnnP_2
P_network_3_1_AI_3
P_network_3_1_AnnP_0
P_network_3_1_AI_1
P_network_3_1_AI_2
P_network_3_1_RI_3
P_network_3_1_RI_1
P_network_3_1_RI_2
P_network_3_1_AskP_3
P_network_3_0_RP_1
P_network_3_2_RP_2
P_network_3_2_AnnP_0
P_network_3_2_RI_2
P_network_3_1_RP_3
P_network_3_1_AnnP_1
P_network_3_0_AskP_1
P_network_3_0_AskP_2
P_network_2_3_RP_3
P_network_3_0_AskP_0
P_network_2_3_RP_1
P_network_2_3_AnnP_3
P_network_2_3_RP_0
P_network_2_3_AnnP_1
P_network_2_3_AI_3
P_network_2_3_AnnP_0
P_network_2_3_AI_2
P_network_2_3_RI_3
P_network_2_3_RI_1
P_network_2_3_RI_2
P_network_2_3_AnsP_3
P_network_2_3_AnsP_2
P_network_2_3_AskP_3
P_network_2_3_AskP_2
P_network_2_2_RP_3
P_network_2_2_RP_1
P_network_2_2_RP_2
P_network_2_2_AnnP_3
P_network_2_2_RP_0
P_network_2_2_AnnP_1
P_network_2_2_AnnP_2
P_network_2_2_AI_3
P_network_2_2_AnnP_0
P_network_2_2_AI_1
P_network_2_2_AI_2
P_network_2_2_RI_3
P_network_2_2_AI_0
P_network_2_2_RI_1
P_network_2_2_RI_2
P_network_2_2_AnsP_3
P_network_2_2_RI_0
P_network_2_2_AnsP_1
P_network_2_2_AnsP_2
P_network_2_2_AskP_3
P_network_2_2_AnsP_0
P_network_2_2_AskP_1
P_network_2_2_AskP_2
P_network_2_1_RP_3
P_network_2_2_AskP_0
P_network_2_1_RP_1
P_network_2_1_RP_2
P_network_2_1_RP_0
P_network_2_1_AnnP_1
P_network_2_1_AnnP_2
P_network_2_1_AnnP_0
P_network_2_1_AI_1
P_network_2_1_AI_2
P_network_2_1_RI_3
P_network_2_1_RI_1
P_network_2_1_RI_2
P_network_2_1_AnsP_2
P_network_2_1_AskP_3
P_network_2_1_AskP_1
P_network_2_1_AskP_2
P_network_2_0_RP_3
P_network_2_0_RP_1
P_network_2_0_RP_2
P_network_2_0_AnnP_3
P_network_2_0_RP_0
P_network_2_0_AnnP_1
P_network_2_0_AnnP_2
P_network_2_0_AI_3
P_network_2_0_AnnP_0
P_network_2_0_AI_1
P_network_2_0_AI_2
P_network_2_0_AI_0
P_network_2_0_RI_1
P_network_2_0_RI_2
P_network_2_0_AnsP_3
P_network_2_0_RI_0
P_network_2_0_AnsP_1
P_network_2_0_AskP_3
P_network_2_0_AnsP_0
P_network_2_0_AskP_1
P_network_1_3_RP_3
P_network_2_0_AskP_0
P_network_1_3_RP_2
P_network_1_3_AnnP_3
P_network_1_3_RP_0
P_network_1_3_AnnP_1
P_network_1_3_AnnP_2
P_network_1_3_AI_3
P_network_1_3_AnnP_0
P_network_1_3_AI_2
P_network_1_3_RI_3
P_network_1_3_RI_2
P_network_3_0_AI_3
P_network_3_0_AI_1
P_network_3_0_AI_2
P_network_3_0_RI_3
P_network_3_0_AI_0
P_network_3_0_RI_1
P_network_3_0_RI_2
P_network_3_0_AnsP_3
P_network_3_0_RI_0
P_network_3_0_AnsP_1
P_network_3_0_AnsP_2
P_network_3_0_AskP_3
P_network_3_0_AnsP_0
P_network_2_3_RP_2
P_network_2_3_AI_1
P_network_2_3_AnnP_2
P_network_2_3_AnsP_1
P_network_2_3_AskP_1
P_network_2_1_AnnP_3
P_network_2_1_AI_3
P_network_2_1_AnsP_3
P_network_2_1_AnsP_1
P_network_2_0_RI_3
P_network_2_0_AnsP_2
P_network_1_3_RP_1
P_network_2_0_AskP_2
P_network_1_3_AI_1
P_network_1_3_RI_1
P_network_1_1_AnsP_3
P_network_1_1_RI_0
P_network_1_1_AnsP_1
P_network_1_1_AnsP_2
P_network_1_1_AnsP_0
P_network_1_1_AskP_1
P_network_1_1_AskP_2
P_network_1_0_RP_3
P_network_1_1_AskP_0
P_network_1_0_RP_2
P_network_1_0_AnnP_3
P_network_1_0_RP_0
P_network_1_0_AnnP_1
P_network_1_0_AnnP_2
P_network_1_3_AnsP_3
P_network_1_0_AnnP_0
P_network_1_3_AnsP_1
P_network_1_3_AnsP_2
P_network_1_3_AskP_3
P_network_1_3_AskP_1
P_network_1_3_AskP_2
P_network_1_2_RP_3
P_network_1_2_RP_1
P_network_1_2_AnnP_3
P_network_1_2_RP_0
P_network_1_2_AnnP_1
P_network_1_2_AnnP_2
P_network_1_2_AI_3
P_network_1_2_AI_1
P_network_1_2_AI_2
P_network_1_2_RI_3
P_network_1_2_RI_1
P_network_1_2_AnsP_3
P_network_1_2_AnsP_1
P_network_1_2_AnsP_2
P_network_1_2_AskP_3
P_network_1_2_AskP_1
P_network_1_2_AskP_2
P_network_1_1_RP_1
P_network_1_1_RP_2
P_network_1_1_AnnP_3
P_network_1_1_RP_0
P_network_1_1_AnnP_2
P_network_1_1_AI_3
P_network_1_1_AnnP_0
P_network_1_1_AI_1
P_network_1_1_AI_2
P_network_1_1_RI_3
P_network_1_1_AI_0
P_network_1_1_RI_1
P_network_1_1_RI_2
P_network_1_1_AskP_3
P_network_1_0_RP_1
P_network_1_2_RP_2
P_network_1_2_AnnP_0
P_network_1_2_RI_2
P_network_1_1_RP_3
P_network_1_1_AnnP_1
P_network_1_0_RI_1
P_network_1_0_RI_2
P_network_1_0_RI_0
P_network_1_0_AnsP_2
P_network_1_0_AnsP_3
P_network_1_0_AI_3
P_network_1_0_AI_1
P_network_1_0_AI_2
P_network_1_0_RI_3
P_network_1_0_AI_0
P_network_0_3_RP_2
P_network_0_3_RP_3
P_network_0_3_RP_0
P_network_0_3_RP_1
P_network_1_0_AnsP_0
P_network_1_0_AnsP_1
P_network_1_0_AskP_2
P_network_1_0_AskP_3
P_network_1_0_AskP_0
P_network_1_0_AskP_1
P_network_0_1_AnnP_2
P_network_0_3_AnnP_3
P_network_0_1_AnnP_0
P_network_0_1_AnnP_1
P_network_0_1_AI_3
P_network_0_1_AI_0
P_network_0_1_AI_1
P_network_0_1_RI_2
P_network_0_1_RI_3
P_network_0_1_RI_1
P_network_0_1_AnsP_2
P_network_0_1_AnsP_3
P_network_0_1_AnsP_0
P_network_0_1_AnsP_1
P_network_0_3_AnnP_2
P_network_0_3_AnnP_0
P_network_0_3_AnnP_1
P_network_0_3_AI_2
P_network_0_3_AI_3
P_network_0_3_AI_0
P_network_0_3_AI_1
P_network_0_3_RI_2
P_network_0_3_RI_3
P_network_0_3_RI_0
P_network_0_3_RI_1
P_network_0_3_AnsP_2
P_network_0_3_AnsP_3
P_network_0_3_AnsP_0
P_network_0_3_AnsP_1
P_network_0_3_AskP_3
P_network_0_3_AskP_0
P_network_0_3_AskP_1
P_network_0_2_RP_2
P_network_0_2_RP_3
P_network_0_2_RP_1
P_network_0_2_AnnP_2
P_network_0_2_AnnP_3
P_network_0_2_AnnP_0
P_network_0_2_AnnP_1
P_network_0_2_AI_2
P_network_0_2_AI_3
P_network_0_2_AI_0
P_network_0_2_AI_1
P_network_0_2_RI_2
P_network_0_2_RI_3
P_network_0_2_RI_0
P_network_0_2_RI_1
P_network_0_2_AnsP_2
P_network_0_2_AnsP_3
P_network_0_2_AnsP_0
P_network_0_2_AnsP_1
P_network_0_2_AskP_2
P_network_0_2_AskP_3
P_network_0_2_AskP_0
P_network_0_2_AskP_1
P_network_0_1_RP_3
P_network_0_1_RP_0
P_network_0_1_RP_1
P_network_0_1_AI_2
P_network_0_1_AnnP_3
P_network_0_1_RI_0
P_network_0_1_AskP_3
P_network_0_3_AskP_2
P_network_0_2_RP_0
P_network_0_1_RP_2
P_negotiation_3_0_DONE
P_negotiation_3_0_NONE
P_negotiation_3_0_CO
P_negotiation_2_2_CO
P_negotiation_2_0_DONE
P_negotiation_1_1_NONE
P_negotiation_1_1_CO
P_negotiation_1_0_CO
P_negotiation_1_0_DONE
P_negotiation_1_0_NONE
P_negotiation_0_3_NONE
P_negotiation_0_3_CO
P_negotiation_0_2_CO
P_negotiation_0_2_DONE
P_negotiation_0_1_DONE
P_negotiation_0_2_NONE
P_negotiation_0_1_NONE
P_negotiation_0_0_CO
P_negotiation_0_0_DONE
P_masterState_3_T_3
P_masterState_3_T_1
P_masterState_3_T_2
P_masterState_3_F_3
P_masterState_3_F_1
P_masterState_3_F_2
P_masterState_3_F_0
P_masterState_2_T_1
P_masterState_2_T_2
P_masterState_2_F_3
P_masterState_2_F_1
P_masterState_2_F_2
P_masterState_1_T_3
P_masterState_1_T_2
P_masterState_1_F_3
P_masterState_1_F_2
P_masterState_0_T_3
P_masterState_0_T_1
P_masterState_0_T_2
P_masterState_0_F_3
P_masterState_0_T_0
P_masterState_0_F_1
P_masterList_3_3_3
P_masterState_0_F_0
P_masterList_3_3_0
P_masterList_3_2_1
P_network_0_1_AskP_2
P_network_0_1_AskP_0
P_network_0_1_AskP_1
P_network_0_0_RP_2
P_network_0_0_RP_3
P_network_0_0_RP_0
P_network_0_0_RP_1
P_network_0_0_AnnP_2
P_network_0_0_AnnP_3
P_network_0_0_AnnP_0
P_network_0_0_AnnP_1
P_network_0_0_AI_2
P_network_0_0_AI_3
P_network_0_0_AI_0
P_network_0_0_AI_1
P_network_0_0_RI_2
P_network_0_0_RI_3
P_network_0_0_RI_0
P_network_0_0_RI_1
P_network_0_0_AnsP_2
P_network_0_0_AnsP_3
P_network_0_0_AnsP_0
P_network_0_0_AnsP_1
P_network_0_0_AskP_2
P_network_0_0_AskP_3
P_network_0_0_AskP_0
P_network_0_0_AskP_1
P_negotiation_3_3_CO
P_negotiation_3_3_NONE
P_negotiation_2_2_NONE
P_poll__networl_1_0_AnnP_0
P_negotiation_2_0_CO
P_negotiation_2_0_NONE
P_negotiation_0_3_DONE
P_negotiation_0_1_CO
P_negotiation_0_0_NONE
P_masterState_2_T_3
P_masterState_1_T_1
P_masterState_1_F_1
P_masterState_0_F_2
P_masterList_3_3_1
P_masterList_3_3_2
P_poll__networl_1_0_AnsP_0
P_poll__networl_1_0_AnsP_2
P_poll__networl_1_0_AnsP_1
P_poll__networl_1_0_AnsP_3
P_poll__networl_1_0_RI_3
P_poll__networl_1_0_RI_2
P_poll__networl_1_0_AI_1
P_poll__networl_1_0_AI_0
P_poll__waitingMessage_1
P_masterList_3_2_3
P_poll__waitingMessage_2
P_poll__waitingMessage_3
P_polling_0
P_sendAnnPs__broadcasting_0_1
P_sendAnnPs__broadcasting_0_2
P_sendAnnPs__broadcasting_0_3
P_sendAnnPs__broadcasting_1_1
P_sendAnnPs__broadcasting_1_2
P_sendAnnPs__broadcasting_1_3
P_sendAnnPs__broadcasting_2_1
P_stage_0_NEG
P_stage_1_SEC
P_startNeg__broadcasting_0_3
P_startNeg__broadcasting_0_2
P_sendAnnPs__broadcasting_2_2
P_sendAnnPs__broadcasting_2_3
P_sendAnnPs__broadcasting_3_1
P_sendAnnPs__broadcasting_3_2
P_startNeg__broadcasting_0_1
P_sendAnnPs__broadcasting_3_3
P_stage_3_SEC
P_stage_0_PRIM
P_stage_0_SEC
P_stage_1_PRIM
P_stage_3_PRIM
P_stage_2_SEC
P_stage_2_PRIM
P_crashed_1
P_crashed_2
P_electedPrimary_2
P_poll__networl_1_0_AI_2
P_crashed_3
P_poll__networl_1_0_AnnP_1
P_poll__networl_1_0_AnnP_2
P_poll__networl_1_0_AI_3
P_dead_1
P_dead_2
P_poll__networl_1_0_RP_2
P_poll__networl_1_0_RP_3
P_poll__networl_1_1_AskP_0
P_poll__networl_1_1_AskP_1
P_electedPrimary_3
P_electedSecondary_0
P_electedSecondary_1
P_electedSecondary_2
P_electedSecondary_3
P_electionFailed_0
P_electionFailed_1
P_dead_3
P_electedPrimary_0
P_electionFailed_2
P_electionFailed_3
P_electionInit_0
P_masterList_0_1_0
P_masterList_0_1_1
P_masterList_0_1_2
P_masterList_0_1_3
P_masterList_0_2_0
P_masterList_0_2_1
P_masterList_0_2_2
P_masterList_0_2_3
P_masterList_0_3_0
P_poll__networl_1_0_AnnP_3
P_poll__networl_1_0_RP_0
P_poll__networl_1_0_RP_1
P_masterList_0_3_1
P_masterList_0_3_2
P_masterList_0_3_3
P_masterList_1_1_0
P_masterList_1_1_1
P_masterList_1_1_3
P_masterList_1_2_0
P_masterList_1_2_1
P_masterList_1_2_2
P_masterList_1_3_0
P_masterList_1_3_1
P_masterList_1_3_2
P_masterList_1_3_3
P_masterList_2_1_0
P_masterList_2_1_2
P_masterList_2_1_3
P_masterList_2_2_0
P_masterList_2_2_1
P_masterList_2_2_2
P_masterList_2_3_0
P_masterList_2_3_1
P_masterList_2_3_2
P_masterList_2_3_3
P_masterList_3_1_0
P_masterList_3_1_2
P_masterList_3_1_3
P_masterList_3_2_0
P_poll__networl_1_1_AskP_2
P_poll__networl_1_1_AskP_3
P_poll__networl_1_1_AnsP_0
P_poll__networl_1_1_AnsP_1
P_poll__networl_1_1_AnsP_2
P_poll__networl_1_1_AnsP_3
P_poll__networl_1_1_RI_0
P_poll__networl_1_1_RI_1
P_poll__networl_1_1_RI_2
P_poll__networl_1_1_RI_3
P_poll__networl_1_1_AI_0
P_poll__networl_1_1_AI_1
P_poll__networl_1_1_AI_2
P_poll__networl_1_1_AI_3
P_poll__networl_1_1_AnnP_0
P_poll__networl_1_1_AnnP_1
P_poll__networl_1_1_AnnP_2
P_poll__networl_1_1_AnnP_3
P_poll__networl_1_1_RP_0
P_poll__networl_1_1_RP_1
P_poll__networl_1_1_RP_2
P_poll__networl_1_1_RP_3
P_poll__networl_1_2_AskP_0
P_poll__networl_1_2_AskP_1
P_poll__networl_1_2_AskP_2
P_poll__networl_1_2_AskP_3
P_poll__networl_1_2_AnsP_0
P_poll__networl_1_2_AnsP_1
P_poll__networl_1_2_AnsP_2
P_poll__networl_1_2_AnsP_3
P_poll__networl_1_2_RI_0
P_poll__networl_1_2_RI_1
P_poll__networl_1_2_RI_2
P_poll__networl_1_2_RI_3
P_poll__networl_1_2_AI_0
P_poll__networl_1_2_AI_1
P_poll__networl_1_2_AI_2
P_poll__networl_1_2_AI_3
P_poll__networl_1_2_AnnP_0
P_poll__networl_1_2_AnnP_1
P_poll__networl_1_2_AnnP_2
P_poll__networl_1_2_AnnP_3
P_poll__networl_1_2_RP_0
P_poll__networl_1_2_RP_1
P_poll__networl_1_2_RP_2
P_poll__networl_1_2_RP_3
P_poll__networl_1_3_AskP_0
P_poll__networl_1_3_AskP_1
P_poll__networl_1_3_AskP_2
P_poll__networl_1_3_AskP_3
P_poll__networl_1_3_AnsP_0
P_poll__networl_1_3_AnsP_1
P_poll__networl_1_3_AnsP_2
P_poll__networl_1_3_AnsP_3
P_poll__networl_1_3_RI_0
P_poll__networl_1_3_RI_1
P_poll__networl_1_3_RI_2
P_poll__networl_1_3_RI_3
P_poll__networl_1_3_AI_0
P_poll__networl_1_3_AI_1
P_poll__networl_1_3_AI_2
P_poll__networl_1_3_AI_3
P_poll__networl_1_3_AnnP_0
P_poll__networl_1_3_AnnP_1
P_poll__networl_1_3_AnnP_2
P_poll__networl_1_3_AnnP_3
P_poll__networl_1_3_RP_0
P_poll__networl_1_3_RP_1
P_poll__networl_1_3_RP_2
P_poll__networl_1_3_RP_3
P_poll__networl_2_0_AskP_0
P_poll__networl_2_0_AskP_1
P_poll__networl_2_0_AskP_2
P_poll__networl_2_0_AskP_3
P_poll__networl_2_0_AnsP_0
P_poll__networl_2_0_AnsP_1
P_poll__networl_2_0_AnsP_2
P_poll__networl_2_0_AnsP_3
P_poll__networl_2_0_RI_0
P_poll__networl_2_0_RI_1
P_poll__networl_2_0_RI_2
P_poll__networl_2_0_RI_3
P_poll__networl_2_0_AI_0
P_poll__networl_2_0_AI_1
P_poll__networl_2_0_AI_2
P_poll__networl_2_0_AI_3
P_poll__networl_2_0_AnnP_0
P_poll__networl_2_0_AnnP_1
P_poll__networl_2_0_AnnP_2
P_poll__networl_2_0_AnnP_3
P_poll__networl_2_0_RP_0
P_poll__networl_2_0_RP_1
P_poll__networl_2_0_RP_2
P_poll__networl_2_0_RP_3
P_poll__networl_2_1_AskP_0
P_poll__networl_2_1_AskP_1
P_poll__networl_2_1_AskP_2
P_poll__networl_2_1_AskP_3
P_poll__networl_2_1_AnsP_0
P_poll__networl_2_1_AnsP_1
P_poll__networl_2_1_AnsP_2
P_poll__networl_2_1_AnsP_3
P_poll__networl_2_1_RI_0
P_poll__networl_2_1_RI_1
P_poll__networl_2_1_RI_2
P_poll__networl_2_1_RI_3
P_poll__networl_2_1_AI_0
P_poll__networl_2_1_AI_1
P_poll__networl_2_1_AI_2
P_poll__networl_2_1_AI_3
P_poll__networl_2_1_AnnP_0
P_poll__networl_2_1_AnnP_1
P_poll__networl_2_1_AnnP_2
P_poll__networl_2_1_AnnP_3
P_poll__networl_2_1_RP_0
P_poll__networl_2_1_RP_1
P_poll__networl_2_1_RP_2
P_poll__networl_2_1_RP_3
P_poll__networl_2_2_AskP_0
P_poll__networl_2_2_AskP_1
P_poll__networl_2_2_AskP_2
P_poll__networl_2_2_AskP_3
P_poll__networl_2_2_AnsP_0
P_poll__networl_2_2_AnsP_1
P_poll__networl_2_2_AnsP_2
P_poll__networl_2_2_AnsP_3
P_poll__networl_2_2_RI_0
P_poll__networl_2_2_RI_1
P_poll__networl_2_2_RI_2
P_poll__networl_2_2_RI_3
P_poll__networl_2_2_AI_0
P_poll__networl_2_2_AI_1
P_poll__networl_2_2_AI_2
P_poll__networl_2_2_AI_3
P_poll__networl_2_2_AnnP_0
P_poll__networl_2_2_AnnP_1
P_poll__networl_2_2_AnnP_2
P_poll__networl_2_2_AnnP_3
P_poll__networl_2_2_RP_0
P_poll__networl_2_2_RP_1
P_poll__networl_2_2_RP_2
P_poll__networl_2_2_RP_3
P_poll__networl_2_3_AskP_0
P_poll__networl_2_3_AskP_1
P_poll__networl_2_3_AskP_2
P_poll__networl_2_3_AskP_3
P_poll__networl_2_3_AnsP_0
P_poll__networl_2_3_AnsP_1
P_poll__networl_2_3_AnsP_2
P_poll__networl_2_3_AnsP_3
P_poll__networl_2_3_RI_0
P_poll__networl_2_3_RI_1
P_poll__networl_2_3_RI_2
P_poll__networl_2_3_RI_3
P_poll__networl_2_3_AI_0
P_poll__networl_2_3_AI_1
P_poll__networl_2_3_AI_2
P_poll__networl_2_3_AI_3
P_poll__networl_2_3_AnnP_0
P_poll__networl_2_3_AnnP_1
P_poll__networl_2_3_AnnP_2
P_poll__networl_2_3_AnnP_3
P_poll__networl_2_3_RP_0
P_poll__networl_2_3_RP_1
P_poll__networl_2_3_RP_2
P_poll__networl_2_3_RP_3
P_poll__networl_3_0_AskP_0
P_poll__networl_3_0_AskP_1
P_poll__networl_3_0_AskP_2
P_poll__networl_3_0_AskP_3
P_poll__networl_3_0_AnsP_0
P_poll__networl_3_0_AnsP_1
P_poll__networl_3_0_AnsP_2
P_poll__networl_3_0_AnsP_3
P_poll__networl_3_0_RI_0
P_poll__networl_3_0_RI_1
P_poll__networl_3_0_RI_2
P_poll__networl_3_0_RI_3
P_poll__networl_3_0_AI_0
P_poll__networl_3_0_AI_1
P_poll__networl_3_0_AI_2
P_poll__networl_3_0_AI_3
P_poll__networl_3_0_AnnP_0
P_poll__networl_3_0_AnnP_1
P_poll__networl_3_0_AnnP_2
P_poll__networl_3_0_AnnP_3
P_poll__networl_3_0_RP_0
P_poll__networl_3_0_RP_1
P_poll__networl_3_0_RP_2
P_poll__networl_3_0_RP_3
P_poll__networl_3_1_AskP_0
P_poll__networl_3_1_AskP_1
P_poll__networl_3_1_AskP_2
P_poll__networl_3_1_AskP_3
P_poll__networl_3_1_AnsP_0
P_poll__networl_3_1_AnsP_1
P_poll__networl_3_1_AnsP_2
P_poll__networl_3_1_AnsP_3
P_poll__networl_3_1_RI_0
P_poll__networl_3_1_RI_1
P_poll__networl_3_1_RI_2
P_poll__networl_3_1_RI_3
P_poll__networl_3_1_AI_0
P_poll__networl_3_1_AI_1
P_poll__networl_3_1_AI_2
P_poll__networl_3_1_AI_3
P_poll__networl_3_1_AnnP_0
P_poll__networl_3_1_AnnP_1
P_poll__networl_3_1_AnnP_2
P_poll__networl_3_1_AnnP_3
P_poll__networl_3_1_RP_0
P_poll__networl_3_1_RP_1
P_poll__networl_3_1_RP_2
P_poll__networl_3_1_RP_3
P_poll__networl_3_2_AskP_0
P_poll__networl_3_2_AskP_1
P_poll__networl_3_2_AskP_2
P_poll__networl_3_2_AskP_3
P_poll__networl_3_2_AnsP_0
P_poll__networl_3_2_AnsP_1
P_poll__networl_3_2_AnsP_2
P_poll__networl_3_2_AnsP_3
P_poll__networl_3_2_RI_0
P_poll__networl_3_2_RI_1
P_poll__networl_3_2_RI_2
P_poll__networl_3_2_RI_3
P_poll__networl_3_2_AI_0
P_poll__networl_3_2_AI_1
P_poll__networl_3_2_AI_2
P_poll__networl_3_2_AI_3
P_poll__networl_3_2_AnnP_0
P_poll__networl_3_2_AnnP_1
P_poll__networl_3_2_AnnP_2
P_poll__networl_3_2_AnnP_3
P_poll__networl_3_2_RP_0
P_poll__networl_3_2_RP_1
P_poll__networl_3_2_RP_2
P_poll__networl_3_2_RP_3
P_poll__networl_3_3_AskP_0
P_poll__networl_3_3_AskP_1
P_poll__networl_3_3_AskP_2
P_poll__networl_3_3_AskP_3
P_poll__networl_3_3_AnsP_0
P_poll__networl_3_3_AnsP_1
P_poll__networl_3_3_AnsP_2
P_poll__networl_3_3_AnsP_3
P_poll__networl_3_3_RI_0
P_poll__networl_3_3_RI_1
P_poll__networl_3_3_RI_2
P_poll__networl_3_3_RI_3
P_poll__networl_3_3_AI_0
P_poll__networl_3_3_AI_1
P_poll__networl_3_3_AI_2
P_poll__networl_3_3_AI_3
P_poll__networl_3_3_AnnP_0
P_poll__networl_3_3_AnnP_1
P_poll__networl_3_3_AnnP_2
P_poll__networl_3_3_AnnP_3
P_poll__networl_3_3_RP_0
P_poll__networl_3_3_RP_1
P_poll__networl_3_3_RP_2
P_poll__networl_3_3_RP_3
P_poll__pollEnd_0
P_poll__waitingMessage_0
The net has transition(s) that can never fire:
T_poll__end_1
T_poll__handleAI1_18
T_poll__handleAI1_1
T_poll__handleAI1_2
T_poll__handleAI1_19
T_poll__handleAI1_3
T_poll__handleAI1_4
T_poll__handleAI1_20
T_poll__handleAI2_10
T_poll__handleAI1_17
T_poll__handleAI1_34
T_poll__handleAI1_21
T_poll__handleAI1_22
T_poll__handleAI1_23
T_poll__handleAI1_24
T_poll__handleAI1_33
T_poll__handleAI1_35
T_poll__handleAI1_36
T_poll__handleAI1_56
T_poll__handleAI1_37
T_poll__handleAI1_39
T_poll__handleAI1_41
T_poll__handleAI1_42
T_poll__handleAI2_11
T_poll__handleAI2_286
T_poll__handleAI1_43
T_poll__handleAI1_44
T_poll__handleAI1_49
T_poll__handleAI1_50
T_poll__handleAI1_51
T_poll__handleAI1_52
T_poll__handleAI1_53
T_poll__handleAI2_51
T_poll__handleAI2_30
T_poll__handleAI2_31
T_poll__handleAI2_25
T_poll__handleAI1_57
T_poll__iAmSecondary_13
T_poll__handleAnnP1_98
T_poll__iAmSecondary_2
T_poll__handleAI1_60
T_poll__iAmSecondary_1
T_poll__handleAI1_61
T_poll__handleAI1_62
T_poll__handleAI1_63
T_poll__handleAI1_64
T_poll__handleAI2_9
T_poll__handleAI2_24
T_poll__handleAI2_52
T_poll__handleAI2_12
T_poll__handleAI2_13
T_poll__handleAI2_14
T_poll__handleAI2_22
T_poll__handleAI2_15
T_poll__handleAI2_16
T_poll__handleAI2_17
T_poll__handleAI2_18
T_poll__handleAI2_19
T_poll__handleAI2_20
T_poll__handleAI2_21
T_poll__handleAI2_46
T_poll__handleAI2_23
T_poll__handleAI2_84
T_poll__handleAI2_26
T_poll__handleAI2_27
T_poll__handleAI2_28
T_poll__handleAI2_29
T_poll__handleAI2_118
T_poll__handleAI2_119
T_poll__handleAI2_120
T_poll__handleAI2_121
T_poll__handleAI2_122
T_poll__handleAI2_32
T_poll__handleAI2_41
T_poll__handleAI2_42
T_poll__handleAI2_43
T_poll__handleAI2_44
T_poll__handleAI2_45
T_poll__handleAI2_47
T_poll__handleAI2_87
T_poll__handleAI2_48
T_poll__handleAI2_49
T_poll__handleAI2_50
T_poll__handleAI2_53
T_poll__handleAI2_148
T_poll__handleAI2_149
T_poll__handleAI2_54
T_poll__handleAI2_55
T_poll__handleAI2_56
T_poll__handleAI2_57
T_poll__handleAI2_58
T_poll__handleAI2_59
T_poll__handleAI2_60
T_poll__handleAI2_61
T_poll__handleAI2_62
T_poll__handleAI2_63
T_poll__handleAI2_64
T_poll__handleAI2_73
T_poll__handleAI2_74
T_poll__handleAI2_75
T_poll__handleAI2_77
T_poll__handleAI2_76
T_poll__handleAI2_78
T_poll__handleAI2_79
T_poll__handleAI2_80
T_poll__handleAI2_81
T_poll__handleAI2_82
T_poll__handleAI2_83
T_poll__handleAI2_243
T_poll__handleAI2_242
T_poll__handleAI2_85
T_poll__handleAI2_86
T_poll__handleAnsP1_3
T_poll__handleAnsP1_4
T_poll__handleAnsP1_5
T_poll__handleAI2_88
T_poll__handleAI2_89
T_poll__handleAI2_90
T_poll__handleAskP_4
T_poll__handleAI2_91
T_poll__handleAI2_92
T_poll__handleAI2_93
T_poll__handleAI2_94
T_poll__handleAI2_95
T_poll__handleAI2_96
T_poll__handleAI2_105
T_poll__handleAI2_106
T_poll__handleAI2_107
T_poll__handleAI2_108
T_poll__handleAI2_109
T_poll__handleAI2_110
T_poll__handleAI2_111
T_poll__handleAI2_112
T_poll__handleAI2_113
T_poll__handleAI2_114
T_poll__handleAI2_115
T_poll__handleAI2_116
T_poll__handleAI2_117
T_poll__handleAnsP3_150
T_poll__handleAnsP3_148
T_poll__handleAnnP1_31
T_poll__handleAnnP1_32
T_poll__handleAnnP1_33
T_poll__handleAnnP1_35
T_poll__handleAnnP1_36
T_poll__handleAnnP1_37
T_poll__handleAnnP1_39
T_poll__handleAnnP1_40
T_poll__handleAnnP1_41
T_poll__handleAnnP1_44
T_poll__handleAnnP1_43
T_poll__handleAI2_123
T_poll__handleAI2_124
T_poll__handleAI2_125
T_poll__handleAI2_126
T_poll__handleAI2_127
T_poll__handleAI2_128
T_poll__handleAI2_145
T_poll__handleAI2_146
T_poll__handleAI2_154
T_poll__handleAI2_147
T_poll__handleAnnP1_63
T_poll__handleAnnP1_64
T_poll__handleAnnP1_65
T_poll__handleAnnP1_66
T_poll__handleAnnP1_68
T_poll__handleAnnP1_69
T_poll__handleAnnP1_70
T_poll__handleAI2_150
T_poll__handleAI2_151
T_poll__handleAI2_152
T_poll__handleAI2_153
T_poll__handleAI2_186
T_poll__handleAI2_155
T_poll__handleAI2_212
T_poll__handleAI2_156
T_poll__handleAI2_157
T_poll__handleAI2_158
T_poll__handleAI2_159
T_poll__handleAI2_160
T_poll__handleAI2_177
T_poll__handleAI2_178
T_poll__handleAI2_179
T_poll__handleAI2_180
T_poll__handleAI2_181
T_poll__handleAI2_182
T_poll__handleAI2_183
T_poll__handleAI2_184
T_poll__handleAI2_185
T_poll__handleAI2_251
T_poll__handleAI2_187
T_poll__handleAI2_188
T_poll__handleAI2_189
T_poll__handleAI2_190
T_poll__handleAI2_191
T_poll__handleAI2_192
T_poll__handleAI2_211
T_poll__handleAI2_210
T_poll__handleAI2_214
T_poll__handleAI2_215
T_poll__handleAI2_216
T_poll__handleAI2_218
T_poll__handleAI2_219
T_poll__handleAI2_220
T_poll__handleAI2_222
T_poll__handleAI2_223
T_poll__handleAI2_224
T_poll__handleAI2_250
T_poll__handleAnsP2_53
T_poll__handleAnsP2_54
T_poll__handleAnsP2_55
T_poll__handleAnsP2_56
T_poll__handleAnsP2_59
T_poll__handleAI2_244
T_poll__handleAI2_246
T_poll__handleAI2_247
T_poll__handleAI2_248
T_poll__handleAnsP3_144
T_poll__handleAnsP3_143
T_poll__handleAI2_252
T_poll__handleAI2_254
T_poll__handleAI2_255
T_poll__handleAI2_256
T_poll__handleAI2_281
T_poll__handleAI2_282
T_poll__handleAI2_283
T_poll__handleAI2_284
T_poll__handleAI2_285
T_poll__handleAI2_350
T_poll__handleAI2_287
T_poll__handleAI2_288
T_poll__handleAI2_314
T_poll__handleAI2_315
T_poll__handleAI2_316
T_poll__handleAI2_318
T_poll__handleAI2_319
T_poll__handleAI2_320
T_poll__handleAI2_345
T_poll__handleAI2_346
T_poll__handleAI2_347
T_poll__handleAI2_348
T_poll__handleAI2_349
T_poll__handleAnnP1_72
T_poll__handleAnnP1_94
T_poll__handleAI2_351
T_poll__handleAI2_352
T_poll__handleAI2_379
T_poll__handleAI2_378
T_poll__handleAI2_380
T_poll__handleAI2_382
T_poll__handleAI2_383
T_poll__handleAI2_384
T_poll__handleAnnP1_2
T_poll__handleAnnP1_3
T_poll__handleAnnP1_4
T_poll__handleAnnP1_6
T_poll__handleAnnP1_8
T_poll__handleAnnP1_7
T_poll__handleAnnP1_10
T_poll__handleAnnP1_11
T_poll__handleAnnP1_12
T_poll__handleAnnP1_14
T_poll__handleAnnP1_16
T_poll__handleAnnP1_15
T_poll__handleAnnP1_18
T_poll__handleAnnP1_19
T_poll__handleAnnP1_20
T_poll__handleAnnP1_22
T_poll__handleAnnP1_24
T_poll__handleAnnP1_23
T_poll__handleAnnP1_26
T_poll__handleAnnP1_27
T_poll__handleAnnP1_61
T_poll__handleAnnP1_28
T_poll__handleAnnP1_30
T_poll__handleAnsP3_152
T_poll__handleAnsP3_154
T_poll__handleAnsP3_155
T_poll__handleAnsP3_158
T_poll__handleAnsP3_159
T_poll__handleAnsP3_171
T_poll__handleAnsP3_172
T_poll__handleAnsP3_175
T_poll__handleAnsP3_176
T_poll__handleAnsP3_178
T_poll__handleAnsP3_180
T_poll__handleAnsP3_182
T_poll__handleAnsP3_184
T_poll__handleAnsP3_186
T_poll__handleAnsP3_187
T_poll__handleAnsP3_190
T_poll__handleAnsP3_191
T_poll__handleAnsP3_203
T_poll__handleAnsP3_204
T_poll__handleAnsP3_207
T_poll__handleAnsP3_208
T_poll__handleAnnP1_45
T_poll__handleAnnP1_47
T_poll__handleAnnP1_48
T_poll__handleAnnP1_49
T_poll__handleAnnP1_51
T_poll__handleAnnP1_52
T_poll__handleAnnP1_53
T_poll__handleAnnP1_55
T_poll__handleAnnP1_56
T_poll__handleAnnP1_57
T_poll__handleAnnP1_59
T_poll__handleAnnP1_60
T_poll__handleAnnP1_93
T_poll__handleAnsP3_459
T_poll__handleAnsP3_460
T_poll__handleAnsP3_463
T_poll__handleAnsP3_464
T_poll__handleAnsP3_466
T_poll__handleAnsP3_468
T_poll__handleAnsP3_470
T_poll__handleAnsP3_472
T_poll__handleAnsP3_474
T_poll__handleAnsP3_475
T_poll__handleAnsP3_478
T_poll__handleAnsP3_479
T_poll__handleAnsP3_491
T_poll__handleAnnP1_73
T_poll__handleAnnP1_74
T_poll__handleAnnP1_76
T_poll__handleAnnP1_77
T_poll__handleAnnP1_78
T_poll__handleAnnP1_80
T_poll__handleAnnP1_81
T_poll__handleAnnP1_82
T_poll__handleAnnP1_84
T_poll__handleAnnP1_85
T_poll__handleAnnP1_86
T_poll__handleAnnP1_88
T_poll__handleAnnP1_89
T_poll__handleAnnP1_90
T_poll__handleAnnP1_92
T_poll__handleAnsP3_344
T_poll__handleAnsP3_342
T_poll__handleAnnP1_96
T_poll__handleAnnP1_97
T_poll__handleAnnP1_103
T_poll__handleAnnP1_119
T_poll__handleAnnP1_99
T_poll__handleAnnP1_101
T_poll__handleAnnP1_102
T_poll__handleAnnP1_105
T_poll__handleAnnP1_106
T_poll__handleAnnP1_111
T_poll__handleAnnP1_107
T_poll__handleAnnP1_109
T_poll__handleAnnP1_110
T_poll__handleAnnP1_113
T_poll__handleAnnP1_114
T_poll__handleAnnP1_115
T_poll__handleAnnP1_117
T_poll__handleAnnP1_118
T_poll__handleAnsP2_103
T_poll__handleAnsP2_123
T_poll__handleAnnP1_121
T_poll__handleAnnP1_122
T_poll__handleAnnP1_123
T_poll__handleAnnP1_125
T_poll__handleAnnP1_127
T_poll__handleAnnP1_126
T_poll__handleAnnP2_1
T_poll__handleAnnP2_2
T_poll__handleAnnP2_3
T_poll__handleAnnP2_4
T_poll__handleAnnP2_5
T_poll__handleAnnP2_6
T_poll__handleAnnP2_7
T_poll__handleAnnP2_8
T_poll__handleAnnP2_9
T_poll__handleAnnP2_10
T_poll__handleAnnP2_11
T_poll__handleAnnP2_12
T_poll__handleAnnP2_13
T_poll__handleAnnP2_14
T_poll__handleAnnP2_15
T_poll__handleAnnP2_16
T_poll__handleAnsP1_1
T_poll__handleAnsP1_2
T_poll__handleAskP_31
T_poll__handleAskP_32
T_poll__handleAskP_33
T_poll__handleAnsP1_6
T_poll__handleAnsP1_9
T_poll__handleAnsP1_11
T_poll__handleAnsP1_13
T_poll__handleAnsP4_30
T_poll__handleAnsP1_16
T_poll__handleAnsP2_3
T_poll__handleAnsP2_4
T_poll__handleAnsP2_5
T_poll__handleAnsP2_6
T_poll__iAmSecondary_4
T_poll__handleAnsP2_7
T_poll__handleAnsP2_8
T_poll__handleAnsP2_11
T_poll__handleAnsP2_12
T_poll__handleAnsP2_13
T_poll__handleAnsP2_14
T_poll__handleAnsP2_15
T_poll__handleAnsP2_16
T_poll__handleAnsP2_19
T_poll__handleAnsP2_20
T_poll__handleAnsP2_21
T_poll__handleAnsP2_22
T_poll__handleAnsP2_23
T_poll__handleAnsP2_24
T_poll__handleAnsP2_27
T_poll__handleAnsP2_28
T_poll__handleAnsP2_29
T_poll__handleAnsP2_30
T_poll__handleAnsP2_31
T_poll__handleAnsP2_32
T_poll__handleAnsP2_35
T_poll__handleAnsP2_36
T_poll__handleAnsP2_37
T_poll__handleAnsP2_38
T_poll__handleAnsP2_39
T_poll__handleAnsP2_40
T_poll__handleAnsP2_43
T_poll__handleAnsP2_44
T_poll__handleAnsP2_45
T_poll__handleAnsP2_46
T_poll__handleAnsP2_47
T_poll__handleAnsP2_48
T_poll__handleAnsP2_51
T_poll__handleAnsP2_52
T_poll__handleAskP_60
T_poll__handleAskP_61
T_poll__handleAskP_62
T_poll__handleAskP_63
T_poll__handleAskP_64
T_poll__handleAskP_65
T_poll__handleAskP_67
T_poll__handleAskP_69
T_poll__handleAskP_70
T_poll__handleAnsP2_60
T_poll__handleAnsP2_61
T_poll__handleAnsP2_62
T_poll__handleAnsP2_63
T_poll__handleAnsP2_64
T_poll__handleAnsP2_67
T_poll__handleAnsP2_68
T_poll__handleAnsP2_69
T_poll__handleAnsP2_70
T_poll__handleAnsP2_71
T_poll__handleAnsP2_72
T_poll__handleAnsP2_75
T_poll__handleAnsP2_76
T_poll__handleAnsP2_77
T_poll__handleAnsP2_78
T_poll__handleAnsP2_79
T_poll__handleAnsP2_80
T_poll__handleAnsP2_83
T_poll__handleAnsP2_84
T_poll__handleAnsP2_85
T_poll__handleAnsP2_86
T_poll__handleAnsP2_87
T_poll__handleAnsP2_88
T_poll__handleAnsP2_91
T_poll__handleAnsP2_92
T_poll__handleAnsP2_93
T_poll__handleAnsP2_94
T_poll__handleAnsP2_95
T_poll__handleAnsP2_96
T_poll__handleAnsP2_99
T_poll__handleAnsP2_100
T_poll__handleAnsP2_101
T_poll__handleAnsP2_102
T_poll__handleAnsP2_104
T_poll__handleAnsP2_107
T_poll__handleAnsP2_108
T_poll__handleAnsP2_109
T_poll__handleAnsP2_110
T_poll__handleAnsP2_111
T_poll__handleAnsP2_112
T_poll__handleAnsP2_115
T_poll__handleAnsP2_116
T_poll__handleAnsP2_117
T_poll__handleAnsP2_118
T_poll__handleAnsP2_119
T_poll__handleAnsP2_120
T_poll__handleAnsP4_112
T_poll__handleAnsP4_111
T_poll__handleAnsP2_124
T_poll__handleAnsP2_125
T_poll__handleAnsP2_126
T_poll__handleAnsP2_127
T_poll__handleAnsP2_128
T_poll__handleAnsP3_11
T_poll__handleAnsP3_12
T_poll__handleAnsP3_15
T_poll__handleAnsP3_16
T_poll__handleAnsP3_18
T_poll__handleAnsP3_20
T_poll__handleAnsP3_22
T_poll__handleAnsP3_24
T_poll__handleAnsP3_26
T_poll__handleAnsP3_27
T_poll__handleAnsP3_30
T_poll__handleAnsP3_31
T_poll__handleAnsP3_43
T_poll__handleAnsP3_44
T_poll__handleAnsP3_47
T_poll__handleAnsP3_48
T_poll__handleAnsP3_50
T_poll__handleAnsP3_52
T_poll__handleAnsP3_54
T_poll__handleAnsP3_56
T_poll__handleAnsP3_58
T_poll__handleAnsP3_59
T_poll__handleAnsP3_62
T_poll__handleAnsP3_63
T_poll__handleAnsP3_75
T_poll__handleAnsP3_76
T_poll__handleAnsP3_79
T_poll__handleAnsP3_80
T_poll__handleAnsP3_82
T_poll__handleAnsP3_84
T_poll__handleAnsP3_86
T_poll__handleAnsP3_88
T_poll__handleAnsP3_90
T_poll__handleAnsP3_91
T_poll__handleAnsP3_94
T_poll__handleAnsP3_95
T_poll__handleAnsP3_107
T_poll__handleAnsP3_108
T_poll__handleAnsP3_111
T_poll__handleAnsP3_112
T_poll__handleAnsP3_114
T_poll__handleAnsP3_116
T_poll__handleAnsP3_118
T_poll__handleAnsP3_120
T_poll__handleAnsP3_122
T_poll__handleAnsP3_123
T_poll__handleAnsP3_127
T_poll__handleAnsP3_126
T_poll__handleAnsP3_140
T_poll__handleAnsP3_139
T_poll__handleAnsP3_146
T_poll__handleAnsP3_210
T_poll__handleAnsP3_212
T_poll__handleAnsP3_214
T_poll__handleAnsP3_216
T_poll__handleAnsP3_218
T_poll__handleAnsP3_219
T_poll__handleAnsP3_222
T_poll__handleAnsP3_223
T_poll__handleAnsP3_235
T_poll__handleAnsP3_236
T_poll__handleAnsP3_239
T_poll__handleAnsP3_240
T_poll__handleAnsP3_242
T_poll__handleAnsP3_244
T_poll__handleAnsP3_246
T_poll__handleAnsP3_248
T_poll__handleAnsP3_250
T_poll__handleAnsP3_251
T_poll__handleAnsP3_254
T_poll__handleAnsP3_255
T_poll__handleAnsP3_267
T_poll__handleAnsP3_268
T_poll__handleAnsP3_271
T_poll__handleAnsP3_272
T_poll__handleAnsP3_274
T_poll__handleAnsP3_276
T_poll__handleAnsP3_278
T_poll__handleAnsP3_280
T_poll__handleAnsP3_282
T_poll__handleAnsP3_283
T_poll__handleAnsP3_286
T_poll__handleAnsP3_287
T_poll__handleAnsP3_299
T_poll__handleAnsP3_300
T_poll__handleAnsP3_303
T_poll__handleAnsP3_304
T_poll__handleAnsP3_306
T_poll__handleAnsP3_308
T_poll__handleAnsP3_310
T_poll__handleAnsP3_312
T_poll__handleAnsP3_314
T_poll__handleAnsP3_315
T_poll__handleAnsP3_318
T_poll__handleAnsP3_319
T_poll__handleAnsP3_331
T_poll__handleAnsP3_332
T_poll__handleAnsP3_335
T_poll__handleAnsP3_336
T_poll__handleAnsP3_338
T_poll__handleAnsP3_340
T_poll__handleAnsP3_346
T_poll__handleAnsP3_347
T_poll__handleAnsP3_350
T_poll__handleAnsP3_351
T_poll__handleAnsP3_363
T_poll__handleAnsP3_364
T_poll__handleAnsP3_367
T_poll__handleAnsP3_368
T_poll__handleAnsP3_370
T_poll__handleAnsP3_372
T_poll__handleAnsP3_374
T_poll__handleAnsP3_376
T_poll__handleAnsP3_378
T_poll__handleAnsP3_379
T_poll__handleAnsP3_382
T_poll__handleAnsP3_383
T_poll__handleAnsP3_395
T_poll__handleAnsP3_399
T_poll__handleAnsP3_396
T_poll__handleAnsP3_400
T_poll__handleAnsP3_402
T_poll__handleAnsP3_404
T_poll__handleAnsP3_406
T_poll__handleAnsP3_408
T_poll__handleAnsP3_410
T_poll__handleAnsP3_411
T_poll__handleAnsP3_414
T_poll__handleAnsP3_415
T_poll__handleAnsP3_427
T_poll__handleAnsP3_428
T_poll__handleAnsP3_431
T_poll__handleAnsP3_432
T_poll__handleAnsP3_434
T_poll__handleAnsP3_436
T_poll__handleAnsP3_438
T_poll__handleAnsP3_440
T_poll__handleAnsP3_442
T_poll__handleAnsP3_443
T_poll__handleAnsP3_446
T_poll__handleAnsP3_447
T_poll__handleAnsP3_492
T_poll__handleAnsP3_495
T_poll__handleAnsP3_496
T_poll__handleAnsP3_498
T_poll__handleAnsP3_500
T_poll__handleAnsP3_502
T_poll__handleAnsP3_504
T_poll__handleAnsP3_506
T_poll__handleAnsP3_507
T_poll__handleAnsP3_510
T_poll__handleAnsP3_511
T_poll__handleAnsP4_3
T_poll__handleAnsP4_4
T_poll__handleAnsP4_5
T_poll__iAmPrimary_3
T_poll__handleAnsP4_6
T_poll__handleAnsP4_7
T_poll__handleAnsP4_8
T_poll__handleAnsP4_11
T_poll__handleAnsP4_12
T_poll__handleAnsP4_13
T_poll__handleAnsP4_14
T_poll__handleAnsP4_15
T_poll__handleAnsP4_16
T_poll__handleAnsP4_19
T_poll__handleAnsP4_20
T_poll__handleAnsP4_21
T_poll__handleAnsP4_22
T_poll__handleAnsP4_23
T_poll__handleAnsP4_24
T_poll__handleAnsP4_27
T_poll__handleAnsP4_28
T_poll__handleAnsP4_29
T_poll__handleAnsP4_31
T_poll__handleAnsP4_32
T_poll__handleAnsP4_35
T_poll__handleAnsP4_36
T_poll__handleAnsP4_37
T_poll__handleAnsP4_38
T_poll__handleAnsP4_39
T_poll__handleAnsP4_40
T_poll__handleAnsP4_43
T_poll__handleAnsP4_44
T_poll__handleAnsP4_45
T_poll__handleAnsP4_46
T_poll__handleAnsP4_47
T_poll__handleAnsP4_48
T_poll__handleAnsP4_51
T_poll__handleAnsP4_52
T_poll__handleAnsP4_53
T_poll__handleAnsP4_54
T_poll__handleAnsP4_55
T_poll__handleAnsP4_56
T_poll__handleAnsP4_59
T_poll__handleAnsP4_60
T_poll__handleAnsP4_61
T_poll__handleAnsP4_62
T_poll__handleAnsP4_63
T_poll__handleAnsP4_64
T_poll__handleAnsP4_67
T_poll__handleAnsP4_68
T_poll__handleAnsP4_69
T_poll__handleAnsP4_70
T_poll__handleAnsP4_71
T_poll__handleAnsP4_72
T_poll__handleAnsP4_75
T_poll__handleAnsP4_76
T_poll__handleAnsP4_77
T_poll__handleAnsP4_78
T_poll__handleAnsP4_79
T_poll__handleAnsP4_80
T_poll__handleAnsP4_83
T_poll__handleAnsP4_84
T_poll__handleAnsP4_85
T_poll__handleAnsP4_86
T_poll__handleAnsP4_87
T_poll__handleAnsP4_88
T_poll__handleAnsP4_91
T_poll__handleAnsP4_92
T_poll__handleAnsP4_93
T_poll__handleAnsP4_110
T_poll__handleAnsP4_94
T_poll__handleAnsP4_95
T_poll__handleAnsP4_96
T_poll__handleAnsP4_99
T_poll__handleAnsP4_100
T_poll__handleAnsP4_101
T_poll__handleAnsP4_102
T_poll__handleAnsP4_103
T_poll__handleAnsP4_104
T_poll__handleAnsP4_107
T_poll__handleAnsP4_108
T_poll__handleAnsP4_109
T_poll__handleAnsP4_115
T_poll__handleAnsP4_116
T_poll__handleAnsP4_117
T_poll__handleAnsP4_118
T_poll__handleAnsP4_119
T_poll__handleAnsP4_120
T_poll__handleAnsP4_123
T_poll__handleAnsP4_124
T_poll__handleAnsP4_125
T_poll__handleAnsP4_126
T_poll__handleAnsP4_127
T_poll__handleAnsP4_128
T_poll__handleAskP_1
T_poll__handleAskP_2
T_poll__handleAskP_3
T_poll__handleAskP_5
T_poll__handleAskP_6
T_poll__handleAskP_7
T_poll__handleAskP_8
T_poll__handleAskP_9
T_poll__handleAskP_10
T_poll__handleAskP_11
T_poll__handleAskP_12
T_poll__handleAskP_13
T_poll__handleAskP_14
T_poll__handleAskP_15
T_poll__handleAskP_16
T_poll__handleAskP_17
T_poll__handleAskP_18
T_poll__handleAskP_19
T_poll__handleAskP_20
T_poll__handleAskP_21
T_poll__handleAskP_22
T_poll__handleAskP_23
T_poll__handleAskP_24
T_poll__handleAskP_25
T_poll__handleAskP_26
T_poll__handleAskP_27
T_poll__handleAskP_28
T_poll__handleAskP_29
T_poll__handleAskP_30
T_poll__handleAskP_34
T_poll__handleAskP_37
T_poll__handleAskP_38
T_poll__handleAskP_39
T_poll__handleAskP_40
T_poll__handleAskP_41
T_poll__handleAskP_42
T_poll__handleAskP_43
T_poll__handleAskP_44
T_poll__handleAskP_45
T_poll__handleAskP_46
T_poll__handleAskP_47
T_poll__handleAskP_48
T_poll__handleAskP_49
T_poll__handleAskP_50
T_poll__handleAskP_53
T_poll__handleAskP_54
T_poll__handleAskP_55
T_poll__iAmPrimary_4
T_poll__handleAskP_56
T_poll__handleAskP_57
T_poll__handleAskP_58
T_poll__handleAskP_59
T_poll__start_1
T_poll__handleAskP_71
T_poll__handleAskP_72
T_poll__handleAskP_73
T_poll__handleAskP_74
T_poll__handleAskP_75
T_poll__handleAskP_76
T_poll__handleAskP_77
T_poll__handleAskP_78
T_poll__handleAskP_79
T_poll__handleAskP_80
T_poll__handleAskP_81
T_poll__handleAskP_83
T_poll__handleAskP_85
T_poll__handleAskP_86
T_poll__handleAskP_87
T_poll__handleAskP_88
T_poll__handleAskP_89
T_poll__handleAskP_90
T_poll__handleAskP_91
T_poll__handleAskP_92
T_poll__handleAskP_93
T_poll__handleAskP_94
T_poll__handleAskP_95
T_poll__handleAskP_96
T_poll__handleAskP_97
T_poll__handleAskP_98
T_poll__handleAskP_99
T_poll__handleAskP_100
T_poll__handleAskP_101
T_poll__handleAskP_102
T_poll__handleAskP_103
T_poll__handleAskP_104
T_poll__handleAskP_105
T_poll__handleAskP_106
T_poll__handleAskP_107
T_poll__handleAskP_108
T_poll__handleAskP_109
T_poll__handleAskP_110
T_poll__handleAskP_111
T_poll__handleAskP_112
T_poll__handleAskP_113
T_poll__handleAskP_116
T_poll__handleAskP_117
T_poll__handleAskP_118
T_poll__handleAskP_119
T_poll__handleAskP_120
T_poll__handleAskP_121
T_poll__handleAskP_122
T_poll__handleAskP_123
T_poll__handleAskP_124
T_poll__handleAskP_125
T_poll__handleAskP_126
T_poll__handleAskP_127
T_poll__iAmSecondary_9
T_poll__handleAskP_128
T_poll__handleRI_2
T_poll__handleRI_1
T_poll__handleRI_3
T_poll__handleRI_4
T_poll__handleRI_5
T_poll__handleRI_6
T_poll__handleRI_9
T_poll__handleRI_11
T_poll__handleRI_13
T_poll__handleRI_16
T_poll__handleRP_1
T_poll__handleRP_2
T_poll__handleRP_3
T_poll__handleRP_4
T_poll__handleRP_5
T_poll__handleRP_6
T_poll__handleRP_7
T_poll__handleRP_8
T_poll__handleRP_9
T_poll__handleRP_10
T_poll__handleRP_11
T_poll__handleRP_12
T_poll__handleRP_13
T_poll__handleRP_14
T_poll__handleRP_15
T_poll__handleRP_16
T_poll__iAmPrimary_1
T_sendAnnPs__end_2
T_poll__iAmPrimary_2
T_poll__iAmSecondary_5
T_poll__iAmSecondary_3
T_poll__iAmSecondary_6
T_poll__iAmSecondary_7
T_poll__iAmSecondary_10
T_poll__iAmSecondary_8
T_poll__iAmSecondary_11
T_poll__iAmSecondary_14
T_poll__iAmSecondary_12
T_poll__iAmSecondary_15
T_poll__iAmSecondary_16
T_sendAnnPs__end_1
T_sendAnnPs__end_3
T_sendAnnPs__end_4
T_sendAnnPs__send_1
T_sendAnnPs__send_2
T_sendAnnPs__send_3
T_sendAnnPs__send_4
T_sendAnnPs__send_5
T_sendAnnPs__send_6
T_sendAnnPs__send_7
T_sendAnnPs__send_8
T_sendAnnPs__send_13
T_sendAnnPs__send_14
T_sendAnnPs__send_15
T_sendAnnPs__send_16
T_sendAnnPs__send_17
T_sendAnnPs__send_18
T_sendAnnPs__send_19
T_sendAnnPs__send_20
T_sendAnnPs__send_25
T_sendAnnPs__send_26
T_sendAnnPs__send_27
T_sendAnnPs__send_28
T_sendAnnPs__send_29
T_sendAnnPs__send_30
T_sendAnnPs__send_31
T_sendAnnPs__send_32
T_sendAnnPs__send_37
T_sendAnnPs__send_38
T_sendAnnPs__send_39
T_sendAnnPs__send_40
T_sendAnnPs__send_41
T_sendAnnPs__send_42
T_sendAnnPs__send_43
T_sendAnnPs__send_44
T_sendAnnPs__start_1
T_sendAnnPs__start_2
T_sendAnnPs__start_3
T_sendAnnPs__start_4
T_startNeg__end_1
T_startNeg__send_1
T_startNeg__send_2
T_startNeg__send_3
T_startNeg__send_4
T_startNeg__send_5
T_startNeg__send_6
T_startNeg__send_7
T_startNeg__send_8
T_startNeg__send_13
T_startNeg__send_14
T_startNeg__send_16
T_startNeg__send_17
T_startNeg__send_18
T_startNeg__send_19
T_startNeg__send_25
T_startNeg__send_27
T_startNeg__send_28
T_startNeg__send_29
T_startNeg__send_30
T_startNeg__send_31
T_startNeg__send_37
T_startNeg__send_39
T_startNeg__send_40
T_startNeg__send_41
T_startNeg__send_42
T_startNeg__send_44
T_startNeg__start_1
T_startSec_1
T_startSec_2
T_startSec_3
T_startSec_4
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m 0.008sec
1848 2767 3409 3674 4186 4641 8645 10863 19702 34624 41454 48712 64913 80436 87198 90732 101028 104489 124146 124160 124177 124233 152050 152057 152088 152116
iterations count:26689 (26), effective:107 (0)
initing FirstDep: 0m 0.008sec
152061
iterations count:1016 (1), effective:0 (0)
152061
iterations count:1016 (1), effective:0 (0)
152061
iterations count:1016 (1), effective:0 (0)
152061
iterations count:1016 (1), effective:0 (0)
152061
iterations count:1056 (1), effective:1 (0)
152061
iterations count:1016 (1), effective:0 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-3"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/root/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-3.tgz
mv NeoElection-PT-3 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is NeoElection-PT-3, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r077kn-smll-146363815900084"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

