About the Execution of Marcie for LamportFastMutEx-PT-2
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 5417.060 | 6605.00 | 6030.00 | 20.00 | TTTFFFTTTFTTTFFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
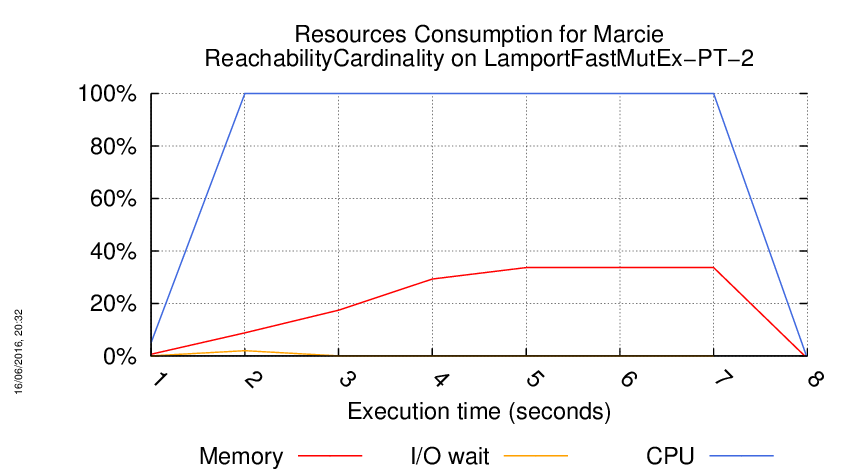
Trace from the execution
Waiting for the VM to be ready (probing ssh)
........
=====================================================================
Generated by BenchKit 2-2979
Executing tool marcie
Input is LamportFastMutEx-PT-2, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r065kn-blw3-146358913500241
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-0
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-1
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-10
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-11
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-12
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-13
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-14
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-15
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-2
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-3
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-4
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-5
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-6
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-7
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-8
FORMULA_NAME LamportFastMutEx-COL-2-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1463730854899
Marcie rev. 8535M (built: crohr on 2016-04-27)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --mcc-mode --memory=6 --suppress
parse successfull
net created successfully
Net: LamportFastMutEx_PT_2
(NrP: 69 NrTr: 96 NrArc: 402)
net check time: 0m 0.000sec
parse formulas
formulas created successfully
place and transition orderings generation:0m 0.000sec
init dd package: 0m 3.740sec
RS generation: 0m 0.061sec
-> reachability set: #nodes 689 (6.9e+02) #states 380
starting MCC model checker
--------------------------
checking: AG [~ [~ [~ [3<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]]]
normalized: ~ [E [true U 3<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]
abstracting: (3<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 0
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.027sec
checking: AG [3<=sum(P_await_13_2, P_await_13_1, P_await_13_0)]
normalized: ~ [E [true U ~ [3<=sum(P_await_13_2, P_await_13_1, P_await_13_0)]]]
abstracting: (3<=sum(P_await_13_2, P_await_13_1, P_await_13_0)) states: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-7 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.053sec
checking: EF [3<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)]
normalized: E [true U 3<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)]
abstracting: (3<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)) states: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.026sec
checking: EF [2<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]
normalized: E [true U 2<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]
abstracting: (2<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 380
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-2 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.029sec
checking: AG [[sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) | ~ [~ [2<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]]]
normalized: ~ [E [true U ~ [[sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) | 2<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]]]
abstracting: (2<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 4
abstracting: (sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 348
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-3 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.097sec
checking: AG [~ [~ [[sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0) | 1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]]
normalized: ~ [E [true U ~ [[sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0) | 1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]]
abstracting: (1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 42
abstracting: (sum(y_2, y_1, y_0)<=sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)) states: 58
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.065sec
checking: EF [[[~ [1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)] | 1<=sum(P_start_1_2, P_start_1_1, P_start_1_0)] | ~ [[1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & 1<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]]]]
normalized: E [true U [~ [[1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & 1<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]] | [1<=sum(P_start_1_2, P_start_1_1, P_start_1_0) | ~ [1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]]]
abstracting: (1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)) states: 32
abstracting: (1<=sum(P_start_1_2, P_start_1_1, P_start_1_0)) states: 69
abstracting: (1<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 24
abstracting: (1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)) states: 32
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-4 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.117sec
checking: EF [~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(x_2, x_1, x_0)]]
normalized: E [true U ~ [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(x_2, x_1, x_0)]]
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(x_2, x_1, x_0)) states: 348
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.057sec
checking: EF [sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]
normalized: E [true U sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]
abstracting: (sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 292
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.041sec
checking: EF [~ [[[1<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] | [sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false) | 2<=sum(P_awaity_2, P_awaity_1, P_awaity_0)]]]]
normalized: E [true U ~ [[[sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false) | 2<=sum(P_awaity_2, P_awaity_1, P_awaity_0)] | [1<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]]
abstracting: (1<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 42
abstracting: (1<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)) states: 32
abstracting: (2<=sum(P_awaity_2, P_awaity_1, P_awaity_0)) states: 0
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 380
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.112sec
checking: EF [[~ [[1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | 3<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]] & [~ [sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)] | sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)]]]
normalized: E [true U [~ [[1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | 3<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]] & [sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0) | ~ [sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]]]
abstracting: (sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 380
abstracting: (sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)) states: 330
abstracting: (3<=sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)) states: 0
abstracting: (1<=sum(P_await_13_2, P_await_13_1, P_await_13_0)) states: 112
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.129sec
checking: EF [~ [[2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0) & [1<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(x_2, x_1, x_0)]]]]
normalized: E [true U ~ [[2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0) & [1<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) & sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(x_2, x_1, x_0)]]]]
abstracting: (sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(x_2, x_1, x_0)) states: 376
abstracting: (1<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)) states: 80
abstracting: (2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)) states: 32
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.086sec
checking: EF [[[3<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) & [3<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0) | sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]] & [1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | [1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]]]]
normalized: E [true U [[1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | [1<=sum(P_await_13_2, P_await_13_1, P_await_13_0) | sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]] & [3<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) & [3<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0) | sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)) states: 324
abstracting: (3<=sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)) states: 0
abstracting: (3<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 0
abstracting: (sum(P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 308
abstracting: (1<=sum(P_await_13_2, P_await_13_1, P_await_13_0)) states: 112
abstracting: (1<=sum(P_await_13_2, P_await_13_1, P_await_13_0)) states: 112
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-13 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.172sec
checking: EF [[[[2<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) | sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)] & 1<=sum(y_2, y_1, y_0)] | 1<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]
normalized: E [true U [1<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false) | [1<=sum(y_2, y_1, y_0) & [2<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0) | sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)]]]]
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)) states: 348
abstracting: (2<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 0
abstracting: (1<=sum(y_2, y_1, y_0)) states: 380
abstracting: (1<=sum(P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 380
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.120sec
checking: AG [[sum(x_2, x_1, x_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | [[sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0) | 1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)] | [sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]]
normalized: ~ [E [true U ~ [[sum(x_2, x_1, x_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | [[sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] | [sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0) | 1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]]]]]
abstracting: (1<=sum(P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)) states: 32
abstracting: (sum(P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)<=sum(P_sety_9_2, P_sety_9_1, P_sety_9_0)) states: 352
abstracting: (sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 380
abstracting: (sum(P_CS_21_2, P_CS_21_1, P_CS_21_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 326
abstracting: (sum(x_2, x_1, x_0)<=sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)) states: 64
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.145sec
checking: AG [~ [[[sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) | sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)] | [sum(y_2, y_1, y_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) | 2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)]]]]
normalized: ~ [E [true U [[sum(y_2, y_1, y_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0) | 2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)] | [sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) | sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]]]
abstracting: (sum(P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 317
abstracting: (sum(P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)<=sum(P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 320
abstracting: (2<=sum(P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_2, P_wait_0_1, P_wait_0_0)) states: 32
abstracting: (sum(y_2, y_1, y_0)<=sum(P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_2, P_done_0_1, P_done_0_0)) states: 80
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-2-ReachabilityCardinality-8 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m 0.117sec
Total processing time: 0m 6.568sec
BK_STOP 1463730861504
--------------------
content from stderr:
check for maximal unmarked siphon
found
The net has a maximal unmarked siphon:
P_start_1_0
P_fordo_12_0
P_wait_0_0
P_await_13_0
P_done_0_0
P_done_0_1
P_done_0_2
P_done_1_0
P_wait_0_1
P_wait_0_2
P_wait_1_0
P_wait_2_0
P_CS_21_0
P_setbi_24_0
P_ify0_4_0
P_sety_9_0
P_setx_3_0
P_b_0_true
P_b_0_false
P_setbi_5_0
P_done_2_0
P_ifyi_15_0
P_awaity_0
P_ifxi_10_0
P_setbi_11_0
The net has transition(s) that can never fire:
T_setx_3_2
T_setbi_11_2
T_setbi_2_1
T_setbi_11_1
T_setx_3_1
T_setbi_2_2
T_setx_3_3
T_yne0_4_2
T_yne0_4_3
T_sety_9_1
T_sety_9_2
T_setbi_5_1
T_setbi_5_2
T_awaity_1
T_yeq0_4_1
T_forod_13_1
T_sety_9_3
T_xnei_10_2
T_xnei_10_3
T_fordo_12_1
T_await_13_1
T_await_13_2
T_await_13_3
T_await_13_4
T_await_13_7
T_ynei_15_2
T_ynei_15_3
T_yeqi_15_1
T_xeqi_10_1
T_sety0_23_1
T_sety0_23_2
T_sety0_23_3
T_setbi_24_1
T_setbi_24_2
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
.........10 708............................................
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="LamportFastMutEx-PT-2"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/home/hulinhub/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/LamportFastMutEx-PT-2.tgz
mv LamportFastMutEx-PT-2 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2979"
echo " Executing tool marcie"
echo " Input is LamportFastMutEx-PT-2, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r065kn-blw3-146358913500241"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "UpperBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

