About the Execution of Marcie for S_Solitaire-PT-SqrNC5x5
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 4297.460 | 81298.00 | 80940.00 | 90.00 | TTTTTTTTTTTTTTTT | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
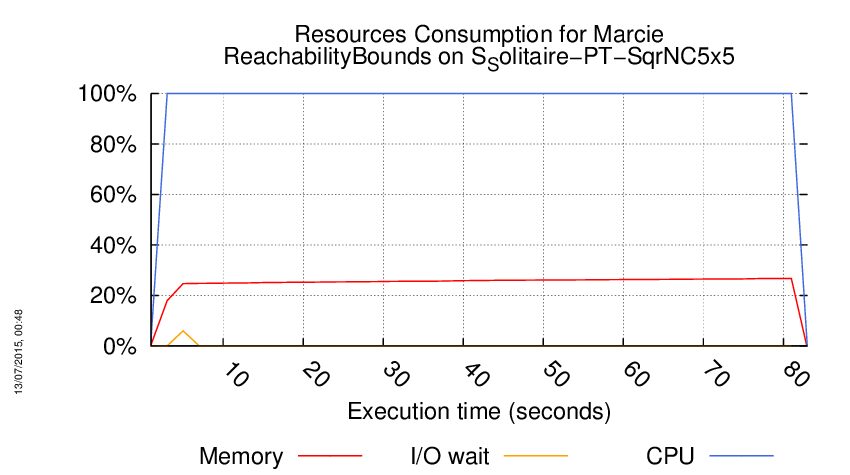
Trace from the execution
Waiting for the VM to be ready (probing ssh)
..................
=====================================================================
Generated by BenchKit 2-2270
Executing tool marcie
Input is S_Solitaire-PT-SqrNC5x5, examination is ReachabilityBounds
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r148st-smll-143305874000203
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-0
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-1
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-10
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-11
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-12
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-13
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-14
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-15
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-2
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-3
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-4
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-5
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-6
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-7
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-8
FORMULA_NAME Solitaire-PT-SqrNC5x5-ReachabilityBounds-9
=== Now, execution of the tool begins
BK_START 1433303053536
Model: S_Solitaire-PT-SqrNC5x5
reachability algorithm:
Saturation-based algorithm
variable ordering algorithm:
Calculated like in [Noa99]
--memory=6 --suppress --rs-algorithm=3 --place-order=5
Marcie rev. 1429:1432M (built: crohr on 2014-10-22)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityBounds.xml --memory=6 --suppress --rs-algorithm=3 --place-order=5
parse successfull
net created successfully
(NrP: 50 NrTr: 84 NrArc: 456)
net check time: 0m0sec
parse formulas successfull
formulas created successfully
place and transition orderings generation:0m0sec
init dd package: 0m3sec
RS generation: 1m11sec
-> reachability set: #nodes 64614 (6.5e+04) #states 16,098,428 (7)
starting MCC model checker
--------------------------
checking: [[[maxVal(F52)<=2 & [maxVal(F64)<=1 & maxVal(F55)<=2]] & maxVal(T64)<=3] & maxVal(F45)<=2]
normalized: [maxVal(F45)<=2 & [maxVal(T64)<=3 & [maxVal(F52)<=2 & [maxVal(F64)<=1 & maxVal(F55)<=2]]]]
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [maxVal(F44)<=2 & maxVal(F65)<=1]
normalized: [maxVal(F44)<=2 & maxVal(F65)<=1]
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [maxVal(T22)<=3 & maxVal(T26)<=3]
normalized: [maxVal(T22)<=3 & maxVal(T26)<=3]
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-2 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [[maxVal(F52)<=3 & maxVal(F26)<=1] & maxVal(T64)<=2]
normalized: [maxVal(T64)<=2 & [maxVal(F52)<=3 & maxVal(F26)<=1]]
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [maxVal(T65)<=1 & maxVal(T55)<=3]
normalized: [maxVal(T65)<=1 & maxVal(T55)<=3]
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-4 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [[maxVal(T64)<=3 & maxVal(F23)<=2] & [[[[[maxVal(T32)<=2 & maxVal(F25)<=3] & [maxVal(F46)<=1 & maxVal(F23)<=3]] & [maxVal(F34)<=1 & [maxVal(T42)<=3 & maxVal(T46)<=2]]] & [maxVal(F43)<=2 & [maxVal(T45)<=3 & [maxVal(T32)<=1 & maxVal(T34)<=2]]]] & [maxVal(F43)<=3 & maxVal(T23)<=1]]]
normalized: [[[maxVal(F43)<=3 & maxVal(T23)<=1] & [[[[maxVal(T32)<=2 & maxVal(F25)<=3] & [maxVal(F46)<=1 & maxVal(F23)<=3]] & [maxVal(F34)<=1 & [maxVal(T42)<=3 & maxVal(T46)<=2]]] & [maxVal(F43)<=2 & [maxVal(T45)<=3 & [maxVal(T32)<=1 & maxVal(T34)<=2]]]]] & [maxVal(T64)<=3 & maxVal(F23)<=2]]
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [maxVal(F33)<=2 & maxVal(T44)<=1]
normalized: [maxVal(F33)<=2 & maxVal(T44)<=1]
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [[[maxVal(F25)<=1 & maxVal(T42)<=1] & maxVal(T56)<=1] & maxVal(T46)<=2]
normalized: [maxVal(T46)<=2 & [maxVal(T56)<=1 & [maxVal(F25)<=1 & maxVal(T42)<=1]]]
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(T44)<=3
normalized: maxVal(T44)<=3
abstracting: (1<=3) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(F45)<=1
normalized: maxVal(F45)<=1
abstracting: (1<=1) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-9 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(T44)<=2
normalized: maxVal(T44)<=2
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [maxVal(T54)<=2 & [maxVal(T56)<=3 & [[[maxVal(F55)<=2 & [maxVal(F23)<=3 & maxVal(T66)<=2]] & [[maxVal(T52)<=1 & maxVal(T62)<=1] & maxVal(F64)<=3]] & [maxVal(T53)<=3 & [maxVal(T54)<=2 & [maxVal(F66)<=3 & maxVal(T65)<=1]]]]]]
normalized: [maxVal(T54)<=2 & [maxVal(T56)<=3 & [[maxVal(T53)<=3 & [maxVal(T54)<=2 & [maxVal(F66)<=3 & maxVal(T65)<=1]]] & [[maxVal(F55)<=2 & [maxVal(F23)<=3 & maxVal(T66)<=2]] & [maxVal(F64)<=3 & [maxVal(T52)<=1 & maxVal(T62)<=1]]]]]]
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-11 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(F34)<=1
normalized: maxVal(F34)<=1
abstracting: (1<=1) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-12 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(F62)<=3
normalized: maxVal(F62)<=3
abstracting: (1<=3) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: [[[[maxVal(F63)<=2 & [[maxVal(T45)<=3 & maxVal(T26)<=3] & [maxVal(F45)<=1 & maxVal(F25)<=2]]] & [[maxVal(F35)<=3 & [maxVal(T55)<=1 & maxVal(F24)<=3]] & [[maxVal(T25)<=2 & maxVal(T22)<=2] & maxVal(T32)<=1]]] & [maxVal(F63)<=1 & maxVal(T42)<=3]] & [maxVal(T22)<=1 & [[maxVal(T33)<=3 & [[maxVal(F23)<=1 & maxVal(T44)<=2] & [maxVal(F32)<=1 & maxVal(T32)<=3]]] & maxVal(T34)<=1]]]
normalized: [[maxVal(T22)<=1 & [maxVal(T34)<=1 & [maxVal(T33)<=3 & [[maxVal(F32)<=1 & maxVal(T32)<=3] & [maxVal(F23)<=1 & maxVal(T44)<=2]]]]] & [[maxVal(F63)<=1 & maxVal(T42)<=3] & [[maxVal(F63)<=2 & [[maxVal(T45)<=3 & maxVal(T26)<=3] & [maxVal(F45)<=1 & maxVal(F25)<=2]]] & [[maxVal(F35)<=3 & [maxVal(T55)<=1 & maxVal(F24)<=3]] & [maxVal(T32)<=1 & [maxVal(T25)<=2 & maxVal(T22)<=2]]]]]]
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=2) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=3) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
abstracting: (1<=1) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: maxVal(F34)<=3
normalized: maxVal(F34)<=3
abstracting: (1<=3) states: 16,098,428 (7)
-> the formula is TRUE
FORMULA Solitaire-PT-SqrNC5x5-ReachabilityBounds-15 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
Total processing time: 1m21sec
BK_STOP 1433303134834
--------------------
content from stderr:
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m0sec
352 853 1296 1071 2160 2578 4672 6752 5809 5264 5870 6692 7467 7192 6979 7087 7076 13917 14067 13857 12286 12114 10829 9910 10009 11940 11012 18515 17685 17350 16947 17721 17946 18113 18159 19008 18909 18069 17990 17755 13580 11933 12466 15208 12535 16728 15974 16428 21545 21155 22898 23004 20769 20650 20851 22021 22817 26478 27592 27597 26724 23052 23190 23880 26543 27039 26053 28990 29328 30843 30679 43477 64142 57626 59349 60069 61826 61902 63381 64477 62584 62895 60266 60582 57375 57561 66924 66403 58870 59515 59474 59857 59705 59764 58946 54952 55990 56179 59906 63235 59600 59044 57346 57102 57305 56570 58016 56829 56687 57966 57774 57794 58160 58022 56981 56719 55309 54878 53785 53286 52561 52904 52896 52479 51870 51109 50533 50775 50062 50219 50148 50297 50459 50375 50319 50221 50108 49708 49560 48659 48242 62599 73843 96659 102621 107103 109928 110876 111945 112471 114318 110522 112042 111181 108634 109234 109259 109557 109939 110363 108647 110040 110545 110327 110258 109646 111715 112003 112079 112460 111473 110402 110172 110096 98109 98766 92240 92327 91603 91442 91908 91742 91555 91226 94721 95739 95786 90894 89427 88323 88066 87359 85099 83130 83468 83471 82655 82521 81724 81772 81672 80322 77798 77419 77250 76473 75719 76008 74431 74575 74733 74672 74806 74244 71767 68428 69345 68984 69159 69353 69129 68550 68507 68418 68639 68145 68142 67982 67705 66648 66336 66311 66371 66024 65951 65668 65491 64968 64624
iterations count:239077 (2846), effective:18445 (219)
initing FirstDep: 0m0sec
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="S_Solitaire-PT-SqrNC5x5"
export BK_EXAMINATION="ReachabilityBounds"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/root/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/S_Solitaire-PT-SqrNC5x5.tgz
mv S_Solitaire-PT-SqrNC5x5 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2270"
echo " Executing tool marcie"
echo " Input is S_Solitaire-PT-SqrNC5x5, examination is ReachabilityBounds"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r148st-smll-143305874000203"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityBounds" = "ReachabilityComputeBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityBounds" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityBounds.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityBounds.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityBounds.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

