About the Execution of Marcie for QuasiCertifProtocol-PT-06
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 7179.070 | 2789617.00 | 2789020.00 | 20.00 | TTTFFTFFTTFTTFTF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
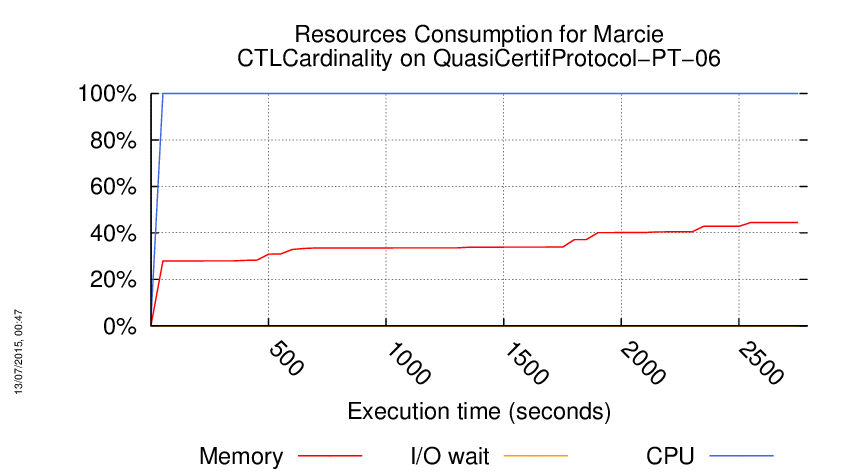
Trace from the execution
Waiting for the VM to be ready (probing ssh)
............
=====================================================================
Generated by BenchKit 2-2265
Executing tool marcie
Input is QuasiCertifProtocol-PT-06, examination is CTLCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r078kn-ebro-143262779400860
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-0
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-1
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-10
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-11
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-12
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-13
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-14
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-15
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-2
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-3
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-4
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-5
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-6
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-7
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-8
FORMULA_NAME QuasiCertifProtocol-COL-06-CTLCardinality-9
=== Now, execution of the tool begins
BK_START 1432913538730
Model: QuasiCertifProtocol-PT-06
reachability algorithm:
Saturation-based algorithm
variable ordering algorithm:
Calculated like in [Noa99]
--memory=6 --suppress --rs-algorithm=3 --place-order=5
Marcie rev. 1429:1432M (built: crohr on 2014-10-22)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=CTLCardinality.xml --memory=6 --suppress --rs-algorithm=3 --place-order=5
parse successfull
net created successfully
(NrP: 270 NrTr: 116 NrArc: 659)
net check time: 0m0sec
parse formulas successfull
formulas created successfully
place and transition orderings generation:0m0sec
init dd package: 0m5sec
RS generation: 0m26sec
-> reachability set: #nodes 218170 (2.2e+05) #states 2,271,960 (6)
starting MCC model checker
--------------------------
checking: E [[[AstopAbort<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1) & sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)] | sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0)<=malicious_reservoir] U [~ [sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)] & sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)]]
normalized: E [[sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0)<=malicious_reservoir | [AstopAbort<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1) & sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)]] U [sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0) & ~ [sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)]]]
abstracting: (sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)) states: 2,255,704 (6)
abstracting: (sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)) states: 2,255,704 (6)
abstracting: (sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)) states: 2,030,944 (6)
abstracting: (AstopAbort<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)) states: 2,255,384 (6)
abstracting: (sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0)<=malicious_reservoir) states: 1,920,522 (6)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 5m29sec
checking: [~ [~ [AX [sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)<=CstopAbort]]] & [~ [1<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)] & ~ [AF [3<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)]]]]
normalized: [[EG [~ [3<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)]] & ~ [1<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)]] & ~ [EX [~ [sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)<=CstopAbort]]]]
abstracting: (sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)<=CstopAbort) states: 581,457 (5)
.abstracting: (1<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)) states: 1,580,304 (6)
abstracting: (3<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)) states: 1,567,760 (6)
..........
EG iterations: 10
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m33sec
checking: EF [E [sum(Cstart_0, Cstart_1, Cstart_6, Cstart_2, Cstart_3, Cstart_4, Cstart_5)<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0) U sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n5_6, n5_1, n5_0, n5_3, n5_2, n5_5, n5_4)]]
normalized: E [true U E [sum(Cstart_0, Cstart_1, Cstart_6, Cstart_2, Cstart_3, Cstart_4, Cstart_5)<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0) U sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n5_6, n5_1, n5_0, n5_3, n5_2, n5_5, n5_4)]]
abstracting: (sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n5_6, n5_1, n5_0, n5_3, n5_2, n5_5, n5_4)) states: 2,256,270 (6)
abstracting: (sum(Cstart_0, Cstart_1, Cstart_6, Cstart_2, Cstart_3, Cstart_4, Cstart_5)<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)) states: 1,916,661 (6)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-2 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m59sec
checking: [[[AF [sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(s5_6, s5_4, s5_5, s5_2, s5_3, s5_0, s5_1)] & [[CstopAbort<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6) | a5<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)] | [3<=a3 & sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)<=a4]]] & sum(n4_0, n4_2, n4_1, n4_4, n4_3, n4_6, n4_5)<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)] & sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=a5]
normalized: [sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=a5 & [sum(n4_0, n4_2, n4_1, n4_4, n4_3, n4_6, n4_5)<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0) & [[[3<=a3 & sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)<=a4] | [CstopAbort<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6) | a5<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)]] & ~ [EG [~ [sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(s5_6, s5_4, s5_5, s5_2, s5_3, s5_0, s5_1)]]]]]]
abstracting: (sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(s5_6, s5_4, s5_5, s5_2, s5_3, s5_0, s5_1)) states: 2,256,270 (6)
.............
EG iterations: 13
abstracting: (a5<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)) states: 2,103,128 (6)
abstracting: (CstopAbort<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)) states: 512,244 (5)
abstracting: (sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)<=a4) states: 2,240,580 (6)
abstracting: (3<=a3) states: 0
abstracting: (sum(n4_0, n4_2, n4_1, n4_4, n4_3, n4_6, n4_5)<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)) states: 2,255,704 (6)
abstracting: (sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)<=a5) states: 2,255,704 (6)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 7m47sec
checking: [E [[AstopAbort<=a3 | a3<=a5] U [1<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0) & 3<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)]] & AG [~ [2<=AstopOK]]]
normalized: [~ [E [true U 2<=AstopOK]] & E [[AstopAbort<=a3 | a3<=a5] U [1<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0) & 3<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)]]]
abstracting: (3<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)) states: 13,852 (4)
abstracting: (1<=sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)) states: 5,232 (3)
abstracting: (a3<=a5) states: 2,263,768 (6)
abstracting: (AstopAbort<=a3) states: 1,465,232 (6)
abstracting: (2<=AstopOK) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-4 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m39sec
checking: EF [~ [EF [3<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)]]]
normalized: E [true U ~ [E [true U 3<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)]]]
abstracting: (3<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)) states: 54,942 (4)
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-5 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m45sec
checking: EG [A [3<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6) U a2<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)]]
normalized: EG [[~ [EG [~ [a2<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)]]] & ~ [E [~ [3<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)] U [~ [3<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)] & ~ [a2<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)]]]]]]
abstracting: (a2<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)) states: 2,271,896 (6)
abstracting: (3<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)) states: 12,672 (4)
abstracting: (3<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)) states: 12,672 (4)
abstracting: (a2<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)) states: 2,271,896 (6)
.....
EG iterations: 5
.
EG iterations: 1
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 5m44sec
checking: ~ [~ [~ [EG [sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=a5]]]]
normalized: ~ [EG [sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=a5]]
abstracting: (sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=a5) states: 2,255,704 (6)
.
EG iterations: 1
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-7 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m18sec
checking: [A [2<=CstopAbort U 2<=a3] | ~ [[AF [malicious_reservoir<=sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)] | 3<=a4]]]
normalized: [~ [[3<=a4 | ~ [EG [~ [malicious_reservoir<=sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)]]]]] | [~ [EG [~ [2<=a3]]] & ~ [E [~ [2<=CstopAbort] U [~ [2<=CstopAbort] & ~ [2<=a3]]]]]]
abstracting: (2<=a3) states: 0
abstracting: (2<=CstopAbort) states: 1,031,121 (6)
abstracting: (2<=CstopAbort) states: 1,031,121 (6)
abstracting: (2<=a3) states: 0
EG iterations: 0
abstracting: (malicious_reservoir<=sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)) states: 2,037,717 (6)
...................................
EG iterations: 35
abstracting: (3<=a4) states: 0
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-8 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m16sec
checking: ~ [EF [EG [sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=malicious_reservoir]]]
normalized: ~ [E [true U EG [sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=malicious_reservoir]]]
abstracting: (sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)<=malicious_reservoir) states: 2,256,516 (6)
.....
EG iterations: 5
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m21sec
checking: ~ [AF [EG [1<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)]]]
normalized: EG [~ [EG [1<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)]]]
abstracting: (1<=sum(n8_3_5, n8_2_5, n8_1_5, n8_0_5, n8_0_6, n8_6_5, n8_5_5, n8_4_5, n8_4_6, n8_3_6, n8_2_6, n8_1_6, n8_6_6, n8_5_6, n8_0_3, n8_1_3, n8_5_2, n8_6_2, n8_4_3, n8_5_3, n8_2_3, n8_3_3, n8_1_4, n8_2_4, n8_6_3, n8_0_4, n8_5_4, n8_6_4, n8_3_4, n8_4_4, n8_1_1, n8_0_1, n8_3_1, n8_2_1, n8_4_0, n8_3_0, n8_6_0, n8_5_0, n8_2_2, n8_1_2, n8_4_2, n8_3_2, n8_5_1, n8_4_1, n8_0_2, n8_6_1, n8_0_0, n8_1_0, n8_2_0)) states: 1,864,152 (6)
...................
EG iterations: 19
...........
EG iterations: 11
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-10 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m25sec
checking: [EX [AF [3<=Astart]] & EF [[~ [a2<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)] & [sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)<=SstopAbort | AstopAbort<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)]]]]
normalized: [E [true U [[sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)<=SstopAbort | AstopAbort<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)] & ~ [a2<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)]]] & EX [~ [EG [~ [3<=Astart]]]]]
abstracting: (3<=Astart) states: 0
EG iterations: 0
.abstracting: (a2<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)) states: 2,271,896 (6)
abstracting: (AstopAbort<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)) states: 1,480,922 (6)
abstracting: (sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)<=SstopAbort) states: 1,191,630 (6)
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 2m59sec
checking: AG [~ [[1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2) & [sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0) | 3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)]]]]
normalized: ~ [E [true U [1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2) & [sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0) | 3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)]]]]
abstracting: (3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)) states: 1,920,039 (6)
abstracting: (sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)) states: 2,029,491 (6)
abstracting: (1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)) states: 1,690,506 (6)
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m55sec
checking: EG [[[a5<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1) | ~ [3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)]] & sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=a2]]
normalized: EG [[sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=a2 & [a5<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1) | ~ [3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)]]]]
abstracting: (3<=sum(c1_6, c1_5, c1_4, c1_3, c1_2, c1_1, c1_0)) states: 1,920,039 (6)
abstracting: (a5<=sum(s2_4, s2_3, s2_6, s2_5, s2_0, s2_2, s2_1)) states: 1,481,744 (6)
abstracting: (sum(s4_6, s4_5, s4_3, s4_4, s4_1, s4_2, s4_0)<=a2) states: 2,029,491 (6)
......
EG iterations: 6
-> the formula is TRUE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 3m23sec
checking: [[[sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)<=sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0) | [~ [3<=a4] | ~ [1<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)]]] & AF [[sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6) & 1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)]]] & ~ [~ [~ [[1<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0) & sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)]]]]]
normalized: [~ [[1<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0) & sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)]] & [~ [EG [~ [[sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6) & 1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)]]]] & [sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)<=sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0) | [~ [1<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)] | ~ [3<=a4]]]]]
abstracting: (3<=a4) states: 0
abstracting: (1<=sum(n1_2, n1_3, n1_4, n1_5, n1_6, n1_1, n1_0)) states: 16,256 (4)
abstracting: (sum(s6_6, s6_4, s6_5, s6_3, s6_2, s6_1, s6_0)<=sum(n7_5_6, n7_6_6, n7_1_6, n7_2_6, n7_3_6, n7_4_6, n7_6_4, n7_5_4, n7_4_4, n7_3_4, n7_2_4, n7_1_4, n7_0_4, n7_6_3, n7_0_6, n7_6_5, n7_5_5, n7_4_5, n7_3_5, n7_2_5, n7_1_5, n7_0_5, n7_3_2, n7_4_2, n7_1_2, n7_2_2, n7_6_1, n7_0_2, n7_4_1, n7_5_1, n7_4_3, n7_5_3, n7_2_3, n7_3_3, n7_0_3, n7_1_3, n7_5_2, n7_6_2, n7_3_0, n7_4_0, n7_5_0, n7_6_0, n7_0_1, n7_1_1, n7_2_1, n7_3_1, n7_0_0, n7_1_0, n7_2_0)) states: 586,686 (5)
abstracting: (1<=sum(SstopOK_5, SstopOK_4, SstopOK_6, SstopOK_1, SstopOK_0, SstopOK_3, SstopOK_2)) states: 1,690,506 (6)
abstracting: (sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n2_0, n2_1, n2_2, n2_3, n2_4, n2_5, n2_6)) states: 2,268,044 (6)
......................
EG iterations: 22
abstracting: (sum(Sstart_4, Sstart_5, Sstart_6, Sstart_0, Sstart_1, Sstart_2, Sstart_3)<=sum(n9_2_6, n9_1_6, n9_4_6, n9_3_6, n9_6_6, n9_5_6, n9_1_5, n9_0_5, n9_3_5, n9_2_5, n9_5_5, n9_4_5, n9_0_6, n9_6_5, n9_1_4, n9_2_4, n9_6_3, n9_0_4, n9_5_4, n9_6_4, n9_3_4, n9_4_4, n9_0_3, n9_1_3, n9_5_2, n9_6_2, n9_4_3, n9_5_3, n9_2_3, n9_3_3, n9_0_2, n9_6_1, n9_5_1, n9_4_1, n9_4_2, n9_3_2, n9_2_2, n9_1_2, n9_6_0, n9_5_0, n9_4_0, n9_3_0, n9_3_1, n9_2_1, n9_1_1, n9_0_1, n9_0_0, n9_1_0, n9_2_0)) states: 2,256,270 (6)
abstracting: (1<=sum(s3_6, s3_3, s3_2, s3_5, s3_4, s3_1, s3_0)) states: 250,410 (5)
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-14 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 5m53sec
checking: [2<=AstopOK | [~ [sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)] | [AF [2<=sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)] | AF [3<=CstopAbort]]]]
normalized: [2<=AstopOK | [[~ [EG [~ [3<=CstopAbort]]] | ~ [EG [~ [2<=sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)]]]] | ~ [sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)]]]
abstracting: (sum(CstopOK_2, CstopOK_3, CstopOK_4, CstopOK_5, CstopOK_6, CstopOK_1, CstopOK_0)<=sum(n6_4, n6_3, n6_6, n6_5, n6_0, n6_2, n6_1)) states: 2,270,216 (6)
abstracting: (2<=sum(n3_5, n3_4, n3_6, n3_0, n3_1, n3_2, n3_3)) states: 15,360 (4)
.
EG iterations: 1
abstracting: (3<=CstopAbort) states: 232,785 (5)
.
EG iterations: 1
abstracting: (2<=AstopOK) states: 0
-> the formula is FALSE
FORMULA QuasiCertifProtocol-COL-06-CTLCardinality-15 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 1m51sec
Total processing time: 46m29sec
BK_STOP 1432916328347
--------------------
content from stderr:
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m0sec
84051 117217 137672 218170
iterations count:4068 (35), effective:116 (1)
initing FirstDep: 0m0sec
iterations count:164 (1), effective:8 (0)
iterations count:116 (1), effective:0 (0)
iterations count:167 (1), effective:11 (0)
iterations count:431 (3), effective:43 (0)
iterations count:766 (6), effective:44 (0)
iterations count:116 (1), effective:0 (0)
iterations count:116 (1), effective:0 (0)
iterations count:243 (2), effective:7 (0)
iterations count:167 (1), effective:9 (0)
164385
iterations count:1146 (9), effective:99 (0)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="QuasiCertifProtocol-PT-06"
export BK_EXAMINATION="CTLCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/QuasiCertifProtocol-PT-06.tgz
mv QuasiCertifProtocol-PT-06 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2265"
echo " Executing tool marcie"
echo " Input is QuasiCertifProtocol-PT-06, examination is CTLCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r078kn-ebro-143262779400860"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "CTLCardinality" = "ReachabilityComputeBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "CTLCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "CTLCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property CTLCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "CTLCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

