About the Execution of Marcie for LamportFastMutEx-PT-3
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 4283.380 | 46370.00 | 46070.00 | 10.00 | TTFFFTTFTTTFTTFF | normal |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
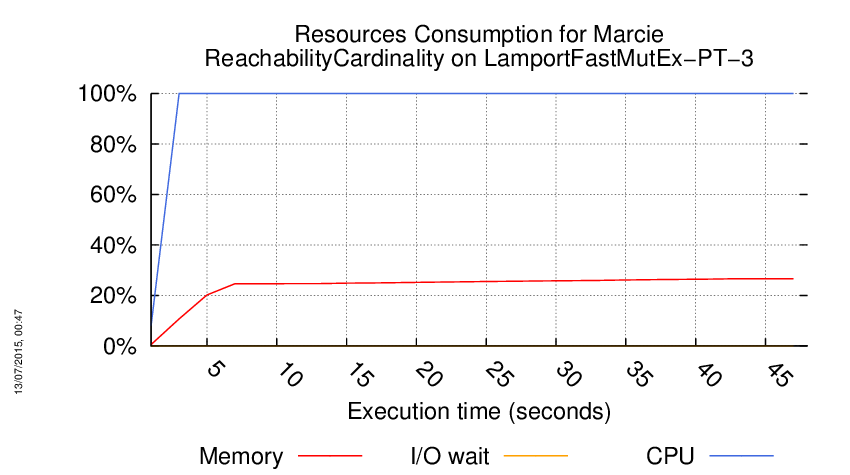
Trace from the execution
Waiting for the VM to be ready (probing ssh)
................................................................
=====================================================================
Generated by BenchKit 2-2265
Executing tool marcie
Input is LamportFastMutEx-PT-3, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 1
Run identifier is r050kn-ebro-143236503900646
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-0
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-1
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-10
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-11
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-12
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-13
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-14
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-15
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-2
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-3
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-4
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-5
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-6
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-7
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-8
FORMULA_NAME LamportFastMutEx-COL-3-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1432545395006
Model: LamportFastMutEx-PT-3
reachability algorithm:
Saturation-based algorithm
variable ordering algorithm:
Calculated like in [Noa99]
--memory=6 --suppress --rs-algorithm=3 --place-order=5
Marcie rev. 1429:1432M (built: crohr on 2014-10-22)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mcc-file=ReachabilityCardinality.xml --memory=6 --suppress --rs-algorithm=3 --place-order=5
parse successfull
net created successfully
(NrP: 100 NrTr: 156 NrArc: 664)
net check time: 0m0sec
parse formulas successfull
formulas created successfully
place and transition orderings generation:0m0sec
init dd package: 0m6sec
RS generation: 0m2sec
-> reachability set: #nodes 5902 (5.9e+03) #states 19,742 (4)
starting MCC model checker
--------------------------
checking: AG [[[[1<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)] & sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(y_3, y_2, y_1, y_0)] | [~ [sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)] | [sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0) | sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)]]]]
normalized: ~ [E [true U ~ [[[sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(y_3, y_2, y_1, y_0) & [1<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]] | [[sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0) | sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)] | ~ [sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)]]]]]]
abstracting: (sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)) states: 18,173 (4)
abstracting: (sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 17,171 (4)
abstracting: (sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)) states: 19,742 (4)
abstracting: (sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 19,742 (4)
abstracting: (1<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 3,954 (3)
abstracting: (sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)<=sum(y_3, y_2, y_1, y_0)) states: 19,519 (4)
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-0 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m1sec
checking: EF [~ [~ [2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)]]]
normalized: E [true U 2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)]
abstracting: (2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)) states: 7,869 (3)
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-1 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m3sec
checking: EF [[[[1<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 1<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)] | [3<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0) | sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)]] & 1<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]]
normalized: E [true U [1<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0) & [[3<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0) | sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)] | [1<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0) & 1<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)]]]]
abstracting: (1<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)) states: 3,985 (3)
abstracting: (1<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)) states: 2,487 (3)
abstracting: (sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)) states: 8,627 (3)
abstracting: (3<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)) states: 4
abstracting: (1<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 1,869 (3)
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-2 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m5sec
checking: EF [[[2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)] & [[3<=sum(x_3, x_2, x_1, x_0) & sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)] | ~ [2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)]]]]
normalized: E [true U [[~ [2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)] | [3<=sum(x_3, x_2, x_1, x_0) & sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)]] & [2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)]]]
abstracting: (sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)) states: 16,787 (4)
abstracting: (2<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)) states: 7,869 (3)
abstracting: (sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)<=sum(P_start_1_3, P_start_1_2, P_start_1_1, P_start_1_0)) states: 16,283 (4)
abstracting: (3<=sum(x_3, x_2, x_1, x_0)) states: 0
abstracting: (2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)) states: 396
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-3 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m2sec
checking: EF [~ [[[3<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)] | ~ [3<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)]]]]
normalized: E [true U ~ [[[3<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)] | ~ [3<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)]]]]
abstracting: (3<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)) states: 12
abstracting: (sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)) states: 16,871 (4)
abstracting: (3<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)) states: 0
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-4 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m2sec
checking: EF [~ [[[2<=sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0) | 2<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)] | [2<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)]]]]
normalized: E [true U ~ [[[2<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)] | [2<=sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0) | 2<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)]]]]
abstracting: (2<=sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)) states: 19,742 (4)
abstracting: (2<=sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0)) states: 8,889 (3)
abstracting: (sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)<=sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)) states: 8,315 (3)
abstracting: (2<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)) states: 219
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-5 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m1sec
checking: EF [[2<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & ~ [sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)]]]
normalized: E [true U [2<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & ~ [sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)]]]
abstracting: (sum(P_wait_3_3, P_wait_3_2, P_wait_3_1, P_wait_3_0, P_wait_2_3, P_wait_2_2, P_wait_2_1, P_wait_2_0, P_wait_1_3, P_wait_1_2, P_wait_1_1, P_wait_1_0, P_wait_0_3, P_wait_0_2, P_wait_0_1, P_wait_0_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)) states: 7,973 (3)
abstracting: (2<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 327
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-6 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m3sec
checking: AG [1<=sum(y_3, y_2, y_1, y_0)]
normalized: ~ [E [true U ~ [1<=sum(y_3, y_2, y_1, y_0)]]]
abstracting: (1<=sum(y_3, y_2, y_1, y_0)) states: 19,742 (4)
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-7 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: EF [[[[3<=sum(P_CS_21_3, P_CS_21_2, P_CS_21_1, P_CS_21_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)] & ~ [sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)]] & ~ [[3<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | 2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)]]]]
normalized: E [true U [~ [[3<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) | 2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)]] & [~ [sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)] & [3<=sum(P_CS_21_3, P_CS_21_2, P_CS_21_1, P_CS_21_0) & sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]]
abstracting: (sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)) states: 16,781 (4)
abstracting: (3<=sum(P_CS_21_3, P_CS_21_2, P_CS_21_1, P_CS_21_0)) states: 0
abstracting: (sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(P_setx_3_3, P_setx_3_2, P_setx_3_1, P_setx_3_0)) states: 17,855 (4)
abstracting: (2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)) states: 129
abstracting: (3<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 9
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-8 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: AG [[[~ [2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)] | [2<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)]] | sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)]]
normalized: ~ [E [true U ~ [[sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) | [[2<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0) & sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)] | ~ [2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)]]]]]]
abstracting: (2<=sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)) states: 396
abstracting: (sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)<=sum(P_fordo_12_3, P_fordo_12_2, P_fordo_12_1, P_fordo_12_0)) states: 16,721 (4)
abstracting: (2<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)) states: 75
abstracting: (sum(P_b_3_true, P_b_3_false, P_b_2_true, P_b_2_false, P_b_1_true, P_b_1_false, P_b_0_true, P_b_0_false)<=sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)) states: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-9 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m4sec
checking: AG [~ [2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)]]
normalized: ~ [E [true U 2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)]]
abstracting: (2<=sum(P_awaity_3, P_awaity_2, P_awaity_1, P_awaity_0)) states: 129
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-10 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m3sec
checking: EF [~ [[[sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) | 2<=sum(y_3, y_2, y_1, y_0)] | [sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(y_3, y_2, y_1, y_0)]]]]
normalized: E [true U ~ [[[sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) | 2<=sum(y_3, y_2, y_1, y_0)] | [sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0) | sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(y_3, y_2, y_1, y_0)]]]]
abstracting: (sum(P_setbi_11_3, P_setbi_11_2, P_setbi_11_1, P_setbi_11_0)<=sum(y_3, y_2, y_1, y_0)) states: 19,667 (4)
abstracting: (sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)<=sum(P_ify0_4_3, P_ify0_4_2, P_ify0_4_1, P_ify0_4_0)) states: 17,039 (4)
abstracting: (2<=sum(y_3, y_2, y_1, y_0)) states: 0
abstracting: (sum(P_setbi_5_3, P_setbi_5_2, P_setbi_5_1, P_setbi_5_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)) states: 18,173 (4)
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-11 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: AG [sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)]
normalized: ~ [E [true U ~ [sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)]]]
abstracting: (sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_sety_9_3, P_sety_9_2, P_sety_9_1, P_sety_9_0)) states: 18,065 (4)
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-12 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m1sec
checking: EF [2<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]
normalized: E [true U 2<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)]
abstracting: (2<=sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)) states: 51
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-13 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m2sec
checking: AG [[sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) | ~ [[sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & 3<=sum(x_3, x_2, x_1, x_0)]]]]
normalized: ~ [E [true U ~ [[sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0) | ~ [[sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0) & 3<=sum(x_3, x_2, x_1, x_0)]]]]]]
abstracting: (3<=sum(x_3, x_2, x_1, x_0)) states: 0
abstracting: (sum(P_ifyi_15_3, P_ifyi_15_2, P_ifyi_15_1, P_ifyi_15_0)<=sum(P_ifxi_10_3, P_ifxi_10_2, P_ifxi_10_1, P_ifxi_10_0)) states: 18,113 (4)
abstracting: (sum(P_setbi_24_3, P_setbi_24_2, P_setbi_24_1, P_setbi_24_0)<=sum(P_done_3_3, P_done_3_2, P_done_3_1, P_done_3_0, P_done_2_3, P_done_2_2, P_done_2_1, P_done_2_0, P_done_1_3, P_done_1_2, P_done_1_1, P_done_1_0, P_done_0_3, P_done_0_2, P_done_0_1, P_done_0_0)) states: 17,261 (4)
-> the formula is TRUE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-14 TRUE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
checking: EF [3<=sum(P_await_13_3, P_await_13_2, P_await_13_1, P_await_13_0)]
normalized: E [true U 3<=sum(P_await_13_3, P_await_13_2, P_await_13_1, P_await_13_0)]
abstracting: (3<=sum(P_await_13_3, P_await_13_2, P_await_13_1, P_await_13_0)) states: 0
-> the formula is FALSE
FORMULA LamportFastMutEx-COL-3-ReachabilityCardinality-15 FALSE TECHNIQUES SEQUENTIAL_PROCESSING DECISION_DIAGRAMS UNFOLDING_TO_PT
MC time: 0m0sec
Total processing time: 0m46sec
BK_STOP 1432545441376
--------------------
content from stderr:
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m0sec
337 573 876 1319 1397 1503 1904 2076 2364 2554 2872 3854 4043 4175 4424 4697 4821 4835 5296 5357 5557 5783 5870 6008
iterations count:24744 (158), effective:633 (4)
initing FirstDep: 0m0sec
4298 4538 4730 5350 6041 6425 6292 6633 6851 6890 6947 6330
iterations count:12856 (82), effective:306 (1)
3027 4362 5421 5609 6043 6295 6609 7135 7474 7606 7217 7258 7024 6967 6361 6331 6938 7255
iterations count:18665 (119), effective:448 (2)
4015 4341 4499 4802 5324 6041 6337 6565 6656 6964 6834 6847 7089 6569 6395
iterations count:15352 (98), effective:360 (2)
665 988 1506 2029 2256 2294 2761 3214 3483 3569 4110 4268 4753 4553 5430 5828 5893
iterations count:17289 (110), effective:426 (2)
881 1328 1504 2431 2984 3043 3367 4642 4991 5972 5903 6473
iterations count:12850 (82), effective:302 (1)
2395 3125 3786 4302 4960 5090 5238 6149 6121 6028 6126 5661 6478
iterations count:13912 (89), effective:342 (2)
1395 3052 3769 4511 5139 5486 5782 5528 5833 5524 6292 6591 6600
iterations count:13416 (86), effective:329 (2)
3999 4823 4968 5443 5813 5790 6646 6800 6289 6283 5996 6214
iterations count:12765 (81), effective:297 (1)
1130 1576 1747 2123 2279 2679 3198 3610 3784 4842 5311 5392 5710 5368 5450 4887 5441 5778 5800
iterations count:19515 (125), effective:441 (2)
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="LamportFastMutEx-PT-3"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="marcie"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/LamportFastMutEx-PT-3.tgz
mv LamportFastMutEx-PT-3 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2265"
echo " Executing tool marcie"
echo " Input is LamportFastMutEx-PT-3, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 1"
echo " Run identifier is r050kn-ebro-143236503900646"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "ReachabilityComputeBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

