About the Execution of TAPAAL(MC) for NeoElection-PT-8
| Execution Summary | |||||
| Max Memory Used (MB) |
Time wait (ms) | CPU Usage (ms) | I/O Wait (ms) | Computed Result | Execution Status |
| 14479.160 | 3600000.00 | 14390195.00 | 20.10 | [undef] | Cannot compute |
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
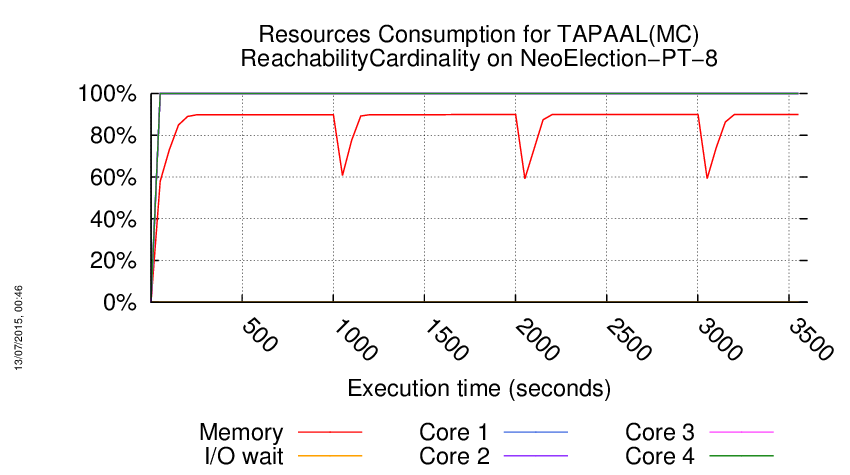
Trace from the execution
Waiting for the VM to be ready (probing ssh)
............................................
=====================================================================
Generated by BenchKit 2-2265
Executing tool classicMC
Input is NeoElection-PT-8, examination is ReachabilityCardinality
Time confinement is 3600 seconds
Memory confinement is 16384 MBytes
Number of cores is 4
Run identifier is r043kn-ebro-143236481900984
=====================================================================
--------------------
content from stdout:
=== Data for post analysis generated by BenchKit (invocation template)
The expected result is a vector of booleans
BOOL_VECTOR
here is the order used to build the result vector(from text file)
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-0
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-1
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-10
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-11
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-12
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-13
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-14
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-15
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-2
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-3
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-4
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-5
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-6
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-7
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-8
FORMULA_NAME NeoElection-COL-8-ReachabilityCardinality-9
=== Now, execution of the tool begins
BK_START 1432412870723
---> classicMC --- TAPAAL Classic Multicore
**********************************************
TAPAAL classicMC verifying ReachabilityCardinality
**********************************************
NeoElection-COL-8-ReachabilityCardinality-0: not EF not ( (((("P-electedPrimary_0" + "P-electedPrimary_1" + "P-electedPrimary_2" + "P-electedPrimary_3" + "P-electedPrimary_4" + "P-electedPrimary_5" + "P-electedPrimary_6" + "P-electedPrimary_7" + "P-electedPrimary_8") <= ("P-masterState_0_F_0" + "P-masterState_0_F_1" + "P-masterState_0_F_2" + "P-masterState_0_F_3" + "P-masterState_0_F_4" + "P-masterState_0_F_5" + "P-masterState_0_F_6" + "P-masterState_0_F_7" + "P-masterState_0_F_8" + "P-masterState_0_T_0" + "P-masterState_0_T_1" + "P-masterState_0_T_2" + "P-masterState_0_T_3" + "P-masterState_0_T_4" + "P-masterState_0_T_5" + "P-masterState_0_T_6" + "P-masterState_0_T_7" + "P-masterState_0_T_8" + "P-masterState_1_F_0" + "P-masterState_1_F_1" + "P-masterState_1_F_2" + "P-masterState_1_F_3" + "P-masterState_1_F_4" + "P-masterState_1_F_5" + "P-masterState_1_F_6" + "P-masterState_1_F_7" + "P-masterState_1_F_8" + "P-masterState_1_T_0" + "P-masterState_1_T_1" + "P-masterState_1_T_2" + "P-masterState_1_T_3" + "P-masterState_1_T_4" + "P-masterState_1_T_5" + "P-masterState_1_T_6" + "P-masterState_1_T_7" + "P-masterState_1_T_8" + "P-masterState_2_F_0" + "P-masterState_2_F_1" + "P-masterState_2_F_2" + "P-masterState_2_F_3" + "P-masterState_2_F_4" + "P-masterState_2_F_5" + "P-masterState_2_F_6" + "P-masterState_2_F_7" + "P-masterState_2_F_8" + "P-masterState_2_T_0" + "P-masterState_2_T_1" + "P-masterState_2_T_2" + "P-masterState_2_T_3" + "P-masterState_2_T_4" + "P-masterState_2_T_5" + "P-masterState_2_T_6" + "P-masterState_2_T_7" + "P-masterState_2_T_8" + "P-masterState_3_F_0" + "P-masterState_3_F_1" + "P-masterState_3_F_2" + "P-masterState_3_F_3" + "P-masterState_3_F_4" + "P-masterState_3_F_5" + "P-masterState_3_F_6" + "P-masterState_3_F_7" + "P-masterState_3_F_8" + "P-masterState_3_T_0" + "P-masterState_3_T_1" + "P-masterState_3_T_2" + "P-masterState_3_T_3" + "P-masterState_3_T_4" + "P-masterState_3_T_5" + "P-masterState_3_T_6" + "P-masterState_3_T_7" + "P-masterState_3_T_8" + "P-masterState_4_F_0" + "P-masterState_4_F_1" + "P-masterState_4_F_2" + "P-masterState_4_F_3" + "P-masterState_4_F_4" + "P-masterState_4_F_5" + "P-masterState_4_F_6" + "P-masterState_4_F_7" + "P-masterState_4_F_8" + "P-masterState_4_T_0" + "P-masterState_4_T_1" + "P-masterState_4_T_2" + "P-masterState_4_T_3" + "P-masterState_4_T_4" + "P-masterState_4_T_5" + "P-masterState_4_T_6" + "P-masterState_4_T_7" + "P-masterState_4_T_8" + "P-masterState_5_F_0" + "P-masterState_5_F_1" + "P-masterState_5_F_2" + "P-masterState_5_F_3" + "P-masterState_5_F_4" + "P-masterState_5_F_5" + "P-masterState_5_F_6" + "P-masterState_5_F_7" + "P-masterState_5_F_8" + "P-masterState_5_T_0" + "P-masterState_5_T_1" + "P-masterState_5_T_2" + "P-masterState_5_T_3" + "P-masterState_5_T_4" + "P-masterState_5_T_5" + "P-masterState_5_T_6" + "P-masterState_5_T_7" + "P-masterState_5_T_8" + "P-masterState_6_F_0" + "P-masterState_6_F_1" + "P-masterState_6_F_2" + "P-masterState_6_F_3" + "P-masterState_6_F_4" + "P-masterState_6_F_5" + "P-masterState_6_F_6" + "P-masterState_6_F_7" + "P-masterState_6_F_8" + "P-masterState_6_T_0" + "P-masterState_6_T_1" + "P-masterState_6_T_2" + "P-masterState_6_T_3" + "P-masterState_6_T_4" + "P-masterState_6_T_5" + "P-masterState_6_T_6" + "P-masterState_6_T_7" + "P-masterState_6_T_8" + "P-masterState_7_F_0" + "P-masterState_7_F_1" + "P-masterState_7_F_2" + "P-masterState_7_F_3" + "P-masterState_7_F_4" + "P-masterState_7_F_5" + "P-masterState_7_F_6" + "P-masterState_7_F_7" + "P-masterState_7_F_8" + "P-masterState_7_T_0" + "P-masterState_7_T_1" + "P-masterState_7_T_2" + "P-masterState_7_T_3" + "P-masterState_7_T_4" + "P-masterState_7_T_5" + "P-masterState_7_T_6" + "P-masterState_7_T_7" + "P-masterState_7_T_8" + "P-masterState_8_F_0" + "P-masterState_8_F_1" + "P-masterState_8_F_2" + "P-masterState_8_F_3" + "P-masterState_8_F_4" + "P-masterState_8_F_5" + "P-masterState_8_F_6" + "P-masterState_8_F_7" + "P-masterState_8_F_8" + "P-masterState_8_T_0" + "P-masterState_8_T_1" + "P-masterState_8_T_2" + "P-masterState_8_T_3" + "P-masterState_8_T_4" + "P-masterState_8_T_5" + "P-masterState_8_T_6" + "P-masterState_8_T_7" + "P-masterState_8_T_8")) and (("P-electedSecondary_0" + "P-electedSecondary_1" + "P-electedSecondary_2" + "P-electedSecondary_3" + "P-electedSecondary_4" + "P-electedSecondary_5" + "P-electedSecondary_6" + "P-electedSecondary_7" + "P-electedSecondary_8") <= ("P-electedSecondary_0" + "P-electedSecondary_1" + "P-electedSecondary_2" + "P-electedSecondary_3" + "P-electedSecondary_4" + "P-electedSecondary_5" + "P-electedSecondary_6" + "P-electedSecondary_7" + "P-electedSecondary_8"))) or (1 <= ("P-poll__networl_0_0_AskP_0" + "P-poll__networl_0_0_AskP_1" + "P-poll__networl_0_0_AskP_2" + "P-poll__networl_0_0_AskP_3" + "P-poll__networl_0_0_AskP_4" + "P-poll__networl_0_0_AskP_5" + "P-poll__networl_0_0_AskP_6" + "P-poll__networl_0_0_AskP_7" + "P-poll__networl_0_0_AskP_8" + "P-poll__networl_0_0_AnsP_0" + "P-poll__networl_0_0_AnsP_1" + "P-poll__networl_0_0_AnsP_2" + "P-poll__networl_0_0_AnsP_3" + "P-poll__networl_0_0_AnsP_4" + "P-poll__networl_0_0_AnsP_5" + "P-poll__networl_0_0_AnsP_6" + "P-poll__networl_0_0_AnsP_7" + "P-poll__networl_0_0_AnsP_8" + "P-poll__networl_0_0_RI_0" + "P-poll__networl_0_0_RI_1" + "P-poll__networl_0_0_RI_2" + "P-poll__networl_0_0_RI_3" + "P-poll__networl_0_0_RI_4" + "P-poll__networl_0_0_RI_5" + "P-poll__networl_0_0_RI_6" + "P-poll__networl_0_0_RI_7" + "P-poll__networl_0_0_RI_8" + "P-poll__networl_0_0_AI_0" + "P-poll__networl_0_0_AI_1" + "P-poll__networl_0_0_AI_2" + "P-poll__networl_0_0_AI_3" + "P-poll__networl_0_0_AI_4" + "P-poll__networl_0_0_AI_5" + "P-poll__networl_0_0_AI_6" + "P-poll__networl_0_0_AI_7" + "P-poll__networl_0_0_AI_8" + "P-poll__networl_0_0_AnnP_0" + "P-poll__networl_0_0_AnnP_1" + "P-poll__networl_0_0_AnnP_2" + "P-poll__networl_0_0_AnnP_3" + "P-poll__networl_0_0_AnnP_4" + "P-poll__networl_0_0_AnnP_5" + "P-poll__networl_0_0_AnnP_6" + "P-poll__networl_0_0_AnnP_7" + "P-poll__networl_0_0_AnnP_8" + "P-poll__networl_0_0_RP_0" + "P-poll__networl_0_0_RP_1" + "P-poll__networl_0_0_RP_2" + "P-poll__networl_0_0_RP_3" + "P-poll__networl_0_0_RP_4" + "P-poll__networl_0_0_RP_5" + "P-poll__networl_0_0_RP_6" + "P-poll__networl_0_0_RP_7" + "P-poll__networl_0_0_RP_8" + "P-poll__networl_0_1_AskP_0" + "P-poll__networl_0_1_AskP_1" + "P-poll__networl_0_1_AskP_2" + "P-poll__networl_0_1_AskP_3" + "P-poll__networl_0_1_AskP_4" + "P-poll__networl_0_1_AskP_5" + "P-poll__networl_0_1_AskP_6" + "P-poll__networl_0_1_AskP_7" + "P-poll__networl_0_1_AskP_8" + "P-poll__networl_0_1_AnsP_0" + "P-poll__networl_0_1_AnsP_1" + "P-poll__networl_0_1_AnsP_2" + "P-poll__networl_0_1_AnsP_3" + "P-poll__networl_0_1_AnsP_4" + "P-poll__networl_0_1_AnsP_5" + "P-poll__networl_0_1_AnsP_6" + "P-poll__networl_0_1_AnsP_7" + "P-poll__networl_0_1_AnsP_8" + "P-poll__networl_0_1_RI_0" + "P-poll__networl_0_1_RI_1" + "P-poll__networl_0_1_RI_2" + "P-poll__networl_0_1_RI_3" + "P-poll__networl_0_1_RI_4" + "P-poll__networl_0_1_RI_5" + "P-poll__networl_0_1_RI_6" + "P-poll__networl_0_1_RI_7" + "P-poll__networl_0_1_RI_8" + "P-poll__networl_0_1_AI_0" + "P-poll__networl_0_1_AI_1" + "P-poll__networl_0_1_AI_2" + "P-poll__networl_0_1_AI_3" + "P-poll__networl_0_1_AI_4" + "P-poll__networl_0_1_AI_5" + "P-poll__networl_0_1_AI_6" + "P-poll__networl_0_1_AI_7" + "P-poll__networl_0_1_AI_8" + "P-poll__networl_0_1_AnnP_0" + "P-poll__networl_0_1_AnnP_1" + "P-poll__networl_0_1_AnnP_2" + "P-poll__networl_0_1_AnnP_3" + "P-poll__networl_0_1_AnnP_4" + "P-poll__networl_0_1_AnnP_5" + "P-poll__networl_0_1_AnnP_6" + "P-poll__networl_0_1_AnnP_7" + "P-poll__networl_0_1_AnnP_8" + "P-poll__networl_0_1_RP_0" + "P-poll__networl_0_1_RP_1" + "P-poll__networl_0_1_RP_2" + "P-poll__networl_0_1_RP_3" + "P-poll__networl_0_1_RP_4" + "P-poll__networl_0_1_RP_5" + "P-poll__networl_0_1_RP_6" + "P-poll__networl_0_1_RP_7" + "P-poll__networl_0_1_RP_8" + "P-poll__networl_0_2_AskP_0" + "P-poll__networl_0_2_AskP_1" + "P-poll__networl_0_2_AskP_2" + "P-poll__networl_0_2_AskP_3" + "P-poll__networl_0_2_AskP_4" + "P-poll__networl_0_2_AskP_5" + "P-poll__networl_0_2_AskP_6" + "P-poll__networl_0_2_AskP_7" + "P-poll__networl_0_2_AskP_8" + "P-poll__networl_0_2_AnsP_0" + "P-poll__networl_0_2_AnsP_1" + "P-poll__networl_0_2_AnsP_2" + "P-poll__networl_0_2_AnsP_3" + "P-poll__networl_0_2_AnsP_4" + "P-poll__networl_0_2_AnsP_5" + "P-poll__networl_0_2_AnsP_6" + "P-poll__networl_0_2_AnsP_7" + "P-poll__networl_0_2_AnsP_8" + "P-poll__networl_0_2_RI_0" + "P-poll__networl_0_2_RI_1" + "P-poll__networl_0_2_RI_2" + "P-poll__networl_0_2_RI_3" + "P-poll__networl_0_2_RI_4" + "P-poll__networl_0_2_RI_5" + "P-poll__networl_0_2_RI_6" + "P-poll__networl_0_2_RI_7" + "P-poll__networl_0_2_RI_8" + "P-poll__networl_0_2_AI_0" + "P-poll__networl_0_2_AI_1" + "P-poll__networl_0_2_AI_2" + "P-poll__networl_0_2_AI_3" + "P-poll__networl_0_2_AI_4" + "P-poll__networl_0_2_AI_5" + "P-poll__networl_0_2_AI_6" + "P-poll__networl_0_2_AI_7" + "P-poll__networl_0_2_AI_8" + "P-poll__networl_0_2_AnnP_0" + "P-poll__networl_0_2_AnnP_1" + "P-poll__networl_0_2_AnnP_2" + "P-poll__networl_0_2_AnnP_3" + "P-poll__networl_0_2_AnnP_4" + "P-poll__networl_0_2_AnnP_5" + "P-poll__networl_0_2_AnnP_6" + "P-poll__networl_0_2_AnnP_7" + "P-poll__networl_0_2_AnnP_8" + "P-poll__networl_0_2_RP_0" + "P-poll__networl_0_2_RP_1" + "P-poll__networl_0_2_RP_2" + "P-poll__networl_0_2_RP_3" + "P-poll__networl_0_2_RP_4" + "P-poll__networl_0_2_RP_5" + "P-poll__networl_0_2_RP_6" + "P-poll__networl_0_2_RP_7" + "P-poll__networl_0_2_RP_8" + "P-poll__networl_0_3_AskP_0" + "P-poll__networl_0_3_AskP_1" + "P-poll__networl_0_3_AskP_2" + "P-poll__networl_0_3_AskP_3" + "P-poll__networl_0_3_AskP_4" + "P-poll__networl_0_3_AskP_5" + "P-poll__networl_0_3_AskP_6" + "P-poll__networl_0_3_AskP_7" + "P-poll__networl_0_3_AskP_8" + "P-poll__networl_0_3_AnsP_0" + "P-poll__networl_0_3_AnsP_1" + "P-poll__networl_0_3_AnsP_2" + "P-poll__networl_0_3_AnsP_3" + "P-poll__networl_0_3_AnsP_4" + "P-poll__networl_0_3_AnsP_5" + "P-poll__networl_0_3_AnsP_6" + "P-poll__networl_0_3_AnsP_7" + "P-poll__networl_0_3_AnsP_8" + "P-poll__networl_0_3_RI_0" + "P-poll__networl_0_3_RI_1" + "P-poll__networl_0_3_RI_2" + "P-poll__networl_0_3_RI_3" + "P-poll__networl_0_3_RI_4" + "P-poll__networl_0_3_RI_5" + "P-poll__networl_0_3_RI_6" + "P-poll__networl_0_3_RI_7" + "P-poll__networl_0_3_RI_8" + "P-poll__networl_0_3_AI_0" + "P-poll__networl_0_3_AI_1" + "P-poll__networl_0_3_AI_2" + "P-poll__networl_0_3_AI_3" + "P-poll__networl_0_3_AI_4" + "P-poll__networl_0_3_AI_5" + "P-poll__networl_0_3_AI_6" + "P-poll__networl_0_3_AI_7" + "P-poll__networl_0_3_AI_8" + "P-poll__networl_0_3_AnnP_0" + "P-poll__networl_0_3_AnnP_1" + "P-poll__networl_0_3_AnnP_2" + "P-poll__networl_0_3_AnnP_3" + "P-poll__networl_0_3_AnnP_4" + "P-poll__networl_0_3_AnnP_5" + "P-poll__networl_0_3_AnnP_6" + "P-poll__networl_0_3_AnnP_7" + "P-poll__networl_0_3_AnnP_8" + "P-poll__networl_0_3_RP_0" + "P-poll__networl_0_3_RP_1" + "P-poll__networl_0_3_RP_2" + "P-poll__networl_0_3_RP_3" + "P-poll__networl_0_3_RP_4" + "P-poll__networl_0_3_RP_5" + "P-poll__networl_0_3_RP_6" + "P-poll__networl_0_3_RP_7" + "P-poll__networl_0_3_RP_8" + "P-poll__networl_0_4_AskP_0" + "P-poll__networl_0_4_AskP_1" + "P-poll__networl_0_4_AskP_2" + "P-poll__networl_0_4_AskP_3" + "P-poll__networl_0_4_AskP_4" + "P-poll__networl_0_4_AskP_5" + "P-poll__networl_0_4_AskP_6" + "P-poll__networl_0_4_AskP_7" + "P-poll__networl_0_4_AskP_8" + "P-poll__networl_0_4_AnsP_0" + "P-poll__networl_0_4_AnsP_1" + "P-poll__networl_0_4_AnsP_2" + "P-poll__networl_0_4_AnsP_3" + "P-poll__networl_0_4_AnsP_4" + "P-poll__networl_0_4_AnsP_5" + "P-poll__networl_0_4_AnsP_6" + "P-poll__networl_0_4_AnsP_7" + "P-poll__networl_0_4_AnsP_8" + "P-poll__networl_0_4_RI_0" + "P-poll__networl_0_4_RI_1" + "P-poll__networl_0_4_RI_2" + "P-poll__networl_0_4_RI_3" + "P-poll__networl_0_4_RI_4" + "P-poll__networl_0_4_RI_5" + "P-poll__networl_0_4_RI_6" + "P-poll__networl_0_4_RI_7" + "P-poll__networl_0_4_RI_8" + "P-poll__networl_0_4_AI_0" + "P-poll__networl_0_4_AI_1" + "P-poll__networl_0_4_AI_2" + "P-poll__networl_0_4_AI_3" + "P-poll__networl_0_4_AI_4" + "P-poll__networl_0_4_AI_5" + "P-poll__networl_0_4_AI_6" + "P-poll__networl_0_4_AI_7" + "P-poll__networl_0_4_AI_8" + "P-poll__networl_0_4_AnnP_0" + "P-poll__networl_0_4_AnnP_1" + "P-poll__networl_0_4_AnnP_2" + "P-poll__networl_0_4_AnnP_3" + "P-poll__networl_0_4_AnnP_4" + "P-poll__networl_0_4_AnnP_5" + "P-poll__networl_0_4_AnnP_6" + "P-poll__networl_0_4_AnnP_7" + "P-poll__networl_0_4_AnnP_8" + "P-poll__networl_0_4_RP_0" + "P-poll__networl_0_4_RP_1" + "P-poll__networl_0_4_RP_2" + "P-poll__networl_0_4_RP_3" + "P-poll__networl_0_4_RP_4" + "P-poll__networl_0_4_RP_5" + "P-poll__networl_0_4_RP_6" + "P-poll__networl_0_4_RP_7" + "P-poll__networl_0_4_RP_8" + "P-poll__networl_0_5_AskP_0" + "P-poll__networl_0_5_AskP_1" + "P-poll__networl_0_5_AskP_2" + "P-poll__networl_0_5_AskP_3" + "P-poll__networl_0_5_AskP_4" + "P-poll__networl_0_5_AskP_5" + "P-poll__networl_0_5_AskP_6" + "P-poll__networl_0_5_AskP_7" + "P-poll__networl_0_5_AskP_8" + "P-poll__networl_0_5_AnsP_0" + "P-poll__networl_0_5_AnsP_1" + "P-poll__networl_0_5_AnsP_2" + "P-poll__networl_0_5_AnsP_3" + "P-poll__networl_0_5_AnsP_4" + "P-poll__networl_0_5_AnsP_5" + "P-poll__networl_0_5_AnsP_6" + "P-poll__networl_0_5_AnsP_7" + "P-poll__networl_0_5_AnsP_8" + "P-poll__networl_0_5_RI_0" + "P-poll__networl_0_5_RI_1" + "P-poll__networl_0_5_RI_2" + "P-poll__networl_0_5_RI_3" + "P-poll__networl_0_5_RI_4" + "P-poll__networl_0_5_RI_5" + "P-poll__networl_0_5_RI_6" + "P-poll__networl_0_5_RI_7" + "P-poll__networl_0_5_RI_8" + "P-poll__networl_0_5_AI_0" + "P-poll__networl_0_5_AI_1" + "P-poll__networl_0_5_AI_2" + "P-poll__networl_0_5_AI_3" + "P-poll__networl_0_5_AI_4" + "P-poll__networl_0_5_AI_5" + "P-poll__networl_0_5_AI_6" + "P-poll__networl_0_5_AI_7" + "P-poll__networl_0_5_AI_8" + "P-poll__networl_0_5_AnnP_0" + "P-poll__networl_0_5_AnnP_1" + "P-poll__networl_0_5_AnnP_2" + "P-poll__networl_0_5_AnnP_3" + "P-poll__networl_0_5_AnnP_4" + "P-poll__networl_0_5_AnnP_5" + "P-poll__networl_0_5_AnnP_6" + "P-poll__networl_0_5_AnnP_7" + "P-poll__networl_0_5_AnnP_8" + "P-poll__networl_0_5_RP_0" + "P-poll__networl_0_5_RP_1" + "P-poll__networl_0_5_RP_2" + "P-poll__networl_0_5_RP_3" + "P-poll__networl_0_5_RP_4" + "P-poll__networl_0_5_RP_5" + "P-poll__networl_0_5_RP_6" + "P-poll__networl_0_5_RP_7" + "P-poll__networl_0_5_RP_8" + "P-poll__networl_0_6_AskP_0" + "P-poll__networl_0_6_AskP_1" + "P-poll__networl_0_6_AskP_2" + "P-poll__networl_0_6_AskP_3" + "P-poll__networl_0_6_AskP_4" + "P-poll__networl_0_6_AskP_5" + "P-poll__networl_0_6_AskP_6" + "P-poll__networl_0_6_AskP_7" + "P-poll__networl_0_6_AskP_8" + "P-poll__networl_0_6_AnsP_0" + "P-poll__networl_0_6_AnsP_1" + "P-poll__networl_0_6_AnsP_2" + "P-poll__networl_0_6_AnsP_3" + "P-poll__networl_0_6_AnsP_4" + "P-poll__networl_0_6_AnsP_5" + "P-poll__networl_0_6_AnsP_6" + "P-poll__networl_0_6_AnsP_7" + "P-poll__networl_0_6_AnsP_8" + "P-poll__networl_0_6_RI_0" + "P-poll__networl_0_6_RI_1" + "P-poll__networl_0_6_RI_2" + "P-poll__networl_0_6_RI_3" + "P-poll__networl_0_6_RI_4" + "P-poll__networl_0_6_RI_5" + "P-poll__networl_0_6_RI_6" + "P-poll__networl_0_6_RI_7" + "P-poll__networl_0_6_RI_8" + "P-poll__networl_0_6_AI_0" + "P-poll__networl_0_6_AI_1" + "P-poll__networl_0_6_AI_2" + "P-poll__networl_0_6_AI_3" + "P-poll__networl_0_6_AI_4" + "P-poll__networl_0_6_AI_5" + "P-poll__networl_0_6_AI_6" + "P-poll__networl_0_6_AI_7" + "P-poll__networl_0_6_AI_8" + "P-poll__networl_0_6_AnnP_0" + "P-poll__networl_0_6_AnnP_1" + "P-poll__networl_0_6_AnnP_2" + "P-poll__networl_0_6_AnnP_3" + "P-poll__networl_0_6_AnnP_4" + "P-poll__networl_0_6_AnnP_5" + "P-poll__networl_0_6_AnnP_6" + "P-poll__networl_0_6_AnnP_7" + "P-poll__networl_0_6_AnnP_8" + "P-poll__networl_0_6_RP_0" + "P-poll__networl_0_6_RP_1" + "P-poll__networl_0_6_RP_2" + "P-poll__networl_0_6_RP_3" + "P-poll__networl_0_6_RP_4" + "P-poll__networl_0_6_RP_5" + "P-poll__networl_0_6_RP_6" + "P-poll__networl_0_6_RP_7" + "P-poll__networl_0_6_RP_8" + "P-poll__networl_0_7_AskP_0" + "P-poll__networl_0_7_AskP_1" + "P-poll__networl_0_7_AskP_2" + "P-poll__networl_0_7_AskP_3" + "P-poll__networl_0_7_AskP_4" + "P-poll__networl_0_7_AskP_5" + "P-poll__networl_0_7_AskP_6" + "P-poll__networl_0_7_AskP_7" + "P-poll__networl_0_7_AskP_8" + "P-poll__networl_0_7_AnsP_0" + "P-poll__networl_0_7_AnsP_1" + "P-poll__networl_0_7_AnsP_2" + "P-poll__networl_0_7_AnsP_3" + "P-poll__networl_0_7_AnsP_4" + "P-poll__networl_0_7_AnsP_5" + "P-poll__networl_0_7_AnsP_6" + "P-poll__networl_0_7_AnsP_7" + "P-poll__networl_0_7_AnsP_8" + "P-poll__networl_0_7_RI_0" + "P-poll__networl_0_7_RI_1" + "P-poll__networl_0_7_RI_2" + "P-poll__networl_0_7_RI_3" + "P-poll__networl_0_7_RI_4" + "P-poll__networl_0_7_RI_5" + "P-poll__networl_0_7_RI_6" + "P-poll__networl_0_7_RI_7" + "P-poll__networl_0_7_RI_8" + "P-poll__networl_0_7_AI_0" + "P-poll__networl_0_7_AI_1" + "P-poll__networl_0_7_AI_2" + "P-poll__networl_0_7_AI_3" + "P-poll__networl_0_7_AI_4" + "P-poll__networl_0_7_AI_5" + "P-poll__networl_0_7_AI_6" + "P-poll__networl_0_7_AI_7" + "P-poll__networl_0_7_AI_8" + "P-poll__networl_0_7_AnnP_0" + "P-poll__networl_0_7_AnnP_1" + "P-poll__networl_0_7_AnnP_2" + "P-poll__networl_0_7_AnnP_3" + "P-poll__networl_0_7_AnnP_4" + "P-poll__networl_0_7_AnnP_5" + "P-poll__networl_0_7_AnnP_6" + "P-poll__networl_0_7_AnnP_7" + "P-poll__networl_0_7_AnnP_8" + "P-poll__networl_0_7_RP_0" + "P-poll__networl_0_7_RP_1" + "P-poll__networl_0_7_RP_2" + "P-poll__networl_0_7_RP_3" + "P-poll__networl_0_7_RP_4" + "P-poll__networl_0_7_RP_5" + "P-poll__networl_0_7_RP_6" + "P-poll__networl_0_7_RP_7" + "P-poll__networl_0_7_RP_8" + "P-poll__networl_0_8_AskP_0" + "P-poll__networl_0_8_AskP_1" + "P-poll__networl_0_8_AskP_2" + "P-poll__networl_0_8_AskP_3" + "P-poll__networl_0_8_AskP_4" + "P-poll__networl_0_8_AskP_5" + "P-poll__networl_0_8_AskP_6" + "P-poll__networl_0_8_AskP_7" + "P-poll__networl_0_8_AskP_8" + "P-poll__networl_0_8_AnsP_0" + "P-poll__networl_0_8_AnsP_1" + "P-poll__networl_0_8_AnsP_2" + "P-poll__networl_0_8_AnsP_3" + "P-poll__networl_0_8_AnsP_4" + "P-poll__networl_0_8_AnsP_5" + "P-poll__networl_0_8_AnsP_6" + "P-poll__networl_0_8_AnsP_7" + "P-poll__networl_0_8_AnsP_8" + "P-poll__networl_0_8_RI_0" + "P-poll__networl_0_8_RI_1" + "P-poll__networl_0_8_RI_2" + "P-poll__networl_0_8_RI_3" + "P-poll__networl_0_8_RI_4" + "P-poll__networl_0_8_RI_5" + "P-poll__networl_0_8_RI_6" + "P-poll__networl_0_8_RI_7" + "P-poll__networl_0_8_RI_8" + "P-poll__networl_0_8_AI_0" + "P-poll__networl_0_8_AI_1" + "P-poll__networl_0_8_AI_2" + "P-poll__networl_0_8_AI_3" + "P-poll__networl_0_8_AI_4" + "P-poll__networl_0_8_AI_5" + "P-poll__networl_0_8_AI_6" + "P-poll__networl_0_8_AI_7" + "P-poll__networl_0_8_AI_8" + "P-poll__networl_0_8_AnnP_0" + "P-poll__networl_0_8_AnnP_1" + "P-poll__networl_0_8_AnnP_2" + "P-poll__networl_0_8_AnnP_3" + "P-poll__networl_0_8_AnnP_4" + "P-poll__networl_0_8_AnnP_5" + "P-poll__networl_0_8_AnnP_6" + "P-poll__networl_0_8_AnnP_7" + "P-poll__networl_0_8_AnnP_8" + "P-poll__networl_0_8_RP_0" + "P-poll__networl_0_8_RP_1" + "P-poll__networl_0_8_RP_2" + "P-poll__networl_0_8_RP_3" + "P-poll__networl_0_8_RP_4" + "P-poll__networl_0_8_RP_5" + "P-poll__networl_0_8_RP_6" + "P-poll__networl_0_8_RP_7" + "P-poll__networl_0_8_RP_8" + "P-poll__networl_1_0_AskP_0" + "P-poll__networl_1_0_AskP_1" + "P-poll__networl_1_0_AskP_2" + "P-poll__networl_1_0_AskP_3" + "P-poll__networl_1_0_AskP_4" + "P-poll__networl_1_0_AskP_5" + "P-poll__networl_1_0_AskP_6" + "P-poll__networl_1_0_AskP_7" + "P-poll__networl_1_0_AskP_8" + "P-poll__networl_1_0_AnsP_0" + "P-poll__networl_1_0_AnsP_1" + "P-poll__networl_1_0_AnsP_2" + "P-poll__networl_1_0_AnsP_3" + "P-poll__networl_1_0_AnsP_4" + "P-poll__networl_1_0_AnsP_5" + "P-poll__networl_1_0_AnsP_6" + "P-poll__networl_1_0_AnsP_7" + "P-poll__networl_1_0_AnsP_8" + "P-poll__networl_1_0_RI_0" + "P-poll__networl_1_0_RI_1" + "P-poll__networl_1_0_RI_2" + "P-poll__networl_1_0_RI_3" + "P-poll__networl_1_0_RI_4" + "P-poll__networl_1_0_RI_5" + "P-poll__networl_1_0_RI_6" + "P-poll__networl_1_0_RI_7" + "P-poll__networl_1_0_RI_8" + "P-poll__networl_1_0_AI_0" + "P-poll__networl_1_0_AI_1" + "P-poll__networl_1_0_AI_2" + "P-poll__networl_1_0_AI_3" + "P-poll__networl_1_0_AI_4" + "P-poll__networl_1_0_AI_5" + "P-poll__networl_1_0_AI_6" + "P-poll__networl_1_0_AI_7" + "P-poll__networl_1_0_AI_8" + "P-poll__networl_1_0_AnnP_0" + "P-poll__networl_1_0_AnnP_1" + "P-poll__networl_1_0_AnnP_2" + "P-poll__networl_1_0_AnnP_3" + "P-poll__networl_1_0_AnnP_4" + "P-poll__networl_1_0_AnnP_5" + "P-poll__networl_1_0_AnnP_6" + "P-poll__networl_1_0_AnnP_7" + "P-poll__networl_1_0_AnnP_8" + "P-poll__networl_1_0_RP_0" + "P-poll__networl_1_0_RP_1" + "P-poll__networl_1_0_RP_2" + "P-poll__networl_1_0_RP_3" + "P-poll__networl_1_0_RP_4" + "P-poll__networl_1_0_RP_5" + "P-poll__networl_1_0_RP_6" + "P-poll__networl_1_0_RP_7" + "P-poll__networl_1_0_RP_8" + "P-poll__networl_1_1_AskP_0" + "P-poll__networl_1_1_AskP_1" + "P-poll__networl_1_1_AskP_2" + "P-poll__networl_1_1_AskP_3" + "P-poll__networl_1_1_AskP_4" + "P-poll__networl_1_1_AskP_5" + "P-poll__networl_1_1_AskP_6" + "P-poll__networl_1_1_AskP_7" + "P-poll__networl_1_1_AskP_8" + "P-poll__networl_1_1_AnsP_0" + "P-poll__networl_1_1_AnsP_1" + "P-poll__networl_1_1_AnsP_2" + "P-poll__networl_1_1_AnsP_3" + "P-poll__networl_1_1_AnsP_4" + "P-poll__networl_1_1_AnsP_5" + "P-poll__networl_1_1_AnsP_6" + "P-poll__networl_1_1_AnsP_7" + "P-poll__networl_1_1_AnsP_8" + "P-poll__networl_1_1_RI_0" + "P-poll__networl_1_1_RI_1" + "P-poll__networl_1_1_RI_2" + "P-poll__networl_1_1_RI_3" + "P-poll__networl_1_1_RI_4" + "P-poll__networl_1_1_RI_5" + "P-poll__networl_1_1_RI_6" + "P-poll__networl_1_1_RI_7" + "P-poll__networl_1_1_RI_8" + "P-poll__networl_1_1_AI_0" + "P-poll__networl_1_1_AI_1" + "P-poll__networl_1_1_AI_2" + "P-poll__networl_1_1_AI_3" + "P-poll__networl_1_1_AI_4" + "P-poll__networl_1_1_AI_5" + "P-poll__networl_1_1_AI_6" + "P-poll__networl_1_1_AI_7" + "P-poll__networl_1_1_AI_8" + "P-poll__networl_1_1_AnnP_0" + "P-poll__networl_1_1_AnnP_1" + "P-poll__networl_1_1_AnnP_2" + "P-poll__networl_1_1_AnnP_3" + "P-poll__networl_1_1_AnnP_4" + "P-poll__networl_1_1_AnnP_5" + "P-poll__networl_1_1_AnnP_6" + "P-poll__networl_1_1_AnnP_7" + "P-poll__networl_1_1_AnnP_8" + "P-poll__networl_1_1_RP_0" + "P-poll__networl_1_1_RP_1" + "P-poll__networl_1_1_RP_2" + "P-poll__networl_1_1_RP_3" + "P-poll__networl_1_1_RP_4" + "P-poll__networl_1_1_RP_5" + "P-poll__networl_1_1_RP_6" + "P-poll__networl_1_1_RP_7" + "P-poll__networl_1_1_RP_8" + "P-poll__networl_1_2_AskP_0" + "P-poll__networl_1_2_AskP_1" + "P-poll__networl_1_2_AskP_2" + "P-poll__networl_1_2_AskP_3" + "P-poll__networl_1_2_AskP_4" + "P-poll__networl_1_2_AskP_5" + "P-poll__networl_1_2_AskP_6" + "P-poll__networl_1_2_AskP_7" + "P-poll__networl_1_2_AskP_8" + "P-poll__networl_1_2_AnsP_0" + "P-poll__networl_1_2_AnsP_1" + "P-poll__networl_1_2_AnsP_2" + "P-poll__networl_1_2_AnsP_3" + "P-poll__networl_1_2_AnsP_4" + "P-poll__networl_1_2_AnsP_5" + "P-poll__networl_1_2_AnsP_6" + "P-poll__networl_1_2_AnsP_7" + "P-poll__networl_1_2_AnsP_8" + "P-poll__networl_1_2_RI_0" + "P-poll__networl_1_2_RI_1" + "P-poll__networl_1_2_RI_2" + "P-poll__networl_1_2_RI_3" + "P-poll__networl_1_2_RI_4" + "P-poll__networl_1_2_RI_5" + "P-poll__networl_1_2_RI_6" + "P-poll__networl_1_2_RI_7" + "P-poll__networl_1_2_RI_8" + "P-poll__networl_1_2_AI_0" + "P-poll__networl_1_2_AI_1" + "P-poll__networl_1_2_AI_2" + "P-poll__networl_1_2_AI_3" + "P-poll__networl_1_2_AI_4" + "P-poll__networl_1_2_AI_5" + "P-poll__networl_1_2_AI_6" + "P-poll__networl_1_2_AI_7" + "P-poll__networl_1_2_AI_8" + "P-poll__networl_1_2_AnnP_0" + "P-poll__networl_1_2_AnnP_1" + "P-poll__networl_1_2_AnnP_2" + "P-poll__networl_1_2_AnnP_3" + "P-poll__networl_1_2_AnnP_4" + "P-poll__networl_1_2_AnnP_5" + "P-poll__networl_1_2_AnnP_6" + "P-poll__networl_1_2_AnnP_7" + "P-poll__networl_1_2_AnnP_8" + "P-poll__networl_1_2_RP_0" + "P-poll__networl_1_2_RP_1" + "P-poll__networl_1_2_RP_2" + "P-poll__networl_1_2_RP_3" + "P-poll__networl_1_2_RP_4" + "P-poll__networl_1_2_RP_5" + "P-poll__networl_1_2_RP_6" + "P-poll__networl_1_2_RP_7" + "P-poll__networl_1_2_RP_8" + "P-poll__networl_1_3_AskP_0" + "P-poll__networl_1_3_AskP_1" + "P-poll__networl_1_3_AskP_2" + "P-poll__networl_1_3_AskP_3" + "P-poll__networl_1_3_AskP_4" + "P-poll__networl_1_3_AskP_5" + "P-poll__networl_1_3_AskP_6" + "P-poll__networl_1_3_AskP_7" + "P-poll__networl_1_3_AskP_8" + "P-poll__networl_1_3_AnsP_0" + "P-poll__networl_1_3_AnsP_1" + "P-poll__networl_1_3_AnsP_2" + "P-poll__networl_1_3_AnsP_3" + "P-poll__networl_1_3_AnsP_4" + "P-poll__networl_1_3_AnsP_5" + "P-poll__networl_1_3_AnsP_6" + "P-poll__networl_1_3_AnsP_7" + "P-poll__networl_1_3_AnsP_8" + "P-poll__networl_1_3_RI_0" + "P-poll__networl_1_3_RI_1" + "P-poll__networl_1_3_RI_2" + "P-poll__networl_1_3_RI_3" + "P-poll__networl_1_3_RI_4" + "P-poll__networl_1_3_RI_5" + "P-poll__networl_1_3_RI_6" + "P-poll__networl_1_3_RI_7" + "P-poll__networl_1_3_RI_8" + "P-poll__networl_1_3_AI_0" + "P-poll__networl_1_3_AI_1" + "P-poll__networl_1_3_AI_2" + "P-poll__networl_1_3_AI_3" + "P-poll__networl_1_3_AI_4" + "P-poll__networl_1_3_AI_5" + "P-poll__networl_1_3_AI_6" + "P-poll__networl_1_3_AI_7" + "P-poll__networl_1_3_AI_8" + "P-poll__networl_1_3_AnnP_0" + "P-poll__networl_1_3_AnnP_1" + "P-poll__networl_1_3_AnnP_2" + "P-poll__networl_1_3_AnnP_3" + "P-poll__networl_1_3_AnnP_4" + "P-poll__networl_1_3_AnnP_5" + "P-poll__networl_1_3_AnnP_6" + "P-poll__networl_1_3_AnnP_7" + "P-poll__networl_1_3_AnnP_8" + "P-poll__networl_1_3_RP_0" + "P-poll__networl_1_3_RP_1" + "P-poll__networl_1_3_RP_2" + "P-poll__networl_1_3_RP_3" + "P-poll__networl_1_3_RP_4" + "P-poll__networl_1_3_RP_5" + "P-poll__networl_1_3_RP_6" + "P-poll__networl_1_3_RP_7" + "P-poll__networl_1_3_RP_8" + "P-poll__networl_1_4_AskP_0" + "P-poll__networl_1_4_AskP_1" + "P-poll__networl_1_4_AskP_2" + "P-poll__networl_1_4_AskP_3" + "P-poll__networl_1_4_AskP_4" + "P-poll__networl_1_4_AskP_5" + "P-poll__networl_1_4_AskP_6" + "P-poll__networl_1_4_AskP_7" + "P-poll__networl_1_4_AskP_8" + "P-poll__networl_1_4_AnsP_0" + "P-poll__networl_1_4_AnsP_1" + "P-poll__networl_1_4_AnsP_2" + "P-poll__networl_1_4_AnsP_3" + "P-poll__networl_1_4_AnsP_4" + "P-poll__networl_1_4_AnsP_5" + "P-poll__networl_1_4_AnsP_6" + "P-poll__networl_1_4_AnsP_7" + "P-poll__networl_1_4_AnsP_8" + "P-poll__networl_1_4_RI_0" + "P-poll__networl_1_4_RI_1" + "P-poll__networl_1_4_RI_2" + "P-poll__networl_1_4_RI_3" + "P-poll__networl_1_4_RI_4" + "P-poll__networl_1_4_RI_5" + "P-poll__networl_1_4_RI_6" + "P-poll__networl_1_4_RI_7" + "P-poll__networl_1_4_RI_8" + "P-poll__networl_1_4_AI_0" + "P-poll__networl_1_4_AI_1" + "P-poll__networl_1_4_AI_2" + "P-poll__networl_1_4_AI_3" + "P-poll__networl_1_4_AI_4" + "P-poll__networl_1_4_AI_5" + "P-poll__networl_1_4_AI_6" + "P-poll__networl_1_4_AI_7" + "P-poll__networl_1_4_AI_8" + "P-poll__networl_1_4_AnnP_0" + "P-poll__networl_1_4_AnnP_1" + "P-poll__networl_1_4_AnnP_2" + "P-poll__networl_1_4_AnnP_3" + "P-poll__networl_1_4_AnnP_4" + "P-poll__networl_1_4_AnnP_5" + "P-poll__networl_1_4_AnnP_6" + "P-poll__networl_1_4_AnnP_7" + "P-poll__networl_1_4_AnnP_8" + "P-poll__networl_1_4_RP_0" + "P-poll__networl_1_4_RP_1" + "P-poll__networl_1_4_RP_2" + "P-poll__networl_1_4_RP_3" + "P-poll__networl_1_4_RP_4" + "P-poll__networl_1_4_RP_5" + "P-poll__networl_1_4_RP_6" + "P-poll__networl_1_4_RP_7" + "P-poll__networl_1_4_RP_8" + "P-poll__networl_1_5_AskP_0" + "P-poll__networl_1_5_AskP_1" + "P-poll__networl_1_5_AskP_2" + "P-poll__networl_1_5_AskP_3" + "P-poll__networl_1_5_AskP_4" + "P-poll__networl_1_5_AskP_5" + "P-poll__networl_1_5_AskP_6" + "P-poll__networl_1_5_AskP_7" + "P-poll__networl_1_5_AskP_8" + "P-poll__networl_1_5_AnsP_0" + "P-poll__networl_1_5_AnsP_1" + "P-poll__networl_1_5_AnsP_2" + "P-poll__networl_1_5_AnsP_3" + "P-poll__networl_1_5_AnsP_4" + "P-poll__networl_1_5_AnsP_5" + "P-poll__networl_1_5_AnsP_6" + "P-poll__networl_1_5_AnsP_7" + "P-poll__networl_1_5_AnsP_8" + "P-poll__networl_1_5_RI_0" + "P-poll__networl_1_5_RI_1" + "P-poll__networl_1_5_RI_2" + "P-poll__networl_1_5_RI_3" + "P-poll__networl_1_5_RI_4" + "P-poll__networl_1_5_RI_5" + "P-poll__networl_1_5_RI_6" + "P-poll__networl_1_5_RI_7" + "P-poll__networl_1_5_RI_8" + "P-poll__networl_1_5_AI_0" + "P-poll__networl_1_5_AI_1" + "P-poll__networl_1_5_AI_2" + "P-poll__networl_1_5_AI_3" + "P-poll__networl_1_5_AI_4" + "P-poll__networl_1_5_AI_5" + "P-poll__networl_1_5_AI_6" + "P-poll__networl_1_5_AI_7" + "P-poll__networl_1_5_AI_8" + "P-poll__networl_1_5_AnnP_0" + "P-poll__networl_1_5_AnnP_1" + "P-poll__networl_1_5_AnnP_2" + "P-poll__networl_1_5_AnnP_3" + "P-poll__networl_1_5_AnnP_4" + "P-poll__networl_1_5_AnnP_5" + "P-poll__networl_1_5_AnnP_6" + "P-poll__networl_1_5_AnnP_7" + "P-poll__networl_1_5_AnnP_8" + "P-poll__networl_1_5_RP_0" + "P-poll__networl_1_5_RP_1" + "P-poll__networl_1_5_RP_2" + "P-poll__networl_1_5_RP_3" + "P-poll__networl_1_5_RP_4" + "P-poll__networl_1_5_RP_5" + "P-poll__networl_1_5_RP_6" + "P-poll__networl_1_5_RP_7" + "P-poll__networl_1_5_RP_8" + "P-poll__networl_1_6_AskP_0" + "P-poll__networl_1_6_AskP_1" + "P-poll__networl_1_6_AskP_2" + "P-poll__networl_1_6_AskP_3" + "P-poll__networl_1_6_AskP_4" + "P-poll__networl_1_6_AskP_5" + "P-poll__networl_1_6_AskP_6" + "P-poll__networl_1_6_AskP_7" + "P-poll__networl_1_6_AskP_8" + "P-poll__networl_1_6_AnsP_0" + "P-poll__networl_1_6_AnsP_1" + "P-poll__networl_1_6_AnsP_2" + "P-poll__networl_1_6_AnsP_3" + "P-poll__networl_1_6_AnsP_4" + "P-poll__networl_1_6_AnsP_5" + "P-poll__networl_1_6_AnsP_6" + "P-poll__networl_1_6_AnsP_7" + "P-poll__networl_1_6_AnsP_8" + "P-poll__networl_1_6_RI_0" + "P-poll__networl_1_6_RI_1" + "P-poll__networl_1_6_RI_2" + "P-poll__networl_1_6_RI_3" + "P-poll__networl_1_6_RI_4" + "P-poll__networl_1_6_RI_5" + "P-poll__networl_1_6_RI_6" + "P-poll__networl_1_6_RI_7" + "P-poll__networl_1_6_RI_8" + "P-poll__networl_1_6_AI_0" + "P-poll__networl_1_6_AI_1" + "P-poll__networl_1_6_AI_2" + "P-poll__networl_1_6_AI_3" + "P-poll__networl_1_6_AI_4" + "P-poll__networl_1_6_AI_5" + "P-poll__networl_1_6_AI_6" + "P-poll__networl_1_6_AI_7" + "P-poll__networl_1_6_AI_8" + "P-poll__networl_1_6_AnnP_0" + "P-poll__networl_1_6_AnnP_1" + "P-poll__networl_1_6_AnnP_2" + "P-poll__networl_1_6_AnnP_3" + "P-poll__networl_1_6_AnnP_4" + "P-poll__networl_1_6_AnnP_5" + "P-poll__networl_1_6_AnnP_6" + "P-poll__networl_1_6_AnnP_7" + "P-poll__networl_1_6_AnnP_8" + "P-poll__networl_1_6_RP_0" + "P-poll__networl_1_6_RP_1" + "P-poll__networl_1_6_RP_2" + "P-poll__networl_1_6_RP_3" + "P-poll__networl_1_6_RP_4" + "P-poll__networl_1_6_RP_5" + "P-poll__networl_1_6_RP_6" + "P-poll__networl_1_6_RP_7" + "P-poll__networl_1_6_RP_8" + "P-poll__networl_1_7_AskP_0" + "P-poll__networl_1_7_AskP_1" + "P-poll__networl_1_7_AskP_2" + "P-poll__networl_1_7_AskP_3" + "P-poll__networl_1_7_AskP_4" + "P-poll__networl_1_7_AskP_5" + "P-poll__networl_1_7_AskP_6" + "P-poll__networl_1_7_AskP_7" + "P-poll__networl_1_7_AskP_8" + "P-poll__networl_1_7_AnsP_0" + "P-poll__networl_1_7_AnsP_1" + "P-poll__networl_1_7_AnsP_2" + "P-poll__networl_1_7_AnsP_3" + "P-poll__networl_1_7_AnsP_4" + "P-poll__networl_1_7_AnsP_5" + "P-poll__networl_1_7_AnsP_6" + "P-poll__networl_1_7_AnsP_7" + "P-poll__networl_1_7_AnsP_8" + "P-poll__networl_1_7_RI_0" + "P-poll__networl_1_7_RI_1" + "P-poll__networl_1_7_RI_2" + "P-poll__networl_1_7_RI_3" + "P-poll__networl_1_7_RI_4" + "P-poll__networl_1_7_RI_5" + "P-poll__networl_1_7_RI_6" + "P-poll__networl_1_7_RI_7" + "P-poll__networl_1_7_RI_8" + "P-poll__networl_1_7_AI_0" + "P-poll__networl_1_7_AI_1" + "P-poll__networl_1_7_AI_2" + "P-poll__networl_1_7_AI_3" + "P-poll__networl_1_7_AI_4" + "P-poll__networl_1_7_AI_5" + "P-poll__networl_1_7_AI_6" + "P-poll__networl_1_7_AI_7" + "P-poll__networl_1_7_AI_8" + "P-poll__networl_1_7_AnnP_0" + "P-poll__networl_1_7_AnnP_1" + "P-poll__networl_1_7_AnnP_2" + "P-poll__networl_1_7_AnnP_3" + "P-poll__networl_1_7_AnnP_4" + "P-poll__networl_1_7_AnnP_5" + "P-poll__networl_1_7_AnnP_6" + "P-poll__networl_1_7_AnnP_7" + "P-poll__networl_1_7_AnnP_8" + "P-poll__networl_1_7_RP_0" + "P-poll__networl_1_7_RP_1" + "P-poll__networl_1_7_RP_2" + "P-poll__networl_1_7_RP_3" + "P-poll__networl_1_7_RP_4" + "P-poll__networl_1_7_RP_5" + "P-poll__networl_1_7_RP_6" + "P-poll__networl_1_7_RP_7" + "P-poll__networl_1_7_RP_8" + "P-poll__networl_1_8_AskP_0" + "P-poll__networl_1_8_AskP_1" + "P-poll__networl_1_8_AskP_2" + "P-poll__networl_1_8_AskP_3" + "P-poll__networl_1_8_AskP_4" + "P-poll__networl_1_8_AskP_5" + "P-poll__networl_1_8_AskP_6" + "P-poll__networl_1_8_AskP_7" + "P-poll__networl_1_8_AskP_8" + "P-poll__networl_1_8_AnsP_0" + "P-poll__networl_1_8_AnsP_1" + "P-poll__networl_1_8_AnsP_2" + "P-poll__networl_1_8_AnsP_3" + "P-poll__networl_1_8_AnsP_4" + "P-poll__networl_1_8_AnsP_5" + "P-poll__networl_1_8_AnsP_6" + "P-poll__networl_1_8_AnsP_7" + "P-poll__networl_1_8_AnsP_8" + "P-poll__networl_1_8_RI_0" + "P-poll__networl_1_8_RI_1" + "P-poll__networl_1_8_RI_2" + "P-poll__networl_1_8_RI_3" + "P-poll__networl_1_8_RI_4" + "P-poll__networl_1_8_RI_5" + "P-poll__networl_1_8_RI_6" + "P-poll__networl_1_8_RI_7" + "P-poll__networl_1_8_RI_8" + "P-poll__networl_1_8_AI_0" + "P-poll__networl_1_8_AI_1" + "P-poll__networl_1_8_AI_2" + "P-poll__networl_1_8_AI_3" + "P-poll__networl_1_8_AI_4" + "P-poll__networl_1_8_AI_5" + "P-poll__networl_1_8_AI_6" + "P-poll__networl_1_8_AI_7" + "P-poll__networl_1_8_AI_8" + "P-poll__networl_1_8_AnnP_0" + "P-poll__networl_1_8_AnnP_1" + "P-poll__networl_1_8_AnnP_2" + "P-poll__networl_1_8_AnnP_3" + "P-poll__networl_1_8_AnnP_4" + "P-poll__networl_1_8_AnnP_5" + "P-poll__networl_1_8_AnnP_6" + "P-poll__networl_1_8_AnnP_7" + "P-poll__networl_1_8_AnnP_8" + "P-poll__networl_1_8_RP_0" + "P-poll__networl_1_8_RP_1" + "P-poll__networl_1_8_RP_2" + "P-poll__networl_1_8_RP_3" + "P-poll__networl_1_8_RP_4" + "P-poll__networl_1_8_RP_5" + "P-poll__networl_1_8_RP_6" + "P-poll__networl_1_8_RP_7" + "P-poll__networl_1_8_RP_8" + "P-poll__networl_2_0_AskP_0" + "P-poll__networl_2_0_AskP_1" + "P-poll__networl_2_0_AskP_2" + "P-poll__networl_2_0_AskP_3" + "P-poll__networl_2_0_AskP_4" + "P-poll__networl_2_0_AskP_5" + "P-poll__networl_2_0_AskP_6" + "P-poll__networl_2_0_AskP_7" + "P-poll__networl_2_0_AskP_8" + "P-poll__networl_2_0_AnsP_0" + "P-poll__networl_2_0_AnsP_1" + "P-poll__networl_2_0_AnsP_2" + "P-poll__networl_2_0_AnsP_3" + "P-poll__networl_2_0_AnsP_4" + "P-poll__networl_2_0_AnsP_5" + "P-poll__networl_2_0_AnsP_6" + "P-poll__networl_2_0_AnsP_7" + "P-poll__networl_2_0_AnsP_8" + "P-poll__networl_2_0_RI_0" + "P-poll__networl_2_0_RI_1" + "P-poll__networl_2_0_RI_2" + "P-poll__networl_2_0_RI_3" + "P-poll__networl_2_0_RI_4" + "P-poll__networl_2_0_RI_5" + "P-poll__networl_2_0_RI_6" + "P-poll__networl_2_0_RI_7" + "P-poll__networl_2_0_RI_8" + "P-poll__networl_2_0_AI_0" + "P-poll__networl_2_0_AI_1" + "P-poll__networl_2_0_AI_2" + "P-poll__networl_2_0_AI_3" + "P-poll__networl_2_0_AI_4" + "P-poll__networl_2_0_AI_5" + "P-poll__networl_2_0_AI_6" + "P-poll__networl_2_0_AI_7" + "P-poll__networl_2_0_AI_8" + "P-poll__networl_2_0_AnnP_0" + "P-poll__networl_2_0_AnnP_1" + "P-poll__networl_2_0_AnnP_2" + "P-poll__networl_2_0_AnnP_3" + "P-poll__networl_2_0_AnnP_4" + "P-poll__networl_2_0_AnnP_5" + "P-poll__networl_2_0_AnnP_6" + "P-poll__networl_2_0_AnnP_7" + "P-poll__networl_2_0_AnnP_8" + "P-poll__networl_2_0_RP_0" + "P-poll__networl_2_0_RP_1" + "P-poll__networl_2_0_RP_2" + "P-poll__networl_2_0_RP_3" + "P-poll__networl_2_0_RP_4" + "P-poll__networl_2_0_RP_5" + "P-poll__networl_2_0_RP_6" + "P-poll__networl_2_0_RP_7" + "P-poll__networl_2_0_RP_8" + "P-poll__networl_2_1_AskP_0" + "P-poll__networl_2_1_AskP_1" + "P-poll__networl_2_1_AskP_2" + "P-poll__networl_2_1_AskP_3" + "P-poll__networl_2_1_AskP_4" + "P-poll__networl_2_1_AskP_5" + "P-poll__networl_2_1_AskP_6" + "P-poll__networl_2_1_AskP_7" + "P-poll__networl_2_1_AskP_8" + "P-poll__networl_2_1_AnsP_0" + "P-poll__networl_2_1_AnsP_1" + "P-poll__networl_2_1_AnsP_2" + "P-poll__networl_2_1_AnsP_3" + "P-poll__networl_2_1_AnsP_4" + "P-poll__networl_2_1_AnsP_5" + "P-poll__networl_2_1_AnsP_6" + "P-poll__networl_2_1_AnsP_7" + "P-poll__networl_2_1_AnsP_8" + "P-poll__networl_2_1_RI_0" + "P-poll__networl_2_1_RI_1" + "P-poll__networl_2_1_RI_2" + "P-poll__networl_2_1_RI_3" + "P-poll__networl_2_1_RI_4" + "P-poll__networl_2_1_RI_5" + "P-poll__networl_2_1_RI_6" + "P-poll__networl_2_1_RI_7" + "P-poll__networl_2_1_RI_8" + "P-poll__networl_2_1_AI_0" + "P-poll__networl_2_1_AI_1" + "P-poll__networl_2_1_AI_2" + "P-poll__networl_2_1_AI_3" + "P-poll__networl_2_1_AI_4" + "P-poll__networl_2_1_AI_5" + "P-poll__networl_2_1_AI_6" + "P-poll__networl_2_1_AI_7" + "P-poll__networl_2_1_AI_8" + "P-poll__networl_2_1_AnnP_0" + "P-poll__networl_2_1_AnnP_1" + "P-poll__networl_2_1_AnnP_2" + "P-poll__networl_2_1_AnnP_3" + "P-poll__networl_2_1_AnnP_4" + "P-poll__networl_2_1_AnnP_5" + "P-poll__networl_2_1_AnnP_6" + "P-poll__networl_2_1_AnnP_7" + "P-poll__networl_2_1_AnnP_8" + "P-poll__networl_2_1_RP_0" + "P-poll__networl_2_1_RP_1" + "P-poll__networl_2_1_RP_2" + "P-poll__networl_2_1_RP_3" + "P-poll__networl_2_1_RP_4" + "P-poll__networl_2_1_RP_5" + "P-poll__networl_2_1_RP_6" + "P-poll__networl_2_1_RP_7" + "P-poll__networl_2_1_RP_8" + "P-poll__networl_2_2_AskP_0" + "P-poll__networl_2_2_AskP_1" + "P-poll__networl_2_2_AskP_2" + "P-poll__networl_2_2_AskP_3" + "P-poll__networl_2_2_AskP_4" + "P-poll__networl_2_2_AskP_5" + "P-poll__networl_2_2_AskP_6" + "P-poll__networl_2_2_AskP_7" + "P-poll__networl_2_2_AskP_8" + "P-poll__networl_2_2_AnsP_0" + "P-poll__networl_2_2_AnsP_1" + "P-poll__networl_2_2_AnsP_2" + "P-poll__networl_2_2_AnsP_3" + "P-poll__networl_2_2_AnsP_4" + "P-poll__networl_2_2_AnsP_5" + "P-poll__networl_2_2_AnsP_6" + "P-poll__networl_2_2_AnsP_7" + "P-poll__networl_2_2_AnsP_8" + "P-poll__networl_2_2_RI_0" + "P-poll__networl_2_2_RI_1" + "P-poll__networl_2_2_RI_2" + "P-poll__networl_2_2_RI_3" + "P-poll__networl_2_2_RI_4" + "P-poll__networl_2_2_RI_5" + "P-poll__networl_2_2_RI_6" + "P-poll__networl_2_2_RI_7" + "P-poll__networl_2_2_RI_8" + "P-poll__networl_2_2_AI_0" + "P-poll__networl_2_2_AI_1" + "P-poll__networl_2_2_AI_2" + "P-poll__networl_2_2_AI_3" + "P-poll__networl_2_2_AI_4" + "P-poll__networl_2_2_AI_5" + "P-poll__networl_2_2_AI_6" + "P-poll__networl_2_2_AI_7" + "P-poll__networl_2_2_AI_8" + "P-poll__networl_2_2_AnnP_0" + "P-poll__networl_2_2_AnnP_1" + "P-poll__networl_2_2_AnnP_2" + "P-poll__networl_2_2_AnnP_3" + "P-poll__networl_2_2_AnnP_4" + "P-poll__networl_2_2_AnnP_5" + "P-poll__networl_2_2_AnnP_6" + "P-poll__networl_2_2_AnnP_7" + "P-poll__networl_2_2_AnnP_8" + "P-poll__networl_2_2_RP_0" + "P-poll__networl_2_2_RP_1" + "P-poll__networl_2_2_RP_2" + "P-poll__networl_2_2_RP_3" + "P-poll__networl_2_2_RP_4" + "P-poll__networl_2_2_RP_5" + "P-poll__networl_2_2_RP_6" + "P-poll__networl_2_2_RP_7" + "P-poll__networl_2_2_RP_8" + "P-poll__networl_2_3_AskP_0" + "P-poll__networl_2_3_AskP_1" + "P-poll__networl_2_3_AskP_2" + "P-poll__networl_2_3_AskP_3" + "P-poll__networl_2_3_AskP_4" + "P-poll__networl_2_3_AskP_5" + "P-poll__networl_2_3_AskP_6" + "P-poll__networl_2_3_AskP_7" + "P-poll__networl_2_3_AskP_8" + "P-poll__networl_2_3_AnsP_0" + "P-poll__networl_2_3_AnsP_1" + "P-poll__networl_2_3_AnsP_2" + "P-poll__networl_2_3_AnsP_3" + "P-poll__networl_2_3_AnsP_4" + "P-poll__networl_2_3_AnsP_5" + "P-poll__networl_2_3_AnsP_6" + "P-poll__networl_2_3_AnsP_7" + "P-poll__networl_2_3_AnsP_8" + "P-poll__networl_2_3_RI_0" + "P-poll__networl_2_3_RI_1" + "P-poll__networl_2_3_RI_2" + "P-poll__networl_2_3_RI_3" + "P-poll__networl_2_3_RI_4" + "P-poll__networl_2_3_RI_5" + "P-poll__networl_2_3_RI_6" + "P-poll__networl_2_3_RI_7" + "P-poll__networl_2_3_RI_8" + "P-poll__networl_2_3_AI_0" + "P-poll__networl_2_3_AI_1" + "P-poll__networl_2_3_AI_2" + "P-poll__networl_2_3_AI_3" + "P-poll__networl_2_3_AI_4" + "P-poll__networl_2_3_AI_5" + "P-poll__networl_2_3_AI_6" + "P-poll__networl_2_3_AI_7" + "P-poll__networl_2_3_AI_8" + "P-poll__networl_2_3_AnnP_0" + "P-poll__networl_2_3_AnnP_1" + "P-poll__networl_2_3_AnnP_2" + "P-poll__networl_2_3_AnnP_3" + "P-poll__networl_2_3_AnnP_4" + "P-poll__networl_2_3_AnnP_5" + "P-poll__networl_2_3_AnnP_6" + "P-poll__networl_2_3_AnnP_7" + "P-poll__networl_2_3_AnnP_8" + "P-poll__networl_2_3_RP_0" + "P-poll__networl_2_3_RP_1" + "P-poll__networl_2_3_RP_2" + "P-poll__networl_2_3_RP_3" + "P-poll__networl_2_3_RP_4" + "P-poll__networl_2_3_RP_5" + "P-poll__networl_2_3_RP_6" + "P-poll__networl_2_3_RP_7" + "P-poll__networl_2_3_RP_8" + "P-poll__networl_2_4_AskP_0" + "P-poll__networl_2_4_AskP_1" + "P-poll__networl_2_4_AskP_2" + "P-poll__networl_2_4_AskP_3" + "P-poll__networl_2_4_AskP_4" + "P-poll__networl_2_4_AskP_5" + "P-poll__networl_2_4_AskP_6" + "P-poll__networl_2_4_AskP_7" + "P-poll__networl_2_4_AskP_8" + "P-poll__networl_2_4_AnsP_0" + "P-poll__networl_2_4_AnsP_1" + "P-poll__networl_2_4_AnsP_2" + "P-poll__networl_2_4_AnsP_3" + "P-poll__networl_2_4_AnsP_4" + "P-poll__networl_2_4_AnsP_5" + "P-poll__networl_2_4_AnsP_6" + "P-poll__networl_2_4_AnsP_7" + "P-poll__networl_2_4_AnsP_8" + "P-poll__networl_2_4_RI_0" + "P-poll__networl_2_4_RI_1" + "P-poll__networl_2_4_RI_2" + "P-poll__networl_2_4_RI_3" + "P-poll__networl_2_4_RI_4" + "P-poll__networl_2_4_RI_5" + "P-poll__networl_2_4_RI_6" + "P-poll__networl_2_4_RI_7" + "P-poll__networl_2_4_RI_8" + "P-poll__networl_2_4_AI_0" + "P-poll__networl_2_4_AI_1" + "P-poll__networl_2_4_AI_2" + "P-poll__networl_2_4_AI_3" + "P-poll__networl_2_4_AI_4" + "P-poll__networl_2_4_AI_5" + "P-poll__networl_2_4_AI_6" + "P-poll__networl_2_4_AI_7" + "P-poll__networl_2_4_AI_8" + "P-poll__networl_2_4_AnnP_0" + "P-poll__networl_2_4_AnnP_1" + "P-poll__networl_2_4_AnnP_2" + "P-poll__networl_2_4_AnnP_3" + "P-poll__networl_2_4_AnnP_4" + "P-poll__networl_2_4_AnnP_5" + "P-poll__networl_2_4_AnnP_6" + "P-poll__networl_2_4_AnnP_7" + "P-poll__networl_2_4_AnnP_8" + "P-poll__networl_2_4_RP_0" + "P-poll__networl_2_4_RP_1" + "P-poll__networl_2_4_RP_2" + "P-poll__networl_2_4_RP_3" + "P-poll__networl_2_4_RP_4" + "P-poll__networl_2_4_RP_5" + "P-poll__networl_2_4_RP_6" + "P-poll__networl_2_4_RP_7" + "P-poll__networl_2_4_RP_8" + "P-poll__networl_2_5_AskP_0" + "P-poll__networl_2_5_AskP_1" + "P-poll__networl_2_5_AskP_2" + "P-poll__networl_2_5_AskP_3" + "P-poll__networl_2_5_AskP_4" + "P-poll__networl_2_5_AskP_5" + "P-poll__networl_2_5_AskP_6" + "P-poll__networl_2_5_AskP_7" + "P-poll__networl_2_5_AskP_8" + "P-poll__networl_2_5_AnsP_0" + "P-poll__networl_2_5_AnsP_1" + "P-poll__networl_2_5_AnsP_2" + "P-poll__networl_2_5_AnsP_3" + "P-poll__networl_2_5_AnsP_4" + "P-poll__networl_2_5_AnsP_5" + "P-poll__networl_2_5_AnsP_6" + "P-poll__networl_2_5_AnsP_7" + "P-poll__networl_2_5_AnsP_8" + "P-poll__networl_2_5_RI_0" + "P-poll__networl_2_5_RI_1" + "P-poll__networl_2_5_RI_2" + "P-poll__networl_2_5_RI_3" + "P-poll__networl_2_5_RI_4" + "P-poll__networl_2_5_RI_5" + "P-poll__networl_2_5_RI_6" + "P-poll__networl_2_5_RI_7" + "P-poll__networl_2_5_RI_8" + "P-poll__networl_2_5_AI_0" + "P-poll__networl_2_5_AI_1" + "P-poll__networl_2_5_AI_2" + "P-poll__networl_2_5_AI_3" + "P-poll__networl_2_5_AI_4" + "P-poll__networl_2_5_AI_5" + "P-poll__networl_2_5_AI_6" + "P-poll__networl_2_5_AI_7" + "P-poll__networl_2_5_AI_8" + "P-poll__networl_2_5_AnnP_0" + "P-poll__networl_2_5_AnnP_1" + "P-poll__networl_2_5_AnnP_2" + "P-poll__networl_2_5_AnnP_3" + "P-poll__networl_2_5_AnnP_4" + "P-poll__networl_2_5_AnnP_5" + "P-poll__networl_2_5_AnnP_6" + "P-poll__networl_2_5_AnnP_7" + "P-poll__networl_2_5_AnnP_8" + "P-poll__networl_2_5_RP_0" + "P-poll__networl_2_5_RP_1" + "P-poll__networl_2_5_RP_2" + "P-poll__networl_2_5_RP_3" + "P-poll__networl_2_5_RP_4" + "P-poll__networl_2_5_RP_5" + "P-poll__networl_2_5_RP_6" + "P-poll__networl_2_5_RP_7" + "P-poll__networl_2_5_RP_8" + "P-poll__networl_2_6_AskP_0" + "P-poll__networl_2_6_AskP_1" + "P-poll__networl_2_6_AskP_2" + "P-poll__networl_2_6_AskP_3" + "P-poll__networl_2_6_AskP_4" + "P-poll__networl_2_6_AskP_5" + "P-poll__networl_2_6_AskP_6" + "P-poll__networl_2_6_AskP_7" + "P-poll__networl_2_6_AskP_8" + "P-poll__networl_2_6_AnsP_0" + "P-poll__networl_2_6_AnsP_1" + "P-poll__networl_2_6_AnsP_2" + "P-poll__networl_2_6_AnsP_3" + "P-poll__networl_2_6_AnsP_4" + "P-poll__networl_2_6_AnsP_5" + "P-poll__networl_2_6_AnsP_6" + "P-poll__networl_2_6_AnsP_7" + "P-poll__networl_2_6_AnsP_8" + "P-poll__networl_2_6_RI_0" + "P-poll__networl_2_6_RI_1" + "P-poll__networl_2_6_RI_2" + "P-poll__networl_2_6_RI_3" + "P-poll__networl_2_6_RI_4" + "P-poll__networl_2_6_RI_5" + "P-poll__networl_2_6_RI_6" + "P-poll__networl_2_6_RI_7" + "P-poll__networl_2_6_RI_8" + "P-poll__networl_2_6_AI_0" + "P-poll__networl_2_6_AI_1" + "P-poll__networl_2_6_AI_2" + "P-poll__networl_2_6_AI_3" + "P-poll__networl_2_6_AI_4" + "P-poll__networl_2_6_AI_5" + "P-poll__networl_2_6_AI_6" + "P-poll__networl_2_6_AI_7" + "P-poll__networl_2_6_AI_8" + "P-poll__networl_2_6_AnnP_0" + "P-poll__networl_2_6_AnnP_1" + "P-poll__networl_2_6_AnnP_2" + "P-poll__networl_2_6_AnnP_3" + "P-poll__networl_2_6_AnnP_4" + "P-poll__networl_2_6_AnnP_5" + "P-poll__networl_2_6_AnnP_6" + "P-poll__networl_2_6_AnnP_7" + "P-poll__networl_2_6_AnnP_8" + "P-poll__networl_2_6_RP_0" + "P-poll__networl_2_6_RP_1" + "P-poll__networl_2_6_RP_2" + "P-poll__networl_2_6_RP_3" + "P-poll__networl_2_6_RP_4" + "P-poll__networl_2_6_RP_5" + "P-poll__networl_2_6_RP_6" + "P-poll__networl_2_6_RP_7" + "P-poll__networl_2_6_RP_8" + "P-poll__networl_2_7_AskP_0" + "P-poll__networl_2_7_AskP_1" + "P-poll__networl_2_7_AskP_2" + "P-poll__networl_2_7_AskP_3" + "P-poll__networl_2_7_AskP_4" + "P-poll__networl_2_7_AskP_5" + "P-poll__networl_2_7_AskP_6" + "P-poll__networl_2_7_AskP_7" + "P-poll__networl_2_7_AskP_8" + "P-poll__networl_2_7_AnsP_0" + "P-poll__networl_2_7_AnsP_1" + "P-poll__networl_2_7_AnsP_2" + "P-poll__networl_2_7_AnsP_3" + "P-poll__networl_2_7_AnsP_4" + "P-poll__networl_2_7_AnsP_5" + "P-poll__networl_2_7_AnsP_6" + "P-poll__networl_2_7_AnsP_7" + "P-poll__networl_2_7_AnsP_8" + "P-poll__networl_2_7_RI_0" + "P-poll__networl_2_7_RI_1" + "P-poll__networl_2_7_RI_2" + "P-poll__networl_2_7_RI_3" + "P-poll__networl_2_7_RI_4" + "P-poll__networl_2_7_RI_5" + "P-poll__networl_2_7_RI_6" + "P-poll__networl_2_7_RI_7" + "P-poll__networl_2_7_RI_8" + "P-poll__networl_2_7_AI_0" + "P-poll__networl_2_7_AI_1" + "P-poll__networl_2_7_AI_2" + "P-poll__networl_2_7_AI_3" + "P-poll__networl_2_7_AI_4" + "P-poll__networl_2_7_AI_5" + "P-poll__networl_2_7_AI_6" + "P-poll__networl_2_7_AI_7" + "P-poll__networl_2_7_AI_8" + "P-poll__networl_2_7_AnnP_0" + "P-poll__networl_2_7_AnnP_1" + "P-poll__networl_2_7_AnnP_2" + "P-poll__networl_2_7_AnnP_3" + "P-poll__networl_2_7_AnnP_4" + "P-poll__networl_2_7_AnnP_5" + "P-poll__networl_2_7_AnnP_6" + "P-poll__networl_2_7_AnnP_7" + "P-poll__networl_2_7_AnnP_8" + "P-poll__networl_2_7_RP_0" + "P-poll__networl_2_7_RP_1" + "P-poll__networl_2_7_RP_2" + "P-poll__networl_2_7_RP_3" + "P-poll__networl_2_7_RP_4" + "P-poll__networl_2_7_RP_5" + "P-poll__networl_2_7_RP_6" + "P-poll__networl_2_7_RP_7" + "P-poll__networl_2_7_RP_8" + "P-poll__networl_2_8_AskP_0" + "P-poll__networl_2_8_AskP_1" + "P-poll__networl_2_8_AskP_2" + "P-poll__networl_2_8_AskP_3" + "P-poll__networl_2_8_AskP_4" + "P-poll__networl_2_8_AskP_5" + "P-poll__networl_2_8_AskP_6" + "P-poll__networl_2_8_AskP_7" + "P-poll__networl_2_8_AskP_8" + "P-poll__networl_2_8_AnsP_0" + "P-poll__networl_2_8_AnsP_1" + "P-poll__networl_2_8_AnsP_2" + "P-poll__networl_2_8_AnsP_3" + "P-poll__networl_2_8_AnsP_4" + "P-poll__networl_2_8_AnsP_5" + "P-poll__networl_2_8_AnsP_6" + "P-poll__networl_2_8_AnsP_7" + "P-poll__networl_2_8_AnsP_8" + "P-poll__networl_2_8_RI_0" + "P-poll__networl_2_8_RI_1" + "P-poll__networl_2_8_RI_2" + "P-poll__networl_2_8_RI_3" + "P-poll__networl_2_8_RI_4" + "P-poll__networl_2_8_RI_5" + "P-poll__networl_2_8_RI_6" + "P-poll__networl_2_8_RI_7" + "P-poll__networl_2_8_RI_8" + "P-poll__networl_2_8_AI_0" + "P-poll__networl_2_8_AI_1" + "P-poll__networl_2_8_AI_2" + "P-poll__networl_2_8_AI_3" + "P-poll__networl_2_8_AI_4" + "P-poll__networl_2_8_AI_5" + "P-poll__networl_2_8_AI_6" + "P-poll__networl_2_8_AI_7" + "P-poll__networl_2_8_AI_8" + "P-poll__networl_2_8_AnnP_0" + "P-poll__networl_2_8_AnnP_1" + "P-poll__networl_2_8_AnnP_2" + "P-poll__networl_2_8_AnnP_3" + "P-poll__networl_2_8_AnnP_4" + "P-poll__networl_2_8_AnnP_5" + "P-poll__networl_2_8_AnnP_6" + "P-poll__networl_2_8_AnnP_7" + "P-poll__networl_2_8_AnnP_8" + "P-poll__networl_2_8_RP_0" + "P-poll__networl_2_8_RP_1" + "P-poll__networl_2_8_RP_2" + "P-poll__networl_2_8_RP_3" + "P-poll__networl_2_8_RP_4" + "P-poll__networl_2_8_RP_5" + "P-poll__networl_2_8_RP_6" + "P-poll__networl_2_8_RP_7" + "P-poll__networl_2_8_RP_8" + "P-poll__networl_3_0_AskP_0" + "P-poll__networl_3_0_AskP_1" + "P-poll__networl_3_0_AskP_2" + "P-poll__networl_3_0_AskP_3" + "P-poll__networl_3_0_AskP_4" + "P-poll__networl_3_0_AskP_5" + "P-poll__networl_3_0_AskP_6" + "P-poll__networl_3_0_AskP_7" + "P-poll__networl_3_0_AskP_8" + "P-poll__networl_3_0_AnsP_0" + "P-poll__networl_3_0_AnsP_1" + "P-poll__networl_3_0_AnsP_2" + "P-poll__networl_3_0_AnsP_3" + "P-poll__networl_3_0_AnsP_4" + "P-poll__networl_3_0_AnsP_5" + "P-poll__networl_3_0_AnsP_6" + "P-poll__networl_3_0_AnsP_7" + "P-poll__networl_3_0_AnsP_8" + "P-poll__networl_3_0_RI_0" + "P-poll__networl_3_0_RI_1" + "P-poll__networl_3_0_RI_2" + "P-poll__networl_3_0_RI_3" + "P-poll__networl_3_0_RI_4" + "P-poll__networl_3_0_RI_5" + "P-poll__networl_3_0_RI_6" + "P-poll__networl_3_0_RI_7" + "P-poll__networl_3_0_RI_8" + "P-poll__networl_3_0_AI_0" + "P-poll__networl_3_0_AI_1" + "P-poll__networl_3_0_AI_2" + "P-poll__networl_3_0_AI_3" + "P-poll__networl_3_0_AI_4" + "P-poll__networl_3_0_AI_5" + "P-poll__networl_3_0_AI_6" + "P-poll__networl_3_0_AI_7" + "P-poll__networl_3_0_AI_8" + "P-poll__networl_3_0_AnnP_0" + "P-poll__networl_3_0_AnnP_1" + "P-poll__networl_3_0_AnnP_2" + "P-poll__networl_3_0_AnnP_3" + "P-poll__networl_3_0_AnnP_4" + "P-poll__networl_3_0_AnnP_5" + "P-poll__networl_3_0_AnnP_6" + "P-poll__networl_3_0_AnnP_7" + "P-poll__networl_3_0_AnnP_8" + "P-poll__networl_3_0_RP_0" + "P-poll__networl_3_0_RP_1" + "P-poll__networl_3_0_RP_2" + "P-poll__networl_3_0_RP_3" + "P-poll__networl_3_0_RP_4" + "P-poll__networl_3_0_RP_5" + "P-poll__networl_3_0_RP_6" + "P-poll__networl_3_0_RP_7" + "P-poll__networl_3_0_RP_8" + "P-poll__networl_3_1_AskP_0" + "P-poll__networl_3_1_AskP_1" + "P-poll__networl_3_1_AskP_2" + "P-poll__networl_3_1_AskP_3" + "P-poll__networl_3_1_AskP_4" + "P-poll__networl_3_1_AskP_5" + "P-poll__networl_3_1_AskP_6" + "P-poll__networl_3_1_AskP_7" + "P-poll__networl_3_1_AskP_8" + "P-poll__networl_3_1_AnsP_0" + "P-poll__networl_3_1_AnsP_1" + "P-poll__networl_3_1_AnsP_2" + "P-poll__networl_3_1_AnsP_3" + "P-poll__networl_3_1_AnsP_4" + "P-poll__networl_3_1_AnsP_5" + "P-poll__networl_3_1_AnsP_6" + "P-poll__networl_3_1_AnsP_7" + "P-poll__networl_3_1_AnsP_8" + "P-poll__networl_3_1_RI_0" + "P-poll__networl_3_1_RI_1" + "P-poll__networl_3_1_RI_2" + "P-poll__networl_3_1_RI_3" + "P-poll__networl_3_1_RI_4" + "P-poll__networl_3_1_RI_5" + "P-poll__networl_3_1_RI_6" + "P-poll__networl_3_1_RI_7" + "P-poll__networl_3_1_RI_8" + "P-poll__networl_3_1_AI_0" + "P-poll__networl_3_1_AI_1" + "P-poll__networl_3_1_AI_2" + "P-poll__networl_3_1_AI_3" + "P-poll__networl_3_1_AI_4" + "P-poll__networl_3_1_AI_5" + "P-poll__networl_3_1_AI_6" + "P-poll__networl_3_1_AI_7" + "P-poll__networl_3_1_AI_8" + "P-poll__networl_3_1_AnnP_0" + "P-poll__networl_3_1_AnnP_1" + "P-poll__networl_3_1_AnnP_2" + "P-poll__networl_3_1_AnnP_3" + "P-poll__networl_3_1_AnnP_4" + "P-poll__networl_3_1_AnnP_5" + "P-poll__networl_3_1_AnnP_6" + "P-poll__networl_3_1_AnnP_7" + "P-poll__networl_3_1_AnnP_8" + "P-poll__networl_3_1_RP_0" + "P-poll__networl_3_1_RP_1" + "P-poll__networl_3_1_RP_2" + "P-poll__networl_3_1_RP_3" + "P-poll__networl_3_1_RP_4" + "P-poll__networl_3_1_RP_5" + "P-poll__networl_3_1_RP_6" + "P-poll__networl_3_1_RP_7" + "P-poll__networl_3_1_RP_8" + "P-poll__networl_3_2_AskP_0" + "P-poll__networl_3_2_AskP_1" + "P-poll__networl_3_2_AskP_2" + "P-poll__networl_3_2_AskP_3" + "P-poll__networl_3_2_AskP_4" + "P-poll__networl_3_2_AskP_5" + "P-poll__networl_3_2_AskP_6" + "P-poll__networl_3_2_AskP_7" + "P-poll__networl_3_2_AskP_8" + "P-poll__networl_3_2_AnsP_0" + "P-poll__networl_3_2_AnsP_1" + "P-poll__networl_3_2_AnsP_2" + "P-poll__networl_3_2_AnsP_3" + "P-poll__networl_3_2_AnsP_4" + "P-poll__networl_3_2_AnsP_5" + "P-poll__networl_3_2_AnsP_6" + "P-poll__networl_3_2_AnsP_7" + "P-poll__networl_3_2_AnsP_8" + "P-poll__networl_3_2_RI_0" + "P-poll__networl_3_2_RI_1" + "P-poll__networl_3_2_RI_2" + "P-poll__networl_3_2_RI_3" + "P-poll__networl_3_2_RI_4" + "P-poll__networl_3_2_RI_5" + "P-poll__networl_3_2_RI_6" + "P-poll__networl_3_2_RI_7" + "P-poll__networl_3_2_RI_8" + "P-poll__networl_3_2_AI_0" + "P-poll__networl_3_2_AI_1" + "P-poll__networl_3_2_AI_2" + "P-poll__networl_3_2_AI_3" + "P-poll__networl_3_2_AI_4" + "P-poll__networl_3_2_AI_5" + "P-poll__networl_3_2_AI_6" + "P-poll__networl_3_2_AI_7" + "P-poll__networl_3_2_AI_8" + "P-poll__networl_3_2_AnnP_0" + "P-poll__networl_3_2_AnnP_1" + "P-poll__networl_3_2_AnnP_2" + "P-poll__networl_3_2_AnnP_3" + "P-poll__networl_3_2_AnnP_4" + "P-poll__networl_3_2_AnnP_5" + "P-poll__networl_3_2_AnnP_6" + "P-poll__networl_3_2_AnnP_7" + "P-poll__networl_3_2_AnnP_8" + "P-poll__networl_3_2_RP_0" + "P-poll__networl_3_2_RP_1" + "P-poll__networl_3_2_RP_2" + "P-poll__networl_3_2_RP_3" + "P-poll__networl_3_2_RP_4" + "P-poll__networl_3_2_RP_5" + "P-poll__networl_3_2_RP_6" + "P-poll__networl_3_2_RP_7" + "P-poll__networl_3_2_RP_8" + "P-poll__networl_3_3_AskP_0" + "P-poll__networl_3_3_AskP_1" + "P-poll__networl_3_3_AskP_2" + "P-poll__networl_3_3_AskP_3" + "P-poll__networl_3_3_AskP_4" + "P-poll__networl_3_3_AskP_5" + "P-poll__networl_3_3_AskP_6" + "P-poll__networl_3_3_AskP_7" + "P-poll__networl_3_3_AskP_8" + "P-poll__networl_3_3_AnsP_0" + "P-poll__networl_3_3_AnsP_1" + "P-poll__networl_3_3_AnsP_2" + "P-poll__networl_3_3_AnsP_3" + "P-poll__networl_3_3_AnsP_4" + "P-poll__networl_3_3_AnsP_5" + "P-poll__networl_3_3_AnsP_6" + "P-poll__networl_3_3_AnsP_7" + "P-poll__networl_3_3_AnsP_8" + "P-poll__networl_3_3_RI_0" + "P-poll__networl_3_3_RI_1" + "P-poll__networl_3_3_RI_2" + "P-poll__networl_3_3_RI_3" + "P-poll__networl_3_3_RI_4" + "P-poll__networl_3_3_RI_5" + "P-poll__networl_3_3_RI_6" + "P-poll__networl_3_3_RI_7" + "P-poll__networl_3_3_RI_8" + "P-poll__networl_3_3_AI_0" + "P-poll__networl_3_3_AI_1" + "P-poll__networl_3_3_AI_2" + "P-poll__networl_3_3_AI_3" + "P-poll__networl_3_3_AI_4" + "P-poll__networl_3_3_AI_5" + "P-poll__networl_3_3_AI_6" + "P-poll__networl_3_3_AI_7" + "P-poll__networl_3_3_AI_8" + "P-poll__networl_3_3_AnnP_0" + "P-poll__networl_3_3_AnnP_1" + "P-poll__networl_3_3_AnnP_2" + "P-poll__networl_3_3_AnnP_3" + "P-poll__networl_3_3_AnnP_4" + "P-poll__networl_3_3_AnnP_5" + "P-poll__networl_3_3_AnnP_6" + "P-poll__networl_3_3_AnnP_7" + "P-poll__networl_3_3_AnnP_8" + "P-poll__networl_3_3_RP_0" + "P-poll__networl_3_3_RP_1" + "P-poll__networl_3_3_RP_2" + "P-poll__networl_3_3_RP_3" + "P-poll__networl_3_3_RP_4" + "P-poll__networl_3_3_RP_5" + "P-poll__networl_3_3_RP_6" + "P-poll__networl_3_3_RP_7" + "P-poll__networl_3_3_RP_8" + "P-poll__networl_3_4_AskP_0" + "P-poll__networl_3_4_AskP_1" + "P-poll__networl_3_4_AskP_2" + "P-poll__networl_3_4_AskP_3" + "P-poll__networl_3_4_AskP_4" + "P-poll__networl_3_4_AskP_5" + "P-poll__networl_3_4_AskP_6" + "P-poll__networl_3_4_AskP_7" + "P-poll__networl_3_4_AskP_8" + "P-poll__networl_3_4_AnsP_0" + "P-poll__networl_3_4_AnsP_1" + "P-poll__networl_3_4_AnsP_2" + "P-poll__networl_3_4_AnsP_3" + "P-poll__networl_3_4_AnsP_4" + "P-poll__networl_3_4_AnsP_5" + "P-poll__networl_3_4_AnsP_6" + "P-poll__networl_3_4_AnsP_7" + "P-poll__networl_3_4_AnsP_8" + "P-poll__networl_3_4_RI_0" + "P-poll__networl_3_4_RI_1" + "P-poll__networl_3_4_RI_2" + "P-poll__networl_3_4_RI_3" + "P-poll__networl_3_4_RI_4" + "P-poll__networl_3_4_RI_5" + "P-poll__networl_3_4_RI_6" + "P-poll__networl_3_4_RI_7" + "P-poll__networl_3_4_RI_8" + "P-poll__networl_3_4_AI_0" + "P-poll__networl_3_4_AI_1" + "P-poll__networl_3_4_AI_2" + "P-poll__networl_3_4_AI_3" + "P-poll__networl_3_4_AI_4" + "P-poll__networl_3_4_AI_5" + "P-poll__networl_3_4_AI_6" + "P-poll__networl_3_4_AI_7" + "P-poll__networl_3_4_AI_8" + "P-poll__networl_3_4_AnnP_0" + "P-poll__networl_3_4_AnnP_1" + "P-poll__networl_3_4_AnnP_2" + "P-poll__networl_3_4_AnnP_3" + "P-poll__networl_3_4_AnnP_4" + "P-poll__networl_3_4_AnnP_5" + "P-poll__networl_3_4_AnnP_6" + "P-poll__networl_3_4_AnnP_7" + "P-poll__networl_3_4_AnnP_8" + "P-poll__networl_3_4_RP_0" + "P-poll__networl_3_4_RP_1" + "P-poll__networl_3_4_RP_2" + "P-poll__networl_3_4_RP_3" + "P-poll__networl_3_4_RP_4" + "P-poll__networl_3_4_RP_5" + "P-poll__networl_3_4_RP_6" + "P-poll__networl_3_4_RP_7" + "P-poll__networl_3_4_RP_8" + "P-poll__networl_3_5_AskP_0" + "P-poll__networl_3_5_AskP_1" + "P-poll__networl_3_5_AskP_2" + "P-poll__networl_3_5_AskP_3" + "P-poll__networl_3_5_AskP_4" + "P-poll__networl_3_5_AskP_5" + "P-poll__networl_3_5_AskP_6" + "P-poll__networl_3_5_AskP_7" + "P-poll__networl_3_5_AskP_8" + "P-poll__networl_3_5_AnsP_0" + "P-poll__networl_3_5_AnsP_1" + "P-poll__networl_3_5_AnsP_2" + "P-poll__networl_3_5_AnsP_3" + "P-poll__networl_3_5_AnsP_4" + "P-poll__networl_3_5_AnsP_5" + "P-poll__networl_3_5_AnsP_6" + "P-poll__networl_3_5_AnsP_7" + "P-poll__networl_3_5_AnsP_8" + "P-poll__networl_3_5_RI_0" + "P-poll__networl_3_5_RI_1" + "P-poll__networl_3_5_RI_2" + "P-poll__networl_3_5_RI_3" + "P-poll__networl_3_5_RI_4" + "P-poll__networl_3_5_RI_5" + "P-poll__networl_3_5_RI_6" + "P-poll__networl_3_5_RI_7" + "P-poll__networl_3_5_RI_8" + "P-poll__networl_3_5_AI_0" + "P-poll__networl_3_5_AI_1" + "P-poll__networl_3_5_AI_2" + "P-poll__networl_3_5_AI_3" + "P-poll__networl_3_5_AI_4" + "P-poll__networl_3_5_AI_5" + "P-poll__networl_3_5_AI_6" + "P-poll__networl_3_5_AI_7" + "P-poll__networl_3_5_AI_8" + "P-poll__networl_3_5_AnnP_0" + "P-poll__networl_3_5_AnnP_1" + "P-poll__networl_3_5_AnnP_2" + "P-poll__networl_3_5_AnnP_3" + "P-poll__networl_3_5_AnnP_4" + "P-poll__networl_3_5_AnnP_5" + "P-poll__networl_3_5_AnnP_6" + "P-poll__networl_3_5_AnnP_7" + "P-poll__networl_3_5_AnnP_8" + "P-poll__networl_3_5_RP_0" + "P-poll__networl_3_5_RP_1" + "P-poll__networl_3_5_RP_2" + "P-poll__networl_3_5_RP_3" + "P-poll__networl_3_5_RP_4" + "P-poll__networl_3_5_RP_5" + "P-poll__networl_3_5_RP_6" + "P-poll__networl_3_5_RP_7" + "P-poll__networl_3_5_RP_8" + "P-poll__networl_3_6_AskP_0" + "P-poll__networl_3_6_AskP_1" + "P-poll__networl_3_6_AskP_2" + "P-poll__networl_3_6_AskP_3" + "P-poll__networl_3_6_AskP_4" + "P-poll__networl_3_6_AskP_5" + "P-poll__networl_3_6_AskP_6" + "P-poll__networl_3_6_AskP_7" + "P-poll__networl_3_6_AskP_8" + "P-poll__networl_3_6_AnsP_0" + "P-poll__networl_3_6_AnsP_1" + "P-poll__networl_3_6_AnsP_2" + "P-poll__networl_3_6_AnsP_3" + "P-poll__networl_3_6_AnsP_4" + "P-poll__networl_3_6_AnsP_5" + "P-poll__networl_3_6_AnsP_6" + "P-poll__networl_3_6_AnsP_7" + "P-poll__networl_3_6_AnsP_8" + "P-poll__networl_3_6_RI_0" + "P-poll__networl_3_6_RI_1" + "P-poll__networl_3_6_RI_2" + "P-poll__networl_3_6_RI_3" + "P-poll__networl_3_6_RI_4" + "P-poll__networl_3_6_RI_5" + "P-poll__networl_3_6_RI_6" + "P-poll__networl_3_6_RI_7" + "P-poll__networl_3_6_RI_8" + "P-poll__networl_3_6_AI_0" + "P-poll__networl_3_6_AI_1" + "P-poll__networl_3_6_AI_2" + "P-poll__networl_3_6_AI_3" + "P-poll__networl_3_6_AI_4" + "P-poll__networl_3_6_AI_5" + "P-poll__networl_3_6_AI_6" + "P-poll__networl_3_6_AI_7" + "P-poll__networl_3_6_AI_8" + "P-poll__networl_3_6_AnnP_0" + "P-poll__networl_3_6_AnnP_1" + "P-poll__networl_3_6_AnnP_2" + "P-poll__networl_3_6_AnnP_3" + "P-poll__networl_3_6_AnnP_4" + "P-poll__networl_3_6_AnnP_5" + "P-poll__networl_3_6_AnnP_6" + "P-poll__networl_3_6_AnnP_7" + "P-poll__networl_3_6_AnnP_8" + "P-poll__networl_3_6_RP_0" + "P-poll__networl_3_6_RP_1" + "P-poll__networl_3_6_RP_2" + "P-poll__networl_3_6_RP_3" + "P-poll__networl_3_6_RP_4" + "P-poll__networl_3_6_RP_5" + "P-poll__networl_3_6_RP_6" + "P-poll__networl_3_6_RP_7" + "P-poll__networl_3_6_RP_8" + "P-poll__networl_3_7_AskP_0" + "P-poll__networl_3_7_AskP_1" + "P-poll__networl_3_7_AskP_2" + "P-poll__networl_3_7_AskP_3" + "P-poll__networl_3_7_AskP_4" + "P-poll__networl_3_7_AskP_5" + "P-poll__networl_3_7_AskP_6" + "P-poll__networl_3_7_AskP_7" + "P-poll__networl_3_7_AskP_8" + "P-poll__networl_3_7_AnsP_0" + "P-poll__networl_3_7_AnsP_1" + "P-poll__networl_3_7_AnsP_2" + "P-poll__networl_3_7_AnsP_3" + "P-poll__networl_3_7_AnsP_4" + "P-poll__networl_3_7_AnsP_5" + "P-poll__networl_3_7_AnsP_6" + "P-poll__networl_3_7_AnsP_7" + "P-poll__networl_3_7_AnsP_8" + "P-poll__networl_3_7_RI_0" + "P-poll__networl_3_7_RI_1" + "P-poll__networl_3_7_RI_2" + "P-poll__networl_3_7_RI_3" + "P-poll__networl_3_7_RI_4" + "P-poll__networl_3_7_RI_5" + "P-poll__networl_3_7_RI_6" + "P-poll__networl_3_7_RI_7" + "P-poll__networl_3_7_RI_8" + "P-poll__networl_3_7_AI_0" + "P-poll__networl_3_7_AI_1" + "P-poll__networl_3_7_AI_2" + "P-poll__networl_3_7_AI_3" + "P-poll__networl_3_7_AI_4" + "P-poll__networl_3_7_AI_5" + "P-poll__networl_3_7_AI_6" + "P-poll__networl_3_7_AI_7" + "P-poll__networl_3_7_AI_8" + "P-poll__networl_3_7_AnnP_0" + "P-poll__networl_3_7_AnnP_1" + "P-poll__networl_3_7_AnnP_2" + "P-poll__networl_3_7_AnnP_3" + "P-poll__networl_3_7_AnnP_4" + "P-poll__networl_3_7_AnnP_5" + "P-poll__networl_3_7_AnnP_6" + "P-poll__networl_3_7_AnnP_7" + "P-poll__networl_3_7_AnnP_8" + "P-poll__networl_3_7_RP_0" + "P-poll__networl_3_7_RP_1" + "P-poll__networl_3_7_RP_2" + "P-poll__networl_3_7_RP_3" + "P-poll__networl_3_7_RP_4" + "P-poll__networl_3_7_RP_5" + "P-poll__networl_3_7_RP_6" + "P-poll__networl_3_7_RP_7" + "P-poll__networl_3_7_RP_8" + "P-poll__networl_3_8_AskP_0" + "P-poll__networl_3_8_AskP_1" + "P-poll__networl_3_8_AskP_2" + "P-poll__networl_3_8_AskP_3" + "P-poll__networl_3_8_AskP_4" + "P-poll__networl_3_8_AskP_5" + "P-poll__networl_3_8_AskP_6" + "P-poll__networl_3_8_AskP_7" + "P-poll__networl_3_8_AskP_8" + "P-poll__networl_3_8_AnsP_0" + "P-poll__networl_3_8_AnsP_1" + "P-poll__networl_3_8_AnsP_2" + "P-poll__networl_3_8_AnsP_3" + "P-poll__networl_3_8_AnsP_4" + "P-poll__networl_3_8_AnsP_5" + "P-poll__networl_3_8_AnsP_6" + "P-poll__networl_3_8_AnsP_7" + "P-poll__networl_3_8_AnsP_8" + "P-poll__networl_3_8_RI_0" + "P-poll__networl_3_8_RI_1" + "P-poll__networl_3_8_RI_2" + "P-poll__networl_3_8_RI_3" + "P-poll__networl_3_8_RI_4" + "P-poll__networl_3_8_RI_5" + "P-poll__networl_3_8_RI_6" + "P-poll__networl_3_8_RI_7" + "P-poll__networl_3_8_RI_8" + "P-poll__networl_3_8_AI_0" + "P-poll__networl_3_8_AI_1" + "P-poll__networl_3_8_AI_2" + "P-poll__networl_3_8_AI_3" + "P-poll__networl_3_8_AI_4" + "P-poll__networl_3_8_AI_5" + "P-poll__networl_3_8_AI_6" + "P-poll__networl_3_8_AI_7" + "P-poll__networl_3_8_AI_8" + "P-poll__networl_3_8_AnnP_0" + "P-poll__networl_3_8_AnnP_1" + "P-poll__networl_3_8_AnnP_2" + "P-poll__networl_3_8_AnnP_3" + "P-poll__networl_3_8_AnnP_4" + "P-poll__networl_3_8_AnnP_5" + "P-poll__networl_3_8_AnnP_6" + "P-poll__networl_3_8_AnnP_7" + "P-poll__networl_3_8_AnnP_8" + "P-poll__networl_3_8_RP_0" + "P-poll__networl_3_8_RP_1" + "P-poll__networl_3_8_RP_2" + "P-poll__networl_3_8_RP_3" + "P-poll__networl_3_8_RP_4" + "P-poll__networl_3_8_RP_5" + "P-poll__networl_3_8_RP_6" + "P-poll__networl_3_8_RP_7" + "P-poll__networl_3_8_RP_8" + "P-poll__networl_4_0_AskP_0" + "P-poll__networl_4_0_AskP_1" + "P-poll__networl_4_0_AskP_2" + "P-poll__networl_4_0_AskP_3" + "P-poll__networl_4_0_AskP_4" + "P-poll__networl_4_0_AskP_5" + "P-poll__networl_4_0_AskP_6" + "P-poll__networl_4_0_AskP_7" + "P-poll__networl_4_0_AskP_8" + "P-poll__networl_4_0_AnsP_0" + "P-poll__networl_4_0_AnsP_1" + "P-poll__networl_4_0_AnsP_2" + "P-poll__networl_4_0_AnsP_3" + "P-poll__networl_4_0_AnsP_4" + "P-poll__networl_4_0_AnsP_5" + "P-poll__networl_4_0_AnsP_6" + "P-poll__networl_4_0_AnsP_7" + "P-poll__networl_4_0_AnsP_8" + "P-poll__networl_4_0_RI_0" + "P-poll__networl_4_0_RI_1" + "P-poll__networl_4_0_RI_2" + "P-poll__networl_4_0_RI_3" + "P-poll__networl_4_0_RI_4" + "P-poll__networl_4_0_RI_5" + "P-poll__networl_4_0_RI_6" + "P-poll__networl_4_0_RI_7" + "P-poll__networl_4_0_RI_8" + "P-poll__networl_4_0_AI_0" + "P-poll__networl_4_0_AI_1" + "P-poll__networl_4_0_AI_2" + "P-poll__networl_4_0_AI_3" + "P-poll__networl_4_0_AI_4" + "P-poll__networl_4_0_AI_5" + "P-poll__networl_4_0_AI_6" + "P-poll__networl_4_0_AI_7" + "P-poll__networl_4_0_AI_8" + "P-poll__networl_4_0_AnnP_0" + "P-poll__networl_4_0_AnnP_1" + "P-poll__networl_4_0_AnnP_2" + "P-poll__networl_4_0_AnnP_3" + "P-poll__networl_4_0_AnnP_4" + "P-poll__networl_4_0_AnnP_5" + "P-poll__networl_4_0_AnnP_6" + "P-poll__networl_4_0_AnnP_7" + "P-poll__networl_4_0_AnnP_8" + "P-poll__networl_4_0_RP_0" + "P-poll__networl_4_0_RP_1" + "P-poll__networl_4_0_RP_2" + "P-poll__networl_4_0_RP_3" + "P-poll__networl_4_0_RP_4" + "P-poll__networl_4_0_RP_5" + "P-poll__networl_4_0_RP_6" + "P-poll__networl_4_0_RP_7" + "P-poll__networl_4_0_RP_8" + "P-poll__networl_4_1_AskP_0" + "P-poll__networl_4_1_AskP_1" + "P-poll__networl_4_1_AskP_2" + "P-poll__networl_4_1_AskP_3" + "P-poll__networl_4_1_AskP_4" + "P-poll__networl_4_1_AskP_5" + "P-poll__networl_4_1_AskP_6" + "P-poll__networl_4_1_AskP_7" + "P-poll__networl_4_1_AskP_8" + "P-poll__networl_4_1_AnsP_0" + "P-poll__networl_4_1_AnsP_1" + "P-poll__networl_4_1_AnsP_2" + "P-poll__networl_4_1_AnsP_3" + "P-poll__networl_4_1_AnsP_4" + "P-poll__networl_4_1_AnsP_5" + "P-poll__networl_4_1_AnsP_6" + "P-poll__networl_4_1_AnsP_7" + "P-poll__networl_4_1_AnsP_8" + "P-poll__networl_4_1_RI_0" + "P-poll__networl_4_1_RI_1" + "P-poll__networl_4_1_RI_2" + "P-poll__networl_4_1_RI_3" + "P-poll__networl_4_1_RI_4" + "P-poll__networl_4_1_RI_5" + "P-poll__networl_4_1_RI_6" + "P-poll__networl_4_1_RI_7" + "P-poll__networl_4_1_RI_8" + "P-poll__networl_4_1_AI_0" + "P-poll__networl_4_1_AI_1" + "P-poll__networl_4_1_AI_2" + "P-poll__networl_4_1_AI_3" + "P-poll__networl_4_1_AI_4" + "P-poll__networl_4_1_AI_5" + "P-poll__networl_4_1_AI_6" + "P-poll__networl_4_1_AI_7" + "P-poll__networl_4_1_AI_8" + "P-poll__networl_4_1_AnnP_0" + "P-poll__networl_4_1_AnnP_1" + "P-poll__networl_4_1_AnnP_2" + "P-poll__networl_4_1_AnnP_3" + "P-poll__networl_4_1_AnnP_4" + "P-poll__networl_4_1_AnnP_5" + "P-poll__networl_4_1_AnnP_6" + "P-poll__networl_4_1_AnnP_7" + "P-poll__networl_4_1_AnnP_8" + "P-poll__networl_4_1_RP_0" + "P-poll__networl_4_1_RP_1" + "P-poll__networl_4_1_RP_2" + "P-poll__networl_4_1_RP_3" + "P-poll__networl_4_1_RP_4" + "P-poll__networl_4_1_RP_5" + "P-poll__networl_4_1_RP_6" + "P-poll__networl_4_1_RP_7" + "P-poll__networl_4_1_RP_8" + "P-poll__networl_4_2_AskP_0" + "P-poll__networl_4_2_AskP_1" + "P-poll__networl_4_2_AskP_2" + "P-poll__networl_4_2_AskP_3" + "P-poll__networl_4_2_AskP_4" + "P-poll__networl_4_2_AskP_5" + "P-poll__networl_4_2_AskP_6" + "P-poll__networl_4_2_AskP_7" + "P-poll__networl_4_2_AskP_8" + "P-poll__networl_4_2_AnsP_0" + "P-poll__networl_4_2_AnsP_1" + "P-poll__networl_4_2_AnsP_2" + "P-poll__networl_4_2_AnsP_3" + "P-poll__networl_4_2_AnsP_4" + "P-poll__networl_4_2_AnsP_5" + "P-poll__networl_4_2_AnsP_6" + "P-poll__networl_4_2_AnsP_7" + "P-poll__networl_4_2_AnsP_8" + "P-poll__networl_4_2_RI_0" + "P-poll__networl_4_2_RI_1" + "P-poll__networl_4_2_RI_2" + "P-poll__networl_4_2_RI_3" + "P-poll__networl_4_2_RI_4" + "P-poll__networl_4_2_RI_5" + "P-poll__networl_4_2_RI_6" + "P-poll__networl_4_2_RI_7" + "P-poll__networl_4_2_RI_8" + "P-poll__networl_4_2_AI_0" + "P-poll__networl_4_2_AI_1" + "P-poll__networl_4_2_AI_2" + "P-poll__networl_4_2_AI_3" + "P-poll__networl_4_2_AI_4" + "P-poll__networl_4_2_AI_5" + "P-poll__networl_4_2_AI_6" + "P-poll__networl_4_2_AI_7" + "P-poll__networl_4_2_AI_8" + "P-poll__networl_4_2_AnnP_0" + "P-poll__networl_4_2_AnnP_1" + "P-poll__networl_4_2_AnnP_2" + "P-poll__networl_4_2_AnnP_3" + "P-poll__networl_4_2_AnnP_4" + "P-poll__networl_4_2_AnnP_5" + "P-poll__networl_4_2_AnnP_6" + "P-poll__networl_4_2_AnnP_7" + "P-poll__networl_4_2_AnnP_8" + "P-poll__networl_4_2_RP_0" + "P-poll__networl_4_2_RP_1" + "P-poll__networl_4_2_RP_2" + "P-poll__networl_4_2_RP_3" + "P-poll__networl_4_2_RP_4" + "P-poll__networl_4_2_RP_5" + "P-poll__networl_4_2_RP_6" + "P-poll__networl_4_2_RP_7" + "P-poll__networl_4_2_RP_8" + "P-poll__networl_4_3_AskP_0" + "P-poll__networl_4_3_AskP_1" + "P-poll__networl_4_3_AskP_2" + "P-poll__networl_4_3_AskP_3" + "P-poll__networl_4_3_AskP_4" + "P-poll__networl_4_3_AskP_5" + "P-poll__networl_4_3_AskP_6" + "P-poll__networl_4_3_AskP_7" + "P-poll__networl_4_3_AskP_8" + "P-poll__networl_4_3_AnsP_0" + "P-poll__networl_4_3_AnsP_1" + "P-poll__networl_4_3_AnsP_2" + "P-poll__networl_4_3_AnsP_3" + "P-poll__networl_4_3_AnsP_4" + "P-poll__networl_4_3_AnsP_5" + "P-poll__networl_4_3_AnsP_6" + "P-poll__networl_4_3_AnsP_7" + "P-poll__networl_4_3_AnsP_8" + "P-poll__networl_4_3_RI_0" + "P-poll__networl_4_3_RI_1" + "P-poll__networl_4_3_RI_2" + "P-poll__networl_4_3_RI_3" + "P-poll__networl_4_3_RI_4" + "P-poll__networl_4_3_RI_5" + "P-poll__networl_4_3_RI_6" + "P-poll__networl_4_3_RI_7" + "P-poll__networl_4_3_RI_8" + "P-poll__networl_4_3_AI_0" + "P-poll__networl_4_3_AI_1" + "P-poll__networl_4_3_AI_2" + "P-poll__networl_4_3_AI_3" + "P-poll__networl_4_3_AI_4" + "P-poll__networl_4_3_AI_5" + "P-poll__networl_4_3_AI_6" + "P-poll__networl_4_3_AI_7" + "P-poll__networl_4_3_AI_8" + "P-poll__networl_4_3_AnnP_0" + "P-poll__networl_4_3_AnnP_1" + "P-poll__networl_4_3_AnnP_2" + "P-poll__networl_4_3_AnnP_3" + "P-poll__networl_4_3_AnnP_4" + "P-poll__networl_4_3_AnnP_5" + "P-poll__networl_4_3_AnnP_6" + "P-poll__networl_4_3_AnnP_7" + "P-poll__networl_4_3_AnnP_8" + "P-poll__networl_4_3_RP_0" + "P-poll__networl_4_3_RP_1" + "P-poll__networl_4_3_RP_2" + "P-poll__networl_4_3_RP_3" + "P-poll__networl_4_3_RP_4" + "P-poll__networl_4_3_RP_5" + "P-poll__networl_4_3_RP_6" + "P-poll__networl_4_3_RP_7" + "P-poll__networl_4_3_RP_8" + "P-poll__networl_4_4_AskP_0" + "P-poll__networl_4_4_AskP_1" + "P-poll__networl_4_4_AskP_2" + "P-poll__networl_4_4_AskP_3" + "P-poll__networl_4_4_AskP_4" + "P-poll__networl_4_4_AskP_5" + "P-poll__networl_4_4_AskP_6" + "P-poll__networl_4_4_AskP_7" + "P-poll__networl_4_4_AskP_8" + "P-poll__networl_4_4_AnsP_0" + "P-poll__networl_4_4_AnsP_1" + "P-poll__networl_4_4_AnsP_2" + "P-poll__networl_4_4_AnsP_3" + "P-poll__networl_4_4_AnsP_4" + "P-poll__networl_4_4_AnsP_5" + "P-poll__networl_4_4_AnsP_6" + "P-poll__networl_4_4_AnsP_7" + "P-poll__networl_4_4_AnsP_8" + "P-poll__networl_4_4_RI_0" + "P-poll__networl_4_4_RI_1" + "P-poll__networl_4_4_RI_2" + "P-poll__networl_4_4_RI_3" + "P-poll__networl_4_4_RI_4" + "P-poll__networl_4_4_RI_5" + "P-poll__networl_4_4_RI_6" + "P-poll__networl_4_4_RI_7" + "P-poll__networl_4_4_RI_8" + "P-poll__networl_4_4_AI_0" + "P-poll__networl_4_4_AI_1" + "P-poll__networl_4_4_AI_2" + "P-poll__networl_4_4_AI_3" + "P-poll__networl_4_4_AI_4" + "P-poll__networl_4_4_AI_5" + "P-poll__networl_4_4_AI_6" + "P-poll__networl_4_4_AI_7" + "P-poll__networl_4_4_AI_8" + "P-poll__networl_4_4_AnnP_0" + "P-poll__networl_4_4_AnnP_1" + "P-poll__networl_4_4_AnnP_2" + "P-poll__networl_4_4_AnnP_3" + "P-poll__networl_4_4_AnnP_4" + "P-poll__networl_4_4_AnnP_5" + "P-poll__networl_4_4_AnnP_6" + "P-poll__networl_4_4_AnnP_7" + "P-poll__networl_4_4_AnnP_8" + "P-poll__networl_4_4_RP_0" + "P-poll__networl_4_4_RP_1" + "P-poll__networl_4_4_RP_2" + "P-poll__networl_4_4_RP_3" + "P-poll__networl_4_4_RP_4" + "P-poll__networl_4_4_RP_5" + "P-poll__networl_4_4_RP_6" + "P-poll__networl_4_4_RP_7" + "P-poll__networl_4_4_RP_8" + "P-poll__networl_4_5_AskP_0" + "P-poll__networl_4_5_AskP_1" + "P-poll__networl_4_5_AskP_2" + "P-poll__networl_4_5_AskP_3" + "P-poll__networl_4_5_AskP_4" + "P-poll__networl_4_5_AskP_5" + "P-poll__networl_4_5_AskP_6" + "P-poll__networl_4_5_AskP_7" + "P-poll__networl_4_5_AskP_8" + "P-poll__networl_4_5_AnsP_0" + "P-poll__networl_4_5_AnsP_1" + "P-poll__networl_4_5_AnsP_2" + "P-poll__networl_4_5_AnsP_3" + "P-poll__networl_4_5_AnsP_4" + "P-poll__networl_4_5_AnsP_5" + "P-poll__networl_4_5_AnsP_6" + "P-poll__networl_4_5_AnsP_7" + "P-poll__networl_4_5_AnsP_8" + "P-poll__networl_4_5_RI_0" + "P-poll__networl_4_5_RI_1" + "P-poll__networl_4_5_RI_2" + "P-poll__networl_4_5_RI_3" + "P-poll__networl_4_5_RI_4" + "P-poll__networl_4_5_RI_5" + "P-poll__networl_4_5_RI_6" + "P-poll__networl_4_5_RI_7" + "P-poll__networl_4_5_RI_8" + "P-poll__networl_4_5_AI_0" + "P-poll__networl_4_5_AI_1" + "P-poll__networl_4_5_AI_2" + "P-poll__networl_4_5_AI_3" + "P-poll__networl_4_5_AI_4" + "P-poll__networl_4_5_AI_5" + "P-poll__networl_4_5_AI_6" + "P-poll__networl_4_5_AI_7" + "P-poll__networl_4_5_AI_8" + "P-poll__networl_4_5_AnnP_0" + "P-poll__networl_4_5_AnnP_1" + "P-poll__networl_4_5_AnnP_2" + "P-poll__networl_4_5_AnnP_3" + "P-poll__networl_4_5_AnnP_4" + "P-poll__networl_4_5_AnnP_5" + "P-poll__networl_4_5_AnnP_6" + "P-poll__networl_4_5_AnnP_7" + "P-poll__networl_4_5_AnnP_8" + "P-poll__networl_4_5_RP_0" + "P-poll__networl_4_5_RP_1" + "P-poll__networl_4_5_RP_2" + "P-poll__networl_4_5_RP_3" + "P-poll__networl_4_5_RP_4" + "P-poll__networl_4_5_RP_5" + "P-poll__networl_4_5_RP_6" + "P-poll__networl_4_5_RP_7" + "P-poll__networl_4_5_RP_8" + "P-poll__networl_4_6_AskP_0" + "P-poll__networl_4_6_AskP_1" + "P-poll__networl_4_6_AskP_2" + "P-poll__networl_4_6_AskP_3" + "P-poll__networl_4_6_AskP_4" + "P-poll__networl_4_6_AskP_5" + "P-poll__networl_4_6_AskP_6" + "P-poll__networl_4_6_AskP_7" + "P-poll__networl_4_6_AskP_8" + "P-poll__networl_4_6_AnsP_0" + "P-poll__networl_4_6_AnsP_1" + "P-poll__networl_4_6_AnsP_2" + "P-poll__networl_4_6_AnsP_3" + "P-poll__networl_4_6_AnsP_4" + "P-poll__networl_4_6_AnsP_5" + "P-poll__networl_4_6_AnsP_6" + "P-poll__networl_4_6_AnsP_7" + "P-poll__networl_4_6_AnsP_8" + "P-poll__networl_4_6_RI_0" + "P-poll__networl_4_6_RI_1" + "P-poll__networl_4_6_RI_2" + "P-poll__networl_4_6_RI_3" + "P-poll__networl_4_6_RI_4" + "P-poll__networl_4_6_RI_5" + "P-poll__networl_4_6_RI_6" + "P-poll__networl_4_6_RI_7" + "P-poll__networl_4_6_RI_8" + "P-poll__networl_4_6_AI_0" + "P-poll__networl_4_6_AI_1" + "P-poll__networl_4_6_AI_2" + "P-poll__networl_4_6_AI_3" + "P-poll__networl_4_6_AI_4" + "P-poll__networl_4_6_AI_5" + "P-poll__networl_4_6_AI_6" + "P-poll__networl_4_6_AI_7" + "P-poll__networl_4_6_AI_8" + "P-poll__networl_4_6_AnnP_0" + "P-poll__networl_4_6_AnnP_1" + "P-poll__networl_4_6_AnnP_2" + "P-poll__networl_4_6_AnnP_3" + "P-poll__networl_4_6_AnnP_4" + "P-poll__networl_4_6_AnnP_5" + "P-poll__networl_4_6_AnnP_6" + "P-poll__networl_4_6_AnnP_7" + "P-poll__networl_4_6_AnnP_8" + "P-poll__networl_4_6_RP_0" + "P-poll__networl_4_6_RP_1" + "P-poll__networl_4_6_RP_2" + "P-poll__networl_4_6_RP_3" + "P-poll__networl_4_6_RP_4" + "P-poll__networl_4_6_RP_5" + "P-poll__networl_4_6_RP_6" + "P-poll__networl_4_6_RP_7" + "P-poll__networl_4_6_RP_8" + "P-poll__networl_4_7_AskP_0" + "P-poll__networl_4_7_AskP_1" + "P-poll__networl_4_7_AskP_2" + "P-poll__networl_4_7_AskP_3" + "P-poll__networl_4_7_AskP_4" + "P-poll__networl_4_7_AskP_5" + "P-poll__networl_4_7_AskP_6" + "P-poll__networl_4_7_AskP_7" + "P-poll__networl_4_7_AskP_8" + "P-poll__networl_4_7_AnsP_0" + "P-poll__networl_4_7_AnsP_1" + "P-poll__networl_4_7_AnsP_2" + "P-poll__networl_4_7_AnsP_3" + "P-poll__networl_4_7_AnsP_4" + "P-poll__networl_4_7_AnsP_5" + "P-poll__networl_4_7_AnsP_6" + "P-poll__networl_4_7_AnsP_7" + "P-poll__networl_4_7_AnsP_8" + "P-poll__networl_4_7_RI_0" + "P-poll__networl_4_7_RI_1" + "P-poll__networl_4_7_RI_2" + "P-poll__networl_4_7_RI_3" + "P-poll__networl_4_7_RI_4" + "P-poll__networl_4_7_RI_5" + "P-poll__networl_4_7_RI_6" + "P-poll__networl_4_7_RI_7" + "P-poll__networl_4_7_RI_8" + "P-poll__networl_4_7_AI_0" + "P-poll__networl_4_7_AI_1" + "P-poll__networl_4_7_AI_2" + "P-poll__networl_4_7_AI_3" + "P-poll__networl_4_7_AI_4" + "P-poll__networl_4_7_AI_5" + "P-poll__networl_4_7_AI_6" + "P-poll__networl_4_7_AI_7" + "P-poll__networl_4_7_AI_8" + "P-poll__networl_4_7_AnnP_0" + "P-poll__networl_4_7_AnnP_1" + "P-poll__networl_4_7_AnnP_2" + "P-poll__networl_4_7_AnnP_3" + "P-poll__networl_4_7_AnnP_4" + "P-poll__networl_4_7_AnnP_5" + "P-poll__networl_4_7_AnnP_6" + "P-poll__networl_4_7_AnnP_7" + "P-poll__networl_4_7_AnnP_8" + "P-poll__networl_4_7_RP_0" + "P-poll__networl_4_7_RP_1" + "P-poll__networl_4_7_RP_2" + "P-poll__networl_4_7_RP_3" + "P-poll__networl_4_7_RP_4" + "P-poll__networl_4_7_RP_5" + "P-poll__networl_4_7_RP_6" + "P-poll__networl_4_7_RP_7" + "P-poll__networl_4_7_RP_8" + "P-poll__networl_4_8_AskP_0" + "P-poll__networl_4_8_AskP_1" + "P-poll__networl_4_8_AskP_2" + "P-poll__networl_4_8_AskP_3" + "P-poll__networl_4_8_AskP_4" + "P-poll__networl_4_8_AskP_5" + "P-poll__networl_4_8_AskP_6" + "P-poll__networl_4_8_AskP_7" + "P-poll__networl_4_8_AskP_8" + "P-poll__networl_4_8_AnsP_0" + "P-poll__networl_4_8_AnsP_1" + "P-poll__networl_4_8_AnsP_2" + "P-poll__networl_4_8_AnsP_3" + "P-poll__networl_4_8_AnsP_4" + "P-poll__networl_4_8_AnsP_5" + "P-poll__networl_4_8_AnsP_6" + "P-poll__networl_4_8_AnsP_7" + "P-poll__networl_4_8_AnsP_8" + "P-poll__networl_4_8_RI_0" + "P-poll__networl_4_8_RI_1" + "P-poll__networl_4_8_RI_2" + "P-poll__networl_4_8_RI_3" + "P-poll__networl_4_8_RI_4" + "P-poll__networl_4_8_RI_5" + "P-poll__networl_4_8_RI_6" + "P-poll__networl_4_8_RI_7" + "P-poll__networl_4_8_RI_8" + "P-poll__networl_4_8_AI_0" + "P-poll__networl_4_8_AI_1" + "P-poll__networl_4_8_AI_2" + "P-poll__networl_4_8_AI_3" + "P-poll__networl_4_8_AI_4" + "P-poll__networl_4_8_AI_5" + "P-poll__networl_4_8_AI_6" + "P-poll__networl_4_8_AI_7" + "P-poll__networl_4_8_AI_8" + "P-poll__networl_4_8_AnnP_0" + "P-poll__networl_4_8_AnnP_1" + "P-poll__networl_4_8_AnnP_2" + "P-poll__networl_4_8_AnnP_3" + "P-poll__networl_4_8_AnnP_4" + "P-poll__networl_4_8_AnnP_5" + "P-poll__networl_4_8_AnnP_6" + "P-poll__networl_4_8_AnnP_7" + "P-poll__networl_4_8_AnnP_8" + "P-poll__networl_4_8_RP_0" + "P-poll__networl_4_8_RP_1" + "P-poll__networl_4_8_RP_2" + "P-poll__networl_4_8_RP_3" + "P-poll__networl_4_8_RP_4" + "P-poll__networl_4_8_RP_5" + "P-poll__networl_4_8_RP_6" + "P-poll__networl_4_8_RP_7" + "P-poll__networl_4_8_RP_8" + "P-poll__networl_5_0_AskP_0" + "P-poll__networl_5_0_AskP_1" + "P-poll__networl_5_0_AskP_2" + "P-poll__networl_5_0_AskP_3" + "P-poll__networl_5_0_AskP_4" + "P-poll__networl_5_0_AskP_5" + "P-poll__networl_5_0_AskP_6" + "P-poll__networl_5_0_AskP_7" + "P-poll__networl_5_0_AskP_8" + "P-poll__networl_5_0_AnsP_0" + "P-poll__networl_5_0_AnsP_1" + "P-poll__networl_5_0_AnsP_2" + "P-poll__networl_5_0_AnsP_3" + "P-poll__networl_5_0_AnsP_4" + "P-poll__networl_5_0_AnsP_5" + "P-poll__networl_5_0_AnsP_6" + "P-poll__networl_5_0_AnsP_7" + "P-poll__networl_5_0_AnsP_8" + "P-poll__networl_5_0_RI_0" + "P-poll__networl_5_0_RI_1" + "P-poll__networl_5_0_RI_2" + "P-poll__networl_5_0_RI_3" + "P-poll__networl_5_0_RI_4" + "P-poll__networl_5_0_RI_5" + "P-poll__networl_5_0_RI_6" + "P-poll__networl_5_0_RI_7" + "P-poll__networl_5_0_RI_8" + "P-poll__networl_5_0_AI_0" + "P-poll__networl_5_0_AI_1" + "P-poll__networl_5_0_AI_2" + "P-poll__networl_5_0_AI_3" + "P-poll__networl_5_0_AI_4" + "P-poll__networl_5_0_AI_5" + "P-poll__networl_5_0_AI_6" + "P-poll__networl_5_0_AI_7" + "P-poll__networl_5_0_AI_8" + "P-poll__networl_5_0_AnnP_0" + "P-poll__networl_5_0_AnnP_1" + "P-poll__networl_5_0_AnnP_2" + "P-poll__networl_5_0_AnnP_3" + "P-poll__networl_5_0_AnnP_4" + "P-poll__networl_5_0_AnnP_5" + "P-poll__networl_5_0_AnnP_6" + "P-poll__networl_5_0_AnnP_7" + "P-poll__networl_5_0_AnnP_8" + "P-poll__networl_5_0_RP_0" + "P-poll__networl_5_0_RP_1" + "P-poll__networl_5_0_RP_2" + "P-poll__networl_5_0_RP_3" + "P-poll__networl_5_0_RP_4" + "P-poll__networl_5_0_RP_5" + "P-poll__networl_5_0_RP_6" + "P-poll__networl_5_0_RP_7" + "P-poll__networl_5_0_RP_8" + "P-poll__networl_5_1_AskP_0" + "P-poll__networl_5_1_AskP_1" + "P-poll__networl_5_1_AskP_2" + "P-poll__networl_5_1_AskP_3" + "P-poll__networl_5_1_AskP_4" + "P-poll__networl_5_1_AskP_5" + "P-poll__networl_5_1_AskP_6" + "P-poll__networl_5_1_AskP_7" + "P-poll__networl_5_1_AskP_8" + "P-poll__networl_5_1_AnsP_0" + "P-poll__networl_5_1_AnsP_1" + "P-poll__networl_5_1_AnsP_2" + "P-poll__networl_5_1_AnsP_3" + "P-poll__networl_5_1_AnsP_4" + "P-poll__networl_5_1_AnsP_5" + "P-poll__networl_5_1_AnsP_6" + "P-poll__networl_5_1_AnsP_7" + "P-poll__networl_5_1_AnsP_8" + "P-poll__networl_5_1_RI_0" + "P-poll__networl_5_1_RI_1" + "P-poll__networl_5_1_RI_2" + "P-poll__networl_5_1_RI_3" + "P-poll__networl_5_1_RI_4" + "P-poll__networl_5_1_RI_5" + "P-poll__networl_5_1_RI_6" + "P-poll__networl_5_1_RI_7" + "P-poll__networl_5_1_RI_8" + "P-poll__networl_5_1_AI_0" + "P-poll__networl_5_1_AI_1" + "P-poll__networl_5_1_AI_2" + "P-poll__networl_5_1_AI_3" + "P-poll__networl_5_1_AI_4" + "P-poll__networl_5_1_AI_5" + "P-poll__networl_5_1_AI_6" + "P-poll__networl_5_1_AI_7" + "P-poll__networl_5_1_AI_8" + "P-poll__networl_5_1_AnnP_0" + "P-poll__networl_5_1_AnnP_1" + "P-poll__networl_5_1_AnnP_2" + "P-poll__networl_5_1_AnnP_3" + "P-poll__networl_5_1_AnnP_4" + "P-poll__networl_5_1_AnnP_5" + "P-poll__networl_5_1_AnnP_6" + "P-poll__networl_5_1_AnnP_7" + "P-poll__networl_5_1_AnnP_8" + "P-poll__networl_5_1_RP_0" + "P-poll__networl_5_1_RP_1" + "P-poll__networl_5_1_RP_2" + "P-poll__networl_5_1_RP_3" + "P-poll__networl_5_1_RP_4" + "P-poll__networl_5_1_RP_5" + "P-poll__networl_5_1_RP_6" + "P-poll__networl_5_1_RP_7" + "P-poll__networl_5_1_RP_8" + "P-poll__networl_5_2_AskP_0" + "P-poll__networl_5_2_AskP_1" + "P-poll__networl_5_2_AskP_2" + "P-poll__networl_5_2_AskP_3" + "P-poll__networl_5_2_AskP_4" + "P-poll__networl_5_2_AskP_5" + "P-poll__networl_5_2_AskP_6" + "P-poll__networl_5_2_AskP_7" + "P-poll__networl_5_2_AskP_8" + "P-poll__networl_5_2_AnsP_0" + "P-poll__networl_5_2_AnsP_1" + "P-poll__networl_5_2_AnsP_2" + "P-poll__networl_5_2_AnsP_3" + "P-poll__networl_5_2_AnsP_4" + "P-poll__networl_5_2_AnsP_5" + "P-poll__networl_5_2_AnsP_6" + "P-poll__networl_5_2_AnsP_7" + "P-poll__networl_5_2_AnsP_8" + "P-poll__networl_5_2_RI_0" + "P-poll__networl_5_2_RI_1" + "P-poll__networl_5_2_RI_2" + "P-poll__networl_5_2_RI_3" + "P-poll__networl_5_2_RI_4" + "P-poll__networl_5_2_RI_5" + "P-poll__networl_5_2_RI_6" + "P-poll__networl_5_2_RI_7" + "P-poll__networl_5_2_RI_8" + "P-poll__networl_5_2_AI_0" + "P-poll__networl_5_2_AI_1" + "P-poll__networl_5_2_AI_2" + "P-poll__networl_5_2_AI_3" + "P-poll__networl_5_2_AI_4" + "P-poll__networl_5_2_AI_5" + "P-poll__networl_5_2_AI_6" + "P-poll__networl_5_2_AI_7" + "P-poll__networl_5_2_AI_8" + "P-poll__networl_5_2_AnnP_0" + "P-poll__networl_5_2_AnnP_1" + "P-poll__networl_5_2_AnnP_2" + "P-poll__networl_5_2_AnnP_3" + "P-poll__networl_5_2_AnnP_4" + "P-poll__networl_5_2_AnnP_5" + "P-poll__networl_5_2_AnnP_6" + "P-poll__networl_5_2_AnnP_7" + "P-poll__networl_5_2_AnnP_8" + "P-poll__networl_5_2_RP_0" + "P-poll__networl_5_2_RP_1" + "P-poll__networl_5_2_RP_2" + "P-poll__networl_5_2_RP_3" + "P-poll__networl_5_2_RP_4" + "P-poll__networl_5_2_RP_5" + "P-poll__networl_5_2_RP_6" + "P-poll__networl_5_2_RP_7" + "P-poll__networl_5_2_RP_8" + "P-poll__networl_5_3_AskP_0" + "P-poll__networl_5_3_AskP_1" + "P-poll__networl_5_3_AskP_2" + "P-poll__networl_5_3_AskP_3" + "P-poll__networl_5_3_AskP_4" + "P-poll__networl_5_3_AskP_5" + "P-poll__networl_5_3_AskP_6" + "P-poll__networl_5_3_AskP_7" + "P-poll__networl_5_3_AskP_8" + "P-poll__networl_5_3_AnsP_0" + "P-poll__networl_5_3_AnsP_1" + "P-poll__networl_5_3_AnsP_2" + "P-poll__networl_5_3_AnsP_3" + "P-poll__networl_5_3_AnsP_4" + "P-poll__networl_5_3_AnsP_5" + "P-poll__networl_5_3_AnsP_6" + "P-poll__networl_5_3_AnsP_7" + "P-poll__networl_5_3_AnsP_8" + "P-poll__networl_5_3_RI_0" + "P-poll__networl_5_3_RI_1" + "P-poll__networl_5_3_RI_2" + "P-poll__networl_5_3_RI_3" + "P-poll__networl_5_3_RI_4" + "P-poll__networl_5_3_RI_5" + "P-poll__networl_5_3_RI_6" + "P-poll__networl_5_3_RI_7" + "P-poll__networl_5_3_RI_8" + "P-poll__networl_5_3_AI_0" + "P-poll__networl_5_3_AI_1" + "P-poll__networl_5_3_AI_2" + "P-poll__networl_5_3_AI_3" + "P-poll__networl_5_3_AI_4" + "P-poll__networl_5_3_AI_5" + "P-poll__networl_5_3_AI_6" + "P-poll__networl_5_3_AI_7" + "P-poll__networl_5_3_AI_8" + "P-poll__networl_5_3_AnnP_0" + "P-poll__networl_5_3_AnnP_1" + "P-poll__networl_5_3_AnnP_2" + "P-poll__networl_5_3_AnnP_3" + "P-poll__networl_5_3_AnnP_4" + "P-poll__networl_5_3_AnnP_5" + "P-poll__networl_5_3_AnnP_6" + "P-poll__networl_5_3_AnnP_7" + "P-poll__networl_5_3_AnnP_8" + "P-poll__networl_5_3_RP_0" + "P-poll__networl_5_3_RP_1" + "P-poll__networl_5_3_RP_2" + "P-poll__networl_5_3_RP_3" + "P-poll__networl_5_3_RP_4" + "P-poll__networl_5_3_RP_5" + "P-poll__networl_5_3_RP_6" + "P-poll__networl_5_3_RP_7" + "P-poll__networl_5_3_RP_8" + "P-poll__networl_5_4_AskP_0" + "P-poll__networl_5_4_AskP_1" + "P-poll__networl_5_4_AskP_2" + "P-poll__networl_5_4_AskP_3" + "P-poll__networl_5_4_AskP_4" + "P-poll__networl_5_4_AskP_5" + "P-poll__networl_5_4_AskP_6" + "P-poll__networl_5_4_AskP_7" + "P-poll__networl_5_4_AskP_8" + "P-poll__networl_5_4_AnsP_0" + "P-poll__networl_5_4_AnsP_1" + "P-poll__networl_5_4_AnsP_2" + "P-poll__networl_5_4_AnsP_3" + "P-poll__networl_5_4_AnsP_4" + "P-poll__networl_5_4_AnsP_5" + "P-poll__networl_5_4_AnsP_6" + "P-poll__networl_5_4_AnsP_7" + "P-poll__networl_5_4_AnsP_8" + "P-poll__networl_5_4_RI_0" + "P-poll__networl_5_4_RI_1" + "P-poll__networl_5_4_RI_2" + "P-poll__networl_5_4_RI_3" + "P-poll__networl_5_4_RI_4" + "P-poll__networl_5_4_RI_5" + "P-poll__networl_5_4_RI_6" + "P-poll__networl_5_4_RI_7" + "P-poll__networl_5_4_RI_8" + "P-poll__networl_5_4_AI_0" + "P-poll__networl_5_4_AI_1" + "P-poll__networl_5_4_AI_2" + "P-poll__networl_5_4_AI_3" + "P-poll__networl_5_4_AI_4" + "P-poll__networl_5_4_AI_5" + "P-poll__networl_5_4_AI_6" + "P-poll__networl_5_4_AI_7" + "P-poll__networl_5_4_AI_8" + "P-poll__networl_5_4_AnnP_0" + "P-poll__networl_5_4_AnnP_1" + "P-poll__networl_5_4_AnnP_2" + "P-poll__networl_5_4_AnnP_3" + "P-poll__networl_5_4_AnnP_4" + "P-poll__networl_5_4_AnnP_5" + "P-poll__networl_5_4_AnnP_6" + "P-poll__networl_5_4_AnnP_7" + "P-poll__networl_5_4_AnnP_8" + "P-poll__networl_5_4_RP_0" + "P-poll__networl_5_4_RP_1" + "P-poll__networl_5_4_RP_2" + "P-poll__networl_5_4_RP_3" + "P-poll__networl_5_4_RP_4" + "P-poll__networl_5_4_RP_5" + "P-poll__networl_5_4_RP_6" + "P-poll__networl_5_4_RP_7" + "P-poll__networl_5_4_RP_8" + "P-poll__networl_5_5_AskP_0" + "P-poll__networl_5_5_AskP_1" + "P-poll__networl_5_5_AskP_2" + "P-poll__networl_5_5_AskP_3" + "P-poll__networl_5_5_AskP_4" + "P-poll__networl_5_5_AskP_5" + "P-poll__networl_5_5_AskP_6" + "P-poll__networl_5_5_AskP_7" + "P-poll__networl_5_5_AskP_8" + "P-poll__networl_5_5_AnsP_0" + "P-poll__networl_5_5_AnsP_1" + "P-poll__networl_5_5_AnsP_2" + "P-poll__networl_5_5_AnsP_3" + "P-poll__networl_5_5_AnsP_4" + "P-poll__networl_5_5_AnsP_5" + "P-poll__networl_5_5_AnsP_6" + "P-poll__networl_5_5_AnsP_7" + "P-poll__networl_5_5_AnsP_8" + "P-poll__networl_5_5_RI_0" + "P-poll__networl_5_5_RI_1" + "P-poll__networl_5_5_RI_2" + "P-poll__networl_5_5_RI_3" + "P-poll__networl_5_5_RI_4" + "P-poll__networl_5_5_RI_5" + "P-poll__networl_5_5_RI_6" + "P-poll__networl_5_5_RI_7" + "P-poll__networl_5_5_RI_8" + "P-poll__networl_5_5_AI_0" + "P-poll__networl_5_5_AI_1" + "P-poll__networl_5_5_AI_2" + "P-poll__networl_5_5_AI_3" + "P-poll__networl_5_5_AI_4" + "P-poll__networl_5_5_AI_5" + "P-poll__networl_5_5_AI_6" + "P-poll__networl_5_5_AI_7" + "P-poll__networl_5_5_AI_8" + "P-poll__networl_5_5_AnnP_0" + "P-poll__networl_5_5_AnnP_1" + "P-poll__networl_5_5_AnnP_2" + "P-poll__networl_5_5_AnnP_3" + "P-poll__networl_5_5_AnnP_4" + "P-poll__networl_5_5_AnnP_5" + "P-poll__networl_5_5_AnnP_6" + "P-poll__networl_5_5_AnnP_7" + "P-poll__networl_5_5_AnnP_8" + "P-poll__networl_5_5_RP_0" + "P-poll__networl_5_5_RP_1" + "P-poll__networl_5_5_RP_2" + "P-poll__networl_5_5_RP_3" + "P-poll__networl_5_5_RP_4" + "P-poll__networl_5_5_RP_5" + "P-poll__networl_5_5_RP_6" + "P-poll__networl_5_5_RP_7" + "P-poll__networl_5_5_RP_8" + "P-poll__networl_5_6_AskP_0" + "P-poll__networl_5_6_AskP_1" + "P-poll__networl_5_6_AskP_2" + "P-poll__networl_5_6_AskP_3" + "P-poll__networl_5_6_AskP_4" + "P-poll__networl_5_6_AskP_5" + "P-poll__networl_5_6_AskP_6" + "P-poll__networl_5_6_AskP_7" + "P-poll__networl_5_6_AskP_8" + "P-poll__networl_5_6_AnsP_0" + "P-poll__networl_5_6_AnsP_1" + "P-poll__networl_5_6_AnsP_2" + "P-poll__networl_5_6_AnsP_3" + "P-poll__networl_5_6_AnsP_4" + "P-poll__networl_5_6_AnsP_5" + "P-poll__networl_5_6_AnsP_6" + "P-poll__networl_5_6_AnsP_7" + "P-poll__networl_5_6_AnsP_8" + "P-poll__networl_5_6_RI_0" + "P-poll__networl_5_6_RI_1" + "P-poll__networl_5_6_RI_2" + "P-poll__networl_5_6_RI_3" + "P-poll__networl_5_6_RI_4" + "P-poll__networl_5_6_RI_5" + "P-poll__networl_5_6_RI_6" + "P-poll__networl_5_6_RI_7" + "P-poll__networl_5_6_RI_8" + "P-poll__networl_5_6_AI_0" + "P-poll__networl_5_6_AI_1" + "P-poll__networl_5_6_AI_2" + "P-poll__networl_5_6_AI_3" + "P-poll__networl_5_6_AI_4" + "P-poll__networl_5_6_AI_5" + "P-poll__networl_5_6_AI_6" + "P-poll__networl_5_6_AI_7" + "P-poll__networl_5_6_AI_8" + "P-poll__networl_5_6_AnnP_0" + "P-poll__networl_5_6_AnnP_1" + "P-poll__networl_5_6_AnnP_2" + "P-poll__networl_5_6_AnnP_3" + "P-poll__networl_5_6_AnnP_4" + "P-poll__networl_5_6_AnnP_5" + "P-poll__networl_5_6_AnnP_6" + "P-poll__networl_5_6_AnnP_7" + "P-poll__networl_5_6_AnnP_8" + "P-poll__networl_5_6_RP_0" + "P-poll__networl_5_6_RP_1" + "P-poll__networl_5_6_RP_2" + "P-poll__networl_5_6_RP_3" + "P-poll__networl_5_6_RP_4" + "P-poll__networl_5_6_RP_5" + "P-poll__networl_5_6_RP_6" + "P-poll__networl_5_6_RP_7" + "P-poll__networl_5_6_RP_8" + "P-poll__networl_5_7_AskP_0" + "P-poll__networl_5_7_AskP_1" + "P-poll__networl_5_7_AskP_2" + "P-poll__networl_5_7_AskP_3" + "P-poll__networl_5_7_AskP_4" + "P-poll__networl_5_7_AskP_5" + "P-poll__networl_5_7_AskP_6" + "P-poll__networl_5_7_AskP_7" + "P-poll__networl_5_7_AskP_8" + "P-poll__networl_5_7_AnsP_0" + "P-poll__networl_5_7_AnsP_1" + "P-poll__networl_5_7_AnsP_2" + "P-poll__networl_5_7_AnsP_3" + "P-poll__networl_5_7_AnsP_4" + "P-poll__networl_5_7_AnsP_5" + "P-poll__networl_5_7_AnsP_6" + "P-poll__networl_5_7_AnsP_7" + "P-poll__networl_5_7_AnsP_8" + "P-poll__networl_5_7_RI_0" + "P-poll__networl_5_7_RI_1" + "P-poll__networl_5_7_RI_2" + "P-poll__networl_5_7_RI_3" + "P-poll__networl_5_7_RI_4" + "P-poll__networl_5_7_RI_5" + "P-poll__networl_5_7_RI_6" + "P-poll__networl_5_7_RI_7" + "P-poll__networl_5_7_RI_8" + "P-poll__networl_5_7_AI_0" + "P-poll__networl_5_7_AI_1" + "P-poll__networl_5_7_AI_2" + "P-poll__networl_5_7_AI_3" + "P-poll__networl_5_7_AI_4" + "P-poll__networl_5_7_AI_5" + "P-poll__networl_5_7_AI_6" + "P-poll__networl_5_7_AI_7" + "P-poll__networl_5_7_AI_8" + "P-poll__networl_5_7_AnnP_0" + "P-poll__networl_5_7_AnnP_1" + "P-poll__networl_5_7_AnnP_2" + "P-poll__networl_5_7_AnnP_3" + "P-poll__networl_5_7_AnnP_4" + "P-poll__networl_5_7_AnnP_5" + "P-poll__networl_5_7_AnnP_6" + "P-poll__networl_5_7_AnnP_7" + "P-poll__networl_5_7_AnnP_8" + "P-poll__networl_5_7_RP_0" + "P-poll__networl_5_7_RP_1" + "P-poll__networl_5_7_RP_2" + "P-poll__networl_5_7_RP_3" + "P-poll__networl_5_7_RP_4" + "P-poll__networl_5_7_RP_5" + "P-poll__networl_5_7_RP_6" + "P-poll__networl_5_7_RP_7" + "P-poll__networl_5_7_RP_8" + "P-poll__networl_5_8_AskP_0" + "P-poll__networl_5_8_AskP_1" + "P-poll__networl_5_8_AskP_2" + "P-poll__networl_5_8_AskP_3" + "P-poll__networl_5_8_AskP_4" + "P-poll__networl_5_8_AskP_5" + "P-poll__networl_5_8_AskP_6" + "P-poll__networl_5_8_AskP_7" + "P-poll__networl_5_8_AskP_8" + "P-poll__networl_5_8_AnsP_0" + "P-poll__networl_5_8_AnsP_1" + "P-poll__networl_5_8_AnsP_2" + "P-poll__networl_5_8_AnsP_3" + "P-poll__networl_5_8_AnsP_4" + "P-poll__networl_5_8_AnsP_5" + "P-poll__networl_5_8_AnsP_6" + "P-poll__networl_5_8_AnsP_7" + "P-poll__networl_5_8_AnsP_8" + "P-poll__networl_5_8_RI_0" + "P-poll__networl_5_8_RI_1" + "P-poll__networl_5_8_RI_2" + "P-poll__networl_5_8_RI_3" + "P-poll__networl_5_8_RI_4" + "P-poll__networl_5_8_RI_5" + "P-poll__networl_5_8_RI_6" + "P-poll__networl_5_8_RI_7" + "P-poll__networl_5_8_RI_8" + "P-poll__networl_5_8_AI_0" + "P-poll__networl_5_8_AI_1" + "P-poll__networl_5_8_AI_2" + "P-poll__networl_5_8_AI_3" + "P-poll__networl_5_8_AI_4" + "P-poll__networl_5_8_AI_5" + "P-poll__networl_5_8_AI_6" + "P-poll__networl_5_8_AI_7" + "P-poll__networl_5_8_AI_8" + "P-poll__networl_5_8_AnnP_0" + "P-poll__networl_5_8_AnnP_1" + "P-poll__networl_5_8_AnnP_2" + "P-poll__networl_5_8_AnnP_3" + "P-poll__networl_5_8_AnnP_4" + "P-poll__networl_5_8_AnnP_5" + "P-poll__networl_5_8_AnnP_6" + "P-poll__networl_5_8_AnnP_7" + "P-poll__networl_5_8_AnnP_8" + "P-poll__networl_5_8_RP_0" + "P-poll__networl_5_8_RP_1" + "P-poll__networl_5_8_RP_2" + "P-poll__networl_5_8_RP_3" + "P-poll__networl_5_8_RP_4" + "P-poll__networl_5_8_RP_5" + "P-poll__networl_5_8_RP_6" + "P-poll__networl_5_8_RP_7" + "P-poll__networl_5_8_RP_8" + "P-poll__networl_6_0_AskP_0" + "P-poll__networl_6_0_AskP_1" + "P-poll__networl_6_0_AskP_2" + "P-poll__networl_6_0_AskP_3" + "P-poll__networl_6_0_AskP_4" + "P-poll__networl_6_0_AskP_5" + "P-poll__networl_6_0_AskP_6" + "P-poll__networl_6_0_AskP_7" + "P-poll__networl_6_0_AskP_8" + "P-poll__networl_6_0_AnsP_0" + "P-poll__networl_6_0_AnsP_1" + "P-poll__networl_6_0_AnsP_2" + "P-poll__networl_6_0_AnsP_3" + "P-poll__networl_6_0_AnsP_4" + "P-poll__networl_6_0_AnsP_5" + "P-poll__networl_6_0_AnsP_6" + "P-poll__networl_6_0_AnsP_7" + "P-poll__networl_6_0_AnsP_8" + "P-poll__networl_6_0_RI_0" + "P-poll__networl_6_0_RI_1" + "P-poll__networl_6_0_RI_2" + "P-poll__networl_6_0_RI_3" + "P-poll__networl_6_0_RI_4" + "P-poll__networl_6_0_RI_5" + "P-poll__networl_6_0_RI_6" + "P-poll__networl_6_0_RI_7" + "P-poll__networl_6_0_RI_8" + "P-poll__networl_6_0_AI_0" + "P-poll__networl_6_0_AI_1" + "P-poll__networl_6_0_AI_2" + "P-poll__networl_6_0_AI_3" + "P-poll__networl_6_0_AI_4" + "P-poll__networl_6_0_AI_5" + "P-poll__networl_6_0_AI_6" + "P-poll__networl_6_0_AI_7" + "P-poll__networl_6_0_AI_8" + "P-poll__networl_6_0_AnnP_0" + "P-poll__networl_6_0_AnnP_1" + "P-poll__networl_6_0_AnnP_2" + "P-poll__networl_6_0_AnnP_3" + "P-poll__networl_6_0_AnnP_4" + "P-poll__networl_6_0_AnnP_5" + "P-poll__networl_6_0_AnnP_6" + "P-poll__networl_6_0_AnnP_7" + "P-poll__networl_6_0_AnnP_8" + "P-poll__networl_6_0_RP_0" + "P-poll__networl_6_0_RP_1" + "P-poll__networl_6_0_RP_2" + "P-poll__networl_6_0_RP_3" + "P-poll__networl_6_0_RP_4" + "P-poll__networl_6_0_RP_5" + "P-poll__networl_6_0_RP_6" + "P-poll__networl_6_0_RP_7" + "P-poll__networl_6_0_RP_8" + "P-poll__networl_6_1_AskP_0" + "P-poll__networl_6_1_AskP_1" + "P-poll__networl_6_1_AskP_2" + "P-poll__networl_6_1_AskP_3" + "P-poll__networl_6_1_AskP_4" + "P-poll__networl_6_1_AskP_5" + "P-poll__networl_6_1_AskP_6" + "P-poll__networl_6_1_AskP_7" + "P-poll__networl_6_1_AskP_8" + "P-poll__networl_6_1_AnsP_0" + "P-poll__networl_6_1_AnsP_1" + "P-poll__networl_6_1_AnsP_2" + "P-poll__networl_6_1_AnsP_3" + "P-poll__networl_6_1_AnsP_4" + "P-poll__networl_6_1_AnsP_5" + "P-poll__networl_6_1_AnsP_6" + "P-poll__networl_6_1_AnsP_7" + "P-poll__networl_6_1_AnsP_8" + "P-poll__networl_6_1_RI_0" + "P-poll__networl_6_1_RI_1" + "P-poll__networl_6_1_RI_2" + "P-poll__networl_6_1_RI_3" + "P-poll__networl_6_1_RI_4" + "P-poll__networl_6_1_RI_5" + "P-poll__networl_6_1_RI_6" + "P-poll__networl_6_1_RI_7" + "P-poll__networl_6_1_RI_8" + "P-poll__networl_6_1_AI_0" + "P-poll__networl_6_1_AI_1" + "P-poll__networl_6_1_AI_2" + "P-poll__networl_6_1_AI_3" + "P-poll__networl_6_1_AI_4" + "P-poll__networl_6_1_AI_5" + "P-poll__networl_6_1_AI_6" + "P-poll__networl_6_1_AI_7" + "P-poll__networl_6_1_AI_8" + "P-poll__networl_6_1_AnnP_0" + "P-poll__networl_6_1_AnnP_1" + "P-poll__networl_6_1_AnnP_2" + "P-poll__networl_6_1_AnnP_3" + "P-poll__networl_6_1_AnnP_4" + "P-poll__networl_6_1_AnnP_5" + "P-poll__networl_6_1_AnnP_6" + "P-poll__networl_6_1_AnnP_7" + "P-poll__networl_6_1_AnnP_8" + "P-poll__networl_6_1_RP_0" + "P-poll__networl_6_1_RP_1" + "P-poll__networl_6_1_RP_2" + "P-poll__networl_6_1_RP_3" + "P-poll__networl_6_1_RP_4" + "P-poll__networl_6_1_RP_5" + "P-poll__networl_6_1_RP_6" + "P-poll__networl_6_1_RP_7" + "P-poll__networl_6_1_RP_8" + "P-poll__networl_6_2_AskP_0" + "P-poll__networl_6_2_AskP_1" + "P-poll__networl_6_2_AskP_2" + "P-poll__networl_6_2_AskP_3" + "P-poll__networl_6_2_AskP_4" + "P-poll__networl_6_2_AskP_5" + "P-poll__networl_6_2_AskP_6" + "P-poll__networl_6_2_AskP_7" + "P-poll__networl_6_2_AskP_8" + "P-poll__networl_6_2_AnsP_0" + "P-poll__networl_6_2_AnsP_1" + "P-poll__networl_6_2_AnsP_2" + "P-poll__networl_6_2_AnsP_3" + "P-poll__networl_6_2_AnsP_4" + "P-poll__networl_6_2_AnsP_5" + "P-poll__networl_6_2_AnsP_6" + "P-poll__networl_6_2_AnsP_7" + "P-poll__networl_6_2_AnsP_8" + "P-poll__networl_6_2_RI_0" + "P-poll__networl_6_2_RI_1" + "P-poll__networl_6_2_RI_2" + "P-poll__networl_6_2_RI_3" + "P-poll__networl_6_2_RI_4" + "P-poll__networl_6_2_RI_5" + "P-poll__networl_6_2_RI_6" + "P-poll__networl_6_2_RI_7" + "P-poll__networl_6_2_RI_8" + "P-poll__networl_6_2_AI_0" + "P-poll__networl_6_2_AI_1" + "P-poll__networl_6_2_AI_2" + "P-poll__networl_6_2_AI_3" + "P-poll__networl_6_2_AI_4" + "P-poll__networl_6_2_AI_5" + "P-poll__networl_6_2_AI_6" + "P-poll__networl_6_2_AI_7" + "P-poll__networl_6_2_AI_8" + "P-poll__networl_6_2_AnnP_0" + "P-poll__networl_6_2_AnnP_1" + "P-poll__networl_6_2_AnnP_2" + "P-poll__networl_6_2_AnnP_3" + "P-poll__networl_6_2_AnnP_4" + "P-poll__networl_6_2_AnnP_5" + "P-poll__networl_6_2_AnnP_6" + "P-poll__networl_6_2_AnnP_7" + "P-poll__networl_6_2_AnnP_8" + "P-poll__networl_6_2_RP_0" + "P-poll__networl_6_2_RP_1" + "P-poll__networl_6_2_RP_2" + "P-poll__networl_6_2_RP_3" + "P-poll__networl_6_2_RP_4" + "P-poll__networl_6_2_RP_5" + "P-poll__networl_6_2_RP_6" + "P-poll__networl_6_2_RP_7" + "P-poll__networl_6_2_RP_8" + "P-poll__networl_6_3_AskP_0" + "P-poll__networl_6_3_AskP_1" + "P-poll__networl_6_3_AskP_2" + "P-poll__networl_6_3_AskP_3" + "P-poll__networl_6_3_AskP_4" + "P-poll__networl_6_3_AskP_5" + "P-poll__networl_6_3_AskP_6" + "P-poll__networl_6_3_AskP_7" + "P-poll__networl_6_3_AskP_8" + "P-poll__networl_6_3_AnsP_0" + "P-poll__networl_6_3_AnsP_1" + "P-poll__networl_6_3_AnsP_2" + "P-poll__networl_6_3_AnsP_3" + "P-poll__networl_6_3_AnsP_4" + "P-poll__networl_6_3_AnsP_5" + "P-poll__networl_6_3_AnsP_6" + "P-poll__networl_6_3_AnsP_7" + "P-poll__networl_6_3_AnsP_8" + "P-poll__networl_6_3_RI_0" + "P-poll__networl_6_3_RI_1" + "P-poll__networl_6_3_RI_2" + "P-poll__networl_6_3_RI_3" + "P-poll__networl_6_3_RI_4" + "P-poll__networl_6_3_RI_5" + "P-poll__networl_6_3_RI_6" + "P-poll__networl_6_3_RI_7" + "P-poll__networl_6_3_RI_8" + "P-poll__networl_6_3_AI_0" + "P-poll__networl_6_3_AI_1" + "P-poll__networl_6_3_AI_2" + "P-poll__networl_6_3_AI_3" + "P-poll__networl_6_3_AI_4" + "P-poll__networl_6_3_AI_5" + "P-poll__networl_6_3_AI_6" + "P-poll__networl_6_3_AI_7" + "P-poll__networl_6_3_AI_8" + "P-poll__networl_6_3_AnnP_0" + "P-poll__networl_6_3_AnnP_1" + "P-poll__networl_6_3_AnnP_2" + "P-poll__networl_6_3_AnnP_3" + "P-poll__networl_6_3_AnnP_4" + "P-poll__networl_6_3_AnnP_5" + "P-poll__networl_6_3_AnnP_6" + "P-poll__networl_6_3_AnnP_7" + "P-poll__networl_6_3_AnnP_8" + "P-poll__networl_6_3_RP_0" + "P-poll__networl_6_3_RP_1" + "P-poll__networl_6_3_RP_2" + "P-poll__networl_6_3_RP_3" + "P-poll__networl_6_3_RP_4" + "P-poll__networl_6_3_RP_5" + "P-poll__networl_6_3_RP_6" + "P-poll__networl_6_3_RP_7" + "P-poll__networl_6_3_RP_8" + "P-poll__networl_6_4_AskP_0" + "P-poll__networl_6_4_AskP_1" + "P-poll__networl_6_4_AskP_2" + "P-poll__networl_6_4_AskP_3" + "P-poll__networl_6_4_AskP_4" + "P-poll__networl_6_4_AskP_5" + "P-poll__networl_6_4_AskP_6" + "P-poll__networl_6_4_AskP_7" + "P-poll__networl_6_4_AskP_8" + "P-poll__networl_6_4_AnsP_0" + "P-poll__networl_6_4_AnsP_1" + "P-poll__networl_6_4_AnsP_2" + "P-poll__networl_6_4_AnsP_3" + "P-poll__networl_6_4_AnsP_4" + "P-poll__networl_6_4_AnsP_5" + "P-poll__networl_6_4_AnsP_6" + "P-poll__networl_6_4_AnsP_7" + "P-poll__networl_6_4_AnsP_8" + "P-poll__networl_6_4_RI_0" + "P-poll__networl_6_4_RI_1" + "P-poll__networl_6_4_RI_2" + "P-poll__networl_6_4_RI_3" + "P-poll__networl_6_4_RI_4" + "P-poll__networl_6_4_RI_5" + "P-poll__networl_6_4_RI_6" + "P-poll__networl_6_4_RI_7" + "P-poll__networl_6_4_RI_8" + "P-poll__networl_6_4_AI_0" + "P-poll__networl_6_4_AI_1" + "P-poll__networl_6_4_AI_2" + "P-poll__networl_6_4_AI_3" + "P-poll__networl_6_4_AI_4" + "P-poll__networl_6_4_AI_5" + "P-poll__networl_6_4_AI_6" + "P-poll__networl_6_4_AI_7" + "P-poll__networl_6_4_AI_8" + "P-poll__networl_6_4_AnnP_0" + "P-poll__networl_6_4_AnnP_1" + "P-poll__networl_6_4_AnnP_2" + "P-poll__networl_6_4_AnnP_3" + "P-poll__networl_6_4_AnnP_4" + "P-poll__networl_6_4_AnnP_5" + "P-poll__networl_6_4_AnnP_6" + "P-poll__networl_6_4_AnnP_7" + "P-poll__networl_6_4_AnnP_8" + "P-poll__networl_6_4_RP_0" + "P-poll__networl_6_4_RP_1" + "P-poll__networl_6_4_RP_2" + "P-poll__networl_6_4_RP_3" + "P-poll__networl_6_4_RP_4" + "P-poll__networl_6_4_RP_5" + "P-poll__networl_6_4_RP_6" + "P-poll__networl_6_4_RP_7" + "P-poll__networl_6_4_RP_8" + "P-poll__networl_6_5_AskP_0" + "P-poll__networl_6_5_AskP_1" + "P-poll__networl_6_5_AskP_2" + "P-poll__networl_6_5_AskP_3" + "P-poll__networl_6_5_AskP_4" + "P-poll__networl_6_5_AskP_5" + "P-poll__networl_6_5_AskP_6" + "P-poll__networl_6_5_AskP_7" + "P-poll__networl_6_5_AskP_8" + "P-poll__networl_6_5_AnsP_0" + "P-poll__networl_6_5_AnsP_1" + "P-poll__networl_6_5_AnsP_2" + "P-poll__networl_6_5_AnsP_3" + "P-poll__networl_6_5_AnsP_4" + "P-poll__networl_6_5_AnsP_5" + "P-poll__networl_6_5_AnsP_6" + "P-poll__networl_6_5_AnsP_7" + "P-poll__networl_6_5_AnsP_8" + "P-poll__networl_6_5_RI_0" + "P-poll__networl_6_5_RI_1" + "P-poll__networl_6_5_RI_2" + "P-poll__networl_6_5_RI_3" + "P-poll__networl_6_5_RI_4" + "P-poll__networl_6_5_RI_5" + "P-poll__networl_6_5_RI_6" + "P-poll__networl_6_5_RI_7" + "P-poll__networl_6_5_RI_8" + "P-poll__networl_6_5_AI_0" + "P-poll__networl_6_5_AI_1" + "P-poll__networl_6_5_AI_2" + "P-poll__networl_6_5_AI_3" + "P-poll__networl_6_5_AI_4" + "P-poll__networl_6_5_AI_5" + "P-poll__networl_6_5_AI_6" + "P-poll__networl_6_5_AI_7" + "P-poll__networl_6_5_AI_8" + "P-poll__networl_6_5_AnnP_0" + "P-poll__networl_6_5_AnnP_1" + "P-poll__networl_6_5_AnnP_2" + "P-poll__networl_6_5_AnnP_3" + "P-poll__networl_6_5_AnnP_4" + "P-poll__networl_6_5_AnnP_5" + "P-poll__networl_6_5_AnnP_6" + "P-poll__networl_6_5_AnnP_7" + "P-poll__networl_6_5_AnnP_8" + "P-poll__networl_6_5_RP_0" + "P-poll__networl_6_5_RP_1" + "P-poll__networl_6_5_RP_2" + "P-poll__networl_6_5_RP_3" + "P-poll__networl_6_5_RP_4" + "P-poll__networl_6_5_RP_5" + "P-poll__networl_6_5_RP_6" + "P-poll__networl_6_5_RP_7" + "P-poll__networl_6_5_RP_8" + "P-poll__networl_6_6_AskP_0" + "P-poll__networl_6_6_AskP_1" + "P-poll__networl_6_6_AskP_2" + "P-poll__networl_6_6_AskP_3" + "P-poll__networl_6_6_AskP_4" + "P-poll__networl_6_6_AskP_5" + "P-poll__networl_6_6_AskP_6" + "P-poll__networl_6_6_AskP_7" + "P-poll__networl_6_6_AskP_8" + "P-poll__networl_6_6_AnsP_0" + "P-poll__networl_6_6_AnsP_1" + "P-poll__networl_6_6_AnsP_2" + "P-poll__networl_6_6_AnsP_3" + "P-poll__networl_6_6_AnsP_4" + "P-poll__networl_6_6_AnsP_5" + "P-poll__networl_6_6_AnsP_6" + "P-poll__networl_6_6_AnsP_7" + "P-poll__networl_6_6_AnsP_8" + "P-poll__networl_6_6_RI_0" + "P-poll__networl_6_6_RI_1" + "P-poll__networl_6_6_RI_2" + "P-poll__networl_6_6_RI_3" + "P-poll__networl_6_6_RI_4" + "P-poll__networl_6_6_RI_5" + "P-poll__networl_6_6_RI_6" + "P-poll__networl_6_6_RI_7" + "P-poll__networl_6_6_RI_8" + "P-poll__networl_6_6_AI_0" + "P-poll__networl_6_6_AI_1" + "P-poll__networl_6_6_AI_2" + "P-poll__networl_6_6_AI_3" + "P-poll__networl_6_6_AI_4" + "P-poll__networl_6_6_AI_5" + "P-poll__networl_6_6_AI_6" + "P-poll__networl_6_6_AI_7" + "P-poll__networl_6_6_AI_8" + "P-poll__networl_6_6_AnnP_0" + "P-poll__networl_6_6_AnnP_1" + "P-poll__networl_6_6_AnnP_2" + "P-poll__networl_6_6_AnnP_3" + "P-poll__networl_6_6_AnnP_4" + "P-poll__networl_6_6_AnnP_5" + "P-poll__networl_6_6_AnnP_6" + "P-poll__networl_6_6_AnnP_7" + "P-poll__networl_6_6_AnnP_8" + "P-poll__networl_6_6_RP_0" + "P-poll__networl_6_6_RP_1" + "P-poll__networl_6_6_RP_2" + "P-poll__networl_6_6_RP_3" + "P-poll__networl_6_6_RP_4" + "P-poll__networl_6_6_RP_5" + "P-poll__networl_6_6_RP_6" + "P-poll__networl_6_6_RP_7" + "P-poll__networl_6_6_RP_8" + "P-poll__networl_6_7_AskP_0" + "P-poll__networl_6_7_AskP_1" + "P-poll__networl_6_7_AskP_2" + "P-poll__networl_6_7_AskP_3" + "P-poll__networl_6_7_AskP_4" + "P-poll__networl_6_7_AskP_5" + "P-poll__networl_6_7_AskP_6" + "P-poll__networl_6_7_AskP_7" + "P-poll__networl_6_7_AskP_8" + "P-poll__networl_6_7_AnsP_0" + "P-poll__networl_6_7_AnsP_1" + "P-poll__networl_6_7_AnsP_2" + "P-poll__networl_6_7_AnsP_3" + "P-poll__networl_6_7_AnsP_4" + "P-poll__networl_6_7_AnsP_5" + "P-poll__networl_6_7_AnsP_6" + "P-poll__networl_6_7_AnsP_7" + "P-poll__networl_6_7_AnsP_8" + "P-poll__networl_6_7_RI_0" + "P-poll__networl_6_7_RI_1" + "P-poll__networl_6_7_RI_2" + "P-poll__networl_6_7_RI_3" + "P-poll__networl_6_7_RI_4" + "P-poll__networl_6_7_RI_5" + "P-poll__networl_6_7_RI_6" + "P-poll__networl_6_7_RI_7" + "P-poll__networl_6_7_RI_8" + "P-poll__networl_6_7_AI_0" + "P-poll__networl_6_7_AI_1" + "P-poll__networl_6_7_AI_2" + "P-poll__networl_6_7_AI_3" + "P-poll__networl_6_7_AI_4" + "P-poll__networl_6_7_AI_5" + "P-poll__networl_6_7_AI_6" + "P-poll__networl_6_7_AI_7" + "P-poll__networl_6_7_AI_8" + "P-poll__networl_6_7_AnnP_0" + "P-poll__networl_6_7_AnnP_1" + "P-poll__networl_6_7_AnnP_2" + "P-poll__networl_6_7_AnnP_3" + "P-poll__networl_6_7_AnnP_4" + "P-poll__networl_6_7_AnnP_5" + "P-poll__networl_6_7_AnnP_6" + "P-poll__networl_6_7_AnnP_7" + "P-poll__networl_6_7_AnnP_8" + "P-poll__networl_6_7_RP_0" + "P-poll__networl_6_7_RP_1" + "P-poll__networl_6_7_RP_2" + "P-poll__networl_6_7_RP_3" + "P-poll__networl_6_7_RP_4" + "P-poll__networl_6_7_RP_5" + "P-poll__networl_6_7_RP_6" + "P-poll__networl_6_7_RP_7" + "P-poll__networl_6_7_RP_8" + "P-poll__networl_6_8_AskP_0" + "P-poll__networl_6_8_AskP_1" + "P-poll__networl_6_8_AskP_2" + "P-poll__networl_6_8_AskP_3" + "P-poll__networl_6_8_AskP_4" + "P-poll__networl_6_8_AskP_5" + "P-poll__networl_6_8_AskP_6" + "P-poll__networl_6_8_AskP_7" + "P-poll__networl_6_8_AskP_8" + "P-poll__networl_6_8_AnsP_0" + "P-poll__networl_6_8_AnsP_1" + "P-poll__networl_6_8_AnsP_2" + "P-poll__networl_6_8_AnsP_3" + "P-poll__networl_6_8_AnsP_4" + "P-poll__networl_6_8_AnsP_5" + "P-poll__networl_6_8_AnsP_6" + "P-poll__networl_6_8_AnsP_7" + "P-poll__networl_6_8_AnsP_8" + "P-poll__networl_6_8_RI_0" + "P-poll__networl_6_8_RI_1" + "P-poll__networl_6_8_RI_2" + "P-poll__networl_6_8_RI_3" + "P-poll__networl_6_8_RI_4" + "P-poll__networl_6_8_RI_5" + "P-poll__networl_6_8_RI_6" + "P-poll__networl_6_8_RI_7" + "P-poll__networl_6_8_RI_8" + "P-poll__networl_6_8_AI_0" + "P-poll__networl_6_8_AI_1" + "P-poll__networl_6_8_AI_2" + "P-poll__networl_6_8_AI_3" + "P-poll__networl_6_8_AI_4" + "P-poll__networl_6_8_AI_5" + "P-poll__networl_6_8_AI_6" + "P-poll__networl_6_8_AI_7" + "P-poll__networl_6_8_AI_8" + "P-poll__networl_6_8_AnnP_0" + "P-poll__networl_6_8_AnnP_1" + "P-poll__networl_6_8_AnnP_2" + "P-poll__networl_6_8_AnnP_3" + "P-poll__networl_6_8_AnnP_4" + "P-poll__networl_6_8_AnnP_5" + "P-poll__networl_6_8_AnnP_6" + "P-poll__networl_6_8_AnnP_7" + "P-poll__networl_6_8_AnnP_8" + "P-poll__networl_6_8_RP_0" + "P-poll__networl_6_8_RP_1" + "P-poll__networl_6_8_RP_2" + "P-poll__networl_6_8_RP_3" + "P-poll__networl_6_8_RP_4" + "P-poll__networl_6_8_RP_5" + "P-poll__networl_6_8_RP_6" + "P-poll__networl_6_8_RP_7" + "P-poll__networl_6_8_RP_8" + "P-poll__networl_7_0_AskP_0" + "P-poll__networl_7_0_AskP_1" + "P-poll__networl_7_0_AskP_2" + "P-poll__networl_7_0_AskP_3" + "P-poll__networl_7_0_AskP_4" + "P-poll__networl_7_0_AskP_5" + "P-poll__networl_7_0_AskP_6" + "P-poll__networl_7_0_AskP_7" + "P-poll__networl_7_0_AskP_8" + "P-poll__networl_7_0_AnsP_0" + "P-poll__networl_7_0_AnsP_1" + "P-poll__networl_7_0_AnsP_2" + "P-poll__networl_7_0_AnsP_3" + "P-poll__networl_7_0_AnsP_4" + "P-poll__networl_7_0_AnsP_5" + "P-poll__networl_7_0_AnsP_6" + "P-poll__networl_7_0_AnsP_7" + "P-poll__networl_7_0_AnsP_8" + "P-poll__networl_7_0_RI_0" + "P-poll__networl_7_0_RI_1" + "P-poll__networl_7_0_RI_2" + "P-poll__networl_7_0_RI_3" + "P-poll__networl_7_0_RI_4" + "P-poll__networl_7_0_RI_5" + "P-poll__networl_7_0_RI_6" + "P-poll__networl_7_0_RI_7" + "P-poll__networl_7_0_RI_8" + "P-poll__networl_7_0_AI_0" + "P-poll__networl_7_0_AI_1" + "P-poll__networl_7_0_AI_2" + "P-poll__networl_7_0_AI_3" + "P-poll__networl_7_0_AI_4" + "P-poll__networl_7_0_AI_5" + "P-poll__networl_7_0_AI_6" + "P-poll__networl_7_0_AI_7" + "P-poll__networl_7_0_AI_8" + "P-poll__networl_7_0_AnnP_0" + "P-poll__networl_7_0_AnnP_1" + "P-poll__networl_7_0_AnnP_2" + "P-poll__networl_7_0_AnnP_3" + "P-poll__networl_7_0_AnnP_4" + "P-poll__networl_7_0_AnnP_5" + "P-poll__networl_7_0_AnnP_6" + "P-poll__networl_7_0_AnnP_7" + "P-poll__networl_7_0_AnnP_8" + "P-poll__networl_7_0_RP_0" + "P-poll__networl_7_0_RP_1" + "P-poll__networl_7_0_RP_2" + "P-poll__networl_7_0_RP_3" + "P-poll__networl_7_0_RP_4" + "P-poll__networl_7_0_RP_5" + "P-poll__networl_7_0_RP_6" + "P-poll__networl_7_0_RP_7" + "P-poll__networl_7_0_RP_8" + "P-poll__networl_7_1_AskP_0" + "P-poll__networl_7_1_AskP_1" + "P-poll__networl_7_1_AskP_2" + "P-poll__networl_7_1_AskP_3" + "P-poll__networl_7_1_AskP_4" + "P-poll__networl_7_1_AskP_5" + "P-poll__networl_7_1_AskP_6" + "P-poll__networl_7_1_AskP_7" + "P-poll__networl_7_1_AskP_8" + "P-poll__networl_7_1_AnsP_0" + "P-poll__networl_7_1_AnsP_1" + "P-poll__networl_7_1_AnsP_2" + "P-poll__networl_7_1_AnsP_3" + "P-poll__networl_7_1_AnsP_4" + "P-poll__networl_7_1_AnsP_5" + "P-poll__networl_7_1_AnsP_6" + "P-poll__networl_7_1_AnsP_7" + "P-poll__networl_7_1_AnsP_8" + "P-poll__networl_7_1_RI_0" + "P-poll__networl_7_1_RI_1" + "P-poll__networl_7_1_RI_2" + "P-poll__networl_7_1_RI_3" + "P-poll__networl_7_1_RI_4" + "P-poll__networl_7_1_RI_5" + "P-poll__networl_7_1_RI_6" + "P-poll__networl_7_1_RI_7" + "P-poll__networl_7_1_RI_8" + "P-poll__networl_7_1_AI_0" + "P-poll__networl_7_1_AI_1" + "P-poll__networl_7_1_AI_2" + "P-poll__networl_7_1_AI_3" + "P-poll__networl_7_1_AI_4" + "P-poll__networl_7_1_AI_5" + "P-poll__networl_7_1_AI_6" + "P-poll__networl_7_1_AI_7" + "P-poll__networl_7_1_AI_8" + "P-poll__networl_7_1_AnnP_0" + "P-poll__networl_7_1_AnnP_1" + "P-poll__networl_7_1_AnnP_2" + "P-poll__networl_7_1_AnnP_3" + "P-poll__networl_7_1_AnnP_4" + "P-poll__networl_7_1_AnnP_5" + "P-poll__networl_7_1_AnnP_6" + "P-poll__networl_7_1_AnnP_7" + "P-poll__networl_7_1_AnnP_8" + "P-poll__networl_7_1_RP_0" + "P-poll__networl_7_1_RP_1" + "P-poll__networl_7_1_RP_2" + "P-poll__networl_7_1_RP_3" + "P-poll__networl_7_1_RP_4" + "P-poll__networl_7_1_RP_5" + "P-poll__networl_7_1_RP_6" + "P-poll__networl_7_1_RP_7" + "P-poll__networl_7_1_RP_8" + "P-poll__networl_7_2_AskP_0" + "P-poll__networl_7_2_AskP_1" + "P-poll__networl_7_2_AskP_2" + "P-poll__networl_7_2_AskP_3" + "P-poll__networl_7_2_AskP_4" + "P-poll__networl_7_2_AskP_5" + "P-poll__networl_7_2_AskP_6" + "P-poll__networl_7_2_AskP_7" + "P-poll__networl_7_2_AskP_8" + "P-poll__networl_7_2_AnsP_0" + "P-poll__networl_7_2_AnsP_1" + "P-poll__networl_7_2_AnsP_2" + "P-poll__networl_7_2_AnsP_3" + "P-poll__networl_7_2_AnsP_4" + "P-poll__networl_7_2_AnsP_5" + "P-poll__networl_7_2_AnsP_6" + "P-poll__networl_7_2_AnsP_7" + "P-poll__networl_7_2_AnsP_8" + "P-poll__networl_7_2_RI_0" + "P-poll__networl_7_2_RI_1" + "P-poll__networl_7_2_RI_2" + "P-poll__networl_7_2_RI_3" + "P-poll__networl_7_2_RI_4" + "P-poll__networl_7_2_RI_5" + "P-poll__networl_7_2_RI_6" + "P-poll__networl_7_2_RI_7" + "P-poll__networl_7_2_RI_8" + "P-poll__networl_7_2_AI_0" + "P-poll__networl_7_2_AI_1" + "P-poll__networl_7_2_AI_2" + "P-poll__networl_7_2_AI_3" + "P-poll__networl_7_2_AI_4" + "P-poll__networl_7_2_AI_5" + "P-poll__networl_7_2_AI_6" + "P-poll__networl_7_2_AI_7" + "P-poll__networl_7_2_AI_8" + "P-poll__networl_7_2_AnnP_0" + "P-poll__networl_7_2_AnnP_1" + "P-poll__networl_7_2_AnnP_2" + "P-poll__networl_7_2_AnnP_3" + "P-poll__networl_7_2_AnnP_4" + "P-poll__networl_7_2_AnnP_5" + "P-poll__networl_7_2_AnnP_6" + "P-poll__networl_7_2_AnnP_7" + "P-poll__networl_7_2_AnnP_8" + "P-poll__networl_7_2_RP_0" + "P-poll__networl_7_2_RP_1" + "P-poll__networl_7_2_RP_2" + "P-poll__networl_7_2_RP_3" + "P-poll__networl_7_2_RP_4" + "P-poll__networl_7_2_RP_5" + "P-poll__networl_7_2_RP_6" + "P-poll__networl_7_2_RP_7" + "P-poll__networl_7_2_RP_8" + "P-poll__networl_7_3_AskP_0" + "P-poll__networl_7_3_AskP_1" + "P-poll__networl_7_3_AskP_2" + "P-poll__networl_7_3_AskP_3" + "P-poll__networl_7_3_AskP_4" + "P-poll__networl_7_3_AskP_5" + "P-poll__networl_7_3_AskP_6" + "P-poll__networl_7_3_AskP_7" + "P-poll__networl_7_3_AskP_8" + "P-poll__networl_7_3_AnsP_0" + "P-poll__networl_7_3_AnsP_1" + "P-poll__networl_7_3_AnsP_2" + "P-poll__networl_7_3_AnsP_3" + "P-poll__networl_7_3_AnsP_4" + "P-poll__networl_7_3_AnsP_5" + "P-poll__networl_7_3_AnsP_6" + "P-poll__networl_7_3_AnsP_7" + "P-poll__networl_7_3_AnsP_8" + "P-poll__networl_7_3_RI_0" + "P-poll__networl_7_3_RI_1" + "P-poll__networl_7_3_RI_2" + "P-poll__networl_7_3_RI_3" + "P-poll__networl_7_3_RI_4" + "P-poll__networl_7_3_RI_5" + "P-poll__networl_7_3_RI_6" + "P-poll__networl_7_3_RI_7" + "P-poll__networl_7_3_RI_8" + "P-poll__networl_7_3_AI_0" + "P-poll__networl_7_3_AI_1" + "P-poll__networl_7_3_AI_2" + "P-poll__networl_7_3_AI_3" + "P-poll__networl_7_3_AI_4" + "P-poll__networl_7_3_AI_5" + "P-poll__networl_7_3_AI_6" + "P-poll__networl_7_3_AI_7" + "P-poll__networl_7_3_AI_8" + "P-poll__networl_7_3_AnnP_0" + "P-poll__networl_7_3_AnnP_1" + "P-poll__networl_7_3_AnnP_2" + "P-poll__networl_7_3_AnnP_3" + "P-poll__networl_7_3_AnnP_4" + "P-poll__networl_7_3_AnnP_5" + "P-poll__networl_7_3_AnnP_6" + "P-poll__networl_7_3_AnnP_7" + "P-poll__networl_7_3_AnnP_8" + "P-poll__networl_7_3_RP_0" + "P-poll__networl_7_3_RP_1" + "P-poll__networl_7_3_RP_2" + "P-poll__networl_7_3_RP_3" + "P-poll__networl_7_3_RP_4" + "P-poll__networl_7_3_RP_5" + "P-poll__networl_7_3_RP_6" + "P-poll__networl_7_3_RP_7" + "P-poll__networl_7_3_RP_8" + "P-poll__networl_7_4_AskP_0" + "P-poll__networl_7_4_AskP_1" + "P-poll__networl_7_4_AskP_2" + "P-poll__networl_7_4_AskP_3" + "P-poll__networl_7_4_AskP_4" + "P-poll__networl_7_4_AskP_5" + "P-poll__networl_7_4_AskP_6" + "P-poll__networl_7_4_AskP_7" + "P-poll__networl_7_4_AskP_8" + "P-poll__networl_7_4_AnsP_0" + "P-poll__networl_7_4_AnsP_1" + "P-poll__networl_7_4_AnsP_2" + "P-poll__networl_7_4_AnsP_3" + "P-poll__networl_7_4_AnsP_4" + "P-poll__networl_7_4_AnsP_5" + "P-poll__networl_7_4_AnsP_6" + "P-poll__networl_7_4_AnsP_7" + "P-poll__networl_7_4_AnsP_8" + "P-poll__networl_7_4_RI_0" + "P-poll__networl_7_4_RI_1" + "P-poll__networl_7_4_RI_2" + "P-poll__networl_7_4_RI_3" + "P-poll__networl_7_4_RI_4" + "P-poll__networl_7_4_RI_5" + "P-poll__networl_7_4_RI_6" + "P-poll__networl_7_4_RI_7" + "P-poll__networl_7_4_RI_8" + "P-poll__networl_7_4_AI_0" + "P-poll__networl_7_4_AI_1" + "P-poll__networl_7_4_AI_2" + "P-poll__networl_7_4_AI_3" + "P-poll__networl_7_4_AI_4" + "P-poll__networl_7_4_AI_5" + "P-poll__networl_7_4_AI_6" + "P-poll__networl_7_4_AI_7" + "P-poll__networl_7_4_AI_8" + "P-poll__networl_7_4_AnnP_0" + "P-poll__networl_7_4_AnnP_1" + "P-poll__networl_7_4_AnnP_2" + "P-poll__networl_7_4_AnnP_3" + "P-poll__networl_7_4_AnnP_4" + "P-poll__networl_7_4_AnnP_5" + "P-poll__networl_7_4_AnnP_6" + "P-poll__networl_7_4_AnnP_7" + "P-poll__networl_7_4_AnnP_8" + "P-poll__networl_7_4_RP_0" + "P-poll__networl_7_4_RP_1" + "P-poll__networl_7_4_RP_2" + "P-poll__networl_7_4_RP_3" + "P-poll__networl_7_4_RP_4" + "P-poll__networl_7_4_RP_5" + "P-poll__networl_7_4_RP_6" + "P-poll__networl_7_4_RP_7" + "P-poll__networl_7_4_RP_8" + "P-poll__networl_7_5_AskP_0" + "P-poll__networl_7_5_AskP_1" + "P-poll__networl_7_5_AskP_2" + "P-poll__networl_7_5_AskP_3" + "P-poll__networl_7_5_AskP_4" + "P-poll__networl_7_5_AskP_5" + "P-poll__networl_7_5_AskP_6" + "P-poll__networl_7_5_AskP_7" + "P-poll__networl_7_5_AskP_8" + "P-poll__networl_7_5_AnsP_0" + "P-poll__networl_7_5_AnsP_1" + "P-poll__networl_7_5_AnsP_2" + "P-poll__networl_7_5_AnsP_3" + "P-poll__networl_7_5_AnsP_4" + "P-poll__networl_7_5_AnsP_5" + "P-poll__networl_7_5_AnsP_6" + "P-poll__networl_7_5_AnsP_7" + "P-poll__networl_7_5_AnsP_8" + "P-poll__networl_7_5_RI_0" + "P-poll__networl_7_5_RI_1" + "P-poll__networl_7_5_RI_2" + "P-poll__networl_7_5_RI_3" + "P-poll__networl_7_5_RI_4" + "P-poll__networl_7_5_RI_5" + "P-poll__networl_7_5_RI_6" + "P-poll__networl_7_5_RI_7" + "P-poll__networl_7_5_RI_8" + "P-poll__networl_7_5_AI_0" + "P-poll__networl_7_5_AI_1" + "P-poll__networl_7_5_AI_2" + "P-poll__networl_7_5_AI_3" + "P-poll__networl_7_5_AI_4" + "P-poll__networl_7_5_AI_5" + "P-poll__networl_7_5_AI_6" + "P-poll__networl_7_5_AI_7" + "P-poll__networl_7_5_AI_8" + "P-poll__networl_7_5_AnnP_0" + "P-poll__networl_7_5_AnnP_1" + "P-poll__networl_7_5_AnnP_2" + "P-poll__networl_7_5_AnnP_3" + "P-poll__networl_7_5_AnnP_4" + "P-poll__networl_7_5_AnnP_5" + "P-poll__networl_7_5_AnnP_6" + "P-poll__networl_7_5_AnnP_7" + "P-poll__networl_7_5_AnnP_8" + "P-poll__networl_7_5_RP_0" + "P-poll__networl_7_5_RP_1" + "P-poll__networl_7_5_RP_2" + "P-poll__networl_7_5_RP_3" + "P-poll__networl_7_5_RP_4" + "P-poll__networl_7_5_RP_5" + "P-poll__networl_7_5_RP_6" + "P-poll__networl_7_5_RP_7" + "P-poll__networl_7_5_RP_8" + "P-poll__networl_7_6_AskP_0" + "P-poll__networl_7_6_AskP_1" + "P-poll__networl_7_6_AskP_2" + "P-poll__networl_7_6_AskP_3" + "P-poll__networl_7_6_AskP_4" + "P-poll__networl_7_6_AskP_5" + "P-poll__networl_7_6_AskP_6" + "P-poll__networl_7_6_AskP_7" + "P-poll__networl_7_6_AskP_8" + "P-poll__networl_7_6_AnsP_0" + "P-poll__networl_7_6_AnsP_1" + "P-poll__networl_7_6_AnsP_2" + "P-poll__networl_7_6_AnsP_3" + "P-poll__networl_7_6_AnsP_4" + "P-poll__networl_7_6_AnsP_5" + "P-poll__networl_7_6_AnsP_6" + "P-poll__networl_7_6_AnsP_7" + "P-poll__networl_7_6_AnsP_8" + "P-poll__networl_7_6_RI_0" + "P-poll__networl_7_6_RI_1" + "P-poll__networl_7_6_RI_2" + "P-poll__networl_7_6_RI_3" + "P-poll__networl_7_6_RI_4" + "P-poll__networl_7_6_RI_5" + "P-poll__networl_7_6_RI_6" + "P-poll__networl_7_6_RI_7" + "P-poll__networl_7_6_RI_8" + "P-poll__networl_7_6_AI_0" + "P-poll__networl_7_6_AI_1" + "P-poll__networl_7_6_AI_2" + "P-poll__networl_7_6_AI_3" + "P-poll__networl_7_6_AI_4" + "P-poll__networl_7_6_AI_5" + "P-poll__networl_7_6_AI_6" + "P-poll__networl_7_6_AI_7" + "P-poll__networl_7_6_AI_8" + "P-poll__networl_7_6_AnnP_0" + "P-poll__networl_7_6_AnnP_1" + "P-poll__networl_7_6_AnnP_2" + "P-poll__networl_7_6_AnnP_3" + "P-poll__networl_7_6_AnnP_4" + "P-poll__networl_7_6_AnnP_5" + "P-poll__networl_7_6_AnnP_6" + "P-poll__networl_7_6_AnnP_7" + "P-poll__networl_7_6_AnnP_8" + "P-poll__networl_7_6_RP_0" + "P-poll__networl_7_6_RP_1" + "P-poll__networl_7_6_RP_2" + "P-poll__networl_7_6_RP_3" + "P-poll__networl_7_6_RP_4" + "P-poll__networl_7_6_RP_5" + "P-poll__networl_7_6_RP_6" + "P-poll__networl_7_6_RP_7" + "P-poll__networl_7_6_RP_8" + "P-poll__networl_7_7_AskP_0" + "P-poll__networl_7_7_AskP_1" + "P-poll__networl_7_7_AskP_2" + "P-poll__networl_7_7_AskP_3" + "P-poll__networl_7_7_AskP_4" + "P-poll__networl_7_7_AskP_5" + "P-poll__networl_7_7_AskP_6" + "P-poll__networl_7_7_AskP_7" + "P-poll__networl_7_7_AskP_8" + "P-poll__networl_7_7_AnsP_0" + "P-poll__networl_7_7_AnsP_1" + "P-poll__networl_7_7_AnsP_2" + "P-poll__networl_7_7_AnsP_3" + "P-poll__networl_7_7_AnsP_4" + "P-poll__networl_7_7_AnsP_5" + "P-poll__networl_7_7_AnsP_6" + "P-poll__networl_7_7_AnsP_7" + "P-poll__networl_7_7_AnsP_8" + "P-poll__networl_7_7_RI_0" + "P-poll__networl_7_7_RI_1" + "P-poll__networl_7_7_RI_2" + "P-poll__networl_7_7_RI_3" + "P-poll__networl_7_7_RI_4" + "P-poll__networl_7_7_RI_5" + "P-poll__networl_7_7_RI_6" + "P-poll__networl_7_7_RI_7" + "P-poll__networl_7_7_RI_8" + "P-poll__networl_7_7_AI_0" + "P-poll__networl_7_7_AI_1" + "P-poll__networl_7_7_AI_2" + "P-poll__networl_7_7_AI_3" + "P-poll__networl_7_7_AI_4" + "P-poll__networl_7_7_AI_5" + "P-poll__networl_7_7_AI_6" + "P-poll__networl_7_7_AI_7" + "P-poll__networl_7_7_AI_8" + "P-poll__networl_7_7_AnnP_0" + "P-poll__networl_7_7_AnnP_1" + "P-poll__networl_7_7_AnnP_2" + "P-poll__networl_7_7_AnnP_3" + "P-poll__networl_7_7_AnnP_4" + "P-poll__networl_7_7_AnnP_5" + "P-poll__networl_7_7_AnnP_6" + "P-poll__networl_7_7_AnnP_7" + "P-poll__networl_7_7_AnnP_8" + "P-poll__networl_7_7_RP_0" + "P-poll__networl_7_7_RP_1" + "P-poll__networl_7_7_RP_2" + "P-poll__networl_7_7_RP_3" + "P-poll__networl_7_7_RP_4" + "P-poll__networl_7_7_RP_5" + "P-poll__networl_7_7_RP_6" + "P-poll__networl_7_7_RP_7" + "P-poll__networl_7_7_RP_8" + "P-poll__networl_7_8_AskP_0" + "P-poll__networl_7_8_AskP_1" + "P-poll__networl_7_8_AskP_2" + "P-poll__networl_7_8_AskP_3" + "P-poll__networl_7_8_AskP_4" + "P-poll__networl_7_8_AskP_5" + "P-poll__networl_7_8_AskP_6" + "P-poll__networl_7_8_AskP_7" + "P-poll__networl_7_8_AskP_8" + "P-poll__networl_7_8_AnsP_0" + "P-poll__networl_7_8_AnsP_1" + "P-poll__networl_7_8_AnsP_2" + "P-poll__networl_7_8_AnsP_3" + "P-poll__networl_7_8_AnsP_4" + "P-poll__networl_7_8_AnsP_5" + "P-poll__networl_7_8_AnsP_6" + "P-poll__networl_7_8_AnsP_7" + "P-poll__networl_7_8_AnsP_8" + "P-poll__networl_7_8_RI_0" + "P-poll__networl_7_8_RI_1" + "P-poll__networl_7_8_RI_2" + "P-poll__networl_7_8_RI_3" + "P-poll__networl_7_8_RI_4" + "P-poll__networl_7_8_RI_5" + "P-poll__networl_7_8_RI_6" + "P-poll__networl_7_8_RI_7" + "P-poll__networl_7_8_RI_8" + "P-poll__networl_7_8_AI_0" + "P-poll__networl_7_8_AI_1" + "P-poll__networl_7_8_AI_2" + "P-poll__networl_7_8_AI_3" + "P-poll__networl_7_8_AI_4" + "P-poll__networl_7_8_AI_5" + "P-poll__networl_7_8_AI_6" + "P-poll__networl_7_8_AI_7" + "P-poll__networl_7_8_AI_8" + "P-poll__networl_7_8_AnnP_0" + "P-poll__networl_7_8_AnnP_1" + "P-poll__networl_7_8_AnnP_2" + "P-poll__networl_7_8_AnnP_3" + "P-poll__networl_7_8_AnnP_4" + "P-poll__networl_7_8_AnnP_5" + "P-poll__networl_7_8_AnnP_6" + "P-poll__networl_7_8_AnnP_7" + "P-poll__networl_7_8_AnnP_8" + "P-poll__networl_7_8_RP_0" + "P-poll__networl_7_8_RP_1" + "P-poll__networl_7_8_RP_2" + "P-poll__networl_7_8_RP_3" + "P-poll__networl_7_8_RP_4" + "P-poll__networl_7_8_RP_5" + "P-poll__networl_7_8_RP_6" + "P-poll__networl_7_8_RP_7" + "P-poll__networl_7_8_RP_8" + "P-poll__networl_8_0_AskP_0" + "P-poll__networl_8_0_AskP_1" + "P-poll__networl_8_0_AskP_2" + "P-poll__networl_8_0_AskP_3" + "P-poll__networl_8_0_AskP_4" + "P-poll__networl_8_0_AskP_5" + "P-poll__networl_8_0_AskP_6" + "P-poll__networl_8_0_AskP_7" + "P-poll__networl_8_0_AskP_8" + "P-poll__networl_8_0_AnsP_0" + "P-poll__networl_8_0_AnsP_1" + "P-poll__networl_8_0_AnsP_2" + "P-poll__networl_8_0_AnsP_3" + "P-poll__networl_8_0_AnsP_4" + "P-poll__networl_8_0_AnsP_5" + "P-poll__networl_8_0_AnsP_6" + "P-poll__networl_8_0_AnsP_7" + "P-poll__networl_8_0_AnsP_8" + "P-poll__networl_8_0_RI_0" + "P-poll__networl_8_0_RI_1" + "P-poll__networl_8_0_RI_2" + "P-poll__networl_8_0_RI_3" + "P-poll__networl_8_0_RI_4" + "P-poll__networl_8_0_RI_5" + "P-poll__networl_8_0_RI_6" + "P-poll__networl_8_0_RI_7" + "P-poll__networl_8_0_RI_8" + "P-poll__networl_8_0_AI_0" + "P-poll__networl_8_0_AI_1" + "P-poll__networl_8_0_AI_2" + "P-poll__networl_8_0_AI_3" + "P-poll__networl_8_0_AI_4" + "P-poll__networl_8_0_AI_5" + "P-poll__networl_8_0_AI_6" + "P-poll__networl_8_0_AI_7" + "P-poll__networl_8_0_AI_8" + "P-poll__networl_8_0_AnnP_0" + "P-poll__networl_8_0_AnnP_1" + "P-poll__networl_8_0_AnnP_2" + "P-poll__networl_8_0_AnnP_3" + "P-poll__networl_8_0_AnnP_4" + "P-poll__networl_8_0_AnnP_5" + "P-poll__networl_8_0_AnnP_6" + "P-poll__networl_8_0_AnnP_7" + "P-poll__networl_8_0_AnnP_8" + "P-poll__networl_8_0_RP_0" + "P-poll__networl_8_0_RP_1" + "P-poll__networl_8_0_RP_2" + "P-poll__networl_8_0_RP_3" + "P-poll__networl_8_0_RP_4" + "P-poll__networl_8_0_RP_5" + "P-poll__networl_8_0_RP_6" + "P-poll__networl_8_0_RP_7" + "P-poll__networl_8_0_RP_8" + "P-poll__networl_8_1_AskP_0" + "P-poll__networl_8_1_AskP_1" + "P-poll__networl_8_1_AskP_2" + "P-poll__networl_8_1_AskP_3" + "P-poll__networl_8_1_AskP_4" + "P-poll__networl_8_1_AskP_5" + "P-poll__networl_8_1_AskP_6" + "P-poll__networl_8_1_AskP_7" + "P-poll__networl_8_1_AskP_8" + "P-poll__networl_8_1_AnsP_0" + "P-poll__networl_8_1_AnsP_1" + "P-poll__networl_8_1_AnsP_2" + "P-poll__networl_8_1_AnsP_3" + "P-poll__networl_8_1_AnsP_4" + "P-poll__networl_8_1_AnsP_5" + "P-poll__networl_8_1_AnsP_6" + "P-poll__networl_8_1_AnsP_7" + "P-poll__networl_8_1_AnsP_8" + "P-poll__networl_8_1_RI_0" + "P-poll__networl_8_1_RI_1" + "P-poll__networl_8_1_RI_2" + "P-poll__networl_8_1_RI_3" + "P-poll__networl_8_1_RI_4" + "P-poll__networl_8_1_RI_5" + "P-poll__networl_8_1_RI_6" + "P-poll__networl_8_1_RI_7" + "P-poll__networl_8_1_RI_8" + "P-poll__networl_8_1_AI_0" + "P-poll__networl_8_1_AI_1" + "P-poll__networl_8_1_AI_2" + "P-poll__networl_8_1_AI_3" + "P-poll__networl_8_1_AI_4" + "P-poll__networl_8_1_AI_5" + "P-poll__networl_8_1_AI_6" + "P-poll__networl_8_1_AI_7" + "P-poll__networl_8_1_AI_8" + "P-poll__networl_8_1_AnnP_0" + "P-poll__networl_8_1_AnnP_1" + "P-poll__networl_8_1_AnnP_2" + "P-poll__networl_8_1_AnnP_3" + "P-poll__networl_8_1_AnnP_4" + "P-poll__networl_8_1_AnnP_5" + "P-poll__networl_8_1_AnnP_6" + "P-poll__networl_8_1_AnnP_7" + "P-poll__networl_8_1_AnnP_8" + "P-poll__networl_8_1_RP_0" + "P-poll__networl_8_1_RP_1" + "P-poll__networl_8_1_RP_2" + "P-poll__networl_8_1_RP_3" + "P-poll__networl_8_1_RP_4" + "P-poll__networl_8_1_RP_5" + "P-poll__networl_8_1_RP_6" + "P-poll__networl_8_1_RP_7" + "P-poll__networl_8_1_RP_8" + "P-poll__networl_8_2_AskP_0" + "P-poll__networl_8_2_AskP_1" + "P-poll__networl_8_2_AskP_2" + "P-poll__networl_8_2_AskP_3" + "P-poll__networl_8_2_AskP_4" + "P-poll__networl_8_2_AskP_5" + "P-poll__networl_8_2_AskP_6" + "P-poll__networl_8_2_AskP_7" + "P-poll__networl_8_2_AskP_8" + "P-poll__networl_8_2_AnsP_0" + "P-poll__networl_8_2_AnsP_1" + "P-poll__networl_8_2_AnsP_2" + "P-poll__networl_8_2_AnsP_3" + "P-poll__networl_8_2_AnsP_4" + "P-poll__networl_8_2_AnsP_5" + "P-poll__networl_8_2_AnsP_6" + "P-poll__networl_8_2_AnsP_7" + "P-poll__networl_8_2_AnsP_8" + "P-poll__networl_8_2_RI_0" + "P-poll__networl_8_2_RI_1" + "P-poll__networl_8_2_RI_2" + "P-poll__networl_8_2_RI_3" + "P-poll__networl_8_2_RI_4" + "P-poll__networl_8_2_RI_5" + "P-poll__networl_8_2_RI_6" + "P-poll__networl_8_2_RI_7" + "P-poll__networl_8_2_RI_8" + "P-poll__networl_8_2_AI_0" + "P-poll__networl_8_2_AI_1" + "P-poll__networl_8_2_AI_2" + "P-poll__networl_8_2_AI_3" + "P-poll__networl_8_2_AI_4" + "P-poll__networl_8_2_AI_5" + "P-poll__networl_8_2_AI_6" + "P-poll__networl_8_2_AI_7" + "P-poll__networl_8_2_AI_8" + "P-poll__networl_8_2_AnnP_0" + "P-poll__networl_8_2_AnnP_1" + "P-poll__networl_8_2_AnnP_2" + "P-poll__networl_8_2_AnnP_3" + "P-poll__networl_8_2_AnnP_4" + "P-poll__networl_8_2_AnnP_5" + "P-poll__networl_8_2_AnnP_6" + "P-poll__networl_8_2_AnnP_7" + "P-poll__networl_8_2_AnnP_8" + "P-poll__networl_8_2_RP_0" + "P-poll__networl_8_2_RP_1" + "P-poll__networl_8_2_RP_2" + "P-poll__networl_8_2_RP_3" + "P-poll__networl_8_2_RP_4" + "P-poll__networl_8_2_RP_5" + "P-poll__networl_8_2_RP_6" + "P-poll__networl_8_2_RP_7" + "P-poll__networl_8_2_RP_8" + "P-poll__networl_8_3_AskP_0" + "P-poll__networl_8_3_AskP_1" + "P-poll__networl_8_3_AskP_2" + "P-poll__networl_8_3_AskP_3" + "P-poll__networl_8_3_AskP_4" + "P-poll__networl_8_3_AskP_5" + "P-poll__networl_8_3_AskP_6" + "P-poll__networl_8_3_AskP_7" + "P-poll__networl_8_3_AskP_8" + "P-poll__networl_8_3_AnsP_0" + "P-poll__networl_8_3_AnsP_1" + "P-poll__networl_8_3_AnsP_2" + "P-poll__networl_8_3_AnsP_3" + "P-poll__networl_8_3_AnsP_4" + "P-poll__networl_8_3_AnsP_5" + "P-poll__networl_8_3_AnsP_6" + "P-poll__networl_8_3_AnsP_7" + "P-poll__networl_8_3_AnsP_8" + "P-poll__networl_8_3_RI_0" + "P-poll__networl_8_3_RI_1" + "P-poll__networl_8_3_RI_2" + "P-poll__networl_8_3_RI_3" + "P-poll__networl_8_3_RI_4" + "P-poll__networl_8_3_RI_5" + "P-poll__networl_8_3_RI_6" + "P-poll__networl_8_3_RI_7" + "P-poll__networl_8_3_RI_8" + "P-poll__networl_8_3_AI_0" + "P-poll__networl_8_3_AI_1" + "P-poll__networl_8_3_AI_2" + "P-poll__networl_8_3_AI_3" + "P-poll__networl_8_3_AI_4" + "P-poll__networl_8_3_AI_5" + "P-poll__networl_8_3_AI_6" + "P-poll__networl_8_3_AI_7" + "P-poll__networl_8_3_AI_8" + "P-poll__networl_8_3_AnnP_0" + "P-poll__networl_8_3_AnnP_1" + "P-poll__networl_8_3_AnnP_2" + "P-poll__networl_8_3_AnnP_3" + "P-poll__networl_8_3_AnnP_4" + "P-poll__networl_8_3_AnnP_5" + "P-poll__networl_8_3_AnnP_6" + "P-poll__networl_8_3_AnnP_7" + "P-poll__networl_8_3_AnnP_8" + "P-poll__networl_8_3_RP_0" + "P-poll__networl_8_3_RP_1" + "P-poll__networl_8_3_RP_2" + "P-poll__networl_8_3_RP_3" + "P-poll__networl_8_3_RP_4" + "P-poll__networl_8_3_RP_5" + "P-poll__networl_8_3_RP_6" + "P-poll__networl_8_3_RP_7" + "P-poll__networl_8_3_RP_8" + "P-poll__networl_8_4_AskP_0" + "P-poll__networl_8_4_AskP_1" + "P-poll__networl_8_4_AskP_2" + "P-poll__networl_8_4_AskP_3" + "P-poll__networl_8_4_AskP_4" + "P-poll__networl_8_4_AskP_5" + "P-poll__networl_8_4_AskP_6" + "P-poll__networl_8_4_AskP_7" + "P-poll__networl_8_4_AskP_8" + "P-poll__networl_8_4_AnsP_0" + "P-poll__networl_8_4_AnsP_1" + "P-poll__networl_8_4_AnsP_2" + "P-poll__networl_8_4_AnsP_3" + "P-poll__networl_8_4_AnsP_4" + "P-poll__networl_8_4_AnsP_5" + "P-poll__networl_8_4_AnsP_6" + "P-poll__networl_8_4_AnsP_7" + "P-poll__networl_8_4_AnsP_8" + "P-poll__networl_8_4_RI_0" + "P-poll__networl_8_4_RI_1" + "P-poll__networl_8_4_RI_2" + "P-poll__networl_8_4_RI_3" + "P-poll__networl_8_4_RI_4" + "P-poll__networl_8_4_RI_5" + "P-poll__networl_8_4_RI_6" + "P-poll__networl_8_4_RI_7" + "P-poll__networl_8_4_RI_8" + "P-poll__networl_8_4_AI_0" + "P-poll__networl_8_4_AI_1" + "P-poll__networl_8_4_AI_2" + "P-poll__networl_8_4_AI_3" + "P-poll__networl_8_4_AI_4" + "P-poll__networl_8_4_AI_5" + "P-poll__networl_8_4_AI_6" + "P-poll__networl_8_4_AI_7" + "P-poll__networl_8_4_AI_8" + "P-poll__networl_8_4_AnnP_0" + "P-poll__networl_8_4_AnnP_1" + "P-poll__networl_8_4_AnnP_2" + "P-poll__networl_8_4_AnnP_3" + "P-poll__networl_8_4_AnnP_4" + "P-poll__networl_8_4_AnnP_5" + "P-poll__networl_8_4_AnnP_6" + "P-poll__networl_8_4_AnnP_7" + "P-poll__networl_8_4_AnnP_8" + "P-poll__networl_8_4_RP_0" + "P-poll__networl_8_4_RP_1" + "P-poll__networl_8_4_RP_2" + "P-poll__networl_8_4_RP_3" + "P-poll__networl_8_4_RP_4" + "P-poll__networl_8_4_RP_5" + "P-poll__networl_8_4_RP_6" + "P-poll__networl_8_4_RP_7" + "P-poll__networl_8_4_RP_8" + "P-poll__networl_8_5_AskP_0" + "P-poll__networl_8_5_AskP_1" + "P-poll__networl_8_5_AskP_2" + "P-poll__networl_8_5_AskP_3" + "P-poll__networl_8_5_AskP_4" + "P-poll__networl_8_5_AskP_5" + "P-poll__networl_8_5_AskP_6" + "P-poll__networl_8_5_AskP_7" + "P-poll__networl_8_5_AskP_8" + "P-poll__networl_8_5_AnsP_0" + "P-poll__networl_8_5_AnsP_1" + "P-poll__networl_8_5_AnsP_2" + "P-poll__networl_8_5_AnsP_3" + "P-poll__networl_8_5_AnsP_4" + "P-poll__networl_8_5_AnsP_5" + "P-poll__networl_8_5_AnsP_6" + "P-poll__networl_8_5_AnsP_7" + "P-poll__networl_8_5_AnsP_8" + "P-poll__networl_8_5_RI_0" + "P-poll__networl_8_5_RI_1" + "P-poll__networl_8_5_RI_2" + "P-poll__networl_8_5_RI_3" + "P-poll__networl_8_5_RI_4" + "P-poll__networl_8_5_RI_5" + "P-poll__networl_8_5_RI_6" + "P-poll__networl_8_5_RI_7" + "P-poll__networl_8_5_RI_8" + "P-poll__networl_8_5_AI_0" + "P-poll__networl_8_5_AI_1" + "P-poll__networl_8_5_AI_2" + "P-poll__networl_8_5_AI_3" + "P-poll__networl_8_5_AI_4" + "P-poll__networl_8_5_AI_5" + "P-poll__networl_8_5_AI_6" + "P-poll__networl_8_5_AI_7" + "P-poll__networl_8_5_AI_8" + "P-poll__networl_8_5_AnnP_0" + "P-poll__networl_8_5_AnnP_1" + "P-poll__networl_8_5_AnnP_2" + "P-poll__networl_8_5_AnnP_3" + "P-poll__networl_8_5_AnnP_4" + "P-poll__networl_8_5_AnnP_5" + "P-poll__networl_8_5_AnnP_6" + "P-poll__networl_8_5_AnnP_7" + "P-poll__networl_8_5_AnnP_8" + "P-poll__networl_8_5_RP_0" + "P-poll__networl_8_5_RP_1" + "P-poll__networl_8_5_RP_2" + "P-poll__networl_8_5_RP_3" + "P-poll__networl_8_5_RP_4" + "P-poll__networl_8_5_RP_5" + "P-poll__networl_8_5_RP_6" + "P-poll__networl_8_5_RP_7" + "P-poll__networl_8_5_RP_8" + "P-poll__networl_8_6_AskP_0" + "P-poll__networl_8_6_AskP_1" + "P-poll__networl_8_6_AskP_2" + "P-poll__networl_8_6_AskP_3" + "P-poll__networl_8_6_AskP_4" + "P-poll__networl_8_6_AskP_5" + "P-poll__networl_8_6_AskP_6" + "P-poll__networl_8_6_AskP_7" + "P-poll__networl_8_6_AskP_8" + "P-poll__networl_8_6_AnsP_0" + "P-poll__networl_8_6_AnsP_1" + "P-poll__networl_8_6_AnsP_2" + "P-poll__networl_8_6_AnsP_3" + "P-poll__networl_8_6_AnsP_4" + "P-poll__networl_8_6_AnsP_5" + "P-poll__networl_8_6_AnsP_6" + "P-poll__networl_8_6_AnsP_7" + "P-poll__networl_8_6_AnsP_8" + "P-poll__networl_8_6_RI_0" + "P-poll__networl_8_6_RI_1" + "P-poll__networl_8_6_RI_2" + "P-poll__networl_8_6_RI_3" + "P-poll__networl_8_6_RI_4" + "P-poll__networl_8_6_RI_5" + "P-poll__networl_8_6_RI_6" + "P-poll__networl_8_6_RI_7" + "P-poll__networl_8_6_RI_8" + "P-poll__networl_8_6_AI_0" + "P-poll__networl_8_6_AI_1" + "P-poll__networl_8_6_AI_2" + "P-poll__networl_8_6_AI_3" + "P-poll__networl_8_6_AI_4" + "P-poll__networl_8_6_AI_5" + "P-poll__networl_8_6_AI_6" + "P-poll__networl_8_6_AI_7" + "P-poll__networl_8_6_AI_8" + "P-poll__networl_8_6_AnnP_0" + "P-poll__networl_8_6_AnnP_1" + "P-poll__networl_8_6_AnnP_2" + "P-poll__networl_8_6_AnnP_3" + "P-poll__networl_8_6_AnnP_4" + "P-poll__networl_8_6_AnnP_5" + "P-poll__networl_8_6_AnnP_6" + "P-poll__networl_8_6_AnnP_7" + "P-poll__networl_8_6_AnnP_8" + "P-poll__networl_8_6_RP_0" + "P-poll__networl_8_6_RP_1" + "P-poll__networl_8_6_RP_2" + "P-poll__networl_8_6_RP_3" + "P-poll__networl_8_6_RP_4" + "P-poll__networl_8_6_RP_5" + "P-poll__networl_8_6_RP_6" + "P-poll__networl_8_6_RP_7" + "P-poll__networl_8_6_RP_8" + "P-poll__networl_8_7_AskP_0" + "P-poll__networl_8_7_AskP_1" + "P-poll__networl_8_7_AskP_2" + "P-poll__networl_8_7_AskP_3" + "P-poll__networl_8_7_AskP_4" + "P-poll__networl_8_7_AskP_5" + "P-poll__networl_8_7_AskP_6" + "P-poll__networl_8_7_AskP_7" + "P-poll__networl_8_7_AskP_8" + "P-poll__networl_8_7_AnsP_0" + "P-poll__networl_8_7_AnsP_1" + "P-poll__networl_8_7_AnsP_2" + "P-poll__networl_8_7_AnsP_3" + "P-poll__networl_8_7_AnsP_4" + "P-poll__networl_8_7_AnsP_5" + "P-poll__networl_8_7_AnsP_6" + "P-poll__networl_8_7_AnsP_7" + "P-poll__networl_8_7_AnsP_8" + "P-poll__networl_8_7_RI_0" + "P-poll__networl_8_7_RI_1" + "P-poll__networl_8_7_RI_2" + "P-poll__networl_8_7_RI_3" + "P-poll__networl_8_7_RI_4" + "P-poll__networl_8_7_RI_5" + "P-poll__networl_8_7_RI_6" + "P-poll__networl_8_7_RI_7" + "P-poll__networl_8_7_RI_8" + "P-poll__networl_8_7_AI_0" + "P-poll__networl_8_7_AI_1" + "P-poll__networl_8_7_AI_2" + "P-poll__networl_8_7_AI_3" + "P-poll__networl_8_7_AI_4" + "P-poll__networl_8_7_AI_5" + "P-poll__networl_8_7_AI_6" + "P-poll__networl_8_7_AI_7" + "P-poll__networl_8_7_AI_8" + "P-poll__networl_8_7_AnnP_0" + "P-poll__networl_8_7_AnnP_1" + "P-poll__networl_8_7_AnnP_2" + "P-poll__networl_8_7_AnnP_3" + "P-poll__networl_8_7_AnnP_4" + "P-poll__networl_8_7_AnnP_5" + "P-poll__networl_8_7_AnnP_6" + "P-poll__networl_8_7_AnnP_7" + "P-poll__networl_8_7_AnnP_8" + "P-poll__networl_8_7_RP_0" + "P-poll__networl_8_7_RP_1" + "P-poll__networl_8_7_RP_2" + "P-poll__networl_8_7_RP_3" + "P-poll__networl_8_7_RP_4" + "P-poll__networl_8_7_RP_5" + "P-poll__networl_8_7_RP_6" + "P-poll__networl_8_7_RP_7" + "P-poll__networl_8_7_RP_8" + "P-poll__networl_8_8_AskP_0" + "P-poll__networl_8_8_AskP_1" + "P-poll__networl_8_8_AskP_2" + "P-poll__networl_8_8_AskP_3" + "P-poll__networl_8_8_AskP_4" + "P-poll__networl_8_8_AskP_5" + "P-poll__networl_8_8_AskP_6" + "P-poll__networl_8_8_AskP_7" + "P-poll__networl_8_8_AskP_8" + "P-poll__networl_8_8_AnsP_0" + "P-poll__networl_8_8_AnsP_1" + "P-poll__networl_8_8_AnsP_2" + "P-poll__networl_8_8_AnsP_3" + "P-poll__networl_8_8_AnsP_4" + "P-poll__networl_8_8_AnsP_5" + "P-poll__networl_8_8_AnsP_6" + "P-poll__networl_8_8_AnsP_7" + "P-poll__networl_8_8_AnsP_8" + "P-poll__networl_8_8_RI_0" + "P-poll__networl_8_8_RI_1" + "P-poll__networl_8_8_RI_2" + "P-poll__networl_8_8_RI_3" + "P-poll__networl_8_8_RI_4" + "P-poll__networl_8_8_RI_5" + "P-poll__networl_8_8_RI_6" + "P-poll__networl_8_8_RI_7" + "P-poll__networl_8_8_RI_8" + "P-poll__networl_8_8_AI_0" + "P-poll__networl_8_8_AI_1" + "P-poll__networl_8_8_AI_2" + "P-poll__networl_8_8_AI_3" + "P-poll__networl_8_8_AI_4" + "P-poll__networl_8_8_AI_5" + "P-poll__networl_8_8_AI_6" + "P-poll__networl_8_8_AI_7" + "P-poll__networl_8_8_AI_8" + "P-poll__networl_8_8_AnnP_0" + "P-poll__networl_8_8_AnnP_1" + "P-poll__networl_8_8_AnnP_2" + "P-poll__networl_8_8_AnnP_3" + "P-poll__networl_8_8_AnnP_4" + "P-poll__networl_8_8_AnnP_5" + "P-poll__networl_8_8_AnnP_6" + "P-poll__networl_8_8_AnnP_7" + "P-poll__networl_8_8_AnnP_8" + "P-poll__networl_8_8_RP_0" + "P-poll__networl_8_8_RP_1" + "P-poll__networl_8_8_RP_2" + "P-poll__networl_8_8_RP_3" + "P-poll__networl_8_8_RP_4" + "P-poll__networl_8_8_RP_5" + "P-poll__networl_8_8_RP_6" + "P-poll__networl_8_8_RP_7" + "P-poll__networl_8_8_RP_8"))) )
NeoElection-COL-8-ReachabilityCardinality-1: EF ( not(((("P-polling_0" + "P-polling_1" + "P-polling_2" + "P-polling_3" + "P-polling_4" + "P-polling_5" + "P-polling_6" + "P-polling_7" + "P-polling_8") <= ("P-startNeg__broadcasting_0_1" + "P-startNeg__broadcasting_0_2" + "P-startNeg__broadcasting_0_3" + "P-startNeg__broadcasting_0_4" + "P-startNeg__broadcasting_0_5" + "P-startNeg__broadcasting_0_6" + "P-startNeg__broadcasting_0_7" + "P-startNeg__broadcasting_0_8" + "P-startNeg__broadcasting_1_1" + "P-startNeg__broadcasting_1_2" + "P-startNeg__broadcasting_1_3" + "P-startNeg__broadcasting_1_4" + "P-startNeg__broadcasting_1_5" + "P-startNeg__broadcasting_1_6" + "P-startNeg__broadcasting_1_7" + "P-startNeg__broadcasting_1_8" + "P-startNeg__broadcasting_2_1" + "P-startNeg__broadcasting_2_2" + "P-startNeg__broadcasting_2_3" + "P-startNeg__broadcasting_2_4" + "P-startNeg__broadcasting_2_5" + "P-startNeg__broadcasting_2_6" + "P-startNeg__broadcasting_2_7" + "P-startNeg__broadcasting_2_8" + "P-startNeg__broadcasting_3_1" + "P-startNeg__broadcasting_3_2" + "P-startNeg__broadcasting_3_3" + "P-startNeg__broadcasting_3_4" + "P-startNeg__broadcasting_3_5" + "P-startNeg__broadcasting_3_6" + "P-startNeg__broadcasting_3_7" + "P-startNeg__broadcasting_3_8" + "P-startNeg__broadcasting_4_1" + "P-startNeg__broadcasting_4_2" + "P-startNeg__broadcasting_4_3" + "P-startNeg__broadcasting_4_4" + "P-startNeg__broadcasting_4_5" + "P-startNeg__broadcasting_4_6" + "P-startNeg__broadcasting_4_7" + "P-startNeg__broadcasting_4_8" + "P-startNeg__broadcasting_5_1" + "P-startNeg__broadcasting_5_2" + "P-startNeg__broadcasting_5_3" + "P-startNeg__broadcasting_5_4" + "P-startNeg__broadcasting_5_5" + "P-startNeg__broadcasting_5_6" + "P-startNeg__broadcasting_5_7" + "P-startNeg__broadcasting_5_8" + "P-startNeg__broadcasting_6_1" + "P-startNeg__broadcasting_6_2" + "P-startNeg__broadcasting_6_3" + "P-startNeg__broadcasting_6_4" + "P-startNeg__broadcasting_6_5" + "P-startNeg__broadcasting_6_6" + "P-startNeg__broadcasting_6_7" + "P-startNeg__broadcasting_6_8" + "P-startNeg__broadcasting_7_1" + "P-startNeg__broadcasting_7_2" + "P-startNeg__broadcasting_7_3" + "P-startNeg__broadcasting_7_4" + "P-startNeg__broadcasting_7_5" + "P-startNeg__broadcasting_7_6" + "P-startNeg__broadcasting_7_7" + "P-startNeg__broadcasting_7_8" + "P-startNeg__broadcasting_8_1" + "P-startNeg__broadcasting_8_2" + "P-startNeg__broadcasting_8_3" + "P-startNeg__broadcasting_8_4" + "P-startNeg__broadcasting_8_5" + "P-startNeg__broadcasting_8_6" + "P-startNeg__broadcasting_8_7" + "P-startNeg__broadcasting_8_8")) and not((("P-masterState_0_F_0" + "P-masterState_0_F_1" + "P-masterState_0_F_2" + "P-masterState_0_F_3" + "P-masterState_0_F_4" + "P-masterState_0_F_5" + "P-masterState_0_F_6" + "P-masterState_0_F_7" + "P-masterState_0_F_8" + "P-masterState_0_T_0" + "P-masterState_0_T_1" + "P-masterState_0_T_2" + "P-masterState_0_T_3" + "P-masterState_0_T_4" + "P-masterState_0_T_5" + "P-masterState_0_T_6" + "P-masterState_0_T_7" + "P-masterState_0_T_8" + "P-masterState_1_F_0" + "P-masterState_1_F_1" + "P-masterState_1_F_2" + "P-masterState_1_F_3" + "P-masterState_1_F_4" + "P-masterState_1_F_5" + "P-masterState_1_F_6" + "P-masterState_1_F_7" + "P-masterState_1_F_8" + "P-masterState_1_T_0" + "P-masterState_1_T_1" + "P-masterState_1_T_2" + "P-masterState_1_T_3" + "P-masterState_1_T_4" + "P-masterState_1_T_5" + "P-masterState_1_T_6" + "P-masterState_1_T_7" + "P-masterState_1_T_8" + "P-masterState_2_F_0" + "P-masterState_2_F_1" + "P-masterState_2_F_2" + "P-masterState_2_F_3" + "P-masterState_2_F_4" + "P-masterState_2_F_5" + "P-masterState_2_F_6" + "P-masterState_2_F_7" + "P-masterState_2_F_8" + "P-masterState_2_T_0" + "P-masterState_2_T_1" + "P-masterState_2_T_2" + "P-masterState_2_T_3" + "P-masterState_2_T_4" + "P-masterState_2_T_5" + "P-masterState_2_T_6" + "P-masterState_2_T_7" + "P-masterState_2_T_8" + "P-masterState_3_F_0" + "P-masterState_3_F_1" + "P-masterState_3_F_2" + "P-masterState_3_F_3" + "P-masterState_3_F_4" + "P-masterState_3_F_5" + "P-masterState_3_F_6" + "P-masterState_3_F_7" + "P-masterState_3_F_8" + "P-masterState_3_T_0" + "P-masterState_3_T_1" + "P-masterState_3_T_2" + "P-masterState_3_T_3" + "P-masterState_3_T_4" + "P-masterState_3_T_5" + "P-masterState_3_T_6" + "P-masterState_3_T_7" + "P-masterState_3_T_8" + "P-masterState_4_F_0" + "P-masterState_4_F_1" + "P-masterState_4_F_2" + "P-masterState_4_F_3" + "P-masterState_4_F_4" + "P-masterState_4_F_5" + "P-masterState_4_F_6" + "P-masterState_4_F_7" + "P-masterState_4_F_8" + "P-masterState_4_T_0" + "P-masterState_4_T_1" + "P-masterState_4_T_2" + "P-masterState_4_T_3" + "P-masterState_4_T_4" + "P-masterState_4_T_5" + "P-masterState_4_T_6" + "P-masterState_4_T_7" + "P-masterState_4_T_8" + "P-masterState_5_F_0" + "P-masterState_5_F_1" + "P-masterState_5_F_2" + "P-masterState_5_F_3" + "P-masterState_5_F_4" + "P-masterState_5_F_5" + "P-masterState_5_F_6" + "P-masterState_5_F_7" + "P-masterState_5_F_8" + "P-masterState_5_T_0" + "P-masterState_5_T_1" + "P-masterState_5_T_2" + "P-masterState_5_T_3" + "P-masterState_5_T_4" + "P-masterState_5_T_5" + "P-masterState_5_T_6" + "P-masterState_5_T_7" + "P-masterState_5_T_8" + "P-masterState_6_F_0" + "P-masterState_6_F_1" + "P-masterState_6_F_2" + "P-masterState_6_F_3" + "P-masterState_6_F_4" + "P-masterState_6_F_5" + "P-masterState_6_F_6" + "P-masterState_6_F_7" + "P-masterState_6_F_8" + "P-masterState_6_T_0" + "P-masterState_6_T_1" + "P-masterState_6_T_2" + "P-masterState_6_T_3" + "P-masterState_6_T_4" + "P-masterState_6_T_5" + "P-masterState_6_T_6" + "P-masterState_6_T_7" + "P-masterState_6_T_8" + "P-masterState_7_F_0" + "P-masterState_7_F_1" + "P-masterState_7_F_2" + "P-masterState_7_F_3" + "P-masterState_7_F_4" + "P-masterState_7_F_5" + "P-masterState_7_F_6" + "P-masterState_7_F_7" + "P-masterState_7_F_8" + "P-masterState_7_T_0" + "P-masterState_7_T_1" + "P-masterState_7_T_2" + "P-masterState_7_T_3" + "P-masterState_7_T_4" + "P-masterState_7_T_5" + "P-masterState_7_T_6" + "P-masterState_7_T_7" + "P-masterState_7_T_8" + "P-masterState_8_F_0" + "P-masterState_8_F_1" + "P-masterState_8_F_2" + "P-masterState_8_F_3" + "P-masterState_8_F_4" + "P-masterState_8_F_5" + "P-masterState_8_F_6" + "P-masterState_8_F_7" + "P-masterState_8_F_8" + "P-masterState_8_T_0" + "P-masterState_8_T_1" + "P-masterState_8_T_2" + "P-masterState_8_T_3" + "P-masterState_8_T_4" + "P-masterState_8_T_5" + "P-masterState_8_T_6" + "P-masterState_8_T_7" + "P-masterState_8_T_8") <= ("P-sendAnnPs__broadcasting_0_1" + "P-sendAnnPs__broadcasting_0_2" + "P-sendAnnPs__broadcasting_0_3" + "P-sendAnnPs__broadcasting_0_4" + "P-sendAnnPs__broadcasting_0_5" + "P-sendAnnPs__broadcasting_0_6" + "P-sendAnnPs__broadcasting_0_7" + "P-sendAnnPs__broadcasting_0_8" + "P-sendAnnPs__broadcasting_1_1" + "P-sendAnnPs__broadcasting_1_2" + "P-sendAnnPs__broadcasting_1_3" + "P-sendAnnPs__broadcasting_1_4" + "P-sendAnnPs__broadcasting_1_5" + "P-sendAnnPs__broadcasting_1_6" + "P-sendAnnPs__broadcasting_1_7" + "P-sendAnnPs__broadcasting_1_8" + "P-sendAnnPs__broadcasting_2_1" + "P-sendAnnPs__broadcasting_2_2" + "P-sendAnnPs__broadcasting_2_3" + "P-sendAnnPs__broadcasting_2_4" + "P-sendAnnPs__broadcasting_2_5" + "P-sendAnnPs__broadcasting_2_6" + "P-sendAnnPs__broadcasting_2_7" + "P-sendAnnPs__broadcasting_2_8" + "P-sendAnnPs__broadcasting_3_1" + "P-sendAnnPs__broadcasting_3_2" + "P-sendAnnPs__broadcasting_3_3" + "P-sendAnnPs__broadcasting_3_4" + "P-sendAnnPs__broadcasting_3_5" + "P-sendAnnPs__broadcasting_3_6" + "P-sendAnnPs__broadcasting_3_7" + "P-sendAnnPs__broadcasting_3_8" + "P-sendAnnPs__broadcasting_4_1" + "P-sendAnnPs__broadcasting_4_2" + "P-sendAnnPs__broadcasting_4_3" + "P-sendAnnPs__broadcasting_4_4" + "P-sendAnnPs__broadcasting_4_5" + "P-sendAnnPs__broadcasting_4_6" + "P-sendAnnPs__broadcasting_4_7" + "P-sendAnnPs__broadcasting_4_8" + "P-sendAnnPs__broadcasting_5_1" + "P-sendAnnPs__broadcasting_5_2" + "P-sendAnnPs__broadcasting_5_3" + "P-sendAnnPs__broadcasting_5_4" + "P-sendAnnPs__broadcasting_5_5" + "P-sendAnnPs__broadcasting_5_6" + "P-sendAnnPs__broadcasting_5_7" + "P-sendAnnPs__broadcasting_5_8" + "P-sendAnnPs__broadcasting_6_1" + "P-sendAnnPs__broadcasting_6_2" + "P-sendAnnPs__broadcasting_6_3" + "P-sendAnnPs__broadcasting_6_4" + "P-sendAnnPs__broadcasting_6_5" + "P-sendAnnPs__broadcasting_6_6" + "P-sendAnnPs__broadcasting_6_7" + "P-sendAnnPs__broadcasting_6_8" + "P-sendAnnPs__broadcasting_7_1" + "P-sendAnnPs__broadcasting_7_2" + "P-sendAnnPs__broadcasting_7_3" + "P-sendAnnPs__broadcasting_7_4" + "P-sendAnnPs__broadcasting_7_5" + "P-sendAnnPs__broadcasting_7_6" + "P-sendAnnPs__broadcasting_7_7" + "P-sendAnnPs__broadcasting_7_8" + "P-sendAnnPs__broadcasting_8_1" + "P-sendAnnPs__broadcasting_8_2" + "P-sendAnnPs__broadcasting_8_3" + "P-sendAnnPs__broadcasting_8_4" + "P-sendAnnPs__broadcasting_8_5" + "P-sendAnnPs__broadcasting_8_6" + "P-sendAnnPs__broadcasting_8_7" + "P-sendAnnPs__broadcasting_8_8"))))) )
NeoElection-COL-8-ReachabilityCardinality-2: not EF not ( (not(((3 <= ("P-electionInit_0" + "P-electionInit_1" + "P-electionInit_2" + "P-electionInit_3" + "P-electionInit_4" + "P-electionInit_5" + "P-electionInit_6" + "P-electionInit_7" + "P-electionInit_8")) and (3 <= ("P-poll__pollEnd_0" + "P-poll__pollEnd_1" + "P-poll__pollEnd_2" + "P-poll__pollEnd_3" + "P-poll__pollEnd_4" + "P-poll__pollEnd_5" + "P-poll__pollEnd_6" + "P-poll__pollEnd_7" + "P-poll__pollEnd_8")))) and not(not((2 <= ("P-masterList_0_1_0" + "P-masterList_0_1_1" + "P-masterList_0_1_2" + "P-masterList_0_1_3" + "P-masterList_0_1_4" + "P-masterList_0_1_5" + "P-masterList_0_1_6" + "P-masterList_0_1_7" + "P-masterList_0_1_8" + "P-masterList_0_2_0" + "P-masterList_0_2_1" + "P-masterList_0_2_2" + "P-masterList_0_2_3" + "P-masterList_0_2_4" + "P-masterList_0_2_5" + "P-masterList_0_2_6" + "P-masterList_0_2_7" + "P-masterList_0_2_8" + "P-masterList_0_3_0" + "P-masterList_0_3_1" + "P-masterList_0_3_2" + "P-masterList_0_3_3" + "P-masterList_0_3_4" + "P-masterList_0_3_5" + "P-masterList_0_3_6" + "P-masterList_0_3_7" + "P-masterList_0_3_8" + "P-masterList_0_4_0" + "P-masterList_0_4_1" + "P-masterList_0_4_2" + "P-masterList_0_4_3" + "P-masterList_0_4_4" + "P-masterList_0_4_5" + "P-masterList_0_4_6" + "P-masterList_0_4_7" + "P-masterList_0_4_8" + "P-masterList_0_5_0" + "P-masterList_0_5_1" + "P-masterList_0_5_2" + "P-masterList_0_5_3" + "P-masterList_0_5_4" + "P-masterList_0_5_5" + "P-masterList_0_5_6" + "P-masterList_0_5_7" + "P-masterList_0_5_8" + "P-masterList_0_6_0" + "P-masterList_0_6_1" + "P-masterList_0_6_2" + "P-masterList_0_6_3" + "P-masterList_0_6_4" + "P-masterList_0_6_5" + "P-masterList_0_6_6" + "P-masterList_0_6_7" + "P-masterList_0_6_8" + "P-masterList_0_7_0" + "P-masterList_0_7_1" + "P-masterList_0_7_2" + "P-masterList_0_7_3" + "P-masterList_0_7_4" + "P-masterList_0_7_5" + "P-masterList_0_7_6" + "P-masterList_0_7_7" + "P-masterList_0_7_8" + "P-masterList_0_8_0" + "P-masterList_0_8_1" + "P-masterList_0_8_2" + "P-masterList_0_8_3" + "P-masterList_0_8_4" + "P-masterList_0_8_5" + "P-masterList_0_8_6" + "P-masterList_0_8_7" + "P-masterList_0_8_8" + "P-masterList_1_1_0" + "P-masterList_1_1_1" + "P-masterList_1_1_2" + "P-masterList_1_1_3" + "P-masterList_1_1_4" + "P-masterList_1_1_5" + "P-masterList_1_1_6" + "P-masterList_1_1_7" + "P-masterList_1_1_8" + "P-masterList_1_2_0" + "P-masterList_1_2_1" + "P-masterList_1_2_2" + "P-masterList_1_2_3" + "P-masterList_1_2_4" + "P-masterList_1_2_5" + "P-masterList_1_2_6" + "P-masterList_1_2_7" + "P-masterList_1_2_8" + "P-masterList_1_3_0" + "P-masterList_1_3_1" + "P-masterList_1_3_2" + "P-masterList_1_3_3" + "P-masterList_1_3_4" + "P-masterList_1_3_5" + "P-masterList_1_3_6" + "P-masterList_1_3_7" + "P-masterList_1_3_8" + "P-masterList_1_4_0" + "P-masterList_1_4_1" + "P-masterList_1_4_2" + "P-masterList_1_4_3" + "P-masterList_1_4_4" + "P-masterList_1_4_5" + "P-masterList_1_4_6" + "P-masterList_1_4_7" + "P-masterList_1_4_8" + "P-masterList_1_5_0" + "P-masterList_1_5_1" + "P-masterList_1_5_2" + "P-masterList_1_5_3" + "P-masterList_1_5_4" + "P-masterList_1_5_5" + "P-masterList_1_5_6" + "P-masterList_1_5_7" + "P-masterList_1_5_8" + "P-masterList_1_6_0" + "P-masterList_1_6_1" + "P-masterList_1_6_2" + "P-masterList_1_6_3" + "P-masterList_1_6_4" + "P-masterList_1_6_5" + "P-masterList_1_6_6" + "P-masterList_1_6_7" + "P-masterList_1_6_8" + "P-masterList_1_7_0" + "P-masterList_1_7_1" + "P-masterList_1_7_2" + "P-masterList_1_7_3" + "P-masterList_1_7_4" + "P-masterList_1_7_5" + "P-masterList_1_7_6" + "P-masterList_1_7_7" + "P-masterList_1_7_8" + "P-masterList_1_8_0" + "P-masterList_1_8_1" + "P-masterList_1_8_2" + "P-masterList_1_8_3" + "P-masterList_1_8_4" + "P-masterList_1_8_5" + "P-masterList_1_8_6" + "P-masterList_1_8_7" + "P-masterList_1_8_8" + "P-masterList_2_1_0" + "P-masterList_2_1_1" + "P-masterList_2_1_2" + "P-masterList_2_1_3" + "P-masterList_2_1_4" + "P-masterList_2_1_5" + "P-masterList_2_1_6" + "P-masterList_2_1_7" + "P-masterList_2_1_8" + "P-masterList_2_2_0" + "P-masterList_2_2_1" + "P-masterList_2_2_2" + "P-masterList_2_2_3" + "P-masterList_2_2_4" + "P-masterList_2_2_5" + "P-masterList_2_2_6" + "P-masterList_2_2_7" + "P-masterList_2_2_8" + "P-masterList_2_3_0" + "P-masterList_2_3_1" + "P-masterList_2_3_2" + "P-masterList_2_3_3" + "P-masterList_2_3_4" + "P-masterList_2_3_5" + "P-masterList_2_3_6" + "P-masterList_2_3_7" + "P-masterList_2_3_8" + "P-masterList_2_4_0" + "P-masterList_2_4_1" + "P-masterList_2_4_2" + "P-masterList_2_4_3" + "P-masterList_2_4_4" + "P-masterList_2_4_5" + "P-masterList_2_4_6" + "P-masterList_2_4_7" + "P-masterList_2_4_8" + "P-masterList_2_5_0" + "P-masterList_2_5_1" + "P-masterList_2_5_2" + "P-masterList_2_5_3" + "P-masterList_2_5_4" + "P-masterList_2_5_5" + "P-masterList_2_5_6" + "P-masterList_2_5_7" + "P-masterList_2_5_8" + "P-masterList_2_6_0" + "P-masterList_2_6_1" + "P-masterList_2_6_2" + "P-masterList_2_6_3" + "P-masterList_2_6_4" + "P-masterList_2_6_5" + "P-masterList_2_6_6" + "P-masterList_2_6_7" + "P-masterList_2_6_8" + "P-masterList_2_7_0" + "P-masterList_2_7_1" + "P-masterList_2_7_2" + "P-masterList_2_7_3" + "P-masterList_2_7_4" + "P-masterList_2_7_5" + "P-masterList_2_7_6" + "P-masterList_2_7_7" + "P-masterList_2_7_8" + "P-masterList_2_8_0" + "P-masterList_2_8_1" + "P-masterList_2_8_2" + "P-masterList_2_8_3" + "P-masterList_2_8_4" + "P-masterList_2_8_5" + "P-masterList_2_8_6" + "P-masterList_2_8_7" + "P-masterList_2_8_8" + "P-masterList_3_1_0" + "P-masterList_3_1_1" + "P-masterList_3_1_2" + "P-masterList_3_1_3" + "P-masterList_3_1_4" + "P-masterList_3_1_5" + "P-masterList_3_1_6" + "P-masterList_3_1_7" + "P-masterList_3_1_8" + "P-masterList_3_2_0" + "P-masterList_3_2_1" + "P-masterList_3_2_2" + "P-masterList_3_2_3" + "P-masterList_3_2_4" + "P-masterList_3_2_5" + "P-masterList_3_2_6" + "P-masterList_3_2_7" + "P-masterList_3_2_8" + "P-masterList_3_3_0" + "P-masterList_3_3_1" + "P-masterList_3_3_2" + "P-masterList_3_3_3" + "P-masterList_3_3_4" + "P-masterList_3_3_5" + "P-masterList_3_3_6" + "P-masterList_3_3_7" + "P-masterList_3_3_8" + "P-masterList_3_4_0" + "P-masterList_3_4_1" + "P-masterList_3_4_2" + "P-masterList_3_4_3" + "P-masterList_3_4_4" + "P-masterList_3_4_5" + "P-masterList_3_4_6" + "P-masterList_3_4_7" + "P-masterList_3_4_8" + "P-masterList_3_5_0" + "P-masterList_3_5_1" + "P-masterList_3_5_2" + "P-masterList_3_5_3" + "P-masterList_3_5_4" + "P-masterList_3_5_5" + "P-masterList_3_5_6" + "P-masterList_3_5_7" + "P-masterList_3_5_8" + "P-masterList_3_6_0" + "P-masterList_3_6_1" + "P-masterList_3_6_2" + "P-masterList_3_6_3" + "P-masterList_3_6_4" + "P-masterList_3_6_5" + "P-masterList_3_6_6" + "P-masterList_3_6_7" + "P-masterList_3_6_8" + "P-masterList_3_7_0" + "P-masterList_3_7_1" + "P-masterList_3_7_2" + "P-masterList_3_7_3" + "P-masterList_3_7_4" + "P-masterList_3_7_5" + "P-masterList_3_7_6" + "P-masterList_3_7_7" + "P-masterList_3_7_8" + "P-masterList_3_8_0" + "P-masterList_3_8_1" + "P-masterList_3_8_2" + "P-masterList_3_8_3" + "P-masterList_3_8_4" + "P-masterList_3_8_5" + "P-masterList_3_8_6" + "P-masterList_3_8_7" + "P-masterList_3_8_8" + "P-masterList_4_1_0" + "P-masterList_4_1_1" + "P-masterList_4_1_2" + "P-masterList_4_1_3" + "P-masterList_4_1_4" + "P-masterList_4_1_5" + "P-masterList_4_1_6" + "P-masterList_4_1_7" + "P-masterList_4_1_8" + "P-masterList_4_2_0" + "P-masterList_4_2_1" + "P-masterList_4_2_2" + "P-masterList_4_2_3" + "P-masterList_4_2_4" + "P-masterList_4_2_5" + "P-masterList_4_2_6" + "P-masterList_4_2_7" + "P-masterList_4_2_8" + "P-masterList_4_3_0" + "P-masterList_4_3_1" + "P-masterList_4_3_2" + "P-masterList_4_3_3" + "P-masterList_4_3_4" + "P-masterList_4_3_5" + "P-masterList_4_3_6" + "P-masterList_4_3_7" + "P-masterList_4_3_8" + "P-masterList_4_4_0" + "P-masterList_4_4_1" + "P-masterList_4_4_2" + "P-masterList_4_4_3" + "P-masterList_4_4_4" + "P-masterList_4_4_5" + "P-masterList_4_4_6" + "P-masterList_4_4_7" + "P-masterList_4_4_8" + "P-masterList_4_5_0" + "P-masterList_4_5_1" + "P-masterList_4_5_2" + "P-masterList_4_5_3" + "P-masterList_4_5_4" + "P-masterList_4_5_5" + "P-masterList_4_5_6" + "P-masterList_4_5_7" + "P-masterList_4_5_8" + "P-masterList_4_6_0" + "P-masterList_4_6_1" + "P-masterList_4_6_2" + "P-masterList_4_6_3" + "P-masterList_4_6_4" + "P-masterList_4_6_5" + "P-masterList_4_6_6" + "P-masterList_4_6_7" + "P-masterList_4_6_8" + "P-masterList_4_7_0" + "P-masterList_4_7_1" + "P-masterList_4_7_2" + "P-masterList_4_7_3" + "P-masterList_4_7_4" + "P-masterList_4_7_5" + "P-masterList_4_7_6" + "P-masterList_4_7_7" + "P-masterList_4_7_8" + "P-masterList_4_8_0" + "P-masterList_4_8_1" + "P-masterList_4_8_2" + "P-masterList_4_8_3" + "P-masterList_4_8_4" + "P-masterList_4_8_5" + "P-masterList_4_8_6" + "P-masterList_4_8_7" + "P-masterList_4_8_8" + "P-masterList_5_1_0" + "P-masterList_5_1_1" + "P-masterList_5_1_2" + "P-masterList_5_1_3" + "P-masterList_5_1_4" + "P-masterList_5_1_5" + "P-masterList_5_1_6" + "P-masterList_5_1_7" + "P-masterList_5_1_8" + "P-masterList_5_2_0" + "P-masterList_5_2_1" + "P-masterList_5_2_2" + "P-masterList_5_2_3" + "P-masterList_5_2_4" + "P-masterList_5_2_5" + "P-masterList_5_2_6" + "P-masterList_5_2_7" + "P-masterList_5_2_8" + "P-masterList_5_3_0" + "P-masterList_5_3_1" + "P-masterList_5_3_2" + "P-masterList_5_3_3" + "P-masterList_5_3_4" + "P-masterList_5_3_5" + "P-masterList_5_3_6" + "P-masterList_5_3_7" + "P-masterList_5_3_8" + "P-masterList_5_4_0" + "P-masterList_5_4_1" + "P-masterList_5_4_2" + "P-masterList_5_4_3" + "P-masterList_5_4_4" + "P-masterList_5_4_5" + "P-masterList_5_4_6" + "P-masterList_5_4_7" + "P-masterList_5_4_8" + "P-masterList_5_5_0" + "P-masterList_5_5_1" + "P-masterList_5_5_2" + "P-masterList_5_5_3" + "P-masterList_5_5_4" + "P-masterList_5_5_5" + "P-masterList_5_5_6" + "P-masterList_5_5_7" + "P-masterList_5_5_8" + "P-masterList_5_6_0" + "P-masterList_5_6_1" + "P-masterList_5_6_2" + "P-masterList_5_6_3" + "P-masterList_5_6_4" + "P-masterList_5_6_5" + "P-masterList_5_6_6" + "P-masterList_5_6_7" + "P-masterList_5_6_8" + "P-masterList_5_7_0" + "P-masterList_5_7_1" + "P-masterList_5_7_2" + "P-masterList_5_7_3" + "P-masterList_5_7_4" + "P-masterList_5_7_5" + "P-masterList_5_7_6" + "P-masterList_5_7_7" + "P-masterList_5_7_8" + "P-masterList_5_8_0" + "P-masterList_5_8_1" + "P-masterList_5_8_2" + "P-masterList_5_8_3" + "P-masterList_5_8_4" + "P-masterList_5_8_5" + "P-masterList_5_8_6" + "P-masterList_5_8_7" + "P-masterList_5_8_8" + "P-masterList_6_1_0" + "P-masterList_6_1_1" + "P-masterList_6_1_2" + "P-masterList_6_1_3" + "P-masterList_6_1_4" + "P-masterList_6_1_5" + "P-masterList_6_1_6" + "P-masterList_6_1_7" + "P-masterList_6_1_8" + "P-masterList_6_2_0" + "P-masterList_6_2_1" + "P-masterList_6_2_2" + "P-masterList_6_2_3" + "P-masterList_6_2_4" + "P-masterList_6_2_5" + "P-masterList_6_2_6" + "P-masterList_6_2_7" + "P-masterList_6_2_8" + "P-masterList_6_3_0" + "P-masterList_6_3_1" + "P-masterList_6_3_2" + "P-masterList_6_3_3" + "P-masterList_6_3_4" + "P-masterList_6_3_5" + "P-masterList_6_3_6" + "P-masterList_6_3_7" + "P-masterList_6_3_8" + "P-masterList_6_4_0" + "P-masterList_6_4_1" + "P-masterList_6_4_2" + "P-masterList_6_4_3" + "P-masterList_6_4_4" + "P-masterList_6_4_5" + "P-masterList_6_4_6" + "P-masterList_6_4_7" + "P-masterList_6_4_8" + "P-masterList_6_5_0" + "P-masterList_6_5_1" + "P-masterList_6_5_2" + "P-masterList_6_5_3" + "P-masterList_6_5_4" + "P-masterList_6_5_5" + "P-masterList_6_5_6" + "P-masterList_6_5_7" + "P-masterList_6_5_8" + "P-masterList_6_6_0" + "P-masterList_6_6_1" + "P-masterList_6_6_2" + "P-masterList_6_6_3" + "P-masterList_6_6_4" + "P-masterList_6_6_5" + "P-masterList_6_6_6" + "P-masterList_6_6_7" + "P-masterList_6_6_8" + "P-masterList_6_7_0" + "P-masterList_6_7_1" + "P-masterList_6_7_2" + "P-masterList_6_7_3" + "P-masterList_6_7_4" + "P-masterList_6_7_5" + "P-masterList_6_7_6" + "P-masterList_6_7_7" + "P-masterList_6_7_8" + "P-masterList_6_8_0" + "P-masterList_6_8_1" + "P-masterList_6_8_2" + "P-masterList_6_8_3" + "P-masterList_6_8_4" + "P-masterList_6_8_5" + "P-masterList_6_8_6" + "P-masterList_6_8_7" + "P-masterList_6_8_8" + "P-masterList_7_1_0" + "P-masterList_7_1_1" + "P-masterList_7_1_2" + "P-masterList_7_1_3" + "P-masterList_7_1_4" + "P-masterList_7_1_5" + "P-masterList_7_1_6" + "P-masterList_7_1_7" + "P-masterList_7_1_8" + "P-masterList_7_2_0" + "P-masterList_7_2_1" + "P-masterList_7_2_2" + "P-masterList_7_2_3" + "P-masterList_7_2_4" + "P-masterList_7_2_5" + "P-masterList_7_2_6" + "P-masterList_7_2_7" + "P-masterList_7_2_8" + "P-masterList_7_3_0" + "P-masterList_7_3_1" + "P-masterList_7_3_2" + "P-masterList_7_3_3" + "P-masterList_7_3_4" + "P-masterList_7_3_5" + "P-masterList_7_3_6" + "P-masterList_7_3_7" + "P-masterList_7_3_8" + "P-masterList_7_4_0" + "P-masterList_7_4_1" + "P-masterList_7_4_2" + "P-masterList_7_4_3" + "P-masterList_7_4_4" + "P-masterList_7_4_5" + "P-masterList_7_4_6" + "P-masterList_7_4_7" + "P-masterList_7_4_8" + "P-masterList_7_5_0" + "P-masterList_7_5_1" + "P-masterList_7_5_2" + "P-masterList_7_5_3" + "P-masterList_7_5_4" + "P-masterList_7_5_5" + "P-masterList_7_5_6" + "P-masterList_7_5_7" + "P-masterList_7_5_8" + "P-masterList_7_6_0" + "P-masterList_7_6_1" + "P-masterList_7_6_2" + "P-masterList_7_6_3" + "P-masterList_7_6_4" + "P-masterList_7_6_5" + "P-masterList_7_6_6" + "P-masterList_7_6_7" + "P-masterList_7_6_8" + "P-masterList_7_7_0" + "P-masterList_7_7_1" + "P-masterList_7_7_2" + "P-masterList_7_7_3" + "P-masterList_7_7_4" + "P-masterList_7_7_5" + "P-masterList_7_7_6" + "P-masterList_7_7_7" + "P-masterList_7_7_8" + "P-masterList_7_8_0" + "P-masterList_7_8_1" + "P-masterList_7_8_2" + "P-masterList_7_8_3" + "P-masterList_7_8_4" + "P-masterList_7_8_5" + "P-masterList_7_8_6" + "P-masterList_7_8_7" + "P-masterList_7_8_8" + "P-masterList_8_1_0" + "P-masterList_8_1_1" + "P-masterList_8_1_2" + "P-masterList_8_1_3" + "P-masterList_8_1_4" + "P-masterList_8_1_5" + "P-masterList_8_1_6" + "P-masterList_8_1_7" + "P-masterList_8_1_8" + "P-masterList_8_2_0" + "P-masterList_8_2_1" + "P-masterList_8_2_2" + "P-masterList_8_2_3" + "P-masterList_8_2_4" + "P-masterList_8_2_5" + "P-masterList_8_2_6" + "P-masterList_8_2_7" + "P-masterList_8_2_8" + "P-masterList_8_3_0" + "P-masterList_8_3_1" + "P-masterList_8_3_2" + "P-masterList_8_3_3" + "P-masterList_8_3_4" + "P-masterList_8_3_5" + "P-masterList_8_3_6" + "P-masterList_8_3_7" + "P-masterList_8_3_8" + "P-masterList_8_4_0" + "P-masterList_8_4_1" + "P-masterList_8_4_2" + "P-masterList_8_4_3" + "P-masterList_8_4_4" + "P-masterList_8_4_5" + "P-masterList_8_4_6" + "P-masterList_8_4_7" + "P-masterList_8_4_8" + "P-masterList_8_5_0" + "P-masterList_8_5_1" + "P-masterList_8_5_2" + "P-masterList_8_5_3" + "P-masterList_8_5_4" + "P-masterList_8_5_5" + "P-masterList_8_5_6" + "P-masterList_8_5_7" + "P-masterList_8_5_8" + "P-masterList_8_6_0" + "P-masterList_8_6_1" + "P-masterList_8_6_2" + "P-masterList_8_6_3" + "P-masterList_8_6_4" + "P-masterList_8_6_5" + "P-masterList_8_6_6" + "P-masterList_8_6_7" + "P-masterList_8_6_8" + "P-masterList_8_7_0" + "P-masterList_8_7_1" + "P-masterList_8_7_2" + "P-masterList_8_7_3" + "P-masterList_8_7_4" + "P-masterList_8_7_5" + "P-masterList_8_7_6" + "P-masterList_8_7_7" + "P-masterList_8_7_8" + "P-masterList_8_8_0" + "P-masterList_8_8_1" + "P-masterList_8_8_2" + "P-masterList_8_8_3" + "P-masterList_8_8_4" + "P-masterList_8_8_5" + "P-masterList_8_8_6" + "P-masterList_8_8_7" + "P-masterList_8_8_8"))))) )
NeoElection-COL-8-ReachabilityCardinality-3: not EF not ( ((not((("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8") <= ("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8"))) or (("P-poll__networl_0_0_AskP_0" + "P-poll__networl_0_0_AskP_1" + "P-poll__networl_0_0_AskP_2" + "P-poll__networl_0_0_AskP_3" + "P-poll__networl_0_0_AskP_4" + "P-poll__networl_0_0_AskP_5" + "P-poll__networl_0_0_AskP_6" + "P-poll__networl_0_0_AskP_7" + "P-poll__networl_0_0_AskP_8" + "P-poll__networl_0_0_AnsP_0" + "P-poll__networl_0_0_AnsP_1" + "P-poll__networl_0_0_AnsP_2" + "P-poll__networl_0_0_AnsP_3" + "P-poll__networl_0_0_AnsP_4" + "P-poll__networl_0_0_AnsP_5" + "P-poll__networl_0_0_AnsP_6" + "P-poll__networl_0_0_AnsP_7" + "P-poll__networl_0_0_AnsP_8" + "P-poll__networl_0_0_RI_0" + "P-poll__networl_0_0_RI_1" + "P-poll__networl_0_0_RI_2" + "P-poll__networl_0_0_RI_3" + "P-poll__networl_0_0_RI_4" + "P-poll__networl_0_0_RI_5" + "P-poll__networl_0_0_RI_6" + "P-poll__networl_0_0_RI_7" + "P-poll__networl_0_0_RI_8" + "P-poll__networl_0_0_AI_0" + "P-poll__networl_0_0_AI_1" + "P-poll__networl_0_0_AI_2" + "P-poll__networl_0_0_AI_3" + "P-poll__networl_0_0_AI_4" + "P-poll__networl_0_0_AI_5" + "P-poll__networl_0_0_AI_6" + "P-poll__networl_0_0_AI_7" + "P-poll__networl_0_0_AI_8" + "P-poll__networl_0_0_AnnP_0" + "P-poll__networl_0_0_AnnP_1" + "P-poll__networl_0_0_AnnP_2" + "P-poll__networl_0_0_AnnP_3" + "P-poll__networl_0_0_AnnP_4" + "P-poll__networl_0_0_AnnP_5" + "P-poll__networl_0_0_AnnP_6" + "P-poll__networl_0_0_AnnP_7" + "P-poll__networl_0_0_AnnP_8" + "P-poll__networl_0_0_RP_0" + "P-poll__networl_0_0_RP_1" + "P-poll__networl_0_0_RP_2" + "P-poll__networl_0_0_RP_3" + "P-poll__networl_0_0_RP_4" + "P-poll__networl_0_0_RP_5" + "P-poll__networl_0_0_RP_6" + "P-poll__networl_0_0_RP_7" + "P-poll__networl_0_0_RP_8" + "P-poll__networl_0_1_AskP_0" + "P-poll__networl_0_1_AskP_1" + "P-poll__networl_0_1_AskP_2" + "P-poll__networl_0_1_AskP_3" + "P-poll__networl_0_1_AskP_4" + "P-poll__networl_0_1_AskP_5" + "P-poll__networl_0_1_AskP_6" + "P-poll__networl_0_1_AskP_7" + "P-poll__networl_0_1_AskP_8" + "P-poll__networl_0_1_AnsP_0" + "P-poll__networl_0_1_AnsP_1" + "P-poll__networl_0_1_AnsP_2" + "P-poll__networl_0_1_AnsP_3" + "P-poll__networl_0_1_AnsP_4" + "P-poll__networl_0_1_AnsP_5" + "P-poll__networl_0_1_AnsP_6" + "P-poll__networl_0_1_AnsP_7" + "P-poll__networl_0_1_AnsP_8" + "P-poll__networl_0_1_RI_0" + "P-poll__networl_0_1_RI_1" + "P-poll__networl_0_1_RI_2" + "P-poll__networl_0_1_RI_3" + "P-poll__networl_0_1_RI_4" + "P-poll__networl_0_1_RI_5" + "P-poll__networl_0_1_RI_6" + "P-poll__networl_0_1_RI_7" + "P-poll__networl_0_1_RI_8" + "P-poll__networl_0_1_AI_0" + "P-poll__networl_0_1_AI_1" + "P-poll__networl_0_1_AI_2" + "P-poll__networl_0_1_AI_3" + "P-poll__networl_0_1_AI_4" + "P-poll__networl_0_1_AI_5" + "P-poll__networl_0_1_AI_6" + "P-poll__networl_0_1_AI_7" + "P-poll__networl_0_1_AI_8" + "P-poll__networl_0_1_AnnP_0" + "P-poll__networl_0_1_AnnP_1" + "P-poll__networl_0_1_AnnP_2" + "P-poll__networl_0_1_AnnP_3" + "P-poll__networl_0_1_AnnP_4" + "P-poll__networl_0_1_AnnP_5" + "P-poll__networl_0_1_AnnP_6" + "P-poll__networl_0_1_AnnP_7" + "P-poll__networl_0_1_AnnP_8" + "P-poll__networl_0_1_RP_0" + "P-poll__networl_0_1_RP_1" + "P-poll__networl_0_1_RP_2" + "P-poll__networl_0_1_RP_3" + "P-poll__networl_0_1_RP_4" + "P-poll__networl_0_1_RP_5" + "P-poll__networl_0_1_RP_6" + "P-poll__networl_0_1_RP_7" + "P-poll__networl_0_1_RP_8" + "P-poll__networl_0_2_AskP_0" + "P-poll__networl_0_2_AskP_1" + "P-poll__networl_0_2_AskP_2" + "P-poll__networl_0_2_AskP_3" + "P-poll__networl_0_2_AskP_4" + "P-poll__networl_0_2_AskP_5" + "P-poll__networl_0_2_AskP_6" + "P-poll__networl_0_2_AskP_7" + "P-poll__networl_0_2_AskP_8" + "P-poll__networl_0_2_AnsP_0" + "P-poll__networl_0_2_AnsP_1" + "P-poll__networl_0_2_AnsP_2" + "P-poll__networl_0_2_AnsP_3" + "P-poll__networl_0_2_AnsP_4" + "P-poll__networl_0_2_AnsP_5" + "P-poll__networl_0_2_AnsP_6" + "P-poll__networl_0_2_AnsP_7" + "P-poll__networl_0_2_AnsP_8" + "P-poll__networl_0_2_RI_0" + "P-poll__networl_0_2_RI_1" + "P-poll__networl_0_2_RI_2" + "P-poll__networl_0_2_RI_3" + "P-poll__networl_0_2_RI_4" + "P-poll__networl_0_2_RI_5" + "P-poll__networl_0_2_RI_6" + "P-poll__networl_0_2_RI_7" + "P-poll__networl_0_2_RI_8" + "P-poll__networl_0_2_AI_0" + "P-poll__networl_0_2_AI_1" + "P-poll__networl_0_2_AI_2" + "P-poll__networl_0_2_AI_3" + "P-poll__networl_0_2_AI_4" + "P-poll__networl_0_2_AI_5" + "P-poll__networl_0_2_AI_6" + "P-poll__networl_0_2_AI_7" + "P-poll__networl_0_2_AI_8" + "P-poll__networl_0_2_AnnP_0" + "P-poll__networl_0_2_AnnP_1" + "P-poll__networl_0_2_AnnP_2" + "P-poll__networl_0_2_AnnP_3" + "P-poll__networl_0_2_AnnP_4" + "P-poll__networl_0_2_AnnP_5" + "P-poll__networl_0_2_AnnP_6" + "P-poll__networl_0_2_AnnP_7" + "P-poll__networl_0_2_AnnP_8" + "P-poll__networl_0_2_RP_0" + "P-poll__networl_0_2_RP_1" + "P-poll__networl_0_2_RP_2" + "P-poll__networl_0_2_RP_3" + "P-poll__networl_0_2_RP_4" + "P-poll__networl_0_2_RP_5" + "P-poll__networl_0_2_RP_6" + "P-poll__networl_0_2_RP_7" + "P-poll__networl_0_2_RP_8" + "P-poll__networl_0_3_AskP_0" + "P-poll__networl_0_3_AskP_1" + "P-poll__networl_0_3_AskP_2" + "P-poll__networl_0_3_AskP_3" + "P-poll__networl_0_3_AskP_4" + "P-poll__networl_0_3_AskP_5" + "P-poll__networl_0_3_AskP_6" + "P-poll__networl_0_3_AskP_7" + "P-poll__networl_0_3_AskP_8" + "P-poll__networl_0_3_AnsP_0" + "P-poll__networl_0_3_AnsP_1" + "P-poll__networl_0_3_AnsP_2" + "P-poll__networl_0_3_AnsP_3" + "P-poll__networl_0_3_AnsP_4" + "P-poll__networl_0_3_AnsP_5" + "P-poll__networl_0_3_AnsP_6" + "P-poll__networl_0_3_AnsP_7" + "P-poll__networl_0_3_AnsP_8" + "P-poll__networl_0_3_RI_0" + "P-poll__networl_0_3_RI_1" + "P-poll__networl_0_3_RI_2" + "P-poll__networl_0_3_RI_3" + "P-poll__networl_0_3_RI_4" + "P-poll__networl_0_3_RI_5" + "P-poll__networl_0_3_RI_6" + "P-poll__networl_0_3_RI_7" + "P-poll__networl_0_3_RI_8" + "P-poll__networl_0_3_AI_0" + "P-poll__networl_0_3_AI_1" + "P-poll__networl_0_3_AI_2" + "P-poll__networl_0_3_AI_3" + "P-poll__networl_0_3_AI_4" + "P-poll__networl_0_3_AI_5" + "P-poll__networl_0_3_AI_6" + "P-poll__networl_0_3_AI_7" + "P-poll__networl_0_3_AI_8" + "P-poll__networl_0_3_AnnP_0" + "P-poll__networl_0_3_AnnP_1" + "P-poll__networl_0_3_AnnP_2" + "P-poll__networl_0_3_AnnP_3" + "P-poll__networl_0_3_AnnP_4" + "P-poll__networl_0_3_AnnP_5" + "P-poll__networl_0_3_AnnP_6" + "P-poll__networl_0_3_AnnP_7" + "P-poll__networl_0_3_AnnP_8" + "P-poll__networl_0_3_RP_0" + "P-poll__networl_0_3_RP_1" + "P-poll__networl_0_3_RP_2" + "P-poll__networl_0_3_RP_3" + "P-poll__networl_0_3_RP_4" + "P-poll__networl_0_3_RP_5" + "P-poll__networl_0_3_RP_6" + "P-poll__networl_0_3_RP_7" + "P-poll__networl_0_3_RP_8" + "P-poll__networl_0_4_AskP_0" + "P-poll__networl_0_4_AskP_1" + "P-poll__networl_0_4_AskP_2" + "P-poll__networl_0_4_AskP_3" + "P-poll__networl_0_4_AskP_4" + "P-poll__networl_0_4_AskP_5" + "P-poll__networl_0_4_AskP_6" + "P-poll__networl_0_4_AskP_7" + "P-poll__networl_0_4_AskP_8" + "P-poll__networl_0_4_AnsP_0" + "P-poll__networl_0_4_AnsP_1" + "P-poll__networl_0_4_AnsP_2" + "P-poll__networl_0_4_AnsP_3" + "P-poll__networl_0_4_AnsP_4" + "P-poll__networl_0_4_AnsP_5" + "P-poll__networl_0_4_AnsP_6" + "P-poll__networl_0_4_AnsP_7" + "P-poll__networl_0_4_AnsP_8" + "P-poll__networl_0_4_RI_0" + "P-poll__networl_0_4_RI_1" + "P-poll__networl_0_4_RI_2" + "P-poll__networl_0_4_RI_3" + "P-poll__networl_0_4_RI_4" + "P-poll__networl_0_4_RI_5" + "P-poll__networl_0_4_RI_6" + "P-poll__networl_0_4_RI_7" + "P-poll__networl_0_4_RI_8" + "P-poll__networl_0_4_AI_0" + "P-poll__networl_0_4_AI_1" + "P-poll__networl_0_4_AI_2" + "P-poll__networl_0_4_AI_3" + "P-poll__networl_0_4_AI_4" + "P-poll__networl_0_4_AI_5" + "P-poll__networl_0_4_AI_6" + "P-poll__networl_0_4_AI_7" + "P-poll__networl_0_4_AI_8" + "P-poll__networl_0_4_AnnP_0" + "P-poll__networl_0_4_AnnP_1" + "P-poll__networl_0_4_AnnP_2" + "P-poll__networl_0_4_AnnP_3" + "P-poll__networl_0_4_AnnP_4" + "P-poll__networl_0_4_AnnP_5" + "P-poll__networl_0_4_AnnP_6" + "P-poll__networl_0_4_AnnP_7" + "P-poll__networl_0_4_AnnP_8" + "P-poll__networl_0_4_RP_0" + "P-poll__networl_0_4_RP_1" + "P-poll__networl_0_4_RP_2" + "P-poll__networl_0_4_RP_3" + "P-poll__networl_0_4_RP_4" + "P-poll__networl_0_4_RP_5" + "P-poll__networl_0_4_RP_6" + "P-poll__networl_0_4_RP_7" + "P-poll__networl_0_4_RP_8" + "P-poll__networl_0_5_AskP_0" + "P-poll__networl_0_5_AskP_1" + "P-poll__networl_0_5_AskP_2" + "P-poll__networl_0_5_AskP_3" + "P-poll__networl_0_5_AskP_4" + "P-poll__networl_0_5_AskP_5" + "P-poll__networl_0_5_AskP_6" + "P-poll__networl_0_5_AskP_7" + "P-poll__networl_0_5_AskP_8" + "P-poll__networl_0_5_AnsP_0" + "P-poll__networl_0_5_AnsP_1" + "P-poll__networl_0_5_AnsP_2" + "P-poll__networl_0_5_AnsP_3" + "P-poll__networl_0_5_AnsP_4" + "P-poll__networl_0_5_AnsP_5" + "P-poll__networl_0_5_AnsP_6" + "P-poll__networl_0_5_AnsP_7" + "P-poll__networl_0_5_AnsP_8" + "P-poll__networl_0_5_RI_0" + "P-poll__networl_0_5_RI_1" + "P-poll__networl_0_5_RI_2" + "P-poll__networl_0_5_RI_3" + "P-poll__networl_0_5_RI_4" + "P-poll__networl_0_5_RI_5" + "P-poll__networl_0_5_RI_6" + "P-poll__networl_0_5_RI_7" + "P-poll__networl_0_5_RI_8" + "P-poll__networl_0_5_AI_0" + "P-poll__networl_0_5_AI_1" + "P-poll__networl_0_5_AI_2" + "P-poll__networl_0_5_AI_3" + "P-poll__networl_0_5_AI_4" + "P-poll__networl_0_5_AI_5" + "P-poll__networl_0_5_AI_6" + "P-poll__networl_0_5_AI_7" + "P-poll__networl_0_5_AI_8" + "P-poll__networl_0_5_AnnP_0" + "P-poll__networl_0_5_AnnP_1" + "P-poll__networl_0_5_AnnP_2" + "P-poll__networl_0_5_AnnP_3" + "P-poll__networl_0_5_AnnP_4" + "P-poll__networl_0_5_AnnP_5" + "P-poll__networl_0_5_AnnP_6" + "P-poll__networl_0_5_AnnP_7" + "P-poll__networl_0_5_AnnP_8" + "P-poll__networl_0_5_RP_0" + "P-poll__networl_0_5_RP_1" + "P-poll__networl_0_5_RP_2" + "P-poll__networl_0_5_RP_3" + "P-poll__networl_0_5_RP_4" + "P-poll__networl_0_5_RP_5" + "P-poll__networl_0_5_RP_6" + "P-poll__networl_0_5_RP_7" + "P-poll__networl_0_5_RP_8" + "P-poll__networl_0_6_AskP_0" + "P-poll__networl_0_6_AskP_1" + "P-poll__networl_0_6_AskP_2" + "P-poll__networl_0_6_AskP_3" + "P-poll__networl_0_6_AskP_4" + "P-poll__networl_0_6_AskP_5" + "P-poll__networl_0_6_AskP_6" + "P-poll__networl_0_6_AskP_7" + "P-poll__networl_0_6_AskP_8" + "P-poll__networl_0_6_AnsP_0" + "P-poll__networl_0_6_AnsP_1" + "P-poll__networl_0_6_AnsP_2" + "P-poll__networl_0_6_AnsP_3" + "P-poll__networl_0_6_AnsP_4" + "P-poll__networl_0_6_AnsP_5" + "P-poll__networl_0_6_AnsP_6" + "P-poll__networl_0_6_AnsP_7" + "P-poll__networl_0_6_AnsP_8" + "P-poll__networl_0_6_RI_0" + "P-poll__networl_0_6_RI_1" + "P-poll__networl_0_6_RI_2" + "P-poll__networl_0_6_RI_3" + "P-poll__networl_0_6_RI_4" + "P-poll__networl_0_6_RI_5" + "P-poll__networl_0_6_RI_6" + "P-poll__networl_0_6_RI_7" + "P-poll__networl_0_6_RI_8" + "P-poll__networl_0_6_AI_0" + "P-poll__networl_0_6_AI_1" + "P-poll__networl_0_6_AI_2" + "P-poll__networl_0_6_AI_3" + "P-poll__networl_0_6_AI_4" + "P-poll__networl_0_6_AI_5" + "P-poll__networl_0_6_AI_6" + "P-poll__networl_0_6_AI_7" + "P-poll__networl_0_6_AI_8" + "P-poll__networl_0_6_AnnP_0" + "P-poll__networl_0_6_AnnP_1" + "P-poll__networl_0_6_AnnP_2" + "P-poll__networl_0_6_AnnP_3" + "P-poll__networl_0_6_AnnP_4" + "P-poll__networl_0_6_AnnP_5" + "P-poll__networl_0_6_AnnP_6" + "P-poll__networl_0_6_AnnP_7" + "P-poll__networl_0_6_AnnP_8" + "P-poll__networl_0_6_RP_0" + "P-poll__networl_0_6_RP_1" + "P-poll__networl_0_6_RP_2" + "P-poll__networl_0_6_RP_3" + "P-poll__networl_0_6_RP_4" + "P-poll__networl_0_6_RP_5" + "P-poll__networl_0_6_RP_6" + "P-poll__networl_0_6_RP_7" + "P-poll__networl_0_6_RP_8" + "P-poll__networl_0_7_AskP_0" + "P-poll__networl_0_7_AskP_1" + "P-poll__networl_0_7_AskP_2" + "P-poll__networl_0_7_AskP_3" + "P-poll__networl_0_7_AskP_4" + "P-poll__networl_0_7_AskP_5" + "P-poll__networl_0_7_AskP_6" + "P-poll__networl_0_7_AskP_7" + "P-poll__networl_0_7_AskP_8" + "P-poll__networl_0_7_AnsP_0" + "P-poll__networl_0_7_AnsP_1" + "P-poll__networl_0_7_AnsP_2" + "P-poll__networl_0_7_AnsP_3" + "P-poll__networl_0_7_AnsP_4" + "P-poll__networl_0_7_AnsP_5" + "P-poll__networl_0_7_AnsP_6" + "P-poll__networl_0_7_AnsP_7" + "P-poll__networl_0_7_AnsP_8" + "P-poll__networl_0_7_RI_0" + "P-poll__networl_0_7_RI_1" + "P-poll__networl_0_7_RI_2" + "P-poll__networl_0_7_RI_3" + "P-poll__networl_0_7_RI_4" + "P-poll__networl_0_7_RI_5" + "P-poll__networl_0_7_RI_6" + "P-poll__networl_0_7_RI_7" + "P-poll__networl_0_7_RI_8" + "P-poll__networl_0_7_AI_0" + "P-poll__networl_0_7_AI_1" + "P-poll__networl_0_7_AI_2" + "P-poll__networl_0_7_AI_3" + "P-poll__networl_0_7_AI_4" + "P-poll__networl_0_7_AI_5" + "P-poll__networl_0_7_AI_6" + "P-poll__networl_0_7_AI_7" + "P-poll__networl_0_7_AI_8" + "P-poll__networl_0_7_AnnP_0" + "P-poll__networl_0_7_AnnP_1" + "P-poll__networl_0_7_AnnP_2" + "P-poll__networl_0_7_AnnP_3" + "P-poll__networl_0_7_AnnP_4" + "P-poll__networl_0_7_AnnP_5" + "P-poll__networl_0_7_AnnP_6" + "P-poll__networl_0_7_AnnP_7" + "P-poll__networl_0_7_AnnP_8" + "P-poll__networl_0_7_RP_0" + "P-poll__networl_0_7_RP_1" + "P-poll__networl_0_7_RP_2" + "P-poll__networl_0_7_RP_3" + "P-poll__networl_0_7_RP_4" + "P-poll__networl_0_7_RP_5" + "P-poll__networl_0_7_RP_6" + "P-poll__networl_0_7_RP_7" + "P-poll__networl_0_7_RP_8" + "P-poll__networl_0_8_AskP_0" + "P-poll__networl_0_8_AskP_1" + "P-poll__networl_0_8_AskP_2" + "P-poll__networl_0_8_AskP_3" + "P-poll__networl_0_8_AskP_4" + "P-poll__networl_0_8_AskP_5" + "P-poll__networl_0_8_AskP_6" + "P-poll__networl_0_8_AskP_7" + "P-poll__networl_0_8_AskP_8" + "P-poll__networl_0_8_AnsP_0" + "P-poll__networl_0_8_AnsP_1" + "P-poll__networl_0_8_AnsP_2" + "P-poll__networl_0_8_AnsP_3" + "P-poll__networl_0_8_AnsP_4" + "P-poll__networl_0_8_AnsP_5" + "P-poll__networl_0_8_AnsP_6" + "P-poll__networl_0_8_AnsP_7" + "P-poll__networl_0_8_AnsP_8" + "P-poll__networl_0_8_RI_0" + "P-poll__networl_0_8_RI_1" + "P-poll__networl_0_8_RI_2" + "P-poll__networl_0_8_RI_3" + "P-poll__networl_0_8_RI_4" + "P-poll__networl_0_8_RI_5" + "P-poll__networl_0_8_RI_6" + "P-poll__networl_0_8_RI_7" + "P-poll__networl_0_8_RI_8" + "P-poll__networl_0_8_AI_0" + "P-poll__networl_0_8_AI_1" + "P-poll__networl_0_8_AI_2" + "P-poll__networl_0_8_AI_3" + "P-poll__networl_0_8_AI_4" + "P-poll__networl_0_8_AI_5" + "P-poll__networl_0_8_AI_6" + "P-poll__networl_0_8_AI_7" + "P-poll__networl_0_8_AI_8" + "P-poll__networl_0_8_AnnP_0" + "P-poll__networl_0_8_AnnP_1" + "P-poll__networl_0_8_AnnP_2" + "P-poll__networl_0_8_AnnP_3" + "P-poll__networl_0_8_AnnP_4" + "P-poll__networl_0_8_AnnP_5" + "P-poll__networl_0_8_AnnP_6" + "P-poll__networl_0_8_AnnP_7" + "P-poll__networl_0_8_AnnP_8" + "P-poll__networl_0_8_RP_0" + "P-poll__networl_0_8_RP_1" + "P-poll__networl_0_8_RP_2" + "P-poll__networl_0_8_RP_3" + "P-poll__networl_0_8_RP_4" + "P-poll__networl_0_8_RP_5" + "P-poll__networl_0_8_RP_6" + "P-poll__networl_0_8_RP_7" + "P-poll__networl_0_8_RP_8" + "P-poll__networl_1_0_AskP_0" + "P-poll__networl_1_0_AskP_1" + "P-poll__networl_1_0_AskP_2" + "P-poll__networl_1_0_AskP_3" + "P-poll__networl_1_0_AskP_4" + "P-poll__networl_1_0_AskP_5" + "P-poll__networl_1_0_AskP_6" + "P-poll__networl_1_0_AskP_7" + "P-poll__networl_1_0_AskP_8" + "P-poll__networl_1_0_AnsP_0" + "P-poll__networl_1_0_AnsP_1" + "P-poll__networl_1_0_AnsP_2" + "P-poll__networl_1_0_AnsP_3" + "P-poll__networl_1_0_AnsP_4" + "P-poll__networl_1_0_AnsP_5" + "P-poll__networl_1_0_AnsP_6" + "P-poll__networl_1_0_AnsP_7" + "P-poll__networl_1_0_AnsP_8" + "P-poll__networl_1_0_RI_0" + "P-poll__networl_1_0_RI_1" + "P-poll__networl_1_0_RI_2" + "P-poll__networl_1_0_RI_3" + "P-poll__networl_1_0_RI_4" + "P-poll__networl_1_0_RI_5" + "P-poll__networl_1_0_RI_6" + "P-poll__networl_1_0_RI_7" + "P-poll__networl_1_0_RI_8" + "P-poll__networl_1_0_AI_0" + "P-poll__networl_1_0_AI_1" + "P-poll__networl_1_0_AI_2" + "P-poll__networl_1_0_AI_3" + "P-poll__networl_1_0_AI_4" + "P-poll__networl_1_0_AI_5" + "P-poll__networl_1_0_AI_6" + "P-poll__networl_1_0_AI_7" + "P-poll__networl_1_0_AI_8" + "P-poll__networl_1_0_AnnP_0" + "P-poll__networl_1_0_AnnP_1" + "P-poll__networl_1_0_AnnP_2" + "P-poll__networl_1_0_AnnP_3" + "P-poll__networl_1_0_AnnP_4" + "P-poll__networl_1_0_AnnP_5" + "P-poll__networl_1_0_AnnP_6" + "P-poll__networl_1_0_AnnP_7" + "P-poll__networl_1_0_AnnP_8" + "P-poll__networl_1_0_RP_0" + "P-poll__networl_1_0_RP_1" + "P-poll__networl_1_0_RP_2" + "P-poll__networl_1_0_RP_3" + "P-poll__networl_1_0_RP_4" + "P-poll__networl_1_0_RP_5" + "P-poll__networl_1_0_RP_6" + "P-poll__networl_1_0_RP_7" + "P-poll__networl_1_0_RP_8" + "P-poll__networl_1_1_AskP_0" + "P-poll__networl_1_1_AskP_1" + "P-poll__networl_1_1_AskP_2" + "P-poll__networl_1_1_AskP_3" + "P-poll__networl_1_1_AskP_4" + "P-poll__networl_1_1_AskP_5" + "P-poll__networl_1_1_AskP_6" + "P-poll__networl_1_1_AskP_7" + "P-poll__networl_1_1_AskP_8" + "P-poll__networl_1_1_AnsP_0" + "P-poll__networl_1_1_AnsP_1" + "P-poll__networl_1_1_AnsP_2" + "P-poll__networl_1_1_AnsP_3" + "P-poll__networl_1_1_AnsP_4" + "P-poll__networl_1_1_AnsP_5" + "P-poll__networl_1_1_AnsP_6" + "P-poll__networl_1_1_AnsP_7" + "P-poll__networl_1_1_AnsP_8" + "P-poll__networl_1_1_RI_0" + "P-poll__networl_1_1_RI_1" + "P-poll__networl_1_1_RI_2" + "P-poll__networl_1_1_RI_3" + "P-poll__networl_1_1_RI_4" + "P-poll__networl_1_1_RI_5" + "P-poll__networl_1_1_RI_6" + "P-poll__networl_1_1_RI_7" + "P-poll__networl_1_1_RI_8" + "P-poll__networl_1_1_AI_0" + "P-poll__networl_1_1_AI_1" + "P-poll__networl_1_1_AI_2" + "P-poll__networl_1_1_AI_3" + "P-poll__networl_1_1_AI_4" + "P-poll__networl_1_1_AI_5" + "P-poll__networl_1_1_AI_6" + "P-poll__networl_1_1_AI_7" + "P-poll__networl_1_1_AI_8" + "P-poll__networl_1_1_AnnP_0" + "P-poll__networl_1_1_AnnP_1" + "P-poll__networl_1_1_AnnP_2" + "P-poll__networl_1_1_AnnP_3" + "P-poll__networl_1_1_AnnP_4" + "P-poll__networl_1_1_AnnP_5" + "P-poll__networl_1_1_AnnP_6" + "P-poll__networl_1_1_AnnP_7" + "P-poll__networl_1_1_AnnP_8" + "P-poll__networl_1_1_RP_0" + "P-poll__networl_1_1_RP_1" + "P-poll__networl_1_1_RP_2" + "P-poll__networl_1_1_RP_3" + "P-poll__networl_1_1_RP_4" + "P-poll__networl_1_1_RP_5" + "P-poll__networl_1_1_RP_6" + "P-poll__networl_1_1_RP_7" + "P-poll__networl_1_1_RP_8" + "P-poll__networl_1_2_AskP_0" + "P-poll__networl_1_2_AskP_1" + "P-poll__networl_1_2_AskP_2" + "P-poll__networl_1_2_AskP_3" + "P-poll__networl_1_2_AskP_4" + "P-poll__networl_1_2_AskP_5" + "P-poll__networl_1_2_AskP_6" + "P-poll__networl_1_2_AskP_7" + "P-poll__networl_1_2_AskP_8" + "P-poll__networl_1_2_AnsP_0" + "P-poll__networl_1_2_AnsP_1" + "P-poll__networl_1_2_AnsP_2" + "P-poll__networl_1_2_AnsP_3" + "P-poll__networl_1_2_AnsP_4" + "P-poll__networl_1_2_AnsP_5" + "P-poll__networl_1_2_AnsP_6" + "P-poll__networl_1_2_AnsP_7" + "P-poll__networl_1_2_AnsP_8" + "P-poll__networl_1_2_RI_0" + "P-poll__networl_1_2_RI_1" + "P-poll__networl_1_2_RI_2" + "P-poll__networl_1_2_RI_3" + "P-poll__networl_1_2_RI_4" + "P-poll__networl_1_2_RI_5" + "P-poll__networl_1_2_RI_6" + "P-poll__networl_1_2_RI_7" + "P-poll__networl_1_2_RI_8" + "P-poll__networl_1_2_AI_0" + "P-poll__networl_1_2_AI_1" + "P-poll__networl_1_2_AI_2" + "P-poll__networl_1_2_AI_3" + "P-poll__networl_1_2_AI_4" + "P-poll__networl_1_2_AI_5" + "P-poll__networl_1_2_AI_6" + "P-poll__networl_1_2_AI_7" + "P-poll__networl_1_2_AI_8" + "P-poll__networl_1_2_AnnP_0" + "P-poll__networl_1_2_AnnP_1" + "P-poll__networl_1_2_AnnP_2" + "P-poll__networl_1_2_AnnP_3" + "P-poll__networl_1_2_AnnP_4" + "P-poll__networl_1_2_AnnP_5" + "P-poll__networl_1_2_AnnP_6" + "P-poll__networl_1_2_AnnP_7" + "P-poll__networl_1_2_AnnP_8" + "P-poll__networl_1_2_RP_0" + "P-poll__networl_1_2_RP_1" + "P-poll__networl_1_2_RP_2" + "P-poll__networl_1_2_RP_3" + "P-poll__networl_1_2_RP_4" + "P-poll__networl_1_2_RP_5" + "P-poll__networl_1_2_RP_6" + "P-poll__networl_1_2_RP_7" + "P-poll__networl_1_2_RP_8" + "P-poll__networl_1_3_AskP_0" + "P-poll__networl_1_3_AskP_1" + "P-poll__networl_1_3_AskP_2" + "P-poll__networl_1_3_AskP_3" + "P-poll__networl_1_3_AskP_4" + "P-poll__networl_1_3_AskP_5" + "P-poll__networl_1_3_AskP_6" + "P-poll__networl_1_3_AskP_7" + "P-poll__networl_1_3_AskP_8" + "P-poll__networl_1_3_AnsP_0" + "P-poll__networl_1_3_AnsP_1" + "P-poll__networl_1_3_AnsP_2" + "P-poll__networl_1_3_AnsP_3" + "P-poll__networl_1_3_AnsP_4" + "P-poll__networl_1_3_AnsP_5" + "P-poll__networl_1_3_AnsP_6" + "P-poll__networl_1_3_AnsP_7" + "P-poll__networl_1_3_AnsP_8" + "P-poll__networl_1_3_RI_0" + "P-poll__networl_1_3_RI_1" + "P-poll__networl_1_3_RI_2" + "P-poll__networl_1_3_RI_3" + "P-poll__networl_1_3_RI_4" + "P-poll__networl_1_3_RI_5" + "P-poll__networl_1_3_RI_6" + "P-poll__networl_1_3_RI_7" + "P-poll__networl_1_3_RI_8" + "P-poll__networl_1_3_AI_0" + "P-poll__networl_1_3_AI_1" + "P-poll__networl_1_3_AI_2" + "P-poll__networl_1_3_AI_3" + "P-poll__networl_1_3_AI_4" + "P-poll__networl_1_3_AI_5" + "P-poll__networl_1_3_AI_6" + "P-poll__networl_1_3_AI_7" + "P-poll__networl_1_3_AI_8" + "P-poll__networl_1_3_AnnP_0" + "P-poll__networl_1_3_AnnP_1" + "P-poll__networl_1_3_AnnP_2" + "P-poll__networl_1_3_AnnP_3" + "P-poll__networl_1_3_AnnP_4" + "P-poll__networl_1_3_AnnP_5" + "P-poll__networl_1_3_AnnP_6" + "P-poll__networl_1_3_AnnP_7" + "P-poll__networl_1_3_AnnP_8" + "P-poll__networl_1_3_RP_0" + "P-poll__networl_1_3_RP_1" + "P-poll__networl_1_3_RP_2" + "P-poll__networl_1_3_RP_3" + "P-poll__networl_1_3_RP_4" + "P-poll__networl_1_3_RP_5" + "P-poll__networl_1_3_RP_6" + "P-poll__networl_1_3_RP_7" + "P-poll__networl_1_3_RP_8" + "P-poll__networl_1_4_AskP_0" + "P-poll__networl_1_4_AskP_1" + "P-poll__networl_1_4_AskP_2" + "P-poll__networl_1_4_AskP_3" + "P-poll__networl_1_4_AskP_4" + "P-poll__networl_1_4_AskP_5" + "P-poll__networl_1_4_AskP_6" + "P-poll__networl_1_4_AskP_7" + "P-poll__networl_1_4_AskP_8" + "P-poll__networl_1_4_AnsP_0" + "P-poll__networl_1_4_AnsP_1" + "P-poll__networl_1_4_AnsP_2" + "P-poll__networl_1_4_AnsP_3" + "P-poll__networl_1_4_AnsP_4" + "P-poll__networl_1_4_AnsP_5" + "P-poll__networl_1_4_AnsP_6" + "P-poll__networl_1_4_AnsP_7" + "P-poll__networl_1_4_AnsP_8" + "P-poll__networl_1_4_RI_0" + "P-poll__networl_1_4_RI_1" + "P-poll__networl_1_4_RI_2" + "P-poll__networl_1_4_RI_3" + "P-poll__networl_1_4_RI_4" + "P-poll__networl_1_4_RI_5" + "P-poll__networl_1_4_RI_6" + "P-poll__networl_1_4_RI_7" + "P-poll__networl_1_4_RI_8" + "P-poll__networl_1_4_AI_0" + "P-poll__networl_1_4_AI_1" + "P-poll__networl_1_4_AI_2" + "P-poll__networl_1_4_AI_3" + "P-poll__networl_1_4_AI_4" + "P-poll__networl_1_4_AI_5" + "P-poll__networl_1_4_AI_6" + "P-poll__networl_1_4_AI_7" + "P-poll__networl_1_4_AI_8" + "P-poll__networl_1_4_AnnP_0" + "P-poll__networl_1_4_AnnP_1" + "P-poll__networl_1_4_AnnP_2" + "P-poll__networl_1_4_AnnP_3" + "P-poll__networl_1_4_AnnP_4" + "P-poll__networl_1_4_AnnP_5" + "P-poll__networl_1_4_AnnP_6" + "P-poll__networl_1_4_AnnP_7" + "P-poll__networl_1_4_AnnP_8" + "P-poll__networl_1_4_RP_0" + "P-poll__networl_1_4_RP_1" + "P-poll__networl_1_4_RP_2" + "P-poll__networl_1_4_RP_3" + "P-poll__networl_1_4_RP_4" + "P-poll__networl_1_4_RP_5" + "P-poll__networl_1_4_RP_6" + "P-poll__networl_1_4_RP_7" + "P-poll__networl_1_4_RP_8" + "P-poll__networl_1_5_AskP_0" + "P-poll__networl_1_5_AskP_1" + "P-poll__networl_1_5_AskP_2" + "P-poll__networl_1_5_AskP_3" + "P-poll__networl_1_5_AskP_4" + "P-poll__networl_1_5_AskP_5" + "P-poll__networl_1_5_AskP_6" + "P-poll__networl_1_5_AskP_7" + "P-poll__networl_1_5_AskP_8" + "P-poll__networl_1_5_AnsP_0" + "P-poll__networl_1_5_AnsP_1" + "P-poll__networl_1_5_AnsP_2" + "P-poll__networl_1_5_AnsP_3" + "P-poll__networl_1_5_AnsP_4" + "P-poll__networl_1_5_AnsP_5" + "P-poll__networl_1_5_AnsP_6" + "P-poll__networl_1_5_AnsP_7" + "P-poll__networl_1_5_AnsP_8" + "P-poll__networl_1_5_RI_0" + "P-poll__networl_1_5_RI_1" + "P-poll__networl_1_5_RI_2" + "P-poll__networl_1_5_RI_3" + "P-poll__networl_1_5_RI_4" + "P-poll__networl_1_5_RI_5" + "P-poll__networl_1_5_RI_6" + "P-poll__networl_1_5_RI_7" + "P-poll__networl_1_5_RI_8" + "P-poll__networl_1_5_AI_0" + "P-poll__networl_1_5_AI_1" + "P-poll__networl_1_5_AI_2" + "P-poll__networl_1_5_AI_3" + "P-poll__networl_1_5_AI_4" + "P-poll__networl_1_5_AI_5" + "P-poll__networl_1_5_AI_6" + "P-poll__networl_1_5_AI_7" + "P-poll__networl_1_5_AI_8" + "P-poll__networl_1_5_AnnP_0" + "P-poll__networl_1_5_AnnP_1" + "P-poll__networl_1_5_AnnP_2" + "P-poll__networl_1_5_AnnP_3" + "P-poll__networl_1_5_AnnP_4" + "P-poll__networl_1_5_AnnP_5" + "P-poll__networl_1_5_AnnP_6" + "P-poll__networl_1_5_AnnP_7" + "P-poll__networl_1_5_AnnP_8" + "P-poll__networl_1_5_RP_0" + "P-poll__networl_1_5_RP_1" + "P-poll__networl_1_5_RP_2" + "P-poll__networl_1_5_RP_3" + "P-poll__networl_1_5_RP_4" + "P-poll__networl_1_5_RP_5" + "P-poll__networl_1_5_RP_6" + "P-poll__networl_1_5_RP_7" + "P-poll__networl_1_5_RP_8" + "P-poll__networl_1_6_AskP_0" + "P-poll__networl_1_6_AskP_1" + "P-poll__networl_1_6_AskP_2" + "P-poll__networl_1_6_AskP_3" + "P-poll__networl_1_6_AskP_4" + "P-poll__networl_1_6_AskP_5" + "P-poll__networl_1_6_AskP_6" + "P-poll__networl_1_6_AskP_7" + "P-poll__networl_1_6_AskP_8" + "P-poll__networl_1_6_AnsP_0" + "P-poll__networl_1_6_AnsP_1" + "P-poll__networl_1_6_AnsP_2" + "P-poll__networl_1_6_AnsP_3" + "P-poll__networl_1_6_AnsP_4" + "P-poll__networl_1_6_AnsP_5" + "P-poll__networl_1_6_AnsP_6" + "P-poll__networl_1_6_AnsP_7" + "P-poll__networl_1_6_AnsP_8" + "P-poll__networl_1_6_RI_0" + "P-poll__networl_1_6_RI_1" + "P-poll__networl_1_6_RI_2" + "P-poll__networl_1_6_RI_3" + "P-poll__networl_1_6_RI_4" + "P-poll__networl_1_6_RI_5" + "P-poll__networl_1_6_RI_6" + "P-poll__networl_1_6_RI_7" + "P-poll__networl_1_6_RI_8" + "P-poll__networl_1_6_AI_0" + "P-poll__networl_1_6_AI_1" + "P-poll__networl_1_6_AI_2" + "P-poll__networl_1_6_AI_3" + "P-poll__networl_1_6_AI_4" + "P-poll__networl_1_6_AI_5" + "P-poll__networl_1_6_AI_6" + "P-poll__networl_1_6_AI_7" + "P-poll__networl_1_6_AI_8" + "P-poll__networl_1_6_AnnP_0" + "P-poll__networl_1_6_AnnP_1" + "P-poll__networl_1_6_AnnP_2" + "P-poll__networl_1_6_AnnP_3" + "P-poll__networl_1_6_AnnP_4" + "P-poll__networl_1_6_AnnP_5" + "P-poll__networl_1_6_AnnP_6" + "P-poll__networl_1_6_AnnP_7" + "P-poll__networl_1_6_AnnP_8" + "P-poll__networl_1_6_RP_0" + "P-poll__networl_1_6_RP_1" + "P-poll__networl_1_6_RP_2" + "P-poll__networl_1_6_RP_3" + "P-poll__networl_1_6_RP_4" + "P-poll__networl_1_6_RP_5" + "P-poll__networl_1_6_RP_6" + "P-poll__networl_1_6_RP_7" + "P-poll__networl_1_6_RP_8" + "P-poll__networl_1_7_AskP_0" + "P-poll__networl_1_7_AskP_1" + "P-poll__networl_1_7_AskP_2" + "P-poll__networl_1_7_AskP_3" + "P-poll__networl_1_7_AskP_4" + "P-poll__networl_1_7_AskP_5" + "P-poll__networl_1_7_AskP_6" + "P-poll__networl_1_7_AskP_7" + "P-poll__networl_1_7_AskP_8" + "P-poll__networl_1_7_AnsP_0" + "P-poll__networl_1_7_AnsP_1" + "P-poll__networl_1_7_AnsP_2" + "P-poll__networl_1_7_AnsP_3" + "P-poll__networl_1_7_AnsP_4" + "P-poll__networl_1_7_AnsP_5" + "P-poll__networl_1_7_AnsP_6" + "P-poll__networl_1_7_AnsP_7" + "P-poll__networl_1_7_AnsP_8" + "P-poll__networl_1_7_RI_0" + "P-poll__networl_1_7_RI_1" + "P-poll__networl_1_7_RI_2" + "P-poll__networl_1_7_RI_3" + "P-poll__networl_1_7_RI_4" + "P-poll__networl_1_7_RI_5" + "P-poll__networl_1_7_RI_6" + "P-poll__networl_1_7_RI_7" + "P-poll__networl_1_7_RI_8" + "P-poll__networl_1_7_AI_0" + "P-poll__networl_1_7_AI_1" + "P-poll__networl_1_7_AI_2" + "P-poll__networl_1_7_AI_3" + "P-poll__networl_1_7_AI_4" + "P-poll__networl_1_7_AI_5" + "P-poll__networl_1_7_AI_6" + "P-poll__networl_1_7_AI_7" + "P-poll__networl_1_7_AI_8" + "P-poll__networl_1_7_AnnP_0" + "P-poll__networl_1_7_AnnP_1" + "P-poll__networl_1_7_AnnP_2" + "P-poll__networl_1_7_AnnP_3" + "P-poll__networl_1_7_AnnP_4" + "P-poll__networl_1_7_AnnP_5" + "P-poll__networl_1_7_AnnP_6" + "P-poll__networl_1_7_AnnP_7" + "P-poll__networl_1_7_AnnP_8" + "P-poll__networl_1_7_RP_0" + "P-poll__networl_1_7_RP_1" + "P-poll__networl_1_7_RP_2" + "P-poll__networl_1_7_RP_3" + "P-poll__networl_1_7_RP_4" + "P-poll__networl_1_7_RP_5" + "P-poll__networl_1_7_RP_6" + "P-poll__networl_1_7_RP_7" + "P-poll__networl_1_7_RP_8" + "P-poll__networl_1_8_AskP_0" + "P-poll__networl_1_8_AskP_1" + "P-poll__networl_1_8_AskP_2" + "P-poll__networl_1_8_AskP_3" + "P-poll__networl_1_8_AskP_4" + "P-poll__networl_1_8_AskP_5" + "P-poll__networl_1_8_AskP_6" + "P-poll__networl_1_8_AskP_7" + "P-poll__networl_1_8_AskP_8" + "P-poll__networl_1_8_AnsP_0" + "P-poll__networl_1_8_AnsP_1" + "P-poll__networl_1_8_AnsP_2" + "P-poll__networl_1_8_AnsP_3" + "P-poll__networl_1_8_AnsP_4" + "P-poll__networl_1_8_AnsP_5" + "P-poll__networl_1_8_AnsP_6" + "P-poll__networl_1_8_AnsP_7" + "P-poll__networl_1_8_AnsP_8" + "P-poll__networl_1_8_RI_0" + "P-poll__networl_1_8_RI_1" + "P-poll__networl_1_8_RI_2" + "P-poll__networl_1_8_RI_3" + "P-poll__networl_1_8_RI_4" + "P-poll__networl_1_8_RI_5" + "P-poll__networl_1_8_RI_6" + "P-poll__networl_1_8_RI_7" + "P-poll__networl_1_8_RI_8" + "P-poll__networl_1_8_AI_0" + "P-poll__networl_1_8_AI_1" + "P-poll__networl_1_8_AI_2" + "P-poll__networl_1_8_AI_3" + "P-poll__networl_1_8_AI_4" + "P-poll__networl_1_8_AI_5" + "P-poll__networl_1_8_AI_6" + "P-poll__networl_1_8_AI_7" + "P-poll__networl_1_8_AI_8" + "P-poll__networl_1_8_AnnP_0" + "P-poll__networl_1_8_AnnP_1" + "P-poll__networl_1_8_AnnP_2" + "P-poll__networl_1_8_AnnP_3" + "P-poll__networl_1_8_AnnP_4" + "P-poll__networl_1_8_AnnP_5" + "P-poll__networl_1_8_AnnP_6" + "P-poll__networl_1_8_AnnP_7" + "P-poll__networl_1_8_AnnP_8" + "P-poll__networl_1_8_RP_0" + "P-poll__networl_1_8_RP_1" + "P-poll__networl_1_8_RP_2" + "P-poll__networl_1_8_RP_3" + "P-poll__networl_1_8_RP_4" + "P-poll__networl_1_8_RP_5" + "P-poll__networl_1_8_RP_6" + "P-poll__networl_1_8_RP_7" + "P-poll__networl_1_8_RP_8" + "P-poll__networl_2_0_AskP_0" + "P-poll__networl_2_0_AskP_1" + "P-poll__networl_2_0_AskP_2" + "P-poll__networl_2_0_AskP_3" + "P-poll__networl_2_0_AskP_4" + "P-poll__networl_2_0_AskP_5" + "P-poll__networl_2_0_AskP_6" + "P-poll__networl_2_0_AskP_7" + "P-poll__networl_2_0_AskP_8" + "P-poll__networl_2_0_AnsP_0" + "P-poll__networl_2_0_AnsP_1" + "P-poll__networl_2_0_AnsP_2" + "P-poll__networl_2_0_AnsP_3" + "P-poll__networl_2_0_AnsP_4" + "P-poll__networl_2_0_AnsP_5" + "P-poll__networl_2_0_AnsP_6" + "P-poll__networl_2_0_AnsP_7" + "P-poll__networl_2_0_AnsP_8" + "P-poll__networl_2_0_RI_0" + "P-poll__networl_2_0_RI_1" + "P-poll__networl_2_0_RI_2" + "P-poll__networl_2_0_RI_3" + "P-poll__networl_2_0_RI_4" + "P-poll__networl_2_0_RI_5" + "P-poll__networl_2_0_RI_6" + "P-poll__networl_2_0_RI_7" + "P-poll__networl_2_0_RI_8" + "P-poll__networl_2_0_AI_0" + "P-poll__networl_2_0_AI_1" + "P-poll__networl_2_0_AI_2" + "P-poll__networl_2_0_AI_3" + "P-poll__networl_2_0_AI_4" + "P-poll__networl_2_0_AI_5" + "P-poll__networl_2_0_AI_6" + "P-poll__networl_2_0_AI_7" + "P-poll__networl_2_0_AI_8" + "P-poll__networl_2_0_AnnP_0" + "P-poll__networl_2_0_AnnP_1" + "P-poll__networl_2_0_AnnP_2" + "P-poll__networl_2_0_AnnP_3" + "P-poll__networl_2_0_AnnP_4" + "P-poll__networl_2_0_AnnP_5" + "P-poll__networl_2_0_AnnP_6" + "P-poll__networl_2_0_AnnP_7" + "P-poll__networl_2_0_AnnP_8" + "P-poll__networl_2_0_RP_0" + "P-poll__networl_2_0_RP_1" + "P-poll__networl_2_0_RP_2" + "P-poll__networl_2_0_RP_3" + "P-poll__networl_2_0_RP_4" + "P-poll__networl_2_0_RP_5" + "P-poll__networl_2_0_RP_6" + "P-poll__networl_2_0_RP_7" + "P-poll__networl_2_0_RP_8" + "P-poll__networl_2_1_AskP_0" + "P-poll__networl_2_1_AskP_1" + "P-poll__networl_2_1_AskP_2" + "P-poll__networl_2_1_AskP_3" + "P-poll__networl_2_1_AskP_4" + "P-poll__networl_2_1_AskP_5" + "P-poll__networl_2_1_AskP_6" + "P-poll__networl_2_1_AskP_7" + "P-poll__networl_2_1_AskP_8" + "P-poll__networl_2_1_AnsP_0" + "P-poll__networl_2_1_AnsP_1" + "P-poll__networl_2_1_AnsP_2" + "P-poll__networl_2_1_AnsP_3" + "P-poll__networl_2_1_AnsP_4" + "P-poll__networl_2_1_AnsP_5" + "P-poll__networl_2_1_AnsP_6" + "P-poll__networl_2_1_AnsP_7" + "P-poll__networl_2_1_AnsP_8" + "P-poll__networl_2_1_RI_0" + "P-poll__networl_2_1_RI_1" + "P-poll__networl_2_1_RI_2" + "P-poll__networl_2_1_RI_3" + "P-poll__networl_2_1_RI_4" + "P-poll__networl_2_1_RI_5" + "P-poll__networl_2_1_RI_6" + "P-poll__networl_2_1_RI_7" + "P-poll__networl_2_1_RI_8" + "P-poll__networl_2_1_AI_0" + "P-poll__networl_2_1_AI_1" + "P-poll__networl_2_1_AI_2" + "P-poll__networl_2_1_AI_3" + "P-poll__networl_2_1_AI_4" + "P-poll__networl_2_1_AI_5" + "P-poll__networl_2_1_AI_6" + "P-poll__networl_2_1_AI_7" + "P-poll__networl_2_1_AI_8" + "P-poll__networl_2_1_AnnP_0" + "P-poll__networl_2_1_AnnP_1" + "P-poll__networl_2_1_AnnP_2" + "P-poll__networl_2_1_AnnP_3" + "P-poll__networl_2_1_AnnP_4" + "P-poll__networl_2_1_AnnP_5" + "P-poll__networl_2_1_AnnP_6" + "P-poll__networl_2_1_AnnP_7" + "P-poll__networl_2_1_AnnP_8" + "P-poll__networl_2_1_RP_0" + "P-poll__networl_2_1_RP_1" + "P-poll__networl_2_1_RP_2" + "P-poll__networl_2_1_RP_3" + "P-poll__networl_2_1_RP_4" + "P-poll__networl_2_1_RP_5" + "P-poll__networl_2_1_RP_6" + "P-poll__networl_2_1_RP_7" + "P-poll__networl_2_1_RP_8" + "P-poll__networl_2_2_AskP_0" + "P-poll__networl_2_2_AskP_1" + "P-poll__networl_2_2_AskP_2" + "P-poll__networl_2_2_AskP_3" + "P-poll__networl_2_2_AskP_4" + "P-poll__networl_2_2_AskP_5" + "P-poll__networl_2_2_AskP_6" + "P-poll__networl_2_2_AskP_7" + "P-poll__networl_2_2_AskP_8" + "P-poll__networl_2_2_AnsP_0" + "P-poll__networl_2_2_AnsP_1" + "P-poll__networl_2_2_AnsP_2" + "P-poll__networl_2_2_AnsP_3" + "P-poll__networl_2_2_AnsP_4" + "P-poll__networl_2_2_AnsP_5" + "P-poll__networl_2_2_AnsP_6" + "P-poll__networl_2_2_AnsP_7" + "P-poll__networl_2_2_AnsP_8" + "P-poll__networl_2_2_RI_0" + "P-poll__networl_2_2_RI_1" + "P-poll__networl_2_2_RI_2" + "P-poll__networl_2_2_RI_3" + "P-poll__networl_2_2_RI_4" + "P-poll__networl_2_2_RI_5" + "P-poll__networl_2_2_RI_6" + "P-poll__networl_2_2_RI_7" + "P-poll__networl_2_2_RI_8" + "P-poll__networl_2_2_AI_0" + "P-poll__networl_2_2_AI_1" + "P-poll__networl_2_2_AI_2" + "P-poll__networl_2_2_AI_3" + "P-poll__networl_2_2_AI_4" + "P-poll__networl_2_2_AI_5" + "P-poll__networl_2_2_AI_6" + "P-poll__networl_2_2_AI_7" + "P-poll__networl_2_2_AI_8" + "P-poll__networl_2_2_AnnP_0" + "P-poll__networl_2_2_AnnP_1" + "P-poll__networl_2_2_AnnP_2" + "P-poll__networl_2_2_AnnP_3" + "P-poll__networl_2_2_AnnP_4" + "P-poll__networl_2_2_AnnP_5" + "P-poll__networl_2_2_AnnP_6" + "P-poll__networl_2_2_AnnP_7" + "P-poll__networl_2_2_AnnP_8" + "P-poll__networl_2_2_RP_0" + "P-poll__networl_2_2_RP_1" + "P-poll__networl_2_2_RP_2" + "P-poll__networl_2_2_RP_3" + "P-poll__networl_2_2_RP_4" + "P-poll__networl_2_2_RP_5" + "P-poll__networl_2_2_RP_6" + "P-poll__networl_2_2_RP_7" + "P-poll__networl_2_2_RP_8" + "P-poll__networl_2_3_AskP_0" + "P-poll__networl_2_3_AskP_1" + "P-poll__networl_2_3_AskP_2" + "P-poll__networl_2_3_AskP_3" + "P-poll__networl_2_3_AskP_4" + "P-poll__networl_2_3_AskP_5" + "P-poll__networl_2_3_AskP_6" + "P-poll__networl_2_3_AskP_7" + "P-poll__networl_2_3_AskP_8" + "P-poll__networl_2_3_AnsP_0" + "P-poll__networl_2_3_AnsP_1" + "P-poll__networl_2_3_AnsP_2" + "P-poll__networl_2_3_AnsP_3" + "P-poll__networl_2_3_AnsP_4" + "P-poll__networl_2_3_AnsP_5" + "P-poll__networl_2_3_AnsP_6" + "P-poll__networl_2_3_AnsP_7" + "P-poll__networl_2_3_AnsP_8" + "P-poll__networl_2_3_RI_0" + "P-poll__networl_2_3_RI_1" + "P-poll__networl_2_3_RI_2" + "P-poll__networl_2_3_RI_3" + "P-poll__networl_2_3_RI_4" + "P-poll__networl_2_3_RI_5" + "P-poll__networl_2_3_RI_6" + "P-poll__networl_2_3_RI_7" + "P-poll__networl_2_3_RI_8" + "P-poll__networl_2_3_AI_0" + "P-poll__networl_2_3_AI_1" + "P-poll__networl_2_3_AI_2" + "P-poll__networl_2_3_AI_3" + "P-poll__networl_2_3_AI_4" + "P-poll__networl_2_3_AI_5" + "P-poll__networl_2_3_AI_6" + "P-poll__networl_2_3_AI_7" + "P-poll__networl_2_3_AI_8" + "P-poll__networl_2_3_AnnP_0" + "P-poll__networl_2_3_AnnP_1" + "P-poll__networl_2_3_AnnP_2" + "P-poll__networl_2_3_AnnP_3" + "P-poll__networl_2_3_AnnP_4" + "P-poll__networl_2_3_AnnP_5" + "P-poll__networl_2_3_AnnP_6" + "P-poll__networl_2_3_AnnP_7" + "P-poll__networl_2_3_AnnP_8" + "P-poll__networl_2_3_RP_0" + "P-poll__networl_2_3_RP_1" + "P-poll__networl_2_3_RP_2" + "P-poll__networl_2_3_RP_3" + "P-poll__networl_2_3_RP_4" + "P-poll__networl_2_3_RP_5" + "P-poll__networl_2_3_RP_6" + "P-poll__networl_2_3_RP_7" + "P-poll__networl_2_3_RP_8" + "P-poll__networl_2_4_AskP_0" + "P-poll__networl_2_4_AskP_1" + "P-poll__networl_2_4_AskP_2" + "P-poll__networl_2_4_AskP_3" + "P-poll__networl_2_4_AskP_4" + "P-poll__networl_2_4_AskP_5" + "P-poll__networl_2_4_AskP_6" + "P-poll__networl_2_4_AskP_7" + "P-poll__networl_2_4_AskP_8" + "P-poll__networl_2_4_AnsP_0" + "P-poll__networl_2_4_AnsP_1" + "P-poll__networl_2_4_AnsP_2" + "P-poll__networl_2_4_AnsP_3" + "P-poll__networl_2_4_AnsP_4" + "P-poll__networl_2_4_AnsP_5" + "P-poll__networl_2_4_AnsP_6" + "P-poll__networl_2_4_AnsP_7" + "P-poll__networl_2_4_AnsP_8" + "P-poll__networl_2_4_RI_0" + "P-poll__networl_2_4_RI_1" + "P-poll__networl_2_4_RI_2" + "P-poll__networl_2_4_RI_3" + "P-poll__networl_2_4_RI_4" + "P-poll__networl_2_4_RI_5" + "P-poll__networl_2_4_RI_6" + "P-poll__networl_2_4_RI_7" + "P-poll__networl_2_4_RI_8" + "P-poll__networl_2_4_AI_0" + "P-poll__networl_2_4_AI_1" + "P-poll__networl_2_4_AI_2" + "P-poll__networl_2_4_AI_3" + "P-poll__networl_2_4_AI_4" + "P-poll__networl_2_4_AI_5" + "P-poll__networl_2_4_AI_6" + "P-poll__networl_2_4_AI_7" + "P-poll__networl_2_4_AI_8" + "P-poll__networl_2_4_AnnP_0" + "P-poll__networl_2_4_AnnP_1" + "P-poll__networl_2_4_AnnP_2" + "P-poll__networl_2_4_AnnP_3" + "P-poll__networl_2_4_AnnP_4" + "P-poll__networl_2_4_AnnP_5" + "P-poll__networl_2_4_AnnP_6" + "P-poll__networl_2_4_AnnP_7" + "P-poll__networl_2_4_AnnP_8" + "P-poll__networl_2_4_RP_0" + "P-poll__networl_2_4_RP_1" + "P-poll__networl_2_4_RP_2" + "P-poll__networl_2_4_RP_3" + "P-poll__networl_2_4_RP_4" + "P-poll__networl_2_4_RP_5" + "P-poll__networl_2_4_RP_6" + "P-poll__networl_2_4_RP_7" + "P-poll__networl_2_4_RP_8" + "P-poll__networl_2_5_AskP_0" + "P-poll__networl_2_5_AskP_1" + "P-poll__networl_2_5_AskP_2" + "P-poll__networl_2_5_AskP_3" + "P-poll__networl_2_5_AskP_4" + "P-poll__networl_2_5_AskP_5" + "P-poll__networl_2_5_AskP_6" + "P-poll__networl_2_5_AskP_7" + "P-poll__networl_2_5_AskP_8" + "P-poll__networl_2_5_AnsP_0" + "P-poll__networl_2_5_AnsP_1" + "P-poll__networl_2_5_AnsP_2" + "P-poll__networl_2_5_AnsP_3" + "P-poll__networl_2_5_AnsP_4" + "P-poll__networl_2_5_AnsP_5" + "P-poll__networl_2_5_AnsP_6" + "P-poll__networl_2_5_AnsP_7" + "P-poll__networl_2_5_AnsP_8" + "P-poll__networl_2_5_RI_0" + "P-poll__networl_2_5_RI_1" + "P-poll__networl_2_5_RI_2" + "P-poll__networl_2_5_RI_3" + "P-poll__networl_2_5_RI_4" + "P-poll__networl_2_5_RI_5" + "P-poll__networl_2_5_RI_6" + "P-poll__networl_2_5_RI_7" + "P-poll__networl_2_5_RI_8" + "P-poll__networl_2_5_AI_0" + "P-poll__networl_2_5_AI_1" + "P-poll__networl_2_5_AI_2" + "P-poll__networl_2_5_AI_3" + "P-poll__networl_2_5_AI_4" + "P-poll__networl_2_5_AI_5" + "P-poll__networl_2_5_AI_6" + "P-poll__networl_2_5_AI_7" + "P-poll__networl_2_5_AI_8" + "P-poll__networl_2_5_AnnP_0" + "P-poll__networl_2_5_AnnP_1" + "P-poll__networl_2_5_AnnP_2" + "P-poll__networl_2_5_AnnP_3" + "P-poll__networl_2_5_AnnP_4" + "P-poll__networl_2_5_AnnP_5" + "P-poll__networl_2_5_AnnP_6" + "P-poll__networl_2_5_AnnP_7" + "P-poll__networl_2_5_AnnP_8" + "P-poll__networl_2_5_RP_0" + "P-poll__networl_2_5_RP_1" + "P-poll__networl_2_5_RP_2" + "P-poll__networl_2_5_RP_3" + "P-poll__networl_2_5_RP_4" + "P-poll__networl_2_5_RP_5" + "P-poll__networl_2_5_RP_6" + "P-poll__networl_2_5_RP_7" + "P-poll__networl_2_5_RP_8" + "P-poll__networl_2_6_AskP_0" + "P-poll__networl_2_6_AskP_1" + "P-poll__networl_2_6_AskP_2" + "P-poll__networl_2_6_AskP_3" + "P-poll__networl_2_6_AskP_4" + "P-poll__networl_2_6_AskP_5" + "P-poll__networl_2_6_AskP_6" + "P-poll__networl_2_6_AskP_7" + "P-poll__networl_2_6_AskP_8" + "P-poll__networl_2_6_AnsP_0" + "P-poll__networl_2_6_AnsP_1" + "P-poll__networl_2_6_AnsP_2" + "P-poll__networl_2_6_AnsP_3" + "P-poll__networl_2_6_AnsP_4" + "P-poll__networl_2_6_AnsP_5" + "P-poll__networl_2_6_AnsP_6" + "P-poll__networl_2_6_AnsP_7" + "P-poll__networl_2_6_AnsP_8" + "P-poll__networl_2_6_RI_0" + "P-poll__networl_2_6_RI_1" + "P-poll__networl_2_6_RI_2" + "P-poll__networl_2_6_RI_3" + "P-poll__networl_2_6_RI_4" + "P-poll__networl_2_6_RI_5" + "P-poll__networl_2_6_RI_6" + "P-poll__networl_2_6_RI_7" + "P-poll__networl_2_6_RI_8" + "P-poll__networl_2_6_AI_0" + "P-poll__networl_2_6_AI_1" + "P-poll__networl_2_6_AI_2" + "P-poll__networl_2_6_AI_3" + "P-poll__networl_2_6_AI_4" + "P-poll__networl_2_6_AI_5" + "P-poll__networl_2_6_AI_6" + "P-poll__networl_2_6_AI_7" + "P-poll__networl_2_6_AI_8" + "P-poll__networl_2_6_AnnP_0" + "P-poll__networl_2_6_AnnP_1" + "P-poll__networl_2_6_AnnP_2" + "P-poll__networl_2_6_AnnP_3" + "P-poll__networl_2_6_AnnP_4" + "P-poll__networl_2_6_AnnP_5" + "P-poll__networl_2_6_AnnP_6" + "P-poll__networl_2_6_AnnP_7" + "P-poll__networl_2_6_AnnP_8" + "P-poll__networl_2_6_RP_0" + "P-poll__networl_2_6_RP_1" + "P-poll__networl_2_6_RP_2" + "P-poll__networl_2_6_RP_3" + "P-poll__networl_2_6_RP_4" + "P-poll__networl_2_6_RP_5" + "P-poll__networl_2_6_RP_6" + "P-poll__networl_2_6_RP_7" + "P-poll__networl_2_6_RP_8" + "P-poll__networl_2_7_AskP_0" + "P-poll__networl_2_7_AskP_1" + "P-poll__networl_2_7_AskP_2" + "P-poll__networl_2_7_AskP_3" + "P-poll__networl_2_7_AskP_4" + "P-poll__networl_2_7_AskP_5" + "P-poll__networl_2_7_AskP_6" + "P-poll__networl_2_7_AskP_7" + "P-poll__networl_2_7_AskP_8" + "P-poll__networl_2_7_AnsP_0" + "P-poll__networl_2_7_AnsP_1" + "P-poll__networl_2_7_AnsP_2" + "P-poll__networl_2_7_AnsP_3" + "P-poll__networl_2_7_AnsP_4" + "P-poll__networl_2_7_AnsP_5" + "P-poll__networl_2_7_AnsP_6" + "P-poll__networl_2_7_AnsP_7" + "P-poll__networl_2_7_AnsP_8" + "P-poll__networl_2_7_RI_0" + "P-poll__networl_2_7_RI_1" + "P-poll__networl_2_7_RI_2" + "P-poll__networl_2_7_RI_3" + "P-poll__networl_2_7_RI_4" + "P-poll__networl_2_7_RI_5" + "P-poll__networl_2_7_RI_6" + "P-poll__networl_2_7_RI_7" + "P-poll__networl_2_7_RI_8" + "P-poll__networl_2_7_AI_0" + "P-poll__networl_2_7_AI_1" + "P-poll__networl_2_7_AI_2" + "P-poll__networl_2_7_AI_3" + "P-poll__networl_2_7_AI_4" + "P-poll__networl_2_7_AI_5" + "P-poll__networl_2_7_AI_6" + "P-poll__networl_2_7_AI_7" + "P-poll__networl_2_7_AI_8" + "P-poll__networl_2_7_AnnP_0" + "P-poll__networl_2_7_AnnP_1" + "P-poll__networl_2_7_AnnP_2" + "P-poll__networl_2_7_AnnP_3" + "P-poll__networl_2_7_AnnP_4" + "P-poll__networl_2_7_AnnP_5" + "P-poll__networl_2_7_AnnP_6" + "P-poll__networl_2_7_AnnP_7" + "P-poll__networl_2_7_AnnP_8" + "P-poll__networl_2_7_RP_0" + "P-poll__networl_2_7_RP_1" + "P-poll__networl_2_7_RP_2" + "P-poll__networl_2_7_RP_3" + "P-poll__networl_2_7_RP_4" + "P-poll__networl_2_7_RP_5" + "P-poll__networl_2_7_RP_6" + "P-poll__networl_2_7_RP_7" + "P-poll__networl_2_7_RP_8" + "P-poll__networl_2_8_AskP_0" + "P-poll__networl_2_8_AskP_1" + "P-poll__networl_2_8_AskP_2" + "P-poll__networl_2_8_AskP_3" + "P-poll__networl_2_8_AskP_4" + "P-poll__networl_2_8_AskP_5" + "P-poll__networl_2_8_AskP_6" + "P-poll__networl_2_8_AskP_7" + "P-poll__networl_2_8_AskP_8" + "P-poll__networl_2_8_AnsP_0" + "P-poll__networl_2_8_AnsP_1" + "P-poll__networl_2_8_AnsP_2" + "P-poll__networl_2_8_AnsP_3" + "P-poll__networl_2_8_AnsP_4" + "P-poll__networl_2_8_AnsP_5" + "P-poll__networl_2_8_AnsP_6" + "P-poll__networl_2_8_AnsP_7" + "P-poll__networl_2_8_AnsP_8" + "P-poll__networl_2_8_RI_0" + "P-poll__networl_2_8_RI_1" + "P-poll__networl_2_8_RI_2" + "P-poll__networl_2_8_RI_3" + "P-poll__networl_2_8_RI_4" + "P-poll__networl_2_8_RI_5" + "P-poll__networl_2_8_RI_6" + "P-poll__networl_2_8_RI_7" + "P-poll__networl_2_8_RI_8" + "P-poll__networl_2_8_AI_0" + "P-poll__networl_2_8_AI_1" + "P-poll__networl_2_8_AI_2" + "P-poll__networl_2_8_AI_3" + "P-poll__networl_2_8_AI_4" + "P-poll__networl_2_8_AI_5" + "P-poll__networl_2_8_AI_6" + "P-poll__networl_2_8_AI_7" + "P-poll__networl_2_8_AI_8" + "P-poll__networl_2_8_AnnP_0" + "P-poll__networl_2_8_AnnP_1" + "P-poll__networl_2_8_AnnP_2" + "P-poll__networl_2_8_AnnP_3" + "P-poll__networl_2_8_AnnP_4" + "P-poll__networl_2_8_AnnP_5" + "P-poll__networl_2_8_AnnP_6" + "P-poll__networl_2_8_AnnP_7" + "P-poll__networl_2_8_AnnP_8" + "P-poll__networl_2_8_RP_0" + "P-poll__networl_2_8_RP_1" + "P-poll__networl_2_8_RP_2" + "P-poll__networl_2_8_RP_3" + "P-poll__networl_2_8_RP_4" + "P-poll__networl_2_8_RP_5" + "P-poll__networl_2_8_RP_6" + "P-poll__networl_2_8_RP_7" + "P-poll__networl_2_8_RP_8" + "P-poll__networl_3_0_AskP_0" + "P-poll__networl_3_0_AskP_1" + "P-poll__networl_3_0_AskP_2" + "P-poll__networl_3_0_AskP_3" + "P-poll__networl_3_0_AskP_4" + "P-poll__networl_3_0_AskP_5" + "P-poll__networl_3_0_AskP_6" + "P-poll__networl_3_0_AskP_7" + "P-poll__networl_3_0_AskP_8" + "P-poll__networl_3_0_AnsP_0" + "P-poll__networl_3_0_AnsP_1" + "P-poll__networl_3_0_AnsP_2" + "P-poll__networl_3_0_AnsP_3" + "P-poll__networl_3_0_AnsP_4" + "P-poll__networl_3_0_AnsP_5" + "P-poll__networl_3_0_AnsP_6" + "P-poll__networl_3_0_AnsP_7" + "P-poll__networl_3_0_AnsP_8" + "P-poll__networl_3_0_RI_0" + "P-poll__networl_3_0_RI_1" + "P-poll__networl_3_0_RI_2" + "P-poll__networl_3_0_RI_3" + "P-poll__networl_3_0_RI_4" + "P-poll__networl_3_0_RI_5" + "P-poll__networl_3_0_RI_6" + "P-poll__networl_3_0_RI_7" + "P-poll__networl_3_0_RI_8" + "P-poll__networl_3_0_AI_0" + "P-poll__networl_3_0_AI_1" + "P-poll__networl_3_0_AI_2" + "P-poll__networl_3_0_AI_3" + "P-poll__networl_3_0_AI_4" + "P-poll__networl_3_0_AI_5" + "P-poll__networl_3_0_AI_6" + "P-poll__networl_3_0_AI_7" + "P-poll__networl_3_0_AI_8" + "P-poll__networl_3_0_AnnP_0" + "P-poll__networl_3_0_AnnP_1" + "P-poll__networl_3_0_AnnP_2" + "P-poll__networl_3_0_AnnP_3" + "P-poll__networl_3_0_AnnP_4" + "P-poll__networl_3_0_AnnP_5" + "P-poll__networl_3_0_AnnP_6" + "P-poll__networl_3_0_AnnP_7" + "P-poll__networl_3_0_AnnP_8" + "P-poll__networl_3_0_RP_0" + "P-poll__networl_3_0_RP_1" + "P-poll__networl_3_0_RP_2" + "P-poll__networl_3_0_RP_3" + "P-poll__networl_3_0_RP_4" + "P-poll__networl_3_0_RP_5" + "P-poll__networl_3_0_RP_6" + "P-poll__networl_3_0_RP_7" + "P-poll__networl_3_0_RP_8" + "P-poll__networl_3_1_AskP_0" + "P-poll__networl_3_1_AskP_1" + "P-poll__networl_3_1_AskP_2" + "P-poll__networl_3_1_AskP_3" + "P-poll__networl_3_1_AskP_4" + "P-poll__networl_3_1_AskP_5" + "P-poll__networl_3_1_AskP_6" + "P-poll__networl_3_1_AskP_7" + "P-poll__networl_3_1_AskP_8" + "P-poll__networl_3_1_AnsP_0" + "P-poll__networl_3_1_AnsP_1" + "P-poll__networl_3_1_AnsP_2" + "P-poll__networl_3_1_AnsP_3" + "P-poll__networl_3_1_AnsP_4" + "P-poll__networl_3_1_AnsP_5" + "P-poll__networl_3_1_AnsP_6" + "P-poll__networl_3_1_AnsP_7" + "P-poll__networl_3_1_AnsP_8" + "P-poll__networl_3_1_RI_0" + "P-poll__networl_3_1_RI_1" + "P-poll__networl_3_1_RI_2" + "P-poll__networl_3_1_RI_3" + "P-poll__networl_3_1_RI_4" + "P-poll__networl_3_1_RI_5" + "P-poll__networl_3_1_RI_6" + "P-poll__networl_3_1_RI_7" + "P-poll__networl_3_1_RI_8" + "P-poll__networl_3_1_AI_0" + "P-poll__networl_3_1_AI_1" + "P-poll__networl_3_1_AI_2" + "P-poll__networl_3_1_AI_3" + "P-poll__networl_3_1_AI_4" + "P-poll__networl_3_1_AI_5" + "P-poll__networl_3_1_AI_6" + "P-poll__networl_3_1_AI_7" + "P-poll__networl_3_1_AI_8" + "P-poll__networl_3_1_AnnP_0" + "P-poll__networl_3_1_AnnP_1" + "P-poll__networl_3_1_AnnP_2" + "P-poll__networl_3_1_AnnP_3" + "P-poll__networl_3_1_AnnP_4" + "P-poll__networl_3_1_AnnP_5" + "P-poll__networl_3_1_AnnP_6" + "P-poll__networl_3_1_AnnP_7" + "P-poll__networl_3_1_AnnP_8" + "P-poll__networl_3_1_RP_0" + "P-poll__networl_3_1_RP_1" + "P-poll__networl_3_1_RP_2" + "P-poll__networl_3_1_RP_3" + "P-poll__networl_3_1_RP_4" + "P-poll__networl_3_1_RP_5" + "P-poll__networl_3_1_RP_6" + "P-poll__networl_3_1_RP_7" + "P-poll__networl_3_1_RP_8" + "P-poll__networl_3_2_AskP_0" + "P-poll__networl_3_2_AskP_1" + "P-poll__networl_3_2_AskP_2" + "P-poll__networl_3_2_AskP_3" + "P-poll__networl_3_2_AskP_4" + "P-poll__networl_3_2_AskP_5" + "P-poll__networl_3_2_AskP_6" + "P-poll__networl_3_2_AskP_7" + "P-poll__networl_3_2_AskP_8" + "P-poll__networl_3_2_AnsP_0" + "P-poll__networl_3_2_AnsP_1" + "P-poll__networl_3_2_AnsP_2" + "P-poll__networl_3_2_AnsP_3" + "P-poll__networl_3_2_AnsP_4" + "P-poll__networl_3_2_AnsP_5" + "P-poll__networl_3_2_AnsP_6" + "P-poll__networl_3_2_AnsP_7" + "P-poll__networl_3_2_AnsP_8" + "P-poll__networl_3_2_RI_0" + "P-poll__networl_3_2_RI_1" + "P-poll__networl_3_2_RI_2" + "P-poll__networl_3_2_RI_3" + "P-poll__networl_3_2_RI_4" + "P-poll__networl_3_2_RI_5" + "P-poll__networl_3_2_RI_6" + "P-poll__networl_3_2_RI_7" + "P-poll__networl_3_2_RI_8" + "P-poll__networl_3_2_AI_0" + "P-poll__networl_3_2_AI_1" + "P-poll__networl_3_2_AI_2" + "P-poll__networl_3_2_AI_3" + "P-poll__networl_3_2_AI_4" + "P-poll__networl_3_2_AI_5" + "P-poll__networl_3_2_AI_6" + "P-poll__networl_3_2_AI_7" + "P-poll__networl_3_2_AI_8" + "P-poll__networl_3_2_AnnP_0" + "P-poll__networl_3_2_AnnP_1" + "P-poll__networl_3_2_AnnP_2" + "P-poll__networl_3_2_AnnP_3" + "P-poll__networl_3_2_AnnP_4" + "P-poll__networl_3_2_AnnP_5" + "P-poll__networl_3_2_AnnP_6" + "P-poll__networl_3_2_AnnP_7" + "P-poll__networl_3_2_AnnP_8" + "P-poll__networl_3_2_RP_0" + "P-poll__networl_3_2_RP_1" + "P-poll__networl_3_2_RP_2" + "P-poll__networl_3_2_RP_3" + "P-poll__networl_3_2_RP_4" + "P-poll__networl_3_2_RP_5" + "P-poll__networl_3_2_RP_6" + "P-poll__networl_3_2_RP_7" + "P-poll__networl_3_2_RP_8" + "P-poll__networl_3_3_AskP_0" + "P-poll__networl_3_3_AskP_1" + "P-poll__networl_3_3_AskP_2" + "P-poll__networl_3_3_AskP_3" + "P-poll__networl_3_3_AskP_4" + "P-poll__networl_3_3_AskP_5" + "P-poll__networl_3_3_AskP_6" + "P-poll__networl_3_3_AskP_7" + "P-poll__networl_3_3_AskP_8" + "P-poll__networl_3_3_AnsP_0" + "P-poll__networl_3_3_AnsP_1" + "P-poll__networl_3_3_AnsP_2" + "P-poll__networl_3_3_AnsP_3" + "P-poll__networl_3_3_AnsP_4" + "P-poll__networl_3_3_AnsP_5" + "P-poll__networl_3_3_AnsP_6" + "P-poll__networl_3_3_AnsP_7" + "P-poll__networl_3_3_AnsP_8" + "P-poll__networl_3_3_RI_0" + "P-poll__networl_3_3_RI_1" + "P-poll__networl_3_3_RI_2" + "P-poll__networl_3_3_RI_3" + "P-poll__networl_3_3_RI_4" + "P-poll__networl_3_3_RI_5" + "P-poll__networl_3_3_RI_6" + "P-poll__networl_3_3_RI_7" + "P-poll__networl_3_3_RI_8" + "P-poll__networl_3_3_AI_0" + "P-poll__networl_3_3_AI_1" + "P-poll__networl_3_3_AI_2" + "P-poll__networl_3_3_AI_3" + "P-poll__networl_3_3_AI_4" + "P-poll__networl_3_3_AI_5" + "P-poll__networl_3_3_AI_6" + "P-poll__networl_3_3_AI_7" + "P-poll__networl_3_3_AI_8" + "P-poll__networl_3_3_AnnP_0" + "P-poll__networl_3_3_AnnP_1" + "P-poll__networl_3_3_AnnP_2" + "P-poll__networl_3_3_AnnP_3" + "P-poll__networl_3_3_AnnP_4" + "P-poll__networl_3_3_AnnP_5" + "P-poll__networl_3_3_AnnP_6" + "P-poll__networl_3_3_AnnP_7" + "P-poll__networl_3_3_AnnP_8" + "P-poll__networl_3_3_RP_0" + "P-poll__networl_3_3_RP_1" + "P-poll__networl_3_3_RP_2" + "P-poll__networl_3_3_RP_3" + "P-poll__networl_3_3_RP_4" + "P-poll__networl_3_3_RP_5" + "P-poll__networl_3_3_RP_6" + "P-poll__networl_3_3_RP_7" + "P-poll__networl_3_3_RP_8" + "P-poll__networl_3_4_AskP_0" + "P-poll__networl_3_4_AskP_1" + "P-poll__networl_3_4_AskP_2" + "P-poll__networl_3_4_AskP_3" + "P-poll__networl_3_4_AskP_4" + "P-poll__networl_3_4_AskP_5" + "P-poll__networl_3_4_AskP_6" + "P-poll__networl_3_4_AskP_7" + "P-poll__networl_3_4_AskP_8" + "P-poll__networl_3_4_AnsP_0" + "P-poll__networl_3_4_AnsP_1" + "P-poll__networl_3_4_AnsP_2" + "P-poll__networl_3_4_AnsP_3" + "P-poll__networl_3_4_AnsP_4" + "P-poll__networl_3_4_AnsP_5" + "P-poll__networl_3_4_AnsP_6" + "P-poll__networl_3_4_AnsP_7" + "P-poll__networl_3_4_AnsP_8" + "P-poll__networl_3_4_RI_0" + "P-poll__networl_3_4_RI_1" + "P-poll__networl_3_4_RI_2" + "P-poll__networl_3_4_RI_3" + "P-poll__networl_3_4_RI_4" + "P-poll__networl_3_4_RI_5" + "P-poll__networl_3_4_RI_6" + "P-poll__networl_3_4_RI_7" + "P-poll__networl_3_4_RI_8" + "P-poll__networl_3_4_AI_0" + "P-poll__networl_3_4_AI_1" + "P-poll__networl_3_4_AI_2" + "P-poll__networl_3_4_AI_3" + "P-poll__networl_3_4_AI_4" + "P-poll__networl_3_4_AI_5" + "P-poll__networl_3_4_AI_6" + "P-poll__networl_3_4_AI_7" + "P-poll__networl_3_4_AI_8" + "P-poll__networl_3_4_AnnP_0" + "P-poll__networl_3_4_AnnP_1" + "P-poll__networl_3_4_AnnP_2" + "P-poll__networl_3_4_AnnP_3" + "P-poll__networl_3_4_AnnP_4" + "P-poll__networl_3_4_AnnP_5" + "P-poll__networl_3_4_AnnP_6" + "P-poll__networl_3_4_AnnP_7" + "P-poll__networl_3_4_AnnP_8" + "P-poll__networl_3_4_RP_0" + "P-poll__networl_3_4_RP_1" + "P-poll__networl_3_4_RP_2" + "P-poll__networl_3_4_RP_3" + "P-poll__networl_3_4_RP_4" + "P-poll__networl_3_4_RP_5" + "P-poll__networl_3_4_RP_6" + "P-poll__networl_3_4_RP_7" + "P-poll__networl_3_4_RP_8" + "P-poll__networl_3_5_AskP_0" + "P-poll__networl_3_5_AskP_1" + "P-poll__networl_3_5_AskP_2" + "P-poll__networl_3_5_AskP_3" + "P-poll__networl_3_5_AskP_4" + "P-poll__networl_3_5_AskP_5" + "P-poll__networl_3_5_AskP_6" + "P-poll__networl_3_5_AskP_7" + "P-poll__networl_3_5_AskP_8" + "P-poll__networl_3_5_AnsP_0" + "P-poll__networl_3_5_AnsP_1" + "P-poll__networl_3_5_AnsP_2" + "P-poll__networl_3_5_AnsP_3" + "P-poll__networl_3_5_AnsP_4" + "P-poll__networl_3_5_AnsP_5" + "P-poll__networl_3_5_AnsP_6" + "P-poll__networl_3_5_AnsP_7" + "P-poll__networl_3_5_AnsP_8" + "P-poll__networl_3_5_RI_0" + "P-poll__networl_3_5_RI_1" + "P-poll__networl_3_5_RI_2" + "P-poll__networl_3_5_RI_3" + "P-poll__networl_3_5_RI_4" + "P-poll__networl_3_5_RI_5" + "P-poll__networl_3_5_RI_6" + "P-poll__networl_3_5_RI_7" + "P-poll__networl_3_5_RI_8" + "P-poll__networl_3_5_AI_0" + "P-poll__networl_3_5_AI_1" + "P-poll__networl_3_5_AI_2" + "P-poll__networl_3_5_AI_3" + "P-poll__networl_3_5_AI_4" + "P-poll__networl_3_5_AI_5" + "P-poll__networl_3_5_AI_6" + "P-poll__networl_3_5_AI_7" + "P-poll__networl_3_5_AI_8" + "P-poll__networl_3_5_AnnP_0" + "P-poll__networl_3_5_AnnP_1" + "P-poll__networl_3_5_AnnP_2" + "P-poll__networl_3_5_AnnP_3" + "P-poll__networl_3_5_AnnP_4" + "P-poll__networl_3_5_AnnP_5" + "P-poll__networl_3_5_AnnP_6" + "P-poll__networl_3_5_AnnP_7" + "P-poll__networl_3_5_AnnP_8" + "P-poll__networl_3_5_RP_0" + "P-poll__networl_3_5_RP_1" + "P-poll__networl_3_5_RP_2" + "P-poll__networl_3_5_RP_3" + "P-poll__networl_3_5_RP_4" + "P-poll__networl_3_5_RP_5" + "P-poll__networl_3_5_RP_6" + "P-poll__networl_3_5_RP_7" + "P-poll__networl_3_5_RP_8" + "P-poll__networl_3_6_AskP_0" + "P-poll__networl_3_6_AskP_1" + "P-poll__networl_3_6_AskP_2" + "P-poll__networl_3_6_AskP_3" + "P-poll__networl_3_6_AskP_4" + "P-poll__networl_3_6_AskP_5" + "P-poll__networl_3_6_AskP_6" + "P-poll__networl_3_6_AskP_7" + "P-poll__networl_3_6_AskP_8" + "P-poll__networl_3_6_AnsP_0" + "P-poll__networl_3_6_AnsP_1" + "P-poll__networl_3_6_AnsP_2" + "P-poll__networl_3_6_AnsP_3" + "P-poll__networl_3_6_AnsP_4" + "P-poll__networl_3_6_AnsP_5" + "P-poll__networl_3_6_AnsP_6" + "P-poll__networl_3_6_AnsP_7" + "P-poll__networl_3_6_AnsP_8" + "P-poll__networl_3_6_RI_0" + "P-poll__networl_3_6_RI_1" + "P-poll__networl_3_6_RI_2" + "P-poll__networl_3_6_RI_3" + "P-poll__networl_3_6_RI_4" + "P-poll__networl_3_6_RI_5" + "P-poll__networl_3_6_RI_6" + "P-poll__networl_3_6_RI_7" + "P-poll__networl_3_6_RI_8" + "P-poll__networl_3_6_AI_0" + "P-poll__networl_3_6_AI_1" + "P-poll__networl_3_6_AI_2" + "P-poll__networl_3_6_AI_3" + "P-poll__networl_3_6_AI_4" + "P-poll__networl_3_6_AI_5" + "P-poll__networl_3_6_AI_6" + "P-poll__networl_3_6_AI_7" + "P-poll__networl_3_6_AI_8" + "P-poll__networl_3_6_AnnP_0" + "P-poll__networl_3_6_AnnP_1" + "P-poll__networl_3_6_AnnP_2" + "P-poll__networl_3_6_AnnP_3" + "P-poll__networl_3_6_AnnP_4" + "P-poll__networl_3_6_AnnP_5" + "P-poll__networl_3_6_AnnP_6" + "P-poll__networl_3_6_AnnP_7" + "P-poll__networl_3_6_AnnP_8" + "P-poll__networl_3_6_RP_0" + "P-poll__networl_3_6_RP_1" + "P-poll__networl_3_6_RP_2" + "P-poll__networl_3_6_RP_3" + "P-poll__networl_3_6_RP_4" + "P-poll__networl_3_6_RP_5" + "P-poll__networl_3_6_RP_6" + "P-poll__networl_3_6_RP_7" + "P-poll__networl_3_6_RP_8" + "P-poll__networl_3_7_AskP_0" + "P-poll__networl_3_7_AskP_1" + "P-poll__networl_3_7_AskP_2" + "P-poll__networl_3_7_AskP_3" + "P-poll__networl_3_7_AskP_4" + "P-poll__networl_3_7_AskP_5" + "P-poll__networl_3_7_AskP_6" + "P-poll__networl_3_7_AskP_7" + "P-poll__networl_3_7_AskP_8" + "P-poll__networl_3_7_AnsP_0" + "P-poll__networl_3_7_AnsP_1" + "P-poll__networl_3_7_AnsP_2" + "P-poll__networl_3_7_AnsP_3" + "P-poll__networl_3_7_AnsP_4" + "P-poll__networl_3_7_AnsP_5" + "P-poll__networl_3_7_AnsP_6" + "P-poll__networl_3_7_AnsP_7" + "P-poll__networl_3_7_AnsP_8" + "P-poll__networl_3_7_RI_0" + "P-poll__networl_3_7_RI_1" + "P-poll__networl_3_7_RI_2" + "P-poll__networl_3_7_RI_3" + "P-poll__networl_3_7_RI_4" + "P-poll__networl_3_7_RI_5" + "P-poll__networl_3_7_RI_6" + "P-poll__networl_3_7_RI_7" + "P-poll__networl_3_7_RI_8" + "P-poll__networl_3_7_AI_0" + "P-poll__networl_3_7_AI_1" + "P-poll__networl_3_7_AI_2" + "P-poll__networl_3_7_AI_3" + "P-poll__networl_3_7_AI_4" + "P-poll__networl_3_7_AI_5" + "P-poll__networl_3_7_AI_6" + "P-poll__networl_3_7_AI_7" + "P-poll__networl_3_7_AI_8" + "P-poll__networl_3_7_AnnP_0" + "P-poll__networl_3_7_AnnP_1" + "P-poll__networl_3_7_AnnP_2" + "P-poll__networl_3_7_AnnP_3" + "P-poll__networl_3_7_AnnP_4" + "P-poll__networl_3_7_AnnP_5" + "P-poll__networl_3_7_AnnP_6" + "P-poll__networl_3_7_AnnP_7" + "P-poll__networl_3_7_AnnP_8" + "P-poll__networl_3_7_RP_0" + "P-poll__networl_3_7_RP_1" + "P-poll__networl_3_7_RP_2" + "P-poll__networl_3_7_RP_3" + "P-poll__networl_3_7_RP_4" + "P-poll__networl_3_7_RP_5" + "P-poll__networl_3_7_RP_6" + "P-poll__networl_3_7_RP_7" + "P-poll__networl_3_7_RP_8" + "P-poll__networl_3_8_AskP_0" + "P-poll__networl_3_8_AskP_1" + "P-poll__networl_3_8_AskP_2" + "P-poll__networl_3_8_AskP_3" + "P-poll__networl_3_8_AskP_4" + "P-poll__networl_3_8_AskP_5" + "P-poll__networl_3_8_AskP_6" + "P-poll__networl_3_8_AskP_7" + "P-poll__networl_3_8_AskP_8" + "P-poll__networl_3_8_AnsP_0" + "P-poll__networl_3_8_AnsP_1" + "P-poll__networl_3_8_AnsP_2" + "P-poll__networl_3_8_AnsP_3" + "P-poll__networl_3_8_AnsP_4" + "P-poll__networl_3_8_AnsP_5" + "P-poll__networl_3_8_AnsP_6" + "P-poll__networl_3_8_AnsP_7" + "P-poll__networl_3_8_AnsP_8" + "P-poll__networl_3_8_RI_0" + "P-poll__networl_3_8_RI_1" + "P-poll__networl_3_8_RI_2" + "P-poll__networl_3_8_RI_3" + "P-poll__networl_3_8_RI_4" + "P-poll__networl_3_8_RI_5" + "P-poll__networl_3_8_RI_6" + "P-poll__networl_3_8_RI_7" + "P-poll__networl_3_8_RI_8" + "P-poll__networl_3_8_AI_0" + "P-poll__networl_3_8_AI_1" + "P-poll__networl_3_8_AI_2" + "P-poll__networl_3_8_AI_3" + "P-poll__networl_3_8_AI_4" + "P-poll__networl_3_8_AI_5" + "P-poll__networl_3_8_AI_6" + "P-poll__networl_3_8_AI_7" + "P-poll__networl_3_8_AI_8" + "P-poll__networl_3_8_AnnP_0" + "P-poll__networl_3_8_AnnP_1" + "P-poll__networl_3_8_AnnP_2" + "P-poll__networl_3_8_AnnP_3" + "P-poll__networl_3_8_AnnP_4" + "P-poll__networl_3_8_AnnP_5" + "P-poll__networl_3_8_AnnP_6" + "P-poll__networl_3_8_AnnP_7" + "P-poll__networl_3_8_AnnP_8" + "P-poll__networl_3_8_RP_0" + "P-poll__networl_3_8_RP_1" + "P-poll__networl_3_8_RP_2" + "P-poll__networl_3_8_RP_3" + "P-poll__networl_3_8_RP_4" + "P-poll__networl_3_8_RP_5" + "P-poll__networl_3_8_RP_6" + "P-poll__networl_3_8_RP_7" + "P-poll__networl_3_8_RP_8" + "P-poll__networl_4_0_AskP_0" + "P-poll__networl_4_0_AskP_1" + "P-poll__networl_4_0_AskP_2" + "P-poll__networl_4_0_AskP_3" + "P-poll__networl_4_0_AskP_4" + "P-poll__networl_4_0_AskP_5" + "P-poll__networl_4_0_AskP_6" + "P-poll__networl_4_0_AskP_7" + "P-poll__networl_4_0_AskP_8" + "P-poll__networl_4_0_AnsP_0" + "P-poll__networl_4_0_AnsP_1" + "P-poll__networl_4_0_AnsP_2" + "P-poll__networl_4_0_AnsP_3" + "P-poll__networl_4_0_AnsP_4" + "P-poll__networl_4_0_AnsP_5" + "P-poll__networl_4_0_AnsP_6" + "P-poll__networl_4_0_AnsP_7" + "P-poll__networl_4_0_AnsP_8" + "P-poll__networl_4_0_RI_0" + "P-poll__networl_4_0_RI_1" + "P-poll__networl_4_0_RI_2" + "P-poll__networl_4_0_RI_3" + "P-poll__networl_4_0_RI_4" + "P-poll__networl_4_0_RI_5" + "P-poll__networl_4_0_RI_6" + "P-poll__networl_4_0_RI_7" + "P-poll__networl_4_0_RI_8" + "P-poll__networl_4_0_AI_0" + "P-poll__networl_4_0_AI_1" + "P-poll__networl_4_0_AI_2" + "P-poll__networl_4_0_AI_3" + "P-poll__networl_4_0_AI_4" + "P-poll__networl_4_0_AI_5" + "P-poll__networl_4_0_AI_6" + "P-poll__networl_4_0_AI_7" + "P-poll__networl_4_0_AI_8" + "P-poll__networl_4_0_AnnP_0" + "P-poll__networl_4_0_AnnP_1" + "P-poll__networl_4_0_AnnP_2" + "P-poll__networl_4_0_AnnP_3" + "P-poll__networl_4_0_AnnP_4" + "P-poll__networl_4_0_AnnP_5" + "P-poll__networl_4_0_AnnP_6" + "P-poll__networl_4_0_AnnP_7" + "P-poll__networl_4_0_AnnP_8" + "P-poll__networl_4_0_RP_0" + "P-poll__networl_4_0_RP_1" + "P-poll__networl_4_0_RP_2" + "P-poll__networl_4_0_RP_3" + "P-poll__networl_4_0_RP_4" + "P-poll__networl_4_0_RP_5" + "P-poll__networl_4_0_RP_6" + "P-poll__networl_4_0_RP_7" + "P-poll__networl_4_0_RP_8" + "P-poll__networl_4_1_AskP_0" + "P-poll__networl_4_1_AskP_1" + "P-poll__networl_4_1_AskP_2" + "P-poll__networl_4_1_AskP_3" + "P-poll__networl_4_1_AskP_4" + "P-poll__networl_4_1_AskP_5" + "P-poll__networl_4_1_AskP_6" + "P-poll__networl_4_1_AskP_7" + "P-poll__networl_4_1_AskP_8" + "P-poll__networl_4_1_AnsP_0" + "P-poll__networl_4_1_AnsP_1" + "P-poll__networl_4_1_AnsP_2" + "P-poll__networl_4_1_AnsP_3" + "P-poll__networl_4_1_AnsP_4" + "P-poll__networl_4_1_AnsP_5" + "P-poll__networl_4_1_AnsP_6" + "P-poll__networl_4_1_AnsP_7" + "P-poll__networl_4_1_AnsP_8" + "P-poll__networl_4_1_RI_0" + "P-poll__networl_4_1_RI_1" + "P-poll__networl_4_1_RI_2" + "P-poll__networl_4_1_RI_3" + "P-poll__networl_4_1_RI_4" + "P-poll__networl_4_1_RI_5" + "P-poll__networl_4_1_RI_6" + "P-poll__networl_4_1_RI_7" + "P-poll__networl_4_1_RI_8" + "P-poll__networl_4_1_AI_0" + "P-poll__networl_4_1_AI_1" + "P-poll__networl_4_1_AI_2" + "P-poll__networl_4_1_AI_3" + "P-poll__networl_4_1_AI_4" + "P-poll__networl_4_1_AI_5" + "P-poll__networl_4_1_AI_6" + "P-poll__networl_4_1_AI_7" + "P-poll__networl_4_1_AI_8" + "P-poll__networl_4_1_AnnP_0" + "P-poll__networl_4_1_AnnP_1" + "P-poll__networl_4_1_AnnP_2" + "P-poll__networl_4_1_AnnP_3" + "P-poll__networl_4_1_AnnP_4" + "P-poll__networl_4_1_AnnP_5" + "P-poll__networl_4_1_AnnP_6" + "P-poll__networl_4_1_AnnP_7" + "P-poll__networl_4_1_AnnP_8" + "P-poll__networl_4_1_RP_0" + "P-poll__networl_4_1_RP_1" + "P-poll__networl_4_1_RP_2" + "P-poll__networl_4_1_RP_3" + "P-poll__networl_4_1_RP_4" + "P-poll__networl_4_1_RP_5" + "P-poll__networl_4_1_RP_6" + "P-poll__networl_4_1_RP_7" + "P-poll__networl_4_1_RP_8" + "P-poll__networl_4_2_AskP_0" + "P-poll__networl_4_2_AskP_1" + "P-poll__networl_4_2_AskP_2" + "P-poll__networl_4_2_AskP_3" + "P-poll__networl_4_2_AskP_4" + "P-poll__networl_4_2_AskP_5" + "P-poll__networl_4_2_AskP_6" + "P-poll__networl_4_2_AskP_7" + "P-poll__networl_4_2_AskP_8" + "P-poll__networl_4_2_AnsP_0" + "P-poll__networl_4_2_AnsP_1" + "P-poll__networl_4_2_AnsP_2" + "P-poll__networl_4_2_AnsP_3" + "P-poll__networl_4_2_AnsP_4" + "P-poll__networl_4_2_AnsP_5" + "P-poll__networl_4_2_AnsP_6" + "P-poll__networl_4_2_AnsP_7" + "P-poll__networl_4_2_AnsP_8" + "P-poll__networl_4_2_RI_0" + "P-poll__networl_4_2_RI_1" + "P-poll__networl_4_2_RI_2" + "P-poll__networl_4_2_RI_3" + "P-poll__networl_4_2_RI_4" + "P-poll__networl_4_2_RI_5" + "P-poll__networl_4_2_RI_6" + "P-poll__networl_4_2_RI_7" + "P-poll__networl_4_2_RI_8" + "P-poll__networl_4_2_AI_0" + "P-poll__networl_4_2_AI_1" + "P-poll__networl_4_2_AI_2" + "P-poll__networl_4_2_AI_3" + "P-poll__networl_4_2_AI_4" + "P-poll__networl_4_2_AI_5" + "P-poll__networl_4_2_AI_6" + "P-poll__networl_4_2_AI_7" + "P-poll__networl_4_2_AI_8" + "P-poll__networl_4_2_AnnP_0" + "P-poll__networl_4_2_AnnP_1" + "P-poll__networl_4_2_AnnP_2" + "P-poll__networl_4_2_AnnP_3" + "P-poll__networl_4_2_AnnP_4" + "P-poll__networl_4_2_AnnP_5" + "P-poll__networl_4_2_AnnP_6" + "P-poll__networl_4_2_AnnP_7" + "P-poll__networl_4_2_AnnP_8" + "P-poll__networl_4_2_RP_0" + "P-poll__networl_4_2_RP_1" + "P-poll__networl_4_2_RP_2" + "P-poll__networl_4_2_RP_3" + "P-poll__networl_4_2_RP_4" + "P-poll__networl_4_2_RP_5" + "P-poll__networl_4_2_RP_6" + "P-poll__networl_4_2_RP_7" + "P-poll__networl_4_2_RP_8" + "P-poll__networl_4_3_AskP_0" + "P-poll__networl_4_3_AskP_1" + "P-poll__networl_4_3_AskP_2" + "P-poll__networl_4_3_AskP_3" + "P-poll__networl_4_3_AskP_4" + "P-poll__networl_4_3_AskP_5" + "P-poll__networl_4_3_AskP_6" + "P-poll__networl_4_3_AskP_7" + "P-poll__networl_4_3_AskP_8" + "P-poll__networl_4_3_AnsP_0" + "P-poll__networl_4_3_AnsP_1" + "P-poll__networl_4_3_AnsP_2" + "P-poll__networl_4_3_AnsP_3" + "P-poll__networl_4_3_AnsP_4" + "P-poll__networl_4_3_AnsP_5" + "P-poll__networl_4_3_AnsP_6" + "P-poll__networl_4_3_AnsP_7" + "P-poll__networl_4_3_AnsP_8" + "P-poll__networl_4_3_RI_0" + "P-poll__networl_4_3_RI_1" + "P-poll__networl_4_3_RI_2" + "P-poll__networl_4_3_RI_3" + "P-poll__networl_4_3_RI_4" + "P-poll__networl_4_3_RI_5" + "P-poll__networl_4_3_RI_6" + "P-poll__networl_4_3_RI_7" + "P-poll__networl_4_3_RI_8" + "P-poll__networl_4_3_AI_0" + "P-poll__networl_4_3_AI_1" + "P-poll__networl_4_3_AI_2" + "P-poll__networl_4_3_AI_3" + "P-poll__networl_4_3_AI_4" + "P-poll__networl_4_3_AI_5" + "P-poll__networl_4_3_AI_6" + "P-poll__networl_4_3_AI_7" + "P-poll__networl_4_3_AI_8" + "P-poll__networl_4_3_AnnP_0" + "P-poll__networl_4_3_AnnP_1" + "P-poll__networl_4_3_AnnP_2" + "P-poll__networl_4_3_AnnP_3" + "P-poll__networl_4_3_AnnP_4" + "P-poll__networl_4_3_AnnP_5" + "P-poll__networl_4_3_AnnP_6" + "P-poll__networl_4_3_AnnP_7" + "P-poll__networl_4_3_AnnP_8" + "P-poll__networl_4_3_RP_0" + "P-poll__networl_4_3_RP_1" + "P-poll__networl_4_3_RP_2" + "P-poll__networl_4_3_RP_3" + "P-poll__networl_4_3_RP_4" + "P-poll__networl_4_3_RP_5" + "P-poll__networl_4_3_RP_6" + "P-poll__networl_4_3_RP_7" + "P-poll__networl_4_3_RP_8" + "P-poll__networl_4_4_AskP_0" + "P-poll__networl_4_4_AskP_1" + "P-poll__networl_4_4_AskP_2" + "P-poll__networl_4_4_AskP_3" + "P-poll__networl_4_4_AskP_4" + "P-poll__networl_4_4_AskP_5" + "P-poll__networl_4_4_AskP_6" + "P-poll__networl_4_4_AskP_7" + "P-poll__networl_4_4_AskP_8" + "P-poll__networl_4_4_AnsP_0" + "P-poll__networl_4_4_AnsP_1" + "P-poll__networl_4_4_AnsP_2" + "P-poll__networl_4_4_AnsP_3" + "P-poll__networl_4_4_AnsP_4" + "P-poll__networl_4_4_AnsP_5" + "P-poll__networl_4_4_AnsP_6" + "P-poll__networl_4_4_AnsP_7" + "P-poll__networl_4_4_AnsP_8" + "P-poll__networl_4_4_RI_0" + "P-poll__networl_4_4_RI_1" + "P-poll__networl_4_4_RI_2" + "P-poll__networl_4_4_RI_3" + "P-poll__networl_4_4_RI_4" + "P-poll__networl_4_4_RI_5" + "P-poll__networl_4_4_RI_6" + "P-poll__networl_4_4_RI_7" + "P-poll__networl_4_4_RI_8" + "P-poll__networl_4_4_AI_0" + "P-poll__networl_4_4_AI_1" + "P-poll__networl_4_4_AI_2" + "P-poll__networl_4_4_AI_3" + "P-poll__networl_4_4_AI_4" + "P-poll__networl_4_4_AI_5" + "P-poll__networl_4_4_AI_6" + "P-poll__networl_4_4_AI_7" + "P-poll__networl_4_4_AI_8" + "P-poll__networl_4_4_AnnP_0" + "P-poll__networl_4_4_AnnP_1" + "P-poll__networl_4_4_AnnP_2" + "P-poll__networl_4_4_AnnP_3" + "P-poll__networl_4_4_AnnP_4" + "P-poll__networl_4_4_AnnP_5" + "P-poll__networl_4_4_AnnP_6" + "P-poll__networl_4_4_AnnP_7" + "P-poll__networl_4_4_AnnP_8" + "P-poll__networl_4_4_RP_0" + "P-poll__networl_4_4_RP_1" + "P-poll__networl_4_4_RP_2" + "P-poll__networl_4_4_RP_3" + "P-poll__networl_4_4_RP_4" + "P-poll__networl_4_4_RP_5" + "P-poll__networl_4_4_RP_6" + "P-poll__networl_4_4_RP_7" + "P-poll__networl_4_4_RP_8" + "P-poll__networl_4_5_AskP_0" + "P-poll__networl_4_5_AskP_1" + "P-poll__networl_4_5_AskP_2" + "P-poll__networl_4_5_AskP_3" + "P-poll__networl_4_5_AskP_4" + "P-poll__networl_4_5_AskP_5" + "P-poll__networl_4_5_AskP_6" + "P-poll__networl_4_5_AskP_7" + "P-poll__networl_4_5_AskP_8" + "P-poll__networl_4_5_AnsP_0" + "P-poll__networl_4_5_AnsP_1" + "P-poll__networl_4_5_AnsP_2" + "P-poll__networl_4_5_AnsP_3" + "P-poll__networl_4_5_AnsP_4" + "P-poll__networl_4_5_AnsP_5" + "P-poll__networl_4_5_AnsP_6" + "P-poll__networl_4_5_AnsP_7" + "P-poll__networl_4_5_AnsP_8" + "P-poll__networl_4_5_RI_0" + "P-poll__networl_4_5_RI_1" + "P-poll__networl_4_5_RI_2" + "P-poll__networl_4_5_RI_3" + "P-poll__networl_4_5_RI_4" + "P-poll__networl_4_5_RI_5" + "P-poll__networl_4_5_RI_6" + "P-poll__networl_4_5_RI_7" + "P-poll__networl_4_5_RI_8" + "P-poll__networl_4_5_AI_0" + "P-poll__networl_4_5_AI_1" + "P-poll__networl_4_5_AI_2" + "P-poll__networl_4_5_AI_3" + "P-poll__networl_4_5_AI_4" + "P-poll__networl_4_5_AI_5" + "P-poll__networl_4_5_AI_6" + "P-poll__networl_4_5_AI_7" + "P-poll__networl_4_5_AI_8" + "P-poll__networl_4_5_AnnP_0" + "P-poll__networl_4_5_AnnP_1" + "P-poll__networl_4_5_AnnP_2" + "P-poll__networl_4_5_AnnP_3" + "P-poll__networl_4_5_AnnP_4" + "P-poll__networl_4_5_AnnP_5" + "P-poll__networl_4_5_AnnP_6" + "P-poll__networl_4_5_AnnP_7" + "P-poll__networl_4_5_AnnP_8" + "P-poll__networl_4_5_RP_0" + "P-poll__networl_4_5_RP_1" + "P-poll__networl_4_5_RP_2" + "P-poll__networl_4_5_RP_3" + "P-poll__networl_4_5_RP_4" + "P-poll__networl_4_5_RP_5" + "P-poll__networl_4_5_RP_6" + "P-poll__networl_4_5_RP_7" + "P-poll__networl_4_5_RP_8" + "P-poll__networl_4_6_AskP_0" + "P-poll__networl_4_6_AskP_1" + "P-poll__networl_4_6_AskP_2" + "P-poll__networl_4_6_AskP_3" + "P-poll__networl_4_6_AskP_4" + "P-poll__networl_4_6_AskP_5" + "P-poll__networl_4_6_AskP_6" + "P-poll__networl_4_6_AskP_7" + "P-poll__networl_4_6_AskP_8" + "P-poll__networl_4_6_AnsP_0" + "P-poll__networl_4_6_AnsP_1" + "P-poll__networl_4_6_AnsP_2" + "P-poll__networl_4_6_AnsP_3" + "P-poll__networl_4_6_AnsP_4" + "P-poll__networl_4_6_AnsP_5" + "P-poll__networl_4_6_AnsP_6" + "P-poll__networl_4_6_AnsP_7" + "P-poll__networl_4_6_AnsP_8" + "P-poll__networl_4_6_RI_0" + "P-poll__networl_4_6_RI_1" + "P-poll__networl_4_6_RI_2" + "P-poll__networl_4_6_RI_3" + "P-poll__networl_4_6_RI_4" + "P-poll__networl_4_6_RI_5" + "P-poll__networl_4_6_RI_6" + "P-poll__networl_4_6_RI_7" + "P-poll__networl_4_6_RI_8" + "P-poll__networl_4_6_AI_0" + "P-poll__networl_4_6_AI_1" + "P-poll__networl_4_6_AI_2" + "P-poll__networl_4_6_AI_3" + "P-poll__networl_4_6_AI_4" + "P-poll__networl_4_6_AI_5" + "P-poll__networl_4_6_AI_6" + "P-poll__networl_4_6_AI_7" + "P-poll__networl_4_6_AI_8" + "P-poll__networl_4_6_AnnP_0" + "P-poll__networl_4_6_AnnP_1" + "P-poll__networl_4_6_AnnP_2" + "P-poll__networl_4_6_AnnP_3" + "P-poll__networl_4_6_AnnP_4" + "P-poll__networl_4_6_AnnP_5" + "P-poll__networl_4_6_AnnP_6" + "P-poll__networl_4_6_AnnP_7" + "P-poll__networl_4_6_AnnP_8" + "P-poll__networl_4_6_RP_0" + "P-poll__networl_4_6_RP_1" + "P-poll__networl_4_6_RP_2" + "P-poll__networl_4_6_RP_3" + "P-poll__networl_4_6_RP_4" + "P-poll__networl_4_6_RP_5" + "P-poll__networl_4_6_RP_6" + "P-poll__networl_4_6_RP_7" + "P-poll__networl_4_6_RP_8" + "P-poll__networl_4_7_AskP_0" + "P-poll__networl_4_7_AskP_1" + "P-poll__networl_4_7_AskP_2" + "P-poll__networl_4_7_AskP_3" + "P-poll__networl_4_7_AskP_4" + "P-poll__networl_4_7_AskP_5" + "P-poll__networl_4_7_AskP_6" + "P-poll__networl_4_7_AskP_7" + "P-poll__networl_4_7_AskP_8" + "P-poll__networl_4_7_AnsP_0" + "P-poll__networl_4_7_AnsP_1" + "P-poll__networl_4_7_AnsP_2" + "P-poll__networl_4_7_AnsP_3" + "P-poll__networl_4_7_AnsP_4" + "P-poll__networl_4_7_AnsP_5" + "P-poll__networl_4_7_AnsP_6" + "P-poll__networl_4_7_AnsP_7" + "P-poll__networl_4_7_AnsP_8" + "P-poll__networl_4_7_RI_0" + "P-poll__networl_4_7_RI_1" + "P-poll__networl_4_7_RI_2" + "P-poll__networl_4_7_RI_3" + "P-poll__networl_4_7_RI_4" + "P-poll__networl_4_7_RI_5" + "P-poll__networl_4_7_RI_6" + "P-poll__networl_4_7_RI_7" + "P-poll__networl_4_7_RI_8" + "P-poll__networl_4_7_AI_0" + "P-poll__networl_4_7_AI_1" + "P-poll__networl_4_7_AI_2" + "P-poll__networl_4_7_AI_3" + "P-poll__networl_4_7_AI_4" + "P-poll__networl_4_7_AI_5" + "P-poll__networl_4_7_AI_6" + "P-poll__networl_4_7_AI_7" + "P-poll__networl_4_7_AI_8" + "P-poll__networl_4_7_AnnP_0" + "P-poll__networl_4_7_AnnP_1" + "P-poll__networl_4_7_AnnP_2" + "P-poll__networl_4_7_AnnP_3" + "P-poll__networl_4_7_AnnP_4" + "P-poll__networl_4_7_AnnP_5" + "P-poll__networl_4_7_AnnP_6" + "P-poll__networl_4_7_AnnP_7" + "P-poll__networl_4_7_AnnP_8" + "P-poll__networl_4_7_RP_0" + "P-poll__networl_4_7_RP_1" + "P-poll__networl_4_7_RP_2" + "P-poll__networl_4_7_RP_3" + "P-poll__networl_4_7_RP_4" + "P-poll__networl_4_7_RP_5" + "P-poll__networl_4_7_RP_6" + "P-poll__networl_4_7_RP_7" + "P-poll__networl_4_7_RP_8" + "P-poll__networl_4_8_AskP_0" + "P-poll__networl_4_8_AskP_1" + "P-poll__networl_4_8_AskP_2" + "P-poll__networl_4_8_AskP_3" + "P-poll__networl_4_8_AskP_4" + "P-poll__networl_4_8_AskP_5" + "P-poll__networl_4_8_AskP_6" + "P-poll__networl_4_8_AskP_7" + "P-poll__networl_4_8_AskP_8" + "P-poll__networl_4_8_AnsP_0" + "P-poll__networl_4_8_AnsP_1" + "P-poll__networl_4_8_AnsP_2" + "P-poll__networl_4_8_AnsP_3" + "P-poll__networl_4_8_AnsP_4" + "P-poll__networl_4_8_AnsP_5" + "P-poll__networl_4_8_AnsP_6" + "P-poll__networl_4_8_AnsP_7" + "P-poll__networl_4_8_AnsP_8" + "P-poll__networl_4_8_RI_0" + "P-poll__networl_4_8_RI_1" + "P-poll__networl_4_8_RI_2" + "P-poll__networl_4_8_RI_3" + "P-poll__networl_4_8_RI_4" + "P-poll__networl_4_8_RI_5" + "P-poll__networl_4_8_RI_6" + "P-poll__networl_4_8_RI_7" + "P-poll__networl_4_8_RI_8" + "P-poll__networl_4_8_AI_0" + "P-poll__networl_4_8_AI_1" + "P-poll__networl_4_8_AI_2" + "P-poll__networl_4_8_AI_3" + "P-poll__networl_4_8_AI_4" + "P-poll__networl_4_8_AI_5" + "P-poll__networl_4_8_AI_6" + "P-poll__networl_4_8_AI_7" + "P-poll__networl_4_8_AI_8" + "P-poll__networl_4_8_AnnP_0" + "P-poll__networl_4_8_AnnP_1" + "P-poll__networl_4_8_AnnP_2" + "P-poll__networl_4_8_AnnP_3" + "P-poll__networl_4_8_AnnP_4" + "P-poll__networl_4_8_AnnP_5" + "P-poll__networl_4_8_AnnP_6" + "P-poll__networl_4_8_AnnP_7" + "P-poll__networl_4_8_AnnP_8" + "P-poll__networl_4_8_RP_0" + "P-poll__networl_4_8_RP_1" + "P-poll__networl_4_8_RP_2" + "P-poll__networl_4_8_RP_3" + "P-poll__networl_4_8_RP_4" + "P-poll__networl_4_8_RP_5" + "P-poll__networl_4_8_RP_6" + "P-poll__networl_4_8_RP_7" + "P-poll__networl_4_8_RP_8" + "P-poll__networl_5_0_AskP_0" + "P-poll__networl_5_0_AskP_1" + "P-poll__networl_5_0_AskP_2" + "P-poll__networl_5_0_AskP_3" + "P-poll__networl_5_0_AskP_4" + "P-poll__networl_5_0_AskP_5" + "P-poll__networl_5_0_AskP_6" + "P-poll__networl_5_0_AskP_7" + "P-poll__networl_5_0_AskP_8" + "P-poll__networl_5_0_AnsP_0" + "P-poll__networl_5_0_AnsP_1" + "P-poll__networl_5_0_AnsP_2" + "P-poll__networl_5_0_AnsP_3" + "P-poll__networl_5_0_AnsP_4" + "P-poll__networl_5_0_AnsP_5" + "P-poll__networl_5_0_AnsP_6" + "P-poll__networl_5_0_AnsP_7" + "P-poll__networl_5_0_AnsP_8" + "P-poll__networl_5_0_RI_0" + "P-poll__networl_5_0_RI_1" + "P-poll__networl_5_0_RI_2" + "P-poll__networl_5_0_RI_3" + "P-poll__networl_5_0_RI_4" + "P-poll__networl_5_0_RI_5" + "P-poll__networl_5_0_RI_6" + "P-poll__networl_5_0_RI_7" + "P-poll__networl_5_0_RI_8" + "P-poll__networl_5_0_AI_0" + "P-poll__networl_5_0_AI_1" + "P-poll__networl_5_0_AI_2" + "P-poll__networl_5_0_AI_3" + "P-poll__networl_5_0_AI_4" + "P-poll__networl_5_0_AI_5" + "P-poll__networl_5_0_AI_6" + "P-poll__networl_5_0_AI_7" + "P-poll__networl_5_0_AI_8" + "P-poll__networl_5_0_AnnP_0" + "P-poll__networl_5_0_AnnP_1" + "P-poll__networl_5_0_AnnP_2" + "P-poll__networl_5_0_AnnP_3" + "P-poll__networl_5_0_AnnP_4" + "P-poll__networl_5_0_AnnP_5" + "P-poll__networl_5_0_AnnP_6" + "P-poll__networl_5_0_AnnP_7" + "P-poll__networl_5_0_AnnP_8" + "P-poll__networl_5_0_RP_0" + "P-poll__networl_5_0_RP_1" + "P-poll__networl_5_0_RP_2" + "P-poll__networl_5_0_RP_3" + "P-poll__networl_5_0_RP_4" + "P-poll__networl_5_0_RP_5" + "P-poll__networl_5_0_RP_6" + "P-poll__networl_5_0_RP_7" + "P-poll__networl_5_0_RP_8" + "P-poll__networl_5_1_AskP_0" + "P-poll__networl_5_1_AskP_1" + "P-poll__networl_5_1_AskP_2" + "P-poll__networl_5_1_AskP_3" + "P-poll__networl_5_1_AskP_4" + "P-poll__networl_5_1_AskP_5" + "P-poll__networl_5_1_AskP_6" + "P-poll__networl_5_1_AskP_7" + "P-poll__networl_5_1_AskP_8" + "P-poll__networl_5_1_AnsP_0" + "P-poll__networl_5_1_AnsP_1" + "P-poll__networl_5_1_AnsP_2" + "P-poll__networl_5_1_AnsP_3" + "P-poll__networl_5_1_AnsP_4" + "P-poll__networl_5_1_AnsP_5" + "P-poll__networl_5_1_AnsP_6" + "P-poll__networl_5_1_AnsP_7" + "P-poll__networl_5_1_AnsP_8" + "P-poll__networl_5_1_RI_0" + "P-poll__networl_5_1_RI_1" + "P-poll__networl_5_1_RI_2" + "P-poll__networl_5_1_RI_3" + "P-poll__networl_5_1_RI_4" + "P-poll__networl_5_1_RI_5" + "P-poll__networl_5_1_RI_6" + "P-poll__networl_5_1_RI_7" + "P-poll__networl_5_1_RI_8" + "P-poll__networl_5_1_AI_0" + "P-poll__networl_5_1_AI_1" + "P-poll__networl_5_1_AI_2" + "P-poll__networl_5_1_AI_3" + "P-poll__networl_5_1_AI_4" + "P-poll__networl_5_1_AI_5" + "P-poll__networl_5_1_AI_6" + "P-poll__networl_5_1_AI_7" + "P-poll__networl_5_1_AI_8" + "P-poll__networl_5_1_AnnP_0" + "P-poll__networl_5_1_AnnP_1" + "P-poll__networl_5_1_AnnP_2" + "P-poll__networl_5_1_AnnP_3" + "P-poll__networl_5_1_AnnP_4" + "P-poll__networl_5_1_AnnP_5" + "P-poll__networl_5_1_AnnP_6" + "P-poll__networl_5_1_AnnP_7" + "P-poll__networl_5_1_AnnP_8" + "P-poll__networl_5_1_RP_0" + "P-poll__networl_5_1_RP_1" + "P-poll__networl_5_1_RP_2" + "P-poll__networl_5_1_RP_3" + "P-poll__networl_5_1_RP_4" + "P-poll__networl_5_1_RP_5" + "P-poll__networl_5_1_RP_6" + "P-poll__networl_5_1_RP_7" + "P-poll__networl_5_1_RP_8" + "P-poll__networl_5_2_AskP_0" + "P-poll__networl_5_2_AskP_1" + "P-poll__networl_5_2_AskP_2" + "P-poll__networl_5_2_AskP_3" + "P-poll__networl_5_2_AskP_4" + "P-poll__networl_5_2_AskP_5" + "P-poll__networl_5_2_AskP_6" + "P-poll__networl_5_2_AskP_7" + "P-poll__networl_5_2_AskP_8" + "P-poll__networl_5_2_AnsP_0" + "P-poll__networl_5_2_AnsP_1" + "P-poll__networl_5_2_AnsP_2" + "P-poll__networl_5_2_AnsP_3" + "P-poll__networl_5_2_AnsP_4" + "P-poll__networl_5_2_AnsP_5" + "P-poll__networl_5_2_AnsP_6" + "P-poll__networl_5_2_AnsP_7" + "P-poll__networl_5_2_AnsP_8" + "P-poll__networl_5_2_RI_0" + "P-poll__networl_5_2_RI_1" + "P-poll__networl_5_2_RI_2" + "P-poll__networl_5_2_RI_3" + "P-poll__networl_5_2_RI_4" + "P-poll__networl_5_2_RI_5" + "P-poll__networl_5_2_RI_6" + "P-poll__networl_5_2_RI_7" + "P-poll__networl_5_2_RI_8" + "P-poll__networl_5_2_AI_0" + "P-poll__networl_5_2_AI_1" + "P-poll__networl_5_2_AI_2" + "P-poll__networl_5_2_AI_3" + "P-poll__networl_5_2_AI_4" + "P-poll__networl_5_2_AI_5" + "P-poll__networl_5_2_AI_6" + "P-poll__networl_5_2_AI_7" + "P-poll__networl_5_2_AI_8" + "P-poll__networl_5_2_AnnP_0" + "P-poll__networl_5_2_AnnP_1" + "P-poll__networl_5_2_AnnP_2" + "P-poll__networl_5_2_AnnP_3" + "P-poll__networl_5_2_AnnP_4" + "P-poll__networl_5_2_AnnP_5" + "P-poll__networl_5_2_AnnP_6" + "P-poll__networl_5_2_AnnP_7" + "P-poll__networl_5_2_AnnP_8" + "P-poll__networl_5_2_RP_0" + "P-poll__networl_5_2_RP_1" + "P-poll__networl_5_2_RP_2" + "P-poll__networl_5_2_RP_3" + "P-poll__networl_5_2_RP_4" + "P-poll__networl_5_2_RP_5" + "P-poll__networl_5_2_RP_6" + "P-poll__networl_5_2_RP_7" + "P-poll__networl_5_2_RP_8" + "P-poll__networl_5_3_AskP_0" + "P-poll__networl_5_3_AskP_1" + "P-poll__networl_5_3_AskP_2" + "P-poll__networl_5_3_AskP_3" + "P-poll__networl_5_3_AskP_4" + "P-poll__networl_5_3_AskP_5" + "P-poll__networl_5_3_AskP_6" + "P-poll__networl_5_3_AskP_7" + "P-poll__networl_5_3_AskP_8" + "P-poll__networl_5_3_AnsP_0" + "P-poll__networl_5_3_AnsP_1" + "P-poll__networl_5_3_AnsP_2" + "P-poll__networl_5_3_AnsP_3" + "P-poll__networl_5_3_AnsP_4" + "P-poll__networl_5_3_AnsP_5" + "P-poll__networl_5_3_AnsP_6" + "P-poll__networl_5_3_AnsP_7" + "P-poll__networl_5_3_AnsP_8" + "P-poll__networl_5_3_RI_0" + "P-poll__networl_5_3_RI_1" + "P-poll__networl_5_3_RI_2" + "P-poll__networl_5_3_RI_3" + "P-poll__networl_5_3_RI_4" + "P-poll__networl_5_3_RI_5" + "P-poll__networl_5_3_RI_6" + "P-poll__networl_5_3_RI_7" + "P-poll__networl_5_3_RI_8" + "P-poll__networl_5_3_AI_0" + "P-poll__networl_5_3_AI_1" + "P-poll__networl_5_3_AI_2" + "P-poll__networl_5_3_AI_3" + "P-poll__networl_5_3_AI_4" + "P-poll__networl_5_3_AI_5" + "P-poll__networl_5_3_AI_6" + "P-poll__networl_5_3_AI_7" + "P-poll__networl_5_3_AI_8" + "P-poll__networl_5_3_AnnP_0" + "P-poll__networl_5_3_AnnP_1" + "P-poll__networl_5_3_AnnP_2" + "P-poll__networl_5_3_AnnP_3" + "P-poll__networl_5_3_AnnP_4" + "P-poll__networl_5_3_AnnP_5" + "P-poll__networl_5_3_AnnP_6" + "P-poll__networl_5_3_AnnP_7" + "P-poll__networl_5_3_AnnP_8" + "P-poll__networl_5_3_RP_0" + "P-poll__networl_5_3_RP_1" + "P-poll__networl_5_3_RP_2" + "P-poll__networl_5_3_RP_3" + "P-poll__networl_5_3_RP_4" + "P-poll__networl_5_3_RP_5" + "P-poll__networl_5_3_RP_6" + "P-poll__networl_5_3_RP_7" + "P-poll__networl_5_3_RP_8" + "P-poll__networl_5_4_AskP_0" + "P-poll__networl_5_4_AskP_1" + "P-poll__networl_5_4_AskP_2" + "P-poll__networl_5_4_AskP_3" + "P-poll__networl_5_4_AskP_4" + "P-poll__networl_5_4_AskP_5" + "P-poll__networl_5_4_AskP_6" + "P-poll__networl_5_4_AskP_7" + "P-poll__networl_5_4_AskP_8" + "P-poll__networl_5_4_AnsP_0" + "P-poll__networl_5_4_AnsP_1" + "P-poll__networl_5_4_AnsP_2" + "P-poll__networl_5_4_AnsP_3" + "P-poll__networl_5_4_AnsP_4" + "P-poll__networl_5_4_AnsP_5" + "P-poll__networl_5_4_AnsP_6" + "P-poll__networl_5_4_AnsP_7" + "P-poll__networl_5_4_AnsP_8" + "P-poll__networl_5_4_RI_0" + "P-poll__networl_5_4_RI_1" + "P-poll__networl_5_4_RI_2" + "P-poll__networl_5_4_RI_3" + "P-poll__networl_5_4_RI_4" + "P-poll__networl_5_4_RI_5" + "P-poll__networl_5_4_RI_6" + "P-poll__networl_5_4_RI_7" + "P-poll__networl_5_4_RI_8" + "P-poll__networl_5_4_AI_0" + "P-poll__networl_5_4_AI_1" + "P-poll__networl_5_4_AI_2" + "P-poll__networl_5_4_AI_3" + "P-poll__networl_5_4_AI_4" + "P-poll__networl_5_4_AI_5" + "P-poll__networl_5_4_AI_6" + "P-poll__networl_5_4_AI_7" + "P-poll__networl_5_4_AI_8" + "P-poll__networl_5_4_AnnP_0" + "P-poll__networl_5_4_AnnP_1" + "P-poll__networl_5_4_AnnP_2" + "P-poll__networl_5_4_AnnP_3" + "P-poll__networl_5_4_AnnP_4" + "P-poll__networl_5_4_AnnP_5" + "P-poll__networl_5_4_AnnP_6" + "P-poll__networl_5_4_AnnP_7" + "P-poll__networl_5_4_AnnP_8" + "P-poll__networl_5_4_RP_0" + "P-poll__networl_5_4_RP_1" + "P-poll__networl_5_4_RP_2" + "P-poll__networl_5_4_RP_3" + "P-poll__networl_5_4_RP_4" + "P-poll__networl_5_4_RP_5" + "P-poll__networl_5_4_RP_6" + "P-poll__networl_5_4_RP_7" + "P-poll__networl_5_4_RP_8" + "P-poll__networl_5_5_AskP_0" + "P-poll__networl_5_5_AskP_1" + "P-poll__networl_5_5_AskP_2" + "P-poll__networl_5_5_AskP_3" + "P-poll__networl_5_5_AskP_4" + "P-poll__networl_5_5_AskP_5" + "P-poll__networl_5_5_AskP_6" + "P-poll__networl_5_5_AskP_7" + "P-poll__networl_5_5_AskP_8" + "P-poll__networl_5_5_AnsP_0" + "P-poll__networl_5_5_AnsP_1" + "P-poll__networl_5_5_AnsP_2" + "P-poll__networl_5_5_AnsP_3" + "P-poll__networl_5_5_AnsP_4" + "P-poll__networl_5_5_AnsP_5" + "P-poll__networl_5_5_AnsP_6" + "P-poll__networl_5_5_AnsP_7" + "P-poll__networl_5_5_AnsP_8" + "P-poll__networl_5_5_RI_0" + "P-poll__networl_5_5_RI_1" + "P-poll__networl_5_5_RI_2" + "P-poll__networl_5_5_RI_3" + "P-poll__networl_5_5_RI_4" + "P-poll__networl_5_5_RI_5" + "P-poll__networl_5_5_RI_6" + "P-poll__networl_5_5_RI_7" + "P-poll__networl_5_5_RI_8" + "P-poll__networl_5_5_AI_0" + "P-poll__networl_5_5_AI_1" + "P-poll__networl_5_5_AI_2" + "P-poll__networl_5_5_AI_3" + "P-poll__networl_5_5_AI_4" + "P-poll__networl_5_5_AI_5" + "P-poll__networl_5_5_AI_6" + "P-poll__networl_5_5_AI_7" + "P-poll__networl_5_5_AI_8" + "P-poll__networl_5_5_AnnP_0" + "P-poll__networl_5_5_AnnP_1" + "P-poll__networl_5_5_AnnP_2" + "P-poll__networl_5_5_AnnP_3" + "P-poll__networl_5_5_AnnP_4" + "P-poll__networl_5_5_AnnP_5" + "P-poll__networl_5_5_AnnP_6" + "P-poll__networl_5_5_AnnP_7" + "P-poll__networl_5_5_AnnP_8" + "P-poll__networl_5_5_RP_0" + "P-poll__networl_5_5_RP_1" + "P-poll__networl_5_5_RP_2" + "P-poll__networl_5_5_RP_3" + "P-poll__networl_5_5_RP_4" + "P-poll__networl_5_5_RP_5" + "P-poll__networl_5_5_RP_6" + "P-poll__networl_5_5_RP_7" + "P-poll__networl_5_5_RP_8" + "P-poll__networl_5_6_AskP_0" + "P-poll__networl_5_6_AskP_1" + "P-poll__networl_5_6_AskP_2" + "P-poll__networl_5_6_AskP_3" + "P-poll__networl_5_6_AskP_4" + "P-poll__networl_5_6_AskP_5" + "P-poll__networl_5_6_AskP_6" + "P-poll__networl_5_6_AskP_7" + "P-poll__networl_5_6_AskP_8" + "P-poll__networl_5_6_AnsP_0" + "P-poll__networl_5_6_AnsP_1" + "P-poll__networl_5_6_AnsP_2" + "P-poll__networl_5_6_AnsP_3" + "P-poll__networl_5_6_AnsP_4" + "P-poll__networl_5_6_AnsP_5" + "P-poll__networl_5_6_AnsP_6" + "P-poll__networl_5_6_AnsP_7" + "P-poll__networl_5_6_AnsP_8" + "P-poll__networl_5_6_RI_0" + "P-poll__networl_5_6_RI_1" + "P-poll__networl_5_6_RI_2" + "P-poll__networl_5_6_RI_3" + "P-poll__networl_5_6_RI_4" + "P-poll__networl_5_6_RI_5" + "P-poll__networl_5_6_RI_6" + "P-poll__networl_5_6_RI_7" + "P-poll__networl_5_6_RI_8" + "P-poll__networl_5_6_AI_0" + "P-poll__networl_5_6_AI_1" + "P-poll__networl_5_6_AI_2" + "P-poll__networl_5_6_AI_3" + "P-poll__networl_5_6_AI_4" + "P-poll__networl_5_6_AI_5" + "P-poll__networl_5_6_AI_6" + "P-poll__networl_5_6_AI_7" + "P-poll__networl_5_6_AI_8" + "P-poll__networl_5_6_AnnP_0" + "P-poll__networl_5_6_AnnP_1" + "P-poll__networl_5_6_AnnP_2" + "P-poll__networl_5_6_AnnP_3" + "P-poll__networl_5_6_AnnP_4" + "P-poll__networl_5_6_AnnP_5" + "P-poll__networl_5_6_AnnP_6" + "P-poll__networl_5_6_AnnP_7" + "P-poll__networl_5_6_AnnP_8" + "P-poll__networl_5_6_RP_0" + "P-poll__networl_5_6_RP_1" + "P-poll__networl_5_6_RP_2" + "P-poll__networl_5_6_RP_3" + "P-poll__networl_5_6_RP_4" + "P-poll__networl_5_6_RP_5" + "P-poll__networl_5_6_RP_6" + "P-poll__networl_5_6_RP_7" + "P-poll__networl_5_6_RP_8" + "P-poll__networl_5_7_AskP_0" + "P-poll__networl_5_7_AskP_1" + "P-poll__networl_5_7_AskP_2" + "P-poll__networl_5_7_AskP_3" + "P-poll__networl_5_7_AskP_4" + "P-poll__networl_5_7_AskP_5" + "P-poll__networl_5_7_AskP_6" + "P-poll__networl_5_7_AskP_7" + "P-poll__networl_5_7_AskP_8" + "P-poll__networl_5_7_AnsP_0" + "P-poll__networl_5_7_AnsP_1" + "P-poll__networl_5_7_AnsP_2" + "P-poll__networl_5_7_AnsP_3" + "P-poll__networl_5_7_AnsP_4" + "P-poll__networl_5_7_AnsP_5" + "P-poll__networl_5_7_AnsP_6" + "P-poll__networl_5_7_AnsP_7" + "P-poll__networl_5_7_AnsP_8" + "P-poll__networl_5_7_RI_0" + "P-poll__networl_5_7_RI_1" + "P-poll__networl_5_7_RI_2" + "P-poll__networl_5_7_RI_3" + "P-poll__networl_5_7_RI_4" + "P-poll__networl_5_7_RI_5" + "P-poll__networl_5_7_RI_6" + "P-poll__networl_5_7_RI_7" + "P-poll__networl_5_7_RI_8" + "P-poll__networl_5_7_AI_0" + "P-poll__networl_5_7_AI_1" + "P-poll__networl_5_7_AI_2" + "P-poll__networl_5_7_AI_3" + "P-poll__networl_5_7_AI_4" + "P-poll__networl_5_7_AI_5" + "P-poll__networl_5_7_AI_6" + "P-poll__networl_5_7_AI_7" + "P-poll__networl_5_7_AI_8" + "P-poll__networl_5_7_AnnP_0" + "P-poll__networl_5_7_AnnP_1" + "P-poll__networl_5_7_AnnP_2" + "P-poll__networl_5_7_AnnP_3" + "P-poll__networl_5_7_AnnP_4" + "P-poll__networl_5_7_AnnP_5" + "P-poll__networl_5_7_AnnP_6" + "P-poll__networl_5_7_AnnP_7" + "P-poll__networl_5_7_AnnP_8" + "P-poll__networl_5_7_RP_0" + "P-poll__networl_5_7_RP_1" + "P-poll__networl_5_7_RP_2" + "P-poll__networl_5_7_RP_3" + "P-poll__networl_5_7_RP_4" + "P-poll__networl_5_7_RP_5" + "P-poll__networl_5_7_RP_6" + "P-poll__networl_5_7_RP_7" + "P-poll__networl_5_7_RP_8" + "P-poll__networl_5_8_AskP_0" + "P-poll__networl_5_8_AskP_1" + "P-poll__networl_5_8_AskP_2" + "P-poll__networl_5_8_AskP_3" + "P-poll__networl_5_8_AskP_4" + "P-poll__networl_5_8_AskP_5" + "P-poll__networl_5_8_AskP_6" + "P-poll__networl_5_8_AskP_7" + "P-poll__networl_5_8_AskP_8" + "P-poll__networl_5_8_AnsP_0" + "P-poll__networl_5_8_AnsP_1" + "P-poll__networl_5_8_AnsP_2" + "P-poll__networl_5_8_AnsP_3" + "P-poll__networl_5_8_AnsP_4" + "P-poll__networl_5_8_AnsP_5" + "P-poll__networl_5_8_AnsP_6" + "P-poll__networl_5_8_AnsP_7" + "P-poll__networl_5_8_AnsP_8" + "P-poll__networl_5_8_RI_0" + "P-poll__networl_5_8_RI_1" + "P-poll__networl_5_8_RI_2" + "P-poll__networl_5_8_RI_3" + "P-poll__networl_5_8_RI_4" + "P-poll__networl_5_8_RI_5" + "P-poll__networl_5_8_RI_6" + "P-poll__networl_5_8_RI_7" + "P-poll__networl_5_8_RI_8" + "P-poll__networl_5_8_AI_0" + "P-poll__networl_5_8_AI_1" + "P-poll__networl_5_8_AI_2" + "P-poll__networl_5_8_AI_3" + "P-poll__networl_5_8_AI_4" + "P-poll__networl_5_8_AI_5" + "P-poll__networl_5_8_AI_6" + "P-poll__networl_5_8_AI_7" + "P-poll__networl_5_8_AI_8" + "P-poll__networl_5_8_AnnP_0" + "P-poll__networl_5_8_AnnP_1" + "P-poll__networl_5_8_AnnP_2" + "P-poll__networl_5_8_AnnP_3" + "P-poll__networl_5_8_AnnP_4" + "P-poll__networl_5_8_AnnP_5" + "P-poll__networl_5_8_AnnP_6" + "P-poll__networl_5_8_AnnP_7" + "P-poll__networl_5_8_AnnP_8" + "P-poll__networl_5_8_RP_0" + "P-poll__networl_5_8_RP_1" + "P-poll__networl_5_8_RP_2" + "P-poll__networl_5_8_RP_3" + "P-poll__networl_5_8_RP_4" + "P-poll__networl_5_8_RP_5" + "P-poll__networl_5_8_RP_6" + "P-poll__networl_5_8_RP_7" + "P-poll__networl_5_8_RP_8" + "P-poll__networl_6_0_AskP_0" + "P-poll__networl_6_0_AskP_1" + "P-poll__networl_6_0_AskP_2" + "P-poll__networl_6_0_AskP_3" + "P-poll__networl_6_0_AskP_4" + "P-poll__networl_6_0_AskP_5" + "P-poll__networl_6_0_AskP_6" + "P-poll__networl_6_0_AskP_7" + "P-poll__networl_6_0_AskP_8" + "P-poll__networl_6_0_AnsP_0" + "P-poll__networl_6_0_AnsP_1" + "P-poll__networl_6_0_AnsP_2" + "P-poll__networl_6_0_AnsP_3" + "P-poll__networl_6_0_AnsP_4" + "P-poll__networl_6_0_AnsP_5" + "P-poll__networl_6_0_AnsP_6" + "P-poll__networl_6_0_AnsP_7" + "P-poll__networl_6_0_AnsP_8" + "P-poll__networl_6_0_RI_0" + "P-poll__networl_6_0_RI_1" + "P-poll__networl_6_0_RI_2" + "P-poll__networl_6_0_RI_3" + "P-poll__networl_6_0_RI_4" + "P-poll__networl_6_0_RI_5" + "P-poll__networl_6_0_RI_6" + "P-poll__networl_6_0_RI_7" + "P-poll__networl_6_0_RI_8" + "P-poll__networl_6_0_AI_0" + "P-poll__networl_6_0_AI_1" + "P-poll__networl_6_0_AI_2" + "P-poll__networl_6_0_AI_3" + "P-poll__networl_6_0_AI_4" + "P-poll__networl_6_0_AI_5" + "P-poll__networl_6_0_AI_6" + "P-poll__networl_6_0_AI_7" + "P-poll__networl_6_0_AI_8" + "P-poll__networl_6_0_AnnP_0" + "P-poll__networl_6_0_AnnP_1" + "P-poll__networl_6_0_AnnP_2" + "P-poll__networl_6_0_AnnP_3" + "P-poll__networl_6_0_AnnP_4" + "P-poll__networl_6_0_AnnP_5" + "P-poll__networl_6_0_AnnP_6" + "P-poll__networl_6_0_AnnP_7" + "P-poll__networl_6_0_AnnP_8" + "P-poll__networl_6_0_RP_0" + "P-poll__networl_6_0_RP_1" + "P-poll__networl_6_0_RP_2" + "P-poll__networl_6_0_RP_3" + "P-poll__networl_6_0_RP_4" + "P-poll__networl_6_0_RP_5" + "P-poll__networl_6_0_RP_6" + "P-poll__networl_6_0_RP_7" + "P-poll__networl_6_0_RP_8" + "P-poll__networl_6_1_AskP_0" + "P-poll__networl_6_1_AskP_1" + "P-poll__networl_6_1_AskP_2" + "P-poll__networl_6_1_AskP_3" + "P-poll__networl_6_1_AskP_4" + "P-poll__networl_6_1_AskP_5" + "P-poll__networl_6_1_AskP_6" + "P-poll__networl_6_1_AskP_7" + "P-poll__networl_6_1_AskP_8" + "P-poll__networl_6_1_AnsP_0" + "P-poll__networl_6_1_AnsP_1" + "P-poll__networl_6_1_AnsP_2" + "P-poll__networl_6_1_AnsP_3" + "P-poll__networl_6_1_AnsP_4" + "P-poll__networl_6_1_AnsP_5" + "P-poll__networl_6_1_AnsP_6" + "P-poll__networl_6_1_AnsP_7" + "P-poll__networl_6_1_AnsP_8" + "P-poll__networl_6_1_RI_0" + "P-poll__networl_6_1_RI_1" + "P-poll__networl_6_1_RI_2" + "P-poll__networl_6_1_RI_3" + "P-poll__networl_6_1_RI_4" + "P-poll__networl_6_1_RI_5" + "P-poll__networl_6_1_RI_6" + "P-poll__networl_6_1_RI_7" + "P-poll__networl_6_1_RI_8" + "P-poll__networl_6_1_AI_0" + "P-poll__networl_6_1_AI_1" + "P-poll__networl_6_1_AI_2" + "P-poll__networl_6_1_AI_3" + "P-poll__networl_6_1_AI_4" + "P-poll__networl_6_1_AI_5" + "P-poll__networl_6_1_AI_6" + "P-poll__networl_6_1_AI_7" + "P-poll__networl_6_1_AI_8" + "P-poll__networl_6_1_AnnP_0" + "P-poll__networl_6_1_AnnP_1" + "P-poll__networl_6_1_AnnP_2" + "P-poll__networl_6_1_AnnP_3" + "P-poll__networl_6_1_AnnP_4" + "P-poll__networl_6_1_AnnP_5" + "P-poll__networl_6_1_AnnP_6" + "P-poll__networl_6_1_AnnP_7" + "P-poll__networl_6_1_AnnP_8" + "P-poll__networl_6_1_RP_0" + "P-poll__networl_6_1_RP_1" + "P-poll__networl_6_1_RP_2" + "P-poll__networl_6_1_RP_3" + "P-poll__networl_6_1_RP_4" + "P-poll__networl_6_1_RP_5" + "P-poll__networl_6_1_RP_6" + "P-poll__networl_6_1_RP_7" + "P-poll__networl_6_1_RP_8" + "P-poll__networl_6_2_AskP_0" + "P-poll__networl_6_2_AskP_1" + "P-poll__networl_6_2_AskP_2" + "P-poll__networl_6_2_AskP_3" + "P-poll__networl_6_2_AskP_4" + "P-poll__networl_6_2_AskP_5" + "P-poll__networl_6_2_AskP_6" + "P-poll__networl_6_2_AskP_7" + "P-poll__networl_6_2_AskP_8" + "P-poll__networl_6_2_AnsP_0" + "P-poll__networl_6_2_AnsP_1" + "P-poll__networl_6_2_AnsP_2" + "P-poll__networl_6_2_AnsP_3" + "P-poll__networl_6_2_AnsP_4" + "P-poll__networl_6_2_AnsP_5" + "P-poll__networl_6_2_AnsP_6" + "P-poll__networl_6_2_AnsP_7" + "P-poll__networl_6_2_AnsP_8" + "P-poll__networl_6_2_RI_0" + "P-poll__networl_6_2_RI_1" + "P-poll__networl_6_2_RI_2" + "P-poll__networl_6_2_RI_3" + "P-poll__networl_6_2_RI_4" + "P-poll__networl_6_2_RI_5" + "P-poll__networl_6_2_RI_6" + "P-poll__networl_6_2_RI_7" + "P-poll__networl_6_2_RI_8" + "P-poll__networl_6_2_AI_0" + "P-poll__networl_6_2_AI_1" + "P-poll__networl_6_2_AI_2" + "P-poll__networl_6_2_AI_3" + "P-poll__networl_6_2_AI_4" + "P-poll__networl_6_2_AI_5" + "P-poll__networl_6_2_AI_6" + "P-poll__networl_6_2_AI_7" + "P-poll__networl_6_2_AI_8" + "P-poll__networl_6_2_AnnP_0" + "P-poll__networl_6_2_AnnP_1" + "P-poll__networl_6_2_AnnP_2" + "P-poll__networl_6_2_AnnP_3" + "P-poll__networl_6_2_AnnP_4" + "P-poll__networl_6_2_AnnP_5" + "P-poll__networl_6_2_AnnP_6" + "P-poll__networl_6_2_AnnP_7" + "P-poll__networl_6_2_AnnP_8" + "P-poll__networl_6_2_RP_0" + "P-poll__networl_6_2_RP_1" + "P-poll__networl_6_2_RP_2" + "P-poll__networl_6_2_RP_3" + "P-poll__networl_6_2_RP_4" + "P-poll__networl_6_2_RP_5" + "P-poll__networl_6_2_RP_6" + "P-poll__networl_6_2_RP_7" + "P-poll__networl_6_2_RP_8" + "P-poll__networl_6_3_AskP_0" + "P-poll__networl_6_3_AskP_1" + "P-poll__networl_6_3_AskP_2" + "P-poll__networl_6_3_AskP_3" + "P-poll__networl_6_3_AskP_4" + "P-poll__networl_6_3_AskP_5" + "P-poll__networl_6_3_AskP_6" + "P-poll__networl_6_3_AskP_7" + "P-poll__networl_6_3_AskP_8" + "P-poll__networl_6_3_AnsP_0" + "P-poll__networl_6_3_AnsP_1" + "P-poll__networl_6_3_AnsP_2" + "P-poll__networl_6_3_AnsP_3" + "P-poll__networl_6_3_AnsP_4" + "P-poll__networl_6_3_AnsP_5" + "P-poll__networl_6_3_AnsP_6" + "P-poll__networl_6_3_AnsP_7" + "P-poll__networl_6_3_AnsP_8" + "P-poll__networl_6_3_RI_0" + "P-poll__networl_6_3_RI_1" + "P-poll__networl_6_3_RI_2" + "P-poll__networl_6_3_RI_3" + "P-poll__networl_6_3_RI_4" + "P-poll__networl_6_3_RI_5" + "P-poll__networl_6_3_RI_6" + "P-poll__networl_6_3_RI_7" + "P-poll__networl_6_3_RI_8" + "P-poll__networl_6_3_AI_0" + "P-poll__networl_6_3_AI_1" + "P-poll__networl_6_3_AI_2" + "P-poll__networl_6_3_AI_3" + "P-poll__networl_6_3_AI_4" + "P-poll__networl_6_3_AI_5" + "P-poll__networl_6_3_AI_6" + "P-poll__networl_6_3_AI_7" + "P-poll__networl_6_3_AI_8" + "P-poll__networl_6_3_AnnP_0" + "P-poll__networl_6_3_AnnP_1" + "P-poll__networl_6_3_AnnP_2" + "P-poll__networl_6_3_AnnP_3" + "P-poll__networl_6_3_AnnP_4" + "P-poll__networl_6_3_AnnP_5" + "P-poll__networl_6_3_AnnP_6" + "P-poll__networl_6_3_AnnP_7" + "P-poll__networl_6_3_AnnP_8" + "P-poll__networl_6_3_RP_0" + "P-poll__networl_6_3_RP_1" + "P-poll__networl_6_3_RP_2" + "P-poll__networl_6_3_RP_3" + "P-poll__networl_6_3_RP_4" + "P-poll__networl_6_3_RP_5" + "P-poll__networl_6_3_RP_6" + "P-poll__networl_6_3_RP_7" + "P-poll__networl_6_3_RP_8" + "P-poll__networl_6_4_AskP_0" + "P-poll__networl_6_4_AskP_1" + "P-poll__networl_6_4_AskP_2" + "P-poll__networl_6_4_AskP_3" + "P-poll__networl_6_4_AskP_4" + "P-poll__networl_6_4_AskP_5" + "P-poll__networl_6_4_AskP_6" + "P-poll__networl_6_4_AskP_7" + "P-poll__networl_6_4_AskP_8" + "P-poll__networl_6_4_AnsP_0" + "P-poll__networl_6_4_AnsP_1" + "P-poll__networl_6_4_AnsP_2" + "P-poll__networl_6_4_AnsP_3" + "P-poll__networl_6_4_AnsP_4" + "P-poll__networl_6_4_AnsP_5" + "P-poll__networl_6_4_AnsP_6" + "P-poll__networl_6_4_AnsP_7" + "P-poll__networl_6_4_AnsP_8" + "P-poll__networl_6_4_RI_0" + "P-poll__networl_6_4_RI_1" + "P-poll__networl_6_4_RI_2" + "P-poll__networl_6_4_RI_3" + "P-poll__networl_6_4_RI_4" + "P-poll__networl_6_4_RI_5" + "P-poll__networl_6_4_RI_6" + "P-poll__networl_6_4_RI_7" + "P-poll__networl_6_4_RI_8" + "P-poll__networl_6_4_AI_0" + "P-poll__networl_6_4_AI_1" + "P-poll__networl_6_4_AI_2" + "P-poll__networl_6_4_AI_3" + "P-poll__networl_6_4_AI_4" + "P-poll__networl_6_4_AI_5" + "P-poll__networl_6_4_AI_6" + "P-poll__networl_6_4_AI_7" + "P-poll__networl_6_4_AI_8" + "P-poll__networl_6_4_AnnP_0" + "P-poll__networl_6_4_AnnP_1" + "P-poll__networl_6_4_AnnP_2" + "P-poll__networl_6_4_AnnP_3" + "P-poll__networl_6_4_AnnP_4" + "P-poll__networl_6_4_AnnP_5" + "P-poll__networl_6_4_AnnP_6" + "P-poll__networl_6_4_AnnP_7" + "P-poll__networl_6_4_AnnP_8" + "P-poll__networl_6_4_RP_0" + "P-poll__networl_6_4_RP_1" + "P-poll__networl_6_4_RP_2" + "P-poll__networl_6_4_RP_3" + "P-poll__networl_6_4_RP_4" + "P-poll__networl_6_4_RP_5" + "P-poll__networl_6_4_RP_6" + "P-poll__networl_6_4_RP_7" + "P-poll__networl_6_4_RP_8" + "P-poll__networl_6_5_AskP_0" + "P-poll__networl_6_5_AskP_1" + "P-poll__networl_6_5_AskP_2" + "P-poll__networl_6_5_AskP_3" + "P-poll__networl_6_5_AskP_4" + "P-poll__networl_6_5_AskP_5" + "P-poll__networl_6_5_AskP_6" + "P-poll__networl_6_5_AskP_7" + "P-poll__networl_6_5_AskP_8" + "P-poll__networl_6_5_AnsP_0" + "P-poll__networl_6_5_AnsP_1" + "P-poll__networl_6_5_AnsP_2" + "P-poll__networl_6_5_AnsP_3" + "P-poll__networl_6_5_AnsP_4" + "P-poll__networl_6_5_AnsP_5" + "P-poll__networl_6_5_AnsP_6" + "P-poll__networl_6_5_AnsP_7" + "P-poll__networl_6_5_AnsP_8" + "P-poll__networl_6_5_RI_0" + "P-poll__networl_6_5_RI_1" + "P-poll__networl_6_5_RI_2" + "P-poll__networl_6_5_RI_3" + "P-poll__networl_6_5_RI_4" + "P-poll__networl_6_5_RI_5" + "P-poll__networl_6_5_RI_6" + "P-poll__networl_6_5_RI_7" + "P-poll__networl_6_5_RI_8" + "P-poll__networl_6_5_AI_0" + "P-poll__networl_6_5_AI_1" + "P-poll__networl_6_5_AI_2" + "P-poll__networl_6_5_AI_3" + "P-poll__networl_6_5_AI_4" + "P-poll__networl_6_5_AI_5" + "P-poll__networl_6_5_AI_6" + "P-poll__networl_6_5_AI_7" + "P-poll__networl_6_5_AI_8" + "P-poll__networl_6_5_AnnP_0" + "P-poll__networl_6_5_AnnP_1" + "P-poll__networl_6_5_AnnP_2" + "P-poll__networl_6_5_AnnP_3" + "P-poll__networl_6_5_AnnP_4" + "P-poll__networl_6_5_AnnP_5" + "P-poll__networl_6_5_AnnP_6" + "P-poll__networl_6_5_AnnP_7" + "P-poll__networl_6_5_AnnP_8" + "P-poll__networl_6_5_RP_0" + "P-poll__networl_6_5_RP_1" + "P-poll__networl_6_5_RP_2" + "P-poll__networl_6_5_RP_3" + "P-poll__networl_6_5_RP_4" + "P-poll__networl_6_5_RP_5" + "P-poll__networl_6_5_RP_6" + "P-poll__networl_6_5_RP_7" + "P-poll__networl_6_5_RP_8" + "P-poll__networl_6_6_AskP_0" + "P-poll__networl_6_6_AskP_1" + "P-poll__networl_6_6_AskP_2" + "P-poll__networl_6_6_AskP_3" + "P-poll__networl_6_6_AskP_4" + "P-poll__networl_6_6_AskP_5" + "P-poll__networl_6_6_AskP_6" + "P-poll__networl_6_6_AskP_7" + "P-poll__networl_6_6_AskP_8" + "P-poll__networl_6_6_AnsP_0" + "P-poll__networl_6_6_AnsP_1" + "P-poll__networl_6_6_AnsP_2" + "P-poll__networl_6_6_AnsP_3" + "P-poll__networl_6_6_AnsP_4" + "P-poll__networl_6_6_AnsP_5" + "P-poll__networl_6_6_AnsP_6" + "P-poll__networl_6_6_AnsP_7" + "P-poll__networl_6_6_AnsP_8" + "P-poll__networl_6_6_RI_0" + "P-poll__networl_6_6_RI_1" + "P-poll__networl_6_6_RI_2" + "P-poll__networl_6_6_RI_3" + "P-poll__networl_6_6_RI_4" + "P-poll__networl_6_6_RI_5" + "P-poll__networl_6_6_RI_6" + "P-poll__networl_6_6_RI_7" + "P-poll__networl_6_6_RI_8" + "P-poll__networl_6_6_AI_0" + "P-poll__networl_6_6_AI_1" + "P-poll__networl_6_6_AI_2" + "P-poll__networl_6_6_AI_3" + "P-poll__networl_6_6_AI_4" + "P-poll__networl_6_6_AI_5" + "P-poll__networl_6_6_AI_6" + "P-poll__networl_6_6_AI_7" + "P-poll__networl_6_6_AI_8" + "P-poll__networl_6_6_AnnP_0" + "P-poll__networl_6_6_AnnP_1" + "P-poll__networl_6_6_AnnP_2" + "P-poll__networl_6_6_AnnP_3" + "P-poll__networl_6_6_AnnP_4" + "P-poll__networl_6_6_AnnP_5" + "P-poll__networl_6_6_AnnP_6" + "P-poll__networl_6_6_AnnP_7" + "P-poll__networl_6_6_AnnP_8" + "P-poll__networl_6_6_RP_0" + "P-poll__networl_6_6_RP_1" + "P-poll__networl_6_6_RP_2" + "P-poll__networl_6_6_RP_3" + "P-poll__networl_6_6_RP_4" + "P-poll__networl_6_6_RP_5" + "P-poll__networl_6_6_RP_6" + "P-poll__networl_6_6_RP_7" + "P-poll__networl_6_6_RP_8" + "P-poll__networl_6_7_AskP_0" + "P-poll__networl_6_7_AskP_1" + "P-poll__networl_6_7_AskP_2" + "P-poll__networl_6_7_AskP_3" + "P-poll__networl_6_7_AskP_4" + "P-poll__networl_6_7_AskP_5" + "P-poll__networl_6_7_AskP_6" + "P-poll__networl_6_7_AskP_7" + "P-poll__networl_6_7_AskP_8" + "P-poll__networl_6_7_AnsP_0" + "P-poll__networl_6_7_AnsP_1" + "P-poll__networl_6_7_AnsP_2" + "P-poll__networl_6_7_AnsP_3" + "P-poll__networl_6_7_AnsP_4" + "P-poll__networl_6_7_AnsP_5" + "P-poll__networl_6_7_AnsP_6" + "P-poll__networl_6_7_AnsP_7" + "P-poll__networl_6_7_AnsP_8" + "P-poll__networl_6_7_RI_0" + "P-poll__networl_6_7_RI_1" + "P-poll__networl_6_7_RI_2" + "P-poll__networl_6_7_RI_3" + "P-poll__networl_6_7_RI_4" + "P-poll__networl_6_7_RI_5" + "P-poll__networl_6_7_RI_6" + "P-poll__networl_6_7_RI_7" + "P-poll__networl_6_7_RI_8" + "P-poll__networl_6_7_AI_0" + "P-poll__networl_6_7_AI_1" + "P-poll__networl_6_7_AI_2" + "P-poll__networl_6_7_AI_3" + "P-poll__networl_6_7_AI_4" + "P-poll__networl_6_7_AI_5" + "P-poll__networl_6_7_AI_6" + "P-poll__networl_6_7_AI_7" + "P-poll__networl_6_7_AI_8" + "P-poll__networl_6_7_AnnP_0" + "P-poll__networl_6_7_AnnP_1" + "P-poll__networl_6_7_AnnP_2" + "P-poll__networl_6_7_AnnP_3" + "P-poll__networl_6_7_AnnP_4" + "P-poll__networl_6_7_AnnP_5" + "P-poll__networl_6_7_AnnP_6" + "P-poll__networl_6_7_AnnP_7" + "P-poll__networl_6_7_AnnP_8" + "P-poll__networl_6_7_RP_0" + "P-poll__networl_6_7_RP_1" + "P-poll__networl_6_7_RP_2" + "P-poll__networl_6_7_RP_3" + "P-poll__networl_6_7_RP_4" + "P-poll__networl_6_7_RP_5" + "P-poll__networl_6_7_RP_6" + "P-poll__networl_6_7_RP_7" + "P-poll__networl_6_7_RP_8" + "P-poll__networl_6_8_AskP_0" + "P-poll__networl_6_8_AskP_1" + "P-poll__networl_6_8_AskP_2" + "P-poll__networl_6_8_AskP_3" + "P-poll__networl_6_8_AskP_4" + "P-poll__networl_6_8_AskP_5" + "P-poll__networl_6_8_AskP_6" + "P-poll__networl_6_8_AskP_7" + "P-poll__networl_6_8_AskP_8" + "P-poll__networl_6_8_AnsP_0" + "P-poll__networl_6_8_AnsP_1" + "P-poll__networl_6_8_AnsP_2" + "P-poll__networl_6_8_AnsP_3" + "P-poll__networl_6_8_AnsP_4" + "P-poll__networl_6_8_AnsP_5" + "P-poll__networl_6_8_AnsP_6" + "P-poll__networl_6_8_AnsP_7" + "P-poll__networl_6_8_AnsP_8" + "P-poll__networl_6_8_RI_0" + "P-poll__networl_6_8_RI_1" + "P-poll__networl_6_8_RI_2" + "P-poll__networl_6_8_RI_3" + "P-poll__networl_6_8_RI_4" + "P-poll__networl_6_8_RI_5" + "P-poll__networl_6_8_RI_6" + "P-poll__networl_6_8_RI_7" + "P-poll__networl_6_8_RI_8" + "P-poll__networl_6_8_AI_0" + "P-poll__networl_6_8_AI_1" + "P-poll__networl_6_8_AI_2" + "P-poll__networl_6_8_AI_3" + "P-poll__networl_6_8_AI_4" + "P-poll__networl_6_8_AI_5" + "P-poll__networl_6_8_AI_6" + "P-poll__networl_6_8_AI_7" + "P-poll__networl_6_8_AI_8" + "P-poll__networl_6_8_AnnP_0" + "P-poll__networl_6_8_AnnP_1" + "P-poll__networl_6_8_AnnP_2" + "P-poll__networl_6_8_AnnP_3" + "P-poll__networl_6_8_AnnP_4" + "P-poll__networl_6_8_AnnP_5" + "P-poll__networl_6_8_AnnP_6" + "P-poll__networl_6_8_AnnP_7" + "P-poll__networl_6_8_AnnP_8" + "P-poll__networl_6_8_RP_0" + "P-poll__networl_6_8_RP_1" + "P-poll__networl_6_8_RP_2" + "P-poll__networl_6_8_RP_3" + "P-poll__networl_6_8_RP_4" + "P-poll__networl_6_8_RP_5" + "P-poll__networl_6_8_RP_6" + "P-poll__networl_6_8_RP_7" + "P-poll__networl_6_8_RP_8" + "P-poll__networl_7_0_AskP_0" + "P-poll__networl_7_0_AskP_1" + "P-poll__networl_7_0_AskP_2" + "P-poll__networl_7_0_AskP_3" + "P-poll__networl_7_0_AskP_4" + "P-poll__networl_7_0_AskP_5" + "P-poll__networl_7_0_AskP_6" + "P-poll__networl_7_0_AskP_7" + "P-poll__networl_7_0_AskP_8" + "P-poll__networl_7_0_AnsP_0" + "P-poll__networl_7_0_AnsP_1" + "P-poll__networl_7_0_AnsP_2" + "P-poll__networl_7_0_AnsP_3" + "P-poll__networl_7_0_AnsP_4" + "P-poll__networl_7_0_AnsP_5" + "P-poll__networl_7_0_AnsP_6" + "P-poll__networl_7_0_AnsP_7" + "P-poll__networl_7_0_AnsP_8" + "P-poll__networl_7_0_RI_0" + "P-poll__networl_7_0_RI_1" + "P-poll__networl_7_0_RI_2" + "P-poll__networl_7_0_RI_3" + "P-poll__networl_7_0_RI_4" + "P-poll__networl_7_0_RI_5" + "P-poll__networl_7_0_RI_6" + "P-poll__networl_7_0_RI_7" + "P-poll__networl_7_0_RI_8" + "P-poll__networl_7_0_AI_0" + "P-poll__networl_7_0_AI_1" + "P-poll__networl_7_0_AI_2" + "P-poll__networl_7_0_AI_3" + "P-poll__networl_7_0_AI_4" + "P-poll__networl_7_0_AI_5" + "P-poll__networl_7_0_AI_6" + "P-poll__networl_7_0_AI_7" + "P-poll__networl_7_0_AI_8" + "P-poll__networl_7_0_AnnP_0" + "P-poll__networl_7_0_AnnP_1" + "P-poll__networl_7_0_AnnP_2" + "P-poll__networl_7_0_AnnP_3" + "P-poll__networl_7_0_AnnP_4" + "P-poll__networl_7_0_AnnP_5" + "P-poll__networl_7_0_AnnP_6" + "P-poll__networl_7_0_AnnP_7" + "P-poll__networl_7_0_AnnP_8" + "P-poll__networl_7_0_RP_0" + "P-poll__networl_7_0_RP_1" + "P-poll__networl_7_0_RP_2" + "P-poll__networl_7_0_RP_3" + "P-poll__networl_7_0_RP_4" + "P-poll__networl_7_0_RP_5" + "P-poll__networl_7_0_RP_6" + "P-poll__networl_7_0_RP_7" + "P-poll__networl_7_0_RP_8" + "P-poll__networl_7_1_AskP_0" + "P-poll__networl_7_1_AskP_1" + "P-poll__networl_7_1_AskP_2" + "P-poll__networl_7_1_AskP_3" + "P-poll__networl_7_1_AskP_4" + "P-poll__networl_7_1_AskP_5" + "P-poll__networl_7_1_AskP_6" + "P-poll__networl_7_1_AskP_7" + "P-poll__networl_7_1_AskP_8" + "P-poll__networl_7_1_AnsP_0" + "P-poll__networl_7_1_AnsP_1" + "P-poll__networl_7_1_AnsP_2" + "P-poll__networl_7_1_AnsP_3" + "P-poll__networl_7_1_AnsP_4" + "P-poll__networl_7_1_AnsP_5" + "P-poll__networl_7_1_AnsP_6" + "P-poll__networl_7_1_AnsP_7" + "P-poll__networl_7_1_AnsP_8" + "P-poll__networl_7_1_RI_0" + "P-poll__networl_7_1_RI_1" + "P-poll__networl_7_1_RI_2" + "P-poll__networl_7_1_RI_3" + "P-poll__networl_7_1_RI_4" + "P-poll__networl_7_1_RI_5" + "P-poll__networl_7_1_RI_6" + "P-poll__networl_7_1_RI_7" + "P-poll__networl_7_1_RI_8" + "P-poll__networl_7_1_AI_0" + "P-poll__networl_7_1_AI_1" + "P-poll__networl_7_1_AI_2" + "P-poll__networl_7_1_AI_3" + "P-poll__networl_7_1_AI_4" + "P-poll__networl_7_1_AI_5" + "P-poll__networl_7_1_AI_6" + "P-poll__networl_7_1_AI_7" + "P-poll__networl_7_1_AI_8" + "P-poll__networl_7_1_AnnP_0" + "P-poll__networl_7_1_AnnP_1" + "P-poll__networl_7_1_AnnP_2" + "P-poll__networl_7_1_AnnP_3" + "P-poll__networl_7_1_AnnP_4" + "P-poll__networl_7_1_AnnP_5" + "P-poll__networl_7_1_AnnP_6" + "P-poll__networl_7_1_AnnP_7" + "P-poll__networl_7_1_AnnP_8" + "P-poll__networl_7_1_RP_0" + "P-poll__networl_7_1_RP_1" + "P-poll__networl_7_1_RP_2" + "P-poll__networl_7_1_RP_3" + "P-poll__networl_7_1_RP_4" + "P-poll__networl_7_1_RP_5" + "P-poll__networl_7_1_RP_6" + "P-poll__networl_7_1_RP_7" + "P-poll__networl_7_1_RP_8" + "P-poll__networl_7_2_AskP_0" + "P-poll__networl_7_2_AskP_1" + "P-poll__networl_7_2_AskP_2" + "P-poll__networl_7_2_AskP_3" + "P-poll__networl_7_2_AskP_4" + "P-poll__networl_7_2_AskP_5" + "P-poll__networl_7_2_AskP_6" + "P-poll__networl_7_2_AskP_7" + "P-poll__networl_7_2_AskP_8" + "P-poll__networl_7_2_AnsP_0" + "P-poll__networl_7_2_AnsP_1" + "P-poll__networl_7_2_AnsP_2" + "P-poll__networl_7_2_AnsP_3" + "P-poll__networl_7_2_AnsP_4" + "P-poll__networl_7_2_AnsP_5" + "P-poll__networl_7_2_AnsP_6" + "P-poll__networl_7_2_AnsP_7" + "P-poll__networl_7_2_AnsP_8" + "P-poll__networl_7_2_RI_0" + "P-poll__networl_7_2_RI_1" + "P-poll__networl_7_2_RI_2" + "P-poll__networl_7_2_RI_3" + "P-poll__networl_7_2_RI_4" + "P-poll__networl_7_2_RI_5" + "P-poll__networl_7_2_RI_6" + "P-poll__networl_7_2_RI_7" + "P-poll__networl_7_2_RI_8" + "P-poll__networl_7_2_AI_0" + "P-poll__networl_7_2_AI_1" + "P-poll__networl_7_2_AI_2" + "P-poll__networl_7_2_AI_3" + "P-poll__networl_7_2_AI_4" + "P-poll__networl_7_2_AI_5" + "P-poll__networl_7_2_AI_6" + "P-poll__networl_7_2_AI_7" + "P-poll__networl_7_2_AI_8" + "P-poll__networl_7_2_AnnP_0" + "P-poll__networl_7_2_AnnP_1" + "P-poll__networl_7_2_AnnP_2" + "P-poll__networl_7_2_AnnP_3" + "P-poll__networl_7_2_AnnP_4" + "P-poll__networl_7_2_AnnP_5" + "P-poll__networl_7_2_AnnP_6" + "P-poll__networl_7_2_AnnP_7" + "P-poll__networl_7_2_AnnP_8" + "P-poll__networl_7_2_RP_0" + "P-poll__networl_7_2_RP_1" + "P-poll__networl_7_2_RP_2" + "P-poll__networl_7_2_RP_3" + "P-poll__networl_7_2_RP_4" + "P-poll__networl_7_2_RP_5" + "P-poll__networl_7_2_RP_6" + "P-poll__networl_7_2_RP_7" + "P-poll__networl_7_2_RP_8" + "P-poll__networl_7_3_AskP_0" + "P-poll__networl_7_3_AskP_1" + "P-poll__networl_7_3_AskP_2" + "P-poll__networl_7_3_AskP_3" + "P-poll__networl_7_3_AskP_4" + "P-poll__networl_7_3_AskP_5" + "P-poll__networl_7_3_AskP_6" + "P-poll__networl_7_3_AskP_7" + "P-poll__networl_7_3_AskP_8" + "P-poll__networl_7_3_AnsP_0" + "P-poll__networl_7_3_AnsP_1" + "P-poll__networl_7_3_AnsP_2" + "P-poll__networl_7_3_AnsP_3" + "P-poll__networl_7_3_AnsP_4" + "P-poll__networl_7_3_AnsP_5" + "P-poll__networl_7_3_AnsP_6" + "P-poll__networl_7_3_AnsP_7" + "P-poll__networl_7_3_AnsP_8" + "P-poll__networl_7_3_RI_0" + "P-poll__networl_7_3_RI_1" + "P-poll__networl_7_3_RI_2" + "P-poll__networl_7_3_RI_3" + "P-poll__networl_7_3_RI_4" + "P-poll__networl_7_3_RI_5" + "P-poll__networl_7_3_RI_6" + "P-poll__networl_7_3_RI_7" + "P-poll__networl_7_3_RI_8" + "P-poll__networl_7_3_AI_0" + "P-poll__networl_7_3_AI_1" + "P-poll__networl_7_3_AI_2" + "P-poll__networl_7_3_AI_3" + "P-poll__networl_7_3_AI_4" + "P-poll__networl_7_3_AI_5" + "P-poll__networl_7_3_AI_6" + "P-poll__networl_7_3_AI_7" + "P-poll__networl_7_3_AI_8" + "P-poll__networl_7_3_AnnP_0" + "P-poll__networl_7_3_AnnP_1" + "P-poll__networl_7_3_AnnP_2" + "P-poll__networl_7_3_AnnP_3" + "P-poll__networl_7_3_AnnP_4" + "P-poll__networl_7_3_AnnP_5" + "P-poll__networl_7_3_AnnP_6" + "P-poll__networl_7_3_AnnP_7" + "P-poll__networl_7_3_AnnP_8" + "P-poll__networl_7_3_RP_0" + "P-poll__networl_7_3_RP_1" + "P-poll__networl_7_3_RP_2" + "P-poll__networl_7_3_RP_3" + "P-poll__networl_7_3_RP_4" + "P-poll__networl_7_3_RP_5" + "P-poll__networl_7_3_RP_6" + "P-poll__networl_7_3_RP_7" + "P-poll__networl_7_3_RP_8" + "P-poll__networl_7_4_AskP_0" + "P-poll__networl_7_4_AskP_1" + "P-poll__networl_7_4_AskP_2" + "P-poll__networl_7_4_AskP_3" + "P-poll__networl_7_4_AskP_4" + "P-poll__networl_7_4_AskP_5" + "P-poll__networl_7_4_AskP_6" + "P-poll__networl_7_4_AskP_7" + "P-poll__networl_7_4_AskP_8" + "P-poll__networl_7_4_AnsP_0" + "P-poll__networl_7_4_AnsP_1" + "P-poll__networl_7_4_AnsP_2" + "P-poll__networl_7_4_AnsP_3" + "P-poll__networl_7_4_AnsP_4" + "P-poll__networl_7_4_AnsP_5" + "P-poll__networl_7_4_AnsP_6" + "P-poll__networl_7_4_AnsP_7" + "P-poll__networl_7_4_AnsP_8" + "P-poll__networl_7_4_RI_0" + "P-poll__networl_7_4_RI_1" + "P-poll__networl_7_4_RI_2" + "P-poll__networl_7_4_RI_3" + "P-poll__networl_7_4_RI_4" + "P-poll__networl_7_4_RI_5" + "P-poll__networl_7_4_RI_6" + "P-poll__networl_7_4_RI_7" + "P-poll__networl_7_4_RI_8" + "P-poll__networl_7_4_AI_0" + "P-poll__networl_7_4_AI_1" + "P-poll__networl_7_4_AI_2" + "P-poll__networl_7_4_AI_3" + "P-poll__networl_7_4_AI_4" + "P-poll__networl_7_4_AI_5" + "P-poll__networl_7_4_AI_6" + "P-poll__networl_7_4_AI_7" + "P-poll__networl_7_4_AI_8" + "P-poll__networl_7_4_AnnP_0" + "P-poll__networl_7_4_AnnP_1" + "P-poll__networl_7_4_AnnP_2" + "P-poll__networl_7_4_AnnP_3" + "P-poll__networl_7_4_AnnP_4" + "P-poll__networl_7_4_AnnP_5" + "P-poll__networl_7_4_AnnP_6" + "P-poll__networl_7_4_AnnP_7" + "P-poll__networl_7_4_AnnP_8" + "P-poll__networl_7_4_RP_0" + "P-poll__networl_7_4_RP_1" + "P-poll__networl_7_4_RP_2" + "P-poll__networl_7_4_RP_3" + "P-poll__networl_7_4_RP_4" + "P-poll__networl_7_4_RP_5" + "P-poll__networl_7_4_RP_6" + "P-poll__networl_7_4_RP_7" + "P-poll__networl_7_4_RP_8" + "P-poll__networl_7_5_AskP_0" + "P-poll__networl_7_5_AskP_1" + "P-poll__networl_7_5_AskP_2" + "P-poll__networl_7_5_AskP_3" + "P-poll__networl_7_5_AskP_4" + "P-poll__networl_7_5_AskP_5" + "P-poll__networl_7_5_AskP_6" + "P-poll__networl_7_5_AskP_7" + "P-poll__networl_7_5_AskP_8" + "P-poll__networl_7_5_AnsP_0" + "P-poll__networl_7_5_AnsP_1" + "P-poll__networl_7_5_AnsP_2" + "P-poll__networl_7_5_AnsP_3" + "P-poll__networl_7_5_AnsP_4" + "P-poll__networl_7_5_AnsP_5" + "P-poll__networl_7_5_AnsP_6" + "P-poll__networl_7_5_AnsP_7" + "P-poll__networl_7_5_AnsP_8" + "P-poll__networl_7_5_RI_0" + "P-poll__networl_7_5_RI_1" + "P-poll__networl_7_5_RI_2" + "P-poll__networl_7_5_RI_3" + "P-poll__networl_7_5_RI_4" + "P-poll__networl_7_5_RI_5" + "P-poll__networl_7_5_RI_6" + "P-poll__networl_7_5_RI_7" + "P-poll__networl_7_5_RI_8" + "P-poll__networl_7_5_AI_0" + "P-poll__networl_7_5_AI_1" + "P-poll__networl_7_5_AI_2" + "P-poll__networl_7_5_AI_3" + "P-poll__networl_7_5_AI_4" + "P-poll__networl_7_5_AI_5" + "P-poll__networl_7_5_AI_6" + "P-poll__networl_7_5_AI_7" + "P-poll__networl_7_5_AI_8" + "P-poll__networl_7_5_AnnP_0" + "P-poll__networl_7_5_AnnP_1" + "P-poll__networl_7_5_AnnP_2" + "P-poll__networl_7_5_AnnP_3" + "P-poll__networl_7_5_AnnP_4" + "P-poll__networl_7_5_AnnP_5" + "P-poll__networl_7_5_AnnP_6" + "P-poll__networl_7_5_AnnP_7" + "P-poll__networl_7_5_AnnP_8" + "P-poll__networl_7_5_RP_0" + "P-poll__networl_7_5_RP_1" + "P-poll__networl_7_5_RP_2" + "P-poll__networl_7_5_RP_3" + "P-poll__networl_7_5_RP_4" + "P-poll__networl_7_5_RP_5" + "P-poll__networl_7_5_RP_6" + "P-poll__networl_7_5_RP_7" + "P-poll__networl_7_5_RP_8" + "P-poll__networl_7_6_AskP_0" + "P-poll__networl_7_6_AskP_1" + "P-poll__networl_7_6_AskP_2" + "P-poll__networl_7_6_AskP_3" + "P-poll__networl_7_6_AskP_4" + "P-poll__networl_7_6_AskP_5" + "P-poll__networl_7_6_AskP_6" + "P-poll__networl_7_6_AskP_7" + "P-poll__networl_7_6_AskP_8" + "P-poll__networl_7_6_AnsP_0" + "P-poll__networl_7_6_AnsP_1" + "P-poll__networl_7_6_AnsP_2" + "P-poll__networl_7_6_AnsP_3" + "P-poll__networl_7_6_AnsP_4" + "P-poll__networl_7_6_AnsP_5" + "P-poll__networl_7_6_AnsP_6" + "P-poll__networl_7_6_AnsP_7" + "P-poll__networl_7_6_AnsP_8" + "P-poll__networl_7_6_RI_0" + "P-poll__networl_7_6_RI_1" + "P-poll__networl_7_6_RI_2" + "P-poll__networl_7_6_RI_3" + "P-poll__networl_7_6_RI_4" + "P-poll__networl_7_6_RI_5" + "P-poll__networl_7_6_RI_6" + "P-poll__networl_7_6_RI_7" + "P-poll__networl_7_6_RI_8" + "P-poll__networl_7_6_AI_0" + "P-poll__networl_7_6_AI_1" + "P-poll__networl_7_6_AI_2" + "P-poll__networl_7_6_AI_3" + "P-poll__networl_7_6_AI_4" + "P-poll__networl_7_6_AI_5" + "P-poll__networl_7_6_AI_6" + "P-poll__networl_7_6_AI_7" + "P-poll__networl_7_6_AI_8" + "P-poll__networl_7_6_AnnP_0" + "P-poll__networl_7_6_AnnP_1" + "P-poll__networl_7_6_AnnP_2" + "P-poll__networl_7_6_AnnP_3" + "P-poll__networl_7_6_AnnP_4" + "P-poll__networl_7_6_AnnP_5" + "P-poll__networl_7_6_AnnP_6" + "P-poll__networl_7_6_AnnP_7" + "P-poll__networl_7_6_AnnP_8" + "P-poll__networl_7_6_RP_0" + "P-poll__networl_7_6_RP_1" + "P-poll__networl_7_6_RP_2" + "P-poll__networl_7_6_RP_3" + "P-poll__networl_7_6_RP_4" + "P-poll__networl_7_6_RP_5" + "P-poll__networl_7_6_RP_6" + "P-poll__networl_7_6_RP_7" + "P-poll__networl_7_6_RP_8" + "P-poll__networl_7_7_AskP_0" + "P-poll__networl_7_7_AskP_1" + "P-poll__networl_7_7_AskP_2" + "P-poll__networl_7_7_AskP_3" + "P-poll__networl_7_7_AskP_4" + "P-poll__networl_7_7_AskP_5" + "P-poll__networl_7_7_AskP_6" + "P-poll__networl_7_7_AskP_7" + "P-poll__networl_7_7_AskP_8" + "P-poll__networl_7_7_AnsP_0" + "P-poll__networl_7_7_AnsP_1" + "P-poll__networl_7_7_AnsP_2" + "P-poll__networl_7_7_AnsP_3" + "P-poll__networl_7_7_AnsP_4" + "P-poll__networl_7_7_AnsP_5" + "P-poll__networl_7_7_AnsP_6" + "P-poll__networl_7_7_AnsP_7" + "P-poll__networl_7_7_AnsP_8" + "P-poll__networl_7_7_RI_0" + "P-poll__networl_7_7_RI_1" + "P-poll__networl_7_7_RI_2" + "P-poll__networl_7_7_RI_3" + "P-poll__networl_7_7_RI_4" + "P-poll__networl_7_7_RI_5" + "P-poll__networl_7_7_RI_6" + "P-poll__networl_7_7_RI_7" + "P-poll__networl_7_7_RI_8" + "P-poll__networl_7_7_AI_0" + "P-poll__networl_7_7_AI_1" + "P-poll__networl_7_7_AI_2" + "P-poll__networl_7_7_AI_3" + "P-poll__networl_7_7_AI_4" + "P-poll__networl_7_7_AI_5" + "P-poll__networl_7_7_AI_6" + "P-poll__networl_7_7_AI_7" + "P-poll__networl_7_7_AI_8" + "P-poll__networl_7_7_AnnP_0" + "P-poll__networl_7_7_AnnP_1" + "P-poll__networl_7_7_AnnP_2" + "P-poll__networl_7_7_AnnP_3" + "P-poll__networl_7_7_AnnP_4" + "P-poll__networl_7_7_AnnP_5" + "P-poll__networl_7_7_AnnP_6" + "P-poll__networl_7_7_AnnP_7" + "P-poll__networl_7_7_AnnP_8" + "P-poll__networl_7_7_RP_0" + "P-poll__networl_7_7_RP_1" + "P-poll__networl_7_7_RP_2" + "P-poll__networl_7_7_RP_3" + "P-poll__networl_7_7_RP_4" + "P-poll__networl_7_7_RP_5" + "P-poll__networl_7_7_RP_6" + "P-poll__networl_7_7_RP_7" + "P-poll__networl_7_7_RP_8" + "P-poll__networl_7_8_AskP_0" + "P-poll__networl_7_8_AskP_1" + "P-poll__networl_7_8_AskP_2" + "P-poll__networl_7_8_AskP_3" + "P-poll__networl_7_8_AskP_4" + "P-poll__networl_7_8_AskP_5" + "P-poll__networl_7_8_AskP_6" + "P-poll__networl_7_8_AskP_7" + "P-poll__networl_7_8_AskP_8" + "P-poll__networl_7_8_AnsP_0" + "P-poll__networl_7_8_AnsP_1" + "P-poll__networl_7_8_AnsP_2" + "P-poll__networl_7_8_AnsP_3" + "P-poll__networl_7_8_AnsP_4" + "P-poll__networl_7_8_AnsP_5" + "P-poll__networl_7_8_AnsP_6" + "P-poll__networl_7_8_AnsP_7" + "P-poll__networl_7_8_AnsP_8" + "P-poll__networl_7_8_RI_0" + "P-poll__networl_7_8_RI_1" + "P-poll__networl_7_8_RI_2" + "P-poll__networl_7_8_RI_3" + "P-poll__networl_7_8_RI_4" + "P-poll__networl_7_8_RI_5" + "P-poll__networl_7_8_RI_6" + "P-poll__networl_7_8_RI_7" + "P-poll__networl_7_8_RI_8" + "P-poll__networl_7_8_AI_0" + "P-poll__networl_7_8_AI_1" + "P-poll__networl_7_8_AI_2" + "P-poll__networl_7_8_AI_3" + "P-poll__networl_7_8_AI_4" + "P-poll__networl_7_8_AI_5" + "P-poll__networl_7_8_AI_6" + "P-poll__networl_7_8_AI_7" + "P-poll__networl_7_8_AI_8" + "P-poll__networl_7_8_AnnP_0" + "P-poll__networl_7_8_AnnP_1" + "P-poll__networl_7_8_AnnP_2" + "P-poll__networl_7_8_AnnP_3" + "P-poll__networl_7_8_AnnP_4" + "P-poll__networl_7_8_AnnP_5" + "P-poll__networl_7_8_AnnP_6" + "P-poll__networl_7_8_AnnP_7" + "P-poll__networl_7_8_AnnP_8" + "P-poll__networl_7_8_RP_0" + "P-poll__networl_7_8_RP_1" + "P-poll__networl_7_8_RP_2" + "P-poll__networl_7_8_RP_3" + "P-poll__networl_7_8_RP_4" + "P-poll__networl_7_8_RP_5" + "P-poll__networl_7_8_RP_6" + "P-poll__networl_7_8_RP_7" + "P-poll__networl_7_8_RP_8" + "P-poll__networl_8_0_AskP_0" + "P-poll__networl_8_0_AskP_1" + "P-poll__networl_8_0_AskP_2" + "P-poll__networl_8_0_AskP_3" + "P-poll__networl_8_0_AskP_4" + "P-poll__networl_8_0_AskP_5" + "P-poll__networl_8_0_AskP_6" + "P-poll__networl_8_0_AskP_7" + "P-poll__networl_8_0_AskP_8" + "P-poll__networl_8_0_AnsP_0" + "P-poll__networl_8_0_AnsP_1" + "P-poll__networl_8_0_AnsP_2" + "P-poll__networl_8_0_AnsP_3" + "P-poll__networl_8_0_AnsP_4" + "P-poll__networl_8_0_AnsP_5" + "P-poll__networl_8_0_AnsP_6" + "P-poll__networl_8_0_AnsP_7" + "P-poll__networl_8_0_AnsP_8" + "P-poll__networl_8_0_RI_0" + "P-poll__networl_8_0_RI_1" + "P-poll__networl_8_0_RI_2" + "P-poll__networl_8_0_RI_3" + "P-poll__networl_8_0_RI_4" + "P-poll__networl_8_0_RI_5" + "P-poll__networl_8_0_RI_6" + "P-poll__networl_8_0_RI_7" + "P-poll__networl_8_0_RI_8" + "P-poll__networl_8_0_AI_0" + "P-poll__networl_8_0_AI_1" + "P-poll__networl_8_0_AI_2" + "P-poll__networl_8_0_AI_3" + "P-poll__networl_8_0_AI_4" + "P-poll__networl_8_0_AI_5" + "P-poll__networl_8_0_AI_6" + "P-poll__networl_8_0_AI_7" + "P-poll__networl_8_0_AI_8" + "P-poll__networl_8_0_AnnP_0" + "P-poll__networl_8_0_AnnP_1" + "P-poll__networl_8_0_AnnP_2" + "P-poll__networl_8_0_AnnP_3" + "P-poll__networl_8_0_AnnP_4" + "P-poll__networl_8_0_AnnP_5" + "P-poll__networl_8_0_AnnP_6" + "P-poll__networl_8_0_AnnP_7" + "P-poll__networl_8_0_AnnP_8" + "P-poll__networl_8_0_RP_0" + "P-poll__networl_8_0_RP_1" + "P-poll__networl_8_0_RP_2" + "P-poll__networl_8_0_RP_3" + "P-poll__networl_8_0_RP_4" + "P-poll__networl_8_0_RP_5" + "P-poll__networl_8_0_RP_6" + "P-poll__networl_8_0_RP_7" + "P-poll__networl_8_0_RP_8" + "P-poll__networl_8_1_AskP_0" + "P-poll__networl_8_1_AskP_1" + "P-poll__networl_8_1_AskP_2" + "P-poll__networl_8_1_AskP_3" + "P-poll__networl_8_1_AskP_4" + "P-poll__networl_8_1_AskP_5" + "P-poll__networl_8_1_AskP_6" + "P-poll__networl_8_1_AskP_7" + "P-poll__networl_8_1_AskP_8" + "P-poll__networl_8_1_AnsP_0" + "P-poll__networl_8_1_AnsP_1" + "P-poll__networl_8_1_AnsP_2" + "P-poll__networl_8_1_AnsP_3" + "P-poll__networl_8_1_AnsP_4" + "P-poll__networl_8_1_AnsP_5" + "P-poll__networl_8_1_AnsP_6" + "P-poll__networl_8_1_AnsP_7" + "P-poll__networl_8_1_AnsP_8" + "P-poll__networl_8_1_RI_0" + "P-poll__networl_8_1_RI_1" + "P-poll__networl_8_1_RI_2" + "P-poll__networl_8_1_RI_3" + "P-poll__networl_8_1_RI_4" + "P-poll__networl_8_1_RI_5" + "P-poll__networl_8_1_RI_6" + "P-poll__networl_8_1_RI_7" + "P-poll__networl_8_1_RI_8" + "P-poll__networl_8_1_AI_0" + "P-poll__networl_8_1_AI_1" + "P-poll__networl_8_1_AI_2" + "P-poll__networl_8_1_AI_3" + "P-poll__networl_8_1_AI_4" + "P-poll__networl_8_1_AI_5" + "P-poll__networl_8_1_AI_6" + "P-poll__networl_8_1_AI_7" + "P-poll__networl_8_1_AI_8" + "P-poll__networl_8_1_AnnP_0" + "P-poll__networl_8_1_AnnP_1" + "P-poll__networl_8_1_AnnP_2" + "P-poll__networl_8_1_AnnP_3" + "P-poll__networl_8_1_AnnP_4" + "P-poll__networl_8_1_AnnP_5" + "P-poll__networl_8_1_AnnP_6" + "P-poll__networl_8_1_AnnP_7" + "P-poll__networl_8_1_AnnP_8" + "P-poll__networl_8_1_RP_0" + "P-poll__networl_8_1_RP_1" + "P-poll__networl_8_1_RP_2" + "P-poll__networl_8_1_RP_3" + "P-poll__networl_8_1_RP_4" + "P-poll__networl_8_1_RP_5" + "P-poll__networl_8_1_RP_6" + "P-poll__networl_8_1_RP_7" + "P-poll__networl_8_1_RP_8" + "P-poll__networl_8_2_AskP_0" + "P-poll__networl_8_2_AskP_1" + "P-poll__networl_8_2_AskP_2" + "P-poll__networl_8_2_AskP_3" + "P-poll__networl_8_2_AskP_4" + "P-poll__networl_8_2_AskP_5" + "P-poll__networl_8_2_AskP_6" + "P-poll__networl_8_2_AskP_7" + "P-poll__networl_8_2_AskP_8" + "P-poll__networl_8_2_AnsP_0" + "P-poll__networl_8_2_AnsP_1" + "P-poll__networl_8_2_AnsP_2" + "P-poll__networl_8_2_AnsP_3" + "P-poll__networl_8_2_AnsP_4" + "P-poll__networl_8_2_AnsP_5" + "P-poll__networl_8_2_AnsP_6" + "P-poll__networl_8_2_AnsP_7" + "P-poll__networl_8_2_AnsP_8" + "P-poll__networl_8_2_RI_0" + "P-poll__networl_8_2_RI_1" + "P-poll__networl_8_2_RI_2" + "P-poll__networl_8_2_RI_3" + "P-poll__networl_8_2_RI_4" + "P-poll__networl_8_2_RI_5" + "P-poll__networl_8_2_RI_6" + "P-poll__networl_8_2_RI_7" + "P-poll__networl_8_2_RI_8" + "P-poll__networl_8_2_AI_0" + "P-poll__networl_8_2_AI_1" + "P-poll__networl_8_2_AI_2" + "P-poll__networl_8_2_AI_3" + "P-poll__networl_8_2_AI_4" + "P-poll__networl_8_2_AI_5" + "P-poll__networl_8_2_AI_6" + "P-poll__networl_8_2_AI_7" + "P-poll__networl_8_2_AI_8" + "P-poll__networl_8_2_AnnP_0" + "P-poll__networl_8_2_AnnP_1" + "P-poll__networl_8_2_AnnP_2" + "P-poll__networl_8_2_AnnP_3" + "P-poll__networl_8_2_AnnP_4" + "P-poll__networl_8_2_AnnP_5" + "P-poll__networl_8_2_AnnP_6" + "P-poll__networl_8_2_AnnP_7" + "P-poll__networl_8_2_AnnP_8" + "P-poll__networl_8_2_RP_0" + "P-poll__networl_8_2_RP_1" + "P-poll__networl_8_2_RP_2" + "P-poll__networl_8_2_RP_3" + "P-poll__networl_8_2_RP_4" + "P-poll__networl_8_2_RP_5" + "P-poll__networl_8_2_RP_6" + "P-poll__networl_8_2_RP_7" + "P-poll__networl_8_2_RP_8" + "P-poll__networl_8_3_AskP_0" + "P-poll__networl_8_3_AskP_1" + "P-poll__networl_8_3_AskP_2" + "P-poll__networl_8_3_AskP_3" + "P-poll__networl_8_3_AskP_4" + "P-poll__networl_8_3_AskP_5" + "P-poll__networl_8_3_AskP_6" + "P-poll__networl_8_3_AskP_7" + "P-poll__networl_8_3_AskP_8" + "P-poll__networl_8_3_AnsP_0" + "P-poll__networl_8_3_AnsP_1" + "P-poll__networl_8_3_AnsP_2" + "P-poll__networl_8_3_AnsP_3" + "P-poll__networl_8_3_AnsP_4" + "P-poll__networl_8_3_AnsP_5" + "P-poll__networl_8_3_AnsP_6" + "P-poll__networl_8_3_AnsP_7" + "P-poll__networl_8_3_AnsP_8" + "P-poll__networl_8_3_RI_0" + "P-poll__networl_8_3_RI_1" + "P-poll__networl_8_3_RI_2" + "P-poll__networl_8_3_RI_3" + "P-poll__networl_8_3_RI_4" + "P-poll__networl_8_3_RI_5" + "P-poll__networl_8_3_RI_6" + "P-poll__networl_8_3_RI_7" + "P-poll__networl_8_3_RI_8" + "P-poll__networl_8_3_AI_0" + "P-poll__networl_8_3_AI_1" + "P-poll__networl_8_3_AI_2" + "P-poll__networl_8_3_AI_3" + "P-poll__networl_8_3_AI_4" + "P-poll__networl_8_3_AI_5" + "P-poll__networl_8_3_AI_6" + "P-poll__networl_8_3_AI_7" + "P-poll__networl_8_3_AI_8" + "P-poll__networl_8_3_AnnP_0" + "P-poll__networl_8_3_AnnP_1" + "P-poll__networl_8_3_AnnP_2" + "P-poll__networl_8_3_AnnP_3" + "P-poll__networl_8_3_AnnP_4" + "P-poll__networl_8_3_AnnP_5" + "P-poll__networl_8_3_AnnP_6" + "P-poll__networl_8_3_AnnP_7" + "P-poll__networl_8_3_AnnP_8" + "P-poll__networl_8_3_RP_0" + "P-poll__networl_8_3_RP_1" + "P-poll__networl_8_3_RP_2" + "P-poll__networl_8_3_RP_3" + "P-poll__networl_8_3_RP_4" + "P-poll__networl_8_3_RP_5" + "P-poll__networl_8_3_RP_6" + "P-poll__networl_8_3_RP_7" + "P-poll__networl_8_3_RP_8" + "P-poll__networl_8_4_AskP_0" + "P-poll__networl_8_4_AskP_1" + "P-poll__networl_8_4_AskP_2" + "P-poll__networl_8_4_AskP_3" + "P-poll__networl_8_4_AskP_4" + "P-poll__networl_8_4_AskP_5" + "P-poll__networl_8_4_AskP_6" + "P-poll__networl_8_4_AskP_7" + "P-poll__networl_8_4_AskP_8" + "P-poll__networl_8_4_AnsP_0" + "P-poll__networl_8_4_AnsP_1" + "P-poll__networl_8_4_AnsP_2" + "P-poll__networl_8_4_AnsP_3" + "P-poll__networl_8_4_AnsP_4" + "P-poll__networl_8_4_AnsP_5" + "P-poll__networl_8_4_AnsP_6" + "P-poll__networl_8_4_AnsP_7" + "P-poll__networl_8_4_AnsP_8" + "P-poll__networl_8_4_RI_0" + "P-poll__networl_8_4_RI_1" + "P-poll__networl_8_4_RI_2" + "P-poll__networl_8_4_RI_3" + "P-poll__networl_8_4_RI_4" + "P-poll__networl_8_4_RI_5" + "P-poll__networl_8_4_RI_6" + "P-poll__networl_8_4_RI_7" + "P-poll__networl_8_4_RI_8" + "P-poll__networl_8_4_AI_0" + "P-poll__networl_8_4_AI_1" + "P-poll__networl_8_4_AI_2" + "P-poll__networl_8_4_AI_3" + "P-poll__networl_8_4_AI_4" + "P-poll__networl_8_4_AI_5" + "P-poll__networl_8_4_AI_6" + "P-poll__networl_8_4_AI_7" + "P-poll__networl_8_4_AI_8" + "P-poll__networl_8_4_AnnP_0" + "P-poll__networl_8_4_AnnP_1" + "P-poll__networl_8_4_AnnP_2" + "P-poll__networl_8_4_AnnP_3" + "P-poll__networl_8_4_AnnP_4" + "P-poll__networl_8_4_AnnP_5" + "P-poll__networl_8_4_AnnP_6" + "P-poll__networl_8_4_AnnP_7" + "P-poll__networl_8_4_AnnP_8" + "P-poll__networl_8_4_RP_0" + "P-poll__networl_8_4_RP_1" + "P-poll__networl_8_4_RP_2" + "P-poll__networl_8_4_RP_3" + "P-poll__networl_8_4_RP_4" + "P-poll__networl_8_4_RP_5" + "P-poll__networl_8_4_RP_6" + "P-poll__networl_8_4_RP_7" + "P-poll__networl_8_4_RP_8" + "P-poll__networl_8_5_AskP_0" + "P-poll__networl_8_5_AskP_1" + "P-poll__networl_8_5_AskP_2" + "P-poll__networl_8_5_AskP_3" + "P-poll__networl_8_5_AskP_4" + "P-poll__networl_8_5_AskP_5" + "P-poll__networl_8_5_AskP_6" + "P-poll__networl_8_5_AskP_7" + "P-poll__networl_8_5_AskP_8" + "P-poll__networl_8_5_AnsP_0" + "P-poll__networl_8_5_AnsP_1" + "P-poll__networl_8_5_AnsP_2" + "P-poll__networl_8_5_AnsP_3" + "P-poll__networl_8_5_AnsP_4" + "P-poll__networl_8_5_AnsP_5" + "P-poll__networl_8_5_AnsP_6" + "P-poll__networl_8_5_AnsP_7" + "P-poll__networl_8_5_AnsP_8" + "P-poll__networl_8_5_RI_0" + "P-poll__networl_8_5_RI_1" + "P-poll__networl_8_5_RI_2" + "P-poll__networl_8_5_RI_3" + "P-poll__networl_8_5_RI_4" + "P-poll__networl_8_5_RI_5" + "P-poll__networl_8_5_RI_6" + "P-poll__networl_8_5_RI_7" + "P-poll__networl_8_5_RI_8" + "P-poll__networl_8_5_AI_0" + "P-poll__networl_8_5_AI_1" + "P-poll__networl_8_5_AI_2" + "P-poll__networl_8_5_AI_3" + "P-poll__networl_8_5_AI_4" + "P-poll__networl_8_5_AI_5" + "P-poll__networl_8_5_AI_6" + "P-poll__networl_8_5_AI_7" + "P-poll__networl_8_5_AI_8" + "P-poll__networl_8_5_AnnP_0" + "P-poll__networl_8_5_AnnP_1" + "P-poll__networl_8_5_AnnP_2" + "P-poll__networl_8_5_AnnP_3" + "P-poll__networl_8_5_AnnP_4" + "P-poll__networl_8_5_AnnP_5" + "P-poll__networl_8_5_AnnP_6" + "P-poll__networl_8_5_AnnP_7" + "P-poll__networl_8_5_AnnP_8" + "P-poll__networl_8_5_RP_0" + "P-poll__networl_8_5_RP_1" + "P-poll__networl_8_5_RP_2" + "P-poll__networl_8_5_RP_3" + "P-poll__networl_8_5_RP_4" + "P-poll__networl_8_5_RP_5" + "P-poll__networl_8_5_RP_6" + "P-poll__networl_8_5_RP_7" + "P-poll__networl_8_5_RP_8" + "P-poll__networl_8_6_AskP_0" + "P-poll__networl_8_6_AskP_1" + "P-poll__networl_8_6_AskP_2" + "P-poll__networl_8_6_AskP_3" + "P-poll__networl_8_6_AskP_4" + "P-poll__networl_8_6_AskP_5" + "P-poll__networl_8_6_AskP_6" + "P-poll__networl_8_6_AskP_7" + "P-poll__networl_8_6_AskP_8" + "P-poll__networl_8_6_AnsP_0" + "P-poll__networl_8_6_AnsP_1" + "P-poll__networl_8_6_AnsP_2" + "P-poll__networl_8_6_AnsP_3" + "P-poll__networl_8_6_AnsP_4" + "P-poll__networl_8_6_AnsP_5" + "P-poll__networl_8_6_AnsP_6" + "P-poll__networl_8_6_AnsP_7" + "P-poll__networl_8_6_AnsP_8" + "P-poll__networl_8_6_RI_0" + "P-poll__networl_8_6_RI_1" + "P-poll__networl_8_6_RI_2" + "P-poll__networl_8_6_RI_3" + "P-poll__networl_8_6_RI_4" + "P-poll__networl_8_6_RI_5" + "P-poll__networl_8_6_RI_6" + "P-poll__networl_8_6_RI_7" + "P-poll__networl_8_6_RI_8" + "P-poll__networl_8_6_AI_0" + "P-poll__networl_8_6_AI_1" + "P-poll__networl_8_6_AI_2" + "P-poll__networl_8_6_AI_3" + "P-poll__networl_8_6_AI_4" + "P-poll__networl_8_6_AI_5" + "P-poll__networl_8_6_AI_6" + "P-poll__networl_8_6_AI_7" + "P-poll__networl_8_6_AI_8" + "P-poll__networl_8_6_AnnP_0" + "P-poll__networl_8_6_AnnP_1" + "P-poll__networl_8_6_AnnP_2" + "P-poll__networl_8_6_AnnP_3" + "P-poll__networl_8_6_AnnP_4" + "P-poll__networl_8_6_AnnP_5" + "P-poll__networl_8_6_AnnP_6" + "P-poll__networl_8_6_AnnP_7" + "P-poll__networl_8_6_AnnP_8" + "P-poll__networl_8_6_RP_0" + "P-poll__networl_8_6_RP_1" + "P-poll__networl_8_6_RP_2" + "P-poll__networl_8_6_RP_3" + "P-poll__networl_8_6_RP_4" + "P-poll__networl_8_6_RP_5" + "P-poll__networl_8_6_RP_6" + "P-poll__networl_8_6_RP_7" + "P-poll__networl_8_6_RP_8" + "P-poll__networl_8_7_AskP_0" + "P-poll__networl_8_7_AskP_1" + "P-poll__networl_8_7_AskP_2" + "P-poll__networl_8_7_AskP_3" + "P-poll__networl_8_7_AskP_4" + "P-poll__networl_8_7_AskP_5" + "P-poll__networl_8_7_AskP_6" + "P-poll__networl_8_7_AskP_7" + "P-poll__networl_8_7_AskP_8" + "P-poll__networl_8_7_AnsP_0" + "P-poll__networl_8_7_AnsP_1" + "P-poll__networl_8_7_AnsP_2" + "P-poll__networl_8_7_AnsP_3" + "P-poll__networl_8_7_AnsP_4" + "P-poll__networl_8_7_AnsP_5" + "P-poll__networl_8_7_AnsP_6" + "P-poll__networl_8_7_AnsP_7" + "P-poll__networl_8_7_AnsP_8" + "P-poll__networl_8_7_RI_0" + "P-poll__networl_8_7_RI_1" + "P-poll__networl_8_7_RI_2" + "P-poll__networl_8_7_RI_3" + "P-poll__networl_8_7_RI_4" + "P-poll__networl_8_7_RI_5" + "P-poll__networl_8_7_RI_6" + "P-poll__networl_8_7_RI_7" + "P-poll__networl_8_7_RI_8" + "P-poll__networl_8_7_AI_0" + "P-poll__networl_8_7_AI_1" + "P-poll__networl_8_7_AI_2" + "P-poll__networl_8_7_AI_3" + "P-poll__networl_8_7_AI_4" + "P-poll__networl_8_7_AI_5" + "P-poll__networl_8_7_AI_6" + "P-poll__networl_8_7_AI_7" + "P-poll__networl_8_7_AI_8" + "P-poll__networl_8_7_AnnP_0" + "P-poll__networl_8_7_AnnP_1" + "P-poll__networl_8_7_AnnP_2" + "P-poll__networl_8_7_AnnP_3" + "P-poll__networl_8_7_AnnP_4" + "P-poll__networl_8_7_AnnP_5" + "P-poll__networl_8_7_AnnP_6" + "P-poll__networl_8_7_AnnP_7" + "P-poll__networl_8_7_AnnP_8" + "P-poll__networl_8_7_RP_0" + "P-poll__networl_8_7_RP_1" + "P-poll__networl_8_7_RP_2" + "P-poll__networl_8_7_RP_3" + "P-poll__networl_8_7_RP_4" + "P-poll__networl_8_7_RP_5" + "P-poll__networl_8_7_RP_6" + "P-poll__networl_8_7_RP_7" + "P-poll__networl_8_7_RP_8" + "P-poll__networl_8_8_AskP_0" + "P-poll__networl_8_8_AskP_1" + "P-poll__networl_8_8_AskP_2" + "P-poll__networl_8_8_AskP_3" + "P-poll__networl_8_8_AskP_4" + "P-poll__networl_8_8_AskP_5" + "P-poll__networl_8_8_AskP_6" + "P-poll__networl_8_8_AskP_7" + "P-poll__networl_8_8_AskP_8" + "P-poll__networl_8_8_AnsP_0" + "P-poll__networl_8_8_AnsP_1" + "P-poll__networl_8_8_AnsP_2" + "P-poll__networl_8_8_AnsP_3" + "P-poll__networl_8_8_AnsP_4" + "P-poll__networl_8_8_AnsP_5" + "P-poll__networl_8_8_AnsP_6" + "P-poll__networl_8_8_AnsP_7" + "P-poll__networl_8_8_AnsP_8" + "P-poll__networl_8_8_RI_0" + "P-poll__networl_8_8_RI_1" + "P-poll__networl_8_8_RI_2" + "P-poll__networl_8_8_RI_3" + "P-poll__networl_8_8_RI_4" + "P-poll__networl_8_8_RI_5" + "P-poll__networl_8_8_RI_6" + "P-poll__networl_8_8_RI_7" + "P-poll__networl_8_8_RI_8" + "P-poll__networl_8_8_AI_0" + "P-poll__networl_8_8_AI_1" + "P-poll__networl_8_8_AI_2" + "P-poll__networl_8_8_AI_3" + "P-poll__networl_8_8_AI_4" + "P-poll__networl_8_8_AI_5" + "P-poll__networl_8_8_AI_6" + "P-poll__networl_8_8_AI_7" + "P-poll__networl_8_8_AI_8" + "P-poll__networl_8_8_AnnP_0" + "P-poll__networl_8_8_AnnP_1" + "P-poll__networl_8_8_AnnP_2" + "P-poll__networl_8_8_AnnP_3" + "P-poll__networl_8_8_AnnP_4" + "P-poll__networl_8_8_AnnP_5" + "P-poll__networl_8_8_AnnP_6" + "P-poll__networl_8_8_AnnP_7" + "P-poll__networl_8_8_AnnP_8" + "P-poll__networl_8_8_RP_0" + "P-poll__networl_8_8_RP_1" + "P-poll__networl_8_8_RP_2" + "P-poll__networl_8_8_RP_3" + "P-poll__networl_8_8_RP_4" + "P-poll__networl_8_8_RP_5" + "P-poll__networl_8_8_RP_6" + "P-poll__networl_8_8_RP_7" + "P-poll__networl_8_8_RP_8") <= ("P-sendAnnPs__broadcasting_0_1" + "P-sendAnnPs__broadcasting_0_2" + "P-sendAnnPs__broadcasting_0_3" + "P-sendAnnPs__broadcasting_0_4" + "P-sendAnnPs__broadcasting_0_5" + "P-sendAnnPs__broadcasting_0_6" + "P-sendAnnPs__broadcasting_0_7" + "P-sendAnnPs__broadcasting_0_8" + "P-sendAnnPs__broadcasting_1_1" + "P-sendAnnPs__broadcasting_1_2" + "P-sendAnnPs__broadcasting_1_3" + "P-sendAnnPs__broadcasting_1_4" + "P-sendAnnPs__broadcasting_1_5" + "P-sendAnnPs__broadcasting_1_6" + "P-sendAnnPs__broadcasting_1_7" + "P-sendAnnPs__broadcasting_1_8" + "P-sendAnnPs__broadcasting_2_1" + "P-sendAnnPs__broadcasting_2_2" + "P-sendAnnPs__broadcasting_2_3" + "P-sendAnnPs__broadcasting_2_4" + "P-sendAnnPs__broadcasting_2_5" + "P-sendAnnPs__broadcasting_2_6" + "P-sendAnnPs__broadcasting_2_7" + "P-sendAnnPs__broadcasting_2_8" + "P-sendAnnPs__broadcasting_3_1" + "P-sendAnnPs__broadcasting_3_2" + "P-sendAnnPs__broadcasting_3_3" + "P-sendAnnPs__broadcasting_3_4" + "P-sendAnnPs__broadcasting_3_5" + "P-sendAnnPs__broadcasting_3_6" + "P-sendAnnPs__broadcasting_3_7" + "P-sendAnnPs__broadcasting_3_8" + "P-sendAnnPs__broadcasting_4_1" + "P-sendAnnPs__broadcasting_4_2" + "P-sendAnnPs__broadcasting_4_3" + "P-sendAnnPs__broadcasting_4_4" + "P-sendAnnPs__broadcasting_4_5" + "P-sendAnnPs__broadcasting_4_6" + "P-sendAnnPs__broadcasting_4_7" + "P-sendAnnPs__broadcasting_4_8" + "P-sendAnnPs__broadcasting_5_1" + "P-sendAnnPs__broadcasting_5_2" + "P-sendAnnPs__broadcasting_5_3" + "P-sendAnnPs__broadcasting_5_4" + "P-sendAnnPs__broadcasting_5_5" + "P-sendAnnPs__broadcasting_5_6" + "P-sendAnnPs__broadcasting_5_7" + "P-sendAnnPs__broadcasting_5_8" + "P-sendAnnPs__broadcasting_6_1" + "P-sendAnnPs__broadcasting_6_2" + "P-sendAnnPs__broadcasting_6_3" + "P-sendAnnPs__broadcasting_6_4" + "P-sendAnnPs__broadcasting_6_5" + "P-sendAnnPs__broadcasting_6_6" + "P-sendAnnPs__broadcasting_6_7" + "P-sendAnnPs__broadcasting_6_8" + "P-sendAnnPs__broadcasting_7_1" + "P-sendAnnPs__broadcasting_7_2" + "P-sendAnnPs__broadcasting_7_3" + "P-sendAnnPs__broadcasting_7_4" + "P-sendAnnPs__broadcasting_7_5" + "P-sendAnnPs__broadcasting_7_6" + "P-sendAnnPs__broadcasting_7_7" + "P-sendAnnPs__broadcasting_7_8" + "P-sendAnnPs__broadcasting_8_1" + "P-sendAnnPs__broadcasting_8_2" + "P-sendAnnPs__broadcasting_8_3" + "P-sendAnnPs__broadcasting_8_4" + "P-sendAnnPs__broadcasting_8_5" + "P-sendAnnPs__broadcasting_8_6" + "P-sendAnnPs__broadcasting_8_7" + "P-sendAnnPs__broadcasting_8_8"))) or (1 <= ("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8"))) )
NeoElection-COL-8-ReachabilityCardinality-4: not EF not ( (("P-dead_0" + "P-dead_1" + "P-dead_2" + "P-dead_3" + "P-dead_4" + "P-dead_5" + "P-dead_6" + "P-dead_7" + "P-dead_8") <= ("P-electedSecondary_0" + "P-electedSecondary_1" + "P-electedSecondary_2" + "P-electedSecondary_3" + "P-electedSecondary_4" + "P-electedSecondary_5" + "P-electedSecondary_6" + "P-electedSecondary_7" + "P-electedSecondary_8")) )
NeoElection-COL-8-ReachabilityCardinality-5: EF ( (not(((("P-sendAnnPs__broadcasting_0_1" + "P-sendAnnPs__broadcasting_0_2" + "P-sendAnnPs__broadcasting_0_3" + "P-sendAnnPs__broadcasting_0_4" + "P-sendAnnPs__broadcasting_0_5" + "P-sendAnnPs__broadcasting_0_6" + "P-sendAnnPs__broadcasting_0_7" + "P-sendAnnPs__broadcasting_0_8" + "P-sendAnnPs__broadcasting_1_1" + "P-sendAnnPs__broadcasting_1_2" + "P-sendAnnPs__broadcasting_1_3" + "P-sendAnnPs__broadcasting_1_4" + "P-sendAnnPs__broadcasting_1_5" + "P-sendAnnPs__broadcasting_1_6" + "P-sendAnnPs__broadcasting_1_7" + "P-sendAnnPs__broadcasting_1_8" + "P-sendAnnPs__broadcasting_2_1" + "P-sendAnnPs__broadcasting_2_2" + "P-sendAnnPs__broadcasting_2_3" + "P-sendAnnPs__broadcasting_2_4" + "P-sendAnnPs__broadcasting_2_5" + "P-sendAnnPs__broadcasting_2_6" + "P-sendAnnPs__broadcasting_2_7" + "P-sendAnnPs__broadcasting_2_8" + "P-sendAnnPs__broadcasting_3_1" + "P-sendAnnPs__broadcasting_3_2" + "P-sendAnnPs__broadcasting_3_3" + "P-sendAnnPs__broadcasting_3_4" + "P-sendAnnPs__broadcasting_3_5" + "P-sendAnnPs__broadcasting_3_6" + "P-sendAnnPs__broadcasting_3_7" + "P-sendAnnPs__broadcasting_3_8" + "P-sendAnnPs__broadcasting_4_1" + "P-sendAnnPs__broadcasting_4_2" + "P-sendAnnPs__broadcasting_4_3" + "P-sendAnnPs__broadcasting_4_4" + "P-sendAnnPs__broadcasting_4_5" + "P-sendAnnPs__broadcasting_4_6" + "P-sendAnnPs__broadcasting_4_7" + "P-sendAnnPs__broadcasting_4_8" + "P-sendAnnPs__broadcasting_5_1" + "P-sendAnnPs__broadcasting_5_2" + "P-sendAnnPs__broadcasting_5_3" + "P-sendAnnPs__broadcasting_5_4" + "P-sendAnnPs__broadcasting_5_5" + "P-sendAnnPs__broadcasting_5_6" + "P-sendAnnPs__broadcasting_5_7" + "P-sendAnnPs__broadcasting_5_8" + "P-sendAnnPs__broadcasting_6_1" + "P-sendAnnPs__broadcasting_6_2" + "P-sendAnnPs__broadcasting_6_3" + "P-sendAnnPs__broadcasting_6_4" + "P-sendAnnPs__broadcasting_6_5" + "P-sendAnnPs__broadcasting_6_6" + "P-sendAnnPs__broadcasting_6_7" + "P-sendAnnPs__broadcasting_6_8" + "P-sendAnnPs__broadcasting_7_1" + "P-sendAnnPs__broadcasting_7_2" + "P-sendAnnPs__broadcasting_7_3" + "P-sendAnnPs__broadcasting_7_4" + "P-sendAnnPs__broadcasting_7_5" + "P-sendAnnPs__broadcasting_7_6" + "P-sendAnnPs__broadcasting_7_7" + "P-sendAnnPs__broadcasting_7_8" + "P-sendAnnPs__broadcasting_8_1" + "P-sendAnnPs__broadcasting_8_2" + "P-sendAnnPs__broadcasting_8_3" + "P-sendAnnPs__broadcasting_8_4" + "P-sendAnnPs__broadcasting_8_5" + "P-sendAnnPs__broadcasting_8_6" + "P-sendAnnPs__broadcasting_8_7" + "P-sendAnnPs__broadcasting_8_8") <= ("P-masterList_0_1_0" + "P-masterList_0_1_1" + "P-masterList_0_1_2" + "P-masterList_0_1_3" + "P-masterList_0_1_4" + "P-masterList_0_1_5" + "P-masterList_0_1_6" + "P-masterList_0_1_7" + "P-masterList_0_1_8" + "P-masterList_0_2_0" + "P-masterList_0_2_1" + "P-masterList_0_2_2" + "P-masterList_0_2_3" + "P-masterList_0_2_4" + "P-masterList_0_2_5" + "P-masterList_0_2_6" + "P-masterList_0_2_7" + "P-masterList_0_2_8" + "P-masterList_0_3_0" + "P-masterList_0_3_1" + "P-masterList_0_3_2" + "P-masterList_0_3_3" + "P-masterList_0_3_4" + "P-masterList_0_3_5" + "P-masterList_0_3_6" + "P-masterList_0_3_7" + "P-masterList_0_3_8" + "P-masterList_0_4_0" + "P-masterList_0_4_1" + "P-masterList_0_4_2" + "P-masterList_0_4_3" + "P-masterList_0_4_4" + "P-masterList_0_4_5" + "P-masterList_0_4_6" + "P-masterList_0_4_7" + "P-masterList_0_4_8" + "P-masterList_0_5_0" + "P-masterList_0_5_1" + "P-masterList_0_5_2" + "P-masterList_0_5_3" + "P-masterList_0_5_4" + "P-masterList_0_5_5" + "P-masterList_0_5_6" + "P-masterList_0_5_7" + "P-masterList_0_5_8" + "P-masterList_0_6_0" + "P-masterList_0_6_1" + "P-masterList_0_6_2" + "P-masterList_0_6_3" + "P-masterList_0_6_4" + "P-masterList_0_6_5" + "P-masterList_0_6_6" + "P-masterList_0_6_7" + "P-masterList_0_6_8" + "P-masterList_0_7_0" + "P-masterList_0_7_1" + "P-masterList_0_7_2" + "P-masterList_0_7_3" + "P-masterList_0_7_4" + "P-masterList_0_7_5" + "P-masterList_0_7_6" + "P-masterList_0_7_7" + "P-masterList_0_7_8" + "P-masterList_0_8_0" + "P-masterList_0_8_1" + "P-masterList_0_8_2" + "P-masterList_0_8_3" + "P-masterList_0_8_4" + "P-masterList_0_8_5" + "P-masterList_0_8_6" + "P-masterList_0_8_7" + "P-masterList_0_8_8" + "P-masterList_1_1_0" + "P-masterList_1_1_1" + "P-masterList_1_1_2" + "P-masterList_1_1_3" + "P-masterList_1_1_4" + "P-masterList_1_1_5" + "P-masterList_1_1_6" + "P-masterList_1_1_7" + "P-masterList_1_1_8" + "P-masterList_1_2_0" + "P-masterList_1_2_1" + "P-masterList_1_2_2" + "P-masterList_1_2_3" + "P-masterList_1_2_4" + "P-masterList_1_2_5" + "P-masterList_1_2_6" + "P-masterList_1_2_7" + "P-masterList_1_2_8" + "P-masterList_1_3_0" + "P-masterList_1_3_1" + "P-masterList_1_3_2" + "P-masterList_1_3_3" + "P-masterList_1_3_4" + "P-masterList_1_3_5" + "P-masterList_1_3_6" + "P-masterList_1_3_7" + "P-masterList_1_3_8" + "P-masterList_1_4_0" + "P-masterList_1_4_1" + "P-masterList_1_4_2" + "P-masterList_1_4_3" + "P-masterList_1_4_4" + "P-masterList_1_4_5" + "P-masterList_1_4_6" + "P-masterList_1_4_7" + "P-masterList_1_4_8" + "P-masterList_1_5_0" + "P-masterList_1_5_1" + "P-masterList_1_5_2" + "P-masterList_1_5_3" + "P-masterList_1_5_4" + "P-masterList_1_5_5" + "P-masterList_1_5_6" + "P-masterList_1_5_7" + "P-masterList_1_5_8" + "P-masterList_1_6_0" + "P-masterList_1_6_1" + "P-masterList_1_6_2" + "P-masterList_1_6_3" + "P-masterList_1_6_4" + "P-masterList_1_6_5" + "P-masterList_1_6_6" + "P-masterList_1_6_7" + "P-masterList_1_6_8" + "P-masterList_1_7_0" + "P-masterList_1_7_1" + "P-masterList_1_7_2" + "P-masterList_1_7_3" + "P-masterList_1_7_4" + "P-masterList_1_7_5" + "P-masterList_1_7_6" + "P-masterList_1_7_7" + "P-masterList_1_7_8" + "P-masterList_1_8_0" + "P-masterList_1_8_1" + "P-masterList_1_8_2" + "P-masterList_1_8_3" + "P-masterList_1_8_4" + "P-masterList_1_8_5" + "P-masterList_1_8_6" + "P-masterList_1_8_7" + "P-masterList_1_8_8" + "P-masterList_2_1_0" + "P-masterList_2_1_1" + "P-masterList_2_1_2" + "P-masterList_2_1_3" + "P-masterList_2_1_4" + "P-masterList_2_1_5" + "P-masterList_2_1_6" + "P-masterList_2_1_7" + "P-masterList_2_1_8" + "P-masterList_2_2_0" + "P-masterList_2_2_1" + "P-masterList_2_2_2" + "P-masterList_2_2_3" + "P-masterList_2_2_4" + "P-masterList_2_2_5" + "P-masterList_2_2_6" + "P-masterList_2_2_7" + "P-masterList_2_2_8" + "P-masterList_2_3_0" + "P-masterList_2_3_1" + "P-masterList_2_3_2" + "P-masterList_2_3_3" + "P-masterList_2_3_4" + "P-masterList_2_3_5" + "P-masterList_2_3_6" + "P-masterList_2_3_7" + "P-masterList_2_3_8" + "P-masterList_2_4_0" + "P-masterList_2_4_1" + "P-masterList_2_4_2" + "P-masterList_2_4_3" + "P-masterList_2_4_4" + "P-masterList_2_4_5" + "P-masterList_2_4_6" + "P-masterList_2_4_7" + "P-masterList_2_4_8" + "P-masterList_2_5_0" + "P-masterList_2_5_1" + "P-masterList_2_5_2" + "P-masterList_2_5_3" + "P-masterList_2_5_4" + "P-masterList_2_5_5" + "P-masterList_2_5_6" + "P-masterList_2_5_7" + "P-masterList_2_5_8" + "P-masterList_2_6_0" + "P-masterList_2_6_1" + "P-masterList_2_6_2" + "P-masterList_2_6_3" + "P-masterList_2_6_4" + "P-masterList_2_6_5" + "P-masterList_2_6_6" + "P-masterList_2_6_7" + "P-masterList_2_6_8" + "P-masterList_2_7_0" + "P-masterList_2_7_1" + "P-masterList_2_7_2" + "P-masterList_2_7_3" + "P-masterList_2_7_4" + "P-masterList_2_7_5" + "P-masterList_2_7_6" + "P-masterList_2_7_7" + "P-masterList_2_7_8" + "P-masterList_2_8_0" + "P-masterList_2_8_1" + "P-masterList_2_8_2" + "P-masterList_2_8_3" + "P-masterList_2_8_4" + "P-masterList_2_8_5" + "P-masterList_2_8_6" + "P-masterList_2_8_7" + "P-masterList_2_8_8" + "P-masterList_3_1_0" + "P-masterList_3_1_1" + "P-masterList_3_1_2" + "P-masterList_3_1_3" + "P-masterList_3_1_4" + "P-masterList_3_1_5" + "P-masterList_3_1_6" + "P-masterList_3_1_7" + "P-masterList_3_1_8" + "P-masterList_3_2_0" + "P-masterList_3_2_1" + "P-masterList_3_2_2" + "P-masterList_3_2_3" + "P-masterList_3_2_4" + "P-masterList_3_2_5" + "P-masterList_3_2_6" + "P-masterList_3_2_7" + "P-masterList_3_2_8" + "P-masterList_3_3_0" + "P-masterList_3_3_1" + "P-masterList_3_3_2" + "P-masterList_3_3_3" + "P-masterList_3_3_4" + "P-masterList_3_3_5" + "P-masterList_3_3_6" + "P-masterList_3_3_7" + "P-masterList_3_3_8" + "P-masterList_3_4_0" + "P-masterList_3_4_1" + "P-masterList_3_4_2" + "P-masterList_3_4_3" + "P-masterList_3_4_4" + "P-masterList_3_4_5" + "P-masterList_3_4_6" + "P-masterList_3_4_7" + "P-masterList_3_4_8" + "P-masterList_3_5_0" + "P-masterList_3_5_1" + "P-masterList_3_5_2" + "P-masterList_3_5_3" + "P-masterList_3_5_4" + "P-masterList_3_5_5" + "P-masterList_3_5_6" + "P-masterList_3_5_7" + "P-masterList_3_5_8" + "P-masterList_3_6_0" + "P-masterList_3_6_1" + "P-masterList_3_6_2" + "P-masterList_3_6_3" + "P-masterList_3_6_4" + "P-masterList_3_6_5" + "P-masterList_3_6_6" + "P-masterList_3_6_7" + "P-masterList_3_6_8" + "P-masterList_3_7_0" + "P-masterList_3_7_1" + "P-masterList_3_7_2" + "P-masterList_3_7_3" + "P-masterList_3_7_4" + "P-masterList_3_7_5" + "P-masterList_3_7_6" + "P-masterList_3_7_7" + "P-masterList_3_7_8" + "P-masterList_3_8_0" + "P-masterList_3_8_1" + "P-masterList_3_8_2" + "P-masterList_3_8_3" + "P-masterList_3_8_4" + "P-masterList_3_8_5" + "P-masterList_3_8_6" + "P-masterList_3_8_7" + "P-masterList_3_8_8" + "P-masterList_4_1_0" + "P-masterList_4_1_1" + "P-masterList_4_1_2" + "P-masterList_4_1_3" + "P-masterList_4_1_4" + "P-masterList_4_1_5" + "P-masterList_4_1_6" + "P-masterList_4_1_7" + "P-masterList_4_1_8" + "P-masterList_4_2_0" + "P-masterList_4_2_1" + "P-masterList_4_2_2" + "P-masterList_4_2_3" + "P-masterList_4_2_4" + "P-masterList_4_2_5" + "P-masterList_4_2_6" + "P-masterList_4_2_7" + "P-masterList_4_2_8" + "P-masterList_4_3_0" + "P-masterList_4_3_1" + "P-masterList_4_3_2" + "P-masterList_4_3_3" + "P-masterList_4_3_4" + "P-masterList_4_3_5" + "P-masterList_4_3_6" + "P-masterList_4_3_7" + "P-masterList_4_3_8" + "P-masterList_4_4_0" + "P-masterList_4_4_1" + "P-masterList_4_4_2" + "P-masterList_4_4_3" + "P-masterList_4_4_4" + "P-masterList_4_4_5" + "P-masterList_4_4_6" + "P-masterList_4_4_7" + "P-masterList_4_4_8" + "P-masterList_4_5_0" + "P-masterList_4_5_1" + "P-masterList_4_5_2" + "P-masterList_4_5_3" + "P-masterList_4_5_4" + "P-masterList_4_5_5" + "P-masterList_4_5_6" + "P-masterList_4_5_7" + "P-masterList_4_5_8" + "P-masterList_4_6_0" + "P-masterList_4_6_1" + "P-masterList_4_6_2" + "P-masterList_4_6_3" + "P-masterList_4_6_4" + "P-masterList_4_6_5" + "P-masterList_4_6_6" + "P-masterList_4_6_7" + "P-masterList_4_6_8" + "P-masterList_4_7_0" + "P-masterList_4_7_1" + "P-masterList_4_7_2" + "P-masterList_4_7_3" + "P-masterList_4_7_4" + "P-masterList_4_7_5" + "P-masterList_4_7_6" + "P-masterList_4_7_7" + "P-masterList_4_7_8" + "P-masterList_4_8_0" + "P-masterList_4_8_1" + "P-masterList_4_8_2" + "P-masterList_4_8_3" + "P-masterList_4_8_4" + "P-masterList_4_8_5" + "P-masterList_4_8_6" + "P-masterList_4_8_7" + "P-masterList_4_8_8" + "P-masterList_5_1_0" + "P-masterList_5_1_1" + "P-masterList_5_1_2" + "P-masterList_5_1_3" + "P-masterList_5_1_4" + "P-masterList_5_1_5" + "P-masterList_5_1_6" + "P-masterList_5_1_7" + "P-masterList_5_1_8" + "P-masterList_5_2_0" + "P-masterList_5_2_1" + "P-masterList_5_2_2" + "P-masterList_5_2_3" + "P-masterList_5_2_4" + "P-masterList_5_2_5" + "P-masterList_5_2_6" + "P-masterList_5_2_7" + "P-masterList_5_2_8" + "P-masterList_5_3_0" + "P-masterList_5_3_1" + "P-masterList_5_3_2" + "P-masterList_5_3_3" + "P-masterList_5_3_4" + "P-masterList_5_3_5" + "P-masterList_5_3_6" + "P-masterList_5_3_7" + "P-masterList_5_3_8" + "P-masterList_5_4_0" + "P-masterList_5_4_1" + "P-masterList_5_4_2" + "P-masterList_5_4_3" + "P-masterList_5_4_4" + "P-masterList_5_4_5" + "P-masterList_5_4_6" + "P-masterList_5_4_7" + "P-masterList_5_4_8" + "P-masterList_5_5_0" + "P-masterList_5_5_1" + "P-masterList_5_5_2" + "P-masterList_5_5_3" + "P-masterList_5_5_4" + "P-masterList_5_5_5" + "P-masterList_5_5_6" + "P-masterList_5_5_7" + "P-masterList_5_5_8" + "P-masterList_5_6_0" + "P-masterList_5_6_1" + "P-masterList_5_6_2" + "P-masterList_5_6_3" + "P-masterList_5_6_4" + "P-masterList_5_6_5" + "P-masterList_5_6_6" + "P-masterList_5_6_7" + "P-masterList_5_6_8" + "P-masterList_5_7_0" + "P-masterList_5_7_1" + "P-masterList_5_7_2" + "P-masterList_5_7_3" + "P-masterList_5_7_4" + "P-masterList_5_7_5" + "P-masterList_5_7_6" + "P-masterList_5_7_7" + "P-masterList_5_7_8" + "P-masterList_5_8_0" + "P-masterList_5_8_1" + "P-masterList_5_8_2" + "P-masterList_5_8_3" + "P-masterList_5_8_4" + "P-masterList_5_8_5" + "P-masterList_5_8_6" + "P-masterList_5_8_7" + "P-masterList_5_8_8" + "P-masterList_6_1_0" + "P-masterList_6_1_1" + "P-masterList_6_1_2" + "P-masterList_6_1_3" + "P-masterList_6_1_4" + "P-masterList_6_1_5" + "P-masterList_6_1_6" + "P-masterList_6_1_7" + "P-masterList_6_1_8" + "P-masterList_6_2_0" + "P-masterList_6_2_1" + "P-masterList_6_2_2" + "P-masterList_6_2_3" + "P-masterList_6_2_4" + "P-masterList_6_2_5" + "P-masterList_6_2_6" + "P-masterList_6_2_7" + "P-masterList_6_2_8" + "P-masterList_6_3_0" + "P-masterList_6_3_1" + "P-masterList_6_3_2" + "P-masterList_6_3_3" + "P-masterList_6_3_4" + "P-masterList_6_3_5" + "P-masterList_6_3_6" + "P-masterList_6_3_7" + "P-masterList_6_3_8" + "P-masterList_6_4_0" + "P-masterList_6_4_1" + "P-masterList_6_4_2" + "P-masterList_6_4_3" + "P-masterList_6_4_4" + "P-masterList_6_4_5" + "P-masterList_6_4_6" + "P-masterList_6_4_7" + "P-masterList_6_4_8" + "P-masterList_6_5_0" + "P-masterList_6_5_1" + "P-masterList_6_5_2" + "P-masterList_6_5_3" + "P-masterList_6_5_4" + "P-masterList_6_5_5" + "P-masterList_6_5_6" + "P-masterList_6_5_7" + "P-masterList_6_5_8" + "P-masterList_6_6_0" + "P-masterList_6_6_1" + "P-masterList_6_6_2" + "P-masterList_6_6_3" + "P-masterList_6_6_4" + "P-masterList_6_6_5" + "P-masterList_6_6_6" + "P-masterList_6_6_7" + "P-masterList_6_6_8" + "P-masterList_6_7_0" + "P-masterList_6_7_1" + "P-masterList_6_7_2" + "P-masterList_6_7_3" + "P-masterList_6_7_4" + "P-masterList_6_7_5" + "P-masterList_6_7_6" + "P-masterList_6_7_7" + "P-masterList_6_7_8" + "P-masterList_6_8_0" + "P-masterList_6_8_1" + "P-masterList_6_8_2" + "P-masterList_6_8_3" + "P-masterList_6_8_4" + "P-masterList_6_8_5" + "P-masterList_6_8_6" + "P-masterList_6_8_7" + "P-masterList_6_8_8" + "P-masterList_7_1_0" + "P-masterList_7_1_1" + "P-masterList_7_1_2" + "P-masterList_7_1_3" + "P-masterList_7_1_4" + "P-masterList_7_1_5" + "P-masterList_7_1_6" + "P-masterList_7_1_7" + "P-masterList_7_1_8" + "P-masterList_7_2_0" + "P-masterList_7_2_1" + "P-masterList_7_2_2" + "P-masterList_7_2_3" + "P-masterList_7_2_4" + "P-masterList_7_2_5" + "P-masterList_7_2_6" + "P-masterList_7_2_7" + "P-masterList_7_2_8" + "P-masterList_7_3_0" + "P-masterList_7_3_1" + "P-masterList_7_3_2" + "P-masterList_7_3_3" + "P-masterList_7_3_4" + "P-masterList_7_3_5" + "P-masterList_7_3_6" + "P-masterList_7_3_7" + "P-masterList_7_3_8" + "P-masterList_7_4_0" + "P-masterList_7_4_1" + "P-masterList_7_4_2" + "P-masterList_7_4_3" + "P-masterList_7_4_4" + "P-masterList_7_4_5" + "P-masterList_7_4_6" + "P-masterList_7_4_7" + "P-masterList_7_4_8" + "P-masterList_7_5_0" + "P-masterList_7_5_1" + "P-masterList_7_5_2" + "P-masterList_7_5_3" + "P-masterList_7_5_4" + "P-masterList_7_5_5" + "P-masterList_7_5_6" + "P-masterList_7_5_7" + "P-masterList_7_5_8" + "P-masterList_7_6_0" + "P-masterList_7_6_1" + "P-masterList_7_6_2" + "P-masterList_7_6_3" + "P-masterList_7_6_4" + "P-masterList_7_6_5" + "P-masterList_7_6_6" + "P-masterList_7_6_7" + "P-masterList_7_6_8" + "P-masterList_7_7_0" + "P-masterList_7_7_1" + "P-masterList_7_7_2" + "P-masterList_7_7_3" + "P-masterList_7_7_4" + "P-masterList_7_7_5" + "P-masterList_7_7_6" + "P-masterList_7_7_7" + "P-masterList_7_7_8" + "P-masterList_7_8_0" + "P-masterList_7_8_1" + "P-masterList_7_8_2" + "P-masterList_7_8_3" + "P-masterList_7_8_4" + "P-masterList_7_8_5" + "P-masterList_7_8_6" + "P-masterList_7_8_7" + "P-masterList_7_8_8" + "P-masterList_8_1_0" + "P-masterList_8_1_1" + "P-masterList_8_1_2" + "P-masterList_8_1_3" + "P-masterList_8_1_4" + "P-masterList_8_1_5" + "P-masterList_8_1_6" + "P-masterList_8_1_7" + "P-masterList_8_1_8" + "P-masterList_8_2_0" + "P-masterList_8_2_1" + "P-masterList_8_2_2" + "P-masterList_8_2_3" + "P-masterList_8_2_4" + "P-masterList_8_2_5" + "P-masterList_8_2_6" + "P-masterList_8_2_7" + "P-masterList_8_2_8" + "P-masterList_8_3_0" + "P-masterList_8_3_1" + "P-masterList_8_3_2" + "P-masterList_8_3_3" + "P-masterList_8_3_4" + "P-masterList_8_3_5" + "P-masterList_8_3_6" + "P-masterList_8_3_7" + "P-masterList_8_3_8" + "P-masterList_8_4_0" + "P-masterList_8_4_1" + "P-masterList_8_4_2" + "P-masterList_8_4_3" + "P-masterList_8_4_4" + "P-masterList_8_4_5" + "P-masterList_8_4_6" + "P-masterList_8_4_7" + "P-masterList_8_4_8" + "P-masterList_8_5_0" + "P-masterList_8_5_1" + "P-masterList_8_5_2" + "P-masterList_8_5_3" + "P-masterList_8_5_4" + "P-masterList_8_5_5" + "P-masterList_8_5_6" + "P-masterList_8_5_7" + "P-masterList_8_5_8" + "P-masterList_8_6_0" + "P-masterList_8_6_1" + "P-masterList_8_6_2" + "P-masterList_8_6_3" + "P-masterList_8_6_4" + "P-masterList_8_6_5" + "P-masterList_8_6_6" + "P-masterList_8_6_7" + "P-masterList_8_6_8" + "P-masterList_8_7_0" + "P-masterList_8_7_1" + "P-masterList_8_7_2" + "P-masterList_8_7_3" + "P-masterList_8_7_4" + "P-masterList_8_7_5" + "P-masterList_8_7_6" + "P-masterList_8_7_7" + "P-masterList_8_7_8" + "P-masterList_8_8_0" + "P-masterList_8_8_1" + "P-masterList_8_8_2" + "P-masterList_8_8_3" + "P-masterList_8_8_4" + "P-masterList_8_8_5" + "P-masterList_8_8_6" + "P-masterList_8_8_7" + "P-masterList_8_8_8")) or (2 <= ("P-poll__networl_0_0_AskP_0" + "P-poll__networl_0_0_AskP_1" + "P-poll__networl_0_0_AskP_2" + "P-poll__networl_0_0_AskP_3" + "P-poll__networl_0_0_AskP_4" + "P-poll__networl_0_0_AskP_5" + "P-poll__networl_0_0_AskP_6" + "P-poll__networl_0_0_AskP_7" + "P-poll__networl_0_0_AskP_8" + "P-poll__networl_0_0_AnsP_0" + "P-poll__networl_0_0_AnsP_1" + "P-poll__networl_0_0_AnsP_2" + "P-poll__networl_0_0_AnsP_3" + "P-poll__networl_0_0_AnsP_4" + "P-poll__networl_0_0_AnsP_5" + "P-poll__networl_0_0_AnsP_6" + "P-poll__networl_0_0_AnsP_7" + "P-poll__networl_0_0_AnsP_8" + "P-poll__networl_0_0_RI_0" + "P-poll__networl_0_0_RI_1" + "P-poll__networl_0_0_RI_2" + "P-poll__networl_0_0_RI_3" + "P-poll__networl_0_0_RI_4" + "P-poll__networl_0_0_RI_5" + "P-poll__networl_0_0_RI_6" + "P-poll__networl_0_0_RI_7" + "P-poll__networl_0_0_RI_8" + "P-poll__networl_0_0_AI_0" + "P-poll__networl_0_0_AI_1" + "P-poll__networl_0_0_AI_2" + "P-poll__networl_0_0_AI_3" + "P-poll__networl_0_0_AI_4" + "P-poll__networl_0_0_AI_5" + "P-poll__networl_0_0_AI_6" + "P-poll__networl_0_0_AI_7" + "P-poll__networl_0_0_AI_8" + "P-poll__networl_0_0_AnnP_0" + "P-poll__networl_0_0_AnnP_1" + "P-poll__networl_0_0_AnnP_2" + "P-poll__networl_0_0_AnnP_3" + "P-poll__networl_0_0_AnnP_4" + "P-poll__networl_0_0_AnnP_5" + "P-poll__networl_0_0_AnnP_6" + "P-poll__networl_0_0_AnnP_7" + "P-poll__networl_0_0_AnnP_8" + "P-poll__networl_0_0_RP_0" + "P-poll__networl_0_0_RP_1" + "P-poll__networl_0_0_RP_2" + "P-poll__networl_0_0_RP_3" + "P-poll__networl_0_0_RP_4" + "P-poll__networl_0_0_RP_5" + "P-poll__networl_0_0_RP_6" + "P-poll__networl_0_0_RP_7" + "P-poll__networl_0_0_RP_8" + "P-poll__networl_0_1_AskP_0" + "P-poll__networl_0_1_AskP_1" + "P-poll__networl_0_1_AskP_2" + "P-poll__networl_0_1_AskP_3" + "P-poll__networl_0_1_AskP_4" + "P-poll__networl_0_1_AskP_5" + "P-poll__networl_0_1_AskP_6" + "P-poll__networl_0_1_AskP_7" + "P-poll__networl_0_1_AskP_8" + "P-poll__networl_0_1_AnsP_0" + "P-poll__networl_0_1_AnsP_1" + "P-poll__networl_0_1_AnsP_2" + "P-poll__networl_0_1_AnsP_3" + "P-poll__networl_0_1_AnsP_4" + "P-poll__networl_0_1_AnsP_5" + "P-poll__networl_0_1_AnsP_6" + "P-poll__networl_0_1_AnsP_7" + "P-poll__networl_0_1_AnsP_8" + "P-poll__networl_0_1_RI_0" + "P-poll__networl_0_1_RI_1" + "P-poll__networl_0_1_RI_2" + "P-poll__networl_0_1_RI_3" + "P-poll__networl_0_1_RI_4" + "P-poll__networl_0_1_RI_5" + "P-poll__networl_0_1_RI_6" + "P-poll__networl_0_1_RI_7" + "P-poll__networl_0_1_RI_8" + "P-poll__networl_0_1_AI_0" + "P-poll__networl_0_1_AI_1" + "P-poll__networl_0_1_AI_2" + "P-poll__networl_0_1_AI_3" + "P-poll__networl_0_1_AI_4" + "P-poll__networl_0_1_AI_5" + "P-poll__networl_0_1_AI_6" + "P-poll__networl_0_1_AI_7" + "P-poll__networl_0_1_AI_8" + "P-poll__networl_0_1_AnnP_0" + "P-poll__networl_0_1_AnnP_1" + "P-poll__networl_0_1_AnnP_2" + "P-poll__networl_0_1_AnnP_3" + "P-poll__networl_0_1_AnnP_4" + "P-poll__networl_0_1_AnnP_5" + "P-poll__networl_0_1_AnnP_6" + "P-poll__networl_0_1_AnnP_7" + "P-poll__networl_0_1_AnnP_8" + "P-poll__networl_0_1_RP_0" + "P-poll__networl_0_1_RP_1" + "P-poll__networl_0_1_RP_2" + "P-poll__networl_0_1_RP_3" + "P-poll__networl_0_1_RP_4" + "P-poll__networl_0_1_RP_5" + "P-poll__networl_0_1_RP_6" + "P-poll__networl_0_1_RP_7" + "P-poll__networl_0_1_RP_8" + "P-poll__networl_0_2_AskP_0" + "P-poll__networl_0_2_AskP_1" + "P-poll__networl_0_2_AskP_2" + "P-poll__networl_0_2_AskP_3" + "P-poll__networl_0_2_AskP_4" + "P-poll__networl_0_2_AskP_5" + "P-poll__networl_0_2_AskP_6" + "P-poll__networl_0_2_AskP_7" + "P-poll__networl_0_2_AskP_8" + "P-poll__networl_0_2_AnsP_0" + "P-poll__networl_0_2_AnsP_1" + "P-poll__networl_0_2_AnsP_2" + "P-poll__networl_0_2_AnsP_3" + "P-poll__networl_0_2_AnsP_4" + "P-poll__networl_0_2_AnsP_5" + "P-poll__networl_0_2_AnsP_6" + "P-poll__networl_0_2_AnsP_7" + "P-poll__networl_0_2_AnsP_8" + "P-poll__networl_0_2_RI_0" + "P-poll__networl_0_2_RI_1" + "P-poll__networl_0_2_RI_2" + "P-poll__networl_0_2_RI_3" + "P-poll__networl_0_2_RI_4" + "P-poll__networl_0_2_RI_5" + "P-poll__networl_0_2_RI_6" + "P-poll__networl_0_2_RI_7" + "P-poll__networl_0_2_RI_8" + "P-poll__networl_0_2_AI_0" + "P-poll__networl_0_2_AI_1" + "P-poll__networl_0_2_AI_2" + "P-poll__networl_0_2_AI_3" + "P-poll__networl_0_2_AI_4" + "P-poll__networl_0_2_AI_5" + "P-poll__networl_0_2_AI_6" + "P-poll__networl_0_2_AI_7" + "P-poll__networl_0_2_AI_8" + "P-poll__networl_0_2_AnnP_0" + "P-poll__networl_0_2_AnnP_1" + "P-poll__networl_0_2_AnnP_2" + "P-poll__networl_0_2_AnnP_3" + "P-poll__networl_0_2_AnnP_4" + "P-poll__networl_0_2_AnnP_5" + "P-poll__networl_0_2_AnnP_6" + "P-poll__networl_0_2_AnnP_7" + "P-poll__networl_0_2_AnnP_8" + "P-poll__networl_0_2_RP_0" + "P-poll__networl_0_2_RP_1" + "P-poll__networl_0_2_RP_2" + "P-poll__networl_0_2_RP_3" + "P-poll__networl_0_2_RP_4" + "P-poll__networl_0_2_RP_5" + "P-poll__networl_0_2_RP_6" + "P-poll__networl_0_2_RP_7" + "P-poll__networl_0_2_RP_8" + "P-poll__networl_0_3_AskP_0" + "P-poll__networl_0_3_AskP_1" + "P-poll__networl_0_3_AskP_2" + "P-poll__networl_0_3_AskP_3" + "P-poll__networl_0_3_AskP_4" + "P-poll__networl_0_3_AskP_5" + "P-poll__networl_0_3_AskP_6" + "P-poll__networl_0_3_AskP_7" + "P-poll__networl_0_3_AskP_8" + "P-poll__networl_0_3_AnsP_0" + "P-poll__networl_0_3_AnsP_1" + "P-poll__networl_0_3_AnsP_2" + "P-poll__networl_0_3_AnsP_3" + "P-poll__networl_0_3_AnsP_4" + "P-poll__networl_0_3_AnsP_5" + "P-poll__networl_0_3_AnsP_6" + "P-poll__networl_0_3_AnsP_7" + "P-poll__networl_0_3_AnsP_8" + "P-poll__networl_0_3_RI_0" + "P-poll__networl_0_3_RI_1" + "P-poll__networl_0_3_RI_2" + "P-poll__networl_0_3_RI_3" + "P-poll__networl_0_3_RI_4" + "P-poll__networl_0_3_RI_5" + "P-poll__networl_0_3_RI_6" + "P-poll__networl_0_3_RI_7" + "P-poll__networl_0_3_RI_8" + "P-poll__networl_0_3_AI_0" + "P-poll__networl_0_3_AI_1" + "P-poll__networl_0_3_AI_2" + "P-poll__networl_0_3_AI_3" + "P-poll__networl_0_3_AI_4" + "P-poll__networl_0_3_AI_5" + "P-poll__networl_0_3_AI_6" + "P-poll__networl_0_3_AI_7" + "P-poll__networl_0_3_AI_8" + "P-poll__networl_0_3_AnnP_0" + "P-poll__networl_0_3_AnnP_1" + "P-poll__networl_0_3_AnnP_2" + "P-poll__networl_0_3_AnnP_3" + "P-poll__networl_0_3_AnnP_4" + "P-poll__networl_0_3_AnnP_5" + "P-poll__networl_0_3_AnnP_6" + "P-poll__networl_0_3_AnnP_7" + "P-poll__networl_0_3_AnnP_8" + "P-poll__networl_0_3_RP_0" + "P-poll__networl_0_3_RP_1" + "P-poll__networl_0_3_RP_2" + "P-poll__networl_0_3_RP_3" + "P-poll__networl_0_3_RP_4" + "P-poll__networl_0_3_RP_5" + "P-poll__networl_0_3_RP_6" + "P-poll__networl_0_3_RP_7" + "P-poll__networl_0_3_RP_8" + "P-poll__networl_0_4_AskP_0" + "P-poll__networl_0_4_AskP_1" + "P-poll__networl_0_4_AskP_2" + "P-poll__networl_0_4_AskP_3" + "P-poll__networl_0_4_AskP_4" + "P-poll__networl_0_4_AskP_5" + "P-poll__networl_0_4_AskP_6" + "P-poll__networl_0_4_AskP_7" + "P-poll__networl_0_4_AskP_8" + "P-poll__networl_0_4_AnsP_0" + "P-poll__networl_0_4_AnsP_1" + "P-poll__networl_0_4_AnsP_2" + "P-poll__networl_0_4_AnsP_3" + "P-poll__networl_0_4_AnsP_4" + "P-poll__networl_0_4_AnsP_5" + "P-poll__networl_0_4_AnsP_6" + "P-poll__networl_0_4_AnsP_7" + "P-poll__networl_0_4_AnsP_8" + "P-poll__networl_0_4_RI_0" + "P-poll__networl_0_4_RI_1" + "P-poll__networl_0_4_RI_2" + "P-poll__networl_0_4_RI_3" + "P-poll__networl_0_4_RI_4" + "P-poll__networl_0_4_RI_5" + "P-poll__networl_0_4_RI_6" + "P-poll__networl_0_4_RI_7" + "P-poll__networl_0_4_RI_8" + "P-poll__networl_0_4_AI_0" + "P-poll__networl_0_4_AI_1" + "P-poll__networl_0_4_AI_2" + "P-poll__networl_0_4_AI_3" + "P-poll__networl_0_4_AI_4" + "P-poll__networl_0_4_AI_5" + "P-poll__networl_0_4_AI_6" + "P-poll__networl_0_4_AI_7" + "P-poll__networl_0_4_AI_8" + "P-poll__networl_0_4_AnnP_0" + "P-poll__networl_0_4_AnnP_1" + "P-poll__networl_0_4_AnnP_2" + "P-poll__networl_0_4_AnnP_3" + "P-poll__networl_0_4_AnnP_4" + "P-poll__networl_0_4_AnnP_5" + "P-poll__networl_0_4_AnnP_6" + "P-poll__networl_0_4_AnnP_7" + "P-poll__networl_0_4_AnnP_8" + "P-poll__networl_0_4_RP_0" + "P-poll__networl_0_4_RP_1" + "P-poll__networl_0_4_RP_2" + "P-poll__networl_0_4_RP_3" + "P-poll__networl_0_4_RP_4" + "P-poll__networl_0_4_RP_5" + "P-poll__networl_0_4_RP_6" + "P-poll__networl_0_4_RP_7" + "P-poll__networl_0_4_RP_8" + "P-poll__networl_0_5_AskP_0" + "P-poll__networl_0_5_AskP_1" + "P-poll__networl_0_5_AskP_2" + "P-poll__networl_0_5_AskP_3" + "P-poll__networl_0_5_AskP_4" + "P-poll__networl_0_5_AskP_5" + "P-poll__networl_0_5_AskP_6" + "P-poll__networl_0_5_AskP_7" + "P-poll__networl_0_5_AskP_8" + "P-poll__networl_0_5_AnsP_0" + "P-poll__networl_0_5_AnsP_1" + "P-poll__networl_0_5_AnsP_2" + "P-poll__networl_0_5_AnsP_3" + "P-poll__networl_0_5_AnsP_4" + "P-poll__networl_0_5_AnsP_5" + "P-poll__networl_0_5_AnsP_6" + "P-poll__networl_0_5_AnsP_7" + "P-poll__networl_0_5_AnsP_8" + "P-poll__networl_0_5_RI_0" + "P-poll__networl_0_5_RI_1" + "P-poll__networl_0_5_RI_2" + "P-poll__networl_0_5_RI_3" + "P-poll__networl_0_5_RI_4" + "P-poll__networl_0_5_RI_5" + "P-poll__networl_0_5_RI_6" + "P-poll__networl_0_5_RI_7" + "P-poll__networl_0_5_RI_8" + "P-poll__networl_0_5_AI_0" + "P-poll__networl_0_5_AI_1" + "P-poll__networl_0_5_AI_2" + "P-poll__networl_0_5_AI_3" + "P-poll__networl_0_5_AI_4" + "P-poll__networl_0_5_AI_5" + "P-poll__networl_0_5_AI_6" + "P-poll__networl_0_5_AI_7" + "P-poll__networl_0_5_AI_8" + "P-poll__networl_0_5_AnnP_0" + "P-poll__networl_0_5_AnnP_1" + "P-poll__networl_0_5_AnnP_2" + "P-poll__networl_0_5_AnnP_3" + "P-poll__networl_0_5_AnnP_4" + "P-poll__networl_0_5_AnnP_5" + "P-poll__networl_0_5_AnnP_6" + "P-poll__networl_0_5_AnnP_7" + "P-poll__networl_0_5_AnnP_8" + "P-poll__networl_0_5_RP_0" + "P-poll__networl_0_5_RP_1" + "P-poll__networl_0_5_RP_2" + "P-poll__networl_0_5_RP_3" + "P-poll__networl_0_5_RP_4" + "P-poll__networl_0_5_RP_5" + "P-poll__networl_0_5_RP_6" + "P-poll__networl_0_5_RP_7" + "P-poll__networl_0_5_RP_8" + "P-poll__networl_0_6_AskP_0" + "P-poll__networl_0_6_AskP_1" + "P-poll__networl_0_6_AskP_2" + "P-poll__networl_0_6_AskP_3" + "P-poll__networl_0_6_AskP_4" + "P-poll__networl_0_6_AskP_5" + "P-poll__networl_0_6_AskP_6" + "P-poll__networl_0_6_AskP_7" + "P-poll__networl_0_6_AskP_8" + "P-poll__networl_0_6_AnsP_0" + "P-poll__networl_0_6_AnsP_1" + "P-poll__networl_0_6_AnsP_2" + "P-poll__networl_0_6_AnsP_3" + "P-poll__networl_0_6_AnsP_4" + "P-poll__networl_0_6_AnsP_5" + "P-poll__networl_0_6_AnsP_6" + "P-poll__networl_0_6_AnsP_7" + "P-poll__networl_0_6_AnsP_8" + "P-poll__networl_0_6_RI_0" + "P-poll__networl_0_6_RI_1" + "P-poll__networl_0_6_RI_2" + "P-poll__networl_0_6_RI_3" + "P-poll__networl_0_6_RI_4" + "P-poll__networl_0_6_RI_5" + "P-poll__networl_0_6_RI_6" + "P-poll__networl_0_6_RI_7" + "P-poll__networl_0_6_RI_8" + "P-poll__networl_0_6_AI_0" + "P-poll__networl_0_6_AI_1" + "P-poll__networl_0_6_AI_2" + "P-poll__networl_0_6_AI_3" + "P-poll__networl_0_6_AI_4" + "P-poll__networl_0_6_AI_5" + "P-poll__networl_0_6_AI_6" + "P-poll__networl_0_6_AI_7" + "P-poll__networl_0_6_AI_8" + "P-poll__networl_0_6_AnnP_0" + "P-poll__networl_0_6_AnnP_1" + "P-poll__networl_0_6_AnnP_2" + "P-poll__networl_0_6_AnnP_3" + "P-poll__networl_0_6_AnnP_4" + "P-poll__networl_0_6_AnnP_5" + "P-poll__networl_0_6_AnnP_6" + "P-poll__networl_0_6_AnnP_7" + "P-poll__networl_0_6_AnnP_8" + "P-poll__networl_0_6_RP_0" + "P-poll__networl_0_6_RP_1" + "P-poll__networl_0_6_RP_2" + "P-poll__networl_0_6_RP_3" + "P-poll__networl_0_6_RP_4" + "P-poll__networl_0_6_RP_5" + "P-poll__networl_0_6_RP_6" + "P-poll__networl_0_6_RP_7" + "P-poll__networl_0_6_RP_8" + "P-poll__networl_0_7_AskP_0" + "P-poll__networl_0_7_AskP_1" + "P-poll__networl_0_7_AskP_2" + "P-poll__networl_0_7_AskP_3" + "P-poll__networl_0_7_AskP_4" + "P-poll__networl_0_7_AskP_5" + "P-poll__networl_0_7_AskP_6" + "P-poll__networl_0_7_AskP_7" + "P-poll__networl_0_7_AskP_8" + "P-poll__networl_0_7_AnsP_0" + "P-poll__networl_0_7_AnsP_1" + "P-poll__networl_0_7_AnsP_2" + "P-poll__networl_0_7_AnsP_3" + "P-poll__networl_0_7_AnsP_4" + "P-poll__networl_0_7_AnsP_5" + "P-poll__networl_0_7_AnsP_6" + "P-poll__networl_0_7_AnsP_7" + "P-poll__networl_0_7_AnsP_8" + "P-poll__networl_0_7_RI_0" + "P-poll__networl_0_7_RI_1" + "P-poll__networl_0_7_RI_2" + "P-poll__networl_0_7_RI_3" + "P-poll__networl_0_7_RI_4" + "P-poll__networl_0_7_RI_5" + "P-poll__networl_0_7_RI_6" + "P-poll__networl_0_7_RI_7" + "P-poll__networl_0_7_RI_8" + "P-poll__networl_0_7_AI_0" + "P-poll__networl_0_7_AI_1" + "P-poll__networl_0_7_AI_2" + "P-poll__networl_0_7_AI_3" + "P-poll__networl_0_7_AI_4" + "P-poll__networl_0_7_AI_5" + "P-poll__networl_0_7_AI_6" + "P-poll__networl_0_7_AI_7" + "P-poll__networl_0_7_AI_8" + "P-poll__networl_0_7_AnnP_0" + "P-poll__networl_0_7_AnnP_1" + "P-poll__networl_0_7_AnnP_2" + "P-poll__networl_0_7_AnnP_3" + "P-poll__networl_0_7_AnnP_4" + "P-poll__networl_0_7_AnnP_5" + "P-poll__networl_0_7_AnnP_6" + "P-poll__networl_0_7_AnnP_7" + "P-poll__networl_0_7_AnnP_8" + "P-poll__networl_0_7_RP_0" + "P-poll__networl_0_7_RP_1" + "P-poll__networl_0_7_RP_2" + "P-poll__networl_0_7_RP_3" + "P-poll__networl_0_7_RP_4" + "P-poll__networl_0_7_RP_5" + "P-poll__networl_0_7_RP_6" + "P-poll__networl_0_7_RP_7" + "P-poll__networl_0_7_RP_8" + "P-poll__networl_0_8_AskP_0" + "P-poll__networl_0_8_AskP_1" + "P-poll__networl_0_8_AskP_2" + "P-poll__networl_0_8_AskP_3" + "P-poll__networl_0_8_AskP_4" + "P-poll__networl_0_8_AskP_5" + "P-poll__networl_0_8_AskP_6" + "P-poll__networl_0_8_AskP_7" + "P-poll__networl_0_8_AskP_8" + "P-poll__networl_0_8_AnsP_0" + "P-poll__networl_0_8_AnsP_1" + "P-poll__networl_0_8_AnsP_2" + "P-poll__networl_0_8_AnsP_3" + "P-poll__networl_0_8_AnsP_4" + "P-poll__networl_0_8_AnsP_5" + "P-poll__networl_0_8_AnsP_6" + "P-poll__networl_0_8_AnsP_7" + "P-poll__networl_0_8_AnsP_8" + "P-poll__networl_0_8_RI_0" + "P-poll__networl_0_8_RI_1" + "P-poll__networl_0_8_RI_2" + "P-poll__networl_0_8_RI_3" + "P-poll__networl_0_8_RI_4" + "P-poll__networl_0_8_RI_5" + "P-poll__networl_0_8_RI_6" + "P-poll__networl_0_8_RI_7" + "P-poll__networl_0_8_RI_8" + "P-poll__networl_0_8_AI_0" + "P-poll__networl_0_8_AI_1" + "P-poll__networl_0_8_AI_2" + "P-poll__networl_0_8_AI_3" + "P-poll__networl_0_8_AI_4" + "P-poll__networl_0_8_AI_5" + "P-poll__networl_0_8_AI_6" + "P-poll__networl_0_8_AI_7" + "P-poll__networl_0_8_AI_8" + "P-poll__networl_0_8_AnnP_0" + "P-poll__networl_0_8_AnnP_1" + "P-poll__networl_0_8_AnnP_2" + "P-poll__networl_0_8_AnnP_3" + "P-poll__networl_0_8_AnnP_4" + "P-poll__networl_0_8_AnnP_5" + "P-poll__networl_0_8_AnnP_6" + "P-poll__networl_0_8_AnnP_7" + "P-poll__networl_0_8_AnnP_8" + "P-poll__networl_0_8_RP_0" + "P-poll__networl_0_8_RP_1" + "P-poll__networl_0_8_RP_2" + "P-poll__networl_0_8_RP_3" + "P-poll__networl_0_8_RP_4" + "P-poll__networl_0_8_RP_5" + "P-poll__networl_0_8_RP_6" + "P-poll__networl_0_8_RP_7" + "P-poll__networl_0_8_RP_8" + "P-poll__networl_1_0_AskP_0" + "P-poll__networl_1_0_AskP_1" + "P-poll__networl_1_0_AskP_2" + "P-poll__networl_1_0_AskP_3" + "P-poll__networl_1_0_AskP_4" + "P-poll__networl_1_0_AskP_5" + "P-poll__networl_1_0_AskP_6" + "P-poll__networl_1_0_AskP_7" + "P-poll__networl_1_0_AskP_8" + "P-poll__networl_1_0_AnsP_0" + "P-poll__networl_1_0_AnsP_1" + "P-poll__networl_1_0_AnsP_2" + "P-poll__networl_1_0_AnsP_3" + "P-poll__networl_1_0_AnsP_4" + "P-poll__networl_1_0_AnsP_5" + "P-poll__networl_1_0_AnsP_6" + "P-poll__networl_1_0_AnsP_7" + "P-poll__networl_1_0_AnsP_8" + "P-poll__networl_1_0_RI_0" + "P-poll__networl_1_0_RI_1" + "P-poll__networl_1_0_RI_2" + "P-poll__networl_1_0_RI_3" + "P-poll__networl_1_0_RI_4" + "P-poll__networl_1_0_RI_5" + "P-poll__networl_1_0_RI_6" + "P-poll__networl_1_0_RI_7" + "P-poll__networl_1_0_RI_8" + "P-poll__networl_1_0_AI_0" + "P-poll__networl_1_0_AI_1" + "P-poll__networl_1_0_AI_2" + "P-poll__networl_1_0_AI_3" + "P-poll__networl_1_0_AI_4" + "P-poll__networl_1_0_AI_5" + "P-poll__networl_1_0_AI_6" + "P-poll__networl_1_0_AI_7" + "P-poll__networl_1_0_AI_8" + "P-poll__networl_1_0_AnnP_0" + "P-poll__networl_1_0_AnnP_1" + "P-poll__networl_1_0_AnnP_2" + "P-poll__networl_1_0_AnnP_3" + "P-poll__networl_1_0_AnnP_4" + "P-poll__networl_1_0_AnnP_5" + "P-poll__networl_1_0_AnnP_6" + "P-poll__networl_1_0_AnnP_7" + "P-poll__networl_1_0_AnnP_8" + "P-poll__networl_1_0_RP_0" + "P-poll__networl_1_0_RP_1" + "P-poll__networl_1_0_RP_2" + "P-poll__networl_1_0_RP_3" + "P-poll__networl_1_0_RP_4" + "P-poll__networl_1_0_RP_5" + "P-poll__networl_1_0_RP_6" + "P-poll__networl_1_0_RP_7" + "P-poll__networl_1_0_RP_8" + "P-poll__networl_1_1_AskP_0" + "P-poll__networl_1_1_AskP_1" + "P-poll__networl_1_1_AskP_2" + "P-poll__networl_1_1_AskP_3" + "P-poll__networl_1_1_AskP_4" + "P-poll__networl_1_1_AskP_5" + "P-poll__networl_1_1_AskP_6" + "P-poll__networl_1_1_AskP_7" + "P-poll__networl_1_1_AskP_8" + "P-poll__networl_1_1_AnsP_0" + "P-poll__networl_1_1_AnsP_1" + "P-poll__networl_1_1_AnsP_2" + "P-poll__networl_1_1_AnsP_3" + "P-poll__networl_1_1_AnsP_4" + "P-poll__networl_1_1_AnsP_5" + "P-poll__networl_1_1_AnsP_6" + "P-poll__networl_1_1_AnsP_7" + "P-poll__networl_1_1_AnsP_8" + "P-poll__networl_1_1_RI_0" + "P-poll__networl_1_1_RI_1" + "P-poll__networl_1_1_RI_2" + "P-poll__networl_1_1_RI_3" + "P-poll__networl_1_1_RI_4" + "P-poll__networl_1_1_RI_5" + "P-poll__networl_1_1_RI_6" + "P-poll__networl_1_1_RI_7" + "P-poll__networl_1_1_RI_8" + "P-poll__networl_1_1_AI_0" + "P-poll__networl_1_1_AI_1" + "P-poll__networl_1_1_AI_2" + "P-poll__networl_1_1_AI_3" + "P-poll__networl_1_1_AI_4" + "P-poll__networl_1_1_AI_5" + "P-poll__networl_1_1_AI_6" + "P-poll__networl_1_1_AI_7" + "P-poll__networl_1_1_AI_8" + "P-poll__networl_1_1_AnnP_0" + "P-poll__networl_1_1_AnnP_1" + "P-poll__networl_1_1_AnnP_2" + "P-poll__networl_1_1_AnnP_3" + "P-poll__networl_1_1_AnnP_4" + "P-poll__networl_1_1_AnnP_5" + "P-poll__networl_1_1_AnnP_6" + "P-poll__networl_1_1_AnnP_7" + "P-poll__networl_1_1_AnnP_8" + "P-poll__networl_1_1_RP_0" + "P-poll__networl_1_1_RP_1" + "P-poll__networl_1_1_RP_2" + "P-poll__networl_1_1_RP_3" + "P-poll__networl_1_1_RP_4" + "P-poll__networl_1_1_RP_5" + "P-poll__networl_1_1_RP_6" + "P-poll__networl_1_1_RP_7" + "P-poll__networl_1_1_RP_8" + "P-poll__networl_1_2_AskP_0" + "P-poll__networl_1_2_AskP_1" + "P-poll__networl_1_2_AskP_2" + "P-poll__networl_1_2_AskP_3" + "P-poll__networl_1_2_AskP_4" + "P-poll__networl_1_2_AskP_5" + "P-poll__networl_1_2_AskP_6" + "P-poll__networl_1_2_AskP_7" + "P-poll__networl_1_2_AskP_8" + "P-poll__networl_1_2_AnsP_0" + "P-poll__networl_1_2_AnsP_1" + "P-poll__networl_1_2_AnsP_2" + "P-poll__networl_1_2_AnsP_3" + "P-poll__networl_1_2_AnsP_4" + "P-poll__networl_1_2_AnsP_5" + "P-poll__networl_1_2_AnsP_6" + "P-poll__networl_1_2_AnsP_7" + "P-poll__networl_1_2_AnsP_8" + "P-poll__networl_1_2_RI_0" + "P-poll__networl_1_2_RI_1" + "P-poll__networl_1_2_RI_2" + "P-poll__networl_1_2_RI_3" + "P-poll__networl_1_2_RI_4" + "P-poll__networl_1_2_RI_5" + "P-poll__networl_1_2_RI_6" + "P-poll__networl_1_2_RI_7" + "P-poll__networl_1_2_RI_8" + "P-poll__networl_1_2_AI_0" + "P-poll__networl_1_2_AI_1" + "P-poll__networl_1_2_AI_2" + "P-poll__networl_1_2_AI_3" + "P-poll__networl_1_2_AI_4" + "P-poll__networl_1_2_AI_5" + "P-poll__networl_1_2_AI_6" + "P-poll__networl_1_2_AI_7" + "P-poll__networl_1_2_AI_8" + "P-poll__networl_1_2_AnnP_0" + "P-poll__networl_1_2_AnnP_1" + "P-poll__networl_1_2_AnnP_2" + "P-poll__networl_1_2_AnnP_3" + "P-poll__networl_1_2_AnnP_4" + "P-poll__networl_1_2_AnnP_5" + "P-poll__networl_1_2_AnnP_6" + "P-poll__networl_1_2_AnnP_7" + "P-poll__networl_1_2_AnnP_8" + "P-poll__networl_1_2_RP_0" + "P-poll__networl_1_2_RP_1" + "P-poll__networl_1_2_RP_2" + "P-poll__networl_1_2_RP_3" + "P-poll__networl_1_2_RP_4" + "P-poll__networl_1_2_RP_5" + "P-poll__networl_1_2_RP_6" + "P-poll__networl_1_2_RP_7" + "P-poll__networl_1_2_RP_8" + "P-poll__networl_1_3_AskP_0" + "P-poll__networl_1_3_AskP_1" + "P-poll__networl_1_3_AskP_2" + "P-poll__networl_1_3_AskP_3" + "P-poll__networl_1_3_AskP_4" + "P-poll__networl_1_3_AskP_5" + "P-poll__networl_1_3_AskP_6" + "P-poll__networl_1_3_AskP_7" + "P-poll__networl_1_3_AskP_8" + "P-poll__networl_1_3_AnsP_0" + "P-poll__networl_1_3_AnsP_1" + "P-poll__networl_1_3_AnsP_2" + "P-poll__networl_1_3_AnsP_3" + "P-poll__networl_1_3_AnsP_4" + "P-poll__networl_1_3_AnsP_5" + "P-poll__networl_1_3_AnsP_6" + "P-poll__networl_1_3_AnsP_7" + "P-poll__networl_1_3_AnsP_8" + "P-poll__networl_1_3_RI_0" + "P-poll__networl_1_3_RI_1" + "P-poll__networl_1_3_RI_2" + "P-poll__networl_1_3_RI_3" + "P-poll__networl_1_3_RI_4" + "P-poll__networl_1_3_RI_5" + "P-poll__networl_1_3_RI_6" + "P-poll__networl_1_3_RI_7" + "P-poll__networl_1_3_RI_8" + "P-poll__networl_1_3_AI_0" + "P-poll__networl_1_3_AI_1" + "P-poll__networl_1_3_AI_2" + "P-poll__networl_1_3_AI_3" + "P-poll__networl_1_3_AI_4" + "P-poll__networl_1_3_AI_5" + "P-poll__networl_1_3_AI_6" + "P-poll__networl_1_3_AI_7" + "P-poll__networl_1_3_AI_8" + "P-poll__networl_1_3_AnnP_0" + "P-poll__networl_1_3_AnnP_1" + "P-poll__networl_1_3_AnnP_2" + "P-poll__networl_1_3_AnnP_3" + "P-poll__networl_1_3_AnnP_4" + "P-poll__networl_1_3_AnnP_5" + "P-poll__networl_1_3_AnnP_6" + "P-poll__networl_1_3_AnnP_7" + "P-poll__networl_1_3_AnnP_8" + "P-poll__networl_1_3_RP_0" + "P-poll__networl_1_3_RP_1" + "P-poll__networl_1_3_RP_2" + "P-poll__networl_1_3_RP_3" + "P-poll__networl_1_3_RP_4" + "P-poll__networl_1_3_RP_5" + "P-poll__networl_1_3_RP_6" + "P-poll__networl_1_3_RP_7" + "P-poll__networl_1_3_RP_8" + "P-poll__networl_1_4_AskP_0" + "P-poll__networl_1_4_AskP_1" + "P-poll__networl_1_4_AskP_2" + "P-poll__networl_1_4_AskP_3" + "P-poll__networl_1_4_AskP_4" + "P-poll__networl_1_4_AskP_5" + "P-poll__networl_1_4_AskP_6" + "P-poll__networl_1_4_AskP_7" + "P-poll__networl_1_4_AskP_8" + "P-poll__networl_1_4_AnsP_0" + "P-poll__networl_1_4_AnsP_1" + "P-poll__networl_1_4_AnsP_2" + "P-poll__networl_1_4_AnsP_3" + "P-poll__networl_1_4_AnsP_4" + "P-poll__networl_1_4_AnsP_5" + "P-poll__networl_1_4_AnsP_6" + "P-poll__networl_1_4_AnsP_7" + "P-poll__networl_1_4_AnsP_8" + "P-poll__networl_1_4_RI_0" + "P-poll__networl_1_4_RI_1" + "P-poll__networl_1_4_RI_2" + "P-poll__networl_1_4_RI_3" + "P-poll__networl_1_4_RI_4" + "P-poll__networl_1_4_RI_5" + "P-poll__networl_1_4_RI_6" + "P-poll__networl_1_4_RI_7" + "P-poll__networl_1_4_RI_8" + "P-poll__networl_1_4_AI_0" + "P-poll__networl_1_4_AI_1" + "P-poll__networl_1_4_AI_2" + "P-poll__networl_1_4_AI_3" + "P-poll__networl_1_4_AI_4" + "P-poll__networl_1_4_AI_5" + "P-poll__networl_1_4_AI_6" + "P-poll__networl_1_4_AI_7" + "P-poll__networl_1_4_AI_8" + "P-poll__networl_1_4_AnnP_0" + "P-poll__networl_1_4_AnnP_1" + "P-poll__networl_1_4_AnnP_2" + "P-poll__networl_1_4_AnnP_3" + "P-poll__networl_1_4_AnnP_4" + "P-poll__networl_1_4_AnnP_5" + "P-poll__networl_1_4_AnnP_6" + "P-poll__networl_1_4_AnnP_7" + "P-poll__networl_1_4_AnnP_8" + "P-poll__networl_1_4_RP_0" + "P-poll__networl_1_4_RP_1" + "P-poll__networl_1_4_RP_2" + "P-poll__networl_1_4_RP_3" + "P-poll__networl_1_4_RP_4" + "P-poll__networl_1_4_RP_5" + "P-poll__networl_1_4_RP_6" + "P-poll__networl_1_4_RP_7" + "P-poll__networl_1_4_RP_8" + "P-poll__networl_1_5_AskP_0" + "P-poll__networl_1_5_AskP_1" + "P-poll__networl_1_5_AskP_2" + "P-poll__networl_1_5_AskP_3" + "P-poll__networl_1_5_AskP_4" + "P-poll__networl_1_5_AskP_5" + "P-poll__networl_1_5_AskP_6" + "P-poll__networl_1_5_AskP_7" + "P-poll__networl_1_5_AskP_8" + "P-poll__networl_1_5_AnsP_0" + "P-poll__networl_1_5_AnsP_1" + "P-poll__networl_1_5_AnsP_2" + "P-poll__networl_1_5_AnsP_3" + "P-poll__networl_1_5_AnsP_4" + "P-poll__networl_1_5_AnsP_5" + "P-poll__networl_1_5_AnsP_6" + "P-poll__networl_1_5_AnsP_7" + "P-poll__networl_1_5_AnsP_8" + "P-poll__networl_1_5_RI_0" + "P-poll__networl_1_5_RI_1" + "P-poll__networl_1_5_RI_2" + "P-poll__networl_1_5_RI_3" + "P-poll__networl_1_5_RI_4" + "P-poll__networl_1_5_RI_5" + "P-poll__networl_1_5_RI_6" + "P-poll__networl_1_5_RI_7" + "P-poll__networl_1_5_RI_8" + "P-poll__networl_1_5_AI_0" + "P-poll__networl_1_5_AI_1" + "P-poll__networl_1_5_AI_2" + "P-poll__networl_1_5_AI_3" + "P-poll__networl_1_5_AI_4" + "P-poll__networl_1_5_AI_5" + "P-poll__networl_1_5_AI_6" + "P-poll__networl_1_5_AI_7" + "P-poll__networl_1_5_AI_8" + "P-poll__networl_1_5_AnnP_0" + "P-poll__networl_1_5_AnnP_1" + "P-poll__networl_1_5_AnnP_2" + "P-poll__networl_1_5_AnnP_3" + "P-poll__networl_1_5_AnnP_4" + "P-poll__networl_1_5_AnnP_5" + "P-poll__networl_1_5_AnnP_6" + "P-poll__networl_1_5_AnnP_7" + "P-poll__networl_1_5_AnnP_8" + "P-poll__networl_1_5_RP_0" + "P-poll__networl_1_5_RP_1" + "P-poll__networl_1_5_RP_2" + "P-poll__networl_1_5_RP_3" + "P-poll__networl_1_5_RP_4" + "P-poll__networl_1_5_RP_5" + "P-poll__networl_1_5_RP_6" + "P-poll__networl_1_5_RP_7" + "P-poll__networl_1_5_RP_8" + "P-poll__networl_1_6_AskP_0" + "P-poll__networl_1_6_AskP_1" + "P-poll__networl_1_6_AskP_2" + "P-poll__networl_1_6_AskP_3" + "P-poll__networl_1_6_AskP_4" + "P-poll__networl_1_6_AskP_5" + "P-poll__networl_1_6_AskP_6" + "P-poll__networl_1_6_AskP_7" + "P-poll__networl_1_6_AskP_8" + "P-poll__networl_1_6_AnsP_0" + "P-poll__networl_1_6_AnsP_1" + "P-poll__networl_1_6_AnsP_2" + "P-poll__networl_1_6_AnsP_3" + "P-poll__networl_1_6_AnsP_4" + "P-poll__networl_1_6_AnsP_5" + "P-poll__networl_1_6_AnsP_6" + "P-poll__networl_1_6_AnsP_7" + "P-poll__networl_1_6_AnsP_8" + "P-poll__networl_1_6_RI_0" + "P-poll__networl_1_6_RI_1" + "P-poll__networl_1_6_RI_2" + "P-poll__networl_1_6_RI_3" + "P-poll__networl_1_6_RI_4" + "P-poll__networl_1_6_RI_5" + "P-poll__networl_1_6_RI_6" + "P-poll__networl_1_6_RI_7" + "P-poll__networl_1_6_RI_8" + "P-poll__networl_1_6_AI_0" + "P-poll__networl_1_6_AI_1" + "P-poll__networl_1_6_AI_2" + "P-poll__networl_1_6_AI_3" + "P-poll__networl_1_6_AI_4" + "P-poll__networl_1_6_AI_5" + "P-poll__networl_1_6_AI_6" + "P-poll__networl_1_6_AI_7" + "P-poll__networl_1_6_AI_8" + "P-poll__networl_1_6_AnnP_0" + "P-poll__networl_1_6_AnnP_1" + "P-poll__networl_1_6_AnnP_2" + "P-poll__networl_1_6_AnnP_3" + "P-poll__networl_1_6_AnnP_4" + "P-poll__networl_1_6_AnnP_5" + "P-poll__networl_1_6_AnnP_6" + "P-poll__networl_1_6_AnnP_7" + "P-poll__networl_1_6_AnnP_8" + "P-poll__networl_1_6_RP_0" + "P-poll__networl_1_6_RP_1" + "P-poll__networl_1_6_RP_2" + "P-poll__networl_1_6_RP_3" + "P-poll__networl_1_6_RP_4" + "P-poll__networl_1_6_RP_5" + "P-poll__networl_1_6_RP_6" + "P-poll__networl_1_6_RP_7" + "P-poll__networl_1_6_RP_8" + "P-poll__networl_1_7_AskP_0" + "P-poll__networl_1_7_AskP_1" + "P-poll__networl_1_7_AskP_2" + "P-poll__networl_1_7_AskP_3" + "P-poll__networl_1_7_AskP_4" + "P-poll__networl_1_7_AskP_5" + "P-poll__networl_1_7_AskP_6" + "P-poll__networl_1_7_AskP_7" + "P-poll__networl_1_7_AskP_8" + "P-poll__networl_1_7_AnsP_0" + "P-poll__networl_1_7_AnsP_1" + "P-poll__networl_1_7_AnsP_2" + "P-poll__networl_1_7_AnsP_3" + "P-poll__networl_1_7_AnsP_4" + "P-poll__networl_1_7_AnsP_5" + "P-poll__networl_1_7_AnsP_6" + "P-poll__networl_1_7_AnsP_7" + "P-poll__networl_1_7_AnsP_8" + "P-poll__networl_1_7_RI_0" + "P-poll__networl_1_7_RI_1" + "P-poll__networl_1_7_RI_2" + "P-poll__networl_1_7_RI_3" + "P-poll__networl_1_7_RI_4" + "P-poll__networl_1_7_RI_5" + "P-poll__networl_1_7_RI_6" + "P-poll__networl_1_7_RI_7" + "P-poll__networl_1_7_RI_8" + "P-poll__networl_1_7_AI_0" + "P-poll__networl_1_7_AI_1" + "P-poll__networl_1_7_AI_2" + "P-poll__networl_1_7_AI_3" + "P-poll__networl_1_7_AI_4" + "P-poll__networl_1_7_AI_5" + "P-poll__networl_1_7_AI_6" + "P-poll__networl_1_7_AI_7" + "P-poll__networl_1_7_AI_8" + "P-poll__networl_1_7_AnnP_0" + "P-poll__networl_1_7_AnnP_1" + "P-poll__networl_1_7_AnnP_2" + "P-poll__networl_1_7_AnnP_3" + "P-poll__networl_1_7_AnnP_4" + "P-poll__networl_1_7_AnnP_5" + "P-poll__networl_1_7_AnnP_6" + "P-poll__networl_1_7_AnnP_7" + "P-poll__networl_1_7_AnnP_8" + "P-poll__networl_1_7_RP_0" + "P-poll__networl_1_7_RP_1" + "P-poll__networl_1_7_RP_2" + "P-poll__networl_1_7_RP_3" + "P-poll__networl_1_7_RP_4" + "P-poll__networl_1_7_RP_5" + "P-poll__networl_1_7_RP_6" + "P-poll__networl_1_7_RP_7" + "P-poll__networl_1_7_RP_8" + "P-poll__networl_1_8_AskP_0" + "P-poll__networl_1_8_AskP_1" + "P-poll__networl_1_8_AskP_2" + "P-poll__networl_1_8_AskP_3" + "P-poll__networl_1_8_AskP_4" + "P-poll__networl_1_8_AskP_5" + "P-poll__networl_1_8_AskP_6" + "P-poll__networl_1_8_AskP_7" + "P-poll__networl_1_8_AskP_8" + "P-poll__networl_1_8_AnsP_0" + "P-poll__networl_1_8_AnsP_1" + "P-poll__networl_1_8_AnsP_2" + "P-poll__networl_1_8_AnsP_3" + "P-poll__networl_1_8_AnsP_4" + "P-poll__networl_1_8_AnsP_5" + "P-poll__networl_1_8_AnsP_6" + "P-poll__networl_1_8_AnsP_7" + "P-poll__networl_1_8_AnsP_8" + "P-poll__networl_1_8_RI_0" + "P-poll__networl_1_8_RI_1" + "P-poll__networl_1_8_RI_2" + "P-poll__networl_1_8_RI_3" + "P-poll__networl_1_8_RI_4" + "P-poll__networl_1_8_RI_5" + "P-poll__networl_1_8_RI_6" + "P-poll__networl_1_8_RI_7" + "P-poll__networl_1_8_RI_8" + "P-poll__networl_1_8_AI_0" + "P-poll__networl_1_8_AI_1" + "P-poll__networl_1_8_AI_2" + "P-poll__networl_1_8_AI_3" + "P-poll__networl_1_8_AI_4" + "P-poll__networl_1_8_AI_5" + "P-poll__networl_1_8_AI_6" + "P-poll__networl_1_8_AI_7" + "P-poll__networl_1_8_AI_8" + "P-poll__networl_1_8_AnnP_0" + "P-poll__networl_1_8_AnnP_1" + "P-poll__networl_1_8_AnnP_2" + "P-poll__networl_1_8_AnnP_3" + "P-poll__networl_1_8_AnnP_4" + "P-poll__networl_1_8_AnnP_5" + "P-poll__networl_1_8_AnnP_6" + "P-poll__networl_1_8_AnnP_7" + "P-poll__networl_1_8_AnnP_8" + "P-poll__networl_1_8_RP_0" + "P-poll__networl_1_8_RP_1" + "P-poll__networl_1_8_RP_2" + "P-poll__networl_1_8_RP_3" + "P-poll__networl_1_8_RP_4" + "P-poll__networl_1_8_RP_5" + "P-poll__networl_1_8_RP_6" + "P-poll__networl_1_8_RP_7" + "P-poll__networl_1_8_RP_8" + "P-poll__networl_2_0_AskP_0" + "P-poll__networl_2_0_AskP_1" + "P-poll__networl_2_0_AskP_2" + "P-poll__networl_2_0_AskP_3" + "P-poll__networl_2_0_AskP_4" + "P-poll__networl_2_0_AskP_5" + "P-poll__networl_2_0_AskP_6" + "P-poll__networl_2_0_AskP_7" + "P-poll__networl_2_0_AskP_8" + "P-poll__networl_2_0_AnsP_0" + "P-poll__networl_2_0_AnsP_1" + "P-poll__networl_2_0_AnsP_2" + "P-poll__networl_2_0_AnsP_3" + "P-poll__networl_2_0_AnsP_4" + "P-poll__networl_2_0_AnsP_5" + "P-poll__networl_2_0_AnsP_6" + "P-poll__networl_2_0_AnsP_7" + "P-poll__networl_2_0_AnsP_8" + "P-poll__networl_2_0_RI_0" + "P-poll__networl_2_0_RI_1" + "P-poll__networl_2_0_RI_2" + "P-poll__networl_2_0_RI_3" + "P-poll__networl_2_0_RI_4" + "P-poll__networl_2_0_RI_5" + "P-poll__networl_2_0_RI_6" + "P-poll__networl_2_0_RI_7" + "P-poll__networl_2_0_RI_8" + "P-poll__networl_2_0_AI_0" + "P-poll__networl_2_0_AI_1" + "P-poll__networl_2_0_AI_2" + "P-poll__networl_2_0_AI_3" + "P-poll__networl_2_0_AI_4" + "P-poll__networl_2_0_AI_5" + "P-poll__networl_2_0_AI_6" + "P-poll__networl_2_0_AI_7" + "P-poll__networl_2_0_AI_8" + "P-poll__networl_2_0_AnnP_0" + "P-poll__networl_2_0_AnnP_1" + "P-poll__networl_2_0_AnnP_2" + "P-poll__networl_2_0_AnnP_3" + "P-poll__networl_2_0_AnnP_4" + "P-poll__networl_2_0_AnnP_5" + "P-poll__networl_2_0_AnnP_6" + "P-poll__networl_2_0_AnnP_7" + "P-poll__networl_2_0_AnnP_8" + "P-poll__networl_2_0_RP_0" + "P-poll__networl_2_0_RP_1" + "P-poll__networl_2_0_RP_2" + "P-poll__networl_2_0_RP_3" + "P-poll__networl_2_0_RP_4" + "P-poll__networl_2_0_RP_5" + "P-poll__networl_2_0_RP_6" + "P-poll__networl_2_0_RP_7" + "P-poll__networl_2_0_RP_8" + "P-poll__networl_2_1_AskP_0" + "P-poll__networl_2_1_AskP_1" + "P-poll__networl_2_1_AskP_2" + "P-poll__networl_2_1_AskP_3" + "P-poll__networl_2_1_AskP_4" + "P-poll__networl_2_1_AskP_5" + "P-poll__networl_2_1_AskP_6" + "P-poll__networl_2_1_AskP_7" + "P-poll__networl_2_1_AskP_8" + "P-poll__networl_2_1_AnsP_0" + "P-poll__networl_2_1_AnsP_1" + "P-poll__networl_2_1_AnsP_2" + "P-poll__networl_2_1_AnsP_3" + "P-poll__networl_2_1_AnsP_4" + "P-poll__networl_2_1_AnsP_5" + "P-poll__networl_2_1_AnsP_6" + "P-poll__networl_2_1_AnsP_7" + "P-poll__networl_2_1_AnsP_8" + "P-poll__networl_2_1_RI_0" + "P-poll__networl_2_1_RI_1" + "P-poll__networl_2_1_RI_2" + "P-poll__networl_2_1_RI_3" + "P-poll__networl_2_1_RI_4" + "P-poll__networl_2_1_RI_5" + "P-poll__networl_2_1_RI_6" + "P-poll__networl_2_1_RI_7" + "P-poll__networl_2_1_RI_8" + "P-poll__networl_2_1_AI_0" + "P-poll__networl_2_1_AI_1" + "P-poll__networl_2_1_AI_2" + "P-poll__networl_2_1_AI_3" + "P-poll__networl_2_1_AI_4" + "P-poll__networl_2_1_AI_5" + "P-poll__networl_2_1_AI_6" + "P-poll__networl_2_1_AI_7" + "P-poll__networl_2_1_AI_8" + "P-poll__networl_2_1_AnnP_0" + "P-poll__networl_2_1_AnnP_1" + "P-poll__networl_2_1_AnnP_2" + "P-poll__networl_2_1_AnnP_3" + "P-poll__networl_2_1_AnnP_4" + "P-poll__networl_2_1_AnnP_5" + "P-poll__networl_2_1_AnnP_6" + "P-poll__networl_2_1_AnnP_7" + "P-poll__networl_2_1_AnnP_8" + "P-poll__networl_2_1_RP_0" + "P-poll__networl_2_1_RP_1" + "P-poll__networl_2_1_RP_2" + "P-poll__networl_2_1_RP_3" + "P-poll__networl_2_1_RP_4" + "P-poll__networl_2_1_RP_5" + "P-poll__networl_2_1_RP_6" + "P-poll__networl_2_1_RP_7" + "P-poll__networl_2_1_RP_8" + "P-poll__networl_2_2_AskP_0" + "P-poll__networl_2_2_AskP_1" + "P-poll__networl_2_2_AskP_2" + "P-poll__networl_2_2_AskP_3" + "P-poll__networl_2_2_AskP_4" + "P-poll__networl_2_2_AskP_5" + "P-poll__networl_2_2_AskP_6" + "P-poll__networl_2_2_AskP_7" + "P-poll__networl_2_2_AskP_8" + "P-poll__networl_2_2_AnsP_0" + "P-poll__networl_2_2_AnsP_1" + "P-poll__networl_2_2_AnsP_2" + "P-poll__networl_2_2_AnsP_3" + "P-poll__networl_2_2_AnsP_4" + "P-poll__networl_2_2_AnsP_5" + "P-poll__networl_2_2_AnsP_6" + "P-poll__networl_2_2_AnsP_7" + "P-poll__networl_2_2_AnsP_8" + "P-poll__networl_2_2_RI_0" + "P-poll__networl_2_2_RI_1" + "P-poll__networl_2_2_RI_2" + "P-poll__networl_2_2_RI_3" + "P-poll__networl_2_2_RI_4" + "P-poll__networl_2_2_RI_5" + "P-poll__networl_2_2_RI_6" + "P-poll__networl_2_2_RI_7" + "P-poll__networl_2_2_RI_8" + "P-poll__networl_2_2_AI_0" + "P-poll__networl_2_2_AI_1" + "P-poll__networl_2_2_AI_2" + "P-poll__networl_2_2_AI_3" + "P-poll__networl_2_2_AI_4" + "P-poll__networl_2_2_AI_5" + "P-poll__networl_2_2_AI_6" + "P-poll__networl_2_2_AI_7" + "P-poll__networl_2_2_AI_8" + "P-poll__networl_2_2_AnnP_0" + "P-poll__networl_2_2_AnnP_1" + "P-poll__networl_2_2_AnnP_2" + "P-poll__networl_2_2_AnnP_3" + "P-poll__networl_2_2_AnnP_4" + "P-poll__networl_2_2_AnnP_5" + "P-poll__networl_2_2_AnnP_6" + "P-poll__networl_2_2_AnnP_7" + "P-poll__networl_2_2_AnnP_8" + "P-poll__networl_2_2_RP_0" + "P-poll__networl_2_2_RP_1" + "P-poll__networl_2_2_RP_2" + "P-poll__networl_2_2_RP_3" + "P-poll__networl_2_2_RP_4" + "P-poll__networl_2_2_RP_5" + "P-poll__networl_2_2_RP_6" + "P-poll__networl_2_2_RP_7" + "P-poll__networl_2_2_RP_8" + "P-poll__networl_2_3_AskP_0" + "P-poll__networl_2_3_AskP_1" + "P-poll__networl_2_3_AskP_2" + "P-poll__networl_2_3_AskP_3" + "P-poll__networl_2_3_AskP_4" + "P-poll__networl_2_3_AskP_5" + "P-poll__networl_2_3_AskP_6" + "P-poll__networl_2_3_AskP_7" + "P-poll__networl_2_3_AskP_8" + "P-poll__networl_2_3_AnsP_0" + "P-poll__networl_2_3_AnsP_1" + "P-poll__networl_2_3_AnsP_2" + "P-poll__networl_2_3_AnsP_3" + "P-poll__networl_2_3_AnsP_4" + "P-poll__networl_2_3_AnsP_5" + "P-poll__networl_2_3_AnsP_6" + "P-poll__networl_2_3_AnsP_7" + "P-poll__networl_2_3_AnsP_8" + "P-poll__networl_2_3_RI_0" + "P-poll__networl_2_3_RI_1" + "P-poll__networl_2_3_RI_2" + "P-poll__networl_2_3_RI_3" + "P-poll__networl_2_3_RI_4" + "P-poll__networl_2_3_RI_5" + "P-poll__networl_2_3_RI_6" + "P-poll__networl_2_3_RI_7" + "P-poll__networl_2_3_RI_8" + "P-poll__networl_2_3_AI_0" + "P-poll__networl_2_3_AI_1" + "P-poll__networl_2_3_AI_2" + "P-poll__networl_2_3_AI_3" + "P-poll__networl_2_3_AI_4" + "P-poll__networl_2_3_AI_5" + "P-poll__networl_2_3_AI_6" + "P-poll__networl_2_3_AI_7" + "P-poll__networl_2_3_AI_8" + "P-poll__networl_2_3_AnnP_0" + "P-poll__networl_2_3_AnnP_1" + "P-poll__networl_2_3_AnnP_2" + "P-poll__networl_2_3_AnnP_3" + "P-poll__networl_2_3_AnnP_4" + "P-poll__networl_2_3_AnnP_5" + "P-poll__networl_2_3_AnnP_6" + "P-poll__networl_2_3_AnnP_7" + "P-poll__networl_2_3_AnnP_8" + "P-poll__networl_2_3_RP_0" + "P-poll__networl_2_3_RP_1" + "P-poll__networl_2_3_RP_2" + "P-poll__networl_2_3_RP_3" + "P-poll__networl_2_3_RP_4" + "P-poll__networl_2_3_RP_5" + "P-poll__networl_2_3_RP_6" + "P-poll__networl_2_3_RP_7" + "P-poll__networl_2_3_RP_8" + "P-poll__networl_2_4_AskP_0" + "P-poll__networl_2_4_AskP_1" + "P-poll__networl_2_4_AskP_2" + "P-poll__networl_2_4_AskP_3" + "P-poll__networl_2_4_AskP_4" + "P-poll__networl_2_4_AskP_5" + "P-poll__networl_2_4_AskP_6" + "P-poll__networl_2_4_AskP_7" + "P-poll__networl_2_4_AskP_8" + "P-poll__networl_2_4_AnsP_0" + "P-poll__networl_2_4_AnsP_1" + "P-poll__networl_2_4_AnsP_2" + "P-poll__networl_2_4_AnsP_3" + "P-poll__networl_2_4_AnsP_4" + "P-poll__networl_2_4_AnsP_5" + "P-poll__networl_2_4_AnsP_6" + "P-poll__networl_2_4_AnsP_7" + "P-poll__networl_2_4_AnsP_8" + "P-poll__networl_2_4_RI_0" + "P-poll__networl_2_4_RI_1" + "P-poll__networl_2_4_RI_2" + "P-poll__networl_2_4_RI_3" + "P-poll__networl_2_4_RI_4" + "P-poll__networl_2_4_RI_5" + "P-poll__networl_2_4_RI_6" + "P-poll__networl_2_4_RI_7" + "P-poll__networl_2_4_RI_8" + "P-poll__networl_2_4_AI_0" + "P-poll__networl_2_4_AI_1" + "P-poll__networl_2_4_AI_2" + "P-poll__networl_2_4_AI_3" + "P-poll__networl_2_4_AI_4" + "P-poll__networl_2_4_AI_5" + "P-poll__networl_2_4_AI_6" + "P-poll__networl_2_4_AI_7" + "P-poll__networl_2_4_AI_8" + "P-poll__networl_2_4_AnnP_0" + "P-poll__networl_2_4_AnnP_1" + "P-poll__networl_2_4_AnnP_2" + "P-poll__networl_2_4_AnnP_3" + "P-poll__networl_2_4_AnnP_4" + "P-poll__networl_2_4_AnnP_5" + "P-poll__networl_2_4_AnnP_6" + "P-poll__networl_2_4_AnnP_7" + "P-poll__networl_2_4_AnnP_8" + "P-poll__networl_2_4_RP_0" + "P-poll__networl_2_4_RP_1" + "P-poll__networl_2_4_RP_2" + "P-poll__networl_2_4_RP_3" + "P-poll__networl_2_4_RP_4" + "P-poll__networl_2_4_RP_5" + "P-poll__networl_2_4_RP_6" + "P-poll__networl_2_4_RP_7" + "P-poll__networl_2_4_RP_8" + "P-poll__networl_2_5_AskP_0" + "P-poll__networl_2_5_AskP_1" + "P-poll__networl_2_5_AskP_2" + "P-poll__networl_2_5_AskP_3" + "P-poll__networl_2_5_AskP_4" + "P-poll__networl_2_5_AskP_5" + "P-poll__networl_2_5_AskP_6" + "P-poll__networl_2_5_AskP_7" + "P-poll__networl_2_5_AskP_8" + "P-poll__networl_2_5_AnsP_0" + "P-poll__networl_2_5_AnsP_1" + "P-poll__networl_2_5_AnsP_2" + "P-poll__networl_2_5_AnsP_3" + "P-poll__networl_2_5_AnsP_4" + "P-poll__networl_2_5_AnsP_5" + "P-poll__networl_2_5_AnsP_6" + "P-poll__networl_2_5_AnsP_7" + "P-poll__networl_2_5_AnsP_8" + "P-poll__networl_2_5_RI_0" + "P-poll__networl_2_5_RI_1" + "P-poll__networl_2_5_RI_2" + "P-poll__networl_2_5_RI_3" + "P-poll__networl_2_5_RI_4" + "P-poll__networl_2_5_RI_5" + "P-poll__networl_2_5_RI_6" + "P-poll__networl_2_5_RI_7" + "P-poll__networl_2_5_RI_8" + "P-poll__networl_2_5_AI_0" + "P-poll__networl_2_5_AI_1" + "P-poll__networl_2_5_AI_2" + "P-poll__networl_2_5_AI_3" + "P-poll__networl_2_5_AI_4" + "P-poll__networl_2_5_AI_5" + "P-poll__networl_2_5_AI_6" + "P-poll__networl_2_5_AI_7" + "P-poll__networl_2_5_AI_8" + "P-poll__networl_2_5_AnnP_0" + "P-poll__networl_2_5_AnnP_1" + "P-poll__networl_2_5_AnnP_2" + "P-poll__networl_2_5_AnnP_3" + "P-poll__networl_2_5_AnnP_4" + "P-poll__networl_2_5_AnnP_5" + "P-poll__networl_2_5_AnnP_6" + "P-poll__networl_2_5_AnnP_7" + "P-poll__networl_2_5_AnnP_8" + "P-poll__networl_2_5_RP_0" + "P-poll__networl_2_5_RP_1" + "P-poll__networl_2_5_RP_2" + "P-poll__networl_2_5_RP_3" + "P-poll__networl_2_5_RP_4" + "P-poll__networl_2_5_RP_5" + "P-poll__networl_2_5_RP_6" + "P-poll__networl_2_5_RP_7" + "P-poll__networl_2_5_RP_8" + "P-poll__networl_2_6_AskP_0" + "P-poll__networl_2_6_AskP_1" + "P-poll__networl_2_6_AskP_2" + "P-poll__networl_2_6_AskP_3" + "P-poll__networl_2_6_AskP_4" + "P-poll__networl_2_6_AskP_5" + "P-poll__networl_2_6_AskP_6" + "P-poll__networl_2_6_AskP_7" + "P-poll__networl_2_6_AskP_8" + "P-poll__networl_2_6_AnsP_0" + "P-poll__networl_2_6_AnsP_1" + "P-poll__networl_2_6_AnsP_2" + "P-poll__networl_2_6_AnsP_3" + "P-poll__networl_2_6_AnsP_4" + "P-poll__networl_2_6_AnsP_5" + "P-poll__networl_2_6_AnsP_6" + "P-poll__networl_2_6_AnsP_7" + "P-poll__networl_2_6_AnsP_8" + "P-poll__networl_2_6_RI_0" + "P-poll__networl_2_6_RI_1" + "P-poll__networl_2_6_RI_2" + "P-poll__networl_2_6_RI_3" + "P-poll__networl_2_6_RI_4" + "P-poll__networl_2_6_RI_5" + "P-poll__networl_2_6_RI_6" + "P-poll__networl_2_6_RI_7" + "P-poll__networl_2_6_RI_8" + "P-poll__networl_2_6_AI_0" + "P-poll__networl_2_6_AI_1" + "P-poll__networl_2_6_AI_2" + "P-poll__networl_2_6_AI_3" + "P-poll__networl_2_6_AI_4" + "P-poll__networl_2_6_AI_5" + "P-poll__networl_2_6_AI_6" + "P-poll__networl_2_6_AI_7" + "P-poll__networl_2_6_AI_8" + "P-poll__networl_2_6_AnnP_0" + "P-poll__networl_2_6_AnnP_1" + "P-poll__networl_2_6_AnnP_2" + "P-poll__networl_2_6_AnnP_3" + "P-poll__networl_2_6_AnnP_4" + "P-poll__networl_2_6_AnnP_5" + "P-poll__networl_2_6_AnnP_6" + "P-poll__networl_2_6_AnnP_7" + "P-poll__networl_2_6_AnnP_8" + "P-poll__networl_2_6_RP_0" + "P-poll__networl_2_6_RP_1" + "P-poll__networl_2_6_RP_2" + "P-poll__networl_2_6_RP_3" + "P-poll__networl_2_6_RP_4" + "P-poll__networl_2_6_RP_5" + "P-poll__networl_2_6_RP_6" + "P-poll__networl_2_6_RP_7" + "P-poll__networl_2_6_RP_8" + "P-poll__networl_2_7_AskP_0" + "P-poll__networl_2_7_AskP_1" + "P-poll__networl_2_7_AskP_2" + "P-poll__networl_2_7_AskP_3" + "P-poll__networl_2_7_AskP_4" + "P-poll__networl_2_7_AskP_5" + "P-poll__networl_2_7_AskP_6" + "P-poll__networl_2_7_AskP_7" + "P-poll__networl_2_7_AskP_8" + "P-poll__networl_2_7_AnsP_0" + "P-poll__networl_2_7_AnsP_1" + "P-poll__networl_2_7_AnsP_2" + "P-poll__networl_2_7_AnsP_3" + "P-poll__networl_2_7_AnsP_4" + "P-poll__networl_2_7_AnsP_5" + "P-poll__networl_2_7_AnsP_6" + "P-poll__networl_2_7_AnsP_7" + "P-poll__networl_2_7_AnsP_8" + "P-poll__networl_2_7_RI_0" + "P-poll__networl_2_7_RI_1" + "P-poll__networl_2_7_RI_2" + "P-poll__networl_2_7_RI_3" + "P-poll__networl_2_7_RI_4" + "P-poll__networl_2_7_RI_5" + "P-poll__networl_2_7_RI_6" + "P-poll__networl_2_7_RI_7" + "P-poll__networl_2_7_RI_8" + "P-poll__networl_2_7_AI_0" + "P-poll__networl_2_7_AI_1" + "P-poll__networl_2_7_AI_2" + "P-poll__networl_2_7_AI_3" + "P-poll__networl_2_7_AI_4" + "P-poll__networl_2_7_AI_5" + "P-poll__networl_2_7_AI_6" + "P-poll__networl_2_7_AI_7" + "P-poll__networl_2_7_AI_8" + "P-poll__networl_2_7_AnnP_0" + "P-poll__networl_2_7_AnnP_1" + "P-poll__networl_2_7_AnnP_2" + "P-poll__networl_2_7_AnnP_3" + "P-poll__networl_2_7_AnnP_4" + "P-poll__networl_2_7_AnnP_5" + "P-poll__networl_2_7_AnnP_6" + "P-poll__networl_2_7_AnnP_7" + "P-poll__networl_2_7_AnnP_8" + "P-poll__networl_2_7_RP_0" + "P-poll__networl_2_7_RP_1" + "P-poll__networl_2_7_RP_2" + "P-poll__networl_2_7_RP_3" + "P-poll__networl_2_7_RP_4" + "P-poll__networl_2_7_RP_5" + "P-poll__networl_2_7_RP_6" + "P-poll__networl_2_7_RP_7" + "P-poll__networl_2_7_RP_8" + "P-poll__networl_2_8_AskP_0" + "P-poll__networl_2_8_AskP_1" + "P-poll__networl_2_8_AskP_2" + "P-poll__networl_2_8_AskP_3" + "P-poll__networl_2_8_AskP_4" + "P-poll__networl_2_8_AskP_5" + "P-poll__networl_2_8_AskP_6" + "P-poll__networl_2_8_AskP_7" + "P-poll__networl_2_8_AskP_8" + "P-poll__networl_2_8_AnsP_0" + "P-poll__networl_2_8_AnsP_1" + "P-poll__networl_2_8_AnsP_2" + "P-poll__networl_2_8_AnsP_3" + "P-poll__networl_2_8_AnsP_4" + "P-poll__networl_2_8_AnsP_5" + "P-poll__networl_2_8_AnsP_6" + "P-poll__networl_2_8_AnsP_7" + "P-poll__networl_2_8_AnsP_8" + "P-poll__networl_2_8_RI_0" + "P-poll__networl_2_8_RI_1" + "P-poll__networl_2_8_RI_2" + "P-poll__networl_2_8_RI_3" + "P-poll__networl_2_8_RI_4" + "P-poll__networl_2_8_RI_5" + "P-poll__networl_2_8_RI_6" + "P-poll__networl_2_8_RI_7" + "P-poll__networl_2_8_RI_8" + "P-poll__networl_2_8_AI_0" + "P-poll__networl_2_8_AI_1" + "P-poll__networl_2_8_AI_2" + "P-poll__networl_2_8_AI_3" + "P-poll__networl_2_8_AI_4" + "P-poll__networl_2_8_AI_5" + "P-poll__networl_2_8_AI_6" + "P-poll__networl_2_8_AI_7" + "P-poll__networl_2_8_AI_8" + "P-poll__networl_2_8_AnnP_0" + "P-poll__networl_2_8_AnnP_1" + "P-poll__networl_2_8_AnnP_2" + "P-poll__networl_2_8_AnnP_3" + "P-poll__networl_2_8_AnnP_4" + "P-poll__networl_2_8_AnnP_5" + "P-poll__networl_2_8_AnnP_6" + "P-poll__networl_2_8_AnnP_7" + "P-poll__networl_2_8_AnnP_8" + "P-poll__networl_2_8_RP_0" + "P-poll__networl_2_8_RP_1" + "P-poll__networl_2_8_RP_2" + "P-poll__networl_2_8_RP_3" + "P-poll__networl_2_8_RP_4" + "P-poll__networl_2_8_RP_5" + "P-poll__networl_2_8_RP_6" + "P-poll__networl_2_8_RP_7" + "P-poll__networl_2_8_RP_8" + "P-poll__networl_3_0_AskP_0" + "P-poll__networl_3_0_AskP_1" + "P-poll__networl_3_0_AskP_2" + "P-poll__networl_3_0_AskP_3" + "P-poll__networl_3_0_AskP_4" + "P-poll__networl_3_0_AskP_5" + "P-poll__networl_3_0_AskP_6" + "P-poll__networl_3_0_AskP_7" + "P-poll__networl_3_0_AskP_8" + "P-poll__networl_3_0_AnsP_0" + "P-poll__networl_3_0_AnsP_1" + "P-poll__networl_3_0_AnsP_2" + "P-poll__networl_3_0_AnsP_3" + "P-poll__networl_3_0_AnsP_4" + "P-poll__networl_3_0_AnsP_5" + "P-poll__networl_3_0_AnsP_6" + "P-poll__networl_3_0_AnsP_7" + "P-poll__networl_3_0_AnsP_8" + "P-poll__networl_3_0_RI_0" + "P-poll__networl_3_0_RI_1" + "P-poll__networl_3_0_RI_2" + "P-poll__networl_3_0_RI_3" + "P-poll__networl_3_0_RI_4" + "P-poll__networl_3_0_RI_5" + "P-poll__networl_3_0_RI_6" + "P-poll__networl_3_0_RI_7" + "P-poll__networl_3_0_RI_8" + "P-poll__networl_3_0_AI_0" + "P-poll__networl_3_0_AI_1" + "P-poll__networl_3_0_AI_2" + "P-poll__networl_3_0_AI_3" + "P-poll__networl_3_0_AI_4" + "P-poll__networl_3_0_AI_5" + "P-poll__networl_3_0_AI_6" + "P-poll__networl_3_0_AI_7" + "P-poll__networl_3_0_AI_8" + "P-poll__networl_3_0_AnnP_0" + "P-poll__networl_3_0_AnnP_1" + "P-poll__networl_3_0_AnnP_2" + "P-poll__networl_3_0_AnnP_3" + "P-poll__networl_3_0_AnnP_4" + "P-poll__networl_3_0_AnnP_5" + "P-poll__networl_3_0_AnnP_6" + "P-poll__networl_3_0_AnnP_7" + "P-poll__networl_3_0_AnnP_8" + "P-poll__networl_3_0_RP_0" + "P-poll__networl_3_0_RP_1" + "P-poll__networl_3_0_RP_2" + "P-poll__networl_3_0_RP_3" + "P-poll__networl_3_0_RP_4" + "P-poll__networl_3_0_RP_5" + "P-poll__networl_3_0_RP_6" + "P-poll__networl_3_0_RP_7" + "P-poll__networl_3_0_RP_8" + "P-poll__networl_3_1_AskP_0" + "P-poll__networl_3_1_AskP_1" + "P-poll__networl_3_1_AskP_2" + "P-poll__networl_3_1_AskP_3" + "P-poll__networl_3_1_AskP_4" + "P-poll__networl_3_1_AskP_5" + "P-poll__networl_3_1_AskP_6" + "P-poll__networl_3_1_AskP_7" + "P-poll__networl_3_1_AskP_8" + "P-poll__networl_3_1_AnsP_0" + "P-poll__networl_3_1_AnsP_1" + "P-poll__networl_3_1_AnsP_2" + "P-poll__networl_3_1_AnsP_3" + "P-poll__networl_3_1_AnsP_4" + "P-poll__networl_3_1_AnsP_5" + "P-poll__networl_3_1_AnsP_6" + "P-poll__networl_3_1_AnsP_7" + "P-poll__networl_3_1_AnsP_8" + "P-poll__networl_3_1_RI_0" + "P-poll__networl_3_1_RI_1" + "P-poll__networl_3_1_RI_2" + "P-poll__networl_3_1_RI_3" + "P-poll__networl_3_1_RI_4" + "P-poll__networl_3_1_RI_5" + "P-poll__networl_3_1_RI_6" + "P-poll__networl_3_1_RI_7" + "P-poll__networl_3_1_RI_8" + "P-poll__networl_3_1_AI_0" + "P-poll__networl_3_1_AI_1" + "P-poll__networl_3_1_AI_2" + "P-poll__networl_3_1_AI_3" + "P-poll__networl_3_1_AI_4" + "P-poll__networl_3_1_AI_5" + "P-poll__networl_3_1_AI_6" + "P-poll__networl_3_1_AI_7" + "P-poll__networl_3_1_AI_8" + "P-poll__networl_3_1_AnnP_0" + "P-poll__networl_3_1_AnnP_1" + "P-poll__networl_3_1_AnnP_2" + "P-poll__networl_3_1_AnnP_3" + "P-poll__networl_3_1_AnnP_4" + "P-poll__networl_3_1_AnnP_5" + "P-poll__networl_3_1_AnnP_6" + "P-poll__networl_3_1_AnnP_7" + "P-poll__networl_3_1_AnnP_8" + "P-poll__networl_3_1_RP_0" + "P-poll__networl_3_1_RP_1" + "P-poll__networl_3_1_RP_2" + "P-poll__networl_3_1_RP_3" + "P-poll__networl_3_1_RP_4" + "P-poll__networl_3_1_RP_5" + "P-poll__networl_3_1_RP_6" + "P-poll__networl_3_1_RP_7" + "P-poll__networl_3_1_RP_8" + "P-poll__networl_3_2_AskP_0" + "P-poll__networl_3_2_AskP_1" + "P-poll__networl_3_2_AskP_2" + "P-poll__networl_3_2_AskP_3" + "P-poll__networl_3_2_AskP_4" + "P-poll__networl_3_2_AskP_5" + "P-poll__networl_3_2_AskP_6" + "P-poll__networl_3_2_AskP_7" + "P-poll__networl_3_2_AskP_8" + "P-poll__networl_3_2_AnsP_0" + "P-poll__networl_3_2_AnsP_1" + "P-poll__networl_3_2_AnsP_2" + "P-poll__networl_3_2_AnsP_3" + "P-poll__networl_3_2_AnsP_4" + "P-poll__networl_3_2_AnsP_5" + "P-poll__networl_3_2_AnsP_6" + "P-poll__networl_3_2_AnsP_7" + "P-poll__networl_3_2_AnsP_8" + "P-poll__networl_3_2_RI_0" + "P-poll__networl_3_2_RI_1" + "P-poll__networl_3_2_RI_2" + "P-poll__networl_3_2_RI_3" + "P-poll__networl_3_2_RI_4" + "P-poll__networl_3_2_RI_5" + "P-poll__networl_3_2_RI_6" + "P-poll__networl_3_2_RI_7" + "P-poll__networl_3_2_RI_8" + "P-poll__networl_3_2_AI_0" + "P-poll__networl_3_2_AI_1" + "P-poll__networl_3_2_AI_2" + "P-poll__networl_3_2_AI_3" + "P-poll__networl_3_2_AI_4" + "P-poll__networl_3_2_AI_5" + "P-poll__networl_3_2_AI_6" + "P-poll__networl_3_2_AI_7" + "P-poll__networl_3_2_AI_8" + "P-poll__networl_3_2_AnnP_0" + "P-poll__networl_3_2_AnnP_1" + "P-poll__networl_3_2_AnnP_2" + "P-poll__networl_3_2_AnnP_3" + "P-poll__networl_3_2_AnnP_4" + "P-poll__networl_3_2_AnnP_5" + "P-poll__networl_3_2_AnnP_6" + "P-poll__networl_3_2_AnnP_7" + "P-poll__networl_3_2_AnnP_8" + "P-poll__networl_3_2_RP_0" + "P-poll__networl_3_2_RP_1" + "P-poll__networl_3_2_RP_2" + "P-poll__networl_3_2_RP_3" + "P-poll__networl_3_2_RP_4" + "P-poll__networl_3_2_RP_5" + "P-poll__networl_3_2_RP_6" + "P-poll__networl_3_2_RP_7" + "P-poll__networl_3_2_RP_8" + "P-poll__networl_3_3_AskP_0" + "P-poll__networl_3_3_AskP_1" + "P-poll__networl_3_3_AskP_2" + "P-poll__networl_3_3_AskP_3" + "P-poll__networl_3_3_AskP_4" + "P-poll__networl_3_3_AskP_5" + "P-poll__networl_3_3_AskP_6" + "P-poll__networl_3_3_AskP_7" + "P-poll__networl_3_3_AskP_8" + "P-poll__networl_3_3_AnsP_0" + "P-poll__networl_3_3_AnsP_1" + "P-poll__networl_3_3_AnsP_2" + "P-poll__networl_3_3_AnsP_3" + "P-poll__networl_3_3_AnsP_4" + "P-poll__networl_3_3_AnsP_5" + "P-poll__networl_3_3_AnsP_6" + "P-poll__networl_3_3_AnsP_7" + "P-poll__networl_3_3_AnsP_8" + "P-poll__networl_3_3_RI_0" + "P-poll__networl_3_3_RI_1" + "P-poll__networl_3_3_RI_2" + "P-poll__networl_3_3_RI_3" + "P-poll__networl_3_3_RI_4" + "P-poll__networl_3_3_RI_5" + "P-poll__networl_3_3_RI_6" + "P-poll__networl_3_3_RI_7" + "P-poll__networl_3_3_RI_8" + "P-poll__networl_3_3_AI_0" + "P-poll__networl_3_3_AI_1" + "P-poll__networl_3_3_AI_2" + "P-poll__networl_3_3_AI_3" + "P-poll__networl_3_3_AI_4" + "P-poll__networl_3_3_AI_5" + "P-poll__networl_3_3_AI_6" + "P-poll__networl_3_3_AI_7" + "P-poll__networl_3_3_AI_8" + "P-poll__networl_3_3_AnnP_0" + "P-poll__networl_3_3_AnnP_1" + "P-poll__networl_3_3_AnnP_2" + "P-poll__networl_3_3_AnnP_3" + "P-poll__networl_3_3_AnnP_4" + "P-poll__networl_3_3_AnnP_5" + "P-poll__networl_3_3_AnnP_6" + "P-poll__networl_3_3_AnnP_7" + "P-poll__networl_3_3_AnnP_8" + "P-poll__networl_3_3_RP_0" + "P-poll__networl_3_3_RP_1" + "P-poll__networl_3_3_RP_2" + "P-poll__networl_3_3_RP_3" + "P-poll__networl_3_3_RP_4" + "P-poll__networl_3_3_RP_5" + "P-poll__networl_3_3_RP_6" + "P-poll__networl_3_3_RP_7" + "P-poll__networl_3_3_RP_8" + "P-poll__networl_3_4_AskP_0" + "P-poll__networl_3_4_AskP_1" + "P-poll__networl_3_4_AskP_2" + "P-poll__networl_3_4_AskP_3" + "P-poll__networl_3_4_AskP_4" + "P-poll__networl_3_4_AskP_5" + "P-poll__networl_3_4_AskP_6" + "P-poll__networl_3_4_AskP_7" + "P-poll__networl_3_4_AskP_8" + "P-poll__networl_3_4_AnsP_0" + "P-poll__networl_3_4_AnsP_1" + "P-poll__networl_3_4_AnsP_2" + "P-poll__networl_3_4_AnsP_3" + "P-poll__networl_3_4_AnsP_4" + "P-poll__networl_3_4_AnsP_5" + "P-poll__networl_3_4_AnsP_6" + "P-poll__networl_3_4_AnsP_7" + "P-poll__networl_3_4_AnsP_8" + "P-poll__networl_3_4_RI_0" + "P-poll__networl_3_4_RI_1" + "P-poll__networl_3_4_RI_2" + "P-poll__networl_3_4_RI_3" + "P-poll__networl_3_4_RI_4" + "P-poll__networl_3_4_RI_5" + "P-poll__networl_3_4_RI_6" + "P-poll__networl_3_4_RI_7" + "P-poll__networl_3_4_RI_8" + "P-poll__networl_3_4_AI_0" + "P-poll__networl_3_4_AI_1" + "P-poll__networl_3_4_AI_2" + "P-poll__networl_3_4_AI_3" + "P-poll__networl_3_4_AI_4" + "P-poll__networl_3_4_AI_5" + "P-poll__networl_3_4_AI_6" + "P-poll__networl_3_4_AI_7" + "P-poll__networl_3_4_AI_8" + "P-poll__networl_3_4_AnnP_0" + "P-poll__networl_3_4_AnnP_1" + "P-poll__networl_3_4_AnnP_2" + "P-poll__networl_3_4_AnnP_3" + "P-poll__networl_3_4_AnnP_4" + "P-poll__networl_3_4_AnnP_5" + "P-poll__networl_3_4_AnnP_6" + "P-poll__networl_3_4_AnnP_7" + "P-poll__networl_3_4_AnnP_8" + "P-poll__networl_3_4_RP_0" + "P-poll__networl_3_4_RP_1" + "P-poll__networl_3_4_RP_2" + "P-poll__networl_3_4_RP_3" + "P-poll__networl_3_4_RP_4" + "P-poll__networl_3_4_RP_5" + "P-poll__networl_3_4_RP_6" + "P-poll__networl_3_4_RP_7" + "P-poll__networl_3_4_RP_8" + "P-poll__networl_3_5_AskP_0" + "P-poll__networl_3_5_AskP_1" + "P-poll__networl_3_5_AskP_2" + "P-poll__networl_3_5_AskP_3" + "P-poll__networl_3_5_AskP_4" + "P-poll__networl_3_5_AskP_5" + "P-poll__networl_3_5_AskP_6" + "P-poll__networl_3_5_AskP_7" + "P-poll__networl_3_5_AskP_8" + "P-poll__networl_3_5_AnsP_0" + "P-poll__networl_3_5_AnsP_1" + "P-poll__networl_3_5_AnsP_2" + "P-poll__networl_3_5_AnsP_3" + "P-poll__networl_3_5_AnsP_4" + "P-poll__networl_3_5_AnsP_5" + "P-poll__networl_3_5_AnsP_6" + "P-poll__networl_3_5_AnsP_7" + "P-poll__networl_3_5_AnsP_8" + "P-poll__networl_3_5_RI_0" + "P-poll__networl_3_5_RI_1" + "P-poll__networl_3_5_RI_2" + "P-poll__networl_3_5_RI_3" + "P-poll__networl_3_5_RI_4" + "P-poll__networl_3_5_RI_5" + "P-poll__networl_3_5_RI_6" + "P-poll__networl_3_5_RI_7" + "P-poll__networl_3_5_RI_8" + "P-poll__networl_3_5_AI_0" + "P-poll__networl_3_5_AI_1" + "P-poll__networl_3_5_AI_2" + "P-poll__networl_3_5_AI_3" + "P-poll__networl_3_5_AI_4" + "P-poll__networl_3_5_AI_5" + "P-poll__networl_3_5_AI_6" + "P-poll__networl_3_5_AI_7" + "P-poll__networl_3_5_AI_8" + "P-poll__networl_3_5_AnnP_0" + "P-poll__networl_3_5_AnnP_1" + "P-poll__networl_3_5_AnnP_2" + "P-poll__networl_3_5_AnnP_3" + "P-poll__networl_3_5_AnnP_4" + "P-poll__networl_3_5_AnnP_5" + "P-poll__networl_3_5_AnnP_6" + "P-poll__networl_3_5_AnnP_7" + "P-poll__networl_3_5_AnnP_8" + "P-poll__networl_3_5_RP_0" + "P-poll__networl_3_5_RP_1" + "P-poll__networl_3_5_RP_2" + "P-poll__networl_3_5_RP_3" + "P-poll__networl_3_5_RP_4" + "P-poll__networl_3_5_RP_5" + "P-poll__networl_3_5_RP_6" + "P-poll__networl_3_5_RP_7" + "P-poll__networl_3_5_RP_8" + "P-poll__networl_3_6_AskP_0" + "P-poll__networl_3_6_AskP_1" + "P-poll__networl_3_6_AskP_2" + "P-poll__networl_3_6_AskP_3" + "P-poll__networl_3_6_AskP_4" + "P-poll__networl_3_6_AskP_5" + "P-poll__networl_3_6_AskP_6" + "P-poll__networl_3_6_AskP_7" + "P-poll__networl_3_6_AskP_8" + "P-poll__networl_3_6_AnsP_0" + "P-poll__networl_3_6_AnsP_1" + "P-poll__networl_3_6_AnsP_2" + "P-poll__networl_3_6_AnsP_3" + "P-poll__networl_3_6_AnsP_4" + "P-poll__networl_3_6_AnsP_5" + "P-poll__networl_3_6_AnsP_6" + "P-poll__networl_3_6_AnsP_7" + "P-poll__networl_3_6_AnsP_8" + "P-poll__networl_3_6_RI_0" + "P-poll__networl_3_6_RI_1" + "P-poll__networl_3_6_RI_2" + "P-poll__networl_3_6_RI_3" + "P-poll__networl_3_6_RI_4" + "P-poll__networl_3_6_RI_5" + "P-poll__networl_3_6_RI_6" + "P-poll__networl_3_6_RI_7" + "P-poll__networl_3_6_RI_8" + "P-poll__networl_3_6_AI_0" + "P-poll__networl_3_6_AI_1" + "P-poll__networl_3_6_AI_2" + "P-poll__networl_3_6_AI_3" + "P-poll__networl_3_6_AI_4" + "P-poll__networl_3_6_AI_5" + "P-poll__networl_3_6_AI_6" + "P-poll__networl_3_6_AI_7" + "P-poll__networl_3_6_AI_8" + "P-poll__networl_3_6_AnnP_0" + "P-poll__networl_3_6_AnnP_1" + "P-poll__networl_3_6_AnnP_2" + "P-poll__networl_3_6_AnnP_3" + "P-poll__networl_3_6_AnnP_4" + "P-poll__networl_3_6_AnnP_5" + "P-poll__networl_3_6_AnnP_6" + "P-poll__networl_3_6_AnnP_7" + "P-poll__networl_3_6_AnnP_8" + "P-poll__networl_3_6_RP_0" + "P-poll__networl_3_6_RP_1" + "P-poll__networl_3_6_RP_2" + "P-poll__networl_3_6_RP_3" + "P-poll__networl_3_6_RP_4" + "P-poll__networl_3_6_RP_5" + "P-poll__networl_3_6_RP_6" + "P-poll__networl_3_6_RP_7" + "P-poll__networl_3_6_RP_8" + "P-poll__networl_3_7_AskP_0" + "P-poll__networl_3_7_AskP_1" + "P-poll__networl_3_7_AskP_2" + "P-poll__networl_3_7_AskP_3" + "P-poll__networl_3_7_AskP_4" + "P-poll__networl_3_7_AskP_5" + "P-poll__networl_3_7_AskP_6" + "P-poll__networl_3_7_AskP_7" + "P-poll__networl_3_7_AskP_8" + "P-poll__networl_3_7_AnsP_0" + "P-poll__networl_3_7_AnsP_1" + "P-poll__networl_3_7_AnsP_2" + "P-poll__networl_3_7_AnsP_3" + "P-poll__networl_3_7_AnsP_4" + "P-poll__networl_3_7_AnsP_5" + "P-poll__networl_3_7_AnsP_6" + "P-poll__networl_3_7_AnsP_7" + "P-poll__networl_3_7_AnsP_8" + "P-poll__networl_3_7_RI_0" + "P-poll__networl_3_7_RI_1" + "P-poll__networl_3_7_RI_2" + "P-poll__networl_3_7_RI_3" + "P-poll__networl_3_7_RI_4" + "P-poll__networl_3_7_RI_5" + "P-poll__networl_3_7_RI_6" + "P-poll__networl_3_7_RI_7" + "P-poll__networl_3_7_RI_8" + "P-poll__networl_3_7_AI_0" + "P-poll__networl_3_7_AI_1" + "P-poll__networl_3_7_AI_2" + "P-poll__networl_3_7_AI_3" + "P-poll__networl_3_7_AI_4" + "P-poll__networl_3_7_AI_5" + "P-poll__networl_3_7_AI_6" + "P-poll__networl_3_7_AI_7" + "P-poll__networl_3_7_AI_8" + "P-poll__networl_3_7_AnnP_0" + "P-poll__networl_3_7_AnnP_1" + "P-poll__networl_3_7_AnnP_2" + "P-poll__networl_3_7_AnnP_3" + "P-poll__networl_3_7_AnnP_4" + "P-poll__networl_3_7_AnnP_5" + "P-poll__networl_3_7_AnnP_6" + "P-poll__networl_3_7_AnnP_7" + "P-poll__networl_3_7_AnnP_8" + "P-poll__networl_3_7_RP_0" + "P-poll__networl_3_7_RP_1" + "P-poll__networl_3_7_RP_2" + "P-poll__networl_3_7_RP_3" + "P-poll__networl_3_7_RP_4" + "P-poll__networl_3_7_RP_5" + "P-poll__networl_3_7_RP_6" + "P-poll__networl_3_7_RP_7" + "P-poll__networl_3_7_RP_8" + "P-poll__networl_3_8_AskP_0" + "P-poll__networl_3_8_AskP_1" + "P-poll__networl_3_8_AskP_2" + "P-poll__networl_3_8_AskP_3" + "P-poll__networl_3_8_AskP_4" + "P-poll__networl_3_8_AskP_5" + "P-poll__networl_3_8_AskP_6" + "P-poll__networl_3_8_AskP_7" + "P-poll__networl_3_8_AskP_8" + "P-poll__networl_3_8_AnsP_0" + "P-poll__networl_3_8_AnsP_1" + "P-poll__networl_3_8_AnsP_2" + "P-poll__networl_3_8_AnsP_3" + "P-poll__networl_3_8_AnsP_4" + "P-poll__networl_3_8_AnsP_5" + "P-poll__networl_3_8_AnsP_6" + "P-poll__networl_3_8_AnsP_7" + "P-poll__networl_3_8_AnsP_8" + "P-poll__networl_3_8_RI_0" + "P-poll__networl_3_8_RI_1" + "P-poll__networl_3_8_RI_2" + "P-poll__networl_3_8_RI_3" + "P-poll__networl_3_8_RI_4" + "P-poll__networl_3_8_RI_5" + "P-poll__networl_3_8_RI_6" + "P-poll__networl_3_8_RI_7" + "P-poll__networl_3_8_RI_8" + "P-poll__networl_3_8_AI_0" + "P-poll__networl_3_8_AI_1" + "P-poll__networl_3_8_AI_2" + "P-poll__networl_3_8_AI_3" + "P-poll__networl_3_8_AI_4" + "P-poll__networl_3_8_AI_5" + "P-poll__networl_3_8_AI_6" + "P-poll__networl_3_8_AI_7" + "P-poll__networl_3_8_AI_8" + "P-poll__networl_3_8_AnnP_0" + "P-poll__networl_3_8_AnnP_1" + "P-poll__networl_3_8_AnnP_2" + "P-poll__networl_3_8_AnnP_3" + "P-poll__networl_3_8_AnnP_4" + "P-poll__networl_3_8_AnnP_5" + "P-poll__networl_3_8_AnnP_6" + "P-poll__networl_3_8_AnnP_7" + "P-poll__networl_3_8_AnnP_8" + "P-poll__networl_3_8_RP_0" + "P-poll__networl_3_8_RP_1" + "P-poll__networl_3_8_RP_2" + "P-poll__networl_3_8_RP_3" + "P-poll__networl_3_8_RP_4" + "P-poll__networl_3_8_RP_5" + "P-poll__networl_3_8_RP_6" + "P-poll__networl_3_8_RP_7" + "P-poll__networl_3_8_RP_8" + "P-poll__networl_4_0_AskP_0" + "P-poll__networl_4_0_AskP_1" + "P-poll__networl_4_0_AskP_2" + "P-poll__networl_4_0_AskP_3" + "P-poll__networl_4_0_AskP_4" + "P-poll__networl_4_0_AskP_5" + "P-poll__networl_4_0_AskP_6" + "P-poll__networl_4_0_AskP_7" + "P-poll__networl_4_0_AskP_8" + "P-poll__networl_4_0_AnsP_0" + "P-poll__networl_4_0_AnsP_1" + "P-poll__networl_4_0_AnsP_2" + "P-poll__networl_4_0_AnsP_3" + "P-poll__networl_4_0_AnsP_4" + "P-poll__networl_4_0_AnsP_5" + "P-poll__networl_4_0_AnsP_6" + "P-poll__networl_4_0_AnsP_7" + "P-poll__networl_4_0_AnsP_8" + "P-poll__networl_4_0_RI_0" + "P-poll__networl_4_0_RI_1" + "P-poll__networl_4_0_RI_2" + "P-poll__networl_4_0_RI_3" + "P-poll__networl_4_0_RI_4" + "P-poll__networl_4_0_RI_5" + "P-poll__networl_4_0_RI_6" + "P-poll__networl_4_0_RI_7" + "P-poll__networl_4_0_RI_8" + "P-poll__networl_4_0_AI_0" + "P-poll__networl_4_0_AI_1" + "P-poll__networl_4_0_AI_2" + "P-poll__networl_4_0_AI_3" + "P-poll__networl_4_0_AI_4" + "P-poll__networl_4_0_AI_5" + "P-poll__networl_4_0_AI_6" + "P-poll__networl_4_0_AI_7" + "P-poll__networl_4_0_AI_8" + "P-poll__networl_4_0_AnnP_0" + "P-poll__networl_4_0_AnnP_1" + "P-poll__networl_4_0_AnnP_2" + "P-poll__networl_4_0_AnnP_3" + "P-poll__networl_4_0_AnnP_4" + "P-poll__networl_4_0_AnnP_5" + "P-poll__networl_4_0_AnnP_6" + "P-poll__networl_4_0_AnnP_7" + "P-poll__networl_4_0_AnnP_8" + "P-poll__networl_4_0_RP_0" + "P-poll__networl_4_0_RP_1" + "P-poll__networl_4_0_RP_2" + "P-poll__networl_4_0_RP_3" + "P-poll__networl_4_0_RP_4" + "P-poll__networl_4_0_RP_5" + "P-poll__networl_4_0_RP_6" + "P-poll__networl_4_0_RP_7" + "P-poll__networl_4_0_RP_8" + "P-poll__networl_4_1_AskP_0" + "P-poll__networl_4_1_AskP_1" + "P-poll__networl_4_1_AskP_2" + "P-poll__networl_4_1_AskP_3" + "P-poll__networl_4_1_AskP_4" + "P-poll__networl_4_1_AskP_5" + "P-poll__networl_4_1_AskP_6" + "P-poll__networl_4_1_AskP_7" + "P-poll__networl_4_1_AskP_8" + "P-poll__networl_4_1_AnsP_0" + "P-poll__networl_4_1_AnsP_1" + "P-poll__networl_4_1_AnsP_2" + "P-poll__networl_4_1_AnsP_3" + "P-poll__networl_4_1_AnsP_4" + "P-poll__networl_4_1_AnsP_5" + "P-poll__networl_4_1_AnsP_6" + "P-poll__networl_4_1_AnsP_7" + "P-poll__networl_4_1_AnsP_8" + "P-poll__networl_4_1_RI_0" + "P-poll__networl_4_1_RI_1" + "P-poll__networl_4_1_RI_2" + "P-poll__networl_4_1_RI_3" + "P-poll__networl_4_1_RI_4" + "P-poll__networl_4_1_RI_5" + "P-poll__networl_4_1_RI_6" + "P-poll__networl_4_1_RI_7" + "P-poll__networl_4_1_RI_8" + "P-poll__networl_4_1_AI_0" + "P-poll__networl_4_1_AI_1" + "P-poll__networl_4_1_AI_2" + "P-poll__networl_4_1_AI_3" + "P-poll__networl_4_1_AI_4" + "P-poll__networl_4_1_AI_5" + "P-poll__networl_4_1_AI_6" + "P-poll__networl_4_1_AI_7" + "P-poll__networl_4_1_AI_8" + "P-poll__networl_4_1_AnnP_0" + "P-poll__networl_4_1_AnnP_1" + "P-poll__networl_4_1_AnnP_2" + "P-poll__networl_4_1_AnnP_3" + "P-poll__networl_4_1_AnnP_4" + "P-poll__networl_4_1_AnnP_5" + "P-poll__networl_4_1_AnnP_6" + "P-poll__networl_4_1_AnnP_7" + "P-poll__networl_4_1_AnnP_8" + "P-poll__networl_4_1_RP_0" + "P-poll__networl_4_1_RP_1" + "P-poll__networl_4_1_RP_2" + "P-poll__networl_4_1_RP_3" + "P-poll__networl_4_1_RP_4" + "P-poll__networl_4_1_RP_5" + "P-poll__networl_4_1_RP_6" + "P-poll__networl_4_1_RP_7" + "P-poll__networl_4_1_RP_8" + "P-poll__networl_4_2_AskP_0" + "P-poll__networl_4_2_AskP_1" + "P-poll__networl_4_2_AskP_2" + "P-poll__networl_4_2_AskP_3" + "P-poll__networl_4_2_AskP_4" + "P-poll__networl_4_2_AskP_5" + "P-poll__networl_4_2_AskP_6" + "P-poll__networl_4_2_AskP_7" + "P-poll__networl_4_2_AskP_8" + "P-poll__networl_4_2_AnsP_0" + "P-poll__networl_4_2_AnsP_1" + "P-poll__networl_4_2_AnsP_2" + "P-poll__networl_4_2_AnsP_3" + "P-poll__networl_4_2_AnsP_4" + "P-poll__networl_4_2_AnsP_5" + "P-poll__networl_4_2_AnsP_6" + "P-poll__networl_4_2_AnsP_7" + "P-poll__networl_4_2_AnsP_8" + "P-poll__networl_4_2_RI_0" + "P-poll__networl_4_2_RI_1" + "P-poll__networl_4_2_RI_2" + "P-poll__networl_4_2_RI_3" + "P-poll__networl_4_2_RI_4" + "P-poll__networl_4_2_RI_5" + "P-poll__networl_4_2_RI_6" + "P-poll__networl_4_2_RI_7" + "P-poll__networl_4_2_RI_8" + "P-poll__networl_4_2_AI_0" + "P-poll__networl_4_2_AI_1" + "P-poll__networl_4_2_AI_2" + "P-poll__networl_4_2_AI_3" + "P-poll__networl_4_2_AI_4" + "P-poll__networl_4_2_AI_5" + "P-poll__networl_4_2_AI_6" + "P-poll__networl_4_2_AI_7" + "P-poll__networl_4_2_AI_8" + "P-poll__networl_4_2_AnnP_0" + "P-poll__networl_4_2_AnnP_1" + "P-poll__networl_4_2_AnnP_2" + "P-poll__networl_4_2_AnnP_3" + "P-poll__networl_4_2_AnnP_4" + "P-poll__networl_4_2_AnnP_5" + "P-poll__networl_4_2_AnnP_6" + "P-poll__networl_4_2_AnnP_7" + "P-poll__networl_4_2_AnnP_8" + "P-poll__networl_4_2_RP_0" + "P-poll__networl_4_2_RP_1" + "P-poll__networl_4_2_RP_2" + "P-poll__networl_4_2_RP_3" + "P-poll__networl_4_2_RP_4" + "P-poll__networl_4_2_RP_5" + "P-poll__networl_4_2_RP_6" + "P-poll__networl_4_2_RP_7" + "P-poll__networl_4_2_RP_8" + "P-poll__networl_4_3_AskP_0" + "P-poll__networl_4_3_AskP_1" + "P-poll__networl_4_3_AskP_2" + "P-poll__networl_4_3_AskP_3" + "P-poll__networl_4_3_AskP_4" + "P-poll__networl_4_3_AskP_5" + "P-poll__networl_4_3_AskP_6" + "P-poll__networl_4_3_AskP_7" + "P-poll__networl_4_3_AskP_8" + "P-poll__networl_4_3_AnsP_0" + "P-poll__networl_4_3_AnsP_1" + "P-poll__networl_4_3_AnsP_2" + "P-poll__networl_4_3_AnsP_3" + "P-poll__networl_4_3_AnsP_4" + "P-poll__networl_4_3_AnsP_5" + "P-poll__networl_4_3_AnsP_6" + "P-poll__networl_4_3_AnsP_7" + "P-poll__networl_4_3_AnsP_8" + "P-poll__networl_4_3_RI_0" + "P-poll__networl_4_3_RI_1" + "P-poll__networl_4_3_RI_2" + "P-poll__networl_4_3_RI_3" + "P-poll__networl_4_3_RI_4" + "P-poll__networl_4_3_RI_5" + "P-poll__networl_4_3_RI_6" + "P-poll__networl_4_3_RI_7" + "P-poll__networl_4_3_RI_8" + "P-poll__networl_4_3_AI_0" + "P-poll__networl_4_3_AI_1" + "P-poll__networl_4_3_AI_2" + "P-poll__networl_4_3_AI_3" + "P-poll__networl_4_3_AI_4" + "P-poll__networl_4_3_AI_5" + "P-poll__networl_4_3_AI_6" + "P-poll__networl_4_3_AI_7" + "P-poll__networl_4_3_AI_8" + "P-poll__networl_4_3_AnnP_0" + "P-poll__networl_4_3_AnnP_1" + "P-poll__networl_4_3_AnnP_2" + "P-poll__networl_4_3_AnnP_3" + "P-poll__networl_4_3_AnnP_4" + "P-poll__networl_4_3_AnnP_5" + "P-poll__networl_4_3_AnnP_6" + "P-poll__networl_4_3_AnnP_7" + "P-poll__networl_4_3_AnnP_8" + "P-poll__networl_4_3_RP_0" + "P-poll__networl_4_3_RP_1" + "P-poll__networl_4_3_RP_2" + "P-poll__networl_4_3_RP_3" + "P-poll__networl_4_3_RP_4" + "P-poll__networl_4_3_RP_5" + "P-poll__networl_4_3_RP_6" + "P-poll__networl_4_3_RP_7" + "P-poll__networl_4_3_RP_8" + "P-poll__networl_4_4_AskP_0" + "P-poll__networl_4_4_AskP_1" + "P-poll__networl_4_4_AskP_2" + "P-poll__networl_4_4_AskP_3" + "P-poll__networl_4_4_AskP_4" + "P-poll__networl_4_4_AskP_5" + "P-poll__networl_4_4_AskP_6" + "P-poll__networl_4_4_AskP_7" + "P-poll__networl_4_4_AskP_8" + "P-poll__networl_4_4_AnsP_0" + "P-poll__networl_4_4_AnsP_1" + "P-poll__networl_4_4_AnsP_2" + "P-poll__networl_4_4_AnsP_3" + "P-poll__networl_4_4_AnsP_4" + "P-poll__networl_4_4_AnsP_5" + "P-poll__networl_4_4_AnsP_6" + "P-poll__networl_4_4_AnsP_7" + "P-poll__networl_4_4_AnsP_8" + "P-poll__networl_4_4_RI_0" + "P-poll__networl_4_4_RI_1" + "P-poll__networl_4_4_RI_2" + "P-poll__networl_4_4_RI_3" + "P-poll__networl_4_4_RI_4" + "P-poll__networl_4_4_RI_5" + "P-poll__networl_4_4_RI_6" + "P-poll__networl_4_4_RI_7" + "P-poll__networl_4_4_RI_8" + "P-poll__networl_4_4_AI_0" + "P-poll__networl_4_4_AI_1" + "P-poll__networl_4_4_AI_2" + "P-poll__networl_4_4_AI_3" + "P-poll__networl_4_4_AI_4" + "P-poll__networl_4_4_AI_5" + "P-poll__networl_4_4_AI_6" + "P-poll__networl_4_4_AI_7" + "P-poll__networl_4_4_AI_8" + "P-poll__networl_4_4_AnnP_0" + "P-poll__networl_4_4_AnnP_1" + "P-poll__networl_4_4_AnnP_2" + "P-poll__networl_4_4_AnnP_3" + "P-poll__networl_4_4_AnnP_4" + "P-poll__networl_4_4_AnnP_5" + "P-poll__networl_4_4_AnnP_6" + "P-poll__networl_4_4_AnnP_7" + "P-poll__networl_4_4_AnnP_8" + "P-poll__networl_4_4_RP_0" + "P-poll__networl_4_4_RP_1" + "P-poll__networl_4_4_RP_2" + "P-poll__networl_4_4_RP_3" + "P-poll__networl_4_4_RP_4" + "P-poll__networl_4_4_RP_5" + "P-poll__networl_4_4_RP_6" + "P-poll__networl_4_4_RP_7" + "P-poll__networl_4_4_RP_8" + "P-poll__networl_4_5_AskP_0" + "P-poll__networl_4_5_AskP_1" + "P-poll__networl_4_5_AskP_2" + "P-poll__networl_4_5_AskP_3" + "P-poll__networl_4_5_AskP_4" + "P-poll__networl_4_5_AskP_5" + "P-poll__networl_4_5_AskP_6" + "P-poll__networl_4_5_AskP_7" + "P-poll__networl_4_5_AskP_8" + "P-poll__networl_4_5_AnsP_0" + "P-poll__networl_4_5_AnsP_1" + "P-poll__networl_4_5_AnsP_2" + "P-poll__networl_4_5_AnsP_3" + "P-poll__networl_4_5_AnsP_4" + "P-poll__networl_4_5_AnsP_5" + "P-poll__networl_4_5_AnsP_6" + "P-poll__networl_4_5_AnsP_7" + "P-poll__networl_4_5_AnsP_8" + "P-poll__networl_4_5_RI_0" + "P-poll__networl_4_5_RI_1" + "P-poll__networl_4_5_RI_2" + "P-poll__networl_4_5_RI_3" + "P-poll__networl_4_5_RI_4" + "P-poll__networl_4_5_RI_5" + "P-poll__networl_4_5_RI_6" + "P-poll__networl_4_5_RI_7" + "P-poll__networl_4_5_RI_8" + "P-poll__networl_4_5_AI_0" + "P-poll__networl_4_5_AI_1" + "P-poll__networl_4_5_AI_2" + "P-poll__networl_4_5_AI_3" + "P-poll__networl_4_5_AI_4" + "P-poll__networl_4_5_AI_5" + "P-poll__networl_4_5_AI_6" + "P-poll__networl_4_5_AI_7" + "P-poll__networl_4_5_AI_8" + "P-poll__networl_4_5_AnnP_0" + "P-poll__networl_4_5_AnnP_1" + "P-poll__networl_4_5_AnnP_2" + "P-poll__networl_4_5_AnnP_3" + "P-poll__networl_4_5_AnnP_4" + "P-poll__networl_4_5_AnnP_5" + "P-poll__networl_4_5_AnnP_6" + "P-poll__networl_4_5_AnnP_7" + "P-poll__networl_4_5_AnnP_8" + "P-poll__networl_4_5_RP_0" + "P-poll__networl_4_5_RP_1" + "P-poll__networl_4_5_RP_2" + "P-poll__networl_4_5_RP_3" + "P-poll__networl_4_5_RP_4" + "P-poll__networl_4_5_RP_5" + "P-poll__networl_4_5_RP_6" + "P-poll__networl_4_5_RP_7" + "P-poll__networl_4_5_RP_8" + "P-poll__networl_4_6_AskP_0" + "P-poll__networl_4_6_AskP_1" + "P-poll__networl_4_6_AskP_2" + "P-poll__networl_4_6_AskP_3" + "P-poll__networl_4_6_AskP_4" + "P-poll__networl_4_6_AskP_5" + "P-poll__networl_4_6_AskP_6" + "P-poll__networl_4_6_AskP_7" + "P-poll__networl_4_6_AskP_8" + "P-poll__networl_4_6_AnsP_0" + "P-poll__networl_4_6_AnsP_1" + "P-poll__networl_4_6_AnsP_2" + "P-poll__networl_4_6_AnsP_3" + "P-poll__networl_4_6_AnsP_4" + "P-poll__networl_4_6_AnsP_5" + "P-poll__networl_4_6_AnsP_6" + "P-poll__networl_4_6_AnsP_7" + "P-poll__networl_4_6_AnsP_8" + "P-poll__networl_4_6_RI_0" + "P-poll__networl_4_6_RI_1" + "P-poll__networl_4_6_RI_2" + "P-poll__networl_4_6_RI_3" + "P-poll__networl_4_6_RI_4" + "P-poll__networl_4_6_RI_5" + "P-poll__networl_4_6_RI_6" + "P-poll__networl_4_6_RI_7" + "P-poll__networl_4_6_RI_8" + "P-poll__networl_4_6_AI_0" + "P-poll__networl_4_6_AI_1" + "P-poll__networl_4_6_AI_2" + "P-poll__networl_4_6_AI_3" + "P-poll__networl_4_6_AI_4" + "P-poll__networl_4_6_AI_5" + "P-poll__networl_4_6_AI_6" + "P-poll__networl_4_6_AI_7" + "P-poll__networl_4_6_AI_8" + "P-poll__networl_4_6_AnnP_0" + "P-poll__networl_4_6_AnnP_1" + "P-poll__networl_4_6_AnnP_2" + "P-poll__networl_4_6_AnnP_3" + "P-poll__networl_4_6_AnnP_4" + "P-poll__networl_4_6_AnnP_5" + "P-poll__networl_4_6_AnnP_6" + "P-poll__networl_4_6_AnnP_7" + "P-poll__networl_4_6_AnnP_8" + "P-poll__networl_4_6_RP_0" + "P-poll__networl_4_6_RP_1" + "P-poll__networl_4_6_RP_2" + "P-poll__networl_4_6_RP_3" + "P-poll__networl_4_6_RP_4" + "P-poll__networl_4_6_RP_5" + "P-poll__networl_4_6_RP_6" + "P-poll__networl_4_6_RP_7" + "P-poll__networl_4_6_RP_8" + "P-poll__networl_4_7_AskP_0" + "P-poll__networl_4_7_AskP_1" + "P-poll__networl_4_7_AskP_2" + "P-poll__networl_4_7_AskP_3" + "P-poll__networl_4_7_AskP_4" + "P-poll__networl_4_7_AskP_5" + "P-poll__networl_4_7_AskP_6" + "P-poll__networl_4_7_AskP_7" + "P-poll__networl_4_7_AskP_8" + "P-poll__networl_4_7_AnsP_0" + "P-poll__networl_4_7_AnsP_1" + "P-poll__networl_4_7_AnsP_2" + "P-poll__networl_4_7_AnsP_3" + "P-poll__networl_4_7_AnsP_4" + "P-poll__networl_4_7_AnsP_5" + "P-poll__networl_4_7_AnsP_6" + "P-poll__networl_4_7_AnsP_7" + "P-poll__networl_4_7_AnsP_8" + "P-poll__networl_4_7_RI_0" + "P-poll__networl_4_7_RI_1" + "P-poll__networl_4_7_RI_2" + "P-poll__networl_4_7_RI_3" + "P-poll__networl_4_7_RI_4" + "P-poll__networl_4_7_RI_5" + "P-poll__networl_4_7_RI_6" + "P-poll__networl_4_7_RI_7" + "P-poll__networl_4_7_RI_8" + "P-poll__networl_4_7_AI_0" + "P-poll__networl_4_7_AI_1" + "P-poll__networl_4_7_AI_2" + "P-poll__networl_4_7_AI_3" + "P-poll__networl_4_7_AI_4" + "P-poll__networl_4_7_AI_5" + "P-poll__networl_4_7_AI_6" + "P-poll__networl_4_7_AI_7" + "P-poll__networl_4_7_AI_8" + "P-poll__networl_4_7_AnnP_0" + "P-poll__networl_4_7_AnnP_1" + "P-poll__networl_4_7_AnnP_2" + "P-poll__networl_4_7_AnnP_3" + "P-poll__networl_4_7_AnnP_4" + "P-poll__networl_4_7_AnnP_5" + "P-poll__networl_4_7_AnnP_6" + "P-poll__networl_4_7_AnnP_7" + "P-poll__networl_4_7_AnnP_8" + "P-poll__networl_4_7_RP_0" + "P-poll__networl_4_7_RP_1" + "P-poll__networl_4_7_RP_2" + "P-poll__networl_4_7_RP_3" + "P-poll__networl_4_7_RP_4" + "P-poll__networl_4_7_RP_5" + "P-poll__networl_4_7_RP_6" + "P-poll__networl_4_7_RP_7" + "P-poll__networl_4_7_RP_8" + "P-poll__networl_4_8_AskP_0" + "P-poll__networl_4_8_AskP_1" + "P-poll__networl_4_8_AskP_2" + "P-poll__networl_4_8_AskP_3" + "P-poll__networl_4_8_AskP_4" + "P-poll__networl_4_8_AskP_5" + "P-poll__networl_4_8_AskP_6" + "P-poll__networl_4_8_AskP_7" + "P-poll__networl_4_8_AskP_8" + "P-poll__networl_4_8_AnsP_0" + "P-poll__networl_4_8_AnsP_1" + "P-poll__networl_4_8_AnsP_2" + "P-poll__networl_4_8_AnsP_3" + "P-poll__networl_4_8_AnsP_4" + "P-poll__networl_4_8_AnsP_5" + "P-poll__networl_4_8_AnsP_6" + "P-poll__networl_4_8_AnsP_7" + "P-poll__networl_4_8_AnsP_8" + "P-poll__networl_4_8_RI_0" + "P-poll__networl_4_8_RI_1" + "P-poll__networl_4_8_RI_2" + "P-poll__networl_4_8_RI_3" + "P-poll__networl_4_8_RI_4" + "P-poll__networl_4_8_RI_5" + "P-poll__networl_4_8_RI_6" + "P-poll__networl_4_8_RI_7" + "P-poll__networl_4_8_RI_8" + "P-poll__networl_4_8_AI_0" + "P-poll__networl_4_8_AI_1" + "P-poll__networl_4_8_AI_2" + "P-poll__networl_4_8_AI_3" + "P-poll__networl_4_8_AI_4" + "P-poll__networl_4_8_AI_5" + "P-poll__networl_4_8_AI_6" + "P-poll__networl_4_8_AI_7" + "P-poll__networl_4_8_AI_8" + "P-poll__networl_4_8_AnnP_0" + "P-poll__networl_4_8_AnnP_1" + "P-poll__networl_4_8_AnnP_2" + "P-poll__networl_4_8_AnnP_3" + "P-poll__networl_4_8_AnnP_4" + "P-poll__networl_4_8_AnnP_5" + "P-poll__networl_4_8_AnnP_6" + "P-poll__networl_4_8_AnnP_7" + "P-poll__networl_4_8_AnnP_8" + "P-poll__networl_4_8_RP_0" + "P-poll__networl_4_8_RP_1" + "P-poll__networl_4_8_RP_2" + "P-poll__networl_4_8_RP_3" + "P-poll__networl_4_8_RP_4" + "P-poll__networl_4_8_RP_5" + "P-poll__networl_4_8_RP_6" + "P-poll__networl_4_8_RP_7" + "P-poll__networl_4_8_RP_8" + "P-poll__networl_5_0_AskP_0" + "P-poll__networl_5_0_AskP_1" + "P-poll__networl_5_0_AskP_2" + "P-poll__networl_5_0_AskP_3" + "P-poll__networl_5_0_AskP_4" + "P-poll__networl_5_0_AskP_5" + "P-poll__networl_5_0_AskP_6" + "P-poll__networl_5_0_AskP_7" + "P-poll__networl_5_0_AskP_8" + "P-poll__networl_5_0_AnsP_0" + "P-poll__networl_5_0_AnsP_1" + "P-poll__networl_5_0_AnsP_2" + "P-poll__networl_5_0_AnsP_3" + "P-poll__networl_5_0_AnsP_4" + "P-poll__networl_5_0_AnsP_5" + "P-poll__networl_5_0_AnsP_6" + "P-poll__networl_5_0_AnsP_7" + "P-poll__networl_5_0_AnsP_8" + "P-poll__networl_5_0_RI_0" + "P-poll__networl_5_0_RI_1" + "P-poll__networl_5_0_RI_2" + "P-poll__networl_5_0_RI_3" + "P-poll__networl_5_0_RI_4" + "P-poll__networl_5_0_RI_5" + "P-poll__networl_5_0_RI_6" + "P-poll__networl_5_0_RI_7" + "P-poll__networl_5_0_RI_8" + "P-poll__networl_5_0_AI_0" + "P-poll__networl_5_0_AI_1" + "P-poll__networl_5_0_AI_2" + "P-poll__networl_5_0_AI_3" + "P-poll__networl_5_0_AI_4" + "P-poll__networl_5_0_AI_5" + "P-poll__networl_5_0_AI_6" + "P-poll__networl_5_0_AI_7" + "P-poll__networl_5_0_AI_8" + "P-poll__networl_5_0_AnnP_0" + "P-poll__networl_5_0_AnnP_1" + "P-poll__networl_5_0_AnnP_2" + "P-poll__networl_5_0_AnnP_3" + "P-poll__networl_5_0_AnnP_4" + "P-poll__networl_5_0_AnnP_5" + "P-poll__networl_5_0_AnnP_6" + "P-poll__networl_5_0_AnnP_7" + "P-poll__networl_5_0_AnnP_8" + "P-poll__networl_5_0_RP_0" + "P-poll__networl_5_0_RP_1" + "P-poll__networl_5_0_RP_2" + "P-poll__networl_5_0_RP_3" + "P-poll__networl_5_0_RP_4" + "P-poll__networl_5_0_RP_5" + "P-poll__networl_5_0_RP_6" + "P-poll__networl_5_0_RP_7" + "P-poll__networl_5_0_RP_8" + "P-poll__networl_5_1_AskP_0" + "P-poll__networl_5_1_AskP_1" + "P-poll__networl_5_1_AskP_2" + "P-poll__networl_5_1_AskP_3" + "P-poll__networl_5_1_AskP_4" + "P-poll__networl_5_1_AskP_5" + "P-poll__networl_5_1_AskP_6" + "P-poll__networl_5_1_AskP_7" + "P-poll__networl_5_1_AskP_8" + "P-poll__networl_5_1_AnsP_0" + "P-poll__networl_5_1_AnsP_1" + "P-poll__networl_5_1_AnsP_2" + "P-poll__networl_5_1_AnsP_3" + "P-poll__networl_5_1_AnsP_4" + "P-poll__networl_5_1_AnsP_5" + "P-poll__networl_5_1_AnsP_6" + "P-poll__networl_5_1_AnsP_7" + "P-poll__networl_5_1_AnsP_8" + "P-poll__networl_5_1_RI_0" + "P-poll__networl_5_1_RI_1" + "P-poll__networl_5_1_RI_2" + "P-poll__networl_5_1_RI_3" + "P-poll__networl_5_1_RI_4" + "P-poll__networl_5_1_RI_5" + "P-poll__networl_5_1_RI_6" + "P-poll__networl_5_1_RI_7" + "P-poll__networl_5_1_RI_8" + "P-poll__networl_5_1_AI_0" + "P-poll__networl_5_1_AI_1" + "P-poll__networl_5_1_AI_2" + "P-poll__networl_5_1_AI_3" + "P-poll__networl_5_1_AI_4" + "P-poll__networl_5_1_AI_5" + "P-poll__networl_5_1_AI_6" + "P-poll__networl_5_1_AI_7" + "P-poll__networl_5_1_AI_8" + "P-poll__networl_5_1_AnnP_0" + "P-poll__networl_5_1_AnnP_1" + "P-poll__networl_5_1_AnnP_2" + "P-poll__networl_5_1_AnnP_3" + "P-poll__networl_5_1_AnnP_4" + "P-poll__networl_5_1_AnnP_5" + "P-poll__networl_5_1_AnnP_6" + "P-poll__networl_5_1_AnnP_7" + "P-poll__networl_5_1_AnnP_8" + "P-poll__networl_5_1_RP_0" + "P-poll__networl_5_1_RP_1" + "P-poll__networl_5_1_RP_2" + "P-poll__networl_5_1_RP_3" + "P-poll__networl_5_1_RP_4" + "P-poll__networl_5_1_RP_5" + "P-poll__networl_5_1_RP_6" + "P-poll__networl_5_1_RP_7" + "P-poll__networl_5_1_RP_8" + "P-poll__networl_5_2_AskP_0" + "P-poll__networl_5_2_AskP_1" + "P-poll__networl_5_2_AskP_2" + "P-poll__networl_5_2_AskP_3" + "P-poll__networl_5_2_AskP_4" + "P-poll__networl_5_2_AskP_5" + "P-poll__networl_5_2_AskP_6" + "P-poll__networl_5_2_AskP_7" + "P-poll__networl_5_2_AskP_8" + "P-poll__networl_5_2_AnsP_0" + "P-poll__networl_5_2_AnsP_1" + "P-poll__networl_5_2_AnsP_2" + "P-poll__networl_5_2_AnsP_3" + "P-poll__networl_5_2_AnsP_4" + "P-poll__networl_5_2_AnsP_5" + "P-poll__networl_5_2_AnsP_6" + "P-poll__networl_5_2_AnsP_7" + "P-poll__networl_5_2_AnsP_8" + "P-poll__networl_5_2_RI_0" + "P-poll__networl_5_2_RI_1" + "P-poll__networl_5_2_RI_2" + "P-poll__networl_5_2_RI_3" + "P-poll__networl_5_2_RI_4" + "P-poll__networl_5_2_RI_5" + "P-poll__networl_5_2_RI_6" + "P-poll__networl_5_2_RI_7" + "P-poll__networl_5_2_RI_8" + "P-poll__networl_5_2_AI_0" + "P-poll__networl_5_2_AI_1" + "P-poll__networl_5_2_AI_2" + "P-poll__networl_5_2_AI_3" + "P-poll__networl_5_2_AI_4" + "P-poll__networl_5_2_AI_5" + "P-poll__networl_5_2_AI_6" + "P-poll__networl_5_2_AI_7" + "P-poll__networl_5_2_AI_8" + "P-poll__networl_5_2_AnnP_0" + "P-poll__networl_5_2_AnnP_1" + "P-poll__networl_5_2_AnnP_2" + "P-poll__networl_5_2_AnnP_3" + "P-poll__networl_5_2_AnnP_4" + "P-poll__networl_5_2_AnnP_5" + "P-poll__networl_5_2_AnnP_6" + "P-poll__networl_5_2_AnnP_7" + "P-poll__networl_5_2_AnnP_8" + "P-poll__networl_5_2_RP_0" + "P-poll__networl_5_2_RP_1" + "P-poll__networl_5_2_RP_2" + "P-poll__networl_5_2_RP_3" + "P-poll__networl_5_2_RP_4" + "P-poll__networl_5_2_RP_5" + "P-poll__networl_5_2_RP_6" + "P-poll__networl_5_2_RP_7" + "P-poll__networl_5_2_RP_8" + "P-poll__networl_5_3_AskP_0" + "P-poll__networl_5_3_AskP_1" + "P-poll__networl_5_3_AskP_2" + "P-poll__networl_5_3_AskP_3" + "P-poll__networl_5_3_AskP_4" + "P-poll__networl_5_3_AskP_5" + "P-poll__networl_5_3_AskP_6" + "P-poll__networl_5_3_AskP_7" + "P-poll__networl_5_3_AskP_8" + "P-poll__networl_5_3_AnsP_0" + "P-poll__networl_5_3_AnsP_1" + "P-poll__networl_5_3_AnsP_2" + "P-poll__networl_5_3_AnsP_3" + "P-poll__networl_5_3_AnsP_4" + "P-poll__networl_5_3_AnsP_5" + "P-poll__networl_5_3_AnsP_6" + "P-poll__networl_5_3_AnsP_7" + "P-poll__networl_5_3_AnsP_8" + "P-poll__networl_5_3_RI_0" + "P-poll__networl_5_3_RI_1" + "P-poll__networl_5_3_RI_2" + "P-poll__networl_5_3_RI_3" + "P-poll__networl_5_3_RI_4" + "P-poll__networl_5_3_RI_5" + "P-poll__networl_5_3_RI_6" + "P-poll__networl_5_3_RI_7" + "P-poll__networl_5_3_RI_8" + "P-poll__networl_5_3_AI_0" + "P-poll__networl_5_3_AI_1" + "P-poll__networl_5_3_AI_2" + "P-poll__networl_5_3_AI_3" + "P-poll__networl_5_3_AI_4" + "P-poll__networl_5_3_AI_5" + "P-poll__networl_5_3_AI_6" + "P-poll__networl_5_3_AI_7" + "P-poll__networl_5_3_AI_8" + "P-poll__networl_5_3_AnnP_0" + "P-poll__networl_5_3_AnnP_1" + "P-poll__networl_5_3_AnnP_2" + "P-poll__networl_5_3_AnnP_3" + "P-poll__networl_5_3_AnnP_4" + "P-poll__networl_5_3_AnnP_5" + "P-poll__networl_5_3_AnnP_6" + "P-poll__networl_5_3_AnnP_7" + "P-poll__networl_5_3_AnnP_8" + "P-poll__networl_5_3_RP_0" + "P-poll__networl_5_3_RP_1" + "P-poll__networl_5_3_RP_2" + "P-poll__networl_5_3_RP_3" + "P-poll__networl_5_3_RP_4" + "P-poll__networl_5_3_RP_5" + "P-poll__networl_5_3_RP_6" + "P-poll__networl_5_3_RP_7" + "P-poll__networl_5_3_RP_8" + "P-poll__networl_5_4_AskP_0" + "P-poll__networl_5_4_AskP_1" + "P-poll__networl_5_4_AskP_2" + "P-poll__networl_5_4_AskP_3" + "P-poll__networl_5_4_AskP_4" + "P-poll__networl_5_4_AskP_5" + "P-poll__networl_5_4_AskP_6" + "P-poll__networl_5_4_AskP_7" + "P-poll__networl_5_4_AskP_8" + "P-poll__networl_5_4_AnsP_0" + "P-poll__networl_5_4_AnsP_1" + "P-poll__networl_5_4_AnsP_2" + "P-poll__networl_5_4_AnsP_3" + "P-poll__networl_5_4_AnsP_4" + "P-poll__networl_5_4_AnsP_5" + "P-poll__networl_5_4_AnsP_6" + "P-poll__networl_5_4_AnsP_7" + "P-poll__networl_5_4_AnsP_8" + "P-poll__networl_5_4_RI_0" + "P-poll__networl_5_4_RI_1" + "P-poll__networl_5_4_RI_2" + "P-poll__networl_5_4_RI_3" + "P-poll__networl_5_4_RI_4" + "P-poll__networl_5_4_RI_5" + "P-poll__networl_5_4_RI_6" + "P-poll__networl_5_4_RI_7" + "P-poll__networl_5_4_RI_8" + "P-poll__networl_5_4_AI_0" + "P-poll__networl_5_4_AI_1" + "P-poll__networl_5_4_AI_2" + "P-poll__networl_5_4_AI_3" + "P-poll__networl_5_4_AI_4" + "P-poll__networl_5_4_AI_5" + "P-poll__networl_5_4_AI_6" + "P-poll__networl_5_4_AI_7" + "P-poll__networl_5_4_AI_8" + "P-poll__networl_5_4_AnnP_0" + "P-poll__networl_5_4_AnnP_1" + "P-poll__networl_5_4_AnnP_2" + "P-poll__networl_5_4_AnnP_3" + "P-poll__networl_5_4_AnnP_4" + "P-poll__networl_5_4_AnnP_5" + "P-poll__networl_5_4_AnnP_6" + "P-poll__networl_5_4_AnnP_7" + "P-poll__networl_5_4_AnnP_8" + "P-poll__networl_5_4_RP_0" + "P-poll__networl_5_4_RP_1" + "P-poll__networl_5_4_RP_2" + "P-poll__networl_5_4_RP_3" + "P-poll__networl_5_4_RP_4" + "P-poll__networl_5_4_RP_5" + "P-poll__networl_5_4_RP_6" + "P-poll__networl_5_4_RP_7" + "P-poll__networl_5_4_RP_8" + "P-poll__networl_5_5_AskP_0" + "P-poll__networl_5_5_AskP_1" + "P-poll__networl_5_5_AskP_2" + "P-poll__networl_5_5_AskP_3" + "P-poll__networl_5_5_AskP_4" + "P-poll__networl_5_5_AskP_5" + "P-poll__networl_5_5_AskP_6" + "P-poll__networl_5_5_AskP_7" + "P-poll__networl_5_5_AskP_8" + "P-poll__networl_5_5_AnsP_0" + "P-poll__networl_5_5_AnsP_1" + "P-poll__networl_5_5_AnsP_2" + "P-poll__networl_5_5_AnsP_3" + "P-poll__networl_5_5_AnsP_4" + "P-poll__networl_5_5_AnsP_5" + "P-poll__networl_5_5_AnsP_6" + "P-poll__networl_5_5_AnsP_7" + "P-poll__networl_5_5_AnsP_8" + "P-poll__networl_5_5_RI_0" + "P-poll__networl_5_5_RI_1" + "P-poll__networl_5_5_RI_2" + "P-poll__networl_5_5_RI_3" + "P-poll__networl_5_5_RI_4" + "P-poll__networl_5_5_RI_5" + "P-poll__networl_5_5_RI_6" + "P-poll__networl_5_5_RI_7" + "P-poll__networl_5_5_RI_8" + "P-poll__networl_5_5_AI_0" + "P-poll__networl_5_5_AI_1" + "P-poll__networl_5_5_AI_2" + "P-poll__networl_5_5_AI_3" + "P-poll__networl_5_5_AI_4" + "P-poll__networl_5_5_AI_5" + "P-poll__networl_5_5_AI_6" + "P-poll__networl_5_5_AI_7" + "P-poll__networl_5_5_AI_8" + "P-poll__networl_5_5_AnnP_0" + "P-poll__networl_5_5_AnnP_1" + "P-poll__networl_5_5_AnnP_2" + "P-poll__networl_5_5_AnnP_3" + "P-poll__networl_5_5_AnnP_4" + "P-poll__networl_5_5_AnnP_5" + "P-poll__networl_5_5_AnnP_6" + "P-poll__networl_5_5_AnnP_7" + "P-poll__networl_5_5_AnnP_8" + "P-poll__networl_5_5_RP_0" + "P-poll__networl_5_5_RP_1" + "P-poll__networl_5_5_RP_2" + "P-poll__networl_5_5_RP_3" + "P-poll__networl_5_5_RP_4" + "P-poll__networl_5_5_RP_5" + "P-poll__networl_5_5_RP_6" + "P-poll__networl_5_5_RP_7" + "P-poll__networl_5_5_RP_8" + "P-poll__networl_5_6_AskP_0" + "P-poll__networl_5_6_AskP_1" + "P-poll__networl_5_6_AskP_2" + "P-poll__networl_5_6_AskP_3" + "P-poll__networl_5_6_AskP_4" + "P-poll__networl_5_6_AskP_5" + "P-poll__networl_5_6_AskP_6" + "P-poll__networl_5_6_AskP_7" + "P-poll__networl_5_6_AskP_8" + "P-poll__networl_5_6_AnsP_0" + "P-poll__networl_5_6_AnsP_1" + "P-poll__networl_5_6_AnsP_2" + "P-poll__networl_5_6_AnsP_3" + "P-poll__networl_5_6_AnsP_4" + "P-poll__networl_5_6_AnsP_5" + "P-poll__networl_5_6_AnsP_6" + "P-poll__networl_5_6_AnsP_7" + "P-poll__networl_5_6_AnsP_8" + "P-poll__networl_5_6_RI_0" + "P-poll__networl_5_6_RI_1" + "P-poll__networl_5_6_RI_2" + "P-poll__networl_5_6_RI_3" + "P-poll__networl_5_6_RI_4" + "P-poll__networl_5_6_RI_5" + "P-poll__networl_5_6_RI_6" + "P-poll__networl_5_6_RI_7" + "P-poll__networl_5_6_RI_8" + "P-poll__networl_5_6_AI_0" + "P-poll__networl_5_6_AI_1" + "P-poll__networl_5_6_AI_2" + "P-poll__networl_5_6_AI_3" + "P-poll__networl_5_6_AI_4" + "P-poll__networl_5_6_AI_5" + "P-poll__networl_5_6_AI_6" + "P-poll__networl_5_6_AI_7" + "P-poll__networl_5_6_AI_8" + "P-poll__networl_5_6_AnnP_0" + "P-poll__networl_5_6_AnnP_1" + "P-poll__networl_5_6_AnnP_2" + "P-poll__networl_5_6_AnnP_3" + "P-poll__networl_5_6_AnnP_4" + "P-poll__networl_5_6_AnnP_5" + "P-poll__networl_5_6_AnnP_6" + "P-poll__networl_5_6_AnnP_7" + "P-poll__networl_5_6_AnnP_8" + "P-poll__networl_5_6_RP_0" + "P-poll__networl_5_6_RP_1" + "P-poll__networl_5_6_RP_2" + "P-poll__networl_5_6_RP_3" + "P-poll__networl_5_6_RP_4" + "P-poll__networl_5_6_RP_5" + "P-poll__networl_5_6_RP_6" + "P-poll__networl_5_6_RP_7" + "P-poll__networl_5_6_RP_8" + "P-poll__networl_5_7_AskP_0" + "P-poll__networl_5_7_AskP_1" + "P-poll__networl_5_7_AskP_2" + "P-poll__networl_5_7_AskP_3" + "P-poll__networl_5_7_AskP_4" + "P-poll__networl_5_7_AskP_5" + "P-poll__networl_5_7_AskP_6" + "P-poll__networl_5_7_AskP_7" + "P-poll__networl_5_7_AskP_8" + "P-poll__networl_5_7_AnsP_0" + "P-poll__networl_5_7_AnsP_1" + "P-poll__networl_5_7_AnsP_2" + "P-poll__networl_5_7_AnsP_3" + "P-poll__networl_5_7_AnsP_4" + "P-poll__networl_5_7_AnsP_5" + "P-poll__networl_5_7_AnsP_6" + "P-poll__networl_5_7_AnsP_7" + "P-poll__networl_5_7_AnsP_8" + "P-poll__networl_5_7_RI_0" + "P-poll__networl_5_7_RI_1" + "P-poll__networl_5_7_RI_2" + "P-poll__networl_5_7_RI_3" + "P-poll__networl_5_7_RI_4" + "P-poll__networl_5_7_RI_5" + "P-poll__networl_5_7_RI_6" + "P-poll__networl_5_7_RI_7" + "P-poll__networl_5_7_RI_8" + "P-poll__networl_5_7_AI_0" + "P-poll__networl_5_7_AI_1" + "P-poll__networl_5_7_AI_2" + "P-poll__networl_5_7_AI_3" + "P-poll__networl_5_7_AI_4" + "P-poll__networl_5_7_AI_5" + "P-poll__networl_5_7_AI_6" + "P-poll__networl_5_7_AI_7" + "P-poll__networl_5_7_AI_8" + "P-poll__networl_5_7_AnnP_0" + "P-poll__networl_5_7_AnnP_1" + "P-poll__networl_5_7_AnnP_2" + "P-poll__networl_5_7_AnnP_3" + "P-poll__networl_5_7_AnnP_4" + "P-poll__networl_5_7_AnnP_5" + "P-poll__networl_5_7_AnnP_6" + "P-poll__networl_5_7_AnnP_7" + "P-poll__networl_5_7_AnnP_8" + "P-poll__networl_5_7_RP_0" + "P-poll__networl_5_7_RP_1" + "P-poll__networl_5_7_RP_2" + "P-poll__networl_5_7_RP_3" + "P-poll__networl_5_7_RP_4" + "P-poll__networl_5_7_RP_5" + "P-poll__networl_5_7_RP_6" + "P-poll__networl_5_7_RP_7" + "P-poll__networl_5_7_RP_8" + "P-poll__networl_5_8_AskP_0" + "P-poll__networl_5_8_AskP_1" + "P-poll__networl_5_8_AskP_2" + "P-poll__networl_5_8_AskP_3" + "P-poll__networl_5_8_AskP_4" + "P-poll__networl_5_8_AskP_5" + "P-poll__networl_5_8_AskP_6" + "P-poll__networl_5_8_AskP_7" + "P-poll__networl_5_8_AskP_8" + "P-poll__networl_5_8_AnsP_0" + "P-poll__networl_5_8_AnsP_1" + "P-poll__networl_5_8_AnsP_2" + "P-poll__networl_5_8_AnsP_3" + "P-poll__networl_5_8_AnsP_4" + "P-poll__networl_5_8_AnsP_5" + "P-poll__networl_5_8_AnsP_6" + "P-poll__networl_5_8_AnsP_7" + "P-poll__networl_5_8_AnsP_8" + "P-poll__networl_5_8_RI_0" + "P-poll__networl_5_8_RI_1" + "P-poll__networl_5_8_RI_2" + "P-poll__networl_5_8_RI_3" + "P-poll__networl_5_8_RI_4" + "P-poll__networl_5_8_RI_5" + "P-poll__networl_5_8_RI_6" + "P-poll__networl_5_8_RI_7" + "P-poll__networl_5_8_RI_8" + "P-poll__networl_5_8_AI_0" + "P-poll__networl_5_8_AI_1" + "P-poll__networl_5_8_AI_2" + "P-poll__networl_5_8_AI_3" + "P-poll__networl_5_8_AI_4" + "P-poll__networl_5_8_AI_5" + "P-poll__networl_5_8_AI_6" + "P-poll__networl_5_8_AI_7" + "P-poll__networl_5_8_AI_8" + "P-poll__networl_5_8_AnnP_0" + "P-poll__networl_5_8_AnnP_1" + "P-poll__networl_5_8_AnnP_2" + "P-poll__networl_5_8_AnnP_3" + "P-poll__networl_5_8_AnnP_4" + "P-poll__networl_5_8_AnnP_5" + "P-poll__networl_5_8_AnnP_6" + "P-poll__networl_5_8_AnnP_7" + "P-poll__networl_5_8_AnnP_8" + "P-poll__networl_5_8_RP_0" + "P-poll__networl_5_8_RP_1" + "P-poll__networl_5_8_RP_2" + "P-poll__networl_5_8_RP_3" + "P-poll__networl_5_8_RP_4" + "P-poll__networl_5_8_RP_5" + "P-poll__networl_5_8_RP_6" + "P-poll__networl_5_8_RP_7" + "P-poll__networl_5_8_RP_8" + "P-poll__networl_6_0_AskP_0" + "P-poll__networl_6_0_AskP_1" + "P-poll__networl_6_0_AskP_2" + "P-poll__networl_6_0_AskP_3" + "P-poll__networl_6_0_AskP_4" + "P-poll__networl_6_0_AskP_5" + "P-poll__networl_6_0_AskP_6" + "P-poll__networl_6_0_AskP_7" + "P-poll__networl_6_0_AskP_8" + "P-poll__networl_6_0_AnsP_0" + "P-poll__networl_6_0_AnsP_1" + "P-poll__networl_6_0_AnsP_2" + "P-poll__networl_6_0_AnsP_3" + "P-poll__networl_6_0_AnsP_4" + "P-poll__networl_6_0_AnsP_5" + "P-poll__networl_6_0_AnsP_6" + "P-poll__networl_6_0_AnsP_7" + "P-poll__networl_6_0_AnsP_8" + "P-poll__networl_6_0_RI_0" + "P-poll__networl_6_0_RI_1" + "P-poll__networl_6_0_RI_2" + "P-poll__networl_6_0_RI_3" + "P-poll__networl_6_0_RI_4" + "P-poll__networl_6_0_RI_5" + "P-poll__networl_6_0_RI_6" + "P-poll__networl_6_0_RI_7" + "P-poll__networl_6_0_RI_8" + "P-poll__networl_6_0_AI_0" + "P-poll__networl_6_0_AI_1" + "P-poll__networl_6_0_AI_2" + "P-poll__networl_6_0_AI_3" + "P-poll__networl_6_0_AI_4" + "P-poll__networl_6_0_AI_5" + "P-poll__networl_6_0_AI_6" + "P-poll__networl_6_0_AI_7" + "P-poll__networl_6_0_AI_8" + "P-poll__networl_6_0_AnnP_0" + "P-poll__networl_6_0_AnnP_1" + "P-poll__networl_6_0_AnnP_2" + "P-poll__networl_6_0_AnnP_3" + "P-poll__networl_6_0_AnnP_4" + "P-poll__networl_6_0_AnnP_5" + "P-poll__networl_6_0_AnnP_6" + "P-poll__networl_6_0_AnnP_7" + "P-poll__networl_6_0_AnnP_8" + "P-poll__networl_6_0_RP_0" + "P-poll__networl_6_0_RP_1" + "P-poll__networl_6_0_RP_2" + "P-poll__networl_6_0_RP_3" + "P-poll__networl_6_0_RP_4" + "P-poll__networl_6_0_RP_5" + "P-poll__networl_6_0_RP_6" + "P-poll__networl_6_0_RP_7" + "P-poll__networl_6_0_RP_8" + "P-poll__networl_6_1_AskP_0" + "P-poll__networl_6_1_AskP_1" + "P-poll__networl_6_1_AskP_2" + "P-poll__networl_6_1_AskP_3" + "P-poll__networl_6_1_AskP_4" + "P-poll__networl_6_1_AskP_5" + "P-poll__networl_6_1_AskP_6" + "P-poll__networl_6_1_AskP_7" + "P-poll__networl_6_1_AskP_8" + "P-poll__networl_6_1_AnsP_0" + "P-poll__networl_6_1_AnsP_1" + "P-poll__networl_6_1_AnsP_2" + "P-poll__networl_6_1_AnsP_3" + "P-poll__networl_6_1_AnsP_4" + "P-poll__networl_6_1_AnsP_5" + "P-poll__networl_6_1_AnsP_6" + "P-poll__networl_6_1_AnsP_7" + "P-poll__networl_6_1_AnsP_8" + "P-poll__networl_6_1_RI_0" + "P-poll__networl_6_1_RI_1" + "P-poll__networl_6_1_RI_2" + "P-poll__networl_6_1_RI_3" + "P-poll__networl_6_1_RI_4" + "P-poll__networl_6_1_RI_5" + "P-poll__networl_6_1_RI_6" + "P-poll__networl_6_1_RI_7" + "P-poll__networl_6_1_RI_8" + "P-poll__networl_6_1_AI_0" + "P-poll__networl_6_1_AI_1" + "P-poll__networl_6_1_AI_2" + "P-poll__networl_6_1_AI_3" + "P-poll__networl_6_1_AI_4" + "P-poll__networl_6_1_AI_5" + "P-poll__networl_6_1_AI_6" + "P-poll__networl_6_1_AI_7" + "P-poll__networl_6_1_AI_8" + "P-poll__networl_6_1_AnnP_0" + "P-poll__networl_6_1_AnnP_1" + "P-poll__networl_6_1_AnnP_2" + "P-poll__networl_6_1_AnnP_3" + "P-poll__networl_6_1_AnnP_4" + "P-poll__networl_6_1_AnnP_5" + "P-poll__networl_6_1_AnnP_6" + "P-poll__networl_6_1_AnnP_7" + "P-poll__networl_6_1_AnnP_8" + "P-poll__networl_6_1_RP_0" + "P-poll__networl_6_1_RP_1" + "P-poll__networl_6_1_RP_2" + "P-poll__networl_6_1_RP_3" + "P-poll__networl_6_1_RP_4" + "P-poll__networl_6_1_RP_5" + "P-poll__networl_6_1_RP_6" + "P-poll__networl_6_1_RP_7" + "P-poll__networl_6_1_RP_8" + "P-poll__networl_6_2_AskP_0" + "P-poll__networl_6_2_AskP_1" + "P-poll__networl_6_2_AskP_2" + "P-poll__networl_6_2_AskP_3" + "P-poll__networl_6_2_AskP_4" + "P-poll__networl_6_2_AskP_5" + "P-poll__networl_6_2_AskP_6" + "P-poll__networl_6_2_AskP_7" + "P-poll__networl_6_2_AskP_8" + "P-poll__networl_6_2_AnsP_0" + "P-poll__networl_6_2_AnsP_1" + "P-poll__networl_6_2_AnsP_2" + "P-poll__networl_6_2_AnsP_3" + "P-poll__networl_6_2_AnsP_4" + "P-poll__networl_6_2_AnsP_5" + "P-poll__networl_6_2_AnsP_6" + "P-poll__networl_6_2_AnsP_7" + "P-poll__networl_6_2_AnsP_8" + "P-poll__networl_6_2_RI_0" + "P-poll__networl_6_2_RI_1" + "P-poll__networl_6_2_RI_2" + "P-poll__networl_6_2_RI_3" + "P-poll__networl_6_2_RI_4" + "P-poll__networl_6_2_RI_5" + "P-poll__networl_6_2_RI_6" + "P-poll__networl_6_2_RI_7" + "P-poll__networl_6_2_RI_8" + "P-poll__networl_6_2_AI_0" + "P-poll__networl_6_2_AI_1" + "P-poll__networl_6_2_AI_2" + "P-poll__networl_6_2_AI_3" + "P-poll__networl_6_2_AI_4" + "P-poll__networl_6_2_AI_5" + "P-poll__networl_6_2_AI_6" + "P-poll__networl_6_2_AI_7" + "P-poll__networl_6_2_AI_8" + "P-poll__networl_6_2_AnnP_0" + "P-poll__networl_6_2_AnnP_1" + "P-poll__networl_6_2_AnnP_2" + "P-poll__networl_6_2_AnnP_3" + "P-poll__networl_6_2_AnnP_4" + "P-poll__networl_6_2_AnnP_5" + "P-poll__networl_6_2_AnnP_6" + "P-poll__networl_6_2_AnnP_7" + "P-poll__networl_6_2_AnnP_8" + "P-poll__networl_6_2_RP_0" + "P-poll__networl_6_2_RP_1" + "P-poll__networl_6_2_RP_2" + "P-poll__networl_6_2_RP_3" + "P-poll__networl_6_2_RP_4" + "P-poll__networl_6_2_RP_5" + "P-poll__networl_6_2_RP_6" + "P-poll__networl_6_2_RP_7" + "P-poll__networl_6_2_RP_8" + "P-poll__networl_6_3_AskP_0" + "P-poll__networl_6_3_AskP_1" + "P-poll__networl_6_3_AskP_2" + "P-poll__networl_6_3_AskP_3" + "P-poll__networl_6_3_AskP_4" + "P-poll__networl_6_3_AskP_5" + "P-poll__networl_6_3_AskP_6" + "P-poll__networl_6_3_AskP_7" + "P-poll__networl_6_3_AskP_8" + "P-poll__networl_6_3_AnsP_0" + "P-poll__networl_6_3_AnsP_1" + "P-poll__networl_6_3_AnsP_2" + "P-poll__networl_6_3_AnsP_3" + "P-poll__networl_6_3_AnsP_4" + "P-poll__networl_6_3_AnsP_5" + "P-poll__networl_6_3_AnsP_6" + "P-poll__networl_6_3_AnsP_7" + "P-poll__networl_6_3_AnsP_8" + "P-poll__networl_6_3_RI_0" + "P-poll__networl_6_3_RI_1" + "P-poll__networl_6_3_RI_2" + "P-poll__networl_6_3_RI_3" + "P-poll__networl_6_3_RI_4" + "P-poll__networl_6_3_RI_5" + "P-poll__networl_6_3_RI_6" + "P-poll__networl_6_3_RI_7" + "P-poll__networl_6_3_RI_8" + "P-poll__networl_6_3_AI_0" + "P-poll__networl_6_3_AI_1" + "P-poll__networl_6_3_AI_2" + "P-poll__networl_6_3_AI_3" + "P-poll__networl_6_3_AI_4" + "P-poll__networl_6_3_AI_5" + "P-poll__networl_6_3_AI_6" + "P-poll__networl_6_3_AI_7" + "P-poll__networl_6_3_AI_8" + "P-poll__networl_6_3_AnnP_0" + "P-poll__networl_6_3_AnnP_1" + "P-poll__networl_6_3_AnnP_2" + "P-poll__networl_6_3_AnnP_3" + "P-poll__networl_6_3_AnnP_4" + "P-poll__networl_6_3_AnnP_5" + "P-poll__networl_6_3_AnnP_6" + "P-poll__networl_6_3_AnnP_7" + "P-poll__networl_6_3_AnnP_8" + "P-poll__networl_6_3_RP_0" + "P-poll__networl_6_3_RP_1" + "P-poll__networl_6_3_RP_2" + "P-poll__networl_6_3_RP_3" + "P-poll__networl_6_3_RP_4" + "P-poll__networl_6_3_RP_5" + "P-poll__networl_6_3_RP_6" + "P-poll__networl_6_3_RP_7" + "P-poll__networl_6_3_RP_8" + "P-poll__networl_6_4_AskP_0" + "P-poll__networl_6_4_AskP_1" + "P-poll__networl_6_4_AskP_2" + "P-poll__networl_6_4_AskP_3" + "P-poll__networl_6_4_AskP_4" + "P-poll__networl_6_4_AskP_5" + "P-poll__networl_6_4_AskP_6" + "P-poll__networl_6_4_AskP_7" + "P-poll__networl_6_4_AskP_8" + "P-poll__networl_6_4_AnsP_0" + "P-poll__networl_6_4_AnsP_1" + "P-poll__networl_6_4_AnsP_2" + "P-poll__networl_6_4_AnsP_3" + "P-poll__networl_6_4_AnsP_4" + "P-poll__networl_6_4_AnsP_5" + "P-poll__networl_6_4_AnsP_6" + "P-poll__networl_6_4_AnsP_7" + "P-poll__networl_6_4_AnsP_8" + "P-poll__networl_6_4_RI_0" + "P-poll__networl_6_4_RI_1" + "P-poll__networl_6_4_RI_2" + "P-poll__networl_6_4_RI_3" + "P-poll__networl_6_4_RI_4" + "P-poll__networl_6_4_RI_5" + "P-poll__networl_6_4_RI_6" + "P-poll__networl_6_4_RI_7" + "P-poll__networl_6_4_RI_8" + "P-poll__networl_6_4_AI_0" + "P-poll__networl_6_4_AI_1" + "P-poll__networl_6_4_AI_2" + "P-poll__networl_6_4_AI_3" + "P-poll__networl_6_4_AI_4" + "P-poll__networl_6_4_AI_5" + "P-poll__networl_6_4_AI_6" + "P-poll__networl_6_4_AI_7" + "P-poll__networl_6_4_AI_8" + "P-poll__networl_6_4_AnnP_0" + "P-poll__networl_6_4_AnnP_1" + "P-poll__networl_6_4_AnnP_2" + "P-poll__networl_6_4_AnnP_3" + "P-poll__networl_6_4_AnnP_4" + "P-poll__networl_6_4_AnnP_5" + "P-poll__networl_6_4_AnnP_6" + "P-poll__networl_6_4_AnnP_7" + "P-poll__networl_6_4_AnnP_8" + "P-poll__networl_6_4_RP_0" + "P-poll__networl_6_4_RP_1" + "P-poll__networl_6_4_RP_2" + "P-poll__networl_6_4_RP_3" + "P-poll__networl_6_4_RP_4" + "P-poll__networl_6_4_RP_5" + "P-poll__networl_6_4_RP_6" + "P-poll__networl_6_4_RP_7" + "P-poll__networl_6_4_RP_8" + "P-poll__networl_6_5_AskP_0" + "P-poll__networl_6_5_AskP_1" + "P-poll__networl_6_5_AskP_2" + "P-poll__networl_6_5_AskP_3" + "P-poll__networl_6_5_AskP_4" + "P-poll__networl_6_5_AskP_5" + "P-poll__networl_6_5_AskP_6" + "P-poll__networl_6_5_AskP_7" + "P-poll__networl_6_5_AskP_8" + "P-poll__networl_6_5_AnsP_0" + "P-poll__networl_6_5_AnsP_1" + "P-poll__networl_6_5_AnsP_2" + "P-poll__networl_6_5_AnsP_3" + "P-poll__networl_6_5_AnsP_4" + "P-poll__networl_6_5_AnsP_5" + "P-poll__networl_6_5_AnsP_6" + "P-poll__networl_6_5_AnsP_7" + "P-poll__networl_6_5_AnsP_8" + "P-poll__networl_6_5_RI_0" + "P-poll__networl_6_5_RI_1" + "P-poll__networl_6_5_RI_2" + "P-poll__networl_6_5_RI_3" + "P-poll__networl_6_5_RI_4" + "P-poll__networl_6_5_RI_5" + "P-poll__networl_6_5_RI_6" + "P-poll__networl_6_5_RI_7" + "P-poll__networl_6_5_RI_8" + "P-poll__networl_6_5_AI_0" + "P-poll__networl_6_5_AI_1" + "P-poll__networl_6_5_AI_2" + "P-poll__networl_6_5_AI_3" + "P-poll__networl_6_5_AI_4" + "P-poll__networl_6_5_AI_5" + "P-poll__networl_6_5_AI_6" + "P-poll__networl_6_5_AI_7" + "P-poll__networl_6_5_AI_8" + "P-poll__networl_6_5_AnnP_0" + "P-poll__networl_6_5_AnnP_1" + "P-poll__networl_6_5_AnnP_2" + "P-poll__networl_6_5_AnnP_3" + "P-poll__networl_6_5_AnnP_4" + "P-poll__networl_6_5_AnnP_5" + "P-poll__networl_6_5_AnnP_6" + "P-poll__networl_6_5_AnnP_7" + "P-poll__networl_6_5_AnnP_8" + "P-poll__networl_6_5_RP_0" + "P-poll__networl_6_5_RP_1" + "P-poll__networl_6_5_RP_2" + "P-poll__networl_6_5_RP_3" + "P-poll__networl_6_5_RP_4" + "P-poll__networl_6_5_RP_5" + "P-poll__networl_6_5_RP_6" + "P-poll__networl_6_5_RP_7" + "P-poll__networl_6_5_RP_8" + "P-poll__networl_6_6_AskP_0" + "P-poll__networl_6_6_AskP_1" + "P-poll__networl_6_6_AskP_2" + "P-poll__networl_6_6_AskP_3" + "P-poll__networl_6_6_AskP_4" + "P-poll__networl_6_6_AskP_5" + "P-poll__networl_6_6_AskP_6" + "P-poll__networl_6_6_AskP_7" + "P-poll__networl_6_6_AskP_8" + "P-poll__networl_6_6_AnsP_0" + "P-poll__networl_6_6_AnsP_1" + "P-poll__networl_6_6_AnsP_2" + "P-poll__networl_6_6_AnsP_3" + "P-poll__networl_6_6_AnsP_4" + "P-poll__networl_6_6_AnsP_5" + "P-poll__networl_6_6_AnsP_6" + "P-poll__networl_6_6_AnsP_7" + "P-poll__networl_6_6_AnsP_8" + "P-poll__networl_6_6_RI_0" + "P-poll__networl_6_6_RI_1" + "P-poll__networl_6_6_RI_2" + "P-poll__networl_6_6_RI_3" + "P-poll__networl_6_6_RI_4" + "P-poll__networl_6_6_RI_5" + "P-poll__networl_6_6_RI_6" + "P-poll__networl_6_6_RI_7" + "P-poll__networl_6_6_RI_8" + "P-poll__networl_6_6_AI_0" + "P-poll__networl_6_6_AI_1" + "P-poll__networl_6_6_AI_2" + "P-poll__networl_6_6_AI_3" + "P-poll__networl_6_6_AI_4" + "P-poll__networl_6_6_AI_5" + "P-poll__networl_6_6_AI_6" + "P-poll__networl_6_6_AI_7" + "P-poll__networl_6_6_AI_8" + "P-poll__networl_6_6_AnnP_0" + "P-poll__networl_6_6_AnnP_1" + "P-poll__networl_6_6_AnnP_2" + "P-poll__networl_6_6_AnnP_3" + "P-poll__networl_6_6_AnnP_4" + "P-poll__networl_6_6_AnnP_5" + "P-poll__networl_6_6_AnnP_6" + "P-poll__networl_6_6_AnnP_7" + "P-poll__networl_6_6_AnnP_8" + "P-poll__networl_6_6_RP_0" + "P-poll__networl_6_6_RP_1" + "P-poll__networl_6_6_RP_2" + "P-poll__networl_6_6_RP_3" + "P-poll__networl_6_6_RP_4" + "P-poll__networl_6_6_RP_5" + "P-poll__networl_6_6_RP_6" + "P-poll__networl_6_6_RP_7" + "P-poll__networl_6_6_RP_8" + "P-poll__networl_6_7_AskP_0" + "P-poll__networl_6_7_AskP_1" + "P-poll__networl_6_7_AskP_2" + "P-poll__networl_6_7_AskP_3" + "P-poll__networl_6_7_AskP_4" + "P-poll__networl_6_7_AskP_5" + "P-poll__networl_6_7_AskP_6" + "P-poll__networl_6_7_AskP_7" + "P-poll__networl_6_7_AskP_8" + "P-poll__networl_6_7_AnsP_0" + "P-poll__networl_6_7_AnsP_1" + "P-poll__networl_6_7_AnsP_2" + "P-poll__networl_6_7_AnsP_3" + "P-poll__networl_6_7_AnsP_4" + "P-poll__networl_6_7_AnsP_5" + "P-poll__networl_6_7_AnsP_6" + "P-poll__networl_6_7_AnsP_7" + "P-poll__networl_6_7_AnsP_8" + "P-poll__networl_6_7_RI_0" + "P-poll__networl_6_7_RI_1" + "P-poll__networl_6_7_RI_2" + "P-poll__networl_6_7_RI_3" + "P-poll__networl_6_7_RI_4" + "P-poll__networl_6_7_RI_5" + "P-poll__networl_6_7_RI_6" + "P-poll__networl_6_7_RI_7" + "P-poll__networl_6_7_RI_8" + "P-poll__networl_6_7_AI_0" + "P-poll__networl_6_7_AI_1" + "P-poll__networl_6_7_AI_2" + "P-poll__networl_6_7_AI_3" + "P-poll__networl_6_7_AI_4" + "P-poll__networl_6_7_AI_5" + "P-poll__networl_6_7_AI_6" + "P-poll__networl_6_7_AI_7" + "P-poll__networl_6_7_AI_8" + "P-poll__networl_6_7_AnnP_0" + "P-poll__networl_6_7_AnnP_1" + "P-poll__networl_6_7_AnnP_2" + "P-poll__networl_6_7_AnnP_3" + "P-poll__networl_6_7_AnnP_4" + "P-poll__networl_6_7_AnnP_5" + "P-poll__networl_6_7_AnnP_6" + "P-poll__networl_6_7_AnnP_7" + "P-poll__networl_6_7_AnnP_8" + "P-poll__networl_6_7_RP_0" + "P-poll__networl_6_7_RP_1" + "P-poll__networl_6_7_RP_2" + "P-poll__networl_6_7_RP_3" + "P-poll__networl_6_7_RP_4" + "P-poll__networl_6_7_RP_5" + "P-poll__networl_6_7_RP_6" + "P-poll__networl_6_7_RP_7" + "P-poll__networl_6_7_RP_8" + "P-poll__networl_6_8_AskP_0" + "P-poll__networl_6_8_AskP_1" + "P-poll__networl_6_8_AskP_2" + "P-poll__networl_6_8_AskP_3" + "P-poll__networl_6_8_AskP_4" + "P-poll__networl_6_8_AskP_5" + "P-poll__networl_6_8_AskP_6" + "P-poll__networl_6_8_AskP_7" + "P-poll__networl_6_8_AskP_8" + "P-poll__networl_6_8_AnsP_0" + "P-poll__networl_6_8_AnsP_1" + "P-poll__networl_6_8_AnsP_2" + "P-poll__networl_6_8_AnsP_3" + "P-poll__networl_6_8_AnsP_4" + "P-poll__networl_6_8_AnsP_5" + "P-poll__networl_6_8_AnsP_6" + "P-poll__networl_6_8_AnsP_7" + "P-poll__networl_6_8_AnsP_8" + "P-poll__networl_6_8_RI_0" + "P-poll__networl_6_8_RI_1" + "P-poll__networl_6_8_RI_2" + "P-poll__networl_6_8_RI_3" + "P-poll__networl_6_8_RI_4" + "P-poll__networl_6_8_RI_5" + "P-poll__networl_6_8_RI_6" + "P-poll__networl_6_8_RI_7" + "P-poll__networl_6_8_RI_8" + "P-poll__networl_6_8_AI_0" + "P-poll__networl_6_8_AI_1" + "P-poll__networl_6_8_AI_2" + "P-poll__networl_6_8_AI_3" + "P-poll__networl_6_8_AI_4" + "P-poll__networl_6_8_AI_5" + "P-poll__networl_6_8_AI_6" + "P-poll__networl_6_8_AI_7" + "P-poll__networl_6_8_AI_8" + "P-poll__networl_6_8_AnnP_0" + "P-poll__networl_6_8_AnnP_1" + "P-poll__networl_6_8_AnnP_2" + "P-poll__networl_6_8_AnnP_3" + "P-poll__networl_6_8_AnnP_4" + "P-poll__networl_6_8_AnnP_5" + "P-poll__networl_6_8_AnnP_6" + "P-poll__networl_6_8_AnnP_7" + "P-poll__networl_6_8_AnnP_8" + "P-poll__networl_6_8_RP_0" + "P-poll__networl_6_8_RP_1" + "P-poll__networl_6_8_RP_2" + "P-poll__networl_6_8_RP_3" + "P-poll__networl_6_8_RP_4" + "P-poll__networl_6_8_RP_5" + "P-poll__networl_6_8_RP_6" + "P-poll__networl_6_8_RP_7" + "P-poll__networl_6_8_RP_8" + "P-poll__networl_7_0_AskP_0" + "P-poll__networl_7_0_AskP_1" + "P-poll__networl_7_0_AskP_2" + "P-poll__networl_7_0_AskP_3" + "P-poll__networl_7_0_AskP_4" + "P-poll__networl_7_0_AskP_5" + "P-poll__networl_7_0_AskP_6" + "P-poll__networl_7_0_AskP_7" + "P-poll__networl_7_0_AskP_8" + "P-poll__networl_7_0_AnsP_0" + "P-poll__networl_7_0_AnsP_1" + "P-poll__networl_7_0_AnsP_2" + "P-poll__networl_7_0_AnsP_3" + "P-poll__networl_7_0_AnsP_4" + "P-poll__networl_7_0_AnsP_5" + "P-poll__networl_7_0_AnsP_6" + "P-poll__networl_7_0_AnsP_7" + "P-poll__networl_7_0_AnsP_8" + "P-poll__networl_7_0_RI_0" + "P-poll__networl_7_0_RI_1" + "P-poll__networl_7_0_RI_2" + "P-poll__networl_7_0_RI_3" + "P-poll__networl_7_0_RI_4" + "P-poll__networl_7_0_RI_5" + "P-poll__networl_7_0_RI_6" + "P-poll__networl_7_0_RI_7" + "P-poll__networl_7_0_RI_8" + "P-poll__networl_7_0_AI_0" + "P-poll__networl_7_0_AI_1" + "P-poll__networl_7_0_AI_2" + "P-poll__networl_7_0_AI_3" + "P-poll__networl_7_0_AI_4" + "P-poll__networl_7_0_AI_5" + "P-poll__networl_7_0_AI_6" + "P-poll__networl_7_0_AI_7" + "P-poll__networl_7_0_AI_8" + "P-poll__networl_7_0_AnnP_0" + "P-poll__networl_7_0_AnnP_1" + "P-poll__networl_7_0_AnnP_2" + "P-poll__networl_7_0_AnnP_3" + "P-poll__networl_7_0_AnnP_4" + "P-poll__networl_7_0_AnnP_5" + "P-poll__networl_7_0_AnnP_6" + "P-poll__networl_7_0_AnnP_7" + "P-poll__networl_7_0_AnnP_8" + "P-poll__networl_7_0_RP_0" + "P-poll__networl_7_0_RP_1" + "P-poll__networl_7_0_RP_2" + "P-poll__networl_7_0_RP_3" + "P-poll__networl_7_0_RP_4" + "P-poll__networl_7_0_RP_5" + "P-poll__networl_7_0_RP_6" + "P-poll__networl_7_0_RP_7" + "P-poll__networl_7_0_RP_8" + "P-poll__networl_7_1_AskP_0" + "P-poll__networl_7_1_AskP_1" + "P-poll__networl_7_1_AskP_2" + "P-poll__networl_7_1_AskP_3" + "P-poll__networl_7_1_AskP_4" + "P-poll__networl_7_1_AskP_5" + "P-poll__networl_7_1_AskP_6" + "P-poll__networl_7_1_AskP_7" + "P-poll__networl_7_1_AskP_8" + "P-poll__networl_7_1_AnsP_0" + "P-poll__networl_7_1_AnsP_1" + "P-poll__networl_7_1_AnsP_2" + "P-poll__networl_7_1_AnsP_3" + "P-poll__networl_7_1_AnsP_4" + "P-poll__networl_7_1_AnsP_5" + "P-poll__networl_7_1_AnsP_6" + "P-poll__networl_7_1_AnsP_7" + "P-poll__networl_7_1_AnsP_8" + "P-poll__networl_7_1_RI_0" + "P-poll__networl_7_1_RI_1" + "P-poll__networl_7_1_RI_2" + "P-poll__networl_7_1_RI_3" + "P-poll__networl_7_1_RI_4" + "P-poll__networl_7_1_RI_5" + "P-poll__networl_7_1_RI_6" + "P-poll__networl_7_1_RI_7" + "P-poll__networl_7_1_RI_8" + "P-poll__networl_7_1_AI_0" + "P-poll__networl_7_1_AI_1" + "P-poll__networl_7_1_AI_2" + "P-poll__networl_7_1_AI_3" + "P-poll__networl_7_1_AI_4" + "P-poll__networl_7_1_AI_5" + "P-poll__networl_7_1_AI_6" + "P-poll__networl_7_1_AI_7" + "P-poll__networl_7_1_AI_8" + "P-poll__networl_7_1_AnnP_0" + "P-poll__networl_7_1_AnnP_1" + "P-poll__networl_7_1_AnnP_2" + "P-poll__networl_7_1_AnnP_3" + "P-poll__networl_7_1_AnnP_4" + "P-poll__networl_7_1_AnnP_5" + "P-poll__networl_7_1_AnnP_6" + "P-poll__networl_7_1_AnnP_7" + "P-poll__networl_7_1_AnnP_8" + "P-poll__networl_7_1_RP_0" + "P-poll__networl_7_1_RP_1" + "P-poll__networl_7_1_RP_2" + "P-poll__networl_7_1_RP_3" + "P-poll__networl_7_1_RP_4" + "P-poll__networl_7_1_RP_5" + "P-poll__networl_7_1_RP_6" + "P-poll__networl_7_1_RP_7" + "P-poll__networl_7_1_RP_8" + "P-poll__networl_7_2_AskP_0" + "P-poll__networl_7_2_AskP_1" + "P-poll__networl_7_2_AskP_2" + "P-poll__networl_7_2_AskP_3" + "P-poll__networl_7_2_AskP_4" + "P-poll__networl_7_2_AskP_5" + "P-poll__networl_7_2_AskP_6" + "P-poll__networl_7_2_AskP_7" + "P-poll__networl_7_2_AskP_8" + "P-poll__networl_7_2_AnsP_0" + "P-poll__networl_7_2_AnsP_1" + "P-poll__networl_7_2_AnsP_2" + "P-poll__networl_7_2_AnsP_3" + "P-poll__networl_7_2_AnsP_4" + "P-poll__networl_7_2_AnsP_5" + "P-poll__networl_7_2_AnsP_6" + "P-poll__networl_7_2_AnsP_7" + "P-poll__networl_7_2_AnsP_8" + "P-poll__networl_7_2_RI_0" + "P-poll__networl_7_2_RI_1" + "P-poll__networl_7_2_RI_2" + "P-poll__networl_7_2_RI_3" + "P-poll__networl_7_2_RI_4" + "P-poll__networl_7_2_RI_5" + "P-poll__networl_7_2_RI_6" + "P-poll__networl_7_2_RI_7" + "P-poll__networl_7_2_RI_8" + "P-poll__networl_7_2_AI_0" + "P-poll__networl_7_2_AI_1" + "P-poll__networl_7_2_AI_2" + "P-poll__networl_7_2_AI_3" + "P-poll__networl_7_2_AI_4" + "P-poll__networl_7_2_AI_5" + "P-poll__networl_7_2_AI_6" + "P-poll__networl_7_2_AI_7" + "P-poll__networl_7_2_AI_8" + "P-poll__networl_7_2_AnnP_0" + "P-poll__networl_7_2_AnnP_1" + "P-poll__networl_7_2_AnnP_2" + "P-poll__networl_7_2_AnnP_3" + "P-poll__networl_7_2_AnnP_4" + "P-poll__networl_7_2_AnnP_5" + "P-poll__networl_7_2_AnnP_6" + "P-poll__networl_7_2_AnnP_7" + "P-poll__networl_7_2_AnnP_8" + "P-poll__networl_7_2_RP_0" + "P-poll__networl_7_2_RP_1" + "P-poll__networl_7_2_RP_2" + "P-poll__networl_7_2_RP_3" + "P-poll__networl_7_2_RP_4" + "P-poll__networl_7_2_RP_5" + "P-poll__networl_7_2_RP_6" + "P-poll__networl_7_2_RP_7" + "P-poll__networl_7_2_RP_8" + "P-poll__networl_7_3_AskP_0" + "P-poll__networl_7_3_AskP_1" + "P-poll__networl_7_3_AskP_2" + "P-poll__networl_7_3_AskP_3" + "P-poll__networl_7_3_AskP_4" + "P-poll__networl_7_3_AskP_5" + "P-poll__networl_7_3_AskP_6" + "P-poll__networl_7_3_AskP_7" + "P-poll__networl_7_3_AskP_8" + "P-poll__networl_7_3_AnsP_0" + "P-poll__networl_7_3_AnsP_1" + "P-poll__networl_7_3_AnsP_2" + "P-poll__networl_7_3_AnsP_3" + "P-poll__networl_7_3_AnsP_4" + "P-poll__networl_7_3_AnsP_5" + "P-poll__networl_7_3_AnsP_6" + "P-poll__networl_7_3_AnsP_7" + "P-poll__networl_7_3_AnsP_8" + "P-poll__networl_7_3_RI_0" + "P-poll__networl_7_3_RI_1" + "P-poll__networl_7_3_RI_2" + "P-poll__networl_7_3_RI_3" + "P-poll__networl_7_3_RI_4" + "P-poll__networl_7_3_RI_5" + "P-poll__networl_7_3_RI_6" + "P-poll__networl_7_3_RI_7" + "P-poll__networl_7_3_RI_8" + "P-poll__networl_7_3_AI_0" + "P-poll__networl_7_3_AI_1" + "P-poll__networl_7_3_AI_2" + "P-poll__networl_7_3_AI_3" + "P-poll__networl_7_3_AI_4" + "P-poll__networl_7_3_AI_5" + "P-poll__networl_7_3_AI_6" + "P-poll__networl_7_3_AI_7" + "P-poll__networl_7_3_AI_8" + "P-poll__networl_7_3_AnnP_0" + "P-poll__networl_7_3_AnnP_1" + "P-poll__networl_7_3_AnnP_2" + "P-poll__networl_7_3_AnnP_3" + "P-poll__networl_7_3_AnnP_4" + "P-poll__networl_7_3_AnnP_5" + "P-poll__networl_7_3_AnnP_6" + "P-poll__networl_7_3_AnnP_7" + "P-poll__networl_7_3_AnnP_8" + "P-poll__networl_7_3_RP_0" + "P-poll__networl_7_3_RP_1" + "P-poll__networl_7_3_RP_2" + "P-poll__networl_7_3_RP_3" + "P-poll__networl_7_3_RP_4" + "P-poll__networl_7_3_RP_5" + "P-poll__networl_7_3_RP_6" + "P-poll__networl_7_3_RP_7" + "P-poll__networl_7_3_RP_8" + "P-poll__networl_7_4_AskP_0" + "P-poll__networl_7_4_AskP_1" + "P-poll__networl_7_4_AskP_2" + "P-poll__networl_7_4_AskP_3" + "P-poll__networl_7_4_AskP_4" + "P-poll__networl_7_4_AskP_5" + "P-poll__networl_7_4_AskP_6" + "P-poll__networl_7_4_AskP_7" + "P-poll__networl_7_4_AskP_8" + "P-poll__networl_7_4_AnsP_0" + "P-poll__networl_7_4_AnsP_1" + "P-poll__networl_7_4_AnsP_2" + "P-poll__networl_7_4_AnsP_3" + "P-poll__networl_7_4_AnsP_4" + "P-poll__networl_7_4_AnsP_5" + "P-poll__networl_7_4_AnsP_6" + "P-poll__networl_7_4_AnsP_7" + "P-poll__networl_7_4_AnsP_8" + "P-poll__networl_7_4_RI_0" + "P-poll__networl_7_4_RI_1" + "P-poll__networl_7_4_RI_2" + "P-poll__networl_7_4_RI_3" + "P-poll__networl_7_4_RI_4" + "P-poll__networl_7_4_RI_5" + "P-poll__networl_7_4_RI_6" + "P-poll__networl_7_4_RI_7" + "P-poll__networl_7_4_RI_8" + "P-poll__networl_7_4_AI_0" + "P-poll__networl_7_4_AI_1" + "P-poll__networl_7_4_AI_2" + "P-poll__networl_7_4_AI_3" + "P-poll__networl_7_4_AI_4" + "P-poll__networl_7_4_AI_5" + "P-poll__networl_7_4_AI_6" + "P-poll__networl_7_4_AI_7" + "P-poll__networl_7_4_AI_8" + "P-poll__networl_7_4_AnnP_0" + "P-poll__networl_7_4_AnnP_1" + "P-poll__networl_7_4_AnnP_2" + "P-poll__networl_7_4_AnnP_3" + "P-poll__networl_7_4_AnnP_4" + "P-poll__networl_7_4_AnnP_5" + "P-poll__networl_7_4_AnnP_6" + "P-poll__networl_7_4_AnnP_7" + "P-poll__networl_7_4_AnnP_8" + "P-poll__networl_7_4_RP_0" + "P-poll__networl_7_4_RP_1" + "P-poll__networl_7_4_RP_2" + "P-poll__networl_7_4_RP_3" + "P-poll__networl_7_4_RP_4" + "P-poll__networl_7_4_RP_5" + "P-poll__networl_7_4_RP_6" + "P-poll__networl_7_4_RP_7" + "P-poll__networl_7_4_RP_8" + "P-poll__networl_7_5_AskP_0" + "P-poll__networl_7_5_AskP_1" + "P-poll__networl_7_5_AskP_2" + "P-poll__networl_7_5_AskP_3" + "P-poll__networl_7_5_AskP_4" + "P-poll__networl_7_5_AskP_5" + "P-poll__networl_7_5_AskP_6" + "P-poll__networl_7_5_AskP_7" + "P-poll__networl_7_5_AskP_8" + "P-poll__networl_7_5_AnsP_0" + "P-poll__networl_7_5_AnsP_1" + "P-poll__networl_7_5_AnsP_2" + "P-poll__networl_7_5_AnsP_3" + "P-poll__networl_7_5_AnsP_4" + "P-poll__networl_7_5_AnsP_5" + "P-poll__networl_7_5_AnsP_6" + "P-poll__networl_7_5_AnsP_7" + "P-poll__networl_7_5_AnsP_8" + "P-poll__networl_7_5_RI_0" + "P-poll__networl_7_5_RI_1" + "P-poll__networl_7_5_RI_2" + "P-poll__networl_7_5_RI_3" + "P-poll__networl_7_5_RI_4" + "P-poll__networl_7_5_RI_5" + "P-poll__networl_7_5_RI_6" + "P-poll__networl_7_5_RI_7" + "P-poll__networl_7_5_RI_8" + "P-poll__networl_7_5_AI_0" + "P-poll__networl_7_5_AI_1" + "P-poll__networl_7_5_AI_2" + "P-poll__networl_7_5_AI_3" + "P-poll__networl_7_5_AI_4" + "P-poll__networl_7_5_AI_5" + "P-poll__networl_7_5_AI_6" + "P-poll__networl_7_5_AI_7" + "P-poll__networl_7_5_AI_8" + "P-poll__networl_7_5_AnnP_0" + "P-poll__networl_7_5_AnnP_1" + "P-poll__networl_7_5_AnnP_2" + "P-poll__networl_7_5_AnnP_3" + "P-poll__networl_7_5_AnnP_4" + "P-poll__networl_7_5_AnnP_5" + "P-poll__networl_7_5_AnnP_6" + "P-poll__networl_7_5_AnnP_7" + "P-poll__networl_7_5_AnnP_8" + "P-poll__networl_7_5_RP_0" + "P-poll__networl_7_5_RP_1" + "P-poll__networl_7_5_RP_2" + "P-poll__networl_7_5_RP_3" + "P-poll__networl_7_5_RP_4" + "P-poll__networl_7_5_RP_5" + "P-poll__networl_7_5_RP_6" + "P-poll__networl_7_5_RP_7" + "P-poll__networl_7_5_RP_8" + "P-poll__networl_7_6_AskP_0" + "P-poll__networl_7_6_AskP_1" + "P-poll__networl_7_6_AskP_2" + "P-poll__networl_7_6_AskP_3" + "P-poll__networl_7_6_AskP_4" + "P-poll__networl_7_6_AskP_5" + "P-poll__networl_7_6_AskP_6" + "P-poll__networl_7_6_AskP_7" + "P-poll__networl_7_6_AskP_8" + "P-poll__networl_7_6_AnsP_0" + "P-poll__networl_7_6_AnsP_1" + "P-poll__networl_7_6_AnsP_2" + "P-poll__networl_7_6_AnsP_3" + "P-poll__networl_7_6_AnsP_4" + "P-poll__networl_7_6_AnsP_5" + "P-poll__networl_7_6_AnsP_6" + "P-poll__networl_7_6_AnsP_7" + "P-poll__networl_7_6_AnsP_8" + "P-poll__networl_7_6_RI_0" + "P-poll__networl_7_6_RI_1" + "P-poll__networl_7_6_RI_2" + "P-poll__networl_7_6_RI_3" + "P-poll__networl_7_6_RI_4" + "P-poll__networl_7_6_RI_5" + "P-poll__networl_7_6_RI_6" + "P-poll__networl_7_6_RI_7" + "P-poll__networl_7_6_RI_8" + "P-poll__networl_7_6_AI_0" + "P-poll__networl_7_6_AI_1" + "P-poll__networl_7_6_AI_2" + "P-poll__networl_7_6_AI_3" + "P-poll__networl_7_6_AI_4" + "P-poll__networl_7_6_AI_5" + "P-poll__networl_7_6_AI_6" + "P-poll__networl_7_6_AI_7" + "P-poll__networl_7_6_AI_8" + "P-poll__networl_7_6_AnnP_0" + "P-poll__networl_7_6_AnnP_1" + "P-poll__networl_7_6_AnnP_2" + "P-poll__networl_7_6_AnnP_3" + "P-poll__networl_7_6_AnnP_4" + "P-poll__networl_7_6_AnnP_5" + "P-poll__networl_7_6_AnnP_6" + "P-poll__networl_7_6_AnnP_7" + "P-poll__networl_7_6_AnnP_8" + "P-poll__networl_7_6_RP_0" + "P-poll__networl_7_6_RP_1" + "P-poll__networl_7_6_RP_2" + "P-poll__networl_7_6_RP_3" + "P-poll__networl_7_6_RP_4" + "P-poll__networl_7_6_RP_5" + "P-poll__networl_7_6_RP_6" + "P-poll__networl_7_6_RP_7" + "P-poll__networl_7_6_RP_8" + "P-poll__networl_7_7_AskP_0" + "P-poll__networl_7_7_AskP_1" + "P-poll__networl_7_7_AskP_2" + "P-poll__networl_7_7_AskP_3" + "P-poll__networl_7_7_AskP_4" + "P-poll__networl_7_7_AskP_5" + "P-poll__networl_7_7_AskP_6" + "P-poll__networl_7_7_AskP_7" + "P-poll__networl_7_7_AskP_8" + "P-poll__networl_7_7_AnsP_0" + "P-poll__networl_7_7_AnsP_1" + "P-poll__networl_7_7_AnsP_2" + "P-poll__networl_7_7_AnsP_3" + "P-poll__networl_7_7_AnsP_4" + "P-poll__networl_7_7_AnsP_5" + "P-poll__networl_7_7_AnsP_6" + "P-poll__networl_7_7_AnsP_7" + "P-poll__networl_7_7_AnsP_8" + "P-poll__networl_7_7_RI_0" + "P-poll__networl_7_7_RI_1" + "P-poll__networl_7_7_RI_2" + "P-poll__networl_7_7_RI_3" + "P-poll__networl_7_7_RI_4" + "P-poll__networl_7_7_RI_5" + "P-poll__networl_7_7_RI_6" + "P-poll__networl_7_7_RI_7" + "P-poll__networl_7_7_RI_8" + "P-poll__networl_7_7_AI_0" + "P-poll__networl_7_7_AI_1" + "P-poll__networl_7_7_AI_2" + "P-poll__networl_7_7_AI_3" + "P-poll__networl_7_7_AI_4" + "P-poll__networl_7_7_AI_5" + "P-poll__networl_7_7_AI_6" + "P-poll__networl_7_7_AI_7" + "P-poll__networl_7_7_AI_8" + "P-poll__networl_7_7_AnnP_0" + "P-poll__networl_7_7_AnnP_1" + "P-poll__networl_7_7_AnnP_2" + "P-poll__networl_7_7_AnnP_3" + "P-poll__networl_7_7_AnnP_4" + "P-poll__networl_7_7_AnnP_5" + "P-poll__networl_7_7_AnnP_6" + "P-poll__networl_7_7_AnnP_7" + "P-poll__networl_7_7_AnnP_8" + "P-poll__networl_7_7_RP_0" + "P-poll__networl_7_7_RP_1" + "P-poll__networl_7_7_RP_2" + "P-poll__networl_7_7_RP_3" + "P-poll__networl_7_7_RP_4" + "P-poll__networl_7_7_RP_5" + "P-poll__networl_7_7_RP_6" + "P-poll__networl_7_7_RP_7" + "P-poll__networl_7_7_RP_8" + "P-poll__networl_7_8_AskP_0" + "P-poll__networl_7_8_AskP_1" + "P-poll__networl_7_8_AskP_2" + "P-poll__networl_7_8_AskP_3" + "P-poll__networl_7_8_AskP_4" + "P-poll__networl_7_8_AskP_5" + "P-poll__networl_7_8_AskP_6" + "P-poll__networl_7_8_AskP_7" + "P-poll__networl_7_8_AskP_8" + "P-poll__networl_7_8_AnsP_0" + "P-poll__networl_7_8_AnsP_1" + "P-poll__networl_7_8_AnsP_2" + "P-poll__networl_7_8_AnsP_3" + "P-poll__networl_7_8_AnsP_4" + "P-poll__networl_7_8_AnsP_5" + "P-poll__networl_7_8_AnsP_6" + "P-poll__networl_7_8_AnsP_7" + "P-poll__networl_7_8_AnsP_8" + "P-poll__networl_7_8_RI_0" + "P-poll__networl_7_8_RI_1" + "P-poll__networl_7_8_RI_2" + "P-poll__networl_7_8_RI_3" + "P-poll__networl_7_8_RI_4" + "P-poll__networl_7_8_RI_5" + "P-poll__networl_7_8_RI_6" + "P-poll__networl_7_8_RI_7" + "P-poll__networl_7_8_RI_8" + "P-poll__networl_7_8_AI_0" + "P-poll__networl_7_8_AI_1" + "P-poll__networl_7_8_AI_2" + "P-poll__networl_7_8_AI_3" + "P-poll__networl_7_8_AI_4" + "P-poll__networl_7_8_AI_5" + "P-poll__networl_7_8_AI_6" + "P-poll__networl_7_8_AI_7" + "P-poll__networl_7_8_AI_8" + "P-poll__networl_7_8_AnnP_0" + "P-poll__networl_7_8_AnnP_1" + "P-poll__networl_7_8_AnnP_2" + "P-poll__networl_7_8_AnnP_3" + "P-poll__networl_7_8_AnnP_4" + "P-poll__networl_7_8_AnnP_5" + "P-poll__networl_7_8_AnnP_6" + "P-poll__networl_7_8_AnnP_7" + "P-poll__networl_7_8_AnnP_8" + "P-poll__networl_7_8_RP_0" + "P-poll__networl_7_8_RP_1" + "P-poll__networl_7_8_RP_2" + "P-poll__networl_7_8_RP_3" + "P-poll__networl_7_8_RP_4" + "P-poll__networl_7_8_RP_5" + "P-poll__networl_7_8_RP_6" + "P-poll__networl_7_8_RP_7" + "P-poll__networl_7_8_RP_8" + "P-poll__networl_8_0_AskP_0" + "P-poll__networl_8_0_AskP_1" + "P-poll__networl_8_0_AskP_2" + "P-poll__networl_8_0_AskP_3" + "P-poll__networl_8_0_AskP_4" + "P-poll__networl_8_0_AskP_5" + "P-poll__networl_8_0_AskP_6" + "P-poll__networl_8_0_AskP_7" + "P-poll__networl_8_0_AskP_8" + "P-poll__networl_8_0_AnsP_0" + "P-poll__networl_8_0_AnsP_1" + "P-poll__networl_8_0_AnsP_2" + "P-poll__networl_8_0_AnsP_3" + "P-poll__networl_8_0_AnsP_4" + "P-poll__networl_8_0_AnsP_5" + "P-poll__networl_8_0_AnsP_6" + "P-poll__networl_8_0_AnsP_7" + "P-poll__networl_8_0_AnsP_8" + "P-poll__networl_8_0_RI_0" + "P-poll__networl_8_0_RI_1" + "P-poll__networl_8_0_RI_2" + "P-poll__networl_8_0_RI_3" + "P-poll__networl_8_0_RI_4" + "P-poll__networl_8_0_RI_5" + "P-poll__networl_8_0_RI_6" + "P-poll__networl_8_0_RI_7" + "P-poll__networl_8_0_RI_8" + "P-poll__networl_8_0_AI_0" + "P-poll__networl_8_0_AI_1" + "P-poll__networl_8_0_AI_2" + "P-poll__networl_8_0_AI_3" + "P-poll__networl_8_0_AI_4" + "P-poll__networl_8_0_AI_5" + "P-poll__networl_8_0_AI_6" + "P-poll__networl_8_0_AI_7" + "P-poll__networl_8_0_AI_8" + "P-poll__networl_8_0_AnnP_0" + "P-poll__networl_8_0_AnnP_1" + "P-poll__networl_8_0_AnnP_2" + "P-poll__networl_8_0_AnnP_3" + "P-poll__networl_8_0_AnnP_4" + "P-poll__networl_8_0_AnnP_5" + "P-poll__networl_8_0_AnnP_6" + "P-poll__networl_8_0_AnnP_7" + "P-poll__networl_8_0_AnnP_8" + "P-poll__networl_8_0_RP_0" + "P-poll__networl_8_0_RP_1" + "P-poll__networl_8_0_RP_2" + "P-poll__networl_8_0_RP_3" + "P-poll__networl_8_0_RP_4" + "P-poll__networl_8_0_RP_5" + "P-poll__networl_8_0_RP_6" + "P-poll__networl_8_0_RP_7" + "P-poll__networl_8_0_RP_8" + "P-poll__networl_8_1_AskP_0" + "P-poll__networl_8_1_AskP_1" + "P-poll__networl_8_1_AskP_2" + "P-poll__networl_8_1_AskP_3" + "P-poll__networl_8_1_AskP_4" + "P-poll__networl_8_1_AskP_5" + "P-poll__networl_8_1_AskP_6" + "P-poll__networl_8_1_AskP_7" + "P-poll__networl_8_1_AskP_8" + "P-poll__networl_8_1_AnsP_0" + "P-poll__networl_8_1_AnsP_1" + "P-poll__networl_8_1_AnsP_2" + "P-poll__networl_8_1_AnsP_3" + "P-poll__networl_8_1_AnsP_4" + "P-poll__networl_8_1_AnsP_5" + "P-poll__networl_8_1_AnsP_6" + "P-poll__networl_8_1_AnsP_7" + "P-poll__networl_8_1_AnsP_8" + "P-poll__networl_8_1_RI_0" + "P-poll__networl_8_1_RI_1" + "P-poll__networl_8_1_RI_2" + "P-poll__networl_8_1_RI_3" + "P-poll__networl_8_1_RI_4" + "P-poll__networl_8_1_RI_5" + "P-poll__networl_8_1_RI_6" + "P-poll__networl_8_1_RI_7" + "P-poll__networl_8_1_RI_8" + "P-poll__networl_8_1_AI_0" + "P-poll__networl_8_1_AI_1" + "P-poll__networl_8_1_AI_2" + "P-poll__networl_8_1_AI_3" + "P-poll__networl_8_1_AI_4" + "P-poll__networl_8_1_AI_5" + "P-poll__networl_8_1_AI_6" + "P-poll__networl_8_1_AI_7" + "P-poll__networl_8_1_AI_8" + "P-poll__networl_8_1_AnnP_0" + "P-poll__networl_8_1_AnnP_1" + "P-poll__networl_8_1_AnnP_2" + "P-poll__networl_8_1_AnnP_3" + "P-poll__networl_8_1_AnnP_4" + "P-poll__networl_8_1_AnnP_5" + "P-poll__networl_8_1_AnnP_6" + "P-poll__networl_8_1_AnnP_7" + "P-poll__networl_8_1_AnnP_8" + "P-poll__networl_8_1_RP_0" + "P-poll__networl_8_1_RP_1" + "P-poll__networl_8_1_RP_2" + "P-poll__networl_8_1_RP_3" + "P-poll__networl_8_1_RP_4" + "P-poll__networl_8_1_RP_5" + "P-poll__networl_8_1_RP_6" + "P-poll__networl_8_1_RP_7" + "P-poll__networl_8_1_RP_8" + "P-poll__networl_8_2_AskP_0" + "P-poll__networl_8_2_AskP_1" + "P-poll__networl_8_2_AskP_2" + "P-poll__networl_8_2_AskP_3" + "P-poll__networl_8_2_AskP_4" + "P-poll__networl_8_2_AskP_5" + "P-poll__networl_8_2_AskP_6" + "P-poll__networl_8_2_AskP_7" + "P-poll__networl_8_2_AskP_8" + "P-poll__networl_8_2_AnsP_0" + "P-poll__networl_8_2_AnsP_1" + "P-poll__networl_8_2_AnsP_2" + "P-poll__networl_8_2_AnsP_3" + "P-poll__networl_8_2_AnsP_4" + "P-poll__networl_8_2_AnsP_5" + "P-poll__networl_8_2_AnsP_6" + "P-poll__networl_8_2_AnsP_7" + "P-poll__networl_8_2_AnsP_8" + "P-poll__networl_8_2_RI_0" + "P-poll__networl_8_2_RI_1" + "P-poll__networl_8_2_RI_2" + "P-poll__networl_8_2_RI_3" + "P-poll__networl_8_2_RI_4" + "P-poll__networl_8_2_RI_5" + "P-poll__networl_8_2_RI_6" + "P-poll__networl_8_2_RI_7" + "P-poll__networl_8_2_RI_8" + "P-poll__networl_8_2_AI_0" + "P-poll__networl_8_2_AI_1" + "P-poll__networl_8_2_AI_2" + "P-poll__networl_8_2_AI_3" + "P-poll__networl_8_2_AI_4" + "P-poll__networl_8_2_AI_5" + "P-poll__networl_8_2_AI_6" + "P-poll__networl_8_2_AI_7" + "P-poll__networl_8_2_AI_8" + "P-poll__networl_8_2_AnnP_0" + "P-poll__networl_8_2_AnnP_1" + "P-poll__networl_8_2_AnnP_2" + "P-poll__networl_8_2_AnnP_3" + "P-poll__networl_8_2_AnnP_4" + "P-poll__networl_8_2_AnnP_5" + "P-poll__networl_8_2_AnnP_6" + "P-poll__networl_8_2_AnnP_7" + "P-poll__networl_8_2_AnnP_8" + "P-poll__networl_8_2_RP_0" + "P-poll__networl_8_2_RP_1" + "P-poll__networl_8_2_RP_2" + "P-poll__networl_8_2_RP_3" + "P-poll__networl_8_2_RP_4" + "P-poll__networl_8_2_RP_5" + "P-poll__networl_8_2_RP_6" + "P-poll__networl_8_2_RP_7" + "P-poll__networl_8_2_RP_8" + "P-poll__networl_8_3_AskP_0" + "P-poll__networl_8_3_AskP_1" + "P-poll__networl_8_3_AskP_2" + "P-poll__networl_8_3_AskP_3" + "P-poll__networl_8_3_AskP_4" + "P-poll__networl_8_3_AskP_5" + "P-poll__networl_8_3_AskP_6" + "P-poll__networl_8_3_AskP_7" + "P-poll__networl_8_3_AskP_8" + "P-poll__networl_8_3_AnsP_0" + "P-poll__networl_8_3_AnsP_1" + "P-poll__networl_8_3_AnsP_2" + "P-poll__networl_8_3_AnsP_3" + "P-poll__networl_8_3_AnsP_4" + "P-poll__networl_8_3_AnsP_5" + "P-poll__networl_8_3_AnsP_6" + "P-poll__networl_8_3_AnsP_7" + "P-poll__networl_8_3_AnsP_8" + "P-poll__networl_8_3_RI_0" + "P-poll__networl_8_3_RI_1" + "P-poll__networl_8_3_RI_2" + "P-poll__networl_8_3_RI_3" + "P-poll__networl_8_3_RI_4" + "P-poll__networl_8_3_RI_5" + "P-poll__networl_8_3_RI_6" + "P-poll__networl_8_3_RI_7" + "P-poll__networl_8_3_RI_8" + "P-poll__networl_8_3_AI_0" + "P-poll__networl_8_3_AI_1" + "P-poll__networl_8_3_AI_2" + "P-poll__networl_8_3_AI_3" + "P-poll__networl_8_3_AI_4" + "P-poll__networl_8_3_AI_5" + "P-poll__networl_8_3_AI_6" + "P-poll__networl_8_3_AI_7" + "P-poll__networl_8_3_AI_8" + "P-poll__networl_8_3_AnnP_0" + "P-poll__networl_8_3_AnnP_1" + "P-poll__networl_8_3_AnnP_2" + "P-poll__networl_8_3_AnnP_3" + "P-poll__networl_8_3_AnnP_4" + "P-poll__networl_8_3_AnnP_5" + "P-poll__networl_8_3_AnnP_6" + "P-poll__networl_8_3_AnnP_7" + "P-poll__networl_8_3_AnnP_8" + "P-poll__networl_8_3_RP_0" + "P-poll__networl_8_3_RP_1" + "P-poll__networl_8_3_RP_2" + "P-poll__networl_8_3_RP_3" + "P-poll__networl_8_3_RP_4" + "P-poll__networl_8_3_RP_5" + "P-poll__networl_8_3_RP_6" + "P-poll__networl_8_3_RP_7" + "P-poll__networl_8_3_RP_8" + "P-poll__networl_8_4_AskP_0" + "P-poll__networl_8_4_AskP_1" + "P-poll__networl_8_4_AskP_2" + "P-poll__networl_8_4_AskP_3" + "P-poll__networl_8_4_AskP_4" + "P-poll__networl_8_4_AskP_5" + "P-poll__networl_8_4_AskP_6" + "P-poll__networl_8_4_AskP_7" + "P-poll__networl_8_4_AskP_8" + "P-poll__networl_8_4_AnsP_0" + "P-poll__networl_8_4_AnsP_1" + "P-poll__networl_8_4_AnsP_2" + "P-poll__networl_8_4_AnsP_3" + "P-poll__networl_8_4_AnsP_4" + "P-poll__networl_8_4_AnsP_5" + "P-poll__networl_8_4_AnsP_6" + "P-poll__networl_8_4_AnsP_7" + "P-poll__networl_8_4_AnsP_8" + "P-poll__networl_8_4_RI_0" + "P-poll__networl_8_4_RI_1" + "P-poll__networl_8_4_RI_2" + "P-poll__networl_8_4_RI_3" + "P-poll__networl_8_4_RI_4" + "P-poll__networl_8_4_RI_5" + "P-poll__networl_8_4_RI_6" + "P-poll__networl_8_4_RI_7" + "P-poll__networl_8_4_RI_8" + "P-poll__networl_8_4_AI_0" + "P-poll__networl_8_4_AI_1" + "P-poll__networl_8_4_AI_2" + "P-poll__networl_8_4_AI_3" + "P-poll__networl_8_4_AI_4" + "P-poll__networl_8_4_AI_5" + "P-poll__networl_8_4_AI_6" + "P-poll__networl_8_4_AI_7" + "P-poll__networl_8_4_AI_8" + "P-poll__networl_8_4_AnnP_0" + "P-poll__networl_8_4_AnnP_1" + "P-poll__networl_8_4_AnnP_2" + "P-poll__networl_8_4_AnnP_3" + "P-poll__networl_8_4_AnnP_4" + "P-poll__networl_8_4_AnnP_5" + "P-poll__networl_8_4_AnnP_6" + "P-poll__networl_8_4_AnnP_7" + "P-poll__networl_8_4_AnnP_8" + "P-poll__networl_8_4_RP_0" + "P-poll__networl_8_4_RP_1" + "P-poll__networl_8_4_RP_2" + "P-poll__networl_8_4_RP_3" + "P-poll__networl_8_4_RP_4" + "P-poll__networl_8_4_RP_5" + "P-poll__networl_8_4_RP_6" + "P-poll__networl_8_4_RP_7" + "P-poll__networl_8_4_RP_8" + "P-poll__networl_8_5_AskP_0" + "P-poll__networl_8_5_AskP_1" + "P-poll__networl_8_5_AskP_2" + "P-poll__networl_8_5_AskP_3" + "P-poll__networl_8_5_AskP_4" + "P-poll__networl_8_5_AskP_5" + "P-poll__networl_8_5_AskP_6" + "P-poll__networl_8_5_AskP_7" + "P-poll__networl_8_5_AskP_8" + "P-poll__networl_8_5_AnsP_0" + "P-poll__networl_8_5_AnsP_1" + "P-poll__networl_8_5_AnsP_2" + "P-poll__networl_8_5_AnsP_3" + "P-poll__networl_8_5_AnsP_4" + "P-poll__networl_8_5_AnsP_5" + "P-poll__networl_8_5_AnsP_6" + "P-poll__networl_8_5_AnsP_7" + "P-poll__networl_8_5_AnsP_8" + "P-poll__networl_8_5_RI_0" + "P-poll__networl_8_5_RI_1" + "P-poll__networl_8_5_RI_2" + "P-poll__networl_8_5_RI_3" + "P-poll__networl_8_5_RI_4" + "P-poll__networl_8_5_RI_5" + "P-poll__networl_8_5_RI_6" + "P-poll__networl_8_5_RI_7" + "P-poll__networl_8_5_RI_8" + "P-poll__networl_8_5_AI_0" + "P-poll__networl_8_5_AI_1" + "P-poll__networl_8_5_AI_2" + "P-poll__networl_8_5_AI_3" + "P-poll__networl_8_5_AI_4" + "P-poll__networl_8_5_AI_5" + "P-poll__networl_8_5_AI_6" + "P-poll__networl_8_5_AI_7" + "P-poll__networl_8_5_AI_8" + "P-poll__networl_8_5_AnnP_0" + "P-poll__networl_8_5_AnnP_1" + "P-poll__networl_8_5_AnnP_2" + "P-poll__networl_8_5_AnnP_3" + "P-poll__networl_8_5_AnnP_4" + "P-poll__networl_8_5_AnnP_5" + "P-poll__networl_8_5_AnnP_6" + "P-poll__networl_8_5_AnnP_7" + "P-poll__networl_8_5_AnnP_8" + "P-poll__networl_8_5_RP_0" + "P-poll__networl_8_5_RP_1" + "P-poll__networl_8_5_RP_2" + "P-poll__networl_8_5_RP_3" + "P-poll__networl_8_5_RP_4" + "P-poll__networl_8_5_RP_5" + "P-poll__networl_8_5_RP_6" + "P-poll__networl_8_5_RP_7" + "P-poll__networl_8_5_RP_8" + "P-poll__networl_8_6_AskP_0" + "P-poll__networl_8_6_AskP_1" + "P-poll__networl_8_6_AskP_2" + "P-poll__networl_8_6_AskP_3" + "P-poll__networl_8_6_AskP_4" + "P-poll__networl_8_6_AskP_5" + "P-poll__networl_8_6_AskP_6" + "P-poll__networl_8_6_AskP_7" + "P-poll__networl_8_6_AskP_8" + "P-poll__networl_8_6_AnsP_0" + "P-poll__networl_8_6_AnsP_1" + "P-poll__networl_8_6_AnsP_2" + "P-poll__networl_8_6_AnsP_3" + "P-poll__networl_8_6_AnsP_4" + "P-poll__networl_8_6_AnsP_5" + "P-poll__networl_8_6_AnsP_6" + "P-poll__networl_8_6_AnsP_7" + "P-poll__networl_8_6_AnsP_8" + "P-poll__networl_8_6_RI_0" + "P-poll__networl_8_6_RI_1" + "P-poll__networl_8_6_RI_2" + "P-poll__networl_8_6_RI_3" + "P-poll__networl_8_6_RI_4" + "P-poll__networl_8_6_RI_5" + "P-poll__networl_8_6_RI_6" + "P-poll__networl_8_6_RI_7" + "P-poll__networl_8_6_RI_8" + "P-poll__networl_8_6_AI_0" + "P-poll__networl_8_6_AI_1" + "P-poll__networl_8_6_AI_2" + "P-poll__networl_8_6_AI_3" + "P-poll__networl_8_6_AI_4" + "P-poll__networl_8_6_AI_5" + "P-poll__networl_8_6_AI_6" + "P-poll__networl_8_6_AI_7" + "P-poll__networl_8_6_AI_8" + "P-poll__networl_8_6_AnnP_0" + "P-poll__networl_8_6_AnnP_1" + "P-poll__networl_8_6_AnnP_2" + "P-poll__networl_8_6_AnnP_3" + "P-poll__networl_8_6_AnnP_4" + "P-poll__networl_8_6_AnnP_5" + "P-poll__networl_8_6_AnnP_6" + "P-poll__networl_8_6_AnnP_7" + "P-poll__networl_8_6_AnnP_8" + "P-poll__networl_8_6_RP_0" + "P-poll__networl_8_6_RP_1" + "P-poll__networl_8_6_RP_2" + "P-poll__networl_8_6_RP_3" + "P-poll__networl_8_6_RP_4" + "P-poll__networl_8_6_RP_5" + "P-poll__networl_8_6_RP_6" + "P-poll__networl_8_6_RP_7" + "P-poll__networl_8_6_RP_8" + "P-poll__networl_8_7_AskP_0" + "P-poll__networl_8_7_AskP_1" + "P-poll__networl_8_7_AskP_2" + "P-poll__networl_8_7_AskP_3" + "P-poll__networl_8_7_AskP_4" + "P-poll__networl_8_7_AskP_5" + "P-poll__networl_8_7_AskP_6" + "P-poll__networl_8_7_AskP_7" + "P-poll__networl_8_7_AskP_8" + "P-poll__networl_8_7_AnsP_0" + "P-poll__networl_8_7_AnsP_1" + "P-poll__networl_8_7_AnsP_2" + "P-poll__networl_8_7_AnsP_3" + "P-poll__networl_8_7_AnsP_4" + "P-poll__networl_8_7_AnsP_5" + "P-poll__networl_8_7_AnsP_6" + "P-poll__networl_8_7_AnsP_7" + "P-poll__networl_8_7_AnsP_8" + "P-poll__networl_8_7_RI_0" + "P-poll__networl_8_7_RI_1" + "P-poll__networl_8_7_RI_2" + "P-poll__networl_8_7_RI_3" + "P-poll__networl_8_7_RI_4" + "P-poll__networl_8_7_RI_5" + "P-poll__networl_8_7_RI_6" + "P-poll__networl_8_7_RI_7" + "P-poll__networl_8_7_RI_8" + "P-poll__networl_8_7_AI_0" + "P-poll__networl_8_7_AI_1" + "P-poll__networl_8_7_AI_2" + "P-poll__networl_8_7_AI_3" + "P-poll__networl_8_7_AI_4" + "P-poll__networl_8_7_AI_5" + "P-poll__networl_8_7_AI_6" + "P-poll__networl_8_7_AI_7" + "P-poll__networl_8_7_AI_8" + "P-poll__networl_8_7_AnnP_0" + "P-poll__networl_8_7_AnnP_1" + "P-poll__networl_8_7_AnnP_2" + "P-poll__networl_8_7_AnnP_3" + "P-poll__networl_8_7_AnnP_4" + "P-poll__networl_8_7_AnnP_5" + "P-poll__networl_8_7_AnnP_6" + "P-poll__networl_8_7_AnnP_7" + "P-poll__networl_8_7_AnnP_8" + "P-poll__networl_8_7_RP_0" + "P-poll__networl_8_7_RP_1" + "P-poll__networl_8_7_RP_2" + "P-poll__networl_8_7_RP_3" + "P-poll__networl_8_7_RP_4" + "P-poll__networl_8_7_RP_5" + "P-poll__networl_8_7_RP_6" + "P-poll__networl_8_7_RP_7" + "P-poll__networl_8_7_RP_8" + "P-poll__networl_8_8_AskP_0" + "P-poll__networl_8_8_AskP_1" + "P-poll__networl_8_8_AskP_2" + "P-poll__networl_8_8_AskP_3" + "P-poll__networl_8_8_AskP_4" + "P-poll__networl_8_8_AskP_5" + "P-poll__networl_8_8_AskP_6" + "P-poll__networl_8_8_AskP_7" + "P-poll__networl_8_8_AskP_8" + "P-poll__networl_8_8_AnsP_0" + "P-poll__networl_8_8_AnsP_1" + "P-poll__networl_8_8_AnsP_2" + "P-poll__networl_8_8_AnsP_3" + "P-poll__networl_8_8_AnsP_4" + "P-poll__networl_8_8_AnsP_5" + "P-poll__networl_8_8_AnsP_6" + "P-poll__networl_8_8_AnsP_7" + "P-poll__networl_8_8_AnsP_8" + "P-poll__networl_8_8_RI_0" + "P-poll__networl_8_8_RI_1" + "P-poll__networl_8_8_RI_2" + "P-poll__networl_8_8_RI_3" + "P-poll__networl_8_8_RI_4" + "P-poll__networl_8_8_RI_5" + "P-poll__networl_8_8_RI_6" + "P-poll__networl_8_8_RI_7" + "P-poll__networl_8_8_RI_8" + "P-poll__networl_8_8_AI_0" + "P-poll__networl_8_8_AI_1" + "P-poll__networl_8_8_AI_2" + "P-poll__networl_8_8_AI_3" + "P-poll__networl_8_8_AI_4" + "P-poll__networl_8_8_AI_5" + "P-poll__networl_8_8_AI_6" + "P-poll__networl_8_8_AI_7" + "P-poll__networl_8_8_AI_8" + "P-poll__networl_8_8_AnnP_0" + "P-poll__networl_8_8_AnnP_1" + "P-poll__networl_8_8_AnnP_2" + "P-poll__networl_8_8_AnnP_3" + "P-poll__networl_8_8_AnnP_4" + "P-poll__networl_8_8_AnnP_5" + "P-poll__networl_8_8_AnnP_6" + "P-poll__networl_8_8_AnnP_7" + "P-poll__networl_8_8_AnnP_8" + "P-poll__networl_8_8_RP_0" + "P-poll__networl_8_8_RP_1" + "P-poll__networl_8_8_RP_2" + "P-poll__networl_8_8_RP_3" + "P-poll__networl_8_8_RP_4" + "P-poll__networl_8_8_RP_5" + "P-poll__networl_8_8_RP_6" + "P-poll__networl_8_8_RP_7" + "P-poll__networl_8_8_RP_8")))) and not(((("P-startNeg__broadcasting_0_1" + "P-startNeg__broadcasting_0_2" + "P-startNeg__broadcasting_0_3" + "P-startNeg__broadcasting_0_4" + "P-startNeg__broadcasting_0_5" + "P-startNeg__broadcasting_0_6" + "P-startNeg__broadcasting_0_7" + "P-startNeg__broadcasting_0_8" + "P-startNeg__broadcasting_1_1" + "P-startNeg__broadcasting_1_2" + "P-startNeg__broadcasting_1_3" + "P-startNeg__broadcasting_1_4" + "P-startNeg__broadcasting_1_5" + "P-startNeg__broadcasting_1_6" + "P-startNeg__broadcasting_1_7" + "P-startNeg__broadcasting_1_8" + "P-startNeg__broadcasting_2_1" + "P-startNeg__broadcasting_2_2" + "P-startNeg__broadcasting_2_3" + "P-startNeg__broadcasting_2_4" + "P-startNeg__broadcasting_2_5" + "P-startNeg__broadcasting_2_6" + "P-startNeg__broadcasting_2_7" + "P-startNeg__broadcasting_2_8" + "P-startNeg__broadcasting_3_1" + "P-startNeg__broadcasting_3_2" + "P-startNeg__broadcasting_3_3" + "P-startNeg__broadcasting_3_4" + "P-startNeg__broadcasting_3_5" + "P-startNeg__broadcasting_3_6" + "P-startNeg__broadcasting_3_7" + "P-startNeg__broadcasting_3_8" + "P-startNeg__broadcasting_4_1" + "P-startNeg__broadcasting_4_2" + "P-startNeg__broadcasting_4_3" + "P-startNeg__broadcasting_4_4" + "P-startNeg__broadcasting_4_5" + "P-startNeg__broadcasting_4_6" + "P-startNeg__broadcasting_4_7" + "P-startNeg__broadcasting_4_8" + "P-startNeg__broadcasting_5_1" + "P-startNeg__broadcasting_5_2" + "P-startNeg__broadcasting_5_3" + "P-startNeg__broadcasting_5_4" + "P-startNeg__broadcasting_5_5" + "P-startNeg__broadcasting_5_6" + "P-startNeg__broadcasting_5_7" + "P-startNeg__broadcasting_5_8" + "P-startNeg__broadcasting_6_1" + "P-startNeg__broadcasting_6_2" + "P-startNeg__broadcasting_6_3" + "P-startNeg__broadcasting_6_4" + "P-startNeg__broadcasting_6_5" + "P-startNeg__broadcasting_6_6" + "P-startNeg__broadcasting_6_7" + "P-startNeg__broadcasting_6_8" + "P-startNeg__broadcasting_7_1" + "P-startNeg__broadcasting_7_2" + "P-startNeg__broadcasting_7_3" + "P-startNeg__broadcasting_7_4" + "P-startNeg__broadcasting_7_5" + "P-startNeg__broadcasting_7_6" + "P-startNeg__broadcasting_7_7" + "P-startNeg__broadcasting_7_8" + "P-startNeg__broadcasting_8_1" + "P-startNeg__broadcasting_8_2" + "P-startNeg__broadcasting_8_3" + "P-startNeg__broadcasting_8_4" + "P-startNeg__broadcasting_8_5" + "P-startNeg__broadcasting_8_6" + "P-startNeg__broadcasting_8_7" + "P-startNeg__broadcasting_8_8") <= ("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8")) or (2 <= ("P-crashed_0" + "P-crashed_1" + "P-crashed_2" + "P-crashed_3" + "P-crashed_4" + "P-crashed_5" + "P-crashed_6" + "P-crashed_7" + "P-crashed_8"))))) )
NeoElection-COL-8-ReachabilityCardinality-6: not EF not ( ((((("P-electionInit_0" + "P-electionInit_1" + "P-electionInit_2" + "P-electionInit_3" + "P-electionInit_4" + "P-electionInit_5" + "P-electionInit_6" + "P-electionInit_7" + "P-electionInit_8") <= ("P-poll__networl_0_0_AskP_0" + "P-poll__networl_0_0_AskP_1" + "P-poll__networl_0_0_AskP_2" + "P-poll__networl_0_0_AskP_3" + "P-poll__networl_0_0_AskP_4" + "P-poll__networl_0_0_AskP_5" + "P-poll__networl_0_0_AskP_6" + "P-poll__networl_0_0_AskP_7" + "P-poll__networl_0_0_AskP_8" + "P-poll__networl_0_0_AnsP_0" + "P-poll__networl_0_0_AnsP_1" + "P-poll__networl_0_0_AnsP_2" + "P-poll__networl_0_0_AnsP_3" + "P-poll__networl_0_0_AnsP_4" + "P-poll__networl_0_0_AnsP_5" + "P-poll__networl_0_0_AnsP_6" + "P-poll__networl_0_0_AnsP_7" + "P-poll__networl_0_0_AnsP_8" + "P-poll__networl_0_0_RI_0" + "P-poll__networl_0_0_RI_1" + "P-poll__networl_0_0_RI_2" + "P-poll__networl_0_0_RI_3" + "P-poll__networl_0_0_RI_4" + "P-poll__networl_0_0_RI_5" + "P-poll__networl_0_0_RI_6" + "P-poll__networl_0_0_RI_7" + "P-poll__networl_0_0_RI_8" + "P-poll__networl_0_0_AI_0" + "P-poll__networl_0_0_AI_1" + "P-poll__networl_0_0_AI_2" + "P-poll__networl_0_0_AI_3" + "P-poll__networl_0_0_AI_4" + "P-poll__networl_0_0_AI_5" + "P-poll__networl_0_0_AI_6" + "P-poll__networl_0_0_AI_7" + "P-poll__networl_0_0_AI_8" + "P-poll__networl_0_0_AnnP_0" + "P-poll__networl_0_0_AnnP_1" + "P-poll__networl_0_0_AnnP_2" + "P-poll__networl_0_0_AnnP_3" + "P-poll__networl_0_0_AnnP_4" + "P-poll__networl_0_0_AnnP_5" + "P-poll__networl_0_0_AnnP_6" + "P-poll__networl_0_0_AnnP_7" + "P-poll__networl_0_0_AnnP_8" + "P-poll__networl_0_0_RP_0" + "P-poll__networl_0_0_RP_1" + "P-poll__networl_0_0_RP_2" + "P-poll__networl_0_0_RP_3" + "P-poll__networl_0_0_RP_4" + "P-poll__networl_0_0_RP_5" + "P-poll__networl_0_0_RP_6" + "P-poll__networl_0_0_RP_7" + "P-poll__networl_0_0_RP_8" + "P-poll__networl_0_1_AskP_0" + "P-poll__networl_0_1_AskP_1" + "P-poll__networl_0_1_AskP_2" + "P-poll__networl_0_1_AskP_3" + "P-poll__networl_0_1_AskP_4" + "P-poll__networl_0_1_AskP_5" + "P-poll__networl_0_1_AskP_6" + "P-poll__networl_0_1_AskP_7" + "P-poll__networl_0_1_AskP_8" + "P-poll__networl_0_1_AnsP_0" + "P-poll__networl_0_1_AnsP_1" + "P-poll__networl_0_1_AnsP_2" + "P-poll__networl_0_1_AnsP_3" + "P-poll__networl_0_1_AnsP_4" + "P-poll__networl_0_1_AnsP_5" + "P-poll__networl_0_1_AnsP_6" + "P-poll__networl_0_1_AnsP_7" + "P-poll__networl_0_1_AnsP_8" + "P-poll__networl_0_1_RI_0" + "P-poll__networl_0_1_RI_1" + "P-poll__networl_0_1_RI_2" + "P-poll__networl_0_1_RI_3" + "P-poll__networl_0_1_RI_4" + "P-poll__networl_0_1_RI_5" + "P-poll__networl_0_1_RI_6" + "P-poll__networl_0_1_RI_7" + "P-poll__networl_0_1_RI_8" + "P-poll__networl_0_1_AI_0" + "P-poll__networl_0_1_AI_1" + "P-poll__networl_0_1_AI_2" + "P-poll__networl_0_1_AI_3" + "P-poll__networl_0_1_AI_4" + "P-poll__networl_0_1_AI_5" + "P-poll__networl_0_1_AI_6" + "P-poll__networl_0_1_AI_7" + "P-poll__networl_0_1_AI_8" + "P-poll__networl_0_1_AnnP_0" + "P-poll__networl_0_1_AnnP_1" + "P-poll__networl_0_1_AnnP_2" + "P-poll__networl_0_1_AnnP_3" + "P-poll__networl_0_1_AnnP_4" + "P-poll__networl_0_1_AnnP_5" + "P-poll__networl_0_1_AnnP_6" + "P-poll__networl_0_1_AnnP_7" + "P-poll__networl_0_1_AnnP_8" + "P-poll__networl_0_1_RP_0" + "P-poll__networl_0_1_RP_1" + "P-poll__networl_0_1_RP_2" + "P-poll__networl_0_1_RP_3" + "P-poll__networl_0_1_RP_4" + "P-poll__networl_0_1_RP_5" + "P-poll__networl_0_1_RP_6" + "P-poll__networl_0_1_RP_7" + "P-poll__networl_0_1_RP_8" + "P-poll__networl_0_2_AskP_0" + "P-poll__networl_0_2_AskP_1" + "P-poll__networl_0_2_AskP_2" + "P-poll__networl_0_2_AskP_3" + "P-poll__networl_0_2_AskP_4" + "P-poll__networl_0_2_AskP_5" + "P-poll__networl_0_2_AskP_6" + "P-poll__networl_0_2_AskP_7" + "P-poll__networl_0_2_AskP_8" + "P-poll__networl_0_2_AnsP_0" + "P-poll__networl_0_2_AnsP_1" + "P-poll__networl_0_2_AnsP_2" + "P-poll__networl_0_2_AnsP_3" + "P-poll__networl_0_2_AnsP_4" + "P-poll__networl_0_2_AnsP_5" + "P-poll__networl_0_2_AnsP_6" + "P-poll__networl_0_2_AnsP_7" + "P-poll__networl_0_2_AnsP_8" + "P-poll__networl_0_2_RI_0" + "P-poll__networl_0_2_RI_1" + "P-poll__networl_0_2_RI_2" + "P-poll__networl_0_2_RI_3" + "P-poll__networl_0_2_RI_4" + "P-poll__networl_0_2_RI_5" + "P-poll__networl_0_2_RI_6" + "P-poll__networl_0_2_RI_7" + "P-poll__networl_0_2_RI_8" + "P-poll__networl_0_2_AI_0" + "P-poll__networl_0_2_AI_1" + "P-poll__networl_0_2_AI_2" + "P-poll__networl_0_2_AI_3" + "P-poll__networl_0_2_AI_4" + "P-poll__networl_0_2_AI_5" + "P-poll__networl_0_2_AI_6" + "P-poll__networl_0_2_AI_7" + "P-poll__networl_0_2_AI_8" + "P-poll__networl_0_2_AnnP_0" + "P-poll__networl_0_2_AnnP_1" + "P-poll__networl_0_2_AnnP_2" + "P-poll__networl_0_2_AnnP_3" + "P-poll__networl_0_2_AnnP_4" + "P-poll__networl_0_2_AnnP_5" + "P-poll__networl_0_2_AnnP_6" + "P-poll__networl_0_2_AnnP_7" + "P-poll__networl_0_2_AnnP_8" + "P-poll__networl_0_2_RP_0" + "P-poll__networl_0_2_RP_1" + "P-poll__networl_0_2_RP_2" + "P-poll__networl_0_2_RP_3" + "P-poll__networl_0_2_RP_4" + "P-poll__networl_0_2_RP_5" + "P-poll__networl_0_2_RP_6" + "P-poll__networl_0_2_RP_7" + "P-poll__networl_0_2_RP_8" + "P-poll__networl_0_3_AskP_0" + "P-poll__networl_0_3_AskP_1" + "P-poll__networl_0_3_AskP_2" + "P-poll__networl_0_3_AskP_3" + "P-poll__networl_0_3_AskP_4" + "P-poll__networl_0_3_AskP_5" + "P-poll__networl_0_3_AskP_6" + "P-poll__networl_0_3_AskP_7" + "P-poll__networl_0_3_AskP_8" + "P-poll__networl_0_3_AnsP_0" + "P-poll__networl_0_3_AnsP_1" + "P-poll__networl_0_3_AnsP_2" + "P-poll__networl_0_3_AnsP_3" + "P-poll__networl_0_3_AnsP_4" + "P-poll__networl_0_3_AnsP_5" + "P-poll__networl_0_3_AnsP_6" + "P-poll__networl_0_3_AnsP_7" + "P-poll__networl_0_3_AnsP_8" + "P-poll__networl_0_3_RI_0" + "P-poll__networl_0_3_RI_1" + "P-poll__networl_0_3_RI_2" + "P-poll__networl_0_3_RI_3" + "P-poll__networl_0_3_RI_4" + "P-poll__networl_0_3_RI_5" + "P-poll__networl_0_3_RI_6" + "P-poll__networl_0_3_RI_7" + "P-poll__networl_0_3_RI_8" + "P-poll__networl_0_3_AI_0" + "P-poll__networl_0_3_AI_1" + "P-poll__networl_0_3_AI_2" + "P-poll__networl_0_3_AI_3" + "P-poll__networl_0_3_AI_4" + "P-poll__networl_0_3_AI_5" + "P-poll__networl_0_3_AI_6" + "P-poll__networl_0_3_AI_7" + "P-poll__networl_0_3_AI_8" + "P-poll__networl_0_3_AnnP_0" + "P-poll__networl_0_3_AnnP_1" + "P-poll__networl_0_3_AnnP_2" + "P-poll__networl_0_3_AnnP_3" + "P-poll__networl_0_3_AnnP_4" + "P-poll__networl_0_3_AnnP_5" + "P-poll__networl_0_3_AnnP_6" + "P-poll__networl_0_3_AnnP_7" + "P-poll__networl_0_3_AnnP_8" + "P-poll__networl_0_3_RP_0" + "P-poll__networl_0_3_RP_1" + "P-poll__networl_0_3_RP_2" + "P-poll__networl_0_3_RP_3" + "P-poll__networl_0_3_RP_4" + "P-poll__networl_0_3_RP_5" + "P-poll__networl_0_3_RP_6" + "P-poll__networl_0_3_RP_7" + "P-poll__networl_0_3_RP_8" + "P-poll__networl_0_4_AskP_0" + "P-poll__networl_0_4_AskP_1" + "P-poll__networl_0_4_AskP_2" + "P-poll__networl_0_4_AskP_3" + "P-poll__networl_0_4_AskP_4" + "P-poll__networl_0_4_AskP_5" + "P-poll__networl_0_4_AskP_6" + "P-poll__networl_0_4_AskP_7" + "P-poll__networl_0_4_AskP_8" + "P-poll__networl_0_4_AnsP_0" + "P-poll__networl_0_4_AnsP_1" + "P-poll__networl_0_4_AnsP_2" + "P-poll__networl_0_4_AnsP_3" + "P-poll__networl_0_4_AnsP_4" + "P-poll__networl_0_4_AnsP_5" + "P-poll__networl_0_4_AnsP_6" + "P-poll__networl_0_4_AnsP_7" + "P-poll__networl_0_4_AnsP_8" + "P-poll__networl_0_4_RI_0" + "P-poll__networl_0_4_RI_1" + "P-poll__networl_0_4_RI_2" + "P-poll__networl_0_4_RI_3" + "P-poll__networl_0_4_RI_4" + "P-poll__networl_0_4_RI_5" + "P-poll__networl_0_4_RI_6" + "P-poll__networl_0_4_RI_7" + "P-poll__networl_0_4_RI_8" + "P-poll__networl_0_4_AI_0" + "P-poll__networl_0_4_AI_1" + "P-poll__networl_0_4_AI_2" + "P-poll__networl_0_4_AI_3" + "P-poll__networl_0_4_AI_4" + "P-poll__networl_0_4_AI_5" + "P-poll__networl_0_4_AI_6" + "P-poll__networl_0_4_AI_7" + "P-poll__networl_0_4_AI_8" + "P-poll__networl_0_4_AnnP_0" + "P-poll__networl_0_4_AnnP_1" + "P-poll__networl_0_4_AnnP_2" + "P-poll__networl_0_4_AnnP_3" + "P-poll__networl_0_4_AnnP_4" + "P-poll__networl_0_4_AnnP_5" + "P-poll__networl_0_4_AnnP_6" + "P-poll__networl_0_4_AnnP_7" + "P-poll__networl_0_4_AnnP_8" + "P-poll__networl_0_4_RP_0" + "P-poll__networl_0_4_RP_1" + "P-poll__networl_0_4_RP_2" + "P-poll__networl_0_4_RP_3" + "P-poll__networl_0_4_RP_4" + "P-poll__networl_0_4_RP_5" + "P-poll__networl_0_4_RP_6" + "P-poll__networl_0_4_RP_7" + "P-poll__networl_0_4_RP_8" + "P-poll__networl_0_5_AskP_0" + "P-poll__networl_0_5_AskP_1" + "P-poll__networl_0_5_AskP_2" + "P-poll__networl_0_5_AskP_3" + "P-poll__networl_0_5_AskP_4" + "P-poll__networl_0_5_AskP_5" + "P-poll__networl_0_5_AskP_6" + "P-poll__networl_0_5_AskP_7" + "P-poll__networl_0_5_AskP_8" + "P-poll__networl_0_5_AnsP_0" + "P-poll__networl_0_5_AnsP_1" + "P-poll__networl_0_5_AnsP_2" + "P-poll__networl_0_5_AnsP_3" + "P-poll__networl_0_5_AnsP_4" + "P-poll__networl_0_5_AnsP_5" + "P-poll__networl_0_5_AnsP_6" + "P-poll__networl_0_5_AnsP_7" + "P-poll__networl_0_5_AnsP_8" + "P-poll__networl_0_5_RI_0" + "P-poll__networl_0_5_RI_1" + "P-poll__networl_0_5_RI_2" + "P-poll__networl_0_5_RI_3" + "P-poll__networl_0_5_RI_4" + "P-poll__networl_0_5_RI_5" + "P-poll__networl_0_5_RI_6" + "P-poll__networl_0_5_RI_7" + "P-poll__networl_0_5_RI_8" + "P-poll__networl_0_5_AI_0" + "P-poll__networl_0_5_AI_1" + "P-poll__networl_0_5_AI_2" + "P-poll__networl_0_5_AI_3" + "P-poll__networl_0_5_AI_4" + "P-poll__networl_0_5_AI_5" + "P-poll__networl_0_5_AI_6" + "P-poll__networl_0_5_AI_7" + "P-poll__networl_0_5_AI_8" + "P-poll__networl_0_5_AnnP_0" + "P-poll__networl_0_5_AnnP_1" + "P-poll__networl_0_5_AnnP_2" + "P-poll__networl_0_5_AnnP_3" + "P-poll__networl_0_5_AnnP_4" + "P-poll__networl_0_5_AnnP_5" + "P-poll__networl_0_5_AnnP_6" + "P-poll__networl_0_5_AnnP_7" + "P-poll__networl_0_5_AnnP_8" + "P-poll__networl_0_5_RP_0" + "P-poll__networl_0_5_RP_1" + "P-poll__networl_0_5_RP_2" + "P-poll__networl_0_5_RP_3" + "P-poll__networl_0_5_RP_4" + "P-poll__networl_0_5_RP_5" + "P-poll__networl_0_5_RP_6" + "P-poll__networl_0_5_RP_7" + "P-poll__networl_0_5_RP_8" + "P-poll__networl_0_6_AskP_0" + "P-poll__networl_0_6_AskP_1" + "P-poll__networl_0_6_AskP_2" + "P-poll__networl_0_6_AskP_3" + "P-poll__networl_0_6_AskP_4" + "P-poll__networl_0_6_AskP_5" + "P-poll__networl_0_6_AskP_6" + "P-poll__networl_0_6_AskP_7" + "P-poll__networl_0_6_AskP_8" + "P-poll__networl_0_6_AnsP_0" + "P-poll__networl_0_6_AnsP_1" + "P-poll__networl_0_6_AnsP_2" + "P-poll__networl_0_6_AnsP_3" + "P-poll__networl_0_6_AnsP_4" + "P-poll__networl_0_6_AnsP_5" + "P-poll__networl_0_6_AnsP_6" + "P-poll__networl_0_6_AnsP_7" + "P-poll__networl_0_6_AnsP_8" + "P-poll__networl_0_6_RI_0" + "P-poll__networl_0_6_RI_1" + "P-poll__networl_0_6_RI_2" + "P-poll__networl_0_6_RI_3" + "P-poll__networl_0_6_RI_4" + "P-poll__networl_0_6_RI_5" + "P-poll__networl_0_6_RI_6" + "P-poll__networl_0_6_RI_7" + "P-poll__networl_0_6_RI_8" + "P-poll__networl_0_6_AI_0" + "P-poll__networl_0_6_AI_1" + "P-poll__networl_0_6_AI_2" + "P-poll__networl_0_6_AI_3" + "P-poll__networl_0_6_AI_4" + "P-poll__networl_0_6_AI_5" + "P-poll__networl_0_6_AI_6" + "P-poll__networl_0_6_AI_7" + "P-poll__networl_0_6_AI_8" + "P-poll__networl_0_6_AnnP_0" + "P-poll__networl_0_6_AnnP_1" + "P-poll__networl_0_6_AnnP_2" + "P-poll__networl_0_6_AnnP_3" + "P-poll__networl_0_6_AnnP_4" + "P-poll__networl_0_6_AnnP_5" + "P-poll__networl_0_6_AnnP_6" + "P-poll__networl_0_6_AnnP_7" + "P-poll__networl_0_6_AnnP_8" + "P-poll__networl_0_6_RP_0" + "P-poll__networl_0_6_RP_1" + "P-poll__networl_0_6_RP_2" + "P-poll__networl_0_6_RP_3" + "P-poll__networl_0_6_RP_4" + "P-poll__networl_0_6_RP_5" + "P-poll__networl_0_6_RP_6" + "P-poll__networl_0_6_RP_7" + "P-poll__networl_0_6_RP_8" + "P-poll__networl_0_7_AskP_0" + "P-poll__networl_0_7_AskP_1" + "P-poll__networl_0_7_AskP_2" + "P-poll__networl_0_7_AskP_3" + "P-poll__networl_0_7_AskP_4" + "P-poll__networl_0_7_AskP_5" + "P-poll__networl_0_7_AskP_6" + "P-poll__networl_0_7_AskP_7" + "P-poll__networl_0_7_AskP_8" + "P-poll__networl_0_7_AnsP_0" + "P-poll__networl_0_7_AnsP_1" + "P-poll__networl_0_7_AnsP_2" + "P-poll__networl_0_7_AnsP_3" + "P-poll__networl_0_7_AnsP_4" + "P-poll__networl_0_7_AnsP_5" + "P-poll__networl_0_7_AnsP_6" + "P-poll__networl_0_7_AnsP_7" + "P-poll__networl_0_7_AnsP_8" + "P-poll__networl_0_7_RI_0" + "P-poll__networl_0_7_RI_1" + "P-poll__networl_0_7_RI_2" + "P-poll__networl_0_7_RI_3" + "P-poll__networl_0_7_RI_4" + "P-poll__networl_0_7_RI_5" + "P-poll__networl_0_7_RI_6" + "P-poll__networl_0_7_RI_7" + "P-poll__networl_0_7_RI_8" + "P-poll__networl_0_7_AI_0" + "P-poll__networl_0_7_AI_1" + "P-poll__networl_0_7_AI_2" + "P-poll__networl_0_7_AI_3" + "P-poll__networl_0_7_AI_4" + "P-poll__networl_0_7_AI_5" + "P-poll__networl_0_7_AI_6" + "P-poll__networl_0_7_AI_7" + "P-poll__networl_0_7_AI_8" + "P-poll__networl_0_7_AnnP_0" + "P-poll__networl_0_7_AnnP_1" + "P-poll__networl_0_7_AnnP_2" + "P-poll__networl_0_7_AnnP_3" + "P-poll__networl_0_7_AnnP_4" + "P-poll__networl_0_7_AnnP_5" + "P-poll__networl_0_7_AnnP_6" + "P-poll__networl_0_7_AnnP_7" + "P-poll__networl_0_7_AnnP_8" + "P-poll__networl_0_7_RP_0" + "P-poll__networl_0_7_RP_1" + "P-poll__networl_0_7_RP_2" + "P-poll__networl_0_7_RP_3" + "P-poll__networl_0_7_RP_4" + "P-poll__networl_0_7_RP_5" + "P-poll__networl_0_7_RP_6" + "P-poll__networl_0_7_RP_7" + "P-poll__networl_0_7_RP_8" + "P-poll__networl_0_8_AskP_0" + "P-poll__networl_0_8_AskP_1" + "P-poll__networl_0_8_AskP_2" + "P-poll__networl_0_8_AskP_3" + "P-poll__networl_0_8_AskP_4" + "P-poll__networl_0_8_AskP_5" + "P-poll__networl_0_8_AskP_6" + "P-poll__networl_0_8_AskP_7" + "P-poll__networl_0_8_AskP_8" + "P-poll__networl_0_8_AnsP_0" + "P-poll__networl_0_8_AnsP_1" + "P-poll__networl_0_8_AnsP_2" + "P-poll__networl_0_8_AnsP_3" + "P-poll__networl_0_8_AnsP_4" + "P-poll__networl_0_8_AnsP_5" + "P-poll__networl_0_8_AnsP_6" + "P-poll__networl_0_8_AnsP_7" + "P-poll__networl_0_8_AnsP_8" + "P-poll__networl_0_8_RI_0" + "P-poll__networl_0_8_RI_1" + "P-poll__networl_0_8_RI_2" + "P-poll__networl_0_8_RI_3" + "P-poll__networl_0_8_RI_4" + "P-poll__networl_0_8_RI_5" + "P-poll__networl_0_8_RI_6" + "P-poll__networl_0_8_RI_7" + "P-poll__networl_0_8_RI_8" + "P-poll__networl_0_8_AI_0" + "P-poll__networl_0_8_AI_1" + "P-poll__networl_0_8_AI_2" + "P-poll__networl_0_8_AI_3" + "P-poll__networl_0_8_AI_4" + "P-poll__networl_0_8_AI_5" + "P-poll__networl_0_8_AI_6" + "P-poll__networl_0_8_AI_7" + "P-poll__networl_0_8_AI_8" + "P-poll__networl_0_8_AnnP_0" + "P-poll__networl_0_8_AnnP_1" + "P-poll__networl_0_8_AnnP_2" + "P-poll__networl_0_8_AnnP_3" + "P-poll__networl_0_8_AnnP_4" + "P-poll__networl_0_8_AnnP_5" + "P-poll__networl_0_8_AnnP_6" + "P-poll__networl_0_8_AnnP_7" + "P-poll__networl_0_8_AnnP_8" + "P-poll__networl_0_8_RP_0" + "P-poll__networl_0_8_RP_1" + "P-poll__networl_0_8_RP_2" + "P-poll__networl_0_8_RP_3" + "P-poll__networl_0_8_RP_4" + "P-poll__networl_0_8_RP_5" + "P-poll__networl_0_8_RP_6" + "P-poll__networl_0_8_RP_7" + "P-poll__networl_0_8_RP_8" + "P-poll__networl_1_0_AskP_0" + "P-poll__networl_1_0_AskP_1" + "P-poll__networl_1_0_AskP_2" + "P-poll__networl_1_0_AskP_3" + "P-poll__networl_1_0_AskP_4" + "P-poll__networl_1_0_AskP_5" + "P-poll__networl_1_0_AskP_6" + "P-poll__networl_1_0_AskP_7" + "P-poll__networl_1_0_AskP_8" + "P-poll__networl_1_0_AnsP_0" + "P-poll__networl_1_0_AnsP_1" + "P-poll__networl_1_0_AnsP_2" + "P-poll__networl_1_0_AnsP_3" + "P-poll__networl_1_0_AnsP_4" + "P-poll__networl_1_0_AnsP_5" + "P-poll__networl_1_0_AnsP_6" + "P-poll__networl_1_0_AnsP_7" + "P-poll__networl_1_0_AnsP_8" + "P-poll__networl_1_0_RI_0" + "P-poll__networl_1_0_RI_1" + "P-poll__networl_1_0_RI_2" + "P-poll__networl_1_0_RI_3" + "P-poll__networl_1_0_RI_4" + "P-poll__networl_1_0_RI_5" + "P-poll__networl_1_0_RI_6" + "P-poll__networl_1_0_RI_7" + "P-poll__networl_1_0_RI_8" + "P-poll__networl_1_0_AI_0" + "P-poll__networl_1_0_AI_1" + "P-poll__networl_1_0_AI_2" + "P-poll__networl_1_0_AI_3" + "P-poll__networl_1_0_AI_4" + "P-poll__networl_1_0_AI_5" + "P-poll__networl_1_0_AI_6" + "P-poll__networl_1_0_AI_7" + "P-poll__networl_1_0_AI_8" + "P-poll__networl_1_0_AnnP_0" + "P-poll__networl_1_0_AnnP_1" + "P-poll__networl_1_0_AnnP_2" + "P-poll__networl_1_0_AnnP_3" + "P-poll__networl_1_0_AnnP_4" + "P-poll__networl_1_0_AnnP_5" + "P-poll__networl_1_0_AnnP_6" + "P-poll__networl_1_0_AnnP_7" + "P-poll__networl_1_0_AnnP_8" + "P-poll__networl_1_0_RP_0" + "P-poll__networl_1_0_RP_1" + "P-poll__networl_1_0_RP_2" + "P-poll__networl_1_0_RP_3" + "P-poll__networl_1_0_RP_4" + "P-poll__networl_1_0_RP_5" + "P-poll__networl_1_0_RP_6" + "P-poll__networl_1_0_RP_7" + "P-poll__networl_1_0_RP_8" + "P-poll__networl_1_1_AskP_0" + "P-poll__networl_1_1_AskP_1" + "P-poll__networl_1_1_AskP_2" + "P-poll__networl_1_1_AskP_3" + "P-poll__networl_1_1_AskP_4" + "P-poll__networl_1_1_AskP_5" + "P-poll__networl_1_1_AskP_6" + "P-poll__networl_1_1_AskP_7" + "P-poll__networl_1_1_AskP_8" + "P-poll__networl_1_1_AnsP_0" + "P-poll__networl_1_1_AnsP_1" + "P-poll__networl_1_1_AnsP_2" + "P-poll__networl_1_1_AnsP_3" + "P-poll__networl_1_1_AnsP_4" + "P-poll__networl_1_1_AnsP_5" + "P-poll__networl_1_1_AnsP_6" + "P-poll__networl_1_1_AnsP_7" + "P-poll__networl_1_1_AnsP_8" + "P-poll__networl_1_1_RI_0" + "P-poll__networl_1_1_RI_1" + "P-poll__networl_1_1_RI_2" + "P-poll__networl_1_1_RI_3" + "P-poll__networl_1_1_RI_4" + "P-poll__networl_1_1_RI_5" + "P-poll__networl_1_1_RI_6" + "P-poll__networl_1_1_RI_7" + "P-poll__networl_1_1_RI_8" + "P-poll__networl_1_1_AI_0" + "P-poll__networl_1_1_AI_1" + "P-poll__networl_1_1_AI_2" + "P-poll__networl_1_1_AI_3" + "P-poll__networl_1_1_AI_4" + "P-poll__networl_1_1_AI_5" + "P-poll__networl_1_1_AI_6" + "P-poll__networl_1_1_AI_7" + "P-poll__networl_1_1_AI_8" + "P-poll__networl_1_1_AnnP_0" + "P-poll__networl_1_1_AnnP_1" + "P-poll__networl_1_1_AnnP_2" + "P-poll__networl_1_1_AnnP_3" + "P-poll__networl_1_1_AnnP_4" + "P-poll__networl_1_1_AnnP_5" + "P-poll__networl_1_1_AnnP_6" + "P-poll__networl_1_1_AnnP_7" + "P-poll__networl_1_1_AnnP_8" + "P-poll__networl_1_1_RP_0" + "P-poll__networl_1_1_RP_1" + "P-poll__networl_1_1_RP_2" + "P-poll__networl_1_1_RP_3" + "P-poll__networl_1_1_RP_4" + "P-poll__networl_1_1_RP_5" + "P-poll__networl_1_1_RP_6" + "P-poll__networl_1_1_RP_7" + "P-poll__networl_1_1_RP_8" + "P-poll__networl_1_2_AskP_0" + "P-poll__networl_1_2_AskP_1" + "P-poll__networl_1_2_AskP_2" + "P-poll__networl_1_2_AskP_3" + "P-poll__networl_1_2_AskP_4" + "P-poll__networl_1_2_AskP_5" + "P-poll__networl_1_2_AskP_6" + "P-poll__networl_1_2_AskP_7" + "P-poll__networl_1_2_AskP_8" + "P-poll__networl_1_2_AnsP_0" + "P-poll__networl_1_2_AnsP_1" + "P-poll__networl_1_2_AnsP_2" + "P-poll__networl_1_2_AnsP_3" + "P-poll__networl_1_2_AnsP_4" + "P-poll__networl_1_2_AnsP_5" + "P-poll__networl_1_2_AnsP_6" + "P-poll__networl_1_2_AnsP_7" + "P-poll__networl_1_2_AnsP_8" + "P-poll__networl_1_2_RI_0" + "P-poll__networl_1_2_RI_1" + "P-poll__networl_1_2_RI_2" + "P-poll__networl_1_2_RI_3" + "P-poll__networl_1_2_RI_4" + "P-poll__networl_1_2_RI_5" + "P-poll__networl_1_2_RI_6" + "P-poll__networl_1_2_RI_7" + "P-poll__networl_1_2_RI_8" + "P-poll__networl_1_2_AI_0" + "P-poll__networl_1_2_AI_1" + "P-poll__networl_1_2_AI_2" + "P-poll__networl_1_2_AI_3" + "P-poll__networl_1_2_AI_4" + "P-poll__networl_1_2_AI_5" + "P-poll__networl_1_2_AI_6" + "P-poll__networl_1_2_AI_7" + "P-poll__networl_1_2_AI_8" + "P-poll__networl_1_2_AnnP_0" + "P-poll__networl_1_2_AnnP_1" + "P-poll__networl_1_2_AnnP_2" + "P-poll__networl_1_2_AnnP_3" + "P-poll__networl_1_2_AnnP_4" + "P-poll__networl_1_2_AnnP_5" + "P-poll__networl_1_2_AnnP_6" + "P-poll__networl_1_2_AnnP_7" + "P-poll__networl_1_2_AnnP_8" + "P-poll__networl_1_2_RP_0" + "P-poll__networl_1_2_RP_1" + "P-poll__networl_1_2_RP_2" + "P-poll__networl_1_2_RP_3" + "P-poll__networl_1_2_RP_4" + "P-poll__networl_1_2_RP_5" + "P-poll__networl_1_2_RP_6" + "P-poll__networl_1_2_RP_7" + "P-poll__networl_1_2_RP_8" + "P-poll__networl_1_3_AskP_0" + "P-poll__networl_1_3_AskP_1" + "P-poll__networl_1_3_AskP_2" + "P-poll__networl_1_3_AskP_3" + "P-poll__networl_1_3_AskP_4" + "P-poll__networl_1_3_AskP_5" + "P-poll__networl_1_3_AskP_6" + "P-poll__networl_1_3_AskP_7" + "P-poll__networl_1_3_AskP_8" + "P-poll__networl_1_3_AnsP_0" + "P-poll__networl_1_3_AnsP_1" + "P-poll__networl_1_3_AnsP_2" + "P-poll__networl_1_3_AnsP_3" + "P-poll__networl_1_3_AnsP_4" + "P-poll__networl_1_3_AnsP_5" + "P-poll__networl_1_3_AnsP_6" + "P-poll__networl_1_3_AnsP_7" + "P-poll__networl_1_3_AnsP_8" + "P-poll__networl_1_3_RI_0" + "P-poll__networl_1_3_RI_1" + "P-poll__networl_1_3_RI_2" + "P-poll__networl_1_3_RI_3" + "P-poll__networl_1_3_RI_4" + "P-poll__networl_1_3_RI_5" + "P-poll__networl_1_3_RI_6" + "P-poll__networl_1_3_RI_7" + "P-poll__networl_1_3_RI_8" + "P-poll__networl_1_3_AI_0" + "P-poll__networl_1_3_AI_1" + "P-poll__networl_1_3_AI_2" + "P-poll__networl_1_3_AI_3" + "P-poll__networl_1_3_AI_4" + "P-poll__networl_1_3_AI_5" + "P-poll__networl_1_3_AI_6" + "P-poll__networl_1_3_AI_7" + "P-poll__networl_1_3_AI_8" + "P-poll__networl_1_3_AnnP_0" + "P-poll__networl_1_3_AnnP_1" + "P-poll__networl_1_3_AnnP_2" + "P-poll__networl_1_3_AnnP_3" + "P-poll__networl_1_3_AnnP_4" + "P-poll__networl_1_3_AnnP_5" + "P-poll__networl_1_3_AnnP_6" + "P-poll__networl_1_3_AnnP_7" + "P-poll__networl_1_3_AnnP_8" + "P-poll__networl_1_3_RP_0" + "P-poll__networl_1_3_RP_1" + "P-poll__networl_1_3_RP_2" + "P-poll__networl_1_3_RP_3" + "P-poll__networl_1_3_RP_4" + "P-poll__networl_1_3_RP_5" + "P-poll__networl_1_3_RP_6" + "P-poll__networl_1_3_RP_7" + "P-poll__networl_1_3_RP_8" + "P-poll__networl_1_4_AskP_0" + "P-poll__networl_1_4_AskP_1" + "P-poll__networl_1_4_AskP_2" + "P-poll__networl_1_4_AskP_3" + "P-poll__networl_1_4_AskP_4" + "P-poll__networl_1_4_AskP_5" + "P-poll__networl_1_4_AskP_6" + "P-poll__networl_1_4_AskP_7" + "P-poll__networl_1_4_AskP_8" + "P-poll__networl_1_4_AnsP_0" + "P-poll__networl_1_4_AnsP_1" + "P-poll__networl_1_4_AnsP_2" + "P-poll__networl_1_4_AnsP_3" + "P-poll__networl_1_4_AnsP_4" + "P-poll__networl_1_4_AnsP_5" + "P-poll__networl_1_4_AnsP_6" + "P-poll__networl_1_4_AnsP_7" + "P-poll__networl_1_4_AnsP_8" + "P-poll__networl_1_4_RI_0" + "P-poll__networl_1_4_RI_1" + "P-poll__networl_1_4_RI_2" + "P-poll__networl_1_4_RI_3" + "P-poll__networl_1_4_RI_4" + "P-poll__networl_1_4_RI_5" + "P-poll__networl_1_4_RI_6" + "P-poll__networl_1_4_RI_7" + "P-poll__networl_1_4_RI_8" + "P-poll__networl_1_4_AI_0" + "P-poll__networl_1_4_AI_1" + "P-poll__networl_1_4_AI_2" + "P-poll__networl_1_4_AI_3" + "P-poll__networl_1_4_AI_4" + "P-poll__networl_1_4_AI_5" + "P-poll__networl_1_4_AI_6" + "P-poll__networl_1_4_AI_7" + "P-poll__networl_1_4_AI_8" + "P-poll__networl_1_4_AnnP_0" + "P-poll__networl_1_4_AnnP_1" + "P-poll__networl_1_4_AnnP_2" + "P-poll__networl_1_4_AnnP_3" + "P-poll__networl_1_4_AnnP_4" + "P-poll__networl_1_4_AnnP_5" + "P-poll__networl_1_4_AnnP_6" + "P-poll__networl_1_4_AnnP_7" + "P-poll__networl_1_4_AnnP_8" + "P-poll__networl_1_4_RP_0" + "P-poll__networl_1_4_RP_1" + "P-poll__networl_1_4_RP_2" + "P-poll__networl_1_4_RP_3" + "P-poll__networl_1_4_RP_4" + "P-poll__networl_1_4_RP_5" + "P-poll__networl_1_4_RP_6" + "P-poll__networl_1_4_RP_7" + "P-poll__networl_1_4_RP_8" + "P-poll__networl_1_5_AskP_0" + "P-poll__networl_1_5_AskP_1" + "P-poll__networl_1_5_AskP_2" + "P-poll__networl_1_5_AskP_3" + "P-poll__networl_1_5_AskP_4" + "P-poll__networl_1_5_AskP_5" + "P-poll__networl_1_5_AskP_6" + "P-poll__networl_1_5_AskP_7" + "P-poll__networl_1_5_AskP_8" + "P-poll__networl_1_5_AnsP_0" + "P-poll__networl_1_5_AnsP_1" + "P-poll__networl_1_5_AnsP_2" + "P-poll__networl_1_5_AnsP_3" + "P-poll__networl_1_5_AnsP_4" + "P-poll__networl_1_5_AnsP_5" + "P-poll__networl_1_5_AnsP_6" + "P-poll__networl_1_5_AnsP_7" + "P-poll__networl_1_5_AnsP_8" + "P-poll__networl_1_5_RI_0" + "P-poll__networl_1_5_RI_1" + "P-poll__networl_1_5_RI_2" + "P-poll__networl_1_5_RI_3" + "P-poll__networl_1_5_RI_4" + "P-poll__networl_1_5_RI_5" + "P-poll__networl_1_5_RI_6" + "P-poll__networl_1_5_RI_7" + "P-poll__networl_1_5_RI_8" + "P-poll__networl_1_5_AI_0" + "P-poll__networl_1_5_AI_1" + "P-poll__networl_1_5_AI_2" + "P-poll__networl_1_5_AI_3" + "P-poll__networl_1_5_AI_4" + "P-poll__networl_1_5_AI_5" + "P-poll__networl_1_5_AI_6" + "P-poll__networl_1_5_AI_7" + "P-poll__networl_1_5_AI_8" + "P-poll__networl_1_5_AnnP_0" + "P-poll__networl_1_5_AnnP_1" + "P-poll__networl_1_5_AnnP_2" + "P-poll__networl_1_5_AnnP_3" + "P-poll__networl_1_5_AnnP_4" + "P-poll__networl_1_5_AnnP_5" + "P-poll__networl_1_5_AnnP_6" + "P-poll__networl_1_5_AnnP_7" + "P-poll__networl_1_5_AnnP_8" + "P-poll__networl_1_5_RP_0" + "P-poll__networl_1_5_RP_1" + "P-poll__networl_1_5_RP_2" + "P-poll__networl_1_5_RP_3" + "P-poll__networl_1_5_RP_4" + "P-poll__networl_1_5_RP_5" + "P-poll__networl_1_5_RP_6" + "P-poll__networl_1_5_RP_7" + "P-poll__networl_1_5_RP_8" + "P-poll__networl_1_6_AskP_0" + "P-poll__networl_1_6_AskP_1" + "P-poll__networl_1_6_AskP_2" + "P-poll__networl_1_6_AskP_3" + "P-poll__networl_1_6_AskP_4" + "P-poll__networl_1_6_AskP_5" + "P-poll__networl_1_6_AskP_6" + "P-poll__networl_1_6_AskP_7" + "P-poll__networl_1_6_AskP_8" + "P-poll__networl_1_6_AnsP_0" + "P-poll__networl_1_6_AnsP_1" + "P-poll__networl_1_6_AnsP_2" + "P-poll__networl_1_6_AnsP_3" + "P-poll__networl_1_6_AnsP_4" + "P-poll__networl_1_6_AnsP_5" + "P-poll__networl_1_6_AnsP_6" + "P-poll__networl_1_6_AnsP_7" + "P-poll__networl_1_6_AnsP_8" + "P-poll__networl_1_6_RI_0" + "P-poll__networl_1_6_RI_1" + "P-poll__networl_1_6_RI_2" + "P-poll__networl_1_6_RI_3" + "P-poll__networl_1_6_RI_4" + "P-poll__networl_1_6_RI_5" + "P-poll__networl_1_6_RI_6" + "P-poll__networl_1_6_RI_7" + "P-poll__networl_1_6_RI_8" + "P-poll__networl_1_6_AI_0" + "P-poll__networl_1_6_AI_1" + "P-poll__networl_1_6_AI_2" + "P-poll__networl_1_6_AI_3" + "P-poll__networl_1_6_AI_4" + "P-poll__networl_1_6_AI_5" + "P-poll__networl_1_6_AI_6" + "P-poll__networl_1_6_AI_7" + "P-poll__networl_1_6_AI_8" + "P-poll__networl_1_6_AnnP_0" + "P-poll__networl_1_6_AnnP_1" + "P-poll__networl_1_6_AnnP_2" + "P-poll__networl_1_6_AnnP_3" + "P-poll__networl_1_6_AnnP_4" + "P-poll__networl_1_6_AnnP_5" + "P-poll__networl_1_6_AnnP_6" + "P-poll__networl_1_6_AnnP_7" + "P-poll__networl_1_6_AnnP_8" + "P-poll__networl_1_6_RP_0" + "P-poll__networl_1_6_RP_1" + "P-poll__networl_1_6_RP_2" + "P-poll__networl_1_6_RP_3" + "P-poll__networl_1_6_RP_4" + "P-poll__networl_1_6_RP_5" + "P-poll__networl_1_6_RP_6" + "P-poll__networl_1_6_RP_7" + "P-poll__networl_1_6_RP_8" + "P-poll__networl_1_7_AskP_0" + "P-poll__networl_1_7_AskP_1" + "P-poll__networl_1_7_AskP_2" + "P-poll__networl_1_7_AskP_3" + "P-poll__networl_1_7_AskP_4" + "P-poll__networl_1_7_AskP_5" + "P-poll__networl_1_7_AskP_6" + "P-poll__networl_1_7_AskP_7" + "P-poll__networl_1_7_AskP_8" + "P-poll__networl_1_7_AnsP_0" + "P-poll__networl_1_7_AnsP_1" + "P-poll__networl_1_7_AnsP_2" + "P-poll__networl_1_7_AnsP_3" + "P-poll__networl_1_7_AnsP_4" + "P-poll__networl_1_7_AnsP_5" + "P-poll__networl_1_7_AnsP_6" + "P-poll__networl_1_7_AnsP_7" + "P-poll__networl_1_7_AnsP_8" + "P-poll__networl_1_7_RI_0" + "P-poll__networl_1_7_RI_1" + "P-poll__networl_1_7_RI_2" + "P-poll__networl_1_7_RI_3" + "P-poll__networl_1_7_RI_4" + "P-poll__networl_1_7_RI_5" + "P-poll__networl_1_7_RI_6" + "P-poll__networl_1_7_RI_7" + "P-poll__networl_1_7_RI_8" + "P-poll__networl_1_7_AI_0" + "P-poll__networl_1_7_AI_1" + "P-poll__networl_1_7_AI_2" + "P-poll__networl_1_7_AI_3" + "P-poll__networl_1_7_AI_4" + "P-poll__networl_1_7_AI_5" + "P-poll__networl_1_7_AI_6" + "P-poll__networl_1_7_AI_7" + "P-poll__networl_1_7_AI_8" + "P-poll__networl_1_7_AnnP_0" + "P-poll__networl_1_7_AnnP_1" + "P-poll__networl_1_7_AnnP_2" + "P-poll__networl_1_7_AnnP_3" + "P-poll__networl_1_7_AnnP_4" + "P-poll__networl_1_7_AnnP_5" + "P-poll__networl_1_7_AnnP_6" + "P-poll__networl_1_7_AnnP_7" + "P-poll__networl_1_7_AnnP_8" + "P-poll__networl_1_7_RP_0" + "P-poll__networl_1_7_RP_1" + "P-poll__networl_1_7_RP_2" + "P-poll__networl_1_7_RP_3" + "P-poll__networl_1_7_RP_4" + "P-poll__networl_1_7_RP_5" + "P-poll__networl_1_7_RP_6" + "P-poll__networl_1_7_RP_7" + "P-poll__networl_1_7_RP_8" + "P-poll__networl_1_8_AskP_0" + "P-poll__networl_1_8_AskP_1" + "P-poll__networl_1_8_AskP_2" + "P-poll__networl_1_8_AskP_3" + "P-poll__networl_1_8_AskP_4" + "P-poll__networl_1_8_AskP_5" + "P-poll__networl_1_8_AskP_6" + "P-poll__networl_1_8_AskP_7" + "P-poll__networl_1_8_AskP_8" + "P-poll__networl_1_8_AnsP_0" + "P-poll__networl_1_8_AnsP_1" + "P-poll__networl_1_8_AnsP_2" + "P-poll__networl_1_8_AnsP_3" + "P-poll__networl_1_8_AnsP_4" + "P-poll__networl_1_8_AnsP_5" + "P-poll__networl_1_8_AnsP_6" + "P-poll__networl_1_8_AnsP_7" + "P-poll__networl_1_8_AnsP_8" + "P-poll__networl_1_8_RI_0" + "P-poll__networl_1_8_RI_1" + "P-poll__networl_1_8_RI_2" + "P-poll__networl_1_8_RI_3" + "P-poll__networl_1_8_RI_4" + "P-poll__networl_1_8_RI_5" + "P-poll__networl_1_8_RI_6" + "P-poll__networl_1_8_RI_7" + "P-poll__networl_1_8_RI_8" + "P-poll__networl_1_8_AI_0" + "P-poll__networl_1_8_AI_1" + "P-poll__networl_1_8_AI_2" + "P-poll__networl_1_8_AI_3" + "P-poll__networl_1_8_AI_4" + "P-poll__networl_1_8_AI_5" + "P-poll__networl_1_8_AI_6" + "P-poll__networl_1_8_AI_7" + "P-poll__networl_1_8_AI_8" + "P-poll__networl_1_8_AnnP_0" + "P-poll__networl_1_8_AnnP_1" + "P-poll__networl_1_8_AnnP_2" + "P-poll__networl_1_8_AnnP_3" + "P-poll__networl_1_8_AnnP_4" + "P-poll__networl_1_8_AnnP_5" + "P-poll__networl_1_8_AnnP_6" + "P-poll__networl_1_8_AnnP_7" + "P-poll__networl_1_8_AnnP_8" + "P-poll__networl_1_8_RP_0" + "P-poll__networl_1_8_RP_1" + "P-poll__networl_1_8_RP_2" + "P-poll__networl_1_8_RP_3" + "P-poll__networl_1_8_RP_4" + "P-poll__networl_1_8_RP_5" + "P-poll__networl_1_8_RP_6" + "P-poll__networl_1_8_RP_7" + "P-poll__networl_1_8_RP_8" + "P-poll__networl_2_0_AskP_0" + "P-poll__networl_2_0_AskP_1" + "P-poll__networl_2_0_AskP_2" + "P-poll__networl_2_0_AskP_3" + "P-poll__networl_2_0_AskP_4" + "P-poll__networl_2_0_AskP_5" + "P-poll__networl_2_0_AskP_6" + "P-poll__networl_2_0_AskP_7" + "P-poll__networl_2_0_AskP_8" + "P-poll__networl_2_0_AnsP_0" + "P-poll__networl_2_0_AnsP_1" + "P-poll__networl_2_0_AnsP_2" + "P-poll__networl_2_0_AnsP_3" + "P-poll__networl_2_0_AnsP_4" + "P-poll__networl_2_0_AnsP_5" + "P-poll__networl_2_0_AnsP_6" + "P-poll__networl_2_0_AnsP_7" + "P-poll__networl_2_0_AnsP_8" + "P-poll__networl_2_0_RI_0" + "P-poll__networl_2_0_RI_1" + "P-poll__networl_2_0_RI_2" + "P-poll__networl_2_0_RI_3" + "P-poll__networl_2_0_RI_4" + "P-poll__networl_2_0_RI_5" + "P-poll__networl_2_0_RI_6" + "P-poll__networl_2_0_RI_7" + "P-poll__networl_2_0_RI_8" + "P-poll__networl_2_0_AI_0" + "P-poll__networl_2_0_AI_1" + "P-poll__networl_2_0_AI_2" + "P-poll__networl_2_0_AI_3" + "P-poll__networl_2_0_AI_4" + "P-poll__networl_2_0_AI_5" + "P-poll__networl_2_0_AI_6" + "P-poll__networl_2_0_AI_7" + "P-poll__networl_2_0_AI_8" + "P-poll__networl_2_0_AnnP_0" + "P-poll__networl_2_0_AnnP_1" + "P-poll__networl_2_0_AnnP_2" + "P-poll__networl_2_0_AnnP_3" + "P-poll__networl_2_0_AnnP_4" + "P-poll__networl_2_0_AnnP_5" + "P-poll__networl_2_0_AnnP_6" + "P-poll__networl_2_0_AnnP_7" + "P-poll__networl_2_0_AnnP_8" + "P-poll__networl_2_0_RP_0" + "P-poll__networl_2_0_RP_1" + "P-poll__networl_2_0_RP_2" + "P-poll__networl_2_0_RP_3" + "P-poll__networl_2_0_RP_4" + "P-poll__networl_2_0_RP_5" + "P-poll__networl_2_0_RP_6" + "P-poll__networl_2_0_RP_7" + "P-poll__networl_2_0_RP_8" + "P-poll__networl_2_1_AskP_0" + "P-poll__networl_2_1_AskP_1" + "P-poll__networl_2_1_AskP_2" + "P-poll__networl_2_1_AskP_3" + "P-poll__networl_2_1_AskP_4" + "P-poll__networl_2_1_AskP_5" + "P-poll__networl_2_1_AskP_6" + "P-poll__networl_2_1_AskP_7" + "P-poll__networl_2_1_AskP_8" + "P-poll__networl_2_1_AnsP_0" + "P-poll__networl_2_1_AnsP_1" + "P-poll__networl_2_1_AnsP_2" + "P-poll__networl_2_1_AnsP_3" + "P-poll__networl_2_1_AnsP_4" + "P-poll__networl_2_1_AnsP_5" + "P-poll__networl_2_1_AnsP_6" + "P-poll__networl_2_1_AnsP_7" + "P-poll__networl_2_1_AnsP_8" + "P-poll__networl_2_1_RI_0" + "P-poll__networl_2_1_RI_1" + "P-poll__networl_2_1_RI_2" + "P-poll__networl_2_1_RI_3" + "P-poll__networl_2_1_RI_4" + "P-poll__networl_2_1_RI_5" + "P-poll__networl_2_1_RI_6" + "P-poll__networl_2_1_RI_7" + "P-poll__networl_2_1_RI_8" + "P-poll__networl_2_1_AI_0" + "P-poll__networl_2_1_AI_1" + "P-poll__networl_2_1_AI_2" + "P-poll__networl_2_1_AI_3" + "P-poll__networl_2_1_AI_4" + "P-poll__networl_2_1_AI_5" + "P-poll__networl_2_1_AI_6" + "P-poll__networl_2_1_AI_7" + "P-poll__networl_2_1_AI_8" + "P-poll__networl_2_1_AnnP_0" + "P-poll__networl_2_1_AnnP_1" + "P-poll__networl_2_1_AnnP_2" + "P-poll__networl_2_1_AnnP_3" + "P-poll__networl_2_1_AnnP_4" + "P-poll__networl_2_1_AnnP_5" + "P-poll__networl_2_1_AnnP_6" + "P-poll__networl_2_1_AnnP_7" + "P-poll__networl_2_1_AnnP_8" + "P-poll__networl_2_1_RP_0" + "P-poll__networl_2_1_RP_1" + "P-poll__networl_2_1_RP_2" + "P-poll__networl_2_1_RP_3" + "P-poll__networl_2_1_RP_4" + "P-poll__networl_2_1_RP_5" + "P-poll__networl_2_1_RP_6" + "P-poll__networl_2_1_RP_7" + "P-poll__networl_2_1_RP_8" + "P-poll__networl_2_2_AskP_0" + "P-poll__networl_2_2_AskP_1" + "P-poll__networl_2_2_AskP_2" + "P-poll__networl_2_2_AskP_3" + "P-poll__networl_2_2_AskP_4" + "P-poll__networl_2_2_AskP_5" + "P-poll__networl_2_2_AskP_6" + "P-poll__networl_2_2_AskP_7" + "P-poll__networl_2_2_AskP_8" + "P-poll__networl_2_2_AnsP_0" + "P-poll__networl_2_2_AnsP_1" + "P-poll__networl_2_2_AnsP_2" + "P-poll__networl_2_2_AnsP_3" + "P-poll__networl_2_2_AnsP_4" + "P-poll__networl_2_2_AnsP_5" + "P-poll__networl_2_2_AnsP_6" + "P-poll__networl_2_2_AnsP_7" + "P-poll__networl_2_2_AnsP_8" + "P-poll__networl_2_2_RI_0" + "P-poll__networl_2_2_RI_1" + "P-poll__networl_2_2_RI_2" + "P-poll__networl_2_2_RI_3" + "P-poll__networl_2_2_RI_4" + "P-poll__networl_2_2_RI_5" + "P-poll__networl_2_2_RI_6" + "P-poll__networl_2_2_RI_7" + "P-poll__networl_2_2_RI_8" + "P-poll__networl_2_2_AI_0" + "P-poll__networl_2_2_AI_1" + "P-poll__networl_2_2_AI_2" + "P-poll__networl_2_2_AI_3" + "P-poll__networl_2_2_AI_4" + "P-poll__networl_2_2_AI_5" + "P-poll__networl_2_2_AI_6" + "P-poll__networl_2_2_AI_7" + "P-poll__networl_2_2_AI_8" + "P-poll__networl_2_2_AnnP_0" + "P-poll__networl_2_2_AnnP_1" + "P-poll__networl_2_2_AnnP_2" + "P-poll__networl_2_2_AnnP_3" + "P-poll__networl_2_2_AnnP_4" + "P-poll__networl_2_2_AnnP_5" + "P-poll__networl_2_2_AnnP_6" + "P-poll__networl_2_2_AnnP_7" + "P-poll__networl_2_2_AnnP_8" + "P-poll__networl_2_2_RP_0" + "P-poll__networl_2_2_RP_1" + "P-poll__networl_2_2_RP_2" + "P-poll__networl_2_2_RP_3" + "P-poll__networl_2_2_RP_4" + "P-poll__networl_2_2_RP_5" + "P-poll__networl_2_2_RP_6" + "P-poll__networl_2_2_RP_7" + "P-poll__networl_2_2_RP_8" + "P-poll__networl_2_3_AskP_0" + "P-poll__networl_2_3_AskP_1" + "P-poll__networl_2_3_AskP_2" + "P-poll__networl_2_3_AskP_3" + "P-poll__networl_2_3_AskP_4" + "P-poll__networl_2_3_AskP_5" + "P-poll__networl_2_3_AskP_6" + "P-poll__networl_2_3_AskP_7" + "P-poll__networl_2_3_AskP_8" + "P-poll__networl_2_3_AnsP_0" + "P-poll__networl_2_3_AnsP_1" + "P-poll__networl_2_3_AnsP_2" + "P-poll__networl_2_3_AnsP_3" + "P-poll__networl_2_3_AnsP_4" + "P-poll__networl_2_3_AnsP_5" + "P-poll__networl_2_3_AnsP_6" + "P-poll__networl_2_3_AnsP_7" + "P-poll__networl_2_3_AnsP_8" + "P-poll__networl_2_3_RI_0" + "P-poll__networl_2_3_RI_1" + "P-poll__networl_2_3_RI_2" + "P-poll__networl_2_3_RI_3" + "P-poll__networl_2_3_RI_4" + "P-poll__networl_2_3_RI_5" + "P-poll__networl_2_3_RI_6" + "P-poll__networl_2_3_RI_7" + "P-poll__networl_2_3_RI_8" + "P-poll__networl_2_3_AI_0" + "P-poll__networl_2_3_AI_1" + "P-poll__networl_2_3_AI_2" + "P-poll__networl_2_3_AI_3" + "P-poll__networl_2_3_AI_4" + "P-poll__networl_2_3_AI_5" + "P-poll__networl_2_3_AI_6" + "P-poll__networl_2_3_AI_7" + "P-poll__networl_2_3_AI_8" + "P-poll__networl_2_3_AnnP_0" + "P-poll__networl_2_3_AnnP_1" + "P-poll__networl_2_3_AnnP_2" + "P-poll__networl_2_3_AnnP_3" + "P-poll__networl_2_3_AnnP_4" + "P-poll__networl_2_3_AnnP_5" + "P-poll__networl_2_3_AnnP_6" + "P-poll__networl_2_3_AnnP_7" + "P-poll__networl_2_3_AnnP_8" + "P-poll__networl_2_3_RP_0" + "P-poll__networl_2_3_RP_1" + "P-poll__networl_2_3_RP_2" + "P-poll__networl_2_3_RP_3" + "P-poll__networl_2_3_RP_4" + "P-poll__networl_2_3_RP_5" + "P-poll__networl_2_3_RP_6" + "P-poll__networl_2_3_RP_7" + "P-poll__networl_2_3_RP_8" + "P-poll__networl_2_4_AskP_0" + "P-poll__networl_2_4_AskP_1" + "P-poll__networl_2_4_AskP_2" + "P-poll__networl_2_4_AskP_3" + "P-poll__networl_2_4_AskP_4" + "P-poll__networl_2_4_AskP_5" + "P-poll__networl_2_4_AskP_6" + "P-poll__networl_2_4_AskP_7" + "P-poll__networl_2_4_AskP_8" + "P-poll__networl_2_4_AnsP_0" + "P-poll__networl_2_4_AnsP_1" + "P-poll__networl_2_4_AnsP_2" + "P-poll__networl_2_4_AnsP_3" + "P-poll__networl_2_4_AnsP_4" + "P-poll__networl_2_4_AnsP_5" + "P-poll__networl_2_4_AnsP_6" + "P-poll__networl_2_4_AnsP_7" + "P-poll__networl_2_4_AnsP_8" + "P-poll__networl_2_4_RI_0" + "P-poll__networl_2_4_RI_1" + "P-poll__networl_2_4_RI_2" + "P-poll__networl_2_4_RI_3" + "P-poll__networl_2_4_RI_4" + "P-poll__networl_2_4_RI_5" + "P-poll__networl_2_4_RI_6" + "P-poll__networl_2_4_RI_7" + "P-poll__networl_2_4_RI_8" + "P-poll__networl_2_4_AI_0" + "P-poll__networl_2_4_AI_1" + "P-poll__networl_2_4_AI_2" + "P-poll__networl_2_4_AI_3" + "P-poll__networl_2_4_AI_4" + "P-poll__networl_2_4_AI_5" + "P-poll__networl_2_4_AI_6" + "P-poll__networl_2_4_AI_7" + "P-poll__networl_2_4_AI_8" + "P-poll__networl_2_4_AnnP_0" + "P-poll__networl_2_4_AnnP_1" + "P-poll__networl_2_4_AnnP_2" + "P-poll__networl_2_4_AnnP_3" + "P-poll__networl_2_4_AnnP_4" + "P-poll__networl_2_4_AnnP_5" + "P-poll__networl_2_4_AnnP_6" + "P-poll__networl_2_4_AnnP_7" + "P-poll__networl_2_4_AnnP_8" + "P-poll__networl_2_4_RP_0" + "P-poll__networl_2_4_RP_1" + "P-poll__networl_2_4_RP_2" + "P-poll__networl_2_4_RP_3" + "P-poll__networl_2_4_RP_4" + "P-poll__networl_2_4_RP_5" + "P-poll__networl_2_4_RP_6" + "P-poll__networl_2_4_RP_7" + "P-poll__networl_2_4_RP_8" + "P-poll__networl_2_5_AskP_0" + "P-poll__networl_2_5_AskP_1" + "P-poll__networl_2_5_AskP_2" + "P-poll__networl_2_5_AskP_3" + "P-poll__networl_2_5_AskP_4" + "P-poll__networl_2_5_AskP_5" + "P-poll__networl_2_5_AskP_6" + "P-poll__networl_2_5_AskP_7" + "P-poll__networl_2_5_AskP_8" + "P-poll__networl_2_5_AnsP_0" + "P-poll__networl_2_5_AnsP_1" + "P-poll__networl_2_5_AnsP_2" + "P-poll__networl_2_5_AnsP_3" + "P-poll__networl_2_5_AnsP_4" + "P-poll__networl_2_5_AnsP_5" + "P-poll__networl_2_5_AnsP_6" + "P-poll__networl_2_5_AnsP_7" + "P-poll__networl_2_5_AnsP_8" + "P-poll__networl_2_5_RI_0" + "P-poll__networl_2_5_RI_1" + "P-poll__networl_2_5_RI_2" + "P-poll__networl_2_5_RI_3" + "P-poll__networl_2_5_RI_4" + "P-poll__networl_2_5_RI_5" + "P-poll__networl_2_5_RI_6" + "P-poll__networl_2_5_RI_7" + "P-poll__networl_2_5_RI_8" + "P-poll__networl_2_5_AI_0" + "P-poll__networl_2_5_AI_1" + "P-poll__networl_2_5_AI_2" + "P-poll__networl_2_5_AI_3" + "P-poll__networl_2_5_AI_4" + "P-poll__networl_2_5_AI_5" + "P-poll__networl_2_5_AI_6" + "P-poll__networl_2_5_AI_7" + "P-poll__networl_2_5_AI_8" + "P-poll__networl_2_5_AnnP_0" + "P-poll__networl_2_5_AnnP_1" + "P-poll__networl_2_5_AnnP_2" + "P-poll__networl_2_5_AnnP_3" + "P-poll__networl_2_5_AnnP_4" + "P-poll__networl_2_5_AnnP_5" + "P-poll__networl_2_5_AnnP_6" + "P-poll__networl_2_5_AnnP_7" + "P-poll__networl_2_5_AnnP_8" + "P-poll__networl_2_5_RP_0" + "P-poll__networl_2_5_RP_1" + "P-poll__networl_2_5_RP_2" + "P-poll__networl_2_5_RP_3" + "P-poll__networl_2_5_RP_4" + "P-poll__networl_2_5_RP_5" + "P-poll__networl_2_5_RP_6" + "P-poll__networl_2_5_RP_7" + "P-poll__networl_2_5_RP_8" + "P-poll__networl_2_6_AskP_0" + "P-poll__networl_2_6_AskP_1" + "P-poll__networl_2_6_AskP_2" + "P-poll__networl_2_6_AskP_3" + "P-poll__networl_2_6_AskP_4" + "P-poll__networl_2_6_AskP_5" + "P-poll__networl_2_6_AskP_6" + "P-poll__networl_2_6_AskP_7" + "P-poll__networl_2_6_AskP_8" + "P-poll__networl_2_6_AnsP_0" + "P-poll__networl_2_6_AnsP_1" + "P-poll__networl_2_6_AnsP_2" + "P-poll__networl_2_6_AnsP_3" + "P-poll__networl_2_6_AnsP_4" + "P-poll__networl_2_6_AnsP_5" + "P-poll__networl_2_6_AnsP_6" + "P-poll__networl_2_6_AnsP_7" + "P-poll__networl_2_6_AnsP_8" + "P-poll__networl_2_6_RI_0" + "P-poll__networl_2_6_RI_1" + "P-poll__networl_2_6_RI_2" + "P-poll__networl_2_6_RI_3" + "P-poll__networl_2_6_RI_4" + "P-poll__networl_2_6_RI_5" + "P-poll__networl_2_6_RI_6" + "P-poll__networl_2_6_RI_7" + "P-poll__networl_2_6_RI_8" + "P-poll__networl_2_6_AI_0" + "P-poll__networl_2_6_AI_1" + "P-poll__networl_2_6_AI_2" + "P-poll__networl_2_6_AI_3" + "P-poll__networl_2_6_AI_4" + "P-poll__networl_2_6_AI_5" + "P-poll__networl_2_6_AI_6" + "P-poll__networl_2_6_AI_7" + "P-poll__networl_2_6_AI_8" + "P-poll__networl_2_6_AnnP_0" + "P-poll__networl_2_6_AnnP_1" + "P-poll__networl_2_6_AnnP_2" + "P-poll__networl_2_6_AnnP_3" + "P-poll__networl_2_6_AnnP_4" + "P-poll__networl_2_6_AnnP_5" + "P-poll__networl_2_6_AnnP_6" + "P-poll__networl_2_6_AnnP_7" + "P-poll__networl_2_6_AnnP_8" + "P-poll__networl_2_6_RP_0" + "P-poll__networl_2_6_RP_1" + "P-poll__networl_2_6_RP_2" + "P-poll__networl_2_6_RP_3" + "P-poll__networl_2_6_RP_4" + "P-poll__networl_2_6_RP_5" + "P-poll__networl_2_6_RP_6" + "P-poll__networl_2_6_RP_7" + "P-poll__networl_2_6_RP_8" + "P-poll__networl_2_7_AskP_0" + "P-poll__networl_2_7_AskP_1" + "P-poll__networl_2_7_AskP_2" + "P-poll__networl_2_7_AskP_3" + "P-poll__networl_2_7_AskP_4" + "P-poll__networl_2_7_AskP_5" + "P-poll__networl_2_7_AskP_6" + "P-poll__networl_2_7_AskP_7" + "P-poll__networl_2_7_AskP_8" + "P-poll__networl_2_7_AnsP_0" + "P-poll__networl_2_7_AnsP_1" + "P-poll__networl_2_7_AnsP_2" + "P-poll__networl_2_7_AnsP_3" + "P-poll__networl_2_7_AnsP_4" + "P-poll__networl_2_7_AnsP_5" + "P-poll__networl_2_7_AnsP_6" + "P-poll__networl_2_7_AnsP_7" + "P-poll__networl_2_7_AnsP_8" + "P-poll__networl_2_7_RI_0" + "P-poll__networl_2_7_RI_1" + "P-poll__networl_2_7_RI_2" + "P-poll__networl_2_7_RI_3" + "P-poll__networl_2_7_RI_4" + "P-poll__networl_2_7_RI_5" + "P-poll__networl_2_7_RI_6" + "P-poll__networl_2_7_RI_7" + "P-poll__networl_2_7_RI_8" + "P-poll__networl_2_7_AI_0" + "P-poll__networl_2_7_AI_1" + "P-poll__networl_2_7_AI_2" + "P-poll__networl_2_7_AI_3" + "P-poll__networl_2_7_AI_4" + "P-poll__networl_2_7_AI_5" + "P-poll__networl_2_7_AI_6" + "P-poll__networl_2_7_AI_7" + "P-poll__networl_2_7_AI_8" + "P-poll__networl_2_7_AnnP_0" + "P-poll__networl_2_7_AnnP_1" + "P-poll__networl_2_7_AnnP_2" + "P-poll__networl_2_7_AnnP_3" + "P-poll__networl_2_7_AnnP_4" + "P-poll__networl_2_7_AnnP_5" + "P-poll__networl_2_7_AnnP_6" + "P-poll__networl_2_7_AnnP_7" + "P-poll__networl_2_7_AnnP_8" + "P-poll__networl_2_7_RP_0" + "P-poll__networl_2_7_RP_1" + "P-poll__networl_2_7_RP_2" + "P-poll__networl_2_7_RP_3" + "P-poll__networl_2_7_RP_4" + "P-poll__networl_2_7_RP_5" + "P-poll__networl_2_7_RP_6" + "P-poll__networl_2_7_RP_7" + "P-poll__networl_2_7_RP_8" + "P-poll__networl_2_8_AskP_0" + "P-poll__networl_2_8_AskP_1" + "P-poll__networl_2_8_AskP_2" + "P-poll__networl_2_8_AskP_3" + "P-poll__networl_2_8_AskP_4" + "P-poll__networl_2_8_AskP_5" + "P-poll__networl_2_8_AskP_6" + "P-poll__networl_2_8_AskP_7" + "P-poll__networl_2_8_AskP_8" + "P-poll__networl_2_8_AnsP_0" + "P-poll__networl_2_8_AnsP_1" + "P-poll__networl_2_8_AnsP_2" + "P-poll__networl_2_8_AnsP_3" + "P-poll__networl_2_8_AnsP_4" + "P-poll__networl_2_8_AnsP_5" + "P-poll__networl_2_8_AnsP_6" + "P-poll__networl_2_8_AnsP_7" + "P-poll__networl_2_8_AnsP_8" + "P-poll__networl_2_8_RI_0" + "P-poll__networl_2_8_RI_1" + "P-poll__networl_2_8_RI_2" + "P-poll__networl_2_8_RI_3" + "P-poll__networl_2_8_RI_4" + "P-poll__networl_2_8_RI_5" + "P-poll__networl_2_8_RI_6" + "P-poll__networl_2_8_RI_7" + "P-poll__networl_2_8_RI_8" + "P-poll__networl_2_8_AI_0" + "P-poll__networl_2_8_AI_1" + "P-poll__networl_2_8_AI_2" + "P-poll__networl_2_8_AI_3" + "P-poll__networl_2_8_AI_4" + "P-poll__networl_2_8_AI_5" + "P-poll__networl_2_8_AI_6" + "P-poll__networl_2_8_AI_7" + "P-poll__networl_2_8_AI_8" + "P-poll__networl_2_8_AnnP_0" + "P-poll__networl_2_8_AnnP_1" + "P-poll__networl_2_8_AnnP_2" + "P-poll__networl_2_8_AnnP_3" + "P-poll__networl_2_8_AnnP_4" + "P-poll__networl_2_8_AnnP_5" + "P-poll__networl_2_8_AnnP_6" + "P-poll__networl_2_8_AnnP_7" + "P-poll__networl_2_8_AnnP_8" + "P-poll__networl_2_8_RP_0" + "P-poll__networl_2_8_RP_1" + "P-poll__networl_2_8_RP_2" + "P-poll__networl_2_8_RP_3" + "P-poll__networl_2_8_RP_4" + "P-poll__networl_2_8_RP_5" + "P-poll__networl_2_8_RP_6" + "P-poll__networl_2_8_RP_7" + "P-poll__networl_2_8_RP_8" + "P-poll__networl_3_0_AskP_0" + "P-poll__networl_3_0_AskP_1" + "P-poll__networl_3_0_AskP_2" + "P-poll__networl_3_0_AskP_3" + "P-poll__networl_3_0_AskP_4" + "P-poll__networl_3_0_AskP_5" + "P-poll__networl_3_0_AskP_6" + "P-poll__networl_3_0_AskP_7" + "P-poll__networl_3_0_AskP_8" + "P-poll__networl_3_0_AnsP_0" + "P-poll__networl_3_0_AnsP_1" + "P-poll__networl_3_0_AnsP_2" + "P-poll__networl_3_0_AnsP_3" + "P-poll__networl_3_0_AnsP_4" + "P-poll__networl_3_0_AnsP_5" + "P-poll__networl_3_0_AnsP_6" + "P-poll__networl_3_0_AnsP_7" + "P-poll__networl_3_0_AnsP_8" + "P-poll__networl_3_0_RI_0" + "P-poll__networl_3_0_RI_1" + "P-poll__networl_3_0_RI_2" + "P-poll__networl_3_0_RI_3" + "P-poll__networl_3_0_RI_4" + "P-poll__networl_3_0_RI_5" + "P-poll__networl_3_0_RI_6" + "P-poll__networl_3_0_RI_7" + "P-poll__networl_3_0_RI_8" + "P-poll__networl_3_0_AI_0" + "P-poll__networl_3_0_AI_1" + "P-poll__networl_3_0_AI_2" + "P-poll__networl_3_0_AI_3" + "P-poll__networl_3_0_AI_4" + "P-poll__networl_3_0_AI_5" + "P-poll__networl_3_0_AI_6" + "P-poll__networl_3_0_AI_7" + "P-poll__networl_3_0_AI_8" + "P-poll__networl_3_0_AnnP_0" + "P-poll__networl_3_0_AnnP_1" + "P-poll__networl_3_0_AnnP_2" + "P-poll__networl_3_0_AnnP_3" + "P-poll__networl_3_0_AnnP_4" + "P-poll__networl_3_0_AnnP_5" + "P-poll__networl_3_0_AnnP_6" + "P-poll__networl_3_0_AnnP_7" + "P-poll__networl_3_0_AnnP_8" + "P-poll__networl_3_0_RP_0" + "P-poll__networl_3_0_RP_1" + "P-poll__networl_3_0_RP_2" + "P-poll__networl_3_0_RP_3" + "P-poll__networl_3_0_RP_4" + "P-poll__networl_3_0_RP_5" + "P-poll__networl_3_0_RP_6" + "P-poll__networl_3_0_RP_7" + "P-poll__networl_3_0_RP_8" + "P-poll__networl_3_1_AskP_0" + "P-poll__networl_3_1_AskP_1" + "P-poll__networl_3_1_AskP_2" + "P-poll__networl_3_1_AskP_3" + "P-poll__networl_3_1_AskP_4" + "P-poll__networl_3_1_AskP_5" + "P-poll__networl_3_1_AskP_6" + "P-poll__networl_3_1_AskP_7" + "P-poll__networl_3_1_AskP_8" + "P-poll__networl_3_1_AnsP_0" + "P-poll__networl_3_1_AnsP_1" + "P-poll__networl_3_1_AnsP_2" + "P-poll__networl_3_1_AnsP_3" + "P-poll__networl_3_1_AnsP_4" + "P-poll__networl_3_1_AnsP_5" + "P-poll__networl_3_1_AnsP_6" + "P-poll__networl_3_1_AnsP_7" + "P-poll__networl_3_1_AnsP_8" + "P-poll__networl_3_1_RI_0" + "P-poll__networl_3_1_RI_1" + "P-poll__networl_3_1_RI_2" + "P-poll__networl_3_1_RI_3" + "P-poll__networl_3_1_RI_4" + "P-poll__networl_3_1_RI_5" + "P-poll__networl_3_1_RI_6" + "P-poll__networl_3_1_RI_7" + "P-poll__networl_3_1_RI_8" + "P-poll__networl_3_1_AI_0" + "P-poll__networl_3_1_AI_1" + "P-poll__networl_3_1_AI_2" + "P-poll__networl_3_1_AI_3" + "P-poll__networl_3_1_AI_4" + "P-poll__networl_3_1_AI_5" + "P-poll__networl_3_1_AI_6" + "P-poll__networl_3_1_AI_7" + "P-poll__networl_3_1_AI_8" + "P-poll__networl_3_1_AnnP_0" + "P-poll__networl_3_1_AnnP_1" + "P-poll__networl_3_1_AnnP_2" + "P-poll__networl_3_1_AnnP_3" + "P-poll__networl_3_1_AnnP_4" + "P-poll__networl_3_1_AnnP_5" + "P-poll__networl_3_1_AnnP_6" + "P-poll__networl_3_1_AnnP_7" + "P-poll__networl_3_1_AnnP_8" + "P-poll__networl_3_1_RP_0" + "P-poll__networl_3_1_RP_1" + "P-poll__networl_3_1_RP_2" + "P-poll__networl_3_1_RP_3" + "P-poll__networl_3_1_RP_4" + "P-poll__networl_3_1_RP_5" + "P-poll__networl_3_1_RP_6" + "P-poll__networl_3_1_RP_7" + "P-poll__networl_3_1_RP_8" + "P-poll__networl_3_2_AskP_0" + "P-poll__networl_3_2_AskP_1" + "P-poll__networl_3_2_AskP_2" + "P-poll__networl_3_2_AskP_3" + "P-poll__networl_3_2_AskP_4" + "P-poll__networl_3_2_AskP_5" + "P-poll__networl_3_2_AskP_6" + "P-poll__networl_3_2_AskP_7" + "P-poll__networl_3_2_AskP_8" + "P-poll__networl_3_2_AnsP_0" + "P-poll__networl_3_2_AnsP_1" + "P-poll__networl_3_2_AnsP_2" + "P-poll__networl_3_2_AnsP_3" + "P-poll__networl_3_2_AnsP_4" + "P-poll__networl_3_2_AnsP_5" + "P-poll__networl_3_2_AnsP_6" + "P-poll__networl_3_2_AnsP_7" + "P-poll__networl_3_2_AnsP_8" + "P-poll__networl_3_2_RI_0" + "P-poll__networl_3_2_RI_1" + "P-poll__networl_3_2_RI_2" + "P-poll__networl_3_2_RI_3" + "P-poll__networl_3_2_RI_4" + "P-poll__networl_3_2_RI_5" + "P-poll__networl_3_2_RI_6" + "P-poll__networl_3_2_RI_7" + "P-poll__networl_3_2_RI_8" + "P-poll__networl_3_2_AI_0" + "P-poll__networl_3_2_AI_1" + "P-poll__networl_3_2_AI_2" + "P-poll__networl_3_2_AI_3" + "P-poll__networl_3_2_AI_4" + "P-poll__networl_3_2_AI_5" + "P-poll__networl_3_2_AI_6" + "P-poll__networl_3_2_AI_7" + "P-poll__networl_3_2_AI_8" + "P-poll__networl_3_2_AnnP_0" + "P-poll__networl_3_2_AnnP_1" + "P-poll__networl_3_2_AnnP_2" + "P-poll__networl_3_2_AnnP_3" + "P-poll__networl_3_2_AnnP_4" + "P-poll__networl_3_2_AnnP_5" + "P-poll__networl_3_2_AnnP_6" + "P-poll__networl_3_2_AnnP_7" + "P-poll__networl_3_2_AnnP_8" + "P-poll__networl_3_2_RP_0" + "P-poll__networl_3_2_RP_1" + "P-poll__networl_3_2_RP_2" + "P-poll__networl_3_2_RP_3" + "P-poll__networl_3_2_RP_4" + "P-poll__networl_3_2_RP_5" + "P-poll__networl_3_2_RP_6" + "P-poll__networl_3_2_RP_7" + "P-poll__networl_3_2_RP_8" + "P-poll__networl_3_3_AskP_0" + "P-poll__networl_3_3_AskP_1" + "P-poll__networl_3_3_AskP_2" + "P-poll__networl_3_3_AskP_3" + "P-poll__networl_3_3_AskP_4" + "P-poll__networl_3_3_AskP_5" + "P-poll__networl_3_3_AskP_6" + "P-poll__networl_3_3_AskP_7" + "P-poll__networl_3_3_AskP_8" + "P-poll__networl_3_3_AnsP_0" + "P-poll__networl_3_3_AnsP_1" + "P-poll__networl_3_3_AnsP_2" + "P-poll__networl_3_3_AnsP_3" + "P-poll__networl_3_3_AnsP_4" + "P-poll__networl_3_3_AnsP_5" + "P-poll__networl_3_3_AnsP_6" + "P-poll__networl_3_3_AnsP_7" + "P-poll__networl_3_3_AnsP_8" + "P-poll__networl_3_3_RI_0" + "P-poll__networl_3_3_RI_1" + "P-poll__networl_3_3_RI_2" + "P-poll__networl_3_3_RI_3" + "P-poll__networl_3_3_RI_4" + "P-poll__networl_3_3_RI_5" + "P-poll__networl_3_3_RI_6" + "P-poll__networl_3_3_RI_7" + "P-poll__networl_3_3_RI_8" + "P-poll__networl_3_3_AI_0" + "P-poll__networl_3_3_AI_1" + "P-poll__networl_3_3_AI_2" + "P-poll__networl_3_3_AI_3" + "P-poll__networl_3_3_AI_4" + "P-poll__networl_3_3_AI_5" + "P-poll__networl_3_3_AI_6" + "P-poll__networl_3_3_AI_7" + "P-poll__networl_3_3_AI_8" + "P-poll__networl_3_3_AnnP_0" + "P-poll__networl_3_3_AnnP_1" + "P-poll__networl_3_3_AnnP_2" + "P-poll__networl_3_3_AnnP_3" + "P-poll__networl_3_3_AnnP_4" + "P-poll__networl_3_3_AnnP_5" + "P-poll__networl_3_3_AnnP_6" + "P-poll__networl_3_3_AnnP_7" + "P-poll__networl_3_3_AnnP_8" + "P-poll__networl_3_3_RP_0" + "P-poll__networl_3_3_RP_1" + "P-poll__networl_3_3_RP_2" + "P-poll__networl_3_3_RP_3" + "P-poll__networl_3_3_RP_4" + "P-poll__networl_3_3_RP_5" + "P-poll__networl_3_3_RP_6" + "P-poll__networl_3_3_RP_7" + "P-poll__networl_3_3_RP_8" + "P-poll__networl_3_4_AskP_0" + "P-poll__networl_3_4_AskP_1" + "P-poll__networl_3_4_AskP_2" + "P-poll__networl_3_4_AskP_3" + "P-poll__networl_3_4_AskP_4" + "P-poll__networl_3_4_AskP_5" + "P-poll__networl_3_4_AskP_6" + "P-poll__networl_3_4_AskP_7" + "P-poll__networl_3_4_AskP_8" + "P-poll__networl_3_4_AnsP_0" + "P-poll__networl_3_4_AnsP_1" + "P-poll__networl_3_4_AnsP_2" + "P-poll__networl_3_4_AnsP_3" + "P-poll__networl_3_4_AnsP_4" + "P-poll__networl_3_4_AnsP_5" + "P-poll__networl_3_4_AnsP_6" + "P-poll__networl_3_4_AnsP_7" + "P-poll__networl_3_4_AnsP_8" + "P-poll__networl_3_4_RI_0" + "P-poll__networl_3_4_RI_1" + "P-poll__networl_3_4_RI_2" + "P-poll__networl_3_4_RI_3" + "P-poll__networl_3_4_RI_4" + "P-poll__networl_3_4_RI_5" + "P-poll__networl_3_4_RI_6" + "P-poll__networl_3_4_RI_7" + "P-poll__networl_3_4_RI_8" + "P-poll__networl_3_4_AI_0" + "P-poll__networl_3_4_AI_1" + "P-poll__networl_3_4_AI_2" + "P-poll__networl_3_4_AI_3" + "P-poll__networl_3_4_AI_4" + "P-poll__networl_3_4_AI_5" + "P-poll__networl_3_4_AI_6" + "P-poll__networl_3_4_AI_7" + "P-poll__networl_3_4_AI_8" + "P-poll__networl_3_4_AnnP_0" + "P-poll__networl_3_4_AnnP_1" + "P-poll__networl_3_4_AnnP_2" + "P-poll__networl_3_4_AnnP_3" + "P-poll__networl_3_4_AnnP_4" + "P-poll__networl_3_4_AnnP_5" + "P-poll__networl_3_4_AnnP_6" + "P-poll__networl_3_4_AnnP_7" + "P-poll__networl_3_4_AnnP_8" + "P-poll__networl_3_4_RP_0" + "P-poll__networl_3_4_RP_1" + "P-poll__networl_3_4_RP_2" + "P-poll__networl_3_4_RP_3" + "P-poll__networl_3_4_RP_4" + "P-poll__networl_3_4_RP_5" + "P-poll__networl_3_4_RP_6" + "P-poll__networl_3_4_RP_7" + "P-poll__networl_3_4_RP_8" + "P-poll__networl_3_5_AskP_0" + "P-poll__networl_3_5_AskP_1" + "P-poll__networl_3_5_AskP_2" + "P-poll__networl_3_5_AskP_3" + "P-poll__networl_3_5_AskP_4" + "P-poll__networl_3_5_AskP_5" + "P-poll__networl_3_5_AskP_6" + "P-poll__networl_3_5_AskP_7" + "P-poll__networl_3_5_AskP_8" + "P-poll__networl_3_5_AnsP_0" + "P-poll__networl_3_5_AnsP_1" + "P-poll__networl_3_5_AnsP_2" + "P-poll__networl_3_5_AnsP_3" + "P-poll__networl_3_5_AnsP_4" + "P-poll__networl_3_5_AnsP_5" + "P-poll__networl_3_5_AnsP_6" + "P-poll__networl_3_5_AnsP_7" + "P-poll__networl_3_5_AnsP_8" + "P-poll__networl_3_5_RI_0" + "P-poll__networl_3_5_RI_1" + "P-poll__networl_3_5_RI_2" + "P-poll__networl_3_5_RI_3" + "P-poll__networl_3_5_RI_4" + "P-poll__networl_3_5_RI_5" + "P-poll__networl_3_5_RI_6" + "P-poll__networl_3_5_RI_7" + "P-poll__networl_3_5_RI_8" + "P-poll__networl_3_5_AI_0" + "P-poll__networl_3_5_AI_1" + "P-poll__networl_3_5_AI_2" + "P-poll__networl_3_5_AI_3" + "P-poll__networl_3_5_AI_4" + "P-poll__networl_3_5_AI_5" + "P-poll__networl_3_5_AI_6" + "P-poll__networl_3_5_AI_7" + "P-poll__networl_3_5_AI_8" + "P-poll__networl_3_5_AnnP_0" + "P-poll__networl_3_5_AnnP_1" + "P-poll__networl_3_5_AnnP_2" + "P-poll__networl_3_5_AnnP_3" + "P-poll__networl_3_5_AnnP_4" + "P-poll__networl_3_5_AnnP_5" + "P-poll__networl_3_5_AnnP_6" + "P-poll__networl_3_5_AnnP_7" + "P-poll__networl_3_5_AnnP_8" + "P-poll__networl_3_5_RP_0" + "P-poll__networl_3_5_RP_1" + "P-poll__networl_3_5_RP_2" + "P-poll__networl_3_5_RP_3" + "P-poll__networl_3_5_RP_4" + "P-poll__networl_3_5_RP_5" + "P-poll__networl_3_5_RP_6" + "P-poll__networl_3_5_RP_7" + "P-poll__networl_3_5_RP_8" + "P-poll__networl_3_6_AskP_0" + "P-poll__networl_3_6_AskP_1" + "P-poll__networl_3_6_AskP_2" + "P-poll__networl_3_6_AskP_3" + "P-poll__networl_3_6_AskP_4" + "P-poll__networl_3_6_AskP_5" + "P-poll__networl_3_6_AskP_6" + "P-poll__networl_3_6_AskP_7" + "P-poll__networl_3_6_AskP_8" + "P-poll__networl_3_6_AnsP_0" + "P-poll__networl_3_6_AnsP_1" + "P-poll__networl_3_6_AnsP_2" + "P-poll__networl_3_6_AnsP_3" + "P-poll__networl_3_6_AnsP_4" + "P-poll__networl_3_6_AnsP_5" + "P-poll__networl_3_6_AnsP_6" + "P-poll__networl_3_6_AnsP_7" + "P-poll__networl_3_6_AnsP_8" + "P-poll__networl_3_6_RI_0" + "P-poll__networl_3_6_RI_1" + "P-poll__networl_3_6_RI_2" + "P-poll__networl_3_6_RI_3" + "P-poll__networl_3_6_RI_4" + "P-poll__networl_3_6_RI_5" + "P-poll__networl_3_6_RI_6" + "P-poll__networl_3_6_RI_7" + "P-poll__networl_3_6_RI_8" + "P-poll__networl_3_6_AI_0" + "P-poll__networl_3_6_AI_1" + "P-poll__networl_3_6_AI_2" + "P-poll__networl_3_6_AI_3" + "P-poll__networl_3_6_AI_4" + "P-poll__networl_3_6_AI_5" + "P-poll__networl_3_6_AI_6" + "P-poll__networl_3_6_AI_7" + "P-poll__networl_3_6_AI_8" + "P-poll__networl_3_6_AnnP_0" + "P-poll__networl_3_6_AnnP_1" + "P-poll__networl_3_6_AnnP_2" + "P-poll__networl_3_6_AnnP_3" + "P-poll__networl_3_6_AnnP_4" + "P-poll__networl_3_6_AnnP_5" + "P-poll__networl_3_6_AnnP_6" + "P-poll__networl_3_6_AnnP_7" + "P-poll__networl_3_6_AnnP_8" + "P-poll__networl_3_6_RP_0" + "P-poll__networl_3_6_RP_1" + "P-poll__networl_3_6_RP_2" + "P-poll__networl_3_6_RP_3" + "P-poll__networl_3_6_RP_4" + "P-poll__networl_3_6_RP_5" + "P-poll__networl_3_6_RP_6" + "P-poll__networl_3_6_RP_7" + "P-poll__networl_3_6_RP_8" + "P-poll__networl_3_7_AskP_0" + "P-poll__networl_3_7_AskP_1" + "P-poll__networl_3_7_AskP_2" + "P-poll__networl_3_7_AskP_3" + "P-poll__networl_3_7_AskP_4" + "P-poll__networl_3_7_AskP_5" + "P-poll__networl_3_7_AskP_6" + "P-poll__networl_3_7_AskP_7" + "P-poll__networl_3_7_AskP_8" + "P-poll__networl_3_7_AnsP_0" + "P-poll__networl_3_7_AnsP_1" + "P-poll__networl_3_7_AnsP_2" + "P-poll__networl_3_7_AnsP_3" + "P-poll__networl_3_7_AnsP_4" + "P-poll__networl_3_7_AnsP_5" + "P-poll__networl_3_7_AnsP_6" + "P-poll__networl_3_7_AnsP_7" + "P-poll__networl_3_7_AnsP_8" + "P-poll__networl_3_7_RI_0" + "P-poll__networl_3_7_RI_1" + "P-poll__networl_3_7_RI_2" + "P-poll__networl_3_7_RI_3" + "P-poll__networl_3_7_RI_4" + "P-poll__networl_3_7_RI_5" + "P-poll__networl_3_7_RI_6" + "P-poll__networl_3_7_RI_7" + "P-poll__networl_3_7_RI_8" + "P-poll__networl_3_7_AI_0" + "P-poll__networl_3_7_AI_1" + "P-poll__networl_3_7_AI_2" + "P-poll__networl_3_7_AI_3" + "P-poll__networl_3_7_AI_4" + "P-poll__networl_3_7_AI_5" + "P-poll__networl_3_7_AI_6" + "P-poll__networl_3_7_AI_7" + "P-poll__networl_3_7_AI_8" + "P-poll__networl_3_7_AnnP_0" + "P-poll__networl_3_7_AnnP_1" + "P-poll__networl_3_7_AnnP_2" + "P-poll__networl_3_7_AnnP_3" + "P-poll__networl_3_7_AnnP_4" + "P-poll__networl_3_7_AnnP_5" + "P-poll__networl_3_7_AnnP_6" + "P-poll__networl_3_7_AnnP_7" + "P-poll__networl_3_7_AnnP_8" + "P-poll__networl_3_7_RP_0" + "P-poll__networl_3_7_RP_1" + "P-poll__networl_3_7_RP_2" + "P-poll__networl_3_7_RP_3" + "P-poll__networl_3_7_RP_4" + "P-poll__networl_3_7_RP_5" + "P-poll__networl_3_7_RP_6" + "P-poll__networl_3_7_RP_7" + "P-poll__networl_3_7_RP_8" + "P-poll__networl_3_8_AskP_0" + "P-poll__networl_3_8_AskP_1" + "P-poll__networl_3_8_AskP_2" + "P-poll__networl_3_8_AskP_3" + "P-poll__networl_3_8_AskP_4" + "P-poll__networl_3_8_AskP_5" + "P-poll__networl_3_8_AskP_6" + "P-poll__networl_3_8_AskP_7" + "P-poll__networl_3_8_AskP_8" + "P-poll__networl_3_8_AnsP_0" + "P-poll__networl_3_8_AnsP_1" + "P-poll__networl_3_8_AnsP_2" + "P-poll__networl_3_8_AnsP_3" + "P-poll__networl_3_8_AnsP_4" + "P-poll__networl_3_8_AnsP_5" + "P-poll__networl_3_8_AnsP_6" + "P-poll__networl_3_8_AnsP_7" + "P-poll__networl_3_8_AnsP_8" + "P-poll__networl_3_8_RI_0" + "P-poll__networl_3_8_RI_1" + "P-poll__networl_3_8_RI_2" + "P-poll__networl_3_8_RI_3" + "P-poll__networl_3_8_RI_4" + "P-poll__networl_3_8_RI_5" + "P-poll__networl_3_8_RI_6" + "P-poll__networl_3_8_RI_7" + "P-poll__networl_3_8_RI_8" + "P-poll__networl_3_8_AI_0" + "P-poll__networl_3_8_AI_1" + "P-poll__networl_3_8_AI_2" + "P-poll__networl_3_8_AI_3" + "P-poll__networl_3_8_AI_4" + "P-poll__networl_3_8_AI_5" + "P-poll__networl_3_8_AI_6" + "P-poll__networl_3_8_AI_7" + "P-poll__networl_3_8_AI_8" + "P-poll__networl_3_8_AnnP_0" + "P-poll__networl_3_8_AnnP_1" + "P-poll__networl_3_8_AnnP_2" + "P-poll__networl_3_8_AnnP_3" + "P-poll__networl_3_8_AnnP_4" + "P-poll__networl_3_8_AnnP_5" + "P-poll__networl_3_8_AnnP_6" + "P-poll__networl_3_8_AnnP_7" + "P-poll__networl_3_8_AnnP_8" + "P-poll__networl_3_8_RP_0" + "P-poll__networl_3_8_RP_1" + "P-poll__networl_3_8_RP_2" + "P-poll__networl_3_8_RP_3" + "P-poll__networl_3_8_RP_4" + "P-poll__networl_3_8_RP_5" + "P-poll__networl_3_8_RP_6" + "P-poll__networl_3_8_RP_7" + "P-poll__networl_3_8_RP_8" + "P-poll__networl_4_0_AskP_0" + "P-poll__networl_4_0_AskP_1" + "P-poll__networl_4_0_AskP_2" + "P-poll__networl_4_0_AskP_3" + "P-poll__networl_4_0_AskP_4" + "P-poll__networl_4_0_AskP_5" + "P-poll__networl_4_0_AskP_6" + "P-poll__networl_4_0_AskP_7" + "P-poll__networl_4_0_AskP_8" + "P-poll__networl_4_0_AnsP_0" + "P-poll__networl_4_0_AnsP_1" + "P-poll__networl_4_0_AnsP_2" + "P-poll__networl_4_0_AnsP_3" + "P-poll__networl_4_0_AnsP_4" + "P-poll__networl_4_0_AnsP_5" + "P-poll__networl_4_0_AnsP_6" + "P-poll__networl_4_0_AnsP_7" + "P-poll__networl_4_0_AnsP_8" + "P-poll__networl_4_0_RI_0" + "P-poll__networl_4_0_RI_1" + "P-poll__networl_4_0_RI_2" + "P-poll__networl_4_0_RI_3" + "P-poll__networl_4_0_RI_4" + "P-poll__networl_4_0_RI_5" + "P-poll__networl_4_0_RI_6" + "P-poll__networl_4_0_RI_7" + "P-poll__networl_4_0_RI_8" + "P-poll__networl_4_0_AI_0" + "P-poll__networl_4_0_AI_1" + "P-poll__networl_4_0_AI_2" + "P-poll__networl_4_0_AI_3" + "P-poll__networl_4_0_AI_4" + "P-poll__networl_4_0_AI_5" + "P-poll__networl_4_0_AI_6" + "P-poll__networl_4_0_AI_7" + "P-poll__networl_4_0_AI_8" + "P-poll__networl_4_0_AnnP_0" + "P-poll__networl_4_0_AnnP_1" + "P-poll__networl_4_0_AnnP_2" + "P-poll__networl_4_0_AnnP_3" + "P-poll__networl_4_0_AnnP_4" + "P-poll__networl_4_0_AnnP_5" + "P-poll__networl_4_0_AnnP_6" + "P-poll__networl_4_0_AnnP_7" + "P-poll__networl_4_0_AnnP_8" + "P-poll__networl_4_0_RP_0" + "P-poll__networl_4_0_RP_1" + "P-poll__networl_4_0_RP_2" + "P-poll__networl_4_0_RP_3" + "P-poll__networl_4_0_RP_4" + "P-poll__networl_4_0_RP_5" + "P-poll__networl_4_0_RP_6" + "P-poll__networl_4_0_RP_7" + "P-poll__networl_4_0_RP_8" + "P-poll__networl_4_1_AskP_0" + "P-poll__networl_4_1_AskP_1" + "P-poll__networl_4_1_AskP_2" + "P-poll__networl_4_1_AskP_3" + "P-poll__networl_4_1_AskP_4" + "P-poll__networl_4_1_AskP_5" + "P-poll__networl_4_1_AskP_6" + "P-poll__networl_4_1_AskP_7" + "P-poll__networl_4_1_AskP_8" + "P-poll__networl_4_1_AnsP_0" + "P-poll__networl_4_1_AnsP_1" + "P-poll__networl_4_1_AnsP_2" + "P-poll__networl_4_1_AnsP_3" + "P-poll__networl_4_1_AnsP_4" + "P-poll__networl_4_1_AnsP_5" + "P-poll__networl_4_1_AnsP_6" + "P-poll__networl_4_1_AnsP_7" + "P-poll__networl_4_1_AnsP_8" + "P-poll__networl_4_1_RI_0" + "P-poll__networl_4_1_RI_1" + "P-poll__networl_4_1_RI_2" + "P-poll__networl_4_1_RI_3" + "P-poll__networl_4_1_RI_4" + "P-poll__networl_4_1_RI_5" + "P-poll__networl_4_1_RI_6" + "P-poll__networl_4_1_RI_7" + "P-poll__networl_4_1_RI_8" + "P-poll__networl_4_1_AI_0" + "P-poll__networl_4_1_AI_1" + "P-poll__networl_4_1_AI_2" + "P-poll__networl_4_1_AI_3" + "P-poll__networl_4_1_AI_4" + "P-poll__networl_4_1_AI_5" + "P-poll__networl_4_1_AI_6" + "P-poll__networl_4_1_AI_7" + "P-poll__networl_4_1_AI_8" + "P-poll__networl_4_1_AnnP_0" + "P-poll__networl_4_1_AnnP_1" + "P-poll__networl_4_1_AnnP_2" + "P-poll__networl_4_1_AnnP_3" + "P-poll__networl_4_1_AnnP_4" + "P-poll__networl_4_1_AnnP_5" + "P-poll__networl_4_1_AnnP_6" + "P-poll__networl_4_1_AnnP_7" + "P-poll__networl_4_1_AnnP_8" + "P-poll__networl_4_1_RP_0" + "P-poll__networl_4_1_RP_1" + "P-poll__networl_4_1_RP_2" + "P-poll__networl_4_1_RP_3" + "P-poll__networl_4_1_RP_4" + "P-poll__networl_4_1_RP_5" + "P-poll__networl_4_1_RP_6" + "P-poll__networl_4_1_RP_7" + "P-poll__networl_4_1_RP_8" + "P-poll__networl_4_2_AskP_0" + "P-poll__networl_4_2_AskP_1" + "P-poll__networl_4_2_AskP_2" + "P-poll__networl_4_2_AskP_3" + "P-poll__networl_4_2_AskP_4" + "P-poll__networl_4_2_AskP_5" + "P-poll__networl_4_2_AskP_6" + "P-poll__networl_4_2_AskP_7" + "P-poll__networl_4_2_AskP_8" + "P-poll__networl_4_2_AnsP_0" + "P-poll__networl_4_2_AnsP_1" + "P-poll__networl_4_2_AnsP_2" + "P-poll__networl_4_2_AnsP_3" + "P-poll__networl_4_2_AnsP_4" + "P-poll__networl_4_2_AnsP_5" + "P-poll__networl_4_2_AnsP_6" + "P-poll__networl_4_2_AnsP_7" + "P-poll__networl_4_2_AnsP_8" + "P-poll__networl_4_2_RI_0" + "P-poll__networl_4_2_RI_1" + "P-poll__networl_4_2_RI_2" + "P-poll__networl_4_2_RI_3" + "P-poll__networl_4_2_RI_4" + "P-poll__networl_4_2_RI_5" + "P-poll__networl_4_2_RI_6" + "P-poll__networl_4_2_RI_7" + "P-poll__networl_4_2_RI_8" + "P-poll__networl_4_2_AI_0" + "P-poll__networl_4_2_AI_1" + "P-poll__networl_4_2_AI_2" + "P-poll__networl_4_2_AI_3" + "P-poll__networl_4_2_AI_4" + "P-poll__networl_4_2_AI_5" + "P-poll__networl_4_2_AI_6" + "P-poll__networl_4_2_AI_7" + "P-poll__networl_4_2_AI_8" + "P-poll__networl_4_2_AnnP_0" + "P-poll__networl_4_2_AnnP_1" + "P-poll__networl_4_2_AnnP_2" + "P-poll__networl_4_2_AnnP_3" + "P-poll__networl_4_2_AnnP_4" + "P-poll__networl_4_2_AnnP_5" + "P-poll__networl_4_2_AnnP_6" + "P-poll__networl_4_2_AnnP_7" + "P-poll__networl_4_2_AnnP_8" + "P-poll__networl_4_2_RP_0" + "P-poll__networl_4_2_RP_1" + "P-poll__networl_4_2_RP_2" + "P-poll__networl_4_2_RP_3" + "P-poll__networl_4_2_RP_4" + "P-poll__networl_4_2_RP_5" + "P-poll__networl_4_2_RP_6" + "P-poll__networl_4_2_RP_7" + "P-poll__networl_4_2_RP_8" + "P-poll__networl_4_3_AskP_0" + "P-poll__networl_4_3_AskP_1" + "P-poll__networl_4_3_AskP_2" + "P-poll__networl_4_3_AskP_3" + "P-poll__networl_4_3_AskP_4" + "P-poll__networl_4_3_AskP_5" + "P-poll__networl_4_3_AskP_6" + "P-poll__networl_4_3_AskP_7" + "P-poll__networl_4_3_AskP_8" + "P-poll__networl_4_3_AnsP_0" + "P-poll__networl_4_3_AnsP_1" + "P-poll__networl_4_3_AnsP_2" + "P-poll__networl_4_3_AnsP_3" + "P-poll__networl_4_3_AnsP_4" + "P-poll__networl_4_3_AnsP_5" + "P-poll__networl_4_3_AnsP_6" + "P-poll__networl_4_3_AnsP_7" + "P-poll__networl_4_3_AnsP_8" + "P-poll__networl_4_3_RI_0" + "P-poll__networl_4_3_RI_1" + "P-poll__networl_4_3_RI_2" + "P-poll__networl_4_3_RI_3" + "P-poll__networl_4_3_RI_4" + "P-poll__networl_4_3_RI_5" + "P-poll__networl_4_3_RI_6" + "P-poll__networl_4_3_RI_7" + "P-poll__networl_4_3_RI_8" + "P-poll__networl_4_3_AI_0" + "P-poll__networl_4_3_AI_1" + "P-poll__networl_4_3_AI_2" + "P-poll__networl_4_3_AI_3" + "P-poll__networl_4_3_AI_4" + "P-poll__networl_4_3_AI_5" + "P-poll__networl_4_3_AI_6" + "P-poll__networl_4_3_AI_7" + "P-poll__networl_4_3_AI_8" + "P-poll__networl_4_3_AnnP_0" + "P-poll__networl_4_3_AnnP_1" + "P-poll__networl_4_3_AnnP_2" + "P-poll__networl_4_3_AnnP_3" + "P-poll__networl_4_3_AnnP_4" + "P-poll__networl_4_3_AnnP_5" + "P-poll__networl_4_3_AnnP_6" + "P-poll__networl_4_3_AnnP_7" + "P-poll__networl_4_3_AnnP_8" + "P-poll__networl_4_3_RP_0" + "P-poll__networl_4_3_RP_1" + "P-poll__networl_4_3_RP_2" + "P-poll__networl_4_3_RP_3" + "P-poll__networl_4_3_RP_4" + "P-poll__networl_4_3_RP_5" + "P-poll__networl_4_3_RP_6" + "P-poll__networl_4_3_RP_7" + "P-poll__networl_4_3_RP_8" + "P-poll__networl_4_4_AskP_0" + "P-poll__networl_4_4_AskP_1" + "P-poll__networl_4_4_AskP_2" + "P-poll__networl_4_4_AskP_3" + "P-poll__networl_4_4_AskP_4" + "P-poll__networl_4_4_AskP_5" + "P-poll__networl_4_4_AskP_6" + "P-poll__networl_4_4_AskP_7" + "P-poll__networl_4_4_AskP_8" + "P-poll__networl_4_4_AnsP_0" + "P-poll__networl_4_4_AnsP_1" + "P-poll__networl_4_4_AnsP_2" + "P-poll__networl_4_4_AnsP_3" + "P-poll__networl_4_4_AnsP_4" + "P-poll__networl_4_4_AnsP_5" + "P-poll__networl_4_4_AnsP_6" + "P-poll__networl_4_4_AnsP_7" + "P-poll__networl_4_4_AnsP_8" + "P-poll__networl_4_4_RI_0" + "P-poll__networl_4_4_RI_1" + "P-poll__networl_4_4_RI_2" + "P-poll__networl_4_4_RI_3" + "P-poll__networl_4_4_RI_4" + "P-poll__networl_4_4_RI_5" + "P-poll__networl_4_4_RI_6" + "P-poll__networl_4_4_RI_7" + "P-poll__networl_4_4_RI_8" + "P-poll__networl_4_4_AI_0" + "P-poll__networl_4_4_AI_1" + "P-poll__networl_4_4_AI_2" + "P-poll__networl_4_4_AI_3" + "P-poll__networl_4_4_AI_4" + "P-poll__networl_4_4_AI_5" + "P-poll__networl_4_4_AI_6" + "P-poll__networl_4_4_AI_7" + "P-poll__networl_4_4_AI_8" + "P-poll__networl_4_4_AnnP_0" + "P-poll__networl_4_4_AnnP_1" + "P-poll__networl_4_4_AnnP_2" + "P-poll__networl_4_4_AnnP_3" + "P-poll__networl_4_4_AnnP_4" + "P-poll__networl_4_4_AnnP_5" + "P-poll__networl_4_4_AnnP_6" + "P-poll__networl_4_4_AnnP_7" + "P-poll__networl_4_4_AnnP_8" + "P-poll__networl_4_4_RP_0" + "P-poll__networl_4_4_RP_1" + "P-poll__networl_4_4_RP_2" + "P-poll__networl_4_4_RP_3" + "P-poll__networl_4_4_RP_4" + "P-poll__networl_4_4_RP_5" + "P-poll__networl_4_4_RP_6" + "P-poll__networl_4_4_RP_7" + "P-poll__networl_4_4_RP_8" + "P-poll__networl_4_5_AskP_0" + "P-poll__networl_4_5_AskP_1" + "P-poll__networl_4_5_AskP_2" + "P-poll__networl_4_5_AskP_3" + "P-poll__networl_4_5_AskP_4" + "P-poll__networl_4_5_AskP_5" + "P-poll__networl_4_5_AskP_6" + "P-poll__networl_4_5_AskP_7" + "P-poll__networl_4_5_AskP_8" + "P-poll__networl_4_5_AnsP_0" + "P-poll__networl_4_5_AnsP_1" + "P-poll__networl_4_5_AnsP_2" + "P-poll__networl_4_5_AnsP_3" + "P-poll__networl_4_5_AnsP_4" + "P-poll__networl_4_5_AnsP_5" + "P-poll__networl_4_5_AnsP_6" + "P-poll__networl_4_5_AnsP_7" + "P-poll__networl_4_5_AnsP_8" + "P-poll__networl_4_5_RI_0" + "P-poll__networl_4_5_RI_1" + "P-poll__networl_4_5_RI_2" + "P-poll__networl_4_5_RI_3" + "P-poll__networl_4_5_RI_4" + "P-poll__networl_4_5_RI_5" + "P-poll__networl_4_5_RI_6" + "P-poll__networl_4_5_RI_7" + "P-poll__networl_4_5_RI_8" + "P-poll__networl_4_5_AI_0" + "P-poll__networl_4_5_AI_1" + "P-poll__networl_4_5_AI_2" + "P-poll__networl_4_5_AI_3" + "P-poll__networl_4_5_AI_4" + "P-poll__networl_4_5_AI_5" + "P-poll__networl_4_5_AI_6" + "P-poll__networl_4_5_AI_7" + "P-poll__networl_4_5_AI_8" + "P-poll__networl_4_5_AnnP_0" + "P-poll__networl_4_5_AnnP_1" + "P-poll__networl_4_5_AnnP_2" + "P-poll__networl_4_5_AnnP_3" + "P-poll__networl_4_5_AnnP_4" + "P-poll__networl_4_5_AnnP_5" + "P-poll__networl_4_5_AnnP_6" + "P-poll__networl_4_5_AnnP_7" + "P-poll__networl_4_5_AnnP_8" + "P-poll__networl_4_5_RP_0" + "P-poll__networl_4_5_RP_1" + "P-poll__networl_4_5_RP_2" + "P-poll__networl_4_5_RP_3" + "P-poll__networl_4_5_RP_4" + "P-poll__networl_4_5_RP_5" + "P-poll__networl_4_5_RP_6" + "P-poll__networl_4_5_RP_7" + "P-poll__networl_4_5_RP_8" + "P-poll__networl_4_6_AskP_0" + "P-poll__networl_4_6_AskP_1" + "P-poll__networl_4_6_AskP_2" + "P-poll__networl_4_6_AskP_3" + "P-poll__networl_4_6_AskP_4" + "P-poll__networl_4_6_AskP_5" + "P-poll__networl_4_6_AskP_6" + "P-poll__networl_4_6_AskP_7" + "P-poll__networl_4_6_AskP_8" + "P-poll__networl_4_6_AnsP_0" + "P-poll__networl_4_6_AnsP_1" + "P-poll__networl_4_6_AnsP_2" + "P-poll__networl_4_6_AnsP_3" + "P-poll__networl_4_6_AnsP_4" + "P-poll__networl_4_6_AnsP_5" + "P-poll__networl_4_6_AnsP_6" + "P-poll__networl_4_6_AnsP_7" + "P-poll__networl_4_6_AnsP_8" + "P-poll__networl_4_6_RI_0" + "P-poll__networl_4_6_RI_1" + "P-poll__networl_4_6_RI_2" + "P-poll__networl_4_6_RI_3" + "P-poll__networl_4_6_RI_4" + "P-poll__networl_4_6_RI_5" + "P-poll__networl_4_6_RI_6" + "P-poll__networl_4_6_RI_7" + "P-poll__networl_4_6_RI_8" + "P-poll__networl_4_6_AI_0" + "P-poll__networl_4_6_AI_1" + "P-poll__networl_4_6_AI_2" + "P-poll__networl_4_6_AI_3" + "P-poll__networl_4_6_AI_4" + "P-poll__networl_4_6_AI_5" + "P-poll__networl_4_6_AI_6" + "P-poll__networl_4_6_AI_7" + "P-poll__networl_4_6_AI_8" + "P-poll__networl_4_6_AnnP_0" + "P-poll__networl_4_6_AnnP_1" + "P-poll__networl_4_6_AnnP_2" + "P-poll__networl_4_6_AnnP_3" + "P-poll__networl_4_6_AnnP_4" + "P-poll__networl_4_6_AnnP_5" + "P-poll__networl_4_6_AnnP_6" + "P-poll__networl_4_6_AnnP_7" + "P-poll__networl_4_6_AnnP_8" + "P-poll__networl_4_6_RP_0" + "P-poll__networl_4_6_RP_1" + "P-poll__networl_4_6_RP_2" + "P-poll__networl_4_6_RP_3" + "P-poll__networl_4_6_RP_4" + "P-poll__networl_4_6_RP_5" + "P-poll__networl_4_6_RP_6" + "P-poll__networl_4_6_RP_7" + "P-poll__networl_4_6_RP_8" + "P-poll__networl_4_7_AskP_0" + "P-poll__networl_4_7_AskP_1" + "P-poll__networl_4_7_AskP_2" + "P-poll__networl_4_7_AskP_3" + "P-poll__networl_4_7_AskP_4" + "P-poll__networl_4_7_AskP_5" + "P-poll__networl_4_7_AskP_6" + "P-poll__networl_4_7_AskP_7" + "P-poll__networl_4_7_AskP_8" + "P-poll__networl_4_7_AnsP_0" + "P-poll__networl_4_7_AnsP_1" + "P-poll__networl_4_7_AnsP_2" + "P-poll__networl_4_7_AnsP_3" + "P-poll__networl_4_7_AnsP_4" + "P-poll__networl_4_7_AnsP_5" + "P-poll__networl_4_7_AnsP_6" + "P-poll__networl_4_7_AnsP_7" + "P-poll__networl_4_7_AnsP_8" + "P-poll__networl_4_7_RI_0" + "P-poll__networl_4_7_RI_1" + "P-poll__networl_4_7_RI_2" + "P-poll__networl_4_7_RI_3" + "P-poll__networl_4_7_RI_4" + "P-poll__networl_4_7_RI_5" + "P-poll__networl_4_7_RI_6" + "P-poll__networl_4_7_RI_7" + "P-poll__networl_4_7_RI_8" + "P-poll__networl_4_7_AI_0" + "P-poll__networl_4_7_AI_1" + "P-poll__networl_4_7_AI_2" + "P-poll__networl_4_7_AI_3" + "P-poll__networl_4_7_AI_4" + "P-poll__networl_4_7_AI_5" + "P-poll__networl_4_7_AI_6" + "P-poll__networl_4_7_AI_7" + "P-poll__networl_4_7_AI_8" + "P-poll__networl_4_7_AnnP_0" + "P-poll__networl_4_7_AnnP_1" + "P-poll__networl_4_7_AnnP_2" + "P-poll__networl_4_7_AnnP_3" + "P-poll__networl_4_7_AnnP_4" + "P-poll__networl_4_7_AnnP_5" + "P-poll__networl_4_7_AnnP_6" + "P-poll__networl_4_7_AnnP_7" + "P-poll__networl_4_7_AnnP_8" + "P-poll__networl_4_7_RP_0" + "P-poll__networl_4_7_RP_1" + "P-poll__networl_4_7_RP_2" + "P-poll__networl_4_7_RP_3" + "P-poll__networl_4_7_RP_4" + "P-poll__networl_4_7_RP_5" + "P-poll__networl_4_7_RP_6" + "P-poll__networl_4_7_RP_7" + "P-poll__networl_4_7_RP_8" + "P-poll__networl_4_8_AskP_0" + "P-poll__networl_4_8_AskP_1" + "P-poll__networl_4_8_AskP_2" + "P-poll__networl_4_8_AskP_3" + "P-poll__networl_4_8_AskP_4" + "P-poll__networl_4_8_AskP_5" + "P-poll__networl_4_8_AskP_6" + "P-poll__networl_4_8_AskP_7" + "P-poll__networl_4_8_AskP_8" + "P-poll__networl_4_8_AnsP_0" + "P-poll__networl_4_8_AnsP_1" + "P-poll__networl_4_8_AnsP_2" + "P-poll__networl_4_8_AnsP_3" + "P-poll__networl_4_8_AnsP_4" + "P-poll__networl_4_8_AnsP_5" + "P-poll__networl_4_8_AnsP_6" + "P-poll__networl_4_8_AnsP_7" + "P-poll__networl_4_8_AnsP_8" + "P-poll__networl_4_8_RI_0" + "P-poll__networl_4_8_RI_1" + "P-poll__networl_4_8_RI_2" + "P-poll__networl_4_8_RI_3" + "P-poll__networl_4_8_RI_4" + "P-poll__networl_4_8_RI_5" + "P-poll__networl_4_8_RI_6" + "P-poll__networl_4_8_RI_7" + "P-poll__networl_4_8_RI_8" + "P-poll__networl_4_8_AI_0" + "P-poll__networl_4_8_AI_1" + "P-poll__networl_4_8_AI_2" + "P-poll__networl_4_8_AI_3" + "P-poll__networl_4_8_AI_4" + "P-poll__networl_4_8_AI_5" + "P-poll__networl_4_8_AI_6" + "P-poll__networl_4_8_AI_7" + "P-poll__networl_4_8_AI_8" + "P-poll__networl_4_8_AnnP_0" + "P-poll__networl_4_8_AnnP_1" + "P-poll__networl_4_8_AnnP_2" + "P-poll__networl_4_8_AnnP_3" + "P-poll__networl_4_8_AnnP_4" + "P-poll__networl_4_8_AnnP_5" + "P-poll__networl_4_8_AnnP_6" + "P-poll__networl_4_8_AnnP_7" + "P-poll__networl_4_8_AnnP_8" + "P-poll__networl_4_8_RP_0" + "P-poll__networl_4_8_RP_1" + "P-poll__networl_4_8_RP_2" + "P-poll__networl_4_8_RP_3" + "P-poll__networl_4_8_RP_4" + "P-poll__networl_4_8_RP_5" + "P-poll__networl_4_8_RP_6" + "P-poll__networl_4_8_RP_7" + "P-poll__networl_4_8_RP_8" + "P-poll__networl_5_0_AskP_0" + "P-poll__networl_5_0_AskP_1" + "P-poll__networl_5_0_AskP_2" + "P-poll__networl_5_0_AskP_3" + "P-poll__networl_5_0_AskP_4" + "P-poll__networl_5_0_AskP_5" + "P-poll__networl_5_0_AskP_6" + "P-poll__networl_5_0_AskP_7" + "P-poll__networl_5_0_AskP_8" + "P-poll__networl_5_0_AnsP_0" + "P-poll__networl_5_0_AnsP_1" + "P-poll__networl_5_0_AnsP_2" + "P-poll__networl_5_0_AnsP_3" + "P-poll__networl_5_0_AnsP_4" + "P-poll__networl_5_0_AnsP_5" + "P-poll__networl_5_0_AnsP_6" + "P-poll__networl_5_0_AnsP_7" + "P-poll__networl_5_0_AnsP_8" + "P-poll__networl_5_0_RI_0" + "P-poll__networl_5_0_RI_1" + "P-poll__networl_5_0_RI_2" + "P-poll__networl_5_0_RI_3" + "P-poll__networl_5_0_RI_4" + "P-poll__networl_5_0_RI_5" + "P-poll__networl_5_0_RI_6" + "P-poll__networl_5_0_RI_7" + "P-poll__networl_5_0_RI_8" + "P-poll__networl_5_0_AI_0" + "P-poll__networl_5_0_AI_1" + "P-poll__networl_5_0_AI_2" + "P-poll__networl_5_0_AI_3" + "P-poll__networl_5_0_AI_4" + "P-poll__networl_5_0_AI_5" + "P-poll__networl_5_0_AI_6" + "P-poll__networl_5_0_AI_7" + "P-poll__networl_5_0_AI_8" + "P-poll__networl_5_0_AnnP_0" + "P-poll__networl_5_0_AnnP_1" + "P-poll__networl_5_0_AnnP_2" + "P-poll__networl_5_0_AnnP_3" + "P-poll__networl_5_0_AnnP_4" + "P-poll__networl_5_0_AnnP_5" + "P-poll__networl_5_0_AnnP_6" + "P-poll__networl_5_0_AnnP_7" + "P-poll__networl_5_0_AnnP_8" + "P-poll__networl_5_0_RP_0" + "P-poll__networl_5_0_RP_1" + "P-poll__networl_5_0_RP_2" + "P-poll__networl_5_0_RP_3" + "P-poll__networl_5_0_RP_4" + "P-poll__networl_5_0_RP_5" + "P-poll__networl_5_0_RP_6" + "P-poll__networl_5_0_RP_7" + "P-poll__networl_5_0_RP_8" + "P-poll__networl_5_1_AskP_0" + "P-poll__networl_5_1_AskP_1" + "P-poll__networl_5_1_AskP_2" + "P-poll__networl_5_1_AskP_3" + "P-poll__networl_5_1_AskP_4" + "P-poll__networl_5_1_AskP_5" + "P-poll__networl_5_1_AskP_6" + "P-poll__networl_5_1_AskP_7" + "P-poll__networl_5_1_AskP_8" + "P-poll__networl_5_1_AnsP_0" + "P-poll__networl_5_1_AnsP_1" + "P-poll__networl_5_1_AnsP_2" + "P-poll__networl_5_1_AnsP_3" + "P-poll__networl_5_1_AnsP_4" + "P-poll__networl_5_1_AnsP_5" + "P-poll__networl_5_1_AnsP_6" + "P-poll__networl_5_1_AnsP_7" + "P-poll__networl_5_1_AnsP_8" + "P-poll__networl_5_1_RI_0" + "P-poll__networl_5_1_RI_1" + "P-poll__networl_5_1_RI_2" + "P-poll__networl_5_1_RI_3" + "P-poll__networl_5_1_RI_4" + "P-poll__networl_5_1_RI_5" + "P-poll__networl_5_1_RI_6" + "P-poll__networl_5_1_RI_7" + "P-poll__networl_5_1_RI_8" + "P-poll__networl_5_1_AI_0" + "P-poll__networl_5_1_AI_1" + "P-poll__networl_5_1_AI_2" + "P-poll__networl_5_1_AI_3" + "P-poll__networl_5_1_AI_4" + "P-poll__networl_5_1_AI_5" + "P-poll__networl_5_1_AI_6" + "P-poll__networl_5_1_AI_7" + "P-poll__networl_5_1_AI_8" + "P-poll__networl_5_1_AnnP_0" + "P-poll__networl_5_1_AnnP_1" + "P-poll__networl_5_1_AnnP_2" + "P-poll__networl_5_1_AnnP_3" + "P-poll__networl_5_1_AnnP_4" + "P-poll__networl_5_1_AnnP_5" + "P-poll__networl_5_1_AnnP_6" + "P-poll__networl_5_1_AnnP_7" + "P-poll__networl_5_1_AnnP_8" + "P-poll__networl_5_1_RP_0" + "P-poll__networl_5_1_RP_1" + "P-poll__networl_5_1_RP_2" + "P-poll__networl_5_1_RP_3" + "P-poll__networl_5_1_RP_4" + "P-poll__networl_5_1_RP_5" + "P-poll__networl_5_1_RP_6" + "P-poll__networl_5_1_RP_7" + "P-poll__networl_5_1_RP_8" + "P-poll__networl_5_2_AskP_0" + "P-poll__networl_5_2_AskP_1" + "P-poll__networl_5_2_AskP_2" + "P-poll__networl_5_2_AskP_3" + "P-poll__networl_5_2_AskP_4" + "P-poll__networl_5_2_AskP_5" + "P-poll__networl_5_2_AskP_6" + "P-poll__networl_5_2_AskP_7" + "P-poll__networl_5_2_AskP_8" + "P-poll__networl_5_2_AnsP_0" + "P-poll__networl_5_2_AnsP_1" + "P-poll__networl_5_2_AnsP_2" + "P-poll__networl_5_2_AnsP_3" + "P-poll__networl_5_2_AnsP_4" + "P-poll__networl_5_2_AnsP_5" + "P-poll__networl_5_2_AnsP_6" + "P-poll__networl_5_2_AnsP_7" + "P-poll__networl_5_2_AnsP_8" + "P-poll__networl_5_2_RI_0" + "P-poll__networl_5_2_RI_1" + "P-poll__networl_5_2_RI_2" + "P-poll__networl_5_2_RI_3" + "P-poll__networl_5_2_RI_4" + "P-poll__networl_5_2_RI_5" + "P-poll__networl_5_2_RI_6" + "P-poll__networl_5_2_RI_7" + "P-poll__networl_5_2_RI_8" + "P-poll__networl_5_2_AI_0" + "P-poll__networl_5_2_AI_1" + "P-poll__networl_5_2_AI_2" + "P-poll__networl_5_2_AI_3" + "P-poll__networl_5_2_AI_4" + "P-poll__networl_5_2_AI_5" + "P-poll__networl_5_2_AI_6" + "P-poll__networl_5_2_AI_7" + "P-poll__networl_5_2_AI_8" + "P-poll__networl_5_2_AnnP_0" + "P-poll__networl_5_2_AnnP_1" + "P-poll__networl_5_2_AnnP_2" + "P-poll__networl_5_2_AnnP_3" + "P-poll__networl_5_2_AnnP_4" + "P-poll__networl_5_2_AnnP_5" + "P-poll__networl_5_2_AnnP_6" + "P-poll__networl_5_2_AnnP_7" + "P-poll__networl_5_2_AnnP_8" + "P-poll__networl_5_2_RP_0" + "P-poll__networl_5_2_RP_1" + "P-poll__networl_5_2_RP_2" + "P-poll__networl_5_2_RP_3" + "P-poll__networl_5_2_RP_4" + "P-poll__networl_5_2_RP_5" + "P-poll__networl_5_2_RP_6" + "P-poll__networl_5_2_RP_7" + "P-poll__networl_5_2_RP_8" + "P-poll__networl_5_3_AskP_0" + "P-poll__networl_5_3_AskP_1" + "P-poll__networl_5_3_AskP_2" + "P-poll__networl_5_3_AskP_3" + "P-poll__networl_5_3_AskP_4" + "P-poll__networl_5_3_AskP_5" + "P-poll__networl_5_3_AskP_6" + "P-poll__networl_5_3_AskP_7" + "P-poll__networl_5_3_AskP_8" + "P-poll__networl_5_3_AnsP_0" + "P-poll__networl_5_3_AnsP_1" + "P-poll__networl_5_3_AnsP_2" + "P-poll__networl_5_3_AnsP_3" + "P-poll__networl_5_3_AnsP_4" + "P-poll__networl_5_3_AnsP_5" + "P-poll__networl_5_3_AnsP_6" + "P-poll__networl_5_3_AnsP_7" + "P-poll__networl_5_3_AnsP_8" + "P-poll__networl_5_3_RI_0" + "P-poll__networl_5_3_RI_1" + "P-poll__networl_5_3_RI_2" + "P-poll__networl_5_3_RI_3" + "P-poll__networl_5_3_RI_4" + "P-poll__networl_5_3_RI_5" + "P-poll__networl_5_3_RI_6" + "P-poll__networl_5_3_RI_7" + "P-poll__networl_5_3_RI_8" + "P-poll__networl_5_3_AI_0" + "P-poll__networl_5_3_AI_1" + "P-poll__networl_5_3_AI_2" + "P-poll__networl_5_3_AI_3" + "P-poll__networl_5_3_AI_4" + "P-poll__networl_5_3_AI_5" + "P-poll__networl_5_3_AI_6" + "P-poll__networl_5_3_AI_7" + "P-poll__networl_5_3_AI_8" + "P-poll__networl_5_3_AnnP_0" + "P-poll__networl_5_3_AnnP_1" + "P-poll__networl_5_3_AnnP_2" + "P-poll__networl_5_3_AnnP_3" + "P-poll__networl_5_3_AnnP_4" + "P-poll__networl_5_3_AnnP_5" + "P-poll__networl_5_3_AnnP_6" + "P-poll__networl_5_3_AnnP_7" + "P-poll__networl_5_3_AnnP_8" + "P-poll__networl_5_3_RP_0" + "P-poll__networl_5_3_RP_1" + "P-poll__networl_5_3_RP_2" + "P-poll__networl_5_3_RP_3" + "P-poll__networl_5_3_RP_4" + "P-poll__networl_5_3_RP_5" + "P-poll__networl_5_3_RP_6" + "P-poll__networl_5_3_RP_7" + "P-poll__networl_5_3_RP_8" + "P-poll__networl_5_4_AskP_0" + "P-poll__networl_5_4_AskP_1" + "P-poll__networl_5_4_AskP_2" + "P-poll__networl_5_4_AskP_3" + "P-poll__networl_5_4_AskP_4" + "P-poll__networl_5_4_AskP_5" + "P-poll__networl_5_4_AskP_6" + "P-poll__networl_5_4_AskP_7" + "P-poll__networl_5_4_AskP_8" + "P-poll__networl_5_4_AnsP_0" + "P-poll__networl_5_4_AnsP_1" + "P-poll__networl_5_4_AnsP_2" + "P-poll__networl_5_4_AnsP_3" + "P-poll__networl_5_4_AnsP_4" + "P-poll__networl_5_4_AnsP_5" + "P-poll__networl_5_4_AnsP_6" + "P-poll__networl_5_4_AnsP_7" + "P-poll__networl_5_4_AnsP_8" + "P-poll__networl_5_4_RI_0" + "P-poll__networl_5_4_RI_1" + "P-poll__networl_5_4_RI_2" + "P-poll__networl_5_4_RI_3" + "P-poll__networl_5_4_RI_4" + "P-poll__networl_5_4_RI_5" + "P-poll__networl_5_4_RI_6" + "P-poll__networl_5_4_RI_7" + "P-poll__networl_5_4_RI_8" + "P-poll__networl_5_4_AI_0" + "P-poll__networl_5_4_AI_1" + "P-poll__networl_5_4_AI_2" + "P-poll__networl_5_4_AI_3" + "P-poll__networl_5_4_AI_4" + "P-poll__networl_5_4_AI_5" + "P-poll__networl_5_4_AI_6" + "P-poll__networl_5_4_AI_7" + "P-poll__networl_5_4_AI_8" + "P-poll__networl_5_4_AnnP_0" + "P-poll__networl_5_4_AnnP_1" + "P-poll__networl_5_4_AnnP_2" + "P-poll__networl_5_4_AnnP_3" + "P-poll__networl_5_4_AnnP_4" + "P-poll__networl_5_4_AnnP_5" + "P-poll__networl_5_4_AnnP_6" + "P-poll__networl_5_4_AnnP_7" + "P-poll__networl_5_4_AnnP_8" + "P-poll__networl_5_4_RP_0" + "P-poll__networl_5_4_RP_1" + "P-poll__networl_5_4_RP_2" + "P-poll__networl_5_4_RP_3" + "P-poll__networl_5_4_RP_4" + "P-poll__networl_5_4_RP_5" + "P-poll__networl_5_4_RP_6" + "P-poll__networl_5_4_RP_7" + "P-poll__networl_5_4_RP_8" + "P-poll__networl_5_5_AskP_0" + "P-poll__networl_5_5_AskP_1" + "P-poll__networl_5_5_AskP_2" + "P-poll__networl_5_5_AskP_3" + "P-poll__networl_5_5_AskP_4" + "P-poll__networl_5_5_AskP_5" + "P-poll__networl_5_5_AskP_6" + "P-poll__networl_5_5_AskP_7" + "P-poll__networl_5_5_AskP_8" + "P-poll__networl_5_5_AnsP_0" + "P-poll__networl_5_5_AnsP_1" + "P-poll__networl_5_5_AnsP_2" + "P-poll__networl_5_5_AnsP_3" + "P-poll__networl_5_5_AnsP_4" + "P-poll__networl_5_5_AnsP_5" + "P-poll__networl_5_5_AnsP_6" + "P-poll__networl_5_5_AnsP_7" + "P-poll__networl_5_5_AnsP_8" + "P-poll__networl_5_5_RI_0" + "P-poll__networl_5_5_RI_1" + "P-poll__networl_5_5_RI_2" + "P-poll__networl_5_5_RI_3" + "P-poll__networl_5_5_RI_4" + "P-poll__networl_5_5_RI_5" + "P-poll__networl_5_5_RI_6" + "P-poll__networl_5_5_RI_7" + "P-poll__networl_5_5_RI_8" + "P-poll__networl_5_5_AI_0" + "P-poll__networl_5_5_AI_1" + "P-poll__networl_5_5_AI_2" + "P-poll__networl_5_5_AI_3" + "P-poll__networl_5_5_AI_4" + "P-poll__networl_5_5_AI_5" + "P-poll__networl_5_5_AI_6" + "P-poll__networl_5_5_AI_7" + "P-poll__networl_5_5_AI_8" + "P-poll__networl_5_5_AnnP_0" + "P-poll__networl_5_5_AnnP_1" + "P-poll__networl_5_5_AnnP_2" + "P-poll__networl_5_5_AnnP_3" + "P-poll__networl_5_5_AnnP_4" + "P-poll__networl_5_5_AnnP_5" + "P-poll__networl_5_5_AnnP_6" + "P-poll__networl_5_5_AnnP_7" + "P-poll__networl_5_5_AnnP_8" + "P-poll__networl_5_5_RP_0" + "P-poll__networl_5_5_RP_1" + "P-poll__networl_5_5_RP_2" + "P-poll__networl_5_5_RP_3" + "P-poll__networl_5_5_RP_4" + "P-poll__networl_5_5_RP_5" + "P-poll__networl_5_5_RP_6" + "P-poll__networl_5_5_RP_7" + "P-poll__networl_5_5_RP_8" + "P-poll__networl_5_6_AskP_0" + "P-poll__networl_5_6_AskP_1" + "P-poll__networl_5_6_AskP_2" + "P-poll__networl_5_6_AskP_3" + "P-poll__networl_5_6_AskP_4" + "P-poll__networl_5_6_AskP_5" + "P-poll__networl_5_6_AskP_6" + "P-poll__networl_5_6_AskP_7" + "P-poll__networl_5_6_AskP_8" + "P-poll__networl_5_6_AnsP_0" + "P-poll__networl_5_6_AnsP_1" + "P-poll__networl_5_6_AnsP_2" + "P-poll__networl_5_6_AnsP_3" + "P-poll__networl_5_6_AnsP_4" + "P-poll__networl_5_6_AnsP_5" + "P-poll__networl_5_6_AnsP_6" + "P-poll__networl_5_6_AnsP_7" + "P-poll__networl_5_6_AnsP_8" + "P-poll__networl_5_6_RI_0" + "P-poll__networl_5_6_RI_1" + "P-poll__networl_5_6_RI_2" + "P-poll__networl_5_6_RI_3" + "P-poll__networl_5_6_RI_4" + "P-poll__networl_5_6_RI_5" + "P-poll__networl_5_6_RI_6" + "P-poll__networl_5_6_RI_7" + "P-poll__networl_5_6_RI_8" + "P-poll__networl_5_6_AI_0" + "P-poll__networl_5_6_AI_1" + "P-poll__networl_5_6_AI_2" + "P-poll__networl_5_6_AI_3" + "P-poll__networl_5_6_AI_4" + "P-poll__networl_5_6_AI_5" + "P-poll__networl_5_6_AI_6" + "P-poll__networl_5_6_AI_7" + "P-poll__networl_5_6_AI_8" + "P-poll__networl_5_6_AnnP_0" + "P-poll__networl_5_6_AnnP_1" + "P-poll__networl_5_6_AnnP_2" + "P-poll__networl_5_6_AnnP_3" + "P-poll__networl_5_6_AnnP_4" + "P-poll__networl_5_6_AnnP_5" + "P-poll__networl_5_6_AnnP_6" + "P-poll__networl_5_6_AnnP_7" + "P-poll__networl_5_6_AnnP_8" + "P-poll__networl_5_6_RP_0" + "P-poll__networl_5_6_RP_1" + "P-poll__networl_5_6_RP_2" + "P-poll__networl_5_6_RP_3" + "P-poll__networl_5_6_RP_4" + "P-poll__networl_5_6_RP_5" + "P-poll__networl_5_6_RP_6" + "P-poll__networl_5_6_RP_7" + "P-poll__networl_5_6_RP_8" + "P-poll__networl_5_7_AskP_0" + "P-poll__networl_5_7_AskP_1" + "P-poll__networl_5_7_AskP_2" + "P-poll__networl_5_7_AskP_3" + "P-poll__networl_5_7_AskP_4" + "P-poll__networl_5_7_AskP_5" + "P-poll__networl_5_7_AskP_6" + "P-poll__networl_5_7_AskP_7" + "P-poll__networl_5_7_AskP_8" + "P-poll__networl_5_7_AnsP_0" + "P-poll__networl_5_7_AnsP_1" + "P-poll__networl_5_7_AnsP_2" + "P-poll__networl_5_7_AnsP_3" + "P-poll__networl_5_7_AnsP_4" + "P-poll__networl_5_7_AnsP_5" + "P-poll__networl_5_7_AnsP_6" + "P-poll__networl_5_7_AnsP_7" + "P-poll__networl_5_7_AnsP_8" + "P-poll__networl_5_7_RI_0" + "P-poll__networl_5_7_RI_1" + "P-poll__networl_5_7_RI_2" + "P-poll__networl_5_7_RI_3" + "P-poll__networl_5_7_RI_4" + "P-poll__networl_5_7_RI_5" + "P-poll__networl_5_7_RI_6" + "P-poll__networl_5_7_RI_7" + "P-poll__networl_5_7_RI_8" + "P-poll__networl_5_7_AI_0" + "P-poll__networl_5_7_AI_1" + "P-poll__networl_5_7_AI_2" + "P-poll__networl_5_7_AI_3" + "P-poll__networl_5_7_AI_4" + "P-poll__networl_5_7_AI_5" + "P-poll__networl_5_7_AI_6" + "P-poll__networl_5_7_AI_7" + "P-poll__networl_5_7_AI_8" + "P-poll__networl_5_7_AnnP_0" + "P-poll__networl_5_7_AnnP_1" + "P-poll__networl_5_7_AnnP_2" + "P-poll__networl_5_7_AnnP_3" + "P-poll__networl_5_7_AnnP_4" + "P-poll__networl_5_7_AnnP_5" + "P-poll__networl_5_7_AnnP_6" + "P-poll__networl_5_7_AnnP_7" + "P-poll__networl_5_7_AnnP_8" + "P-poll__networl_5_7_RP_0" + "P-poll__networl_5_7_RP_1" + "P-poll__networl_5_7_RP_2" + "P-poll__networl_5_7_RP_3" + "P-poll__networl_5_7_RP_4" + "P-poll__networl_5_7_RP_5" + "P-poll__networl_5_7_RP_6" + "P-poll__networl_5_7_RP_7" + "P-poll__networl_5_7_RP_8" + "P-poll__networl_5_8_AskP_0" + "P-poll__networl_5_8_AskP_1" + "P-poll__networl_5_8_AskP_2" + "P-poll__networl_5_8_AskP_3" + "P-poll__networl_5_8_AskP_4" + "P-poll__networl_5_8_AskP_5" + "P-poll__networl_5_8_AskP_6" + "P-poll__networl_5_8_AskP_7" + "P-poll__networl_5_8_AskP_8" + "P-poll__networl_5_8_AnsP_0" + "P-poll__networl_5_8_AnsP_1" + "P-poll__networl_5_8_AnsP_2" + "P-poll__networl_5_8_AnsP_3" + "P-poll__networl_5_8_AnsP_4" + "P-poll__networl_5_8_AnsP_5" + "P-poll__networl_5_8_AnsP_6" + "P-poll__networl_5_8_AnsP_7" + "P-poll__networl_5_8_AnsP_8" + "P-poll__networl_5_8_RI_0" + "P-poll__networl_5_8_RI_1" + "P-poll__networl_5_8_RI_2" + "P-poll__networl_5_8_RI_3" + "P-poll__networl_5_8_RI_4" + "P-poll__networl_5_8_RI_5" + "P-poll__networl_5_8_RI_6" + "P-poll__networl_5_8_RI_7" + "P-poll__networl_5_8_RI_8" + "P-poll__networl_5_8_AI_0" + "P-poll__networl_5_8_AI_1" + "P-poll__networl_5_8_AI_2" + "P-poll__networl_5_8_AI_3" + "P-poll__networl_5_8_AI_4" + "P-poll__networl_5_8_AI_5" + "P-poll__networl_5_8_AI_6" + "P-poll__networl_5_8_AI_7" + "P-poll__networl_5_8_AI_8" + "P-poll__networl_5_8_AnnP_0" + "P-poll__networl_5_8_AnnP_1" + "P-poll__networl_5_8_AnnP_2" + "P-poll__networl_5_8_AnnP_3" + "P-poll__networl_5_8_AnnP_4" + "P-poll__networl_5_8_AnnP_5" + "P-poll__networl_5_8_AnnP_6" + "P-poll__networl_5_8_AnnP_7" + "P-poll__networl_5_8_AnnP_8" + "P-poll__networl_5_8_RP_0" + "P-poll__networl_5_8_RP_1" + "P-poll__networl_5_8_RP_2" + "P-poll__networl_5_8_RP_3" + "P-poll__networl_5_8_RP_4" + "P-poll__networl_5_8_RP_5" + "P-poll__networl_5_8_RP_6" + "P-poll__networl_5_8_RP_7" + "P-poll__networl_5_8_RP_8" + "P-poll__networl_6_0_AskP_0" + "P-poll__networl_6_0_AskP_1" + "P-poll__networl_6_0_AskP_2" + "P-poll__networl_6_0_AskP_3" + "P-poll__networl_6_0_AskP_4" + "P-poll__networl_6_0_AskP_5" + "P-poll__networl_6_0_AskP_6" + "P-poll__networl_6_0_AskP_7" + "P-poll__networl_6_0_AskP_8" + "P-poll__networl_6_0_AnsP_0" + "P-poll__networl_6_0_AnsP_1" + "P-poll__networl_6_0_AnsP_2" + "P-poll__networl_6_0_AnsP_3" + "P-poll__networl_6_0_AnsP_4" + "P-poll__networl_6_0_AnsP_5" + "P-poll__networl_6_0_AnsP_6" + "P-poll__networl_6_0_AnsP_7" + "P-poll__networl_6_0_AnsP_8" + "P-poll__networl_6_0_RI_0" + "P-poll__networl_6_0_RI_1" + "P-poll__networl_6_0_RI_2" + "P-poll__networl_6_0_RI_3" + "P-poll__networl_6_0_RI_4" + "P-poll__networl_6_0_RI_5" + "P-poll__networl_6_0_RI_6" + "P-poll__networl_6_0_RI_7" + "P-poll__networl_6_0_RI_8" + "P-poll__networl_6_0_AI_0" + "P-poll__networl_6_0_AI_1" + "P-poll__networl_6_0_AI_2" + "P-poll__networl_6_0_AI_3" + "P-poll__networl_6_0_AI_4" + "P-poll__networl_6_0_AI_5" + "P-poll__networl_6_0_AI_6" + "P-poll__networl_6_0_AI_7" + "P-poll__networl_6_0_AI_8" + "P-poll__networl_6_0_AnnP_0" + "P-poll__networl_6_0_AnnP_1" + "P-poll__networl_6_0_AnnP_2" + "P-poll__networl_6_0_AnnP_3" + "P-poll__networl_6_0_AnnP_4" + "P-poll__networl_6_0_AnnP_5" + "P-poll__networl_6_0_AnnP_6" + "P-poll__networl_6_0_AnnP_7" + "P-poll__networl_6_0_AnnP_8" + "P-poll__networl_6_0_RP_0" + "P-poll__networl_6_0_RP_1" + "P-poll__networl_6_0_RP_2" + "P-poll__networl_6_0_RP_3" + "P-poll__networl_6_0_RP_4" + "P-poll__networl_6_0_RP_5" + "P-poll__networl_6_0_RP_6" + "P-poll__networl_6_0_RP_7" + "P-poll__networl_6_0_RP_8" + "P-poll__networl_6_1_AskP_0" + "P-poll__networl_6_1_AskP_1" + "P-poll__networl_6_1_AskP_2" + "P-poll__networl_6_1_AskP_3" + "P-poll__networl_6_1_AskP_4" + "P-poll__networl_6_1_AskP_5" + "P-poll__networl_6_1_AskP_6" + "P-poll__networl_6_1_AskP_7" + "P-poll__networl_6_1_AskP_8" + "P-poll__networl_6_1_AnsP_0" + "P-poll__networl_6_1_AnsP_1" + "P-poll__networl_6_1_AnsP_2" + "P-poll__networl_6_1_AnsP_3" + "P-poll__networl_6_1_AnsP_4" + "P-poll__networl_6_1_AnsP_5" + "P-poll__networl_6_1_AnsP_6" + "P-poll__networl_6_1_AnsP_7" + "P-poll__networl_6_1_AnsP_8" + "P-poll__networl_6_1_RI_0" + "P-poll__networl_6_1_RI_1" + "P-poll__networl_6_1_RI_2" + "P-poll__networl_6_1_RI_3" + "P-poll__networl_6_1_RI_4" + "P-poll__networl_6_1_RI_5" + "P-poll__networl_6_1_RI_6" + "P-poll__networl_6_1_RI_7" + "P-poll__networl_6_1_RI_8" + "P-poll__networl_6_1_AI_0" + "P-poll__networl_6_1_AI_1" + "P-poll__networl_6_1_AI_2" + "P-poll__networl_6_1_AI_3" + "P-poll__networl_6_1_AI_4" + "P-poll__networl_6_1_AI_5" + "P-poll__networl_6_1_AI_6" + "P-poll__networl_6_1_AI_7" + "P-poll__networl_6_1_AI_8" + "P-poll__networl_6_1_AnnP_0" + "P-poll__networl_6_1_AnnP_1" + "P-poll__networl_6_1_AnnP_2" + "P-poll__networl_6_1_AnnP_3" + "P-poll__networl_6_1_AnnP_4" + "P-poll__networl_6_1_AnnP_5" + "P-poll__networl_6_1_AnnP_6" + "P-poll__networl_6_1_AnnP_7" + "P-poll__networl_6_1_AnnP_8" + "P-poll__networl_6_1_RP_0" + "P-poll__networl_6_1_RP_1" + "P-poll__networl_6_1_RP_2" + "P-poll__networl_6_1_RP_3" + "P-poll__networl_6_1_RP_4" + "P-poll__networl_6_1_RP_5" + "P-poll__networl_6_1_RP_6" + "P-poll__networl_6_1_RP_7" + "P-poll__networl_6_1_RP_8" + "P-poll__networl_6_2_AskP_0" + "P-poll__networl_6_2_AskP_1" + "P-poll__networl_6_2_AskP_2" + "P-poll__networl_6_2_AskP_3" + "P-poll__networl_6_2_AskP_4" + "P-poll__networl_6_2_AskP_5" + "P-poll__networl_6_2_AskP_6" + "P-poll__networl_6_2_AskP_7" + "P-poll__networl_6_2_AskP_8" + "P-poll__networl_6_2_AnsP_0" + "P-poll__networl_6_2_AnsP_1" + "P-poll__networl_6_2_AnsP_2" + "P-poll__networl_6_2_AnsP_3" + "P-poll__networl_6_2_AnsP_4" + "P-poll__networl_6_2_AnsP_5" + "P-poll__networl_6_2_AnsP_6" + "P-poll__networl_6_2_AnsP_7" + "P-poll__networl_6_2_AnsP_8" + "P-poll__networl_6_2_RI_0" + "P-poll__networl_6_2_RI_1" + "P-poll__networl_6_2_RI_2" + "P-poll__networl_6_2_RI_3" + "P-poll__networl_6_2_RI_4" + "P-poll__networl_6_2_RI_5" + "P-poll__networl_6_2_RI_6" + "P-poll__networl_6_2_RI_7" + "P-poll__networl_6_2_RI_8" + "P-poll__networl_6_2_AI_0" + "P-poll__networl_6_2_AI_1" + "P-poll__networl_6_2_AI_2" + "P-poll__networl_6_2_AI_3" + "P-poll__networl_6_2_AI_4" + "P-poll__networl_6_2_AI_5" + "P-poll__networl_6_2_AI_6" + "P-poll__networl_6_2_AI_7" + "P-poll__networl_6_2_AI_8" + "P-poll__networl_6_2_AnnP_0" + "P-poll__networl_6_2_AnnP_1" + "P-poll__networl_6_2_AnnP_2" + "P-poll__networl_6_2_AnnP_3" + "P-poll__networl_6_2_AnnP_4" + "P-poll__networl_6_2_AnnP_5" + "P-poll__networl_6_2_AnnP_6" + "P-poll__networl_6_2_AnnP_7" + "P-poll__networl_6_2_AnnP_8" + "P-poll__networl_6_2_RP_0" + "P-poll__networl_6_2_RP_1" + "P-poll__networl_6_2_RP_2" + "P-poll__networl_6_2_RP_3" + "P-poll__networl_6_2_RP_4" + "P-poll__networl_6_2_RP_5" + "P-poll__networl_6_2_RP_6" + "P-poll__networl_6_2_RP_7" + "P-poll__networl_6_2_RP_8" + "P-poll__networl_6_3_AskP_0" + "P-poll__networl_6_3_AskP_1" + "P-poll__networl_6_3_AskP_2" + "P-poll__networl_6_3_AskP_3" + "P-poll__networl_6_3_AskP_4" + "P-poll__networl_6_3_AskP_5" + "P-poll__networl_6_3_AskP_6" + "P-poll__networl_6_3_AskP_7" + "P-poll__networl_6_3_AskP_8" + "P-poll__networl_6_3_AnsP_0" + "P-poll__networl_6_3_AnsP_1" + "P-poll__networl_6_3_AnsP_2" + "P-poll__networl_6_3_AnsP_3" + "P-poll__networl_6_3_AnsP_4" + "P-poll__networl_6_3_AnsP_5" + "P-poll__networl_6_3_AnsP_6" + "P-poll__networl_6_3_AnsP_7" + "P-poll__networl_6_3_AnsP_8" + "P-poll__networl_6_3_RI_0" + "P-poll__networl_6_3_RI_1" + "P-poll__networl_6_3_RI_2" + "P-poll__networl_6_3_RI_3" + "P-poll__networl_6_3_RI_4" + "P-poll__networl_6_3_RI_5" + "P-poll__networl_6_3_RI_6" + "P-poll__networl_6_3_RI_7" + "P-poll__networl_6_3_RI_8" + "P-poll__networl_6_3_AI_0" + "P-poll__networl_6_3_AI_1" + "P-poll__networl_6_3_AI_2" + "P-poll__networl_6_3_AI_3" + "P-poll__networl_6_3_AI_4" + "P-poll__networl_6_3_AI_5" + "P-poll__networl_6_3_AI_6" + "P-poll__networl_6_3_AI_7" + "P-poll__networl_6_3_AI_8" + "P-poll__networl_6_3_AnnP_0" + "P-poll__networl_6_3_AnnP_1" + "P-poll__networl_6_3_AnnP_2" + "P-poll__networl_6_3_AnnP_3" + "P-poll__networl_6_3_AnnP_4" + "P-poll__networl_6_3_AnnP_5" + "P-poll__networl_6_3_AnnP_6" + "P-poll__networl_6_3_AnnP_7" + "P-poll__networl_6_3_AnnP_8" + "P-poll__networl_6_3_RP_0" + "P-poll__networl_6_3_RP_1" + "P-poll__networl_6_3_RP_2" + "P-poll__networl_6_3_RP_3" + "P-poll__networl_6_3_RP_4" + "P-poll__networl_6_3_RP_5" + "P-poll__networl_6_3_RP_6" + "P-poll__networl_6_3_RP_7" + "P-poll__networl_6_3_RP_8" + "P-poll__networl_6_4_AskP_0" + "P-poll__networl_6_4_AskP_1" + "P-poll__networl_6_4_AskP_2" + "P-poll__networl_6_4_AskP_3" + "P-poll__networl_6_4_AskP_4" + "P-poll__networl_6_4_AskP_5" + "P-poll__networl_6_4_AskP_6" + "P-poll__networl_6_4_AskP_7" + "P-poll__networl_6_4_AskP_8" + "P-poll__networl_6_4_AnsP_0" + "P-poll__networl_6_4_AnsP_1" + "P-poll__networl_6_4_AnsP_2" + "P-poll__networl_6_4_AnsP_3" + "P-poll__networl_6_4_AnsP_4" + "P-poll__networl_6_4_AnsP_5" + "P-poll__networl_6_4_AnsP_6" + "P-poll__networl_6_4_AnsP_7" + "P-poll__networl_6_4_AnsP_8" + "P-poll__networl_6_4_RI_0" + "P-poll__networl_6_4_RI_1" + "P-poll__networl_6_4_RI_2" + "P-poll__networl_6_4_RI_3" + "P-poll__networl_6_4_RI_4" + "P-poll__networl_6_4_RI_5" + "P-poll__networl_6_4_RI_6" + "P-poll__networl_6_4_RI_7" + "P-poll__networl_6_4_RI_8" + "P-poll__networl_6_4_AI_0" + "P-poll__networl_6_4_AI_1" + "P-poll__networl_6_4_AI_2" + "P-poll__networl_6_4_AI_3" + "P-poll__networl_6_4_AI_4" + "P-poll__networl_6_4_AI_5" + "P-poll__networl_6_4_AI_6" + "P-poll__networl_6_4_AI_7" + "P-poll__networl_6_4_AI_8" + "P-poll__networl_6_4_AnnP_0" + "P-poll__networl_6_4_AnnP_1" + "P-poll__networl_6_4_AnnP_2" + "P-poll__networl_6_4_AnnP_3" + "P-poll__networl_6_4_AnnP_4" + "P-poll__networl_6_4_AnnP_5" + "P-poll__networl_6_4_AnnP_6" + "P-poll__networl_6_4_AnnP_7" + "P-poll__networl_6_4_AnnP_8" + "P-poll__networl_6_4_RP_0" + "P-poll__networl_6_4_RP_1" + "P-poll__networl_6_4_RP_2" + "P-poll__networl_6_4_RP_3" + "P-poll__networl_6_4_RP_4" + "P-poll__networl_6_4_RP_5" + "P-poll__networl_6_4_RP_6" + "P-poll__networl_6_4_RP_7" + "P-poll__networl_6_4_RP_8" + "P-poll__networl_6_5_AskP_0" + "P-poll__networl_6_5_AskP_1" + "P-poll__networl_6_5_AskP_2" + "P-poll__networl_6_5_AskP_3" + "P-poll__networl_6_5_AskP_4" + "P-poll__networl_6_5_AskP_5" + "P-poll__networl_6_5_AskP_6" + "P-poll__networl_6_5_AskP_7" + "P-poll__networl_6_5_AskP_8" + "P-poll__networl_6_5_AnsP_0" + "P-poll__networl_6_5_AnsP_1" + "P-poll__networl_6_5_AnsP_2" + "P-poll__networl_6_5_AnsP_3" + "P-poll__networl_6_5_AnsP_4" + "P-poll__networl_6_5_AnsP_5" + "P-poll__networl_6_5_AnsP_6" + "P-poll__networl_6_5_AnsP_7" + "P-poll__networl_6_5_AnsP_8" + "P-poll__networl_6_5_RI_0" + "P-poll__networl_6_5_RI_1" + "P-poll__networl_6_5_RI_2" + "P-poll__networl_6_5_RI_3" + "P-poll__networl_6_5_RI_4" + "P-poll__networl_6_5_RI_5" + "P-poll__networl_6_5_RI_6" + "P-poll__networl_6_5_RI_7" + "P-poll__networl_6_5_RI_8" + "P-poll__networl_6_5_AI_0" + "P-poll__networl_6_5_AI_1" + "P-poll__networl_6_5_AI_2" + "P-poll__networl_6_5_AI_3" + "P-poll__networl_6_5_AI_4" + "P-poll__networl_6_5_AI_5" + "P-poll__networl_6_5_AI_6" + "P-poll__networl_6_5_AI_7" + "P-poll__networl_6_5_AI_8" + "P-poll__networl_6_5_AnnP_0" + "P-poll__networl_6_5_AnnP_1" + "P-poll__networl_6_5_AnnP_2" + "P-poll__networl_6_5_AnnP_3" + "P-poll__networl_6_5_AnnP_4" + "P-poll__networl_6_5_AnnP_5" + "P-poll__networl_6_5_AnnP_6" + "P-poll__networl_6_5_AnnP_7" + "P-poll__networl_6_5_AnnP_8" + "P-poll__networl_6_5_RP_0" + "P-poll__networl_6_5_RP_1" + "P-poll__networl_6_5_RP_2" + "P-poll__networl_6_5_RP_3" + "P-poll__networl_6_5_RP_4" + "P-poll__networl_6_5_RP_5" + "P-poll__networl_6_5_RP_6" + "P-poll__networl_6_5_RP_7" + "P-poll__networl_6_5_RP_8" + "P-poll__networl_6_6_AskP_0" + "P-poll__networl_6_6_AskP_1" + "P-poll__networl_6_6_AskP_2" + "P-poll__networl_6_6_AskP_3" + "P-poll__networl_6_6_AskP_4" + "P-poll__networl_6_6_AskP_5" + "P-poll__networl_6_6_AskP_6" + "P-poll__networl_6_6_AskP_7" + "P-poll__networl_6_6_AskP_8" + "P-poll__networl_6_6_AnsP_0" + "P-poll__networl_6_6_AnsP_1" + "P-poll__networl_6_6_AnsP_2" + "P-poll__networl_6_6_AnsP_3" + "P-poll__networl_6_6_AnsP_4" + "P-poll__networl_6_6_AnsP_5" + "P-poll__networl_6_6_AnsP_6" + "P-poll__networl_6_6_AnsP_7" + "P-poll__networl_6_6_AnsP_8" + "P-poll__networl_6_6_RI_0" + "P-poll__networl_6_6_RI_1" + "P-poll__networl_6_6_RI_2" + "P-poll__networl_6_6_RI_3" + "P-poll__networl_6_6_RI_4" + "P-poll__networl_6_6_RI_5" + "P-poll__networl_6_6_RI_6" + "P-poll__networl_6_6_RI_7" + "P-poll__networl_6_6_RI_8" + "P-poll__networl_6_6_AI_0" + "P-poll__networl_6_6_AI_1" + "P-poll__networl_6_6_AI_2" + "P-poll__networl_6_6_AI_3" + "P-poll__networl_6_6_AI_4" + "P-poll__networl_6_6_AI_5" + "P-poll__networl_6_6_AI_6" + "P-poll__networl_6_6_AI_7" + "P-poll__networl_6_6_AI_8" + "P-poll__networl_6_6_AnnP_0" + "P-poll__networl_6_6_AnnP_1" + "P-poll__networl_6_6_AnnP_2" + "P-poll__networl_6_6_AnnP_3" + "P-poll__networl_6_6_AnnP_4" + "P-poll__networl_6_6_AnnP_5" + "P-poll__networl_6_6_AnnP_6" + "P-poll__networl_6_6_AnnP_7" + "P-poll__networl_6_6_AnnP_8" + "P-poll__networl_6_6_RP_0" + "P-poll__networl_6_6_RP_1" + "P-poll__networl_6_6_RP_2" + "P-poll__networl_6_6_RP_3" + "P-poll__networl_6_6_RP_4" + "P-poll__networl_6_6_RP_5" + "P-poll__networl_6_6_RP_6" + "P-poll__networl_6_6_RP_7" + "P-poll__networl_6_6_RP_8" + "P-poll__networl_6_7_AskP_0" + "P-poll__networl_6_7_AskP_1" + "P-poll__networl_6_7_AskP_2" + "P-poll__networl_6_7_AskP_3" + "P-poll__networl_6_7_AskP_4" + "P-poll__networl_6_7_AskP_5" + "P-poll__networl_6_7_AskP_6" + "P-poll__networl_6_7_AskP_7" + "P-poll__networl_6_7_AskP_8" + "P-poll__networl_6_7_AnsP_0" + "P-poll__networl_6_7_AnsP_1" + "P-poll__networl_6_7_AnsP_2" + "P-poll__networl_6_7_AnsP_3" + "P-poll__networl_6_7_AnsP_4" + "P-poll__networl_6_7_AnsP_5" + "P-poll__networl_6_7_AnsP_6" + "P-poll__networl_6_7_AnsP_7" + "P-poll__networl_6_7_AnsP_8" + "P-poll__networl_6_7_RI_0" + "P-poll__networl_6_7_RI_1" + "P-poll__networl_6_7_RI_2" + "P-poll__networl_6_7_RI_3" + "P-poll__networl_6_7_RI_4" + "P-poll__networl_6_7_RI_5" + "P-poll__networl_6_7_RI_6" + "P-poll__networl_6_7_RI_7" + "P-poll__networl_6_7_RI_8" + "P-poll__networl_6_7_AI_0" + "P-poll__networl_6_7_AI_1" + "P-poll__networl_6_7_AI_2" + "P-poll__networl_6_7_AI_3" + "P-poll__networl_6_7_AI_4" + "P-poll__networl_6_7_AI_5" + "P-poll__networl_6_7_AI_6" + "P-poll__networl_6_7_AI_7" + "P-poll__networl_6_7_AI_8" + "P-poll__networl_6_7_AnnP_0" + "P-poll__networl_6_7_AnnP_1" + "P-poll__networl_6_7_AnnP_2" + "P-poll__networl_6_7_AnnP_3" + "P-poll__networl_6_7_AnnP_4" + "P-poll__networl_6_7_AnnP_5" + "P-poll__networl_6_7_AnnP_6" + "P-poll__networl_6_7_AnnP_7" + "P-poll__networl_6_7_AnnP_8" + "P-poll__networl_6_7_RP_0" + "P-poll__networl_6_7_RP_1" + "P-poll__networl_6_7_RP_2" + "P-poll__networl_6_7_RP_3" + "P-poll__networl_6_7_RP_4" + "P-poll__networl_6_7_RP_5" + "P-poll__networl_6_7_RP_6" + "P-poll__networl_6_7_RP_7" + "P-poll__networl_6_7_RP_8" + "P-poll__networl_6_8_AskP_0" + "P-poll__networl_6_8_AskP_1" + "P-poll__networl_6_8_AskP_2" + "P-poll__networl_6_8_AskP_3" + "P-poll__networl_6_8_AskP_4" + "P-poll__networl_6_8_AskP_5" + "P-poll__networl_6_8_AskP_6" + "P-poll__networl_6_8_AskP_7" + "P-poll__networl_6_8_AskP_8" + "P-poll__networl_6_8_AnsP_0" + "P-poll__networl_6_8_AnsP_1" + "P-poll__networl_6_8_AnsP_2" + "P-poll__networl_6_8_AnsP_3" + "P-poll__networl_6_8_AnsP_4" + "P-poll__networl_6_8_AnsP_5" + "P-poll__networl_6_8_AnsP_6" + "P-poll__networl_6_8_AnsP_7" + "P-poll__networl_6_8_AnsP_8" + "P-poll__networl_6_8_RI_0" + "P-poll__networl_6_8_RI_1" + "P-poll__networl_6_8_RI_2" + "P-poll__networl_6_8_RI_3" + "P-poll__networl_6_8_RI_4" + "P-poll__networl_6_8_RI_5" + "P-poll__networl_6_8_RI_6" + "P-poll__networl_6_8_RI_7" + "P-poll__networl_6_8_RI_8" + "P-poll__networl_6_8_AI_0" + "P-poll__networl_6_8_AI_1" + "P-poll__networl_6_8_AI_2" + "P-poll__networl_6_8_AI_3" + "P-poll__networl_6_8_AI_4" + "P-poll__networl_6_8_AI_5" + "P-poll__networl_6_8_AI_6" + "P-poll__networl_6_8_AI_7" + "P-poll__networl_6_8_AI_8" + "P-poll__networl_6_8_AnnP_0" + "P-poll__networl_6_8_AnnP_1" + "P-poll__networl_6_8_AnnP_2" + "P-poll__networl_6_8_AnnP_3" + "P-poll__networl_6_8_AnnP_4" + "P-poll__networl_6_8_AnnP_5" + "P-poll__networl_6_8_AnnP_6" + "P-poll__networl_6_8_AnnP_7" + "P-poll__networl_6_8_AnnP_8" + "P-poll__networl_6_8_RP_0" + "P-poll__networl_6_8_RP_1" + "P-poll__networl_6_8_RP_2" + "P-poll__networl_6_8_RP_3" + "P-poll__networl_6_8_RP_4" + "P-poll__networl_6_8_RP_5" + "P-poll__networl_6_8_RP_6" + "P-poll__networl_6_8_RP_7" + "P-poll__networl_6_8_RP_8" + "P-poll__networl_7_0_AskP_0" + "P-poll__networl_7_0_AskP_1" + "P-poll__networl_7_0_AskP_2" + "P-poll__networl_7_0_AskP_3" + "P-poll__networl_7_0_AskP_4" + "P-poll__networl_7_0_AskP_5" + "P-poll__networl_7_0_AskP_6" + "P-poll__networl_7_0_AskP_7" + "P-poll__networl_7_0_AskP_8" + "P-poll__networl_7_0_AnsP_0" + "P-poll__networl_7_0_AnsP_1" + "P-poll__networl_7_0_AnsP_2" + "P-poll__networl_7_0_AnsP_3" + "P-poll__networl_7_0_AnsP_4" + "P-poll__networl_7_0_AnsP_5" + "P-poll__networl_7_0_AnsP_6" + "P-poll__networl_7_0_AnsP_7" + "P-poll__networl_7_0_AnsP_8" + "P-poll__networl_7_0_RI_0" + "P-poll__networl_7_0_RI_1" + "P-poll__networl_7_0_RI_2" + "P-poll__networl_7_0_RI_3" + "P-poll__networl_7_0_RI_4" + "P-poll__networl_7_0_RI_5" + "P-poll__networl_7_0_RI_6" + "P-poll__networl_7_0_RI_7" + "P-poll__networl_7_0_RI_8" + "P-poll__networl_7_0_AI_0" + "P-poll__networl_7_0_AI_1" + "P-poll__networl_7_0_AI_2" + "P-poll__networl_7_0_AI_3" + "P-poll__networl_7_0_AI_4" + "P-poll__networl_7_0_AI_5" + "P-poll__networl_7_0_AI_6" + "P-poll__networl_7_0_AI_7" + "P-poll__networl_7_0_AI_8" + "P-poll__networl_7_0_AnnP_0" + "P-poll__networl_7_0_AnnP_1" + "P-poll__networl_7_0_AnnP_2" + "P-poll__networl_7_0_AnnP_3" + "P-poll__networl_7_0_AnnP_4" + "P-poll__networl_7_0_AnnP_5" + "P-poll__networl_7_0_AnnP_6" + "P-poll__networl_7_0_AnnP_7" + "P-poll__networl_7_0_AnnP_8" + "P-poll__networl_7_0_RP_0" + "P-poll__networl_7_0_RP_1" + "P-poll__networl_7_0_RP_2" + "P-poll__networl_7_0_RP_3" + "P-poll__networl_7_0_RP_4" + "P-poll__networl_7_0_RP_5" + "P-poll__networl_7_0_RP_6" + "P-poll__networl_7_0_RP_7" + "P-poll__networl_7_0_RP_8" + "P-poll__networl_7_1_AskP_0" + "P-poll__networl_7_1_AskP_1" + "P-poll__networl_7_1_AskP_2" + "P-poll__networl_7_1_AskP_3" + "P-poll__networl_7_1_AskP_4" + "P-poll__networl_7_1_AskP_5" + "P-poll__networl_7_1_AskP_6" + "P-poll__networl_7_1_AskP_7" + "P-poll__networl_7_1_AskP_8" + "P-poll__networl_7_1_AnsP_0" + "P-poll__networl_7_1_AnsP_1" + "P-poll__networl_7_1_AnsP_2" + "P-poll__networl_7_1_AnsP_3" + "P-poll__networl_7_1_AnsP_4" + "P-poll__networl_7_1_AnsP_5" + "P-poll__networl_7_1_AnsP_6" + "P-poll__networl_7_1_AnsP_7" + "P-poll__networl_7_1_AnsP_8" + "P-poll__networl_7_1_RI_0" + "P-poll__networl_7_1_RI_1" + "P-poll__networl_7_1_RI_2" + "P-poll__networl_7_1_RI_3" + "P-poll__networl_7_1_RI_4" + "P-poll__networl_7_1_RI_5" + "P-poll__networl_7_1_RI_6" + "P-poll__networl_7_1_RI_7" + "P-poll__networl_7_1_RI_8" + "P-poll__networl_7_1_AI_0" + "P-poll__networl_7_1_AI_1" + "P-poll__networl_7_1_AI_2" + "P-poll__networl_7_1_AI_3" + "P-poll__networl_7_1_AI_4" + "P-poll__networl_7_1_AI_5" + "P-poll__networl_7_1_AI_6" + "P-poll__networl_7_1_AI_7" + "P-poll__networl_7_1_AI_8" + "P-poll__networl_7_1_AnnP_0" + "P-poll__networl_7_1_AnnP_1" + "P-poll__networl_7_1_AnnP_2" + "P-poll__networl_7_1_AnnP_3" + "P-poll__networl_7_1_AnnP_4" + "P-poll__networl_7_1_AnnP_5" + "P-poll__networl_7_1_AnnP_6" + "P-poll__networl_7_1_AnnP_7" + "P-poll__networl_7_1_AnnP_8" + "P-poll__networl_7_1_RP_0" + "P-poll__networl_7_1_RP_1" + "P-poll__networl_7_1_RP_2" + "P-poll__networl_7_1_RP_3" + "P-poll__networl_7_1_RP_4" + "P-poll__networl_7_1_RP_5" + "P-poll__networl_7_1_RP_6" + "P-poll__networl_7_1_RP_7" + "P-poll__networl_7_1_RP_8" + "P-poll__networl_7_2_AskP_0" + "P-poll__networl_7_2_AskP_1" + "P-poll__networl_7_2_AskP_2" + "P-poll__networl_7_2_AskP_3" + "P-poll__networl_7_2_AskP_4" + "P-poll__networl_7_2_AskP_5" + "P-poll__networl_7_2_AskP_6" + "P-poll__networl_7_2_AskP_7" + "P-poll__networl_7_2_AskP_8" + "P-poll__networl_7_2_AnsP_0" + "P-poll__networl_7_2_AnsP_1" + "P-poll__networl_7_2_AnsP_2" + "P-poll__networl_7_2_AnsP_3" + "P-poll__networl_7_2_AnsP_4" + "P-poll__networl_7_2_AnsP_5" + "P-poll__networl_7_2_AnsP_6" + "P-poll__networl_7_2_AnsP_7" + "P-poll__networl_7_2_AnsP_8" + "P-poll__networl_7_2_RI_0" + "P-poll__networl_7_2_RI_1" + "P-poll__networl_7_2_RI_2" + "P-poll__networl_7_2_RI_3" + "P-poll__networl_7_2_RI_4" + "P-poll__networl_7_2_RI_5" + "P-poll__networl_7_2_RI_6" + "P-poll__networl_7_2_RI_7" + "P-poll__networl_7_2_RI_8" + "P-poll__networl_7_2_AI_0" + "P-poll__networl_7_2_AI_1" + "P-poll__networl_7_2_AI_2" + "P-poll__networl_7_2_AI_3" + "P-poll__networl_7_2_AI_4" + "P-poll__networl_7_2_AI_5" + "P-poll__networl_7_2_AI_6" + "P-poll__networl_7_2_AI_7" + "P-poll__networl_7_2_AI_8" + "P-poll__networl_7_2_AnnP_0" + "P-poll__networl_7_2_AnnP_1" + "P-poll__networl_7_2_AnnP_2" + "P-poll__networl_7_2_AnnP_3" + "P-poll__networl_7_2_AnnP_4" + "P-poll__networl_7_2_AnnP_5" + "P-poll__networl_7_2_AnnP_6" + "P-poll__networl_7_2_AnnP_7" + "P-poll__networl_7_2_AnnP_8" + "P-poll__networl_7_2_RP_0" + "P-poll__networl_7_2_RP_1" + "P-poll__networl_7_2_RP_2" + "P-poll__networl_7_2_RP_3" + "P-poll__networl_7_2_RP_4" + "P-poll__networl_7_2_RP_5" + "P-poll__networl_7_2_RP_6" + "P-poll__networl_7_2_RP_7" + "P-poll__networl_7_2_RP_8" + "P-poll__networl_7_3_AskP_0" + "P-poll__networl_7_3_AskP_1" + "P-poll__networl_7_3_AskP_2" + "P-poll__networl_7_3_AskP_3" + "P-poll__networl_7_3_AskP_4" + "P-poll__networl_7_3_AskP_5" + "P-poll__networl_7_3_AskP_6" + "P-poll__networl_7_3_AskP_7" + "P-poll__networl_7_3_AskP_8" + "P-poll__networl_7_3_AnsP_0" + "P-poll__networl_7_3_AnsP_1" + "P-poll__networl_7_3_AnsP_2" + "P-poll__networl_7_3_AnsP_3" + "P-poll__networl_7_3_AnsP_4" + "P-poll__networl_7_3_AnsP_5" + "P-poll__networl_7_3_AnsP_6" + "P-poll__networl_7_3_AnsP_7" + "P-poll__networl_7_3_AnsP_8" + "P-poll__networl_7_3_RI_0" + "P-poll__networl_7_3_RI_1" + "P-poll__networl_7_3_RI_2" + "P-poll__networl_7_3_RI_3" + "P-poll__networl_7_3_RI_4" + "P-poll__networl_7_3_RI_5" + "P-poll__networl_7_3_RI_6" + "P-poll__networl_7_3_RI_7" + "P-poll__networl_7_3_RI_8" + "P-poll__networl_7_3_AI_0" + "P-poll__networl_7_3_AI_1" + "P-poll__networl_7_3_AI_2" + "P-poll__networl_7_3_AI_3" + "P-poll__networl_7_3_AI_4" + "P-poll__networl_7_3_AI_5" + "P-poll__networl_7_3_AI_6" + "P-poll__networl_7_3_AI_7" + "P-poll__networl_7_3_AI_8" + "P-poll__networl_7_3_AnnP_0" + "P-poll__networl_7_3_AnnP_1" + "P-poll__networl_7_3_AnnP_2" + "P-poll__networl_7_3_AnnP_3" + "P-poll__networl_7_3_AnnP_4" + "P-poll__networl_7_3_AnnP_5" + "P-poll__networl_7_3_AnnP_6" + "P-poll__networl_7_3_AnnP_7" + "P-poll__networl_7_3_AnnP_8" + "P-poll__networl_7_3_RP_0" + "P-poll__networl_7_3_RP_1" + "P-poll__networl_7_3_RP_2" + "P-poll__networl_7_3_RP_3" + "P-poll__networl_7_3_RP_4" + "P-poll__networl_7_3_RP_5" + "P-poll__networl_7_3_RP_6" + "P-poll__networl_7_3_RP_7" + "P-poll__networl_7_3_RP_8" + "P-poll__networl_7_4_AskP_0" + "P-poll__networl_7_4_AskP_1" + "P-poll__networl_7_4_AskP_2" + "P-poll__networl_7_4_AskP_3" + "P-poll__networl_7_4_AskP_4" + "P-poll__networl_7_4_AskP_5" + "P-poll__networl_7_4_AskP_6" + "P-poll__networl_7_4_AskP_7" + "P-poll__networl_7_4_AskP_8" + "P-poll__networl_7_4_AnsP_0" + "P-poll__networl_7_4_AnsP_1" + "P-poll__networl_7_4_AnsP_2" + "P-poll__networl_7_4_AnsP_3" + "P-poll__networl_7_4_AnsP_4" + "P-poll__networl_7_4_AnsP_5" + "P-poll__networl_7_4_AnsP_6" + "P-poll__networl_7_4_AnsP_7" + "P-poll__networl_7_4_AnsP_8" + "P-poll__networl_7_4_RI_0" + "P-poll__networl_7_4_RI_1" + "P-poll__networl_7_4_RI_2" + "P-poll__networl_7_4_RI_3" + "P-poll__networl_7_4_RI_4" + "P-poll__networl_7_4_RI_5" + "P-poll__networl_7_4_RI_6" + "P-poll__networl_7_4_RI_7" + "P-poll__networl_7_4_RI_8" + "P-poll__networl_7_4_AI_0" + "P-poll__networl_7_4_AI_1" + "P-poll__networl_7_4_AI_2" + "P-poll__networl_7_4_AI_3" + "P-poll__networl_7_4_AI_4" + "P-poll__networl_7_4_AI_5" + "P-poll__networl_7_4_AI_6" + "P-poll__networl_7_4_AI_7" + "P-poll__networl_7_4_AI_8" + "P-poll__networl_7_4_AnnP_0" + "P-poll__networl_7_4_AnnP_1" + "P-poll__networl_7_4_AnnP_2" + "P-poll__networl_7_4_AnnP_3" + "P-poll__networl_7_4_AnnP_4" + "P-poll__networl_7_4_AnnP_5" + "P-poll__networl_7_4_AnnP_6" + "P-poll__networl_7_4_AnnP_7" + "P-poll__networl_7_4_AnnP_8" + "P-poll__networl_7_4_RP_0" + "P-poll__networl_7_4_RP_1" + "P-poll__networl_7_4_RP_2" + "P-poll__networl_7_4_RP_3" + "P-poll__networl_7_4_RP_4" + "P-poll__networl_7_4_RP_5" + "P-poll__networl_7_4_RP_6" + "P-poll__networl_7_4_RP_7" + "P-poll__networl_7_4_RP_8" + "P-poll__networl_7_5_AskP_0" + "P-poll__networl_7_5_AskP_1" + "P-poll__networl_7_5_AskP_2" + "P-poll__networl_7_5_AskP_3" + "P-poll__networl_7_5_AskP_4" + "P-poll__networl_7_5_AskP_5" + "P-poll__networl_7_5_AskP_6" + "P-poll__networl_7_5_AskP_7" + "P-poll__networl_7_5_AskP_8" + "P-poll__networl_7_5_AnsP_0" + "P-poll__networl_7_5_AnsP_1" + "P-poll__networl_7_5_AnsP_2" + "P-poll__networl_7_5_AnsP_3" + "P-poll__networl_7_5_AnsP_4" + "P-poll__networl_7_5_AnsP_5" + "P-poll__networl_7_5_AnsP_6" + "P-poll__networl_7_5_AnsP_7" + "P-poll__networl_7_5_AnsP_8" + "P-poll__networl_7_5_RI_0" + "P-poll__networl_7_5_RI_1" + "P-poll__networl_7_5_RI_2" + "P-poll__networl_7_5_RI_3" + "P-poll__networl_7_5_RI_4" + "P-poll__networl_7_5_RI_5" + "P-poll__networl_7_5_RI_6" + "P-poll__networl_7_5_RI_7" + "P-poll__networl_7_5_RI_8" + "P-poll__networl_7_5_AI_0" + "P-poll__networl_7_5_AI_1" + "P-poll__networl_7_5_AI_2" + "P-poll__networl_7_5_AI_3" + "P-poll__networl_7_5_AI_4" + "P-poll__networl_7_5_AI_5" + "P-poll__networl_7_5_AI_6" + "P-poll__networl_7_5_AI_7" + "P-poll__networl_7_5_AI_8" + "P-poll__networl_7_5_AnnP_0" + "P-poll__networl_7_5_AnnP_1" + "P-poll__networl_7_5_AnnP_2" + "P-poll__networl_7_5_AnnP_3" + "P-poll__networl_7_5_AnnP_4" + "P-poll__networl_7_5_AnnP_5" + "P-poll__networl_7_5_AnnP_6" + "P-poll__networl_7_5_AnnP_7" + "P-poll__networl_7_5_AnnP_8" + "P-poll__networl_7_5_RP_0" + "P-poll__networl_7_5_RP_1" + "P-poll__networl_7_5_RP_2" + "P-poll__networl_7_5_RP_3" + "P-poll__networl_7_5_RP_4" + "P-poll__networl_7_5_RP_5" + "P-poll__networl_7_5_RP_6" + "P-poll__networl_7_5_RP_7" + "P-poll__networl_7_5_RP_8" + "P-poll__networl_7_6_AskP_0" + "P-poll__networl_7_6_AskP_1" + "P-poll__networl_7_6_AskP_2" + "P-poll__networl_7_6_AskP_3" + "P-poll__networl_7_6_AskP_4" + "P-poll__networl_7_6_AskP_5" + "P-poll__networl_7_6_AskP_6" + "P-poll__networl_7_6_AskP_7" + "P-poll__networl_7_6_AskP_8" + "P-poll__networl_7_6_AnsP_0" + "P-poll__networl_7_6_AnsP_1" + "P-poll__networl_7_6_AnsP_2" + "P-poll__networl_7_6_AnsP_3" + "P-poll__networl_7_6_AnsP_4" + "P-poll__networl_7_6_AnsP_5" + "P-poll__networl_7_6_AnsP_6" + "P-poll__networl_7_6_AnsP_7" + "P-poll__networl_7_6_AnsP_8" + "P-poll__networl_7_6_RI_0" + "P-poll__networl_7_6_RI_1" + "P-poll__networl_7_6_RI_2" + "P-poll__networl_7_6_RI_3" + "P-poll__networl_7_6_RI_4" + "P-poll__networl_7_6_RI_5" + "P-poll__networl_7_6_RI_6" + "P-poll__networl_7_6_RI_7" + "P-poll__networl_7_6_RI_8" + "P-poll__networl_7_6_AI_0" + "P-poll__networl_7_6_AI_1" + "P-poll__networl_7_6_AI_2" + "P-poll__networl_7_6_AI_3" + "P-poll__networl_7_6_AI_4" + "P-poll__networl_7_6_AI_5" + "P-poll__networl_7_6_AI_6" + "P-poll__networl_7_6_AI_7" + "P-poll__networl_7_6_AI_8" + "P-poll__networl_7_6_AnnP_0" + "P-poll__networl_7_6_AnnP_1" + "P-poll__networl_7_6_AnnP_2" + "P-poll__networl_7_6_AnnP_3" + "P-poll__networl_7_6_AnnP_4" + "P-poll__networl_7_6_AnnP_5" + "P-poll__networl_7_6_AnnP_6" + "P-poll__networl_7_6_AnnP_7" + "P-poll__networl_7_6_AnnP_8" + "P-poll__networl_7_6_RP_0" + "P-poll__networl_7_6_RP_1" + "P-poll__networl_7_6_RP_2" + "P-poll__networl_7_6_RP_3" + "P-poll__networl_7_6_RP_4" + "P-poll__networl_7_6_RP_5" + "P-poll__networl_7_6_RP_6" + "P-poll__networl_7_6_RP_7" + "P-poll__networl_7_6_RP_8" + "P-poll__networl_7_7_AskP_0" + "P-poll__networl_7_7_AskP_1" + "P-poll__networl_7_7_AskP_2" + "P-poll__networl_7_7_AskP_3" + "P-poll__networl_7_7_AskP_4" + "P-poll__networl_7_7_AskP_5" + "P-poll__networl_7_7_AskP_6" + "P-poll__networl_7_7_AskP_7" + "P-poll__networl_7_7_AskP_8" + "P-poll__networl_7_7_AnsP_0" + "P-poll__networl_7_7_AnsP_1" + "P-poll__networl_7_7_AnsP_2" + "P-poll__networl_7_7_AnsP_3" + "P-poll__networl_7_7_AnsP_4" + "P-poll__networl_7_7_AnsP_5" + "P-poll__networl_7_7_AnsP_6" + "P-poll__networl_7_7_AnsP_7" + "P-poll__networl_7_7_AnsP_8" + "P-poll__networl_7_7_RI_0" + "P-poll__networl_7_7_RI_1" + "P-poll__networl_7_7_RI_2" + "P-poll__networl_7_7_RI_3" + "P-poll__networl_7_7_RI_4" + "P-poll__networl_7_7_RI_5" + "P-poll__networl_7_7_RI_6" + "P-poll__networl_7_7_RI_7" + "P-poll__networl_7_7_RI_8" + "P-poll__networl_7_7_AI_0" + "P-poll__networl_7_7_AI_1" + "P-poll__networl_7_7_AI_2" + "P-poll__networl_7_7_AI_3" + "P-poll__networl_7_7_AI_4" + "P-poll__networl_7_7_AI_5" + "P-poll__networl_7_7_AI_6" + "P-poll__networl_7_7_AI_7" + "P-poll__networl_7_7_AI_8" + "P-poll__networl_7_7_AnnP_0" + "P-poll__networl_7_7_AnnP_1" + "P-poll__networl_7_7_AnnP_2" + "P-poll__networl_7_7_AnnP_3" + "P-poll__networl_7_7_AnnP_4" + "P-poll__networl_7_7_AnnP_5" + "P-poll__networl_7_7_AnnP_6" + "P-poll__networl_7_7_AnnP_7" + "P-poll__networl_7_7_AnnP_8" + "P-poll__networl_7_7_RP_0" + "P-poll__networl_7_7_RP_1" + "P-poll__networl_7_7_RP_2" + "P-poll__networl_7_7_RP_3" + "P-poll__networl_7_7_RP_4" + "P-poll__networl_7_7_RP_5" + "P-poll__networl_7_7_RP_6" + "P-poll__networl_7_7_RP_7" + "P-poll__networl_7_7_RP_8" + "P-poll__networl_7_8_AskP_0" + "P-poll__networl_7_8_AskP_1" + "P-poll__networl_7_8_AskP_2" + "P-poll__networl_7_8_AskP_3" + "P-poll__networl_7_8_AskP_4" + "P-poll__networl_7_8_AskP_5" + "P-poll__networl_7_8_AskP_6" + "P-poll__networl_7_8_AskP_7" + "P-poll__networl_7_8_AskP_8" + "P-poll__networl_7_8_AnsP_0" + "P-poll__networl_7_8_AnsP_1" + "P-poll__networl_7_8_AnsP_2" + "P-poll__networl_7_8_AnsP_3" + "P-poll__networl_7_8_AnsP_4" + "P-poll__networl_7_8_AnsP_5" + "P-poll__networl_7_8_AnsP_6" + "P-poll__networl_7_8_AnsP_7" + "P-poll__networl_7_8_AnsP_8" + "P-poll__networl_7_8_RI_0" + "P-poll__networl_7_8_RI_1" + "P-poll__networl_7_8_RI_2" + "P-poll__networl_7_8_RI_3" + "P-poll__networl_7_8_RI_4" + "P-poll__networl_7_8_RI_5" + "P-poll__networl_7_8_RI_6" + "P-poll__networl_7_8_RI_7" + "P-poll__networl_7_8_RI_8" + "P-poll__networl_7_8_AI_0" + "P-poll__networl_7_8_AI_1" + "P-poll__networl_7_8_AI_2" + "P-poll__networl_7_8_AI_3" + "P-poll__networl_7_8_AI_4" + "P-poll__networl_7_8_AI_5" + "P-poll__networl_7_8_AI_6" + "P-poll__networl_7_8_AI_7" + "P-poll__networl_7_8_AI_8" + "P-poll__networl_7_8_AnnP_0" + "P-poll__networl_7_8_AnnP_1" + "P-poll__networl_7_8_AnnP_2" + "P-poll__networl_7_8_AnnP_3" + "P-poll__networl_7_8_AnnP_4" + "P-poll__networl_7_8_AnnP_5" + "P-poll__networl_7_8_AnnP_6" + "P-poll__networl_7_8_AnnP_7" + "P-poll__networl_7_8_AnnP_8" + "P-poll__networl_7_8_RP_0" + "P-poll__networl_7_8_RP_1" + "P-poll__networl_7_8_RP_2" + "P-poll__networl_7_8_RP_3" + "P-poll__networl_7_8_RP_4" + "P-poll__networl_7_8_RP_5" + "P-poll__networl_7_8_RP_6" + "P-poll__networl_7_8_RP_7" + "P-poll__networl_7_8_RP_8" + "P-poll__networl_8_0_AskP_0" + "P-poll__networl_8_0_AskP_1" + "P-poll__networl_8_0_AskP_2" + "P-poll__networl_8_0_AskP_3" + "P-poll__networl_8_0_AskP_4" + "P-poll__networl_8_0_AskP_5" + "P-poll__networl_8_0_AskP_6" + "P-poll__networl_8_0_AskP_7" + "P-poll__networl_8_0_AskP_8" + "P-poll__networl_8_0_AnsP_0" + "P-poll__networl_8_0_AnsP_1" + "P-poll__networl_8_0_AnsP_2" + "P-poll__networl_8_0_AnsP_3" + "P-poll__networl_8_0_AnsP_4" + "P-poll__networl_8_0_AnsP_5" + "P-poll__networl_8_0_AnsP_6" + "P-poll__networl_8_0_AnsP_7" + "P-poll__networl_8_0_AnsP_8" + "P-poll__networl_8_0_RI_0" + "P-poll__networl_8_0_RI_1" + "P-poll__networl_8_0_RI_2" + "P-poll__networl_8_0_RI_3" + "P-poll__networl_8_0_RI_4" + "P-poll__networl_8_0_RI_5" + "P-poll__networl_8_0_RI_6" + "P-poll__networl_8_0_RI_7" + "P-poll__networl_8_0_RI_8" + "P-poll__networl_8_0_AI_0" + "P-poll__networl_8_0_AI_1" + "P-poll__networl_8_0_AI_2" + "P-poll__networl_8_0_AI_3" + "P-poll__networl_8_0_AI_4" + "P-poll__networl_8_0_AI_5" + "P-poll__networl_8_0_AI_6" + "P-poll__networl_8_0_AI_7" + "P-poll__networl_8_0_AI_8" + "P-poll__networl_8_0_AnnP_0" + "P-poll__networl_8_0_AnnP_1" + "P-poll__networl_8_0_AnnP_2" + "P-poll__networl_8_0_AnnP_3" + "P-poll__networl_8_0_AnnP_4" + "P-poll__networl_8_0_AnnP_5" + "P-poll__networl_8_0_AnnP_6" + "P-poll__networl_8_0_AnnP_7" + "P-poll__networl_8_0_AnnP_8" + "P-poll__networl_8_0_RP_0" + "P-poll__networl_8_0_RP_1" + "P-poll__networl_8_0_RP_2" + "P-poll__networl_8_0_RP_3" + "P-poll__networl_8_0_RP_4" + "P-poll__networl_8_0_RP_5" + "P-poll__networl_8_0_RP_6" + "P-poll__networl_8_0_RP_7" + "P-poll__networl_8_0_RP_8" + "P-poll__networl_8_1_AskP_0" + "P-poll__networl_8_1_AskP_1" + "P-poll__networl_8_1_AskP_2" + "P-poll__networl_8_1_AskP_3" + "P-poll__networl_8_1_AskP_4" + "P-poll__networl_8_1_AskP_5" + "P-poll__networl_8_1_AskP_6" + "P-poll__networl_8_1_AskP_7" + "P-poll__networl_8_1_AskP_8" + "P-poll__networl_8_1_AnsP_0" + "P-poll__networl_8_1_AnsP_1" + "P-poll__networl_8_1_AnsP_2" + "P-poll__networl_8_1_AnsP_3" + "P-poll__networl_8_1_AnsP_4" + "P-poll__networl_8_1_AnsP_5" + "P-poll__networl_8_1_AnsP_6" + "P-poll__networl_8_1_AnsP_7" + "P-poll__networl_8_1_AnsP_8" + "P-poll__networl_8_1_RI_0" + "P-poll__networl_8_1_RI_1" + "P-poll__networl_8_1_RI_2" + "P-poll__networl_8_1_RI_3" + "P-poll__networl_8_1_RI_4" + "P-poll__networl_8_1_RI_5" + "P-poll__networl_8_1_RI_6" + "P-poll__networl_8_1_RI_7" + "P-poll__networl_8_1_RI_8" + "P-poll__networl_8_1_AI_0" + "P-poll__networl_8_1_AI_1" + "P-poll__networl_8_1_AI_2" + "P-poll__networl_8_1_AI_3" + "P-poll__networl_8_1_AI_4" + "P-poll__networl_8_1_AI_5" + "P-poll__networl_8_1_AI_6" + "P-poll__networl_8_1_AI_7" + "P-poll__networl_8_1_AI_8" + "P-poll__networl_8_1_AnnP_0" + "P-poll__networl_8_1_AnnP_1" + "P-poll__networl_8_1_AnnP_2" + "P-poll__networl_8_1_AnnP_3" + "P-poll__networl_8_1_AnnP_4" + "P-poll__networl_8_1_AnnP_5" + "P-poll__networl_8_1_AnnP_6" + "P-poll__networl_8_1_AnnP_7" + "P-poll__networl_8_1_AnnP_8" + "P-poll__networl_8_1_RP_0" + "P-poll__networl_8_1_RP_1" + "P-poll__networl_8_1_RP_2" + "P-poll__networl_8_1_RP_3" + "P-poll__networl_8_1_RP_4" + "P-poll__networl_8_1_RP_5" + "P-poll__networl_8_1_RP_6" + "P-poll__networl_8_1_RP_7" + "P-poll__networl_8_1_RP_8" + "P-poll__networl_8_2_AskP_0" + "P-poll__networl_8_2_AskP_1" + "P-poll__networl_8_2_AskP_2" + "P-poll__networl_8_2_AskP_3" + "P-poll__networl_8_2_AskP_4" + "P-poll__networl_8_2_AskP_5" + "P-poll__networl_8_2_AskP_6" + "P-poll__networl_8_2_AskP_7" + "P-poll__networl_8_2_AskP_8" + "P-poll__networl_8_2_AnsP_0" + "P-poll__networl_8_2_AnsP_1" + "P-poll__networl_8_2_AnsP_2" + "P-poll__networl_8_2_AnsP_3" + "P-poll__networl_8_2_AnsP_4" + "P-poll__networl_8_2_AnsP_5" + "P-poll__networl_8_2_AnsP_6" + "P-poll__networl_8_2_AnsP_7" + "P-poll__networl_8_2_AnsP_8" + "P-poll__networl_8_2_RI_0" + "P-poll__networl_8_2_RI_1" + "P-poll__networl_8_2_RI_2" + "P-poll__networl_8_2_RI_3" + "P-poll__networl_8_2_RI_4" + "P-poll__networl_8_2_RI_5" + "P-poll__networl_8_2_RI_6" + "P-poll__networl_8_2_RI_7" + "P-poll__networl_8_2_RI_8" + "P-poll__networl_8_2_AI_0" + "P-poll__networl_8_2_AI_1" + "P-poll__networl_8_2_AI_2" + "P-poll__networl_8_2_AI_3" + "P-poll__networl_8_2_AI_4" + "P-poll__networl_8_2_AI_5" + "P-poll__networl_8_2_AI_6" + "P-poll__networl_8_2_AI_7" + "P-poll__networl_8_2_AI_8" + "P-poll__networl_8_2_AnnP_0" + "P-poll__networl_8_2_AnnP_1" + "P-poll__networl_8_2_AnnP_2" + "P-poll__networl_8_2_AnnP_3" + "P-poll__networl_8_2_AnnP_4" + "P-poll__networl_8_2_AnnP_5" + "P-poll__networl_8_2_AnnP_6" + "P-poll__networl_8_2_AnnP_7" + "P-poll__networl_8_2_AnnP_8" + "P-poll__networl_8_2_RP_0" + "P-poll__networl_8_2_RP_1" + "P-poll__networl_8_2_RP_2" + "P-poll__networl_8_2_RP_3" + "P-poll__networl_8_2_RP_4" + "P-poll__networl_8_2_RP_5" + "P-poll__networl_8_2_RP_6" + "P-poll__networl_8_2_RP_7" + "P-poll__networl_8_2_RP_8" + "P-poll__networl_8_3_AskP_0" + "P-poll__networl_8_3_AskP_1" + "P-poll__networl_8_3_AskP_2" + "P-poll__networl_8_3_AskP_3" + "P-poll__networl_8_3_AskP_4" + "P-poll__networl_8_3_AskP_5" + "P-poll__networl_8_3_AskP_6" + "P-poll__networl_8_3_AskP_7" + "P-poll__networl_8_3_AskP_8" + "P-poll__networl_8_3_AnsP_0" + "P-poll__networl_8_3_AnsP_1" + "P-poll__networl_8_3_AnsP_2" + "P-poll__networl_8_3_AnsP_3" + "P-poll__networl_8_3_AnsP_4" + "P-poll__networl_8_3_AnsP_5" + "P-poll__networl_8_3_AnsP_6" + "P-poll__networl_8_3_AnsP_7" + "P-poll__networl_8_3_AnsP_8" + "P-poll__networl_8_3_RI_0" + "P-poll__networl_8_3_RI_1" + "P-poll__networl_8_3_RI_2" + "P-poll__networl_8_3_RI_3" + "P-poll__networl_8_3_RI_4" + "P-poll__networl_8_3_RI_5" + "P-poll__networl_8_3_RI_6" + "P-poll__networl_8_3_RI_7" + "P-poll__networl_8_3_RI_8" + "P-poll__networl_8_3_AI_0" + "P-poll__networl_8_3_AI_1" + "P-poll__networl_8_3_AI_2" + "P-poll__networl_8_3_AI_3" + "P-poll__networl_8_3_AI_4" + "P-poll__networl_8_3_AI_5" + "P-poll__networl_8_3_AI_6" + "P-poll__networl_8_3_AI_7" + "P-poll__networl_8_3_AI_8" + "P-poll__networl_8_3_AnnP_0" + "P-poll__networl_8_3_AnnP_1" + "P-poll__networl_8_3_AnnP_2" + "P-poll__networl_8_3_AnnP_3" + "P-poll__networl_8_3_AnnP_4" + "P-poll__networl_8_3_AnnP_5" + "P-poll__networl_8_3_AnnP_6" + "P-poll__networl_8_3_AnnP_7" + "P-poll__networl_8_3_AnnP_8" + "P-poll__networl_8_3_RP_0" + "P-poll__networl_8_3_RP_1" + "P-poll__networl_8_3_RP_2" + "P-poll__networl_8_3_RP_3" + "P-poll__networl_8_3_RP_4" + "P-poll__networl_8_3_RP_5" + "P-poll__networl_8_3_RP_6" + "P-poll__networl_8_3_RP_7" + "P-poll__networl_8_3_RP_8" + "P-poll__networl_8_4_AskP_0" + "P-poll__networl_8_4_AskP_1" + "P-poll__networl_8_4_AskP_2" + "P-poll__networl_8_4_AskP_3" + "P-poll__networl_8_4_AskP_4" + "P-poll__networl_8_4_AskP_5" + "P-poll__networl_8_4_AskP_6" + "P-poll__networl_8_4_AskP_7" + "P-poll__networl_8_4_AskP_8" + "P-poll__networl_8_4_AnsP_0" + "P-poll__networl_8_4_AnsP_1" + "P-poll__networl_8_4_AnsP_2" + "P-poll__networl_8_4_AnsP_3" + "P-poll__networl_8_4_AnsP_4" + "P-poll__networl_8_4_AnsP_5" + "P-poll__networl_8_4_AnsP_6" + "P-poll__networl_8_4_AnsP_7" + "P-poll__networl_8_4_AnsP_8" + "P-poll__networl_8_4_RI_0" + "P-poll__networl_8_4_RI_1" + "P-poll__networl_8_4_RI_2" + "P-poll__networl_8_4_RI_3" + "P-poll__networl_8_4_RI_4" + "P-poll__networl_8_4_RI_5" + "P-poll__networl_8_4_RI_6" + "P-poll__networl_8_4_RI_7" + "P-poll__networl_8_4_RI_8" + "P-poll__networl_8_4_AI_0" + "P-poll__networl_8_4_AI_1" + "P-poll__networl_8_4_AI_2" + "P-poll__networl_8_4_AI_3" + "P-poll__networl_8_4_AI_4" + "P-poll__networl_8_4_AI_5" + "P-poll__networl_8_4_AI_6" + "P-poll__networl_8_4_AI_7" + "P-poll__networl_8_4_AI_8" + "P-poll__networl_8_4_AnnP_0" + "P-poll__networl_8_4_AnnP_1" + "P-poll__networl_8_4_AnnP_2" + "P-poll__networl_8_4_AnnP_3" + "P-poll__networl_8_4_AnnP_4" + "P-poll__networl_8_4_AnnP_5" + "P-poll__networl_8_4_AnnP_6" + "P-poll__networl_8_4_AnnP_7" + "P-poll__networl_8_4_AnnP_8" + "P-poll__networl_8_4_RP_0" + "P-poll__networl_8_4_RP_1" + "P-poll__networl_8_4_RP_2" + "P-poll__networl_8_4_RP_3" + "P-poll__networl_8_4_RP_4" + "P-poll__networl_8_4_RP_5" + "P-poll__networl_8_4_RP_6" + "P-poll__networl_8_4_RP_7" + "P-poll__networl_8_4_RP_8" + "P-poll__networl_8_5_AskP_0" + "P-poll__networl_8_5_AskP_1" + "P-poll__networl_8_5_AskP_2" + "P-poll__networl_8_5_AskP_3" + "P-poll__networl_8_5_AskP_4" + "P-poll__networl_8_5_AskP_5" + "P-poll__networl_8_5_AskP_6" + "P-poll__networl_8_5_AskP_7" + "P-poll__networl_8_5_AskP_8" + "P-poll__networl_8_5_AnsP_0" + "P-poll__networl_8_5_AnsP_1" + "P-poll__networl_8_5_AnsP_2" + "P-poll__networl_8_5_AnsP_3" + "P-poll__networl_8_5_AnsP_4" + "P-poll__networl_8_5_AnsP_5" + "P-poll__networl_8_5_AnsP_6" + "P-poll__networl_8_5_AnsP_7" + "P-poll__networl_8_5_AnsP_8" + "P-poll__networl_8_5_RI_0" + "P-poll__networl_8_5_RI_1" + "P-poll__networl_8_5_RI_2" + "P-poll__networl_8_5_RI_3" + "P-poll__networl_8_5_RI_4" + "P-poll__networl_8_5_RI_5" + "P-poll__networl_8_5_RI_6" + "P-poll__networl_8_5_RI_7" + "P-poll__networl_8_5_RI_8" + "P-poll__networl_8_5_AI_0" + "P-poll__networl_8_5_AI_1" + "P-poll__networl_8_5_AI_2" + "P-poll__networl_8_5_AI_3" + "P-poll__networl_8_5_AI_4" + "P-poll__networl_8_5_AI_5" + "P-poll__networl_8_5_AI_6" + "P-poll__networl_8_5_AI_7" + "P-poll__networl_8_5_AI_8" + "P-poll__networl_8_5_AnnP_0" + "P-poll__networl_8_5_AnnP_1" + "P-poll__networl_8_5_AnnP_2" + "P-poll__networl_8_5_AnnP_3" + "P-poll__networl_8_5_AnnP_4" + "P-poll__networl_8_5_AnnP_5" + "P-poll__networl_8_5_AnnP_6" + "P-poll__networl_8_5_AnnP_7" + "P-poll__networl_8_5_AnnP_8" + "P-poll__networl_8_5_RP_0" + "P-poll__networl_8_5_RP_1" + "P-poll__networl_8_5_RP_2" + "P-poll__networl_8_5_RP_3" + "P-poll__networl_8_5_RP_4" + "P-poll__networl_8_5_RP_5" + "P-poll__networl_8_5_RP_6" + "P-poll__networl_8_5_RP_7" + "P-poll__networl_8_5_RP_8" + "P-poll__networl_8_6_AskP_0" + "P-poll__networl_8_6_AskP_1" + "P-poll__networl_8_6_AskP_2" + "P-poll__networl_8_6_AskP_3" + "P-poll__networl_8_6_AskP_4" + "P-poll__networl_8_6_AskP_5" + "P-poll__networl_8_6_AskP_6" + "P-poll__networl_8_6_AskP_7" + "P-poll__networl_8_6_AskP_8" + "P-poll__networl_8_6_AnsP_0" + "P-poll__networl_8_6_AnsP_1" + "P-poll__networl_8_6_AnsP_2" + "P-poll__networl_8_6_AnsP_3" + "P-poll__networl_8_6_AnsP_4" + "P-poll__networl_8_6_AnsP_5" + "P-poll__networl_8_6_AnsP_6" + "P-poll__networl_8_6_AnsP_7" + "P-poll__networl_8_6_AnsP_8" + "P-poll__networl_8_6_RI_0" + "P-poll__networl_8_6_RI_1" + "P-poll__networl_8_6_RI_2" + "P-poll__networl_8_6_RI_3" + "P-poll__networl_8_6_RI_4" + "P-poll__networl_8_6_RI_5" + "P-poll__networl_8_6_RI_6" + "P-poll__networl_8_6_RI_7" + "P-poll__networl_8_6_RI_8" + "P-poll__networl_8_6_AI_0" + "P-poll__networl_8_6_AI_1" + "P-poll__networl_8_6_AI_2" + "P-poll__networl_8_6_AI_3" + "P-poll__networl_8_6_AI_4" + "P-poll__networl_8_6_AI_5" + "P-poll__networl_8_6_AI_6" + "P-poll__networl_8_6_AI_7" + "P-poll__networl_8_6_AI_8" + "P-poll__networl_8_6_AnnP_0" + "P-poll__networl_8_6_AnnP_1" + "P-poll__networl_8_6_AnnP_2" + "P-poll__networl_8_6_AnnP_3" + "P-poll__networl_8_6_AnnP_4" + "P-poll__networl_8_6_AnnP_5" + "P-poll__networl_8_6_AnnP_6" + "P-poll__networl_8_6_AnnP_7" + "P-poll__networl_8_6_AnnP_8" + "P-poll__networl_8_6_RP_0" + "P-poll__networl_8_6_RP_1" + "P-poll__networl_8_6_RP_2" + "P-poll__networl_8_6_RP_3" + "P-poll__networl_8_6_RP_4" + "P-poll__networl_8_6_RP_5" + "P-poll__networl_8_6_RP_6" + "P-poll__networl_8_6_RP_7" + "P-poll__networl_8_6_RP_8" + "P-poll__networl_8_7_AskP_0" + "P-poll__networl_8_7_AskP_1" + "P-poll__networl_8_7_AskP_2" + "P-poll__networl_8_7_AskP_3" + "P-poll__networl_8_7_AskP_4" + "P-poll__networl_8_7_AskP_5" + "P-poll__networl_8_7_AskP_6" + "P-poll__networl_8_7_AskP_7" + "P-poll__networl_8_7_AskP_8" + "P-poll__networl_8_7_AnsP_0" + "P-poll__networl_8_7_AnsP_1" + "P-poll__networl_8_7_AnsP_2" + "P-poll__networl_8_7_AnsP_3" + "P-poll__networl_8_7_AnsP_4" + "P-poll__networl_8_7_AnsP_5" + "P-poll__networl_8_7_AnsP_6" + "P-poll__networl_8_7_AnsP_7" + "P-poll__networl_8_7_AnsP_8" + "P-poll__networl_8_7_RI_0" + "P-poll__networl_8_7_RI_1" + "P-poll__networl_8_7_RI_2" + "P-poll__networl_8_7_RI_3" + "P-poll__networl_8_7_RI_4" + "P-poll__networl_8_7_RI_5" + "P-poll__networl_8_7_RI_6" + "P-poll__networl_8_7_RI_7" + "P-poll__networl_8_7_RI_8" + "P-poll__networl_8_7_AI_0" + "P-poll__networl_8_7_AI_1" + "P-poll__networl_8_7_AI_2" + "P-poll__networl_8_7_AI_3" + "P-poll__networl_8_7_AI_4" + "P-poll__networl_8_7_AI_5" + "P-poll__networl_8_7_AI_6" + "P-poll__networl_8_7_AI_7" + "P-poll__networl_8_7_AI_8" + "P-poll__networl_8_7_AnnP_0" + "P-poll__networl_8_7_AnnP_1" + "P-poll__networl_8_7_AnnP_2" + "P-poll__networl_8_7_AnnP_3" + "P-poll__networl_8_7_AnnP_4" + "P-poll__networl_8_7_AnnP_5" + "P-poll__networl_8_7_AnnP_6" + "P-poll__networl_8_7_AnnP_7" + "P-poll__networl_8_7_AnnP_8" + "P-poll__networl_8_7_RP_0" + "P-poll__networl_8_7_RP_1" + "P-poll__networl_8_7_RP_2" + "P-poll__networl_8_7_RP_3" + "P-poll__networl_8_7_RP_4" + "P-poll__networl_8_7_RP_5" + "P-poll__networl_8_7_RP_6" + "P-poll__networl_8_7_RP_7" + "P-poll__networl_8_7_RP_8" + "P-poll__networl_8_8_AskP_0" + "P-poll__networl_8_8_AskP_1" + "P-poll__networl_8_8_AskP_2" + "P-poll__networl_8_8_AskP_3" + "P-poll__networl_8_8_AskP_4" + "P-poll__networl_8_8_AskP_5" + "P-poll__networl_8_8_AskP_6" + "P-poll__networl_8_8_AskP_7" + "P-poll__networl_8_8_AskP_8" + "P-poll__networl_8_8_AnsP_0" + "P-poll__networl_8_8_AnsP_1" + "P-poll__networl_8_8_AnsP_2" + "P-poll__networl_8_8_AnsP_3" + "P-poll__networl_8_8_AnsP_4" + "P-poll__networl_8_8_AnsP_5" + "P-poll__networl_8_8_AnsP_6" + "P-poll__networl_8_8_AnsP_7" + "P-poll__networl_8_8_AnsP_8" + "P-poll__networl_8_8_RI_0" + "P-poll__networl_8_8_RI_1" + "P-poll__networl_8_8_RI_2" + "P-poll__networl_8_8_RI_3" + "P-poll__networl_8_8_RI_4" + "P-poll__networl_8_8_RI_5" + "P-poll__networl_8_8_RI_6" + "P-poll__networl_8_8_RI_7" + "P-poll__networl_8_8_RI_8" + "P-poll__networl_8_8_AI_0" + "P-poll__networl_8_8_AI_1" + "P-poll__networl_8_8_AI_2" + "P-poll__networl_8_8_AI_3" + "P-poll__networl_8_8_AI_4" + "P-poll__networl_8_8_AI_5" + "P-poll__networl_8_8_AI_6" + "P-poll__networl_8_8_AI_7" + "P-poll__networl_8_8_AI_8" + "P-poll__networl_8_8_AnnP_0" + "P-poll__networl_8_8_AnnP_1" + "P-poll__networl_8_8_AnnP_2" + "P-poll__networl_8_8_AnnP_3" + "P-poll__networl_8_8_AnnP_4" + "P-poll__networl_8_8_AnnP_5" + "P-poll__networl_8_8_AnnP_6" + "P-poll__networl_8_8_AnnP_7" + "P-poll__networl_8_8_AnnP_8" + "P-poll__networl_8_8_RP_0" + "P-poll__networl_8_8_RP_1" + "P-poll__networl_8_8_RP_2" + "P-poll__networl_8_8_RP_3" + "P-poll__networl_8_8_RP_4" + "P-poll__networl_8_8_RP_5" + "P-poll__networl_8_8_RP_6" + "P-poll__networl_8_8_RP_7" + "P-poll__networl_8_8_RP_8")) or (("P-electedSecondary_0" + "P-electedSecondary_1" + "P-electedSecondary_2" + "P-electedSecondary_3" + "P-electedSecondary_4" + "P-electedSecondary_5" + "P-electedSecondary_6" + "P-electedSecondary_7" + "P-electedSecondary_8") <= ("P-poll__pollEnd_0" + "P-poll__pollEnd_1" + "P-poll__pollEnd_2" + "P-poll__pollEnd_3" + "P-poll__pollEnd_4" + "P-poll__pollEnd_5" + "P-poll__pollEnd_6" + "P-poll__pollEnd_7" + "P-poll__pollEnd_8"))) and (3 <= ("P-masterState_0_F_0" + "P-masterState_0_F_1" + "P-masterState_0_F_2" + "P-masterState_0_F_3" + "P-masterState_0_F_4" + "P-masterState_0_F_5" + "P-masterState_0_F_6" + "P-masterState_0_F_7" + "P-masterState_0_F_8" + "P-masterState_0_T_0" + "P-masterState_0_T_1" + "P-masterState_0_T_2" + "P-masterState_0_T_3" + "P-masterState_0_T_4" + "P-masterState_0_T_5" + "P-masterState_0_T_6" + "P-masterState_0_T_7" + "P-masterState_0_T_8" + "P-masterState_1_F_0" + "P-masterState_1_F_1" + "P-masterState_1_F_2" + "P-masterState_1_F_3" + "P-masterState_1_F_4" + "P-masterState_1_F_5" + "P-masterState_1_F_6" + "P-masterState_1_F_7" + "P-masterState_1_F_8" + "P-masterState_1_T_0" + "P-masterState_1_T_1" + "P-masterState_1_T_2" + "P-masterState_1_T_3" + "P-masterState_1_T_4" + "P-masterState_1_T_5" + "P-masterState_1_T_6" + "P-masterState_1_T_7" + "P-masterState_1_T_8" + "P-masterState_2_F_0" + "P-masterState_2_F_1" + "P-masterState_2_F_2" + "P-masterState_2_F_3" + "P-masterState_2_F_4" + "P-masterState_2_F_5" + "P-masterState_2_F_6" + "P-masterState_2_F_7" + "P-masterState_2_F_8" + "P-masterState_2_T_0" + "P-masterState_2_T_1" + "P-masterState_2_T_2" + "P-masterState_2_T_3" + "P-masterState_2_T_4" + "P-masterState_2_T_5" + "P-masterState_2_T_6" + "P-masterState_2_T_7" + "P-masterState_2_T_8" + "P-masterState_3_F_0" + "P-masterState_3_F_1" + "P-masterState_3_F_2" + "P-masterState_3_F_3" + "P-masterState_3_F_4" + "P-masterState_3_F_5" + "P-masterState_3_F_6" + "P-masterState_3_F_7" + "P-masterState_3_F_8" + "P-masterState_3_T_0" + "P-masterState_3_T_1" + "P-masterState_3_T_2" + "P-masterState_3_T_3" + "P-masterState_3_T_4" + "P-masterState_3_T_5" + "P-masterState_3_T_6" + "P-masterState_3_T_7" + "P-masterState_3_T_8" + "P-masterState_4_F_0" + "P-masterState_4_F_1" + "P-masterState_4_F_2" + "P-masterState_4_F_3" + "P-masterState_4_F_4" + "P-masterState_4_F_5" + "P-masterState_4_F_6" + "P-masterState_4_F_7" + "P-masterState_4_F_8" + "P-masterState_4_T_0" + "P-masterState_4_T_1" + "P-masterState_4_T_2" + "P-masterState_4_T_3" + "P-masterState_4_T_4" + "P-masterState_4_T_5" + "P-masterState_4_T_6" + "P-masterState_4_T_7" + "P-masterState_4_T_8" + "P-masterState_5_F_0" + "P-masterState_5_F_1" + "P-masterState_5_F_2" + "P-masterState_5_F_3" + "P-masterState_5_F_4" + "P-masterState_5_F_5" + "P-masterState_5_F_6" + "P-masterState_5_F_7" + "P-masterState_5_F_8" + "P-masterState_5_T_0" + "P-masterState_5_T_1" + "P-masterState_5_T_2" + "P-masterState_5_T_3" + "P-masterState_5_T_4" + "P-masterState_5_T_5" + "P-masterState_5_T_6" + "P-masterState_5_T_7" + "P-masterState_5_T_8" + "P-masterState_6_F_0" + "P-masterState_6_F_1" + "P-masterState_6_F_2" + "P-masterState_6_F_3" + "P-masterState_6_F_4" + "P-masterState_6_F_5" + "P-masterState_6_F_6" + "P-masterState_6_F_7" + "P-masterState_6_F_8" + "P-masterState_6_T_0" + "P-masterState_6_T_1" + "P-masterState_6_T_2" + "P-masterState_6_T_3" + "P-masterState_6_T_4" + "P-masterState_6_T_5" + "P-masterState_6_T_6" + "P-masterState_6_T_7" + "P-masterState_6_T_8" + "P-masterState_7_F_0" + "P-masterState_7_F_1" + "P-masterState_7_F_2" + "P-masterState_7_F_3" + "P-masterState_7_F_4" + "P-masterState_7_F_5" + "P-masterState_7_F_6" + "P-masterState_7_F_7" + "P-masterState_7_F_8" + "P-masterState_7_T_0" + "P-masterState_7_T_1" + "P-masterState_7_T_2" + "P-masterState_7_T_3" + "P-masterState_7_T_4" + "P-masterState_7_T_5" + "P-masterState_7_T_6" + "P-masterState_7_T_7" + "P-masterState_7_T_8" + "P-masterState_8_F_0" + "P-masterState_8_F_1" + "P-masterState_8_F_2" + "P-masterState_8_F_3" + "P-masterState_8_F_4" + "P-masterState_8_F_5" + "P-masterState_8_F_6" + "P-masterState_8_F_7" + "P-masterState_8_F_8" + "P-masterState_8_T_0" + "P-masterState_8_T_1" + "P-masterState_8_T_2" + "P-masterState_8_T_3" + "P-masterState_8_T_4" + "P-masterState_8_T_5" + "P-masterState_8_T_6" + "P-masterState_8_T_7" + "P-masterState_8_T_8"))) or (("P-poll__handlingMessage_0" + "P-poll__handlingMessage_1" + "P-poll__handlingMessage_2" + "P-poll__handlingMessage_3" + "P-poll__handlingMessage_4" + "P-poll__handlingMessage_5" + "P-poll__handlingMessage_6" + "P-poll__handlingMessage_7" + "P-poll__handlingMessage_8") <= ("P-dead_0" + "P-dead_1" + "P-dead_2" + "P-dead_3" + "P-dead_4" + "P-dead_5" + "P-dead_6" + "P-dead_7" + "P-dead_8"))) )
NeoElection-COL-8-ReachabilityCardinality-7: EF ( not((("P-stage_0_NEG" + "P-stage_0_PRIM" + "P-stage_0_SEC" + "P-stage_1_NEG" + "P-stage_1_PRIM" + "P-stage_1_SEC" + "P-stage_2_NEG" + "P-stage_2_PRIM" + "P-stage_2_SEC" + "P-stage_3_NEG" + "P-stage_3_PRIM" + "P-stage_3_SEC" + "P-stage_4_NEG" + "P-stage_4_PRIM" + "P-stage_4_SEC" + "P-stage_5_NEG" + "P-stage_5_PRIM" + "P-stage_5_SEC" + "P-stage_6_NEG" + "P-stage_6_PRIM" + "P-stage_6_SEC" + "P-stage_7_NEG" + "P-stage_7_PRIM" + "P-stage_7_SEC" + "P-stage_8_NEG" + "P-stage_8_PRIM" + "P-stage_8_SEC") <= ("P-negotiation_0_0_NONE" + "P-negotiation_0_0_CO" + "P-negotiation_0_0_DONE" + "P-negotiation_0_1_NONE" + "P-negotiation_0_1_CO" + "P-negotiation_0_1_DONE" + "P-negotiation_0_2_NONE" + "P-negotiation_0_2_CO" + "P-negotiation_0_2_DONE" + "P-negotiation_0_3_NONE" + "P-negotiation_0_3_CO" + "P-negotiation_0_3_DONE" + "P-negotiation_0_4_NONE" + "P-negotiation_0_4_CO" + "P-negotiation_0_4_DONE" + "P-negotiation_0_5_NONE" + "P-negotiation_0_5_CO" + "P-negotiation_0_5_DONE" + "P-negotiation_0_6_NONE" + "P-negotiation_0_6_CO" + "P-negotiation_0_6_DONE" + "P-negotiation_0_7_NONE" + "P-negotiation_0_7_CO" + "P-negotiation_0_7_DONE" + "P-negotiation_0_8_NONE" + "P-negotiation_0_8_CO" + "P-negotiation_0_8_DONE" + "P-negotiation_1_0_NONE" + "P-negotiation_1_0_CO" + "P-negotiation_1_0_DONE" + "P-negotiation_1_1_NONE" + "P-negotiation_1_1_CO" + "P-negotiation_1_1_DONE" + "P-negotiation_1_2_NONE" + "P-negotiation_1_2_CO" + "P-negotiation_1_2_DONE" + "P-negotiation_1_3_NONE" + "P-negotiation_1_3_CO" + "P-negotiation_1_3_DONE" + "P-negotiation_1_4_NONE" + "P-negotiation_1_4_CO" + "P-negotiation_1_4_DONE" + "P-negotiation_1_5_NONE" + "P-negotiation_1_5_CO" + "P-negotiation_1_5_DONE" + "P-negotiation_1_6_NONE" + "P-negotiation_1_6_CO" + "P-negotiation_1_6_DONE" + "P-negotiation_1_7_NONE" + "P-negotiation_1_7_CO" + "P-negotiation_1_7_DONE" + "P-negotiation_1_8_NONE" + "P-negotiation_1_8_CO" + "P-negotiation_1_8_DONE" + "P-negotiation_2_0_NONE" + "P-negotiation_2_0_CO" + "P-negotiation_2_0_DONE" + "P-negotiation_2_1_NONE" + "P-negotiation_2_1_CO" + "P-negotiation_2_1_DONE" + "P-negotiation_2_2_NONE" + "P-negotiation_2_2_CO" + "P-negotiation_2_2_DONE" + "P-negotiation_2_3_NONE" + "P-negotiation_2_3_CO" + "P-negotiation_2_3_DONE" + "P-negotiation_2_4_NONE" + "P-negotiation_2_4_CO" + "P-negotiation_2_4_DONE" + "P-negotiation_2_5_NONE" + "P-negotiation_2_5_CO" + "P-negotiation_2_5_DONE" + "P-negotiation_2_6_NONE" + "P-negotiation_2_6_CO" + "P-negotiation_2_6_DONE" + "P-negotiation_2_7_NONE" + "P-negotiation_2_7_CO" + "P-negotiation_2_7_DONE" + "P-negotiation_2_8_NONE" + "P-negotiation_2_8_CO" + "P-negotiation_2_8_DONE" + "P-negotiation_3_0_NONE" + "P-negotiation_3_0_CO" + "P-negotiation_3_0_DONE" + "P-negotiation_3_1_NONE" + "P-negotiation_3_1_CO" + "P-negotiation_3_1_DONE" + "P-negotiation_3_2_NONE" + "P-negotiation_3_2_CO" + "P-negotiation_3_2_DONE" + "P-negotiation_3_3_NONE" + "P-negotiation_3_3_CO" + "P-negotiation_3_3_DONE" + "P-negotiation_3_4_NONE" + "P-negotiation_3_4_CO" + "P-negotiation_3_4_DONE" + "P-negotiation_3_5_NONE" + "P-negotiation_3_5_CO" + "P-negotiation_3_5_DONE" + "P-negotiation_3_6_NONE" + "P-negotiation_3_6_CO" + "P-negotiation_3_6_DONE" + "P-negotiation_3_7_NONE" + "P-negotiation_3_7_CO" + "P-negotiation_3_7_DONE" + "P-negotiation_3_8_NONE" + "P-negotiation_3_8_CO" + "P-negotiation_3_8_DONE" + "P-negotiation_4_0_NONE" + "P-negotiation_4_0_CO" + "P-negotiation_4_0_DONE" + "P-negotiation_4_1_NONE" + "P-negotiation_4_1_CO" + "P-negotiation_4_1_DONE" + "P-negotiation_4_2_NONE" + "P-negotiation_4_2_CO" + "P-negotiation_4_2_DONE" + "P-negotiation_4_3_NONE" + "P-negotiation_4_3_CO" + "P-negotiation_4_3_DONE" + "P-negotiation_4_4_NONE" + "P-negotiation_4_4_CO" + "P-negotiation_4_4_DONE" + "P-negotiation_4_5_NONE" + "P-negotiation_4_5_CO" + "P-negotiation_4_5_DONE" + "P-negotiation_4_6_NONE" + "P-negotiation_4_6_CO" + "P-negotiation_4_6_DONE" + "P-negotiation_4_7_NONE" + "P-negotiation_4_7_CO" + "P-negotiation_4_7_DONE" + "P-negotiation_4_8_NONE" + "P-negotiation_4_8_CO" + "P-negotiation_4_8_DONE" + "P-negotiation_5_0_NONE" + "P-negotiation_5_0_CO" + "P-negotiation_5_0_DONE" + "P-negotiation_5_1_NONE" + "P-negotiation_5_1_CO" + "P-negotiation_5_1_DONE" + "P-negotiation_5_2_NONE" + "P-negotiation_5_2_CO" + "P-negotiation_5_2_DONE" + "P-negotiation_5_3_NONE" + "P-negotiation_5_3_CO" + "P-negotiation_5_3_DONE" + "P-negotiation_5_4_NONE" + "P-negotiation_5_4_CO" + "P-negotiation_5_4_DONE" + "P-negotiation_5_5_NONE" + "P-negotiation_5_5_CO" + "P-negotiation_5_5_DONE" + "P-negotiation_5_6_NONE" + "P-negotiation_5_6_CO" + "P-negotiation_5_6_DONE" + "P-negotiation_5_7_NONE" + "P-negotiation_5_7_CO" + "P-negotiation_5_7_DONE" + "P-negotiation_5_8_NONE" + "P-negotiation_5_8_CO" + "P-negotiation_5_8_DONE" + "P-negotiation_6_0_NONE" + "P-negotiation_6_0_CO" + "P-negotiation_6_0_DONE" + "P-negotiation_6_1_NONE" + "P-negotiation_6_1_CO" + "P-negotiation_6_1_DONE" + "P-negotiation_6_2_NONE" + "P-negotiation_6_2_CO" + "P-negotiation_6_2_DONE" + "P-negotiation_6_3_NONE" + "P-negotiation_6_3_CO" + "P-negotiation_6_3_DONE" + "P-negotiation_6_4_NONE" + "P-negotiation_6_4_CO" + "P-negotiation_6_4_DONE" + "P-negotiation_6_5_NONE" + "P-negotiation_6_5_CO" + "P-negotiation_6_5_DONE" + "P-negotiation_6_6_NONE" + "P-negotiation_6_6_CO" + "P-negotiation_6_6_DONE" + "P-negotiation_6_7_NONE" + "P-negotiation_6_7_CO" + "P-negotiation_6_7_DONE" + "P-negotiation_6_8_NONE" + "P-negotiation_6_8_CO" + "P-negotiation_6_8_DONE" + "P-negotiation_7_0_NONE" + "P-negotiation_7_0_CO" + "P-negotiation_7_0_DONE" + "P-negotiation_7_1_NONE" + "P-negotiation_7_1_CO" + "P-negotiation_7_1_DONE" + "P-negotiation_7_2_NONE" + "P-negotiation_7_2_CO" + "P-negotiation_7_2_DONE" + "P-negotiation_7_3_NONE" + "P-negotiation_7_3_CO" + "P-negotiation_7_3_DONE" + "P-negotiation_7_4_NONE" + "P-negotiation_7_4_CO" + "P-negotiation_7_4_DONE" + "P-negotiation_7_5_NONE" + "P-negotiation_7_5_CO" + "P-negotiation_7_5_DONE" + "P-negotiation_7_6_NONE" + "P-negotiation_7_6_CO" + "P-negotiation_7_6_DONE" + "P-negotiation_7_7_NONE" + "P-negotiation_7_7_CO" + "P-negotiation_7_7_DONE" + "P-negotiation_7_8_NONE" + "P-negotiation_7_8_CO" + "P-negotiation_7_8_DONE" + "P-negotiation_8_0_NONE" + "P-negotiation_8_0_CO" + "P-negotiation_8_0_DONE" + "P-negotiation_8_1_NONE" + "P-negotiation_8_1_CO" + "P-negotiation_8_1_DONE" + "P-negotiation_8_2_NONE" + "P-negotiation_8_2_CO" + "P-negotiation_8_2_DONE" + "P-negotiation_8_3_NONE" + "P-negotiation_8_3_CO" + "P-negotiation_8_3_DONE" + "P-negotiation_8_4_NONE" + "P-negotiation_8_4_CO" + "P-negotiation_8_4_DONE" + "P-negotiation_8_5_NONE" + "P-negotiation_8_5_CO" + "P-negotiation_8_5_DONE" + "P-negotiation_8_6_NONE" + "P-negotiation_8_6_CO" + "P-negotiation_8_6_DONE" + "P-negotiation_8_7_NONE" + "P-negotiation_8_7_CO" + "P-negotiation_8_7_DONE" + "P-negotiation_8_8_NONE" + "P-negotiation_8_8_CO" + "P-negotiation_8_8_DONE"))) )
NeoElection-COL-8-ReachabilityCardinality-8: EF ( ((3 <= ("P-startNeg__broadcasting_0_1" + "P-startNeg__broadcasting_0_2" + "P-startNeg__broadcasting_0_3" + "P-startNeg__broadcasting_0_4" + "P-startNeg__broadcasting_0_5" + "P-startNeg__broadcasting_0_6" + "P-startNeg__broadcasting_0_7" + "P-startNeg__broadcasting_0_8" + "P-startNeg__broadcasting_1_1" + "P-startNeg__broadcasting_1_2" + "P-startNeg__broadcasting_1_3" + "P-startNeg__broadcasting_1_4" + "P-startNeg__broadcasting_1_5" + "P-startNeg__broadcasting_1_6" + "P-startNeg__broadcasting_1_7" + "P-startNeg__broadcasting_1_8" + "P-startNeg__broadcasting_2_1" + "P-startNeg__broadcasting_2_2" + "P-startNeg__broadcasting_2_3" + "P-startNeg__broadcasting_2_4" + "P-startNeg__broadcasting_2_5" + "P-startNeg__broadcasting_2_6" + "P-startNeg__broadcasting_2_7" + "P-startNeg__broadcasting_2_8" + "P-startNeg__broadcasting_3_1" + "P-startNeg__broadcasting_3_2" + "P-startNeg__broadcasting_3_3" + "P-startNeg__broadcasting_3_4" + "P-startNeg__broadcasting_3_5" + "P-startNeg__broadcasting_3_6" + "P-startNeg__broadcasting_3_7" + "P-startNeg__broadcasting_3_8" + "P-startNeg__broadcasting_4_1" + "P-startNeg__broadcasting_4_2" + "P-startNeg__broadcasting_4_3" + "P-startNeg__broadcasting_4_4" + "P-startNeg__broadcasting_4_5" + "P-startNeg__broadcasting_4_6" + "P-startNeg__broadcasting_4_7" + "P-startNeg__broadcasting_4_8" + "P-startNeg__broadcasting_5_1" + "P-startNeg__broadcasting_5_2" + "P-startNeg__broadcasting_5_3" + "P-startNeg__broadcasting_5_4" + "P-startNeg__broadcasting_5_5" + "P-startNeg__broadcasting_5_6" + "P-startNeg__broadcasting_5_7" + "P-startNeg__broadcasting_5_8" + "P-startNeg__broadcasting_6_1" + "P-startNeg__broadcasting_6_2" + "P-startNeg__broadcasting_6_3" + "P-startNeg__broadcasting_6_4" + "P-startNeg__broadcasting_6_5" + "P-startNeg__broadcasting_6_6" + "P-startNeg__broadcasting_6_7" + "P-startNeg__broadcasting_6_8" + "P-startNeg__broadcasting_7_1" + "P-startNeg__broadcasting_7_2" + "P-startNeg__broadcasting_7_3" + "P-startNeg__broadcasting_7_4" + "P-startNeg__broadcasting_7_5" + "P-startNeg__broadcasting_7_6" + "P-startNeg__broadcasting_7_7" + "P-startNeg__broadcasting_7_8" + "P-startNeg__broadcasting_8_1" + "P-startNeg__broadcasting_8_2" + "P-startNeg__broadcasting_8_3" + "P-startNeg__broadcasting_8_4" + "P-startNeg__broadcasting_8_5" + "P-startNeg__broadcasting_8_6" + "P-startNeg__broadcasting_8_7" + "P-startNeg__broadcasting_8_8")) and (((2 <= ("P-stage_0_NEG" + "P-stage_0_PRIM" + "P-stage_0_SEC" + "P-stage_1_NEG" + "P-stage_1_PRIM" + "P-stage_1_SEC" + "P-stage_2_NEG" + "P-stage_2_PRIM" + "P-stage_2_SEC" + "P-stage_3_NEG" + "P-stage_3_PRIM" + "P-stage_3_SEC" + "P-stage_4_NEG" + "P-stage_4_PRIM" + "P-stage_4_SEC" + "P-stage_5_NEG" + "P-stage_5_PRIM" + "P-stage_5_SEC" + "P-stage_6_NEG" + "P-stage_6_PRIM" + "P-stage_6_SEC" + "P-stage_7_NEG" + "P-stage_7_PRIM" + "P-stage_7_SEC" + "P-stage_8_NEG" + "P-stage_8_PRIM" + "P-stage_8_SEC")) and (("P-crashed_0" + "P-crashed_1" + "P-crashed_2" + "P-crashed_3" + "P-crashed_4" + "P-crashed_5" + "P-crashed_6" + "P-crashed_7" + "P-crashed_8") <= ("P-masterList_0_1_0" + "P-masterList_0_1_1" + "P-masterList_0_1_2" + "P-masterList_0_1_3" + "P-masterList_0_1_4" + "P-masterList_0_1_5" + "P-masterList_0_1_6" + "P-masterList_0_1_7" + "P-masterList_0_1_8" + "P-masterList_0_2_0" + "P-masterList_0_2_1" + "P-masterList_0_2_2" + "P-masterList_0_2_3" + "P-masterList_0_2_4" + "P-masterList_0_2_5" + "P-masterList_0_2_6" + "P-masterList_0_2_7" + "P-masterList_0_2_8" + "P-masterList_0_3_0" + "P-masterList_0_3_1" + "P-masterList_0_3_2" + "P-masterList_0_3_3" + "P-masterList_0_3_4" + "P-masterList_0_3_5" + "P-masterList_0_3_6" + "P-masterList_0_3_7" + "P-masterList_0_3_8" + "P-masterList_0_4_0" + "P-masterList_0_4_1" + "P-masterList_0_4_2" + "P-masterList_0_4_3" + "P-masterList_0_4_4" + "P-masterList_0_4_5" + "P-masterList_0_4_6" + "P-masterList_0_4_7" + "P-masterList_0_4_8" + "P-masterList_0_5_0" + "P-masterList_0_5_1" + "P-masterList_0_5_2" + "P-masterList_0_5_3" + "P-masterList_0_5_4" + "P-masterList_0_5_5" + "P-masterList_0_5_6" + "P-masterList_0_5_7" + "P-masterList_0_5_8" + "P-masterList_0_6_0" + "P-masterList_0_6_1" + "P-masterList_0_6_2" + "P-masterList_0_6_3" + "P-masterList_0_6_4" + "P-masterList_0_6_5" + "P-masterList_0_6_6" + "P-masterList_0_6_7" + "P-masterList_0_6_8" + "P-masterList_0_7_0" + "P-masterList_0_7_1" + "P-masterList_0_7_2" + "P-masterList_0_7_3" + "P-masterList_0_7_4" + "P-masterList_0_7_5" + "P-masterList_0_7_6" + "P-masterList_0_7_7" + "P-masterList_0_7_8" + "P-masterList_0_8_0" + "P-masterList_0_8_1" + "P-masterList_0_8_2" + "P-masterList_0_8_3" + "P-masterList_0_8_4" + "P-masterList_0_8_5" + "P-masterList_0_8_6" + "P-masterList_0_8_7" + "P-masterList_0_8_8" + "P-masterList_1_1_0" + "P-masterList_1_1_1" + "P-masterList_1_1_2" + "P-masterList_1_1_3" + "P-masterList_1_1_4" + "P-masterList_1_1_5" + "P-masterList_1_1_6" + "P-masterList_1_1_7" + "P-masterList_1_1_8" + "P-masterList_1_2_0" + "P-masterList_1_2_1" + "P-masterList_1_2_2" + "P-masterList_1_2_3" + "P-masterList_1_2_4" + "P-masterList_1_2_5" + "P-masterList_1_2_6" + "P-masterList_1_2_7" + "P-masterList_1_2_8" + "P-masterList_1_3_0" + "P-masterList_1_3_1" + "P-masterList_1_3_2" + "P-masterList_1_3_3" + "P-masterList_1_3_4" + "P-masterList_1_3_5" + "P-masterList_1_3_6" + "P-masterList_1_3_7" + "P-masterList_1_3_8" + "P-masterList_1_4_0" + "P-masterList_1_4_1" + "P-masterList_1_4_2" + "P-masterList_1_4_3" + "P-masterList_1_4_4" + "P-masterList_1_4_5" + "P-masterList_1_4_6" + "P-masterList_1_4_7" + "P-masterList_1_4_8" + "P-masterList_1_5_0" + "P-masterList_1_5_1" + "P-masterList_1_5_2" + "P-masterList_1_5_3" + "P-masterList_1_5_4" + "P-masterList_1_5_5" + "P-masterList_1_5_6" + "P-masterList_1_5_7" + "P-masterList_1_5_8" + "P-masterList_1_6_0" + "P-masterList_1_6_1" + "P-masterList_1_6_2" + "P-masterList_1_6_3" + "P-masterList_1_6_4" + "P-masterList_1_6_5" + "P-masterList_1_6_6" + "P-masterList_1_6_7" + "P-masterList_1_6_8" + "P-masterList_1_7_0" + "P-masterList_1_7_1" + "P-masterList_1_7_2" + "P-masterList_1_7_3" + "P-masterList_1_7_4" + "P-masterList_1_7_5" + "P-masterList_1_7_6" + "P-masterList_1_7_7" + "P-masterList_1_7_8" + "P-masterList_1_8_0" + "P-masterList_1_8_1" + "P-masterList_1_8_2" + "P-masterList_1_8_3" + "P-masterList_1_8_4" + "P-masterList_1_8_5" + "P-masterList_1_8_6" + "P-masterList_1_8_7" + "P-masterList_1_8_8" + "P-masterList_2_1_0" + "P-masterList_2_1_1" + "P-masterList_2_1_2" + "P-masterList_2_1_3" + "P-masterList_2_1_4" + "P-masterList_2_1_5" + "P-masterList_2_1_6" + "P-masterList_2_1_7" + "P-masterList_2_1_8" + "P-masterList_2_2_0" + "P-masterList_2_2_1" + "P-masterList_2_2_2" + "P-masterList_2_2_3" + "P-masterList_2_2_4" + "P-masterList_2_2_5" + "P-masterList_2_2_6" + "P-masterList_2_2_7" + "P-masterList_2_2_8" + "P-masterList_2_3_0" + "P-masterList_2_3_1" + "P-masterList_2_3_2" + "P-masterList_2_3_3" + "P-masterList_2_3_4" + "P-masterList_2_3_5" + "P-masterList_2_3_6" + "P-masterList_2_3_7" + "P-masterList_2_3_8" + "P-masterList_2_4_0" + "P-masterList_2_4_1" + "P-masterList_2_4_2" + "P-masterList_2_4_3" + "P-masterList_2_4_4" + "P-masterList_2_4_5" + "P-masterList_2_4_6" + "P-masterList_2_4_7" + "P-masterList_2_4_8" + "P-masterList_2_5_0" + "P-masterList_2_5_1" + "P-masterList_2_5_2" + "P-masterList_2_5_3" + "P-masterList_2_5_4" + "P-masterList_2_5_5" + "P-masterList_2_5_6" + "P-masterList_2_5_7" + "P-masterList_2_5_8" + "P-masterList_2_6_0" + "P-masterList_2_6_1" + "P-masterList_2_6_2" + "P-masterList_2_6_3" + "P-masterList_2_6_4" + "P-masterList_2_6_5" + "P-masterList_2_6_6" + "P-masterList_2_6_7" + "P-masterList_2_6_8" + "P-masterList_2_7_0" + "P-masterList_2_7_1" + "P-masterList_2_7_2" + "P-masterList_2_7_3" + "P-masterList_2_7_4" + "P-masterList_2_7_5" + "P-masterList_2_7_6" + "P-masterList_2_7_7" + "P-masterList_2_7_8" + "P-masterList_2_8_0" + "P-masterList_2_8_1" + "P-masterList_2_8_2" + "P-masterList_2_8_3" + "P-masterList_2_8_4" + "P-masterList_2_8_5" + "P-masterList_2_8_6" + "P-masterList_2_8_7" + "P-masterList_2_8_8" + "P-masterList_3_1_0" + "P-masterList_3_1_1" + "P-masterList_3_1_2" + "P-masterList_3_1_3" + "P-masterList_3_1_4" + "P-masterList_3_1_5" + "P-masterList_3_1_6" + "P-masterList_3_1_7" + "P-masterList_3_1_8" + "P-masterList_3_2_0" + "P-masterList_3_2_1" + "P-masterList_3_2_2" + "P-masterList_3_2_3" + "P-masterList_3_2_4" + "P-masterList_3_2_5" + "P-masterList_3_2_6" + "P-masterList_3_2_7" + "P-masterList_3_2_8" + "P-masterList_3_3_0" + "P-masterList_3_3_1" + "P-masterList_3_3_2" + "P-masterList_3_3_3" + "P-masterList_3_3_4" + "P-masterList_3_3_5" + "P-masterList_3_3_6" + "P-masterList_3_3_7" + "P-masterList_3_3_8" + "P-masterList_3_4_0" + "P-masterList_3_4_1" + "P-masterList_3_4_2" + "P-masterList_3_4_3" + "P-masterList_3_4_4" + "P-masterList_3_4_5" + "P-masterList_3_4_6" + "P-masterList_3_4_7" + "P-masterList_3_4_8" + "P-masterList_3_5_0" + "P-masterList_3_5_1" + "P-masterList_3_5_2" + "P-masterList_3_5_3" + "P-masterList_3_5_4" + "P-masterList_3_5_5" + "P-masterList_3_5_6" + "P-masterList_3_5_7" + "P-masterList_3_5_8" + "P-masterList_3_6_0" + "P-masterList_3_6_1" + "P-masterList_3_6_2" + "P-masterList_3_6_3" + "P-masterList_3_6_4" + "P-masterList_3_6_5" + "P-masterList_3_6_6" + "P-masterList_3_6_7" + "P-masterList_3_6_8" + "P-masterList_3_7_0" + "P-masterList_3_7_1" + "P-masterList_3_7_2" + "P-masterList_3_7_3" + "P-masterList_3_7_4" + "P-masterList_3_7_5" + "P-masterList_3_7_6" + "P-masterList_3_7_7" + "P-masterList_3_7_8" + "P-masterList_3_8_0" + "P-masterList_3_8_1" + "P-masterList_3_8_2" + "P-masterList_3_8_3" + "P-masterList_3_8_4" + "P-masterList_3_8_5" + "P-masterList_3_8_6" + "P-masterList_3_8_7" + "P-masterList_3_8_8" + "P-masterList_4_1_0" + "P-masterList_4_1_1" + "P-masterList_4_1_2" + "P-masterList_4_1_3" + "P-masterList_4_1_4" + "P-masterList_4_1_5" + "P-masterList_4_1_6" + "P-masterList_4_1_7" + "P-masterList_4_1_8" + "P-masterList_4_2_0" + "P-masterList_4_2_1" + "P-masterList_4_2_2" + "P-masterList_4_2_3" + "P-masterList_4_2_4" + "P-masterList_4_2_5" + "P-masterList_4_2_6" + "P-masterList_4_2_7" + "P-masterList_4_2_8" + "P-masterList_4_3_0" + "P-masterList_4_3_1" + "P-masterList_4_3_2" + "P-masterList_4_3_3" + "P-masterList_4_3_4" + "P-masterList_4_3_5" + "P-masterList_4_3_6" + "P-masterList_4_3_7" + "P-masterList_4_3_8" + "P-masterList_4_4_0" + "P-masterList_4_4_1" + "P-masterList_4_4_2" + "P-masterList_4_4_3" + "P-masterList_4_4_4" + "P-masterList_4_4_5" + "P-masterList_4_4_6" + "P-masterList_4_4_7" + "P-masterList_4_4_8" + "P-masterList_4_5_0" + "P-masterList_4_5_1" + "P-masterList_4_5_2" + "P-masterList_4_5_3" + "P-masterList_4_5_4" + "P-masterList_4_5_5" + "P-masterList_4_5_6" + "P-masterList_4_5_7" + "P-masterList_4_5_8" + "P-masterList_4_6_0" + "P-masterList_4_6_1" + "P-masterList_4_6_2" + "P-masterList_4_6_3" + "P-masterList_4_6_4" + "P-masterList_4_6_5" + "P-masterList_4_6_6" + "P-masterList_4_6_7" + "P-masterList_4_6_8" + "P-masterList_4_7_0" + "P-masterList_4_7_1" + "P-masterList_4_7_2" + "P-masterList_4_7_3" + "P-masterList_4_7_4" + "P-masterList_4_7_5" + "P-masterList_4_7_6" + "P-masterList_4_7_7" + "P-masterList_4_7_8" + "P-masterList_4_8_0" + "P-masterList_4_8_1" + "P-masterList_4_8_2" + "P-masterList_4_8_3" + "P-masterList_4_8_4" + "P-masterList_4_8_5" + "P-masterList_4_8_6" + "P-masterList_4_8_7" + "P-masterList_4_8_8" + "P-masterList_5_1_0" + "P-masterList_5_1_1" + "P-masterList_5_1_2" + "P-masterList_5_1_3" + "P-masterList_5_1_4" + "P-masterList_5_1_5" + "P-masterList_5_1_6" + "P-masterList_5_1_7" + "P-masterList_5_1_8" + "P-masterList_5_2_0" + "P-masterList_5_2_1" + "P-masterList_5_2_2" + "P-masterList_5_2_3" + "P-masterList_5_2_4" + "P-masterList_5_2_5" + "P-masterList_5_2_6" + "P-masterList_5_2_7" + "P-masterList_5_2_8" + "P-masterList_5_3_0" + "P-masterList_5_3_1" + "P-masterList_5_3_2" + "P-masterList_5_3_3" + "P-masterList_5_3_4" + "P-masterList_5_3_5" + "P-masterList_5_3_6" + "P-masterList_5_3_7" + "P-masterList_5_3_8" + "P-masterList_5_4_0" + "P-masterList_5_4_1" + "P-masterList_5_4_2" + "P-masterList_5_4_3" + "P-masterList_5_4_4" + "P-masterList_5_4_5" + "P-masterList_5_4_6" + "P-masterList_5_4_7" + "P-masterList_5_4_8" + "P-masterList_5_5_0" + "P-masterList_5_5_1" + "P-masterList_5_5_2" + "P-masterList_5_5_3" + "P-masterList_5_5_4" + "P-masterList_5_5_5" + "P-masterList_5_5_6" + "P-masterList_5_5_7" + "P-masterList_5_5_8" + "P-masterList_5_6_0" + "P-masterList_5_6_1" + "P-masterList_5_6_2" + "P-masterList_5_6_3" + "P-masterList_5_6_4" + "P-masterList_5_6_5" + "P-masterList_5_6_6" + "P-masterList_5_6_7" + "P-masterList_5_6_8" + "P-masterList_5_7_0" + "P-masterList_5_7_1" + "P-masterList_5_7_2" + "P-masterList_5_7_3" + "P-masterList_5_7_4" + "P-masterList_5_7_5" + "P-masterList_5_7_6" + "P-masterList_5_7_7" + "P-masterList_5_7_8" + "P-masterList_5_8_0" + "P-masterList_5_8_1" + "P-masterList_5_8_2" + "P-masterList_5_8_3" + "P-masterList_5_8_4" + "P-masterList_5_8_5" + "P-masterList_5_8_6" + "P-masterList_5_8_7" + "P-masterList_5_8_8" + "P-masterList_6_1_0" + "P-masterList_6_1_1" + "P-masterList_6_1_2" + "P-masterList_6_1_3" + "P-masterList_6_1_4" + "P-masterList_6_1_5" + "P-masterList_6_1_6" + "P-masterList_6_1_7" + "P-masterList_6_1_8" + "P-masterList_6_2_0" + "P-masterList_6_2_1" + "P-masterList_6_2_2" + "P-masterList_6_2_3" + "P-masterList_6_2_4" + "P-masterList_6_2_5" + "P-masterList_6_2_6" + "P-masterList_6_2_7" + "P-masterList_6_2_8" + "P-masterList_6_3_0" + "P-masterList_6_3_1" + "P-masterList_6_3_2" + "P-masterList_6_3_3" + "P-masterList_6_3_4" + "P-masterList_6_3_5" + "P-masterList_6_3_6" + "P-masterList_6_3_7" + "P-masterList_6_3_8" + "P-masterList_6_4_0" + "P-masterList_6_4_1" + "P-masterList_6_4_2" + "P-masterList_6_4_3" + "P-masterList_6_4_4" + "P-masterList_6_4_5" + "P-masterList_6_4_6" + "P-masterList_6_4_7" + "P-masterList_6_4_8" + "P-masterList_6_5_0" + "P-masterList_6_5_1" + "P-masterList_6_5_2" + "P-masterList_6_5_3" + "P-masterList_6_5_4" + "P-masterList_6_5_5" + "P-masterList_6_5_6" + "P-masterList_6_5_7" + "P-masterList_6_5_8" + "P-masterList_6_6_0" + "P-masterList_6_6_1" + "P-masterList_6_6_2" + "P-masterList_6_6_3" + "P-masterList_6_6_4" + "P-masterList_6_6_5" + "P-masterList_6_6_6" + "P-masterList_6_6_7" + "P-masterList_6_6_8" + "P-masterList_6_7_0" + "P-masterList_6_7_1" + "P-masterList_6_7_2" + "P-masterList_6_7_3" + "P-masterList_6_7_4" + "P-masterList_6_7_5" + "P-masterList_6_7_6" + "P-masterList_6_7_7" + "P-masterList_6_7_8" + "P-masterList_6_8_0" + "P-masterList_6_8_1" + "P-masterList_6_8_2" + "P-masterList_6_8_3" + "P-masterList_6_8_4" + "P-masterList_6_8_5" + "P-masterList_6_8_6" + "P-masterList_6_8_7" + "P-masterList_6_8_8" + "P-masterList_7_1_0" + "P-masterList_7_1_1" + "P-masterList_7_1_2" + "P-masterList_7_1_3" + "P-masterList_7_1_4" + "P-masterList_7_1_5" + "P-masterList_7_1_6" + "P-masterList_7_1_7" + "P-masterList_7_1_8" + "P-masterList_7_2_0" + "P-masterList_7_2_1" + "P-masterList_7_2_2" + "P-masterList_7_2_3" + "P-masterList_7_2_4" + "P-masterList_7_2_5" + "P-masterList_7_2_6" + "P-masterList_7_2_7" + "P-masterList_7_2_8" + "P-masterList_7_3_0" + "P-masterList_7_3_1" + "P-masterList_7_3_2" + "P-masterList_7_3_3" + "P-masterList_7_3_4" + "P-masterList_7_3_5" + "P-masterList_7_3_6" + "P-masterList_7_3_7" + "P-masterList_7_3_8" + "P-masterList_7_4_0" + "P-masterList_7_4_1" + "P-masterList_7_4_2" + "P-masterList_7_4_3" + "P-masterList_7_4_4" + "P-masterList_7_4_5" + "P-masterList_7_4_6" + "P-masterList_7_4_7" + "P-masterList_7_4_8" + "P-masterList_7_5_0" + "P-masterList_7_5_1" + "P-masterList_7_5_2" + "P-masterList_7_5_3" + "P-masterList_7_5_4" + "P-masterList_7_5_5" + "P-masterList_7_5_6" + "P-masterList_7_5_7" + "P-masterList_7_5_8" + "P-masterList_7_6_0" + "P-masterList_7_6_1" + "P-masterList_7_6_2" + "P-masterList_7_6_3" + "P-masterList_7_6_4" + "P-masterList_7_6_5" + "P-masterList_7_6_6" + "P-masterList_7_6_7" + "P-masterList_7_6_8" + "P-masterList_7_7_0" + "P-masterList_7_7_1" + "P-masterList_7_7_2" + "P-masterList_7_7_3" + "P-masterList_7_7_4" + "P-masterList_7_7_5" + "P-masterList_7_7_6" + "P-masterList_7_7_7" + "P-masterList_7_7_8" + "P-masterList_7_8_0" + "P-masterList_7_8_1" + "P-masterList_7_8_2" + "P-masterList_7_8_3" + "P-masterList_7_8_4" + "P-masterList_7_8_5" + "P-masterList_7_8_6" + "P-masterList_7_8_7" + "P-masterList_7_8_8" + "P-masterList_8_1_0" + "P-masterList_8_1_1" + "P-masterList_8_1_2" + "P-masterList_8_1_3" + "P-masterList_8_1_4" + "P-masterList_8_1_5" + "P-masterList_8_1_6" + "P-masterList_8_1_7" + "P-masterList_8_1_8" + "P-masterList_8_2_0" + "P-masterList_8_2_1" + "P-masterList_8_2_2" + "P-masterList_8_2_3" + "P-masterList_8_2_4" + "P-masterList_8_2_5" + "P-masterList_8_2_6" + "P-masterList_8_2_7" + "P-masterList_8_2_8" + "P-masterList_8_3_0" + "P-masterList_8_3_1" + "P-masterList_8_3_2" + "P-masterList_8_3_3" + "P-masterList_8_3_4" + "P-masterList_8_3_5" + "P-masterList_8_3_6" + "P-masterList_8_3_7" + "P-masterList_8_3_8" + "P-masterList_8_4_0" + "P-masterList_8_4_1" + "P-masterList_8_4_2" + "P-masterList_8_4_3" + "P-masterList_8_4_4" + "P-masterList_8_4_5" + "P-masterList_8_4_6" + "P-masterList_8_4_7" + "P-masterList_8_4_8" + "P-masterList_8_5_0" + "P-masterList_8_5_1" + "P-masterList_8_5_2" + "P-masterList_8_5_3" + "P-masterList_8_5_4" + "P-masterList_8_5_5" + "P-masterList_8_5_6" + "P-masterList_8_5_7" + "P-masterList_8_5_8" + "P-masterList_8_6_0" + "P-masterList_8_6_1" + "P-masterList_8_6_2" + "P-masterList_8_6_3" + "P-masterList_8_6_4" + "P-masterList_8_6_5" + "P-masterList_8_6_6" + "P-masterList_8_6_7" + "P-masterList_8_6_8" + "P-masterList_8_7_0" + "P-masterList_8_7_1" + "P-masterList_8_7_2" + "P-masterList_8_7_3" + "P-masterList_8_7_4" + "P-masterList_8_7_5" + "P-masterList_8_7_6" + "P-masterList_8_7_7" + "P-masterList_8_7_8" + "P-masterList_8_8_0" + "P-masterList_8_8_1" + "P-masterList_8_8_2" + "P-masterList_8_8_3" + "P-masterList_8_8_4" + "P-masterList_8_8_5" + "P-masterList_8_8_6" + "P-masterList_8_8_7" + "P-masterList_8_8_8"))) and ((2 <= ("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8")) and (("P-polling_0" + "P-polling_1" + "P-polling_2" + "P-polling_3" + "P-polling_4" + "P-polling_5" + "P-polling_6" + "P-polling_7" + "P-polling_8") <= ("P-negotiation_0_0_NONE" + "P-negotiation_0_0_CO" + "P-negotiation_0_0_DONE" + "P-negotiation_0_1_NONE" + "P-negotiation_0_1_CO" + "P-negotiation_0_1_DONE" + "P-negotiation_0_2_NONE" + "P-negotiation_0_2_CO" + "P-negotiation_0_2_DONE" + "P-negotiation_0_3_NONE" + "P-negotiation_0_3_CO" + "P-negotiation_0_3_DONE" + "P-negotiation_0_4_NONE" + "P-negotiation_0_4_CO" + "P-negotiation_0_4_DONE" + "P-negotiation_0_5_NONE" + "P-negotiation_0_5_CO" + "P-negotiation_0_5_DONE" + "P-negotiation_0_6_NONE" + "P-negotiation_0_6_CO" + "P-negotiation_0_6_DONE" + "P-negotiation_0_7_NONE" + "P-negotiation_0_7_CO" + "P-negotiation_0_7_DONE" + "P-negotiation_0_8_NONE" + "P-negotiation_0_8_CO" + "P-negotiation_0_8_DONE" + "P-negotiation_1_0_NONE" + "P-negotiation_1_0_CO" + "P-negotiation_1_0_DONE" + "P-negotiation_1_1_NONE" + "P-negotiation_1_1_CO" + "P-negotiation_1_1_DONE" + "P-negotiation_1_2_NONE" + "P-negotiation_1_2_CO" + "P-negotiation_1_2_DONE" + "P-negotiation_1_3_NONE" + "P-negotiation_1_3_CO" + "P-negotiation_1_3_DONE" + "P-negotiation_1_4_NONE" + "P-negotiation_1_4_CO" + "P-negotiation_1_4_DONE" + "P-negotiation_1_5_NONE" + "P-negotiation_1_5_CO" + "P-negotiation_1_5_DONE" + "P-negotiation_1_6_NONE" + "P-negotiation_1_6_CO" + "P-negotiation_1_6_DONE" + "P-negotiation_1_7_NONE" + "P-negotiation_1_7_CO" + "P-negotiation_1_7_DONE" + "P-negotiation_1_8_NONE" + "P-negotiation_1_8_CO" + "P-negotiation_1_8_DONE" + "P-negotiation_2_0_NONE" + "P-negotiation_2_0_CO" + "P-negotiation_2_0_DONE" + "P-negotiation_2_1_NONE" + "P-negotiation_2_1_CO" + "P-negotiation_2_1_DONE" + "P-negotiation_2_2_NONE" + "P-negotiation_2_2_CO" + "P-negotiation_2_2_DONE" + "P-negotiation_2_3_NONE" + "P-negotiation_2_3_CO" + "P-negotiation_2_3_DONE" + "P-negotiation_2_4_NONE" + "P-negotiation_2_4_CO" + "P-negotiation_2_4_DONE" + "P-negotiation_2_5_NONE" + "P-negotiation_2_5_CO" + "P-negotiation_2_5_DONE" + "P-negotiation_2_6_NONE" + "P-negotiation_2_6_CO" + "P-negotiation_2_6_DONE" + "P-negotiation_2_7_NONE" + "P-negotiation_2_7_CO" + "P-negotiation_2_7_DONE" + "P-negotiation_2_8_NONE" + "P-negotiation_2_8_CO" + "P-negotiation_2_8_DONE" + "P-negotiation_3_0_NONE" + "P-negotiation_3_0_CO" + "P-negotiation_3_0_DONE" + "P-negotiation_3_1_NONE" + "P-negotiation_3_1_CO" + "P-negotiation_3_1_DONE" + "P-negotiation_3_2_NONE" + "P-negotiation_3_2_CO" + "P-negotiation_3_2_DONE" + "P-negotiation_3_3_NONE" + "P-negotiation_3_3_CO" + "P-negotiation_3_3_DONE" + "P-negotiation_3_4_NONE" + "P-negotiation_3_4_CO" + "P-negotiation_3_4_DONE" + "P-negotiation_3_5_NONE" + "P-negotiation_3_5_CO" + "P-negotiation_3_5_DONE" + "P-negotiation_3_6_NONE" + "P-negotiation_3_6_CO" + "P-negotiation_3_6_DONE" + "P-negotiation_3_7_NONE" + "P-negotiation_3_7_CO" + "P-negotiation_3_7_DONE" + "P-negotiation_3_8_NONE" + "P-negotiation_3_8_CO" + "P-negotiation_3_8_DONE" + "P-negotiation_4_0_NONE" + "P-negotiation_4_0_CO" + "P-negotiation_4_0_DONE" + "P-negotiation_4_1_NONE" + "P-negotiation_4_1_CO" + "P-negotiation_4_1_DONE" + "P-negotiation_4_2_NONE" + "P-negotiation_4_2_CO" + "P-negotiation_4_2_DONE" + "P-negotiation_4_3_NONE" + "P-negotiation_4_3_CO" + "P-negotiation_4_3_DONE" + "P-negotiation_4_4_NONE" + "P-negotiation_4_4_CO" + "P-negotiation_4_4_DONE" + "P-negotiation_4_5_NONE" + "P-negotiation_4_5_CO" + "P-negotiation_4_5_DONE" + "P-negotiation_4_6_NONE" + "P-negotiation_4_6_CO" + "P-negotiation_4_6_DONE" + "P-negotiation_4_7_NONE" + "P-negotiation_4_7_CO" + "P-negotiation_4_7_DONE" + "P-negotiation_4_8_NONE" + "P-negotiation_4_8_CO" + "P-negotiation_4_8_DONE" + "P-negotiation_5_0_NONE" + "P-negotiation_5_0_CO" + "P-negotiation_5_0_DONE" + "P-negotiation_5_1_NONE" + "P-negotiation_5_1_CO" + "P-negotiation_5_1_DONE" + "P-negotiation_5_2_NONE" + "P-negotiation_5_2_CO" + "P-negotiation_5_2_DONE" + "P-negotiation_5_3_NONE" + "P-negotiation_5_3_CO" + "P-negotiation_5_3_DONE" + "P-negotiation_5_4_NONE" + "P-negotiation_5_4_CO" + "P-negotiation_5_4_DONE" + "P-negotiation_5_5_NONE" + "P-negotiation_5_5_CO" + "P-negotiation_5_5_DONE" + "P-negotiation_5_6_NONE" + "P-negotiation_5_6_CO" + "P-negotiation_5_6_DONE" + "P-negotiation_5_7_NONE" + "P-negotiation_5_7_CO" + "P-negotiation_5_7_DONE" + "P-negotiation_5_8_NONE" + "P-negotiation_5_8_CO" + "P-negotiation_5_8_DONE" + "P-negotiation_6_0_NONE" + "P-negotiation_6_0_CO" + "P-negotiation_6_0_DONE" + "P-negotiation_6_1_NONE" + "P-negotiation_6_1_CO" + "P-negotiation_6_1_DONE" + "P-negotiation_6_2_NONE" + "P-negotiation_6_2_CO" + "P-negotiation_6_2_DONE" + "P-negotiation_6_3_NONE" + "P-negotiation_6_3_CO" + "P-negotiation_6_3_DONE" + "P-negotiation_6_4_NONE" + "P-negotiation_6_4_CO" + "P-negotiation_6_4_DONE" + "P-negotiation_6_5_NONE" + "P-negotiation_6_5_CO" + "P-negotiation_6_5_DONE" + "P-negotiation_6_6_NONE" + "P-negotiation_6_6_CO" + "P-negotiation_6_6_DONE" + "P-negotiation_6_7_NONE" + "P-negotiation_6_7_CO" + "P-negotiation_6_7_DONE" + "P-negotiation_6_8_NONE" + "P-negotiation_6_8_CO" + "P-negotiation_6_8_DONE" + "P-negotiation_7_0_NONE" + "P-negotiation_7_0_CO" + "P-negotiation_7_0_DONE" + "P-negotiation_7_1_NONE" + "P-negotiation_7_1_CO" + "P-negotiation_7_1_DONE" + "P-negotiation_7_2_NONE" + "P-negotiation_7_2_CO" + "P-negotiation_7_2_DONE" + "P-negotiation_7_3_NONE" + "P-negotiation_7_3_CO" + "P-negotiation_7_3_DONE" + "P-negotiation_7_4_NONE" + "P-negotiation_7_4_CO" + "P-negotiation_7_4_DONE" + "P-negotiation_7_5_NONE" + "P-negotiation_7_5_CO" + "P-negotiation_7_5_DONE" + "P-negotiation_7_6_NONE" + "P-negotiation_7_6_CO" + "P-negotiation_7_6_DONE" + "P-negotiation_7_7_NONE" + "P-negotiation_7_7_CO" + "P-negotiation_7_7_DONE" + "P-negotiation_7_8_NONE" + "P-negotiation_7_8_CO" + "P-negotiation_7_8_DONE" + "P-negotiation_8_0_NONE" + "P-negotiation_8_0_CO" + "P-negotiation_8_0_DONE" + "P-negotiation_8_1_NONE" + "P-negotiation_8_1_CO" + "P-negotiation_8_1_DONE" + "P-negotiation_8_2_NONE" + "P-negotiation_8_2_CO" + "P-negotiation_8_2_DONE" + "P-negotiation_8_3_NONE" + "P-negotiation_8_3_CO" + "P-negotiation_8_3_DONE" + "P-negotiation_8_4_NONE" + "P-negotiation_8_4_CO" + "P-negotiation_8_4_DONE" + "P-negotiation_8_5_NONE" + "P-negotiation_8_5_CO" + "P-negotiation_8_5_DONE" + "P-negotiation_8_6_NONE" + "P-negotiation_8_6_CO" + "P-negotiation_8_6_DONE" + "P-negotiation_8_7_NONE" + "P-negotiation_8_7_CO" + "P-negotiation_8_7_DONE" + "P-negotiation_8_8_NONE" + "P-negotiation_8_8_CO" + "P-negotiation_8_8_DONE"))))) )
NeoElection-COL-8-ReachabilityCardinality-9: not EF not ( (3 <= ("P-masterList_0_1_0" + "P-masterList_0_1_1" + "P-masterList_0_1_2" + "P-masterList_0_1_3" + "P-masterList_0_1_4" + "P-masterList_0_1_5" + "P-masterList_0_1_6" + "P-masterList_0_1_7" + "P-masterList_0_1_8" + "P-masterList_0_2_0" + "P-masterList_0_2_1" + "P-masterList_0_2_2" + "P-masterList_0_2_3" + "P-masterList_0_2_4" + "P-masterList_0_2_5" + "P-masterList_0_2_6" + "P-masterList_0_2_7" + "P-masterList_0_2_8" + "P-masterList_0_3_0" + "P-masterList_0_3_1" + "P-masterList_0_3_2" + "P-masterList_0_3_3" + "P-masterList_0_3_4" + "P-masterList_0_3_5" + "P-masterList_0_3_6" + "P-masterList_0_3_7" + "P-masterList_0_3_8" + "P-masterList_0_4_0" + "P-masterList_0_4_1" + "P-masterList_0_4_2" + "P-masterList_0_4_3" + "P-masterList_0_4_4" + "P-masterList_0_4_5" + "P-masterList_0_4_6" + "P-masterList_0_4_7" + "P-masterList_0_4_8" + "P-masterList_0_5_0" + "P-masterList_0_5_1" + "P-masterList_0_5_2" + "P-masterList_0_5_3" + "P-masterList_0_5_4" + "P-masterList_0_5_5" + "P-masterList_0_5_6" + "P-masterList_0_5_7" + "P-masterList_0_5_8" + "P-masterList_0_6_0" + "P-masterList_0_6_1" + "P-masterList_0_6_2" + "P-masterList_0_6_3" + "P-masterList_0_6_4" + "P-masterList_0_6_5" + "P-masterList_0_6_6" + "P-masterList_0_6_7" + "P-masterList_0_6_8" + "P-masterList_0_7_0" + "P-masterList_0_7_1" + "P-masterList_0_7_2" + "P-masterList_0_7_3" + "P-masterList_0_7_4" + "P-masterList_0_7_5" + "P-masterList_0_7_6" + "P-masterList_0_7_7" + "P-masterList_0_7_8" + "P-masterList_0_8_0" + "P-masterList_0_8_1" + "P-masterList_0_8_2" + "P-masterList_0_8_3" + "P-masterList_0_8_4" + "P-masterList_0_8_5" + "P-masterList_0_8_6" + "P-masterList_0_8_7" + "P-masterList_0_8_8" + "P-masterList_1_1_0" + "P-masterList_1_1_1" + "P-masterList_1_1_2" + "P-masterList_1_1_3" + "P-masterList_1_1_4" + "P-masterList_1_1_5" + "P-masterList_1_1_6" + "P-masterList_1_1_7" + "P-masterList_1_1_8" + "P-masterList_1_2_0" + "P-masterList_1_2_1" + "P-masterList_1_2_2" + "P-masterList_1_2_3" + "P-masterList_1_2_4" + "P-masterList_1_2_5" + "P-masterList_1_2_6" + "P-masterList_1_2_7" + "P-masterList_1_2_8" + "P-masterList_1_3_0" + "P-masterList_1_3_1" + "P-masterList_1_3_2" + "P-masterList_1_3_3" + "P-masterList_1_3_4" + "P-masterList_1_3_5" + "P-masterList_1_3_6" + "P-masterList_1_3_7" + "P-masterList_1_3_8" + "P-masterList_1_4_0" + "P-masterList_1_4_1" + "P-masterList_1_4_2" + "P-masterList_1_4_3" + "P-masterList_1_4_4" + "P-masterList_1_4_5" + "P-masterList_1_4_6" + "P-masterList_1_4_7" + "P-masterList_1_4_8" + "P-masterList_1_5_0" + "P-masterList_1_5_1" + "P-masterList_1_5_2" + "P-masterList_1_5_3" + "P-masterList_1_5_4" + "P-masterList_1_5_5" + "P-masterList_1_5_6" + "P-masterList_1_5_7" + "P-masterList_1_5_8" + "P-masterList_1_6_0" + "P-masterList_1_6_1" + "P-masterList_1_6_2" + "P-masterList_1_6_3" + "P-masterList_1_6_4" + "P-masterList_1_6_5" + "P-masterList_1_6_6" + "P-masterList_1_6_7" + "P-masterList_1_6_8" + "P-masterList_1_7_0" + "P-masterList_1_7_1" + "P-masterList_1_7_2" + "P-masterList_1_7_3" + "P-masterList_1_7_4" + "P-masterList_1_7_5" + "P-masterList_1_7_6" + "P-masterList_1_7_7" + "P-masterList_1_7_8" + "P-masterList_1_8_0" + "P-masterList_1_8_1" + "P-masterList_1_8_2" + "P-masterList_1_8_3" + "P-masterList_1_8_4" + "P-masterList_1_8_5" + "P-masterList_1_8_6" + "P-masterList_1_8_7" + "P-masterList_1_8_8" + "P-masterList_2_1_0" + "P-masterList_2_1_1" + "P-masterList_2_1_2" + "P-masterList_2_1_3" + "P-masterList_2_1_4" + "P-masterList_2_1_5" + "P-masterList_2_1_6" + "P-masterList_2_1_7" + "P-masterList_2_1_8" + "P-masterList_2_2_0" + "P-masterList_2_2_1" + "P-masterList_2_2_2" + "P-masterList_2_2_3" + "P-masterList_2_2_4" + "P-masterList_2_2_5" + "P-masterList_2_2_6" + "P-masterList_2_2_7" + "P-masterList_2_2_8" + "P-masterList_2_3_0" + "P-masterList_2_3_1" + "P-masterList_2_3_2" + "P-masterList_2_3_3" + "P-masterList_2_3_4" + "P-masterList_2_3_5" + "P-masterList_2_3_6" + "P-masterList_2_3_7" + "P-masterList_2_3_8" + "P-masterList_2_4_0" + "P-masterList_2_4_1" + "P-masterList_2_4_2" + "P-masterList_2_4_3" + "P-masterList_2_4_4" + "P-masterList_2_4_5" + "P-masterList_2_4_6" + "P-masterList_2_4_7" + "P-masterList_2_4_8" + "P-masterList_2_5_0" + "P-masterList_2_5_1" + "P-masterList_2_5_2" + "P-masterList_2_5_3" + "P-masterList_2_5_4" + "P-masterList_2_5_5" + "P-masterList_2_5_6" + "P-masterList_2_5_7" + "P-masterList_2_5_8" + "P-masterList_2_6_0" + "P-masterList_2_6_1" + "P-masterList_2_6_2" + "P-masterList_2_6_3" + "P-masterList_2_6_4" + "P-masterList_2_6_5" + "P-masterList_2_6_6" + "P-masterList_2_6_7" + "P-masterList_2_6_8" + "P-masterList_2_7_0" + "P-masterList_2_7_1" + "P-masterList_2_7_2" + "P-masterList_2_7_3" + "P-masterList_2_7_4" + "P-masterList_2_7_5" + "P-masterList_2_7_6" + "P-masterList_2_7_7" + "P-masterList_2_7_8" + "P-masterList_2_8_0" + "P-masterList_2_8_1" + "P-masterList_2_8_2" + "P-masterList_2_8_3" + "P-masterList_2_8_4" + "P-masterList_2_8_5" + "P-masterList_2_8_6" + "P-masterList_2_8_7" + "P-masterList_2_8_8" + "P-masterList_3_1_0" + "P-masterList_3_1_1" + "P-masterList_3_1_2" + "P-masterList_3_1_3" + "P-masterList_3_1_4" + "P-masterList_3_1_5" + "P-masterList_3_1_6" + "P-masterList_3_1_7" + "P-masterList_3_1_8" + "P-masterList_3_2_0" + "P-masterList_3_2_1" + "P-masterList_3_2_2" + "P-masterList_3_2_3" + "P-masterList_3_2_4" + "P-masterList_3_2_5" + "P-masterList_3_2_6" + "P-masterList_3_2_7" + "P-masterList_3_2_8" + "P-masterList_3_3_0" + "P-masterList_3_3_1" + "P-masterList_3_3_2" + "P-masterList_3_3_3" + "P-masterList_3_3_4" + "P-masterList_3_3_5" + "P-masterList_3_3_6" + "P-masterList_3_3_7" + "P-masterList_3_3_8" + "P-masterList_3_4_0" + "P-masterList_3_4_1" + "P-masterList_3_4_2" + "P-masterList_3_4_3" + "P-masterList_3_4_4" + "P-masterList_3_4_5" + "P-masterList_3_4_6" + "P-masterList_3_4_7" + "P-masterList_3_4_8" + "P-masterList_3_5_0" + "P-masterList_3_5_1" + "P-masterList_3_5_2" + "P-masterList_3_5_3" + "P-masterList_3_5_4" + "P-masterList_3_5_5" + "P-masterList_3_5_6" + "P-masterList_3_5_7" + "P-masterList_3_5_8" + "P-masterList_3_6_0" + "P-masterList_3_6_1" + "P-masterList_3_6_2" + "P-masterList_3_6_3" + "P-masterList_3_6_4" + "P-masterList_3_6_5" + "P-masterList_3_6_6" + "P-masterList_3_6_7" + "P-masterList_3_6_8" + "P-masterList_3_7_0" + "P-masterList_3_7_1" + "P-masterList_3_7_2" + "P-masterList_3_7_3" + "P-masterList_3_7_4" + "P-masterList_3_7_5" + "P-masterList_3_7_6" + "P-masterList_3_7_7" + "P-masterList_3_7_8" + "P-masterList_3_8_0" + "P-masterList_3_8_1" + "P-masterList_3_8_2" + "P-masterList_3_8_3" + "P-masterList_3_8_4" + "P-masterList_3_8_5" + "P-masterList_3_8_6" + "P-masterList_3_8_7" + "P-masterList_3_8_8" + "P-masterList_4_1_0" + "P-masterList_4_1_1" + "P-masterList_4_1_2" + "P-masterList_4_1_3" + "P-masterList_4_1_4" + "P-masterList_4_1_5" + "P-masterList_4_1_6" + "P-masterList_4_1_7" + "P-masterList_4_1_8" + "P-masterList_4_2_0" + "P-masterList_4_2_1" + "P-masterList_4_2_2" + "P-masterList_4_2_3" + "P-masterList_4_2_4" + "P-masterList_4_2_5" + "P-masterList_4_2_6" + "P-masterList_4_2_7" + "P-masterList_4_2_8" + "P-masterList_4_3_0" + "P-masterList_4_3_1" + "P-masterList_4_3_2" + "P-masterList_4_3_3" + "P-masterList_4_3_4" + "P-masterList_4_3_5" + "P-masterList_4_3_6" + "P-masterList_4_3_7" + "P-masterList_4_3_8" + "P-masterList_4_4_0" + "P-masterList_4_4_1" + "P-masterList_4_4_2" + "P-masterList_4_4_3" + "P-masterList_4_4_4" + "P-masterList_4_4_5" + "P-masterList_4_4_6" + "P-masterList_4_4_7" + "P-masterList_4_4_8" + "P-masterList_4_5_0" + "P-masterList_4_5_1" + "P-masterList_4_5_2" + "P-masterList_4_5_3" + "P-masterList_4_5_4" + "P-masterList_4_5_5" + "P-masterList_4_5_6" + "P-masterList_4_5_7" + "P-masterList_4_5_8" + "P-masterList_4_6_0" + "P-masterList_4_6_1" + "P-masterList_4_6_2" + "P-masterList_4_6_3" + "P-masterList_4_6_4" + "P-masterList_4_6_5" + "P-masterList_4_6_6" + "P-masterList_4_6_7" + "P-masterList_4_6_8" + "P-masterList_4_7_0" + "P-masterList_4_7_1" + "P-masterList_4_7_2" + "P-masterList_4_7_3" + "P-masterList_4_7_4" + "P-masterList_4_7_5" + "P-masterList_4_7_6" + "P-masterList_4_7_7" + "P-masterList_4_7_8" + "P-masterList_4_8_0" + "P-masterList_4_8_1" + "P-masterList_4_8_2" + "P-masterList_4_8_3" + "P-masterList_4_8_4" + "P-masterList_4_8_5" + "P-masterList_4_8_6" + "P-masterList_4_8_7" + "P-masterList_4_8_8" + "P-masterList_5_1_0" + "P-masterList_5_1_1" + "P-masterList_5_1_2" + "P-masterList_5_1_3" + "P-masterList_5_1_4" + "P-masterList_5_1_5" + "P-masterList_5_1_6" + "P-masterList_5_1_7" + "P-masterList_5_1_8" + "P-masterList_5_2_0" + "P-masterList_5_2_1" + "P-masterList_5_2_2" + "P-masterList_5_2_3" + "P-masterList_5_2_4" + "P-masterList_5_2_5" + "P-masterList_5_2_6" + "P-masterList_5_2_7" + "P-masterList_5_2_8" + "P-masterList_5_3_0" + "P-masterList_5_3_1" + "P-masterList_5_3_2" + "P-masterList_5_3_3" + "P-masterList_5_3_4" + "P-masterList_5_3_5" + "P-masterList_5_3_6" + "P-masterList_5_3_7" + "P-masterList_5_3_8" + "P-masterList_5_4_0" + "P-masterList_5_4_1" + "P-masterList_5_4_2" + "P-masterList_5_4_3" + "P-masterList_5_4_4" + "P-masterList_5_4_5" + "P-masterList_5_4_6" + "P-masterList_5_4_7" + "P-masterList_5_4_8" + "P-masterList_5_5_0" + "P-masterList_5_5_1" + "P-masterList_5_5_2" + "P-masterList_5_5_3" + "P-masterList_5_5_4" + "P-masterList_5_5_5" + "P-masterList_5_5_6" + "P-masterList_5_5_7" + "P-masterList_5_5_8" + "P-masterList_5_6_0" + "P-masterList_5_6_1" + "P-masterList_5_6_2" + "P-masterList_5_6_3" + "P-masterList_5_6_4" + "P-masterList_5_6_5" + "P-masterList_5_6_6" + "P-masterList_5_6_7" + "P-masterList_5_6_8" + "P-masterList_5_7_0" + "P-masterList_5_7_1" + "P-masterList_5_7_2" + "P-masterList_5_7_3" + "P-masterList_5_7_4" + "P-masterList_5_7_5" + "P-masterList_5_7_6" + "P-masterList_5_7_7" + "P-masterList_5_7_8" + "P-masterList_5_8_0" + "P-masterList_5_8_1" + "P-masterList_5_8_2" + "P-masterList_5_8_3" + "P-masterList_5_8_4" + "P-masterList_5_8_5" + "P-masterList_5_8_6" + "P-masterList_5_8_7" + "P-masterList_5_8_8" + "P-masterList_6_1_0" + "P-masterList_6_1_1" + "P-masterList_6_1_2" + "P-masterList_6_1_3" + "P-masterList_6_1_4" + "P-masterList_6_1_5" + "P-masterList_6_1_6" + "P-masterList_6_1_7" + "P-masterList_6_1_8" + "P-masterList_6_2_0" + "P-masterList_6_2_1" + "P-masterList_6_2_2" + "P-masterList_6_2_3" + "P-masterList_6_2_4" + "P-masterList_6_2_5" + "P-masterList_6_2_6" + "P-masterList_6_2_7" + "P-masterList_6_2_8" + "P-masterList_6_3_0" + "P-masterList_6_3_1" + "P-masterList_6_3_2" + "P-masterList_6_3_3" + "P-masterList_6_3_4" + "P-masterList_6_3_5" + "P-masterList_6_3_6" + "P-masterList_6_3_7" + "P-masterList_6_3_8" + "P-masterList_6_4_0" + "P-masterList_6_4_1" + "P-masterList_6_4_2" + "P-masterList_6_4_3" + "P-masterList_6_4_4" + "P-masterList_6_4_5" + "P-masterList_6_4_6" + "P-masterList_6_4_7" + "P-masterList_6_4_8" + "P-masterList_6_5_0" + "P-masterList_6_5_1" + "P-masterList_6_5_2" + "P-masterList_6_5_3" + "P-masterList_6_5_4" + "P-masterList_6_5_5" + "P-masterList_6_5_6" + "P-masterList_6_5_7" + "P-masterList_6_5_8" + "P-masterList_6_6_0" + "P-masterList_6_6_1" + "P-masterList_6_6_2" + "P-masterList_6_6_3" + "P-masterList_6_6_4" + "P-masterList_6_6_5" + "P-masterList_6_6_6" + "P-masterList_6_6_7" + "P-masterList_6_6_8" + "P-masterList_6_7_0" + "P-masterList_6_7_1" + "P-masterList_6_7_2" + "P-masterList_6_7_3" + "P-masterList_6_7_4" + "P-masterList_6_7_5" + "P-masterList_6_7_6" + "P-masterList_6_7_7" + "P-masterList_6_7_8" + "P-masterList_6_8_0" + "P-masterList_6_8_1" + "P-masterList_6_8_2" + "P-masterList_6_8_3" + "P-masterList_6_8_4" + "P-masterList_6_8_5" + "P-masterList_6_8_6" + "P-masterList_6_8_7" + "P-masterList_6_8_8" + "P-masterList_7_1_0" + "P-masterList_7_1_1" + "P-masterList_7_1_2" + "P-masterList_7_1_3" + "P-masterList_7_1_4" + "P-masterList_7_1_5" + "P-masterList_7_1_6" + "P-masterList_7_1_7" + "P-masterList_7_1_8" + "P-masterList_7_2_0" + "P-masterList_7_2_1" + "P-masterList_7_2_2" + "P-masterList_7_2_3" + "P-masterList_7_2_4" + "P-masterList_7_2_5" + "P-masterList_7_2_6" + "P-masterList_7_2_7" + "P-masterList_7_2_8" + "P-masterList_7_3_0" + "P-masterList_7_3_1" + "P-masterList_7_3_2" + "P-masterList_7_3_3" + "P-masterList_7_3_4" + "P-masterList_7_3_5" + "P-masterList_7_3_6" + "P-masterList_7_3_7" + "P-masterList_7_3_8" + "P-masterList_7_4_0" + "P-masterList_7_4_1" + "P-masterList_7_4_2" + "P-masterList_7_4_3" + "P-masterList_7_4_4" + "P-masterList_7_4_5" + "P-masterList_7_4_6" + "P-masterList_7_4_7" + "P-masterList_7_4_8" + "P-masterList_7_5_0" + "P-masterList_7_5_1" + "P-masterList_7_5_2" + "P-masterList_7_5_3" + "P-masterList_7_5_4" + "P-masterList_7_5_5" + "P-masterList_7_5_6" + "P-masterList_7_5_7" + "P-masterList_7_5_8" + "P-masterList_7_6_0" + "P-masterList_7_6_1" + "P-masterList_7_6_2" + "P-masterList_7_6_3" + "P-masterList_7_6_4" + "P-masterList_7_6_5" + "P-masterList_7_6_6" + "P-masterList_7_6_7" + "P-masterList_7_6_8" + "P-masterList_7_7_0" + "P-masterList_7_7_1" + "P-masterList_7_7_2" + "P-masterList_7_7_3" + "P-masterList_7_7_4" + "P-masterList_7_7_5" + "P-masterList_7_7_6" + "P-masterList_7_7_7" + "P-masterList_7_7_8" + "P-masterList_7_8_0" + "P-masterList_7_8_1" + "P-masterList_7_8_2" + "P-masterList_7_8_3" + "P-masterList_7_8_4" + "P-masterList_7_8_5" + "P-masterList_7_8_6" + "P-masterList_7_8_7" + "P-masterList_7_8_8" + "P-masterList_8_1_0" + "P-masterList_8_1_1" + "P-masterList_8_1_2" + "P-masterList_8_1_3" + "P-masterList_8_1_4" + "P-masterList_8_1_5" + "P-masterList_8_1_6" + "P-masterList_8_1_7" + "P-masterList_8_1_8" + "P-masterList_8_2_0" + "P-masterList_8_2_1" + "P-masterList_8_2_2" + "P-masterList_8_2_3" + "P-masterList_8_2_4" + "P-masterList_8_2_5" + "P-masterList_8_2_6" + "P-masterList_8_2_7" + "P-masterList_8_2_8" + "P-masterList_8_3_0" + "P-masterList_8_3_1" + "P-masterList_8_3_2" + "P-masterList_8_3_3" + "P-masterList_8_3_4" + "P-masterList_8_3_5" + "P-masterList_8_3_6" + "P-masterList_8_3_7" + "P-masterList_8_3_8" + "P-masterList_8_4_0" + "P-masterList_8_4_1" + "P-masterList_8_4_2" + "P-masterList_8_4_3" + "P-masterList_8_4_4" + "P-masterList_8_4_5" + "P-masterList_8_4_6" + "P-masterList_8_4_7" + "P-masterList_8_4_8" + "P-masterList_8_5_0" + "P-masterList_8_5_1" + "P-masterList_8_5_2" + "P-masterList_8_5_3" + "P-masterList_8_5_4" + "P-masterList_8_5_5" + "P-masterList_8_5_6" + "P-masterList_8_5_7" + "P-masterList_8_5_8" + "P-masterList_8_6_0" + "P-masterList_8_6_1" + "P-masterList_8_6_2" + "P-masterList_8_6_3" + "P-masterList_8_6_4" + "P-masterList_8_6_5" + "P-masterList_8_6_6" + "P-masterList_8_6_7" + "P-masterList_8_6_8" + "P-masterList_8_7_0" + "P-masterList_8_7_1" + "P-masterList_8_7_2" + "P-masterList_8_7_3" + "P-masterList_8_7_4" + "P-masterList_8_7_5" + "P-masterList_8_7_6" + "P-masterList_8_7_7" + "P-masterList_8_7_8" + "P-masterList_8_8_0" + "P-masterList_8_8_1" + "P-masterList_8_8_2" + "P-masterList_8_8_3" + "P-masterList_8_8_4" + "P-masterList_8_8_5" + "P-masterList_8_8_6" + "P-masterList_8_8_7" + "P-masterList_8_8_8")) )
NeoElection-COL-8-ReachabilityCardinality-10: EF ( not(not(not((("P-poll__networl_0_0_AskP_0" + "P-poll__networl_0_0_AskP_1" + "P-poll__networl_0_0_AskP_2" + "P-poll__networl_0_0_AskP_3" + "P-poll__networl_0_0_AskP_4" + "P-poll__networl_0_0_AskP_5" + "P-poll__networl_0_0_AskP_6" + "P-poll__networl_0_0_AskP_7" + "P-poll__networl_0_0_AskP_8" + "P-poll__networl_0_0_AnsP_0" + "P-poll__networl_0_0_AnsP_1" + "P-poll__networl_0_0_AnsP_2" + "P-poll__networl_0_0_AnsP_3" + "P-poll__networl_0_0_AnsP_4" + "P-poll__networl_0_0_AnsP_5" + "P-poll__networl_0_0_AnsP_6" + "P-poll__networl_0_0_AnsP_7" + "P-poll__networl_0_0_AnsP_8" + "P-poll__networl_0_0_RI_0" + "P-poll__networl_0_0_RI_1" + "P-poll__networl_0_0_RI_2" + "P-poll__networl_0_0_RI_3" + "P-poll__networl_0_0_RI_4" + "P-poll__networl_0_0_RI_5" + "P-poll__networl_0_0_RI_6" + "P-poll__networl_0_0_RI_7" + "P-poll__networl_0_0_RI_8" + "P-poll__networl_0_0_AI_0" + "P-poll__networl_0_0_AI_1" + "P-poll__networl_0_0_AI_2" + "P-poll__networl_0_0_AI_3" + "P-poll__networl_0_0_AI_4" + "P-poll__networl_0_0_AI_5" + "P-poll__networl_0_0_AI_6" + "P-poll__networl_0_0_AI_7" + "P-poll__networl_0_0_AI_8" + "P-poll__networl_0_0_AnnP_0" + "P-poll__networl_0_0_AnnP_1" + "P-poll__networl_0_0_AnnP_2" + "P-poll__networl_0_0_AnnP_3" + "P-poll__networl_0_0_AnnP_4" + "P-poll__networl_0_0_AnnP_5" + "P-poll__networl_0_0_AnnP_6" + "P-poll__networl_0_0_AnnP_7" + "P-poll__networl_0_0_AnnP_8" + "P-poll__networl_0_0_RP_0" + "P-poll__networl_0_0_RP_1" + "P-poll__networl_0_0_RP_2" + "P-poll__networl_0_0_RP_3" + "P-poll__networl_0_0_RP_4" + "P-poll__networl_0_0_RP_5" + "P-poll__networl_0_0_RP_6" + "P-poll__networl_0_0_RP_7" + "P-poll__networl_0_0_RP_8" + "P-poll__networl_0_1_AskP_0" + "P-poll__networl_0_1_AskP_1" + "P-poll__networl_0_1_AskP_2" + "P-poll__networl_0_1_AskP_3" + "P-poll__networl_0_1_AskP_4" + "P-poll__networl_0_1_AskP_5" + "P-poll__networl_0_1_AskP_6" + "P-poll__networl_0_1_AskP_7" + "P-poll__networl_0_1_AskP_8" + "P-poll__networl_0_1_AnsP_0" + "P-poll__networl_0_1_AnsP_1" + "P-poll__networl_0_1_AnsP_2" + "P-poll__networl_0_1_AnsP_3" + "P-poll__networl_0_1_AnsP_4" + "P-poll__networl_0_1_AnsP_5" + "P-poll__networl_0_1_AnsP_6" + "P-poll__networl_0_1_AnsP_7" + "P-poll__networl_0_1_AnsP_8" + "P-poll__networl_0_1_RI_0" + "P-poll__networl_0_1_RI_1" + "P-poll__networl_0_1_RI_2" + "P-poll__networl_0_1_RI_3" + "P-poll__networl_0_1_RI_4" + "P-poll__networl_0_1_RI_5" + "P-poll__networl_0_1_RI_6" + "P-poll__networl_0_1_RI_7" + "P-poll__networl_0_1_RI_8" + "P-poll__networl_0_1_AI_0" + "P-poll__networl_0_1_AI_1" + "P-poll__networl_0_1_AI_2" + "P-poll__networl_0_1_AI_3" + "P-poll__networl_0_1_AI_4" + "P-poll__networl_0_1_AI_5" + "P-poll__networl_0_1_AI_6" + "P-poll__networl_0_1_AI_7" + "P-poll__networl_0_1_AI_8" + "P-poll__networl_0_1_AnnP_0" + "P-poll__networl_0_1_AnnP_1" + "P-poll__networl_0_1_AnnP_2" + "P-poll__networl_0_1_AnnP_3" + "P-poll__networl_0_1_AnnP_4" + "P-poll__networl_0_1_AnnP_5" + "P-poll__networl_0_1_AnnP_6" + "P-poll__networl_0_1_AnnP_7" + "P-poll__networl_0_1_AnnP_8" + "P-poll__networl_0_1_RP_0" + "P-poll__networl_0_1_RP_1" + "P-poll__networl_0_1_RP_2" + "P-poll__networl_0_1_RP_3" + "P-poll__networl_0_1_RP_4" + "P-poll__networl_0_1_RP_5" + "P-poll__networl_0_1_RP_6" + "P-poll__networl_0_1_RP_7" + "P-poll__networl_0_1_RP_8" + "P-poll__networl_0_2_AskP_0" + "P-poll__networl_0_2_AskP_1" + "P-poll__networl_0_2_AskP_2" + "P-poll__networl_0_2_AskP_3" + "P-poll__networl_0_2_AskP_4" + "P-poll__networl_0_2_AskP_5" + "P-poll__networl_0_2_AskP_6" + "P-poll__networl_0_2_AskP_7" + "P-poll__networl_0_2_AskP_8" + "P-poll__networl_0_2_AnsP_0" + "P-poll__networl_0_2_AnsP_1" + "P-poll__networl_0_2_AnsP_2" + "P-poll__networl_0_2_AnsP_3" + "P-poll__networl_0_2_AnsP_4" + "P-poll__networl_0_2_AnsP_5" + "P-poll__networl_0_2_AnsP_6" + "P-poll__networl_0_2_AnsP_7" + "P-poll__networl_0_2_AnsP_8" + "P-poll__networl_0_2_RI_0" + "P-poll__networl_0_2_RI_1" + "P-poll__networl_0_2_RI_2" + "P-poll__networl_0_2_RI_3" + "P-poll__networl_0_2_RI_4" + "P-poll__networl_0_2_RI_5" + "P-poll__networl_0_2_RI_6" + "P-poll__networl_0_2_RI_7" + "P-poll__networl_0_2_RI_8" + "P-poll__networl_0_2_AI_0" + "P-poll__networl_0_2_AI_1" + "P-poll__networl_0_2_AI_2" + "P-poll__networl_0_2_AI_3" + "P-poll__networl_0_2_AI_4" + "P-poll__networl_0_2_AI_5" + "P-poll__networl_0_2_AI_6" + "P-poll__networl_0_2_AI_7" + "P-poll__networl_0_2_AI_8" + "P-poll__networl_0_2_AnnP_0" + "P-poll__networl_0_2_AnnP_1" + "P-poll__networl_0_2_AnnP_2" + "P-poll__networl_0_2_AnnP_3" + "P-poll__networl_0_2_AnnP_4" + "P-poll__networl_0_2_AnnP_5" + "P-poll__networl_0_2_AnnP_6" + "P-poll__networl_0_2_AnnP_7" + "P-poll__networl_0_2_AnnP_8" + "P-poll__networl_0_2_RP_0" + "P-poll__networl_0_2_RP_1" + "P-poll__networl_0_2_RP_2" + "P-poll__networl_0_2_RP_3" + "P-poll__networl_0_2_RP_4" + "P-poll__networl_0_2_RP_5" + "P-poll__networl_0_2_RP_6" + "P-poll__networl_0_2_RP_7" + "P-poll__networl_0_2_RP_8" + "P-poll__networl_0_3_AskP_0" + "P-poll__networl_0_3_AskP_1" + "P-poll__networl_0_3_AskP_2" + "P-poll__networl_0_3_AskP_3" + "P-poll__networl_0_3_AskP_4" + "P-poll__networl_0_3_AskP_5" + "P-poll__networl_0_3_AskP_6" + "P-poll__networl_0_3_AskP_7" + "P-poll__networl_0_3_AskP_8" + "P-poll__networl_0_3_AnsP_0" + "P-poll__networl_0_3_AnsP_1" + "P-poll__networl_0_3_AnsP_2" + "P-poll__networl_0_3_AnsP_3" + "P-poll__networl_0_3_AnsP_4" + "P-poll__networl_0_3_AnsP_5" + "P-poll__networl_0_3_AnsP_6" + "P-poll__networl_0_3_AnsP_7" + "P-poll__networl_0_3_AnsP_8" + "P-poll__networl_0_3_RI_0" + "P-poll__networl_0_3_RI_1" + "P-poll__networl_0_3_RI_2" + "P-poll__networl_0_3_RI_3" + "P-poll__networl_0_3_RI_4" + "P-poll__networl_0_3_RI_5" + "P-poll__networl_0_3_RI_6" + "P-poll__networl_0_3_RI_7" + "P-poll__networl_0_3_RI_8" + "P-poll__networl_0_3_AI_0" + "P-poll__networl_0_3_AI_1" + "P-poll__networl_0_3_AI_2" + "P-poll__networl_0_3_AI_3" + "P-poll__networl_0_3_AI_4" + "P-poll__networl_0_3_AI_5" + "P-poll__networl_0_3_AI_6" + "P-poll__networl_0_3_AI_7" + "P-poll__networl_0_3_AI_8" + "P-poll__networl_0_3_AnnP_0" + "P-poll__networl_0_3_AnnP_1" + "P-poll__networl_0_3_AnnP_2" + "P-poll__networl_0_3_AnnP_3" + "P-poll__networl_0_3_AnnP_4" + "P-poll__networl_0_3_AnnP_5" + "P-poll__networl_0_3_AnnP_6" + "P-poll__networl_0_3_AnnP_7" + "P-poll__networl_0_3_AnnP_8" + "P-poll__networl_0_3_RP_0" + "P-poll__networl_0_3_RP_1" + "P-poll__networl_0_3_RP_2" + "P-poll__networl_0_3_RP_3" + "P-poll__networl_0_3_RP_4" + "P-poll__networl_0_3_RP_5" + "P-poll__networl_0_3_RP_6" + "P-poll__networl_0_3_RP_7" + "P-poll__networl_0_3_RP_8" + "P-poll__networl_0_4_AskP_0" + "P-poll__networl_0_4_AskP_1" + "P-poll__networl_0_4_AskP_2" + "P-poll__networl_0_4_AskP_3" + "P-poll__networl_0_4_AskP_4" + "P-poll__networl_0_4_AskP_5" + "P-poll__networl_0_4_AskP_6" + "P-poll__networl_0_4_AskP_7" + "P-poll__networl_0_4_AskP_8" + "P-poll__networl_0_4_AnsP_0" + "P-poll__networl_0_4_AnsP_1" + "P-poll__networl_0_4_AnsP_2" + "P-poll__networl_0_4_AnsP_3" + "P-poll__networl_0_4_AnsP_4" + "P-poll__networl_0_4_AnsP_5" + "P-poll__networl_0_4_AnsP_6" + "P-poll__networl_0_4_AnsP_7" + "P-poll__networl_0_4_AnsP_8" + "P-poll__networl_0_4_RI_0" + "P-poll__networl_0_4_RI_1" + "P-poll__networl_0_4_RI_2" + "P-poll__networl_0_4_RI_3" + "P-poll__networl_0_4_RI_4" + "P-poll__networl_0_4_RI_5" + "P-poll__networl_0_4_RI_6" + "P-poll__networl_0_4_RI_7" + "P-poll__networl_0_4_RI_8" + "P-poll__networl_0_4_AI_0" + "P-poll__networl_0_4_AI_1" + "P-poll__networl_0_4_AI_2" + "P-poll__networl_0_4_AI_3" + "P-poll__networl_0_4_AI_4" + "P-poll__networl_0_4_AI_5" + "P-poll__networl_0_4_AI_6" + "P-poll__networl_0_4_AI_7" + "P-poll__networl_0_4_AI_8" + "P-poll__networl_0_4_AnnP_0" + "P-poll__networl_0_4_AnnP_1" + "P-poll__networl_0_4_AnnP_2" + "P-poll__networl_0_4_AnnP_3" + "P-poll__networl_0_4_AnnP_4" + "P-poll__networl_0_4_AnnP_5" + "P-poll__networl_0_4_AnnP_6" + "P-poll__networl_0_4_AnnP_7" + "P-poll__networl_0_4_AnnP_8" + "P-poll__networl_0_4_RP_0" + "P-poll__networl_0_4_RP_1" + "P-poll__networl_0_4_RP_2" + "P-poll__networl_0_4_RP_3" + "P-poll__networl_0_4_RP_4" + "P-poll__networl_0_4_RP_5" + "P-poll__networl_0_4_RP_6" + "P-poll__networl_0_4_RP_7" + "P-poll__networl_0_4_RP_8" + "P-poll__networl_0_5_AskP_0" + "P-poll__networl_0_5_AskP_1" + "P-poll__networl_0_5_AskP_2" + "P-poll__networl_0_5_AskP_3" + "P-poll__networl_0_5_AskP_4" + "P-poll__networl_0_5_AskP_5" + "P-poll__networl_0_5_AskP_6" + "P-poll__networl_0_5_AskP_7" + "P-poll__networl_0_5_AskP_8" + "P-poll__networl_0_5_AnsP_0" + "P-poll__networl_0_5_AnsP_1" + "P-poll__networl_0_5_AnsP_2" + "P-poll__networl_0_5_AnsP_3" + "P-poll__networl_0_5_AnsP_4" + "P-poll__networl_0_5_AnsP_5" + "P-poll__networl_0_5_AnsP_6" + "P-poll__networl_0_5_AnsP_7" + "P-poll__networl_0_5_AnsP_8" + "P-poll__networl_0_5_RI_0" + "P-poll__networl_0_5_RI_1" + "P-poll__networl_0_5_RI_2" + "P-poll__networl_0_5_RI_3" + "P-poll__networl_0_5_RI_4" + "P-poll__networl_0_5_RI_5" + "P-poll__networl_0_5_RI_6" + "P-poll__networl_0_5_RI_7" + "P-poll__networl_0_5_RI_8" + "P-poll__networl_0_5_AI_0" + "P-poll__networl_0_5_AI_1" + "P-poll__networl_0_5_AI_2" + "P-poll__networl_0_5_AI_3" + "P-poll__networl_0_5_AI_4" + "P-poll__networl_0_5_AI_5" + "P-poll__networl_0_5_AI_6" + "P-poll__networl_0_5_AI_7" + "P-poll__networl_0_5_AI_8" + "P-poll__networl_0_5_AnnP_0" + "P-poll__networl_0_5_AnnP_1" + "P-poll__networl_0_5_AnnP_2" + "P-poll__networl_0_5_AnnP_3" + "P-poll__networl_0_5_AnnP_4" + "P-poll__networl_0_5_AnnP_5" + "P-poll__networl_0_5_AnnP_6" + "P-poll__networl_0_5_AnnP_7" + "P-poll__networl_0_5_AnnP_8" + "P-poll__networl_0_5_RP_0" + "P-poll__networl_0_5_RP_1" + "P-poll__networl_0_5_RP_2" + "P-poll__networl_0_5_RP_3" + "P-poll__networl_0_5_RP_4" + "P-poll__networl_0_5_RP_5" + "P-poll__networl_0_5_RP_6" + "P-poll__networl_0_5_RP_7" + "P-poll__networl_0_5_RP_8" + "P-poll__networl_0_6_AskP_0" + "P-poll__networl_0_6_AskP_1" + "P-poll__networl_0_6_AskP_2" + "P-poll__networl_0_6_AskP_3" + "P-poll__networl_0_6_AskP_4" + "P-poll__networl_0_6_AskP_5" + "P-poll__networl_0_6_AskP_6" + "P-poll__networl_0_6_AskP_7" + "P-poll__networl_0_6_AskP_8" + "P-poll__networl_0_6_AnsP_0" + "P-poll__networl_0_6_AnsP_1" + "P-poll__networl_0_6_AnsP_2" + "P-poll__networl_0_6_AnsP_3" + "P-poll__networl_0_6_AnsP_4" + "P-poll__networl_0_6_AnsP_5" + "P-poll__networl_0_6_AnsP_6" + "P-poll__networl_0_6_AnsP_7" + "P-poll__networl_0_6_AnsP_8" + "P-poll__networl_0_6_RI_0" + "P-poll__networl_0_6_RI_1" + "P-poll__networl_0_6_RI_2" + "P-poll__networl_0_6_RI_3" + "P-poll__networl_0_6_RI_4" + "P-poll__networl_0_6_RI_5" + "P-poll__networl_0_6_RI_6" + "P-poll__networl_0_6_RI_7" + "P-poll__networl_0_6_RI_8" + "P-poll__networl_0_6_AI_0" + "P-poll__networl_0_6_AI_1" + "P-poll__networl_0_6_AI_2" + "P-poll__networl_0_6_AI_3" + "P-poll__networl_0_6_AI_4" + "P-poll__networl_0_6_AI_5" + "P-poll__networl_0_6_AI_6" + "P-poll__networl_0_6_AI_7" + "P-poll__networl_0_6_AI_8" + "P-poll__networl_0_6_AnnP_0" + "P-poll__networl_0_6_AnnP_1" + "P-poll__networl_0_6_AnnP_2" + "P-poll__networl_0_6_AnnP_3" + "P-poll__networl_0_6_AnnP_4" + "P-poll__networl_0_6_AnnP_5" + "P-poll__networl_0_6_AnnP_6" + "P-poll__networl_0_6_AnnP_7" + "P-poll__networl_0_6_AnnP_8" + "P-poll__networl_0_6_RP_0" + "P-poll__networl_0_6_RP_1" + "P-poll__networl_0_6_RP_2" + "P-poll__networl_0_6_RP_3" + "P-poll__networl_0_6_RP_4" + "P-poll__networl_0_6_RP_5" + "P-poll__networl_0_6_RP_6" + "P-poll__networl_0_6_RP_7" + "P-poll__networl_0_6_RP_8" + "P-poll__networl_0_7_AskP_0" + "P-poll__networl_0_7_AskP_1" + "P-poll__networl_0_7_AskP_2" + "P-poll__networl_0_7_AskP_3" + "P-poll__networl_0_7_AskP_4" + "P-poll__networl_0_7_AskP_5" + "P-poll__networl_0_7_AskP_6" + "P-poll__networl_0_7_AskP_7" + "P-poll__networl_0_7_AskP_8" + "P-poll__networl_0_7_AnsP_0" + "P-poll__networl_0_7_AnsP_1" + "P-poll__networl_0_7_AnsP_2" + "P-poll__networl_0_7_AnsP_3" + "P-poll__networl_0_7_AnsP_4" + "P-poll__networl_0_7_AnsP_5" + "P-poll__networl_0_7_AnsP_6" + "P-poll__networl_0_7_AnsP_7" + "P-poll__networl_0_7_AnsP_8" + "P-poll__networl_0_7_RI_0" + "P-poll__networl_0_7_RI_1" + "P-poll__networl_0_7_RI_2" + "P-poll__networl_0_7_RI_3" + "P-poll__networl_0_7_RI_4" + "P-poll__networl_0_7_RI_5" + "P-poll__networl_0_7_RI_6" + "P-poll__networl_0_7_RI_7" + "P-poll__networl_0_7_RI_8" + "P-poll__networl_0_7_AI_0" + "P-poll__networl_0_7_AI_1" + "P-poll__networl_0_7_AI_2" + "P-poll__networl_0_7_AI_3" + "P-poll__networl_0_7_AI_4" + "P-poll__networl_0_7_AI_5" + "P-poll__networl_0_7_AI_6" + "P-poll__networl_0_7_AI_7" + "P-poll__networl_0_7_AI_8" + "P-poll__networl_0_7_AnnP_0" + "P-poll__networl_0_7_AnnP_1" + "P-poll__networl_0_7_AnnP_2" + "P-poll__networl_0_7_AnnP_3" + "P-poll__networl_0_7_AnnP_4" + "P-poll__networl_0_7_AnnP_5" + "P-poll__networl_0_7_AnnP_6" + "P-poll__networl_0_7_AnnP_7" + "P-poll__networl_0_7_AnnP_8" + "P-poll__networl_0_7_RP_0" + "P-poll__networl_0_7_RP_1" + "P-poll__networl_0_7_RP_2" + "P-poll__networl_0_7_RP_3" + "P-poll__networl_0_7_RP_4" + "P-poll__networl_0_7_RP_5" + "P-poll__networl_0_7_RP_6" + "P-poll__networl_0_7_RP_7" + "P-poll__networl_0_7_RP_8" + "P-poll__networl_0_8_AskP_0" + "P-poll__networl_0_8_AskP_1" + "P-poll__networl_0_8_AskP_2" + "P-poll__networl_0_8_AskP_3" + "P-poll__networl_0_8_AskP_4" + "P-poll__networl_0_8_AskP_5" + "P-poll__networl_0_8_AskP_6" + "P-poll__networl_0_8_AskP_7" + "P-poll__networl_0_8_AskP_8" + "P-poll__networl_0_8_AnsP_0" + "P-poll__networl_0_8_AnsP_1" + "P-poll__networl_0_8_AnsP_2" + "P-poll__networl_0_8_AnsP_3" + "P-poll__networl_0_8_AnsP_4" + "P-poll__networl_0_8_AnsP_5" + "P-poll__networl_0_8_AnsP_6" + "P-poll__networl_0_8_AnsP_7" + "P-poll__networl_0_8_AnsP_8" + "P-poll__networl_0_8_RI_0" + "P-poll__networl_0_8_RI_1" + "P-poll__networl_0_8_RI_2" + "P-poll__networl_0_8_RI_3" + "P-poll__networl_0_8_RI_4" + "P-poll__networl_0_8_RI_5" + "P-poll__networl_0_8_RI_6" + "P-poll__networl_0_8_RI_7" + "P-poll__networl_0_8_RI_8" + "P-poll__networl_0_8_AI_0" + "P-poll__networl_0_8_AI_1" + "P-poll__networl_0_8_AI_2" + "P-poll__networl_0_8_AI_3" + "P-poll__networl_0_8_AI_4" + "P-poll__networl_0_8_AI_5" + "P-poll__networl_0_8_AI_6" + "P-poll__networl_0_8_AI_7" + "P-poll__networl_0_8_AI_8" + "P-poll__networl_0_8_AnnP_0" + "P-poll__networl_0_8_AnnP_1" + "P-poll__networl_0_8_AnnP_2" + "P-poll__networl_0_8_AnnP_3" + "P-poll__networl_0_8_AnnP_4" + "P-poll__networl_0_8_AnnP_5" + "P-poll__networl_0_8_AnnP_6" + "P-poll__networl_0_8_AnnP_7" + "P-poll__networl_0_8_AnnP_8" + "P-poll__networl_0_8_RP_0" + "P-poll__networl_0_8_RP_1" + "P-poll__networl_0_8_RP_2" + "P-poll__networl_0_8_RP_3" + "P-poll__networl_0_8_RP_4" + "P-poll__networl_0_8_RP_5" + "P-poll__networl_0_8_RP_6" + "P-poll__networl_0_8_RP_7" + "P-poll__networl_0_8_RP_8" + "P-poll__networl_1_0_AskP_0" + "P-poll__networl_1_0_AskP_1" + "P-poll__networl_1_0_AskP_2" + "P-poll__networl_1_0_AskP_3" + "P-poll__networl_1_0_AskP_4" + "P-poll__networl_1_0_AskP_5" + "P-poll__networl_1_0_AskP_6" + "P-poll__networl_1_0_AskP_7" + "P-poll__networl_1_0_AskP_8" + "P-poll__networl_1_0_AnsP_0" + "P-poll__networl_1_0_AnsP_1" + "P-poll__networl_1_0_AnsP_2" + "P-poll__networl_1_0_AnsP_3" + "P-poll__networl_1_0_AnsP_4" + "P-poll__networl_1_0_AnsP_5" + "P-poll__networl_1_0_AnsP_6" + "P-poll__networl_1_0_AnsP_7" + "P-poll__networl_1_0_AnsP_8" + "P-poll__networl_1_0_RI_0" + "P-poll__networl_1_0_RI_1" + "P-poll__networl_1_0_RI_2" + "P-poll__networl_1_0_RI_3" + "P-poll__networl_1_0_RI_4" + "P-poll__networl_1_0_RI_5" + "P-poll__networl_1_0_RI_6" + "P-poll__networl_1_0_RI_7" + "P-poll__networl_1_0_RI_8" + "P-poll__networl_1_0_AI_0" + "P-poll__networl_1_0_AI_1" + "P-poll__networl_1_0_AI_2" + "P-poll__networl_1_0_AI_3" + "P-poll__networl_1_0_AI_4" + "P-poll__networl_1_0_AI_5" + "P-poll__networl_1_0_AI_6" + "P-poll__networl_1_0_AI_7" + "P-poll__networl_1_0_AI_8" + "P-poll__networl_1_0_AnnP_0" + "P-poll__networl_1_0_AnnP_1" + "P-poll__networl_1_0_AnnP_2" + "P-poll__networl_1_0_AnnP_3" + "P-poll__networl_1_0_AnnP_4" + "P-poll__networl_1_0_AnnP_5" + "P-poll__networl_1_0_AnnP_6" + "P-poll__networl_1_0_AnnP_7" + "P-poll__networl_1_0_AnnP_8" + "P-poll__networl_1_0_RP_0" + "P-poll__networl_1_0_RP_1" + "P-poll__networl_1_0_RP_2" + "P-poll__networl_1_0_RP_3" + "P-poll__networl_1_0_RP_4" + "P-poll__networl_1_0_RP_5" + "P-poll__networl_1_0_RP_6" + "P-poll__networl_1_0_RP_7" + "P-poll__networl_1_0_RP_8" + "P-poll__networl_1_1_AskP_0" + "P-poll__networl_1_1_AskP_1" + "P-poll__networl_1_1_AskP_2" + "P-poll__networl_1_1_AskP_3" + "P-poll__networl_1_1_AskP_4" + "P-poll__networl_1_1_AskP_5" + "P-poll__networl_1_1_AskP_6" + "P-poll__networl_1_1_AskP_7" + "P-poll__networl_1_1_AskP_8" + "P-poll__networl_1_1_AnsP_0" + "P-poll__networl_1_1_AnsP_1" + "P-poll__networl_1_1_AnsP_2" + "P-poll__networl_1_1_AnsP_3" + "P-poll__networl_1_1_AnsP_4" + "P-poll__networl_1_1_AnsP_5" + "P-poll__networl_1_1_AnsP_6" + "P-poll__networl_1_1_AnsP_7" + "P-poll__networl_1_1_AnsP_8" + "P-poll__networl_1_1_RI_0" + "P-poll__networl_1_1_RI_1" + "P-poll__networl_1_1_RI_2" + "P-poll__networl_1_1_RI_3" + "P-poll__networl_1_1_RI_4" + "P-poll__networl_1_1_RI_5" + "P-poll__networl_1_1_RI_6" + "P-poll__networl_1_1_RI_7" + "P-poll__networl_1_1_RI_8" + "P-poll__networl_1_1_AI_0" + "P-poll__networl_1_1_AI_1" + "P-poll__networl_1_1_AI_2" + "P-poll__networl_1_1_AI_3" + "P-poll__networl_1_1_AI_4" + "P-poll__networl_1_1_AI_5" + "P-poll__networl_1_1_AI_6" + "P-poll__networl_1_1_AI_7" + "P-poll__networl_1_1_AI_8" + "P-poll__networl_1_1_AnnP_0" + "P-poll__networl_1_1_AnnP_1" + "P-poll__networl_1_1_AnnP_2" + "P-poll__networl_1_1_AnnP_3" + "P-poll__networl_1_1_AnnP_4" + "P-poll__networl_1_1_AnnP_5" + "P-poll__networl_1_1_AnnP_6" + "P-poll__networl_1_1_AnnP_7" + "P-poll__networl_1_1_AnnP_8" + "P-poll__networl_1_1_RP_0" + "P-poll__networl_1_1_RP_1" + "P-poll__networl_1_1_RP_2" + "P-poll__networl_1_1_RP_3" + "P-poll__networl_1_1_RP_4" + "P-poll__networl_1_1_RP_5" + "P-poll__networl_1_1_RP_6" + "P-poll__networl_1_1_RP_7" + "P-poll__networl_1_1_RP_8" + "P-poll__networl_1_2_AskP_0" + "P-poll__networl_1_2_AskP_1" + "P-poll__networl_1_2_AskP_2" + "P-poll__networl_1_2_AskP_3" + "P-poll__networl_1_2_AskP_4" + "P-poll__networl_1_2_AskP_5" + "P-poll__networl_1_2_AskP_6" + "P-poll__networl_1_2_AskP_7" + "P-poll__networl_1_2_AskP_8" + "P-poll__networl_1_2_AnsP_0" + "P-poll__networl_1_2_AnsP_1" + "P-poll__networl_1_2_AnsP_2" + "P-poll__networl_1_2_AnsP_3" + "P-poll__networl_1_2_AnsP_4" + "P-poll__networl_1_2_AnsP_5" + "P-poll__networl_1_2_AnsP_6" + "P-poll__networl_1_2_AnsP_7" + "P-poll__networl_1_2_AnsP_8" + "P-poll__networl_1_2_RI_0" + "P-poll__networl_1_2_RI_1" + "P-poll__networl_1_2_RI_2" + "P-poll__networl_1_2_RI_3" + "P-poll__networl_1_2_RI_4" + "P-poll__networl_1_2_RI_5" + "P-poll__networl_1_2_RI_6" + "P-poll__networl_1_2_RI_7" + "P-poll__networl_1_2_RI_8" + "P-poll__networl_1_2_AI_0" + "P-poll__networl_1_2_AI_1" + "P-poll__networl_1_2_AI_2" + "P-poll__networl_1_2_AI_3" + "P-poll__networl_1_2_AI_4" + "P-poll__networl_1_2_AI_5" + "P-poll__networl_1_2_AI_6" + "P-poll__networl_1_2_AI_7" + "P-poll__networl_1_2_AI_8" + "P-poll__networl_1_2_AnnP_0" + "P-poll__networl_1_2_AnnP_1" + "P-poll__networl_1_2_AnnP_2" + "P-poll__networl_1_2_AnnP_3" + "P-poll__networl_1_2_AnnP_4" + "P-poll__networl_1_2_AnnP_5" + "P-poll__networl_1_2_AnnP_6" + "P-poll__networl_1_2_AnnP_7" + "P-poll__networl_1_2_AnnP_8" + "P-poll__networl_1_2_RP_0" + "P-poll__networl_1_2_RP_1" + "P-poll__networl_1_2_RP_2" + "P-poll__networl_1_2_RP_3" + "P-poll__networl_1_2_RP_4" + "P-poll__networl_1_2_RP_5" + "P-poll__networl_1_2_RP_6" + "P-poll__networl_1_2_RP_7" + "P-poll__networl_1_2_RP_8" + "P-poll__networl_1_3_AskP_0" + "P-poll__networl_1_3_AskP_1" + "P-poll__networl_1_3_AskP_2" + "P-poll__networl_1_3_AskP_3" + "P-poll__networl_1_3_AskP_4" + "P-poll__networl_1_3_AskP_5" + "P-poll__networl_1_3_AskP_6" + "P-poll__networl_1_3_AskP_7" + "P-poll__networl_1_3_AskP_8" + "P-poll__networl_1_3_AnsP_0" + "P-poll__networl_1_3_AnsP_1" + "P-poll__networl_1_3_AnsP_2" + "P-poll__networl_1_3_AnsP_3" + "P-poll__networl_1_3_AnsP_4" + "P-poll__networl_1_3_AnsP_5" + "P-poll__networl_1_3_AnsP_6" + "P-poll__networl_1_3_AnsP_7" + "P-poll__networl_1_3_AnsP_8" + "P-poll__networl_1_3_RI_0" + "P-poll__networl_1_3_RI_1" + "P-poll__networl_1_3_RI_2" + "P-poll__networl_1_3_RI_3" + "P-poll__networl_1_3_RI_4" + "P-poll__networl_1_3_RI_5" + "P-poll__networl_1_3_RI_6" + "P-poll__networl_1_3_RI_7" + "P-poll__networl_1_3_RI_8" + "P-poll__networl_1_3_AI_0" + "P-poll__networl_1_3_AI_1" + "P-poll__networl_1_3_AI_2" + "P-poll__networl_1_3_AI_3" + "P-poll__networl_1_3_AI_4" + "P-poll__networl_1_3_AI_5" + "P-poll__networl_1_3_AI_6" + "P-poll__networl_1_3_AI_7" + "P-poll__networl_1_3_AI_8" + "P-poll__networl_1_3_AnnP_0" + "P-poll__networl_1_3_AnnP_1" + "P-poll__networl_1_3_AnnP_2" + "P-poll__networl_1_3_AnnP_3" + "P-poll__networl_1_3_AnnP_4" + "P-poll__networl_1_3_AnnP_5" + "P-poll__networl_1_3_AnnP_6" + "P-poll__networl_1_3_AnnP_7" + "P-poll__networl_1_3_AnnP_8" + "P-poll__networl_1_3_RP_0" + "P-poll__networl_1_3_RP_1" + "P-poll__networl_1_3_RP_2" + "P-poll__networl_1_3_RP_3" + "P-poll__networl_1_3_RP_4" + "P-poll__networl_1_3_RP_5" + "P-poll__networl_1_3_RP_6" + "P-poll__networl_1_3_RP_7" + "P-poll__networl_1_3_RP_8" + "P-poll__networl_1_4_AskP_0" + "P-poll__networl_1_4_AskP_1" + "P-poll__networl_1_4_AskP_2" + "P-poll__networl_1_4_AskP_3" + "P-poll__networl_1_4_AskP_4" + "P-poll__networl_1_4_AskP_5" + "P-poll__networl_1_4_AskP_6" + "P-poll__networl_1_4_AskP_7" + "P-poll__networl_1_4_AskP_8" + "P-poll__networl_1_4_AnsP_0" + "P-poll__networl_1_4_AnsP_1" + "P-poll__networl_1_4_AnsP_2" + "P-poll__networl_1_4_AnsP_3" + "P-poll__networl_1_4_AnsP_4" + "P-poll__networl_1_4_AnsP_5" + "P-poll__networl_1_4_AnsP_6" + "P-poll__networl_1_4_AnsP_7" + "P-poll__networl_1_4_AnsP_8" + "P-poll__networl_1_4_RI_0" + "P-poll__networl_1_4_RI_1" + "P-poll__networl_1_4_RI_2" + "P-poll__networl_1_4_RI_3" + "P-poll__networl_1_4_RI_4" + "P-poll__networl_1_4_RI_5" + "P-poll__networl_1_4_RI_6" + "P-poll__networl_1_4_RI_7" + "P-poll__networl_1_4_RI_8" + "P-poll__networl_1_4_AI_0" + "P-poll__networl_1_4_AI_1" + "P-poll__networl_1_4_AI_2" + "P-poll__networl_1_4_AI_3" + "P-poll__networl_1_4_AI_4" + "P-poll__networl_1_4_AI_5" + "P-poll__networl_1_4_AI_6" + "P-poll__networl_1_4_AI_7" + "P-poll__networl_1_4_AI_8" + "P-poll__networl_1_4_AnnP_0" + "P-poll__networl_1_4_AnnP_1" + "P-poll__networl_1_4_AnnP_2" + "P-poll__networl_1_4_AnnP_3" + "P-poll__networl_1_4_AnnP_4" + "P-poll__networl_1_4_AnnP_5" + "P-poll__networl_1_4_AnnP_6" + "P-poll__networl_1_4_AnnP_7" + "P-poll__networl_1_4_AnnP_8" + "P-poll__networl_1_4_RP_0" + "P-poll__networl_1_4_RP_1" + "P-poll__networl_1_4_RP_2" + "P-poll__networl_1_4_RP_3" + "P-poll__networl_1_4_RP_4" + "P-poll__networl_1_4_RP_5" + "P-poll__networl_1_4_RP_6" + "P-poll__networl_1_4_RP_7" + "P-poll__networl_1_4_RP_8" + "P-poll__networl_1_5_AskP_0" + "P-poll__networl_1_5_AskP_1" + "P-poll__networl_1_5_AskP_2" + "P-poll__networl_1_5_AskP_3" + "P-poll__networl_1_5_AskP_4" + "P-poll__networl_1_5_AskP_5" + "P-poll__networl_1_5_AskP_6" + "P-poll__networl_1_5_AskP_7" + "P-poll__networl_1_5_AskP_8" + "P-poll__networl_1_5_AnsP_0" + "P-poll__networl_1_5_AnsP_1" + "P-poll__networl_1_5_AnsP_2" + "P-poll__networl_1_5_AnsP_3" + "P-poll__networl_1_5_AnsP_4" + "P-poll__networl_1_5_AnsP_5" + "P-poll__networl_1_5_AnsP_6" + "P-poll__networl_1_5_AnsP_7" + "P-poll__networl_1_5_AnsP_8" + "P-poll__networl_1_5_RI_0" + "P-poll__networl_1_5_RI_1" + "P-poll__networl_1_5_RI_2" + "P-poll__networl_1_5_RI_3" + "P-poll__networl_1_5_RI_4" + "P-poll__networl_1_5_RI_5" + "P-poll__networl_1_5_RI_6" + "P-poll__networl_1_5_RI_7" + "P-poll__networl_1_5_RI_8" + "P-poll__networl_1_5_AI_0" + "P-poll__networl_1_5_AI_1" + "P-poll__networl_1_5_AI_2" + "P-poll__networl_1_5_AI_3" + "P-poll__networl_1_5_AI_4" + "P-poll__networl_1_5_AI_5" + "P-poll__networl_1_5_AI_6" + "P-poll__networl_1_5_AI_7" + "P-poll__networl_1_5_AI_8" + "P-poll__networl_1_5_AnnP_0" + "P-poll__networl_1_5_AnnP_1" + "P-poll__networl_1_5_AnnP_2" + "P-poll__networl_1_5_AnnP_3" + "P-poll__networl_1_5_AnnP_4" + "P-poll__networl_1_5_AnnP_5" + "P-poll__networl_1_5_AnnP_6" + "P-poll__networl_1_5_AnnP_7" + "P-poll__networl_1_5_AnnP_8" + "P-poll__networl_1_5_RP_0" + "P-poll__networl_1_5_RP_1" + "P-poll__networl_1_5_RP_2" + "P-poll__networl_1_5_RP_3" + "P-poll__networl_1_5_RP_4" + "P-poll__networl_1_5_RP_5" + "P-poll__networl_1_5_RP_6" + "P-poll__networl_1_5_RP_7" + "P-poll__networl_1_5_RP_8" + "P-poll__networl_1_6_AskP_0" + "P-poll__networl_1_6_AskP_1" + "P-poll__networl_1_6_AskP_2" + "P-poll__networl_1_6_AskP_3" + "P-poll__networl_1_6_AskP_4" + "P-poll__networl_1_6_AskP_5" + "P-poll__networl_1_6_AskP_6" + "P-poll__networl_1_6_AskP_7" + "P-poll__networl_1_6_AskP_8" + "P-poll__networl_1_6_AnsP_0" + "P-poll__networl_1_6_AnsP_1" + "P-poll__networl_1_6_AnsP_2" + "P-poll__networl_1_6_AnsP_3" + "P-poll__networl_1_6_AnsP_4" + "P-poll__networl_1_6_AnsP_5" + "P-poll__networl_1_6_AnsP_6" + "P-poll__networl_1_6_AnsP_7" + "P-poll__networl_1_6_AnsP_8" + "P-poll__networl_1_6_RI_0" + "P-poll__networl_1_6_RI_1" + "P-poll__networl_1_6_RI_2" + "P-poll__networl_1_6_RI_3" + "P-poll__networl_1_6_RI_4" + "P-poll__networl_1_6_RI_5" + "P-poll__networl_1_6_RI_6" + "P-poll__networl_1_6_RI_7" + "P-poll__networl_1_6_RI_8" + "P-poll__networl_1_6_AI_0" + "P-poll__networl_1_6_AI_1" + "P-poll__networl_1_6_AI_2" + "P-poll__networl_1_6_AI_3" + "P-poll__networl_1_6_AI_4" + "P-poll__networl_1_6_AI_5" + "P-poll__networl_1_6_AI_6" + "P-poll__networl_1_6_AI_7" + "P-poll__networl_1_6_AI_8" + "P-poll__networl_1_6_AnnP_0" + "P-poll__networl_1_6_AnnP_1" + "P-poll__networl_1_6_AnnP_2" + "P-poll__networl_1_6_AnnP_3" + "P-poll__networl_1_6_AnnP_4" + "P-poll__networl_1_6_AnnP_5" + "P-poll__networl_1_6_AnnP_6" + "P-poll__networl_1_6_AnnP_7" + "P-poll__networl_1_6_AnnP_8" + "P-poll__networl_1_6_RP_0" + "P-poll__networl_1_6_RP_1" + "P-poll__networl_1_6_RP_2" + "P-poll__networl_1_6_RP_3" + "P-poll__networl_1_6_RP_4" + "P-poll__networl_1_6_RP_5" + "P-poll__networl_1_6_RP_6" + "P-poll__networl_1_6_RP_7" + "P-poll__networl_1_6_RP_8" + "P-poll__networl_1_7_AskP_0" + "P-poll__networl_1_7_AskP_1" + "P-poll__networl_1_7_AskP_2" + "P-poll__networl_1_7_AskP_3" + "P-poll__networl_1_7_AskP_4" + "P-poll__networl_1_7_AskP_5" + "P-poll__networl_1_7_AskP_6" + "P-poll__networl_1_7_AskP_7" + "P-poll__networl_1_7_AskP_8" + "P-poll__networl_1_7_AnsP_0" + "P-poll__networl_1_7_AnsP_1" + "P-poll__networl_1_7_AnsP_2" + "P-poll__networl_1_7_AnsP_3" + "P-poll__networl_1_7_AnsP_4" + "P-poll__networl_1_7_AnsP_5" + "P-poll__networl_1_7_AnsP_6" + "P-poll__networl_1_7_AnsP_7" + "P-poll__networl_1_7_AnsP_8" + "P-poll__networl_1_7_RI_0" + "P-poll__networl_1_7_RI_1" + "P-poll__networl_1_7_RI_2" + "P-poll__networl_1_7_RI_3" + "P-poll__networl_1_7_RI_4" + "P-poll__networl_1_7_RI_5" + "P-poll__networl_1_7_RI_6" + "P-poll__networl_1_7_RI_7" + "P-poll__networl_1_7_RI_8" + "P-poll__networl_1_7_AI_0" + "P-poll__networl_1_7_AI_1" + "P-poll__networl_1_7_AI_2" + "P-poll__networl_1_7_AI_3" + "P-poll__networl_1_7_AI_4" + "P-poll__networl_1_7_AI_5" + "P-poll__networl_1_7_AI_6" + "P-poll__networl_1_7_AI_7" + "P-poll__networl_1_7_AI_8" + "P-poll__networl_1_7_AnnP_0" + "P-poll__networl_1_7_AnnP_1" + "P-poll__networl_1_7_AnnP_2" + "P-poll__networl_1_7_AnnP_3" + "P-poll__networl_1_7_AnnP_4" + "P-poll__networl_1_7_AnnP_5" + "P-poll__networl_1_7_AnnP_6" + "P-poll__networl_1_7_AnnP_7" + "P-poll__networl_1_7_AnnP_8" + "P-poll__networl_1_7_RP_0" + "P-poll__networl_1_7_RP_1" + "P-poll__networl_1_7_RP_2" + "P-poll__networl_1_7_RP_3" + "P-poll__networl_1_7_RP_4" + "P-poll__networl_1_7_RP_5" + "P-poll__networl_1_7_RP_6" + "P-poll__networl_1_7_RP_7" + "P-poll__networl_1_7_RP_8" + "P-poll__networl_1_8_AskP_0" + "P-poll__networl_1_8_AskP_1" + "P-poll__networl_1_8_AskP_2" + "P-poll__networl_1_8_AskP_3" + "P-poll__networl_1_8_AskP_4" + "P-poll__networl_1_8_AskP_5" + "P-poll__networl_1_8_AskP_6" + "P-poll__networl_1_8_AskP_7" + "P-poll__networl_1_8_AskP_8" + "P-poll__networl_1_8_AnsP_0" + "P-poll__networl_1_8_AnsP_1" + "P-poll__networl_1_8_AnsP_2" + "P-poll__networl_1_8_AnsP_3" + "P-poll__networl_1_8_AnsP_4" + "P-poll__networl_1_8_AnsP_5" + "P-poll__networl_1_8_AnsP_6" + "P-poll__networl_1_8_AnsP_7" + "P-poll__networl_1_8_AnsP_8" + "P-poll__networl_1_8_RI_0" + "P-poll__networl_1_8_RI_1" + "P-poll__networl_1_8_RI_2" + "P-poll__networl_1_8_RI_3" + "P-poll__networl_1_8_RI_4" + "P-poll__networl_1_8_RI_5" + "P-poll__networl_1_8_RI_6" + "P-poll__networl_1_8_RI_7" + "P-poll__networl_1_8_RI_8" + "P-poll__networl_1_8_AI_0" + "P-poll__networl_1_8_AI_1" + "P-poll__networl_1_8_AI_2" + "P-poll__networl_1_8_AI_3" + "P-poll__networl_1_8_AI_4" + "P-poll__networl_1_8_AI_5" + "P-poll__networl_1_8_AI_6" + "P-poll__networl_1_8_AI_7" + "P-poll__networl_1_8_AI_8" + "P-poll__networl_1_8_AnnP_0" + "P-poll__networl_1_8_AnnP_1" + "P-poll__networl_1_8_AnnP_2" + "P-poll__networl_1_8_AnnP_3" + "P-poll__networl_1_8_AnnP_4" + "P-poll__networl_1_8_AnnP_5" + "P-poll__networl_1_8_AnnP_6" + "P-poll__networl_1_8_AnnP_7" + "P-poll__networl_1_8_AnnP_8" + "P-poll__networl_1_8_RP_0" + "P-poll__networl_1_8_RP_1" + "P-poll__networl_1_8_RP_2" + "P-poll__networl_1_8_RP_3" + "P-poll__networl_1_8_RP_4" + "P-poll__networl_1_8_RP_5" + "P-poll__networl_1_8_RP_6" + "P-poll__networl_1_8_RP_7" + "P-poll__networl_1_8_RP_8" + "P-poll__networl_2_0_AskP_0" + "P-poll__networl_2_0_AskP_1" + "P-poll__networl_2_0_AskP_2" + "P-poll__networl_2_0_AskP_3" + "P-poll__networl_2_0_AskP_4" + "P-poll__networl_2_0_AskP_5" + "P-poll__networl_2_0_AskP_6" + "P-poll__networl_2_0_AskP_7" + "P-poll__networl_2_0_AskP_8" + "P-poll__networl_2_0_AnsP_0" + "P-poll__networl_2_0_AnsP_1" + "P-poll__networl_2_0_AnsP_2" + "P-poll__networl_2_0_AnsP_3" + "P-poll__networl_2_0_AnsP_4" + "P-poll__networl_2_0_AnsP_5" + "P-poll__networl_2_0_AnsP_6" + "P-poll__networl_2_0_AnsP_7" + "P-poll__networl_2_0_AnsP_8" + "P-poll__networl_2_0_RI_0" + "P-poll__networl_2_0_RI_1" + "P-poll__networl_2_0_RI_2" + "P-poll__networl_2_0_RI_3" + "P-poll__networl_2_0_RI_4" + "P-poll__networl_2_0_RI_5" + "P-poll__networl_2_0_RI_6" + "P-poll__networl_2_0_RI_7" + "P-poll__networl_2_0_RI_8" + "P-poll__networl_2_0_AI_0" + "P-poll__networl_2_0_AI_1" + "P-poll__networl_2_0_AI_2" + "P-poll__networl_2_0_AI_3" + "P-poll__networl_2_0_AI_4" + "P-poll__networl_2_0_AI_5" + "P-poll__networl_2_0_AI_6" + "P-poll__networl_2_0_AI_7" + "P-poll__networl_2_0_AI_8" + "P-poll__networl_2_0_AnnP_0" + "P-poll__networl_2_0_AnnP_1" + "P-poll__networl_2_0_AnnP_2" + "P-poll__networl_2_0_AnnP_3" + "P-poll__networl_2_0_AnnP_4" + "P-poll__networl_2_0_AnnP_5" + "P-poll__networl_2_0_AnnP_6" + "P-poll__networl_2_0_AnnP_7" + "P-poll__networl_2_0_AnnP_8" + "P-poll__networl_2_0_RP_0" + "P-poll__networl_2_0_RP_1" + "P-poll__networl_2_0_RP_2" + "P-poll__networl_2_0_RP_3" + "P-poll__networl_2_0_RP_4" + "P-poll__networl_2_0_RP_5" + "P-poll__networl_2_0_RP_6" + "P-poll__networl_2_0_RP_7" + "P-poll__networl_2_0_RP_8" + "P-poll__networl_2_1_AskP_0" + "P-poll__networl_2_1_AskP_1" + "P-poll__networl_2_1_AskP_2" + "P-poll__networl_2_1_AskP_3" + "P-poll__networl_2_1_AskP_4" + "P-poll__networl_2_1_AskP_5" + "P-poll__networl_2_1_AskP_6" + "P-poll__networl_2_1_AskP_7" + "P-poll__networl_2_1_AskP_8" + "P-poll__networl_2_1_AnsP_0" + "P-poll__networl_2_1_AnsP_1" + "P-poll__networl_2_1_AnsP_2" + "P-poll__networl_2_1_AnsP_3" + "P-poll__networl_2_1_AnsP_4" + "P-poll__networl_2_1_AnsP_5" + "P-poll__networl_2_1_AnsP_6" + "P-poll__networl_2_1_AnsP_7" + "P-poll__networl_2_1_AnsP_8" + "P-poll__networl_2_1_RI_0" + "P-poll__networl_2_1_RI_1" + "P-poll__networl_2_1_RI_2" + "P-poll__networl_2_1_RI_3" + "P-poll__networl_2_1_RI_4" + "P-poll__networl_2_1_RI_5" + "P-poll__networl_2_1_RI_6" + "P-poll__networl_2_1_RI_7" + "P-poll__networl_2_1_RI_8" + "P-poll__networl_2_1_AI_0" + "P-poll__networl_2_1_AI_1" + "P-poll__networl_2_1_AI_2" + "P-poll__networl_2_1_AI_3" + "P-poll__networl_2_1_AI_4" + "P-poll__networl_2_1_AI_5" + "P-poll__networl_2_1_AI_6" + "P-poll__networl_2_1_AI_7" + "P-poll__networl_2_1_AI_8" + "P-poll__networl_2_1_AnnP_0" + "P-poll__networl_2_1_AnnP_1" + "P-poll__networl_2_1_AnnP_2" + "P-poll__networl_2_1_AnnP_3" + "P-poll__networl_2_1_AnnP_4" + "P-poll__networl_2_1_AnnP_5" + "P-poll__networl_2_1_AnnP_6" + "P-poll__networl_2_1_AnnP_7" + "P-poll__networl_2_1_AnnP_8" + "P-poll__networl_2_1_RP_0" + "P-poll__networl_2_1_RP_1" + "P-poll__networl_2_1_RP_2" + "P-poll__networl_2_1_RP_3" + "P-poll__networl_2_1_RP_4" + "P-poll__networl_2_1_RP_5" + "P-poll__networl_2_1_RP_6" + "P-poll__networl_2_1_RP_7" + "P-poll__networl_2_1_RP_8" + "P-poll__networl_2_2_AskP_0" + "P-poll__networl_2_2_AskP_1" + "P-poll__networl_2_2_AskP_2" + "P-poll__networl_2_2_AskP_3" + "P-poll__networl_2_2_AskP_4" + "P-poll__networl_2_2_AskP_5" + "P-poll__networl_2_2_AskP_6" + "P-poll__networl_2_2_AskP_7" + "P-poll__networl_2_2_AskP_8" + "P-poll__networl_2_2_AnsP_0" + "P-poll__networl_2_2_AnsP_1" + "P-poll__networl_2_2_AnsP_2" + "P-poll__networl_2_2_AnsP_3" + "P-poll__networl_2_2_AnsP_4" + "P-poll__networl_2_2_AnsP_5" + "P-poll__networl_2_2_AnsP_6" + "P-poll__networl_2_2_AnsP_7" + "P-poll__networl_2_2_AnsP_8" + "P-poll__networl_2_2_RI_0" + "P-poll__networl_2_2_RI_1" + "P-poll__networl_2_2_RI_2" + "P-poll__networl_2_2_RI_3" + "P-poll__networl_2_2_RI_4" + "P-poll__networl_2_2_RI_5" + "P-poll__networl_2_2_RI_6" + "P-poll__networl_2_2_RI_7" + "P-poll__networl_2_2_RI_8" + "P-poll__networl_2_2_AI_0" + "P-poll__networl_2_2_AI_1" + "P-poll__networl_2_2_AI_2" + "P-poll__networl_2_2_AI_3" + "P-poll__networl_2_2_AI_4" + "P-poll__networl_2_2_AI_5" + "P-poll__networl_2_2_AI_6" + "P-poll__networl_2_2_AI_7" + "P-poll__networl_2_2_AI_8" + "P-poll__networl_2_2_AnnP_0" + "P-poll__networl_2_2_AnnP_1" + "P-poll__networl_2_2_AnnP_2" + "P-poll__networl_2_2_AnnP_3" + "P-poll__networl_2_2_AnnP_4" + "P-poll__networl_2_2_AnnP_5" + "P-poll__networl_2_2_AnnP_6" + "P-poll__networl_2_2_AnnP_7" + "P-poll__networl_2_2_AnnP_8" + "P-poll__networl_2_2_RP_0" + "P-poll__networl_2_2_RP_1" + "P-poll__networl_2_2_RP_2" + "P-poll__networl_2_2_RP_3" + "P-poll__networl_2_2_RP_4" + "P-poll__networl_2_2_RP_5" + "P-poll__networl_2_2_RP_6" + "P-poll__networl_2_2_RP_7" + "P-poll__networl_2_2_RP_8" + "P-poll__networl_2_3_AskP_0" + "P-poll__networl_2_3_AskP_1" + "P-poll__networl_2_3_AskP_2" + "P-poll__networl_2_3_AskP_3" + "P-poll__networl_2_3_AskP_4" + "P-poll__networl_2_3_AskP_5" + "P-poll__networl_2_3_AskP_6" + "P-poll__networl_2_3_AskP_7" + "P-poll__networl_2_3_AskP_8" + "P-poll__networl_2_3_AnsP_0" + "P-poll__networl_2_3_AnsP_1" + "P-poll__networl_2_3_AnsP_2" + "P-poll__networl_2_3_AnsP_3" + "P-poll__networl_2_3_AnsP_4" + "P-poll__networl_2_3_AnsP_5" + "P-poll__networl_2_3_AnsP_6" + "P-poll__networl_2_3_AnsP_7" + "P-poll__networl_2_3_AnsP_8" + "P-poll__networl_2_3_RI_0" + "P-poll__networl_2_3_RI_1" + "P-poll__networl_2_3_RI_2" + "P-poll__networl_2_3_RI_3" + "P-poll__networl_2_3_RI_4" + "P-poll__networl_2_3_RI_5" + "P-poll__networl_2_3_RI_6" + "P-poll__networl_2_3_RI_7" + "P-poll__networl_2_3_RI_8" + "P-poll__networl_2_3_AI_0" + "P-poll__networl_2_3_AI_1" + "P-poll__networl_2_3_AI_2" + "P-poll__networl_2_3_AI_3" + "P-poll__networl_2_3_AI_4" + "P-poll__networl_2_3_AI_5" + "P-poll__networl_2_3_AI_6" + "P-poll__networl_2_3_AI_7" + "P-poll__networl_2_3_AI_8" + "P-poll__networl_2_3_AnnP_0" + "P-poll__networl_2_3_AnnP_1" + "P-poll__networl_2_3_AnnP_2" + "P-poll__networl_2_3_AnnP_3" + "P-poll__networl_2_3_AnnP_4" + "P-poll__networl_2_3_AnnP_5" + "P-poll__networl_2_3_AnnP_6" + "P-poll__networl_2_3_AnnP_7" + "P-poll__networl_2_3_AnnP_8" + "P-poll__networl_2_3_RP_0" + "P-poll__networl_2_3_RP_1" + "P-poll__networl_2_3_RP_2" + "P-poll__networl_2_3_RP_3" + "P-poll__networl_2_3_RP_4" + "P-poll__networl_2_3_RP_5" + "P-poll__networl_2_3_RP_6" + "P-poll__networl_2_3_RP_7" + "P-poll__networl_2_3_RP_8" + "P-poll__networl_2_4_AskP_0" + "P-poll__networl_2_4_AskP_1" + "P-poll__networl_2_4_AskP_2" + "P-poll__networl_2_4_AskP_3" + "P-poll__networl_2_4_AskP_4" + "P-poll__networl_2_4_AskP_5" + "P-poll__networl_2_4_AskP_6" + "P-poll__networl_2_4_AskP_7" + "P-poll__networl_2_4_AskP_8" + "P-poll__networl_2_4_AnsP_0" + "P-poll__networl_2_4_AnsP_1" + "P-poll__networl_2_4_AnsP_2" + "P-poll__networl_2_4_AnsP_3" + "P-poll__networl_2_4_AnsP_4" + "P-poll__networl_2_4_AnsP_5" + "P-poll__networl_2_4_AnsP_6" + "P-poll__networl_2_4_AnsP_7" + "P-poll__networl_2_4_AnsP_8" + "P-poll__networl_2_4_RI_0" + "P-poll__networl_2_4_RI_1" + "P-poll__networl_2_4_RI_2" + "P-poll__networl_2_4_RI_3" + "P-poll__networl_2_4_RI_4" + "P-poll__networl_2_4_RI_5" + "P-poll__networl_2_4_RI_6" + "P-poll__networl_2_4_RI_7" + "P-poll__networl_2_4_RI_8" + "P-poll__networl_2_4_AI_0" + "P-poll__networl_2_4_AI_1" + "P-poll__networl_2_4_AI_2" + "P-poll__networl_2_4_AI_3" + "P-poll__networl_2_4_AI_4" + "P-poll__networl_2_4_AI_5" + "P-poll__networl_2_4_AI_6" + "P-poll__networl_2_4_AI_7" + "P-poll__networl_2_4_AI_8" + "P-poll__networl_2_4_AnnP_0" + "P-poll__networl_2_4_AnnP_1" + "P-poll__networl_2_4_AnnP_2" + "P-poll__networl_2_4_AnnP_3" + "P-poll__networl_2_4_AnnP_4" + "P-poll__networl_2_4_AnnP_5" + "P-poll__networl_2_4_AnnP_6" + "P-poll__networl_2_4_AnnP_7" + "P-poll__networl_2_4_AnnP_8" + "P-poll__networl_2_4_RP_0" + "P-poll__networl_2_4_RP_1" + "P-poll__networl_2_4_RP_2" + "P-poll__networl_2_4_RP_3" + "P-poll__networl_2_4_RP_4" + "P-poll__networl_2_4_RP_5" + "P-poll__networl_2_4_RP_6" + "P-poll__networl_2_4_RP_7" + "P-poll__networl_2_4_RP_8" + "P-poll__networl_2_5_AskP_0" + "P-poll__networl_2_5_AskP_1" + "P-poll__networl_2_5_AskP_2" + "P-poll__networl_2_5_AskP_3" + "P-poll__networl_2_5_AskP_4" + "P-poll__networl_2_5_AskP_5" + "P-poll__networl_2_5_AskP_6" + "P-poll__networl_2_5_AskP_7" + "P-poll__networl_2_5_AskP_8" + "P-poll__networl_2_5_AnsP_0" + "P-poll__networl_2_5_AnsP_1" + "P-poll__networl_2_5_AnsP_2" + "P-poll__networl_2_5_AnsP_3" + "P-poll__networl_2_5_AnsP_4" + "P-poll__networl_2_5_AnsP_5" + "P-poll__networl_2_5_AnsP_6" + "P-poll__networl_2_5_AnsP_7" + "P-poll__networl_2_5_AnsP_8" + "P-poll__networl_2_5_RI_0" + "P-poll__networl_2_5_RI_1" + "P-poll__networl_2_5_RI_2" + "P-poll__networl_2_5_RI_3" + "P-poll__networl_2_5_RI_4" + "P-poll__networl_2_5_RI_5" + "P-poll__networl_2_5_RI_6" + "P-poll__networl_2_5_RI_7" + "P-poll__networl_2_5_RI_8" + "P-poll__networl_2_5_AI_0" + "P-poll__networl_2_5_AI_1" + "P-poll__networl_2_5_AI_2" + "P-poll__networl_2_5_AI_3" + "P-poll__networl_2_5_AI_4" + "P-poll__networl_2_5_AI_5" + "P-poll__networl_2_5_AI_6" + "P-poll__networl_2_5_AI_7" + "P-poll__networl_2_5_AI_8" + "P-poll__networl_2_5_AnnP_0" + "P-poll__networl_2_5_AnnP_1" + "P-poll__networl_2_5_AnnP_2" + "P-poll__networl_2_5_AnnP_3" + "P-poll__networl_2_5_AnnP_4" + "P-poll__networl_2_5_AnnP_5" + "P-poll__networl_2_5_AnnP_6" + "P-poll__networl_2_5_AnnP_7" + "P-poll__networl_2_5_AnnP_8" + "P-poll__networl_2_5_RP_0" + "P-poll__networl_2_5_RP_1" + "P-poll__networl_2_5_RP_2" + "P-poll__networl_2_5_RP_3" + "P-poll__networl_2_5_RP_4" + "P-poll__networl_2_5_RP_5" + "P-poll__networl_2_5_RP_6" + "P-poll__networl_2_5_RP_7" + "P-poll__networl_2_5_RP_8" + "P-poll__networl_2_6_AskP_0" + "P-poll__networl_2_6_AskP_1" + "P-poll__networl_2_6_AskP_2" + "P-poll__networl_2_6_AskP_3" + "P-poll__networl_2_6_AskP_4" + "P-poll__networl_2_6_AskP_5" + "P-poll__networl_2_6_AskP_6" + "P-poll__networl_2_6_AskP_7" + "P-poll__networl_2_6_AskP_8" + "P-poll__networl_2_6_AnsP_0" + "P-poll__networl_2_6_AnsP_1" + "P-poll__networl_2_6_AnsP_2" + "P-poll__networl_2_6_AnsP_3" + "P-poll__networl_2_6_AnsP_4" + "P-poll__networl_2_6_AnsP_5" + "P-poll__networl_2_6_AnsP_6" + "P-poll__networl_2_6_AnsP_7" + "P-poll__networl_2_6_AnsP_8" + "P-poll__networl_2_6_RI_0" + "P-poll__networl_2_6_RI_1" + "P-poll__networl_2_6_RI_2" + "P-poll__networl_2_6_RI_3" + "P-poll__networl_2_6_RI_4" + "P-poll__networl_2_6_RI_5" + "P-poll__networl_2_6_RI_6" + "P-poll__networl_2_6_RI_7" + "P-poll__networl_2_6_RI_8" + "P-poll__networl_2_6_AI_0" + "P-poll__networl_2_6_AI_1" + "P-poll__networl_2_6_AI_2" + "P-poll__networl_2_6_AI_3" + "P-poll__networl_2_6_AI_4" + "P-poll__networl_2_6_AI_5" + "P-poll__networl_2_6_AI_6" + "P-poll__networl_2_6_AI_7" + "P-poll__networl_2_6_AI_8" + "P-poll__networl_2_6_AnnP_0" + "P-poll__networl_2_6_AnnP_1" + "P-poll__networl_2_6_AnnP_2" + "P-poll__networl_2_6_AnnP_3" + "P-poll__networl_2_6_AnnP_4" + "P-poll__networl_2_6_AnnP_5" + "P-poll__networl_2_6_AnnP_6" + "P-poll__networl_2_6_AnnP_7" + "P-poll__networl_2_6_AnnP_8" + "P-poll__networl_2_6_RP_0" + "P-poll__networl_2_6_RP_1" + "P-poll__networl_2_6_RP_2" + "P-poll__networl_2_6_RP_3" + "P-poll__networl_2_6_RP_4" + "P-poll__networl_2_6_RP_5" + "P-poll__networl_2_6_RP_6" + "P-poll__networl_2_6_RP_7" + "P-poll__networl_2_6_RP_8" + "P-poll__networl_2_7_AskP_0" + "P-poll__networl_2_7_AskP_1" + "P-poll__networl_2_7_AskP_2" + "P-poll__networl_2_7_AskP_3" + "P-poll__networl_2_7_AskP_4" + "P-poll__networl_2_7_AskP_5" + "P-poll__networl_2_7_AskP_6" + "P-poll__networl_2_7_AskP_7" + "P-poll__networl_2_7_AskP_8" + "P-poll__networl_2_7_AnsP_0" + "P-poll__networl_2_7_AnsP_1" + "P-poll__networl_2_7_AnsP_2" + "P-poll__networl_2_7_AnsP_3" + "P-poll__networl_2_7_AnsP_4" + "P-poll__networl_2_7_AnsP_5" + "P-poll__networl_2_7_AnsP_6" + "P-poll__networl_2_7_AnsP_7" + "P-poll__networl_2_7_AnsP_8" + "P-poll__networl_2_7_RI_0" + "P-poll__networl_2_7_RI_1" + "P-poll__networl_2_7_RI_2" + "P-poll__networl_2_7_RI_3" + "P-poll__networl_2_7_RI_4" + "P-poll__networl_2_7_RI_5" + "P-poll__networl_2_7_RI_6" + "P-poll__networl_2_7_RI_7" + "P-poll__networl_2_7_RI_8" + "P-poll__networl_2_7_AI_0" + "P-poll__networl_2_7_AI_1" + "P-poll__networl_2_7_AI_2" + "P-poll__networl_2_7_AI_3" + "P-poll__networl_2_7_AI_4" + "P-poll__networl_2_7_AI_5" + "P-poll__networl_2_7_AI_6" + "P-poll__networl_2_7_AI_7" + "P-poll__networl_2_7_AI_8" + "P-poll__networl_2_7_AnnP_0" + "P-poll__networl_2_7_AnnP_1" + "P-poll__networl_2_7_AnnP_2" + "P-poll__networl_2_7_AnnP_3" + "P-poll__networl_2_7_AnnP_4" + "P-poll__networl_2_7_AnnP_5" + "P-poll__networl_2_7_AnnP_6" + "P-poll__networl_2_7_AnnP_7" + "P-poll__networl_2_7_AnnP_8" + "P-poll__networl_2_7_RP_0" + "P-poll__networl_2_7_RP_1" + "P-poll__networl_2_7_RP_2" + "P-poll__networl_2_7_RP_3" + "P-poll__networl_2_7_RP_4" + "P-poll__networl_2_7_RP_5" + "P-poll__networl_2_7_RP_6" + "P-poll__networl_2_7_RP_7" + "P-poll__networl_2_7_RP_8" + "P-poll__networl_2_8_AskP_0" + "P-poll__networl_2_8_AskP_1" + "P-poll__networl_2_8_AskP_2" + "P-poll__networl_2_8_AskP_3" + "P-poll__networl_2_8_AskP_4" + "P-poll__networl_2_8_AskP_5" + "P-poll__networl_2_8_AskP_6" + "P-poll__networl_2_8_AskP_7" + "P-poll__networl_2_8_AskP_8" + "P-poll__networl_2_8_AnsP_0" + "P-poll__networl_2_8_AnsP_1" + "P-poll__networl_2_8_AnsP_2" + "P-poll__networl_2_8_AnsP_3" + "P-poll__networl_2_8_AnsP_4" + "P-poll__networl_2_8_AnsP_5" + "P-poll__networl_2_8_AnsP_6" + "P-poll__networl_2_8_AnsP_7" + "P-poll__networl_2_8_AnsP_8" + "P-poll__networl_2_8_RI_0" + "P-poll__networl_2_8_RI_1" + "P-poll__networl_2_8_RI_2" + "P-poll__networl_2_8_RI_3" + "P-poll__networl_2_8_RI_4" + "P-poll__networl_2_8_RI_5" + "P-poll__networl_2_8_RI_6" + "P-poll__networl_2_8_RI_7" + "P-poll__networl_2_8_RI_8" + "P-poll__networl_2_8_AI_0" + "P-poll__networl_2_8_AI_1" + "P-poll__networl_2_8_AI_2" + "P-poll__networl_2_8_AI_3" + "P-poll__networl_2_8_AI_4" + "P-poll__networl_2_8_AI_5" + "P-poll__networl_2_8_AI_6" + "P-poll__networl_2_8_AI_7" + "P-poll__networl_2_8_AI_8" + "P-poll__networl_2_8_AnnP_0" + "P-poll__networl_2_8_AnnP_1" + "P-poll__networl_2_8_AnnP_2" + "P-poll__networl_2_8_AnnP_3" + "P-poll__networl_2_8_AnnP_4" + "P-poll__networl_2_8_AnnP_5" + "P-poll__networl_2_8_AnnP_6" + "P-poll__networl_2_8_AnnP_7" + "P-poll__networl_2_8_AnnP_8" + "P-poll__networl_2_8_RP_0" + "P-poll__networl_2_8_RP_1" + "P-poll__networl_2_8_RP_2" + "P-poll__networl_2_8_RP_3" + "P-poll__networl_2_8_RP_4" + "P-poll__networl_2_8_RP_5" + "P-poll__networl_2_8_RP_6" + "P-poll__networl_2_8_RP_7" + "P-poll__networl_2_8_RP_8" + "P-poll__networl_3_0_AskP_0" + "P-poll__networl_3_0_AskP_1" + "P-poll__networl_3_0_AskP_2" + "P-poll__networl_3_0_AskP_3" + "P-poll__networl_3_0_AskP_4" + "P-poll__networl_3_0_AskP_5" + "P-poll__networl_3_0_AskP_6" + "P-poll__networl_3_0_AskP_7" + "P-poll__networl_3_0_AskP_8" + "P-poll__networl_3_0_AnsP_0" + "P-poll__networl_3_0_AnsP_1" + "P-poll__networl_3_0_AnsP_2" + "P-poll__networl_3_0_AnsP_3" + "P-poll__networl_3_0_AnsP_4" + "P-poll__networl_3_0_AnsP_5" + "P-poll__networl_3_0_AnsP_6" + "P-poll__networl_3_0_AnsP_7" + "P-poll__networl_3_0_AnsP_8" + "P-poll__networl_3_0_RI_0" + "P-poll__networl_3_0_RI_1" + "P-poll__networl_3_0_RI_2" + "P-poll__networl_3_0_RI_3" + "P-poll__networl_3_0_RI_4" + "P-poll__networl_3_0_RI_5" + "P-poll__networl_3_0_RI_6" + "P-poll__networl_3_0_RI_7" + "P-poll__networl_3_0_RI_8" + "P-poll__networl_3_0_AI_0" + "P-poll__networl_3_0_AI_1" + "P-poll__networl_3_0_AI_2" + "P-poll__networl_3_0_AI_3" + "P-poll__networl_3_0_AI_4" + "P-poll__networl_3_0_AI_5" + "P-poll__networl_3_0_AI_6" + "P-poll__networl_3_0_AI_7" + "P-poll__networl_3_0_AI_8" + "P-poll__networl_3_0_AnnP_0" + "P-poll__networl_3_0_AnnP_1" + "P-poll__networl_3_0_AnnP_2" + "P-poll__networl_3_0_AnnP_3" + "P-poll__networl_3_0_AnnP_4" + "P-poll__networl_3_0_AnnP_5" + "P-poll__networl_3_0_AnnP_6" + "P-poll__networl_3_0_AnnP_7" + "P-poll__networl_3_0_AnnP_8" + "P-poll__networl_3_0_RP_0" + "P-poll__networl_3_0_RP_1" + "P-poll__networl_3_0_RP_2" + "P-poll__networl_3_0_RP_3" + "P-poll__networl_3_0_RP_4" + "P-poll__networl_3_0_RP_5" + "P-poll__networl_3_0_RP_6" + "P-poll__networl_3_0_RP_7" + "P-poll__networl_3_0_RP_8" + "P-poll__networl_3_1_AskP_0" + "P-poll__networl_3_1_AskP_1" + "P-poll__networl_3_1_AskP_2" + "P-poll__networl_3_1_AskP_3" + "P-poll__networl_3_1_AskP_4" + "P-poll__networl_3_1_AskP_5" + "P-poll__networl_3_1_AskP_6" + "P-poll__networl_3_1_AskP_7" + "P-poll__networl_3_1_AskP_8" + "P-poll__networl_3_1_AnsP_0" + "P-poll__networl_3_1_AnsP_1" + "P-poll__networl_3_1_AnsP_2" + "P-poll__networl_3_1_AnsP_3" + "P-poll__networl_3_1_AnsP_4" + "P-poll__networl_3_1_AnsP_5" + "P-poll__networl_3_1_AnsP_6" + "P-poll__networl_3_1_AnsP_7" + "P-poll__networl_3_1_AnsP_8" + "P-poll__networl_3_1_RI_0" + "P-poll__networl_3_1_RI_1" + "P-poll__networl_3_1_RI_2" + "P-poll__networl_3_1_RI_3" + "P-poll__networl_3_1_RI_4" + "P-poll__networl_3_1_RI_5" + "P-poll__networl_3_1_RI_6" + "P-poll__networl_3_1_RI_7" + "P-poll__networl_3_1_RI_8" + "P-poll__networl_3_1_AI_0" + "P-poll__networl_3_1_AI_1" + "P-poll__networl_3_1_AI_2" + "P-poll__networl_3_1_AI_3" + "P-poll__networl_3_1_AI_4" + "P-poll__networl_3_1_AI_5" + "P-poll__networl_3_1_AI_6" + "P-poll__networl_3_1_AI_7" + "P-poll__networl_3_1_AI_8" + "P-poll__networl_3_1_AnnP_0" + "P-poll__networl_3_1_AnnP_1" + "P-poll__networl_3_1_AnnP_2" + "P-poll__networl_3_1_AnnP_3" + "P-poll__networl_3_1_AnnP_4" + "P-poll__networl_3_1_AnnP_5" + "P-poll__networl_3_1_AnnP_6" + "P-poll__networl_3_1_AnnP_7" + "P-poll__networl_3_1_AnnP_8" + "P-poll__networl_3_1_RP_0" + "P-poll__networl_3_1_RP_1" + "P-poll__networl_3_1_RP_2" + "P-poll__networl_3_1_RP_3" + "P-poll__networl_3_1_RP_4" + "P-poll__networl_3_1_RP_5" + "P-poll__networl_3_1_RP_6" + "P-poll__networl_3_1_RP_7" + "P-poll__networl_3_1_RP_8" + "P-poll__networl_3_2_AskP_0" + "P-poll__networl_3_2_AskP_1" + "P-poll__networl_3_2_AskP_2" + "P-poll__networl_3_2_AskP_3" + "P-poll__networl_3_2_AskP_4" + "P-poll__networl_3_2_AskP_5" + "P-poll__networl_3_2_AskP_6" + "P-poll__networl_3_2_AskP_7" + "P-poll__networl_3_2_AskP_8" + "P-poll__networl_3_2_AnsP_0" + "P-poll__networl_3_2_AnsP_1" + "P-poll__networl_3_2_AnsP_2" + "P-poll__networl_3_2_AnsP_3" + "P-poll__networl_3_2_AnsP_4" + "P-poll__networl_3_2_AnsP_5" + "P-poll__networl_3_2_AnsP_6" + "P-poll__networl_3_2_AnsP_7" + "P-poll__networl_3_2_AnsP_8" + "P-poll__networl_3_2_RI_0" + "P-poll__networl_3_2_RI_1" + "P-poll__networl_3_2_RI_2" + "P-poll__networl_3_2_RI_3" + "P-poll__networl_3_2_RI_4" + "P-poll__networl_3_2_RI_5" + "P-poll__networl_3_2_RI_6" + "P-poll__networl_3_2_RI_7" + "P-poll__networl_3_2_RI_8" + "P-poll__networl_3_2_AI_0" + "P-poll__networl_3_2_AI_1" + "P-poll__networl_3_2_AI_2" + "P-poll__networl_3_2_AI_3" + "P-poll__networl_3_2_AI_4" + "P-poll__networl_3_2_AI_5" + "P-poll__networl_3_2_AI_6" + "P-poll__networl_3_2_AI_7" + "P-poll__networl_3_2_AI_8" + "P-poll__networl_3_2_AnnP_0" + "P-poll__networl_3_2_AnnP_1" + "P-poll__networl_3_2_AnnP_2" + "P-poll__networl_3_2_AnnP_3" + "P-poll__networl_3_2_AnnP_4" + "P-poll__networl_3_2_AnnP_5" + "P-poll__networl_3_2_AnnP_6" + "P-poll__networl_3_2_AnnP_7" + "P-poll__networl_3_2_AnnP_8" + "P-poll__networl_3_2_RP_0" + "P-poll__networl_3_2_RP_1" + "P-poll__networl_3_2_RP_2" + "P-poll__networl_3_2_RP_3" + "P-poll__networl_3_2_RP_4" + "P-poll__networl_3_2_RP_5" + "P-poll__networl_3_2_RP_6" + "P-poll__networl_3_2_RP_7" + "P-poll__networl_3_2_RP_8" + "P-poll__networl_3_3_AskP_0" + "P-poll__networl_3_3_AskP_1" + "P-poll__networl_3_3_AskP_2" + "P-poll__networl_3_3_AskP_3" + "P-poll__networl_3_3_AskP_4" + "P-poll__networl_3_3_AskP_5" + "P-poll__networl_3_3_AskP_6" + "P-poll__networl_3_3_AskP_7" + "P-poll__networl_3_3_AskP_8" + "P-poll__networl_3_3_AnsP_0" + "P-poll__networl_3_3_AnsP_1" + "P-poll__networl_3_3_AnsP_2" + "P-poll__networl_3_3_AnsP_3" + "P-poll__networl_3_3_AnsP_4" + "P-poll__networl_3_3_AnsP_5" + "P-poll__networl_3_3_AnsP_6" + "P-poll__networl_3_3_AnsP_7" + "P-poll__networl_3_3_AnsP_8" + "P-poll__networl_3_3_RI_0" + "P-poll__networl_3_3_RI_1" + "P-poll__networl_3_3_RI_2" + "P-poll__networl_3_3_RI_3" + "P-poll__networl_3_3_RI_4" + "P-poll__networl_3_3_RI_5" + "P-poll__networl_3_3_RI_6" + "P-poll__networl_3_3_RI_7" + "P-poll__networl_3_3_RI_8" + "P-poll__networl_3_3_AI_0" + "P-poll__networl_3_3_AI_1" + "P-poll__networl_3_3_AI_2" + "P-poll__networl_3_3_AI_3" + "P-poll__networl_3_3_AI_4" + "P-poll__networl_3_3_AI_5" + "P-poll__networl_3_3_AI_6" + "P-poll__networl_3_3_AI_7" + "P-poll__networl_3_3_AI_8" + "P-poll__networl_3_3_AnnP_0" + "P-poll__networl_3_3_AnnP_1" + "P-poll__networl_3_3_AnnP_2" + "P-poll__networl_3_3_AnnP_3" + "P-poll__networl_3_3_AnnP_4" + "P-poll__networl_3_3_AnnP_5" + "P-poll__networl_3_3_AnnP_6" + "P-poll__networl_3_3_AnnP_7" + "P-poll__networl_3_3_AnnP_8" + "P-poll__networl_3_3_RP_0" + "P-poll__networl_3_3_RP_1" + "P-poll__networl_3_3_RP_2" + "P-poll__networl_3_3_RP_3" + "P-poll__networl_3_3_RP_4" + "P-poll__networl_3_3_RP_5" + "P-poll__networl_3_3_RP_6" + "P-poll__networl_3_3_RP_7" + "P-poll__networl_3_3_RP_8" + "P-poll__networl_3_4_AskP_0" + "P-poll__networl_3_4_AskP_1" + "P-poll__networl_3_4_AskP_2" + "P-poll__networl_3_4_AskP_3" + "P-poll__networl_3_4_AskP_4" + "P-poll__networl_3_4_AskP_5" + "P-poll__networl_3_4_AskP_6" + "P-poll__networl_3_4_AskP_7" + "P-poll__networl_3_4_AskP_8" + "P-poll__networl_3_4_AnsP_0" + "P-poll__networl_3_4_AnsP_1" + "P-poll__networl_3_4_AnsP_2" + "P-poll__networl_3_4_AnsP_3" + "P-poll__networl_3_4_AnsP_4" + "P-poll__networl_3_4_AnsP_5" + "P-poll__networl_3_4_AnsP_6" + "P-poll__networl_3_4_AnsP_7" + "P-poll__networl_3_4_AnsP_8" + "P-poll__networl_3_4_RI_0" + "P-poll__networl_3_4_RI_1" + "P-poll__networl_3_4_RI_2" + "P-poll__networl_3_4_RI_3" + "P-poll__networl_3_4_RI_4" + "P-poll__networl_3_4_RI_5" + "P-poll__networl_3_4_RI_6" + "P-poll__networl_3_4_RI_7" + "P-poll__networl_3_4_RI_8" + "P-poll__networl_3_4_AI_0" + "P-poll__networl_3_4_AI_1" + "P-poll__networl_3_4_AI_2" + "P-poll__networl_3_4_AI_3" + "P-poll__networl_3_4_AI_4" + "P-poll__networl_3_4_AI_5" + "P-poll__networl_3_4_AI_6" + "P-poll__networl_3_4_AI_7" + "P-poll__networl_3_4_AI_8" + "P-poll__networl_3_4_AnnP_0" + "P-poll__networl_3_4_AnnP_1" + "P-poll__networl_3_4_AnnP_2" + "P-poll__networl_3_4_AnnP_3" + "P-poll__networl_3_4_AnnP_4" + "P-poll__networl_3_4_AnnP_5" + "P-poll__networl_3_4_AnnP_6" + "P-poll__networl_3_4_AnnP_7" + "P-poll__networl_3_4_AnnP_8" + "P-poll__networl_3_4_RP_0" + "P-poll__networl_3_4_RP_1" + "P-poll__networl_3_4_RP_2" + "P-poll__networl_3_4_RP_3" + "P-poll__networl_3_4_RP_4" + "P-poll__networl_3_4_RP_5" + "P-poll__networl_3_4_RP_6" + "P-poll__networl_3_4_RP_7" + "P-poll__networl_3_4_RP_8" + "P-poll__networl_3_5_AskP_0" + "P-poll__networl_3_5_AskP_1" + "P-poll__networl_3_5_AskP_2" + "P-poll__networl_3_5_AskP_3" + "P-poll__networl_3_5_AskP_4" + "P-poll__networl_3_5_AskP_5" + "P-poll__networl_3_5_AskP_6" + "P-poll__networl_3_5_AskP_7" + "P-poll__networl_3_5_AskP_8" + "P-poll__networl_3_5_AnsP_0" + "P-poll__networl_3_5_AnsP_1" + "P-poll__networl_3_5_AnsP_2" + "P-poll__networl_3_5_AnsP_3" + "P-poll__networl_3_5_AnsP_4" + "P-poll__networl_3_5_AnsP_5" + "P-poll__networl_3_5_AnsP_6" + "P-poll__networl_3_5_AnsP_7" + "P-poll__networl_3_5_AnsP_8" + "P-poll__networl_3_5_RI_0" + "P-poll__networl_3_5_RI_1" + "P-poll__networl_3_5_RI_2" + "P-poll__networl_3_5_RI_3" + "P-poll__networl_3_5_RI_4" + "P-poll__networl_3_5_RI_5" + "P-poll__networl_3_5_RI_6" + "P-poll__networl_3_5_RI_7" + "P-poll__networl_3_5_RI_8" + "P-poll__networl_3_5_AI_0" + "P-poll__networl_3_5_AI_1" + "P-poll__networl_3_5_AI_2" + "P-poll__networl_3_5_AI_3" + "P-poll__networl_3_5_AI_4" + "P-poll__networl_3_5_AI_5" + "P-poll__networl_3_5_AI_6" + "P-poll__networl_3_5_AI_7" + "P-poll__networl_3_5_AI_8" + "P-poll__networl_3_5_AnnP_0" + "P-poll__networl_3_5_AnnP_1" + "P-poll__networl_3_5_AnnP_2" + "P-poll__networl_3_5_AnnP_3" + "P-poll__networl_3_5_AnnP_4" + "P-poll__networl_3_5_AnnP_5" + "P-poll__networl_3_5_AnnP_6" + "P-poll__networl_3_5_AnnP_7" + "P-poll__networl_3_5_AnnP_8" + "P-poll__networl_3_5_RP_0" + "P-poll__networl_3_5_RP_1" + "P-poll__networl_3_5_RP_2" + "P-poll__networl_3_5_RP_3" + "P-poll__networl_3_5_RP_4" + "P-poll__networl_3_5_RP_5" + "P-poll__networl_3_5_RP_6" + "P-poll__networl_3_5_RP_7" + "P-poll__networl_3_5_RP_8" + "P-poll__networl_3_6_AskP_0" + "P-poll__networl_3_6_AskP_1" + "P-poll__networl_3_6_AskP_2" + "P-poll__networl_3_6_AskP_3" + "P-poll__networl_3_6_AskP_4" + "P-poll__networl_3_6_AskP_5" + "P-poll__networl_3_6_AskP_6" + "P-poll__networl_3_6_AskP_7" + "P-poll__networl_3_6_AskP_8" + "P-poll__networl_3_6_AnsP_0" + "P-poll__networl_3_6_AnsP_1" + "P-poll__networl_3_6_AnsP_2" + "P-poll__networl_3_6_AnsP_3" + "P-poll__networl_3_6_AnsP_4" + "P-poll__networl_3_6_AnsP_5" + "P-poll__networl_3_6_AnsP_6" + "P-poll__networl_3_6_AnsP_7" + "P-poll__networl_3_6_AnsP_8" + "P-poll__networl_3_6_RI_0" + "P-poll__networl_3_6_RI_1" + "P-poll__networl_3_6_RI_2" + "P-poll__networl_3_6_RI_3" + "P-poll__networl_3_6_RI_4" + "P-poll__networl_3_6_RI_5" + "P-poll__networl_3_6_RI_6" + "P-poll__networl_3_6_RI_7" + "P-poll__networl_3_6_RI_8" + "P-poll__networl_3_6_AI_0" + "P-poll__networl_3_6_AI_1" + "P-poll__networl_3_6_AI_2" + "P-poll__networl_3_6_AI_3" + "P-poll__networl_3_6_AI_4" + "P-poll__networl_3_6_AI_5" + "P-poll__networl_3_6_AI_6" + "P-poll__networl_3_6_AI_7" + "P-poll__networl_3_6_AI_8" + "P-poll__networl_3_6_AnnP_0" + "P-poll__networl_3_6_AnnP_1" + "P-poll__networl_3_6_AnnP_2" + "P-poll__networl_3_6_AnnP_3" + "P-poll__networl_3_6_AnnP_4" + "P-poll__networl_3_6_AnnP_5" + "P-poll__networl_3_6_AnnP_6" + "P-poll__networl_3_6_AnnP_7" + "P-poll__networl_3_6_AnnP_8" + "P-poll__networl_3_6_RP_0" + "P-poll__networl_3_6_RP_1" + "P-poll__networl_3_6_RP_2" + "P-poll__networl_3_6_RP_3" + "P-poll__networl_3_6_RP_4" + "P-poll__networl_3_6_RP_5" + "P-poll__networl_3_6_RP_6" + "P-poll__networl_3_6_RP_7" + "P-poll__networl_3_6_RP_8" + "P-poll__networl_3_7_AskP_0" + "P-poll__networl_3_7_AskP_1" + "P-poll__networl_3_7_AskP_2" + "P-poll__networl_3_7_AskP_3" + "P-poll__networl_3_7_AskP_4" + "P-poll__networl_3_7_AskP_5" + "P-poll__networl_3_7_AskP_6" + "P-poll__networl_3_7_AskP_7" + "P-poll__networl_3_7_AskP_8" + "P-poll__networl_3_7_AnsP_0" + "P-poll__networl_3_7_AnsP_1" + "P-poll__networl_3_7_AnsP_2" + "P-poll__networl_3_7_AnsP_3" + "P-poll__networl_3_7_AnsP_4" + "P-poll__networl_3_7_AnsP_5" + "P-poll__networl_3_7_AnsP_6" + "P-poll__networl_3_7_AnsP_7" + "P-poll__networl_3_7_AnsP_8" + "P-poll__networl_3_7_RI_0" + "P-poll__networl_3_7_RI_1" + "P-poll__networl_3_7_RI_2" + "P-poll__networl_3_7_RI_3" + "P-poll__networl_3_7_RI_4" + "P-poll__networl_3_7_RI_5" + "P-poll__networl_3_7_RI_6" + "P-poll__networl_3_7_RI_7" + "P-poll__networl_3_7_RI_8" + "P-poll__networl_3_7_AI_0" + "P-poll__networl_3_7_AI_1" + "P-poll__networl_3_7_AI_2" + "P-poll__networl_3_7_AI_3" + "P-poll__networl_3_7_AI_4" + "P-poll__networl_3_7_AI_5" + "P-poll__networl_3_7_AI_6" + "P-poll__networl_3_7_AI_7" + "P-poll__networl_3_7_AI_8" + "P-poll__networl_3_7_AnnP_0" + "P-poll__networl_3_7_AnnP_1" + "P-poll__networl_3_7_AnnP_2" + "P-poll__networl_3_7_AnnP_3" + "P-poll__networl_3_7_AnnP_4" + "P-poll__networl_3_7_AnnP_5" + "P-poll__networl_3_7_AnnP_6" + "P-poll__networl_3_7_AnnP_7" + "P-poll__networl_3_7_AnnP_8" + "P-poll__networl_3_7_RP_0" + "P-poll__networl_3_7_RP_1" + "P-poll__networl_3_7_RP_2" + "P-poll__networl_3_7_RP_3" + "P-poll__networl_3_7_RP_4" + "P-poll__networl_3_7_RP_5" + "P-poll__networl_3_7_RP_6" + "P-poll__networl_3_7_RP_7" + "P-poll__networl_3_7_RP_8" + "P-poll__networl_3_8_AskP_0" + "P-poll__networl_3_8_AskP_1" + "P-poll__networl_3_8_AskP_2" + "P-poll__networl_3_8_AskP_3" + "P-poll__networl_3_8_AskP_4" + "P-poll__networl_3_8_AskP_5" + "P-poll__networl_3_8_AskP_6" + "P-poll__networl_3_8_AskP_7" + "P-poll__networl_3_8_AskP_8" + "P-poll__networl_3_8_AnsP_0" + "P-poll__networl_3_8_AnsP_1" + "P-poll__networl_3_8_AnsP_2" + "P-poll__networl_3_8_AnsP_3" + "P-poll__networl_3_8_AnsP_4" + "P-poll__networl_3_8_AnsP_5" + "P-poll__networl_3_8_AnsP_6" + "P-poll__networl_3_8_AnsP_7" + "P-poll__networl_3_8_AnsP_8" + "P-poll__networl_3_8_RI_0" + "P-poll__networl_3_8_RI_1" + "P-poll__networl_3_8_RI_2" + "P-poll__networl_3_8_RI_3" + "P-poll__networl_3_8_RI_4" + "P-poll__networl_3_8_RI_5" + "P-poll__networl_3_8_RI_6" + "P-poll__networl_3_8_RI_7" + "P-poll__networl_3_8_RI_8" + "P-poll__networl_3_8_AI_0" + "P-poll__networl_3_8_AI_1" + "P-poll__networl_3_8_AI_2" + "P-poll__networl_3_8_AI_3" + "P-poll__networl_3_8_AI_4" + "P-poll__networl_3_8_AI_5" + "P-poll__networl_3_8_AI_6" + "P-poll__networl_3_8_AI_7" + "P-poll__networl_3_8_AI_8" + "P-poll__networl_3_8_AnnP_0" + "P-poll__networl_3_8_AnnP_1" + "P-poll__networl_3_8_AnnP_2" + "P-poll__networl_3_8_AnnP_3" + "P-poll__networl_3_8_AnnP_4" + "P-poll__networl_3_8_AnnP_5" + "P-poll__networl_3_8_AnnP_6" + "P-poll__networl_3_8_AnnP_7" + "P-poll__networl_3_8_AnnP_8" + "P-poll__networl_3_8_RP_0" + "P-poll__networl_3_8_RP_1" + "P-poll__networl_3_8_RP_2" + "P-poll__networl_3_8_RP_3" + "P-poll__networl_3_8_RP_4" + "P-poll__networl_3_8_RP_5" + "P-poll__networl_3_8_RP_6" + "P-poll__networl_3_8_RP_7" + "P-poll__networl_3_8_RP_8" + "P-poll__networl_4_0_AskP_0" + "P-poll__networl_4_0_AskP_1" + "P-poll__networl_4_0_AskP_2" + "P-poll__networl_4_0_AskP_3" + "P-poll__networl_4_0_AskP_4" + "P-poll__networl_4_0_AskP_5" + "P-poll__networl_4_0_AskP_6" + "P-poll__networl_4_0_AskP_7" + "P-poll__networl_4_0_AskP_8" + "P-poll__networl_4_0_AnsP_0" + "P-poll__networl_4_0_AnsP_1" + "P-poll__networl_4_0_AnsP_2" + "P-poll__networl_4_0_AnsP_3" + "P-poll__networl_4_0_AnsP_4" + "P-poll__networl_4_0_AnsP_5" + "P-poll__networl_4_0_AnsP_6" + "P-poll__networl_4_0_AnsP_7" + "P-poll__networl_4_0_AnsP_8" + "P-poll__networl_4_0_RI_0" + "P-poll__networl_4_0_RI_1" + "P-poll__networl_4_0_RI_2" + "P-poll__networl_4_0_RI_3" + "P-poll__networl_4_0_RI_4" + "P-poll__networl_4_0_RI_5" + "P-poll__networl_4_0_RI_6" + "P-poll__networl_4_0_RI_7" + "P-poll__networl_4_0_RI_8" + "P-poll__networl_4_0_AI_0" + "P-poll__networl_4_0_AI_1" + "P-poll__networl_4_0_AI_2" + "P-poll__networl_4_0_AI_3" + "P-poll__networl_4_0_AI_4" + "P-poll__networl_4_0_AI_5" + "P-poll__networl_4_0_AI_6" + "P-poll__networl_4_0_AI_7" + "P-poll__networl_4_0_AI_8" + "P-poll__networl_4_0_AnnP_0" + "P-poll__networl_4_0_AnnP_1" + "P-poll__networl_4_0_AnnP_2" + "P-poll__networl_4_0_AnnP_3" + "P-poll__networl_4_0_AnnP_4" + "P-poll__networl_4_0_AnnP_5" + "P-poll__networl_4_0_AnnP_6" + "P-poll__networl_4_0_AnnP_7" + "P-poll__networl_4_0_AnnP_8" + "P-poll__networl_4_0_RP_0" + "P-poll__networl_4_0_RP_1" + "P-poll__networl_4_0_RP_2" + "P-poll__networl_4_0_RP_3" + "P-poll__networl_4_0_RP_4" + "P-poll__networl_4_0_RP_5" + "P-poll__networl_4_0_RP_6" + "P-poll__networl_4_0_RP_7" + "P-poll__networl_4_0_RP_8" + "P-poll__networl_4_1_AskP_0" + "P-poll__networl_4_1_AskP_1" + "P-poll__networl_4_1_AskP_2" + "P-poll__networl_4_1_AskP_3" + "P-poll__networl_4_1_AskP_4" + "P-poll__networl_4_1_AskP_5" + "P-poll__networl_4_1_AskP_6" + "P-poll__networl_4_1_AskP_7" + "P-poll__networl_4_1_AskP_8" + "P-poll__networl_4_1_AnsP_0" + "P-poll__networl_4_1_AnsP_1" + "P-poll__networl_4_1_AnsP_2" + "P-poll__networl_4_1_AnsP_3" + "P-poll__networl_4_1_AnsP_4" + "P-poll__networl_4_1_AnsP_5" + "P-poll__networl_4_1_AnsP_6" + "P-poll__networl_4_1_AnsP_7" + "P-poll__networl_4_1_AnsP_8" + "P-poll__networl_4_1_RI_0" + "P-poll__networl_4_1_RI_1" + "P-poll__networl_4_1_RI_2" + "P-poll__networl_4_1_RI_3" + "P-poll__networl_4_1_RI_4" + "P-poll__networl_4_1_RI_5" + "P-poll__networl_4_1_RI_6" + "P-poll__networl_4_1_RI_7" + "P-poll__networl_4_1_RI_8" + "P-poll__networl_4_1_AI_0" + "P-poll__networl_4_1_AI_1" + "P-poll__networl_4_1_AI_2" + "P-poll__networl_4_1_AI_3" + "P-poll__networl_4_1_AI_4" + "P-poll__networl_4_1_AI_5" + "P-poll__networl_4_1_AI_6" + "P-poll__networl_4_1_AI_7" + "P-poll__networl_4_1_AI_8" + "P-poll__networl_4_1_AnnP_0" + "P-poll__networl_4_1_AnnP_1" + "P-poll__networl_4_1_AnnP_2" + "P-poll__networl_4_1_AnnP_3" + "P-poll__networl_4_1_AnnP_4" + "P-poll__networl_4_1_AnnP_5" + "P-poll__networl_4_1_AnnP_6" + "P-poll__networl_4_1_AnnP_7" + "P-poll__networl_4_1_AnnP_8" + "P-poll__networl_4_1_RP_0" + "P-poll__networl_4_1_RP_1" + "P-poll__networl_4_1_RP_2" + "P-poll__networl_4_1_RP_3" + "P-poll__networl_4_1_RP_4" + "P-poll__networl_4_1_RP_5" + "P-poll__networl_4_1_RP_6" + "P-poll__networl_4_1_RP_7" + "P-poll__networl_4_1_RP_8" + "P-poll__networl_4_2_AskP_0" + "P-poll__networl_4_2_AskP_1" + "P-poll__networl_4_2_AskP_2" + "P-poll__networl_4_2_AskP_3" + "P-poll__networl_4_2_AskP_4" + "P-poll__networl_4_2_AskP_5" + "P-poll__networl_4_2_AskP_6" + "P-poll__networl_4_2_AskP_7" + "P-poll__networl_4_2_AskP_8" + "P-poll__networl_4_2_AnsP_0" + "P-poll__networl_4_2_AnsP_1" + "P-poll__networl_4_2_AnsP_2" + "P-poll__networl_4_2_AnsP_3" + "P-poll__networl_4_2_AnsP_4" + "P-poll__networl_4_2_AnsP_5" + "P-poll__networl_4_2_AnsP_6" + "P-poll__networl_4_2_AnsP_7" + "P-poll__networl_4_2_AnsP_8" + "P-poll__networl_4_2_RI_0" + "P-poll__networl_4_2_RI_1" + "P-poll__networl_4_2_RI_2" + "P-poll__networl_4_2_RI_3" + "P-poll__networl_4_2_RI_4" + "P-poll__networl_4_2_RI_5" + "P-poll__networl_4_2_RI_6" + "P-poll__networl_4_2_RI_7" + "P-poll__networl_4_2_RI_8" + "P-poll__networl_4_2_AI_0" + "P-poll__networl_4_2_AI_1" + "P-poll__networl_4_2_AI_2" + "P-poll__networl_4_2_AI_3" + "P-poll__networl_4_2_AI_4" + "P-poll__networl_4_2_AI_5" + "P-poll__networl_4_2_AI_6" + "P-poll__networl_4_2_AI_7" + "P-poll__networl_4_2_AI_8" + "P-poll__networl_4_2_AnnP_0" + "P-poll__networl_4_2_AnnP_1" + "P-poll__networl_4_2_AnnP_2" + "P-poll__networl_4_2_AnnP_3" + "P-poll__networl_4_2_AnnP_4" + "P-poll__networl_4_2_AnnP_5" + "P-poll__networl_4_2_AnnP_6" + "P-poll__networl_4_2_AnnP_7" + "P-poll__networl_4_2_AnnP_8" + "P-poll__networl_4_2_RP_0" + "P-poll__networl_4_2_RP_1" + "P-poll__networl_4_2_RP_2" + "P-poll__networl_4_2_RP_3" + "P-poll__networl_4_2_RP_4" + "P-poll__networl_4_2_RP_5" + "P-poll__networl_4_2_RP_6" + "P-poll__networl_4_2_RP_7" + "P-poll__networl_4_2_RP_8" + "P-poll__networl_4_3_AskP_0" + "P-poll__networl_4_3_AskP_1" + "P-poll__networl_4_3_AskP_2" + "P-poll__networl_4_3_AskP_3" + "P-poll__networl_4_3_AskP_4" + "P-poll__networl_4_3_AskP_5" + "P-poll__networl_4_3_AskP_6" + "P-poll__networl_4_3_AskP_7" + "P-poll__networl_4_3_AskP_8" + "P-poll__networl_4_3_AnsP_0" + "P-poll__networl_4_3_AnsP_1" + "P-poll__networl_4_3_AnsP_2" + "P-poll__networl_4_3_AnsP_3" + "P-poll__networl_4_3_AnsP_4" + "P-poll__networl_4_3_AnsP_5" + "P-poll__networl_4_3_AnsP_6" + "P-poll__networl_4_3_AnsP_7" + "P-poll__networl_4_3_AnsP_8" + "P-poll__networl_4_3_RI_0" + "P-poll__networl_4_3_RI_1" + "P-poll__networl_4_3_RI_2" + "P-poll__networl_4_3_RI_3" + "P-poll__networl_4_3_RI_4" + "P-poll__networl_4_3_RI_5" + "P-poll__networl_4_3_RI_6" + "P-poll__networl_4_3_RI_7" + "P-poll__networl_4_3_RI_8" + "P-poll__networl_4_3_AI_0" + "P-poll__networl_4_3_AI_1" + "P-poll__networl_4_3_AI_2" + "P-poll__networl_4_3_AI_3" + "P-poll__networl_4_3_AI_4" + "P-poll__networl_4_3_AI_5" + "P-poll__networl_4_3_AI_6" + "P-poll__networl_4_3_AI_7" + "P-poll__networl_4_3_AI_8" + "P-poll__networl_4_3_AnnP_0" + "P-poll__networl_4_3_AnnP_1" + "P-poll__networl_4_3_AnnP_2" + "P-poll__networl_4_3_AnnP_3" + "P-poll__networl_4_3_AnnP_4" + "P-poll__networl_4_3_AnnP_5" + "P-poll__networl_4_3_AnnP_6" + "P-poll__networl_4_3_AnnP_7" + "P-poll__networl_4_3_AnnP_8" + "P-poll__networl_4_3_RP_0" + "P-poll__networl_4_3_RP_1" + "P-poll__networl_4_3_RP_2" + "P-poll__networl_4_3_RP_3" + "P-poll__networl_4_3_RP_4" + "P-poll__networl_4_3_RP_5" + "P-poll__networl_4_3_RP_6" + "P-poll__networl_4_3_RP_7" + "P-poll__networl_4_3_RP_8" + "P-poll__networl_4_4_AskP_0" + "P-poll__networl_4_4_AskP_1" + "P-poll__networl_4_4_AskP_2" + "P-poll__networl_4_4_AskP_3" + "P-poll__networl_4_4_AskP_4" + "P-poll__networl_4_4_AskP_5" + "P-poll__networl_4_4_AskP_6" + "P-poll__networl_4_4_AskP_7" + "P-poll__networl_4_4_AskP_8" + "P-poll__networl_4_4_AnsP_0" + "P-poll__networl_4_4_AnsP_1" + "P-poll__networl_4_4_AnsP_2" + "P-poll__networl_4_4_AnsP_3" + "P-poll__networl_4_4_AnsP_4" + "P-poll__networl_4_4_AnsP_5" + "P-poll__networl_4_4_AnsP_6" + "P-poll__networl_4_4_AnsP_7" + "P-poll__networl_4_4_AnsP_8" + "P-poll__networl_4_4_RI_0" + "P-poll__networl_4_4_RI_1" + "P-poll__networl_4_4_RI_2" + "P-poll__networl_4_4_RI_3" + "P-poll__networl_4_4_RI_4" + "P-poll__networl_4_4_RI_5" + "P-poll__networl_4_4_RI_6" + "P-poll__networl_4_4_RI_7" + "P-poll__networl_4_4_RI_8" + "P-poll__networl_4_4_AI_0" + "P-poll__networl_4_4_AI_1" + "P-poll__networl_4_4_AI_2" + "P-poll__networl_4_4_AI_3" + "P-poll__networl_4_4_AI_4" + "P-poll__networl_4_4_AI_5" + "P-poll__networl_4_4_AI_6" + "P-poll__networl_4_4_AI_7" + "P-poll__networl_4_4_AI_8" + "P-poll__networl_4_4_AnnP_0" + "P-poll__networl_4_4_AnnP_1" + "P-poll__networl_4_4_AnnP_2" + "P-poll__networl_4_4_AnnP_3" + "P-poll__networl_4_4_AnnP_4" + "P-poll__networl_4_4_AnnP_5" + "P-poll__networl_4_4_AnnP_6" + "P-poll__networl_4_4_AnnP_7" + "P-poll__networl_4_4_AnnP_8" + "P-poll__networl_4_4_RP_0" + "P-poll__networl_4_4_RP_1" + "P-poll__networl_4_4_RP_2" + "P-poll__networl_4_4_RP_3" + "P-poll__networl_4_4_RP_4" + "P-poll__networl_4_4_RP_5" + "P-poll__networl_4_4_RP_6" + "P-poll__networl_4_4_RP_7" + "P-poll__networl_4_4_RP_8" + "P-poll__networl_4_5_AskP_0" + "P-poll__networl_4_5_AskP_1" + "P-poll__networl_4_5_AskP_2" + "P-poll__networl_4_5_AskP_3" + "P-poll__networl_4_5_AskP_4" + "P-poll__networl_4_5_AskP_5" + "P-poll__networl_4_5_AskP_6" + "P-poll__networl_4_5_AskP_7" + "P-poll__networl_4_5_AskP_8" + "P-poll__networl_4_5_AnsP_0" + "P-poll__networl_4_5_AnsP_1" + "P-poll__networl_4_5_AnsP_2" + "P-poll__networl_4_5_AnsP_3" + "P-poll__networl_4_5_AnsP_4" + "P-poll__networl_4_5_AnsP_5" + "P-poll__networl_4_5_AnsP_6" + "P-poll__networl_4_5_AnsP_7" + "P-poll__networl_4_5_AnsP_8" + "P-poll__networl_4_5_RI_0" + "P-poll__networl_4_5_RI_1" + "P-poll__networl_4_5_RI_2" + "P-poll__networl_4_5_RI_3" + "P-poll__networl_4_5_RI_4" + "P-poll__networl_4_5_RI_5" + "P-poll__networl_4_5_RI_6" + "P-poll__networl_4_5_RI_7" + "P-poll__networl_4_5_RI_8" + "P-poll__networl_4_5_AI_0" + "P-poll__networl_4_5_AI_1" + "P-poll__networl_4_5_AI_2" + "P-poll__networl_4_5_AI_3" + "P-poll__networl_4_5_AI_4" + "P-poll__networl_4_5_AI_5" + "P-poll__networl_4_5_AI_6" + "P-poll__networl_4_5_AI_7" + "P-poll__networl_4_5_AI_8" + "P-poll__networl_4_5_AnnP_0" + "P-poll__networl_4_5_AnnP_1" + "P-poll__networl_4_5_AnnP_2" + "P-poll__networl_4_5_AnnP_3" + "P-poll__networl_4_5_AnnP_4" + "P-poll__networl_4_5_AnnP_5" + "P-poll__networl_4_5_AnnP_6" + "P-poll__networl_4_5_AnnP_7" + "P-poll__networl_4_5_AnnP_8" + "P-poll__networl_4_5_RP_0" + "P-poll__networl_4_5_RP_1" + "P-poll__networl_4_5_RP_2" + "P-poll__networl_4_5_RP_3" + "P-poll__networl_4_5_RP_4" + "P-poll__networl_4_5_RP_5" + "P-poll__networl_4_5_RP_6" + "P-poll__networl_4_5_RP_7" + "P-poll__networl_4_5_RP_8" + "P-poll__networl_4_6_AskP_0" + "P-poll__networl_4_6_AskP_1" + "P-poll__networl_4_6_AskP_2" + "P-poll__networl_4_6_AskP_3" + "P-poll__networl_4_6_AskP_4" + "P-poll__networl_4_6_AskP_5" + "P-poll__networl_4_6_AskP_6" + "P-poll__networl_4_6_AskP_7" + "P-poll__networl_4_6_AskP_8" + "P-poll__networl_4_6_AnsP_0" + "P-poll__networl_4_6_AnsP_1" + "P-poll__networl_4_6_AnsP_2" + "P-poll__networl_4_6_AnsP_3" + "P-poll__networl_4_6_AnsP_4" + "P-poll__networl_4_6_AnsP_5" + "P-poll__networl_4_6_AnsP_6" + "P-poll__networl_4_6_AnsP_7" + "P-poll__networl_4_6_AnsP_8" + "P-poll__networl_4_6_RI_0" + "P-poll__networl_4_6_RI_1" + "P-poll__networl_4_6_RI_2" + "P-poll__networl_4_6_RI_3" + "P-poll__networl_4_6_RI_4" + "P-poll__networl_4_6_RI_5" + "P-poll__networl_4_6_RI_6" + "P-poll__networl_4_6_RI_7" + "P-poll__networl_4_6_RI_8" + "P-poll__networl_4_6_AI_0" + "P-poll__networl_4_6_AI_1" + "P-poll__networl_4_6_AI_2" + "P-poll__networl_4_6_AI_3" + "P-poll__networl_4_6_AI_4" + "P-poll__networl_4_6_AI_5" + "P-poll__networl_4_6_AI_6" + "P-poll__networl_4_6_AI_7" + "P-poll__networl_4_6_AI_8" + "P-poll__networl_4_6_AnnP_0" + "P-poll__networl_4_6_AnnP_1" + "P-poll__networl_4_6_AnnP_2" + "P-poll__networl_4_6_AnnP_3" + "P-poll__networl_4_6_AnnP_4" + "P-poll__networl_4_6_AnnP_5" + "P-poll__networl_4_6_AnnP_6" + "P-poll__networl_4_6_AnnP_7" + "P-poll__networl_4_6_AnnP_8" + "P-poll__networl_4_6_RP_0" + "P-poll__networl_4_6_RP_1" + "P-poll__networl_4_6_RP_2" + "P-poll__networl_4_6_RP_3" + "P-poll__networl_4_6_RP_4" + "P-poll__networl_4_6_RP_5" + "P-poll__networl_4_6_RP_6" + "P-poll__networl_4_6_RP_7" + "P-poll__networl_4_6_RP_8" + "P-poll__networl_4_7_AskP_0" + "P-poll__networl_4_7_AskP_1" + "P-poll__networl_4_7_AskP_2" + "P-poll__networl_4_7_AskP_3" + "P-poll__networl_4_7_AskP_4" + "P-poll__networl_4_7_AskP_5" + "P-poll__networl_4_7_AskP_6" + "P-poll__networl_4_7_AskP_7" + "P-poll__networl_4_7_AskP_8" + "P-poll__networl_4_7_AnsP_0" + "P-poll__networl_4_7_AnsP_1" + "P-poll__networl_4_7_AnsP_2" + "P-poll__networl_4_7_AnsP_3" + "P-poll__networl_4_7_AnsP_4" + "P-poll__networl_4_7_AnsP_5" + "P-poll__networl_4_7_AnsP_6" + "P-poll__networl_4_7_AnsP_7" + "P-poll__networl_4_7_AnsP_8" + "P-poll__networl_4_7_RI_0" + "P-poll__networl_4_7_RI_1" + "P-poll__networl_4_7_RI_2" + "P-poll__networl_4_7_RI_3" + "P-poll__networl_4_7_RI_4" + "P-poll__networl_4_7_RI_5" + "P-poll__networl_4_7_RI_6" + "P-poll__networl_4_7_RI_7" + "P-poll__networl_4_7_RI_8" + "P-poll__networl_4_7_AI_0" + "P-poll__networl_4_7_AI_1" + "P-poll__networl_4_7_AI_2" + "P-poll__networl_4_7_AI_3" + "P-poll__networl_4_7_AI_4" + "P-poll__networl_4_7_AI_5" + "P-poll__networl_4_7_AI_6" + "P-poll__networl_4_7_AI_7" + "P-poll__networl_4_7_AI_8" + "P-poll__networl_4_7_AnnP_0" + "P-poll__networl_4_7_AnnP_1" + "P-poll__networl_4_7_AnnP_2" + "P-poll__networl_4_7_AnnP_3" + "P-poll__networl_4_7_AnnP_4" + "P-poll__networl_4_7_AnnP_5" + "P-poll__networl_4_7_AnnP_6" + "P-poll__networl_4_7_AnnP_7" + "P-poll__networl_4_7_AnnP_8" + "P-poll__networl_4_7_RP_0" + "P-poll__networl_4_7_RP_1" + "P-poll__networl_4_7_RP_2" + "P-poll__networl_4_7_RP_3" + "P-poll__networl_4_7_RP_4" + "P-poll__networl_4_7_RP_5" + "P-poll__networl_4_7_RP_6" + "P-poll__networl_4_7_RP_7" + "P-poll__networl_4_7_RP_8" + "P-poll__networl_4_8_AskP_0" + "P-poll__networl_4_8_AskP_1" + "P-poll__networl_4_8_AskP_2" + "P-poll__networl_4_8_AskP_3" + "P-poll__networl_4_8_AskP_4" + "P-poll__networl_4_8_AskP_5" + "P-poll__networl_4_8_AskP_6" + "P-poll__networl_4_8_AskP_7" + "P-poll__networl_4_8_AskP_8" + "P-poll__networl_4_8_AnsP_0" + "P-poll__networl_4_8_AnsP_1" + "P-poll__networl_4_8_AnsP_2" + "P-poll__networl_4_8_AnsP_3" + "P-poll__networl_4_8_AnsP_4" + "P-poll__networl_4_8_AnsP_5" + "P-poll__networl_4_8_AnsP_6" + "P-poll__networl_4_8_AnsP_7" + "P-poll__networl_4_8_AnsP_8" + "P-poll__networl_4_8_RI_0" + "P-poll__networl_4_8_RI_1" + "P-poll__networl_4_8_RI_2" + "P-poll__networl_4_8_RI_3" + "P-poll__networl_4_8_RI_4" + "P-poll__networl_4_8_RI_5" + "P-poll__networl_4_8_RI_6" + "P-poll__networl_4_8_RI_7" + "P-poll__networl_4_8_RI_8" + "P-poll__networl_4_8_AI_0" + "P-poll__networl_4_8_AI_1" + "P-poll__networl_4_8_AI_2" + "P-poll__networl_4_8_AI_3" + "P-poll__networl_4_8_AI_4" + "P-poll__networl_4_8_AI_5" + "P-poll__networl_4_8_AI_6" + "P-poll__networl_4_8_AI_7" + "P-poll__networl_4_8_AI_8" + "P-poll__networl_4_8_AnnP_0" + "P-poll__networl_4_8_AnnP_1" + "P-poll__networl_4_8_AnnP_2" + "P-poll__networl_4_8_AnnP_3" + "P-poll__networl_4_8_AnnP_4" + "P-poll__networl_4_8_AnnP_5" + "P-poll__networl_4_8_AnnP_6" + "P-poll__networl_4_8_AnnP_7" + "P-poll__networl_4_8_AnnP_8" + "P-poll__networl_4_8_RP_0" + "P-poll__networl_4_8_RP_1" + "P-poll__networl_4_8_RP_2" + "P-poll__networl_4_8_RP_3" + "P-poll__networl_4_8_RP_4" + "P-poll__networl_4_8_RP_5" + "P-poll__networl_4_8_RP_6" + "P-poll__networl_4_8_RP_7" + "P-poll__networl_4_8_RP_8" + "P-poll__networl_5_0_AskP_0" + "P-poll__networl_5_0_AskP_1" + "P-poll__networl_5_0_AskP_2" + "P-poll__networl_5_0_AskP_3" + "P-poll__networl_5_0_AskP_4" + "P-poll__networl_5_0_AskP_5" + "P-poll__networl_5_0_AskP_6" + "P-poll__networl_5_0_AskP_7" + "P-poll__networl_5_0_AskP_8" + "P-poll__networl_5_0_AnsP_0" + "P-poll__networl_5_0_AnsP_1" + "P-poll__networl_5_0_AnsP_2" + "P-poll__networl_5_0_AnsP_3" + "P-poll__networl_5_0_AnsP_4" + "P-poll__networl_5_0_AnsP_5" + "P-poll__networl_5_0_AnsP_6" + "P-poll__networl_5_0_AnsP_7" + "P-poll__networl_5_0_AnsP_8" + "P-poll__networl_5_0_RI_0" + "P-poll__networl_5_0_RI_1" + "P-poll__networl_5_0_RI_2" + "P-poll__networl_5_0_RI_3" + "P-poll__networl_5_0_RI_4" + "P-poll__networl_5_0_RI_5" + "P-poll__networl_5_0_RI_6" + "P-poll__networl_5_0_RI_7" + "P-poll__networl_5_0_RI_8" + "P-poll__networl_5_0_AI_0" + "P-poll__networl_5_0_AI_1" + "P-poll__networl_5_0_AI_2" + "P-poll__networl_5_0_AI_3" + "P-poll__networl_5_0_AI_4" + "P-poll__networl_5_0_AI_5" + "P-poll__networl_5_0_AI_6" + "P-poll__networl_5_0_AI_7" + "P-poll__networl_5_0_AI_8" + "P-poll__networl_5_0_AnnP_0" + "P-poll__networl_5_0_AnnP_1" + "P-poll__networl_5_0_AnnP_2" + "P-poll__networl_5_0_AnnP_3" + "P-poll__networl_5_0_AnnP_4" + "P-poll__networl_5_0_AnnP_5" + "P-poll__networl_5_0_AnnP_6" + "P-poll__networl_5_0_AnnP_7" + "P-poll__networl_5_0_AnnP_8" + "P-poll__networl_5_0_RP_0" + "P-poll__networl_5_0_RP_1" + "P-poll__networl_5_0_RP_2" + "P-poll__networl_5_0_RP_3" + "P-poll__networl_5_0_RP_4" + "P-poll__networl_5_0_RP_5" + "P-poll__networl_5_0_RP_6" + "P-poll__networl_5_0_RP_7" + "P-poll__networl_5_0_RP_8" + "P-poll__networl_5_1_AskP_0" + "P-poll__networl_5_1_AskP_1" + "P-poll__networl_5_1_AskP_2" + "P-poll__networl_5_1_AskP_3" + "P-poll__networl_5_1_AskP_4" + "P-poll__networl_5_1_AskP_5" + "P-poll__networl_5_1_AskP_6" + "P-poll__networl_5_1_AskP_7" + "P-poll__networl_5_1_AskP_8" + "P-poll__networl_5_1_AnsP_0" + "P-poll__networl_5_1_AnsP_1" + "P-poll__networl_5_1_AnsP_2" + "P-poll__networl_5_1_AnsP_3" + "P-poll__networl_5_1_AnsP_4" + "P-poll__networl_5_1_AnsP_5" + "P-poll__networl_5_1_AnsP_6" + "P-poll__networl_5_1_AnsP_7" + "P-poll__networl_5_1_AnsP_8" + "P-poll__networl_5_1_RI_0" + "P-poll__networl_5_1_RI_1" + "P-poll__networl_5_1_RI_2" + "P-poll__networl_5_1_RI_3" + "P-poll__networl_5_1_RI_4" + "P-poll__networl_5_1_RI_5" + "P-poll__networl_5_1_RI_6" + "P-poll__networl_5_1_RI_7" + "P-poll__networl_5_1_RI_8" + "P-poll__networl_5_1_AI_0" + "P-poll__networl_5_1_AI_1" + "P-poll__networl_5_1_AI_2" + "P-poll__networl_5_1_AI_3" + "P-poll__networl_5_1_AI_4" + "P-poll__networl_5_1_AI_5" + "P-poll__networl_5_1_AI_6" + "P-poll__networl_5_1_AI_7" + "P-poll__networl_5_1_AI_8" + "P-poll__networl_5_1_AnnP_0" + "P-poll__networl_5_1_AnnP_1" + "P-poll__networl_5_1_AnnP_2" + "P-poll__networl_5_1_AnnP_3" + "P-poll__networl_5_1_AnnP_4" + "P-poll__networl_5_1_AnnP_5" + "P-poll__networl_5_1_AnnP_6" + "P-poll__networl_5_1_AnnP_7" + "P-poll__networl_5_1_AnnP_8" + "P-poll__networl_5_1_RP_0" + "P-poll__networl_5_1_RP_1" + "P-poll__networl_5_1_RP_2" + "P-poll__networl_5_1_RP_3" + "P-poll__networl_5_1_RP_4" + "P-poll__networl_5_1_RP_5" + "P-poll__networl_5_1_RP_6" + "P-poll__networl_5_1_RP_7" + "P-poll__networl_5_1_RP_8" + "P-poll__networl_5_2_AskP_0" + "P-poll__networl_5_2_AskP_1" + "P-poll__networl_5_2_AskP_2" + "P-poll__networl_5_2_AskP_3" + "P-poll__networl_5_2_AskP_4" + "P-poll__networl_5_2_AskP_5" + "P-poll__networl_5_2_AskP_6" + "P-poll__networl_5_2_AskP_7" + "P-poll__networl_5_2_AskP_8" + "P-poll__networl_5_2_AnsP_0" + "P-poll__networl_5_2_AnsP_1" + "P-poll__networl_5_2_AnsP_2" + "P-poll__networl_5_2_AnsP_3" + "P-poll__networl_5_2_AnsP_4" + "P-poll__networl_5_2_AnsP_5" + "P-poll__networl_5_2_AnsP_6" + "P-poll__networl_5_2_AnsP_7" + "P-poll__networl_5_2_AnsP_8" + "P-poll__networl_5_2_RI_0" + "P-poll__networl_5_2_RI_1" + "P-poll__networl_5_2_RI_2" + "P-poll__networl_5_2_RI_3" + "P-poll__networl_5_2_RI_4" + "P-poll__networl_5_2_RI_5" + "P-poll__networl_5_2_RI_6" + "P-poll__networl_5_2_RI_7" + "P-poll__networl_5_2_RI_8" + "P-poll__networl_5_2_AI_0" + "P-poll__networl_5_2_AI_1" + "P-poll__networl_5_2_AI_2" + "P-poll__networl_5_2_AI_3" + "P-poll__networl_5_2_AI_4" + "P-poll__networl_5_2_AI_5" + "P-poll__networl_5_2_AI_6" + "P-poll__networl_5_2_AI_7" + "P-poll__networl_5_2_AI_8" + "P-poll__networl_5_2_AnnP_0" + "P-poll__networl_5_2_AnnP_1" + "P-poll__networl_5_2_AnnP_2" + "P-poll__networl_5_2_AnnP_3" + "P-poll__networl_5_2_AnnP_4" + "P-poll__networl_5_2_AnnP_5" + "P-poll__networl_5_2_AnnP_6" + "P-poll__networl_5_2_AnnP_7" + "P-poll__networl_5_2_AnnP_8" + "P-poll__networl_5_2_RP_0" + "P-poll__networl_5_2_RP_1" + "P-poll__networl_5_2_RP_2" + "P-poll__networl_5_2_RP_3" + "P-poll__networl_5_2_RP_4" + "P-poll__networl_5_2_RP_5" + "P-poll__networl_5_2_RP_6" + "P-poll__networl_5_2_RP_7" + "P-poll__networl_5_2_RP_8" + "P-poll__networl_5_3_AskP_0" + "P-poll__networl_5_3_AskP_1" + "P-poll__networl_5_3_AskP_2" + "P-poll__networl_5_3_AskP_3" + "P-poll__networl_5_3_AskP_4" + "P-poll__networl_5_3_AskP_5" + "P-poll__networl_5_3_AskP_6" + "P-poll__networl_5_3_AskP_7" + "P-poll__networl_5_3_AskP_8" + "P-poll__networl_5_3_AnsP_0" + "P-poll__networl_5_3_AnsP_1" + "P-poll__networl_5_3_AnsP_2" + "P-poll__networl_5_3_AnsP_3" + "P-poll__networl_5_3_AnsP_4" + "P-poll__networl_5_3_AnsP_5" + "P-poll__networl_5_3_AnsP_6" + "P-poll__networl_5_3_AnsP_7" + "P-poll__networl_5_3_AnsP_8" + "P-poll__networl_5_3_RI_0" + "P-poll__networl_5_3_RI_1" + "P-poll__networl_5_3_RI_2" + "P-poll__networl_5_3_RI_3" + "P-poll__networl_5_3_RI_4" + "P-poll__networl_5_3_RI_5" + "P-poll__networl_5_3_RI_6" + "P-poll__networl_5_3_RI_7" + "P-poll__networl_5_3_RI_8" + "P-poll__networl_5_3_AI_0" + "P-poll__networl_5_3_AI_1" + "P-poll__networl_5_3_AI_2" + "P-poll__networl_5_3_AI_3" + "P-poll__networl_5_3_AI_4" + "P-poll__networl_5_3_AI_5" + "P-poll__networl_5_3_AI_6" + "P-poll__networl_5_3_AI_7" + "P-poll__networl_5_3_AI_8" + "P-poll__networl_5_3_AnnP_0" + "P-poll__networl_5_3_AnnP_1" + "P-poll__networl_5_3_AnnP_2" + "P-poll__networl_5_3_AnnP_3" + "P-poll__networl_5_3_AnnP_4" + "P-poll__networl_5_3_AnnP_5" + "P-poll__networl_5_3_AnnP_6" + "P-poll__networl_5_3_AnnP_7" + "P-poll__networl_5_3_AnnP_8" + "P-poll__networl_5_3_RP_0" + "P-poll__networl_5_3_RP_1" + "P-poll__networl_5_3_RP_2" + "P-poll__networl_5_3_RP_3" + "P-poll__networl_5_3_RP_4" + "P-poll__networl_5_3_RP_5" + "P-poll__networl_5_3_RP_6" + "P-poll__networl_5_3_RP_7" + "P-poll__networl_5_3_RP_8" + "P-poll__networl_5_4_AskP_0" + "P-poll__networl_5_4_AskP_1" + "P-poll__networl_5_4_AskP_2" + "P-poll__networl_5_4_AskP_3" + "P-poll__networl_5_4_AskP_4" + "P-poll__networl_5_4_AskP_5" + "P-poll__networl_5_4_AskP_6" + "P-poll__networl_5_4_AskP_7" + "P-poll__networl_5_4_AskP_8" + "P-poll__networl_5_4_AnsP_0" + "P-poll__networl_5_4_AnsP_1" + "P-poll__networl_5_4_AnsP_2" + "P-poll__networl_5_4_AnsP_3" + "P-poll__networl_5_4_AnsP_4" + "P-poll__networl_5_4_AnsP_5" + "P-poll__networl_5_4_AnsP_6" + "P-poll__networl_5_4_AnsP_7" + "P-poll__networl_5_4_AnsP_8" + "P-poll__networl_5_4_RI_0" + "P-poll__networl_5_4_RI_1" + "P-poll__networl_5_4_RI_2" + "P-poll__networl_5_4_RI_3" + "P-poll__networl_5_4_RI_4" + "P-poll__networl_5_4_RI_5" + "P-poll__networl_5_4_RI_6" + "P-poll__networl_5_4_RI_7" + "P-poll__networl_5_4_RI_8" + "P-poll__networl_5_4_AI_0" + "P-poll__networl_5_4_AI_1" + "P-poll__networl_5_4_AI_2" + "P-poll__networl_5_4_AI_3" + "P-poll__networl_5_4_AI_4" + "P-poll__networl_5_4_AI_5" + "P-poll__networl_5_4_AI_6" + "P-poll__networl_5_4_AI_7" + "P-poll__networl_5_4_AI_8" + "P-poll__networl_5_4_AnnP_0" + "P-poll__networl_5_4_AnnP_1" + "P-poll__networl_5_4_AnnP_2" + "P-poll__networl_5_4_AnnP_3" + "P-poll__networl_5_4_AnnP_4" + "P-poll__networl_5_4_AnnP_5" + "P-poll__networl_5_4_AnnP_6" + "P-poll__networl_5_4_AnnP_7" + "P-poll__networl_5_4_AnnP_8" + "P-poll__networl_5_4_RP_0" + "P-poll__networl_5_4_RP_1" + "P-poll__networl_5_4_RP_2" + "P-poll__networl_5_4_RP_3" + "P-poll__networl_5_4_RP_4" + "P-poll__networl_5_4_RP_5" + "P-poll__networl_5_4_RP_6" + "P-poll__networl_5_4_RP_7" + "P-poll__networl_5_4_RP_8" + "P-poll__networl_5_5_AskP_0" + "P-poll__networl_5_5_AskP_1" + "P-poll__networl_5_5_AskP_2" + "P-poll__networl_5_5_AskP_3" + "P-poll__networl_5_5_AskP_4" + "P-poll__networl_5_5_AskP_5" + "P-poll__networl_5_5_AskP_6" + "P-poll__networl_5_5_AskP_7" + "P-poll__networl_5_5_AskP_8" + "P-poll__networl_5_5_AnsP_0" + "P-poll__networl_5_5_AnsP_1" + "P-poll__networl_5_5_AnsP_2" + "P-poll__networl_5_5_AnsP_3" + "P-poll__networl_5_5_AnsP_4" + "P-poll__networl_5_5_AnsP_5" + "P-poll__networl_5_5_AnsP_6" + "P-poll__networl_5_5_AnsP_7" + "P-poll__networl_5_5_AnsP_8" + "P-poll__networl_5_5_RI_0" + "P-poll__networl_5_5_RI_1" + "P-poll__networl_5_5_RI_2" + "P-poll__networl_5_5_RI_3" + "P-poll__networl_5_5_RI_4" + "P-poll__networl_5_5_RI_5" + "P-poll__networl_5_5_RI_6" + "P-poll__networl_5_5_RI_7" + "P-poll__networl_5_5_RI_8" + "P-poll__networl_5_5_AI_0" + "P-poll__networl_5_5_AI_1" + "P-poll__networl_5_5_AI_2" + "P-poll__networl_5_5_AI_3" + "P-poll__networl_5_5_AI_4" + "P-poll__networl_5_5_AI_5" + "P-poll__networl_5_5_AI_6" + "P-poll__networl_5_5_AI_7" + "P-poll__networl_5_5_AI_8" + "P-poll__networl_5_5_AnnP_0" + "P-poll__networl_5_5_AnnP_1" + "P-poll__networl_5_5_AnnP_2" + "P-poll__networl_5_5_AnnP_3" + "P-poll__networl_5_5_AnnP_4" + "P-poll__networl_5_5_AnnP_5" + "P-poll__networl_5_5_AnnP_6" + "P-poll__networl_5_5_AnnP_7" + "P-poll__networl_5_5_AnnP_8" + "P-poll__networl_5_5_RP_0" + "P-poll__networl_5_5_RP_1" + "P-poll__networl_5_5_RP_2" + "P-poll__networl_5_5_RP_3" + "P-poll__networl_5_5_RP_4" + "P-poll__networl_5_5_RP_5" + "P-poll__networl_5_5_RP_6" + "P-poll__networl_5_5_RP_7" + "P-poll__networl_5_5_RP_8" + "P-poll__networl_5_6_AskP_0" + "P-poll__networl_5_6_AskP_1" + "P-poll__networl_5_6_AskP_2" + "P-poll__networl_5_6_AskP_3" + "P-poll__networl_5_6_AskP_4" + "P-poll__networl_5_6_AskP_5" + "P-poll__networl_5_6_AskP_6" + "P-poll__networl_5_6_AskP_7" + "P-poll__networl_5_6_AskP_8" + "P-poll__networl_5_6_AnsP_0" + "P-poll__networl_5_6_AnsP_1" + "P-poll__networl_5_6_AnsP_2" + "P-poll__networl_5_6_AnsP_3" + "P-poll__networl_5_6_AnsP_4" + "P-poll__networl_5_6_AnsP_5" + "P-poll__networl_5_6_AnsP_6" + "P-poll__networl_5_6_AnsP_7" + "P-poll__networl_5_6_AnsP_8" + "P-poll__networl_5_6_RI_0" + "P-poll__networl_5_6_RI_1" + "P-poll__networl_5_6_RI_2" + "P-poll__networl_5_6_RI_3" + "P-poll__networl_5_6_RI_4" + "P-poll__networl_5_6_RI_5" + "P-poll__networl_5_6_RI_6" + "P-poll__networl_5_6_RI_7" + "P-poll__networl_5_6_RI_8" + "P-poll__networl_5_6_AI_0" + "P-poll__networl_5_6_AI_1" + "P-poll__networl_5_6_AI_2" + "P-poll__networl_5_6_AI_3" + "P-poll__networl_5_6_AI_4" + "P-poll__networl_5_6_AI_5" + "P-poll__networl_5_6_AI_6" + "P-poll__networl_5_6_AI_7" + "P-poll__networl_5_6_AI_8" + "P-poll__networl_5_6_AnnP_0" + "P-poll__networl_5_6_AnnP_1" + "P-poll__networl_5_6_AnnP_2" + "P-poll__networl_5_6_AnnP_3" + "P-poll__networl_5_6_AnnP_4" + "P-poll__networl_5_6_AnnP_5" + "P-poll__networl_5_6_AnnP_6" + "P-poll__networl_5_6_AnnP_7" + "P-poll__networl_5_6_AnnP_8" + "P-poll__networl_5_6_RP_0" + "P-poll__networl_5_6_RP_1" + "P-poll__networl_5_6_RP_2" + "P-poll__networl_5_6_RP_3" + "P-poll__networl_5_6_RP_4" + "P-poll__networl_5_6_RP_5" + "P-poll__networl_5_6_RP_6" + "P-poll__networl_5_6_RP_7" + "P-poll__networl_5_6_RP_8" + "P-poll__networl_5_7_AskP_0" + "P-poll__networl_5_7_AskP_1" + "P-poll__networl_5_7_AskP_2" + "P-poll__networl_5_7_AskP_3" + "P-poll__networl_5_7_AskP_4" + "P-poll__networl_5_7_AskP_5" + "P-poll__networl_5_7_AskP_6" + "P-poll__networl_5_7_AskP_7" + "P-poll__networl_5_7_AskP_8" + "P-poll__networl_5_7_AnsP_0" + "P-poll__networl_5_7_AnsP_1" + "P-poll__networl_5_7_AnsP_2" + "P-poll__networl_5_7_AnsP_3" + "P-poll__networl_5_7_AnsP_4" + "P-poll__networl_5_7_AnsP_5" + "P-poll__networl_5_7_AnsP_6" + "P-poll__networl_5_7_AnsP_7" + "P-poll__networl_5_7_AnsP_8" + "P-poll__networl_5_7_RI_0" + "P-poll__networl_5_7_RI_1" + "P-poll__networl_5_7_RI_2" + "P-poll__networl_5_7_RI_3" + "P-poll__networl_5_7_RI_4" + "P-poll__networl_5_7_RI_5" + "P-poll__networl_5_7_RI_6" + "P-poll__networl_5_7_RI_7" + "P-poll__networl_5_7_RI_8" + "P-poll__networl_5_7_AI_0" + "P-poll__networl_5_7_AI_1" + "P-poll__networl_5_7_AI_2" + "P-poll__networl_5_7_AI_3" + "P-poll__networl_5_7_AI_4" + "P-poll__networl_5_7_AI_5" + "P-poll__networl_5_7_AI_6" + "P-poll__networl_5_7_AI_7" + "P-poll__networl_5_7_AI_8" + "P-poll__networl_5_7_AnnP_0" + "P-poll__networl_5_7_AnnP_1" + "P-poll__networl_5_7_AnnP_2" + "P-poll__networl_5_7_AnnP_3" + "P-poll__networl_5_7_AnnP_4" + "P-poll__networl_5_7_AnnP_5" + "P-poll__networl_5_7_AnnP_6" + "P-poll__networl_5_7_AnnP_7" + "P-poll__networl_5_7_AnnP_8" + "P-poll__networl_5_7_RP_0" + "P-poll__networl_5_7_RP_1" + "P-poll__networl_5_7_RP_2" + "P-poll__networl_5_7_RP_3" + "P-poll__networl_5_7_RP_4" + "P-poll__networl_5_7_RP_5" + "P-poll__networl_5_7_RP_6" + "P-poll__networl_5_7_RP_7" + "P-poll__networl_5_7_RP_8" + "P-poll__networl_5_8_AskP_0" + "P-poll__networl_5_8_AskP_1" + "P-poll__networl_5_8_AskP_2" + "P-poll__networl_5_8_AskP_3" + "P-poll__networl_5_8_AskP_4" + "P-poll__networl_5_8_AskP_5" + "P-poll__networl_5_8_AskP_6" + "P-poll__networl_5_8_AskP_7" + "P-poll__networl_5_8_AskP_8" + "P-poll__networl_5_8_AnsP_0" + "P-poll__networl_5_8_AnsP_1" + "P-poll__networl_5_8_AnsP_2" + "P-poll__networl_5_8_AnsP_3" + "P-poll__networl_5_8_AnsP_4" + "P-poll__networl_5_8_AnsP_5" + "P-poll__networl_5_8_AnsP_6" + "P-poll__networl_5_8_AnsP_7" + "P-poll__networl_5_8_AnsP_8" + "P-poll__networl_5_8_RI_0" + "P-poll__networl_5_8_RI_1" + "P-poll__networl_5_8_RI_2" + "P-poll__networl_5_8_RI_3" + "P-poll__networl_5_8_RI_4" + "P-poll__networl_5_8_RI_5" + "P-poll__networl_5_8_RI_6" + "P-poll__networl_5_8_RI_7" + "P-poll__networl_5_8_RI_8" + "P-poll__networl_5_8_AI_0" + "P-poll__networl_5_8_AI_1" + "P-poll__networl_5_8_AI_2" + "P-poll__networl_5_8_AI_3" + "P-poll__networl_5_8_AI_4" + "P-poll__networl_5_8_AI_5" + "P-poll__networl_5_8_AI_6" + "P-poll__networl_5_8_AI_7" + "P-poll__networl_5_8_AI_8" + "P-poll__networl_5_8_AnnP_0" + "P-poll__networl_5_8_AnnP_1" + "P-poll__networl_5_8_AnnP_2" + "P-poll__networl_5_8_AnnP_3" + "P-poll__networl_5_8_AnnP_4" + "P-poll__networl_5_8_AnnP_5" + "P-poll__networl_5_8_AnnP_6" + "P-poll__networl_5_8_AnnP_7" + "P-poll__networl_5_8_AnnP_8" + "P-poll__networl_5_8_RP_0" + "P-poll__networl_5_8_RP_1" + "P-poll__networl_5_8_RP_2" + "P-poll__networl_5_8_RP_3" + "P-poll__networl_5_8_RP_4" + "P-poll__networl_5_8_RP_5" + "P-poll__networl_5_8_RP_6" + "P-poll__networl_5_8_RP_7" + "P-poll__networl_5_8_RP_8" + "P-poll__networl_6_0_AskP_0" + "P-poll__networl_6_0_AskP_1" + "P-poll__networl_6_0_AskP_2" + "P-poll__networl_6_0_AskP_3" + "P-poll__networl_6_0_AskP_4" + "P-poll__networl_6_0_AskP_5" + "P-poll__networl_6_0_AskP_6" + "P-poll__networl_6_0_AskP_7" + "P-poll__networl_6_0_AskP_8" + "P-poll__networl_6_0_AnsP_0" + "P-poll__networl_6_0_AnsP_1" + "P-poll__networl_6_0_AnsP_2" + "P-poll__networl_6_0_AnsP_3" + "P-poll__networl_6_0_AnsP_4" + "P-poll__networl_6_0_AnsP_5" + "P-poll__networl_6_0_AnsP_6" + "P-poll__networl_6_0_AnsP_7" + "P-poll__networl_6_0_AnsP_8" + "P-poll__networl_6_0_RI_0" + "P-poll__networl_6_0_RI_1" + "P-poll__networl_6_0_RI_2" + "P-poll__networl_6_0_RI_3" + "P-poll__networl_6_0_RI_4" + "P-poll__networl_6_0_RI_5" + "P-poll__networl_6_0_RI_6" + "P-poll__networl_6_0_RI_7" + "P-poll__networl_6_0_RI_8" + "P-poll__networl_6_0_AI_0" + "P-poll__networl_6_0_AI_1" + "P-poll__networl_6_0_AI_2" + "P-poll__networl_6_0_AI_3" + "P-poll__networl_6_0_AI_4" + "P-poll__networl_6_0_AI_5" + "P-poll__networl_6_0_AI_6" + "P-poll__networl_6_0_AI_7" + "P-poll__networl_6_0_AI_8" + "P-poll__networl_6_0_AnnP_0" + "P-poll__networl_6_0_AnnP_1" + "P-poll__networl_6_0_AnnP_2" + "P-poll__networl_6_0_AnnP_3" + "P-poll__networl_6_0_AnnP_4" + "P-poll__networl_6_0_AnnP_5" + "P-poll__networl_6_0_AnnP_6" + "P-poll__networl_6_0_AnnP_7" + "P-poll__networl_6_0_AnnP_8" + "P-poll__networl_6_0_RP_0" + "P-poll__networl_6_0_RP_1" + "P-poll__networl_6_0_RP_2" + "P-poll__networl_6_0_RP_3" + "P-poll__networl_6_0_RP_4" + "P-poll__networl_6_0_RP_5" + "P-poll__networl_6_0_RP_6" + "P-poll__networl_6_0_RP_7" + "P-poll__networl_6_0_RP_8" + "P-poll__networl_6_1_AskP_0" + "P-poll__networl_6_1_AskP_1" + "P-poll__networl_6_1_AskP_2" + "P-poll__networl_6_1_AskP_3" + "P-poll__networl_6_1_AskP_4" + "P-poll__networl_6_1_AskP_5" + "P-poll__networl_6_1_AskP_6" + "P-poll__networl_6_1_AskP_7" + "P-poll__networl_6_1_AskP_8" + "P-poll__networl_6_1_AnsP_0" + "P-poll__networl_6_1_AnsP_1" + "P-poll__networl_6_1_AnsP_2" + "P-poll__networl_6_1_AnsP_3" + "P-poll__networl_6_1_AnsP_4" + "P-poll__networl_6_1_AnsP_5" + "P-poll__networl_6_1_AnsP_6" + "P-poll__networl_6_1_AnsP_7" + "P-poll__networl_6_1_AnsP_8" + "P-poll__networl_6_1_RI_0" + "P-poll__networl_6_1_RI_1" + "P-poll__networl_6_1_RI_2" + "P-poll__networl_6_1_RI_3" + "P-poll__networl_6_1_RI_4" + "P-poll__networl_6_1_RI_5" + "P-poll__networl_6_1_RI_6" + "P-poll__networl_6_1_RI_7" + "P-poll__networl_6_1_RI_8" + "P-poll__networl_6_1_AI_0" + "P-poll__networl_6_1_AI_1" + "P-poll__networl_6_1_AI_2" + "P-poll__networl_6_1_AI_3" + "P-poll__networl_6_1_AI_4" + "P-poll__networl_6_1_AI_5" + "P-poll__networl_6_1_AI_6" + "P-poll__networl_6_1_AI_7" + "P-poll__networl_6_1_AI_8" + "P-poll__networl_6_1_AnnP_0" + "P-poll__networl_6_1_AnnP_1" + "P-poll__networl_6_1_AnnP_2" + "P-poll__networl_6_1_AnnP_3" + "P-poll__networl_6_1_AnnP_4" + "P-poll__networl_6_1_AnnP_5" + "P-poll__networl_6_1_AnnP_6" + "P-poll__networl_6_1_AnnP_7" + "P-poll__networl_6_1_AnnP_8" + "P-poll__networl_6_1_RP_0" + "P-poll__networl_6_1_RP_1" + "P-poll__networl_6_1_RP_2" + "P-poll__networl_6_1_RP_3" + "P-poll__networl_6_1_RP_4" + "P-poll__networl_6_1_RP_5" + "P-poll__networl_6_1_RP_6" + "P-poll__networl_6_1_RP_7" + "P-poll__networl_6_1_RP_8" + "P-poll__networl_6_2_AskP_0" + "P-poll__networl_6_2_AskP_1" + "P-poll__networl_6_2_AskP_2" + "P-poll__networl_6_2_AskP_3" + "P-poll__networl_6_2_AskP_4" + "P-poll__networl_6_2_AskP_5" + "P-poll__networl_6_2_AskP_6" + "P-poll__networl_6_2_AskP_7" + "P-poll__networl_6_2_AskP_8" + "P-poll__networl_6_2_AnsP_0" + "P-poll__networl_6_2_AnsP_1" + "P-poll__networl_6_2_AnsP_2" + "P-poll__networl_6_2_AnsP_3" + "P-poll__networl_6_2_AnsP_4" + "P-poll__networl_6_2_AnsP_5" + "P-poll__networl_6_2_AnsP_6" + "P-poll__networl_6_2_AnsP_7" + "P-poll__networl_6_2_AnsP_8" + "P-poll__networl_6_2_RI_0" + "P-poll__networl_6_2_RI_1" + "P-poll__networl_6_2_RI_2" + "P-poll__networl_6_2_RI_3" + "P-poll__networl_6_2_RI_4" + "P-poll__networl_6_2_RI_5" + "P-poll__networl_6_2_RI_6" + "P-poll__networl_6_2_RI_7" + "P-poll__networl_6_2_RI_8" + "P-poll__networl_6_2_AI_0" + "P-poll__networl_6_2_AI_1" + "P-poll__networl_6_2_AI_2" + "P-poll__networl_6_2_AI_3" + "P-poll__networl_6_2_AI_4" + "P-poll__networl_6_2_AI_5" + "P-poll__networl_6_2_AI_6" + "P-poll__networl_6_2_AI_7" + "P-poll__networl_6_2_AI_8" + "P-poll__networl_6_2_AnnP_0" + "P-poll__networl_6_2_AnnP_1" + "P-poll__networl_6_2_AnnP_2" + "P-poll__networl_6_2_AnnP_3" + "P-poll__networl_6_2_AnnP_4" + "P-poll__networl_6_2_AnnP_5" + "P-poll__networl_6_2_AnnP_6" + "P-poll__networl_6_2_AnnP_7" + "P-poll__networl_6_2_AnnP_8" + "P-poll__networl_6_2_RP_0" + "P-poll__networl_6_2_RP_1" + "P-poll__networl_6_2_RP_2" + "P-poll__networl_6_2_RP_3" + "P-poll__networl_6_2_RP_4" + "P-poll__networl_6_2_RP_5" + "P-poll__networl_6_2_RP_6" + "P-poll__networl_6_2_RP_7" + "P-poll__networl_6_2_RP_8" + "P-poll__networl_6_3_AskP_0" + "P-poll__networl_6_3_AskP_1" + "P-poll__networl_6_3_AskP_2" + "P-poll__networl_6_3_AskP_3" + "P-poll__networl_6_3_AskP_4" + "P-poll__networl_6_3_AskP_5" + "P-poll__networl_6_3_AskP_6" + "P-poll__networl_6_3_AskP_7" + "P-poll__networl_6_3_AskP_8" + "P-poll__networl_6_3_AnsP_0" + "P-poll__networl_6_3_AnsP_1" + "P-poll__networl_6_3_AnsP_2" + "P-poll__networl_6_3_AnsP_3" + "P-poll__networl_6_3_AnsP_4" + "P-poll__networl_6_3_AnsP_5" + "P-poll__networl_6_3_AnsP_6" + "P-poll__networl_6_3_AnsP_7" + "P-poll__networl_6_3_AnsP_8" + "P-poll__networl_6_3_RI_0" + "P-poll__networl_6_3_RI_1" + "P-poll__networl_6_3_RI_2" + "P-poll__networl_6_3_RI_3" + "P-poll__networl_6_3_RI_4" + "P-poll__networl_6_3_RI_5" + "P-poll__networl_6_3_RI_6" + "P-poll__networl_6_3_RI_7" + "P-poll__networl_6_3_RI_8" + "P-poll__networl_6_3_AI_0" + "P-poll__networl_6_3_AI_1" + "P-poll__networl_6_3_AI_2" + "P-poll__networl_6_3_AI_3" + "P-poll__networl_6_3_AI_4" + "P-poll__networl_6_3_AI_5" + "P-poll__networl_6_3_AI_6" + "P-poll__networl_6_3_AI_7" + "P-poll__networl_6_3_AI_8" + "P-poll__networl_6_3_AnnP_0" + "P-poll__networl_6_3_AnnP_1" + "P-poll__networl_6_3_AnnP_2" + "P-poll__networl_6_3_AnnP_3" + "P-poll__networl_6_3_AnnP_4" + "P-poll__networl_6_3_AnnP_5" + "P-poll__networl_6_3_AnnP_6" + "P-poll__networl_6_3_AnnP_7" + "P-poll__networl_6_3_AnnP_8" + "P-poll__networl_6_3_RP_0" + "P-poll__networl_6_3_RP_1" + "P-poll__networl_6_3_RP_2" + "P-poll__networl_6_3_RP_3" + "P-poll__networl_6_3_RP_4" + "P-poll__networl_6_3_RP_5" + "P-poll__networl_6_3_RP_6" + "P-poll__networl_6_3_RP_7" + "P-poll__networl_6_3_RP_8" + "P-poll__networl_6_4_AskP_0" + "P-poll__networl_6_4_AskP_1" + "P-poll__networl_6_4_AskP_2" + "P-poll__networl_6_4_AskP_3" + "P-poll__networl_6_4_AskP_4" + "P-poll__networl_6_4_AskP_5" + "P-poll__networl_6_4_AskP_6" + "P-poll__networl_6_4_AskP_7" + "P-poll__networl_6_4_AskP_8" + "P-poll__networl_6_4_AnsP_0" + "P-poll__networl_6_4_AnsP_1" + "P-poll__networl_6_4_AnsP_2" + "P-poll__networl_6_4_AnsP_3" + "P-poll__networl_6_4_AnsP_4" + "P-poll__networl_6_4_AnsP_5" + "P-poll__networl_6_4_AnsP_6" + "P-poll__networl_6_4_AnsP_7" + "P-poll__networl_6_4_AnsP_8" + "P-poll__networl_6_4_RI_0" + "P-poll__networl_6_4_RI_1" + "P-poll__networl_6_4_RI_2" + "P-poll__networl_6_4_RI_3" + "P-poll__networl_6_4_RI_4" + "P-poll__networl_6_4_RI_5" + "P-poll__networl_6_4_RI_6" + "P-poll__networl_6_4_RI_7" + "P-poll__networl_6_4_RI_8" + "P-poll__networl_6_4_AI_0" + "P-poll__networl_6_4_AI_1" + "P-poll__networl_6_4_AI_2" + "P-poll__networl_6_4_AI_3" + "P-poll__networl_6_4_AI_4" + "P-poll__networl_6_4_AI_5" + "P-poll__networl_6_4_AI_6" + "P-poll__networl_6_4_AI_7" + "P-poll__networl_6_4_AI_8" + "P-poll__networl_6_4_AnnP_0" + "P-poll__networl_6_4_AnnP_1" + "P-poll__networl_6_4_AnnP_2" + "P-poll__networl_6_4_AnnP_3" + "P-poll__networl_6_4_AnnP_4" + "P-poll__networl_6_4_AnnP_5" + "P-poll__networl_6_4_AnnP_6" + "P-poll__networl_6_4_AnnP_7" + "P-poll__networl_6_4_AnnP_8" + "P-poll__networl_6_4_RP_0" + "P-poll__networl_6_4_RP_1" + "P-poll__networl_6_4_RP_2" + "P-poll__networl_6_4_RP_3" + "P-poll__networl_6_4_RP_4" + "P-poll__networl_6_4_RP_5" + "P-poll__networl_6_4_RP_6" + "P-poll__networl_6_4_RP_7" + "P-poll__networl_6_4_RP_8" + "P-poll__networl_6_5_AskP_0" + "P-poll__networl_6_5_AskP_1" + "P-poll__networl_6_5_AskP_2" + "P-poll__networl_6_5_AskP_3" + "P-poll__networl_6_5_AskP_4" + "P-poll__networl_6_5_AskP_5" + "P-poll__networl_6_5_AskP_6" + "P-poll__networl_6_5_AskP_7" + "P-poll__networl_6_5_AskP_8" + "P-poll__networl_6_5_AnsP_0" + "P-poll__networl_6_5_AnsP_1" + "P-poll__networl_6_5_AnsP_2" + "P-poll__networl_6_5_AnsP_3" + "P-poll__networl_6_5_AnsP_4" + "P-poll__networl_6_5_AnsP_5" + "P-poll__networl_6_5_AnsP_6" + "P-poll__networl_6_5_AnsP_7" + "P-poll__networl_6_5_AnsP_8" + "P-poll__networl_6_5_RI_0" + "P-poll__networl_6_5_RI_1" + "P-poll__networl_6_5_RI_2" + "P-poll__networl_6_5_RI_3" + "P-poll__networl_6_5_RI_4" + "P-poll__networl_6_5_RI_5" + "P-poll__networl_6_5_RI_6" + "P-poll__networl_6_5_RI_7" + "P-poll__networl_6_5_RI_8" + "P-poll__networl_6_5_AI_0" + "P-poll__networl_6_5_AI_1" + "P-poll__networl_6_5_AI_2" + "P-poll__networl_6_5_AI_3" + "P-poll__networl_6_5_AI_4" + "P-poll__networl_6_5_AI_5" + "P-poll__networl_6_5_AI_6" + "P-poll__networl_6_5_AI_7" + "P-poll__networl_6_5_AI_8" + "P-poll__networl_6_5_AnnP_0" + "P-poll__networl_6_5_AnnP_1" + "P-poll__networl_6_5_AnnP_2" + "P-poll__networl_6_5_AnnP_3" + "P-poll__networl_6_5_AnnP_4" + "P-poll__networl_6_5_AnnP_5" + "P-poll__networl_6_5_AnnP_6" + "P-poll__networl_6_5_AnnP_7" + "P-poll__networl_6_5_AnnP_8" + "P-poll__networl_6_5_RP_0" + "P-poll__networl_6_5_RP_1" + "P-poll__networl_6_5_RP_2" + "P-poll__networl_6_5_RP_3" + "P-poll__networl_6_5_RP_4" + "P-poll__networl_6_5_RP_5" + "P-poll__networl_6_5_RP_6" + "P-poll__networl_6_5_RP_7" + "P-poll__networl_6_5_RP_8" + "P-poll__networl_6_6_AskP_0" + "P-poll__networl_6_6_AskP_1" + "P-poll__networl_6_6_AskP_2" + "P-poll__networl_6_6_AskP_3" + "P-poll__networl_6_6_AskP_4" + "P-poll__networl_6_6_AskP_5" + "P-poll__networl_6_6_AskP_6" + "P-poll__networl_6_6_AskP_7" + "P-poll__networl_6_6_AskP_8" + "P-poll__networl_6_6_AnsP_0" + "P-poll__networl_6_6_AnsP_1" + "P-poll__networl_6_6_AnsP_2" + "P-poll__networl_6_6_AnsP_3" + "P-poll__networl_6_6_AnsP_4" + "P-poll__networl_6_6_AnsP_5" + "P-poll__networl_6_6_AnsP_6" + "P-poll__networl_6_6_AnsP_7" + "P-poll__networl_6_6_AnsP_8" + "P-poll__networl_6_6_RI_0" + "P-poll__networl_6_6_RI_1" + "P-poll__networl_6_6_RI_2" + "P-poll__networl_6_6_RI_3" + "P-poll__networl_6_6_RI_4" + "P-poll__networl_6_6_RI_5" + "P-poll__networl_6_6_RI_6" + "P-poll__networl_6_6_RI_7" + "P-poll__networl_6_6_RI_8" + "P-poll__networl_6_6_AI_0" + "P-poll__networl_6_6_AI_1" + "P-poll__networl_6_6_AI_2" + "P-poll__networl_6_6_AI_3" + "P-poll__networl_6_6_AI_4" + "P-poll__networl_6_6_AI_5" + "P-poll__networl_6_6_AI_6" + "P-poll__networl_6_6_AI_7" + "P-poll__networl_6_6_AI_8" + "P-poll__networl_6_6_AnnP_0" + "P-poll__networl_6_6_AnnP_1" + "P-poll__networl_6_6_AnnP_2" + "P-poll__networl_6_6_AnnP_3" + "P-poll__networl_6_6_AnnP_4" + "P-poll__networl_6_6_AnnP_5" + "P-poll__networl_6_6_AnnP_6" + "P-poll__networl_6_6_AnnP_7" + "P-poll__networl_6_6_AnnP_8" + "P-poll__networl_6_6_RP_0" + "P-poll__networl_6_6_RP_1" + "P-poll__networl_6_6_RP_2" + "P-poll__networl_6_6_RP_3" + "P-poll__networl_6_6_RP_4" + "P-poll__networl_6_6_RP_5" + "P-poll__networl_6_6_RP_6" + "P-poll__networl_6_6_RP_7" + "P-poll__networl_6_6_RP_8" + "P-poll__networl_6_7_AskP_0" + "P-poll__networl_6_7_AskP_1" + "P-poll__networl_6_7_AskP_2" + "P-poll__networl_6_7_AskP_3" + "P-poll__networl_6_7_AskP_4" + "P-poll__networl_6_7_AskP_5" + "P-poll__networl_6_7_AskP_6" + "P-poll__networl_6_7_AskP_7" + "P-poll__networl_6_7_AskP_8" + "P-poll__networl_6_7_AnsP_0" + "P-poll__networl_6_7_AnsP_1" + "P-poll__networl_6_7_AnsP_2" + "P-poll__networl_6_7_AnsP_3" + "P-poll__networl_6_7_AnsP_4" + "P-poll__networl_6_7_AnsP_5" + "P-poll__networl_6_7_AnsP_6" + "P-poll__networl_6_7_AnsP_7" + "P-poll__networl_6_7_AnsP_8" + "P-poll__networl_6_7_RI_0" + "P-poll__networl_6_7_RI_1" + "P-poll__networl_6_7_RI_2" + "P-poll__networl_6_7_RI_3" + "P-poll__networl_6_7_RI_4" + "P-poll__networl_6_7_RI_5" + "P-poll__networl_6_7_RI_6" + "P-poll__networl_6_7_RI_7" + "P-poll__networl_6_7_RI_8" + "P-poll__networl_6_7_AI_0" + "P-poll__networl_6_7_AI_1" + "P-poll__networl_6_7_AI_2" + "P-poll__networl_6_7_AI_3" + "P-poll__networl_6_7_AI_4" + "P-poll__networl_6_7_AI_5" + "P-poll__networl_6_7_AI_6" + "P-poll__networl_6_7_AI_7" + "P-poll__networl_6_7_AI_8" + "P-poll__networl_6_7_AnnP_0" + "P-poll__networl_6_7_AnnP_1" + "P-poll__networl_6_7_AnnP_2" + "P-poll__networl_6_7_AnnP_3" + "P-poll__networl_6_7_AnnP_4" + "P-poll__networl_6_7_AnnP_5" + "P-poll__networl_6_7_AnnP_6" + "P-poll__networl_6_7_AnnP_7" + "P-poll__networl_6_7_AnnP_8" + "P-poll__networl_6_7_RP_0" + "P-poll__networl_6_7_RP_1" + "P-poll__networl_6_7_RP_2" + "P-poll__networl_6_7_RP_3" + "P-poll__networl_6_7_RP_4" + "P-poll__networl_6_7_RP_5" + "P-poll__networl_6_7_RP_6" + "P-poll__networl_6_7_RP_7" + "P-poll__networl_6_7_RP_8" + "P-poll__networl_6_8_AskP_0" + "P-poll__networl_6_8_AskP_1" + "P-poll__networl_6_8_AskP_2" + "P-poll__networl_6_8_AskP_3" + "P-poll__networl_6_8_AskP_4" + "P-poll__networl_6_8_AskP_5" + "P-poll__networl_6_8_AskP_6" + "P-poll__networl_6_8_AskP_7" + "P-poll__networl_6_8_AskP_8" + "P-poll__networl_6_8_AnsP_0" + "P-poll__networl_6_8_AnsP_1" + "P-poll__networl_6_8_AnsP_2" + "P-poll__networl_6_8_AnsP_3" + "P-poll__networl_6_8_AnsP_4" + "P-poll__networl_6_8_AnsP_5" + "P-poll__networl_6_8_AnsP_6" + "P-poll__networl_6_8_AnsP_7" + "P-poll__networl_6_8_AnsP_8" + "P-poll__networl_6_8_RI_0" + "P-poll__networl_6_8_RI_1" + "P-poll__networl_6_8_RI_2" + "P-poll__networl_6_8_RI_3" + "P-poll__networl_6_8_RI_4" + "P-poll__networl_6_8_RI_5" + "P-poll__networl_6_8_RI_6" + "P-poll__networl_6_8_RI_7" + "P-poll__networl_6_8_RI_8" + "P-poll__networl_6_8_AI_0" + "P-poll__networl_6_8_AI_1" + "P-poll__networl_6_8_AI_2" + "P-poll__networl_6_8_AI_3" + "P-poll__networl_6_8_AI_4" + "P-poll__networl_6_8_AI_5" + "P-poll__networl_6_8_AI_6" + "P-poll__networl_6_8_AI_7" + "P-poll__networl_6_8_AI_8" + "P-poll__networl_6_8_AnnP_0" + "P-poll__networl_6_8_AnnP_1" + "P-poll__networl_6_8_AnnP_2" + "P-poll__networl_6_8_AnnP_3" + "P-poll__networl_6_8_AnnP_4" + "P-poll__networl_6_8_AnnP_5" + "P-poll__networl_6_8_AnnP_6" + "P-poll__networl_6_8_AnnP_7" + "P-poll__networl_6_8_AnnP_8" + "P-poll__networl_6_8_RP_0" + "P-poll__networl_6_8_RP_1" + "P-poll__networl_6_8_RP_2" + "P-poll__networl_6_8_RP_3" + "P-poll__networl_6_8_RP_4" + "P-poll__networl_6_8_RP_5" + "P-poll__networl_6_8_RP_6" + "P-poll__networl_6_8_RP_7" + "P-poll__networl_6_8_RP_8" + "P-poll__networl_7_0_AskP_0" + "P-poll__networl_7_0_AskP_1" + "P-poll__networl_7_0_AskP_2" + "P-poll__networl_7_0_AskP_3" + "P-poll__networl_7_0_AskP_4" + "P-poll__networl_7_0_AskP_5" + "P-poll__networl_7_0_AskP_6" + "P-poll__networl_7_0_AskP_7" + "P-poll__networl_7_0_AskP_8" + "P-poll__networl_7_0_AnsP_0" + "P-poll__networl_7_0_AnsP_1" + "P-poll__networl_7_0_AnsP_2" + "P-poll__networl_7_0_AnsP_3" + "P-poll__networl_7_0_AnsP_4" + "P-poll__networl_7_0_AnsP_5" + "P-poll__networl_7_0_AnsP_6" + "P-poll__networl_7_0_AnsP_7" + "P-poll__networl_7_0_AnsP_8" + "P-poll__networl_7_0_RI_0" + "P-poll__networl_7_0_RI_1" + "P-poll__networl_7_0_RI_2" + "P-poll__networl_7_0_RI_3" + "P-poll__networl_7_0_RI_4" + "P-poll__networl_7_0_RI_5" + "P-poll__networl_7_0_RI_6" + "P-poll__networl_7_0_RI_7" + "P-poll__networl_7_0_RI_8" + "P-poll__networl_7_0_AI_0" + "P-poll__networl_7_0_AI_1" + "P-poll__networl_7_0_AI_2" + "P-poll__networl_7_0_AI_3" + "P-poll__networl_7_0_AI_4" + "P-poll__networl_7_0_AI_5" + "P-poll__networl_7_0_AI_6" + "P-poll__networl_7_0_AI_7" + "P-poll__networl_7_0_AI_8" + "P-poll__networl_7_0_AnnP_0" + "P-poll__networl_7_0_AnnP_1" + "P-poll__networl_7_0_AnnP_2" + "P-poll__networl_7_0_AnnP_3" + "P-poll__networl_7_0_AnnP_4" + "P-poll__networl_7_0_AnnP_5" + "P-poll__networl_7_0_AnnP_6" + "P-poll__networl_7_0_AnnP_7" + "P-poll__networl_7_0_AnnP_8" + "P-poll__networl_7_0_RP_0" + "P-poll__networl_7_0_RP_1" + "P-poll__networl_7_0_RP_2" + "P-poll__networl_7_0_RP_3" + "P-poll__networl_7_0_RP_4" + "P-poll__networl_7_0_RP_5" + "P-poll__networl_7_0_RP_6" + "P-poll__networl_7_0_RP_7" + "P-poll__networl_7_0_RP_8" + "P-poll__networl_7_1_AskP_0" + "P-poll__networl_7_1_AskP_1" + "P-poll__networl_7_1_AskP_2" + "P-poll__networl_7_1_AskP_3" + "P-poll__networl_7_1_AskP_4" + "P-poll__networl_7_1_AskP_5" + "P-poll__networl_7_1_AskP_6" + "P-poll__networl_7_1_AskP_7" + "P-poll__networl_7_1_AskP_8" + "P-poll__networl_7_1_AnsP_0" + "P-poll__networl_7_1_AnsP_1" + "P-poll__networl_7_1_AnsP_2" + "P-poll__networl_7_1_AnsP_3" + "P-poll__networl_7_1_AnsP_4" + "P-poll__networl_7_1_AnsP_5" + "P-poll__networl_7_1_AnsP_6" + "P-poll__networl_7_1_AnsP_7" + "P-poll__networl_7_1_AnsP_8" + "P-poll__networl_7_1_RI_0" + "P-poll__networl_7_1_RI_1" + "P-poll__networl_7_1_RI_2" + "P-poll__networl_7_1_RI_3" + "P-poll__networl_7_1_RI_4" + "P-poll__networl_7_1_RI_5" + "P-poll__networl_7_1_RI_6" + "P-poll__networl_7_1_RI_7" + "P-poll__networl_7_1_RI_8" + "P-poll__networl_7_1_AI_0" + "P-poll__networl_7_1_AI_1" + "P-poll__networl_7_1_AI_2" + "P-poll__networl_7_1_AI_3" + "P-poll__networl_7_1_AI_4" + "P-poll__networl_7_1_AI_5" + "P-poll__networl_7_1_AI_6" + "P-poll__networl_7_1_AI_7" + "P-poll__networl_7_1_AI_8" + "P-poll__networl_7_1_AnnP_0" + "P-poll__networl_7_1_AnnP_1" + "P-poll__networl_7_1_AnnP_2" + "P-poll__networl_7_1_AnnP_3" + "P-poll__networl_7_1_AnnP_4" + "P-poll__networl_7_1_AnnP_5" + "P-poll__networl_7_1_AnnP_6" + "P-poll__networl_7_1_AnnP_7" + "P-poll__networl_7_1_AnnP_8" + "P-poll__networl_7_1_RP_0" + "P-poll__networl_7_1_RP_1" + "P-poll__networl_7_1_RP_2" + "P-poll__networl_7_1_RP_3" + "P-poll__networl_7_1_RP_4" + "P-poll__networl_7_1_RP_5" + "P-poll__networl_7_1_RP_6" + "P-poll__networl_7_1_RP_7" + "P-poll__networl_7_1_RP_8" + "P-poll__networl_7_2_AskP_0" + "P-poll__networl_7_2_AskP_1" + "P-poll__networl_7_2_AskP_2" + "P-poll__networl_7_2_AskP_3" + "P-poll__networl_7_2_AskP_4" + "P-poll__networl_7_2_AskP_5" + "P-poll__networl_7_2_AskP_6" + "P-poll__networl_7_2_AskP_7" + "P-poll__networl_7_2_AskP_8" + "P-poll__networl_7_2_AnsP_0" + "P-poll__networl_7_2_AnsP_1" + "P-poll__networl_7_2_AnsP_2" + "P-poll__networl_7_2_AnsP_3" + "P-poll__networl_7_2_AnsP_4" + "P-poll__networl_7_2_AnsP_5" + "P-poll__networl_7_2_AnsP_6" + "P-poll__networl_7_2_AnsP_7" + "P-poll__networl_7_2_AnsP_8" + "P-poll__networl_7_2_RI_0" + "P-poll__networl_7_2_RI_1" + "P-poll__networl_7_2_RI_2" + "P-poll__networl_7_2_RI_3" + "P-poll__networl_7_2_RI_4" + "P-poll__networl_7_2_RI_5" + "P-poll__networl_7_2_RI_6" + "P-poll__networl_7_2_RI_7" + "P-poll__networl_7_2_RI_8" + "P-poll__networl_7_2_AI_0" + "P-poll__networl_7_2_AI_1" + "P-poll__networl_7_2_AI_2" + "P-poll__networl_7_2_AI_3" + "P-poll__networl_7_2_AI_4" + "P-poll__networl_7_2_AI_5" + "P-poll__networl_7_2_AI_6" + "P-poll__networl_7_2_AI_7" + "P-poll__networl_7_2_AI_8" + "P-poll__networl_7_2_AnnP_0" + "P-poll__networl_7_2_AnnP_1" + "P-poll__networl_7_2_AnnP_2" + "P-poll__networl_7_2_AnnP_3" + "P-poll__networl_7_2_AnnP_4" + "P-poll__networl_7_2_AnnP_5" + "P-poll__networl_7_2_AnnP_6" + "P-poll__networl_7_2_AnnP_7" + "P-poll__networl_7_2_AnnP_8" + "P-poll__networl_7_2_RP_0" + "P-poll__networl_7_2_RP_1" + "P-poll__networl_7_2_RP_2" + "P-poll__networl_7_2_RP_3" + "P-poll__networl_7_2_RP_4" + "P-poll__networl_7_2_RP_5" + "P-poll__networl_7_2_RP_6" + "P-poll__networl_7_2_RP_7" + "P-poll__networl_7_2_RP_8" + "P-poll__networl_7_3_AskP_0" + "P-poll__networl_7_3_AskP_1" + "P-poll__networl_7_3_AskP_2" + "P-poll__networl_7_3_AskP_3" + "P-poll__networl_7_3_AskP_4" + "P-poll__networl_7_3_AskP_5" + "P-poll__networl_7_3_AskP_6" + "P-poll__networl_7_3_AskP_7" + "P-poll__networl_7_3_AskP_8" + "P-poll__networl_7_3_AnsP_0" + "P-poll__networl_7_3_AnsP_1" + "P-poll__networl_7_3_AnsP_2" + "P-poll__networl_7_3_AnsP_3" + "P-poll__networl_7_3_AnsP_4" + "P-poll__networl_7_3_AnsP_5" + "P-poll__networl_7_3_AnsP_6" + "P-poll__networl_7_3_AnsP_7" + "P-poll__networl_7_3_AnsP_8" + "P-poll__networl_7_3_RI_0" + "P-poll__networl_7_3_RI_1" + "P-poll__networl_7_3_RI_2" + "P-poll__networl_7_3_RI_3" + "P-poll__networl_7_3_RI_4" + "P-poll__networl_7_3_RI_5" + "P-poll__networl_7_3_RI_6" + "P-poll__networl_7_3_RI_7" + "P-poll__networl_7_3_RI_8" + "P-poll__networl_7_3_AI_0" + "P-poll__networl_7_3_AI_1" + "P-poll__networl_7_3_AI_2" + "P-poll__networl_7_3_AI_3" + "P-poll__networl_7_3_AI_4" + "P-poll__networl_7_3_AI_5" + "P-poll__networl_7_3_AI_6" + "P-poll__networl_7_3_AI_7" + "P-poll__networl_7_3_AI_8" + "P-poll__networl_7_3_AnnP_0" + "P-poll__networl_7_3_AnnP_1" + "P-poll__networl_7_3_AnnP_2" + "P-poll__networl_7_3_AnnP_3" + "P-poll__networl_7_3_AnnP_4" + "P-poll__networl_7_3_AnnP_5" + "P-poll__networl_7_3_AnnP_6" + "P-poll__networl_7_3_AnnP_7" + "P-poll__networl_7_3_AnnP_8" + "P-poll__networl_7_3_RP_0" + "P-poll__networl_7_3_RP_1" + "P-poll__networl_7_3_RP_2" + "P-poll__networl_7_3_RP_3" + "P-poll__networl_7_3_RP_4" + "P-poll__networl_7_3_RP_5" + "P-poll__networl_7_3_RP_6" + "P-poll__networl_7_3_RP_7" + "P-poll__networl_7_3_RP_8" + "P-poll__networl_7_4_AskP_0" + "P-poll__networl_7_4_AskP_1" + "P-poll__networl_7_4_AskP_2" + "P-poll__networl_7_4_AskP_3" + "P-poll__networl_7_4_AskP_4" + "P-poll__networl_7_4_AskP_5" + "P-poll__networl_7_4_AskP_6" + "P-poll__networl_7_4_AskP_7" + "P-poll__networl_7_4_AskP_8" + "P-poll__networl_7_4_AnsP_0" + "P-poll__networl_7_4_AnsP_1" + "P-poll__networl_7_4_AnsP_2" + "P-poll__networl_7_4_AnsP_3" + "P-poll__networl_7_4_AnsP_4" + "P-poll__networl_7_4_AnsP_5" + "P-poll__networl_7_4_AnsP_6" + "P-poll__networl_7_4_AnsP_7" + "P-poll__networl_7_4_AnsP_8" + "P-poll__networl_7_4_RI_0" + "P-poll__networl_7_4_RI_1" + "P-poll__networl_7_4_RI_2" + "P-poll__networl_7_4_RI_3" + "P-poll__networl_7_4_RI_4" + "P-poll__networl_7_4_RI_5" + "P-poll__networl_7_4_RI_6" + "P-poll__networl_7_4_RI_7" + "P-poll__networl_7_4_RI_8" + "P-poll__networl_7_4_AI_0" + "P-poll__networl_7_4_AI_1" + "P-poll__networl_7_4_AI_2" + "P-poll__networl_7_4_AI_3" + "P-poll__networl_7_4_AI_4" + "P-poll__networl_7_4_AI_5" + "P-poll__networl_7_4_AI_6" + "P-poll__networl_7_4_AI_7" + "P-poll__networl_7_4_AI_8" + "P-poll__networl_7_4_AnnP_0" + "P-poll__networl_7_4_AnnP_1" + "P-poll__networl_7_4_AnnP_2" + "P-poll__networl_7_4_AnnP_3" + "P-poll__networl_7_4_AnnP_4" + "P-poll__networl_7_4_AnnP_5" + "P-poll__networl_7_4_AnnP_6" + "P-poll__networl_7_4_AnnP_7" + "P-poll__networl_7_4_AnnP_8" + "P-poll__networl_7_4_RP_0" + "P-poll__networl_7_4_RP_1" + "P-poll__networl_7_4_RP_2" + "P-poll__networl_7_4_RP_3" + "P-poll__networl_7_4_RP_4" + "P-poll__networl_7_4_RP_5" + "P-poll__networl_7_4_RP_6" + "P-poll__networl_7_4_RP_7" + "P-poll__networl_7_4_RP_8" + "P-poll__networl_7_5_AskP_0" + "P-poll__networl_7_5_AskP_1" + "P-poll__networl_7_5_AskP_2" + "P-poll__networl_7_5_AskP_3" + "P-poll__networl_7_5_AskP_4" + "P-poll__networl_7_5_AskP_5" + "P-poll__networl_7_5_AskP_6" + "P-poll__networl_7_5_AskP_7" + "P-poll__networl_7_5_AskP_8" + "P-poll__networl_7_5_AnsP_0" + "P-poll__networl_7_5_AnsP_1" + "P-poll__networl_7_5_AnsP_2" + "P-poll__networl_7_5_AnsP_3" + "P-poll__networl_7_5_AnsP_4" + "P-poll__networl_7_5_AnsP_5" + "P-poll__networl_7_5_AnsP_6" + "P-poll__networl_7_5_AnsP_7" + "P-poll__networl_7_5_AnsP_8" + "P-poll__networl_7_5_RI_0" + "P-poll__networl_7_5_RI_1" + "P-poll__networl_7_5_RI_2" + "P-poll__networl_7_5_RI_3" + "P-poll__networl_7_5_RI_4" + "P-poll__networl_7_5_RI_5" + "P-poll__networl_7_5_RI_6" + "P-poll__networl_7_5_RI_7" + "P-poll__networl_7_5_RI_8" + "P-poll__networl_7_5_AI_0" + "P-poll__networl_7_5_AI_1" + "P-poll__networl_7_5_AI_2" + "P-poll__networl_7_5_AI_3" + "P-poll__networl_7_5_AI_4" + "P-poll__networl_7_5_AI_5" + "P-poll__networl_7_5_AI_6" + "P-poll__networl_7_5_AI_7" + "P-poll__networl_7_5_AI_8" + "P-poll__networl_7_5_AnnP_0" + "P-poll__networl_7_5_AnnP_1" + "P-poll__networl_7_5_AnnP_2" + "P-poll__networl_7_5_AnnP_3" + "P-poll__networl_7_5_AnnP_4" + "P-poll__networl_7_5_AnnP_5" + "P-poll__networl_7_5_AnnP_6" + "P-poll__networl_7_5_AnnP_7" + "P-poll__networl_7_5_AnnP_8" + "P-poll__networl_7_5_RP_0" + "P-poll__networl_7_5_RP_1" + "P-poll__networl_7_5_RP_2" + "P-poll__networl_7_5_RP_3" + "P-poll__networl_7_5_RP_4" + "P-poll__networl_7_5_RP_5" + "P-poll__networl_7_5_RP_6" + "P-poll__networl_7_5_RP_7" + "P-poll__networl_7_5_RP_8" + "P-poll__networl_7_6_AskP_0" + "P-poll__networl_7_6_AskP_1" + "P-poll__networl_7_6_AskP_2" + "P-poll__networl_7_6_AskP_3" + "P-poll__networl_7_6_AskP_4" + "P-poll__networl_7_6_AskP_5" + "P-poll__networl_7_6_AskP_6" + "P-poll__networl_7_6_AskP_7" + "P-poll__networl_7_6_AskP_8" + "P-poll__networl_7_6_AnsP_0" + "P-poll__networl_7_6_AnsP_1" + "P-poll__networl_7_6_AnsP_2" + "P-poll__networl_7_6_AnsP_3" + "P-poll__networl_7_6_AnsP_4" + "P-poll__networl_7_6_AnsP_5" + "P-poll__networl_7_6_AnsP_6" + "P-poll__networl_7_6_AnsP_7" + "P-poll__networl_7_6_AnsP_8" + "P-poll__networl_7_6_RI_0" + "P-poll__networl_7_6_RI_1" + "P-poll__networl_7_6_RI_2" + "P-poll__networl_7_6_RI_3" + "P-poll__networl_7_6_RI_4" + "P-poll__networl_7_6_RI_5" + "P-poll__networl_7_6_RI_6" + "P-poll__networl_7_6_RI_7" + "P-poll__networl_7_6_RI_8" + "P-poll__networl_7_6_AI_0" + "P-poll__networl_7_6_AI_1" + "P-poll__networl_7_6_AI_2" + "P-poll__networl_7_6_AI_3" + "P-poll__networl_7_6_AI_4" + "P-poll__networl_7_6_AI_5" + "P-poll__networl_7_6_AI_6" + "P-poll__networl_7_6_AI_7" + "P-poll__networl_7_6_AI_8" + "P-poll__networl_7_6_AnnP_0" + "P-poll__networl_7_6_AnnP_1" + "P-poll__networl_7_6_AnnP_2" + "P-poll__networl_7_6_AnnP_3" + "P-poll__networl_7_6_AnnP_4" + "P-poll__networl_7_6_AnnP_5" + "P-poll__networl_7_6_AnnP_6" + "P-poll__networl_7_6_AnnP_7" + "P-poll__networl_7_6_AnnP_8" + "P-poll__networl_7_6_RP_0" + "P-poll__networl_7_6_RP_1" + "P-poll__networl_7_6_RP_2" + "P-poll__networl_7_6_RP_3" + "P-poll__networl_7_6_RP_4" + "P-poll__networl_7_6_RP_5" + "P-poll__networl_7_6_RP_6" + "P-poll__networl_7_6_RP_7" + "P-poll__networl_7_6_RP_8" + "P-poll__networl_7_7_AskP_0" + "P-poll__networl_7_7_AskP_1" + "P-poll__networl_7_7_AskP_2" + "P-poll__networl_7_7_AskP_3" + "P-poll__networl_7_7_AskP_4" + "P-poll__networl_7_7_AskP_5" + "P-poll__networl_7_7_AskP_6" + "P-poll__networl_7_7_AskP_7" + "P-poll__networl_7_7_AskP_8" + "P-poll__networl_7_7_AnsP_0" + "P-poll__networl_7_7_AnsP_1" + "P-poll__networl_7_7_AnsP_2" + "P-poll__networl_7_7_AnsP_3" + "P-poll__networl_7_7_AnsP_4" + "P-poll__networl_7_7_AnsP_5" + "P-poll__networl_7_7_AnsP_6" + "P-poll__networl_7_7_AnsP_7" + "P-poll__networl_7_7_AnsP_8" + "P-poll__networl_7_7_RI_0" + "P-poll__networl_7_7_RI_1" + "P-poll__networl_7_7_RI_2" + "P-poll__networl_7_7_RI_3" + "P-poll__networl_7_7_RI_4" + "P-poll__networl_7_7_RI_5" + "P-poll__networl_7_7_RI_6" + "P-poll__networl_7_7_RI_7" + "P-poll__networl_7_7_RI_8" + "P-poll__networl_7_7_AI_0" + "P-poll__networl_7_7_AI_1" + "P-poll__networl_7_7_AI_2" + "P-poll__networl_7_7_AI_3" + "P-poll__networl_7_7_AI_4" + "P-poll__networl_7_7_AI_5" + "P-poll__networl_7_7_AI_6" + "P-poll__networl_7_7_AI_7" + "P-poll__networl_7_7_AI_8" + "P-poll__networl_7_7_AnnP_0" + "P-poll__networl_7_7_AnnP_1" + "P-poll__networl_7_7_AnnP_2" + "P-poll__networl_7_7_AnnP_3" + "P-poll__networl_7_7_AnnP_4" + "P-poll__networl_7_7_AnnP_5" + "P-poll__networl_7_7_AnnP_6" + "P-poll__networl_7_7_AnnP_7" + "P-poll__networl_7_7_AnnP_8" + "P-poll__networl_7_7_RP_0" + "P-poll__networl_7_7_RP_1" + "P-poll__networl_7_7_RP_2" + "P-poll__networl_7_7_RP_3" + "P-poll__networl_7_7_RP_4" + "P-poll__networl_7_7_RP_5" + "P-poll__networl_7_7_RP_6" + "P-poll__networl_7_7_RP_7" + "P-poll__networl_7_7_RP_8" + "P-poll__networl_7_8_AskP_0" + "P-poll__networl_7_8_AskP_1" + "P-poll__networl_7_8_AskP_2" + "P-poll__networl_7_8_AskP_3" + "P-poll__networl_7_8_AskP_4" + "P-poll__networl_7_8_AskP_5" + "P-poll__networl_7_8_AskP_6" + "P-poll__networl_7_8_AskP_7" + "P-poll__networl_7_8_AskP_8" + "P-poll__networl_7_8_AnsP_0" + "P-poll__networl_7_8_AnsP_1" + "P-poll__networl_7_8_AnsP_2" + "P-poll__networl_7_8_AnsP_3" + "P-poll__networl_7_8_AnsP_4" + "P-poll__networl_7_8_AnsP_5" + "P-poll__networl_7_8_AnsP_6" + "P-poll__networl_7_8_AnsP_7" + "P-poll__networl_7_8_AnsP_8" + "P-poll__networl_7_8_RI_0" + "P-poll__networl_7_8_RI_1" + "P-poll__networl_7_8_RI_2" + "P-poll__networl_7_8_RI_3" + "P-poll__networl_7_8_RI_4" + "P-poll__networl_7_8_RI_5" + "P-poll__networl_7_8_RI_6" + "P-poll__networl_7_8_RI_7" + "P-poll__networl_7_8_RI_8" + "P-poll__networl_7_8_AI_0" + "P-poll__networl_7_8_AI_1" + "P-poll__networl_7_8_AI_2" + "P-poll__networl_7_8_AI_3" + "P-poll__networl_7_8_AI_4" + "P-poll__networl_7_8_AI_5" + "P-poll__networl_7_8_AI_6" + "P-poll__networl_7_8_AI_7" + "P-poll__networl_7_8_AI_8" + "P-poll__networl_7_8_AnnP_0" + "P-poll__networl_7_8_AnnP_1" + "P-poll__networl_7_8_AnnP_2" + "P-poll__networl_7_8_AnnP_3" + "P-poll__networl_7_8_AnnP_4" + "P-poll__networl_7_8_AnnP_5" + "P-poll__networl_7_8_AnnP_6" + "P-poll__networl_7_8_AnnP_7" + "P-poll__networl_7_8_AnnP_8" + "P-poll__networl_7_8_RP_0" + "P-poll__networl_7_8_RP_1" + "P-poll__networl_7_8_RP_2" + "P-poll__networl_7_8_RP_3" + "P-poll__networl_7_8_RP_4" + "P-poll__networl_7_8_RP_5" + "P-poll__networl_7_8_RP_6" + "P-poll__networl_7_8_RP_7" + "P-poll__networl_7_8_RP_8" + "P-poll__networl_8_0_AskP_0" + "P-poll__networl_8_0_AskP_1" + "P-poll__networl_8_0_AskP_2" + "P-poll__networl_8_0_AskP_3" + "P-poll__networl_8_0_AskP_4" + "P-poll__networl_8_0_AskP_5" + "P-poll__networl_8_0_AskP_6" + "P-poll__networl_8_0_AskP_7" + "P-poll__networl_8_0_AskP_8" + "P-poll__networl_8_0_AnsP_0" + "P-poll__networl_8_0_AnsP_1" + "P-poll__networl_8_0_AnsP_2" + "P-poll__networl_8_0_AnsP_3" + "P-poll__networl_8_0_AnsP_4" + "P-poll__networl_8_0_AnsP_5" + "P-poll__networl_8_0_AnsP_6" + "P-poll__networl_8_0_AnsP_7" + "P-poll__networl_8_0_AnsP_8" + "P-poll__networl_8_0_RI_0" + "P-poll__networl_8_0_RI_1" + "P-poll__networl_8_0_RI_2" + "P-poll__networl_8_0_RI_3" + "P-poll__networl_8_0_RI_4" + "P-poll__networl_8_0_RI_5" + "P-poll__networl_8_0_RI_6" + "P-poll__networl_8_0_RI_7" + "P-poll__networl_8_0_RI_8" + "P-poll__networl_8_0_AI_0" + "P-poll__networl_8_0_AI_1" + "P-poll__networl_8_0_AI_2" + "P-poll__networl_8_0_AI_3" + "P-poll__networl_8_0_AI_4" + "P-poll__networl_8_0_AI_5" + "P-poll__networl_8_0_AI_6" + "P-poll__networl_8_0_AI_7" + "P-poll__networl_8_0_AI_8" + "P-poll__networl_8_0_AnnP_0" + "P-poll__networl_8_0_AnnP_1" + "P-poll__networl_8_0_AnnP_2" + "P-poll__networl_8_0_AnnP_3" + "P-poll__networl_8_0_AnnP_4" + "P-poll__networl_8_0_AnnP_5" + "P-poll__networl_8_0_AnnP_6" + "P-poll__networl_8_0_AnnP_7" + "P-poll__networl_8_0_AnnP_8" + "P-poll__networl_8_0_RP_0" + "P-poll__networl_8_0_RP_1" + "P-poll__networl_8_0_RP_2" + "P-poll__networl_8_0_RP_3" + "P-poll__networl_8_0_RP_4" + "P-poll__networl_8_0_RP_5" + "P-poll__networl_8_0_RP_6" + "P-poll__networl_8_0_RP_7" + "P-poll__networl_8_0_RP_8" + "P-poll__networl_8_1_AskP_0" + "P-poll__networl_8_1_AskP_1" + "P-poll__networl_8_1_AskP_2" + "P-poll__networl_8_1_AskP_3" + "P-poll__networl_8_1_AskP_4" + "P-poll__networl_8_1_AskP_5" + "P-poll__networl_8_1_AskP_6" + "P-poll__networl_8_1_AskP_7" + "P-poll__networl_8_1_AskP_8" + "P-poll__networl_8_1_AnsP_0" + "P-poll__networl_8_1_AnsP_1" + "P-poll__networl_8_1_AnsP_2" + "P-poll__networl_8_1_AnsP_3" + "P-poll__networl_8_1_AnsP_4" + "P-poll__networl_8_1_AnsP_5" + "P-poll__networl_8_1_AnsP_6" + "P-poll__networl_8_1_AnsP_7" + "P-poll__networl_8_1_AnsP_8" + "P-poll__networl_8_1_RI_0" + "P-poll__networl_8_1_RI_1" + "P-poll__networl_8_1_RI_2" + "P-poll__networl_8_1_RI_3" + "P-poll__networl_8_1_RI_4" + "P-poll__networl_8_1_RI_5" + "P-poll__networl_8_1_RI_6" + "P-poll__networl_8_1_RI_7" + "P-poll__networl_8_1_RI_8" + "P-poll__networl_8_1_AI_0" + "P-poll__networl_8_1_AI_1" + "P-poll__networl_8_1_AI_2" + "P-poll__networl_8_1_AI_3" + "P-poll__networl_8_1_AI_4" + "P-poll__networl_8_1_AI_5" + "P-poll__networl_8_1_AI_6" + "P-poll__networl_8_1_AI_7" + "P-poll__networl_8_1_AI_8" + "P-poll__networl_8_1_AnnP_0" + "P-poll__networl_8_1_AnnP_1" + "P-poll__networl_8_1_AnnP_2" + "P-poll__networl_8_1_AnnP_3" + "P-poll__networl_8_1_AnnP_4" + "P-poll__networl_8_1_AnnP_5" + "P-poll__networl_8_1_AnnP_6" + "P-poll__networl_8_1_AnnP_7" + "P-poll__networl_8_1_AnnP_8" + "P-poll__networl_8_1_RP_0" + "P-poll__networl_8_1_RP_1" + "P-poll__networl_8_1_RP_2" + "P-poll__networl_8_1_RP_3" + "P-poll__networl_8_1_RP_4" + "P-poll__networl_8_1_RP_5" + "P-poll__networl_8_1_RP_6" + "P-poll__networl_8_1_RP_7" + "P-poll__networl_8_1_RP_8" + "P-poll__networl_8_2_AskP_0" + "P-poll__networl_8_2_AskP_1" + "P-poll__networl_8_2_AskP_2" + "P-poll__networl_8_2_AskP_3" + "P-poll__networl_8_2_AskP_4" + "P-poll__networl_8_2_AskP_5" + "P-poll__networl_8_2_AskP_6" + "P-poll__networl_8_2_AskP_7" + "P-poll__networl_8_2_AskP_8" + "P-poll__networl_8_2_AnsP_0" + "P-poll__networl_8_2_AnsP_1" + "P-poll__networl_8_2_AnsP_2" + "P-poll__networl_8_2_AnsP_3" + "P-poll__networl_8_2_AnsP_4" + "P-poll__networl_8_2_AnsP_5" + "P-poll__networl_8_2_AnsP_6" + "P-poll__networl_8_2_AnsP_7" + "P-poll__networl_8_2_AnsP_8" + "P-poll__networl_8_2_RI_0" + "P-poll__networl_8_2_RI_1" + "P-poll__networl_8_2_RI_2" + "P-poll__networl_8_2_RI_3" + "P-poll__networl_8_2_RI_4" + "P-poll__networl_8_2_RI_5" + "P-poll__networl_8_2_RI_6" + "P-poll__networl_8_2_RI_7" + "P-poll__networl_8_2_RI_8" + "P-poll__networl_8_2_AI_0" + "P-poll__networl_8_2_AI_1" + "P-poll__networl_8_2_AI_2" + "P-poll__networl_8_2_AI_3" + "P-poll__networl_8_2_AI_4" + "P-poll__networl_8_2_AI_5" + "P-poll__networl_8_2_AI_6" + "P-poll__networl_8_2_AI_7" + "P-poll__networl_8_2_AI_8" + "P-poll__networl_8_2_AnnP_0" + "P-poll__networl_8_2_AnnP_1" + "P-poll__networl_8_2_AnnP_2" + "P-poll__networl_8_2_AnnP_3" + "P-poll__networl_8_2_AnnP_4" + "P-poll__networl_8_2_AnnP_5" + "P-poll__networl_8_2_AnnP_6" + "P-poll__networl_8_2_AnnP_7" + "P-poll__networl_8_2_AnnP_8" + "P-poll__networl_8_2_RP_0" + "P-poll__networl_8_2_RP_1" + "P-poll__networl_8_2_RP_2" + "P-poll__networl_8_2_RP_3" + "P-poll__networl_8_2_RP_4" + "P-poll__networl_8_2_RP_5" + "P-poll__networl_8_2_RP_6" + "P-poll__networl_8_2_RP_7" + "P-poll__networl_8_2_RP_8" + "P-poll__networl_8_3_AskP_0" + "P-poll__networl_8_3_AskP_1" + "P-poll__networl_8_3_AskP_2" + "P-poll__networl_8_3_AskP_3" + "P-poll__networl_8_3_AskP_4" + "P-poll__networl_8_3_AskP_5" + "P-poll__networl_8_3_AskP_6" + "P-poll__networl_8_3_AskP_7" + "P-poll__networl_8_3_AskP_8" + "P-poll__networl_8_3_AnsP_0" + "P-poll__networl_8_3_AnsP_1" + "P-poll__networl_8_3_AnsP_2" + "P-poll__networl_8_3_AnsP_3" + "P-poll__networl_8_3_AnsP_4" + "P-poll__networl_8_3_AnsP_5" + "P-poll__networl_8_3_AnsP_6" + "P-poll__networl_8_3_AnsP_7" + "P-poll__networl_8_3_AnsP_8" + "P-poll__networl_8_3_RI_0" + "P-poll__networl_8_3_RI_1" + "P-poll__networl_8_3_RI_2" + "P-poll__networl_8_3_RI_3" + "P-poll__networl_8_3_RI_4" + "P-poll__networl_8_3_RI_5" + "P-poll__networl_8_3_RI_6" + "P-poll__networl_8_3_RI_7" + "P-poll__networl_8_3_RI_8" + "P-poll__networl_8_3_AI_0" + "P-poll__networl_8_3_AI_1" + "P-poll__networl_8_3_AI_2" + "P-poll__networl_8_3_AI_3" + "P-poll__networl_8_3_AI_4" + "P-poll__networl_8_3_AI_5" + "P-poll__networl_8_3_AI_6" + "P-poll__networl_8_3_AI_7" + "P-poll__networl_8_3_AI_8" + "P-poll__networl_8_3_AnnP_0" + "P-poll__networl_8_3_AnnP_1" + "P-poll__networl_8_3_AnnP_2" + "P-poll__networl_8_3_AnnP_3" + "P-poll__networl_8_3_AnnP_4" + "P-poll__networl_8_3_AnnP_5" + "P-poll__networl_8_3_AnnP_6" + "P-poll__networl_8_3_AnnP_7" + "P-poll__networl_8_3_AnnP_8" + "P-poll__networl_8_3_RP_0" + "P-poll__networl_8_3_RP_1" + "P-poll__networl_8_3_RP_2" + "P-poll__networl_8_3_RP_3" + "P-poll__networl_8_3_RP_4" + "P-poll__networl_8_3_RP_5" + "P-poll__networl_8_3_RP_6" + "P-poll__networl_8_3_RP_7" + "P-poll__networl_8_3_RP_8" + "P-poll__networl_8_4_AskP_0" + "P-poll__networl_8_4_AskP_1" + "P-poll__networl_8_4_AskP_2" + "P-poll__networl_8_4_AskP_3" + "P-poll__networl_8_4_AskP_4" + "P-poll__networl_8_4_AskP_5" + "P-poll__networl_8_4_AskP_6" + "P-poll__networl_8_4_AskP_7" + "P-poll__networl_8_4_AskP_8" + "P-poll__networl_8_4_AnsP_0" + "P-poll__networl_8_4_AnsP_1" + "P-poll__networl_8_4_AnsP_2" + "P-poll__networl_8_4_AnsP_3" + "P-poll__networl_8_4_AnsP_4" + "P-poll__networl_8_4_AnsP_5" + "P-poll__networl_8_4_AnsP_6" + "P-poll__networl_8_4_AnsP_7" + "P-poll__networl_8_4_AnsP_8" + "P-poll__networl_8_4_RI_0" + "P-poll__networl_8_4_RI_1" + "P-poll__networl_8_4_RI_2" + "P-poll__networl_8_4_RI_3" + "P-poll__networl_8_4_RI_4" + "P-poll__networl_8_4_RI_5" + "P-poll__networl_8_4_RI_6" + "P-poll__networl_8_4_RI_7" + "P-poll__networl_8_4_RI_8" + "P-poll__networl_8_4_AI_0" + "P-poll__networl_8_4_AI_1" + "P-poll__networl_8_4_AI_2" + "P-poll__networl_8_4_AI_3" + "P-poll__networl_8_4_AI_4" + "P-poll__networl_8_4_AI_5" + "P-poll__networl_8_4_AI_6" + "P-poll__networl_8_4_AI_7" + "P-poll__networl_8_4_AI_8" + "P-poll__networl_8_4_AnnP_0" + "P-poll__networl_8_4_AnnP_1" + "P-poll__networl_8_4_AnnP_2" + "P-poll__networl_8_4_AnnP_3" + "P-poll__networl_8_4_AnnP_4" + "P-poll__networl_8_4_AnnP_5" + "P-poll__networl_8_4_AnnP_6" + "P-poll__networl_8_4_AnnP_7" + "P-poll__networl_8_4_AnnP_8" + "P-poll__networl_8_4_RP_0" + "P-poll__networl_8_4_RP_1" + "P-poll__networl_8_4_RP_2" + "P-poll__networl_8_4_RP_3" + "P-poll__networl_8_4_RP_4" + "P-poll__networl_8_4_RP_5" + "P-poll__networl_8_4_RP_6" + "P-poll__networl_8_4_RP_7" + "P-poll__networl_8_4_RP_8" + "P-poll__networl_8_5_AskP_0" + "P-poll__networl_8_5_AskP_1" + "P-poll__networl_8_5_AskP_2" + "P-poll__networl_8_5_AskP_3" + "P-poll__networl_8_5_AskP_4" + "P-poll__networl_8_5_AskP_5" + "P-poll__networl_8_5_AskP_6" + "P-poll__networl_8_5_AskP_7" + "P-poll__networl_8_5_AskP_8" + "P-poll__networl_8_5_AnsP_0" + "P-poll__networl_8_5_AnsP_1" + "P-poll__networl_8_5_AnsP_2" + "P-poll__networl_8_5_AnsP_3" + "P-poll__networl_8_5_AnsP_4" + "P-poll__networl_8_5_AnsP_5" + "P-poll__networl_8_5_AnsP_6" + "P-poll__networl_8_5_AnsP_7" + "P-poll__networl_8_5_AnsP_8" + "P-poll__networl_8_5_RI_0" + "P-poll__networl_8_5_RI_1" + "P-poll__networl_8_5_RI_2" + "P-poll__networl_8_5_RI_3" + "P-poll__networl_8_5_RI_4" + "P-poll__networl_8_5_RI_5" + "P-poll__networl_8_5_RI_6" + "P-poll__networl_8_5_RI_7" + "P-poll__networl_8_5_RI_8" + "P-poll__networl_8_5_AI_0" + "P-poll__networl_8_5_AI_1" + "P-poll__networl_8_5_AI_2" + "P-poll__networl_8_5_AI_3" + "P-poll__networl_8_5_AI_4" + "P-poll__networl_8_5_AI_5" + "P-poll__networl_8_5_AI_6" + "P-poll__networl_8_5_AI_7" + "P-poll__networl_8_5_AI_8" + "P-poll__networl_8_5_AnnP_0" + "P-poll__networl_8_5_AnnP_1" + "P-poll__networl_8_5_AnnP_2" + "P-poll__networl_8_5_AnnP_3" + "P-poll__networl_8_5_AnnP_4" + "P-poll__networl_8_5_AnnP_5" + "P-poll__networl_8_5_AnnP_6" + "P-poll__networl_8_5_AnnP_7" + "P-poll__networl_8_5_AnnP_8" + "P-poll__networl_8_5_RP_0" + "P-poll__networl_8_5_RP_1" + "P-poll__networl_8_5_RP_2" + "P-poll__networl_8_5_RP_3" + "P-poll__networl_8_5_RP_4" + "P-poll__networl_8_5_RP_5" + "P-poll__networl_8_5_RP_6" + "P-poll__networl_8_5_RP_7" + "P-poll__networl_8_5_RP_8" + "P-poll__networl_8_6_AskP_0" + "P-poll__networl_8_6_AskP_1" + "P-poll__networl_8_6_AskP_2" + "P-poll__networl_8_6_AskP_3" + "P-poll__networl_8_6_AskP_4" + "P-poll__networl_8_6_AskP_5" + "P-poll__networl_8_6_AskP_6" + "P-poll__networl_8_6_AskP_7" + "P-poll__networl_8_6_AskP_8" + "P-poll__networl_8_6_AnsP_0" + "P-poll__networl_8_6_AnsP_1" + "P-poll__networl_8_6_AnsP_2" + "P-poll__networl_8_6_AnsP_3" + "P-poll__networl_8_6_AnsP_4" + "P-poll__networl_8_6_AnsP_5" + "P-poll__networl_8_6_AnsP_6" + "P-poll__networl_8_6_AnsP_7" + "P-poll__networl_8_6_AnsP_8" + "P-poll__networl_8_6_RI_0" + "P-poll__networl_8_6_RI_1" + "P-poll__networl_8_6_RI_2" + "P-poll__networl_8_6_RI_3" + "P-poll__networl_8_6_RI_4" + "P-poll__networl_8_6_RI_5" + "P-poll__networl_8_6_RI_6" + "P-poll__networl_8_6_RI_7" + "P-poll__networl_8_6_RI_8" + "P-poll__networl_8_6_AI_0" + "P-poll__networl_8_6_AI_1" + "P-poll__networl_8_6_AI_2" + "P-poll__networl_8_6_AI_3" + "P-poll__networl_8_6_AI_4" + "P-poll__networl_8_6_AI_5" + "P-poll__networl_8_6_AI_6" + "P-poll__networl_8_6_AI_7" + "P-poll__networl_8_6_AI_8" + "P-poll__networl_8_6_AnnP_0" + "P-poll__networl_8_6_AnnP_1" + "P-poll__networl_8_6_AnnP_2" + "P-poll__networl_8_6_AnnP_3" + "P-poll__networl_8_6_AnnP_4" + "P-poll__networl_8_6_AnnP_5" + "P-poll__networl_8_6_AnnP_6" + "P-poll__networl_8_6_AnnP_7" + "P-poll__networl_8_6_AnnP_8" + "P-poll__networl_8_6_RP_0" + "P-poll__networl_8_6_RP_1" + "P-poll__networl_8_6_RP_2" + "P-poll__networl_8_6_RP_3" + "P-poll__networl_8_6_RP_4" + "P-poll__networl_8_6_RP_5" + "P-poll__networl_8_6_RP_6" + "P-poll__networl_8_6_RP_7" + "P-poll__networl_8_6_RP_8" + "P-poll__networl_8_7_AskP_0" + "P-poll__networl_8_7_AskP_1" + "P-poll__networl_8_7_AskP_2" + "P-poll__networl_8_7_AskP_3" + "P-poll__networl_8_7_AskP_4" + "P-poll__networl_8_7_AskP_5" + "P-poll__networl_8_7_AskP_6" + "P-poll__networl_8_7_AskP_7" + "P-poll__networl_8_7_AskP_8" + "P-poll__networl_8_7_AnsP_0" + "P-poll__networl_8_7_AnsP_1" + "P-poll__networl_8_7_AnsP_2" + "P-poll__networl_8_7_AnsP_3" + "P-poll__networl_8_7_AnsP_4" + "P-poll__networl_8_7_AnsP_5" + "P-poll__networl_8_7_AnsP_6" + "P-poll__networl_8_7_AnsP_7" + "P-poll__networl_8_7_AnsP_8" + "P-poll__networl_8_7_RI_0" + "P-poll__networl_8_7_RI_1" + "P-poll__networl_8_7_RI_2" + "P-poll__networl_8_7_RI_3" + "P-poll__networl_8_7_RI_4" + "P-poll__networl_8_7_RI_5" + "P-poll__networl_8_7_RI_6" + "P-poll__networl_8_7_RI_7" + "P-poll__networl_8_7_RI_8" + "P-poll__networl_8_7_AI_0" + "P-poll__networl_8_7_AI_1" + "P-poll__networl_8_7_AI_2" + "P-poll__networl_8_7_AI_3" + "P-poll__networl_8_7_AI_4" + "P-poll__networl_8_7_AI_5" + "P-poll__networl_8_7_AI_6" + "P-poll__networl_8_7_AI_7" + "P-poll__networl_8_7_AI_8" + "P-poll__networl_8_7_AnnP_0" + "P-poll__networl_8_7_AnnP_1" + "P-poll__networl_8_7_AnnP_2" + "P-poll__networl_8_7_AnnP_3" + "P-poll__networl_8_7_AnnP_4" + "P-poll__networl_8_7_AnnP_5" + "P-poll__networl_8_7_AnnP_6" + "P-poll__networl_8_7_AnnP_7" + "P-poll__networl_8_7_AnnP_8" + "P-poll__networl_8_7_RP_0" + "P-poll__networl_8_7_RP_1" + "P-poll__networl_8_7_RP_2" + "P-poll__networl_8_7_RP_3" + "P-poll__networl_8_7_RP_4" + "P-poll__networl_8_7_RP_5" + "P-poll__networl_8_7_RP_6" + "P-poll__networl_8_7_RP_7" + "P-poll__networl_8_7_RP_8" + "P-poll__networl_8_8_AskP_0" + "P-poll__networl_8_8_AskP_1" + "P-poll__networl_8_8_AskP_2" + "P-poll__networl_8_8_AskP_3" + "P-poll__networl_8_8_AskP_4" + "P-poll__networl_8_8_AskP_5" + "P-poll__networl_8_8_AskP_6" + "P-poll__networl_8_8_AskP_7" + "P-poll__networl_8_8_AskP_8" + "P-poll__networl_8_8_AnsP_0" + "P-poll__networl_8_8_AnsP_1" + "P-poll__networl_8_8_AnsP_2" + "P-poll__networl_8_8_AnsP_3" + "P-poll__networl_8_8_AnsP_4" + "P-poll__networl_8_8_AnsP_5" + "P-poll__networl_8_8_AnsP_6" + "P-poll__networl_8_8_AnsP_7" + "P-poll__networl_8_8_AnsP_8" + "P-poll__networl_8_8_RI_0" + "P-poll__networl_8_8_RI_1" + "P-poll__networl_8_8_RI_2" + "P-poll__networl_8_8_RI_3" + "P-poll__networl_8_8_RI_4" + "P-poll__networl_8_8_RI_5" + "P-poll__networl_8_8_RI_6" + "P-poll__networl_8_8_RI_7" + "P-poll__networl_8_8_RI_8" + "P-poll__networl_8_8_AI_0" + "P-poll__networl_8_8_AI_1" + "P-poll__networl_8_8_AI_2" + "P-poll__networl_8_8_AI_3" + "P-poll__networl_8_8_AI_4" + "P-poll__networl_8_8_AI_5" + "P-poll__networl_8_8_AI_6" + "P-poll__networl_8_8_AI_7" + "P-poll__networl_8_8_AI_8" + "P-poll__networl_8_8_AnnP_0" + "P-poll__networl_8_8_AnnP_1" + "P-poll__networl_8_8_AnnP_2" + "P-poll__networl_8_8_AnnP_3" + "P-poll__networl_8_8_AnnP_4" + "P-poll__networl_8_8_AnnP_5" + "P-poll__networl_8_8_AnnP_6" + "P-poll__networl_8_8_AnnP_7" + "P-poll__networl_8_8_AnnP_8" + "P-poll__networl_8_8_RP_0" + "P-poll__networl_8_8_RP_1" + "P-poll__networl_8_8_RP_2" + "P-poll__networl_8_8_RP_3" + "P-poll__networl_8_8_RP_4" + "P-poll__networl_8_8_RP_5" + "P-poll__networl_8_8_RP_6" + "P-poll__networl_8_8_RP_7" + "P-poll__networl_8_8_RP_8") <= ("P-electionFailed_0" + "P-electionFailed_1" + "P-electionFailed_2" + "P-electionFailed_3" + "P-electionFailed_4" + "P-electionFailed_5" + "P-electionFailed_6" + "P-electionFailed_7" + "P-electionFailed_8"))))) )
NeoElection-COL-8-ReachabilityCardinality-11: EF ( (1 <= ("P-poll__waitingMessage_0" + "P-poll__waitingMessage_1" + "P-poll__waitingMessage_2" + "P-poll__waitingMessage_3" + "P-poll__waitingMessage_4" + "P-poll__waitingMessage_5" + "P-poll__waitingMessage_6" + "P-poll__waitingMessage_7" + "P-poll__waitingMessage_8")) )
BK_TIME_CONFINEMENT_REACHED
--------------------
content from stderr:
perl: warning: Setting locale failed.
perl: warning: Please check that your locale settings:
LANGUAGE = (unset),
LC_ALL = (unset),
LANG = "fr_FR.UTF-8"
are supported and installed on your system.
perl: warning: Falling back to the standard locale ("C").
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
set -x
# this is for BenchKit: configuration of major elements for the test
export BK_INPUT="NeoElection-PT-8"
export BK_EXAMINATION="ReachabilityCardinality"
export BK_TOOL="classicMC"
export BK_RESULT_DIR="/users/gast00/fkordon/BK_RESULTS/OUTPUTS"
export BK_TIME_CONFINEMENT="3600"
export BK_MEMORY_CONFINEMENT="16384"
# this is specific to your benchmark or test
export BIN_DIR="$HOME/BenchKit/bin"
# remove the execution directoty if it exists (to avoid increse of .vmdk images)
if [ -d execution ] ; then
rm -rf execution
fi
tar xzf /home/mcc/BenchKit/INPUTS/NeoElection-PT-8.tgz
mv NeoElection-PT-8 execution
# this is for BenchKit: explicit launching of the test
cd execution
echo "====================================================================="
echo " Generated by BenchKit 2-2265"
echo " Executing tool classicMC"
echo " Input is NeoElection-PT-8, examination is ReachabilityCardinality"
echo " Time confinement is $BK_TIME_CONFINEMENT seconds"
echo " Memory confinement is 16384 MBytes"
echo " Number of cores is 4"
echo " Run identifier is r043kn-ebro-143236481900984"
echo "====================================================================="
echo
echo "--------------------"
echo "content from stdout:"
echo
echo "=== Data for post analysis generated by BenchKit (invocation template)"
echo
if [ "ReachabilityCardinality" = "ReachabilityComputeBounds" ] ; then
echo "The expected result is a vector of positive values"
echo NUM_VECTOR
elif [ "ReachabilityCardinality" != "StateSpace" ] ; then
echo "The expected result is a vector of booleans"
echo BOOL_VECTOR
else
echo "no data necessary for post analysis"
fi
echo
if [ -f "ReachabilityCardinality.txt" ] ; then
echo "here is the order used to build the result vector(from text file)"
for x in $(grep Property ReachabilityCardinality.txt | cut -d ' ' -f 2 | sort -u) ; do
echo "FORMULA_NAME $x"
done
elif [ -f "ReachabilityCardinality.xml" ] ; then # for cunf (txt files deleted;-)
echo echo "here is the order used to build the result vector(from xml file)"
for x in $(grep '
echo "FORMULA_NAME $x"
done
fi
echo
echo "=== Now, execution of the tool begins"
echo
echo -n "BK_START "
date -u +%s%3N
echo
timeout -s 9 $BK_TIME_CONFINEMENT bash -c "/home/mcc/BenchKit/BenchKit_head.sh 2> STDERR ; echo ; echo -n \"BK_STOP \" ; date -u +%s%3N"
if [ $? -eq 137 ] ; then
echo
echo "BK_TIME_CONFINEMENT_REACHED"
fi
echo
echo "--------------------"
echo "content from stderr:"
echo
cat STDERR ;

