Introduction
This page shows the outputs produced by the execution of marcie on NeoElection/3 (P/T). We provide:
- A short summary,
- the execution chart (evolution of CPU and memory over the execution),
- the sequence of actions to be executed by the VM,
- the results of these actions.
About the Execution
| Execution Summary | |||
| Memory (MB) | CPU (s) | End | |
| 800.81 | 11.61 | normal | |
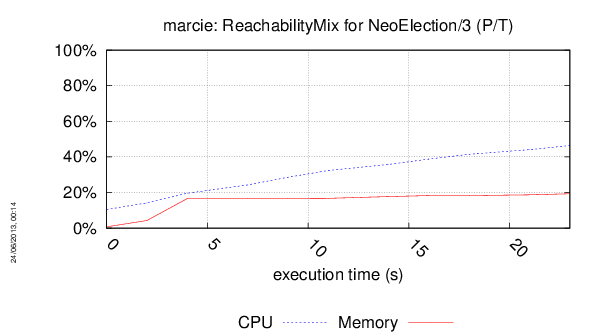
Execution Chart
We display below the execution chart for this examination (boot time has been removed).
Sequence of Actions to be Executed by the VM
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
export BK_INPUT=NeoElection-PT-3
export BK_EXAMINATION=ReachabilityMix
export BK_TOOL=marcie
export BK_RESULT_DIR=/tmp
export BK_LOG_FILE=/tmp/BenchKit_head_log_file.1654
export BIN_DIR=/home/mcc/BenchKit/bin
cd /home/mcc/BenchKit/INPUTS/NeoElection-PT-3
echo =====================================================================
echo ' Generated by BenchKit 1.0'
echo ' Executing tool marcie:'
echo ' Test is NeoElection-PT-3, examination is ReachabilityMix'
echo =====================================================================
echo
echo --------------------
echo 'content from stdout:'
echo
bash /home/mcc/BenchKit/BenchKit_head.sh
Execution Outputs of marcie for NeoElection/3 (P/T)
This is useful if one wants to reexecute the tool in the VM from the submitted image disk.
execution on node 32: cluster1u34.lip6.fr (runId=136959876701521_n_32)
=====================================================================
runnning marcie on NeoElection-PT-3 (ReachabilityMix)
We got on stdout:
Probing ssh
Waiting ssh to respond
Ssh up and responding
=====================================================================
Generated by BenchKit 1.0
Executing tool marcie:
Test is NeoElection-PT-3, examination is ReachabilityMix
=====================================================================
--------------------
content from stdout:
START 1369634148
Marcie rev. 1103M (build: rohrch on 2013-02-17)
A model checker for Generalized Stochastic Petri nets
authors: Alex Tovchigrechko (IDD package and CTL model checking)
Martin Schwarick (Symbolic numerical analysis and CSL model checking)
Christian Rohr (Simulative and approximative numerical model checking)
marcie@informatik.tu-cottbus.de
called as: marcie --net-file=model.pnml --mem=4 --mcc-file=ReachabilityMix.txt
constant oo registered with value < INFINITY >
parse successfull!
(NrP: 972 NrTr: 1016)
net check time: 0m0sec
parse mcc successfull!
place and transition orderings generation:0m0sec
init dd package: 0m1sec
RS generation: 0m7sec
-> reachability set: #nodes 19347 (1.9e+04) #states 974,325 (5)
starting CTL model checker
--------------------------
checking: AG [[[poll__handlingMessage_1=dead_1 & [poll__handlingMessage_0=dead_0 & [poll__handlingMessage_3=dead_3 & [poll__handlingMessage_2=dead_2 & true]]]] & [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]]]]]]]]]]]]]
normalized: ~ [E [true U ~ [[[poll__handlingMessage_1=dead_1 & [poll__handlingMessage_0=dead_0 & [poll__handlingMessage_3=dead_3 & [poll__handlingMessage_2=dead_2 & true]]]] & [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]]]]]]]]]]]]]]]
-> the formula is FALSE
FORMULA p_37_mix_eq_and FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m4sec
checking: AG [[[[[[true & poll__handlingMessage_2=dead_2] & poll__handlingMessage_3=dead_3] & poll__handlingMessage_0=dead_0] & poll__handlingMessage_1=dead_1] | [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [[startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [[[startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [[[[startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]] & startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1] & startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2] & startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3]] & startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3] & startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2]] & startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2]]]]
normalized: ~ [E [true U ~ [[[[[startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [[[[startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [[startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]]] & startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2]] & startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1] & startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3] & startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2]] & startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2] & startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3] | [poll__handlingMessage_1=dead_1 & [[[true & poll__handlingMessage_2=dead_2] & poll__handlingMessage_3=dead_3] & poll__handlingMessage_0=dead_0]]]]]]
-> the formula is FALSE
FORMULA p_38_mix_eq_or FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[[[[[poll__handlingMessage_2=dead_2 & true] & poll__handlingMessage_3=dead_3] & poll__handlingMessage_0=dead_0] & poll__handlingMessage_1=dead_1] & [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [[startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [[startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [[[true & startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1] & startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2] & startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1]]]] & startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1]] & startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2]]]]]]
normalized: ~ [E [true U ~ [[[poll__handlingMessage_1=dead_1 & [poll__handlingMessage_0=dead_0 & [poll__handlingMessage_3=dead_3 & [poll__handlingMessage_2=dead_2 & true]]]] & [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [[true & startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1] & startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2]]]]]]]]]]]]]]]
-> the formula is FALSE
FORMULA p_39_mix_eq_and_notx FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[[[poll__handlingMessage_0=dead_0 & [[poll__handlingMessage_2=dead_2 & true] & poll__handlingMessage_3=dead_3]] & poll__handlingMessage_1=dead_1] | [[startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [[startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [[startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [[[startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [[[startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true] & startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2] & startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1]] & startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2] & startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3]] & startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3]] & startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3]] & startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3]]]
normalized: ~ [E [true U ~ [[[poll__handlingMessage_1=dead_1 & [poll__handlingMessage_0=dead_0 & [poll__handlingMessage_3=dead_3 & [poll__handlingMessage_2=dead_2 & true]]]] | [startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]]]]]]]]]]]]]]]
-> the formula is FALSE
FORMULA p_40_mix_eq_or_notx FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[[startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [[startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [[startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [[startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [[startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [[startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [true & startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1]] & startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1]] & startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2]] & startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1]] & startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2]] & startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2]] -> [[poll__handlingMessage_0=dead_0 & [[poll__handlingMessage_2=dead_2 & true] & poll__handlingMessage_3=dead_3]] & poll__handlingMessage_1=dead_1]]]
normalized: ~ [E [true U ~ [[[poll__handlingMessage_1=dead_1 & [poll__handlingMessage_0=dead_0 & [poll__handlingMessage_3=dead_3 & [poll__handlingMessage_2=dead_2 & true]]]] | ~ [[startNeg__broadcasting_1_3!=sendAnnPs__broadcasting_1_3 & [startNeg__broadcasting_1_2!=sendAnnPs__broadcasting_1_2 & [startNeg__broadcasting_2_3!=sendAnnPs__broadcasting_2_3 & [startNeg__broadcasting_3_2!=sendAnnPs__broadcasting_3_2 & [startNeg__broadcasting_3_3!=sendAnnPs__broadcasting_3_3 & [startNeg__broadcasting_2_1!=sendAnnPs__broadcasting_2_1 & [startNeg__broadcasting_0_3!=sendAnnPs__broadcasting_0_3 & [startNeg__broadcasting_2_2!=sendAnnPs__broadcasting_2_2 & [startNeg__broadcasting_1_1!=sendAnnPs__broadcasting_1_1 & [startNeg__broadcasting_3_1!=sendAnnPs__broadcasting_3_1 & [startNeg__broadcasting_0_2!=sendAnnPs__broadcasting_0_2 & [startNeg__broadcasting_0_1!=sendAnnPs__broadcasting_0_1 & true]]]]]]]]]]]]]]]]]
-> the formula is TRUE
FORMULA p_41_mix_eq_x TRUE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[[true & [network_2_2_RP_2>poll__networl_2_2_RP_2 & [network_1_0_RI_0>poll__networl_1_0_RI_0 & [network_0_0_AnnP_2>poll__networl_0_0_AnnP_2 & [network_1_3_AskP_0>poll__networl_1_3_AskP_0 & [network_2_3_RP_0>poll__networl_2_3_RP_0 & [network_2_1_AnsP_2>poll__networl_2_1_AnsP_2 & [network_1_2_RI_0>poll__networl_1_2_RI_0 & [network_2_0_AI_2>poll__networl_2_0_AI_2 & [network_0_3_AnnP_0>poll__networl_0_3_AnnP_0 & [network_0_1_AI_2>poll__networl_0_1_AI_2 & [network_2_3_RI_0>poll__networl_2_3_RI_0 & [network_2_3_AnsP_3>poll__networl_2_3_AnsP_3 & [network_2_3_AskP_3>poll__networl_2_3_AskP_3 & [network_0_2_AI_0>poll__networl_0_2_AI_0 & [network_3_1_AnsP_0>poll__networl_3_1_AnsP_0 & [network_0_0_AnnP_0>poll__networl_0_0_AnnP_0 & [network_0_2_AnnP_0>poll__networl_0_2_AnnP_0 & [network_1_1_AnsP_0>poll__networl_1_1_AnsP_0 & [network_3_1_AI_1>poll__networl_3_1_AI_1 & [network_1_1_AskP_3>poll__networl_1_1_AskP_3 & [network_0_2_RI_2>poll__networl_0_2_RI_2 & [network_3_3_RI_0>poll__networl_3_3_RI_0 & [network_3_1_RI_3>poll__networl_3_1_RI_3 & [network_3_2_AnnP_0>poll__networl_3_2_AnnP_0 & [network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [network_1_2_AnsP_2>poll__networl_1_2_AnsP_2 & [network_3_0_AskP_2>poll__networl_3_0_AskP_2 & [network_1_0_AnsP_3>poll__networl_1_0_AnsP_3 & [network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [[[[[[[[[network_1_1_RI_1>poll__networl_1_1_RI_1 & [[network_3_2_RI_0>poll__networl_3_2_RI_0 & [[network_1_0_RP_2>poll__networl_1_0_RP_2 & [[network_3_1_AnnP_0>poll__networl_3_1_AnnP_0 & [network_1_1_AnnP_3>poll__networl_1_1_AnnP_3 & [[[[[[[[network_2_0_AnsP_2>poll__networl_2_0_AnsP_2 & [[[[[[[[[[[[[[[[network_0_1_AnnP_1>poll__networl_0_1_AnnP_1 & [[[network_2_2_RI_1>poll__networl_2_2_RI_1 & [[network_2_3_AnnP_1>poll__networl_2_3_AnnP_1 & [[[[[network_2_0_RI_0>poll__networl_2_0_RI_0 & [[[[[[[[[[[[[[[[[[[[[[[[network_1_3_AnsP_1>poll__networl_1_3_AnsP_1 & [network_0_3_RP_3>poll__networl_0_3_RP_3 & [[[[network_2_2_RI_2>poll__networl_2_2_RI_2 & [network_1_2_AskP_0>poll__networl_1_2_AskP_0 & [[[network_1_1_AnnP_2>poll__networl_1_1_AnnP_2 & [[[[[[[[network_0_1_RI_0>poll__networl_0_1_RI_0 & [[network_1_3_RP_3>poll__networl_1_3_RP_3 & [[[network_0_0_RP_0>poll__networl_0_0_RP_0 & [[network_0_1_AI_0>poll__networl_0_1_AI_0 & [[[network_3_2_RI_3>poll__networl_3_2_RI_3 & [[[[network_2_0_RI_1>poll__networl_2_0_RI_1 & [[[[network_3_1_AnnP_1>poll__networl_3_1_AnnP_1 & [[network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [[[[[[[[network_0_1_AI_3>poll__networl_0_1_AI_3 & [network_2_1_AI_0>poll__networl_2_1_AI_0 & [network_2_1_RP_3>poll__networl_2_1_RP_3 & [[network_2_3_AI_2>poll__networl_2_3_AI_2 & [network_1_2_AskP_2>poll__networl_1_2_AskP_2 & [network_3_1_AskP_3>poll__networl_3_1_AskP_3 & [network_0_0_RP_2>poll__networl_0_0_RP_2 & [[network_3_0_AI_0>poll__networl_3_0_AI_0 & [network_2_0_RP_1>poll__networl_2_0_RP_1 & [network_3_1_RI_0>poll__networl_3_1_RI_0 & [network_2_0_AI_3>poll__networl_2_0_AI_3 & [[network_0_2_RP_3>poll__networl_0_2_RP_3 & [network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [network_2_2_AskP_0>poll__networl_2_2_AskP_0 & [[network_0_1_AnnP_2>poll__networl_0_1_AnnP_2 & [network_3_2_RI_2>poll__networl_3_2_RI_2 & [network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [[network_3_1_AnnP_3>poll__networl_3_1_AnnP_3 & [network_3_2_AskP_1>poll__networl_3_2_AskP_1 & [network_3_1_AI_0>poll__networl_3_1_AI_0 & [network_3_1_AnsP_3>poll__networl_3_1_AnsP_3 & [[network_2_3_RP_3>poll__networl_2_3_RP_3 & [network_1_2_AI_1>poll__networl_1_2_AI_1 & [network_1_1_RP_3>poll__networl_1_1_RP_3 & [network_2_2_AnsP_0>poll__networl_2_2_AnsP_0 & [[network_2_1_RI_2>poll__networl_2_1_RI_2 & [network_2_3_AnsP_1>poll__networl_2_3_AnsP_1 & [network_2_1_RI_0>poll__networl_2_1_RI_0 & [network_3_0_AnnP_3>poll__networl_3_0_AnnP_3 & [network_0_0_RI_1>poll__networl_0_0_RI_1 & [[network_2_3_AI_0>poll__networl_2_3_AI_0 & [[network_0_3_AnsP_0>poll__networl_0_3_AnsP_0 & [network_0_1_AnnP_0>poll__networl_0_1_AnnP_0 & [network_2_2_AnnP_0>poll__networl_2_2_AnnP_0 & [network_3_3_AskP_1>poll__networl_3_3_AskP_1 & [network_1_1_AI_3>poll__networl_1_1_AI_3 & [network_3_3_RI_2>poll__networl_3_3_RI_2 & [[network_0_1_AnsP_2>poll__networl_0_1_AnsP_2 & [network_0_0_AnsP_0>poll__networl_0_0_AnsP_0 & [network_1_1_RI_3>poll__networl_1_1_RI_3 & [network_1_0_RI_3>poll__networl_1_0_RI_3 & [network_0_0_RI_0>poll__networl_0_0_RI_0 & [network_0_0_AskP_2>poll__networl_0_0_AskP_2 & [network_3_2_AnsP_2>poll__networl_3_2_AnsP_2 & [[network_2_3_AnnP_3>poll__networl_2_3_AnnP_3 & [network_2_1_RI_3>poll__networl_2_1_RI_3 & [network_2_0_RI_2>poll__networl_2_0_RI_2 & [[network_3_1_AI_3>poll__networl_3_1_AI_3 & [network_0_3_RI_2>poll__networl_0_3_RI_2 & [network_2_3_AnnP_2>poll__networl_2_3_AnnP_2 & [network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [network_1_0_AnnP_3>poll__networl_1_0_AnnP_3 & [network_1_1_RI_2>poll__networl_1_1_RI_2 & [network_3_2_AI_0>poll__networl_3_2_AI_0 & [network_3_0_AnsP_3>poll__networl_3_0_AnsP_3 & [network_0_3_AnnP_1>poll__networl_0_3_AnnP_1 & [network_3_3_RI_3>poll__networl_3_3_RI_3 & [network_3_3_AI_1>poll__networl_3_3_AI_1 & [[network_0_1_RP_3>poll__networl_0_1_RP_3 & [network_2_2_RP_3>poll__networl_2_2_RP_3 & [network_0_0_RI_3>poll__networl_0_0_RI_3 & [network_3_3_RP_3>poll__networl_3_3_RP_3 & [network_0_0_AI_0>poll__networl_0_0_AI_0 & [network_3_0_RI_0>poll__networl_3_0_RI_0 & [network_3_2_RP_3>poll__networl_3_2_RP_3 & [network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [network_3_3_AskP_0>poll__networl_3_3_AskP_0 & [network_2_2_AnsP_1>poll__networl_2_2_AnsP_1 & [network_0_2_RI_0>poll__networl_0_2_RI_0 & [network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [network_3_0_AI_2>poll__networl_3_0_AI_2 & [network_1_2_RP_1>poll__networl_1_2_RP_1 & [network_1_2_AnsP_3>poll__networl_1_2_AnsP_3 & [network_3_0_AskP_3>poll__networl_3_0_AskP_3 & [network_2_1_RI_1>poll__networl_2_1_RI_1 & [network_0_0_AnsP_1>poll__networl_0_0_AnsP_1 & [network_3_3_AnsP_1>poll__networl_3_3_AnsP_1 & [network_3_1_RI_1>poll__networl_3_1_RI_1 & [network_1_2_AI_3>poll__networl_1_2_AI_3 & [network_0_3_RI_0>poll__networl_0_3_RI_0 & [[[network_3_3_RP_1>poll__networl_3_3_RP_1 & [[network_1_3_AI_1>poll__networl_1_3_AI_1 & [[network_3_3_AI_2>poll__networl_3_3_AI_2 & [[network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [[[[[[[[[[network_1_0_RP_3>poll__networl_1_0_RP_3 & [[network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [[[[[[[[[[[[network_0_1_RI_2>poll__networl_0_1_RI_2 & [[[network_3_0_RI_3>poll__networl_3_0_RI_3 & [network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [[network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [[[network_0_2_AnsP_0>poll__networl_0_2_AnsP_0 & [network_0_3_AnnP_3>poll__networl_0_3_AnnP_3 & [network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [network_2_2_AnnP_1>poll__networl_2_2_AnnP_1 & [network_1_1_AnnP_0>poll__networl_1_1_AnnP_0 & [network_3_2_AnnP_3>poll__networl_3_2_AnnP_3 & [network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [network_1_0_AI_0>poll__networl_1_0_AI_0 & [network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [network_1_2_AI_0>poll__networl_1_2_AI_0 & [network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [network_1_1_AnnP_1>poll__networl_1_1_AnnP_1 & [network_1_3_AI_0>poll__networl_1_3_AI_0 & [[network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [[network_1_2_RP_0>poll__networl_1_2_RP_0 & [network_1_2_RI_3>poll__networl_1_2_RI_3 & [[[network_0_2_AskP_3>poll__networl_0_2_AskP_3 & [network_1_3_AI_2>poll__networl_1_3_AI_2 & [network_1_3_AnsP_2>poll__networl_1_3_AnsP_2 & [network_0_2_AI_3>poll__networl_0_2_AI_3 & [network_1_2_AI_2>poll__networl_1_2_AI_2 & [[network_3_2_RP_0>poll__networl_3_2_RP_0 & [[network_1_0_RP_0>poll__networl_1_0_RP_0 & [network_0_2_AnsP_2>poll__networl_0_2_AnsP_2 & [network_2_0_AI_0>poll__networl_2_0_AI_0 & [[network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [network_3_0_RP_2>poll__networl_3_0_RP_2 & [network_2_2_AI_2>poll__networl_2_2_AI_2 & [network_0_1_AskP_3>poll__networl_0_1_AskP_3 & [network_1_1_RI_0>poll__networl_1_1_RI_0 & [network_0_1_RI_3>poll__networl_0_1_RI_3 & [network_1_2_RP_2>poll__networl_1_2_RP_2 & [network_0_3_AnnP_2>poll__networl_0_3_AnnP_2 & [network_3_1_AnsP_2>poll__networl_3_1_AnsP_2 & [network_1_3_AnnP_2>poll__networl_1_3_AnnP_2 & [network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [network_0_0_AI_2>poll__networl_0_0_AI_2 & [network_2_3_AI_3>poll__networl_2_3_AI_3 & [network_3_2_AskP_2>poll__networl_3_2_AskP_2 & [network_2_1_AnsP_0>poll__networl_2_1_AnsP_0 & [network_3_0_AnnP_0>poll__networl_3_0_AnnP_0 & [network_1_3_RP_1>poll__networl_1_3_RP_1 & [network_3_3_AskP_2>poll__networl_3_3_AskP_2 & [network_3_3_RP_2>poll__networl_3_3_RP_2 & [network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [network_1_0_RI_2>poll__networl_1_0_RI_2 & [network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [network_0_0_RI_2>poll__networl_0_0_RI_2 & [network_3_3_AI_0>poll__networl_3_3_AI_0 & [network_1_2_AnsP_0>poll__networl_1_2_AnsP_0 & [network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [network_3_2_AnsP_3>poll__networl_3_2_AnsP_3 & [network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [network_3_2_AI_3>poll__networl_3_2_AI_3 & [network_1_3_RP_2>poll__networl_1_3_RP_2 & [network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [network_3_3_AnnP_2>poll__networl_3_3_AnnP_2 & [network_1_0_AnsP_2>poll__networl_1_0_AnsP_2 & [network_0_1_AnsP_0>poll__networl_0_1_AnsP_0 & [network_0_2_RP_0>poll__networl_0_2_RP_0 & [network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [network_1_3_RI_2>poll__networl_1_3_RI_2 & [network_0_0_RP_3>poll__networl_0_0_RP_3 & [network_1_0_AI_2>poll__networl_1_0_AI_2 & [network_3_0_AI_3>poll__networl_3_0_AI_3 & [network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [network_2_2_AnsP_3>poll__networl_2_2_AnsP_3 & [network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [[[[[[network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [[network_2_3_RI_2>poll__networl_2_3_RI_2 & true] & network_1_1_RP_2>poll__networl_1_1_RP_2]] & network_1_1_AnsP_3>poll__networl_1_1_AnsP_3] & network_3_0_RP_1>poll__networl_3_0_RP_1] & network_1_3_RI_0>poll__networl_1_3_RI_0] & network_1_0_AskP_3>poll__networl_1_0_AskP_3] & network_1_1_RP_0>poll__networl_1_1_RP_0]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & network_3_2_RI_1>poll__networl_3_2_RI_1]]]] & network_2_1_AskP_1>poll__networl_2_1_AskP_1]] & network_2_0_RP_0>poll__networl_2_0_RP_0]]]]]] & network_1_1_AnsP_1>poll__networl_1_1_AnsP_1] & network_2_0_AskP_0>poll__networl_2_0_AskP_0]]] & network_2_1_AskP_2>poll__networl_2_1_AskP_2]] & network_0_2_RP_1>poll__networl_0_2_RP_1]]]]]]]]]]]]]]]]] & network_2_1_AnsP_3>poll__networl_2_1_AnsP_3] & network_3_3_AI_3>poll__networl_3_3_AI_3]] & network_2_3_AskP_1>poll__networl_2_3_AskP_1]]]] & network_3_3_RI_1>poll__networl_3_3_RI_1] & network_2_3_AskP_2>poll__networl_2_3_AskP_2]] & network_2_1_RP_1>poll__networl_2_1_RP_1] & network_2_2_AskP_3>poll__networl_2_2_AskP_3] & network_1_3_RI_3>poll__networl_1_3_RI_3] & network_3_2_AI_1>poll__networl_3_2_AI_1] & network_1_2_RP_3>poll__networl_1_2_RP_3] & network_2_2_AI_1>poll__networl_2_2_AI_1] & network_2_3_RI_1>poll__networl_2_3_RI_1] & network_0_1_AskP_1>poll__networl_0_1_AskP_1] & network_1_3_AskP_3>poll__networl_1_3_AskP_3] & network_0_3_AI_0>poll__networl_0_3_AI_0] & network_1_2_AnnP_0>poll__networl_1_2_AnnP_0]] & network_0_2_AnnP_2>poll__networl_0_2_AnnP_2]] & network_3_3_AnnP_1>poll__networl_3_3_AnnP_1] & network_3_0_RP_0>poll__networl_3_0_RP_0] & network_0_3_AskP_0>poll__networl_0_3_AskP_0] & network_3_2_RP_2>poll__networl_3_2_RP_2] & network_3_2_RP_1>poll__networl_3_2_RP_1] & network_1_0_AnnP_2>poll__networl_1_0_AnnP_2] & network_2_0_AnsP_3>poll__networl_2_0_AnsP_3] & network_3_1_RP_0>poll__networl_3_1_RP_0] & network_2_2_RP_1>poll__networl_2_2_RP_1]] & network_0_3_AnsP_1>poll__networl_0_3_AnsP_1]] & network_0_3_AI_3>poll__networl_0_3_AI_3]] & network_0_2_AskP_0>poll__networl_0_2_AskP_0]] & network_2_1_AnsP_1>poll__networl_2_1_AnsP_1] & network_3_0_AnsP_2>poll__networl_3_0_AnsP_2]]]]]]]]]]]]]]]]]]]]]]]] & network_1_0_AI_1>poll__networl_1_0_AI_1]]]]]]]]]]]]] & network_3_1_RP_1>poll__networl_3_1_RP_1]]]] & network_1_0_AnnP_1>poll__networl_1_0_AnnP_1]]]]]]]] & network_2_0_RI_3>poll__networl_2_0_RI_3]]]]]]] & network_3_2_AI_2>poll__networl_3_2_AI_2]] & network_2_0_RP_2>poll__networl_2_0_RP_2]]]]]] & network_0_3_RI_1>poll__networl_0_3_RI_1]]]]] & network_1_3_AnsP_0>poll__networl_1_3_AnsP_0]]]]] & network_1_0_AI_3>poll__networl_1_0_AI_3]]]]] & network_1_1_AI_2>poll__networl_1_1_AI_2]]]]] & network_0_2_RP_2>poll__networl_0_2_RP_2]]]]] & network_1_3_RI_1>poll__networl_1_3_RI_1]]]]] & network_3_0_RI_1>poll__networl_3_0_RI_1]]]] & network_1_3_AskP_1>poll__networl_1_3_AskP_1] & network_2_0_AnsP_0>poll__networl_2_0_AnsP_0] & network_1_2_AnnP_1>poll__networl_1_2_AnnP_1] & network_0_3_RI_3>poll__networl_0_3_RI_3] & network_0_1_RP_0>poll__networl_0_1_RP_0] & network_3_1_RI_2>poll__networl_3_1_RI_2] & network_0_0_AI_3>poll__networl_0_0_AI_3]] & network_3_3_AnsP_0>poll__networl_3_3_AnsP_0]] & network_2_1_AI_3>poll__networl_2_1_AI_3] & network_0_3_AnsP_3>poll__networl_0_3_AnsP_3] & network_2_1_AI_1>poll__networl_2_1_AI_1]] & network_2_1_AnnP_2>poll__networl_2_1_AnnP_2] & network_2_3_AI_1>poll__networl_2_3_AI_1] & network_0_1_AI_1>poll__networl_0_1_AI_1]] & network_3_0_AnsP_1>poll__networl_3_0_AnsP_1] & network_3_3_AnnP_0>poll__networl_3_3_AnnP_0]] & network_3_2_AnsP_0>poll__networl_3_2_AnsP_0]] & network_2_1_AskP_3>poll__networl_2_1_AskP_3] & network_3_0_AI_1>poll__networl_3_0_AI_1]] & network_2_3_RP_1>poll__networl_2_3_RP_1]] & network_3_0_RP_3>poll__networl_3_0_RP_3] & network_0_2_AnsP_1>poll__networl_0_2_AnsP_1] & network_1_2_AnsP_1>poll__networl_1_2_AnsP_1] & network_1_3_AnnP_1>poll__networl_1_3_AnnP_1] & network_2_0_AnnP_1>poll__networl_2_0_AnnP_1] & network_0_1_RP_2>poll__networl_0_1_RP_2] & network_2_0_RP_3>poll__networl_2_0_RP_3]] & network_2_0_AnnP_2>poll__networl_2_0_AnnP_2] & network_2_3_AskP_0>poll__networl_2_3_AskP_0]]] & network_0_0_AnnP_3>poll__networl_0_0_AnnP_3] & network_0_3_RP_0>poll__networl_0_3_RP_0] & network_1_0_RI_1>poll__networl_1_0_RI_1]]] & network_3_0_AnnP_2>poll__networl_3_0_AnnP_2] & network_3_2_AnnP_1>poll__networl_3_2_AnnP_1] & network_0_3_AskP_3>poll__networl_0_3_AskP_3] & network_1_2_RI_2>poll__networl_1_2_RI_2] & network_0_3_AI_1>poll__networl_0_3_AI_1] & network_1_3_RP_0>poll__networl_1_3_RP_0] & network_0_0_AnsP_3>poll__networl_0_0_AnsP_3] & network_2_1_AnnP_0>poll__networl_2_1_AnnP_0] & network_1_1_AskP_2>poll__networl_1_1_AskP_2] & network_0_3_AnsP_2>poll__networl_0_3_AnsP_2] & network_2_0_AskP_2>poll__networl_2_0_AskP_2] & network_2_1_AskP_0>poll__networl_2_1_AskP_0] & network_1_2_AskP_1>poll__networl_1_2_AskP_1] & network_2_2_AI_0>poll__networl_2_2_AI_0] & network_2_1_AI_2>poll__networl_2_1_AI_2] & network_3_3_AnsP_3>poll__networl_3_3_AnsP_3] & network_3_1_RP_3>poll__networl_3_1_RP_3] & network_3_1_AI_2>poll__networl_3_1_AI_2] & network_2_1_RP_0>poll__networl_2_1_RP_0] & network_1_0_AnsP_0>poll__networl_1_0_AnsP_0] & network_0_3_AI_2>poll__networl_0_3_AI_2] & network_2_0_AnsP_1>poll__networl_2_0_AnsP_1] & network_3_0_AnsP_0>poll__networl_3_0_AnsP_0]] & network_0_2_AskP_1>poll__networl_0_2_AskP_1] & network_2_2_RP_0>poll__networl_2_2_RP_0] & network_0_2_AnnP_3>poll__networl_0_2_AnnP_3] & network_0_0_AI_1>poll__networl_0_0_AI_1]] & network_3_1_AskP_2>poll__networl_3_1_AskP_2]] & network_2_2_AskP_2>poll__networl_2_2_AskP_2] & network_1_1_AI_0>poll__networl_1_1_AI_0]] & network_1_2_AnnP_2>poll__networl_1_2_AnnP_2] & network_3_2_AskP_3>poll__networl_3_2_AskP_3] & network_0_3_RP_2>poll__networl_0_3_RP_2] & network_1_1_RP_1>poll__networl_1_1_RP_1] & network_1_0_AnsP_1>poll__networl_1_0_AnsP_1] & network_2_3_AnsP_2>poll__networl_2_3_AnsP_2] & network_1_0_AnnP_0>poll__networl_1_0_AnnP_0] & network_0_0_AskP_0>poll__networl_0_0_AskP_0] & network_1_0_AskP_1>poll__networl_1_0_AskP_1] & network_0_1_RI_1>poll__networl_0_1_RI_1] & network_2_3_AnsP_0>poll__networl_2_3_AnsP_0] & network_2_3_AnnP_0>poll__networl_2_3_AnnP_0] & network_1_0_RP_1>poll__networl_1_0_RP_1] & network_3_3_AnnP_3>poll__networl_3_3_AnnP_3] & network_0_1_AnnP_3>poll__networl_0_1_AnnP_3]] & network_2_2_AnsP_2>poll__networl_2_2_AnsP_2] & network_2_1_AnnP_3>poll__networl_2_1_AnnP_3] & network_0_2_RI_3>poll__networl_0_2_RI_3] & network_3_3_RP_0>poll__networl_3_3_RP_0] & network_3_1_AskP_0>poll__networl_3_1_AskP_0] & network_0_1_RP_1>poll__networl_0_1_RP_1] & network_0_2_AskP_2>poll__networl_0_2_AskP_2]]] & network_0_1_AnsP_3>poll__networl_0_1_AnsP_3]] & network_3_2_AnnP_2>poll__networl_3_2_AnnP_2]] & network_0_0_RP_1>poll__networl_0_0_RP_1]] & network_3_3_AnsP_2>poll__networl_3_3_AnsP_2] & network_3_1_AnsP_1>poll__networl_3_1_AnsP_1] & network_2_2_AnnP_2>poll__networl_2_2_AnnP_2] & network_0_0_AskP_3>poll__networl_0_0_AskP_3] & network_2_3_RP_2>poll__networl_2_3_RP_2] & network_0_2_AI_2>poll__networl_0_2_AI_2] & network_2_0_AI_1>poll__networl_2_0_AI_1] & network_2_2_AskP_1>poll__networl_2_2_AskP_1]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) ]]
normalized: ~ [E [true U ~ [[ ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) & [[network_2_2_RP_2>poll__networl_2_2_RP_2 & [network_1_0_RI_0>poll__networl_1_0_RI_0 & [network_0_0_AnnP_2>poll__networl_0_0_AnnP_2 & [network_1_3_AskP_0>poll__networl_1_3_AskP_0 & [network_2_3_RP_0>poll__networl_2_3_RP_0 & [network_2_1_AnsP_2>poll__networl_2_1_AnsP_2 & [network_1_2_RI_0>poll__networl_1_2_RI_0 & [network_2_0_AI_2>poll__networl_2_0_AI_2 & [network_0_3_AnnP_0>poll__networl_0_3_AnnP_0 & [network_0_1_AI_2>poll__networl_0_1_AI_2 & [network_2_3_RI_0>poll__networl_2_3_RI_0 & [network_2_3_AnsP_3>poll__networl_2_3_AnsP_3 & [network_2_3_AskP_3>poll__networl_2_3_AskP_3 & [network_0_2_AI_0>poll__networl_0_2_AI_0 & [network_3_1_AnsP_0>poll__networl_3_1_AnsP_0 & [network_0_0_AnnP_0>poll__networl_0_0_AnnP_0 & [network_0_2_AnnP_0>poll__networl_0_2_AnnP_0 & [network_1_1_AnsP_0>poll__networl_1_1_AnsP_0 & [network_3_1_AI_1>poll__networl_3_1_AI_1 & [network_1_1_AskP_3>poll__networl_1_1_AskP_3 & [network_0_2_RI_2>poll__networl_0_2_RI_2 & [network_3_3_RI_0>poll__networl_3_3_RI_0 & [network_3_1_RI_3>poll__networl_3_1_RI_3 & [network_3_2_AnnP_0>poll__networl_3_2_AnnP_0 & [network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [network_1_2_AnsP_2>poll__networl_1_2_AnsP_2 & [network_3_0_AskP_2>poll__networl_3_0_AskP_2 & [network_1_0_AnsP_3>poll__networl_1_0_AnsP_3 & [network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [network_2_2_AskP_1>poll__networl_2_2_AskP_1 & [network_2_0_AI_1>poll__networl_2_0_AI_1 & [network_0_2_AI_2>poll__networl_0_2_AI_2 & [network_2_3_RP_2>poll__networl_2_3_RP_2 & [network_0_0_AskP_3>poll__networl_0_0_AskP_3 & [network_2_2_AnnP_2>poll__networl_2_2_AnnP_2 & [network_3_1_AnsP_1>poll__networl_3_1_AnsP_1 & [network_3_3_AnsP_2>poll__networl_3_3_AnsP_2 & [network_1_1_RI_1>poll__networl_1_1_RI_1 & [network_0_0_RP_1>poll__networl_0_0_RP_1 & [network_3_2_RI_0>poll__networl_3_2_RI_0 & [network_3_2_AnnP_2>poll__networl_3_2_AnnP_2 & [network_1_0_RP_2>poll__networl_1_0_RP_2 & [network_0_1_AnsP_3>poll__networl_0_1_AnsP_3 & [network_3_1_AnnP_0>poll__networl_3_1_AnnP_0 & [network_1_1_AnnP_3>poll__networl_1_1_AnnP_3 & [network_0_2_AskP_2>poll__networl_0_2_AskP_2 & [network_0_1_RP_1>poll__networl_0_1_RP_1 & [network_3_1_AskP_0>poll__networl_3_1_AskP_0 & [network_3_3_RP_0>poll__networl_3_3_RP_0 & [network_0_2_RI_3>poll__networl_0_2_RI_3 & [network_2_1_AnnP_3>poll__networl_2_1_AnnP_3 & [network_2_2_AnsP_2>poll__networl_2_2_AnsP_2 & [network_2_0_AnsP_2>poll__networl_2_0_AnsP_2 & [network_0_1_AnnP_3>poll__networl_0_1_AnnP_3 & [network_3_3_AnnP_3>poll__networl_3_3_AnnP_3 & [network_1_0_RP_1>poll__networl_1_0_RP_1 & [network_2_3_AnnP_0>poll__networl_2_3_AnnP_0 & [network_2_3_AnsP_0>poll__networl_2_3_AnsP_0 & [network_0_1_RI_1>poll__networl_0_1_RI_1 & [network_1_0_AskP_1>poll__networl_1_0_AskP_1 & [network_0_0_AskP_0>poll__networl_0_0_AskP_0 & [network_1_0_AnnP_0>poll__networl_1_0_AnnP_0 & [network_2_3_AnsP_2>poll__networl_2_3_AnsP_2 & [network_1_0_AnsP_1>poll__networl_1_0_AnsP_1 & [network_1_1_RP_1>poll__networl_1_1_RP_1 & [network_0_3_RP_2>poll__networl_0_3_RP_2 & [network_3_2_AskP_3>poll__networl_3_2_AskP_3 & [network_1_2_AnnP_2>poll__networl_1_2_AnnP_2 & [network_0_1_AnnP_1>poll__networl_0_1_AnnP_1 & [network_1_1_AI_0>poll__networl_1_1_AI_0 & [network_2_2_AskP_2>poll__networl_2_2_AskP_2 & [network_2_2_RI_1>poll__networl_2_2_RI_1 & [network_3_1_AskP_2>poll__networl_3_1_AskP_2 & [network_2_3_AnnP_1>poll__networl_2_3_AnnP_1 & [network_0_0_AI_1>poll__networl_0_0_AI_1 & [network_0_2_AnnP_3>poll__networl_0_2_AnnP_3 & [network_2_2_RP_0>poll__networl_2_2_RP_0 & [network_0_2_AskP_1>poll__networl_0_2_AskP_1 & [network_2_0_RI_0>poll__networl_2_0_RI_0 & [network_3_0_AnsP_0>poll__networl_3_0_AnsP_0 & [network_2_0_AnsP_1>poll__networl_2_0_AnsP_1 & [network_0_3_AI_2>poll__networl_0_3_AI_2 & [network_1_0_AnsP_0>poll__networl_1_0_AnsP_0 & [network_2_1_RP_0>poll__networl_2_1_RP_0 & [network_3_1_AI_2>poll__networl_3_1_AI_2 & [network_3_1_RP_3>poll__networl_3_1_RP_3 & [network_3_3_AnsP_3>poll__networl_3_3_AnsP_3 & [network_2_1_AI_2>poll__networl_2_1_AI_2 & [network_2_2_AI_0>poll__networl_2_2_AI_0 & [network_1_2_AskP_1>poll__networl_1_2_AskP_1 & [network_2_1_AskP_0>poll__networl_2_1_AskP_0 & [network_2_0_AskP_2>poll__networl_2_0_AskP_2 & [network_0_3_AnsP_2>poll__networl_0_3_AnsP_2 & [network_1_1_AskP_2>poll__networl_1_1_AskP_2 & [network_2_1_AnnP_0>poll__networl_2_1_AnnP_0 & [network_0_0_AnsP_3>poll__networl_0_0_AnsP_3 & [network_1_3_RP_0>poll__networl_1_3_RP_0 & [network_0_3_AI_1>poll__networl_0_3_AI_1 & [network_1_2_RI_2>poll__networl_1_2_RI_2 & [network_0_3_AskP_3>poll__networl_0_3_AskP_3 & [network_3_2_AnnP_1>poll__networl_3_2_AnnP_1 & [network_3_0_AnnP_2>poll__networl_3_0_AnnP_2 & [network_1_3_AnsP_1>poll__networl_1_3_AnsP_1 & [network_0_3_RP_3>poll__networl_0_3_RP_3 & [network_1_0_RI_1>poll__networl_1_0_RI_1 & [network_0_3_RP_0>poll__networl_0_3_RP_0 & [network_0_0_AnnP_3>poll__networl_0_0_AnnP_3 & [network_2_2_RI_2>poll__networl_2_2_RI_2 & [network_1_2_AskP_0>poll__networl_1_2_AskP_0 & [network_2_3_AskP_0>poll__networl_2_3_AskP_0 & [network_2_0_AnnP_2>poll__networl_2_0_AnnP_2 & [network_1_1_AnnP_2>poll__networl_1_1_AnnP_2 & [network_2_0_RP_3>poll__networl_2_0_RP_3 & [network_0_1_RP_2>poll__networl_0_1_RP_2 & [network_2_0_AnnP_1>poll__networl_2_0_AnnP_1 & [network_1_3_AnnP_1>poll__networl_1_3_AnnP_1 & [network_1_2_AnsP_1>poll__networl_1_2_AnsP_1 & [network_0_2_AnsP_1>poll__networl_0_2_AnsP_1 & [network_3_0_RP_3>poll__networl_3_0_RP_3 & [network_0_1_RI_0>poll__networl_0_1_RI_0 & [network_2_3_RP_1>poll__networl_2_3_RP_1 & [network_1_3_RP_3>poll__networl_1_3_RP_3 & [network_3_0_AI_1>poll__networl_3_0_AI_1 & [network_2_1_AskP_3>poll__networl_2_1_AskP_3 & [network_0_0_RP_0>poll__networl_0_0_RP_0 & [network_3_2_AnsP_0>poll__networl_3_2_AnsP_0 & [network_0_1_AI_0>poll__networl_0_1_AI_0 & [network_3_3_AnnP_0>poll__networl_3_3_AnnP_0 & [network_3_0_AnsP_1>poll__networl_3_0_AnsP_1 & [network_3_2_RI_3>poll__networl_3_2_RI_3 & [network_0_1_AI_1>poll__networl_0_1_AI_1 & [network_2_3_AI_1>poll__networl_2_3_AI_1 & [network_2_1_AnnP_2>poll__networl_2_1_AnnP_2 & [network_2_0_RI_1>poll__networl_2_0_RI_1 & [network_2_1_AI_1>poll__networl_2_1_AI_1 & [network_0_3_AnsP_3>poll__networl_0_3_AnsP_3 & [network_2_1_AI_3>poll__networl_2_1_AI_3 & [network_3_1_AnnP_1>poll__networl_3_1_AnnP_1 & [network_3_3_AnsP_0>poll__networl_3_3_AnsP_0 & [network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [network_0_0_AI_3>poll__networl_0_0_AI_3 & [network_3_1_RI_2>poll__networl_3_1_RI_2 & [network_0_1_RP_0>poll__networl_0_1_RP_0 & [network_0_3_RI_3>poll__networl_0_3_RI_3 & [network_1_2_AnnP_1>poll__networl_1_2_AnnP_1 & [network_2_0_AnsP_0>poll__networl_2_0_AnsP_0 & [network_1_3_AskP_1>poll__networl_1_3_AskP_1 & [network_0_1_AI_3>poll__networl_0_1_AI_3 & [network_2_1_AI_0>poll__networl_2_1_AI_0 & [network_2_1_RP_3>poll__networl_2_1_RP_3 & [network_3_0_RI_1>poll__networl_3_0_RI_1 & [network_2_3_AI_2>poll__networl_2_3_AI_2 & [network_1_2_AskP_2>poll__networl_1_2_AskP_2 & [network_3_1_AskP_3>poll__networl_3_1_AskP_3 & [network_0_0_RP_2>poll__networl_0_0_RP_2 & [network_1_3_RI_1>poll__networl_1_3_RI_1 & [network_3_0_AI_0>poll__networl_3_0_AI_0 & [network_2_0_RP_1>poll__networl_2_0_RP_1 & [network_3_1_RI_0>poll__networl_3_1_RI_0 & [network_2_0_AI_3>poll__networl_2_0_AI_3 & [network_0_2_RP_2>poll__networl_0_2_RP_2 & [network_0_2_RP_3>poll__networl_0_2_RP_3 & [network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [network_2_2_AskP_0>poll__networl_2_2_AskP_0 & [network_1_1_AI_2>poll__networl_1_1_AI_2 & [network_0_1_AnnP_2>poll__networl_0_1_AnnP_2 & [network_3_2_RI_2>poll__networl_3_2_RI_2 & [network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [network_1_0_AI_3>poll__networl_1_0_AI_3 & [network_3_1_AnnP_3>poll__networl_3_1_AnnP_3 & [network_3_2_AskP_1>poll__networl_3_2_AskP_1 & [network_3_1_AI_0>poll__networl_3_1_AI_0 & [network_3_1_AnsP_3>poll__networl_3_1_AnsP_3 & [network_1_3_AnsP_0>poll__networl_1_3_AnsP_0 & [network_2_3_RP_3>poll__networl_2_3_RP_3 & [network_1_2_AI_1>poll__networl_1_2_AI_1 & [network_1_1_RP_3>poll__networl_1_1_RP_3 & [network_2_2_AnsP_0>poll__networl_2_2_AnsP_0 & [network_0_3_RI_1>poll__networl_0_3_RI_1 & [network_2_1_RI_2>poll__networl_2_1_RI_2 & [network_2_3_AnsP_1>poll__networl_2_3_AnsP_1 & [network_2_1_RI_0>poll__networl_2_1_RI_0 & [network_3_0_AnnP_3>poll__networl_3_0_AnnP_3 & [network_0_0_RI_1>poll__networl_0_0_RI_1 & [network_2_0_RP_2>poll__networl_2_0_RP_2 & [network_2_3_AI_0>poll__networl_2_3_AI_0 & [network_3_2_AI_2>poll__networl_3_2_AI_2 & [network_0_3_AnsP_0>poll__networl_0_3_AnsP_0 & [network_0_1_AnnP_0>poll__networl_0_1_AnnP_0 & [network_2_2_AnnP_0>poll__networl_2_2_AnnP_0 & [network_3_3_AskP_1>poll__networl_3_3_AskP_1 & [network_1_1_AI_3>poll__networl_1_1_AI_3 & [network_3_3_RI_2>poll__networl_3_3_RI_2 & [network_2_0_RI_3>poll__networl_2_0_RI_3 & [network_0_1_AnsP_2>poll__networl_0_1_AnsP_2 & [network_0_0_AnsP_0>poll__networl_0_0_AnsP_0 & [network_1_1_RI_3>poll__networl_1_1_RI_3 & [network_1_0_RI_3>poll__networl_1_0_RI_3 & [network_0_0_RI_0>poll__networl_0_0_RI_0 & [network_0_0_AskP_2>poll__networl_0_0_AskP_2 & [network_3_2_AnsP_2>poll__networl_3_2_AnsP_2 & [network_1_0_AnnP_1>poll__networl_1_0_AnnP_1 & [network_2_3_AnnP_3>poll__networl_2_3_AnnP_3 & [network_2_1_RI_3>poll__networl_2_1_RI_3 & [network_2_0_RI_2>poll__networl_2_0_RI_2 & [network_3_1_RP_1>poll__networl_3_1_RP_1 & [network_3_1_AI_3>poll__networl_3_1_AI_3 & [network_0_3_RI_2>poll__networl_0_3_RI_2 & [network_2_3_AnnP_2>poll__networl_2_3_AnnP_2 & [network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [network_1_0_AnnP_3>poll__networl_1_0_AnnP_3 & [network_1_1_RI_2>poll__networl_1_1_RI_2 & [network_3_2_AI_0>poll__networl_3_2_AI_0 & [network_3_0_AnsP_3>poll__networl_3_0_AnsP_3 & [network_0_3_AnnP_1>poll__networl_0_3_AnnP_1 & [network_3_3_RI_3>poll__networl_3_3_RI_3 & [network_3_3_AI_1>poll__networl_3_3_AI_1 & [network_1_0_AI_1>poll__networl_1_0_AI_1 & [network_0_1_RP_3>poll__networl_0_1_RP_3 & [network_2_2_RP_3>poll__networl_2_2_RP_3 & [network_0_0_RI_3>poll__networl_0_0_RI_3 & [network_3_3_RP_3>poll__networl_3_3_RP_3 & [network_0_0_AI_0>poll__networl_0_0_AI_0 & [network_3_0_RI_0>poll__networl_3_0_RI_0 & [network_3_2_RP_3>poll__networl_3_2_RP_3 & [network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [network_3_3_AskP_0>poll__networl_3_3_AskP_0 & [network_2_2_AnsP_1>poll__networl_2_2_AnsP_1 & [network_0_2_RI_0>poll__networl_0_2_RI_0 & [network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [network_3_0_AI_2>poll__networl_3_0_AI_2 & [network_1_2_RP_1>poll__networl_1_2_RP_1 & [network_1_2_AnsP_3>poll__networl_1_2_AnsP_3 & [network_3_0_AskP_3>poll__networl_3_0_AskP_3 & [network_2_1_RI_1>poll__networl_2_1_RI_1 & [network_0_0_AnsP_1>poll__networl_0_0_AnsP_1 & [network_3_3_AnsP_1>poll__networl_3_3_AnsP_1 & [network_3_1_RI_1>poll__networl_3_1_RI_1 & [network_1_2_AI_3>poll__networl_1_2_AI_3 & [network_0_3_RI_0>poll__networl_0_3_RI_0 & [network_3_0_AnsP_2>poll__networl_3_0_AnsP_2 & [network_2_1_AnsP_1>poll__networl_2_1_AnsP_1 & [network_3_3_RP_1>poll__networl_3_3_RP_1 & [network_0_2_AskP_0>poll__networl_0_2_AskP_0 & [network_1_3_AI_1>poll__networl_1_3_AI_1 & [network_0_3_AI_3>poll__networl_0_3_AI_3 & [network_3_3_AI_2>poll__networl_3_3_AI_2 & [network_0_3_AnsP_1>poll__networl_0_3_AnsP_1 & [network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [network_2_2_RP_1>poll__networl_2_2_RP_1 & [network_3_1_RP_0>poll__networl_3_1_RP_0 & [network_2_0_AnsP_3>poll__networl_2_0_AnsP_3 & [network_1_0_AnnP_2>poll__networl_1_0_AnnP_2 & [network_3_2_RP_1>poll__networl_3_2_RP_1 & [network_3_2_RP_2>poll__networl_3_2_RP_2 & [network_0_3_AskP_0>poll__networl_0_3_AskP_0 & [network_3_0_RP_0>poll__networl_3_0_RP_0 & [network_3_3_AnnP_1>poll__networl_3_3_AnnP_1 & [network_1_0_RP_3>poll__networl_1_0_RP_3 & [network_0_2_AnnP_2>poll__networl_0_2_AnnP_2 & [network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [network_1_2_AnnP_0>poll__networl_1_2_AnnP_0 & [network_0_3_AI_0>poll__networl_0_3_AI_0 & [network_1_3_AskP_3>poll__networl_1_3_AskP_3 & [network_0_1_AskP_1>poll__networl_0_1_AskP_1 & [network_2_3_RI_1>poll__networl_2_3_RI_1 & [network_2_2_AI_1>poll__networl_2_2_AI_1 & [network_1_2_RP_3>poll__networl_1_2_RP_3 & [network_3_2_AI_1>poll__networl_3_2_AI_1 & [network_1_3_RI_3>poll__networl_1_3_RI_3 & [network_2_2_AskP_3>poll__networl_2_2_AskP_3 & [network_2_1_RP_1>poll__networl_2_1_RP_1 & [network_0_1_RI_2>poll__networl_0_1_RI_2 & [network_2_3_AskP_2>poll__networl_2_3_AskP_2 & [network_3_3_RI_1>poll__networl_3_3_RI_1 & [network_3_0_RI_3>poll__networl_3_0_RI_3 & [network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [network_2_3_AskP_1>poll__networl_2_3_AskP_1 & [network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [network_3_3_AI_3>poll__networl_3_3_AI_3 & [network_2_1_AnsP_3>poll__networl_2_1_AnsP_3 & [network_0_2_AnsP_0>poll__networl_0_2_AnsP_0 & [network_0_3_AnnP_3>poll__networl_0_3_AnnP_3 & [network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [network_2_2_AnnP_1>poll__networl_2_2_AnnP_1 & [network_1_1_AnnP_0>poll__networl_1_1_AnnP_0 & [network_3_2_AnnP_3>poll__networl_3_2_AnnP_3 & [network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [network_1_0_AI_0>poll__networl_1_0_AI_0 & [network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [network_1_2_AI_0>poll__networl_1_2_AI_0 & [network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [network_1_1_AnnP_1>poll__networl_1_1_AnnP_1 & [network_1_3_AI_0>poll__networl_1_3_AI_0 & [network_0_2_RP_1>poll__networl_0_2_RP_1 & [network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [network_2_1_AskP_2>poll__networl_2_1_AskP_2 & [network_1_2_RP_0>poll__networl_1_2_RP_0 & [network_1_2_RI_3>poll__networl_1_2_RI_3 & [network_2_0_AskP_0>poll__networl_2_0_AskP_0 & [network_1_1_AnsP_1>poll__networl_1_1_AnsP_1 & [network_0_2_AskP_3>poll__networl_0_2_AskP_3 & [network_1_3_AI_2>poll__networl_1_3_AI_2 & [network_1_3_AnsP_2>poll__networl_1_3_AnsP_2 & [network_0_2_AI_3>poll__networl_0_2_AI_3 & [network_1_2_AI_2>poll__networl_1_2_AI_2 & [network_2_0_RP_0>poll__networl_2_0_RP_0 & [network_3_2_RP_0>poll__networl_3_2_RP_0 & [network_2_1_AskP_1>poll__networl_2_1_AskP_1 & [network_1_0_RP_0>poll__networl_1_0_RP_0 & [network_0_2_AnsP_2>poll__networl_0_2_AnsP_2 & [network_2_0_AI_0>poll__networl_2_0_AI_0 & [network_3_2_RI_1>poll__networl_3_2_RI_1 & [network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [network_3_0_RP_2>poll__networl_3_0_RP_2 & [network_2_2_AI_2>poll__networl_2_2_AI_2 & [network_0_1_AskP_3>poll__networl_0_1_AskP_3 & [network_1_1_RI_0>poll__networl_1_1_RI_0 & [network_0_1_RI_3>poll__networl_0_1_RI_3 & [network_1_2_RP_2>poll__networl_1_2_RP_2 & [network_0_3_AnnP_2>poll__networl_0_3_AnnP_2 & [network_3_1_AnsP_2>poll__networl_3_1_AnsP_2 & [network_1_3_AnnP_2>poll__networl_1_3_AnnP_2 & [network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [network_0_0_AI_2>poll__networl_0_0_AI_2 & [network_2_3_AI_3>poll__networl_2_3_AI_3 & [network_3_2_AskP_2>poll__networl_3_2_AskP_2 & [network_2_1_AnsP_0>poll__networl_2_1_AnsP_0 & [network_3_0_AnnP_0>poll__networl_3_0_AnnP_0 & [network_1_3_RP_1>poll__networl_1_3_RP_1 & [network_3_3_AskP_2>poll__networl_3_3_AskP_2 & [network_3_3_RP_2>poll__networl_3_3_RP_2 & [network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [network_1_0_RI_2>poll__networl_1_0_RI_2 & [network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [network_0_0_RI_2>poll__networl_0_0_RI_2 & [network_3_3_AI_0>poll__networl_3_3_AI_0 & [network_1_2_AnsP_0>poll__networl_1_2_AnsP_0 & [network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [network_3_2_AnsP_3>poll__networl_3_2_AnsP_3 & [network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [network_3_2_AI_3>poll__networl_3_2_AI_3 & [network_1_3_RP_2>poll__networl_1_3_RP_2 & [network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [network_3_3_AnnP_2>poll__networl_3_3_AnnP_2 & [network_1_0_AnsP_2>poll__networl_1_0_AnsP_2 & [network_0_1_AnsP_0>poll__networl_0_1_AnsP_0 & [network_0_2_RP_0>poll__networl_0_2_RP_0 & [network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [network_1_3_RI_2>poll__networl_1_3_RI_2 & [network_0_0_RP_3>poll__networl_0_0_RP_3 & [network_1_0_AI_2>poll__networl_1_0_AI_2 & [network_3_0_AI_3>poll__networl_3_0_AI_3 & [network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [network_2_2_AnsP_3>poll__networl_2_2_AnsP_3 & [network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [network_1_1_RP_0>poll__networl_1_1_RP_0 & [network_1_0_AskP_3>poll__networl_1_0_AskP_3 & [network_1_3_RI_0>poll__networl_1_3_RI_0 & [network_3_0_RP_1>poll__networl_3_0_RP_1 & [network_1_1_AnsP_3>poll__networl_1_1_AnsP_3 & [network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [network_1_1_RP_2>poll__networl_1_1_RP_2 & [network_2_3_RI_2>poll__networl_2_3_RI_2 & true]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & true]]]]]
-> the formula is FALSE
FORMULA p_42_mix_full_and FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[[true & [network_2_2_RP_2>poll__networl_2_2_RP_2 & [[[[[[[[[[[[[[[[[network_1_1_AnsP_0>poll__networl_1_1_AnsP_0 & [network_3_1_AI_1>poll__networl_3_1_AI_1 & [network_1_1_AskP_3>poll__networl_1_1_AskP_3 & [network_0_2_RI_2>poll__networl_0_2_RI_2 & [network_3_3_RI_0>poll__networl_3_3_RI_0 & [network_3_1_RI_3>poll__networl_3_1_RI_3 & [network_3_2_AnnP_0>poll__networl_3_2_AnnP_0 & [network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [network_1_2_AnsP_2>poll__networl_1_2_AnsP_2 & [network_3_0_AskP_2>poll__networl_3_0_AskP_2 & [network_1_0_AnsP_3>poll__networl_1_0_AnsP_3 & [network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [network_2_2_AskP_1>poll__networl_2_2_AskP_1 & [network_2_0_AI_1>poll__networl_2_0_AI_1 & [[network_2_3_RP_2>poll__networl_2_3_RP_2 & [network_0_0_AskP_3>poll__networl_0_0_AskP_3 & [network_2_2_AnnP_2>poll__networl_2_2_AnnP_2 & [network_3_1_AnsP_1>poll__networl_3_1_AnsP_1 & [network_3_3_AnsP_2>poll__networl_3_3_AnsP_2 & [network_1_1_RI_1>poll__networl_1_1_RI_1 & [network_0_0_RP_1>poll__networl_0_0_RP_1 & [network_3_2_RI_0>poll__networl_3_2_RI_0 & [network_3_2_AnnP_2>poll__networl_3_2_AnnP_2 & [network_1_0_RP_2>poll__networl_1_0_RP_2 & [network_0_1_AnsP_3>poll__networl_0_1_AnsP_3 & [network_3_1_AnnP_0>poll__networl_3_1_AnnP_0 & [network_1_1_AnnP_3>poll__networl_1_1_AnnP_3 & [network_0_2_AskP_2>poll__networl_0_2_AskP_2 & [network_0_1_RP_1>poll__networl_0_1_RP_1 & [network_3_1_AskP_0>poll__networl_3_1_AskP_0 & [network_3_3_RP_0>poll__networl_3_3_RP_0 & [network_0_2_RI_3>poll__networl_0_2_RI_3 & [network_2_1_AnnP_3>poll__networl_2_1_AnnP_3 & [[[network_0_1_AnnP_3>poll__networl_0_1_AnnP_3 & [[network_1_0_RP_1>poll__networl_1_0_RP_1 & [[[[[[[network_2_3_AnsP_2>poll__networl_2_3_AnsP_2 & [[[[[[[[[network_2_2_RI_1>poll__networl_2_2_RI_1 & [[[[network_0_2_AnnP_3>poll__networl_0_2_AnnP_3 & [[network_0_2_AskP_1>poll__networl_0_2_AskP_1 & [[[[[[network_2_1_RP_0>poll__networl_2_1_RP_0 & [[network_3_1_RP_3>poll__networl_3_1_RP_3 & [[network_2_1_AI_2>poll__networl_2_1_AI_2 & [network_2_2_AI_0>poll__networl_2_2_AI_0 & [network_1_2_AskP_1>poll__networl_1_2_AskP_1 & [[network_2_0_AskP_2>poll__networl_2_0_AskP_2 & [[network_1_1_AskP_2>poll__networl_1_1_AskP_2 & [network_2_1_AnnP_0>poll__networl_2_1_AnnP_0 & [network_0_0_AnsP_3>poll__networl_0_0_AnsP_3 & [[[network_1_2_RI_2>poll__networl_1_2_RI_2 & [network_0_3_AskP_3>poll__networl_0_3_AskP_3 & [network_3_2_AnnP_1>poll__networl_3_2_AnnP_1 & [network_3_0_AnnP_2>poll__networl_3_0_AnnP_2 & [network_1_3_AnsP_1>poll__networl_1_3_AnsP_1 & [network_0_3_RP_3>poll__networl_0_3_RP_3 & [network_1_0_RI_1>poll__networl_1_0_RI_1 & [network_0_3_RP_0>poll__networl_0_3_RP_0 & [network_0_0_AnnP_3>poll__networl_0_0_AnnP_3 & [network_2_2_RI_2>poll__networl_2_2_RI_2 & [network_1_2_AskP_0>poll__networl_1_2_AskP_0 & [network_2_3_AskP_0>poll__networl_2_3_AskP_0 & [network_2_0_AnnP_2>poll__networl_2_0_AnnP_2 & [network_1_1_AnnP_2>poll__networl_1_1_AnnP_2 & [network_2_0_RP_3>poll__networl_2_0_RP_3 & [[network_2_0_AnnP_1>poll__networl_2_0_AnnP_1 & [network_1_3_AnnP_1>poll__networl_1_3_AnnP_1 & [network_1_2_AnsP_1>poll__networl_1_2_AnsP_1 & [network_0_2_AnsP_1>poll__networl_0_2_AnsP_1 & [network_3_0_RP_3>poll__networl_3_0_RP_3 & [network_0_1_RI_0>poll__networl_0_1_RI_0 & [network_2_3_RP_1>poll__networl_2_3_RP_1 & [network_1_3_RP_3>poll__networl_1_3_RP_3 & [[network_2_1_AskP_3>poll__networl_2_1_AskP_3 & [network_0_0_RP_0>poll__networl_0_0_RP_0 & [network_3_2_AnsP_0>poll__networl_3_2_AnsP_0 & [network_0_1_AI_0>poll__networl_0_1_AI_0 & [network_3_3_AnnP_0>poll__networl_3_3_AnnP_0 & [network_3_0_AnsP_1>poll__networl_3_0_AnsP_1 & [network_3_2_RI_3>poll__networl_3_2_RI_3 & [network_0_1_AI_1>poll__networl_0_1_AI_1 & [network_2_3_AI_1>poll__networl_2_3_AI_1 & [network_2_1_AnnP_2>poll__networl_2_1_AnnP_2 & [network_2_0_RI_1>poll__networl_2_0_RI_1 & [network_2_1_AI_1>poll__networl_2_1_AI_1 & [network_0_3_AnsP_3>poll__networl_0_3_AnsP_3 & [network_2_1_AI_3>poll__networl_2_1_AI_3 & [network_3_1_AnnP_1>poll__networl_3_1_AnnP_1 & [network_3_3_AnsP_0>poll__networl_3_3_AnsP_0 & [network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [network_0_0_AI_3>poll__networl_0_0_AI_3 & [network_3_1_RI_2>poll__networl_3_1_RI_2 & [network_0_1_RP_0>poll__networl_0_1_RP_0 & [network_0_3_RI_3>poll__networl_0_3_RI_3 & [network_1_2_AnnP_1>poll__networl_1_2_AnnP_1 & [network_2_0_AnsP_0>poll__networl_2_0_AnsP_0 & [network_1_3_AskP_1>poll__networl_1_3_AskP_1 & [network_0_1_AI_3>poll__networl_0_1_AI_3 & [network_2_1_AI_0>poll__networl_2_1_AI_0 & [network_2_1_RP_3>poll__networl_2_1_RP_3 & [network_3_0_RI_1>poll__networl_3_0_RI_1 & [network_2_3_AI_2>poll__networl_2_3_AI_2 & [network_1_2_AskP_2>poll__networl_1_2_AskP_2 & [network_3_1_AskP_3>poll__networl_3_1_AskP_3 & [network_0_0_RP_2>poll__networl_0_0_RP_2 & [network_1_3_RI_1>poll__networl_1_3_RI_1 & [network_3_0_AI_0>poll__networl_3_0_AI_0 & [network_2_0_RP_1>poll__networl_2_0_RP_1 & [network_3_1_RI_0>poll__networl_3_1_RI_0 & [network_2_0_AI_3>poll__networl_2_0_AI_3 & [network_0_2_RP_2>poll__networl_0_2_RP_2 & [network_0_2_RP_3>poll__networl_0_2_RP_3 & [network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [network_2_2_AskP_0>poll__networl_2_2_AskP_0 & [network_1_1_AI_2>poll__networl_1_1_AI_2 & [network_0_1_AnnP_2>poll__networl_0_1_AnnP_2 & [network_3_2_RI_2>poll__networl_3_2_RI_2 & [network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [network_1_0_AI_3>poll__networl_1_0_AI_3 & [network_3_1_AnnP_3>poll__networl_3_1_AnnP_3 & [[network_3_1_AI_0>poll__networl_3_1_AI_0 & [network_3_1_AnsP_3>poll__networl_3_1_AnsP_3 & [network_1_3_AnsP_0>poll__networl_1_3_AnsP_0 & [network_2_3_RP_3>poll__networl_2_3_RP_3 & [[network_1_1_RP_3>poll__networl_1_1_RP_3 & [network_2_2_AnsP_0>poll__networl_2_2_AnsP_0 & [[[network_2_3_AnsP_1>poll__networl_2_3_AnsP_1 & [[[[[network_2_3_AI_0>poll__networl_2_3_AI_0 & [[[[[[[network_3_3_RI_2>poll__networl_3_3_RI_2 & [[network_0_1_AnsP_2>poll__networl_0_1_AnsP_2 & [network_0_0_AnsP_0>poll__networl_0_0_AnsP_0 & [network_1_1_RI_3>poll__networl_1_1_RI_3 & [[network_0_0_RI_0>poll__networl_0_0_RI_0 & [[[[network_2_3_AnnP_3>poll__networl_2_3_AnnP_3 & [[network_2_0_RI_2>poll__networl_2_0_RI_2 & [network_3_1_RP_1>poll__networl_3_1_RP_1 & [[[[network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [network_1_0_AnnP_3>poll__networl_1_0_AnnP_3 & [network_1_1_RI_2>poll__networl_1_1_RI_2 & [network_3_2_AI_0>poll__networl_3_2_AI_0 & [network_3_0_AnsP_3>poll__networl_3_0_AnsP_3 & [network_0_3_AnnP_1>poll__networl_0_3_AnnP_1 & [network_3_3_RI_3>poll__networl_3_3_RI_3 & [network_3_3_AI_1>poll__networl_3_3_AI_1 & [network_1_0_AI_1>poll__networl_1_0_AI_1 & [network_0_1_RP_3>poll__networl_0_1_RP_3 & [network_2_2_RP_3>poll__networl_2_2_RP_3 & [network_0_0_RI_3>poll__networl_0_0_RI_3 & [network_3_3_RP_3>poll__networl_3_3_RP_3 & [network_0_0_AI_0>poll__networl_0_0_AI_0 & [network_3_0_RI_0>poll__networl_3_0_RI_0 & [network_3_2_RP_3>poll__networl_3_2_RP_3 & [network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [network_3_3_AskP_0>poll__networl_3_3_AskP_0 & [network_2_2_AnsP_1>poll__networl_2_2_AnsP_1 & [network_0_2_RI_0>poll__networl_0_2_RI_0 & [network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [network_3_0_AI_2>poll__networl_3_0_AI_2 & [network_1_2_RP_1>poll__networl_1_2_RP_1 & [network_1_2_AnsP_3>poll__networl_1_2_AnsP_3 & [network_3_0_AskP_3>poll__networl_3_0_AskP_3 & [network_2_1_RI_1>poll__networl_2_1_RI_1 & [network_0_0_AnsP_1>poll__networl_0_0_AnsP_1 & [network_3_3_AnsP_1>poll__networl_3_3_AnsP_1 & [network_3_1_RI_1>poll__networl_3_1_RI_1 & [network_1_2_AI_3>poll__networl_1_2_AI_3 & [network_0_3_RI_0>poll__networl_0_3_RI_0 & [network_3_0_AnsP_2>poll__networl_3_0_AnsP_2 & [network_2_1_AnsP_1>poll__networl_2_1_AnsP_1 & [network_3_3_RP_1>poll__networl_3_3_RP_1 & [network_0_2_AskP_0>poll__networl_0_2_AskP_0 & [network_1_3_AI_1>poll__networl_1_3_AI_1 & [network_0_3_AI_3>poll__networl_0_3_AI_3 & [network_3_3_AI_2>poll__networl_3_3_AI_2 & [network_0_3_AnsP_1>poll__networl_0_3_AnsP_1 & [network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [network_2_2_RP_1>poll__networl_2_2_RP_1 & [network_3_1_RP_0>poll__networl_3_1_RP_0 & [network_2_0_AnsP_3>poll__networl_2_0_AnsP_3 & [network_1_0_AnnP_2>poll__networl_1_0_AnnP_2 & [network_3_2_RP_1>poll__networl_3_2_RP_1 & [network_3_2_RP_2>poll__networl_3_2_RP_2 & [network_0_3_AskP_0>poll__networl_0_3_AskP_0 & [network_3_0_RP_0>poll__networl_3_0_RP_0 & [network_3_3_AnnP_1>poll__networl_3_3_AnnP_1 & [network_1_0_RP_3>poll__networl_1_0_RP_3 & [network_0_2_AnnP_2>poll__networl_0_2_AnnP_2 & [network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [network_1_2_AnnP_0>poll__networl_1_2_AnnP_0 & [network_0_3_AI_0>poll__networl_0_3_AI_0 & [network_1_3_AskP_3>poll__networl_1_3_AskP_3 & [network_0_1_AskP_1>poll__networl_0_1_AskP_1 & [network_2_3_RI_1>poll__networl_2_3_RI_1 & [network_2_2_AI_1>poll__networl_2_2_AI_1 & [network_1_2_RP_3>poll__networl_1_2_RP_3 & [network_3_2_AI_1>poll__networl_3_2_AI_1 & [network_1_3_RI_3>poll__networl_1_3_RI_3 & [network_2_2_AskP_3>poll__networl_2_2_AskP_3 & [network_2_1_RP_1>poll__networl_2_1_RP_1 & [network_0_1_RI_2>poll__networl_0_1_RI_2 & [network_2_3_AskP_2>poll__networl_2_3_AskP_2 & [network_3_3_RI_1>poll__networl_3_3_RI_1 & [network_3_0_RI_3>poll__networl_3_0_RI_3 & [network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [network_2_3_AskP_1>poll__networl_2_3_AskP_1 & [network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [network_3_3_AI_3>poll__networl_3_3_AI_3 & [network_2_1_AnsP_3>poll__networl_2_1_AnsP_3 & [network_0_2_AnsP_0>poll__networl_0_2_AnsP_0 & [network_0_3_AnnP_3>poll__networl_0_3_AnnP_3 & [network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [network_2_2_AnnP_1>poll__networl_2_2_AnnP_1 & [network_1_1_AnnP_0>poll__networl_1_1_AnnP_0 & [network_3_2_AnnP_3>poll__networl_3_2_AnnP_3 & [network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [network_1_0_AI_0>poll__networl_1_0_AI_0 & [network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [network_1_2_AI_0>poll__networl_1_2_AI_0 & [network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [network_1_1_AnnP_1>poll__networl_1_1_AnnP_1 & [network_1_3_AI_0>poll__networl_1_3_AI_0 & [network_0_2_RP_1>poll__networl_0_2_RP_1 & [network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [network_2_1_AskP_2>poll__networl_2_1_AskP_2 & [network_1_2_RP_0>poll__networl_1_2_RP_0 & [network_1_2_RI_3>poll__networl_1_2_RI_3 & [network_2_0_AskP_0>poll__networl_2_0_AskP_0 & [network_1_1_AnsP_1>poll__networl_1_1_AnsP_1 & [network_0_2_AskP_3>poll__networl_0_2_AskP_3 & [network_1_3_AI_2>poll__networl_1_3_AI_2 & [network_1_3_AnsP_2>poll__networl_1_3_AnsP_2 & [network_0_2_AI_3>poll__networl_0_2_AI_3 & [network_1_2_AI_2>poll__networl_1_2_AI_2 & [network_2_0_RP_0>poll__networl_2_0_RP_0 & [network_3_2_RP_0>poll__networl_3_2_RP_0 & [network_2_1_AskP_1>poll__networl_2_1_AskP_1 & [network_1_0_RP_0>poll__networl_1_0_RP_0 & [network_0_2_AnsP_2>poll__networl_0_2_AnsP_2 & [network_2_0_AI_0>poll__networl_2_0_AI_0 & [network_3_2_RI_1>poll__networl_3_2_RI_1 & [network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [network_3_0_RP_2>poll__networl_3_0_RP_2 & [network_2_2_AI_2>poll__networl_2_2_AI_2 & [network_0_1_AskP_3>poll__networl_0_1_AskP_3 & [network_1_1_RI_0>poll__networl_1_1_RI_0 & [network_0_1_RI_3>poll__networl_0_1_RI_3 & [network_1_2_RP_2>poll__networl_1_2_RP_2 & [network_0_3_AnnP_2>poll__networl_0_3_AnnP_2 & [network_3_1_AnsP_2>poll__networl_3_1_AnsP_2 & [network_1_3_AnnP_2>poll__networl_1_3_AnnP_2 & [network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [network_0_0_AI_2>poll__networl_0_0_AI_2 & [network_2_3_AI_3>poll__networl_2_3_AI_3 & [network_3_2_AskP_2>poll__networl_3_2_AskP_2 & [network_2_1_AnsP_0>poll__networl_2_1_AnsP_0 & [network_3_0_AnnP_0>poll__networl_3_0_AnnP_0 & [network_1_3_RP_1>poll__networl_1_3_RP_1 & [network_3_3_AskP_2>poll__networl_3_3_AskP_2 & [network_3_3_RP_2>poll__networl_3_3_RP_2 & [network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [network_1_0_RI_2>poll__networl_1_0_RI_2 & [network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [network_0_0_RI_2>poll__networl_0_0_RI_2 & [network_3_3_AI_0>poll__networl_3_3_AI_0 & [network_1_2_AnsP_0>poll__networl_1_2_AnsP_0 & [network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [network_3_2_AnsP_3>poll__networl_3_2_AnsP_3 & [network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [network_3_2_AI_3>poll__networl_3_2_AI_3 & [network_1_3_RP_2>poll__networl_1_3_RP_2 & [network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [network_3_3_AnnP_2>poll__networl_3_3_AnnP_2 & [network_1_0_AnsP_2>poll__networl_1_0_AnsP_2 & [network_0_1_AnsP_0>poll__networl_0_1_AnsP_0 & [network_0_2_RP_0>poll__networl_0_2_RP_0 & [network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [network_1_3_RI_2>poll__networl_1_3_RI_2 & [network_0_0_RP_3>poll__networl_0_0_RP_3 & [network_1_0_AI_2>poll__networl_1_0_AI_2 & [network_3_0_AI_3>poll__networl_3_0_AI_3 & [network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [network_2_2_AnsP_3>poll__networl_2_2_AnsP_3 & [network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [network_1_1_RP_0>poll__networl_1_1_RP_0 & [network_1_0_AskP_3>poll__networl_1_0_AskP_3 & [network_1_3_RI_0>poll__networl_1_3_RI_0 & [network_3_0_RP_1>poll__networl_3_0_RP_1 & [network_1_1_AnsP_3>poll__networl_1_1_AnsP_3 & [network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [network_1_1_RP_2>poll__networl_1_1_RP_2 & [network_2_3_RI_2>poll__networl_2_3_RI_2 & true]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & network_2_3_AnnP_2>poll__networl_2_3_AnnP_2] & network_0_3_RI_2>poll__networl_0_3_RI_2] & network_3_1_AI_3>poll__networl_3_1_AI_3]]] & network_2_1_RI_3>poll__networl_2_1_RI_3]] & network_1_0_AnnP_1>poll__networl_1_0_AnnP_1] & network_3_2_AnsP_2>poll__networl_3_2_AnsP_2] & network_0_0_AskP_2>poll__networl_0_0_AskP_2]] & network_1_0_RI_3>poll__networl_1_0_RI_3]]]] & network_2_0_RI_3>poll__networl_2_0_RI_3]] & network_1_1_AI_3>poll__networl_1_1_AI_3] & network_3_3_AskP_1>poll__networl_3_3_AskP_1] & network_2_2_AnnP_0>poll__networl_2_2_AnnP_0] & network_0_1_AnnP_0>poll__networl_0_1_AnnP_0] & network_0_3_AnsP_0>poll__networl_0_3_AnsP_0] & network_3_2_AI_2>poll__networl_3_2_AI_2]] & network_2_0_RP_2>poll__networl_2_0_RP_2] & network_0_0_RI_1>poll__networl_0_0_RI_1] & network_3_0_AnnP_3>poll__networl_3_0_AnnP_3] & network_2_1_RI_0>poll__networl_2_1_RI_0]] & network_2_1_RI_2>poll__networl_2_1_RI_2] & network_0_3_RI_1>poll__networl_0_3_RI_1]]] & network_1_2_AI_1>poll__networl_1_2_AI_1]]]]] & network_3_2_AskP_1>poll__networl_3_2_AskP_1]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & network_3_0_AI_1>poll__networl_3_0_AI_1]]]]]]]]] & network_0_1_RP_2>poll__networl_0_1_RP_2]]]]]]]]]]]]]]]] & network_0_3_AI_1>poll__networl_0_3_AI_1] & network_1_3_RP_0>poll__networl_1_3_RP_0]]]] & network_0_3_AnsP_2>poll__networl_0_3_AnsP_2]] & network_2_1_AskP_0>poll__networl_2_1_AskP_0]]]] & network_3_3_AnsP_3>poll__networl_3_3_AnsP_3]] & network_3_1_AI_2>poll__networl_3_1_AI_2]] & network_1_0_AnsP_0>poll__networl_1_0_AnsP_0] & network_0_3_AI_2>poll__networl_0_3_AI_2] & network_2_0_AnsP_1>poll__networl_2_0_AnsP_1] & network_3_0_AnsP_0>poll__networl_3_0_AnsP_0] & network_2_0_RI_0>poll__networl_2_0_RI_0]] & network_2_2_RP_0>poll__networl_2_2_RP_0]] & network_0_0_AI_1>poll__networl_0_0_AI_1] & network_2_3_AnnP_1>poll__networl_2_3_AnnP_1] & network_3_1_AskP_2>poll__networl_3_1_AskP_2]] & network_2_2_AskP_2>poll__networl_2_2_AskP_2] & network_1_1_AI_0>poll__networl_1_1_AI_0] & network_0_1_AnnP_1>poll__networl_0_1_AnnP_1] & network_1_2_AnnP_2>poll__networl_1_2_AnnP_2] & network_3_2_AskP_3>poll__networl_3_2_AskP_3] & network_0_3_RP_2>poll__networl_0_3_RP_2] & network_1_1_RP_1>poll__networl_1_1_RP_1] & network_1_0_AnsP_1>poll__networl_1_0_AnsP_1]] & network_1_0_AnnP_0>poll__networl_1_0_AnnP_0] & network_0_0_AskP_0>poll__networl_0_0_AskP_0] & network_1_0_AskP_1>poll__networl_1_0_AskP_1] & network_0_1_RI_1>poll__networl_0_1_RI_1] & network_2_3_AnsP_0>poll__networl_2_3_AnsP_0] & network_2_3_AnnP_0>poll__networl_2_3_AnnP_0]] & network_3_3_AnnP_3>poll__networl_3_3_AnnP_3]] & network_2_0_AnsP_2>poll__networl_2_0_AnsP_2] & network_2_2_AnsP_2>poll__networl_2_2_AnsP_2]]]]]]]]]]]]]]]]]]]] & network_0_2_AI_2>poll__networl_0_2_AI_2]]]]]]]]]]]]]]] & network_0_2_AnnP_0>poll__networl_0_2_AnnP_0] & network_0_0_AnnP_0>poll__networl_0_0_AnnP_0] & network_3_1_AnsP_0>poll__networl_3_1_AnsP_0] & network_0_2_AI_0>poll__networl_0_2_AI_0] & network_2_3_AskP_3>poll__networl_2_3_AskP_3] & network_2_3_AnsP_3>poll__networl_2_3_AnsP_3] & network_2_3_RI_0>poll__networl_2_3_RI_0] & network_0_1_AI_2>poll__networl_0_1_AI_2] & network_0_3_AnnP_0>poll__networl_0_3_AnnP_0] & network_2_0_AI_2>poll__networl_2_0_AI_2] & network_1_2_RI_0>poll__networl_1_2_RI_0] & network_2_1_AnsP_2>poll__networl_2_1_AnsP_2] & network_2_3_RP_0>poll__networl_2_3_RP_0] & network_1_3_AskP_0>poll__networl_1_3_AskP_0] & network_0_0_AnnP_2>poll__networl_0_0_AnnP_2] & network_1_0_RI_0>poll__networl_1_0_RI_0]]] | ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) ]]
normalized: ~ [E [true U ~ [[ ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) | [[network_2_2_RP_2>poll__networl_2_2_RP_2 & [network_1_0_RI_0>poll__networl_1_0_RI_0 & [network_0_0_AnnP_2>poll__networl_0_0_AnnP_2 & [network_1_3_AskP_0>poll__networl_1_3_AskP_0 & [network_2_3_RP_0>poll__networl_2_3_RP_0 & [network_2_1_AnsP_2>poll__networl_2_1_AnsP_2 & [network_1_2_RI_0>poll__networl_1_2_RI_0 & [network_2_0_AI_2>poll__networl_2_0_AI_2 & [network_0_3_AnnP_0>poll__networl_0_3_AnnP_0 & [network_0_1_AI_2>poll__networl_0_1_AI_2 & [network_2_3_RI_0>poll__networl_2_3_RI_0 & [network_2_3_AnsP_3>poll__networl_2_3_AnsP_3 & [network_2_3_AskP_3>poll__networl_2_3_AskP_3 & [network_0_2_AI_0>poll__networl_0_2_AI_0 & [network_3_1_AnsP_0>poll__networl_3_1_AnsP_0 & [network_0_0_AnnP_0>poll__networl_0_0_AnnP_0 & [network_0_2_AnnP_0>poll__networl_0_2_AnnP_0 & [network_1_1_AnsP_0>poll__networl_1_1_AnsP_0 & [network_3_1_AI_1>poll__networl_3_1_AI_1 & [network_1_1_AskP_3>poll__networl_1_1_AskP_3 & [network_0_2_RI_2>poll__networl_0_2_RI_2 & [network_3_3_RI_0>poll__networl_3_3_RI_0 & [network_3_1_RI_3>poll__networl_3_1_RI_3 & [network_3_2_AnnP_0>poll__networl_3_2_AnnP_0 & [network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [network_1_2_AnsP_2>poll__networl_1_2_AnsP_2 & [network_3_0_AskP_2>poll__networl_3_0_AskP_2 & [network_1_0_AnsP_3>poll__networl_1_0_AnsP_3 & [network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [network_2_2_AskP_1>poll__networl_2_2_AskP_1 & [network_2_0_AI_1>poll__networl_2_0_AI_1 & [network_0_2_AI_2>poll__networl_0_2_AI_2 & [network_2_3_RP_2>poll__networl_2_3_RP_2 & [network_0_0_AskP_3>poll__networl_0_0_AskP_3 & [network_2_2_AnnP_2>poll__networl_2_2_AnnP_2 & [network_3_1_AnsP_1>poll__networl_3_1_AnsP_1 & [network_3_3_AnsP_2>poll__networl_3_3_AnsP_2 & [network_1_1_RI_1>poll__networl_1_1_RI_1 & [network_0_0_RP_1>poll__networl_0_0_RP_1 & [network_3_2_RI_0>poll__networl_3_2_RI_0 & [network_3_2_AnnP_2>poll__networl_3_2_AnnP_2 & [network_1_0_RP_2>poll__networl_1_0_RP_2 & [network_0_1_AnsP_3>poll__networl_0_1_AnsP_3 & [network_3_1_AnnP_0>poll__networl_3_1_AnnP_0 & [network_1_1_AnnP_3>poll__networl_1_1_AnnP_3 & [network_0_2_AskP_2>poll__networl_0_2_AskP_2 & [network_0_1_RP_1>poll__networl_0_1_RP_1 & [network_3_1_AskP_0>poll__networl_3_1_AskP_0 & [network_3_3_RP_0>poll__networl_3_3_RP_0 & [network_0_2_RI_3>poll__networl_0_2_RI_3 & [network_2_1_AnnP_3>poll__networl_2_1_AnnP_3 & [network_2_2_AnsP_2>poll__networl_2_2_AnsP_2 & [network_2_0_AnsP_2>poll__networl_2_0_AnsP_2 & [network_0_1_AnnP_3>poll__networl_0_1_AnnP_3 & [network_3_3_AnnP_3>poll__networl_3_3_AnnP_3 & [network_1_0_RP_1>poll__networl_1_0_RP_1 & [network_2_3_AnnP_0>poll__networl_2_3_AnnP_0 & [network_2_3_AnsP_0>poll__networl_2_3_AnsP_0 & [network_0_1_RI_1>poll__networl_0_1_RI_1 & [network_1_0_AskP_1>poll__networl_1_0_AskP_1 & [network_0_0_AskP_0>poll__networl_0_0_AskP_0 & [network_1_0_AnnP_0>poll__networl_1_0_AnnP_0 & [network_2_3_AnsP_2>poll__networl_2_3_AnsP_2 & [network_1_0_AnsP_1>poll__networl_1_0_AnsP_1 & [network_1_1_RP_1>poll__networl_1_1_RP_1 & [network_0_3_RP_2>poll__networl_0_3_RP_2 & [network_3_2_AskP_3>poll__networl_3_2_AskP_3 & [network_1_2_AnnP_2>poll__networl_1_2_AnnP_2 & [network_0_1_AnnP_1>poll__networl_0_1_AnnP_1 & [network_1_1_AI_0>poll__networl_1_1_AI_0 & [network_2_2_AskP_2>poll__networl_2_2_AskP_2 & [network_2_2_RI_1>poll__networl_2_2_RI_1 & [network_3_1_AskP_2>poll__networl_3_1_AskP_2 & [network_2_3_AnnP_1>poll__networl_2_3_AnnP_1 & [network_0_0_AI_1>poll__networl_0_0_AI_1 & [network_0_2_AnnP_3>poll__networl_0_2_AnnP_3 & [network_2_2_RP_0>poll__networl_2_2_RP_0 & [network_0_2_AskP_1>poll__networl_0_2_AskP_1 & [network_2_0_RI_0>poll__networl_2_0_RI_0 & [network_3_0_AnsP_0>poll__networl_3_0_AnsP_0 & [network_2_0_AnsP_1>poll__networl_2_0_AnsP_1 & [network_0_3_AI_2>poll__networl_0_3_AI_2 & [network_1_0_AnsP_0>poll__networl_1_0_AnsP_0 & [network_2_1_RP_0>poll__networl_2_1_RP_0 & [network_3_1_AI_2>poll__networl_3_1_AI_2 & [network_3_1_RP_3>poll__networl_3_1_RP_3 & [network_3_3_AnsP_3>poll__networl_3_3_AnsP_3 & [network_2_1_AI_2>poll__networl_2_1_AI_2 & [network_2_2_AI_0>poll__networl_2_2_AI_0 & [network_1_2_AskP_1>poll__networl_1_2_AskP_1 & [network_2_1_AskP_0>poll__networl_2_1_AskP_0 & [network_2_0_AskP_2>poll__networl_2_0_AskP_2 & [network_0_3_AnsP_2>poll__networl_0_3_AnsP_2 & [network_1_1_AskP_2>poll__networl_1_1_AskP_2 & [network_2_1_AnnP_0>poll__networl_2_1_AnnP_0 & [network_0_0_AnsP_3>poll__networl_0_0_AnsP_3 & [network_1_3_RP_0>poll__networl_1_3_RP_0 & [network_0_3_AI_1>poll__networl_0_3_AI_1 & [network_1_2_RI_2>poll__networl_1_2_RI_2 & [network_0_3_AskP_3>poll__networl_0_3_AskP_3 & [network_3_2_AnnP_1>poll__networl_3_2_AnnP_1 & [network_3_0_AnnP_2>poll__networl_3_0_AnnP_2 & [network_1_3_AnsP_1>poll__networl_1_3_AnsP_1 & [network_0_3_RP_3>poll__networl_0_3_RP_3 & [network_1_0_RI_1>poll__networl_1_0_RI_1 & [network_0_3_RP_0>poll__networl_0_3_RP_0 & [network_0_0_AnnP_3>poll__networl_0_0_AnnP_3 & [network_2_2_RI_2>poll__networl_2_2_RI_2 & [network_1_2_AskP_0>poll__networl_1_2_AskP_0 & [network_2_3_AskP_0>poll__networl_2_3_AskP_0 & [network_2_0_AnnP_2>poll__networl_2_0_AnnP_2 & [network_1_1_AnnP_2>poll__networl_1_1_AnnP_2 & [network_2_0_RP_3>poll__networl_2_0_RP_3 & [network_0_1_RP_2>poll__networl_0_1_RP_2 & [network_2_0_AnnP_1>poll__networl_2_0_AnnP_1 & [network_1_3_AnnP_1>poll__networl_1_3_AnnP_1 & [network_1_2_AnsP_1>poll__networl_1_2_AnsP_1 & [network_0_2_AnsP_1>poll__networl_0_2_AnsP_1 & [network_3_0_RP_3>poll__networl_3_0_RP_3 & [network_0_1_RI_0>poll__networl_0_1_RI_0 & [network_2_3_RP_1>poll__networl_2_3_RP_1 & [network_1_3_RP_3>poll__networl_1_3_RP_3 & [network_3_0_AI_1>poll__networl_3_0_AI_1 & [network_2_1_AskP_3>poll__networl_2_1_AskP_3 & [network_0_0_RP_0>poll__networl_0_0_RP_0 & [network_3_2_AnsP_0>poll__networl_3_2_AnsP_0 & [network_0_1_AI_0>poll__networl_0_1_AI_0 & [network_3_3_AnnP_0>poll__networl_3_3_AnnP_0 & [network_3_0_AnsP_1>poll__networl_3_0_AnsP_1 & [network_3_2_RI_3>poll__networl_3_2_RI_3 & [network_0_1_AI_1>poll__networl_0_1_AI_1 & [network_2_3_AI_1>poll__networl_2_3_AI_1 & [network_2_1_AnnP_2>poll__networl_2_1_AnnP_2 & [network_2_0_RI_1>poll__networl_2_0_RI_1 & [network_2_1_AI_1>poll__networl_2_1_AI_1 & [network_0_3_AnsP_3>poll__networl_0_3_AnsP_3 & [network_2_1_AI_3>poll__networl_2_1_AI_3 & [network_3_1_AnnP_1>poll__networl_3_1_AnnP_1 & [network_3_3_AnsP_0>poll__networl_3_3_AnsP_0 & [network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [network_0_0_AI_3>poll__networl_0_0_AI_3 & [network_3_1_RI_2>poll__networl_3_1_RI_2 & [network_0_1_RP_0>poll__networl_0_1_RP_0 & [network_0_3_RI_3>poll__networl_0_3_RI_3 & [network_1_2_AnnP_1>poll__networl_1_2_AnnP_1 & [network_2_0_AnsP_0>poll__networl_2_0_AnsP_0 & [network_1_3_AskP_1>poll__networl_1_3_AskP_1 & [network_0_1_AI_3>poll__networl_0_1_AI_3 & [network_2_1_AI_0>poll__networl_2_1_AI_0 & [network_2_1_RP_3>poll__networl_2_1_RP_3 & [network_3_0_RI_1>poll__networl_3_0_RI_1 & [network_2_3_AI_2>poll__networl_2_3_AI_2 & [network_1_2_AskP_2>poll__networl_1_2_AskP_2 & [network_3_1_AskP_3>poll__networl_3_1_AskP_3 & [network_0_0_RP_2>poll__networl_0_0_RP_2 & [network_1_3_RI_1>poll__networl_1_3_RI_1 & [network_3_0_AI_0>poll__networl_3_0_AI_0 & [network_2_0_RP_1>poll__networl_2_0_RP_1 & [network_3_1_RI_0>poll__networl_3_1_RI_0 & [network_2_0_AI_3>poll__networl_2_0_AI_3 & [network_0_2_RP_2>poll__networl_0_2_RP_2 & [network_0_2_RP_3>poll__networl_0_2_RP_3 & [network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [network_2_2_AskP_0>poll__networl_2_2_AskP_0 & [network_1_1_AI_2>poll__networl_1_1_AI_2 & [network_0_1_AnnP_2>poll__networl_0_1_AnnP_2 & [network_3_2_RI_2>poll__networl_3_2_RI_2 & [network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [network_1_0_AI_3>poll__networl_1_0_AI_3 & [network_3_1_AnnP_3>poll__networl_3_1_AnnP_3 & [network_3_2_AskP_1>poll__networl_3_2_AskP_1 & [network_3_1_AI_0>poll__networl_3_1_AI_0 & [network_3_1_AnsP_3>poll__networl_3_1_AnsP_3 & [network_1_3_AnsP_0>poll__networl_1_3_AnsP_0 & [network_2_3_RP_3>poll__networl_2_3_RP_3 & [network_1_2_AI_1>poll__networl_1_2_AI_1 & [network_1_1_RP_3>poll__networl_1_1_RP_3 & [network_2_2_AnsP_0>poll__networl_2_2_AnsP_0 & [network_0_3_RI_1>poll__networl_0_3_RI_1 & [network_2_1_RI_2>poll__networl_2_1_RI_2 & [network_2_3_AnsP_1>poll__networl_2_3_AnsP_1 & [network_2_1_RI_0>poll__networl_2_1_RI_0 & [network_3_0_AnnP_3>poll__networl_3_0_AnnP_3 & [network_0_0_RI_1>poll__networl_0_0_RI_1 & [network_2_0_RP_2>poll__networl_2_0_RP_2 & [network_2_3_AI_0>poll__networl_2_3_AI_0 & [network_3_2_AI_2>poll__networl_3_2_AI_2 & [network_0_3_AnsP_0>poll__networl_0_3_AnsP_0 & [network_0_1_AnnP_0>poll__networl_0_1_AnnP_0 & [network_2_2_AnnP_0>poll__networl_2_2_AnnP_0 & [network_3_3_AskP_1>poll__networl_3_3_AskP_1 & [network_1_1_AI_3>poll__networl_1_1_AI_3 & [network_3_3_RI_2>poll__networl_3_3_RI_2 & [network_2_0_RI_3>poll__networl_2_0_RI_3 & [network_0_1_AnsP_2>poll__networl_0_1_AnsP_2 & [network_0_0_AnsP_0>poll__networl_0_0_AnsP_0 & [network_1_1_RI_3>poll__networl_1_1_RI_3 & [network_1_0_RI_3>poll__networl_1_0_RI_3 & [network_0_0_RI_0>poll__networl_0_0_RI_0 & [network_0_0_AskP_2>poll__networl_0_0_AskP_2 & [network_3_2_AnsP_2>poll__networl_3_2_AnsP_2 & [network_1_0_AnnP_1>poll__networl_1_0_AnnP_1 & [network_2_3_AnnP_3>poll__networl_2_3_AnnP_3 & [network_2_1_RI_3>poll__networl_2_1_RI_3 & [network_2_0_RI_2>poll__networl_2_0_RI_2 & [network_3_1_RP_1>poll__networl_3_1_RP_1 & [network_3_1_AI_3>poll__networl_3_1_AI_3 & [network_0_3_RI_2>poll__networl_0_3_RI_2 & [network_2_3_AnnP_2>poll__networl_2_3_AnnP_2 & [network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [network_1_0_AnnP_3>poll__networl_1_0_AnnP_3 & [network_1_1_RI_2>poll__networl_1_1_RI_2 & [network_3_2_AI_0>poll__networl_3_2_AI_0 & [network_3_0_AnsP_3>poll__networl_3_0_AnsP_3 & [network_0_3_AnnP_1>poll__networl_0_3_AnnP_1 & [network_3_3_RI_3>poll__networl_3_3_RI_3 & [network_3_3_AI_1>poll__networl_3_3_AI_1 & [network_1_0_AI_1>poll__networl_1_0_AI_1 & [network_0_1_RP_3>poll__networl_0_1_RP_3 & [network_2_2_RP_3>poll__networl_2_2_RP_3 & [network_0_0_RI_3>poll__networl_0_0_RI_3 & [network_3_3_RP_3>poll__networl_3_3_RP_3 & [network_0_0_AI_0>poll__networl_0_0_AI_0 & [network_3_0_RI_0>poll__networl_3_0_RI_0 & [network_3_2_RP_3>poll__networl_3_2_RP_3 & [network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [network_3_3_AskP_0>poll__networl_3_3_AskP_0 & [network_2_2_AnsP_1>poll__networl_2_2_AnsP_1 & [network_0_2_RI_0>poll__networl_0_2_RI_0 & [network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [network_3_0_AI_2>poll__networl_3_0_AI_2 & [network_1_2_RP_1>poll__networl_1_2_RP_1 & [network_1_2_AnsP_3>poll__networl_1_2_AnsP_3 & [network_3_0_AskP_3>poll__networl_3_0_AskP_3 & [network_2_1_RI_1>poll__networl_2_1_RI_1 & [network_0_0_AnsP_1>poll__networl_0_0_AnsP_1 & [network_3_3_AnsP_1>poll__networl_3_3_AnsP_1 & [network_3_1_RI_1>poll__networl_3_1_RI_1 & [network_1_2_AI_3>poll__networl_1_2_AI_3 & [network_0_3_RI_0>poll__networl_0_3_RI_0 & [network_3_0_AnsP_2>poll__networl_3_0_AnsP_2 & [network_2_1_AnsP_1>poll__networl_2_1_AnsP_1 & [network_3_3_RP_1>poll__networl_3_3_RP_1 & [network_0_2_AskP_0>poll__networl_0_2_AskP_0 & [network_1_3_AI_1>poll__networl_1_3_AI_1 & [network_0_3_AI_3>poll__networl_0_3_AI_3 & [network_3_3_AI_2>poll__networl_3_3_AI_2 & [network_0_3_AnsP_1>poll__networl_0_3_AnsP_1 & [network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [network_2_2_RP_1>poll__networl_2_2_RP_1 & [network_3_1_RP_0>poll__networl_3_1_RP_0 & [network_2_0_AnsP_3>poll__networl_2_0_AnsP_3 & [network_1_0_AnnP_2>poll__networl_1_0_AnnP_2 & [network_3_2_RP_1>poll__networl_3_2_RP_1 & [network_3_2_RP_2>poll__networl_3_2_RP_2 & [network_0_3_AskP_0>poll__networl_0_3_AskP_0 & [network_3_0_RP_0>poll__networl_3_0_RP_0 & [network_3_3_AnnP_1>poll__networl_3_3_AnnP_1 & [network_1_0_RP_3>poll__networl_1_0_RP_3 & [network_0_2_AnnP_2>poll__networl_0_2_AnnP_2 & [network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [network_1_2_AnnP_0>poll__networl_1_2_AnnP_0 & [network_0_3_AI_0>poll__networl_0_3_AI_0 & [network_1_3_AskP_3>poll__networl_1_3_AskP_3 & [network_0_1_AskP_1>poll__networl_0_1_AskP_1 & [network_2_3_RI_1>poll__networl_2_3_RI_1 & [network_2_2_AI_1>poll__networl_2_2_AI_1 & [network_1_2_RP_3>poll__networl_1_2_RP_3 & [network_3_2_AI_1>poll__networl_3_2_AI_1 & [network_1_3_RI_3>poll__networl_1_3_RI_3 & [network_2_2_AskP_3>poll__networl_2_2_AskP_3 & [network_2_1_RP_1>poll__networl_2_1_RP_1 & [network_0_1_RI_2>poll__networl_0_1_RI_2 & [network_2_3_AskP_2>poll__networl_2_3_AskP_2 & [network_3_3_RI_1>poll__networl_3_3_RI_1 & [network_3_0_RI_3>poll__networl_3_0_RI_3 & [network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [network_2_3_AskP_1>poll__networl_2_3_AskP_1 & [network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [network_3_3_AI_3>poll__networl_3_3_AI_3 & [network_2_1_AnsP_3>poll__networl_2_1_AnsP_3 & [network_0_2_AnsP_0>poll__networl_0_2_AnsP_0 & [network_0_3_AnnP_3>poll__networl_0_3_AnnP_3 & [network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [network_2_2_AnnP_1>poll__networl_2_2_AnnP_1 & [network_1_1_AnnP_0>poll__networl_1_1_AnnP_0 & [network_3_2_AnnP_3>poll__networl_3_2_AnnP_3 & [network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [network_1_0_AI_0>poll__networl_1_0_AI_0 & [network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [network_1_2_AI_0>poll__networl_1_2_AI_0 & [network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [network_1_1_AnnP_1>poll__networl_1_1_AnnP_1 & [network_1_3_AI_0>poll__networl_1_3_AI_0 & [network_0_2_RP_1>poll__networl_0_2_RP_1 & [network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [network_2_1_AskP_2>poll__networl_2_1_AskP_2 & [network_1_2_RP_0>poll__networl_1_2_RP_0 & [network_1_2_RI_3>poll__networl_1_2_RI_3 & [network_2_0_AskP_0>poll__networl_2_0_AskP_0 & [network_1_1_AnsP_1>poll__networl_1_1_AnsP_1 & [network_0_2_AskP_3>poll__networl_0_2_AskP_3 & [network_1_3_AI_2>poll__networl_1_3_AI_2 & [network_1_3_AnsP_2>poll__networl_1_3_AnsP_2 & [network_0_2_AI_3>poll__networl_0_2_AI_3 & [network_1_2_AI_2>poll__networl_1_2_AI_2 & [network_2_0_RP_0>poll__networl_2_0_RP_0 & [network_3_2_RP_0>poll__networl_3_2_RP_0 & [network_2_1_AskP_1>poll__networl_2_1_AskP_1 & [network_1_0_RP_0>poll__networl_1_0_RP_0 & [network_0_2_AnsP_2>poll__networl_0_2_AnsP_2 & [network_2_0_AI_0>poll__networl_2_0_AI_0 & [network_3_2_RI_1>poll__networl_3_2_RI_1 & [network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [network_3_0_RP_2>poll__networl_3_0_RP_2 & [network_2_2_AI_2>poll__networl_2_2_AI_2 & [network_0_1_AskP_3>poll__networl_0_1_AskP_3 & [network_1_1_RI_0>poll__networl_1_1_RI_0 & [network_0_1_RI_3>poll__networl_0_1_RI_3 & [network_1_2_RP_2>poll__networl_1_2_RP_2 & [network_0_3_AnnP_2>poll__networl_0_3_AnnP_2 & [network_3_1_AnsP_2>poll__networl_3_1_AnsP_2 & [network_1_3_AnnP_2>poll__networl_1_3_AnnP_2 & [network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [network_0_0_AI_2>poll__networl_0_0_AI_2 & [network_2_3_AI_3>poll__networl_2_3_AI_3 & [network_3_2_AskP_2>poll__networl_3_2_AskP_2 & [network_2_1_AnsP_0>poll__networl_2_1_AnsP_0 & [network_3_0_AnnP_0>poll__networl_3_0_AnnP_0 & [network_1_3_RP_1>poll__networl_1_3_RP_1 & [network_3_3_AskP_2>poll__networl_3_3_AskP_2 & [network_3_3_RP_2>poll__networl_3_3_RP_2 & [network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [network_1_0_RI_2>poll__networl_1_0_RI_2 & [network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [network_0_0_RI_2>poll__networl_0_0_RI_2 & [network_3_3_AI_0>poll__networl_3_3_AI_0 & [network_1_2_AnsP_0>poll__networl_1_2_AnsP_0 & [network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [network_3_2_AnsP_3>poll__networl_3_2_AnsP_3 & [network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [network_3_2_AI_3>poll__networl_3_2_AI_3 & [network_1_3_RP_2>poll__networl_1_3_RP_2 & [network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [network_3_3_AnnP_2>poll__networl_3_3_AnnP_2 & [network_1_0_AnsP_2>poll__networl_1_0_AnsP_2 & [network_0_1_AnsP_0>poll__networl_0_1_AnsP_0 & [network_0_2_RP_0>poll__networl_0_2_RP_0 & [network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [network_1_3_RI_2>poll__networl_1_3_RI_2 & [network_0_0_RP_3>poll__networl_0_0_RP_3 & [network_1_0_AI_2>poll__networl_1_0_AI_2 & [network_3_0_AI_3>poll__networl_3_0_AI_3 & [network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [network_2_2_AnsP_3>poll__networl_2_2_AnsP_3 & [network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [network_1_1_RP_0>poll__networl_1_1_RP_0 & [network_1_0_AskP_3>poll__networl_1_0_AskP_3 & [network_1_3_RI_0>poll__networl_1_3_RI_0 & [network_3_0_RP_1>poll__networl_3_0_RP_1 & [network_1_1_AnsP_3>poll__networl_1_1_AnsP_3 & [network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [network_1_1_RP_2>poll__networl_1_1_RP_2 & [network_2_3_RI_2>poll__networl_2_3_RI_2 & true]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & true]]]]]
-> the formula is FALSE
FORMULA p_43_mix_full_or FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
checking: AG [[ ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) & [true & [[[network_0_0_AnnP_2>poll__networl_0_0_AnnP_2 & [[network_2_3_RP_0>poll__networl_2_3_RP_0 & [[[[[[network_2_3_RI_0>poll__networl_2_3_RI_0 & [[[[[[[[[[[[[[network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [[[[network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [[[[[[[[[network_1_1_RI_1>poll__networl_1_1_RI_1 & [network_0_0_RP_1>poll__networl_0_0_RP_1 & [[[[[[[[[[[network_0_2_RI_3>poll__networl_0_2_RI_3 & [network_2_1_AnnP_3>poll__networl_2_1_AnnP_3 & [[network_2_0_AnsP_2>poll__networl_2_0_AnsP_2 & [[network_3_3_AnnP_3>poll__networl_3_3_AnnP_3 & [[[network_2_3_AnsP_0>poll__networl_2_3_AnsP_0 & [[[network_0_0_AskP_0>poll__networl_0_0_AskP_0 & [[network_2_3_AnsP_2>poll__networl_2_3_AnsP_2 & [network_1_0_AnsP_1>poll__networl_1_0_AnsP_1 & [[[[network_1_2_AnnP_2>poll__networl_1_2_AnnP_2 & [network_0_1_AnnP_1>poll__networl_0_1_AnnP_1 & [network_1_1_AI_0>poll__networl_1_1_AI_0 & [[network_2_2_RI_1>poll__networl_2_2_RI_1 & [network_3_1_AskP_2>poll__networl_3_1_AskP_2 & [network_2_3_AnnP_1>poll__networl_2_3_AnnP_1 & [[[[[[[[network_0_3_AI_2>poll__networl_0_3_AI_2 & [network_1_0_AnsP_0>poll__networl_1_0_AnsP_0 & [network_2_1_RP_0>poll__networl_2_1_RP_0 & [network_3_1_AI_2>poll__networl_3_1_AI_2 & [network_3_1_RP_3>poll__networl_3_1_RP_3 & [[[[network_1_2_AskP_1>poll__networl_1_2_AskP_1 & [network_2_1_AskP_0>poll__networl_2_1_AskP_0 & [network_2_0_AskP_2>poll__networl_2_0_AskP_2 & [network_0_3_AnsP_2>poll__networl_0_3_AnsP_2 & [network_1_1_AskP_2>poll__networl_1_1_AskP_2 & [[network_0_0_AnsP_3>poll__networl_0_0_AnsP_3 & [network_1_3_RP_0>poll__networl_1_3_RP_0 & [network_0_3_AI_1>poll__networl_0_3_AI_1 & [[[network_3_2_AnnP_1>poll__networl_3_2_AnnP_1 & [[[network_0_3_RP_3>poll__networl_0_3_RP_3 & [network_1_0_RI_1>poll__networl_1_0_RI_1 & [network_0_3_RP_0>poll__networl_0_3_RP_0 & [network_0_0_AnnP_3>poll__networl_0_0_AnnP_3 & [[[network_2_3_AskP_0>poll__networl_2_3_AskP_0 & [[[network_2_0_RP_3>poll__networl_2_0_RP_3 & [[[network_1_3_AnnP_1>poll__networl_1_3_AnnP_1 & [[[network_3_0_RP_3>poll__networl_3_0_RP_3 & [[[[[[network_0_0_RP_0>poll__networl_0_0_RP_0 & [[[network_3_3_AnnP_0>poll__networl_3_3_AnnP_0 & [[[network_0_1_AI_1>poll__networl_0_1_AI_1 & [[[network_2_0_RI_1>poll__networl_2_0_RI_1 & [[network_0_3_AnsP_3>poll__networl_0_3_AnsP_3 & [[[[network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [network_0_0_AI_3>poll__networl_0_0_AI_3 & [network_3_1_RI_2>poll__networl_3_1_RI_2 & [[[[network_2_0_AnsP_0>poll__networl_2_0_AnsP_0 & [[[network_2_1_AI_0>poll__networl_2_1_AI_0 & [[[network_2_3_AI_2>poll__networl_2_3_AI_2 & [[[[[[[[[[[network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [[network_1_1_AI_2>poll__networl_1_1_AI_2 & [[[network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [[[network_3_2_AskP_1>poll__networl_3_2_AskP_1 & [[[[[[network_1_1_RP_3>poll__networl_1_1_RP_3 & [[[network_2_1_RI_2>poll__networl_2_1_RI_2 & [[network_2_1_RI_0>poll__networl_2_1_RI_0 & [network_3_0_AnnP_3>poll__networl_3_0_AnnP_3 & [[[[[[network_0_1_AnnP_0>poll__networl_0_1_AnnP_0 & [[[[[[[[network_1_1_RI_3>poll__networl_1_1_RI_3 & [[[[[[[network_2_1_RI_3>poll__networl_2_1_RI_3 & [[[network_3_1_AI_3>poll__networl_3_1_AI_3 & [network_0_3_RI_2>poll__networl_0_3_RI_2 & [[network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [[[[[[[[[[network_2_2_RP_3>poll__networl_2_2_RP_3 & [[network_3_3_RP_3>poll__networl_3_3_RP_3 & [[[[network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [[[[network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [[[[[[[[[[network_0_3_RI_0>poll__networl_0_3_RI_0 & [network_3_0_AnsP_2>poll__networl_3_0_AnsP_2 & [network_2_1_AnsP_1>poll__networl_2_1_AnsP_1 & [[network_0_2_AskP_0>poll__networl_0_2_AskP_0 & [[network_0_3_AI_3>poll__networl_0_3_AI_3 & [[[network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [network_2_2_RP_1>poll__networl_2_2_RP_1 & [network_3_1_RP_0>poll__networl_3_1_RP_0 & [network_2_0_AnsP_3>poll__networl_2_0_AnsP_3 & [network_1_0_AnnP_2>poll__networl_1_0_AnnP_2 & [[network_3_2_RP_2>poll__networl_3_2_RP_2 & [network_0_3_AskP_0>poll__networl_0_3_AskP_0 & [network_3_0_RP_0>poll__networl_3_0_RP_0 & [network_3_3_AnnP_1>poll__networl_3_3_AnnP_1 & [network_1_0_RP_3>poll__networl_1_0_RP_3 & [network_0_2_AnnP_2>poll__networl_0_2_AnnP_2 & [network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [[network_0_3_AI_0>poll__networl_0_3_AI_0 & [network_1_3_AskP_3>poll__networl_1_3_AskP_3 & [network_0_1_AskP_1>poll__networl_0_1_AskP_1 & [network_2_3_RI_1>poll__networl_2_3_RI_1 & [network_2_2_AI_1>poll__networl_2_2_AI_1 & [network_1_2_RP_3>poll__networl_1_2_RP_3 & [network_3_2_AI_1>poll__networl_3_2_AI_1 & [[network_2_2_AskP_3>poll__networl_2_2_AskP_3 & [[[network_2_3_AskP_2>poll__networl_2_3_AskP_2 & [[[network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [[network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [[[[[network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [[[[network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [[network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [[network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [[network_1_3_AI_0>poll__networl_1_3_AI_0 & [network_0_2_RP_1>poll__networl_0_2_RP_1 & [network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [network_2_1_AskP_2>poll__networl_2_1_AskP_2 & [network_1_2_RP_0>poll__networl_1_2_RP_0 & [[[[[[[[[[[[[[[[network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [[[[[[[[[[network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [[network_2_3_AI_3>poll__networl_2_3_AI_3 & [[[[network_1_3_RP_1>poll__networl_1_3_RP_1 & [[[network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [[network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [[network_3_3_AI_0>poll__networl_3_3_AI_0 & [[network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [[network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [[[network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [[[[[network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [[[[[network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [[network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [network_1_1_RP_0>poll__networl_1_1_RP_0 & [network_1_0_AskP_3>poll__networl_1_0_AskP_3 & [network_1_3_RI_0>poll__networl_1_3_RI_0 & [network_3_0_RP_1>poll__networl_3_0_RP_1 & [network_1_1_AnsP_3>poll__networl_1_1_AnsP_3 & [network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [network_1_1_RP_2>poll__networl_1_1_RP_2 & [network_2_3_RI_2>poll__networl_2_3_RI_2 & true]]]]]]]]]] & network_2_2_AnsP_3>poll__networl_2_2_AnsP_3]]] & network_3_0_AI_3>poll__networl_3_0_AI_3] & network_1_0_AI_2>poll__networl_1_0_AI_2] & network_0_0_RP_3>poll__networl_0_0_RP_3] & network_1_3_RI_2>poll__networl_1_3_RI_2]]] & network_0_2_RP_0>poll__networl_0_2_RP_0] & network_0_1_AnsP_0>poll__networl_0_1_AnsP_0] & network_1_0_AnsP_2>poll__networl_1_0_AnsP_2] & network_3_3_AnnP_2>poll__networl_3_3_AnnP_2]]] & network_1_3_RP_2>poll__networl_1_3_RP_2] & network_3_2_AI_3>poll__networl_3_2_AI_3]] & network_3_2_AnsP_3>poll__networl_3_2_AnsP_3]] & network_1_2_AnsP_0>poll__networl_1_2_AnsP_0]] & network_0_0_RI_2>poll__networl_0_0_RI_2]]]] & network_1_0_RI_2>poll__networl_1_0_RI_2]] & network_3_3_RP_2>poll__networl_3_3_RP_2] & network_3_3_AskP_2>poll__networl_3_3_AskP_2]] & network_3_0_AnnP_0>poll__networl_3_0_AnnP_0] & network_2_1_AnsP_0>poll__networl_2_1_AnsP_0] & network_3_2_AskP_2>poll__networl_3_2_AskP_2]] & network_0_0_AI_2>poll__networl_0_0_AI_2]]]]]]] & network_1_3_AnnP_2>poll__networl_1_3_AnnP_2] & network_3_1_AnsP_2>poll__networl_3_1_AnsP_2] & network_0_3_AnnP_2>poll__networl_0_3_AnnP_2] & network_1_2_RP_2>poll__networl_1_2_RP_2] & network_0_1_RI_3>poll__networl_0_1_RI_3] & network_1_1_RI_0>poll__networl_1_1_RI_0] & network_0_1_AskP_3>poll__networl_0_1_AskP_3] & network_2_2_AI_2>poll__networl_2_2_AI_2] & network_3_0_RP_2>poll__networl_3_0_RP_2]]] & network_3_2_RI_1>poll__networl_3_2_RI_1] & network_2_0_AI_0>poll__networl_2_0_AI_0] & network_0_2_AnsP_2>poll__networl_0_2_AnsP_2] & network_1_0_RP_0>poll__networl_1_0_RP_0] & network_2_1_AskP_1>poll__networl_2_1_AskP_1] & network_3_2_RP_0>poll__networl_3_2_RP_0] & network_2_0_RP_0>poll__networl_2_0_RP_0] & network_1_2_AI_2>poll__networl_1_2_AI_2] & network_0_2_AI_3>poll__networl_0_2_AI_3] & network_1_3_AnsP_2>poll__networl_1_3_AnsP_2] & network_1_3_AI_2>poll__networl_1_3_AI_2] & network_0_2_AskP_3>poll__networl_0_2_AskP_3] & network_1_1_AnsP_1>poll__networl_1_1_AnsP_1] & network_2_0_AskP_0>poll__networl_2_0_AskP_0] & network_1_2_RI_3>poll__networl_1_2_RI_3]]]]]] & network_1_1_AnnP_1>poll__networl_1_1_AnnP_1]] & network_1_2_AI_0>poll__networl_1_2_AI_0]] & network_1_0_AI_0>poll__networl_1_0_AI_0]]]] & network_3_2_AnnP_3>poll__networl_3_2_AnnP_3] & network_1_1_AnnP_0>poll__networl_1_1_AnnP_0] & network_2_2_AnnP_1>poll__networl_2_2_AnnP_1]]] & network_0_3_AnnP_3>poll__networl_0_3_AnnP_3] & network_0_2_AnsP_0>poll__networl_0_2_AnsP_0] & network_2_1_AnsP_3>poll__networl_2_1_AnsP_3] & network_3_3_AI_3>poll__networl_3_3_AI_3]] & network_2_3_AskP_1>poll__networl_2_3_AskP_1]]] & network_3_0_RI_3>poll__networl_3_0_RI_3] & network_3_3_RI_1>poll__networl_3_3_RI_1]] & network_0_1_RI_2>poll__networl_0_1_RI_2] & network_2_1_RP_1>poll__networl_2_1_RP_1]] & network_1_3_RI_3>poll__networl_1_3_RI_3]]]]]]]] & network_1_2_AnnP_0>poll__networl_1_2_AnnP_0]]]]]]]] & network_3_2_RP_1>poll__networl_3_2_RP_1]]]]]] & network_0_3_AnsP_1>poll__networl_0_3_AnsP_1] & network_3_3_AI_2>poll__networl_3_3_AI_2]] & network_1_3_AI_1>poll__networl_1_3_AI_1]] & network_3_3_RP_1>poll__networl_3_3_RP_1]]]] & network_1_2_AI_3>poll__networl_1_2_AI_3] & network_3_1_RI_1>poll__networl_3_1_RI_1] & network_3_3_AnsP_1>poll__networl_3_3_AnsP_1] & network_0_0_AnsP_1>poll__networl_0_0_AnsP_1] & network_2_1_RI_1>poll__networl_2_1_RI_1] & network_3_0_AskP_3>poll__networl_3_0_AskP_3] & network_1_2_AnsP_3>poll__networl_1_2_AnsP_3] & network_1_2_RP_1>poll__networl_1_2_RP_1] & network_3_0_AI_2>poll__networl_3_0_AI_2]] & network_0_2_RI_0>poll__networl_0_2_RI_0] & network_2_2_AnsP_1>poll__networl_2_2_AnsP_1] & network_3_3_AskP_0>poll__networl_3_3_AskP_0]]] & network_3_2_RP_3>poll__networl_3_2_RP_3] & network_3_0_RI_0>poll__networl_3_0_RI_0] & network_0_0_AI_0>poll__networl_0_0_AI_0]] & network_0_0_RI_3>poll__networl_0_0_RI_3]] & network_0_1_RP_3>poll__networl_0_1_RP_3] & network_1_0_AI_1>poll__networl_1_0_AI_1] & network_3_3_AI_1>poll__networl_3_3_AI_1] & network_3_3_RI_3>poll__networl_3_3_RI_3] & network_0_3_AnnP_1>poll__networl_0_3_AnnP_1] & network_3_0_AnsP_3>poll__networl_3_0_AnsP_3] & network_3_2_AI_0>poll__networl_3_2_AI_0] & network_1_1_RI_2>poll__networl_1_1_RI_2] & network_1_0_AnnP_3>poll__networl_1_0_AnnP_3]]] & network_2_3_AnnP_2>poll__networl_2_3_AnnP_2]]] & network_3_1_RP_1>poll__networl_3_1_RP_1] & network_2_0_RI_2>poll__networl_2_0_RI_2]] & network_2_3_AnnP_3>poll__networl_2_3_AnnP_3] & network_1_0_AnnP_1>poll__networl_1_0_AnnP_1] & network_3_2_AnsP_2>poll__networl_3_2_AnsP_2] & network_0_0_AskP_2>poll__networl_0_0_AskP_2] & network_0_0_RI_0>poll__networl_0_0_RI_0] & network_1_0_RI_3>poll__networl_1_0_RI_3]] & network_0_0_AnsP_0>poll__networl_0_0_AnsP_0] & network_0_1_AnsP_2>poll__networl_0_1_AnsP_2] & network_2_0_RI_3>poll__networl_2_0_RI_3] & network_3_3_RI_2>poll__networl_3_3_RI_2] & network_1_1_AI_3>poll__networl_1_1_AI_3] & network_3_3_AskP_1>poll__networl_3_3_AskP_1] & network_2_2_AnnP_0>poll__networl_2_2_AnnP_0]] & network_0_3_AnsP_0>poll__networl_0_3_AnsP_0] & network_3_2_AI_2>poll__networl_3_2_AI_2] & network_2_3_AI_0>poll__networl_2_3_AI_0] & network_2_0_RP_2>poll__networl_2_0_RP_2] & network_0_0_RI_1>poll__networl_0_0_RI_1]]] & network_2_3_AnsP_1>poll__networl_2_3_AnsP_1]] & network_0_3_RI_1>poll__networl_0_3_RI_1] & network_2_2_AnsP_0>poll__networl_2_2_AnsP_0]] & network_1_2_AI_1>poll__networl_1_2_AI_1] & network_2_3_RP_3>poll__networl_2_3_RP_3] & network_1_3_AnsP_0>poll__networl_1_3_AnsP_0] & network_3_1_AnsP_3>poll__networl_3_1_AnsP_3] & network_3_1_AI_0>poll__networl_3_1_AI_0]] & network_3_1_AnnP_3>poll__networl_3_1_AnnP_3] & network_1_0_AI_3>poll__networl_1_0_AI_3]]] & network_3_2_RI_2>poll__networl_3_2_RI_2] & network_0_1_AnnP_2>poll__networl_0_1_AnnP_2]] & network_2_2_AskP_0>poll__networl_2_2_AskP_0]]] & network_0_2_RP_3>poll__networl_0_2_RP_3] & network_0_2_RP_2>poll__networl_0_2_RP_2] & network_2_0_AI_3>poll__networl_2_0_AI_3] & network_3_1_RI_0>poll__networl_3_1_RI_0] & network_2_0_RP_1>poll__networl_2_0_RP_1] & network_3_0_AI_0>poll__networl_3_0_AI_0] & network_1_3_RI_1>poll__networl_1_3_RI_1] & network_0_0_RP_2>poll__networl_0_0_RP_2] & network_3_1_AskP_3>poll__networl_3_1_AskP_3] & network_1_2_AskP_2>poll__networl_1_2_AskP_2]] & network_3_0_RI_1>poll__networl_3_0_RI_1] & network_2_1_RP_3>poll__networl_2_1_RP_3]] & network_0_1_AI_3>poll__networl_0_1_AI_3] & network_1_3_AskP_1>poll__networl_1_3_AskP_1]] & network_1_2_AnnP_1>poll__networl_1_2_AnnP_1] & network_0_3_RI_3>poll__networl_0_3_RI_3] & network_0_1_RP_0>poll__networl_0_1_RP_0]]]] & network_3_3_AnsP_0>poll__networl_3_3_AnsP_0] & network_3_1_AnnP_1>poll__networl_3_1_AnnP_1] & network_2_1_AI_3>poll__networl_2_1_AI_3]] & network_2_1_AI_1>poll__networl_2_1_AI_1]] & network_2_1_AnnP_2>poll__networl_2_1_AnnP_2] & network_2_3_AI_1>poll__networl_2_3_AI_1]] & network_3_2_RI_3>poll__networl_3_2_RI_3] & network_3_0_AnsP_1>poll__networl_3_0_AnsP_1]] & network_0_1_AI_0>poll__networl_0_1_AI_0] & network_3_2_AnsP_0>poll__networl_3_2_AnsP_0]] & network_2_1_AskP_3>poll__networl_2_1_AskP_3] & network_3_0_AI_1>poll__networl_3_0_AI_1] & network_1_3_RP_3>poll__networl_1_3_RP_3] & network_2_3_RP_1>poll__networl_2_3_RP_1] & network_0_1_RI_0>poll__networl_0_1_RI_0]] & network_0_2_AnsP_1>poll__networl_0_2_AnsP_1] & network_1_2_AnsP_1>poll__networl_1_2_AnsP_1]] & network_2_0_AnnP_1>poll__networl_2_0_AnnP_1] & network_0_1_RP_2>poll__networl_0_1_RP_2]] & network_1_1_AnnP_2>poll__networl_1_1_AnnP_2] & network_2_0_AnnP_2>poll__networl_2_0_AnnP_2]] & network_1_2_AskP_0>poll__networl_1_2_AskP_0] & network_2_2_RI_2>poll__networl_2_2_RI_2]]]]] & network_1_3_AnsP_1>poll__networl_1_3_AnsP_1] & network_3_0_AnnP_2>poll__networl_3_0_AnnP_2]] & network_0_3_AskP_3>poll__networl_0_3_AskP_3] & network_1_2_RI_2>poll__networl_1_2_RI_2]]]] & network_2_1_AnnP_0>poll__networl_2_1_AnnP_0]]]]]] & network_2_2_AI_0>poll__networl_2_2_AI_0] & network_2_1_AI_2>poll__networl_2_1_AI_2] & network_3_3_AnsP_3>poll__networl_3_3_AnsP_3]]]]]] & network_2_0_AnsP_1>poll__networl_2_0_AnsP_1] & network_3_0_AnsP_0>poll__networl_3_0_AnsP_0] & network_2_0_RI_0>poll__networl_2_0_RI_0] & network_0_2_AskP_1>poll__networl_0_2_AskP_1] & network_2_2_RP_0>poll__networl_2_2_RP_0] & network_0_2_AnnP_3>poll__networl_0_2_AnnP_3] & network_0_0_AI_1>poll__networl_0_0_AI_1]]]] & network_2_2_AskP_2>poll__networl_2_2_AskP_2]]]] & network_3_2_AskP_3>poll__networl_3_2_AskP_3] & network_0_3_RP_2>poll__networl_0_3_RP_2] & network_1_1_RP_1>poll__networl_1_1_RP_1]]] & network_1_0_AnnP_0>poll__networl_1_0_AnnP_0]] & network_1_0_AskP_1>poll__networl_1_0_AskP_1] & network_0_1_RI_1>poll__networl_0_1_RI_1]] & network_2_3_AnnP_0>poll__networl_2_3_AnnP_0] & network_1_0_RP_1>poll__networl_1_0_RP_1]] & network_0_1_AnnP_3>poll__networl_0_1_AnnP_3]] & network_2_2_AnsP_2>poll__networl_2_2_AnsP_2]]] & network_3_3_RP_0>poll__networl_3_3_RP_0] & network_3_1_AskP_0>poll__networl_3_1_AskP_0] & network_0_1_RP_1>poll__networl_0_1_RP_1] & network_0_2_AskP_2>poll__networl_0_2_AskP_2] & network_1_1_AnnP_3>poll__networl_1_1_AnnP_3] & network_3_1_AnnP_0>poll__networl_3_1_AnnP_0] & network_0_1_AnsP_3>poll__networl_0_1_AnsP_3] & network_1_0_RP_2>poll__networl_1_0_RP_2] & network_3_2_AnnP_2>poll__networl_3_2_AnnP_2] & network_3_2_RI_0>poll__networl_3_2_RI_0]]] & network_3_3_AnsP_2>poll__networl_3_3_AnsP_2] & network_3_1_AnsP_1>poll__networl_3_1_AnsP_1] & network_2_2_AnnP_2>poll__networl_2_2_AnnP_2] & network_0_0_AskP_3>poll__networl_0_0_AskP_3] & network_2_3_RP_2>poll__networl_2_3_RP_2] & network_0_2_AI_2>poll__networl_0_2_AI_2] & network_2_0_AI_1>poll__networl_2_0_AI_1] & network_2_2_AskP_1>poll__networl_2_2_AskP_1]] & network_1_0_AnsP_3>poll__networl_1_0_AnsP_3] & network_3_0_AskP_2>poll__networl_3_0_AskP_2] & network_1_2_AnsP_2>poll__networl_1_2_AnsP_2]] & network_3_2_AnnP_0>poll__networl_3_2_AnnP_0] & network_3_1_RI_3>poll__networl_3_1_RI_3] & network_3_3_RI_0>poll__networl_3_3_RI_0] & network_0_2_RI_2>poll__networl_0_2_RI_2] & network_1_1_AskP_3>poll__networl_1_1_AskP_3] & network_3_1_AI_1>poll__networl_3_1_AI_1] & network_1_1_AnsP_0>poll__networl_1_1_AnsP_0] & network_0_2_AnnP_0>poll__networl_0_2_AnnP_0] & network_0_0_AnnP_0>poll__networl_0_0_AnnP_0] & network_3_1_AnsP_0>poll__networl_3_1_AnsP_0] & network_0_2_AI_0>poll__networl_0_2_AI_0] & network_2_3_AskP_3>poll__networl_2_3_AskP_3] & network_2_3_AnsP_3>poll__networl_2_3_AnsP_3]] & network_0_1_AI_2>poll__networl_0_1_AI_2] & network_0_3_AnnP_0>poll__networl_0_3_AnnP_0] & network_2_0_AI_2>poll__networl_2_0_AI_2] & network_1_2_RI_0>poll__networl_1_2_RI_0] & network_2_1_AnsP_2>poll__networl_2_1_AnsP_2]] & network_1_3_AskP_0>poll__networl_1_3_AskP_0]] & network_1_0_RI_0>poll__networl_1_0_RI_0] & network_2_2_RP_2>poll__networl_2_2_RP_2]]]]
normalized: ~ [E [true U ~ [[ ( ( ( electedPrimary_2 + electedPrimary_1 ) + electedPrimary_0 ) + electedPrimary_3 ) < ( ( ( electionInit_1 + electionInit_2 ) + electionInit_0 ) + electionInit_3 ) & [[network_2_2_RP_2>poll__networl_2_2_RP_2 & [network_1_0_RI_0>poll__networl_1_0_RI_0 & [network_0_0_AnnP_2>poll__networl_0_0_AnnP_2 & [network_1_3_AskP_0>poll__networl_1_3_AskP_0 & [network_2_3_RP_0>poll__networl_2_3_RP_0 & [network_2_1_AnsP_2>poll__networl_2_1_AnsP_2 & [network_1_2_RI_0>poll__networl_1_2_RI_0 & [network_2_0_AI_2>poll__networl_2_0_AI_2 & [network_0_3_AnnP_0>poll__networl_0_3_AnnP_0 & [network_0_1_AI_2>poll__networl_0_1_AI_2 & [network_2_3_RI_0>poll__networl_2_3_RI_0 & [network_2_3_AnsP_3>poll__networl_2_3_AnsP_3 & [network_2_3_AskP_3>poll__networl_2_3_AskP_3 & [network_0_2_AI_0>poll__networl_0_2_AI_0 & [network_3_1_AnsP_0>poll__networl_3_1_AnsP_0 & [network_0_0_AnnP_0>poll__networl_0_0_AnnP_0 & [network_0_2_AnnP_0>poll__networl_0_2_AnnP_0 & [network_1_1_AnsP_0>poll__networl_1_1_AnsP_0 & [network_3_1_AI_1>poll__networl_3_1_AI_1 & [network_1_1_AskP_3>poll__networl_1_1_AskP_3 & [network_0_2_RI_2>poll__networl_0_2_RI_2 & [network_3_3_RI_0>poll__networl_3_3_RI_0 & [network_3_1_RI_3>poll__networl_3_1_RI_3 & [network_3_2_AnnP_0>poll__networl_3_2_AnnP_0 & [network_2_0_AskP_3>poll__networl_2_0_AskP_3 & [network_1_2_AnsP_2>poll__networl_1_2_AnsP_2 & [network_3_0_AskP_2>poll__networl_3_0_AskP_2 & [network_1_0_AnsP_3>poll__networl_1_0_AnsP_3 & [network_1_3_AnnP_0>poll__networl_1_3_AnnP_0 & [network_2_2_AskP_1>poll__networl_2_2_AskP_1 & [network_2_0_AI_1>poll__networl_2_0_AI_1 & [network_0_2_AI_2>poll__networl_0_2_AI_2 & [network_2_3_RP_2>poll__networl_2_3_RP_2 & [network_0_0_AskP_3>poll__networl_0_0_AskP_3 & [network_2_2_AnnP_2>poll__networl_2_2_AnnP_2 & [network_3_1_AnsP_1>poll__networl_3_1_AnsP_1 & [network_3_3_AnsP_2>poll__networl_3_3_AnsP_2 & [network_1_1_RI_1>poll__networl_1_1_RI_1 & [network_0_0_RP_1>poll__networl_0_0_RP_1 & [network_3_2_RI_0>poll__networl_3_2_RI_0 & [network_3_2_AnnP_2>poll__networl_3_2_AnnP_2 & [network_1_0_RP_2>poll__networl_1_0_RP_2 & [network_0_1_AnsP_3>poll__networl_0_1_AnsP_3 & [network_3_1_AnnP_0>poll__networl_3_1_AnnP_0 & [network_1_1_AnnP_3>poll__networl_1_1_AnnP_3 & [network_0_2_AskP_2>poll__networl_0_2_AskP_2 & [network_0_1_RP_1>poll__networl_0_1_RP_1 & [network_3_1_AskP_0>poll__networl_3_1_AskP_0 & [network_3_3_RP_0>poll__networl_3_3_RP_0 & [network_0_2_RI_3>poll__networl_0_2_RI_3 & [network_2_1_AnnP_3>poll__networl_2_1_AnnP_3 & [network_2_2_AnsP_2>poll__networl_2_2_AnsP_2 & [network_2_0_AnsP_2>poll__networl_2_0_AnsP_2 & [network_0_1_AnnP_3>poll__networl_0_1_AnnP_3 & [network_3_3_AnnP_3>poll__networl_3_3_AnnP_3 & [network_1_0_RP_1>poll__networl_1_0_RP_1 & [network_2_3_AnnP_0>poll__networl_2_3_AnnP_0 & [network_2_3_AnsP_0>poll__networl_2_3_AnsP_0 & [network_0_1_RI_1>poll__networl_0_1_RI_1 & [network_1_0_AskP_1>poll__networl_1_0_AskP_1 & [network_0_0_AskP_0>poll__networl_0_0_AskP_0 & [network_1_0_AnnP_0>poll__networl_1_0_AnnP_0 & [network_2_3_AnsP_2>poll__networl_2_3_AnsP_2 & [network_1_0_AnsP_1>poll__networl_1_0_AnsP_1 & [network_1_1_RP_1>poll__networl_1_1_RP_1 & [network_0_3_RP_2>poll__networl_0_3_RP_2 & [network_3_2_AskP_3>poll__networl_3_2_AskP_3 & [network_1_2_AnnP_2>poll__networl_1_2_AnnP_2 & [network_0_1_AnnP_1>poll__networl_0_1_AnnP_1 & [network_1_1_AI_0>poll__networl_1_1_AI_0 & [network_2_2_AskP_2>poll__networl_2_2_AskP_2 & [network_2_2_RI_1>poll__networl_2_2_RI_1 & [network_3_1_AskP_2>poll__networl_3_1_AskP_2 & [network_2_3_AnnP_1>poll__networl_2_3_AnnP_1 & [network_0_0_AI_1>poll__networl_0_0_AI_1 & [network_0_2_AnnP_3>poll__networl_0_2_AnnP_3 & [network_2_2_RP_0>poll__networl_2_2_RP_0 & [network_0_2_AskP_1>poll__networl_0_2_AskP_1 & [network_2_0_RI_0>poll__networl_2_0_RI_0 & [network_3_0_AnsP_0>poll__networl_3_0_AnsP_0 & [network_2_0_AnsP_1>poll__networl_2_0_AnsP_1 & [network_0_3_AI_2>poll__networl_0_3_AI_2 & [network_1_0_AnsP_0>poll__networl_1_0_AnsP_0 & [network_2_1_RP_0>poll__networl_2_1_RP_0 & [network_3_1_AI_2>poll__networl_3_1_AI_2 & [network_3_1_RP_3>poll__networl_3_1_RP_3 & [network_3_3_AnsP_3>poll__networl_3_3_AnsP_3 & [network_2_1_AI_2>poll__networl_2_1_AI_2 & [network_2_2_AI_0>poll__networl_2_2_AI_0 & [network_1_2_AskP_1>poll__networl_1_2_AskP_1 & [network_2_1_AskP_0>poll__networl_2_1_AskP_0 & [network_2_0_AskP_2>poll__networl_2_0_AskP_2 & [network_0_3_AnsP_2>poll__networl_0_3_AnsP_2 & [network_1_1_AskP_2>poll__networl_1_1_AskP_2 & [network_2_1_AnnP_0>poll__networl_2_1_AnnP_0 & [network_0_0_AnsP_3>poll__networl_0_0_AnsP_3 & [network_1_3_RP_0>poll__networl_1_3_RP_0 & [network_0_3_AI_1>poll__networl_0_3_AI_1 & [network_1_2_RI_2>poll__networl_1_2_RI_2 & [network_0_3_AskP_3>poll__networl_0_3_AskP_3 & [network_3_2_AnnP_1>poll__networl_3_2_AnnP_1 & [network_3_0_AnnP_2>poll__networl_3_0_AnnP_2 & [network_1_3_AnsP_1>poll__networl_1_3_AnsP_1 & [network_0_3_RP_3>poll__networl_0_3_RP_3 & [network_1_0_RI_1>poll__networl_1_0_RI_1 & [network_0_3_RP_0>poll__networl_0_3_RP_0 & [network_0_0_AnnP_3>poll__networl_0_0_AnnP_3 & [network_2_2_RI_2>poll__networl_2_2_RI_2 & [network_1_2_AskP_0>poll__networl_1_2_AskP_0 & [network_2_3_AskP_0>poll__networl_2_3_AskP_0 & [network_2_0_AnnP_2>poll__networl_2_0_AnnP_2 & [network_1_1_AnnP_2>poll__networl_1_1_AnnP_2 & [network_2_0_RP_3>poll__networl_2_0_RP_3 & [network_0_1_RP_2>poll__networl_0_1_RP_2 & [network_2_0_AnnP_1>poll__networl_2_0_AnnP_1 & [network_1_3_AnnP_1>poll__networl_1_3_AnnP_1 & [network_1_2_AnsP_1>poll__networl_1_2_AnsP_1 & [network_0_2_AnsP_1>poll__networl_0_2_AnsP_1 & [network_3_0_RP_3>poll__networl_3_0_RP_3 & [network_0_1_RI_0>poll__networl_0_1_RI_0 & [network_2_3_RP_1>poll__networl_2_3_RP_1 & [network_1_3_RP_3>poll__networl_1_3_RP_3 & [network_3_0_AI_1>poll__networl_3_0_AI_1 & [network_2_1_AskP_3>poll__networl_2_1_AskP_3 & [network_0_0_RP_0>poll__networl_0_0_RP_0 & [network_3_2_AnsP_0>poll__networl_3_2_AnsP_0 & [network_0_1_AI_0>poll__networl_0_1_AI_0 & [network_3_3_AnnP_0>poll__networl_3_3_AnnP_0 & [network_3_0_AnsP_1>poll__networl_3_0_AnsP_1 & [network_3_2_RI_3>poll__networl_3_2_RI_3 & [network_0_1_AI_1>poll__networl_0_1_AI_1 & [network_2_3_AI_1>poll__networl_2_3_AI_1 & [network_2_1_AnnP_2>poll__networl_2_1_AnnP_2 & [network_2_0_RI_1>poll__networl_2_0_RI_1 & [network_2_1_AI_1>poll__networl_2_1_AI_1 & [network_0_3_AnsP_3>poll__networl_0_3_AnsP_3 & [network_2_1_AI_3>poll__networl_2_1_AI_3 & [network_3_1_AnnP_1>poll__networl_3_1_AnnP_1 & [network_3_3_AnsP_0>poll__networl_3_3_AnsP_0 & [network_1_3_AnnP_3>poll__networl_1_3_AnnP_3 & [network_0_0_AI_3>poll__networl_0_0_AI_3 & [network_3_1_RI_2>poll__networl_3_1_RI_2 & [network_0_1_RP_0>poll__networl_0_1_RP_0 & [network_0_3_RI_3>poll__networl_0_3_RI_3 & [network_1_2_AnnP_1>poll__networl_1_2_AnnP_1 & [network_2_0_AnsP_0>poll__networl_2_0_AnsP_0 & [network_1_3_AskP_1>poll__networl_1_3_AskP_1 & [network_0_1_AI_3>poll__networl_0_1_AI_3 & [network_2_1_AI_0>poll__networl_2_1_AI_0 & [network_2_1_RP_3>poll__networl_2_1_RP_3 & [network_3_0_RI_1>poll__networl_3_0_RI_1 & [network_2_3_AI_2>poll__networl_2_3_AI_2 & [network_1_2_AskP_2>poll__networl_1_2_AskP_2 & [network_3_1_AskP_3>poll__networl_3_1_AskP_3 & [network_0_0_RP_2>poll__networl_0_0_RP_2 & [network_1_3_RI_1>poll__networl_1_3_RI_1 & [network_3_0_AI_0>poll__networl_3_0_AI_0 & [network_2_0_RP_1>poll__networl_2_0_RP_1 & [network_3_1_RI_0>poll__networl_3_1_RI_0 & [network_2_0_AI_3>poll__networl_2_0_AI_3 & [network_0_2_RP_2>poll__networl_0_2_RP_2 & [network_0_2_RP_3>poll__networl_0_2_RP_3 & [network_2_2_AnnP_3>poll__networl_2_2_AnnP_3 & [network_3_0_AskP_0>poll__networl_3_0_AskP_0 & [network_2_2_AskP_0>poll__networl_2_2_AskP_0 & [network_1_1_AI_2>poll__networl_1_1_AI_2 & [network_0_1_AnnP_2>poll__networl_0_1_AnnP_2 & [network_3_2_RI_2>poll__networl_3_2_RI_2 & [network_1_3_AnsP_3>poll__networl_1_3_AnsP_3 & [network_0_3_RP_1>poll__networl_0_3_RP_1 & [network_1_0_AI_3>poll__networl_1_0_AI_3 & [network_3_1_AnnP_3>poll__networl_3_1_AnnP_3 & [network_3_2_AskP_1>poll__networl_3_2_AskP_1 & [network_3_1_AI_0>poll__networl_3_1_AI_0 & [network_3_1_AnsP_3>poll__networl_3_1_AnsP_3 & [network_1_3_AnsP_0>poll__networl_1_3_AnsP_0 & [network_2_3_RP_3>poll__networl_2_3_RP_3 & [network_1_2_AI_1>poll__networl_1_2_AI_1 & [network_1_1_RP_3>poll__networl_1_1_RP_3 & [network_2_2_AnsP_0>poll__networl_2_2_AnsP_0 & [network_0_3_RI_1>poll__networl_0_3_RI_1 & [network_2_1_RI_2>poll__networl_2_1_RI_2 & [network_2_3_AnsP_1>poll__networl_2_3_AnsP_1 & [network_2_1_RI_0>poll__networl_2_1_RI_0 & [network_3_0_AnnP_3>poll__networl_3_0_AnnP_3 & [network_0_0_RI_1>poll__networl_0_0_RI_1 & [network_2_0_RP_2>poll__networl_2_0_RP_2 & [network_2_3_AI_0>poll__networl_2_3_AI_0 & [network_3_2_AI_2>poll__networl_3_2_AI_2 & [network_0_3_AnsP_0>poll__networl_0_3_AnsP_0 & [network_0_1_AnnP_0>poll__networl_0_1_AnnP_0 & [network_2_2_AnnP_0>poll__networl_2_2_AnnP_0 & [network_3_3_AskP_1>poll__networl_3_3_AskP_1 & [network_1_1_AI_3>poll__networl_1_1_AI_3 & [network_3_3_RI_2>poll__networl_3_3_RI_2 & [network_2_0_RI_3>poll__networl_2_0_RI_3 & [network_0_1_AnsP_2>poll__networl_0_1_AnsP_2 & [network_0_0_AnsP_0>poll__networl_0_0_AnsP_0 & [network_1_1_RI_3>poll__networl_1_1_RI_3 & [network_1_0_RI_3>poll__networl_1_0_RI_3 & [network_0_0_RI_0>poll__networl_0_0_RI_0 & [network_0_0_AskP_2>poll__networl_0_0_AskP_2 & [network_3_2_AnsP_2>poll__networl_3_2_AnsP_2 & [network_1_0_AnnP_1>poll__networl_1_0_AnnP_1 & [network_2_3_AnnP_3>poll__networl_2_3_AnnP_3 & [network_2_1_RI_3>poll__networl_2_1_RI_3 & [network_2_0_RI_2>poll__networl_2_0_RI_2 & [network_3_1_RP_1>poll__networl_3_1_RP_1 & [network_3_1_AI_3>poll__networl_3_1_AI_3 & [network_0_3_RI_2>poll__networl_0_3_RI_2 & [network_2_3_AnnP_2>poll__networl_2_3_AnnP_2 & [network_2_2_AI_3>poll__networl_2_2_AI_3 & [network_3_0_RI_2>poll__networl_3_0_RI_2 & [network_1_0_AnnP_3>poll__networl_1_0_AnnP_3 & [network_1_1_RI_2>poll__networl_1_1_RI_2 & [network_3_2_AI_0>poll__networl_3_2_AI_0 & [network_3_0_AnsP_3>poll__networl_3_0_AnsP_3 & [network_0_3_AnnP_1>poll__networl_0_3_AnnP_1 & [network_3_3_RI_3>poll__networl_3_3_RI_3 & [network_3_3_AI_1>poll__networl_3_3_AI_1 & [network_1_0_AI_1>poll__networl_1_0_AI_1 & [network_0_1_RP_3>poll__networl_0_1_RP_3 & [network_2_2_RP_3>poll__networl_2_2_RP_3 & [network_0_0_RI_3>poll__networl_0_0_RI_3 & [network_3_3_RP_3>poll__networl_3_3_RP_3 & [network_0_0_AI_0>poll__networl_0_0_AI_0 & [network_3_0_RI_0>poll__networl_3_0_RI_0 & [network_3_2_RP_3>poll__networl_3_2_RP_3 & [network_1_1_AI_1>poll__networl_1_1_AI_1 & [network_1_2_AnnP_3>poll__networl_1_2_AnnP_3 & [network_3_3_AskP_0>poll__networl_3_3_AskP_0 & [network_2_2_AnsP_1>poll__networl_2_2_AnsP_1 & [network_0_2_RI_0>poll__networl_0_2_RI_0 & [network_0_1_AnsP_1>poll__networl_0_1_AnsP_1 & [network_3_0_AI_2>poll__networl_3_0_AI_2 & [network_1_2_RP_1>poll__networl_1_2_RP_1 & [network_1_2_AnsP_3>poll__networl_1_2_AnsP_3 & [network_3_0_AskP_3>poll__networl_3_0_AskP_3 & [network_2_1_RI_1>poll__networl_2_1_RI_1 & [network_0_0_AnsP_1>poll__networl_0_0_AnsP_1 & [network_3_3_AnsP_1>poll__networl_3_3_AnsP_1 & [network_3_1_RI_1>poll__networl_3_1_RI_1 & [network_1_2_AI_3>poll__networl_1_2_AI_3 & [network_0_3_RI_0>poll__networl_0_3_RI_0 & [network_3_0_AnsP_2>poll__networl_3_0_AnsP_2 & [network_2_1_AnsP_1>poll__networl_2_1_AnsP_1 & [network_3_3_RP_1>poll__networl_3_3_RP_1 & [network_0_2_AskP_0>poll__networl_0_2_AskP_0 & [network_1_3_AI_1>poll__networl_1_3_AI_1 & [network_0_3_AI_3>poll__networl_0_3_AI_3 & [network_3_3_AI_2>poll__networl_3_3_AI_2 & [network_0_3_AnsP_1>poll__networl_0_3_AnsP_1 & [network_0_1_AskP_0>poll__networl_0_1_AskP_0 & [network_2_2_RP_1>poll__networl_2_2_RP_1 & [network_3_1_RP_0>poll__networl_3_1_RP_0 & [network_2_0_AnsP_3>poll__networl_2_0_AnsP_3 & [network_1_0_AnnP_2>poll__networl_1_0_AnnP_2 & [network_3_2_RP_1>poll__networl_3_2_RP_1 & [network_3_2_RP_2>poll__networl_3_2_RP_2 & [network_0_3_AskP_0>poll__networl_0_3_AskP_0 & [network_3_0_RP_0>poll__networl_3_0_RP_0 & [network_3_3_AnnP_1>poll__networl_3_3_AnnP_1 & [network_1_0_RP_3>poll__networl_1_0_RP_3 & [network_0_2_AnnP_2>poll__networl_0_2_AnnP_2 & [network_0_0_AskP_1>poll__networl_0_0_AskP_1 & [network_1_2_AnnP_0>poll__networl_1_2_AnnP_0 & [network_0_3_AI_0>poll__networl_0_3_AI_0 & [network_1_3_AskP_3>poll__networl_1_3_AskP_3 & [network_0_1_AskP_1>poll__networl_0_1_AskP_1 & [network_2_3_RI_1>poll__networl_2_3_RI_1 & [network_2_2_AI_1>poll__networl_2_2_AI_1 & [network_1_2_RP_3>poll__networl_1_2_RP_3 & [network_3_2_AI_1>poll__networl_3_2_AI_1 & [network_1_3_RI_3>poll__networl_1_3_RI_3 & [network_2_2_AskP_3>poll__networl_2_2_AskP_3 & [network_2_1_RP_1>poll__networl_2_1_RP_1 & [network_0_1_RI_2>poll__networl_0_1_RI_2 & [network_2_3_AskP_2>poll__networl_2_3_AskP_2 & [network_3_3_RI_1>poll__networl_3_3_RI_1 & [network_3_0_RI_3>poll__networl_3_0_RI_3 & [network_2_1_RP_2>poll__networl_2_1_RP_2 & [network_3_2_AnsP_1>poll__networl_3_2_AnsP_1 & [network_2_3_AskP_1>poll__networl_2_3_AskP_1 & [network_3_1_AnnP_2>poll__networl_3_1_AnnP_2 & [network_3_3_AI_3>poll__networl_3_3_AI_3 & [network_2_1_AnsP_3>poll__networl_2_1_AnsP_3 & [network_0_2_AnsP_0>poll__networl_0_2_AnsP_0 & [network_0_3_AnnP_3>poll__networl_0_3_AnnP_3 & [network_1_1_AskP_1>poll__networl_1_1_AskP_1 & [network_3_2_AskP_0>poll__networl_3_2_AskP_0 & [network_2_2_AnnP_1>poll__networl_2_2_AnnP_1 & [network_1_1_AnnP_0>poll__networl_1_1_AnnP_0 & [network_3_2_AnnP_3>poll__networl_3_2_AnnP_3 & [network_3_3_AskP_3>poll__networl_3_3_AskP_3 & [network_3_1_RP_2>poll__networl_3_1_RP_2 & [network_1_2_RI_1>poll__networl_1_2_RI_1 & [network_1_0_AI_0>poll__networl_1_0_AI_0 & [network_0_2_AnnP_1>poll__networl_0_2_AnnP_1 & [network_1_2_AI_0>poll__networl_1_2_AI_0 & [network_2_1_AnnP_1>poll__networl_2_1_AnnP_1 & [network_1_1_AnnP_1>poll__networl_1_1_AnnP_1 & [network_1_3_AI_0>poll__networl_1_3_AI_0 & [network_0_2_RP_1>poll__networl_0_2_RP_1 & [network_0_0_AnsP_2>poll__networl_0_0_AnsP_2 & [network_2_1_AskP_2>poll__networl_2_1_AskP_2 & [network_1_2_RP_0>poll__networl_1_2_RP_0 & [network_1_2_RI_3>poll__networl_1_2_RI_3 & [network_2_0_AskP_0>poll__networl_2_0_AskP_0 & [network_1_1_AnsP_1>poll__networl_1_1_AnsP_1 & [network_0_2_AskP_3>poll__networl_0_2_AskP_3 & [network_1_3_AI_2>poll__networl_1_3_AI_2 & [network_1_3_AnsP_2>poll__networl_1_3_AnsP_2 & [network_0_2_AI_3>poll__networl_0_2_AI_3 & [network_1_2_AI_2>poll__networl_1_2_AI_2 & [network_2_0_RP_0>poll__networl_2_0_RP_0 & [network_3_2_RP_0>poll__networl_3_2_RP_0 & [network_2_1_AskP_1>poll__networl_2_1_AskP_1 & [network_1_0_RP_0>poll__networl_1_0_RP_0 & [network_0_2_AnsP_2>poll__networl_0_2_AnsP_2 & [network_2_0_AI_0>poll__networl_2_0_AI_0 & [network_3_2_RI_1>poll__networl_3_2_RI_1 & [network_0_2_AI_1>poll__networl_0_2_AI_1 & [network_1_1_AnsP_2>poll__networl_1_1_AnsP_2 & [network_3_0_RP_2>poll__networl_3_0_RP_2 & [network_2_2_AI_2>poll__networl_2_2_AI_2 & [network_0_1_AskP_3>poll__networl_0_1_AskP_3 & [network_1_1_RI_0>poll__networl_1_1_RI_0 & [network_0_1_RI_3>poll__networl_0_1_RI_3 & [network_1_2_RP_2>poll__networl_1_2_RP_2 & [network_0_3_AnnP_2>poll__networl_0_3_AnnP_2 & [network_3_1_AnsP_2>poll__networl_3_1_AnsP_2 & [network_1_3_AnnP_2>poll__networl_1_3_AnnP_2 & [network_1_1_AskP_0>poll__networl_1_1_AskP_0 & [network_0_0_AnnP_1>poll__networl_0_0_AnnP_1 & [network_1_2_AskP_3>poll__networl_1_2_AskP_3 & [network_1_0_AskP_0>poll__networl_1_0_AskP_0 & [network_1_3_AskP_2>poll__networl_1_3_AskP_2 & [network_2_2_RI_0>poll__networl_2_2_RI_0 & [network_0_0_AI_2>poll__networl_0_0_AI_2 & [network_2_3_AI_3>poll__networl_2_3_AI_3 & [network_3_2_AskP_2>poll__networl_3_2_AskP_2 & [network_2_1_AnsP_0>poll__networl_2_1_AnsP_0 & [network_3_0_AnnP_0>poll__networl_3_0_AnnP_0 & [network_1_3_RP_1>poll__networl_1_3_RP_1 & [network_3_3_AskP_2>poll__networl_3_3_AskP_2 & [network_3_3_RP_2>poll__networl_3_3_RP_2 & [network_0_1_AskP_2>poll__networl_0_1_AskP_2 & [network_1_0_RI_2>poll__networl_1_0_RI_2 & [network_2_2_RI_3>poll__networl_2_2_RI_3 & [network_3_0_AskP_1>poll__networl_3_0_AskP_1 & [network_0_3_AskP_1>poll__networl_0_3_AskP_1 & [network_0_0_RI_2>poll__networl_0_0_RI_2 & [network_3_3_AI_0>poll__networl_3_3_AI_0 & [network_1_2_AnsP_0>poll__networl_1_2_AnsP_0 & [network_3_0_AnnP_1>poll__networl_3_0_AnnP_1 & [network_3_2_AnsP_3>poll__networl_3_2_AnsP_3 & [network_2_0_AskP_1>poll__networl_2_0_AskP_1 & [network_3_2_AI_3>poll__networl_3_2_AI_3 & [network_1_3_RP_2>poll__networl_1_3_RP_2 & [network_1_0_AskP_2>poll__networl_1_0_AskP_2 & [network_1_3_AI_3>poll__networl_1_3_AI_3 & [network_3_3_AnnP_2>poll__networl_3_3_AnnP_2 & [network_1_0_AnsP_2>poll__networl_1_0_AnsP_2 & [network_0_1_AnsP_0>poll__networl_0_1_AnsP_0 & [network_0_2_RP_0>poll__networl_0_2_RP_0 & [network_2_0_AnnP_3>poll__networl_2_0_AnnP_3 & [network_0_2_RI_1>poll__networl_0_2_RI_1 & [network_1_3_RI_2>poll__networl_1_3_RI_2 & [network_0_0_RP_3>poll__networl_0_0_RP_3 & [network_1_0_AI_2>poll__networl_1_0_AI_2 & [network_3_0_AI_3>poll__networl_3_0_AI_3 & [network_2_3_RI_3>poll__networl_2_3_RI_3 & [network_3_1_AskP_1>poll__networl_3_1_AskP_1 & [network_2_2_AnsP_3>poll__networl_2_2_AnsP_3 & [network_2_0_AnnP_0>poll__networl_2_0_AnnP_0 & [network_0_2_AnsP_3>poll__networl_0_2_AnsP_3 & [network_1_1_RP_0>poll__networl_1_1_RP_0 & [network_1_0_AskP_3>poll__networl_1_0_AskP_3 & [network_1_3_RI_0>poll__networl_1_3_RI_0 & [network_3_0_RP_1>poll__networl_3_0_RP_1 & [network_1_1_AnsP_3>poll__networl_1_1_AnsP_3 & [network_0_3_AskP_2>poll__networl_0_3_AskP_2 & [network_1_1_RP_2>poll__networl_1_1_RP_2 & [network_2_3_RI_2>poll__networl_2_3_RI_2 & true]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]] & true]]]]]
-> the formula is FALSE
FORMULA p_44_mix_full_and_notx FALSE TECHNIQUES DECISION_DIAGRAMS
mc time: 0m0sec
total processing time: 0m23sec
STOP 1369634171
--------------------
content from stderr:
check if there are places and transitions
ok
check if there are transitions without pre-places
ok
check if at least one transition is enabled in m0
ok
check if there are transitions that can never fire
ok
initing FirstDep: 0m0sec
2413 2983 4406 5170 8021 8230 9312 9485 12146 12633 13261 15641 17360 19352
iterations count:14854 (14), effective:108 (0)
initing FirstDep: 0m0sec
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
19347
iterations count:1016 (1), effective:0 (0)
--------------------
content from /tmp/BenchKit_head_log_file.1654:

